Decoding Strategies in Large Language Models

Community Article Published October 29, 2024

In LLMs, most of the focus is on model architectures, data processing, and optimization. However, decoding strategies like beam search play a crucial role in text generation and are often overlooked. In this article, we will explore how LLMs generate text by looking into the mechanics of greedy search and beam search, as well as sampling techniques with top-k and nucleus sampling.

By the end of this article, you'll know how these decoding strategies work and how to tune important parameters like temperature, num_beams, top_k, and top_p.

The code for this article can be found on GitHub and Google Colab for reference and further exploration.

📚 Background

To kick things off, let’s start with an example. We'll feed the text “I have a dream” to a GPT-2 model and ask it to generate the next five tokens (words or subwords).

from transformers import GPT2LMHeadModel, GPT2Tokenizer
import torch

device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = GPT2LMHeadModel.from_pretrained('gpt2').to(device)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
model.eval()

text = "I have a dream"
input_ids = tokenizer.encode(text, return_tensors='pt').to(device)

outputs = model.generate(input_ids, max_length=len(input_ids.squeeze())+5)
generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print(f"Generated text: {generated_text}")

Generated text: I have a dream of being a doctor.

The sentence “I have a dream of being a doctor” appears to have been generated by GPT-2. However, GPT-2 didn’t exactly produce this sentence.

There’s a common misconception that LLMs like GPT-2 directly produce text. This isn’t the case. Instead, LLMs calculate logits, which are scores assigned to every possible token in their vocabulary. To simplify, here’s an illustrative breakdown of the process:

The tokenizer, Byte-Pair Encoding in this instance, translates each token in the input text into a corresponding token ID. Then, GPT-2 uses these token IDs as input and tries to predict the next most likely token. Finally, the model generates logits, which are converted into probabilities using a softmax function.

For example, the model assigns a probability of 17% to the token for "of" being the next token after "I have a dream". This output essentially represents a ranked list of potential next tokens in the sequence. More formally, we denote this probability as $P(\text{of } | \text{ I have a dream}) = 17%$.

Autoregressive models like GPT predict the next token in a sequence based on the preceding tokens. Consider a sequence of tokens $w = (w_1, w_2, \ldots, w_t)$. The joint probability of this sequence $P(w)$ can be broken down as:

$\begin{align} P(w) &= P(w_1, w_2, \ldots, w_t) \\ &= P(w_1) P(w_2 | w_1) P(w_3 | w_2, w_1) \ldots P(w_t | w_1, \ldots, w_{t-1}) \\ &= \prod_{i=1}^t P(w_i | w_1, \dots, w_{i-1}). \end{align}$

For each token $w_i$ in the sequence, $P(w_i | w_1, \ldots, w_{i-1})$ represents the conditional probability of $w_i$ given all the preceding tokens $(w_1, \ldots, w_{i-1})$. GPT-2 calculates this conditional probability for each of the 50,257 tokens in its vocabulary.

This leads to the question: how do we use these probabilities to generate text? This is where decoding strategies, such as greedy search and beam search, come into play.

🏃‍♂️ Greedy Search

Greedy search is a decoding method that takes the most probable token at each step as the next token in the sequence. To put it simply, it only retains the most likely token at each stage, discarding all other potential options. Using our example:

Step 1: Input: “I have a dream” → Most likely token: “ of”
Step 2: Input: “I have a dream of” → Most likely token: “ being”
Step 3: Input: “I have a dream of being” → Most likely token: “ a”
Step 4: Input: “I have a dream of being a” → Most likely token: “ doctor”
Step 5: Input: “I have a dream of being a doctor” → Most likely token: “.”

While this approach might sound intuitive, it’s important to note that the greedy search is short-sighted: it only considers the most probable token at each step without considering the overall effect on the sequence. This property makes it fast and efficient as it doesn’t need to keep track of multiple sequences, but it also means that it can miss out on better sequences that might have appeared with slightly less probable next tokens.

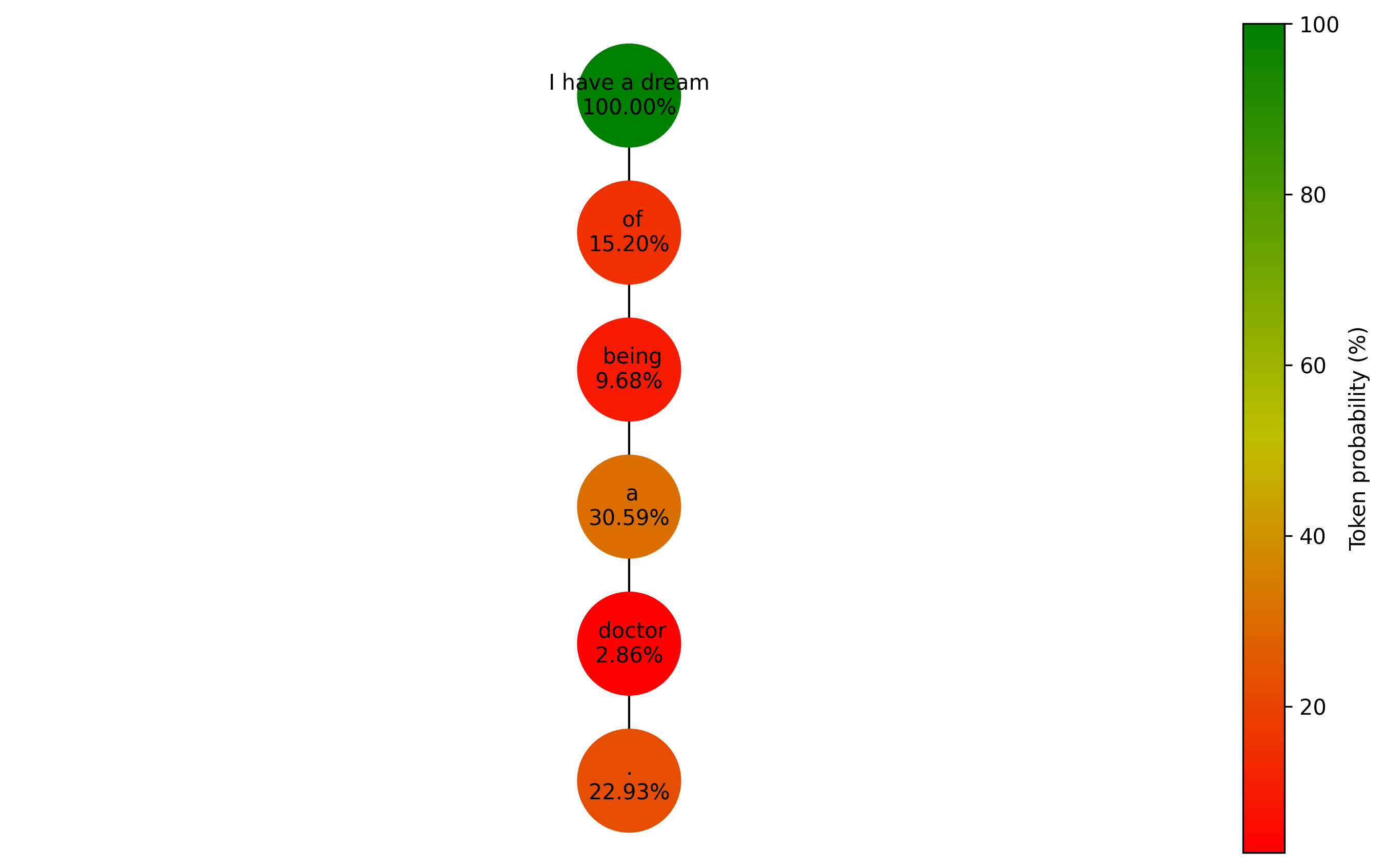
Next, let’s illustrate the greedy search implementation using graphviz and networkx. We select the ID with the highest score, compute its log probability (we take the log to simplify calculations), and add it to the tree. We’ll repeat this process for five tokens.

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import time

def get_log_prob(logits, token_id):
    # Compute the softmax of the logits
    probabilities = torch.nn.functional.softmax(logits, dim=-1)
    log_probabilities = torch.log(probabilities)
    
    # Get the log probability of the token
    token_log_probability = log_probabilities[token_id].item()
    return token_log_probability

def greedy_search(input_ids, node, length=5):
    if length == 0:
        return input_ids

    outputs = model(input_ids)
    predictions = outputs.logits

    # Get the predicted next sub-word (here we use top-k search)
    logits = predictions[0, -1, :]
    token_id = torch.argmax(logits).unsqueeze(0)

    # Compute the score of the predicted token
    token_score = get_log_prob(logits, token_id)

    # Add the predicted token to the list of input ids
    new_input_ids = torch.cat([input_ids, token_id.unsqueeze(0)], dim=-1)

    # Add node and edge to graph
    next_token = tokenizer.decode(token_id, skip_special_tokens=True)
    current_node = list(graph.successors(node))[0]
    graph.nodes[current_node]['tokenscore'] = np.exp(token_score) * 100
    graph.nodes[current_node]['token'] = next_token + f"_{length}"

    # Recursive call
    input_ids = greedy_search(new_input_ids, current_node, length-1)
    
    return input_ids

# Parameters
length = 5
beams = 1

# Create a balanced tree with height 'length'
graph = nx.balanced_tree(1, length, create_using=nx.DiGraph())

# Add 'tokenscore', 'cumscore', and 'token' attributes to each node
for node in graph.nodes:
    graph.nodes[node]['tokenscore'] = 100
    graph.nodes[node]['token'] = text

# Start generating text
output_ids = greedy_search(input_ids, 0, length=length)
output = tokenizer.decode(output_ids.squeeze().tolist(), skip_special_tokens=True)
print(f"Generated text: {output}")

Generated text: I have a dream of being a doctor.

Our greedy search generates the same text as the one from the transformers library: “I have a dream of being a doctor.” Let’s visualize the tree we created.

    import matplotlib.pyplot as plt
    import networkx as nx
    import matplotlib.colors as mcolors
    from matplotlib.colors import LinearSegmentedColormap
    
    def plot_graph(graph, length, beams, score):
        fig, ax = plt.subplots(figsize=(3+1.2*beams**length, max(5, 2+length)), dpi=300, facecolor='white')
    
        # Create positions for each node
        pos = nx.nx_agraph.graphviz_layout(graph, prog="dot")
    
        # Normalize the colors along the range of token scores
        if score == 'token':
            scores = [data['tokenscore'] for _, data in graph.nodes(data=True) if data['token'] is not None]
        elif score == 'sequence':
            scores = [data['sequencescore'] for _, data in graph.nodes(data=True) if data['token'] is not None]
        vmin = min(scores)
        vmax = max(scores)
        norm = mcolors.Normalize(vmin=vmin, vmax=vmax)
        cmap = LinearSegmentedColormap.from_list('rg', ["r", "y", "g"], N=256) 
    
        # Draw the nodes
        nx.draw_networkx_nodes(graph, pos, node_size=2000, node_shape='o', alpha=1, linewidths=4, 
                              node_color=scores, cmap=cmap)
    
        # Draw the edges
        nx.draw_networkx_edges(graph, pos)
    
        # Draw the labels
        if score == 'token':
            labels = {node: data['token'].split('_')[0] + f"\n{data['tokenscore']:.2f}%" for node, data in graph.nodes(data=True) if data['token'] is not None}
        elif score == 'sequence':
            labels = {node: data['token'].split('_')[0] + f"\n{data['sequencescore']:.2f}" for node, data in graph.nodes(data=True) if data['token'] is not None}
        nx.draw_networkx_labels(graph, pos, labels=labels, font_size=10)
        plt.box(False)
    
        # Add a colorbar
        sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
        sm.set_array([])
        if score == 'token':
            fig.colorbar(sm, ax=ax, orientation='vertical', pad=0, label='Token probability (%)')
        elif score == 'sequence':
            fig.colorbar(sm, ax=ax, orientation='vertical', pad=0, label='Sequence score')
        plt.show()
    
    # Plot graph
    plot_graph(graph, length, 1.5, 'token')

In this graph, the top node stores the input token (thus with a 100% probability), while all other nodes represent generated tokens. Although each token in this sequence was the most likely at the time of prediction, "being" and "doctor" were assigned relatively low probabilities of 9.68% and 2.86%, respectively. This suggests that "of", our first predicted token, may not have been the most suitable choice as it led to "being", which is quite unlikely.

In the following section, we'll explore how beam search can address this problem.

⚖️ Beam Search

Unlike greedy search, which only considers the next most probable token, beam search takes into account the $n$ most likely tokens, where $n$ represents the number of beams. This procedure is repeated until a predefined maximum length is reached or an end-of-sequence token appears. At this point, the sequence (or "beam") with the highest overall score is chosen as the output.

We can adapt the previous function to consider the $n$ most probable tokens instead of just one. Here, we'll maintain the sequence score $\log P(w)$, which is the cumulative sum of the log probability of every token in the beam. We normalize this score by the sequence length to prevent bias towards longer sequences (this factor can be adjusted). Once again, we'll generate five additional tokens to complete the sentence "I have a dream."

from tqdm.notebook import tqdm

def greedy_sampling(logits, beams):
    return torch.topk(logits, beams).indices
    
def beam_search(input_ids, node, bar, length, beams, sampling, temperature=0.1):
    if length == 0:
        return None

    outputs = model(input_ids)
    predictions = outputs.logits

    # Get the predicted next sub-word (here we use top-k search)
    logits = predictions[0, -1, :]

    if sampling == 'greedy':
        top_token_ids = greedy_sampling(logits, beams)
    elif sampling == 'top_k':
        top_token_ids = top_k_sampling(logits, temperature, 20, beams)
    elif sampling == 'nucleus':
        top_token_ids = nucleus_sampling(logits, temperature, 0.5, beams)

    for j, token_id in enumerate(top_token_ids):
        bar.update(1)

        # Compute the score of the predicted token
        token_score = get_log_prob(logits, token_id)
        cumulative_score = graph.nodes[node]['cumscore'] + token_score

        # Add the predicted token to the list of input ids
        new_input_ids = torch.cat([input_ids, token_id.unsqueeze(0).unsqueeze(0)], dim=-1)

        # Add node and edge to graph
        token = tokenizer.decode(token_id, skip_special_tokens=True)
        current_node = list(graph.successors(node))[j]
        graph.nodes[current_node]['tokenscore'] = np.exp(token_score) * 100
        graph.nodes[current_node]['cumscore'] = cumulative_score
        graph.nodes[current_node]['sequencescore'] = 1/(len(new_input_ids.squeeze())) * cumulative_score
        graph.nodes[current_node]['token'] = token + f"_{length}_{j}"

        # Recursive call
        beam_search(new_input_ids, current_node, bar, length-1, beams, sampling, 1)

# Parameters
length = 5
beams = 2

# Create a balanced tree with height 'length' and branching factor 'k'
graph = nx.balanced_tree(beams, length, create_using=nx.DiGraph())
bar = tqdm(total=len(graph.nodes))

# Add 'tokenscore', 'cumscore', and 'token' attributes to each node
for node in graph.nodes:
    graph.nodes[node]['tokenscore'] = 100
    graph.nodes[node]['cumscore'] = 0
    graph.nodes[node]['sequencescore'] = 0
    graph.nodes[node]['token'] = text

# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'greedy', 1)

The function computes the scores for 63 tokens and beams^length = 5² = 25 possible sequences. In our implementation, all the information is stored in the graph. Our next step is to extract the best sequence.

First, we identify the leaf node with the highest sequence score. Next, we find the shortest path from the root to this leaf. Every node along this path contains a token from the optimal sequence. Here's how we can implement it:

def get_best_sequence(G):
    # Create a list of leaf nodes
    leaf_nodes = [node for node in G.nodes() if G.out_degree(node)==0]

    # Get the leaf node with the highest cumscore
    max_score_node = None
    max_score = float('-inf')
    for node in leaf_nodes:
        if G.nodes[node]['sequencescore'] > max_score:
            max_score = G.nodes[node]['sequencescore']
            max_score_node = node

    # Retrieve the sequence of nodes from this leaf node to the root node in a list
    path = nx.shortest_path(G, source=0, target=max_score_node)

    # Return the string of token attributes of this sequence
    sequence = "".join([G.nodes[node]['token'].split('_')[0] for node in path])
    
    return sequence, max_score

sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}")

Generated text: I have a dream. I have a dream

The best sequence seems to be "I have a dream. I have a dream," which is a common response from GPT-2, even though it may be surprising. To verify this, let's plot the graph.

In this visualization, we'll display the sequence score for each node, which represents the score of the sequence up to that point. If the function get_best_sequence() is correct, the "dream" node in the sequence "I have a dream. I have a dream" should have the highest score among all the leaf nodes.

# Plot graph
plot_graph(graph, length, beams, 'sequence')

Indeed, the "dream" token has the highest sequence score with a value of -0.69. Interestingly, we can see the score of the greedy sequence "I have a dream of being a doctor." on the left with a value of -1.16.

As expected, the greedy search leads to suboptimal results. But, to be honest, our new outcome is not particularly compelling either. To generate more varied sequences, we'll implement two sampling algorithms: top-k and nucleus.

🎲 Top-k sampling

Top-k sampling is a technique that leverages the probability distribution generated by the language model to select a token randomly from the k most likely options.

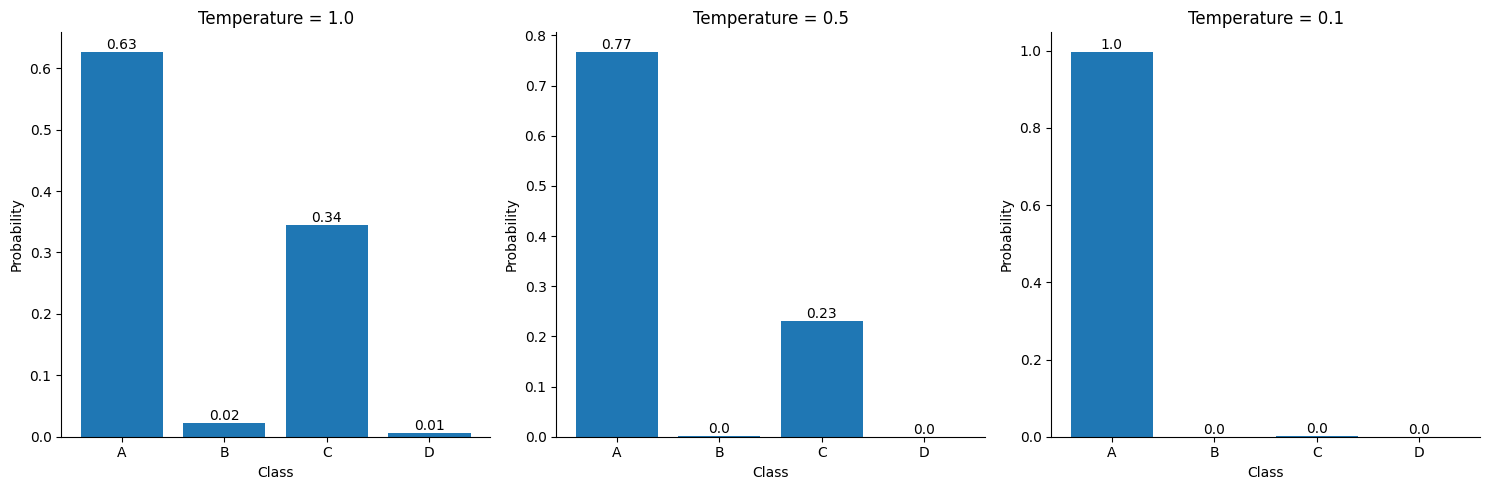
To illustrate, suppose we have $k = 3$ and four tokens: A, B, C, and D, with respective probabilities: $P(A) = 30%$, $P(B) = 15%$, $P(C) = 5%$, and $P(D) = 1%$. In top-k sampling, token D is disregarded, and the algorithm will output A 60% of the time, B 30% of the time, and C 10% of the time. This approach ensures that we prioritize the most probable tokens while introducing an element of randomness in the selection process.

Another way of introducing randomness is the concept of temperature. The temperature $T$ is a parameter that ranges from 0 to 1, which affects the probabilities generated by the softmax function, making the most likely tokens more influential. In practice, it simply consists of dividing the input logits by a value we call temperature:

$\text{softmax}(x_i) = \frac{e^{x_i / T}}{\sum_{j} e^{x_j / T}}$

Here is a chart that demonstrates the impact of temperature on the probabilities generated for a given set of input logits [1.5, -1.8, 0.9, -3.2]. We've plotted three different temperature values to observe the differences.

A temperature of 1.0 is equivalent to a default softmax with no temperature at all. On the other hand, a low temperature setting (0.1) significantly alters the probability distribution. This is commonly used in text generation to control the level of "creativity" in the generated output. By adjusting the temperature, we can influence the extent to which the model produces more diverse or predictable responses.

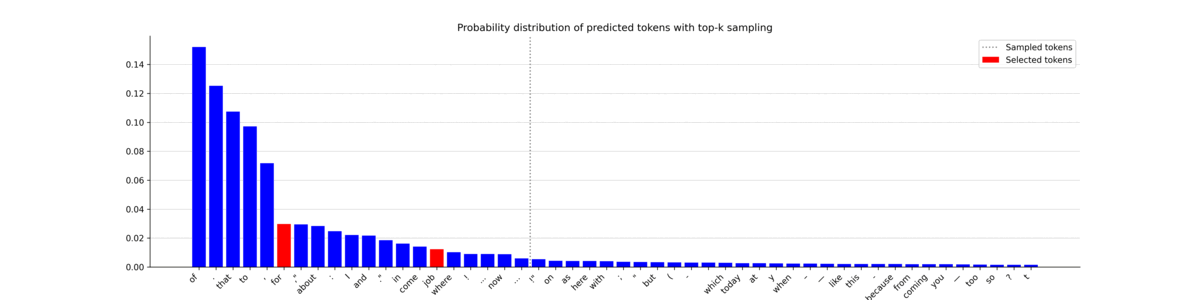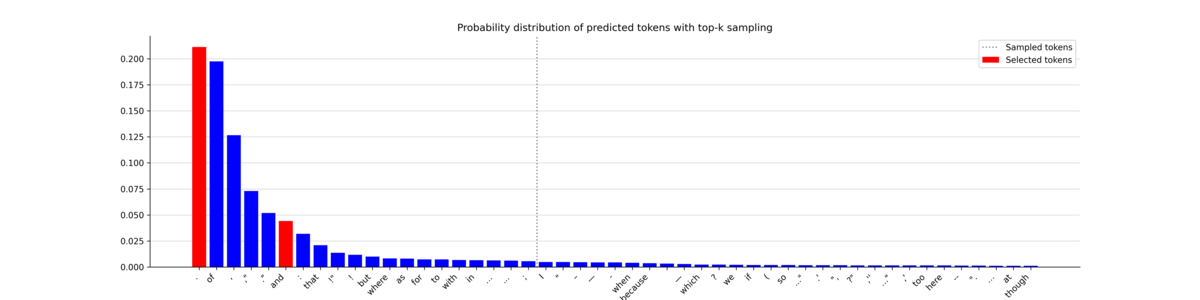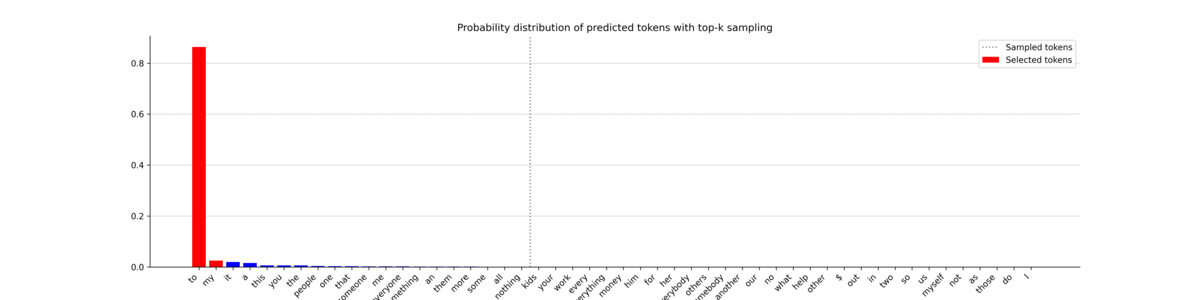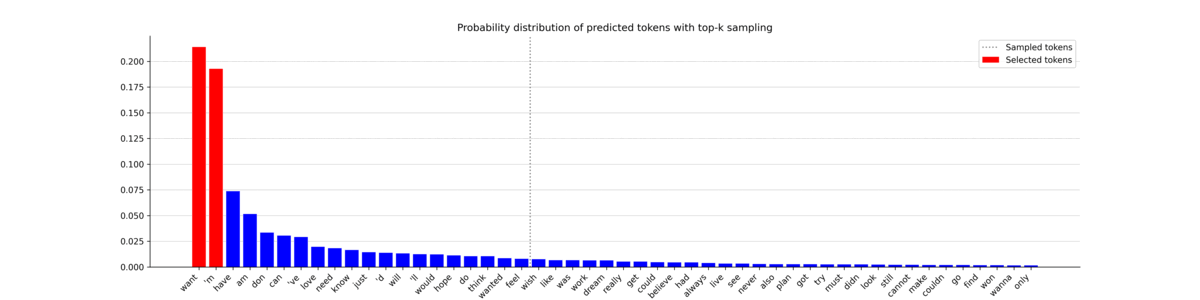
Let’s now implement the top k sampling algorithm. We’ll use it in the beam_search() function by providing the “top_k” argument. To illustrate how the algorithm works, we will also plot the probability distributions for top_k = 20.

def plot_prob_distribution(probabilities, next_tokens, sampling, potential_nb, total_nb=50):
    # Get top k tokens
    top_k_prob, top_k_indices = torch.topk(probabilities, total_nb)
    top_k_tokens = [tokenizer.decode([idx]) for idx in top_k_indices.tolist()]

    # Get next tokens and their probabilities
    next_tokens_list = [tokenizer.decode([idx]) for idx in next_tokens.tolist()]
    next_token_prob = probabilities[next_tokens].tolist()

    # Create figure
    plt.figure(figsize=(0.4*total_nb, 5), dpi=300, facecolor='white')
    plt.rc('axes', axisbelow=True)
    plt.grid(axis='y', linestyle='-', alpha=0.5)
    if potential_nb < total_nb:
        plt.axvline(x=potential_nb-0.5, ls=':', color='grey', label='Sampled tokens')
    plt.bar(top_k_tokens, top_k_prob.tolist(), color='blue')
    plt.bar(next_tokens_list, next_token_prob, color='red', label='Selected tokens')
    plt.xticks(rotation=45, ha='right', va='top')
    plt.gca().spines['top'].set_visible(False)
    plt.gca().spines['right'].set_visible(False)
    if sampling == 'top_k':
        plt.title('Probability distribution of predicted tokens with top-k sampling')
    elif sampling == 'nucleus':
        plt.title('Probability distribution of predicted tokens with nucleus sampling')
    plt.legend()
    plt.savefig(f'{sampling}_{time.time()}.png', dpi=300)
    plt.close()

def top_k_sampling(logits, temperature, top_k, beams, plot=True):
    assert top_k >= 1
    assert beams <= top_k

    indices_to_remove = logits < torch.topk(logits, top_k)[0][..., -1, None]
    new_logits = torch.clone(logits)
    new_logits[indices_to_remove] = float('-inf')

    # Convert logits to probabilities
    probabilities = torch.nn.functional.softmax(new_logits / temperature, dim=-1)

    # Sample n tokens from the resulting distribution
    next_tokens = torch.multinomial(probabilities, beams)

    # Plot distribution
    if plot:
        total_prob = torch.nn.functional.softmax(logits / temperature, dim=-1)
        plot_prob_distribution(total_prob, next_tokens, 'top_k', top_k)

    return next_tokens

# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'top_k', 1)

These plots give a good intuition of how top-k sampling works, with all the potentially selected tokens on the left of the horizontal bar. While the most probable tokens are selected (in red) most of the time, it also allows less likely tokens to be chosen. This offers an interesting tradeoff that can steer a sequence towards a less predictable but more natural-sounding sentence. Now let’s print the text it generated.

sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}")

Generated text: I have a dream job and I want to

The top-k sampling found a new sequence: “I have a dream job and I want to”, which feels significantly more natural than “I have a dream. I have a dream”. We’re making progress!

Let’s see how this decision tree differs from the previous one.

# Plot graph
plot_graph(graph, length, beams, 'sequence')

You can see how the nodes differ significantly from the previous iteration, making more diverse choices. Although the sequence score of this new outcome might not be the highest (-1.01 instead of -0.69 previously), it’s important to remember that higher scores do not always lead to more realistic or meaningful sequences.

Now that we’ve introduced top-k sampling, we have to present the other most popular sampling technique: nucleus sampling.

🔬 Nucleus sampling

Nucleus sampling, also known as top-p sampling, takes a different approach from top-k sampling. Rather than selecting the top $k$ most probable tokens, nucleus sampling chooses a cutoff value $p$ such that the sum of the probabilities of the selected tokens exceeds $p$. This forms a "nucleus" of tokens from which to randomly choose the next token.

In other words, the model examines its top probable tokens in descending order and keeps adding them to the list until the total probability surpasses the threshold $p$. Unlike top-k sampling, the number of tokens included in the nucleus can vary from step to step. This variability often results in a more diverse and creative output, making nucleus sampling popular for tasks such as text generation.

To implement the nucleus sampling method, we can use the "nucleus" parameter in the beam_search() function. In this example, we'll set the value of $p$ to 0.5. To make it easier, we'll include a minimum number of tokens equal to the number of beams. We'll also consider tokens with cumulative probabilities lower than $p$, rather than higher. It's worth noting that while the details may differ, the core idea of nucleus sampling remains the same.

def nucleus_sampling(logits, temperature, p, beams, plot=True):
    assert p > 0
    assert p <= 1

    # Sort the probabilities in descending order and compute cumulative probabilities
    sorted_logits, sorted_indices = torch.sort(logits, descending=True)
    probabilities = torch.nn.functional.softmax(sorted_logits / temperature, dim=-1)
    cumulative_probabilities = torch.cumsum(probabilities, dim=-1)

    # Create a mask for probabilities that are in the top-p
    mask = cumulative_probabilities < p

    # If there's not n index where cumulative_probabilities < p, we use the top n tokens instead
    if mask.sum() > beams:
        top_p_index_to_keep = torch.where(mask)[0][-1].detach().cpu().tolist()
    else:
        top_p_index_to_keep = beams

    # Only keep top-p indices
    indices_to_remove = sorted_indices[top_p_index_to_keep:]
    sorted_logits[indices_to_remove] = float('-inf')

    # Sample n tokens from the resulting distribution
    probabilities = torch.nn.functional.softmax(sorted_logits / temperature, dim=-1)
    next_tokens = torch.multinomial(probabilities, beams)

    # Plot distribution
    if plot:
        total_prob = torch.nn.functional.softmax(logits / temperature, dim=-1)
        plot_prob_distribution(total_prob, next_tokens, 'nucleus', top_p_index_to_keep)

    return next_tokens

# Start generating text
beam_search(input_ids, 0, bar, length, beams, 'nucleus', 1)

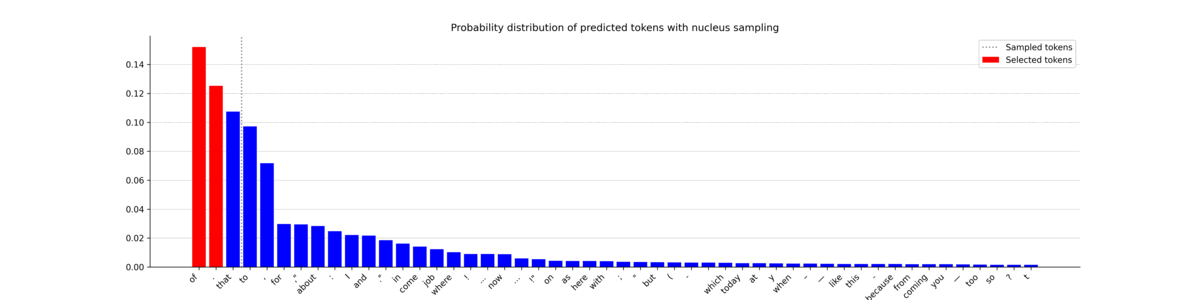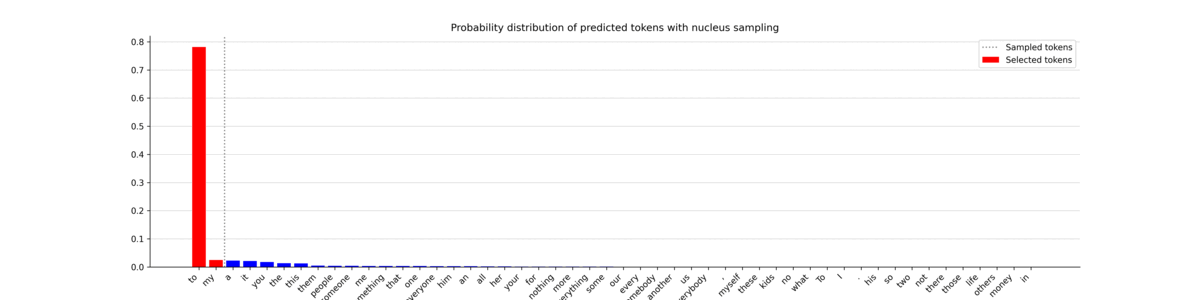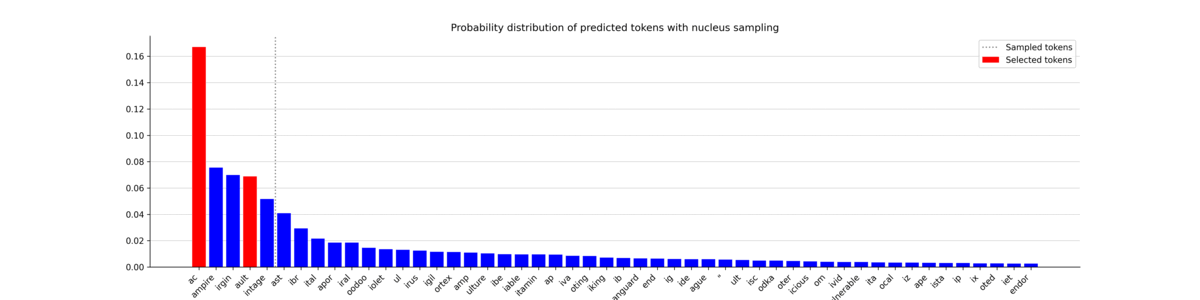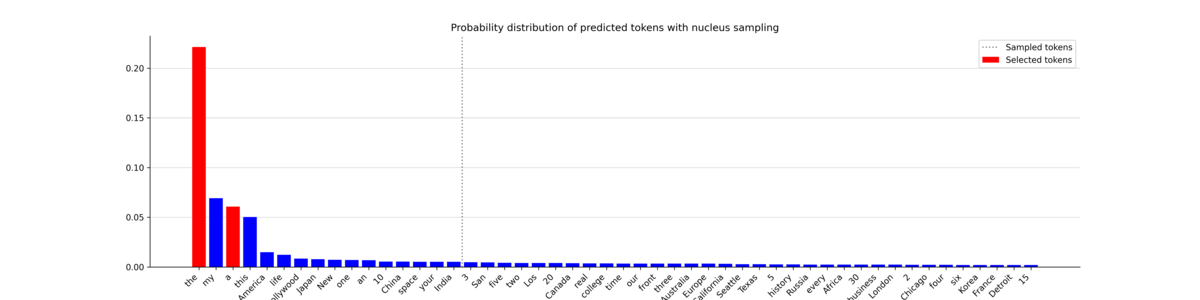
In this plot, you can see that the number of tokens included in the nucleus (left of the vertical bar) fluctuates a lot. The generated probability distributions vary considerably, leading to the selection of tokens that are not always among the most probable ones. This opens the door to the generation of unique and varied sequences. Now, let’s observe the text it generated.

sequence, max_score = get_best_sequence(graph)
print(f"Generated text: {sequence}")

Generated text: I have a dream. I'm going to

The nucleus sampling algorithm produces the sequence: “I have a dream. I’m going to”, which shows a notable enhancement in semantic coherence compared to greedy sampling.

To compare the decision paths, let’s visualize the new tree nucleus sampling generated.

# Plot graph
plot_graph(graph, length, beams, 'sequence')

As with top-k sampling, this tree is very different from the one generated with greedy sampling, displaying more variety. Both top-k and nucleus sampling offer unique advantages when generating text, enhancing diversity, and introducing creativity into the output. Your choice between the two methods (or even greedy search) will depend on the specific requirements and constraints of your project.

Conclusion

In this article, we have delved deep into various decoding methods used by LLMs, specifically GPT-2. We started with a simple greedy search and its immediate (yet often suboptimal) selection of the most probable next token. Next, we introduced the beam search technique, which considers several of the most likely tokens at each step. Although it offers more nuanced results, beam search can sometimes fall short in generating diverse and creative sequences.

To bring more variability into the process, we then moved on to top-k sampling and nucleus sampling. Top-k sampling diversifies the text generation by randomly selecting among the k most probable tokens, while nucleus sampling takes a different path by dynamically forming a nucleus of tokens based on cumulative probability. Each of these methods brings unique strengths and potential drawbacks to the table, and the specific requirements of your project will largely dictate the choice among them.

Ultimately, understanding these techniques and their trade-offs will equip you to better guide the LLMs toward producing increasingly realistic, nuanced, and compelling textual output.

If you’re interested in more technical content around LLMs, you can follow me on Twitter @maximelabonne.

Upvote