Update Thinking Like Transformers-cn.md
Browse files- Thinking Like Transformers-cn.md +28 -25
Thinking Like Transformers-cn.md
CHANGED
|
@@ -1,3 +1,4 @@
|
|
|
|
|
| 1 |
|
| 2 |
- [论文](https://arxiv.org/pdf/2106.06981.pdf) 来自 Gail Weiss, Yoav Goldberg,Eran Yahav.
|
| 3 |
- 博客参考 [Sasha Rush](https://rush-nlp.com/) 和 [Gail Weiss](https://sgailw.cswp.cs.technion.ac.il/)
|
|
@@ -35,16 +36,17 @@ flip()
|
|
| 35 |
|
| 36 |
|
| 37 |
</center>
|
|
|
|
| 38 |
## 表格目录
|
| 39 |
|
| 40 |
-
- 部分一:
|
| 41 |
-
-
|
| 42 |
|
| 43 |
## Transformers 作为代码
|
| 44 |
|
| 45 |
-
我们的目标是定义一套计算形式来最小化 Transformers 的表达。我们将通过类比进行此过程,描述其 Transformers 方面的每个语言构造。(正式语言规范请看[全文](https://arxiv.org/pdf/2106.06981.pdf))
|
| 46 |
|
| 47 |
-
这个语言的核心单元是将一个序列转换成相同长度的另一个序列的序列操作。我后面将其称之为 transforms
|
| 48 |
|
| 49 |
### 输入
|
| 50 |
|
|
@@ -56,7 +58,7 @@ flip()
|
|
| 56 |
|
| 57 |
</center>
|
| 58 |
|
| 59 |
-
在代码中,
|
| 60 |
|
| 61 |
```python
|
| 62 |
tokens
|
|
@@ -80,7 +82,7 @@ tokens.input([5, 2, 4, 5, 2, 2])
|
|
| 80 |
|
| 81 |
</center>
|
| 82 |
|
| 83 |
-
作为 Transformers
|
| 84 |
|
| 85 |
```python
|
| 86 |
indices
|
|
@@ -125,7 +127,7 @@ tokens == "l"
|
|
| 125 |
|
| 126 |
</center>
|
| 127 |
|
| 128 |
-
结果是一个新的 transform
|
| 129 |
|
| 130 |
```python
|
| 131 |
model = tokens * 2 - 1
|
|
@@ -138,7 +140,7 @@ model.input([1, 2, 3, 5, 2])
|
|
| 138 |
|
| 139 |
</center>
|
| 140 |
|
| 141 |
-
该运算可以组合多个 Transforms
|
| 142 |
|
| 143 |
```python
|
| 144 |
model = tokens - 5 + indices
|
|
@@ -161,7 +163,7 @@ model.input([1, 2, 3, 5, 2])
|
|
| 161 |
|
| 162 |
</center>
|
| 163 |
|
| 164 |
-
我们提供了一些辅助函数让写 transforms
|
| 165 |
|
| 166 |
```python
|
| 167 |
where((tokens == "h") | (tokens == "l"), tokens, "q")
|
|
@@ -173,7 +175,7 @@ where((tokens == "h") | (tokens == "l"), tokens, "q")
|
|
| 173 |
|
| 174 |
</center>
|
| 175 |
|
| 176 |
-
`map` 使我们可以定义自己的操作,例如一个字符串以 int 转换。(用户应谨慎使用可以使用的简单神经网络计算的操作)
|
| 177 |
|
| 178 |
```python
|
| 179 |
atoi = tokens.map(lambda x: ord(x) - ord('0'))
|
|
@@ -186,7 +188,7 @@ atoi.input("31234")
|
|
| 186 |
|
| 187 |
</center>
|
| 188 |
|
| 189 |
-
当连接了这些 transforms
|
| 190 |
|
| 191 |
```python
|
| 192 |
def atoi(seq=tokens):
|
|
@@ -211,7 +213,7 @@ op.input("02-13")
|
|
| 211 |
|
| 212 |
</center>
|
| 213 |
|
| 214 |
-
我们开始定义
|
| 215 |
|
| 216 |
```python
|
| 217 |
key(tokens)
|
|
@@ -223,7 +225,7 @@ key(tokens)
|
|
| 223 |
|
| 224 |
</center>
|
| 225 |
|
| 226 |
-
对于 query 也一样
|
| 227 |
|
| 228 |
```python
|
| 229 |
query(tokens)
|
|
@@ -235,7 +237,7 @@ query(tokens)
|
|
| 235 |
|
| 236 |
</center>
|
| 237 |
|
| 238 |
-
标量可以作为 key 或 query
|
| 239 |
|
| 240 |
```python
|
| 241 |
query(1)
|
|
@@ -261,7 +263,8 @@ eq
|
|
| 261 |
</center>
|
| 262 |
|
| 263 |
一些例子:
|
| 264 |
-
|
|
|
|
| 265 |
|
| 266 |
```python
|
| 267 |
offset = (key(indices) == query(indices - 1))
|
|
@@ -274,7 +277,7 @@ offset
|
|
| 274 |
|
| 275 |
</center>
|
| 276 |
|
| 277 |
-
- key 早于 query
|
| 278 |
|
| 279 |
```python
|
| 280 |
before = key(indices) < query(indices)
|
|
@@ -287,7 +290,7 @@ before
|
|
| 287 |
|
| 288 |
</center>
|
| 289 |
|
| 290 |
-
- key 晚于 query
|
| 291 |
|
| 292 |
```python
|
| 293 |
after = key(indices) > query(indices)
|
|
@@ -329,7 +332,7 @@ before & eq
|
|
| 329 |
|
| 330 |
</center>
|
| 331 |
|
| 332 |
-
视觉上我们遵循图表结构,
|
| 333 |
|
| 334 |
<center>
|
| 335 |
|
|
@@ -353,7 +356,7 @@ length
|
|
| 353 |
|
| 354 |
这里有更多复杂的例子,下面将一步一步展示。(这有点像做采访一样)
|
| 355 |
|
| 356 |
-
|
| 357 |
|
| 358 |
```python
|
| 359 |
WINDOW=3
|
|
@@ -367,7 +370,7 @@ s1
|
|
| 367 |
|
| 368 |
</center>
|
| 369 |
|
| 370 |
-
|
| 371 |
|
| 372 |
```python
|
| 373 |
s2 = (key(indices) <= query(indices))
|
|
@@ -379,7 +382,7 @@ s2
|
|
| 379 |
|
| 380 |
</center>
|
| 381 |
|
| 382 |
-
|
| 383 |
|
| 384 |
```python
|
| 385 |
sel = s1 & s2
|
|
@@ -392,7 +395,7 @@ sel
|
|
| 392 |
|
| 393 |
</center>
|
| 394 |
|
| 395 |
-
|
| 396 |
|
| 397 |
```python
|
| 398 |
sum2 = sel.value(tokens)
|
|
@@ -526,7 +529,7 @@ first("l")
|
|
| 526 |
|
| 527 |
### 挑战五 :右对齐
|
| 528 |
|
| 529 |
-
右对齐一个填充序列。例:
|
| 530 |
|
| 531 |
```python
|
| 532 |
def ralign(default="-", sop=tokens):
|
|
@@ -544,7 +547,7 @@ ralign()("xyz__")
|
|
| 544 |
|
| 545 |
### 挑战六:分离
|
| 546 |
|
| 547 |
-
把一个序列在 token "v" 处分离成两部分然后右对齐 (2 层)
|
| 548 |
|
| 549 |
```python
|
| 550 |
def split(v, i, sop=tokens):
|
|
@@ -577,7 +580,7 @@ split("+", 0)("xyz+zyr")
|
|
| 577 |
|
| 578 |
### 挑战七:滑动
|
| 579 |
|
| 580 |
-
将特殊 token
|
| 581 |
|
| 582 |
```python
|
| 583 |
def slide(match, seq=tokens):
|
|
|
|
| 1 |
+
# 了解 Transformers 是如何“思考”的
|
| 2 |
|
| 3 |
- [论文](https://arxiv.org/pdf/2106.06981.pdf) 来自 Gail Weiss, Yoav Goldberg,Eran Yahav.
|
| 4 |
- 博客参考 [Sasha Rush](https://rush-nlp.com/) 和 [Gail Weiss](https://sgailw.cswp.cs.technion.ac.il/)
|
|
|
|
| 36 |

|
| 37 |
|
| 38 |
</center>
|
| 39 |
+
|
| 40 |
## 表格目录
|
| 41 |
|
| 42 |
+
- 部分一:Transformers 作为代码
|
| 43 |
+
- 部分二:用 Transformers 编写程序
|
| 44 |
|
| 45 |
## Transformers 作为代码
|
| 46 |
|
| 47 |
+
我们的目标是定义一套计算形式来最小化 Transformers 的表达。我们将通过类比进行此过程,描述其 Transformers 方面的每个语言构造。(正式语言规范请看 [全文](https://arxiv.org/pdf/2106.06981.pdf))
|
| 48 |
|
| 49 |
+
这个语言的核心单元是将一个序列转换成相同长度的另一个序列的序列操作。我后面将其称之为 transforms。
|
| 50 |
|
| 51 |
### 输入
|
| 52 |
|
|
|
|
| 58 |
|
| 59 |
</center>
|
| 60 |
|
| 61 |
+
在代码中,tokens 的特征表示最简单的 transform,它返回经过模型的 tokens,默认输入序列是 "hello":
|
| 62 |
|
| 63 |
```python
|
| 64 |
tokens
|
|
|
|
| 82 |
|
| 83 |
</center>
|
| 84 |
|
| 85 |
+
作为 Transformers,我们不能直接接受这些序列的位置。但是为了模拟位置嵌入,我们可以获取位置的索引:
|
| 86 |
|
| 87 |
```python
|
| 88 |
indices
|
|
|
|
| 127 |
|
| 128 |
</center>
|
| 129 |
|
| 130 |
+
结果是一个新的 transform,一旦重构新的输入就会按照重构方式计算:
|
| 131 |
|
| 132 |
```python
|
| 133 |
model = tokens * 2 - 1
|
|
|
|
| 140 |
|
| 141 |
</center>
|
| 142 |
|
| 143 |
+
该运算可以组合多个 Transforms,举个例子,以上述的 token 和 indices 为例,这里可以类别 Transformer 可以跟踪多个片段信息:
|
| 144 |
|
| 145 |
```python
|
| 146 |
model = tokens - 5 + indices
|
|
|
|
| 163 |
|
| 164 |
</center>
|
| 165 |
|
| 166 |
+
我们提供了一些辅助函数让写 transforms 变得更简单,举例来说,`where` 提供了一个类似 `if` 功能的结构。
|
| 167 |
|
| 168 |
```python
|
| 169 |
where((tokens == "h") | (tokens == "l"), tokens, "q")
|
|
|
|
| 175 |
|
| 176 |
</center>
|
| 177 |
|
| 178 |
+
`map` 使我们可以定义自己的操作,例如一个字符串以 `int` 转换。(用户应谨慎使用可以使用的简单神经网络计算的操作)
|
| 179 |
|
| 180 |
```python
|
| 181 |
atoi = tokens.map(lambda x: ord(x) - ord('0'))
|
|
|
|
| 188 |
|
| 189 |
</center>
|
| 190 |
|
| 191 |
+
当连接了这些 transforms,可以更容易的编写功能。举例来说,下面是应用了 where 和 atoi 和加 2 的操作
|
| 192 |
|
| 193 |
```python
|
| 194 |
def atoi(seq=tokens):
|
|
|
|
| 213 |
|
| 214 |
</center>
|
| 215 |
|
| 216 |
+
我们开始定义 key 和 query 的标记,Keys 和 Queries 可以直接从上面的 transforms 创建。举个例子,如果我们想要定义一个 key 我们称作 `key`。
|
| 217 |
|
| 218 |
```python
|
| 219 |
key(tokens)
|
|
|
|
| 225 |
|
| 226 |
</center>
|
| 227 |
|
| 228 |
+
对于 `query` 也一样
|
| 229 |
|
| 230 |
```python
|
| 231 |
query(tokens)
|
|
|
|
| 237 |
|
| 238 |
</center>
|
| 239 |
|
| 240 |
+
标量可以作为 `key` 或 `query` 使用,他们会广播到基础序列的长度。
|
| 241 |
|
| 242 |
```python
|
| 243 |
query(1)
|
|
|
|
| 263 |
</center>
|
| 264 |
|
| 265 |
一些例子:
|
| 266 |
+
|
| 267 |
+
- 选择器的匹配位置偏移 1:
|
| 268 |
|
| 269 |
```python
|
| 270 |
offset = (key(indices) == query(indices - 1))
|
|
|
|
| 277 |
|
| 278 |
</center>
|
| 279 |
|
| 280 |
+
- key 早于 query 的选择器:
|
| 281 |
|
| 282 |
```python
|
| 283 |
before = key(indices) < query(indices)
|
|
|
|
| 290 |
|
| 291 |
</center>
|
| 292 |
|
| 293 |
+
- key 晚于 query 的选择器:
|
| 294 |
|
| 295 |
```python
|
| 296 |
after = key(indices) > query(indices)
|
|
|
|
| 332 |
|
| 333 |
</center>
|
| 334 |
|
| 335 |
+
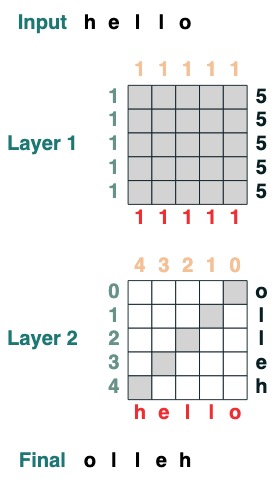
视觉上我们遵循图表结构,Query 在左边,Key 在上边,Value 在下面,输出在右边
|
| 336 |
|
| 337 |
<center>
|
| 338 |
|
|
|
|
| 356 |
|
| 357 |
这里有更多复杂的例子,下面将一步一步展示。(这有点像做采访一样)
|
| 358 |
|
| 359 |
+
我们想要计算一个序列的相邻值的和,首先我们向前截断:
|
| 360 |
|
| 361 |
```python
|
| 362 |
WINDOW=3
|
|
|
|
| 370 |
|
| 371 |
</center>
|
| 372 |
|
| 373 |
+
然后我们向后截断:
|
| 374 |
|
| 375 |
```python
|
| 376 |
s2 = (key(indices) <= query(indices))
|
|
|
|
| 382 |
|
| 383 |
</center>
|
| 384 |
|
| 385 |
+
两者相交:
|
| 386 |
|
| 387 |
```python
|
| 388 |
sel = s1 & s2
|
|
|
|
| 395 |
|
| 396 |
</center>
|
| 397 |
|
| 398 |
+
最终聚合:
|
| 399 |
|
| 400 |
```python
|
| 401 |
sum2 = sel.value(tokens)
|
|
|
|
| 529 |
|
| 530 |
### 挑战五 :右对齐
|
| 531 |
|
| 532 |
+
右对齐一个填充序列。例:"`ralign().inputs('xyz___') ='—xyz'`" (2 层)
|
| 533 |
|
| 534 |
```python
|
| 535 |
def ralign(default="-", sop=tokens):
|
|
|
|
| 547 |
|
| 548 |
### 挑战六:分离
|
| 549 |
|
| 550 |
+
把一个序列在 token "v" 处分离成两部分然后右对齐 (2 层):
|
| 551 |
|
| 552 |
```python
|
| 553 |
def split(v, i, sop=tokens):
|
|
|
|
| 580 |
|
| 581 |
### 挑战七:滑动
|
| 582 |
|
| 583 |
+
将特殊 token "<" 替换为最接近的 "<" value (2 层):
|
| 584 |
|
| 585 |
```python
|
| 586 |
def slide(match, seq=tokens):
|