code
stringlengths 2.5k
836k
| kind
stringclasses 2
values | parsed_code
stringlengths 2
404k
| quality_prob
float64 0.6
0.98
| learning_prob
float64 0.3
1
|
|---|---|---|---|---|
# Visualizing Logistic Regression
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('data/', one_hot=True)
trainimg = mnist.train.images
trainlabel = mnist.train.labels
testimg = mnist.test.images
testlabel = mnist.test.labels
```
# Define the graph
```
# Parameters of Logistic Regression
learning_rate = 0.01
training_epochs = 20
batch_size = 100
display_step = 5
# Create Graph for Logistic Regression
x = tf.placeholder("float", [None, 784], name="INPUT_x")
y = tf.placeholder("float", [None, 10], name="OUTPUT_y")
W = tf.Variable(tf.zeros([784, 10]), name="WEIGHT_W")
b = tf.Variable(tf.zeros([10]), name="BIAS_b")
# Activation, Cost, and Optimizing functions
pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))
optm = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accr = tf.reduce_mean(tf.cast(corr, "float"))
init = tf.initialize_all_variables()
```
# Launch the graph
```
sess = tf.Session()
sess.run(init)
```
# Summary writer
```
summary_path = '/tmp/tf_logs/logistic_regression_mnist'
summary_writer = tf.summary.FileWriter(summary_path, graph=sess.graph)
print ("Summary writer ready")
```
# Run
```
print ("Summary writer ready")
for epoch in range(training_epochs):
sum_cost = 0.
num_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(num_batch):
randidx = np.random.randint(trainimg.shape[0], size=batch_size)
batch_xs = trainimg[randidx, :]
batch_ys = trainlabel[randidx, :]
# Fit training using batch data
feeds = {x: batch_xs, y: batch_ys}
sess.run(optm, feed_dict=feeds)
# Compute average loss
sum_cost += sess.run(cost, feed_dict=feeds)
avg_cost = sum_cost / num_batch
# Display logs per epoch step
if epoch % display_step == 0:
train_acc = sess.run(accr, feed_dict={x: batch_xs, y: batch_ys})
print ("Epoch: %03d/%03d cost: %.9f train_acc: %.3f"
% (epoch, training_epochs, avg_cost, train_acc))
print ("Optimization Finished!")
# Test model
test_acc = sess.run(accr, feed_dict={x: testimg, y: testlabel})
print (("Test Accuracy: %.3f") % (test_acc))
float(epoch)
```
### Run the command line
##### tensorboard --logdir=/tmp/tf_logs/logistic_regression_mnist
### Open http://localhost:6006/ into your web browser
<img src="images/tsboard/logistic_regression_mnist.png">
|
github_jupyter
|
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('data/', one_hot=True)
trainimg = mnist.train.images
trainlabel = mnist.train.labels
testimg = mnist.test.images
testlabel = mnist.test.labels
# Parameters of Logistic Regression
learning_rate = 0.01
training_epochs = 20
batch_size = 100
display_step = 5
# Create Graph for Logistic Regression
x = tf.placeholder("float", [None, 784], name="INPUT_x")
y = tf.placeholder("float", [None, 10], name="OUTPUT_y")
W = tf.Variable(tf.zeros([784, 10]), name="WEIGHT_W")
b = tf.Variable(tf.zeros([10]), name="BIAS_b")
# Activation, Cost, and Optimizing functions
pred = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))
optm = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accr = tf.reduce_mean(tf.cast(corr, "float"))
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
summary_path = '/tmp/tf_logs/logistic_regression_mnist'
summary_writer = tf.summary.FileWriter(summary_path, graph=sess.graph)
print ("Summary writer ready")
print ("Summary writer ready")
for epoch in range(training_epochs):
sum_cost = 0.
num_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(num_batch):
randidx = np.random.randint(trainimg.shape[0], size=batch_size)
batch_xs = trainimg[randidx, :]
batch_ys = trainlabel[randidx, :]
# Fit training using batch data
feeds = {x: batch_xs, y: batch_ys}
sess.run(optm, feed_dict=feeds)
# Compute average loss
sum_cost += sess.run(cost, feed_dict=feeds)
avg_cost = sum_cost / num_batch
# Display logs per epoch step
if epoch % display_step == 0:
train_acc = sess.run(accr, feed_dict={x: batch_xs, y: batch_ys})
print ("Epoch: %03d/%03d cost: %.9f train_acc: %.3f"
% (epoch, training_epochs, avg_cost, train_acc))
print ("Optimization Finished!")
# Test model
test_acc = sess.run(accr, feed_dict={x: testimg, y: testlabel})
print (("Test Accuracy: %.3f") % (test_acc))
float(epoch)
| 0.676086 | 0.913252 |
# Final Project Submission
* Student name: `Reno Vieira Neto`
* Student pace: `self paced`
* Scheduled project review date/time: `Fri Oct 15, 2021 3pm – 3:45pm (PDT)`
* Instructor name: `James Irving`
* Blog post URL: https://renoneto.github.io/using_streamlit
#### This project originated the [following app](https://movie-recommender-reno.herokuapp.com/). I'd recommend playing with the app and then coming back here to understand how the model behind it works.
# Table of Contents <a class="anchor" id="toc"></a>
- **[Business Case and Goals](#bc)**
- **[The Dataset](#td)**
- **[Dataset Exploration and Cleaning](#dec)**
- **[No. of Movies by Genre](#mg)**
- **[No. of Ratings per Year](#ry)**
- **[No. of Users rating movies per Year](#urm)**
- **[Recommender System](#rs)**
- **[Create Popularity Model](#pop)**
- **[Collaborative-Based Filtering](#colab)**
- **[Hyperparameter Tuning](#grid)**
- **[Try different models](#dif)**
- **[Model Evaluation](#eval)**
- **[Create function to take user input and give recommendations (+ hint of content-based attribute)](#func)**
- **[Conclusion](#conclusion)**
- **[Export files to create app](#lit)**
- **[Improvements](#improvements)**
# Business Case and Goal <a class="anchor" id="bc"></a>
In this project, I'm creating a movie recommender using the [MovieLens dataset](https://grouplens.org/datasets/movielens/) to build a model that provides top 5 movie recommendations to a user, based on their ratings of other movies. I'm going to be addressing the cold start problem as well by being able to deal with users with no movie ratings.
# The Dataset <a class="anchor" id="td"></a>
The MovieLens dataset is a "classic" recommendation system dataset used in numerous academic papers and machine learning proofs-of-concept.
[You can find more about it here](https://grouplens.org/datasets/movielens/)
# Dataset Exploration and Cleaning <a class="anchor" id="dec"></a>
## Import necessary packages
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import re
import time
from surprise import Reader, Dataset, dump
from surprise.model_selection import cross_validate, GridSearchCV
from surprise.prediction_algorithms import KNNBasic, KNNBaseline, SVD, SVDpp
from surprise.accuracy import rmse
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
# Import datasets
df_movies = pd.read_csv('./app/data/movies.csv')
df_ratings = pd.read_csv('./app/data/ratings.csv')
# Show first rows
display(df_movies.head())
display(df_ratings.head())
```
#### Notes
- Breakdown genres into different columns (one-hot encoding)
- `title` seems to have the release year of the movie. It might be interesting to have title and year in different columns.
```
# Check for nulls and data types
display(df_movies.info())
display(df_ratings.info())
```
#### Notes
- No nulls
- Might need to convert timestamps to `datetime`
- There are 9742 movies in the dataset
- 100836 ratings
### `df_movies`
First, I'm going to start exploring the movies dataset to understand what I'm dealing with.
```
# Create column with array of genres and calculate the Number of Genres per movie
df_movies['genres_array'] = df_movies['genres'].str.split('|')
# Flattened genres
stacked_genres = df_movies['genres_array'].apply(pd.Series).stack(level=0).reset_index()
stacked_genres.columns = ['index', 'level_1', 'genre']
# Combine original dataframe with flattened genres using the index
df_movies_new = pd.merge(df_movies, stacked_genres, how='left', left_index=True, right_on=['index'])
df_movies_new = df_movies_new[['movieId', 'title', 'genre']]
# One-hot Encoding of Genre column
one_hot = pd.get_dummies(df_movies_new['genre'])
# Get list of genres (it's going to be useful soon)
list_of_genres = list(one_hot.columns)
# Combine the new dataframe with the one-hot encoded dataframe
df_movies_new = pd.merge(df_movies_new, one_hot, left_index=True, right_index=True)
df_movies_new = df_movies_new.drop('genre', axis=1)
# Use groupby to have one row per movie
df_movies_new = df_movies_new.groupby(['movieId', 'title']).sum()[list_of_genres].reset_index()
# Split year and title
df_movies_new['release_year'] = df_movies_new.apply(lambda x: x['title'].strip()[-5:][:-1], axis=1)
df_movies_new['release_year'] = df_movies_new.apply(lambda x:
x['release_year']
if len(re.findall("[0-9]{4}", x['release_year'])) == 1
else np.nan, axis=1)
df_movies_new['title'] = df_movies_new.apply(lambda x:
x['title'][:-6].strip()
if x['release_year'] != np.nan
else x['title'], axis=1)
```
### No. of Movies by genre <a class="anchor" id="mg"></a>
**[Go back to Table of Contents](#toc)**
```
# Create empty dictionary to store the no of movies by genre
no_of_movies_by_genre = {}
for genre in list_of_genres:
no_of_movies = df_movies_new[genre].sum()
no_of_movies_by_genre[genre] = no_of_movies
# Transform that into a dataframe
to_plot = pd.DataFrame.from_dict(no_of_movies_by_genre, orient='index').reset_index()
to_plot.columns = ['genre', 'no_of_movies']
to_plot = to_plot.sort_values('no_of_movies', ascending=False).reset_index(drop=True)
# Plot
plt.figure(figsize=(10,8))
sns.barplot(x="no_of_movies", y="genre", data=to_plot)
plt.title('No of Movies by Genre', size=14)
plt.xlabel('No. of Movies', size=13)
plt.ylabel(None)
plt.show()
```
#### Note
- We are dealing with an unbalanced dataset from the perspective of the genres. There are way more Drama and Comedy movies than other genres. The consequence of that to the model is that certain genres will have a smaller set of options to choose from.
### `df_ratings`
### No. of Ratings per Year <a class="anchor" id="ry"></a>
I wonder how many ratings were created per year.
**[Go back to Table of Contents](#toc)**
```
# Convert timestamp column to datetime
df_ratings['datetime'] = pd.to_datetime(df_ratings['timestamp'], unit='s')
df_ratings['year'] = df_ratings['datetime'].dt.year
# Create plot with No. of ratings per year
to_plot = df_ratings.groupby('year').count()['rating'].reset_index()
plt.figure(figsize=(17,5))
sns.barplot(x='year', y='rating', data=to_plot, color='blue', alpha=0.5)
plt.title('No of Ratings per Year')
plt.show()
```
**Note**
- I don't see any trends. It's great to see that the last 4 years of the dataset had almost the same number of ratings.
### No. of Users rating movies per Year <a class="anchor" id="urm"></a>
**[Go back to Table of Contents](#toc)**
```
# Create Plot with No. of Unique Users giving ratings
to_plot = df_ratings.groupby('year').nunique()['userId'].reset_index()
plt.figure(figsize=(17,5))
sns.barplot(x='year', y='userId', data=to_plot, color='blue', alpha=0.5)
plt.title('No. of Users rating movies per Year')
plt.show()
```
**Note**
- Not many users rating movies. Around 40 per year.
# Recommender System <a class="anchor" id="rs"></a>
## Create Popularity Model <a class="anchor" id="pop"></a>
The first model is going to be very simple. It's a popularity model. Basically I'm going to rank movies by popularity. However, I need to find a way to scale the ratings because a movie with 100 ratings with an average of 4.5 and another with 2 with an average of 4.75 are completely different. I'd argue that the first movie actually has a higher rating score than the second one since more users have rated it with a high score.
To address that problem I'm using the IMDB's Weighted Rating Method I found [online](https://math.stackexchange.com/questions/169032/understanding-the-imdb-weighted-rating-function-for-usage-on-my-own-website) that does a good job at weighting the ratings.
#### Calculation

where,
* v is the number of votes for the movie;
* m is the minimum votes required to be listed in the chart;
* R is the average rating of the movie; And
* C is the mean vote across the whole report
#### C: Calculate mean vote across the whole dataset
```
# Calculate Mean and Count the No. of Ratings to a given movie
mean_ratings_df = df_ratings.groupby('movieId').agg(avg_rating=('rating', 'mean'),
count_rating=('rating', 'count')).reset_index()
# Calculate the Overall Average Rating
mean_ratings_df['overall_avg_rating'] = mean_ratings_df['avg_rating'].mean()
mean_ratings_df.head()
```
#### m: Define the minimum number of ratings required to be listed
To define the minimum number of votes I'm going to look at the distribution of No. of Ratings by Movies.
```
# Plot
plt.figure(figsize=(15,5))
sns.boxplot(x=mean_ratings_df['count_rating'])
plt.title('Boxplot of No. of Ratings given to movies')
plt.show()
```
Not super helpful. I'm going to print different quantiles
```
# Calculate different quatiles
n_of_users = df_ratings['userId'].nunique()
n_of_movies = len(mean_ratings_df)
quantiles_list = []
for n in range(10, 100, 5):
q = mean_ratings_df['count_rating'].quantile(n/100)
n_of_selected_movies = len(mean_ratings_df[mean_ratings_df['count_rating'] >= q])
quantiles_list.append([n, q, n_of_selected_movies])
pd.DataFrame(quantiles_list, columns=['quantile', 'quantile_value', 'number_of_movies'])
```
Before deciding the Minimum No. of Ratings, I'm going to look at the number of movies users have rated.
```
df_ratings.groupby('userId').count()['movieId'].describe()
```
The Median number of movies a user has rated is 70 movies and the 75th quantile is 168 movies.
Therefore, I'm comfortable moving forward with having the Minimum Number of Ratings (or `m`) of 47 ratings since that represents 491 Movies which is more than most users have rated.
> **Disclamer**: I have tried a minimum of 27/17 ratings as well, however, the model resulted in weird recommendations. So I'm picking 47 after iteratively trying 17 and 27.
#### m = 47
#### Create function to apply to the dataset
```
def weighted_rating(df):
"""
Calculates the IMDB's Weighted Rating using the following formula:
(v / (v+m) * R) + (m / (m+v) * C)
where:
- v is the number of votes for the movie;
- m is the minimum votes required to be listed in the chart;
- R is the average rating of the movie; And
- C is the mean vote across the whole report
"""
v = df['count_rating']
m = df['minimum_no_of_ratings']
R = df['avg_rating']
C = df['overall_avg_rating']
return (v / (v+m) * R) + (m / (m+v) * C)
# Create Copy
popularity_df = mean_ratings_df.copy()
# Calculate the 95th quantile and the weighted rating
popularity_df['minimum_no_of_ratings'] = popularity_df['count_rating'].quantile(0.95)
popularity_df['weighted_rating'] = popularity_df.apply(weighted_rating, axis=1)
```
I'm going to look at the top 10 movies with the highest ratings.
```
# Grab the top 10 ids
top_ten_ids = popularity_df.sort_values('weighted_rating', ascending=False)['movieId'][:10].values
# Print them
for idx, movie_id in enumerate(top_ten_ids):
print((idx + 1), df_movies[df_movies['movieId'] == movie_id]['title'].item())
```
Not too bad, I agree with these being the top 10. _However, that's very personal._
**[Go back to Table of Contents](#toc)**
## Collaborative-Based Filtering <a class="anchor" id="colab"></a>
Collaborative Filtering is based on the idea that users similar to a me can be utilized to predict how much I will like a particular product or service that those same users have used/experienced but I have not.
The strategy is to use different models and compare their performances. The metric to optimize for is RMSE. However, most likely, the best model will be the Singular Value Decomposition (SVD) or SVD++ based on what I have seen in different places. Nonetheless, I think it's worth trying different models rather than simply trying only these two models.
Moreover, I'm also considering the fit time, otherwise, I might end up with a model that would not be _deployable_.
```
# Create a new dataframe to train the model.
df_ratings_clean = df_ratings[['userId', 'movieId', 'rating']]
```
#### Reduce dataset to decrease runtime
The dataset is too big and it's going to take too long to train the models if I use the whole dataset (_I've learned that the hard way_). Therefore, I'm picking only 50% of it to identify the best hyperparameters for the SVD model and I'm running GridSearchCV only for 50% of that. Once I identify the best hyperparameters, I'll then train the model using the whole dataset.
```
# Randomly pick 50,000 datapoints fmor the dataset
sample_df = df_ratings_clean.sample(n=50000, random_state=111)
# Split the sample data in two so I can test the best hyperparameters later on
train_df, test_df = train_test_split(sample_df, train_size=.50, random_state=111)
# Create reader and dataset objects
reader = Reader()
traindata = Dataset.load_from_df(train_df, reader)
testdata = Dataset.load_from_df(test_df, reader)
```
### GridSearchCV - Hyperparameter Tunning of SVD <a class="anchor" id="grid"></a>
**[Go back to Table of Contents](#toc)**
```
# Perform a gridsearch with SVD
param_grid = {'n_factors':[10, 15, 20]
, 'n_epochs': [10, 20]
, 'lr_all': [0.008, 0.012]
, 'reg_all': [0.06, 0.1]
, 'random_state': [111]}
gs_model = GridSearchCV(SVD, param_grid=param_grid, n_jobs = -1, joblib_verbose=False)
%time gs_model.fit(traindata)
print('The best parameters are:')
gs_model.best_params['rmse']
```
### GridSearchCV Metrics Analysis
Let's analyze the metrics of each run and pick the best parameters given the RMSE and Fit Time. Sometimes simply choosing the best parameters is not the best option since the only goal of the Grid is to minimize RMSE. We should also consider the Fit Time if we are planning on having this model as a service running online.
```
# Convert results from the GridSearchCV to dataframes
df_params = pd.DataFrame(gs_model.cv_results['params'])
df_rmse = pd.DataFrame(gs_model.cv_results['mean_test_rmse'], columns=['mean_test_rmse'])
df_time = pd.DataFrame(gs_model.cv_results['mean_fit_time'], columns=['mean_fit_time'])
df_results = pd.concat([df_params, df_rmse, df_time], axis=1)
```
Create a function to print metrics so we can see the impact of hyperparameters in RMSE and Fit Time.
```
def compare_metrics_chart(df, column_a, column_b):
"""
Function to plot the comparison of two metrics in a GridSearchCV run.
Args:
df(pd.Dataframe): Pandas Dataframe with GridSearchCV metrics.
column_a(str): First metric
column_b(str): Second Metric
"""
# Create Figure
fig = plt.figure(figsize=(10,5))
# Create first axis
ax = fig.add_subplot(111)
# Plot Column A
sns.lineplot(data=df[column_a], color="g", ax=ax)
# Set Y Label
ax.set_ylabel(column_a, color='g', size=10)
# Create axis 2
ax2 = plt.twinx()
# Plot Column B
sns.lineplot(data=df[column_b], color="b", ax=ax2)
# Set Y Label
ax2.set_ylabel(column_b, color='b', size=10)
# Change the format of the title
column_a_title = column_a.replace('_', ' ').title()
column_b_title = column_b.replace('_', ' ').title()
plt.title(column_a_title + ' vs. ' + column_b_title)
plt.show();
```
#### Number of Factors
```
compare_metrics_chart(df_results, 'n_factors', 'mean_test_rmse')
compare_metrics_chart(df_results, 'n_factors', 'mean_fit_time')
```
The lowest values for RMSE is reached regardless of the Number of Factors. It's arguable that we should have more factors to decrease RMSE since that's the expectation. However, it comes at a cost: fit time increase. Since the data is showing we can achieve low RMSE with only `10` factors then I'm going to choose that.
#### Number of Epochs
```
compare_metrics_chart(df_results, 'n_epochs', 'mean_test_rmse')
compare_metrics_chart(df_results, 'n_epochs', 'mean_fit_time')
```
The Number of Epochs reduces RMSE, but it's possible to see an increase of 50%-80% in Fit Time, which is more than the positive impact in RMSE. Therefore, I'll go with `20` epochs.
#### Regularization Term
```
compare_metrics_chart(df_results, 'reg_all', 'mean_test_rmse')
compare_metrics_chart(df_results, 'reg_all', 'mean_fit_time')
```
Low regularization term achieves better results with no impact in fit time.
#### Learning Rate
```
compare_metrics_chart(df_results, 'lr_all', 'mean_test_rmse')
compare_metrics_chart(df_results, 'lr_all', 'mean_fit_time')
```
Having high Learning Rate has a positive impact in RMSE with now impact in Fit Time.
#### Final hyperparameters:
- `n_factors`: 15
- `n_epochs`: 20
- `lr_all`: 0.012
- `reg_all`: 0.06
**[Go back to Table of Contents](#toc)**
### Try different models <a class="anchor" id="dif"></a>
#### Create a function to easily test different models
```
def full_model_training_evaluation(model, model_name, traindata, testdata):
"""
Train and test different models and collect fit time and train/test RMSE.
Args:
model(surprise.prediction_algorithms): Model instances from the surprise package.
model_name(str): Model name created by the User. A way to identify the model.
traindata(surprise.dataset.DatasetAutoFolds): Train dataset
testdata(surprise.dataset.DatasetAutoFolds): Test dataset
Returns:
results(dict): A dictionary with the model name, fit time and RMSE's (train/test).
"""
# Stor results in dictionary
results = {}
results['model_name'] = model_name
print('Training', model_name, 'model')
# Fit on train data
start_time = time.time()
model.fit(traindata.build_full_trainset())
end_time = time.time()
total_time = round(end_time - start_time, 2)
results['fit_time_in_seconds'] = total_time
# Get RMSE on train data
predictions_train = model.test(traindata.build_full_trainset().build_testset())
rmse_train = rmse(predictions_train, verbose=False).round(2)
results['rmse_train'] = rmse_train
# Get RMSE on test data
predictions_test = model.test(testdata.build_full_trainset().build_testset())
rmse_test = rmse(predictions_test, verbose=False).round(2)
results['rmse_test'] = rmse_test
return results
```
Instantiate different models
```
# Create SVD model with the best hyperparameters
svd = SVD(n_factors=15, n_epochs=20, lr_all=0.012, reg_all=0.06, random_state=111)
# SVD++: Use the same hyperparameters
svd_pp = SVDpp(n_factors=15, n_epochs=20, lr_all=0.012, reg_all=0.06, random_state=111)
# Different instances of KNN Basic models with different hyperparameters
knn_basic_person_baseline = KNNBasic(sim_options={'name':'pearson_baseline', 'user_based':True}, verbose=False)
knn_basic_person = KNNBasic(sim_options={'name':'pearson', 'user_based':True}, verbose=False)
knn_basic_cosine = KNNBasic(sim_options={'name':'cosine', 'user_based':True}, verbose=False)
# Different instances of KNN Baseline models with different hyperparameters
knn_base_person_baseline = KNNBaseline(sim_options={'name':'pearson_baseline', 'user_based':True}, verbose=False)
knn_base_person = KNNBaseline(sim_options={'name':'pearson', 'user_based':True}, verbose=False)
knn_base_cosine = KNNBaseline(sim_options={'name':'cosine', 'user_based':True}, verbose=False)
# Put all models in a dictionary
models = {'SVD': svd,
'SVD++': svd_pp,
'KNNBasic Cosine': knn_basic_cosine,
'KNNBasic Person': knn_basic_person,
'KNNBasic Person Baseline': knn_basic_person_baseline,
'KNNBaseline Cosine': knn_base_cosine,
'KNNBaseline Person': knn_base_person,
'KNNBaseline Person Baseline': knn_base_person_baseline}
# Loop through different models and evaluate them
model_results = []
for model_name, model_instance in models.items():
results = full_model_training_evaluation(model_instance, model_name, traindata, testdata)
model_results.append(results)
```
**[Go back to Table of Contents](#toc)**
### Model Evaluation <a class="anchor" id="eval"></a>
```
pd.DataFrame(model_results)
```
#### Notes:
- **Fit Time**: `SVD++` is by far the worst model. All KNN models have somewhat the same Fit Time, which is 4 times faster than `SVD`. However, they are all very fast relative to the `SVD++` model.
- **RMSE Train**: The KNN Models using `person_baseline` is overfitting the train set. When comparing both Singular Value Decomposition models, the `SVD++` is performing better than the `SVD`.
- **RMSE Test**: Both Singular Value Decomposition models had the same performance numbers and performed better than all KNN models.
### Conclusion
I'll move forward with the `SVD` model given the fit time and RMSE scores.
**[Go back to Table of Contents](#toc)**
## Create function to take user input and give recommendations (+ hint of content-based attribute) <a class="anchor" id="func"></a>
Finally, I'm going to create a function that takes a genre and ratings from a user who has no ratings in the dataset. In the process, I'm going to focus my recommendations based on the chosen genre (content-based part of the recommendation).
```
# Create list of genres
list_of_genres = stacked_genres['genre'].sort_values().unique()[1:]
# Combine mean ratings and movies details
ratings_movies_df = pd.merge(mean_ratings_df, df_movies, on='movieId')
```
#### Filter the dataset by removing movies with not enough ratings
```
def filtered_dataset(genre):
"""
Function to filter the dataset given the genre and remove outliers.
Args:
genre(str): The genre the user has chosen to come with recommendations.
Returns:
genre_df(pd.DataFrame): Filtered Dataframe with only the chosen genre.
"""
# Keep only the selected genre
genre_df = ratings_movies_df[ratings_movies_df['genres'].str.contains(genre)]
# Calculate the 95th quantile and the weighted rating
minimum_no_of_ratings = genre_df['count_rating'].quantile(0.95)
genre_df['minimum_no_of_ratings'] = minimum_no_of_ratings
genre_df['weighted_rating'] = genre_df.apply(weighted_rating, axis=1)
# Remove movies with not enough ratings
genre_df = genre_df[genre_df['count_rating'] >= minimum_no_of_ratings]
# Sorted it by weighted rating so we have the highest ratings on the top
genre_df = genre_df.sort_values('weighted_rating', ascending=False)
genre_df = genre_df.reset_index(drop=True)
# Keep certain relevant columns
genre_df = genre_df[['movieId', 'title',
'genres', 'count_rating',
'minimum_no_of_ratings', 'weighted_rating']]
return genre_df
```
#### Create first a function to let the user rate five movies
```
def rate_movie(n_of_movies=5, default_user_id=9999999):
"""
Function to request a new user to review some movies.
Args:
n_of_movies(int): Number of ratings the new will have to give.
default_user_id(int): Random user id that will be given to the user to be able to reference to it later.
Returns:
new_ratings_df(pd.DataFrame): Pandas Dataframe with the new ratings
favorite_genre(str): The User's favorite genre
"""
# Print a list of the available genres
print('List of Available Genres: ', ", ".join(list_of_genres))
# Gather input from user on which genre will be analyzed
favorite_genre = input('Choose one genre from the following (case-sensitive): ')
# Filter the dataset
df_movies_popularity = filtered_dataset(favorite_genre)
# Keep only movies that contain the chosen genre
favorite_genre_movies = df_movies_popularity[df_movies_popularity['genres'].str.contains(favorite_genre)]
# Keep the highest rated movies
favorite_genre_movies = favorite_genre_movies.iloc[:20].sample(frac=1, random_state=111)
favorite_genre_movies = favorite_genre_movies.iloc[:n_of_movies]
print('')
# Created to store ratings from user
ratings_list = []
# Loop through dataframe with movies to be rated
for row in favorite_genre_movies.iterrows():
# Extract Title and ID
movie_title = row[1]['title']
movie_id = row[1]['movieId']
print('Movie to rate: ', movie_title)
# Gather rating from user
rating = input('How do you rate this movie on a scale of 1-5, press n if you have not seen :\n')
# Deal with users not typing a number and create a new variable with the integer
try:
rating_int = int(rating)
except:
rating_int = 1
# While the Rating is not valid, keep asking the user
while (rating != 'n') and not (1 <= rating_int <=5):
rating = input('Please rate the movie between 1-5 or n if you have not seen : \n')
else:
# If the rating is different from 'n' then we need to add the rating to the list
if rating != 'n':
ratings_list.append({'userId': default_user_id,
'movieId': movie_id,
'rating': rating_int})
print('')
# Convert to DataFrame
new_ratings_df = pd.DataFrame(ratings_list)
return new_ratings_df, favorite_genre, df_movies_popularity
```
#### Create a function to give the recommendations
```
def give_n_recommendations(model, default_user_id=9999999, n_recommendations=5):
"""
Function to request a new user to review movies and give recommendations based on that.
Args:
model(surprise.prediction_algorithms): Model instances from the surprise package.
default_user_id(int): Random user id that will be given to the user to be able to reference to it later.
n_recommendations(int): Number of recommendations that will be given to the user.
"""
# Extract ratings from the user
new_ratings_df, favorite_genre, df_movies_popularity = rate_movie(default_user_id=default_user_id)
watched_movies_id = new_ratings_df['movieId']
## add the new ratings to the original ratings DataFrame
updated_df = pd.concat([new_ratings_df, df_ratings_clean])
new_data = Dataset.load_from_df(updated_df, reader)
new_dataset = new_data.build_full_trainset()
# Fit new dataset
model.fit(new_dataset)
# make predictions for the user
results = []
for movie_id in df_movies_popularity['movieId'].unique():
predicted_score = model.predict(default_user_id, movie_id)[3]
results.append((movie_id, predicted_score))
# order the predictions from highest to lowest rated
ranked_movies = pd.DataFrame(results, columns=['movieId', 'predicted_score'])
ranked_movies = ranked_movies[~ranked_movies['movieId'].isin(watched_movies_id)]
ranked_movies = ranked_movies.sort_values('predicted_score', ascending=False).reset_index(drop=True)
ranked_movies = pd.merge(ranked_movies, df_movies, on='movieId')
# ranked_movies = ranked_movies[ranked_movies['genres'].str.contains(favorite_genre)]
print('The recommendations are the following:')
if len(ranked_movies) < n_recommendations:
n_recommendations = len(ranked_movies)
for row in range(n_recommendations):
movie_id = ranked_movies.iloc[row]['movieId']
recommended_title = df_movies[df_movies['movieId'] == movie_id]['title'].item()
print(f'No. {row+1} is {recommended_title}')
```
#### Let's test it out!
I'm going to try different genres to see how the model behaves.
#### `Action`
```
give_n_recommendations(svd)
```
#### `Documentary`
```
give_n_recommendations(svd)
```
#### `Crime`
```
give_n_recommendations(svd)
```
#### `Romance`
```
give_n_recommendations(svd)
```
# Conclusion <a class="anchor" id="conclusion"></a>
I'm happy with the results. However, I think the function is a bit limited. I'd like to have the recommender in an app. To do that, I'm going to use Streamlit.
**[Go back to Table of Contents](#toc)**
# Export files to create app <a class="anchor" id="lit"></a>
I'm going to export some files so I can use them in Streamlit
```
# Export it to use it on streamlit
ratings_movies_df.to_csv('./app/data/movies_by_rating.csv', index=0)
df_ratings_clean.to_csv('./app/data/user_movie_ratings.csv', index=0)
dump.dump('./app/data/svd.pkl', algo=svd)
```
# [Check out the App!](https://movie-recommender-reno.herokuapp.com/)
# Improvements <a class="anchor" id="improvements"></a>
- Use Normalized Discounted Cumulative Gain (NDCG) to evaluate models.
- Develop a Content-Based layer using `tags` and `genres` or even `title`/`year`.
- Sometimes I rate Star Wars with 1 star and the recommender outputs more Start Wars movies.
**[Go back to Table of Contents](#toc)**
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import re
import time
from surprise import Reader, Dataset, dump
from surprise.model_selection import cross_validate, GridSearchCV
from surprise.prediction_algorithms import KNNBasic, KNNBaseline, SVD, SVDpp
from surprise.accuracy import rmse
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
# Import datasets
df_movies = pd.read_csv('./app/data/movies.csv')
df_ratings = pd.read_csv('./app/data/ratings.csv')
# Show first rows
display(df_movies.head())
display(df_ratings.head())
# Check for nulls and data types
display(df_movies.info())
display(df_ratings.info())
# Create column with array of genres and calculate the Number of Genres per movie
df_movies['genres_array'] = df_movies['genres'].str.split('|')
# Flattened genres
stacked_genres = df_movies['genres_array'].apply(pd.Series).stack(level=0).reset_index()
stacked_genres.columns = ['index', 'level_1', 'genre']
# Combine original dataframe with flattened genres using the index
df_movies_new = pd.merge(df_movies, stacked_genres, how='left', left_index=True, right_on=['index'])
df_movies_new = df_movies_new[['movieId', 'title', 'genre']]
# One-hot Encoding of Genre column
one_hot = pd.get_dummies(df_movies_new['genre'])
# Get list of genres (it's going to be useful soon)
list_of_genres = list(one_hot.columns)
# Combine the new dataframe with the one-hot encoded dataframe
df_movies_new = pd.merge(df_movies_new, one_hot, left_index=True, right_index=True)
df_movies_new = df_movies_new.drop('genre', axis=1)
# Use groupby to have one row per movie
df_movies_new = df_movies_new.groupby(['movieId', 'title']).sum()[list_of_genres].reset_index()
# Split year and title
df_movies_new['release_year'] = df_movies_new.apply(lambda x: x['title'].strip()[-5:][:-1], axis=1)
df_movies_new['release_year'] = df_movies_new.apply(lambda x:
x['release_year']
if len(re.findall("[0-9]{4}", x['release_year'])) == 1
else np.nan, axis=1)
df_movies_new['title'] = df_movies_new.apply(lambda x:
x['title'][:-6].strip()
if x['release_year'] != np.nan
else x['title'], axis=1)
# Create empty dictionary to store the no of movies by genre
no_of_movies_by_genre = {}
for genre in list_of_genres:
no_of_movies = df_movies_new[genre].sum()
no_of_movies_by_genre[genre] = no_of_movies
# Transform that into a dataframe
to_plot = pd.DataFrame.from_dict(no_of_movies_by_genre, orient='index').reset_index()
to_plot.columns = ['genre', 'no_of_movies']
to_plot = to_plot.sort_values('no_of_movies', ascending=False).reset_index(drop=True)
# Plot
plt.figure(figsize=(10,8))
sns.barplot(x="no_of_movies", y="genre", data=to_plot)
plt.title('No of Movies by Genre', size=14)
plt.xlabel('No. of Movies', size=13)
plt.ylabel(None)
plt.show()
# Convert timestamp column to datetime
df_ratings['datetime'] = pd.to_datetime(df_ratings['timestamp'], unit='s')
df_ratings['year'] = df_ratings['datetime'].dt.year
# Create plot with No. of ratings per year
to_plot = df_ratings.groupby('year').count()['rating'].reset_index()
plt.figure(figsize=(17,5))
sns.barplot(x='year', y='rating', data=to_plot, color='blue', alpha=0.5)
plt.title('No of Ratings per Year')
plt.show()
# Create Plot with No. of Unique Users giving ratings
to_plot = df_ratings.groupby('year').nunique()['userId'].reset_index()
plt.figure(figsize=(17,5))
sns.barplot(x='year', y='userId', data=to_plot, color='blue', alpha=0.5)
plt.title('No. of Users rating movies per Year')
plt.show()
# Calculate Mean and Count the No. of Ratings to a given movie
mean_ratings_df = df_ratings.groupby('movieId').agg(avg_rating=('rating', 'mean'),
count_rating=('rating', 'count')).reset_index()
# Calculate the Overall Average Rating
mean_ratings_df['overall_avg_rating'] = mean_ratings_df['avg_rating'].mean()
mean_ratings_df.head()
# Plot
plt.figure(figsize=(15,5))
sns.boxplot(x=mean_ratings_df['count_rating'])
plt.title('Boxplot of No. of Ratings given to movies')
plt.show()
# Calculate different quatiles
n_of_users = df_ratings['userId'].nunique()
n_of_movies = len(mean_ratings_df)
quantiles_list = []
for n in range(10, 100, 5):
q = mean_ratings_df['count_rating'].quantile(n/100)
n_of_selected_movies = len(mean_ratings_df[mean_ratings_df['count_rating'] >= q])
quantiles_list.append([n, q, n_of_selected_movies])
pd.DataFrame(quantiles_list, columns=['quantile', 'quantile_value', 'number_of_movies'])
df_ratings.groupby('userId').count()['movieId'].describe()
def weighted_rating(df):
"""
Calculates the IMDB's Weighted Rating using the following formula:
(v / (v+m) * R) + (m / (m+v) * C)
where:
- v is the number of votes for the movie;
- m is the minimum votes required to be listed in the chart;
- R is the average rating of the movie; And
- C is the mean vote across the whole report
"""
v = df['count_rating']
m = df['minimum_no_of_ratings']
R = df['avg_rating']
C = df['overall_avg_rating']
return (v / (v+m) * R) + (m / (m+v) * C)
# Create Copy
popularity_df = mean_ratings_df.copy()
# Calculate the 95th quantile and the weighted rating
popularity_df['minimum_no_of_ratings'] = popularity_df['count_rating'].quantile(0.95)
popularity_df['weighted_rating'] = popularity_df.apply(weighted_rating, axis=1)
# Grab the top 10 ids
top_ten_ids = popularity_df.sort_values('weighted_rating', ascending=False)['movieId'][:10].values
# Print them
for idx, movie_id in enumerate(top_ten_ids):
print((idx + 1), df_movies[df_movies['movieId'] == movie_id]['title'].item())
# Create a new dataframe to train the model.
df_ratings_clean = df_ratings[['userId', 'movieId', 'rating']]
# Randomly pick 50,000 datapoints fmor the dataset
sample_df = df_ratings_clean.sample(n=50000, random_state=111)
# Split the sample data in two so I can test the best hyperparameters later on
train_df, test_df = train_test_split(sample_df, train_size=.50, random_state=111)
# Create reader and dataset objects
reader = Reader()
traindata = Dataset.load_from_df(train_df, reader)
testdata = Dataset.load_from_df(test_df, reader)
# Perform a gridsearch with SVD
param_grid = {'n_factors':[10, 15, 20]
, 'n_epochs': [10, 20]
, 'lr_all': [0.008, 0.012]
, 'reg_all': [0.06, 0.1]
, 'random_state': [111]}
gs_model = GridSearchCV(SVD, param_grid=param_grid, n_jobs = -1, joblib_verbose=False)
%time gs_model.fit(traindata)
print('The best parameters are:')
gs_model.best_params['rmse']
# Convert results from the GridSearchCV to dataframes
df_params = pd.DataFrame(gs_model.cv_results['params'])
df_rmse = pd.DataFrame(gs_model.cv_results['mean_test_rmse'], columns=['mean_test_rmse'])
df_time = pd.DataFrame(gs_model.cv_results['mean_fit_time'], columns=['mean_fit_time'])
df_results = pd.concat([df_params, df_rmse, df_time], axis=1)
def compare_metrics_chart(df, column_a, column_b):
"""
Function to plot the comparison of two metrics in a GridSearchCV run.
Args:
df(pd.Dataframe): Pandas Dataframe with GridSearchCV metrics.
column_a(str): First metric
column_b(str): Second Metric
"""
# Create Figure
fig = plt.figure(figsize=(10,5))
# Create first axis
ax = fig.add_subplot(111)
# Plot Column A
sns.lineplot(data=df[column_a], color="g", ax=ax)
# Set Y Label
ax.set_ylabel(column_a, color='g', size=10)
# Create axis 2
ax2 = plt.twinx()
# Plot Column B
sns.lineplot(data=df[column_b], color="b", ax=ax2)
# Set Y Label
ax2.set_ylabel(column_b, color='b', size=10)
# Change the format of the title
column_a_title = column_a.replace('_', ' ').title()
column_b_title = column_b.replace('_', ' ').title()
plt.title(column_a_title + ' vs. ' + column_b_title)
plt.show();
compare_metrics_chart(df_results, 'n_factors', 'mean_test_rmse')
compare_metrics_chart(df_results, 'n_factors', 'mean_fit_time')
compare_metrics_chart(df_results, 'n_epochs', 'mean_test_rmse')
compare_metrics_chart(df_results, 'n_epochs', 'mean_fit_time')
compare_metrics_chart(df_results, 'reg_all', 'mean_test_rmse')
compare_metrics_chart(df_results, 'reg_all', 'mean_fit_time')
compare_metrics_chart(df_results, 'lr_all', 'mean_test_rmse')
compare_metrics_chart(df_results, 'lr_all', 'mean_fit_time')
def full_model_training_evaluation(model, model_name, traindata, testdata):
"""
Train and test different models and collect fit time and train/test RMSE.
Args:
model(surprise.prediction_algorithms): Model instances from the surprise package.
model_name(str): Model name created by the User. A way to identify the model.
traindata(surprise.dataset.DatasetAutoFolds): Train dataset
testdata(surprise.dataset.DatasetAutoFolds): Test dataset
Returns:
results(dict): A dictionary with the model name, fit time and RMSE's (train/test).
"""
# Stor results in dictionary
results = {}
results['model_name'] = model_name
print('Training', model_name, 'model')
# Fit on train data
start_time = time.time()
model.fit(traindata.build_full_trainset())
end_time = time.time()
total_time = round(end_time - start_time, 2)
results['fit_time_in_seconds'] = total_time
# Get RMSE on train data
predictions_train = model.test(traindata.build_full_trainset().build_testset())
rmse_train = rmse(predictions_train, verbose=False).round(2)
results['rmse_train'] = rmse_train
# Get RMSE on test data
predictions_test = model.test(testdata.build_full_trainset().build_testset())
rmse_test = rmse(predictions_test, verbose=False).round(2)
results['rmse_test'] = rmse_test
return results
# Create SVD model with the best hyperparameters
svd = SVD(n_factors=15, n_epochs=20, lr_all=0.012, reg_all=0.06, random_state=111)
# SVD++: Use the same hyperparameters
svd_pp = SVDpp(n_factors=15, n_epochs=20, lr_all=0.012, reg_all=0.06, random_state=111)
# Different instances of KNN Basic models with different hyperparameters
knn_basic_person_baseline = KNNBasic(sim_options={'name':'pearson_baseline', 'user_based':True}, verbose=False)
knn_basic_person = KNNBasic(sim_options={'name':'pearson', 'user_based':True}, verbose=False)
knn_basic_cosine = KNNBasic(sim_options={'name':'cosine', 'user_based':True}, verbose=False)
# Different instances of KNN Baseline models with different hyperparameters
knn_base_person_baseline = KNNBaseline(sim_options={'name':'pearson_baseline', 'user_based':True}, verbose=False)
knn_base_person = KNNBaseline(sim_options={'name':'pearson', 'user_based':True}, verbose=False)
knn_base_cosine = KNNBaseline(sim_options={'name':'cosine', 'user_based':True}, verbose=False)
# Put all models in a dictionary
models = {'SVD': svd,
'SVD++': svd_pp,
'KNNBasic Cosine': knn_basic_cosine,
'KNNBasic Person': knn_basic_person,
'KNNBasic Person Baseline': knn_basic_person_baseline,
'KNNBaseline Cosine': knn_base_cosine,
'KNNBaseline Person': knn_base_person,
'KNNBaseline Person Baseline': knn_base_person_baseline}
# Loop through different models and evaluate them
model_results = []
for model_name, model_instance in models.items():
results = full_model_training_evaluation(model_instance, model_name, traindata, testdata)
model_results.append(results)
pd.DataFrame(model_results)
# Create list of genres
list_of_genres = stacked_genres['genre'].sort_values().unique()[1:]
# Combine mean ratings and movies details
ratings_movies_df = pd.merge(mean_ratings_df, df_movies, on='movieId')
def filtered_dataset(genre):
"""
Function to filter the dataset given the genre and remove outliers.
Args:
genre(str): The genre the user has chosen to come with recommendations.
Returns:
genre_df(pd.DataFrame): Filtered Dataframe with only the chosen genre.
"""
# Keep only the selected genre
genre_df = ratings_movies_df[ratings_movies_df['genres'].str.contains(genre)]
# Calculate the 95th quantile and the weighted rating
minimum_no_of_ratings = genre_df['count_rating'].quantile(0.95)
genre_df['minimum_no_of_ratings'] = minimum_no_of_ratings
genre_df['weighted_rating'] = genre_df.apply(weighted_rating, axis=1)
# Remove movies with not enough ratings
genre_df = genre_df[genre_df['count_rating'] >= minimum_no_of_ratings]
# Sorted it by weighted rating so we have the highest ratings on the top
genre_df = genre_df.sort_values('weighted_rating', ascending=False)
genre_df = genre_df.reset_index(drop=True)
# Keep certain relevant columns
genre_df = genre_df[['movieId', 'title',
'genres', 'count_rating',
'minimum_no_of_ratings', 'weighted_rating']]
return genre_df
def rate_movie(n_of_movies=5, default_user_id=9999999):
"""
Function to request a new user to review some movies.
Args:
n_of_movies(int): Number of ratings the new will have to give.
default_user_id(int): Random user id that will be given to the user to be able to reference to it later.
Returns:
new_ratings_df(pd.DataFrame): Pandas Dataframe with the new ratings
favorite_genre(str): The User's favorite genre
"""
# Print a list of the available genres
print('List of Available Genres: ', ", ".join(list_of_genres))
# Gather input from user on which genre will be analyzed
favorite_genre = input('Choose one genre from the following (case-sensitive): ')
# Filter the dataset
df_movies_popularity = filtered_dataset(favorite_genre)
# Keep only movies that contain the chosen genre
favorite_genre_movies = df_movies_popularity[df_movies_popularity['genres'].str.contains(favorite_genre)]
# Keep the highest rated movies
favorite_genre_movies = favorite_genre_movies.iloc[:20].sample(frac=1, random_state=111)
favorite_genre_movies = favorite_genre_movies.iloc[:n_of_movies]
print('')
# Created to store ratings from user
ratings_list = []
# Loop through dataframe with movies to be rated
for row in favorite_genre_movies.iterrows():
# Extract Title and ID
movie_title = row[1]['title']
movie_id = row[1]['movieId']
print('Movie to rate: ', movie_title)
# Gather rating from user
rating = input('How do you rate this movie on a scale of 1-5, press n if you have not seen :\n')
# Deal with users not typing a number and create a new variable with the integer
try:
rating_int = int(rating)
except:
rating_int = 1
# While the Rating is not valid, keep asking the user
while (rating != 'n') and not (1 <= rating_int <=5):
rating = input('Please rate the movie between 1-5 or n if you have not seen : \n')
else:
# If the rating is different from 'n' then we need to add the rating to the list
if rating != 'n':
ratings_list.append({'userId': default_user_id,
'movieId': movie_id,
'rating': rating_int})
print('')
# Convert to DataFrame
new_ratings_df = pd.DataFrame(ratings_list)
return new_ratings_df, favorite_genre, df_movies_popularity
def give_n_recommendations(model, default_user_id=9999999, n_recommendations=5):
"""
Function to request a new user to review movies and give recommendations based on that.
Args:
model(surprise.prediction_algorithms): Model instances from the surprise package.
default_user_id(int): Random user id that will be given to the user to be able to reference to it later.
n_recommendations(int): Number of recommendations that will be given to the user.
"""
# Extract ratings from the user
new_ratings_df, favorite_genre, df_movies_popularity = rate_movie(default_user_id=default_user_id)
watched_movies_id = new_ratings_df['movieId']
## add the new ratings to the original ratings DataFrame
updated_df = pd.concat([new_ratings_df, df_ratings_clean])
new_data = Dataset.load_from_df(updated_df, reader)
new_dataset = new_data.build_full_trainset()
# Fit new dataset
model.fit(new_dataset)
# make predictions for the user
results = []
for movie_id in df_movies_popularity['movieId'].unique():
predicted_score = model.predict(default_user_id, movie_id)[3]
results.append((movie_id, predicted_score))
# order the predictions from highest to lowest rated
ranked_movies = pd.DataFrame(results, columns=['movieId', 'predicted_score'])
ranked_movies = ranked_movies[~ranked_movies['movieId'].isin(watched_movies_id)]
ranked_movies = ranked_movies.sort_values('predicted_score', ascending=False).reset_index(drop=True)
ranked_movies = pd.merge(ranked_movies, df_movies, on='movieId')
# ranked_movies = ranked_movies[ranked_movies['genres'].str.contains(favorite_genre)]
print('The recommendations are the following:')
if len(ranked_movies) < n_recommendations:
n_recommendations = len(ranked_movies)
for row in range(n_recommendations):
movie_id = ranked_movies.iloc[row]['movieId']
recommended_title = df_movies[df_movies['movieId'] == movie_id]['title'].item()
print(f'No. {row+1} is {recommended_title}')
give_n_recommendations(svd)
give_n_recommendations(svd)
give_n_recommendations(svd)
give_n_recommendations(svd)
# Export it to use it on streamlit
ratings_movies_df.to_csv('./app/data/movies_by_rating.csv', index=0)
df_ratings_clean.to_csv('./app/data/user_movie_ratings.csv', index=0)
dump.dump('./app/data/svd.pkl', algo=svd)
| 0.662906 | 0.885829 |
```
#all_slow
#export
from fastai.basics import *
#hide
from nbdev.showdoc import *
#default_exp callback.tensorboard
```
# Tensorboard
> Integration with [tensorboard](https://www.tensorflow.org/tensorboard)
First thing first, you need to install tensorboard with
```
pip install tensorboard
```
Then launch tensorboard with
```
tensorboard --logdir=runs
```
in your terminal. You can change the logdir as long as it matches the `log_dir` you pass to `TensorBoardCallback` (default is `runs` in the working directory).
## Tensorboard Embedding Projector support
> Tensorboard Embedding Projector is currently only supported for image classification
### Export Embeddings during Training
Tensorboard [Embedding Projector](https://www.tensorflow.org/tensorboard/tensorboard_projector_plugin) is supported in `TensorBoardCallback` (set parameter `projector=True`) during training. The validation set embeddings will be written after each epoch.
```
cbs = [TensorBoardCallback(projector=True)]
learn = cnn_learner(dls, resnet18, metrics=accuracy, cbs=cbs)
```
### Export Embeddings for a custom dataset
To write the embeddings for a custom dataset (e. g. after loading a learner) use `TensorBoardProjectorCallback`. Add the callback manually to the learner.
```
learn = load_learner('path/to/export.pkl')
learn.add_cb(TensorBoardProjectorCallback())
dl = learn.dls.test_dl(files, with_labels=True)
_ = learn.get_preds(dl=dl)
```
If using a custom model (non fastai-resnet) pass the layer where the embeddings should be extracted as a callback-parameter.
```
layer = learn.model[1][1]
learn.add_cb(TensorBoardProjectorCallback(layer=layer))
```
```
#export
import tensorboard
from torch.utils.tensorboard import SummaryWriter
from fastai.callback.fp16 import ModelToHalf
from fastai.callback.hook import hook_output
#export
class TensorBoardBaseCallback(Callback):
def __init__(self):
self.run_projector = False
def after_pred(self):
if self.run_projector: self.feat = _add_projector_features(self.learn, self.h, self.feat)
def after_validate(self):
if not self.run_projector: return
self.run_projector = False
self._remove()
_write_projector_embedding(self.learn, self.writer, self.feat)
def after_fit(self):
if self.run: self.writer.close()
def _setup_projector(self):
self.run_projector = True
self.h = hook_output(self.learn.model[1][1] if not self.layer else self.layer)
self.feat = {}
def _setup_writer(self):
self.writer = SummaryWriter(log_dir=self.log_dir)
def _remove(self):
if getattr(self, 'h', None): self.h.remove()
def __del__(self): self._remove()
#export
class TensorBoardCallback(TensorBoardBaseCallback):
"Saves model topology, losses & metrics"
def __init__(self, log_dir=None, trace_model=True, log_preds=True, n_preds=9, projector=False, layer=None):
super().__init__()
store_attr()
def before_fit(self):
self.run = not hasattr(self.learn, 'lr_finder') and not hasattr(self, "gather_preds") and rank_distrib()==0
if not self.run: return
self._setup_writer()
if self.trace_model:
if hasattr(self.learn, 'mixed_precision'):
raise Exception("Can't trace model in mixed precision, pass `trace_model=False` or don't use FP16.")
b = self.dls.one_batch()
self.learn._split(b)
self.writer.add_graph(self.model, *self.xb)
def after_batch(self):
self.writer.add_scalar('train_loss', self.smooth_loss, self.train_iter)
for i,h in enumerate(self.opt.hypers):
for k,v in h.items(): self.writer.add_scalar(f'{k}_{i}', v, self.train_iter)
def after_epoch(self):
for n,v in zip(self.recorder.metric_names[2:-1], self.recorder.log[2:-1]):
self.writer.add_scalar(n, v, self.train_iter)
if self.log_preds:
b = self.dls.valid.one_batch()
self.learn.one_batch(0, b)
preds = getattr(self.loss_func, 'activation', noop)(self.pred)
out = getattr(self.loss_func, 'decodes', noop)(preds)
x,y,its,outs = self.dls.valid.show_results(b, out, show=False, max_n=self.n_preds)
tensorboard_log(x, y, its, outs, self.writer, self.train_iter)
def before_validate(self):
if self.projector: self._setup_projector()
#export
class TensorBoardProjectorCallback(TensorBoardBaseCallback):
"Saves Embeddings for Tensorboard Projector"
def __init__(self, log_dir=None, layer=None):
super().__init__()
store_attr()
def before_fit(self):
self.run = not hasattr(self.learn, 'lr_finder') and hasattr(self, "gather_preds") and rank_distrib()==0
if not self.run: return
self._setup_writer()
def before_validate(self):
self._setup_projector()
#export
def _write_projector_embedding(learn, writer, feat):
lbls = [learn.dl.vocab[l] for l in feat['lbl']] if getattr(learn.dl, 'vocab', None) else None
writer.add_embedding(feat['vec'], metadata=lbls, label_img=feat['img'], global_step=learn.train_iter)
#export
def _add_projector_features(learn, hook, feat):
img = normalize_for_projector(learn.x)
first_epoch = True if learn.iter == 0 else False
feat['vec'] = hook.stored if first_epoch else torch.cat((feat['vec'], hook.stored),0)
feat['img'] = img if first_epoch else torch.cat((feat['img'], img),0)
if getattr(learn.dl, 'vocab', None):
feat['lbl'] = learn.y if first_epoch else torch.cat((feat['lbl'], learn.y),0)
return feat
#export
@typedispatch
def normalize_for_projector(x:TensorImage):
# normalize tensor to be between 0-1
img = x.clone()
sz = img.shape
img = img.view(x.size(0), -1)
img -= img.min(1, keepdim=True)[0]
img /= img.max(1, keepdim=True)[0]
img = img.view(*sz)
return img
#export
from fastai.vision.data import *
#export
@typedispatch
def tensorboard_log(x:TensorImage, y: TensorCategory, samples, outs, writer, step):
fig,axs = get_grid(len(samples), add_vert=1, return_fig=True)
for i in range(2):
axs = [b.show(ctx=c) for b,c in zip(samples.itemgot(i),axs)]
axs = [r.show(ctx=c, color='green' if b==r else 'red')
for b,r,c in zip(samples.itemgot(1),outs.itemgot(0),axs)]
writer.add_figure('Sample results', fig, step)
#export
from fastai.vision.core import TensorPoint,TensorBBox
#export
@typedispatch
def tensorboard_log(x:TensorImage, y: (TensorImageBase, TensorPoint, TensorBBox), samples, outs, writer, step):
fig,axs = get_grid(len(samples), add_vert=1, return_fig=True, double=True)
for i in range(2):
axs[::2] = [b.show(ctx=c) for b,c in zip(samples.itemgot(i),axs[::2])]
for x in [samples,outs]:
axs[1::2] = [b.show(ctx=c) for b,c in zip(x.itemgot(0),axs[1::2])]
writer.add_figure('Sample results', fig, step)
```
## Test
```
from fastai.vision.all import Resize, RandomSubsetSplitter, aug_transforms, cnn_learner, resnet18
```
## TensorBoardCallback
```
path = untar_data(URLs.PETS)
db = DataBlock(blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
item_tfms=Resize(128),
splitter=RandomSubsetSplitter(train_sz=0.1, valid_sz=0.01),
batch_tfms=aug_transforms(size=64),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.*$'), 'name'))
dls = db.dataloaders(path/'images')
learn = cnn_learner(dls, resnet18, metrics=accuracy)
learn.unfreeze()
learn.fit_one_cycle(3, cbs=TensorBoardCallback(Path.home()/'tmp'/'runs', trace_model=True))
```
## Projector
### Projector in TensorBoardCallback
```
path = untar_data(URLs.PETS)
db = DataBlock(blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
item_tfms=Resize(128),
splitter=RandomSubsetSplitter(train_sz=0.05, valid_sz=0.01),
batch_tfms=aug_transforms(size=64),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.*$'), 'name'))
dls = db.dataloaders(path/'images')
cbs = [TensorBoardCallback(log_dir=Path.home()/'tmp'/'runs', projector=True)]
learn = cnn_learner(dls, resnet18, metrics=accuracy, cbs=cbs)
learn.unfreeze()
learn.fit_one_cycle(3)
```
### TensorBoardProjectorCallback
```
path = untar_data(URLs.PETS)
db = DataBlock(blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
item_tfms=Resize(128),
splitter=RandomSubsetSplitter(train_sz=0.1, valid_sz=0.01),
batch_tfms=aug_transforms(size=64),
get_y=using_attr(RegexLabeller(r'(.+)_\d+.*$'), 'name'))
dls = db.dataloaders(path/'images')
files = get_image_files(path/'images')
files = files[:256]
learn = cnn_learner(dls, resnet18, metrics=accuracy)
learn.add_cb(TensorBoardProjectorCallback(log_dir=Path.home()/'tmp'/'runs'))
dl = learn.dls.test_dl(files, with_labels=True)
_ = learn.get_preds(dl=dl)
```
### Validate results in tensorboard
Run the following command in the command line to check if the projector embeddings have been correctly wirtten:
```
tensorboard --logdir=~/tmp/runs
```
Open http://localhost:6006 in browser (TensorBoard Projector doesn't work correctly in Safari!)
## Export -
```
#hide
from nbdev.export import *
notebook2script()
```
|
github_jupyter
|
#all_slow
#export
from fastai.basics import *
#hide
from nbdev.showdoc import *
#default_exp callback.tensorboard
pip install tensorboard
in your terminal. You can change the logdir as long as it matches the `log_dir` you pass to `TensorBoardCallback` (default is `runs` in the working directory).
## Tensorboard Embedding Projector support
> Tensorboard Embedding Projector is currently only supported for image classification
### Export Embeddings during Training
Tensorboard [Embedding Projector](https://www.tensorflow.org/tensorboard/tensorboard_projector_plugin) is supported in `TensorBoardCallback` (set parameter `projector=True`) during training. The validation set embeddings will be written after each epoch.
### Export Embeddings for a custom dataset
To write the embeddings for a custom dataset (e. g. after loading a learner) use `TensorBoardProjectorCallback`. Add the callback manually to the learner.
If using a custom model (non fastai-resnet) pass the layer where the embeddings should be extracted as a callback-parameter.
## Test
## TensorBoardCallback
## Projector
### Projector in TensorBoardCallback
### TensorBoardProjectorCallback
### Validate results in tensorboard
Run the following command in the command line to check if the projector embeddings have been correctly wirtten:
Open http://localhost:6006 in browser (TensorBoard Projector doesn't work correctly in Safari!)
## Export -
| 0.718496 | 0.86511 |
<a href="https://colab.research.google.com/github/Victoooooor/SimpleJobs/blob/main/movenet.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title
!pip install -q imageio
!pip install -q opencv-python
!pip install -q git+https://github.com/tensorflow/docs
#@title
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow_docs.vis import embed
import numpy as np
import cv2
import os
# Import matplotlib libraries
from matplotlib import pyplot as plt
from matplotlib.collections import LineCollection
import matplotlib.patches as patches
import imageio
from IPython.display import HTML, display
from google.colab import files
import sys
import time
import shutil
from google.colab.patches import cv2_imshow
import copy
from base64 import b64encode
#@title
KEYPOINT_DICT = {
'nose': 0,
'left_eye': 1,
'right_eye': 2,
'left_ear': 3,
'right_ear': 4,
'left_shoulder': 5,
'right_shoulder': 6,
'left_elbow': 7,
'right_elbow': 8,
'left_wrist': 9,
'right_wrist': 10,
'left_hip': 11,
'right_hip': 12,
'left_knee': 13,
'right_knee': 14,
'left_ankle': 15,
'right_ankle': 16
}
# Maps bones to a matplotlib color name.
KEYPOINT_EDGE_INDS_TO_COLOR = {
(0, 1): 'm',
(0, 2): 'c',
(1, 3): 'm',
(2, 4): 'c',
(0, 5): 'm',
(0, 6): 'c',
(5, 7): 'm',
(7, 9): 'm',
(6, 8): 'c',
(8, 10): 'c',
(5, 6): 'y',
(5, 11): 'm',
(6, 12): 'c',
(11, 12): 'y',
(11, 13): 'm',
(13, 15): 'm',
(12, 14): 'c',
(14, 16): 'c'
}
def _keypoints_and_edges_for_display(keypoints_with_scores,
height,
width,
keypoint_threshold=0.11):
"""Returns high confidence keypoints and edges for visualization.
Args:
keypoints_with_scores: A numpy array with shape [1, 1, 17, 3] representing
the keypoint coordinates and scores returned from the MoveNet model.
height: height of the image in pixels.
width: width of the image in pixels.
keypoint_threshold: minimum confidence score for a keypoint to be
visualized.
Returns:
A (keypoints_xy, edges_xy, edge_colors) containing:
* the coordinates of all keypoints of all detected entities;
* the coordinates of all skeleton edges of all detected entities;
* the colors in which the edges should be plotted.
"""
keypoints_all = []
keypoint_edges_all = []
edge_colors = []
num_instances, _, _, _ = keypoints_with_scores.shape
for idx in range(num_instances):
kpts_x = keypoints_with_scores[0, idx, :, 1]
kpts_y = keypoints_with_scores[0, idx, :, 0]
kpts_scores = keypoints_with_scores[0, idx, :, 2]
kpts_absolute_xy = np.stack(
[width * np.array(kpts_x), height * np.array(kpts_y)], axis=-1)
kpts_above_thresh_absolute = kpts_absolute_xy[
kpts_scores > keypoint_threshold, :]
keypoints_all.append(kpts_above_thresh_absolute)
for edge_pair, color in KEYPOINT_EDGE_INDS_TO_COLOR.items():
if (kpts_scores[edge_pair[0]] > keypoint_threshold and
kpts_scores[edge_pair[1]] > keypoint_threshold):
x_start = kpts_absolute_xy[edge_pair[0], 0]
y_start = kpts_absolute_xy[edge_pair[0], 1]
x_end = kpts_absolute_xy[edge_pair[1], 0]
y_end = kpts_absolute_xy[edge_pair[1], 1]
line_seg = np.array([[x_start, y_start], [x_end, y_end]])
keypoint_edges_all.append(line_seg)
edge_colors.append(color)
if keypoints_all:
keypoints_xy = np.concatenate(keypoints_all, axis=0)
else:
keypoints_xy = np.zeros((0, 17, 2))
if keypoint_edges_all:
edges_xy = np.stack(keypoint_edges_all, axis=0)
else:
edges_xy = np.zeros((0, 2, 2))
return keypoints_xy, edges_xy, edge_colors
def draw_prediction_on_image(
image, keypoints_with_scores, crop_region=None, close_figure=False,
output_image_height=None):
"""Draws the keypoint predictions on image.
Args:
image: A numpy array with shape [height, width, channel] representing the
pixel values of the input image.
keypoints_with_scores: A numpy array with shape [1, 1, 17, 3] representing
the keypoint coordinates and scores returned from the MoveNet model.
crop_region: A dictionary that defines the coordinates of the bounding box
of the crop region in normalized coordinates (see the init_crop_region
function below for more detail). If provided, this function will also
draw the bounding box on the image.
output_image_height: An integer indicating the height of the output image.
Note that the image aspect ratio will be the same as the input image.
Returns:
A numpy array with shape [out_height, out_width, channel] representing the
image overlaid with keypoint predictions.
"""
height, width, channel = image.shape
aspect_ratio = float(width) / height
fig, ax = plt.subplots(figsize=(12 * aspect_ratio, 12))
# To remove the huge white borders
fig.tight_layout(pad=0)
ax.margins(0)
ax.set_yticklabels([])
ax.set_xticklabels([])
plt.axis('off')
im = ax.imshow(image)
line_segments = LineCollection([], linewidths=(4), linestyle='solid')
ax.add_collection(line_segments)
# Turn off tick labels
scat = ax.scatter([], [], s=60, color='#FF1493', zorder=3)
(keypoint_locs, keypoint_edges,
edge_colors) = _keypoints_and_edges_for_display(
keypoints_with_scores, height, width)
line_segments.set_segments(keypoint_edges)
line_segments.set_color(edge_colors)
if keypoint_edges.shape[0]:
line_segments.set_segments(keypoint_edges)
line_segments.set_color(edge_colors)
if keypoint_locs.shape[0]:
scat.set_offsets(keypoint_locs)
if crop_region is not None:
xmin = max(crop_region['x_min'] * width, 0.0)
ymin = max(crop_region['y_min'] * height, 0.0)
rec_width = min(crop_region['x_max'], 0.99) * width - xmin
rec_height = min(crop_region['y_max'], 0.99) * height - ymin
rect = patches.Rectangle(
(xmin,ymin),rec_width,rec_height,
linewidth=1,edgecolor='b',facecolor='none')
ax.add_patch(rect)
fig.canvas.draw()
image_from_plot = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)
image_from_plot = image_from_plot.reshape(
fig.canvas.get_width_height()[::-1] + (3,))
plt.close(fig)
if output_image_height is not None:
output_image_width = int(output_image_height / height * width)
image_from_plot = cv2.resize(
image_from_plot, dsize=(output_image_width, output_image_height),
interpolation=cv2.INTER_CUBIC)
return image_from_plot
def to_gif(images, fps):
"""Converts image sequence (4D numpy array) to gif."""
imageio.mimsave('./animation.gif', images, fps=fps)
return embed.embed_file('./animation.gif')
def progress(value, max=100):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 100%'
>
{value}
</progress>
""".format(value=value, max=max))
def show_video(video_path, video_width = 600):
video_file = open(video_path, "r+b").read()
video_url = f"data:video/mp4;base64,{b64encode(video_file).decode()}"
return HTML(f"""<video width={video_width} controls><source src="{video_url}"></video>""")
# Load the input image.
def get_pose(image, thresh = 0.2):
detection_threshold = thresh
image = tf.expand_dims(image, axis=0)
image_origin = copy.copy(image)
image = tf.cast(tf.image.resize_with_pad(
image, 256, 256), dtype=tf.int32)
_, image_height, image_width, channel = image_origin.shape
# print(image_height, image_width)
if channel != 3:
sys.exit('Image isn\'t in RGB format.')
output = movenet(image)
people = output['output_0'].numpy()[:, :, :51].reshape((6, 17, 3))
if image_width > image_height:
# print('scaling')
dif = people - 0.5
people[:,:,0] = 0.5 + image_width/image_height * dif[:,:,0]
elif image_width < image_height:
# print('scaling')
dif = people - 0.5
people[:,:,1] = 0.5 + image_height/image_width * dif[:,:,1]
# Save landmarks if all landmarks were detected
ppl = []
for i in range(6):
# print(output['output_0'][0, i, -1])
if output['output_0'][0, i, -1] > detection_threshold:
ppl.append(people[i])
should_keep_image = len(ppl) > 0
if not should_keep_image:
print('No pose was confidentlly detected.')
#draw all
merged_img = np.squeeze(image_origin.numpy(), axis=0)
for pp in ppl:
merged_img = draw_prediction_on_image(
merged_img, np.array([[pp]]), output_image_height=image_height)
return merged_img, ppl
def get_vid(filename, fhandle, desti = 'processed.mp4', interval = 5):
video_file = desti
video = cv2.VideoCapture(filename)
if not video.isOpened():
sys.exit('video does not exist')
fps = int(video.get(cv2.CAP_PROP_FPS))
frame_num = int(video.get(cv2.CAP_PROP_FRAME_COUNT))
frame_width = int(video.get(cv2.CAP_PROP_FRAME_WIDTH))
frame_height = int(video.get(cv2.CAP_PROP_FRAME_HEIGHT))
fourcc = cv2.VideoWriter_fourcc(*'mp4v')
video_writer = cv2.VideoWriter(video_file,fourcc,fps,(frame_width,frame_height))
print("Frames per second using video.get(cv2.CAP_PROP_FPS) : {0}".format(fps))
frame_counter = 0
while True:
ret, frame = video.read()
if ret == True:
tfframe= tf.convert_to_tensor(frame)
new_frame, data = get_pose(tfframe)
video_writer.write(new_frame)
if frame_counter % interval == 0:
data=np.delete(data,2,2)
data[:,:,[0,1]] = data[:,:,[1,0]]
np.savetxt(fhandle, data.flatten(),
fmt='%.18e', newline=',')
fhandle.write(b"\n")
frame_counter += 1
if ret == False:
break
video.release()
video_writer.release()
cv2.destroyAllWindows()
return video_file
#@title
model = hub.load("https://tfhub.dev/google/movenet/multipose/lightning/1")
movenet = model.signatures['serving_default']
#params
interval = 5 #meaning save to csv every 5 frames
uploaded = files.upload()
filename = next(iter(uploaded))
#@title
text_name = 'pose.csv'
try:
os.remove(text_name)
except:
None
with open(text_name, "ab") as csv:
# numpy.savetxt(csv, a)
gen = get_vid(filename, csv, interval = interval)
csv.close()
audiofile = '_sound.mp3'
withsound = 'output.mp4'
!ffmpeg -i {filename} -f mp3 -ab 192000 -vn {audiofile}
!ffmpeg -i {gen} -i {audiofile} -map 0:0 -map 1:0 -c:v copy -c:a copy {withsound}
!zip -r file.zip {text_name} {withsound}
files.download('file.zip')
try:
os.remove(text_name)
os.remove(filename)
os.remove(audiofile)
os.remove(gen)
os.remove(withsound)
except:
None
```
|
github_jupyter
|
#@title
!pip install -q imageio
!pip install -q opencv-python
!pip install -q git+https://github.com/tensorflow/docs
#@title
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow_docs.vis import embed
import numpy as np
import cv2
import os
# Import matplotlib libraries
from matplotlib import pyplot as plt
from matplotlib.collections import LineCollection
import matplotlib.patches as patches
import imageio
from IPython.display import HTML, display
from google.colab import files
import sys
import time
import shutil
from google.colab.patches import cv2_imshow
import copy
from base64 import b64encode
#@title
KEYPOINT_DICT = {
'nose': 0,
'left_eye': 1,
'right_eye': 2,
'left_ear': 3,
'right_ear': 4,
'left_shoulder': 5,
'right_shoulder': 6,
'left_elbow': 7,
'right_elbow': 8,
'left_wrist': 9,
'right_wrist': 10,
'left_hip': 11,
'right_hip': 12,
'left_knee': 13,
'right_knee': 14,
'left_ankle': 15,
'right_ankle': 16
}
# Maps bones to a matplotlib color name.
KEYPOINT_EDGE_INDS_TO_COLOR = {
(0, 1): 'm',
(0, 2): 'c',
(1, 3): 'm',
(2, 4): 'c',
(0, 5): 'm',
(0, 6): 'c',
(5, 7): 'm',
(7, 9): 'm',
(6, 8): 'c',
(8, 10): 'c',
(5, 6): 'y',
(5, 11): 'm',
(6, 12): 'c',
(11, 12): 'y',
(11, 13): 'm',
(13, 15): 'm',
(12, 14): 'c',
(14, 16): 'c'
}
def _keypoints_and_edges_for_display(keypoints_with_scores,
height,
width,
keypoint_threshold=0.11):
"""Returns high confidence keypoints and edges for visualization.
Args:
keypoints_with_scores: A numpy array with shape [1, 1, 17, 3] representing
the keypoint coordinates and scores returned from the MoveNet model.
height: height of the image in pixels.
width: width of the image in pixels.
keypoint_threshold: minimum confidence score for a keypoint to be
visualized.
Returns:
A (keypoints_xy, edges_xy, edge_colors) containing:
* the coordinates of all keypoints of all detected entities;
* the coordinates of all skeleton edges of all detected entities;
* the colors in which the edges should be plotted.
"""
keypoints_all = []
keypoint_edges_all = []
edge_colors = []
num_instances, _, _, _ = keypoints_with_scores.shape
for idx in range(num_instances):
kpts_x = keypoints_with_scores[0, idx, :, 1]
kpts_y = keypoints_with_scores[0, idx, :, 0]
kpts_scores = keypoints_with_scores[0, idx, :, 2]
kpts_absolute_xy = np.stack(
[width * np.array(kpts_x), height * np.array(kpts_y)], axis=-1)
kpts_above_thresh_absolute = kpts_absolute_xy[
kpts_scores > keypoint_threshold, :]
keypoints_all.append(kpts_above_thresh_absolute)
for edge_pair, color in KEYPOINT_EDGE_INDS_TO_COLOR.items():
if (kpts_scores[edge_pair[0]] > keypoint_threshold and
kpts_scores[edge_pair[1]] > keypoint_threshold):
x_start = kpts_absolute_xy[edge_pair[0], 0]
y_start = kpts_absolute_xy[edge_pair[0], 1]
x_end = kpts_absolute_xy[edge_pair[1], 0]
y_end = kpts_absolute_xy[edge_pair[1], 1]
line_seg = np.array([[x_start, y_start], [x_end, y_end]])
keypoint_edges_all.append(line_seg)
edge_colors.append(color)
if keypoints_all:
keypoints_xy = np.concatenate(keypoints_all, axis=0)
else:
keypoints_xy = np.zeros((0, 17, 2))
if keypoint_edges_all:
edges_xy = np.stack(keypoint_edges_all, axis=0)
else:
edges_xy = np.zeros((0, 2, 2))
return keypoints_xy, edges_xy, edge_colors
def draw_prediction_on_image(
image, keypoints_with_scores, crop_region=None, close_figure=False,
output_image_height=None):
"""Draws the keypoint predictions on image.
Args:
image: A numpy array with shape [height, width, channel] representing the
pixel values of the input image.
keypoints_with_scores: A numpy array with shape [1, 1, 17, 3] representing
the keypoint coordinates and scores returned from the MoveNet model.
crop_region: A dictionary that defines the coordinates of the bounding box
of the crop region in normalized coordinates (see the init_crop_region
function below for more detail). If provided, this function will also
draw the bounding box on the image.
output_image_height: An integer indicating the height of the output image.
Note that the image aspect ratio will be the same as the input image.
Returns:
A numpy array with shape [out_height, out_width, channel] representing the
image overlaid with keypoint predictions.
"""
height, width, channel = image.shape
aspect_ratio = float(width) / height
fig, ax = plt.subplots(figsize=(12 * aspect_ratio, 12))
# To remove the huge white borders
fig.tight_layout(pad=0)
ax.margins(0)
ax.set_yticklabels([])
ax.set_xticklabels([])
plt.axis('off')
im = ax.imshow(image)
line_segments = LineCollection([], linewidths=(4), linestyle='solid')
ax.add_collection(line_segments)
# Turn off tick labels
scat = ax.scatter([], [], s=60, color='#FF1493', zorder=3)
(keypoint_locs, keypoint_edges,
edge_colors) = _keypoints_and_edges_for_display(
keypoints_with_scores, height, width)
line_segments.set_segments(keypoint_edges)
line_segments.set_color(edge_colors)
if keypoint_edges.shape[0]:
line_segments.set_segments(keypoint_edges)
line_segments.set_color(edge_colors)
if keypoint_locs.shape[0]:
scat.set_offsets(keypoint_locs)
if crop_region is not None:
xmin = max(crop_region['x_min'] * width, 0.0)
ymin = max(crop_region['y_min'] * height, 0.0)
rec_width = min(crop_region['x_max'], 0.99) * width - xmin
rec_height = min(crop_region['y_max'], 0.99) * height - ymin
rect = patches.Rectangle(
(xmin,ymin),rec_width,rec_height,
linewidth=1,edgecolor='b',facecolor='none')
ax.add_patch(rect)
fig.canvas.draw()
image_from_plot = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)
image_from_plot = image_from_plot.reshape(
fig.canvas.get_width_height()[::-1] + (3,))
plt.close(fig)
if output_image_height is not None:
output_image_width = int(output_image_height / height * width)
image_from_plot = cv2.resize(
image_from_plot, dsize=(output_image_width, output_image_height),
interpolation=cv2.INTER_CUBIC)
return image_from_plot
def to_gif(images, fps):
"""Converts image sequence (4D numpy array) to gif."""
imageio.mimsave('./animation.gif', images, fps=fps)
return embed.embed_file('./animation.gif')
def progress(value, max=100):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 100%'
>
{value}
</progress>
""".format(value=value, max=max))
def show_video(video_path, video_width = 600):
video_file = open(video_path, "r+b").read()
video_url = f"data:video/mp4;base64,{b64encode(video_file).decode()}"
return HTML(f"""<video width={video_width} controls><source src="{video_url}"></video>""")
# Load the input image.
def get_pose(image, thresh = 0.2):
detection_threshold = thresh
image = tf.expand_dims(image, axis=0)
image_origin = copy.copy(image)
image = tf.cast(tf.image.resize_with_pad(
image, 256, 256), dtype=tf.int32)
_, image_height, image_width, channel = image_origin.shape
# print(image_height, image_width)
if channel != 3:
sys.exit('Image isn\'t in RGB format.')
output = movenet(image)
people = output['output_0'].numpy()[:, :, :51].reshape((6, 17, 3))
if image_width > image_height:
# print('scaling')
dif = people - 0.5
people[:,:,0] = 0.5 + image_width/image_height * dif[:,:,0]
elif image_width < image_height:
# print('scaling')
dif = people - 0.5
people[:,:,1] = 0.5 + image_height/image_width * dif[:,:,1]
# Save landmarks if all landmarks were detected
ppl = []
for i in range(6):
# print(output['output_0'][0, i, -1])
if output['output_0'][0, i, -1] > detection_threshold:
ppl.append(people[i])
should_keep_image = len(ppl) > 0
if not should_keep_image:
print('No pose was confidentlly detected.')
#draw all
merged_img = np.squeeze(image_origin.numpy(), axis=0)
for pp in ppl:
merged_img = draw_prediction_on_image(
merged_img, np.array([[pp]]), output_image_height=image_height)
return merged_img, ppl
def get_vid(filename, fhandle, desti = 'processed.mp4', interval = 5):
video_file = desti
video = cv2.VideoCapture(filename)
if not video.isOpened():
sys.exit('video does not exist')
fps = int(video.get(cv2.CAP_PROP_FPS))
frame_num = int(video.get(cv2.CAP_PROP_FRAME_COUNT))
frame_width = int(video.get(cv2.CAP_PROP_FRAME_WIDTH))
frame_height = int(video.get(cv2.CAP_PROP_FRAME_HEIGHT))
fourcc = cv2.VideoWriter_fourcc(*'mp4v')
video_writer = cv2.VideoWriter(video_file,fourcc,fps,(frame_width,frame_height))
print("Frames per second using video.get(cv2.CAP_PROP_FPS) : {0}".format(fps))
frame_counter = 0
while True:
ret, frame = video.read()
if ret == True:
tfframe= tf.convert_to_tensor(frame)
new_frame, data = get_pose(tfframe)
video_writer.write(new_frame)
if frame_counter % interval == 0:
data=np.delete(data,2,2)
data[:,:,[0,1]] = data[:,:,[1,0]]
np.savetxt(fhandle, data.flatten(),
fmt='%.18e', newline=',')
fhandle.write(b"\n")
frame_counter += 1
if ret == False:
break
video.release()
video_writer.release()
cv2.destroyAllWindows()
return video_file
#@title
model = hub.load("https://tfhub.dev/google/movenet/multipose/lightning/1")
movenet = model.signatures['serving_default']
#params
interval = 5 #meaning save to csv every 5 frames
uploaded = files.upload()
filename = next(iter(uploaded))
#@title
text_name = 'pose.csv'
try:
os.remove(text_name)
except:
None
with open(text_name, "ab") as csv:
# numpy.savetxt(csv, a)
gen = get_vid(filename, csv, interval = interval)
csv.close()
audiofile = '_sound.mp3'
withsound = 'output.mp4'
!ffmpeg -i {filename} -f mp3 -ab 192000 -vn {audiofile}
!ffmpeg -i {gen} -i {audiofile} -map 0:0 -map 1:0 -c:v copy -c:a copy {withsound}
!zip -r file.zip {text_name} {withsound}
files.download('file.zip')
try:
os.remove(text_name)
os.remove(filename)
os.remove(audiofile)
os.remove(gen)
os.remove(withsound)
except:
None
| 0.760651 | 0.820001 |
# Getting started with Captum Insights: a simple model on CIFAR10 dataset
Demonstrates how to use Captum Insights embedded in a notebook to debug a CIFAR model and test samples. This is a slight modification of the CIFAR_TorchVision_Interpret notebook.
More details about the model can be found here: https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html#sphx-glr-beginner-blitz-cifar10-tutorial-py
**Note:** Before running this tutorial, please install the torchvision, and IPython packages.
```
import os
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
from captum.insights import AttributionVisualizer, Batch
from captum.insights.features import ImageFeature
```
Define functions for classification classes and pretrained model.
```
def get_classes():
classes = [
"Plane",
"Car",
"Bird",
"Cat",
"Deer",
"Dog",
"Frog",
"Horse",
"Ship",
"Truck",
]
return classes
def get_pretrained_model():
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool1 = nn.MaxPool2d(2, 2)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
self.relu1 = nn.ReLU()
self.relu2 = nn.ReLU()
self.relu3 = nn.ReLU()
self.relu4 = nn.ReLU()
def forward(self, x):
x = self.pool1(self.relu1(self.conv1(x)))
x = self.pool2(self.relu2(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = self.relu3(self.fc1(x))
x = self.relu4(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
net.load_state_dict(torch.load("models/cifar_torchvision.pt"))
return net
def baseline_func(input):
return input * 0
def formatted_data_iter():
dataset = torchvision.datasets.CIFAR10(
root="data/test", train=False, download=True, transform=transforms.ToTensor()
)
dataloader = iter(
torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=False, num_workers=2)
)
while True:
images, labels = next(dataloader)
yield Batch(inputs=images, labels=labels)
```
Run the visualizer and render inside notebook for interactive debugging.
```
normalize = transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
model = get_pretrained_model()
visualizer = AttributionVisualizer(
models=[model],
score_func=lambda o: torch.nn.functional.softmax(o, 1),
classes=get_classes(),
features=[
ImageFeature(
"Photo",
baseline_transforms=[baseline_func],
input_transforms=[normalize],
)
],
dataset=formatted_data_iter(),
)
visualizer.render()
# show a screenshot if using notebook non-interactively
from IPython.display import Image
Image(filename='img/captum_insights.png')
```
|
github_jupyter
|
import os
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
from captum.insights import AttributionVisualizer, Batch
from captum.insights.features import ImageFeature
def get_classes():
classes = [
"Plane",
"Car",
"Bird",
"Cat",
"Deer",
"Dog",
"Frog",
"Horse",
"Ship",
"Truck",
]
return classes
def get_pretrained_model():
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool1 = nn.MaxPool2d(2, 2)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
self.relu1 = nn.ReLU()
self.relu2 = nn.ReLU()
self.relu3 = nn.ReLU()
self.relu4 = nn.ReLU()
def forward(self, x):
x = self.pool1(self.relu1(self.conv1(x)))
x = self.pool2(self.relu2(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = self.relu3(self.fc1(x))
x = self.relu4(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
net.load_state_dict(torch.load("models/cifar_torchvision.pt"))
return net
def baseline_func(input):
return input * 0
def formatted_data_iter():
dataset = torchvision.datasets.CIFAR10(
root="data/test", train=False, download=True, transform=transforms.ToTensor()
)
dataloader = iter(
torch.utils.data.DataLoader(dataset, batch_size=4, shuffle=False, num_workers=2)
)
while True:
images, labels = next(dataloader)
yield Batch(inputs=images, labels=labels)
normalize = transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
model = get_pretrained_model()
visualizer = AttributionVisualizer(
models=[model],
score_func=lambda o: torch.nn.functional.softmax(o, 1),
classes=get_classes(),
features=[
ImageFeature(
"Photo",
baseline_transforms=[baseline_func],
input_transforms=[normalize],
)
],
dataset=formatted_data_iter(),
)
visualizer.render()
# show a screenshot if using notebook non-interactively
from IPython.display import Image
Image(filename='img/captum_insights.png')
| 0.905044 | 0.978935 |
# Loading Image Data
So far we've been working with fairly artificial datasets that you wouldn't typically be using in real projects. Instead, you'll likely be dealing with full-sized images like you'd get from smart phone cameras. In this notebook, we'll look at how to load images and use them to train neural networks.
We'll be using a [dataset of cat and dog photos](https://www.kaggle.com/c/dogs-vs-cats) available from Kaggle. Here are a couple example images:
<img src='assets/dog_cat.png'>
We'll use this dataset to train a neural network that can differentiate between cats and dogs. These days it doesn't seem like a big accomplishment, but five years ago it was a serious challenge for computer vision systems.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
```
The easiest way to load image data is with `datasets.ImageFolder` from `torchvision` ([documentation](http://pytorch.org/docs/master/torchvision/datasets.html#imagefolder)). In general you'll use `ImageFolder` like so:
```python
dataset = datasets.ImageFolder('path/to/data', transform=transform)
```
where `'path/to/data'` is the file path to the data directory and `transform` is a list of processing steps built with the [`transforms`](http://pytorch.org/docs/master/torchvision/transforms.html) module from `torchvision`. ImageFolder expects the files and directories to be constructed like so:
```
root/dog/xxx.png
root/dog/xxy.png
root/dog/xxz.png
root/cat/123.png
root/cat/nsdf3.png
root/cat/asd932_.png
```
where each class has it's own directory (`cat` and `dog`) for the images. The images are then labeled with the class taken from the directory name. So here, the image `123.png` would be loaded with the class label `cat`. You can download the dataset already structured like this [from here](https://s3.amazonaws.com/content.udacity-data.com/nd089/Cat_Dog_data.zip). I've also split it into a training set and test set.
### Transforms
When you load in the data with `ImageFolder`, you'll need to define some transforms. For example, the images are different sizes but we'll need them to all be the same size for training. You can either resize them with `transforms.Resize()` or crop with `transforms.CenterCrop()`, `transforms.RandomResizedCrop()`, etc. We'll also need to convert the images to PyTorch tensors with `transforms.ToTensor()`. Typically you'll combine these transforms into a pipeline with `transforms.Compose()`, which accepts a list of transforms and runs them in sequence. It looks something like this to scale, then crop, then convert to a tensor:
```python
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
```
There are plenty of transforms available, I'll cover more in a bit and you can read through the [documentation](http://pytorch.org/docs/master/torchvision/transforms.html).
### Data Loaders
With the `ImageFolder` loaded, you have to pass it to a [`DataLoader`](http://pytorch.org/docs/master/data.html#torch.utils.data.DataLoader). The `DataLoader` takes a dataset (such as you would get from `ImageFolder`) and returns batches of images and the corresponding labels. You can set various parameters like the batch size and if the data is shuffled after each epoch.
```python
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
```
Here `dataloader` is a [generator](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/). To get data out of it, you need to loop through it or convert it to an iterator and call `next()`.
```python
# Looping through it, get a batch on each loop
for images, labels in dataloader:
pass
# Get one batch
images, labels = next(iter(dataloader))
```
>**Exercise:** Load images from the `Cat_Dog_data/train` folder, define a few transforms, then build the dataloader.
```
data_dir = '/Users/mohamedabdelbary/Documents/Dev/deep-learning-v2-pytorch/dogs-vs-cats/'
transform = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()
])
dataset = datasets.ImageFolder(data_dir, transform=transform)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# Run this to test your data loader
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
```
If you loaded the data correctly, you should see something like this (your image will be different):
<img src='assets/cat_cropped.png' width=244>
## Data Augmentation
A common strategy for training neural networks is to introduce randomness in the input data itself. For example, you can randomly rotate, mirror, scale, and/or crop your images during training. This will help your network generalize as it's seeing the same images but in different locations, with different sizes, in different orientations, etc.
To randomly rotate, scale and crop, then flip your images you would define your transforms like this:
```python
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5],
[0.5, 0.5, 0.5])])
```
You'll also typically want to normalize images with `transforms.Normalize`. You pass in a list of means and list of standard deviations, then the color channels are normalized like so
```input[channel] = (input[channel] - mean[channel]) / std[channel]```
Subtracting `mean` centers the data around zero and dividing by `std` squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
You can find a list of all [the available transforms here](http://pytorch.org/docs/0.3.0/torchvision/transforms.html). When you're testing however, you'll want to use images that aren't altered (except you'll need to normalize the same way). So, for validation/test images, you'll typically just resize and crop.
>**Exercise:** Define transforms for training data and testing data below. Leave off normalization for now.
```
data_dir = '/Users/mohamedabdelbary/Documents/Dev/deep-learning-v2-pytorch/dogs-vs-cats'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5],
[0.5, 0.5, 0.5])
])
test_transforms = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()
])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=32)
testloader = torch.utils.data.DataLoader(test_data, batch_size=32)
# change this to the trainloader or testloader
data_iter = iter(testloader)
images, labels = next(data_iter)
fig, axes = plt.subplots(figsize=(10,4), ncols=4)
for ii in range(4):
ax = axes[ii]
helper.imshow(images[ii], ax=ax, normalize=False)
```
Your transformed images should look something like this.
<center>Training examples:</center>
<img src='assets/train_examples.png' width=500px>
<center>Testing examples:</center>
<img src='assets/test_examples.png' width=500px>
At this point you should be able to load data for training and testing. Now, you should try building a network that can classify cats vs dogs. This is quite a bit more complicated than before with the MNIST and Fashion-MNIST datasets. To be honest, you probably won't get it to work with a fully-connected network, no matter how deep. These images have three color channels and at a higher resolution (so far you've seen 28x28 images which are tiny).
In the next part, I'll show you how to use a pre-trained network to build a model that can actually solve this problem.
```
# Optional TODO: Attempt to build a network to classify cats vs dogs from this dataset
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
dataset = datasets.ImageFolder('path/to/data', transform=transform)
root/dog/xxx.png
root/dog/xxy.png
root/dog/xxz.png
root/cat/123.png
root/cat/nsdf3.png
root/cat/asd932_.png
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# Looping through it, get a batch on each loop
for images, labels in dataloader:
pass
# Get one batch
images, labels = next(iter(dataloader))
data_dir = '/Users/mohamedabdelbary/Documents/Dev/deep-learning-v2-pytorch/dogs-vs-cats/'
transform = transforms.Compose([
transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()
])
dataset = datasets.ImageFolder(data_dir, transform=transform)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# Run this to test your data loader
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5],
[0.5, 0.5, 0.5])])
Subtracting `mean` centers the data around zero and dividing by `std` squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
You can find a list of all [the available transforms here](http://pytorch.org/docs/0.3.0/torchvision/transforms.html). When you're testing however, you'll want to use images that aren't altered (except you'll need to normalize the same way). So, for validation/test images, you'll typically just resize and crop.
>**Exercise:** Define transforms for training data and testing data below. Leave off normalization for now.
Your transformed images should look something like this.
<center>Training examples:</center>
<img src='assets/train_examples.png' width=500px>
<center>Testing examples:</center>
<img src='assets/test_examples.png' width=500px>
At this point you should be able to load data for training and testing. Now, you should try building a network that can classify cats vs dogs. This is quite a bit more complicated than before with the MNIST and Fashion-MNIST datasets. To be honest, you probably won't get it to work with a fully-connected network, no matter how deep. These images have three color channels and at a higher resolution (so far you've seen 28x28 images which are tiny).
In the next part, I'll show you how to use a pre-trained network to build a model that can actually solve this problem.
| 0.829561 | 0.991161 |
```
# Visualization of the KO+ChIP Gold Standard from:
# Miraldi et al. (2018) "Leveraging chromatin accessibility for transcriptional regulatory network inference in Th17 Cells"
# TO START: In the menu above, choose "Cell" --> "Run All", and network + heatmap will load
# Change "canvas" to "SVG" (drop-down menu in cell below) to enable drag interactions with nodes & labels
# More info about jp_gene_viz and user interface instructions are available on Github:
# https://github.com/simonsfoundation/jp_gene_viz/blob/master/doc/dNetwork%20widget%20overview.ipynb
# Info specific to the "Multi-network" view:
# https://github.com/simonsfoundation/jp_gene_viz/blob/master/doc/Combined%20widgets.ipynb
# directory containing gene expression data and network folder
directory = "."
# folder containing networks
netPath = 'Networks'
# name of gene expression file
expressionFile = 'Th0_Th17_48hTh.txt'
# sample condition for initial gene node color
sampleConditionOfInt = 'Th17(48h)'
# The starting conditions for each of the networks is a list of tuples. Tuple entries are:
# 0. network file name (column format) (as found in directory)
# 1. column of the expression matrix that you want the nodes to be colored by
# 2. network title, to which we'll add the gene and peak cutoffs
# 3. cut off for edge strength, note TRN edges strengths are quantile for 15 TFs/gene, to see top 10 TFs/gene,
# increase cutoff to .33, etc.
networkInits = [
('ChIP_A17_KOall_ATh_bias50_maxComb_sp.tsv',sampleConditionOfInt,' Final ChIP/ATAC(Th17)+KO+ATAC(Th) TRN',.93),
('ATAC_Th17_bias50_maxComb_sp.tsv',sampleConditionOfInt,'Final ATAC-only TRN', .93),
("KO75_KOrk_1norm_sp.tsv",sampleConditionOfInt,'KO G.S. (25 TFs)',0),
("KC1p5_sp.tsv",sampleConditionOfInt,'KO-ChIP G.S. (9 TFs)',0)]
tfFocus = 1 # If 1, automatically applies the "TF only" function, so we can focus on TFs
# If 0, all genes shown
# Uncomment to run without install (in binder, for example)
import sys
if ".." not in sys.path:
sys.path.append("..")
from jp_gene_viz import dNetwork
dNetwork.load_javascript_support()
from jp_gene_viz import multiple_network
from jp_gene_viz import LExpression
LExpression.load_javascript_support()
networkList = list() # this list will contain heatmap-linked network objects
for networkInit in networkInits:
networkFile = networkInit[0]
curr = LExpression.LinkedExpressionNetwork()
print directory + '/' + networkFile
curr.load_network(directory + '/' + netPath + '/' + networkFile)
networkList.append(curr)
# visualize the networks -- HARD CODED for 4 networks:
M = multiple_network.MultipleNetworks(
[[networkList[0], networkList[1]],
[networkList[2], networkList[3]]])
M.svg_width = 500
M.show()
# Set network preferences
count = 0
for curr in networkList:
networkInit = networkInits[count]
# get title information + curr column for shading of figures
currCol = networkInit[1]
titleInf = networkInit[2]
threshhold = networkInit[3]
# set threshold
curr.network.threshhold_slider.value = threshhold
curr.network.apply_click(None)
curr.network.restore_click(None)
if tfFocus:
# focus on TF core
curr.network.tf_only_click(None)
curr.network.layout_click(None)
# layout network
curr.network.connected_only_click()
curr.network.layout_dropdown.value = 'fruchterman_reingold'
curr.network.layout_click()
# set title
curr.network.title_html.value = titleInf
# add labels
curr.network.labels_button.value=True
curr.network.draw_click(None)
# Load heatmap
curr.load_heatmap(directory + '/' + expressionFile)
# color nodes according to a sample column in the gene expression matrix
curr.gene_click(None)
curr.expression.transform_dropdown.value = 'Z score'
curr.expression.apply_transform()
curr.expression.col = currCol
curr.condition_click(None)
count += 1
```
|
github_jupyter
|
# Visualization of the KO+ChIP Gold Standard from:
# Miraldi et al. (2018) "Leveraging chromatin accessibility for transcriptional regulatory network inference in Th17 Cells"
# TO START: In the menu above, choose "Cell" --> "Run All", and network + heatmap will load
# Change "canvas" to "SVG" (drop-down menu in cell below) to enable drag interactions with nodes & labels
# More info about jp_gene_viz and user interface instructions are available on Github:
# https://github.com/simonsfoundation/jp_gene_viz/blob/master/doc/dNetwork%20widget%20overview.ipynb
# Info specific to the "Multi-network" view:
# https://github.com/simonsfoundation/jp_gene_viz/blob/master/doc/Combined%20widgets.ipynb
# directory containing gene expression data and network folder
directory = "."
# folder containing networks
netPath = 'Networks'
# name of gene expression file
expressionFile = 'Th0_Th17_48hTh.txt'
# sample condition for initial gene node color
sampleConditionOfInt = 'Th17(48h)'
# The starting conditions for each of the networks is a list of tuples. Tuple entries are:
# 0. network file name (column format) (as found in directory)
# 1. column of the expression matrix that you want the nodes to be colored by
# 2. network title, to which we'll add the gene and peak cutoffs
# 3. cut off for edge strength, note TRN edges strengths are quantile for 15 TFs/gene, to see top 10 TFs/gene,
# increase cutoff to .33, etc.
networkInits = [
('ChIP_A17_KOall_ATh_bias50_maxComb_sp.tsv',sampleConditionOfInt,' Final ChIP/ATAC(Th17)+KO+ATAC(Th) TRN',.93),
('ATAC_Th17_bias50_maxComb_sp.tsv',sampleConditionOfInt,'Final ATAC-only TRN', .93),
("KO75_KOrk_1norm_sp.tsv",sampleConditionOfInt,'KO G.S. (25 TFs)',0),
("KC1p5_sp.tsv",sampleConditionOfInt,'KO-ChIP G.S. (9 TFs)',0)]
tfFocus = 1 # If 1, automatically applies the "TF only" function, so we can focus on TFs
# If 0, all genes shown
# Uncomment to run without install (in binder, for example)
import sys
if ".." not in sys.path:
sys.path.append("..")
from jp_gene_viz import dNetwork
dNetwork.load_javascript_support()
from jp_gene_viz import multiple_network
from jp_gene_viz import LExpression
LExpression.load_javascript_support()
networkList = list() # this list will contain heatmap-linked network objects
for networkInit in networkInits:
networkFile = networkInit[0]
curr = LExpression.LinkedExpressionNetwork()
print directory + '/' + networkFile
curr.load_network(directory + '/' + netPath + '/' + networkFile)
networkList.append(curr)
# visualize the networks -- HARD CODED for 4 networks:
M = multiple_network.MultipleNetworks(
[[networkList[0], networkList[1]],
[networkList[2], networkList[3]]])
M.svg_width = 500
M.show()
# Set network preferences
count = 0
for curr in networkList:
networkInit = networkInits[count]
# get title information + curr column for shading of figures
currCol = networkInit[1]
titleInf = networkInit[2]
threshhold = networkInit[3]
# set threshold
curr.network.threshhold_slider.value = threshhold
curr.network.apply_click(None)
curr.network.restore_click(None)
if tfFocus:
# focus on TF core
curr.network.tf_only_click(None)
curr.network.layout_click(None)
# layout network
curr.network.connected_only_click()
curr.network.layout_dropdown.value = 'fruchterman_reingold'
curr.network.layout_click()
# set title
curr.network.title_html.value = titleInf
# add labels
curr.network.labels_button.value=True
curr.network.draw_click(None)
# Load heatmap
curr.load_heatmap(directory + '/' + expressionFile)
# color nodes according to a sample column in the gene expression matrix
curr.gene_click(None)
curr.expression.transform_dropdown.value = 'Z score'
curr.expression.apply_transform()
curr.expression.col = currCol
curr.condition_click(None)
count += 1
| 0.609757 | 0.747455 |
# Bagging
This notebook introduces a very natural strategy to build ensembles of
machine learning models named "bagging".
"Bagging" stands for Bootstrap AGGregatING. It uses bootstrap resampling
(random sampling with replacement) to learn several models on random
variations of the training set. At predict time, the predictions of each
learner are aggregated to give the final predictions.
First, we will generate a simple synthetic dataset to get insights regarding
bootstraping.
```
import pandas as pd
import numpy as np
# create a random number generator that will be used to set the randomness
rng = np.random.RandomState(1)
def generate_data(n_samples=30):
"""Generate synthetic dataset. Returns `data_train`, `data_test`,
`target_train`."""
x_min, x_max = -3, 3
x = rng.uniform(x_min, x_max, size=n_samples)
noise = 4.0 * rng.randn(n_samples)
y = x ** 3 - 0.5 * (x + 1) ** 2 + noise
y /= y.std()
data_train = pd.DataFrame(x, columns=["Feature"])
data_test = pd.DataFrame(
np.linspace(x_max, x_min, num=300), columns=["Feature"])
target_train = pd.Series(y, name="Target")
return data_train, data_test, target_train
import matplotlib.pyplot as plt
import seaborn as sns
data_train, data_test, target_train = generate_data(n_samples=30)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
_ = plt.title("Synthetic regression dataset")
```
The relationship between our feature and the target to predict is non-linear.
However, a decision tree is capable of approximating such a non-linear
dependency:
```
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
tree.fit(data_train, target_train)
y_pred = tree.predict(data_test)
```
Remember that the term "test" here refers to data that was not used for
training and computing an evaluation metric on such a synthetic test set
would be meaningless.
```
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
plt.plot(data_test["Feature"], y_pred, label="Fitted tree")
plt.legend()
_ = plt.title("Predictions by a single decision tree")
```
Let's see how we can use bootstraping to learn several trees.
## Bootstrap resampling
A bootstrap sample corresponds to a resampling with replacement, of the
original dataset, a sample that is the same size as the original dataset.
Thus, the bootstrap sample will contain some data points several times while
some of the original data points will not be present.
We will create a function that given `data` and `target` will return a
resampled variation `data_bootstrap` and `target_bootstrap`.
```
def bootstrap_sample(data, target):
# Indices corresponding to a sampling with replacement of the same sample
# size than the original data
bootstrap_indices = rng.choice(
np.arange(target.shape[0]), size=target.shape[0], replace=True,
)
# In pandas, we need to use `.iloc` to extract rows using an integer
# position index:
data_bootstrap = data.iloc[bootstrap_indices]
target_bootstrap = target.iloc[bootstrap_indices]
return data_bootstrap, target_bootstrap
```
We will generate 3 bootstrap samples and qualitatively check the difference
with the original dataset.
```
n_bootstraps = 3
for bootstrap_idx in range(n_bootstraps):
# draw a bootstrap from the original data
data_bootstrap, target_booststrap = bootstrap_sample(
data_train, target_train,
)
plt.figure()
plt.scatter(data_bootstrap["Feature"], target_booststrap,
color="tab:blue", facecolors="none",
alpha=0.5, label="Resampled data", s=180, linewidth=5)
plt.scatter(data_train["Feature"], target_train,
color="black", s=60,
alpha=1, label="Original data")
plt.title(f"Resampled data #{bootstrap_idx}")
plt.legend()
```
Observe that the 3 variations all share common points with the original
dataset. Some of the points are randomly resampled several times and appear
as darker blue circles.
The 3 generated bootstrap samples are all different from the original dataset
and from each other. To confirm this intuition, we can check the number of
unique samples in the bootstrap samples.
```
data_train_huge, data_test_huge, target_train_huge = generate_data(
n_samples=100_000)
data_bootstrap_sample, target_bootstrap_sample = bootstrap_sample(
data_train_huge, target_train_huge)
ratio_unique_sample = (np.unique(data_bootstrap_sample).size /
data_bootstrap_sample.size)
print(
f"Percentage of samples present in the original dataset: "
f"{ratio_unique_sample * 100:.1f}%"
)
```
On average, ~63.2% of the original data points of the original dataset will
be present in a given bootstrap sample. The other ~36.8% are repeated
samples.
We are able to generate many datasets, all slightly different.
Now, we can fit a decision tree for each of these datasets and they all shall
be slightly different as well.
```
bag_of_trees = []
for bootstrap_idx in range(n_bootstraps):
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
data_bootstrap_sample, target_bootstrap_sample = bootstrap_sample(
data_train, target_train)
tree.fit(data_bootstrap_sample, target_bootstrap_sample)
bag_of_trees.append(tree)
```
Now that we created a bag of different trees, we can use each of the trees to
predict the samples within the range of data. They shall give slightly
different predictions.
```
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
for tree_idx, tree in enumerate(bag_of_trees):
tree_predictions = tree.predict(data_test)
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.8,
label=f"Tree #{tree_idx} predictions")
plt.legend()
_ = plt.title("Predictions of trees trained on different bootstraps")
```
## Aggregating
Once our trees are fitted and we are able to get predictions for each of
them. In regression, the most straightforward way to combine those
predictions is just to average them: for a given test data point, we feed the
input feature values to each of the `n` trained models in the ensemble and as
a result compute `n` predicted values for the target variable. The final
prediction of the ensemble for the test data point is the average of those
`n` values.
We can plot the averaged predictions from the previous example.
```
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bag_predictions = []
for tree_idx, tree in enumerate(bag_of_trees):
tree_predictions = tree.predict(data_test)
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.8,
label=f"Tree #{tree_idx} predictions")
bag_predictions.append(tree_predictions)
bag_predictions = np.mean(bag_predictions, axis=0)
plt.plot(data_test["Feature"], bag_predictions, label="Averaged predictions",
linestyle="-")
plt.legend(bbox_to_anchor=(1.05, 0.8), loc="upper left")
_ = plt.title("Predictions of bagged trees")
```
The unbroken red line shows the averaged predictions, which would be the
final predictions given by our 'bag' of decision tree regressors. Note that
the predictions of the ensemble is more stable because of the averaging
operation. As a result, the bag of trees as a whole is less likely to overfit
than the individual trees.
## Bagging in scikit-learn
Scikit-learn implements the bagging procedure as a "meta-estimator", that is
an estimator that wraps another estimator: it takes a base model that is
cloned several times and trained independently on each bootstrap sample.
The following code snippet shows how to build a bagging ensemble of decision
trees. We set `n_estimators=100` instead of 3 in our manual implementation
above to get a stronger smoothing effect.
```
from sklearn.ensemble import BaggingRegressor
bagged_trees = BaggingRegressor(
base_estimator=DecisionTreeRegressor(max_depth=3),
n_estimators=100,
)
_ = bagged_trees.fit(data_train, target_train)
```
Let us visualize the predictions of the ensemble on the same interval of data:
```
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagged_trees_predictions = bagged_trees.predict(data_test)
plt.plot(data_test["Feature"], bagged_trees_predictions)
_ = plt.title("Predictions from a bagging classifier")
```
Because we use 100 trees in the ensemble, the average prediction is indeed
slightly smoother but very similar to our previous average plot.
It is possible to access the internal models of the ensemble stored as a
Python list in the `bagged_trees.estimators_` attribute after fitting.
Let us compare the based model predictions with their average:
```
for tree_idx, tree in enumerate(bagged_trees.estimators_):
label = "Predictions of individual trees" if tree_idx == 0 else None
# we convert `data_test` into a NumPy array to avoid a warning raised in scikit-learn
tree_predictions = tree.predict(data_test.to_numpy())
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.1,
color="tab:blue", label=label)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagged_trees_predictions = bagged_trees.predict(data_test)
plt.plot(data_test["Feature"], bagged_trees_predictions,
color="tab:orange", label="Predictions of ensemble")
_ = plt.legend()
```
We used a low value of the opacity parameter `alpha` to better appreciate the
overlap in the prediction functions of the individual trees.
This visualization gives some insights on the uncertainty in the predictions
in different areas of the feature space.
## Bagging complex pipelines
While we used a decision tree as a base model, nothing prevents us of using
any other type of model.
As we know that the original data generating function is a noisy polynomial
transformation of the input variable, let us try to fit a bagged polynomial
regression pipeline on this dataset:
```
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import make_pipeline
polynomial_regressor = make_pipeline(
MinMaxScaler(),
PolynomialFeatures(degree=4),
Ridge(alpha=1e-10),
)
```
This pipeline first scales the data to the 0-1 range with `MinMaxScaler`.
Then it extracts degree-4 polynomial features. The resulting features will
all stay in the 0-1 range by construction: if `x` lies in the 0-1 range then
`x ** n` also lies in the 0-1 range for any value of `n`.
Then the pipeline feeds the resulting non-linear features to a regularized
linear regression model for the final prediction of the target variable.
Note that we intentionally use a small value for the regularization parameter
`alpha` as we expect the bagging ensemble to work well with slightly overfit
base models.
The ensemble itself is simply built by passing the resulting pipeline as the
`base_estimator` parameter of the `BaggingRegressor` class:
```
bagging = BaggingRegressor(
base_estimator=polynomial_regressor,
n_estimators=100,
random_state=0,
)
_ = bagging.fit(data_train, target_train)
for i, regressor in enumerate(bagging.estimators_):
# we convert `data_test` into a NumPy array to avoid a warning raised in scikit-learn
regressor_predictions = regressor.predict(data_test.to_numpy())
base_model_line = plt.plot(
data_test["Feature"], regressor_predictions, linestyle="--", alpha=0.2,
label="Predictions of base models" if i == 0 else None,
color="tab:blue"
)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagging_predictions = bagging.predict(data_test)
plt.plot(data_test["Feature"], bagging_predictions,
color="tab:orange", label="Predictions of ensemble")
plt.ylim(target_train.min(), target_train.max())
plt.legend()
_ = plt.title("Bagged polynomial regression")
```
The predictions of this bagged polynomial regression model looks
qualitatively better than the bagged trees. This is somewhat expected since
the base model better reflects our knowldege of the true data generating
process.
Again the different shades induced by the overlapping blue lines let us
appreciate the uncertainty in the prediction of the bagged ensemble.
To conclude this notebook, we note that the bootstrapping procedure is a
generic tool of statistics and is not limited to build ensemble of machine
learning models. The interested reader can learn more on the [Wikipedia
article on
bootstrapping](https://en.wikipedia.org/wiki/Bootstrapping_(statistics)).
|
github_jupyter
|
import pandas as pd
import numpy as np
# create a random number generator that will be used to set the randomness
rng = np.random.RandomState(1)
def generate_data(n_samples=30):
"""Generate synthetic dataset. Returns `data_train`, `data_test`,
`target_train`."""
x_min, x_max = -3, 3
x = rng.uniform(x_min, x_max, size=n_samples)
noise = 4.0 * rng.randn(n_samples)
y = x ** 3 - 0.5 * (x + 1) ** 2 + noise
y /= y.std()
data_train = pd.DataFrame(x, columns=["Feature"])
data_test = pd.DataFrame(
np.linspace(x_max, x_min, num=300), columns=["Feature"])
target_train = pd.Series(y, name="Target")
return data_train, data_test, target_train
import matplotlib.pyplot as plt
import seaborn as sns
data_train, data_test, target_train = generate_data(n_samples=30)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
_ = plt.title("Synthetic regression dataset")
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
tree.fit(data_train, target_train)
y_pred = tree.predict(data_test)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
plt.plot(data_test["Feature"], y_pred, label="Fitted tree")
plt.legend()
_ = plt.title("Predictions by a single decision tree")
def bootstrap_sample(data, target):
# Indices corresponding to a sampling with replacement of the same sample
# size than the original data
bootstrap_indices = rng.choice(
np.arange(target.shape[0]), size=target.shape[0], replace=True,
)
# In pandas, we need to use `.iloc` to extract rows using an integer
# position index:
data_bootstrap = data.iloc[bootstrap_indices]
target_bootstrap = target.iloc[bootstrap_indices]
return data_bootstrap, target_bootstrap
n_bootstraps = 3
for bootstrap_idx in range(n_bootstraps):
# draw a bootstrap from the original data
data_bootstrap, target_booststrap = bootstrap_sample(
data_train, target_train,
)
plt.figure()
plt.scatter(data_bootstrap["Feature"], target_booststrap,
color="tab:blue", facecolors="none",
alpha=0.5, label="Resampled data", s=180, linewidth=5)
plt.scatter(data_train["Feature"], target_train,
color="black", s=60,
alpha=1, label="Original data")
plt.title(f"Resampled data #{bootstrap_idx}")
plt.legend()
data_train_huge, data_test_huge, target_train_huge = generate_data(
n_samples=100_000)
data_bootstrap_sample, target_bootstrap_sample = bootstrap_sample(
data_train_huge, target_train_huge)
ratio_unique_sample = (np.unique(data_bootstrap_sample).size /
data_bootstrap_sample.size)
print(
f"Percentage of samples present in the original dataset: "
f"{ratio_unique_sample * 100:.1f}%"
)
bag_of_trees = []
for bootstrap_idx in range(n_bootstraps):
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
data_bootstrap_sample, target_bootstrap_sample = bootstrap_sample(
data_train, target_train)
tree.fit(data_bootstrap_sample, target_bootstrap_sample)
bag_of_trees.append(tree)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
for tree_idx, tree in enumerate(bag_of_trees):
tree_predictions = tree.predict(data_test)
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.8,
label=f"Tree #{tree_idx} predictions")
plt.legend()
_ = plt.title("Predictions of trees trained on different bootstraps")
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bag_predictions = []
for tree_idx, tree in enumerate(bag_of_trees):
tree_predictions = tree.predict(data_test)
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.8,
label=f"Tree #{tree_idx} predictions")
bag_predictions.append(tree_predictions)
bag_predictions = np.mean(bag_predictions, axis=0)
plt.plot(data_test["Feature"], bag_predictions, label="Averaged predictions",
linestyle="-")
plt.legend(bbox_to_anchor=(1.05, 0.8), loc="upper left")
_ = plt.title("Predictions of bagged trees")
from sklearn.ensemble import BaggingRegressor
bagged_trees = BaggingRegressor(
base_estimator=DecisionTreeRegressor(max_depth=3),
n_estimators=100,
)
_ = bagged_trees.fit(data_train, target_train)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagged_trees_predictions = bagged_trees.predict(data_test)
plt.plot(data_test["Feature"], bagged_trees_predictions)
_ = plt.title("Predictions from a bagging classifier")
for tree_idx, tree in enumerate(bagged_trees.estimators_):
label = "Predictions of individual trees" if tree_idx == 0 else None
# we convert `data_test` into a NumPy array to avoid a warning raised in scikit-learn
tree_predictions = tree.predict(data_test.to_numpy())
plt.plot(data_test["Feature"], tree_predictions, linestyle="--", alpha=0.1,
color="tab:blue", label=label)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagged_trees_predictions = bagged_trees.predict(data_test)
plt.plot(data_test["Feature"], bagged_trees_predictions,
color="tab:orange", label="Predictions of ensemble")
_ = plt.legend()
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import make_pipeline
polynomial_regressor = make_pipeline(
MinMaxScaler(),
PolynomialFeatures(degree=4),
Ridge(alpha=1e-10),
)
bagging = BaggingRegressor(
base_estimator=polynomial_regressor,
n_estimators=100,
random_state=0,
)
_ = bagging.fit(data_train, target_train)
for i, regressor in enumerate(bagging.estimators_):
# we convert `data_test` into a NumPy array to avoid a warning raised in scikit-learn
regressor_predictions = regressor.predict(data_test.to_numpy())
base_model_line = plt.plot(
data_test["Feature"], regressor_predictions, linestyle="--", alpha=0.2,
label="Predictions of base models" if i == 0 else None,
color="tab:blue"
)
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
bagging_predictions = bagging.predict(data_test)
plt.plot(data_test["Feature"], bagging_predictions,
color="tab:orange", label="Predictions of ensemble")
plt.ylim(target_train.min(), target_train.max())
plt.legend()
_ = plt.title("Bagged polynomial regression")
| 0.856317 | 0.963057 |
### Dependencies for the interactive plots apart from rdkit, oechem and other qc* packages
!conda install -c conda-forge plotly -y
!conda install -c plotly jupyter-dash -y
!conda install -c plotly plotly-orca -y
```
#imports
import numpy as np
from scipy import stats
import fragmenter
from openeye import oechem
TD_datasets = [
'Fragment Stability Benchmark',
# 'Fragmenter paper',
# 'OpenFF DANCE 1 eMolecules t142 v1.0',
'OpenFF Fragmenter Validation 1.0',
'OpenFF Full TorsionDrive Benchmark 1',
'OpenFF Gen 2 Torsion Set 1 Roche 2',
'OpenFF Gen 2 Torsion Set 2 Coverage 2',
'OpenFF Gen 2 Torsion Set 3 Pfizer Discrepancy 2',
'OpenFF Gen 2 Torsion Set 4 eMolecules Discrepancy 2',
'OpenFF Gen 2 Torsion Set 5 Bayer 2',
'OpenFF Gen 2 Torsion Set 6 Supplemental 2',
'OpenFF Group1 Torsions 2',
'OpenFF Group1 Torsions 3',
'OpenFF Primary Benchmark 1 Torsion Set',
'OpenFF Primary Benchmark 2 Torsion Set',
'OpenFF Primary TorsionDrive Benchmark 1',
'OpenFF Rowley Biaryl v1.0',
'OpenFF Substituted Phenyl Set 1',
'OpenFF-benchmark-ligand-fragments-v1.0',
'Pfizer Discrepancy Torsion Dataset 1',
'SMIRNOFF Coverage Torsion Set 1',
# 'SiliconTX Torsion Benchmark Set 1',
'TorsionDrive Paper'
]
def oeb2oemol(oebfile):
"""
Takes in oebfile and generates oemolList
Parameters
----------
oebfile : String
Title of an oeb file
Returns
-------
mollist : List of objects
List of OEMols in the .oeb file
"""
ifs = oechem.oemolistream(oebfile)
mollist = []
for mol in ifs.GetOEGraphMols():
mollist.append(oechem.OEGraphMol(mol))
return mollist
def compute_r_ci(wbos, max_energies):
return (stats.linregress(wbos, max_energies)[2])**2
def plot_interactive(fileList, t_id):
"""
Takes in a list of oeb files and plots wbo vs torsion barrier, combining all the datasets and plotting by each tid in the combined dataset
Note: ***Plot is interactive (or returns chemical structures) only for the last usage
Parameters
----------
fileList: list of strings
each string is a oeb file name
Eg. ['rowley.oeb'] or ['rowley.oeb', 'phenyl.oeb']
t_id: str
torsion id, eg., 't43'
"""
import plotly.express as px
from jupyter_dash import JupyterDash
import dash_core_components as dcc
import dash_html_components as html
import pandas as pd
import plotly.graph_objects as go
from dash.dependencies import Input, Output
from rdkit import Chem
from rdkit.Chem.Draw import MolsToGridImage
import base64
from io import BytesIO
from plotly.validators.scatter.marker import SymbolValidator
import ntpath
df = pd.DataFrame(columns = ['tid', 'tb', 'wbo', 'cmiles', 'TDindices', 'filename'])
fig = go.Figure({'layout' : go.Layout(height=900, width=1000,
xaxis={'title': 'Wiberg Bond Order'},
yaxis={'title': 'Torsion barrier (kJ/mol)'},
#paper_bgcolor='white',
plot_bgcolor='rgba(0,0,0,0)',
margin={'l': 40, 'b': 200, 't': 40, 'r': 10},
legend={'orientation': 'h', 'y': -0.2},
legend_font=dict(family='Arial', color='black', size=15),
hovermode=False,
dragmode='select')})
fig.update_xaxes(title_font=dict(size=26, family='Arial', color='black'),
ticks="outside", tickwidth=2, tickcolor='black', ticklen=10,
tickfont=dict(family='Arial', color='black', size=20),
showgrid=False, gridwidth=1, gridcolor='black',
mirror=True, linewidth=2, linecolor='black', showline=True)
fig.update_yaxes(title_font=dict(size=26, family='Arial', color='black'),
ticks="outside", tickwidth=2, tickcolor='black', ticklen=10,
tickfont=dict(family='Arial', color='black', size=20),
showgrid=False, gridwidth=1, gridcolor='black',
mirror=True, linewidth=2, linecolor='black', showline=True)
colors = fragmenter.chemi._KELLYS_COLORS
colors = colors * 2
raw_symbols = SymbolValidator().values
symbols = []
for i in range(0,len(raw_symbols),8):
symbols.append(raw_symbols[i])
count = 0
fname = []
for fileName in fileList:
molList = []
fname = fileName
molList = oeb2oemol(fname)
for m in molList:
tid = m.GetData("IDMatch")
fname = ntpath.basename(fileName)
df = df.append({'tid': tid,
'tb': m.GetData("TB"),
'wbo' : m.GetData("WBO"),
'cmiles' : m.GetData("cmiles"),
'TDindices' : m.GetData("TDindices"),
'filename' : fname},
ignore_index = True)
x = df[(df.filename == fname) & (df.tid == t_id)].wbo
y = df.loc[x.index].tb
fig.add_scatter(x=x,
y=y,
mode="markers",
name=fname,
marker_color=colors[count],
marker_symbol=count,
marker_size=13)
count += 1
x = df[df.tid == t_id].wbo
y = df.loc[x.index].tb
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
print("tid: ", t_id, "r_value: ", r_value,
"slope: ", slope, "intercept: ", intercept)
fig.add_traces(go.Scatter(
x=np.unique(x),
y=np.poly1d([slope, intercept])(np.unique(x)),
showlegend=False, mode ='lines'))
slope_text = 'slope: '+str('%.2f' % slope)
r_value = 'r_val: '+str('%.2f' % r_value)
fig_text = slope_text + ', '+ r_value
fig.add_annotation(text=fig_text,
font = {'family': "Arial", 'size': 22, 'color': 'black'},
xref="paper", yref="paper", x=1, y=1,
showarrow=False)
graph_component = dcc.Graph(id="graph_id", figure=fig)
image_component = html.Img(id="structure-image")
external_stylesheets = ['https://codepen.io/chriddyp/pen/bWLwgP.css']
app = JupyterDash(__name__)
app.layout = html.Div([
html.Div([graph_component]),
html.Div([image_component])])
@app.callback(
Output('structure-image', 'src'),
[Input('graph_id', 'selectedData')])
def display_selected_data(selectedData):
max_structs = 40
structs_per_row = 1
empty_plot = "data:image/gif;base64,R0lGODlhAQABAAAAACwAAAAAAQABAAA="
if selectedData:
if len(selectedData['points']) == 0:
return empty_plot
print("# of points selected = ", len(selectedData['points']))
xval = [x['x'] for x in selectedData['points']]
yval = [x['y'] for x in selectedData['points']]
match_df = df[df['tb'].isin(yval) & df['tid'].isin([t_id])]
smiles_list = list(match_df.cmiles)
name_list = list(match_df.tid)
name_list = []
hl_atoms = []
for i in range(len(smiles_list)):
print(smiles_list[i])
indices_tup = match_df.iloc[i].TDindices
indices_list = [x + 1 for x in list(indices_tup)]
hl_atoms.append(indices_list)
tid = match_df.iloc[i].tid
tor_bar = match_df.iloc[i].tb
wbo_tor = match_df.iloc[i].wbo
cmiles_str = match_df.iloc[i].cmiles
tmp = [str(tid), ':', 'TDindices [', str(indices_tup[0]+1),
str(indices_tup[1]+1), str(indices_tup[2]+1),
str(indices_tup[3]+1), ']',
'wbo:', str('%.2f'%(wbo_tor)),
'TB:', str('%.2f'%(tor_bar)), '(kJ/mol)']
name_list.append(' '.join(tmp))
mol_list = [Chem.MolFromSmiles(x) for x in smiles_list]
print(len(mol_list))
img = MolsToGridImage(mol_list[0:max_structs],
subImgSize=(500, 500),
molsPerRow=structs_per_row,
legends=name_list)
# ,
# highlightAtomLists=hl_atoms)
buffered = BytesIO()
img.save(buffered, format="PNG", legendFontSize=60)
encoded_image = base64.b64encode(buffered.getvalue())
src_str = 'data:image/png;base64,{}'.format(encoded_image.decode())
else:
return empty_plot
return src_str
if __name__ == '__main__':
app.run_server(mode='inline', port=8061, debug=True)
return fig
```
`rowley_t43 = plot_interactive(['./FF_1.2.1/OpenFF Rowley Biaryl v1.0.oeb'], t_id='t43')`
```
folder_name = './FF_1.3.0-tig-8/'
TD_datasets = [
'Fragment Stability Benchmark',
# 'Fragmenter paper',
# 'OpenFF DANCE 1 eMolecules t142 v1.0',
'OpenFF Fragmenter Validation 1.0',
'OpenFF Full TorsionDrive Benchmark 1',
'OpenFF Gen 2 Torsion Set 1 Roche 2',
'OpenFF Gen 2 Torsion Set 2 Coverage 2',
'OpenFF Gen 2 Torsion Set 3 Pfizer Discrepancy 2',
'OpenFF Gen 2 Torsion Set 4 eMolecules Discrepancy 2',
'OpenFF Gen 2 Torsion Set 5 Bayer 2',
'OpenFF Gen 2 Torsion Set 6 Supplemental 2',
'OpenFF Group1 Torsions 2',
'OpenFF Group1 Torsions 3',
'OpenFF Primary Benchmark 1 Torsion Set',
'OpenFF Primary Benchmark 2 Torsion Set',
'OpenFF Primary TorsionDrive Benchmark 1',
'OpenFF Rowley Biaryl v1.0',
'OpenFF Substituted Phenyl Set 1',
'OpenFF-benchmark-ligand-fragments-v1.0',
'Pfizer Discrepancy Torsion Dataset 1',
'SMIRNOFF Coverage Torsion Set 1',
# 'SiliconTX Torsion Benchmark Set 1',
'TorsionDrive Paper'
]
TD_working_oeb = [folder_name+x+'.oeb' for x in TD_datasets]
# all_t43 = plot_interactive(TD_working_oeb, t_id='t43')
tig_ids = ['TIG2']
for iid in tig_ids:
tmp = plot_interactive(TD_working_oeb, t_id=iid)
# tmp.write_image(folder_name+"fig_"+str(iid)+".pdf")
```
|
github_jupyter
|
#imports
import numpy as np
from scipy import stats
import fragmenter
from openeye import oechem
TD_datasets = [
'Fragment Stability Benchmark',
# 'Fragmenter paper',
# 'OpenFF DANCE 1 eMolecules t142 v1.0',
'OpenFF Fragmenter Validation 1.0',
'OpenFF Full TorsionDrive Benchmark 1',
'OpenFF Gen 2 Torsion Set 1 Roche 2',
'OpenFF Gen 2 Torsion Set 2 Coverage 2',
'OpenFF Gen 2 Torsion Set 3 Pfizer Discrepancy 2',
'OpenFF Gen 2 Torsion Set 4 eMolecules Discrepancy 2',
'OpenFF Gen 2 Torsion Set 5 Bayer 2',
'OpenFF Gen 2 Torsion Set 6 Supplemental 2',
'OpenFF Group1 Torsions 2',
'OpenFF Group1 Torsions 3',
'OpenFF Primary Benchmark 1 Torsion Set',
'OpenFF Primary Benchmark 2 Torsion Set',
'OpenFF Primary TorsionDrive Benchmark 1',
'OpenFF Rowley Biaryl v1.0',
'OpenFF Substituted Phenyl Set 1',
'OpenFF-benchmark-ligand-fragments-v1.0',
'Pfizer Discrepancy Torsion Dataset 1',
'SMIRNOFF Coverage Torsion Set 1',
# 'SiliconTX Torsion Benchmark Set 1',
'TorsionDrive Paper'
]
def oeb2oemol(oebfile):
"""
Takes in oebfile and generates oemolList
Parameters
----------
oebfile : String
Title of an oeb file
Returns
-------
mollist : List of objects
List of OEMols in the .oeb file
"""
ifs = oechem.oemolistream(oebfile)
mollist = []
for mol in ifs.GetOEGraphMols():
mollist.append(oechem.OEGraphMol(mol))
return mollist
def compute_r_ci(wbos, max_energies):
return (stats.linregress(wbos, max_energies)[2])**2
def plot_interactive(fileList, t_id):
"""
Takes in a list of oeb files and plots wbo vs torsion barrier, combining all the datasets and plotting by each tid in the combined dataset
Note: ***Plot is interactive (or returns chemical structures) only for the last usage
Parameters
----------
fileList: list of strings
each string is a oeb file name
Eg. ['rowley.oeb'] or ['rowley.oeb', 'phenyl.oeb']
t_id: str
torsion id, eg., 't43'
"""
import plotly.express as px
from jupyter_dash import JupyterDash
import dash_core_components as dcc
import dash_html_components as html
import pandas as pd
import plotly.graph_objects as go
from dash.dependencies import Input, Output
from rdkit import Chem
from rdkit.Chem.Draw import MolsToGridImage
import base64
from io import BytesIO
from plotly.validators.scatter.marker import SymbolValidator
import ntpath
df = pd.DataFrame(columns = ['tid', 'tb', 'wbo', 'cmiles', 'TDindices', 'filename'])
fig = go.Figure({'layout' : go.Layout(height=900, width=1000,
xaxis={'title': 'Wiberg Bond Order'},
yaxis={'title': 'Torsion barrier (kJ/mol)'},
#paper_bgcolor='white',
plot_bgcolor='rgba(0,0,0,0)',
margin={'l': 40, 'b': 200, 't': 40, 'r': 10},
legend={'orientation': 'h', 'y': -0.2},
legend_font=dict(family='Arial', color='black', size=15),
hovermode=False,
dragmode='select')})
fig.update_xaxes(title_font=dict(size=26, family='Arial', color='black'),
ticks="outside", tickwidth=2, tickcolor='black', ticklen=10,
tickfont=dict(family='Arial', color='black', size=20),
showgrid=False, gridwidth=1, gridcolor='black',
mirror=True, linewidth=2, linecolor='black', showline=True)
fig.update_yaxes(title_font=dict(size=26, family='Arial', color='black'),
ticks="outside", tickwidth=2, tickcolor='black', ticklen=10,
tickfont=dict(family='Arial', color='black', size=20),
showgrid=False, gridwidth=1, gridcolor='black',
mirror=True, linewidth=2, linecolor='black', showline=True)
colors = fragmenter.chemi._KELLYS_COLORS
colors = colors * 2
raw_symbols = SymbolValidator().values
symbols = []
for i in range(0,len(raw_symbols),8):
symbols.append(raw_symbols[i])
count = 0
fname = []
for fileName in fileList:
molList = []
fname = fileName
molList = oeb2oemol(fname)
for m in molList:
tid = m.GetData("IDMatch")
fname = ntpath.basename(fileName)
df = df.append({'tid': tid,
'tb': m.GetData("TB"),
'wbo' : m.GetData("WBO"),
'cmiles' : m.GetData("cmiles"),
'TDindices' : m.GetData("TDindices"),
'filename' : fname},
ignore_index = True)
x = df[(df.filename == fname) & (df.tid == t_id)].wbo
y = df.loc[x.index].tb
fig.add_scatter(x=x,
y=y,
mode="markers",
name=fname,
marker_color=colors[count],
marker_symbol=count,
marker_size=13)
count += 1
x = df[df.tid == t_id].wbo
y = df.loc[x.index].tb
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
print("tid: ", t_id, "r_value: ", r_value,
"slope: ", slope, "intercept: ", intercept)
fig.add_traces(go.Scatter(
x=np.unique(x),
y=np.poly1d([slope, intercept])(np.unique(x)),
showlegend=False, mode ='lines'))
slope_text = 'slope: '+str('%.2f' % slope)
r_value = 'r_val: '+str('%.2f' % r_value)
fig_text = slope_text + ', '+ r_value
fig.add_annotation(text=fig_text,
font = {'family': "Arial", 'size': 22, 'color': 'black'},
xref="paper", yref="paper", x=1, y=1,
showarrow=False)
graph_component = dcc.Graph(id="graph_id", figure=fig)
image_component = html.Img(id="structure-image")
external_stylesheets = ['https://codepen.io/chriddyp/pen/bWLwgP.css']
app = JupyterDash(__name__)
app.layout = html.Div([
html.Div([graph_component]),
html.Div([image_component])])
@app.callback(
Output('structure-image', 'src'),
[Input('graph_id', 'selectedData')])
def display_selected_data(selectedData):
max_structs = 40
structs_per_row = 1
empty_plot = "data:image/gif;base64,R0lGODlhAQABAAAAACwAAAAAAQABAAA="
if selectedData:
if len(selectedData['points']) == 0:
return empty_plot
print("# of points selected = ", len(selectedData['points']))
xval = [x['x'] for x in selectedData['points']]
yval = [x['y'] for x in selectedData['points']]
match_df = df[df['tb'].isin(yval) & df['tid'].isin([t_id])]
smiles_list = list(match_df.cmiles)
name_list = list(match_df.tid)
name_list = []
hl_atoms = []
for i in range(len(smiles_list)):
print(smiles_list[i])
indices_tup = match_df.iloc[i].TDindices
indices_list = [x + 1 for x in list(indices_tup)]
hl_atoms.append(indices_list)
tid = match_df.iloc[i].tid
tor_bar = match_df.iloc[i].tb
wbo_tor = match_df.iloc[i].wbo
cmiles_str = match_df.iloc[i].cmiles
tmp = [str(tid), ':', 'TDindices [', str(indices_tup[0]+1),
str(indices_tup[1]+1), str(indices_tup[2]+1),
str(indices_tup[3]+1), ']',
'wbo:', str('%.2f'%(wbo_tor)),
'TB:', str('%.2f'%(tor_bar)), '(kJ/mol)']
name_list.append(' '.join(tmp))
mol_list = [Chem.MolFromSmiles(x) for x in smiles_list]
print(len(mol_list))
img = MolsToGridImage(mol_list[0:max_structs],
subImgSize=(500, 500),
molsPerRow=structs_per_row,
legends=name_list)
# ,
# highlightAtomLists=hl_atoms)
buffered = BytesIO()
img.save(buffered, format="PNG", legendFontSize=60)
encoded_image = base64.b64encode(buffered.getvalue())
src_str = 'data:image/png;base64,{}'.format(encoded_image.decode())
else:
return empty_plot
return src_str
if __name__ == '__main__':
app.run_server(mode='inline', port=8061, debug=True)
return fig
folder_name = './FF_1.3.0-tig-8/'
TD_datasets = [
'Fragment Stability Benchmark',
# 'Fragmenter paper',
# 'OpenFF DANCE 1 eMolecules t142 v1.0',
'OpenFF Fragmenter Validation 1.0',
'OpenFF Full TorsionDrive Benchmark 1',
'OpenFF Gen 2 Torsion Set 1 Roche 2',
'OpenFF Gen 2 Torsion Set 2 Coverage 2',
'OpenFF Gen 2 Torsion Set 3 Pfizer Discrepancy 2',
'OpenFF Gen 2 Torsion Set 4 eMolecules Discrepancy 2',
'OpenFF Gen 2 Torsion Set 5 Bayer 2',
'OpenFF Gen 2 Torsion Set 6 Supplemental 2',
'OpenFF Group1 Torsions 2',
'OpenFF Group1 Torsions 3',
'OpenFF Primary Benchmark 1 Torsion Set',
'OpenFF Primary Benchmark 2 Torsion Set',
'OpenFF Primary TorsionDrive Benchmark 1',
'OpenFF Rowley Biaryl v1.0',
'OpenFF Substituted Phenyl Set 1',
'OpenFF-benchmark-ligand-fragments-v1.0',
'Pfizer Discrepancy Torsion Dataset 1',
'SMIRNOFF Coverage Torsion Set 1',
# 'SiliconTX Torsion Benchmark Set 1',
'TorsionDrive Paper'
]
TD_working_oeb = [folder_name+x+'.oeb' for x in TD_datasets]
# all_t43 = plot_interactive(TD_working_oeb, t_id='t43')
tig_ids = ['TIG2']
for iid in tig_ids:
tmp = plot_interactive(TD_working_oeb, t_id=iid)
# tmp.write_image(folder_name+"fig_"+str(iid)+".pdf")
| 0.668015 | 0.692207 |
# Noisy Convolutional Neural Network Example
Build a noisy convolutional neural network with TensorFlow v2.
- Author: Gagandeep Singh
- Project: https://github.com/czgdp1807/noisy_weights
Experimental Details
- Datasets: The MNIST database of handwritten digits has been used for training and testing.
Observations
- It has been observed that accuracy of the model isn't affected on testing it with MNIST digits.
- The uncertainty expressed by the model is low which is expected since train and test disitributions are same.
References
- [1] https://github.com/aymericdamien/TensorFlow-Examples/
```
from __future__ import absolute_import, division, print_function
import tensorflow as tf
from tensorflow.keras import Model, layers
import numpy as np
# MNIST dataset parameters.
num_classes = 10 # total classes (0-9 digits).
# Training parameters.
learning_rate = 0.001
training_steps = 200
batch_size = 128
display_step = 10
# Network parameters.
conv1_filters = 32 # number of filters for 1st conv layer.
conv2_filters = 64 # number of filters for 2nd conv layer.
fc1_units = 1024 # number of neurons for 1st fully-connected layer.
# Prepare MNIST data.
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Convert to float32.
x_train, x_test = np.array(x_train, np.float32), np.array(x_test, np.float32)
# Normalize images value from [0, 255] to [0, 1].
x_train, x_test = x_train / 255., x_test / 255.
# Use tf.data API to shuffle and batch data.
train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_data = train_data.repeat().shuffle(5000).batch(batch_size).prefetch(1)
# Create TF Model.
class ConvNet(Model):
# Set layers.
def __init__(self):
super(ConvNet, self).__init__()
# Convolution Layer with 32 filters and a kernel size of 5.
self.conv1 = layers.Conv2D(32, kernel_size=5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with kernel size of 2 and strides of 2.
self.maxpool1 = layers.MaxPool2D(2, strides=2)
# Convolution Layer with 64 filters and a kernel size of 3.
self.conv2 = layers.Conv2D(64, kernel_size=3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with kernel size of 2 and strides of 2.
self.maxpool2 = layers.MaxPool2D(2, strides=2)
# Flatten the data to a 1-D vector for the fully connected layer.
self.flatten = layers.Flatten()
# Fully connected layer.
self.fc1 = layers.Dense(1024)
# Apply Dropout (if is_training is False, dropout is not applied).
self.dropout = layers.Dropout(rate=0.5)
# Output layer, class prediction.
self.out = layers.Dense(num_classes)
# Set forward pass.
def call(self, x, is_training=False):
def add_noise(_layer):
noisy_weights = []
for weight in _layer.get_weights():
noisy_weights.append(weight + tf.random.normal(weight.shape, 0., 0.001))
_layer.set_weights(noisy_weights)
if not is_training:
add_noise(self.conv1)
add_noise(self.conv2)
add_noise(self.fc1)
add_noise(self.out)
x = tf.reshape(x, [-1, 28, 28, 1])
x = self.conv1(x)
x = self.maxpool1(x)
x = self.conv2(x)
x = self.maxpool2(x)
x = self.flatten(x)
x = self.fc1(x)
x = self.dropout(x, training=is_training)
x = self.out(x)
if not is_training:
# tf cross entropy expect logits without softmax, so only
# apply softmax when not training.
x = tf.nn.softmax(x)
return x
# Build neural network model.
conv_net = ConvNet()
# Cross-Entropy Loss.
# Note that this will apply 'softmax' to the logits.
def cross_entropy_loss(x, y):
# Convert labels to int 64 for tf cross-entropy function.
y = tf.cast(y, tf.int64)
# Apply softmax to logits and compute cross-entropy.
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=x)
# Average loss across the batch.
return tf.reduce_mean(loss)
# Accuracy metric.
def accuracy(y_pred, y_true):
# Predicted class is the index of highest score in prediction vector (i.e. argmax).
correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64))
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis=-1)
# Stochastic gradient descent optimizer.
optimizer = tf.optimizers.Adam(learning_rate)
# Optimization process.
def run_optimization(x, y):
# Wrap computation inside a GradientTape for automatic differentiation.
with tf.GradientTape() as g:
# Forward pass.
pred = conv_net(x, is_training=True)
# Compute loss.
loss = cross_entropy_loss(pred, y)
# Variables to update, i.e. trainable variables.
trainable_variables = conv_net.trainable_variables
# Compute gradients.
gradients = g.gradient(loss, trainable_variables)
# Update W and b following gradients.
optimizer.apply_gradients(zip(gradients, trainable_variables))
# Run training for the given number of steps.
for step, (batch_x, batch_y) in enumerate(train_data.take(training_steps), 1):
# Run the optimization to update W and b values.
run_optimization(batch_x, batch_y)
if step % display_step == 0:
pred = conv_net(batch_x)
loss = cross_entropy_loss(pred, batch_y)
acc = accuracy(pred, batch_y)
print("step: %i, loss: %f, accuracy: %f" % (step, loss, acc))
# Test model on validation set.
pred = conv_net(x_test)
print("Test Accuracy: %f" % accuracy(pred, y_test))
# Visualize predictions.
import matplotlib.pyplot as plt
def compute_entropy(preds):
uncertainties = []
for i in range(preds.shape[0]):
uncertainties.append(-tf.reduce_mean(tf.math.multiply(preds[i], tf.math.log(preds[i]))))
return tf.convert_to_tensor(uncertainties)
n_images = 5
test_images = x_test[:n_images]
n_samples = 10
predictions = []
for i in range(n_samples):
predictions.append(conv_net(test_images))
predictions = tf.convert_to_tensor(predictions)
predictions = tf.reduce_mean(predictions, 0)
uncertainty = compute_entropy(predictions)
print(uncertainty)
# Display image and model prediction.
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction: %i" % np.argmax(predictions.numpy()[i]))
```
|
github_jupyter
|
from __future__ import absolute_import, division, print_function
import tensorflow as tf
from tensorflow.keras import Model, layers
import numpy as np
# MNIST dataset parameters.
num_classes = 10 # total classes (0-9 digits).
# Training parameters.
learning_rate = 0.001
training_steps = 200
batch_size = 128
display_step = 10
# Network parameters.
conv1_filters = 32 # number of filters for 1st conv layer.
conv2_filters = 64 # number of filters for 2nd conv layer.
fc1_units = 1024 # number of neurons for 1st fully-connected layer.
# Prepare MNIST data.
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Convert to float32.
x_train, x_test = np.array(x_train, np.float32), np.array(x_test, np.float32)
# Normalize images value from [0, 255] to [0, 1].
x_train, x_test = x_train / 255., x_test / 255.
# Use tf.data API to shuffle and batch data.
train_data = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_data = train_data.repeat().shuffle(5000).batch(batch_size).prefetch(1)
# Create TF Model.
class ConvNet(Model):
# Set layers.
def __init__(self):
super(ConvNet, self).__init__()
# Convolution Layer with 32 filters and a kernel size of 5.
self.conv1 = layers.Conv2D(32, kernel_size=5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with kernel size of 2 and strides of 2.
self.maxpool1 = layers.MaxPool2D(2, strides=2)
# Convolution Layer with 64 filters and a kernel size of 3.
self.conv2 = layers.Conv2D(64, kernel_size=3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with kernel size of 2 and strides of 2.
self.maxpool2 = layers.MaxPool2D(2, strides=2)
# Flatten the data to a 1-D vector for the fully connected layer.
self.flatten = layers.Flatten()
# Fully connected layer.
self.fc1 = layers.Dense(1024)
# Apply Dropout (if is_training is False, dropout is not applied).
self.dropout = layers.Dropout(rate=0.5)
# Output layer, class prediction.
self.out = layers.Dense(num_classes)
# Set forward pass.
def call(self, x, is_training=False):
def add_noise(_layer):
noisy_weights = []
for weight in _layer.get_weights():
noisy_weights.append(weight + tf.random.normal(weight.shape, 0., 0.001))
_layer.set_weights(noisy_weights)
if not is_training:
add_noise(self.conv1)
add_noise(self.conv2)
add_noise(self.fc1)
add_noise(self.out)
x = tf.reshape(x, [-1, 28, 28, 1])
x = self.conv1(x)
x = self.maxpool1(x)
x = self.conv2(x)
x = self.maxpool2(x)
x = self.flatten(x)
x = self.fc1(x)
x = self.dropout(x, training=is_training)
x = self.out(x)
if not is_training:
# tf cross entropy expect logits without softmax, so only
# apply softmax when not training.
x = tf.nn.softmax(x)
return x
# Build neural network model.
conv_net = ConvNet()
# Cross-Entropy Loss.
# Note that this will apply 'softmax' to the logits.
def cross_entropy_loss(x, y):
# Convert labels to int 64 for tf cross-entropy function.
y = tf.cast(y, tf.int64)
# Apply softmax to logits and compute cross-entropy.
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=x)
# Average loss across the batch.
return tf.reduce_mean(loss)
# Accuracy metric.
def accuracy(y_pred, y_true):
# Predicted class is the index of highest score in prediction vector (i.e. argmax).
correct_prediction = tf.equal(tf.argmax(y_pred, 1), tf.cast(y_true, tf.int64))
return tf.reduce_mean(tf.cast(correct_prediction, tf.float32), axis=-1)
# Stochastic gradient descent optimizer.
optimizer = tf.optimizers.Adam(learning_rate)
# Optimization process.
def run_optimization(x, y):
# Wrap computation inside a GradientTape for automatic differentiation.
with tf.GradientTape() as g:
# Forward pass.
pred = conv_net(x, is_training=True)
# Compute loss.
loss = cross_entropy_loss(pred, y)
# Variables to update, i.e. trainable variables.
trainable_variables = conv_net.trainable_variables
# Compute gradients.
gradients = g.gradient(loss, trainable_variables)
# Update W and b following gradients.
optimizer.apply_gradients(zip(gradients, trainable_variables))
# Run training for the given number of steps.
for step, (batch_x, batch_y) in enumerate(train_data.take(training_steps), 1):
# Run the optimization to update W and b values.
run_optimization(batch_x, batch_y)
if step % display_step == 0:
pred = conv_net(batch_x)
loss = cross_entropy_loss(pred, batch_y)
acc = accuracy(pred, batch_y)
print("step: %i, loss: %f, accuracy: %f" % (step, loss, acc))
# Test model on validation set.
pred = conv_net(x_test)
print("Test Accuracy: %f" % accuracy(pred, y_test))
# Visualize predictions.
import matplotlib.pyplot as plt
def compute_entropy(preds):
uncertainties = []
for i in range(preds.shape[0]):
uncertainties.append(-tf.reduce_mean(tf.math.multiply(preds[i], tf.math.log(preds[i]))))
return tf.convert_to_tensor(uncertainties)
n_images = 5
test_images = x_test[:n_images]
n_samples = 10
predictions = []
for i in range(n_samples):
predictions.append(conv_net(test_images))
predictions = tf.convert_to_tensor(predictions)
predictions = tf.reduce_mean(predictions, 0)
uncertainty = compute_entropy(predictions)
print(uncertainty)
# Display image and model prediction.
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction: %i" % np.argmax(predictions.numpy()[i]))
| 0.939519 | 0.974893 |
This is a "Neural Network" toy example which implements the basic logical gates.
Here we don't use any method to train the NN model. We just guess correct weight.
It is meant to show how in principle NN works.
```
import math
def sigmoid(x):
return 1./(1+ math.exp(-x))
def neuron(inputs, weights):
return sigmoid(sum([x*y for x,y in zip(inputs,weights)]))
def almost_equal(x,y,epsilon=0.001):
return abs(x-y) < epsilon
```
### We "implement" NN that computes OR operation:
| x1| x2| OR|
|---|---|---|
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 1
### Input:
* x0 = 1 (bias term)
* x1,x2 in [0,1]
### Weights:
We "guess" e.g. w0 = -5, w1= 10 and w2= 10 weights.
```
def NN_OR(x1,x2):
weights =[-10, 20, 20]
inputs = [1, x1, x2]
return neuron(weights,inputs)
print(NN_OR(1,0))
print(NN_OR(0,0))
assert almost_equal(NN_OR(0,0),0)
assert almost_equal(NN_OR(0,1),1)
assert almost_equal(NN_OR(1,0),1)
assert almost_equal(NN_OR(1,1),1)
```
### Analogically we "implement" NN that computes AND operation:
| x1| x2| AND|
|---|---|---|
0 | 0 | 0
0 | 1 | 0
1 | 0 | 0
1 | 1 | 1
### Input:
* x0 = 1 (bias term)
* x1,x2 in [0,1]
### Weights:
We "guess" e.g. w0 = -30, w1= 20 and w2 = 20 weights.
```
def NN_AND(x1,x2):
weights =[-30, 20, 20]
inputs = [1, x1, x2]
return neuron(weights,inputs)
print(NN_AND(1,0))
print(NN_AND(1,1))
assert almost_equal(NN_AND(0,0),0)
assert almost_equal(NN_AND(0,1),0)
assert almost_equal(NN_AND(1,0),0)
assert almost_equal(NN_AND(1,1),1)
```
### Analogically we "implement" NN that computes NOT operation:
| x | NOT|
|---|--- |
| 0 | 1
| 1 | 0
### Input:
* x0 = 1 (bias term)
* x in [0,1]
### Weights:
We "guess w0=20 and w1 =-30
```
def NN_NOT(x):
weights =[20, -30]
inputs = [1, x]
return neuron(weights,inputs)
print(NN_NOT(1))
print(NN_NOT(0))
assert almost_equal(NN_NOT(1),0)
assert almost_equal(NN_NOT(0),1)
```
### XOR operation
| x1| x2| XOR|
|---|---|---|
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 0
It's known that we cannot express XOR with one layer.
XOR is equivalent to (x1 OR x2) AND NOT(x1 AND x2)
### Input:
* x0 = 1 (bias term)
* x1,x2 in [0,1]
We will use combination of already existing GATES
```
def NN_XOR(x1,x2):
first = NN_OR(x1,x2)
second = NN_AND(x1,x2)
return NN_AND(first, NN_NOT(second))
print(NN_XOR(1,0))
print(NN_XOR(0,0))
print(NN_XOR(1,1))
assert almost_equal(NN_XOR(0,0),0)
assert almost_equal(NN_XOR(0,1),1)
assert almost_equal(NN_XOR(1,0),1)
assert almost_equal(NN_XOR(1,1),0)
```
|
github_jupyter
|
import math
def sigmoid(x):
return 1./(1+ math.exp(-x))
def neuron(inputs, weights):
return sigmoid(sum([x*y for x,y in zip(inputs,weights)]))
def almost_equal(x,y,epsilon=0.001):
return abs(x-y) < epsilon
def NN_OR(x1,x2):
weights =[-10, 20, 20]
inputs = [1, x1, x2]
return neuron(weights,inputs)
print(NN_OR(1,0))
print(NN_OR(0,0))
assert almost_equal(NN_OR(0,0),0)
assert almost_equal(NN_OR(0,1),1)
assert almost_equal(NN_OR(1,0),1)
assert almost_equal(NN_OR(1,1),1)
def NN_AND(x1,x2):
weights =[-30, 20, 20]
inputs = [1, x1, x2]
return neuron(weights,inputs)
print(NN_AND(1,0))
print(NN_AND(1,1))
assert almost_equal(NN_AND(0,0),0)
assert almost_equal(NN_AND(0,1),0)
assert almost_equal(NN_AND(1,0),0)
assert almost_equal(NN_AND(1,1),1)
def NN_NOT(x):
weights =[20, -30]
inputs = [1, x]
return neuron(weights,inputs)
print(NN_NOT(1))
print(NN_NOT(0))
assert almost_equal(NN_NOT(1),0)
assert almost_equal(NN_NOT(0),1)
def NN_XOR(x1,x2):
first = NN_OR(x1,x2)
second = NN_AND(x1,x2)
return NN_AND(first, NN_NOT(second))
print(NN_XOR(1,0))
print(NN_XOR(0,0))
print(NN_XOR(1,1))
assert almost_equal(NN_XOR(0,0),0)
assert almost_equal(NN_XOR(0,1),1)
assert almost_equal(NN_XOR(1,0),1)
assert almost_equal(NN_XOR(1,1),0)
| 0.609292 | 0.978073 |
```
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to change the path if needed.)
school_data_to_load = "Resources/schools_complete.csv"
student_data_to_load = "Resources/students_complete.csv"
# Read the School Data and Student Data and store into a Pandas DataFrame
school_data_df = pd.read_csv(school_data_to_load)
student_data_df = pd.read_csv(student_data_to_load)
# Cleaning Student Names and Replacing Substrings in a Python String
# Add each prefix and suffix to remove to a list.
prefixes_suffixes = ["Dr. ", "Mr. ","Ms. ", "Mrs. ", "Miss ", " MD", " DDS", " DVM", " PhD"]
# Iterate through the words in the "prefixes_suffixes" list and replace them with an empty space, "".
for word in prefixes_suffixes:
student_data_df["student_name"] = student_data_df["student_name"].str.replace(word,"")
# Check names.
student_data_df.head(10)
```
## Deliverable 1: Replace the reading and math scores.
### Replace the 9th grade reading and math scores at Thomas High School with NaN.
```
# Install numpy using conda install numpy or pip install numpy.
# Step 1. Import numpy as np.
import numpy as np
# Step 2. Use the loc method on the student_data_df to select all the reading scores from the 9th grade at Thomas High School and replace them with NaN.
reading_score_df = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "9th") &
(student_data_df["reading_score"] > 0), "reading_score"] = np.nan
student_data_df
# Step 2. Use the loc method on the student_data_df to select all the math scores from the 9th grade at Thomas High School and replace them with NaN.
math_score_df = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "9th") &
(student_data_df["math_score"] > 0), "math_score"] = np.nan
# Step 4. Check the student data for NaN's.
student_data_df
```
## Deliverable 2 : Repeat the school district analysis
### District Summary
```
# Combine the data into a single dataset
school_data_complete_df = pd.merge(student_data_df, school_data_df, how = "left" , on =["school_name", "school_name"])
# Calculate the Totals (Schools and Students)
school_count = len(school_data_complete_df["school_name"].unique())
student_count = school_data_complete_df["Student ID"].count()
# Calculate the Total Budget
total_budget = school_data_df["budget"].sum()
# Calculate the Average Scores using the "clean_student_data".
average_reading_score = school_data_complete_df["reading_score"].mean()
average_math_score = school_data_complete_df["math_score"].mean()
# Step 1. Get the number of students that are in ninth grade at Thomas High School.
# These students have no grades.
missing_grades = school_data_complete_df[(school_data_complete_df["math_score"].isna())].count()["student_name"]
# Get the total student count
student_count = school_data_complete_df["Student ID"].count()
# Step 2. Subtract the number of students that are in ninth grade at
# Thomas High School from the total student count to get the new total student count.
new_student_count = (student_count - missing_grades)
# Calculate the passing rates using the "clean_student_data".
passing_math_count = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)].count()["student_name"]
passing_reading_count = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)].count()["student_name"]
# Step 3. Calculate the passing percentages with the new total student count.
passing_math_percentage = passing_math_count/ float(new_student_count) * 100
passing_reading_percentage = passing_reading_count/ float(new_student_count) * 100
# Calculate the students who passed both reading and math.
passing_math_reading = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)
& (school_data_complete_df["reading_score"] >= 70)]
# Calculate the number of students that passed both reading and math.
overall_passing_math_reading_count = passing_math_reading["student_name"].count()
# Step 4.Calculate the overall passing percentage with new total student count.
overall_passing_percentage = overall_passing_math_reading_count/ new_student_count * 100
# Create a DataFrame
district_summary_df = pd.DataFrame(
[{"Total Schools": school_count,
"Total Students": student_count,
"Total Budget": total_budget,
"Average Math Score": average_math_score,
"Average Reading Score": average_reading_score,
"% Passing Math": passing_math_percentage,
"% Passing Reading": passing_reading_percentage,
"% Overall Passing": overall_passing_percentage}])
# Format the "Total Students" to have the comma for a thousands separator.
district_summary_df["Total Students"] = district_summary_df["Total Students"].map("{:,}".format)
# Format the "Total Budget" to have the comma for a thousands separator, a decimal separator and a "$".
district_summary_df["Total Budget"] = district_summary_df["Total Budget"].map("${:,.2f}".format)
# Format the columns.
district_summary_df["Average Math Score"] = district_summary_df["Average Math Score"].map("{:.1f}".format)
district_summary_df["Average Reading Score"] = district_summary_df["Average Reading Score"].map("{:.1f}".format)
district_summary_df["% Passing Math"] = district_summary_df["% Passing Math"].map("{:.1f}".format)
district_summary_df["% Passing Reading"] = district_summary_df["% Passing Reading"].map("{:.1f}".format)
district_summary_df["% Overall Passing"] = district_summary_df["% Overall Passing"].map("{:.1f}".format)
# Display the data frame
district_summary_df
```
## School Summary
```
# Determine the School Type
per_school_types = school_data_df.set_index(["school_name"])["type"]
# Calculate the total student count.
per_school_counts = school_data_complete_df["school_name"].value_counts()
# Calculate the total school budget and per capita spending
per_school_budget = school_data_complete_df.groupby(["school_name"]).mean()["budget"]
# Calculate the per capita spending.
per_school_capita = per_school_budget / per_school_counts
# Calculate the average test scores.
per_school_math = school_data_complete_df.groupby(["school_name"]).mean()["math_score"]
per_school_reading = school_data_complete_df.groupby(["school_name"]).mean()["reading_score"]
# Calculate the passing scores by creating a filtered DataFrame.
per_school_passing_math = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)]
per_school_passing_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)]
# Calculate the number of students passing math and passing reading by school.
per_school_passing_math = per_school_passing_math.groupby(["school_name"]).count()["student_name"]
per_school_passing_reading = per_school_passing_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of passing math and reading scores per school.
per_school_passing_math = per_school_passing_math / per_school_counts * 100
per_school_passing_reading = per_school_passing_reading / per_school_counts * 100
# Calculate the students who passed both reading and math.
per_passing_math_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)
& (school_data_complete_df["math_score"] >= 70)]
# Calculate the number of students passing math and passing reading by school.
per_passing_math_reading = per_passing_math_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of passing math and reading scores per school.
per_overall_passing_percentage = per_passing_math_reading / per_school_counts * 100
# Create the DataFrame
per_school_summary_df = pd.DataFrame({
"School Type": per_school_types,
"Total Students": per_school_counts,
"Total School Budget": per_school_budget,
"Per Student Budget": per_school_capita,
"Average Math Score": per_school_math,
"Average Reading Score": per_school_reading,
"% Passing Math": per_school_passing_math,
"% Passing Reading": per_school_passing_reading,
"% Overall Passing": per_overall_passing_percentage})
# per_school_summary_df.head()
# Format the Total School Budget and the Per Student Budget
per_school_summary_df["Total School Budget"] = per_school_summary_df["Total School Budget"].map("${:,.2f}".format)
per_school_summary_df["Per Student Budget"] = per_school_summary_df["Per Student Budget"].map("${:,.2f}".format)
# Display the data frame
per_school_summary_df
THS_summary = (per_school_summary_df.loc[["Thomas High School"]])
# Step 5. Get the number of 10th-12th graders from Thomas High School (THS).
THS_tenth_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th")].count()["Student ID"]
THS_eleventh_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th")].count()["Student ID"]
THS_twelfth_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th")].count()["Student ID"]
# Step 6. Get all the students passing math from THS
THS_tenth_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
# Step 7. Get all the students passing reading from THS
THS_tenth_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
# Step 8. Get all the students passing math and reading from THS
THS_tenth_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
# Step 9. Calculate the percentage of 10th-12th grade students passing math from Thomas High School.
THS_tenth_graders_passing_math_percentage = THS_tenth_graders_passing_math/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_math_percentage = THS_eleventh_graders_passing_math/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_math_percentage = THS_twelfth_graders_passing_math/ float(THS_twelfth_graders) * 100
# Step 10. Calculate the percentage of 10th-12th grade students passing reading from Thomas High School.
THS_tenth_graders_passing_reading_percentage = THS_tenth_graders_passing_reading/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_reading_percentage = THS_eleventh_graders_passing_reading/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_reading_percentage = THS_twelfth_graders_passing_reading/ float(THS_twelfth_graders) * 100
# Step 11. Calculate the overall passing percentage of 10th-12th grade from Thomas High School.
THS_tenth_graders_passing_overall_percentage = THS_tenth_graders_passing_overall/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_overall_percentage = THS_eleventh_graders_passing_overall/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_overall_percentage = THS_twelfth_graders_passing_overall/ float(THS_twelfth_graders) * 100
# Step 12. Replace the passing math percent for Thomas High School in the per_school_summary_df.
THS_passing_math = (THS_tenth_graders_passing_math + THS_eleventh_graders_passing_math + THS_twelfth_graders_passing_math)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_math_percentage = THS_passing_math/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Passing Math'] = THS_passing_math_percentage * 100
# Step 13. Replace the passing reading percentage for Thomas High School in the per_school_summary_df.
THS_passing_reading = (THS_tenth_graders_passing_reading + THS_eleventh_graders_passing_reading + THS_twelfth_graders_passing_reading)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_reading_percentage = THS_passing_reading/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Passing Reading'] = THS_passing_reading_percentage * 100
# Step 14. Replace the overall passing percentage for Thomas High School in the per_school_summary_df.
THS_passing_overall = (THS_tenth_graders_passing_overall + THS_eleventh_graders_passing_overall + THS_twelfth_graders_passing_overall)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_overall_percentage = THS_passing_overall/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Overall Passing'] = THS_passing_overall_percentage * 100
per_school_summary_df
THS_summary = (per_school_summary_df.loc[["Thomas High School"]])
```
## High and Low Performing Schools
```
# Sort and show top five schools.
top_schools = per_school_summary_df.sort_values([ "% Overall Passing"], ascending = False)
top_schools.head()
# Sort and show top five schools.
bottom_schools = per_school_summary_df.sort_values ([ "% Overall Passing"] , ascending = True)
bottom_schools.head()
```
## Math and Reading Scores by Grade
```
# Create a Series of scores by grade levels using conditionals.
ninth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "9th")]
tenth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "10th")]
eleventh_graders = school_data_complete_df[(school_data_complete_df["grade"] == "11th")]
twelfth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "12th")]
# Group each school Series by the school name for the average math score.
ninth_graders_math_scores = ninth_graders.groupby(["school_name"]).mean()["math_score"]
tenth_graders_math_scores = tenth_graders.groupby(["school_name"]).mean()["math_score"]
eleventh_graders_math_scores = eleventh_graders.groupby(["school_name"]).mean()["math_score"]
twelfth_graders_math_scores = twelfth_graders.groupby(["school_name"]).mean()["math_score"]
# Group each school Series by the school name for the average reading score.
ninth_graders_reading_scores = ninth_graders.groupby(["school_name"]).mean()["reading_score"]
tenth_graders_reading_scores = tenth_graders.groupby(["school_name"]).mean()["reading_score"]
eleventh_graders_reading_scores = eleventh_graders.groupby(["school_name"]).mean()["reading_score"]
twelfth_graders_reading_scores = twelfth_graders.groupby(["school_name"]).mean()["reading_score"]
# Combine each Series for average math scores by school into single data frame.
math_scores_by_grade = pd.DataFrame({
"9th": ninth_graders_math_scores,
"10th": tenth_graders_math_scores,
"11th": eleventh_graders_math_scores,
"12th": twelfth_graders_math_scores
})
# Combine each Series for average reading scores by school into single data frame.
reading_scores_by_grade = pd.DataFrame({
"9th": ninth_graders_reading_scores,
"10th": tenth_graders_reading_scores,
"11th": eleventh_graders_reading_scores,
"12th": twelfth_graders_reading_scores
})
# Format each grade column.
math_scores_by_grade["9th"] = math_scores_by_grade["9th"].map("{:,.1f}".format)
math_scores_by_grade["10th"] = math_scores_by_grade["10th"].map("{:,.1f}".format)
math_scores_by_grade["11th"] = math_scores_by_grade["11th"].map("{:,.1f}".format)
math_scores_by_grade["12th"] = math_scores_by_grade["12th"].map("{:,.1f}".format)
# Format each grade column.
reading_scores_by_grade["9th"] = reading_scores_by_grade["9th"].map("{:,.1f}".format)
reading_scores_by_grade["10th"] = reading_scores_by_grade["10th"].map("{:,.1f}".format)
reading_scores_by_grade["11th"] = reading_scores_by_grade["11th"].map("{:,.1f}".format)
reading_scores_by_grade["12th"] = reading_scores_by_grade["12th"].map("{:,.1f}".format)
# Remove the index.
reading_scores_by_grade = reading_scores_by_grade[["9th", "10th", "11th", "12th"]]
reading_scores_by_grade.index.name = None
# Display the data frame
reading_scores_by_grade
# Remove the index.
math_scores_by_grade = math_scores_by_grade[["9th", "10th", "11th", "12th"]]
math_scores_by_grade.index.name = None
# Display the data frame
math_scores_by_grade
```
## Scores by School Spending
```
# Establish the spending bins and group names.
spending_bins = [0, 585, 630, 645, 675]
group_name = ["<$584", "$585 - $629", "$630 - $644" , "$645 - $675"]
per_school_summary_df["Spending Ranges (Per Student)"] = pd.cut(per_school_capita, spending_bins, labels = group_name)
# Calculate averages for the desired columns.
spending_math_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Math Score"]
spending_reading_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Reading Score"]
spending_passing_math = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Math"]
spending_passing_reading = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Reading"]
spending_passing_overall = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Overall Passing"]
# Create the DataFrame
spending_summary_df = pd.DataFrame({
"Average Math Score" : spending_math_scores,
"Average Reading Score" : spending_reading_scores,
"% Passing Math" : spending_passing_math,
"% Passing Reading" : spending_passing_reading,
"% Passing Overall": spending_passing_overall
})
# Format the DataFrame
spending_summary_df["Average Math Score"] = spending_summary_df["Average Math Score"].map("{:.1f}".format)
spending_summary_df["Average Reading Score"] = spending_summary_df["Average Reading Score"].map("{:.1f}".format)
spending_summary_df["% Passing Math"] = spending_summary_df["% Passing Math"].map("{:.1f}".format)
spending_summary_df["% Passing Reading"] = spending_summary_df["% Passing Reading"].map("{:.1f}".format)
spending_summary_df["% Passing Overall"] = spending_summary_df["% Passing Overall"].map("{:.1f}".format)
spending_summary_df
```
## Scores by School Size
```
# Establish the bins.
size_bins = [0, 1000, 2000, 5000]
group_names = ["Small (<1000)", "Medium (1000-2000)", "Large(2000 -5000)"]
# Categorize spending based on the bins.
per_school_summary_df["School Size"] = pd.cut(per_school_summary_df["Total Students"], size_bins, labels=group_names)
# Calculate averages for the desired columns.
size_math_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Math Score"]
size_reading_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Reading Score"]
size_passing_math = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Math"]
size_passing_reading = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Reading"]
size_passing_overall = per_school_summary_df.groupby(["School Size"]).mean()["% Overall Passing"]
# Assemble into DataFrame.
size_summary_df = pd.DataFrame({
"Average Math Score" : size_math_scores,
"Average Reading Score" : size_reading_scores,
"% Passing Math" : size_passing_math,
"% Passing Reading" : size_passing_reading,
"% Passing Overall": size_passing_overall
})
# Format the DataFrame
size_summary_df["Average Math Score"] = size_summary_df["Average Math Score"].map("{:.1f}".format)
size_summary_df["Average Reading Score"] = size_summary_df["Average Reading Score"].map("{:.1f}".format)
size_summary_df["% Passing Math"] = size_summary_df["% Passing Math"].map("{:.1f}".format)
size_summary_df["% Passing Reading"] = size_summary_df["% Passing Reading"].map("{:.1f}".format)
size_summary_df["% Passing Overall"] = size_summary_df["% Passing Overall"].map("{:.1f}".format)
size_summary_df
```
## Scores by School Type
```
# Calculate averages for the desired columns.
type_math_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Math Score"]
type_reading_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Reading Score"]
type_passing_math = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Math"]
type_passing_reading = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Reading"]
type_passing_overall = per_school_summary_df.groupby(["School Type"]).mean()["% Overall Passing"]
# Assemble into DataFrame.
type_summary_df = pd.DataFrame({
"Average Math Score" : type_math_scores,
"Average Reading Score" : type_reading_scores,
"% Passing Math" : type_passing_math,
"% Passing Reading" : type_passing_reading,
"% Passing Overall": type_passing_overall
})
# # Format the DataFrame
type_summary_df["Average Math Score"] = type_summary_df["Average Math Score"].map("{:.1f}".format)
type_summary_df["Average Reading Score"] = type_summary_df["Average Reading Score"].map("{:.1f}".format)
type_summary_df["% Passing Math"] = type_summary_df["% Passing Math"].map("{:.1f}".format)
type_summary_df["% Passing Reading"] = type_summary_df["% Passing Reading"].map("{:.1f}".format)
type_summary_df["% Passing Overall"] = type_summary_df["% Passing Overall"].map("{:.1f}".format)
type_summary_df
```
|
github_jupyter
|
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to change the path if needed.)
school_data_to_load = "Resources/schools_complete.csv"
student_data_to_load = "Resources/students_complete.csv"
# Read the School Data and Student Data and store into a Pandas DataFrame
school_data_df = pd.read_csv(school_data_to_load)
student_data_df = pd.read_csv(student_data_to_load)
# Cleaning Student Names and Replacing Substrings in a Python String
# Add each prefix and suffix to remove to a list.
prefixes_suffixes = ["Dr. ", "Mr. ","Ms. ", "Mrs. ", "Miss ", " MD", " DDS", " DVM", " PhD"]
# Iterate through the words in the "prefixes_suffixes" list and replace them with an empty space, "".
for word in prefixes_suffixes:
student_data_df["student_name"] = student_data_df["student_name"].str.replace(word,"")
# Check names.
student_data_df.head(10)
# Install numpy using conda install numpy or pip install numpy.
# Step 1. Import numpy as np.
import numpy as np
# Step 2. Use the loc method on the student_data_df to select all the reading scores from the 9th grade at Thomas High School and replace them with NaN.
reading_score_df = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "9th") &
(student_data_df["reading_score"] > 0), "reading_score"] = np.nan
student_data_df
# Step 2. Use the loc method on the student_data_df to select all the math scores from the 9th grade at Thomas High School and replace them with NaN.
math_score_df = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "9th") &
(student_data_df["math_score"] > 0), "math_score"] = np.nan
# Step 4. Check the student data for NaN's.
student_data_df
# Combine the data into a single dataset
school_data_complete_df = pd.merge(student_data_df, school_data_df, how = "left" , on =["school_name", "school_name"])
# Calculate the Totals (Schools and Students)
school_count = len(school_data_complete_df["school_name"].unique())
student_count = school_data_complete_df["Student ID"].count()
# Calculate the Total Budget
total_budget = school_data_df["budget"].sum()
# Calculate the Average Scores using the "clean_student_data".
average_reading_score = school_data_complete_df["reading_score"].mean()
average_math_score = school_data_complete_df["math_score"].mean()
# Step 1. Get the number of students that are in ninth grade at Thomas High School.
# These students have no grades.
missing_grades = school_data_complete_df[(school_data_complete_df["math_score"].isna())].count()["student_name"]
# Get the total student count
student_count = school_data_complete_df["Student ID"].count()
# Step 2. Subtract the number of students that are in ninth grade at
# Thomas High School from the total student count to get the new total student count.
new_student_count = (student_count - missing_grades)
# Calculate the passing rates using the "clean_student_data".
passing_math_count = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)].count()["student_name"]
passing_reading_count = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)].count()["student_name"]
# Step 3. Calculate the passing percentages with the new total student count.
passing_math_percentage = passing_math_count/ float(new_student_count) * 100
passing_reading_percentage = passing_reading_count/ float(new_student_count) * 100
# Calculate the students who passed both reading and math.
passing_math_reading = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)
& (school_data_complete_df["reading_score"] >= 70)]
# Calculate the number of students that passed both reading and math.
overall_passing_math_reading_count = passing_math_reading["student_name"].count()
# Step 4.Calculate the overall passing percentage with new total student count.
overall_passing_percentage = overall_passing_math_reading_count/ new_student_count * 100
# Create a DataFrame
district_summary_df = pd.DataFrame(
[{"Total Schools": school_count,
"Total Students": student_count,
"Total Budget": total_budget,
"Average Math Score": average_math_score,
"Average Reading Score": average_reading_score,
"% Passing Math": passing_math_percentage,
"% Passing Reading": passing_reading_percentage,
"% Overall Passing": overall_passing_percentage}])
# Format the "Total Students" to have the comma for a thousands separator.
district_summary_df["Total Students"] = district_summary_df["Total Students"].map("{:,}".format)
# Format the "Total Budget" to have the comma for a thousands separator, a decimal separator and a "$".
district_summary_df["Total Budget"] = district_summary_df["Total Budget"].map("${:,.2f}".format)
# Format the columns.
district_summary_df["Average Math Score"] = district_summary_df["Average Math Score"].map("{:.1f}".format)
district_summary_df["Average Reading Score"] = district_summary_df["Average Reading Score"].map("{:.1f}".format)
district_summary_df["% Passing Math"] = district_summary_df["% Passing Math"].map("{:.1f}".format)
district_summary_df["% Passing Reading"] = district_summary_df["% Passing Reading"].map("{:.1f}".format)
district_summary_df["% Overall Passing"] = district_summary_df["% Overall Passing"].map("{:.1f}".format)
# Display the data frame
district_summary_df
# Determine the School Type
per_school_types = school_data_df.set_index(["school_name"])["type"]
# Calculate the total student count.
per_school_counts = school_data_complete_df["school_name"].value_counts()
# Calculate the total school budget and per capita spending
per_school_budget = school_data_complete_df.groupby(["school_name"]).mean()["budget"]
# Calculate the per capita spending.
per_school_capita = per_school_budget / per_school_counts
# Calculate the average test scores.
per_school_math = school_data_complete_df.groupby(["school_name"]).mean()["math_score"]
per_school_reading = school_data_complete_df.groupby(["school_name"]).mean()["reading_score"]
# Calculate the passing scores by creating a filtered DataFrame.
per_school_passing_math = school_data_complete_df[(school_data_complete_df["math_score"] >= 70)]
per_school_passing_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)]
# Calculate the number of students passing math and passing reading by school.
per_school_passing_math = per_school_passing_math.groupby(["school_name"]).count()["student_name"]
per_school_passing_reading = per_school_passing_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of passing math and reading scores per school.
per_school_passing_math = per_school_passing_math / per_school_counts * 100
per_school_passing_reading = per_school_passing_reading / per_school_counts * 100
# Calculate the students who passed both reading and math.
per_passing_math_reading = school_data_complete_df[(school_data_complete_df["reading_score"] >= 70)
& (school_data_complete_df["math_score"] >= 70)]
# Calculate the number of students passing math and passing reading by school.
per_passing_math_reading = per_passing_math_reading.groupby(["school_name"]).count()["student_name"]
# Calculate the percentage of passing math and reading scores per school.
per_overall_passing_percentage = per_passing_math_reading / per_school_counts * 100
# Create the DataFrame
per_school_summary_df = pd.DataFrame({
"School Type": per_school_types,
"Total Students": per_school_counts,
"Total School Budget": per_school_budget,
"Per Student Budget": per_school_capita,
"Average Math Score": per_school_math,
"Average Reading Score": per_school_reading,
"% Passing Math": per_school_passing_math,
"% Passing Reading": per_school_passing_reading,
"% Overall Passing": per_overall_passing_percentage})
# per_school_summary_df.head()
# Format the Total School Budget and the Per Student Budget
per_school_summary_df["Total School Budget"] = per_school_summary_df["Total School Budget"].map("${:,.2f}".format)
per_school_summary_df["Per Student Budget"] = per_school_summary_df["Per Student Budget"].map("${:,.2f}".format)
# Display the data frame
per_school_summary_df
THS_summary = (per_school_summary_df.loc[["Thomas High School"]])
# Step 5. Get the number of 10th-12th graders from Thomas High School (THS).
THS_tenth_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th")].count()["Student ID"]
THS_eleventh_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th")].count()["Student ID"]
THS_twelfth_graders = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th")].count()["Student ID"]
# Step 6. Get all the students passing math from THS
THS_tenth_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_math = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["math_score"] >= 70)].count()["Student ID"]
# Step 7. Get all the students passing reading from THS
THS_tenth_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_reading = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["reading_score"] >= 70)].count()["Student ID"]
# Step 8. Get all the students passing math and reading from THS
THS_tenth_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "10th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_eleventh_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "11th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
THS_twelfth_graders_passing_overall = student_data_df.loc[
(student_data_df["school_name"] == "Thomas High School")&
(student_data_df["grade"] == "12th") &
(student_data_df["math_score"] >= 70) & (student_data_df["reading_score"] >= 70)].count()["Student ID"]
# Step 9. Calculate the percentage of 10th-12th grade students passing math from Thomas High School.
THS_tenth_graders_passing_math_percentage = THS_tenth_graders_passing_math/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_math_percentage = THS_eleventh_graders_passing_math/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_math_percentage = THS_twelfth_graders_passing_math/ float(THS_twelfth_graders) * 100
# Step 10. Calculate the percentage of 10th-12th grade students passing reading from Thomas High School.
THS_tenth_graders_passing_reading_percentage = THS_tenth_graders_passing_reading/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_reading_percentage = THS_eleventh_graders_passing_reading/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_reading_percentage = THS_twelfth_graders_passing_reading/ float(THS_twelfth_graders) * 100
# Step 11. Calculate the overall passing percentage of 10th-12th grade from Thomas High School.
THS_tenth_graders_passing_overall_percentage = THS_tenth_graders_passing_overall/ float(THS_tenth_graders) * 100
THS_eleventh_graders_passing_overall_percentage = THS_eleventh_graders_passing_overall/ float(THS_eleventh_graders) * 100
THS_twelfth_graders_passing_overall_percentage = THS_twelfth_graders_passing_overall/ float(THS_twelfth_graders) * 100
# Step 12. Replace the passing math percent for Thomas High School in the per_school_summary_df.
THS_passing_math = (THS_tenth_graders_passing_math + THS_eleventh_graders_passing_math + THS_twelfth_graders_passing_math)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_math_percentage = THS_passing_math/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Passing Math'] = THS_passing_math_percentage * 100
# Step 13. Replace the passing reading percentage for Thomas High School in the per_school_summary_df.
THS_passing_reading = (THS_tenth_graders_passing_reading + THS_eleventh_graders_passing_reading + THS_twelfth_graders_passing_reading)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_reading_percentage = THS_passing_reading/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Passing Reading'] = THS_passing_reading_percentage * 100
# Step 14. Replace the overall passing percentage for Thomas High School in the per_school_summary_df.
THS_passing_overall = (THS_tenth_graders_passing_overall + THS_eleventh_graders_passing_overall + THS_twelfth_graders_passing_overall)
THS_studentbody = (THS_tenth_graders + THS_eleventh_graders + THS_twelfth_graders )
THS_passing_overall_percentage = THS_passing_overall/ THS_studentbody
per_school_summary_df.at['Thomas High School','% Overall Passing'] = THS_passing_overall_percentage * 100
per_school_summary_df
THS_summary = (per_school_summary_df.loc[["Thomas High School"]])
# Sort and show top five schools.
top_schools = per_school_summary_df.sort_values([ "% Overall Passing"], ascending = False)
top_schools.head()
# Sort and show top five schools.
bottom_schools = per_school_summary_df.sort_values ([ "% Overall Passing"] , ascending = True)
bottom_schools.head()
# Create a Series of scores by grade levels using conditionals.
ninth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "9th")]
tenth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "10th")]
eleventh_graders = school_data_complete_df[(school_data_complete_df["grade"] == "11th")]
twelfth_graders = school_data_complete_df[(school_data_complete_df["grade"] == "12th")]
# Group each school Series by the school name for the average math score.
ninth_graders_math_scores = ninth_graders.groupby(["school_name"]).mean()["math_score"]
tenth_graders_math_scores = tenth_graders.groupby(["school_name"]).mean()["math_score"]
eleventh_graders_math_scores = eleventh_graders.groupby(["school_name"]).mean()["math_score"]
twelfth_graders_math_scores = twelfth_graders.groupby(["school_name"]).mean()["math_score"]
# Group each school Series by the school name for the average reading score.
ninth_graders_reading_scores = ninth_graders.groupby(["school_name"]).mean()["reading_score"]
tenth_graders_reading_scores = tenth_graders.groupby(["school_name"]).mean()["reading_score"]
eleventh_graders_reading_scores = eleventh_graders.groupby(["school_name"]).mean()["reading_score"]
twelfth_graders_reading_scores = twelfth_graders.groupby(["school_name"]).mean()["reading_score"]
# Combine each Series for average math scores by school into single data frame.
math_scores_by_grade = pd.DataFrame({
"9th": ninth_graders_math_scores,
"10th": tenth_graders_math_scores,
"11th": eleventh_graders_math_scores,
"12th": twelfth_graders_math_scores
})
# Combine each Series for average reading scores by school into single data frame.
reading_scores_by_grade = pd.DataFrame({
"9th": ninth_graders_reading_scores,
"10th": tenth_graders_reading_scores,
"11th": eleventh_graders_reading_scores,
"12th": twelfth_graders_reading_scores
})
# Format each grade column.
math_scores_by_grade["9th"] = math_scores_by_grade["9th"].map("{:,.1f}".format)
math_scores_by_grade["10th"] = math_scores_by_grade["10th"].map("{:,.1f}".format)
math_scores_by_grade["11th"] = math_scores_by_grade["11th"].map("{:,.1f}".format)
math_scores_by_grade["12th"] = math_scores_by_grade["12th"].map("{:,.1f}".format)
# Format each grade column.
reading_scores_by_grade["9th"] = reading_scores_by_grade["9th"].map("{:,.1f}".format)
reading_scores_by_grade["10th"] = reading_scores_by_grade["10th"].map("{:,.1f}".format)
reading_scores_by_grade["11th"] = reading_scores_by_grade["11th"].map("{:,.1f}".format)
reading_scores_by_grade["12th"] = reading_scores_by_grade["12th"].map("{:,.1f}".format)
# Remove the index.
reading_scores_by_grade = reading_scores_by_grade[["9th", "10th", "11th", "12th"]]
reading_scores_by_grade.index.name = None
# Display the data frame
reading_scores_by_grade
# Remove the index.
math_scores_by_grade = math_scores_by_grade[["9th", "10th", "11th", "12th"]]
math_scores_by_grade.index.name = None
# Display the data frame
math_scores_by_grade
# Establish the spending bins and group names.
spending_bins = [0, 585, 630, 645, 675]
group_name = ["<$584", "$585 - $629", "$630 - $644" , "$645 - $675"]
per_school_summary_df["Spending Ranges (Per Student)"] = pd.cut(per_school_capita, spending_bins, labels = group_name)
# Calculate averages for the desired columns.
spending_math_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Math Score"]
spending_reading_scores = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["Average Reading Score"]
spending_passing_math = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Math"]
spending_passing_reading = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Passing Reading"]
spending_passing_overall = per_school_summary_df.groupby(["Spending Ranges (Per Student)"]).mean()["% Overall Passing"]
# Create the DataFrame
spending_summary_df = pd.DataFrame({
"Average Math Score" : spending_math_scores,
"Average Reading Score" : spending_reading_scores,
"% Passing Math" : spending_passing_math,
"% Passing Reading" : spending_passing_reading,
"% Passing Overall": spending_passing_overall
})
# Format the DataFrame
spending_summary_df["Average Math Score"] = spending_summary_df["Average Math Score"].map("{:.1f}".format)
spending_summary_df["Average Reading Score"] = spending_summary_df["Average Reading Score"].map("{:.1f}".format)
spending_summary_df["% Passing Math"] = spending_summary_df["% Passing Math"].map("{:.1f}".format)
spending_summary_df["% Passing Reading"] = spending_summary_df["% Passing Reading"].map("{:.1f}".format)
spending_summary_df["% Passing Overall"] = spending_summary_df["% Passing Overall"].map("{:.1f}".format)
spending_summary_df
# Establish the bins.
size_bins = [0, 1000, 2000, 5000]
group_names = ["Small (<1000)", "Medium (1000-2000)", "Large(2000 -5000)"]
# Categorize spending based on the bins.
per_school_summary_df["School Size"] = pd.cut(per_school_summary_df["Total Students"], size_bins, labels=group_names)
# Calculate averages for the desired columns.
size_math_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Math Score"]
size_reading_scores = per_school_summary_df.groupby(["School Size"]).mean()["Average Reading Score"]
size_passing_math = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Math"]
size_passing_reading = per_school_summary_df.groupby(["School Size"]).mean()["% Passing Reading"]
size_passing_overall = per_school_summary_df.groupby(["School Size"]).mean()["% Overall Passing"]
# Assemble into DataFrame.
size_summary_df = pd.DataFrame({
"Average Math Score" : size_math_scores,
"Average Reading Score" : size_reading_scores,
"% Passing Math" : size_passing_math,
"% Passing Reading" : size_passing_reading,
"% Passing Overall": size_passing_overall
})
# Format the DataFrame
size_summary_df["Average Math Score"] = size_summary_df["Average Math Score"].map("{:.1f}".format)
size_summary_df["Average Reading Score"] = size_summary_df["Average Reading Score"].map("{:.1f}".format)
size_summary_df["% Passing Math"] = size_summary_df["% Passing Math"].map("{:.1f}".format)
size_summary_df["% Passing Reading"] = size_summary_df["% Passing Reading"].map("{:.1f}".format)
size_summary_df["% Passing Overall"] = size_summary_df["% Passing Overall"].map("{:.1f}".format)
size_summary_df
# Calculate averages for the desired columns.
type_math_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Math Score"]
type_reading_scores = per_school_summary_df.groupby(["School Type"]).mean()["Average Reading Score"]
type_passing_math = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Math"]
type_passing_reading = per_school_summary_df.groupby(["School Type"]).mean()["% Passing Reading"]
type_passing_overall = per_school_summary_df.groupby(["School Type"]).mean()["% Overall Passing"]
# Assemble into DataFrame.
type_summary_df = pd.DataFrame({
"Average Math Score" : type_math_scores,
"Average Reading Score" : type_reading_scores,
"% Passing Math" : type_passing_math,
"% Passing Reading" : type_passing_reading,
"% Passing Overall": type_passing_overall
})
# # Format the DataFrame
type_summary_df["Average Math Score"] = type_summary_df["Average Math Score"].map("{:.1f}".format)
type_summary_df["Average Reading Score"] = type_summary_df["Average Reading Score"].map("{:.1f}".format)
type_summary_df["% Passing Math"] = type_summary_df["% Passing Math"].map("{:.1f}".format)
type_summary_df["% Passing Reading"] = type_summary_df["% Passing Reading"].map("{:.1f}".format)
type_summary_df["% Passing Overall"] = type_summary_df["% Passing Overall"].map("{:.1f}".format)
type_summary_df
| 0.641198 | 0.861538 |
# 探索过拟合和欠拟合
在前面的两个例子中(电影影评分类和预测燃油效率),我们看到,在训练许多周期之后,我们的模型对验证数据的准确性会到达峰值,然后开始下降。
换句话说,我们的模型会过度拟合训练数据,学习如果处理过拟合很重要,尽管通常可以在训练集上实现高精度,但我们真正想要的是开发能够很好泛化测试数据(或之前未见过的数据)的模型。
过拟合的反面是欠拟合,当测试数据仍有改进空间会发生欠拟合,出现这种情况的原因有很多:模型不够强大,过度正则化,或者根本没有经过足够长的时间训练,这意味着网络尚未学习训练数据中的相关模式。
如果训练时间过长,模型将开始过度拟合,并从训练数据中学习模式,而这些模式可能并不适用于测试数据,我们需要取得平衡,了解如何训练适当数量的周期,我们将在下面讨论,这是一项有用的技能。
为了防止过拟合,最好的解决方案是使用更多的训练数据,受过更多数据训练的模型自然会更好的泛化。当没有更多的训练数据时,另外一个最佳解决方案是使用正则化等技术,这些限制了模型可以存储的信息的数据量和类型,如果网络只能记住少量模式,那么优化过程将迫使它专注于最突出的模式,这些模式有更好的泛化性。
在本章节中,我们将探索两种常见的正则化技术:权重正则化和dropout丢弃正则化,并使用它们来改进我们的IMDB电影评论分类。
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## 下载IMDB数据集
我们不会像以前一样使用嵌入,而是对句子进行多重编码。这个模型将很快适应训练集。它将用于证明何时发生过拟合,以及如何处理它。
对我们的列表进行多热编码意味着将它们转换为0和1的向量,具体地说,这将意味着例如将序列[3,5]转换为10000维向量,除了索引3和5的值是1之外,其他全零。
```
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
# Create an all-zero matrix of shape (len(sequences), dimension)
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0 # set specific indices of results[i] to 1s
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)
```
让我们看一下生成的多热矢量,单词索引按频率排序,因此预计索引零附近有更多的1值,我们可以在下图中看到:
```
plt.plot(train_data[0])
```
## 演示过拟合
防止过度拟合的最简单方法是减小模型的大小,即模型中可学习参数的数量(由层数和每层单元数决定)。在深度学习中,模型中可学习参数的数量通常被称为模型的“容量”。直观地,具有更多参数的模型将具有更多的“记忆能力”,因此将能够容易地学习训练样本与其目标之间的完美的字典式映射,没有任何泛化能力的映射,但是在对未见过的数据做出预测时这将是无用的。
始终牢记这一点:深度学习模型往往善于适应训练数据,但真正的挑战是泛化,而不是适应。
另一方面,如果网络具有有限的记忆资源,则将不能容易地学习映射。为了最大限度地减少损失,它必须学习具有更强预测能力的压缩表示。同时,如果您使模型太小,则难以适应训练数据。“太多容量”和“容量不足”之间存在平衡。
不幸的是,没有神奇的公式来确定模型的正确大小或架构(就层数而言,或每层的正确大小),您将不得不尝试使用一系列不同的架构。
要找到合适的模型大小,最好从相对较少的层和参数开始,然后开始增加层的大小或添加新层,直到您看到验证损失的收益递减为止。让我们在电影评论分类网络上试试。
我们将仅适用`Dense`层作为基线创建一个简单模型,然后创建更小和更大的版本,并进行比较。
### 创建一个基线模型
```
baseline_model = keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
baseline_model.summary()
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### 创建一个更小的模型
让我们创建一个隐藏单元较少的模型,与我们刚刚创建的基线模型进行比较:
```
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.summary()
```
用相同的数据训练模型:
```
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### 创建一个较大的模型
作为练习,您可以创建一个更大的模型,并查看它开始过拟合的速度。
接下来,让我们在这个基准测试中添加一个容量更大的网络,远远超出问题的范围:
```
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
bigger_model.summary()
```
并且,再次使用相同的数据训练模型:
```
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### 绘制训练和验证损失
<!--TODO(markdaoust): This should be a one-liner with tensorboard -->
实线表示训练损失,虚线表示验证损失(记住:较低的验证损失表示更好的模型)。在这里,较小的网络开始过拟合晚于基线模型(在6个周期之后而不是4个周期),并且一旦开始过拟合,其性能下降得慢得多。
```
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])
```
请注意,较大的网络在仅仅一个周期之后几乎立即开始过度拟合,并且更严重。网络容量越大,能够越快地对训练数据进行建模(导致训练损失低),但过拟合的可能性越大(导致训练和验证损失之间的差异很大)。
## 防止过拟合的策略
### 添加权重正则化
你可能熟悉奥卡姆的剃刀原则:给出两个解释的东西,最可能正确的解释是“最简单”的解释,即做出最少量假设的解释。这也适用于神经网络学习的模型:给定一些训练数据和网络架构,有多组权重值(多个模型)可以解释数据,而简单模型比复杂模型更不容易过度拟合。
在这种情况下,“简单模型”是参数值分布的熵更小的模型(或参数更少的模型,如我们在上一节中看到的)。因此,减轻过度拟合的一种常见方法是通过强制网络的权值只取较小的值来限制网络的复杂性,这使得权值的分布更加“规则”。这被称为“权重正则化”,它是通过在网络的损失函数中增加与权重过大相关的成本来实现的。这种成本有两种:
- [L1 正则化](https://developers.google.cn/machine-learning/glossary/#L1_regularization)其中添加的成本与权重系数的绝对值成正比(即与权重的“L1范数”成正比)。
- [L2 正则化](https://developers.google.cn/machine-learning/glossary/#L2_regularization), 其中增加的成本与权重系数值的平方成正比(即与权重的平方“L2范数”成正比)。L2正则化在神经网络中也称为权值衰减。不要让不同的名称迷惑你:权重衰减在数学上与L2正则化是完全相同的。
L2正则化引入了稀疏性,使一些权重参数为零。L2正则化将惩罚权重参数而不会使它们稀疏,这是L2更常见的一个原因。
在`tf.keras`中,通过将权重正则化实例作为关键字参数传递给层来添加权重正则化。我们现在添加L2权重正则化。
```
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
```l2(0.001)```表示该层的权重矩阵中的每个系数都会将```0.001 * weight_coefficient_value**2```添加到网络的总损失中。请注意,由于此惩罚仅在训练时添加,因此在训练时该网络的损失将远高于测试时。
这是我们的L2正则化惩罚的影响:
```
plot_history([('baseline', baseline_history),
('l2', l2_model_history)])
```
正如你所看到的,L2正则化模型比基线模型更能抵抗过拟合,即使两个模型具有相同数量的参数。
### 添加Dropout(丢弃正则化)
Dropout是由Hinton和他在多伦多大学的学生开发的最有效和最常用的神经网络正则化技术之一。Dropout应用于层主要就是在训练期间随机“丢弃”(即设置为零)该层的多个输出特征。假设一个给定的层通常会在训练期间为给定的输入样本返回一个向量[0.2,0.5,1.3,0.8,1.1],在应用了Dropout之后,该向量将具有随机分布的几个零条目,例如,[0,0.5,1.3,0,1.1]。“丢弃率”是被归零的特征的一部分,它通常设置在0.2和0.5之间,
在测试时,没有单元被剔除,而是将层的输出值按与丢弃率相等的因子缩小,以平衡实际活动的单元多余训练时的单元。
在`tf.keras`中,您可以通过`Dropout`层在网络中引入dropout,该层将在之前应用于层的输出。
让我们在IMDB网络中添加两个`Dropout`层,看看它们在减少过度拟合方面做得如何:
```
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dropout(0.5),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid')
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('baseline', baseline_history),
('dropout', dpt_model_history)])
```
从上图可以看出,添加dropout时对基线模型的明显改进。
回顾一下,以下是防止神经网络中过度拟合的最常用方法:
- 获取更多训练数据
- 减少网络的容量
- 添加权重正则化
- 添加dropout
本指南未涉及的两个重要方法是数据增强和批量标准化。
|
github_jupyter
|
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
# Create an all-zero matrix of shape (len(sequences), dimension)
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0 # set specific indices of results[i] to 1s
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)
plt.plot(train_data[0])
baseline_model = keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
baseline_model.summary()
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.summary()
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
bigger_model.summary()
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('baseline', baseline_history),
('l2', l2_model_history)])
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dropout(0.5),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid')
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('baseline', baseline_history),
('dropout', dpt_model_history)])
| 0.894657 | 0.938745 |
# Ex2 - Getting and Knowing your Data
Check out [Chipotle Exercises Video Tutorial](https://www.youtube.com/watch?v=lpuYZ5EUyS8&list=PLgJhDSE2ZLxaY_DigHeiIDC1cD09rXgJv&index=2) to watch a data scientist go through the exercises
This time we are going to pull data directly from the internet.
Special thanks to: https://github.com/justmarkham for sharing the dataset and materials.
### Step 1. Import the necessary libraries
```
import pandas as pd
import numpy as np
```
### Step 2. Import the dataset from this [address](https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv).
### Step 3. Assign it to a variable called chipo.
```
url = 'https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv'
chipo = pd.read_csv(url, sep = '\t')
```
### Step 4. See the first 10 entries
```
chipo.head(10)
```
### Step 5. What is the number of observations in the dataset?
```
# Solution 1
chipo.shape[0] # entries <= 4622 observations
# Solution 2
chipo.info() # entries <= 4622 observations
```
### Step 6. What is the number of columns in the dataset?
```
chipo.shape[1]
```
### Step 7. Print the name of all the columns.
```
chipo.columns
```
### Step 8. How is the dataset indexed?
```
chipo.index
```
### Step 9. Which was the most-ordered item?
```
c = chipo.groupby('item_name')
c = c.sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
```
### Step 10. For the most-ordered item, how many items were ordered?
```
c = chipo.groupby('item_name')
c = c.sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
```
### Step 11. What was the most ordered item in the choice_description column?
```
c = chipo.groupby('choice_description').sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
# Diet Coke 159
```
### Step 12. How many items were orderd in total?
```
total_items_orders = chipo.quantity.sum()
total_items_orders
```
### Step 13. Turn the item price into a float
#### Step 13.a. Check the item price type
```
chipo.item_price.dtype
```
#### Step 13.b. Create a lambda function and change the type of item price
```
dollarizer = lambda x: float(x[1:-1])
chipo.item_price = chipo.item_price.apply(dollarizer)
```
#### Step 13.c. Check the item price type
```
chipo.item_price.dtype
```
### Step 14. How much was the revenue for the period in the dataset?
```
revenue = (chipo['quantity']* chipo['item_price']).sum()
print('Revenue was: $' + str(np.round(revenue,2)))
```
### Step 15. How many orders were made in the period?
```
orders = chipo.order_id.value_counts().count()
orders
```
### Step 16. What is the average revenue amount per order?
```
# Solution 1
chipo['revenue'] = chipo['quantity'] * chipo['item_price']
order_grouped = chipo.groupby(by=['order_id']).sum()
order_grouped.mean()['revenue']
# Solution 2
chipo.groupby(by=['order_id']).sum().mean()['revenue']
```
### Step 17. How many different items are sold?
```
chipo.item_name.value_counts().count()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
url = 'https://raw.githubusercontent.com/justmarkham/DAT8/master/data/chipotle.tsv'
chipo = pd.read_csv(url, sep = '\t')
chipo.head(10)
# Solution 1
chipo.shape[0] # entries <= 4622 observations
# Solution 2
chipo.info() # entries <= 4622 observations
chipo.shape[1]
chipo.columns
chipo.index
c = chipo.groupby('item_name')
c = c.sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
c = chipo.groupby('item_name')
c = c.sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
c = chipo.groupby('choice_description').sum()
c = c.sort_values(['quantity'], ascending=False)
c.head(1)
# Diet Coke 159
total_items_orders = chipo.quantity.sum()
total_items_orders
chipo.item_price.dtype
dollarizer = lambda x: float(x[1:-1])
chipo.item_price = chipo.item_price.apply(dollarizer)
chipo.item_price.dtype
revenue = (chipo['quantity']* chipo['item_price']).sum()
print('Revenue was: $' + str(np.round(revenue,2)))
orders = chipo.order_id.value_counts().count()
orders
# Solution 1
chipo['revenue'] = chipo['quantity'] * chipo['item_price']
order_grouped = chipo.groupby(by=['order_id']).sum()
order_grouped.mean()['revenue']
# Solution 2
chipo.groupby(by=['order_id']).sum().mean()['revenue']
chipo.item_name.value_counts().count()
| 0.628179 | 0.988199 |
# Simulation of Ball drop and Spring mass damper system
"Simulation of dynamic systems for dummies".
<img src="for_dummies.jpg" width="200" align="right">
This is a very simple description of how to do time simulations of a dynamic system using SciPy ODE (Ordinary Differnetial Equation) Solver.
```
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
```
## Simulation of a static system to introduce ODEint
Define a method that takes a system state and describe how this state will change in time. The method does this by returning time derivatives for each state. The ODE solver will use these time derivatives to calculate new states, for the next time step.
Here is a method that takes a system to simulate a train that travels with constant speed:
(The system has only one state, the position of the train)
```
V_start = 150*10**3/3600 # [m/s] Train velocity at start
def train(states,t):
# states:
# [x]
x = states[0] # Position of train
dxdt = V_start # The position state will change by the speed of the train
# Time derivative of the states:
d_states_dt = np.array([dxdt])
return d_states_dt
x_start = 0 # [m] Train position at start
# The states at start of the simulation, the train is traveling with constant speed V at position x = 0.
states_0 = np.array([x_start])
# Create a time vector for the simulation:
t = np.linspace(0,10,100)
# Simulate with the "train" method and start states for the times in t:
states = odeint(func = train,y0 = states_0,t = t)
# The result is the time series of the states:
x = states[:,0]
fig,ax = plt.subplots()
ax.plot(t,x,label = 'Train position')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
```
The speed can hower be a state too:
```
def train_2_states(states,t):
# states:
# [x,V]
x = states[0] # Position of train
V = states[1] # Speed of train
dxdt = V # The position state will change by the speed of the train
dVdt = 0 # The velocity will not change (No acceleration)
# Time derivative of the states:
d_states_dt = np.array([dxdt,dVdt])
return d_states_dt
# The states at start of the simulation, the train is traveling with constant speed V at position x = 0.
states_0 = np.array([x_start,V_start])
# Create a time vector for the simulation:
t = np.linspace(0,10,100)
# Simulate with the "train" method and start states for the times in t:
states = odeint(func = train_2_states,y0 = states_0,t = t)
# The result is the time series of the states:
x = states[:,0]
dxdt = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Train position')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Train speed')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
```
## Ball drop
Here is a system where the speed is not constant.
A simulation of a ball drop under the influence of gravity force.
```
g = 9.81
m = 1
def ball_drop(states,t):
# states:
# [x,v]
# F = g*m = m*dv/dt
# --> dv/dt = (g*m) / m
x = states[0]
dxdt = states[1]
dvdt = (g*m) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
states_0 = np.array([0,0])
t = np.linspace(0,10,100)
states = odeint(func = ball_drop,y0 = states_0,t = t)
x = states[:,0]
dxdt = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Ball position')
ax.set_title('Ball drop')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Ball speed')
ax.set_title('Ball drop')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
```
Simulating in air, where the ball has a resistance due aerodynamic drag.
```
cd = 0.01
def ball_drop_air(states,t):
# states:
# [x,u]
# F = g*m - cd*u = m*du/dt
# --> du/dt = (g*m - cd*u**2) / m
x = states[0]
u = states[1]
dxdt = u
dudt = (g*m - cd*u**2) / m
d_states_dt = np.array([dxdt,dudt])
return d_states_dt
states = odeint(func = ball_drop_air,y0 = states_0,t = t)
x_air = states[:,0]
dxdt_air = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Vacuum')
ax.plot(t,x_air,label = 'Air')
ax.set_title('Ball drop in vacuum and air')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Vacuum')
ax.plot(t,dxdt_air,label = 'Air')
ax.set_title('Ball drop in vacuum and air')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
```
The very classical dynamic system with a spring, a mass and a damper.

```
k = 3 # The stiffnes of the spring (relates to position)
c = 0.1 # Damping term (relates to velocity)
m = 0.1 # The mass (relates to acceleration)
def spring_mass_damp(states,t):
# states:
# [x,v]
# F = -k*x -c*v = m*dv/dt
# --> dv/dt = (-kx -c*v) / m
x = states[0]
dxdt = states[1]
dvdt = (-k*x -c*dxdt) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
y0 = np.array([1,0])
t = np.linspace(0,10,100)
states = odeint(func = spring_mass_damp,y0 = y0,t = t)
x = states[:,0]
dxdt = states[:,1]
fig,ax = plt.subplots()
ax.plot(t,x)
ax.set_title('Spring mass damper simulation')
ax.set_xlabel('time [s]')
a = ax.set_ylabel('x [m]')
```
Also add a gravity force
```
g = 9.81
def spring_mass_damp_g(states,t):
# states:
# [x,v]
# F = g*m -k*x -c*v = m*dv/dt
# --> dv/dt = (g*m -kx -c*v) / m
x = states[0]
dxdt = states[1]
dvdt = (g*m -k*x -c*dxdt) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
states_g = odeint(func = spring_mass_damp_g,y0 = y0,t = t)
x_g = states_g[:,0]
dxdt_g = states_g[:,1]
fig,ax = plt.subplots()
ax.plot(t,x,label = 'No gravity force')
ax.plot(t,x_g,label = 'Gravity force')
ax.set_title('Spring mass damper simulation with and without gravity')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
```
## SymPy solution
```
import sympy as sym
import sympy.physics.mechanics as me
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax')
x, v = me.dynamicsymbols('x v')
m, c, k, g, t = sym.symbols('m c k g t')
ceiling = me.ReferenceFrame('C')
O = me.Point('O')
P = me.Point('P')
O.set_vel(ceiling, 0)
P.set_pos(O, x * ceiling.x)
P.set_vel(ceiling, v * ceiling.x)
P.vel(ceiling)
damping = -c * P.vel(ceiling)
stiffness = -k * P.pos_from(O)
gravity = m * g * ceiling.x
forces = damping + stiffness + gravity
forces
```
|
github_jupyter
|
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
V_start = 150*10**3/3600 # [m/s] Train velocity at start
def train(states,t):
# states:
# [x]
x = states[0] # Position of train
dxdt = V_start # The position state will change by the speed of the train
# Time derivative of the states:
d_states_dt = np.array([dxdt])
return d_states_dt
x_start = 0 # [m] Train position at start
# The states at start of the simulation, the train is traveling with constant speed V at position x = 0.
states_0 = np.array([x_start])
# Create a time vector for the simulation:
t = np.linspace(0,10,100)
# Simulate with the "train" method and start states for the times in t:
states = odeint(func = train,y0 = states_0,t = t)
# The result is the time series of the states:
x = states[:,0]
fig,ax = plt.subplots()
ax.plot(t,x,label = 'Train position')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
def train_2_states(states,t):
# states:
# [x,V]
x = states[0] # Position of train
V = states[1] # Speed of train
dxdt = V # The position state will change by the speed of the train
dVdt = 0 # The velocity will not change (No acceleration)
# Time derivative of the states:
d_states_dt = np.array([dxdt,dVdt])
return d_states_dt
# The states at start of the simulation, the train is traveling with constant speed V at position x = 0.
states_0 = np.array([x_start,V_start])
# Create a time vector for the simulation:
t = np.linspace(0,10,100)
# Simulate with the "train" method and start states for the times in t:
states = odeint(func = train_2_states,y0 = states_0,t = t)
# The result is the time series of the states:
x = states[:,0]
dxdt = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Train position')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Train speed')
ax.set_title('Train traveling at constant speed')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
g = 9.81
m = 1
def ball_drop(states,t):
# states:
# [x,v]
# F = g*m = m*dv/dt
# --> dv/dt = (g*m) / m
x = states[0]
dxdt = states[1]
dvdt = (g*m) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
states_0 = np.array([0,0])
t = np.linspace(0,10,100)
states = odeint(func = ball_drop,y0 = states_0,t = t)
x = states[:,0]
dxdt = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Ball position')
ax.set_title('Ball drop')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Ball speed')
ax.set_title('Ball drop')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
cd = 0.01
def ball_drop_air(states,t):
# states:
# [x,u]
# F = g*m - cd*u = m*du/dt
# --> du/dt = (g*m - cd*u**2) / m
x = states[0]
u = states[1]
dxdt = u
dudt = (g*m - cd*u**2) / m
d_states_dt = np.array([dxdt,dudt])
return d_states_dt
states = odeint(func = ball_drop_air,y0 = states_0,t = t)
x_air = states[:,0]
dxdt_air = states[:,1]
fig,axes = plt.subplots(ncols = 2)
fig.set_size_inches(11,5)
ax = axes[0]
ax.plot(t,x,label = 'Vacuum')
ax.plot(t,x_air,label = 'Air')
ax.set_title('Ball drop in vacuum and air')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
ax = axes[1]
ax.plot(t,dxdt,label = 'Vacuum')
ax.plot(t,dxdt_air,label = 'Air')
ax.set_title('Ball drop in vacuum and air')
ax.set_xlabel('time [s]')
ax.set_ylabel('dx/dt [m/s]')
a = ax.legend()
k = 3 # The stiffnes of the spring (relates to position)
c = 0.1 # Damping term (relates to velocity)
m = 0.1 # The mass (relates to acceleration)
def spring_mass_damp(states,t):
# states:
# [x,v]
# F = -k*x -c*v = m*dv/dt
# --> dv/dt = (-kx -c*v) / m
x = states[0]
dxdt = states[1]
dvdt = (-k*x -c*dxdt) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
y0 = np.array([1,0])
t = np.linspace(0,10,100)
states = odeint(func = spring_mass_damp,y0 = y0,t = t)
x = states[:,0]
dxdt = states[:,1]
fig,ax = plt.subplots()
ax.plot(t,x)
ax.set_title('Spring mass damper simulation')
ax.set_xlabel('time [s]')
a = ax.set_ylabel('x [m]')
g = 9.81
def spring_mass_damp_g(states,t):
# states:
# [x,v]
# F = g*m -k*x -c*v = m*dv/dt
# --> dv/dt = (g*m -kx -c*v) / m
x = states[0]
dxdt = states[1]
dvdt = (g*m -k*x -c*dxdt) / m
d_states_dt = np.array([dxdt,dvdt])
return d_states_dt
states_g = odeint(func = spring_mass_damp_g,y0 = y0,t = t)
x_g = states_g[:,0]
dxdt_g = states_g[:,1]
fig,ax = plt.subplots()
ax.plot(t,x,label = 'No gravity force')
ax.plot(t,x_g,label = 'Gravity force')
ax.set_title('Spring mass damper simulation with and without gravity')
ax.set_xlabel('time [s]')
ax.set_ylabel('x [m]')
a = ax.legend()
import sympy as sym
import sympy.physics.mechanics as me
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax')
x, v = me.dynamicsymbols('x v')
m, c, k, g, t = sym.symbols('m c k g t')
ceiling = me.ReferenceFrame('C')
O = me.Point('O')
P = me.Point('P')
O.set_vel(ceiling, 0)
P.set_pos(O, x * ceiling.x)
P.set_vel(ceiling, v * ceiling.x)
P.vel(ceiling)
damping = -c * P.vel(ceiling)
stiffness = -k * P.pos_from(O)
gravity = m * g * ceiling.x
forces = damping + stiffness + gravity
forces
| 0.782372 | 0.981382 |
# Heart Rate Varability (HRV)
NeuroKit2 is the most comprehensive software for computing HRV indices, and the list of features is available below:
| Domains | Indices | NeuroKit | heartpy | HRV | pyHRV | |
|-------------------|:-------:|:---------------:|:-------:|:---:|:-----:|---|
| Time Domain | | | | | | |
| | | CVNN | ✔️ | | | |
| | | CVSD | ✔️ | | | |
| | | MAD | | ✔️ | | |
| | | MHR | | | ✔️ | |
| | | MRRI | | | ✔️ | |
| | | NNI parameters | | | | ✔️ |
| | | ΔNNI parameters | | | | ✔️ |
| | | MadNN | ✔️ | | | |
| | | MeanNN | ✔️ | | | |
| | | MedianNN | ✔️ | | | |
| | | MCVNN | ✔️ | | | |
| | | pNN20 | ✔️ | ✔️ | | ✔️ |
| | | pNN50 | ✔️ | ✔️ | ✔️ | ✔️ |
| | | RMSSD | ✔️ | ✔️ | ✔️ | ✔️ |
| | | SDANN | | | | ✔️ |
| | | SDNN | ✔️ | ✔️ | ✔️ | ✔️ |
| | | SDNN_index | | | | ✔️ |
| | | SDSD | ✔️ | ✔️ | ✔️ | ✔️ |
| | | TINN | ✔️ | | | ✔️ |
| Frequency Domain | | | | | | |
| | | ULF | ✔️ | | | ✔️ |
| | | VLF | ✔️ | | ✔️ | ✔️ |
| | | LF | ✔️ | ✔️ | ✔️ | ✔️ |
| | | LFn | ✔️ | | ✔️ | ✔️ |
| | | LF Peak | | | | ✔️ |
| | | LF Relative | | | | ✔️ |
| | | HF | ✔️ | ✔️ | ✔️ | ✔️ |
| | | HFnu | ✔️ | | ✔️ | ✔️ |
| | | HF Peak | | | | ✔️ |
| | | HF Relative | | | | ✔️ |
| | | LF/HF | ✔️ | ✔️ | ✔️ | ✔️ |
| Non-Linear Domain | | | | | | |
| | | SD1 | ✔️ | ✔️ | ✔️ | ✔️ |
| | | SD2 | ✔️ | ✔️ | ✔️ | ✔️ |
| | | S | ✔️ | ✔️ | | ✔️ |
| | | SD1/SD2 | ✔️ | ✔️ | | ✔️ |
| | | SampEn | ✔️ | | | ✔️ |
| | | DFA | | | | ✔️ |
| | | CSI | ✔️ | | | |
| | | Modified CSI | ✔️ | | | |
| | | CVI | ✔️ | | | |
## Compute HRV features
This example can be referenced by [citing the package](https://github.com/neuropsychology/NeuroKit#citation).
The example shows how to use NeuroKit2 to compute heart rate variability (HRV) indices in the time-, frequency-, and non-linear domain.
```
# Load the NeuroKit package and other useful packages
import neurokit2 as nk
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [15, 9] # Bigger images
```
## Download Dataset
First, let's download the resting rate data (sampled at 100Hz) using `nk.data()`.
```
data = nk.data("bio_resting_5min_100hz")
data.head() # Print first 5 rows
```
You can see that it consists of three different signals, pertaining to ECG, PPG (an alternative determinant of heart rate as compared to ECG), and RSP (respiration). Now, let's extract the ECG signal in the shape of a vector (i.e., a one-dimensional array), and find the peaks using [ecg_peaks()](https://neurokit2.readthedocs.io/en/latest/functions.html#neurokit2.ecg_peaks).
```
# Find peaks
peaks, info = nk.ecg_peaks(data["ECG"], sampling_rate=100)
```
*Note: It is critical that you specify the correct sampling rate of your signal throughout many processing functions, as this allows NeuroKit to have a time reference.*
This produces two elements, `peaks` which is a DataFrame of same length as the input signal in which occurences of R-peaks are marked with 1 in a list of zeros. `info` is a dictionary of the sample points at which these R-peaks occur.
HRV is the temporal variation between consecutive heartbeats (**RR intervals**). Here, we will use `peaks` i.e. occurrences of the heartbeat peaks, as the input argument in the following HRV functions to extract the indices.
## Time-Domain Analysis
First, let's extract the time-domain indices.
```
# Extract clean EDA and SCR features
hrv_time = nk.hrv_time(peaks, sampling_rate=100, show=True)
hrv_time
```
These features include the RMSSD (square root of the mean of the sum of successive differences between adjacent RR intervals), MeanNN (mean of RR intervals) so on and so forth. You can also visualize the distribution of R-R intervals by specifying `show=True` in [hrv_time()](https://neurokit2.readthedocs.io/en/latest/functions.html#neurokit2.hrv_time).
## Frequency-Domain Analysis
Now, let's extract the frequency domain features, which involve extracting for example the spectral power density pertaining to different frequency bands. Again, you can visualize the power across frequency bands by specifying `show=True` in [hrv_frequency()](https://neurokit2.readthedocs.io/en/latest/functions.html#neurokit2.hrv_frequency).
```
hrv_freq = nk.hrv_frequency(peaks, sampling_rate=100, show=True)
hrv_freq
```
## Non-Linear Domain Analysis
Now, let's compute the non-linear indices with [hrv_nonlinear()](https://neurokit2.readthedocs.io/en/latest/functions.html#neurokit2.hrv_nonlinear).
```
hrv_non = nk.hrv_nonlinear(peaks, sampling_rate=100, show=True)
hrv_non
```
This will produce a Poincaré plot which plots each RR interval against the next successive one.
## All Domains
Finally, if you'd like to extract HRV indices from all three domains, you can simply input `peaks` into [hrv()](https://neurokit2.readthedocs.io/en/latest/functions.html#neurokit2.hrv), where you can specify `show=True` to visualize the combination of plots depicting the RR intervals distribution, power spectral density for frequency domains, and the poincare scattergram.
```
hrv_indices = nk.hrv(peaks, sampling_rate=100, show=True)
hrv_indices
```
## Resources
There are several other packages more focused on HRV in which you might find a more in depth explanation and documentation. See their documentation here:
- [HeartPy](https://python-heart-rate-analysis-toolkit.readthedocs.io/en/latest/)
- [HRV](https://hrv.readthedocs.io/en/latest/)
- [pyHRV](https://pyhrv.readthedocs.io/en/latest/_pages/api/nonlinear.html)
|
github_jupyter
|
# Load the NeuroKit package and other useful packages
import neurokit2 as nk
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [15, 9] # Bigger images
data = nk.data("bio_resting_5min_100hz")
data.head() # Print first 5 rows
# Find peaks
peaks, info = nk.ecg_peaks(data["ECG"], sampling_rate=100)
# Extract clean EDA and SCR features
hrv_time = nk.hrv_time(peaks, sampling_rate=100, show=True)
hrv_time
hrv_freq = nk.hrv_frequency(peaks, sampling_rate=100, show=True)
hrv_freq
hrv_non = nk.hrv_nonlinear(peaks, sampling_rate=100, show=True)
hrv_non
hrv_indices = nk.hrv(peaks, sampling_rate=100, show=True)
hrv_indices
| 0.673514 | 0.92054 |
```
import numpy as np
import os
import torch
import torchvision
import torchvision.transforms as transforms
### Load dataset - Preprocessing
DATA_PATH = '/tmp/data'
BATCH_SIZE = 64
def load_mnist(path, batch_size):
if not os.path.exists(path): os.mkdir(path)
trans = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (1.0,))])
train_set = torchvision.datasets.MNIST(root=path, train=True,
transform=trans, download=True)
test_set = torchvision.datasets.MNIST(root=path, train=False,
transform=trans, download=True)
train_loader = torch.utils.data.DataLoader(
dataset=train_set,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(
dataset=test_set,
batch_size=batch_size,
shuffle = False)
return train_loader, test_loader
train_loader, test_loader = load_mnist(DATA_PATH, BATCH_SIZE)
### Build network
IN_SIZE = 28*28
HIDDEN_SIZE = 50
OUT_SIZE = 10
LR=0.001
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(IN_SIZE , HIDDEN_SIZE)
self.l2 = torch.nn.Linear(HIDDEN_SIZE, OUT_SIZE)
def forward(self, x):
x = x.view(-1, IN_SIZE)
x = torch.relu(self.l1(x))
y_logits = self.l2(x)
return y_logits
net = Net()
criterion = torch.nn.CrossEntropyLoss(reduction='sum')
opti = torch.optim.SGD(net.parameters(), lr=LR)
### Training
NEPOCHS = 5
for epoch in range(NEPOCHS):
for batch_idx, (X, y) in enumerate(train_loader):
net.zero_grad()
y_logits = net(X)
loss = criterion(y_logits, y)
loss.backward()
opti.step()
preds = torch.empty(len(train_loader.dataset))
y = torch.empty(len(train_loader.dataset))
loss = 0
for batch_idx, (bX, by) in enumerate(train_loader):
y_logits = net(bX)
bloss = criterion(y_logits, by)
bpreds = torch.argmax(y_logits, dim=1)
preds[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = bpreds
y[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = by
loss += bloss
acc = y.eq(preds).sum().float() / len(y)
print('Epoch {}: Loss = {}, Accuracy = {}'.format(epoch+1,
loss.data,
acc))
### Evaluate
preds = torch.empty(len(test_loader.dataset))
y = torch.empty(len(test_loader.dataset))
loss = 0
for batch_idx, (bX, by) in enumerate(test_loader):
y_logits = net(bX)
bloss = criterion(y_logits, by)
bpreds = torch.argmax(y_logits, dim=1)
preds[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = bpreds
y[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = by
loss += bloss
acc = y.eq(preds).sum().float() / len(y)
print('Test Accuracy = {}'.format(acc))
```
|
github_jupyter
|
import numpy as np
import os
import torch
import torchvision
import torchvision.transforms as transforms
### Load dataset - Preprocessing
DATA_PATH = '/tmp/data'
BATCH_SIZE = 64
def load_mnist(path, batch_size):
if not os.path.exists(path): os.mkdir(path)
trans = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (1.0,))])
train_set = torchvision.datasets.MNIST(root=path, train=True,
transform=trans, download=True)
test_set = torchvision.datasets.MNIST(root=path, train=False,
transform=trans, download=True)
train_loader = torch.utils.data.DataLoader(
dataset=train_set,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(
dataset=test_set,
batch_size=batch_size,
shuffle = False)
return train_loader, test_loader
train_loader, test_loader = load_mnist(DATA_PATH, BATCH_SIZE)
### Build network
IN_SIZE = 28*28
HIDDEN_SIZE = 50
OUT_SIZE = 10
LR=0.001
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(IN_SIZE , HIDDEN_SIZE)
self.l2 = torch.nn.Linear(HIDDEN_SIZE, OUT_SIZE)
def forward(self, x):
x = x.view(-1, IN_SIZE)
x = torch.relu(self.l1(x))
y_logits = self.l2(x)
return y_logits
net = Net()
criterion = torch.nn.CrossEntropyLoss(reduction='sum')
opti = torch.optim.SGD(net.parameters(), lr=LR)
### Training
NEPOCHS = 5
for epoch in range(NEPOCHS):
for batch_idx, (X, y) in enumerate(train_loader):
net.zero_grad()
y_logits = net(X)
loss = criterion(y_logits, y)
loss.backward()
opti.step()
preds = torch.empty(len(train_loader.dataset))
y = torch.empty(len(train_loader.dataset))
loss = 0
for batch_idx, (bX, by) in enumerate(train_loader):
y_logits = net(bX)
bloss = criterion(y_logits, by)
bpreds = torch.argmax(y_logits, dim=1)
preds[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = bpreds
y[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = by
loss += bloss
acc = y.eq(preds).sum().float() / len(y)
print('Epoch {}: Loss = {}, Accuracy = {}'.format(epoch+1,
loss.data,
acc))
### Evaluate
preds = torch.empty(len(test_loader.dataset))
y = torch.empty(len(test_loader.dataset))
loss = 0
for batch_idx, (bX, by) in enumerate(test_loader):
y_logits = net(bX)
bloss = criterion(y_logits, by)
bpreds = torch.argmax(y_logits, dim=1)
preds[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = bpreds
y[batch_idx*BATCH_SIZE:batch_idx*BATCH_SIZE+len(bX)] = by
loss += bloss
acc = y.eq(preds).sum().float() / len(y)
print('Test Accuracy = {}'.format(acc))
| 0.807537 | 0.641029 |
# Numpy
" NumPy is the fundamental package for scientific computing with Python. It contains among other things:
* a powerful N-dimensional array object
* sophisticated (broadcasting) functions
* useful linear algebra, Fourier transform, and random number capabilities "
-- From the [NumPy](http://www.numpy.org/) landing page.
Before learning about numpy, we introduce..
### The NXOR Function
Many of the exercises involve working with the $\mathrm{NXOR} \colon \; [-1, 1]^2 \rightarrow \{-1, +1\}$ function defined as
$$ (x_1, x_2) \longmapsto \mathrm{sgn}(x_1 \cdot x_2) .$$
where for $x_1 \cdot x_2 = 0$ we let $\mathrm{NXOR}(x_1, x_2) = -1$.
We can visualize this function as
![A set of points in \[-1, +1\]^2 with green and red markers denoting the value assigned to them by the NXOR function](https://github.com/tmlss2018/PracticalSessions/blob/master/assets/nxor_labels.png?raw=true)
where each point in $ [-1, 1]^2$ is marked by green (+1) or red (-1) according to the value assigned to it by the NXOR function.
Over the course of the intro lab exercises we will
1. Generate such data with numpy.
2. Create the plot above with matplotlib.
3. Train a model to learn this function.
### Setup and imports. Run the following cell.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import numpy as np
```
### Random numbers in numpy
```
np.random.random((3, 2)) # Array of shape (3, 2), entries uniform in [0, 1).
```
Note that (as usual in computing) numpy produces pseudo-random numbers based on a seed, or more precisely a random state. In order to make random sequences and calculations based on reproducible, use
* the [`np.random.seed()`](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.seed.html) function to set the default global seed, or
* the [`np.random.RandomState`](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.RandomState.html) class which is a container for a pseudo-random number generator and exposes methods for generating random numbers.
```
np.random.seed(0)
print(np.random.random(2))
# Reset the global random state to the same state.
np.random.seed(0)
print(np.random.random(2))
```
### Numpy Array Operations 1
There are a large number of operations you can run on any numpy array. Here we showcase some common ones.
```
# Create one from hard-coded data:
ar = np.array([
[0.0, 0.2],
[0.9, 0.5],
[0.3, 0.7],
], dtype=np.float64) # float64 is the default.
print('The array:\n', ar)
print()
print('data type', ar.dtype)
print('transpose\n', ar.T)
print('shape', ar.shape)
print('reshaping an array', ar.reshape((6)))
```
Many numpy operations are available both as np module functions as well as array methods. For example, we can also reshape as
```
print('reshape v2', np.reshape(ar, (6, 1)))
```
### Numpy Indexing and selectors
Here are some basic indexing examples from numpy.
```
ar
ar[0, 1] # row, column
ar[:, 1] # slices: select all elements across the first (0th) axis.
ar[1:2, 1] # slices with syntax from:to, selecting [from, to).
ar[1:, 1] # Omit `to` to go all the way to the end
ar[:2, 1] # Omit `from` to start from the beginning
ar[0:-1, 1] # Use negative indexing to count elements from the back.
```
We can also pass boolean arrays as indices. These will exactly define which elements to select.
```
ar[np.array([
[True, False],
[False, True],
[True, False],
])]
```
Boolean arrays can be created with logical operations, then used as selectors. Logical operators apply elementwise.
```
ar_2 = np.array([ # Nearly the same as ar
[0.0, 0.1],
[0.9, 0.5],
[0.0, 0.7],
])
# Where ar_2 is smaller than ar, let ar_2 be -inf.
ar_2[ar_2 < ar] = -np.inf
ar_2
```
### Numpy Operations 2
```
print('array:\n', ar)
print()
print('sum across axis 0 (rows):', ar.sum(axis=0))
print('mean', ar.mean())
print('min', ar.min())
print('row-wise min', ar.min(axis=1))
```
We can also take element-wise minimums between two arrays.
We may want to do this when "clipping" values in a matrix, that is, setting any values larger than, say, 0.6, to 0.6. We would do this in numpy with..
### Broadcasting (and selectors)
```
np.minimum(ar, 0.6)
```
Numpy automatically turns the scalar 0.6 into an array the same size as `ar` in order to take element-wise minimum.
Broadcasting can save us a lot of typing, but in complicated cases it may require a good understanding of the exact rules followed.
Some references:
* [Numpy page that explains broadcasting](https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
* [Similar content with some visualizations](http://scipy.github.io/old-wiki/pages/EricsBroadcastingDoc)
Here we follow with a selection of other useful broadcasting examples.
```
# Centering our array.
print('centered array:\n', ar - np.mean(ar))
```
Note that `np.mean()` was a scalar, but it is automatically subtracted from every element.
We can write the minimum function ourselves, as well.
```
clipped_ar = ar.copy() # So that ar is not modified.
clipped_ar[clipped_ar > 0.6] = 0.6
clipped_ar
```
A few things happened here:
1. 0.6 was broadcast in for the greater than (>) operation
2. The greater than operation defined a selector, selecting a subset of the elements of the array
3. 0.6 was broadcast to the right number of elements for assignment.
Vectors may also be broadcast into matrices.
```
vec = np.array([1, 2])
ar + vec
```
Here the shapes of the involved arrays are:
```
ar (2d array): 2 x 2
vec (1d array): 2
Result (2d array): 2 x 2
```
When either of the dimensions compared is one (even implicitly, like in the case of `vec`), the other is used. In other words, dimensions with size 1 are stretched or “copied” to match the other.
Here, this meant that the `[1, 2]` row was repeated to match the number of rows in `ar`, then added together.
If there is a shape mismatch, you will be informed. To try, uncomment the line below and run it.
```
#ar + np.array([[1, 2, 3]])
```
#### Exercise
Broadcast and add the vector `[10, 20, 30]` across the columns of `ar`.
You should get
```
array([[10. , 10.2],
[20.9, 20.5],
[30.3, 30.7]])
```
```
#@title Code
# Recall that you can use vec.shape to verify that your array has the
# shape you expect.
### Your code here ###
#@title Solution
vec = np.array([[10], [20], [30]])
ar + vec
```
### `np.newaxis`
We can use another numpy feature, `np.newaxis` to simply form the column vector that was required for the example above. It adds a singleton dimension to arrays at the desired location:
```
vec = np.array([1, 2])
vec.shape
vec[np.newaxis, :].shape
vec[:, np.newaxis].shape
```
Now you know more than enough to generate some example data for our `NXOR` function.
### Exercise: Generate Data for NXOR
Write a function `get_data(num_examples)` that returns two numpy arrays
* `inputs` of shape `num_examples x 2` with points selected uniformly from the $[-1, 1]^2$ domain.
* `labels` of shape `num_examples` with the associated output of `NXOR`.
```
#@title Code
def get_data(num_examples):
# Replace with your code.
return np.zeros((num_examples, 2)), np.zeros((num_examples))
#@title Solution
# Solution 1.
def get_data(num_examples):
inputs = 2*np.random.random((num_examples, 2)) - 1
labels = np.prod(inputs, axis=1)
labels[labels <= 0] = -1
labels[labels > 0] = 1
return inputs, labels
# Solution 1.
# def get_data(num_examples):
# inputs = 2*np.random.random((num_examples, 2)) - 1
# labels = np.sign(np.prod(inputs, axis=1))
# labels[labels == 0] = -1
# return inputs, labels
get_data(4)
```
## That's all, folks!
For now.
```
```
|
github_jupyter
|
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import numpy as np
np.random.random((3, 2)) # Array of shape (3, 2), entries uniform in [0, 1).
np.random.seed(0)
print(np.random.random(2))
# Reset the global random state to the same state.
np.random.seed(0)
print(np.random.random(2))
# Create one from hard-coded data:
ar = np.array([
[0.0, 0.2],
[0.9, 0.5],
[0.3, 0.7],
], dtype=np.float64) # float64 is the default.
print('The array:\n', ar)
print()
print('data type', ar.dtype)
print('transpose\n', ar.T)
print('shape', ar.shape)
print('reshaping an array', ar.reshape((6)))
print('reshape v2', np.reshape(ar, (6, 1)))
ar
ar[0, 1] # row, column
ar[:, 1] # slices: select all elements across the first (0th) axis.
ar[1:2, 1] # slices with syntax from:to, selecting [from, to).
ar[1:, 1] # Omit `to` to go all the way to the end
ar[:2, 1] # Omit `from` to start from the beginning
ar[0:-1, 1] # Use negative indexing to count elements from the back.
ar[np.array([
[True, False],
[False, True],
[True, False],
])]
ar_2 = np.array([ # Nearly the same as ar
[0.0, 0.1],
[0.9, 0.5],
[0.0, 0.7],
])
# Where ar_2 is smaller than ar, let ar_2 be -inf.
ar_2[ar_2 < ar] = -np.inf
ar_2
print('array:\n', ar)
print()
print('sum across axis 0 (rows):', ar.sum(axis=0))
print('mean', ar.mean())
print('min', ar.min())
print('row-wise min', ar.min(axis=1))
np.minimum(ar, 0.6)
# Centering our array.
print('centered array:\n', ar - np.mean(ar))
clipped_ar = ar.copy() # So that ar is not modified.
clipped_ar[clipped_ar > 0.6] = 0.6
clipped_ar
vec = np.array([1, 2])
ar + vec
ar (2d array): 2 x 2
vec (1d array): 2
Result (2d array): 2 x 2
#ar + np.array([[1, 2, 3]])
array([[10. , 10.2],
[20.9, 20.5],
[30.3, 30.7]])
```
### `np.newaxis`
We can use another numpy feature, `np.newaxis` to simply form the column vector that was required for the example above. It adds a singleton dimension to arrays at the desired location:
Now you know more than enough to generate some example data for our `NXOR` function.
### Exercise: Generate Data for NXOR
Write a function `get_data(num_examples)` that returns two numpy arrays
* `inputs` of shape `num_examples x 2` with points selected uniformly from the $[-1, 1]^2$ domain.
* `labels` of shape `num_examples` with the associated output of `NXOR`.
## That's all, folks!
For now.
| 0.719581 | 0.988165 |
```
import numpy as np
import pandas as pd
import mxnet as mx
import matplotlib.pyplot as plt
import plotly.plotly as py
import logging
logging.basicConfig(level=logging.DEBUG)
train1=pd.read_csv('../data/train.csv')
train1.shape
train1.iloc[0:4, 0:15]
train=np.asarray(train1.iloc[0:33600,:])
cv=np.asarray(train1.iloc[33600:,:])
_train=train[:,1:]
_train.shape
_cv=cv[:,1:]
_cv.shape
trainx=np.reshape(_train, (_train.shape[0],1,28,28))/255
cvx=np.reshape(_cv, (_cv.shape[0],1,28,28))/255
ix=3
img=np.asarray(np.matrix(trainx[ix,0,:,:]))
plt.imshow(img, cmap='Greys_r')
plt.show()
trainy=np.asarray(train[:,0])
cvy=np.asarray(cv[:,0])
trainy.shape
```
FULLY CONNECTED NEURAL NETWORK
===========================
```
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first fullc layer
flatten = mx.sym.flatten(data=data)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc1, act_type="relu")
# output fullc
fc3 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
SNN = mx.symbol.SoftmaxOutput(data=fc3, label=Y, name="SNN")
SNN_model = mx.mod.Module(symbol=SNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
SNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
```
DEEP FULLY CONNECTED NEURAL NETWORK
===========================
```
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first fullc layer
flatten = mx.sym.flatten(data=data)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin1 = mx.sym.Activation(data=fc1, act_type="relu")
# second fullc layer
fc2 = mx.symbol.FullyConnected(data=nlin1, num_hidden=500)
nlin2 = mx.sym.Activation(data=fc2, act_type="relu")
# third fullc layer
fc3 = mx.symbol.FullyConnected(data=nlin2, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc3, act_type="relu")
# output fullc
fc4 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
DNN = mx.symbol.SoftmaxOutput(data=fc4, label=Y, name="DNN")
DNN_model = mx.mod.Module(symbol=DNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
DNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
```
CONVOLUTIONAL NEURAL NETWORK
===========================
```
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first conv layer
conv1 = mx.sym.Convolution(data=data, kernel=(5,5), num_filter=20)
nlin1 = mx.sym.Activation(data=conv1, act_type="relu")
pool1 = mx.sym.Pooling(data=nlin1, pool_type="max", kernel=(2,2), stride=(2,2))
drop1 = mx.symbol.Dropout(data=pool1,p=0.5)
# second conv layer
conv2 = mx.sym.Convolution(data=drop1, kernel=(5,5), num_filter=40)
nlin2 = mx.sym.Activation(data=conv2, act_type="relu")
pool2 = mx.sym.Pooling(data=nlin2, pool_type="max", kernel=(2,2), stride=(2,2))
drop2 = mx.symbol.Dropout(data=pool2,p=0.5)
# first fullc layer
flatten = mx.sym.flatten(data=drop2)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc1, act_type="relu")
# output fullc
fc2 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
CNN = mx.symbol.SoftmaxOutput(data=fc2, label=Y,name="CCN")
CNN_model = mx.mod.Module(symbol=CNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
CNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import mxnet as mx
import matplotlib.pyplot as plt
import plotly.plotly as py
import logging
logging.basicConfig(level=logging.DEBUG)
train1=pd.read_csv('../data/train.csv')
train1.shape
train1.iloc[0:4, 0:15]
train=np.asarray(train1.iloc[0:33600,:])
cv=np.asarray(train1.iloc[33600:,:])
_train=train[:,1:]
_train.shape
_cv=cv[:,1:]
_cv.shape
trainx=np.reshape(_train, (_train.shape[0],1,28,28))/255
cvx=np.reshape(_cv, (_cv.shape[0],1,28,28))/255
ix=3
img=np.asarray(np.matrix(trainx[ix,0,:,:]))
plt.imshow(img, cmap='Greys_r')
plt.show()
trainy=np.asarray(train[:,0])
cvy=np.asarray(cv[:,0])
trainy.shape
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first fullc layer
flatten = mx.sym.flatten(data=data)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc1, act_type="relu")
# output fullc
fc3 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
SNN = mx.symbol.SoftmaxOutput(data=fc3, label=Y, name="SNN")
SNN_model = mx.mod.Module(symbol=SNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
SNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first fullc layer
flatten = mx.sym.flatten(data=data)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin1 = mx.sym.Activation(data=fc1, act_type="relu")
# second fullc layer
fc2 = mx.symbol.FullyConnected(data=nlin1, num_hidden=500)
nlin2 = mx.sym.Activation(data=fc2, act_type="relu")
# third fullc layer
fc3 = mx.symbol.FullyConnected(data=nlin2, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc3, act_type="relu")
# output fullc
fc4 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
DNN = mx.symbol.SoftmaxOutput(data=fc4, label=Y, name="DNN")
DNN_model = mx.mod.Module(symbol=DNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
DNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
data = mx.sym.var('data')
Y= mx.symbol.Variable('softmax_label')
# first conv layer
conv1 = mx.sym.Convolution(data=data, kernel=(5,5), num_filter=20)
nlin1 = mx.sym.Activation(data=conv1, act_type="relu")
pool1 = mx.sym.Pooling(data=nlin1, pool_type="max", kernel=(2,2), stride=(2,2))
drop1 = mx.symbol.Dropout(data=pool1,p=0.5)
# second conv layer
conv2 = mx.sym.Convolution(data=drop1, kernel=(5,5), num_filter=40)
nlin2 = mx.sym.Activation(data=conv2, act_type="relu")
pool2 = mx.sym.Pooling(data=nlin2, pool_type="max", kernel=(2,2), stride=(2,2))
drop2 = mx.symbol.Dropout(data=pool2,p=0.5)
# first fullc layer
flatten = mx.sym.flatten(data=drop2)
fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
nlin3 = mx.sym.Activation(data=fc1, act_type="relu")
# output fullc
fc2 = mx.sym.FullyConnected(data=nlin3, num_hidden=10)
# Softmax output
CNN = mx.symbol.SoftmaxOutput(data=fc2, label=Y,name="CCN")
CNN_model = mx.mod.Module(symbol=CNN, label_names =['softmax_label'], context=mx.cpu())
batch_size = 100
train_iter = mx.io.NDArrayIter(trainx, trainy, batch_size, shuffle=True)
val_iter = mx.io.NDArrayIter(cvx, cvy, batch_size)
CNN_model.fit(train_iter, # train data
eval_data=val_iter, # validation data
optimizer='sgd',
optimizer_params={'learning_rate':0.05, 'momentum': 0.9},
eval_metric='acc',
batch_end_callback = mx.callback.Speedometer(batch_size=batch_size, frequent=200),
num_epoch=15)
| 0.610686 | 0.707922 |
```
# Hidden code cell for setup
# Imports and setup
import astropixie
import astropixie_widgets
import enum
import ipywidgets
import numpy
astropixie_widgets.config.setup_notebook()
from astropixie.data import pprint as show_data_in_table
from numpy import intersect1d as stars_in_both
class SortOrder(enum.Enum):
BrightestToDimmest = enum.auto()
DimmestToBrightest = enum.auto()
HottestToCoolest = enum.auto()
CoolestToHottest = enum.auto()
def filter_star_data(data, sortOrder, percent=100):
if sortOrder in [SortOrder.BrightestToDimmest, SortOrder.DimmestToBrightest]:
order = 'luminosity'
elif sortOrder in [SortOrder.HottestToCoolest, SortOrder.CoolestToHottest]:
order = 'temperature'
sortedData = numpy.sort(data, axis=None, order=order)
if sortOrder in [SortOrder.HottestToCoolest, SortOrder.BrightestToDimmest]:
sortedData = sortedData[::-1]
filteredStarCount = int(len(sortedData) * percent / 100)
return sortedData[0:filteredStarCount]
```
## Introduction and Background
Today you will be using a data visualization tool called the [H-R Diagram](https://en.wikipedia.org/wiki/Hertzsprung–Russell_diagram), first developed more than a century ago by [Ejnar Hertzsprung](https://en.wikipedia.org/wiki/Ejnar_Hertzsprung) from Denmark, and [Henry Norris Russell](https://en.wikipedia.org/wiki/Henry_Norris_Russell), an American. The H-R Diagram will enable you to create your own "window" to the stars and explore what it can reveal about star properties such as size, temperature, and energy output.
In order to accurately compare stars to each other and measure properties such as their energy outputs, it is important to account for the fact that two stars of the same brightness will look very different if one is farther away from Earth than the other. One way to address this issue is to collect data from a group of stars in a [star cluster](https://en.wikipedia.org/wiki/Star_cluster), in which all the stars are the same distance away. Today you will collect and analyze data for the stars in one cluster, which will allow you to determine the variation that exists in stellar properties.
In this investigation, the term [luminosity](https://en.wikipedia.org/wiki/Luminosity) refers to the total energy output from a star per unit of time. Luminosity is typically reported as a ratio of the star's energy output compared to the energy emitted by the Sun. For example, a star with a _solar luminosity_ of "10" emits ten times more energy than the Sun.
# Procedure and Data
First call up the information and data for your star cluster.
*Type in the name of your cluster and press Enter:*
```
# Hidden code cell
cluster = astropixie.data.Berkeley20SDSS()
hr_diagram = astropixie_widgets.visual.SHRD(cluster)
hr_diagram.show()
def show_data_in_hr_diagram(data):
# Note, pulling the ranges from the H-R diagram widget.
astropixie_widgets.visual.hr_diagram_from_data(data, hr_diagram.x_range, hr_diagram.y_range)
```
####  *Make your best estimate of which stars in the image belong to the cluster.*
####  *Use your mouse to outline the boundary of the cluster.*
#### You will now see a plot of all the data for the stars you selected displayed on an H-R Diagram.
####  Notice that most stars occupy a region stretching from the upper left to the lower right of the diagram. This is known as the [main sequence](https://cnx.org/contents/[email protected]:EVgehrPG@9/The-HR-Diagram).
####  Answer the next question about the main sequence of your cluster.
```
# Hidden code cell for question
astropixie_widgets.question.show_question("1. Where on the main sequence are stars the most numerous? What color are these stars?")
```
#### You will now begin to work with code to define the characteristics of the stars in the cluster. The code in the gray below calls up all data in the cluster and displays it as a data table.
####  Click on the gray code box below, and hold down SHIFT and press ENTER to run this code.
```
all_star_data = hr_diagram.filtered_data
show_data_in_table(all_star_data)
```
####  Run the code below to sort the data by temperature. Record the maximum and minimum temperatures:
```
# The code below sorts the star data from coolest stars to hottest stars,
# and stores it in the new list named 'coolToHot'
coolToHot = filter_star_data(all_star_data, SortOrder.CoolestToHottest)
# Show the new list 'coolToHot' in a table.
show_data_in_table(coolToHot)
astropixie_widgets.question.show_question("2. Record the hottest and coolest temperatures for the stars in your cluster.")
```
#### Now you will use code to define a selected set of stars on the H-R Diagram. The next box contains code that displays only the hottest stars (hottest = top 20% of cluster data ordered by temperature).
####  Run the code and observe where the stars appear on the diagram:
```
hottestStars = filter_star_data(all_star_data, SortOrder.HottestToCoolest, percent=20)
show_data_in_hr_diagram(hottestStars)
```
#### The next box contains code that displays only the coolest stars (coolest = bottom 20% of cluster data ordered by temperature).
####  Run the code and observe where the stars appear on the diagram:
```
coolestStars = filter_star_data(all_star_data, SortOrder.CoolestToHottest, percent=20)
show_data_in_hr_diagram(coolestStars)
```
####  The next code box sorts the data by luminosity (brightness). Run it and record the maximum and minimum luminosity values:
```
# The code below sorts the star data from dimmest stars to the brightest stars,
# and stores it in the new list named 'dimToBright'
dimToBright = filter_star_data(all_star_data, SortOrder.DimmestToBrightest)
# Show the new list 'dimToBright' in a table.
show_data_in_table(dimToBright)
astropixie_widgets.question.show_question("3. Record the largest and smallest luminosities for the stars in your cluster.")
```
#### The next box contains code that displays only the most luminous (brightest) stars (brightest = top 20% of cluster data ordered by luminosity).
####  Run the code and observe where the stars appear on the diagram:
```
brightestStars = filter_star_data(all_star_data, SortOrder.BrightestToDimmest, percent=20)
show_data_in_hr_diagram(brightestStars)
```
#### The next box contains code that displays only the least luminous (dimmest) stars (dimmest = bottom 20% of cluster data ordered by luminosity).
####  Run the code and observe where the stars appear on the diagram:
```
dimmestStars = filter_star_data(all_star_data, SortOrder.DimmestToBrightest, percent=20)
show_data_in_hr_diagram(dimmestStars)
```
#### It's possible to define a set of stars that share two common characterisitics.
####  For the next questions (4a, b, c and d), answer each part by first running the code then describing the area of the H-R Diagram where the stars appear. Answer with a combination of two of these words: *left, right, top, bottom*, and a color or colors.
####  Run the code and observe where cool and dim stars appear on the diagram:
```
coolAndDimStars = stars_in_both(coolestStars, dimmestStars)
show_data_in_hr_diagram(coolAndDimStars)
astropixie_widgets.question.show_question("4a. Where on the H-R diagram are cool, dim stars located? What color are these stars?")
```
####  Run the code and observe where cool and bright stars appear on the diagram:
```
coolAndBrightStars = stars_in_both(coolestStars, brightestStars)
show_data_in_hr_diagram(coolAndBrightStars)
astropixie_widgets.question.show_question("4b. Where on the H-R diagram are bright, cool stars located? What color are these stars?")
```
####  Run the code and observe where hot and bright stars appear on the diagram:
```
hotAndBrightStars = stars_in_both(hottestStars, brightestStars)
show_data_in_hr_diagram(hotAndBrightStars)
astropixie_widgets.question.show_question("4c. Where on the H-R diagram are hot, bright stars located? What color are these stars?")
```
####  Run the code and observe where hot and dim stars appear on the diagram:
```
hotAndDimStars = stars_in_both(hottestStars, dimmestStars)
show_data_in_hr_diagram(hotAndDimStars)
astropixie_widgets.question.show_question("4d. Where on the H-R diagram are dim, hot stars located? What color are these stars?")
```
#  Discuss and report
#### *Take a few minutes with your partner or small group to investigate and discuss the following:*
```
astropixie_widgets.question.show_question("5. The Sun’s surface temperature is about 6000K. Suppose a main sequence star has a temperature three times greater than the Sun’s. How much more luminous than the Sun is the hotter star? Use your diagram to estimate an answer.")
astropixie_widgets.question.show_question("6. Two stars have the same luminosity but differ in color. What physical property of the stars could explain this?")
astropixie_widgets.question.show_question("7. Two giant stars have the same luminosity. One is yellow and the other is orange. Which one is larger? Explain your reasoning.")
astropixie_widgets.question.show_question("8. What physical property of stars could explain why stars in the lower left of the H-R Diagram are dimmer than the stars in the upper left, since they are both very hot?")
```
### *Be prepared to report out and discuss your observations.*
#  Summary
```
astropixie_widgets.question.show_question("9. Now that you have had a chance to discuss your observations, write a summary in the text box below that explains what you have learned about star temperatures, sizes and luminosities.", rows=6)
```
## Challenge Problem
#### Use what you have learned to write code that will display only the *blue stars* in your cluster.
####  Write your code in the box below, and hold down SHIFT and press ENTER to run your code. You can edit your code and run it as many times as you like.
####  Answer the next question based on the code you wrote.
```
astropixie_widgets.question.show_question("10. What percentage (number value) did you enter to display only the blue stars in your data set?")
```
|
github_jupyter
|
# Hidden code cell for setup
# Imports and setup
import astropixie
import astropixie_widgets
import enum
import ipywidgets
import numpy
astropixie_widgets.config.setup_notebook()
from astropixie.data import pprint as show_data_in_table
from numpy import intersect1d as stars_in_both
class SortOrder(enum.Enum):
BrightestToDimmest = enum.auto()
DimmestToBrightest = enum.auto()
HottestToCoolest = enum.auto()
CoolestToHottest = enum.auto()
def filter_star_data(data, sortOrder, percent=100):
if sortOrder in [SortOrder.BrightestToDimmest, SortOrder.DimmestToBrightest]:
order = 'luminosity'
elif sortOrder in [SortOrder.HottestToCoolest, SortOrder.CoolestToHottest]:
order = 'temperature'
sortedData = numpy.sort(data, axis=None, order=order)
if sortOrder in [SortOrder.HottestToCoolest, SortOrder.BrightestToDimmest]:
sortedData = sortedData[::-1]
filteredStarCount = int(len(sortedData) * percent / 100)
return sortedData[0:filteredStarCount]
# Hidden code cell
cluster = astropixie.data.Berkeley20SDSS()
hr_diagram = astropixie_widgets.visual.SHRD(cluster)
hr_diagram.show()
def show_data_in_hr_diagram(data):
# Note, pulling the ranges from the H-R diagram widget.
astropixie_widgets.visual.hr_diagram_from_data(data, hr_diagram.x_range, hr_diagram.y_range)
# Hidden code cell for question
astropixie_widgets.question.show_question("1. Where on the main sequence are stars the most numerous? What color are these stars?")
all_star_data = hr_diagram.filtered_data
show_data_in_table(all_star_data)
# The code below sorts the star data from coolest stars to hottest stars,
# and stores it in the new list named 'coolToHot'
coolToHot = filter_star_data(all_star_data, SortOrder.CoolestToHottest)
# Show the new list 'coolToHot' in a table.
show_data_in_table(coolToHot)
astropixie_widgets.question.show_question("2. Record the hottest and coolest temperatures for the stars in your cluster.")
hottestStars = filter_star_data(all_star_data, SortOrder.HottestToCoolest, percent=20)
show_data_in_hr_diagram(hottestStars)
coolestStars = filter_star_data(all_star_data, SortOrder.CoolestToHottest, percent=20)
show_data_in_hr_diagram(coolestStars)
# The code below sorts the star data from dimmest stars to the brightest stars,
# and stores it in the new list named 'dimToBright'
dimToBright = filter_star_data(all_star_data, SortOrder.DimmestToBrightest)
# Show the new list 'dimToBright' in a table.
show_data_in_table(dimToBright)
astropixie_widgets.question.show_question("3. Record the largest and smallest luminosities for the stars in your cluster.")
brightestStars = filter_star_data(all_star_data, SortOrder.BrightestToDimmest, percent=20)
show_data_in_hr_diagram(brightestStars)
dimmestStars = filter_star_data(all_star_data, SortOrder.DimmestToBrightest, percent=20)
show_data_in_hr_diagram(dimmestStars)
coolAndDimStars = stars_in_both(coolestStars, dimmestStars)
show_data_in_hr_diagram(coolAndDimStars)
astropixie_widgets.question.show_question("4a. Where on the H-R diagram are cool, dim stars located? What color are these stars?")
coolAndBrightStars = stars_in_both(coolestStars, brightestStars)
show_data_in_hr_diagram(coolAndBrightStars)
astropixie_widgets.question.show_question("4b. Where on the H-R diagram are bright, cool stars located? What color are these stars?")
hotAndBrightStars = stars_in_both(hottestStars, brightestStars)
show_data_in_hr_diagram(hotAndBrightStars)
astropixie_widgets.question.show_question("4c. Where on the H-R diagram are hot, bright stars located? What color are these stars?")
hotAndDimStars = stars_in_both(hottestStars, dimmestStars)
show_data_in_hr_diagram(hotAndDimStars)
astropixie_widgets.question.show_question("4d. Where on the H-R diagram are dim, hot stars located? What color are these stars?")
astropixie_widgets.question.show_question("5. The Sun’s surface temperature is about 6000K. Suppose a main sequence star has a temperature three times greater than the Sun’s. How much more luminous than the Sun is the hotter star? Use your diagram to estimate an answer.")
astropixie_widgets.question.show_question("6. Two stars have the same luminosity but differ in color. What physical property of the stars could explain this?")
astropixie_widgets.question.show_question("7. Two giant stars have the same luminosity. One is yellow and the other is orange. Which one is larger? Explain your reasoning.")
astropixie_widgets.question.show_question("8. What physical property of stars could explain why stars in the lower left of the H-R Diagram are dimmer than the stars in the upper left, since they are both very hot?")
astropixie_widgets.question.show_question("9. Now that you have had a chance to discuss your observations, write a summary in the text box below that explains what you have learned about star temperatures, sizes and luminosities.", rows=6)
astropixie_widgets.question.show_question("10. What percentage (number value) did you enter to display only the blue stars in your data set?")
| 0.615781 | 0.910704 |
# Compare Robustness
## Set up the Environment
```
# Import everything that's needed to run the notebook
import os
import pickle
import dill
import pathlib
import datetime
import random
import time
from IPython.display import display, Markdown, Latex
import pandas as pd
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.neural_network import MLPClassifier
import scipy.stats
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import util
import robust
from ipynb.fs.defs.descriptor_based_neural_networks import DescriptorBuilder
from ipynb.fs.defs.construct_sbnn import SBNNPreprocessor
from sklearn.model_selection import learning_curve
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
plt.rc('axes', labelsize=15)
# Define the path to the configuration dictionary
config_path = 'configuration.p'
# Load the configuration dictionary
with open(config_path, 'rb') as f:
configuration = pickle.load(f)
# Get the paths to the relevant directories
data_directory_path = configuration['data']['directory_path']
classifiers_directory_path = configuration['classifiers']['directory_path']
```
## Load the Storages of Results and Reports
```
dbnn_storage1 = dbnn_storage
dbnn_storage = {}
results_directory_path = configuration['results']['directory_path']
path = os.path.join(results_directory_path, 'dbnn_results.p')
with open(path, 'rb') as f:
dbnn_storage['results'] = pickle.load(f)
reports_directory_path = configuration['reports']['directory_path']
path = os.path.join(reports_directory_path, 'dbnn')
path = os.path.join(path, 'dbnn_reports.p')
with open(path, 'rb') as f:
dbnn_storage['reports'] = pickle.load(f)
```
## Load the DBNNs
```
with open('dbnns1.p', 'rb') as f:
dbnns = dill.load(f)
```
## Load and Prepare Set $\mathcal{F}$
```
# Define the dictionary to store the actual datasets, indexed by their names
datasets = {}
# Load the datasets
for set_name in ['F-left', 'F-right', 'F-central', 'F-symmetric']:
set_path = configuration['data']['datasets'][set_name]['path']
print('Loading {} from {}'.format(set_name, set_path))
datasets[set_name] = util.load_from_file(set_path)
print('Done.')
for set_name in datasets:
labels = [sample.pop() for sample in datasets[set_name]]
samples = datasets[set_name]
datasets[set_name] = {'samples' : samples, 'labels' : labels}
```
## Load the Tests
```
# Make a dictionary to hold the tests
test_classifiers = {}
# Specify the classical tests
codes = ['SW', 'SF', 'LF', 'JB', 'DP', 'AD', 'CVM', 'FSSD']
# Load the classical tests
for test_code in codes:
test, statistic = util.get_test(test_code)
for alpha in [0.01, 0.05]:
test_classifiers[(test_code, alpha)] = util.TestClassifier(test, statistic, alpha)
# Although SBNN is not technically a test, consider it too.
with open(os.path.join('classifiers', 'sbnn.p'), 'rb') as f:
sbnn = pickle.load(f)
test_classifiers[('SBNN', '/')] = sbnn
codes += ['SBNN']
# Specify the robustified tests
robust_codes = ['MMRT1', 'MMRT2', 'TTRT1', 'TTRT2', 'RSW', 'RLM']
# Load the robustified tests
for test_code in robust_codes:
test, statistic = robust.get_robust_test(test_code)
for alpha in [0.01, 0.05]:
test_classifiers[(test_code, alpha)] = util.TestClassifier(test, statistic, alpha)
```
## Evaluate the Tests
```
# Specify the sample sizes
n_range = range(10, 101, 10)
# Specify the metrics to calculate
metrics = ['TNR']
# Evaluate the tests on each group of samples in set F
for group in ['F-left', 'F-right', 'F-central', 'F-symmetric']:
print(group)
samples = datasets[group]['samples']
labels = datasets[group]['labels']
# Create a dictionary to store the results
all_test_results = {}
for (test_code, alpha) in test_classifiers:
# Evaluate the tests (and SBNN)
print('\t', test_code, alpha, end='')
# Get the test
test_clf = test_classifiers[(test_code, alpha)]
# Evaluate it
start = time.time()
test_results_df = util.evaluate_pretty(samples,
labels,
test_clf,
metrics=metrics,
n_range=n_range,
index='n')
end = time.time()
# Show how long its evaluation took and display the results
print('\t', end - start)
display(test_results_df.T)
# Memorize the results
all_test_results[(test_code, alpha)] = test_results_df
# Put the results into the storage for persistence
for key in all_test_results:
test_results = all_test_results[key]
memory = dbnn_storage['results']['comparison'].get(group, {})
memory[key] = test_results
dbnn_storage['results']['comparison'][group] = memory
```
## Create the Dataframes of Results
```
F_results = {}
for group in dbnn_storage['results']['comparison']:
if group[0] != 'F':
continue
print(group)
results = dbnn_storage['results']['comparison'][group]
results_dict = {test_key: results[test_key]['TNR'] for test_key in results}
results_df = pd.concat(results_dict, axis=1)
results_df = results_df[sorted(results_df.columns)]
for name in sorted(dbnns.keys()):
if '0.01' in name:
new_name = 'DBNN$_{0.01}$'
alpha = 0.01
elif '0.05' in name:
new_name = 'DBNN$_{0.05}$'
alpha = 0.05
elif 'opt' in name:
new_name = 'DBNN$_{opt}$'
alpha = '/'
elif '0.1' in name:
continue
else:
new_name = 'DBNN'
alpha = '/'
results_df[(new_name, alpha)] = dbnn_storage['results']['evaluation'][name][group]['TNR']
# list(sorted(dbnns.keys()))
results_df = results_df[[col for col in results_df.columns]]
F_results[group] = results_df
display(results_df.T)
```
## Make $\LaTeX$ Tables and Plot the Figures
```
#(F_results['F-left'].xs('/', level=1, axis=1) <= 0.05*2).T#.sum(axis=0)
#F_results['F-symmetric'].xs('/', level=1, axis=1)
competitors = list(test_classifiers.keys())
dbnn_cols = [('DBNN', '/'), ('DBNN$_{opt}$', '/'),
('DBNN$_{0.01}$', 0.01), ('DBNN$_{0.05}$', 0.05)]
selected_results = {}
for group in F_results:
print(group)
df_competition = F_results[group][competitors].T.sort_values(by='overall', ascending=True).head(5)
df_dbnn = F_results[group][dbnn_cols].T
selected_results[group] = df_dbnn.append(df_competition)
display(selected_results[group])
figures = {'reports' : {'comparison' : {}}}
for group in selected_results:
df = selected_results[group].T
fig = df[df.index != 'overall'].plot(kind='line', style=['o-', 'v-', '^-', 's-', 'D--', 'p--', 'x--', 'X-.', 'd--'],
#color=['navy', 'darkred', 'red', 'orangered', 'orange'],
linewidth=3,
markersize=13,
figsize=(10,7), use_index=True)
plt.legend(fontsize=11)
plt.ylabel('$TNR$')
plt.legend(bbox_to_anchor=(0, 1.01), loc='lower left', ncol=5)
plt.tight_layout()
#plt.plot(range(0, 101, 100), [0.05, 0.05])
latex = util.get_latex_table(F_results[group].T, float_format='$%.2f$',
index=True, caption=group, label=group)
dbnn_storage['reports']['comparison'][group] = {'fig' : fig, 'latex': latex}
figures['reports']['comparison'][group] = {'fig' : fig}
print(latex)
```
## Save
```
results_directory_path = configuration['results']['directory_path']
path = os.path.join(results_directory_path, 'dbnn_results.p')
with open(path, 'wb') as f:
pickle.dump(dbnn_storage['results'], f)
reports_directory_path = configuration['reports']['directory_path']
path = os.path.join(reports_directory_path, 'dbnn')
pathlib.Path(*path.split(os.sep)).mkdir(parents=True, exist_ok=True)
reports_directory_path = path
path = os.path.join(reports_directory_path, 'dbnn_reports.p')
with open(path, 'wb') as f:
pickle.dump(dbnn_storage['reports'], f)
util.traverse_and_save(figures, reports_directory_path)
```
|
github_jupyter
|
# Import everything that's needed to run the notebook
import os
import pickle
import dill
import pathlib
import datetime
import random
import time
from IPython.display import display, Markdown, Latex
import pandas as pd
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.neural_network import MLPClassifier
import scipy.stats
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import util
import robust
from ipynb.fs.defs.descriptor_based_neural_networks import DescriptorBuilder
from ipynb.fs.defs.construct_sbnn import SBNNPreprocessor
from sklearn.model_selection import learning_curve
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
plt.rc('axes', labelsize=15)
# Define the path to the configuration dictionary
config_path = 'configuration.p'
# Load the configuration dictionary
with open(config_path, 'rb') as f:
configuration = pickle.load(f)
# Get the paths to the relevant directories
data_directory_path = configuration['data']['directory_path']
classifiers_directory_path = configuration['classifiers']['directory_path']
dbnn_storage1 = dbnn_storage
dbnn_storage = {}
results_directory_path = configuration['results']['directory_path']
path = os.path.join(results_directory_path, 'dbnn_results.p')
with open(path, 'rb') as f:
dbnn_storage['results'] = pickle.load(f)
reports_directory_path = configuration['reports']['directory_path']
path = os.path.join(reports_directory_path, 'dbnn')
path = os.path.join(path, 'dbnn_reports.p')
with open(path, 'rb') as f:
dbnn_storage['reports'] = pickle.load(f)
with open('dbnns1.p', 'rb') as f:
dbnns = dill.load(f)
# Define the dictionary to store the actual datasets, indexed by their names
datasets = {}
# Load the datasets
for set_name in ['F-left', 'F-right', 'F-central', 'F-symmetric']:
set_path = configuration['data']['datasets'][set_name]['path']
print('Loading {} from {}'.format(set_name, set_path))
datasets[set_name] = util.load_from_file(set_path)
print('Done.')
for set_name in datasets:
labels = [sample.pop() for sample in datasets[set_name]]
samples = datasets[set_name]
datasets[set_name] = {'samples' : samples, 'labels' : labels}
# Make a dictionary to hold the tests
test_classifiers = {}
# Specify the classical tests
codes = ['SW', 'SF', 'LF', 'JB', 'DP', 'AD', 'CVM', 'FSSD']
# Load the classical tests
for test_code in codes:
test, statistic = util.get_test(test_code)
for alpha in [0.01, 0.05]:
test_classifiers[(test_code, alpha)] = util.TestClassifier(test, statistic, alpha)
# Although SBNN is not technically a test, consider it too.
with open(os.path.join('classifiers', 'sbnn.p'), 'rb') as f:
sbnn = pickle.load(f)
test_classifiers[('SBNN', '/')] = sbnn
codes += ['SBNN']
# Specify the robustified tests
robust_codes = ['MMRT1', 'MMRT2', 'TTRT1', 'TTRT2', 'RSW', 'RLM']
# Load the robustified tests
for test_code in robust_codes:
test, statistic = robust.get_robust_test(test_code)
for alpha in [0.01, 0.05]:
test_classifiers[(test_code, alpha)] = util.TestClassifier(test, statistic, alpha)
# Specify the sample sizes
n_range = range(10, 101, 10)
# Specify the metrics to calculate
metrics = ['TNR']
# Evaluate the tests on each group of samples in set F
for group in ['F-left', 'F-right', 'F-central', 'F-symmetric']:
print(group)
samples = datasets[group]['samples']
labels = datasets[group]['labels']
# Create a dictionary to store the results
all_test_results = {}
for (test_code, alpha) in test_classifiers:
# Evaluate the tests (and SBNN)
print('\t', test_code, alpha, end='')
# Get the test
test_clf = test_classifiers[(test_code, alpha)]
# Evaluate it
start = time.time()
test_results_df = util.evaluate_pretty(samples,
labels,
test_clf,
metrics=metrics,
n_range=n_range,
index='n')
end = time.time()
# Show how long its evaluation took and display the results
print('\t', end - start)
display(test_results_df.T)
# Memorize the results
all_test_results[(test_code, alpha)] = test_results_df
# Put the results into the storage for persistence
for key in all_test_results:
test_results = all_test_results[key]
memory = dbnn_storage['results']['comparison'].get(group, {})
memory[key] = test_results
dbnn_storage['results']['comparison'][group] = memory
F_results = {}
for group in dbnn_storage['results']['comparison']:
if group[0] != 'F':
continue
print(group)
results = dbnn_storage['results']['comparison'][group]
results_dict = {test_key: results[test_key]['TNR'] for test_key in results}
results_df = pd.concat(results_dict, axis=1)
results_df = results_df[sorted(results_df.columns)]
for name in sorted(dbnns.keys()):
if '0.01' in name:
new_name = 'DBNN$_{0.01}$'
alpha = 0.01
elif '0.05' in name:
new_name = 'DBNN$_{0.05}$'
alpha = 0.05
elif 'opt' in name:
new_name = 'DBNN$_{opt}$'
alpha = '/'
elif '0.1' in name:
continue
else:
new_name = 'DBNN'
alpha = '/'
results_df[(new_name, alpha)] = dbnn_storage['results']['evaluation'][name][group]['TNR']
# list(sorted(dbnns.keys()))
results_df = results_df[[col for col in results_df.columns]]
F_results[group] = results_df
display(results_df.T)
#(F_results['F-left'].xs('/', level=1, axis=1) <= 0.05*2).T#.sum(axis=0)
#F_results['F-symmetric'].xs('/', level=1, axis=1)
competitors = list(test_classifiers.keys())
dbnn_cols = [('DBNN', '/'), ('DBNN$_{opt}$', '/'),
('DBNN$_{0.01}$', 0.01), ('DBNN$_{0.05}$', 0.05)]
selected_results = {}
for group in F_results:
print(group)
df_competition = F_results[group][competitors].T.sort_values(by='overall', ascending=True).head(5)
df_dbnn = F_results[group][dbnn_cols].T
selected_results[group] = df_dbnn.append(df_competition)
display(selected_results[group])
figures = {'reports' : {'comparison' : {}}}
for group in selected_results:
df = selected_results[group].T
fig = df[df.index != 'overall'].plot(kind='line', style=['o-', 'v-', '^-', 's-', 'D--', 'p--', 'x--', 'X-.', 'd--'],
#color=['navy', 'darkred', 'red', 'orangered', 'orange'],
linewidth=3,
markersize=13,
figsize=(10,7), use_index=True)
plt.legend(fontsize=11)
plt.ylabel('$TNR$')
plt.legend(bbox_to_anchor=(0, 1.01), loc='lower left', ncol=5)
plt.tight_layout()
#plt.plot(range(0, 101, 100), [0.05, 0.05])
latex = util.get_latex_table(F_results[group].T, float_format='$%.2f$',
index=True, caption=group, label=group)
dbnn_storage['reports']['comparison'][group] = {'fig' : fig, 'latex': latex}
figures['reports']['comparison'][group] = {'fig' : fig}
print(latex)
results_directory_path = configuration['results']['directory_path']
path = os.path.join(results_directory_path, 'dbnn_results.p')
with open(path, 'wb') as f:
pickle.dump(dbnn_storage['results'], f)
reports_directory_path = configuration['reports']['directory_path']
path = os.path.join(reports_directory_path, 'dbnn')
pathlib.Path(*path.split(os.sep)).mkdir(parents=True, exist_ok=True)
reports_directory_path = path
path = os.path.join(reports_directory_path, 'dbnn_reports.p')
with open(path, 'wb') as f:
pickle.dump(dbnn_storage['reports'], f)
util.traverse_and_save(figures, reports_directory_path)
| 0.652906 | 0.773216 |
## Example. Probability of a girl birth given placenta previa
**Analysis using a uniform prior distribution**
```
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
from scipy.special import expit
az.style.use('arviz-darkgrid')
%config Inline.figure_formats = ['retina']
%load_ext watermark
births = 987
fem_births = 437
with pm.Model() as model_1:
theta = pm.Uniform('theta', lower=0, upper=1)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
with model_1:
trace_1 = pm.sample(draws=20_000, tune=50_000)
az.plot_trace(trace_1);
df = az.summary(trace_1, round_to=4)
df
```
The summary shows the mean and the standard deviation, it also shows the 95% posterior interval [0.4112, 0.4732]. The next plot is the plot for the posterior distribution.
```
az.plot_posterior(trace_1); # same as pm.plot_posterior()
```
The true posterior distribution is $\textsf{Beta}(438, 544)$. Let's compare it with the one we found using `pymc`.
```
from scipy.stats import beta
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, 438, 544)
mean_t = df['mean'].values[0]
sd_t = df['sd'].values[0]
alpha_t = (mean_t**2 * (1 - mean_t)) / (sd_t**2) - mean_t
beta_t = (1 - mean_t) * (mean_t * (1 - mean_t) / sd_t**2 - 1)
y_pred = beta.pdf(x, alpha_t, beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='True', linewidth=5)
plt.plot(x, y_pred, 'o', label='Predicted', linewidth=4, alpha=0.6)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
```
Just like in the book, `phi` is the ratio of male to female births and `trans` is the logit transform of `theta`.
```
with pm.Model() as model_2:
theta = pm.Uniform('theta', lower=0, upper=1)
trans = pm.Deterministic('trans', pm.logit(theta))
phi = pm.Deterministic('phi', (1 - theta) / theta)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
```
Try looking at the model's test point to see if your model has problems.
```
model_2.check_test_point()
```
For comparison's sake, we change the value for `observed` to a negative number to see what happens:
```
with pm.Model() as model_2_bad:
theta = pm.Uniform('theta', lower=0, upper=1)
trans = pm.Deterministic('trans', pm.logit(theta))
phi = pm.Deterministic('phi', (1 - theta) / theta)
obs = pm.Binomial('observed', n=births, p=theta, observed=-2)
model_2_bad.check_test_point()
with model_2:
trace_2 = pm.sample(draws=5000, tune=2000)
az.plot_trace(trace_2);
df2 = az.summary(trace_2, round_to=4)
df2
```
You can plot the posterior distribution for the logit transform, `trans`; the male-to-female sex ratio, `phi`.
```
fig, axes = plt.subplots(ncols=2, nrows=1, figsize=(11, 4))
az.plot_posterior(trace_2, var_names=['trans', 'phi'], ax=axes);
```
If you want the interval for `trans`, you have to invert the 95% interval on the logit scale
```
lldd = expit(df2.loc['trans','hpd_3%'])
llii = expit(df2.loc['trans','hpd_97%'])
print(f'The interval is [{lldd:.3f}, {llii:.3f}]')
```
**Analysis using a nonconjugate prior distribution**
And with a custom prior distribution, a triangular one with a uniform distribution to the left and a uniform distribution to the right.
```
import theano.tensor as tt
def triangular(central_num, width):
left_num = central_num - width
right_num = central_num + width
theta = pm.Triangular('theta', lower=left_num, upper=right_num, c=central_num)
# Comment these lines to see some changes
if tt.lt(left_num, theta):
theta = pm.Uniform('theta1', lower=0, upper=left_num)
if tt.gt(right_num, theta):
theta = pm.Uniform('theta2', lower=right_num, upper=1)
return theta
```
Remember, you can play with `width`. In this case, `width=0.09`
```
central_num = 0.485
width = 0.09
with pm.Model() as model_3:
theta = triangular(central_num, width)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
with model_3:
trace_3 = pm.sample(draws=15_000, tune=15_000, target_accept=0.95)
az.plot_trace(trace_3, var_names=['theta']);
az.summary(trace_3, var_names='theta', round_to=4)
```
And the posterior distribution for `theta` is this.
```
az.plot_posterior(trace_3, var_names='theta');
```
## Estimating a rate from Poisson data: an idealized example
```
with pm.Model() as poisson_model:
theta = pm.Gamma('theta', alpha=3, beta=5)
post = pm.Poisson('post', mu=2 * theta, observed=3)
poisson_model.check_test_point()
pm.model_to_graphviz(poisson_model)
with poisson_model:
trace_poisson = pm.sample(draws=20_000, tune=10_000, target_accept=0.95)
az.plot_trace(trace_poisson);
df4 = az.summary(trace_poisson, round_to=4)
df4
```
The plot of the posterior distribution
```
pm.plot_posterior(trace_poisson);
```
The true posterior distribution is $\textsf{Gamma}(6,7)$. Let's compare it with the one we found using `pymc`.
```
from scipy.stats import gamma
x = np.linspace(0, 3, 1000)
y = gamma.pdf(x, 6, scale=1/7)
mean_t = df4['mean'].values[0]
sd_t = df4['sd'].values[0]
alpha_t = mean_t**2 / sd_t**2
beta_t = mean_t / sd_t**2
y_pred = gamma.pdf(x, alpha_t, scale=1/beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, 'k', label='True', linewidth=7)
plt.plot(x, y_pred, 'C1', label='Predicted', linewidth=3, alpha=0.9)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
```
If we add additional data, `mu` changes.
```
with pm.Model() as poisson_model_2:
theta = pm.Gamma('theta', alpha=3, beta=5)
post = pm.Poisson('post', mu=20 * theta, observed=30)
with poisson_model_2:
trace_poisson_2 = pm.sample(draws=10_000, tune=15_000, target_accept=0.95)
az.plot_trace(trace_poisson_2);
df5 = pm.summary(trace_poisson_2, round_to=4)
df5
az.plot_posterior(trace_poisson_2);
```
The true posterior distribution is $\textsf{Gamma}(33, 25)$
```
x = np.linspace(0, 3, 1000)
y = gamma.pdf(x, 33, scale=1/25) # How you write alpha and beta
mean_t = df5['mean'].values[0]
sd_t = df5['sd'].values[0]
alpha_t = mean_t**2 / sd_t**2
beta_t = mean_t / sd_t**2
y_pred = gamma.pdf(x, alpha_t, scale=1/beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, 'k', label='True', linewidth=5)
plt.plot(x, y_pred, 'oC1', label='Predicted', alpha=0.15)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
val = np.mean(trace_poisson_2['theta'] >= 1)
print(f'The posterior probability that theta exceeds 1.0 is {val:.2f}.')
%watermark -iv -v -p theano,scipy,matplotlib,arviz -m
```
|
github_jupyter
|
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
from scipy.special import expit
az.style.use('arviz-darkgrid')
%config Inline.figure_formats = ['retina']
%load_ext watermark
births = 987
fem_births = 437
with pm.Model() as model_1:
theta = pm.Uniform('theta', lower=0, upper=1)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
with model_1:
trace_1 = pm.sample(draws=20_000, tune=50_000)
az.plot_trace(trace_1);
df = az.summary(trace_1, round_to=4)
df
az.plot_posterior(trace_1); # same as pm.plot_posterior()
from scipy.stats import beta
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, 438, 544)
mean_t = df['mean'].values[0]
sd_t = df['sd'].values[0]
alpha_t = (mean_t**2 * (1 - mean_t)) / (sd_t**2) - mean_t
beta_t = (1 - mean_t) * (mean_t * (1 - mean_t) / sd_t**2 - 1)
y_pred = beta.pdf(x, alpha_t, beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='True', linewidth=5)
plt.plot(x, y_pred, 'o', label='Predicted', linewidth=4, alpha=0.6)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
with pm.Model() as model_2:
theta = pm.Uniform('theta', lower=0, upper=1)
trans = pm.Deterministic('trans', pm.logit(theta))
phi = pm.Deterministic('phi', (1 - theta) / theta)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
model_2.check_test_point()
with pm.Model() as model_2_bad:
theta = pm.Uniform('theta', lower=0, upper=1)
trans = pm.Deterministic('trans', pm.logit(theta))
phi = pm.Deterministic('phi', (1 - theta) / theta)
obs = pm.Binomial('observed', n=births, p=theta, observed=-2)
model_2_bad.check_test_point()
with model_2:
trace_2 = pm.sample(draws=5000, tune=2000)
az.plot_trace(trace_2);
df2 = az.summary(trace_2, round_to=4)
df2
fig, axes = plt.subplots(ncols=2, nrows=1, figsize=(11, 4))
az.plot_posterior(trace_2, var_names=['trans', 'phi'], ax=axes);
lldd = expit(df2.loc['trans','hpd_3%'])
llii = expit(df2.loc['trans','hpd_97%'])
print(f'The interval is [{lldd:.3f}, {llii:.3f}]')
import theano.tensor as tt
def triangular(central_num, width):
left_num = central_num - width
right_num = central_num + width
theta = pm.Triangular('theta', lower=left_num, upper=right_num, c=central_num)
# Comment these lines to see some changes
if tt.lt(left_num, theta):
theta = pm.Uniform('theta1', lower=0, upper=left_num)
if tt.gt(right_num, theta):
theta = pm.Uniform('theta2', lower=right_num, upper=1)
return theta
central_num = 0.485
width = 0.09
with pm.Model() as model_3:
theta = triangular(central_num, width)
obs = pm.Binomial('observed', n=births, p=theta, observed=fem_births)
with model_3:
trace_3 = pm.sample(draws=15_000, tune=15_000, target_accept=0.95)
az.plot_trace(trace_3, var_names=['theta']);
az.summary(trace_3, var_names='theta', round_to=4)
az.plot_posterior(trace_3, var_names='theta');
with pm.Model() as poisson_model:
theta = pm.Gamma('theta', alpha=3, beta=5)
post = pm.Poisson('post', mu=2 * theta, observed=3)
poisson_model.check_test_point()
pm.model_to_graphviz(poisson_model)
with poisson_model:
trace_poisson = pm.sample(draws=20_000, tune=10_000, target_accept=0.95)
az.plot_trace(trace_poisson);
df4 = az.summary(trace_poisson, round_to=4)
df4
pm.plot_posterior(trace_poisson);
from scipy.stats import gamma
x = np.linspace(0, 3, 1000)
y = gamma.pdf(x, 6, scale=1/7)
mean_t = df4['mean'].values[0]
sd_t = df4['sd'].values[0]
alpha_t = mean_t**2 / sd_t**2
beta_t = mean_t / sd_t**2
y_pred = gamma.pdf(x, alpha_t, scale=1/beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, 'k', label='True', linewidth=7)
plt.plot(x, y_pred, 'C1', label='Predicted', linewidth=3, alpha=0.9)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
with pm.Model() as poisson_model_2:
theta = pm.Gamma('theta', alpha=3, beta=5)
post = pm.Poisson('post', mu=20 * theta, observed=30)
with poisson_model_2:
trace_poisson_2 = pm.sample(draws=10_000, tune=15_000, target_accept=0.95)
az.plot_trace(trace_poisson_2);
df5 = pm.summary(trace_poisson_2, round_to=4)
df5
az.plot_posterior(trace_poisson_2);
x = np.linspace(0, 3, 1000)
y = gamma.pdf(x, 33, scale=1/25) # How you write alpha and beta
mean_t = df5['mean'].values[0]
sd_t = df5['sd'].values[0]
alpha_t = mean_t**2 / sd_t**2
beta_t = mean_t / sd_t**2
y_pred = gamma.pdf(x, alpha_t, scale=1/beta_t)
plt.figure(figsize=(10, 5))
plt.plot(x, y, 'k', label='True', linewidth=5)
plt.plot(x, y_pred, 'oC1', label='Predicted', alpha=0.15)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\theta$', fontsize=14);
val = np.mean(trace_poisson_2['theta'] >= 1)
print(f'The posterior probability that theta exceeds 1.0 is {val:.2f}.')
%watermark -iv -v -p theano,scipy,matplotlib,arviz -m
| 0.709623 | 0.987436 |
# Klasyfikatory
### Pakiety
```
import pandas as pd
import numpy as np
import category_encoders as ce
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import recall_score
from sklearn.pipeline import Pipeline
from sklearn.metrics import precision_score
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
import random
import warnings
warnings.filterwarnings('ignore')
from xgboost import XGBClassifier
```
### Ustawienie ziarna gwarantuje reprodukowalność wyników
```
np.random.seed(123)
```
### Wczytanie danych
```
data = pd.read_csv('australia.csv')
data = pd.DataFrame(data)
```
### Sprawdzenia zrównoważenia zbioru ze względu na zmienną celu, w celu doboru odpowiednich miar oceny klasyfikacji
```
data.filter(["RainTomorrow"]).hist()
```
Dane są niezrównoważone, więc jako miary jakości predykcji klasy przez klasyfikatory będziemy używać precision i recall (nie accuracy)
# 1. Podział na zbiory treningowy i testowy
* 80% obserwacji należy do zbioru treningowego, pozostałe do testowego.
* Odseparowujemy zmienną celu od zmiennych objaśniających.
```
X_train, X_test, Y_train, Y_test = train_test_split(data.drop('RainTomorrow', axis=1), data['RainTomorrow'])
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
```
# 2. Klasyfikatory
## 2.1. Random Forest
```
# Stworzenie modelu
rf_classifier = RandomForestClassifier(n_estimators=1000, max_depth=8, max_features='sqrt', bootstrap=True,
min_samples_leaf=2, min_samples_split=2, random_state=42)
```
### Objaśnienie wybranych hiperparametrów
Wybrane hiperparametry:
**n_estimators** - ilość drzew składowych (int, domyślnie 100)
**max_depth** - maksymalna głębokość drzewa (int, domyślnie None)
**min_samples_split** - minimalna liczba obserwacji wymagana do podziału węzła wewnętrznego (int/float, domyślnie 2)
**min_samples_leaf** - minimalna liczba obserwacji wymagana względem liścia (int, domyślnie 1)
**max_features** - ilość cech branych pod uwagę podczas poszukiwania najlepszego podziału (string). Jeśli “sqrt”, to max_features=sqrt(n_features), jeśli “log2”, to max_features=log2(n_features).
**bootstrap** - stosowanie bootstrap (bool, domyślnie True)
**random_state** - kontroluje losowość procedury bootstrap
```
# Trenowanie modelu
rf_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class1 = rf_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba1 = rf_classifier.predict_proba(X_test)[:, 1]
```
## 2.2. XGBoost
```
# Stworzenie modelu
xgb_classifier = XGBClassifier(n_estimators = 1000, booster = 'gbtree', colsample_bytree = 0.8, max_depth = 5,
gamma = 1.5, min_child_weight = 1, subsample = 0.8, random_state = 42)
```
### Objaśnienie wybranych hiperparametrów
**booster** - typ boostera, gbtree, gblinear lub dart. Dwa pierwsze oparte na modelach drzewiastych, ostatni na funkcjach liniowych.
**colsample_bytree** - to frakcja kolumn (losowo wybranych), które zostaną wykorzystane przy konstruowaniu każdego drzewa.
**gamma** - odpowiada za częstość przycinania drzewa, im wyższa gamma, tym częściej przycinamy.
**min_child_weight** - minimalna waga wymagana względem 'dziecka'
**subsample** - odpowiada części obserwacji (wierszy) do podpróbkowania na każdym etapie. Domyślnie jest ustawiony na 1, co oznacza, że używamy wszystkich wierszy.
Pozostałe jak wyżej.
```
# Trenowanie modelu
xgb_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class2 = xgb_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba2 = xgb_classifier.predict_proba(X_test)[:, 1]
```
## 2.3. Regresja logistyczna
```
from sklearn.linear_model import LogisticRegression
# Budowanie modelu
lr_classifier = LogisticRegression(penalty = 'l1', class_weight='balanced', C = 0.01, solver = 'saga')
```
### Objaśnienie wybranych hiperparametrów
**penalty** - norma kary.
**class_weight** - wagi klas.
**C** - odwrotny parametr regularyzacji, wyższe wartości C odpowiadają mniejszej regularyzacji.
**solver** - algorytm używany w procedurze optymalizacji.
```
lr_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class3 = lr_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba3 = lr_classifier.predict_proba(X_test)[:, 1]
```
# 3. Zestawienie rezultatów
## 3.1. Miary precision i recall
Wartości miary recall na zbiorze testowym dla klasyfikatorów Random Forest, XGBoost i regresji logistycznej wynoszą odpowiednio:
```
pd.DataFrame({"Metoda" : ["Random Forest", "XGBoost", "Regresja logistyczna"],
"Recall" : [recall_score(Y_test, predict_class1), recall_score(Y_test, predict_class2), recall_score(Y_test, predict_class3)],
"Precision" : [precision_score(Y_test, predict_class1, average='macro'), precision_score(Y_test, predict_class2, average='macro'), precision_score(Y_test, predict_class3, average='macro')]})
```
## Krzywe Precision-Recall
```
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import plot_precision_recall_curve
disp1 = plot_precision_recall_curve(rf_classifier, X_test, Y_test)
disp1.ax_.set_title('Krzywa Precision-Recall dla klasyfikatora Random Forest')
disp2 = plot_precision_recall_curve(xgb_classifier, X_test, Y_test)
disp2.ax_.set_title('Krzywa Precision-Recall dla klasyfikatora XGBoost')
disp3 = plot_precision_recall_curve(lr_classifier, X_test, Y_test)
disp3.ax_.set_title('Krzywa Precision-Recall dla regresji logistycznej')
```
## Wnioski:
Przy predykcji klasy okazuje się, że osiągnięte przez klasyfikatory wartości precision i recall są zróżnicowane. Względem miary precision najlepsze rezultaty osiągnął Random Forest, natomiast względem recall regresja logistyczna.
Moim zdaniem, ocena który klasyfikator jest lepszy od pozostałych zależy od konkretnej sytuacji i zmiennej celu, którą chcemy przewidywać. Mianowicie ważne jest to, czy chcemy aby klasyfikator wykrywał jak największą frakcję wyników dodatnich (maksymalizacja recall), czy aby jak największa część obserwacji wskazanych przez klasyfikator jako dodatnia faktycznie taka była (maksymalizacja precision).
W przypadku przewidywania deszczu, skupiłabym się bardziej na zmiennej recall.
## 3.2. Krzywa ROCR i miara AUC
```
# Krzywa ROCR
fpr1, tpr1, thresholds1 = metrics.roc_curve(Y_test, predict_proba1) # false & true positive rates
fpr2, tpr2, thresholds2 = metrics.roc_curve(Y_test, predict_proba2) # false & true positive rates
fpr3, tpr3, thresholds3 = metrics.roc_curve(Y_test, predict_proba3) # false & true positive rates
plt.figure()
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr1, tpr1, label='Random Forest')
plt.plot(fpr2, tpr2, label='XGBoost')
plt.plot(fpr3, tpr3, label='Regresja Logistyczna')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()
# Miara AUC
pd.DataFrame({"Klasyfikator" : ["Random Forest", "XGBoost", "Regresja Logistyczna"],
"AUC": [metrics.auc(fpr1, tpr1), metrics.auc(fpr2, tpr2), metrics.auc(fpr3, tpr3)]})
```
## Wnioski
Rezultaty osiągnięte przez klasyfikatory w przypadku predykcji prawdopodobieństwa są niemalże identyczne (krzywe ROCR pokrywają się) i dość wysokie. Jak widać najwyższy wynik względem miary AUC osiągnęła regresja logistyczna, nie mniej jednak, różnice są znikome. Jak wynika z literatury, wyniki wszystkich klasyfikatorów świadczą o tym, że każdy z nich może być postrzegany jako co najmniej dobry, a nawet bardzo dobry.
# Część dodatkowa - model regresyjny
# Regresja liniowa
```
import category_encoders as ce
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
```
### Wczytanie danych
```
df = pd.read_csv('allegro-api-transactions.csv')
df = pd.DataFrame(df)
df = df.drop(['lp', 'date'], axis = 1)
Y = df.price
cols = ['categories', 'seller','it_location', 'main_category']
```
## 1. Target Encoding
```
te = ce.TargetEncoder(cols = cols)
# Podział na zbiory treningowy i testowy
train_X1, test_X1, train_Y1, test_Y1 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
encoded_train_X1 = te.fit_transform(train_X1, train_Y1)
encoded_test_X1 = te.transform(test_X1, test_Y1)
# Model
linreg1 = LinearRegression()
linreg1.fit(encoded_train_X1, train_Y1)
# Predykcja
y_pred1 = linreg1.predict(encoded_test_X1)
```
## 2. James Stein Encoding
```
js = ce.james_stein.JamesSteinEncoder(df, cols = cols)
# Podział na zbiory treningowy i testowy
train_X2, test_X2, train_Y2, test_Y2 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
encoded_train_X2 = js.fit_transform(train_X2, train_Y2)
encoded_test_X2 = js.transform(test_X2, test_Y2)
# Model
linreg2 = LinearRegression()
linreg2.fit(encoded_train_X2, train_Y2)
# Predykcja
y_pred2 = linreg2.predict(encoded_test_X2)
```
## 3. CatBoost Encoding
```
cb = ce.CatBoostEncoder(cols = cols)
# Podział na zbiory treningowy i testowy
train_X3, test_X3, train_Y3, test_Y3 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
train_X3_copy = train_X3.copy()
train_Y3_copy = train_Y3.copy()
test_X3_copy = test_X3.copy()
test_Y3_copy = test_Y3.copy()
## Losowa permutacja wierszy (zabieg zalecane w dokumentacji)
train_permutation = np.random.permutation(len(train_X3_copy))
train_X3_copy = train_X3_copy.iloc[train_permutation].reset_index(drop = True)
train_Y3_copy = train_Y3_copy.iloc[train_permutation].reset_index(drop = True)
test_permutation = np.random.permutation(len(test_X3_copy))
test_X3_copy = test_X3_copy.iloc[test_permutation].reset_index(drop = True)
test_Y3_copy = test_Y3_copy.iloc[test_permutation].reset_index(drop = True)
## Kodowanie
encoded_train_X3 = cb.fit_transform(train_X3_copy, train_Y3_copy)
encoded_test_X3 = cb.transform(test_X3_copy, test_Y3_copy)
# Model
linreg3 = LinearRegression()
linreg3.fit(encoded_train_X3, train_Y3_copy)
# Predykcja
y_pred3 = linreg3.predict(encoded_test_X3)
```
## Zestawienie wyników
```
pd.DataFrame({"Metoda" : ["Target Encoding", "James Stein Encoding", "CatBoost Encoding"],
"R2" : [r2_score(test_Y1, y_pred1), r2_score(test_Y2, y_pred2), r2_score(test_Y3_copy, y_pred3)],
"RMSE" : [mean_squared_error(test_Y1, y_pred1, squared=False), mean_squared_error(test_Y2, y_pred2, squared=False), mean_squared_error(test_Y3_copy, y_pred3, squared=False)]})
```
## Wnioski
Zgodnie z początkową intuicją rezultaty regresji względem rozważanych miar, dla danych poddanych podobnym metodom kodowania zmiennych kategorycznych, są zróżnicowane w nieznacznym stopniu.
Pierwsze co rzuca się w oczy w powyższych wynikach, to niskie wartości współczynników determinacji. Wartość R<sup>2</sup> wynosząca ok. 0.1-0.15, gdzie maksymalna możliwa wartość wynosi 1, jest niezwykle mała. Pokazuje, że nasze modele regresji praktycznie nie przedstawiają zmienności próbki. Wartości błędów średniokwadratowych dla rozważanych encodingów są nieco bardziej zróżnicowane.
Nie mniej jednak w tym wywołaniu, najlepiej względem obydwu miar wypadł CatBoost Encoding. (Odnoszę się do konkretnego wywołania, ponieważ wyniki nie są ściśle reprodukowalne)
|
github_jupyter
|
import pandas as pd
import numpy as np
import category_encoders as ce
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import recall_score
from sklearn.pipeline import Pipeline
from sklearn.metrics import precision_score
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
import random
import warnings
warnings.filterwarnings('ignore')
from xgboost import XGBClassifier
np.random.seed(123)
data = pd.read_csv('australia.csv')
data = pd.DataFrame(data)
data.filter(["RainTomorrow"]).hist()
X_train, X_test, Y_train, Y_test = train_test_split(data.drop('RainTomorrow', axis=1), data['RainTomorrow'])
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Stworzenie modelu
rf_classifier = RandomForestClassifier(n_estimators=1000, max_depth=8, max_features='sqrt', bootstrap=True,
min_samples_leaf=2, min_samples_split=2, random_state=42)
# Trenowanie modelu
rf_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class1 = rf_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba1 = rf_classifier.predict_proba(X_test)[:, 1]
# Stworzenie modelu
xgb_classifier = XGBClassifier(n_estimators = 1000, booster = 'gbtree', colsample_bytree = 0.8, max_depth = 5,
gamma = 1.5, min_child_weight = 1, subsample = 0.8, random_state = 42)
# Trenowanie modelu
xgb_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class2 = xgb_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba2 = xgb_classifier.predict_proba(X_test)[:, 1]
from sklearn.linear_model import LogisticRegression
# Budowanie modelu
lr_classifier = LogisticRegression(penalty = 'l1', class_weight='balanced', C = 0.01, solver = 'saga')
lr_classifier.fit(X_train, Y_train)
# Predykcja klasy
predict_class3 = lr_classifier.predict(X_test)
# Predykcja prawdopodobieństwa
predict_proba3 = lr_classifier.predict_proba(X_test)[:, 1]
pd.DataFrame({"Metoda" : ["Random Forest", "XGBoost", "Regresja logistyczna"],
"Recall" : [recall_score(Y_test, predict_class1), recall_score(Y_test, predict_class2), recall_score(Y_test, predict_class3)],
"Precision" : [precision_score(Y_test, predict_class1, average='macro'), precision_score(Y_test, predict_class2, average='macro'), precision_score(Y_test, predict_class3, average='macro')]})
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import plot_precision_recall_curve
disp1 = plot_precision_recall_curve(rf_classifier, X_test, Y_test)
disp1.ax_.set_title('Krzywa Precision-Recall dla klasyfikatora Random Forest')
disp2 = plot_precision_recall_curve(xgb_classifier, X_test, Y_test)
disp2.ax_.set_title('Krzywa Precision-Recall dla klasyfikatora XGBoost')
disp3 = plot_precision_recall_curve(lr_classifier, X_test, Y_test)
disp3.ax_.set_title('Krzywa Precision-Recall dla regresji logistycznej')
# Krzywa ROCR
fpr1, tpr1, thresholds1 = metrics.roc_curve(Y_test, predict_proba1) # false & true positive rates
fpr2, tpr2, thresholds2 = metrics.roc_curve(Y_test, predict_proba2) # false & true positive rates
fpr3, tpr3, thresholds3 = metrics.roc_curve(Y_test, predict_proba3) # false & true positive rates
plt.figure()
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr1, tpr1, label='Random Forest')
plt.plot(fpr2, tpr2, label='XGBoost')
plt.plot(fpr3, tpr3, label='Regresja Logistyczna')
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()
# Miara AUC
pd.DataFrame({"Klasyfikator" : ["Random Forest", "XGBoost", "Regresja Logistyczna"],
"AUC": [metrics.auc(fpr1, tpr1), metrics.auc(fpr2, tpr2), metrics.auc(fpr3, tpr3)]})
import category_encoders as ce
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
df = pd.read_csv('allegro-api-transactions.csv')
df = pd.DataFrame(df)
df = df.drop(['lp', 'date'], axis = 1)
Y = df.price
cols = ['categories', 'seller','it_location', 'main_category']
te = ce.TargetEncoder(cols = cols)
# Podział na zbiory treningowy i testowy
train_X1, test_X1, train_Y1, test_Y1 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
encoded_train_X1 = te.fit_transform(train_X1, train_Y1)
encoded_test_X1 = te.transform(test_X1, test_Y1)
# Model
linreg1 = LinearRegression()
linreg1.fit(encoded_train_X1, train_Y1)
# Predykcja
y_pred1 = linreg1.predict(encoded_test_X1)
js = ce.james_stein.JamesSteinEncoder(df, cols = cols)
# Podział na zbiory treningowy i testowy
train_X2, test_X2, train_Y2, test_Y2 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
encoded_train_X2 = js.fit_transform(train_X2, train_Y2)
encoded_test_X2 = js.transform(test_X2, test_Y2)
# Model
linreg2 = LinearRegression()
linreg2.fit(encoded_train_X2, train_Y2)
# Predykcja
y_pred2 = linreg2.predict(encoded_test_X2)
cb = ce.CatBoostEncoder(cols = cols)
# Podział na zbiory treningowy i testowy
train_X3, test_X3, train_Y3, test_Y3 = train_test_split(df.drop('price', axis=1), df['price'])
# Kodowanie po podziale na podzbiory
train_X3_copy = train_X3.copy()
train_Y3_copy = train_Y3.copy()
test_X3_copy = test_X3.copy()
test_Y3_copy = test_Y3.copy()
## Losowa permutacja wierszy (zabieg zalecane w dokumentacji)
train_permutation = np.random.permutation(len(train_X3_copy))
train_X3_copy = train_X3_copy.iloc[train_permutation].reset_index(drop = True)
train_Y3_copy = train_Y3_copy.iloc[train_permutation].reset_index(drop = True)
test_permutation = np.random.permutation(len(test_X3_copy))
test_X3_copy = test_X3_copy.iloc[test_permutation].reset_index(drop = True)
test_Y3_copy = test_Y3_copy.iloc[test_permutation].reset_index(drop = True)
## Kodowanie
encoded_train_X3 = cb.fit_transform(train_X3_copy, train_Y3_copy)
encoded_test_X3 = cb.transform(test_X3_copy, test_Y3_copy)
# Model
linreg3 = LinearRegression()
linreg3.fit(encoded_train_X3, train_Y3_copy)
# Predykcja
y_pred3 = linreg3.predict(encoded_test_X3)
pd.DataFrame({"Metoda" : ["Target Encoding", "James Stein Encoding", "CatBoost Encoding"],
"R2" : [r2_score(test_Y1, y_pred1), r2_score(test_Y2, y_pred2), r2_score(test_Y3_copy, y_pred3)],
"RMSE" : [mean_squared_error(test_Y1, y_pred1, squared=False), mean_squared_error(test_Y2, y_pred2, squared=False), mean_squared_error(test_Y3_copy, y_pred3, squared=False)]})
| 0.605799 | 0.797596 |
# Statistics
:label:`sec_statistics`
Undoubtedly, to be a top deep learning practitioner, the ability to train the state-of-the-art and high accurate models is crucial. However, it is often unclear when improvements are significant, or only the result of random fluctuations in the training process. To be able to discuss uncertainty in estimated values, we must learn some statistics.
The earliest reference of *statistics* can be traced back to an Arab scholar Al-Kindi in the $9^{\mathrm{th}}$-century, who gave a detailed description of how to use statistics and frequency analysis to decipher encrypted messages. After 800 years, the modern statistics arose from Germany in 1700s, when the researchers focused on the demographic and economic data collection and analysis. Today, statistics is the science subject that concerns the collection, processing, analysis, interpretation and visualization of data. What is more, the core theory of statistics has been widely used in the research within academia, industry, and government.
More specifically, statistics can be divided to *descriptive statistics* and *statistical inference*. The former focus on summarizing and illustrating the features of a collection of observed data, which is referred to as a *sample*. The sample is drawn from a *population*, denotes the total set of similar individuals, items, or events of our experiment interests. Contrary to descriptive statistics, *statistical inference* further deduces the characteristics of a population from the given *samples*, based on the assumptions that the sample distribution can replicate the population distribution at some degree.
You may wonder: “What is the essential difference between machine learning and statistics?” Fundamentally speaking, statistics focuses on the inference problem. This type of problems includes modeling the relationship between the variables, such as causal inference, and testing the statistically significance of model parameters, such as A/B testing. In contrast, machine learning emphasizes on making accurate predictions, without explicitly programming and understanding each parameter's functionality.
In this section, we will introduce three types of statistics inference methods: evaluating and comparing estimators, conducting hypothesis tests, and constructing confidence intervals. These methods can help us infer the characteristics of a given population, i.e., the true parameter $\theta$. For brevity, we assume that the true parameter $\theta$ of a given population is a scalar value. It is straightforward to extend to the case where $\theta$ is a vector or a tensor, thus we omit it in our discussion.
## Evaluating and Comparing Estimators
In statistics, an *estimator* is a function of given samples used to estimate the true parameter $\theta$. We will write $\hat{\theta}_n = \hat{f}(x_1, \ldots, x_n)$ for the estimate of $\theta$ after observing the samples {$x_1, x_2, \ldots, x_n$}.
We have seen simple examples of estimators before in section :numref:`sec_maximum_likelihood`. If you have a number of samples from a Bernoulli random variable, then the maximum likelihood estimate for the probability the random variable is one can be obtained by counting the number of ones observed and dividing by the total number of samples. Similarly, an exercise asked you to show that the maximum likelihood estimate of the mean of a Gaussian given a number of samples is given by the average value of all the samples. These estimators will almost never give the true value of the parameter, but ideally for a large number of samples the estimate will be close.
As an example, we show below the true density of a Gaussian random variable with mean zero and variance one, along with a collection samples from that Gaussian. We constructed the $y$ coordinate so every point is visible and the relationship to the original density is clearer.
```
import random
from mxnet import np, npx
from d2l import mxnet as d2l
npx.set_np()
# Sample datapoints and create y coordinate
epsilon = 0.1
random.seed(8675309)
xs = np.random.normal(loc=0, scale=1, size=(300,))
ys = [
np.sum(
np.exp(-(xs[:i] - xs[i])**2 /
(2 * epsilon**2)) / np.sqrt(2 * np.pi * epsilon**2)) / len(xs)
for i in range(len(xs))]
# Compute true density
xd = np.arange(np.min(xs), np.max(xs), 0.01)
yd = np.exp(-xd**2 / 2) / np.sqrt(2 * np.pi)
# Plot the results
d2l.plot(xd, yd, 'x', 'density')
d2l.plt.scatter(xs, ys)
d2l.plt.axvline(x=0)
d2l.plt.axvline(x=np.mean(xs), linestyle='--', color='purple')
d2l.plt.title(f'sample mean: {float(np.mean(xs)):.2f}')
d2l.plt.show()
```
There can be many ways to compute an estimator of a parameter $\hat{\theta}_n$. In this section, we introduce three common methods to evaluate and compare estimators: the mean squared error, the standard deviation, and statistical bias.
### Mean Squared Error
Perhaps the simplest metric used to evaluate estimators is the *mean squared error (MSE)* (or $l_2$ loss) of an estimator can be defined as
$$\mathrm{MSE} (\hat{\theta}_n, \theta) = E[(\hat{\theta}_n - \theta)^2].$$
:eqlabel:`eq_mse_est`
This allows us to quantify the average squared deviation from the true value. MSE is always non-negative. If you have read :numref:`sec_linear_regression`, you will recognize it as the most commonly used regression loss function. As a measure to evaluate an estimator, the closer its value to zero, the closer the estimator is close to the true parameter $\theta$.
### Statistical Bias
The MSE provides a natural metric, but we can easily imagine multiple different phenomena that might make it large. Two fundamentally important are fluctuation in the estimator due to randomness in the dataset, and systematic error in the estimator due to the estimation procedure.
First, let us measure the systematic error. For an estimator $\hat{\theta}_n$, the mathematical illustration of *statistical bias* can be defined as
$$\mathrm{bias}(\hat{\theta}_n) = E(\hat{\theta}_n - \theta) = E(\hat{\theta}_n) - \theta.$$
:eqlabel:`eq_bias`
Note that when $\mathrm{bias}(\hat{\theta}_n) = 0$, the expectation of the estimator $\hat{\theta}_n$ is equal to the true value of parameter. In this case, we say $\hat{\theta}_n$ is an unbiased estimator. In general, an unbiased estimator is better than a biased estimator since its expectation is the same as the true parameter.
It is worth being aware, however, that biased estimators are frequently used in practice. There are cases where unbiased estimators do not exist without further assumptions, or are intractable to compute. This may seem like a significant flaw in an estimator, however the majority of estimators encountered in practice are at least asymptotically unbiased in the sense that the bias tends to zero as the number of available samples tends to infinity: $\lim_{n \rightarrow \infty} \mathrm{bias}(\hat{\theta}_n) = 0$.
### Variance and Standard Deviation
Second, let us measure the randomness in the estimator. Recall from :numref:`sec_random_variables`, the *standard deviation* (or *standard error*) is defined as the squared root of the variance. We may measure the degree of fluctuation of an estimator by measuring the standard deviation or variance of that estimator.
$$\sigma_{\hat{\theta}_n} = \sqrt{\mathrm{Var} (\hat{\theta}_n )} = \sqrt{E[(\hat{\theta}_n - E(\hat{\theta}_n))^2]}.$$
:eqlabel:`eq_var_est`
It is important to compare :eqref:`eq_var_est` to :eqref:`eq_mse_est`. In this equation we do not compare to the true population value $\theta$, but instead to $E(\hat{\theta}_n)$, the expected sample mean. Thus we are not measuring how far the estimator tends to be from the true value, but instead we measuring the fluctuation of the estimator itself.
### The Bias-Variance Trade-off
It is intuitively clear that these two main components contribute to the mean squared error. What is somewhat shocking is that we can show that this is actually a *decomposition* of the mean squared error into these two contributions plus a third one. That is to say that we can write the mean squared error as the sum of the square of the bias, the variance and the irreducible error.
$$
\begin{aligned}
\mathrm{MSE} (\hat{\theta}_n, \theta) &= E[(\hat{\theta}_n - \theta)^2] \\
&= E[(\hat{\theta}_n)^2] + E[\theta^2] - 2E[\hat{\theta}_n\theta] \\
&= \mathrm{Var} [\hat{\theta}_n] + E[\hat{\theta}_n]^2 + \mathrm{Var} [\theta] + E[\theta]^2 - 2E[\hat{\theta}_n]E[\theta] \\
&= (E[\hat{\theta}_n] - E[\theta])^2 + \mathrm{Var} [\hat{\theta}_n] + \mathrm{Var} [\theta] \\
&= (E[\hat{\theta}_n - \theta])^2 + \mathrm{Var} [\hat{\theta}_n] + \mathrm{Var} [\theta] \\
&= (\mathrm{bias} [\hat{\theta}_n])^2 + \mathrm{Var} (\hat{\theta}_n) + \mathrm{Var} [\theta].\\
\end{aligned}
$$
We refer the above formula as *bias-variance trade-off*. The mean squared error can be divided into three sources of error: the error from high bias, the error from high variance and the irreducible error. The bias error is commonly seen in a simple model (such as a linear regression model), which cannot extract high dimensional relations between the features and the outputs. If a model suffers from high bias error, we often say it is *underfitting* or lack of *flexibilty* as introduced in (:numref:`sec_model_selection`). The high variance usually results from a too complex model, which overfits the training data. As a result, an *overfitting* model is sensitive to small fluctuations in the data. If a model suffers from high variance, we often say it is *overfitting* and lack of *generalization* as introduced in (:numref:`sec_model_selection`). The irreducible error is the result from noise in the $\theta$ itself.
### Evaluating Estimators in Code
Since the standard deviation of an estimator has been implementing by simply calling `a.std()` for a tensor `a`, we will skip it but implement the statistical bias and the mean squared error.
```
# Statistical bias
def stat_bias(true_theta, est_theta):
return (np.mean(est_theta) - true_theta)
# Mean squared error
def mse(data, true_theta):
return (np.mean(np.square(data - true_theta)))
```
To illustrate the equation of the bias-variance trade-off, let us simulate of normal distribution $\mathcal{N}(\theta, \sigma^2)$ with $10,000$ samples. Here, we use a $\theta = 1$ and $\sigma = 4$. As the estimator is a function of the given samples, here we use the mean of the samples as an estimator for true $\theta$ in this normal distribution $\mathcal{N}(\theta, \sigma^2)$ .
```
theta_true = 1
sigma = 4
sample_len = 10000
samples = np.random.normal(theta_true, sigma, sample_len)
theta_est = np.mean(samples)
theta_est
```
Let us validate the trade-off equation by calculating the summation of the squared bias and the variance of our estimator. First, calculate the MSE of our estimator.
```
mse(samples, theta_true)
```
Next, we calculate $\mathrm{Var} (\hat{\theta}_n) + [\mathrm{bias} (\hat{\theta}_n)]^2$ as below. As you can see, the two values agree to numerical precision.
```
bias = stat_bias(theta_true, theta_est)
np.square(samples.std()) + np.square(bias)
```
## Conducting Hypothesis Tests
The most commonly encountered topic in statistical inference is hypothesis testing. While hypothesis testing was popularized in the early 20th century, the first use can be traced back to John Arbuthnot in the 1700s. John tracked 80-year birth records in London and concluded that more men were born than women each year. Following that, the modern significance testing is the intelligence heritage by Karl Pearson who invented $p$-value and Pearson's chi-squared test, William Gosset who is the father of Student's t-distribution, and Ronald Fisher who initialed the null hypothesis and the significance test.
A *hypothesis test* is a way of evaluating some evidence against the default statement about a population. We refer the default statement as the *null hypothesis* $H_0$, which we try to reject using the observed data. Here, we use $H_0$ as a starting point for the statistical significance testing. The *alternative hypothesis* $H_A$ (or $H_1$) is a statement that is contrary to the null hypothesis. A null hypothesis is often stated in a declarative form which posits a relationship between variables. It should reflect the brief as explicit as possible, and be testable by statistics theory.
Imagine you are a chemist. After spending thousands of hours in the lab, you develop a new medicine which can dramatically improve one's ability to understand math. To show its magic power, you need to test it. Naturally, you may need some volunteers to take the medicine and see whether it can help them learn math better. How do you get started?
First, you will need carefully random selected two groups of volunteers, so that there is no difference between their math understanding ability measured by some metrics. The two groups are commonly referred to as the test group and the control group. The *test group* (or *treatment group*) is a group of individuals who will experience the medicine, while the *control group* represents the group of users who are set aside as a benchmark, i.e., identical environment setups except taking this medicine. In this way, the influence of all the variables are minimized, except the impact of the independent variable in the treatment.
Second, after a period of taking the medicine, you will need to measure the two groups' math understanding by the same metrics, such as letting the volunteers do the same tests after learning a new math formula. Then, you can collect their performance and compare the results. In this case, our null hypothesis will be that there is no difference between the two groups, and our alternate will be that there is.
This is still not fully formal. There are many details you have to think of carefully. For example, what is the suitable metrics to test their math understanding ability? How many volunteers for your test so you can be confident to claim the effectiveness of your medicine? How long should you run the test? How do you decide if there is a difference between the two groups? Do you care about the average performance only, or also the range of variation of the scores? And so on.
In this way, hypothesis testing provides a framework for experimental design and reasoning about certainty in observed results. If we can now show that the null hypothesis is very unlikely to be true, we may reject it with confidence.
To complete the story of how to work with hypothesis testing, we need to now introduce some additional terminology and make some of our concepts above formal.
### Statistical Significance
The *statistical significance* measures the probability of erroneously rejecting the null hypothesis, $H_0$, when it should not be rejected, i.e.,
$$ \text{statistical significance }= 1 - \alpha = 1 - P(\text{reject } H_0 \mid H_0 \text{ is true} ).$$
It is also referred to as the *type I error* or *false positive*. The $\alpha$, is called as the *significance level* and its commonly used value is $5\%$, i.e., $1-\alpha = 95\%$. The significance level can be explained as the level of risk that we are willing to take, when we reject a true null hypothesis.
:numref:`fig_statistical_significance` shows the observations' values and probability of a given normal distribution in a two-sample hypothesis test. If the observation data example is located outsides the $95\%$ threshold, it will be a very unlikely observation under the null hypothesis assumption. Hence, there might be something wrong with the null hypothesis and we will reject it.

:label:`fig_statistical_significance`
### Statistical Power
The *statistical power* (or *sensitivity*) measures the probability of reject the null hypothesis, $H_0$, when it should be rejected, i.e.,
$$ \text{statistical power }= 1 - \beta = 1 - P(\text{ fail to reject } H_0 \mid H_0 \text{ is false} ).$$
Recall that a *type I error* is error caused by rejecting the null hypothesis when it is true, whereas a *type II error* is resulted from failing to reject the null hypothesis when it is false. A type II error is usually denoted as $\beta$, and hence the corresponding statistical power is $1-\beta$.
Intuitively, statistical power can be interpreted as how likely our test will detect a real discrepancy of some minimum magnitude at a desired statistical significance level. $80\%$ is a commonly used statistical power threshold. The higher the statistical power, the more likely we are to detect true differences.
One of the most common uses of statistical power is in determining the number of samples needed. The probability you reject the null hypothesis when it is false depends on the degree to which it is false (known as the *effect size*) and the number of samples you have. As you might expect, small effect sizes will require a very large number of samples to be detectable with high probability. While beyond the scope of this brief appendix to derive in detail, as an example, want to be able to reject a null hypothesis that our sample came from a mean zero variance one Gaussian, and we believe that our sample's mean is actually close to one, we can do so with acceptable error rates with a sample size of only $8$. However, if we think our sample population true mean is close to $0.01$, then we'd need a sample size of nearly $80000$ to detect the difference.
We can imagine the power as a water filter. In this analogy, a high power hypothesis test is like a high quality water filtration system that will reduce harmful substances in the water as much as possible. On the other hand, a smaller discrepancy is like a low quality water filter, where some relative small substances may easily escape from the gaps. Similarly, if the statistical power is not of enough high power, then the test may not catch the smaller discrepancy.
### Test Statistic
A *test statistic* $T(x)$ is a scalar which summarizes some characteristic of the sample data. The goal of defining such a statistic is that it should allow us to distinguish between different distributions and conduct our hypothesis test. Thinking back to our chemist example, if we wish to show that one population performs better than the other, it could be reasonable to take the mean as the test statistic. Different choices of test statistic can lead to statistical test with drastically different statistical power.
Often, $T(X)$ (the distribution of the test statistic under our null hypothesis) will follow, at least approximately, a common probability distribution such as a normal distribution when considered under the null hypothesis. If we can derive explicitly such a distribution, and then measure our test statistic on our dataset, we can safely reject the null hypothesis if our statistic is far outside the range that we would expect. Making this quantitative leads us to the notion of $p$-values.
### $p$-value
The $p$-value (or the *probability value*) is the probability that $T(X)$ is at least as extreme as the observed test statistic $T(x)$ assuming that the null hypothesis is *true*, i.e.,
$$ p\text{-value} = P_{H_0}(T(X) \geq T(x)).$$
If the $p$-value is smaller than or equal to a predefined and fixed statistical significance level $\alpha$, we may reject the null hypothesis. Otherwise, we will conclude that we are lack of evidence to reject the null hypothesis. For a given population distribution, the *region of rejection* will be the interval contained of all the points which has a $p$-value smaller than the statistical significance level $\alpha$.
### One-side Test and Two-sided Test
Normally there are two kinds of significance test: the one-sided test and the two-sided test. The *one-sided test* (or *one-tailed test*) is applicable when the null hypothesis and the alternative hypothesis only have one direction. For example, the null hypothesis may state that the true parameter $\theta$ is less than or equal to a value $c$. The alternative hypothesis would be that $\theta$ is greater than $c$. That is, the region of rejection is on only one side of the sampling distribution. Contrary to the one-sided test, the *two-sided test* (or *two-tailed test*) is applicable when the region of rejection is on both sides of the sampling distribution. An example in this case may have a null hypothesis state that the true parameter $\theta$ is equal to a value $c$. The alternative hypothesis would be that $\theta$ is not equal to $c$.
### General Steps of Hypothesis Testing
After getting familiar with the above concepts, let us go through the general steps of hypothesis testing.
1. State the question and establish a null hypotheses $H_0$.
2. Set the statistical significance level $\alpha$ and a statistical power ($1 - \beta$).
3. Obtain samples through experiments. The number of samples needed will depend on the statistical power, and the expected effect size.
4. Calculate the test statistic and the $p$-value.
5. Make the decision to keep or reject the null hypothesis based on the $p$-value and the statistical significance level $\alpha$.
To conduct a hypothesis test, we start by defining a null hypothesis and a level of risk that we are willing to take. Then we calculate the test statistic of the sample, taking an extreme value of the test statistic as evidence against the null hypothesis. If the test statistic falls within the reject region, we may reject the null hypothesis in favor of the alternative.
Hypothesis testing is applicable in a variety of scenarios such as the clinical trails and A/B testing.
## Constructing Confidence Intervals
When estimating the value of a parameter $\theta$, point estimators like $\hat \theta$ are of limited utility since they contain no notion of uncertainty. Rather, it would be far better if we could produce an interval that would contain the true parameter $\theta$ with high probability. If you were interested in such ideas a century ago, then you would have been excited to read "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability" by Jerzy Neyman :cite:`Neyman.1937`, who first introduced the concept of confidence interval in 1937.
To be useful, a confidence interval should be as small as possible for a given degree of certainty. Let us see how to derive it.
### Definition
Mathematically, a *confidence interval* for the true parameter $\theta$ is an interval $C_n$ that computed from the sample data such that
$$P_{\theta} (C_n \ni \theta) \geq 1 - \alpha, \forall \theta.$$
:eqlabel:`eq_confidence`
Here $\alpha \in (0, 1)$, and $1 - \alpha$ is called the *confidence level* or *coverage* of the interval. This is the same $\alpha$ as the significance level as we discussed about above.
Note that :eqref:`eq_confidence` is about variable $C_n$, not about the fixed $\theta$. To emphasize this, we write $P_{\theta} (C_n \ni \theta)$ rather than $P_{\theta} (\theta \in C_n)$.
### Interpretation
It is very tempting to interpret a $95\%$ confidence interval as an interval where you can be $95\%$ sure the true parameter lies, however this is sadly not true. The true parameter is fixed, and it is the interval that is random. Thus a better interpretation would be to say that if you generated a large number of confidence intervals by this procedure, $95\%$ of the generated intervals would contain the true parameter.
This may seem pedantic, but it can have real implications for the interpretation of the results. In particular, we may satisfy :eqref:`eq_confidence` by constructing intervals that we are *almost certain* do not contain the true value, as long as we only do so rarely enough. We close this section by providing three tempting but false statements. An in-depth discussion of these points can be found in :cite:`Morey.Hoekstra.Rouder.ea.2016`.
* **Fallacy 1**. Narrow confidence intervals mean we can estimate the parameter precisely.
* **Fallacy 2**. The values inside the confidence interval are more likely to be the true value than those outside the interval.
* **Fallacy 3**. The probability that a particular observed $95\%$ confidence interval contains the true value is $95\%$.
Sufficed to say, confidence intervals are subtle objects. However, if you keep the interpretation clear, they can be powerful tools.
### A Gaussian Example
Let us discuss the most classical example, the confidence interval for the mean of a Gaussian of unknown mean and variance. Suppose we collect $n$ samples $\{x_i\}_{i=1}^n$ from our Gaussian $\mathcal{N}(\mu, \sigma^2)$. We can compute estimators for the mean and standard deviation by taking
$$\hat\mu_n = \frac{1}{n}\sum_{i=1}^n x_i \;\text{and}\; \hat\sigma^2_n = \frac{1}{n-1}\sum_{i=1}^n (x_i - \hat\mu)^2.$$
If we now consider the random variable
$$
T = \frac{\hat\mu_n - \mu}{\hat\sigma_n/\sqrt{n}},
$$
we obtain a random variable following a well-known distribution called the *Student's t-distribution on* $n-1$ *degrees of freedom*.
This distribution is very well studied, and it is known, for instance, that as $n\rightarrow \infty$, it is approximately a standard Gaussian, and thus by looking up values of the Gaussian c.d.f. in a table, we may conclude that the value of $T$ is in the interval $[-1.96, 1.96]$ at least $95\%$ of the time. For finite values of $n$, the interval needs to be somewhat larger, but are well known and precomputed in tables.
Thus, we may conclude that for large $n$,
$$
P\left(\frac{\hat\mu_n - \mu}{\hat\sigma_n/\sqrt{n}} \in [-1.96, 1.96]\right) \ge 0.95.
$$
Rearranging this by multiplying both sides by $\hat\sigma_n/\sqrt{n}$ and then adding $\hat\mu_n$, we obtain
$$
P\left(\mu \in \left[\hat\mu_n - 1.96\frac{\hat\sigma_n}{\sqrt{n}}, \hat\mu_n + 1.96\frac{\hat\sigma_n}{\sqrt{n}}\right]\right) \ge 0.95.
$$
Thus we know that we have found our $95\%$ confidence interval:
$$\left[\hat\mu_n - 1.96\frac{\hat\sigma_n}{\sqrt{n}}, \hat\mu_n + 1.96\frac{\hat\sigma_n}{\sqrt{n}}\right].$$
:eqlabel:`eq_gauss_confidence`
It is safe to say that :eqref:`eq_gauss_confidence` is one of the most used formula in statistics. Let us close our discussion of statistics by implementing it. For simplicity, we assume we are in the asymptotic regime. Small values of $N$ should include the correct value of `t_star` obtained either programmatically or from a $t$-table.
```
# Number of samples
N = 1000
# Sample dataset
samples = np.random.normal(loc=0, scale=1, size=(N,))
# Lookup Students's t-distribution c.d.f.
t_star = 1.96
# Construct interval
mu_hat = np.mean(samples)
sigma_hat = samples.std(ddof=1)
(mu_hat - t_star * sigma_hat / np.sqrt(N),
mu_hat + t_star * sigma_hat / np.sqrt(N))
```
## Summary
* Statistics focuses on inference problems, whereas deep learning emphasizes on making accurate predictions without explicitly programming and understanding.
* There are three common statistics inference methods: evaluating and comparing estimators, conducting hypothesis tests, and constructing confidence intervals.
* There are three most common estimators: statistical bias, standard deviation, and mean square error.
* A confidence interval is an estimated range of a true population parameter that we can construct by given the samples.
* Hypothesis testing is a way of evaluating some evidence against the default statement about a population.
## Exercises
1. Let $X_1, X_2, \ldots, X_n \overset{\text{iid}}{\sim} \mathrm{Unif}(0, \theta)$, where "iid" stands for *independent and identically distributed*. Consider the following estimators of $\theta$:
$$\hat{\theta} = \max \{X_1, X_2, \ldots, X_n \};$$
$$\tilde{\theta} = 2 \bar{X_n} = \frac{2}{n} \sum_{i=1}^n X_i.$$
* Find the statistical bias, standard deviation, and mean square error of $\hat{\theta}.$
* Find the statistical bias, standard deviation, and mean square error of $\tilde{\theta}.$
* Which estimator is better?
1. For our chemist example in introduction, can you derive the 5 steps to conduct a two-sided hypothesis testing? Given the statistical significance level $\alpha = 0.05$ and the statistical power $1 - \beta = 0.8$.
1. Run the confidence interval code with $N=2$ and $\alpha = 0.5$ for $100$ independently generated dataset, and plot the resulting intervals (in this case `t_star = 1.0`). You will see several very short intervals which are very far from containing the true mean $0$. Does this contradict the interpretation of the confidence interval? Do you feel comfortable using short intervals to indicate high precision estimates?
[Discussions](https://discuss.d2l.ai/t/419)
|
github_jupyter
|
import random
from mxnet import np, npx
from d2l import mxnet as d2l
npx.set_np()
# Sample datapoints and create y coordinate
epsilon = 0.1
random.seed(8675309)
xs = np.random.normal(loc=0, scale=1, size=(300,))
ys = [
np.sum(
np.exp(-(xs[:i] - xs[i])**2 /
(2 * epsilon**2)) / np.sqrt(2 * np.pi * epsilon**2)) / len(xs)
for i in range(len(xs))]
# Compute true density
xd = np.arange(np.min(xs), np.max(xs), 0.01)
yd = np.exp(-xd**2 / 2) / np.sqrt(2 * np.pi)
# Plot the results
d2l.plot(xd, yd, 'x', 'density')
d2l.plt.scatter(xs, ys)
d2l.plt.axvline(x=0)
d2l.plt.axvline(x=np.mean(xs), linestyle='--', color='purple')
d2l.plt.title(f'sample mean: {float(np.mean(xs)):.2f}')
d2l.plt.show()
# Statistical bias
def stat_bias(true_theta, est_theta):
return (np.mean(est_theta) - true_theta)
# Mean squared error
def mse(data, true_theta):
return (np.mean(np.square(data - true_theta)))
theta_true = 1
sigma = 4
sample_len = 10000
samples = np.random.normal(theta_true, sigma, sample_len)
theta_est = np.mean(samples)
theta_est
mse(samples, theta_true)
bias = stat_bias(theta_true, theta_est)
np.square(samples.std()) + np.square(bias)
# Number of samples
N = 1000
# Sample dataset
samples = np.random.normal(loc=0, scale=1, size=(N,))
# Lookup Students's t-distribution c.d.f.
t_star = 1.96
# Construct interval
mu_hat = np.mean(samples)
sigma_hat = samples.std(ddof=1)
(mu_hat - t_star * sigma_hat / np.sqrt(N),
mu_hat + t_star * sigma_hat / np.sqrt(N))
| 0.76533 | 0.994396 |
# Style Transfer on ONNX Models with OpenVINO

This notebook demonstrates [Fast Neural Style Transfer](https://github.com/onnx/models/tree/master/vision/style_transfer/fast_neural_style) on ONNX models with OpenVINO. Style Transfer models mix the content of an image with the style of another image.
For this notebook, we use five pretrained models, for the following styles: Mosaic, Rain Princess, Candy, Udnie and Pointilism. The models are from the [ONNX Model Repository](https://github.com/onnx/models) and are based on the research paper [Perceptual Losses for Real-Time Style Transfer and Super-Resolution](https://arxiv.org/abs/1603.08155) by Justin Johnson, Alexandre Alahi and Li Fei-Fei.
## Preparation
### Imports
```
import sys
from enum import Enum
from pathlib import Path
import cv2
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import HTML, FileLink, clear_output, display
from openvino.runtime import Core, PartialShape
from yaspin import yaspin
sys.path.append("../utils")
from notebook_utils import download_file
```
### Download Models
The `Style` Enum lists the supported styles with url, title and model path properties. Models for all supported styles will be downloaded to `MODEL_DIR` if they have not been downloaded before.
```
BASE_URL = "https://github.com/onnx/models/raw/main/vision/style_transfer/fast_neural_style/model"
MODEL_DIR = "model"
class Style(Enum):
MOSAIC = "mosaic"
RAIN_PRINCESS = "rain-princess"
CANDY = "candy"
UDNIE = "udnie"
POINTILISM = "pointilism"
def __init__(self, *args):
self.model_path = Path(f"{self.value}-9.onnx")
self.title = self.value.replace("-", " ").title()
self.url = f"{BASE_URL}/{self.model_path}"
for style in Style:
if not Path(f"{MODEL_DIR}/{style.model_path}").exists():
download_file(style.url, directory=MODEL_DIR)
```
### Load Image
Load an image with OpenCV and convert it to RGB. The style transfer model will be resized to the image shape. This gives the most detailed results, but for larger images, inference will take longer and use more memory. The `resize_to_max` function optionally resizes the image to a maximum size.
```
IMAGE_FILE = "data/coco_square.jpg"
image = cv2.cvtColor(cv2.imread(IMAGE_FILE), cv2.COLOR_BGR2RGB)
def resize_to_max(image: np.ndarray, max_side: int) -> np.ndarray:
"""
Resize image to an image where the largest side has a maximum length of max_side
while keeping aspect ratio. Example: if an original image has width and height of (1000, 500)
and max_side is 300, the resized image will have a width and height of (300, 150).
:param image: Array of image to resize
:param max_side: Maximum length of largest image side
:return: Resized image
"""
if max(image.shape) <= max_side:
new_image = image
else:
index = np.argmax(image.shape)
factor = max_side / image.shape[index]
height, width = image.shape[:2]
new_height, new_width = int(factor * height), int(factor * width)
new_image = cv2.resize(image, (new_width, new_height))
return new_image
# Uncomment the line below to resize large images to a max side length to improve inference speed.
# image = resize_to_max(image=image, max_side=1024)
```
## Do Inference and Show Results
For all five models: do inference, convert the result to an 8-bit image, show the results, and save the results to disk.
```
# Set SAVE_RESULTS to False to disable saving the result images.
SAVE_RESULTS = True
# find reasonable dimensions for matplotlib plot
wh_ratio = image.shape[1] / image.shape[0]
figwidth = 15
figheight = (figwidth * 0.75) // wh_ratio
# Create matplotlib plot and show source image
fig, ax = plt.subplots(2, 3, figsize=(figwidth, figheight))
axs = ax.ravel()
axs[0].imshow(image)
axs[0].set_title("Source Image")
axs[0].axis("off")
# Create Core instance, prepare output folder
ie = Core()
output_folder = Path("output")
output_folder.mkdir(exist_ok=True)
# Transpose input image to network dimensions and extract image name and shape
input_image = np.expand_dims(image.transpose(2, 0, 1), axis=0)
image_name = Path(IMAGE_FILE).stem
image_shape_str = f"{image.shape[1]}x{image.shape[0]}"
file_links = []
for i, style in enumerate(Style):
# Load model and get model info
model = ie.read_model(model=Path(MODEL_DIR) / style.model_path)
input_key = list(model.inputs)[0]
# Reshape network to image shape and load network to device
model.reshape({input_key: PartialShape([1, 3, image.shape[0], image.shape[1]])})
compiled_model = ie.compile_model(model=model, device_name="CPU")
output_key = list(compiled_model.outputs)[0]
# Do inference
with yaspin(text=f"Doing inference on {style.title} model") as sp:
request = compiled_model.create_infer_request()
request.infer(inputs={input_key.any_name: input_image})
result = request.get_output_tensor(output_key.index).data
result = compiled_model([input_image])[output_key]
sp.ok("✔")
# Convert inference result to image shape and apply postprocessing
# Postprocessing is described in the model documentation:
# https://github.com/onnx/models/tree/master/vision/style_transfer/fast_neural_style
result = result.squeeze().transpose(1, 2, 0)
result = np.clip(result, 0, 255).astype(np.uint8)
# Show the result
axs[i + 1].imshow(result)
axs[i + 1].set_title(style.title)
axs[i + 1].axis("off")
# Optionally save results to disk
if SAVE_RESULTS:
image_path = f"{image_name}_{style.model_path.stem}_{image_shape_str}.png"
output_path = output_folder / image_path
cv2.imwrite(str(output_path), cv2.cvtColor(result, cv2.COLOR_BGR2RGB))
file_link = FileLink(output_path, result_html_prefix=f"{style.title} image: ")
file_link.html_link_str = "<a href='%s' download>%s</a>"
file_links.append(file_link)
del model
del compiled_model
clear_output(wait=True)
fig.tight_layout()
plt.show()
if SAVE_RESULTS:
output_path = output_folder / f"{image_name}_{image_shape_str}_style_transfer.jpg"
fig.savefig(str(output_path), dpi=300, bbox_inches="tight", pad_inches=0.1)
file_link = FileLink(output_path, result_html_prefix="Overview image: ")
file_link.html_link_str = "<a href='%s' download>%s</a>"
file_links.append(file_link)
display(HTML("Saved image files:"))
for file_link in file_links:
display(HTML(file_link._repr_html_()))
```
|
github_jupyter
|
import sys
from enum import Enum
from pathlib import Path
import cv2
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import HTML, FileLink, clear_output, display
from openvino.runtime import Core, PartialShape
from yaspin import yaspin
sys.path.append("../utils")
from notebook_utils import download_file
BASE_URL = "https://github.com/onnx/models/raw/main/vision/style_transfer/fast_neural_style/model"
MODEL_DIR = "model"
class Style(Enum):
MOSAIC = "mosaic"
RAIN_PRINCESS = "rain-princess"
CANDY = "candy"
UDNIE = "udnie"
POINTILISM = "pointilism"
def __init__(self, *args):
self.model_path = Path(f"{self.value}-9.onnx")
self.title = self.value.replace("-", " ").title()
self.url = f"{BASE_URL}/{self.model_path}"
for style in Style:
if not Path(f"{MODEL_DIR}/{style.model_path}").exists():
download_file(style.url, directory=MODEL_DIR)
IMAGE_FILE = "data/coco_square.jpg"
image = cv2.cvtColor(cv2.imread(IMAGE_FILE), cv2.COLOR_BGR2RGB)
def resize_to_max(image: np.ndarray, max_side: int) -> np.ndarray:
"""
Resize image to an image where the largest side has a maximum length of max_side
while keeping aspect ratio. Example: if an original image has width and height of (1000, 500)
and max_side is 300, the resized image will have a width and height of (300, 150).
:param image: Array of image to resize
:param max_side: Maximum length of largest image side
:return: Resized image
"""
if max(image.shape) <= max_side:
new_image = image
else:
index = np.argmax(image.shape)
factor = max_side / image.shape[index]
height, width = image.shape[:2]
new_height, new_width = int(factor * height), int(factor * width)
new_image = cv2.resize(image, (new_width, new_height))
return new_image
# Uncomment the line below to resize large images to a max side length to improve inference speed.
# image = resize_to_max(image=image, max_side=1024)
# Set SAVE_RESULTS to False to disable saving the result images.
SAVE_RESULTS = True
# find reasonable dimensions for matplotlib plot
wh_ratio = image.shape[1] / image.shape[0]
figwidth = 15
figheight = (figwidth * 0.75) // wh_ratio
# Create matplotlib plot and show source image
fig, ax = plt.subplots(2, 3, figsize=(figwidth, figheight))
axs = ax.ravel()
axs[0].imshow(image)
axs[0].set_title("Source Image")
axs[0].axis("off")
# Create Core instance, prepare output folder
ie = Core()
output_folder = Path("output")
output_folder.mkdir(exist_ok=True)
# Transpose input image to network dimensions and extract image name and shape
input_image = np.expand_dims(image.transpose(2, 0, 1), axis=0)
image_name = Path(IMAGE_FILE).stem
image_shape_str = f"{image.shape[1]}x{image.shape[0]}"
file_links = []
for i, style in enumerate(Style):
# Load model and get model info
model = ie.read_model(model=Path(MODEL_DIR) / style.model_path)
input_key = list(model.inputs)[0]
# Reshape network to image shape and load network to device
model.reshape({input_key: PartialShape([1, 3, image.shape[0], image.shape[1]])})
compiled_model = ie.compile_model(model=model, device_name="CPU")
output_key = list(compiled_model.outputs)[0]
# Do inference
with yaspin(text=f"Doing inference on {style.title} model") as sp:
request = compiled_model.create_infer_request()
request.infer(inputs={input_key.any_name: input_image})
result = request.get_output_tensor(output_key.index).data
result = compiled_model([input_image])[output_key]
sp.ok("✔")
# Convert inference result to image shape and apply postprocessing
# Postprocessing is described in the model documentation:
# https://github.com/onnx/models/tree/master/vision/style_transfer/fast_neural_style
result = result.squeeze().transpose(1, 2, 0)
result = np.clip(result, 0, 255).astype(np.uint8)
# Show the result
axs[i + 1].imshow(result)
axs[i + 1].set_title(style.title)
axs[i + 1].axis("off")
# Optionally save results to disk
if SAVE_RESULTS:
image_path = f"{image_name}_{style.model_path.stem}_{image_shape_str}.png"
output_path = output_folder / image_path
cv2.imwrite(str(output_path), cv2.cvtColor(result, cv2.COLOR_BGR2RGB))
file_link = FileLink(output_path, result_html_prefix=f"{style.title} image: ")
file_link.html_link_str = "<a href='%s' download>%s</a>"
file_links.append(file_link)
del model
del compiled_model
clear_output(wait=True)
fig.tight_layout()
plt.show()
if SAVE_RESULTS:
output_path = output_folder / f"{image_name}_{image_shape_str}_style_transfer.jpg"
fig.savefig(str(output_path), dpi=300, bbox_inches="tight", pad_inches=0.1)
file_link = FileLink(output_path, result_html_prefix="Overview image: ")
file_link.html_link_str = "<a href='%s' download>%s</a>"
file_links.append(file_link)
display(HTML("Saved image files:"))
for file_link in file_links:
display(HTML(file_link._repr_html_()))
| 0.610453 | 0.951051 |
```
!wget https://download.pytorch.org/tutorial/hymenoptera_data.zip -P data/
!unzip -d data data/hymenoptera_data.zip
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
import torchvision
from torchvision import datasets, models
from torchvision import transforms as T
import numpy as np
import matplotlib.pyplot as plt
import time
import os
import copy
plt.ion()
data_transforms = {
'train': T.Compose([
T.RandomResizedCrop(224),
T.RandomHorizontalFlip(),
T.ToTensor(),
T.Normalize(
[0.485, 0.456, 0.406], [0.229, 0.224, 0.225]
)
]),
'val': T.Compose([
T.Resize(256),
T.CenterCrop(224),
T.ToTensor(),
T.Normalize(
[0.485, 0.456, 0.406], [0.229, 0.224, 0.225]
)
])
}
data_dir = './data/hymenoptera_data'
image_datasets = {x: datasets.ImageFolder(os.path.join(data_dir, x), data_transforms[x]) for x in ['train', 'val']}
dataloaders = {x: torch.utils.data.DataLoader(image_datasets[x], batch_size=4, shuffle=True, num_workers=4) for x in ['train', 'val']}
dataset_sizes = {x: len(image_datasets[x]) for x in ['train', 'val']}
class_names = image_datasets['train'].classes
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
def imshow(inp, title=None):
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.01)
inputs, classes = next(iter(dataloaders['train']))
out = torchvision.utils.make_grid(inputs)
imshow(out, title=[class_names[x] for x in classes])
def train_model(model, criterion, optimizer, scheduler, num_epochs=25):
since = time.time()
best_model_weights = copy.deepcopy(model.state_dict())
best_acc = 0.0
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch, num_epochs - 1))
print('-' * 10)
for phase in ['train', 'val']:
if phase == 'train':
model.train()
else:
model.eval()
running_loss = 0.0
running_corrects = 0
for inputs, labels in dataloaders[phase]:
inputs, labels = inputs.to(device), labels.to(device)
optimizer.zero_grad()
with torch.set_grad_enabled(phase == 'train'):
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
if phase == 'train':
loss.backward()
optimizer.step()
running_loss += loss.item() * inputs.size(0)
running_corrects += torch.sum(preds == labels.data)
if phase == 'train':
scheduler.step()
epoch_loss = running_loss / dataset_sizes[phase]
epoch_acc = running_corrects.double() / dataset_size[phase]
print('{} Loss: {:.4f} Acc: {:.4f}'.format(phase, epoch_loss, epoch_acc))
if phase == 'val' and epoch_acc > best_acc:
best_acc = epoch_acc
best_model_weights = copy.deepcopy(model.state_dict())
print()
time_elapsed = time.time() - since
print('Training complete in {:.0f}m {:.0f}s'.format(time_elapsed // 60, time_elapsed % 60))
print('Best val Acc: {:4f}'.format(best_acc))
model.load_state_dict(best_model_weights)
return model
def visualize_model(model, num_images=6):
was_training = model.training
model.eval()
images_so_far = 0
fig = plt.figure()
with torch.no_grad():
for i, (inputs, labels) in enumerate(dataloaders['val']):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images//2, 2, images_so_far)
ax.axis('off')
ax.set_title('predicted: {}'.format(class_names[preds[j]]))
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
model.train(mode=was_training)
return
model.train(mode=was_training)
model_ft = models.resnet18(pretrained=True)
num_features = model_ft.fc.in_features
model_ft.fc = nn.Linear(num_features, 2)
model_ft = model_ft.to(device)
criterion = nn.CrossEntropyLoss()
optimizer_ft = optim.SGD(model_ft.parameters(), lr=0.001, momentum=0.9)
exp_lr_scheduler = lr_scheduler.StepLR(optimizer_ft, step_size=7, gamma=0.1)
model_ft = train_model(model_ft, criterion, optimizer_ft, exp_lr_scheduler, num_epochs=25)
visualize_model(model_ft)
model_conv = models.resnet18(pretrained=True)
for param in model_conv.parameters():
param.requires_grad = False
num_features = model_conv.fc.in_features
model_conv.fc = nn.Linear(num_features, 2)
model_conv = model_conv.to(device)
criterion = nn.CrossEntropyLoss()
optim_conv = optim.SGD(model_conv.parameters(), lr=0.001, momentum=0.9)
exp_lr_scheduler = lr_scheduler.StepLR(optim_conv, step_size=7, gamma=0.1)
model_conv = train_model(model_conv, criterion, optim_conv, exp_lr_scheduler, num_epochs=25)
visualize_model(model_conv)
```
|
github_jupyter
|
!wget https://download.pytorch.org/tutorial/hymenoptera_data.zip -P data/
!unzip -d data data/hymenoptera_data.zip
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
import torchvision
from torchvision import datasets, models
from torchvision import transforms as T
import numpy as np
import matplotlib.pyplot as plt
import time
import os
import copy
plt.ion()
data_transforms = {
'train': T.Compose([
T.RandomResizedCrop(224),
T.RandomHorizontalFlip(),
T.ToTensor(),
T.Normalize(
[0.485, 0.456, 0.406], [0.229, 0.224, 0.225]
)
]),
'val': T.Compose([
T.Resize(256),
T.CenterCrop(224),
T.ToTensor(),
T.Normalize(
[0.485, 0.456, 0.406], [0.229, 0.224, 0.225]
)
])
}
data_dir = './data/hymenoptera_data'
image_datasets = {x: datasets.ImageFolder(os.path.join(data_dir, x), data_transforms[x]) for x in ['train', 'val']}
dataloaders = {x: torch.utils.data.DataLoader(image_datasets[x], batch_size=4, shuffle=True, num_workers=4) for x in ['train', 'val']}
dataset_sizes = {x: len(image_datasets[x]) for x in ['train', 'val']}
class_names = image_datasets['train'].classes
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
def imshow(inp, title=None):
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.01)
inputs, classes = next(iter(dataloaders['train']))
out = torchvision.utils.make_grid(inputs)
imshow(out, title=[class_names[x] for x in classes])
def train_model(model, criterion, optimizer, scheduler, num_epochs=25):
since = time.time()
best_model_weights = copy.deepcopy(model.state_dict())
best_acc = 0.0
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch, num_epochs - 1))
print('-' * 10)
for phase in ['train', 'val']:
if phase == 'train':
model.train()
else:
model.eval()
running_loss = 0.0
running_corrects = 0
for inputs, labels in dataloaders[phase]:
inputs, labels = inputs.to(device), labels.to(device)
optimizer.zero_grad()
with torch.set_grad_enabled(phase == 'train'):
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
if phase == 'train':
loss.backward()
optimizer.step()
running_loss += loss.item() * inputs.size(0)
running_corrects += torch.sum(preds == labels.data)
if phase == 'train':
scheduler.step()
epoch_loss = running_loss / dataset_sizes[phase]
epoch_acc = running_corrects.double() / dataset_size[phase]
print('{} Loss: {:.4f} Acc: {:.4f}'.format(phase, epoch_loss, epoch_acc))
if phase == 'val' and epoch_acc > best_acc:
best_acc = epoch_acc
best_model_weights = copy.deepcopy(model.state_dict())
print()
time_elapsed = time.time() - since
print('Training complete in {:.0f}m {:.0f}s'.format(time_elapsed // 60, time_elapsed % 60))
print('Best val Acc: {:4f}'.format(best_acc))
model.load_state_dict(best_model_weights)
return model
def visualize_model(model, num_images=6):
was_training = model.training
model.eval()
images_so_far = 0
fig = plt.figure()
with torch.no_grad():
for i, (inputs, labels) in enumerate(dataloaders['val']):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images//2, 2, images_so_far)
ax.axis('off')
ax.set_title('predicted: {}'.format(class_names[preds[j]]))
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
model.train(mode=was_training)
return
model.train(mode=was_training)
model_ft = models.resnet18(pretrained=True)
num_features = model_ft.fc.in_features
model_ft.fc = nn.Linear(num_features, 2)
model_ft = model_ft.to(device)
criterion = nn.CrossEntropyLoss()
optimizer_ft = optim.SGD(model_ft.parameters(), lr=0.001, momentum=0.9)
exp_lr_scheduler = lr_scheduler.StepLR(optimizer_ft, step_size=7, gamma=0.1)
model_ft = train_model(model_ft, criterion, optimizer_ft, exp_lr_scheduler, num_epochs=25)
visualize_model(model_ft)
model_conv = models.resnet18(pretrained=True)
for param in model_conv.parameters():
param.requires_grad = False
num_features = model_conv.fc.in_features
model_conv.fc = nn.Linear(num_features, 2)
model_conv = model_conv.to(device)
criterion = nn.CrossEntropyLoss()
optim_conv = optim.SGD(model_conv.parameters(), lr=0.001, momentum=0.9)
exp_lr_scheduler = lr_scheduler.StepLR(optim_conv, step_size=7, gamma=0.1)
model_conv = train_model(model_conv, criterion, optim_conv, exp_lr_scheduler, num_epochs=25)
visualize_model(model_conv)
| 0.836688 | 0.817319 |
```
!pip install coremltools
# Initialise packages
from u2net import U2NETP
import coremltools as ct
from coremltools.proto import FeatureTypes_pb2 as ft
import torch
import torch.nn as nn
from torch.autograd import Variable
import os
import numpy as np
from PIL import Image
from torchvision import transforms
from skimage import io, transform
class WrappedModel(nn.Module):
def __init__(self):
super(WrappedModel, self).__init__()
self.model = U2NETP(3,1)
self.model.load_state_dict(torch.load("u2netp.pth", map_location=torch.device('cpu')))
self.model.cpu()
self.model.eval()
def normPRED(self, d):
ma = torch.max(d)
mi = torch.min(d)
dn = (d-mi)/(ma-mi)
return dn
def forward(self, x):
d1,d2,d3,d4,d5,d6,d7 = self.model(x)
'''
d1 = self.normPRED(d1)
d2 = self.normPRED(d2)
d3 = self.normPRED(d3)
d4 = self.normPRED(d4)
d5 = self.normPRED(d5)
d6 = self.normPRED(d6)
d7 = self.normPRED(d7)
'''
return d1,d2,d3,d4,d5,d6,d7
from torchvision import transforms
def save_output(pred, image):
print(pred.shape)
predict = pred
predict = predict.squeeze()
print(predict.shape)
predict_np = predict.cpu().data.numpy()
im = Image.fromarray(predict_np * 255).convert('RGB')
imo = im.resize((image.size[0],image.size[1]),resample=Image.BILINEAR)
display(imo)
def tensor_lab(sample):
image = sample
tmpImg = np.zeros((image.shape[0],image.shape[1],3))
image = image/np.max(image)
tmpImg[:,:,0] = (image[:,:,0]-0.485)/0.229
tmpImg[:,:,1] = (image[:,:,1]-0.456)/0.224
tmpImg[:,:,2] = (image[:,:,2]-0.406)/0.225
# change the r,g,b to b,r,g from [0,255] to [0,1]
tmpImg = tmpImg.transpose((2, 0, 1))
return torch.from_numpy(tmpImg)
# Pre-processing
def input_test_image(image_name):
inputs_test = Image.open(image_name)
inputs_test = inputs_test.resize((320, 320))
inputs_test = np.asarray(inputs_test)
inputs_test = tensor_lab(inputs_test)
inputs_test = inputs_test.unsqueeze_(0)
inputs_test = inputs_test.type(torch.FloatTensor)
return inputs_test
'''
def input_test_image(image_name):
inputs_test = Image.open(image_name)
inputs_test = inputs_test.resize((320, 320))
inputs_test = transforms.ToTensor()(inputs_test).unsqueeze_(0)
inputs_test = inputs_test.type(torch.FloatTensor)
return inputs_test
'''
image_name = "0002-01.jpg"
input_image = input_test_image(image_name)
net = WrappedModel()
d1,d2,d3,d4,d5,d6,d7 = net(input_image)
save_output(d1, Image.open(image_name))
# Initialise Baseline UNETP model.
net = U2NETP(3,1)
device = torch.device('cpu')
net.load_state_dict(torch.load("u2netp.pth", map_location=device))
net.cpu()
net.eval()
# Trace the model.
image_name = "0002-01.jpg"
input_image = input_test_image(image_name)
print(input_image.shape)
traced_model = torch.jit.trace(net, input_image)
# Convert the model
_inputs = ct.ImageType(
name= "input_1",
shape= input_image.shape,
bias=[-0.485/0.229,
-0.456/0.224,
-0.406/0.225],
scale=1.0/255.0
)
model = ct.convert(traced_model, inputs=[_inputs])
# Add metadata
model.short_description = "U2-Net: Going Deeper with Nested U-Structure for Salient Object Detection"
model.license = "Apache 2.0"
model.author = "Qin, Xuebin and Zhang, Zichen and Huang, Chenyang and Dehghan, Masood and Zaiane, Osmar and Jagersand, Martin"
# Rename inputs
spec = model.get_spec()
ct.utils.rename_feature(spec, "input_1", "in_0")
ct.utils.rename_feature(spec,"2169","out_a0")
ct.utils.rename_feature(spec,"2170","out_a1")
ct.utils.rename_feature(spec,"2171","out_a2")
ct.utils.rename_feature(spec,"2172","out_a3")
ct.utils.rename_feature(spec,"2173","out_a4")
ct.utils.rename_feature(spec,"2174","out_a5")
ct.utils.rename_feature(spec,"2175","out_a6")
model = ct.models.MLModel(spec)
model.save("u2netp_temp.mlmodel")
# Re-open model for modification
model = ct.models.MLModel("u2netp_temp.mlmodel")
# Get the model specifications
spec = model.get_spec()
# Change model input and save
input = spec.description.input[0]
input.type.imageType.colorSpace = ft.ImageFeatureType.BGR
input.type.imageType.height = 320
input.type.imageType.width = 320
ct.utils.save_spec(spec, "u2netp_temp_new_input.mlmodel")
# Re-open model for modification
model = ct.models.MLModel("u2netp_temp_new_input.mlmodel")
spec = model.get_spec()
spec_layers = getattr(spec, spec.WhichOneof("Type")).layers
output_layers = spec_layers[476:] # Get only the last output layers, may change with full-size U^2net
# Append new layers
new_layers = []
layernum = 0;
for layer in output_layers:
new_layer = spec_layers.add()
new_layer.name = 'out_p' + str(layernum)
new_layers.append('out_p' + str(layernum))
new_layer.activation.linear.alpha = 255
new_layer.activation.linear.beta = 0
new_layer.input.append('out_a' + str(layernum))
new_layer.output.append('out_p' + str(layernum))
output_description = next(x for x in spec.description.output if x.name==output_layers[layernum].output[0])
output_description.name = new_layer.name
layernum = layernum + 1
# Specify the outputs as grayscale images.
for output in spec.description.output:
if output.name not in new_layers:
continue
if output.type.WhichOneof('Type') != 'multiArrayType':
raise ValueError("%s is not a multiarray type" % output.name)
array_shape = tuple(output.type.multiArrayType.shape)
# print(array_shape)
# print(output.type)
output.type.imageType.colorSpace = ft.ImageFeatureType.ColorSpace.Value('GRAYSCALE')
output.type.imageType.width = 320
output.type.imageType.height = 320
updated_model = ct.models.MLModel(spec)
model.short_description = "U2-Net: Going Deeper with Nested U-Structure for Salient Object Detection"
model.license = "Apache 2.0"
model.author = "Qin, Xuebin and Zhang, Zichen and Huang, Chenyang and Dehghan, Masood and Zaiane, Osmar and Jagersand, Martin"
updated_model.save("updated_model.mlmodel")
```
|
github_jupyter
|
!pip install coremltools
# Initialise packages
from u2net import U2NETP
import coremltools as ct
from coremltools.proto import FeatureTypes_pb2 as ft
import torch
import torch.nn as nn
from torch.autograd import Variable
import os
import numpy as np
from PIL import Image
from torchvision import transforms
from skimage import io, transform
class WrappedModel(nn.Module):
def __init__(self):
super(WrappedModel, self).__init__()
self.model = U2NETP(3,1)
self.model.load_state_dict(torch.load("u2netp.pth", map_location=torch.device('cpu')))
self.model.cpu()
self.model.eval()
def normPRED(self, d):
ma = torch.max(d)
mi = torch.min(d)
dn = (d-mi)/(ma-mi)
return dn
def forward(self, x):
d1,d2,d3,d4,d5,d6,d7 = self.model(x)
'''
d1 = self.normPRED(d1)
d2 = self.normPRED(d2)
d3 = self.normPRED(d3)
d4 = self.normPRED(d4)
d5 = self.normPRED(d5)
d6 = self.normPRED(d6)
d7 = self.normPRED(d7)
'''
return d1,d2,d3,d4,d5,d6,d7
from torchvision import transforms
def save_output(pred, image):
print(pred.shape)
predict = pred
predict = predict.squeeze()
print(predict.shape)
predict_np = predict.cpu().data.numpy()
im = Image.fromarray(predict_np * 255).convert('RGB')
imo = im.resize((image.size[0],image.size[1]),resample=Image.BILINEAR)
display(imo)
def tensor_lab(sample):
image = sample
tmpImg = np.zeros((image.shape[0],image.shape[1],3))
image = image/np.max(image)
tmpImg[:,:,0] = (image[:,:,0]-0.485)/0.229
tmpImg[:,:,1] = (image[:,:,1]-0.456)/0.224
tmpImg[:,:,2] = (image[:,:,2]-0.406)/0.225
# change the r,g,b to b,r,g from [0,255] to [0,1]
tmpImg = tmpImg.transpose((2, 0, 1))
return torch.from_numpy(tmpImg)
# Pre-processing
def input_test_image(image_name):
inputs_test = Image.open(image_name)
inputs_test = inputs_test.resize((320, 320))
inputs_test = np.asarray(inputs_test)
inputs_test = tensor_lab(inputs_test)
inputs_test = inputs_test.unsqueeze_(0)
inputs_test = inputs_test.type(torch.FloatTensor)
return inputs_test
'''
def input_test_image(image_name):
inputs_test = Image.open(image_name)
inputs_test = inputs_test.resize((320, 320))
inputs_test = transforms.ToTensor()(inputs_test).unsqueeze_(0)
inputs_test = inputs_test.type(torch.FloatTensor)
return inputs_test
'''
image_name = "0002-01.jpg"
input_image = input_test_image(image_name)
net = WrappedModel()
d1,d2,d3,d4,d5,d6,d7 = net(input_image)
save_output(d1, Image.open(image_name))
# Initialise Baseline UNETP model.
net = U2NETP(3,1)
device = torch.device('cpu')
net.load_state_dict(torch.load("u2netp.pth", map_location=device))
net.cpu()
net.eval()
# Trace the model.
image_name = "0002-01.jpg"
input_image = input_test_image(image_name)
print(input_image.shape)
traced_model = torch.jit.trace(net, input_image)
# Convert the model
_inputs = ct.ImageType(
name= "input_1",
shape= input_image.shape,
bias=[-0.485/0.229,
-0.456/0.224,
-0.406/0.225],
scale=1.0/255.0
)
model = ct.convert(traced_model, inputs=[_inputs])
# Add metadata
model.short_description = "U2-Net: Going Deeper with Nested U-Structure for Salient Object Detection"
model.license = "Apache 2.0"
model.author = "Qin, Xuebin and Zhang, Zichen and Huang, Chenyang and Dehghan, Masood and Zaiane, Osmar and Jagersand, Martin"
# Rename inputs
spec = model.get_spec()
ct.utils.rename_feature(spec, "input_1", "in_0")
ct.utils.rename_feature(spec,"2169","out_a0")
ct.utils.rename_feature(spec,"2170","out_a1")
ct.utils.rename_feature(spec,"2171","out_a2")
ct.utils.rename_feature(spec,"2172","out_a3")
ct.utils.rename_feature(spec,"2173","out_a4")
ct.utils.rename_feature(spec,"2174","out_a5")
ct.utils.rename_feature(spec,"2175","out_a6")
model = ct.models.MLModel(spec)
model.save("u2netp_temp.mlmodel")
# Re-open model for modification
model = ct.models.MLModel("u2netp_temp.mlmodel")
# Get the model specifications
spec = model.get_spec()
# Change model input and save
input = spec.description.input[0]
input.type.imageType.colorSpace = ft.ImageFeatureType.BGR
input.type.imageType.height = 320
input.type.imageType.width = 320
ct.utils.save_spec(spec, "u2netp_temp_new_input.mlmodel")
# Re-open model for modification
model = ct.models.MLModel("u2netp_temp_new_input.mlmodel")
spec = model.get_spec()
spec_layers = getattr(spec, spec.WhichOneof("Type")).layers
output_layers = spec_layers[476:] # Get only the last output layers, may change with full-size U^2net
# Append new layers
new_layers = []
layernum = 0;
for layer in output_layers:
new_layer = spec_layers.add()
new_layer.name = 'out_p' + str(layernum)
new_layers.append('out_p' + str(layernum))
new_layer.activation.linear.alpha = 255
new_layer.activation.linear.beta = 0
new_layer.input.append('out_a' + str(layernum))
new_layer.output.append('out_p' + str(layernum))
output_description = next(x for x in spec.description.output if x.name==output_layers[layernum].output[0])
output_description.name = new_layer.name
layernum = layernum + 1
# Specify the outputs as grayscale images.
for output in spec.description.output:
if output.name not in new_layers:
continue
if output.type.WhichOneof('Type') != 'multiArrayType':
raise ValueError("%s is not a multiarray type" % output.name)
array_shape = tuple(output.type.multiArrayType.shape)
# print(array_shape)
# print(output.type)
output.type.imageType.colorSpace = ft.ImageFeatureType.ColorSpace.Value('GRAYSCALE')
output.type.imageType.width = 320
output.type.imageType.height = 320
updated_model = ct.models.MLModel(spec)
model.short_description = "U2-Net: Going Deeper with Nested U-Structure for Salient Object Detection"
model.license = "Apache 2.0"
model.author = "Qin, Xuebin and Zhang, Zichen and Huang, Chenyang and Dehghan, Masood and Zaiane, Osmar and Jagersand, Martin"
updated_model.save("updated_model.mlmodel")
| 0.821617 | 0.38523 |
# Basics of Deep Learning
In this notebook, we will cover the basics behind Deep Learning. I'm talking about building a brain....

Only kidding. Deep learning is a fascinating new field that has exploded over the last few years. From being used as facial recognition in apps such as Snapchat or challenger banks, to more advanced use cases such as being used in [protein-folding](https://www.independent.co.uk/life-style/gadgets-and-tech/protein-folding-ai-deepmind-google-cancer-covid-b1764008.html).
In this notebook we will:
- Explain the building blocks of neural networks
- Go over some applications of Deep Learning
## Building blocks of Neural Networks
I have no doubt that you have heard/seen how similar neural networks are to....our brains.
### The Perceptron
The building block of neural networks. The perceptron has a rich history (covered in the background section of this book). The perceptron was created in 1958 by Frank Rosenblatt (I love that name) in Cornell, however, that story is for another day....or section in this book (backgrounds!),
The perceptron is an algorithm that can learn a binary classifier (e.g. is that a cat or dog?). This is known as a threshold function, which maps an input vector *x* to an output decision *$f(x)$ = output*. Here is the formal maths to better explain my verbal fluff:
$ f(x) = { 1 (if: w.x+b > 0), 0 (otherwise) $
### The Artificial neural network
Lets take a look at the high level architecture first.

The gif above of a neural network classifying images is one of the best visual ways of understanding how neural networks, work. The neural network is made up of a few key concepts:
- An input: this is the data you pass into the network. For example, data relating to a customer (e.g. height, weight etc) or the pixels of an image
- An output: this is the prediction of the neural network
- A hidden layer: more on this later
- Neuron: the network is made up of neurons, that take an input, and give an output
Now, we have a slightly better understanding of what a neuron is. Lets look at a very simple neuron:
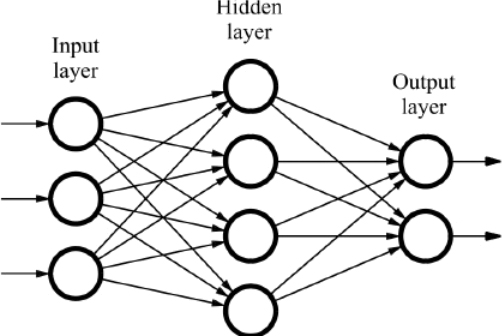
From the above image, you can clearly see the three components listed above together.
### But Abdi, what is the goal of a neural network?
Isn't it obvious? To me, it definitely was not when I first started to learn about neural networks. Neural networks are beautifully complex to understand, but with enough time and lots of youtube videos, you'll be able to master this topic.
The goal of a neural network is to make a pretty good guess of something. For example, a phone may have a face unlock feature. The phone probably got you to take a short video/images of yourself in order to set up this security feature, and when it **learned** your face, you were then able to use it to unlock your phone. This is pretty much what we do with neural networks. We teach it by giving it data, and making sure it gets better at making predictions by adjusting the weights between neurons. More on this soon.
## Gradient Descent Algo
One of the best videos on neural networks, by 3Blue1Brown:
<figure class="video_container">
<iframe src="https://www.youtube.com/watch?v=aircAruvnKk" frameborder="0" allowfullscreen="true"> </iframe>
</figure>
His series on Neural networks and Linear algebra are golden sources for learning Deep Learning.
### Simple Gradient Descent Implementation
with the help from our friends over at Udacity, please view below an implementation of the Gradient Descent Algo. This is a very basic neural network that only has its inputs linked directly to the outputs.
We begin by defining some functions.
```
import numpy as np
# We will be using a sigmoid activation function
def sigmoid(x):
return 1/(1+np.exp(-x))
# derivation of sigmoid(x) - will be used for backpropagating errors through the network
def sigmoid_prime(x):
return sigmoid(x)*(1-sigmoid(x))
```
We begin by defining a simple neural network:
- two input neurons: x1 and x2
- one output neuron: y1
```
x = np.array([1,5])
y = 0.4
```
We now define the weights, w1 and w2 for the two input neurons; x1 and x2. Also, we define a learning rate that will help us control our gradient descent step
```
weights = np.array([-0.2,0.4])
learnrate = 0.5
```
we now start moving forwards through the network, known as feed forward. We can combine the input vector with the weight vector using numpy's dot product
```
# linear combination
# h = x[0]*weights[0] + x[1]*weights[1]
h = np.dot(x, weights)
```
We now apply our non-linearity, this will provide us with our output.
```
# apply non-linearity
output = sigmoid(h)
```
Now that we have our prediction, we are able to determine the error of our neural network. Here, we will use the difference between our actual and predicted.
```
error = y - output
```
The goal now is to determine how to change our weights in order to reduce the error above. This is where our good friend gradient descent and the chain rule come into play:
- we determine the derivative of our error with respect to our input weights. Hence:
- change in weights = $ \frac{d}{dw_{i}} \frac{1}{2}{(y - \hat{y})^2}$
- simplifies to = learning rate * error term * $ x_{i}$
- where:
- learning rate = $ n $
- error term = $ (y - \hat{y}) * f'(h) $
- h = $ \sum_{i} W_{i} x_{i} $
We begin by calculating our f'(h)
```
# output gradient - derivative of activation function
output_gradient = sigmoid_prime(h)
```
Now, we can calcualte our error term
```
error_trm = error * output_gradient
```
With that, we can update our weights by combining the error term, learning rate and our x
```
#gradient desc step - updating the weights
dsc_step = [
learnrate * error_trm * x[0],
learnrate * error_trm * x[1]
]
```
Which leaves...
```
print(f'Actual: {y}')
print(f'NN output: {output}')
print(f'Error: {error}')
print(f'Weight change: {dsc_step}')
```
### More in depth...
Lets now build our own end to end example. we will begin by creating some fake data, followed by implementing our neural network.
```
x = np.random.rand(200,2)
y = np.random.randint(low=0, high=2, size=(200,1))
no_data_points, no_features = x.shape
def sig(x):
'''Calc for sigmoid'''
return 1 / (1+np.exp(-x))
weights = np.random.normal(scale=1/no_features**.5, size=no_features)
epochs = 1000
learning_rate = 0.5
last_loss = None
for single_data_pass in range(epochs):
# Creating a weight change tracker
change_in_weights = np.zeros(weights.shape)
for x_i, y_i in zip(x, y):
h = np.dot(x_i, weights)
y_hat = sigmoid(h)
error = y_i - y_hat
# error term = error * f'(h)
error_term = error * (y_hat * (1-y_hat))
# now multiply this by the current x & add to our weight update
change_in_weights += (error_term * x_i)
# now update the actual weights
weights += (learning_rate * change_in_weights / no_data_points)
# print the loss every 100th pass
if single_data_pass % (epochs/10) == 0:
# use current weights in NN to determine outputs
output = sigmoid(np.dot(x_i,weights))
# find the loss
loss = np.mean((output-y_i)**2)
#
if last_loss and last_loss < loss:
print(f'Train loss: {loss}, WARNING - Loss is inscreasing')
else:
print(f'Training loss: {loss}')
last_loss = loss
```
## Multilayer NN
Now, lets build upon our neural network, but this time, we have a hidden layer.
Lets first see how to build the network to make predictions.
```
X = np.random.randn(4)
weights_input_to_hidden = np.random.normal(0, scale=0.1, size=(4, 3))
weights_hidden_to_output = np.random.normal(0, scale=0.1, size=(3, 2))
sum_input = np.dot(X, weights_input_to_hidden)
h = sigmoid(sum_input)
sum_h = np.dot(h, weights_hidden_to_output)
y_pred = sigmoid(sum_h)
```
## Backpropa what?
Ok, so now, how do we refine our weights? Well, this is where **backpropagation** comes in. After feeding our data forwards through the network, using feed forward, we propagate our errors backwards, making use of things such as the chain rule.
Lets do an implementation.
```
# we have three input nodes
x = np.array([0.5, 0.2, -0.3])
# one output node
y = 0.7
learnrate = 0.5
# 2 nodes in hidden layer
weights_input_hidden = np.array(
[
[0.5, -0.6], [0.1, -0.2], [0.1, 0.7]
]
)
weights_hidden_output = np.array([
0.1,-0.3
])
# feeding data forwards through the network
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
#---
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output)
y_hat = sigmoid(output_layer_input)
# backward propagate the errors to tune the weights
# 1. calculate errors
error = y - y_hat
output_node_error_term = error * (y_hat * (1-y_hat))
#----
hidden_node_error_term = weights_hidden_output * output_node_error_term *(hidden_layer_output * (1-hidden_layer_output))
# 2. calculate weight changes
delta_w_output_node = learnrate * output_node_error_term * hidden_layer_output
#-----
delta_w_hidden_node = learnrate * hidden_node_error_term * x[:,None]
print(f'Original weights:\n{weights_input_hidden}\n{weights_hidden_output}')
print()
print('Change in weights for hidden layer to output layer:')
print(delta_w_output_node)
print('Change in weights for input layer to hidden layer:')
print(delta_w_hidden_node)
```
## Putting it all together
```
features = np.random.rand(200,2)
target = np.random.randint(low=0, high=2, size=(200,1))
def complete_backprop(x,y):
'''Complete implementation of backpropagation'''
n_hidden_units = 2
epochs = 900
learnrate = 0.005
n_records, n_features = features.shape
last_loss = None
w_input_to_hidden = np.random.normal(scale=1/n_features**.5,size=(n_features, n_hidden_units))
w_hidden_to_output = np.random.normal(scale=1/n_features**.5, size=n_hidden_units)
for single_epoch in range(epochs):
delw_input_to_hidden = np.zeros(w_input_to_hidden.shape)
delw_hidden_to_output = np.zeros(w_hidden_to_output.shape)
for x,y in zip(features, target):
# ----------------------
# 1. Feed data forwards
# ----------------------
hidden_layer_input = np.dot(x,w_input_to_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, w_hidden_to_output)
output_layer_output = sigmoid(output_layer_input)
# ----------------------
# 2. Backpropagate the errors
# ----------------------
# error at output layer
prediction_error = y - output_layer_output
output_error_term = prediction_error * (output_layer_output * (1-output_layer_output))
# error at hidden layer (propagated from output layer)
# scale error from output layer by weights
hidden_layer_error = np.multiply(output_error_term, w_hidden_to_output)
hidden_error_term = hidden_layer_error * (hidden_layer_output * (1-hidden_layer_output))
# ----------------------
# 3. Find change of weights for each data point
# ----------------------
delw_hidden_to_output += output_error_term * hidden_layer_output
delw_input_to_hidden += hidden_error_term * x[:,None]
# Now update the actual weights
w_hidden_to_output += learnrate * delw_hidden_to_output / n_records
w_input_to_hidden += learnrate * delw_input_to_hidden / n_records
# Printing out the mean square error on the training set
if single_epoch % (epochs / 10) == 0:
hidden_output = sigmoid(np.dot(x, w_input_to_hidden))
out = sigmoid(np.dot(hidden_output,
w_hidden_to_output))
loss = np.mean((out - target) ** 2)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
complete_backprop(features,target)
```
|
github_jupyter
|
import numpy as np
# We will be using a sigmoid activation function
def sigmoid(x):
return 1/(1+np.exp(-x))
# derivation of sigmoid(x) - will be used for backpropagating errors through the network
def sigmoid_prime(x):
return sigmoid(x)*(1-sigmoid(x))
x = np.array([1,5])
y = 0.4
weights = np.array([-0.2,0.4])
learnrate = 0.5
# linear combination
# h = x[0]*weights[0] + x[1]*weights[1]
h = np.dot(x, weights)
# apply non-linearity
output = sigmoid(h)
error = y - output
# output gradient - derivative of activation function
output_gradient = sigmoid_prime(h)
error_trm = error * output_gradient
#gradient desc step - updating the weights
dsc_step = [
learnrate * error_trm * x[0],
learnrate * error_trm * x[1]
]
print(f'Actual: {y}')
print(f'NN output: {output}')
print(f'Error: {error}')
print(f'Weight change: {dsc_step}')
x = np.random.rand(200,2)
y = np.random.randint(low=0, high=2, size=(200,1))
no_data_points, no_features = x.shape
def sig(x):
'''Calc for sigmoid'''
return 1 / (1+np.exp(-x))
weights = np.random.normal(scale=1/no_features**.5, size=no_features)
epochs = 1000
learning_rate = 0.5
last_loss = None
for single_data_pass in range(epochs):
# Creating a weight change tracker
change_in_weights = np.zeros(weights.shape)
for x_i, y_i in zip(x, y):
h = np.dot(x_i, weights)
y_hat = sigmoid(h)
error = y_i - y_hat
# error term = error * f'(h)
error_term = error * (y_hat * (1-y_hat))
# now multiply this by the current x & add to our weight update
change_in_weights += (error_term * x_i)
# now update the actual weights
weights += (learning_rate * change_in_weights / no_data_points)
# print the loss every 100th pass
if single_data_pass % (epochs/10) == 0:
# use current weights in NN to determine outputs
output = sigmoid(np.dot(x_i,weights))
# find the loss
loss = np.mean((output-y_i)**2)
#
if last_loss and last_loss < loss:
print(f'Train loss: {loss}, WARNING - Loss is inscreasing')
else:
print(f'Training loss: {loss}')
last_loss = loss
X = np.random.randn(4)
weights_input_to_hidden = np.random.normal(0, scale=0.1, size=(4, 3))
weights_hidden_to_output = np.random.normal(0, scale=0.1, size=(3, 2))
sum_input = np.dot(X, weights_input_to_hidden)
h = sigmoid(sum_input)
sum_h = np.dot(h, weights_hidden_to_output)
y_pred = sigmoid(sum_h)
# we have three input nodes
x = np.array([0.5, 0.2, -0.3])
# one output node
y = 0.7
learnrate = 0.5
# 2 nodes in hidden layer
weights_input_hidden = np.array(
[
[0.5, -0.6], [0.1, -0.2], [0.1, 0.7]
]
)
weights_hidden_output = np.array([
0.1,-0.3
])
# feeding data forwards through the network
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
#---
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output)
y_hat = sigmoid(output_layer_input)
# backward propagate the errors to tune the weights
# 1. calculate errors
error = y - y_hat
output_node_error_term = error * (y_hat * (1-y_hat))
#----
hidden_node_error_term = weights_hidden_output * output_node_error_term *(hidden_layer_output * (1-hidden_layer_output))
# 2. calculate weight changes
delta_w_output_node = learnrate * output_node_error_term * hidden_layer_output
#-----
delta_w_hidden_node = learnrate * hidden_node_error_term * x[:,None]
print(f'Original weights:\n{weights_input_hidden}\n{weights_hidden_output}')
print()
print('Change in weights for hidden layer to output layer:')
print(delta_w_output_node)
print('Change in weights for input layer to hidden layer:')
print(delta_w_hidden_node)
features = np.random.rand(200,2)
target = np.random.randint(low=0, high=2, size=(200,1))
def complete_backprop(x,y):
'''Complete implementation of backpropagation'''
n_hidden_units = 2
epochs = 900
learnrate = 0.005
n_records, n_features = features.shape
last_loss = None
w_input_to_hidden = np.random.normal(scale=1/n_features**.5,size=(n_features, n_hidden_units))
w_hidden_to_output = np.random.normal(scale=1/n_features**.5, size=n_hidden_units)
for single_epoch in range(epochs):
delw_input_to_hidden = np.zeros(w_input_to_hidden.shape)
delw_hidden_to_output = np.zeros(w_hidden_to_output.shape)
for x,y in zip(features, target):
# ----------------------
# 1. Feed data forwards
# ----------------------
hidden_layer_input = np.dot(x,w_input_to_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, w_hidden_to_output)
output_layer_output = sigmoid(output_layer_input)
# ----------------------
# 2. Backpropagate the errors
# ----------------------
# error at output layer
prediction_error = y - output_layer_output
output_error_term = prediction_error * (output_layer_output * (1-output_layer_output))
# error at hidden layer (propagated from output layer)
# scale error from output layer by weights
hidden_layer_error = np.multiply(output_error_term, w_hidden_to_output)
hidden_error_term = hidden_layer_error * (hidden_layer_output * (1-hidden_layer_output))
# ----------------------
# 3. Find change of weights for each data point
# ----------------------
delw_hidden_to_output += output_error_term * hidden_layer_output
delw_input_to_hidden += hidden_error_term * x[:,None]
# Now update the actual weights
w_hidden_to_output += learnrate * delw_hidden_to_output / n_records
w_input_to_hidden += learnrate * delw_input_to_hidden / n_records
# Printing out the mean square error on the training set
if single_epoch % (epochs / 10) == 0:
hidden_output = sigmoid(np.dot(x, w_input_to_hidden))
out = sigmoid(np.dot(hidden_output,
w_hidden_to_output))
loss = np.mean((out - target) ** 2)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
complete_backprop(features,target)
| 0.678753 | 0.989712 |
# Convolutional Neural Network Example
Build a convolutional neural network with TensorFlow.
This example is using TensorFlow layers API, see 'convolutional_network_raw' example
for a raw TensorFlow implementation with variables.
- Author: Aymeric Damien
- Project: https://github.com/aymericdamien/TensorFlow-Examples/
## CNN Overview
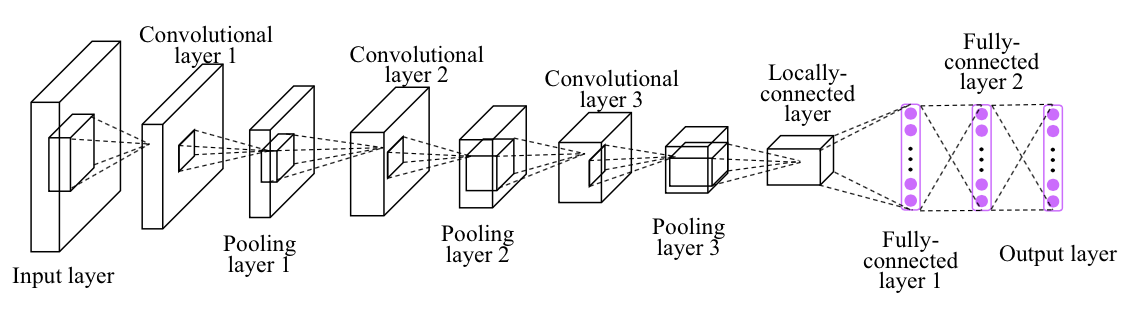
## MNIST Dataset Overview
This example is using MNIST handwritten digits. The dataset contains 60,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/
```
from __future__ import division, print_function, absolute_import
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
# Training Parameters
learning_rate = 0.001
num_steps = 2000
batch_size = 128
# Network Parameters
num_input = 784 # MNIST data input (img shape: 28*28)
num_classes = 10 # MNIST total classes (0-9 digits)
dropout = 0.25 # Dropout, probability to drop a unit
# Create the neural network
def conv_net(x_dict, n_classes, dropout, reuse, is_training):
# Define a scope for reusing the variables
with tf.variable_scope('ConvNet', reuse=reuse):
# TF Estimator input is a dict, in case of multiple inputs
x = x_dict['images']
# MNIST data input is a 1-D vector of 784 features (28*28 pixels)
# Reshape to match picture format [Height x Width x Channel]
# Tensor input become 4-D: [Batch Size, Height, Width, Channel]
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# Convolution Layer with 32 filters and a kernel size of 5
conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv1 = tf.layers.max_pooling2d(conv1, 2, 2)
# Convolution Layer with 64 filters and a kernel size of 3
conv2 = tf.layers.conv2d(conv1, 64, 3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv2 = tf.layers.max_pooling2d(conv2, 2, 2)
# Flatten the data to a 1-D vector for the fully connected layer
fc1 = tf.contrib.layers.flatten(conv2)
# Fully connected layer (in tf contrib folder for now)
fc1 = tf.layers.dense(fc1, 1024)
# Apply Dropout (if is_training is False, dropout is not applied)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)
# Output layer, class prediction
out = tf.layers.dense(fc1, n_classes)
return out
# Define the model function (following TF Estimator Template)
def model_fn(features, labels, mode):
# Build the neural network
# Because Dropout have different behavior at training and prediction time, we
# need to create 2 distinct computation graphs that still share the same weights.
logits_train = conv_net(features, num_classes, dropout, reuse=False, is_training=True)
logits_test = conv_net(features, num_classes, dropout, reuse=True, is_training=False)
# Predictions
pred_classes = tf.argmax(logits_test, axis=1)
pred_probas = tf.nn.softmax(logits_test)
# If prediction mode, early return
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode, predictions=pred_classes)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits_train, labels=tf.cast(labels, dtype=tf.int32)))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op, global_step=tf.train.get_global_step())
# Evaluate the accuracy of the model
acc_op = tf.metrics.accuracy(labels=labels, predictions=pred_classes)
# TF Estimators requires to return a EstimatorSpec, that specify
# the different ops for training, evaluating, ...
estim_specs = tf.estimator.EstimatorSpec(
mode=mode,
predictions=pred_classes,
loss=loss_op,
train_op=train_op,
eval_metric_ops={'accuracy': acc_op})
return estim_specs
# Build the Estimator
model = tf.estimator.Estimator(model_fn)
# Define the input function for training
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.train.images}, y=mnist.train.labels,
batch_size=batch_size, num_epochs=None, shuffle=True)
# Train the Model
model.train(input_fn, steps=num_steps)
# Evaluate the Model
# Define the input function for evaluating
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.test.images}, y=mnist.test.labels,
batch_size=batch_size, shuffle=False)
# Use the Estimator 'evaluate' method
model.evaluate(input_fn)
# Predict single images
n_images = 4
# Get images from test set
test_images = mnist.test.images[:n_images]
# Prepare the input data
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': test_images}, shuffle=False)
# Use the model to predict the images class
preds = list(model.predict(input_fn))
# Display
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction:", preds[i])
```
|
github_jupyter
|
from __future__ import division, print_function, absolute_import
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
# Training Parameters
learning_rate = 0.001
num_steps = 2000
batch_size = 128
# Network Parameters
num_input = 784 # MNIST data input (img shape: 28*28)
num_classes = 10 # MNIST total classes (0-9 digits)
dropout = 0.25 # Dropout, probability to drop a unit
# Create the neural network
def conv_net(x_dict, n_classes, dropout, reuse, is_training):
# Define a scope for reusing the variables
with tf.variable_scope('ConvNet', reuse=reuse):
# TF Estimator input is a dict, in case of multiple inputs
x = x_dict['images']
# MNIST data input is a 1-D vector of 784 features (28*28 pixels)
# Reshape to match picture format [Height x Width x Channel]
# Tensor input become 4-D: [Batch Size, Height, Width, Channel]
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# Convolution Layer with 32 filters and a kernel size of 5
conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv1 = tf.layers.max_pooling2d(conv1, 2, 2)
# Convolution Layer with 64 filters and a kernel size of 3
conv2 = tf.layers.conv2d(conv1, 64, 3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv2 = tf.layers.max_pooling2d(conv2, 2, 2)
# Flatten the data to a 1-D vector for the fully connected layer
fc1 = tf.contrib.layers.flatten(conv2)
# Fully connected layer (in tf contrib folder for now)
fc1 = tf.layers.dense(fc1, 1024)
# Apply Dropout (if is_training is False, dropout is not applied)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)
# Output layer, class prediction
out = tf.layers.dense(fc1, n_classes)
return out
# Define the model function (following TF Estimator Template)
def model_fn(features, labels, mode):
# Build the neural network
# Because Dropout have different behavior at training and prediction time, we
# need to create 2 distinct computation graphs that still share the same weights.
logits_train = conv_net(features, num_classes, dropout, reuse=False, is_training=True)
logits_test = conv_net(features, num_classes, dropout, reuse=True, is_training=False)
# Predictions
pred_classes = tf.argmax(logits_test, axis=1)
pred_probas = tf.nn.softmax(logits_test)
# If prediction mode, early return
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode, predictions=pred_classes)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits_train, labels=tf.cast(labels, dtype=tf.int32)))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op, global_step=tf.train.get_global_step())
# Evaluate the accuracy of the model
acc_op = tf.metrics.accuracy(labels=labels, predictions=pred_classes)
# TF Estimators requires to return a EstimatorSpec, that specify
# the different ops for training, evaluating, ...
estim_specs = tf.estimator.EstimatorSpec(
mode=mode,
predictions=pred_classes,
loss=loss_op,
train_op=train_op,
eval_metric_ops={'accuracy': acc_op})
return estim_specs
# Build the Estimator
model = tf.estimator.Estimator(model_fn)
# Define the input function for training
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.train.images}, y=mnist.train.labels,
batch_size=batch_size, num_epochs=None, shuffle=True)
# Train the Model
model.train(input_fn, steps=num_steps)
# Evaluate the Model
# Define the input function for evaluating
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.test.images}, y=mnist.test.labels,
batch_size=batch_size, shuffle=False)
# Use the Estimator 'evaluate' method
model.evaluate(input_fn)
# Predict single images
n_images = 4
# Get images from test set
test_images = mnist.test.images[:n_images]
# Prepare the input data
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': test_images}, shuffle=False)
# Use the model to predict the images class
preds = list(model.predict(input_fn))
# Display
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction:", preds[i])
| 0.828973 | 0.987017 |
```
%load_ext autoreload
%autoreload 2
import gust # library for loading graph data
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.sparse as sp
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist
import time
import random
from scipy.spatial.distance import squareform
torch.set_default_tensor_type('torch.cuda.FloatTensor')
%matplotlib inline
sns.set_style('whitegrid')
# Load the dataset using `gust` library
# graph.standardize() makes the graph unweighted, undirected and selects
# the largest connected component
# graph.unpack() returns the necessary vectors / matrices
A, X, _, y = gust.load_dataset('cora').standardize().unpack()
# A - adjacency matrix
# X - attribute matrix - not needed
# y - node labels
A=A[:10,:10]
if (A != A.T).sum() > 0:
raise RuntimeError("The graph must be undirected!")
if (A.data != 1).sum() > 0:
raise RuntimeError("The graph must be unweighted!")
adj = torch.FloatTensor(A.toarray()).cuda()
# Make it stochastic
adj = torch.FloatTensor(A.toarray()).cuda()
'''
from the paper Sampling from Large Graphs:
We first choose node v uniformly at random. We then generate a random number x that is geometrically distributed
with mean pf /(1 − pf ). Node v selects x out-links incident
to nodes that were not yet visited. Let w1, w2, . . . , wx denote the other ends of these selected links. We then apply
this step recursively to each of w1, w2, . . . , wx until enough
nodes have been burned. As the process continues, nodes
cannot be visited a second time, preventing the construction
from cycling. If the fire dies, then we restart it, i.e. select
new node v uniformly at random. We call the parameter pf
the forward burning probability.
'''
#1. choose first node v uniformly at random and store it
v_new = np.random.randint(len(adj))
nodes = torch.tensor([v_new])
print('nodes: ', nodes)
#2. generate random number x from geometrix distribution with mean pf/(1-pf)
pf=0.3 #burning probability, evaluated as best from the given paper
x = np.random.geometric(pf/(1-pf))
#3. let idx choose x out-links
w = (adj[v_new]==1).nonzero()
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
w=w[idx_w]
#4. loop until 15% of the dataset is covered
while len(nodes)<20:
v_new = w[0].item()
w = (adj[v_new]==1).nonzero()
for i in w:
for j in nodes:
if w[i]==nodes[j]:
w[i]=0
w = w.remove(0)
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
v_new = torch.tensor([v_new])
nodes = torch.cat((nodes,v_new),0)
print(nodes)
num_nodes = A.shape[0]
num_edges = A.sum()
# Convert adjacency matrix to a CUDA Tensor
adj = torch.FloatTensor(A.toarray()).cuda()
#torch.manual_seed(123)
# Define the embedding matrix
embedding_dim = 64
emb = nn.Parameter(torch.empty(num_nodes, embedding_dim).normal_(0.0, 1.0))
# Initialize the bias
# The bias is initialized in such a way that if the dot product between two embedding vectors is 0
# (i.e. z_i^T z_j = 0), then their connection probability is sigmoid(b) equals to the
# background edge probability in the graph. This significantly speeds up training
edge_proba = num_edges / (num_nodes**2 - num_nodes)
bias_init = np.log(edge_proba / (1 - edge_proba))
b = nn.Parameter(torch.Tensor([bias_init]))
# Regularize the embeddings but don't regularize the bias
# The value of weight_decay has a significant effect on the performance of the model (don't set too high!)
opt = torch.optim.Adam([
{'params': [emb], 'weight_decay': 1e-7}, {'params': [b]}],
lr=1e-2)
def compute_loss_ber_sig(adj, emb, b=0.1):
#kernel: theta(z_i,z_j)=sigma(z_i^Tz_j+b)
# Initialization
N,d=emb.shape
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
logits =dot+b
#transform adj
ind=torch.triu_indices(N,N,offset=1)
logits = logits[ind[0], ind[1]]
labels = adj[ind[0],ind[1]]
#compute p(A|Z)
loss = F.binary_cross_entropy_with_logits(logits, labels, weight=None, size_average=None, reduce=None, reduction='mean')
return loss
def compute_loss_d1(adj, emb, b=0.0):
"""Compute the rdf distance of the Bernoulli model."""
# Initialization
start_time = time.time()
N,d=emb.shape
squared_euclidian = torch.zeros(N,N).cuda()
gamma= 0.1
end_time= time.time()
duration= end_time -start_time
#print(f' Time for initialization = {duration:.5f}')
# Compute squared euclidian
start_time = time.time()
for index, embedding in enumerate(emb):
sub = embedding-emb + 10e-9
squared_euclidian[index,:]= torch.sum(torch.pow(sub,2),1)
end_time= time.time()
duration= end_time -start_time
#print(f' Time for euclidian = {duration:.5f}')
# Compute exponentianl
start_time = time.time()
radial_exp = torch.exp (-gamma * torch.sqrt(squared_euclidian))
loss = F.binary_cross_entropy(radial_exp, adj, reduction='none')
loss[np.diag_indices(adj.shape[0])] = 0.0
end_time= time.time()
duration= end_time -start_time
#print(f' Time for loss = {duration:.5f}')
return loss.mean()
def compute_loss_ber_exp2(adj, emb, b=0.1):
#Init
N,d=emb.shape
#get indices of upper triangular matrix
ind=torch.triu_indices(N,N,offset=1)
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
print('dist: ', dot, dot.size(), type(dot))
logits=1-torch.exp(-dot)
logits=logits[ind[0],ind[1]]
labels = adj[ind[0],ind[1]]
print('logits: ', logits, logits.size(), type(logits))
#compute loss
loss = F.binary_cross_entropy_with_logits(logits, labels, reduction='mean')
return loss
def compute_loss_KL(adj, emb, b=0.0):
#adj = torch.FloatTensor(A.toarray()).cuda()
degree= torch.from_numpy(adj.sum(axis=1))
print('degree: ', degree, type(degree), degree.size())
inv_degree=torch.diagflat(1/degree).cuda()
print('invdegree: ', invdegree, type(invdegree), invdegree.size())
P = inv_degree.mm(adj)
print('P: ', invdegree, type(invdegree), invdegree.size())
loss = -(P*torch.log( 10e-9+ F.softmax(emb.mm(emb.t() ),dim=1,dtype=torch.float)))
return loss.mean()
max_epochs = 1000
display_step = 250
compute_loss = compute_loss_KL
for epoch in range(max_epochs):
opt.zero_grad()
loss = compute_loss(adj, emb, b)
loss.backward()
opt.step()
# Training loss is printed every display_step epochs
if epoch == 0 or (epoch + 1) % display_step == 0:
print(f'Epoch {epoch+1:4d}, loss = {loss.item():.5f}')
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import gust # library for loading graph data
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.sparse as sp
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist
import time
import random
from scipy.spatial.distance import squareform
torch.set_default_tensor_type('torch.cuda.FloatTensor')
%matplotlib inline
sns.set_style('whitegrid')
# Load the dataset using `gust` library
# graph.standardize() makes the graph unweighted, undirected and selects
# the largest connected component
# graph.unpack() returns the necessary vectors / matrices
A, X, _, y = gust.load_dataset('cora').standardize().unpack()
# A - adjacency matrix
# X - attribute matrix - not needed
# y - node labels
A=A[:10,:10]
if (A != A.T).sum() > 0:
raise RuntimeError("The graph must be undirected!")
if (A.data != 1).sum() > 0:
raise RuntimeError("The graph must be unweighted!")
adj = torch.FloatTensor(A.toarray()).cuda()
# Make it stochastic
adj = torch.FloatTensor(A.toarray()).cuda()
'''
from the paper Sampling from Large Graphs:
We first choose node v uniformly at random. We then generate a random number x that is geometrically distributed
with mean pf /(1 − pf ). Node v selects x out-links incident
to nodes that were not yet visited. Let w1, w2, . . . , wx denote the other ends of these selected links. We then apply
this step recursively to each of w1, w2, . . . , wx until enough
nodes have been burned. As the process continues, nodes
cannot be visited a second time, preventing the construction
from cycling. If the fire dies, then we restart it, i.e. select
new node v uniformly at random. We call the parameter pf
the forward burning probability.
'''
#1. choose first node v uniformly at random and store it
v_new = np.random.randint(len(adj))
nodes = torch.tensor([v_new])
print('nodes: ', nodes)
#2. generate random number x from geometrix distribution with mean pf/(1-pf)
pf=0.3 #burning probability, evaluated as best from the given paper
x = np.random.geometric(pf/(1-pf))
#3. let idx choose x out-links
w = (adj[v_new]==1).nonzero()
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
w=w[idx_w]
#4. loop until 15% of the dataset is covered
while len(nodes)<20:
v_new = w[0].item()
w = (adj[v_new]==1).nonzero()
for i in w:
for j in nodes:
if w[i]==nodes[j]:
w[i]=0
w = w.remove(0)
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
v_new = torch.tensor([v_new])
nodes = torch.cat((nodes,v_new),0)
print(nodes)
num_nodes = A.shape[0]
num_edges = A.sum()
# Convert adjacency matrix to a CUDA Tensor
adj = torch.FloatTensor(A.toarray()).cuda()
#torch.manual_seed(123)
# Define the embedding matrix
embedding_dim = 64
emb = nn.Parameter(torch.empty(num_nodes, embedding_dim).normal_(0.0, 1.0))
# Initialize the bias
# The bias is initialized in such a way that if the dot product between two embedding vectors is 0
# (i.e. z_i^T z_j = 0), then their connection probability is sigmoid(b) equals to the
# background edge probability in the graph. This significantly speeds up training
edge_proba = num_edges / (num_nodes**2 - num_nodes)
bias_init = np.log(edge_proba / (1 - edge_proba))
b = nn.Parameter(torch.Tensor([bias_init]))
# Regularize the embeddings but don't regularize the bias
# The value of weight_decay has a significant effect on the performance of the model (don't set too high!)
opt = torch.optim.Adam([
{'params': [emb], 'weight_decay': 1e-7}, {'params': [b]}],
lr=1e-2)
def compute_loss_ber_sig(adj, emb, b=0.1):
#kernel: theta(z_i,z_j)=sigma(z_i^Tz_j+b)
# Initialization
N,d=emb.shape
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
logits =dot+b
#transform adj
ind=torch.triu_indices(N,N,offset=1)
logits = logits[ind[0], ind[1]]
labels = adj[ind[0],ind[1]]
#compute p(A|Z)
loss = F.binary_cross_entropy_with_logits(logits, labels, weight=None, size_average=None, reduce=None, reduction='mean')
return loss
def compute_loss_d1(adj, emb, b=0.0):
"""Compute the rdf distance of the Bernoulli model."""
# Initialization
start_time = time.time()
N,d=emb.shape
squared_euclidian = torch.zeros(N,N).cuda()
gamma= 0.1
end_time= time.time()
duration= end_time -start_time
#print(f' Time for initialization = {duration:.5f}')
# Compute squared euclidian
start_time = time.time()
for index, embedding in enumerate(emb):
sub = embedding-emb + 10e-9
squared_euclidian[index,:]= torch.sum(torch.pow(sub,2),1)
end_time= time.time()
duration= end_time -start_time
#print(f' Time for euclidian = {duration:.5f}')
# Compute exponentianl
start_time = time.time()
radial_exp = torch.exp (-gamma * torch.sqrt(squared_euclidian))
loss = F.binary_cross_entropy(radial_exp, adj, reduction='none')
loss[np.diag_indices(adj.shape[0])] = 0.0
end_time= time.time()
duration= end_time -start_time
#print(f' Time for loss = {duration:.5f}')
return loss.mean()
def compute_loss_ber_exp2(adj, emb, b=0.1):
#Init
N,d=emb.shape
#get indices of upper triangular matrix
ind=torch.triu_indices(N,N,offset=1)
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
print('dist: ', dot, dot.size(), type(dot))
logits=1-torch.exp(-dot)
logits=logits[ind[0],ind[1]]
labels = adj[ind[0],ind[1]]
print('logits: ', logits, logits.size(), type(logits))
#compute loss
loss = F.binary_cross_entropy_with_logits(logits, labels, reduction='mean')
return loss
def compute_loss_KL(adj, emb, b=0.0):
#adj = torch.FloatTensor(A.toarray()).cuda()
degree= torch.from_numpy(adj.sum(axis=1))
print('degree: ', degree, type(degree), degree.size())
inv_degree=torch.diagflat(1/degree).cuda()
print('invdegree: ', invdegree, type(invdegree), invdegree.size())
P = inv_degree.mm(adj)
print('P: ', invdegree, type(invdegree), invdegree.size())
loss = -(P*torch.log( 10e-9+ F.softmax(emb.mm(emb.t() ),dim=1,dtype=torch.float)))
return loss.mean()
max_epochs = 1000
display_step = 250
compute_loss = compute_loss_KL
for epoch in range(max_epochs):
opt.zero_grad()
loss = compute_loss(adj, emb, b)
loss.backward()
opt.step()
# Training loss is printed every display_step epochs
if epoch == 0 or (epoch + 1) % display_step == 0:
print(f'Epoch {epoch+1:4d}, loss = {loss.item():.5f}')
| 0.79158 | 0.604487 |
# Analyzing Portfolio Risk and Return
In this Challenge, you'll assume the role of a quantitative analyst for a FinTech investing platform. This platform aims to offer clients a one-stop online investment solution for their retirement portfolios that’s both inexpensive and high quality. (Think about [Wealthfront](https://www.wealthfront.com/) or [Betterment](https://www.betterment.com/)). To keep the costs low, the firm uses algorithms to build each client's portfolio. The algorithms choose from various investment styles and options.
You've been tasked with evaluating four new investment options for inclusion in the client portfolios. Legendary fund and hedge-fund managers run all four selections. (People sometimes refer to these managers as **whales**, because of the large amount of money that they manage). You’ll need to determine the fund with the most investment potential based on key risk-management metrics: the daily returns, standard deviations, Sharpe ratios, and betas.
## Instructions
### Import the Data
Use the `whale_analysis.ipynb` file to complete the following steps:
1. Import the required libraries and dependencies.
2. Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
3. Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
### Analyze the Performance
Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents. To do so, complete the following steps:
1. Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
2. Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
3. Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
### Analyze the Volatility
Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots. To do so, complete the following steps:
1. Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
2. Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
> **Hint** Save this new DataFrame—the one that contains the data for just the four fund portfolios. You’ll use it throughout the analysis.
3. Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
### Analyze the Risk
Evaluate the risk profile of each portfolio by using the standard deviation and the beta. To do so, complete the following steps:
1. Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
2. Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
3. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
5. Answer the following three questions:
* Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
* Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
* Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
### Analyze the Risk-Return Profile
To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio. To do so, complete the following steps:
1. Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
2. Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
3. Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
#### Diversify the Portfolio
Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options. To start your analysis, complete the following step:
* Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
Next, for each of the two portfolios that you chose, complete the following steps:
1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
Finally, answer the following two questions:
* Which of the two portfolios seem more sensitive to movements in the S&P 500?
* Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
### Import the Data
#### Step 1: Import the required libraries and dependencies.
```
# Import the required libraries and dependencies
import pandas as pd
from pathlib import Path
%matplotlib inline
import numpy as np
import os
#understanding where we are in the dir in order to have Path work correctly
os.getcwd()
```
#### Step 2: Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
```
# Import the data by reading in the CSV file and setting the DatetimeIndex
# Review the first 5 rows of the DataFrame
whale_df = pd.read_csv(
Path('Resources/whale_navs.csv'),
index_col = 'date',
parse_dates = True,
infer_datetime_format = True
)
whale_df.head()
```
#### Step 3: Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
```
# Prepare for the analysis by converting the dataframe of NAVs and prices to daily returns
# Drop any rows with all missing values
# Review the first five rows of the daily returns DataFrame.
whale_daily_returns = whale_df.pct_change().dropna()
whale_daily_returns.head(5)
```
---
## Quantative Analysis
The analysis has several components: performance, volatility, risk, risk-return profile, and portfolio diversification. You’ll analyze each component one at a time.
### Analyze the Performance
Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents.
#### Step 1: Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the daily return data of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(figsize =(15,5), title = 'Daily returns of the whales and S&P 500')
```
#### Step 2: Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
```
# Calculate and plot the cumulative returns of the 4 fund portfolios and the S&P 500
# Review the last 5 rows of the cumulative returns DataFrame
whale_cumulative_returns = (1 + whale_daily_returns).cumprod()
whale_cumulative_returns.tail()
```
#### Step 3: Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Visualize the cumulative returns using the Pandas plot function
# Include a title parameter and adjust the figure size
whale_cumulative_returns.plot(figsize =(20,10), title = 'Cumulative returns of whales and the S&P 500')
```
#### Step 4: Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
**Question** Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
**Answer** # No they do not. In fact, the S&P 500 outperforms every whale fund by a signifigant amount
---
### Analyze the Volatility
Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots.
#### Step 1: Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Use the daily return data to create box plots to visualize the volatility of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(kind ='box', title = 'Box plot of daily returns of the whales and SPX')
```
#### Step 2: Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Create a new DataFrame containing only the 4 fund portfolios by dropping the S&P 500 column from the DataFrame
# Create box plots to reflect the return data for only the 4 fund portfolios
# Include a title parameter and adjust the figure size
whales_only = whale_daily_returns.drop(['S&P 500'], axis = 1)
whales_only.plot(kind = 'box', figsize =(15, 7), title = 'Whale only data ex-SPX')
```
#### Step 3: Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
**Question** Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
**Answer** # It appears that Berkshire Hathaway has the largest spread as per the box spread daily return data.
---
### Analyze the Risk
Evaluate the risk profile of each portfolio by using the standard deviation and the beta.
#### Step 1: Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
```
# Calculate and sort the standard deviation for all 4 portfolios and the S&P 500
# Review the standard deviations sorted smallest to largest
whale_std = whale_daily_returns.std()
whale_std.sort_values()
```
#### Step 2: Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
```
# Calculate and sort the annualized standard deviation (252 trading days) of the 4 portfolios and the S&P 500
# Review the annual standard deviations smallest to largest
whale_std_annualized = whale_std *np.sqrt(252)
whale_std_annualized.sort_values()
```
#### Step 3: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Using the daily returns DataFrame and a 21-day rolling window,
# plot the rolling standard deviation of the 4 portfolios and the S&P 500
# Include a title parameter and adjust the figure size
whale_std_21d = whale_daily_returns.rolling(window = 21).std()
whale_std_21d.plot(figsize=(15,10), title = 'Rolling 21d std deviations of Whales and SPX')
```
#### Step 4: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Using the daily return data and a 21-day rolling window, plot the rolling standard deviation of just the 4 portfolios.
# Include a title parameter and adjust the figure size
rolling_std_deviaton_21d = whales_only.rolling(21).std()
rolling_std_deviaton_21d.plot(figsize = (15,7), title = 'Rolling Std Deviations -- 21d using daily return data')
```
#### Step 5: Answer the following three questions:
1. Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
2. Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
3. Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
**Question 1** Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
**Answer 1** # Based on the std deviations, Berkshire and Tiger pose more risk with annualized std deviations of 66 and 11.9 respectvly.
**Question 2** Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
**Answer 2** # Most of the time yes though the SPX has considerably higher spikes in standard deviation.
**Question 3** Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
**Answer 3** # The Berkshire fund poses the most risk out of the 4 funds. Since 2019, the Paulson fund has increased risk and std deviations close to Berkshire.
---
### Analyze the Risk-Return Profile
To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio.
#### Step 1: Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
```
# Calculate the annual average return data for the for fund portfolios and the S&P 500
# Use 252 as the number of trading days in the year
# Review the annual average returns sorted from lowest to highest
annualized_average_returns = whale_daily_returns.mean()*(252)
annualized_average_returns.sort_values()
```
#### Step 2: Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
```
# Calculate the annualized Sharpe Ratios for each of the 4 portfolios and the S&P 500.
# Review the Sharpe ratios sorted lowest to highest
sharpe = annualized_average_returns / whale_std_annualized
sharpe.sort_values()
```
#### Step 3: Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Visualize the Sharpe ratios as a bar chart
# Include a title parameter and adjust the figure size
sharpe.plot(kind = 'bar', figsize = (12,5), title = 'Sharpe Ratios of the Whales and the SPX')
```
#### Step 4: Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
**Question** Which of the four portfolios offers the best risk-return profile? Which offers the worst?
**Answer** # Tiger Global offeres the best risk return profile (per the Sharpe Ratio) while Paulson offers the wors risk return profile.
---
### Diversify the Portfolio
Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options.
#### Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
```
# Calculate the variance of the S&P 500 using a rolling 60-day window.
spx_var_60d = whale_daily_returns['S&P 500'].rolling(window = 60).var()
spx_var_60d.tail()
```
#### For each of the two portfolios that you chose, complete the following steps:
1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
##### Portfolio 1 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
```
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
berkshire_spx_cov_60d = whale_daily_returns['BERKSHIRE HATHAWAY INC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
berkshire_spx_cov_60d.tail()
```
##### Portfolio 1 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
```
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
berkshire_beta = berkshire_spx_cov_60d / spx_var_60d
berkshire_beta.tail()
#covariance = whale_daily_returns['BERKSHIRE HATHAWAY INC'].cov(whale_daily_returns['S&P 500'])
#variance = whale_daily_returns['S&P 500'].var()
#beta = covariance/variance
#beta
```
##### Portfolio 1 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
```
# Calculate the average of the 60-day rolling beta
berkshire_average_60d_beta = berkshire_beta.mean()
berkshire_average_60d_beta
```
##### Portfolio 1 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the rolling beta
# Include a title parameter and adjust the figure size
berkshire_beta.plot(figsize =(15,7), title = 'Berkshire 60d rolling beta')
```
##### Portfolio 2 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
```
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
tiger_spx_cov_60d = whale_daily_returns['TIGER GLOBAL MANAGEMENT LLC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
tiger_spx_cov_60d.tail()
```
##### Portfolio 2 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
```
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
tiger_beta = tiger_spx_cov_60d / spx_var_60d
```
##### Portfolio 2 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
```
# Calculate the average of the 60-day rolling beta
tiger_average_60d_beta = tiger_beta.mean()
tiger_average_60d_beta
```
##### Portfolio 2 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the rolling beta
# Include a title parameter and adjust the figure size
tiger_beta.plot(figsize =(15,7), title = 'Tiger 60d rolling beta')
```
#### Answer the following two questions:
1. Which of the two portfolios seem more sensitive to movements in the S&P 500?
2. Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
**Question 1** Which of the two portfolios seem more sensitive to movements in the S&P 500?
**Answer 1** # It appears that the Berkshuire Hathway portfolio is more seneitive to the S&P 500
**Question 2** Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
**Answer 2** # Despite the increased risk I would recommend the Berkshire portfolio. This is largely due to the higher Sharpe ratio for berkshire is 0.71 vs Tiger which is 0.57.
---
|
github_jupyter
|
# Import the required libraries and dependencies
import pandas as pd
from pathlib import Path
%matplotlib inline
import numpy as np
import os
#understanding where we are in the dir in order to have Path work correctly
os.getcwd()
# Import the data by reading in the CSV file and setting the DatetimeIndex
# Review the first 5 rows of the DataFrame
whale_df = pd.read_csv(
Path('Resources/whale_navs.csv'),
index_col = 'date',
parse_dates = True,
infer_datetime_format = True
)
whale_df.head()
# Prepare for the analysis by converting the dataframe of NAVs and prices to daily returns
# Drop any rows with all missing values
# Review the first five rows of the daily returns DataFrame.
whale_daily_returns = whale_df.pct_change().dropna()
whale_daily_returns.head(5)
# Plot the daily return data of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(figsize =(15,5), title = 'Daily returns of the whales and S&P 500')
# Calculate and plot the cumulative returns of the 4 fund portfolios and the S&P 500
# Review the last 5 rows of the cumulative returns DataFrame
whale_cumulative_returns = (1 + whale_daily_returns).cumprod()
whale_cumulative_returns.tail()
# Visualize the cumulative returns using the Pandas plot function
# Include a title parameter and adjust the figure size
whale_cumulative_returns.plot(figsize =(20,10), title = 'Cumulative returns of whales and the S&P 500')
# Use the daily return data to create box plots to visualize the volatility of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(kind ='box', title = 'Box plot of daily returns of the whales and SPX')
# Create a new DataFrame containing only the 4 fund portfolios by dropping the S&P 500 column from the DataFrame
# Create box plots to reflect the return data for only the 4 fund portfolios
# Include a title parameter and adjust the figure size
whales_only = whale_daily_returns.drop(['S&P 500'], axis = 1)
whales_only.plot(kind = 'box', figsize =(15, 7), title = 'Whale only data ex-SPX')
# Calculate and sort the standard deviation for all 4 portfolios and the S&P 500
# Review the standard deviations sorted smallest to largest
whale_std = whale_daily_returns.std()
whale_std.sort_values()
# Calculate and sort the annualized standard deviation (252 trading days) of the 4 portfolios and the S&P 500
# Review the annual standard deviations smallest to largest
whale_std_annualized = whale_std *np.sqrt(252)
whale_std_annualized.sort_values()
# Using the daily returns DataFrame and a 21-day rolling window,
# plot the rolling standard deviation of the 4 portfolios and the S&P 500
# Include a title parameter and adjust the figure size
whale_std_21d = whale_daily_returns.rolling(window = 21).std()
whale_std_21d.plot(figsize=(15,10), title = 'Rolling 21d std deviations of Whales and SPX')
# Using the daily return data and a 21-day rolling window, plot the rolling standard deviation of just the 4 portfolios.
# Include a title parameter and adjust the figure size
rolling_std_deviaton_21d = whales_only.rolling(21).std()
rolling_std_deviaton_21d.plot(figsize = (15,7), title = 'Rolling Std Deviations -- 21d using daily return data')
# Calculate the annual average return data for the for fund portfolios and the S&P 500
# Use 252 as the number of trading days in the year
# Review the annual average returns sorted from lowest to highest
annualized_average_returns = whale_daily_returns.mean()*(252)
annualized_average_returns.sort_values()
# Calculate the annualized Sharpe Ratios for each of the 4 portfolios and the S&P 500.
# Review the Sharpe ratios sorted lowest to highest
sharpe = annualized_average_returns / whale_std_annualized
sharpe.sort_values()
# Visualize the Sharpe ratios as a bar chart
# Include a title parameter and adjust the figure size
sharpe.plot(kind = 'bar', figsize = (12,5), title = 'Sharpe Ratios of the Whales and the SPX')
# Calculate the variance of the S&P 500 using a rolling 60-day window.
spx_var_60d = whale_daily_returns['S&P 500'].rolling(window = 60).var()
spx_var_60d.tail()
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
berkshire_spx_cov_60d = whale_daily_returns['BERKSHIRE HATHAWAY INC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
berkshire_spx_cov_60d.tail()
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
berkshire_beta = berkshire_spx_cov_60d / spx_var_60d
berkshire_beta.tail()
#covariance = whale_daily_returns['BERKSHIRE HATHAWAY INC'].cov(whale_daily_returns['S&P 500'])
#variance = whale_daily_returns['S&P 500'].var()
#beta = covariance/variance
#beta
# Calculate the average of the 60-day rolling beta
berkshire_average_60d_beta = berkshire_beta.mean()
berkshire_average_60d_beta
# Plot the rolling beta
# Include a title parameter and adjust the figure size
berkshire_beta.plot(figsize =(15,7), title = 'Berkshire 60d rolling beta')
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
tiger_spx_cov_60d = whale_daily_returns['TIGER GLOBAL MANAGEMENT LLC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
tiger_spx_cov_60d.tail()
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
tiger_beta = tiger_spx_cov_60d / spx_var_60d
# Calculate the average of the 60-day rolling beta
tiger_average_60d_beta = tiger_beta.mean()
tiger_average_60d_beta
# Plot the rolling beta
# Include a title parameter and adjust the figure size
tiger_beta.plot(figsize =(15,7), title = 'Tiger 60d rolling beta')
| 0.851089 | 0.995805 |
```
# install: tqdm (progress bars)
!pip install tqdm
import torch
import torch.nn as nn
import numpy as np
from tqdm.auto import tqdm
from torch.utils.data import DataLoader, Dataset, TensorDataset
import torchvision.datasets as ds
```
## Load the data (CIFAR-10)
```
def load_cifar(datadir='./data_cache'): # will download ~400MB of data into this dir. Change the dir if neccesary. If using paperspace, you can make this /storage
train_ds = ds.CIFAR10(root=datadir, train=True,
download=True, transform=None)
test_ds = ds.CIFAR10(root=datadir, train=False,
download=True, transform=None)
def to_xy(dataset):
X = torch.Tensor(np.transpose(dataset.data, (0, 3, 1, 2))).float() / 255.0 # [0, 1]
Y = torch.Tensor(np.array(dataset.targets)).long()
return X, Y
X_tr, Y_tr = to_xy(train_ds)
X_te, Y_te = to_xy(test_ds)
return X_tr, Y_tr, X_te, Y_te
def make_loader(dataset, batch_size=128):
return torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=4, pin_memory=True)
X_tr, Y_tr, X_te, Y_te = load_cifar()
train_dl = make_loader(TensorDataset(X_tr, Y_tr))
test_dl = make_loader(TensorDataset(X_te, Y_te))
```
## Training helper functions
```
def train_epoch(model, train_dl : DataLoader, opt, k = 50):
''' Trains model for one epoch on the provided dataloader, with optimizer opt. Logs stats every k batches.'''
loss_func = nn.CrossEntropyLoss()
model.train()
model.cuda()
netLoss = 0.0
nCorrect = 0
nTotal = 0
for i, (xB, yB) in enumerate(tqdm(train_dl)):
opt.zero_grad()
xB, yB = xB.cuda(), yB.cuda()
outputs = model(xB)
loss = loss_func(outputs, yB)
loss.backward()
opt.step()
netLoss += loss.item() * len(xB)
with torch.no_grad():
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yB).float().sum()
nTotal += preds.size(0)
if (i+1) % k == 0:
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
print(f'\t [Batch {i+1} / {len(train_dl)}] Train Loss: {avg_loss:.3f} \t Train Acc: {train_acc:.3f}')
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
return avg_loss, train_acc
def evaluate(model, test_dl, loss_func=nn.CrossEntropyLoss().cuda()):
''' Returns loss, acc'''
model.eval()
model.cuda()
nCorrect = 0.0
nTotal = 0
net_loss = 0.0
with torch.no_grad():
for (xb, yb) in test_dl:
xb, yb = xb.cuda(), yb.cuda()
outputs = model(xb)
loss = len(xb) * loss_func(outputs, yb)
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yb).float().sum()
net_loss += loss
nTotal += preds.size(0)
acc = nCorrect.cpu().item() / float(nTotal)
loss = net_loss.cpu().item() / float(nTotal)
return loss, acc
## Define model
## 5-Layer CNN for CIFAR
## This is the Myrtle5 network by David Page (https://myrtle.ai/learn/how-to-train-your-resnet-4-architecture/)
class Flatten(nn.Module):
def forward(self, x): return x.view(x.size(0), x.size(1))
def make_cnn(c=64, num_classes=10):
''' Returns a 5-layer CNN with width parameter c. '''
return nn.Sequential(
# Layer 0
nn.Conv2d(3, c, kernel_size=3, stride=1,
padding=1, bias=True),
nn.BatchNorm2d(c),
nn.ReLU(),
# Layer 1
nn.Conv2d(c, c*2, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*2),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 2
nn.Conv2d(c*2, c*4, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*4),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 3
nn.Conv2d(c*4, c*8, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*8),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 4
nn.MaxPool2d(4),
Flatten(),
nn.Linear(c*8, num_classes, bias=True)
)
## Train
model = make_cnn()
opt = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 20
for i in range(epochs):
print(f'Starting Epoch {i}')
train_loss, train_acc = train_epoch(model, train_dl, opt)
test_loss, test_acc = evaluate(model, test_dl)
print(f'Epoch {i}:\t Train Loss: {train_loss:.3f} \t Train Acc: {train_acc:.3f}\t Test Acc: {test_acc:.3f}')
```
|
github_jupyter
|
# install: tqdm (progress bars)
!pip install tqdm
import torch
import torch.nn as nn
import numpy as np
from tqdm.auto import tqdm
from torch.utils.data import DataLoader, Dataset, TensorDataset
import torchvision.datasets as ds
def load_cifar(datadir='./data_cache'): # will download ~400MB of data into this dir. Change the dir if neccesary. If using paperspace, you can make this /storage
train_ds = ds.CIFAR10(root=datadir, train=True,
download=True, transform=None)
test_ds = ds.CIFAR10(root=datadir, train=False,
download=True, transform=None)
def to_xy(dataset):
X = torch.Tensor(np.transpose(dataset.data, (0, 3, 1, 2))).float() / 255.0 # [0, 1]
Y = torch.Tensor(np.array(dataset.targets)).long()
return X, Y
X_tr, Y_tr = to_xy(train_ds)
X_te, Y_te = to_xy(test_ds)
return X_tr, Y_tr, X_te, Y_te
def make_loader(dataset, batch_size=128):
return torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=4, pin_memory=True)
X_tr, Y_tr, X_te, Y_te = load_cifar()
train_dl = make_loader(TensorDataset(X_tr, Y_tr))
test_dl = make_loader(TensorDataset(X_te, Y_te))
def train_epoch(model, train_dl : DataLoader, opt, k = 50):
''' Trains model for one epoch on the provided dataloader, with optimizer opt. Logs stats every k batches.'''
loss_func = nn.CrossEntropyLoss()
model.train()
model.cuda()
netLoss = 0.0
nCorrect = 0
nTotal = 0
for i, (xB, yB) in enumerate(tqdm(train_dl)):
opt.zero_grad()
xB, yB = xB.cuda(), yB.cuda()
outputs = model(xB)
loss = loss_func(outputs, yB)
loss.backward()
opt.step()
netLoss += loss.item() * len(xB)
with torch.no_grad():
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yB).float().sum()
nTotal += preds.size(0)
if (i+1) % k == 0:
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
print(f'\t [Batch {i+1} / {len(train_dl)}] Train Loss: {avg_loss:.3f} \t Train Acc: {train_acc:.3f}')
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
return avg_loss, train_acc
def evaluate(model, test_dl, loss_func=nn.CrossEntropyLoss().cuda()):
''' Returns loss, acc'''
model.eval()
model.cuda()
nCorrect = 0.0
nTotal = 0
net_loss = 0.0
with torch.no_grad():
for (xb, yb) in test_dl:
xb, yb = xb.cuda(), yb.cuda()
outputs = model(xb)
loss = len(xb) * loss_func(outputs, yb)
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yb).float().sum()
net_loss += loss
nTotal += preds.size(0)
acc = nCorrect.cpu().item() / float(nTotal)
loss = net_loss.cpu().item() / float(nTotal)
return loss, acc
## Define model
## 5-Layer CNN for CIFAR
## This is the Myrtle5 network by David Page (https://myrtle.ai/learn/how-to-train-your-resnet-4-architecture/)
class Flatten(nn.Module):
def forward(self, x): return x.view(x.size(0), x.size(1))
def make_cnn(c=64, num_classes=10):
''' Returns a 5-layer CNN with width parameter c. '''
return nn.Sequential(
# Layer 0
nn.Conv2d(3, c, kernel_size=3, stride=1,
padding=1, bias=True),
nn.BatchNorm2d(c),
nn.ReLU(),
# Layer 1
nn.Conv2d(c, c*2, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*2),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 2
nn.Conv2d(c*2, c*4, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*4),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 3
nn.Conv2d(c*4, c*8, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*8),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 4
nn.MaxPool2d(4),
Flatten(),
nn.Linear(c*8, num_classes, bias=True)
)
## Train
model = make_cnn()
opt = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 20
for i in range(epochs):
print(f'Starting Epoch {i}')
train_loss, train_acc = train_epoch(model, train_dl, opt)
test_loss, test_acc = evaluate(model, test_dl)
print(f'Epoch {i}:\t Train Loss: {train_loss:.3f} \t Train Acc: {train_acc:.3f}\t Test Acc: {test_acc:.3f}')
| 0.879858 | 0.832475 |
# Introduction to Deep Learning with PyTorch
In this notebook, you will get an introduction to [PyTorch](http://pytorch.org/), which is a framework for building and training neural networks (NN). ``PyTorch`` in a lot of ways behaves like the arrays you know and love from Numpy. These Numpy arrays, after all, are just *tensors*. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with **Python** and the ``Numpy/Scipy`` stack compared to *TensorFlow* and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
!pip install torch==1.10.1
!pip install matplotlib==3.5.0
!pip install numpy==1.21.4
!pip install omegaconf==2.1.1
!pip install optuna==2.10.0
!pip install Pillow==9.0.0
!pip install scikit_learn==1.0.2
!pip install torchvision==0.11.2
!pip install transformers==4.15.0
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
print(bias)
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second tensor. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view) and [`torch.transpose(weights,0,1)`](https://pytorch.org/docs/master/generated/torch.transpose.html).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
* `torch.transpose(weights,0,1)` will return transposed weights tensor. This returns transposed version of inpjut tensor along dim 0 and dim 1. This is efficient since we do not specify to actual dimesions of weights.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
One more approach is to use `.t()` to transpose vector of weights, in our case from (1,5) to (5,1) shape.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
print('Hello pycharm')
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units are a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
np.set_printoptions(precision=8)
a = np.random.rand(4,3)
a
torch.set_printoptions(precision=8)
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
|
github_jupyter
|
# First, import PyTorch
!pip install torch==1.10.1
!pip install matplotlib==3.5.0
!pip install numpy==1.21.4
!pip install omegaconf==2.1.1
!pip install optuna==2.10.0
!pip install Pillow==9.0.0
!pip install scikit_learn==1.0.2
!pip install torchvision==0.11.2
!pip install transformers==4.15.0
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
print(bias)
## Calculate the output of this network using the weights and bias tensors
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
## Calculate the output of this network using matrix multiplication
print('Hello pycharm')
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
## Your solution here
import numpy as np
np.set_printoptions(precision=8)
a = np.random.rand(4,3)
a
torch.set_printoptions(precision=8)
b = torch.from_numpy(a)
b
b.numpy()
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
| 0.708616 | 0.988949 |
<h1>PCA Training with BotNet (02-03-2018)</h1>
```
import os
import tensorflow as tf
import numpy as np
import itertools
import matplotlib.pyplot as plt
import gc
from datetime import datetime
from sklearn.utils import shuffle
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.metrics import confusion_matrix
input_label = []
output_label = []
a,b = 0,0
ficheiro = open("..\\DatasetTratado\\02-03-2018.csv", "r")
nome_label = ficheiro.readline().split(",")
ficheiro.readline()
ficheiro.readline()
linha = ficheiro.readline()
while(linha != ""):
linha = linha.split(",")
out = linha.pop(37)
if(out == "Benign"):
out = 0
b += 1
else:
out = 1
a += 1
output_label.append(out)
input_label.append(linha)
linha = ficheiro.readline()
ficheiro.close()
print(str(a) + " " + str(b))
backup_input_label = input_label[:]
backup_output_label = output_label[:]
input_label = backup_input_label[:]
output_label = backup_output_label[:]
```
## "STANDARDIZATION"
```
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(input_label)
input_label = scaler.transform(input_label)
input_label
```
<h2>NUMBER OF PARAMETERS WITH PCA</h2>
```
from sklearn.decomposition import PCA
pca=PCA(n_components=18)
pca.fit(input_label)
x_pca = pca.transform(input_label)
input_label.shape
x_pca.shape
input_label
x_pca
# plt.figure(figsize=(8,6))
# plt.scatter(range(1000), x_pca[:,0][:1000])
# plt.scatter(range(1000), x_pca[:,1][:1000], c="red")
# plt.xlabel('First principle component')
# plt.ylabel('Second principle component')
```
<h2>MATPLOTLIB</h2>
```
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0][:200000],x_pca[:,1][:200000])
plt.xlabel('First principle component')
plt.ylabel('Second principle component')
```
<h2>MODEL TRAINING</h2>
```
x_pca = x_pca.reshape(len(x_pca), 18, 1)
y_pca = np.array(output_label)
x_pca, y_pca = shuffle(x_pca, y_pca)
inp_train, inp_test, out_train, out_test = train_test_split(x_pca, y_pca, test_size = 0.2)
model = keras.Sequential([
layers.Input(shape = (18, 1)),
layers.Conv1D(filters = 32, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Conv1D(filters = 16, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Flatten(),
layers.Dense(units = 2, activation = "softmax")
])
model.compile(optimizer= keras.optimizers.SGD(learning_rate= 0.08), loss="sparse_categorical_crossentropy", metrics=['accuracy'])
treino = model.fit(x = inp_train, y = out_train, validation_split= 0.1, epochs = 5, shuffle = True,verbose = 1)
res = [np.argmax(resu) for resu in model.predict(inp_test)]
cm = confusion_matrix(y_true = out_test.reshape(len(out_test)), y_pred = np.array(res))
def plot_confusion_matrix(cm, classes, normaliza = False, title = "Confusion matrix", cmap = plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normaliza:
cm = cm.astype('float') / cm.sum(axis = 1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print("Confusion matrix, without normalization")
print(cm)
thresh = cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i,j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
labels = ["Benign", "Bot"]
plot_confusion_matrix(cm = cm, classes = labels, title = "Bot IDS")
model.save("CNN1BotNet(02-03-2018)PCA2.h5")
```
|
github_jupyter
|
import os
import tensorflow as tf
import numpy as np
import itertools
import matplotlib.pyplot as plt
import gc
from datetime import datetime
from sklearn.utils import shuffle
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.metrics import confusion_matrix
input_label = []
output_label = []
a,b = 0,0
ficheiro = open("..\\DatasetTratado\\02-03-2018.csv", "r")
nome_label = ficheiro.readline().split(",")
ficheiro.readline()
ficheiro.readline()
linha = ficheiro.readline()
while(linha != ""):
linha = linha.split(",")
out = linha.pop(37)
if(out == "Benign"):
out = 0
b += 1
else:
out = 1
a += 1
output_label.append(out)
input_label.append(linha)
linha = ficheiro.readline()
ficheiro.close()
print(str(a) + " " + str(b))
backup_input_label = input_label[:]
backup_output_label = output_label[:]
input_label = backup_input_label[:]
output_label = backup_output_label[:]
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(input_label)
input_label = scaler.transform(input_label)
input_label
from sklearn.decomposition import PCA
pca=PCA(n_components=18)
pca.fit(input_label)
x_pca = pca.transform(input_label)
input_label.shape
x_pca.shape
input_label
x_pca
# plt.figure(figsize=(8,6))
# plt.scatter(range(1000), x_pca[:,0][:1000])
# plt.scatter(range(1000), x_pca[:,1][:1000], c="red")
# plt.xlabel('First principle component')
# plt.ylabel('Second principle component')
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0][:200000],x_pca[:,1][:200000])
plt.xlabel('First principle component')
plt.ylabel('Second principle component')
x_pca = x_pca.reshape(len(x_pca), 18, 1)
y_pca = np.array(output_label)
x_pca, y_pca = shuffle(x_pca, y_pca)
inp_train, inp_test, out_train, out_test = train_test_split(x_pca, y_pca, test_size = 0.2)
model = keras.Sequential([
layers.Input(shape = (18, 1)),
layers.Conv1D(filters = 32, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Conv1D(filters = 16, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Flatten(),
layers.Dense(units = 2, activation = "softmax")
])
model.compile(optimizer= keras.optimizers.SGD(learning_rate= 0.08), loss="sparse_categorical_crossentropy", metrics=['accuracy'])
treino = model.fit(x = inp_train, y = out_train, validation_split= 0.1, epochs = 5, shuffle = True,verbose = 1)
res = [np.argmax(resu) for resu in model.predict(inp_test)]
cm = confusion_matrix(y_true = out_test.reshape(len(out_test)), y_pred = np.array(res))
def plot_confusion_matrix(cm, classes, normaliza = False, title = "Confusion matrix", cmap = plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normaliza:
cm = cm.astype('float') / cm.sum(axis = 1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print("Confusion matrix, without normalization")
print(cm)
thresh = cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i,j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
labels = ["Benign", "Bot"]
plot_confusion_matrix(cm = cm, classes = labels, title = "Bot IDS")
model.save("CNN1BotNet(02-03-2018)PCA2.h5")
| 0.623377 | 0.711042 |
<a href="https://colab.research.google.com/github/awikner/CHyPP/blob/master/TREND_Logistic_Regression.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Import libraries and sklearn and skimage modules.
```
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from skimage.util import invert
```
## Load in the mnist handwritten number dataset from the openml library. The X array contains images of handwritten numbers, while the y array contains their known classification.
```
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
```
## We plot a few of the number images and their known classifications in greyscale.
```
plt.imshow(invert(X[0].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[0]))
plt.show()
plt.imshow(invert(X[1].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[1]))
plt.show()
plt.imshow(invert(X[2].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[2]))
plt.show()
```
## Before we can begin classification, we must train our model. We begin by breaking up our data set into training and testing sets.
```
train_samples = 800
# train_samples = 8000
test_samples = 10000
X_train, X_test, y_train, y_test = train_test_split(X,y,train_size = train_samples, test_size = test_samples)
```
## We use sklearn to create our logistic regression classifier. We then fit it to our training data.
```
classifier = LogisticRegression(solver = 'saga', penalty = 'l1', tol = 1e-2)
classifier.fit(X_train, y_train)
```
## We test the accuracy of our trained classifier using the accuracy score method on the training and testing data sets. This computes the number of accurately predicted classes over the total number of samples. Note that the in-sample (training) accuracy is much higher than the out-of-sample (test) accuracy.
```
score_train = classifier.score(X_train,y_train)
score_test = classifier.score(X_test,y_test)
print('Accuracy score for training data: ',score_train)
print('Accuracy score for test data: ',score_test)
```
## Finally, we plot a few test images to show how our classifier has classified them.
```
offset = 23
y0_test = classifier.predict(X_test[0 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[0 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y0_test+', True number: '+y_test[0+offset])
plt.show()
y1_test = classifier.predict(X_test[1 + offset ].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[1 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y1_test+', True number: '+y_test[1+offset])
plt.show()
y2_test = classifier.predict(X_test[2 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[2 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y2_test+', True number: '+y_test[2+offset])
plt.show()
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from skimage.util import invert
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
plt.imshow(invert(X[0].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[0]))
plt.show()
plt.imshow(invert(X[1].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[1]))
plt.show()
plt.imshow(invert(X[2].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[2]))
plt.show()
train_samples = 800
# train_samples = 8000
test_samples = 10000
X_train, X_test, y_train, y_test = train_test_split(X,y,train_size = train_samples, test_size = test_samples)
classifier = LogisticRegression(solver = 'saga', penalty = 'l1', tol = 1e-2)
classifier.fit(X_train, y_train)
score_train = classifier.score(X_train,y_train)
score_test = classifier.score(X_test,y_test)
print('Accuracy score for training data: ',score_train)
print('Accuracy score for test data: ',score_test)
offset = 23
y0_test = classifier.predict(X_test[0 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[0 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y0_test+', True number: '+y_test[0+offset])
plt.show()
y1_test = classifier.predict(X_test[1 + offset ].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[1 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y1_test+', True number: '+y_test[1+offset])
plt.show()
y2_test = classifier.predict(X_test[2 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[2 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y2_test+', True number: '+y_test[2+offset])
plt.show()
| 0.611034 | 0.99066 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Algorithms/Segmentation/segmentation_snic.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# imageCollection = ee.ImageCollection("USDA/NAIP/DOQQ"),
# geometry = ee.Geometry.Polygon(
# [[[-121.89511299133301, 38.98496606984683],
# [-121.89511299133301, 38.909335196675435],
# [-121.69358253479004, 38.909335196675435],
# [-121.69358253479004, 38.98496606984683]]], {}, False),
# geometry2 = ee.Geometry.Polygon(
# [[[-108.34304809570307, 36.66975278349341],
# [-108.34225416183466, 36.66977859999848],
# [-108.34226489067072, 36.67042400981031],
# [-108.34308028221125, 36.670380982657925]]]),
# imageCollection2 = ee.ImageCollection("USDA/NASS/CDL"),
# cdl2016 = ee.Image("USDA/NASS/CDL/2016")
# Map.centerObject(geometry, {}, 'roi')
# # Map.addLayer(ee.Image(1), {'palette': "white"})
# cdl2016 = cdl2016.select(0).clip(geometry)
# function erode(img, distance) {
# d = (img.Not().unmask(1) \
# .fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return img.updateMask(d.gt(distance))
# }
# function dilate(img, distance) {
# d = (img.fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return d.lt(distance)
# }
# function expandSeeds(seeds) {
# seeds = seeds.unmask(0).focal_max()
# return seeds.updateMask(seeds)
# }
# bands = ["R", "G", "B", "N"]
# img = imageCollection \
# .filterDate('2015-01-01', '2017-01-01') \
# .filterBounds(geometry) \
# .mosaic()
# img = ee.Image(img).clip(geometry).divide(255).select(bands)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN", False)
# seeds = ee.Algorithms.Image.Segmentation.seedGrid(36)
# # Apply a softening.
# kernel = ee.Kernel.gaussian(3)
# img = img.convolve(kernel)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN blur", False)
# # Compute and display NDVI, NDVI slices and NDVI gradient.
# ndvi = img.normalizedDifference(["N", "R"])
# # print(ui.Chart.image.histogram(ndvi, geometry, 10))
# Map.addLayer(ndvi, {'min':0, 'max':1, 'palette': ["black", "tan", "green", "darkgreen"]}, "NDVI", False)
# Map.addLayer(ndvi.gt([0, 0.2, 0.40, 0.60, 0.80, 1.00]).reduce('sum'), {'min':0, 'max': 6}, "NDVI steps", False)
# ndviGradient = ndvi.gradient().pow(2).reduce('sum').sqrt()
# Map.addLayer(ndviGradient, {'min':0, 'max':0.01}, "NDVI gradient", False)
# gradient = img.spectralErosion().spectralGradient('emd')
# Map.addLayer(gradient, {'min':0, 'max': 0.3}, "emd", False)
# # Run SNIC on the regular square grid.
# snic = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize:256,
# seeds: seeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters = snic.select("clusters")
# Map.addLayer(clusters.randomVisualizer(), {}, "clusters")
# Map.addLayer(snic, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# Map.addLayer(expandSeeds(seeds))
# # Compute per-cluster stdDev.
# stdDev = img.addBands(clusters).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev, {'min':0, 'max':0.1}, "StdDev")
# # Display outliers as transparent
# outliers = stdDev.reduce('sum').gt(0.25)
# Map.addLayer(outliers.updateMask(outliers.Not()), {}, "Outliers", False)
# # Within each outlier, find most distant member.
# distance = img.select(bands).spectralDistance(snic.select(bands), "sam").updateMask(outliers)
# maxDistance = distance.addBands(clusters).reduceConnectedComponents(ee.Reducer.max(), "clusters", 256)
# Map.addLayer(distance, {'min':0, 'max':0.3}, "max distance")
# Map.addLayer(expandSeeds(expandSeeds(distance.eq(maxDistance))), {'palette': ["red"]}, "second seeds")
# newSeeds = seeds.unmask(0).add(distance.eq(maxDistance).unmask(0))
# newSeeds = newSeeds.updateMask(newSeeds)
# # Run SNIC again with both sets of seeds.
# snic2 = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize: 256,
# seeds: newSeeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters2 = snic2.select("clusters")
# Map.addLayer(clusters2.randomVisualizer(), {}, "clusters 2")
# Map.addLayer(snic2, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# # Compute outliers again.
# stdDev2 = img.addBands(clusters2).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev2, {'min':0, 'max':0.1}, "StdDev 2")
# outliers2 = stdDev2.reduce('sum').gt(0.25)
# outliers2 = outliers2.updateMask(outliers2.Not())
# Map.addLayer(outliers2, {}, "Outliers 2", False)
# # Show the final set of seeds.
# Map.addLayer(expandSeeds(newSeeds), {'palette': "white"}, "newSeeds")
# Map.addLayer(expandSeeds(distance.eq(maxDistance)), {'palette': ["red"]}, "second seeds")
# # Area, Perimeter, Width and Height (using snic1 for speed)
# area = ee.Image.pixelArea().addBands(clusters).reduceConnectedComponents(ee.Reducer.sum(), "clusters", 256)
# Map.addLayer(area, {'min':50000, 'max': 500000}, "Cluster Area")
# minMax = clusters.reduceNeighborhood(ee.Reducer.minMax(), ee.Kernel.square(1))
# perimeterPixels = minMax.select(0).neq(minMax.select(1)).rename('perimeter')
# Map.addLayer(perimeterPixels, {'min': 0, 'max': 1}, 'perimeterPixels')
# perimeter = perimeterPixels.addBands(clusters) \
# .reduceConnectedComponents(ee.Reducer.sum(), 'clusters', 256)
# Map.addLayer(perimeter, {'min': 100, 'max': 400}, 'Perimeter size', False)
# sizes = ee.Image.pixelLonLat().addBands(clusters).reduceConnectedComponents(ee.Reducer.minMax(), "clusters", 256)
# width = sizes.select("longitude_max").subtract(sizes.select("longitude_min"))
# height = sizes.select("latitude_max").subtract(sizes.select("latitude_min"))
# Map.addLayer(width, {'min':0, 'max':0.02}, "Cluster width")
# Map.addLayer(height, {'min':0, 'max':0.02}, "Cluster height")
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# Add Earth Engine dataset
# imageCollection = ee.ImageCollection("USDA/NAIP/DOQQ"),
# geometry = ee.Geometry.Polygon(
# [[[-121.89511299133301, 38.98496606984683],
# [-121.89511299133301, 38.909335196675435],
# [-121.69358253479004, 38.909335196675435],
# [-121.69358253479004, 38.98496606984683]]], {}, False),
# geometry2 = ee.Geometry.Polygon(
# [[[-108.34304809570307, 36.66975278349341],
# [-108.34225416183466, 36.66977859999848],
# [-108.34226489067072, 36.67042400981031],
# [-108.34308028221125, 36.670380982657925]]]),
# imageCollection2 = ee.ImageCollection("USDA/NASS/CDL"),
# cdl2016 = ee.Image("USDA/NASS/CDL/2016")
# Map.centerObject(geometry, {}, 'roi')
# # Map.addLayer(ee.Image(1), {'palette': "white"})
# cdl2016 = cdl2016.select(0).clip(geometry)
# function erode(img, distance) {
# d = (img.Not().unmask(1) \
# .fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return img.updateMask(d.gt(distance))
# }
# function dilate(img, distance) {
# d = (img.fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return d.lt(distance)
# }
# function expandSeeds(seeds) {
# seeds = seeds.unmask(0).focal_max()
# return seeds.updateMask(seeds)
# }
# bands = ["R", "G", "B", "N"]
# img = imageCollection \
# .filterDate('2015-01-01', '2017-01-01') \
# .filterBounds(geometry) \
# .mosaic()
# img = ee.Image(img).clip(geometry).divide(255).select(bands)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN", False)
# seeds = ee.Algorithms.Image.Segmentation.seedGrid(36)
# # Apply a softening.
# kernel = ee.Kernel.gaussian(3)
# img = img.convolve(kernel)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN blur", False)
# # Compute and display NDVI, NDVI slices and NDVI gradient.
# ndvi = img.normalizedDifference(["N", "R"])
# # print(ui.Chart.image.histogram(ndvi, geometry, 10))
# Map.addLayer(ndvi, {'min':0, 'max':1, 'palette': ["black", "tan", "green", "darkgreen"]}, "NDVI", False)
# Map.addLayer(ndvi.gt([0, 0.2, 0.40, 0.60, 0.80, 1.00]).reduce('sum'), {'min':0, 'max': 6}, "NDVI steps", False)
# ndviGradient = ndvi.gradient().pow(2).reduce('sum').sqrt()
# Map.addLayer(ndviGradient, {'min':0, 'max':0.01}, "NDVI gradient", False)
# gradient = img.spectralErosion().spectralGradient('emd')
# Map.addLayer(gradient, {'min':0, 'max': 0.3}, "emd", False)
# # Run SNIC on the regular square grid.
# snic = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize:256,
# seeds: seeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters = snic.select("clusters")
# Map.addLayer(clusters.randomVisualizer(), {}, "clusters")
# Map.addLayer(snic, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# Map.addLayer(expandSeeds(seeds))
# # Compute per-cluster stdDev.
# stdDev = img.addBands(clusters).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev, {'min':0, 'max':0.1}, "StdDev")
# # Display outliers as transparent
# outliers = stdDev.reduce('sum').gt(0.25)
# Map.addLayer(outliers.updateMask(outliers.Not()), {}, "Outliers", False)
# # Within each outlier, find most distant member.
# distance = img.select(bands).spectralDistance(snic.select(bands), "sam").updateMask(outliers)
# maxDistance = distance.addBands(clusters).reduceConnectedComponents(ee.Reducer.max(), "clusters", 256)
# Map.addLayer(distance, {'min':0, 'max':0.3}, "max distance")
# Map.addLayer(expandSeeds(expandSeeds(distance.eq(maxDistance))), {'palette': ["red"]}, "second seeds")
# newSeeds = seeds.unmask(0).add(distance.eq(maxDistance).unmask(0))
# newSeeds = newSeeds.updateMask(newSeeds)
# # Run SNIC again with both sets of seeds.
# snic2 = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize: 256,
# seeds: newSeeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters2 = snic2.select("clusters")
# Map.addLayer(clusters2.randomVisualizer(), {}, "clusters 2")
# Map.addLayer(snic2, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# # Compute outliers again.
# stdDev2 = img.addBands(clusters2).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev2, {'min':0, 'max':0.1}, "StdDev 2")
# outliers2 = stdDev2.reduce('sum').gt(0.25)
# outliers2 = outliers2.updateMask(outliers2.Not())
# Map.addLayer(outliers2, {}, "Outliers 2", False)
# # Show the final set of seeds.
# Map.addLayer(expandSeeds(newSeeds), {'palette': "white"}, "newSeeds")
# Map.addLayer(expandSeeds(distance.eq(maxDistance)), {'palette': ["red"]}, "second seeds")
# # Area, Perimeter, Width and Height (using snic1 for speed)
# area = ee.Image.pixelArea().addBands(clusters).reduceConnectedComponents(ee.Reducer.sum(), "clusters", 256)
# Map.addLayer(area, {'min':50000, 'max': 500000}, "Cluster Area")
# minMax = clusters.reduceNeighborhood(ee.Reducer.minMax(), ee.Kernel.square(1))
# perimeterPixels = minMax.select(0).neq(minMax.select(1)).rename('perimeter')
# Map.addLayer(perimeterPixels, {'min': 0, 'max': 1}, 'perimeterPixels')
# perimeter = perimeterPixels.addBands(clusters) \
# .reduceConnectedComponents(ee.Reducer.sum(), 'clusters', 256)
# Map.addLayer(perimeter, {'min': 100, 'max': 400}, 'Perimeter size', False)
# sizes = ee.Image.pixelLonLat().addBands(clusters).reduceConnectedComponents(ee.Reducer.minMax(), "clusters", 256)
# width = sizes.select("longitude_max").subtract(sizes.select("longitude_min"))
# height = sizes.select("latitude_max").subtract(sizes.select("latitude_min"))
# Map.addLayer(width, {'min':0, 'max':0.02}, "Cluster width")
# Map.addLayer(height, {'min':0, 'max':0.02}, "Cluster height")
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 0.665845 | 0.958654 |
# Introduction to XGBoost Spark with GPU
Taxi is an example of xgboost regressor. In this notebook, we will show you how to load data, train the xgboost model and use this model to predict "fare_amount" of your taxi trip.
A few libraries are required:
1. NumPy
2. cudf jar
3. xgboost4j jar
4. xgboost4j-spark jar
#### Import All Libraries
```
from ml.dmlc.xgboost4j.scala.spark import XGBoostRegressionModel, XGBoostRegressor
from ml.dmlc.xgboost4j.scala.spark.rapids import GpuDataReader
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
```
Note on CPU version: `GpuDataReader` is not necessary, but two extra libraries are required.
```Python
from pyspark.ml.feature import VectorAssembler
from pyspark.sql.functions import col
```
#### Create Spark Session
```
spark = SparkSession.builder.getOrCreate()
```
#### Specify the Data Schema and Load the Data
```
label = 'fare_amount'
schema = StructType([
StructField('vendor_id', FloatType()),
StructField('passenger_count', FloatType()),
StructField('trip_distance', FloatType()),
StructField('pickup_longitude', FloatType()),
StructField('pickup_latitude', FloatType()),
StructField('rate_code', FloatType()),
StructField('store_and_fwd', FloatType()),
StructField('dropoff_longitude', FloatType()),
StructField('dropoff_latitude', FloatType()),
StructField(label, FloatType()),
StructField('hour', FloatType()),
StructField('year', IntegerType()),
StructField('month', IntegerType()),
StructField('day', FloatType()),
StructField('day_of_week', FloatType()),
StructField('is_weekend', FloatType()),
])
features = [ x.name for x in schema if x.name != label ]
train_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
```
Note on CPU version: Data reader is created with `spark.read` instead of `GpuDataReader(spark)`. Also vectorization is required, which means you need to assemble all feature columns into one column.
```Python
def vectorize(data_frame):
to_floats = [ col(x.name).cast(FloatType()) for x in data_frame.schema ]
return (VectorAssembler()
.setInputCols(features)
.setOutputCol('features')
.transform(data_frame.select(to_floats))
.select(col('features'), col(label)))
train_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
train_data = vectorize(train_data)
eval_data = vectorize(eval_data)
```
#### Create XGBoostRegressor
```
params = {
'eta': 0.05,
'treeMethod': 'gpu_hist',
'maxDepth': 8,
'subsample': 0.8,
'gamma': 1.0,
'numRound': 100,
'numWorkers': 1,
}
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCols(features)
```
Note on CPU version: The CPU version provides the `setFeaturesCol` function, that's why vectorization is required. The parameter `num_workers` should be set to the number of machines with GPU in Spark cluster in GPU version, while it can be set to the number of your CPU cores in CPU version. The tree method `gpu_hist` is designed for GPU training, while tree method `hist` is designed for CPU training.
```Python
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCol('features')
```
#### Train the Data with Benchmark
```
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Training', lambda: regressor.fit(train_data))
```
#### Save and Reload the Model
```
model.write().overwrite().save('/data/new-model-path')
loaded_model = XGBoostRegressionModel().load('/data/new-model-path')
```
#### Transformation and Show Result Sample
```
def transform():
result = loaded_model.transform(eval_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transformation', transform)
result.select('vendor_id', 'passenger_count', 'trip_distance', label, 'prediction').show(5)
```
Note on CPU version: You cannot `select` the feature columns after vectorization. So please use `result.show(5)` instead.
#### Evaluation
```
accuracy = with_benchmark(
'Evaluation',
lambda: RegressionEvaluator().setLabelCol(label).evaluate(result))
print('RMSI is ' + str(accuracy))
```
#### Stop
```
spark.stop()
```
|
github_jupyter
|
from ml.dmlc.xgboost4j.scala.spark import XGBoostRegressionModel, XGBoostRegressor
from ml.dmlc.xgboost4j.scala.spark.rapids import GpuDataReader
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
from pyspark.ml.feature import VectorAssembler
from pyspark.sql.functions import col
spark = SparkSession.builder.getOrCreate()
label = 'fare_amount'
schema = StructType([
StructField('vendor_id', FloatType()),
StructField('passenger_count', FloatType()),
StructField('trip_distance', FloatType()),
StructField('pickup_longitude', FloatType()),
StructField('pickup_latitude', FloatType()),
StructField('rate_code', FloatType()),
StructField('store_and_fwd', FloatType()),
StructField('dropoff_longitude', FloatType()),
StructField('dropoff_latitude', FloatType()),
StructField(label, FloatType()),
StructField('hour', FloatType()),
StructField('year', IntegerType()),
StructField('month', IntegerType()),
StructField('day', FloatType()),
StructField('day_of_week', FloatType()),
StructField('is_weekend', FloatType()),
])
features = [ x.name for x in schema if x.name != label ]
train_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
def vectorize(data_frame):
to_floats = [ col(x.name).cast(FloatType()) for x in data_frame.schema ]
return (VectorAssembler()
.setInputCols(features)
.setOutputCol('features')
.transform(data_frame.select(to_floats))
.select(col('features'), col(label)))
train_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
train_data = vectorize(train_data)
eval_data = vectorize(eval_data)
params = {
'eta': 0.05,
'treeMethod': 'gpu_hist',
'maxDepth': 8,
'subsample': 0.8,
'gamma': 1.0,
'numRound': 100,
'numWorkers': 1,
}
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCols(features)
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCol('features')
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Training', lambda: regressor.fit(train_data))
model.write().overwrite().save('/data/new-model-path')
loaded_model = XGBoostRegressionModel().load('/data/new-model-path')
def transform():
result = loaded_model.transform(eval_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transformation', transform)
result.select('vendor_id', 'passenger_count', 'trip_distance', label, 'prediction').show(5)
accuracy = with_benchmark(
'Evaluation',
lambda: RegressionEvaluator().setLabelCol(label).evaluate(result))
print('RMSI is ' + str(accuracy))
spark.stop()
| 0.730001 | 0.960731 |
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
*No changes were made to the contents of this notebook from the original.*
<!--NAVIGATION-->
< [Geographic Data with Basemap](04.13-Geographic-Data-With-Basemap.ipynb) | [Contents](Index.ipynb) | [Further Resources](04.15-Further-Resources.ipynb) >
# Visualization with Seaborn
Matplotlib has proven to be an incredibly useful and popular visualization tool, but even avid users will admit it often leaves much to be desired.
There are several valid complaints about Matplotlib that often come up:
- Prior to version 2.0, Matplotlib's defaults are not exactly the best choices. It was based off of MATLAB circa 1999, and this often shows.
- Matplotlib's API is relatively low level. Doing sophisticated statistical visualization is possible, but often requires a *lot* of boilerplate code.
- Matplotlib predated Pandas by more than a decade, and thus is not designed for use with Pandas ``DataFrame``s. In order to visualize data from a Pandas ``DataFrame``, you must extract each ``Series`` and often concatenate them together into the right format. It would be nicer to have a plotting library that can intelligently use the ``DataFrame`` labels in a plot.
An answer to these problems is [Seaborn](http://seaborn.pydata.org/). Seaborn provides an API on top of Matplotlib that offers sane choices for plot style and color defaults, defines simple high-level functions for common statistical plot types, and integrates with the functionality provided by Pandas ``DataFrame``s.
To be fair, the Matplotlib team is addressing this: it has recently added the ``plt.style`` tools discussed in [Customizing Matplotlib: Configurations and Style Sheets](04.11-Settings-and-Stylesheets.ipynb), and is starting to handle Pandas data more seamlessly.
The 2.0 release of the library will include a new default stylesheet that will improve on the current status quo.
But for all the reasons just discussed, Seaborn remains an extremely useful addon.
## Seaborn Versus Matplotlib
Here is an example of a simple random-walk plot in Matplotlib, using its classic plot formatting and colors.
We start with the typical imports:
```
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
import pandas as pd
```
Now we create some random walk data:
```
# Create some data
rng = np.random.RandomState(0)
x = np.linspace(0, 10, 500)
y = np.cumsum(rng.randn(500, 6), 0)
```
And do a simple plot:
```
# Plot the data with Matplotlib defaults
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
```
Although the result contains all the information we'd like it to convey, it does so in a way that is not all that aesthetically pleasing, and even looks a bit old-fashioned in the context of 21st-century data visualization.
Now let's take a look at how it works with Seaborn.
As we will see, Seaborn has many of its own high-level plotting routines, but it can also overwrite Matplotlib's default parameters and in turn get even simple Matplotlib scripts to produce vastly superior output.
We can set the style by calling Seaborn's ``set()`` method.
By convention, Seaborn is imported as ``sns``:
```
import seaborn as sns
sns.set()
```
Now let's rerun the same two lines as before:
```
# same plotting code as above!
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
```
Ah, much better!
## Exploring Seaborn Plots
The main idea of Seaborn is that it provides high-level commands to create a variety of plot types useful for statistical data exploration, and even some statistical model fitting.
Let's take a look at a few of the datasets and plot types available in Seaborn. Note that all of the following *could* be done using raw Matplotlib commands (this is, in fact, what Seaborn does under the hood) but the Seaborn API is much more convenient.
### Histograms, KDE, and densities
Often in statistical data visualization, all you want is to plot histograms and joint distributions of variables.
We have seen that this is relatively straightforward in Matplotlib:
```
data = np.random.multivariate_normal([0, 0], [[5, 2], [2, 2]], size=2000)
data = pd.DataFrame(data, columns=['x', 'y'])
for col in 'xy':
plt.hist(data[col], normed=True, alpha=0.5)
```
Rather than a histogram, we can get a smooth estimate of the distribution using a kernel density estimation, which Seaborn does with ``sns.kdeplot``:
```
for col in 'xy':
sns.kdeplot(data[col], shade=True)
```
Histograms and KDE can be combined using ``distplot``:
```
sns.distplot(data['x'])
sns.distplot(data['y']);
```
If we pass the full two-dimensional dataset to ``kdeplot``, we will get a two-dimensional visualization of the data:
```
sns.kdeplot(data);
```
We can see the joint distribution and the marginal distributions together using ``sns.jointplot``.
For this plot, we'll set the style to a white background:
```
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='kde');
```
There are other parameters that can be passed to ``jointplot``—for example, we can use a hexagonally based histogram instead:
```
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='hex')
```
### Pair plots
When you generalize joint plots to datasets of larger dimensions, you end up with *pair plots*. This is very useful for exploring correlations between multidimensional data, when you'd like to plot all pairs of values against each other.
We'll demo this with the well-known Iris dataset, which lists measurements of petals and sepals of three iris species:
```
iris = sns.load_dataset("iris")
iris.head()
```
Visualizing the multidimensional relationships among the samples is as easy as calling ``sns.pairplot``:
```
sns.pairplot(iris, hue='species', size=2.5);
```
### Faceted histograms
Sometimes the best way to view data is via histograms of subsets. Seaborn's ``FacetGrid`` makes this extremely simple.
We'll take a look at some data that shows the amount that restaurant staff receive in tips based on various indicator data:
```
tips = sns.load_dataset('tips')
tips.head()
tips['tip_pct'] = 100 * tips['tip'] / tips['total_bill']
grid = sns.FacetGrid(tips, row="sex", col="time", margin_titles=True)
grid.map(plt.hist, "tip_pct", bins=np.linspace(0, 40, 15));
```
### Factor plots
Factor plots can be useful for this kind of visualization as well. This allows you to view the distribution of a parameter within bins defined by any other parameter:
```
with sns.axes_style(style='ticks'):
g = sns.factorplot("day", "total_bill", "sex", data=tips, kind="box")
g.set_axis_labels("Day", "Total Bill");
```
### Joint distributions
Similar to the pairplot we saw earlier, we can use ``sns.jointplot`` to show the joint distribution between different datasets, along with the associated marginal distributions:
```
with sns.axes_style('white'):
sns.jointplot("total_bill", "tip", data=tips, kind='hex')
```
The joint plot can even do some automatic kernel density estimation and regression:
```
sns.jointplot("total_bill", "tip", data=tips, kind='reg');
```
### Bar plots
Time series can be plotted using ``sns.factorplot``. In the following example, we'll use the Planets data that we first saw in [Aggregation and Grouping](03.08-Aggregation-and-Grouping.ipynb):
```
planets = sns.load_dataset('planets')
planets.head()
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=2,
kind="count", color='steelblue')
g.set_xticklabels(step=5)
```
We can learn more by looking at the *method* of discovery of each of these planets:
```
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=4.0, kind='count',
hue='method', order=range(2001, 2015))
g.set_ylabels('Number of Planets Discovered')
```
For more information on plotting with Seaborn, see the [Seaborn documentation](http://seaborn.pydata.org/), a [tutorial](http://seaborn.pydata.org/
tutorial.htm), and the [Seaborn gallery](http://seaborn.pydata.org/examples/index.html).
## Example: Exploring Marathon Finishing Times
Here we'll look at using Seaborn to help visualize and understand finishing results from a marathon.
I've scraped the data from sources on the Web, aggregated it and removed any identifying information, and put it on GitHub where it can be downloaded
(if you are interested in using Python for web scraping, I would recommend [*Web Scraping with Python*](http://shop.oreilly.com/product/0636920034391.do) by Ryan Mitchell).
We will start by downloading the data from
the Web, and loading it into Pandas:
```
#!curl -O https://raw.githubusercontent.com/jakevdp/marathon-data/master/marathon-data.csv
data = pd.read_csv('marathon-data.csv')
data.head()
```
By default, Pandas loaded the time columns as Python strings (type ``object``); we can see this by looking at the ``dtypes`` attribute of the DataFrame:
```
data.dtypes
```
Let's fix this by providing a converter for the times:
```
import datetime as dt #pd.datatools.timedelta deprecated
def convert_time(s):
h, m, s = map(int, s.split(':'))
return dt.timedelta(hours=h, minutes=m, seconds=s)
data = pd.read_csv('marathon-data.csv',
converters={'split':convert_time, 'final':convert_time})
data.head()
data.dtypes
```
That looks much better. For the purpose of our Seaborn plotting utilities, let's next add columns that give the times in seconds:
```
data['split_sec'] = data['split'].astype(int) / 1E9
data['final_sec'] = data['final'].astype(int) / 1E9
data.head()
```
To get an idea of what the data looks like, we can plot a ``jointplot`` over the data:
```
with sns.axes_style('white'):
g = sns.jointplot("split_sec", "final_sec", data, kind='hex')
g.ax_joint.plot(np.linspace(4000, 16000),
np.linspace(8000, 32000), ':k')
```
The dotted line shows where someone's time would lie if they ran the marathon at a perfectly steady pace. The fact that the distribution lies above this indicates (as you might expect) that most people slow down over the course of the marathon.
If you have run competitively, you'll know that those who do the opposite—run faster during the second half of the race—are said to have "negative-split" the race.
Let's create another column in the data, the split fraction, which measures the degree to which each runner negative-splits or positive-splits the race:
```
data['split_frac'] = 1 - 2 * data['split_sec'] / data['final_sec']
data.head()
```
Where this split difference is less than zero, the person negative-split the race by that fraction.
Let's do a distribution plot of this split fraction:
```
sns.distplot(data['split_frac'], kde=False);
plt.axvline(0, color="k", linestyle="--");
sum(data.split_frac < 0)
```
Out of nearly 40,000 participants, there were only 250 people who negative-split their marathon.
Let's see whether there is any correlation between this split fraction and other variables. We'll do this using a ``pairgrid``, which draws plots of all these correlations:
```
g = sns.PairGrid(data, vars=['age', 'split_sec', 'final_sec', 'split_frac'],
hue='gender', palette='RdBu_r')
g.map(plt.scatter, alpha=0.8)
g.add_legend();
```
It looks like the split fraction does not correlate particularly with age, but does correlate with the final time: faster runners tend to have closer to even splits on their marathon time.
(We see here that Seaborn is no panacea for Matplotlib's ills when it comes to plot styles: in particular, the x-axis labels overlap. Because the output is a simple Matplotlib plot, however, the methods in [Customizing Ticks](04.10-Customizing-Ticks.ipynb) can be used to adjust such things if desired.)
The difference between men and women here is interesting. Let's look at the histogram of split fractions for these two groups:
```
sns.kdeplot(data.split_frac[data.gender=='M'], label='men', shade=True)
sns.kdeplot(data.split_frac[data.gender=='W'], label='women', shade=True)
plt.xlabel('split_frac');
```
The interesting thing here is that there are many more men than women who are running close to an even split!
This almost looks like some kind of bimodal distribution among the men and women. Let's see if we can suss-out what's going on by looking at the distributions as a function of age.
A nice way to compare distributions is to use a *violin plot*
```
sns.violinplot("gender", "split_frac", data=data,
palette=["lightblue", "lightpink"]);
```
This is yet another way to compare the distributions between men and women.
Let's look a little deeper, and compare these violin plots as a function of age. We'll start by creating a new column in the array that specifies the decade of age that each person is in:
```
data['age_dec'] = data.age.map(lambda age: 10 * (age // 10))
data.head()
men = (data.gender == 'M')
women = (data.gender == 'W')
with sns.axes_style(style=None):
sns.violinplot("age_dec", "split_frac", hue="gender", data=data,
split=True, inner="quartile",
palette=["lightblue", "lightpink"]);
```
Looking at this, we can see where the distributions of men and women differ: the split distributions of men in their 20s to 50s show a pronounced over-density toward lower splits when compared to women of the same age (or of any age, for that matter).
Also surprisingly, the 80-year-old women seem to outperform *everyone* in terms of their split time. This is probably due to the fact that we're estimating the distribution from small numbers, as there are only a handful of runners in that range:
```
(data.age > 80).sum()
```
Back to the men with negative splits: who are these runners? Does this split fraction correlate with finishing quickly? We can plot this very easily. We'll use ``regplot``, which will automatically fit a linear regression to the data:
```
g = sns.lmplot('final_sec', 'split_frac', col='gender', data=data,
markers=".", scatter_kws=dict(color='c'))
g.map(plt.axhline, y=0.1, color="k", ls=":");
```
Apparently the people with fast splits are the elite runners who are finishing within ~15,000 seconds, or about 4 hours. People slower than that are much less likely to have a fast second split.
<!--NAVIGATION-->
< [Geographic Data with Basemap](04.13-Geographic-Data-With-Basemap.ipynb) | [Contents](Index.ipynb) | [Further Resources](04.15-Further-Resources.ipynb) >
|
github_jupyter
|
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
import pandas as pd
# Create some data
rng = np.random.RandomState(0)
x = np.linspace(0, 10, 500)
y = np.cumsum(rng.randn(500, 6), 0)
# Plot the data with Matplotlib defaults
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
import seaborn as sns
sns.set()
# same plotting code as above!
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
data = np.random.multivariate_normal([0, 0], [[5, 2], [2, 2]], size=2000)
data = pd.DataFrame(data, columns=['x', 'y'])
for col in 'xy':
plt.hist(data[col], normed=True, alpha=0.5)
for col in 'xy':
sns.kdeplot(data[col], shade=True)
sns.distplot(data['x'])
sns.distplot(data['y']);
sns.kdeplot(data);
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='kde');
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='hex')
iris = sns.load_dataset("iris")
iris.head()
sns.pairplot(iris, hue='species', size=2.5);
tips = sns.load_dataset('tips')
tips.head()
tips['tip_pct'] = 100 * tips['tip'] / tips['total_bill']
grid = sns.FacetGrid(tips, row="sex", col="time", margin_titles=True)
grid.map(plt.hist, "tip_pct", bins=np.linspace(0, 40, 15));
with sns.axes_style(style='ticks'):
g = sns.factorplot("day", "total_bill", "sex", data=tips, kind="box")
g.set_axis_labels("Day", "Total Bill");
with sns.axes_style('white'):
sns.jointplot("total_bill", "tip", data=tips, kind='hex')
sns.jointplot("total_bill", "tip", data=tips, kind='reg');
planets = sns.load_dataset('planets')
planets.head()
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=2,
kind="count", color='steelblue')
g.set_xticklabels(step=5)
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=4.0, kind='count',
hue='method', order=range(2001, 2015))
g.set_ylabels('Number of Planets Discovered')
#!curl -O https://raw.githubusercontent.com/jakevdp/marathon-data/master/marathon-data.csv
data = pd.read_csv('marathon-data.csv')
data.head()
data.dtypes
import datetime as dt #pd.datatools.timedelta deprecated
def convert_time(s):
h, m, s = map(int, s.split(':'))
return dt.timedelta(hours=h, minutes=m, seconds=s)
data = pd.read_csv('marathon-data.csv',
converters={'split':convert_time, 'final':convert_time})
data.head()
data.dtypes
data['split_sec'] = data['split'].astype(int) / 1E9
data['final_sec'] = data['final'].astype(int) / 1E9
data.head()
with sns.axes_style('white'):
g = sns.jointplot("split_sec", "final_sec", data, kind='hex')
g.ax_joint.plot(np.linspace(4000, 16000),
np.linspace(8000, 32000), ':k')
data['split_frac'] = 1 - 2 * data['split_sec'] / data['final_sec']
data.head()
sns.distplot(data['split_frac'], kde=False);
plt.axvline(0, color="k", linestyle="--");
sum(data.split_frac < 0)
g = sns.PairGrid(data, vars=['age', 'split_sec', 'final_sec', 'split_frac'],
hue='gender', palette='RdBu_r')
g.map(plt.scatter, alpha=0.8)
g.add_legend();
sns.kdeplot(data.split_frac[data.gender=='M'], label='men', shade=True)
sns.kdeplot(data.split_frac[data.gender=='W'], label='women', shade=True)
plt.xlabel('split_frac');
sns.violinplot("gender", "split_frac", data=data,
palette=["lightblue", "lightpink"]);
data['age_dec'] = data.age.map(lambda age: 10 * (age // 10))
data.head()
men = (data.gender == 'M')
women = (data.gender == 'W')
with sns.axes_style(style=None):
sns.violinplot("age_dec", "split_frac", hue="gender", data=data,
split=True, inner="quartile",
palette=["lightblue", "lightpink"]);
(data.age > 80).sum()
g = sns.lmplot('final_sec', 'split_frac', col='gender', data=data,
markers=".", scatter_kws=dict(color='c'))
g.map(plt.axhline, y=0.1, color="k", ls=":");
| 0.669096 | 0.988906 |
# SMARTS selection and depiction
## Depict molecular components selected by a particular SMARTS
This notebook focuses on selecting molecules containing fragments matching a particular SMARTS query, and then depicting the components (i.e. bonds, angles, torsions) matching that particular query.
```
import openeye.oechem as oechem
import openeye.oedepict as oedepict
from IPython.display import display
import os
from __future__ import print_function
def depictMatch(mol, match, width=500, height=200):
"""Take in an OpenEye molecule and a substructure match and display the results
with (optionally) specified resolution."""
from IPython.display import Image
dopt = oedepict.OEPrepareDepictionOptions()
dopt.SetDepictOrientation( oedepict.OEDepictOrientation_Horizontal)
dopt.SetSuppressHydrogens(True)
oedepict.OEPrepareDepiction(mol, dopt)
opts = oedepict.OE2DMolDisplayOptions(width, height, oedepict.OEScale_AutoScale)
disp = oedepict.OE2DMolDisplay(mol, opts)
hstyle = oedepict.OEHighlightStyle_Color
hcolor = oechem.OEColor(oechem.OELightBlue)
oedepict.OEAddHighlighting(disp, hcolor, hstyle, match)
ofs = oechem.oeosstream()
oedepict.OERenderMolecule(ofs, 'png', disp)
ofs.flush()
return Image(data = "".join(ofs.str()))
import parmed
def createOpenMMSystem(mol):
"""
Generate OpenMM System and positions from an OEMol.
Parameters
----------
mol : OEMol
The molecule
Returns
-------
system : simtk.openmm.System
The OpenMM System
positions : simtk.unit.Quantity wrapped
Positions of the molecule
"""
# write mol2 file
ofsmol2 = oechem.oemolostream('molecule.mol2')
ofsmol2.SetFlavor( oechem.OEFormat_MOL2, oechem.OEOFlavor_MOL2_Forcefield );
oechem.OEWriteConstMolecule(ofsmol2, mol)
ofsmol2.close()
# write tleap input file
leap_input = """
lig = loadMol2 molecule.mol2
saveAmberParm lig prmtop inpcrd
quit
"""
outfile = open('leap.in', 'w')
outfile.write(leap_input)
outfile.close()
# run tleap
leaprc = 'leaprc.Frosst_AlkEthOH'
os.system( 'tleap -f %s -f leap.in > leap.out' % leaprc )
# check if param file was not saved (implies parameterization problems)
paramsNotSaved = 'Parameter file was not saved'
leaplog = open( 'leap.out', 'r' ).read()
if paramsNotSaved in leaplog:
raise Exception('Parameter file was not saved.')
# Read prmtop and inpcrd
amberparm = parmed.amber.AmberParm( 'prmtop', 'inpcrd' )
system = amberparm.createSystem()
return (system, amberparm.positions)
import copy
from simtk import openmm, unit
def getValenceEnergyComponent(system, positions, atoms):
"""
Get the OpenMM valence energy corresponding to a specified set of atoms (bond, angle, torsion).
Parameters
----------
system : simtk.openmm.System
The OpenMM System object for the molecule
positions : simtk.unit.Quantity of dimension (natoms,3) with units compatible with angstroms
The positions of the molecule
atoms : list or set of int
The set of atoms in the bond, angle, or torsion.
Returns
-------
potential : simtk.unit.Quantity with units compatible with kilocalories_per_mole
The energy of the valence component.
"""
atoms = set(atoms)
natoms = len(atoms) # number of atoms
# Create a copy of the original System object so we can manipulate it
system = copy.deepcopy(system)
# Determine Force types to keep
if natoms == 2:
forcename = 'HarmonicBondForce'
elif natoms == 3:
forcename = 'HarmonicAngleForce'
elif natoms == 4:
forcename = 'PeriodicTorsionForce'
else:
raise Exception('len(atoms) = %d, but must be in [2,3,4] for bond, angle, or torsion' % len(atoms))
# Discard Force objects we don't need
for force_index in reversed(range(system.getNumForces())):
if system.getForce(force_index).__class__.__name__ != forcename:
system.removeForce(force_index)
# Report on constraints
if forcename == 'HarmonicBondForce':
for constraint_index in range(system.getNumConstraints()):
[i, j, r0] = system.getConstraintParameters(constraint_index)
if set([i,j]) == atoms:
print('Bond is constrained')
# Zero out force components that don't involve the atoms
for force_index in range(system.getNumForces()):
force = system.getForce(force_index)
if forcename == 'HarmonicBondForce':
for param_index in range(force.getNumBonds()):
[i, j, r0, K] = force.getBondParameters(param_index)
if set([i,j]) != atoms:
K *= 0
else:
print('Match found: bond parameter %d : r0 = %s, K = %s' % (param_index, str(r0), str(K)))
force.setBondParameters(param_index, i, j, r0, K)
elif forcename == 'HarmonicAngleForce':
for param_index in range(force.getNumAngles()):
[i, j, k, theta0, K] = force.getAngleParameters(param_index)
if set([i,j,k]) != atoms:
K *= 0
else:
print('Match found: angle parameter %d : theta0 = %s, K = %s' % (param_index, str(theta0), str(K)))
force.setAngleParameters(param_index, i, j, k, theta0, K)
elif forcename == 'PeriodicTorsionForce':
for param_index in range(force.getNumTorsions()):
[i, j, k, l, periodicity, phase, K] = force.getTorsionParameters(param_index)
if set([i,j,k,l]) != atoms:
K *= 0
else:
print('Match found: torsion parameter %d : periodicity = %s, phase = %s, K = %s' % (param_index, str(periodicity), str(phase), str(K)))
force.setTorsionParameters(param_index, i, j, k, l, periodicity, phase, K)
# Compute energy
platform = openmm.Platform.getPlatformByName('Reference')
integrator = openmm.VerletIntegrator(1.0 * unit.femtoseconds)
context = openmm.Context(system, integrator, platform)
context.setPositions(positions)
potential = context.getState(getEnergy=True).getPotentialEnergy()
del context, integrator, system
# Return energy
return potential
#SMARTS query defining your search (and potentially forcefield term of interest)
#Note currently this must specify an angle term for the OpenMM energy to be
Smarts = '[#6X4]-[#6X4]-[#8X2]' # angle example
Smarts = '[a,A]-[#6X4]-[#8X2]-[#1]' # torsion example
Smarts = '[#6X4]-[#6X4]' # bond example
#Set up substructure query
qmol = oechem.OEQMol()
if not oechem.OEParseSmarts( qmol, Smarts ):
print( 'OEParseSmarts failed')
ss = oechem.OESubSearch( qmol)
#File to search for this substructure
fileprefix= 'AlkEthOH_dvrs1'
ifs = oechem.oemolistream(fileprefix+'.oeb')
#Do substructure search and depiction
mol = oechem.OEMol()
#Loop over molecules in file
for mol in ifs.GetOEMols():
# Get OpenMM System and positions.
[system, positions] = createOpenMMSystem(mol)
goodMol = True
oechem.OEPrepareSearch(mol, ss)
unique = True
#Loop over matches within this molecule in file and depict
for match in ss.Match(mol, unique):
display( depictMatch(mol, match))
atoms = list()
for ma in match.GetAtoms():
print(ma.target.GetIdx(), end=" ")
#print(ma.pattern.GetIdx(), end=" ")
atoms.append( ma.target.GetIdx() )
print('')
#Get OpenMM angle energy and print IF it's an angle term
potential = getValenceEnergyComponent(system, positions, atoms)
print('%16.10f kcal/mol' % (potential / unit.kilocalories_per_mole))
ifs.close()
```
|
github_jupyter
|
import openeye.oechem as oechem
import openeye.oedepict as oedepict
from IPython.display import display
import os
from __future__ import print_function
def depictMatch(mol, match, width=500, height=200):
"""Take in an OpenEye molecule and a substructure match and display the results
with (optionally) specified resolution."""
from IPython.display import Image
dopt = oedepict.OEPrepareDepictionOptions()
dopt.SetDepictOrientation( oedepict.OEDepictOrientation_Horizontal)
dopt.SetSuppressHydrogens(True)
oedepict.OEPrepareDepiction(mol, dopt)
opts = oedepict.OE2DMolDisplayOptions(width, height, oedepict.OEScale_AutoScale)
disp = oedepict.OE2DMolDisplay(mol, opts)
hstyle = oedepict.OEHighlightStyle_Color
hcolor = oechem.OEColor(oechem.OELightBlue)
oedepict.OEAddHighlighting(disp, hcolor, hstyle, match)
ofs = oechem.oeosstream()
oedepict.OERenderMolecule(ofs, 'png', disp)
ofs.flush()
return Image(data = "".join(ofs.str()))
import parmed
def createOpenMMSystem(mol):
"""
Generate OpenMM System and positions from an OEMol.
Parameters
----------
mol : OEMol
The molecule
Returns
-------
system : simtk.openmm.System
The OpenMM System
positions : simtk.unit.Quantity wrapped
Positions of the molecule
"""
# write mol2 file
ofsmol2 = oechem.oemolostream('molecule.mol2')
ofsmol2.SetFlavor( oechem.OEFormat_MOL2, oechem.OEOFlavor_MOL2_Forcefield );
oechem.OEWriteConstMolecule(ofsmol2, mol)
ofsmol2.close()
# write tleap input file
leap_input = """
lig = loadMol2 molecule.mol2
saveAmberParm lig prmtop inpcrd
quit
"""
outfile = open('leap.in', 'w')
outfile.write(leap_input)
outfile.close()
# run tleap
leaprc = 'leaprc.Frosst_AlkEthOH'
os.system( 'tleap -f %s -f leap.in > leap.out' % leaprc )
# check if param file was not saved (implies parameterization problems)
paramsNotSaved = 'Parameter file was not saved'
leaplog = open( 'leap.out', 'r' ).read()
if paramsNotSaved in leaplog:
raise Exception('Parameter file was not saved.')
# Read prmtop and inpcrd
amberparm = parmed.amber.AmberParm( 'prmtop', 'inpcrd' )
system = amberparm.createSystem()
return (system, amberparm.positions)
import copy
from simtk import openmm, unit
def getValenceEnergyComponent(system, positions, atoms):
"""
Get the OpenMM valence energy corresponding to a specified set of atoms (bond, angle, torsion).
Parameters
----------
system : simtk.openmm.System
The OpenMM System object for the molecule
positions : simtk.unit.Quantity of dimension (natoms,3) with units compatible with angstroms
The positions of the molecule
atoms : list or set of int
The set of atoms in the bond, angle, or torsion.
Returns
-------
potential : simtk.unit.Quantity with units compatible with kilocalories_per_mole
The energy of the valence component.
"""
atoms = set(atoms)
natoms = len(atoms) # number of atoms
# Create a copy of the original System object so we can manipulate it
system = copy.deepcopy(system)
# Determine Force types to keep
if natoms == 2:
forcename = 'HarmonicBondForce'
elif natoms == 3:
forcename = 'HarmonicAngleForce'
elif natoms == 4:
forcename = 'PeriodicTorsionForce'
else:
raise Exception('len(atoms) = %d, but must be in [2,3,4] for bond, angle, or torsion' % len(atoms))
# Discard Force objects we don't need
for force_index in reversed(range(system.getNumForces())):
if system.getForce(force_index).__class__.__name__ != forcename:
system.removeForce(force_index)
# Report on constraints
if forcename == 'HarmonicBondForce':
for constraint_index in range(system.getNumConstraints()):
[i, j, r0] = system.getConstraintParameters(constraint_index)
if set([i,j]) == atoms:
print('Bond is constrained')
# Zero out force components that don't involve the atoms
for force_index in range(system.getNumForces()):
force = system.getForce(force_index)
if forcename == 'HarmonicBondForce':
for param_index in range(force.getNumBonds()):
[i, j, r0, K] = force.getBondParameters(param_index)
if set([i,j]) != atoms:
K *= 0
else:
print('Match found: bond parameter %d : r0 = %s, K = %s' % (param_index, str(r0), str(K)))
force.setBondParameters(param_index, i, j, r0, K)
elif forcename == 'HarmonicAngleForce':
for param_index in range(force.getNumAngles()):
[i, j, k, theta0, K] = force.getAngleParameters(param_index)
if set([i,j,k]) != atoms:
K *= 0
else:
print('Match found: angle parameter %d : theta0 = %s, K = %s' % (param_index, str(theta0), str(K)))
force.setAngleParameters(param_index, i, j, k, theta0, K)
elif forcename == 'PeriodicTorsionForce':
for param_index in range(force.getNumTorsions()):
[i, j, k, l, periodicity, phase, K] = force.getTorsionParameters(param_index)
if set([i,j,k,l]) != atoms:
K *= 0
else:
print('Match found: torsion parameter %d : periodicity = %s, phase = %s, K = %s' % (param_index, str(periodicity), str(phase), str(K)))
force.setTorsionParameters(param_index, i, j, k, l, periodicity, phase, K)
# Compute energy
platform = openmm.Platform.getPlatformByName('Reference')
integrator = openmm.VerletIntegrator(1.0 * unit.femtoseconds)
context = openmm.Context(system, integrator, platform)
context.setPositions(positions)
potential = context.getState(getEnergy=True).getPotentialEnergy()
del context, integrator, system
# Return energy
return potential
#SMARTS query defining your search (and potentially forcefield term of interest)
#Note currently this must specify an angle term for the OpenMM energy to be
Smarts = '[#6X4]-[#6X4]-[#8X2]' # angle example
Smarts = '[a,A]-[#6X4]-[#8X2]-[#1]' # torsion example
Smarts = '[#6X4]-[#6X4]' # bond example
#Set up substructure query
qmol = oechem.OEQMol()
if not oechem.OEParseSmarts( qmol, Smarts ):
print( 'OEParseSmarts failed')
ss = oechem.OESubSearch( qmol)
#File to search for this substructure
fileprefix= 'AlkEthOH_dvrs1'
ifs = oechem.oemolistream(fileprefix+'.oeb')
#Do substructure search and depiction
mol = oechem.OEMol()
#Loop over molecules in file
for mol in ifs.GetOEMols():
# Get OpenMM System and positions.
[system, positions] = createOpenMMSystem(mol)
goodMol = True
oechem.OEPrepareSearch(mol, ss)
unique = True
#Loop over matches within this molecule in file and depict
for match in ss.Match(mol, unique):
display( depictMatch(mol, match))
atoms = list()
for ma in match.GetAtoms():
print(ma.target.GetIdx(), end=" ")
#print(ma.pattern.GetIdx(), end=" ")
atoms.append( ma.target.GetIdx() )
print('')
#Get OpenMM angle energy and print IF it's an angle term
potential = getValenceEnergyComponent(system, positions, atoms)
print('%16.10f kcal/mol' % (potential / unit.kilocalories_per_mole))
ifs.close()
| 0.676086 | 0.783119 |
# <span style="color:red">Seaborn | Part-14: FacetGrid:</span>
Welcome to another lecture on *Seaborn*! Our journey began with assigning *style* and *color* to our plots as per our requirement. Then we moved on to *visualize distribution of a dataset*, and *Linear relationships*, and further we dived into topics covering *plots for Categorical data*. Every now and then, we've also roughly touched customization aspects using underlying Matplotlib code. That indeed is the end of the types of plots offered by Seaborn, and only leaves us with widening the scope of usage of all the plots that we have learnt till now.
Our discussion in upcoming lectures is majorly going to focus on using the core of Seaborn, based on which, *Seaborn* allows us to plot these amazing figures, that we had been detailing previously. This ofcourse isn't going to be a brand new topic because every now & then I have used these in previous lectures but hereon we're going to specifically deal with each one of those.
To introduce our new topic, i.e. **<span style="color:red">Grids</span>**, we shall at first list the options available. Majorly, there are just two aspects to our discussion on *Grids* that includes:
- **<span style="color:red">FacetGrid</span>**
- **<span style="color:red">PairGrid</span>**
Additionally, we also have a companion function for *PairGrid* to enhance execution speed of *PairGrid*, i.e.
- **<span style="color:red">Pairplot</span>**
Our discourse shall detail each one of these topics in-length for better understanding. As we have already covered the statistical inference of each type of plot, our emphasis shall mostly be on scaling and parameter variety of known plots on these grids. So let us commence our journey with **FacetGrid** in this lecture.
## <span style="color:red">FacetGrid:</span>
The term **Facet** here refers to *a dimension* or say, an *aspect* or a feature of a *multi-dimensional dataset*. This analysis is extremely useful when working with a multi-variate dataset which has a varied blend of datatypes, specially in *Data Science* & *Machine Learning* domain, where generally you would be dealing with huge datasets. If you're a *working pofessional*, you know what I am talking about. And if you're a *fresher* or a *student*, just to give you an idea, in this era of *Big Data*, an average *CSV file* (which is generally the most common form), or even a RDBMS size would vary from Gigabytes to Terabytes of data. If you are dealing with *Image/Video/Audio datasets*, then you may easily expect those to be in *hundreds of gigabyte*.
On the other hand, the term **Grid** refers to any *framework with spaced bars that are parallel to or cross each other, to form a series of squares or rectangles*. Statistically, these *Grids* are also used to represent and understand an entire *population* or just a *sample space* out of it. In general, these are pretty powerful tool for presentation, to describe our dataset and to study the *interrelationship*, or *correlation* between *each facet* of any *environment*.
To kill our curiousity, let us plot a simple **<span style="color:red">FacetGrid</span>** before continuing on with our discussion. And to do that, we shall once again quickly import our package dependencies and set the aesthetics for future use with built-in datasets.
```
# Importing intrinsic libraries:
import numpy as np
import pandas as pd
np.random.seed(101)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(style="whitegrid", palette="rocket")
import warnings
warnings.filterwarnings("ignore")
# Let us also get tableau colors we defined earlier:
tableau_20 = [(31, 119, 180), (174, 199, 232), (255, 127, 14), (255, 187, 120),
(44, 160, 44), (152, 223, 138), (214, 39, 40), (255, 152, 150),
(148, 103, 189), (197, 176, 213), (140, 86, 75), (196, 156, 148),
(227, 119, 194), (247, 182, 210), (127, 127, 127), (199, 199, 199),
(188, 189, 34), (219, 219, 141), (23, 190, 207), (158, 218, 229)]
# Scaling above RGB values to [0, 1] range, which is Matplotlib acceptable format:
for i in range(len(tableau_20)):
r, g, b = tableau_20[i]
tableau_20[i] = (r / 255., g / 255., b / 255.)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Plotting a basic FacetGrid with Scatterplot representation:
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
```
This is a combined scatter representation of Tips dataset that we have seen earlier as well, where Total tip generated against Total Bill amount is drawn in accordance with their Gender and Smoking practice. With this we can conclude how **FacetGrid** helps us visualize distribution of a variable or the relationship between multiple variables separately within subsets of our dataset. Important to note here is that Seaborn FacetGrid can only support upto **3-Dimensional figures**, using `row`, `column` and `hue` dimensions of the grid for *Categorical* and *Discrete* variables within our dataset.
Let us now have a look at the *parameters* offered or supported by Seaborn for a **FacetGrid**:
`seaborn.FacetGrid(data, row=None, col=None, hue=None, col_wrap=None, sharex=True, sharey=True, size=3, aspect=1, palette=None, row_order=None, col_order=None, hue_order=None, hue_kws=None, dropna=True, legend_out=True, despine=True, margin_titles=False, xlim=None, ylim=None, subplot_kws=None, gridspec_kws=None`
There seems to be few new parameters out here for us, so let us one-by-one understand their scope before we start experimenting with those on our plots:
- We are well acquainted with mandatory `data`, `row`, `col` and `hue` parameters.
- Next is `col_wrap` that defines the **width of our variable** selected as `col` dimension, so that the *column facets* can span multiple rows.
- `sharex` helps us **draft dedicated Y-axis** for each sub-plot, if declared `False`. Same concept holds good for `sharey` as well.
- `size` helps us determine the size of our grid-frame.
- We may also declare `hue_kws` parameter that lets us **control other aesthetics** of our plot.
- `dropna` drops all the **NULL variables** from the selected features; and `legend_out` places the Legend either inside or outside our plot, as we've already seen.
- `margin_titles` fetch the **feature names** from our dataset; and `xlim` & `ylim` additionally offers Matplotlib style limitation to each of our axes on the grid.
That pretty much seems to cover *intrinsic parameters* so let us now try to use them one-by-one with slight modifications:
Let us begin by pulling the *Legend inside* our FacetGrid and *creating a Header* for our grid:
```
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5, legend_out=False)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
plt.suptitle('Tip Collection based on Gender and Smoking', fontsize=11)
```
So declaring `legend_out` as `False` and creating a **Superhead title** using *Matplotlib* seems to be working great on our Grid. Customization on *Header size* gives us an add-on capability as well. Right now, we are going by default `palette` for **marker colors** which can be customized by setting to a different one. Let us try other parameters as well:
Actually, before we jump further into utilization of other parameters, let me quickly take you behind the curtain of this plot. As visible, we assigned `ax` as a variable to our **FacetGrid** for creating a visualizaion figure, and then plotted a **Scatterplot** on top of it, before decorating further with a *Legend* and a *Super Title*. So when we initialized the assignment of `ax`, the grid actually gets created using backend *Matplotlib figure and axes*, though doesn't plot anything on top of it. This is when we call Scatterplot on our sample data, that in turn at the backend calls `FacetGrid.map()` function to map this grid to our Scatterplot. We intended to draw a linear relation plot, and thus entered multiple variable names, i.e. `Total Bill` and associated `Tip` to form *facets*, or dimensions of our grid.
Also important to note is the use the [matplotlib.pyplot.gca()](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.gca.html) function, if required to *set the current axes* on our Grid. This shall fetch the current Axes instance on our current figure matching the given keyword arguments or params, & if unavailable, it shall even create one.
```
# Let us create a dummy DataFrame:
football = pd.DataFrame({
"Wins": [76, 64, 38, 78, 63, 45, 32, 46, 13, 40, 59, 80],
"Loss": [55, 67, 70, 56, 59, 69, 72, 24, 45, 21, 58, 22],
"Team": ["Arsenal"] * 4 + ["Liverpool"] * 4 + ["Chelsea"] * 4,
"Year": ["2015", "2016", "2017", "2018"] * 3})
```
Before I begin illustration using this DataFrame, on a lighter note, I would add a disclosure that this is a dummy dataset and holds no resemblance whatsoever to actual records of respective Soccer clubs. So if you're one among those die-hard fans of any of these clubs, kindly excuse me if the numbers don't tally, as they are all fabricated.
Here, **football** is kind of a *Time-series Pandas DataFrame* that in entirety reflects 4 features, where `Wins` and `Loss` variables represent the quarterly Scorecard of three soccer `Teams` for last four `Years`, from 2015 to 2018. Let us check how this DataFrame looks like:
```
football
```
This looks pretty good for our purpose so now let us initialize our FacetGrid on top of it and try to obtain a time-indexed with further plotting. In production environment, to keep our solution scalable, this is generally done by defining a function for data manipulation so we shall try that in this example:
```
# Defining a customizable function to be precise with our requirements & shall discuss it a little later:
# We shall be using a new type of plot here that I shall discuss in detail later on.
def football_plot(data, color):
sns.heatmap(data[["Wins", "Loss"]])
# 'margin_titles' won't necessarily guarantee desired results so better to be cautious:
ax = sns.FacetGrid(football, col="Team", size=5, margin_titles=True)
ax.map_dataframe(football_plot)
ax = sns.FacetGrid(football, col="Team", size=5)
ax.map(sns.kdeplot, "Wins", "Year", hist=True, lw=2)
```
As visible, **Heatmap** plots rectangular boxes for data points as a color-encoded matrix, and this is a topic we shall be discussing in detail in another Lecture but for now, I just wanted you to have a preview of it, and hence used it on top of our **FacetGrid**. Another good thing to know with *FacetGrid* is **gridspec** module which allows Matplotlib params to be passed for drawing attention to a particular facet by increasing its size. To better understand, let us try to use this module now:
```
# Loading built-in Titanic Dataset:
titanic = sns.load_dataset("titanic")
# Assigning reformed `deck` column:
titanic = titanic.assign(deck=titanic.deck.astype(object)).sort_values("deck")
# Creating Grid and Plot:
ax = sns.FacetGrid(titanic, col="class", sharex=False, size=7,
gridspec_kws={"width_ratios": [3.5, 2, 2]})
ax.map(sns.boxplot, "deck", "age")
ax.set_titles(fontweight='bold', size=17)
```
Breaking it down, at first we import our built-in Titanic dataset, and then assign a new column, i.e. `deck` using Pandas `.assign()` function. Here we declare this new column as a component of pre-existing `deck` column from Titanic dataset, but as a sorted object. Then we create our *FacetGrid* mentioning the DataFrame, the column on which Grids get segregated but with shared across *Y-axis*; for `chosen deck` against `Age` of passengers. Next in action is our **grid keyword specifications**, where we decide the *width ratio* of the plot that shall be passed on to these grids. Finally, we have our **Box Plot** representing values of `Age` feature across respective decks.
Now let us try to use different axes with same size for multivariate plotting on Tips dataset:
```
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Mapping a Scatterplot to our FacetGrid:
ax = sns.FacetGrid(tips, col="smoker", row="sex", size=3.5)
ax = (ax.map(plt.scatter, "total_bill", "tip", color=tableau_20[6]).set_axis_labels("Total Bill Generated (USD)", "Tip Amount"))
# Increasing size for subplot Titles & making it appear Bolder:
ax.set_titles(fontweight='bold', size=11)
```
**Scatterplot** dealing with data that has multiple variables is no new science for us so instead let me highlight what `.map()` does for us. This function actually allows us to project our figure axes, in accordance to which our Scatterplot spreads the feature datapoints across the grids, depending upon the segregators. Here we have `sex` and `smoker` as our segregators (When I use the general term "segregator", it just refers to the columns on which we decide to determine the layout). This comes in really handy as we can pass *Matplotlib parrameters* for further customization of our plot. At the end, when we add `.set_axis_labels()` it gets easy for us to label our axes but please note that this method shall work for you only when you're dealing with grids, hence you didn't observe me adapting to this function, while detailing various other plots.
- Let us now talk about the `football_plot` function we defined earlier with **football** DataFrame. The only reason I didn't speak of it then was because I wanted you to go through a few more parameter implementation before getting into this. There are **3 important rules for defining such functions** that are supported by [FacetGrid.map](http://xarray.pydata.org/en/stable/generated/xarray.plot.FacetGrid.map.html):
-They must take array-like inputs as positional arguments, with the first argument corresponding to the `X-Axis`, and the second argument corresponding to `y-Axis`.
-They must also accept two keyword arguments: `color`, and `label`. If you want to use a `hue` variable, than these should get passed to the underlying plotting function (As a side note: You may just catch `**kwargs` and not do anything with them, if it's not relevant to the specific plot you're making.
-Lastly, when called, they must draw a plot on the "currently active" matplotlib Axes.
- Important to note is that there may be cases where your function draws a plot that looks correct without taking `x`, `y`, positional inputs and then it is better to just call the plot, like: `ax.set_axis_labels("Column_1", "Column_2")` after you use `.map()`, which should rename your axes properly. Alternatively, you may also want to do something like `ax.set(xticklabels=)` to get more meaningful ticks.
- Well I am also quite stoked to mention another important function (though not that comonly used), that is [FacetGrid.map_dataframe()](http://nullege.com/codes/search/axisgrid.FacetGrid.map_dataframe). The rules here are similar to `FacetGrid.map()`, but the function you pass must accept a DataFrame input in a parameter called `data`, and instead of taking *array-like positional* inputs it takes *strings* that correspond to variables in that dataframe. Then on each iteration through the *facets*, the function will be called with the *Input dataframe*, masked to just the values for that combination of `row`, `col`, and `hue` levels.
**Another important to note with both the above-mentioned functions is that the `return` value is ignored so you don't really have to worry about it.** Just for illustration purpose, let us consider drafting a function that just *draws a horizontal line in each `facet` at `y=2` and ignores all the Input data*:
```
# That is all you require in your function:
def plot_func(x, y, color=None, label=None):
ax.map(plt.axhline, y=2)
```
I know this function concept might look little hazy at the moment but once you have covered more on dates and maptplotlib syntax in particular, the picture shall get much more clearer for you.
Let us look at one more example of `FacetGrid()` and this time let us again create a synthetic DataFrame for this demonstration:
```
# Creating synthetic Data (Don't focus on how it's getting created):
units = np.linspace(0, 50)
A = [1., 18., 40., 100.]
df = []
for i in A:
V1 = np.sin(i * units)
V2 = np.cos(i * units)
df.append(pd.DataFrame({"units": units, "V_1": V1, "V_2": V2, "A": i}))
sample = pd.concat(df, axis=0)
# Previewing DataFrame:
sample.head(10)
sample.describe()
# Melting our sample DataFrame:
sample_melt = sample.melt(id_vars=['A', 'units'], value_vars=['V_1', 'V_2'])
# Creating plot:
ax = sns.FacetGrid(sample_melt, col='A', hue='A', palette="icefire", row='variable', sharey='row', margin_titles=True)
ax.map(plt.plot, 'units', 'value')
ax.add_legend()
```
This process shall come in handy if you ever wish to vertically stack rows of subplots on top of one another. You do not really have to focus on the process of creating dataset, as generally you will have your dataset provided with a problem statement. For our plot, yu may just consider these visual variations as [Sinusoidal waves](https://en.wikipedia.org/wiki/Sine_wave). I shall attach a link in our notebook, if you wish to dig deeper into what these are and how are they actually computed.
Our next lecture would be pretty much a small follow up to this lecture, where we would try to bring more of *Categorical data* to our **FacetGrid()**. Meanwhile, I would again suggest you to play around with analyzing and plotting datasets, as much as you can because visualization is a very important facet of *Data Science & Research*. And, I shall see you in our next lecture.
|
github_jupyter
|
# Importing intrinsic libraries:
import numpy as np
import pandas as pd
np.random.seed(101)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(style="whitegrid", palette="rocket")
import warnings
warnings.filterwarnings("ignore")
# Let us also get tableau colors we defined earlier:
tableau_20 = [(31, 119, 180), (174, 199, 232), (255, 127, 14), (255, 187, 120),
(44, 160, 44), (152, 223, 138), (214, 39, 40), (255, 152, 150),
(148, 103, 189), (197, 176, 213), (140, 86, 75), (196, 156, 148),
(227, 119, 194), (247, 182, 210), (127, 127, 127), (199, 199, 199),
(188, 189, 34), (219, 219, 141), (23, 190, 207), (158, 218, 229)]
# Scaling above RGB values to [0, 1] range, which is Matplotlib acceptable format:
for i in range(len(tableau_20)):
r, g, b = tableau_20[i]
tableau_20[i] = (r / 255., g / 255., b / 255.)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Plotting a basic FacetGrid with Scatterplot representation:
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5, legend_out=False)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
plt.suptitle('Tip Collection based on Gender and Smoking', fontsize=11)
# Let us create a dummy DataFrame:
football = pd.DataFrame({
"Wins": [76, 64, 38, 78, 63, 45, 32, 46, 13, 40, 59, 80],
"Loss": [55, 67, 70, 56, 59, 69, 72, 24, 45, 21, 58, 22],
"Team": ["Arsenal"] * 4 + ["Liverpool"] * 4 + ["Chelsea"] * 4,
"Year": ["2015", "2016", "2017", "2018"] * 3})
football
# Defining a customizable function to be precise with our requirements & shall discuss it a little later:
# We shall be using a new type of plot here that I shall discuss in detail later on.
def football_plot(data, color):
sns.heatmap(data[["Wins", "Loss"]])
# 'margin_titles' won't necessarily guarantee desired results so better to be cautious:
ax = sns.FacetGrid(football, col="Team", size=5, margin_titles=True)
ax.map_dataframe(football_plot)
ax = sns.FacetGrid(football, col="Team", size=5)
ax.map(sns.kdeplot, "Wins", "Year", hist=True, lw=2)
# Loading built-in Titanic Dataset:
titanic = sns.load_dataset("titanic")
# Assigning reformed `deck` column:
titanic = titanic.assign(deck=titanic.deck.astype(object)).sort_values("deck")
# Creating Grid and Plot:
ax = sns.FacetGrid(titanic, col="class", sharex=False, size=7,
gridspec_kws={"width_ratios": [3.5, 2, 2]})
ax.map(sns.boxplot, "deck", "age")
ax.set_titles(fontweight='bold', size=17)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Mapping a Scatterplot to our FacetGrid:
ax = sns.FacetGrid(tips, col="smoker", row="sex", size=3.5)
ax = (ax.map(plt.scatter, "total_bill", "tip", color=tableau_20[6]).set_axis_labels("Total Bill Generated (USD)", "Tip Amount"))
# Increasing size for subplot Titles & making it appear Bolder:
ax.set_titles(fontweight='bold', size=11)
# That is all you require in your function:
def plot_func(x, y, color=None, label=None):
ax.map(plt.axhline, y=2)
# Creating synthetic Data (Don't focus on how it's getting created):
units = np.linspace(0, 50)
A = [1., 18., 40., 100.]
df = []
for i in A:
V1 = np.sin(i * units)
V2 = np.cos(i * units)
df.append(pd.DataFrame({"units": units, "V_1": V1, "V_2": V2, "A": i}))
sample = pd.concat(df, axis=0)
# Previewing DataFrame:
sample.head(10)
sample.describe()
# Melting our sample DataFrame:
sample_melt = sample.melt(id_vars=['A', 'units'], value_vars=['V_1', 'V_2'])
# Creating plot:
ax = sns.FacetGrid(sample_melt, col='A', hue='A', palette="icefire", row='variable', sharey='row', margin_titles=True)
ax.map(plt.plot, 'units', 'value')
ax.add_legend()
| 0.677581 | 0.986071 |
# MIST101 Pratical 1: Introduction to Tensorflow (Basics of Tensorflow)
## What is Tensor
The central unit of data in TensorFlow is the tensor. A tensor consists of a set of primitive values shaped into an array of any number of dimensions. A tensor's rank is its number of dimensions. Here are some examples of tensors:
```
3 # a rank 0 tensor; this is a scalar with shape []
[1., 2., 3.] # a rank 1 tensor; this is a vector with shape [3]
[[1., 2., 3.], [4., 5., 6.]] # a rank 2 tensor; a matrix with shape [2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # a rank 3 tensor with shape [2, 1, 3]
```
## What is Tensorflow - Building and Running the Computational Graph
The canonical import statement for TensorFlow programs is as follows:
```
import tensorflow as tf
```
This gives Python access to all of TensorFlow's classes, methods, and symbols.
You might think of TensorFlow Core programs as consisting of two discrete sections:
1. Building the computational graph.
2. Running the computational graph.
A computational graph is a series of TensorFlow operations arranged into a graph of nodes. Now, we are going to introduce some basic nodes.
## Basic Nodes
Let's start with building a simple computational graph. Each node takes zero or more tensors as inputs and produces a tensor as an output. One type of node is a constant. Like all TensorFlow constants, it takes no inputs, and it outputs a value it stores internally. We can create two floating point Tensors node1 and node2 as follows:
```
node1 = tf.constant(3.0, dtype=tf.float32)
node2 = tf.constant(4.0) # also tf.float32 implicitly
print(node1, node2)
```
Notice that printing the nodes does not output the values 3.0 and 4.0 as you might expect. Instead, they are nodes that, when evaluated, would produce 3.0 and 4.0, respectively. To actually evaluate the nodes, we must run the computational graph within a session. A session encapsulates the control and state of the TensorFlow runtime.
The following code creates a **Session** object and then invokes its run method to run enough of the computational graph to evaluate node1 and node2. By running the computational graph in a session as follows:
```
sess = tf.Session()
print(sess.run([node1, node2]))
```
We can build more complicated computations by combining Tensor nodes with operations (Operations are also nodes). For example, we can add our two constant nodes and produce a new graph as follows:
```
node3 = tf.add(node1, node2)
print(node3)
print(sess.run(node3))
```
This graph is not especially interesting because it always produces a constant result. A graph can be modified to accept external inputs, known as **placeholders**. A placeholder is a promise to provide a value later.
```
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b # + provides a shortcut for tf.add(a, b)
# This will give an error because the placeholders are not provided with any values
print(sess.run(adder_node))
```
To feed values to the placeholders, we need to add a dictionary to the "sess.run" function. In this dictionary, we pair up the placeholder nodes and the values we want to feed in.
```
print(sess.run(adder_node, {a: 3, b: 4.5}))
# Feeding multiple values for multiple runs
print(sess.run(adder_node, {a: [1, 3], b: [2, 4]}))
```
In machine learning we will typically want a model that can take arbitrary inputs, such as the one above. To make the model trainable, we need to be able to modify the graph to get new outputs with the same input. **Variables** allow us to add trainable parameters to a graph. They are constructed with a type and initial value:
```
W = tf.Variable([0.3], dtype=tf.float32)
b = tf.Variable([-0.3], dtype=tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b
```
Constants are initialized when you call tf.constant, and their value can never change. By contrast, variables are not initialized when you call tf.Variable.
```
# This will give you an error when the variables are not yet initialized
sess.run(W)
```
To initialize all the variables in a TensorFlow program, you must explicitly call a special operation as follows:
```
init = tf.global_variables_initializer()
sess.run(init)
```
It is important to realize init is a handle to the TensorFlow sub-graph that initializes all the global variables. Until we call sess.run, the variables are uninitialized.
```
# This will not you an error after the variables are initialized
sess.run([W, b])
```
Since x is a placeholder, we can evaluate linear_model for several values of x simultaneously as follows:
```
# Evaluate the values from the linear model
print(sess.run(linear_model, {x: [1, 2, 3, 4]}))
```
We've created a model, but we don't know how good it is yet. To evaluate the model on training data, we need another placeholder (**y**) to provide the desired values, and we need to write a loss function.
A loss function measures how far apart the current model is from the provided data. We'll use a standard loss model for linear regression, which sums the squares of the deltas between the current model and the provided data. **linear_model - y** creates a vector where each element is the corresponding example's error delta. We call **tf.square** to square that error. Then, we sum all the squared errors to create a single scalar that abstracts the error of all examples using **tf.reduce_sum**:
```
# The desired values
y = tf.placeholder(tf.float32)
# Loss function
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
# Evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
```
We could improve this manually by reassigning the values of W and b to the perfect values of -1 and 1. A variable is initialized to the value provided to **tf.Variable** but can be changed using operations like **tf.assign**. For example, W=-1 and b=1 are the optimal parameters for our model. We can change W and b accordingly:
```
# Define the assign nodes for both variables
fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
# Reassign the values of W and b
sess.run([fixW, fixb])
# Re-evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
```
We have encountered several tensor nodes in this tutorial. In summary:
#### Tensor Nodes
Tensor nodes provide a tensor as output.
1. tf.Placeholder: A promise to provide a value
2. tf.Variable: The value can be changed after initialization
3. tf.Constant: The value never changes
### Training Nodes
Manually changing the variables to improve the model is not ideal. Luckily, TensorFlow provides optimizers that slowly change each variable in order to minimize the loss function. The simplest optimizer is gradient descent. It modifies each variable according to the magnitude of the derivative of loss with respect to that variable. In general, computing symbolic derivatives manually is tedious and error-prone. Consequently, TensorFlow can automatically produce derivatives given only a description of the model using the function **tf.gradients**. For simplicity, optimizers typically do this for you. For example,
```
# Create nodes for optimizer and training
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# Reset variable values to incorrect defaults.
sess.run(init)
# Show the initial variable values
print("Variables Before training: " + str(sess.run([W, b])))
# Run the training node for 1000 times
for i in range(1000):
sess.run(train, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})
# Show the new variable values
print("Variables After training: " + str(sess.run([W, b])))
# Loss re-evaluation
print("Loss After training: " + str(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})))
```
*This tutorial is modified from https://www.tensorflow.org/get_started/*
|
github_jupyter
|
3 # a rank 0 tensor; this is a scalar with shape []
[1., 2., 3.] # a rank 1 tensor; this is a vector with shape [3]
[[1., 2., 3.], [4., 5., 6.]] # a rank 2 tensor; a matrix with shape [2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # a rank 3 tensor with shape [2, 1, 3]
import tensorflow as tf
node1 = tf.constant(3.0, dtype=tf.float32)
node2 = tf.constant(4.0) # also tf.float32 implicitly
print(node1, node2)
sess = tf.Session()
print(sess.run([node1, node2]))
node3 = tf.add(node1, node2)
print(node3)
print(sess.run(node3))
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b # + provides a shortcut for tf.add(a, b)
# This will give an error because the placeholders are not provided with any values
print(sess.run(adder_node))
print(sess.run(adder_node, {a: 3, b: 4.5}))
# Feeding multiple values for multiple runs
print(sess.run(adder_node, {a: [1, 3], b: [2, 4]}))
W = tf.Variable([0.3], dtype=tf.float32)
b = tf.Variable([-0.3], dtype=tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b
# This will give you an error when the variables are not yet initialized
sess.run(W)
init = tf.global_variables_initializer()
sess.run(init)
# This will not you an error after the variables are initialized
sess.run([W, b])
# Evaluate the values from the linear model
print(sess.run(linear_model, {x: [1, 2, 3, 4]}))
# The desired values
y = tf.placeholder(tf.float32)
# Loss function
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
# Evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
# Define the assign nodes for both variables
fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
# Reassign the values of W and b
sess.run([fixW, fixb])
# Re-evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
# Create nodes for optimizer and training
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# Reset variable values to incorrect defaults.
sess.run(init)
# Show the initial variable values
print("Variables Before training: " + str(sess.run([W, b])))
# Run the training node for 1000 times
for i in range(1000):
sess.run(train, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})
# Show the new variable values
print("Variables After training: " + str(sess.run([W, b])))
# Loss re-evaluation
print("Loss After training: " + str(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})))
| 0.872836 | 0.996264 |
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [cbe61622](https://jckantor.github.io/cbe61622);
content is available [on Github](https://github.com/jckantor/cbe61622.git).*
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
# 4.10 Potentiostats and Galvanostats
## 4.10.1 References
---
Adams, Scott D., et al. "MiniStat: Development and evaluation of a mini-potentiostat for electrochemical measurements." Ieee Access 7 (2019): 31903-31912. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8657694
---
Ainla, Alar, et al. "Open-source potentiostat for wireless electrochemical detection with smartphones." Analytical chemistry 90.10 (2018): 6240-6246. https://gmwgroup.harvard.edu/files/gmwgroup/files/1308.pdf
---
Bianchi, Valentina, et al. "A Wi-Fi cloud-based portable potentiostat for electrochemical biosensors." IEEE Transactions on Instrumentation and Measurement 69.6 (2019): 3232-3240.
---
Dobbelaere, Thomas, Philippe M. Vereecken, and Christophe Detavernier. "A USB-controlled potentiostat/galvanostat for thin-film battery characterization." HardwareX 2 (2017): 34-49. https://doi.org/10.1016/j.ohx.2017.08.001
---
Hoilett, Orlando S., et al. "KickStat: A coin-sized potentiostat for high-resolution electrochemical analysis." Sensors 20.8 (2020): 2407. https://www.mdpi.com/1424-8220/20/8/2407/htm
---
Irving, P., R. Cecil, and M. Z. Yates. "MYSTAT: A compact potentiostat/galvanostat for general electrochemistry measurements." HardwareX 9 (2021): e00163. https://www.sciencedirect.com/science/article/pii/S2468067220300729
> 2, 3, and 4 wire cell configurations with +/- 12 volts at 200ma.
---
Lopin, Prattana, and Kyle V. Lopin. "PSoC-Stat: A single chip open source potentiostat based on a Programmable System on a Chip." PloS one 13.7 (2018): e0201353. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0201353
---
Matsubara, Yasuo. "A Small yet Complete Framework for a Potentiostat, Galvanostat, and Electrochemical Impedance Spectrometer." (2021): 3362-3370. https://pubs.acs.org/doi/full/10.1021/acs.jchemed.1c00228
> Elegant 2 omp amp current source for a galvanostat.
---
## 4.10.2 Application to Electrical Impedence Spectroscopy
---
Wang, Shangshang, et al. "Electrochemical impedance spectroscopy." Nature Reviews Methods Primers 1.1 (2021): 1-21. https://www.nature.com/articles/s43586-021-00039-w.pdf
> Tutorial presentation of EIS, including instrumentation and data analysis.
---
Magar, Hend S., Rabeay YA Hassan, and Ashok Mulchandani. "Electrochemical Impedance Spectroscopy (EIS): Principles, Construction, and Biosensing Applications." Sensors 21.19 (2021): 6578. https://www.mdpi.com/1424-8220/21/19/6578/pdf
> Tutorial introduction with descriptions of application to solutions and reactions at surfaces.
---
Instruments, Gamry. "Basics of electrochemical impedance spectroscopy." G. Instruments, Complex impedance in Corrosion (2007): 1-30. https://www.c3-analysentechnik.eu/downloads/applikationsberichte/gamry/5657-Application-Note-EIS.pdf
> Tutorial introduction to EIS with extensive modeling discussion.
---
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
|
github_jupyter
|
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [cbe61622](https://jckantor.github.io/cbe61622);
content is available [on Github](https://github.com/jckantor/cbe61622.git).*
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
# 4.10 Potentiostats and Galvanostats
## 4.10.1 References
---
Adams, Scott D., et al. "MiniStat: Development and evaluation of a mini-potentiostat for electrochemical measurements." Ieee Access 7 (2019): 31903-31912. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8657694
---
Ainla, Alar, et al. "Open-source potentiostat for wireless electrochemical detection with smartphones." Analytical chemistry 90.10 (2018): 6240-6246. https://gmwgroup.harvard.edu/files/gmwgroup/files/1308.pdf
---
Bianchi, Valentina, et al. "A Wi-Fi cloud-based portable potentiostat for electrochemical biosensors." IEEE Transactions on Instrumentation and Measurement 69.6 (2019): 3232-3240.
---
Dobbelaere, Thomas, Philippe M. Vereecken, and Christophe Detavernier. "A USB-controlled potentiostat/galvanostat for thin-film battery characterization." HardwareX 2 (2017): 34-49. https://doi.org/10.1016/j.ohx.2017.08.001
---
Hoilett, Orlando S., et al. "KickStat: A coin-sized potentiostat for high-resolution electrochemical analysis." Sensors 20.8 (2020): 2407. https://www.mdpi.com/1424-8220/20/8/2407/htm
---
Irving, P., R. Cecil, and M. Z. Yates. "MYSTAT: A compact potentiostat/galvanostat for general electrochemistry measurements." HardwareX 9 (2021): e00163. https://www.sciencedirect.com/science/article/pii/S2468067220300729
> 2, 3, and 4 wire cell configurations with +/- 12 volts at 200ma.
---
Lopin, Prattana, and Kyle V. Lopin. "PSoC-Stat: A single chip open source potentiostat based on a Programmable System on a Chip." PloS one 13.7 (2018): e0201353. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0201353
---
Matsubara, Yasuo. "A Small yet Complete Framework for a Potentiostat, Galvanostat, and Electrochemical Impedance Spectrometer." (2021): 3362-3370. https://pubs.acs.org/doi/full/10.1021/acs.jchemed.1c00228
> Elegant 2 omp amp current source for a galvanostat.
---
## 4.10.2 Application to Electrical Impedence Spectroscopy
---
Wang, Shangshang, et al. "Electrochemical impedance spectroscopy." Nature Reviews Methods Primers 1.1 (2021): 1-21. https://www.nature.com/articles/s43586-021-00039-w.pdf
> Tutorial presentation of EIS, including instrumentation and data analysis.
---
Magar, Hend S., Rabeay YA Hassan, and Ashok Mulchandani. "Electrochemical Impedance Spectroscopy (EIS): Principles, Construction, and Biosensing Applications." Sensors 21.19 (2021): 6578. https://www.mdpi.com/1424-8220/21/19/6578/pdf
> Tutorial introduction with descriptions of application to solutions and reactions at surfaces.
---
Instruments, Gamry. "Basics of electrochemical impedance spectroscopy." G. Instruments, Complex impedance in Corrosion (2007): 1-30. https://www.c3-analysentechnik.eu/downloads/applikationsberichte/gamry/5657-Application-Note-EIS.pdf
> Tutorial introduction to EIS with extensive modeling discussion.
---
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
| 0.672762 | 0.703193 |
<a href="https://colab.research.google.com/github/linked0/deep-learning/blob/master/AAMY/cifar10_cnn_my.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
'''
#Train a simple deep CNN on the CIFAR10 small images dataset.
It gets to 75% validation accuracy in 25 epochs, and 79% after 50 epochs.
(It's still underfitting at that point, though).
'''
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 100
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
print(x_train.shape)
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3,3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3,3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_aumentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size = batch_size,
epochs = epochs,
validation_data = (x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set imput mean to 0 over the dataset
samplewise_center=False, # set each samle mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_ntd_normalization=False, # divide each input by tis std
)
```
|
github_jupyter
|
'''
#Train a simple deep CNN on the CIFAR10 small images dataset.
It gets to 75% validation accuracy in 25 epochs, and 79% after 50 epochs.
(It's still underfitting at that point, though).
'''
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 100
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
print(x_train.shape)
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3,3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3,3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_aumentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size = batch_size,
epochs = epochs,
validation_data = (x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set imput mean to 0 over the dataset
samplewise_center=False, # set each samle mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_ntd_normalization=False, # divide each input by tis std
)
| 0.873701 | 0.925634 |
# Hello Image Segmentation
A very basic introduction to using segmentation models with OpenVINO.
We use the pre-trained [road-segmentation-adas-0001](https://docs.openvinotoolkit.org/latest/omz_models_model_road_segmentation_adas_0001.html) model from the [Open Model Zoo](https://github.com/openvinotoolkit/open_model_zoo/). ADAS stands for Advanced Driver Assistance Services. The model recognizes four classes: background, road, curb and mark.
## Imports
```
import cv2
import matplotlib.pyplot as plt
import numpy as np
import sys
from openvino.runtime import Core
sys.path.append("../utils")
from notebook_utils import segmentation_map_to_image
```
## Load the Model
```
ie = Core()
model = ie.read_model(model="model/road-segmentation-adas-0001.xml")
compiled_model = ie.compile_model(model=model, device_name="CPU")
input_layer_ir = compiled_model.input(0)
output_layer_ir = compiled_model.output(0)
```
## Load an Image
A sample image from the [Mapillary Vistas](https://www.mapillary.com/dataset/vistas) dataset is provided.
```
# The segmentation network expects images in BGR format
image = cv2.imread("data/empty_road_mapillary.jpg")
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_h, image_w, _ = image.shape
# N,C,H,W = batch size, number of channels, height, width
N, C, H, W = input_layer_ir.shape
# OpenCV resize expects the destination size as (width, height)
resized_image = cv2.resize(image, (W, H))
# reshape to network input shape
input_image = np.expand_dims(
resized_image.transpose(2, 0, 1), 0
)
plt.imshow(rgb_image)
```
## Do Inference
```
# Run the inference
result = compiled_model([input_image])[output_layer_ir]
# Prepare data for visualization
segmentation_mask = np.argmax(result, axis=1)
plt.imshow(segmentation_mask.transpose(1, 2, 0))
```
## Prepare Data for Visualization
```
# Define colormap, each color represents a class
colormap = np.array([[68, 1, 84], [48, 103, 141], [53, 183, 120], [199, 216, 52]])
# Define the transparency of the segmentation mask on the photo
alpha = 0.3
# Use function from notebook_utils.py to transform mask to an RGB image
mask = segmentation_map_to_image(segmentation_mask, colormap)
resized_mask = cv2.resize(mask, (image_w, image_h))
# Create image with mask put on
image_with_mask = cv2.addWeighted(resized_mask, alpha, rgb_image, 1 - alpha, 0)
```
## Visualize data
```
# Define titles with images
data = {"Base Photo": rgb_image, "Segmentation": mask, "Masked Photo": image_with_mask}
# Create subplot to visualize images
fig, axs = plt.subplots(1, len(data.items()), figsize=(15, 10))
# Fill subplot
for ax, (name, image) in zip(axs, data.items()):
ax.axis('off')
ax.set_title(name)
ax.imshow(image)
# Display image
plt.show(fig)
```
|
github_jupyter
|
import cv2
import matplotlib.pyplot as plt
import numpy as np
import sys
from openvino.runtime import Core
sys.path.append("../utils")
from notebook_utils import segmentation_map_to_image
ie = Core()
model = ie.read_model(model="model/road-segmentation-adas-0001.xml")
compiled_model = ie.compile_model(model=model, device_name="CPU")
input_layer_ir = compiled_model.input(0)
output_layer_ir = compiled_model.output(0)
# The segmentation network expects images in BGR format
image = cv2.imread("data/empty_road_mapillary.jpg")
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_h, image_w, _ = image.shape
# N,C,H,W = batch size, number of channels, height, width
N, C, H, W = input_layer_ir.shape
# OpenCV resize expects the destination size as (width, height)
resized_image = cv2.resize(image, (W, H))
# reshape to network input shape
input_image = np.expand_dims(
resized_image.transpose(2, 0, 1), 0
)
plt.imshow(rgb_image)
# Run the inference
result = compiled_model([input_image])[output_layer_ir]
# Prepare data for visualization
segmentation_mask = np.argmax(result, axis=1)
plt.imshow(segmentation_mask.transpose(1, 2, 0))
# Define colormap, each color represents a class
colormap = np.array([[68, 1, 84], [48, 103, 141], [53, 183, 120], [199, 216, 52]])
# Define the transparency of the segmentation mask on the photo
alpha = 0.3
# Use function from notebook_utils.py to transform mask to an RGB image
mask = segmentation_map_to_image(segmentation_mask, colormap)
resized_mask = cv2.resize(mask, (image_w, image_h))
# Create image with mask put on
image_with_mask = cv2.addWeighted(resized_mask, alpha, rgb_image, 1 - alpha, 0)
# Define titles with images
data = {"Base Photo": rgb_image, "Segmentation": mask, "Masked Photo": image_with_mask}
# Create subplot to visualize images
fig, axs = plt.subplots(1, len(data.items()), figsize=(15, 10))
# Fill subplot
for ax, (name, image) in zip(axs, data.items()):
ax.axis('off')
ax.set_title(name)
ax.imshow(image)
# Display image
plt.show(fig)
| 0.636466 | 0.988414 |
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Gaussian Probabilities
```
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Introduction
The last chapter ended by discussing some of the drawbacks of the Discrete Bayesian filter. For many tracking and filtering problems our desire is to have a filter that is *unimodal* and *continuous*. That is, we want to model our system using floating point math (continuous) and to have only one belief represented (unimodal). For example, we want to say an aircraft is at (12.34, -95.54, 2389.5) where that is latitude, longitude, and altitude. We do not want our filter to tell us "it might be at (1.65, -78.01, 2100.45) or it might be at (34.36, -98.23, 2543.79)." That doesn't match our physical intuition of how the world works, and as we discussed, it can be prohibitively expensive to compute the multimodal case. And, of course, multiple position estimates makes navigating impossible.
We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate. As you might guess from the chapter name, Gaussian distributions provide all of these features.
## Mean, Variance, and Standard Deviations
### Random Variables
Each time you roll a die the *outcome* will be between 1 and 6. If we rolled a fair die a million times we'd expect to get 1 1/6 of the time. Thus we say the *probability*, or *odds* of the outcome 1 is 1/6. Likewise, if I asked you the chance of 1 being the result of the next roll you'd reply 1/6.
This combination of values and associated probabilities is called a [*random variable*](https://en.wikipedia.org/wiki/Random_variable). *Random* does not mean the process is nondeterministic, only that we lack information. The result of a die toss is deterministic, but we lack enough information to compute the result. We don't know what will happen, except probabilistically.
While we are defining things, the range of values is called the [*sample space*](https://en.wikipedia.org/wiki/Sample_space). For a die the sample space is {1, 2, 3, 4, 5, 6}. For a coin the sample space is {H, T}. *Space* is a mathematical term which means a set with structure. The sample space for the die is a subset of the natural numbers in the range of 1 to 6.
Another example of a random variable is the heights of students in a university. Here the sample space is a range of values in the real numbers between two limits defined by biology.
Random variables such as coin tosses and die rolls are *discrete random variables*. This means their sample space is represented by either a finite number of values or a countably infinite number of values such as the natural numbers. Heights of humans are called *continuous random variables* since they can take on any real value between two limits.
Do not confuse the *measurement* of the random variable with the actual value. If we can only measure the height of a person to 0.1 meters we would only record values from 0.1, 0.2, 0.3...2.7, yielding 27 discrete choices. Nonetheless a person's height can vary between any arbitrary real value between those ranges, and so height is a continuous random variable.
In statistics capital letters are used for random variables, usually from the latter half of the alphabet. So, we might say that $X$ is the random variable representing the die toss, or $Y$ are the heights of the students in the freshmen poetry class. In later chapters we will follow the convention of using lower case for vectors, and upper case for matrices. Unfortunately these conventions clash, and you will have to determine which an author is using from context.
## Probability Distribution
The [*probability distribution*](https://en.wikipedia.org/wiki/Probability_distribution) gives the probability for the random variable to take any value in a sample space. For example, for a fair six sided die we might say:
|Value|Probability|
|-----|-----------|
|1|1/6|
|2|1/6|
|3|1/6|
|4|1/6|
|5|1/6|
|6|1/6|
Some sources call this the *probability function*. Using ordinary function notation, we would write:
$$P(X{=}4) = f(4) = \frac{1}{6}$$
This states that the probability of the die landing on 4 is $\frac{1}{6}$. $P(X{=}x_k)$ is notation for "the probability of $X$ being $x_k$. Some texts use $Pr$ or $Prob$ instead of $P$.
Another example is a fair coin. It has the sample space {H, T}. The coin is fair, so the probability for heads (H) is 50%, and the probability for tails (T) is 50%. We write this as
$$\begin{gathered}P(X{=}H) = 0.5\\P(X{=}T)=0.5\end{gathered}$$
Sample spaces are not unique. One sample space for a die is {1, 2, 3, 4, 5, 6}. Another valid sample space would be {even, odd}. Another might be {dots in all corners, not dots in all corners}. A sample space is valid so long as it covers all possibilities, and any single event is described by only one element. {even, 1, 3, 4, 5} is not a valid sample space for a die since a value of 4 is matched both by 'even' and '4'.
The probabilities for all values of a *discrete random value* is known as the *discrete probability distribution* and the probabilities for all values of a *continuous random value* is known as the *continuous probability distribution*.
To be a probability distribution the probability of each value $x_i$ must be $x_i \ge 0$, since no probability can be less than zero. Secondly, the sum of the probabilities for all values must equal one. This should be intuitively clear for a coin toss: if the odds of getting heads is 70%, then the odds of getting tails must be 30%. We formulize this requirement as
$$\sum\limits_u P(X{=}u)= 1$$
for discrete distributions, and as
$$\int P(X{=}u) \,du= 1$$
for continuous distributions.
### The Mean, Median, and Mode of a Random Variable
Given a set of data we often want to know a representative or average value for that set. There are many measures for this, and the concept is called a [*measure of central tendency*](https://en.wikipedia.org/wiki/Central_tendency). For example we will want to know the *average* height of the students. We all know how to find the average, but let me belabor the point so I can introduce more formal notation and terminology. Another word for average is the *mean*. We compute the mean by summing the values and dividing by the number of values. If the heights of the students in meters is
$$X = \{1.8, 2.0, 1.7, 1.9, 1.6\}$$
we compute the mean as
$$\mu = \frac{1.8 + 2.0 + 1.7 + 1.9 + 1.6}{5} = 1.8$$
It is traditional to use the symbol $\mu$ (mu) to denote the mean.
We can formalize this computation with the equation
$$ \mu = \frac{1}{n}\sum^n_{i=1} x_i$$
NumPy provides `numpy.mean()` for computing the mean.
```
import numpy as np
x = [1.85, 2.0, 1.7, 1.9, 1.6]
print(np.mean(x))
```
The *mode* of a set of numbers is the number that occurs most often. If only one number occurs most often we say it is a *unimodal* set, and if two or more numbers occur the most with equal frequency than te set is *multimodal*. For example the set {1, 2, 2, 2, 3, 4, 4, 4} has modes 2 and 4, which is multimodal, and the set {5, 7, 7, 13} has the mode 7, and so it is unimodal. We will not be computing the mode in this manner in this book, but we do use the concepts of unimodal and multimodal in a more general sense. For example, in the **Discrete Bayes** chapter we talked about our belief in the dog's position as a *multimodal distribution* because we assigned different probabilities to different positions.
Finally, the *median* of a set of numbers is the middle point of the set so that half the values are below the median and half are above the median. Here, above and below is in relation to the set being sorted. If the set contains an even number of values then the two middle numbers are averaged together.
Numpy provides `numpy.median()` to compute the median. As you can see the median of {1.85, 2.0, 1.7, 1.9, 1.6} is 1.85, because 1.85 is the third element of this set after being sorted.
```
print(np.median(x))
```
## Expected Value of a Random Variable
The [*expected value*](https://en.wikipedia.org/wiki/Expected_value) of a random variable is the average value it would have if we took an infinite number of samples of it and then averaged those samples together. Let's say we have $x=[1,3,5]$ and each value is equally probable. What would we *expect* $x$ to have, on average?
It would be the average of 1, 3, and 5, of course, which is 3. That should make sense; we would expect equal numbers of 1, 3, and 5 to occur, so $(1+3+5)/3=3$ is clearly the average of that infinite series of samples. In other words, here the expected value is the *mean* of the sample space.
Now suppose that each value has a different probability of happening. Say 1 has an 80% chance of occurring, 3 has an 15% chance, and 5 has only a 5% chance. In this case we compute the expected value by multiplying each value of $x$ by the percent chance of it occurring, and summing the result. For this case we could compute
$$\mathbb E[X] = (1)(0.8) + (3)(0.15) + (5)(0.05) = 1.5$$
Here I have introduced the notation $\mathbb E[X]$ for the expected value of $x$. Some texts use $E(x)$. The value 1.5 for $x$ makes intuitive sense because $x$ is far more likely to be 1 than 3 or 5, and 3 is more likely than 5 as well.
We can formalize this by letting $x_i$ be the $i^{th}$ value of $X$, and $p_i$ be the probability of its occurrence. This gives us
$$\mathbb E[X] = \sum_{i=1}^n p_ix_i$$
A trivial bit of algebra shows that if the probabilities are all equal, the expected value is the same as the mean:
$$\mathbb E[X] = \sum_{i=1}^n p_ix_i = \sum_{i=1}^n \frac{1}{n}x_i = \mu_x$$
If $x$ is continuous we substitute the sum for an integral, like so
$$\mathbb E[X] = \int_{-\infty}^\infty x\, f(x) \,dx$$
where $f(x)$ is the probability distribution function of $x$. We won't be using this equation yet, but we will be using it in the next chapter.
### Variance of a Random Variable
The computation above tells us the average height of the students, but it doesn't tell us everything we might want to know. For example, suppose we have three classes of students, which we label $X$, $Y$, and $Z$, with these heights:
```
X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]
```
Using NumPy we see that the mean height of each class is the same.
```
print(np.mean(X))
print(np.mean(Y))
print(np.mean(Z))
```
The mean of each class is 1.8 meters, but notice that there is a much greater amount of variation in the heights in the second class than in the first class, and that there is no variation at all in the third class.
The mean tells us something about the data, but not the whole story. We want to be able to specify how much *variation* there is between the heights of the students. You can imagine a number of reasons for this. Perhaps a school district needs to order 5,000 desks, and they want to be sure they buy sizes that accommodate the range of heights of the students.
Statistics has formalized this concept of measuring variation into the notion of [*standard deviation*](https://en.wikipedia.org/wiki/Standard_deviation) and [*variance*](https://en.wikipedia.org/wiki/Variance). The equation for computing the variance is
$$\mathit{VAR}(X) = E[(X - \mu)^2]$$
Ignoring the squared terms for a moment, you can see that the variance is the *expected value* for how much the sample space ($X$) varies from the mean (squared, of course). We have the formula for the expected value $E[X] = \sum\limits_{i=1}^n p_ix_i$, and we will assume that any height is equally probable, so we can substitute that into the equation above to get
$$\mathit{VAR}(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2$$
Let's compute the variance of the three classes to see what values we get and to become familiar with this concept.
The mean of $X$ is 1.8 ($\mu_x = 1.8$) so we compute
$$
\begin{aligned}
\mathit{VAR}(X) &=\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5} \\
&= \frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5} \\
\mathit{VAR}(X)&= 0.02 \, m^2
\end{aligned}$$
NumPy provides the function `var()` to compute the variance:
```
print(np.var(X), "meters squared")
```
This is perhaps a bit hard to interpret. Heights are in meters, yet the variance is meters squared. Thus we have a more commonly used measure, the *standard deviation*, which is defined as the square root of the variance:
$$\sigma = \sqrt{\mathit{VAR}(X)}=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2}$$
It is typical to use $\sigma$ for the *standard deviation* and $\sigma^2$ for the *variance*. In most of this book I will be using $\sigma^2$ instead of $\mathit{VAR}(X)$ for the variance; they symbolize the same thing.
For the first class we compute the standard deviation with
$$
\begin{aligned}
\sigma_x &=\sqrt{\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5}} \\
&= \sqrt{\frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5}} \\
\sigma_x&= 0.1414
\end{aligned}$$
We can verify this computation with the NumPy method `numpy.std()` which computes the standard deviation. 'std' is a common abbreviation for standard deviation.
```
print('std {:.4f}'.format(np.std(X)))
print('var {:.4f}'.format(np.std(X)**2))
```
And, of course, $0.1414^2 = 0.02$, which agrees with our earlier computation of the variance.
What does the standard deviation signify? It tells us how much the heights vary amongst themselves. "How much" is not a mathematical term. We will be able to define it much more precisely once we introduce the concept of a Gaussian in the next section. For now I'll say that for many things 68% of all values lie within one standard deviation of the mean. In other words we can conclude that for a random class 68% of the students will have heights between 1.66 (1.8-0.1414) meters and 1.94 (1.8+0.1414) meters.
We can view this in a plot:
```
from book_format import set_figsize, figsize
from code.book_plots import interactive_plot
from code.gaussian_internal import plot_height_std
import matplotlib.pyplot as plt
with interactive_plot():
plot_height_std(X)
```
For only 5 students we obviously will not get exactly 68% within one standard deviation. We do see that 3 out of 5 students are within $\pm1\sigma$, or 60%, which is as close as you can get to 68% with only 5 samples. I haven't yet introduced enough math or Python for you to fully understand the next bit of code, but let's look at the results for a class with 100 students.
> We write one standard deviation as $1\sigma$, which is pronounced "one standard deviation", not "one sigma". Two standard deviations is $2\sigma$, and so on.
```
from numpy.random import randn
data = [1.8 + .1414*randn() for i in range(100)]
with interactive_plot():
plot_height_std(data, lw=2)
print('mean = {:.3f}'.format(np.mean(data)))
print('std = {:.3f}'.format(np.std(data)))
```
We can see by eye that roughly 68% of the heights lie within $\pm1\sigma$ of the mean 1.8.
We'll discuss this in greater depth soon. For now let's compute the standard deviation for
$$Y = [2.2, 1.5, 2.3, 1.7, 1.3]$$
The mean of $Y$ is $\mu=1.8$ m, so
$$
\begin{aligned}
\sigma_y &=\sqrt{\frac{(2.2-1.8)^2 + (1.5-1.8)^2 + (2.3-1.8)^2 + (1.7-1.8)^2 + (1.3-1.8)^2} {5}} \\
&= \sqrt{0.152} = 0.39 \ m
\end{aligned}$$
We will verify that with NumPy with
```
print('std of Y is {:.4f} m'.format(np.std(Y)))
```
This corresponds with what we would expect. There is more variation in the heights for $Y$, and the standard deviation is larger.
Finally, let's compute the standard deviation for $Z$. There is no variation in the values, so we would expect the standard deviation to be zero. We show this to be true with
$$
\begin{aligned}
\sigma_z &=\sqrt{\frac{(1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2} {5}} \\
&= \sqrt{\frac{0+0+0+0+0}{5}} \\
\sigma_z&= 0.0 \ m
\end{aligned}$$
```
print(np.std(Z))
```
Before we continue I need to point out that I'm ignoring that on average men are taller than women. In general the height variance of a class that contains only men or women will be smaller than a class with both sexes. This is true for other factors as well. Well nourished children are taller than malnourished children. Scandinavians are taller than Italians. When designing experiments statisticians need to take these factors into account.
I suggested we might be performing this analysis to order desks for a school district. For each age group there are likely to be two different means - one clustered around the mean height of the females, and a second mean clustered around the mean heights of the males. The mean of the entire class will be somewhere between the two. If we bought desks for the mean of all students we are likely to end up with desks that fit neither the males or females in the school!
It's too early to understand why, but we will not normally be faced with these problems in this book. Consult any standard probability text if you need to learn techniques to deal with these issues.
### Why the Square of the Differences
Why are we taking the *square* of the differences for the variance? I could go into a lot of math, but let's look at this in a simple way. Here is a chart of the values of $X$ plotted against the mean for $X=[3,-3,3,-3]$
```
with interactive_plot():
X = [3, -3, 3, -3]
mean = np.average(X)
for i in range(len(X)):
plt.plot([i ,i], [mean, X[i]], color='k')
plt.axhline(mean)
plt.xlim(-1, len(X))
plt.tick_params(axis='x', labelbottom='off')
```
If we didn't take the square of the differences the signs would cancel everything out:
$$\frac{(3-0) + (-3-0) + (3-0) + (-3-0)}{4} = 0$$
This is clearly incorrect, as there is more than 0 variance in the data.
Maybe we can use the absolute value? We can see by inspection that the result is $12/4=3$ which is certainly correct — each value varies by 3 from the mean. But what if we have $Y=[6, -2, -3, 1]$? In this case we get $12/4=3$. $Y$ is clearly more spread out than $X$, but the computation yields the same variance. If we use the correct formula we get a variance of 3.5 for $Y$, which reflects its larger variation.
This is not a proof of correctness. Indeed, Carl Friedrich Gauss, the inventor of the technique, recognized that is is somewhat arbitrary. If there are outliers then squaring the difference gives disproportionate weight to that term. For example, let's see what happens if we have $X = [1,-1,1,-2,3,2,100]$.
```
X = [1, -1, 1, -2, 3, 2, 100]
print('Variance of X = {:.2f}'.format(np.var(X)))
```
Is this "correct"? You tell me. Without the outlier of 100 we get $\sigma^2=2.89$, which accurately reflects how $X$ is varying absent the outlier. The one outlier swamps the computation. I will not continue down this path; if you are interested you might want to look at the work that James Berger has done on this problem, in a field called *Bayesian robustness*, or the excellent publications on *robust statistics* by Peter J. Huber [3].
## Gaussians
We are now ready to learn about [Gaussians](https://en.wikipedia.org/wiki/Gaussian_function). Let's remind ourselves of the motivation for this chapter.
> We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate.
Let's look at a graph of a Gaussian distribution to get a sense of what we are talking about.
```
from filterpy.stats import plot_gaussian_pdf
plt.figure()
ax = plot_gaussian_pdf(mean=1.8, variance=0.1414**2,
xlabel='Student Height', ylabel='pdf')
```
This curve is a [*probability density function*](https://en.wikipedia.org/wiki/Probability_density_function) or *pdf* for short. It shows the relative likelihood for the random variable to take on a value. In the chart above, a student is somewhat more likely to have a height near 1.8 m than 1.7 m, and far more likely to have a height of 1.9 m vs 1.1 m.
> I explain how to plot Gaussians, and much more, in the Notebook *Computing_and_Plotting_PDFs* in the
Supporting_Notebooks folder. You can read it online [here](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb) [1].
This may be recognizable to you as a 'bell curve'. This curve is ubiquitous because under real world conditions many observations are distributed in such a manner. In fact, this is the curve for the student heights given earlier. I will not use the term 'bell curve' to refer to a Gaussian because many probability distributions have a similar bell curve shape. Non-mathematical sources might not be as precise, so be judicious in what you conclude when you see the term used without definition.
This curve is not unique to heights — a vast amount of natural phenomena exhibits this sort of distribution, including the sensors that we use in filtering problems. As we will see, it also has all the attributes that we are looking for — it represents a unimodal belief or value as a probability, it is continuous, and it is computationally efficient. We will soon discover that it also has other desirable qualities which we may not realize we desire.
To further motivate you, recall the shapes of the probability distributions in the *Discrete Bayes* chapter. They were not perfect Gaussian curves, but they were similar, as in the plot below. We will be using Gaussians to replace the discrete probabilities used in that chapter!
```
import code.book_plots as book_plots
belief = [ 0.,0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]
with interactive_plot():
book_plots.bar_plot(belief)
```
## Nomenclature
A bit of nomenclature before we continue - this chart depicts the *probability density* of a *random variable* having any value between ($-\infty..\infty)$. What does that mean? Imagine we take an infinite number of infinitely precise measurements of the speed of automobiles on a section of highway. We could then plot the results by showing the relative number of cars going past at any given speed. If the average was 120 kph, it might look like this:
```
with interactive_plot():
ax = plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)')
```
The y-axis depicts the *probability density* — the relative amount of cars that are going the speed at the corresponding x-axis.
You may object that human heights or automobile speeds cannot be less than zero, let alone $-\infty$ or $\infty$. This is true, but this is a common limitation of mathematical modeling. “The map is not the territory” is a common expression, and it is true for Bayesian filtering and statistics. The Gaussian distribution above models the distribution of the measured automobile speeds, but being a model it is necessarily imperfect. The difference between model and reality will come up again and again in these filters. Gaussians are used in many branches of mathematics, not because they perfectly model reality, but because they are easier to use than any other relatively accurate choice. However, even in this book Gaussians will fail to model reality, forcing us to use computationally expensive alternatives.
You will see these distributions called *Gaussian distributions* or *normal distributions*. *Gaussian* and *normal* both mean the same thing in this context, and are used interchangeably. I will use both throughout this book as different sources will use either term, and I want you to be used to seeing both. Finally, as in this paragraph, it is typical to shorten the name and talk about a *Gaussian* or *normal* — these are both typical shortcut names for the *Gaussian distribution*.
## Gaussian Distributions
Let's explore how Gaussians work. A Gaussian is a *continuous probability distribution* that is completely described with two parameters, the mean ($\mu$) and the variance ($\sigma^2$). It is defined as:
$$
f(x, \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp\big [{-\frac{(x-\mu)^2}{2\sigma^2} }\big ]
$$
$\exp[x]$ is notation for $e^x$.
<p> Don't be dissuaded by the equation if you haven't seen it before; you will not need to memorize or manipulate it. The computation of this function is stored in `stats.py` with the function `gaussian(x, mean, var)`.
> **Optional:** Let's remind ourselves how to look at a function stored in a file by using the *%load* magic. If you type *%load -s gaussian stats.py* into a code cell and then press CTRL-Enter, the notebook will create a new input cell and load the function into it.
```python
%load -s gaussian stats.py
def gaussian(x, mean, var):
"""returns normal distribution for x given a
gaussian with the specified mean and variance.
"""
return (np.exp((-0.5*(np.asarray(x)-mean)**2)/var) /
math.sqrt(2*math.pi*var))
```
<p><p><p><p>We will plot a Gaussian with a mean of 22 $(\mu=22)$, with a variance of 4 $(\sigma^2=4)$, and then discuss what this means.
```
from filterpy.stats import gaussian, norm_cdf
with interactive_plot():
ax = plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$')
```
What does this curve *mean*? Assume we have a thermometer which reads 22°C. No thermometer is perfectly accurate, and so we expect that each reading will be slightly off the actual value. However, a theorem called [*Central Limit Theorem*](https://en.wikipedia.org/wiki/Central_limit_theorem) states that if we make many measurements that the measurements will be normally distributed. When we look at this chart we can "sort of" think of it as representing the probability of the thermometer reading a particular value given the actual temperature of 22°C.
Recall that a Gaussian distribution is *continuous*. Think of an infinitely long straight line - what is the probability that a point you pick randomly is at 2. Clearly 0%, as there is an infinite number of choices to choose from. The same is true for normal distributions; in the graph above the probability of being *exactly* 2°C is 0% because there are an infinite number of values the reading can take.
What is this curve? It is something we call the *probability density function.* The area under the curve at any region gives you the probability of those values. So, for example, if you compute the area under the curve between 20 and 22 the resulting area will be the probability of the temperature reading being between those two temperatures.
We can think of this in Bayesian terms or frequentist terms. As a Bayesian, if the thermometer reads exactly 22°C, then our belief is described by the curve - our belief that the actual (system) temperature is near 22 is very high, and our belief that the actual temperature is near 18 is very low. As a frequentist we would say that if we took 1 billion temperature measurements of a system at exactly 22°C, then a histogram of the measurements would look like this curve.
How do you compute the probability, or area under the curve? You integrate the equation for the Gaussian
$$ \int^{x_1}_{x_0} \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}{(x-\mu)^2}/\sigma^2 } dx$$
I wrote `filterpy.stats.norm_cdf` which computes the integral for you. For example, we can compute
```
print('Probability of range 21.5 to 22.5 is {:.2f}%'.format(
norm_cdf((21.5, 22.5), 22,4)*100))
print('Probability of range 23.5 to 24.5 is {:.2f}%'.format(
norm_cdf((23.5, 24.5), 22,4)*100))
```
The mean ($\mu$) is what it sounds like — the average of all possible probabilities. Because of the symmetric shape of the curve it is also the tallest part of the curve. The thermometer reads 22°C, so that is what we used for the mean.
The notation for a normal distribution for a random variable $X$ is $X \sim\ \mathcal{N}(\mu,\sigma^2)$ where $\sim$ means *distributed according to*. This means I can express the temperature reading of our thermometer as
$$\text{temp} \sim \mathcal{N}(22,4)$$
This is an extremely important result. Gaussians allow me to capture an infinite number of possible values with only two numbers! With the values $\mu=22$ and $\sigma^2=4$ I can compute the distribution of measurements for over any range.
> Some sources use $\mathcal N (\mu, \sigma)$ instead of $\mathcal N (\mu, \sigma^2)$. Either is fine, they are both conventions. You need to keep in mind which form is being used if you see a term such as $\mathcal{N}(22,4)$. In this book I always use $\mathcal N (\mu, \sigma^2)$, so $\sigma=2$, $\sigma^2=4$ for this example.
## The Variance and Belief
Since this is a probability density distribution it is required that the area under the curve always equals one. This should be intuitively clear — the area under the curve represents all possible outcomes, *something* happened, and the probability of *something happening* is one, so the density must sum to one. We can prove this ourselves with a bit of code. (If you are mathematically inclined, integrate the Gaussian equation from $-\infty$ to $\infty$)
```
print(norm_cdf((-1e8, 1e8), mu=0, var=4))
```
This leads to an important insight. If the variance is small the curve will be narrow. this is because the variance is a measure of *how much* the samples vary from the mean. To keep the area equal to 1, the curve must also be tall. On the other hand if the variance is large the curve will be wide, and thus it will also have to be short to make the area equal to 1.
Let's look at that graphically:
```
import numpy as np
import matplotlib.pyplot as plt
xs = np.arange(15, 30, 0.05)
with interactive_plot():
plt.plot(xs, gaussian(xs, 23, 0.05), label='$\sigma^2$=0.05', c='b')
plt.plot(xs, gaussian(xs, 23, 1), label='$\sigma^2$=1', ls=':', c='b')
plt.plot(xs, gaussian(xs, 23, 5), label='$\sigma^2$=5', ls='--', c='b')
plt.legend()
```
What is this telling us? The Gaussian with $\sigma^2=0.05$ is very narrow. It is saying that we believe $x=23$, and that we are very sure about that. In contrast, the Gaussian with $\sigma^2=5$ also believes that $x=23$, but we are much less sure about that. Our believe that $x=23$ is lower, and so our belief about the likely possible values for $x$ is spread out — we think it is quite likely that $x=20$ or $x=26$, for example. $\sigma^2=0.05$ has almost completely eliminated $22$ or $24$ as possible values, whereas $\sigma^2=5$ considers them nearly as likely as $23$.
If we think back to the thermometer, we can consider these three curves as representing the readings from three different thermometers. The curve for $\sigma^2=0.05$ represents a very accurate thermometer, and curve for $\sigma^2=5$ represents a fairly inaccurate one. Note the very powerful property the Gaussian distribution affords us — we can entirely represent both the reading and the error of a thermometer with only two numbers — the mean and the variance.
An equivalent formation for a Gaussian is $\mathcal{N}(\mu,1/\tau)$ where $\mu$ is the *mean* and $\tau$ the *precision*. $1/\tau = \sigma^2$; it is the reciprocal of the variance. While we do not use this formulation in this book, it underscores that the variance is a measure of how precise our data is. A small variance yields large precision — our measurement is very precise. Conversely, a large variance yields low precision — our belief is spread out across a large area. You should become comfortable with thinking about Gaussians in these equivalent forms. In Bayesian terms Gaussians reflect our *belief* about a measurement, they express the *precision* of the measurement, and they express how much *variance* there is in the measurements. These are all different ways of stating the same fact.
I'm getting ahead of myself, but in the next chapters we will use Gaussians to express our belief in things like the estimated position of the object we are tracking, or the accuracy of the sensors we are using.
## The 68-95-99.7 Rule
It is worth spending a few words on standard deviation now. The standard deviation is a measure of how much variation from the mean exists. For Gaussian distributions, 68% of all the data falls within one standard deviation ($\pm1\sigma$) of the mean, 95% falls within two standard deviations ($\pm2\sigma$), and 99.7% within three ($\pm3\sigma$). This is often called the [68-95-99.7 rule](https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule). If you were told that the average test score in a class was 71 with a standard deviation of 9.4, you could conclude that 95% of the students received a score between 52.2 and 89.8 if the distribution is normal (that is calculated with $71 \pm (2 * 9.4)$).
Finally, these are not arbitrary numbers. If the Gaussian for our position is $\mu=22$ meters, then the standard deviation also has units meters. Thus $\sigma=0.2$ implies that 68% of the measurements range from 21.8 to 22.2 meters. Variance is the standard deviation squared, thus $\sigma^2 = .04$ meters$^2$.
The following graph depicts the relationship between the standard deviation and the normal distribution.
```
from code.gaussian_internal import display_stddev_plot
with interactive_plot():
display_stddev_plot()
```
## Interactive Gaussians
For those that are reading this in a Jupyter Notebook, here is an interactive version of the Gaussian plots. Use the sliders to modify $\mu$ and $\sigma^2$. Adjusting $\mu$ will move the graph to the left and right because you are adjusting the mean, and adjusting $\sigma^2$ will make the bell curve thicker and thinner.
```
import math
from IPython.html.widgets import interact, interactive, fixed
set_figsize(y=3)
def plt_g(mu,variance):
plt.figure()
xs = np.arange(2, 8, 0.1)
ys = gaussian(xs, mu, variance)
plt.plot(xs, ys)
plt.ylim((0, 1))
interact (plt_g, mu=(0., 10), variance = (.2, 1.));
```
Finally, if you are reading this online, here is an animation of a Gaussian. First, the mean is shifted to the right. Then the mean is centered at $\mu=5$ and the variance is modified.
<img src='animations/04_gaussian_animate.gif'>
## Computational Properties of Gaussians
A remarkable property of Gaussians is that the product of two independent Gaussians is another Gaussian! The sum is not Gaussian, but proportional to a Gaussian.
The discrete Bayes filter works by multiplying and adding probabilities. I'm getting ahead of myself, but the Kalman filter uses Gaussians instead of probabilities, but the rest of the algorithm remains the same. This means we will need to multiply and add Gaussians.
The Gaussian is a nonlinear function, and typically if you multiply a nonlinear equation with itself you end up with a different equation. For example, the shape of `sin(x)sin(x)` is very different from `sin(x)`. But the result of multiplying two Gaussians is yet another Gaussian. This is a fundamental property, and a key reason why Kalman filters are computationally feasible. Said another way, Kalman filters use Gaussians *because* they are computationally nice.
The remainder of this section is optional. I will derive the equations for the sum and product of two Gaussians. You will not need to understand this material to understand the rest of the book, so long as you accept the results.
### Product of Gaussians
The product of two independent Gaussians is given by:
$$\begin{aligned}\mu &=\frac{\sigma_1^2\mu_2 + \sigma_2^2\mu_1}{\sigma_1^2+\sigma_2^2}\\
\sigma^2 &=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}
\end{aligned}$$
You can find this result by multiplying the equation for two Gaussians together and combining terms. The algebra gets messy. I will derive it using Bayes theorem. We can state the problem as: let the prior be $N(\bar\mu, \bar\sigma^2)$, and measurement be $z \propto N(z, \sigma_z^2)$. What is the posterior x given the measurement z?
Write the posterior as $P(x \mid z)$. Now we can use Bayes Theorem to state
$$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
$P(z)$ is a normalizing constant, so we can create a proportinality
$$P(x \mid z) \propto P(z|x)P(x)$$
Now we subtitute in the equations for the Gaussians, which are
$$P(z \mid x) = \frac{1}{\sqrt{2\pi\sigma_z^2}}\exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big]$$
$$P(x) = \frac{1}{\sqrt{2\pi\bar\sigma^2}}\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big]$$
We can drop the leading terms, as they are constants, giving us
$$\begin{aligned}
P(x \mid z) &\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big]\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big]\\
&\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big] \\
&\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z-x)^2-\sigma_z^2(x-\bar\mu)^2]\Big]
\end{aligned}$$
Now we multiply out the squared terms and group in terms of the posterior $x$.
$$\begin{aligned}
P(x \mid z) &\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z^2 -2xz + x^2) + \sigma_z^2(x^2 - 2x\bar\mu+\bar\mu^2)]\Big ] \\
&\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z) + (\bar\sigma^2z^2+\sigma_z^2\bar\mu^2)]\Big ]
\end{aligned}$$
The last parentheses do not contain the posterior $x$, so it can be treated as a constant and discarded.
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z)}{\sigma_z^2\bar\sigma^2}\Big ]
$$
Divide numerator and denominator by $\bar\sigma^2+\sigma_z^2$ to get
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{x^2-2x(\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2})}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\Big ]
$$
Proportionality lets us create or delete constants at will, so we can factor this into
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{(x-\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2})^2}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\Big ]
$$
A Gaussian is
$$N(\mu,\, \sigma^2) \propto \exp\Big [-\frac{1}{2}\frac{(x - \mu)^2}{\sigma^2}\Big ]$$
So we can see that $P(x \mid z)$ has a mean of
$$\mu_\mathtt{posterior} = \frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2}$$
and a variance of
$$
\sigma_\mathtt{posterior} = \frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}
$$
I've dropped the constants, and so the result is not a normal, but proportional to one. Bayes theorem normalizes with the $P(z)$ divisor, ensuring that the result is normal. We normalize in the update step of our filters, ensuring the filter estimate is Gaussian.
$$\mathcal N_1 = \| \mathcal N_2\cdot \mathcal N_3\|$$
### Sum of Gaussians
The sum of two Gaussians is given by
$$\begin{gathered}\mu = \mu_1 + \mu_2 \\
\sigma^2 = \sigma^2_1 + \sigma^2_2
\end{gathered}$$
There are several proofs for this. I will use convolution since we used convolution in the previous chapter for the histograms of probabilities.
To find the density function of the sum of two Gaussian random variables we sum the density functions of each. They are nonlinear, continuous functions, so we need to compute the sum with an integral. If the random variables $p$ and $z$ (e.g. prior and measurement) are independent we can compute this with
$p(x) = \int\limits_{-\infty}^\infty f_p(x-z)f_z(z)\, dx$
This is the equation for a convolution. Now we just do some math:
$p(x) = \int\limits_{-\infty}^\infty f_2(x-x_1)f_1(x_1)\, dx$
$= \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\sigma_z}\exp\left[-\frac{x - z - \mu_z}{2\sigma^2_z}\right]
\frac{1}{\sqrt{2\pi}\sigma_p}\exp\left[-\frac{x - \mu_p}{2\sigma^2_p}\right] \, dx$
$= \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right]
\frac{1}{\sqrt{2\pi}\frac{\sigma_p\sigma_z}{\sqrt{\sigma_p^2 + \sigma_z^2}}} \exp\left[ -\frac{(x - \frac{\sigma_p^2(x-\mu_z) + \sigma_z^2\mu_p}{}))^2}{2\left(\frac{\sigma_p\sigma_x}{\sqrt{\sigma_z^2+\sigma_p^2}}\right)^2}\right] \, dx$
$= \frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right] \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\frac{\sigma_p\sigma_z}{\sqrt{\sigma_p^2 + \sigma_z^2}}} \exp\left[ -\frac{(x - \frac{\sigma_p^2(x-\mu_z) + \sigma_z^2\mu_p}{}))^2}{2\left(\frac{\sigma_p\sigma_x}{\sqrt{\sigma_z^2+\sigma_p^2}}\right)^2}\right] \, dx$
The expression inside the integral is a normal distribution. The sum of a normal distribution is one, hence the integral is one. This gives us
$$p(x) = \frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right]$$
This is in the form of a normal, where
$$\begin{gathered}\mu_x = \mu_p + \mu_z \\
\sigma_x^2 = \sigma_z^2+\sigma_p^2\, \square\end{gathered}$$
## Computing Probabilities with scipy.stats
In this chapter I used code from [FilterPy](https://github.com/rlabbe/filterpy) to compute and plot Gaussians. I did that to give you a chance to look at the code and see how these functions are implemented. However, Python comes with "batteries included" as the saying goes, and it comes with a wide range of statistics functions in the module `scipy.stats`. So let's walk through how to use scipy.stats to compute statistics and probabilities.
The `scipy.stats` module contains a number of objects which you can use to compute attributes of various probability distributions. The full documentation for this module is here: http://docs.scipy.org/doc/scipy/reference/stats.html. We will focus on the norm variable, which implements the normal distribution. Let's look at some code that uses `scipy.stats.norm` to compute a Gaussian, and compare its value to the value returned by the `gaussian()` function from FilterPy.
```
from scipy.stats import norm
import filterpy.stats
print(norm(2, 3).pdf(1.5))
print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))
```
The call `norm(2, 3)` creates what scipy calls a 'frozen' distribution - it creates and returns an object with a mean of 2 and a standard deviation of 3. You can then use this object multiple times to get the probability density of various values, like so:
```
n23 = norm(2, 3)
print('pdf of 1.5 is %.4f' % n23.pdf(1.5))
print('pdf of 2.5 is also %.4f' % n23.pdf(2.5))
print('pdf of 2 is %.4f' % n23.pdf(2))
```
The documentation for [scipy.stats.norm](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html#scipy.stats.normfor) [2] lists many other functions. For example, we can generate $n$ samples from the distribution with the `rvs()` function.
```
np.set_printoptions(precision=3, linewidth=50)
print(n23.rvs(size=15))
```
We can get the [*cumulative distribution function (CDF)*](https://en.wikipedia.org/wiki/Cumulative_distribution_function), which is the probability that a randomly drawn value from the distribution is less than or equal to $x$.
```
# probability that a random value is less than the mean 2
print(n23.cdf(2))
```
We can get various properties of the distribution:
```
print('variance is', n23.var())
print('standard deviation is', n23.std())
print('mean is', n23.mean())
```
## Fat Tails
Earlier I mentioned the *central limit theorem*, which states that under certain conditions the arithmetic sum of any independent random variable will be normally distributed, regardless of how the random variables are distributed. This is important to us because nature is full of distributions which are not normal, but when we apply the central limit theorem over large populations we end up with normal distributions.
However, a key part of the proof is “under certain conditions”. These conditions often do not hold for the physical world. The resulting distributions are called *fat tailed*. Tails is a colloquial term for the far left and right side parts of the curve where the probability density is close to zero.
Let's consider a trivial example. We think of things like test scores as being normally distributed. If you have ever had a professor “grade on a curve” you have been subject to this assumption. But of course test scores cannot follow a normal distribution. This is because the distribution assigns a nonzero probability distribution for *any* value, no matter how far from the mean. So, for example, say your mean is 90 and the standard deviation is 13. The normal distribution assumes that there is a large chance of somebody getting a 90, and a small chance of somebody getting a 40. However, it also implies that there is a tiny chance of somebody getting a grade of -10, or 150. It assigns an infinitesimal chance of getting a score of $-10^{300}$ or $10^{32986}$. The *tails* of a Gaussian distribution are infinitely long.
But for a test we know this is not true. Ignoring extra credit, you cannot get less than 0, or more than 100. Let's plot this range of values using a normal distribution.
```
xs = np.arange(10,100, 0.05)
ys = [gaussian(x, 90, 30) for x in xs]
with interactive_plot():
plt.plot(xs, ys, label='var=0.2')
plt.xlim((0,120))
plt.ylim(0, 0.09);
```
The area under the curve cannot equal 1, so it is not a probability distribution. What actually happens is that more students than predicted by a normal distribution get scores nearer the upper end of the range (for example), and that tail becomes “fat”. Also, the test is probably not able to perfectly distinguish incredibly minute differences in skill in the students, so the distribution to the left of the mean is also probably a bit bunched up in places. The resulting distribution is called a [*fat tail distribution*](https://en.wikipedia.org/wiki/Fat-tailed_distribution).
Kalman filters use sensors to measure the world. The errors in a sensor's measurements are rarely truly Gaussian. It is far too early to be talking about the difficulties that this presents to the Kalman filter designer. It is worth keeping in the back of your mind the fact that the Kalman filter math is based on an idealized model of the world. For now I will present a bit of code that I will be using later in the book to form fat tail distributions to simulate various processes and sensors. This distribution is called the [*Student's $t$-distribution*](https://en.wikipedia.org/wiki/Student%27s_t-distribution).
Let's say I want to model a sensor that has some white noise in the output. For simplicity, let's say the signal is a constant 10, and the standard deviation of the noise is 2. We can use the function `numpy.random.randn()` to get a random number with a mean of 0 and a standard deviation of 1. I can simulate this with:
```
from numpy.random import randn
def sense():
return 10 + randn()*2
```
Let's plot that signal and see what it looks like.
```
zs = [sense() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
```
That looks like I would expect. The signal is centered around 10. A standard deviation of 2 means that 68% of the measurements will be within $\pm$ 2 of 10, and 99% will be within $\pm$ 6 of 10, and that looks like what is happening.
Now let's look at a fat tailed distribution generated with the Student's $t$-distribution. I will not go into the math, but just give you the source code for it and then plot a distribution using it.
```
import random
import math
def rand_student_t(df, mu=0, std=1):
"""return random number distributed by Student's t
distribution with `df` degrees of freedom with the
specified mean and standard deviation.
"""
x = random.gauss(0, std)
y = 2.0*random.gammavariate(0.5*df, 2.0)
return x / (math.sqrt(y / df)) + mu
def sense_t():
return 10 + rand_student_t(7)*2
zs = [sense_t() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
```
We can see from the plot that while the output is similar to the normal distribution there are outliers that go far more than 3 standard deviations from the mean (7 to 13). This is what causes the 'fat tail'.
It is unlikely that the Student's $t$-distribution is an accurate model of how your sensor (say, a GPS or Doppler) performs, and this is not a book on how to model physical systems. However, it does produce reasonable data to test your filter's performance when presented with real world noise. We will be using distributions like these throughout the rest of the book in our simulations and tests.
This is not an idle concern. The Kalman filter equations assume the noise is normally distributed, and perform sub-optimally if this is not true. Designers for mission critical filters, such as the filters on spacecraft, need to master a lot of theory and empirical knowledge about the performance of the sensors on their spacecraft.
The code for rand_student_t is included in `filterpy.stats`. You may use it with
```python
from filterpy.stats import rand_student_t
```
## Summary and Key Points
This chapter is a poor introduction to statistics in general. I've only covered the concepts that needed to use Gaussians in the remainder of the book, no more. What I've covered will not get you very far if you intend to read the Kalman filter literature. If this is a new topic to you I suggest reading a statistics textbook. I've always liked the Schaum series for self study, and Alan Downey's *Think Stats* [5] is also very good.
The following points **must** be understood by you before we continue:
* Normals express a continuous probability distribution
* They are completely described by two parameters: the mean ($\mu$) and variance ($\sigma^2$)
* $\mu$ is the average of all possible values
* The variance $\sigma^2$ represents how much our measurements vary from the mean
* The standard deviation ($\sigma$) is the square root of the variance ($\sigma^2$)
* Many things in nature approximate a normal distribution
## References
[1] https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb
[2] http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html
[3] http://docs.scipy.org/doc/scipy/reference/tutorial/stats.html
[4] Huber, Peter J. *Robust Statistical Procedures*, Second Edition. Society for Industrial and Applied Mathematics, 1996.
[5] Downey, Alan. *Think Stats*, Second Edition. O'Reilly Media.
https://github.com/AllenDowney/ThinkStats2
http://greenteapress.com/thinkstats/
|
github_jupyter
|
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
import numpy as np
x = [1.85, 2.0, 1.7, 1.9, 1.6]
print(np.mean(x))
print(np.median(x))
X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]
print(np.mean(X))
print(np.mean(Y))
print(np.mean(Z))
print(np.var(X), "meters squared")
print('std {:.4f}'.format(np.std(X)))
print('var {:.4f}'.format(np.std(X)**2))
from book_format import set_figsize, figsize
from code.book_plots import interactive_plot
from code.gaussian_internal import plot_height_std
import matplotlib.pyplot as plt
with interactive_plot():
plot_height_std(X)
from numpy.random import randn
data = [1.8 + .1414*randn() for i in range(100)]
with interactive_plot():
plot_height_std(data, lw=2)
print('mean = {:.3f}'.format(np.mean(data)))
print('std = {:.3f}'.format(np.std(data)))
print('std of Y is {:.4f} m'.format(np.std(Y)))
print(np.std(Z))
with interactive_plot():
X = [3, -3, 3, -3]
mean = np.average(X)
for i in range(len(X)):
plt.plot([i ,i], [mean, X[i]], color='k')
plt.axhline(mean)
plt.xlim(-1, len(X))
plt.tick_params(axis='x', labelbottom='off')
X = [1, -1, 1, -2, 3, 2, 100]
print('Variance of X = {:.2f}'.format(np.var(X)))
from filterpy.stats import plot_gaussian_pdf
plt.figure()
ax = plot_gaussian_pdf(mean=1.8, variance=0.1414**2,
xlabel='Student Height', ylabel='pdf')
import code.book_plots as book_plots
belief = [ 0.,0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]
with interactive_plot():
book_plots.bar_plot(belief)
with interactive_plot():
ax = plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)')
%load -s gaussian stats.py
def gaussian(x, mean, var):
"""returns normal distribution for x given a
gaussian with the specified mean and variance.
"""
return (np.exp((-0.5*(np.asarray(x)-mean)**2)/var) /
math.sqrt(2*math.pi*var))
from filterpy.stats import gaussian, norm_cdf
with interactive_plot():
ax = plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$')
print('Probability of range 21.5 to 22.5 is {:.2f}%'.format(
norm_cdf((21.5, 22.5), 22,4)*100))
print('Probability of range 23.5 to 24.5 is {:.2f}%'.format(
norm_cdf((23.5, 24.5), 22,4)*100))
print(norm_cdf((-1e8, 1e8), mu=0, var=4))
import numpy as np
import matplotlib.pyplot as plt
xs = np.arange(15, 30, 0.05)
with interactive_plot():
plt.plot(xs, gaussian(xs, 23, 0.05), label='$\sigma^2$=0.05', c='b')
plt.plot(xs, gaussian(xs, 23, 1), label='$\sigma^2$=1', ls=':', c='b')
plt.plot(xs, gaussian(xs, 23, 5), label='$\sigma^2$=5', ls='--', c='b')
plt.legend()
from code.gaussian_internal import display_stddev_plot
with interactive_plot():
display_stddev_plot()
import math
from IPython.html.widgets import interact, interactive, fixed
set_figsize(y=3)
def plt_g(mu,variance):
plt.figure()
xs = np.arange(2, 8, 0.1)
ys = gaussian(xs, mu, variance)
plt.plot(xs, ys)
plt.ylim((0, 1))
interact (plt_g, mu=(0., 10), variance = (.2, 1.));
from scipy.stats import norm
import filterpy.stats
print(norm(2, 3).pdf(1.5))
print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))
n23 = norm(2, 3)
print('pdf of 1.5 is %.4f' % n23.pdf(1.5))
print('pdf of 2.5 is also %.4f' % n23.pdf(2.5))
print('pdf of 2 is %.4f' % n23.pdf(2))
np.set_printoptions(precision=3, linewidth=50)
print(n23.rvs(size=15))
# probability that a random value is less than the mean 2
print(n23.cdf(2))
print('variance is', n23.var())
print('standard deviation is', n23.std())
print('mean is', n23.mean())
xs = np.arange(10,100, 0.05)
ys = [gaussian(x, 90, 30) for x in xs]
with interactive_plot():
plt.plot(xs, ys, label='var=0.2')
plt.xlim((0,120))
plt.ylim(0, 0.09);
from numpy.random import randn
def sense():
return 10 + randn()*2
zs = [sense() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
import random
import math
def rand_student_t(df, mu=0, std=1):
"""return random number distributed by Student's t
distribution with `df` degrees of freedom with the
specified mean and standard deviation.
"""
x = random.gauss(0, std)
y = 2.0*random.gammavariate(0.5*df, 2.0)
return x / (math.sqrt(y / df)) + mu
def sense_t():
return 10 + rand_student_t(7)*2
zs = [sense_t() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
from filterpy.stats import rand_student_t
| 0.68056 | 0.992386 |
```
import numpy as np
import logging
import torch
import torch.nn.functional as F
import numpy as np
from tqdm import trange
from pytorch_pretrained_bert import GPT2Tokenizer, GPT2Model, GPT2LMHeadModel
# Load pre-trained model tokenizer (vocabulary)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
text_1 = "It was nearly two weeks later when the cosmonaut was jolted out of sleep, "
text_2 = "snug against"
indexed_tokens_1 = tokenizer.encode(text_1)
indexed_tokens_2 = tokenizer.encode(text_2)
# Convert inputs to PyTorch tensors
tokens_tensor_1 = torch.tensor([indexed_tokens_1])
tokens_tensor_2 = torch.tensor([indexed_tokens_2])
# Load pre-trained model (weights)
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.eval()
# If you have a GPU, put everything on cuda
tokens_tensor_1 = tokens_tensor_1.to('cuda')
tokens_tensor_2 = tokens_tensor_2.to('cuda')
model.to('cuda')
# Predict all tokens
with torch.no_grad():
predictions_1, past = model(tokens_tensor_1)
# past can be used to reuse precomputed hidden state in a subsequent predictions
# (see beam-search examples in the run_gpt2.py example).
predictions_2, past = model(tokens_tensor_2, past=past)
# get the predicted last token
predicted_index = torch.argmax(predictions_2[0, -1, :]).item()
predicted_token = tokenizer.decode([predicted_index])
predicted_token
```
lol
```
logging.basicConfig(format = '%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt = '%m/%d/%Y %H:%M:%S',
level = logging.INFO)
logger = logging.getLogger(__name__)
def top_k_logits(logits, k):
"""
Masks everything but the k top entries as -infinity (1e10).
Used to mask logits such that e^-infinity -> 0 won't contribute to the
sum of the denominator.
"""
if k == 0:
return logits
else:
values = torch.topk(logits, k)[0]
batch_mins = values[:, -1].view(-1, 1).expand_as(logits)
return torch.where(logits < batch_mins, torch.ones_like(logits) * -1e10, logits)
def sample_sequence(model, length, start_token=None, batch_size=None, context=None, temperature=1, top_k=0, device='cuda', sample=True):
if start_token is None:
assert context is not None, 'Specify exactly one of start_token and context!'
context = torch.tensor(context, device=device, dtype=torch.long).unsqueeze(0).repeat(batch_size, 1)
else:
assert context is None, 'Specify exactly one of start_token and context!'
context = torch.full((batch_size, 1), start_token, device=device, dtype=torch.long)
prev = context
output = context
past = None
with torch.no_grad():
for i in trange(length):
logits, past = model(prev, past=past)
logits = logits[:, -1, :] / temperature
logits = top_k_logits(logits, k=top_k)
log_probs = F.softmax(logits, dim=-1)
if sample:
prev = torch.multinomial(log_probs, num_samples=1)
else:
_, prev = torch.topk(log_probs, k=1, dim=-1)
output = torch.cat((output, prev), dim=1)
return output
def run_model(input_text, length=-1, nsamples=1, batch_size=1, temperature=1.0, top_k=0, seed=0):
assert nsamples % batch_size == 0
np.random.seed(seed)
torch.random.manual_seed(seed)
torch.cuda.manual_seed(seed)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
enc = GPT2Tokenizer.from_pretrained('gpt2')
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.to(device)
model.eval()
if length == -1:
length = model.config.n_ctx // 2
elif length > model.config.n_ctx:
raise ValueError("Can't get samples longer than window size: %s" % model.config.n_ctx)
while True:
context_tokens = []
if input_text:
context_tokens = enc.encode(input_text)
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=context_tokens,
start_token=None,
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:, len(context_tokens):].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
else:
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=None,
start_token=enc.encoder['<|endoftext|>'],
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:,1:].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
run_model("It was nearly two weeks later when the cosmonaut was jolted out of sleep, jolted by")
```
|
github_jupyter
|
import numpy as np
import logging
import torch
import torch.nn.functional as F
import numpy as np
from tqdm import trange
from pytorch_pretrained_bert import GPT2Tokenizer, GPT2Model, GPT2LMHeadModel
# Load pre-trained model tokenizer (vocabulary)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
text_1 = "It was nearly two weeks later when the cosmonaut was jolted out of sleep, "
text_2 = "snug against"
indexed_tokens_1 = tokenizer.encode(text_1)
indexed_tokens_2 = tokenizer.encode(text_2)
# Convert inputs to PyTorch tensors
tokens_tensor_1 = torch.tensor([indexed_tokens_1])
tokens_tensor_2 = torch.tensor([indexed_tokens_2])
# Load pre-trained model (weights)
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.eval()
# If you have a GPU, put everything on cuda
tokens_tensor_1 = tokens_tensor_1.to('cuda')
tokens_tensor_2 = tokens_tensor_2.to('cuda')
model.to('cuda')
# Predict all tokens
with torch.no_grad():
predictions_1, past = model(tokens_tensor_1)
# past can be used to reuse precomputed hidden state in a subsequent predictions
# (see beam-search examples in the run_gpt2.py example).
predictions_2, past = model(tokens_tensor_2, past=past)
# get the predicted last token
predicted_index = torch.argmax(predictions_2[0, -1, :]).item()
predicted_token = tokenizer.decode([predicted_index])
predicted_token
logging.basicConfig(format = '%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt = '%m/%d/%Y %H:%M:%S',
level = logging.INFO)
logger = logging.getLogger(__name__)
def top_k_logits(logits, k):
"""
Masks everything but the k top entries as -infinity (1e10).
Used to mask logits such that e^-infinity -> 0 won't contribute to the
sum of the denominator.
"""
if k == 0:
return logits
else:
values = torch.topk(logits, k)[0]
batch_mins = values[:, -1].view(-1, 1).expand_as(logits)
return torch.where(logits < batch_mins, torch.ones_like(logits) * -1e10, logits)
def sample_sequence(model, length, start_token=None, batch_size=None, context=None, temperature=1, top_k=0, device='cuda', sample=True):
if start_token is None:
assert context is not None, 'Specify exactly one of start_token and context!'
context = torch.tensor(context, device=device, dtype=torch.long).unsqueeze(0).repeat(batch_size, 1)
else:
assert context is None, 'Specify exactly one of start_token and context!'
context = torch.full((batch_size, 1), start_token, device=device, dtype=torch.long)
prev = context
output = context
past = None
with torch.no_grad():
for i in trange(length):
logits, past = model(prev, past=past)
logits = logits[:, -1, :] / temperature
logits = top_k_logits(logits, k=top_k)
log_probs = F.softmax(logits, dim=-1)
if sample:
prev = torch.multinomial(log_probs, num_samples=1)
else:
_, prev = torch.topk(log_probs, k=1, dim=-1)
output = torch.cat((output, prev), dim=1)
return output
def run_model(input_text, length=-1, nsamples=1, batch_size=1, temperature=1.0, top_k=0, seed=0):
assert nsamples % batch_size == 0
np.random.seed(seed)
torch.random.manual_seed(seed)
torch.cuda.manual_seed(seed)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
enc = GPT2Tokenizer.from_pretrained('gpt2')
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.to(device)
model.eval()
if length == -1:
length = model.config.n_ctx // 2
elif length > model.config.n_ctx:
raise ValueError("Can't get samples longer than window size: %s" % model.config.n_ctx)
while True:
context_tokens = []
if input_text:
context_tokens = enc.encode(input_text)
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=context_tokens,
start_token=None,
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:, len(context_tokens):].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
else:
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=None,
start_token=enc.encoder['<|endoftext|>'],
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:,1:].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
run_model("It was nearly two weeks later when the cosmonaut was jolted out of sleep, jolted by")
| 0.871297 | 0.707859 |
```
from typing import Tuple, Dict, Callable, Iterator, Union, Optional, List
import os
import sys
import yaml
import numpy as np
import torch
from torch import Tensor
import gym
# To import module code.
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from src.environment_api import EnvironmentObjective, manipulate_reward
from src.policy_parameterizations import MLP, discretize
from src.evaluate import (
offline_reward_evaluation,
postprocessing_interpolate_x,
plot_rewards_over_calls,
)
import matplotlib.pyplot as plt
%config Completer.use_jedi = False
plt.style.use('seaborn-whitegrid')
tex_fonts = {
# Use LaTeX to write all text
"text.usetex": True,
"font.family": "serif",
# Use 10pt font in plots, to match 10pt font in document
"axes.labelsize": 9,
"font.size": 9,
# Make the legend/label fonts a little smaller
"legend.fontsize": 8,
"xtick.labelsize": 8,
"ytick.labelsize": 8
}
plt.rcParams.update(tex_fonts)
def plot_rewards_over_calls(
rewards_optimizer: List[torch.tensor],
names_optimizer: List[str],
title: str,
marker: List[str] = ["o", ">"],
steps: int = 100,
markevery: int = 5,
figsize: Tuple[float] = (2.8, 1.7),
path_savefig: Optional[str] = None,
):
"""Generate plot showing rewards over objective calls for multiple optimizer.
Args:
rewards_optimizer: List of torch tensors for every optimizer.
title: Plot title.
marker: Plot marker.
steps: Number which defines the x-th reward that should be plotted.
markevery: Number which defines the x-th reward which should be marked (after steps).
path_savefig: Path where to save the resulting figure.
"""
plt.figure(figsize=figsize)
for index_optimizer, rewards in enumerate(rewards_optimizer):
max_calls = rewards.shape[-1]
m = torch.mean(rewards, dim=0)[::steps]
std = torch.std(rewards, dim=0)[::steps]
plt.plot(
torch.linspace(0, max_calls, max_calls // steps),
m,
marker=marker[index_optimizer],
markevery=markevery,
markersize=3,
label=names_optimizer[index_optimizer],
)
plt.fill_between(
torch.linspace(0, max_calls, max_calls // steps),
m - std,
m + std,
alpha=0.2,
)
plt.xlabel("\# of evaluations")
plt.ylabel("Average Reward")
plt.legend(loc="lower right")
plt.title(title)
plt.xlim([0, max_calls])
if path_savefig:
plt.savefig(path_savefig, bbox_inches="tight")
def postprocess_data(configs: List[str], postprocess: bool = True):
method_to_name = {'gibo': 'GIBO', 'rs': 'ARS', 'vbo': 'Vanilla BO'}
list_interpolated_rewards = []
list_names_optimizer = []
for cfg_str in configs:
with open(cfg_str, 'r') as f:
cfg = yaml.load(f, Loader=yaml.Loader)
directory = '.' + cfg['out_dir']
if postprocess:
print('Postprocess tracked parameters over optimization procedure.')
# Usecase 1: optimizing policy for a reinforcement learning environment.
mlp = MLP(*cfg['mlp']['layers'], add_bias=cfg['mlp']['add_bias'])
len_params = mlp.len_params
# In evaluation mode manipulation of state and reward is always None.
objective_env = EnvironmentObjective(
env=gym.make(cfg['environment_name']),
policy=mlp,
manipulate_state=None,
manipulate_reward=None,
)
# Load data.
print(f'Load data from {directory}.')
parameters = np.load(
os.path.join(directory, 'parameters.npy'), allow_pickle=True
).item()
calls = np.load(
os.path.join(directory, 'calls.npy'), allow_pickle=True
).item()
# Postprocess data (offline evaluation and interpolation).
print('Postprocess data: offline evaluation and interpolation.')
offline_rewards = offline_reward_evaluation(parameters, objective_env)
interpolated_rewards = postprocessing_interpolate_x(
offline_rewards, calls, max_calls=cfg['max_objective_calls']
)
# Save postprocessed data.
print(f'Save postprocessed data in {directory}.')
torch.save(
interpolated_rewards, os.path.join(directory, 'interpolated_rewards.pt')
)
torch.save(offline_rewards, os.path.join(directory, 'offline_rewards.pt'))
else:
interpolated_rewards = torch.load(
os.path.join(directory, 'interpolated_rewards.pt')
)
list_names_optimizer.append(method_to_name[cfg['method']])
list_interpolated_rewards.append(interpolated_rewards)
return list_names_optimizer, list_interpolated_rewards
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/cartpole/rs_10runs.yaml',
'../configs/rl_experiment/cartpole/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Cartpole-v1',
marker=['o', '>'],
steps=10,
markevery=1,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/cartpole/cartpole_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/swimmer/rs_10runs.yaml',
'../configs/rl_experiment/swimmer/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Swimmer-v1',
marker=['o', '>'],
steps=50,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/swimmer/swimmer_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/hopper/rs_10runs.yaml',
'../configs/rl_experiment/hopper/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Hopper-v1',
marker=['o', '>'],
steps=200,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/hopper/hopper_v1_10runs.pdf',
)
```
|
github_jupyter
|
from typing import Tuple, Dict, Callable, Iterator, Union, Optional, List
import os
import sys
import yaml
import numpy as np
import torch
from torch import Tensor
import gym
# To import module code.
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from src.environment_api import EnvironmentObjective, manipulate_reward
from src.policy_parameterizations import MLP, discretize
from src.evaluate import (
offline_reward_evaluation,
postprocessing_interpolate_x,
plot_rewards_over_calls,
)
import matplotlib.pyplot as plt
%config Completer.use_jedi = False
plt.style.use('seaborn-whitegrid')
tex_fonts = {
# Use LaTeX to write all text
"text.usetex": True,
"font.family": "serif",
# Use 10pt font in plots, to match 10pt font in document
"axes.labelsize": 9,
"font.size": 9,
# Make the legend/label fonts a little smaller
"legend.fontsize": 8,
"xtick.labelsize": 8,
"ytick.labelsize": 8
}
plt.rcParams.update(tex_fonts)
def plot_rewards_over_calls(
rewards_optimizer: List[torch.tensor],
names_optimizer: List[str],
title: str,
marker: List[str] = ["o", ">"],
steps: int = 100,
markevery: int = 5,
figsize: Tuple[float] = (2.8, 1.7),
path_savefig: Optional[str] = None,
):
"""Generate plot showing rewards over objective calls for multiple optimizer.
Args:
rewards_optimizer: List of torch tensors for every optimizer.
title: Plot title.
marker: Plot marker.
steps: Number which defines the x-th reward that should be plotted.
markevery: Number which defines the x-th reward which should be marked (after steps).
path_savefig: Path where to save the resulting figure.
"""
plt.figure(figsize=figsize)
for index_optimizer, rewards in enumerate(rewards_optimizer):
max_calls = rewards.shape[-1]
m = torch.mean(rewards, dim=0)[::steps]
std = torch.std(rewards, dim=0)[::steps]
plt.plot(
torch.linspace(0, max_calls, max_calls // steps),
m,
marker=marker[index_optimizer],
markevery=markevery,
markersize=3,
label=names_optimizer[index_optimizer],
)
plt.fill_between(
torch.linspace(0, max_calls, max_calls // steps),
m - std,
m + std,
alpha=0.2,
)
plt.xlabel("\# of evaluations")
plt.ylabel("Average Reward")
plt.legend(loc="lower right")
plt.title(title)
plt.xlim([0, max_calls])
if path_savefig:
plt.savefig(path_savefig, bbox_inches="tight")
def postprocess_data(configs: List[str], postprocess: bool = True):
method_to_name = {'gibo': 'GIBO', 'rs': 'ARS', 'vbo': 'Vanilla BO'}
list_interpolated_rewards = []
list_names_optimizer = []
for cfg_str in configs:
with open(cfg_str, 'r') as f:
cfg = yaml.load(f, Loader=yaml.Loader)
directory = '.' + cfg['out_dir']
if postprocess:
print('Postprocess tracked parameters over optimization procedure.')
# Usecase 1: optimizing policy for a reinforcement learning environment.
mlp = MLP(*cfg['mlp']['layers'], add_bias=cfg['mlp']['add_bias'])
len_params = mlp.len_params
# In evaluation mode manipulation of state and reward is always None.
objective_env = EnvironmentObjective(
env=gym.make(cfg['environment_name']),
policy=mlp,
manipulate_state=None,
manipulate_reward=None,
)
# Load data.
print(f'Load data from {directory}.')
parameters = np.load(
os.path.join(directory, 'parameters.npy'), allow_pickle=True
).item()
calls = np.load(
os.path.join(directory, 'calls.npy'), allow_pickle=True
).item()
# Postprocess data (offline evaluation and interpolation).
print('Postprocess data: offline evaluation and interpolation.')
offline_rewards = offline_reward_evaluation(parameters, objective_env)
interpolated_rewards = postprocessing_interpolate_x(
offline_rewards, calls, max_calls=cfg['max_objective_calls']
)
# Save postprocessed data.
print(f'Save postprocessed data in {directory}.')
torch.save(
interpolated_rewards, os.path.join(directory, 'interpolated_rewards.pt')
)
torch.save(offline_rewards, os.path.join(directory, 'offline_rewards.pt'))
else:
interpolated_rewards = torch.load(
os.path.join(directory, 'interpolated_rewards.pt')
)
list_names_optimizer.append(method_to_name[cfg['method']])
list_interpolated_rewards.append(interpolated_rewards)
return list_names_optimizer, list_interpolated_rewards
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/cartpole/rs_10runs.yaml',
'../configs/rl_experiment/cartpole/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Cartpole-v1',
marker=['o', '>'],
steps=10,
markevery=1,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/cartpole/cartpole_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/swimmer/rs_10runs.yaml',
'../configs/rl_experiment/swimmer/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Swimmer-v1',
marker=['o', '>'],
steps=50,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/swimmer/swimmer_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/hopper/rs_10runs.yaml',
'../configs/rl_experiment/hopper/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Hopper-v1',
marker=['o', '>'],
steps=200,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/hopper/hopper_v1_10runs.pdf',
)
| 0.727782 | 0.433382 |
Universidade Federal do Rio Grande do Sul (UFRGS)
Programa de Pós-Graduação em Engenharia Civil (PPGEC)
# Project PETROBRAS (2018/00147-5):
## Attenuation of dynamic loading along mooring lines embedded in clay
---
_Prof. Marcelo M. Rocha, Dr.techn._ [(ORCID)](https://orcid.org/0000-0001-5640-1020)
Porto Alegre, RS, Brazil
___
[1. Introduction](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/01_Introduction.ipynb?flush_cache=true)
[2. Reduced model scaling](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/02_Reduced_model.ipynb?flush_cache=true)
[3. Typical soil](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/03_Typical_soil.ipynb?flush_cache=true)
[4. The R4 studless 120mm chain](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/04_R4_studless_chain.ipynb?flush_cache=true)
[5. Dynamic load definition](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/05_Dynamic_load.ipynb?flush_cache=true)
[6. Design of chain anchoring system](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/06_Chain_anchor.ipynb?flush_cache=true)
[7. Design of uniaxial load cell with inclinometer](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/07_Load_cell.ipynb?flush_cache=true)
[8. Location of experimental sites](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/08_Experimental_sites.ipynb?flush_cache=true)
```
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Importing "pandas dataframe" with dimension exponents for scales calculation
DimData = pd.read_excel('resources/DimData.xlsx', sheet_name='DimData', index_col=0)
print(DimData)
```
## 2. Reduced model scaling
[(Link for PEC00144 class on Dimensional Analysis)](https://nbviewer.jupyter.org/github/mmaiarocha/PEC00144/blob/master/2_Dimensional_analysis.ipynb)
Experiments must be designed with a reduced length scale specified as $\lambda_L = 1:10$.
By considering that the soil in the experimental field satisfactorily resembles the
specified _typical soil_ (see [section 3](https://nbviewer.jupyter.org/urls/dl.dropbox.com/s/z35uz1iz5be4mq2/03_Typical_soil.ipynb?flush_cache=true)), the further scale-restricted
quantities are the soil density, $\rho_{\rm soil} = 1600{\rm kg/m^3}$ with scale $\lambda_\rho = 1:1$,
and the gravity acceleration, $g = 9.81{\rm m/s^2}$ also with scale $\lambda_g = 1:1$.
All other quantities have derived scales that must be calculated and used for the
interpretation of experimental results.
The choice of these three control quantities, $L$, $\rho$, and $g$, is based on the very
basic assumption that _the most important parameter governing the soil reaction for large
displacements is the undrained shear resistance_, $s_{\rm u}$. This parameter is assumed
to have the general form:
$$ s_{\rm u} = k\rho_{\rm soil} g z $$
where $k$ is a non-dimensional factor and $z$ the depth measured from soil surface.
Under this assumption, the scale of $s_{\rm u}$ will be correct at any depth $z$.
The three control quantities allow the definition of an new dimensional base to be used
for calculating the derived scales of further relevant quantities.
Dimension exponents are read from ``pandas`` dataframe ``DimData``:
```
ABC = ['L', 'ρ', 'a'] # control quantities are length, density and acceleration
LMT = ['L', 'M', 'T'] # dimension exponents (last three columns of DimData dataframe)
base = DimData.loc[ABC, LMT]
print(base)
```
Scales calculation requires the inversion of this new base, what is carried out with
``numpy`` method ``linalg.inv``:
```
i_base = np.linalg.inv(base)
print(i_base)
```
Now we specify a list of all quantities for which derived scales are to be calculated.
We choose, for instance:
* Force, $F$, (for chain tension),
* Frequency, $f$, (for dynamic loading spectral density),
* Mass per unit length, $\mu_L$, (for specifying the grade of model chain),
* Stress, $\sigma$, (for soil resistance)
A list with the identifiers of these quantities is used to read their dimension
exponents from ``DimData`` dataframe, given the problem dimension matrix also as
a dataframe:
```
param = ['F', 'f', 'μL', 'σ'] # parameters which scales must be calculated
npar = len(param) # number of parameters in the previous list
DimMat = DimData.loc[param, LMT]
print(DimMat)
```
The code snipet below calculates a new dimension matrix with the dimension exponents
corresponding to the new base. This new matrix is directly formatted as a ``pandas`` dataframe:
```
NewMat = pd.DataFrame(data = np.dot(DimMat,i_base),
index = DimMat.index,
columns = ABC)
print(NewMat)
```
To check the results above, let us take a look in the force dimensions:
\begin{align*}
[F] &= [L]^3 \, [\rho]^1 \, [a]^1 \\
&= {\rm (m)^3 \, (kg/m^3)^1 \, (m/s^2)^1} \\
&= {\rm kg \, m \, / \, s^2} \\
&= {\rm N}
\end{align*}
where $[\cdot]$ means ''unit of''. One may conclude that the computational procedure is _ok_,
despite its conciseness.
The next step is the especification of experimental scales for the control quantities, as
previously discussed:
```
λ_L = 1/10 # length scale for the reduced model
λ_ρ = 1/1 # same soil, with same density
λ_a = 1/1 # gravity will not be changed!
scales = np.tile([λ_L, λ_ρ, λ_a],(npar,1))
```
A last code line calculates the derived scales and includes them as an additional column in
dataframe ``NewMat``:
```
NewMat['scale'] = np.prod(scales**NewMat[ABC], axis=1)
print(NewMat)
```
where it can be seen, for instance, that the forces in the reduced model will be
one thousandth of the real scale forces. On the other hand, model time passes $\approx$3.16 times
faster, what makes frequencies the same amount higher.
The stress scale calculated above applies to the undrained soil shear resistance, $s_{\rm u}$,
for this resistance depends on the product of the base quantities. However, elastic stresses
and stiffness properties (Young's and shear modulae) _are not expected to follow this
scale_. It is important to keep in mind that these quantities are not likely to be relevant
for the experimental results, for large plastic displacements are to dominate the process.
These scales will be used in the following sections to design all experimental features.
|
github_jupyter
|
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Importing "pandas dataframe" with dimension exponents for scales calculation
DimData = pd.read_excel('resources/DimData.xlsx', sheet_name='DimData', index_col=0)
print(DimData)
ABC = ['L', 'ρ', 'a'] # control quantities are length, density and acceleration
LMT = ['L', 'M', 'T'] # dimension exponents (last three columns of DimData dataframe)
base = DimData.loc[ABC, LMT]
print(base)
i_base = np.linalg.inv(base)
print(i_base)
param = ['F', 'f', 'μL', 'σ'] # parameters which scales must be calculated
npar = len(param) # number of parameters in the previous list
DimMat = DimData.loc[param, LMT]
print(DimMat)
NewMat = pd.DataFrame(data = np.dot(DimMat,i_base),
index = DimMat.index,
columns = ABC)
print(NewMat)
λ_L = 1/10 # length scale for the reduced model
λ_ρ = 1/1 # same soil, with same density
λ_a = 1/1 # gravity will not be changed!
scales = np.tile([λ_L, λ_ρ, λ_a],(npar,1))
NewMat['scale'] = np.prod(scales**NewMat[ABC], axis=1)
print(NewMat)
| 0.626238 | 0.941007 |
<center>
<img src="https://raw.githubusercontent.com/Yorko/mlcourse.ai/master/img/ods_stickers.jpg" />
## [mlcourse.ai](https://mlcourse.ai) - Open Machine Learning Course
<center>
Auteur: [Yury Kashnitskiy](https://yorko.github.io). Traduit par Anna Larionova et [Ousmane Cissé](https://fr.linkedin.com/in/ousmane-cisse).
Ce matériel est soumis aux termes et conditions de la licence [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/).
L'utilisation gratuite est autorisée à des fins non commerciales.
# <center> Sujet 6. Régression</center>
## <center>Lasso et Regression Ridge</center>
*Le programme du cours diffère cette semaine du plan de l'article, car le sujet 4 (modèles linéaires) est trop vaste et important, nous couvrons donc la régression cette semaine.*
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set() # just to use the seaborn theme
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso, LassoCV, Ridge, RidgeCV
from sklearn.model_selection import KFold, cross_val_score
```
**Nous travaillerons avec les données sur les prix des logements à Boston (référentiel UCI).**
**Téléchargez les données.**
```
boston = load_boston()
X, y = boston["data"], boston["target"]
```
**Description des données:**
```
print(boston.DESCR)
boston.feature_names
```
**Regardons les deux premiers enregistrements.**
```
X[:2]
```
## Régression Lasso
La régression Lasso minimise l'erreur quadratique moyenne avec la régularisation L1:
$$\Large error(X, y, w) = \frac{1}{2} \sum_{i=1}^\ell {(y_i - w^Tx_i)}^2 + \alpha \sum_{i=1}^d |w_i|$$
où l'équation d'hyperplan $y = w^Tx$ en fonction des paramètres du modèle $w$, $\ell$ est le nombre d'observations dans les données $X$, $d$ est le nombre d'entités, valeurs cibles $y$, coefficient de régularisation $\alpha$.
**Ajustons la régression Lasso avec le petit coefficient $\alpha$ (régularisation faible). Le coefficient lié à la caractéristique NOX (concentration en oxydes nitriques) sera nul. Cela signifie que cette caractéristique est la moins importante pour la prévision des prix médians des logements dans cette région.**
```
lasso = Lasso(alpha=0.1)
lasso.fit(X, y)
lasso.coef_
```
**Entraînons la régression Lasso avec $\alpha=10$. Tous les coefficients sont égaux à zéro, à l'exception des caractéristiques ZN (proportion de terrains résidentiels zonés pour des lots de plus de 25 000 pieds carrés), TAXE (taux de taxe foncière de pleine valeur), B (proportion de Noirs par ville) et LSTAT (% de statut inférieur de la population).**
```
lasso = Lasso(alpha=10)
lasso.fit(X, y)
lasso.coef_
```
**Cela signifie que la régression Lasso peut servir de méthode de sélection des caractéristiques.**
```
n_alphas = 200
alphas = np.linspace(0.1, 10, n_alphas)
model = Lasso()
coefs = []
for a in alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
plt.rcParams["figure.figsize"] = (12, 8)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Lasso coefficients as a function of the regularization")
plt.axis("tight")
plt.show();
```
**Maintenant, trouvons la meilleure valeur de $\alpha$ lors de la validation croisée.**
```
lasso_cv = LassoCV(alphas=alphas, cv=3, random_state=17)
lasso_cv.fit(X, y)
lasso_cv.coef_
lasso_cv.alpha_
```
**Dans Scikit-learn, les métriques sont généralement * maximisées *, donc pour MSE il y a une solution: `neg_mean_squared_error` est plutôt minimisé. Pas vraiment pratique.**
```
cross_val_score(Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error")
abs(
cross_val_score(
Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error"
).mean()
)
abs(np.mean(cross_val_score(Lasso(9.95), X, y, cv=3, scoring="neg_mean_squared_error")))
```
**Encore un point ambigu: LassoCV trie les valeurs des paramètres par ordre décroissant pour faciliter l'optimisation. Il peut sembler que l’optimisation $\alpha$ ne fonctionne pas correctement.**
```
lasso_cv.alphas[:10]
lasso_cv.alphas_[:10]
plt.plot(lasso_cv.alphas, lasso_cv.mse_path_.mean(1)) # incorrect
plt.axvline(lasso_cv.alpha_, c="g");
plt.plot(lasso_cv.alphas_, lasso_cv.mse_path_.mean(1)) # correct
plt.axvline(lasso_cv.alpha_, c="g");
```
## Régression Ridge
La régression Ridge minimise l'erreur quadratique moyenne avec la régularisation L2:
$$\Large error(X, y, w) = \frac{1}{2} \sum_{i=1}^\ell {(y_i - w^Tx_i)}^2 + \alpha \sum_{i=1}^d w_i^2$$
où l'équation d'hyperplan $y = w^Tx$ en fonction des paramètres du modèle $w$, $\ell$ est le nombre d'observations dans les données $X$, $d$ est le nombre d'entités, valeurs cibles $y$, coefficient de régularisation $\alpha$.
Il existe une classe spéciale [RidgeCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear _model.RidgeCV.html # sklearn.linear_ model.RidgeCV) pour la régression Ridge validation croisée.
```
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
ridge_cv = RidgeCV(alphas=ridge_alphas, scoring="neg_mean_squared_error", cv=3)
ridge_cv.fit(X, y)
ridge_cv.alpha_
```
**En cas de régression Ridge, aucun des paramètres ne se réduit à zéro. La valeur peut être petite mais non nulle.**
```
ridge_cv.coef_
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
model = Ridge()
coefs = []
for a in ridge_alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(ridge_alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge coefficients as a function of the regularization")
plt.axis("tight")
plt.show()
```
## Références
- [Generalized linear models](http://scikit-learn.org/stable/modules/linear_model.html) (Generalized Linear Models, GLM) in Scikit-learn
- [LinearRegression](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression), [Lasso](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html#sklearn.linear_model.Lasso), [LassoCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LassoCV.html#sklearn.linear_model.LassoCV), [Ridge](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html) and [RidgeCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html#sklearn.linear_model.RidgeCV) in Scikit-learn
|
github_jupyter
|
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set() # just to use the seaborn theme
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso, LassoCV, Ridge, RidgeCV
from sklearn.model_selection import KFold, cross_val_score
boston = load_boston()
X, y = boston["data"], boston["target"]
print(boston.DESCR)
boston.feature_names
X[:2]
lasso = Lasso(alpha=0.1)
lasso.fit(X, y)
lasso.coef_
lasso = Lasso(alpha=10)
lasso.fit(X, y)
lasso.coef_
n_alphas = 200
alphas = np.linspace(0.1, 10, n_alphas)
model = Lasso()
coefs = []
for a in alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
plt.rcParams["figure.figsize"] = (12, 8)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Lasso coefficients as a function of the regularization")
plt.axis("tight")
plt.show();
lasso_cv = LassoCV(alphas=alphas, cv=3, random_state=17)
lasso_cv.fit(X, y)
lasso_cv.coef_
lasso_cv.alpha_
cross_val_score(Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error")
abs(
cross_val_score(
Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error"
).mean()
)
abs(np.mean(cross_val_score(Lasso(9.95), X, y, cv=3, scoring="neg_mean_squared_error")))
lasso_cv.alphas[:10]
lasso_cv.alphas_[:10]
plt.plot(lasso_cv.alphas, lasso_cv.mse_path_.mean(1)) # incorrect
plt.axvline(lasso_cv.alpha_, c="g");
plt.plot(lasso_cv.alphas_, lasso_cv.mse_path_.mean(1)) # correct
plt.axvline(lasso_cv.alpha_, c="g");
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
ridge_cv = RidgeCV(alphas=ridge_alphas, scoring="neg_mean_squared_error", cv=3)
ridge_cv.fit(X, y)
ridge_cv.alpha_
ridge_cv.coef_
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
model = Ridge()
coefs = []
for a in ridge_alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(ridge_alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge coefficients as a function of the regularization")
plt.axis("tight")
plt.show()
| 0.764716 | 0.984094 |
```
!pip install gluoncv # -i https://opentuna.cn/pypi/web/simple
%matplotlib inline
```
4. Transfer Learning with Your Own Image Dataset
=======================================================
Dataset size is a big factor in the performance of deep learning models.
``ImageNet`` has over one million labeled images, but
we often don't have so much labeled data in other domains.
Training a deep learning models on small datasets may lead to severe overfitting.
Transfer learning is a technique that addresses this problem.
The idea is simple: we can start training with a pre-trained model,
instead of starting from scratch.
As Isaac Newton said, "If I have seen further it is by standing on the
shoulders of Giants".
In this tutorial, we will explain the basics of transfer
learning, and apply it to the ``MINC-2500`` dataset.
Data Preparation
----------------
`MINC <http://opensurfaces.cs.cornell.edu/publications/minc/>`__ is
short for Materials in Context Database, provided by Cornell.
``MINC-2500`` is a resized subset of ``MINC`` with 23 classes, and 2500
images in each class. It is well labeled and has a moderate size thus is
perfect to be our example.
|image-minc|
To start, we first download ``MINC-2500`` from
`here <http://opensurfaces.cs.cornell.edu/publications/minc/>`__.
Suppose we have the data downloaded to ``~/data/`` and
extracted to ``~/data/minc-2500``.
After extraction, it occupies around 2.6GB disk space with the following
structure:
::
minc-2500
├── README.txt
├── categories.txt
├── images
└── labels
The ``images`` folder has 23 sub-folders for 23 classes, and ``labels``
folder contains five different splits for training, validation, and test.
We have written a script to prepare the data for you:
:download:`Download prepare_minc.py<../../../scripts/classification/finetune/prepare_minc.py>`
Run it with
::
python prepare_minc.py --data ~/data/minc-2500 --split 1
Now we have the following structure:
::
minc-2500
├── categories.txt
├── images
├── labels
├── README.txt
├── test
├── train
└── val
In order to go through this tutorial within a reasonable amount of time,
we have prepared a small subset of the ``MINC-2500`` dataset,
but you should substitute it with the original dataset for your experiments.
We can download and extract it with:
Hyperparameters
----------
First, let's import all other necessary libraries.
```
import mxnet as mx
import numpy as np
import os, time, shutil
from mxnet import gluon, image, init, nd
from mxnet import autograd as ag
from mxnet.gluon import nn
from mxnet.gluon.data.vision import transforms
from gluoncv.utils import makedirs
from gluoncv.model_zoo import get_model
```
We set the hyperparameters as following:
```
classes = 5
epochs = 100
lr = 0.001
per_device_batch_size = 32
momentum = 0.9
wd = 0.0001
lr_factor = 0.75
lr_steps = [10, 20, 30, np.inf]
num_gpus = 1
num_workers = 8
ctx = [mx.gpu(i) for i in range(num_gpus)] if num_gpus > 0 else [mx.cpu()]
batch_size = per_device_batch_size * max(num_gpus, 1)
```
Things to keep in mind:
1. ``epochs = 5`` is just for this tutorial with the tiny dataset. please change it to a larger number in your experiments, for instance 40.
2. ``per_device_batch_size`` is also set to a small number. In your experiments you can try larger number like 64.
3. remember to tune ``num_gpus`` and ``num_workers`` according to your machine.
4. A pre-trained model is already in a pretty good status. So we can start with a small ``lr``.
Data Augmentation
-----------------
In transfer learning, data augmentation can also help.
We use the following augmentation in training:
2. Randomly crop the image and resize it to 224x224
3. Randomly flip the image horizontally
4. Randomly jitter color and add noise
5. Transpose the data from height*width*num_channels to num_channels*height*width, and map values from [0, 255] to [0, 1]
6. Normalize with the mean and standard deviation from the ImageNet dataset.
```
jitter_param = 0.4
lighting_param = 0.1
transform_train = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomFlipLeftRight(),
transforms.RandomColorJitter(brightness=jitter_param, contrast=jitter_param,
saturation=jitter_param),
transforms.RandomLighting(lighting_param),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
transform_test = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
```
With the data augmentation functions, we can define our data loaders:
```
!wget -O image_classification.zip "https://datalab.s3.amazonaws.com/data/image_classification.zip?AWSAccessKeyId=AKIAYNUCDPLSDWHHQJ7Y&Signature=LV6WeQbTIHylCBov79KW8iRigPg%3D&Expires=1637340066"
!unzip -q image_classification.zip
!mkdir -p data/train
!mkdir -p data/test
import os
base_dir = 'image_classification'
filenames = os.listdir(base_dir)
class_names = []
for filename in filenames:
if os.path.isdir(os.path.join(base_dir, filename)) and not filename.startswith('.'):
class_names.append(filename)
if not os.path.exists(os.path.join('data/train/', filename)):
os.mkdir(os.path.join('data/train/', filename))
os.mkdir(os.path.join('data/test/', filename))
from sklearn.model_selection import train_test_split
for name in class_names:
filenames = os.listdir(os.path.join(base_dir, name))
print(name, len(filenames))
train_filenames, test_filenames = train_test_split(filenames, test_size=0.3)
for filename in train_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/train/', name, filename))
for filename in test_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/test/', name, filename))
path = './data'
train_path = os.path.join(path, 'train')
val_path = os.path.join(path, 'test')
test_path = os.path.join(path, 'test')
train_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(train_path).transform_first(transform_train),
batch_size=batch_size, shuffle=True, num_workers=num_workers)
val_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(val_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
test_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(test_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
print(gluon.data.vision.ImageFolderDataset(train_path).synsets)
print(gluon.data.vision.ImageFolderDataset(val_path).synsets)
print(gluon.data.vision.ImageFolderDataset(test_path).synsets)
```
Note that only ``train_data`` uses ``transform_train``, while
``val_data`` and ``test_data`` use ``transform_test`` to produce deterministic
results for evaluation.
Model and Trainer
-----------------
We use a pre-trained ``ResNet50_v2`` model, which has balanced accuracy and
computation cost.
```
model_name = 'ResNet50_v2'
# model_name = 'ResNet152_v1d'
finetune_net = get_model(model_name, pretrained=True)
with finetune_net.name_scope():
finetune_net.output = nn.Dense(classes)
finetune_net.output.initialize(init.Xavier(), ctx = ctx)
finetune_net.collect_params().reset_ctx(ctx)
finetune_net.hybridize()
trainer = gluon.Trainer(finetune_net.collect_params(), 'sgd', {
'learning_rate': lr, 'momentum': momentum, 'wd': wd})
metric = mx.metric.Accuracy()
L = gluon.loss.SoftmaxCrossEntropyLoss()
```
Here's an illustration of the pre-trained model
and our newly defined model:
|image-model|
Specifically, we define the new model by::
1. load the pre-trained model
2. re-define the output layer for the new task
3. train the network
This is called "fine-tuning", i.e. we have a model trained on another task,
and we would like to tune it for the dataset we have in hand.
We define a evaluation function for validation and testing.
```
def test(net, val_data, ctx):
metric = mx.metric.Accuracy()
for i, batch in enumerate(val_data):
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
outputs = [net(X) for X in data]
metric.update(label, outputs)
# print(label, outputs)
return metric.get()
```
Training Loop
-------------
Following is the main training loop. It is the same as the loop in
`CIFAR10 <dive_deep_cifar10.html>`__
and ImageNet.
<div class="alert alert-info"><h4>Note</h4><p>Once again, in order to go through the tutorial faster, we are training on a small
subset of the original ``MINC-2500`` dataset, and for only 5 epochs. By training on the
full dataset with 40 epochs, it is expected to get accuracy around 80% on test data.</p></div>
```
lr_counter = 0
num_batch = len(train_data)
for epoch in range(epochs):
if epoch == lr_steps[lr_counter]:
trainer.set_learning_rate(trainer.learning_rate*lr_factor)
lr_counter += 1
tic = time.time()
train_loss = 0
metric.reset()
for i, batch in enumerate(train_data):
# print(i)
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
# print(label)
with ag.record():
outputs = [finetune_net(X) for X in data]
loss = [L(yhat, y) for yhat, y in zip(outputs, label)]
for l in loss:
l.backward()
trainer.step(batch_size)
train_loss += sum([l.mean().asscalar() for l in loss]) / len(loss)
metric.update(label, outputs)
_, train_acc = metric.get()
train_loss /= num_batch
_, val_acc = test(finetune_net, val_data, ctx)
print('[Epoch %d] Train-acc: %.3f, loss: %.3f | Val-acc: %.3f | time: %.1f' %
(epoch, train_acc, train_loss, val_acc, time.time() - tic))
_, test_acc = test(finetune_net, test_data, ctx)
print('[Finished] Test-acc: %.3f' % (test_acc))
print('[Finished] Test-acc: %.3f' % (test_acc))
!mkdir endpoint/model
finetune_net.save_parameters('endpoint/model/model-0000.params')
```
Next
----
Now that you have learned to muster the power of transfer
learning, to learn more about training a model on
ImageNet, please read `this tutorial <dive_deep_imagenet.html>`__.
The idea of transfer learning is the basis of
`object detection <../examples_detection/index.html>`_ and
`semantic segmentation <../examples_segmentation/index.html>`_,
the next two chapters of our tutorial.
.. |image-minc| image:: https://raw.githubusercontent.com/dmlc/web-data/master/gluoncv/datasets/MINC-2500.png
.. |image-model| image:: https://zh.gluon.ai/_images/fine-tuning.svg
|
github_jupyter
|
!pip install gluoncv # -i https://opentuna.cn/pypi/web/simple
%matplotlib inline
import mxnet as mx
import numpy as np
import os, time, shutil
from mxnet import gluon, image, init, nd
from mxnet import autograd as ag
from mxnet.gluon import nn
from mxnet.gluon.data.vision import transforms
from gluoncv.utils import makedirs
from gluoncv.model_zoo import get_model
classes = 5
epochs = 100
lr = 0.001
per_device_batch_size = 32
momentum = 0.9
wd = 0.0001
lr_factor = 0.75
lr_steps = [10, 20, 30, np.inf]
num_gpus = 1
num_workers = 8
ctx = [mx.gpu(i) for i in range(num_gpus)] if num_gpus > 0 else [mx.cpu()]
batch_size = per_device_batch_size * max(num_gpus, 1)
jitter_param = 0.4
lighting_param = 0.1
transform_train = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomFlipLeftRight(),
transforms.RandomColorJitter(brightness=jitter_param, contrast=jitter_param,
saturation=jitter_param),
transforms.RandomLighting(lighting_param),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
transform_test = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
!wget -O image_classification.zip "https://datalab.s3.amazonaws.com/data/image_classification.zip?AWSAccessKeyId=AKIAYNUCDPLSDWHHQJ7Y&Signature=LV6WeQbTIHylCBov79KW8iRigPg%3D&Expires=1637340066"
!unzip -q image_classification.zip
!mkdir -p data/train
!mkdir -p data/test
import os
base_dir = 'image_classification'
filenames = os.listdir(base_dir)
class_names = []
for filename in filenames:
if os.path.isdir(os.path.join(base_dir, filename)) and not filename.startswith('.'):
class_names.append(filename)
if not os.path.exists(os.path.join('data/train/', filename)):
os.mkdir(os.path.join('data/train/', filename))
os.mkdir(os.path.join('data/test/', filename))
from sklearn.model_selection import train_test_split
for name in class_names:
filenames = os.listdir(os.path.join(base_dir, name))
print(name, len(filenames))
train_filenames, test_filenames = train_test_split(filenames, test_size=0.3)
for filename in train_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/train/', name, filename))
for filename in test_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/test/', name, filename))
path = './data'
train_path = os.path.join(path, 'train')
val_path = os.path.join(path, 'test')
test_path = os.path.join(path, 'test')
train_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(train_path).transform_first(transform_train),
batch_size=batch_size, shuffle=True, num_workers=num_workers)
val_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(val_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
test_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(test_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
print(gluon.data.vision.ImageFolderDataset(train_path).synsets)
print(gluon.data.vision.ImageFolderDataset(val_path).synsets)
print(gluon.data.vision.ImageFolderDataset(test_path).synsets)
model_name = 'ResNet50_v2'
# model_name = 'ResNet152_v1d'
finetune_net = get_model(model_name, pretrained=True)
with finetune_net.name_scope():
finetune_net.output = nn.Dense(classes)
finetune_net.output.initialize(init.Xavier(), ctx = ctx)
finetune_net.collect_params().reset_ctx(ctx)
finetune_net.hybridize()
trainer = gluon.Trainer(finetune_net.collect_params(), 'sgd', {
'learning_rate': lr, 'momentum': momentum, 'wd': wd})
metric = mx.metric.Accuracy()
L = gluon.loss.SoftmaxCrossEntropyLoss()
def test(net, val_data, ctx):
metric = mx.metric.Accuracy()
for i, batch in enumerate(val_data):
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
outputs = [net(X) for X in data]
metric.update(label, outputs)
# print(label, outputs)
return metric.get()
lr_counter = 0
num_batch = len(train_data)
for epoch in range(epochs):
if epoch == lr_steps[lr_counter]:
trainer.set_learning_rate(trainer.learning_rate*lr_factor)
lr_counter += 1
tic = time.time()
train_loss = 0
metric.reset()
for i, batch in enumerate(train_data):
# print(i)
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
# print(label)
with ag.record():
outputs = [finetune_net(X) for X in data]
loss = [L(yhat, y) for yhat, y in zip(outputs, label)]
for l in loss:
l.backward()
trainer.step(batch_size)
train_loss += sum([l.mean().asscalar() for l in loss]) / len(loss)
metric.update(label, outputs)
_, train_acc = metric.get()
train_loss /= num_batch
_, val_acc = test(finetune_net, val_data, ctx)
print('[Epoch %d] Train-acc: %.3f, loss: %.3f | Val-acc: %.3f | time: %.1f' %
(epoch, train_acc, train_loss, val_acc, time.time() - tic))
_, test_acc = test(finetune_net, test_data, ctx)
print('[Finished] Test-acc: %.3f' % (test_acc))
print('[Finished] Test-acc: %.3f' % (test_acc))
!mkdir endpoint/model
finetune_net.save_parameters('endpoint/model/model-0000.params')
| 0.679179 | 0.925769 |
## Diffusion Tensor Imaging (DTI)
Diffusion tensor imaging or "DTI" refers to images describing diffusion with a tensor model. DTI is derived from preprocessed diffusion weighted imaging (DWI) data. First proposed by Basser and colleagues ([Basser, 1994](https://www.ncbi.nlm.nih.gov/pubmed/8130344)), the diffusion tensor model describes diffusion characteristics within an imaging voxel. This model has been very influential in demonstrating the utility of the diffusion MRI in characterizing the microstructure of white matter and the biophysical properties (inferred from local diffusion properties). The DTI model is still a commonly used model to investigate white matter.
The tensor models the diffusion signal mathematically as:

Where  is a unit vector in 3D space indicating the direction of measurement and b are the parameters of the measurement, such as the strength and duration of diffusion-weighting gradient.  is the diffusion-weighted signal measured and  is the signal conducted in a measurement with no diffusion weighting.  is a positive-definite quadratic form, which contains six free parameters to be fit. These six parameters are:

The diffusion matrix is a variance-covariance matrix of the diffusivity along the three spatial dimensions. Note that we can assume that the diffusivity has antipodal symmetry, so elements across the diagonal of the matrix are equal. For example: . This is why there are only 6 free parameters to estimate here.
Tensors are represented by ellipsoids characterized by calculated eigenvalues () and eigenvectors () from the previously described matrix. The computed eigenvalues and eigenvectors are normally sorted in descending magnitude (i.e. ). Eigenvalues are always strictly positive in the context of dMRI and are measured in mm^2/s. In the DTI model, the largest eigenvalue gives the principal direction of the diffusion tensor, and the other two eigenvectors span the orthogonal plane to the former direction.

_Adapted from Jelison et al., 2004_
In the following example, we will walk through how to model a diffusion dataset. While there are a number of diffusion models, many of which are implemented in `DIPY`. However, for the purposes of this lesson, we will focus on the tensor model described above.
### Reconstruction with the `dipy.reconst` module
The `reconst` module contains implementations of the following models:
* Tensor (Basser et al., 1994)
* Constrained Spherical Deconvolution (Tournier et al. 2007)
* Diffusion Kurtosis (Jensen et al. 2005)
* DSI (Wedeen et al. 2008)
* DSI with deconvolution (Canales-Rodriguez et al. 2010)
* Generalized Q Imaging (Yeh et al. 2010)
* MAPMRI (Özarslan et al. 2013)
* SHORE (Özarslan et al. 2008)
* CSA (Aganj et al. 2009)
* Q ball (Descoteaux et al. 2007)
* OPDT (Tristan-Vega et al. 2010)
* Sparse Fascicle Model (Rokem et al. 2015)
The different algorithms implemented in the module all share a similar conceptual structure:
* `ReconstModel` objects (e.g. `TensorModel`) carry the parameters that are required in order to fit a model. For example, the directions and magnitudes of the gradients that were applied in the experiment. `TensorModel` objects have a `fit` method, which takes in data, and returns a `ReconstFit` object. This is where a lot of the heavy lifting of the processing will take place.
* `ReconstFit` objects carry the model that was used to generate the object. They also include the parameters that were estimated during fitting of the data. They have methods to calculate derived statistics, which can differ from model to model. All objects also have an orientation distribution function (`odf`), and most (but not all) contain a `predict` method, which enables the prediction of another dataset based on the current gradient table.
### Reconstruction with the DTI model
Let's get started! First, we will need to grab **preprocessed** DWI files and load them! We will also load in the anatomical image to use as a reference later on!
```
import bids
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
from nilearn import image as img
import nibabel as nib
bids.config.set_option('extension_initial_dot', True)
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
# Grab the transformed t1 file for reference
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
# Recall the preprocessed data is no longer in BIDS - we will directly grab these files
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
```
Next, we need to create the tensor model using our gradient table and then fit the model using our data! We will start by creating a mask from our data and apply it to avoid calculating tensors on the background! This can be done using `DIPY`'s mask module. Then, we will our data!
```
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
dwi_data = dwi_data.get_fdata() # We re-use the variable for memory purposes
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1) # Specify the volume index to the b0 volumes
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
```
The fit method creates a <code>TensorFit</code> object which contains the fitting parameters and other attributes of the model. A number of quantitative scalar metrics can be derived from the eigenvalues! In this tutorial, we will cover fractional anisotropy, mean diffusivity, axial diffusivity, and radial diffusivity. Each of these scalar, rotationally invariant metrics were calculated in the previous fitting step!
### Fractional anisotropy (FA)
Fractional anisotropy (FA) characterizes the degree to which the distribution of diffusion in an imaging voxel is directional. That is, whether there is relatively unrestricted diffusion in a particular direction.
Mathematically, FA is defined as the normalized variance of the eigenvalues of the tensor:

Values of FA vary between 0 and 1 (unitless). In the cases of perfect, isotropic diffusion, , the diffusion tensor is a sphere and FA = 0. If the first two eigenvalues are equal the tensor will be oblate or planar, whereas if the first eigenvalue is larger than the other two, it will have the mentioned ellipsoid shape: as diffusion progressively becomes more anisotropic, eigenvalues become more unequal, causing the tensor to be elongated, with FA approaching 1. Note that FA should be interpreted carefully. It may be an indication of the density of packing fibers in a voxel and the amount of myelin wrapped around those axons, but it is not always a measure of "tissue integrity".
Let's take a look at what the FA map looks like! An FA map is a gray-scale image, where higher intensities reflect more anisotropic diffuse regions.
_Note: we will have to first create the image from the array, making use of the reference anatomical_
```
from nilearn import plotting as plot
import matplotlib.pyplot as plt # To enable plotting
%matplotlib inline
fa_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.fa)
plot.plot_anat(fa_img, cut_coords=(0, -29, 20))
```
Derived from partial volume effects in imaging voxels due to the presence of different tissues, noise in the measurements and numerical errors, the DTI model estimation may yield negative eigenvalues. Such *degenerate* case is not physically meaningful. These values are usually revealed as black or 0-valued pixels in FA maps.
FA is a central value in dMRI: large FA values imply that the underlying fiber populations have a very coherent orientation, whereas lower FA values point to voxels containing multiple fiber crossings. Lowest FA values are indicative of non-white matter tissue in healthy brains (see, for example, Alexander et al.'s "Diffusion Tensor Imaging of the Brain". Neurotherapeutics 4, 316-329 (2007), and Jeurissen et al.'s "Investigating the Prevalence of Complex Fiber Configurations in White Matter Tissue with Diffusion Magnetic Resonance Imaging". Hum. Brain Mapp. 2012, 34(11) pp. 2747-2766).
### Mean diffusivity (MD)
An often used complimentary measure to FA is mean diffusivity (MD). MD is a measure of the degree of diffusion, independent of direction. This is sometimes known as the apparent diffusion coefficient (ADC). Mathematically, MD is computed as the mean eigenvalues of the tensor and is measured in mm^2/s.

Similar to the previous FA image, let's take a look at what the MD map looks like. Again, higher intensities reflect higher mean diffusivity!
```
%matplotlib inline
md_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.md)
# Arbitrarily set min and max of color bar
plot.plot_anat(md_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
```
### Axial and radial diffusivity (AD & RD)
The final two metrics we will discuss are axial diffusivity (AD) and radial diffusivity (RD). Two tensors with different shapes may yield the same FA values, and additional measures such as AD and RD are required to further characterize the tensor. AD describes the diffusion rate along the primary axis of diffusion, along , or parallel to the axon (and hence, some works refer to it as the *parallel diffusivity*). On the other hand, RD reflects the average diffusivity along the other two minor axes (being named as *perpendicular diffusivity* in some works) (). Both are measured in mm^2/s.

### Tensor visualizations
There are several ways of visualizing tensors. One way is using an RGB map, which overlays the primary diffusion orientation on an FA map. The colours of this map encodes the diffusion orientation. Note that this map provides no directional information (e.g. whether the diffusion flows from right-to-left or vice-versa). To do this with <code>DIPY</code>, we can use the <code>color_fa</code> function. The colours map to the following orientations:
* Red = Left / Right
* Green = Anterior / Posterior
* Blue = Superior / Inferior
_Note: The plotting functions in <code>nilearn</code> are unable to visualize these RGB maps. However, we can use the <code>matplotlib</code> library to view these images._
```
from scipy import ndimage # To rotate image for visualization purposes
from dipy.reconst.dti import color_fa
%matplotlib inline
RGB_map = color_fa(dti_fit.fa, dti_fit.evecs)
fig, ax = plt.subplots(1, 3, figsize=(10, 10))
ax[0].imshow(ndimage.rotate(
RGB_map[:, RGB_map.shape[1]//2, :, :], 90, reshape=False))
ax[1].imshow(ndimage.rotate(
RGB_map[RGB_map.shape[0]//2, :, :, :], 90, reshape=False))
ax[2].imshow(ndimage.rotate(
RGB_map[:, :, RGB_map.shape[2]//2, :], 90, reshape=False))
```
Another way of viewing the tensors is to visualize the diffusion tensor in each imaging voxel with colour encoding (we will refer you to the [`Dipy` documentation](https://dipy.org/tutorials/) for the steps to perform this type of visualization as it can be memory intensive). Below is an example image of such tensor visualization.

### Some notes on DTI
DTI is only one of many models and is one of the simplest models available for modelling diffusion. While it is used for many studies, there are also some drawbacks (e.g. ability to distinguish multiple fibre orientations in an imaging voxel). Examples of this can be seen below!

_Sourced from Sotiropoulos and Zalesky (2017). Building connectomes using diffusion MRI: why, how, and but. NMR in Biomedicine. 4(32). e3752. doi:10.1002/nbm.3752._
Though other models are outside the scope of this lesson, we recommend looking into some of the pros and cons of each model (listed previously) to choose one best suited for your data!
## Exercise 1
Plot the axial and radial diffusivity maps of the example given. Start from fitting the preprocessed diffusion image.
## Solution
```
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
from nilearn import image as img
import nibabel as nib
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
dwi_data = dwi_data.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)
# Fit dti model
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
# Plot axial diffusivity map
ad_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.ad)
plot.plot_anat(ad_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
# Plot radial diffusivity map
rd_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.rd)
plot.plot_anat(rd_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
```
|
github_jupyter
|
import bids
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
from nilearn import image as img
import nibabel as nib
bids.config.set_option('extension_initial_dot', True)
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
# Grab the transformed t1 file for reference
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
# Recall the preprocessed data is no longer in BIDS - we will directly grab these files
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
dwi_data = dwi_data.get_fdata() # We re-use the variable for memory purposes
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1) # Specify the volume index to the b0 volumes
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
from nilearn import plotting as plot
import matplotlib.pyplot as plt # To enable plotting
%matplotlib inline
fa_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.fa)
plot.plot_anat(fa_img, cut_coords=(0, -29, 20))
%matplotlib inline
md_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.md)
# Arbitrarily set min and max of color bar
plot.plot_anat(md_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
from scipy import ndimage # To rotate image for visualization purposes
from dipy.reconst.dti import color_fa
%matplotlib inline
RGB_map = color_fa(dti_fit.fa, dti_fit.evecs)
fig, ax = plt.subplots(1, 3, figsize=(10, 10))
ax[0].imshow(ndimage.rotate(
RGB_map[:, RGB_map.shape[1]//2, :, :], 90, reshape=False))
ax[1].imshow(ndimage.rotate(
RGB_map[RGB_map.shape[0]//2, :, :, :], 90, reshape=False))
ax[2].imshow(ndimage.rotate(
RGB_map[:, :, RGB_map.shape[2]//2, :], 90, reshape=False))
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
from nilearn import image as img
import nibabel as nib
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
dwi_data = dwi_data.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)
# Fit dti model
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
# Plot axial diffusivity map
ad_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.ad)
plot.plot_anat(ad_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
# Plot radial diffusivity map
rd_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.rd)
plot.plot_anat(rd_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
| 0.68616 | 0.99153 |
```
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats import norm
# Getting the database
df_data = pd.read_excel('proshares_analysis_data.xlsx', header=0, index_col=0, sheet_name='merrill_factors')
df_data.head()
```
# Section 1 - Short answer
1.1 Mean-variance optimization goes long the highest Sharpe-Ratio assets and shorts the lowest Sharpe-ratio assets.
False. The mean-variance optimization takes into account not only the mean returns and volatilities but also the correlation structure among assets. If an asset has low covariance with other assets it can have a high weight even if its sharpe ratio is not so big.
1.2 Investing in an ETF makes more sense for a long-term horizon than a short-term horizon.
True. An ETF is a portfolio of stocks. It should show better performance metrics over long horizons then short horizons.
1.3 Do you suggest that we (in a year) estimate the regression with an intercept or without an
intercept? Why?
We should include the intercept in the regression. As we have a small sample of data the estimate of mean returns will not be trustable. As a result, we should not force the betas of the regression to try to replicate both the trend and the variation of the asset returns.
1.4 Is HDG effective at tracking HFRI in-sample? And out of sample?
Yes, the out-of-sample replication performs very well in comparison to the target. In terms of the in-sample comparison, the annualized tracking error is 0.023 which is acceptable.
1.5 A hedge fund claims to beat the market by having a very high alpha. After regressing the hedge fund returns on the
6 Merrill-Lynch style factors, you find the alpha to be negative. Explain why this discrepancy can happen.
The difference can be in terms of the benchmark you are comparing the returns. If for example, the hedge fund is comparing its returns with a smaller set of factors, the regression can show a positive and high alpha. But in this case is just because you have ommited variables.
# Section 2 - Allocation
```
# 2.1 What are the weights of the tangency portfolio, wtan?
rf_lab = 'USGG3M Index'
df_excess = df_data.apply(lambda x: x - df_data.loc[:, rf_lab]).drop(rf_lab, axis=1)
df_excess.head()
mu = df_excess.mean()
cov_matrix = df_excess.cov()
inv_cov = np.linalg.inv(cov_matrix)
wtan = (1 / (np.ones(len(mu)) @ inv_cov @ mu)) * (inv_cov @ mu)
df_wtan = pd.DataFrame(wtan, index = df_excess.columns.values, columns=['Weights'])
df_wtan
# 2.2 What are the weights of the optimal portfolio, w* with a targeted excess mean return of .02 per month?
# Is the optimal portfolio, w*, invested in the risk-free rate?
mu_target = 0.02
k = len(mu)
delta = mu_target * ((np.ones((1, k)) @ inv_cov @ mu) / (mu.T @ inv_cov @ mu))
wstar = delta * wtan
df_wstar = pd.DataFrame(wstar, index = df_excess.columns.values, columns=['Weights'])
df_wstar
print('The optimal mean-variance portfolio is positioned by {:.2f}% in the risk free rate.'.format(100 * (1 - delta[0])))
# 2.3 Report the mean, volatility, and Sharpe ratio of the optimized portfolio. Annualize all three statistics
df_retstar = pd.DataFrame(df_excess.values @ wstar, index=df_excess.index, columns=['Mean-variance'])
df_stats = pd.DataFrame(index = ['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats['Mean'] = 12 * df_retstar.mean().values
df_stats['Volatility'] = np.sqrt(12) * df_retstar.std().values
df_stats['Sharpe'] = df_stats['Mean'].values / df_stats['Volatility'].values
df_stats
# 2.4 Re-calculate the optimal portfolio, w∗ with target excess mean of .02 per month. But this time only use data through
# 2018 in doing the calculation. Calculate the return in 2019-2021 based on those optimal weights.
df_excess_IS = df_excess.loc['2018', :]
df_excess_OOS = df_excess.loc['2019':, :]
mu_IS = df_excess_IS.mean()
cov_matrix_IS = df_excess_IS.cov()
inv_cov_IS = np.linalg.inv(cov_matrix_IS)
wtan_IS = (1 / (np.ones(len(mu_IS)) @ inv_cov_IS @ mu_IS)) * (inv_cov_IS @ mu_IS)
delta_IS = mu_target * ((np.ones((1, len(mu_IS))) @ inv_cov_IS @ mu_IS) / (mu_IS.T @ inv_cov_IS @ mu_IS))
wstar_IS = delta_IS * wtan_IS
pd.DataFrame(wstar_IS, index=df_excess_IS.columns.values, columns=['MV portfolio'])
# Report the mean, volatility, and Sharpe ratio of the 2019-2021 performance.
df_retstar_OOS = pd.DataFrame(df_excess_OOS.values @ wstar_IS, index=df_excess_OOS.index, columns=['MV portfolio'])
df_stats_OOS = pd.DataFrame(index=['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_OOS['Mean'] = 12 * df_retstar_OOS.mean().values
df_stats_OOS['Volatility'] = np.sqrt(12) * df_retstar_OOS.std().values
df_stats_OOS['Sharpe'] = df_stats_OOS['Mean'] / df_stats_OOS['Volatility']
df_stats_OOS
```
2.5 Suppose that instead of optimizing these 5 risky assets, we optimized 5 commodity futures: oil, coffee, cocoa, lumber, cattle, and gold. Do you think the out-of-sample fragility problem would be better or worse than what we have seen optimizing equities?
It will depend on how accurate is our estimate for the parameters of mean and covariance matrix of those assets. The weak out-of-sample performance of the mean-variance approach is driven by the fact that the mean and covariance matrix are not robust statistics and both change over time. In my opinion the out-of-sample fragility would be even worse in the case of the commodity futures because we will have very correlated assets. The determinant of the covariance matrix should be very low, which will make the weights very sensitive to any change in the mean return.
# Section 3 - Hedging and replication
```
# Suppose we want to invest in EEM, but hedge out SPY. Do this by estimating a regression of EEM on SPY
y = df_excess.loc[:, 'EEM US Equity']
x = df_excess.loc[:, 'SPY US Equity']
model_factor = sm.OLS(y, x).fit()
print(model_factor.summary())
```
3.1 What is the optimal hedge ratio over the full sample of data? That is, for every dollar invested in EEM, what would you invest in SPY?
The optimal hedge ratio will be the beta parameter of the above regression. As a result, the optimal hedge ratio will be 0.9257 invested in S&P for every dollar you invested in EEM.
```
# 3.2 What is the mean, volatility, and Sharpe ratio of the hedged position, had we applied that hedge throughout the
# full sample?
beta = model_factor.params[0]
df_position = pd.DataFrame(y.values - beta * x.values, index=y.index, columns=['Hedged position'])
df_stats_hedged = pd.DataFrame(index=['Hedged position'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_hedged['Mean'] = 12 * df_position.mean().values
df_stats_hedged['Volatility'] = np.sqrt(12) * df_position.std().values
df_stats_hedged['Sharpe'] = df_stats_hedged['Mean'] / df_stats_hedged['Volatility']
df_stats_hedged
```
3.3 Does it have the same mean as EEM? Why or why not?
No it does not have the same mean as EEM. As we are hedging against the S&P, our position is shorting the S&P index so that we can hedge against market movements. As a result, our hedged position will subtract the beta multiplied by the mean of the S&P returns.
3.4 Suppose we estimated a multifactor regression where in addition to SPY, we had IWM as a regressor. Why might this regression be difficult to use for attribution or even hedging?
Because our regressors will be very correlated. As the IWM is an ETF of stocks, its correlation with the S&P should be very high.
# Section 4 - Modeling Risk
```
df_total = df_data.loc[:, ['SPY US Equity', 'EFA US Equity']]
df_total.head()
df_total['Diff'] = df_total['EFA US Equity'] - df_total['SPY US Equity']
mu = 12 * np.log(1 + df_total['Diff']).mean()
sigma = np.sqrt(12) * np.log(1 + df_total['Diff']).std()
threshold = 0
h = 10
# Calculatiing the probability
prob = norm.cdf((threshold - mu) / (sigma / np.sqrt(h)))
print('The probability that the S&P will outperform EFA is: {:.2f}%.'.format(100 * prob))
# 4.2 Calculate the 60-month rolling volatility of EFA
vol_rolling = ((df_total.loc[:, 'EFA US Equity'].shift(1) ** 2).rolling(window=60).mean()) ** 0.5
vol_current = vol_rolling.values[-1]
# Use the latest estimate of the volatility (Sep 2021), along with the normality formula, to calculate a Sep 2021 estimate
# of the 1-month, 1% VaR. In using the VaR formula, assume that the mean is zero.
var_5 = -2.33 * vol_current
print('The estimated 1% VaR is {:.3f}%.'.format(var_5 * 100))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats import norm
# Getting the database
df_data = pd.read_excel('proshares_analysis_data.xlsx', header=0, index_col=0, sheet_name='merrill_factors')
df_data.head()
# 2.1 What are the weights of the tangency portfolio, wtan?
rf_lab = 'USGG3M Index'
df_excess = df_data.apply(lambda x: x - df_data.loc[:, rf_lab]).drop(rf_lab, axis=1)
df_excess.head()
mu = df_excess.mean()
cov_matrix = df_excess.cov()
inv_cov = np.linalg.inv(cov_matrix)
wtan = (1 / (np.ones(len(mu)) @ inv_cov @ mu)) * (inv_cov @ mu)
df_wtan = pd.DataFrame(wtan, index = df_excess.columns.values, columns=['Weights'])
df_wtan
# 2.2 What are the weights of the optimal portfolio, w* with a targeted excess mean return of .02 per month?
# Is the optimal portfolio, w*, invested in the risk-free rate?
mu_target = 0.02
k = len(mu)
delta = mu_target * ((np.ones((1, k)) @ inv_cov @ mu) / (mu.T @ inv_cov @ mu))
wstar = delta * wtan
df_wstar = pd.DataFrame(wstar, index = df_excess.columns.values, columns=['Weights'])
df_wstar
print('The optimal mean-variance portfolio is positioned by {:.2f}% in the risk free rate.'.format(100 * (1 - delta[0])))
# 2.3 Report the mean, volatility, and Sharpe ratio of the optimized portfolio. Annualize all three statistics
df_retstar = pd.DataFrame(df_excess.values @ wstar, index=df_excess.index, columns=['Mean-variance'])
df_stats = pd.DataFrame(index = ['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats['Mean'] = 12 * df_retstar.mean().values
df_stats['Volatility'] = np.sqrt(12) * df_retstar.std().values
df_stats['Sharpe'] = df_stats['Mean'].values / df_stats['Volatility'].values
df_stats
# 2.4 Re-calculate the optimal portfolio, w∗ with target excess mean of .02 per month. But this time only use data through
# 2018 in doing the calculation. Calculate the return in 2019-2021 based on those optimal weights.
df_excess_IS = df_excess.loc['2018', :]
df_excess_OOS = df_excess.loc['2019':, :]
mu_IS = df_excess_IS.mean()
cov_matrix_IS = df_excess_IS.cov()
inv_cov_IS = np.linalg.inv(cov_matrix_IS)
wtan_IS = (1 / (np.ones(len(mu_IS)) @ inv_cov_IS @ mu_IS)) * (inv_cov_IS @ mu_IS)
delta_IS = mu_target * ((np.ones((1, len(mu_IS))) @ inv_cov_IS @ mu_IS) / (mu_IS.T @ inv_cov_IS @ mu_IS))
wstar_IS = delta_IS * wtan_IS
pd.DataFrame(wstar_IS, index=df_excess_IS.columns.values, columns=['MV portfolio'])
# Report the mean, volatility, and Sharpe ratio of the 2019-2021 performance.
df_retstar_OOS = pd.DataFrame(df_excess_OOS.values @ wstar_IS, index=df_excess_OOS.index, columns=['MV portfolio'])
df_stats_OOS = pd.DataFrame(index=['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_OOS['Mean'] = 12 * df_retstar_OOS.mean().values
df_stats_OOS['Volatility'] = np.sqrt(12) * df_retstar_OOS.std().values
df_stats_OOS['Sharpe'] = df_stats_OOS['Mean'] / df_stats_OOS['Volatility']
df_stats_OOS
# Suppose we want to invest in EEM, but hedge out SPY. Do this by estimating a regression of EEM on SPY
y = df_excess.loc[:, 'EEM US Equity']
x = df_excess.loc[:, 'SPY US Equity']
model_factor = sm.OLS(y, x).fit()
print(model_factor.summary())
# 3.2 What is the mean, volatility, and Sharpe ratio of the hedged position, had we applied that hedge throughout the
# full sample?
beta = model_factor.params[0]
df_position = pd.DataFrame(y.values - beta * x.values, index=y.index, columns=['Hedged position'])
df_stats_hedged = pd.DataFrame(index=['Hedged position'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_hedged['Mean'] = 12 * df_position.mean().values
df_stats_hedged['Volatility'] = np.sqrt(12) * df_position.std().values
df_stats_hedged['Sharpe'] = df_stats_hedged['Mean'] / df_stats_hedged['Volatility']
df_stats_hedged
df_total = df_data.loc[:, ['SPY US Equity', 'EFA US Equity']]
df_total.head()
df_total['Diff'] = df_total['EFA US Equity'] - df_total['SPY US Equity']
mu = 12 * np.log(1 + df_total['Diff']).mean()
sigma = np.sqrt(12) * np.log(1 + df_total['Diff']).std()
threshold = 0
h = 10
# Calculatiing the probability
prob = norm.cdf((threshold - mu) / (sigma / np.sqrt(h)))
print('The probability that the S&P will outperform EFA is: {:.2f}%.'.format(100 * prob))
# 4.2 Calculate the 60-month rolling volatility of EFA
vol_rolling = ((df_total.loc[:, 'EFA US Equity'].shift(1) ** 2).rolling(window=60).mean()) ** 0.5
vol_current = vol_rolling.values[-1]
# Use the latest estimate of the volatility (Sep 2021), along with the normality formula, to calculate a Sep 2021 estimate
# of the 1-month, 1% VaR. In using the VaR formula, assume that the mean is zero.
var_5 = -2.33 * vol_current
print('The estimated 1% VaR is {:.3f}%.'.format(var_5 * 100))
| 0.777638 | 0.904777 |
```
try:
import openmdao.api as om
except ImportError:
!python -m pip install openmdao[notebooks]
import openmdao.api as om
```
# BoundsEnforceLS
The BoundsEnforceLS only backtracks until variables violate their upper and lower bounds.
Here is a simple example where BoundsEnforceLS is used to backtrack during the Newton solver's iteration on
a system that contains an implicit component with 3 states that are confined to a small range of values.
```
import numpy as np
import openmdao.api as om
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS()
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
from openmdao.utils.assert_utils import assert_near_equal
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
```
## BoundsEnforceLS Options
```
om.show_options_table("openmdao.solvers.linesearch.backtracking.BoundsEnforceLS")
```
## BoundsEnforceLS Constructor
The call signature for the `BoundsEnforceLS` constructor is:
```{eval-rst}
.. automethod:: openmdao.solvers.linesearch.backtracking.BoundsEnforceLS.__init__
:noindex:
```
## BoundsEnforceLS Option Examples
**bound_enforcement**
BoundsEnforceLS includes the `bound_enforcement` option in its options dictionary. This option has a dual role:
1. Behavior of the non-bounded variables when the bounded ones are capped.
2. Direction of the further backtracking.
There are three difference bounds enforcement schemes available in this option.
With "scalar" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the
remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that
it still moves in the direction of the initial point. This is the default bounds enforcement for `BoundsEnforceLS`.

With "vector" bounds enforcement, the solution in the output vector is pulled back in unison to a point where none of the
variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the
initial point.

With "wall" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.
```{Note}
When using BoundsEnforceLS linesearch, the `scalar` and `wall` methods are exactly the same because no further
backtracking is performed.
```

Here are a few examples of this option:
- bound_enforcement: vector
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "vector", the output vector is rolled back along the computed gradient until
it reaches a point where the earliest bound violation occurred. The backtracking continues along the original
computed gradient.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='vector')
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
```
- bound_enforcement: scalar
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "scaler", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='scalar')
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
top.run_model()
# Test lower bounds: should stop just short of the lower bound
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
```
- bound_enforcement: wall
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "wall", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient
direction that follows the boundary of the violated output bounds.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='wall')
top.setup()
top.set_val('x', np.array([0.5, 0.5, 0.5]).reshape(3, 1))
# Test upper bounds: should go to the upper bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 2.4)
top.run_model()
print(top.get_val('comp.z', indices=0))
print(top.get_val('comp.z', indices=1))
print(top.get_val('comp.z', indices=2))
assert_near_equal(top.get_val('comp.z', indices=0), [2.6], 1e-8)
assert_near_equal(top.get_val('comp.z', indices=1), [2.5], 1e-8)
assert_near_equal(top.get_val('comp.z', indices=2), [2.65], 1e-8)
```
|
github_jupyter
|
try:
import openmdao.api as om
except ImportError:
!python -m pip install openmdao[notebooks]
import openmdao.api as om
import numpy as np
import openmdao.api as om
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS()
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
from openmdao.utils.assert_utils import assert_near_equal
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
om.show_options_table("openmdao.solvers.linesearch.backtracking.BoundsEnforceLS")
## BoundsEnforceLS Option Examples
**bound_enforcement**
BoundsEnforceLS includes the `bound_enforcement` option in its options dictionary. This option has a dual role:
1. Behavior of the non-bounded variables when the bounded ones are capped.
2. Direction of the further backtracking.
There are three difference bounds enforcement schemes available in this option.
With "scalar" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the
remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that
it still moves in the direction of the initial point. This is the default bounds enforcement for `BoundsEnforceLS`.

With "vector" bounds enforcement, the solution in the output vector is pulled back in unison to a point where none of the
variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the
initial point.

With "wall" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.

Here are a few examples of this option:
- bound_enforcement: vector
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "vector", the output vector is rolled back along the computed gradient until
it reaches a point where the earliest bound violation occurred. The backtracking continues along the original
computed gradient.
- bound_enforcement: scalar
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "scaler", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.
- bound_enforcement: wall
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "wall", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient
direction that follows the boundary of the violated output bounds.
| 0.825379 | 0.8059 |
# Classroom exercise: energy calculation
## Diffusion model in 1D
Description: A one-dimensional diffusion model. (Could be a gas of particles, or a bunch of crowded people in a corridor, or animals in a valley habitat...)
- Agents are on a 1d axis
- Agents do not want to be where there are other agents
- This is represented as an 'energy': the higher the energy, the more unhappy the agents.
Implementation:
- Given a vector $n$ of positive integers, and of arbitrary length
- Compute the energy, $E(n) = \sum_i n_i(n_i - 1)$
- Later, we will have the likelyhood of an agent moving depend on the change in energy.
```
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
density = np.array([0, 0, 3, 5, 8, 4, 2, 1])
fig, ax = plt.subplots()
ax.bar(np.arange(len(density)) - 0.5, density)
ax.xrange = [-0.5, len(density) - 0.5]
ax.set_ylabel("Particle count $n_i$")
ax.set_xlabel("Position $i$")
```
Here, the total energy due to position 2 is $3 (3-1)=6$, and due to column 7 is $1 (1-1)=0$. We need to sum these to get the
total energy.
## Starting point
Create a Python module:
```
%%bash
rm -rf diffusion
mkdir diffusion
install -m 644 /dev/null diffusion/__init__.py
```
**Windows:** You will need to run the following instead
```cmd
%%cmd
rmdir /s diffusion
mkdir diffusion
type nul > diffusion/__init__.py
```
**NB.** If you are using the Windows command prompt, you will also have to replace all subsequent `%%bash` directives with `%%cmd`
* Implementation file: diffusion_model.py
```
%%writefile diffusion/model.py
def energy(density, coeff=1.0):
"""Energy associated with the diffusion model
Parameters
----------
density: array of positive integers
Number of particles at each position i in the array
coeff: float
Diffusion coefficient.
"""
# implementation goes here
```
* Testing file: test_diffusion_model.py
```
%%writefile diffusion/test_model.py
from .model import energy
def test_energy():
"""Optional description for nose reporting."""
# Test something
```
Invoke the tests:
```
%%bash
cd diffusion
py.test
```
Now, write your code (in `model.py`), and tests (in `test_model.py`), testing as you do.
## Solution
Don't look until after you've tried!
In the spirit of test-driven development let's first consider our tests.
```
%%writefile diffusion/test_model.py
"""Unit tests for a diffusion model."""
from pytest import raises
from .model import energy
def test_energy_fails_on_non_integer_density():
with raises(TypeError) as exception:
energy([1.0, 2, 3])
def test_energy_fails_on_negative_density():
with raises(ValueError) as exception:
energy([-1, 2, 3])
def test_energy_fails_ndimensional_density():
with raises(ValueError) as exception:
energy([[1, 2, 3], [3, 4, 5]])
def test_zero_energy_cases():
# Zero energy at zero density
densities = [[], [0], [0, 0, 0]]
for density in densities:
assert energy(density) == 0
def test_derivative():
from numpy.random import randint
# Loop over vectors of different sizes (but not empty)
for vector_size in randint(1, 1000, size=30):
# Create random density of size N
density = randint(50, size=vector_size)
# will do derivative at this index
element_index = randint(vector_size)
# modified densities
density_plus_one = density.copy()
density_plus_one[element_index] += 1
# Compute and check result
# d(n^2-1)/dn = 2n
expected = 2.0 * density[element_index] if density[element_index] > 0 else 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
def test_derivative_no_self_energy():
"""If particle is alone, then its participation to energy is zero."""
from numpy import array
density = array([1, 0, 1, 10, 15, 0])
density_plus_one = density.copy()
density[1] += 1
expected = 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
```
Now let's write an implementation that passes the tests.
```
%%writefile diffusion/model.py
"""Simplistic 1-dimensional diffusion model."""
from numpy import array, any, sum
def energy(density):
"""Energy associated with the diffusion model
:Parameters:
density: array of positive integers
Number of particles at each position i in the array/geometry
"""
# Make sure input is an numpy array
density = array(density)
# ...of the right kind (integer). Unless it is zero length,
# in which case type does not matter.
if density.dtype.kind != "i" and len(density) > 0:
raise TypeError("Density should be a array of *integers*.")
# and the right values (positive or null)
if any(density < 0):
raise ValueError("Density should be an array of *positive* integers.")
if density.ndim != 1:
raise ValueError(
"Density should be an a *1-dimensional*" + "array of positive integers."
)
return sum(density * (density - 1))
%%bash
cd diffusion
py.test
```
## Coverage
With py.test, you can use the ["pytest-cov" plugin](https://github.com/pytest-dev/pytest-cov) to measure test coverage
```
%%bash
cd diffusion
py.test --cov
```
Or an html report:
```
%%bash
#%%cmd (windows)
cd diffusion
py.test --cov --cov-report html
```
Look at the [coverage results](./diffusion/htmlcov/index.html)
|
github_jupyter
|
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
density = np.array([0, 0, 3, 5, 8, 4, 2, 1])
fig, ax = plt.subplots()
ax.bar(np.arange(len(density)) - 0.5, density)
ax.xrange = [-0.5, len(density) - 0.5]
ax.set_ylabel("Particle count $n_i$")
ax.set_xlabel("Position $i$")
%%bash
rm -rf diffusion
mkdir diffusion
install -m 644 /dev/null diffusion/__init__.py
%%cmd
rmdir /s diffusion
mkdir diffusion
type nul > diffusion/__init__.py
%%writefile diffusion/model.py
def energy(density, coeff=1.0):
"""Energy associated with the diffusion model
Parameters
----------
density: array of positive integers
Number of particles at each position i in the array
coeff: float
Diffusion coefficient.
"""
# implementation goes here
%%writefile diffusion/test_model.py
from .model import energy
def test_energy():
"""Optional description for nose reporting."""
# Test something
%%bash
cd diffusion
py.test
%%writefile diffusion/test_model.py
"""Unit tests for a diffusion model."""
from pytest import raises
from .model import energy
def test_energy_fails_on_non_integer_density():
with raises(TypeError) as exception:
energy([1.0, 2, 3])
def test_energy_fails_on_negative_density():
with raises(ValueError) as exception:
energy([-1, 2, 3])
def test_energy_fails_ndimensional_density():
with raises(ValueError) as exception:
energy([[1, 2, 3], [3, 4, 5]])
def test_zero_energy_cases():
# Zero energy at zero density
densities = [[], [0], [0, 0, 0]]
for density in densities:
assert energy(density) == 0
def test_derivative():
from numpy.random import randint
# Loop over vectors of different sizes (but not empty)
for vector_size in randint(1, 1000, size=30):
# Create random density of size N
density = randint(50, size=vector_size)
# will do derivative at this index
element_index = randint(vector_size)
# modified densities
density_plus_one = density.copy()
density_plus_one[element_index] += 1
# Compute and check result
# d(n^2-1)/dn = 2n
expected = 2.0 * density[element_index] if density[element_index] > 0 else 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
def test_derivative_no_self_energy():
"""If particle is alone, then its participation to energy is zero."""
from numpy import array
density = array([1, 0, 1, 10, 15, 0])
density_plus_one = density.copy()
density[1] += 1
expected = 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
%%writefile diffusion/model.py
"""Simplistic 1-dimensional diffusion model."""
from numpy import array, any, sum
def energy(density):
"""Energy associated with the diffusion model
:Parameters:
density: array of positive integers
Number of particles at each position i in the array/geometry
"""
# Make sure input is an numpy array
density = array(density)
# ...of the right kind (integer). Unless it is zero length,
# in which case type does not matter.
if density.dtype.kind != "i" and len(density) > 0:
raise TypeError("Density should be a array of *integers*.")
# and the right values (positive or null)
if any(density < 0):
raise ValueError("Density should be an array of *positive* integers.")
if density.ndim != 1:
raise ValueError(
"Density should be an a *1-dimensional*" + "array of positive integers."
)
return sum(density * (density - 1))
%%bash
cd diffusion
py.test
%%bash
cd diffusion
py.test --cov
%%bash
#%%cmd (windows)
cd diffusion
py.test --cov --cov-report html
| 0.724188 | 0.982305 |
<a href="https://colab.research.google.com/github/krakowiakpawel9/convnet-course/blob/master/02_mnist_cnn.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Trenowanie prostej sieci neuronowej na zbiorze MNIST
```
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import warnings
warnings.filterwarnings('ignore')
```
### Załadowanie danych
```
# zdefiniowanie wymiarów obrazu wejsciowego
img_rows, img_cols = 28, 28
(X_train, y_train), (X_test, y_test) = mnist.load_data()
```
### Eksploracja danych
```
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
print('Liczba dabych treningowych:', X_train.shape[0])
print('Liczba danych testowych:', X_test.shape[0])
print('Rozmiar pojedynczego obrazka:', X_train[0].shape)
```
### Wyświetlenie obrazka
```
import matplotlib.pyplot as plt
plt.imshow(X_train[0], cmap='Greys')
plt.axis('off')
```
### Wyświetlenie kilku obrazków
```
plt.figure(figsize=(13, 13))
for i in range(1, 11):
plt.subplot(1, 10, i)
plt.axis('off')
plt.imshow(X_train[i], cmap='Greys')
plt.show()
```
### Wyświetlenie danych
```
print(X_train[0][10])
# dolna połówka obrazka
plt.imshow(X_train[0][14:], cmap='Greys')
# górna połówka obrazka
plt.imshow(X_train[0][:14], cmap='Greys')
```
### Przycinanie obrazka
```
plt.imshow(X_train[0][5:20, 5:20], cmap='Greys')
```
### Obsługa problemu zapisu obrazów wejściowych - channel first vs. channel last
```
print(K.image_data_format())
if K.image_data_format() == 'channel_first':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print(input_shape)
```
### Wyświetlenie etykiet
```
print('y_train:', y_train)
print('y_train shape:', y_train.shape)
```
## Przygotowanie danych
```
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape)
print(X_test.shape)
```
### Przygotowanie etykiet
```
y_train = keras.utils.to_categorical(y_train, num_classes=10)
y_test = keras.utils.to_categorical(y_test, num_classes=10)
print(y_train.shape)
print(y_test.shape)
print(y_train[0])
```
### Budowa modelu
```
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(units=128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.summary()
```
### Kompilacja modelu
```
model.compile(optimizer='adadelta',
loss='categorical_crossentropy',
metrics=['accuracy'])
```
### Trenowanie modelu
```
history = model.fit(X_train, y_train,
batch_size=128,
epochs=20,
validation_data=(X_test, y_test))
```
### Ocena modelu
```
score = model.evaluate(X_test, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
### Wykres dokładności
```
def make_accuracy_plot(history):
"""
Funkcja zwraca wykres dokładności (accuracy) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
acc, val_acc = history.history['acc'], history.history['val_acc']
epochs = range(1, len(acc) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, acc, label='Dokładność trenowania', marker='o')
plt.plot(epochs, val_acc, label='Dokładność walidacji', marker='o')
plt.legend()
plt.title('Dokładność trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Dokładność')
plt.show()
def make_loss_plot(history):
"""
Funkcja zwraca wykres straty (loss) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
loss, val_loss = history.history['loss'], history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss, label='Strata trenowania', marker='o')
plt.plot(epochs, val_loss, label='Strata walidacji', marker='o')
plt.legend()
plt.title('Strata trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.show()
make_accuracy_plot(history)
make_loss_plot(history)
```
|
github_jupyter
|
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import warnings
warnings.filterwarnings('ignore')
# zdefiniowanie wymiarów obrazu wejsciowego
img_rows, img_cols = 28, 28
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
print('Liczba dabych treningowych:', X_train.shape[0])
print('Liczba danych testowych:', X_test.shape[0])
print('Rozmiar pojedynczego obrazka:', X_train[0].shape)
import matplotlib.pyplot as plt
plt.imshow(X_train[0], cmap='Greys')
plt.axis('off')
plt.figure(figsize=(13, 13))
for i in range(1, 11):
plt.subplot(1, 10, i)
plt.axis('off')
plt.imshow(X_train[i], cmap='Greys')
plt.show()
print(X_train[0][10])
# dolna połówka obrazka
plt.imshow(X_train[0][14:], cmap='Greys')
# górna połówka obrazka
plt.imshow(X_train[0][:14], cmap='Greys')
plt.imshow(X_train[0][5:20, 5:20], cmap='Greys')
print(K.image_data_format())
if K.image_data_format() == 'channel_first':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print(input_shape)
print('y_train:', y_train)
print('y_train shape:', y_train.shape)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape)
print(X_test.shape)
y_train = keras.utils.to_categorical(y_train, num_classes=10)
y_test = keras.utils.to_categorical(y_test, num_classes=10)
print(y_train.shape)
print(y_test.shape)
print(y_train[0])
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(units=128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.summary()
model.compile(optimizer='adadelta',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_train, y_train,
batch_size=128,
epochs=20,
validation_data=(X_test, y_test))
score = model.evaluate(X_test, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
def make_accuracy_plot(history):
"""
Funkcja zwraca wykres dokładności (accuracy) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
acc, val_acc = history.history['acc'], history.history['val_acc']
epochs = range(1, len(acc) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, acc, label='Dokładność trenowania', marker='o')
plt.plot(epochs, val_acc, label='Dokładność walidacji', marker='o')
plt.legend()
plt.title('Dokładność trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Dokładność')
plt.show()
def make_loss_plot(history):
"""
Funkcja zwraca wykres straty (loss) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
loss, val_loss = history.history['loss'], history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss, label='Strata trenowania', marker='o')
plt.plot(epochs, val_loss, label='Strata walidacji', marker='o')
plt.legend()
plt.title('Strata trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.show()
make_accuracy_plot(history)
make_loss_plot(history)
| 0.728941 | 0.950915 |
# Think Bayes: Chapter 7
This notebook presents code and exercises from Think Bayes, second edition.
Copyright 2016 Allen B. Downey
MIT License: https://opensource.org/licenses/MIT
```
from __future__ import print_function, division
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import math
import numpy as np
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkbayes2
import thinkplot
```
## Warm-up exercises
**Exercise:** Suppose that goal scoring in hockey is well modeled by a
Poisson process, and that the long-run goal-scoring rate of the
Boston Bruins against the Vancouver Canucks is 2.9 goals per game.
In their next game, what is the probability
that the Bruins score exactly 3 goals? Plot the PMF of `k`, the number
of goals they score in a game.
```
### Solution
```
**Exercise:** Assuming again that the goal scoring rate is 2.9, what is the probability of scoring a total of 9 goals in three games? Answer this question two ways:
1. Compute the distribution of goals scored in one game and then add it to itself twice to find the distribution of goals scored in 3 games.
2. Use the Poisson PMF with parameter $\lambda t$, where $\lambda$ is the rate in goals per game and $t$ is the duration in games.
```
### Solution
```
**Exercise:** Suppose that the long-run goal-scoring rate of the
Canucks against the Bruins is 2.6 goals per game. Plot the distribution
of `t`, the time until the Canucks score their first goal.
In their next game, what is the probability that the Canucks score
during the first period (that is, the first third of the game)?
Hint: `thinkbayes2` provides `MakeExponentialPmf` and `EvalExponentialCdf`.
```
### Solution
```
**Exercise:** Assuming again that the goal scoring rate is 2.8, what is the probability that the Canucks get shut out (that is, don't score for an entire game)? Answer this question two ways, using the CDF of the exponential distribution and the PMF of the Poisson distribution.
```
### Solution
```
## The Boston Bruins problem
The `Hockey` suite contains hypotheses about the goal scoring rate for one team against the other. The prior is Gaussian, with mean and variance based on previous games in the league.
The Likelihood function takes as data the number of goals scored in a game.
```
from thinkbayes2 import MakeNormalPmf
from thinkbayes2 import EvalPoissonPmf
class Hockey(thinkbayes2.Suite):
"""Represents hypotheses about the scoring rate for a team."""
def __init__(self, label=None):
"""Initializes the Hockey object.
label: string
"""
mu = 2.8
sigma = 0.3
pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)
thinkbayes2.Suite.__init__(self, pmf, label=label)
def Likelihood(self, data, hypo):
"""Computes the likelihood of the data under the hypothesis.
Evaluates the Poisson PMF for lambda k.
hypo: goal scoring rate in goals per game
data: goals scored in one game
"""
lam = hypo
k = data
like = EvalPoissonPmf(k, lam)
return like
```
Now we can initialize a suite for each team:
```
suite1 = Hockey('bruins')
suite2 = Hockey('canucks')
```
Here's what the priors look like:
```
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
```
And we can update each suite with the scores from the first 4 games.
```
suite1.UpdateSet([0, 2, 8, 4])
suite2.UpdateSet([1, 3, 1, 0])
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.Mean(), suite2.Mean()
```
To predict the number of goals scored in the next game we can compute, for each hypothetical value of $\lambda$, a Poisson distribution of goals scored, then make a weighted mixture of Poissons:
```
from thinkbayes2 import MakeMixture
from thinkbayes2 import MakePoissonPmf
def MakeGoalPmf(suite, high=10):
"""Makes the distribution of goals scored, given distribution of lam.
suite: distribution of goal-scoring rate
high: upper bound
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakePoissonPmf(lam, high)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the results look like.
```
goal_dist1 = MakeGoalPmf(suite1)
goal_dist2 = MakeGoalPmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(goal_dist1)
thinkplot.Pmf(goal_dist2)
thinkplot.Config(xlabel='Goals',
ylabel='Probability',
xlim=[-0.7, 11.5])
goal_dist1.Mean(), goal_dist2.Mean()
```
Now we can compute the probability that the Bruins win, lose, or tie in regulation time.
```
diff = goal_dist1 - goal_dist2
p_win = diff.ProbGreater(0)
p_loss = diff.ProbLess(0)
p_tie = diff.Prob(0)
print('Prob win, loss, tie:', p_win, p_loss, p_tie)
```
If the game goes into overtime, we have to compute the distribution of `t`, the time until the first goal, for each team. For each hypothetical value of $\lambda$, the distribution of `t` is exponential, so the predictive distribution is a mixture of exponentials.
```
from thinkbayes2 import MakeExponentialPmf
def MakeGoalTimePmf(suite):
"""Makes the distribution of time til first goal.
suite: distribution of goal-scoring rate
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakeExponentialPmf(lam, high=2.5, n=1001)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the predictive distributions for `t` look like.
```
time_dist1 = MakeGoalTimePmf(suite1)
time_dist2 = MakeGoalTimePmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(time_dist1)
thinkplot.Pmf(time_dist2)
thinkplot.Config(xlabel='Games until goal',
ylabel='Probability')
time_dist1.Mean(), time_dist2.Mean()
```
In overtime the first team to score wins, so the probability of winning is the probability of generating a smaller value of `t`:
```
p_win_in_overtime = time_dist1.ProbLess(time_dist2)
p_adjust = time_dist1.ProbEqual(time_dist2)
p_win_in_overtime += p_adjust / 2
print('p_win_in_overtime', p_win_in_overtime)
```
Finally, we can compute the overall chance that the Bruins win, either in regulation or overtime.
```
p_win_overall = p_win + p_tie * p_win_in_overtime
print('p_win_overall', p_win_overall)
```
## Exercises
**Exercise:** To make the model of overtime more correct, we could update both suites with 0 goals in one game, before computing the predictive distribution of `t`. Make this change and see what effect it has on the results.
```
### Solution
```
**Exercise:** In the final match of the 2014 FIFA World Cup, Germany defeated Argentina 1-0. What is the probability that Germany had the better team? What is the probability that Germany would win a rematch?
For a prior distribution on the goal-scoring rate for each team, use a gamma distribution with parameter 1.3.
```
from thinkbayes2 import MakeGammaPmf
xs = np.linspace(0, 8, 101)
pmf = MakeGammaPmf(xs, 1.3)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Goals per game')
pmf.Mean()
### Solution
```
**Exercise:** In the 2014 FIFA World Cup, Germany played Brazil in a semifinal match. Germany scored after 11 minutes and again at the 23 minute mark. At that point in the match, how many goals would you expect Germany to score after 90 minutes? What was the probability that they would score 5 more goals (as, in fact, they did)?
Note: for this one you will need a new suite that provides a Likelihood function that takes as data the time between goals, rather than the number of goals in a game.
```
### Solution
```
**Exercise:** Which is a better way to break a tie: overtime or penalty shots?
**Exercise:** Suppose that you are an ecologist sampling the insect population in a new environment. You deploy 100 traps in a test area and come back the next day to check on them. You find that 37 traps have been triggered, trapping an insect inside. Once a trap triggers, it cannot trap another insect until it has been reset.
If you reset the traps and come back in two days, how many traps do you expect to find triggered? Compute a posterior predictive distribution for the number of traps.
```
### Solution
```
|
github_jupyter
|
from __future__ import print_function, division
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import math
import numpy as np
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkbayes2
import thinkplot
### Solution
### Solution
### Solution
### Solution
from thinkbayes2 import MakeNormalPmf
from thinkbayes2 import EvalPoissonPmf
class Hockey(thinkbayes2.Suite):
"""Represents hypotheses about the scoring rate for a team."""
def __init__(self, label=None):
"""Initializes the Hockey object.
label: string
"""
mu = 2.8
sigma = 0.3
pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)
thinkbayes2.Suite.__init__(self, pmf, label=label)
def Likelihood(self, data, hypo):
"""Computes the likelihood of the data under the hypothesis.
Evaluates the Poisson PMF for lambda k.
hypo: goal scoring rate in goals per game
data: goals scored in one game
"""
lam = hypo
k = data
like = EvalPoissonPmf(k, lam)
return like
suite1 = Hockey('bruins')
suite2 = Hockey('canucks')
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.UpdateSet([0, 2, 8, 4])
suite2.UpdateSet([1, 3, 1, 0])
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.Mean(), suite2.Mean()
from thinkbayes2 import MakeMixture
from thinkbayes2 import MakePoissonPmf
def MakeGoalPmf(suite, high=10):
"""Makes the distribution of goals scored, given distribution of lam.
suite: distribution of goal-scoring rate
high: upper bound
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakePoissonPmf(lam, high)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
goal_dist1 = MakeGoalPmf(suite1)
goal_dist2 = MakeGoalPmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(goal_dist1)
thinkplot.Pmf(goal_dist2)
thinkplot.Config(xlabel='Goals',
ylabel='Probability',
xlim=[-0.7, 11.5])
goal_dist1.Mean(), goal_dist2.Mean()
diff = goal_dist1 - goal_dist2
p_win = diff.ProbGreater(0)
p_loss = diff.ProbLess(0)
p_tie = diff.Prob(0)
print('Prob win, loss, tie:', p_win, p_loss, p_tie)
from thinkbayes2 import MakeExponentialPmf
def MakeGoalTimePmf(suite):
"""Makes the distribution of time til first goal.
suite: distribution of goal-scoring rate
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakeExponentialPmf(lam, high=2.5, n=1001)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
time_dist1 = MakeGoalTimePmf(suite1)
time_dist2 = MakeGoalTimePmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(time_dist1)
thinkplot.Pmf(time_dist2)
thinkplot.Config(xlabel='Games until goal',
ylabel='Probability')
time_dist1.Mean(), time_dist2.Mean()
p_win_in_overtime = time_dist1.ProbLess(time_dist2)
p_adjust = time_dist1.ProbEqual(time_dist2)
p_win_in_overtime += p_adjust / 2
print('p_win_in_overtime', p_win_in_overtime)
p_win_overall = p_win + p_tie * p_win_in_overtime
print('p_win_overall', p_win_overall)
### Solution
from thinkbayes2 import MakeGammaPmf
xs = np.linspace(0, 8, 101)
pmf = MakeGammaPmf(xs, 1.3)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Goals per game')
pmf.Mean()
### Solution
### Solution
### Solution
| 0.772788 | 0.983738 |
### **Heavy Machinery Image Recognition**
We are going to build a Machine Learning which can recognize a heavy machinery images, whether it is a truck or an excavator
```
from IPython.display import display
import os
import requests
from PIL import Image
from io import BytesIO
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing.image import load_img, img_to_array
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten, Activation
from sklearn.svm import SVC
from matplotlib import pyplot as plt
```
## **Connect to Google Drive**
Our data is stored in Google Drive, so we need to mount/connect our Google Colab session to Google Drive folder
```
from google.colab import drive
drive.mount('/content/gdrive')
```
**Define the path of the folder in our Google Drive**
```
DATA_SOURCE = "/content/gdrive/My Drive/Colab Notebooks/images_data/"
PATH_TRUCK_IMAGES = DATA_SOURCE + "Trucks/"
PATH_EXCAVATOR_IMAGES = DATA_SOURCE + "Excavators/"
```
## **Let's try to read and image and do Some Processing**
```
HEIGHT = 200
WIDTH = 300
IMAGE_SIZE = (HEIGHT, WIDTH, 1)
img = load_img(PATH_TRUCK_IMAGES + "6-image-Komatsu-960E-1.jpg", target_size=IMAGE_SIZE)
display(img)
```
An image is actually just an array. Our photos above is a colored image, or we can call it an RGB image.
RGB image is a 3D array, which first dimension indicates height, second dimension indicates width, and the third dimension indicates th intensity of color red, green, and blue
```
img_array = img_to_array(img)
img_array.shape
```
**Converting to Grayscale**
In our case, we can clearly see that trucks and excavators have very different shape. Also, most of them are colored yellow (or yellow-ish). Therefore, it is okay to ignore colors and convert our image to grayscale to save some resources.
Converting RGB image to Grayscale image means we reduce data-size to 1/3, thus saving a lot computing resources
```
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None)[:,:,0]/255
img_array_grayscale.shape
plt.imshow(img_array_grayscale, cmap='gray', vmin=0, vmax=1)
plt.show()
img_array_grayscale_flat = img_array.flatten()
img_array_grayscale_flat.shape
img_array_grayscale_flat
```
## **Building The Machine Learning**
## **Load images from directory**
```
train_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="training", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
validation_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="validation", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
```
## Design our Machine Learning
## 1. Simple Flattened Image + Support Vector Machine (SVM)
```
simple_ML = tf.keras.Sequential()
simple_ML.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
simple_ML.add(tf.keras.layers.Flatten())
simple_ML.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
simple_ML.summary()
for images, labels in train_data.take(1):
X_train = images.numpy()
train_labels = labels.numpy()
X_train = simple_ML.predict(X_train)
train_labels = train_labels.flatten()
for images, labels in validation_data.take(1):
X_validation = images.numpy()
validation_labels = labels.numpy()
X_validation = simple_ML.predict(X_validation)
validation_labels = validation_labels.flatten()
SVC_classifier = SVC()
SVC_classifier.fit(X=X_train, y=train_labels)
y_training = SVC_classifier.predict(X_train)
y_predict = SVC_classifier.predict(X_validation)
accuracy_t = np.sum([y_training == train_labels])/len(train_labels)
accuracy_v = np.sum([y_predict == validation_labels])/len(validation_labels)
print("Accuracy on Training Set: {}".format(accuracy_t))
print("Accuracy on Validation Set: {}".format(accuracy_v))
```
## 2. Convolutional Neural Network (CNN)
```
CNN_model = tf.keras.Sequential()
CNN_model.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
CNN_model.add(Conv2D(30, (5,5), input_shape=IMAGE_SIZE, activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Conv2D(30, (3,3), activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Dropout(0.2))
CNN_model.add(Flatten())
CNN_model.add(Dense(100, activation='relu'))
CNN_model.add(Dense(20, activation='relu'))
CNN_model.add(Dense(1, activation='sigmoid'))
CNN_model.compile(optimizer='adam', loss="binary_crossentropy", metrics=['accuracy'])
CNN_model.summary()
training = CNN_model.fit(train_data, validation_data=validation_data, batch_size=80, epochs=10)
def predict_image(url, model):
response = requests.get(url)
img = Image.open(BytesIO(response.content))
img_resize = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]))
img_resize_display = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]), Image.ANTIALIAS)
img_array = tf.keras.preprocessing.image.img_to_array(
img_resize, data_format=None, dtype=None
)
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None).numpy()
img_array_grayscale.shape
img_array_grayscale =img_array_grayscale.reshape(1, 200, 300, 1)
prediction = model.predict(img_array_grayscale)[0][0]
predict_label = "Excavator" if prediction < 0.5 else "Dump Truck"
predict_score = 1-prediction if prediction < 0.5 else prediction
print("{0} (Confidence: {1:.2f}%)".format(predict_label, predict_score*100))
display(img_resize_display)
url = "https://baumaschinen-modelle.net/de/sammlung/Dresser_730E.jpg"
predict_image(url=url, model=CNN_model)
```
|
github_jupyter
|
from IPython.display import display
import os
import requests
from PIL import Image
from io import BytesIO
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing.image import load_img, img_to_array
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten, Activation
from sklearn.svm import SVC
from matplotlib import pyplot as plt
from google.colab import drive
drive.mount('/content/gdrive')
DATA_SOURCE = "/content/gdrive/My Drive/Colab Notebooks/images_data/"
PATH_TRUCK_IMAGES = DATA_SOURCE + "Trucks/"
PATH_EXCAVATOR_IMAGES = DATA_SOURCE + "Excavators/"
HEIGHT = 200
WIDTH = 300
IMAGE_SIZE = (HEIGHT, WIDTH, 1)
img = load_img(PATH_TRUCK_IMAGES + "6-image-Komatsu-960E-1.jpg", target_size=IMAGE_SIZE)
display(img)
img_array = img_to_array(img)
img_array.shape
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None)[:,:,0]/255
img_array_grayscale.shape
plt.imshow(img_array_grayscale, cmap='gray', vmin=0, vmax=1)
plt.show()
img_array_grayscale_flat = img_array.flatten()
img_array_grayscale_flat.shape
img_array_grayscale_flat
train_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="training", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
validation_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="validation", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
simple_ML = tf.keras.Sequential()
simple_ML.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
simple_ML.add(tf.keras.layers.Flatten())
simple_ML.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
simple_ML.summary()
for images, labels in train_data.take(1):
X_train = images.numpy()
train_labels = labels.numpy()
X_train = simple_ML.predict(X_train)
train_labels = train_labels.flatten()
for images, labels in validation_data.take(1):
X_validation = images.numpy()
validation_labels = labels.numpy()
X_validation = simple_ML.predict(X_validation)
validation_labels = validation_labels.flatten()
SVC_classifier = SVC()
SVC_classifier.fit(X=X_train, y=train_labels)
y_training = SVC_classifier.predict(X_train)
y_predict = SVC_classifier.predict(X_validation)
accuracy_t = np.sum([y_training == train_labels])/len(train_labels)
accuracy_v = np.sum([y_predict == validation_labels])/len(validation_labels)
print("Accuracy on Training Set: {}".format(accuracy_t))
print("Accuracy on Validation Set: {}".format(accuracy_v))
CNN_model = tf.keras.Sequential()
CNN_model.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
CNN_model.add(Conv2D(30, (5,5), input_shape=IMAGE_SIZE, activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Conv2D(30, (3,3), activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Dropout(0.2))
CNN_model.add(Flatten())
CNN_model.add(Dense(100, activation='relu'))
CNN_model.add(Dense(20, activation='relu'))
CNN_model.add(Dense(1, activation='sigmoid'))
CNN_model.compile(optimizer='adam', loss="binary_crossentropy", metrics=['accuracy'])
CNN_model.summary()
training = CNN_model.fit(train_data, validation_data=validation_data, batch_size=80, epochs=10)
def predict_image(url, model):
response = requests.get(url)
img = Image.open(BytesIO(response.content))
img_resize = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]))
img_resize_display = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]), Image.ANTIALIAS)
img_array = tf.keras.preprocessing.image.img_to_array(
img_resize, data_format=None, dtype=None
)
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None).numpy()
img_array_grayscale.shape
img_array_grayscale =img_array_grayscale.reshape(1, 200, 300, 1)
prediction = model.predict(img_array_grayscale)[0][0]
predict_label = "Excavator" if prediction < 0.5 else "Dump Truck"
predict_score = 1-prediction if prediction < 0.5 else prediction
print("{0} (Confidence: {1:.2f}%)".format(predict_label, predict_score*100))
display(img_resize_display)
url = "https://baumaschinen-modelle.net/de/sammlung/Dresser_730E.jpg"
predict_image(url=url, model=CNN_model)
| 0.652795 | 0.90261 |
<small><i>This notebook was put together by [Jake Vanderplas](http://www.vanderplas.com). Source and license info is on [GitHub](https://github.com/jakevdp/sklearn_tutorial/).</i></small>
```
! git clone https://github.com/data-psl/lectures2021
import sys
sys.path.append('lectures2021/notebooks/02_sklearn')
%cd 'lectures2021/notebooks/02_sklearn'
```
# Density Estimation: Gaussian Mixture Models
Here we'll explore **Gaussian Mixture Models**, which is an unsupervised clustering & density estimation technique.
We'll start with our standard set of initial imports
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use('seaborn')
```
## Introducing Gaussian Mixture Models
We previously saw an example of K-Means, which is a clustering algorithm which is most often fit using an expectation-maximization approach.
Here we'll consider an extension to this which is suitable for both **clustering** and **density estimation**.
For example, imagine we have some one-dimensional data in a particular distribution:
```
np.random.seed(2)
x = np.concatenate([np.random.normal(0, 2, 2000),
np.random.normal(5, 5, 2000),
np.random.normal(3, 0.5, 600)])
plt.hist(x, 80, density=True)
plt.xlim(-10, 20);
```
Gaussian mixture models will allow us to approximate this density:
```
from sklearn.mixture import GaussianMixture as GMM
X = x[:, np.newaxis]
clf = GMM(4, max_iter=500, random_state=3).fit(X)
xpdf = np.linspace(-10, 20, 1000)
density = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-r')
plt.xlim(-10, 20);
```
Note that this density is fit using a **mixture of Gaussians**, which we can examine by looking at the ``means_``, ``covars_``, and ``weights_`` attributes:
```
clf.means_
clf.covariances_
clf.weights_
plt.hist(x, 80, density=True, alpha=0.3)
plt.plot(xpdf, density, '-r')
for i in range(clf.n_components):
pdf = clf.weights_[i] * stats.norm(clf.means_[i, 0],
np.sqrt(clf.covariances_[i, 0])).pdf(xpdf)
plt.fill(xpdf, pdf, facecolor='gray',
edgecolor='none', alpha=0.3)
plt.xlim(-10, 20);
```
These individual Gaussian distributions are fit using an expectation-maximization method, much as in K means, except that rather than explicit cluster assignment, the **posterior probability** is used to compute the weighted mean and covariance.
Somewhat surprisingly, this algorithm **provably** converges to the optimum (though the optimum is not necessarily global).
## How many Gaussians?
Given a model, we can use one of several means to evaluate how well it fits the data.
For example, there is the Aikaki Information Criterion (AIC) and the Bayesian Information Criterion (BIC)
```
print(clf.bic(X))
print(clf.aic(X))
```
Let's take a look at these as a function of the number of gaussians:
```
n_estimators = np.arange(1, 10)
clfs = [GMM(n, max_iter=1000).fit(X) for n in n_estimators]
bics = [clf.bic(X) for clf in clfs]
aics = [clf.aic(X) for clf in clfs]
plt.plot(n_estimators, bics, label='BIC')
plt.plot(n_estimators, aics, label='AIC')
plt.legend();
```
It appears that for both the AIC and BIC, 4 components is preferred.
## Example: GMM For Outlier Detection
GMM is what's known as a **Generative Model**: it's a probabilistic model from which a dataset can be generated.
One thing that generative models can be useful for is **outlier detection**: we can simply evaluate the likelihood of each point under the generative model; the points with a suitably low likelihood (where "suitable" is up to your own bias/variance preference) can be labeld outliers.
Let's take a look at this by defining a new dataset with some outliers:
```
np.random.seed(0)
# Add 20 outliers
true_outliers = np.sort(np.random.randint(0, len(x), 20))
y = x.copy()
y[true_outliers] += 50 * np.random.randn(20)
clf = GMM(4, max_iter=500, random_state=0).fit(y[:, np.newaxis])
xpdf = np.linspace(-10, 20, 1000)
density_noise = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(y, 80, density=True, alpha=0.5)
plt.plot(xpdf, density_noise, '-r')
plt.xlim(-15, 30);
```
Now let's evaluate the log-likelihood of each point under the model, and plot these as a function of ``y``:
```
log_likelihood = np.array([clf.score_samples([[yy]]) for yy in y])
# log_likelihood = clf.score_samples(y[:, np.newaxis])[0]
plt.plot(y, log_likelihood, '.k');
detected_outliers = np.where(log_likelihood < -9)[0]
print("true outliers:")
print(true_outliers)
print("\ndetected outliers:")
print(detected_outliers)
```
The algorithm misses a few of these points, which is to be expected (some of the "outliers" actually land in the middle of the distribution!)
Here are the outliers that were missed:
```
set(true_outliers) - set(detected_outliers)
```
And here are the non-outliers which were spuriously labeled outliers:
```
set(detected_outliers) - set(true_outliers)
```
Finally, we should note that although all of the above is done in one dimension, GMM does generalize to multiple dimensions, as we'll see in the breakout session.
## Other Density Estimators
The other main density estimator that you might find useful is *Kernel Density Estimation*, which is available via ``sklearn.neighbors.KernelDensity``. In some ways, this can be thought of as a generalization of GMM where there is a gaussian placed at the location of *every* training point!
```
from sklearn.neighbors import KernelDensity
kde = KernelDensity(0.15).fit(x[:, None])
density_kde = np.exp(kde.score_samples(xpdf[:, None]))
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-b', label='GMM')
plt.plot(xpdf, density_kde, '-r', label='KDE')
plt.xlim(-10, 20)
plt.legend();
```
All of these density estimators can be viewed as **Generative models** of the data: that is, that is, the model tells us how more data can be created which fits the model.
|
github_jupyter
|
! git clone https://github.com/data-psl/lectures2021
import sys
sys.path.append('lectures2021/notebooks/02_sklearn')
%cd 'lectures2021/notebooks/02_sklearn'
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use('seaborn')
np.random.seed(2)
x = np.concatenate([np.random.normal(0, 2, 2000),
np.random.normal(5, 5, 2000),
np.random.normal(3, 0.5, 600)])
plt.hist(x, 80, density=True)
plt.xlim(-10, 20);
from sklearn.mixture import GaussianMixture as GMM
X = x[:, np.newaxis]
clf = GMM(4, max_iter=500, random_state=3).fit(X)
xpdf = np.linspace(-10, 20, 1000)
density = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-r')
plt.xlim(-10, 20);
clf.means_
clf.covariances_
clf.weights_
plt.hist(x, 80, density=True, alpha=0.3)
plt.plot(xpdf, density, '-r')
for i in range(clf.n_components):
pdf = clf.weights_[i] * stats.norm(clf.means_[i, 0],
np.sqrt(clf.covariances_[i, 0])).pdf(xpdf)
plt.fill(xpdf, pdf, facecolor='gray',
edgecolor='none', alpha=0.3)
plt.xlim(-10, 20);
print(clf.bic(X))
print(clf.aic(X))
n_estimators = np.arange(1, 10)
clfs = [GMM(n, max_iter=1000).fit(X) for n in n_estimators]
bics = [clf.bic(X) for clf in clfs]
aics = [clf.aic(X) for clf in clfs]
plt.plot(n_estimators, bics, label='BIC')
plt.plot(n_estimators, aics, label='AIC')
plt.legend();
np.random.seed(0)
# Add 20 outliers
true_outliers = np.sort(np.random.randint(0, len(x), 20))
y = x.copy()
y[true_outliers] += 50 * np.random.randn(20)
clf = GMM(4, max_iter=500, random_state=0).fit(y[:, np.newaxis])
xpdf = np.linspace(-10, 20, 1000)
density_noise = np.array([np.exp(clf.score([[xp]])) for xp in xpdf])
plt.hist(y, 80, density=True, alpha=0.5)
plt.plot(xpdf, density_noise, '-r')
plt.xlim(-15, 30);
log_likelihood = np.array([clf.score_samples([[yy]]) for yy in y])
# log_likelihood = clf.score_samples(y[:, np.newaxis])[0]
plt.plot(y, log_likelihood, '.k');
detected_outliers = np.where(log_likelihood < -9)[0]
print("true outliers:")
print(true_outliers)
print("\ndetected outliers:")
print(detected_outliers)
set(true_outliers) - set(detected_outliers)
set(detected_outliers) - set(true_outliers)
from sklearn.neighbors import KernelDensity
kde = KernelDensity(0.15).fit(x[:, None])
density_kde = np.exp(kde.score_samples(xpdf[:, None]))
plt.hist(x, 80, density=True, alpha=0.5)
plt.plot(xpdf, density, '-b', label='GMM')
plt.plot(xpdf, density_kde, '-r', label='KDE')
plt.xlim(-10, 20)
plt.legend();
| 0.694199 | 0.984679 |
While taking the **Intro to Deep Learning with PyTorch** course by Udacity, I really liked exercise that was based on building a character-level language model using LSTMs. I was unable to complete all on my own since NLP is still a very new field to me. I decided to give the exercise a try with `tensorflow 2.0` and because of the ease of use you get in `keras`, I could develop a very simple LSTM-based language model able to predict a single character given a set of characters.
The exercise uses the **Anna Karenina** nodel written by Leo Tolstoy as its data. I used a small subset of it in this notebook, though.
```
!pip install tensorflow-gpu==2.0.0-beta1
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
import numpy as np
from tensorflow.keras.preprocessing.sequence import pad_sequences
print(tf.__version__)
```
I start by loading the novel.
```
# Open text file and read in data as `text`
with open('anna.txt', 'r') as f:
text = f.read()
# First hundred characters
text[:100]
```
The text will start look ugly now :(
```
# Strip all the new lines
tokens = text.split()
text_without_nlines = ' '.join(tokens)
```
I will be using LSTMs for developing the language model. A sequence in an one-hot-encoded form is needed to be given as its input. Each input sequence will be 50 characters with one output character, making each sequence 51 characters long.
We can create the sequences by enumerating the characters in the text, starting at the 51st character at index 50.
```
# Prepare the sequences for the model
length = 50
sequences = []
for i in range(length, len(text_without_nlines)):
# Select sequence of tokens
seq = text_without_nlines[i-length:i+1]
sequences.append(seq)
print('Total Sequences: {}'.format(len(sequences)))
# Save these sequences for later use
filename = 'char_sequences.txt'
data = '\n'.join(sequences)
file = open(filename, 'w')
file.write(data)
file.close()
print('File saved!')
# Preview
!head -5 char_sequences.txt
# Load up the data
sequences_from_file = open('char_sequences.txt')
text = sequences_from_file.read()
lines = text.split('\n')
# Cause computers understand only numbers
# Assigning each character a unique integer
# Charater -> Integer
chars = sorted(list(set(text)))
mapping = dict((c, i) for i, c in enumerate(chars))
# Convert the sequences to integer encodings
int_sequences = []
for line in lines:
encoded_seq = [mapping[char] for char in line]
int_sequences.append(encoded_seq)
# How big is the corpus?
vocab_size = len(mapping)
print('Voacabulary size', vocab_size)
# X -> y mapping of input sequence in this form
int_sequences = np.array(int_sequences)
X, y = int_sequences[:,:-1], int_sequences[:,-1]
```
I will be using a very small subset of data.
```
X[:10000].shape, y[:10000].shape
```
The characters will have to be one-hot-encoded before they are fed to the language model. It also preserves a concise input representation but when the input feature space is very very large, Character Embeddings should be used before.
```
one_hot_sequences = [tf.keras.utils.to_categorical(x, num_classes=vocab_size) for x in X[:10000]]
X = np.array(one_hot_sequences)
y = tf.keras.utils.to_categorical(y[:10000], num_classes=vocab_size)
# Mini language model :)
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.LSTM(256, input_shape=(X.shape[1], X.shape[2])))
model.add(tf.keras.layers.Dense(vocab_size, activation='softmax'))
print(model.summary())
```
There can be a problem of exploding gradients and to prevent that I am going to specify the `clipnorm` term in the optimizer.
```
adam = Adam(lr=.001, clipnorm=0.5)
model.compile(loss='categorical_crossentropy', optimizer=adam, metrics=['accuracy'])
model.fit(X, y, epochs=200, verbose=2)
```
The training loss keeps on decreasing and the accuracy keeps getting increased. This is a good sign.
Now that the model is trained, we can employ it to generate characters on given sequences of characters. For doing this, the model would require the given inputs to be exactly in the shape with which it was trained. If we give an input sequence that does not *exactly* match with that of the training input sequences, we will get errors.
We will use the `pad_sequences()` function which will truncate the characters from first the half of the test input sequences and padd extra characters if needed (0 essentially). We will define a small helper function for generating characters of user-specified length. The user will have to provide some initial text to the model, though.
```
def generate_seq(model, mapping, seq_length, init_text, n_chars):
in_text = init_text
# Generate a fixed number of characters
for _ in range(n_chars):
# Encode to integers
encoded = [mapping[char] for char in in_text]
# Map sequences to a fixed length
encoded = pad_sequences([encoded], maxlen=seq_length, padding='pre', truncating='pre')
# print(encoded.shape)
# One-hot encode
encoded = tf.keras.utils.to_categorical(encoded, num_classes=vocab_size)
# print(encoded.shape)
# Predict character
yhat = model.predict_classes(encoded, verbose=0)
# Integer -> Character
out_char = ''
for char, index in mapping.items():
if index == yhat:
out_char = char
break
# We append the characters after the input sequence
in_text += char
return in_text
# Let's test
print(generate_seq(model, mapping, 50, 'And Levin said', 20))
print(generate_seq(model, mapping, 50, 'Happy families', 20))
```
The model does generate something meaningful. At this stage it is really nothing apart from just one LSTM layer (and its power is evident).
|
github_jupyter
|
!pip install tensorflow-gpu==2.0.0-beta1
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
import numpy as np
from tensorflow.keras.preprocessing.sequence import pad_sequences
print(tf.__version__)
# Open text file and read in data as `text`
with open('anna.txt', 'r') as f:
text = f.read()
# First hundred characters
text[:100]
# Strip all the new lines
tokens = text.split()
text_without_nlines = ' '.join(tokens)
# Prepare the sequences for the model
length = 50
sequences = []
for i in range(length, len(text_without_nlines)):
# Select sequence of tokens
seq = text_without_nlines[i-length:i+1]
sequences.append(seq)
print('Total Sequences: {}'.format(len(sequences)))
# Save these sequences for later use
filename = 'char_sequences.txt'
data = '\n'.join(sequences)
file = open(filename, 'w')
file.write(data)
file.close()
print('File saved!')
# Preview
!head -5 char_sequences.txt
# Load up the data
sequences_from_file = open('char_sequences.txt')
text = sequences_from_file.read()
lines = text.split('\n')
# Cause computers understand only numbers
# Assigning each character a unique integer
# Charater -> Integer
chars = sorted(list(set(text)))
mapping = dict((c, i) for i, c in enumerate(chars))
# Convert the sequences to integer encodings
int_sequences = []
for line in lines:
encoded_seq = [mapping[char] for char in line]
int_sequences.append(encoded_seq)
# How big is the corpus?
vocab_size = len(mapping)
print('Voacabulary size', vocab_size)
# X -> y mapping of input sequence in this form
int_sequences = np.array(int_sequences)
X, y = int_sequences[:,:-1], int_sequences[:,-1]
X[:10000].shape, y[:10000].shape
one_hot_sequences = [tf.keras.utils.to_categorical(x, num_classes=vocab_size) for x in X[:10000]]
X = np.array(one_hot_sequences)
y = tf.keras.utils.to_categorical(y[:10000], num_classes=vocab_size)
# Mini language model :)
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.LSTM(256, input_shape=(X.shape[1], X.shape[2])))
model.add(tf.keras.layers.Dense(vocab_size, activation='softmax'))
print(model.summary())
adam = Adam(lr=.001, clipnorm=0.5)
model.compile(loss='categorical_crossentropy', optimizer=adam, metrics=['accuracy'])
model.fit(X, y, epochs=200, verbose=2)
def generate_seq(model, mapping, seq_length, init_text, n_chars):
in_text = init_text
# Generate a fixed number of characters
for _ in range(n_chars):
# Encode to integers
encoded = [mapping[char] for char in in_text]
# Map sequences to a fixed length
encoded = pad_sequences([encoded], maxlen=seq_length, padding='pre', truncating='pre')
# print(encoded.shape)
# One-hot encode
encoded = tf.keras.utils.to_categorical(encoded, num_classes=vocab_size)
# print(encoded.shape)
# Predict character
yhat = model.predict_classes(encoded, verbose=0)
# Integer -> Character
out_char = ''
for char, index in mapping.items():
if index == yhat:
out_char = char
break
# We append the characters after the input sequence
in_text += char
return in_text
# Let's test
print(generate_seq(model, mapping, 50, 'And Levin said', 20))
print(generate_seq(model, mapping, 50, 'Happy families', 20))
| 0.701713 | 0.947381 |
## Example. Estimating the speed of light
Simon Newcomb's measurements of the speed of light, from
> Stigler, S. M. (1977). Do robust estimators work with real data? (with discussion). *Annals of
Statistics* **5**, 1055–1098.
The data are recorded as deviations from $24\ 800$
nanoseconds. Table 3.1 of Bayesian Data Analysis.
28 26 33 24 34 -44 27 16 40 -2
29 22 24 21 25 30 23 29 31 19
24 20 36 32 36 28 25 21 28 29
37 25 28 26 30 32 36 26 30 22
36 23 27 27 28 27 31 27 26 33
26 32 32 24 39 28 24 25 32 25
29 27 28 29 16 23
```
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from scipy.optimize import brentq
plt.style.use('seaborn-darkgrid')
plt.rc('font', size=12)
%config Inline.figure_formats = ['retina']
numbs = "28 26 33 24 34 -44 27 16 40 -2 29 22 \
24 21 25 30 23 29 31 19 24 20 36 32 36 28 25 21 28 29 \
37 25 28 26 30 32 36 26 30 22 36 23 27 27 28 27 31 27 26 \
33 26 32 32 24 39 28 24 25 32 25 29 27 28 29 16 23"
nums = np.array([int(i) for i in numbs.split(' ')])
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(nums, bins=35, edgecolor='w')
plt.title('Distribution of the measurements');
mean_t = np.mean(nums)
print(f'The mean of the 66 measurements is {mean_t:.1f}')
std_t = np.std(nums, ddof=1)
print(f'The standard deviation of the 66 measurements is {std_t:.1f}')
```
And now, we use `pymc` to estimate the mean and the standard deviation from the data.
```
with pm.Model() as model_1:
mu = pm.Uniform('mu', lower=10, upper=30)
sigma = pm.Uniform('sigma', lower=0, upper=20)
post = pm.Normal('post', mu=mu, sd=sigma, observed=nums)
with model_1:
trace_1 = pm.sample(draws=50_000, tune=50_000)
az.plot_trace(trace_1);
df = pm.summary(trace_1)
df.style.format('{:.4f}')
```
As you can see, the highest posterior interval for `mu` is [23.69, 28.77].
```
pm.plot_posterior(trace_1, var_names=['mu'], kind = 'hist');
```
The true posterior distribution is $t_{65}$
```
from scipy.stats import t
x = np.linspace(22, 30, 500)
y = t.pdf(x, 65, loc=mean_t)
y_pred = t.pdf(x, 65, loc=df['mean'].values[0])
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='True', linewidth=5)
plt.plot(x, y_pred, 'o', label='Predicted', alpha=0.2)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\mu$', fontsize=14);
```
The book says you can find the posterior interval by simulation, so let's do that with Python. First, draw random values of $\sigma^2$ and $\mu$.
```
mu_estim = []
for i in range(10_000):
y = np.random.chisquare(65)
y2 = 65 * std_t**2 / y
yy = np.random.normal(loc=mean_t, scale=y2/66)
mu_estim.append(yy)
```
To visualize `mu_estim`, we plot a histogram.
```
plt.figure(figsize=(8,5))
rang, bins1, _ = plt.hist(mu_estim, bins=1000, density=True)
plt.xlabel(r'$\mu$', fontsize=14);
```
The advantage here is that you can find the median and the central posterior interval. Well, the median is...
```
idx = bins1.shape[0] // 2
print((bins1[idx] + bins1[idx + 1]) / 2)
```
And the central posterior interval is... not that easy to find. We have to find $a$ such as:
$$\int_{\mu -a}^{\mu +a} f(x)\, dx = 0.95,$$
with $\mu$ the median. We need to define $dx$ and $f(x)$.
```
delta_bin = bins1[1] - bins1[0]
print(f'This is delta x: {delta_bin}')
```
We define a function to find $a$ (in fact, $a$ is an index). `rang` is $f(x)$.
```
def func3(a):
return sum(rang[idx - int(a):idx + int(a)] * delta_bin) - 0.95
idx_sol = brentq(func3, 0, idx)
idx_sol
```
That number is an index, therefore the interval is:
```
l_i = bins1[idx - int(idx_sol)]
l_d = bins1[idx + int(idx_sol)]
print(f'The central posterior interval is [{l_i:.2f}, {l_d:.2f}]')
```
## Example. Pre-election polling
Let's put that in code.
```
obs = np.array([727, 583, 137])
bush_supp = obs[0] / sum(obs)
dukakis_supp = obs[1] / sum(obs)
other_supp = obs[2] / sum(obs)
arr = np.array([bush_supp, dukakis_supp, other_supp])
print('The proportion array is', arr)
print('The supporters array is', obs)
```
Remember that we want to find the distribution of $\theta_1 - \theta_2$. In this case, the prior distribution on each $\theta$ is a uniform distribution; the data $(y_1, y_2, y_3)$ follow a multinomial distribution, with parameters $(\theta_1, \theta_2, \theta_3)$.
```
import theano
import theano.tensor as tt
with pm.Model() as model_3:
theta1 = pm.Uniform('theta1', lower=0, upper=1)
theta2 = pm.Uniform('theta2', lower=0, upper=1)
theta3 = pm.Uniform('theta3', lower=0, upper=1)
post = pm.Multinomial('post', n=obs.sum(), p=[theta1, theta2, theta3], observed=obs)
diff = pm.Deterministic('diff', theta1 - theta2)
model_3.check_test_point()
pm.model_to_graphviz(model_3)
with model_3:
trace_3 = pm.sample(draws=50_000, tune=50_000)
az.plot_trace(trace_3);
pm.summary(trace_3, kind = "stats")
pm.summary(trace_3, kind = "diagnostics")
```
As you can see, the way we write the model is not good, that's why you see a lot of divergences and `ess_bulk` (the bulk effective sample size) as well as `ess_tail` (the tail effective sample size) are very, very low. This can be improved.
```
with pm.Model() as model_4:
theta = pm.Dirichlet('theta', a=np.ones_like(obs))
post = pm.Multinomial('post', n=obs.sum(), p=theta, observed=obs)
with model_4:
trace_4 = pm.sample(10_000, tune=5000)
az.plot_trace(trace_4);
pm.summary(trace_4)
```
Better trace plot and better `ess_bulk`/`ess_tail`. Now we can estimate $\theta_1 - \theta_2$, we draw 4000 points from the posterior distribution.
```
post_samples = pm.sample_posterior_predictive(trace_4, samples=4_000, model=model_4)
diff = []
sum_post_sample = post_samples['post'].sum(axis=1)[0]
for i in range(post_samples['post'].shape[0]):
diff.append((post_samples['post'][i, 0] -
post_samples['post'][i, 1]) / sum_post_sample)
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(diff, bins=25, edgecolor='w', density=True)
plt.title(r'Distribution of $\theta_1 - \theta_2$ using Pymc3');
```
Of course you can compare this result with the true posterior distribution
```
from scipy.stats import dirichlet
ddd = dirichlet([728, 584, 138])
rad = []
for i in range(4_000):
rad.append(ddd.rvs()[0][0] - ddd.rvs()[0][1])
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(rad, color='C5', bins=25, edgecolor='w', density=True)
plt.title(r'Distribution of $\theta_1 - \theta_2$');
plt.figure(figsize=(10, 6))
sns.kdeplot(rad, label='True')
sns.kdeplot(diff, label='Predicted');
plt.title('Comparison between both methods')
plt.xlabel(r'$\theta_1 - \theta_2$', fontsize=14);
```
## Example: analysis of a bioassay experiment
This information is in Table 3.1
```
x_dose = np.array([-0.86, -0.3, -0.05, 0.73])
n_anim = np.array([5, 5, 5, 5])
y_deat = np.array([0, 1, 3, 5])
with pm.Model() as model_5:
alpha = pm.Uniform('alpha', lower=-5, upper=7)
beta = pm.Uniform('beta', lower=0, upper=50)
theta = pm.math.invlogit(alpha + beta * x_dose)
post = pm.Binomial('post', n=n_anim, p=theta, observed=y_deat)
with model_5:
trace_5 = pm.sample(draws=10_000, tune=15_000)
az.plot_trace(trace_5);
df5 = pm.summary(trace_5)
df5.style.format('{:.4f}')
```
The next plots are a scatter plot, a plot for the posterior for `alpha` and `beta` and a countour plot.
```
az.plot_pair(trace_5, figsize=(8, 7), divergences=True, kind = "hexbin");
fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(13, 5))
az.plot_posterior(trace_5, ax=ax, kind='hist');
fig, ax = plt.subplots(figsize=(10,6))
sns.kdeplot(trace_5['alpha'][30000:40000], trace_5['beta'][30000:40000],
cmap=plt.cm.viridis, ax=ax, n_levels=10)
ax.set_xlim(-2, 4)
ax.set_ylim(-2, 27)
ax.set_xlabel('alpha')
ax.set_ylabel('beta');
```
Histogram of the draws from the posterior distribution of the LD50
```
ld50 = []
begi = 1500
for i in range(1000):
ld50.append( - trace_5['alpha'][begi + i] / trace_5['beta'][begi + i])
plt.figure(figsize=(10, 6))
_, _, _, = plt.hist(ld50, bins=25, edgecolor='w')
plt.xlabel('LD50', fontsize=14);
%load_ext watermark
%watermark -iv -v -p theano,scipy,matplotlib -m
```
|
github_jupyter
|
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from scipy.optimize import brentq
plt.style.use('seaborn-darkgrid')
plt.rc('font', size=12)
%config Inline.figure_formats = ['retina']
numbs = "28 26 33 24 34 -44 27 16 40 -2 29 22 \
24 21 25 30 23 29 31 19 24 20 36 32 36 28 25 21 28 29 \
37 25 28 26 30 32 36 26 30 22 36 23 27 27 28 27 31 27 26 \
33 26 32 32 24 39 28 24 25 32 25 29 27 28 29 16 23"
nums = np.array([int(i) for i in numbs.split(' ')])
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(nums, bins=35, edgecolor='w')
plt.title('Distribution of the measurements');
mean_t = np.mean(nums)
print(f'The mean of the 66 measurements is {mean_t:.1f}')
std_t = np.std(nums, ddof=1)
print(f'The standard deviation of the 66 measurements is {std_t:.1f}')
with pm.Model() as model_1:
mu = pm.Uniform('mu', lower=10, upper=30)
sigma = pm.Uniform('sigma', lower=0, upper=20)
post = pm.Normal('post', mu=mu, sd=sigma, observed=nums)
with model_1:
trace_1 = pm.sample(draws=50_000, tune=50_000)
az.plot_trace(trace_1);
df = pm.summary(trace_1)
df.style.format('{:.4f}')
pm.plot_posterior(trace_1, var_names=['mu'], kind = 'hist');
from scipy.stats import t
x = np.linspace(22, 30, 500)
y = t.pdf(x, 65, loc=mean_t)
y_pred = t.pdf(x, 65, loc=df['mean'].values[0])
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='True', linewidth=5)
plt.plot(x, y_pred, 'o', label='Predicted', alpha=0.2)
plt.legend()
plt.title('The posterior distribution')
plt.xlabel(r'$\mu$', fontsize=14);
mu_estim = []
for i in range(10_000):
y = np.random.chisquare(65)
y2 = 65 * std_t**2 / y
yy = np.random.normal(loc=mean_t, scale=y2/66)
mu_estim.append(yy)
plt.figure(figsize=(8,5))
rang, bins1, _ = plt.hist(mu_estim, bins=1000, density=True)
plt.xlabel(r'$\mu$', fontsize=14);
idx = bins1.shape[0] // 2
print((bins1[idx] + bins1[idx + 1]) / 2)
delta_bin = bins1[1] - bins1[0]
print(f'This is delta x: {delta_bin}')
def func3(a):
return sum(rang[idx - int(a):idx + int(a)] * delta_bin) - 0.95
idx_sol = brentq(func3, 0, idx)
idx_sol
l_i = bins1[idx - int(idx_sol)]
l_d = bins1[idx + int(idx_sol)]
print(f'The central posterior interval is [{l_i:.2f}, {l_d:.2f}]')
obs = np.array([727, 583, 137])
bush_supp = obs[0] / sum(obs)
dukakis_supp = obs[1] / sum(obs)
other_supp = obs[2] / sum(obs)
arr = np.array([bush_supp, dukakis_supp, other_supp])
print('The proportion array is', arr)
print('The supporters array is', obs)
import theano
import theano.tensor as tt
with pm.Model() as model_3:
theta1 = pm.Uniform('theta1', lower=0, upper=1)
theta2 = pm.Uniform('theta2', lower=0, upper=1)
theta3 = pm.Uniform('theta3', lower=0, upper=1)
post = pm.Multinomial('post', n=obs.sum(), p=[theta1, theta2, theta3], observed=obs)
diff = pm.Deterministic('diff', theta1 - theta2)
model_3.check_test_point()
pm.model_to_graphviz(model_3)
with model_3:
trace_3 = pm.sample(draws=50_000, tune=50_000)
az.plot_trace(trace_3);
pm.summary(trace_3, kind = "stats")
pm.summary(trace_3, kind = "diagnostics")
with pm.Model() as model_4:
theta = pm.Dirichlet('theta', a=np.ones_like(obs))
post = pm.Multinomial('post', n=obs.sum(), p=theta, observed=obs)
with model_4:
trace_4 = pm.sample(10_000, tune=5000)
az.plot_trace(trace_4);
pm.summary(trace_4)
post_samples = pm.sample_posterior_predictive(trace_4, samples=4_000, model=model_4)
diff = []
sum_post_sample = post_samples['post'].sum(axis=1)[0]
for i in range(post_samples['post'].shape[0]):
diff.append((post_samples['post'][i, 0] -
post_samples['post'][i, 1]) / sum_post_sample)
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(diff, bins=25, edgecolor='w', density=True)
plt.title(r'Distribution of $\theta_1 - \theta_2$ using Pymc3');
from scipy.stats import dirichlet
ddd = dirichlet([728, 584, 138])
rad = []
for i in range(4_000):
rad.append(ddd.rvs()[0][0] - ddd.rvs()[0][1])
plt.figure(figsize=(10, 6))
_, _, _ = plt.hist(rad, color='C5', bins=25, edgecolor='w', density=True)
plt.title(r'Distribution of $\theta_1 - \theta_2$');
plt.figure(figsize=(10, 6))
sns.kdeplot(rad, label='True')
sns.kdeplot(diff, label='Predicted');
plt.title('Comparison between both methods')
plt.xlabel(r'$\theta_1 - \theta_2$', fontsize=14);
x_dose = np.array([-0.86, -0.3, -0.05, 0.73])
n_anim = np.array([5, 5, 5, 5])
y_deat = np.array([0, 1, 3, 5])
with pm.Model() as model_5:
alpha = pm.Uniform('alpha', lower=-5, upper=7)
beta = pm.Uniform('beta', lower=0, upper=50)
theta = pm.math.invlogit(alpha + beta * x_dose)
post = pm.Binomial('post', n=n_anim, p=theta, observed=y_deat)
with model_5:
trace_5 = pm.sample(draws=10_000, tune=15_000)
az.plot_trace(trace_5);
df5 = pm.summary(trace_5)
df5.style.format('{:.4f}')
az.plot_pair(trace_5, figsize=(8, 7), divergences=True, kind = "hexbin");
fig, ax = plt.subplots(ncols=2, nrows=1, figsize=(13, 5))
az.plot_posterior(trace_5, ax=ax, kind='hist');
fig, ax = plt.subplots(figsize=(10,6))
sns.kdeplot(trace_5['alpha'][30000:40000], trace_5['beta'][30000:40000],
cmap=plt.cm.viridis, ax=ax, n_levels=10)
ax.set_xlim(-2, 4)
ax.set_ylim(-2, 27)
ax.set_xlabel('alpha')
ax.set_ylabel('beta');
ld50 = []
begi = 1500
for i in range(1000):
ld50.append( - trace_5['alpha'][begi + i] / trace_5['beta'][begi + i])
plt.figure(figsize=(10, 6))
_, _, _, = plt.hist(ld50, bins=25, edgecolor='w')
plt.xlabel('LD50', fontsize=14);
%load_ext watermark
%watermark -iv -v -p theano,scipy,matplotlib -m
| 0.627495 | 0.955693 |
```
%matplotlib inline
```
# Net file
This is the Net file for the clique problem: state and output transition function definition
```
import tensorflow as tf
import numpy as np
def weight_variable(shape, nm):
'''function to initialize weights'''
initial = tf.truncated_normal(shape, stddev=0.1)
tf.summary.histogram(nm, initial, collections=['always'])
return tf.Variable(initial, name=nm)
class Net:
'''class to define state and output network'''
def __init__(self, input_dim, state_dim, output_dim):
'''initialize weight and parameter'''
self.EPSILON = 0.00000001
self.input_dim = input_dim
self.state_dim = state_dim
self.output_dim = output_dim
self.state_input = self.input_dim - 1 + state_dim
#### TO BE SET FOR A SPECIFIC PROBLEM
self.state_l1 = 15
self.state_l2 = self.state_dim
self.output_l1 = 10
self.output_l2 = self.output_dim
# list of weights
self.weights = {'State_L1': weight_variable([self.state_input, self.state_l1], "WEIGHT_STATE_L1"),
'State_L2': weight_variable([ self.state_l1, self.state_l2], "WEIGHT_STATE_L1"),
'Output_L1':weight_variable([self.state_l2,self.output_l1], "WEIGHT_OUTPUT_L1"),
'Output_L2': weight_variable([self.output_l1, self.output_l2], "WEIGHT_OUTPUT_L2")
}
# list of biases
self.biases = {'State_L1': weight_variable([self.state_l1],"BIAS_STATE_L1"),
'State_L2': weight_variable([self.state_l2], "BIAS_STATE_L2"),
'Output_L1':weight_variable([self.output_l1],"BIAS_OUTPUT_L1"),
'Output_L2': weight_variable([ self.output_l2], "BIAS_OUTPUT_L2")
}
def netSt(self, inp):
with tf.variable_scope('State_net'):
# method to define the architecture of the state network
layer1 = tf.nn.tanh(tf.add(tf.matmul(inp,self.weights["State_L1"]),self.biases["State_L1"]))
layer2 = tf.nn.tanh(tf.add(tf.matmul(layer1, self.weights["State_L2"]), self.biases["State_L2"]))
return layer2
def netOut(self, inp):
# method to define the architecture of the output network
with tf.variable_scope('Out_net'):
layer1 = tf.nn.tanh(tf.add(tf.matmul(inp, self.weights["Output_L1"]), self.biases["Output_L1"]))
layer2 = tf.nn.softmax(tf.add(tf.matmul(layer1, self.weights["Output_L2"]), self.biases["Output_L2"]))
return layer2
def Loss(self, output, target, output_weight=None):
# method to define the loss function
#lo=tf.losses.softmax_cross_entropy(target,output)
output = tf.maximum(output, self.EPSILON, name="Avoiding_explosions") # to avoid explosions
xent = -tf.reduce_sum(target * tf.log(output), 1)
lo = tf.reduce_mean(xent)
return lo
def Metric(self, target, output, output_weight=None):
# method to define the evaluation metric
correct_prediction = tf.equal(tf.argmax(output, 1), tf.argmax(target, 1))
metric = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
return metric
```
|
github_jupyter
|
%matplotlib inline
import tensorflow as tf
import numpy as np
def weight_variable(shape, nm):
'''function to initialize weights'''
initial = tf.truncated_normal(shape, stddev=0.1)
tf.summary.histogram(nm, initial, collections=['always'])
return tf.Variable(initial, name=nm)
class Net:
'''class to define state and output network'''
def __init__(self, input_dim, state_dim, output_dim):
'''initialize weight and parameter'''
self.EPSILON = 0.00000001
self.input_dim = input_dim
self.state_dim = state_dim
self.output_dim = output_dim
self.state_input = self.input_dim - 1 + state_dim
#### TO BE SET FOR A SPECIFIC PROBLEM
self.state_l1 = 15
self.state_l2 = self.state_dim
self.output_l1 = 10
self.output_l2 = self.output_dim
# list of weights
self.weights = {'State_L1': weight_variable([self.state_input, self.state_l1], "WEIGHT_STATE_L1"),
'State_L2': weight_variable([ self.state_l1, self.state_l2], "WEIGHT_STATE_L1"),
'Output_L1':weight_variable([self.state_l2,self.output_l1], "WEIGHT_OUTPUT_L1"),
'Output_L2': weight_variable([self.output_l1, self.output_l2], "WEIGHT_OUTPUT_L2")
}
# list of biases
self.biases = {'State_L1': weight_variable([self.state_l1],"BIAS_STATE_L1"),
'State_L2': weight_variable([self.state_l2], "BIAS_STATE_L2"),
'Output_L1':weight_variable([self.output_l1],"BIAS_OUTPUT_L1"),
'Output_L2': weight_variable([ self.output_l2], "BIAS_OUTPUT_L2")
}
def netSt(self, inp):
with tf.variable_scope('State_net'):
# method to define the architecture of the state network
layer1 = tf.nn.tanh(tf.add(tf.matmul(inp,self.weights["State_L1"]),self.biases["State_L1"]))
layer2 = tf.nn.tanh(tf.add(tf.matmul(layer1, self.weights["State_L2"]), self.biases["State_L2"]))
return layer2
def netOut(self, inp):
# method to define the architecture of the output network
with tf.variable_scope('Out_net'):
layer1 = tf.nn.tanh(tf.add(tf.matmul(inp, self.weights["Output_L1"]), self.biases["Output_L1"]))
layer2 = tf.nn.softmax(tf.add(tf.matmul(layer1, self.weights["Output_L2"]), self.biases["Output_L2"]))
return layer2
def Loss(self, output, target, output_weight=None):
# method to define the loss function
#lo=tf.losses.softmax_cross_entropy(target,output)
output = tf.maximum(output, self.EPSILON, name="Avoiding_explosions") # to avoid explosions
xent = -tf.reduce_sum(target * tf.log(output), 1)
lo = tf.reduce_mean(xent)
return lo
def Metric(self, target, output, output_weight=None):
# method to define the evaluation metric
correct_prediction = tf.equal(tf.argmax(output, 1), tf.argmax(target, 1))
metric = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
return metric
| 0.738575 | 0.843186 |
<a href="https://colab.research.google.com/github/seyrankhademi/introduction2AI/blob/main/linear_vs_mlp.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Computer Programming vs Machine Learning
This notebook is written by Dr. Seyran Khademi to familiarize the students with the concept of machine learning and its difference with computer programming. The code is developed in Jupyter notebook and it is compatible with the Google Colab platform.
---
## What is fundamentally different between machine learning and computer programming?
Let's look at an example project. Suppose that university wants to automate the process of granting scholarship to the students. They need a computer to make a decision whether an applicant is eligible for the scholarship or not based on some handcrafted features extracted by people at university including 1) grade point average (GPA) 2) quality of portfolio(QP) 3) Age and 4) whether the applicant has other loans or not. So for each applicant, there is a given tabular data like the following:
| Features | Applicant
|------|------|
| GPA | a number between [0,10]|
| QP |a number between [0,10] |
| Age |an integer between [18,40]|
| Loan |1 or 0 for loan/no loan|
Weighted-sum program
In the first attempt, we use a piece of code that computes the weighted sum of the given features as the final score for the applicant. In computer programming, the program (the rules) are set by the human explicitly. In our scholarship project, the rules are the weights for each feature,i.e., $[w_1,w_2,w_3,w_4]$. Note that each weight is the importance of the corresponding feature in the final score. Suppose that the committee for the scholarship assignment proposes the following weights $[0.4.0.3,0.2,0.1]$ respectively. The following cell is the code snippet that computes the final score of the applicant by the given weights.
```
# The weighet-sum function takes as an input the feature values for the applicant
# and outputs the final score.
import numpy as np
def weighted_sum(GPA,QP,Age,Loan):
#check that the points for GPA and QP are in range between 0 and 10
x=GPA
y=QP
points = np.array([x,y])
if (points < 0).all() and (points > 10).all():
print("Error: The GPA and PQ points must be between 0 and 10.")
#check that the age in range between 18 and 40
z=Age
if (z < 18) or (z > 40):
print("Note: Applicants younger than 18 and older than 40 are not eligible for the scholorship.")
#check that the loan feature is specified as binary
v=Loan
if (z ==0 or z==1):
print("Error: If the applicant has other loans currently enter 1 otherwise enter 0 for the Loan feature.")
#compute the weighed sum score
w1=0.4
w2=0.3
w3=0.2
w4=0.1
Score=w1*x+w2*y+w3*z+w4*v
print("Final score for the applicant is", + Score)
```
Let's see what is the score for Sara given the folowing records:
| Features | Sara
|------|------|
| GPA | 7.8|
| QP |6.5 |
| Age |26|
| Loan |0|
We call the function ```weighted_sum``` to compute the score ...
```
weighted_sum(7.8,6.5,26,0)
```
By running the code cell you found out what is the final score for Sara. In case the scholarship is competitive you need to compute the scores for other applicants and see whether Sara is in, e.g., the top 50% or not but we stop here as we made already our point. The weights (the selection rule) are given to the computer for this task by the human experts that learned the weightings empirically over the years of doing their job!
## Machine Learning (ML)
University collected enough digital records from the students who have applied for the scholarship together with the outcome based on the following criteria that Whether the student
1. finished master studies in less than two year
2. has returned the loan within 10 years
Given the amount of data the university decided to replace the averaging software with an ML model that can be *trained* on the available data to *learn* the selection rules.
---
In the following code cell, we generate some synthetic data for this task as we don't really have the students record. For the sake of visualization purposes, we only take two features per applicant lets to say GPA and QP.
```
# generate syntatic data with two features (GPA and QP) and two class labels (sucsesful or not)
from sklearn.datasets import make_moons, make_circles, make_classification,make_gaussian_quantiles
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# The random-state in the data generator is set to fix for reproducibility.
data,labels = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=2, class_sep=0.9, random_state=42)
# fit the features in the range [0 10]
scaler = MinMaxScaler(feature_range=(0, 10))
data_scaled = scaler.fit_transform(data)
# plot samples of data points with their labels
plt.scatter(data_scaled [:, 0], data_scaled [:, 1], marker='o', c=labels, s=100, edgecolor='k')
plt.xlabel('Quality of portfolio')
plt.ylabel('GPA')
plt.show()
```
So you should see a figure with two classes "Purple" and "Yellow". Can you guess which class represents the "successful" students?
Next we train a simple ML model on these data to classify "Purple" from "Yellow".
---
We need to split our data into the test and train sets. The test set is used for evaluation of the model and the training set is for the model to learn the best decision-making rule from.
```
from sklearn.model_selection import train_test_split
# normalizing data to get best performance
X = StandardScaler().fit_transform(data)
# splitting data to train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=.4, random_state=42)
from sklearn import metrics
# evalution function takes the test data and the clf and calculates the accuracy of the model
def evaluate(X_test,clf):
y_pred = clf.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
```
Our first model is a simple linear classifer to be trained and evaluted on the train and the test data respectively.
```
from sklearn import svm
clf = svm.SVC(kernel='linear')
clf.fit(X_train,y_train)
evaluate(X_test,clf)
```
Our simple ML model performs with $86\%$ accuracy. Is that acceptable for our application?
---
Let's look closer to the data again and the decision boundry of our trained classifier.
```
# the function gets the training data, labels and the classifier and plots decision boundry
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
def plot_decision_boundary(X_train,y_train,clf):
gs = gridspec.GridSpec(2, 2)
fig = plot_decision_regions(X_train, y_train.astype(np.integer),clf=clf, legend=2)
plot_decision_boundary(X_train,y_train,clf)
```
As you can see the linear classifier called support vector machine (SVM) may not be flexible enough to separate our (normalized) data.
## Neural Network
The next classifier that we try is a very simple Neural Network that is a very basic nonlinear model that is called a multi-layer perceptron (MLP).
MLP is more flexible than our simple SVM.
```
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(solver='adam', alpha=1e-3, hidden_layer_sizes=(5, 2), learning_rate_init=0.005, max_iter=1000, random_state=1)
clf.fit(X_train,y_train)
evaluate(X_test,clf)
```
Our accuracy improved to $90\%$ using the MLP. Let's look at the decision plot to get a glance at our neural network classifier.
```
plot_decision_boundary(X_train,y_train,clf)
```
It is clear that our MLP model with more parameters (thus more complex) can adapt better to our synthetic dataset. In deep learning, the computer model is much more complex with thousands and millions of parameters to adapt to data with a complex nature. Nevertheless, training deep learning models requires great computational power and training time so we skip it in this tutorial. For real data and proper deep learning models, you can visit https://github.com/seyrankhademi/ResNet_CIFAR10.
## Conclusion
Once we have complex data, we need complex models to analyze that. Our synthetic data is way more simple in terms of dimensionality compared to real data captured from our world. However, we observed the effect of introducing a relatively more complex model compared to the linear model for the task of classification even in this simplified setting. Note that deep learning follows the same rules of statistical learning as developed for years in machine learning, however, we had not had enough computational power up to just recent years and such a huge amount of data to process in order to deploy deep learning.
|
github_jupyter
|
# The weighet-sum function takes as an input the feature values for the applicant
# and outputs the final score.
import numpy as np
def weighted_sum(GPA,QP,Age,Loan):
#check that the points for GPA and QP are in range between 0 and 10
x=GPA
y=QP
points = np.array([x,y])
if (points < 0).all() and (points > 10).all():
print("Error: The GPA and PQ points must be between 0 and 10.")
#check that the age in range between 18 and 40
z=Age
if (z < 18) or (z > 40):
print("Note: Applicants younger than 18 and older than 40 are not eligible for the scholorship.")
#check that the loan feature is specified as binary
v=Loan
if (z ==0 or z==1):
print("Error: If the applicant has other loans currently enter 1 otherwise enter 0 for the Loan feature.")
#compute the weighed sum score
w1=0.4
w2=0.3
w3=0.2
w4=0.1
Score=w1*x+w2*y+w3*z+w4*v
print("Final score for the applicant is", + Score)
weighted_sum(7.8,6.5,26,0)
# generate syntatic data with two features (GPA and QP) and two class labels (sucsesful or not)
from sklearn.datasets import make_moons, make_circles, make_classification,make_gaussian_quantiles
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# The random-state in the data generator is set to fix for reproducibility.
data,labels = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=2, class_sep=0.9, random_state=42)
# fit the features in the range [0 10]
scaler = MinMaxScaler(feature_range=(0, 10))
data_scaled = scaler.fit_transform(data)
# plot samples of data points with their labels
plt.scatter(data_scaled [:, 0], data_scaled [:, 1], marker='o', c=labels, s=100, edgecolor='k')
plt.xlabel('Quality of portfolio')
plt.ylabel('GPA')
plt.show()
from sklearn.model_selection import train_test_split
# normalizing data to get best performance
X = StandardScaler().fit_transform(data)
# splitting data to train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=.4, random_state=42)
from sklearn import metrics
# evalution function takes the test data and the clf and calculates the accuracy of the model
def evaluate(X_test,clf):
y_pred = clf.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
from sklearn import svm
clf = svm.SVC(kernel='linear')
clf.fit(X_train,y_train)
evaluate(X_test,clf)
# the function gets the training data, labels and the classifier and plots decision boundry
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
def plot_decision_boundary(X_train,y_train,clf):
gs = gridspec.GridSpec(2, 2)
fig = plot_decision_regions(X_train, y_train.astype(np.integer),clf=clf, legend=2)
plot_decision_boundary(X_train,y_train,clf)
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(solver='adam', alpha=1e-3, hidden_layer_sizes=(5, 2), learning_rate_init=0.005, max_iter=1000, random_state=1)
clf.fit(X_train,y_train)
evaluate(X_test,clf)
plot_decision_boundary(X_train,y_train,clf)
| 0.651022 | 0.989501 |
# The Fourier Transform
*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Properties
The Fourier transform has a number of specific properties. They can be concluded from its definition. The most important ones in the context of signals and systems are reviewed in the following.
### Invertibility
According to the [Fourier inversion theorem](https://en.wikipedia.org/wiki/Fourier_inversion_theorem), for many types of signals it is possible to recover the signal $x(t)$ from its Fourier transformation $X(j \omega) = \mathcal{F} \{ x(t) \}$
\begin{equation}
x(t) = \mathcal{F}^{-1} \left\{ \mathcal{F} \{ x(t) \} \right\}
\end{equation}
A sufficient condition for the theorem to hold is that both the signal $x(t)$ and its Fourier transformation are absolutely integrable and $x(t)$ is continuous at the considered time $t$. For this type of signals, above relation can be proven by applying the definition of the Fourier transform and its inverse and rearranging terms. However, the invertibility of the Fourier transformation holds also for more general signals $x(t)$, composed for instance from Dirac delta distributions.
**Example**
The invertibility of the Fourier transform is illustrated at the example of the [rectangular signal](../continuous_signals/standard_signals.ipynb#Rectangular-Signal) $x(t) = \text{rect}(t)$. The inverse of [its Fourier transform](definition.ipynb#Transformation-of-the-Rectangular-Signal) $X(j \omega) = \text{sinc} \left( \frac{\omega}{2} \right)$ is computed to show that the rectangular signal, although it has discontinuities, can be recovered by inverse Fourier transformation.
```
%matplotlib inline
import sympy as sym
sym.init_printing()
def fourier_transform(x):
return sym.transforms._fourier_transform(x, t, w, 1, -1, 'Fourier')
def inverse_fourier_transform(X):
return sym.transforms._fourier_transform(X, w, t, 1/(2*sym.pi), 1, 'Inverse Fourier')
t, w = sym.symbols('t omega')
X = sym.sinc(w/2)
x = inverse_fourier_transform(X)
x
sym.plot(x, (t,-1,1), ylabel=r'$x(t)$');
```
### Duality
Comparing the [definition of the Fourier transform](definition.ipynb) with its inverse
\begin{align}
X(j \omega) &= \int_{-\infty}^{\infty} x(t) \, e^{-j \omega t} \; dt \\
x(t) &= \frac{1}{2 \pi} \int_{-\infty}^{\infty} X(j \omega) \, e^{j \omega t} \; d\omega
\end{align}
reveals that both are very similar in their structure. They differ only with respect to the normalization factor $2 \pi$ and the sign of the exponential function. The duality principle of the Fourier transform can be deduced from this observation. Let's assume that we know the Fourier transformation $x_2(j \omega)$ of a signal $x_1(t)$
\begin{equation}
x_2(j \omega) = \mathcal{F} \{ x_1(t) \}
\end{equation}
It follows that the Fourier transformation of the signal
\begin{equation}
x_2(j t) = x_2(j \omega) \big\vert_{\omega=t}
\end{equation}
is given as
\begin{equation}
\mathcal{F} \{ x_2(j t) \} = 2 \pi \cdot x_1(- \omega)
\end{equation}
The duality principle of the Fourier transformation allows to carry over results from the time-domain to the spectral-domain and vice-versa. It can be used to derive new transforms from known transforms. This is illustrated at an example. Note, that the Laplace transformation shows no duality. This is due to the mapping of a complex signal $x(t)$ with real valued independent variable $t \in \mathbb{R}$ to its complex transform $X(s) \in \mathbb{C}$ with complex valued independent variable $s \in \mathbb{C}$.
#### Transformation of the exponential signal
The Fourier transform of a shifted Dirac impulse $\delta(t - \tau)$ is derived by introducing it into the definition of the Fourier transform and exploiting the sifting property of the Dirac delta function
\begin{equation}
\mathcal{F} \{ \delta(t - \tau) \} = \int_{-\infty}^{\infty} \delta(t - \tau) \, e^{-j \omega t} \; dt = e^{-j \omega \tau}
\end{equation}
Using the duality principle, the Fourier transform of $e^{-j \omega_0 t}$ can be derived from this result by
1. substituting $\omega$ with $t$ and $\tau$ with $\omega_0$ on the right-hand side to yield the time-domain signal $e^{-j \omega_0 t}$
2. substituting $t$ by $- \omega$, $\tau$ with $\omega_0$ and multiplying the result by $2 \pi$ on the left-hand side
\begin{equation}
\mathcal{F} \{ e^{-j \omega_0 t} \} = 2 \pi \cdot \delta(\omega + \omega_0)
\end{equation}
### Linearity
The Fourier transform is a linear operation. For two signals $x_1(t)$ and $x_2(t)$ with Fourier transforms $X_1(j \omega) = \mathcal{F} \{ x_1(t) \}$ and $X_2(j \omega) = \mathcal{F} \{ x_2(t) \}$ the following holds
\begin{equation}
\mathcal{F} \{ A \cdot x_1(t) + B \cdot x_2(t) \} = A \cdot X_1(j \omega) + B \cdot X_2(j \omega)
\end{equation}
with $A, B \in \mathbb{C}$. The Fourier transform of a weighted superposition of signals is equal to the weighted superposition of the individual Fourier transforms. This property is useful to derive the Fourier transform of signals that can be expressed as superposition of other signals for which the Fourier transform is known or can be calculated easier. Linearity holds also for the inverse Fourier transform.
#### Transformation of the cosine and sine signal
The Fourier transform of $\cos(\omega_0 t)$ and $\sin(\omega_0 t)$ is derived by expressing both as harmonic exponential signals using [Euler's formula](https://en.wikipedia.org/wiki/Euler's_formula)
\begin{align}
\cos(\omega_0 t) &= \frac{1}{2} \left( e^{j \omega_0 t} + e^{-j \omega_0 t} \right) \\
\sin(\omega_0 t) &= \frac{1}{2j} \left( e^{j \omega_0 t} - e^{-j \omega_0 t} \right)
\end{align}
together with the Fourier transform $\mathcal{F} \{ e^{-j \omega_0 t} \} = 2 \pi \cdot \delta(\omega - \omega_0)$ from above yields
\begin{align}
\mathcal{F} \{ \cos(\omega_0 t) \} &= \pi \left( \delta(\omega + \omega_0) + \delta(\omega - \omega_0) \right) \\
\mathcal{F} \{ \sin(\omega_0 t) \} &= j \pi \left( \delta(\omega + \omega_0) - \delta(\omega - \omega_0) \right)
\end{align}
### Symmetries
In order to investigate the symmetries of the Fourier transform $X(j \omega) = \mathcal{F} \{ x(t) \}$ of a signal $x(t)$, first the case of a real valued signal $x(t) \in \mathbb{R}$ is considered. The results are then generalized to complex signals $x(t) \in \mathbb{C}$.
#### Real valued signals
Decomposing a real valued signal $x(t) \in \mathbb{R}$ into its even and odd part $x(t) = x_\text{e}(t) + x_\text{o}(t)$ and introducing these into the definition of the Fourier transform yields
\begin{align}
X(j \omega) &= \int_{-\infty}^{\infty} \left[ x_\text{e}(t) + x_\text{o}(t) \right] e^{-j \omega t} \; dt \\
&= \int_{-\infty}^{\infty} \left[ x_\text{e}(t) + x_\text{o}(t) \right] \cdot \left[ \cos(\omega t) - j \sin(\omega t) \right] \; dt \\
&= \underbrace{\int_{-\infty}^{\infty} x_\text{e}(t) \cos(\omega t) \; dt}_{X_\text{e}(j \omega)} +
j \underbrace{\int_{-\infty}^{\infty} - x_\text{o}(t) \sin(\omega t) \; dt}_{X_\text{o}(j \omega)}
\end{align}
For the last equality the fact was exploited that an integral with symmetric limits is zero for odd functions. Note that the multiplication of an odd function with an even/odd function results in an even/odd function. In order to conclude on the symmetry of $X(j \omega)$ its behavior for a reverse of the sign of $\omega$ has to be investigated. Due to the symmetry properties of $\cos(\omega t)$ and $\sin(\omega t)$, it follows that the Fourier transform of the
* even part $x_\text{e}(t)$ is real valued with even symmetry $X_\text{e}(j \omega) = X_\text{e}(-j \omega)$
* odd part $x_\text{o}(t)$ is imaginary valued with odd symmetry $X_\text{o}(j \omega) = - X_\text{o}(-j \omega)$
Combining this, it can be concluded that the Fourier transform $X(j \omega)$ of a real-valued signal $x(t) \in \mathbb{R}$ shows complex conjugate symmetry
\begin{equation}
X(j \omega) = X^*(- j \omega)
\end{equation}
It follows that the magnitude spectrum $|X(j \omega)|$ of a real-valued signal shows even symmetry
\begin{equation}
|X(j \omega)| = |X(- j \omega)|
\end{equation}
and the phase $\varphi(j \omega) = \arg \{ X(j \omega) \}$ odd symmetry
\begin{equation}
\varphi(j \omega) = - \varphi(- j \omega)
\end{equation}
Due to these symmetries, both are often plotted only for positive frequencies $\omega \geq 0$. However, without the information that the signal is real-valued it is not possible to conclude on the magnitude spectrum and phase for the negative frequencies $\omega < 0$.
#### Complex Signals
By following the same procedure as above for an imaginary signal, the symmetries of the Fourier transform of the even and odd part of an imaginary signal can be derived. The results can be combined, by decomposing a complex signal $x(t) \in \mathbb{C}$ and its Fourier transform into its even and odd part for both the real and imaginary part. This results in the following symmetry relations of the Fourier transform

**Example**
The Fourier transform $X(j \omega)$ of the signal $x(t) = \text{sgn}(t) \cdot \text{rect}(t)$ is computed. The signal is real valued with odd symmetry due to the sign function. It follows from the symmetry realations of the Fourier transform, that $X(j \omega)$ is imaginary with odd symmetry.
```
class rect(sym.Function):
@classmethod
def eval(cls, arg):
return sym.Heaviside(arg + sym.S.Half) - sym.Heaviside(arg - sym.S.Half)
x = sym.sign(t)*rect(t)
sym.plot(x, (t, -2, 2), xlabel=r'$t$', ylabel=r'$x(t)$');
X = fourier_transform(x)
X = X.rewrite(sym.cos).simplify()
X
sym.plot(sym.im(X), (w, -30, 30), xlabel=r'$\omega$', ylabel=r'$\Im \{ X(j \omega) \}$');
```
**Exercise**
* What symmetry do you expect for the Fourier transform of the signal $x(t) = j \cdot \text{sgn}(t) \cdot \text{rect}(t)$? Check your results by modifying above example.
**Copyright**
The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors.
|
github_jupyter
|
%matplotlib inline
import sympy as sym
sym.init_printing()
def fourier_transform(x):
return sym.transforms._fourier_transform(x, t, w, 1, -1, 'Fourier')
def inverse_fourier_transform(X):
return sym.transforms._fourier_transform(X, w, t, 1/(2*sym.pi), 1, 'Inverse Fourier')
t, w = sym.symbols('t omega')
X = sym.sinc(w/2)
x = inverse_fourier_transform(X)
x
sym.plot(x, (t,-1,1), ylabel=r'$x(t)$');
class rect(sym.Function):
@classmethod
def eval(cls, arg):
return sym.Heaviside(arg + sym.S.Half) - sym.Heaviside(arg - sym.S.Half)
x = sym.sign(t)*rect(t)
sym.plot(x, (t, -2, 2), xlabel=r'$t$', ylabel=r'$x(t)$');
X = fourier_transform(x)
X = X.rewrite(sym.cos).simplify()
X
sym.plot(sym.im(X), (w, -30, 30), xlabel=r'$\omega$', ylabel=r'$\Im \{ X(j \omega) \}$');
| 0.706089 | 0.99311 |
# Pyspark & Astrophysical data: IMAGE
Let's play with Image. In this example, we load an image data from a FITS file (CFHTLens), and identify sources with a simple astropy algorithm. The workflow is described below. For simplicity, we only focus on one CCD in this notebook. For full scale, see the pyspark [im2cat.py](https://github.com/astrolabsoftware/spark-fits/blob/master/examples/python/im2cat.py) script.

```
## Import SparkSession from Spark
from pyspark.sql import SparkSession
## Create a DataFrame from the HDU data of a FITS file
fn = "../../src/test/resources/image.fits"
hdu = 1
df = spark.read.format("fits").option("hdu", hdu).load(fn)
## By default, spark-fits distributes the rows of the image
df.printSchema()
df.show(5)
```
# Find objects on CCD
```
## In order to work on the full image, one needs to
## re-partition the image by gathering all rows.
## For simplicity, we work with only one image, but in real life
## we would just have all CCDs distributed, one per Spark mapper.
## For a real life example, see the full example at spark-fits/example/python/im2cat.py
def rowdf_into_imagerdd(df, final_num_partition=1):
"""
Reshape a DataFrame of rows into a RDD containing the full image
in one partition.
Parameters
----------
df : DataFrame
DataFrame of image rows.
final_num_partition : Int
The final number of partitions. Must be one (default) unless you
know what you are doing.
Returns
----------
imageRDD : RDD
RDD containing the full image in one partition
"""
return df.rdd.coalesce(final_num_partition).glom()
imRDD = rowdf_into_imagerdd(df, 1)
## Let's run a simple object finder on our image,
## and collect the catalog.
import numpy as np
from photutils import DAOStarFinder
from astropy.stats import sigma_clipped_stats
def reshape_image(im):
"""
By default, Spark shapes images into (nx, 1, ny).
This routine reshapes images into (nx, ny)
Parameters
----------
im : 3D array
Original image with shape (nx, 1, ny)
Returns
----------
im_reshaped : 2D array
Original image with shape (nx, ny)
"""
shape = np.shape(im)
return im.reshape((shape[0], shape[2]))
def get_stat(data, sigma=3.0, iters=3):
"""
Estimate the background and background noise using
sigma-clipped statistics.
Parameters
----------
data : 2D array
2d array containing the data.
sigma : float
sigma.
iters : int
Number of iteration to perform to get accurate estimate.
The higher the better, but it will be longer.
"""
mean, median, std = sigma_clipped_stats(data, sigma=sigma, iters=iters)
return mean, median, std
## Source detection: build the catalogs for each CCD in parallel
## Only one CCD in this example.
cat = imRDD.map(
lambda im: reshape_image(np.array(im)))\
.map(
lambda im: (im, get_stat(im)))\
.map(
lambda im_stat: (
im_stat[0],
im_stat[1][1],
DAOStarFinder(fwhm=3.0, threshold=5.*im_stat[1][2])))\
.map(
lambda im_mean_starfinder: im_mean_starfinder[2](
im_mean_starfinder[0] - im_mean_starfinder[1]))
final_cat = cat.collect()
print(final_cat)
## Let's visualise our objects found
from astropy.io import fits
from photutils import CircularAperture
from astropy.visualization import SqrtStretch
from astropy.visualization.mpl_normalize import ImageNormalize
import matplotlib.pyplot as pl
## Grab initial data for plot
data = fits.open(fn)
data = data[hdu].data
## Plot the result on top of the CCD
fig = pl.figure(0, (10, 10))
positions = (
final_cat[hdu-1]['xcentroid'],
final_cat[hdu-1]['ycentroid'])
apertures = CircularAperture(positions, r=10.)
norm = ImageNormalize(stretch=SqrtStretch())
pl.imshow(data, cmap='Greys', origin="lower", norm=norm)
apertures.plot(color='blue', lw=1.0, alpha=0.5)
pl.show()
## Of course, one could use different algorithms, like the ones in the Stack!
```
|
github_jupyter
|
## Import SparkSession from Spark
from pyspark.sql import SparkSession
## Create a DataFrame from the HDU data of a FITS file
fn = "../../src/test/resources/image.fits"
hdu = 1
df = spark.read.format("fits").option("hdu", hdu).load(fn)
## By default, spark-fits distributes the rows of the image
df.printSchema()
df.show(5)
## In order to work on the full image, one needs to
## re-partition the image by gathering all rows.
## For simplicity, we work with only one image, but in real life
## we would just have all CCDs distributed, one per Spark mapper.
## For a real life example, see the full example at spark-fits/example/python/im2cat.py
def rowdf_into_imagerdd(df, final_num_partition=1):
"""
Reshape a DataFrame of rows into a RDD containing the full image
in one partition.
Parameters
----------
df : DataFrame
DataFrame of image rows.
final_num_partition : Int
The final number of partitions. Must be one (default) unless you
know what you are doing.
Returns
----------
imageRDD : RDD
RDD containing the full image in one partition
"""
return df.rdd.coalesce(final_num_partition).glom()
imRDD = rowdf_into_imagerdd(df, 1)
## Let's run a simple object finder on our image,
## and collect the catalog.
import numpy as np
from photutils import DAOStarFinder
from astropy.stats import sigma_clipped_stats
def reshape_image(im):
"""
By default, Spark shapes images into (nx, 1, ny).
This routine reshapes images into (nx, ny)
Parameters
----------
im : 3D array
Original image with shape (nx, 1, ny)
Returns
----------
im_reshaped : 2D array
Original image with shape (nx, ny)
"""
shape = np.shape(im)
return im.reshape((shape[0], shape[2]))
def get_stat(data, sigma=3.0, iters=3):
"""
Estimate the background and background noise using
sigma-clipped statistics.
Parameters
----------
data : 2D array
2d array containing the data.
sigma : float
sigma.
iters : int
Number of iteration to perform to get accurate estimate.
The higher the better, but it will be longer.
"""
mean, median, std = sigma_clipped_stats(data, sigma=sigma, iters=iters)
return mean, median, std
## Source detection: build the catalogs for each CCD in parallel
## Only one CCD in this example.
cat = imRDD.map(
lambda im: reshape_image(np.array(im)))\
.map(
lambda im: (im, get_stat(im)))\
.map(
lambda im_stat: (
im_stat[0],
im_stat[1][1],
DAOStarFinder(fwhm=3.0, threshold=5.*im_stat[1][2])))\
.map(
lambda im_mean_starfinder: im_mean_starfinder[2](
im_mean_starfinder[0] - im_mean_starfinder[1]))
final_cat = cat.collect()
print(final_cat)
## Let's visualise our objects found
from astropy.io import fits
from photutils import CircularAperture
from astropy.visualization import SqrtStretch
from astropy.visualization.mpl_normalize import ImageNormalize
import matplotlib.pyplot as pl
## Grab initial data for plot
data = fits.open(fn)
data = data[hdu].data
## Plot the result on top of the CCD
fig = pl.figure(0, (10, 10))
positions = (
final_cat[hdu-1]['xcentroid'],
final_cat[hdu-1]['ycentroid'])
apertures = CircularAperture(positions, r=10.)
norm = ImageNormalize(stretch=SqrtStretch())
pl.imshow(data, cmap='Greys', origin="lower", norm=norm)
apertures.plot(color='blue', lw=1.0, alpha=0.5)
pl.show()
## Of course, one could use different algorithms, like the ones in the Stack!
| 0.880045 | 0.986442 |
# Data Manipulation
It is impossible to get anything done if we cannot manipulate data. Generally, there are two important things we need to do with data: (i) acquire it and (ii) process it once it is inside the computer. There is no point in acquiring data if we do not even know how to store it, so let's get our hands dirty first by playing with synthetic data. We will start by introducing the tensor,
PyTorch's primary tool for storing and transforming data. If you have worked with NumPy before, you will notice that tensors are, by design, similar to NumPy's multi-dimensional array. Tensors support asynchronous computation on CPU, GPU and provide support for automatic differentiation.
## Getting Started
```
import torch
```
Tensors represent (possibly multi-dimensional) arrays of numerical values.
The simplest object we can create is a vector. To start, we can use `arange` to create a row vector with 12 consecutive integers.
```
x = torch.arange(12, dtype=torch.float64)
x
# We can get the tensor shape through the shape attribute.
x.shape
# .shape is an alias for .size(), and was added to more closely match numpy
x.size()
```
We use the `reshape` function to change the shape of one (possibly multi-dimensional) array, to another that contains the same number of elements.
For example, we can transform the shape of our line vector `x` to (3, 4), which contains the same values but interprets them as a matrix containing 3 rows and 4 columns. Note that although the shape has changed, the elements in `x` have not.
```
x = x.reshape((3, 4))
x
```
Reshaping by manually specifying each of the dimensions can get annoying. Once we know one of the dimensions, why should we have to perform the division our selves to determine the other? For example, above, to get a matrix with 3 rows, we had to specify that it should have 4 columns (to account for the 12 elements). Fortunately, PyTorch can automatically work out one dimension given the other.
We can invoke this capability by placing `-1` for the dimension that we would like PyTorch to automatically infer. In our case, instead of
`x.reshape((3, 4))`, we could have equivalently used `x.reshape((-1, 4))` or `x.reshape((3, -1))`.
```
torch.FloatTensor(2, 3)
torch.Tensor(2, 3)
torch.empty(2, 3)
```
torch.Tensor() is just an alias to torch.FloatTensor() which is the default type of tensor, when no dtype is specified during tensor construction.
From the torch for numpy users notes, it seems that torch.Tensor() is a drop-in replacement of numpy.empty()
So, in essence torch.FloatTensor() and torch.empty() does the same job.
The `empty` method just grabs some memory and hands us back a matrix without setting the values of any of its entries. This is very efficient but it means that the entries might take any arbitrary values, including very big ones! Typically, we'll want our matrices initialized either with ones, zeros, some known constant or numbers randomly sampled from a known distribution.
Perhaps most often, we want an array of all zeros. To create tensor with all elements set to 0 and a shape of (2, 3, 4) we can invoke:
```
torch.zeros((2, 3, 4))
```
We can create tensors with each element set to 1 works via
```
torch.ones((2, 3, 4))
```
We can also specify the value of each element in the desired NDArray by supplying a Python list containing the numerical values.
```
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
y
```
In some cases, we will want to randomly sample the values of each element in the tensor according to some known probability distribution. This is especially common when we intend to use the tensor as a parameter in a neural network. The following snippet creates an tensor with a shape of (3,4). Each of its elements is randomly sampled in a normal distribution with zero mean and unit variance.
```
torch.randn(3, 4)
```
## Operations
Oftentimes, we want to apply functions to arrays. Some of the simplest and most useful functions are the element-wise functions. These operate by performing a single scalar operation on the corresponding elements of two arrays. We can create an element-wise function from any function that maps from the scalars to the scalars. In math notations we would denote such a function as $f: \mathbb{R} \rightarrow \mathbb{R}$. Given any two vectors $\mathbf{u}$ and $\mathbf{v}$ *of the same shape*, and the function f,
we can produce a vector $\mathbf{c} = F(\mathbf{u},\mathbf{v})$ by setting $c_i \gets f(u_i, v_i)$ for all $i$. Here, we produced the vector-valued $F: \mathbb{R}^d \rightarrow \mathbb{R}^d$ by *lifting* the scalar function to an element-wise vector operation. In PyTorch, the common standard arithmetic operators (+,-,/,\*,\*\*) have all been *lifted* to element-wise operations for identically-shaped tensors of arbitrary shape. We can call element-wise operations on any two tensors of the same shape, including matrices.
```
x = torch.tensor([1, 2, 4, 8], dtype=torch.float32)
y = torch.ones_like(x) * 2
print('x =', x)
print('x + y', x + y)
print('x - y', x - y)
print('x * y', x * y)
print('x / y', x / y)
```
Many more operations can be applied element-wise, such as exponentiation:
```
torch.exp(x)
# Note: torch.exp is not implemented for 'torch.LongTensor'.
```
In addition to computations by element, we can also perform matrix operations, like matrix multiplication using the `mm` or `matmul` function. Next, we will perform matrix multiplication of `x` and the transpose of `y`. We define `x` as a matrix of 3 rows and 4 columns, and `y` is transposed into a matrix of 4 rows and 3 columns. The two matrices are multiplied to obtain a matrix of 3 rows and 3 columns.
```
x = torch.arange(12, dtype=torch.float32).reshape((3,4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]], dtype=torch.float32)
print(x.dtype)
print(y)
torch.mm(x, y.t())
```
Note that torch.dot() behaves differently to np.dot(). There's been some discussion about what would be desirable here. Specifically, torch.dot() treats both a and b as 1D vectors (irrespective of their original shape) and computes their inner product.
We can also merge multiple tensors. For that, we need to tell the system along which dimension to merge. The example below merges two matrices along dimension 0 (along rows) and dimension 1 (along columns) respectively.
```
torch.cat((x, y), dim=0)
torch.cat((x, y), dim=1)
```
Sometimes, we may want to construct binary tensors via logical statements. Take `x == y` as an example. If `x` and `y` are equal for some entry, the new tensor has a value of 1 at the same position; otherwise it is 0.
```
x == y
```
Summing all the elements in the tensor yields an tensor with only one element.
```
x.sum()
```
We can transform the result into a scalar in Python using the `asscalar` function of `numpy`. In the following example, the $\ell_2$ norm of `x` yields a single element tensor. The final result is transformed into a scalar.
```
import numpy as np
np.asscalar(x.norm())
```
## Broadcast Mechanism
In the above section, we saw how to perform operations on two tensors of the same shape. When their shapes differ, a broadcasting mechanism may be triggered analogous to NumPy: first, copy the elements appropriately so that the two tensors have the same shape, and then carry out operations by element.
```
a = torch.arange(3, dtype=torch.float).reshape((3, 1))
b = torch.arange(2, dtype=torch.float).reshape((1, 2))
a, b
```
Since `a` and `b` are (3x1) and (1x2) matrices respectively, their shapes do not match up if we want to add them. PyTorch addresses this by 'broadcasting' the entries of both matrices into a larger (3x2) matrix as follows: for matrix `a` it replicates the columns, for matrix `b` it replicates the rows before adding up both element-wise.
```
a + b
```
## Indexing and Slicing
Just like in any other Python array, elements in a tensor can be accessed by its index. In good Python tradition the first element has index 0 and ranges are specified to include the first but not the last element. By this logic `1:3` selects the second and third element. Let's try this out by selecting the respective rows in a matrix.
```
x[1:3]
```
Beyond reading, we can also write elements of a matrix.
```
x[1, 2] = 9
x
```
If we want to assign multiple elements the same value, we simply index all of them and then assign them the value. For instance, `[0:2, :]` accesses the first and second rows. While we discussed indexing for matrices, this obviously also works for vectors and for tensors of more than 2 dimensions.
```
x[0:2, :] = 12
x
```
## Saving Memory
In the previous example, every time we ran an operation, we allocated new memory to host its results. For example, if we write `y = x + y`, we will dereference the matrix that `y` used to point to and instead point it at the newly allocated memory. In the following example we demonstrate this with Python's `id()` function, which gives us the exact address of the referenced object in memory. After running `y = y + x`, we will find that `id(y)` points to a different location. That is because Python first evaluates `y + x`, allocating new memory for the result and then subsequently redirects `y` to point at this new location in memory.
```
before = id(y)
y = y + x
id(y) == before
```
This might be undesirable for two reasons. First, we do not want to run around allocating memory unnecessarily all the time. In machine learning, we might have hundreds of megabytes of parameters and update all of them multiple times per second. Typically, we will want to perform these updates *in place*. Second, we might point at the same parameters from multiple variables. If we do not update in place, this could cause a memory leak, making it possible for us to inadvertently reference stale parameters.
Fortunately, performing in-place operations in PyTorch is easy. We can assign the result of an operation to a previously allocated array with slice notation, e.g., `y[:] = <expression>`. To illustrate the behavior, we first clone the shape of a matrix using `zeros_like` to allocate a block of 0 entries.
```
z = torch.zeros_like(y)
print('id(z):', id(z))
z[:] = x + y
print('id(z):', id(z))
```
While this looks pretty, `x+y` here will still allocate a temporary buffer to store the result of `x+y` before copying it to `z[:]`. To make even better use of memory, we can directly invoke the underlying `tensor` operation, in this case `add`, avoiding temporary buffers. We do this by specifying the `out` keyword argument, which every `tensor` operator supports:
```
before = id(z)
torch.add(x, y, out=z)
id(z) == before
```
If the value of `x ` is not reused in subsequent computations, we can also use `x[:] = x + y` or `x += y` to reduce the memory overhead of the operation.
```
before = id(x)
x += y
id(x) == before
```
## Mutual Transformation of PyTorch and NumPy
Converting PyTorch Tensors to and from NumPy Arrays is easy. The converted arrays do *not* share memory. This minor inconvenience is actually quite important: when you perform operations on the CPU or one of the GPUs, you do not want PyTorch having to wait whether NumPy might want to be doing something else with the same chunk of memory. `.tensor` and `.numpy` do the trick.
```
a = x.numpy()
print(type(a))
b = torch.tensor(a)
print(type(b))
```
## Exercises
1. Run the code in this section. Change the conditional statement `x == y` in this section to `x < y` or `x > y`, and then see what kind of tensor you can get.
1. Replace the two tensors that operate by element in the broadcast mechanism with other shapes, e.g. three dimensional tensors. Is the result the same as expected?
1. Assume that we have three matrices `a`, `b` and `c`. Rewrite `c = torch.mm(a, b.t()) + c` in the most memory efficient manner.
|
github_jupyter
|
import torch
x = torch.arange(12, dtype=torch.float64)
x
# We can get the tensor shape through the shape attribute.
x.shape
# .shape is an alias for .size(), and was added to more closely match numpy
x.size()
x = x.reshape((3, 4))
x
torch.FloatTensor(2, 3)
torch.Tensor(2, 3)
torch.empty(2, 3)
torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
y
torch.randn(3, 4)
x = torch.tensor([1, 2, 4, 8], dtype=torch.float32)
y = torch.ones_like(x) * 2
print('x =', x)
print('x + y', x + y)
print('x - y', x - y)
print('x * y', x * y)
print('x / y', x / y)
torch.exp(x)
# Note: torch.exp is not implemented for 'torch.LongTensor'.
x = torch.arange(12, dtype=torch.float32).reshape((3,4))
y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]], dtype=torch.float32)
print(x.dtype)
print(y)
torch.mm(x, y.t())
torch.cat((x, y), dim=0)
torch.cat((x, y), dim=1)
x == y
x.sum()
import numpy as np
np.asscalar(x.norm())
a = torch.arange(3, dtype=torch.float).reshape((3, 1))
b = torch.arange(2, dtype=torch.float).reshape((1, 2))
a, b
a + b
x[1:3]
x[1, 2] = 9
x
x[0:2, :] = 12
x
before = id(y)
y = y + x
id(y) == before
z = torch.zeros_like(y)
print('id(z):', id(z))
z[:] = x + y
print('id(z):', id(z))
before = id(z)
torch.add(x, y, out=z)
id(z) == before
before = id(x)
x += y
id(x) == before
a = x.numpy()
print(type(a))
b = torch.tensor(a)
print(type(b))
| 0.644113 | 0.994129 |
## GANs
Credits: \
https://pytorch.org/tutorials/beginner/dcgan_faces_tutorial.html \
https://jovian.ai/aakashns/06-mnist-gan
```
from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
# Root directory for dataset
dataroot = "../data/celeba/"
# Number of workers for dataloader
workers = 2
# Batch size during training
batch_size = 128
# Spatial size of training images. All images will be resized to this
# size using a transformer.
image_size = 64
# Number of channels in the training images. For color images this is 3
nc = 3
# Size of z latent vector (i.e. size of generator input)
nz = 100
# Size of feature maps in generator
ngf = 64
# Size of feature maps in discriminator
ndf = 64
# Number of training epochs
num_epochs = 5
# Learning rate for optimizers
lr = 0.0002
# Beta1 hyperparam for Adam optimizers
beta1 = 0.5
# Number of GPUs available. Use 0 for CPU mode.
ngpu = 0
# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=workers)
# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
# Plot some training images
real_batch = next(iter(dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64],
padding=2, normalize=True).cpu(),(1,2,0)))
```
|
github_jupyter
|
from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
# Root directory for dataset
dataroot = "../data/celeba/"
# Number of workers for dataloader
workers = 2
# Batch size during training
batch_size = 128
# Spatial size of training images. All images will be resized to this
# size using a transformer.
image_size = 64
# Number of channels in the training images. For color images this is 3
nc = 3
# Size of z latent vector (i.e. size of generator input)
nz = 100
# Size of feature maps in generator
ngf = 64
# Size of feature maps in discriminator
ndf = 64
# Number of training epochs
num_epochs = 5
# Learning rate for optimizers
lr = 0.0002
# Beta1 hyperparam for Adam optimizers
beta1 = 0.5
# Number of GPUs available. Use 0 for CPU mode.
ngpu = 0
# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=workers)
# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
# Plot some training images
real_batch = next(iter(dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64],
padding=2, normalize=True).cpu(),(1,2,0)))
| 0.838548 | 0.843638 |
<table> <tr>
<td style="background-color:#ffffff;">
<a href="http://qworld.lu.lv" target="_blank"><img src="../images/qworld.jpg" width="25%" align="left"> </a></td>
<td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
prepared by <a href="http://abu.lu.lv" target="_blank">Abuzer Yakaryilmaz</a> (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
</td>
</tr></table>
<table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
$ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
$ \newcommand{\bstate}[1]{ [ \mspace{-1mu} #1 \mspace{-1.5mu} ] } $
## Project | Implementing Quantum Teleportation
We simulate the standard quantum teleportation protocol between Asja to Balvis.
- _Please do not use any quantum programming library or any scientific python library such as `NumPy`._
- _Each qubit starts in state $ \ket{0} $, and each quantum operator should be implemented one by one._
- _The state of quantum system should not be set automatically to certain quantum states._
- _Please write your own code for matrix multiplication and tensoring matrices._
### Create a python class called `quantum_teleportation`
This class simulates a quantum system with three qubits. Asja has the qubits $q_2$ and $q_1$ and Balvis has the qubit $q_0$. The computation of your system is traced by a 8-dimensional vector and so each quantum operator is represented as a ($8 \times 8$)-dimensional matrix. The qubits are combined as $ q_2 \otimes q_1 \otimes q_0 $.
### The methods
For each new instance, the state of $q_2$ is set to a random (real-valued) quantum state.
1. `print_quantum_message()`: Print the initial quantum state of $ q_2 $.
1. `print_state()`: Print the state of system.
Each method given below should be called in the given order. Otherwise, an error should be returned with a warning message.
_The state of the system should be updated after each quantum operator including the measurements on $ q_2 $ and $q_1$._
3. `create_entanglement()`: Create entanglements between the qubits $q_1$ and $q_0$.
1. `balvis_travels()`: Assume that Balvis takes his qubits and go away.
1. `asja_measures()`: Asja measures her qubits $q_2$ and $q_1$ and return the measurement outcomes. Remark that the qubit $ q_0 $ is not measured.
Asja observes one of these four results: `00`, `01`, `10`, or `11`.
To implement this measurement operator, we define four different matrices: $ M_{00} $, $ M_{01} $, $ M_{10} $, and $M_{11}$, where $ M_{ab}$ = $ (\ket{ab}\bra{ab}) \otimes I_2 $ is a ($ 8 \times 8 $)-dimensional matrix.
- Remark that $ \ket{ab} $ is a 4-dimensional column vector and $ \bra{ab} $ is the (conjugate) transpose of $ \ket{ab} $, which is a 4-dimensional row vector.
- Therefore, $ \ket{ab}\bra{ab} $ is a matrix multiplication and the result is a ($4 \times 4$)-dimensional matrix.
- $I_2$ is the 2x2-dimensional identity matrix.
Let $\ket{v}$ be the state vector before the measurement. Each outcome has the same probability (1/4) in our case. One of them is selected randomly, say `01`. The new state becomes the normalized version of the vector that is obtained by $ \ket{\widetilde{v_{01}}} = M_{01} \ket{v} $, i.e., the length of $\ket{\widetilde{v_{01}}}$ is less than 1 and so this vector must be multiplied with a factor to make its length 1.
6. `asja_sends_measument_outcomes(outcome)`: Asja sends the measurement outcomes to Balvis such as `10`.
1. `balvis_post_processing()`: Apply post-processing quantum operators to Balvis’ qubit (if necessary) depending on the measurement outcomes recivied from Asja.
Test your class by checking the quantum state after each step and also verify whether the quantum message prepared by Asja is teleported to Balvis' qubit or not.
|
github_jupyter
|
<table> <tr>
<td style="background-color:#ffffff;">
<a href="http://qworld.lu.lv" target="_blank"><img src="../images/qworld.jpg" width="25%" align="left"> </a></td>
<td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
prepared by <a href="http://abu.lu.lv" target="_blank">Abuzer Yakaryilmaz</a> (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
</td>
</tr></table>
<table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
$ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
$ \newcommand{\bstate}[1]{ [ \mspace{-1mu} #1 \mspace{-1.5mu} ] } $
## Project | Implementing Quantum Teleportation
We simulate the standard quantum teleportation protocol between Asja to Balvis.
- _Please do not use any quantum programming library or any scientific python library such as `NumPy`._
- _Each qubit starts in state $ \ket{0} $, and each quantum operator should be implemented one by one._
- _The state of quantum system should not be set automatically to certain quantum states._
- _Please write your own code for matrix multiplication and tensoring matrices._
### Create a python class called `quantum_teleportation`
This class simulates a quantum system with three qubits. Asja has the qubits $q_2$ and $q_1$ and Balvis has the qubit $q_0$. The computation of your system is traced by a 8-dimensional vector and so each quantum operator is represented as a ($8 \times 8$)-dimensional matrix. The qubits are combined as $ q_2 \otimes q_1 \otimes q_0 $.
### The methods
For each new instance, the state of $q_2$ is set to a random (real-valued) quantum state.
1. `print_quantum_message()`: Print the initial quantum state of $ q_2 $.
1. `print_state()`: Print the state of system.
Each method given below should be called in the given order. Otherwise, an error should be returned with a warning message.
_The state of the system should be updated after each quantum operator including the measurements on $ q_2 $ and $q_1$._
3. `create_entanglement()`: Create entanglements between the qubits $q_1$ and $q_0$.
1. `balvis_travels()`: Assume that Balvis takes his qubits and go away.
1. `asja_measures()`: Asja measures her qubits $q_2$ and $q_1$ and return the measurement outcomes. Remark that the qubit $ q_0 $ is not measured.
Asja observes one of these four results: `00`, `01`, `10`, or `11`.
To implement this measurement operator, we define four different matrices: $ M_{00} $, $ M_{01} $, $ M_{10} $, and $M_{11}$, where $ M_{ab}$ = $ (\ket{ab}\bra{ab}) \otimes I_2 $ is a ($ 8 \times 8 $)-dimensional matrix.
- Remark that $ \ket{ab} $ is a 4-dimensional column vector and $ \bra{ab} $ is the (conjugate) transpose of $ \ket{ab} $, which is a 4-dimensional row vector.
- Therefore, $ \ket{ab}\bra{ab} $ is a matrix multiplication and the result is a ($4 \times 4$)-dimensional matrix.
- $I_2$ is the 2x2-dimensional identity matrix.
Let $\ket{v}$ be the state vector before the measurement. Each outcome has the same probability (1/4) in our case. One of them is selected randomly, say `01`. The new state becomes the normalized version of the vector that is obtained by $ \ket{\widetilde{v_{01}}} = M_{01} \ket{v} $, i.e., the length of $\ket{\widetilde{v_{01}}}$ is less than 1 and so this vector must be multiplied with a factor to make its length 1.
6. `asja_sends_measument_outcomes(outcome)`: Asja sends the measurement outcomes to Balvis such as `10`.
1. `balvis_post_processing()`: Apply post-processing quantum operators to Balvis’ qubit (if necessary) depending on the measurement outcomes recivied from Asja.
Test your class by checking the quantum state after each step and also verify whether the quantum message prepared by Asja is teleported to Balvis' qubit or not.
| 0.712932 | 0.969985 |
```
from google.colab import drive
drive.mount('/content/drive')
import os
os.chdir('/content/drive/My Drive/Colab Notebooks/Udacity/deep-learning-v2-pytorch/convolutional-neural-networks/conv-visualization')
```
# Maxpooling Layer
In this notebook, we add and visualize the output of a maxpooling layer in a CNN.
A convolutional layer + activation function, followed by a pooling layer, and a linear layer (to create a desired output size) make up the basic layers of a CNN.
<img src='notebook_ims/CNN_all_layers.png' height=50% width=50% />
### Import the image
```
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'data/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# normalize, rescale entries to lie in [0,1]
gray_img = gray_img.astype("float32")/255
# plot image
plt.imshow(gray_img, cmap='gray')
plt.show()
```
### Define and visualize the filters
```
import numpy as np
## TODO: Feel free to modify the numbers here, to try out another filter!
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
print('Filter shape: ', filter_vals.shape)
# Defining four different filters,
# all of which are linear combinations of the `filter_vals` defined above
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# For an example, print out the values of filter 1
print('Filter 1: \n', filter_1)
```
### Define convolutional and pooling layers
You've seen how to define a convolutional layer, next is a:
* Pooling layer
In the next cell, we initialize a convolutional layer so that it contains all the created filters. Then add a maxpooling layer, [documented here](http://pytorch.org/docs/stable/_modules/torch/nn/modules/pooling.html), with a kernel size of (2x2) so you can see that the image resolution has been reduced after this step!
A maxpooling layer reduces the x-y size of an input and only keeps the most *active* pixel values. Below is an example of a 2x2 pooling kernel, with a stride of 2, applied to a small patch of grayscale pixel values; reducing the x-y size of the patch by a factor of 2. Only the maximum pixel values in 2x2 remain in the new, pooled output.
<img src='notebook_ims/maxpooling_ex.png' height=50% width=50% />
```
import torch
import torch.nn as nn
import torch.nn.functional as F
# define a neural network with a convolutional layer with four filters
# AND a pooling layer of size (2, 2)
class Net(nn.Module):
def __init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# assumes there are 4 grayscale filters
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(2, 2)
def forward(self, x):
# calculates the output of a convolutional layer
# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layers
return conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
```
### Visualize the output of each filter
First, we'll define a helper function, `viz_layer` that takes in a specific layer and number of filters (optional argument), and displays the output of that layer once an image has been passed through.
```
# helper function for visualizing the output of a given layer
# default number of filters is 4
def viz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1)
# grab layer outputs
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
```
Let's look at the output of a convolutional layer after a ReLu activation function is applied.
#### ReLu activation
A ReLu function turns all negative pixel values in 0's (black). See the equation pictured below for input pixel values, `x`.
<img src='notebook_ims/relu_ex.png' height=50% width=50% />
```
# plot original image
plt.imshow(gray_img, cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# convert the image into an input Tensor
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
# get all the layers
conv_layer, activated_layer, pooled_layer = model(gray_img_tensor)
# visualize the output of the activated conv layer
viz_layer(activated_layer)
```
### Visualize the output of the pooling layer
Then, take a look at the output of a pooling layer. The pooling layer takes as input the feature maps pictured above and reduces the dimensionality of those maps, by some pooling factor, by constructing a new, smaller image of only the maximum (brightest) values in a given kernel area.
Take a look at the values on the x, y axes to see how the image has changed size.
```
# visualize the output of the pooling layer
viz_layer(pooled_layer)
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
import os
os.chdir('/content/drive/My Drive/Colab Notebooks/Udacity/deep-learning-v2-pytorch/convolutional-neural-networks/conv-visualization')
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'data/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# normalize, rescale entries to lie in [0,1]
gray_img = gray_img.astype("float32")/255
# plot image
plt.imshow(gray_img, cmap='gray')
plt.show()
import numpy as np
## TODO: Feel free to modify the numbers here, to try out another filter!
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
print('Filter shape: ', filter_vals.shape)
# Defining four different filters,
# all of which are linear combinations of the `filter_vals` defined above
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# For an example, print out the values of filter 1
print('Filter 1: \n', filter_1)
import torch
import torch.nn as nn
import torch.nn.functional as F
# define a neural network with a convolutional layer with four filters
# AND a pooling layer of size (2, 2)
class Net(nn.Module):
def __init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# assumes there are 4 grayscale filters
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(2, 2)
def forward(self, x):
# calculates the output of a convolutional layer
# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layers
return conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
# helper function for visualizing the output of a given layer
# default number of filters is 4
def viz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1)
# grab layer outputs
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
# plot original image
plt.imshow(gray_img, cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# convert the image into an input Tensor
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
# get all the layers
conv_layer, activated_layer, pooled_layer = model(gray_img_tensor)
# visualize the output of the activated conv layer
viz_layer(activated_layer)
# visualize the output of the pooling layer
viz_layer(pooled_layer)
| 0.6488 | 0.862757 |
To start this Jupyter Dash app, please run all the cells below. Then, click on the **temporary** URL at the end of the last cell to open the app.
```
!pip install -q jupyter-dash==0.3.0rc1 dash-bootstrap-components transformers
import time
import dash
import dash_html_components as html
import dash_core_components as dcc
import dash_bootstrap_components as dbc
from dash.dependencies import Input, Output, State
from jupyter_dash import JupyterDash
from transformers import BartTokenizer, BartForConditionalGeneration
import torch
device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"Device: {device}")
# Load Model
pretrained = "sshleifer/distilbart-xsum-12-6"
model = BartForConditionalGeneration.from_pretrained(pretrained)
tokenizer = BartTokenizer.from_pretrained(pretrained)
# Switch to cuda, eval mode, and FP16 for faster inference
if device == "cuda":
model = model.half()
model.to(device)
model.eval();
# Define app
app = JupyterDash(__name__, external_stylesheets=[dbc.themes.BOOTSTRAP])
server = app.server
controls = dbc.Card(
[
dbc.FormGroup(
[
dbc.Label("Output Length (# Tokens)"),
dcc.Slider(
id="max-length",
min=10,
max=50,
value=30,
marks={i: str(i) for i in range(10, 51, 10)},
),
]
),
dbc.FormGroup(
[
dbc.Label("Beam Size"),
dcc.Slider(
id="num-beams",
min=2,
max=6,
value=4,
marks={i: str(i) for i in [2, 4, 6]},
),
]
),
dbc.FormGroup(
[
dbc.Spinner(
[
dbc.Button("Summarize", id="button-run"),
html.Div(id="time-taken"),
]
)
]
),
],
body=True,
style={"height": "275px"},
)
# Define Layout
app.layout = dbc.Container(
fluid=True,
children=[
html.H1("Dash Automatic Summarization (with DistilBART)"),
html.Hr(),
dbc.Row(
[
dbc.Col(
width=5,
children=[
controls,
dbc.Card(
body=True,
children=[
dbc.FormGroup(
[
dbc.Label("Summarized Content"),
dcc.Textarea(
id="summarized-content",
style={
"width": "100%",
"height": "calc(75vh - 275px)",
},
),
]
)
],
),
],
),
dbc.Col(
width=7,
children=[
dbc.Card(
body=True,
children=[
dbc.FormGroup(
[
dbc.Label("Original Text (Paste here)"),
dcc.Textarea(
id="original-text",
style={"width": "100%", "height": "75vh"},
),
]
)
],
)
],
),
]
),
],
)
@app.callback(
[Output("summarized-content", "value"), Output("time-taken", "children")],
[
Input("button-run", "n_clicks"),
Input("max-length", "value"),
Input("num-beams", "value"),
],
[State("original-text", "value")],
)
def summarize(n_clicks, max_len, num_beams, original_text):
if original_text is None or original_text == "":
return "", "Did not run"
t0 = time.time()
inputs = tokenizer.batch_encode_plus(
[original_text], max_length=1024, return_tensors="pt"
)
inputs = inputs.to(device)
# Generate Summary
summary_ids = model.generate(
inputs["input_ids"],
num_beams=num_beams,
max_length=max_len,
early_stopping=True,
)
out = [
tokenizer.decode(
g, skip_special_tokens=True, clean_up_tokenization_spaces=False
)
for g in summary_ids
]
t1 = time.time()
time_taken = f"Summarized on {device} in {t1-t0:.2f}s"
return out[0], time_taken
```
Run the cell below to run your Jupyter Dash app. Click on the **temporary** URL to access the app.
```
app.run_server(mode='inline')
```
|
github_jupyter
|
!pip install -q jupyter-dash==0.3.0rc1 dash-bootstrap-components transformers
import time
import dash
import dash_html_components as html
import dash_core_components as dcc
import dash_bootstrap_components as dbc
from dash.dependencies import Input, Output, State
from jupyter_dash import JupyterDash
from transformers import BartTokenizer, BartForConditionalGeneration
import torch
device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"Device: {device}")
# Load Model
pretrained = "sshleifer/distilbart-xsum-12-6"
model = BartForConditionalGeneration.from_pretrained(pretrained)
tokenizer = BartTokenizer.from_pretrained(pretrained)
# Switch to cuda, eval mode, and FP16 for faster inference
if device == "cuda":
model = model.half()
model.to(device)
model.eval();
# Define app
app = JupyterDash(__name__, external_stylesheets=[dbc.themes.BOOTSTRAP])
server = app.server
controls = dbc.Card(
[
dbc.FormGroup(
[
dbc.Label("Output Length (# Tokens)"),
dcc.Slider(
id="max-length",
min=10,
max=50,
value=30,
marks={i: str(i) for i in range(10, 51, 10)},
),
]
),
dbc.FormGroup(
[
dbc.Label("Beam Size"),
dcc.Slider(
id="num-beams",
min=2,
max=6,
value=4,
marks={i: str(i) for i in [2, 4, 6]},
),
]
),
dbc.FormGroup(
[
dbc.Spinner(
[
dbc.Button("Summarize", id="button-run"),
html.Div(id="time-taken"),
]
)
]
),
],
body=True,
style={"height": "275px"},
)
# Define Layout
app.layout = dbc.Container(
fluid=True,
children=[
html.H1("Dash Automatic Summarization (with DistilBART)"),
html.Hr(),
dbc.Row(
[
dbc.Col(
width=5,
children=[
controls,
dbc.Card(
body=True,
children=[
dbc.FormGroup(
[
dbc.Label("Summarized Content"),
dcc.Textarea(
id="summarized-content",
style={
"width": "100%",
"height": "calc(75vh - 275px)",
},
),
]
)
],
),
],
),
dbc.Col(
width=7,
children=[
dbc.Card(
body=True,
children=[
dbc.FormGroup(
[
dbc.Label("Original Text (Paste here)"),
dcc.Textarea(
id="original-text",
style={"width": "100%", "height": "75vh"},
),
]
)
],
)
],
),
]
),
],
)
@app.callback(
[Output("summarized-content", "value"), Output("time-taken", "children")],
[
Input("button-run", "n_clicks"),
Input("max-length", "value"),
Input("num-beams", "value"),
],
[State("original-text", "value")],
)
def summarize(n_clicks, max_len, num_beams, original_text):
if original_text is None or original_text == "":
return "", "Did not run"
t0 = time.time()
inputs = tokenizer.batch_encode_plus(
[original_text], max_length=1024, return_tensors="pt"
)
inputs = inputs.to(device)
# Generate Summary
summary_ids = model.generate(
inputs["input_ids"],
num_beams=num_beams,
max_length=max_len,
early_stopping=True,
)
out = [
tokenizer.decode(
g, skip_special_tokens=True, clean_up_tokenization_spaces=False
)
for g in summary_ids
]
t1 = time.time()
time_taken = f"Summarized on {device} in {t1-t0:.2f}s"
return out[0], time_taken
app.run_server(mode='inline')
| 0.727395 | 0.54468 |
```
from google.colab import drive
drive.mount('/content/drive')
```
Importing all the dependencies
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications import MobileNetV2, ResNet50, VGG19
from tensorflow.keras.layers import AveragePooling2D
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.applications.mobilenet_v2 import preprocess_input
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.preprocessing.image import load_img
from tensorflow.keras.models import load_model
from sklearn.preprocessing import OneHotEncoder
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import warnings
warnings.filterwarnings("ignore")
from imutils import paths
import matplotlib.pyplot as plt
import numpy as np
import argparse
import os
import cv2
```
####Preprocessing
Load all the images and labels and preprocess them, convert to numpy arrays and append them to the respective lists and converting those to numpy arrays
```
path = '/content/drive/My Drive/Face-Mask-Detector/resources/dataset/'
imagePaths = list(paths.list_images(path))
images = []
labels = []
for imagePath in imagePaths:
label = imagePath.split(os.path.sep)[-2]
image = load_img(imagePath, target_size=(224, 224))
image = img_to_array(image)
image = preprocess_input(image)
images.append(image)
labels.append(label)
images = np.array(images, dtype="float32")
labels = np.array(labels)
```
Getting the shapes of the arrays
```
print(images.shape)
print(labels.shape)
np.unique(labels)
```
One-hot encode the labels as they are categorical
```
encoder = LabelBinarizer()
labels = encoder.fit_transform(labels)
labels = to_categorical(labels)
```
Perform the train test split by forming giving 20% dataset to test our model.
```
X_train, X_test, y_train, y_test = train_test_split(images, labels,
test_size=0.20, stratify=labels)
```
Training image generator for data augmentation
```
datagen = ImageDataGenerator(
rotation_range=20,
zoom_range=0.15,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.15,
horizontal_flip=True,
fill_mode="nearest")
```
###MobileNetV2 Models Building Block
<img src="https://drive.google.com/uc?id=1yKgIXSDFdadQNcD5sjmqmJ07a6lQPCzq" width="500" height = '500' layout="centre">
For this task, we will be fine-tuning the MobileNet V2 architecture, a highly efficient architecture which works well with limited computational capacity.
Keras Functional API has been used to made the architecture of the model.
```
baseModel = MobileNetV2(weights="imagenet", include_top=False,
input_tensor=Input(shape=(224, 224, 3)))
X = baseModel.output
X = AveragePooling2D(pool_size=(7, 7))(X)
X = Flatten()(X)
X = Dense(128, activation="relu")(X)
X = Dropout(0.5)(X)
X = Dense(2, activation="softmax")(X)
model = Model(inputs=baseModel.input, outputs=X)
```
As we are using Transfer Learning i.e Pretrained MobileNetV2 we need to freeze its layers and train only last two dense layers.
```
for layer in baseModel.layers:
layer.trainable = False
```
Final Architecture of our model.
```
model.summary()
```
Defining few parameters
```
batch_size = 128
epochs = 15
```
Defining the optimzer and compiling the model.
```
optimizer = Adam(lr=1e-4, decay=1e-3)
model.compile(loss="binary_crossentropy", optimizer=optimizer, metrics=["accuracy"])
```
Training the model.
```
hist = model.fit(datagen.flow(X_train, y_train, batch_size=batch_size),
steps_per_epoch=len(X_train) // batch_size,
validation_data=(X_test, y_test),
validation_steps=len(X_test) // batch_size,
epochs=epochs)
```
We need to find the index of the label with corresponding largest predicted probability for each image in text set.
```
y_pred = model.predict(X_test, batch_size=batch_size)
y_pred = np.argmax(y_pred, axis=1)
print(classification_report(y_test.argmax(axis=1), y_pred, target_names=encoder.classes_))
```
Saving the model.h5 file so that it can loaded later to use for mask detection.
```
model.save("model", save_format="h5")
```
Plot the train and validation loss for our model using matplotlib library.
```
plt.plot(np.arange(0, epochs), hist.history["loss"], label="train_loss")
plt.plot(np.arange(0, epochs), hist.history["val_loss"], label="val_loss")
plt.title("Training and Validation Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(loc="upper right")
```
We have use used pretrained model to detect faces in images and used opencv deep neural network module to read model and its config file.
Weights of trained mask classifier model is loaded.
```
prototxtPath = '/content/drive/My Drive/Face-Mask-Detector/resources/face_detector/deploy.prototxt'
weightsPath = '/content/drive/My Drive/Face-Mask-Detector/resources/face_detector/res10_300x300_ssd_iter_140000.caffemodel'
face_model = cv2.dnn.readNet(prototxtPath, weightsPath)
model = load_model("model")
```
Preprocess the images using Blob module of opencv which resizes and crops image from center, subtract mean values, scales values by scalefactor, swap Blue and Red channels and them pass the blob throught our network to obtain the face which are detected by the model.
```
im_path='people2.jpg'
image = cv2.imdecode(np.fromfile(im_path, dtype=np.uint8), cv2.IMREAD_UNCHANGED)
# image = cv2.imread('/content/drive/My Drive/maskclassifier/test/people2.jpg')
height, width = image.shape[:2]
blob = cv2.dnn.blobFromImage(image, 1.0, (300, 300), (104.0, 177.0, 123.0))
face_model.setInput(blob)
detections = face_model.forward() #detecting the faces
```
In this part we have loop through all the detections and if their score is greater than certain threshold then we have find the dimensions of face and use preprocessing steps used for training images. Then we have used model trained to predict the class of the face image by passing the image through it.
Then Opencv functions are used to create bounding boxes, put text and show the image.
```
from google.colab.patches import cv2_imshow
threshold = 0.2
person_with_mask = 0;
person_without_mask = 0;
for i in range(0, detections.shape[2]):
score = detections[0, 0, i, 2]
if score > threshold:
#coordinates of the bounding box
box = detections[0, 0, i, 3:7] * np.array([width, height, width, height])
X_start, Y_start, X_end, Y_end = box.astype("int")
X_start, Y_start = (max(0, X_start), max(0, Y_start))
X_end, Y_end = (min(width - 1, X_end), min(height - 1, Y_end))
face = image[Y_start:Y_end, X_start:X_end]
face = cv2.cvtColor(face, cv2.COLOR_BGR2RGB) #Convert to rgb
face = cv2.resize(face, (224, 224)) #resize
face = img_to_array(face)
face = preprocess_input(face)
face = np.expand_dims(face, axis=0)
mask, withoutMask = model.predict(face)[0]
if mask > withoutMask:
label = "Mask"
person_with_mask += 1
else:
label = "No Mask"
person_without_mask += 1
if label == "Mask":
color = (0, 255, 0)
else:
color = (0, 0, 255)
label = "{}: {:.2f}%".format(label, max(mask, withoutMask) * 100)
cv2.putText(image, label, (X_start, Y_start - 10), cv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)
cv2.rectangle(image, (X_start, Y_start), (X_end, Y_end), color, 2)
print("Number of person with mask : {}".format(person_with_mask))
print("Number of person without mask : {}".format(person_without_mask))
cv2_imshow(image)
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications import MobileNetV2, ResNet50, VGG19
from tensorflow.keras.layers import AveragePooling2D
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.applications.mobilenet_v2 import preprocess_input
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.preprocessing.image import load_img
from tensorflow.keras.models import load_model
from sklearn.preprocessing import OneHotEncoder
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import warnings
warnings.filterwarnings("ignore")
from imutils import paths
import matplotlib.pyplot as plt
import numpy as np
import argparse
import os
import cv2
path = '/content/drive/My Drive/Face-Mask-Detector/resources/dataset/'
imagePaths = list(paths.list_images(path))
images = []
labels = []
for imagePath in imagePaths:
label = imagePath.split(os.path.sep)[-2]
image = load_img(imagePath, target_size=(224, 224))
image = img_to_array(image)
image = preprocess_input(image)
images.append(image)
labels.append(label)
images = np.array(images, dtype="float32")
labels = np.array(labels)
print(images.shape)
print(labels.shape)
np.unique(labels)
encoder = LabelBinarizer()
labels = encoder.fit_transform(labels)
labels = to_categorical(labels)
X_train, X_test, y_train, y_test = train_test_split(images, labels,
test_size=0.20, stratify=labels)
datagen = ImageDataGenerator(
rotation_range=20,
zoom_range=0.15,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.15,
horizontal_flip=True,
fill_mode="nearest")
baseModel = MobileNetV2(weights="imagenet", include_top=False,
input_tensor=Input(shape=(224, 224, 3)))
X = baseModel.output
X = AveragePooling2D(pool_size=(7, 7))(X)
X = Flatten()(X)
X = Dense(128, activation="relu")(X)
X = Dropout(0.5)(X)
X = Dense(2, activation="softmax")(X)
model = Model(inputs=baseModel.input, outputs=X)
for layer in baseModel.layers:
layer.trainable = False
model.summary()
batch_size = 128
epochs = 15
optimizer = Adam(lr=1e-4, decay=1e-3)
model.compile(loss="binary_crossentropy", optimizer=optimizer, metrics=["accuracy"])
hist = model.fit(datagen.flow(X_train, y_train, batch_size=batch_size),
steps_per_epoch=len(X_train) // batch_size,
validation_data=(X_test, y_test),
validation_steps=len(X_test) // batch_size,
epochs=epochs)
y_pred = model.predict(X_test, batch_size=batch_size)
y_pred = np.argmax(y_pred, axis=1)
print(classification_report(y_test.argmax(axis=1), y_pred, target_names=encoder.classes_))
model.save("model", save_format="h5")
plt.plot(np.arange(0, epochs), hist.history["loss"], label="train_loss")
plt.plot(np.arange(0, epochs), hist.history["val_loss"], label="val_loss")
plt.title("Training and Validation Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(loc="upper right")
prototxtPath = '/content/drive/My Drive/Face-Mask-Detector/resources/face_detector/deploy.prototxt'
weightsPath = '/content/drive/My Drive/Face-Mask-Detector/resources/face_detector/res10_300x300_ssd_iter_140000.caffemodel'
face_model = cv2.dnn.readNet(prototxtPath, weightsPath)
model = load_model("model")
im_path='people2.jpg'
image = cv2.imdecode(np.fromfile(im_path, dtype=np.uint8), cv2.IMREAD_UNCHANGED)
# image = cv2.imread('/content/drive/My Drive/maskclassifier/test/people2.jpg')
height, width = image.shape[:2]
blob = cv2.dnn.blobFromImage(image, 1.0, (300, 300), (104.0, 177.0, 123.0))
face_model.setInput(blob)
detections = face_model.forward() #detecting the faces
from google.colab.patches import cv2_imshow
threshold = 0.2
person_with_mask = 0;
person_without_mask = 0;
for i in range(0, detections.shape[2]):
score = detections[0, 0, i, 2]
if score > threshold:
#coordinates of the bounding box
box = detections[0, 0, i, 3:7] * np.array([width, height, width, height])
X_start, Y_start, X_end, Y_end = box.astype("int")
X_start, Y_start = (max(0, X_start), max(0, Y_start))
X_end, Y_end = (min(width - 1, X_end), min(height - 1, Y_end))
face = image[Y_start:Y_end, X_start:X_end]
face = cv2.cvtColor(face, cv2.COLOR_BGR2RGB) #Convert to rgb
face = cv2.resize(face, (224, 224)) #resize
face = img_to_array(face)
face = preprocess_input(face)
face = np.expand_dims(face, axis=0)
mask, withoutMask = model.predict(face)[0]
if mask > withoutMask:
label = "Mask"
person_with_mask += 1
else:
label = "No Mask"
person_without_mask += 1
if label == "Mask":
color = (0, 255, 0)
else:
color = (0, 0, 255)
label = "{}: {:.2f}%".format(label, max(mask, withoutMask) * 100)
cv2.putText(image, label, (X_start, Y_start - 10), cv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)
cv2.rectangle(image, (X_start, Y_start), (X_end, Y_end), color, 2)
print("Number of person with mask : {}".format(person_with_mask))
print("Number of person without mask : {}".format(person_without_mask))
cv2_imshow(image)
| 0.673621 | 0.855489 |
```
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras import layers, optimizers, models
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from pandas.plotting import register_matplotlib_converters
%matplotlib inline
register_matplotlib_converters()
sns.set(style="darkgrid", font_scale=1.5)
LENGTH = 90
SUBSAMPLING = 2 #once every 20 seconds predict
```
# Train Model
```
def preprocessTestingData(data, length):
hist = []
target = []
for i in range(len(data)-length):
x = data[i:i+length]
y = data[i+length]
hist.append(x)
target.append(y)
# Convert into numpy arrays and shape correctly (len(dataset), length) and (len(dataset), 1) respectivly
hist = np.array(hist)
target = np.array(target)
target = target.reshape(-1,1)
#Reshape the input into (len(dataset), length, 1)
hist = hist.reshape((len(hist), length, 1))
return(hist, target)
def trainModel(datasets, length, model=None, quiet=False):
for dataset in datasets:
X_train, y_train = preprocessTestingData(dataset, length)
if not model:
# Create model and compile
model = tf.keras.Sequential()
model.add(layers.LSTM(units=32, return_sequences=True, input_shape=(length,1), dropout=0.2))
model.add(layers.LSTM(units=32, return_sequences=True, dropout=0.2))
model.add(layers.LSTM(units=32, dropout=0.2))
model.add(layers.Dense(units=1))
optimizer = optimizers.Adam()
model.compile(optimizer=optimizer, loss='mean_squared_error')
# Perform training
output = 1
if quiet:
output = 0
history = model.fit(X_train, y_train, epochs=6, batch_size=32, verbose=output)
# Show loss
if not quiet:
loss = history.history['loss']
epoch_count = range(1, len(loss) + 1)
plt.figure(figsize=(6,4))
plt.plot(epoch_count, loss, 'r--')
plt.legend(['Training Loss'])
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()
return model
def scaleData(paths):
scaler = MinMaxScaler()
datasets = []
for path in paths:
# perform partial fits on all datasets
# datasets.append(pd.read_csv(path)[['price']][::SUBSAMPLING]) # TODO remove, 120 subsample for every two minues
new_df = pd.DataFrame()
new_df["price"] = from_csv[["high_price","low_price"]].mean(axis=1)
datasets.append(new_df[::SUBSAMPLING])
scaler = scaler.partial_fit(datasets[-1])
for i in range(len(datasets)):
# once all partial fits have been performed, transform every file
datasets[i] = scaler.transform(datasets[i])
return (datasets, scaler)
paths = ["../../data/ETH.csv"]
datasets, scaler = scaleData(paths)
model = trainModel(datasets, LENGTH)
```
# Test Model
## Evaluation Helpers
```
def sub_sample(arr1, arr2, sub):
return (arr1[::sub], arr2[::sub])
def evaluate_model(real_data, predicted_data, inherent_loss=2):
real_data = real_data.reshape(len(real_data))
predicted_data = predicted_data.reshape(len(predicted_data))
real_diff = np.diff(real_data)
predicted_diff = np.diff(predicted_data)
correct_slopes = 0
profit = 0
for i in range(len(real_data)-1):
if np.sign(real_diff[i]) == np.sign(predicted_diff[i]):
correct_slopes = correct_slopes + 1
# If we have a positive slope calculate profit
if real_diff[i] > 0:
# we subtract inherent_loss due to the limit market mechanics
revenue = (real_data[i+1] - real_data[i]) - inherent_loss
if revenue > 0:
# print(f"Found a profit where current value is {real_data[i+1]} last was {real_data[i]} net {revenue}")
profit = profit + revenue
else:
# We guessed wrong
if predicted_diff[i] > 0:
# we would have bought
revenue = (real_data[i+1] - real_data[i]) - inherent_loss
# print(f"Selling at a loss of {revenue}")
profit = profit + revenue
return (correct_slopes, profit)
def eval_model_on_dataset(actual, prediction, subsampling, inherent_loss):
# Subsample the test points, this seems to increase accuracy
real_subbed, pred_subbed = sub_sample(actual, prediction, subsampling)
# Determine the number of cases in which we predicted a correct increase
correct_slopes, profit = evaluate_model(real_subbed, pred_subbed, inherent_loss)
print(f"Found {correct_slopes} out of {len(real_subbed)-1}")
precent_success = (correct_slopes/(len(real_subbed)-1)) * 100
print(f"{precent_success}%")
print("Profit:", profit)
return profit
```
## Test Model
```
def testModel(model, path_to_testing_dataset, quiet=False):
datasets, scaler = scaleData([path_to_testing_dataset])
hist, actual = preprocessTestingData(datasets[0], LENGTH)
pred = model.predict(hist)
pred_transformed = scaler.inverse_transform(pred)
actual_transformed = scaler.inverse_transform(actual)
if not quiet:
plt.figure(figsize=(12,8))
plt.plot(actual_transformed, color='blue', label='Real')
plt.plot(pred_transformed, color='red', label='Prediction')
plt.title('ETH Price Prediction')
plt.legend()
plt.show()
return eval_model_on_dataset(actual=actual_transformed, prediction=pred_transformed, subsampling=1, inherent_loss=2)
testModel(model, "../../data/MorningTest4.csv")
```
# Single Prediction
```
# For example, if we just want to predict the next timestep in the dataset we can prepare it as such:
# 1. get the [length] last points from the data set since that's what we care about
length = LENGTH
most_recent_period = pd.read_csv('../../data/MorningTest2.csv')[['price']].tail(length)
# 2. convert to numpy array
most_recent_period = np.array(most_recent_period)
# 3. normalize data
scaler = MinMaxScaler()
most_recent_period_scaled = scaler.fit_transform(most_recent_period)
# 4. reshape to the 3D tensor we expected (1, length, 1)
most_recent_period_scaled_shaped = most_recent_period_scaled.reshape((1, length, 1))
# 5. Predict
prediction = model.predict(most_recent_period_scaled_shaped)
# 6. Un-normalize the data
result = scaler.inverse_transform(prediction)
print(f"${result[0][0]}")
```
# Prediction Success Evaluation
```
model.save("my_model")
pink = models.load_model("my_model")
profits = []
for length in np.arange(5, 360, 5):
for sub in np.arange(10, 480, 5):
try:
LENGTH = length
SUBSAMPLING = sub
model = trainModel(datasets, LENGTH, quiet=True)
profit = testModel(model, "../../data/MorningTest.csv", quiet=True)
profits.append((profit, length, sub))
print(sorted(profits, key=lambda tup: -tup[0])[0:20])
except:
pass
print("FINAL RESULTS")
sorted(profits, key=lambda tup: tup[0])[0:20]
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras import layers, optimizers, models
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from pandas.plotting import register_matplotlib_converters
%matplotlib inline
register_matplotlib_converters()
sns.set(style="darkgrid", font_scale=1.5)
LENGTH = 90
SUBSAMPLING = 2 #once every 20 seconds predict
def preprocessTestingData(data, length):
hist = []
target = []
for i in range(len(data)-length):
x = data[i:i+length]
y = data[i+length]
hist.append(x)
target.append(y)
# Convert into numpy arrays and shape correctly (len(dataset), length) and (len(dataset), 1) respectivly
hist = np.array(hist)
target = np.array(target)
target = target.reshape(-1,1)
#Reshape the input into (len(dataset), length, 1)
hist = hist.reshape((len(hist), length, 1))
return(hist, target)
def trainModel(datasets, length, model=None, quiet=False):
for dataset in datasets:
X_train, y_train = preprocessTestingData(dataset, length)
if not model:
# Create model and compile
model = tf.keras.Sequential()
model.add(layers.LSTM(units=32, return_sequences=True, input_shape=(length,1), dropout=0.2))
model.add(layers.LSTM(units=32, return_sequences=True, dropout=0.2))
model.add(layers.LSTM(units=32, dropout=0.2))
model.add(layers.Dense(units=1))
optimizer = optimizers.Adam()
model.compile(optimizer=optimizer, loss='mean_squared_error')
# Perform training
output = 1
if quiet:
output = 0
history = model.fit(X_train, y_train, epochs=6, batch_size=32, verbose=output)
# Show loss
if not quiet:
loss = history.history['loss']
epoch_count = range(1, len(loss) + 1)
plt.figure(figsize=(6,4))
plt.plot(epoch_count, loss, 'r--')
plt.legend(['Training Loss'])
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()
return model
def scaleData(paths):
scaler = MinMaxScaler()
datasets = []
for path in paths:
# perform partial fits on all datasets
# datasets.append(pd.read_csv(path)[['price']][::SUBSAMPLING]) # TODO remove, 120 subsample for every two minues
new_df = pd.DataFrame()
new_df["price"] = from_csv[["high_price","low_price"]].mean(axis=1)
datasets.append(new_df[::SUBSAMPLING])
scaler = scaler.partial_fit(datasets[-1])
for i in range(len(datasets)):
# once all partial fits have been performed, transform every file
datasets[i] = scaler.transform(datasets[i])
return (datasets, scaler)
paths = ["../../data/ETH.csv"]
datasets, scaler = scaleData(paths)
model = trainModel(datasets, LENGTH)
def sub_sample(arr1, arr2, sub):
return (arr1[::sub], arr2[::sub])
def evaluate_model(real_data, predicted_data, inherent_loss=2):
real_data = real_data.reshape(len(real_data))
predicted_data = predicted_data.reshape(len(predicted_data))
real_diff = np.diff(real_data)
predicted_diff = np.diff(predicted_data)
correct_slopes = 0
profit = 0
for i in range(len(real_data)-1):
if np.sign(real_diff[i]) == np.sign(predicted_diff[i]):
correct_slopes = correct_slopes + 1
# If we have a positive slope calculate profit
if real_diff[i] > 0:
# we subtract inherent_loss due to the limit market mechanics
revenue = (real_data[i+1] - real_data[i]) - inherent_loss
if revenue > 0:
# print(f"Found a profit where current value is {real_data[i+1]} last was {real_data[i]} net {revenue}")
profit = profit + revenue
else:
# We guessed wrong
if predicted_diff[i] > 0:
# we would have bought
revenue = (real_data[i+1] - real_data[i]) - inherent_loss
# print(f"Selling at a loss of {revenue}")
profit = profit + revenue
return (correct_slopes, profit)
def eval_model_on_dataset(actual, prediction, subsampling, inherent_loss):
# Subsample the test points, this seems to increase accuracy
real_subbed, pred_subbed = sub_sample(actual, prediction, subsampling)
# Determine the number of cases in which we predicted a correct increase
correct_slopes, profit = evaluate_model(real_subbed, pred_subbed, inherent_loss)
print(f"Found {correct_slopes} out of {len(real_subbed)-1}")
precent_success = (correct_slopes/(len(real_subbed)-1)) * 100
print(f"{precent_success}%")
print("Profit:", profit)
return profit
def testModel(model, path_to_testing_dataset, quiet=False):
datasets, scaler = scaleData([path_to_testing_dataset])
hist, actual = preprocessTestingData(datasets[0], LENGTH)
pred = model.predict(hist)
pred_transformed = scaler.inverse_transform(pred)
actual_transformed = scaler.inverse_transform(actual)
if not quiet:
plt.figure(figsize=(12,8))
plt.plot(actual_transformed, color='blue', label='Real')
plt.plot(pred_transformed, color='red', label='Prediction')
plt.title('ETH Price Prediction')
plt.legend()
plt.show()
return eval_model_on_dataset(actual=actual_transformed, prediction=pred_transformed, subsampling=1, inherent_loss=2)
testModel(model, "../../data/MorningTest4.csv")
# For example, if we just want to predict the next timestep in the dataset we can prepare it as such:
# 1. get the [length] last points from the data set since that's what we care about
length = LENGTH
most_recent_period = pd.read_csv('../../data/MorningTest2.csv')[['price']].tail(length)
# 2. convert to numpy array
most_recent_period = np.array(most_recent_period)
# 3. normalize data
scaler = MinMaxScaler()
most_recent_period_scaled = scaler.fit_transform(most_recent_period)
# 4. reshape to the 3D tensor we expected (1, length, 1)
most_recent_period_scaled_shaped = most_recent_period_scaled.reshape((1, length, 1))
# 5. Predict
prediction = model.predict(most_recent_period_scaled_shaped)
# 6. Un-normalize the data
result = scaler.inverse_transform(prediction)
print(f"${result[0][0]}")
model.save("my_model")
pink = models.load_model("my_model")
profits = []
for length in np.arange(5, 360, 5):
for sub in np.arange(10, 480, 5):
try:
LENGTH = length
SUBSAMPLING = sub
model = trainModel(datasets, LENGTH, quiet=True)
profit = testModel(model, "../../data/MorningTest.csv", quiet=True)
profits.append((profit, length, sub))
print(sorted(profits, key=lambda tup: -tup[0])[0:20])
except:
pass
print("FINAL RESULTS")
sorted(profits, key=lambda tup: tup[0])[0:20]
| 0.699254 | 0.822688 |
<a href="https://colab.research.google.com/github/paulowe/ml-lambda/blob/main/colab-train1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Import packages
```
import sklearn
import pandas as pd
import numpy as np
import csv as csv
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import classification_report
from sklearn import metrics
from sklearn.externals import joblib
from sklearn.preprocessing import label_binarize
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import roc_auc_score
```
- Verify you are running Version 0.23.1 of sklearn. Some of the packages used for model evaluation only work with this version or higher.
- Run <> to upgrade sklearn
```
sklearn.__version__
```
## Import Data
X - all training examples
y - all true labels
```
data = pd.read_csv('./syntheticData.csv')
X, y = data.iloc[:, 1:], data.iloc[:,0]
```
## Visualize Data
(80100 * 377) training matrix
(801 * 1) label vector
```
print(X.head())
print(X.shape)
print(y.head())
print(y.shape)
```
## Split into training, cross validation and test sets
- Shuffle dataset
- Perform Split (60-20-20)
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40, stratify=y)
X_cv, X_test, y_cv, y_test = train_test_split(X_test, y_test, test_size=0.5, stratify=y_test)
print("Training data dimensions")
print(X_train.shape)
print(y_train.shape)
print("Cross validation data dimensions")
print(X_cv.shape)
print(y_cv.shape)
print("Test data dimensions")
print(X_test.shape)
print(y_test.shape)
```
## Train default MLP Classifier
```
clf = MLPClassifier()
clf = clf.fit(X_train, y_train)
```
## Training Variant: Bottom Up implementation
In this variant I will implement an identical classifier to the one we trained above. The objective here is to expose underlying components of the training process and perform direct optimization and monitoring techniques.
- Random initialization for weights
- Feedforward Propagation - Prediction function
- Neural Network Cost Function
- Backpropagation
- Sigmoid Gradient
### Random initialization
Select values for $\Theta^{(l)}$ uniformly in the range $[-\epsilon_{init} , \epsilon_{init}]$
One effective strategy for choosing $\epsilon_{init}$ is to base it on the number of units in the network
$\epsilon_{init} = \frac{\sqrt{6}}{\sqrt{L_{in} + L_{out}}}$
```
def randInitializeWeights(L_in, L_out):
"""
randomly initializes the weights of a layer with L_in incoming connections and L_out outgoing connections.
"""
epi = (6**1/2) / (L_in + L_out)**1/2
W = np.random.rand(L_out,L_in +1) *(2*epi) -epi
return W
```
Initialize Theta Vectors
Here we will randomly intialize theta vecotrs for each layer
```
input_layer_size = 400
hidden_layer_size = 25
num_labels = 801
Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size)
Theta2 = randInitializeWeights(hidden_layer_size, num_labels)
nn_params = np.append(Theta1.flatten(),Theta2.flatten())
def sigmoidGradient(z):
"""
computes the gradient of the sigmoid function
"""
sigmoid = 1/(1 + np.exp(-z))
return sigmoid *(1-sigmoid)
def predict(Theta1, Theta2, X):
"""
Predict the label of an input given a trained neural network
"""
m= X.shape[0]
X = np.hstack((np.ones((m,1)),X))
a1 = sigmoid(X @ Theta1.T)
a1 = np.hstack((np.ones((m,1)), a1)) # hidden layer
a2 = sigmoid(a1 @ Theta2.T) # output layer
#find out why its +1
return np.argmax(a2,axis=1)+1
pred = predict(Theta1, Theta2, X)
# numEx - is the number of examples in the training set
print("Training Set Accuracy:",sum(pred[:,np.newaxis]==y)[0]/numEx*100,"%")
```
## Computing Neural Network Cost function
$J(\Theta) = \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^k [-y_k^{(i)} log(h_\Theta(x^{(i)})_k) - ( 1 -y_k^{(i)} log (1-h_\Theta(x^{(i)})_k)] + \frac{\lambda}{2m}[\sum_{j=1}^{25} \sum_{k=1}^{400} (\Theta_{j,k}^{(1)})^2 + \sum_{j=1}^{10} \sum_{k=1}^{25} (\Theta_{j,k}^{(2)})^2]$
## Computing Backpropagation
Implementation of Backpropagation to compute gradients.
```
def nnCostFunction(nn_params,input_layer_size, hidden_layer_size, num_labels,X, y,Lambda):
"""
nn_params contains the parameters unrolled into a vector
compute the cost and gradient of the neural network
"""
# Reshape nn_params back into the parameters Theta1 and Theta2
Theta1 = nn_params[:((input_layer_size+1) * hidden_layer_size)].reshape(hidden_layer_size,input_layer_size+1)
Theta2 = nn_params[((input_layer_size +1)* hidden_layer_size ):].reshape(num_labels,hidden_layer_size+1)
m = X.shape[0]
J=0
X = np.hstack((np.ones((m,1)),X))
y10 = np.zeros((m,num_labels))
a1 = sigmoid(X @ Theta1.T)
a1 = np.hstack((np.ones((m,1)), a1)) # hidden layer
a2 = sigmoid(a1 @ Theta2.T) # output layer
for i in range(1,num_labels+1):
y10[:,i-1][:,np.newaxis] = np.where(y==i,1,0)
for j in range(num_labels):
J = J + sum(-y10[:,j] * np.log(a2[:,j]) - (1-y10[:,j])*np.log(1-a2[:,j]))
cost = 1/m* J
reg_J = cost + Lambda/(2*m) * (np.sum(Theta1[:,1:]**2) + np.sum(Theta2[:,1:]**2))
# Implement the backpropagation algorithm to compute the gradients
grad1 = np.zeros((Theta1.shape))
grad2 = np.zeros((Theta2.shape))
for i in range(m):
xi= X[i,:] # 1 X 401
a1i = a1[i,:] # 1 X 26
a2i =a2[i,:] # 1 X 10
d2 = a2i - y10[i,:]
d1 = Theta2.T @ d2.T * sigmoidGradient(np.hstack((1,xi @ Theta1.T)))
grad1= grad1 + d1[1:][:,np.newaxis] @ xi[:,np.newaxis].T
grad2 = grad2 + d2.T[:,np.newaxis] @ a1i[:,np.newaxis].T
grad1 = 1/m * grad1
grad2 = 1/m*grad2
grad1_reg = grad1 + (Lambda/m) * np.hstack((np.zeros((Theta1.shape[0],1)),Theta1[:,1:]))
grad2_reg = grad2 + (Lambda/m) * np.hstack((np.zeros((Theta2.shape[0],1)),Theta2[:,1:]))
return cost, grad1, grad2,reg_J, grad1_reg,grad2_reg
def sigmoidGradient(z):
"""
computes the gradient of the sigmoid function
"""
sigmoid = 1/(1 + np.exp(-z))
return sigmoid *(1-sigmoid)
```
## In Action: Cost Function
Piece up different components defined above to compute cost of our Neural Network (regularized and unregularized)
** predicting an underfitted model
```
J,reg_J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, 1)[0:4:3]
print("Cost at parameters (non-regularized):",J,"\nCost at parameters (Regularized):",reg_J)
```
## Model Evaluation
Model Evaluation is an important part of understanding your model performance.
For that matter it is crucial to choose a good evaluation metric you can monitor. In our case Accuracy makes the most sense.
We will monitor
- Accuracy on Test (clf)
- AUC (implementation requires sklearn v0.23.1 +)
- Accuracy on Test (eng)
- AUC
- Accuracy other vairants (vnt)
- AUC
```
# Accuracy
testsetPred = clf.predict(X_test)
accuracy_score(y_test, testsetPred)
#AUC
#roc_auc_score(y_test, testsetPred, multi_class='ovr')
```
## Serialize Model Variant
Serialize the classifier you like
(1) Default Sklearn Model (clf)
(2) Variant 1 (eng)
(3) Variant 2
(4) Variant 3
```
"""
Serialize Model
"""
joblib.dump(clf, 'mlp.pkl')
```
|
github_jupyter
|
import sklearn
import pandas as pd
import numpy as np
import csv as csv
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import classification_report
from sklearn import metrics
from sklearn.externals import joblib
from sklearn.preprocessing import label_binarize
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import roc_auc_score
sklearn.__version__
data = pd.read_csv('./syntheticData.csv')
X, y = data.iloc[:, 1:], data.iloc[:,0]
print(X.head())
print(X.shape)
print(y.head())
print(y.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40, stratify=y)
X_cv, X_test, y_cv, y_test = train_test_split(X_test, y_test, test_size=0.5, stratify=y_test)
print("Training data dimensions")
print(X_train.shape)
print(y_train.shape)
print("Cross validation data dimensions")
print(X_cv.shape)
print(y_cv.shape)
print("Test data dimensions")
print(X_test.shape)
print(y_test.shape)
clf = MLPClassifier()
clf = clf.fit(X_train, y_train)
def randInitializeWeights(L_in, L_out):
"""
randomly initializes the weights of a layer with L_in incoming connections and L_out outgoing connections.
"""
epi = (6**1/2) / (L_in + L_out)**1/2
W = np.random.rand(L_out,L_in +1) *(2*epi) -epi
return W
input_layer_size = 400
hidden_layer_size = 25
num_labels = 801
Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size)
Theta2 = randInitializeWeights(hidden_layer_size, num_labels)
nn_params = np.append(Theta1.flatten(),Theta2.flatten())
def sigmoidGradient(z):
"""
computes the gradient of the sigmoid function
"""
sigmoid = 1/(1 + np.exp(-z))
return sigmoid *(1-sigmoid)
def predict(Theta1, Theta2, X):
"""
Predict the label of an input given a trained neural network
"""
m= X.shape[0]
X = np.hstack((np.ones((m,1)),X))
a1 = sigmoid(X @ Theta1.T)
a1 = np.hstack((np.ones((m,1)), a1)) # hidden layer
a2 = sigmoid(a1 @ Theta2.T) # output layer
#find out why its +1
return np.argmax(a2,axis=1)+1
pred = predict(Theta1, Theta2, X)
# numEx - is the number of examples in the training set
print("Training Set Accuracy:",sum(pred[:,np.newaxis]==y)[0]/numEx*100,"%")
def nnCostFunction(nn_params,input_layer_size, hidden_layer_size, num_labels,X, y,Lambda):
"""
nn_params contains the parameters unrolled into a vector
compute the cost and gradient of the neural network
"""
# Reshape nn_params back into the parameters Theta1 and Theta2
Theta1 = nn_params[:((input_layer_size+1) * hidden_layer_size)].reshape(hidden_layer_size,input_layer_size+1)
Theta2 = nn_params[((input_layer_size +1)* hidden_layer_size ):].reshape(num_labels,hidden_layer_size+1)
m = X.shape[0]
J=0
X = np.hstack((np.ones((m,1)),X))
y10 = np.zeros((m,num_labels))
a1 = sigmoid(X @ Theta1.T)
a1 = np.hstack((np.ones((m,1)), a1)) # hidden layer
a2 = sigmoid(a1 @ Theta2.T) # output layer
for i in range(1,num_labels+1):
y10[:,i-1][:,np.newaxis] = np.where(y==i,1,0)
for j in range(num_labels):
J = J + sum(-y10[:,j] * np.log(a2[:,j]) - (1-y10[:,j])*np.log(1-a2[:,j]))
cost = 1/m* J
reg_J = cost + Lambda/(2*m) * (np.sum(Theta1[:,1:]**2) + np.sum(Theta2[:,1:]**2))
# Implement the backpropagation algorithm to compute the gradients
grad1 = np.zeros((Theta1.shape))
grad2 = np.zeros((Theta2.shape))
for i in range(m):
xi= X[i,:] # 1 X 401
a1i = a1[i,:] # 1 X 26
a2i =a2[i,:] # 1 X 10
d2 = a2i - y10[i,:]
d1 = Theta2.T @ d2.T * sigmoidGradient(np.hstack((1,xi @ Theta1.T)))
grad1= grad1 + d1[1:][:,np.newaxis] @ xi[:,np.newaxis].T
grad2 = grad2 + d2.T[:,np.newaxis] @ a1i[:,np.newaxis].T
grad1 = 1/m * grad1
grad2 = 1/m*grad2
grad1_reg = grad1 + (Lambda/m) * np.hstack((np.zeros((Theta1.shape[0],1)),Theta1[:,1:]))
grad2_reg = grad2 + (Lambda/m) * np.hstack((np.zeros((Theta2.shape[0],1)),Theta2[:,1:]))
return cost, grad1, grad2,reg_J, grad1_reg,grad2_reg
def sigmoidGradient(z):
"""
computes the gradient of the sigmoid function
"""
sigmoid = 1/(1 + np.exp(-z))
return sigmoid *(1-sigmoid)
J,reg_J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, 1)[0:4:3]
print("Cost at parameters (non-regularized):",J,"\nCost at parameters (Regularized):",reg_J)
# Accuracy
testsetPred = clf.predict(X_test)
accuracy_score(y_test, testsetPred)
#AUC
#roc_auc_score(y_test, testsetPred, multi_class='ovr')
"""
Serialize Model
"""
joblib.dump(clf, 'mlp.pkl')
| 0.615897 | 0.972753 |
# Periodic Motion: Kinematic Exploration of Pendulum
Working with observations to develop a conceptual representation of periodic motion in the context of a pendulum.
### Dependencies
This is my usual spectrum of dependencies that seem to be generally useful. We'll see if I need additional ones. When needed I will use the newer version of the random number generator since the older version is being deprecated. If you have troubles with any random numbers check for python updates for your Anaconda install.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import default_rng
rng = default_rng()
```
### Conceptual Observations
From the video in the [Periodic Motion breadcrumb ](http://coccweb.cocc.edu/bemerson/PhysicsGlobal/Courses/PH213/PH213Materials/PH213Breadcrumbs/PH213BCHarmonic.html) we sought to extract a sense of position, velocity and acceleration at different points in the process. In a simplified (not overthinking it) sense there are three general ways to describe the motion of the pendulum. Horizontal, vertical, and angular. In each case there is a midpoint or neutral position that one might reasonably label as 0 in x,y, or $\theta$. In each case there is an extreme in each direction from the neutral position which is repeated. Where I start counting time from is totally up in the air but it seems like each section the motion is taking the same amount of time. Dropping some rough data into an array and plotting it would look something like this....
```
conceptX = [-5., 0., 5., 0., -5., 0]
conceptY = [-.6, 0.,0.6,0.,-0.6,0.]
conceptTheta = [- 15. , 0., 15., 0., -15.,0.]
conceptTime = [0., 1.,2.,3.,4.,5.]
fig, ax = plt.subplots()
ax.scatter(conceptTime, conceptX ,s = 150, marker = '+',color = 'blue', label = 'x motion')
ax.scatter(conceptTime, conceptY , s = 150, marker = 'o', color = 'red', label = 'y motion')
ax.scatter(conceptTime, conceptTheta , s = 150, marker = '*', color = 'green', label = 'theta motion')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax.set(xlabel='conceptual time', ylabel='position',
title='Conceptual motion')
fig.set_size_inches(10, 5)
plt.legend(loc= 2)
ax.grid()
fig.savefig("images/allThree.png")
plt.show()
```
Generally this seems to match the general sense of the motion. The horizontal motion is 'larger' than the vertical motion and the angular motion also goes back and forth in some units. To minimize confusion with multiple data sets I'll move to a single data set for a bit -- the horizontal one.
```
fig2, ax2 = plt.subplots()
ax2.scatter(conceptTime, conceptX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax2.set(xlabel='conceptual time', ylabel='position',
title='Conceptual motion')
fig2.set_size_inches(10, 5)
plt.legend(loc= 2)
ax2.grid()
fig2.savefig("images/justHorizontal.png")
plt.show()
```
### Velocity at Each Point
In examining the video one hopes that we notice that the pendulum stops at each extreme of motion. After some thought (particularly in the horizontal direction) it seems plausible that gravity is pulling the pendulum 'down' until it reaches it's lowest point (speeding it up) and then pulls it 'back' (slowing it down) during the next part of the cycle. One can also arrive at this observation by considering the gravitational potential energy and our energy bar charts. All of this leads to the idea that the velocity reachs a maximum when the pendulum is at it's 'neutral' point. If we were to draw lines to indicate the local slope of the x(t) function we might see something like this.....
Consider which of the three possibilities illustrated in the set of plots is consistent with a function that speeds up and slows down as you observe.
```
# first extreme
min0x = [-.4,0.,.4]
min0y = [-5.,-5.,-5.]
# first neutral
min1xa = [.5,1.,1.5]
min1ya = [-1.,0.,1.]
min1xb = [.5,1.,1.5]
min1yb = [-2.5,0.,2.5]
min1xc = [.8,1.,1.2]
min1yc = [-2.5,0.,2.5]
# second extreme
min2x = [1.6,2.,2.4]
min2y = [5.,5.,5.]
# second neutral
min3xa = [2.5,3.,3.5]
min3ya = [1.,0.,-1.]
min3xb = [2.5,3.,3.5]
min3yb = [2.5,0.,-2.5]
min3xc = [2.8,3.,3.2]
min3yc = [2.5,0.,-2.5]
# third extreme
min4x = [3.6,4.,4.4]
min4y = [-5.,-5.,-5.]
fig3, (bx1,bx2,bx3) = plt.subplots(3,1)
# First, the low max velocity
bx1.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx1.plot(min0x, min0y, color = 'red')
bx1.plot(min2x, min2y, color = 'red')
bx1.plot(min4x, min4y, color = 'red')
# max velocity points first
bx1.plot(min1xa, min1ya, color = 'red')
# max velocity points second
bx1.plot(min3xa, min3ya, color = 'red')
# second, max velocity as constant
bx2.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx2.plot(min0x, min0y, color = 'red')
bx2.plot(min2x, min2y, color = 'red')
bx2.plot(min4x, min4y, color = 'red')
# max velocity points first
bx2.plot(min1xb, min1yb, color = 'red')
# max velocity points second
bx2.plot(min3xb, min3yb, color = 'red')
# Third, max velocity with 'room to decrease'
bx3.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx3.plot(min0x, min0y, color = 'red')
bx3.plot(min2x, min2y, color = 'red')
bx3.plot(min4x, min4y, color = 'red')
# max velocity points first
bx3.plot(min1xc, min1yc, color = 'red')
# max velocity points second
bx3.plot(min3xc, min3yc, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
bx1.set(xlabel='', ylabel='position',
title='low velocity at neutral point')
bx2.set(xlabel='', ylabel='position',
title='average velocity at neutral point')
bx3.set(xlabel='conceptual time', ylabel='position',
title='higher velocity at neutral point')
fig3.set_size_inches(10, 15)
#plt.legend(loc= 2)
bx1.grid()
bx2.grid()
bx3.grid()
fig3.savefig("images/possibleConcepts.png")
plt.show()
```
### Which one is consistent?
Hopefully you see that only the last plot with a higher velocity at the neutral point is a possible representation of the kinematics.
### Elapsed Time for a Cycle
Counting 'elephants' the time to complete one cycle in the horizontal direction seems to be between 5 and 6 seconds. If I take 6 s to be the cycle time then each section of the plot above takes 1.5 s.
### Scale of Horizontal Motion
It is hard to know how to scale the horizontal motion though it seems likely that it isn't 10 m from side to side. Hard to say but it feels more reasonable to assume the maximum horizontal distance from the neutral point is more like 1.2 m. I wouldn't argue with you if you thought it was a bit more or less.
### Tidying Up
Let's put all of this last estimation into the plot and see what happens.....
```
scaledX = [-1.2, 0., 1.2, 0., -1.2, 0]
scaledTime = [0., 1.5,3.,4.5,6.,7.5]
# s on end indicates scaled values of position and time
min0xs = [-.4,0.,.4]
min0ys = [-1.2,-1.2,-1.2]
# first neutral
min1xs = [1.2,1.5,1.8]
min1ys = [-.4,0.,.4]
# second extreme
min2xs = [2.6,3.,3.4]
min2ys = [1.2,1.2,1.2]
# second neutral
min3xs = [4.2,4.5,4.8]
min3ys = [.4,0.,-.4]
# third extreme
min4xs = [5.6,6.,6.4]
min4ys= [-1.2,-1.2,-1.2]
fig4, ax4 = plt.subplots()
ax4.scatter(scaledTime, scaledX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
ax4.plot(min0xs, min0ys, color = 'red')
ax4.plot(min2xs, min2ys, color = 'red')
ax4.plot(min4xs, min4ys, color = 'red')
# max velocity points first
ax4.plot(min1xs, min1ys, color = 'red')
# max velocity points second
ax4.plot(min3xs, min3ys, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax4.set(xlabel='scaled time (s)', ylabel='position (m)',
title='Estimated Motion')
fig4.set_size_inches(10, 5)
plt.legend(loc= 2)
ax4.grid()
fig4.savefig("images/bestConcept.png")
plt.show()
```
## Adding a Model
So what sort of mathematical function might be plausible to model this with? No surprise that sine and cosine are very reasonable choices. This particular set of data looks most like the negative of the cosine function so I will use that. Because the cos($\theta$) ranges between 1 and -1 I need to multiply by some scalar to get it to hit the peaks and troughs of my data. This factor is called the amplitude and is often abbreviated A.
$$ \large x(t) = A \: cos(\theta) $$
In this expression the time dependence muct be hiding in the $\theta$ term. $\theta = \theta (t)$ . Then there is the question about how to stretch or shrink the cosine function so that it completes a full cycle in 6 s. You could go back to your trig class and try to remember this but I'll save you the trouble. Since the cosine function completes a full cycle in 2$\pi$ radians what we need is:
$$ \large \theta (t) \: = \: \frac{2\pi}{T}\:t $$
T is called the period of the motion which we have estimated to be 6 s. Notice that when t = 6 s then t/T = 1 and $\theta$ = 2$\pi$.
This is implemented in the next cell and then plotted on top of our conceptual sketch....
```
amplitude = 1.2
omega = 2*np.pi/6.
modelTime = np.linspace(0, 8, 500)
modelX = -amplitude * np.cos(omega*modelTime)
fig5, ax5 = plt.subplots()
ax5.scatter(scaledTime, scaledX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
ax5.plot(modelTime, modelX, color = 'green', label = 'harmonic model')
# 0 velocity points
ax5.plot(min0xs, min0ys, color = 'red')
ax5.plot(min2xs, min2ys, color = 'red')
ax5.plot(min4xs, min4ys, color = 'red')
# max velocity points first
ax5.plot(min1xs, min1ys, color = 'red')
# max velocity points second
ax5.plot(min3xs, min3ys, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax5.set(xlabel='scaled time (s)', ylabel='position (m)',
title='Estimated Motion')
fig5.set_size_inches(10, 5)
plt.legend(loc= 2)
ax5.grid()
fig5.savefig("images/dataWithModel.png")
plt.show()
```
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import default_rng
rng = default_rng()
conceptX = [-5., 0., 5., 0., -5., 0]
conceptY = [-.6, 0.,0.6,0.,-0.6,0.]
conceptTheta = [- 15. , 0., 15., 0., -15.,0.]
conceptTime = [0., 1.,2.,3.,4.,5.]
fig, ax = plt.subplots()
ax.scatter(conceptTime, conceptX ,s = 150, marker = '+',color = 'blue', label = 'x motion')
ax.scatter(conceptTime, conceptY , s = 150, marker = 'o', color = 'red', label = 'y motion')
ax.scatter(conceptTime, conceptTheta , s = 150, marker = '*', color = 'green', label = 'theta motion')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax.set(xlabel='conceptual time', ylabel='position',
title='Conceptual motion')
fig.set_size_inches(10, 5)
plt.legend(loc= 2)
ax.grid()
fig.savefig("images/allThree.png")
plt.show()
fig2, ax2 = plt.subplots()
ax2.scatter(conceptTime, conceptX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax2.set(xlabel='conceptual time', ylabel='position',
title='Conceptual motion')
fig2.set_size_inches(10, 5)
plt.legend(loc= 2)
ax2.grid()
fig2.savefig("images/justHorizontal.png")
plt.show()
# first extreme
min0x = [-.4,0.,.4]
min0y = [-5.,-5.,-5.]
# first neutral
min1xa = [.5,1.,1.5]
min1ya = [-1.,0.,1.]
min1xb = [.5,1.,1.5]
min1yb = [-2.5,0.,2.5]
min1xc = [.8,1.,1.2]
min1yc = [-2.5,0.,2.5]
# second extreme
min2x = [1.6,2.,2.4]
min2y = [5.,5.,5.]
# second neutral
min3xa = [2.5,3.,3.5]
min3ya = [1.,0.,-1.]
min3xb = [2.5,3.,3.5]
min3yb = [2.5,0.,-2.5]
min3xc = [2.8,3.,3.2]
min3yc = [2.5,0.,-2.5]
# third extreme
min4x = [3.6,4.,4.4]
min4y = [-5.,-5.,-5.]
fig3, (bx1,bx2,bx3) = plt.subplots(3,1)
# First, the low max velocity
bx1.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx1.plot(min0x, min0y, color = 'red')
bx1.plot(min2x, min2y, color = 'red')
bx1.plot(min4x, min4y, color = 'red')
# max velocity points first
bx1.plot(min1xa, min1ya, color = 'red')
# max velocity points second
bx1.plot(min3xa, min3ya, color = 'red')
# second, max velocity as constant
bx2.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx2.plot(min0x, min0y, color = 'red')
bx2.plot(min2x, min2y, color = 'red')
bx2.plot(min4x, min4y, color = 'red')
# max velocity points first
bx2.plot(min1xb, min1yb, color = 'red')
# max velocity points second
bx2.plot(min3xb, min3yb, color = 'red')
# Third, max velocity with 'room to decrease'
bx3.scatter(conceptTime, conceptX , marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
bx3.plot(min0x, min0y, color = 'red')
bx3.plot(min2x, min2y, color = 'red')
bx3.plot(min4x, min4y, color = 'red')
# max velocity points first
bx3.plot(min1xc, min1yc, color = 'red')
# max velocity points second
bx3.plot(min3xc, min3yc, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
bx1.set(xlabel='', ylabel='position',
title='low velocity at neutral point')
bx2.set(xlabel='', ylabel='position',
title='average velocity at neutral point')
bx3.set(xlabel='conceptual time', ylabel='position',
title='higher velocity at neutral point')
fig3.set_size_inches(10, 15)
#plt.legend(loc= 2)
bx1.grid()
bx2.grid()
bx3.grid()
fig3.savefig("images/possibleConcepts.png")
plt.show()
scaledX = [-1.2, 0., 1.2, 0., -1.2, 0]
scaledTime = [0., 1.5,3.,4.5,6.,7.5]
# s on end indicates scaled values of position and time
min0xs = [-.4,0.,.4]
min0ys = [-1.2,-1.2,-1.2]
# first neutral
min1xs = [1.2,1.5,1.8]
min1ys = [-.4,0.,.4]
# second extreme
min2xs = [2.6,3.,3.4]
min2ys = [1.2,1.2,1.2]
# second neutral
min3xs = [4.2,4.5,4.8]
min3ys = [.4,0.,-.4]
# third extreme
min4xs = [5.6,6.,6.4]
min4ys= [-1.2,-1.2,-1.2]
fig4, ax4 = plt.subplots()
ax4.scatter(scaledTime, scaledX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
# 0 velocity points
ax4.plot(min0xs, min0ys, color = 'red')
ax4.plot(min2xs, min2ys, color = 'red')
ax4.plot(min4xs, min4ys, color = 'red')
# max velocity points first
ax4.plot(min1xs, min1ys, color = 'red')
# max velocity points second
ax4.plot(min3xs, min3ys, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax4.set(xlabel='scaled time (s)', ylabel='position (m)',
title='Estimated Motion')
fig4.set_size_inches(10, 5)
plt.legend(loc= 2)
ax4.grid()
fig4.savefig("images/bestConcept.png")
plt.show()
amplitude = 1.2
omega = 2*np.pi/6.
modelTime = np.linspace(0, 8, 500)
modelX = -amplitude * np.cos(omega*modelTime)
fig5, ax5 = plt.subplots()
ax5.scatter(scaledTime, scaledX ,s = 150, marker = '.',color = 'blue', label = 'x motion')
ax5.plot(modelTime, modelX, color = 'green', label = 'harmonic model')
# 0 velocity points
ax5.plot(min0xs, min0ys, color = 'red')
ax5.plot(min2xs, min2ys, color = 'red')
ax5.plot(min4xs, min4ys, color = 'red')
# max velocity points first
ax5.plot(min1xs, min1ys, color = 'red')
# max velocity points second
ax5.plot(min3xs, min3ys, color = 'red')
plt.rcParams.update({'font.size': 12}) # make labels easier to read
ax5.set(xlabel='scaled time (s)', ylabel='position (m)',
title='Estimated Motion')
fig5.set_size_inches(10, 5)
plt.legend(loc= 2)
ax5.grid()
fig5.savefig("images/dataWithModel.png")
plt.show()
| 0.611614 | 0.978426 |
```
%matplotlib inline
```
A Gentle Introduction to ``torch.autograd``
---------------------------------
``torch.autograd`` is PyTorch’s automatic differentiation engine that powers
neural network training. In this section, you will get a conceptual
understanding of how autograd helps a neural network train.
Background
~~~~~~~~~~
Neural networks (NNs) are a collection of nested functions that are
executed on some input data. These functions are defined by *parameters*
(consisting of weights and biases), which in PyTorch are stored in
tensors.
Training a NN happens in two steps:
**Forward Propagation**: In forward prop, the NN makes its best guess
about the correct output. It runs the input data through each of its
functions to make this guess.
**Backward Propagation**: In backprop, the NN adjusts its parameters
proportionate to the error in its guess. It does this by traversing
backwards from the output, collecting the derivatives of the error with
respect to the parameters of the functions (*gradients*), and optimizing
the parameters using gradient descent. For a more detailed walkthrough
of backprop, check out this `video from
3Blue1Brown <https://www.youtube.com/watch?v=tIeHLnjs5U8>`__.
Usage in PyTorch
~~~~~~~~~~~
Let's take a look at a single training step.
For this example, we load a pretrained resnet18 model from ``torchvision``.
We create a random data tensor to represent a single image with 3 channels, and height & width of 64,
and its corresponding ``label`` initialized to some random values.
```
import torch, torchvision
model = torchvision.models.resnet18(pretrained=True)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)
```
Next, we run the input data through the model through each of its layers to make a prediction.
This is the **forward pass**.
```
prediction = model(data) # forward pass
```
We use the model's prediction and the corresponding label to calculate the error (``loss``).
The next step is to backpropagate this error through the network.
Backward propagation is kicked off when we call ``.backward()`` on the error tensor.
Autograd then calculates and stores the gradients for each model parameter in the parameter's ``.grad`` attribute.
```
loss = (prediction - labels).sum()
loss.backward() # backward pass
```
Next, we load an optimizer, in this case SGD with a learning rate of 0.01 and momentum of 0.9.
We register all the parameters of the model in the optimizer.
```
optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
```
Finally, we call ``.step()`` to initiate gradient descent. The optimizer adjusts each parameter by its gradient stored in ``.grad``.
```
optim.step() #gradient descent
```
At this point, you have everything you need to train your neural network.
The below sections detail the workings of autograd - feel free to skip them.
--------------
Differentiation in Autograd
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's take a look at how ``autograd`` collects gradients. We create two tensors ``a`` and ``b`` with
``requires_grad=True``. This signals to ``autograd`` that every operation on them should be tracked.
```
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
```
We create another tensor ``Q`` from ``a`` and ``b``.
\begin{align}Q = 3a^3 - b^2\end{align}
```
Q = 3*a**3 - b**2
```
Let's assume ``a`` and ``b`` to be parameters of an NN, and ``Q``
to be the error. In NN training, we want gradients of the error
w.r.t. parameters, i.e.
\begin{align}\frac{\partial Q}{\partial a} = 9a^2\end{align}
\begin{align}\frac{\partial Q}{\partial b} = -2b\end{align}
When we call ``.backward()`` on ``Q``, autograd calculates these gradients
and stores them in the respective tensors' ``.grad`` attribute.
We need to explicitly pass a ``gradient`` argument in ``Q.backward()`` because it is a vector.
``gradient`` is a tensor of the same shape as ``Q``, and it represents the
gradient of Q w.r.t. itself, i.e.
\begin{align}\frac{dQ}{dQ} = 1\end{align}
Equivalently, we can also aggregate Q into a scalar and call backward implicitly, like ``Q.sum().backward()``.
```
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
```
Gradients are now deposited in ``a.grad`` and ``b.grad``
```
# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)
```
Optional Reading - Vector Calculus using ``autograd``
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Mathematically, if you have a vector valued function
$\vec{y}=f(\vec{x})$, then the gradient of $\vec{y}$ with
respect to $\vec{x}$ is a Jacobian matrix $J$:
\begin{align}J
=
\left(\begin{array}{cc}
\frac{\partial \bf{y}}{\partial x_{1}} &
... &
\frac{\partial \bf{y}}{\partial x_{n}}
\end{array}\right)
=
\left(\begin{array}{ccc}
\frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\
\vdots & \ddots & \vdots\\
\frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}
\end{array}\right)\end{align}
Generally speaking, ``torch.autograd`` is an engine for computing
vector-Jacobian product. That is, given any vector $\vec{v}$, compute the product
$J^{T}\cdot \vec{v}$
If $v$ happens to be the gradient of a scalar function
\begin{align}l
=
g\left(\vec{y}\right)
=
\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\end{align}
then by the chain rule, the vector-Jacobian product would be the
gradient of $l$ with respect to $\vec{x}$:
\begin{align}J^{T}\cdot \vec{v}=\left(\begin{array}{ccc}
\frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\
\vdots & \ddots & \vdots\\
\frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}
\end{array}\right)\left(\begin{array}{c}
\frac{\partial l}{\partial y_{1}}\\
\vdots\\
\frac{\partial l}{\partial y_{m}}
\end{array}\right)=\left(\begin{array}{c}
\frac{\partial l}{\partial x_{1}}\\
\vdots\\
\frac{\partial l}{\partial x_{n}}
\end{array}\right)\end{align}
This characteristic of vector-Jacobian product is what we use in the above example;
``external_grad`` represents $\vec{v}$.
Computational Graph
~~~~~~~~~~~~~~~~~~~
Conceptually, autograd keeps a record of data (tensors) & all executed
operations (along with the resulting new tensors) in a directed acyclic
graph (DAG) consisting of
`Function <https://pytorch.org/docs/stable/autograd.html#torch.autograd.Function>`__
objects. In this DAG, leaves are the input tensors, roots are the output
tensors. By tracing this graph from roots to leaves, you can
automatically compute the gradients using the chain rule.
In a forward pass, autograd does two things simultaneously:
- run the requested operation to compute a resulting tensor, and
- maintain the operation’s *gradient function* in the DAG.
The backward pass kicks off when ``.backward()`` is called on the DAG
root. ``autograd`` then:
- computes the gradients from each ``.grad_fn``,
- accumulates them in the respective tensor’s ``.grad`` attribute, and
- using the chain rule, propagates all the way to the leaf tensors.
Below is a visual representation of the DAG in our example. In the graph,
the arrows are in the direction of the forward pass. The nodes represent the backward functions
of each operation in the forward pass. The leaf nodes in blue represent our leaf tensors ``a`` and ``b``.
.. figure:: /_static/img/dag_autograd.png
<div class="alert alert-info"><h4>Note</h4><p>**DAGs are dynamic in PyTorch**
An important thing to note is that the graph is recreated from scratch; after each
``.backward()`` call, autograd starts populating a new graph. This is
exactly what allows you to use control flow statements in your model;
you can change the shape, size and operations at every iteration if
needed.</p></div>
Exclusion from the DAG
^^^^^^^^^^^^^^^^^^^^^^
``torch.autograd`` tracks operations on all tensors which have their
``requires_grad`` flag set to ``True``. For tensors that don’t require
gradients, setting this attribute to ``False`` excludes it from the
gradient computation DAG.
The output tensor of an operation will require gradients even if only a
single input tensor has ``requires_grad=True``.
```
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)
a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
```
In a NN, parameters that don't compute gradients are usually called **frozen parameters**.
It is useful to "freeze" part of your model if you know in advance that you won't need the gradients of those parameters
(this offers some performance benefits by reducing autograd computations).
Another common usecase where exclusion from the DAG is important is for
`finetuning a pretrained network <https://pytorch.org/tutorials/beginner/finetuning_torchvision_models_tutorial.html>`__
In finetuning, we freeze most of the model and typically only modify the classifier layers to make predictions on new labels.
Let's walk through a small example to demonstrate this. As before, we load a pretrained resnet18 model, and freeze all the parameters.
```
from torch import nn, optim
model = torchvision.models.resnet18(pretrained=True)
# Freeze all the parameters in the network
for param in model.parameters():
param.requires_grad = False
```
Let's say we want to finetune the model on a new dataset with 10 labels.
In resnet, the classifier is the last linear layer ``model.fc``.
We can simply replace it with a new linear layer (unfrozen by default)
that acts as our classifier.
```
model.fc = nn.Linear(512, 10)
```
Now all parameters in the model, except the parameters of ``model.fc``, are frozen.
The only parameters that compute gradients are the weights and bias of ``model.fc``.
```
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)
```
Notice although we register all the parameters in the optimizer,
the only parameters that are computing gradients (and hence updated in gradient descent)
are the weights and bias of the classifier.
The same exclusionary functionality is available as a context manager in
`torch.no_grad() <https://pytorch.org/docs/stable/generated/torch.no_grad.html>`__
--------------
Further readings:
~~~~~~~~~~~~~~~~~~~
- `In-place operations & Multithreaded Autograd <https://pytorch.org/docs/stable/notes/autograd.html>`__
- `Example implementation of reverse-mode autodiff <https://colab.research.google.com/drive/1VpeE6UvEPRz9HmsHh1KS0XxXjYu533EC>`__
|
github_jupyter
|
%matplotlib inline
import torch, torchvision
model = torchvision.models.resnet18(pretrained=True)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)
prediction = model(data) # forward pass
loss = (prediction - labels).sum()
loss.backward() # backward pass
optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
optim.step() #gradient descent
import torch
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)
a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
from torch import nn, optim
model = torchvision.models.resnet18(pretrained=True)
# Freeze all the parameters in the network
for param in model.parameters():
param.requires_grad = False
model.fc = nn.Linear(512, 10)
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)
| 0.861101 | 0.992393 |
# Financial Planning with APIs and Simulations
In this Challenge, you’ll create two financial analysis tools by using a single Jupyter notebook:
Part 1: A financial planner for emergencies. The members will be able to use this tool to visualize their current savings. The members can then determine if they have enough reserves for an emergency fund.
Part 2: A financial planner for retirement. This tool will forecast the performance of their retirement portfolio in 30 years. To do this, the tool will make an Alpaca API call via the Alpaca SDK to get historical price data for use in Monte Carlo simulations.
You’ll use the information from the Monte Carlo simulation to answer questions about the portfolio in your Jupyter notebook.
```
# Import the required libraries and dependencies
import os
import requests
import json
import pandas as pd
from dotenv import load_dotenv
import alpaca_trade_api as tradeapi
from MCForecastTools import MCSimulation
%matplotlib inline
# Load the environment variables from the .env file
#by calling the load_dotenv function
load_dotenv()
```
## Part 1: Create a Financial Planner for Emergencies
### Evaluate the Cryptocurrency Wallet by Using the Requests Library
In this section, you’ll determine the current value of a member’s cryptocurrency wallet. You’ll collect the current prices for the Bitcoin and Ethereum cryptocurrencies by using the Python Requests library. For the prototype, you’ll assume that the member holds the 1.2 Bitcoins (BTC) and 5.3 Ethereum coins (ETH). To do all this, complete the following steps:
1. Create a variable named `monthly_income`, and set its value to `12000`.
2. Use the Requests library to get the current price (in US dollars) of Bitcoin (BTC) and Ethereum (ETH) by using the API endpoints that the starter code supplies.
3. Navigate the JSON response object to access the current price of each coin, and store each in a variable.
> **Hint** Note the specific identifier for each cryptocurrency in the API JSON response. The Bitcoin identifier is `1`, and the Ethereum identifier is `1027`.
4. Calculate the value, in US dollars, of the current amount of each cryptocurrency and of the entire cryptocurrency wallet.
```
# The current number of coins for each cryptocurrency asset held in the portfolio.
BTC_coins = 1.2
ETH_coins = 5.3
```
#### Step 1: Create a variable named `monthly_income`, and set its value to `12000`.
```
# The monthly amount for the member's household income
monthly_income = 12000
```
#### Review the endpoint URLs for the API calls to Free Crypto API in order to get the current pricing information for both BTC and ETH.
```
# The Free Crypto API Call endpoint URLs for the held cryptocurrency assets
BTC_url = "https://api.alternative.me/v2/ticker/Bitcoin/?convert=USD"
ETH_url = "https://api.alternative.me/v2/ticker/Ethereum/?convert=USD"
```
#### Step 2. Use the Requests library to get the current price (in US dollars) of Bitcoin (BTC) and Ethereum (ETH) by using the API endpoints that the starter code supplied.
```
# Using the Python requests library, make an API call to access the current price of BTC
BTC_response = requests.get(BTC_url).json()
# Use the json.dumps function to review the response data from the API call
# Use the indent and sort_keys parameters to make the response object readable
print(json.dumps(BTC_response, indent=4, sort_keys=True))
# Using the Python requests library, make an API call to access the current price ETH
ETH_response = requests.get(ETH_url).json()
# Use the json.dumps function to review the response data from the API call
# Use the indent and sort_keys parameters to make the response object readable
print(json.dumps(ETH_response, indent=4, sort_keys=True))
```
#### Step 3: Navigate the JSON response object to access the current price of each coin, and store each in a variable.
```
# Navigate the BTC response object to access the current price of BTC
BTC_price = BTC_response['data']['1']['quotes']['USD']['price']
# Print the current price of BTC
print(f"The current price of Bitcoin is ${BTC_price}")
# Navigate the BTC response object to access the current price of ETH
ETH_price = ETH_response['data']['1027']['quotes']['USD']['price']
# Print the current price of ETH
print(f"The current price of Ethereum is ${ETH_price}")
```
### Step 4: Calculate the value, in US dollars, of the current amount of each cryptocurrency and of the entire cryptocurrency wallet.
```
# Compute the current value of the BTC holding
BTC_value = BTC_price * BTC_coins
# Print current value of your holding in BTC
print(f"The current value of Bitcoin is ${BTC_value}")
# Compute the current value of the ETH holding
ETH_value = ETH_price * ETH_coins
# Print current value of your holding in ETH
print(f"The current value of Ethereum is ${ETH_value}")
# Compute the total value of the cryptocurrency wallet
# Add the value of the BTC holding to the value of the ETH holding
crypto_wallet_value = BTC_value + ETH_value
# Print current cryptocurrency wallet balance
print(f"The current cryptocurrency wallet balance is ${crypto_wallet_value}")
```
### Evaluate the Stock and Bond Holdings by Using the Alpaca SDK
In this section, you’ll determine the current value of a member’s stock and bond holdings. You’ll make an API call to Alpaca via the Alpaca SDK to get the current closing prices of the SPDR S&P 500 ETF Trust (ticker: SPY) and of the iShares Core US Aggregate Bond ETF (ticker: AGG). For the prototype, assume that the member holds 110 shares of SPY, which represents the stock portion of their portfolio, and 200 shares of AGG, which represents the bond portion. To do all this, complete the following steps:
1. In the `Starter_Code` folder, create an environment file (`.env`) to store the values of your Alpaca API key and Alpaca secret key.
2. Set the variables for the Alpaca API and secret keys. Using the Alpaca SDK, create the Alpaca `tradeapi.REST` object. In this object, include the parameters for the Alpaca API key, the secret key, and the version number.
3. Set the following parameters for the Alpaca API call:
- `tickers`: Use the tickers for the member’s stock and bond holdings.
- `timeframe`: Use a time frame of one day.
- `start_date` and `end_date`: Use the same date for these parameters, and format them with the date of the previous weekday (or `2020-08-07`). This is because you want the one closing price for the most-recent trading day.
4. Get the current closing prices for `SPY` and `AGG` by using the Alpaca `get_barset` function. Format the response as a Pandas DataFrame by including the `df` property at the end of the `get_barset` function.
5. Navigating the Alpaca response DataFrame, select the `SPY` and `AGG` closing prices, and store them as variables.
6. Calculate the value, in US dollars, of the current amount of shares in each of the stock and bond portions of the portfolio, and print the results.
#### Review the total number of shares held in both (SPY) and (AGG).
```
# Current amount of shares held in both the stock (SPY) and bond (AGG) portion of the portfolio.
SPY_shares = 110
AGG_shares = 200
```
#### Step 1: In the `Starter_Code` folder, create an environment file (`.env`) to store the values of your Alpaca API key and Alpaca secret key.
#### Step 2: Set the variables for the Alpaca API and secret keys. Using the Alpaca SDK, create the Alpaca `tradeapi.REST` object. In this object, include the parameters for the Alpaca API key, the secret key, and the version number.
```
# Set the variables for the Alpaca API and secret keys
alpaca_api_key = os.getenv("ALPACA_API_KEY")
alpaca_secret_key = os.getenv("ALPACA_SECRET_KEY")
# Create the Alpaca tradeapi.REST object
alpaca = tradeapi.REST(
alpaca_api_key,
alpaca_secret_key,
api_version="v2")
```
#### Step 3: Set the following parameters for the Alpaca API call:
- `tickers`: Use the tickers for the member’s stock and bond holdings.
- `timeframe`: Use a time frame of one day.
- `start_date` and `end_date`: Use the same date for these parameters, and format them with the date of the previous weekday (or `2020-08-07`). This is because you want the one closing price for the most-recent trading day.
```
# Set the tickers for both the bond and stock portion of the portfolio
tickers = ["AGG", "SPY"]
# Set timeframe to 1D
timeframe = "1D"
# Format current date as ISO format
# Set both the start and end date at the date of your prior weekday
# This will give you the closing price of the previous trading day
# Alternatively you can use a start and end date of 2020-08-07
start_date = pd.Timestamp("2020-08-07")
end_date = pd.Timestamp("2020-08-07")
```
#### Step 4: Get the current closing prices for `SPY` and `AGG` by using the Alpaca `get_barset` function. Format the response as a Pandas DataFrame by including the `df` property at the end of the `get_barset` function.
```
# Use the Alpaca get_barset function to get current closing prices the portfolio
# Be sure to set the `df` property after the function to format the response object as a DataFrame
portfolio_closing_prices = alpaca.get_barset(
tickers,
timeframe,
start = start_date,
end = end_date
).df
# Review the first 5 rows of the Alpaca DataFrame
portfolio_closing_prices.head()
```
#### Step 5: Navigating the Alpaca response DataFrame, select the `SPY` and `AGG` closing prices, and store them as variables.
```
# Access the closing price for AGG from the Alpaca DataFrame
# Converting the value to a floating point number
AGG_close_price = float(portfolio_closing_prices["AGG"]["close"][0])
# Print the AGG closing price
print(AGG_close_price)
# Access the closing price for SPY from the Alpaca DataFrame
# Converting the value to a floating point number
SPY_close_price = float(portfolio_closing_prices["SPY"]["close"][0])
# Print the SPY closing price
print(SPY_close_price)
```
#### Step 6: Calculate the value, in US dollars, of the current amount of shares in each of the stock and bond portions of the portfolio, and print the results.
```
# Calculate the current value of the bond portion of the portfolio
AGG_value = AGG_close_price * AGG_shares
# Print the current value of the bond portfolio
print(f"The current value of the bond portfolio is ${AGG_value}")
# Calculate the current value of the stock portion of the portfolio
SPY_value = SPY_close_price * SPY_shares
# Print the current value of the stock portfolio
print(f"The current value of the stock portfolio is ${SPY_value}")
# Calculate the total value of the stock and bond portion of the portfolio
total_stocks_bonds = SPY_value + AGG_value
# Print the current balance of the stock and bond portion of the portfolio
print(f"The current balance of the stock and bond portion is ${total_stocks_bonds}")
# Calculate the total value of the member's entire savings portfolio
# Add the value of the cryptocurrency wallet to the value of the total stocks and bonds
total_portfolio = crypto_wallet_value + total_stocks_bonds
# Print current cryptocurrency wallet balance
print(f"The current cryptocurrency wallet balance is ${crypto_wallet_value}")
```
### Evaluate the Emergency Fund
In this section, you’ll use the valuations for the cryptocurrency wallet and for the stock and bond portions of the portfolio to determine if the credit union member has enough savings to build an emergency fund into their financial plan. To do this, complete the following steps:
1. Create a Python list named `savings_data` that has two elements. The first element contains the total value of the cryptocurrency wallet. The second element contains the total value of the stock and bond portions of the portfolio.
2. Use the `savings_data` list to create a Pandas DataFrame named `savings_df`, and then display this DataFrame. The function to create the DataFrame should take the following three parameters:
- `savings_data`: Use the list that you just created.
- `columns`: Set this parameter equal to a Python list with a single value called `amount`.
- `index`: Set this parameter equal to a Python list with the values of `crypto` and `stock/bond`.
3. Use the `savings_df` DataFrame to plot a pie chart that visualizes the composition of the member’s portfolio. The y-axis of the pie chart uses `amount`. Be sure to add a title.
4. Using Python, determine if the current portfolio has enough to create an emergency fund as part of the member’s financial plan. Ideally, an emergency fund should equal to three times the member’s monthly income. To do this, implement the following steps:
1. Create a variable named `emergency_fund_value`, and set it equal to three times the value of the member’s `monthly_income` of $12000. (You set this earlier in Part 1).
2. Create a series of three if statements to determine if the member’s total portfolio is large enough to fund the emergency portfolio:
1. If the total portfolio value is greater than the emergency fund value, display a message congratulating the member for having enough money in this fund.
2. Else if the total portfolio value is equal to the emergency fund value, display a message congratulating the member on reaching this important financial goal.
3. Else the total portfolio is less than the emergency fund value, so display a message showing how many dollars away the member is from reaching the goal. (Subtract the total portfolio value from the emergency fund value.)
#### Step 1: Create a Python list named `savings_data` that has two elements. The first element contains the total value of the cryptocurrency wallet. The second element contains the total value of the stock and bond portions of the portfolio.
```
# Consolidate financial assets data into a Python list
savings_data = crypto_wallet_value + total_stocks_bonds
# Review the Python list savings_data
savings_data
```
#### Step 2: Use the `savings_data` list to create a Pandas DataFrame named `savings_df`, and then display this DataFrame. The function to create the DataFrame should take the following three parameters:
- `savings_data`: Use the list that you just created.
- `columns`: Set this parameter equal to a Python list with a single value called `amount`.
- `index`: Set this parameter equal to a Python list with the values of `crypto` and `stock/bond`.
```
# Create a Pandas DataFrame called savings_df
savings_df = pd.DataFrame(
{'Amount': [crypto_wallet_value, total_stocks_bonds]},
index=['Crypto', 'Stock/Bond']
)
# Display the savings_df DataFrame
savings_df
```
#### Step 3: Use the `savings_df` DataFrame to plot a pie chart that visualizes the composition of the member’s portfolio. The y-axis of the pie chart uses `amount`. Be sure to add a title.
```
# Plot the total value of the member's portfolio (crypto and stock/bond) in a pie chart
savings_df.plot.pie(y='Amount', title="Portfolio Composition - 2020-08-07", figsize=(7,8))
```
#### Step 4: Using Python, determine if the current portfolio has enough to create an emergency fund as part of the member’s financial plan. Ideally, an emergency fund should equal to three times the member’s monthly income. To do this, implement the following steps:
Step 1. Create a variable named `emergency_fund_value`, and set it equal to three times the value of the member’s `monthly_income` of 12000. (You set this earlier in Part 1).
Step 2. Create a series of three if statements to determine if the member’s total portfolio is large enough to fund the emergency portfolio:
* If the total portfolio value is greater than the emergency fund value, display a message congratulating the member for having enough money in this fund.
* Else if the total portfolio value is equal to the emergency fund value, display a message congratulating the member on reaching this important financial goal.
* Else the total portfolio is less than the emergency fund value, so display a message showing how many dollars away the member is from reaching the goal. (Subtract the total portfolio value from the emergency fund value.)
##### Step 4-1: Create a variable named `emergency_fund_value`, and set it equal to three times the value of the member’s `monthly_income` of 12000. (You set this earlier in Part 1).
```
# Create a variable named emergency_fund_value
emergency_fund_value = monthly_income * 3
emergency_fund_value
```
##### Step 4-2: Create a series of three if statements to determine if the member’s total portfolio is large enough to fund the emergency portfolio:
* If the total portfolio value is greater than the emergency fund value, display a message congratulating the member for having enough money in this fund.
* Else if the total portfolio value is equal to the emergency fund value, display a message congratulating the member on reaching this important financial goal.
* Else the total portfolio is less than the emergency fund value, so display a message showing how many dollars away the member is from reaching the goal. (Subtract the total portfolio value from the emergency fund value.)
```
amt_from_goal = savings_data - emergency_fund_value
print(amt_from_goal)
# Evaluate the possibility of creating an emergency fund with 3 conditions:
if savings_data > emergency_fund_value:
print("Congrats! you have enough money in this fund")
elif savings_data == emergency_fund_value:
print("Congrats! you have reached your financial goal")
else:
print("You are $ {amt_from_goal}")
```
## Part 2: Create a Financial Planner for Retirement
### Create the Monte Carlo Simulation
In this section, you’ll use the MCForecastTools library to create a Monte Carlo simulation for the member’s savings portfolio. To do this, complete the following steps:
1. Make an API call via the Alpaca SDK to get 3 years of historical closing prices for a traditional 60/40 portfolio split: 60% stocks (SPY) and 40% bonds (AGG).
2. Run a Monte Carlo simulation of 500 samples and 30 years for the 60/40 portfolio, and then plot the results.The following image shows the overlay line plot resulting from a simulation with these characteristics. However, because a random number generator is used to run each live Monte Carlo simulation, your image will differ slightly from this exact image:

3. Plot the probability distribution of the Monte Carlo simulation. Plot the probability distribution of the Monte Carlo simulation. The following image shows the histogram plot resulting from a simulation with these characteristics. However, because a random number generator is used to run each live Monte Carlo simulation, your image will differ slightly from this exact image:

4. Generate the summary statistics for the Monte Carlo simulation.
#### Step 1: Make an API call via the Alpaca SDK to get 3 years of historical closing prices for a traditional 60/40 portfolio split: 60% stocks (SPY) and 40% bonds (AGG).
```
# Set start and end dates of 3 years back from your current date
# Alternatively, you can use an end date of 2020-08-07 and work 3 years back from that date
start_date = pd.Timestamp("2017-08-07", tz="America/New_York").isoformat()
end_date = pd.Timestamp("2020-08-07", tz="America/New_York").isoformat()
# Set number of rows to 1000 to retrieve the maximum amount of rows
limit_rows = 1000
# Use the Alpaca get_barset function to make the API call to get the 3 years worth of pricing data
# The tickers and timeframe parameters should have been set in Part 1 of this activity
# The start and end dates should be updated with the information set above
# Remember to add the df property to the end of the call so the response is returned as a DataFrame
three_year_pricing = alpaca.get_barset(
tickers,
timeframe,
start=start_date,
end=end_date,
limit=limit_rows
).df
# Display both the first and last five rows of the DataFrame
three_year_pricing.head()
three_year_pricing.tail()
```
#### Step 2: Run a Monte Carlo simulation of 500 samples and 30 years for the 60/40 portfolio, and then plot the results.
```
# Configure the Monte Carlo simulation to forecast 30 years cumulative returns
# The weights should be split 40% to AGG and 60% to SPY.
# Run 500 samples.
MC_thirtyyear = MCSimulation(
portfolio_data = three_year_pricing,
weights = [.40,.60],
num_simulation = 500,
num_trading_days = 252*30
)
# Review the simulation input data
MC_thirtyyear.portfolio_data
# Run the Monte Carlo simulation to forecast 30 years cumulative returns
MC_thirtyyear.calc_cumulative_return()
# Visualize the 30-year Monte Carlo simulation by creating an
# overlay line plot
MC_simulation_lineplot = MC_thirtyyear.plot_simulation()
MC_simulation_lineplot.get_figure().savefig("MC_thirtyyear_sim_plot.png", bbox_inches="tight")
```
#### Step 3: Plot the probability distribution of the Monte Carlo simulation.
```
# Visualize the probability distribution of the 30-year Monte Carlo simulation
# by plotting a histogram
MC_distribution_plot = MC_thirtyyear.plot_distribution()
MC_distribution_plot.get_figure().savefig("MC_thirtyyear_dist_plot.png", bbox_inches="tight")
```
#### Step 4: Generate the summary statistics for the Monte Carlo simulation.
```
# Generate summary statistics from the 30-year Monte Carlo simulation results
# Save the results as a variable
MC_summary_statistics = MC_thirtyyear.summarize_cumulative_return()
# Review the 30-year Monte Carlo summary statistics
MC_summary_statistics
```
### Analyze the Retirement Portfolio Forecasts
Using the current value of only the stock and bond portion of the member's portfolio and the summary statistics that you generated from the Monte Carlo simulation, answer the following question in your Jupyter notebook:
- What are the lower and upper bounds for the expected value of the portfolio with a 95% confidence interval?
```
# Print the current balance of the stock and bond portion of the members portfolio
total_stocks_bonds
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes for the current stock/bond portfolio
ci_lower_thirty_cumulative_return = MC_summary_statistics[8] * 65737.189
ci_upper_thirty_cumulative_return = MC_summary_statistics[9] * 65737.189
# Print the result of your calculations
print(f"There is a 95% chance that an initial investment of $67,737.189 in the portfolio"
f" over the next 30 years will end within in the range of"
f" ${ci_lower_thirty_cumulative_return: .2f} and ${ci_upper_thirty_cumulative_return: .2f}.")
```
### Forecast Cumulative Returns in 10 Years
The CTO of the credit union is impressed with your work on these planning tools but wonders if 30 years is a long time to wait until retirement. So, your next task is to adjust the retirement portfolio and run a new Monte Carlo simulation to find out if the changes will allow members to retire earlier.
For this new Monte Carlo simulation, do the following:
- Forecast the cumulative returns for 10 years from now. Because of the shortened investment horizon (30 years to 10 years), the portfolio needs to invest more heavily in the riskier asset—that is, stock—to help accumulate wealth for retirement.
- Adjust the weights of the retirement portfolio so that the composition for the Monte Carlo simulation consists of 20% bonds and 80% stocks.
- Run the simulation over 500 samples, and use the same data that the API call to Alpaca generated.
- Based on the new Monte Carlo simulation, answer the following questions in your Jupyter notebook:
- Using the current value of only the stock and bond portion of the member's portfolio and the summary statistics that you generated from the new Monte Carlo simulation, what are the lower and upper bounds for the expected value of the portfolio (with the new weights) with a 95% confidence interval?
- Will weighting the portfolio more heavily toward stocks allow the credit union members to retire after only 10 years?
```
# Configure a Monte Carlo simulation to forecast 10 years cumulative returns
# The weights should be split 20% to AGG and 80% to SPY.
# Run 500 samples.
MC_tenyear = MCSimulation(
portfolio_data = three_year_pricing,
weights = [.20,.80],
num_simulation = 500,
num_trading_days = 252*10
)
# Review the simulation input data
MC_tenyear.portfolio_data
# Run the Monte Carlo simulation to forecast 10 years cumulative returns
MC_tenyear.calc_cumulative_return()
# Visualize the 10-year Monte Carlo simulation by creating an
# overlay line plot
MC_simulation_lineplot = MC_tenyear.plot_simulation()
MC_simulation_lineplot.get_figure().savefig("MC_tenyear_sim_plot.png", bbox_inches="tight")
# Visualize the probability distribution of the 10-year Monte Carlo simulation
# by plotting a histogram
MC_distribution_plot = MC_tenyear.plot_distribution()
MC_distribution_plot.get_figure().savefig("MC_tenyear_dist_plot.png", bbox_inches="tight")
# Generate summary statistics from the 10-year Monte Carlo simulation results
# Save the results as a variable
MC_summary_statistics = MC_tenyear.summarize_cumulative_return()
# Review the 10-year Monte Carlo summary statistics
MC_summary_statistics
```
### Answer the following questions:
#### Question: Using the current value of only the stock and bond portion of the member's portfolio and the summary statistics that you generated from the new Monte Carlo simulation, what are the lower and upper bounds for the expected value of the portfolio (with the new weights) with a 95% confidence interval?
```
# Print the current balance of the stock and bond portion of the members portfolio
total_stocks_bonds
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes for the current stock/bond portfolio
ci_lower_ten_cumulative_return = MC_summary_statistics[8] * 65737.189
ci_upper_ten_cumulative_return = MC_summary_statistics[9] * 65737.189
# Print the result of your calculations
print(f"There is a 95% chance that an initial investment of $67,737.189 in the portfolio"
f" over the next 10 years will end within in the range of"
f" ${ci_lower_ten_cumulative_return: .2f} and ${ci_upper_ten_cumulative_return: .2f}.")
```
#### Question: Will weighting the portfolio more heavily to stocks allow the credit union members to retire after only 10 years?
|
github_jupyter
|
# Import the required libraries and dependencies
import os
import requests
import json
import pandas as pd
from dotenv import load_dotenv
import alpaca_trade_api as tradeapi
from MCForecastTools import MCSimulation
%matplotlib inline
# Load the environment variables from the .env file
#by calling the load_dotenv function
load_dotenv()
# The current number of coins for each cryptocurrency asset held in the portfolio.
BTC_coins = 1.2
ETH_coins = 5.3
# The monthly amount for the member's household income
monthly_income = 12000
# The Free Crypto API Call endpoint URLs for the held cryptocurrency assets
BTC_url = "https://api.alternative.me/v2/ticker/Bitcoin/?convert=USD"
ETH_url = "https://api.alternative.me/v2/ticker/Ethereum/?convert=USD"
# Using the Python requests library, make an API call to access the current price of BTC
BTC_response = requests.get(BTC_url).json()
# Use the json.dumps function to review the response data from the API call
# Use the indent and sort_keys parameters to make the response object readable
print(json.dumps(BTC_response, indent=4, sort_keys=True))
# Using the Python requests library, make an API call to access the current price ETH
ETH_response = requests.get(ETH_url).json()
# Use the json.dumps function to review the response data from the API call
# Use the indent and sort_keys parameters to make the response object readable
print(json.dumps(ETH_response, indent=4, sort_keys=True))
# Navigate the BTC response object to access the current price of BTC
BTC_price = BTC_response['data']['1']['quotes']['USD']['price']
# Print the current price of BTC
print(f"The current price of Bitcoin is ${BTC_price}")
# Navigate the BTC response object to access the current price of ETH
ETH_price = ETH_response['data']['1027']['quotes']['USD']['price']
# Print the current price of ETH
print(f"The current price of Ethereum is ${ETH_price}")
# Compute the current value of the BTC holding
BTC_value = BTC_price * BTC_coins
# Print current value of your holding in BTC
print(f"The current value of Bitcoin is ${BTC_value}")
# Compute the current value of the ETH holding
ETH_value = ETH_price * ETH_coins
# Print current value of your holding in ETH
print(f"The current value of Ethereum is ${ETH_value}")
# Compute the total value of the cryptocurrency wallet
# Add the value of the BTC holding to the value of the ETH holding
crypto_wallet_value = BTC_value + ETH_value
# Print current cryptocurrency wallet balance
print(f"The current cryptocurrency wallet balance is ${crypto_wallet_value}")
# Current amount of shares held in both the stock (SPY) and bond (AGG) portion of the portfolio.
SPY_shares = 110
AGG_shares = 200
# Set the variables for the Alpaca API and secret keys
alpaca_api_key = os.getenv("ALPACA_API_KEY")
alpaca_secret_key = os.getenv("ALPACA_SECRET_KEY")
# Create the Alpaca tradeapi.REST object
alpaca = tradeapi.REST(
alpaca_api_key,
alpaca_secret_key,
api_version="v2")
# Set the tickers for both the bond and stock portion of the portfolio
tickers = ["AGG", "SPY"]
# Set timeframe to 1D
timeframe = "1D"
# Format current date as ISO format
# Set both the start and end date at the date of your prior weekday
# This will give you the closing price of the previous trading day
# Alternatively you can use a start and end date of 2020-08-07
start_date = pd.Timestamp("2020-08-07")
end_date = pd.Timestamp("2020-08-07")
# Use the Alpaca get_barset function to get current closing prices the portfolio
# Be sure to set the `df` property after the function to format the response object as a DataFrame
portfolio_closing_prices = alpaca.get_barset(
tickers,
timeframe,
start = start_date,
end = end_date
).df
# Review the first 5 rows of the Alpaca DataFrame
portfolio_closing_prices.head()
# Access the closing price for AGG from the Alpaca DataFrame
# Converting the value to a floating point number
AGG_close_price = float(portfolio_closing_prices["AGG"]["close"][0])
# Print the AGG closing price
print(AGG_close_price)
# Access the closing price for SPY from the Alpaca DataFrame
# Converting the value to a floating point number
SPY_close_price = float(portfolio_closing_prices["SPY"]["close"][0])
# Print the SPY closing price
print(SPY_close_price)
# Calculate the current value of the bond portion of the portfolio
AGG_value = AGG_close_price * AGG_shares
# Print the current value of the bond portfolio
print(f"The current value of the bond portfolio is ${AGG_value}")
# Calculate the current value of the stock portion of the portfolio
SPY_value = SPY_close_price * SPY_shares
# Print the current value of the stock portfolio
print(f"The current value of the stock portfolio is ${SPY_value}")
# Calculate the total value of the stock and bond portion of the portfolio
total_stocks_bonds = SPY_value + AGG_value
# Print the current balance of the stock and bond portion of the portfolio
print(f"The current balance of the stock and bond portion is ${total_stocks_bonds}")
# Calculate the total value of the member's entire savings portfolio
# Add the value of the cryptocurrency wallet to the value of the total stocks and bonds
total_portfolio = crypto_wallet_value + total_stocks_bonds
# Print current cryptocurrency wallet balance
print(f"The current cryptocurrency wallet balance is ${crypto_wallet_value}")
# Consolidate financial assets data into a Python list
savings_data = crypto_wallet_value + total_stocks_bonds
# Review the Python list savings_data
savings_data
# Create a Pandas DataFrame called savings_df
savings_df = pd.DataFrame(
{'Amount': [crypto_wallet_value, total_stocks_bonds]},
index=['Crypto', 'Stock/Bond']
)
# Display the savings_df DataFrame
savings_df
# Plot the total value of the member's portfolio (crypto and stock/bond) in a pie chart
savings_df.plot.pie(y='Amount', title="Portfolio Composition - 2020-08-07", figsize=(7,8))
# Create a variable named emergency_fund_value
emergency_fund_value = monthly_income * 3
emergency_fund_value
amt_from_goal = savings_data - emergency_fund_value
print(amt_from_goal)
# Evaluate the possibility of creating an emergency fund with 3 conditions:
if savings_data > emergency_fund_value:
print("Congrats! you have enough money in this fund")
elif savings_data == emergency_fund_value:
print("Congrats! you have reached your financial goal")
else:
print("You are $ {amt_from_goal}")
# Set start and end dates of 3 years back from your current date
# Alternatively, you can use an end date of 2020-08-07 and work 3 years back from that date
start_date = pd.Timestamp("2017-08-07", tz="America/New_York").isoformat()
end_date = pd.Timestamp("2020-08-07", tz="America/New_York").isoformat()
# Set number of rows to 1000 to retrieve the maximum amount of rows
limit_rows = 1000
# Use the Alpaca get_barset function to make the API call to get the 3 years worth of pricing data
# The tickers and timeframe parameters should have been set in Part 1 of this activity
# The start and end dates should be updated with the information set above
# Remember to add the df property to the end of the call so the response is returned as a DataFrame
three_year_pricing = alpaca.get_barset(
tickers,
timeframe,
start=start_date,
end=end_date,
limit=limit_rows
).df
# Display both the first and last five rows of the DataFrame
three_year_pricing.head()
three_year_pricing.tail()
# Configure the Monte Carlo simulation to forecast 30 years cumulative returns
# The weights should be split 40% to AGG and 60% to SPY.
# Run 500 samples.
MC_thirtyyear = MCSimulation(
portfolio_data = three_year_pricing,
weights = [.40,.60],
num_simulation = 500,
num_trading_days = 252*30
)
# Review the simulation input data
MC_thirtyyear.portfolio_data
# Run the Monte Carlo simulation to forecast 30 years cumulative returns
MC_thirtyyear.calc_cumulative_return()
# Visualize the 30-year Monte Carlo simulation by creating an
# overlay line plot
MC_simulation_lineplot = MC_thirtyyear.plot_simulation()
MC_simulation_lineplot.get_figure().savefig("MC_thirtyyear_sim_plot.png", bbox_inches="tight")
# Visualize the probability distribution of the 30-year Monte Carlo simulation
# by plotting a histogram
MC_distribution_plot = MC_thirtyyear.plot_distribution()
MC_distribution_plot.get_figure().savefig("MC_thirtyyear_dist_plot.png", bbox_inches="tight")
# Generate summary statistics from the 30-year Monte Carlo simulation results
# Save the results as a variable
MC_summary_statistics = MC_thirtyyear.summarize_cumulative_return()
# Review the 30-year Monte Carlo summary statistics
MC_summary_statistics
# Print the current balance of the stock and bond portion of the members portfolio
total_stocks_bonds
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes for the current stock/bond portfolio
ci_lower_thirty_cumulative_return = MC_summary_statistics[8] * 65737.189
ci_upper_thirty_cumulative_return = MC_summary_statistics[9] * 65737.189
# Print the result of your calculations
print(f"There is a 95% chance that an initial investment of $67,737.189 in the portfolio"
f" over the next 30 years will end within in the range of"
f" ${ci_lower_thirty_cumulative_return: .2f} and ${ci_upper_thirty_cumulative_return: .2f}.")
# Configure a Monte Carlo simulation to forecast 10 years cumulative returns
# The weights should be split 20% to AGG and 80% to SPY.
# Run 500 samples.
MC_tenyear = MCSimulation(
portfolio_data = three_year_pricing,
weights = [.20,.80],
num_simulation = 500,
num_trading_days = 252*10
)
# Review the simulation input data
MC_tenyear.portfolio_data
# Run the Monte Carlo simulation to forecast 10 years cumulative returns
MC_tenyear.calc_cumulative_return()
# Visualize the 10-year Monte Carlo simulation by creating an
# overlay line plot
MC_simulation_lineplot = MC_tenyear.plot_simulation()
MC_simulation_lineplot.get_figure().savefig("MC_tenyear_sim_plot.png", bbox_inches="tight")
# Visualize the probability distribution of the 10-year Monte Carlo simulation
# by plotting a histogram
MC_distribution_plot = MC_tenyear.plot_distribution()
MC_distribution_plot.get_figure().savefig("MC_tenyear_dist_plot.png", bbox_inches="tight")
# Generate summary statistics from the 10-year Monte Carlo simulation results
# Save the results as a variable
MC_summary_statistics = MC_tenyear.summarize_cumulative_return()
# Review the 10-year Monte Carlo summary statistics
MC_summary_statistics
# Print the current balance of the stock and bond portion of the members portfolio
total_stocks_bonds
# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes for the current stock/bond portfolio
ci_lower_ten_cumulative_return = MC_summary_statistics[8] * 65737.189
ci_upper_ten_cumulative_return = MC_summary_statistics[9] * 65737.189
# Print the result of your calculations
print(f"There is a 95% chance that an initial investment of $67,737.189 in the portfolio"
f" over the next 10 years will end within in the range of"
f" ${ci_lower_ten_cumulative_return: .2f} and ${ci_upper_ten_cumulative_return: .2f}.")
| 0.729327 | 0.989254 |
<a href="https://colab.research.google.com/github/chadeowen/DS-Sprint-03-Creating-Professional-Portfolios/blob/master/ChadOwen_DS_Unit_1_Sprint_Challenge_3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Data Science Unit 1 Sprint Challenge 3
# Creating Professional Portfolios
For your Sprint Challenge, you will **write about your upcoming [data storytelling portfolio project](https://learn.lambdaschool.com/ds/module/recedjanlbpqxic2r)**.
(Don't worry, you don't have to choose your final idea now. For this challenge, you can write about any idea you're considering.)
# Part 1
**Describe an idea** you could work on for your upcoming data storytelling project. What's your hypothesis?
#### Write a [lede](https://www.thoughtco.com/how-to-write-a-great-lede-2074346) (first paragraph)
- Put the bottom line up front.
- Use 60 words or fewer. (The [Hemingway App](http://www.hemingwayapp.com/) gives you word count.)
[This is hard](https://quoteinvestigator.com/2012/04/28/shorter-letter/), but you can do it!
#### Stretch goals
- Write more about your idea. Tell us what the story's about. Show us why it's interesting. Continue to follow the inverted pyramid structure.
- Improve your readability. Post your "before & after" scores from the Hemingway App.
- Who what where when why = States, Population Growth Rates, USA, From Civil War until now, Multitude of factors
- I want my title to **pop**... maybe something like: '_A Second Civil War is Approaching; Why The North Might Be in More Trouble Than it Thinks_'
- Controversial, I'm aware... Must tread lightly and be cautious of language, I'm also aware...
- Lede: Population growth rates in Southern States have significantly outpaced those in Northern States since the Civil War; how __*might*__ this affect the current political divide?
# Part 2
#### Find sources
- Link to at least 2 relevant sources for your topic. Sources could include any data or writing about your topic.
- Use [Markdown](https://commonmark.org/help/) to format your links.
- Summarize each source in 1-2 sentences.
#### Stretch goals
- Find more sources.
- Use Markdown to add images from your sources.
- Critically evaluate your sources in writing.
[Facts and Trends Article](https://factsandtrends.net/2018/01/18/southern-states-continue-outpace-rest-u-s-population-growth/)
- Numerical Growth top ten list and Percentage Growth top ten list
[Bloomberg Opinion](https://www.bloomberg.com/opinion/articles/2018-01-04/america-s-heartland-has-moved-to-the-south-and-west)
- Opinion piece on Southern and Western Population Growth
- Some great visuals to keep in mind when making my report
# Part 3
#### Plan your next steps
- Describe at least 2 actions you'd take to get started with your project.
- Use Markdown headings and lists to organize your plan.
#### Stretch goals
- Add detail to your plan.
- Publish your project proposal on your GitHub Pages site.
# Story
- The story I want to tell with the data is the most important part. Although I do not intend on being a data scientist with 'clickbait' or 'attention grabbing' reports, I do not mind using those practices given time constraints (project timelines). After collecting regional growth rates and state growth rates (speaking strictly population), I will paint a picture as to *why* the shifts are occuring and *how* this could play a factor given today's two-party divide.
## Data
- The next step is to find the data. I'm finding that it's a bit trickier to track down historical census data (every seven years) and coupling that with census estimates (yearly) in a clean csv file, but I should be able to build my own if worst comes to worst. I have a broad idea of what the data will look like, but this weekend and next is when I'll spend time finding it.
## Data Viz
- Last action is choosing my data visualizations. I intend to provide different visualizations to portray multiple perspectives. The bloomberg article linked above looks helpful, but I will select data viz's that support my 'story'
|
github_jupyter
|
<a href="https://colab.research.google.com/github/chadeowen/DS-Sprint-03-Creating-Professional-Portfolios/blob/master/ChadOwen_DS_Unit_1_Sprint_Challenge_3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Data Science Unit 1 Sprint Challenge 3
# Creating Professional Portfolios
For your Sprint Challenge, you will **write about your upcoming [data storytelling portfolio project](https://learn.lambdaschool.com/ds/module/recedjanlbpqxic2r)**.
(Don't worry, you don't have to choose your final idea now. For this challenge, you can write about any idea you're considering.)
# Part 1
**Describe an idea** you could work on for your upcoming data storytelling project. What's your hypothesis?
#### Write a [lede](https://www.thoughtco.com/how-to-write-a-great-lede-2074346) (first paragraph)
- Put the bottom line up front.
- Use 60 words or fewer. (The [Hemingway App](http://www.hemingwayapp.com/) gives you word count.)
[This is hard](https://quoteinvestigator.com/2012/04/28/shorter-letter/), but you can do it!
#### Stretch goals
- Write more about your idea. Tell us what the story's about. Show us why it's interesting. Continue to follow the inverted pyramid structure.
- Improve your readability. Post your "before & after" scores from the Hemingway App.
- Who what where when why = States, Population Growth Rates, USA, From Civil War until now, Multitude of factors
- I want my title to **pop**... maybe something like: '_A Second Civil War is Approaching; Why The North Might Be in More Trouble Than it Thinks_'
- Controversial, I'm aware... Must tread lightly and be cautious of language, I'm also aware...
- Lede: Population growth rates in Southern States have significantly outpaced those in Northern States since the Civil War; how __*might*__ this affect the current political divide?
# Part 2
#### Find sources
- Link to at least 2 relevant sources for your topic. Sources could include any data or writing about your topic.
- Use [Markdown](https://commonmark.org/help/) to format your links.
- Summarize each source in 1-2 sentences.
#### Stretch goals
- Find more sources.
- Use Markdown to add images from your sources.
- Critically evaluate your sources in writing.
[Facts and Trends Article](https://factsandtrends.net/2018/01/18/southern-states-continue-outpace-rest-u-s-population-growth/)
- Numerical Growth top ten list and Percentage Growth top ten list
[Bloomberg Opinion](https://www.bloomberg.com/opinion/articles/2018-01-04/america-s-heartland-has-moved-to-the-south-and-west)
- Opinion piece on Southern and Western Population Growth
- Some great visuals to keep in mind when making my report
# Part 3
#### Plan your next steps
- Describe at least 2 actions you'd take to get started with your project.
- Use Markdown headings and lists to organize your plan.
#### Stretch goals
- Add detail to your plan.
- Publish your project proposal on your GitHub Pages site.
# Story
- The story I want to tell with the data is the most important part. Although I do not intend on being a data scientist with 'clickbait' or 'attention grabbing' reports, I do not mind using those practices given time constraints (project timelines). After collecting regional growth rates and state growth rates (speaking strictly population), I will paint a picture as to *why* the shifts are occuring and *how* this could play a factor given today's two-party divide.
## Data
- The next step is to find the data. I'm finding that it's a bit trickier to track down historical census data (every seven years) and coupling that with census estimates (yearly) in a clean csv file, but I should be able to build my own if worst comes to worst. I have a broad idea of what the data will look like, but this weekend and next is when I'll spend time finding it.
## Data Viz
- Last action is choosing my data visualizations. I intend to provide different visualizations to portray multiple perspectives. The bloomberg article linked above looks helpful, but I will select data viz's that support my 'story'
| 0.63273 | 0.747017 |
```
%matplotlib inline
```
Tensors
--------------------------------------------
Tensors are a specialized data structure that are very similar to arrays
and matrices. In PyTorch, we use tensors to encode the inputs and
outputs of a model, as well as the model’s parameters.
Tensors are similar to NumPy’s ndarrays, except that tensors can run on
GPUs or other specialized hardware to accelerate computing. If you’re familiar with ndarrays, you’ll
be right at home with the Tensor API. If not, follow along in this quick
API walkthrough.
```
import torch
import numpy as np
```
Tensor Initialization
~~~~~~~~~~~~~~~~~~~~~
Tensors can be initialized in various ways. Take a look at the following examples:
**Directly from data**
Tensors can be created directly from data. The data type is automatically inferred.
```
data = [[1, 2], [3, 4]]
x_data = torch.tensor(data)
x_data.dtype
x_data
```
**From a NumPy array**
Tensors can be created from NumPy arrays (and vice versa - see `bridge-to-np-label`).
```
np_array = np.array(data)
x_np = torch.from_numpy(np_array)
np_array
x_np
```
**From another tensor:**
The new tensor retains the properties (shape, datatype) of the argument tensor, unless explicitly overridden.
```
x_ones = torch.ones_like(x_data) # retains the properties of x_data
print(f"Ones Tensor: \n {x_ones} \n")
x_rand = torch.rand_like(x_data, dtype=torch.float) # overrides the datatype of x_data
print(f"Random Tensor: \n {x_rand} \n")
```
**With random or constant values:**
``shape`` is a tuple of tensor dimensions. In the functions below, it determines the dimensionality of the output tensor.
```
shape = (2, 3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)
print(f"Random Tensor: \n {rand_tensor} \n")
print(f"Ones Tensor: \n {ones_tensor} \n")
print(f"Zeros Tensor: \n {zeros_tensor}")
```
--------------
Tensor Attributes
~~~~~~~~~~~~~~~~~
Tensor attributes describe their shape, datatype, and the device on which they are stored.
```
tensor = torch.rand(3, 4)
print(f"Shape of tensor: {tensor.shape}")
print(f"Datatype of tensor: {tensor.dtype}")
print(f"Device tensor is stored on: {tensor.device}")
```
--------------
Tensor Operations
~~~~~~~~~~~~~~~~~
Over 100 tensor operations, including transposing, indexing, slicing,
mathematical operations, linear algebra, random sampling, and more are
comprehensively described
`here <https://pytorch.org/docs/stable/torch.html>`__.
Each of them can be run on the GPU (at typically higher speeds than on a
CPU). If you’re using Colab, allocate a GPU by going to Edit > Notebook
Settings.
```
# We move our tensor to the GPU if available
if torch.cuda.is_available():
tensor = tensor.to('cuda')
print(f"Device tensor is stored on: {tensor.device}")
```
Try out some of the operations from the list.
If you're familiar with the NumPy API, you'll find the Tensor API a breeze to use.
**Standard numpy-like indexing and slicing:**
```
tensor = torch.ones(4, 4)
tensor[:,1] = 0
print(tensor)
tensor[:,0]=0
print(tensor)
```
**Joining tensors** You can use ``torch.cat`` to concatenate a sequence of tensors along a given dimension.
See also `torch.stack <https://pytorch.org/docs/stable/generated/torch.stack.html>`__,
another tensor joining op that is subtly different from ``torch.cat``.
```
t1 = torch.cat([tensor, tensor, tensor], dim=1)
print(t1)
t2=torch.cat([tensor, tensor,tensor], dim=0)
print(t2)
```
**Multiplying tensors**
```
# This computes the element-wise product
print(f"tensor.mul(tensor) \n {tensor.mul(tensor)} \n")
# Alternative syntax:
print(f"tensor * tensor \n {tensor * tensor}")
```
This computes the matrix multiplication between two tensors
```
print(f"tensor.matmul(tensor.T) \n {tensor.matmul(tensor.T)} \n")
# Alternative syntax:
print(f"tensor @ tensor.T \n {tensor @ tensor.T}")
```
**In-place operations**
Operations that have a ``_`` suffix are in-place. For example: ``x.copy_(y)``, ``x.t_()``, will change ``x``.
```
print(tensor, "\n")
tensor.add_(5)
print(tensor)
```
<div class="alert alert-info"><h4>Note</h4><p>In-place operations save some memory, but can be problematic when computing derivatives because of an immediate loss
of history. Hence, their use is discouraged.</p></div>
--------------
Bridge with NumPy
~~~~~~~~~~~~~~~~~
Tensors on the CPU and NumPy arrays can share their underlying memory
locations, and changing one will change the other.
Tensor to NumPy array
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
```
t = torch.ones(5)
print(f"t: {t}")
n = t.numpy()
print(f"n: {n}")
```
A change in the tensor reflects in the NumPy array.
```
t.add_(1)
print(f"t: {t}")
print(f"n: {n}")
```
NumPy array to Tensor
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
```
n = np.ones(5)
t = torch.from_numpy(n)
t
```
Changes in the NumPy array reflects in the tensor.
```
np.add(n, 1, out=n)
print(f"t: {t}")
print(f"n: {n}")
```
|
github_jupyter
|
%matplotlib inline
import torch
import numpy as np
data = [[1, 2], [3, 4]]
x_data = torch.tensor(data)
x_data.dtype
x_data
np_array = np.array(data)
x_np = torch.from_numpy(np_array)
np_array
x_np
x_ones = torch.ones_like(x_data) # retains the properties of x_data
print(f"Ones Tensor: \n {x_ones} \n")
x_rand = torch.rand_like(x_data, dtype=torch.float) # overrides the datatype of x_data
print(f"Random Tensor: \n {x_rand} \n")
shape = (2, 3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)
print(f"Random Tensor: \n {rand_tensor} \n")
print(f"Ones Tensor: \n {ones_tensor} \n")
print(f"Zeros Tensor: \n {zeros_tensor}")
tensor = torch.rand(3, 4)
print(f"Shape of tensor: {tensor.shape}")
print(f"Datatype of tensor: {tensor.dtype}")
print(f"Device tensor is stored on: {tensor.device}")
# We move our tensor to the GPU if available
if torch.cuda.is_available():
tensor = tensor.to('cuda')
print(f"Device tensor is stored on: {tensor.device}")
tensor = torch.ones(4, 4)
tensor[:,1] = 0
print(tensor)
tensor[:,0]=0
print(tensor)
t1 = torch.cat([tensor, tensor, tensor], dim=1)
print(t1)
t2=torch.cat([tensor, tensor,tensor], dim=0)
print(t2)
# This computes the element-wise product
print(f"tensor.mul(tensor) \n {tensor.mul(tensor)} \n")
# Alternative syntax:
print(f"tensor * tensor \n {tensor * tensor}")
print(f"tensor.matmul(tensor.T) \n {tensor.matmul(tensor.T)} \n")
# Alternative syntax:
print(f"tensor @ tensor.T \n {tensor @ tensor.T}")
print(tensor, "\n")
tensor.add_(5)
print(tensor)
t = torch.ones(5)
print(f"t: {t}")
n = t.numpy()
print(f"n: {n}")
t.add_(1)
print(f"t: {t}")
print(f"n: {n}")
n = np.ones(5)
t = torch.from_numpy(n)
t
np.add(n, 1, out=n)
print(f"t: {t}")
print(f"n: {n}")
| 0.671255 | 0.983518 |
```
%matplotlib inline
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8, 4.5))
plt.subplots_adjust(left=0.02, right=0.98, top=0.98, bottom=0.00)
m = Basemap(projection='robin',lon_0=0,resolution='c')
m.fillcontinents(color='gray',lake_color='white')
m.drawcoastlines()
plt.savefig('world.png',dpi=75)
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
from matplotlib.collections import PathCollection
from matplotlib.path import Path
fig = plt.figure(figsize=(8, 4.5))
plt.subplots_adjust(left=0.02, right=0.98, top=0.98, bottom=0.00)
# MPL searches for ne_10m_land.shp in the directory 'D:\\ne_10m_land'
m = Basemap(projection='robin',lon_0=0,resolution='c')
shp_info = m.readshapefile('D:\\ne_10m_land', 'scalerank', drawbounds=True)
ax = plt.gca()
ax.cla()
paths = []
for line in shp_info[4]._paths:
paths.append(Path(line.vertices, codes=line.codes))
coll = PathCollection(paths, linewidths=0, facecolors='grey', zorder=2)
m = Basemap(projection='robin',lon_0=0,resolution='c')
# drawing something seems necessary to 'initiate' the map properly
m.drawcoastlines(color='white', zorder=0)
ax = plt.gca()
ax.add_collection(coll)
plt.savefig('world.png',dpi=75)
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
# setup Lambert Conformal basemap.
# set resolution=None to skip processing of boundary datasets.
m = Basemap(width=12000000,height=9000000,projection='lcc',
resolution=None,lat_1=45.,lat_2=55,lat_0=50,lon_0=-107.)
m.bluemarble()
plt.show()
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
# setup Lambert Conformal basemap.
# set resolution=None to skip processing of boundary datasets.
m = Basemap(width=1200000,height=900000,projection='lcc',
resolution=None,lat_1=45.,lat_2=65,lat_0=55,lon_0=-3.)
m.etopo()
plt.show()
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import numpy as np
# set up orthographic map projection with
# perspective of satellite looking down at 50N, 100W.
# use low resolution coastlines.
map = Basemap(projection='ortho',lat_0=45,lon_0=0,resolution='l')
# draw coastlines, country boundaries, fill continents.
map.drawcoastlines(linewidth=0.25)
map.drawcountries(linewidth=0.25)
map.fillcontinents(color='coral',lake_color='aqua')
# draw the edge of the map projection region (the projection limb)
map.drawmapboundary(fill_color='aqua')
# draw lat/lon grid lines every 30 degrees.
map.drawmeridians(np.arange(0,360,30))
map.drawparallels(np.arange(-90,90,30))
# make up some data on a regular lat/lon grid.
nlats = 73; nlons = 145; delta = 2.*np.pi/(nlons-1)
lats = (0.5*np.pi-delta*np.indices((nlats,nlons))[0,:,:])
lons = (delta*np.indices((nlats,nlons))[1,:,:])
wave = 0.75*(np.sin(2.*lats)**8*np.cos(4.*lons))
mean = 0.5*np.cos(2.*lats)*((np.sin(2.*lats))**2 + 2.)
# compute native map projection coordinates of lat/lon grid.
x, y = map(lons*180./np.pi, lats*180./np.pi)
# contour data over the map.
cs = map.contour(x,y,wave+mean,15,linewidths=1.5)
plt.title('contour lines over filled continent background')
plt.show()
```
|
github_jupyter
|
%matplotlib inline
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8, 4.5))
plt.subplots_adjust(left=0.02, right=0.98, top=0.98, bottom=0.00)
m = Basemap(projection='robin',lon_0=0,resolution='c')
m.fillcontinents(color='gray',lake_color='white')
m.drawcoastlines()
plt.savefig('world.png',dpi=75)
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
from matplotlib.collections import PathCollection
from matplotlib.path import Path
fig = plt.figure(figsize=(8, 4.5))
plt.subplots_adjust(left=0.02, right=0.98, top=0.98, bottom=0.00)
# MPL searches for ne_10m_land.shp in the directory 'D:\\ne_10m_land'
m = Basemap(projection='robin',lon_0=0,resolution='c')
shp_info = m.readshapefile('D:\\ne_10m_land', 'scalerank', drawbounds=True)
ax = plt.gca()
ax.cla()
paths = []
for line in shp_info[4]._paths:
paths.append(Path(line.vertices, codes=line.codes))
coll = PathCollection(paths, linewidths=0, facecolors='grey', zorder=2)
m = Basemap(projection='robin',lon_0=0,resolution='c')
# drawing something seems necessary to 'initiate' the map properly
m.drawcoastlines(color='white', zorder=0)
ax = plt.gca()
ax.add_collection(coll)
plt.savefig('world.png',dpi=75)
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
# setup Lambert Conformal basemap.
# set resolution=None to skip processing of boundary datasets.
m = Basemap(width=12000000,height=9000000,projection='lcc',
resolution=None,lat_1=45.,lat_2=55,lat_0=50,lon_0=-107.)
m.bluemarble()
plt.show()
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
# setup Lambert Conformal basemap.
# set resolution=None to skip processing of boundary datasets.
m = Basemap(width=1200000,height=900000,projection='lcc',
resolution=None,lat_1=45.,lat_2=65,lat_0=55,lon_0=-3.)
m.etopo()
plt.show()
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import numpy as np
# set up orthographic map projection with
# perspective of satellite looking down at 50N, 100W.
# use low resolution coastlines.
map = Basemap(projection='ortho',lat_0=45,lon_0=0,resolution='l')
# draw coastlines, country boundaries, fill continents.
map.drawcoastlines(linewidth=0.25)
map.drawcountries(linewidth=0.25)
map.fillcontinents(color='coral',lake_color='aqua')
# draw the edge of the map projection region (the projection limb)
map.drawmapboundary(fill_color='aqua')
# draw lat/lon grid lines every 30 degrees.
map.drawmeridians(np.arange(0,360,30))
map.drawparallels(np.arange(-90,90,30))
# make up some data on a regular lat/lon grid.
nlats = 73; nlons = 145; delta = 2.*np.pi/(nlons-1)
lats = (0.5*np.pi-delta*np.indices((nlats,nlons))[0,:,:])
lons = (delta*np.indices((nlats,nlons))[1,:,:])
wave = 0.75*(np.sin(2.*lats)**8*np.cos(4.*lons))
mean = 0.5*np.cos(2.*lats)*((np.sin(2.*lats))**2 + 2.)
# compute native map projection coordinates of lat/lon grid.
x, y = map(lons*180./np.pi, lats*180./np.pi)
# contour data over the map.
cs = map.contour(x,y,wave+mean,15,linewidths=1.5)
plt.title('contour lines over filled continent background')
plt.show()
| 0.633977 | 0.774157 |
# 250-D Multivariate Normal
Let's go for broke here.
## Setup
First, let's set up some environmental dependencies. These just make the numerics easier and adjust some of the plotting defaults to make things more legible.
```
# Python 3 compatability
from __future__ import division, print_function
from builtins import range
# system functions that are always useful to have
import time, sys, os
# basic numeric setup
import numpy as np
import math
from numpy import linalg
# inline plotting
%matplotlib inline
# plotting
import matplotlib
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# seed the random number generator
np.random.seed(2018)
# re-defining plotting defaults
from matplotlib import rcParams
rcParams.update({'xtick.major.pad': '7.0'})
rcParams.update({'xtick.major.size': '7.5'})
rcParams.update({'xtick.major.width': '1.5'})
rcParams.update({'xtick.minor.pad': '7.0'})
rcParams.update({'xtick.minor.size': '3.5'})
rcParams.update({'xtick.minor.width': '1.0'})
rcParams.update({'ytick.major.pad': '7.0'})
rcParams.update({'ytick.major.size': '7.5'})
rcParams.update({'ytick.major.width': '1.5'})
rcParams.update({'ytick.minor.pad': '7.0'})
rcParams.update({'ytick.minor.size': '3.5'})
rcParams.update({'ytick.minor.width': '1.0'})
rcParams.update({'font.size': 30})
import dynesty
```
Here we will quickly demonstrate that slice sampling is able to cope with very high-dimensional problems without the use of gradients. Our target will in this case be a 250-D uncorrelated multivariate normal distribution with an identical prior.
```
from scipy.special import ndtri
ndim = 250 # number of dimensions
C = np.identity(ndim) # set covariance to identity matrix
Cinv = linalg.inv(C) # precision matrix
lnorm = -0.5 * (np.log(2 * np.pi) * ndim + np.log(linalg.det(C))) # ln(normalization)
# 250-D iid standard normal log-likelihood
def loglikelihood(x):
"""Multivariate normal log-likelihood."""
return -0.5 * np.dot(x, np.dot(Cinv, x)) + lnorm
# prior transform (iid standard normal prior)
def prior_transform(u):
"""Transforms our unit cube samples `u` to a flat prior between -10. and 10. in each variable."""
return ndtri(u)
# ln(evidence)
lnz_truth = lnorm - 0.5 * ndim * np.log(2)
print(lnz_truth)
```
We will use Hamiltonian Slice Sampling (`'hslice'`) to sample in high dimensions. We will also utilize a small number of overall particles ($K < N$) to demonstrate that we can be quite sparsely sampled in this regime and still perform decently well.
```
# hamiltonian slice sampling ('hslice')
sampler = dynesty.DynamicNestedSampler(loglikelihood, prior_transform, ndim,
bound='none', sample='hslice', slices=10)
sampler.run_nested(nlive_init=100, nlive_batch=100)
res = sampler.results
```
Let's dump our results to disk to avoid losing all that work!
```
import pickle
# dump results
output = open('250d_gauss.pkl', 'wb')
pickle.dump(sampler.results, output)
output.close()
import pickle
output = open('250d_gauss.pkl', 'rb')
res = pickle.load(output)
output.close()
```
Now let's see how our sampling went.
```
from dynesty import plotting as dyplot
# evidence check
fig, axes = dyplot.runplot(res, color='red', lnz_truth=lnz_truth, truth_color='black', logplot=True)
fig.tight_layout()
# posterior check
dims = [-1, -2, -3, -4, -5]
fig, ax = plt.subplots(5, 5, figsize=(25, 25))
samps, samps_t = res.samples, res.samples[:,dims]
res.samples = samps_t
fg, ax = dyplot.cornerplot(res, color='red', truths=np.zeros(ndim), truth_color='black',
span=[(-3.5, 3.5) for i in range(len(dims))],
show_titles=True, title_kwargs={'y': 1.05},
quantiles=None, fig=(fig, ax))
res.samples = samps
print(1./np.sqrt(2))
```
That looks good! Obviously we can't plot the full 250x250 plot, but 5x5 subplots should do.
Now we can finally check how well our mean and covariances agree.
```
# let's confirm we actually got the entire distribution
from dynesty import utils
weights = np.exp(res.logwt - res.logz[-1])
mu, cov = utils.mean_and_cov(samps, weights)
# plot residuals
from scipy.stats.kde import gaussian_kde
mu_kde = gaussian_kde(mu)
xgrid = np.linspace(-0.5, 0.5, 1000)
mu_pdf = mu_kde.pdf(xgrid)
cov_kde = gaussian_kde((cov - C).flatten())
xgrid2 = np.linspace(-0.3, 0.3, 1000)
cov_pdf = cov_kde.pdf(xgrid2)
plt.figure(figsize=(16, 6))
plt.subplot(1, 2, 1)
plt.plot(xgrid, mu_pdf, lw=3, color='black')
plt.xlabel('Mean Offset')
plt.ylabel('PDF')
plt.subplot(1, 2, 2)
plt.plot(xgrid2, cov_pdf, lw=3, color='red')
plt.xlabel('Covariance Offset')
plt.ylabel('PDF')
# print values
print('Means (0.):', np.mean(mu), '+/-', np.std(mu))
print('Variance (0.5):', np.mean(np.diag(cov)), '+/-', np.std(np.diag(cov)))
cov_up = np.triu(cov, k=1).flatten()
cov_low = np.tril(cov,k=-1).flatten()
cov_offdiag = np.append(cov_up[abs(cov_up) != 0.], cov_low[cov_low != 0.])
print('Covariance (0.):', np.mean(cov_offdiag), '+/-', np.std(cov_offdiag))
plt.tight_layout()
# plot individual values
plt.figure(figsize=(20,6))
plt.subplot(1, 3, 1)
plt.plot(mu, 'k.')
plt.ylabel('Mean')
plt.xlabel('Dimension')
plt.tight_layout()
plt.subplot(1, 3, 2)
plt.plot(np.diag(cov) - 0.5, 'r.')
plt.ylabel('Variance')
plt.xlabel('Dimension')
plt.tight_layout()
plt.subplot(1, 3, 3)
plt.plot(cov_low[cov_low != 0.], 'b.')
plt.plot(cov_up[cov_up != 0.], 'b.')
plt.ylabel('Covariance')
plt.xlabel('Cross-Term')
plt.tight_layout()
```
|
github_jupyter
|
# Python 3 compatability
from __future__ import division, print_function
from builtins import range
# system functions that are always useful to have
import time, sys, os
# basic numeric setup
import numpy as np
import math
from numpy import linalg
# inline plotting
%matplotlib inline
# plotting
import matplotlib
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# seed the random number generator
np.random.seed(2018)
# re-defining plotting defaults
from matplotlib import rcParams
rcParams.update({'xtick.major.pad': '7.0'})
rcParams.update({'xtick.major.size': '7.5'})
rcParams.update({'xtick.major.width': '1.5'})
rcParams.update({'xtick.minor.pad': '7.0'})
rcParams.update({'xtick.minor.size': '3.5'})
rcParams.update({'xtick.minor.width': '1.0'})
rcParams.update({'ytick.major.pad': '7.0'})
rcParams.update({'ytick.major.size': '7.5'})
rcParams.update({'ytick.major.width': '1.5'})
rcParams.update({'ytick.minor.pad': '7.0'})
rcParams.update({'ytick.minor.size': '3.5'})
rcParams.update({'ytick.minor.width': '1.0'})
rcParams.update({'font.size': 30})
import dynesty
from scipy.special import ndtri
ndim = 250 # number of dimensions
C = np.identity(ndim) # set covariance to identity matrix
Cinv = linalg.inv(C) # precision matrix
lnorm = -0.5 * (np.log(2 * np.pi) * ndim + np.log(linalg.det(C))) # ln(normalization)
# 250-D iid standard normal log-likelihood
def loglikelihood(x):
"""Multivariate normal log-likelihood."""
return -0.5 * np.dot(x, np.dot(Cinv, x)) + lnorm
# prior transform (iid standard normal prior)
def prior_transform(u):
"""Transforms our unit cube samples `u` to a flat prior between -10. and 10. in each variable."""
return ndtri(u)
# ln(evidence)
lnz_truth = lnorm - 0.5 * ndim * np.log(2)
print(lnz_truth)
# hamiltonian slice sampling ('hslice')
sampler = dynesty.DynamicNestedSampler(loglikelihood, prior_transform, ndim,
bound='none', sample='hslice', slices=10)
sampler.run_nested(nlive_init=100, nlive_batch=100)
res = sampler.results
import pickle
# dump results
output = open('250d_gauss.pkl', 'wb')
pickle.dump(sampler.results, output)
output.close()
import pickle
output = open('250d_gauss.pkl', 'rb')
res = pickle.load(output)
output.close()
from dynesty import plotting as dyplot
# evidence check
fig, axes = dyplot.runplot(res, color='red', lnz_truth=lnz_truth, truth_color='black', logplot=True)
fig.tight_layout()
# posterior check
dims = [-1, -2, -3, -4, -5]
fig, ax = plt.subplots(5, 5, figsize=(25, 25))
samps, samps_t = res.samples, res.samples[:,dims]
res.samples = samps_t
fg, ax = dyplot.cornerplot(res, color='red', truths=np.zeros(ndim), truth_color='black',
span=[(-3.5, 3.5) for i in range(len(dims))],
show_titles=True, title_kwargs={'y': 1.05},
quantiles=None, fig=(fig, ax))
res.samples = samps
print(1./np.sqrt(2))
# let's confirm we actually got the entire distribution
from dynesty import utils
weights = np.exp(res.logwt - res.logz[-1])
mu, cov = utils.mean_and_cov(samps, weights)
# plot residuals
from scipy.stats.kde import gaussian_kde
mu_kde = gaussian_kde(mu)
xgrid = np.linspace(-0.5, 0.5, 1000)
mu_pdf = mu_kde.pdf(xgrid)
cov_kde = gaussian_kde((cov - C).flatten())
xgrid2 = np.linspace(-0.3, 0.3, 1000)
cov_pdf = cov_kde.pdf(xgrid2)
plt.figure(figsize=(16, 6))
plt.subplot(1, 2, 1)
plt.plot(xgrid, mu_pdf, lw=3, color='black')
plt.xlabel('Mean Offset')
plt.ylabel('PDF')
plt.subplot(1, 2, 2)
plt.plot(xgrid2, cov_pdf, lw=3, color='red')
plt.xlabel('Covariance Offset')
plt.ylabel('PDF')
# print values
print('Means (0.):', np.mean(mu), '+/-', np.std(mu))
print('Variance (0.5):', np.mean(np.diag(cov)), '+/-', np.std(np.diag(cov)))
cov_up = np.triu(cov, k=1).flatten()
cov_low = np.tril(cov,k=-1).flatten()
cov_offdiag = np.append(cov_up[abs(cov_up) != 0.], cov_low[cov_low != 0.])
print('Covariance (0.):', np.mean(cov_offdiag), '+/-', np.std(cov_offdiag))
plt.tight_layout()
# plot individual values
plt.figure(figsize=(20,6))
plt.subplot(1, 3, 1)
plt.plot(mu, 'k.')
plt.ylabel('Mean')
plt.xlabel('Dimension')
plt.tight_layout()
plt.subplot(1, 3, 2)
plt.plot(np.diag(cov) - 0.5, 'r.')
plt.ylabel('Variance')
plt.xlabel('Dimension')
plt.tight_layout()
plt.subplot(1, 3, 3)
plt.plot(cov_low[cov_low != 0.], 'b.')
plt.plot(cov_up[cov_up != 0.], 'b.')
plt.ylabel('Covariance')
plt.xlabel('Cross-Term')
plt.tight_layout()
| 0.685423 | 0.874023 |
# Transfer Learning
In this notebook, you'll learn how to use pre-trained networks to solved challenging problems in computer vision. Specifically, you'll use networks trained on [ImageNet](http://www.image-net.org/) [available from torchvision](http://pytorch.org/docs/0.3.0/torchvision/models.html).
ImageNet is a massive dataset with over 1 million labeled images in 1000 categories. It's used to train deep neural networks using an architecture called convolutional layers. I'm not going to get into the details of convolutional networks here, but if you want to learn more about them, please [watch this](https://www.youtube.com/watch?v=2-Ol7ZB0MmU).
Once trained, these models work astonishingly well as feature detectors for images they weren't trained on. Using a pre-trained network on images not in the training set is called transfer learning. Here we'll use transfer learning to train a network that can classify our cat and dog photos with near perfect accuracy.
With `torchvision.models` you can download these pre-trained networks and use them in your applications. We'll include `models` in our imports now.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
```
Most of the pretrained models require the input to be 224x224 images. Also, we'll need to match the normalization used when the models were trained. Each color channel was normalized separately, the means are `[0.485, 0.456, 0.406]` and the standard deviations are `[0.229, 0.224, 0.225]`.
```
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(test_data, batch_size=64)
```
We can load in a model such as [DenseNet](http://pytorch.org/docs/0.3.0/torchvision/models.html#id5). Let's print out the model architecture so we can see what's going on.
```
model = models.densenet121(pretrained=True)
model
```
This model is built out of two main parts, the features and the classifier. The features part is a stack of convolutional layers and overall works as a feature detector that can be fed into a classifier. The classifier part is a single fully-connected layer `(classifier): Linear(in_features=1024, out_features=1000)`. This layer was trained on the ImageNet dataset, so it won't work for our specific problem. That means we need to replace the classifier, but the features will work perfectly on their own. In general, I think about pre-trained networks as amazingly good feature detectors that can be used as the input for simple feed-forward classifiers.
```
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(1024, 500)),
('relu', nn.ReLU()),
('fc2', nn.Linear(500, 2)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
```
With our model built, we need to train the classifier. However, now we're using a **really deep** neural network. If you try to train this on a CPU like normal, it will take a long, long time. Instead, we're going to use the GPU to do the calculations. The linear algebra computations are done in parallel on the GPU leading to 100x increased training speeds. It's also possible to train on multiple GPUs, further decreasing training time.
PyTorch, along with pretty much every other deep learning framework, uses [CUDA](https://developer.nvidia.com/cuda-zone) to efficiently compute the forward and backwards passes on the GPU. In PyTorch, you move your model parameters and other tensors to the GPU memory using `model.to('cuda')`. You can move them back from the GPU with `model.to('cpu')` which you'll commonly do when you need to operate on the network output outside of PyTorch. As a demonstration of the increased speed, I'll compare how long it takes to perform a forward and backward pass with and without a GPU.
```
import time
for device in ['cpu', 'cuda']:
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.001)
model.to(device)
for ii, (inputs, labels) in enumerate(trainloader):
# Move input and label tensors to the GPU
inputs, labels = inputs.to(device), labels.to(device)
start = time.time()
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if ii==3:
break
print(f"Device = {device}; Time per batch: {(time.time() - start)/3:.3f} seconds")
```
You can write device agnostic code which will automatically use CUDA if it's enabled like so:
```python
# at beginning of the script
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
...
# then whenever you get a new Tensor or Module
# this won't copy if they are already on the desired device
input = data.to(device)
model = MyModule(...).to(device)
```
From here, I'll let you finish training the model. The process is the same as before except now your model is much more powerful. You should get better than 95% accuracy easily.
>**Exercise:** Train a pretrained models to classify the cat and dog images. Continue with the DenseNet model, or try ResNet, it's also a good model to try out first. Make sure you are only training the classifier and the parameters for the features part are frozen.
```
## TODO: Use a pretrained model to classify the cat and dog images
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = models.resnet50(pretrained=True)
# Turn of gradients for the model
for param in model.parameters():
param.requires_grad = False
# Define new classifier
clsssifier = nn.Sequential(nn.Linear(2048, 512),
nn.ReLU(),
nn.Dropout(p=0.2),
nn.Linear(512,2),
nn.LogSoftmax(dim=1))
model.fc = clsssifier
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.fc.parameters(), lr=0.003)
model.to(device)
epochs = 1
steps = 0
running_loss = 0
print_every = 5
for epoch in range(epochs):
for images, labels in trainloader:
steps += 1
if steps == 50:
break;
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
logps = model(images)
loss = criterion(logps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % print_every == 0:
model.eval()
test_loss = 0
accuracy = 0
for images, labels in testloader:
images, labels = images.to(device), labels.to(device)
logps = model(images)
loss = criterion(logps, labels)
test_loss += loss.item()
# calculate the accuracy
ps = torch.exp(logps)
top_ps, top_class = ps.topk(1, dim=1)
equality = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equality.type(torch.FloatTensor)).item()
print(f"Epoch {epoch+1}/{epochs}.. "
f"Train loss: {running_loss/print_every:.3f}.. "
f"Test loss: {test_loss/len(testloader):.3f}.. "
f"Test accuracy: {accuracy/len(testloader):.3f}")
running_loss = 0
model.train()
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(test_data, batch_size=64)
model = models.densenet121(pretrained=True)
model
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(1024, 500)),
('relu', nn.ReLU()),
('fc2', nn.Linear(500, 2)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
import time
for device in ['cpu', 'cuda']:
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.001)
model.to(device)
for ii, (inputs, labels) in enumerate(trainloader):
# Move input and label tensors to the GPU
inputs, labels = inputs.to(device), labels.to(device)
start = time.time()
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if ii==3:
break
print(f"Device = {device}; Time per batch: {(time.time() - start)/3:.3f} seconds")
# at beginning of the script
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
...
# then whenever you get a new Tensor or Module
# this won't copy if they are already on the desired device
input = data.to(device)
model = MyModule(...).to(device)
## TODO: Use a pretrained model to classify the cat and dog images
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = models.resnet50(pretrained=True)
# Turn of gradients for the model
for param in model.parameters():
param.requires_grad = False
# Define new classifier
clsssifier = nn.Sequential(nn.Linear(2048, 512),
nn.ReLU(),
nn.Dropout(p=0.2),
nn.Linear(512,2),
nn.LogSoftmax(dim=1))
model.fc = clsssifier
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.fc.parameters(), lr=0.003)
model.to(device)
epochs = 1
steps = 0
running_loss = 0
print_every = 5
for epoch in range(epochs):
for images, labels in trainloader:
steps += 1
if steps == 50:
break;
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
logps = model(images)
loss = criterion(logps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % print_every == 0:
model.eval()
test_loss = 0
accuracy = 0
for images, labels in testloader:
images, labels = images.to(device), labels.to(device)
logps = model(images)
loss = criterion(logps, labels)
test_loss += loss.item()
# calculate the accuracy
ps = torch.exp(logps)
top_ps, top_class = ps.topk(1, dim=1)
equality = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equality.type(torch.FloatTensor)).item()
print(f"Epoch {epoch+1}/{epochs}.. "
f"Train loss: {running_loss/print_every:.3f}.. "
f"Test loss: {test_loss/len(testloader):.3f}.. "
f"Test accuracy: {accuracy/len(testloader):.3f}")
running_loss = 0
model.train()
| 0.67694 | 0.989582 |
```
import gym
import math
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import time as t
from gym import envs
envids = [spec.id for spec in envs.registry.all()]
'''for envid in sorted(envids):
print(envid) '''
#To improve the velocity, run it on the GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('Device ', device)
#Create the enviorment
env = gym.make('LunarLander-v2')
env.seed(101) #To ensure it's the same situation always simulated, even if it's random
np.random.seed(101)
#check the properties of the enviorment
print('observation space:', env.observation_space) #states, is continuous 2-D (a box)
print('action space:', env.action_space) #actions, 1 discrete action, with 3 possible values
# print(' - low:', env.action_space.low) #minimum speed
# print(' - high:', env.action_space.high) #maximus speed
#t.sleep(10)
print( env.observation_space.shape[0] ) #First layer number of states+
h_size=16
# 1 action ,0 nothing, 1 left, 2 up , 3 right
#In this case exist 4 movements which can be positive or 0
#Creation of a class to chosse the actions, the policy
class Agent(nn.Module):
def __init__(self, env, h_size=16):
super(Agent, self).__init__() #Equivalent to super().__init__()
#Means that this class heritage the init from nn.Module class
# nn.Module it's the base class for all the neural net networks
# https://pytorch.org/docs/stable/_modules/torch/nn/modules/module.html#Module
# https://pytorch.org/docs/stable/nn.html
self.env = env #Save the enviorment as the Gym enviorment
# state, hidden layer, action sizes
self.s_size = env.observation_space.shape[0] #First layer number of states+
self.h_size = h_size #hidden layer
self.a_size = 1 #Last layer number of actions ( 0 don't do nothing, 1 left, 2 up,3right)
# define layers
self.fc1 = nn.Linear(self.s_size, self.h_size) # A linear layer that connect the states with the hidden layer
self.fc2 = nn.Linear(self.h_size, self.a_size) # Hidden layer the from hidden layer to actions
def set_weights(self, weights):
s_size = self.s_size
h_size = self.h_size
a_size = self.a_size
# print(s_size)
# print(h_size)
# print(a_size)
# Are linear layers so
# weight _w and b it's the bias.
#https://medium.com/datathings/linear-layers-explained-in-a-simple-way-2319a9c2d1aa
#The bias learns a constant value, independent of the input.
# Learns that all the positive states need at least a bias constant + something dependant
# a linear layer learns that the output ,it's the Activation Function ( input * pendent (the weight) + constant)
# linear neuron output = input *w + b
# separate the weights for each layer
# so we are saying that (state1 * wl1 + bl1)*wl2 +bl2, so we belive it follows a 1st order equation * activation function
fc1_end = (s_size*h_size)+h_size
#The first states * number of hidden layers are the weights of the first layer, each network has different weights for each state input
fc1_W = torch.from_numpy(weights[:s_size*h_size].reshape(s_size, h_size))
#From the previous end , the follwing hidden layer neurons number weights are the bias, each neuron has only 1 bias, doesn't depend on the state input
fc1_b = torch.from_numpy(weights[s_size*h_size:fc1_end])
#Every neuron has a weight for each action output
fc2_W = torch.from_numpy(weights[fc1_end:fc1_end+(h_size*a_size)].reshape(h_size, a_size))
fc2_b = torch.from_numpy(weights[fc1_end+(h_size*a_size):])
# set the weights for each layer
self.fc1.weight.data.copy_(fc1_W.view_as(self.fc1.weight.data))
self.fc1.bias.data.copy_(fc1_b.view_as(self.fc1.bias.data))
self.fc2.weight.data.copy_(fc2_W.view_as(self.fc2.weight.data))
self.fc2.bias.data.copy_(fc2_b.view_as(self.fc2.bias.data))
def get_weights_dim(self):
#In reality its returning the weights + bias dimensions, the +1 its the bias
return (self.s_size+1)*self.h_size + (self.h_size+1)*self.a_size
def forward(self, x):
#forward its Method to be able to pass the data as batches of data
# It passes the data as Matrices adding the activation functions at the same time
#They have activation functions to
#https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
x = F.relu(self.fc1(x)) # Only possitive values pass
#x = F.tanh(self.fc2(x))
x = torch.sigmoid(self.fc2(x)) # Only from 0 to 1, to have easy to do 4 groups
return x.cpu().data
def evaluate(self, weights, gamma=1.0, max_t=5000):
# Obtain the accumulative reward from the actions selected by the neural net
self.set_weights(weights)
episode_return = 0.0
state = self.env.reset()
for t in range(max_t):
state = torch.from_numpy(state).float().to(device)
action = self.forward(state)
#print(action)
action = action *3
if(action >= 2.5):
action = 3
elif (action >= 1.5):
action = 2
elif (action >= 0.5):
action = 1
else:
action = 0
state, reward, done, _ = self.env.step(action)
episode_return += reward * math.pow(gamma, t)
if done:
break
return episode_return
#End of class
agent = Agent(env).to(device) # Creation of a neural net in the device, in my case the GPU
#Cross Entrophy Method, to choose the weights
def cem(n_iterations=1000, max_t=1000, gamma=1.0, print_every=10, pop_size=50, elite_frac=0.2, sigma=0.5):
"""PyTorch implementation of the cross-entropy method.
Params
======
n_iterations (int): maximum number of training iterations
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
pop_size (int): size of population at each iteration
elite_frac (float): percentage of top performers to use in update
sigma (float): standard deviation of additive noise
"""
#Fracció de millors pesos que et quedas
n_elite=int(pop_size*elite_frac)
#scores doble end queee , from 100 values
scores_deque = deque(maxlen=100)
#intial scores empty
scores = []
#Initial best weights, are from 0 to 1, it's good to be small the weights, but they should be different from 0.
# small to avoid overfiting , different from 0 to update them
best_weight = sigma*np.random.randn(agent.get_weights_dim())
#Each iteration, modify + 1 to 0 the best weight randomly
#Computes the reward with these weights
#Sort the reward to get the best ones
# Save the best weights
# the Best weight it's the mean of the best one
#compute the main reward of the main best rewards ones
#this it's show to evalute how good its
for i_iteration in range(1, n_iterations+1):
weights_pop = [best_weight + (sigma*np.random.randn(agent.get_weights_dim())) for i in range(pop_size)]
rewards = np.array([agent.evaluate(weights, gamma, max_t) for weights in weights_pop])
elite_idxs = rewards.argsort()[-n_elite:]
elite_weights = [weights_pop[i] for i in elite_idxs]
best_weight = np.array(elite_weights).mean(axis=0)
reward = agent.evaluate(best_weight, gamma=1.0)
scores_deque.append(reward)
scores.append(reward)
#save the check point
torch.save(agent.state_dict(), 'checkpointLunar.pth')
if i_iteration % print_every == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_iteration, np.mean(scores_deque)))
if np.mean(scores_deque)>=90.0:
print('\nEnvironment solved in {:d} iterations!\tAverage Score: {:.2f}'.format(i_iteration-100, np.mean(scores_deque)))
break
return scores
#Execute the cross entrophy method with default Values
#scores = cem()
#To don't ask the GPU as much reduce the pop_size, it's the amount of elemts try
scores = cem(pop_size=30)
#
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# load the weights from file
agent.load_state_dict(torch.load('checkpoint.pth'))
state = env.reset()
while True:
state = torch.from_numpy(state).float().to(device)
with torch.no_grad():
action = agent(state)
action = action *3
if(action >= 2.5):
action = 3
elif (action >= 1.5):
action = 2
elif (action >= 0.5):
action = 1
else:
action = 0
env.render()
t.sleep(0.1)
next_state, reward, done, _ = env.step(action)
state = next_state
if done:
break
env.close()
env.close()
#save the check point
torch.save(agent.state_dict(), 'checkpointLunar.pth')
```
|
github_jupyter
|
import gym
import math
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import time as t
from gym import envs
envids = [spec.id for spec in envs.registry.all()]
'''for envid in sorted(envids):
print(envid) '''
#To improve the velocity, run it on the GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('Device ', device)
#Create the enviorment
env = gym.make('LunarLander-v2')
env.seed(101) #To ensure it's the same situation always simulated, even if it's random
np.random.seed(101)
#check the properties of the enviorment
print('observation space:', env.observation_space) #states, is continuous 2-D (a box)
print('action space:', env.action_space) #actions, 1 discrete action, with 3 possible values
# print(' - low:', env.action_space.low) #minimum speed
# print(' - high:', env.action_space.high) #maximus speed
#t.sleep(10)
print( env.observation_space.shape[0] ) #First layer number of states+
h_size=16
# 1 action ,0 nothing, 1 left, 2 up , 3 right
#In this case exist 4 movements which can be positive or 0
#Creation of a class to chosse the actions, the policy
class Agent(nn.Module):
def __init__(self, env, h_size=16):
super(Agent, self).__init__() #Equivalent to super().__init__()
#Means that this class heritage the init from nn.Module class
# nn.Module it's the base class for all the neural net networks
# https://pytorch.org/docs/stable/_modules/torch/nn/modules/module.html#Module
# https://pytorch.org/docs/stable/nn.html
self.env = env #Save the enviorment as the Gym enviorment
# state, hidden layer, action sizes
self.s_size = env.observation_space.shape[0] #First layer number of states+
self.h_size = h_size #hidden layer
self.a_size = 1 #Last layer number of actions ( 0 don't do nothing, 1 left, 2 up,3right)
# define layers
self.fc1 = nn.Linear(self.s_size, self.h_size) # A linear layer that connect the states with the hidden layer
self.fc2 = nn.Linear(self.h_size, self.a_size) # Hidden layer the from hidden layer to actions
def set_weights(self, weights):
s_size = self.s_size
h_size = self.h_size
a_size = self.a_size
# print(s_size)
# print(h_size)
# print(a_size)
# Are linear layers so
# weight _w and b it's the bias.
#https://medium.com/datathings/linear-layers-explained-in-a-simple-way-2319a9c2d1aa
#The bias learns a constant value, independent of the input.
# Learns that all the positive states need at least a bias constant + something dependant
# a linear layer learns that the output ,it's the Activation Function ( input * pendent (the weight) + constant)
# linear neuron output = input *w + b
# separate the weights for each layer
# so we are saying that (state1 * wl1 + bl1)*wl2 +bl2, so we belive it follows a 1st order equation * activation function
fc1_end = (s_size*h_size)+h_size
#The first states * number of hidden layers are the weights of the first layer, each network has different weights for each state input
fc1_W = torch.from_numpy(weights[:s_size*h_size].reshape(s_size, h_size))
#From the previous end , the follwing hidden layer neurons number weights are the bias, each neuron has only 1 bias, doesn't depend on the state input
fc1_b = torch.from_numpy(weights[s_size*h_size:fc1_end])
#Every neuron has a weight for each action output
fc2_W = torch.from_numpy(weights[fc1_end:fc1_end+(h_size*a_size)].reshape(h_size, a_size))
fc2_b = torch.from_numpy(weights[fc1_end+(h_size*a_size):])
# set the weights for each layer
self.fc1.weight.data.copy_(fc1_W.view_as(self.fc1.weight.data))
self.fc1.bias.data.copy_(fc1_b.view_as(self.fc1.bias.data))
self.fc2.weight.data.copy_(fc2_W.view_as(self.fc2.weight.data))
self.fc2.bias.data.copy_(fc2_b.view_as(self.fc2.bias.data))
def get_weights_dim(self):
#In reality its returning the weights + bias dimensions, the +1 its the bias
return (self.s_size+1)*self.h_size + (self.h_size+1)*self.a_size
def forward(self, x):
#forward its Method to be able to pass the data as batches of data
# It passes the data as Matrices adding the activation functions at the same time
#They have activation functions to
#https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
x = F.relu(self.fc1(x)) # Only possitive values pass
#x = F.tanh(self.fc2(x))
x = torch.sigmoid(self.fc2(x)) # Only from 0 to 1, to have easy to do 4 groups
return x.cpu().data
def evaluate(self, weights, gamma=1.0, max_t=5000):
# Obtain the accumulative reward from the actions selected by the neural net
self.set_weights(weights)
episode_return = 0.0
state = self.env.reset()
for t in range(max_t):
state = torch.from_numpy(state).float().to(device)
action = self.forward(state)
#print(action)
action = action *3
if(action >= 2.5):
action = 3
elif (action >= 1.5):
action = 2
elif (action >= 0.5):
action = 1
else:
action = 0
state, reward, done, _ = self.env.step(action)
episode_return += reward * math.pow(gamma, t)
if done:
break
return episode_return
#End of class
agent = Agent(env).to(device) # Creation of a neural net in the device, in my case the GPU
#Cross Entrophy Method, to choose the weights
def cem(n_iterations=1000, max_t=1000, gamma=1.0, print_every=10, pop_size=50, elite_frac=0.2, sigma=0.5):
"""PyTorch implementation of the cross-entropy method.
Params
======
n_iterations (int): maximum number of training iterations
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
pop_size (int): size of population at each iteration
elite_frac (float): percentage of top performers to use in update
sigma (float): standard deviation of additive noise
"""
#Fracció de millors pesos que et quedas
n_elite=int(pop_size*elite_frac)
#scores doble end queee , from 100 values
scores_deque = deque(maxlen=100)
#intial scores empty
scores = []
#Initial best weights, are from 0 to 1, it's good to be small the weights, but they should be different from 0.
# small to avoid overfiting , different from 0 to update them
best_weight = sigma*np.random.randn(agent.get_weights_dim())
#Each iteration, modify + 1 to 0 the best weight randomly
#Computes the reward with these weights
#Sort the reward to get the best ones
# Save the best weights
# the Best weight it's the mean of the best one
#compute the main reward of the main best rewards ones
#this it's show to evalute how good its
for i_iteration in range(1, n_iterations+1):
weights_pop = [best_weight + (sigma*np.random.randn(agent.get_weights_dim())) for i in range(pop_size)]
rewards = np.array([agent.evaluate(weights, gamma, max_t) for weights in weights_pop])
elite_idxs = rewards.argsort()[-n_elite:]
elite_weights = [weights_pop[i] for i in elite_idxs]
best_weight = np.array(elite_weights).mean(axis=0)
reward = agent.evaluate(best_weight, gamma=1.0)
scores_deque.append(reward)
scores.append(reward)
#save the check point
torch.save(agent.state_dict(), 'checkpointLunar.pth')
if i_iteration % print_every == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_iteration, np.mean(scores_deque)))
if np.mean(scores_deque)>=90.0:
print('\nEnvironment solved in {:d} iterations!\tAverage Score: {:.2f}'.format(i_iteration-100, np.mean(scores_deque)))
break
return scores
#Execute the cross entrophy method with default Values
#scores = cem()
#To don't ask the GPU as much reduce the pop_size, it's the amount of elemts try
scores = cem(pop_size=30)
#
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# load the weights from file
agent.load_state_dict(torch.load('checkpoint.pth'))
state = env.reset()
while True:
state = torch.from_numpy(state).float().to(device)
with torch.no_grad():
action = agent(state)
action = action *3
if(action >= 2.5):
action = 3
elif (action >= 1.5):
action = 2
elif (action >= 0.5):
action = 1
else:
action = 0
env.render()
t.sleep(0.1)
next_state, reward, done, _ = env.step(action)
state = next_state
if done:
break
env.close()
env.close()
#save the check point
torch.save(agent.state_dict(), 'checkpointLunar.pth')
| 0.805058 | 0.615897 |
(IN)=
# 1.7 Integración Numérica
```{admonition} Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar `<ruta a mi directorio>` por la ruta de directorio que se desea mapear a `/datos` dentro del contenedor de docker.
`docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:2.1.4`
password para jupyterlab: `qwerty`
Detener el contenedor de docker:
`docker stop jupyterlab_optimizacion`
Documentación de la imagen de docker `palmoreck/jupyterlab_optimizacion:2.1.4` en [liga](https://github.com/palmoreck/dockerfiles/tree/master/jupyterlab/optimizacion).
```
---
Nota generada a partir de la [liga1](https://www.dropbox.com/s/jfrxanjls8kndjp/Diferenciacion_e_Integracion.pdf?dl=0) y [liga2](https://www.dropbox.com/s/k3y7h9yn5d3yf3t/Integracion_por_Monte_Carlo.pdf?dl=0).
```{admonition} Al final de esta nota el y la lectora:
:class: tip
* Aprenderá que el método de integración numérica es un método estable numéricamente respecto al redondeo.
* Aprenderá a aproximar integrales de forma numérica por el método de Monte Carlo y tendrá una alternativa a los métodos por Newton-Cotes para el caso de más de una dimensión.
```
```{admonition} Comentario
Los métodos revisados en esta nota de integración numérica serán utilizados más adelante para revisión de herramientas en Python de **perfilamiento de código: uso de cpu y memoria**. También serán referidos en el capítulo de **cómputo en paralelo**.
```
En lo siguiente consideramos que las funciones del integrando están en $\mathcal{C}^2$ en el conjunto de integración (ver {ref}`Definición de función, continuidad y derivada <FCD>` para definición de $\mathcal{C}^2$).
Las reglas o métodos por cuadratura nos ayudan a aproximar integrales con sumas de la forma:
$$\displaystyle \int_a^bf(x)dx \approx \displaystyle \sum_{i=0}^nw_if(x_i)$$
donde: $w_i$ es el **peso** para el **nodo** $x_i$, $f$ se llama integrando y $[a,b]$ intervalo de integración. Los valores $f(x_i)$ se asumen conocidos.
Una gran cantidad de reglas o métodos por cuadratura se obtienen con interpoladores polinomiales del integrando (por ejemplo usando la representación de Lagrange) o también con el teorema Taylor (ver nota {ref}`Polinomios de Taylor y diferenciación numérica <PTDN>` para éste teorema).
Se realizan aproximaciones numéricas por:
* Desconocimiento de la función en todo el intervalo $[a,b]$ y sólo se conoce en los nodos su valor.
* Inexistencia de antiderivada o primitiva del integrando. Por ejemplo:
$$\displaystyle \int_a^be^{-\frac{x^2}{2}}dx$$ con $a,b$ números reales.
```{admonition} Observación
:class: tip
Si existe antiderivada o primitiva del integrando puede usarse el cómputo simbólico o algebraico para obtener el resultado de la integral y evaluarse. Un paquete de Python que nos ayuda a lo anterior es [SymPy](https://www.sympy.org/en/index.html).
```
Dependiendo de la ubicación de los nodos y pesos es el método de cuadratura que resulta:
* Newton-Cotes si los nodos y pesos son equidistantes como la regla del rectángulo, trapecio y Simpson (con el teorema de Taylor o interpolación es posible obtener tales fórmulas).
* Cuadratura Gaussiana si se desea obtener reglas o fórmulas que tengan la mayor exactitud posible (los nodos y pesos se eligen para cumplir con lo anterior). Ejemplos de este tipo de cuadratura se tiene la regla por cuadratura Gauss-Legendre en $[-1,1]$ (que usa [polinomos de Legendre](https://en.wikipedia.org/wiki/Legendre_polynomials)) o Gauss-Hermite (que usa [polinomios de Hermite](https://en.wikipedia.org/wiki/Hermite_polynomials)) para el caso de integrales en $[-\infty, \infty]$ con integrando $e^{-x^2}f(x)$.
```{margin}
En este dibujo se muestra que puede subdivirse el intervalo de integración en una mayor cantidad de subintervalos, lo cual para la función $f$ mostrada es benéfico pues se tiene mejor aproximación (¿en la práctica esto será bueno? recuérdese los errores de redondeo de la nota {ref}`Sistema de punto flotante <SPF>`).
```
<img src="https://dl.dropboxusercontent.com/s/baf7eauuwm347zk/integracion_numerica.png?dl=0" heigth="500" width="500">
En el dibujo: a),b) y c) se integra numéricamente por Newton-Cotes. d) es por cuadratura Gaussiana.
```{admonition} Observación
:class: tip
Si la fórmula por Newton-Cotes involucra el valor de la función en los extremos se nombra cerrada, si no los involucra se les nombra abiertas. En el dibujo d) es abierta.
```
```{admonition} Definición
Los métodos que utilizan la idea anterior de dividir en subintervalos se les conoce como **métodos de integración numérica compuestos** en contraste con los simples:
Para las reglas compuestas se divide el intervalo $[a,b]$ en $n_\text{sub}$ subinteralos $[a_{i-1},a_i], i=1,\dots,n_\text{sub}$ con $a_0=a<a_1<\dots<a_{n_\text{sub}-1}<a_{n_\text{sub}}=b$ y se considera una partición regular, esto es: $a_i-a_{i-1}=\hat{h}$ con $\hat{h}=\frac{h}{n_\text{sub}}$ y $h=b-a$. En este contexto se realiza la aproximación:
$$\displaystyle \int_a^bf(x)dx = \sum_{i=1}^{n_\text{sub}}\int_{a_{i-1}}^{a_i}f(x)dx.$$
```
```{admonition} Comentario
Los métodos de integración numérica por Newton-Cotes o cuadratura Gaussiana pueden extenderse a más dimensiones, sin embargo incurren en lo que se conoce como la **maldición de la dimensionalidad** que para el caso de integración numérica consiste en la gran cantidad de evaluaciones que deben realizarse de la función del integrando para tener una exactitud pequeña. Por ejemplo con un número de nodos igual a $10^4$, una distancia entre ellos de $.1$ y una integral en $4$ dimensiones para la regla por Newton Cotes del rectángulo, se obtiene una exactitud de $2$ dígitos. Como alternativa a los métodos por cuadratura anteriores para las integrales de más dimensiones se tienen los {ref}`métodos de integración por el método Monte Carlo <IMC>` que generan aproximaciones con una exactitud moderada (del orden de $\mathcal{O}(n^{-1/2})$ con $n$ número de nodos) para un número de puntos moderado **independiente** de la dimensión.
```
## Newton-Cotes
Si los nodos $x_i, i=0,1,\dots,$ cumplen $x_{i+1}-x_i=h, \forall i=0,1,\dots,$ con $h$ (espaciado) constante y se aproxima la función del integrando $f$ con un polinomio en $(x_i,f(x_i)) \forall i=0,1,\dots,$ entonces se tiene un método de integración numérica por Newton-Cotes (o reglas o fórmulas por Newton-Cotes).
## Ejemplo de una integral que no tiene antiderivada
En las siguientes reglas se considerará la función $f(x)=e^{-x^2}$ la cual tiene una forma:
```
import math
import numpy as np
import pandas as pd
from scipy.integrate import quad
import matplotlib.pyplot as plt
f=lambda x: np.exp(-x**2)
x=np.arange(-1,1,.01)
plt.plot(x,f(x))
plt.title('f(x)=exp(-x^2)')
plt.show()
```
El valor de la integral $\int_0^1e^{-x^2}dx$ es:
```
obj, err = quad(f, 0, 1)
print((obj,err))
```
```{admonition} Observación
:class: tip
El segundo valor regresado `err`, es una cota superior del error.
```
## Regla simple del rectángulo
Denotaremos a esta regla como $Rf$. En este caso se aproxima el integrando $f$ por un polinomio de grado **cero** con nodo en $x_1 = \frac{a+b}{2}$. Entonces:
$$\displaystyle \int_a^bf(x)dx \approx \int_a^bf(x_1)dx = (b-a)f(x_1)=(b-a)f\left( \frac{a+b}{2} \right ) = hf(x_1)$$
con $h=b-a, x_1=\frac{a+b}{2}$.
<img src="https://dl.dropboxusercontent.com/s/mzlmnvgnltqamz3/rectangulo_simple.png?dl=0" heigth="200" width="200">
### Ejemplo de implementación de regla simple de rectángulo: usando math
Utilizar la regla simple del rectángulo para aproximar la integral $\displaystyle \int_0^1e^{-x^2}dx$.
```
f=lambda x: math.exp(-x**2) #using math library
def Rf(f,a,b):
"""
Compute numerical approximation using simple rectangle or midpoint method in
an interval.
"""
node=a+(b-a)/2.0 #mid point formula to minimize rounding errors
return f(node) #zero degree polynomial
rf_simple = Rf(f,0,1)
print(rf_simple)
```
```{admonition} Observación
:class: tip
Para cualquier aproximación calculada siempre es una muy buena idea reportar el error relativo de la aproximación si tenemos el valor del objetivo. No olvidar esto :)
```
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un valor `obj`:**
```
def compute_error(obj,approx):
'''
Relative or absolute error between obj and approx.
'''
if math.fabs(obj) > np.finfo(float).eps:
Err = math.fabs(obj-approx)/math.fabs(obj)
else:
Err = math.fabs(obj-approx)
return Err
print(compute_error(obj, rf_simple))
```
**El error relativo es de $4.2\%$ aproximadamente.**
## Regla compuesta del rectángulo
En cada subintervalo construído como $[a_{i-1},a_i]$ con $i=1,\dots,n_{\text{sub}}$ se aplica la regla simple $Rf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx R_i(f) \forall i=1,\dots,n_{\text{sub}}.$$
De forma sencilla se puede ver que la regla compuesta del rectángulo $R_c(f)$ se escribe:
$$\begin{eqnarray}
R_c(f) &=& \displaystyle \sum_{i=1}^{n_\text{sub}}(a_i-a_{i-1})f\left( \frac{a_i+a_{i-1}}{2}\right) \nonumber\\
&=& \frac{h}{n_\text{sub}}\sum_{i=1}^{n_\text{sub}}f\left( \frac{a_i+a_{i-1}}{2}\right) \nonumber\\
&=&\frac{h}{n_\text{sub}}\sum_{i=1}^{n_\text{sub}}f\left( x_i\right) \nonumber
\end{eqnarray}
$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/j2wmiyoms7gxrzp/rectangulo_compuesto.png?dl=0" heigth="200" width="200">
```{admonition} Observación
:class: tip
Los nodos para el caso del rectángulo se obtienen con la fórmula: $x_i = a +(i+\frac{1}{2})\hat{h}, \forall i=0,\dots,n_\text{sub}-1, \hat{h}=\frac{h}{n_\text{sub}}$. Por ejemplo si $a=1, b=2$ y $\hat{h}=\frac{1}{4}$ (por tanto $n_\text{sub}=4$ subintervalos) entonces:
Los subintervalos que tenemos son: $\left[1,\frac{5}{4}\right], \left[\frac{5}{4}, \frac{6}{4}\right], \left[\frac{6}{4}, \frac{7}{4}\right]$ y $\left[\frac{7}{4}, 2\right]$.
Los nodos están dados por:
$$x_0 = 1 + \left(0 + \frac{1}{2} \right)\frac{1}{4} = 1 + \frac{1}{8} = \frac{9}{8}$$
$$x_1 = 1 + \left(1 + \frac{1}{2}\right)\frac{1}{4} = 1 + \frac{3}{2}\cdot \frac{1}{4} = \frac{11}{8}$$
$$x_2 = 1 + \left(2 + \frac{1}{2}\right)\frac{1}{4} = 1 + \frac{5}{8}\cdot \frac{1}{4} = \frac{13}{8}$$
$$x_3 = 1 + \left(3 + \frac{1}{2}\right)\frac{1}{4} = 1 + \frac{7}{2}\cdot \frac{1}{4} = \frac{15}{8}$$
```
```{admonition} Observación
:class: tip
Obsérvese que para el caso de la regla del rectángulo Rcf $n = n_\text{sub}$ con $n$ número de nodos.
```
### Ejemplo de implementación de regla compuesta de rectángulo: usando math
Utilizar la regla compuesta del rectángulo para aproximar la integral $\int_0^1e^{-x^2}dx$.
```
f=lambda x: math.exp(-x**2) #using math library
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
"""
Compute numerical approximation using rectangle or mid-point method in
an interval.
Nodes are generated via formula: x_i = a+(i+1/2)h_hat for i=0,1,...,n-1 and h_hat=(b-a)/n
Args:
f (function): function expression of integrand
a (float): left point of interval
b (float): right point of interval
n (float): number of subintervals
Returns:
sum_res (float): numerical approximation to integral of f in the interval a,b
"""
h_hat=(b-a)/n
nodes=[a+(i+1/2)*h_hat for i in range(0,n)]
sum_res=0
for node in nodes:
sum_res=sum_res+f(node)
return h_hat*sum_res
a = 0; b = 1
```
**1 nodo**
```
n = 1
rcf_1 = Rcf(f,a, b, n)
print(rcf_1)
```
**2 nodos**
```
n = 2
rcf_2 = Rcf(f,a, b, n)
print(rcf_2)
```
**$10^3$ nodos**
```
n = 10**3
rcf_3 = Rcf(f, a, b, n)
print(rcf_3)
```
**Errores relativos:**
```
rel_err_rcf_1 = compute_error(obj, rcf_1)
rel_err_rcf_2 = compute_error(obj, rcf_2)
rel_err_rcf_3 = compute_error(obj, rcf_3)
dic = {"Aproximaciones Rcf": [
"Rcf_1",
"Rcf_2",
"Rcf_3"
],
"Número de nodos" : [
1,
2,
1e3
],
"Errores relativos": [
rel_err_rcf_1,
rel_err_rcf_2,
rel_err_rcf_3
]
}
print(pd.DataFrame(dic))
```
### Comentario: `pytest`
Otra forma de evaluar las aproximaciones realizadas es con módulos o paquetes de Python creados para este propósito en lugar de crear nuestras funciones como la de `compute_error`. Uno de estos es el paquete [pytest](https://docs.pytest.org/en/latest/) y la función [approx](https://docs.pytest.org/en/latest/reference.html#pytest-approx) de este paquete:
```
from pytest import approx
print(rcf_1 == approx(obj))
print(rcf_2 == approx(obj))
print(rcf_3 == approx(obj))
```
Y podemos usar un valor definido de tolerancia definido para hacer la prueba (por default se tiene una tolerancia de $10^{-6}$):
```
print(rcf_1 == approx(obj, abs=1e-1, rel=1e-1))
```
### Pregunta
**Será el método del rectángulo un método estable numéricamente bajo el redondeo?** Ver nota {ref}`Condición de un problema y estabilidad de un algoritmo <CPEA>` para definición de estabilidad numérica de un algoritmo.
Para responder la pregunta anterior aproximamos la integral con más nodos: $10^5$ nodos
```
n = 10**5
rcf_4 = Rcf(f, a, b, n)
print(rcf_4)
print(compute_error(obj, rcf_4))
```
Al menos para este ejemplo con $10^5$ nodos parece ser **numéricamente estable...**
## Regla compuesta del trapecio
En cada subintervalo se aplica la regla simple $Tf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx T_i(f) \forall i=1,\dots,n_\text{sub}.$$
Con $T_i(f) = \frac{(a_i-a_{i-1})}{2}(f(a_i)+f(a_{i-1}))$ para $i=1,\dots,n_\text{sub}$.
De forma sencilla se puede ver que la regla compuesta del trapecio $T_c(f)$ se escribe como:
$$T_c(f) = \displaystyle \frac{h}{2n_\text{sub}}\left[f(x_0)+f(x_{n_\text{sub}})+2\displaystyle\sum_{i=1}^{n_\text{sub}-1}f(x_i)\right]$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/4dl2btndrftdorp/trapecio_compuesto.png?dl=0" heigth="200" width="200">
```{admonition} Observaciones
:class: tip
* Los nodos para el caso del trapecio se obtienen con la fórmula: $x_i = a +i\hat{h}, \forall i=0,\dots,n_\text{sub}, \hat{h}=\frac{h}{n_\text{sub}}$.
* Obsérvese que para el caso de la regla del trapecio Tcf $n = n_\text{sub}+1$ con $n$ número de nodos.
```
### Ejemplo de implementación de regla compuesta del trapecio: usando numpy
Con la regla compuesta del trapecio se aproximará la integral $\int_0^1e^{-x^2}dx$. Se calculará el error relativo y graficará $n_\text{sub}$ vs Error relativo para $n_\text{sub}=1,10,100,1000,10000$.
```
f=lambda x: np.exp(-x**2) #using numpy library
def Tcf(n,f,a,b): #Tcf: trapecio compuesto para f
"""
Compute numerical approximation using trapezoidal method in
an interval.
Nodes are generated via formula: x_i = a+ih_hat for i=0,1,...,n and h_hat=(b-a)/n
Args:
f (function): function expression of integrand
a (float): left point of interval
b (float): right point of interval
n (float): number of subintervals
Returns:
sum_res (float): numerical approximation to integral of f in the interval a,b
"""
h=b-a
nodes=np.linspace(a,b,n+1)
sum_res=sum(f(nodes[1:-1]))
return h/(2*n)*(f(nodes[0])+f(nodes[-1])+2*sum_res)
```
Graficamos:
```
numb_of_subintervals=(1,10,100,1000,10000)
tcf_approx = np.array([Tcf(n,f,0,1) for n in numb_of_subintervals])
```
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un varios valores `obj`:**
```
def compute_error_point_wise(obj,approx):
'''
Relative or absolute error between obj and approx.
'''
if np.abs(obj) > np.nextafter(0,1):
Err = np.abs(obj-approx)/np.abs(obj)
else:
Err = np.abs(obj-approx)
return Err
relative_errors = compute_error_point_wise(obj, tcf_approx)
print(relative_errors)
plt.plot(numb_of_subintervals, relative_errors,'o')
plt.xlabel('number of subintervals')
plt.ylabel('Relative error')
plt.title('Error relativo en la regla del Trapecio')
plt.show()
```
Si no nos interesa el valor de los errores relativos y sólo la gráfica podemos utilizar la siguiente opción:
```
from functools import partial
```
Ver [functools.partial](https://docs.python.org/2/library/functools.html#functools.partial) para documentación, [liga](https://stackoverflow.com/questions/15331726/how-does-functools-partial-do-what-it-does) para una explicación de `partial` y [liga2](https://stackoverflow.com/questions/10834960/how-to-do-multiple-arguments-to-map-function-where-one-remains-the-same-in-pytho), [liga3](https://stackoverflow.com/questions/47859209/how-to-map-over-a-function-with-multiple-arguments-in-python) para ejemplos de uso.
```
tcf_approx_2 = map(partial(Tcf,f=f,a=a,b=b),
numb_of_subintervals) #map returns an iterator
```
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un varios valores `obj`:**
```
def compute_error_point_wise_2(obj, approx):
for ap in approx:
yield math.fabs(ap-obj)/math.fabs(obj) #using math library
```
```{admonition} Observación
:class: tip
La función `compute_error_point_wise_2` anterior es un [generator](https://wiki.python.org/moin/Generators), ver [liga](https://stackoverflow.com/questions/231767/what-does-the-yield-keyword-do) para conocer el uso de `yield`.
```
```
relative_errors_2 = compute_error_point_wise_2(obj, tcf_approx_2)
plt.plot(numb_of_subintervals,list(relative_errors_2),'o')
plt.xlabel('number of subintervals')
plt.ylabel('Relative error')
plt.title('Error relativo en la regla del Trapecio')
plt.show()
```
**Otra forma con [scatter](https://matplotlib.org/3.3.0/api/_as_gen/matplotlib.pyplot.scatter.html):**
```
tcf_approx_2 = map(partial(Tcf,f=f,a=a,b=b),
numb_of_subintervals) #map returns an iterator
relative_errors_2 = compute_error_point_wise_2(obj, tcf_approx_2)
[plt.scatter(n,rel_err) for n,rel_err in zip(numb_of_subintervals,relative_errors_2)]
plt.xlabel('number of subintervals')
plt.ylabel('Relative error')
plt.title('Error relativo en la regla del Trapecio')
plt.show()
```
## Regla compuesta de Simpson
En cada subintervalo se aplica la regla simple $Sf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx S_i(f) \forall i=1,\dots,n_\text{sub}$$
con $S_i(f) = \frac{h}{6}\left[f(x_{2i})+f(x_{2i-2})+4f(x_{2i-1})\right]$ para el subintervalo $[a_{i-1},a_i]$ con $i=1,\dots,n_\text{sub}$.
De forma sencilla se puede ver que la regla compuesta de Simpson compuesta $S_c(f)$ se escribe como:
$$S_c(f) = \displaystyle \frac{h}{3(2n_\text{sub})} \left [ f(x_0) + f(x_{2n_\text{sub}}) + 2 \sum_{i=1}^{n_\text{sub}-1}f(x_{2i}) + 4 \sum_{i=1}^{n_\text{sub}}f(x_{2i-1})\right ]$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/8rx32vdtulpdflm/Simpson_compuesto.png?dl=0" heigth="200" width="200">
```{admonition} Observaciones
:class: tip
* Los nodos para el caso de Simpson se obtienen con la fórmula: $x_i = a +\frac{i}{2}\hat{h}, \forall i=0,\dots,2n, \hat{h}=\frac{h}{n_\text{sub}}$.
* Obsérvese que para el caso de la regla de Simpson Scf $n = 2n_\text{sub}+1$ con $n$ número de nodos.
```
```{margin}
En esta [liga](https://www.dropbox.com/s/qrbcs5n57kp5150/Simpson-6-subintervalos.pdf?dl=0) está un apoyo visual para la regla Scf.
```
```{admonition} Ejercicio
:class: tip
Implementar la regla compuesta de Simpson para aproximar la integral $\int_0^1e^{-x^2}dx$. Calcular error relativo y realizar una gráfica de $n$ vs Error relativo para $n=1,10,100,1000,10000$ utilizando *Numpy* e `iterators`.
```
## Expresiones de los errores para las reglas compuestas del rectángulo, trapecio y Simpson
La forma de los errores de las reglas del rectángulo, trapecio y Simpson se pueden obtener con interpolación o con el teorema de Taylor. Ver [Diferenciación e Integración](https://www.dropbox.com/s/jfrxanjls8kndjp/Diferenciacion_e_Integracion.pdf?dl=0) para detalles y {ref}`Polinomios de Taylor y diferenciación numérica <PTDN>` para el teorema. Suponiendo que $f$ cumple con condiciones sobre sus derivadas, tales errores son:
$$\text{Err}Rc(f) = \frac{b-a}{6}f^{(2)}(\xi_r)\hat{h}^2, \xi_r \in [a,b]$$
$$\text{Err}Tc(f)=-\frac{b-a}{12}f^{(2)}(\xi_t)\hat{h}^2, \xi_t \in [a,b]$$
$$\text{Err}Sc(f)=-\frac{b-a}{180}f^{(4)}(\xi_S)\hat{h}^4, \xi_S \in [a,b].$$
(IMC)=
## Integración por el método de Monte Carlo
Los métodos de integración numérica por Monte Carlo son similares a los métodos por cuadratura en el sentido que se eligen puntos en los que se evaluará el integrando para sumar sus valores. La diferencia esencial con los métodos por cuadratura es que en el método de integración por Monte Carlo los puntos son **seleccionados de una forma *aleatoria*** (de hecho es pseudo-aleatoria pues se generan con un programa de computadora) en lugar de generarse con una fórmula.
### Problema
En esta sección consideramos $n$ número de nodos.
Aproximar numéricamente la integral $\displaystyle \int_{\Omega}f(x)dx$ para $x \in \mathbb{R}^\mathcal{D}, \Omega \subseteq \mathbb{R}^\mathcal{D}, f: \mathbb{R}^\mathcal{D} \rightarrow \mathbb{R}$ función tal que la integral esté bien definida en $\Omega$.
Por ejemplo para $\mathcal{D}=2:$
<img src="https://dl.dropboxusercontent.com/s/xktwjmgbf8aiekw/integral_2_dimensiones.png?dl=0" heigth="500" width="500">
Para resolver el problema anterior con $\Omega$ un rectángulo, podemos utilizar las reglas por cuadratura por Newton-Cotes o cuadratura Gaussiana en una dimensión manteniendo fija la otra dimensión. Sin embargo considérese la siguiente situación:
La regla del rectángulo (o del punto medio) y del trapecio tienen un error de orden $\mathcal{O}(h^2)$ independientemente de si se está aproximando integrales de una o más dimensiones. Supóngase que se utilizan $n$ nodos para tener un valor de espaciado igual a $\hat{h}$ en una dimensión, entonces para $\mathcal{D}$ dimensiones se requerirían $N=n^\mathcal{D}$ evaluaciones del integrando, o bien, si se tiene un valor de $N$ igual a $10, 000$ y $\mathcal{D}=4$ dimensiones el error sería del orden $\mathcal{O}(N^{-2/\mathcal{D}})$ lo que implicaría un valor de $\hat{h}=.1$ para aproximadamente sólo **dos dígitos** correctos en la aproximación (para el enunciado anterior recuérdese que $\hat{h}$ es proporcional a $n^{-1}$ y $n$ = $N^{1/\mathcal{D}}$). Este esfuerzo enorme de evaluar $N$ veces el integrando para una exactitud pequeña se debe al problema de generar puntos para *llenar* un espacio $\mathcal{D}$-dimensional y se conoce con el nombre de la maldición de la dimensionalidad, [***the curse of dimensionality***](https://en.wikipedia.org/wiki/Curse_of_dimensionality).
Una opción para resolver la situación anterior si no se desea una precisión alta (por ejemplo con una precisión de $10^{-4}$ o $4$ dígitos es suficiente) es con el método de integración por Monte Carlo (tal nombre por el uso de números aleatorios). La integración por el método de Monte Carlo está basada en la interpretación geométrica de las integrales: calcular la integral del problema inicial requiere calcular el **hipervolumen** de $\Omega$.
### Ejemplo
Supóngase que se desea aproximar el área de un círculo centrado en el origen de radio igual a $1$:
<img src="https://dl.dropboxusercontent.com/s/xmtcxw3wntfxuau/monte_carlo_1.png?dl=0" heigth="300" width="300">
entonces el área de este círculo es $\pi r^2 = \pi$.
Para lo anterior **encerramos** al círculo con un cuadrado de lado $2$:
<img src="https://dl.dropboxusercontent.com/s/igsn57vuahem0il/monte_carlo_2.png?dl=0" heigth="200" width="200">
Si tenemos $n$ puntos en el cuadrado:
<img src="https://dl.dropboxusercontent.com/s/a4krdneo0jaerqz/monte_carlo_3.png?dl=0" heigth="200" width="200">
y consideramos los $m$ puntos que están dentro del círculo:
<img src="https://dl.dropboxusercontent.com/s/pr4c5e57r4fawdt/monte_carlo_4.png?dl=0" heigth="200" width="200">
Entonces: $\frac{\text{Área del círculo}}{\text{Área del cuadrado}} \approx \frac{m}{n}$ y se tiene: Área del círculo $\approx$Área del cuadrado$\frac{m}{n}$ y si $n$ crece entonces la aproximación es mejor.
prueba numérica:
```
density_p=int(2.5*10**3)
x_p=np.random.uniform(-1,1,(density_p,2))
plt.scatter(x_p[:,0],x_p[:,1],marker='.',color='g')
density=1e-5
x=np.arange(-1,1,density)
y1=np.sqrt(1-x**2)
y2=-np.sqrt(1-x**2)
plt.plot(x,y1,'r',x,y2,'r')
plt.title('Integración por Monte Carlo')
plt.grid()
plt.show()
f=lambda x: np.sqrt(x[:,0]**2 + x[:,1]**2) #norm2 definition
ind=f(x_p)<=1
x_p_subset=x_p[ind]
plt.scatter(x_p_subset[:,0],x_p_subset[:,1],marker='.',color='r')
plt.title('Integración por Monte Carlo')
plt.grid()
plt.show()
```
Área del círculo es aproximadamente:
```
square_area = 4
print(square_area*len(x_p_subset)/len(x_p))
```
Si aumentamos el número de puntos...
```
density_p=int(10**4)
x_p=np.random.uniform(-1,1,(density_p,2))
ind=f(x_p)<=1
x_p_subset=x_p[ind]
print(square_area*len(x_p_subset)/len(x_p))
density_p=int(10**5)
x_p=np.random.uniform(-1,1,(density_p,2))
ind=f(x_p)<=1
x_p_subset=x_p[ind]
print(square_area*len(x_p_subset)/len(x_p))
```
```{admonition} Comentarios
* El método de Monte Carlo revisado en el ejemplo anterior nos indica que debemos encerrar a la región de integración $\Omega$. Por ejemplo para una región $\Omega$ más general:
<img src="https://dl.dropboxusercontent.com/s/ke6hngwue3ovpaz/monte_carlo_5.png?dl=0" heigth="300" width="300">
entonces la integración por el método de Monte Carlo será:
$$\displaystyle \int_\Omega f d\Omega \approx V \overline{f}$$
donde: $V$ es el hipervolumen de $\Omega_E$ que encierra a $\Omega$, esto es $\Omega \subseteq \Omega_E$, $\{x_1,\dots,x_n\}$ es un conjunto de puntos distribuidos uniformemente en $\Omega_E$ y $\overline{f}=\frac{1}{n}\displaystyle \sum_{i=1}^nf(x_i)$
* Consideramos $\overline{f}$ pues $\displaystyle \sum_{i=1}^nf(x_i)$ representa el valor de $m$ si pensamos a $f$ como una restricción que deben cumplir los $n$ puntos en el ejemplo de aproximación al área del círculo: Área del círculo $\approx$Área del cuadrado$\frac{m}{n}$ (en este caso Área del cuadrado es el hipervolumen $V$).
* Algunas características para regiones $\Omega_E$ que encierren a $\Omega$ es que:
* Sea sencillo generar números aleatorios uniformes.
* Sea sencillo obtener su hipervolumen.
```
### Ejemplos
**Aproximar las siguientes integrales:**
```
density_p=int(10**4)
```
* $\displaystyle \int_0^1\frac{4}{1+x^2}dx = \pi$
```
f = lambda x: 4/(1+x**2)
x_p = np.random.uniform(0,1,density_p)
obj = math.pi
a = 0
b = 1
vol = b-a
ex_1 = vol*np.mean(f(x_p))
print("error relativo: {:0.4e}".format(compute_error(obj, ex_1)))
```
* $\displaystyle \int_1^2 \frac{1}{x}dx = \log{2}$.
```
f = lambda x: 1/x
x_p = np.random.uniform(1,2,density_p)
obj = math.log(2)
a = 1
b = 2
vol = b-a
ex_2 = vol*np.mean(f(x_p))
print("error relativo: {:0.4e}".format(compute_error(obj, ex_2)))
```
* $\displaystyle \int_{-1}^1 \int_0^1x^2+y^2dxdy = \frac{4}{3}$.
```
f = lambda x,y:x**2+y**2
a1 = -1
b1 = 1
a2 = 0
b2 = 1
x_p = np.random.uniform(a1,b1,density_p)
y_p = np.random.uniform(a2,b2,density_p)
obj = 4/3
vol = (b1-a1)*(b2-a2)
ex_3 = vol*np.mean(f(x_p,y_p))
print("error relativo: {:0.4e}".format(compute_error(obj, ex_3)))
```
* $\displaystyle \int_0^{\frac{\pi}{2}} \int_0^{\frac{\pi}{2}}\cos(x)\sin(y)dxdy=1$.
```
f = lambda x,y:np.cos(x)*np.sin(y)
a1 = 0
b1 = math.pi/2
a2 = 0
b2 = math.pi/2
x_p = np.random.uniform(a1,b1,density_p)
y_p = np.random.uniform(a2,b2,density_p)
obj = 1
vol = (b1-a1)*(b2-a2)
ex_4 = vol*np.mean(f(x_p,y_p))
print("error relativo: {:0.4e}".format(compute_error(obj, ex_4)))
```
* $\displaystyle \int_0^1\int_{\frac{-1}{2}}^0\int_0^{\frac{1}{3}}(x+2y+3z)^2dxdydz =\frac{1}{12}$.
```
f = lambda x,y,z:(x+2*y+3*z)**2
a1 = 0
b1 = 1
a2 = -1/2
b2 = 0
a3 = 0
b3 = 1/3
x_p = np.random.uniform(a1,b1,density_p)
y_p = np.random.uniform(a2,b2,density_p)
z_p = np.random.uniform(a3,b3,density_p)
obj = 1/12
vol = (b1-a1)*(b2-a2)*(b3-a3)
ex_5 = vol*np.mean(f(x_p,y_p,z_p))
print("error relativo: {:0.4e}".format(compute_error(obj, ex_5)))
```
### ¿Cuál es el error en la aproximación por el método de integración por Monte Carlo?
Para obtener la expresión del error en esta aproximación supóngase que $x_1, x_2,\dots x_n$ son variables aleatorias independientes uniformemente distribuidas. Entonces:
$$\text{Err}(\overline{f})=\sqrt{\text{Var}(\overline{f})}=\sqrt{\text{Var}\left( \frac{1}{n} \displaystyle \sum_{i=1}^nf(x_i)\right)}=\dots=\sqrt{\frac{\text{Var}(f(x))}{n}}$$
con $x$ variable aleatoria uniformemente distribuida.
Un estimador de $\text{Var}(f(x))$ es: $\frac{1}{n}\displaystyle \sum_{i=1}^n(f(x_i)-\overline{f})^2=\overline{f^2}-\overline{f}^2$ por lo que $\hat{\text{Err}}(\overline{f}) = \sqrt{\frac{\overline{f^2}-\overline{f}^2}{n}}$.
Se tiene entonces que $\displaystyle \int_\Omega f d\Omega$ estará en el intervalo:
$$V(\overline{f} \pm \text{Err}(\overline{f})) \approx V(\overline{f} \pm \hat{\text{Err}}(\overline{f}))=V\overline{f} \pm V\sqrt{\frac{\overline{f^2}-\overline{f}^2}{n}}$$
```{admonition} Comentarios
* Los signos $\pm$ en el error de aproximación **no** representan una cota rigurosa, es una desviación estándar.
* A diferencia de la aproximación por las reglas por cuadratura tenemos una precisión con $n$ puntos independientemente de la dimensión $\mathcal{D}$.
* Si $\mathcal{D} \rightarrow \infty$ entonces $\hat{\text{Err}}(\overline{f}) = \mathcal{O}\left(\frac{1}{\sqrt{n}} \right)$ por lo que para ganar un decimal extra de precisión en la integración por el método de Monte Carlo se requiere incrementar el número de puntos por un factor de $10^2$.
```
```{admonition} Observación
:class: tip
Obsérvese que si $f$ es constante entonces $\hat{\text{Err}}(\overline{f})=0$. Esto implica que si $f$ es casi constante y $\Omega_E$ encierra muy bien a $\Omega$ entonces se tendrá una estimación muy precisa de $\displaystyle \int_\Omega f d\Omega$, por esto en la integración por el método de Monte Carlo se realizan cambios de variable de modo que transformen a $f$ en aproximadamente constante y que esto resulte además en regiones $\Omega_E$ que encierren a $\Omega$ casi de manera exacta (y que además sea sencillo generar números pseudo aleatorios en ellas!).
```
### Ejemplo
Para el ejemplo anterior $\displaystyle \int_0^1\frac{4}{1+x^2}dx = \pi$ se tiene:
```
f = lambda x: 4/(1+x**2)
x_p = np.random.uniform(0,1,density_p)
obj = math.pi
a = 0
b = 1
vol = b-a
f_bar = np.mean(f(x_p))
ex_6 = vol*f_bar
print("error relativo: {:0.4e}".format(compute_error(obj,ex_6 )))
error_std = math.sqrt(sum((f(x_p)-f_bar)**2)/density_p**2)
print(error_std)
```
intervalo:
```
print((ex_6-vol*error_std, ex_6+vol*error_std))
```
```{admonition} Ejercicios
:class: tip
Aproximar, reportar errores relativos e intervalo de estimación en una tabla:
* $\displaystyle \int_0^1\int_0^1\sqrt{x+y}dydx=\frac{2}{3}\left(\frac{2}{5}2^{5/2}-\frac{4}{5}\right)$.
* $\displaystyle \int_D \int \sqrt{x+y}dydx=8\frac{\sqrt{2}}{15}$ donde: $D=\{(x,y) \in \mathbb{R}^2 | 0 \leq x \leq 1, -x \leq y \leq x\}$.
* $\displaystyle \int_D \int \exp{(x^2+y^2)}dydx = \pi(e^9-1)$ donde $D=\{(x,y) \in \mathbb{R}^2 | x^2+y^2 \leq 9\}$.
* $\displaystyle \int_0^2 \int_{-1}^1 \int_0^1 (2x+3y+z)dzdydx = 10$.
```
### Aproximación de características de variables aleatorias
La integración por el método de Monte Carlo se utiliza para aproximar características de variables aleatorias continuas. Por ejemplo, si $x$ es variable aleatoria continua, entonces su media está dada por:
$$E_f[h(X)] = \displaystyle \int_{S_X}h(x)f(x)dx$$
donde: $f$ es función de densidad de $X$, $S_X$ es el soporte de $X$ y $h$ es una transformación. Entonces:
$$E_f[h(X)] \approx \frac{1}{n} \displaystyle \sum_{i=1}^nh(x_i)=\overline{h}_n$$
con $\{x_1,x_2,\dots,x_n\}$ muestra de $f$. Y por la ley de los grandes números se tiene:
$$\overline{h}_n \xrightarrow{n \rightarrow \infty} E_f[h(X)]$$
con **convergencia casi segura**. Aún más: si $E_f[h^2(X)] < \infty$ entonces el error de aproximación de $\overline{h}_n$ es del orden $\mathcal{O}\left(\frac{1}{\sqrt{n}} \right)$ y una estimación de este error es: $\hat{\text{Err}}(\overline{h}) = \sqrt{\frac{\overline{h^2}-\overline{h}^2}{n}}$. Por el teorema del límite central:
$$\frac{\overline{h}_n-E_f[h(X)]}{\hat{\text{Err}}(\overline{h})} \xrightarrow{n \rightarrow \infty} N(0,1)$$
con $N(0,1)$ una distribución Normal con $\mu=0,\sigma=1$ $\therefore$ si $n \rightarrow \infty$ un intervalo de confianza al $95\%$ para $E_f[h(X)]$ es: $\overline{h}_n \pm z_{.975} \hat{\text{Err}}(\overline{h})$.
Uno de los pasos complicados en el desarrollo anterior es obtener una muestra de $f$. Para el caso de variables continuas se puede utilizar el teorema de transformación inversa o integral de probabilidad. Otros métodos son los nombrados [métodos de monte Carlo con cadenas de Markov](https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo) o MCMC.
```{admonition} Ejercicios
:class: tip
1. Resuelve los ejercicios y preguntas de la nota.
**Referencias**
1. R. L. Burden, J. D. Faires, Numerical Analysis, Brooks/Cole Cengage Learning, 2005.
2. M. T. Heath, Scientific Computing. An Introductory Survey, McGraw-Hill, 2002.
|
github_jupyter
|
---
Nota generada a partir de la [liga1](https://www.dropbox.com/s/jfrxanjls8kndjp/Diferenciacion_e_Integracion.pdf?dl=0) y [liga2](https://www.dropbox.com/s/k3y7h9yn5d3yf3t/Integracion_por_Monte_Carlo.pdf?dl=0).
En lo siguiente consideramos que las funciones del integrando están en $\mathcal{C}^2$ en el conjunto de integración (ver {ref}`Definición de función, continuidad y derivada <FCD>` para definición de $\mathcal{C}^2$).
Las reglas o métodos por cuadratura nos ayudan a aproximar integrales con sumas de la forma:
$$\displaystyle \int_a^bf(x)dx \approx \displaystyle \sum_{i=0}^nw_if(x_i)$$
donde: $w_i$ es el **peso** para el **nodo** $x_i$, $f$ se llama integrando y $[a,b]$ intervalo de integración. Los valores $f(x_i)$ se asumen conocidos.
Una gran cantidad de reglas o métodos por cuadratura se obtienen con interpoladores polinomiales del integrando (por ejemplo usando la representación de Lagrange) o también con el teorema Taylor (ver nota {ref}`Polinomios de Taylor y diferenciación numérica <PTDN>` para éste teorema).
Se realizan aproximaciones numéricas por:
* Desconocimiento de la función en todo el intervalo $[a,b]$ y sólo se conoce en los nodos su valor.
* Inexistencia de antiderivada o primitiva del integrando. Por ejemplo:
$$\displaystyle \int_a^be^{-\frac{x^2}{2}}dx$$ con $a,b$ números reales.
Dependiendo de la ubicación de los nodos y pesos es el método de cuadratura que resulta:
* Newton-Cotes si los nodos y pesos son equidistantes como la regla del rectángulo, trapecio y Simpson (con el teorema de Taylor o interpolación es posible obtener tales fórmulas).
* Cuadratura Gaussiana si se desea obtener reglas o fórmulas que tengan la mayor exactitud posible (los nodos y pesos se eligen para cumplir con lo anterior). Ejemplos de este tipo de cuadratura se tiene la regla por cuadratura Gauss-Legendre en $[-1,1]$ (que usa [polinomos de Legendre](https://en.wikipedia.org/wiki/Legendre_polynomials)) o Gauss-Hermite (que usa [polinomios de Hermite](https://en.wikipedia.org/wiki/Hermite_polynomials)) para el caso de integrales en $[-\infty, \infty]$ con integrando $e^{-x^2}f(x)$.
<img src="https://dl.dropboxusercontent.com/s/baf7eauuwm347zk/integracion_numerica.png?dl=0" heigth="500" width="500">
En el dibujo: a),b) y c) se integra numéricamente por Newton-Cotes. d) es por cuadratura Gaussiana.
## Newton-Cotes
Si los nodos $x_i, i=0,1,\dots,$ cumplen $x_{i+1}-x_i=h, \forall i=0,1,\dots,$ con $h$ (espaciado) constante y se aproxima la función del integrando $f$ con un polinomio en $(x_i,f(x_i)) \forall i=0,1,\dots,$ entonces se tiene un método de integración numérica por Newton-Cotes (o reglas o fórmulas por Newton-Cotes).
## Ejemplo de una integral que no tiene antiderivada
En las siguientes reglas se considerará la función $f(x)=e^{-x^2}$ la cual tiene una forma:
El valor de la integral $\int_0^1e^{-x^2}dx$ es:
## Regla simple del rectángulo
Denotaremos a esta regla como $Rf$. En este caso se aproxima el integrando $f$ por un polinomio de grado **cero** con nodo en $x_1 = \frac{a+b}{2}$. Entonces:
$$\displaystyle \int_a^bf(x)dx \approx \int_a^bf(x_1)dx = (b-a)f(x_1)=(b-a)f\left( \frac{a+b}{2} \right ) = hf(x_1)$$
con $h=b-a, x_1=\frac{a+b}{2}$.
<img src="https://dl.dropboxusercontent.com/s/mzlmnvgnltqamz3/rectangulo_simple.png?dl=0" heigth="200" width="200">
### Ejemplo de implementación de regla simple de rectángulo: usando math
Utilizar la regla simple del rectángulo para aproximar la integral $\displaystyle \int_0^1e^{-x^2}dx$.
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un valor `obj`:**
**El error relativo es de $4.2\%$ aproximadamente.**
## Regla compuesta del rectángulo
En cada subintervalo construído como $[a_{i-1},a_i]$ con $i=1,\dots,n_{\text{sub}}$ se aplica la regla simple $Rf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx R_i(f) \forall i=1,\dots,n_{\text{sub}}.$$
De forma sencilla se puede ver que la regla compuesta del rectángulo $R_c(f)$ se escribe:
$$\begin{eqnarray}
R_c(f) &=& \displaystyle \sum_{i=1}^{n_\text{sub}}(a_i-a_{i-1})f\left( \frac{a_i+a_{i-1}}{2}\right) \nonumber\\
&=& \frac{h}{n_\text{sub}}\sum_{i=1}^{n_\text{sub}}f\left( \frac{a_i+a_{i-1}}{2}\right) \nonumber\\
&=&\frac{h}{n_\text{sub}}\sum_{i=1}^{n_\text{sub}}f\left( x_i\right) \nonumber
\end{eqnarray}
$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/j2wmiyoms7gxrzp/rectangulo_compuesto.png?dl=0" heigth="200" width="200">
### Ejemplo de implementación de regla compuesta de rectángulo: usando math
Utilizar la regla compuesta del rectángulo para aproximar la integral $\int_0^1e^{-x^2}dx$.
**1 nodo**
**2 nodos**
**$10^3$ nodos**
**Errores relativos:**
### Comentario: `pytest`
Otra forma de evaluar las aproximaciones realizadas es con módulos o paquetes de Python creados para este propósito en lugar de crear nuestras funciones como la de `compute_error`. Uno de estos es el paquete [pytest](https://docs.pytest.org/en/latest/) y la función [approx](https://docs.pytest.org/en/latest/reference.html#pytest-approx) de este paquete:
Y podemos usar un valor definido de tolerancia definido para hacer la prueba (por default se tiene una tolerancia de $10^{-6}$):
### Pregunta
**Será el método del rectángulo un método estable numéricamente bajo el redondeo?** Ver nota {ref}`Condición de un problema y estabilidad de un algoritmo <CPEA>` para definición de estabilidad numérica de un algoritmo.
Para responder la pregunta anterior aproximamos la integral con más nodos: $10^5$ nodos
Al menos para este ejemplo con $10^5$ nodos parece ser **numéricamente estable...**
## Regla compuesta del trapecio
En cada subintervalo se aplica la regla simple $Tf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx T_i(f) \forall i=1,\dots,n_\text{sub}.$$
Con $T_i(f) = \frac{(a_i-a_{i-1})}{2}(f(a_i)+f(a_{i-1}))$ para $i=1,\dots,n_\text{sub}$.
De forma sencilla se puede ver que la regla compuesta del trapecio $T_c(f)$ se escribe como:
$$T_c(f) = \displaystyle \frac{h}{2n_\text{sub}}\left[f(x_0)+f(x_{n_\text{sub}})+2\displaystyle\sum_{i=1}^{n_\text{sub}-1}f(x_i)\right]$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/4dl2btndrftdorp/trapecio_compuesto.png?dl=0" heigth="200" width="200">
### Ejemplo de implementación de regla compuesta del trapecio: usando numpy
Con la regla compuesta del trapecio se aproximará la integral $\int_0^1e^{-x^2}dx$. Se calculará el error relativo y graficará $n_\text{sub}$ vs Error relativo para $n_\text{sub}=1,10,100,1000,10000$.
Graficamos:
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un varios valores `obj`:**
Si no nos interesa el valor de los errores relativos y sólo la gráfica podemos utilizar la siguiente opción:
Ver [functools.partial](https://docs.python.org/2/library/functools.html#functools.partial) para documentación, [liga](https://stackoverflow.com/questions/15331726/how-does-functools-partial-do-what-it-does) para una explicación de `partial` y [liga2](https://stackoverflow.com/questions/10834960/how-to-do-multiple-arguments-to-map-function-where-one-remains-the-same-in-pytho), [liga3](https://stackoverflow.com/questions/47859209/how-to-map-over-a-function-with-multiple-arguments-in-python) para ejemplos de uso.
**Para el cálculo del error utilizamos {ref}`fórmulas para calcular errores absolutos y relativos <FORERRABSERRREL>`:**
$$\text{ErrRel(aprox)} = \frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$
**La siguiente función calcula un error relativo para un varios valores `obj`:**
**Otra forma con [scatter](https://matplotlib.org/3.3.0/api/_as_gen/matplotlib.pyplot.scatter.html):**
## Regla compuesta de Simpson
En cada subintervalo se aplica la regla simple $Sf$, esto es:
$$\displaystyle \int_{a_{i-1}}^{a_i}f(x)dx \approx S_i(f) \forall i=1,\dots,n_\text{sub}$$
con $S_i(f) = \frac{h}{6}\left[f(x_{2i})+f(x_{2i-2})+4f(x_{2i-1})\right]$ para el subintervalo $[a_{i-1},a_i]$ con $i=1,\dots,n_\text{sub}$.
De forma sencilla se puede ver que la regla compuesta de Simpson compuesta $S_c(f)$ se escribe como:
$$S_c(f) = \displaystyle \frac{h}{3(2n_\text{sub})} \left [ f(x_0) + f(x_{2n_\text{sub}}) + 2 \sum_{i=1}^{n_\text{sub}-1}f(x_{2i}) + 4 \sum_{i=1}^{n_\text{sub}}f(x_{2i-1})\right ]$$
con $h=b-a$ y $n_\text{sub}$ número de subintervalos.
<img src="https://dl.dropboxusercontent.com/s/8rx32vdtulpdflm/Simpson_compuesto.png?dl=0" heigth="200" width="200">
## Expresiones de los errores para las reglas compuestas del rectángulo, trapecio y Simpson
La forma de los errores de las reglas del rectángulo, trapecio y Simpson se pueden obtener con interpolación o con el teorema de Taylor. Ver [Diferenciación e Integración](https://www.dropbox.com/s/jfrxanjls8kndjp/Diferenciacion_e_Integracion.pdf?dl=0) para detalles y {ref}`Polinomios de Taylor y diferenciación numérica <PTDN>` para el teorema. Suponiendo que $f$ cumple con condiciones sobre sus derivadas, tales errores son:
$$\text{Err}Rc(f) = \frac{b-a}{6}f^{(2)}(\xi_r)\hat{h}^2, \xi_r \in [a,b]$$
$$\text{Err}Tc(f)=-\frac{b-a}{12}f^{(2)}(\xi_t)\hat{h}^2, \xi_t \in [a,b]$$
$$\text{Err}Sc(f)=-\frac{b-a}{180}f^{(4)}(\xi_S)\hat{h}^4, \xi_S \in [a,b].$$
(IMC)=
## Integración por el método de Monte Carlo
Los métodos de integración numérica por Monte Carlo son similares a los métodos por cuadratura en el sentido que se eligen puntos en los que se evaluará el integrando para sumar sus valores. La diferencia esencial con los métodos por cuadratura es que en el método de integración por Monte Carlo los puntos son **seleccionados de una forma *aleatoria*** (de hecho es pseudo-aleatoria pues se generan con un programa de computadora) en lugar de generarse con una fórmula.
### Problema
En esta sección consideramos $n$ número de nodos.
Aproximar numéricamente la integral $\displaystyle \int_{\Omega}f(x)dx$ para $x \in \mathbb{R}^\mathcal{D}, \Omega \subseteq \mathbb{R}^\mathcal{D}, f: \mathbb{R}^\mathcal{D} \rightarrow \mathbb{R}$ función tal que la integral esté bien definida en $\Omega$.
Por ejemplo para $\mathcal{D}=2:$
<img src="https://dl.dropboxusercontent.com/s/xktwjmgbf8aiekw/integral_2_dimensiones.png?dl=0" heigth="500" width="500">
Para resolver el problema anterior con $\Omega$ un rectángulo, podemos utilizar las reglas por cuadratura por Newton-Cotes o cuadratura Gaussiana en una dimensión manteniendo fija la otra dimensión. Sin embargo considérese la siguiente situación:
La regla del rectángulo (o del punto medio) y del trapecio tienen un error de orden $\mathcal{O}(h^2)$ independientemente de si se está aproximando integrales de una o más dimensiones. Supóngase que se utilizan $n$ nodos para tener un valor de espaciado igual a $\hat{h}$ en una dimensión, entonces para $\mathcal{D}$ dimensiones se requerirían $N=n^\mathcal{D}$ evaluaciones del integrando, o bien, si se tiene un valor de $N$ igual a $10, 000$ y $\mathcal{D}=4$ dimensiones el error sería del orden $\mathcal{O}(N^{-2/\mathcal{D}})$ lo que implicaría un valor de $\hat{h}=.1$ para aproximadamente sólo **dos dígitos** correctos en la aproximación (para el enunciado anterior recuérdese que $\hat{h}$ es proporcional a $n^{-1}$ y $n$ = $N^{1/\mathcal{D}}$). Este esfuerzo enorme de evaluar $N$ veces el integrando para una exactitud pequeña se debe al problema de generar puntos para *llenar* un espacio $\mathcal{D}$-dimensional y se conoce con el nombre de la maldición de la dimensionalidad, [***the curse of dimensionality***](https://en.wikipedia.org/wiki/Curse_of_dimensionality).
Una opción para resolver la situación anterior si no se desea una precisión alta (por ejemplo con una precisión de $10^{-4}$ o $4$ dígitos es suficiente) es con el método de integración por Monte Carlo (tal nombre por el uso de números aleatorios). La integración por el método de Monte Carlo está basada en la interpretación geométrica de las integrales: calcular la integral del problema inicial requiere calcular el **hipervolumen** de $\Omega$.
### Ejemplo
Supóngase que se desea aproximar el área de un círculo centrado en el origen de radio igual a $1$:
<img src="https://dl.dropboxusercontent.com/s/xmtcxw3wntfxuau/monte_carlo_1.png?dl=0" heigth="300" width="300">
entonces el área de este círculo es $\pi r^2 = \pi$.
Para lo anterior **encerramos** al círculo con un cuadrado de lado $2$:
<img src="https://dl.dropboxusercontent.com/s/igsn57vuahem0il/monte_carlo_2.png?dl=0" heigth="200" width="200">
Si tenemos $n$ puntos en el cuadrado:
<img src="https://dl.dropboxusercontent.com/s/a4krdneo0jaerqz/monte_carlo_3.png?dl=0" heigth="200" width="200">
y consideramos los $m$ puntos que están dentro del círculo:
<img src="https://dl.dropboxusercontent.com/s/pr4c5e57r4fawdt/monte_carlo_4.png?dl=0" heigth="200" width="200">
Entonces: $\frac{\text{Área del círculo}}{\text{Área del cuadrado}} \approx \frac{m}{n}$ y se tiene: Área del círculo $\approx$Área del cuadrado$\frac{m}{n}$ y si $n$ crece entonces la aproximación es mejor.
prueba numérica:
Área del círculo es aproximadamente:
Si aumentamos el número de puntos...
### Ejemplos
**Aproximar las siguientes integrales:**
* $\displaystyle \int_0^1\frac{4}{1+x^2}dx = \pi$
* $\displaystyle \int_1^2 \frac{1}{x}dx = \log{2}$.
* $\displaystyle \int_{-1}^1 \int_0^1x^2+y^2dxdy = \frac{4}{3}$.
* $\displaystyle \int_0^{\frac{\pi}{2}} \int_0^{\frac{\pi}{2}}\cos(x)\sin(y)dxdy=1$.
* $\displaystyle \int_0^1\int_{\frac{-1}{2}}^0\int_0^{\frac{1}{3}}(x+2y+3z)^2dxdydz =\frac{1}{12}$.
### ¿Cuál es el error en la aproximación por el método de integración por Monte Carlo?
Para obtener la expresión del error en esta aproximación supóngase que $x_1, x_2,\dots x_n$ son variables aleatorias independientes uniformemente distribuidas. Entonces:
$$\text{Err}(\overline{f})=\sqrt{\text{Var}(\overline{f})}=\sqrt{\text{Var}\left( \frac{1}{n} \displaystyle \sum_{i=1}^nf(x_i)\right)}=\dots=\sqrt{\frac{\text{Var}(f(x))}{n}}$$
con $x$ variable aleatoria uniformemente distribuida.
Un estimador de $\text{Var}(f(x))$ es: $\frac{1}{n}\displaystyle \sum_{i=1}^n(f(x_i)-\overline{f})^2=\overline{f^2}-\overline{f}^2$ por lo que $\hat{\text{Err}}(\overline{f}) = \sqrt{\frac{\overline{f^2}-\overline{f}^2}{n}}$.
Se tiene entonces que $\displaystyle \int_\Omega f d\Omega$ estará en el intervalo:
$$V(\overline{f} \pm \text{Err}(\overline{f})) \approx V(\overline{f} \pm \hat{\text{Err}}(\overline{f}))=V\overline{f} \pm V\sqrt{\frac{\overline{f^2}-\overline{f}^2}{n}}$$
### Ejemplo
Para el ejemplo anterior $\displaystyle \int_0^1\frac{4}{1+x^2}dx = \pi$ se tiene:
intervalo:
### Aproximación de características de variables aleatorias
La integración por el método de Monte Carlo se utiliza para aproximar características de variables aleatorias continuas. Por ejemplo, si $x$ es variable aleatoria continua, entonces su media está dada por:
$$E_f[h(X)] = \displaystyle \int_{S_X}h(x)f(x)dx$$
donde: $f$ es función de densidad de $X$, $S_X$ es el soporte de $X$ y $h$ es una transformación. Entonces:
$$E_f[h(X)] \approx \frac{1}{n} \displaystyle \sum_{i=1}^nh(x_i)=\overline{h}_n$$
con $\{x_1,x_2,\dots,x_n\}$ muestra de $f$. Y por la ley de los grandes números se tiene:
$$\overline{h}_n \xrightarrow{n \rightarrow \infty} E_f[h(X)]$$
con **convergencia casi segura**. Aún más: si $E_f[h^2(X)] < \infty$ entonces el error de aproximación de $\overline{h}_n$ es del orden $\mathcal{O}\left(\frac{1}{\sqrt{n}} \right)$ y una estimación de este error es: $\hat{\text{Err}}(\overline{h}) = \sqrt{\frac{\overline{h^2}-\overline{h}^2}{n}}$. Por el teorema del límite central:
$$\frac{\overline{h}_n-E_f[h(X)]}{\hat{\text{Err}}(\overline{h})} \xrightarrow{n \rightarrow \infty} N(0,1)$$
con $N(0,1)$ una distribución Normal con $\mu=0,\sigma=1$ $\therefore$ si $n \rightarrow \infty$ un intervalo de confianza al $95\%$ para $E_f[h(X)]$ es: $\overline{h}_n \pm z_{.975} \hat{\text{Err}}(\overline{h})$.
Uno de los pasos complicados en el desarrollo anterior es obtener una muestra de $f$. Para el caso de variables continuas se puede utilizar el teorema de transformación inversa o integral de probabilidad. Otros métodos son los nombrados [métodos de monte Carlo con cadenas de Markov](https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo) o MCMC.
| 0.742795 | 0.898009 |
# Use Case 1: Kögur
In this example we will subsample a dataset stored on SciServer using methods resembling field-work procedures.
Specifically, we will estimate volume fluxes through the [Kögur section](http://kogur.whoi.edu) using (i) mooring arrays, and (ii) ship surveys.
```
# Import oceanspy
import oceanspy as ospy
# Import additional packages used in this notebook
import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
```
The following cell starts a dask client (see the [Dask Client section in the tutorial](Tutorial.ipynb#Dask-Client)).
```
# Start client
from dask.distributed import Client
client = Client()
client
```
This command opens one of the datasets avaiable on SciServer.
```
# Open dataset stored on SciServer.
od = ospy.open_oceandataset.from_catalog('EGshelfIIseas2km_ASR_full')
```
The following cell changes the default parameters used by the plotting functions.
```
import matplotlib as mpl
%matplotlib inline
mpl.rcParams['figure.figsize'] = [10.0, 5.0]
```
## Mooring array
The following diagram shows the instrumentation deployed by observational oceanographers to monitor the Kögur section (source: http://kogur.whoi.edu/img/array_boxes.png).
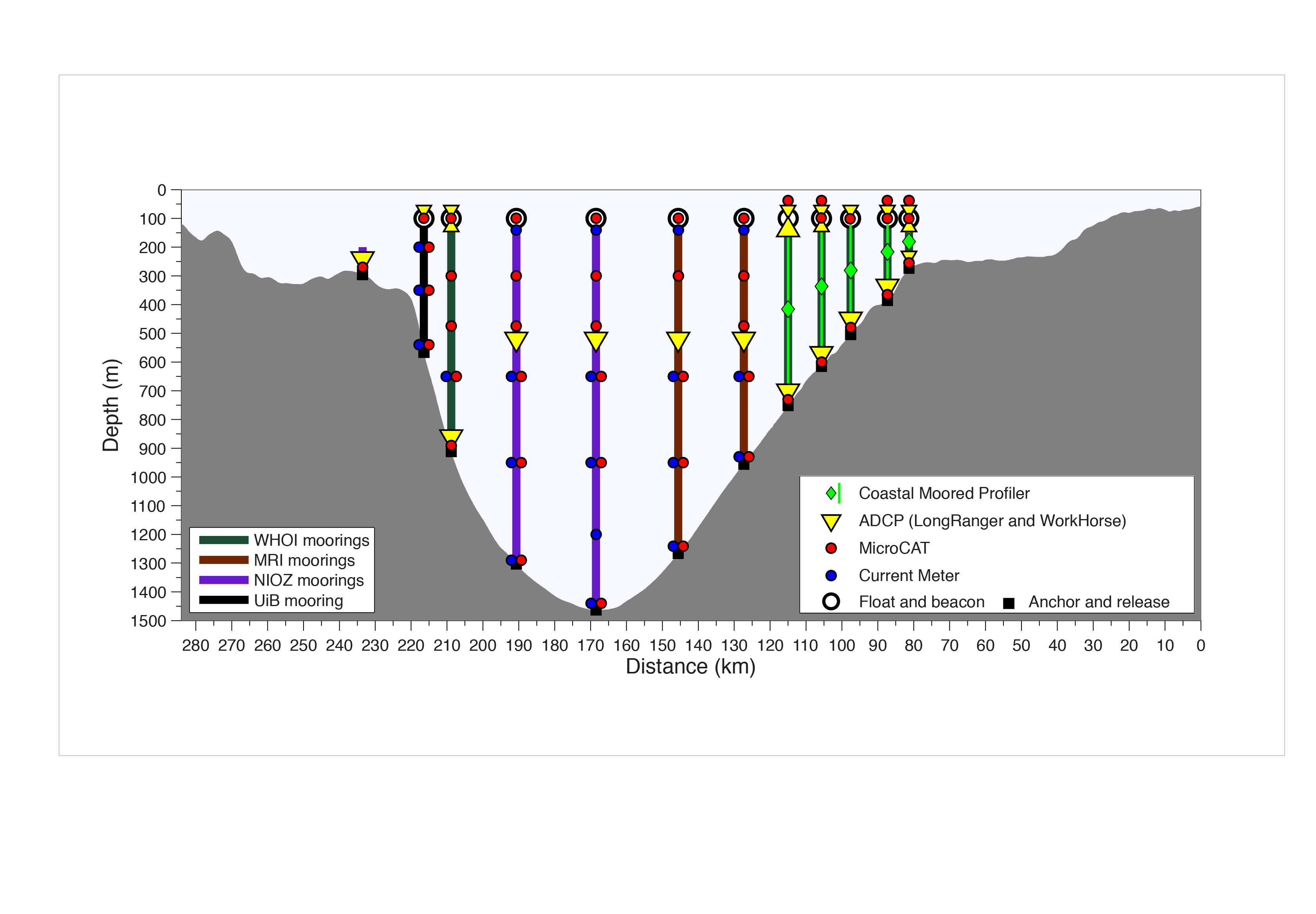
The analogous OceanSpy function (`compute.mooring_array`) extracts vertical sections from the model using two criteria:
* Vertical sections follow great circle paths (unless cartesian coordinates are used).
* Vertical sections follow the grid of the model (extracted moorings are adjacent to each other, and the native grid of the model is preserved).
```
# Kögur information
lats_Kogur = [ 68.68, 67.52, 66.49]
lons_Kogur = [-26.28, -23.77, -22.99]
depth_Kogur = [0, -1750]
# Select time range:
# September 2007, extracting one snapshot every 3 days
timeRange = ['2007-09-01', '2007-09-30T18']
timeFreq = '3D'
# Extract mooring array and fields used by this notebook
od_moor = od.subsample.mooring_array(Xmoor=lons_Kogur,
Ymoor=lats_Kogur,
ZRange=depth_Kogur,
timeRange=timeRange,
timeFreq=timeFreq,
varList=['Temp', 'S',
'U', 'V',
'dyG', 'dxG',
'drF',
'HFacS', 'HFacW'])
```
The following cell shows how to store the mooring array in a NetCDF file. In this use case, we only use this feature to create a checkpoint. Another option could be to move the file to other servers or computers. If the NetCDF is re-opened using OceanSpy (as shown below), all OceanSpy functions are enabled and can be applied to the `oceandataset`.
```
# Store the new mooring dataset
filename = 'Kogur_mooring.nc'
od_moor.to_netcdf(filename)
# The NetCDF can now be re-opened with oceanspy at any time,
# and on any computer
od_moor = ospy.open_oceandataset.from_netcdf(filename)
# Print size
print('Size:')
print(' * Original dataset: {0:.1f} TB'.format(od.dataset.nbytes*1.E-12))
print(' * Mooring dataset: {0:.1f} MB'.format(od_moor.dataset.nbytes*1.E-6))
print()
```
The following map shows the location of the moorings forming the Kögur section.
```
# Plot map and mooring locations
fig = plt.figure(figsize=(5, 5))
ax = od.plot.horizontal_section(varName='Depth')
XC = od_moor.dataset['XC'].squeeze()
YC = od_moor.dataset['YC'].squeeze()
line = ax.plot(XC, YC, 'r.',
transform=ccrs.PlateCarree())
```
The following figure shows the grid structure of the mooring array. The original grid structure of the model is unchaged, and each mooring is associated with one C-gridpoint (e.g., hydrography), two U-gridpoint and two V-gridpoint (e.g., velocities), and four G-gripoint (e.g., vertical component of relative vorticity).
```
# Print grid
print(od_moor.grid)
print()
print(od_moor.dataset.coords)
print()
# Plot 10 moorings and their grid points
fig, ax = plt.subplots(1, 1)
n_moorings = 10
# Markers:
for _, (pos, mark, col) in enumerate(zip(['C', 'G', 'U', 'V'],
['o', 'x', '>', '^'],
['k', 'm', 'r', 'b'])):
X = od_moor.dataset['X'+pos].values[:n_moorings].flatten()
Y = od_moor.dataset['Y'+pos].values[:n_moorings].flatten()
ax.plot(X, Y, col+mark, markersize=20, label=pos)
if pos == 'C':
for i in range(n_moorings):
ax.annotate(str(i), (X[i], Y[i]),
size=15, weight="bold", color='w', ha='center', va='center')
ax.set_xticks(X, minor=False)
ax.set_yticks(Y, minor=False)
elif pos == 'G':
ax.set_xticks(X, minor=True)
ax.set_yticks(Y, minor=True)
ax.legend(prop={'size': 20})
ax.grid(which='major', linestyle='-')
ax.grid(which='minor', linestyle='--')
```
## Plots
### Vertical sections
We can now use OceanSpy to plot vertical sections. Here we plot isopycnal contours on top of the mean meridional velocities (`V`). Although there are two V-points associated with each mooring, the plot can be displayed because OceanSpy automatically performs a linear interpolation using the grid object.
```
# Plot time mean
ax = od_moor.plot.vertical_section(varName='V', contourName='Sigma0', meanAxes='time',
robust=True, cmap='coolwarm')
```
It is possible to visualize all the snapshots by omitting the `meanAxes='time'` argument:
```
# Plot all snapshots
ax = od_moor.plot.vertical_section(varName='V', contourName='Sigma0',
robust=True, cmap='coolwarm', col_wrap=5)
# Alternatively, use the following command to produce a movie:
# anim = od_moor.animate.vertical_section(varName='V', contourName='Sigma0', ...)
```
### TS-diagrams
Here we use OceanSpy to plot a Temperature-Salinity diagram.
```
ax = od_moor.plot.TS_diagram()
# Alternatively, use the following command
# to explore how the water masses change with time:
# anim = od_moor.animate.TS_diagram()
```
We can also color each TS point using any field in the original dataset, or any field computed by OceanSpy. Fields that are not on the same grid of temperature and salinity are automatically regridded by OceanSpy.
```
ax = od_moor.plot.TS_diagram(colorName='V',
meanAxes='time',
cmap_kwargs={'robust': True,
'cmap': 'coolwarm'})
```
## Volume flux
OceanSpy can be used to compute accurate volume fluxes through vertical sections.
The function `compute.mooring_volume_transport` calculates the inflow/outflow through all grid faces of the vertical section.
This function creates a new dimension named `path` because transports can be computed using two paths (see the plot below).
```
# Show volume flux variables
ds_Vflux = ospy.compute.mooring_volume_transport(od_moor)
od_moor = od_moor.merge_into_oceandataset(ds_Vflux)
print(ds_Vflux)
# Plot 10 moorings and volume flux directions.
fig, ax = plt.subplots(1, 1)
ms = 10
s = 100
ds = od_moor.dataset
_ = ax.step(ds['XU'].isel(Xp1=0).squeeze().values,
ds['YV'].isel(Yp1=0).squeeze().values, 'C0.-', ms=ms, label='path0')
_ = ax.step(ds['XU'].isel(Xp1=1).squeeze().values,
ds['YV'].isel(Yp1=1).squeeze().values, 'C1.-', ms=ms, label='path1')
_ = ax.plot(ds['XC'].squeeze(),
ds['YC'].squeeze(), 'k.', ms=ms, label='mooring')
_ = ax.scatter(ds['X_Vtransport'].where(ds['dir_Vtransport'] == 1),
ds['Y_Vtransport'].where(ds['dir_Vtransport'] == 1),
s=s, c='k', marker='^', label='meridional direction')
_ = ax.scatter(ds['X_Utransport'].where(ds['dir_Utransport'] == 1),
ds['Y_Utransport'].where(ds['dir_Utransport'] == 1),
s=s, c='k', marker='>', label='zonal direction')
_ = ax.scatter(ds['X_Vtransport'].where(ds['dir_Vtransport'] == -1),
ds['Y_Vtransport'].where(ds['dir_Vtransport'] == -1),
s=s, c='k', marker='v', label='meridional direction')
_ = ax.scatter(ds['X_Utransport'].where(ds['dir_Utransport'] == -1),
ds['Y_Utransport'].where(ds['dir_Utransport'] == -1),
s=s, c='k', marker='<', label='zonal direction')
# Only show a few moorings
m_start = 50
m_end = 70
xlim = ax.set_xlim(sorted([ds['XC'].isel(mooring=m_start).values,
ds['XC'].isel(mooring=m_end).values]))
ylim = ax.set_ylim(sorted([ds['YC'].isel(mooring=m_start).values,
ds['YC'].isel(mooring=m_end).values]))
ax.legend()
```
Here we compute and plot the cumulative mean transport through the Kögur mooring array.
```
# Compute cumulative transport
tran_moor = od_moor.dataset['transport']
cum_tran_moor = tran_moor.sum('Z').mean('time').cumsum('mooring')
cum_tran_moor.attrs = tran_moor.attrs
fig, ax = plt.subplots(1, 1)
lines = cum_tran_moor.squeeze().plot.line(hue='path', linewidth=3)
tot_mean_tran_moor = cum_tran_moor.isel(mooring=-1).mean('path')
title = ax.set_title('TOTAL MEAN TRANSPORT: {0:.1f} Sv'
''.format(tot_mean_tran_moor.values))
```
Here we compute the transport of the overflow, defined as water with density greater than 27.8 kg m$^{-3}$.
```
# Mask transport using density
od_moor = od_moor.compute.potential_density_anomaly()
density = od_moor.dataset['Sigma0'].squeeze()
oflow_moor = tran_moor.where(density>27.8)
# Compute cumulative transport as before
cum_oflow_moor = oflow_moor.sum('Z').mean('time').cumsum('mooring')
cum_oflow_moor.attrs = oflow_moor.attrs
fig, ax = plt.subplots(1, 1)
lines = cum_oflow_moor.squeeze().plot.line(hue='path', linewidth=3)
tot_mean_oflow_moor = cum_oflow_moor.isel(mooring=-1).mean('path')
title = ax.set_title('TOTAL MEAN OVERFLOW TRANSPORT: {0:.1f} Sv'
''.format(tot_mean_oflow_moor.values))
```
## Ship survey
The following picture shows the NATO Research Vessel Alliance, a ship designed to carry out research at sea (source: http://www.marina.difesa.it/noi-siamo-la-marina/mezzi/forze-navali/PublishingImages/_alliance.jpg).

The OceanSpy function analogous to a ship survey (`compute.survey_stations`) extracts vertical sections from the model using two criteria:
* Vertical sections follow great circle paths (unless cartesian coordinates are used) with constant horizontal spacing between stations.
* Interpolation is performed and all fields are returned at the same locations (the native grid of the model is NOT preserved).
```
# Spacing between interpolated stations
delta_Kogur = 2 # km
# Extract survey stations
# Reduce dataset to speed things up:
od_surv = od.subsample.survey_stations(Xsurv=lons_Kogur,
Ysurv=lats_Kogur,
delta=delta_Kogur,
ZRange=depth_Kogur,
timeRange=timeRange,
timeFreq=timeFreq,
varList=['Temp', 'S',
'U', 'V',
'drC', 'drF',
'HFacC', 'HFacW', 'HFacS'])
# Plot map and survey stations
fig = plt.figure(figsize=(5, 5))
ax = od.plot.horizontal_section(varName='Depth')
XC = od_surv.dataset['XC'].squeeze()
YC = od_surv.dataset['YC'].squeeze()
line = ax.plot(XC, YC, 'r.',
transform=ccrs.PlateCarree())
```
## Orthogonal velocities
We can use OceanSpy to compute the velocity components orthogonal and tangential to the Kögur section.
```
od_surv = od_surv.compute.survey_aligned_velocities()
```
The following animation shows isopycnal contours on top of the velocity component orthogonal to the Kögur section.
```
anim = od_surv.animate.vertical_section(varName='ort_Vel', contourName='Sigma0',
robust=True, cmap='coolwarm',
display=False)
# The following code is necessary to display the animation in the documentation.
# When the notebook is executed, remove the code below and set
# display=True in the command above to show the animation.
import matplotlib.pyplot as plt
dirName = '_static'
import os
try:
os.mkdir(dirName)
except FileExistsError:
pass
anim.save('{}/Kogur.mp4'.format(dirName))
plt.close()
!ffmpeg -loglevel panic -y -i _static/Kogur.mp4 -filter_complex "[0:v] fps=12,scale=480:-1,split [a][b];[a] palettegen [p];[b][p] paletteuse" _static/Kogur.gif
!rm -f _static/Kogur.mp4
```

Finally, we can infer the volume flux by integrating the orthogonal velocities.
```
# Integrate along Z
od_surv = od_surv.compute.integral(varNameList='ort_Vel',
axesList=['Z'])
# Compute transport using weights
od_surv = od_surv.compute.weighted_mean(varNameList='I(ort_Vel)dZ',
axesList=['station'])
transport_surv = (od_surv.dataset['I(ort_Vel)dZ'] *
od_surv.dataset['weight_I(ort_Vel)dZ'])
# Convert in Sverdrup
transport_surv = transport_surv * 1.E-6
# Compute cumulative transport
cum_transport_surv = transport_surv.cumsum('station').rename('Horizontal volume transport')
cum_transport_surv.attrs['units'] = 'Sv'
```
Here we plot the cumulative transport for each snapshot.
```
# Plot
fig, ax = plt.subplots(figsize=(13,5))
lines = cum_transport_surv.squeeze().plot.line(hue='time', linewidth=3)
tot_mean_transport = cum_transport_surv.isel(station=-1).mean('time')
title = ax.set_title('TOTAL MEAN TRANSPORT: {0:.1f} Sv'.format(tot_mean_transport.values))
```
|
github_jupyter
|
# Import oceanspy
import oceanspy as ospy
# Import additional packages used in this notebook
import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
# Start client
from dask.distributed import Client
client = Client()
client
# Open dataset stored on SciServer.
od = ospy.open_oceandataset.from_catalog('EGshelfIIseas2km_ASR_full')
import matplotlib as mpl
%matplotlib inline
mpl.rcParams['figure.figsize'] = [10.0, 5.0]
# Kögur information
lats_Kogur = [ 68.68, 67.52, 66.49]
lons_Kogur = [-26.28, -23.77, -22.99]
depth_Kogur = [0, -1750]
# Select time range:
# September 2007, extracting one snapshot every 3 days
timeRange = ['2007-09-01', '2007-09-30T18']
timeFreq = '3D'
# Extract mooring array and fields used by this notebook
od_moor = od.subsample.mooring_array(Xmoor=lons_Kogur,
Ymoor=lats_Kogur,
ZRange=depth_Kogur,
timeRange=timeRange,
timeFreq=timeFreq,
varList=['Temp', 'S',
'U', 'V',
'dyG', 'dxG',
'drF',
'HFacS', 'HFacW'])
# Store the new mooring dataset
filename = 'Kogur_mooring.nc'
od_moor.to_netcdf(filename)
# The NetCDF can now be re-opened with oceanspy at any time,
# and on any computer
od_moor = ospy.open_oceandataset.from_netcdf(filename)
# Print size
print('Size:')
print(' * Original dataset: {0:.1f} TB'.format(od.dataset.nbytes*1.E-12))
print(' * Mooring dataset: {0:.1f} MB'.format(od_moor.dataset.nbytes*1.E-6))
print()
# Plot map and mooring locations
fig = plt.figure(figsize=(5, 5))
ax = od.plot.horizontal_section(varName='Depth')
XC = od_moor.dataset['XC'].squeeze()
YC = od_moor.dataset['YC'].squeeze()
line = ax.plot(XC, YC, 'r.',
transform=ccrs.PlateCarree())
# Print grid
print(od_moor.grid)
print()
print(od_moor.dataset.coords)
print()
# Plot 10 moorings and their grid points
fig, ax = plt.subplots(1, 1)
n_moorings = 10
# Markers:
for _, (pos, mark, col) in enumerate(zip(['C', 'G', 'U', 'V'],
['o', 'x', '>', '^'],
['k', 'm', 'r', 'b'])):
X = od_moor.dataset['X'+pos].values[:n_moorings].flatten()
Y = od_moor.dataset['Y'+pos].values[:n_moorings].flatten()
ax.plot(X, Y, col+mark, markersize=20, label=pos)
if pos == 'C':
for i in range(n_moorings):
ax.annotate(str(i), (X[i], Y[i]),
size=15, weight="bold", color='w', ha='center', va='center')
ax.set_xticks(X, minor=False)
ax.set_yticks(Y, minor=False)
elif pos == 'G':
ax.set_xticks(X, minor=True)
ax.set_yticks(Y, minor=True)
ax.legend(prop={'size': 20})
ax.grid(which='major', linestyle='-')
ax.grid(which='minor', linestyle='--')
# Plot time mean
ax = od_moor.plot.vertical_section(varName='V', contourName='Sigma0', meanAxes='time',
robust=True, cmap='coolwarm')
# Plot all snapshots
ax = od_moor.plot.vertical_section(varName='V', contourName='Sigma0',
robust=True, cmap='coolwarm', col_wrap=5)
# Alternatively, use the following command to produce a movie:
# anim = od_moor.animate.vertical_section(varName='V', contourName='Sigma0', ...)
ax = od_moor.plot.TS_diagram()
# Alternatively, use the following command
# to explore how the water masses change with time:
# anim = od_moor.animate.TS_diagram()
ax = od_moor.plot.TS_diagram(colorName='V',
meanAxes='time',
cmap_kwargs={'robust': True,
'cmap': 'coolwarm'})
# Show volume flux variables
ds_Vflux = ospy.compute.mooring_volume_transport(od_moor)
od_moor = od_moor.merge_into_oceandataset(ds_Vflux)
print(ds_Vflux)
# Plot 10 moorings and volume flux directions.
fig, ax = plt.subplots(1, 1)
ms = 10
s = 100
ds = od_moor.dataset
_ = ax.step(ds['XU'].isel(Xp1=0).squeeze().values,
ds['YV'].isel(Yp1=0).squeeze().values, 'C0.-', ms=ms, label='path0')
_ = ax.step(ds['XU'].isel(Xp1=1).squeeze().values,
ds['YV'].isel(Yp1=1).squeeze().values, 'C1.-', ms=ms, label='path1')
_ = ax.plot(ds['XC'].squeeze(),
ds['YC'].squeeze(), 'k.', ms=ms, label='mooring')
_ = ax.scatter(ds['X_Vtransport'].where(ds['dir_Vtransport'] == 1),
ds['Y_Vtransport'].where(ds['dir_Vtransport'] == 1),
s=s, c='k', marker='^', label='meridional direction')
_ = ax.scatter(ds['X_Utransport'].where(ds['dir_Utransport'] == 1),
ds['Y_Utransport'].where(ds['dir_Utransport'] == 1),
s=s, c='k', marker='>', label='zonal direction')
_ = ax.scatter(ds['X_Vtransport'].where(ds['dir_Vtransport'] == -1),
ds['Y_Vtransport'].where(ds['dir_Vtransport'] == -1),
s=s, c='k', marker='v', label='meridional direction')
_ = ax.scatter(ds['X_Utransport'].where(ds['dir_Utransport'] == -1),
ds['Y_Utransport'].where(ds['dir_Utransport'] == -1),
s=s, c='k', marker='<', label='zonal direction')
# Only show a few moorings
m_start = 50
m_end = 70
xlim = ax.set_xlim(sorted([ds['XC'].isel(mooring=m_start).values,
ds['XC'].isel(mooring=m_end).values]))
ylim = ax.set_ylim(sorted([ds['YC'].isel(mooring=m_start).values,
ds['YC'].isel(mooring=m_end).values]))
ax.legend()
# Compute cumulative transport
tran_moor = od_moor.dataset['transport']
cum_tran_moor = tran_moor.sum('Z').mean('time').cumsum('mooring')
cum_tran_moor.attrs = tran_moor.attrs
fig, ax = plt.subplots(1, 1)
lines = cum_tran_moor.squeeze().plot.line(hue='path', linewidth=3)
tot_mean_tran_moor = cum_tran_moor.isel(mooring=-1).mean('path')
title = ax.set_title('TOTAL MEAN TRANSPORT: {0:.1f} Sv'
''.format(tot_mean_tran_moor.values))
# Mask transport using density
od_moor = od_moor.compute.potential_density_anomaly()
density = od_moor.dataset['Sigma0'].squeeze()
oflow_moor = tran_moor.where(density>27.8)
# Compute cumulative transport as before
cum_oflow_moor = oflow_moor.sum('Z').mean('time').cumsum('mooring')
cum_oflow_moor.attrs = oflow_moor.attrs
fig, ax = plt.subplots(1, 1)
lines = cum_oflow_moor.squeeze().plot.line(hue='path', linewidth=3)
tot_mean_oflow_moor = cum_oflow_moor.isel(mooring=-1).mean('path')
title = ax.set_title('TOTAL MEAN OVERFLOW TRANSPORT: {0:.1f} Sv'
''.format(tot_mean_oflow_moor.values))
# Spacing between interpolated stations
delta_Kogur = 2 # km
# Extract survey stations
# Reduce dataset to speed things up:
od_surv = od.subsample.survey_stations(Xsurv=lons_Kogur,
Ysurv=lats_Kogur,
delta=delta_Kogur,
ZRange=depth_Kogur,
timeRange=timeRange,
timeFreq=timeFreq,
varList=['Temp', 'S',
'U', 'V',
'drC', 'drF',
'HFacC', 'HFacW', 'HFacS'])
# Plot map and survey stations
fig = plt.figure(figsize=(5, 5))
ax = od.plot.horizontal_section(varName='Depth')
XC = od_surv.dataset['XC'].squeeze()
YC = od_surv.dataset['YC'].squeeze()
line = ax.plot(XC, YC, 'r.',
transform=ccrs.PlateCarree())
od_surv = od_surv.compute.survey_aligned_velocities()
anim = od_surv.animate.vertical_section(varName='ort_Vel', contourName='Sigma0',
robust=True, cmap='coolwarm',
display=False)
# The following code is necessary to display the animation in the documentation.
# When the notebook is executed, remove the code below and set
# display=True in the command above to show the animation.
import matplotlib.pyplot as plt
dirName = '_static'
import os
try:
os.mkdir(dirName)
except FileExistsError:
pass
anim.save('{}/Kogur.mp4'.format(dirName))
plt.close()
!ffmpeg -loglevel panic -y -i _static/Kogur.mp4 -filter_complex "[0:v] fps=12,scale=480:-1,split [a][b];[a] palettegen [p];[b][p] paletteuse" _static/Kogur.gif
!rm -f _static/Kogur.mp4
# Integrate along Z
od_surv = od_surv.compute.integral(varNameList='ort_Vel',
axesList=['Z'])
# Compute transport using weights
od_surv = od_surv.compute.weighted_mean(varNameList='I(ort_Vel)dZ',
axesList=['station'])
transport_surv = (od_surv.dataset['I(ort_Vel)dZ'] *
od_surv.dataset['weight_I(ort_Vel)dZ'])
# Convert in Sverdrup
transport_surv = transport_surv * 1.E-6
# Compute cumulative transport
cum_transport_surv = transport_surv.cumsum('station').rename('Horizontal volume transport')
cum_transport_surv.attrs['units'] = 'Sv'
# Plot
fig, ax = plt.subplots(figsize=(13,5))
lines = cum_transport_surv.squeeze().plot.line(hue='time', linewidth=3)
tot_mean_transport = cum_transport_surv.isel(station=-1).mean('time')
title = ax.set_title('TOTAL MEAN TRANSPORT: {0:.1f} Sv'.format(tot_mean_transport.values))
| 0.639961 | 0.982691 |
# CS229: Problem Set 4
## Problem 4: Independent Component Analysis
**C. Combier**
This iPython Notebook provides solutions to Stanford's CS229 (Machine Learning, Fall 2017) graduate course problem set 3, taught by Andrew Ng.
The problem set can be found here: [./ps4.pdf](ps4.pdf)
I chose to write the solutions to the coding questions in Python, whereas the Stanford class is taught with Matlab/Octave.
## Notation
- $x_i$ is the $i^{th}$ feature vector
- $y_i$ is the expected outcome for the $i^{th}$ training example
- $z_i$'s are the latent (hidden) variables
- $m$ is the number of training examples
- $n$ is the number of features
For clarity, I've inlined the code of the provided helper function ```belsej.py```.
## Dependencies
I installed ```sounddevice``` to Anaconda with the following command:
```conda install -c conda-forge python-sounddevice ```
First, let's set up the environment and write helper functions:
- ```normalize``` ensures all mixes have the same volume
- ```load_data``` loads the mix
- ```play``` plays the audio using ```sounddevice```
```
### Independent Components Analysis
###
### This program requires a working installation of:
###
### On Mac:
### conda install -c conda-forge python-sounddevice
###
import sounddevice as sd
import numpy as np
Fs = 11025
def normalize(dat):
return 0.99 * dat / np.max(np.abs(dat))
def load_data():
mix = np.loadtxt('data/mix.dat')
return mix
def play(vec):
sd.play(vec, Fs, blocking=True)
```
Next we write a numerically stable sigmoid function, to avoid overflows:
```
# Numerically stable sigmoid
def sigmoid(x):
return np.where(x >= 0, 1 / (1 + np.exp(-x)), np.exp(x) / (1 + np.exp(x)))
```
The following functions calculates the weights to separate the independent components of the five mixes, using stochastic gradient descent and annealing to speed up convergence.
```
def unmixer(X):
M, N = X.shape
W = np.eye(N)
anneal = [0.1, 0.1, 0.1, 0.05, 0.05, 0.05, 0.02, 0.02, 0.01, 0.01,
0.005, 0.005, 0.002, 0.002, 0.001, 0.001]
print('Separating tracks ...')
for alpha in anneal:
for xi in X:
W += alpha * (np.outer(1 - 2 * sigmoid(np.dot(W, xi.T)), xi) + np.linalg.inv(W.T))
return W
```
Finally, this last function unmixes the 5 mixes to extract the independent components.
```
def unmix(X, W):
S = np.zeros(X.shape)
S = X.dot(W.T)
return S
```
Now, we load the mix data:
```
X = normalize(load_data())
for i in range(X.shape[1]):
print('Playing mixed track %d' % i)
play(X[:, i])
```
Next, we run Independent Component Analysis and separate the components in the mix:
```
W = unmixer(X)
S = normalize(unmix(X, W))
```
Finally, we play the separated components:
```
for i in range(S.shape[1]):
print('Playing separated track %d' % i)
play(S[:, i])
```
|
github_jupyter
|
First, let's set up the environment and write helper functions:
- ```normalize``` ensures all mixes have the same volume
- ```load_data``` loads the mix
- ```play``` plays the audio using ```sounddevice```
Next we write a numerically stable sigmoid function, to avoid overflows:
The following functions calculates the weights to separate the independent components of the five mixes, using stochastic gradient descent and annealing to speed up convergence.
Finally, this last function unmixes the 5 mixes to extract the independent components.
Now, we load the mix data:
Next, we run Independent Component Analysis and separate the components in the mix:
Finally, we play the separated components:
| 0.80147 | 0.98752 |
Lorenz equations as a model of atmospheric convection:
This is one of the classic systems in non-linear differential equations. It exhibits a range of different behaviors as the parameters (σ, β, ρ) are varied.
x˙ = σ(y−x)
y˙ = ρx−y−xz
z˙ = −βz+xy
The Lorenz equations also arise in simplified models for lasers, dynamos, thermosyphons, brushless DC motors, electric circuits, chemical reactions, and forward osmosis.
The Lorenz system is nonlinear, non-periodic, three-dimensional and deterministic.
The Lorenz equations are derived from the Oberbeck-Boussinesq approximation to the equations describing fluid circulation in a shallow layer of fluid, heated uniformly from below and cooled uniformly from above. This fluid circulation is known as Rayleigh-Bénard convection. The fluid is assumed to circulate in two dimensions (vertical and horizontal) with periodic rectangular boundary conditions.
The partial differential equations modeling the system's stream function and temperature are subjected to a spectral Galerkin approximation: the hydrodynamic fields are expanded in Fourier series, which are then severely truncated to a single term for the stream function and two terms for the temperature. This reduces the model equations to a set of three coupled, nonlinear ordinary differential equations.
```
%matplotlib inline
from ipywidgets import interact, interactive
from IPython.display import clear_output, display, HTML
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import cnames
from matplotlib import animation
#Computing the trajectories and plotting the result.
def solve_lorenz(
N =10,
angle = 0.0,
max_time = 4.0,
sigma = 10.0,
beta = 8./3,
rho = 28.0):
'''
We define a function that can integrate the differential
equations numerically and then plot the solutions.
This function has arguments that control the parameters of the
differential equation (σ, β, ρ),
the numerical integration (N, max_time),
and the visualization (angle).
'''
fig = plt.figure();
ax = fig.add_axes([0, 0, 1, 1], projection = '3d');
ax.axis('on')
#Prepare the axes limits.
ax.set_xlim((-25, 25))
ax.set_ylim((-35, 35))
ax.set_zlim((5, 55))
def lorenz_deriv(
x_y_z,
t0,
sigma = sigma,
beta = beta,
rho = rho):
'''
Computes the time-derivate of a Lorenz System.
'''
x, y, z = x_y_z
return[
sigma * (y - x),
x * (rho - z) - y,
x * y - beta * z]
#Choose random starting points, uniformly distributed from -15 to 15.
np.random.seed(1)
x0 = -15 + 30 * np.random.random((N, 3))
#Solve for the trajectories.
t = np.linspace(0, max_time, int(250*max_time))
x_t = np.asarray([integrate.odeint(lorenz_deriv, x0i, t) for x0i in x0])
#Choose a different color for each trajectory.
colors = plt.cm.jet(np.linspace(0, 1, N));
for i in range(N):
x, y, z = x_t[i,:,:].T
lines = ax.plot(x, y, z, '-', c = colors[i])
_ = plt.setp(lines, linewidth = 2);
ax.view_init(30, angle)
_ = plt.show();
return t, x_t
t, x_t = solve_lorenz(angle = 0, N = 10)
w = interactive(
solve_lorenz,
angle = (0., 360.),
N = (0, 50),
sigma = (0.0, 50.0),
rho = (0.0, 50.0),
)
display(w)
```
|
github_jupyter
|
%matplotlib inline
from ipywidgets import interact, interactive
from IPython.display import clear_output, display, HTML
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import cnames
from matplotlib import animation
#Computing the trajectories and plotting the result.
def solve_lorenz(
N =10,
angle = 0.0,
max_time = 4.0,
sigma = 10.0,
beta = 8./3,
rho = 28.0):
'''
We define a function that can integrate the differential
equations numerically and then plot the solutions.
This function has arguments that control the parameters of the
differential equation (σ, β, ρ),
the numerical integration (N, max_time),
and the visualization (angle).
'''
fig = plt.figure();
ax = fig.add_axes([0, 0, 1, 1], projection = '3d');
ax.axis('on')
#Prepare the axes limits.
ax.set_xlim((-25, 25))
ax.set_ylim((-35, 35))
ax.set_zlim((5, 55))
def lorenz_deriv(
x_y_z,
t0,
sigma = sigma,
beta = beta,
rho = rho):
'''
Computes the time-derivate of a Lorenz System.
'''
x, y, z = x_y_z
return[
sigma * (y - x),
x * (rho - z) - y,
x * y - beta * z]
#Choose random starting points, uniformly distributed from -15 to 15.
np.random.seed(1)
x0 = -15 + 30 * np.random.random((N, 3))
#Solve for the trajectories.
t = np.linspace(0, max_time, int(250*max_time))
x_t = np.asarray([integrate.odeint(lorenz_deriv, x0i, t) for x0i in x0])
#Choose a different color for each trajectory.
colors = plt.cm.jet(np.linspace(0, 1, N));
for i in range(N):
x, y, z = x_t[i,:,:].T
lines = ax.plot(x, y, z, '-', c = colors[i])
_ = plt.setp(lines, linewidth = 2);
ax.view_init(30, angle)
_ = plt.show();
return t, x_t
t, x_t = solve_lorenz(angle = 0, N = 10)
w = interactive(
solve_lorenz,
angle = (0., 360.),
N = (0, 50),
sigma = (0.0, 50.0),
rho = (0.0, 50.0),
)
display(w)
| 0.702836 | 0.981875 |
## Neural Networks
- This was adopted from the PyTorch Tutorials.
- http://pytorch.org/tutorials/beginner/pytorch_with_examples.html
## Neural Networks
- Neural networks are the foundation of deep learning, which has revolutionized the
```In the mathematical theory of artificial neural networks, the universal approximation theorem states[1] that a feed-forward network with a single hidden layer containing a finite number of neurons (i.e., a multilayer perceptron), can approximate continuous functions on compact subsets of Rn, under mild assumptions on the activation function.```
### Generate Fake Data
- `D_in` is the number of dimensions of an input varaible.
- `D_out` is the number of dimentions of an output variable.
- Here we are learning some special "fake" data that represents the xor problem.
- Here, the dv is 1 if either the first or second variable is
```
# -*- coding: utf-8 -*-
import numpy as np
#This is our independent and dependent variables.
x = np.array([ [0,0,0],[1,0,0],[0,1,0],[0,0,0] ])
y = np.array([[0,1,1,0]]).T
print("Input data:\n",x,"\n Output data:\n",y)
```
### A Simple Neural Network
- Here we are going to build a neural network with 2 hidden layers.
-
```
np.random.seed(seed=83832)
#D_in is the number of input variables.
#H is the hidden dimension.
#D_out is the number of dimensions for the output.
D_in, H, D_out = 3, 2, 1
# Randomly initialize weights og out 2 hidden layer network.
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
bias = np.random.randn(H, 1)
```
### Learn the Appropriate Weights via Backpropogation
- Learning rate adjust how quickly the model will adjust parameters.
```
# -*- coding: utf-8 -*-
learning_rate = .01
for t in range(500):
# Forward pass: compute predicted y
h = x.dot(w1)
#A relu is just the activation.
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
# Compute and print loss
loss = np.square(y_pred - y).sum()
print(t, loss)
# Backprop to compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
# Update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
```
#CFully connected
```
pred = np.maximum(x.dot(w1),0).dot(w2)
print (pred, "\n", y)
```
### Hidden Layers are Often Viewed as Unknown
- Just a weighting matrix
```
#However
w1
w2
# Relu just removes the negative numbers.
h_relu
```
|
github_jupyter
|
### Generate Fake Data
- `D_in` is the number of dimensions of an input varaible.
- `D_out` is the number of dimentions of an output variable.
- Here we are learning some special "fake" data that represents the xor problem.
- Here, the dv is 1 if either the first or second variable is
### A Simple Neural Network
- Here we are going to build a neural network with 2 hidden layers.
-
### Learn the Appropriate Weights via Backpropogation
- Learning rate adjust how quickly the model will adjust parameters.
#CFully connected
### Hidden Layers are Often Viewed as Unknown
- Just a weighting matrix
| 0.802981 | 0.989899 |
# Saving and Loading Models
In this notebook, I'll show you how to save and load models with PyTorch. This is important because you'll often want to load previously trained models to use in making predictions or to continue training on new data.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import helper
import fc_model
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
```
# Train a network
To make things more concise here, I moved the model architecture and training code from the last part to a file called `fc_model`. Importing this, we can easily create a fully-connected network with `fc_model.Network`, and train the network using `fc_model.train`. I'll use this model (once it's trained) to demonstrate how we can save and load models.
```
# Create the network, define the criterion and optimizer
model = fc_model.Network(784, 10, [512, 256, 128])
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
fc_model.train(model, trainloader, testloader, criterion, optimizer, epochs=2)
```
## Saving and loading networks
As you can imagine, it's impractical to train a network every time you need to use it. Instead, we can save trained networks then load them later to train more or use them for predictions.
The parameters for PyTorch networks are stored in a model's `state_dict`. We can see the state dict contains the weight and bias matrices for each of our layers.
```
print("Our model: \n\n", model, '\n')
print("The state dict keys: \n\n", model.state_dict().keys())
```
The simplest thing to do is simply save the state dict with `torch.save`. For example, we can save it to a file `'checkpoint.pth'`.
```
torch.save(model.state_dict(), 'checkpoint.pth')
```
Then we can load the state dict with `torch.load`.
```
state_dict = torch.load('checkpoint.pth')
print(state_dict.keys())
```
And to load the state dict in to the network, you do `model.load_state_dict(state_dict)`.
```
model.load_state_dict(state_dict)
```
Seems pretty straightforward, but as usual it's a bit more complicated. Loading the state dict works only if the model architecture is exactly the same as the checkpoint architecture. If I create a model with a different architecture, this fails.
```
# Try this
model = fc_model.Network(784, 10, [400, 200, 100])
# This will throw an error because the tensor sizes are wrong!
model.load_state_dict(state_dict)
```
This means we need to rebuild the model exactly as it was when trained. Information about the model architecture needs to be saved in the checkpoint, along with the state dict. To do this, you build a dictionary with all the information you need to compeletely rebuild the model.
```
checkpoint = {'input_size': 784,
'output_size': 10,
'hidden_layers': [each.out_features for each in model.hidden_layers],
'state_dict': model.state_dict()}
torch.save(checkpoint, 'checkpoint.pth')
```
Now the checkpoint has all the necessary information to rebuild the trained model. You can easily make that a function if you want. Similarly, we can write a function to load checkpoints.
```
def load_checkpoint(filepath):
checkpoint = torch.load(filepath)
model = fc_model.Network(checkpoint['input_size'],
checkpoint['output_size'],
checkpoint['hidden_layers'])
model.load_state_dict(checkpoint['state_dict'])
return model
model = load_checkpoint('checkpoint.pth')
print(model)
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import helper
import fc_model
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
# Create the network, define the criterion and optimizer
model = fc_model.Network(784, 10, [512, 256, 128])
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
fc_model.train(model, trainloader, testloader, criterion, optimizer, epochs=2)
print("Our model: \n\n", model, '\n')
print("The state dict keys: \n\n", model.state_dict().keys())
torch.save(model.state_dict(), 'checkpoint.pth')
state_dict = torch.load('checkpoint.pth')
print(state_dict.keys())
model.load_state_dict(state_dict)
# Try this
model = fc_model.Network(784, 10, [400, 200, 100])
# This will throw an error because the tensor sizes are wrong!
model.load_state_dict(state_dict)
checkpoint = {'input_size': 784,
'output_size': 10,
'hidden_layers': [each.out_features for each in model.hidden_layers],
'state_dict': model.state_dict()}
torch.save(checkpoint, 'checkpoint.pth')
def load_checkpoint(filepath):
checkpoint = torch.load(filepath)
model = fc_model.Network(checkpoint['input_size'],
checkpoint['output_size'],
checkpoint['hidden_layers'])
model.load_state_dict(checkpoint['state_dict'])
return model
model = load_checkpoint('checkpoint.pth')
print(model)
| 0.799011 | 0.989791 |
```
import time
import os
import pandas as pd
import numpy as np
np.set_printoptions(precision=6, suppress=True)
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
import tensorflow as tf
from tensorflow.keras import *
tf.__version__
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
from tensorflow.keras.metrics import Metric
class RSquare(Metric):
"""Compute R^2 score.
This is also called as coefficient of determination.
It tells how close are data to the fitted regression line.
- Highest score can be 1.0 and it indicates that the predictors
perfectly accounts for variation in the target.
- Score 0.0 indicates that the predictors do not
account for variation in the target.
- It can also be negative if the model is worse.
Usage:
```python
actuals = tf.constant([1, 4, 3], dtype=tf.float32)
preds = tf.constant([2, 4, 4], dtype=tf.float32)
result = tf.keras.metrics.RSquare()
result.update_state(actuals, preds)
print('R^2 score is: ', r1.result().numpy()) # 0.57142866
```
"""
def __init__(self, name='r_square', dtype=tf.float32):
super(RSquare, self).__init__(name=name, dtype=dtype)
self.squared_sum = self.add_weight("squared_sum", initializer="zeros")
self.sum = self.add_weight("sum", initializer="zeros")
self.res = self.add_weight("residual", initializer="zeros")
self.count = self.add_weight("count", initializer="zeros")
def update_state(self, y_true, y_pred):
y_true = tf.convert_to_tensor(y_true, tf.float32)
y_pred = tf.convert_to_tensor(y_pred, tf.float32)
self.squared_sum.assign_add(tf.reduce_sum(y_true**2))
self.sum.assign_add(tf.reduce_sum(y_true))
self.res.assign_add(
tf.reduce_sum(tf.square(tf.subtract(y_true, y_pred))))
self.count.assign_add(tf.cast(tf.shape(y_true)[0], tf.float32))
def result(self):
mean = self.sum / self.count
total = self.squared_sum - 2 * self.sum * mean + self.count * mean**2
return 1 - (self.res / total)
def reset_states(self):
# The state of the metric will be reset at the start of each epoch.
self.squared_sum.assign(0.0)
self.sum.assign(0.0)
self.res.assign(0.0)
self.count.assign(0.0)
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = ((8/2.54), (6/2.54))
plt.rcParams["font.family"] = "Arial"
plt.rcParams["mathtext.default"] = "rm"
plt.rcParams.update({'font.size': 11})
MARKER_SIZE = 15
cmap_m = ["#f4a6ad", "#f6957e", "#fccfa2", "#8de7be", "#86d6f2", "#24a9e4", "#b586e0", "#d7f293"]
cmap = ["#e94d5b", "#ef4d28", "#f9a54f", "#25b575", "#1bb1e7", "#1477a2", "#a662e5", "#c2f442"]
plt.rcParams['axes.spines.top'] = False
# plt.rcParams['axes.edgecolor'] =
plt.rcParams['axes.linewidth'] = 1
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['xtick.major.width'] = 1
plt.rcParams['xtick.minor.width'] = 1
plt.rcParams['ytick.major.width'] = 1
plt.rcParams['ytick.minor.width'] = 1
```
# Model training
## hyperparameters
```
SIZE = 50
LOSS_RATES = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95]
DISP_STEPS = 100
TRAINING_EPOCHS = 500
BATCH_SIZE = 32
LEARNING_RATE = 0.001
class ConvBlock(layers.Layer):
def __init__(self, filters, kernel_size, dropout_rate):
super(ConvBlock, self).__init__()
self.filters = filters
self.kernel_size = kernel_size
self.dropout_rate = dropout_rate
self.conv1 = layers.Conv2D(self.filters, self.kernel_size,
activation='relu', kernel_initializer='he_normal', padding='same')
self.batch1 = layers.BatchNormalization()
self.drop = layers.Dropout(self.dropout_rate)
self.conv2 = layers.Conv2D(self.filters, self.kernel_size,
activation='relu', kernel_initializer='he_normal', padding='same')
self.batch2 = layers.BatchNormalization()
def call(self, inp):
inp = self.batch1(self.conv1(inp))
inp = self.drop(inp)
inp = self.batch2(self.conv2(inp))
return inp
class DeconvBlock(layers.Layer):
def __init__(self, filters, kernel_size, strides):
super(DeconvBlock, self).__init__()
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.deconv1 = layers.Conv2DTranspose(self.filters, self.kernel_size, strides=self.strides, padding='same')
def call(self, inp):
inp = self.deconv1(inp)
return inp
class UNet(Model):
def __init__(self):
super(UNet, self).__init__()
self.conv_block1 = ConvBlock(64, (2, 2), 0.1)
self.pool1 = layers.MaxPooling2D()
self.conv_block2 = ConvBlock(128, (2, 2), 0.2)
self.pool2 = layers.MaxPooling2D()
self.conv_block3 = ConvBlock(256, (2, 2), 0.2)
self.deconv_block1 = DeconvBlock(128, (2, 2), (2, 2))
self.conv_block4 = ConvBlock(128, (2, 2), 0.2)
self.deconv_block2 = DeconvBlock(32, (2, 2), (2, 2))
self.padding = layers.ZeroPadding2D(((1, 0), (0, 1)))
self.conv_block5 = ConvBlock(64, (2, 2), 0.1)
self.output_conv = layers.Conv2D(1, (1, 1), activation='sigmoid')
def call(self, inp):
conv1 = self.conv_block1(inp)
pooled1 = self.pool1(conv1)
conv2 = self.conv_block2(pooled1)
pooled2 = self.pool2(conv2)
bottom = self.conv_block3(pooled2)
deconv1 = self.padding(self.deconv_block1(bottom))
deconv1 = layers.concatenate([deconv1, conv2])
deconv1 = self.conv_block4(deconv1)
deconv2 = self.deconv_block2(deconv1)
deconv2 = layers.concatenate([deconv2, conv1])
deconv2 = self.conv_block5(deconv2)
return self.output_conv(deconv2)
#loss inputs should be masked.
loss_object = tf.keras.losses.MeanSquaredError()
def loss_function(model, inp, tar):
masked_real = tar * (1 - inp[..., 1:2])
masked_pred = model(inp) * (1 - inp[..., 1:2])
return loss_object(masked_real, masked_pred)
```
# Mining
```
for LOSS_RATE in LOSS_RATES:
l = np.load('./data/tot_dataset_loss_%.2f.npz' % LOSS_RATE)
raw_input = l['raw_input']
raw_label = l['raw_label']
test_input = l['test_input']
test_label = l['test_label']
MAXS = l['MAXS']
MINS = l['MINS']
SCREEN_SIZE = l['SCREEN_SIZE']
raw_input = raw_input.astype(np.float32)
raw_label = raw_label.astype(np.float32)
test_input = test_input.astype(np.float32)
test_label = test_label.astype(np.float32)
num_train = int(raw_input.shape[0]*.7)
raw_input, raw_label = shuffle(raw_input, raw_label, random_state=4574)
train_input, train_label = raw_input[:num_train, ...], raw_label[:num_train, ...]
val_input, val_label = raw_input[num_train:, ...], raw_label[num_train:, ...]
train_dataset = tf.data.Dataset.from_tensor_slices((train_input, train_label))
train_dataset = train_dataset.cache().shuffle(BATCH_SIZE*50).batch(BATCH_SIZE)
val_dataset = tf.data.Dataset.from_tensor_slices((val_input, val_label))
val_dataset = val_dataset.cache().shuffle(BATCH_SIZE*50).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices((test_input, test_label))
test_dataset = test_dataset.batch(BATCH_SIZE)
print('Training for loss rate %.2f start.' % LOSS_RATE)
BEST_PATH = './checkpoints/UNet_best_loss_%.2fp' % LOSS_RATE
@tf.function
def train(loss_function, model, opt, inp, tar):
with tf.GradientTape() as tape:
gradients = tape.gradient(loss_function(model, inp, tar), model.trainable_variables)
gradient_variables = zip(gradients, model.trainable_variables)
opt.apply_gradients(gradient_variables)
unet_model = UNet()
opt = tf.optimizers.Adam(learning_rate=LEARNING_RATE)
checkpoint_path = BEST_PATH
ckpt = tf.train.Checkpoint(unet_model=unet_model, opt=opt)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=10)
writer = tf.summary.create_file_writer('tmp')
prev_test_loss = 100.0
early_stop_buffer = 500
with writer.as_default():
with tf.summary.record_if(True):
for epoch in range(TRAINING_EPOCHS):
for step, (inp, tar) in enumerate(train_dataset):
train(loss_function, unet_model, opt, inp, tar)
loss_values = loss_function(unet_model, inp, tar)
tf.summary.scalar('loss', loss_values, step=step)
if step % DISP_STEPS == 0:
test_loss = 0
for step_, (inp_, tar_) in enumerate(test_dataset):
test_loss += loss_function(unet_model, inp_, tar_)
if step_ > DISP_STEPS:
test_loss /= DISP_STEPS
break
if test_loss.numpy() < prev_test_loss:
ckpt_save_path = ckpt_manager.save()
prev_test_loss = test_loss.numpy()
print('Saving checkpoint at {}'.format(ckpt_save_path))
else:
early_stop_buffer -= 1
print('Epoch {} batch {} train loss: {:.4f} test loss: {:.4f}'
.format(epoch, step, loss_values.numpy(), test_loss.numpy()))
if early_stop_buffer <= 0:
print('early stop.')
break
if early_stop_buffer <= 0:
break
i = -1
if ckpt_manager.checkpoints:
ckpt.restore(ckpt_manager.checkpoints[i])
print ('Checkpoint ' + ckpt_manager.checkpoints[i][-2:] +' restored!!')
unet_model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate=LEARNING_RATE),
loss = tf.keras.losses.MeanSquaredError())
test_loss = unet_model.evaluate(test_dataset)
pred_result = unet_model.predict(test_dataset)
avg_pred = []
OUTLIER = 2
for __ in range(5):
temp = []
for _ in range(int(pred_result.shape[1]/5)):
temp.append(pred_result[..., _*5:(_+1)*5, 0][..., __])
temp = np.stack(temp, axis=2)
temp.sort(axis=2)
avg_pred.append(temp[..., OUTLIER:-OUTLIER].mean(axis=2))
avg_pred = np.stack(avg_pred, axis=2)
masking = test_input[..., 1]
avg_masking = masking[..., :5]
masked_pred = np.ma.array(pred_result[..., 0], mask=masking)
masked_avg_pred = np.ma.array(avg_pred, mask=avg_masking)
masked_label = np.ma.array(test_label[..., 0], mask=masking)
plot_label = ((MAXS[:5]-MINS[:5])*masked_label[..., :5] + MINS[:5])
plot_label.fill_value = np.nan
plot_avg_pred = ((MAXS[:5]-MINS[:5])*masked_avg_pred[..., :5] + MINS[:5])
plot_avg_pred.fill_value = np.nan
f = open('./results/UNet_best_loss_%.2fp.npz' % LOSS_RATE, 'wb')
np.savez(f,
test_label = plot_label.filled(),
test_pred = plot_avg_pred.filled()
)
f.close()
```
|
github_jupyter
|
import time
import os
import pandas as pd
import numpy as np
np.set_printoptions(precision=6, suppress=True)
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
import tensorflow as tf
from tensorflow.keras import *
tf.__version__
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
from tensorflow.keras.metrics import Metric
class RSquare(Metric):
"""Compute R^2 score.
This is also called as coefficient of determination.
It tells how close are data to the fitted regression line.
- Highest score can be 1.0 and it indicates that the predictors
perfectly accounts for variation in the target.
- Score 0.0 indicates that the predictors do not
account for variation in the target.
- It can also be negative if the model is worse.
Usage:
```python
actuals = tf.constant([1, 4, 3], dtype=tf.float32)
preds = tf.constant([2, 4, 4], dtype=tf.float32)
result = tf.keras.metrics.RSquare()
result.update_state(actuals, preds)
print('R^2 score is: ', r1.result().numpy()) # 0.57142866
```
"""
def __init__(self, name='r_square', dtype=tf.float32):
super(RSquare, self).__init__(name=name, dtype=dtype)
self.squared_sum = self.add_weight("squared_sum", initializer="zeros")
self.sum = self.add_weight("sum", initializer="zeros")
self.res = self.add_weight("residual", initializer="zeros")
self.count = self.add_weight("count", initializer="zeros")
def update_state(self, y_true, y_pred):
y_true = tf.convert_to_tensor(y_true, tf.float32)
y_pred = tf.convert_to_tensor(y_pred, tf.float32)
self.squared_sum.assign_add(tf.reduce_sum(y_true**2))
self.sum.assign_add(tf.reduce_sum(y_true))
self.res.assign_add(
tf.reduce_sum(tf.square(tf.subtract(y_true, y_pred))))
self.count.assign_add(tf.cast(tf.shape(y_true)[0], tf.float32))
def result(self):
mean = self.sum / self.count
total = self.squared_sum - 2 * self.sum * mean + self.count * mean**2
return 1 - (self.res / total)
def reset_states(self):
# The state of the metric will be reset at the start of each epoch.
self.squared_sum.assign(0.0)
self.sum.assign(0.0)
self.res.assign(0.0)
self.count.assign(0.0)
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = ((8/2.54), (6/2.54))
plt.rcParams["font.family"] = "Arial"
plt.rcParams["mathtext.default"] = "rm"
plt.rcParams.update({'font.size': 11})
MARKER_SIZE = 15
cmap_m = ["#f4a6ad", "#f6957e", "#fccfa2", "#8de7be", "#86d6f2", "#24a9e4", "#b586e0", "#d7f293"]
cmap = ["#e94d5b", "#ef4d28", "#f9a54f", "#25b575", "#1bb1e7", "#1477a2", "#a662e5", "#c2f442"]
plt.rcParams['axes.spines.top'] = False
# plt.rcParams['axes.edgecolor'] =
plt.rcParams['axes.linewidth'] = 1
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['xtick.major.width'] = 1
plt.rcParams['xtick.minor.width'] = 1
plt.rcParams['ytick.major.width'] = 1
plt.rcParams['ytick.minor.width'] = 1
SIZE = 50
LOSS_RATES = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95]
DISP_STEPS = 100
TRAINING_EPOCHS = 500
BATCH_SIZE = 32
LEARNING_RATE = 0.001
class ConvBlock(layers.Layer):
def __init__(self, filters, kernel_size, dropout_rate):
super(ConvBlock, self).__init__()
self.filters = filters
self.kernel_size = kernel_size
self.dropout_rate = dropout_rate
self.conv1 = layers.Conv2D(self.filters, self.kernel_size,
activation='relu', kernel_initializer='he_normal', padding='same')
self.batch1 = layers.BatchNormalization()
self.drop = layers.Dropout(self.dropout_rate)
self.conv2 = layers.Conv2D(self.filters, self.kernel_size,
activation='relu', kernel_initializer='he_normal', padding='same')
self.batch2 = layers.BatchNormalization()
def call(self, inp):
inp = self.batch1(self.conv1(inp))
inp = self.drop(inp)
inp = self.batch2(self.conv2(inp))
return inp
class DeconvBlock(layers.Layer):
def __init__(self, filters, kernel_size, strides):
super(DeconvBlock, self).__init__()
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.deconv1 = layers.Conv2DTranspose(self.filters, self.kernel_size, strides=self.strides, padding='same')
def call(self, inp):
inp = self.deconv1(inp)
return inp
class UNet(Model):
def __init__(self):
super(UNet, self).__init__()
self.conv_block1 = ConvBlock(64, (2, 2), 0.1)
self.pool1 = layers.MaxPooling2D()
self.conv_block2 = ConvBlock(128, (2, 2), 0.2)
self.pool2 = layers.MaxPooling2D()
self.conv_block3 = ConvBlock(256, (2, 2), 0.2)
self.deconv_block1 = DeconvBlock(128, (2, 2), (2, 2))
self.conv_block4 = ConvBlock(128, (2, 2), 0.2)
self.deconv_block2 = DeconvBlock(32, (2, 2), (2, 2))
self.padding = layers.ZeroPadding2D(((1, 0), (0, 1)))
self.conv_block5 = ConvBlock(64, (2, 2), 0.1)
self.output_conv = layers.Conv2D(1, (1, 1), activation='sigmoid')
def call(self, inp):
conv1 = self.conv_block1(inp)
pooled1 = self.pool1(conv1)
conv2 = self.conv_block2(pooled1)
pooled2 = self.pool2(conv2)
bottom = self.conv_block3(pooled2)
deconv1 = self.padding(self.deconv_block1(bottom))
deconv1 = layers.concatenate([deconv1, conv2])
deconv1 = self.conv_block4(deconv1)
deconv2 = self.deconv_block2(deconv1)
deconv2 = layers.concatenate([deconv2, conv1])
deconv2 = self.conv_block5(deconv2)
return self.output_conv(deconv2)
#loss inputs should be masked.
loss_object = tf.keras.losses.MeanSquaredError()
def loss_function(model, inp, tar):
masked_real = tar * (1 - inp[..., 1:2])
masked_pred = model(inp) * (1 - inp[..., 1:2])
return loss_object(masked_real, masked_pred)
for LOSS_RATE in LOSS_RATES:
l = np.load('./data/tot_dataset_loss_%.2f.npz' % LOSS_RATE)
raw_input = l['raw_input']
raw_label = l['raw_label']
test_input = l['test_input']
test_label = l['test_label']
MAXS = l['MAXS']
MINS = l['MINS']
SCREEN_SIZE = l['SCREEN_SIZE']
raw_input = raw_input.astype(np.float32)
raw_label = raw_label.astype(np.float32)
test_input = test_input.astype(np.float32)
test_label = test_label.astype(np.float32)
num_train = int(raw_input.shape[0]*.7)
raw_input, raw_label = shuffle(raw_input, raw_label, random_state=4574)
train_input, train_label = raw_input[:num_train, ...], raw_label[:num_train, ...]
val_input, val_label = raw_input[num_train:, ...], raw_label[num_train:, ...]
train_dataset = tf.data.Dataset.from_tensor_slices((train_input, train_label))
train_dataset = train_dataset.cache().shuffle(BATCH_SIZE*50).batch(BATCH_SIZE)
val_dataset = tf.data.Dataset.from_tensor_slices((val_input, val_label))
val_dataset = val_dataset.cache().shuffle(BATCH_SIZE*50).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices((test_input, test_label))
test_dataset = test_dataset.batch(BATCH_SIZE)
print('Training for loss rate %.2f start.' % LOSS_RATE)
BEST_PATH = './checkpoints/UNet_best_loss_%.2fp' % LOSS_RATE
@tf.function
def train(loss_function, model, opt, inp, tar):
with tf.GradientTape() as tape:
gradients = tape.gradient(loss_function(model, inp, tar), model.trainable_variables)
gradient_variables = zip(gradients, model.trainable_variables)
opt.apply_gradients(gradient_variables)
unet_model = UNet()
opt = tf.optimizers.Adam(learning_rate=LEARNING_RATE)
checkpoint_path = BEST_PATH
ckpt = tf.train.Checkpoint(unet_model=unet_model, opt=opt)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=10)
writer = tf.summary.create_file_writer('tmp')
prev_test_loss = 100.0
early_stop_buffer = 500
with writer.as_default():
with tf.summary.record_if(True):
for epoch in range(TRAINING_EPOCHS):
for step, (inp, tar) in enumerate(train_dataset):
train(loss_function, unet_model, opt, inp, tar)
loss_values = loss_function(unet_model, inp, tar)
tf.summary.scalar('loss', loss_values, step=step)
if step % DISP_STEPS == 0:
test_loss = 0
for step_, (inp_, tar_) in enumerate(test_dataset):
test_loss += loss_function(unet_model, inp_, tar_)
if step_ > DISP_STEPS:
test_loss /= DISP_STEPS
break
if test_loss.numpy() < prev_test_loss:
ckpt_save_path = ckpt_manager.save()
prev_test_loss = test_loss.numpy()
print('Saving checkpoint at {}'.format(ckpt_save_path))
else:
early_stop_buffer -= 1
print('Epoch {} batch {} train loss: {:.4f} test loss: {:.4f}'
.format(epoch, step, loss_values.numpy(), test_loss.numpy()))
if early_stop_buffer <= 0:
print('early stop.')
break
if early_stop_buffer <= 0:
break
i = -1
if ckpt_manager.checkpoints:
ckpt.restore(ckpt_manager.checkpoints[i])
print ('Checkpoint ' + ckpt_manager.checkpoints[i][-2:] +' restored!!')
unet_model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate=LEARNING_RATE),
loss = tf.keras.losses.MeanSquaredError())
test_loss = unet_model.evaluate(test_dataset)
pred_result = unet_model.predict(test_dataset)
avg_pred = []
OUTLIER = 2
for __ in range(5):
temp = []
for _ in range(int(pred_result.shape[1]/5)):
temp.append(pred_result[..., _*5:(_+1)*5, 0][..., __])
temp = np.stack(temp, axis=2)
temp.sort(axis=2)
avg_pred.append(temp[..., OUTLIER:-OUTLIER].mean(axis=2))
avg_pred = np.stack(avg_pred, axis=2)
masking = test_input[..., 1]
avg_masking = masking[..., :5]
masked_pred = np.ma.array(pred_result[..., 0], mask=masking)
masked_avg_pred = np.ma.array(avg_pred, mask=avg_masking)
masked_label = np.ma.array(test_label[..., 0], mask=masking)
plot_label = ((MAXS[:5]-MINS[:5])*masked_label[..., :5] + MINS[:5])
plot_label.fill_value = np.nan
plot_avg_pred = ((MAXS[:5]-MINS[:5])*masked_avg_pred[..., :5] + MINS[:5])
plot_avg_pred.fill_value = np.nan
f = open('./results/UNet_best_loss_%.2fp.npz' % LOSS_RATE, 'wb')
np.savez(f,
test_label = plot_label.filled(),
test_pred = plot_avg_pred.filled()
)
f.close()
| 0.825414 | 0.674855 |
<a href="https://colab.research.google.com/github/prachi-lad17/Python-Case-Studies/blob/main/Case_Study_2%3A%20Figuring_out_which_customer_may_leave.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# **Figuring out which customer may leave**
```
```
# Figuring Our Which Customers May Leave - Churn Analysis
### About our Dataset
Source - https://www.kaggle.com/blastchar/telco-customer-churn
1. We have customer information for a Telecommunications company
2. We've got customer IDs, general customer info, the servies they've subscribed too, type of contract and monthly charges.
3. This is a historic customer information so we have a field stating whether that customer has **churnded**
**Field Descriptions**
- customerID - Customer ID
- gender - Whether the customer is a male or a female
- SeniorCitizen - Whether the customer is a senior citizen or not (1, 0)
- Partner - Whether the customer has a partner or not (Yes, No)
- Dependents - Whether the customer has dependents or not (Yes, No)
- tenure - Number of months the customer has stayed with the company
- PhoneService - Whether the customer has a phone service or not (Yes, No)
- MultipleLines - Whether the customer has multiple lines or not (Yes, No, No phone service)
- InternetService - Customer’s internet service provider (DSL, Fiber optic, No)
- OnlineSecurity - Whether the customer has online security or not (Yes, No, No internet service)
- OnlineBackup - Whether the customer has online backup or not (Yes, No, No internet service)
- DeviceProtection - Whether the customer has device protection or not (Yes, No, No internet service)
- TechSupport - Whether the customer has tech support or not (Yes, No, No internet service)
- StreamingTV - Whether the customer has streaming TV or not (Yes, No, No internet service)
- StreamingMovies - Whether the customer has streaming movies or not (Yes, No, No internet service)
- Contract - The contract term of the customer (Month-to-month, One year, Two year)
- PaperlessBilling - Whether the customer has paperless billing or not (Yes, No)
- PaymentMethod - The customer’s payment method (Electronic check, Mailed check Bank transfer (automatic), Credit card (automatic))
- MonthlyCharges - The amount charged to the customer monthly
- TotalCharges - The total amount charged to the customer
- Churn - Whether the customer churned or not (Yes or No)
***Customer Churn*** - churn is when an existing customer, user, player, subscriber or any kind of return client stops doing business or ends the relationship with a company.
**Aim -** is to figure our which customers may likely churn in future
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
## Loading files
file_name = "https://raw.githubusercontent.com/rajeevratan84/datascienceforbusiness/master/WA_Fn-UseC_-Telco-Customer-Churn.csv"
churn_df = pd.read_csv(file_name)
# Using .head() function to check if file is uploaded. It will print first 5 records.
churn_df.head()
## To check last 5 records, we use .tail() funtion
churn_df.tail()
## To get summary on numeric columns
churn_df.describe()
## To get summary on each column
churn_df.describe(include="all")
## TO check categorical variables in dataset
churn_df.select_dtypes(exclude=['int64','float']).columns
## To check numerical variables
churn_df.select_dtypes(exclude=['object']).columns
## To check the unique values
churn_df.SeniorCitizen.unique()
## To check unique levels of tenure
churn_df.tenure.unique()
## Printing unique levels of Churn variable
churn_df.Churn.unique()
## How many unique values are there in MonthlyChaerges variable
len(churn_df.MonthlyCharges.unique())
## How many unique values are there in Churn variable
len(churn_df.Churn.unique())
## Another way of showing information of data in a single output
print("No_of_Rows: ", churn_df.shape[0])
print()
print("No_of_Columns: ", churn_df.shape[1])
print()
print("Features: ", churn_df.columns.to_list)
print("\nMissing_Values: ", churn_df.isnull().sum().values.sum())
print("\nMissing_Values: ", churn_df.isnull().sum())
print("\nUnique_Values: \n", churn_df.nunique())
## Print how many churn and not churn
churn_df['Churn'].value_counts(sort = False)
```
## **Exporatory Data Analysis**
```
## It is a best practice to keep a copy, in case we need to check at original dataset in future
churn_df_copy = churn_df.copy()
## Dropping the columns which are not necessary for the plots we are gonna do.
churn_df_copy.drop(['customerID','MonthlyCharges', 'TotalCharges', 'tenure'], axis=1, inplace=True)
churn_df_copy.head()
```
### **pd.crosstab() == if we want to work upon more variable at a time then we use pd.crosstab()**
* The pandas crosstab function builds a cross-tabulation table that can show the frequency with which certain groups of data appear.
* The crosstab function can operate on numpy arrays, series or columns in a dataframe.
* Pandas does that work behind the scenes to count how many occurrences there are of each combination.
* The pandas crosstab function is a useful tool for summarizing data. The functionality overlaps with some of the other pandas tools but it occupies a useful place in your data analysis toolbox.
```
## By using this code we can apply crosstab function for each column
summary = pd.concat([pd.crosstab(churn_df_copy[x], churn_df_copy.Churn) for x in churn_df_copy.columns[:-1]], keys=churn_df_copy.columns[:-1])
summary
## Printing churn rate by gender
pd.crosstab(churn_df_copy['Churn'],churn_df_copy['gender'])
## Printing churn rate by gender with margins
pd.crosstab(churn_df_copy['Churn'],churn_df_copy['gender'],margins=True,margins_name="Total",normalize=True)
## Checking margins
pd.concat([pd.crosstab(churn_df_copy[x], churn_df_copy.Churn,margins=True,margins_name="Total",normalize=True) for x in churn_df_copy.columns[:-1]], keys=churn_df_copy.columns[:-1])
"""Making a % column for summary"""
summary['Churn_%'] = summary['Yes'] / summary['No'] + summary['Yes']
summary
```
## **Visualization and EDA**
```
import matplotlib.pyplot as plt # this is used for the plot the graph
import seaborn as sns # used for plot interactive graph.
from pylab import rcParams # Customize Matplotlib plots using rcParams
# Data to plot
labels = churn_df['Churn'].value_counts(sort = True).index
sizes = churn_df['Churn'].value_counts(sort = True)
colors = ["pink","lightblue"]
explode = (0.05,0) # explode 1st slice
rcParams['figure.figsize'] = 7,7
# Plot
plt.pie(sizes, explode=explode, labels=labels, colors=colors, autopct='%1.1f%%', shadow=True, startangle=90,)
plt.title('Customer Churn Breakdown')
plt.show()
# Correlation plot doesn't end up being too informative
import matplotlib.pyplot as plt
def plot_corr(df,size=10):
'''Function plots a graphical correlation matrix for each pair of columns in the dataframe.
Input:
df: pandas DataFrame
size: vertical and horizontal size of the plot'''
corr = df.corr()
fig, ax = plt.subplots(figsize=(size, size))
ax.legend()
cax = ax.matshow(corr)
fig.colorbar(cax)
plt.xticks(range(len(corr.columns)), corr.columns, rotation='vertical')
plt.yticks(range(len(corr.columns)), corr.columns)
plot_corr(churn_df)
# Create a Violin Plot showing how monthy charges relate to Churn
# We an see that Churned customers tend to be higher paying customers
g = sns.factorplot(x="Churn", y = "MonthlyCharges",data = churn_df, kind="violin", palette = "Pastel1")
# Let's look at Tenure
g = sns.factorplot(x="Churn", y = "tenure",data = churn_df, kind="violin", palette = "Pastel1")
plt.figure(figsize= (10,10))
sns.countplot(churn_df['Churn'])
```
## **Preparing our dataset for Machine Learning**
```
# Check for empty fields, Note, " " is not Null but a spaced character
len(churn_df[churn_df['TotalCharges'] == " "])
## Drop missing data
churn_df = churn_df[churn_df['TotalCharges'] != " "]
len(churn_df[churn_df['TotalCharges'] == " "])
## Here we are making diff col - id_col, target_col,
## Next we are writing a code to check the unique levels in each categorical variable and if it is <6 then it is applying label encoding.
## Label Encoding takes binary column and changes the values to 0 and 1. We do label encoding because our can only understand 0 and 1 language.
## cat_col - will store categorical variables which are having less than 6 unique levels
## id_col - stores customerID column
## target_col - stores Churn column
## num_cols - stores all the numerical columns except id_cols, target_cols, cat_col
## bin_cols - stores the binary variables
## multi_cols - stores the categorical columns which are not binary
## Then next we do label encoding for binary columns
## And duplicating columns for multi value columns
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
#customer id col
id_col = ['customerID']
#Target columns
target_col = ["Churn"]
#categorical columns
cat_cols = churn_df.nunique()[churn_df.nunique() < 6].keys().tolist()
cat_cols = [x for x in cat_cols if x not in target_col]
#numerical columns
num_cols = [x for x in churn_df.columns if x not in cat_cols + target_col + id_col]
#Binary columns with 2 values
bin_cols = churn_df.nunique()[churn_df.nunique() == 2].keys().tolist()
#Columns more than 2 values
multi_cols = [i for i in cat_cols if i not in bin_cols]
#Label encoding Binary columns
le = LabelEncoder()
for i in bin_cols :
churn_df[i] = le.fit_transform(churn_df[i])
#Duplicating columns for multi value columns
churn_df = pd.get_dummies(data = churn_df, columns = multi_cols )
churn_df.head()
len(churn_df.columns)
num_cols
id_col
cat_cols
## Scaling Numerical columns
std = StandardScaler()
## Scale data
scaled = std.fit_transform(churn_df[num_cols])
scaled = pd.DataFrame(scaled,columns = num_cols)
## Dropping original values merging scaled values for numerical columns
df_telcom_og = churn_df.copy()
churn_df = churn_df.drop(columns = num_cols,axis = 1)
churn_df = churn_df.merge(scaled, left_index = True, right_index = True, how = "left")
## Churn_df.info()
churn_df.head()
churn_df.drop(['customerID'], axis=1, inplace=True)
churn_df.head()
churn_df[churn_df.isnull().any(axis=1)]
print(len(churn_df.isnull().sum()))
## Since there are only 11 NA values, we drop them.
churn_df = churn_df.dropna()
# Double check that nulls have been removed
churn_df[churn_df.isnull().any(axis=1)]
```
# **Splitting into training and testing**
```
from sklearn.model_selection import train_test_split
# We remove our label values from train data
X = churn_df.drop(['Churn'],axis=1).values
# We assigned our label variable to test data
Y = churn_df['Churn'].values
# Split it to a 70:30 Ratio Train:Test
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.3)
type(x_train)
df_train = pd.DataFrame(x_train)
df_train.head()
print(len(churn_df.columns))
churn_df.columns
churn_df.head()
```
# **Training LOGISTIC REGRESSION model**
```
from sklearn.linear_model import LogisticRegression
### creating a model
classifier_model = LogisticRegression()
### passing training data to model
classifier_model.fit(x_train,y_train)
### predicting values x_test using model and storing the values in y_pred
y_pred = classifier_model.predict(x_test)
### interception and coefficient of model
print(classifier_model.intercept_)
print(classifier_model.coef_)
print()
### printing values for better understanding
print(list(zip(y_test, y_pred)))
from sklearn.metrics import accuracy_score,confusion_matrix,classification_report
### creating and printing confusion matrix
conf_matrix = confusion_matrix(y_test,y_pred)
print(conf_matrix)
### Creating and printing classification report
print("Classification Report: ")
print(classification_report(y_test,y_pred))
### Creating and printing accuracy score
acc = accuracy_score(y_test,y_pred)
print("Accuracy {0:.2f}%".format(100*accuracy_score(y_pred, y_test)))
```
## **Feature Importance using Logistic Regression**
```
# Let's see what features mattered most i.e. Feature Importance
# We sort on the co-efficients with the largest weights as those impact the resulting output the most
coef = classifier_model.coef_[0]
coef = [abs(number) for number in coef]
print(coef)
# Finding and deleting the label column
cols = list(churn_df.columns)
cols.index('Churn')
del cols[6]
cols
# Sorting on Feature Importance
sorted_index = sorted(range(len(coef)), key = lambda k: coef[k], reverse = True)
for idx in sorted_index:
print(cols[idx])
```
## **Try Random Forests**
```
from sklearn.ensemble import RandomForestClassifier
random_forest_model = RandomForestClassifier(n_estimators=100,random_state=10) ## it will built 100 DT in background
#fit the model on the data and predict the values
random_forest_model.fit(x_train,y_train)
y_pred_rf = random_forest_model.predict(x_test)
from sklearn.metrics import accuracy_score,confusion_matrix,classification_report
### creating and printing confusion matrix
conf_matrix_rf = confusion_matrix(y_test,y_pred_rf)
print(conf_matrix_rf)
### Creating and printing classification report
print("Classification Report: ")
print(classification_report(y_test,y_pred_rf))
### Creating and printing accuracy score
acc = accuracy_score(y_test,y_pred_rf)
print("Accuracy {0:.2f}%".format(100*accuracy_score(y_pred_rf, y_test)))
```
# **Saving a model**
```
import pickle
# save
with open('model.pkl','wb') as f:
pickle.dump(random_forest_model, f)
# load
with open('model.pkl', 'rb') as f:
loaded_model_rf = pickle.load(f)
predictions = loaded_model_rf.predict(x_test)
predictions
```
# **Deep Learning Model**
```
## Using the newest version of Tensorflow 2.0
%tensorflow_version 2.x
## Checking to ensure we are using our GPU
import tensorflow as tf
tf.test.gpu_device_name()
# Create a simple model
import tensorflow.keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(20, kernel_initializer = "uniform",activation = "relu", input_dim=40))
model.add(Dense(1, kernel_initializer = "uniform",activation = "sigmoid"))
model.compile(optimizer= "adam",loss = "binary_crossentropy",metrics = ["accuracy"])
# Display Model Summary and Show Parameters
model.summary()
# Start Training Our Classifier
batch_size = 64
epochs = 25
history = model.fit(x_train,
y_train,
batch_size = batch_size,
epochs = epochs,
verbose = 1,
validation_data = (x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
predictions = model.predict(x_test)
predictions = (predictions > 0.5)
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
```
# **Saving Model**
```
## Simple cnn = simple convolutional neural network
## You mean a HDF5/H5 file, which is a file format to store structured data, its not a model by itself.
## Keras saves models in this format as it can easily store the weights and model configuration in a single file.
model.save("simple_cnn_25_epochs.h5")
## Loading our model
from tensorflow.keras.models import load_model
classifier_DL_simple_cnn = load_model('simple_cnn_25_epochs.h5')
```
# **Trying deeper models, checkpoints and stopping early.**
```
from tensorflow.keras.regularizers import l2
from tensorflow.keras.layers import Dropout
from tensorflow.keras.callbacks import ModelCheckpoint
model2 = Sequential()
# Hidden Layer 1
model2.add(Dense(2000, activation='relu', input_dim=40, kernel_regularizer=l2(0.01)))
model2.add(Dropout(0.3, noise_shape=None, seed=None))
# Hidden Layer 2
model2.add(Dense(1000, activation='relu', input_dim=18, kernel_regularizer=l2(0.01)))
model2.add(Dropout(0.3, noise_shape=None, seed=None))
# Hidden Layer 3
model2.add(Dense(500, activation = 'relu', kernel_regularizer=l2(0.01)))
model2.add(Dropout(0.3, noise_shape=None, seed=None))
model2.add(Dense(1, activation='sigmoid'))
model2.summary()
# Create our checkpoint so that we save model after each epoch
checkpoint = ModelCheckpoint("deep_model_checkpoint.h5",
monitor="val_loss",
mode="min",
save_best_only = True,
verbose=1)
model2.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Defining our early stoppping criteria
from tensorflow.keras.callbacks import EarlyStopping
earlystop = EarlyStopping(monitor = 'val_loss', # value being monitored for improvement
min_delta = 0, #Abs value and is the min change required before we stop
patience = 2, #Number of epochs we wait before stopping
verbose = 1,
restore_best_weights = True) #keeps the best weigths once stopped
# we put our call backs into a callback list
callbacks = [earlystop, checkpoint]
batch_size = 32
epochs = 10
history = model2.fit(x_train,
y_train,
batch_size = batch_size,
epochs = epochs,
verbose = 1,
# NOTE We are adding our callbacks here
callbacks = callbacks,
validation_data = (x_test, y_test))
score = model2.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
|
github_jupyter
|
```
# Figuring Our Which Customers May Leave - Churn Analysis
### About our Dataset
Source - https://www.kaggle.com/blastchar/telco-customer-churn
1. We have customer information for a Telecommunications company
2. We've got customer IDs, general customer info, the servies they've subscribed too, type of contract and monthly charges.
3. This is a historic customer information so we have a field stating whether that customer has **churnded**
**Field Descriptions**
- customerID - Customer ID
- gender - Whether the customer is a male or a female
- SeniorCitizen - Whether the customer is a senior citizen or not (1, 0)
- Partner - Whether the customer has a partner or not (Yes, No)
- Dependents - Whether the customer has dependents or not (Yes, No)
- tenure - Number of months the customer has stayed with the company
- PhoneService - Whether the customer has a phone service or not (Yes, No)
- MultipleLines - Whether the customer has multiple lines or not (Yes, No, No phone service)
- InternetService - Customer’s internet service provider (DSL, Fiber optic, No)
- OnlineSecurity - Whether the customer has online security or not (Yes, No, No internet service)
- OnlineBackup - Whether the customer has online backup or not (Yes, No, No internet service)
- DeviceProtection - Whether the customer has device protection or not (Yes, No, No internet service)
- TechSupport - Whether the customer has tech support or not (Yes, No, No internet service)
- StreamingTV - Whether the customer has streaming TV or not (Yes, No, No internet service)
- StreamingMovies - Whether the customer has streaming movies or not (Yes, No, No internet service)
- Contract - The contract term of the customer (Month-to-month, One year, Two year)
- PaperlessBilling - Whether the customer has paperless billing or not (Yes, No)
- PaymentMethod - The customer’s payment method (Electronic check, Mailed check Bank transfer (automatic), Credit card (automatic))
- MonthlyCharges - The amount charged to the customer monthly
- TotalCharges - The total amount charged to the customer
- Churn - Whether the customer churned or not (Yes or No)
***Customer Churn*** - churn is when an existing customer, user, player, subscriber or any kind of return client stops doing business or ends the relationship with a company.
**Aim -** is to figure our which customers may likely churn in future
## **Exporatory Data Analysis**
### **pd.crosstab() == if we want to work upon more variable at a time then we use pd.crosstab()**
* The pandas crosstab function builds a cross-tabulation table that can show the frequency with which certain groups of data appear.
* The crosstab function can operate on numpy arrays, series or columns in a dataframe.
* Pandas does that work behind the scenes to count how many occurrences there are of each combination.
* The pandas crosstab function is a useful tool for summarizing data. The functionality overlaps with some of the other pandas tools but it occupies a useful place in your data analysis toolbox.
## **Visualization and EDA**
## **Preparing our dataset for Machine Learning**
# **Splitting into training and testing**
# **Training LOGISTIC REGRESSION model**
## **Feature Importance using Logistic Regression**
## **Try Random Forests**
# **Saving a model**
# **Deep Learning Model**
# **Saving Model**
# **Trying deeper models, checkpoints and stopping early.**
| 0.719285 | 0.934634 |
# 04 - Full waveform inversion with Devito and Dask
## Introduction
In this tutorial we show how [Devito](http://www.devitoproject.org/devito-public) and [scipy.optimize.minimize](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) are used with [Dask](https://dask.pydata.org/en/latest/#dask) to perform [full waveform inversion](https://www.slim.eos.ubc.ca/research/inversion) (FWI) on distributed memory parallel computers.
## scipy.optimize.minimize
In this tutorial we use [scipy.optimize.minimize](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) to solve the FWI gradient based minimization problem rather than the simple grdient decent algorithm in the previous tutorial.
```python
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
```
> Minimization of scalar function of one or more variables.
>
> In general, the optimization problems are of the form:
>
> minimize f(x) subject to
>
> g_i(x) >= 0, i = 1,...,m
> h_j(x) = 0, j = 1,...,p
> where x is a vector of one or more variables. g_i(x) are the inequality constraints. h_j(x) are the equality constrains.
[scipy.optimize.minimize](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) provides a wide variety of methods for solving minimization problems depending on the context. Here we are going to focus on using L-BFGS via [scipy.optimize.minimize(method=’L-BFGS-B’)](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html#optimize-minimize-lbfgsb)
```python
scipy.optimize.minimize(fun, x0, args=(), method='L-BFGS-B', jac=None, bounds=None, tol=None, callback=None, options={'disp': None, 'maxls': 20, 'iprint': -1, 'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000, 'ftol': 2.220446049250313e-09, 'maxcor': 10, 'maxfun': 15000})```
The argument `fun` is a callable function that returns the misfit between the simulated and the observed data. If `jac` is a Boolean and is `True`, `fun` is assumed to return the gradient along with the objective function - as is our case when applying the adjoint-state method.
## What is Dask?
> [Dask](https://dask.pydata.org/en/latest/#dask) is a flexible parallel computing library for analytic computing.
>
> Dask is composed of two components:
>
> * Dynamic task scheduling optimized for computation...
> * “Big Data” collections like parallel arrays, dataframes, and lists that extend common interfaces like NumPy, Pandas, or Python iterators to larger-than-memory or distributed environments. These parallel collections run on top of the dynamic task schedulers.
>
> Dask emphasizes the following virtues:
>
> * Familiar: Provides parallelized NumPy array and Pandas DataFrame objects
> * Flexible: Provides a task scheduling interface for more custom workloads and integration with other projects.
> * Native: Enables distributed computing in Pure Python with access to the PyData stack.
> * Fast: Operates with low overhead, low latency, and minimal serialization necessary for fast numerical algorithms
> * Scales up: Runs resiliently on clusters with 1000s of cores
> * Scales down: Trivial to set up and run on a laptop in a single process
> * Responsive: Designed with interactive computing in mind it provides rapid feedback and diagnostics to aid humans
**We are going to use it here to parallelise the computation of the functional and gradient as this is the vast bulk of the computational expense of FWI and it is trivially parallel over data shots.**
## Setting up (synthetic) data
In a real world scenario we work with collected seismic data; for the tutorial we know what the actual solution is and we are using the workers to also generate the synthetic data.
```
#NBVAL_IGNORE_OUTPUT
# Set up inversion parameters.
param = {'t0': 0.,
'tn': 1000., # Simulation last 1 second (1000 ms)
'f0': 0.010, # Source peak frequency is 10Hz (0.010 kHz)
'nshots': 5, # Number of shots to create gradient from
'm_bounds': (0.08, 0.25), # Set the min and max slowness
'shape': (101, 101), # Number of grid points (nx, nz).
'spacing': (10., 10.), # Grid spacing in m. The domain size is now 1km by 1km.
'origin': (0, 0), # Need origin to define relative source and receiver locations.
'nbl': 40} # nbl thickness.
import numpy as np
import scipy
from scipy import signal, optimize
from devito import Grid
from distributed import Client, LocalCluster, wait
import cloudpickle as pickle
# Import acoustic solver, source and receiver modules.
from examples.seismic import Model, demo_model, AcquisitionGeometry, Receiver
from examples.seismic.acoustic import AcousticWaveSolver
from examples.seismic import AcquisitionGeometry
# Import convenience function for plotting results
from examples.seismic import plot_image
def get_true_model():
''' Define the test phantom; in this case we are using
a simple circle so we can easily see what is going on.
'''
return demo_model('circle-isotropic', vp=3.0, vp_background=2.5,
origin=param['origin'], shape=param['shape'],
spacing=param['spacing'], nbl=param['nbl'])
def get_initial_model():
'''The initial guess for the subsurface model.
'''
# Make sure both model are on the same grid
grid = get_true_model().grid
return demo_model('circle-isotropic', vp=2.5, vp_background=2.5,
origin=param['origin'], shape=param['shape'],
spacing=param['spacing'], nbl=param['nbl'],
grid=grid)
def wrap_model(x, astype=None):
'''Wrap a flat array as a subsurface model.
'''
model = get_initial_model()
if astype:
model.vp = x.astype(astype).reshape(model.vp.data.shape)
else:
model.vp = x.reshape(model.vp.data.shape)
return model
def load_model(filename):
""" Returns the current model. This is used by the
worker to get the current model.
"""
pkl = pickle.load(open(filename, "rb"))
return pkl['model']
def dump_model(filename, model):
''' Dump model to disk.
'''
pickle.dump({'model':model}, open(filename, "wb"))
def load_shot_data(shot_id, dt):
''' Load shot data from disk, resampling to the model time step.
'''
pkl = pickle.load(open("shot_%d.p"%shot_id, "rb"))
return pkl['geometry'].resample(dt), pkl['rec'].resample(dt)
def dump_shot_data(shot_id, rec, geometry):
''' Dump shot data to disk.
'''
pickle.dump({'rec':rec, 'geometry': geometry}, open('shot_%d.p'%shot_id, "wb"))
def generate_shotdata_i(param):
""" Inversion crime alert! Here the worker is creating the
'observed' data using the real model. For a real case
the worker would be reading seismic data from disk.
"""
true_model = get_true_model()
shot_id = param['shot_id']
src_coordinates = np.empty((1, len(param['shape'])))
src_coordinates[0, :] = [30, param['shot_id']*1000./(param['nshots']-1)]
# Number of receiver locations per shot.
nreceivers = 101
# Set up receiver data and geometry.
rec_coordinates = np.empty((nreceivers, len(param['shape'])))
rec_coordinates[:, 1] = np.linspace(0, true_model.domain_size[0], num=nreceivers)
rec_coordinates[:, 0] = 980. # 20m from the right end
# Geometry
geometry = AcquisitionGeometry(true_model, rec_coordinates, src_coordinates,
param['t0'], param['tn'], src_type='Ricker',
f0=param['f0'])
# Set up solver.
solver = AcousticWaveSolver(true_model, geometry, space_order=4)
# Generate synthetic receiver data from true model.
true_d, _, _ = solver.forward(vp=true_model.vp)
dump_shot_data(shot_id, true_d, geometry)
def generate_shotdata(param):
# Define work list
work = [dict(param) for i in range(param['nshots'])]
for i in range(param['nshots']):
work[i]['shot_id'] = i
generate_shotdata_i(work[i])
# Map worklist to cluster
futures = client.map(generate_shotdata_i, work)
# Wait for all futures
wait(futures)
#NBVAL_IGNORE_OUTPUT
# Start Dask cluster
cluster = LocalCluster(n_workers=2, death_timeout=600)
client = Client(cluster)
# Generate shot data.
generate_shotdata(param)
```
## Dask specifics
Previously we defined a function to calculate the individual contribution to the functional and gradient for each shot, which was then used in a loop over all shots. However, when using distributed frameworks such as Dask we instead think in terms of creating a worklist which gets *mapped* onto the worker pool. The sum reduction is also performed in parallel. For now however we assume that the scipy.optimize.minimize itself is running on the *master* process; this is a reasonable simplification because the computational cost of calculating (f, g) far exceeds the other compute costs.
Because we want to be able to use standard reduction operators such as sum on (f, g) we first define it as a type so that we can define the `__add__` (and `__rand__` method).
```
# Define a type to store the functional and gradient.
class fg_pair:
def __init__(self, f, g):
self.f = f
self.g = g
def __add__(self, other):
f = self.f + other.f
g = self.g + other.g
return fg_pair(f, g)
def __radd__(self, other):
if other == 0:
return self
else:
return self.__add__(other)
```
## Create operators for gradient based inversion
To perform the inversion we are going to use [scipy.optimize.minimize(method=’L-BFGS-B’)](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html#optimize-minimize-lbfgsb).
First we define the functional, ```f```, and gradient, ```g```, operator (i.e. the function ```fun```) for a single shot of data. This is the work that is going to be performed by the worker on a unit of data.
```
from devito import Function
# Create FWI gradient kernel for a single shot
def fwi_gradient_i(param):
# Load the current model and the shot data for this worker.
# Note, unlike the serial example the model is not passed in
# as an argument. Broadcasting large datasets is considered
# a programming anti-pattern and at the time of writing it
# it only worked relaiably with Dask master. Therefore, the
# the model is communicated via a file.
model0 = load_model(param['model'])
dt = model0.critical_dt
geometry, rec = load_shot_data(param['shot_id'], dt)
geometry.model = model0
# Set up solver.
solver = AcousticWaveSolver(model0, geometry, space_order=4)
# Compute simulated data and full forward wavefield u0
d, u0, _ = solver.forward(save=True)
# Compute the data misfit (residual) and objective function
residual = Receiver(name='rec', grid=model0.grid,
time_range=geometry.time_axis,
coordinates=geometry.rec_positions)
residual.data[:] = d.data[:residual.shape[0], :] - rec.data[:residual.shape[0], :]
f = .5*np.linalg.norm(residual.data.flatten())**2
# Compute gradient using the adjoint-state method. Note, this
# backpropagates the data misfit through the model.
grad = Function(name="grad", grid=model0.grid)
solver.gradient(rec=residual, u=u0, grad=grad)
# Copying here to avoid a (probably overzealous) destructor deleting
# the gradient before Dask has had a chance to communicate it.
g = np.array(grad.data[:])
# return the objective functional and gradient.
return fg_pair(f, g)
```
Define the global functional-gradient operator. This does the following:
* Maps the worklist (shots) to the workers so that the invidual contributions to (f, g) are computed.
* Sum individual contributions to (f, g) and returns the result.
```
def fwi_gradient(model, param):
# Dump a copy of the current model for the workers
# to pick up when they are ready.
param['model'] = "model_0.p"
dump_model(param['model'], wrap_model(model))
# Define work list
work = [dict(param) for i in range(param['nshots'])]
for i in range(param['nshots']):
work[i]['shot_id'] = i
# Distribute worklist to workers.
fgi = client.map(fwi_gradient_i, work, retries=1)
# Perform reduction.
fg = client.submit(sum, fgi).result()
# L-BFGS in scipy expects a flat array in 64-bit floats.
return fg.f, -fg.g.flatten().astype(np.float64)
```
## FWI with L-BFGS-B
Equipped with a function to calculate the functional and gradient, we are finally ready to define the optimization function.
```
from scipy import optimize
# Define bounding box constraints on the solution.
def apply_box_constraint(vp):
# Maximum possible 'realistic' velocity is 3.5 km/sec
# Minimum possible 'realistic' velocity is 2 km/sec
return np.clip(vp, 2.0, 3.5)
# Many optimization methods in scipy.optimize.minimize accept a callback
# function that can operate on the solution after every iteration. Here
# we use this to apply box constraints and to monitor the true relative
# solution error.
relative_error = []
def fwi_callbacks(x):
# Apply boundary constraint
x.data[:] = apply_box_constraint(x)
# Calculate true relative error
true_x = get_true_model().vp.data.flatten()
relative_error.append(np.linalg.norm((x-true_x)/true_x))
def fwi(model, param, ftol=0.1, maxiter=5):
result = optimize.minimize(fwi_gradient,
model.vp.data.flatten().astype(np.float64),
args=(param, ), method='L-BFGS-B', jac=True,
callback=fwi_callbacks,
options={'ftol':ftol,
'maxiter':maxiter,
'disp':True})
return result
```
We now apply our FWI function and have a look at the result.
```
#NBVAL_IGNORE_OUTPUT
model0 = get_initial_model()
# Baby steps
result = fwi(model0, param)
# Print out results of optimizer.
print(result)
#NBVAL_SKIP
# Show what the update does to the model
from examples.seismic import plot_image, plot_velocity
model0.vp = result.x.astype(np.float32).reshape(model0.vp.data.shape)
plot_velocity(model0)
#NBVAL_SKIP
# Plot percentage error
plot_image(100*np.abs(model0.vp.data-get_true_model().vp.data)/get_true_model().vp.data, vmax=15, cmap="hot")
#NBVAL_SKIP
import matplotlib.pyplot as plt
# Plot objective function decrease
plt.figure()
plt.loglog(relative_error)
plt.xlabel('Iteration number')
plt.ylabel('True relative error')
plt.title('Convergence')
plt.show()
```
<sup>This notebook is part of the tutorial "Optimised Symbolic Finite Difference Computation with Devito" presented at the Intel® HPC Developer Conference 2017.</sup>
|
github_jupyter
|
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
scipy.optimize.minimize(fun, x0, args=(), method='L-BFGS-B', jac=None, bounds=None, tol=None, callback=None, options={'disp': None, 'maxls': 20, 'iprint': -1, 'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000, 'ftol': 2.220446049250313e-09, 'maxcor': 10, 'maxfun': 15000})```
The argument `fun` is a callable function that returns the misfit between the simulated and the observed data. If `jac` is a Boolean and is `True`, `fun` is assumed to return the gradient along with the objective function - as is our case when applying the adjoint-state method.
## What is Dask?
> [Dask](https://dask.pydata.org/en/latest/#dask) is a flexible parallel computing library for analytic computing.
>
> Dask is composed of two components:
>
> * Dynamic task scheduling optimized for computation...
> * “Big Data” collections like parallel arrays, dataframes, and lists that extend common interfaces like NumPy, Pandas, or Python iterators to larger-than-memory or distributed environments. These parallel collections run on top of the dynamic task schedulers.
>
> Dask emphasizes the following virtues:
>
> * Familiar: Provides parallelized NumPy array and Pandas DataFrame objects
> * Flexible: Provides a task scheduling interface for more custom workloads and integration with other projects.
> * Native: Enables distributed computing in Pure Python with access to the PyData stack.
> * Fast: Operates with low overhead, low latency, and minimal serialization necessary for fast numerical algorithms
> * Scales up: Runs resiliently on clusters with 1000s of cores
> * Scales down: Trivial to set up and run on a laptop in a single process
> * Responsive: Designed with interactive computing in mind it provides rapid feedback and diagnostics to aid humans
**We are going to use it here to parallelise the computation of the functional and gradient as this is the vast bulk of the computational expense of FWI and it is trivially parallel over data shots.**
## Setting up (synthetic) data
In a real world scenario we work with collected seismic data; for the tutorial we know what the actual solution is and we are using the workers to also generate the synthetic data.
## Dask specifics
Previously we defined a function to calculate the individual contribution to the functional and gradient for each shot, which was then used in a loop over all shots. However, when using distributed frameworks such as Dask we instead think in terms of creating a worklist which gets *mapped* onto the worker pool. The sum reduction is also performed in parallel. For now however we assume that the scipy.optimize.minimize itself is running on the *master* process; this is a reasonable simplification because the computational cost of calculating (f, g) far exceeds the other compute costs.
Because we want to be able to use standard reduction operators such as sum on (f, g) we first define it as a type so that we can define the `__add__` (and `__rand__` method).
## Create operators for gradient based inversion
To perform the inversion we are going to use [scipy.optimize.minimize(method=’L-BFGS-B’)](https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html#optimize-minimize-lbfgsb).
First we define the functional, ```f```, and gradient, ```g```, operator (i.e. the function ```fun```) for a single shot of data. This is the work that is going to be performed by the worker on a unit of data.
Define the global functional-gradient operator. This does the following:
* Maps the worklist (shots) to the workers so that the invidual contributions to (f, g) are computed.
* Sum individual contributions to (f, g) and returns the result.
## FWI with L-BFGS-B
Equipped with a function to calculate the functional and gradient, we are finally ready to define the optimization function.
We now apply our FWI function and have a look at the result.
| 0.857231 | 0.968081 |
# Code
**Date: February, 2017**
```
%matplotlib inline
import numpy as np
import scipy as sp
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# For linear regression
from scipy.stats import multivariate_normal
from scipy.integrate import dblquad
# Shut down warnings for nicer output
import warnings
warnings.filterwarnings('ignore')
colors = sns.color_palette()
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
```
**Coin tossing example**
```
#===================================================
# FUNCTIONS
#===================================================
def relative_entropy(theta0, a):
return theta0 * np.log(theta0/a) + (1 - theta0) * np.log((1 - theta0)/(1 - a))
def quadratic_loss(theta0, a):
return (a - theta0)**2
def loss_distribution(l, dr, loss, true_dist, theta0, y_grid):
"""
Uses the formula for the change of discrete random variable. It takes care of the
fact that relative entropy is not monotone.
"""
eps = 1e-16
if loss == 'relative_entropy':
a1 = sp.optimize.bisect(lambda a: relative_entropy(theta0, a) - l, a = eps, b = theta0)
a2 = sp.optimize.bisect(lambda a: relative_entropy(theta0, a) - l, a = theta0, b = 1 - eps)
elif loss == 'quadratic':
a1 = theta0 - np.sqrt(l)
a2 = theta0 + np.sqrt(l)
if np.isclose(a1, dr).any():
y1 = y_grid[np.isclose(a1, dr)][0]
prob1 = true_dist.pmf(y1)
else:
prob1 = 0.0
if np.isclose(a2, dr).any():
y2 = y_grid[np.isclose(a2, dr)][0]
prob2 = true_dist.pmf(y2)
else:
prob2 = 0.0
if np.isclose(a1, a2):
# around zero loss, the two sides might find the same a
return prob1
else:
return prob1 + prob2
def risk_quadratic(theta0, n, alpha=0, beta=0):
"""
See Casella and Berger, p.332
"""
first_term = n * theta0 * (1 - theta0)/(alpha + beta + n)**2
second_term = ((n * theta0 + alpha)/(alpha + beta + n) - theta0)**2
return first_term + second_term
def loss_figures(theta0, n, alpha, beta, mle=True, entropy=True):
true_dist = stats.binom(n, theta0)
y_grid = np.arange(n + 1) # sum of ones in a sample
a_grid = np.linspace(0, 1, 100) # action space represented as [0, 1]
# The two decision functions (as a function of Y)
decision_rule = y_grid/n
decision_rule_bayes = (y_grid + alpha)/(n + alpha + beta)
if mle and entropy:
"""
MLE with relative entropy loss
"""
loss = relative_entropy(theta0, decision_rule)
loss_dist = np.asarray([loss_distribution(i, decision_rule, "relative_entropy",
true_dist, theta0,
y_grid) for i in loss[1:-1]])
loss_dist = np.hstack([true_dist.pmf(y_grid[0]), loss_dist, true_dist.pmf(y_grid[-1])])
risk = loss @ loss_dist
elif mle and not entropy:
"""
MLE with quadratic loss
"""
loss = quadratic_loss(theta0, decision_rule)
loss_dist = np.asarray([loss_distribution(i, decision_rule, "quadratic",
true_dist, theta0,
y_grid) for i in loss])
risk = risk_quadratic(theta0, n)
elif not mle and entropy:
"""
Bayes with realtive entropy loss
"""
loss = relative_entropy(theta0, decision_rule_bayes)
loss_dist = np.asarray([loss_distribution(i, decision_rule_bayes, "relative_entropy",
true_dist, theta0, y_grid) for i in loss])
risk = loss @ loss_dist
elif not mle and not entropy:
"""
Bayes with quadratic loss
"""
loss = quadratic_loss(theta0, decision_rule_bayes)
loss_dist = np.asarray([loss_distribution(i, decision_rule_bayes, "quadratic",
true_dist, theta0, y_grid) for i in loss])
risk = risk_quadratic(theta0, n, alpha, beta)
return loss, loss_dist, risk
theta0 = .79
n = 25
alpha, beta = 7, 2
#=========================
# Elements of Figure 1
#=========================
true_dist = stats.binom(n, theta0)
y_grid = np.arange(n + 1) # sum of ones in a sample
a_grid = np.linspace(0, 1, 100) # action space represented as [0, 1]
rel_ent = relative_entropy(theta0, a_grid) # form of the loss function
quadratic = quadratic_loss(theta0, a_grid) # form of the loss function
#=========================
# Elements of Figure 2
#=========================
theta0_alt = .39
true_dist_alt = stats.binom(n, theta0_alt)
# The two decision functions (as a function of Y)
decision_rule = y_grid/n
decision_rule_bayes = (y_grid + alpha)/(n + alpha + beta)
#=========================
# Elements of Figure 3
#=========================
loss_re_mle, loss_dist_re_mle, risk_re_mle = loss_figures(theta0, n, alpha, beta)
loss_quad_mle, loss_dist_quad_mle, risk_quad_mle = loss_figures(theta0, n, alpha, beta,
entropy=False)
loss_re_bayes, loss_dist_re_bayes, risk_re_bayes = loss_figures(theta0, n, alpha, beta,
mle=False)
loss_quad_bayes, loss_dist_quad_bayes, risk_quad_bayes = loss_figures(theta0, n, alpha, beta,
mle=False, entropy=False)
loss_re_mle_alt, loss_dist_re_mle_alt, risk_re_mle_alt = loss_figures(theta0_alt,
n, alpha, beta)
loss_quad_mle_alt, loss_dist_quad_mle_alt, risk_quad_mle_alt = loss_figures(theta0_alt, n,
alpha, beta, entropy=False)
loss_re_bayes_alt, loss_dist_re_bayes_alt, risk_re_bayes_alt = loss_figures(theta0_alt, n,
alpha, beta, mle=False)
loss_quad_bayes_alt, loss_dist_quad_bayes_alt, risk_quad_bayes_alt = loss_figures(theta0_alt,
n, alpha, beta,
mle=False, entropy=False)
fig, ax = plt.subplots(1, 2, figsize = (12, 4))
ax[0].set_title('True distribution over Y', fontsize = 14)
ax[0].plot(y_grid, true_dist.pmf(y_grid), 'o', color = sns.color_palette()[3])
ax[0].vlines(y_grid, 0, true_dist.pmf(y_grid), lw = 4, color = sns.color_palette()[3], alpha = .7)
ax[0].set_xlabel(r'Number of ones in the sample', fontsize = 12)
ax[1].set_title('Loss functions over the action space', fontsize = 14)
ax[1].plot(a_grid, rel_ent, lw = 2, label = 'relative entropy loss')
ax[1].plot(a_grid, quadratic, lw = 2, label = 'quadratic loss')
ax[1].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
ax[1].legend(loc = 'best', fontsize = 12)
ax[1].set_xlabel(r'Actions $(a)$', fontsize = 12)
plt.tight_layout()
plt.savefig("./example1_fig1.png", dpi=800)
fig, ax = plt.subplots(1, 2, figsize = (12, 4))
ax[0].set_title('Induced action distribution of the MLE estimator', fontsize = 14)
# Small bias
ax[0].plot(decision_rule, true_dist.pmf(y_grid), 'o')
ax[0].vlines(decision_rule, 0, true_dist.pmf(y_grid), lw = 5, alpha = .9, color = sns.color_palette()[0])
ax[0].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
# Large bias for Bayes
ax[0].plot(decision_rule, true_dist_alt.pmf(y_grid), 'o', color = sns.color_palette()[0], alpha = .4)
ax[0].vlines(decision_rule, 0, true_dist_alt.pmf(y_grid), lw = 4, alpha = .4, color = sns.color_palette()[0])
ax[0].axvline(theta0_alt, color = sns.color_palette()[2], lw = 2, alpha = .4,
label = r'$\theta=${t}'.format(t=theta0_alt))
ax[0].legend(loc = 'best', fontsize = 12)
ax[0].set_ylim([0, .2])
ax[0].set_xlim([0, 1])
ax[0].set_xlabel(r'Actions $(a)$', fontsize = 12)
ax[1].set_title('Induced action distribution of the Bayes estimator', fontsize = 14)
# Small bias
ax[1].plot(decision_rule_bayes, true_dist.pmf(y_grid), 'o', color = sns.color_palette()[1])
ax[1].vlines(decision_rule_bayes, 0, true_dist.pmf(y_grid), lw = 5, alpha = .9,
color = sns.color_palette()[1])
ax[1].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
# Large bias for Bayes
ax[1].plot(decision_rule_bayes, true_dist_alt.pmf(y_grid), 'o', color = sns.color_palette()[1], alpha = .4)
ax[1].vlines(decision_rule_bayes, 0, true_dist_alt.pmf(y_grid), lw = 4, alpha = .4,
color = sns.color_palette()[1])
ax[1].axvline(theta0_alt, color = sns.color_palette()[2], lw = 2, alpha = .4,
label = r'$\theta=${t}'.format(t=theta0_alt))
ax[1].legend(loc = 'best', fontsize = 12)
ax[1].set_ylim([0, .2])
ax[1].set_xlim([0, 1])
ax[1].set_xlabel(r'Actions $(a)$', fontsize = 12)
plt.tight_layout()
plt.savefig("./example1_fig2.png", dpi=800)
fig, ax = plt.subplots(2, 2, figsize = (12, 6))
ax[0, 0].set_title('Induced entropy loss distribution (MLE estimator)', fontsize = 14)
ax[0, 0].vlines(loss_re_mle, 0, loss_dist_re_mle, lw = 9, alpha = .9, color = sns.color_palette()[0])
ax[0, 0].axvline(risk_re_mle, lw = 3, linestyle = '--',
color = sns.color_palette()[0], label = r"Entropy risk ($\theta_0={t}$)".format(t=theta0))
ax[0, 0].vlines(loss_re_mle_alt, 0, loss_dist_re_mle_alt, lw = 9, alpha = .3, color = sns.color_palette()[0])
ax[0, 0].axvline(risk_re_mle_alt, lw = 3, linestyle = '--', alpha = .4,
color = sns.color_palette()[0], label = r"Entropy risk ($\theta={t}$)".format(t=theta0_alt))
ax[0, 0].set_xlim([0, .1])
ax[0, 0].set_ylim([0, .2])
ax[0, 0].set_xlabel('Loss', fontsize=12)
ax[0, 0].legend(loc = 'best', fontsize = 12)
ax[1, 0].set_title('Induced entropy loss distribution (Bayes estimator)', fontsize=14)
ax[1, 0].vlines(loss_re_bayes, 0, loss_dist_re_bayes, lw=9, alpha=.9, color=sns.color_palette()[1])
ax[1, 0].axvline(risk_re_bayes, lw=3, linestyle='--',
color = sns.color_palette()[1], label=r"Entropy risk ($\theta_0={t}$)".format(t=theta0))
ax[1, 0].vlines(loss_re_bayes_alt, 0, loss_dist_re_bayes_alt, lw=9, alpha=.3, color=sns.color_palette()[1])
ax[1, 0].axvline(risk_re_bayes_alt, lw=3, linestyle='--', alpha=.4, color=sns.color_palette()[1],
label=r"Entropy risk ($\theta={t}$)".format(t=theta0_alt))
ax[1, 0].set_xlim([0, .1])
ax[1, 0].set_ylim([0, .2])
ax[1, 0].set_xlabel('Loss')
ax[1, 0].legend(loc='best', fontsize=12)
ax[0, 1].set_title('Induced quadratic loss distribution (MLE estimator)', fontsize=14)
ax[0, 1].vlines(loss_quad_mle, 0, loss_dist_quad_mle, lw=9, alpha=.9, color=sns.color_palette()[0])
ax[0, 1].axvline(risk_quad_mle, lw=3, linestyle='--',
color = sns.color_palette()[0], label=r"Quadratic risk ($\theta_0={t}$)".format(t=theta0))
ax[0, 1].vlines(loss_quad_mle_alt, 0, loss_dist_quad_mle_alt, lw=9, alpha=.3, color=sns.color_palette()[0])
ax[0, 1].axvline(risk_quad_mle_alt, lw=3, linestyle='--', alpha=.4,
color=sns.color_palette()[0], label=r"Quadratic risk ($\theta={t}$)".format(t=theta0_alt))
ax[0, 1].set_xlim([0, .05])
ax[0, 1].set_ylim([0, .2])
ax[0, 1].set_xlabel('Loss', fontsize=12)
ax[0, 1].legend(loc='best', fontsize=12)
ax[1, 1].set_title('Induced quadratic loss distribution (Bayes estimator)', fontsize=14)
ax[1, 1].vlines(loss_quad_bayes, 0, loss_dist_quad_bayes, lw=9, alpha=.9, color=sns.color_palette()[1])
ax[1, 1].axvline(risk_quad_bayes, lw=3, linestyle='--',
color = sns.color_palette()[1], label=r"Quadratic risk ($\theta_0={t}$)".format(t=theta0))
ax[1, 1].vlines(loss_quad_bayes_alt, 0, loss_dist_quad_bayes_alt, lw=9, alpha=.3, color=sns.color_palette()[1])
ax[1, 1].axvline(risk_quad_bayes_alt, lw=3, linestyle = '--', alpha=.4,
color=sns.color_palette()[1], label=r"Quadratic risk ($\theta={t}$)".format(t=theta0_alt))
ax[1, 1].set_xlim([0, .05])
ax[1, 1].set_ylim([0, .2])
ax[1, 1].set_xlabel('Loss', fontsize=12)
ax[1, 1].legend(loc='best', fontsize=12)
plt.tight_layout()
plt.savefig("./example1_fig3.png", dpi=800)
```
**Bayes OLS example**
```
mu = np.array([1, 3]) # mean
sigma = np.array([[4, 1], [1, 8]]) # covariance matrix
n = 50 # sample size
# Bayes priors
mu_bayes = np.array([2, 2])
precis_bayes = np.array([[6, -3], [-3, 6]])
# joint normal rv for (Y,X)
mvnorm = multivariate_normal(mu, sigma)
# decision rule -- OLS estimator
def d_OLS(Z, n):
Y = Z[:, 0]
X = np.stack((np.ones(n), Z[:,1]), axis=-1)
return np.linalg.inv(X.T @ X) @ X.T @ Y
# decision rule -- Bayes
def d_bayes(Z, n):
Y = Z[:, 0]
X = np.stack((np.ones(n), Z[:,1]), axis=-1)
return np.linalg.inv(X.T @ X + precis_bayes) @ (precis_bayes @ mu_bayes + X.T @ Y)
# loss -- define integrand
def loss_int(y, x, b):
'''Defines the integrand under mvnorm distribution.'''
return (y - b[0] - b[1]*x)**2*mvnorm.pdf((y,x))
# simulate distribution over actions and over losses
B_OLS = []
L_OLS = []
B_bayes = []
L_bayes = []
for i in range(1000):
# generate sample
Z = mvnorm.rvs(n)
# get OLS action corrsponding to realized sample
b_OLS = d_OLS(Z, n)
# get Bayes action
b_bayes = d_bayes(Z, n)
# get loss through integration
l_OLS = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_OLS,)) # get loss
l_bayes = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_bayes,)) # get loss
# record action
B_OLS.append(b_OLS)
B_bayes.append(b_bayes)
# record loss
L_OLS.append(l_OLS)
L_bayes.append(l_bayes)
# take first column if integrating
L_OLS = np.array(L_OLS)[:, 0]
L_bayes = np.array(L_bayes)[:, 0]
B_OLS = pd.DataFrame(B_OLS, columns=["$\\beta_0$", "$\\beta_1$"])
B_bayes = pd.DataFrame(B_bayes, columns=["$\\beta_0$", "$\\beta_1$"])
g1 = sns.jointplot(x = "$\\beta_0$", y = "$\\beta_1$", data=B_OLS, kind="kde",
space=0.3, color = sns.color_palette()[0], size=5, xlim = (-.5, 1.6), ylim = (-.1, .4))
g1.ax_joint.plot([mu[0] - sigma[0,1]/sigma[1,1]*mu[1]],[sigma[0,1]/sigma[1,1]], 'ro', color='r', label='best-in-class')
g1.set_axis_labels(r'$\beta_0$', r'$\beta_1$', fontsize=14)
g1.fig.suptitle('Induced action distribution -- OLS', fontsize=14, y=1.04)
plt.savefig("./example2_fig1a.png", dpi=800)
g2 = sns.jointplot(x = "$\\beta_0$", y = "$\\beta_1$", data=B_bayes, kind="kde",
space=0.3, color = sns.color_palette()[0], size=5, xlim = (-.5, 1.6), ylim = (-.1, .4))
g2.ax_joint.plot([mu[0] - sigma[0,1]/sigma[1,1]*mu[1]],[sigma[0,1]/sigma[1,1]], 'ro', color='r', label='best-in-class')
g2.set_axis_labels(r'$\beta_0$', r'$\beta_1$', fontsize=14)
g2.fig.suptitle('Induced action distribution -- Bayes', fontsize=14, y=1.04)
plt.savefig("./example2_fig1b.png", dpi=800)
plt.show()
b_best = [mu[0] - sigma[0,1]/sigma[1,1]*mu[1], sigma[0,1]/sigma[1,1]]
l_best = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_best,))
print(l_best[0])
plt.figure(figsize=(11, 5))
plt.axvline(x=l_best[0], ymin=0, ymax=1, linewidth=3, color = colors[4], label='Best-in-class loss')
plt.axvline(x=L_OLS.mean(), ymin=0, ymax=1, linewidth=3, color = colors[2], label='Risk of OLS')
plt.axvline(x=L_bayes.mean(), ymin=0, ymax=1, linewidth=3, color = colors[3], label='Risk of Bayes')
sns.distplot(L_OLS, bins=50, kde=False, color = colors[0], label='OLS')
sns.distplot(L_bayes, bins=50, kde=False, color = colors[1], label='Bayes')
plt.title('Induced loss distribution', fontsize = 14, y=1.02)
plt.legend(fontsize=12)
plt.xlabel('Loss', fontsize=12)
plt.xlim([3.8, 4.5])
plt.tight_layout()
plt.savefig("./example2_fig2.png", dpi=800)
beta_0 = mu[0] - sigma[0,1]/sigma[1,1]*mu[1]
beta_1 = sigma[0,1]/sigma[1,1]
print('Bias of OLS')
print('==========================')
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_0, B_OLS.mean()[0], beta_0 - B_OLS.mean()[0]))
print('{:.4f} - {:.4f} = {:.4f}\n\n'.format(beta_1, B_OLS.mean()[1], beta_1 - B_OLS.mean()[1]))
print('Bias of Bayes')
print('==========================')
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_0, B_bayes.mean()[0], beta_0 - B_bayes.mean()[0]))
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_1, B_bayes.mean()[1], beta_1 - B_bayes.mean()[1]))
print('Variance of OLS')
print('======================')
print(B_OLS.var())
print('\n\nVarinace of Bayes')
print('======================')
print(B_bayes.var())
print('Risk of OLS: {:.4f} \nRisk of Bayes: {:.4f}'.format(L_OLS.mean(), L_bayes.mean()))
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import scipy as sp
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# For linear regression
from scipy.stats import multivariate_normal
from scipy.integrate import dblquad
# Shut down warnings for nicer output
import warnings
warnings.filterwarnings('ignore')
colors = sns.color_palette()
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
#===================================================
# FUNCTIONS
#===================================================
def relative_entropy(theta0, a):
return theta0 * np.log(theta0/a) + (1 - theta0) * np.log((1 - theta0)/(1 - a))
def quadratic_loss(theta0, a):
return (a - theta0)**2
def loss_distribution(l, dr, loss, true_dist, theta0, y_grid):
"""
Uses the formula for the change of discrete random variable. It takes care of the
fact that relative entropy is not monotone.
"""
eps = 1e-16
if loss == 'relative_entropy':
a1 = sp.optimize.bisect(lambda a: relative_entropy(theta0, a) - l, a = eps, b = theta0)
a2 = sp.optimize.bisect(lambda a: relative_entropy(theta0, a) - l, a = theta0, b = 1 - eps)
elif loss == 'quadratic':
a1 = theta0 - np.sqrt(l)
a2 = theta0 + np.sqrt(l)
if np.isclose(a1, dr).any():
y1 = y_grid[np.isclose(a1, dr)][0]
prob1 = true_dist.pmf(y1)
else:
prob1 = 0.0
if np.isclose(a2, dr).any():
y2 = y_grid[np.isclose(a2, dr)][0]
prob2 = true_dist.pmf(y2)
else:
prob2 = 0.0
if np.isclose(a1, a2):
# around zero loss, the two sides might find the same a
return prob1
else:
return prob1 + prob2
def risk_quadratic(theta0, n, alpha=0, beta=0):
"""
See Casella and Berger, p.332
"""
first_term = n * theta0 * (1 - theta0)/(alpha + beta + n)**2
second_term = ((n * theta0 + alpha)/(alpha + beta + n) - theta0)**2
return first_term + second_term
def loss_figures(theta0, n, alpha, beta, mle=True, entropy=True):
true_dist = stats.binom(n, theta0)
y_grid = np.arange(n + 1) # sum of ones in a sample
a_grid = np.linspace(0, 1, 100) # action space represented as [0, 1]
# The two decision functions (as a function of Y)
decision_rule = y_grid/n
decision_rule_bayes = (y_grid + alpha)/(n + alpha + beta)
if mle and entropy:
"""
MLE with relative entropy loss
"""
loss = relative_entropy(theta0, decision_rule)
loss_dist = np.asarray([loss_distribution(i, decision_rule, "relative_entropy",
true_dist, theta0,
y_grid) for i in loss[1:-1]])
loss_dist = np.hstack([true_dist.pmf(y_grid[0]), loss_dist, true_dist.pmf(y_grid[-1])])
risk = loss @ loss_dist
elif mle and not entropy:
"""
MLE with quadratic loss
"""
loss = quadratic_loss(theta0, decision_rule)
loss_dist = np.asarray([loss_distribution(i, decision_rule, "quadratic",
true_dist, theta0,
y_grid) for i in loss])
risk = risk_quadratic(theta0, n)
elif not mle and entropy:
"""
Bayes with realtive entropy loss
"""
loss = relative_entropy(theta0, decision_rule_bayes)
loss_dist = np.asarray([loss_distribution(i, decision_rule_bayes, "relative_entropy",
true_dist, theta0, y_grid) for i in loss])
risk = loss @ loss_dist
elif not mle and not entropy:
"""
Bayes with quadratic loss
"""
loss = quadratic_loss(theta0, decision_rule_bayes)
loss_dist = np.asarray([loss_distribution(i, decision_rule_bayes, "quadratic",
true_dist, theta0, y_grid) for i in loss])
risk = risk_quadratic(theta0, n, alpha, beta)
return loss, loss_dist, risk
theta0 = .79
n = 25
alpha, beta = 7, 2
#=========================
# Elements of Figure 1
#=========================
true_dist = stats.binom(n, theta0)
y_grid = np.arange(n + 1) # sum of ones in a sample
a_grid = np.linspace(0, 1, 100) # action space represented as [0, 1]
rel_ent = relative_entropy(theta0, a_grid) # form of the loss function
quadratic = quadratic_loss(theta0, a_grid) # form of the loss function
#=========================
# Elements of Figure 2
#=========================
theta0_alt = .39
true_dist_alt = stats.binom(n, theta0_alt)
# The two decision functions (as a function of Y)
decision_rule = y_grid/n
decision_rule_bayes = (y_grid + alpha)/(n + alpha + beta)
#=========================
# Elements of Figure 3
#=========================
loss_re_mle, loss_dist_re_mle, risk_re_mle = loss_figures(theta0, n, alpha, beta)
loss_quad_mle, loss_dist_quad_mle, risk_quad_mle = loss_figures(theta0, n, alpha, beta,
entropy=False)
loss_re_bayes, loss_dist_re_bayes, risk_re_bayes = loss_figures(theta0, n, alpha, beta,
mle=False)
loss_quad_bayes, loss_dist_quad_bayes, risk_quad_bayes = loss_figures(theta0, n, alpha, beta,
mle=False, entropy=False)
loss_re_mle_alt, loss_dist_re_mle_alt, risk_re_mle_alt = loss_figures(theta0_alt,
n, alpha, beta)
loss_quad_mle_alt, loss_dist_quad_mle_alt, risk_quad_mle_alt = loss_figures(theta0_alt, n,
alpha, beta, entropy=False)
loss_re_bayes_alt, loss_dist_re_bayes_alt, risk_re_bayes_alt = loss_figures(theta0_alt, n,
alpha, beta, mle=False)
loss_quad_bayes_alt, loss_dist_quad_bayes_alt, risk_quad_bayes_alt = loss_figures(theta0_alt,
n, alpha, beta,
mle=False, entropy=False)
fig, ax = plt.subplots(1, 2, figsize = (12, 4))
ax[0].set_title('True distribution over Y', fontsize = 14)
ax[0].plot(y_grid, true_dist.pmf(y_grid), 'o', color = sns.color_palette()[3])
ax[0].vlines(y_grid, 0, true_dist.pmf(y_grid), lw = 4, color = sns.color_palette()[3], alpha = .7)
ax[0].set_xlabel(r'Number of ones in the sample', fontsize = 12)
ax[1].set_title('Loss functions over the action space', fontsize = 14)
ax[1].plot(a_grid, rel_ent, lw = 2, label = 'relative entropy loss')
ax[1].plot(a_grid, quadratic, lw = 2, label = 'quadratic loss')
ax[1].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
ax[1].legend(loc = 'best', fontsize = 12)
ax[1].set_xlabel(r'Actions $(a)$', fontsize = 12)
plt.tight_layout()
plt.savefig("./example1_fig1.png", dpi=800)
fig, ax = plt.subplots(1, 2, figsize = (12, 4))
ax[0].set_title('Induced action distribution of the MLE estimator', fontsize = 14)
# Small bias
ax[0].plot(decision_rule, true_dist.pmf(y_grid), 'o')
ax[0].vlines(decision_rule, 0, true_dist.pmf(y_grid), lw = 5, alpha = .9, color = sns.color_palette()[0])
ax[0].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
# Large bias for Bayes
ax[0].plot(decision_rule, true_dist_alt.pmf(y_grid), 'o', color = sns.color_palette()[0], alpha = .4)
ax[0].vlines(decision_rule, 0, true_dist_alt.pmf(y_grid), lw = 4, alpha = .4, color = sns.color_palette()[0])
ax[0].axvline(theta0_alt, color = sns.color_palette()[2], lw = 2, alpha = .4,
label = r'$\theta=${t}'.format(t=theta0_alt))
ax[0].legend(loc = 'best', fontsize = 12)
ax[0].set_ylim([0, .2])
ax[0].set_xlim([0, 1])
ax[0].set_xlabel(r'Actions $(a)$', fontsize = 12)
ax[1].set_title('Induced action distribution of the Bayes estimator', fontsize = 14)
# Small bias
ax[1].plot(decision_rule_bayes, true_dist.pmf(y_grid), 'o', color = sns.color_palette()[1])
ax[1].vlines(decision_rule_bayes, 0, true_dist.pmf(y_grid), lw = 5, alpha = .9,
color = sns.color_palette()[1])
ax[1].axvline(theta0, color = sns.color_palette()[2], lw = 2, label = r'$\theta_0=${t}'.format(t=theta0))
# Large bias for Bayes
ax[1].plot(decision_rule_bayes, true_dist_alt.pmf(y_grid), 'o', color = sns.color_palette()[1], alpha = .4)
ax[1].vlines(decision_rule_bayes, 0, true_dist_alt.pmf(y_grid), lw = 4, alpha = .4,
color = sns.color_palette()[1])
ax[1].axvline(theta0_alt, color = sns.color_palette()[2], lw = 2, alpha = .4,
label = r'$\theta=${t}'.format(t=theta0_alt))
ax[1].legend(loc = 'best', fontsize = 12)
ax[1].set_ylim([0, .2])
ax[1].set_xlim([0, 1])
ax[1].set_xlabel(r'Actions $(a)$', fontsize = 12)
plt.tight_layout()
plt.savefig("./example1_fig2.png", dpi=800)
fig, ax = plt.subplots(2, 2, figsize = (12, 6))
ax[0, 0].set_title('Induced entropy loss distribution (MLE estimator)', fontsize = 14)
ax[0, 0].vlines(loss_re_mle, 0, loss_dist_re_mle, lw = 9, alpha = .9, color = sns.color_palette()[0])
ax[0, 0].axvline(risk_re_mle, lw = 3, linestyle = '--',
color = sns.color_palette()[0], label = r"Entropy risk ($\theta_0={t}$)".format(t=theta0))
ax[0, 0].vlines(loss_re_mle_alt, 0, loss_dist_re_mle_alt, lw = 9, alpha = .3, color = sns.color_palette()[0])
ax[0, 0].axvline(risk_re_mle_alt, lw = 3, linestyle = '--', alpha = .4,
color = sns.color_palette()[0], label = r"Entropy risk ($\theta={t}$)".format(t=theta0_alt))
ax[0, 0].set_xlim([0, .1])
ax[0, 0].set_ylim([0, .2])
ax[0, 0].set_xlabel('Loss', fontsize=12)
ax[0, 0].legend(loc = 'best', fontsize = 12)
ax[1, 0].set_title('Induced entropy loss distribution (Bayes estimator)', fontsize=14)
ax[1, 0].vlines(loss_re_bayes, 0, loss_dist_re_bayes, lw=9, alpha=.9, color=sns.color_palette()[1])
ax[1, 0].axvline(risk_re_bayes, lw=3, linestyle='--',
color = sns.color_palette()[1], label=r"Entropy risk ($\theta_0={t}$)".format(t=theta0))
ax[1, 0].vlines(loss_re_bayes_alt, 0, loss_dist_re_bayes_alt, lw=9, alpha=.3, color=sns.color_palette()[1])
ax[1, 0].axvline(risk_re_bayes_alt, lw=3, linestyle='--', alpha=.4, color=sns.color_palette()[1],
label=r"Entropy risk ($\theta={t}$)".format(t=theta0_alt))
ax[1, 0].set_xlim([0, .1])
ax[1, 0].set_ylim([0, .2])
ax[1, 0].set_xlabel('Loss')
ax[1, 0].legend(loc='best', fontsize=12)
ax[0, 1].set_title('Induced quadratic loss distribution (MLE estimator)', fontsize=14)
ax[0, 1].vlines(loss_quad_mle, 0, loss_dist_quad_mle, lw=9, alpha=.9, color=sns.color_palette()[0])
ax[0, 1].axvline(risk_quad_mle, lw=3, linestyle='--',
color = sns.color_palette()[0], label=r"Quadratic risk ($\theta_0={t}$)".format(t=theta0))
ax[0, 1].vlines(loss_quad_mle_alt, 0, loss_dist_quad_mle_alt, lw=9, alpha=.3, color=sns.color_palette()[0])
ax[0, 1].axvline(risk_quad_mle_alt, lw=3, linestyle='--', alpha=.4,
color=sns.color_palette()[0], label=r"Quadratic risk ($\theta={t}$)".format(t=theta0_alt))
ax[0, 1].set_xlim([0, .05])
ax[0, 1].set_ylim([0, .2])
ax[0, 1].set_xlabel('Loss', fontsize=12)
ax[0, 1].legend(loc='best', fontsize=12)
ax[1, 1].set_title('Induced quadratic loss distribution (Bayes estimator)', fontsize=14)
ax[1, 1].vlines(loss_quad_bayes, 0, loss_dist_quad_bayes, lw=9, alpha=.9, color=sns.color_palette()[1])
ax[1, 1].axvline(risk_quad_bayes, lw=3, linestyle='--',
color = sns.color_palette()[1], label=r"Quadratic risk ($\theta_0={t}$)".format(t=theta0))
ax[1, 1].vlines(loss_quad_bayes_alt, 0, loss_dist_quad_bayes_alt, lw=9, alpha=.3, color=sns.color_palette()[1])
ax[1, 1].axvline(risk_quad_bayes_alt, lw=3, linestyle = '--', alpha=.4,
color=sns.color_palette()[1], label=r"Quadratic risk ($\theta={t}$)".format(t=theta0_alt))
ax[1, 1].set_xlim([0, .05])
ax[1, 1].set_ylim([0, .2])
ax[1, 1].set_xlabel('Loss', fontsize=12)
ax[1, 1].legend(loc='best', fontsize=12)
plt.tight_layout()
plt.savefig("./example1_fig3.png", dpi=800)
mu = np.array([1, 3]) # mean
sigma = np.array([[4, 1], [1, 8]]) # covariance matrix
n = 50 # sample size
# Bayes priors
mu_bayes = np.array([2, 2])
precis_bayes = np.array([[6, -3], [-3, 6]])
# joint normal rv for (Y,X)
mvnorm = multivariate_normal(mu, sigma)
# decision rule -- OLS estimator
def d_OLS(Z, n):
Y = Z[:, 0]
X = np.stack((np.ones(n), Z[:,1]), axis=-1)
return np.linalg.inv(X.T @ X) @ X.T @ Y
# decision rule -- Bayes
def d_bayes(Z, n):
Y = Z[:, 0]
X = np.stack((np.ones(n), Z[:,1]), axis=-1)
return np.linalg.inv(X.T @ X + precis_bayes) @ (precis_bayes @ mu_bayes + X.T @ Y)
# loss -- define integrand
def loss_int(y, x, b):
'''Defines the integrand under mvnorm distribution.'''
return (y - b[0] - b[1]*x)**2*mvnorm.pdf((y,x))
# simulate distribution over actions and over losses
B_OLS = []
L_OLS = []
B_bayes = []
L_bayes = []
for i in range(1000):
# generate sample
Z = mvnorm.rvs(n)
# get OLS action corrsponding to realized sample
b_OLS = d_OLS(Z, n)
# get Bayes action
b_bayes = d_bayes(Z, n)
# get loss through integration
l_OLS = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_OLS,)) # get loss
l_bayes = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_bayes,)) # get loss
# record action
B_OLS.append(b_OLS)
B_bayes.append(b_bayes)
# record loss
L_OLS.append(l_OLS)
L_bayes.append(l_bayes)
# take first column if integrating
L_OLS = np.array(L_OLS)[:, 0]
L_bayes = np.array(L_bayes)[:, 0]
B_OLS = pd.DataFrame(B_OLS, columns=["$\\beta_0$", "$\\beta_1$"])
B_bayes = pd.DataFrame(B_bayes, columns=["$\\beta_0$", "$\\beta_1$"])
g1 = sns.jointplot(x = "$\\beta_0$", y = "$\\beta_1$", data=B_OLS, kind="kde",
space=0.3, color = sns.color_palette()[0], size=5, xlim = (-.5, 1.6), ylim = (-.1, .4))
g1.ax_joint.plot([mu[0] - sigma[0,1]/sigma[1,1]*mu[1]],[sigma[0,1]/sigma[1,1]], 'ro', color='r', label='best-in-class')
g1.set_axis_labels(r'$\beta_0$', r'$\beta_1$', fontsize=14)
g1.fig.suptitle('Induced action distribution -- OLS', fontsize=14, y=1.04)
plt.savefig("./example2_fig1a.png", dpi=800)
g2 = sns.jointplot(x = "$\\beta_0$", y = "$\\beta_1$", data=B_bayes, kind="kde",
space=0.3, color = sns.color_palette()[0], size=5, xlim = (-.5, 1.6), ylim = (-.1, .4))
g2.ax_joint.plot([mu[0] - sigma[0,1]/sigma[1,1]*mu[1]],[sigma[0,1]/sigma[1,1]], 'ro', color='r', label='best-in-class')
g2.set_axis_labels(r'$\beta_0$', r'$\beta_1$', fontsize=14)
g2.fig.suptitle('Induced action distribution -- Bayes', fontsize=14, y=1.04)
plt.savefig("./example2_fig1b.png", dpi=800)
plt.show()
b_best = [mu[0] - sigma[0,1]/sigma[1,1]*mu[1], sigma[0,1]/sigma[1,1]]
l_best = dblquad(loss_int, -np.inf, np.inf, lambda x: -np.inf, lambda x: np.inf, args=(b_best,))
print(l_best[0])
plt.figure(figsize=(11, 5))
plt.axvline(x=l_best[0], ymin=0, ymax=1, linewidth=3, color = colors[4], label='Best-in-class loss')
plt.axvline(x=L_OLS.mean(), ymin=0, ymax=1, linewidth=3, color = colors[2], label='Risk of OLS')
plt.axvline(x=L_bayes.mean(), ymin=0, ymax=1, linewidth=3, color = colors[3], label='Risk of Bayes')
sns.distplot(L_OLS, bins=50, kde=False, color = colors[0], label='OLS')
sns.distplot(L_bayes, bins=50, kde=False, color = colors[1], label='Bayes')
plt.title('Induced loss distribution', fontsize = 14, y=1.02)
plt.legend(fontsize=12)
plt.xlabel('Loss', fontsize=12)
plt.xlim([3.8, 4.5])
plt.tight_layout()
plt.savefig("./example2_fig2.png", dpi=800)
beta_0 = mu[0] - sigma[0,1]/sigma[1,1]*mu[1]
beta_1 = sigma[0,1]/sigma[1,1]
print('Bias of OLS')
print('==========================')
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_0, B_OLS.mean()[0], beta_0 - B_OLS.mean()[0]))
print('{:.4f} - {:.4f} = {:.4f}\n\n'.format(beta_1, B_OLS.mean()[1], beta_1 - B_OLS.mean()[1]))
print('Bias of Bayes')
print('==========================')
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_0, B_bayes.mean()[0], beta_0 - B_bayes.mean()[0]))
print('{:.4f} - {:.4f} = {:.4f}'.format(beta_1, B_bayes.mean()[1], beta_1 - B_bayes.mean()[1]))
print('Variance of OLS')
print('======================')
print(B_OLS.var())
print('\n\nVarinace of Bayes')
print('======================')
print(B_bayes.var())
print('Risk of OLS: {:.4f} \nRisk of Bayes: {:.4f}'.format(L_OLS.mean(), L_bayes.mean()))
| 0.713232 | 0.832849 |
## Classes
```
from abc import ABC, abstractmethod
class Account(ABC):
def __init__(self, account_number, balance):
self._account_number = account_number
self._balance = balance
def deposit(self, value):
if value > 0:
self._balance += value
else:
print("Invalid value to deposit:", value)
def withdraw(self, value):
if value > 0 and value <= self._balance:
self._balance -= value
else:
print("Invalid value to withdraw:", value)
@property
def account_number(self):
return self._account_number
@property
def balance(self):
return self._balance
@abstractmethod
def description(self):
pass
class SavingsAccount(Account):
def __init__(self, account_number, balance, interest=0.02):
super().__init__(account_number, balance)
self._interest = interest
def annual_interest(self):
return self.balance * self._interest
@property
def interest(self):
'''
This method is not part of the exercise
'''
return self._interest
def description(self):
return "savings"
class CurrentAccount(Account):
def __init__(self, account_number, balance, overdraft=100):
super().__init__(account_number, balance)
self._overdraft = overdraft
def withdraw(self, value):
if value > 0 and value <= (self._balance + self._overdraft):
self._balance -= value
else:
print("Invalid value to withdraw:", value)
@property
def overdraft(self):
'''
This method is not part of the exercise
'''
return self._overdraft
def description(self):
return "current"
```
## Testing
```
s = SavingsAccount("1", 1000)
s.balance
s.interest
s.annual_interest()
c = CurrentAccount("2", 50)
c.balance
c.overdraft
c.withdraw(200)
```
## List of Accounts
```
accounts = []
# let's add some accounts
accounts.append(SavingsAccount("1000", 1000))
accounts.append(SavingsAccount("1001", 5000))
accounts.append(CurrentAccount("2000", 10000, 1000))
accounts.append(CurrentAccount("2001", 500))
accounts.append(SavingsAccount("1002", 10, 0.1))
accounts.append(SavingsAccount("1003", 100000, 0.05))
accounts.append(CurrentAccount("2002", 10, 0.0))
accounts.append(CurrentAccount("2003", 50, 100))
accounts.append(CurrentAccount("2004", 5))
accounts.append(CurrentAccount("2005", 1000, 10))
accounts.append(CurrentAccount("2006", 500, 1000))
for account in accounts:
if isinstance(account, CurrentAccount):
if account.overdraft > account.balance:
print("Account", account.account_number, ": overdraft =", account.overdraft, ", balance = ", account.balance)
```
|
github_jupyter
|
from abc import ABC, abstractmethod
class Account(ABC):
def __init__(self, account_number, balance):
self._account_number = account_number
self._balance = balance
def deposit(self, value):
if value > 0:
self._balance += value
else:
print("Invalid value to deposit:", value)
def withdraw(self, value):
if value > 0 and value <= self._balance:
self._balance -= value
else:
print("Invalid value to withdraw:", value)
@property
def account_number(self):
return self._account_number
@property
def balance(self):
return self._balance
@abstractmethod
def description(self):
pass
class SavingsAccount(Account):
def __init__(self, account_number, balance, interest=0.02):
super().__init__(account_number, balance)
self._interest = interest
def annual_interest(self):
return self.balance * self._interest
@property
def interest(self):
'''
This method is not part of the exercise
'''
return self._interest
def description(self):
return "savings"
class CurrentAccount(Account):
def __init__(self, account_number, balance, overdraft=100):
super().__init__(account_number, balance)
self._overdraft = overdraft
def withdraw(self, value):
if value > 0 and value <= (self._balance + self._overdraft):
self._balance -= value
else:
print("Invalid value to withdraw:", value)
@property
def overdraft(self):
'''
This method is not part of the exercise
'''
return self._overdraft
def description(self):
return "current"
s = SavingsAccount("1", 1000)
s.balance
s.interest
s.annual_interest()
c = CurrentAccount("2", 50)
c.balance
c.overdraft
c.withdraw(200)
accounts = []
# let's add some accounts
accounts.append(SavingsAccount("1000", 1000))
accounts.append(SavingsAccount("1001", 5000))
accounts.append(CurrentAccount("2000", 10000, 1000))
accounts.append(CurrentAccount("2001", 500))
accounts.append(SavingsAccount("1002", 10, 0.1))
accounts.append(SavingsAccount("1003", 100000, 0.05))
accounts.append(CurrentAccount("2002", 10, 0.0))
accounts.append(CurrentAccount("2003", 50, 100))
accounts.append(CurrentAccount("2004", 5))
accounts.append(CurrentAccount("2005", 1000, 10))
accounts.append(CurrentAccount("2006", 500, 1000))
for account in accounts:
if isinstance(account, CurrentAccount):
if account.overdraft > account.balance:
print("Account", account.account_number, ": overdraft =", account.overdraft, ", balance = ", account.balance)
| 0.6488 | 0.646446 |
```
import pandas as pd
docs = pd.read_table('SMSSpamCollection', header=None, names=['Class', 'sms'])
docs.head()
#df.column_name.value_counts() - gives no. of unique inputs in that columns
docs.Class.value_counts()
ham_spam=docs.Class.value_counts()
ham_spam
print("Spam % is ",(ham_spam[1]/float(ham_spam[0]+ham_spam[1]))*100)
# mapping labels to 1 and 0
docs['label'] = docs.Class.map({'ham':0, 'spam':1})
docs.head()
X=docs.sms
y=docs.label
X = docs.sms
y = docs.label
print(X.shape)
print(y.shape)
# splitting into test and train
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
X_train.head()
from sklearn.feature_extraction.text import CountVectorizer
# vectorising the text
vect = CountVectorizer(stop_words='english')
vect.fit(X_train)
vect.vocabulary_
vect.get_feature_names()
# transform
X_train_transformed = vect.transform(X_train)
X_test_tranformed =vect.transform(X_test)
from sklearn.naive_bayes import BernoulliNB
# instantiate bernoulli NB object
bnb = BernoulliNB()
# fit
bnb.fit(X_train_transformed,y_train)
# predict class
y_pred_class = bnb.predict(X_test_tranformed)
# predict probability
y_pred_proba =bnb.predict_proba(X_test_tranformed)
# accuracy
from sklearn import metrics
metrics.accuracy_score(y_test, y_pred_class)
bnb
metrics.confusion_matrix(y_test, y_pred_class)
confusion = metrics.confusion_matrix(y_test, y_pred_class)
print(confusion)
#[row, column]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
TP = confusion[1, 1]
sensitivity = TP / float(FN + TP)
print("sensitivity",sensitivity)
specificity = TN / float(TN + FP)
print("specificity",specificity)
precision = TP / float(TP + FP)
print("precision",precision)
print(metrics.precision_score(y_test, y_pred_class))
print("precision",precision)
print("PRECISION SCORE :",metrics.precision_score(y_test, y_pred_class))
print("RECALL SCORE :", metrics.recall_score(y_test, y_pred_class))
print("F1 SCORE :",metrics.f1_score(y_test, y_pred_class))
y_pred_proba
from sklearn.metrics import confusion_matrix as sk_confusion_matrix
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_pred_proba[:,1])
roc_auc = auc(false_positive_rate, true_positive_rate)
print (roc_auc)
print(true_positive_rate)
print(false_positive_rate)
print(thresholds)
%matplotlib inline
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.title('ROC')
plt.plot(false_positive_rate, true_positive_rate)
```
|
github_jupyter
|
import pandas as pd
docs = pd.read_table('SMSSpamCollection', header=None, names=['Class', 'sms'])
docs.head()
#df.column_name.value_counts() - gives no. of unique inputs in that columns
docs.Class.value_counts()
ham_spam=docs.Class.value_counts()
ham_spam
print("Spam % is ",(ham_spam[1]/float(ham_spam[0]+ham_spam[1]))*100)
# mapping labels to 1 and 0
docs['label'] = docs.Class.map({'ham':0, 'spam':1})
docs.head()
X=docs.sms
y=docs.label
X = docs.sms
y = docs.label
print(X.shape)
print(y.shape)
# splitting into test and train
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
X_train.head()
from sklearn.feature_extraction.text import CountVectorizer
# vectorising the text
vect = CountVectorizer(stop_words='english')
vect.fit(X_train)
vect.vocabulary_
vect.get_feature_names()
# transform
X_train_transformed = vect.transform(X_train)
X_test_tranformed =vect.transform(X_test)
from sklearn.naive_bayes import BernoulliNB
# instantiate bernoulli NB object
bnb = BernoulliNB()
# fit
bnb.fit(X_train_transformed,y_train)
# predict class
y_pred_class = bnb.predict(X_test_tranformed)
# predict probability
y_pred_proba =bnb.predict_proba(X_test_tranformed)
# accuracy
from sklearn import metrics
metrics.accuracy_score(y_test, y_pred_class)
bnb
metrics.confusion_matrix(y_test, y_pred_class)
confusion = metrics.confusion_matrix(y_test, y_pred_class)
print(confusion)
#[row, column]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
TP = confusion[1, 1]
sensitivity = TP / float(FN + TP)
print("sensitivity",sensitivity)
specificity = TN / float(TN + FP)
print("specificity",specificity)
precision = TP / float(TP + FP)
print("precision",precision)
print(metrics.precision_score(y_test, y_pred_class))
print("precision",precision)
print("PRECISION SCORE :",metrics.precision_score(y_test, y_pred_class))
print("RECALL SCORE :", metrics.recall_score(y_test, y_pred_class))
print("F1 SCORE :",metrics.f1_score(y_test, y_pred_class))
y_pred_proba
from sklearn.metrics import confusion_matrix as sk_confusion_matrix
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, y_pred_proba[:,1])
roc_auc = auc(false_positive_rate, true_positive_rate)
print (roc_auc)
print(true_positive_rate)
print(false_positive_rate)
print(thresholds)
%matplotlib inline
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.title('ROC')
plt.plot(false_positive_rate, true_positive_rate)
| 0.616936 | 0.544378 |
Straightforward translation of https://github.com/rmeinl/apricot-julia/blob/5f130f846f8b7f93bb4429e2b182f0765a61035c/notebooks/python_reimpl.ipynb
See also https://github.com/genkuroki/public/blob/main/0016/apricot/python_reimpl.ipynb
```
using Seaborn
using ScikitLearn: @sk_import
@sk_import datasets: fetch_covtype
using Random
using StatsBase: sample
digits_data = fetch_covtype()
X_digits = permutedims(abs.(digits_data["data"]))
summary(X_digits)
"""`calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)` mutates `gains` only"""
function calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)
Threads.@threads for i in eachindex(idxs)
@inbounds idx = idxs[i]
@inbounds gains[i] = sum(j -> sqrt(current_values[j] + X[j, idx]), axes(X, 1))
end
gains .-= current_concave_values_sum
end
@doc calculate_gains!
function fit(X, k; calculate_gains! = calculate_gains!)
d, n = size(X)
cost = 0.0
ranking = Int[]
total_gains = Float64[]
current_values = zeros(d)
current_concave_values_sum = sum(sqrt, current_values)
idxs = collect(1:n)
gains = zeros(n)
while cost < k
calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)
idx = argmax(gains)
best_idx = idxs[idx]
curr_cost = 1.0
cost + curr_cost > k && break
cost += curr_cost
# Calculate gains
gain = gains[idx] * curr_cost
# Select next
current_values .+= @view X[:, best_idx]
current_concave_values_sum = sum(sqrt, current_values)
push!(ranking, best_idx)
push!(total_gains, gain)
popat!(idxs, idx)
end
return ranking, total_gains
end
k = 1000
@time ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!);
@time ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!);
tic = time()
ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!)
toc0 = time() - tic
toc0
@time begin
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
end;
@time begin
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
end;
tic = time()
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
toc1 = time() - tic
toc1
plt.figure(figsize=(9, 4.5))
plt.subplot(121)
plt.plot(cumsum(gains0), label="Naive")
plt.plot(gains1, label="Random")
plt.ylabel("F(S)")
plt.xlabel("Subset Size")
plt.legend()
plt.grid(lw=0.3)
plt.subplot(122)
plt.bar(1:2, [toc0, toc1])
plt.ylabel("Time (s)")
plt.xticks(1:2, ["Naive", "Random"], rotation=90)
plt.grid(lw=0.3)
plt.title("Julia 1.6.2")
plt.tight_layout()
#plt.show()
```
|
github_jupyter
|
using Seaborn
using ScikitLearn: @sk_import
@sk_import datasets: fetch_covtype
using Random
using StatsBase: sample
digits_data = fetch_covtype()
X_digits = permutedims(abs.(digits_data["data"]))
summary(X_digits)
"""`calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)` mutates `gains` only"""
function calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)
Threads.@threads for i in eachindex(idxs)
@inbounds idx = idxs[i]
@inbounds gains[i] = sum(j -> sqrt(current_values[j] + X[j, idx]), axes(X, 1))
end
gains .-= current_concave_values_sum
end
@doc calculate_gains!
function fit(X, k; calculate_gains! = calculate_gains!)
d, n = size(X)
cost = 0.0
ranking = Int[]
total_gains = Float64[]
current_values = zeros(d)
current_concave_values_sum = sum(sqrt, current_values)
idxs = collect(1:n)
gains = zeros(n)
while cost < k
calculate_gains!(X, gains, current_values, idxs, current_concave_values_sum)
idx = argmax(gains)
best_idx = idxs[idx]
curr_cost = 1.0
cost + curr_cost > k && break
cost += curr_cost
# Calculate gains
gain = gains[idx] * curr_cost
# Select next
current_values .+= @view X[:, best_idx]
current_concave_values_sum = sum(sqrt, current_values)
push!(ranking, best_idx)
push!(total_gains, gain)
popat!(idxs, idx)
end
return ranking, total_gains
end
k = 1000
@time ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!);
@time ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!);
tic = time()
ranking0, gains0 = fit(X_digits, k; calculate_gains! = calculate_gains!)
toc0 = time() - tic
toc0
@time begin
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
end;
@time begin
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
end;
tic = time()
idxs = sample(axes(X_digits, 2), k; replace=false)
X_subset = X_digits[:, idxs]
gains1 = cumsum(X_subset; dims=2)
gains1 = vec(sum(sqrt, gains1; dims=1))
toc1 = time() - tic
toc1
plt.figure(figsize=(9, 4.5))
plt.subplot(121)
plt.plot(cumsum(gains0), label="Naive")
plt.plot(gains1, label="Random")
plt.ylabel("F(S)")
plt.xlabel("Subset Size")
plt.legend()
plt.grid(lw=0.3)
plt.subplot(122)
plt.bar(1:2, [toc0, toc1])
plt.ylabel("Time (s)")
plt.xticks(1:2, ["Naive", "Random"], rotation=90)
plt.grid(lw=0.3)
plt.title("Julia 1.6.2")
plt.tight_layout()
#plt.show()
| 0.66454 | 0.868882 |
**Pandas Exercises - With the NY Times Covid data**
Run the cell below to pull get the data from the nytimes github
```
!git clone https://github.com/nytimes/covid-19-data.git
```
**1. Import Pandas and Check your Version of Pandas**
```
import pandas as pd
pd.__version__
```
**2. Read the *us-counties.csv* data into a new Dataframe**
```
covid_data = pd.read_csv('/content/covid-19-data/us-counties.csv')
```
**3. Display the first 5 Rows**
```
covid_data.head(5)
```
**4. Drop the 'fips' Column**
```
covid_data = covid_data.drop('fips', axis=1)
```
**5. Check dtypes of the data**
```
covid_data.dtypes
```
**6. Change the 'date' column to Date dtype**
```
covid_data.date = pd.to_datetime(covid_data.date)
```
**7. Set the data index to 'date'**
```
covid_data = covid_data.set_index('date')
```
**8. Find how many weeks worth of data we have**
```
print('Weeks:', (covid_data.index.max() - covid_data.index.min()).days / 7)
```
**9. Create a seperate Dataframe representing only California and display the first 5 data entries**
```
CA_data = covid_data[covid_data['state'].str.contains("California")]
CA_data.head()
```
**10. How many counties in California do we have data for?**
```
CA_data['county'].nunique()
```
**11. How many data entries do we have for each county?**
```
CA_data['county'].value_counts()
# Alternatively the count and totals can be done with collections Counter
from collections import Counter
count = Counter(CA_data['county'])
count
```
**12. How many counties in California have experienced over 1000 cases?**
```
len(CA_data[CA_data['cases'] > 1000]['county'].value_counts())
# nunique will tell you how for each Column
CA_data[CA_data['cases'] > 1000].nunique()
```
**13. Which county has experienced the highest death toll?**
```
CA_data[CA_data['deaths'] > max(CA_data['deaths']) - 1]
```
**14. Slice the Data for that County Seperately into a new Dataframe**
```
la_ca_data = CA_data[CA_data['county'].str.contains('Los Angeles')]
```
**15. Create and populate new Columns for New Cases per Day and Deaths per day**
```
# Creating a New Column this way will Raise a SettingWithCopyWarning
pd.set_option('mode.chained_assignment',None)
# The Code above surpresses that warning
la_ca_data['cases_per_day'] = la_ca_data['cases'].diff(1).fillna(0)
la_ca_data['deaths_per_day'] = la_ca_data['deaths'].diff(1).fillna(0)
# This code turns the warning back on
# See the Pandas documentation here for more on SettingWithCopyWarning
# https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
pd.set_option('mode.chained_assignment', 'warn')
```
**16. What date had the most cases for LA county?**
```
la_ca_data[la_ca_data['cases_per_day'] > max(la_ca_data['cases_per_day']) - 1]
```
**17. Inspect the data in the month of April for Los Angeles County**
```
april_la_ca_data = la_ca_data['2020-04-01':'2020-04-30']
april_la_ca_data
```
**18. Find the mean [cases per day] for April**
```
april_la_ca_data = la_ca_data['2020-04-01':'2020-04-30']
april_la_ca_data.describe()
```
**19. Plot cases per day for the month of April in Los Angeles county**
```
la_cases_plot = april_la_ca_data['cases_per_day'].plot(title='LA County Cases per Day')
fig = la_cases_plot.get_figure()
fig.set_size_inches(8,4)
```
**20. Plot Deaths per Day for the month of March**
```
march_la_ca_data = la_ca_data['2020-03-01':'2020-03-31']
la_march_plot = march_la_ca_data['deaths_per_day'].plot(title='LA County Deaths per Day')
fig = la_march_plot.get_figure()
fig.set_size_inches(8,4)
```
**Armed with basics in Pandas - Answer your own questions about the data! Happy exploring**
Don't hesitate to send me suggestions / a message / or make change requests. There is more than one way to do everything here!
```
```
|
github_jupyter
|
!git clone https://github.com/nytimes/covid-19-data.git
import pandas as pd
pd.__version__
covid_data = pd.read_csv('/content/covid-19-data/us-counties.csv')
covid_data.head(5)
covid_data = covid_data.drop('fips', axis=1)
covid_data.dtypes
covid_data.date = pd.to_datetime(covid_data.date)
covid_data = covid_data.set_index('date')
print('Weeks:', (covid_data.index.max() - covid_data.index.min()).days / 7)
CA_data = covid_data[covid_data['state'].str.contains("California")]
CA_data.head()
CA_data['county'].nunique()
CA_data['county'].value_counts()
# Alternatively the count and totals can be done with collections Counter
from collections import Counter
count = Counter(CA_data['county'])
count
len(CA_data[CA_data['cases'] > 1000]['county'].value_counts())
# nunique will tell you how for each Column
CA_data[CA_data['cases'] > 1000].nunique()
CA_data[CA_data['deaths'] > max(CA_data['deaths']) - 1]
la_ca_data = CA_data[CA_data['county'].str.contains('Los Angeles')]
# Creating a New Column this way will Raise a SettingWithCopyWarning
pd.set_option('mode.chained_assignment',None)
# The Code above surpresses that warning
la_ca_data['cases_per_day'] = la_ca_data['cases'].diff(1).fillna(0)
la_ca_data['deaths_per_day'] = la_ca_data['deaths'].diff(1).fillna(0)
# This code turns the warning back on
# See the Pandas documentation here for more on SettingWithCopyWarning
# https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
pd.set_option('mode.chained_assignment', 'warn')
la_ca_data[la_ca_data['cases_per_day'] > max(la_ca_data['cases_per_day']) - 1]
april_la_ca_data = la_ca_data['2020-04-01':'2020-04-30']
april_la_ca_data
april_la_ca_data = la_ca_data['2020-04-01':'2020-04-30']
april_la_ca_data.describe()
la_cases_plot = april_la_ca_data['cases_per_day'].plot(title='LA County Cases per Day')
fig = la_cases_plot.get_figure()
fig.set_size_inches(8,4)
march_la_ca_data = la_ca_data['2020-03-01':'2020-03-31']
la_march_plot = march_la_ca_data['deaths_per_day'].plot(title='LA County Deaths per Day')
fig = la_march_plot.get_figure()
fig.set_size_inches(8,4)
| 0.65202 | 0.966505 |
## Welcome to Coding Exercise 5.
We'll only have 2 questions and both of them will be difficult. You may import other libraries to help you here. Clue: find out more about the ```itertools``` and ```math``` library.
### Question 1.
* List item
* List item
### "Greatest Possible Combination"
We have a function as such:
```f(x1, x2, x3) = (x1^2 + x2 * x3) modulo 20 ```
Given 3 list/array/vector containing possible values of x1, x2, and x3, find the maximum output possible.
#### Explanation:
If x1 = 2, x2 = 5, x3 = 3, then...
The function's output is: (2^2 + 5 * 3) modulo 20 = (4 + 15) modulo 20 = 19 modulo 20 = 19.
If x1 = 3, x2 = 5, x3 = 3, then...
The function's output is: (3^2 + 5 * 3) modulo 20 = (9 + 15) modulo 20 = 24 modulo 20 = 4.
In this case, since 19 > 4, the combination of (X1 = 2, X2 = 5, X3 = 3) gives a *greater* output value than the combination of (X1 = 3, X2 = 5, X3 = 3).
#### Example:
- Array X1: [2, 4]
- Array X2: [1, 2, 3]
- Array x3: [5, 6]
How many combinations do we have?
1. X1 = 2, X2 = 1, X3 = 5. Output = (2^2 + 1 * 5) modulo 20 = 9 modulo 20 = 9.
2. X1 = 2, X2 = 1, X3 = 6. Output = 10
3. X1 = 2, X2 = 2, X3 = 5. Output = 14
4. X1 = 2, X2 = 2, X3 = 6. Output = 16
5. X1 = 2, X2 = 3, X3 = 5. Output = 19
6. X1 = 2, X2 = 3, X3 = 6. Output = (2^2 + 3 * 6) modulo 20 = 22 modulo 20 = 2
7. X1 = 4, X2 = 1, X3 = 5. Output = 1
8. X1 = 4, X2 = 1, X3 = 6. Output = 2
9. X1 = 4, X2 = 2, X3 = 5. Output = 6
10. X1 = 4, X2 = 2, X3 = 6. Output = 8
11. X1 = 4, X2 = 3, X3 = 5. Output = 11
12. X1 = 4, X2 = 3, X3 = 6. Output = 14
Out of these 12 combinations, what is the maximum output of our function?
The maximum output is 19, achieved with X1 = 2, X2 = 3, X3 = 5.
Answer : 19
(No need to specify the values of X1, X2, X3).
```
### Write your solution here ###
def maximum(x1, x2, x3):
return
```
### Question 2.
### "Position in Repeating Series"
Your function will be called ```position``` and it has 3 inputs.
This problem has 3 inputs:
- The first input, (n), is the maximum number in our series
- The second input, (r), is how many times our series will be repeated
- The third input, (p), is the position of the desired output.
Here are a few examples:
- If n = 3, and r = 1, then our series will be: 1,2,3,2,1
- If n = 4, and r = 1, then our series will be: 1,2,3,4,3,2,1
- If n = 3, and r = 2, then our series will be: 1,2,3,2,1,2,3,2,1
- If n = 4, and r = 2, then our series will be: 1,2,3,4,3,2,1,2,3,4,3,2,1
- If n = 5, and r = 3, then our series will be: 1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1
Now, what is the meaning of the third input?
We want to know what's the value of the number in the position of p. The first number in the series is the first position. This is not the same as index! Indexing in Python starts at 0, and indexing in R starts at 1, so we want to make a standard that applies to both Python and R.
#### Example 1
n = 3, r = 1, p = 4
The series is : 1, 2, 3, 2, 1
The 4th number of the series = suku ke - 4 dari barisan tersebut = 2.
Answer = 2.
#### Example 2
n = 3, r = 2, p = 7
The series is : 1, 2, 3, 2, 1, 2, 3, 2, 1
The 7th number of the series = suku ke - 7 dari barisan tersebut = 3.
Answer = 3.
#### Example 3
n = 4, r = 2, p = 7
The series is : 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1
The 7th number of the series = suku ke - 7 dari barisan tersebut = 1.
Answer = 1.
```
### Write your solution here ###
def position(n, r, p):
return
```
|
github_jupyter
|
Given 3 list/array/vector containing possible values of x1, x2, and x3, find the maximum output possible.
#### Explanation:
If x1 = 2, x2 = 5, x3 = 3, then...
The function's output is: (2^2 + 5 * 3) modulo 20 = (4 + 15) modulo 20 = 19 modulo 20 = 19.
If x1 = 3, x2 = 5, x3 = 3, then...
The function's output is: (3^2 + 5 * 3) modulo 20 = (9 + 15) modulo 20 = 24 modulo 20 = 4.
In this case, since 19 > 4, the combination of (X1 = 2, X2 = 5, X3 = 3) gives a *greater* output value than the combination of (X1 = 3, X2 = 5, X3 = 3).
#### Example:
- Array X1: [2, 4]
- Array X2: [1, 2, 3]
- Array x3: [5, 6]
How many combinations do we have?
1. X1 = 2, X2 = 1, X3 = 5. Output = (2^2 + 1 * 5) modulo 20 = 9 modulo 20 = 9.
2. X1 = 2, X2 = 1, X3 = 6. Output = 10
3. X1 = 2, X2 = 2, X3 = 5. Output = 14
4. X1 = 2, X2 = 2, X3 = 6. Output = 16
5. X1 = 2, X2 = 3, X3 = 5. Output = 19
6. X1 = 2, X2 = 3, X3 = 6. Output = (2^2 + 3 * 6) modulo 20 = 22 modulo 20 = 2
7. X1 = 4, X2 = 1, X3 = 5. Output = 1
8. X1 = 4, X2 = 1, X3 = 6. Output = 2
9. X1 = 4, X2 = 2, X3 = 5. Output = 6
10. X1 = 4, X2 = 2, X3 = 6. Output = 8
11. X1 = 4, X2 = 3, X3 = 5. Output = 11
12. X1 = 4, X2 = 3, X3 = 6. Output = 14
Out of these 12 combinations, what is the maximum output of our function?
The maximum output is 19, achieved with X1 = 2, X2 = 3, X3 = 5.
Answer : 19
(No need to specify the values of X1, X2, X3).
### Question 2.
### "Position in Repeating Series"
Your function will be called ```position``` and it has 3 inputs.
This problem has 3 inputs:
- The first input, (n), is the maximum number in our series
- The second input, (r), is how many times our series will be repeated
- The third input, (p), is the position of the desired output.
Here are a few examples:
- If n = 3, and r = 1, then our series will be: 1,2,3,2,1
- If n = 4, and r = 1, then our series will be: 1,2,3,4,3,2,1
- If n = 3, and r = 2, then our series will be: 1,2,3,2,1,2,3,2,1
- If n = 4, and r = 2, then our series will be: 1,2,3,4,3,2,1,2,3,4,3,2,1
- If n = 5, and r = 3, then our series will be: 1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1
Now, what is the meaning of the third input?
We want to know what's the value of the number in the position of p. The first number in the series is the first position. This is not the same as index! Indexing in Python starts at 0, and indexing in R starts at 1, so we want to make a standard that applies to both Python and R.
#### Example 1
n = 3, r = 1, p = 4
The series is : 1, 2, 3, 2, 1
The 4th number of the series = suku ke - 4 dari barisan tersebut = 2.
Answer = 2.
#### Example 2
n = 3, r = 2, p = 7
The series is : 1, 2, 3, 2, 1, 2, 3, 2, 1
The 7th number of the series = suku ke - 7 dari barisan tersebut = 3.
Answer = 3.
#### Example 3
n = 4, r = 2, p = 7
The series is : 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1
The 7th number of the series = suku ke - 7 dari barisan tersebut = 1.
Answer = 1.
| 0.883324 | 0.989977 |
```
"""Bond Breaking"""
__authors__ = "Victor H. Chavez", "Lyudmila Slipchenko"
__credits__ = ["Victor H. Chavez", "Lyudmila Slipchenko"]
__email__ = ["[email protected]", "[email protected]"]
__copyright__ = "(c) 2008-2019, The Psi4Education Developers"
__license__ = "BSD-3-Clause"
__date__ = "2019-11-18"
```
---
## Lab 2. Bond-breaking in $H_2$
In this lab, you will:
* Investigate the bond-breaking reaction in $H_2$ molecule.
* Compare the performance of restricted and unrestricted Hartree-Fock, and Density Functional Theory for bond breaking.
* Benchmark these results with respect to the Full Configuration Interaction (FCI) values obtained using the coupled cluster with single and double excitations (CCSD) calculations, which give the exact answer for the two-electron system.
* Calculate the correlation energy.
* Distinguish dynamic and static contributions to the correlation energy.
Authors: Lyudmila Slipchenko ([email protected]; ORCID: 0000-0002-0445-2990) and Victor H. Chavez ([email protected]; ORCID: 0000-0003-3765-2961).
***
```
#Import modules
import psi4
import numpy as np
import os
import matplotlib.pyplot as plt
```
***
To perform a basic calculation we use the ```psi4.energy``` function. The function needs to know what method and basis set to use, and what molecule you are interested in (if you have defined more than one geometry inside your Jupyter Notebook). Let say that we want to get the HF energy of the Helium atom. We would need to do the following:
```
#Define Helium Geometry
#The first line referst to the charge and spin multiplicity.
he_geo = psi4.geometry("""
0 1
He 0.0 0.0 0.0
""")
#Request the HF calculation using the correlation consistent basis set cc-pvdz.
e = psi4.energy("HF/cc-pvdz", molecule=he_geo)
#Print the energy. The units are given in atomic units or hartrees.
print(f"The HF energy of He is {e}")
#We made us of *f-strings* which allow us to combine strings and numbers in a print statement.
```
If you were to try the Helium example on a Hydrogen atom as it is, you would find that Psi4 will throw an error. This is because when running a calculation, Psi4 defaults to a *Restricted Hartree-Fock* or *RHF*, (i.e. a system with an even number of electrons where all electrons are paired). This means that electrons of opposite spin occupy (or are "restricted") to the same spatial orbital.
In cases like Hydrogen, where the numbers of alpha and beta spin electrons are different, we lift this restriction allowing both electrons to have different spatial orbitals.
<br>
<img src="./restricted.png">
<br>
We need to tell Psi4 that we want an UHF calculation. This is done by setting the global option "reference" as "UHF". In the cell below, type: ```psi4.set_options({"reference" : "UHF"})```. You may need to switch between UHF and RHF many times throughout the lab.
***
We want to produce a binding energy curve for the $H_2$ molecule using different levels of theory. The binding energy is given by:
$$E_{bind} = E(H_2) - 2E(H) \tag{1} $$
For a molecule with one degree of freedom, just like the $H_2$ molecule, the potential energy surface is just a 1D curve. Notice that the second term on the right hand side of the equation is just constant that is equal to two times the energy of the Hydrogen atom. Your first task is to obtain this value for each method:
### Part 1
#### **1.** Calculate and store the energy of a single H atom with the methods: HF, PBE, B3LYP and CCSD. Use 6-31G** basis for all the calculation in this lab. Change the reference and multiplicity of the atom accordingly.
<div class="alert alert-info">
Hint: Notice that the first argument of `psi4.energy` is a string. You could quickly go through the calculations by creating a list with the different methods and then use them in a for loop to to run each of them. Consider that the string also contains the basis set. In order to overcome this predicament, remember that strings can be concatenated by using the `+` operator (e.g. "HF"+"/cc-pvdz").
</div>
#### **2.** Explain the origin of errors in each method and why HF and CCSD energies are the same for the H atom.
```
### RESPONSE
```
---
Let us now concentrate on the first term of equation 1. We require to run a series of calculations for each method at different H-H separations in Angstroms (e.g. 0.3, 0.4, 0.5, ... ,4.9, 5.0).
<div class="alert alert-info">
Hint : Given that the argument of a psi4.geometry is a string, we can take advantage of that by looking at the following example:
</div>
```
#Define string with psi4.geometry syntax.
#Identify what you want to change and use a particular label that you know that won't get repeated.
molecule = """
**atom1** 0.0 0.0 0.0
"""
#Create a list with the things that you want to go through.
atoms = [ "H", "He", "Li" ]
#Cycle through them.
for atom in atoms:
print(molecule.replace("**atom1**", atom))
```
#### **3.** Using the previous example and the following distances, write a snippet that will calculate the energy at each separation for a **RHF** calculation. You will need to change the reference to "RHF" (Psi4 still thinks you want to run UHF calculations).
Make sure you store the wavefunction object for each separation since it will be used later in the lab: ```energy, wfn = psi4.energy("method/basis", return_wfn=True)```
```
#We use more points closer to where we would expect to have the ground state geometry to create a nice and smooth function.
distances = np.zeros(20)
distances[0:16] = np.linspace(0.3, 2.5, 16)
distances[16:] = np.linspace(2.7, 5.0, 4)
```
Here we are using the `numpy` library first to create an empty array filled with zeros using `np.zeros`, where the argument specifies the size of the array. The other function `np.linspace` creates a sequence of evenly spaced values within an interval. This means, we generated a linear space with 16 points from 0.3 to 2.5 and one with 4 points from 2.7 to 5.0.
```
#RESPONSE:
```
---
#### **4.** Calculate the energies at the same distances at the **UHF** level. You can recycle the code that you just wrote (just remember to change the name of your variables). We will need extra information that can ony be found in the output.
In order to save the output to a file we require the additional option: ```psi4.core.set_output_file("filename.txt", True)```.
<div class="alert alert-info">
Hint: In order to obtain the correct UHF energies, we need to set the extra following options:
<\div>
```
psi4.set_options({'reference' : 'UHF',
'guess_mix' : True,
'guess' : "gwh"})
#RESPONSE
```
#### **5.** Store the values for $S^2$. This information is found in each outputfile close to the end of your calculation (look for Spin Contamination Metric).
You can go through each of the files and copy the value, but you can also think about how can you let python automatize this process. Think carefully about the steps required for this. Given a path you would need to import the file ( `f = open(path, 'r')` ) and proceed to extract the lines ( `f.read().splitlines()` ). With those lines available, you may concentrate on determining whether or not each line contains the `S^2` string.
If you require a more thorough review of parsing files. You can look at [this tutorial](https://education.molssi.org/python_scripting_cms/02-file_parsing/index.html) to learn more about file parsing.
```
#Response
```
#### **6.** Make a table or plot of $S^2$ values from the UHF calculations. Explain why $S^2$ deteriorates when the H-H bond is stretched.
```
#Response
```
---
#### 7. Calculate the same potential energy surface at the DFT level. Use the PBE functional and a restricted wavefunction.
```
#RESPONSE
```
#### **8.** Calculate the same potential energy surface at the FCI level.
For a two-electron system, the FCI results may be obtained by using the CCSD method. This is true because CCSD includes determinants that are singly and doubly excited. For a two electron system that includes all electrons available, thus CCSD includes all possible excitations in the system.
#### **9.** You will need to save the output file generated by Psi4 again. From the output file, record total CCSD ampltitudes: CCSD $T_1^2$ and $T_2^2$, and the value of the largest $T_2$ amplitude for the ground state geometry and for a split geometry.
Consider T as a sum of operators that that act on a reference determinant. In CCSD $T = T_1 + T_2$ where $T_1$ refers with single excitations and $T_2$ with double excitations.
The values of amplitudes show a relative weight of singly and doubly excited determinants in the wavefunction. If $T_1$ and/or $T_2$ are large (generally speaking, if a particular |$T_2| > 0.1$), the wavefunction is considered to be multi-configurational, i.e., containing several important Slater determinants. In other words, this is a region where non-dynamic (static) correlation is significant. Several small $T_1$ and $T_2$ amplitudes tell about (almost always present) dynamic correlation.
In each output you should look at the values of *Largest {TIA, Tia, TIjAb} Amplitudes*, where the $T$ refers to the previously mentioned operator, and the following indices refer to the orbitals used according to the notation:
| | Occupied Molecular Orbitals | Virtual Molecular Orbitals | | |
|-------|-----------------------------|----------------------------|---|---|
| Alpha | i,j | a, b | | |
| Beta | I, J | A, B | | |
```
#RESPONSE
```
---
#### **10.** Plot on the same graph the RHF, DFT and FCI binding energies in $H_2$ versus the separation distance. Plot in kcal/mol energy units (1 Hartree = 627.5 kcal/mol)
```
#Response
```
#### **11.** Using your results, compare CCSD, UHF and RHF dissociation energies.
```
#RESPONSE
```
---
#### **12.** Comment on the behaviour of RHF with respect to FCI at short (around 0.7 Angstroms) and long distances. For more information, you can read paragraph 3.8.7 from Reference 1 (found below) for a discussion of RHF and UHF solutions.
#RESPONSE
---
#### **13.** Plot the first two $H_2$ molecular orbitals from your RHF and UHF calculations at equilibrium , 0.7 and 5.0 Angstroms. Remember to use the appropriate global settings. Comment on qualitative changes in the shape of the orbitals.
##### You may use the function `generate_orbitals` from the orbital_helper file in the same directory to plot both HOMO and HOMO for the $H_2$ molecule. The syntax is the following:
```
from orbital_helper import generate_orbitals
x, alpha_orbitals, beta_orbitals = generate_orbitals(wfn, [1,2,3])
#Where the arguments are the wavefunction object and the integer values of the orbitals.
#The function returns a numpy array with the domain, and a set of lists with alpha and beta orbitals.
```
##### If you have the package `moly` installed. You may visualize the orbitals in 3D with the following:
```
import moly
fig = moly.Figure(figsize=(300,500))
fig.add_orbital("Name", wfn, orbital_number, iso, colorscale="portland_r")
fig.show()
```
```
from orbital_helper import generate_orbitals
#RESPONSE
```
---
#### **14.** Difference between FCI and HF energies is the correlation energy. What is the nature of the correlation energy (dynamic vs non-dynamic) in $H_2$ at equilibrium and long distances? At what distance does the non-dynamic correlation become important?
#RESPONSE
---
#### **15.** Comment on the behaviour of DFT at equilibrium and long distances. What is the reason of DFT failure for bond-breaking?
#RESPONSE
---
#### **Bonus.** From the previously computed energy of a Hydrogen atom with the hybrid B3LYP functional. Compare the energy of the atom computed with HF, B3LYP and the exact energy. Do you see any discrepancy with B3LYP? If so, what is/are the reasons for such discrepancies?
```
#RESPONSE
```
***
## Part 2
Your friend, who is an experimental chemist, seeks your help knowing that you have expertise in running quantum chemistry simulations. Their research group has measured the singlet-triplet gap of ozone recently. They want to see if computational simulations can support their measurement. How will you measure the singlet-triplet gap in ozone?
Use the ideas from the previous part of this lab and the follwoing hints:
**1.** Assume that the singlet and triplet ozone molecules have the same geometry.
**2.** You will have to optimize the geometry of ozone to start with. Psi4 can let you import geometries from PubChem. The sytax is: `h2o_geometry = psi4.geometry("pubchem:water")`. You may use the common name or its molecular formula. Alternatively, you can use a database such as [CCCBDB](https://cccbdb.nist.gov/).
**3.** Use RHF/6-31G* for simulating the singlet ozone molecule. Use UHF/6-31G* for simulating the triplet ozone molecule. Use the energy difference to compute the gap.
**4.** Write the electronic energies corresponding to singlet and triplet ozone molecules. the singlet-triplet gap in eV, and the $<S^2>$ value for triplet ozone. Information about spin contamination is given by $<S^2>$ and can be found close to the end of your calculation (look for Spin Contamination Metric).
```
#Response
```
---
Now, compute the singlet-triplet gap between the $^1\Delta_g$ and $^3\Sigma_g$ states of oxygen molecule and report it in eV. Compare the singlet-triplet gap you computed in this lab with the ones availiable in CCBDB. Is it an exact match (http://cccbdb.nist.gov/stgap1.asp)?
<img src="./ozone.png">
##### Compare the expected $<S^2>$ with observed $<S^2>$ and respond: Of all the four cases you have computed so far, which one suffers the most spin contamination?
```
#RESPONSE
```
---
Bonus. Compute the singlet-triplet gap between $^1\Sigma_g ^+$ and $^3\Sigma_g ^-$ states of oxygen atom.
<div class="alert alert-info">
Hint: Start with $^1 \Delta_g$ geometry. Use the maximum overlap method (MOM) to force the highest beta electron to occupy the second $\pi^*$ ortibal: ```psi4.set_options({"MOM_START":1})```
</div>
```
#Response
```
# ---
## Further Reading:
#### General:
1. Szabo, A., & Ostlund, N. S. (2012). Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation.
2. Cramer, Christopher J. Essentials of computational chemistry: theories and models. John Wiley & Sons, 2013.
3. Krylov. A. Theory and Practice of Molecular Electronic Structure: [link](http://iopenshell.usc.edu/chem545/lectures2016/chem545_2016.pdf)
4. Sherrill. D. Non-Dynamical (Static) Electron Correlation: Bond Breaking in Quantum Chemistry [link](https://youtu.be/coGVX7HCCQE)
#### Bond stretching:
1. Dutta, Antara, and C. David Sherrill. "Full configuration interaction potential energy curves for breaking bonds to hydrogen: An assessment of single-reference correlation methods." The Journal of chemical physics 118.4 (2003): 1610-1619.
#### Singlet-triplet gaps:
1. Slipchenko, Lyudmila V., and Anna I. Krylov. "Singlet-triplet gaps in diradicals by the spin-flip approach: A benchmark study." The Journal of chemical physics 117.10 (2002): 4694-4708.
|
github_jupyter
|
"""Bond Breaking"""
__authors__ = "Victor H. Chavez", "Lyudmila Slipchenko"
__credits__ = ["Victor H. Chavez", "Lyudmila Slipchenko"]
__email__ = ["[email protected]", "[email protected]"]
__copyright__ = "(c) 2008-2019, The Psi4Education Developers"
__license__ = "BSD-3-Clause"
__date__ = "2019-11-18"
#Import modules
import psi4
import numpy as np
import os
import matplotlib.pyplot as plt
#Define Helium Geometry
#The first line referst to the charge and spin multiplicity.
he_geo = psi4.geometry("""
0 1
He 0.0 0.0 0.0
""")
#Request the HF calculation using the correlation consistent basis set cc-pvdz.
e = psi4.energy("HF/cc-pvdz", molecule=he_geo)
#Print the energy. The units are given in atomic units or hartrees.
print(f"The HF energy of He is {e}")
#We made us of *f-strings* which allow us to combine strings and numbers in a print statement.
### RESPONSE
#Define string with psi4.geometry syntax.
#Identify what you want to change and use a particular label that you know that won't get repeated.
molecule = """
**atom1** 0.0 0.0 0.0
"""
#Create a list with the things that you want to go through.
atoms = [ "H", "He", "Li" ]
#Cycle through them.
for atom in atoms:
print(molecule.replace("**atom1**", atom))
Here we are using the `numpy` library first to create an empty array filled with zeros using `np.zeros`, where the argument specifies the size of the array. The other function `np.linspace` creates a sequence of evenly spaced values within an interval. This means, we generated a linear space with 16 points from 0.3 to 2.5 and one with 4 points from 2.7 to 5.0.
---
#### **4.** Calculate the energies at the same distances at the **UHF** level. You can recycle the code that you just wrote (just remember to change the name of your variables). We will need extra information that can ony be found in the output.
In order to save the output to a file we require the additional option: ```psi4.core.set_output_file("filename.txt", True)```.
<div class="alert alert-info">
Hint: In order to obtain the correct UHF energies, we need to set the extra following options:
<\div>
#### **5.** Store the values for $S^2$. This information is found in each outputfile close to the end of your calculation (look for Spin Contamination Metric).
You can go through each of the files and copy the value, but you can also think about how can you let python automatize this process. Think carefully about the steps required for this. Given a path you would need to import the file ( `f = open(path, 'r')` ) and proceed to extract the lines ( `f.read().splitlines()` ). With those lines available, you may concentrate on determining whether or not each line contains the `S^2` string.
If you require a more thorough review of parsing files. You can look at [this tutorial](https://education.molssi.org/python_scripting_cms/02-file_parsing/index.html) to learn more about file parsing.
#### **6.** Make a table or plot of $S^2$ values from the UHF calculations. Explain why $S^2$ deteriorates when the H-H bond is stretched.
---
#### 7. Calculate the same potential energy surface at the DFT level. Use the PBE functional and a restricted wavefunction.
#### **8.** Calculate the same potential energy surface at the FCI level.
For a two-electron system, the FCI results may be obtained by using the CCSD method. This is true because CCSD includes determinants that are singly and doubly excited. For a two electron system that includes all electrons available, thus CCSD includes all possible excitations in the system.
#### **9.** You will need to save the output file generated by Psi4 again. From the output file, record total CCSD ampltitudes: CCSD $T_1^2$ and $T_2^2$, and the value of the largest $T_2$ amplitude for the ground state geometry and for a split geometry.
Consider T as a sum of operators that that act on a reference determinant. In CCSD $T = T_1 + T_2$ where $T_1$ refers with single excitations and $T_2$ with double excitations.
The values of amplitudes show a relative weight of singly and doubly excited determinants in the wavefunction. If $T_1$ and/or $T_2$ are large (generally speaking, if a particular |$T_2| > 0.1$), the wavefunction is considered to be multi-configurational, i.e., containing several important Slater determinants. In other words, this is a region where non-dynamic (static) correlation is significant. Several small $T_1$ and $T_2$ amplitudes tell about (almost always present) dynamic correlation.
In each output you should look at the values of *Largest {TIA, Tia, TIjAb} Amplitudes*, where the $T$ refers to the previously mentioned operator, and the following indices refer to the orbitals used according to the notation:
| | Occupied Molecular Orbitals | Virtual Molecular Orbitals | | |
|-------|-----------------------------|----------------------------|---|---|
| Alpha | i,j | a, b | | |
| Beta | I, J | A, B | | |
---
#### **10.** Plot on the same graph the RHF, DFT and FCI binding energies in $H_2$ versus the separation distance. Plot in kcal/mol energy units (1 Hartree = 627.5 kcal/mol)
#### **11.** Using your results, compare CCSD, UHF and RHF dissociation energies.
---
#### **12.** Comment on the behaviour of RHF with respect to FCI at short (around 0.7 Angstroms) and long distances. For more information, you can read paragraph 3.8.7 from Reference 1 (found below) for a discussion of RHF and UHF solutions.
#RESPONSE
---
#### **13.** Plot the first two $H_2$ molecular orbitals from your RHF and UHF calculations at equilibrium , 0.7 and 5.0 Angstroms. Remember to use the appropriate global settings. Comment on qualitative changes in the shape of the orbitals.
##### You may use the function `generate_orbitals` from the orbital_helper file in the same directory to plot both HOMO and HOMO for the $H_2$ molecule. The syntax is the following:
##### If you have the package `moly` installed. You may visualize the orbitals in 3D with the following:
---
#### **14.** Difference between FCI and HF energies is the correlation energy. What is the nature of the correlation energy (dynamic vs non-dynamic) in $H_2$ at equilibrium and long distances? At what distance does the non-dynamic correlation become important?
#RESPONSE
---
#### **15.** Comment on the behaviour of DFT at equilibrium and long distances. What is the reason of DFT failure for bond-breaking?
#RESPONSE
---
#### **Bonus.** From the previously computed energy of a Hydrogen atom with the hybrid B3LYP functional. Compare the energy of the atom computed with HF, B3LYP and the exact energy. Do you see any discrepancy with B3LYP? If so, what is/are the reasons for such discrepancies?
***
## Part 2
Your friend, who is an experimental chemist, seeks your help knowing that you have expertise in running quantum chemistry simulations. Their research group has measured the singlet-triplet gap of ozone recently. They want to see if computational simulations can support their measurement. How will you measure the singlet-triplet gap in ozone?
Use the ideas from the previous part of this lab and the follwoing hints:
**1.** Assume that the singlet and triplet ozone molecules have the same geometry.
**2.** You will have to optimize the geometry of ozone to start with. Psi4 can let you import geometries from PubChem. The sytax is: `h2o_geometry = psi4.geometry("pubchem:water")`. You may use the common name or its molecular formula. Alternatively, you can use a database such as [CCCBDB](https://cccbdb.nist.gov/).
**3.** Use RHF/6-31G* for simulating the singlet ozone molecule. Use UHF/6-31G* for simulating the triplet ozone molecule. Use the energy difference to compute the gap.
**4.** Write the electronic energies corresponding to singlet and triplet ozone molecules. the singlet-triplet gap in eV, and the $<S^2>$ value for triplet ozone. Information about spin contamination is given by $<S^2>$ and can be found close to the end of your calculation (look for Spin Contamination Metric).
---
Now, compute the singlet-triplet gap between the $^1\Delta_g$ and $^3\Sigma_g$ states of oxygen molecule and report it in eV. Compare the singlet-triplet gap you computed in this lab with the ones availiable in CCBDB. Is it an exact match (http://cccbdb.nist.gov/stgap1.asp)?
<img src="./ozone.png">
##### Compare the expected $<S^2>$ with observed $<S^2>$ and respond: Of all the four cases you have computed so far, which one suffers the most spin contamination?
---
Bonus. Compute the singlet-triplet gap between $^1\Sigma_g ^+$ and $^3\Sigma_g ^-$ states of oxygen atom.
<div class="alert alert-info">
Hint: Start with $^1 \Delta_g$ geometry. Use the maximum overlap method (MOM) to force the highest beta electron to occupy the second $\pi^*$ ortibal: ```psi4.set_options({"MOM_START":1})```
</div>
| 0.79657 | 0.925095 |
# Named Entity Recognition using Transformers
**Author:** [Varun Singh](https://www.linkedin.com/in/varunsingh2/)<br>
**Date created:** Jun 23, 2021<br>
**Last modified:** Jun 24, 2021<br>
**Description:** NER using the Transformers and data from CoNLL 2003 shared task.
## Introduction
Named Entity Recognition (NER) is the process of identifying named entities in text.
Example of named entities are: "Person", "Location", "Organization", "Dates" etc. NER is
essentially a token classification task where every token is classified into one or more
predetermined categories.
In this exercise, we will train a simple Transformer based model to perform NER. We will
be using the data from CoNLL 2003 shared task. For more information about the dataset,
please visit [the dataset website](https://www.clips.uantwerpen.be/conll2003/ner/).
However, since obtaining this data requires an additional step of getting a free license, we will be using
HuggingFace's datasets library which contains a processed version of this dataset.
## Install the open source datasets library from HuggingFace
```
!pip3 install datasets
!wget https://raw.githubusercontent.com/sighsmile/conlleval/master/conlleval.py
import os
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from datasets import load_dataset
from collections import Counter
from conlleval import evaluate
```
We will be using the transformer implementation from this fantastic
[example](https://keras.io/examples/nlp/text_classification_with_transformer/).
Let's start by defining a `TransformerBlock` layer:
```
class TransformerBlock(layers.Layer):
def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):
super(TransformerBlock, self).__init__()
self.att = keras.layers.MultiHeadAttention(
num_heads=num_heads, key_dim=embed_dim
)
self.ffn = keras.Sequential(
[
keras.layers.Dense(ff_dim, activation="relu"),
keras.layers.Dense(embed_dim),
]
)
self.layernorm1 = keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = keras.layers.Dropout(rate)
self.dropout2 = keras.layers.Dropout(rate)
def call(self, inputs, training=False):
attn_output = self.att(inputs, inputs)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output, training=training)
return self.layernorm2(out1 + ffn_output)
```
Next, let's define a `TokenAndPositionEmbedding` layer:
```
class TokenAndPositionEmbedding(layers.Layer):
def __init__(self, maxlen, vocab_size, embed_dim):
super(TokenAndPositionEmbedding, self).__init__()
self.token_emb = keras.layers.Embedding(
input_dim=vocab_size, output_dim=embed_dim
)
self.pos_emb = keras.layers.Embedding(input_dim=maxlen, output_dim=embed_dim)
def call(self, inputs):
maxlen = tf.shape(inputs)[-1]
positions = tf.range(start=0, limit=maxlen, delta=1)
position_embeddings = self.pos_emb(positions)
token_embeddings = self.token_emb(inputs)
return token_embeddings + position_embeddings
```
## Build the NER model class as a `keras.Model` subclass
```
class NERModel(keras.Model):
def __init__(
self, num_tags, vocab_size, maxlen=128, embed_dim=32, num_heads=2, ff_dim=32
):
super(NERModel, self).__init__()
self.embedding_layer = TokenAndPositionEmbedding(maxlen, vocab_size, embed_dim)
self.transformer_block = TransformerBlock(embed_dim, num_heads, ff_dim)
self.dropout1 = layers.Dropout(0.1)
self.ff = layers.Dense(ff_dim, activation="relu")
self.dropout2 = layers.Dropout(0.1)
self.ff_final = layers.Dense(num_tags, activation="softmax")
def call(self, inputs, training=False):
x = self.embedding_layer(inputs)
x = self.transformer_block(x)
x = self.dropout1(x, training=training)
x = self.ff(x)
x = self.dropout2(x, training=training)
x = self.ff_final(x)
return x
```
## Load the CoNLL 2003 dataset from the datasets library and process it
```
conll_data = load_dataset("conll2003")
```
We will export this data to a tab-separated file format which will be easy to read as a
`tf.data.Dataset` object.
```
def export_to_file(export_file_path, data):
with open(export_file_path, "w") as f:
for record in data:
ner_tags = record["ner_tags"]
tokens = record["tokens"]
f.write(
str(len(tokens))
+ "\t"
+ "\t".join(tokens)
+ "\t"
+ "\t".join(map(str, ner_tags))
+ "\n"
)
os.mkdir("data")
export_to_file("./data/conll_train.txt", conll_data["train"])
export_to_file("./data/conll_val.txt", conll_data["validation"])
```
## Make the NER label lookup table
NER labels are usually provided in IOB, IOB2 or IOBES formats. Checkout this link for
more information:
[Wikipedia](https://en.wikipedia.org/wiki/Inside%E2%80%93outside%E2%80%93beginning_(tagging))
Note that we start our label numbering from 1 since 0 will be reserved for padding. We
have a total of 10 labels: 9 from the NER dataset and one for padding.
```
def make_tag_lookup_table():
iob_labels = ["B", "I"]
ner_labels = ["PER", "ORG", "LOC", "MISC"]
all_labels = [(label1, label2) for label2 in ner_labels for label1 in iob_labels]
all_labels = ["-".join([a, b]) for a, b in all_labels]
all_labels = ["[PAD]", "O"] + all_labels
return dict(zip(range(0, len(all_labels) + 1), all_labels))
mapping = make_tag_lookup_table()
print(mapping)
```
Get a list of all tokens in the training dataset. This will be used to create the
vocabulary.
```
all_tokens = sum(conll_data["train"]["tokens"], [])
all_tokens_array = np.array(list(map(str.lower, all_tokens)))
counter = Counter(all_tokens_array)
print(len(counter))
num_tags = len(mapping)
vocab_size = 20000
# We only take (vocab_size - 2) most commons words from the training data since
# the `StringLookup` class uses 2 additional tokens - one denoting an unknown
# token and another one denoting a masking token
vocabulary = [token for token, count in counter.most_common(vocab_size - 2)]
# The StringLook class will convert tokens to token IDs
lookup_layer = keras.layers.experimental.preprocessing.StringLookup(
vocabulary=vocabulary
)
```
Create 2 new `Dataset` objects from the training and validation data
```
train_data = tf.data.TextLineDataset("./data/conll_train.txt")
val_data = tf.data.TextLineDataset("./data/conll_val.txt")
```
Print out one line to make sure it looks good. The first record in the line is the number of tokens.
After that we will have all the tokens followed by all the ner tags.
```
print(list(train_data.take(1).as_numpy_iterator()))
```
We will be using the following map function to transform the data in the dataset:
```
def map_record_to_training_data(record):
record = tf.strings.split(record, sep="\t")
length = tf.strings.to_number(record[0], out_type=tf.int32)
tokens = record[1 : length + 1]
tags = record[length + 1 :]
tags = tf.strings.to_number(tags, out_type=tf.int64)
tags += 1
return tokens, tags
def lowercase_and_convert_to_ids(tokens):
tokens = tf.strings.lower(tokens)
return lookup_layer(tokens)
# We use `padded_batch` here because each record in the dataset has a
# different length.
batch_size = 32
train_dataset = (
train_data.map(map_record_to_training_data)
.map(lambda x, y: (lowercase_and_convert_to_ids(x), y))
.padded_batch(batch_size)
)
val_dataset = (
val_data.map(map_record_to_training_data)
.map(lambda x, y: (lowercase_and_convert_to_ids(x), y))
.padded_batch(batch_size)
)
ner_model = NERModel(num_tags, vocab_size, embed_dim=32, num_heads=4, ff_dim=64)
```
We will be using a custom loss function that will ignore the loss from padded tokens.
```
class CustomNonPaddingTokenLoss(keras.losses.Loss):
def __init__(self, name="custom_ner_loss"):
super().__init__(name=name)
def call(self, y_true, y_pred):
loss_fn = keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction=keras.losses.Reduction.NONE
)
loss = loss_fn(y_true, y_pred)
mask = tf.cast((y_true > 0), dtype=tf.float32)
loss = loss * mask
return tf.reduce_sum(loss) / tf.reduce_sum(mask)
loss = CustomNonPaddingTokenLoss()
```
## Compile and fit the model
```
ner_model.compile(optimizer="adam", loss=loss)
ner_model.fit(train_dataset, epochs=10)
def tokenize_and_convert_to_ids(text):
tokens = text.split()
return lowercase_and_convert_to_ids(tokens)
# Sample inference using the trained model
sample_input = tokenize_and_convert_to_ids(
"eu rejects german call to boycott british lamb"
)
sample_input = tf.reshape(sample_input, shape=[1, -1])
print(sample_input)
output = ner_model.predict(sample_input)
prediction = np.argmax(output, axis=-1)[0]
prediction = [mapping[i] for i in prediction]
# eu -> B-ORG, german -> B-MISC, british -> B-MISC
print(prediction)
```
## Metrics calculation
Here is a function to calculate the metrics. The function calculates F1 score for the
overall NER dataset as well as individual scores for each NER tag.
```
def calculate_metrics(dataset):
all_true_tag_ids, all_predicted_tag_ids = [], []
for x, y in dataset:
output = ner_model.predict(x)
predictions = np.argmax(output, axis=-1)
predictions = np.reshape(predictions, [-1])
true_tag_ids = np.reshape(y, [-1])
mask = (true_tag_ids > 0) & (predictions > 0)
true_tag_ids = true_tag_ids[mask]
predicted_tag_ids = predictions[mask]
all_true_tag_ids.append(true_tag_ids)
all_predicted_tag_ids.append(predicted_tag_ids)
all_true_tag_ids = np.concatenate(all_true_tag_ids)
all_predicted_tag_ids = np.concatenate(all_predicted_tag_ids)
predicted_tags = [mapping[tag] for tag in all_predicted_tag_ids]
real_tags = [mapping[tag] for tag in all_true_tag_ids]
evaluate(real_tags, predicted_tags)
calculate_metrics(val_dataset)
```
## Conclusions
In this exercise, we created a simple transformer based named entity recognition model.
We trained it on the CoNLL 2003 shared task data and got an overall F1 score of around 70%.
State of the art NER models fine-tuned on pretrained models such as BERT or ELECTRA can easily
get much higher F1 score -between 90-95% on this dataset owing to the inherent knowledge
of words as part of the pretraining process and the usage of subword tokenization.
|
github_jupyter
|
!pip3 install datasets
!wget https://raw.githubusercontent.com/sighsmile/conlleval/master/conlleval.py
import os
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from datasets import load_dataset
from collections import Counter
from conlleval import evaluate
class TransformerBlock(layers.Layer):
def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):
super(TransformerBlock, self).__init__()
self.att = keras.layers.MultiHeadAttention(
num_heads=num_heads, key_dim=embed_dim
)
self.ffn = keras.Sequential(
[
keras.layers.Dense(ff_dim, activation="relu"),
keras.layers.Dense(embed_dim),
]
)
self.layernorm1 = keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = keras.layers.Dropout(rate)
self.dropout2 = keras.layers.Dropout(rate)
def call(self, inputs, training=False):
attn_output = self.att(inputs, inputs)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output, training=training)
return self.layernorm2(out1 + ffn_output)
class TokenAndPositionEmbedding(layers.Layer):
def __init__(self, maxlen, vocab_size, embed_dim):
super(TokenAndPositionEmbedding, self).__init__()
self.token_emb = keras.layers.Embedding(
input_dim=vocab_size, output_dim=embed_dim
)
self.pos_emb = keras.layers.Embedding(input_dim=maxlen, output_dim=embed_dim)
def call(self, inputs):
maxlen = tf.shape(inputs)[-1]
positions = tf.range(start=0, limit=maxlen, delta=1)
position_embeddings = self.pos_emb(positions)
token_embeddings = self.token_emb(inputs)
return token_embeddings + position_embeddings
class NERModel(keras.Model):
def __init__(
self, num_tags, vocab_size, maxlen=128, embed_dim=32, num_heads=2, ff_dim=32
):
super(NERModel, self).__init__()
self.embedding_layer = TokenAndPositionEmbedding(maxlen, vocab_size, embed_dim)
self.transformer_block = TransformerBlock(embed_dim, num_heads, ff_dim)
self.dropout1 = layers.Dropout(0.1)
self.ff = layers.Dense(ff_dim, activation="relu")
self.dropout2 = layers.Dropout(0.1)
self.ff_final = layers.Dense(num_tags, activation="softmax")
def call(self, inputs, training=False):
x = self.embedding_layer(inputs)
x = self.transformer_block(x)
x = self.dropout1(x, training=training)
x = self.ff(x)
x = self.dropout2(x, training=training)
x = self.ff_final(x)
return x
conll_data = load_dataset("conll2003")
def export_to_file(export_file_path, data):
with open(export_file_path, "w") as f:
for record in data:
ner_tags = record["ner_tags"]
tokens = record["tokens"]
f.write(
str(len(tokens))
+ "\t"
+ "\t".join(tokens)
+ "\t"
+ "\t".join(map(str, ner_tags))
+ "\n"
)
os.mkdir("data")
export_to_file("./data/conll_train.txt", conll_data["train"])
export_to_file("./data/conll_val.txt", conll_data["validation"])
def make_tag_lookup_table():
iob_labels = ["B", "I"]
ner_labels = ["PER", "ORG", "LOC", "MISC"]
all_labels = [(label1, label2) for label2 in ner_labels for label1 in iob_labels]
all_labels = ["-".join([a, b]) for a, b in all_labels]
all_labels = ["[PAD]", "O"] + all_labels
return dict(zip(range(0, len(all_labels) + 1), all_labels))
mapping = make_tag_lookup_table()
print(mapping)
all_tokens = sum(conll_data["train"]["tokens"], [])
all_tokens_array = np.array(list(map(str.lower, all_tokens)))
counter = Counter(all_tokens_array)
print(len(counter))
num_tags = len(mapping)
vocab_size = 20000
# We only take (vocab_size - 2) most commons words from the training data since
# the `StringLookup` class uses 2 additional tokens - one denoting an unknown
# token and another one denoting a masking token
vocabulary = [token for token, count in counter.most_common(vocab_size - 2)]
# The StringLook class will convert tokens to token IDs
lookup_layer = keras.layers.experimental.preprocessing.StringLookup(
vocabulary=vocabulary
)
train_data = tf.data.TextLineDataset("./data/conll_train.txt")
val_data = tf.data.TextLineDataset("./data/conll_val.txt")
print(list(train_data.take(1).as_numpy_iterator()))
def map_record_to_training_data(record):
record = tf.strings.split(record, sep="\t")
length = tf.strings.to_number(record[0], out_type=tf.int32)
tokens = record[1 : length + 1]
tags = record[length + 1 :]
tags = tf.strings.to_number(tags, out_type=tf.int64)
tags += 1
return tokens, tags
def lowercase_and_convert_to_ids(tokens):
tokens = tf.strings.lower(tokens)
return lookup_layer(tokens)
# We use `padded_batch` here because each record in the dataset has a
# different length.
batch_size = 32
train_dataset = (
train_data.map(map_record_to_training_data)
.map(lambda x, y: (lowercase_and_convert_to_ids(x), y))
.padded_batch(batch_size)
)
val_dataset = (
val_data.map(map_record_to_training_data)
.map(lambda x, y: (lowercase_and_convert_to_ids(x), y))
.padded_batch(batch_size)
)
ner_model = NERModel(num_tags, vocab_size, embed_dim=32, num_heads=4, ff_dim=64)
class CustomNonPaddingTokenLoss(keras.losses.Loss):
def __init__(self, name="custom_ner_loss"):
super().__init__(name=name)
def call(self, y_true, y_pred):
loss_fn = keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction=keras.losses.Reduction.NONE
)
loss = loss_fn(y_true, y_pred)
mask = tf.cast((y_true > 0), dtype=tf.float32)
loss = loss * mask
return tf.reduce_sum(loss) / tf.reduce_sum(mask)
loss = CustomNonPaddingTokenLoss()
ner_model.compile(optimizer="adam", loss=loss)
ner_model.fit(train_dataset, epochs=10)
def tokenize_and_convert_to_ids(text):
tokens = text.split()
return lowercase_and_convert_to_ids(tokens)
# Sample inference using the trained model
sample_input = tokenize_and_convert_to_ids(
"eu rejects german call to boycott british lamb"
)
sample_input = tf.reshape(sample_input, shape=[1, -1])
print(sample_input)
output = ner_model.predict(sample_input)
prediction = np.argmax(output, axis=-1)[0]
prediction = [mapping[i] for i in prediction]
# eu -> B-ORG, german -> B-MISC, british -> B-MISC
print(prediction)
def calculate_metrics(dataset):
all_true_tag_ids, all_predicted_tag_ids = [], []
for x, y in dataset:
output = ner_model.predict(x)
predictions = np.argmax(output, axis=-1)
predictions = np.reshape(predictions, [-1])
true_tag_ids = np.reshape(y, [-1])
mask = (true_tag_ids > 0) & (predictions > 0)
true_tag_ids = true_tag_ids[mask]
predicted_tag_ids = predictions[mask]
all_true_tag_ids.append(true_tag_ids)
all_predicted_tag_ids.append(predicted_tag_ids)
all_true_tag_ids = np.concatenate(all_true_tag_ids)
all_predicted_tag_ids = np.concatenate(all_predicted_tag_ids)
predicted_tags = [mapping[tag] for tag in all_predicted_tag_ids]
real_tags = [mapping[tag] for tag in all_true_tag_ids]
evaluate(real_tags, predicted_tags)
calculate_metrics(val_dataset)
| 0.889966 | 0.936807 |
# Machine Learning
> A Summary of lecture "Introduction to Computational Thinking and Data Science", via MITx-6.00.2x (edX)
- toc: true
- badges: true
- comments: true
- author: Chanseok Kang
- categories: [Python, edX, Machine_Learning]
- image: images/ml_block.png
- What is Machine Learning
- Many useful programs learn something
> Note: "Field of study that gives computers the ability to learn without being explicitly programmed" - Arthur Samuel
- Modern statistics meets optimization

- Basic Paradigm
- Observe set of examples: **training data**
- Infer something about process that generated that data
- Use inference to make predictions about previously unseen data: **test data**
- All ML Methods Require
- Representation of the features
- Distance metric for feature vectors
- Objective function and constraints
- Optimization method for learning the model
- Evaluation method
- Supervised Learning
- Start with set of feature vector / value pairs
- Goal : find a model that predicts a value for a previously unseen feature vector
- **Regression** models predict a real
- E.g. linear regression
- **Classification** models predict a label (chosen from a finite set of labels)
- Unsupervied Learning
- Start with a set of feature vectors
- Goal : uncover some latent structure in the set of feature vectors
- **Clustering** the most common technique
- Define some metric that captures how similar one feature vector is to another
- Group examples based on this metric
- Choosing Features
- Features never fully describe the situation
- Feature Engineering
- Represent examples by feature vectors that will facilitate generalization
- Suppose I want to use 100 examples from past to predict which students will pass the final exam
- Some features surely helpful, e.g., their grade on the midterm, did they do the problem sets, etc.
- Others might cause me to overfit, e.g., birth month
- Whant to maximize ratio of useful input to irrelevant input
- Signal-to-Noise Ratio (SNR)
- K-Nearest Neighbors
- Distance between vectors
- Minkowski metric
$$ dist(X_1, X_2, p) = (\sum_{k=1}^{len}abs({X_1}_k - {X_2}_k)^p)^{\frac{1}{p}} \\
p=1 : \text{Manhattan Distance} \\
p=2 : \text{Euclidean Distance}$$
```
from lecture12_segment2 import *
cobra = Animal('cobra', [1,1,1,1,0])
rattlesnake = Animal('rattlesnake', [1,1,1,1,0])
boa = Animal('boa\nconstrictor', [0,1,0,1,0])
chicken = Animal('chicken', [1,1,0,1,2])
alligator = Animal('alligator', [1,1,0,1,4])
dartFrog = Animal('dart frog', [1,0,1,0,4])
zebra = Animal('zebra', [0,0,0,0,4])
python = Animal('python', [1,1,0,1,0])
guppy = Animal('guppy', [0,1,0,0,0])
animals = [cobra, rattlesnake, boa, chicken, guppy,
dartFrog, zebra, python, alligator]
compareAnimals(animals, 3) # k=3
```
- Using Distance Matrix for classification
- Simplest approach is probably nearest neighbor
- Remember training data
- When predicting the label of a new example
- Find the nearest example in the training data
- Predict the label associated with that example
- Advantage and Disadvantage of KNN
- Advantages
- Learning fase, no explicit training
- No theory required
- Easy to explain method and results
- Disadvantages
- Memory intensive and predictions can take a long time
- Are better algorithms than brute force
- No model to shed light on process that generated data
```
# Applying scaling
cobra = Animal('cobra', [1,1,1,1,0])
rattlesnake = Animal('rattlesnake', [1,1,1,1,0])
boa = Animal('boa\nconstrictor', [0,1,0,1,0])
chicken = Animal('chicken', [1,1,0,1,2])
alligator = Animal('alligator', [1,1,0,1,1])
dartFrog = Animal('dart frog', [1,0,1,0,1])
zebra = Animal('zebra', [0,0,0,0,1])
python = Animal('python', [1,1,0,1,0])
guppy = Animal('guppy', [0,1,0,0,0])
animals = [cobra, rattlesnake, boa, chicken, guppy,
dartFrog, zebra, python, alligator]
compareAnimals(animals, 3) k = 3
```
- A more General Approach: Scaling
- Z-scaling
- Each feature has a mean of 0 & a standard deviation of 1
- Interpolation
- Map minimum value to 0, maximum value to 1, and linearly interpolate
```python
def zScaleFeatures(vals):
"""Assumes vals is a sequence of floats"""
result = np.array(vals)
mean = np.mean(vals)
result = result - mean
return result/np.std(result)
def iScaleFeatures(vals):
"""Assumes vals is a sequence of floats"""
minVal, maxVal = min(vals), max(vals)
fit = np.polyfit([minVal, maxVal], [0, 1], 1)
return np.polyval(fit, vals)
```
- Clustering
- Partition examples into groups (clusters) such that examples in a group are more similar to each other than to examples in other groups
- Unlike classification, there is not typically a "right answer"
- Answer dictated by feature vector and distance metric, not by a group truth label
- Optimization Problem
$$ variability(c) = \sum_{e \in c} distance(mean(c), e)^2 \\
dissimilarity(C) = \sum_{c \in C} variability(c) \\
c :\text{one cluster} \\
C : \text{all of the clusters}$$
- Why not divide variability by size of cluster?
- Big and bad worse than small and bad
- Is optimization problem finding a $C$ that minimizes $dissimilarity(C)$?
- No, otherwise could put each example in its own cluster
- Need constraints, e.g.
- Minimum distance between clusters
- Number of clusters
- K-means Clustering
- Constraint: exactly k non-empty clusters
- Use a greedy algorithm to find an approximation to minimizing objective function
- Algorithm
```
randomly chose k examples as initial centroids
while true:
create k clusters by assigning each example to closest centroid
compute k new centroids by averaging examples in each cluster
if centroids don`t change:
break
```
```
from lecture12_segment3 import *
centers = [(2, 3), (4, 6), (7, 4), (7,7)]
examples = []
random.seed(0)
for c in centers:
for i in range(5):
xVal = (c[0] + random.gauss(0, .5))
yVal = (c[1] + random.gauss(0, .5))
name = str(c) + '-' + str(i)
example = Example(name, pylab.array([xVal, yVal]))
examples.append(example)
xVals, yVals = [], []
for e in examples:
xVals.append(e.getFeatures()[0])
yVals.append(e.getFeatures()[1])
random.seed(2)
kmeans(examples, 4, True)
```
- Mitigating Dependence on Initial Centroids
```python
best = kMeans(points)
for t in range(numTrials):
C = kMeans(points)
if dissimilarity(C) < dissimilarity(best):
best = C
return best
```
- A Pretty Example
- User k-means to cluster groups of pixels in an image by their color
- Get the color associated with the centroid of each cluster, i.e., the average color of the cluster
- For each pixel in the original image, find the centroid that is its nearest neighbor
- Replaced the pixel by that centroid
|
github_jupyter
|
from lecture12_segment2 import *
cobra = Animal('cobra', [1,1,1,1,0])
rattlesnake = Animal('rattlesnake', [1,1,1,1,0])
boa = Animal('boa\nconstrictor', [0,1,0,1,0])
chicken = Animal('chicken', [1,1,0,1,2])
alligator = Animal('alligator', [1,1,0,1,4])
dartFrog = Animal('dart frog', [1,0,1,0,4])
zebra = Animal('zebra', [0,0,0,0,4])
python = Animal('python', [1,1,0,1,0])
guppy = Animal('guppy', [0,1,0,0,0])
animals = [cobra, rattlesnake, boa, chicken, guppy,
dartFrog, zebra, python, alligator]
compareAnimals(animals, 3) # k=3
# Applying scaling
cobra = Animal('cobra', [1,1,1,1,0])
rattlesnake = Animal('rattlesnake', [1,1,1,1,0])
boa = Animal('boa\nconstrictor', [0,1,0,1,0])
chicken = Animal('chicken', [1,1,0,1,2])
alligator = Animal('alligator', [1,1,0,1,1])
dartFrog = Animal('dart frog', [1,0,1,0,1])
zebra = Animal('zebra', [0,0,0,0,1])
python = Animal('python', [1,1,0,1,0])
guppy = Animal('guppy', [0,1,0,0,0])
animals = [cobra, rattlesnake, boa, chicken, guppy,
dartFrog, zebra, python, alligator]
compareAnimals(animals, 3) k = 3
def zScaleFeatures(vals):
"""Assumes vals is a sequence of floats"""
result = np.array(vals)
mean = np.mean(vals)
result = result - mean
return result/np.std(result)
def iScaleFeatures(vals):
"""Assumes vals is a sequence of floats"""
minVal, maxVal = min(vals), max(vals)
fit = np.polyfit([minVal, maxVal], [0, 1], 1)
return np.polyval(fit, vals)
randomly chose k examples as initial centroids
while true:
create k clusters by assigning each example to closest centroid
compute k new centroids by averaging examples in each cluster
if centroids don`t change:
break
from lecture12_segment3 import *
centers = [(2, 3), (4, 6), (7, 4), (7,7)]
examples = []
random.seed(0)
for c in centers:
for i in range(5):
xVal = (c[0] + random.gauss(0, .5))
yVal = (c[1] + random.gauss(0, .5))
name = str(c) + '-' + str(i)
example = Example(name, pylab.array([xVal, yVal]))
examples.append(example)
xVals, yVals = [], []
for e in examples:
xVals.append(e.getFeatures()[0])
yVals.append(e.getFeatures()[1])
random.seed(2)
kmeans(examples, 4, True)
best = kMeans(points)
for t in range(numTrials):
C = kMeans(points)
if dissimilarity(C) < dissimilarity(best):
best = C
return best
| 0.641759 | 0.984246 |
# Workshop 12: Introduction to Numerical ODE Solutions
*Source: Eric Ayars, PHYS 312 @ CSU Chico*
**Submit this notebook to bCourses to receive a grade for this Workshop.**
Please complete workshop activities in code cells in this iPython notebook. The activities titled **Practice** are purely for you to explore Python, and no particular output is expected. Some of them have some code written, and you should try to modify it in different ways to understand how it works. Although no particular output is expected at submission time, it is _highly_ recommended that you read and work through the practice activities before or alongside the exercises. However, the activities titled **Exercise** have specific tasks and specific outputs expected. Include comments in your code when necessary. Enter your name in the cell at the top of the notebook.
**The workshop should be submitted on bCourses under the Assignments tab (both the .ipynb and .pdf files).**
```
# Run this cell before preceding
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
```
## Ordinary Differential Equation (ODE)
An ordinary differential equation is an equation that takes the following form:
$$F(t,x,x',x'',\dots) = 0$$
where $x$ is a function of $t$ and the $'$ symbol denotes derivatives:
$$x' = \frac{dx}{dt}$$
$$x'' = \frac{d^2x}{dt^2}$$
$$\vdots$$
An example is
$$x' + x = 0$$
To solve such an equation, we need to specify an *initial condition*: a set of values $(t_0, x_0)$ that our solution must pass through. This is because there are multiple solutions which can satisfy that equation. Any solution of the form
$$x(t) = Ae^{-t}$$
satisfies the differential equation above. So by requiring that this curve pass through a particular point $(t_0, x_0)$, we can determine $A$:
$$A = \frac{x_0}{e^{-t_0}}$$
Another way to visualize is this is with the aid of a "slope field": a plot that, for various points $(t,x)$ shows what $x(t)$ must look like locally by evaluating the derivative $x'$ at that point:
```
# Initial condition
t0 = 0.0
x0 = 0.75
# Make a grid of x,t values
t_values = np.linspace(t0, t0+3, 20)
x_values = np.linspace(-np.abs(x0)*1.2, np.abs(x0)*1.2, 20)
t, x = np.meshgrid(t_values, x_values)
# Evaluate derivative at each x point
xdot = -x
plt.figure()
# Plot slope field arrows
plt.quiver(t,x, np.ones(t.shape), xdot,color='b')
# Plot solution
A = x0 / np.exp(-t0)
plt.plot(t_values,A * np.exp(-t_values),color='r')
# Plot initial condition
plt.plot(t0,x0,'go',markersize=8)
plt.xlabel('t')
plt.ylabel('x(t)')
plt.title("Slope field and a solution of $x'=x$")
plt.show()
```
With those two pieces of information--the differential equation and an initial condition--we are able to write down a closed-form solution $x(t)$. But for a general differential equation, even if you have an initial condition, it is difficult to write down $x(t)$ in closed form. For example, if the equation is nonlinear or, if you have a set of *coupled* differential equations, as we frequently encounter in physics, numerical methods are indispensable.
## Outline of this Workshop
1. Basic setup and numerical solution of a first-order ODE
2. Set up a second-order ODE--the harmonic oscillator
3. Numerical stability issue
4. Phase portraits
## Euler method
### Definition of the Euler method
Suppose we have the differential equation
$$\frac{dx}{dt} = f(x,t)$$
This means that, given a point in the system $(x_0, t_0)$, we have a way to compute the derivative $dx/dt$ at that point. But it may be difficult or impossible to analytically integrate $f(x,t)$ to find a closed form for $x(t)$. Instead, we rely on numerical methods to estimate solutions. More specifically, given an *initial condition* $(x_0, t_0)$, where $x(t_0) = x_0$, the goal is to find a numerical method to calculate $x(t)$ for $t > t_0$.
The most basic Euler method is based on the simple observation that
$$x(t+\Delta t) = x(t) + \int_{t}^{t+\Delta t} \left(\frac{dx}{dt}\right) dt = x(t) + \int_{t}^{t+\Delta t} f(x(t),t) dt $$
If we cannot explicitly take that integral, but we have a way to calculate $f(x,t)$, then the first thing we would try is
$$x(t+\Delta t) \approx x(t) + f(x(t), t) \cdot \Delta t$$
Now let us try to make this into code. Suppose we have a list of times $\{t_i\}$ such that $t_{i+1} - t_i = \Delta t$ (generated by `np.arange` or `np.linspace`, for example). Then given $x_0$ at $t_0$, we calculate $x_i$ according to the rule
$$x_i = x_{i-1} + f(x_{i-1},t_{i-1})\Delta t$$
So as long as we can write the first derivative in the form above, we have a way to attack this problem.
For example, we can numerically solve a problem like
$$v' = 1-v^2$$
$$\rightarrow v_i = v_{i-1} + f(v_{i-1}, t_{i-1}) \Delta t = v_{i-1} + (1-v_{i-1}^2)\Delta t$$
Given an initial $(t_0, v_0)$, we can use the Euler method to solve this equation, which describes the velocity (denoted $v$ here) of a particle falling but experiencing a drag force (see lecture). We know that the solution of such an equation should be that the velocity of the particle should increase quickly at first (due to constant gravitational force) but then asymptote to some terminal value because the drag force increases with velocity. Let's see this:
```
# Basic example of Euler method
t_0 = 0.0 # initial time condition
v_0 = 0.0 # initial velocity condition
# Generate some times t_i
t_data = np.linspace(0,100,1000)
# Placeholder array for velocities v_i
v_data = np.zeros(1000)
v_data[0] = v_0
N = len(t_data)
# use Euler method to estimate v_i for each i
for i in range(1,N):
f = 1 - v_data[i-1]**2 # f(v_{i-1})
dt = t_data[i] - t_data[i-1] # time interval
v_data[i] = v_data[i-1] + f * dt # calculate v_i
# Plot results
plt.figure()
plt.plot(t_data, v_data)
plt.xlabel("Time")
plt.ylabel("Velocity")
plt.title("Velocity of particle falling and experiencing drag")
plt.show()
```
So we have established a technique to approximate solutions to some first-order differential equations. Note that these solutions still have some error--flip back to the workshop on integration techniques to remind yourself of this.
At first, being able to solve only first-order differential equations seems very restrictive. But actually, it is enough for us to start modeling real systems and observing interesting behaviors. First, let us try to convert a second order differential equation, such as Newton's second law, into a set of first order differential equations, which we now know how to solve.
### Example: Euler Method and a Second-Order ODE
Commonly we have a set of *second-order* differential equations. For example, the harmonic oscillator takes this form:
$$F = ma = m\frac{d^2x}{dt^2} = -kx$$
$$\rightarrow \frac{d^2x}{dt^2} + \frac{k}{m}x = 0$$
But we can rewrite as a set of first-order differential equations by noting that
$$a = \frac{dv}{dt}$$
and
$$v = \frac{dx}{dt}$$
So the force equation above becomes a pair of equations:
\begin{align}
x' &= \frac{dx}{dt} = v \\
v' &= \frac{dv}{dt} = -\frac{k}{m}x
\end{align}
This means that to form a solution, we need three numbers for the initial condition, $(t_0, x_0, v_0)$ where $x(t_0) = x_0$ and $v(t_0) = v_0$. As we did above, let us write this down in terms of the values $x_i$, $v_i$, and $t_i$:
\begin{align}
x_i &= x_{i-1} + v_{i-1} \Delta t \\
v_i &= v_{i-1} + \left(-\frac{k}{m}x_{i-1}\right)\Delta t
\end{align}
In the examples below, I will continue to take $t_0 = 0$
```
# Use Euler method to solve coupled first order ODE
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
km = 0.3 # value of k / m
# Initial conditions
x_0 = 1.0
v_0 = 0.0
# Number of timesteps
T = 1000
dt = 0.1 #size of time step (Delta t)
def Euler(t0, x0, v0, T, dt):
x_data = np.zeros(T)
v_data = np.zeros(T)
t_data = np.arange(T) * dt + t0
x_data[0] = x0
v_data[0] = v0
for i in range(1,T):
x_data[i] = x_data[i-1] + v_data[i-1] * dt
v_data[i] = v_data[i-1] + (-km * x_data[i-1]) * dt
return t_data, x_data, v_data
t_data, x_data, v_data = Euler(0.0, x_0, v_0, T, dt)
# Analytical solutions for (x(t), v(t)) assuming x_0 = 1.0, v_0 = 0, t_0 = 0
analytical_x = np.cos(np.sqrt(km)*t_data)
analytical_v = -np.sqrt(km)*np.sin(np.sqrt(km)*t_data)
plt.figure(figsize=(8,8))
plt.subplot(211)
plt.plot(t_data, x_data, label="numerical")
plt.plot(t_data, analytical_x,label="analytical")
plt.ylabel("Position")
plt.legend()
plt.title("Position of the mass on spring")
plt.subplot(212)
plt.plot(t_data, v_data, label="numerical")
plt.plot(t_data, analytical_v, label="analytical")
plt.ylabel("Velocity")
plt.xlabel("Time")
plt.legend()
plt.title("Velocity of the mass on spring")
# Plot error in position as a function of time
plt.figure()
plt.plot(t_data, np.abs(x_data - analytical_x))
plt.ylabel("$|x_i - x_{analytical}|$")
plt.xlabel("Time")
plt.title("Absolute error in position")
plt.show()
```
### Exercise 1:
The damped harmonic oscillator (DHO) satisfies the following differential equation:
$$\frac{d^2x}{dt^2}+\frac{c}{m}\frac{dx}{dt}+\frac{k}{m}x = 0$$
It differs from the previous example by the addition of the $(c/m) dx/dt$ term. Like we did above, we can unwrap this second-order ODE into two first-order ODEs using two separate variables $x(t)$ and $v(t)$
\begin{align}
x' &= v \\
v' &= -\frac{c}{m}v - \frac{k}{m}x
\end{align}
1. Like in the example above, write down the update rules for $x_i$ and $v_i$.
1. Then write some code to implement your rules to estimate a numerical solution for $x(t)$ and $v(t)$ for a given initial condition $x_0$ and $v_0$ (you can assume $t_0 = 0$ like above).
1. Plot your results for $x(t)$ and $v(t)$ and make sure that they make sense. You may use the code in the example as a template.
*Hint*: Recall that the qualitative behavior of the oscillator is different depending on the (dimensionless) value of the ratio
$$\frac{(c/m)^2}{k/m}$$
So you should be able to see the effect of this by trying out different values for $c/m$ and $k/m$.
```
# Code for Exercise 1
```
## But wait...
But you know that for a closed system, like the SHO, we actually have a special constraint on the system--the total energy (kinetic + potential) must be constant! So at every point of our solution, we should check whether this is true. How do we evaluate the total energy?
$$E = T + U = \frac{1}{2}mv^2 + \frac{1}{2}kx^2$$
Let's define a rescaled energy $\tilde{E}$ as $(1/m)E$:
$$\tilde{E} = \frac{1}{2}v^2 + \frac{1}{2}\frac{k}{m} x^2$$
### Exercise 2:
1. Copy the code from the example using the SHO above, in which we solved the SHO using the Euler Method. Add code to calculate the rescaled energy $\tilde{E}_i$ for each time step.
1. Plot $\tilde{E}(t)$ vs. the time. Does the energy stay constant, fluctuate around some constant value, or does it diverge/decay?
```
# Code for Exercise 2
```
## Euler-Cromer/Symplectic Euler Method
There exists a way to keep the energy fluctuations from growing, using a just a slight variant of the update rules described above. This update rule is called the
\begin{align}
v_i &= v_{i-1} + \left(-\frac{k}{m}x_{i-1}\right)\Delta t \\
x_i &= x_{i-1} + v_{i} \Delta t
\end{align}
In this version, you use the approximate velocity at time $t_i$ instead of the velocity at time $t_{i-1}$ to calculate $x_i$.
### Exercise 3:
1. Modify the code from Exercise 2 to instead implement the update rule in the Euler-Cromer method. You can either modify the it in-place or copy it to the cell below and modify it.
1. Now run your code to calculate and plot $x(t)$, $v(t)$, and $\tilde{E}(t)$. Does the energy stay constant, fluctuate around some constant value, or does it diverge/decay?
```
# Code for Exercise 3
```
There are also higher order ODE integration schemes, like Runge-Kutta, which make better estimates of the change in $(x(t),v(t)...)$ between $t_{i-1}$ and $t_i$. The shortcoming of our simple method above is that we are typically using the value of the derivative ($x'$ or $v'$) at $t_i$ or $t_{i-1}$ as a subsitute for the derivative over the entire interval $(t_{i-1}, t_i)$. These higher order schemes try to make better estimates of the derivatives inside this interval to make a better estimate of $\Delta x$ and $\Delta v$.
## Visualizing Phase Space
Here we generalize the use of the slope field above to visualize our error in the Euler method. The tool below is called a phase portrait and is ubiquitous in physics and mathematics, and students studying dynamical systems for their capstone projects may find it useful as a nice visualization. In the cell below, we examine the phase portrait of the SHO and study the numerical and analytical solutions. Before you run this cell, run the SHO example cell again with `x_0 = 1.0` and `v_0 = 0.0` so that `km`, `x_data`, and `v_data` are properly populated.
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
xvalues, yvalues = np.meshgrid(np.arange(min(x_data),max(x_data), 0.2), np.arange(min(v_data), max(v_data), 0.5))
xdot = yvalues
ydot = - km * xvalues
plt.figure(figsize=(8,8))
plt.streamplot(xvalues, yvalues, xdot, ydot)
plt.plot(x_data[0],v_data[0],'go',markersize=8)
plt.plot(x_data, v_data,color='r', label="numerical")
plt.plot(analytical_x, analytical_v, color='k', label="analytical")
plt.ylabel("Velocity")
plt.xlabel("Position")
plt.title("Phase Portrait")
plt.legend()
plt.grid()
plt.show()
```
You can make phase portraits for just about any system! Here's a phase portrait for the DHO. How does the phase portrait change qualitatively, as you vary $c/m$ and $k/m$?
```
cm = 0.2 # c / m
km = 0.3 # k / m
xvalues, yvalues = np.meshgrid(np.arange(-3,3, 0.5), np.arange(-3,3, 0.5))
xdot = yvalues
ydot = - cm * yvalues - km * xvalues
plt.figure(figsize=(8,8))
plt.streamplot(xvalues, yvalues, xdot, ydot)
plt.ylabel("Velocity")
plt.xlabel("Position")
plt.title("Phase Portrait")
plt.grid()
plt.show()
```
|
github_jupyter
|
# Run this cell before preceding
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# Initial condition
t0 = 0.0
x0 = 0.75
# Make a grid of x,t values
t_values = np.linspace(t0, t0+3, 20)
x_values = np.linspace(-np.abs(x0)*1.2, np.abs(x0)*1.2, 20)
t, x = np.meshgrid(t_values, x_values)
# Evaluate derivative at each x point
xdot = -x
plt.figure()
# Plot slope field arrows
plt.quiver(t,x, np.ones(t.shape), xdot,color='b')
# Plot solution
A = x0 / np.exp(-t0)
plt.plot(t_values,A * np.exp(-t_values),color='r')
# Plot initial condition
plt.plot(t0,x0,'go',markersize=8)
plt.xlabel('t')
plt.ylabel('x(t)')
plt.title("Slope field and a solution of $x'=x$")
plt.show()
# Basic example of Euler method
t_0 = 0.0 # initial time condition
v_0 = 0.0 # initial velocity condition
# Generate some times t_i
t_data = np.linspace(0,100,1000)
# Placeholder array for velocities v_i
v_data = np.zeros(1000)
v_data[0] = v_0
N = len(t_data)
# use Euler method to estimate v_i for each i
for i in range(1,N):
f = 1 - v_data[i-1]**2 # f(v_{i-1})
dt = t_data[i] - t_data[i-1] # time interval
v_data[i] = v_data[i-1] + f * dt # calculate v_i
# Plot results
plt.figure()
plt.plot(t_data, v_data)
plt.xlabel("Time")
plt.ylabel("Velocity")
plt.title("Velocity of particle falling and experiencing drag")
plt.show()
# Use Euler method to solve coupled first order ODE
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
km = 0.3 # value of k / m
# Initial conditions
x_0 = 1.0
v_0 = 0.0
# Number of timesteps
T = 1000
dt = 0.1 #size of time step (Delta t)
def Euler(t0, x0, v0, T, dt):
x_data = np.zeros(T)
v_data = np.zeros(T)
t_data = np.arange(T) * dt + t0
x_data[0] = x0
v_data[0] = v0
for i in range(1,T):
x_data[i] = x_data[i-1] + v_data[i-1] * dt
v_data[i] = v_data[i-1] + (-km * x_data[i-1]) * dt
return t_data, x_data, v_data
t_data, x_data, v_data = Euler(0.0, x_0, v_0, T, dt)
# Analytical solutions for (x(t), v(t)) assuming x_0 = 1.0, v_0 = 0, t_0 = 0
analytical_x = np.cos(np.sqrt(km)*t_data)
analytical_v = -np.sqrt(km)*np.sin(np.sqrt(km)*t_data)
plt.figure(figsize=(8,8))
plt.subplot(211)
plt.plot(t_data, x_data, label="numerical")
plt.plot(t_data, analytical_x,label="analytical")
plt.ylabel("Position")
plt.legend()
plt.title("Position of the mass on spring")
plt.subplot(212)
plt.plot(t_data, v_data, label="numerical")
plt.plot(t_data, analytical_v, label="analytical")
plt.ylabel("Velocity")
plt.xlabel("Time")
plt.legend()
plt.title("Velocity of the mass on spring")
# Plot error in position as a function of time
plt.figure()
plt.plot(t_data, np.abs(x_data - analytical_x))
plt.ylabel("$|x_i - x_{analytical}|$")
plt.xlabel("Time")
plt.title("Absolute error in position")
plt.show()
# Code for Exercise 1
# Code for Exercise 2
# Code for Exercise 3
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
xvalues, yvalues = np.meshgrid(np.arange(min(x_data),max(x_data), 0.2), np.arange(min(v_data), max(v_data), 0.5))
xdot = yvalues
ydot = - km * xvalues
plt.figure(figsize=(8,8))
plt.streamplot(xvalues, yvalues, xdot, ydot)
plt.plot(x_data[0],v_data[0],'go',markersize=8)
plt.plot(x_data, v_data,color='r', label="numerical")
plt.plot(analytical_x, analytical_v, color='k', label="analytical")
plt.ylabel("Velocity")
plt.xlabel("Position")
plt.title("Phase Portrait")
plt.legend()
plt.grid()
plt.show()
cm = 0.2 # c / m
km = 0.3 # k / m
xvalues, yvalues = np.meshgrid(np.arange(-3,3, 0.5), np.arange(-3,3, 0.5))
xdot = yvalues
ydot = - cm * yvalues - km * xvalues
plt.figure(figsize=(8,8))
plt.streamplot(xvalues, yvalues, xdot, ydot)
plt.ylabel("Velocity")
plt.xlabel("Position")
plt.title("Phase Portrait")
plt.grid()
plt.show()
| 0.828766 | 0.989928 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.