Spaces:
Running
Running
File size: 4,776 Bytes
ada8661 afc1f9a ada8661 00fe769 ada8661 afc1f9a ada8661 afc1f9a |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
---
title: MAPE
emoji: 🤗
colorFrom: blue
colorTo: red
sdk: gradio
sdk_version: 3.19.1
app_file: app.py
pinned: false
tags:
- evaluate
- metric
description: >-
Mean Absolute Percentage Error (MAPE) is the mean percentage error difference between the predicted and actual
values.
---
# Metric Card for MAPE
## Metric Description
Mean Absolute Error (MAPE) is the mean of the percentage error of difference between the predicted $x_i$ and actual $y_i$ numeric values:
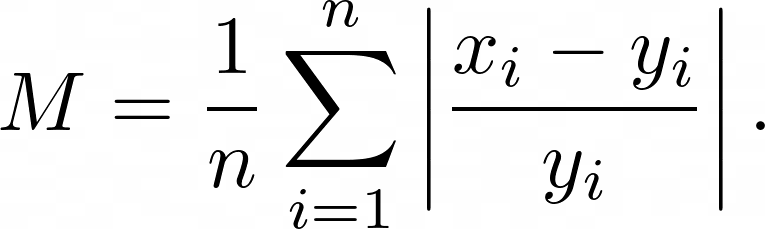
## How to Use
At minimum, this metric requires predictions and references as inputs.
```python
>>> mape_metric = evaluate.load("mape")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = mape_metric.compute(predictions=predictions, references=references)
```
### Inputs
Mandatory inputs:
- `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values.
- `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values.
Optional arguments:
- `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`.
- `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`.
- `raw_values` returns a full set of errors in case of multioutput input.
- `uniform_average` means that the errors of all outputs are averaged with uniform weight.
- the array-like value defines weights used to average errors.
### Output Values
This metric outputs a dictionary, containing the mean absolute error score, which is of type:
- `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned.
- numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately.
Each MAPE `float` value is postive with the best value being 0.0.
Output Example(s):
```python
{'mape': 0.5}
```
If `multioutput="raw_values"`:
```python
{'mape': array([0.5, 1. ])}
```
#### Values from Popular Papers
### Examples
Example with the `uniform_average` config:
```python
>>> mape_metric = evaluate.load("mape")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = mape_metric.compute(predictions=predictions, references=references)
>>> print(results)
{'mape': 0.3273...}
```
Example with multi-dimensional lists, and the `raw_values` config:
```python
>>> mape_metric = evaluate.load("mape", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0.1, 2], [-1, 2], [8, -5]]
>>> results = mape_metric.compute(predictions=predictions, references=references)
>>> print(results)
{'mape': 0.8874...}
>>> results = mape_metric.compute(predictions=predictions, references=references, multioutput='raw_values')
>>> print(results)
{'mape': array([1.3749..., 0.4])}
```
## Limitations and Bias
One limitation of MAPE is that it cannot be used if the ground truth is zero or close to zero. This metric is also asymmetric in that it puts a heavier penalty on predictions less than the ground truth and a smaller penalty on predictions bigger than the ground truth and thus can lead to a bias of methods being select which under-predict if selected via this metric.
## Citation(s)
```bibtex
@article{scikit-learn,
title={Scikit-learn: Machine Learning in {P}ython},
author={Pedregosa, F. and Varoquaux, G. and Gramfort, A. and Michel, V.
and Thirion, B. and Grisel, O. and Blondel, M. and Prettenhofer, P.
and Weiss, R. and Dubourg, V. and Vanderplas, J. and Passos, A. and
Cournapeau, D. and Brucher, M. and Perrot, M. and Duchesnay, E.},
journal={Journal of Machine Learning Research},
volume={12},
pages={2825--2830},
year={2011}
}
```
```bibtex
@article{DEMYTTENAERE201638,
title = {Mean Absolute Percentage Error for regression models},
journal = {Neurocomputing},
volume = {192},
pages = {38--48},
year = {2016},
note = {Advances in artificial neural networks, machine learning and computational intelligence},
issn = {0925-2312},
doi = {https://doi.org/10.1016/j.neucom.2015.12.114},
url = {https://www.sciencedirect.com/science/article/pii/S0925231216003325},
author = {Arnaud {de Myttenaere} and Boris Golden and Bénédicte {Le Grand} and Fabrice Rossi},
}
```
## Further References
- [Mean absolute percentage error - Wikipedia](https://en.wikipedia.org/wiki/Mean_absolute_percentage_error)
|