Spaces:
Running
Running
File size: 4,794 Bytes
745aead e4482cc 74c0426 e4482cc 745aead e4482cc 74c0426 13bba78 9791485 74c0426 e4482cc |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 |
---
title: MSE
emoji: 🤗
colorFrom: blue
colorTo: red
sdk: gradio
sdk_version: 3.0.2
app_file: app.py
pinned: false
tags:
- evaluate
- metric
description: >-
Mean Squared Error(MSE) is the average of the square of difference between the predicted
and actual values.
---
# Metric Card for MSE
## Metric Description
Mean Squared Error(MSE) represents the average of the squares of errors -- i.e. the average squared difference between the estimated values and the actual values.
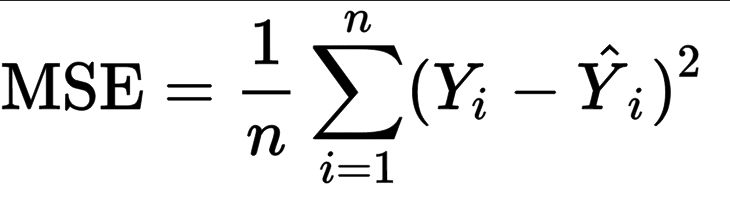
## How to Use
At minimum, this metric requires predictions and references as inputs.
```python
>>> mse_metric = evaluate.load("mse")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = mse_metric.compute(predictions=predictions, references=references)
```
### Inputs
Mandatory inputs:
- `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values.
- `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values.
Optional arguments:
- `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`.
- `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`.
- `raw_values` returns a full set of errors in case of multioutput input.
- `uniform_average` means that the errors of all outputs are averaged with uniform weight.
- the array-like value defines weights used to average errors.
- `squared` (`bool`): If `True` returns MSE value, if `False` returns RMSE (Root Mean Squared Error). The default value is `True`.
### Output Values
This metric outputs a dictionary, containing the mean squared error score, which is of type:
- `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned.
- numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately.
Each MSE `float` value ranges from `0.0` to `1.0`, with the best value being `0.0`.
Output Example(s):
```python
{'mse': 0.5}
```
If `multioutput="raw_values"`:
```python
{'mse': array([0.41666667, 1. ])}
```
#### Values from Popular Papers
### Examples
Example with the `uniform_average` config:
```python
>>> mse_metric = evaluate.load("mse")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = mse_metric.compute(predictions=predictions, references=references)
>>> print(results)
{'mse': 0.375}
```
Example with `squared = True`, which returns the RMSE:
```python
>>> mse_metric = evaluate.load("mse")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> rmse_result = mse_metric.compute(predictions=predictions, references=references, squared=False)
>>> print(rmse_result)
{'mse': 0.6123724356957945}
```
Example with multi-dimensional lists, and the `raw_values` config:
```python
>>> mse_metric = evaluate.load("mse", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0, 2], [-1, 2], [8, -5]]
>>> results = mse_metric.compute(predictions=predictions, references=references, multioutput='raw_values')
>>> print(results)
{'mse': array([0.41666667, 1. ])}
"""
```
## Limitations and Bias
MSE has the disadvantage of heavily weighting outliers -- given that it squares them, this results in large errors weighing more heavily than small ones. It can be used alongside [MAE](https://huggingface.co/metrics/mae), which is complementary given that it does not square the errors.
## Citation(s)
```bibtex
@article{scikit-learn,
title={Scikit-learn: Machine Learning in {P}ython},
author={Pedregosa, F. and Varoquaux, G. and Gramfort, A. and Michel, V.
and Thirion, B. and Grisel, O. and Blondel, M. and Prettenhofer, P.
and Weiss, R. and Dubourg, V. and Vanderplas, J. and Passos, A. and
Cournapeau, D. and Brucher, M. and Perrot, M. and Duchesnay, E.},
journal={Journal of Machine Learning Research},
volume={12},
pages={2825--2830},
year={2011}
}
```
```bibtex
@article{willmott2005advantages,
title={Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance},
author={Willmott, Cort J and Matsuura, Kenji},
journal={Climate research},
volume={30},
number={1},
pages={79--82},
year={2005}
}
```
## Further References
- [Mean Squared Error - Wikipedia](https://en.wikipedia.org/wiki/Mean_squared_error)
|