Spaces:
Running
Running
File size: 3,840 Bytes
f1834c2 36e833c f1834c2 f6abea4 f1834c2 36e833c f1834c2 36e833c |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 |
---
title: sMAPE
emoji: 🤗
colorFrom: blue
colorTo: red
sdk: gradio
sdk_version: 3.19.1
app_file: app.py
pinned: false
tags:
- evaluate
- metric
description: >-
Symmetric Mean Absolute Percentage Error (sMAPE) is the symmetric mean percentage error difference between the predicted and actual values defined by Chen and Yang (2004).
---
# Metric Card for sMAPE
## Metric Description
Symmetric Mean Absolute Error (sMAPE) is the symmetric mean of the percentage error of difference between the predicted $x_i$ and actual $y_i$ numeric values:
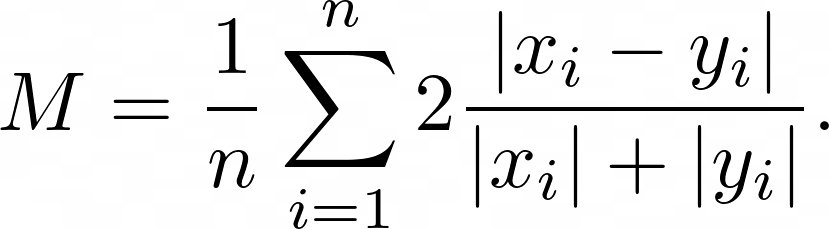
## How to Use
At minimum, this metric requires predictions and references as inputs.
```python
>>> smape_metric = evaluate.load("smape")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = smape_metric.compute(predictions=predictions, references=references)
```
### Inputs
Mandatory inputs:
- `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values.
- `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values.
Optional arguments:
- `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`.
- `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`.
- `raw_values` returns a full set of errors in case of multioutput input.
- `uniform_average` means that the errors of all outputs are averaged with uniform weight.
- the array-like value defines weights used to average errors.
### Output Values
This metric outputs a dictionary, containing the mean absolute error score, which is of type:
- `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned.
- numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately.
Each sMAPE `float` value ranges from `0.0` to `2.0`, with the best value being 0.0.
Output Example(s):
```python
{'smape': 0.5}
```
If `multioutput="raw_values"`:
```python
{'smape': array([0.5, 1.5 ])}
```
#### Values from Popular Papers
### Examples
Example with the `uniform_average` config:
```python
>>> smape_metric = evaluate.load("smape")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> results = smape_metric.compute(predictions=predictions, references=references)
>>> print(results)
{'smape': 0.5787...}
```
Example with multi-dimensional lists, and the `raw_values` config:
```python
>>> smape_metric = evaluate.load("smape", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0.1, 2], [-1, 2], [8, -5]]
>>> results = smape_metric.compute(predictions=predictions, references=references)
>>> print(results)
{'smape': 0.8874...}
>>> results = smape_metric.compute(predictions=predictions, references=references, multioutput='raw_values')
>>> print(results)
{'smape': array([1.3749..., 0.4])}
```
## Limitations and Bias
This metric is called a measure of "percentage error" even though there is no multiplier of 100. The range is between (0, 2) with it being two when the target and prediction are both zero.
## Citation(s)
```bibtex
@article{article,
author = {Chen, Zhuo and Yang, Yuhong},
year = {2004},
month = {04},
pages = {},
title = {Assessing forecast accuracy measures}
}
```
## Further References
- [Symmetric Mean absolute percentage error - Wikipedia](https://en.wikipedia.org/wiki/Symmetric_mean_absolute_percentage_error)
|