title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python simple and very short DP solution | stone-game-iv | 0 | 1 | ```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0]*(n+1)\n for i in range(1, n+1):\n j = 1\n while j*j <= i and not dp[i]:\n dp[i] = dp[i-j*j]^1\n j+=1\n return dp[n]\n```\n**Like it? please upvote...** | 6 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there are `n` stones in a pile. On each player's turn, that player makes a _move_ consisting of removing **any** non-zero **square number** of stones in the pile.
Also, if a player cannot make a move, he/she loses the game.
Given a positive integer `n`, return `true` if and only if Alice wins the game otherwise return `false`, assuming both players play optimally.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** Alice can remove 1 stone winning the game because Bob doesn't have any moves.
**Example 2:**
**Input:** n = 2
**Output:** false
**Explanation:** Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).
**Example 3:**
**Input:** n = 4
**Output:** true
**Explanation:** n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).
**Constraints:**
* `1 <= n <= 105` | Count the frequency of each integer in the array. Get all lucky numbers and return the largest of them. |
Python simple and very short DP solution | stone-game-iv | 0 | 1 | ```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = [0]*(n+1)\n for i in range(1, n+1):\n j = 1\n while j*j <= i and not dp[i]:\n dp[i] = dp[i-j*j]^1\n j+=1\n return dp[n]\n```\n**Like it? please upvote...** | 6 | There are `n` cities numbered from `1` to `n`. You are given an array `edges` of size `n-1`, where `edges[i] = [ui, vi]` represents a bidirectional edge between cities `ui` and `vi`. There exists a unique path between each pair of cities. In other words, the cities form a **tree**.
A **subtree** is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.
For each `d` from `1` to `n-1`, find the number of subtrees in which the **maximum distance** between any two cities in the subtree is equal to `d`.
Return _an array of size_ `n-1` _where the_ `dth` _element **(1-indexed)** is the number of subtrees in which the **maximum distance** between any two cities is equal to_ `d`.
**Notice** that the **distance** between the two cities is the number of edges in the path between them.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,3\],\[2,4\]\]
**Output:** \[3,4,0\]
**Explanation:**
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\]
**Output:** \[1\]
**Example 3:**
**Input:** n = 3, edges = \[\[1,2\],\[2,3\]\]
**Output:** \[2,1\]
**Constraints:**
* `2 <= n <= 15`
* `edges.length == n-1`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* All pairs `(ui, vi)` are distinct. | Use dynamic programming to keep track of winning and losing states. Given some number of stones, Alice can win if she can force Bob onto a losing state. |
Stone Game IV solution in Python with rigorous explaination. | stone-game-iv | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nLet $i$ be variable with the current leftmost stone index and $turn$ be the variable which indicates whose turn it is. $-1\\to Bob, 1\\to Alice$ \nLet\'s first look at the base cases:\n- If the end of the sequence is reached, then whoevers turn it is currently loses the game.\n- Thus, if $i==n$ and it is $Alice$ to play, then $Alice$ loses and $Bob$ wins, and vice versa if it is $Bob$ to play.\n\nNow, we look at all possible number of stones that can be removed in the current turn, ie. a square number that is less than or equal to the number of stones remaining, and remove them. Once the stones are removed the turn must pass to the next player, thus the line\n```\na, b = util(i + k**2, -turn) #-turn means turn passes to the next player\n```\nFor explaination on why we look from the greatest possible $$k$$ to the smallest (1), refer to the Time Complexity section.\nNow, the following cases arise, \n1) If in the current turn it was $$Alice$$ to play and choosing $$k^2$$ in current turn results in a win for $$Alice$$ ($$a==True$$), then by making optimal choices $$Alice$$ wins.\n2) If it was $$Bob$$ to play on the other hand, and $$k^2$$ in the current turn results in a win for $$Bob$$ ($$b==True$$), then with optimal choices $$Bob$$ wins.\n\nIn both of the above cases, we update $$dp[(i, turn)]$$ with the optimal choice for current stage $$(i, turn)$$\n```\nk = int((n - i) ** 0.5)\nwhile k>=1:\n a, b = util(i + k**2, -turn)\n if (turn==1 and a) or (turn==-1 and b):\n # Case 1. or Case 2. as explained above.\n dp[(i, turn)] = [a, b]\n break\n k -= 1\n```\nAlso, as soon as we find a win for the player with the current turn, we exit the loop. This is because, We are told in the problem that the players make optimal choices for them to win and thus any choice that yields a win in the current turn for the current player is optimal. Before exiting the loop however, we cache the current result.\n\n```\nif (i, turn) in dp:\n return dp[(i, turn)]\nif (i, -turn) in dp:\n a, b = dp[(i, -turn)]\n return [not a, not b]\n```\nHere, if result for $$(i, turn)$$ is already known then we just return the result. But if result for $$(i, -turn)$$(same $i$ but it was the other players turn) is known then we know that we would have the same result in our current case as well, with the roles reversed for the players. ie. winner in $$dp[(i, -turn)]$$ becomes the losser in $$dp[(i, turn)]$$ and vice versa.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\forall i\\in{[0, n-1]}$$ we run a loop from $k=\\lfloor\\sqrt{n-i}\\rfloor\\to1$. Thus the time complexity is $$O(n\\sqrt{n})$$. It is to note that running a loop for $k=1\\to\\lfloor\\sqrt{n-i}\\rfloor$ is also correct approach wise, but I got poor run times ~$9000ms$ with this, although the time complexity remains the same. My intuition tells me that using the greatest number of stones that gives a win to the player with the turn gives the fastest runtime ( ~$$600ms$$ with my code). This should work because as soon as you find a perfect square to remove at current turn that gives the win to the current player, that would be an optimal choice to make. Among possibly multiple optimal choices for the square number to remove at current stage, removing the greatest feasible square that is an optimal choice, gives the best runtime in this approach.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nHere, a cache of the form $$dp[i][j]$$ is used. $$i$$ takes values from $0 \\to n-1$ and $j\\in{\\{1,-1\\}}$. Thus the space complexity is $$O(n)$$.\n# Code\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = {}\n def util(i, turn=1):\n if i==n and turn==1:\n return [False, True]\n elif i==n:\n return [True, False]\n\n if (i, turn) in dp:\n return dp[(i, turn)]\n if (i, -turn) in dp:\n a, b = dp[(i, -turn)]\n return [not a, not b]\n if turn==1:\n dp[(i, turn)] = [False, True]\n else:\n dp[(i, turn)] = [True, False]\n k = int((n - i) ** 0.5)\n while k>=1:\n a, b = util(i + k**2, -turn)\n if (turn==1 and a) or (turn==-1 and b):\n dp[(i, turn)] = [a, b]\n break\n \n k -= 1\n \n return dp[(i, turn)]\n \n return util(0, 1)[0]\n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there are `n` stones in a pile. On each player's turn, that player makes a _move_ consisting of removing **any** non-zero **square number** of stones in the pile.
Also, if a player cannot make a move, he/she loses the game.
Given a positive integer `n`, return `true` if and only if Alice wins the game otherwise return `false`, assuming both players play optimally.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** Alice can remove 1 stone winning the game because Bob doesn't have any moves.
**Example 2:**
**Input:** n = 2
**Output:** false
**Explanation:** Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).
**Example 3:**
**Input:** n = 4
**Output:** true
**Explanation:** n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).
**Constraints:**
* `1 <= n <= 105` | Count the frequency of each integer in the array. Get all lucky numbers and return the largest of them. |
Stone Game IV solution in Python with rigorous explaination. | stone-game-iv | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nLet $i$ be variable with the current leftmost stone index and $turn$ be the variable which indicates whose turn it is. $-1\\to Bob, 1\\to Alice$ \nLet\'s first look at the base cases:\n- If the end of the sequence is reached, then whoevers turn it is currently loses the game.\n- Thus, if $i==n$ and it is $Alice$ to play, then $Alice$ loses and $Bob$ wins, and vice versa if it is $Bob$ to play.\n\nNow, we look at all possible number of stones that can be removed in the current turn, ie. a square number that is less than or equal to the number of stones remaining, and remove them. Once the stones are removed the turn must pass to the next player, thus the line\n```\na, b = util(i + k**2, -turn) #-turn means turn passes to the next player\n```\nFor explaination on why we look from the greatest possible $$k$$ to the smallest (1), refer to the Time Complexity section.\nNow, the following cases arise, \n1) If in the current turn it was $$Alice$$ to play and choosing $$k^2$$ in current turn results in a win for $$Alice$$ ($$a==True$$), then by making optimal choices $$Alice$$ wins.\n2) If it was $$Bob$$ to play on the other hand, and $$k^2$$ in the current turn results in a win for $$Bob$$ ($$b==True$$), then with optimal choices $$Bob$$ wins.\n\nIn both of the above cases, we update $$dp[(i, turn)]$$ with the optimal choice for current stage $$(i, turn)$$\n```\nk = int((n - i) ** 0.5)\nwhile k>=1:\n a, b = util(i + k**2, -turn)\n if (turn==1 and a) or (turn==-1 and b):\n # Case 1. or Case 2. as explained above.\n dp[(i, turn)] = [a, b]\n break\n k -= 1\n```\nAlso, as soon as we find a win for the player with the current turn, we exit the loop. This is because, We are told in the problem that the players make optimal choices for them to win and thus any choice that yields a win in the current turn for the current player is optimal. Before exiting the loop however, we cache the current result.\n\n```\nif (i, turn) in dp:\n return dp[(i, turn)]\nif (i, -turn) in dp:\n a, b = dp[(i, -turn)]\n return [not a, not b]\n```\nHere, if result for $$(i, turn)$$ is already known then we just return the result. But if result for $$(i, -turn)$$(same $i$ but it was the other players turn) is known then we know that we would have the same result in our current case as well, with the roles reversed for the players. ie. winner in $$dp[(i, -turn)]$$ becomes the losser in $$dp[(i, turn)]$$ and vice versa.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\forall i\\in{[0, n-1]}$$ we run a loop from $k=\\lfloor\\sqrt{n-i}\\rfloor\\to1$. Thus the time complexity is $$O(n\\sqrt{n})$$. It is to note that running a loop for $k=1\\to\\lfloor\\sqrt{n-i}\\rfloor$ is also correct approach wise, but I got poor run times ~$9000ms$ with this, although the time complexity remains the same. My intuition tells me that using the greatest number of stones that gives a win to the player with the turn gives the fastest runtime ( ~$$600ms$$ with my code). This should work because as soon as you find a perfect square to remove at current turn that gives the win to the current player, that would be an optimal choice to make. Among possibly multiple optimal choices for the square number to remove at current stage, removing the greatest feasible square that is an optimal choice, gives the best runtime in this approach.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nHere, a cache of the form $$dp[i][j]$$ is used. $$i$$ takes values from $0 \\to n-1$ and $j\\in{\\{1,-1\\}}$. Thus the space complexity is $$O(n)$$.\n# Code\n```\nclass Solution:\n def winnerSquareGame(self, n: int) -> bool:\n dp = {}\n def util(i, turn=1):\n if i==n and turn==1:\n return [False, True]\n elif i==n:\n return [True, False]\n\n if (i, turn) in dp:\n return dp[(i, turn)]\n if (i, -turn) in dp:\n a, b = dp[(i, -turn)]\n return [not a, not b]\n if turn==1:\n dp[(i, turn)] = [False, True]\n else:\n dp[(i, turn)] = [True, False]\n k = int((n - i) ** 0.5)\n while k>=1:\n a, b = util(i + k**2, -turn)\n if (turn==1 and a) or (turn==-1 and b):\n dp[(i, turn)] = [a, b]\n break\n \n k -= 1\n \n return dp[(i, turn)]\n \n return util(0, 1)[0]\n``` | 0 | There are `n` cities numbered from `1` to `n`. You are given an array `edges` of size `n-1`, where `edges[i] = [ui, vi]` represents a bidirectional edge between cities `ui` and `vi`. There exists a unique path between each pair of cities. In other words, the cities form a **tree**.
A **subtree** is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.
For each `d` from `1` to `n-1`, find the number of subtrees in which the **maximum distance** between any two cities in the subtree is equal to `d`.
Return _an array of size_ `n-1` _where the_ `dth` _element **(1-indexed)** is the number of subtrees in which the **maximum distance** between any two cities is equal to_ `d`.
**Notice** that the **distance** between the two cities is the number of edges in the path between them.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,3\],\[2,4\]\]
**Output:** \[3,4,0\]
**Explanation:**
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\]
**Output:** \[1\]
**Example 3:**
**Input:** n = 3, edges = \[\[1,2\],\[2,3\]\]
**Output:** \[2,1\]
**Constraints:**
* `2 <= n <= 15`
* `edges.length == n-1`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* All pairs `(ui, vi)` are distinct. | Use dynamic programming to keep track of winning and losing states. Given some number of stones, Alice can win if she can force Bob onto a losing state. |
Python3 || recursive DP || easy to understand | stone-game-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code uses dynamic programming to determine if Alice can win a game where the players take turns removing a non-zero square number of stones from a pile. It\'s built around the idea of calculating whether, starting with a certain number of stones, the current player can force a win if they play optimally.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe rec function is a recursive function that takes the remaining stones rem as input. It returns True if the current player can win with rem stones and False otherwise.\n\nIf rem is 0, it means no stones are left, and the current player has lost the game, so the function returns False.\n\nIf the result for the current rem has already been calculated and stored in dp, it is returned.\n\nThe variable ans is initialized as False, representing whether the current player can win from the current state. This will be updated as the function explores different possible moves.\n\nThe function iterates through the list of square numbers self.sq. For each square number t, it checks if t is greater than the remaining stones rem. If t is greater, it breaks the loop because it\'s not possible to use that square number in the current state.\n\nFor each square number t, it checks if there\'s a move such that the other player loses the game (i.e., the recursive call with rem - t returns False). If such a move exists, ans is set to True.\n\nThe result ans is stored in the dp array at index rem.\n\nThe winnerSquareGame function initializes the list of square numbers, self.sq, and the dynamic programming array, self.dp. It then calls the rec function with n as input and returns the result of whether Alice can win the game with n stones.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is determined by the rec function\'s recursive calls. In the worst case, the function explores all possible moves, which could be up to sqrt(n) possibilities, and it is called for all values from 1 to n. Therefore, the time complexity is O(n * sqrt(n)).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) because of the dynamic programming array self.dp, and the list self.sq has a maximum size of sqrt(n).\n\n# Code\n```\nclass Solution:\n #dp[rem] is there atleast a way in which if someone plays he/she will win for sure\n def rec(self,rem):\n if rem==0:\n return False\n if self.dp[rem]!=-1:\n return self.dp[rem]\n ans=False\n for t in self.sq:\n if t>rem:\n break\n ans= ans or (not self.rec(rem-t))\n self.dp[rem]=ans\n return ans\n\n\n def winnerSquareGame(self, n: int) -> bool:\n self.sq=[]\n for i in range(1,n+1):\n if i*i>n:\n break\n self.sq.append(i*i)\n self.dp=[-1]*(n+1)\n return self.rec(n)\n\n \n``` | 0 | Alice and Bob take turns playing a game, with Alice starting first.
Initially, there are `n` stones in a pile. On each player's turn, that player makes a _move_ consisting of removing **any** non-zero **square number** of stones in the pile.
Also, if a player cannot make a move, he/she loses the game.
Given a positive integer `n`, return `true` if and only if Alice wins the game otherwise return `false`, assuming both players play optimally.
**Example 1:**
**Input:** n = 1
**Output:** true
**Explanation:** Alice can remove 1 stone winning the game because Bob doesn't have any moves.
**Example 2:**
**Input:** n = 2
**Output:** false
**Explanation:** Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).
**Example 3:**
**Input:** n = 4
**Output:** true
**Explanation:** n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).
**Constraints:**
* `1 <= n <= 105` | Count the frequency of each integer in the array. Get all lucky numbers and return the largest of them. |
Python3 || recursive DP || easy to understand | stone-game-iv | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code uses dynamic programming to determine if Alice can win a game where the players take turns removing a non-zero square number of stones from a pile. It\'s built around the idea of calculating whether, starting with a certain number of stones, the current player can force a win if they play optimally.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe rec function is a recursive function that takes the remaining stones rem as input. It returns True if the current player can win with rem stones and False otherwise.\n\nIf rem is 0, it means no stones are left, and the current player has lost the game, so the function returns False.\n\nIf the result for the current rem has already been calculated and stored in dp, it is returned.\n\nThe variable ans is initialized as False, representing whether the current player can win from the current state. This will be updated as the function explores different possible moves.\n\nThe function iterates through the list of square numbers self.sq. For each square number t, it checks if t is greater than the remaining stones rem. If t is greater, it breaks the loop because it\'s not possible to use that square number in the current state.\n\nFor each square number t, it checks if there\'s a move such that the other player loses the game (i.e., the recursive call with rem - t returns False). If such a move exists, ans is set to True.\n\nThe result ans is stored in the dp array at index rem.\n\nThe winnerSquareGame function initializes the list of square numbers, self.sq, and the dynamic programming array, self.dp. It then calls the rec function with n as input and returns the result of whether Alice can win the game with n stones.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is determined by the rec function\'s recursive calls. In the worst case, the function explores all possible moves, which could be up to sqrt(n) possibilities, and it is called for all values from 1 to n. Therefore, the time complexity is O(n * sqrt(n)).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) because of the dynamic programming array self.dp, and the list self.sq has a maximum size of sqrt(n).\n\n# Code\n```\nclass Solution:\n #dp[rem] is there atleast a way in which if someone plays he/she will win for sure\n def rec(self,rem):\n if rem==0:\n return False\n if self.dp[rem]!=-1:\n return self.dp[rem]\n ans=False\n for t in self.sq:\n if t>rem:\n break\n ans= ans or (not self.rec(rem-t))\n self.dp[rem]=ans\n return ans\n\n\n def winnerSquareGame(self, n: int) -> bool:\n self.sq=[]\n for i in range(1,n+1):\n if i*i>n:\n break\n self.sq.append(i*i)\n self.dp=[-1]*(n+1)\n return self.rec(n)\n\n \n``` | 0 | There are `n` cities numbered from `1` to `n`. You are given an array `edges` of size `n-1`, where `edges[i] = [ui, vi]` represents a bidirectional edge between cities `ui` and `vi`. There exists a unique path between each pair of cities. In other words, the cities form a **tree**.
A **subtree** is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.
For each `d` from `1` to `n-1`, find the number of subtrees in which the **maximum distance** between any two cities in the subtree is equal to `d`.
Return _an array of size_ `n-1` _where the_ `dth` _element **(1-indexed)** is the number of subtrees in which the **maximum distance** between any two cities is equal to_ `d`.
**Notice** that the **distance** between the two cities is the number of edges in the path between them.
**Example 1:**
**Input:** n = 4, edges = \[\[1,2\],\[2,3\],\[2,4\]\]
**Output:** \[3,4,0\]
**Explanation:**
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\]
**Output:** \[1\]
**Example 3:**
**Input:** n = 3, edges = \[\[1,2\],\[2,3\]\]
**Output:** \[2,1\]
**Constraints:**
* `2 <= n <= 15`
* `edges.length == n-1`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* All pairs `(ui, vi)` are distinct. | Use dynamic programming to keep track of winning and losing states. Given some number of stones, Alice can win if she can force Bob onto a losing state. |
Video Solution | Explanation With Drawings | In Depth | C++ | Java | Python 3 | number-of-good-pairs | 1 | 1 | # Intuition and approach dicussed in detail in video solution\nhttps://youtu.be/iE2klzxiLHE\n\n# Complexity\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int numIdenticalPairs(vector<int>& nums) {\n unordered_map<int, int> numFreqMp;\n int answer = 0;\n for(auto num : nums){\n answer += numFreqMp[num];\n numFreqMp[num]++;\n }\n return answer;\n }\n};\n```\nJava\n```\nclass Solution {\n public int numIdenticalPairs(int[] nums) {\n Map<Integer, Integer> numFreqMp = new HashMap<>();\n int answer = 0;\n for(var num : nums){\n answer += numFreqMp.getOrDefault(num, 0);\n numFreqMp.put(num, numFreqMp.getOrDefault(num, 0) + 1);\n }\n return answer;\n }\n}\n```\nPython 3\n```\nclass Solution:\n def numIdenticalPairs(self, nums):\n numFreqMp = {}\n \n answer = 0\n for num in nums:\n answer += numFreqMp.get(num, 0)\n numFreqMp[num] = numFreqMp.get(num, 0) + 1\n return answer\n``` | 2 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
✅one line|BEATS 100% Runtime||Explanation✅ | number-of-good-pairs | 1 | 1 | # Intution\nwe have to count the occurrence of the same elements\nwith` A[i] == A[j]` and `i < j`\n\n# Approach\n- We will `intiliaze ans with 0` and an empty` unordered map` to store the occurrence of the element \n- For each element in the given array:\n- Here there will be 2 cases\n 1. if element/number is `present in the map` that means for example at any time in unordered map we saw count of num(element) 1 is 2 thats means currunt element can form 2 pair with previous 1, so at that time `we will add this count in answer` and also` increase the count of the element in out map`\n 2. If element/number is `not present in the map`, it means this is the first time we\'re seeing this number, so we `initialize its count to 1.`\n- At last we will return our answer\n\n# Complexity\n- Time complexity : `O(N)`\n- Space complexity : `O(N)`\n# Codes\n```C++_one_line []\nclass Solution {\npublic:\n int numIdenticalPairs(vector<int>& A) {\n return accumulate(A.begin(), A.end(), 0, [count = unordered_map<int, int> {}] (auto x, auto y) mutable {\n return x + count[y]++;\n });\n }\n};\n```\n```C++ []\nclass Solution {\npublic:\n int numIdenticalPairs(vector<int>& A) {\n int ans = 0;\n unordered_map<int, int> cnt;\n for (int x: A) {\n ans += cnt[x]++;\n }\n return ans;\n }\n};\n```\n```java []\nclass Solution {\n public int numIdenticalPairs(int[] A) {\n int ans = 0, cnt[] = new int[101];\n for (int a: A) {\n ans += cnt[a]++;\n }\n return ans;\n }\n}\n```\n```Python []\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n return sum([math.comb(n, 2) for n in collections.Counter(nums).values()]) \n```\n```C# []\n\npublic class Solution\n{\n public int NumIdenticalPairs(int[] A)\n {\n int ans = 0;\n Dictionary<int, int> cnt = new Dictionary<int, int>();\n foreach (int x in A)\n {\n if (cnt.ContainsKey(x))\n ans += cnt[x]++;\n else\n cnt[x] = 1;\n }\n return ans;\n }\n}\n\n```\n```Rust []\n\nuse std::collections::HashMap;\nimpl Solution {\n pub fn num_identical_pairs(a: Vec<i32>) -> i32 {\n let mut ans = 0;\n let mut cnt = HashMap::new();\n \n for x in a.iter() {\n ans += cnt.get(x).unwrap_or(&0);\n *cnt.entry(*x).or_insert(0) += 1;\n }\n \n ans\n }\n}\n\n```\n```ruby []\ndef num_identical_pairs(a)\n ans = 0\n cnt = Hash.new(0)\n \n a.each do |x|\n ans += cnt[x]\n cnt[x] += 1\n end\n \n ans\nend\n\n```\n```javascript []\nfunction numIdenticalPairs(A) {\n let ans = 0;\n const cnt = {};\n \n for (let x of A) {\n ans += cnt[x] || 0;\n cnt[x] = (cnt[x] || 0) + 1;\n }\n \n return ans;\n}\n\n\n```\n```Go []\npackage main\n\nfunc numIdenticalPairs(A []int) int {\n ans := 0\n cnt := make(map[int]int)\n \n for _, x := range A {\n ans += cnt[x]\n cnt[x]++\n }\n \n return ans\n}\n\n```\n```PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function numIdenticalPairs($A) {\n $ans = 0;\n $cnt = [];\n \n foreach ($A as $x) {\n $ans += $cnt[$x] ?? 0;\n $cnt[$x] = ($cnt[$x] ?? 0) + 1;\n }\n \n return $ans;\n}\n\n}\n```\n\n\nIf you really found my solution helpful **please upvote it**, as it motivates me to post such kind of codes.\n**Let me know in comment if i can do better.**\nLet\'s Connect on **[LINKDIN](https://www.linkedin.com/in/mahesh-vishnoi-a4a47a193)**\n\n\n\n\n\n | 161 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
NOOB CODE : Easy to Understand | number-of-good-pairs | 0 | 1 | \n\n# Approach\n1. Initialize a variable `c` to 0. This variable will be used to count the number of identical pairs.\n\n2. Use nested loops to iterate through the elements in the `nums` list. The outer loop runs from index 0 to `len(nums) - 2`, and the inner loop runs from `i+1` to `len(nums) - 1`. This combination of loops ensures that each pair of elements in the list is compared exactly once, avoiding duplicate counts.\n\n3. Check if the elements at the current indices `i` and `j` are equal using the condition `if nums[i] == nums[j]`.\n\n4. If the elements are equal, increment the count `c` by 1. This indicates that you have found an identical pair.\n\n5. Continue iterating through all possible pairs in the list, checking for identical elements.\n\n6. After both loops have finished running, return the final value of `c`, which represents the total number of identical pairs in the input list.\n\n# Complexity\n- Time complexity: ***O(n^2)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n c=0\n for i in range(0,len(nums)-1):\n for j in range((i+1),len(nums)):\n if nums[i]==nums[j]:\n c+=1\n return(c)\n\n``` | 2 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
Using dictionary | number-of-good-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n d={}\n for i in nums:\n if i in d:\n d[i]+=1\n else:\n d[i]=1\n count=0\n for i in d:\n a=d[i]\n if(a>1):\n count+=(a*(a-1))//2\n return count\n``` | 1 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
Title: Unveiling Good Pairs with a One-Liner: A Pythonic Approach | number-of-good-pairs | 0 | 1 | # Simple Efficient One-Line Code for Identical Pairs\n\n## Intuition\nUpon reading the problem, it becomes evident that we need to count the number of pairs where the elements are identical. This is reminiscent of the combination formula, where we choose 2 items out of `n` items. The formula for this is `n(n-1)/2`. Given this insight, we can leverage Python\'s `Counter` to count occurrences of each number and then apply the combination formula to each count.\n\n## Approach\n1. **Utilize Counter**: The `Counter` from the `collections` module is used to count the occurrences of each number in the input list `nums`.\n2. **Apply Combination Formula**: For each unique number count `n` from the `Counter`, calculate the number of good pairs using the combination formula `n * (n-1) / 2`.\n3. **Sum Up Pairs**: Sum all the good pairs calculated for each unique number to get the total number of good pairs.\n\n## Complexity\n- **Time complexity**: \\(O(n)\\) - The `Counter` creates a count dictionary in linear time, and the combination calculations and sum are also linear.\n \n- **Space complexity**: \\(O(m)\\) - Where `m` is the number of unique elements in `nums`. The space is used to store the count dictionary from the `Counter`.\n\n## Code\n```python\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n from collections import Counter\n \n # Count occurrences of each number in nums\n num_counts = Counter(nums)\n \n # Calculate the number of good pairs\n output = sum(val * (val - 1) // 2 for val in num_counts.values())\n \n return output\n | 0 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
Easy apporach for beginners | number-of-good-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt the beinging of reading the question we will know that we need two loops one for ith index and other for the jth index.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we need to sort the list. So that we decrease the time complexity.\nAs i and j can\'t be equal form the question .So the jth index starts from the i+1.\n\n\n# Complexity\n- Time complexity: O(n2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n nums.sort()\n count=0\n for i in range(0,len(nums)):\n for j in range(i+1,len(nums)):\n if(nums[i]==nums[j]):\n count+=1\n else:\n break\n return count\n \n``` | 1 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
Number of Good Pairs Solution | number-of-good-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key intuition behind this code is to efficiently count the number of good pairs without explicitly checking all pairs in a nested loop. By using a dictionary to keep track of the count of each number, you can determine how many good pairs can be formed with each number as you iterate through the array. This approach reduces the time complexity from O(n^2) to O(n), where n is the length of the nums array, making it a more efficient solution.\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n pair = 0\n num_count = {}\n for num in nums :\n if num in num_count :\n pair += num_count[num]\n num_count[num] += 1\n else :\n num_count[num] = 1\n return pair\n \n``` | 1 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
Beats 94% runtime Easy python solution | number-of-good-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind the frequency of each number and if it is greater than 1 then caluculate the nC2 value for that and add the result to sum \n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n hashtable={}\n for i in nums:\n if i in hashtable:\n hashtable[i]=hashtable[i]+1\n else:\n hashtable[i]=1\n sum=0\n for i in hashtable:\n n=hashtable[i]\n if n>1:\n sum=sum+(n*(n-1))/2\n return int(sum)\n \n\n \n``` | 1 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
range, len, for loop | number-of-good-pairs | 0 | 1 | # Code\n```\nclass Solution:\n def numIdenticalPairs(self, nums: List[int]) -> int:\n count = 0\n for i in range(len(nums)):\n for j in range(i + 1, len(nums)):\n if nums[i] == nums[j]:\n count += 1\n return count\n``` | 1 | Given an array of integers `nums`, return _the number of **good pairs**_.
A pair `(i, j)` is called _good_ if `nums[i] == nums[j]` and `i` < `j`.
**Example 1:**
**Input:** nums = \[1,2,3,1,1,3\]
**Output:** 4
**Explanation:** There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.
**Example 2:**
**Input:** nums = \[1,1,1,1\]
**Output:** 6
**Explanation:** Each pair in the array are _good_.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Use two hash tables. The first to save the check-in time for a customer and the second to update the total time between two stations. |
[Python] Sum of Arithmetic Progression with explanation **100.00% Faster** | number-of-substrings-with-only-1s | 0 | 1 | There is a ***pattern***, you will find that the ***result is the sum of arithmetic progression***.\nArithmetic progression: **t(n) = a + d(n-1)**\nSum of arithmetic progression: **s(n) = (n / 2) * (2a + d(n-1))**\n\nIn this problem, the first term(a) will be the the length of "1" and the number of terms will also be the length of "1".\n\nThe common difference(d) is **-1**.\n\n**E.g. input is "111111"**\nThen, \n**n = 6\na = 6\nd = -1**\nAfterthat, calculate the sum of arithmetic progression with the formula of **s(n) = (n / 2) * (2a + d(n-1))**,\nCalculate step by step: **(6-0) + (6-1) + (6-2) + (6-3) + (6-4) + (6-5) = 21**,\nwhich is the result of this problem.\n\n***Solution***\n*100% Faster, Memory Usage less than 100.00% of Python3 online submissions.*\n```\nclass Solution:\n def numSub(self, s: str) -> int: \n res = 0\n s = s.split("0")\n\n for one in s:\n if one == "":\n continue\n \n n = len(one)\n temp = (n / 2)*(2*n + (n-1)*-1)\n \n if temp >= 1000000007:\n res += temp % 1000000007\n else:\n res += temp\n return int(res)\n``` | 8 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
[Python] Sum of Arithmetic Progression with explanation **100.00% Faster** | number-of-substrings-with-only-1s | 0 | 1 | There is a ***pattern***, you will find that the ***result is the sum of arithmetic progression***.\nArithmetic progression: **t(n) = a + d(n-1)**\nSum of arithmetic progression: **s(n) = (n / 2) * (2a + d(n-1))**\n\nIn this problem, the first term(a) will be the the length of "1" and the number of terms will also be the length of "1".\n\nThe common difference(d) is **-1**.\n\n**E.g. input is "111111"**\nThen, \n**n = 6\na = 6\nd = -1**\nAfterthat, calculate the sum of arithmetic progression with the formula of **s(n) = (n / 2) * (2a + d(n-1))**,\nCalculate step by step: **(6-0) + (6-1) + (6-2) + (6-3) + (6-4) + (6-5) = 21**,\nwhich is the result of this problem.\n\n***Solution***\n*100% Faster, Memory Usage less than 100.00% of Python3 online submissions.*\n```\nclass Solution:\n def numSub(self, s: str) -> int: \n res = 0\n s = s.split("0")\n\n for one in s:\n if one == "":\n continue\n \n n = len(one)\n temp = (n / 2)*(2*n + (n-1)*-1)\n \n if temp >= 1000000007:\n res += temp % 1000000007\n else:\n res += temp\n return int(res)\n``` | 8 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
ONE-LINER || FASTER THAN 98% || SC 90% || | number-of-substrings-with-only-1s | 0 | 1 | ```\n return sum(map(lambda x: ((1+len(x))*len(x)//2)%(10**9+7), s.split(\'0\')))\n```\nIF THIS HELP U KINDLY UPVOTE THIS TO HELP OTHERS TO GET THIS SOLUTION\nIF U DONT GET IT KINDLY COMMENT AND FEEL FREE TO ASK\nAND CORRECT MEIF I AM WRONG | 3 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
ONE-LINER || FASTER THAN 98% || SC 90% || | number-of-substrings-with-only-1s | 0 | 1 | ```\n return sum(map(lambda x: ((1+len(x))*len(x)//2)%(10**9+7), s.split(\'0\')))\n```\nIF THIS HELP U KINDLY UPVOTE THIS TO HELP OTHERS TO GET THIS SOLUTION\nIF U DONT GET IT KINDLY COMMENT AND FEEL FREE TO ASK\nAND CORRECT MEIF I AM WRONG | 3 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Easy Python Solution | number-of-substrings-with-only-1s | 0 | 1 | # Code\n```\nclass Solution:\n def numSub(self, nums: str) -> int:\n # stores the count of ones\n count = 0\n\n # stores the final answer\n answer = 0\n\n for i in range(len(nums)):\n if nums[i] == \'1\':\n count = count + 1\n else:\n answer = answer + ((count * (count + 1)) / 2) % ((10 ** 9) + 7)\n count = 0\n \n answer = answer + ((count * (count + 1)) / 2) % ((10 ** 9) + 7)\n\n return int(answer)\n``` | 0 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
Easy Python Solution | number-of-substrings-with-only-1s | 0 | 1 | # Code\n```\nclass Solution:\n def numSub(self, nums: str) -> int:\n # stores the count of ones\n count = 0\n\n # stores the final answer\n answer = 0\n\n for i in range(len(nums)):\n if nums[i] == \'1\':\n count = count + 1\n else:\n answer = answer + ((count * (count + 1)) / 2) % ((10 ** 9) + 7)\n count = 0\n \n answer = answer + ((count * (count + 1)) / 2) % ((10 ** 9) + 7)\n\n return int(answer)\n``` | 0 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Just iterate and count consecutive 1s | number-of-substrings-with-only-1s | 0 | 1 | # Intuition\nJust traverse the string and count consecutive 1s and then calculate the output using the formula [(n * (n+1))//2]. \n\n\n\n# Complexity\n- Time complexity:\nO(N): Linear time, because we are iterating only once\n\n- Space complexity:\nO(1): Constant space complexity\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n count = 0\n ans = 0\n for i in s:\n if i == \'1\':\n count += 1\n else:\n ans += ( count * (count + 1)) // 2\n count = 0\n\n ans += (count * (count+1))//2\n\n return (ans % (10**9 + 7))\n \n\n \n``` | 0 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
Just iterate and count consecutive 1s | number-of-substrings-with-only-1s | 0 | 1 | # Intuition\nJust traverse the string and count consecutive 1s and then calculate the output using the formula [(n * (n+1))//2]. \n\n\n\n# Complexity\n- Time complexity:\nO(N): Linear time, because we are iterating only once\n\n- Space complexity:\nO(1): Constant space complexity\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n count = 0\n ans = 0\n for i in s:\n if i == \'1\':\n count += 1\n else:\n ans += ( count * (count + 1)) // 2\n count = 0\n\n ans += (count * (count+1))//2\n\n return (ans % (10**9 + 7))\n \n\n \n``` | 0 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Simple approach defeat 100% | number-of-substrings-with-only-1s | 0 | 1 | \n\n\n\n# Complexity\nO(n) (n = len(s))\n\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n vals = s.split(\'0\')\n _sum = 0\n for _bin in vals:\n n = len(_bin)\n _sum += n * (n+1) // 2\n return _sum % (10**9 + 7)\n \n``` | 0 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
Simple approach defeat 100% | number-of-substrings-with-only-1s | 0 | 1 | \n\n\n\n# Complexity\nO(n) (n = len(s))\n\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n vals = s.split(\'0\')\n _sum = 0\n for _bin in vals:\n n = len(_bin)\n _sum += n * (n+1) // 2\n return _sum % (10**9 + 7)\n \n``` | 0 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Sum of natural numbers , beats 98% | number-of-substrings-with-only-1s | 0 | 1 | # Intuition\nuse sum of first n natural numbers\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSplit the string using 0s and for each element in the array use sum of n natural numbers to count total combinations\n\nfor example for string 111111\n\nso split array will be [\'111111\'] and length of element will be 6\n\nif take only 1 "1" then total ways = 6\nif take only 2 "1" then total ways = 5\nif take only 3 "1" then total ways = 4\nif take only 4 "1" then total ways = 3\nif take only 5 "1" then total ways = 2\nif take only 6 "1" then total ways = 1\n\ntotal =6+5+4+3+2+1 or we can use n(n+1)/2 where n=6\n\nsimilary for test case "0110111"\narray will be ["11","111"]\n\nyou can now apply same then you will get for "11" =2+1\nand for "111" = 3+2+1\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n count=s.split("0")\n ans=0.0\n for i in count:\n if(i == ""):\n continue\n else:\n ans+=(((len(i))*(len(i)+1))/2)%1000000007\n\n return(int(ans)) \n \n``` | 0 | Given a binary string `s`, return _the number of substrings with all characters_ `1`_'s_. Since the answer may be too large, return it modulo `109 + 7`.
**Example 1:**
**Input:** s = "0110111 "
**Output:** 9
**Explanation:** There are 9 substring in total with only 1's characters.
"1 " -> 5 times.
"11 " -> 3 times.
"111 " -> 1 time.
**Example 2:**
**Input:** s = "101 "
**Output:** 2
**Explanation:** Substring "1 " is shown 2 times in s.
**Example 3:**
**Input:** s = "111111 "
**Output:** 21
**Explanation:** Each substring contains only 1's characters.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Use DP with 4 states (pos: Int, posEvil: Int, equalToS1: Bool, equalToS2: Bool) which compute the number of valid strings of size "pos" where the maximum common suffix with string "evil" has size "posEvil". When "equalToS1" is "true", the current valid string is equal to "S1" otherwise it is greater. In a similar way when equalToS2 is "true" the current valid string is equal to "S2" otherwise it is smaller. To update the maximum common suffix with string "evil" use KMP preprocessing. |
Sum of natural numbers , beats 98% | number-of-substrings-with-only-1s | 0 | 1 | # Intuition\nuse sum of first n natural numbers\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSplit the string using 0s and for each element in the array use sum of n natural numbers to count total combinations\n\nfor example for string 111111\n\nso split array will be [\'111111\'] and length of element will be 6\n\nif take only 1 "1" then total ways = 6\nif take only 2 "1" then total ways = 5\nif take only 3 "1" then total ways = 4\nif take only 4 "1" then total ways = 3\nif take only 5 "1" then total ways = 2\nif take only 6 "1" then total ways = 1\n\ntotal =6+5+4+3+2+1 or we can use n(n+1)/2 where n=6\n\nsimilary for test case "0110111"\narray will be ["11","111"]\n\nyou can now apply same then you will get for "11" =2+1\nand for "111" = 3+2+1\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSub(self, s: str) -> int:\n count=s.split("0")\n ans=0.0\n for i in count:\n if(i == ""):\n continue\n else:\n ans+=(((len(i))*(len(i)+1))/2)%1000000007\n\n return(int(ans)) \n \n``` | 0 | Given an array of integers `nums`, sort the array in **increasing** order based on the frequency of the values. If multiple values have the same frequency, sort them in **decreasing** order.
Return the _sorted array_.
**Example 1:**
**Input:** nums = \[1,1,2,2,2,3\]
**Output:** \[3,1,1,2,2,2\]
**Explanation:** '3' has a frequency of 1, '1' has a frequency of 2, and '2' has a frequency of 3.
**Example 2:**
**Input:** nums = \[2,3,1,3,2\]
**Output:** \[1,3,3,2,2\]
**Explanation:** '2' and '3' both have a frequency of 2, so they are sorted in decreasing order.
**Example 3:**
**Input:** nums = \[-1,1,-6,4,5,-6,1,4,1\]
**Output:** \[5,-1,4,4,-6,-6,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 100`
* `-100 <= nums[i] <= 100` | Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the total contribution of it to the final answer is (n + 1) * n // 2. |
Python BFS Solution with Intuition and Approach | path-with-maximum-probability | 0 | 1 | # Intuition and Approach\nStart by building a `hashmap (graph)`, where `key` is the `node` and value is the value of `(probability, neighbor_node)`\n\nNext just like in a `standard breadth first search` we use a `queue` in this we will use a `priority queue` aka a `maxHeap`.\n\nKeep a dictionary `dist` to keep track of value of `probability` it took to reach the node. (Remember the probability of our `start` node is `1` as in maximum).\n\nEverytime we pop from `minHeap` we have 2 options. If the node has never been visited before according to our `dist` dictionary, then we will multiply `current node\'s probability` and the `node we are trying to visit\'s probability` and add them to our `heap` and `dist` dictionary.\nOtherwise if the multiplication of `current node\'s probability` and the `node we are trying to visit\'s probability` is greater than the value in our dictionary then we update the value and add the node to our `heap`.\nIn summary this is the implementation of `Djikstra\'s shortest path algorithm`.\n\nNote: In python there is no maxHeap, so we have to negate our values to pretend like we are using the maximum. For example `prob=1` becomes `prob=-1`\n\n# Complexity\n- Time complexity:\nE*logV (Time complexity of Djikstra)\n\n- Space complexity:\nO(edges + n) Since to build the graph we atleast need to store n nodes and it\'s edges.\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n def build_graph(n, edges, probability):\n graph = {}\n for i in range(n):\n graph[i] = []\n for i in range(len(edges)):\n frm, to = edges[i]\n graph[frm].append((probability[i], to))\n graph[to].append((probability[i], frm))\n return graph\n def bfs(graph):\n import heapq as hq\n dist = {start:-1}\n heap = [(-1, start)]\n hq.heapify(heap)\n while len(heap) > 0:\n prob, node = hq.heappop(heap)\n for child in graph[node]:\n p,c = child\n if c in dist:\n if abs(p*prob) > abs(dist[c]):\n hq.heappush(heap, (-abs(p*prob), c))\n dist[c] = -abs(p*prob)\n else:\n hq.heappush(heap, (-abs(p * prob), c))\n dist[c] = -abs(p * prob)\n return 0 if end not in dist else -dist[end]\n\n return bfs(build_graph(n, edges, succProb))\n``` | 1 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
Python BFS Solution with Intuition and Approach | path-with-maximum-probability | 0 | 1 | # Intuition and Approach\nStart by building a `hashmap (graph)`, where `key` is the `node` and value is the value of `(probability, neighbor_node)`\n\nNext just like in a `standard breadth first search` we use a `queue` in this we will use a `priority queue` aka a `maxHeap`.\n\nKeep a dictionary `dist` to keep track of value of `probability` it took to reach the node. (Remember the probability of our `start` node is `1` as in maximum).\n\nEverytime we pop from `minHeap` we have 2 options. If the node has never been visited before according to our `dist` dictionary, then we will multiply `current node\'s probability` and the `node we are trying to visit\'s probability` and add them to our `heap` and `dist` dictionary.\nOtherwise if the multiplication of `current node\'s probability` and the `node we are trying to visit\'s probability` is greater than the value in our dictionary then we update the value and add the node to our `heap`.\nIn summary this is the implementation of `Djikstra\'s shortest path algorithm`.\n\nNote: In python there is no maxHeap, so we have to negate our values to pretend like we are using the maximum. For example `prob=1` becomes `prob=-1`\n\n# Complexity\n- Time complexity:\nE*logV (Time complexity of Djikstra)\n\n- Space complexity:\nO(edges + n) Since to build the graph we atleast need to store n nodes and it\'s edges.\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n def build_graph(n, edges, probability):\n graph = {}\n for i in range(n):\n graph[i] = []\n for i in range(len(edges)):\n frm, to = edges[i]\n graph[frm].append((probability[i], to))\n graph[to].append((probability[i], frm))\n return graph\n def bfs(graph):\n import heapq as hq\n dist = {start:-1}\n heap = [(-1, start)]\n hq.heapify(heap)\n while len(heap) > 0:\n prob, node = hq.heappop(heap)\n for child in graph[node]:\n p,c = child\n if c in dist:\n if abs(p*prob) > abs(dist[c]):\n hq.heappush(heap, (-abs(p*prob), c))\n dist[c] = -abs(p*prob)\n else:\n hq.heappush(heap, (-abs(p * prob), c))\n dist[c] = -abs(p * prob)\n return 0 if end not in dist else -dist[end]\n\n return bfs(build_graph(n, edges, succProb))\n``` | 1 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
Python | Dijkstra | Beats 100% | Easy to Understand | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be solved using Dijkstra\'s algorithm to find the path with the maximum probability of success. We can represent the graph as an adjacency list, where each node has a list of its neighbors and the corresponding edge probabilities.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of Dijkstra\'s algorithm is O((V+E)logV), where V is the number of nodes and E is the number of edges in the graph. In the worst case, all edges need to be explored.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(V) to store the adjacency list, probabilities array, and priority queue, where V is the number of nodes in the graph.\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n # Step 1: Create adjacency list\n adj = [[] for _ in range(n)] # Initialize adjacency list\n for i, (a, b) in enumerate(edges):\n adj[a].append((b, succProb[i])) # Add neighbor and edge probability to adjacency list of node \'a\'\n adj[b].append((a, succProb[i])) # Add neighbor and edge probability to adjacency list of node \'b\'\n\n # Step 2: Initialize probabilities\n probabilities = [0] * n # Initialize probability array\n probabilities[start] = 1 # Set probability of start node to 1\n\n # Step 3: Initialize priority queue\n pq = [] # Initialize priority queue\n heapq.heappush(pq, (-1, start)) # Push start node to priority queue with probability -1 (negative for max heap)\n\n # Step 4: Dijkstra\'s algorithm\n while pq:\n probability, node = heapq.heappop(pq) # Pop node with highest probability from priority queue\n probability *= -1 # Invert probability back to positive\n\n if node == end: # If end node is reached, return the probability\n return probability\n\n if probability < probabilities[node]: # If a lower probability is already recorded, skip this node\n continue\n\n for neighbor, edge_prob in adj[node]: # Iterate through neighbors of the current node\n new_prob = probability * edge_prob # Calculate the new probability to reach the neighbor\n if new_prob > probabilities[neighbor]: # If the new probability is higher than the recorded probability\n probabilities[neighbor] = new_prob # Update the probability of reaching the neighbor\n heapq.heappush(pq, (-new_prob, neighbor)) # Push the neighbor to the priority queue with the new probability\n\n # Step 5: No path found\n return 0 | 1 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
Python | Dijkstra | Beats 100% | Easy to Understand | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be solved using Dijkstra\'s algorithm to find the path with the maximum probability of success. We can represent the graph as an adjacency list, where each node has a list of its neighbors and the corresponding edge probabilities.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of Dijkstra\'s algorithm is O((V+E)logV), where V is the number of nodes and E is the number of edges in the graph. In the worst case, all edges need to be explored.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(V) to store the adjacency list, probabilities array, and priority queue, where V is the number of nodes in the graph.\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n # Step 1: Create adjacency list\n adj = [[] for _ in range(n)] # Initialize adjacency list\n for i, (a, b) in enumerate(edges):\n adj[a].append((b, succProb[i])) # Add neighbor and edge probability to adjacency list of node \'a\'\n adj[b].append((a, succProb[i])) # Add neighbor and edge probability to adjacency list of node \'b\'\n\n # Step 2: Initialize probabilities\n probabilities = [0] * n # Initialize probability array\n probabilities[start] = 1 # Set probability of start node to 1\n\n # Step 3: Initialize priority queue\n pq = [] # Initialize priority queue\n heapq.heappush(pq, (-1, start)) # Push start node to priority queue with probability -1 (negative for max heap)\n\n # Step 4: Dijkstra\'s algorithm\n while pq:\n probability, node = heapq.heappop(pq) # Pop node with highest probability from priority queue\n probability *= -1 # Invert probability back to positive\n\n if node == end: # If end node is reached, return the probability\n return probability\n\n if probability < probabilities[node]: # If a lower probability is already recorded, skip this node\n continue\n\n for neighbor, edge_prob in adj[node]: # Iterate through neighbors of the current node\n new_prob = probability * edge_prob # Calculate the new probability to reach the neighbor\n if new_prob > probabilities[neighbor]: # If the new probability is higher than the recorded probability\n probabilities[neighbor] = new_prob # Update the probability of reaching the neighbor\n heapq.heappush(pq, (-new_prob, neighbor)) # Push the neighbor to the priority queue with the new probability\n\n # Step 5: No path found\n return 0 | 1 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
Problem Of the Day 28/06/2023 | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n # Adjacency list\n adj = [[] for _ in range(n)]\n for i in range(len(edges)):\n u, v = edges[i]\n p = succProb[i]\n adj[u].append((v, p))\n adj[v].append((u, p))\n\n # Distances array\n dist = [0.0] * n\n dist[start] = 1.0\n\n # Queue for BFS\n queue = deque([start])\n\n while queue:\n curr = queue.popleft()\n\n for node, prob in adj[curr]:\n new_prob = dist[curr] * prob\n\n if new_prob > dist[node]:\n dist[node] = new_prob\n queue.append(node)\n\n return dist[end]\n``` | 1 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
Problem Of the Day 28/06/2023 | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n # Adjacency list\n adj = [[] for _ in range(n)]\n for i in range(len(edges)):\n u, v = edges[i]\n p = succProb[i]\n adj[u].append((v, p))\n adj[v].append((u, p))\n\n # Distances array\n dist = [0.0] * n\n dist[start] = 1.0\n\n # Queue for BFS\n queue = deque([start])\n\n while queue:\n curr = queue.popleft()\n\n for node, prob in adj[curr]:\n new_prob = dist[curr] * prob\n\n if new_prob > dist[node]:\n dist[node] = new_prob\n queue.append(node)\n\n return dist[end]\n``` | 1 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
SIMPLE PYTHON SOLUTION | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSHORTEST PATH\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n adj=[[] for _ in range(n)]\n for i in range(len(edges)):\n adj[edges[i][0]].append((-1*succProb[i],edges[i][1]))\n adj[edges[i][1]].append((-1*succProb[i],edges[i][0]))\n dst=[0]*n\n st=[(-1,start)]\n heapq.heapify(st)\n dst[start]=-1\n while st:\n d,x=heapq.heappop(st)\n for dt,i in adj[x]:\n print(i,d,dt,dst[i])\n if -1*(d*dt)<dst[i]:\n dst[i]=-1*(d*dt)\n if i!=end:\n heapq.heappush(st,(-1*(d*dt),i))\n return -1*dst[end]\n\n``` | 1 | You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.2\], start = 0, end = 2
**Output:** 0.25000
**Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\],\[0,2\]\], succProb = \[0.5,0.5,0.3\], start = 0, end = 2
**Output:** 0.30000
**Example 3:**
**Input:** n = 3, edges = \[\[0,1\]\], succProb = \[0.5\], start = 0, end = 2
**Output:** 0.00000
**Explanation:** There is no path between 0 and 2.
**Constraints:**
* `2 <= n <= 10^4`
* `0 <= start, end < n`
* `start != end`
* `0 <= a, b < n`
* `a != b`
* `0 <= succProb.length == edges.length <= 2*10^4`
* `0 <= succProb[i] <= 1`
* There is at most one edge between every two nodes. | Find the minimum prefix sum. |
SIMPLE PYTHON SOLUTION | path-with-maximum-probability | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSHORTEST PATH\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:\n adj=[[] for _ in range(n)]\n for i in range(len(edges)):\n adj[edges[i][0]].append((-1*succProb[i],edges[i][1]))\n adj[edges[i][1]].append((-1*succProb[i],edges[i][0]))\n dst=[0]*n\n st=[(-1,start)]\n heapq.heapify(st)\n dst[start]=-1\n while st:\n d,x=heapq.heappop(st)\n for dt,i in adj[x]:\n print(i,d,dt,dst[i])\n if -1*(d*dt)<dst[i]:\n dst[i]=-1*(d*dt)\n if i!=end:\n heapq.heappush(st,(-1*(d*dt),i))\n return -1*dst[end]\n\n``` | 1 | Given a binary tree `root` and an integer `target`, delete all the **leaf nodes** with value `target`.
Note that once you delete a leaf node with value `target`**,** if its parent node becomes a leaf node and has the value `target`, it should also be deleted (you need to continue doing that until you cannot).
**Example 1:**
**Input:** root = \[1,2,3,2,null,2,4\], target = 2
**Output:** \[1,null,3,null,4\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed (Picture in left).
After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).
**Example 2:**
**Input:** root = \[1,3,3,3,2\], target = 3
**Output:** \[1,3,null,null,2\]
**Example 3:**
**Input:** root = \[1,2,null,2,null,2\], target = 2
**Output:** \[1\]
**Explanation:** Leaf nodes in green with value (target = 2) are removed at each step.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 3000]`.
* `1 <= Node.val, target <= 1000` | Multiplying probabilities will result in precision errors. Take log probabilities to sum up numbers instead of multiplying them. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs. |
[Python3] geometric median | best-position-for-a-service-centre | 0 | 1 | This problem is to compute a quantity called "geometric median". There are algorithms dedicated to solve such problems such as Weiszfeld\'s algorithm. But those algorithms leverages on statistical routines such as weighted least squares. \n\nSince this is a 2d toy problem, we could use some "brute force" grid searching method to find an approximation. Suppose you think `x, y` is a candidate. Then, you could perturb the point along `x` and `y` by a small amount (`chg` in the implementation) and check if the new point provides a smaller distance. If so, the new point becomes the new candidate. \n\nThe trick is to progressively decrease `chg` to a satisfying precision (`1e-5` in this setting). One could reduce it by half or any chosen factor. In the meantime, centroid is a good starting point. \n\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n #euclidean distance \n fn = lambda x, y: sum(sqrt((x-xx)**2 + (y-yy)**2) for xx, yy in positions)\n #centroid as starting point\n x = sum(x for x, _ in positions)/len(positions)\n y = sum(y for _, y in positions)/len(positions)\n \n ans = fn(x, y)\n chg = 100 #change since 0 <= positions[i][0], positions[i][1] <= 100\n while chg > 1e-6: #accuracy within 1e-5\n zoom = True\n for dx, dy in (-1, 0), (0, -1), (0, 1), (1, 0):\n xx = x + chg * dx\n yy = y + chg * dy\n dd = fn(xx, yy)\n if dd < ans: \n ans = dd \n x, y = xx, yy\n zoom = False \n break \n if zoom: chg /= 2\n return ans \n``` | 72 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
[Python3] geometric median | best-position-for-a-service-centre | 0 | 1 | This problem is to compute a quantity called "geometric median". There are algorithms dedicated to solve such problems such as Weiszfeld\'s algorithm. But those algorithms leverages on statistical routines such as weighted least squares. \n\nSince this is a 2d toy problem, we could use some "brute force" grid searching method to find an approximation. Suppose you think `x, y` is a candidate. Then, you could perturb the point along `x` and `y` by a small amount (`chg` in the implementation) and check if the new point provides a smaller distance. If so, the new point becomes the new candidate. \n\nThe trick is to progressively decrease `chg` to a satisfying precision (`1e-5` in this setting). One could reduce it by half or any chosen factor. In the meantime, centroid is a good starting point. \n\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n #euclidean distance \n fn = lambda x, y: sum(sqrt((x-xx)**2 + (y-yy)**2) for xx, yy in positions)\n #centroid as starting point\n x = sum(x for x, _ in positions)/len(positions)\n y = sum(y for _, y in positions)/len(positions)\n \n ans = fn(x, y)\n chg = 100 #change since 0 <= positions[i][0], positions[i][1] <= 100\n while chg > 1e-6: #accuracy within 1e-5\n zoom = True\n for dx, dy in (-1, 0), (0, -1), (0, 1), (1, 0):\n xx = x + chg * dx\n yy = y + chg * dy\n dd = fn(xx, yy)\n if dd < ans: \n ans = dd \n x, y = xx, yy\n zoom = False \n break \n if zoom: chg /= 2\n return ans \n``` | 72 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python solution gradient descent. Explanation | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to find the minimum distance sum of all the given positions. We can approach this problem using an optimization technique called gradient descent. Gradient descent is an iterative process in which the solution is gradually approximated. We start with a random point and then search for a point that is closer to the minimum distance sum. We can use a step size to determine how far away from the current point we need to search for the new point. We can continuously repeat this process until we find the points that give us the minimum distance sum. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a gradient descent approach to solve this problem. We start with a random point and calculate the total distance sum of this point with respect to all the given positions. We then search for a point that is closer to the minimum distance sum by incrementing or decrementing the current point by a step size. We repeat this process until we reach a point that gives us the minimum distance sum. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n def dist(x, y):\n return sum(((x - a) ** 2 + (y - b) ** 2) ** 0.5 for a, b in positions)\n x, y = sum(a for a, b in positions) / len(positions), sum(b for a, b in positions) / len(positions)\n step = 100\n while step > 1e-6:\n for dx, dy in [[0, 1], [1, 0], [0, -1], [-1, 0]]:\n nx, ny = x + step * dx, y + step * dy\n if dist(nx, ny) < dist(x, y):\n x, y = nx, ny\n break\n else:\n step /= 2\n return dist(x, y)\n``` | 2 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python solution gradient descent. Explanation | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to find the minimum distance sum of all the given positions. We can approach this problem using an optimization technique called gradient descent. Gradient descent is an iterative process in which the solution is gradually approximated. We start with a random point and then search for a point that is closer to the minimum distance sum. We can use a step size to determine how far away from the current point we need to search for the new point. We can continuously repeat this process until we find the points that give us the minimum distance sum. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use a gradient descent approach to solve this problem. We start with a random point and calculate the total distance sum of this point with respect to all the given positions. We then search for a point that is closer to the minimum distance sum by incrementing or decrementing the current point by a step size. We repeat this process until we reach a point that gives us the minimum distance sum. \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n def dist(x, y):\n return sum(((x - a) ** 2 + (y - b) ** 2) ** 0.5 for a, b in positions)\n x, y = sum(a for a, b in positions) / len(positions), sum(b for a, b in positions) / len(positions)\n step = 100\n while step > 1e-6:\n for dx, dy in [[0, 1], [1, 0], [0, -1], [-1, 0]]:\n nx, ny = x + step * dx, y + step * dy\n if dist(nx, ny) < dist(x, y):\n x, y = nx, ny\n break\n else:\n step /= 2\n return dist(x, y)\n``` | 2 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
[Python] Gradient Descent with Armijo stepsize rule | best-position-for-a-service-centre | 0 | 1 | The problem is written as:\n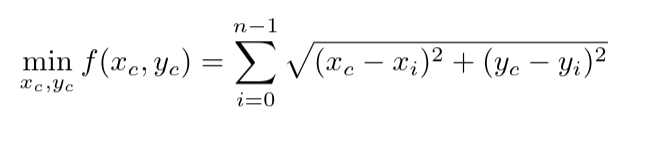.\nThe gradient is\n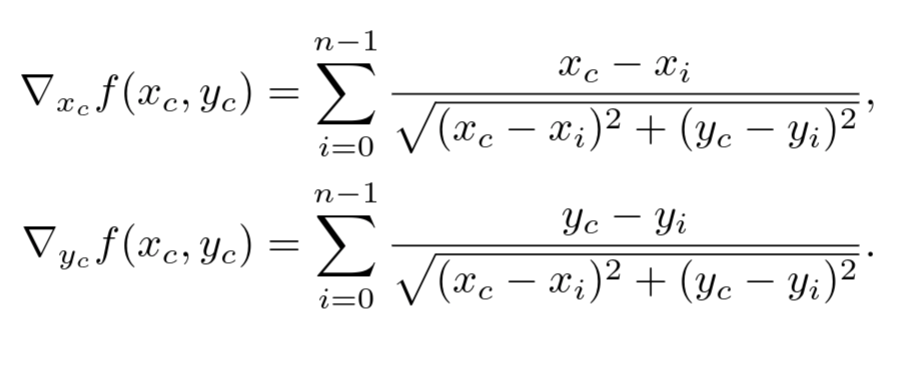\n\n\n\n```python\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n EPSILON = 1.0\n ALPHA = 0.5\n BETA = 0.8\n N = len(positions)\n def calcgradient(x, y):\n ans = [0, 0]\n for i in range(N):\n denom = math.sqrt(pow(positions[i][0]-x, 2) + pow(positions[i][1] - y, 2))\n \n ans[0] += (x - positions[i][0])/denom\n ans[1] += (y - positions[i][1])/denom\n return ans\n \n def object(x, y):\n res = 0.0\n for i in range(N):\n res += math.sqrt(pow(positions[i][0]-x, 2) + pow(positions[i][1] - y, 2)) \n # print("x:", x, " obj:", res)\n return res\n \n def armijo(x, y, epsilon):\n grad = calcgradient(x, y)\n left = object(x - epsilon * grad[0], y - epsilon * grad[1]) - object(x, y)\n right = -1 * ALPHA * epsilon * (grad[0] * grad[0] + grad[1] * grad[1])\n res = left <= right\n # print(left, right)\n return res\n def backtrack(x, y):\n eps = EPSILON\n while armijo(x, y, eps) is False:\n eps = BETA * eps\n return eps\n x = 0.1\n y = 0.1\n res = object(x, y)\n flag = True\n while flag:\n # print(i)\n stepsize = backtrack(x, y)\n grad = calcgradient(x, y)\n x -= stepsize * grad[0]\n y -= stepsize * grad[1]\n nres = object(x, y)\n # print(x, y, nres)\n if nres < res - 0.00000001:\n flag = True\n else:\n flag = False\n res = nres\n return res\n```\n\n In order to deal with zero denominator while calculating gradient, I set initial values for x and y as\n ```python\n x = 0.1\n y = 0.1\n ```\n \n Peformance:\n Runtime: 380 ms, faster than 71.43% of Python3 online submissions for Best Position for a Service Centre.\nMemory Usage: 13.9 MB, less than 100.00% of Python3 online submissions for Best Position for a Service Centre. | 23 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
[Python] Gradient Descent with Armijo stepsize rule | best-position-for-a-service-centre | 0 | 1 | The problem is written as:\n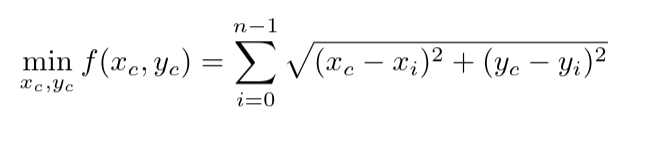.\nThe gradient is\n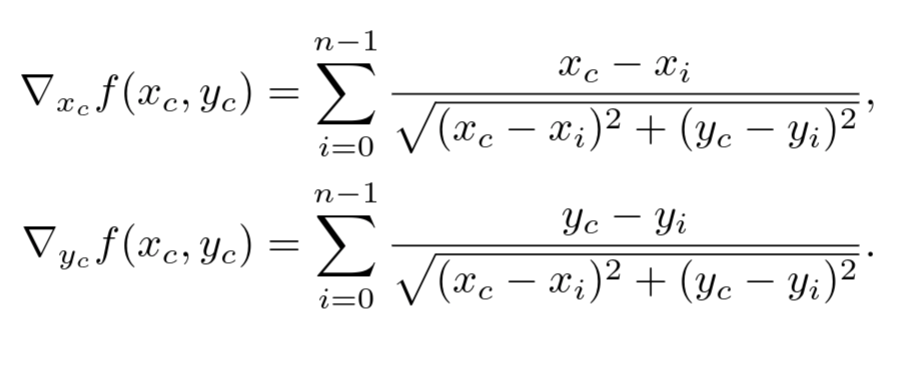\n\n\n\n```python\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n EPSILON = 1.0\n ALPHA = 0.5\n BETA = 0.8\n N = len(positions)\n def calcgradient(x, y):\n ans = [0, 0]\n for i in range(N):\n denom = math.sqrt(pow(positions[i][0]-x, 2) + pow(positions[i][1] - y, 2))\n \n ans[0] += (x - positions[i][0])/denom\n ans[1] += (y - positions[i][1])/denom\n return ans\n \n def object(x, y):\n res = 0.0\n for i in range(N):\n res += math.sqrt(pow(positions[i][0]-x, 2) + pow(positions[i][1] - y, 2)) \n # print("x:", x, " obj:", res)\n return res\n \n def armijo(x, y, epsilon):\n grad = calcgradient(x, y)\n left = object(x - epsilon * grad[0], y - epsilon * grad[1]) - object(x, y)\n right = -1 * ALPHA * epsilon * (grad[0] * grad[0] + grad[1] * grad[1])\n res = left <= right\n # print(left, right)\n return res\n def backtrack(x, y):\n eps = EPSILON\n while armijo(x, y, eps) is False:\n eps = BETA * eps\n return eps\n x = 0.1\n y = 0.1\n res = object(x, y)\n flag = True\n while flag:\n # print(i)\n stepsize = backtrack(x, y)\n grad = calcgradient(x, y)\n x -= stepsize * grad[0]\n y -= stepsize * grad[1]\n nres = object(x, y)\n # print(x, y, nres)\n if nres < res - 0.00000001:\n flag = True\n else:\n flag = False\n res = nres\n return res\n```\n\n In order to deal with zero denominator while calculating gradient, I set initial values for x and y as\n ```python\n x = 0.1\n y = 0.1\n ```\n \n Peformance:\n Runtime: 380 ms, faster than 71.43% of Python3 online submissions for Best Position for a Service Centre.\nMemory Usage: 13.9 MB, less than 100.00% of Python3 online submissions for Best Position for a Service Centre. | 23 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Simple gradient descent. | best-position-for-a-service-centre | 0 | 1 | \n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n if len(positions) == 1:\n return 0\n def grad(x, y, xs, ys):\n norm = [ sqrt( (x-xi)**2 + (y-yi) **2 ) for xi, yi in zip(xs, ys)] \n dx = sum([ (x - xi) / ni for xi, ni in zip(xs, norm)])\n dy = sum([ (y - yi) / ni for yi, ni in zip(ys, norm)])\n return dx, dy\n def f(x, y, xs, ys):\n return sum([ sqrt( (x-xi)**2 + (y-yi) **2 ) for xi, yi in zip(xs, ys)] )\n\n xs = [x for x, _ in positions] \n ys = [y for _, y in positions] \n\n x = sum(xs) / len(positions) + 0.01\n y = sum(ys) / len(positions) + 0.01\n loss = f(x,y, xs, ys)\n chg = float("inf")\n stepsize = 1\n cnt = 1\n while chg > 1e-7 and cnt < 5000:\n cnt += 1\n old_loss = loss\n dx, dy = grad(x, y, xs, ys)\n\n\n while True and abs(dx**2 + dy**2) > 1e-9:\n cnt += 1\n new_x = x - stepsize * dx\n new_y = y - stepsize * dy\n new_loss = f(new_x, new_y, xs, ys)\n if new_loss < loss:\n x = new_x\n y = new_y\n loss = new_loss\n break\n stepsize = stepsize / cnt\n\n\n chg = abs(old_loss - loss)\n\n return loss\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Simple gradient descent. | best-position-for-a-service-centre | 0 | 1 | \n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n if len(positions) == 1:\n return 0\n def grad(x, y, xs, ys):\n norm = [ sqrt( (x-xi)**2 + (y-yi) **2 ) for xi, yi in zip(xs, ys)] \n dx = sum([ (x - xi) / ni for xi, ni in zip(xs, norm)])\n dy = sum([ (y - yi) / ni for yi, ni in zip(ys, norm)])\n return dx, dy\n def f(x, y, xs, ys):\n return sum([ sqrt( (x-xi)**2 + (y-yi) **2 ) for xi, yi in zip(xs, ys)] )\n\n xs = [x for x, _ in positions] \n ys = [y for _, y in positions] \n\n x = sum(xs) / len(positions) + 0.01\n y = sum(ys) / len(positions) + 0.01\n loss = f(x,y, xs, ys)\n chg = float("inf")\n stepsize = 1\n cnt = 1\n while chg > 1e-7 and cnt < 5000:\n cnt += 1\n old_loss = loss\n dx, dy = grad(x, y, xs, ys)\n\n\n while True and abs(dx**2 + dy**2) > 1e-9:\n cnt += 1\n new_x = x - stepsize * dx\n new_y = y - stepsize * dy\n new_loss = f(new_x, new_y, xs, ys)\n if new_loss < loss:\n x = new_x\n y = new_y\n loss = new_loss\n break\n stepsize = stepsize / cnt\n\n\n chg = abs(old_loss - loss)\n\n return loss\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
The Alternating Direction Method of Multipliers (ADMM) | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe objective is convex, decomposible but not everywhere differentiable. It is suitable for the alternating direction method of multipliers (ADMM), but not gradient descent.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nhttps://arxiv.org/pdf/1501.03879.pdf\n\n# Code\n```\nimport numpy as np\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n a = np.asarray(positions) * 1.0\n\n n = a.shape[0]\n z = np.zeros(2)\n z_prev = np.zeros(2)\n\n # ADMM variables\n x = np.zeros((n, 2))\n y = np.zeros((n, 2))\n mu = 0.05\n nit = 0\n lam = 1.0 / mu\n\n while True:\n nit += 1\n v = z - y * lam\n vma = v - a\n d = np.linalg.norm(vma, axis=1, keepdims=True).clip(1e-8)\n x = v - np.minimum(lam/d, 1) * vma \n r = (x + y * lam).sum(0)\n z = r / n\n y += mu * (x - z)\n \n if nit > 500:\n break\n \n z_prev[:] = z\n\n dist = np.sqrt(np.power(z - a, 2.0).sum(1)).sum()\n\n return dist \n\n```\n | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
The Alternating Direction Method of Multipliers (ADMM) | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe objective is convex, decomposible but not everywhere differentiable. It is suitable for the alternating direction method of multipliers (ADMM), but not gradient descent.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nhttps://arxiv.org/pdf/1501.03879.pdf\n\n# Code\n```\nimport numpy as np\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n a = np.asarray(positions) * 1.0\n\n n = a.shape[0]\n z = np.zeros(2)\n z_prev = np.zeros(2)\n\n # ADMM variables\n x = np.zeros((n, 2))\n y = np.zeros((n, 2))\n mu = 0.05\n nit = 0\n lam = 1.0 / mu\n\n while True:\n nit += 1\n v = z - y * lam\n vma = v - a\n d = np.linalg.norm(vma, axis=1, keepdims=True).clip(1e-8)\n x = v - np.minimum(lam/d, 1) * vma \n r = (x + y * lam).sum(0)\n z = r / n\n y += mu * (x - z)\n \n if nit > 500:\n break\n \n z_prev[:] = z\n\n dist = np.sqrt(np.power(z - a, 2.0).sum(1)).sum()\n\n return dist \n\n```\n | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python: Weiszfeld's algorithm for Geometric Median | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first I thought "gee, why isn\'t this an Easy problem? I\'ll just compute the center of gravity (2D mean) of the points, then sum up the distance from the center to all the points. But when I tried it, it became clear that this wasn\'t going to work. That\'s when I read the Hint and learned that the problem calls for computing the *Geometric Median* of the points. Turning to Wikipedia, I learned that unlike the center of gravity, there\'s no closed form solution for the Geometric Median. The Hint suggests an algorithmic approach to search for the smallest circle that contains the points, while the Wikipedia article suggested *Weiszfeld\'s algorithm*, which iteratively refines the estimate of the Geometric Median.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe implementation consists of several steps: First, the center of the minimum circle is approximated by the center of gravity, a straightforward computation. Second, the nested ```while``` loop implements the Weiszfeld\'s algorithm, iteratively updating the variables ```ctr_x``` and ```ctr_y```. The approximation loop is exited once the change in the variables is below a threshold. Once the center point has been calculated, the third step is simply to sum up the distances to all the ```positions```.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe running time complexity is determined by how quickly Weiszfeld\'s algorithm converges. I\'m afraid I really have no intuition as to how the convergence rate depends on the number or disposition of the input points. Each *iteration* evaluates expressions involving all of the ```positions``` and so it is $$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nAll of the variables, excluding the input, are scalar and thus the space complexity is $$O(1)$$, not dependent on the size of the inputs.\n\n# Code\n```\nfrom math import sqrt\n\nclass Solution:\n def getMinDistSum(self, positions: list[list[int]]) -> float:\n # First, compute the center of gravity as a starting point for an\n # iterative solution.\n n = len(positions)\n sum_x = sum(map(lambda pos: pos[0], positions))\n sum_y = sum(map(lambda pos: pos[1], positions))\n ctr_x = sum_x / n\n ctr_y = sum_y / n\n # Next, use the iterative"Weiszfeld\'s algorithm" to refine the estimate\n # the geometric median, which the Hint notes is the formalization of\n # the problem (https://en.wikipedia.org/wiki/Geometric_median):\n prev_ctr_x = ctr_x\n prev_ctr_y = ctr_y\n while True:\n top_sum_x = top_sum_y = bot_sum_x = bot_sum_y = 0.0\n for posn_x, posn_y in positions:\n denom = self.distance(posn_x, posn_y, ctr_x, ctr_y)\n if denom == 0.0:\n continue\n top_sum_x += posn_x / denom\n top_sum_y += posn_y / denom\n bot_sum_x += 1 / denom\n bot_sum_y += 1 / denom\n if bot_sum_x == 0 or bot_sum_y == 0:\n break\n ctr_x = top_sum_x / bot_sum_x\n ctr_y = top_sum_y / bot_sum_y\n if self.distance(prev_ctr_x, prev_ctr_y, ctr_x, ctr_y) < 10 ** -7:\n break\n else:\n prev_ctr_x = ctr_x\n prev_ctr_y = ctr_y\n # Calculate sum of distances to approximated geometric median\n total_distance = 0\n for posn_x, posn_y in positions:\n total_distance += self.distance( posn_x, posn_y, ctr_x, ctr_y )\n return total_distance\n\n def distance(self, x1, y1, x2, y2):\n return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)\n\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python: Weiszfeld's algorithm for Geometric Median | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first I thought "gee, why isn\'t this an Easy problem? I\'ll just compute the center of gravity (2D mean) of the points, then sum up the distance from the center to all the points. But when I tried it, it became clear that this wasn\'t going to work. That\'s when I read the Hint and learned that the problem calls for computing the *Geometric Median* of the points. Turning to Wikipedia, I learned that unlike the center of gravity, there\'s no closed form solution for the Geometric Median. The Hint suggests an algorithmic approach to search for the smallest circle that contains the points, while the Wikipedia article suggested *Weiszfeld\'s algorithm*, which iteratively refines the estimate of the Geometric Median.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe implementation consists of several steps: First, the center of the minimum circle is approximated by the center of gravity, a straightforward computation. Second, the nested ```while``` loop implements the Weiszfeld\'s algorithm, iteratively updating the variables ```ctr_x``` and ```ctr_y```. The approximation loop is exited once the change in the variables is below a threshold. Once the center point has been calculated, the third step is simply to sum up the distances to all the ```positions```.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe running time complexity is determined by how quickly Weiszfeld\'s algorithm converges. I\'m afraid I really have no intuition as to how the convergence rate depends on the number or disposition of the input points. Each *iteration* evaluates expressions involving all of the ```positions``` and so it is $$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nAll of the variables, excluding the input, are scalar and thus the space complexity is $$O(1)$$, not dependent on the size of the inputs.\n\n# Code\n```\nfrom math import sqrt\n\nclass Solution:\n def getMinDistSum(self, positions: list[list[int]]) -> float:\n # First, compute the center of gravity as a starting point for an\n # iterative solution.\n n = len(positions)\n sum_x = sum(map(lambda pos: pos[0], positions))\n sum_y = sum(map(lambda pos: pos[1], positions))\n ctr_x = sum_x / n\n ctr_y = sum_y / n\n # Next, use the iterative"Weiszfeld\'s algorithm" to refine the estimate\n # the geometric median, which the Hint notes is the formalization of\n # the problem (https://en.wikipedia.org/wiki/Geometric_median):\n prev_ctr_x = ctr_x\n prev_ctr_y = ctr_y\n while True:\n top_sum_x = top_sum_y = bot_sum_x = bot_sum_y = 0.0\n for posn_x, posn_y in positions:\n denom = self.distance(posn_x, posn_y, ctr_x, ctr_y)\n if denom == 0.0:\n continue\n top_sum_x += posn_x / denom\n top_sum_y += posn_y / denom\n bot_sum_x += 1 / denom\n bot_sum_y += 1 / denom\n if bot_sum_x == 0 or bot_sum_y == 0:\n break\n ctr_x = top_sum_x / bot_sum_x\n ctr_y = top_sum_y / bot_sum_y\n if self.distance(prev_ctr_x, prev_ctr_y, ctr_x, ctr_y) < 10 ** -7:\n break\n else:\n prev_ctr_x = ctr_x\n prev_ctr_y = ctr_y\n # Calculate sum of distances to approximated geometric median\n total_distance = 0\n for posn_x, posn_y in positions:\n total_distance += self.distance( posn_x, posn_y, ctr_x, ctr_y )\n return total_distance\n\n def distance(self, x1, y1, x2, y2):\n return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)\n\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python simple gradient descent | best-position-for-a-service-centre | 0 | 1 | # Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n step_size = 50\n alpha = 0.7\n cur_pos = (0, 0)\n directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]\n while step_size > 10**(-9):\n cur_distance = get_distance(positions, cur_pos)\n for d in directions:\n new_dist = get_distance(positions, move(cur_pos, mag_mul(d, step_size)))\n if new_dist < cur_distance:\n cur_pos = move(cur_pos, mag_mul(d, step_size))\n break\n if new_dist >= cur_distance:\n step_size *= alpha\n return get_distance(positions, cur_pos)\n\ndef move(pos, added_vec):\n return pos[0] + added_vec[0], pos[1] + added_vec[1]\n\ndef mag_mul(vec, mag):\n return vec[0] * mag , vec[1] * mag\n\ndef get_distance(positions, pos):\n total_dist = 0\n for i in positions:\n total_dist += ((i[0]- pos[0])**2 + (i[1] - pos[1])**2) ** (1/2)\n return total_dist\n\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python simple gradient descent | best-position-for-a-service-centre | 0 | 1 | # Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n step_size = 50\n alpha = 0.7\n cur_pos = (0, 0)\n directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]\n while step_size > 10**(-9):\n cur_distance = get_distance(positions, cur_pos)\n for d in directions:\n new_dist = get_distance(positions, move(cur_pos, mag_mul(d, step_size)))\n if new_dist < cur_distance:\n cur_pos = move(cur_pos, mag_mul(d, step_size))\n break\n if new_dist >= cur_distance:\n step_size *= alpha\n return get_distance(positions, cur_pos)\n\ndef move(pos, added_vec):\n return pos[0] + added_vec[0], pos[1] + added_vec[1]\n\ndef mag_mul(vec, mag):\n return vec[0] * mag , vec[1] * mag\n\ndef get_distance(positions, pos):\n total_dist = 0\n for i in positions:\n total_dist += ((i[0]- pos[0])**2 + (i[1] - pos[1])**2) ** (1/2)\n return total_dist\n\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Weiszfeld's algorithm | Commented and Explained | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBest position for a service is a geometric median. These are related to Fermat\'s theorem and are part of the higher level algorithmic problems on Leetcode. Check the wiki here for more : https://en.wikipedia.org/wiki/Geometric_median\n\nTo calculate this appropriately and give a set up that\'s useful for those in AI / ML, we focus on a non-dimensionally bound version of euclidean distance. This lets us have a more generalized approach for our work. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo get set up, we need a few variables first \nset P as the size of the positions array \nset epsilon as 10^-7 \nset center as [0.0] * len(positions[0]) (a point of 0.0 for the center of the space that is of dimension to match) \nset cL as the length of the center (our dimensionality) \n\nfor each point in position \n- for index, point_vector in enumerate point \n - center[index] += point_vector\n\nfor each center_vector in center \n- normalize by P \n\nset distance flag as True \n\nSet a euclidean distance function using point 1 and 2 as parameters \n- value is 0 \n- for i in range len point 1 \n - value is incremented by square of difference of point 1 at i and point 2 at i \n- return square root of value \n\nwhile distance flag is true \n- set up numerators as 0.0 array of size cL \n- set up denominator as 0 \n- for position in positions \n - find distance from cener to position\n - if distance gt epsilon\n - for index, position_vector in enumerate position \n - numerators[index] += position_vector / distance \n - denominator += 1/distance \n- if denominator is 0 return 0 \n- otherwise, set new center as [num_i / denominator for num_i in numerators] \n- distance flag is then equal to distance of center and new center is gte epsilon\n- if distance flag \n - center is new center \n\ntotal distance is 0 \nfor position in positions \n- total distance += distance of center to position \n\nreturn rounded form of total distance to 5 places \n\n# Complexity\n- Time complexity : O(P^?)\n - Time P to build center originally \n - Time to converge is difficult to ascertain \n - based on others work, it is likely monotonic https://www.ncbi.nlm.nih.gov/pmc/articles/PMC26449/\n - It involves work P, so we can estimate it as a power of P \n - It involves work D for dimensionality, so we can estimate as a combined power of both \n - Last portion is O(P) \n - Total is some power form of O(P) as P subsumes D \n\n- Space complexity : O(D) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - We store the center of size O(D) \n - We store numerators of size O(D) \n - We store new center of size O(D) \n - All O(D)\n\n# Code\n```\nimport math\nfrom typing import List\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float :\n # get number of points, set up epsilon and set center as average x and y \n P = len(positions)\n epsilon = 1e-7\n center = [0.0]*len(positions[0])\n cL = len(center)\n # sum up over positions \n for p_i in range(P) : \n # and over each dimensions of each position \n for index, p_v in enumerate(positions[p_i]) : \n center[index] += p_v\n\n # then divide these all out by number of points \n for c_i in range(cL) : \n center[c_i] = center[c_i] / P\n\n # set distance flag for a do while loop \n distance_flag = True \n\n # euclidean distance in n dimensional space \n def euclidean(p1, p2) : \n # build value over dimensions \n value = 0 \n # loop over each option \n for i in range(len(p1)) : \n # sum up power value \n value += ((p1[i] - p2[i])*(p1[i]-p2[i]))\n # sqrt at end \n return math.sqrt(value)\n\n # following is based off of https://en.wikipedia.org/wiki/Geometric_median\n # where we utilize Weiszfeld\'s algorithm\n # and notice that we have an epsilon value as our stopping threshold \n # in this case we find the new center for y_k as the sum of the values of interest \n # which are those whose distance is greater than epsilon for euclidean center, position \n # divided by the distance and then all eventually divided by 1 / sum of the distances of interest \n # when you have read the above from lines 36 to here and think you understand it, go read the lines 46 - 65\n # this will be your check to see if you have it \n\n # do while procession \n while distance_flag :\n # reset numerators and denominator\n numerators = [0.0]*cL\n denominator = 0 \n # loop over positions \n for position in positions : \n # get distance \n distance = euclidean(center, position)\n # if distance gt epsilon \n if distance > epsilon : \n # update numerators accordingly \n for index, p_v in enumerate(position) : \n numerators[index] += p_v / distance\n # update denominator \n denominator += 1 / distance\n \n # if denominator is 0 return 0 \n if denominator == 0 : \n return 0 \n\n # otherwise, establish new center as the ith numerator / denominator for numerator in numerators\n new_center = [num_i / denominator for num_i in numerators]\n\n # set distance flag as euclidean of center and new center is gte epsilon\n distance_flag = euclidean(center, new_center) >= epsilon \n # if we are continuing, update center. Otherwise, leave be\n if distance_flag : \n center = new_center\n\n # When done, calculate distance \n total_distance = 0 \n # as accumulated map of euclidean of center and positions\n for position in positions : \n total_distance += euclidean(center, position)\n \n # return rounded value to 5 decimal places \n return round(total_distance, 5)\n\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Weiszfeld's algorithm | Commented and Explained | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBest position for a service is a geometric median. These are related to Fermat\'s theorem and are part of the higher level algorithmic problems on Leetcode. Check the wiki here for more : https://en.wikipedia.org/wiki/Geometric_median\n\nTo calculate this appropriately and give a set up that\'s useful for those in AI / ML, we focus on a non-dimensionally bound version of euclidean distance. This lets us have a more generalized approach for our work. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo get set up, we need a few variables first \nset P as the size of the positions array \nset epsilon as 10^-7 \nset center as [0.0] * len(positions[0]) (a point of 0.0 for the center of the space that is of dimension to match) \nset cL as the length of the center (our dimensionality) \n\nfor each point in position \n- for index, point_vector in enumerate point \n - center[index] += point_vector\n\nfor each center_vector in center \n- normalize by P \n\nset distance flag as True \n\nSet a euclidean distance function using point 1 and 2 as parameters \n- value is 0 \n- for i in range len point 1 \n - value is incremented by square of difference of point 1 at i and point 2 at i \n- return square root of value \n\nwhile distance flag is true \n- set up numerators as 0.0 array of size cL \n- set up denominator as 0 \n- for position in positions \n - find distance from cener to position\n - if distance gt epsilon\n - for index, position_vector in enumerate position \n - numerators[index] += position_vector / distance \n - denominator += 1/distance \n- if denominator is 0 return 0 \n- otherwise, set new center as [num_i / denominator for num_i in numerators] \n- distance flag is then equal to distance of center and new center is gte epsilon\n- if distance flag \n - center is new center \n\ntotal distance is 0 \nfor position in positions \n- total distance += distance of center to position \n\nreturn rounded form of total distance to 5 places \n\n# Complexity\n- Time complexity : O(P^?)\n - Time P to build center originally \n - Time to converge is difficult to ascertain \n - based on others work, it is likely monotonic https://www.ncbi.nlm.nih.gov/pmc/articles/PMC26449/\n - It involves work P, so we can estimate it as a power of P \n - It involves work D for dimensionality, so we can estimate as a combined power of both \n - Last portion is O(P) \n - Total is some power form of O(P) as P subsumes D \n\n- Space complexity : O(D) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - We store the center of size O(D) \n - We store numerators of size O(D) \n - We store new center of size O(D) \n - All O(D)\n\n# Code\n```\nimport math\nfrom typing import List\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float :\n # get number of points, set up epsilon and set center as average x and y \n P = len(positions)\n epsilon = 1e-7\n center = [0.0]*len(positions[0])\n cL = len(center)\n # sum up over positions \n for p_i in range(P) : \n # and over each dimensions of each position \n for index, p_v in enumerate(positions[p_i]) : \n center[index] += p_v\n\n # then divide these all out by number of points \n for c_i in range(cL) : \n center[c_i] = center[c_i] / P\n\n # set distance flag for a do while loop \n distance_flag = True \n\n # euclidean distance in n dimensional space \n def euclidean(p1, p2) : \n # build value over dimensions \n value = 0 \n # loop over each option \n for i in range(len(p1)) : \n # sum up power value \n value += ((p1[i] - p2[i])*(p1[i]-p2[i]))\n # sqrt at end \n return math.sqrt(value)\n\n # following is based off of https://en.wikipedia.org/wiki/Geometric_median\n # where we utilize Weiszfeld\'s algorithm\n # and notice that we have an epsilon value as our stopping threshold \n # in this case we find the new center for y_k as the sum of the values of interest \n # which are those whose distance is greater than epsilon for euclidean center, position \n # divided by the distance and then all eventually divided by 1 / sum of the distances of interest \n # when you have read the above from lines 36 to here and think you understand it, go read the lines 46 - 65\n # this will be your check to see if you have it \n\n # do while procession \n while distance_flag :\n # reset numerators and denominator\n numerators = [0.0]*cL\n denominator = 0 \n # loop over positions \n for position in positions : \n # get distance \n distance = euclidean(center, position)\n # if distance gt epsilon \n if distance > epsilon : \n # update numerators accordingly \n for index, p_v in enumerate(position) : \n numerators[index] += p_v / distance\n # update denominator \n denominator += 1 / distance\n \n # if denominator is 0 return 0 \n if denominator == 0 : \n return 0 \n\n # otherwise, establish new center as the ith numerator / denominator for numerator in numerators\n new_center = [num_i / denominator for num_i in numerators]\n\n # set distance flag as euclidean of center and new center is gte epsilon\n distance_flag = euclidean(center, new_center) >= epsilon \n # if we are continuing, update center. Otherwise, leave be\n if distance_flag : \n center = new_center\n\n # When done, calculate distance \n total_distance = 0 \n # as accumulated map of euclidean of center and positions\n for position in positions : \n total_distance += euclidean(center, position)\n \n # return rounded value to 5 decimal places \n return round(total_distance, 5)\n\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
3-Line Python Solution by using Scipy for Optimization | best-position-for-a-service-centre | 0 | 1 | # Approach\nThis is a typical optimization problem. The object is to find the optimal $$(\\bar{x}, \\bar{y})$$ pair that minimizes $$ \\sum_{i}{\\sqrt{ (\\bar{x}-x_i)^2 + \\sqrt{(\\bar{y} - y_i)^2} } }$$. The answer $$(\\bar{x}, \\bar{y})$$ can be obtained by a multivariate optimization algorithm such as gradient descend. For a lazy Python user, a collection of optimization algorithms are handy in `scipy.optimize`. The default solver is BFGS, and the only concern is the tolerance that should be smaller than $$10^{-5}$$ as stated in the problem description. \n\n# Code\n```\nimport numpy as np\nfrom scipy.optimize import minimize\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n def cost(p):\n return sum(sqrt((p[0]-x)*(p[0]-x) + (p[1]-y)*(p[1]-y)) for x, y in positions)\n positions = np.array(positions)\n return cost(minimize(cost, x0=[0, 0], tol=10**(-6)).x)\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
3-Line Python Solution by using Scipy for Optimization | best-position-for-a-service-centre | 0 | 1 | # Approach\nThis is a typical optimization problem. The object is to find the optimal $$(\\bar{x}, \\bar{y})$$ pair that minimizes $$ \\sum_{i}{\\sqrt{ (\\bar{x}-x_i)^2 + \\sqrt{(\\bar{y} - y_i)^2} } }$$. The answer $$(\\bar{x}, \\bar{y})$$ can be obtained by a multivariate optimization algorithm such as gradient descend. For a lazy Python user, a collection of optimization algorithms are handy in `scipy.optimize`. The default solver is BFGS, and the only concern is the tolerance that should be smaller than $$10^{-5}$$ as stated in the problem description. \n\n# Code\n```\nimport numpy as np\nfrom scipy.optimize import minimize\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n def cost(p):\n return sum(sqrt((p[0]-x)*(p[0]-x) + (p[1]-y)*(p[1]-y)) for x, y in positions)\n positions = np.array(positions)\n return cost(minimize(cost, x0=[0, 0], tol=10**(-6)).x)\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python (Geometric Median) | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions):\n def dist(x,y):\n return sum([math.sqrt((x-a)**2 + (y-b)**2) for a,b in positions])\n\n x,y = sum([i[0] for i in positions])/len(positions), sum([i[1] for i in positions])/len(positions)\n step = 100\n\n while step > 1e-6:\n for dx,dy in [[0,1],[0,-1],[1,0],[-1,0]]:\n nx,ny = x+step*dx,y+step*dy\n if dist(nx,ny) < dist(x,y):\n x,y = nx,ny\n break\n else:\n step = step/2\n\n return dist(x,y)\n\n \n\n\n\n\n\n\n \n\n \n\n\n\n\n \n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python (Geometric Median) | best-position-for-a-service-centre | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions):\n def dist(x,y):\n return sum([math.sqrt((x-a)**2 + (y-b)**2) for a,b in positions])\n\n x,y = sum([i[0] for i in positions])/len(positions), sum([i[1] for i in positions])/len(positions)\n step = 100\n\n while step > 1e-6:\n for dx,dy in [[0,1],[0,-1],[1,0],[-1,0]]:\n nx,ny = x+step*dx,y+step*dy\n if dist(nx,ny) < dist(x,y):\n x,y = nx,ny\n break\n else:\n step = step/2\n\n return dist(x,y)\n\n \n\n\n\n\n\n\n \n\n \n\n\n\n\n \n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
NOT effective but easy to understand solution O(11200*n) | best-position-for-a-service-centre | 0 | 1 | # Intuition\nSorry for my english, I know it can be bad + this is the first solution I post\nI hope this helps someone understand the problem\n\n\n# Approach\nSo, I determine the best position first with an accuracy of integers then to tenths, to hundredths and thousandths\nI do it by brute force, over and over again approaching the best position\n(You can look inside the code, there are comments with explanations)\n(At the very bottom there will be a shorter version of the code)\n\n# Complexity\nI think it is O(11200*n)\n11200 is the approximate number of iterations in the "for" loops to achieve accuracy to thousandths\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n ms = 10**10 # the value that the function will return\n best_pos = ()\n # So, here is the first loop, where I determine best position\n # with an accuracy to integers\n for y in range(101):\n for x in range(101):\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x - x1)**2 + (y - y1)**2)**0.5\n if s < ms:\n best_pos = (x, y)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n # now I have integer best_pos, and I will \n # determine best position with an accuracy of tenths\n # To do this, I have to receive float values \u200B\u200Bin the loop,\n # so I need to multiply the integers by 10, \n # and also take an indent (step), \n # in case the desired position is far beyond \n # the previously obtained integer values\n ml = 10\n step = 10\n for x in range(ml*X - step, ml*X + step+1):\n for y in range(ml*Y - step, ml*Y + step+1):\n x0 = x/ml \n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n # now I do absolutely the same thing, but \n # with an accuracy of hundreds\n # (that\'s why ml = 100)\n ml = 100\n x_range = int(ml*X) - step, int(ml*X) + step+1\n y_range = int(ml*Y) - step, int(ml*Y) + step+1\n for x in range(*x_range):\n for y in range(*y_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n # and now thousandths\n X = best_pos[0]\n Y = best_pos[1]\n ml = 1000\n x_range = int(ml*X) - step, int(ml*X) + step+1\n y_range = int(ml*Y) - step, int(ml*Y) + step+1\n for x in range(*x_range):\n for y in range(*y_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n ms = s\n\n \n return ms\n\n\n\n\n\n# also this code could be written much shorter\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n ms = 10**10 \n s = 0\n best_pos = ()\n ml = 1\n for k in range(4):\n x_range = (0, 101) if k == 0 else (int(ml*X) - 10, int(ml*X) + 11)\n y_range = (0, 101) if k == 0 else (int(ml*Y) - 10, int(ml*Y) + 11)\n for y in range(*y_range):\n for x in range(*x_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n ml *= 10\n return ms\n \n\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
NOT effective but easy to understand solution O(11200*n) | best-position-for-a-service-centre | 0 | 1 | # Intuition\nSorry for my english, I know it can be bad + this is the first solution I post\nI hope this helps someone understand the problem\n\n\n# Approach\nSo, I determine the best position first with an accuracy of integers then to tenths, to hundredths and thousandths\nI do it by brute force, over and over again approaching the best position\n(You can look inside the code, there are comments with explanations)\n(At the very bottom there will be a shorter version of the code)\n\n# Complexity\nI think it is O(11200*n)\n11200 is the approximate number of iterations in the "for" loops to achieve accuracy to thousandths\n\n# Code\n```\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n ms = 10**10 # the value that the function will return\n best_pos = ()\n # So, here is the first loop, where I determine best position\n # with an accuracy to integers\n for y in range(101):\n for x in range(101):\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x - x1)**2 + (y - y1)**2)**0.5\n if s < ms:\n best_pos = (x, y)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n # now I have integer best_pos, and I will \n # determine best position with an accuracy of tenths\n # To do this, I have to receive float values \u200B\u200Bin the loop,\n # so I need to multiply the integers by 10, \n # and also take an indent (step), \n # in case the desired position is far beyond \n # the previously obtained integer values\n ml = 10\n step = 10\n for x in range(ml*X - step, ml*X + step+1):\n for y in range(ml*Y - step, ml*Y + step+1):\n x0 = x/ml \n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n # now I do absolutely the same thing, but \n # with an accuracy of hundreds\n # (that\'s why ml = 100)\n ml = 100\n x_range = int(ml*X) - step, int(ml*X) + step+1\n y_range = int(ml*Y) - step, int(ml*Y) + step+1\n for x in range(*x_range):\n for y in range(*y_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n # and now thousandths\n X = best_pos[0]\n Y = best_pos[1]\n ml = 1000\n x_range = int(ml*X) - step, int(ml*X) + step+1\n y_range = int(ml*Y) - step, int(ml*Y) + step+1\n for x in range(*x_range):\n for y in range(*y_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n ms = s\n\n \n return ms\n\n\n\n\n\n# also this code could be written much shorter\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n ms = 10**10 \n s = 0\n best_pos = ()\n ml = 1\n for k in range(4):\n x_range = (0, 101) if k == 0 else (int(ml*X) - 10, int(ml*X) + 11)\n y_range = (0, 101) if k == 0 else (int(ml*Y) - 10, int(ml*Y) + 11)\n for y in range(*y_range):\n for x in range(*x_range):\n x0 = x/ml\n y0 = y/ml\n s = 0\n for house in positions:\n x1 = house[0]\n y1 = house[1]\n s += ((x0 - x1)**2 + (y0 - y1)**2)**0.5\n if s < ms:\n best_pos = (x0, y0)\n ms = s\n X = best_pos[0]\n Y = best_pos[1]\n ml *= 10\n return ms\n \n\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Python Gradient Descent With Weight Decay | best-position-for-a-service-centre | 0 | 1 | # Code\n```\nfrom math import sqrt\n\ndef f(xcenter: float, ycenter: float, positions: List[List[int]]) -> float:\n return sum(fdist(xcenter,ycenter,positions))\n\ndef fdist(xcenter: float, ycenter: float,positions: List[List[int]]) -> List[int]:\n return [sqrt((xcenter - x)**2 + (ycenter - y)**2) for x,y in positions]\n\ndef dx(x: float, y: float, xcenter: float, ycenter: float) -> float:\n denom = sqrt((-x + xcenter)**2 + (-y + ycenter)**2)\n if denom == 0:\n return 0\n return (-x + xcenter)/denom\n\ndef dy(x: float, y: float, xcenter: float, ycenter: float) -> float:\n denom = sqrt((-x + xcenter)**2 + (-y + ycenter)**2)\n if denom == 0:\n return 0\n return (-y + ycenter)/denom\n\ndef grad_desc(xcenter: float, ycenter: float, positions: List[List[int]], eta: float = 0.1, iter: int = 1000, eps:float = 1e-8, decay=1) -> float:\n #print(xcenter,ycenter,f(xcenter,ycenter,positions))\n for i in range(iter):\n acc_dx = 0.0\n acc_dy = 0.0\n for x,y in positions:\n acc_dx += dx(float(x),float(y),xcenter,ycenter)\n acc_dy += dy(float(x),float(y),xcenter,ycenter)\n xcenter_next = xcenter - eta * acc_dx/len(positions)\n ycenter_next = ycenter - eta * acc_dy/len(positions)\n if abs(xcenter_next - xcenter) <= eps and \\\n abs(ycenter_next - ycenter) <= eps:\n break\n xcenter = xcenter_next\n ycenter = ycenter_next\n eta *= decay\n #print(xcenter,ycenter,f(xcenter,ycenter,positions))\n\n return i,xcenter,ycenter\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n if len(positions) == 1:\n return 0.0\n\n xcenter = sum([x for x,_ in positions])/len(positions)\n ycenter = sum([y for _,y in positions])/len(positions)\n max_iter = 10000\n i,xcenter,ycenter = grad_desc(xcenter,ycenter,positions,eta = 0.9, iter = max_iter, eps=10e-6,decay=0.9999)\n if i == max_iter-1:\n i,xcenter,ycenter = grad_desc(xcenter,ycenter,positions,eta = 0.09, iter = max_iter, eps=10e-8,decay=0.99)\n print(f\'End Iteration: {i}\')\n return f(xcenter,ycenter,positions)\n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Python Gradient Descent With Weight Decay | best-position-for-a-service-centre | 0 | 1 | # Code\n```\nfrom math import sqrt\n\ndef f(xcenter: float, ycenter: float, positions: List[List[int]]) -> float:\n return sum(fdist(xcenter,ycenter,positions))\n\ndef fdist(xcenter: float, ycenter: float,positions: List[List[int]]) -> List[int]:\n return [sqrt((xcenter - x)**2 + (ycenter - y)**2) for x,y in positions]\n\ndef dx(x: float, y: float, xcenter: float, ycenter: float) -> float:\n denom = sqrt((-x + xcenter)**2 + (-y + ycenter)**2)\n if denom == 0:\n return 0\n return (-x + xcenter)/denom\n\ndef dy(x: float, y: float, xcenter: float, ycenter: float) -> float:\n denom = sqrt((-x + xcenter)**2 + (-y + ycenter)**2)\n if denom == 0:\n return 0\n return (-y + ycenter)/denom\n\ndef grad_desc(xcenter: float, ycenter: float, positions: List[List[int]], eta: float = 0.1, iter: int = 1000, eps:float = 1e-8, decay=1) -> float:\n #print(xcenter,ycenter,f(xcenter,ycenter,positions))\n for i in range(iter):\n acc_dx = 0.0\n acc_dy = 0.0\n for x,y in positions:\n acc_dx += dx(float(x),float(y),xcenter,ycenter)\n acc_dy += dy(float(x),float(y),xcenter,ycenter)\n xcenter_next = xcenter - eta * acc_dx/len(positions)\n ycenter_next = ycenter - eta * acc_dy/len(positions)\n if abs(xcenter_next - xcenter) <= eps and \\\n abs(ycenter_next - ycenter) <= eps:\n break\n xcenter = xcenter_next\n ycenter = ycenter_next\n eta *= decay\n #print(xcenter,ycenter,f(xcenter,ycenter,positions))\n\n return i,xcenter,ycenter\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n if len(positions) == 1:\n return 0.0\n\n xcenter = sum([x for x,_ in positions])/len(positions)\n ycenter = sum([y for _,y in positions])/len(positions)\n max_iter = 10000\n i,xcenter,ycenter = grad_desc(xcenter,ycenter,positions,eta = 0.9, iter = max_iter, eps=10e-6,decay=0.9999)\n if i == max_iter-1:\n i,xcenter,ycenter = grad_desc(xcenter,ycenter,positions,eta = 0.09, iter = max_iter, eps=10e-8,decay=0.99)\n print(f\'End Iteration: {i}\')\n return f(xcenter,ycenter,positions)\n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Linear Descend Technique - Python Solution | best-position-for-a-service-centre | 0 | 1 | \n# Code\n```\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n\n def total_distance(positions, x, y):\n res = 0\n for a, b in positions:\n res += math.sqrt((x - a)**2 + (y - b)**2)\n return res\n\n limit = 10**-5\n step = 1\n currx = 0\n curry = 0\n minDistance = total_distance(positions, currx, curry)\n while step > limit:\n reduceStep = True\n dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n for dx, dy in dirs:\n newx, newy = currx + dx*step, curry + dy*step\n newDistance = total_distance(positions, newx, newy)\n if newDistance < minDistance:\n minDistance = newDistance\n currx = newx\n curry = newy\n reduceStep = False\n\n if reduceStep:\n step /= 10\n\n return minDistance\n\n \n``` | 0 | A delivery company wants to build a new service center in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new center in a position such that **the sum of the euclidean distances to all customers is minimum**.
Given an array `positions` where `positions[i] = [xi, yi]` is the position of the `ith` customer on the map, return _the minimum sum of the euclidean distances_ to all customers.
In other words, you need to choose the position of the service center `[xcentre, ycentre]` such that the following formula is minimized:
Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** positions = \[\[0,1\],\[1,0\],\[1,2\],\[2,1\]\]
**Output:** 4.00000
**Explanation:** As shown, you can see that choosing \[xcentre, ycentre\] = \[1, 1\] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.
**Example 2:**
**Input:** positions = \[\[1,1\],\[3,3\]\]
**Output:** 2.82843
**Explanation:** The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843
**Constraints:**
* `1 <= positions.length <= 50`
* `positions[i].length == 2`
* `0 <= xi, yi <= 100`
F(0) = 0, F(1) = 1, F(n) = F(n - 1) + F(n - 2) for n >= 2. | Generate all Fibonacci numbers up to the limit (they are few). Use greedy solution, taking at every time the greatest Fibonacci number which is smaller than or equal to the current number. Subtract this Fibonacci number from the current number and repeat again the process. |
Linear Descend Technique - Python Solution | best-position-for-a-service-centre | 0 | 1 | \n# Code\n```\n\nclass Solution:\n def getMinDistSum(self, positions: List[List[int]]) -> float:\n\n def total_distance(positions, x, y):\n res = 0\n for a, b in positions:\n res += math.sqrt((x - a)**2 + (y - b)**2)\n return res\n\n limit = 10**-5\n step = 1\n currx = 0\n curry = 0\n minDistance = total_distance(positions, currx, curry)\n while step > limit:\n reduceStep = True\n dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n for dx, dy in dirs:\n newx, newy = currx + dx*step, curry + dy*step\n newDistance = total_distance(positions, newx, newy)\n if newDistance < minDistance:\n minDistance = newDistance\n currx = newx\n curry = newy\n reduceStep = False\n\n if reduceStep:\n step /= 10\n\n return minDistance\n\n \n``` | 0 | Given two strings `s` and `t`, find the number of ways you can choose a non-empty substring of `s` and replace a **single character** by a different character such that the resulting substring is a substring of `t`. In other words, find the number of substrings in `s` that differ from some substring in `t` by **exactly** one character.
For example, the underlined substrings in `"computer "` and `"computation "` only differ by the `'e'`/`'a'`, so this is a valid way.
Return _the number of substrings that satisfy the condition above._
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aba ", t = "baba "
**Output:** 6
**Explanation:** The following are the pairs of substrings from s and t that differ by exactly 1 character:
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
( "aba ", "baba ")
The underlined portions are the substrings that are chosen from s and t.
**Example 2:**
**Input:** s = "ab ", t = "bb "
**Output:** 3
**Explanation:** The following are the pairs of substrings from s and t that differ by 1 character:
( "ab ", "bb ")
( "ab ", "bb ")
( "ab ", "bb ")
The underlined portions are the substrings that are chosen from s and t.
**Constraints:**
* `1 <= s.length, t.length <= 100`
* `s` and `t` consist of lowercase English letters only. | The problem can be reworded as, giving a set of points on a 2d-plane, return the geometric median. Loop over each triplet of points (positions[i], positions[j], positions[k]) where i < j < k, get the centre of the circle which goes throw the 3 points, check if all other points lie in this circle. |
Pandas vs SQL | Elegant & Short | All 30 Days of Pandas solutions ✅ | find-users-with-valid-e-mails | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n``` Python []\ndef valid_emails(users: pd.DataFrame) -> pd.DataFrame:\n return users[\n users[\'mail\'].str.match(r\'^[a-zA-Z][a-zA-Z\\d_.-]*@leetcode\\.com\')\n ]\n```\n```SQL []\nSELECT *\n FROM Users \n WHERE mail REGEXP \'^[a-zA-Z][a-zA-Z0-9_.-]*@leetcode[.]com$\';\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n | 23 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
Easy to understand.....! | find-users-with-valid-e-mails | 0 | 1 | \n# Code\n```\nimport pandas as pd\n\ndef isValid(row):\n temp = row[\'mail\'].split(\'@\')\n \n if len(temp) <=1:\n return False\n if temp[1] !=\'leetcode.com\':\n return False\n prefix = temp[0]\n if not prefix[0].isalpha():\n return False\n t = [\'_\', \'.\', \'-\', \'/\']\n ok = True\n for i in prefix:\n a = i in t\n b = i.isalpha()\n c = i.isnumeric()\n ok = (a or b or c)\n if not ok:\n return ok \n return ok \n\n\n\n\ndef ssd(row):\n if isValid(row):\n \n return True\n else:\n return False\n\n \ndef valid_emails(users: pd.DataFrame) -> pd.DataFrame:\n\n users[\'valid\'] = users.apply(ssd, axis=1)\n users = users[users[\'valid\'] == True]\n\n return users[[\'user_id\', \'name\', \'mail\']]\n``` | 5 | You are given an integer array `nums`. You can choose **exactly one** index (**0-indexed**) and remove the element. Notice that the index of the elements may change after the removal.
For example, if `nums = [6,1,7,4,1]`:
* Choosing to remove index `1` results in `nums = [6,7,4,1]`.
* Choosing to remove index `2` results in `nums = [6,1,4,1]`.
* Choosing to remove index `4` results in `nums = [6,1,7,4]`.
An array is **fair** if the sum of the odd-indexed values equals the sum of the even-indexed values.
Return the _**number** of indices that you could choose such that after the removal,_ `nums` _is **fair**._
**Example 1:**
**Input:** nums = \[2,1,6,4\]
**Output:** 1
**Explanation:**
Remove index 0: \[1,6,4\] -> Even sum: 1 + 4 = 5. Odd sum: 6. Not fair.
Remove index 1: \[2,6,4\] -> Even sum: 2 + 4 = 6. Odd sum: 6. Fair.
Remove index 2: \[2,1,4\] -> Even sum: 2 + 4 = 6. Odd sum: 1. Not fair.
Remove index 3: \[2,1,6\] -> Even sum: 2 + 6 = 8. Odd sum: 1. Not fair.
There is 1 index that you can remove to make nums fair.
**Example 2:**
**Input:** nums = \[1,1,1\]
**Output:** 3
**Explanation:** You can remove any index and the remaining array is fair.
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** 0
**Explanation:** You cannot make a fair array after removing any index.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 104` | null |
Simple Logic | water-bottles | 0 | 1 | **Just keep track of** :\n1. How many bottles can we sell.\n2. How many bottles will remain after we sell.\n3. How many bottles we get back after we have made the sale.\n\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n drink_bottle = 0\n \n while True:\n \n # check how many will remain if we sell the empty bottle\n remainingBottle = numBottles % numExchange\n # print(remainingBottle)\n\n # sell only those bottle that will yeild use one bottle\n sell_full_bottle = numBottles - remainingBottle\n # print(sell_full_bottle)\n\n # in the end if suppose we have some bottle left\n if sell_full_bottle == 0:\n drink_bottle += numBottles\n break\n\n # when we sell this is the number of bottle we did drink\n drink_bottle += sell_full_bottle\n\n # how many bottle did we get back after selling the empty ones\n extra_bottle_obtained = sell_full_bottle // numExchange\n # print(extra_bottle_obtained)\n\n # add them to the bottle we previously had\n numBottles = remainingBottle + extra_bottle_obtained\n # print(numBottles)\n \n # print("\\n")\n \n # print(drink_bottle)\n return drink_bottle\n``` | 1 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
Simple Logic | water-bottles | 0 | 1 | **Just keep track of** :\n1. How many bottles can we sell.\n2. How many bottles will remain after we sell.\n3. How many bottles we get back after we have made the sale.\n\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n drink_bottle = 0\n \n while True:\n \n # check how many will remain if we sell the empty bottle\n remainingBottle = numBottles % numExchange\n # print(remainingBottle)\n\n # sell only those bottle that will yeild use one bottle\n sell_full_bottle = numBottles - remainingBottle\n # print(sell_full_bottle)\n\n # in the end if suppose we have some bottle left\n if sell_full_bottle == 0:\n drink_bottle += numBottles\n break\n\n # when we sell this is the number of bottle we did drink\n drink_bottle += sell_full_bottle\n\n # how many bottle did we get back after selling the empty ones\n extra_bottle_obtained = sell_full_bottle // numExchange\n # print(extra_bottle_obtained)\n\n # add them to the bottle we previously had\n numBottles = remainingBottle + extra_bottle_obtained\n # print(numBottles)\n \n # print("\\n")\n \n # print(drink_bottle)\n return drink_bottle\n``` | 1 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
Simple python solution | while loop | water-bottles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = numBottles + (numBottles // numExchange) \n rem = (numBottles // numExchange) + (numBottles % numExchange)\n if numBottles < numExchange:\n return numBottles\n elif rem >= numExchange:\n while rem >= numExchange:\n numBottles = rem\n rem = (numBottles // numExchange) + (numBottles % numExchange)\n ans += (numBottles // numExchange)\n return ans\n \n return ans\n\n\n```\n\n\n\n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = numBottles\n\n while numBottles >= numExchange:\n # Calculate the number of bottles obtained through exchange\n newBottles = numBottles // numExchange\n\n # Update the total count of bottles\n ans += newBottles\n\n # Calculate the remaining bottles after exchange\n numBottles = newBottles + numBottles % numExchange\n\n return ans\n\n\n\n```\n\n\n | 1 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
Simple python solution | while loop | water-bottles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = numBottles + (numBottles // numExchange) \n rem = (numBottles // numExchange) + (numBottles % numExchange)\n if numBottles < numExchange:\n return numBottles\n elif rem >= numExchange:\n while rem >= numExchange:\n numBottles = rem\n rem = (numBottles // numExchange) + (numBottles % numExchange)\n ans += (numBottles // numExchange)\n return ans\n \n return ans\n\n\n```\n\n\n\n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = numBottles\n\n while numBottles >= numExchange:\n # Calculate the number of bottles obtained through exchange\n newBottles = numBottles // numExchange\n\n # Update the total count of bottles\n ans += newBottles\n\n # Calculate the remaining bottles after exchange\n numBottles = newBottles + numBottles % numExchange\n\n return ans\n\n\n\n```\n\n\n | 1 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
[Python3 | C++] Two beautiful solutions | water-bottles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are two ways to solve this problem and we will analyze both:\n1) The way of an honest programmer\n2) A tricky but mathematical way\n# Approach 1 (Honest Programmer)\n<!-- Describe your approach to solving the problem. -->\nIteratively we get the number of available and empty bottles for drinking. The number of bottles available for drinking is added to the `result` and to the number of empty bottles (we drank them), and then we continue the procedure while we can still drink something.\nWe use the `divmod` function, which returns a tuple from the result of the integer division of the first number by the second and the remainder of the division of the first number by the second.\n\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n result = numBottles\n drunk, empty = divmod(numBottles, numExchange)\n while drunk:\n result += drunk\n drunk, empty = divmod(empty + drunk, numExchange)\n return result\n```\n```C++ []\nclass Solution {\npublic:\n pair<int, int> divmod(int dividend, int divisor) {\n int quotient = dividend / divisor;\n int remainder = dividend % divisor;\n return make_pair(quotient, remainder);\n }\n int numWaterBottles(int numBottles, int numExchange) {\n int result = numBottles;\n pair<int, int> div = divmod(numBottles, numExchange);\n int drunk = div.first;\n int empty = div.second;\n while(drunk) {\n result += drunk;\n div = divmod(drunk + empty, numExchange);\n drunk = div.first;\n empty = div.second;\n }\n return result;\n }\n};\n```\n# Complexity\n- Time complexity: $$O(\\frac{\\log_{} nB}{\\log_{} nE})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBut this approach is boring, you can have more fun!\n\n# Approach 2 (Tricky Mathematician)\nLet\'s forget that we are dealing with integer operations, let\'s imagine that we can have a fractional number of bottles (that is, for example, with $$numExchange = 3$$, we could exchange one empty bottle for $$1/3$$ filled).\nLet:\n$$N = numBottles $$\n$$d = numExchange$$\n\nThen, all we need to calculate is the sum of this sequence:\n$$N, $$ $$N/d, $$ $$N/d^2, $$ $$N/d^3, $$ $$...$$\nWhere each i-th element of the sequence shows how much water we can drink at the i-th step.\n$$S = N + N/d + N/d^2 + N/d^3 + ... = N(1 + 1/d + 1/d^2 + 1/d^3 + ...)$$\nIn parentheses there is nothing else than the sum of an infinite geometric progression, we can write this using the limit of the partial sum of the geometric progression:\n$$S = \\lim_{n \\to \\infty} N\\frac{((1/d)^n-1)}{1/d-1}$$, taking into account the formula $$S_n=\\frac{b_1(q^n-1)}{q-1}$$, where $$q$$ - common ratio and $$b_1$$ - the first term of the geometric progression.\nIn our case $$b_1 = 1$$ and $$q = \\frac 1 d$$.\nSince $$d > 1$$, then $$1/d < 1$$, and $$(1/d)^n \\rightarrow 0$$ at $$n \\rightarrow \\infty$$\nThus $$S = N\\frac{(0^+-1)}{1/d-1} = \\frac{N}{1-1/d} = \\frac{Nd}{d-1}$$\nGreat! We have obtained a formula for the number of bottles that we can eventually drink if we allow fractional filling of bottles.\nBut is everything so simple and can we just return the amount received? Let\'s look at an example:\nLet $$N = 8$$ and $$d = 3$$.\n$$result = 8 + \\lfloor \\frac 8 3\\rfloor + \\lfloor \\frac {(2+2)} 3 \\rfloor + \\lfloor \\frac {(1+1)} 3 \\rfloor = 8 + 2 + 1 + 0= 11$$\nAnd according to our formula: $$result = \\frac{8*3}{3-1}=12$$\nBut why didn\'t the results match?\nThe thing is that $$N * d$$ is completely divisible by $$d-1$$\nAssuming fractional filling of bottles, we allowed ourselves to drink one additional bottle with the help of an infinite number of iterations of the exchange, eventually summed up in one whole bottle.\nThe solution is simply an additional check for the divisibility of $$N * d$$ by $$d-1$$, in which case we need to subtract 1 from the final result.\n$$result = \\lfloor\\frac{Nd}{d-1}\\rfloor$$ if $$(Nd)mod(d-1)$$ $$!= 0$$ else $$\\lfloor\\frac{Nd}{d-1}\\rfloor - 1$$\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n result = (numBottles * numExchange) // (numExchange - 1)\n return result if (numBottles * numExchange) % (numExchange - 1) else result-1\n```\n```C++ []\nclass Solution {\npublic:\n int numWaterBottles(int numBottles, int numExchange) {\n int result = (numBottles * numExchange) / (numExchange - 1);\n return (numBottles * numExchange) % (numExchange - 1) ? result : result-1;\n }\n```\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBy the way, exactly the same result can be achieved by subtracting an arbitrarily small $$\\varepsilon>0$$ from the numerator to avoid the case of integer division of the numerator by the denominator.\n$$result = \\lfloor\\frac{Nd-\\varepsilon}{d-1}\\rfloor$$\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n epsilon = 1e-8\n return int((numBottles * numExchange - epsilon) // (numExchange - 1))\n\n```\n```C++ []\nclass Solution {\npublic:\n int numWaterBottles(int numBottles, int numExchange) {\n int result = (numBottles * numExchange - 1e-8) / (numExchange - 1);\n return result; \n }\n```\n | 10 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
[Python3 | C++] Two beautiful solutions | water-bottles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are two ways to solve this problem and we will analyze both:\n1) The way of an honest programmer\n2) A tricky but mathematical way\n# Approach 1 (Honest Programmer)\n<!-- Describe your approach to solving the problem. -->\nIteratively we get the number of available and empty bottles for drinking. The number of bottles available for drinking is added to the `result` and to the number of empty bottles (we drank them), and then we continue the procedure while we can still drink something.\nWe use the `divmod` function, which returns a tuple from the result of the integer division of the first number by the second and the remainder of the division of the first number by the second.\n\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n result = numBottles\n drunk, empty = divmod(numBottles, numExchange)\n while drunk:\n result += drunk\n drunk, empty = divmod(empty + drunk, numExchange)\n return result\n```\n```C++ []\nclass Solution {\npublic:\n pair<int, int> divmod(int dividend, int divisor) {\n int quotient = dividend / divisor;\n int remainder = dividend % divisor;\n return make_pair(quotient, remainder);\n }\n int numWaterBottles(int numBottles, int numExchange) {\n int result = numBottles;\n pair<int, int> div = divmod(numBottles, numExchange);\n int drunk = div.first;\n int empty = div.second;\n while(drunk) {\n result += drunk;\n div = divmod(drunk + empty, numExchange);\n drunk = div.first;\n empty = div.second;\n }\n return result;\n }\n};\n```\n# Complexity\n- Time complexity: $$O(\\frac{\\log_{} nB}{\\log_{} nE})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBut this approach is boring, you can have more fun!\n\n# Approach 2 (Tricky Mathematician)\nLet\'s forget that we are dealing with integer operations, let\'s imagine that we can have a fractional number of bottles (that is, for example, with $$numExchange = 3$$, we could exchange one empty bottle for $$1/3$$ filled).\nLet:\n$$N = numBottles $$\n$$d = numExchange$$\n\nThen, all we need to calculate is the sum of this sequence:\n$$N, $$ $$N/d, $$ $$N/d^2, $$ $$N/d^3, $$ $$...$$\nWhere each i-th element of the sequence shows how much water we can drink at the i-th step.\n$$S = N + N/d + N/d^2 + N/d^3 + ... = N(1 + 1/d + 1/d^2 + 1/d^3 + ...)$$\nIn parentheses there is nothing else than the sum of an infinite geometric progression, we can write this using the limit of the partial sum of the geometric progression:\n$$S = \\lim_{n \\to \\infty} N\\frac{((1/d)^n-1)}{1/d-1}$$, taking into account the formula $$S_n=\\frac{b_1(q^n-1)}{q-1}$$, where $$q$$ - common ratio and $$b_1$$ - the first term of the geometric progression.\nIn our case $$b_1 = 1$$ and $$q = \\frac 1 d$$.\nSince $$d > 1$$, then $$1/d < 1$$, and $$(1/d)^n \\rightarrow 0$$ at $$n \\rightarrow \\infty$$\nThus $$S = N\\frac{(0^+-1)}{1/d-1} = \\frac{N}{1-1/d} = \\frac{Nd}{d-1}$$\nGreat! We have obtained a formula for the number of bottles that we can eventually drink if we allow fractional filling of bottles.\nBut is everything so simple and can we just return the amount received? Let\'s look at an example:\nLet $$N = 8$$ and $$d = 3$$.\n$$result = 8 + \\lfloor \\frac 8 3\\rfloor + \\lfloor \\frac {(2+2)} 3 \\rfloor + \\lfloor \\frac {(1+1)} 3 \\rfloor = 8 + 2 + 1 + 0= 11$$\nAnd according to our formula: $$result = \\frac{8*3}{3-1}=12$$\nBut why didn\'t the results match?\nThe thing is that $$N * d$$ is completely divisible by $$d-1$$\nAssuming fractional filling of bottles, we allowed ourselves to drink one additional bottle with the help of an infinite number of iterations of the exchange, eventually summed up in one whole bottle.\nThe solution is simply an additional check for the divisibility of $$N * d$$ by $$d-1$$, in which case we need to subtract 1 from the final result.\n$$result = \\lfloor\\frac{Nd}{d-1}\\rfloor$$ if $$(Nd)mod(d-1)$$ $$!= 0$$ else $$\\lfloor\\frac{Nd}{d-1}\\rfloor - 1$$\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n result = (numBottles * numExchange) // (numExchange - 1)\n return result if (numBottles * numExchange) % (numExchange - 1) else result-1\n```\n```C++ []\nclass Solution {\npublic:\n int numWaterBottles(int numBottles, int numExchange) {\n int result = (numBottles * numExchange) / (numExchange - 1);\n return (numBottles * numExchange) % (numExchange - 1) ? result : result-1;\n }\n```\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBy the way, exactly the same result can be achieved by subtracting an arbitrarily small $$\\varepsilon>0$$ from the numerator to avoid the case of integer division of the numerator by the denominator.\n$$result = \\lfloor\\frac{Nd-\\varepsilon}{d-1}\\rfloor$$\n# Code\n```Python3 []\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n epsilon = 1e-8\n return int((numBottles * numExchange - epsilon) // (numExchange - 1))\n\n```\n```C++ []\nclass Solution {\npublic:\n int numWaterBottles(int numBottles, int numExchange) {\n int result = (numBottles * numExchange - 1e-8) / (numExchange - 1);\n return result; \n }\n```\n | 10 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
One-liner in Python | water-bottles | 0 | 1 | ```\ndef numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n return int(numBottles + (numBottles - 1) / (numExchange - 1))\n```\nPlease upvote if you like it | 20 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
One-liner in Python | water-bottles | 0 | 1 | ```\ndef numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n return int(numBottles + (numBottles - 1) / (numExchange - 1))\n```\nPlease upvote if you like it | 20 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
O(1) solution 3 line | water-bottles | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numWaterBottles(int numBottles, int numExchange) {\n int x=(numBottles*numExchange)-1;\n int y=numExchange-1;\n int z=(x/y);\n return z;\n }\n}\n``` | 1 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
O(1) solution 3 line | water-bottles | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numWaterBottles(int numBottles, int numExchange) {\n int x=(numBottles*numExchange)-1;\n int y=numExchange-1;\n int z=(x/y);\n return z;\n }\n}\n``` | 1 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
Python3 easy | while-loop | Comments - added | water-bottles | 0 | 1 | **PLease Upvote,** if it helped !\nit motivates me :)\n```\n#just keep in mind that when you exhange empty bottles for filled ones they will also get empty after drinking \n#don\'t miss counting them\n\ndef numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n if numBottles<numExchange:\n return numBottles\n else:\n tot=numBottles\n empty=numBottles\n while(empty>=numExchange):\n tot+=(empty//numExchange)\n empty=empty%numExchange+(empty//numExchange)\n return tot\n```\n\n**please upvote , if it helped you :)** | 7 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
Python3 easy | while-loop | Comments - added | water-bottles | 0 | 1 | **PLease Upvote,** if it helped !\nit motivates me :)\n```\n#just keep in mind that when you exhange empty bottles for filled ones they will also get empty after drinking \n#don\'t miss counting them\n\ndef numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n if numBottles<numExchange:\n return numBottles\n else:\n tot=numBottles\n empty=numBottles\n while(empty>=numExchange):\n tot+=(empty//numExchange)\n empty=empty%numExchange+(empty//numExchange)\n return tot\n```\n\n**please upvote , if it helped you :)** | 7 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
[Python3] Simple Solution | water-bottles | 0 | 1 | ```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n drank , left = [numBottles] * 2\n \n while left >= numExchange:\n left -= numExchange - 1\n drank += 1\n \n return drank\n``` | 5 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
[Python3] Simple Solution | water-bottles | 0 | 1 | ```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n drank , left = [numBottles] * 2\n \n while left >= numExchange:\n left -= numExchange - 1\n drank += 1\n \n return drank\n``` | 5 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
[Python3] 5-line iterative | water-bottles | 0 | 1 | \n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = r = 0\n while numBottles:\n ans += numBottles\n numBottles, r = divmod(numBottles + r, numExchange)\n return ans \n``` | 9 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
[Python3] 5-line iterative | water-bottles | 0 | 1 | \n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = r = 0\n while numBottles:\n ans += numBottles\n numBottles, r = divmod(numBottles + r, numExchange)\n return ans \n``` | 9 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
Python Beats 93.2% | water-bottles | 0 | 1 | \n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = 0\n cant = 0\n while numBottles>0:\n take = (numBottles+cant)//numExchange\n cant = (numBottles+cant)%numExchange\n ans += numBottles\n\n numBottles = take\n\n return ans\n \n``` | 2 | There are `numBottles` water bottles that are initially full of water. You can exchange `numExchange` empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers `numBottles` and `numExchange`, return _the **maximum** number of water bottles you can drink_.
**Example 1:**
**Input:** numBottles = 9, numExchange = 3
**Output:** 13
**Explanation:** You can exchange 3 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 9 + 3 + 1 = 13.
**Example 2:**
**Input:** numBottles = 15, numExchange = 4
**Output:** 19
**Explanation:** You can exchange 4 empty bottles to get 1 full water bottle.
Number of water bottles you can drink: 15 + 3 + 1 = 19.
**Constraints:**
* `1 <= numBottles <= 100`
* `2 <= numExchange <= 100` | null |
Python Beats 93.2% | water-bottles | 0 | 1 | \n# Code\n```\nclass Solution:\n def numWaterBottles(self, numBottles: int, numExchange: int) -> int:\n ans = 0\n cant = 0\n while numBottles>0:\n take = (numBottles+cant)//numExchange\n cant = (numBottles+cant)%numExchange\n ans += numBottles\n\n numBottles = take\n\n return ans\n \n``` | 2 | You are given an integer array `heights` representing the heights of buildings, some `bricks`, and some `ladders`.
You start your journey from building `0` and move to the next building by possibly using bricks or ladders.
While moving from building `i` to building `i+1` (**0-indexed**),
* If the current building's height is **greater than or equal** to the next building's height, you do **not** need a ladder or bricks.
* If the current building's height is **less than** the next building's height, you can either use **one ladder** or `(h[i+1] - h[i])` **bricks**.
_Return the furthest building index (0-indexed) you can reach if you use the given ladders and bricks optimally._
**Example 1:**
**Input:** heights = \[4,2,7,6,9,14,12\], bricks = 5, ladders = 1
**Output:** 4
**Explanation:** Starting at building 0, you can follow these steps:
- Go to building 1 without using ladders nor bricks since 4 >= 2.
- Go to building 2 using 5 bricks. You must use either bricks or ladders because 2 < 7.
- Go to building 3 without using ladders nor bricks since 7 >= 6.
- Go to building 4 using your only ladder. You must use either bricks or ladders because 6 < 9.
It is impossible to go beyond building 4 because you do not have any more bricks or ladders.
**Example 2:**
**Input:** heights = \[4,12,2,7,3,18,20,3,19\], bricks = 10, ladders = 2
**Output:** 7
**Example 3:**
**Input:** heights = \[14,3,19,3\], bricks = 17, ladders = 0
**Output:** 3
**Constraints:**
* `1 <= heights.length <= 105`
* `1 <= heights[i] <= 106`
* `0 <= bricks <= 109`
* `0 <= ladders <= heights.length` | Simulate the process until there are not enough empty bottles for even one full bottle of water. |
Python | O(1) Space | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n\n**Disclaimer**: first, we talk about "additional" space here, so output parameters like `ans` do not count. Second, I do not consider the graph to take additional space, since it\'s a result of a poor input format choice.\n\n# Approach\n\nLet\'s imagine that we run a timed depth first search on our tree. "Timed" as in "a counter is incremented when entering and exiting a vertex". We\'ll denote entrance and exit (in and out) times for a vertex $$v$$ as $$t_i(v)$$ and $$t_o(v)$$ respectively. Further denote the set of visited vertices at time $$t$$ as $$S(t)$$.\n\n**Lemma**: A subtree of a vertex $$v$$ is $$S(t_o(v)) \\setminus S(t_i(v))$$.\n_Proof_: all vertices in a subtree of $$v$$ get exited before $$v$$, so they all belong to $$S(t_o(v))$$. All vertices in a subtree of $$v$$ are entered after $$v$$, so none of them belongs to $$S(t_i(v))$$.\n\nNow let\'s maintain a frequency table of labels during the dfs. The answer for a given vertex will be the difference between the label\'s frequencies at times $$t_o$$ and $$t_i$$ due to the above lemma. \n\nUpvote so that more people learn this trick!\n\n_Note_ (in case you are wondering why this is so important). Imagine that labels are integers instead of letters. Then all $$O(n)$$ of your hashmaps from a naive solution suddenly take $$O(n)$$ space. Merging them takes $$O(n)$$ time too, for a total of $$O(n^2)$$. However, this solution will remain $$O(n + n) = O(n)$$.\n\n# Complexity\n\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$, or $$O(|\\Sigma| + h)$$ if you want to be pedantic.\n\n# Code\n\n```python\nimport collections\n\n\nclass Solution:\n def countSubTrees(self, n: int, edges: list[list[int]], labels: str) -> list[int]:\n graph = [[] for _ in range(n)]\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n\n ans = [0] * n\n\n def dfs(vertex: int, parent: int, cnt: collections.Counter) -> None:\n before = cnt[labels[vertex]]\n\n for adjacent in graph[vertex]:\n if adjacent != parent:\n dfs(adjacent, vertex, cnt)\n\n cnt[labels[vertex]] += 1\n ans[vertex] = cnt[labels[vertex]] - before\n\n dfs(0, 0, collections.Counter())\n return ans\n \n``` | 11 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python | O(1) Space | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n\n**Disclaimer**: first, we talk about "additional" space here, so output parameters like `ans` do not count. Second, I do not consider the graph to take additional space, since it\'s a result of a poor input format choice.\n\n# Approach\n\nLet\'s imagine that we run a timed depth first search on our tree. "Timed" as in "a counter is incremented when entering and exiting a vertex". We\'ll denote entrance and exit (in and out) times for a vertex $$v$$ as $$t_i(v)$$ and $$t_o(v)$$ respectively. Further denote the set of visited vertices at time $$t$$ as $$S(t)$$.\n\n**Lemma**: A subtree of a vertex $$v$$ is $$S(t_o(v)) \\setminus S(t_i(v))$$.\n_Proof_: all vertices in a subtree of $$v$$ get exited before $$v$$, so they all belong to $$S(t_o(v))$$. All vertices in a subtree of $$v$$ are entered after $$v$$, so none of them belongs to $$S(t_i(v))$$.\n\nNow let\'s maintain a frequency table of labels during the dfs. The answer for a given vertex will be the difference between the label\'s frequencies at times $$t_o$$ and $$t_i$$ due to the above lemma. \n\nUpvote so that more people learn this trick!\n\n_Note_ (in case you are wondering why this is so important). Imagine that labels are integers instead of letters. Then all $$O(n)$$ of your hashmaps from a naive solution suddenly take $$O(n)$$ space. Merging them takes $$O(n)$$ time too, for a total of $$O(n^2)$$. However, this solution will remain $$O(n + n) = O(n)$$.\n\n# Complexity\n\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(1)$$, or $$O(|\\Sigma| + h)$$ if you want to be pedantic.\n\n# Code\n\n```python\nimport collections\n\n\nclass Solution:\n def countSubTrees(self, n: int, edges: list[list[int]], labels: str) -> list[int]:\n graph = [[] for _ in range(n)]\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n\n ans = [0] * n\n\n def dfs(vertex: int, parent: int, cnt: collections.Counter) -> None:\n before = cnt[labels[vertex]]\n\n for adjacent in graph[vertex]:\n if adjacent != parent:\n dfs(adjacent, vertex, cnt)\n\n cnt[labels[vertex]] += 1\n ans[vertex] = cnt[labels[vertex]] - before\n\n dfs(0, 0, collections.Counter())\n return ans\n \n``` | 11 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
MOST OPTIMIZED PYTHON SOLUTION || DFS TRAVERSAL | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(V+E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V*E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self,node,grid,visited,fst,labels):\n visited[node]=1\n lst=[0]*26\n lst[ord(labels[node])-97]=1\n for i in grid[node]:\n if visited[i]==1:\n continue\n x=self.dfs(i,grid,visited,fst,labels)\n for j in range(26):\n lst[j]+=x[j]\n fst[node]=lst[ord(labels[node])-97]\n return lst\n\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n grid=[[] for _ in range(n)]\n for i,j in edges:\n grid[i].append(j)\n grid[j].append(i)\n\n visited=[0]*n\n fst=[0]*n\n self.dfs(0,grid,visited,fst,labels)\n return fst\n\n``` | 3 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
MOST OPTIMIZED PYTHON SOLUTION || DFS TRAVERSAL | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(V+E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V*E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self,node,grid,visited,fst,labels):\n visited[node]=1\n lst=[0]*26\n lst[ord(labels[node])-97]=1\n for i in grid[node]:\n if visited[i]==1:\n continue\n x=self.dfs(i,grid,visited,fst,labels)\n for j in range(26):\n lst[j]+=x[j]\n fst[node]=lst[ord(labels[node])-97]\n return lst\n\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n grid=[[] for _ in range(n)]\n for i,j in edges:\n grid[i].append(j)\n grid[j].append(i)\n\n visited=[0]*n\n fst=[0]*n\n self.dfs(0,grid,visited,fst,labels)\n return fst\n\n``` | 3 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python3 DFS with quick explanation | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n\nTraverse the tree and each node should return a vector to its parent node. The vector should have the count of all the labels in the sub-tree of this node.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we make a graph of the tree so we can traverse it. Then we use a dfs algorithm to traverse the tree and count the number of all characters in its subtree. As we traverse, we discard the parent node from the graph of the child node so the parent node will not be revisited by the child node.\n\nWe use ret as our return array and we use count as our hashtable to add up all characters in the subtree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n # get vector of counts of all letters for subtree\n def dfs(node):\n count = Counter(labels[node])\n for child in graph[node]:\n # discard so no repeat\n graph[child].discard(node)\n\n # add characters of all subtrees\n count += dfs(child)\n\n ret[node] = count[labels[node]]\n return count\n # make graph of the tree\n graph = collections.defaultdict(set)\n for x, y in edges:\n graph[x].add(y)\n graph[y].add(x)\n \n ret = [0] * n\n dfs(0)\n return ret\n \n\n``` | 3 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python3 DFS with quick explanation | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n\nTraverse the tree and each node should return a vector to its parent node. The vector should have the count of all the labels in the sub-tree of this node.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we make a graph of the tree so we can traverse it. Then we use a dfs algorithm to traverse the tree and count the number of all characters in its subtree. As we traverse, we discard the parent node from the graph of the child node so the parent node will not be revisited by the child node.\n\nWe use ret as our return array and we use count as our hashtable to add up all characters in the subtree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n # get vector of counts of all letters for subtree\n def dfs(node):\n count = Counter(labels[node])\n for child in graph[node]:\n # discard so no repeat\n graph[child].discard(node)\n\n # add characters of all subtrees\n count += dfs(child)\n\n ret[node] = count[labels[node]]\n return count\n # make graph of the tree\n graph = collections.defaultdict(set)\n for x, y in edges:\n graph[x].add(y)\n graph[y].add(x)\n \n ret = [0] * n\n dfs(0)\n return ret\n \n\n``` | 3 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
C# & Python 3 Solutions | Dictionary | DFS | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Approach\nIn this approach, we traverse from the root nodes to the leaf node and count the number of characters using DFS. \nWe don\u2019t need to create counts array and iterate over it in every call. Instead, we can store single array for all calls, which has counts of visited labels for all time. Then, the answer for some node is the difference between this label visits count before and after handling this node. Thanks to **@8symbols**.\n\n**If you like it, please upvote. Thanks**\n\n\n\n\n# Code - C#\n```\npublic class Solution {\n public int[] CountSubTrees(int n, int[][] edges, string labels) {\n int[] answer = new int[n];\n Dictionary<char, int> counts = new();\n Dictionary<int,List<int>> tree = BuildTree(edges);\n void DFS(int node, int parent) {\n if(!counts.ContainsKey(labels[node]))\n counts.Add(labels[node], 0);\n\n int previous = counts[labels[node]];\n counts[labels[node]]++;\n\n foreach (int child in tree[node])\n if (child != parent) DFS(child, node);\n \n answer[node] = counts[labels[node]] - previous;\n }\n DFS(0, -1);\n return answer;\n }\n\n public Dictionary<int,List<int>> BuildTree(int[][] edges){\n Dictionary<int,List<int>> tree = new();\n foreach(var edge in edges){\n int a = edge[0], b = edge[1];\n if(!tree.ContainsKey(a)) tree.Add(a,new List<int>());\n if(!tree.ContainsKey(b)) tree.Add(b, new List<int>());\n tree[a].Add(b);\n tree[b].Add(a);\n }\n return tree;\n }\n}\n```\n\n\n# Code - Python 3\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n graph = [[] for _ in range(n)]\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n \n counts = {}\n answer = [0] * n\n \n def dfs(node, parent):\n if labels[node] not in counts:\n counts[labels[node]] = 0\n\n previous = counts[labels[node]]\n counts[labels[node]] += 1\n \n for child in graph[node]:\n if child != parent:\n dfs(child, node)\n \n answer[node] = counts[labels[node]] - previous\n \n dfs(0, -1)\n return answer\n``` | 2 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
C# & Python 3 Solutions | Dictionary | DFS | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Approach\nIn this approach, we traverse from the root nodes to the leaf node and count the number of characters using DFS. \nWe don\u2019t need to create counts array and iterate over it in every call. Instead, we can store single array for all calls, which has counts of visited labels for all time. Then, the answer for some node is the difference between this label visits count before and after handling this node. Thanks to **@8symbols**.\n\n**If you like it, please upvote. Thanks**\n\n\n\n\n# Code - C#\n```\npublic class Solution {\n public int[] CountSubTrees(int n, int[][] edges, string labels) {\n int[] answer = new int[n];\n Dictionary<char, int> counts = new();\n Dictionary<int,List<int>> tree = BuildTree(edges);\n void DFS(int node, int parent) {\n if(!counts.ContainsKey(labels[node]))\n counts.Add(labels[node], 0);\n\n int previous = counts[labels[node]];\n counts[labels[node]]++;\n\n foreach (int child in tree[node])\n if (child != parent) DFS(child, node);\n \n answer[node] = counts[labels[node]] - previous;\n }\n DFS(0, -1);\n return answer;\n }\n\n public Dictionary<int,List<int>> BuildTree(int[][] edges){\n Dictionary<int,List<int>> tree = new();\n foreach(var edge in edges){\n int a = edge[0], b = edge[1];\n if(!tree.ContainsKey(a)) tree.Add(a,new List<int>());\n if(!tree.ContainsKey(b)) tree.Add(b, new List<int>());\n tree[a].Add(b);\n tree[b].Add(a);\n }\n return tree;\n }\n}\n```\n\n\n# Code - Python 3\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n graph = [[] for _ in range(n)]\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n \n counts = {}\n answer = [0] * n\n \n def dfs(node, parent):\n if labels[node] not in counts:\n counts[labels[node]] = 0\n\n previous = counts[labels[node]]\n counts[labels[node]] += 1\n \n for child in graph[node]:\n if child != parent:\n dfs(child, node)\n \n answer[node] = counts[labels[node]] - previous\n \n dfs(0, -1)\n return answer\n``` | 2 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python solution beats 99.38% | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n adj = [[] for _ in range(n)]\n\n for a, b in edges:\n adj[a].append(b)\n adj[b].append(a)\n\n count = [0]*len(string.ascii_lowercase)\n answer = [0]*n\n\n def dfs(node, parent):\n index = ord(labels[node]) - ord(\'a\')\n previous = count[index]\n\n count[index] += 1\n\n for child in adj[node]:\n if child != parent:\n dfs(child,node)\n answer[node] = count[index] - previous\n dfs(0,-1)\n return answer\n\n \n``` | 2 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
Python solution beats 99.38% | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n adj = [[] for _ in range(n)]\n\n for a, b in edges:\n adj[a].append(b)\n adj[b].append(a)\n\n count = [0]*len(string.ascii_lowercase)\n answer = [0]*n\n\n def dfs(node, parent):\n index = ord(labels[node]) - ord(\'a\')\n previous = count[index]\n\n count[index] += 1\n\n for child in adj[node]:\n if child != parent:\n dfs(child,node)\n answer[node] = count[index] - previous\n dfs(0,-1)\n return answer\n\n \n``` | 2 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
🧑💻Python3 Simple Solution | DFS + Dictionary | Great explanation | 97% optimal | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | Note: Skip to "**How to Solve**" section if you have basic understanding of DFS.\nAlso the **code has proper comments**, skips to the code directly if you prefer :)\n\n# Approach\nSo heres the deal, first of all the questions asks us to consider about undirected trees, by that what they are implying is to consider your data structure as a graph instead of a tree. Secondly, after readin the question, you should be able to understand it is somehow related to depth first search, though you might not know what exactly to do, your intiution would have suggested to use Depth First Search.\n\n# Concentration\nWe need to keep track of all the labels in a subtree along with their frequencies. You can do this with a dictionary where the key is the label and the frequency is the value. Dotn forget to the add the label of the current node to dictionary of it\'s subtree\'s labels\n\n# Recursion vs Iterative approach\nAs you would know, there are 2 ways of performing DFS in graphs, one using recurrsion and another using a stack datastructure. But for this particular question, we will be using recursion as it will be easier to keep track of the labels. labels of each child node will be passed to the parent node and in the parent node, we add all the labels of all its\'s children\'s subtrees.\n\n# DFS initiation\nOur plan here is to perform DFS on the given data structure which we will assume to be a graph. To perform DFS on a graph, we need to know the neighbours of each node. We can construct a dictionary using edges list.\nYou do it in the following way:\n```\nd = collections.defaultdict(list)\nfor i in edges:\n d[i[0]].append(i[1])\n d[i[1]].append(i[0])\n```\n\nNow we can perform DFS. Also remeber to keep track of the nodes that you have visited using a list/set. \n\n# How to solve\nNote: For better understanding, read this along with the code. \n\nPerforming a DFS is a trival task, but we also need to keep track of the labels and their frequency for each subtree. We can create a dictionary and call it labels_dict. In this dict, we keep track of all the labels in a node\'s subtree. Then we return labels_dict at the end of dfs, which means, we will be passing a subtree\'s result to its parent(except for root).\n\nHow to keep track of subtree\'s labels:\n1. Add the current label to the dictionary.\n2. Perform dfs on each child node, this returns the labels in each child\'s subtree which we will add to our current dictionary\n3. Update the results array\n4. return the labels_dict(current dictionary) at the end of dfs(in this step we return the subtree\'s labels to its parent node where we continue steps 2-4)\n\nLet me know any questions or concerns\n\nHope my solution helps. Happy coding:)\n\n# Time Complexity : $$$O(n^2)$$$\n\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n neighbours = collections.defaultdict(list) # Dictioanry to keep track of neighbours for each node\n result = [-1]*n # result vector with -1 for all positions\n for edge in edges: # Populate d with neighbours\n neighbours[edge[0]].append(edge[1])\n neighbours[edge[1]].append(edge[0])\n\n visited = [-1]*n # Visited vector to keep track of visited nodes\n\n def dfs(edge):\n labels_dict = collections.defaultdict(int) # Dictionary to keep track of all the labels in the subtree\n labels_dict[labels[edge]] += 1 # Update the dictionary with the current label\n for i in neighbours[edge]: # Iterate through all neighbours\n if visited[i] == -1:\n visited[i] = 1\n subtree_labels = dfs(i) # Call dfs(edge) if the edge has not been visited yet, it returns labels of subtree\n for j in subtree_labels: # Add all the contents of subtree_labels to current labels\n if j in labels_dict:\n labels_dict[j]+= subtree_labels[j]\n else:\n labels_dict[j] = subtree_labels[j]\n # Now labels contains all the labels in its subtree along with their frequency \n result[edge] = labels_dict[labels[edge]] # Update results with the label count\n return labels_dict # Return labels to its parent\n\n visited[0] = 1 # Update visited of root to 1\n dfs(0) # Call dfs on the root node\n return result #Return the result\n\n\n``` | 2 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
🧑💻Python3 Simple Solution | DFS + Dictionary | Great explanation | 97% optimal | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | Note: Skip to "**How to Solve**" section if you have basic understanding of DFS.\nAlso the **code has proper comments**, skips to the code directly if you prefer :)\n\n# Approach\nSo heres the deal, first of all the questions asks us to consider about undirected trees, by that what they are implying is to consider your data structure as a graph instead of a tree. Secondly, after readin the question, you should be able to understand it is somehow related to depth first search, though you might not know what exactly to do, your intiution would have suggested to use Depth First Search.\n\n# Concentration\nWe need to keep track of all the labels in a subtree along with their frequencies. You can do this with a dictionary where the key is the label and the frequency is the value. Dotn forget to the add the label of the current node to dictionary of it\'s subtree\'s labels\n\n# Recursion vs Iterative approach\nAs you would know, there are 2 ways of performing DFS in graphs, one using recurrsion and another using a stack datastructure. But for this particular question, we will be using recursion as it will be easier to keep track of the labels. labels of each child node will be passed to the parent node and in the parent node, we add all the labels of all its\'s children\'s subtrees.\n\n# DFS initiation\nOur plan here is to perform DFS on the given data structure which we will assume to be a graph. To perform DFS on a graph, we need to know the neighbours of each node. We can construct a dictionary using edges list.\nYou do it in the following way:\n```\nd = collections.defaultdict(list)\nfor i in edges:\n d[i[0]].append(i[1])\n d[i[1]].append(i[0])\n```\n\nNow we can perform DFS. Also remeber to keep track of the nodes that you have visited using a list/set. \n\n# How to solve\nNote: For better understanding, read this along with the code. \n\nPerforming a DFS is a trival task, but we also need to keep track of the labels and their frequency for each subtree. We can create a dictionary and call it labels_dict. In this dict, we keep track of all the labels in a node\'s subtree. Then we return labels_dict at the end of dfs, which means, we will be passing a subtree\'s result to its parent(except for root).\n\nHow to keep track of subtree\'s labels:\n1. Add the current label to the dictionary.\n2. Perform dfs on each child node, this returns the labels in each child\'s subtree which we will add to our current dictionary\n3. Update the results array\n4. return the labels_dict(current dictionary) at the end of dfs(in this step we return the subtree\'s labels to its parent node where we continue steps 2-4)\n\nLet me know any questions or concerns\n\nHope my solution helps. Happy coding:)\n\n# Time Complexity : $$$O(n^2)$$$\n\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n neighbours = collections.defaultdict(list) # Dictioanry to keep track of neighbours for each node\n result = [-1]*n # result vector with -1 for all positions\n for edge in edges: # Populate d with neighbours\n neighbours[edge[0]].append(edge[1])\n neighbours[edge[1]].append(edge[0])\n\n visited = [-1]*n # Visited vector to keep track of visited nodes\n\n def dfs(edge):\n labels_dict = collections.defaultdict(int) # Dictionary to keep track of all the labels in the subtree\n labels_dict[labels[edge]] += 1 # Update the dictionary with the current label\n for i in neighbours[edge]: # Iterate through all neighbours\n if visited[i] == -1:\n visited[i] = 1\n subtree_labels = dfs(i) # Call dfs(edge) if the edge has not been visited yet, it returns labels of subtree\n for j in subtree_labels: # Add all the contents of subtree_labels to current labels\n if j in labels_dict:\n labels_dict[j]+= subtree_labels[j]\n else:\n labels_dict[j] = subtree_labels[j]\n # Now labels contains all the labels in its subtree along with their frequency \n result[edge] = labels_dict[labels[edge]] # Update results with the label count\n return labels_dict # Return labels to its parent\n\n visited[0] = 1 # Update visited of root to 1\n dfs(0) # Call dfs on the root node\n return result #Return the result\n\n\n``` | 2 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
✅Python3 solution. Beats 100% in time and memory | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\nMy idea was that you need to know only two things when building the final array - the count when the node was first visited and the current count.\nThe code is higly optimized for memory efficiency and not for readability. I\'m sorry for that, but I tried to add comments on the parts where weird things are happenning according to me. If you have any questions - feel free to ask.\n\n# Approach\nI\'m using DFS to traverse the tree. When visiting a node for the first time, store the number of labels like the node\'s seen so far. Then add all the children of the current node to the DFS stack. When we pop back to the node after visiting the whole subtree, we can calculate how many labels like the current were found by simply substracting the initial count from the running total.\n\n# Complexity\n- Time complexity: $$O(n)$$ since we visit each of the $$n$$ nodes exactly twice\n\n- Space complexity: $$O(n)$$ since the largest portion of memory we need is an array of `n` integers to store the `first_seen` values, and then we use the same array as the result\n<!-- Add your space complexity here, e.g. -->\n\n# Code\n```\nORD_A = ord(\'a\')\n\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n adj_list = [[] for _ in range(n)]\n for a, b in edges:\n adj_list[a].append(b)\n adj_list[b].append(a)\n\n # storing the total seen characters until the given moment\n count = [0] * 26\n # first_seen is used to store the number of labels equal to the current node\'s\n # at the moment of the first visit\n first_seen = [-1] * n\n\n # iterative DFS\n stack = [0]\n while stack:\n node = stack[-1]\n\n label = ord(labels[node]) - ORD_A\n \n # each node is visited exactly twice\n if first_seen[node] == -1:\n first_seen[node] = count[label]\n count[label] += 1\n \n for neigh in adj_list[node]:\n if first_seen[neigh] == -1:\n stack.append(neigh)\n else:\n stack.pop()\n # the number of nodes with the same label in the subtree is\n # the total number of labels seen so far minus the number of\n # such labels seen at the moment of the first visit\n # NOTE: we use first_seen as a result array, because after visiting\n # the whole subtree of node, first_seen[node] is no longer needed\n first_seen[node] = count[label] - first_seen[node]\n \n return first_seen\n``` | 1 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
✅Python3 solution. Beats 100% in time and memory | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\nMy idea was that you need to know only two things when building the final array - the count when the node was first visited and the current count.\nThe code is higly optimized for memory efficiency and not for readability. I\'m sorry for that, but I tried to add comments on the parts where weird things are happenning according to me. If you have any questions - feel free to ask.\n\n# Approach\nI\'m using DFS to traverse the tree. When visiting a node for the first time, store the number of labels like the node\'s seen so far. Then add all the children of the current node to the DFS stack. When we pop back to the node after visiting the whole subtree, we can calculate how many labels like the current were found by simply substracting the initial count from the running total.\n\n# Complexity\n- Time complexity: $$O(n)$$ since we visit each of the $$n$$ nodes exactly twice\n\n- Space complexity: $$O(n)$$ since the largest portion of memory we need is an array of `n` integers to store the `first_seen` values, and then we use the same array as the result\n<!-- Add your space complexity here, e.g. -->\n\n# Code\n```\nORD_A = ord(\'a\')\n\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n adj_list = [[] for _ in range(n)]\n for a, b in edges:\n adj_list[a].append(b)\n adj_list[b].append(a)\n\n # storing the total seen characters until the given moment\n count = [0] * 26\n # first_seen is used to store the number of labels equal to the current node\'s\n # at the moment of the first visit\n first_seen = [-1] * n\n\n # iterative DFS\n stack = [0]\n while stack:\n node = stack[-1]\n\n label = ord(labels[node]) - ORD_A\n \n # each node is visited exactly twice\n if first_seen[node] == -1:\n first_seen[node] = count[label]\n count[label] += 1\n \n for neigh in adj_list[node]:\n if first_seen[neigh] == -1:\n stack.append(neigh)\n else:\n stack.pop()\n # the number of nodes with the same label in the subtree is\n # the total number of labels seen so far minus the number of\n # such labels seen at the moment of the first visit\n # NOTE: we use first_seen as a result array, because after visiting\n # the whole subtree of node, first_seen[node] is no longer needed\n first_seen[node] = count[label] - first_seen[node]\n \n return first_seen\n``` | 1 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
PYTHON || EASY TO UNDERSTAND || WELL EXPLAINED | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\nThe intuition behind this solution is to use a depth-first search (dfs) to traverse the tree and keep track of the counts of each label in the subtree of each node.\n\n# Approach\nThe approach is as follows:\n\n1. Create an adjacency list representation of the tree using the edges array.\n2. Initialize an array (ans) to store the number of nodes in the subtree of each node that have the same label as that node.\n3. Use a dfs function to traverse the tree, starting from the root (node 0).\n4. For each child of the current node, recursively call the dfs function and update the count of each label using a Counter object.\n5. Update the ans array for the current node with the count of the label at that node.\n6. Return the counts of all labels in the subtree rooted at the current node.\n7. The ans array will now contain the number of nodes in the subtree of each node that have the same label as that node.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n graph = collections.defaultdict(list)\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n ans = [0] * n\n def dfs(node, parent):\n counts = collections.Counter()\n for child in graph[node]:\n if child != parent:\n counts += dfs(child, node)\n counts[labels[node]] += 1\n ans[node] = counts[labels[node]]\n return counts\n\n dfs(0, None)\n return ans\n\n``` | 1 | You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` `edges`. The **root** of the tree is the node `0`, and each node of the tree has **a label** which is a lower-case character given in the string `labels` (i.e. The node with the number `i` has the label `labels[i]`).
The `edges` array is given on the form `edges[i] = [ai, bi]`, which means there is an edge between nodes `ai` and `bi` in the tree.
Return _an array of size `n`_ where `ans[i]` is the number of nodes in the subtree of the `ith` node which have the same label as node `i`.
A subtree of a tree `T` is the tree consisting of a node in `T` and all of its descendant nodes.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[0,2\],\[1,4\],\[1,5\],\[2,3\],\[2,6\]\], labels = "abaedcd "
**Output:** \[2,1,1,1,1,1,1\]
**Explanation:** Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[1,2\],\[0,3\]\], labels = "bbbb "
**Output:** \[4,2,1,1\]
**Explanation:** The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.
**Example 3:**
**Input:** n = 5, edges = \[\[0,1\],\[0,2\],\[1,3\],\[0,4\]\], labels = "aabab "
**Output:** \[3,2,1,1,1\]
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `labels.length == n`
* `labels` is consisting of only of lowercase English letters. | Sort elements and take each element from the largest until accomplish the conditions. |
PYTHON || EASY TO UNDERSTAND || WELL EXPLAINED | number-of-nodes-in-the-sub-tree-with-the-same-label | 0 | 1 | # Intuition\nThe intuition behind this solution is to use a depth-first search (dfs) to traverse the tree and keep track of the counts of each label in the subtree of each node.\n\n# Approach\nThe approach is as follows:\n\n1. Create an adjacency list representation of the tree using the edges array.\n2. Initialize an array (ans) to store the number of nodes in the subtree of each node that have the same label as that node.\n3. Use a dfs function to traverse the tree, starting from the root (node 0).\n4. For each child of the current node, recursively call the dfs function and update the count of each label using a Counter object.\n5. Update the ans array for the current node with the count of the label at that node.\n6. Return the counts of all labels in the subtree rooted at the current node.\n7. The ans array will now contain the number of nodes in the subtree of each node that have the same label as that node.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:\n graph = collections.defaultdict(list)\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n ans = [0] * n\n def dfs(node, parent):\n counts = collections.Counter()\n for child in graph[node]:\n if child != parent:\n counts += dfs(child, node)\n counts[labels[node]] += 1\n ans[node] = counts[labels[node]]\n return counts\n\n dfs(0, None)\n return ans\n\n``` | 1 | Bob is standing at cell `(0, 0)`, and he wants to reach `destination`: `(row, column)`. He can only travel **right** and **down**. You are going to help Bob by providing **instructions** for him to reach `destination`.
The **instructions** are represented as a string, where each character is either:
* `'H'`, meaning move horizontally (go **right**), or
* `'V'`, meaning move vertically (go **down**).
Multiple **instructions** will lead Bob to `destination`. For example, if `destination` is `(2, 3)`, both `"HHHVV "` and `"HVHVH "` are valid **instructions**.
However, Bob is very picky. Bob has a lucky number `k`, and he wants the `kth` **lexicographically smallest instructions** that will lead him to `destination`. `k` is **1-indexed**.
Given an integer array `destination` and an integer `k`, return _the_ `kth` _**lexicographically smallest instructions** that will take Bob to_ `destination`.
**Example 1:**
**Input:** destination = \[2,3\], k = 1
**Output:** "HHHVV "
**Explanation:** All the instructions that reach (2, 3) in lexicographic order are as follows:
\[ "HHHVV ", "HHVHV ", "HHVVH ", "HVHHV ", "HVHVH ", "HVVHH ", "VHHHV ", "VHHVH ", "VHVHH ", "VVHHH "\].
**Example 2:**
**Input:** destination = \[2,3\], k = 2
**Output:** "HHVHV "
**Example 3:**
**Input:** destination = \[2,3\], k = 3
**Output:** "HHVVH "
**Constraints:**
* `destination.length == 2`
* `1 <= row, column <= 15`
* `1 <= k <= nCr(row + column, row)`, where `nCr(a, b)` denotes `a` choose `b`. | Start traversing the tree and each node should return a vector to its parent node. The vector should be of length 26 and have the count of all the labels in the sub-tree of this node. |
Python Easy to Read solution with explanation | maximum-number-of-non-overlapping-substrings | 0 | 1 | This is a slightly modified version based on the discussion here\nhttps://leetcode.com/problems/maximum-number-of-non-overlapping-substrings/discuss/743402/21-lines-Python-greedy-solution\n\n[Explanation]\n1. Get the first and last occurance of each characters\n2. For the range of each letter, we need to update the range according to all the characters within the range. For example: `abab` we would have the initial range as `a: [0,2], b: [1:3]`. Since the range of `a` which is `[0,2]` will include `b`, we need to update the range of `a` to also include all occurances of `b` as well. \n3. Finally, we sort all the ranges according to it\'s `end` (since we want to take smallest range possible) and take as much as we can as long as the `start` of the current range is `>=` the `end` of the previous range.\n\n[Time/Space]\n**This is a bit tricky, but I\'ll try my best. Please correct me if I made any mistakes below.**\n1. Loop through `s` once, so `O(N)` where N is the length of `s`\n2. Loop through all ranges, and there could be at most `26` ranges so `O(26)`. Depending on how many other characters included in each range, we would be spending another `26` loops within the loop, so total `O(26*26)`\n3. We are basically looping through the dictionary `ranges` which could have at most `26` items that was generated from #1, so it\'s `O(26)`. We also spent `O(26log26)` to sort it\n\nOverall, I personally think it\'s `O(N)` for time and `O(26)` at most to store ranges for all letters.\nAgain, please correct me if I am wrong. Much appreciated. \n\n```Python\ndef maxNumOfSubstrings(self, s: str) -> List[str]:\n\tranges = collections.defaultdict(list)\n\t# 1\n\tfor idx, ch in enumerate(s):\n\t\tranges[ch].append(idx)\n\t# 2\n\tfor r in ranges:\n\t\tleft, right = ranges[r][0], ranges[r][-1]+1\n\t\ttempl, tempr = left, right\n\t\twhile True:\n\t\t\tfor ch in set(s[templ:tempr]):\n\t\t\t\ttempl = min(templ, ranges[ch][0])\n\t\t\t\ttempr = max(tempr, ranges[ch][-1]+1)\n\t\t\tif (templ, tempr) == (left, right): break\n\t\t\tleft, right = templ, tempr\n\t\tranges[r] = (templ, tempr)\n\t# 3\t\n\tsorted_ranges = sorted(ranges.values(), key=lambda pair: pair[1])\n\tans, prev = [], 0\n\tfor start, end in sorted_ranges:\n\t\tif start >= prev:\n\t\t\tans.append(s[start:end])\n\t\t\tprev = end\n\treturn ans | 31 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
Python Easy to Read solution with explanation | maximum-number-of-non-overlapping-substrings | 0 | 1 | This is a slightly modified version based on the discussion here\nhttps://leetcode.com/problems/maximum-number-of-non-overlapping-substrings/discuss/743402/21-lines-Python-greedy-solution\n\n[Explanation]\n1. Get the first and last occurance of each characters\n2. For the range of each letter, we need to update the range according to all the characters within the range. For example: `abab` we would have the initial range as `a: [0,2], b: [1:3]`. Since the range of `a` which is `[0,2]` will include `b`, we need to update the range of `a` to also include all occurances of `b` as well. \n3. Finally, we sort all the ranges according to it\'s `end` (since we want to take smallest range possible) and take as much as we can as long as the `start` of the current range is `>=` the `end` of the previous range.\n\n[Time/Space]\n**This is a bit tricky, but I\'ll try my best. Please correct me if I made any mistakes below.**\n1. Loop through `s` once, so `O(N)` where N is the length of `s`\n2. Loop through all ranges, and there could be at most `26` ranges so `O(26)`. Depending on how many other characters included in each range, we would be spending another `26` loops within the loop, so total `O(26*26)`\n3. We are basically looping through the dictionary `ranges` which could have at most `26` items that was generated from #1, so it\'s `O(26)`. We also spent `O(26log26)` to sort it\n\nOverall, I personally think it\'s `O(N)` for time and `O(26)` at most to store ranges for all letters.\nAgain, please correct me if I am wrong. Much appreciated. \n\n```Python\ndef maxNumOfSubstrings(self, s: str) -> List[str]:\n\tranges = collections.defaultdict(list)\n\t# 1\n\tfor idx, ch in enumerate(s):\n\t\tranges[ch].append(idx)\n\t# 2\n\tfor r in ranges:\n\t\tleft, right = ranges[r][0], ranges[r][-1]+1\n\t\ttempl, tempr = left, right\n\t\twhile True:\n\t\t\tfor ch in set(s[templ:tempr]):\n\t\t\t\ttempl = min(templ, ranges[ch][0])\n\t\t\t\ttempr = max(tempr, ranges[ch][-1]+1)\n\t\t\tif (templ, tempr) == (left, right): break\n\t\t\tleft, right = templ, tempr\n\t\tranges[r] = (templ, tempr)\n\t# 3\t\n\tsorted_ranges = sorted(ranges.values(), key=lambda pair: pair[1])\n\tans, prev = [], 0\n\tfor start, end in sorted_ranges:\n\t\tif start >= prev:\n\t\t\tans.append(s[start:end])\n\t\t\tprev = end\n\treturn ans | 31 | Given the `root` of a binary tree, return _the lowest common ancestor (LCA) of two given nodes,_ `p` _and_ `q`. If either node `p` or `q` **does not exist** in the tree, return `null`. All values of the nodes in the tree are **unique**.
According to the **[definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor)**: "The lowest common ancestor of two nodes `p` and `q` in a binary tree `T` is the lowest node that has both `p` and `q` as **descendants** (where we allow **a node to be a descendant of itself**) ". A **descendant** of a node `x` is a node `y` that is on the path from node `x` to some leaf node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 1
**Output:** 3
**Explanation:** The LCA of nodes 5 and 1 is 3.
**Example 2:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 4
**Output:** 5
**Explanation:** The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.
**Example 3:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], p = 5, q = 10
**Output:** null
**Explanation:** Node 10 does not exist in the tree, so return null.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 104]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
**Follow up:** Can you find the LCA traversing the tree, without checking nodes existence? | Notice that it's impossible for any two valid substrings to overlap unless one is inside another. We can start by finding the starting and ending index for each character. From these indices, we can form the substrings by expanding each character's range if necessary (if another character exists in the range with smaller/larger starting/ending index). Sort the valid substrings by length and greedily take those with the smallest length, discarding the ones that overlap those we took. |
python solution | maximum-number-of-non-overlapping-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nnear about O(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nnear about O(n)\n\n# Code\n```\nclass Solution:\n def maxNumOfSubstrings(self, s: str) -> List[str]:\n\n # storing the intervals of characters\n\n intervals = {}\n for i in range(len(s)):\n if s[i] not in intervals :\n intervals[s[i]] = [i,i]\n else :\n intervals[s[i]].pop()\n intervals[s[i]].append(i)\n \n # merging overlapping intervals\n\n for i in intervals:\n start,end = intervals[i]\n for j in range(start+1,end):\n curStart, curEnd = intervals[s[j]]\n if curStart < start :\n start = curStart\n if curEnd > end :\n end = curEnd\n intervals[i] = [start,end]\n\n # merging overlapping intervals\n\n for i in intervals:\n start,end = intervals[i]\n for j in range(start+1,end):\n curStart, curEnd = intervals[s[j]]\n if curStart < start :\n start = curStart\n if curEnd > end :\n end = curEnd\n intervals[i] = [start,end]\n \n # storing intervals in list\n\n res = []\n for i in intervals:\n res.append(intervals[i])\n res = sorted(res,key = lambda x : x[1])\n\n # finding ans and sotring in ansArr\n\n end = res[0][1]\n start = res[0][0]\n ansArr = [s[res[0][0] : end+1]]\n for i in range(1,len(res)):\n if res[i][0] > end :\n ansArr.append(s[res[i][0] : res[i][1]+1])\n end = res[i][1]\n start = res[i][0]\n\n return ansArr\n\n``` | 0 | Given a string `s` of lowercase letters, you need to find the maximum number of **non-empty** substrings of `s` that meet the following conditions:
1. The substrings do not overlap, that is for any two substrings `s[i..j]` and `s[x..y]`, either `j < x` or `i > y` is true.
2. A substring that contains a certain character `c` must also contain all occurrences of `c`.
Find _the maximum number of substrings that meet the above conditions_. If there are multiple solutions with the same number of substrings, _return the one with minimum total length._ It can be shown that there exists a unique solution of minimum total length.
Notice that you can return the substrings in **any** order.
**Example 1:**
**Input:** s = "adefaddaccc "
**Output:** \[ "e ", "f ", "ccc "\]
**Explanation:** The following are all the possible substrings that meet the conditions:
\[
"adefaddaccc "
"adefadda ",
"ef ",
"e ",
"f ",
"ccc ",
\]
If we choose the first string, we cannot choose anything else and we'd get only 1. If we choose "adefadda ", we are left with "ccc " which is the only one that doesn't overlap, thus obtaining 2 substrings. Notice also, that it's not optimal to choose "ef " since it can be split into two. Therefore, the optimal way is to choose \[ "e ", "f ", "ccc "\] which gives us 3 substrings. No other solution of the same number of substrings exist.
**Example 2:**
**Input:** s = "abbaccd "
**Output:** \[ "d ", "bb ", "cc "\]
**Explanation:** Notice that while the set of substrings \[ "d ", "abba ", "cc "\] also has length 3, it's considered incorrect since it has larger total length.
**Constraints:**
* `1 <= s.length <= 105`
* `s` contains only lowercase English letters. | Read the string from right to left, if the string ends in '0' then the number is even otherwise it is odd. Simulate the steps described in the binary string. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.