title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | maximum-subarray | 1 | 1 | # Intuition\nThe Intuition behind the code is to find the maximum sum of a contiguous subarray within the given array `nums`. It does this by scanning through the array and keeping track of the current sum of the subarray. Whenever the current sum becomes greater than the maximum sum encountered so far, it updates the maximum sum. If the current sum becomes negative, it resets the sum to 0 and starts a new subarray. By the end of the loop, the code returns the maximum sum found.\n\n# Approach:\n\n1. We start by initializing two variables: `maxSum` and `currentSum`.\n - `maxSum` represents the maximum sum encountered so far and is initially set to the minimum possible integer value to ensure that any valid subarray sum will be greater than it.\n - `currentSum` represents the current sum of the subarray being considered and is initially set to 0.\n2. We iterate through the `nums` array using a for loop, starting from the first element and going up to the last element.\n3. For each element in the array, we add it to the current sum `currentSum`. This calculates the sum of the subarray ending at the current element.\n4. Next, we check if the current sum `currentSum` is greater than the current maximum sum `maxSum`.\n - If it is, we update `maxSum` with the new value of `currentSum`. This means we have found a new maximum subarray sum.\n5. If the current sum `currentSum` becomes negative, it indicates that including the current element in the subarray would reduce the overall sum. In such cases, we reset `currentSum` to 0. This effectively discards the current subarray and allows us to start a fresh subarray from the next element.\n6. We repeat steps 3 to 5 for each element in the array.\n7. After iterating through the entire array, the variable `maxSum` will contain the maximum subarray sum encountered.\n8. Finally, we return the value of `maxSum` as the result, representing the maximum sum of a contiguous subarray within the given array `nums`.\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int maxSubArray(vector<int>& nums) {\n int maxSum = INT_MIN;\n int currentSum = 0;\n \n for (int i = 0; i < nums.size(); i++) {\n currentSum += nums[i];\n \n if (currentSum > maxSum) {\n maxSum = currentSum;\n }\n \n if (currentSum < 0) {\n currentSum = 0;\n }\n }\n \n return maxSum;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxSubArray(int[] nums) {\n int maxSum = Integer.MIN_VALUE;\n int currentSum = 0;\n \n for (int i = 0; i < nums.length; i++) {\n currentSum += nums[i];\n \n if (currentSum > maxSum) {\n maxSum = currentSum;\n }\n \n if (currentSum < 0) {\n currentSum = 0;\n }\n }\n \n return maxSum;\n }\n}\n```\n```Python3 []\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n maxSum = float(\'-inf\')\n currentSum = 0\n \n for num in nums:\n currentSum += num\n \n if currentSum > maxSum:\n maxSum = currentSum\n \n if currentSum < 0:\n currentSum = 0\n \n return maxSum\n```\n\n# clean code\n\n```C++ []\nclass Solution {\npublic:\n int maxSubArray(vector<int>& nums) {\n int maxSum = nums[0];\n int currentSum = nums[0];\n\n for (int i = 1; i < nums.size(); i++) {\n currentSum = max(nums[i], currentSum + nums[i]);\n maxSum = max(maxSum, currentSum);\n }\n\n return maxSum;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxSubArray(int[] nums) {\n int maxSum = nums[0];\n int currentSum = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n currentSum = Math.max(nums[i], currentSum + nums[i]);\n maxSum = Math.max(maxSum, currentSum);\n }\n\n return maxSum;\n }\n}\n```\n```Python3 []\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n maxSum = nums[0]\n currentSum = nums[0]\n\n for num in nums[1:]:\n currentSum = max(num, currentSum + num)\n maxSum = max(maxSum, currentSum)\n\n return maxSum\n```\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote for more questions.**\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 324 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
90% intuitive Python solution -- Imagine you are walking through a mountain range | maximum-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n Imagine the array is a list of steps up and down in the mountain. You are traversing the mountain from left to right.\n You are wondering what is the longest way up there is in this mountain.\n\n Keep track of the lowest point you have been to so far.\n Every time, compare your current elevation with the lowest point. This is how high you have come since the last lowest point.\n If this way up is the highest so far, then it\'s your new longest way up.\n\n Oonce you are done traversing the whole mountain, then this is the largest way up, i.e. your largest contiguous subarray.\n\n# Complexity\n- Time complexity: O(n) -- One pass of the list\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) -- Keep track of current lowest elevation, and current largest increase in elevation\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n return my_solution_mountain_range(nums)\n\ndef my_solution_mountain_range(nums: List[int]) -> int:\n """\n Imagine the array is a list of steps up and down in the mountain. You are traversing the mountain from left to right.\n You are wondering what is the longest way up there is in this mountain.\n\n Keep track of the lowest point you have been to so far.\n Every time, compare your current elevation with the lowest point. This is how high you have come since the last lowest point.\n If this way up is the highest so far, then it\'s your new longest way up.\n\n Oonce you are done traversing the whole mountain, then this is the largest way up, i.e. your largest contiguous subarray.\n """\n # special case: if all numbers are negative, then just the "least small" is the greatest sum\n _max_neg_all = - float("inf")\n all_neg = True\n for n in nums:\n if n > 0:\n all_neg = False\n break\n if n > _max_neg_all:\n _max_neg_all = n\n if all_neg:\n return _max_neg_all\n\n current_elevation = 0\n min_elevation = 0\n current_largest_increase = 0\n for n in nums:\n current_elevation += n\n if current_elevation < min_elevation:\n min_elevation = current_elevation\n if current_largest_increase < current_elevation - min_elevation:\n current_largest_increase = current_elevation - min_elevation\n return current_largest_increase\n\n``` | 1 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
Simple Python Solution | maximum-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSolve Problem using basic and simple python knowledge\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nKadane\'s algorithm\n\n**Explanation:**\n\n Initialization:\n\n---\n\n\n- arr: The input array for which we want to find the maximum sum subarray.\n- l and r: Pointers indicating the left and right boundaries of the current subarray.\n- res: Variable to store the maximum sum found so far (initialized to negative infinity for comparison).\n- prod: Current sum of the subarray.\n- \n\n---\n\n Main Loop:\n\n- The algorithm iterates through the array using the right pointer r.\n- For each element at index r, it adds the element to the current sum prod.\n- The result res is updated to be the maximum of the current result and the current sum.\n- \n\n---\n\nHandling Negative Sums:\n\n- If the current sum becomes negative (prod < 0), it means that continuing the current subarray would not yield a maximum sum.\n- In this case, the subarray is reset by moving the left pointer l to the next position after r, and the current sum prod is reset to 0.\n- \n\n---\n\nUpdating Pointers:\n\n- The right pointer r is incremented to move to the next element in the array.\n- \n\n---\n\nResult:\n\n- The final result res contains the maximum sum of a subarray in the given array.\n\n\n---\n\nThis algorithm has a time complexity of O(n), where n is the length of the input array. It\'s an efficient way to find the maximum sum subarray.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n l = 0\n r = 0\n res = float(\'-inf\') # Initialize res to negative infinity for comparison\n prod = 0\n length = len(nums)\n\n while r < length:\n prod = prod + nums[r]\n res = max(res, prod)\n \n if prod < 0:\n # If the current sum is negative, reset the window\n prod = 0\n l = r + 1\n \n r += 1\n\n return(res)\n\n \n``` | 1 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
Kadane's Algo || O(n) time and O(1) space || Easiest Beginner friendly Sol | maximum-subarray | 1 | 1 | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem:\nWe can solve this problem using **Kadane\'s Algorithm**\n\n**LETS DRY RUN THIS CODE WITH ONE EXAPMPLE :**\n\nSuppose we have the following input vector: **[-2, 1, -3, 4, -1, 2, 1, -5, 4].**\n\nWe initialize the maximumSum = INT_MIN (-2147483648) and currSumSubarray = 0.\n\nWe loop through the input vector and perform the following operations:\n\nAt the first iteration, currSumSubarray becomes -2 and since it is less than 0, we set it to 0. maximumSum remains at INT_MIN.\n\nAt the second iteration, currSumSubarray becomes 1, which is greater than 0, so we keep it as it is. We update maximumSum to 1.\n\nAt the third iteration, currSumSubarray becomes -2, which is less than 0, so we set it to 0. maximumSum remains at 1.\n\nAt the fourth iteration, currSumSubarray becomes 4, which is greater than 0, so we keep it as it is. We update maximumSum to 4.\n\nAt the fifth iteration, currSumSubarray becomes 3, which is greater than 0, so we keep it as it is. maximumSum remains at 4.\n\nAt the sixth iteration, currSumSubarray becomes 5, which is greater than 0, so we keep it as it is. We update maximumSum to 5.\n\nAt the seventh iteration, currSumSubarray becomes 6, which is greater than 0, so we keep it as it is. We update maximumSum to 6.\n\nAt the eighth iteration, currSumSubarray becomes 1, which is greater than 0, so we keep it as it is. maximumSum remains at 6.\n\nAt the ninth iteration, currSumSubarray becomes 5, which is greater than 0, so we keep it as it is. maximumSum remains at 6.\n\nAfter iterating through the input vector, we return maximumSum which is equal to 6. Therefore, the maximum sum subarray of the given input vector is [4, -1, 2, 1], and the sum of this subarray is 6.\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem:\n1. Initialize two variables, maximumSum and currSumSubarray to the minimum integer value (INT_MIN) and 0, respectively.\n2. Loop through the array from index 0 to n-1, where n is the size of the array.\n3. In each iteration, add the current element of the array to the currSumSubarray variable.\n4. Take the maximum between maximumSum and currSumSubarray and store it in the maximumSum variable.\n5. Take the maximum between currSumSubarray and 0 and store it in currSumSubarray. This is done because if the currSumSubarray becomes negative, it means that we should start a new subarray, so we reset currSumSubarray to 0.\n6. After the loop ends, return the maximumSum variable, which contains the maximum sum of a subarray.\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int maxSubArray(vector<int>& nums) {\n int n = nums.size();\n //maximumSum will calculate our ans and currSumSubarray will calculate maximum sum subarray till ith position \n int maximumSum = INT_MIN, currSumSubarray = 0;\n for (int i = 0; i < n; i++) {\n currSumSubarray += nums[i]; \n maximumSum = max(maximumSum, currSumSubarray);\n //here we are taking max with 0 bcz if currSumSubarray = -1 or any negative value then it again starts with currSumSubarray = 0\n currSumSubarray = max(currSumSubarray, 0);\n } \n return maximumSum;\n }\n};\n```\n```Java []\nclass Solution {\n public int maxSubArray(int[] nums) {\n int n = nums.length;\n int maximumSum = Integer.MIN_VALUE, currSumSubarray = 0;\n for (int i = 0; i < n; i++) {\n currSumSubarray += nums[i]; \n maximumSum = Math.max(maximumSum, currSumSubarray);\n currSumSubarray = Math.max(currSumSubarray, 0);\n } \n return maximumSum;\n }\n}\n\n```\n```Python []\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n n = len(nums)\n maximumSum, currSumSubarray = float(\'-inf\'), 0\n for i in range(n):\n currSumSubarray += nums[i]\n maximumSum = max(maximumSum, currSumSubarray)\n currSumSubarray = max(currSumSubarray, 0)\n return maximumSum\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the size of the input array. The algorithm has to loop through the array only once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, since the algorithm is using only a constant amount of extra space regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 103 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
Simplest Python Solution using Kadane's Algorithm | maximum-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Code\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n maxi = float(\'-inf\')\n temp = 0\n for i in nums:\n temp += i \n maxi = max(maxi,temp)\n temp = 0 if temp <0 else temp\n return maxi\n``` | 1 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
153. Solution | maximum-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing Kadan\'s Algorithm\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n max_so_far = float("-inf")\n max_ending_here = 0\n\n for i in range (len(nums)):\n max_ending_here = max_ending_here + nums[i]\n if (max_so_far < max_ending_here):\n max_so_far = max_ending_here\n if (max_ending_here < 0):\n max_ending_here = 0\n return max_so_far\n``` | 1 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
Very Easy 100% (Fully Explained)(Java, C++, Python, JavaScript, C, Python3) | maximum-subarray | 1 | 1 | # **Java Solution (Dynamic Programming Approach):**\nRuntime: 1 ms, faster than 89.13% of Java online submissions for Maximum Subarray.\n```\nclass Solution {\n public int maxSubArray(int[] nums) {\n // Initialize currMaxSum & take first element of array from which we start to do sum...\n int maxSum = nums[0];\n // Initialize the current sum of our subarray as nums[0]...\n int currSum = nums[0];\n // Traverse all the element through the loop...\n for (int i = 1; i < nums.length; i++) {\n // Do sum of elements contigous with curr sum...\n // Compare it with array element to get maximum result...\n currSum = Math.max(currSum + nums[i], nums[i]);\n // Compare current sum and max sum.\n maxSum = Math.max(maxSum, currSum);\n }\n return maxSum; // return the contiguous subarray which has the largest sum...\n }\n}\n```\n\n# **C++ Solution (Kadane\u2019s approach):**\n```\nclass Solution {\npublic:\n int maxSubArray(vector<int>& nums) {\n // Initialize maxSum as an integer that cannot store any value below the limit...\n int maxSum = INT_MIN;\n // Initialize maxSum...\n int maxSumSoFar = 0;\n // Traverse all the element through the loop...\n for(int i = 0; i < nums.size(); i++){\n // Keep adding the current value...\n maxSumSoFar += nums[i];\n // Update maxSum to maxSum and maxSumSoFar...\n if(maxSum < maxSumSoFar){\n maxSum = maxSumSoFar;\n }\n // if maxSumSoFar is less than 0 then update it to 0...\n if(maxSumSoFar < 0){\n maxSumSoFar = 0;\n }\n }\n return maxSum; // Return the contiguous subarray which has the largest sum...\n }\n};\n```\n\n# **Python Solution (Dynamic Programming Approach):**\nRuntime: 585 ms, faster than 95.18% of Python online submissions for Maximum Subarray.\nMemory Usage: 25.3 MB, less than 97.76% of Python online submissions for Maximum Subarray.\n```\nclass Solution(object):\n def maxSubArray(self, nums):\n # Create an array...\n arr = []\n arr.append(nums[0])\n # Initialize the max sum...\n maxSum = arr[0]\n # Traverse all the element through the loop...\n for i in range(1, len(nums)):\n # arr[i] represents the largest sum of all subarrays ending with index i...\n # then its value should be the larger one between nums[i]...\n # arr[i-1] + nums[i] (largest sum plus current number with using prefix)...\n # calculate arr[0], arr[1]\u2026, arr[n] while comparing each one with current largest sum...\n arr.append(max(arr[i-1] + nums[i], nums[i]))\n # if arr[i] > maxSum then maxSum = arr[i].\n if arr[i] > maxSum:\n maxSum = arr[i]\n return maxSum # Return the contiguous subarray which has the largest sum...\n```\n \n# **JavaScript Solution (Dynamic Programming Approach):**\nRuntime: 103 ms, faster than 75.34% of JavaScript online submissions for Maximum Subarray.\n```\nvar maxSubArray = function(nums) {\n // Initialize the max sum...\n let maxSum = nums[0];\n // Traverse all the element through the loop...\n for (let i = 1; i < nums.length; i++) {\n // nums[i] represents the largest sum of all subarrays ending with index i...\n // then its value should be the larger one between nums[i]...\n // nums[i-1] + nums[i] (largest sum plus current number with using prefix)...\n // calculate nums[0], nums[1]\u2026, nums[n] while comparing each one with current largest sum...\n nums[i] = Math.max(0, nums[i - 1]) + nums[i];\n // if nums[i] > maxSum then maxSum = nums[i]...\n if (nums[i] > maxSum)\n maxSum = nums[i];\n }\n return maxSum; // return the contiguous subarray which has the largest sum...\n};\n```\n\n# **C Language (Kadane\u2019s approach):**\n```\nint maxSubArray(int* nums, int numsSize){\n // Initialize maxSum as an integer that cannot store any value below the limit...\n int maxSum = nums[0];\n // Initialize maxSum...\n int maxSumSoFar = 0;\n // Traverse all the element through the loop...\n for(int i = 0; i < numsSize; i++){\n // Keep adding the current value...\n maxSumSoFar += nums[i];\n // Update maxSum to maxSum and maxSumSoFar...\n if(maxSum < maxSumSoFar){\n maxSum = maxSumSoFar;\n }\n // if maxSumSoFar is less than 0 then update it to 0...\n if(maxSumSoFar < 0){\n maxSumSoFar = 0;\n }\n }\n return maxSum; // Return the contiguous subarray which has the largest sum...\n}\n```\n\n# **Python3 Solution (Dynamic Programming Approach):**\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n # Create an array...\n arr = []\n arr.append(nums[0])\n # Initialize the max sum...\n maxSum = arr[0]\n for i in range(1, len(nums)):\n # arr[i] represents the largest sum of all subarrays ending with index i...\n # then its value should be the larger one between nums[i]...\n # arr[i-1] + nums[i] (largest sum plus current number with using prefix)...\n # calculate arr[0], arr[1]\u2026, arr[n] while comparing each one with current largest sum...\n arr.append(max(arr[i-1] + nums[i], nums[i]))\n # if arr[i] > maxSum then maxSum = arr[i].\n if arr[i] > maxSum:\n maxSum = arr[i]\n return maxSum # Return the contiguous subarray which has the largest sum...\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 151 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
pyhton clean & simple ✅ | | kaden algo. O(n) | | beats 93%🔥🔥🔥 | maximum-subarray | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSubArray(self, nums: List[int]) -> int:\n s = 0 \n maxi = -10001\n \n for i in range(len(nums)):\n s += nums[i]\n if s > maxi: maxi = s\n if s < 0:\n s = 0\n return maxi\n\n``` | 4 | Given an integer array `nums`, find the subarray with the largest sum, and return _its sum_.
**Example 1:**
**Input:** nums = \[-2,1,-3,4,-1,2,1,-5,4\]
**Output:** 6
**Explanation:** The subarray \[4,-1,2,1\] has the largest sum 6.
**Example 2:**
**Input:** nums = \[1\]
**Output:** 1
**Explanation:** The subarray \[1\] has the largest sum 1.
**Example 3:**
**Input:** nums = \[5,4,-1,7,8\]
**Output:** 23
**Explanation:** The subarray \[5,4,-1,7,8\] has the largest sum 23.
**Constraints:**
* `1 <= nums.length <= 105`
* `-104 <= nums[i] <= 104`
**Follow up:** If you have figured out the `O(n)` solution, try coding another solution using the **divide and conquer** approach, which is more subtle. | null |
Binbin the charismatic scientist is back! | spiral-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n L=[]\n m = len(matrix)\n n = len(matrix[0])\n if m == 1:\n for j in range(n):\n L.append(matrix[0][j])\n return L\n if n == 1:\n for i in range(m):\n L.append(matrix[i][0])\n return L\n r = 1\n\n while m- 2*r >= 0 and n-2*r >=-1:\n for j in range(-1+r,n-r):\n L.append(matrix[r-1][j])\n #print(L)\n for i in range(r-1,m-r):\n L.append(matrix[i][n-r])\n # print(L)\n if m == 2*r-1:\n return L\n for j in range(n-r,r-1,-1):\n i = m-r\n L.append(matrix[i][j])\n #print(L)\n if n == 2*r -1:\n L.append(matrix[m-r][n-r])\n return L\n for i in range(m-r,r-1,-1):\n j = r-1\n L.append(matrix[i][j])\n #print(L)\n r += 1\n #print(r)\n if m - 2*r == -1 and n-2*r >= -1:\n for j in range (r-1,n-r+1):\n L.append(matrix[r-1][j])\n\n return L\n\n\n \n``` | 1 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Binbin the charismatic scientist is back! | spiral-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n L=[]\n m = len(matrix)\n n = len(matrix[0])\n if m == 1:\n for j in range(n):\n L.append(matrix[0][j])\n return L\n if n == 1:\n for i in range(m):\n L.append(matrix[i][0])\n return L\n r = 1\n\n while m- 2*r >= 0 and n-2*r >=-1:\n for j in range(-1+r,n-r):\n L.append(matrix[r-1][j])\n #print(L)\n for i in range(r-1,m-r):\n L.append(matrix[i][n-r])\n # print(L)\n if m == 2*r-1:\n return L\n for j in range(n-r,r-1,-1):\n i = m-r\n L.append(matrix[i][j])\n #print(L)\n if n == 2*r -1:\n L.append(matrix[m-r][n-r])\n return L\n for i in range(m-r,r-1,-1):\n j = r-1\n L.append(matrix[i][j])\n #print(L)\n r += 1\n #print(r)\n if m - 2*r == -1 and n-2*r >= -1:\n for j in range (r-1,n-r+1):\n L.append(matrix[r-1][j])\n\n return L\n\n\n \n``` | 1 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | spiral-matrix | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. I planned to give for next 10,000 Subscribers as well. If you\'re interested **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution \n\n# Search \uD83D\uDC49 `Spiral Matrix by Tech Wired `\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\n- We will use a while loop to traverse the matrix in a clockwise spiral order.\n- We will define four variables: left, right, top, bottom to represent the four boundaries of the current spiral.\n- We will use four for loops to traverse each edge of the current spiral in clockwise order and add the elements to the result list.\n- We will update the boundaries of the current spiral and continue the process until all elements have been traversed.\n\n# Intuition:\n\n- We start with the outermost layer of the matrix and traverse it in a clockwise spiral order, adding the elements to the result list.\n- Then we move on to the next inner layer of the matrix and repeat the process until we have traversed all layers.\n- To traverse each layer, we need to keep track of the four boundaries of the current spiral.\n- We start at the top-left corner of the current spiral and move right until we hit the top-right corner.\n- Then we move down to the bottom-right corner and move left until we hit the bottom-left corner.\n- Finally, we move up to the top-left corner of the next spiral and repeat the process until we have traversed all elements in the matrix.\n\n\n\n\n\n```Python []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n if not matrix:\n return []\n\n rows, cols = len(matrix), len(matrix[0])\n top, bottom, left, right = 0, rows-1, 0, cols-1\n result = []\n \n while len(result) < rows * cols:\n for i in range(left, right+1):\n result.append(matrix[top][i])\n top += 1\n \n for i in range(top, bottom+1):\n result.append(matrix[i][right])\n right -= 1\n \n if top <= bottom:\n for i in range(right, left-1, -1):\n result.append(matrix[bottom][i])\n bottom -= 1\n \n if left <= right:\n for i in range(bottom, top-1, -1):\n result.append(matrix[i][left])\n left += 1\n \n return result\n\n```\n```Java []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n List<Integer> result = new ArrayList<>();\n if (matrix == null || matrix.length == 0) {\n return result;\n }\n \n int rows = matrix.length, cols = matrix[0].length;\n int left = 0, right = cols-1, top = 0, bottom = rows-1;\n \n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n result.add(matrix[top][i]);\n }\n top++;\n \n for (int i = top; i <= bottom; i++) {\n result.add(matrix[i][right]);\n }\n right--;\n \n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n result.add(matrix[bottom][i]);\n }\n bottom--;\n }\n \n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n result.add(matrix[i][left]);\n }\n left++;\n }\n }\n \n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n vector<int> result;\n if (matrix.empty() || matrix[0].empty()) {\n return result;\n }\n \n int rows = matrix.size(), cols = matrix[0].size();\n int left = 0, right = cols-1, top = 0, bottom = rows-1;\n \n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n result.push_back(matrix[top][i]);\n }\n top++;\n \n for (int i = top; i <= bottom; i++) {\n result.push_back(matrix[i][right]);\n }\n right--;\n \n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n result.push_back(matrix[bottom][i]);\n }\n bottom--;\n }\n \n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n result.push_back(matrix[i][left]);\n }\n left++;\n }\n }\n \n return result;\n }\n};\n\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D | 215 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | spiral-matrix | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. I planned to give for next 10,000 Subscribers as well. If you\'re interested **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution \n\n# Search \uD83D\uDC49 `Spiral Matrix by Tech Wired `\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\n- We will use a while loop to traverse the matrix in a clockwise spiral order.\n- We will define four variables: left, right, top, bottom to represent the four boundaries of the current spiral.\n- We will use four for loops to traverse each edge of the current spiral in clockwise order and add the elements to the result list.\n- We will update the boundaries of the current spiral and continue the process until all elements have been traversed.\n\n# Intuition:\n\n- We start with the outermost layer of the matrix and traverse it in a clockwise spiral order, adding the elements to the result list.\n- Then we move on to the next inner layer of the matrix and repeat the process until we have traversed all layers.\n- To traverse each layer, we need to keep track of the four boundaries of the current spiral.\n- We start at the top-left corner of the current spiral and move right until we hit the top-right corner.\n- Then we move down to the bottom-right corner and move left until we hit the bottom-left corner.\n- Finally, we move up to the top-left corner of the next spiral and repeat the process until we have traversed all elements in the matrix.\n\n\n\n\n\n```Python []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n if not matrix:\n return []\n\n rows, cols = len(matrix), len(matrix[0])\n top, bottom, left, right = 0, rows-1, 0, cols-1\n result = []\n \n while len(result) < rows * cols:\n for i in range(left, right+1):\n result.append(matrix[top][i])\n top += 1\n \n for i in range(top, bottom+1):\n result.append(matrix[i][right])\n right -= 1\n \n if top <= bottom:\n for i in range(right, left-1, -1):\n result.append(matrix[bottom][i])\n bottom -= 1\n \n if left <= right:\n for i in range(bottom, top-1, -1):\n result.append(matrix[i][left])\n left += 1\n \n return result\n\n```\n```Java []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n List<Integer> result = new ArrayList<>();\n if (matrix == null || matrix.length == 0) {\n return result;\n }\n \n int rows = matrix.length, cols = matrix[0].length;\n int left = 0, right = cols-1, top = 0, bottom = rows-1;\n \n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n result.add(matrix[top][i]);\n }\n top++;\n \n for (int i = top; i <= bottom; i++) {\n result.add(matrix[i][right]);\n }\n right--;\n \n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n result.add(matrix[bottom][i]);\n }\n bottom--;\n }\n \n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n result.add(matrix[i][left]);\n }\n left++;\n }\n }\n \n return result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n vector<int> result;\n if (matrix.empty() || matrix[0].empty()) {\n return result;\n }\n \n int rows = matrix.size(), cols = matrix[0].size();\n int left = 0, right = cols-1, top = 0, bottom = rows-1;\n \n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n result.push_back(matrix[top][i]);\n }\n top++;\n \n for (int i = top; i <= bottom; i++) {\n result.push_back(matrix[i][right]);\n }\n right--;\n \n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n result.push_back(matrix[bottom][i]);\n }\n bottom--;\n }\n \n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n result.push_back(matrix[i][left]);\n }\n left++;\n }\n }\n \n return result;\n }\n};\n\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D | 215 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
✔💯 DAY 404 | BRUTE->BETTER->OPTIMAL->1- LINER | 0MS-100% | | [PYTHON/JAVA/C++] | EXPLAINED 🆙🆙🆙 | spiral-matrix | 1 | 1 | \n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# BRUTE\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\nBrute Force Approach:\n\nUse a stack and a 2D array to traverse the matrix in spiral order. It starts at the top-left corner of the matrix and pushes the coordinates onto the stack. It then pops the coordinates from the stack and checks if they are within the boundaries of the matrix and if they have been visited before. If they have not been visited, the value at that coordinate is added to the answer list and the coordinate is marked as visited. The program then checks the next coordinate in the direction of traversal (which is determined by the direction array) and pushes it onto the stack. If the next coordinate is out of bounds or has been visited before, the direction of traversal is changed by incrementing the index of the direction array. The program continues to pop coordinates from the stack until it is empty, at which point it returns the answer list.\n\n```java []\npublic List<Integer> spiralOrder(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n List<Integer> answer = new ArrayList<>();\n int[][] direction = {{1,0}, {0,-1}, {-1,0}, {0,1}};\n int[][] visited = new int[m][n];\n for(int i = 0; i < m; i++) {\n Arrays.fill(visited[i], 0);\n }\n Consumer<int[]> traverse = (coord) -> {\n int index = 3;\n Stack<int[]> stack = new Stack<>();\n stack.push(coord);\n while(!stack.isEmpty()) {\n coord = stack.pop();\n if(coord[0] >= m || coord[0] < 0 || coord[1] >= n || coord[1] < 0 || visited[coord[0]][coord[1]] == 1) {\n continue;\n }\n answer.add(matrix[coord[0]][coord[1]]);\n visited[coord[0]][coord[1]] = 1;\n int[] coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n if(coord2[0] >= m || coord2[0] < 0 || coord2[1] >= n || coord2[1] < 0 || visited[coord2[0]][coord2[1]] == 1) {\n index = (index + 1) % 4;\n }\n coord2 = new int[]{coord[0] + direction[index][0], coord[1] + direction[index][1]};\n stack.push(coord2);\n }\n };\n traverse.accept(new int[]{0,0});\n return answer;\n}\n```\n```c++ []\nvector<int> spiralOrder(vector<vector<int>>& matrix) {\n int m = matrix.size();\n int n = matrix[0].size();\n vector<int> answer;\n vector<vector<int>> direction = {{1,0}, {0,-1}, {-1,0}, {0,1}};\n vector<vector<int>> visited(m, vector<int>(n, 0));\n function<void(vector<int>, int)> traverse = [&](vector<int> coord, int index) {\n if(coord[0] >= m || coord[0] < 0 || coord[1] >= n || coord[1] < 0 || visited[coord[0]][coord[1]] == 1) {\n return;\n }\n answer.push_back(matrix[coord[0]][coord[1]]);\n visited[coord[0]][coord[1]] = 1;\n vector<int> coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n if(coord2[0] >= m || coord2[0] < 0 || coord2[1] >= n || coord2[1] < 0 || visited[coord2[0]][coord2[1]] == 1) {\n index = (index + 1) % 4;\n }\n coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n traverse(coord2, index);\n };\n traverse({0,0}, 3);\n return answer;\n}\n```\n```python []\ndef spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n m = len(matrix)\n n = len(matrix[0])\n answer = []\n direction = [[1,0],[0,-1],[-1,0],[0,1]]\n visited = []\n for i in range(m):\n visited.append([0]*n)\n def traverse(coord, index):\n if coord[0] >= m or coord[0] < 0 or coord[1] >= n or coord[0] < 0 or visited[coord[0]][coord[1]] == 1:\n return\n answer.append(matrix[coord[0]][coord[1]])\n visited[coord[0]][coord[1]] = 1\n coord2 = [a + b for a, b in zip(coord, direction[index])]\n if coord2[0] >= m or coord2[0] < 0 or coord2[1] >= n or coord2[0] < 0 or visited[coord2[0]][coord2[1]] == 1:\n index = (index + 1) % 4\n coord2 = [a + b for a, b in zip(coord, direction[index])]\n traverse(coord2, index)\n traverse([0,0],3)\n return answer\n```\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# BETTER \n\nBetter Approach:\n\nThis approach uses four variables to keep track of the boundaries of the matrix and a variable to keep track of the direction of traversal. It starts at the top-left corner of the matrix and adds the value at that coordinate to the result list. It then checks the direction of traversal and increments or decrements the row or column index accordingly. If the index reaches a boundary, the boundary is updated and the direction of traversal is changed. The program continues to add values to the result list until it has added all the values in the matrix. Finally, it returns the result list. This approach is similar to the previous approaches, but it uses boundary variables and a character variable to keep track of the direction of traversal instead of a 2D array.\n\n\n# Code\n```java []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n int nrow = matrix.length;\n int ncol = matrix[0].length;\n int l_wall = -1, r_wall = ncol, u_wall = 0, d_wall = nrow;\n char direction = \'r\';\n List<Integer> result = new ArrayList<>();\n int i = 0, j = 0;\n while(result.size() < nrow * ncol) {\n result.add(matrix[i][j]);\n if(direction == \'r\') {\n j++;\n if(j == r_wall) {\n r_wall--;\n j = r_wall;\n direction = \'d\';\n i++;\n }\n }\n else if(direction == \'d\') {\n i++;\n if(i == d_wall) {\n d_wall--;\n i = d_wall;\n direction = \'l\';\n j--;\n }\n }\n else if(direction == \'l\') {\n j--;\n if(j == l_wall) {\n l_wall++;\n j = l_wall;\n direction = \'u\';\n i--;\n }\n }\n else if(direction == \'u\') {\n i--;\n if(i == u_wall) {\n u_wall++;\n i = u_wall;\n direction = \'r\';\n j++;\n }\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n int nrow = matrix.size();\n int ncol = matrix[0].size();\n int l_wall = -1, r_wall = ncol, u_wall = 0, d_wall = nrow;\n char direction = \'r\';\n vector<int> result;\n int i = 0, j = 0;\n while(result.size() < nrow * ncol) {\n result.push_back(matrix[i][j]);\n if(direction == \'r\') {\n j++;\n if(j == r_wall) {\n r_wall--;\n j = r_wall;\n direction = \'d\';\n i++;\n }\n }\n else if(direction == \'d\') {\n i++;\n if(i == d_wall) {\n d_wall--;\n i = d_wall;\n direction = \'l\';\n j--;\n }\n }\n else if(direction == \'l\') {\n j--;\n if(j == l_wall) {\n l_wall++;\n j = l_wall;\n direction = \'u\';\n i--;\n }\n }\n else if(direction == \'u\') {\n i--;\n if(i == u_wall) {\n u_wall++;\n i = u_wall;\n direction = \'r\';\n j++;\n }\n }\n }\n return result;\n }\n};\n```\n```PYTHON []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n nrow, ncol = len(matrix), len(matrix[0])\n l_wall, r_wall = -1, ncol\n u_wall, d_wall = 0, nrow\n direction = \'r\'\n result = []\n i, j = 0, 0\n while len(result) < nrow * ncol:\n result.append(matrix[i][j])\n if direction == \'r\':\n j += 1\n if j == r_wall:\n r_wall -= 1\n j = r_wall\n direction = \'d\'\n i += 1\n elif direction == \'d\':\n i += 1\n if i == d_wall:\n d_wall -= 1\n i = d_wall\n direction = \'l\'\n j -= 1\n elif direction == \'l\':\n j -= 1\n if j == l_wall:\n l_wall += 1\n j = l_wall\n direction = \'u\'\n i -= 1\n elif direction == \'u\':\n i -= 1\n if i == u_wall:\n u_wall += 1\n i = u_wall\n direction = \'r\'\n j += 1\n return result\n```\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# Optimal\n\nOptimal Approach:\n\nWe can further optimize the above approach by using a single loop to traverse the matrix in a spiral order. We start by initializing the top, bottom, left, and right pointers to the edges of the matrix. We then use a single loop to traverse the matrix in a spiral order by moving the pointers inward after each traversal. We continue this process until we have visited all elements of the matrix.\n\n\n```JAVA []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n List<Integer> result = new ArrayList<>();\n if(matrix == null || matrix.length == 0) {\n return result;\n }\n int m = matrix.length;\n int n = matrix[0].length;\n int top = 0, bottom = m - 1, left = 0, right = n - 1;\n while(top <= bottom && left <= right) {\n // Traverse right\n for(int i = left; i <= right; i++) {\n result.add(matrix[top][i]);\n }\n top++;\n // Traverse down\n for(int i = top; i <= bottom; i++) {\n result.add(matrix[i][right]);\n }\n right--;\n // Traverse left\n if(top <= bottom) {\n for(int i = right; i >= left; i--) {\n result.add(matrix[bottom][i]);\n }\n bottom--;\n }\n // Traverse up\n if(left <= right) {\n for(int i = bottom; i >= top; i--) {\n result.add(matrix[i][left]);\n }\n left++;\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n vector<int> result;\n if(matrix.empty() || matrix[0].empty()) {\n return result;\n }\n int m = matrix.size();\n int n = matrix[0].size();\n int top = 0, bottom = m - 1, left = 0, right = n - 1;\n while(top <= bottom && left <= right) {\n // Traverse right\n for(int i = left; i <= right; i++) {\n result.push_back(matrix[top][i]);\n }\n top++;\n // Traverse down\n for(int i = top; i <= bottom; i++) {\n result.push_back(matrix[i][right]);\n }\n right--;\n // Traverse left\n if(top <= bottom) {\n for(int i = right; i >= left; i--) {\n result.push_back(matrix[bottom][i]);\n }\n bottom--;\n }\n // Traverse up\n if(left <= right) {\n for(int i = bottom; i >= top; i--) {\n result.push_back(matrix[i][left]);\n }\n left++;\n }\n }\n return result;\n }\n};\n```\n```PYTHON []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n result = []\n if not matrix or not matrix[0]:\n return result\n m, n = len(matrix), len(matrix[0])\n top, bottom, left, right = 0, m - 1, 0, n - 1\n while top <= bottom and left <= right:\n # Traverse right\n for i in range(left, right + 1):\n result.append(matrix[top][i])\n top += 1\n # Traverse down\n for i in range(top, bottom + 1):\n result.append(matrix[i][right])\n right -= 1\n # Traverse left\n if top <= bottom:\n for i in range(right, left - 1, -1):\n result.append(matrix[bottom][i])\n bottom -= 1\n # Traverse up\n if left <= right:\n for i in range(bottom, top - 1, -1):\n result.append(matrix[i][left])\n left += 1\n return result\n```\n\n# ONE LINER \n```PYTHON []\ndef spiralOrder(self, matrix):\n return matrix and list(matrix.pop(0)) + self.spiralOrder(zip(*matrix)[::-1])\n```\n```PYTHON3 []\ndef spiralOrder(self, matrix):\n return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\n```\n```py []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n result = []\n while matrix:\n result += matrix.pop(0) # pop the first row each time\n matrix = list(zip(*matrix))[::-1] # left rotate matrix 90 degree each time\n return result\n```\n# how it works step by step.\n\nThe first line of the code checks if the matrix is not empty. If the matrix is empty, it returns an empty list. If the matrix is not empty, it proceeds with the traversal.\n\n##### \u2022return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\nThe second line of the code uses a list comprehension to extract the first row of the matrix and add it to the result list. It then uses the pop() method to remove the first row from the matrix.\n\n##### \u2022[*matrix.pop(0)]\nThe third line of the code uses the zip() function to transpose the matrix and then reverses the order of the rows using slicing. This creates a new matrix that can be traversed in the next recursive call.\n\n##### \u2022[*zip(*matrix)][::-1]\nThe fourth line of the code uses recursion to traverse the new matrix in a spiral order. The result of the recursive call is added to the result list using the + operator.\n\n##### \u2022self.spiralOrder([*zip(*matrix)][::-1])\nFinally, the result list is returned.\n\n##### \u2022return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\nusing recursive approach to traverse the matrix in a spiral order. It extracts the first row of the matrix, removes it from the matrix, transposes the matrix, and then reverses the order of the rows to create a new matrix that can be traversed in the next recursive call. The process continues until all elements of the matrix have been added to the result list.\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# DRY RUN\n\n\n##### \u2022\tExample 1:\n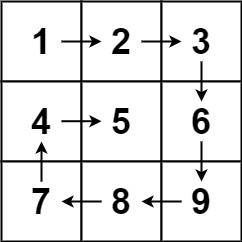\n##### \u2022\tInput: matrix = [[1,2,3],[4,5,6],[7,8,9]]\n##### \u2022\tOutput: [1,2,3,6,9,8,7,4,5]\n##### \u2022\tStep-by-Step Explanation:\n##### \u2022\tInitialize the result list as an empty list.\n##### \u2022\tSet the top, bottom, left, and right pointers to the edges of the matrix. top = 0, bottom = 2, left = 0, right = 2.\n##### \u2022\tTraverse the first row from left to right and add the elements to the result list. result = [1, 2, 3]. Increment the top pointer to 1.\n##### \u2022\tTraverse the last column from top to bottom and add the elements to the result list. result = [1, 2, 3, 6, 9]. Decrement the right pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is true, traverse the last row from right to left and add the elements to the result list. result = [1, 2, 3, 6, 9, 8, 7]. Decrement the bottom pointer to 1.\n##### \u2022\tCheck if left <= right. Since it is true, traverse the first column from bottom to top and add the elements to the result list. result = [1, 2, 3, 6, 9, 8, 7, 4, 5]. Increment the left pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is false, the traversal is complete. Return the result list.\n##### \u2022\tExample 2:\n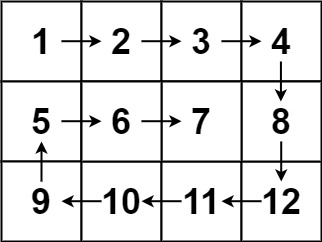\n##### \u2022\tInput: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]\n##### \u2022\tOutput: [1,2,3,4,8,12,11,10,9,5,6,7]\n##### \u2022\tStep-by-Step Explanation:\n##### \u2022\tInitialize the result list as an empty list.\n##### \u2022\tSet the top, bottom, left, and right pointers to the edges of the matrix. top = 0, bottom = 2, left = 0, right = 3.\n##### \u2022\tTraverse the first row from left to right and add the elements to the result list. result = [1, 2, 3, 4]. Increment the top pointer to 1.\n##### \u2022\tTraverse the last column from top to bottom and add the elements to the result list. result = [1, 2, 3, 4, 8, 12]. Decrement the right pointer to 2.\n##### \u2022\tCheck if top <= bottom. Since it is true, traverse the last row from right to left and add the elements to the result list. result = [1, 2, 3, 4, 8, 12, 11, 10, 9]. Decrement the bottom pointer to 1.\n##### \u2022\tCheck if left <= right. Since it is true, traverse the first column from bottom to top and add the elements to the result list. result = [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]. Increment the left pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is false, the traversal is complete. Return the result list.\n\n\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A | 114 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
✔💯 DAY 404 | BRUTE->BETTER->OPTIMAL->1- LINER | 0MS-100% | | [PYTHON/JAVA/C++] | EXPLAINED 🆙🆙🆙 | spiral-matrix | 1 | 1 | \n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# BRUTE\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\nBrute Force Approach:\n\nUse a stack and a 2D array to traverse the matrix in spiral order. It starts at the top-left corner of the matrix and pushes the coordinates onto the stack. It then pops the coordinates from the stack and checks if they are within the boundaries of the matrix and if they have been visited before. If they have not been visited, the value at that coordinate is added to the answer list and the coordinate is marked as visited. The program then checks the next coordinate in the direction of traversal (which is determined by the direction array) and pushes it onto the stack. If the next coordinate is out of bounds or has been visited before, the direction of traversal is changed by incrementing the index of the direction array. The program continues to pop coordinates from the stack until it is empty, at which point it returns the answer list.\n\n```java []\npublic List<Integer> spiralOrder(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n List<Integer> answer = new ArrayList<>();\n int[][] direction = {{1,0}, {0,-1}, {-1,0}, {0,1}};\n int[][] visited = new int[m][n];\n for(int i = 0; i < m; i++) {\n Arrays.fill(visited[i], 0);\n }\n Consumer<int[]> traverse = (coord) -> {\n int index = 3;\n Stack<int[]> stack = new Stack<>();\n stack.push(coord);\n while(!stack.isEmpty()) {\n coord = stack.pop();\n if(coord[0] >= m || coord[0] < 0 || coord[1] >= n || coord[1] < 0 || visited[coord[0]][coord[1]] == 1) {\n continue;\n }\n answer.add(matrix[coord[0]][coord[1]]);\n visited[coord[0]][coord[1]] = 1;\n int[] coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n if(coord2[0] >= m || coord2[0] < 0 || coord2[1] >= n || coord2[1] < 0 || visited[coord2[0]][coord2[1]] == 1) {\n index = (index + 1) % 4;\n }\n coord2 = new int[]{coord[0] + direction[index][0], coord[1] + direction[index][1]};\n stack.push(coord2);\n }\n };\n traverse.accept(new int[]{0,0});\n return answer;\n}\n```\n```c++ []\nvector<int> spiralOrder(vector<vector<int>>& matrix) {\n int m = matrix.size();\n int n = matrix[0].size();\n vector<int> answer;\n vector<vector<int>> direction = {{1,0}, {0,-1}, {-1,0}, {0,1}};\n vector<vector<int>> visited(m, vector<int>(n, 0));\n function<void(vector<int>, int)> traverse = [&](vector<int> coord, int index) {\n if(coord[0] >= m || coord[0] < 0 || coord[1] >= n || coord[1] < 0 || visited[coord[0]][coord[1]] == 1) {\n return;\n }\n answer.push_back(matrix[coord[0]][coord[1]]);\n visited[coord[0]][coord[1]] = 1;\n vector<int> coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n if(coord2[0] >= m || coord2[0] < 0 || coord2[1] >= n || coord2[1] < 0 || visited[coord2[0]][coord2[1]] == 1) {\n index = (index + 1) % 4;\n }\n coord2 = {coord[0] + direction[index][0], coord[1] + direction[index][1]};\n traverse(coord2, index);\n };\n traverse({0,0}, 3);\n return answer;\n}\n```\n```python []\ndef spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n m = len(matrix)\n n = len(matrix[0])\n answer = []\n direction = [[1,0],[0,-1],[-1,0],[0,1]]\n visited = []\n for i in range(m):\n visited.append([0]*n)\n def traverse(coord, index):\n if coord[0] >= m or coord[0] < 0 or coord[1] >= n or coord[0] < 0 or visited[coord[0]][coord[1]] == 1:\n return\n answer.append(matrix[coord[0]][coord[1]])\n visited[coord[0]][coord[1]] = 1\n coord2 = [a + b for a, b in zip(coord, direction[index])]\n if coord2[0] >= m or coord2[0] < 0 or coord2[1] >= n or coord2[0] < 0 or visited[coord2[0]][coord2[1]] == 1:\n index = (index + 1) % 4\n coord2 = [a + b for a, b in zip(coord, direction[index])]\n traverse(coord2, index)\n traverse([0,0],3)\n return answer\n```\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# BETTER \n\nBetter Approach:\n\nThis approach uses four variables to keep track of the boundaries of the matrix and a variable to keep track of the direction of traversal. It starts at the top-left corner of the matrix and adds the value at that coordinate to the result list. It then checks the direction of traversal and increments or decrements the row or column index accordingly. If the index reaches a boundary, the boundary is updated and the direction of traversal is changed. The program continues to add values to the result list until it has added all the values in the matrix. Finally, it returns the result list. This approach is similar to the previous approaches, but it uses boundary variables and a character variable to keep track of the direction of traversal instead of a 2D array.\n\n\n# Code\n```java []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n int nrow = matrix.length;\n int ncol = matrix[0].length;\n int l_wall = -1, r_wall = ncol, u_wall = 0, d_wall = nrow;\n char direction = \'r\';\n List<Integer> result = new ArrayList<>();\n int i = 0, j = 0;\n while(result.size() < nrow * ncol) {\n result.add(matrix[i][j]);\n if(direction == \'r\') {\n j++;\n if(j == r_wall) {\n r_wall--;\n j = r_wall;\n direction = \'d\';\n i++;\n }\n }\n else if(direction == \'d\') {\n i++;\n if(i == d_wall) {\n d_wall--;\n i = d_wall;\n direction = \'l\';\n j--;\n }\n }\n else if(direction == \'l\') {\n j--;\n if(j == l_wall) {\n l_wall++;\n j = l_wall;\n direction = \'u\';\n i--;\n }\n }\n else if(direction == \'u\') {\n i--;\n if(i == u_wall) {\n u_wall++;\n i = u_wall;\n direction = \'r\';\n j++;\n }\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n int nrow = matrix.size();\n int ncol = matrix[0].size();\n int l_wall = -1, r_wall = ncol, u_wall = 0, d_wall = nrow;\n char direction = \'r\';\n vector<int> result;\n int i = 0, j = 0;\n while(result.size() < nrow * ncol) {\n result.push_back(matrix[i][j]);\n if(direction == \'r\') {\n j++;\n if(j == r_wall) {\n r_wall--;\n j = r_wall;\n direction = \'d\';\n i++;\n }\n }\n else if(direction == \'d\') {\n i++;\n if(i == d_wall) {\n d_wall--;\n i = d_wall;\n direction = \'l\';\n j--;\n }\n }\n else if(direction == \'l\') {\n j--;\n if(j == l_wall) {\n l_wall++;\n j = l_wall;\n direction = \'u\';\n i--;\n }\n }\n else if(direction == \'u\') {\n i--;\n if(i == u_wall) {\n u_wall++;\n i = u_wall;\n direction = \'r\';\n j++;\n }\n }\n }\n return result;\n }\n};\n```\n```PYTHON []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n nrow, ncol = len(matrix), len(matrix[0])\n l_wall, r_wall = -1, ncol\n u_wall, d_wall = 0, nrow\n direction = \'r\'\n result = []\n i, j = 0, 0\n while len(result) < nrow * ncol:\n result.append(matrix[i][j])\n if direction == \'r\':\n j += 1\n if j == r_wall:\n r_wall -= 1\n j = r_wall\n direction = \'d\'\n i += 1\n elif direction == \'d\':\n i += 1\n if i == d_wall:\n d_wall -= 1\n i = d_wall\n direction = \'l\'\n j -= 1\n elif direction == \'l\':\n j -= 1\n if j == l_wall:\n l_wall += 1\n j = l_wall\n direction = \'u\'\n i -= 1\n elif direction == \'u\':\n i -= 1\n if i == u_wall:\n u_wall += 1\n i = u_wall\n direction = \'r\'\n j += 1\n return result\n```\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# Optimal\n\nOptimal Approach:\n\nWe can further optimize the above approach by using a single loop to traverse the matrix in a spiral order. We start by initializing the top, bottom, left, and right pointers to the edges of the matrix. We then use a single loop to traverse the matrix in a spiral order by moving the pointers inward after each traversal. We continue this process until we have visited all elements of the matrix.\n\n\n```JAVA []\nclass Solution {\n public List<Integer> spiralOrder(int[][] matrix) {\n List<Integer> result = new ArrayList<>();\n if(matrix == null || matrix.length == 0) {\n return result;\n }\n int m = matrix.length;\n int n = matrix[0].length;\n int top = 0, bottom = m - 1, left = 0, right = n - 1;\n while(top <= bottom && left <= right) {\n // Traverse right\n for(int i = left; i <= right; i++) {\n result.add(matrix[top][i]);\n }\n top++;\n // Traverse down\n for(int i = top; i <= bottom; i++) {\n result.add(matrix[i][right]);\n }\n right--;\n // Traverse left\n if(top <= bottom) {\n for(int i = right; i >= left; i--) {\n result.add(matrix[bottom][i]);\n }\n bottom--;\n }\n // Traverse up\n if(left <= right) {\n for(int i = bottom; i >= top; i--) {\n result.add(matrix[i][left]);\n }\n left++;\n }\n }\n return result;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> spiralOrder(vector<vector<int>>& matrix) {\n vector<int> result;\n if(matrix.empty() || matrix[0].empty()) {\n return result;\n }\n int m = matrix.size();\n int n = matrix[0].size();\n int top = 0, bottom = m - 1, left = 0, right = n - 1;\n while(top <= bottom && left <= right) {\n // Traverse right\n for(int i = left; i <= right; i++) {\n result.push_back(matrix[top][i]);\n }\n top++;\n // Traverse down\n for(int i = top; i <= bottom; i++) {\n result.push_back(matrix[i][right]);\n }\n right--;\n // Traverse left\n if(top <= bottom) {\n for(int i = right; i >= left; i--) {\n result.push_back(matrix[bottom][i]);\n }\n bottom--;\n }\n // Traverse up\n if(left <= right) {\n for(int i = bottom; i >= top; i--) {\n result.push_back(matrix[i][left]);\n }\n left++;\n }\n }\n return result;\n }\n};\n```\n```PYTHON []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n result = []\n if not matrix or not matrix[0]:\n return result\n m, n = len(matrix), len(matrix[0])\n top, bottom, left, right = 0, m - 1, 0, n - 1\n while top <= bottom and left <= right:\n # Traverse right\n for i in range(left, right + 1):\n result.append(matrix[top][i])\n top += 1\n # Traverse down\n for i in range(top, bottom + 1):\n result.append(matrix[i][right])\n right -= 1\n # Traverse left\n if top <= bottom:\n for i in range(right, left - 1, -1):\n result.append(matrix[bottom][i])\n bottom -= 1\n # Traverse up\n if left <= right:\n for i in range(bottom, top - 1, -1):\n result.append(matrix[i][left])\n left += 1\n return result\n```\n\n# ONE LINER \n```PYTHON []\ndef spiralOrder(self, matrix):\n return matrix and list(matrix.pop(0)) + self.spiralOrder(zip(*matrix)[::-1])\n```\n```PYTHON3 []\ndef spiralOrder(self, matrix):\n return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\n```\n```py []\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n result = []\n while matrix:\n result += matrix.pop(0) # pop the first row each time\n matrix = list(zip(*matrix))[::-1] # left rotate matrix 90 degree each time\n return result\n```\n# how it works step by step.\n\nThe first line of the code checks if the matrix is not empty. If the matrix is empty, it returns an empty list. If the matrix is not empty, it proceeds with the traversal.\n\n##### \u2022return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\nThe second line of the code uses a list comprehension to extract the first row of the matrix and add it to the result list. It then uses the pop() method to remove the first row from the matrix.\n\n##### \u2022[*matrix.pop(0)]\nThe third line of the code uses the zip() function to transpose the matrix and then reverses the order of the rows using slicing. This creates a new matrix that can be traversed in the next recursive call.\n\n##### \u2022[*zip(*matrix)][::-1]\nThe fourth line of the code uses recursion to traverse the new matrix in a spiral order. The result of the recursive call is added to the result list using the + operator.\n\n##### \u2022self.spiralOrder([*zip(*matrix)][::-1])\nFinally, the result list is returned.\n\n##### \u2022return matrix and [*matrix.pop(0)] + self.spiralOrder([*zip(*matrix)][::-1])\nusing recursive approach to traverse the matrix in a spiral order. It extracts the first row of the matrix, removes it from the matrix, transposes the matrix, and then reverses the order of the rows to create a new matrix that can be traversed in the next recursive call. The process continues until all elements of the matrix have been added to the result list.\n# Complexity\n- Time complexity:O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# DRY RUN\n\n\n##### \u2022\tExample 1:\n\n##### \u2022\tInput: matrix = [[1,2,3],[4,5,6],[7,8,9]]\n##### \u2022\tOutput: [1,2,3,6,9,8,7,4,5]\n##### \u2022\tStep-by-Step Explanation:\n##### \u2022\tInitialize the result list as an empty list.\n##### \u2022\tSet the top, bottom, left, and right pointers to the edges of the matrix. top = 0, bottom = 2, left = 0, right = 2.\n##### \u2022\tTraverse the first row from left to right and add the elements to the result list. result = [1, 2, 3]. Increment the top pointer to 1.\n##### \u2022\tTraverse the last column from top to bottom and add the elements to the result list. result = [1, 2, 3, 6, 9]. Decrement the right pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is true, traverse the last row from right to left and add the elements to the result list. result = [1, 2, 3, 6, 9, 8, 7]. Decrement the bottom pointer to 1.\n##### \u2022\tCheck if left <= right. Since it is true, traverse the first column from bottom to top and add the elements to the result list. result = [1, 2, 3, 6, 9, 8, 7, 4, 5]. Increment the left pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is false, the traversal is complete. Return the result list.\n##### \u2022\tExample 2:\n\n##### \u2022\tInput: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]\n##### \u2022\tOutput: [1,2,3,4,8,12,11,10,9,5,6,7]\n##### \u2022\tStep-by-Step Explanation:\n##### \u2022\tInitialize the result list as an empty list.\n##### \u2022\tSet the top, bottom, left, and right pointers to the edges of the matrix. top = 0, bottom = 2, left = 0, right = 3.\n##### \u2022\tTraverse the first row from left to right and add the elements to the result list. result = [1, 2, 3, 4]. Increment the top pointer to 1.\n##### \u2022\tTraverse the last column from top to bottom and add the elements to the result list. result = [1, 2, 3, 4, 8, 12]. Decrement the right pointer to 2.\n##### \u2022\tCheck if top <= bottom. Since it is true, traverse the last row from right to left and add the elements to the result list. result = [1, 2, 3, 4, 8, 12, 11, 10, 9]. Decrement the bottom pointer to 1.\n##### \u2022\tCheck if left <= right. Since it is true, traverse the first column from bottom to top and add the elements to the result list. result = [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]. Increment the left pointer to 1.\n##### \u2022\tCheck if top <= bottom. Since it is false, the traversal is complete. Return the result list.\n\n\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A | 114 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Best Java || c++ || Python || JavaScript with 100% beat in both space and time complexity. | spiral-matrix | 1 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI made 4 distinct points (& their initialization.)\n1. Left = 0\n2. Right = Number of columns - 1 \n3. Down = Number of rows - 1\n4. Top = 0\n\n- // Basically left and down here, denoting rows.\n// And right and top here, denoting columns \n\nStep 1 :\n\n---\n\n At first add element from top to right. \n Then increment right by 1 bcz my first row is covered completely.\n \nStep 2 :\n\n---\n\n Then add elements from left to down.\n Then decrement left by 1 bcz last column (which right was denoting is covered.)\n\nStep 3 :\n\n---\n\n Then add elements from right to top.\n Then decrement down by 1 bcz last row is covered now.\n\nStep 4 : (The final Step after which same paradigm will be followed)\n\n---\n\n Now add elements from down to left.\n And increment the top by 1 bcz first column is covered now.\n\n - At every step take care that (left <= down) and (top <= right) else break the loop.\n- Hopes so you got that !! Follow the code for more apprehendment. :)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n```\no(n*m) Since we are traversing each elements of loop 1 by 1.\n```\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n```\nCode block\n```o(n*m) Since we are creating an ArrayList or List on samne order. \n```\n# Code\n \nclass Solution {\n\n public List<Integer> spiralOrder(int[][] matrix) {\n ArrayList<Integer> l = new ArrayList<>();\n int left = 0, right = matrix[0].length - 1, down = matrix.length - 1, top = 0;\n while (true) {\n for (int i = top; i <= right; i++)\n l.add(matrix[left][i]);\n left++;\n if (left > down)\n break;\n for (int i = left; i <= down; i++)\n l.add(matrix[i][right]);\n right--;\n if (top > right)\n break;\n for (int i = right; i >= top; i--)\n l.add(matrix[down][i]);\n down--;\n if (left > down)\n break;\n for (int i = down; i >= left; i--)\n l.add(matrix[i][top]);\n top++;\n if (top > right)\n break;\n }\n\n return l;\n }\n}\n``` | 1 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Best Java || c++ || Python || JavaScript with 100% beat in both space and time complexity. | spiral-matrix | 1 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI made 4 distinct points (& their initialization.)\n1. Left = 0\n2. Right = Number of columns - 1 \n3. Down = Number of rows - 1\n4. Top = 0\n\n- // Basically left and down here, denoting rows.\n// And right and top here, denoting columns \n\nStep 1 :\n\n---\n\n At first add element from top to right. \n Then increment right by 1 bcz my first row is covered completely.\n \nStep 2 :\n\n---\n\n Then add elements from left to down.\n Then decrement left by 1 bcz last column (which right was denoting is covered.)\n\nStep 3 :\n\n---\n\n Then add elements from right to top.\n Then decrement down by 1 bcz last row is covered now.\n\nStep 4 : (The final Step after which same paradigm will be followed)\n\n---\n\n Now add elements from down to left.\n And increment the top by 1 bcz first column is covered now.\n\n - At every step take care that (left <= down) and (top <= right) else break the loop.\n- Hopes so you got that !! Follow the code for more apprehendment. :)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n```\no(n*m) Since we are traversing each elements of loop 1 by 1.\n```\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n```\nCode block\n```o(n*m) Since we are creating an ArrayList or List on samne order. \n```\n# Code\n \nclass Solution {\n\n public List<Integer> spiralOrder(int[][] matrix) {\n ArrayList<Integer> l = new ArrayList<>();\n int left = 0, right = matrix[0].length - 1, down = matrix.length - 1, top = 0;\n while (true) {\n for (int i = top; i <= right; i++)\n l.add(matrix[left][i]);\n left++;\n if (left > down)\n break;\n for (int i = left; i <= down; i++)\n l.add(matrix[i][right]);\n right--;\n if (top > right)\n break;\n for (int i = right; i >= top; i--)\n l.add(matrix[down][i]);\n down--;\n if (left > down)\n break;\n for (int i = down; i >= left; i--)\n l.add(matrix[i][top]);\n top++;\n if (top > right)\n break;\n }\n\n return l;\n }\n}\n``` | 1 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
🐍Python3 simple and easy solution🔥🔥 | spiral-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using property of array**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- there are 4 stages of this problem\n - **1**) pop first row and put as it is\n - **2**) now we need last column in downwards order\n - **3**) now we need last row backwards\n - **4**) now we need first column upwards.\n- simple as it is.\n- we perform these 4 steps recursively till wed have empty matrix.\n- retutn answer array.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n ans = []\n while matrix: # traverse till matrix is nonempty\n ans += matrix[0] # push the first row as it is\n matrix.pop(0) # pop it from main matrix\n if matrix:\n for i in matrix: # now push last column if matrix is nonempty\n if i:\n ans.append(i.pop()) # pop while pushing\n if matrix and matrix[-1]: # we need last row reversed\n ans += matrix[-1][::-1]\n matrix.pop() # also pop it\n if matrix:\n # reverse it and add because when we traverse it is up->down, we need down->up\n for i in matrix[::-1]: # now we go for step 4 first column\n if i:\n ans.append(i.pop(0))\n return ans\n```\n# Please upvote and comment below for any suggestion( \u0361\u2688\u202F\u035C\u0296 \u0361\u2688) \uD83D\uDC49 | 3 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
🐍Python3 simple and easy solution🔥🔥 | spiral-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using property of array**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- there are 4 stages of this problem\n - **1**) pop first row and put as it is\n - **2**) now we need last column in downwards order\n - **3**) now we need last row backwards\n - **4**) now we need first column upwards.\n- simple as it is.\n- we perform these 4 steps recursively till wed have empty matrix.\n- retutn answer array.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n ans = []\n while matrix: # traverse till matrix is nonempty\n ans += matrix[0] # push the first row as it is\n matrix.pop(0) # pop it from main matrix\n if matrix:\n for i in matrix: # now push last column if matrix is nonempty\n if i:\n ans.append(i.pop()) # pop while pushing\n if matrix and matrix[-1]: # we need last row reversed\n ans += matrix[-1][::-1]\n matrix.pop() # also pop it\n if matrix:\n # reverse it and add because when we traverse it is up->down, we need down->up\n for i in matrix[::-1]: # now we go for step 4 first column\n if i:\n ans.append(i.pop(0))\n return ans\n```\n# Please upvote and comment below for any suggestion( \u0361\u2688\u202F\u035C\u0296 \u0361\u2688) \uD83D\uDC49 | 3 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
python 3 solution for spiral matrix one of the most easiest you will never forget | spiral-matrix | 0 | 1 | # UPVOTE \n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n res = []\n if len(matrix) == 0:\n return res\n row_begin = 0\n col_begin = 0\n row_end = len(matrix)-1 \n col_end = len(matrix[0])-1\n while (row_begin <= row_end and col_begin <= col_end):\n for i in range(col_begin,col_end+1):\n res.append(matrix[row_begin][i])\n row_begin += 1\n for i in range(row_begin,row_end+1):\n res.append(matrix[i][col_end])\n col_end -= 1\n if (row_begin <= row_end):\n for i in range(col_end,col_begin-1,-1):\n res.append(matrix[row_end][i])\n row_end -= 1\n if (col_begin <= col_end):\n for i in range(row_end,row_begin-1,-1):\n res.append(matrix[i][col_begin])\n col_begin += 1\n return res\n \n \n \n``` | 319 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
python 3 solution for spiral matrix one of the most easiest you will never forget | spiral-matrix | 0 | 1 | # UPVOTE \n```\nclass Solution:\n def spiralOrder(self, matrix: List[List[int]]) -> List[int]:\n res = []\n if len(matrix) == 0:\n return res\n row_begin = 0\n col_begin = 0\n row_end = len(matrix)-1 \n col_end = len(matrix[0])-1\n while (row_begin <= row_end and col_begin <= col_end):\n for i in range(col_begin,col_end+1):\n res.append(matrix[row_begin][i])\n row_begin += 1\n for i in range(row_begin,row_end+1):\n res.append(matrix[i][col_end])\n col_end -= 1\n if (row_begin <= row_end):\n for i in range(col_end,col_begin-1,-1):\n res.append(matrix[row_end][i])\n row_end -= 1\n if (col_begin <= col_end):\n for i in range(row_end,row_begin-1,-1):\n res.append(matrix[i][col_begin])\n col_begin += 1\n return res\n \n \n \n``` | 319 | Given an `m x n` `matrix`, return _all elements of the_ `matrix` _in spiral order_.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[1,2,3,6,9,8,7,4,5\]
**Example 2:**
**Input:** matrix = \[\[1,2,3,4\],\[5,6,7,8\],\[9,10,11,12\]\]
**Output:** \[1,2,3,4,8,12,11,10,9,5,6,7\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 10`
* `-100 <= matrix[i][j] <= 100` | Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do. We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need. Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row.
Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not. |
Easy O(n) without dp | jump-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n\n reachable = 0\n\n for i in range(len(nums)):\n\n if i>reachable:\n return False \n\n reachable = max(reachable, i+nums[i])\n \n return True\n \n``` | 27 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Binbin little princess is back with her knight | jump-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n I=len(nums)-1\n if I == 0:\n return True\n for i in nums[-2::-1]:\n I -= 1\n L=len(nums)\n #print(L)\n if i+I>= L-1:\n nums = nums[0:I+1]\n #print(i,I,nums)\n if I == 0:\n #print(i,I,nums,L)\n if i >= L-1:\n return True\n if i < L-1:\n return False\n\n``` | 1 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Beats 98% || Mind blowing intuition explained | jump-game | 0 | 1 | # Intuition\nChange the destination point backwards. \n# Approach\nInitially, first destination point is last index. Change destination point to index of first previous element that can jump to current goal. That way we can, tecnically, consider this new goal as destination point cause once we can reach to it we can automatically get to original goal as well. In the end, if last updated goal happens to be very first element or zero index then it means that we can get to the original last index destination point from zero index.\n# Complexity\n- Time complexity:\nO(N)\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n #original destination is last index\n goal = len(nums)-1\n\n #check backwards\n for i in range(len(nums)-2,-1,-1):\n #if we can jump then update\n if i+nums[i] >= goal:\n goal = i\n\n #check if we can reach from first index\n return True if goal == 0 else False #return goal == 0\n\n``` | 30 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Very Easy 100%(Fully Explained)(Java,C++, Python, JS, C, Python3) | jump-game | 1 | 1 | # **Java Solution:**\n```\nclass Solution {\n public boolean canJump(int[] nums) {\n // Take curr variable to keep the current maximum jump...\n int curr = 0;\n // Traverse all the elements through loop...\n for (int i = 0; i < nums.length; i++) {\n // If the current index \'i\' is less than current maximum jump \'curr\'...\n // It means there is no way to jump to current index...\n // so we should return false...\n if (i > curr) {\n return false;\n }\n // Update the current maximum jump...\n curr = Math.max(curr, i + nums[i]); // It\u2019s possible to reach the end of the array...\n }\n return true;\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n bool canJump(vector<int>& nums) {\n int idx = 0;\n //check what is the maximum index we can reach from that index...\n for (int maximum = 0; idx < nums.size() && idx <= maximum; ++idx)\n maximum = max(idx + nums[idx], maximum); //if the maximum index reached is the last index of the array...\n return idx == nums.size();\n }\n};\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def canJump(self, nums):\n # Take curr variable to keep the current maximum jump...\n curr = nums[0]\n # Traverse all the elements through loop...\n for i in range(1,len(nums)):\n # If the current index \'i\' is less than current maximum jump \'curr\'...\n # It means there is no way to jump to current index...\n # so we should return false...\n if curr == 0:\n return False\n curr -= 1\n # Update the current maximum jump...\n curr = max(curr, nums[i]) # It\u2019s possible to reach the end of the array...\n return True\n```\n\n# **JavaScript Solution:**\n```\nvar canJump = function(nums) {\n // Base condition...\n if(nums.length <= 1)\n return true;\n // To keep the maximum index that can be reached...\n let maximum = nums[0];\n // Traverse all the elements through loop...\n for(let i = 0; i < nums.length; i++){\n //if there is no way to jump to next...\n // so we should return false...\n if(maximum <= i && nums[i] == 0) \n return false;\n //update the maximum jump... \n if(i + nums[i] > maximum){\n maximum = i + nums[i];\n }\n //maximum is enough to reach the end...\n if(maximum >= nums.length-1) \n return true;\n }\n return false; \n};\n```\n\n# **C Language:**\n```\nbool canJump(int* nums, int numsSize){\n int jump = 0;\n for (int i = 0; i < numsSize; i++) {\n if (jump < i) {\n break;\n }\n if (jump < i + nums[i]) {\n jump = i + nums[i];\n }\n if (jump >= numsSize - 1) {\n return true;\n }\n }\n return false;\n}\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n # Take curr variable to keep the current maximum jump...\n curr = nums[0]\n # Traverse all the elements through loop...\n for i in range(1,len(nums)):\n # If the current index \'i\' is less than current maximum jump \'curr\'...\n # It means there is no way to jump to current index...\n # so we should return false...\n if curr == 0:\n return False\n curr -= 1\n # Update the current maximum jump...\n curr = max(curr, nums[i]) # It\u2019s possible to reach the end of the array...\n return True\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 107 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Use a counter to count on your step! | jump-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key mindset here is to use a counter to count on residual steps.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTake k as your residual steps. Everytime you move, k-1. If nums[i] offers you more steps, take it! If you run out of your move and can\'t move to finishing line, you fail. Otherwise, return True.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n if len(nums)==1:\n return True\n k = nums[0]\n for i in range(len(nums)-1):\n if nums[i] > k:\n k = nums[i]\n k = k - 1\n if k < 0 :\n return False\n return True\n\n``` | 7 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Python DP + Memo solution | jump-game | 0 | 1 | # Approach\nCreate an array containing information whether you can get to the i-th position.\nWe can simply go through all elements of the array and then iterate over all possible jump lengths updating information in our boolean array.\n\n# Complexity\n- Time complexity: $$O(nk)$$, where k is a sum of all jumps (sum of nums array)\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n n=len(nums)\n dp=[False for _ in range(n)]\n dp[0]=True\n\n for i in range(n):\n if dp[i]: # if this position is reachable\n for j in range(1,nums[i]+1):\n if i+j<n:\n dp[i+j]=True\n if i+j==n-1:\n return True\n return dp[n-1]\n``` | 8 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Python Simple Solution || Beats 81.14% | jump-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI can start from the finish line and problems only appear when there is a zero\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code uses a greedy approach to iterate from the last index `j` towards the first index. It starts with `j` set to the last index of `nums`.\n\nIn each iteration, it checks if the element at index `j-1` is greater than 0. If it is, it means we can jump from index `j-1` to index `j`. In this case, it decrements `j` by 1 and continues to the next iteration.\n\nIf the element at index `j-1` is 0, it means we cannot jump from index `j-1` to index `j`. In this case, it enters a nested loop starting from index `i` set to `j-1` and iterates towards the first index (`i <= 0`).\n\nWithin the nested loop, it checks if the value at index `i` (`nums[i]`) is less than the distance between `j` and `i` (`j-i`). If it is, it means it is not possible to jump from index `i` to index `j` based on the value at index `i`. In this case, it decrements `i` by 1 and continues to check the previous indices.\n\nIf the nested loop reaches the first index (`i <= 0`) without finding a suitable index to jump from, it means it is not possible to reach the last index of `nums`. In this case, the code returns `False`.\n\nIf the outer loop completes and exits without encountering any issues, it means it is possible to reach the last index of `nums` based on the given jump values. The code then returns `True`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n j=len(nums)-1\n\n while j>0:\n if nums[j-1]>0:\n j-=1\n else:\n i=j-1\n while nums[i]<j-i:\n if i<=0:\n return False\n i-=1\n j=i\n return True\n\n``` | 10 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
O(N) & O(1) | jump-game | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n # t.c/s.c -> O(N)/O(1)\n goal = len(nums)-1\n\n for i in range(len(nums)-2,-1,-1):\n if i + nums[i] >= goal:\n goal = i\n return True if goal == 0 else False\n # return goal == 0\n\n \n``` | 1 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Python Every possible solution Greedy, DP, Recurssive | jump-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n### Greedy TO(n) SO(1)\nMaintain a reachable variable and update it on every iteration, if we are ahead of reachable that means it\'s not possible. else reachle will be equal to n\n\n### DP TO(n^2) SO(n)\nUsing a 1d array to mark evry reachable destination by True and then check if we reached on then end or not.\n\n\n### Recurssive TO(n^n) SO(1)\nTry running DFS on every possible value and check if reached in the end or not.\n\n\n\n# Code\n```\n#Greedy\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n reacable = 0\n for i in range(len(nums)):\n if reacable < i :\n return False\n reacable = max(reacable, i+nums[i])\n return True\n```\n```\n#DP\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n n =len(nums)\n dp = [False for i in range(n)]\n dp[0] = True\n \n for i in range(n):\n if dp[i]:\n for j in range(i+1, i+nums[i]+1):\n if j < n:\n dp[j] = True\n if j == n - 1:\n return True\n return dp[n-1]\n```\n```\n#Recurssive\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n def dfs(i, n, nums):\n if i > n:\n return False\n if i == n:\n return True\n ans = False\n for e in range(1, nums[i]+1):\n ans = ans or dfs(e+i, n, nums)\n return ans\n return dfs(0, len(nums)-1, nums)\n```\n\n# Upvote if it\'s helpfulll. | 6 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Python dynamic programming solution | jump-game | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n i = 1\n prev = nums[0]\n if len(nums) == 1:\n return True\n if prev == 0:\n return False\n while i < len(nums)-1:\n prev = max(prev-1, nums[i])\n if not prev:\n return False\n i+=1 \n return True\n \n``` | 1 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Python3 Deadly easy code only 9 lines beats 94.08% in runtime | jump-game | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n if len(nums) == 1:return True\n i = 0;j = i\n for i in range(100000):\n if j > i+nums[i]:pass\n else:j = i+nums[i]\n i+=1\n if i > j:break\n if j >= len(nums)-1:return True\n return False\n \n``` | 4 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Simple recursive solution | time beats 95.86% | jump-game | 0 | 1 | # Approach\nConsider a variable last_index that points to the element which we are trying to reach. Initialize it to len(nums) - 1.\nRecursively traverse from las_index towards the beginning of the array, searching for the index from which the last_index is reachable. \nIf the last_index is reachable from a preceding index, call the function by updating last_index to current index value\nBase-case: return true if the last_index is 0.\n\n# Complexity\n- Time complexity:$$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rec(self, nums, last_idx) -> bool:\n if last_idx == 0:\n return True\n \n i = last_idx-1\n while i >= 0:\n if i + nums[i] >= last_idx:\n return self.rec(nums, i)\n i -= 1\n return False\n \n def canJump(self, nums: List[int]) -> bool:\n return self.rec(nums, len(nums)-1)\n``` | 1 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
C++ - Easiest Beginner Friendly Sol || Greedy || O(n) time and O(1) space | jump-game | 1 | 1 | # Intuition of this Problem:\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Initialize a variable reach to 0, which represents the farthest index that can be reached so far.\n2. Loop through the array nums and for each index i, do the following:\n - a. If i is greater than reach or reach is greater than or equal to nums.length - 1, break the loop as it means reaching the last index is not possible.\n - b. Update the value of reach as the maximum of reach and i + nums[i].\n1. Return reach >= nums.length - 1, which means that the last index can be reached or not.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n bool canJump(vector<int>& nums) {\n int n = nums.size();\n int reach = 0;\n for (int i = 0; i < n; i++) {\n // (i > reach) will cover [1,1,0,1,2] or [0,0,0....]\n if(i > reach || reach >= n-1)\n break;\n //this reach will store upto which index we can jump from that ith index\n reach = max(reach, i + nums[i]);\n }\n if (reach >= n-1)\n return true;\n //this "return false" means definitely (i > reach) at any point\n return false;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean canJump(int[] nums) {\n int reach = 0;\n for (int i = 0; i < nums.length; i++) {\n if (i > reach || reach >= nums.length - 1) break;\n reach = Math.max(reach, i + nums[i]);\n }\n return reach >= nums.length - 1;\n }\n}\n\n```\n```Python []\nclass Solution:\n def canJump(self, nums: List[int]) -> bool:\n reach = 0\n for i in range(len(nums)):\n if i > reach or reach >= len(nums) - 1:\n break\n reach = max(reach, i + nums[i])\n return reach >= len(nums) - 1\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n)**, where n is the length of the array nums. This is because we are looping through the entire nums array once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**, as we are using a single integer variable reach.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 27 | You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
Return `true` _if you can reach the last index, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,3,1,1,4\]
**Output:** true
**Explanation:** Jump 1 step from index 0 to 1, then 3 steps to the last index.
**Example 2:**
**Input:** nums = \[3,2,1,0,4\]
**Output:** false
**Explanation:** You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 105` | null |
Solution | merge-intervals | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> merge(vector<vector<int>>& intervals) {\n \n if(intervals.size()==1)\n return intervals;\n vector<pair<int,int>> p;\n for(int i=0;i<intervals.size();i++)\n {\n p.push_back({intervals[i][0],intervals[i][1]});\n } \n sort(p.begin(),p.end());\n\n vector<vector<int>> ans;\n int f=p[0].first,s=p[0].second;\n for(int i=0;i<p.size()-1;i++)\n {\n vector<int> a(2);\n if(s>=p[i+1].first)\n {\n s=max(s,p[i+1].second);\n }\n else\n {\n a[0]=f;\n a[1]=s;\n f=p[i+1].first;\n s=p[i+1].second;\n ans.push_back(a);\n }\n } \n int n=intervals.size();\n ans.push_back({f,s});\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n intervals = sorted(intervals, key=lambda x: x [0])\n\n ans = []\n\n for interval in intervals:\n if not ans or ans[-1][1] < interval[0]:\n ans.append(interval)\n else:\n ans[-1][1] = max(ans[-1][1], interval[1])\n \n return ans\n```\n\n```Java []\nclass Solution {\n public int[][] merge(int[][] intervals) {\n\t\tint min = Integer.MAX_VALUE;\n\t\tint max = Integer.MIN_VALUE;\n\t\t\n\t\tfor (int i = 0; i < intervals.length; i++) {\n\t\t\tmin = Math.min(min, intervals[i][0]);\n\t\t\tmax = Math.max(max, intervals[i][0]);\n\t\t}\n\t\t\n\t\tint[] range = new int[max - min + 1];\n\t\tfor (int i = 0; i < intervals.length; i++) {\n\t\t\trange[intervals[i][0] - min] = Math.max(intervals[i][1] - min, range[intervals[i][0] - min]); \n\t\t}\n\t\t\n\t\tint start = 0, end = 0;\n\t\tLinkedList<int[]> result = new LinkedList<>();\n\t\tfor (int i = 0; i < range.length; i++) {\n\t\t\tif (range[i] == 0) {\n\t\t\t\tcontinue;\n\t\t\t}\n\t\t\tif (i <= end) {\n\t\t\t\tend = Math.max(range[i], end);\n\t\t\t} else {\n\t\t\t\tresult.add(new int[] {start + min, end + min});\n\t\t\t\tstart = i;\n\t\t\t\tend = range[i];\n\t\t\t}\n\t\t}\n\t\tresult.add(new int[] {start + min, end + min});\n\t\treturn result.toArray(new int[result.size()][]);\n\t}\n}\n```\n | 482 | Given an array of `intervals` where `intervals[i] = [starti, endi]`, merge all overlapping intervals, and return _an array of the non-overlapping intervals that cover all the intervals in the input_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[2,6\],\[8,10\],\[15,18\]\]
**Output:** \[\[1,6\],\[8,10\],\[15,18\]\]
**Explanation:** Since intervals \[1,3\] and \[2,6\] overlap, merge them into \[1,6\].
**Example 2:**
**Input:** intervals = \[\[1,4\],\[4,5\]\]
**Output:** \[\[1,5\]\]
**Explanation:** Intervals \[1,4\] and \[4,5\] are considered overlapping.
**Constraints:**
* `1 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 104` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | merge-intervals | 1 | 1 | # My youtube channel - KeetCode(Ex-Amazon)\nI create 158 videos for leetcode questions as of April 28, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\n\nhttps://youtu.be/IuzSG0YEdXU\n\n---\n\n# Intuition\nSort intervals with start points. It takes advantage of the fact that the intervals are sorted by start point, which allows us to avoid comparing every interval to every other interval.\n\n# Approach\nThis is based on Python code. Other languages might be different.\n\n1. The merge method takes a list of lists as an argument. Each inner list represents an interval, and the first element of the inner list is the start point, and the second element is the end point.\n\n2. Check if the given list is empty, if yes, return an empty list.\n\n3. Initialize an empty list named merged to store the merged intervals.\n\n4. Sort the given list of intervals by the first element of each interval using the sort method and a lambda function.\n\n5. Set the variable prev to the first interval of the sorted intervals list.\n\n6. Iterate over the sorted intervals list, starting from the second interval.\n\n7. Check if the start point of the current interval is less than or equal to the end point of the previous interval.\n\n8. If yes, then update the end point of the previous interval with the maximum of the current interval\'s end point and the previous interval\'s end point.\n9. If no, then append the previous interval to the merged list and set prev to the current interval.\n\n10. After the loop, append the last interval (prev) to the merged list.\nReturn the merged list containing the merged intervals.\n\n# Complexity\nThis is based on Python code. Other languages might be different.\n\n- Time complexity: O(n log n)\nn is the length of the input list \'intervals\'. This is because the code sorts the intervals list in O(n log n) time using the built-in Python sorting algorithm, and then iterates over the sorted list once in O(n) time to merge overlapping intervals.\n\n- Space complexity: O(n)\nn is the length of the input list \'intervals\'. This is because the code creates a new list \'merged\' to store the merged intervals, which can contain up to n elements if there are no overlapping intervals. Additionally, the code uses a constant amount of space to store the \'prev\' variable and other temporary variables, which does not depend on the size of the input.\n\n---\n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\nhttps://leetcode.com/niits/\n\n---\n\n# Python\n```\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n if not intervals:\n return []\n \n merged = []\n intervals.sort(key=lambda x: x[0])\n\n prev = intervals[0]\n\n for interval in intervals[1:]:\n if interval[0] <= prev[1]:\n prev[1] = max(prev[1], interval[1])\n else:\n merged.append(prev)\n prev = interval\n \n merged.append(prev)\n\n return merged\n```\n# JavaScript\n```\n/**\n * @param {number[][]} intervals\n * @return {number[][]}\n */\nvar merge = function(intervals) {\n if (!intervals || intervals.length === 0) {\n return [];\n }\n\n let merged = [];\n intervals.sort((a, b) => a[0] - b[0]);\n\n let mergedInterval = intervals[0];\n\n for (let i = 1; i < intervals.length; i++) {\n let interval = intervals[i];\n\n if (interval[0] <= mergedInterval[1]) {\n mergedInterval[1] = Math.max(mergedInterval[1], interval[1]);\n } else {\n merged.push(mergedInterval);\n mergedInterval = interval;\n }\n }\n\n merged.push(mergedInterval);\n\n return merged; \n};\n```\n# Java\n```\nclass Solution {\n public int[][] merge(int[][] intervals) {\n if (intervals == null || intervals.length == 0) {\n return new int[0][];\n }\n\n Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));\n\n List<int[]> merged = new ArrayList<>();\n int[] mergedInterval = intervals[0];\n\n for (int i = 1; i < intervals.length; i++) {\n int[] interval = intervals[i];\n \n if (interval[0] <= mergedInterval[1]) {\n mergedInterval[1] = Math.max(mergedInterval[1], interval[1]);\n } else {\n merged.add(mergedInterval);\n mergedInterval = interval; \n }\n }\n\n merged.add(mergedInterval);\n\n return merged.toArray(new int[merged.size()][]); \n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n vector<vector<int>> merge(vector<vector<int>>& intervals) {\n if (intervals.empty()) {\n return {};\n }\n\n sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0];\n });\n\n vector<vector<int>> merged;\n vector<int> mergedInterval = intervals[0];\n\n for (int i = 1; i < intervals.size(); i++) {\n const vector<int>& interval = intervals[i];\n \n if (interval[0] <= mergedInterval[1]) {\n mergedInterval[1] = max(mergedInterval[1], interval[1]);\n } else {\n merged.push_back(mergedInterval);\n mergedInterval = interval;\n }\n }\n\n merged.push_back(mergedInterval);\n\n return merged; \n }\n};\n``` | 27 | Given an array of `intervals` where `intervals[i] = [starti, endi]`, merge all overlapping intervals, and return _an array of the non-overlapping intervals that cover all the intervals in the input_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[2,6\],\[8,10\],\[15,18\]\]
**Output:** \[\[1,6\],\[8,10\],\[15,18\]\]
**Explanation:** Since intervals \[1,3\] and \[2,6\] overlap, merge them into \[1,6\].
**Example 2:**
**Input:** intervals = \[\[1,4\],\[4,5\]\]
**Output:** \[\[1,5\]\]
**Explanation:** Intervals \[1,4\] and \[4,5\] are considered overlapping.
**Constraints:**
* `1 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 104` | null |
[Python3] Sort O(Nlog(N)) | merge-intervals | 0 | 1 | ```\nintervals [[1, 3], [2, 6], [8, 10], [15, 18]]\nintervals.sort [[1, 3], [2, 6], [8, 10], [15, 18]]\n\ninterval = [1,3]\nmerged =[]\nnot merged:\n\tmerged =[ [1,3] ]\n\ninterval =[2,6]\nmerged = [ [1,3] ]\nmerged[-1][-1] = 3 > interval[0] = 2:\n\tmerged[-1][-1] = max(merged[-1][-1] = 3 ,interval[-1] = 6) =6\nmerged = [[1,6]]\n```\n```\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n intervals.sort(key =lambda x: x[0])\n merged =[]\n for i in intervals:\n\t\t\t# if the list of merged intervals is empty \n\t\t\t# or if the current interval does not overlap with the previous,\n\t\t\t# simply append it.\n if not merged or merged[-1][-1] < i[0]:\n merged.append(i)\n\t\t\t# otherwise, there is overlap,\n\t\t\t#so we merge the current and previous intervals.\n else:\n merged[-1][-1] = max(merged[-1][-1], i[-1])\n return merged\n```\n\n* Time complexity:\n\tIn python, use sort method to a list costs [O(nlogn)](https://wiki.python.org/moin/TimeComplexity), where n is the length of the list.\n\tThe for-loop used to merge intervals, costs O(n).\n\tO(nlogn)+O(n) = O(nlogn)\n\tSo the total time complexity is O(nlogn).\n* Space complexity\n\tThe algorithm used a merged list and a variable i.\n\tIn the worst case, the merged list is equal to the length of the input intervals list. So the space complexity is O(n), where n is the length of the input list.\n\n```\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n intervals.sort()\n merged = []\n for i in range(len(intervals)):\n if merged == []:\n merged.append(intervals[i])\n else:\n previous_end = merged[-1][1]\n current_start = intervals[i][0]\n current_end = intervals[i][1]\n if previous_end >= current_start: # overlap\n merged[-1][1] = max(previous_end,current_end)\n else:\n merged.append(intervals[i])\n return merged\n \n``` | 182 | Given an array of `intervals` where `intervals[i] = [starti, endi]`, merge all overlapping intervals, and return _an array of the non-overlapping intervals that cover all the intervals in the input_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[2,6\],\[8,10\],\[15,18\]\]
**Output:** \[\[1,6\],\[8,10\],\[15,18\]\]
**Explanation:** Since intervals \[1,3\] and \[2,6\] overlap, merge them into \[1,6\].
**Example 2:**
**Input:** intervals = \[\[1,4\],\[4,5\]\]
**Output:** \[\[1,5\]\]
**Explanation:** Intervals \[1,4\] and \[4,5\] are considered overlapping.
**Constraints:**
* `1 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 104` | null |
Binbin is not guade | merge-intervals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n intervals = sorted(intervals)\n ret = [intervals[0]]\n for a,b in intervals:\n if not ret or a > ret[-1][1]:\n ret.append([a,b])\n else:\n ret[-1][1] = max(ret[-1][1],b)\n return ret\n``` | 1 | Given an array of `intervals` where `intervals[i] = [starti, endi]`, merge all overlapping intervals, and return _an array of the non-overlapping intervals that cover all the intervals in the input_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[2,6\],\[8,10\],\[15,18\]\]
**Output:** \[\[1,6\],\[8,10\],\[15,18\]\]
**Explanation:** Since intervals \[1,3\] and \[2,6\] overlap, merge them into \[1,6\].
**Example 2:**
**Input:** intervals = \[\[1,4\],\[4,5\]\]
**Output:** \[\[1,5\]\]
**Explanation:** Intervals \[1,4\] and \[4,5\] are considered overlapping.
**Constraints:**
* `1 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 104` | null |
binbin is guade | merge-intervals | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def merge(self, intervals: List[List[int]]) -> List[List[int]]:\n ret = [intervals[0]]\n for i in range(1, len(intervals)):\n # print(i)\n current_sublist = intervals[i]\n ret.append(current_sublist)\n for j in ret[:-1]:\n previous_sublist = j \n #print(previous_sublist)\n if current_sublist[0] <= previous_sublist[1] and current_sublist[1] >= previous_sublist[0]:\n #print(current_sublist,previous_sublist)\n ret.remove(current_sublist)\n ret.remove(previous_sublist)\n ret.append([min(current_sublist[0],previous_sublist[0]),max(current_sublist[1],previous_sublist[1])])\n current_sublist = ret[-1]\n #print(ret)\n \n return ret\n``` | 1 | Given an array of `intervals` where `intervals[i] = [starti, endi]`, merge all overlapping intervals, and return _an array of the non-overlapping intervals that cover all the intervals in the input_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[2,6\],\[8,10\],\[15,18\]\]
**Output:** \[\[1,6\],\[8,10\],\[15,18\]\]
**Explanation:** Since intervals \[1,3\] and \[2,6\] overlap, merge them into \[1,6\].
**Example 2:**
**Input:** intervals = \[\[1,4\],\[4,5\]\]
**Output:** \[\[1,5\]\]
**Explanation:** Intervals \[1,4\] and \[4,5\] are considered overlapping.
**Constraints:**
* `1 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 104` | null |
SIMPLE STRAIGHTFORWARD PYTHON (BEATS 93%) | insert-interval | 0 | 1 | \n# Approach\n1. Append new interval into `intervals`\n2. Sort `intervals` by starting times (default sort behavior)\n3. Append to `ans` if `ans` is empty or if the current start time is greater than the last time, indicating no overlap and meaning we need to add a new interval\n4. Or update last `ans` end time if the current start is less than or equal to last end AND current end is greater than last end\n\n\n# Complexity\n- Time complexity:\n$$O(n \\; log \\; n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n intervals.append(newInterval)\n intervals.sort()\n\n ans = []\n for start, end in intervals:\n if not ans or start > ans[-1][1]:\n ans.append([start, end])\n elif start <= ans[-1][1] and end > ans[-1][1]:\n ans[-1][1] = end\n \n return ans\n``` | 1 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Detailed solution in Python3/Go/Ts with O(n) time and space complexity | insert-interval | 0 | 1 | # Intuition\n\nAs we iterate through the intervals we only need to merge intervals that overlap each other and insert our new interval if it ends before the next iterated interval\n\n# Approach\n\nWe begin by creating an empty list which will contain our final **output**.\n\nIterate through all of the provided `intervals`. For each iterated interval:\n- If it begins after our new interval ends,\n - Insert new interval to our **output**\n - **Add** all remaining intervals from the current interval to our **output** container.\n - **Exit** the loop by returning _the currently generated output._\n- If it ends before our new interval begins\n - **Add** it directly to our **output**, as new interval does not need to be processed yet and is still yet to come somewhere in the future time intervals.\n- If it overlaps with our new interval\n - **Redefine** new interval by taking the **minimum** of _compared beginnings_ as the **start** and the **maximum** of _compared beginnings_ as the **end**. _DO NOT INSERT IT YET!_\n\nNotice that after we **exit** out of our defined loop without hitting the **return** statement within our **first condition**, we have yet to **insert** our new interval to our **output**. So, before _returning_ the **output** at this point, have our _new interval_ inserted into the returned **output**.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n # Initialize an output container\n output = []\n\n # Iterate through all intervals\n for i in range(len(intervals)):\n # If the new interval ends before the current interval\n # - Append the new interval to the output\n # - Append the rest of the remaining intervals to the output\n # - Return the output\n if newInterval[1] < intervals[i][0]:\n output.append(newInterval)\n return output + intervals[i:]\n \n # If the new interval begins after the current interval\n # - Append the current interval to the output\n elif newInterval[0] > intervals[i][1]:\n output.append(intervals[i])\n\n # If the new interval overlaps with the current interval\n # merge intervals to create a new interval where\n # - Interval begins at the earliest of beginnings\n # - Interval ends at the latest of ends\n #\n # ! Do not add the new interval to the output just yet!\n # ! Further merging may be required\n else:\n newInterval = [\n min(newInterval[0], intervals[i][0]),\n max(newInterval[1], intervals[i][1])\n ]\n\n # Add the new interval to the output if not added already\n # ! No need for conditions as we would not reach this point otherwise\n output.append(newInterval)\n\n # Return the final output\n return output\n```\n```Go []\nfunc insert(intervals [][]int, newInterval []int) [][]int {\n // Initialize an output container\n output := [][]int{}\n\n // Iterate through all intervals\n for i := 0; i < len(intervals); i++ {\n if newInterval[1] < intervals[i][0] {\n // If the new interval ends before the current interval\n // - Append the new interval to the output\n // - Append the rest of the remaining intervals to the output\n // - Return the output\n output = append(output, newInterval)\n return append(output, intervals[i:]...)\n } else if newInterval[0] > intervals[i][1] {\n // If the new interval begins after the current interval\n // - Append the current interval to the output\n output = append(output, intervals[i])\n } else {\n // If the new interval overlaps with the current interval\n // merge intervals to create a new interval where\n // - Interval begins at the earliest of beginnings\n // - Interval ends at the latest of ends\n //\n // ! Do not add the new interval to the output just yet!\n // ! Further merging may be required\n newInterval = []int {\n min(newInterval[0], intervals[i][0]),\n max(newInterval[1], intervals[i][1]),\n }\n }\n }\n\n // Add the new interval to the output if not added already\n // ! No need for conditions as we would not reach this point otherwise\n output = append(output, newInterval)\n\n // Return the final output\n return output\n}\n```\n```typescript []\nfunction insert(intervals: number[][], newInterval: number[]): number[][] {\n // Initialize an output container\n const output: number[][] = [];\n\n // Iterate through all intervals\n for(let i = 0; i < intervals.length; i++) {\n // If the new interval ends before the current interval\n // - Append the new interval to the output\n // - Append the rest of the remaining intervals to the output\n // - Return the output\n if (newInterval[1] < intervals[i][0]) {\n output.push(newInterval);\n intervals.slice(i).forEach(interval => output.push(interval));\n return output;\n }\n\n // If the new interval begins after the current interval\n // - Append the current interval to the output\n else if (newInterval[0] > intervals[i][1])\n output.push(intervals[i])\n\n // If the new interval overlaps with the current interval\n // merge intervals to create a new interval where\n // - Interval begins at the earliest of beginnings\n // - Interval ends at the latest of ends\n //\n // ! Do not add the new interval to the output just yet!\n // ! Further merging may be required\n else\n newInterval = [\n Math.min(newInterval[0], intervals[i][0]),\n Math.max(newInterval[1], intervals[i][1])\n ];\n }\n\n // Add the new interval to the output if not added already\n // ! No need for conditions as we would not reach this point otherwise\n output.push(newInterval);\n\n // Return the final output\n return output;\n};\n```\n | 6 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Python Super Short, Simple & Clean Solution 99% faster | insert-interval | 0 | 1 | the main idea is that when iterating over the intervals there are three cases:\n\n1. the new interval is in the range of the other interval\n2. the new interval\'s range is before the other\n3. the new interval is after the range of other interval\n\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n result = []\n \n for interval in intervals:\n\t\t\t# the new interval is after the range of other interval, so we can leave the current interval baecause the new one does not overlap with it\n if interval[1] < newInterval[0]:\n result.append(interval)\n # the new interval\'s range is before the other, so we can add the new interval and update it to the current one\n elif interval[0] > newInterval[1]:\n result.append(newInterval)\n newInterval = interval\n # the new interval is in the range of the other interval, we have an overlap, so we must choose the min for start and max for end of interval \n elif interval[1] >= newInterval[0] or interval[0] <= newInterval[1]:\n newInterval[0] = min(interval[0], newInterval[0])\n newInterval[1] = max(newInterval[1], interval[1])\n\n \n result.append(newInterval); \n return result\n``` | 114 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Simple Python solution using insort | insert-interval | 0 | 1 | \n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n insort(intervals, newInterval)\n ans = [intervals[0]]\n for s, e in intervals[1:]:\n if ans[-1][-1] >= s:\n ans[-1][-1] = max(ans[-1][-1], e)\n else:\n ans.append([s, e])\n return ans\n \n``` | 3 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
57. Insert Interval with step by step explanation | insert-interval | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, we handle the edge case where intervals is empty by returning [newInterval].\n2. Then, we use binary search to find the right place to insert newInterval into intervals.\n3. Next, we initialize a result list with the first interval from intervals.\n4. Finally, we iterate through intervals and merge overlapping intervals by updating the end of the last interval in result. If there is no overlap, we append the current interval to result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n # edge case where intervals is empty\n if not intervals:\n return [newInterval]\n \n # initialize start and end pointers\n start, end = 0, len(intervals) - 1\n \n # find the right place to insert the newInterval\n while start <= end:\n mid = (start + end) // 2\n if intervals[mid][0] < newInterval[0]:\n start = mid + 1\n else:\n end = mid - 1\n \n # insert the newInterval\n intervals.insert(start, newInterval)\n \n # initialize result list and the first interval\n result = [intervals[0]]\n \n # iterate through intervals and merge overlapping intervals\n for i in range(1, len(intervals)):\n prev_interval = result[-1]\n curr_interval = intervals[i]\n if prev_interval[1] >= curr_interval[0]:\n result[-1] = [prev_interval[0], max(prev_interval[1], curr_interval[1])]\n else:\n result.append(curr_interval)\n \n return result\n\n``` | 2 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Simple Python Solution | TC: O(N) | SC: O(N) | insert-interval | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty result array.\n2. Iterate through the existing intervals and compare the start and end times of each interval with the start and end times of the new interval.\n3. If the current interval starts before the new interval and ends before it, add it to the result array.\n4. If the current interval starts before the new interval and overlaps with it, update the start time of the new interval to the start time of the current interval.\n5. If the current interval starts after the new interval, add the new interval to the result array and set the new interval to the current interval.\n6. If the current interval starts after the new interval and overlaps with it, update the end time of the new interval to the end time of the current interval.\n7. After the iteration, add the new interval to the result array if it has not been added yet.\n8. Return the result array as the final output.\n# Complexity\n- Time complexity: $$ O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n result = []\n i = 0\n while i < len(intervals):\n if intervals[i][1] < newInterval[0]:\n result.append(intervals[i])\n elif newInterval[1] < intervals[i][0]:\n result.append(newInterval)\n newInterval = intervals[i]\n else:\n newInterval[0] = min(intervals[i][0], newInterval[0])\n newInterval[1] = max(intervals[i][1], newInterval[1])\n i += 1\n result.append(newInterval)\n return result\n\n\n\n\n\n\n``` | 1 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Python Binary search | insert-interval | 0 | 1 | # Complexity\n- Time complexity:\nStill $$O(n)$$ for bad worse cases.\n\n\n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n i = bisect.bisect_left(intervals, newInterval)\n res = intervals[:i]\n \n if res and newInterval[0] <= res[-1][1] :\n res[-1][1] = max(res[-1][1], newInterval[1])\n else:\n res.append(newInterval)\n\n for i in range(i,len(intervals)):\n if intervals[i][0]<=res[-1][1]:\n res[-1][1] = max(res[-1][1], intervals[i][1])\n else:\n return res+ intervals[i:]\n return res\n\n``` | 1 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
✅ Explained - Simple and Clear Python3 Code✅ | insert-interval | 0 | 1 | \n# Approach\nThe solution follows the logic of iterating through the intervals to find the correct position to insert the new interval while maintaining the sorted order. After insertion, it iterates over the modified array to merge any overlapping intervals by updating the end time of the previous interval if necessary. Finally, it returns the modified array with the new interval inserted and any overlapping intervals merged.\n\n# Code\n```\nclass Solution:\n def insert(self, inv: List[List[int]], nw: List[int]) -> List[List[int]]:\n #insert nw\n test=True\n for i in range(len(inv)):\n if inv[i][0]>nw[0]:\n test=False\n inv.insert(i,nw)\n if test:\n inv.append(nw)\n\n i=1\n while i<len(inv):\n if inv[i-1][1]>=inv[i][0]:\n inv[i-1][1]=max (inv[i-1][1],inv[i][1])\n inv.pop(i)\n else:\n i+=1\n \n return inv\n``` | 9 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Easiest Solution | insert-interval | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n l = []\n for i in intervals:\n if i[1] < newInterval[0]:\n l.append(i)\n elif i[0] > newInterval[1]:\n l.append(newInterval)\n newInterval = i\n elif i[1] >= newInterval[0] or i[0] <= newInterval[1]:\n newInterval[0] = min(i[0],newInterval[0])\n newInterval[1] = max(newInterval[1],i[1])\n l.append(newInterval)\n return l\n\n\n\n\n\n``` | 5 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
Python3 || 79 ms, faster than 93.12% of Python3 || Clean and Easy to Understand | insert-interval | 0 | 1 | ```\ndef insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:\n result = []\n for i in range(len(intervals)):\n if newInterval[1] < intervals[i][0]:\n result.append(newInterval)\n return result + intervals[i:]\n elif newInterval[0] > intervals[i][1]:\n result.append(intervals[i])\n else:\n newInterval = [min(newInterval[0], intervals[i][0]), max(newInterval[1], intervals[i][1])]\n result.append(newInterval)\n return result\n``` | 16 | You are given an array of non-overlapping intervals `intervals` where `intervals[i] = [starti, endi]` represent the start and the end of the `ith` interval and `intervals` is sorted in ascending order by `starti`. You are also given an interval `newInterval = [start, end]` that represents the start and end of another interval.
Insert `newInterval` into `intervals` such that `intervals` is still sorted in ascending order by `starti` and `intervals` still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return `intervals` _after the insertion_.
**Example 1:**
**Input:** intervals = \[\[1,3\],\[6,9\]\], newInterval = \[2,5\]
**Output:** \[\[1,5\],\[6,9\]\]
**Example 2:**
**Input:** intervals = \[\[1,2\],\[3,5\],\[6,7\],\[8,10\],\[12,16\]\], newInterval = \[4,8\]
**Output:** \[\[1,2\],\[3,10\],\[12,16\]\]
**Explanation:** Because the new interval \[4,8\] overlaps with \[3,5\],\[6,7\],\[8,10\].
**Constraints:**
* `0 <= intervals.length <= 104`
* `intervals[i].length == 2`
* `0 <= starti <= endi <= 105`
* `intervals` is sorted by `starti` in **ascending** order.
* `newInterval.length == 2`
* `0 <= start <= end <= 105` | null |
[VIDEO] Step-by-Step Explanation - Traverse from Back | length-of-last-word | 0 | 1 | https://youtu.be/rxb7umOJScc?si=bc9dzIPqjSn9davE\n\nOne way of solving this would be to use the `split()` method to split the string on whitespaces, then return the length of the last word in the array:\n```\narray = s.split()\nreturn len(array[-1])\n```\nHowever, this is inefficient because you have to split on <i>every</i> whitespace in the string, when really, you only need the last word. An optimized solution would be to traverse the string from the back instead.\n\nThe first `while` loop moves the pointer `i` backwards through the string until the first non-whitespace character is found. Then we\'re ready to start counting the length of the word we just hit, so the second loop increments `length` and moves `i` backwards until a whitespace character is found.\n\nOnce that whitespace character is found, that means we\'ve finished traversing the word, so the only thing left to do is to return `length`.\n\n\n# Code\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n length = 0\n i = len(s) - 1\n while i >= 0 and s[i] == \' \':\n i -= 1\n while i >= 0 and s[i] != \' \':\n length += 1\n i -= 1\n return length\n``` | 8 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
Easy Python Solution with Briefly Explanation ✅✅ | length-of-last-word | 0 | 1 | # Approach\nThis code defines a class `Solution` with a method `lengthOfLastWord` that calculates the length of the last word in a given input string `s`. Here\'s a brief explanation of each part of the code:\n\n1. `stripped = s.strip()`: This line removes leading and trailing whitespace from the input string `s` using the `strip` method. This is done to handle cases where there might be spaces at the beginning or end of the string.\n\n2. `strList = stripped.split(" ")`: This line splits the stripped string `stripped` into a list of words using a space as the delimiter. It uses the `split` method, which separates the string into a list of substrings wherever it encounters a space character.\n\n3. `lastWord = strList[-1]`: This line extracts the last element (which is the last word) from the `strList` by using the index `-1`. This assumes that words in the string are separated by spaces.\n\n4. `return len(lastWord)`: Finally, the code returns the length of the `lastWord` using the `len` function. This length represents the number of characters in the last word of the input string.\n\nIn summary, the code takes a string as input, removes leading and trailing spaces, splits the string into words, extracts the last word, and returns the length of that last word.\n\n# Code\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n stripped = s.strip()\n strList = stripped.split(" ")\n lastWord = strList[-1]\n return len(lastWord)\n```\n\n**Please upvote if you like the solution.\nHappy Coding! \uD83D\uDE0A** | 15 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
Python3 Two Liner beats 97.14% 🚀 with Explanation | length-of-last-word | 0 | 1 | # Approach\n- First we will convert given String of words into array of strings on basis of white spaces using python\'s `.split()` which converts the string into Array \n\n- for example:\n```\nstr = "Hello World"\narr = str.split()\n\n# arr will be\narr = ["Hello" , "World"]\n```\n- So we will just return the length of last string from the array \n\n# Code\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n arr = s.split()\n return len(arr[-1])\n```\n# proof \n\n\n | 9 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
phew! by13 year old boy( solution) | length-of-last-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLastWord(self, x: str) -> int:\n y = list()\n y = x.split(" ")\n while y[-1] == "":\n\n \n y.pop()\n\n p = y[-1]\n return len(p)\n \n\n\n \n``` | 1 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
Simple Python solution | length-of-last-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n return len(s.split()[-1])\n``` | 5 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
Simple method in two line | length-of-last-word | 0 | 1 | this is the one of the easiest method for beginners\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n word_list=s.split()\n return len(word_list[-1])\n \n``` | 0 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
🌺C# ,Java ,Python3, JavaScript solutions ( iteration or trim ) | length-of-last-word | 1 | 1 | The easist way may be iterate from the end of the string, can we do that with a different way?\n**Of course !**\n\n\u2B50**See more Code and Explanation : [https://zyrastory.com/en/coding-en/leetcode-en/leetcode-58-length-of-last-word-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-58-length-of-last-word-solution-and-explanation-en/)**\n\n##### C# Examples\n**1. Iteration**\n```\npublic class Solution {\n public int LengthOfLastWord(string s) {\n \n int cnt = 0;\n \n for(int i = s.Length-1;i>=0;i--)\n {\n if(Char.IsWhiteSpace(s[i]))\n {\n if(cnt>0)\n {\n return cnt; \n }\n continue;\n }\n \n cnt+=1;\n }\n return cnt;\n }\n}\n```\n\n**2. Split + Trim**\n```\npublic class Solution {\n public int LengthOfLastWord(string s) {\n s = s.TrimEnd(); //or you can use Trim()\n string[] tmp = s.Split(\' \');\n return tmp[tmp.Length-1].Length; \n }\n}\n```\nIs there an easier way in C#? Yes!\n\n---\n\n\n##### Java Solution\n**1. Iteration**\n```\nclass Solution {\n public int lengthOfLastWord(String s) {\n int cnt = 0;\n \n for(int i = s.length()-1;i>=0;i--)\n {\n if(s.charAt(i)==\' \')\n {\n if(cnt>0)\n {\n return cnt; \n }\n continue;\n }\n \n cnt+=1;\n }\n return cnt;\n }\n}\n```\n\n\n**2.**\n```\nclass Solution {\n public int lengthOfLastWord(String s) {\n s = s.trim();\n String[] arr = s.split("\\\\s+");\n \n return arr[arr.length-1].length();\n }\n}\n```\n\n---\n\n\n\n##### Python3 Solution\n**1. Iteration**\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n cnt = 0;\n for i in range(len(s)-1,-1,-1):\n if(s[i]== \' \'):\n if cnt>0 :\n return cnt\n continue\n cnt+=1;\n return cnt\n```\n\n**2.**\n```\nclass Solution:\n def lengthOfLastWord(self, s: str) -> int:\n s = s.rstrip() #or strip\n return len(s.split()[-1])\n```\n\n---\n\n\n##### JavaScript Solution\n**1. Iteration**\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar lengthOfLastWord = function(s) {\n var cnt = 0;\n\n for(var i = s.length-1;i>=0;i--)\n {\n if(s[i]==\' \')\n {\n if(cnt>0)\n {\n return cnt; \n }\n continue;\n }\n\n cnt+=1;\n }\n return cnt;\n};\n```\n\n\n**2.**\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar lengthOfLastWord = function(s) {\n s = s.trim();\n var arr = s.split(\' \');\n return arr[arr.length-1].length;\n};\n```\n\n\n\nIf you got any problem about the explanation or you need other programming language solution, please feel free to leave your comment.\n\n\uD83E\uDDE1See more problems solutions - **[Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)**\n\nThanks! | 15 | Given a string `s` consisting of words and spaces, return _the length of the **last** word in the string._
A **word** is a maximal substring consisting of non-space characters only.
**Example 1:**
**Input:** s = "Hello World "
**Output:** 5
**Explanation:** The last word is "World " with length 5.
**Example 2:**
**Input:** s = " fly me to the moon "
**Output:** 4
**Explanation:** The last word is "moon " with length 4.
**Example 3:**
**Input:** s = "luffy is still joyboy "
**Output:** 6
**Explanation:** The last word is "joyboy " with length 6.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of only English letters and spaces `' '`.
* There will be at least one word in `s`. | null |
PYTHON3 || SIMPLE TO UNDERSTAND SOLUTION || 100% WORKING | spiral-matrix-ii | 0 | 1 | # Code\n```\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n res = [[0]*n for i in range(n)]\n if n < 2:\n res[0][0]=1\n return res\n else:\n track = 1\n cycle = 1\n k = 0\n i = 0\n while k < n:\n # For 1st Cycle --> Left to Right\n if cycle == 1:\n for j in range(k,n):\n res[i][j] = track\n track += 1\n \n # For 2nd Cycle --> Top to Bottom\n if cycle == 2:\n for j in range(k+1,n):\n res[j][i] = track\n track += 1\n \n # For 3rd Cycle --> Right to Left\n if cycle == 3:\n for j in range(n-2,k-1,-1):\n res[i][j] = track\n track += 1\n \n # For 4th Cycle --> Bottom to Top\n if cycle == 4:\n for j in range(n-2,k,-1):\n res[j][i] = track\n track += 1\n i=j\n if cycle == 4:\n cycle = 1\n k += 1\n n -= 1\n else:\n cycle += 1\n\n return res\n``` | 1 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Enchanting Spiral Matrix Generation: Unveiling the Elegance of Python Magic! | spiral-matrix-ii | 0 | 1 | # Spiral Matrix Generation\n\n## Intuition\nThe code generates a 2D matrix of size `n x n` in a spiral order, starting from the top-left corner and moving in a clockwise direction.\n\n## Approach\n1. Initialize variables to keep track of the total number of elements (`total`), the current count (`count`), and the starting and ending positions of rows and columns.\n2. Create an empty `n x n` matrix (`ans`) filled with zeros.\n3. Use a while loop to iterate until all elements are filled in the matrix.\n4. For each iteration, perform the following steps:\n - Fill the top row from `startingcol` to `endingcol`.\n - Increment `startingrow` to move to the next row.\n - Fill the rightmost column from `startingrow` to `endingrow`.\n - Decrement `endingcol` to move to the next column.\n - Fill the bottom row from `endingcol` to `startingcol`.\n - Decrement `endingrow` to move to the next row.\n - Fill the leftmost column from `endingrow` to `startingrow`.\n - Increment `startingcol` to move to the next column.\n5. Return the generated matrix.\n\n## Complexity\n- Time complexity: $$O(n^2)$$, where n is the input size.\n- Space complexity: $$O(n^2)$$, due to the space used to store the generated matrix.\n\n# Code\n```python\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n total = n * n\n count = 1\n startingrow = 0\n endingrow = n - 1\n startingcol = 0\n endingcol = n - 1\n \n ans = [[0 for _ in range(n)] for _ in range(n)]\n \n while count <= total:\n for i in range(startingcol, endingcol + 1):\n ans[startingrow][i] = count\n count += 1\n startingrow += 1\n\n for i in range(startingrow, endingrow + 1):\n ans[i][endingcol] = count\n count += 1\n endingcol -= 1\n\n for i in range(endingcol, startingcol - 1, -1):\n ans[endingrow][i] = count\n count += 1\n endingrow -= 1\n\n for i in range(endingrow, startingrow - 1, -1):\n ans[i][startingcol] = count\n count += 1\n startingcol += 1\n return ans\n | 1 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Binbin golden again today! Big big applause for her! | spiral-matrix-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n M = [[0 for j in range(n)] for i in range(n)]\n if n == 1:\n return [[1]]\n a=0\n b=n-1\n r = 1\n while 2*r <= n:\n for i in range(r-1, n-r):\n a += 1\n b += 1\n M[r-1][i]=a\n M[i][n-r]=b\n a = b\n b = a + n -2*r+1\n for j in range(n-r,r-1,-1):\n a +=1\n b += 1\n M[n-r][j]=a\n M[j][r-1]=b\n r += 1\n a = b\n b = a + n -2*r+1\n \n #print(r)\n if 2*r == n+1:\n M[r-1][r-1]=b+1\n return M\n \n``` | 1 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Simple Python Solution | spiral-matrix-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n matrix = [[0] * n for _ in range(n)]\n \n count = 1\n rowStart = 0\n rowEnd = n-1\n colStart = 0\n colEnd = n-1\n \n while(rowStart <= rowEnd and colStart <= colEnd):\n for i in range(colStart, colEnd+1):\n matrix[rowStart][i] = count\n count += 1\n rowStart += 1\n \n if rowStart > rowEnd:\n break\n \n for i in range(rowStart, rowEnd+1):\n matrix[i][colEnd] = count\n count += 1\n colEnd -= 1\n \n if colStart > colEnd:\n break\n \n for i in range(colEnd, colStart-1, -1):\n matrix[rowEnd][i] = count\n count += 1\n rowEnd -= 1\n \n if rowStart > rowEnd:\n break\n \n for i in range(rowEnd, rowStart-1, -1):\n matrix[i][colStart] = count\n count += 1\n colStart += 1\n return matrix\n``` | 1 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Python short and clean. Iterative solution. | spiral-matrix-ii | 0 | 1 | # Approach\n1. Reuse the `inwards_spiral` function from [Spiral Matrix I](https://leetcode.com/problems/spiral-matrix/solutions/1467615/python-short-and-clean-iterative-solution/?orderBy=most_votes) to generate indices in spiral order.\n\n2. Zip through indices and counter, assigning count to the corresponding index of the `matrix`.\n\n# Complexity\n- Time complexity: $$O(n * m)$$\n\n- Space complexity: $$O(1)$$, ignoring the returned list.\n\nwhere,\n`m * n is the dimensions of matrix.`\n\n# Code\n```python\nclass Solution:\n def generateMatrix(self, n: int) -> list[list[int]]:\n \n def inwards_spiral(m: int, n: int) -> Iterator[Tuple[int, int]]:\n """Return list of (i, j) indices of a m * n matrix in spiral order"""\n \n for k in range((min(m, n) + 1) // 2):\n (i1, j1), (i2, j2) = (k, k), (m - k - 1, n - k - 1)\n \n if (i1, j1) == (i2, j2): yield (i1, j1); return # Center\n \n yield from ((i1, j) for j in range(j1, j2)) # Left to Right\n yield from ((i, j2) for i in range(i1, i2)) # Top to Bottom\n yield from ((i2, j) for j in range(j2, j1, -1)) if i1 != i2 else ((i2, j2),) # Right to Left\n yield from ((i, j1) for i in range(i2, i1, -1)) if j1 != j2 else ((i2, j1),) # Bottom to Top\n \n matrix = [[0] * n for _ in range(n)]\n for (i, j), x in zip(inwards_spiral(n, n), count(1)): matrix[i][j] = x\n return matrix\n\n\n``` | 2 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🔥🔥Easy Solution Using 4 Pointers!!🔥🔥 | spiral-matrix-ii | 0 | 1 | # Intuition\nWe have to make a matrix then traverse it spirally!\n\n# Approach\nFirst of all we have to create a 2-D matrix of size NxN and assign each cell with value 1. Then after that we have to start traversing it spirally and while traversing each cell we have to calculate its value from its previous cell.\n\n# Complexity\n- Time complexity:\nO(N*N)\n\n- Space complexity:\nO(N*N)\n\n# Code\n```\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n matrix=[[1 for _ in range(n)]for _ in range(n)]\n print(matrix)\n top,left=0,0\n down,right=len(matrix)-1,len(matrix[0])-1\n direction=0\n while top<=down and left<=right:\n if direction==0:\n if top==0:\n for i in range(left+1,right+1):\n matrix[top][i]+=matrix[top][i-1]\n top+=1\n else:\n for i in range(left,right+1):\n matrix[top][i]+=matrix[top][i-1]\n top+=1\n\n elif direction==1:\n for i in range(top,down+1):\n matrix[i][right]+=matrix[i-1][right]\n right-=1\n elif direction==2:\n for i in range(right,left-1,-1):\n matrix[down][i]+=matrix[down][i+1]\n down-=1\n elif direction==3:\n for i in range(down,top-1,-1):\n matrix[i][left]+=matrix[i+1][left]\n left+=1\n direction=(direction+1)%4\n return matrix\n``` | 1 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | spiral-matrix-ii | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. I planned to give for next 10,000 Subscribers as well. If you\'re interested **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Initialize an empty matrix of size n x n with all elements set to zero.\n- Define variables left, right, top, bottom, and num.\n- Use a while loop to iterate over the matrix in a spiral order.\n- In each iteration, fill in the top row, right column, bottom row, and left column of the remaining submatrix, in that order.\n- Increment/decrement the values of left, right, top, and bottom accordingly after each iteration, and update the value of num to be filled in the next iteration.\n- Return the generated matrix.\n# Intuition:\n\nThe code generates the matrix by filling in its elements in a spiral order, starting from the top-left corner and moving clockwise. It uses the variables left, right, top, and bottom to keep track of the current submatrix being filled in, and the variable num to keep track of the next number to be filled in the matrix. The algorithm fills in the matrix in four steps:\n\n- Fill in the top row from left to right.\n- Fill in the right column from top to bottom.\n- Fill in the bottom row from right to left.\n- Fill in the left column from bottom to top.\n\nAfter each step, the corresponding variable (left, right, top, or bottom) is incremented or decremented to exclude the already filled elements in the next iteration. The algorithm stops when the submatrix being filled in becomes empty, i.e., left > right or top > bottom. Finally, the generated matrix is returned.\n\n\n```Python []\nclass Solution:\n def generateMatrix(self, n: int) -> List[List[int]]:\n if not n:\n return []\n matrix = [[0 for _ in range(n)] for _ in range(n)]\n left, right, top, bottom, num = 0, n-1, 0, n-1, 1\n while left <= right and top <= bottom:\n for i in range(left, right+1):\n matrix[top][i] = num \n num += 1\n top += 1\n for i in range(top, bottom+1):\n matrix[i][right] = num\n num += 1\n right -= 1\n if top <= bottom:\n for i in range(right, left-1, -1):\n matrix[bottom][i] = num\n num += 1\n bottom -= 1\n if left <= right:\n for i in range(bottom, top-1, -1):\n matrix[i][left] = num\n num += 1\n left += 1\n return matrix\n\n```\n```Java []\nclass Solution {\n public int[][] generateMatrix(int n) {\n if (n == 0) {\n return new int[0][0];\n }\n int[][] matrix = new int[n][n];\n int left = 0, right = n-1, top = 0, bottom = n-1, num = 1;\n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num++;\n }\n top++;\n for (int i = top; i <= bottom; i++) {\n matrix[i][right] = num++;\n }\n right--;\n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n matrix[bottom][i] = num++;\n }\n bottom--;\n }\n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n matrix[i][left] = num++;\n }\n left++;\n }\n }\n return matrix;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> generateMatrix(int n) {\n if (n == 0) {\n return {};\n }\n vector<vector<int>> matrix(n, vector<int>(n, 0));\n int left = 0, right = n-1, top = 0, bottom = n-1, num = 1;\n while (left <= right && top <= bottom) {\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num++;\n }\n top++;\n for (int i = top; i <= bottom; i++) {\n matrix[i][right] = num++;\n }\n right--;\n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n matrix[bottom][i] = num++;\n }\n bottom--;\n }\n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n matrix[i][left] = num++;\n }\n left++;\n }\n }\n return matrix;\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 61 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
✔💯 DAY 405 | BRUTE->BETTER->OPTIMAL->3-LINER | 0MS-100% | | [PYTHON/JAVA/C++] | EXPLAINED 🆙🆙🆙 | spiral-matrix-ii | 1 | 1 | \n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n\n# BRUTE\nThe brute force solution to generate a matrix in spiral order is to simulate the process of filling the matrix in a spiral order. We can start by initializing the matrix with zeros and then fill the matrix in a spiral order by moving right, down, left, and up. We keep track of the current position in the matrix and the direction of movement. Whenever we reach the boundary of the matrix or encounter a non-zero element, we change the direction of movement. We continue this process until all the elements in the matrix are filled.\n\n```java []\npublic int[][] generateMatrix(int n) {\n int[][] matrix = new int[n][n];\n int num = 1;\n int row = 0;\n int col = 0;\n int direction = 0;\n int[] dr = {0, 1, 0, -1};\n int[] dc = {1, 0, -1, 0};\n while (num <= n * n) {\n matrix[row][col] = num;\n num++;\n int nextRow = row + dr[direction];\n int nextCol = col + dc[direction];\n if (nextRow < 0 || nextRow >= n || nextCol < 0 || nextCol >= n || matrix[nextRow][nextCol] != 0) {\n direction = (direction + 1) % 4;\n }\n row += dr[direction];\n col += dc[direction];\n }\n return matrix;\n }\n```\n```c++ []\nvector<vector<int>> generateMatrix(int n) {\n vector<vector<int>> matrix(n, vector<int>(n));\n int num = 1;\n int row = 0;\n int col = 0;\n int direction = 0;\n vector<int> dr = {0, 1, 0, -1};\n vector<int> dc = {1, 0, -1, 0};\n while (num <= n * n) {\n matrix[row][col] = num;\n num++;\n int nextRow = row + dr[direction];\n int nextCol = col + dc[direction];\n if (nextRow < 0 || nextRow >= n || nextCol < 0 || nextCol >= n || matrix[nextRow][nextCol] != 0) {\n direction = (direction + 1) % 4;\n }\n row += dr[direction];\n col += dc[direction];\n }\n return matrix;\n}\n```\n```python []\ndef generateMatrix(n: int) -> List[List[int]]:\n matrix = [[0] * n for _ in range(n)]\n num = 1\n row = 0\n col = 0\n direction = 0\n dr = [0, 1, 0, -1]\n dc = [1, 0, -1, 0]\n while num <= n * n:\n matrix[row][col] = num\n num += 1\n nextRow = row + dr[direction]\n nextCol = col + dc[direction]\n if nextRow < 0 or nextRow >= n or nextCol < 0 or nextCol >= n or matrix[nextRow][nextCol] != 0:\n direction = (direction + 1) % 4\n row += dr[direction]\n col += dc[direction]\n return matrix\n```\n# Complexity\nThe time complexity of the brute force solution is O(n^2) because we need to fill all the elements in the matrix. The space complexity is also O(n^2)+2*O(1D) because we need to create a matrix of size n x n to store the elements and two direction 1D arrays.\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n# Better Solution:\n\nA better solution to generate a matrix in spiral order is to use a recursive approach. We can divide the matrix into four sub-matrices and fill each sub-matrix in a spiral order recursively. We start by filling the top row of the matrix, then fill the right column, then the bottom row, and finally the left column. We repeat this process for the remaining sub-matrix until all the elements in the matrix are filled.\n\n```java []\npublic int[][] generateMatrix(int n) {\n int[][] matrix = new int[n][n];\n fillMatrix(matrix, 0, n - 1, 0, n - 1, 1);\n return matrix;\n }\n\n public void fillMatrix(int[][] matrix, int top, int bottom, int left, int right, int num) {\n if (top > bottom || left > right) {\n return;\n }\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num;\n num++;\n }\n for (int i = top + 1; i <= bottom; i++) {\n matrix[i][right] = num;\n num++;\n }\n if (top < bottom && left < right) {\n for (int i = right - 1; i >= left; i--) {\n matrix[bottom][i] = num;\n num++;\n }\n for (int i = bottom - 1; i > top; i--) {\n matrix[i][left] = num;\n num++;\n }\n }\n fillMatrix(matrix, top + 1, bottom - 1, left + 1, right - 1, num);\n }\n\n```\n```c++ []\nvector<vector<int>> generateMatrix(int n) {\n vector<vector<int>> matrix(n, vector<int>(n));\n fillMatrix(matrix, 0, n - 1, 0, n - 1, 1);\n return matrix;\n}\n\nvoid fillMatrix(vector<vector<int>>& matrix, int top, int bottom, int left, int right, int num) {\n if (top > bottom || left > right) {\n return;\n }\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num;\n num++;\n }\n for (int i = top + 1; i <= bottom; i++) {\n matrix[i][right] = num;\n num++;\n }\n if (top < bottom && left < right) {\n for (int i = right - 1; i >= left; i--) {\n matrix[bottom][i] = num;\n num++;\n }\n for (int i = bottom - 1; i > top; i--) {\n matrix[i][left] = num;\n num++;\n }\n }\n fillMatrix(matrix, top + 1, bottom - 1, left + 1, right - 1, num);\n}\n```\n```python []\ndef generateMatrix(n: int) -> List[List[int]]:\n matrix = [[0] * n for _ in range(n)]\n fillMatrix(matrix, 0, n - 1, 0, n - 1, 1)\n return matrix\n\ndef fillMatrix(matrix: List[List[int]], top: int, bottom: int, left: int, right: int, num: int) -> None:\n if top > bottom or left > right:\n return\n for i in range(left, right + 1):\n matrix[top][i] = num\n num += 1\n for i in range(top + 1, bottom + 1):\n matrix[i][right] = num\n num += 1\n if top < bottom and left < right:\n for i in range(right - 1, left - 1, -1):\n matrix[bottom][i] = num\n num += 1\n for i in range(bottom - 1, top, -1):\n matrix[i][left] = num\n num += 1\n fillMatrix(matrix, top + 1, bottom - 1, left + 1, right - 1, num)\n```\n# Complexity\nThe time complexity of the better solution is O(n^2) because we need to fill all the elements in the matrix. The space complexity is also O(n^2) because we need to create a matrix of size n x n to store the elements. However, the space complexity of the recursive approach is O(n2)+o(log n) because we use the call stack to store the recursive calls, which has a maximum depth of log n.\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n# optimal\n\n```java []\npublic int[][] generateMatrix(int n) {\n int[][] matrix = new int[n][n];\n int top = 0;\n int bottom = n - 1;\n int left = 0;\n int right = n - 1;\n int num = 1;\n while (top <= bottom && left <= right) {\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num;\n num++;\n }\n top++;\n for (int i = top; i <= bottom; i++) {\n matrix[i][right] = num;\n num++;\n }\n right--;\n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n matrix[bottom][i] = num;\n num++;\n }\n bottom--;\n }\n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n matrix[i][left] = num;\n num++;\n }\n left++;\n }\n }\n return matrix;\n }\n```\n```c++ []\nvector<vector<int>> generateMatrix(int n) {\n vector<vector<int>> matrix(n, vector<int>(n));\n int top = 0;\n int bottom = n - 1;\n int left = 0;\n int right = n - 1;\n int num = 1;\n while (top <= bottom && <= right) {\n for (int i = left; i <= right; i++) {\n matrix[top][i] = num;\n num++;\n }\n top++;\n for (int i = top; i <= bottom; i++) {\n matrix[i][right] = num;\n num++;\n }\n right--;\n if (top <= bottom) {\n for (int i = right; i >= left; i--) {\n matrix[bottom][i] = num;\n num++;\n }\n bottom--;\n }\n if (left <= right) {\n for (int i = bottom; i >= top; i--) {\n matrix[i][left] = num;\n num++;\n }\n left++;\n }\n }\n return matrix;\n}\n```\n```python []\ndef generateMatrix(n: int) -> List[List[int]]:\n matrix = [[0] * n for _ in range(n)]\n top = 0\n bottom = n - 1\n left = 0\n right = n - 1\n num = 1\n while top <= bottom and left <= right:\n for i in range(left, right + 1):\n matrix[top][i] = num\n num += 1\n top += 1\n for i in range(top, bottom + 1):\n matrix[i][right] = num\n num += 1\n right -= 1\n if top <= bottom:\n for i in range(right, left - 1, -1):\n matrix[bottom][i] = num\n num += 1\n bottom -= 1\n if left <= right:\n for i in range(bottom, top - 1, -1):\n matrix[i][left] = num\n num += 1\n left += 1\n return matrix\n```\n# Complexity\nThe time complexity of the optimal solution is O(n^2) because we need to fill all the elements in the matrix. The space complexity is o(n2)+ O(1) because we only need to create a constant number of variables to store the boundaries of the matrix and the current number to fill.\n\nIn terms of time complexity, the optimal solution is the best because it has the same time complexity as the other two solutions but uses a single loop instead of recursion or simulating the process of filling the matrix. In terms of space complexity, the optimal solution is the best because it only uses a constant amount of space, whereas the other two solutions use a matrix of size n x n or a call stack of size log n.\n\n# concise code\n# Algorithm\n##### \u2022\tUse four variables i, j, di, and dj to keep track of the current position and direction\n##### \u2022\tThen starts by initializing the matrix with all zeros\n##### \u2022\tIt then fills the matrix in a spiral order by moving in the current direction and changing direction when it encounters a non-zero element\n##### \u2022\tThe loop variable k starts from 1 and goes up to n * n\n##### \u2022\tIn each iteration, then sets the value of the current position (i, j) to k\n##### \u2022\tIt then checks if the next position in the current direction (i + di, j + dj) is already filled with a non-zero value\n##### \u2022\tIf it is, changes the direction by swapping di and dj and negating one of them\n##### \u2022\tFinally, updates the current position by adding di to i and dj to j\n##### \u2022\tOnce the loop is complete, the matrix is filled in a spiral order and returns the matrix\n\n```java []\npublic int[][] generateMatrix(int n) {\n int matrix[][] = new int[n][n],i = 0, j = 0, di = 0, dj = 1;\n for (int k = 1; k <= n * n; k++) {\n matrix[i][j] = k;\n if (matrix[(i + di + n) % n][(j + dj + n) % n] != 0) {\n int temp = di;\n di = dj;\n dj = -temp;\n }\n i += di;\n j += dj;\n } return matrix;\n}\n```\n```c++ []\nvector<vector<int>> generateMatrix(int n) {\n vector<vector<int>> matrix(n, vector<int>(n));\n int i = 0, j = 0, di = 0, dj = 1;\n for (int k = 1; k <= n * n; k++) {\n matrix[i][j] = k;\n if (matrix[(i + di + n) % n][(j + dj + n) % n] != 0) {\n int temp = di;\n di = dj;\n dj = -temp;\n }\n i += di;\n j += dj;\n }\n return matrix;\n}\n```\n```python []\ndef generateMatrix(self, n):\n A = [[0] * n for _ in range(n)]\n i, j, di, dj = 0, 0, 0, 1\n for k in xrange(n*n):\n A[i][j] = k + 1\n if A[(i+di)%n][(j+dj)%n]:\n di, dj = dj, -di\n i += di\n j += dj\n return A\n```\n\n# dry run for n=3\n##### \u2022\tInitially, we create a new n x n matrix filled with zeros\n##### \u2022\tWe also initialize i and j to 0, and di and dj to 0 and 1 respectively\n##### \u2022\tWe then enter a loop that runs from k=1 to k=n*n\n##### \u2022\tIn each iteration of the loop, we do the following:We set the value of the current cell to k\n##### \u2022\tWe check if the next cell in the direction of (di, dj) is already filled\n##### \u2022\tIf it is, we change the direction of motion by swapping di and dj and negating the new value of dj\n##### \u2022\tWe update the values of i and j by adding di and dj respectively\n##### \u2022\tAfter the loop completes, we return the filled matrix\n##### \u2022\tThe final matrix is:\n```\n1 2 3\n8 9 4\n7 6 5\n```\n# 3 LINES code\n# Algorithm\n##### \u2022\tFirst initializes an empty list A and a variable lo to n*n+1\n##### \u2022\tIt then enters a loop that continues until lo is less than or equal to 1\n##### \u2022\tIn each iteration, set hi to the current value of lo and updates lo to lo - len(A)\n##### \u2022\tIt then creates a new list of integers from lo to hi and appends it to the beginning of A\n##### \u2022\tThen reverses the order of the remaining elements in A and transposes the resulting list of lists using the zip() function\n##### \u2022\tThis effectively rotates the matrix by 90 degrees counterclockwise\n##### \u2022\tThe loop continues until lo is less than or equal to 1, at which point the matrix is filled in a spiral order and returns A\n\n```PYTHON []\ndef generateMatrix(self, n):\n A = [[n*n]]\n while A[0][0] > 1:\n A = [range(A[0][0] - len(A), A[0][0])] + zip(*A[::-1])\n return A * (n>0)\n```\n```PYTHON []\ndef generateMatrix(self, n):\n A, lo = [], n*n+1\n while lo > 1:\n lo, hi = lo - len(A), lo\n A = [range(lo, hi)] + zip(*A[::-1])\n return A\n```\n# dry run for n=3\n##### \u2022\tInitially, A is set to [[9]]\n##### \u2022\tIn the while loop, we check if the first element of A is greater than 1\n##### \u2022\tSince it is, we perform the following steps:We create a new list B containing a range of numbers from A[0][0] - len(A) to A[0][0] - 1\n##### \u2022\tIn this case, B is equal to range(7, 9)\n##### \u2022\tWe then take the transpose of A using zip(*A[::-1])\n##### \u2022\tThe [::-1] reverses the order of the elements in A, and the * unpacks the elements of A as arguments to zip\n##### \u2022\tThe zip function then groups the elements of each sub-list of A with the corresponding elements of B, effectively rotating the matrix by 90 degrees counterclockwise\n##### \u2022\tWe concatenate B with the result of step 2 to form a new matrix A\n##### \u2022\tWe repeat steps 1-3 until the first element of A is equal to 1\n##### \u2022\tFinally, we return A multiplied by (n>0), which is equivalent to returning A if n is positive and an empty list if n is zero\n\nAt each iteration, the code fills in one element of the matrix in a spiral order. The final matrix is filled in the following order:\n1 2 3\n8 9 4\n7 6 5\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A | 46 | Given a positive integer `n`, generate an `n x n` `matrix` filled with elements from `1` to `n2` in spiral order.
**Example 1:**
**Input:** n = 3
**Output:** \[\[1,2,3\],\[8,9,4\],\[7,6,5\]\]
**Example 2:**
**Input:** n = 1
**Output:** \[\[1\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Simplest solution | BEATS 94.5% | permutation-sequence | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n total, ret, digits = 1, "", [i for i in range(1, n+1)]\n for i in range(2, n):\n total*= i\n k-=1\n\n for i in range(n-1, -1, -1):\n #choose digit and remove it from digits\n val = k // total\n ret+= str(digits[val])\n del digits[val]\n k-= val*total\n\n total = total//i if i>0 else total\n return ret\n\n\n\n``` | 1 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Easy Python Implementation: Beat 88% in time. | permutation-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nConsider the example: n = 3, k = 3. The result is 213. Let\'s think about how to obtain 213 given k=3. The total number of permutation is n! = 3! = 6. \n\n**Observation:** The number of permutation that start with digit 1/2/3 are all **(n-1)!**=2!. If k = 1 or 2, we know the result must be started by digit 1; if k = 3 or 4, the first digit in the result is 2; if k = 5 or 6, the first digit must be 3. \n\nBy this observation, we can decide what the first digit in the result should be. In this example, the first digit is 2. Now we now subtract 2 from k, and now k becomes 1. This is because we will find our results from cases that start with 2, and we ignore all the cases that start with 1 and there are totally 2 cases that start with 1.\n\nThere are 2 cases associated with permutations that start with 2: 213 and 231. To get the second digit, we consider the permutations of this list [1,3]. Notice that the permutations can start with either 1 or 3; and for both digits, there are only (n-1)!=1!=1 permutation, where n is the length of the list. Notice now k is 1, which implies the digit is 1. So we have obtained our second digit as 2. \n\nThe last digit is decided more easily since there are only one digit remains in the list: if n==1, return the only digit in the list directly. \n\nNotice that the step of deciding each digit is similar, so we use recursion to solve the problem. Also, you might be more comfortable to do the matrix indexing if k is 0-indexed.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math \nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n nums = [i+1 for i in range(n)]\n return self.getPermutation2(k-1, nums) # we want k be 0-indexed\n \n def getPermutation2(self, k, nums) -> str:\n n = len(nums) \n if n == 1: \n return str(nums[0])\n if k == 0: return "".join([str(i) for i in nums]) # shortcut for speeding up\n p_n_1 = math.factorial(n-1) # permutations of n-1 \n idx = k//p_n_1 # idx of the chosen digit\n return str(nums[idx]) + self.getPermutation2(k%p_n_1, nums[:idx]+nums[idx+1:])\n \n``` | 1 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Solution | permutation-sequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> v={0};\n int tmp=1;\n for(int i=1;i<=n;i++){\n v.push_back(i);\n tmp*=i;\n }\n string s;\n cout<<tmp<<" ";\n for(int i=n;i>=2;i--){\n tmp/=i;\n int fl=(k+tmp-1)/tmp;\n s.push_back(v[fl]+\'0\');\n k-=(fl-1)*tmp;\n for(int j=fl;j<v.size()-1;j++){\n v[j]=v[j+1];\n }\n }\n s.push_back(v[1]+\'0\'); \n return s;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n nums = [i for i in range(1, n+1)] # list of numbers from 1 to n\n factorial = [1] * n\n for i in range(1, n):\n factorial[i] = factorial[i-1] * i\n \n k -= 1\n result = []\n for i in range(n-1, -1, -1):\n index = k // factorial[i]\n result.append(str(nums[index]))\n nums.pop(index)\n k = k % factorial[i]\n \n return \'\'.join(result)\n```\n\n```Java []\nclass Solution {\n private static int[] fact = {0, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n private String getPermutation(int n, int k, boolean[] nums, char[] str, int index) {\n int i = 0, m = nums.length;\n if(n == 1) {\n while(i < m && nums[i]) ++i;\n str[index++]=(char)(\'0\'+i+1);\n return String.valueOf(str);\n }\n if(k == 0) {\n while(i < m) {\n if(!nums[i]) str[index++]=(char)(\'0\'+i+1);\n ++i;\n }\n return String.valueOf(str);\n }\n \n int div = k/fact[n-1], mod = k%fact[n-1], j = -1;\n while(i < m-1 && div != j) {\n if(!nums[i]) ++j;\n if(j == div) break;\n ++i;\n }\n str[index++]=(char)(\'0\'+i+1);\n if(i < m) nums[i]=true;\n return getPermutation(n-1, mod, nums, str, index); \n }\n\n public String getPermutation(int n, int k) {\n boolean[] nums = new boolean[n];\n char[] charArr = new char[n];\n return getPermutation(n, k-1, nums, charArr, 0);\n }\n}\n```\n | 23 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Beats 99.7% 60. Permutation Sequence with step by step explanation | permutation-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere, we use a simple factorial approach. First, we calculate all the factorials up to n, and use that to find the next number to add to the result. We start from the last factorial and keep adding numbers to the result, decrementing k and removing the selected number from the list. This continues until all numbers have been added to the result and k becomes 0. We return the result as a single string.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n nums = [i for i in range(1, n+1)] # list of numbers from 1 to n\n factorial = [1] * n # initialize factorial with n factorial of 1\n for i in range(1, n):\n factorial[i] = factorial[i-1] * i # calculate the factorials\n \n k -= 1 # decrement k by 1, since k is 1-indexed\n result = []\n for i in range(n-1, -1, -1):\n index = k // factorial[i] # calculate the index of the number to be picked\n result.append(str(nums[index])) # add the number to result\n nums.pop(index) # remove the number from the list\n k = k % factorial[i] # update k\n \n return \'\'.join(result) # join the result list into a single string and return\n\n``` | 2 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Most optimal solution without using recursion and backtracking with complete exaplanation | permutation-sequence | 1 | 1 | \n\n# Approach\nThe given solution aims to find the kth permutation sequence of numbers from 1 to n. It uses a mathematical approach to determine the digits of the kth permutation by repeatedly calculating the factorial of (n-1), identifying the next digit in the permutation, and updating the remaining digits.\n\nHere\'s the explanation of the solution steps:\n\n1. Calculate the factorial of (n-1) to determine the count of permutations that can be formed with the remaining digits.\n2. Create a list called nums containing numbers from 1 to n.\n3. Adjust k to be 0-based (k = k - 1).\n4. Repeatedly find the next digit in the permutation by dividing k by the current factorial value. This indicates which digit from the remaining digits list should be added to the answer.\n5. Remove the selected digit from the nums list.\n6. Update k by taking the remainder after division by the current factorial value.\n7. Update the factorial value by dividing it by the size of the nums list.\n8. Repeat steps 4-7 until all digits are added to the answer.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact = 1;\n vector<int> nums;\n \n for (int i = 1; i < n; i++) {\n fact = fact * i;\n nums.push_back(i);\n }\n nums.push_back(n);\n \n string ans = "";\n k = k - 1;\n \n while (true) {\n ans = ans + to_string(nums[k / fact]);\n nums.erase(nums.begin() + k / fact);\n \n if (nums.size() == 0) {\n break;\n }\n \n k = k % fact;\n fact = fact / nums.size();\n }\n \n return ans;\n }\n};\n\n```\n```JAVA []\nclass Solution {\n public String getPermutation(int n, int k) {\n int fact = 1;\n List<Integer> nums = new ArrayList<>();\n \n for (int i = 1; i < n; i++) {\n fact *= i;\n nums.add(i);\n }\n nums.add(n);\n \n StringBuilder ans = new StringBuilder();\n k--;\n \n while (true) {\n ans.append(nums.get(k / fact));\n nums.remove(k / fact);\n \n if (nums.isEmpty()) {\n break;\n }\n \n k %= fact;\n fact /= nums.size();\n }\n \n return ans.toString();\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n fact = 1\n nums = list(range(1, n + 1))\n \n for i in range(1, n):\n fact *= i\n \n ans = []\n k -= 1\n \n while True:\n ans.append(str(nums[k // fact]))\n nums.pop(k // fact)\n \n if not nums:\n break\n \n k %= fact\n fact //= len(nums)\n \n return \'\'.join(ans)\n**Bold**\n```\n\n | 3 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
1 Liner Code 😎 | Python | permutation-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Using the `Permutations` to find all the possible permutations.\n2. Sorting in the ascending order.\n3. Getting the `k-1` th value, which is a tuple\n4. Converting that tuple in string format.\n5. Returning the result.\n\n# Code\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n return \'\'.join([str(i) for i in sorted(list(permutations([i for i in range(1, n+1)], n)))[k-1]])\n \n\n\n \n``` | 3 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Python With Recursion | permutation-sequence | 0 | 1 | # Intuition\nThe intuition behind this code is to find the k-th permutation of numbers from 1 to n. To understand the intuition, let\'s break down the approach step by step:\n\n\n\nThe key insight here is to break down the problem into smaller subproblems by calculating `offset` and determining how many times to "skip" the first digit in the remaining validInt list. This allows you to build the k-th permutation efficiently using recursion.\n\n# Approach\n1. **Initialization**: Initialize `validInt` as a list of numbers from 1 to n, representing the available digits for the permutation. Also, initialize `ans` as 0, which will be used to build the k-th permutation.\n\n2. **Recursive Approach**:\n\n - In each recursion, you are trying to find the next digit in the permutation.\n - Calculate `offset`, which is the number of permutations for the remaining (n-1) digits. This is done by computing `math.factorial(n - 1)`.\n - Find `skip`, which represents how many times you can "skip" the first digit in the remaining validInt list to get closer to the k-th permutation. It\'s calculated as `(k - 1) // offset`.\n - Update `ans` by adding the digit at `validInt[skip]` to the end. This digit is chosen because you are effectively choosing the `(skip+1)-th` number in the remaining validInt list.\n - Remove the chosen digit from `validInt` to ensure it\'s not used again.\n - The remaining task is to find the k-th permutation of the remaining (n-1) digits. So, recursively call `getPermutationtemp` with the updated `n`, `k % offset`, and the modified `validInt` list.\n\n3. **Base Case**: When `n` becomes zero, there are no more digits to add to the permutation, and the function returns `str(ans)` which represents the k-th permutation.\n\n# Complexity\n- Time complexity:\nThe time complexity is primarily determined by the recursive function getPermutationtemp. In each recursive call, you perform a few basic arithmetic operations and list operations (like popping a value). The critical operation is calculating the factorial, which has a time complexity of O(n) since it iterates through the numbers from 1 to n. The recursion also runs for n levels.\n\nTherefore, the time complexity of the getPermutation function is O(n^2).\n\n- Space Complexity:\n\nThe space complexity of this code is determined by the memory used for the recursion stack and the validInt list.\n\nThe recursion stack can have at most n levels, so the space used for the recursion stack is O(n).\n\nThe validInt list initially contains n elements, and in each recursive call, you pop one element from it. The space used for validInt is O(n).\n\nOverall, the space complexity is O(n) due to the recursion stack and the validInt list.\n\n# Code\n```\ndef getPermutationtemp(n,k,validInt,ans=0):\n if n<=0:\n return str(ans)\n #validInt = [i+1 for i in range(n)]\n offset = math.factorial(n-1)\n skip = (k-1)//offset\n ans = ans*10+validInt[skip]\n validInt.pop(skip)\n return getPermutationtemp(n-1,k%offset,validInt,ans)\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n validInt = [i+1 for i in range(n)]\n return getPermutationtemp(n,k,validInt)\n \n \n \n``` | 1 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Python || 99.74% Faster || Easy || Recursion | permutation-sequence | 0 | 1 | ```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n def solve(arr,k,n,ans):\n if n==1:\n ans+=str(arr[0])\n return ans\n f=factorial(n-1)\n ind=k//f\n ans+=str(arr[ind])\n arr.pop(ind)\n k%=f\n return solve(arr,k,n-1,ans)\n \n arr=[i for i in range(1,n+1)]\n k-=1\n ans=\'\'\n return solve(arr,k,n,ans)\n```\n**An upvote will be encouraging** | 1 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Python ✅- beats 98%- Easy&Optimum Solution | permutation-sequence | 0 | 1 | **This is optimum question **\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n s=[]\n for i in range(n):\n s.append(str(i+1))\n \n def fun(s,k,l):\n p=[]\n fact=factorial(l)\n #print(fact)\n while (s!=[]): \n fact=fact//l\n #print(fact)\n i,k=divmod(k,fact)\n #print(i,k)\n x=s[i] \n p.append(x) \n s=s[:i]+s[i+1:]\n #print(s)\n l-=1\n #print(p)\n return "".join(p)\n \n return fun(s,k-1,n)\n``` | 2 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Python3 Solution Explained With a Tip For Faster Execution | Beats 99.8% | permutation-sequence | 0 | 1 | My solution is basically the same with the many others but here is another explanation:\n\nLet\'s go over an example:\n```\nn=4 k=9\n1234 ------ start here\n1243 ------ third digit changes here \n1324 ------ second digit changes here \n1342\n1423\n1432 \n2134 ------ first digit changes here \n2143\n2314 -> k=9\n2341\n2413\n2431\n3124 ------ first digit changes here \n.\n.\n.\n```\nAs you can see first digit changes after 6 occurances which is (n-1)! and the second digit changes after 2 occurances which is (n-2)!. Similarly third digit changes after 1 occurances which is (n-3)!. Is this a coincidance? Of course not. Since it is a permutation we compute it like this:\n```(n)(n-1)(n-2)...(1)``` each paranthesis represents a digit. for the first place, we have n options. After using one of the numbers, we cannot use it again. So we have n-1 number options for the second place. In the end we multiply them to get the total number of permutations. Let\'s say we picked \'1\' for the first place. now we have (n-1)! options for the rest of the number. This is why at each step a number is repeated that many time. \n\nLet\'s go back to our example:\n\nSince the first digit is repeated (n-1)! times, by dividing the k by n we can find our first digit. Division must be integer division because we are only interested in the integer part.\n``` \nk=9, n=4\n(n-1)! = 6\nk /(n-1)! = 1\nremainder = 3\n```\nNumbers that we can use as digits are = ```[1,2,...,n]```\n\nSo, our first digit is the digit at index 1 which is ```2```. We take the digit at 1 because our list is sorted so we are sure that the second smallest digit is at index 1.\n\nSince we used ```2```, we need to remove it from our list and k takes the value of the remainder. You can think of lit ike this: we decided on our first digit so we can discard that part and deal with the rest of the number. As you can see the problem is the same! but this time we have (n-2)! instead of (n-1)!, k=remainder and we have one less number in our list. \n\n\n\nHere is my code:\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n factor = factorial(n-1)\n k -= 1 # index starts from 1 in the question but our list indexs starts from 0\n ans = []\n numbers_left = list(range(1,n+1))\n \n for m in range(n-1,0,-1):\n index = int(k // factor)\n ans += str(numbers_left[index])\n numbers_left.pop(index)\n k %= factor\n factor /= m\n \n ans += str(numbers_left[0])\n return \'\'.join(ans)\n```\n\n**Tips:**\n* Don\'t make ```ans``` a string because strings are not modified in place. It creates another copy of the string which makes your code slower. Instead of string, use a list which is pretty easy to append at the end, and then concatenate them in the end with join function. | 15 | The set `[1, 2, 3, ..., n]` contains a total of `n!` unique permutations.
By listing and labeling all of the permutations in order, we get the following sequence for `n = 3`:
1. `"123 "`
2. `"132 "`
3. `"213 "`
4. `"231 "`
5. `"312 "`
6. `"321 "`
Given `n` and `k`, return the `kth` permutation sequence.
**Example 1:**
**Input:** n = 3, k = 3
**Output:** "213"
**Example 2:**
**Input:** n = 4, k = 9
**Output:** "2314"
**Example 3:**
**Input:** n = 3, k = 1
**Output:** "123"
**Constraints:**
* `1 <= n <= 9`
* `1 <= k <= n!` | null |
Best Python Solution || O(N) Time Beats 90% || Two Pointers | rotate-list | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe create two pointers f and s initially we send f to k moves forward. If k exceeds the length of list then we take k % length to get the exact number of moves f should move. And finally we start moving both s and f until f reaches the end then just cut the list from s to f and attach it in the front :) \n\nComment down for more clarification and please Upvote if you like the solution\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if not head or not head.next or k==0:\n return head\n f = s = head\n count = 0\n for i in range(k):\n count +=1\n if not f.next:\n f = s\n break\n f = f.next \n for i in range(k%count):\n f = f.next\n if f == s:\n return f\n while f.next:\n f = f.next\n s = s.next\n temp = s.next\n s.next = None\n f.next = head\n return temp\n``` | 1 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
[96% faster] Simple python solution with explanation | rotate-list | 0 | 1 | Please upvote if you liked the solution \n\n\n```\n\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, x):\n# self.val = x\n# self.next = None\n\nclass Solution:\n def rotateRight(self, head: ListNode, k: int) -> ListNode:\n \n if not head:\n return None\n \n lastElement = head\n length = 1\n # get the length of the list and the last node in the list\n while ( lastElement.next ):\n lastElement = lastElement.next\n length += 1\n\n # If k is equal to the length of the list then k == 0\n # ElIf k is greater than the length of the list then k = k % length\n k = k % length\n \n # Set the last node to point to head node\n # The list is now a circular linked list with last node pointing to first node\n lastElement.next = head\n \n # Traverse the list to get to the node just before the ( length - k )th node.\n # Example: In 1->2->3->4->5, and k = 2\n # we need to get to the Node(3)\n tempNode = head\n for _ in range( length - k - 1 ):\n tempNode = tempNode.next\n \n # Get the next node from the tempNode and then set the tempNode.next as None\n # Example: In 1->2->3->4->5, and k = 2\n # tempNode = Node(3)\n # answer = Node(3).next => Node(4)\n # Node(3).next = None ( cut the linked list from here )\n answer = tempNode.next\n tempNode.next = None\n \n return answer\n\n\n``` | 321 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Simple and Elegant Python Solution | rotate-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor this problem it tells us that we want to rotate right k times. This tells us that after the end of k right rotations, the tail of the new linked list should be the node k elements from the end of the original linked list. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Figure out the length of the list + get pointer to last node in list\n2. Connect the end of the list to the beginning of the list\n3. Find the node that should be the new tail of our list\n4. Grab the new tail\'s next (our new LL\'s head) and then set tail.next to None to break the circular LL\n5. Return the head!\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n # base cases\n if head is None or k == 0:\n return head\n if head.next is None:\n return head\n \n # get end of list as well as length of list\n temp = head\n nodeCount = 1\n while temp.next != None:\n temp = temp.next\n nodeCount += 1\n tail = temp\n\n # connect end of list to head\n tail.next = head\n\n # find the node to shift from\n k = k % nodeCount\n shifts = nodeCount - k - 1\n temp = head\n while shifts > 0:\n temp = temp.next \n shifts -= 1\n\n # reset head and cut connection to break loop\n head = temp.next\n temp.next = None\n\n return head\n\n``` | 1 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Python 3 recursive solution | rotate-list | 0 | 1 | \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if not head: return head\n\n if head.next == None: return head\n new_head = head\n t = head\n c = 0\n while t:\n t = t.next\n c = c + 1\n\n n = int(k%c)\n\n while n != 0:\n new_head = self.rotate(new_head)\n n = n - 1\n\n return new_head\n\n def rotate(self,head):\n dummy = ListNode(-200,head)\n ls = head\n cur = head.next\n while cur:\n if cur.next == None:\n break\n cur = cur.next\n ls = ls.next\n\n ls.next = None\n cur.next = dummy.next\n dummy.next = cur\n return dummy.next\n\n``` | 1 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Best Python Solution || O(N) Time Beats 90% || Two Pointers | rotate-list | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe create two pointers f and s initially we send f to k moves forward. If k exceeds the length of list then we take k % length to get the exact number of moves f should move. And finally we start moving both s and f until f reaches the end then just cut the list from s to f and attach it in the front :) \n\nComment down for more clarification and please Upvote if like the solution\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if not head or not head.next or k==0:\n return head\n f = s = head\n count = 0\n for i in range(k):\n count +=1\n if not f.next:\n f = s\n break\n f = f.next \n for i in range(k%count):\n f = f.next\n if f == s:\n return f\n while f.next:\n f = f.next\n s = s.next\n temp = s.next\n s.next = None\n f.next = head\n return temp\n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Easy to understand explained linear solution | rotate-list | 0 | 1 | # Intuition\n- pointer approach\n- connect end and start\n- and break at k\n\n\n# Approach\n- if n=0 or 1 or k=0 just return head bcuz it cant be rotated\n- calculate lengh of linkedlist\n- now mod k by n bcuz rotaion by n gives the given rotation only\n- now connect last node to first node\n- now travel current till n-k\n- now modify head to current next element\n- make current next null\n- return head dont have to worry about last node bcuz we already connected first and last\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n\n if not head or not head.next or k==0:return head \n curr,size=head,1\n \n while curr.next:\n size+=1\n curr=curr.next\n \n k=k%size\n k=size-k\n curr.next=head\n while k:\n curr=curr.next\n k-=1\n \n head=curr.next\n curr.next=None\n \n return head\n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Runtime : Beats 71.05%✅ /// Memory : Beats 51.16%✅ | rotate-list | 0 | 1 | # Complexity\n- Time complexity:\nO(n) + O(k)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n\n if not head or k == 0:\n return head\n \n # Find the length of the node list\n length = 1\n temp = head\n while temp.next:\n length += 1\n temp = temp.next\n \n # Optimize the value of k \n k = k % length\n if k == 0:\n return head\n \n # Find the new start node\n fast = head\n slow = head\n for _ in range(k):\n fast = fast.next\n \n while fast.next:\n fast = fast.next\n slow = slow.next\n \n # Change the new connections\n new_head = slow.next\n slow.next = None\n fast.next = head\n \n return new_head\n\n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
✅ 🔥 Python3 || ⚡easy solution | rotate-list | 0 | 1 | \n```\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if head is None or head.next is None or k == 0:\n return head\n \n # Obtener la longitud de la lista enlazada\n length = 0\n itr = head\n while itr:\n length += 1\n itr = itr.next\n \n # Obtener la cantidad de pasos necesarios para rotar\n k = k % length\n \n # Si k es igual a 0, no es necesario rotar\n if k == 0:\n return head\n \n # Obtener el nodo en la posici\xF3n (length - k)\n itr = head\n for i in range(length - k - 1):\n itr = itr.next\n \n # Hacer la rotaci\xF3n\n new_head = itr.next\n itr.next = None\n itr = new_head\n while itr.next:\n itr = itr.next\n itr.next = head\n \n return new_head\n``` | 1 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
✅ [Python] | [VISUAL] | Easy to Understand | O(N) Time | O(1) Space | rotate-list | 0 | 1 | \uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A\n\n**Approach**\nHere we modify the linked list in place by visiting the last node and then moving a certain number of nodes to find the new head of the linked list. The example below shows a visual of the algorithm working on the given example [1,2,3,4,5] k=2.\n\n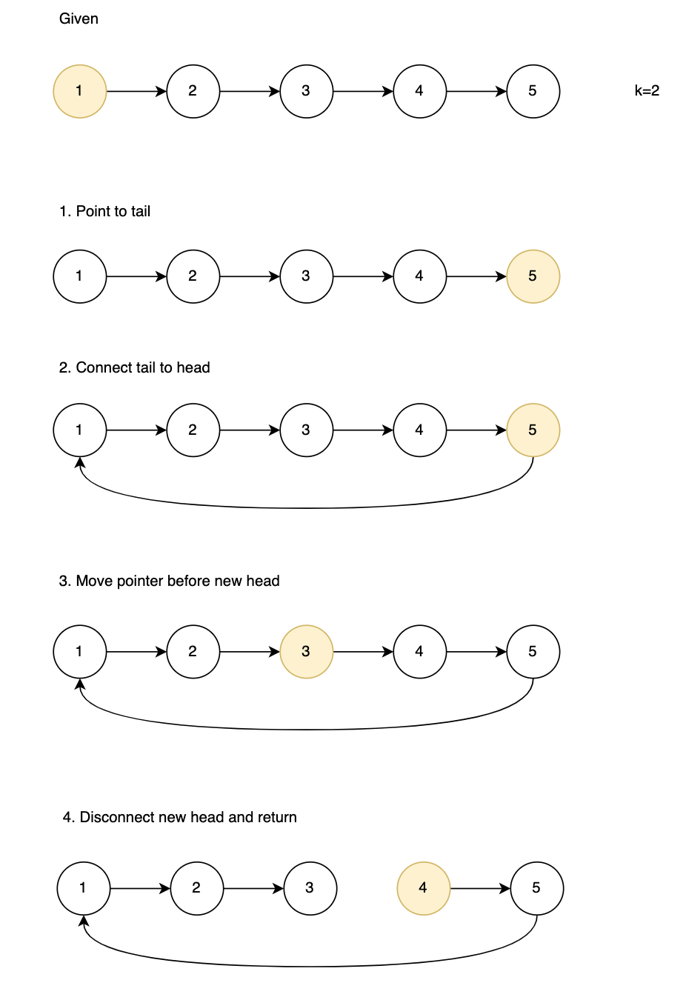\n\n\n\n**Code**\nSee the code below related to the visual above.\n\n<iframe src="https://leetcode.com/playground/WwHR5WaM/shared" frameBorder="0" width="800" height="600"></iframe>\n\n\t\nHope you enjoyed! Please leave a comment if anything is missed. Thanks!\n\uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A | 58 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
61. Rotate List with step by step explanation | rotate-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. If the head is None or the head.next is None, return head, because there is no need to rotate.\n2. Get the length of the linked list and the tail node.\n3. Get the kth node from the beginning, which is the new head.\n4. Connect the tail to the head to make a circle.\n5. Set the next of the kth node to None, because it is the end of the linked list.\n6. Return the new head.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n\nclass Solution:\n def rotateRight(self, head: ListNode, k: int) -> ListNode:\n if not head or not head.next:\n return head\n length = 0\n cur = head\n tail = None\n while cur:\n length += 1\n tail = cur\n cur = cur.next\n k = k % length\n if k == 0:\n return head\n k = length - k\n cur = head\n for i in range(k - 1):\n cur = cur.next\n new_head = cur.next\n tail.next = head\n cur.next = None\n return new_head\n\n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Yahooooo Binbin loves linked list, much understandable than (> >) tree | rotate-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if k == 0 or not head :\n return head\n \n cur = head\n l = 1 #length of linked list\n while cur.next:\n cur = cur.next\n l += 1\n rot = k % l\n cur.next = head #connect tail to head\n\n new_tail = head\n for _ in range(l-rot-1):\n new_tail = new_tail.next\n\n anw = new_tail.next\n new_tail.next = None #cut the circular link\n \n\n return anw\n \n\n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
✔️ [Python3] ROTATE ( •́ .̫ •̀ ), Explained | rotate-list | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nFirst of all, we notice that `k` can be greater than the length of the list. In this case, rotations will be repeated. To avoid useless operations, we convert `k` as follows: `k = k % length` (if `k` is equal to the length, the k becomes 0 so we don\'t need to rotate anything). Thus, we need to know the length of the list and also the last element to attach it to the head. After we figure out the true `k`, we can find the node where we have to cut the list.\n\nTime: **O(n)** - traversing\nSpace: **O(1)**\n\nRuntime: 38 ms, faster than **86.22%** of Python3 online submissions for Rotate List.\nMemory Usage: 13.9 MB, less than **88.66%** of Python3 online submissions for Rotate List.\n\n```\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n if not head: return head\n \n zero = ListNode(next=head) # dummy node\n \n count, tail = 0, zero\n while tail.next:\n count, tail = count + 1, tail.next\n \n k = k % count\n if not k: return head\n\n newTail = zero\n for _ in range(0, count - k):\n newTail = newTail.next\n\n zero.next, tail.next, newTail.next = newTail.next, head, None\n \n return zero.next\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 27 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Solution of the probem in Python | rotate-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n temp1=head\n temp2=head\n driver1=ListNode()\n temp3=driver1\n driver2=ListNode()\n temp4=driver2\n if not temp1 and not temp2:\n return driver1.next\n i=0\n while temp2:\n temp2=temp2.next\n i+=1\n k=k%i\n temp2=head\n for i in range(k):\n temp2=temp2.next\n while temp2:\n temp4.next=ListNode(temp1.val)\n temp4=temp4.next\n temp1=temp1.next\n temp2=temp2.next\n while temp1:\n temp3.next=ListNode(temp1.val)\n temp3=temp3.next\n temp1=temp1.next\n temp3.next=driver2.next\n return driver1.next\n \n``` | 1 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
Clear Explanation with Images || Python || Very Easy to Understand | rotate-list | 0 | 1 | 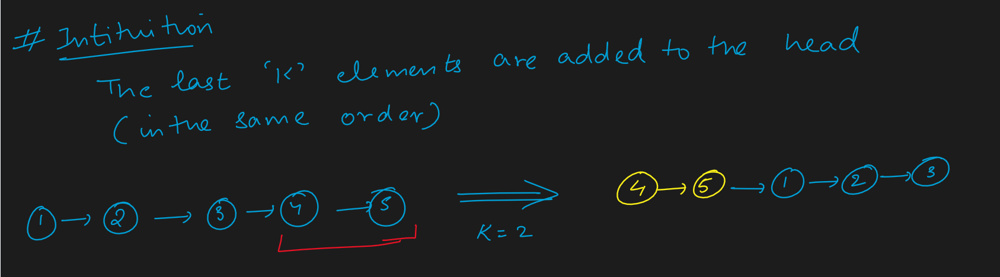\n\n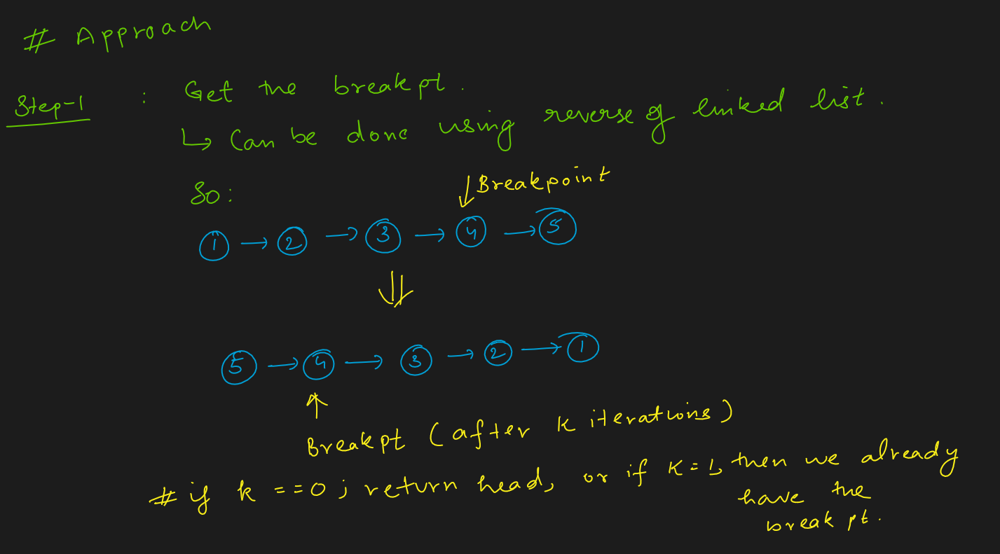\n\n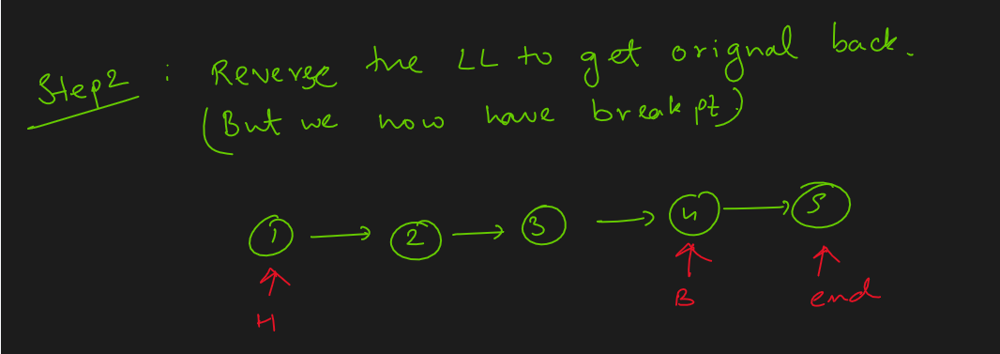\n\n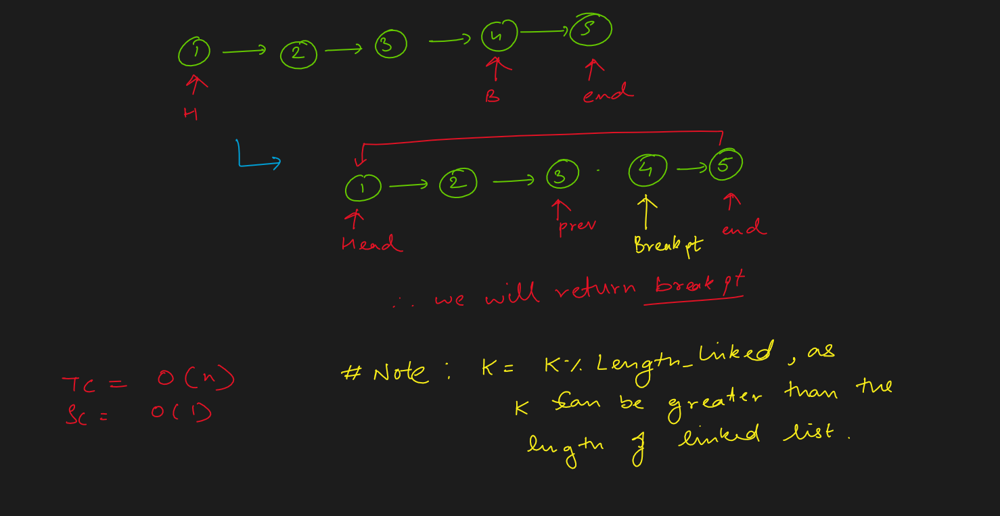\n\n\n\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def reverse(self,root) :\n if root is None or root.next is None :\n return root\n prev,cur,fut = None,root,root.next\n \n while cur.next :\n cur.next = prev\n prev = cur\n cur = fut\n fut = cur.next\n cur.next = prev\n\n head,end = cur,None\n while cur :\n end = cur\n cur = cur.next\n return head,end\n\n\n def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:\n \n if k == 0 or head is None or head.next is None:\n return head\n\n linked_length = 0\n cur = head\n\n while cur :\n linked_length += 1\n cur = cur.next\n \n k = k % linked_length\n if k == 0 :\n return head\n \n temp_head,end = self.reverse(head)\n breakpt = temp_head\n \n while k > 1 :\n k -= 1\n breakpt = breakpt.next\n \n \n cur,end = self.reverse(temp_head)\n \n while cur :\n if cur.next == breakpt :\n cur.next = None\n end.next = head\n return breakpt\n cur = cur.next\n \n``` | 2 | Given the `head` of a linked list, rotate the list to the right by `k` places.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], k = 2
**Output:** \[4,5,1,2,3\]
**Example 2:**
**Input:** head = \[0,1,2\], k = 4
**Output:** \[2,0,1\]
**Constraints:**
* The number of nodes in the list is in the range `[0, 500]`.
* `-100 <= Node.val <= 100`
* `0 <= k <= 2 * 109` | null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++ | unique-paths | 1 | 1 | # Intuition\nThe main idea to solve the unique paths question is to use dynamic programming to calculate the number of unique paths from the top-left corner of a grid to the bottom-right corner. \n\nThis approach efficiently solves the problem by breaking it down into smaller subproblems and avoiding redundant calculations. It\'s a classic example of dynamic programming used for finding solutions to grid-related problems.\n\n---\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 253 videos as of September 3rd, 2023.\n\nhttps://youtu.be/6NorAYw7NMU\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\n### \u2B50\uFE0F Don\'t forget to subscribe to my channel!\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python. Other might be differnt a bit.\n\n1. **Initialization of the AboveRow list**\n - Main Point: Initialize the aboveRow list with `n` elements, all set to 1.\n - Detailed Explanation: This list represents the number of unique paths for each column in the top row of the grid. It\'s initialized with 1 because there\'s only one way to reach each cell in the top row, which is by moving horizontally.\n\n2. **Iteration through Rows**\n - Main Point: Loop `m - 1` times, where `m` is the number of rows in the grid.\n - Detailed Explanation: This loop iterates over each row below the top row. The `-1` is used because the top row was already initialized, and there\'s no need to recompute it.\n\n3. **Creating a New Row**\n - Main Point: Inside the loop, create a new list called currentRow with `n` elements, all set to 1.\n - Detailed Explanation: For each row below the top row, we create a new list to store the number of unique paths for each column in that row. All values are initialized to 1 because there are no previous paths to consider yet.\n\n4. **Nested Loop for Columns**\n - Main Point: Iterate over each column in the currentRow from index 1 to `n - 1`.\n - Detailed Explanation: This nested loop starts from index 1 because the cell at index 0 already has one unique path, and we want to calculate the number of unique paths for the remaining cells in the current row.\n\n5. **Updating Cell Values**\n - Main Point: In the nested loop, update the currentRow list at index `i` by adding the value at index `i-1` of the currentRow and the value at index `i` of the aboveRow.\n - Detailed Explanation: This step implements the dynamic programming logic. The number of unique paths to reach a cell in the current row is the sum of the number of paths to reach the cell immediately to the left (in the same row) and the number of paths to reach the cell above it (from the aboveRow).\n\n6. **Updating aboveRow**\n - Main Point: After the nested loop completes, update the aboveRow to be equal to the currentRow.\n - Detailed Explanation: We update the aboveRow to be the same as the currentRow because it becomes the reference for the next row calculation.\n\n7. **Returning the Result**\n - Main Point: Once the outer loop finishes, return the last element of the aboveRow list, which represents the number of unique paths to reach the bottom-right cell of the grid.\n - Detailed Explanation: The final result is stored in the last element of the aboveRow list because it represents the number of unique paths to reach the last column in the last row, which is the destination cell.\n\nThis algorithm efficiently calculates the number of unique paths to traverse an `m x n` grid from the top-left corner to the bottom-right corner using dynamic programming.\n\n# Complexity\n- Time complexity: O(m * n)\n\n- Space complexity: O(n)\nn is the number of columns in the grid\n\n```python []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n\n aboveRow = [1] * n\n\n for _ in range(m - 1):\n currentRow = [1] * n\n for i in range(1, n):\n currentRow[i] = currentRow[i-1] + aboveRow[i]\n aboveRow = currentRow\n \n return aboveRow[-1]\n```\n```javascript []\n/**\n * @param {number} m\n * @param {number} n\n * @return {number}\n */\nvar uniquePaths = function(m, n) {\n let aboveRow = Array(n).fill(1);\n\n for (let row = 1; row < m; row++) {\n let currentRow = Array(n).fill(1);\n for (let col = 1; col < n; col++) {\n currentRow[col] = currentRow[col - 1] + aboveRow[col];\n }\n aboveRow = currentRow;\n }\n\n return aboveRow[n - 1]; \n};\n```\n```java []\nclass Solution {\n public int uniquePaths(int m, int n) {\n int[] aboveRow = new int[n];\n Arrays.fill(aboveRow, 1);\n\n for (int row = 1; row < m; row++) {\n int[] currentRow = new int[n];\n Arrays.fill(currentRow, 1);\n for (int col = 1; col < n; col++) {\n currentRow[col] = currentRow[col - 1] + aboveRow[col];\n }\n aboveRow = currentRow;\n }\n\n return aboveRow[n - 1]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n std::vector<int> aboveRow(n, 1);\n\n for (int row = 1; row < m; row++) {\n std::vector<int> currentRow(n, 1);\n for (int col = 1; col < n; col++) {\n currentRow[col] = currentRow[col - 1] + aboveRow[col];\n }\n aboveRow = currentRow;\n }\n\n return aboveRow[n - 1]; \n }\n};\n```\n | 22 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
✅ 98.83% Easy DP & Math | unique-paths | 1 | 1 | # Interview Guide - Unique Paths in a Grid\n\n## Problem Understanding\n\nThe problem describes a robot situated on a $$ m \\times n $$ grid, starting at the top-left corner (i.e., $$ \\text{grid}[0][0] $$). The robot can move either to the right or downwards at any given time, and the objective is to reach the bottom-right corner of the grid. The challenge is to find the number of unique paths the robot can take to reach this goal.\n\n### Key Points to Consider\n\n1. **Grid Dimensions**: \n The grid dimensions are $$ m $$ (rows) and $$ n $$ (columns), with $$ 1 \\leq m, n \\leq 100 $$.\n \n2. **Movement Constraints**: \n The robot can only move either down or to the right at any given point. It cannot move diagonally or backwards.\n\n3. **Dynamic Programming and Combinatorial Mathematics**: \n The problem can be solved using either a Dynamic Programming approach or using Combinatorial Mathematics.\n\n---\n\n## Live Coding & More - 3 Solutions\nhttps://youtu.be/-0OSF4u0cjQ?si=zup18xLotShahabI\n\n## Solution #1: Dynamic Programming\n\n### Intuition and Logic Behind the Solution\n\nThe idea behind this approach is to use a 2D Dynamic Programming (DP) array to store the number of unique paths to each cell. A cell $$ (i, j) $$ can be reached either from $$ (i-1, j) $$ or $$ (i, j-1) $$, and thus the number of unique paths to $$ (i, j) $$ is the sum of the number of unique paths to these two cells.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Create a $$ m \\times n $$ DP array, initializing the first row and first column to 1 because there\'s only one way to reach those cells from the starting point.\n\n2. **Main Algorithm**: \n - Iterate over the DP array starting from cell $$ (1, 1) $$.\n - For each cell $$ (i, j) $$, set $$ \\text{dp}[i][j] = \\text{dp}[i-1][j] + \\text{dp}[i][j-1] $$.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(m \\times n) $$ \u2014 We iterate through each cell once.\n- **Space Complexity**: $$ O(m \\times n) $$ \u2014 For the DP array.\n\n---\n\n## Solution #2: Memory-Optimized Dynamic Programming\n\n### Intuition and Logic Behind the Solution\n\nThe original DP solution used a $$ m \\times n $$ array to store the number of unique paths to each cell. However, since we only need information from the previous row and the current row to compute the number of unique paths for a given cell, we can optimize the solution to use only two rows at a time. This reduces the space complexity from $$ O(m \\times n) $$ to $$ O(n) $$.\n\n### Transitioning from $$ O(m \\times n) $$ to $$ O(n) $$\n\nIn the original $$ O(m \\times n) $$ approach, we used a 2D array `dp` where $$ \\text{dp}[i][j] $$ represented the number of unique paths to reach cell $$ (i, j) $$. To optimize this to $$ O(n) $$, we can maintain only two 1D arrays: `prev_row` and `curr_row`, each of length $$ n $$.\n\n- `prev_row[j]` will represent $$ \\text{dp}[i-1][j] $$, the number of unique paths to reach the cell in the previous row and $$ j $$-th column.\n- `curr_row[j]` will represent $$ \\text{dp}[i][j] $$, the number of unique paths to reach the cell in the current row and $$ j $$-th column.\n\n### Step-by-step Explanation\n\n1. **Initialization**: \n - Initialize two 1D arrays `curr_row` and `prev_row` with $$ n $$ elements, setting all elements to 1.\n\n2. **Main Algorithm**: \n - Iterate over the rows starting from 1 (the second row).\n - For each cell $$ (i, j) $$, set `curr_row[j] = curr_row[j-1] + prev_row[j]` .\n - Swap `curr_row` and `prev_row` for the next iteration.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(m \\times n) $$ \u2014 We still iterate through each cell once.\n- **Space Complexity**: $$ O(n) $$ \u2014 For the two 1D arrays.\n\n---\n\n## Solution #3: Combinatorial Mathematics\n\n### Intuition\n\nThe number of unique paths can be seen as the number of ways to choose $$ m-1 $$ downs and $$ n-1 $$ rights, regardless of the order. In combinatorial terms, this is equivalent to $$ \\binom{m+n-2}{m-1} $$.\n\n### Algorithm\n\n1. **Use the Combinatorial Formula**: \n $$ \\binom{m+n-2}{m-1} $$ or $$ \\binom{m+n-2}{n-1} $$ to calculate the number of unique paths.\n\n2. **Python\'s Math Library**: \n Python provides a built-in function $$ \\text{math.comb(n, k)} $$ to calculate $$ \\binom{n}{k} $$ efficiently.\n\n### Complexity Analysis\n\n- **Time Complexity**: $$ O(m) $$ or $$ O(n) $$ \u2014 For calculating the combination.\n- **Space Complexity**: $$ O(1) $$ \u2014 Constant space.\n\n---\n\n# Performance\n### Dynamic Programming\n\n| Language | Time (ms) | Memory (MB) |\n|-----------|-----------|-------------|\n| Rust | 0 ms | 2.2 MB |\n| C++ | 0 ms | 6.5 MB |\n| Java | 0 ms | 39.9 MB |\n| Go | 1 ms | 2.1 MB |\n| PHP | 10 ms | 19.3 MB |\n| C# | 23 ms | 26.6 MB |\n| Python3 (1D) | 26 ms | 16.3 MB |\n| Python3 (2D) | 28 ms | 16.3 MB |\n| JavaScript| 52 ms | 41.6 MB |\n\n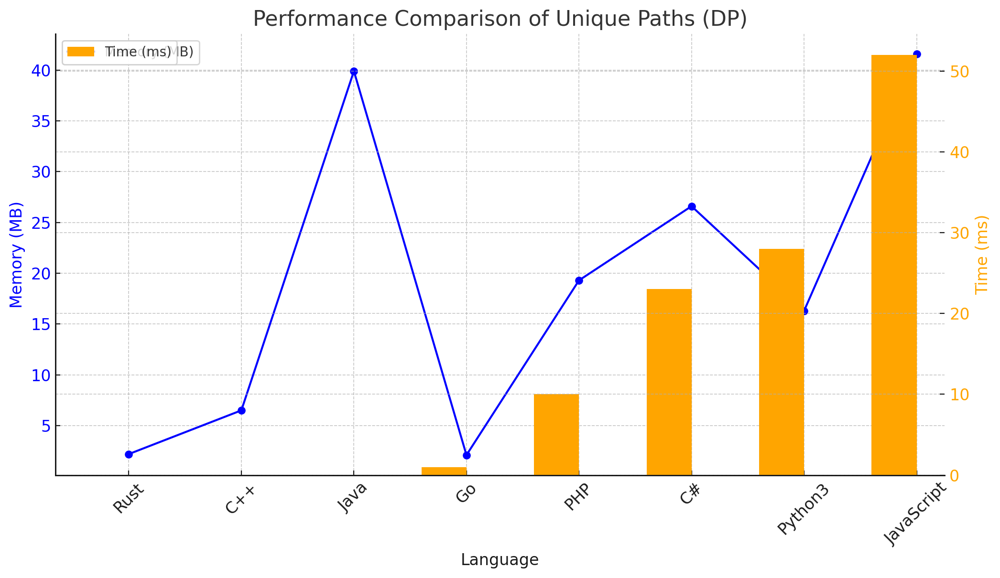\n\n\n## Combinatorial Mathematics\n\n| Language | Time (ms) | Memory (MB) |\n|-----------|-----------|-------------|\n| Rust | 0 ms | 2.2 MB |\n| C++ | 0 ms | 5.9 MB |\n| PHP | 0 ms | 18.9 MB |\n| Java | 0 ms | 39.8 MB |\n| Go | 1 ms | 1.9 MB |\n| C# | 22 ms | 26.5 MB |\n| Python3 | 27 ms | 16.4 MB |\n| JavaScript| 55 ms | 41.3 MB |\n\n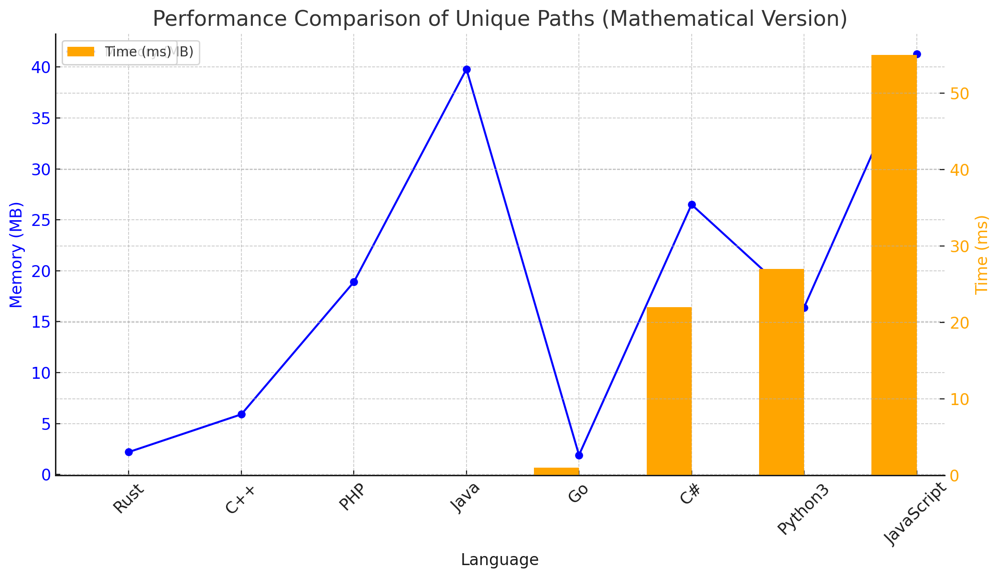\n\n# Code Math\n``` Python []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n return math.comb(m+n-2, m-1)\n```\n``` Rust []\nimpl Solution {\n pub fn unique_paths(m: i32, n: i32) -> i32 {\n let mut ans: i64 = 1;\n for i in 1..=m as i64 - 1 {\n ans = ans * (n as i64 - 1 + i) / i;\n }\n ans as i32\n }\n}\n```\n``` Go []\nfunc uniquePaths(m int, n int) int {\n ans := 1\n for i := 1; i <= m - 1; i++ {\n ans = ans * (n - 1 + i) / i\n }\n return ans\n}\n```\n``` C++ []\n#include <cmath>\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n long long ans = 1;\n for (int i = 1; i <= m - 1; ++i) {\n ans = ans * (n - 1 + i) / i;\n }\n return (int)ans;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int uniquePaths(int m, int n) {\n long ans = 1;\n for (int i = 1; i <= m - 1; i++) {\n ans = ans * (n - 1 + i) / i;\n }\n return (int)ans;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int UniquePaths(int m, int n) {\n long ans = 1;\n for (int i = 1; i <= m - 1; i++) {\n ans = ans * (n - 1 + i) / i;\n }\n return (int)ans;\n }\n}\n```\n``` PHP []\nclass Solution {\n function uniquePaths($m, $n) {\n $ans = 1;\n for ($i = 1; $i <= $m - 1; ++$i) {\n $ans = $ans * ($n - 1 + $i) / $i;\n }\n return (int)$ans;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} m\n * @param {number} n\n * @return {number}\n */\nvar uniquePaths = function(m, n) {\n let ans = 1;\n for (let i = 1; i <= m - 1; i++) {\n ans = ans * (n - 1 + i) / i;\n }\n return ans;\n};\n```\n# Code DP - 2D\n``` Python []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp = [[1 if i == 0 or j == 0 else 0 for j in range(n)] for i in range(m)]\n \n for i in range(1, m):\n for j in range(1, n):\n dp[i][j] = dp[i-1][j] + dp[i][j-1]\n \n return dp[-1][-1]\n```\n``` C++ []\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n vector<vector<int>> dp(m, vector<int>(n, 0));\n \n for (int i = 0; i < m; ++i) {\n dp[i][0] = 1;\n }\n for (int j = 0; j < n; ++j) {\n dp[0][j] = 1;\n }\n \n for (int i = 1; i < m; ++i) {\n for (int j = 1; j < n; ++j) {\n dp[i][j] = dp[i-1][j] + dp[i][j-1];\n }\n }\n \n return dp[m-1][n-1];\n }\n};\n```\n``` Java []\npublic class Solution {\n public int uniquePaths(int m, int n) {\n int[][] dp = new int[m][n];\n \n for (int i = 0; i < m; i++) {\n dp[i][0] = 1;\n }\n for (int j = 0; j < n; j++) {\n dp[0][j] = 1;\n }\n \n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n dp[i][j] = dp[i-1][j] + dp[i][j-1];\n }\n }\n \n return dp[m-1][n-1];\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn unique_paths(m: i32, n: i32) -> i32 {\n let mut dp: Vec<Vec<i32>> = vec![vec![1; n as usize]; m as usize];\n \n for i in 1..m as usize {\n for j in 1..n as usize {\n dp[i][j] = dp[i-1][j] + dp[i][j-1];\n }\n }\n \n dp[(m-1) as usize][(n-1) as usize]\n }\n}\n```\n``` Go []\nfunc uniquePaths(m int, n int) int {\n dp := make([][]int, m)\n for i := range dp {\n dp[i] = make([]int, n)\n }\n \n for i := 0; i < m; i++ {\n dp[i][0] = 1\n }\n for j := 0; j < n; j++ {\n dp[0][j] = 1\n }\n \n for i := 1; i < m; i++ {\n for j := 1; j < n; j++ {\n dp[i][j] = dp[i-1][j] + dp[i][j-1]\n }\n }\n \n return dp[m-1][n-1]\n}\n```\n``` C# []\npublic class Solution {\n public int UniquePaths(int m, int n) {\n int[,] dp = new int[m, n];\n \n for (int i = 0; i < m; i++) {\n dp[i, 0] = 1;\n }\n for (int j = 0; j < n; j++) {\n dp[0, j] = 1;\n }\n \n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n dp[i, j] = dp[i-1, j] + dp[i, j-1];\n }\n }\n \n return dp[m-1, n-1];\n }\n}\n```\n``` PHP []\nclass Solution {\n function uniquePaths($m, $n) {\n $dp = array_fill(0, $m, array_fill(0, $n, 0));\n \n for ($i = 0; $i < $m; ++$i) {\n $dp[$i][0] = 1;\n }\n for ($j = 0; $j < $n; ++$j) {\n $dp[0][$j] = 1;\n }\n \n for ($i = 1; $i < $m; ++$i) {\n for ($j = 1; $j < $n; ++$j) {\n $dp[$i][$j] = $dp[$i-1][$j] + $dp[$i][$j-1];\n }\n }\n \n return $dp[$m-1][$n-1];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} m\n * @param {number} n\n * @return {number}\n */\nvar uniquePaths = function(m, n) {\n const dp = Array.from({ length: m }, () => Array(n).fill(0));\n \n for (let i = 0; i < m; ++i) {\n dp[i][0] = 1;\n }\n for (let j = 0; j < n; ++j) {\n dp[0][j] = 1;\n }\n \n for (let i = 1; i < m; ++i) {\n for (let j = 1; j < n; ++j) {\n dp[i][j] = dp[i-1][j] + dp[i][j-1];\n }\n }\n \n return dp[m-1][n-1];\n};\n```\n# Code DP - 1D\n``` Python []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n curr_row = [1] * n\n prev_row = [1] * n\n\n for i in range(1, m):\n for j in range(1, n):\n curr_row[j] = curr_row[j - 1] + prev_row[j] \n curr_row, prev_row = prev_row, curr_row\n \n return prev_row[-1]\n```\n\n## Final Thoughts\n\nBoth solutions are valid for the given problem constraints. The Dynamic Programming approach is more general and can be extended to more complex scenarios, such as when some cells are blocked. On the other hand, the Combinatorial Mathematics approach is more efficient for this specific problem.\n\nTackling this problem offers a deep dive into Dynamic Programming and Combinatorial Mathematics. Whether you use a dynamic table or mathematical combinations, each approach is a lesson in computational thinking. This isn\'t just a problem; it\'s a tool for honing your optimization and math skills. So dive in and advance your algorithm mastery. \uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB\uD83C\uDF1F | 113 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
✅Step by step🔥Beginner Friendly🔥||DP||✅3 Approaches||full explanation🔥|| DP | unique-paths | 1 | 1 | # Question Understanding-\n\n**Given are only two valid moves :**\n- **Move right**\n- **Move down**\nHence, it is clear number of paths from cell (i,j) = sum of paths from cell( i+1,j) and cell(i,j+1)\n\n**It becomes a DP problem.**\nBut implementing DP directly **will lead to TLE**.\n**So memoization is useful -> Storing a result** so that we donot need to calculate it again.\n\ndp[i][j] = d[i+1][j] + dp[i][j+1]\n\n# BASE CASES\n\n**If we are in last row**, i == m-1, we only have the choice to move RIGHT, Hence number of moves will be 1.\n**If we are in last column**, j == n-1, we only have the choice to move DOWN, Hence number of moves will be 1.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Step-by-Step Solution:\n\n---\n\n\n---\n# **Bottom-Up Dynamic Programming:**\n\n**Step 1: Initialize the DP Table**\n- Create a 2D DP (dynamic programming) table of **size m x n** to store the number of unique paths for each cell.\n- **Initialize the rightmost column and bottom row of the DP table to 1** because there\'s only one way to reach each cell in those rows/columns (by moving all the way right or all the way down).\n\n**Step 2: Fill in the DP Table**\n\n- **Start from the second-to-last** row and second-to-last column (i.e., i = m - 2 and j = n - 2).\n- **For each cell (i, j) in the grid:**\n - Calculate the **number of unique paths to reach (i, j)** as the sum of the unique paths from the cell below (i+1, j) and **the cell to the right (i, j+1)**. Use this formula: **dp[i][j] = dp[i+1][j] + dp[i][j+1].**\n - **Continue filling** in the DP table row by row and column by column until you reach the top-left corner (dp[0][0]).\n\n**Step 3: Return the Result**\n\n- Return the value stored in the top-left corner of the DP table (dp[0][0]), which represents the number of unique paths from the top-left corner to the bottom-right corner.\n<!-- Describe your approach to solving the problem. -->\n\n---\n\n\n---\n\n\n# **Top-Down Dynamic Programming:**\n\n**Step 1: Initialize the Memoization Table**\n\n- **Create a memoization table** (an auxiliary 2D array) of size m x n to store computed results. Initialize all entries to -1 to indicate that no results have been computed yet.\n\n**Step 2: Recursive Function**\n- **Implement a recursive function**, say **uniquePathsRecursive(x, y, m, n, memo)**, which calculates the number of unique paths to reach cell (x, y) from the top-left corner.\n- **In this function:**\n - **Check if (x, y) is the destination cell** (m - 1, n - 1). If yes, return 1 since there is one way to reach the destination.\n - **Check if the result for (x, y) is already computed** in the memoization table (memo[x][y] != -1). **If yes, return the stored result.** \n\n - **Otherwise, calculate the number of unique paths** by recursively moving right and down (if valid) and adding the results. **Use the following logic:**\n \u27A1**If (x, y) can move right** (i.e., x < m - 1), calculate rightPaths = uniquePathsRecursive(x + 1, y, m, n, memo).\n \u27A1 **If (x, y) can move down** (i.e., y < n - 1), calculate downPaths = uniquePathsRecursive(x, y + 1, m, n, memo).\n \u27A1 **The total unique paths to (x, y) are rightPaths + downPaths.**\n \u27A1** Store the result** in the memoization table (memo[x][y]) and return it. \n\n**Step 3: Invoke the Recursive Function**\n\n- Call the recursive function with the initial arguments (0, 0, m, n, memo) to find the number of unique paths.\n\n**Step 4: Return the Result**\n\n- The result obtained from the recursive function call represents the number of unique paths from the top-left corner to the bottom-right corner.\n # Complexity\n\n---\n\n\n**Bottom-Up Dynamic Programming:**\n**Time Complexity (TC):** The bottom-up approach fills in the DP table iteratively, visiting each cell once. There are m rows and n columns in the grid, so the TC is **O(m * n)**.\n**Space Complexity (SC):** The space complexity is determined by the DP table, which is of size m x n. Therefore, **the SC is O(m * n)** to store the DP table.\n\n---\n\n\n**Top-Down Dynamic Programming (with Memoization):**\n**Time Complexity (TC):** O(m * n).\n**Space Complexity (SC):** O(m + n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n---\n\n\n\n# \uD83D\uDE0A\uD83D\uDE0ASMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n---\n\n\n# Bottom up Approach Code\n```C++ []\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n vector<vector<int>> dp(m, vector<int>(n, 0));\n \n // Initialize the rightmost column and bottom row to 1 because there is only one way to reach each cell in those rows/columns.\n for (int i = 0; i < m; i++) {\n dp[i][n-1] = 1;\n }\n for (int j = 0; j < n; j++) {\n dp[m-1][j] = 1;\n }\n \n // Fill in the dp table bottom-up\n for (int i = m - 2; i >= 0; i--) {\n for (int j = n - 2; j >= 0; j--) {\n dp[i][j] = dp[i+1][j] + dp[i][j+1];\n }\n }\n \n return dp[0][0];\n }\n};\n\n```\n```python3 []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n # Create a 2D DP table filled with zeros\n dp = [[0] * n for _ in range(m)]\n \n # Initialize the rightmost column and bottom row to 1\n for i in range(m):\n dp[i][n-1] = 1\n for j in range(n):\n dp[m-1][j] = 1\n \n # Fill in the DP table bottom-up\n for i in range(m - 2, -1, -1):\n for j in range(n - 2, -1, -1):\n dp[i][j] = dp[i+1][j] + dp[i][j+1]\n \n # Return the result stored in the top-left corner\n return dp[0][0]\n\n```\n```Java []\nclass Solution {\n public int uniquePaths(int m, int n) {\n // Create a 2D DP array filled with zeros\n int[][] dp = new int[m][n];\n \n // Initialize the rightmost column and bottom row to 1\n for (int i = 0; i < m; i++) {\n dp[i][n-1] = 1;\n }\n for (int j = 0; j < n; j++) {\n dp[m-1][j] = 1;\n }\n \n // Fill in the DP array bottom-up\n for (int i = m - 2; i >= 0; i--) {\n for (int j = n - 2; j >= 0; j--) {\n dp[i][j] = dp[i+1][j] + dp[i][j+1];\n }\n }\n \n // Return the result stored in the top-left corner\n return dp[0][0];\n }\n}\n\n```\n```Javascript []\nvar uniquePaths = function(m, n) {\n // Create a 2D DP array filled with zeros\n let dp = new Array(m).fill().map(() => new Array(n).fill(0));\n \n // Initialize the rightmost column and bottom row to 1\n for (let i = 0; i < m; i++) {\n dp[i][n-1] = 1;\n }\n for (let j = 0; j < n; j++) {\n dp[m-1][j] = 1;\n }\n \n // Fill in the DP array bottom-up\n for (let i = m - 2; i >= 0; i--) {\n for (let j = n - 2; j >= 0; j--) {\n dp[i][j] = dp[i+1][j] + dp[i][j+1];\n }\n }\n \n // Return the result stored in the top-left corner\n return dp[0][0];\n};\n\n```\n# Top-Down Approach Code\n\n```C++ []\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n // Create a memoization table to store computed results\n vector<vector<int>> memo(m, vector<int>(n, -1));\n \n // Call the recursive function to compute unique paths\n return uniquePathsRecursive(0, 0, m, n, memo);\n }\n \n int uniquePathsRecursive(int x, int y, int m, int n, vector<vector<int>>& memo) {\n // If we reach the destination (bottom-right corner), return 1\n if (x == m - 1 && y == n - 1) {\n return 1;\n }\n \n // If we have already computed the result for this cell, return it from the memo table\n if (memo[x][y] != -1) {\n return memo[x][y];\n }\n \n // Calculate the number of unique paths by moving right and down\n int rightPaths = 0;\n int downPaths = 0;\n \n // Check if it\'s valid to move right\n if (x < m - 1) {\n rightPaths = uniquePathsRecursive(x + 1, y, m, n, memo);\n }\n \n // Check if it\'s valid to move down\n if (y < n - 1) {\n downPaths = uniquePathsRecursive(x, y + 1, m, n, memo);\n }\n \n // Store the result in the memo table and return it\n memo[x][y] = rightPaths + downPaths;\n return memo[x][y];\n }\n};\n\n```\n```python3 []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n # Create a memoization table to store computed results\n memo = [[-1 for _ in range(n)] for _ in range(m)]\n \n # Call the recursive function to compute unique paths\n return self.uniquePathsRecursive(0, 0, m, n, memo)\n \n def uniquePathsRecursive(self, x: int, y: int, m: int, n: int, memo: List[List[int]]) -> int:\n # If we reach the destination (bottom-right corner), return 1\n if x == m - 1 and y == n - 1:\n return 1\n \n # If we have already computed the result for this cell, return it from the memo table\n if memo[x][y] != -1:\n return memo[x][y]\n \n # Calculate the number of unique paths by moving right and down\n rightPaths = 0\n downPaths = 0\n \n # Check if it\'s valid to move right\n if x < m - 1:\n rightPaths = self.uniquePathsRecursive(x + 1, y, m, n, memo)\n \n # Check if it\'s valid to move down\n if y < n - 1:\n downPaths = self.uniquePathsRecursive(x, y + 1, m, n, memo)\n \n # Store the result in the memo table and return it\n memo[x][y] = rightPaths + downPaths\n return memo[x][y]\n\n```\n```Java []\nclass Solution {\n public int uniquePaths(int m, int n) {\n // Create a memoization table to store computed results\n int[][] memo = new int[m][n];\n \n // Initialize the memoization table with -1 to indicate uncomputed results\n for (int i = 0; i < m; i++) {\n Arrays.fill(memo[i], -1);\n }\n \n // Call the recursive function to compute unique paths\n return uniquePathsRecursive(0, 0, m, n, memo);\n }\n \n public int uniquePathsRecursive(int x, int y, int m, int n, int[][] memo) {\n // If we reach the destination (bottom-right corner), return 1\n if (x == m - 1 && y == n - 1) {\n return 1;\n }\n \n // If we have already computed the result for this cell, return it from the memo table\n if (memo[x][y] != -1) {\n return memo[x][y];\n }\n \n // Calculate the number of unique paths by moving right and down\n int rightPaths = 0;\n int downPaths = 0;\n \n // Check if it\'s valid to move right\n if (x < m - 1) {\n rightPaths = uniquePathsRecursive(x + 1, y, m, n, memo);\n }\n \n // Check if it\'s valid to move down\n if (y < n - 1) {\n downPaths = uniquePathsRecursive(x, y + 1, m, n, memo);\n }\n \n // Store the result in the memo table and return it\n memo[x][y] = rightPaths + downPaths;\n return memo[x][y];\n }\n}\n\n```\n```Javascript []\nvar uniquePaths = function(m, n) {\n // Create a memoization table to store computed results\n let memo = new Array(m).fill(null).map(() => new Array(n).fill(-1));\n \n // Call the recursive function to compute unique paths\n return uniquePathsRecursive(0, 0, m, n, memo);\n};\n\nvar uniquePathsRecursive = function(x, y, m, n, memo) {\n // If we reach the destination (bottom-right corner), return 1\n if (x === m - 1 && y === n - 1) {\n return 1;\n }\n \n // If we have already computed the result for this cell, return it from the memo table\n if (memo[x][y] !== -1) {\n return memo[x][y];\n }\n \n // Calculate the number of unique paths by moving right and down\n let rightPaths = 0;\n let downPaths = 0;\n \n // Check if it\'s valid to move right\n if (x < m - 1) {\n rightPaths = uniquePathsRecursive(x + 1, y, m, n, memo);\n }\n \n // Check if it\'s valid to move down\n if (y < n - 1) {\n downPaths = uniquePathsRecursive(x, y + 1, m, n, memo);\n }\n \n // Store the result in the memo table and return it\n memo[x][y] = rightPaths + downPaths;\n return memo[x][y];\n};\n\n```\n# \uD83D\uDE0A\uD83D\uDE0ASMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n | 103 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
testing123 | unique-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ntesting123\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic programming approach where we save the count of the possible paths that past through each index. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(M * N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(M * N)\n\n# Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp = [[0 for _ in range(n)] for _ in range(m)]\n dp[0][0] = 1\n\n for i in range(m):\n for j in range(n):\n # val1 = left val, val2 = top val\n val1 = 0\n val2 = 0\n if(j-1 >= 0):\n val1 = dp[i][j-1]\n if(i-1 >= 0):\n val2 = dp[i-1][j]\n dp[i][j] = dp[i][j] + val1 + val2\n \n\n return dp[m-1][n-1]\n\n \n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Top-Down Dynamic Programming in Python3 | unique-paths | 0 | 1 | # Intuition\nThe problem description is the following: \n\n- there\'s a robot, that\'s standing at (0, 0)\n- our goal is to calculate **HOW** many **UNIQUE** paths can we explore by moving robot at directions\n\n\n---\n\n\nLets consider an example:\n```py\ngrid = [[R, 0]\n [0, 0]]\n# starting point is (0, 0)\n# and robot can achieve (1, 1) only in TWO steps\n# (0, 0) => (0, 1) => (1, 1)\n# (0, 0) => (1, 0) => (1, 1)\n```\nThe idea behind is quite simple:\n- start from ending point `(n - 1, m - 1)`\n- we only need to consider a move into another `row` or `column`\n- if the robot **is out of boundary**, this path is **invalid** one\n- otherwise increment the answer!\n\n---\n\nIf you haven\'t already familiar with [Dynamic Programming](https://en.wikipedia.org/wiki/Dynamic_programming), follow the link.\n\n# Approach\n1. declare `dp` function and here is the signature:\n```\n# state: row and col, that\'ll represent current cell, \n# where robot is standing\n# \n# recurrence relation: because the robot goes only over ROW, and COL\n# it moves in X and in Y-axis => check if the robot is still \n# INSIDE of a grid and let him go UP or LEFT\n\n# at each step we want to know a number of unique ways\n```\n2. if the robot has reached (0, 0), this path will be considered as a **valid**, so return `1`\n3. return `dp(m - 1, n - 1)`\n\n# Complexity\n- Time complexity: **O(m*n)**, because of iterating over a grid \n\n- Space complexity: **O(m*n)**, because of storing inside `cache` `row` and `col`\n\n# Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n @cache\n def dp(row, col):\n if (row, col) == (0, 0): return 1\n \n ways = 0\n \n if row: ways += dp(row - 1, col) \n if col: ways += dp(row, col - 1) \n\n return ways\n \n return dp(m - 1, n - 1)\n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Paths | unique-paths | 1 | 1 | # Intuition\nWhen first encountering this problem, my initial thought was to approach it using dynamic programming. I recognized that this is a classic problem of finding the number of unique paths from the top-left corner to the bottom-right corner of a grid, where you can only move down or to the right. \n\n# Approach\nTo solve this problem, I used dynamic programming to build a 2D array to store the number of unique paths for each cell in the grid. I started with initializing the top-left cell with a value of 1 since there is only one way to reach it. Then, I iterated through the grid row by row and calculated the number of unique paths for each cell by adding the number of unique paths from the cell above it and the cell to the left of it. This way, I filled in the entire grid, and the value in the bottom-right cell represents the total number of unique paths.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(m * n), where m is the number of rows and n is the number of columns in the grid. This is because we iterate through the entire grid once to calculate the unique paths for each cell.\n\n- Space complexity: The space complexity is O(m * n) as well since we use a 2D array of the same size as the grid to store the intermediate results.\n\n# Code\n```Java []\nclass Solution {\n public int uniquePaths(int m, int n) {\n int dp[][] = new int[m][n];\n dp[0][0] = 1;\n \n // Initialize the first column and first row with 1\n for (int i = 1; i < m; i++) {\n dp[i][0] = 1;\n }\n for (int j = 1; j < n; j++) {\n dp[0][j] = 1;\n }\n \n // Calculate unique paths for each cell\n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n dp[i][j] = dp[i - 1][j] + dp[i][j - 1];\n }\n }\n \n return dp[m - 1][n - 1];\n }\n}\n```\n```python []\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp = [[0] * n for _ in range(m)]\n dp[0][0] = 1\n\n # Initialize the first column and first row with 1\n for i in range(1, m):\n dp[i][0] = 1\n for j in range(1, n):\n dp[0][j] = 1\n\n # Calculate unique paths for each cell\n for i in range(1, m):\n for j in range(1, n):\n dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\n\n return dp[m - 1][n - 1]\n\n```\n```C++ []\nclass Solution {\npublic:\n int uniquePaths(int m, int n) {\n vector<vector<int>> dp(m, vector<int>(n, 0));\n dp[0][0] = 1;\n\n // Initialize the first column and first row with 1\n for (int i = 1; i < m; i++) {\n dp[i][0] = 1;\n }\n for (int j = 1; j < n; j++) {\n dp[0][j] = 1;\n }\n\n // Calculate unique paths for each cell\n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n dp[i][j] = dp[i - 1][j] + dp[i][j - 1];\n }\n }\n\n return dp[m - 1][n - 1];\n }\n};\n```\n\n\nThis code provides a straightforward and efficient solution to the problem of finding the number of unique paths in a grid. | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Python easy solutions | unique-paths | 0 | 1 | # Intuition\n\n\n# Approach\nm*n = 3*7\n[28, 21, 15, 10, 6, 3, 1] 0\n[7, 6, 5, 4, 3, 2, 1] 0\n[1, 1, 1, 1, 1, 1, 1] 0\n 0 0 0 0 0 0 0\n\nWe see this matrix, that assign 1\'s to bottom row and right most column. Then in reverse direction sum up thr right ane down value.\nThat is at place 5*1 we have 1 at right value and 1 at down. So at 5*1 we have 2. Similarly at 5*0 we have 2+1 that is 3.\n\nWe put all 1\'s because all the bottom side we consider it is 0 ane same for right.\nThen finally return row[0], That is 28\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n row = [1]*n\n\n for i in range(m-1):\n newRow = [1]*n\n\n for j in range(n-2, -1, -1):\n newRow[j] = newRow[j+1] + row[j]\n row = newRow \n\n return row[0]\n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
python3 easy beats 7% | unique-paths | 0 | 1 | # Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n #bottom additional row of all the ones\n oldrow = [1]*n\n for i in range(m-1):\n #for each row we are calculating newrow\n newrow = [1]*n\n #traverse through columns in reverse order excluding last column \n for j in range(n-2, -1, -1):\n #at each postion \'i\' answer is answer at \'i+1\' block of same row + answer\n #at ith position of bottom row \n newrow[j] = newrow[j+1] + oldrow[j]\n oldrow = newrow\n return oldrow[0]\n \n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Binbin solved this question at light speed! | unique-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n if m == 1 and n == 1:\n return 1\n L_n=[0]\n for t in range(n-1):\n L_n.append(1)\n \n for i in range(m-1):\n L_o=L_n\n L_n=[1]\n for j in range(1,n):\n L_n.append(L_n[j-1]+L_o[j])\n return L_n[-1]\n \n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
4 Different Approaches---->DP | unique-paths | 0 | 1 | # 1. Recursive Approach-------->Top to Down\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n def solve(ind1,ind2):\n if ind1==0 and ind2==0:\n return 1\n if ind1<0 or ind2<0:\n return 0\n return solve(ind1-1,ind2)+solve(ind1,ind2-1)\n return solve(m-1,n-1)\n ```\n # 2. Memorization Approach\n ```\n class Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp=[[-1]*(n+1) for i in range(m)]\n def solve(ind1,ind2):\n if ind1==0 and ind2==0:\n return 1\n if ind1<0 or ind2<0:\n return 0\n if dp[ind1][ind2]!=-1:\n return dp[ind1][ind2]\n left=solve(ind1,ind2-1)\n up=solve(ind1-1,ind2)\n dp[ind1][ind2]=up+left\n return left+up\n return solve(m-1,n-1)\n```\n# 3. Tabulation------>Bottom to Up Approach\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp=[[0]*(n+1) for i in range(m+1)]\n for ind1 in range(1,m+1):\n for ind2 in range(1,n+1):\n if ind1==ind2==1:\n dp[ind1][ind2]=1\n else:\n left=up=0\n if ind2-1>=0:\n left=dp[ind1][ind2-1]\n if ind1-1>=0:\n up=dp[ind1-1][ind2]\n dp[ind1][ind2]=up+left\n return dp[-1][-1]\n```\n# 4. Space Optimization\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n prev=[0]*(n+1)\n for ind1 in range(1,m+1):\n cur=[0]*(n+1)\n for ind2 in range(1,n+1):\n if ind1==ind2==1:\n cur[ind2]=1\n else:\n left=up=0\n if ind2-1>=0:\n left=cur[ind2-1]\n if ind1-1>=0:\n up=prev[ind2]\n cur[ind2]=up+left\n prev=cur\n return cur[-1]\n```\n# please upvote me it would encourage me alot\n | 5 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Python| binomial coefficients | n+m choose n (or m) | formula with factorial | unique-paths | 0 | 1 | # Intuition\n\n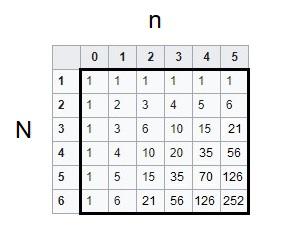\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n\n def fact(n):\n fact = 1\n for num in range(2, n + 1):\n fact *= num\n return fact\n\n k = m+n-2\n\n return int(fact(k)/(fact(m-1)*fact(k-m+1)))\n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Python || Dynamic Programming || BackTracking 🔥 | unique-paths | 0 | 1 | # Code\n```\nclass Solution:\n def uniquePaths(self, m: int, n: int) -> int:\n dp = [[0]*101 for i in range(101)]\n def count(r,c):\n if r == 1 or c == 1:\n return 1\n if dp[r][c]:\n return dp[r][c]\n left = count(r - 1, c)\n right = count(r, c - 1)\n dp[r][c] = left + right\n return dp[r][c]\n return count(m,n)\n``` | 1 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
Given the two integers `m` and `n`, return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The test cases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** m = 3, n = 7
**Output:** 28
**Example 2:**
**Input:** m = 3, n = 2
**Output:** 3
**Explanation:** From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
**Constraints:**
* `1 <= m, n <= 100` | null |
Python3 Solution | unique-paths-ii | 0 | 1 | \n```\nclass Solution:\n def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:\n m=len(obstacleGrid)\n n=len(obstacleGrid[0])\n dp=[[0 for _ in range(n)] for _ in range(m)]\n for col in range(n):\n if obstacleGrid[0][col]==1:\n break\n dp[0][col]=1\n for row in range(m):\n if obstacleGrid[row][0]==1:\n break\n\n dp[row][0]=1\n\n for row in range(1,m):\n for col in range(1,n):\n if obstacleGrid[row][col]==1:\n continue\n\n dp[row][col]=dp[row-1][col]+dp[row][col-1]\n\n return dp[-1][-1] \n``` | 3 | You are given an `m x n` integer array `grid`. There is a robot initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
An obstacle and space are marked as `1` or `0` respectively in `grid`. A path that the robot takes cannot include **any** square that is an obstacle.
Return _the number of possible unique paths that the robot can take to reach the bottom-right corner_.
The testcases are generated so that the answer will be less than or equal to `2 * 109`.
**Example 1:**
**Input:** obstacleGrid = \[\[0,0,0\],\[0,1,0\],\[0,0,0\]\]
**Output:** 2
**Explanation:** There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
**Example 2:**
**Input:** obstacleGrid = \[\[0,1\],\[0,0\]\]
**Output:** 1
**Constraints:**
* `m == obstacleGrid.length`
* `n == obstacleGrid[i].length`
* `1 <= m, n <= 100`
* `obstacleGrid[i][j]` is `0` or `1`. | The robot can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it. However, if any cell has an obstacle, you don't let that cell contribute to any path. So, for the first row, the number of ways will simply be
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1]
else
obstacleGrid[i,j] = 0
You can do a similar processing for finding out the number of ways of reaching the cells in the first column. For any other cell, we can find out the number of ways of reaching it, by making use of the number of ways of reaching the cell directly above it and the cell to the left of it in the grid. This is because these are the only two directions from which the robot can come to the current cell. Since we are making use of pre-computed values along the iteration, this becomes a dynamic programming problem.
if obstacleGrid[i][j] is not an obstacle
obstacleGrid[i,j] = obstacleGrid[i,j - 1] + obstacleGrid[i - 1][j]
else
obstacleGrid[i,j] = 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.