title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | grid-illumination | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> gridIllumination(int n, vector<vector<int>>& l, vector<vector<int>>& q) {\n unordered_map<int,int>lx,ly,ld,rd;\n vector<int>a;\n vector<vector<int>>dir;\n unordered_set<long>lamp;\n for(auto &i:l){\n long s=(long)i[0]*n+i[1];\n if(!lamp.count(s)){\n lamp.insert(s);\n lx[i[0]]++;\n ly[i[1]]++;\n ld[i[0]-i[1]]++;\n rd[i[0]+i[1]]++;\n }\n }\n dir={{-1,-1},{-1,0},{-1,1},{0,-1},{0,0},{0,1},{1,-1},{1,0},{1,1}};\n for(auto &i:q){\n int x=i[0],y=i[1];\n if(lx.count(x)||ly.count(y)||ld.count(x-y)||rd.count(x+y)){\n a.push_back(1);\n }\n else{\n a.push_back(0);\n continue;\n }\n for(auto &d:dir){\n int nx=x+d[0],ny=y+d[1];\n if(nx>=0 && nx<n && ny>=0 && ny<n ){ \n long s=(long)nx*n+ny;\n if(lamp.count(s)){\n if(lx.count(nx)){\n lx[nx]--;\n if(lx[nx]<1)\n lx.erase(nx);\n }\n if(ly.count(ny)){\n ly[ny]--;\n if(ly[ny]<1)\n ly.erase(ny);\n }\n if(ld.count(nx-ny)){\n ld[nx-ny]--;\n if(ld[nx-ny]<1)\n ld.erase(nx-ny);\n }\n if(rd.count(nx+ny)){\n rd[nx+ny]--;\n if(rd[nx+ny]<1)\n rd.erase(nx+ny);\n }\n lamp.erase(s);\n }\n }\n }\n }\n return a;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n rows, cols, pd, sd, lighted = {}, {}, {}, {}, set()\n for a,b in lamps:\n if (a,b) in lighted:\n continue\n rows[a] = rows.get(a, 0) + 1\n cols[b] = cols.get(b, 0) + 1\n pd[a-b] = pd.get(a-b, 0) + 1\n sd[a+b] = sd.get(a+b, 0) + 1\n lighted.add((a,b))\n \n res = []\n moves = [[0,0], [-1,0], [-1,1], [0,1], [1,1], [1,0], [1,-1], [0,-1], [-1,-1]]\n for a, b in queries:\n if rows.get(a, 0) > 0 or cols.get(b, 0) > 0 or pd.get(a-b, 0) > 0 or sd.get(a+b, 0) > 0:\n res.append(1)\n for i, j in moves:\n na, nb = a + i, b + j\n if (na, nb) in lighted:\n lighted.remove((na, nb))\n rows[na] -= 1\n cols[nb] -= 1\n pd[na-nb] -= 1\n sd[na+nb] -= 1\n else:\n res.append(0)\n return res\n```\n\n```Java []\nclass Solution {\n private int n;\n private HashMap<Integer, Integer> rowIllum;\n private HashMap<Integer, Integer> colIllum;\n private HashMap<Integer, Integer> dia1Illum;\n private HashMap<Integer, Integer> dia2Illum;\n private HashMap<Integer, ArrayList<Integer>> lamps;\n\n public boolean isIlluminated(int x, int y) {\n return rowIllum.getOrDefault(x, 0) > 0 || colIllum.getOrDefault(y, 0) > 0 || \n dia1Illum.getOrDefault(x - y, 0) > 0 || dia2Illum.getOrDefault(x + y, 0) > 0;\n }\n public void turnOff(int x, int y) {\n for(int i = Math.max(x - 1, 0); i < Math.min(x + 2, n); i++) {\n if(lamps.containsKey(i)) {\n ArrayList<Integer> l = lamps.get(i);\n for(int j = Math.max(y - 1, 0); j < Math.min(y + 2, n); j++) {\n if(l.contains(j)) {\n rowIllum.put(i, rowIllum.get(i) - 1);\n colIllum.put(j, colIllum.get(j) - 1);\n dia1Illum.put(i - j, dia1Illum.get(i - j) - 1);\n dia2Illum.put(i + j, dia2Illum.get(i + j) - 1);\n l.remove((Integer)j);\n }\n if(l.isEmpty()) {\n lamps.remove(i);\n }\n }\n }\n }\n }\n public void turnOn(int x, int y) {\n if(!lamps.containsKey(x) || !lamps.get(x).contains(y)) {\n lamps.computeIfAbsent(x, k -> {\n return new ArrayList<Integer>();\n }).add(y);\n rowIllum.put(x, rowIllum.getOrDefault(x, 0) + 1);\n colIllum.put(y, colIllum.getOrDefault(y, 0) + 1);\n dia1Illum.put(x - y, dia1Illum.getOrDefault(x - y, 0) + 1);\n dia2Illum.put(x + y, dia2Illum.getOrDefault(x + y, 0) + 1);\n }\n }\n public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {\n this.n = n;\n rowIllum = new HashMap<Integer, Integer>();\n colIllum = new HashMap<Integer, Integer>();\n dia1Illum = new HashMap<Integer, Integer>();\n dia2Illum = new HashMap<Integer, Integer>();\n this.lamps = new HashMap<Integer, ArrayList<Integer>>();\n\n for(int[] l : lamps) {\n turnOn(l[0], l[1]);\n }\n int[] ans = new int[queries.length];\n int index = 0;\n for(int[] q : queries) {\n if(isIlluminated(q[0], q[1])) {\n ans[index] = 1;\n turnOff(q[0], q[1]);\n }\n index++;\n }\n return ans;\n }\n}\n``` | 1 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Solution | grid-illumination | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> gridIllumination(int n, vector<vector<int>>& l, vector<vector<int>>& q) {\n unordered_map<int,int>lx,ly,ld,rd;\n vector<int>a;\n vector<vector<int>>dir;\n unordered_set<long>lamp;\n for(auto &i:l){\n long s=(long)i[0]*n+i[1];\n if(!lamp.count(s)){\n lamp.insert(s);\n lx[i[0]]++;\n ly[i[1]]++;\n ld[i[0]-i[1]]++;\n rd[i[0]+i[1]]++;\n }\n }\n dir={{-1,-1},{-1,0},{-1,1},{0,-1},{0,0},{0,1},{1,-1},{1,0},{1,1}};\n for(auto &i:q){\n int x=i[0],y=i[1];\n if(lx.count(x)||ly.count(y)||ld.count(x-y)||rd.count(x+y)){\n a.push_back(1);\n }\n else{\n a.push_back(0);\n continue;\n }\n for(auto &d:dir){\n int nx=x+d[0],ny=y+d[1];\n if(nx>=0 && nx<n && ny>=0 && ny<n ){ \n long s=(long)nx*n+ny;\n if(lamp.count(s)){\n if(lx.count(nx)){\n lx[nx]--;\n if(lx[nx]<1)\n lx.erase(nx);\n }\n if(ly.count(ny)){\n ly[ny]--;\n if(ly[ny]<1)\n ly.erase(ny);\n }\n if(ld.count(nx-ny)){\n ld[nx-ny]--;\n if(ld[nx-ny]<1)\n ld.erase(nx-ny);\n }\n if(rd.count(nx+ny)){\n rd[nx+ny]--;\n if(rd[nx+ny]<1)\n rd.erase(nx+ny);\n }\n lamp.erase(s);\n }\n }\n }\n }\n return a;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n rows, cols, pd, sd, lighted = {}, {}, {}, {}, set()\n for a,b in lamps:\n if (a,b) in lighted:\n continue\n rows[a] = rows.get(a, 0) + 1\n cols[b] = cols.get(b, 0) + 1\n pd[a-b] = pd.get(a-b, 0) + 1\n sd[a+b] = sd.get(a+b, 0) + 1\n lighted.add((a,b))\n \n res = []\n moves = [[0,0], [-1,0], [-1,1], [0,1], [1,1], [1,0], [1,-1], [0,-1], [-1,-1]]\n for a, b in queries:\n if rows.get(a, 0) > 0 or cols.get(b, 0) > 0 or pd.get(a-b, 0) > 0 or sd.get(a+b, 0) > 0:\n res.append(1)\n for i, j in moves:\n na, nb = a + i, b + j\n if (na, nb) in lighted:\n lighted.remove((na, nb))\n rows[na] -= 1\n cols[nb] -= 1\n pd[na-nb] -= 1\n sd[na+nb] -= 1\n else:\n res.append(0)\n return res\n```\n\n```Java []\nclass Solution {\n private int n;\n private HashMap<Integer, Integer> rowIllum;\n private HashMap<Integer, Integer> colIllum;\n private HashMap<Integer, Integer> dia1Illum;\n private HashMap<Integer, Integer> dia2Illum;\n private HashMap<Integer, ArrayList<Integer>> lamps;\n\n public boolean isIlluminated(int x, int y) {\n return rowIllum.getOrDefault(x, 0) > 0 || colIllum.getOrDefault(y, 0) > 0 || \n dia1Illum.getOrDefault(x - y, 0) > 0 || dia2Illum.getOrDefault(x + y, 0) > 0;\n }\n public void turnOff(int x, int y) {\n for(int i = Math.max(x - 1, 0); i < Math.min(x + 2, n); i++) {\n if(lamps.containsKey(i)) {\n ArrayList<Integer> l = lamps.get(i);\n for(int j = Math.max(y - 1, 0); j < Math.min(y + 2, n); j++) {\n if(l.contains(j)) {\n rowIllum.put(i, rowIllum.get(i) - 1);\n colIllum.put(j, colIllum.get(j) - 1);\n dia1Illum.put(i - j, dia1Illum.get(i - j) - 1);\n dia2Illum.put(i + j, dia2Illum.get(i + j) - 1);\n l.remove((Integer)j);\n }\n if(l.isEmpty()) {\n lamps.remove(i);\n }\n }\n }\n }\n }\n public void turnOn(int x, int y) {\n if(!lamps.containsKey(x) || !lamps.get(x).contains(y)) {\n lamps.computeIfAbsent(x, k -> {\n return new ArrayList<Integer>();\n }).add(y);\n rowIllum.put(x, rowIllum.getOrDefault(x, 0) + 1);\n colIllum.put(y, colIllum.getOrDefault(y, 0) + 1);\n dia1Illum.put(x - y, dia1Illum.getOrDefault(x - y, 0) + 1);\n dia2Illum.put(x + y, dia2Illum.getOrDefault(x + y, 0) + 1);\n }\n }\n public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {\n this.n = n;\n rowIllum = new HashMap<Integer, Integer>();\n colIllum = new HashMap<Integer, Integer>();\n dia1Illum = new HashMap<Integer, Integer>();\n dia2Illum = new HashMap<Integer, Integer>();\n this.lamps = new HashMap<Integer, ArrayList<Integer>>();\n\n for(int[] l : lamps) {\n turnOn(l[0], l[1]);\n }\n int[] ans = new int[queries.length];\n int index = 0;\n for(int[] q : queries) {\n if(isIlluminated(q[0], q[1])) {\n ans[index] = 1;\n turnOff(q[0], q[1]);\n }\n index++;\n }\n return ans;\n }\n}\n``` | 1 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python3 solution | Hashmap | Explained | grid-illumination | 0 | 1 | \'\'\'\n1. The idea is to store every lamp light in 4 hashmaps: for row, column, p diag, s diag (every direction of light) and store the lamps position in a set (cuz we need to access them quickly and also, they may repeat themselves)\n2. Check for light iterating queries (if there is light then we have to check for lamps). If we find a lamp in 3x3 range (all directions in that range from our [queries[i][0], queries[i][1]] position we delete the light from that lamp and remove the lamp from our set. ) \n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n def check(i, j, dRow, dCol, dDiagS, dDiagP):\n if (i in dRow and dRow[i] > 0) or (j in dCol and dCol[j] > 0) or (\n i + j in dDiagS and dDiagS[i + j] > 0) or (\n i - j in dDiagP and dDiagP[i - j] > 0):\n return True\n return False\n \n def decrement(i, j, dRow, dCol, dDiagS, dDiagP):\n dRow[i] -= 1\n dCol[j] -= 1\n dDiagS[i + j] -= 1\n dDiagP[i - j] -= 1\n \n my_set = set()\n dRow, dCol, dDiagS, dDiagP = {}, {}, {}, {} \n for i in range(len(lamps)):\n if (lamps[i][0], lamps[i][1]) not in my_set:\n if lamps[i][0] not in dRow:\n dRow[lamps[i][0]] = 1\n else:\n dRow[lamps[i][0]] += 1\n if lamps[i][1] not in dCol:\n dCol[lamps[i][1]] = 1\n else:\n dCol[lamps[i][1]] += 1\n if sum(lamps[i]) not in dDiagS:\n dDiagS[sum(lamps[i])] = 1\n else:\n dDiagS[sum(lamps[i])] += 1\n if lamps[i][0] - lamps[i][1] not in dDiagP:\n dDiagP[lamps[i][0] - lamps[i][1]] = 1\n else:\n dDiagP[lamps[i][0] - lamps[i][1]] += 1\n my_set.add((lamps[i][0], lamps[i][1]))\n ans = []\n directions = [(-1, -1), (-1, 0), (0, -1), (0, 0), (0, 1), (1, 0), (1, 1), (1, -1), (-1, 1)]\n for i in range(len(queries)):\n # check if it\'s lighted up\n if check(queries[i][0], queries[i][1], dRow, dCol, dDiagS, dDiagP):\n ans.append(1)\n # check for lamp at 9 blocks\n for x in directions:\n if (queries[i][0]+x[0], queries[i][1]+x[1]) in my_set:\n decrement(queries[i][0]+x[0], queries[i][1]+x[1], dRow, dCol, dDiagS, dDiagP)\n my_set.remove((queries[i][0]+x[0], queries[i][1]+x[1]))\n else:\n ans.append(0)\n return ans\n```\n\'\'\'\nIf you like it, please upvote! ^^ | 1 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python3 solution | Hashmap | Explained | grid-illumination | 0 | 1 | \'\'\'\n1. The idea is to store every lamp light in 4 hashmaps: for row, column, p diag, s diag (every direction of light) and store the lamps position in a set (cuz we need to access them quickly and also, they may repeat themselves)\n2. Check for light iterating queries (if there is light then we have to check for lamps). If we find a lamp in 3x3 range (all directions in that range from our [queries[i][0], queries[i][1]] position we delete the light from that lamp and remove the lamp from our set. ) \n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n def check(i, j, dRow, dCol, dDiagS, dDiagP):\n if (i in dRow and dRow[i] > 0) or (j in dCol and dCol[j] > 0) or (\n i + j in dDiagS and dDiagS[i + j] > 0) or (\n i - j in dDiagP and dDiagP[i - j] > 0):\n return True\n return False\n \n def decrement(i, j, dRow, dCol, dDiagS, dDiagP):\n dRow[i] -= 1\n dCol[j] -= 1\n dDiagS[i + j] -= 1\n dDiagP[i - j] -= 1\n \n my_set = set()\n dRow, dCol, dDiagS, dDiagP = {}, {}, {}, {} \n for i in range(len(lamps)):\n if (lamps[i][0], lamps[i][1]) not in my_set:\n if lamps[i][0] not in dRow:\n dRow[lamps[i][0]] = 1\n else:\n dRow[lamps[i][0]] += 1\n if lamps[i][1] not in dCol:\n dCol[lamps[i][1]] = 1\n else:\n dCol[lamps[i][1]] += 1\n if sum(lamps[i]) not in dDiagS:\n dDiagS[sum(lamps[i])] = 1\n else:\n dDiagS[sum(lamps[i])] += 1\n if lamps[i][0] - lamps[i][1] not in dDiagP:\n dDiagP[lamps[i][0] - lamps[i][1]] = 1\n else:\n dDiagP[lamps[i][0] - lamps[i][1]] += 1\n my_set.add((lamps[i][0], lamps[i][1]))\n ans = []\n directions = [(-1, -1), (-1, 0), (0, -1), (0, 0), (0, 1), (1, 0), (1, 1), (1, -1), (-1, 1)]\n for i in range(len(queries)):\n # check if it\'s lighted up\n if check(queries[i][0], queries[i][1], dRow, dCol, dDiagS, dDiagP):\n ans.append(1)\n # check for lamp at 9 blocks\n for x in directions:\n if (queries[i][0]+x[0], queries[i][1]+x[1]) in my_set:\n decrement(queries[i][0]+x[0], queries[i][1]+x[1], dRow, dCol, dDiagS, dDiagP)\n my_set.remove((queries[i][0]+x[0], queries[i][1]+x[1]))\n else:\n ans.append(0)\n return ans\n```\n\'\'\'\nIf you like it, please upvote! ^^ | 1 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python Easy to Understand O(L+Q) Solution | grid-illumination | 0 | 1 | # Code\n``` python3 \nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n on = set()\n onv = Counter() # number of turned-on-lights in | direction at given index\n onh = Counter() # number of turned-on-lights in - direction at given index\n ona = Counter() # number of turned-on-lights in \\ direction at given index\n ons = Counter() # number of turned-on-lights in / direction at given index\n\n for i,j in lamps:\n if (i,j) in on: continue\n on.add((i,j))\n onv[i]+=1\n onh[j]+=1\n ona[i+j]+=1\n ons[i-j]+=1\n \n ans = []\n\n def turnoff_if_on(i,j):\n if not (i,j) in on: return\n on.remove((i,j))\n onv[i]-=1\n onh[j]-=1\n ona[i+j]-=1\n ons[i-j]-=1\n\n for i,j in queries:\n if onv[i] or onh[j] or ona[i+j] or ons[i-j]: \n ans.append(1)\n turnoff_if_on(i,j)\n turnoff_if_on(i+1,j)\n turnoff_if_on(i-1,j)\n turnoff_if_on(i,j-1)\n turnoff_if_on(i+1,j-1)\n turnoff_if_on(i-1,j-1)\n turnoff_if_on(i,j+1)\n turnoff_if_on(i+1,j+1)\n turnoff_if_on(i-1,j+1)\n else:\n ans.append(0)\n \n return ans\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python Easy to Understand O(L+Q) Solution | grid-illumination | 0 | 1 | # Code\n``` python3 \nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n on = set()\n onv = Counter() # number of turned-on-lights in | direction at given index\n onh = Counter() # number of turned-on-lights in - direction at given index\n ona = Counter() # number of turned-on-lights in \\ direction at given index\n ons = Counter() # number of turned-on-lights in / direction at given index\n\n for i,j in lamps:\n if (i,j) in on: continue\n on.add((i,j))\n onv[i]+=1\n onh[j]+=1\n ona[i+j]+=1\n ons[i-j]+=1\n \n ans = []\n\n def turnoff_if_on(i,j):\n if not (i,j) in on: return\n on.remove((i,j))\n onv[i]-=1\n onh[j]-=1\n ona[i+j]-=1\n ons[i-j]-=1\n\n for i,j in queries:\n if onv[i] or onh[j] or ona[i+j] or ons[i-j]: \n ans.append(1)\n turnoff_if_on(i,j)\n turnoff_if_on(i+1,j)\n turnoff_if_on(i-1,j)\n turnoff_if_on(i,j-1)\n turnoff_if_on(i+1,j-1)\n turnoff_if_on(i-1,j-1)\n turnoff_if_on(i,j+1)\n turnoff_if_on(i+1,j+1)\n turnoff_if_on(i-1,j+1)\n else:\n ans.append(0)\n \n return ans\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python 4 Hash Maps, O(n) | grid-illumination | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n on = set()\n yOn = {}\n xOn = {}\n dy = {}\n dx = {}\n\n res = []\n\n for i,l in enumerate(lamps):\n if (tuple(l)) not in on:\n on.add(tuple(l))\n if l[1] not in yOn:\n yOn[l[1]] = 1\n else:\n yOn[l[1]] += 1\n \n if l[0] not in xOn:\n xOn[l[0]] = 1\n else:\n xOn[l[0]] += 1\n\n if l[1] - l[0] not in dy:\n dy[l[1] - l[0]] = 1\n else:\n dy[l[1] - l[0]] += 1\n \n if l[0] + l[1] not in dx:\n dx[l[0] + l[1]] = 1\n else:\n dx[l[0] + l[1]] += 1\n \n def checkIsOn(x, y):\n if (\n x in xOn or\n y in yOn or \n y - x in dy or\n x + y in dx\n ):\n return True\n return False\n\n def turnOffSpot(x,y):\n def turnOff(x0,y0):\n if (x0, y0) in on:\n on.remove((x0,y0))\n xOn[x0] -= 1\n yOn[y0] -= 1\n dy[y0 - x0] -= 1\n dx[x0 + y0] -= 1\n\n if xOn[x0] == 0:\n xOn.pop(x0, None)\n \n if yOn[y0] == 0:\n yOn.pop(y0, None)\n\n if dy[y0 - x0] == 0:\n dy.pop(y0 - x0, None)\n\n if dx[x0 + y0] == 0:\n dx.pop(x0 + y0, None)\n \n for i in range(-1,2,1):\n for j in range(-1,2,1):\n turnOff(x + i, y + j)\n\n for q in queries:\n if checkIsOn(q[0], q[1]):\n res.append(1)\n else:\n res.append(0)\n turnOffSpot(q[0], q[1])\n\n return res\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python 4 Hash Maps, O(n) | grid-illumination | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n on = set()\n yOn = {}\n xOn = {}\n dy = {}\n dx = {}\n\n res = []\n\n for i,l in enumerate(lamps):\n if (tuple(l)) not in on:\n on.add(tuple(l))\n if l[1] not in yOn:\n yOn[l[1]] = 1\n else:\n yOn[l[1]] += 1\n \n if l[0] not in xOn:\n xOn[l[0]] = 1\n else:\n xOn[l[0]] += 1\n\n if l[1] - l[0] not in dy:\n dy[l[1] - l[0]] = 1\n else:\n dy[l[1] - l[0]] += 1\n \n if l[0] + l[1] not in dx:\n dx[l[0] + l[1]] = 1\n else:\n dx[l[0] + l[1]] += 1\n \n def checkIsOn(x, y):\n if (\n x in xOn or\n y in yOn or \n y - x in dy or\n x + y in dx\n ):\n return True\n return False\n\n def turnOffSpot(x,y):\n def turnOff(x0,y0):\n if (x0, y0) in on:\n on.remove((x0,y0))\n xOn[x0] -= 1\n yOn[y0] -= 1\n dy[y0 - x0] -= 1\n dx[x0 + y0] -= 1\n\n if xOn[x0] == 0:\n xOn.pop(x0, None)\n \n if yOn[y0] == 0:\n yOn.pop(y0, None)\n\n if dy[y0 - x0] == 0:\n dy.pop(y0 - x0, None)\n\n if dx[x0 + y0] == 0:\n dx.pop(x0 + y0, None)\n \n for i in range(-1,2,1):\n for j in range(-1,2,1):\n turnOff(x + i, y + j)\n\n for q in queries:\n if checkIsOn(q[0], q[1]):\n res.append(1)\n else:\n res.append(0)\n turnOffSpot(q[0], q[1])\n\n return res\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Easy to understand, step wise explanation😸 | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInitial thought to update the grid on each operation but then it was taking too long as each iteration we need to visit row, col and 2 diagonals. So ditched the idea of updating grid. then used hashmap to store the lamp position in each row, col , primary diagonal and secodnary. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe put lamps in a set. \nthen make 4 hasmaps to store the lamp ignited in each row, column, primary & secondary diagonal. \nthen we traverse through the queries lamps, if they exist in any of the hashtable we append value as 1 in result else 0. \nThen we check if need to turnoff any bulb by checking them in initial set, if any iginited bulb exist in 3*3 grid we remove it from hashtables. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(lamps + 9* queries)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(lamps)\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n res = []\n # lamp set to store all ignited lamps \n lamp_set = {(i, j) for i, j in lamps}\n rows = defaultdict(int)\n cols = defaultdict(int)\n primary = defaultdict(int)\n secondary = defaultdict(int)\n\n # store the rows , cols & diagonals where bulbs are on.\n for i, j in lamp_set: \n rows[i] += 1\n cols[j] += 1\n primary[i+j] += 1\n secondary[i-j] += 1\n\n for i, j in queries:\n if rows[i] or cols[j] or primary[i+j] or secondary[i-j]:\n res.append(1)\n else:\n res.append(0)\n \n for delrow in range(i-1, i+2):\n for delcol in range(j-1, j+2):\n if (delrow, delcol) in lamp_set:\n lamp_set.remove((delrow, delcol))\n rows[delrow] -= 1\n cols[delcol] -= 1\n primary[delrow+delcol] -= 1\n secondary[delrow-delcol] -= 1\n return res\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Easy to understand, step wise explanation😸 | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInitial thought to update the grid on each operation but then it was taking too long as each iteration we need to visit row, col and 2 diagonals. So ditched the idea of updating grid. then used hashmap to store the lamp position in each row, col , primary diagonal and secodnary. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe put lamps in a set. \nthen make 4 hasmaps to store the lamp ignited in each row, column, primary & secondary diagonal. \nthen we traverse through the queries lamps, if they exist in any of the hashtable we append value as 1 in result else 0. \nThen we check if need to turnoff any bulb by checking them in initial set, if any iginited bulb exist in 3*3 grid we remove it from hashtables. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(lamps + 9* queries)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(lamps)\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n res = []\n # lamp set to store all ignited lamps \n lamp_set = {(i, j) for i, j in lamps}\n rows = defaultdict(int)\n cols = defaultdict(int)\n primary = defaultdict(int)\n secondary = defaultdict(int)\n\n # store the rows , cols & diagonals where bulbs are on.\n for i, j in lamp_set: \n rows[i] += 1\n cols[j] += 1\n primary[i+j] += 1\n secondary[i-j] += 1\n\n for i, j in queries:\n if rows[i] or cols[j] or primary[i+j] or secondary[i-j]:\n res.append(1)\n else:\n res.append(0)\n \n for delrow in range(i-1, i+2):\n for delcol in range(j-1, j+2):\n if (delrow, delcol) in lamp_set:\n lamp_set.remove((delrow, delcol))\n rows[delrow] -= 1\n cols[delcol] -= 1\n primary[delrow+delcol] -= 1\n secondary[delrow-delcol] -= 1\n return res\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python3||O(Queries*8) | grid-illumination | 0 | 1 | # Intuition\n- We create hashMaps for rows, cols, diag and anti diagonal and update the count as we come across each lamp\n- And we then move on to the queries, in it we try removing the lamps that are neighboring the current query point.\n\n# Approach\n- Intuition pretty much covers the approach\n\n# Complexity\n- Time complexity:\n-O(Queries*8)\n\n- Space complexity:\n- O(Lamps)\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n\n def antiDiagNum(row,col):\n return row+col\n\n def solve(n,lamps,queries):\n row = defaultdict(int)\n col = defaultdict(int)\n diag = defaultdict(int)\n anti = defaultdict(int)\n ans = []\n mp = {}\n \n for i in range(len(lamps)):\n if tuple(lamps[i]) not in mp:\n # print(lamps[i])\n row[lamps[i][0]]+=1\n col[lamps[i][1]]+=1\n d = None\n if lamps[i][0] > lamps[i][1]:\n d = n - (lamps[i][0] - lamps[i][1])\n elif lamps[i][1] > lamps[i][0]:\n d = n+(lamps[i][1]-lamps[i][0])\n else:\n d = n\n diag[d]+=1\n anti[antiDiagNum(lamps[i][0],lamps[i][1])]+=1\n\n\n if tuple(lamps[i]) not in mp:\n mp[tuple(lamps[i])] = []\n mp[tuple(lamps[i])].extend([lamps[i][0],lamps[i][1],d])\n \n \n for i in range(len(queries)):\n #row\n r = queries[i][0]\n c = queries[i][1]\n d = None\n if queries[i][0] > queries[i][1]:\n d = n - (queries[i][0]-queries[i][1])\n elif queries[i][1] > queries[i][0]:\n d = n+(queries[i][1]-queries[i][0])\n else:\n d = n\n \n if row[r] > 0:\n ans.append(1)\n elif col[c] > 0:\n ans.append(1)\n elif diag[d] > 0:\n ans.append(1)\n elif anti[antiDiagNum(r,c)] > 0:\n ans.append(1)\n else:\n ans.append(0)\n \n ng = [(r,c),(r+1,c),(r+1,c-1),(r+1,c+1),(r,c+1),(r,c-1),(r-1,c),(r-1,c+1),(r-1,c-1)]\n\n for n1 in ng:\n # print(n1)\n if n1 in mp:\n r = n1[0]\n c = n1[1]\n d = None\n if n1[0] > n1[1]:\n d = n - (n1[0]-n1[1])\n elif n1[1] > n1[0]:\n d = n+(n1[1]-n1[0])\n else:\n d = n\n row[r]-=1\n col[c]-=1\n diag[d]-=1\n anti[antiDiagNum(n1[0],n1[1])]-=1\n mp.pop(tuple(n1))\n\n return ans\n\n return solve(n,lamps,queries)\n # return [0,0] \n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python3||O(Queries*8) | grid-illumination | 0 | 1 | # Intuition\n- We create hashMaps for rows, cols, diag and anti diagonal and update the count as we come across each lamp\n- And we then move on to the queries, in it we try removing the lamps that are neighboring the current query point.\n\n# Approach\n- Intuition pretty much covers the approach\n\n# Complexity\n- Time complexity:\n-O(Queries*8)\n\n- Space complexity:\n- O(Lamps)\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n\n def antiDiagNum(row,col):\n return row+col\n\n def solve(n,lamps,queries):\n row = defaultdict(int)\n col = defaultdict(int)\n diag = defaultdict(int)\n anti = defaultdict(int)\n ans = []\n mp = {}\n \n for i in range(len(lamps)):\n if tuple(lamps[i]) not in mp:\n # print(lamps[i])\n row[lamps[i][0]]+=1\n col[lamps[i][1]]+=1\n d = None\n if lamps[i][0] > lamps[i][1]:\n d = n - (lamps[i][0] - lamps[i][1])\n elif lamps[i][1] > lamps[i][0]:\n d = n+(lamps[i][1]-lamps[i][0])\n else:\n d = n\n diag[d]+=1\n anti[antiDiagNum(lamps[i][0],lamps[i][1])]+=1\n\n\n if tuple(lamps[i]) not in mp:\n mp[tuple(lamps[i])] = []\n mp[tuple(lamps[i])].extend([lamps[i][0],lamps[i][1],d])\n \n \n for i in range(len(queries)):\n #row\n r = queries[i][0]\n c = queries[i][1]\n d = None\n if queries[i][0] > queries[i][1]:\n d = n - (queries[i][0]-queries[i][1])\n elif queries[i][1] > queries[i][0]:\n d = n+(queries[i][1]-queries[i][0])\n else:\n d = n\n \n if row[r] > 0:\n ans.append(1)\n elif col[c] > 0:\n ans.append(1)\n elif diag[d] > 0:\n ans.append(1)\n elif anti[antiDiagNum(r,c)] > 0:\n ans.append(1)\n else:\n ans.append(0)\n \n ng = [(r,c),(r+1,c),(r+1,c-1),(r+1,c+1),(r,c+1),(r,c-1),(r-1,c),(r-1,c+1),(r-1,c-1)]\n\n for n1 in ng:\n # print(n1)\n if n1 in mp:\n r = n1[0]\n c = n1[1]\n d = None\n if n1[0] > n1[1]:\n d = n - (n1[0]-n1[1])\n elif n1[1] > n1[0]:\n d = n+(n1[1]-n1[0])\n else:\n d = n\n row[r]-=1\n col[c]-=1\n diag[d]-=1\n anti[antiDiagNum(n1[0],n1[1])]-=1\n mp.pop(tuple(n1))\n\n return ans\n\n return solve(n,lamps,queries)\n # return [0,0] \n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
[Python] Easy hashmaps | grid-illumination | 0 | 1 | \n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n rows = defaultdict(int)\n cols = defaultdict(int)\n d1 = defaultdict(int)\n d2 = defaultdict(int)\n baseLights = set()\n for r, c in lamps:\n if (r,c) in baseLights:\n continue\n rows[r]+=1\n cols[c]+=1\n d1[r-c]+=1\n d2[r+c]+=1\n baseLights.add((r,c))\n\n res = []\n for r,c in queries:\n if rows[r] > 0 or cols[c] > 0 or d1[r-c] > 0 or d2[r+c] > 0:\n res.append(1)\n else:\n res.append(0)\n \n #bullshit:\n rZero = r - 1 >= 0\n rLen = r+1 < n\n cZero = c - 1 >= 0\n cLen = c+1 < n\n\n toIterate = [(r,c)]\n if rZero and cZero:\n toIterate.append((r-1,c-1))\n if rZero:\n toIterate.append((r-1,c))\n if rZero and cLen:\n toIterate.append((r-1, c+1))\n if cZero:\n toIterate.append((r,c-1))\n if cZero and rLen:\n toIterate.append((r+1, c-1))\n if rLen:\n toIterate.append((r+1,c))\n if cLen and rLen:\n toIterate.append((r+1, c+1))\n if cLen:\n toIterate.append((r, c+1))\n\n for r, c in toIterate:\n if (r,c) in baseLights:\n rows[r]-=1\n cols[c]-=1\n d1[r-c]-=1\n d2[r+c]-=1\n baseLights.remove((r,c))\n\n return res\n\n\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
[Python] Easy hashmaps | grid-illumination | 0 | 1 | \n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n rows = defaultdict(int)\n cols = defaultdict(int)\n d1 = defaultdict(int)\n d2 = defaultdict(int)\n baseLights = set()\n for r, c in lamps:\n if (r,c) in baseLights:\n continue\n rows[r]+=1\n cols[c]+=1\n d1[r-c]+=1\n d2[r+c]+=1\n baseLights.add((r,c))\n\n res = []\n for r,c in queries:\n if rows[r] > 0 or cols[c] > 0 or d1[r-c] > 0 or d2[r+c] > 0:\n res.append(1)\n else:\n res.append(0)\n \n #bullshit:\n rZero = r - 1 >= 0\n rLen = r+1 < n\n cZero = c - 1 >= 0\n cLen = c+1 < n\n\n toIterate = [(r,c)]\n if rZero and cZero:\n toIterate.append((r-1,c-1))\n if rZero:\n toIterate.append((r-1,c))\n if rZero and cLen:\n toIterate.append((r-1, c+1))\n if cZero:\n toIterate.append((r,c-1))\n if cZero and rLen:\n toIterate.append((r+1, c-1))\n if rLen:\n toIterate.append((r+1,c))\n if cLen and rLen:\n toIterate.append((r+1, c+1))\n if cLen:\n toIterate.append((r, c+1))\n\n for r, c in toIterate:\n if (r,c) in baseLights:\n rows[r]-=1\n cols[c]-=1\n d1[r-c]-=1\n d2[r+c]-=1\n baseLights.remove((r,c))\n\n return res\n\n\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python Solution | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n ans = []\n xrr = [0,0,1,1,1,0,-1,-1,-1]\n yrr = [0,1,1,0,-1,-1,-1,0,1]\n rows,cols,pos,neg = Counter(),Counter(),Counter(),Counter()\n lamps = {tuple(lamp) for lamp in lamps}\n for i,j in lamps:\n rows[i] += 1\n cols[j] += 1\n pos[i+j] += 1\n neg[i-j] += 1\n for i,j in queries:\n if rows[i] or cols[j] or pos[i+j] or neg[i-j]:\n ans.append(1)\n else:\n ans.append(0)\n for k in range(9):\n x_val = i + xrr[k]\n y_val = j + yrr[k]\n if (x_val,y_val) not in lamps:\n continue\n lamps.remove((x_val,y_val))\n rows[x_val] -= 1\n cols[y_val] -= 1\n pos[x_val + y_val] -= 1\n neg[x_val - y_val] -= 1\n return ans\n\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python Solution | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n ans = []\n xrr = [0,0,1,1,1,0,-1,-1,-1]\n yrr = [0,1,1,0,-1,-1,-1,0,1]\n rows,cols,pos,neg = Counter(),Counter(),Counter(),Counter()\n lamps = {tuple(lamp) for lamp in lamps}\n for i,j in lamps:\n rows[i] += 1\n cols[j] += 1\n pos[i+j] += 1\n neg[i-j] += 1\n for i,j in queries:\n if rows[i] or cols[j] or pos[i+j] or neg[i-j]:\n ans.append(1)\n else:\n ans.append(0)\n for k in range(9):\n x_val = i + xrr[k]\n y_val = j + yrr[k]\n if (x_val,y_val) not in lamps:\n continue\n lamps.remove((x_val,y_val))\n rows[x_val] -= 1\n cols[y_val] -= 1\n pos[x_val + y_val] -= 1\n neg[x_val - y_val] -= 1\n return ans\n\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
SOLID Principles Practice | Commented and Explained | Set and Dictionaries | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI wanted to solve this in as object oriented a process as possible and try to really focus on my solid principles, so I decided to work this a bit of a long way around. The goal of this was to increase software engineering capability, not just solve the problem. \n\nIn this problem, we need a way to quickly access and update linear spaces of a grid quickly and efficiently. One way of doing that is by splitting this up into the eight orthogonals as 4 directionals. To those that that was gibberish, we want to split North, South, East, West, and NorthEast, NorthWest, SouthEast, SouthWest into 4 sector lines. So we\'d have lines that ran NorthSouth and EastWest, and so on. \n\nTo do this we need to realize a scheme for notating what is where. For ease of reference and relation to the process of diagonal grids, we do this with rows, cols, rows+cols, rows-cols as the four lines to represent West->East, North->South, SouthWest->NorthEast, NorthWest->SouthEast respectively. \n\nThese are set up in the object initiation function as they are needed by all instances of such an object. \n\nThen, we can get location entries for such a state by passing in a row and column index (note, we make no guarantees about spatial awareness, so anything that is physically out of bounds could be present. To limit this, we\'d want to know actual grid size) This will return respectively row index, column index, row index + column index, row index - column index as a list\n\nWe make an is illuminated function that will be given a row and column index. We start by getting the location entries for this row and column index using the prior function described. We then check each by enumerating these location entries. Of those, if any of our location maps at index and position are greater than 0, we are illuminated, so return 1. Otherwise, return 0. \n\nWe make an increment location status function that takes a row, col, and increment. We get the location entries as described above, enumerate over positional relationships, and increment by the passed increment\n\nWe make a get neighborhood function that, when given a row index and column index, returns the N8 neighborhood. A more useful form should allow user to specify type of neighborhood to return and then based on that return a pass to the actual sub function necessary\n\nWe make a turn off neighborhood function that when given a row and column index first gets the neighborhood needed, then for each neighbor in the neighborhood, if that neighbor is in on, it removes them from there, and then increments the location status using the appropriate function with a passed increment of -1. \n\nWe make an initialize illumination function that is given a list of lamps and then iterates over each lamp in the list of lamps. It extracts row and col from lamp, then if not already processed, turns them on and increments location status appropriately \n\nWe make a process queries function that given a set of queries sets up an illumination status by query index of 0 for each query in queries\nWe then enumerate our queries, getting row and col out of the specific query current, then setting the appropriate index of our illumination status array to the result of our call to is illuminated. We then turn off the neighborhood after processing. When done with all queries we return the illumination status by query. \n\nWe then finalize our gridIllumination function as requested by initializing the lamps with the initialize illumination function and then returning the result of a call to process queries. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach to the problem was to design an object oriented system representation that could quickly access the assignments in optimized directionality locations appropriately. \n\n# Complexity\n- Time complexity: O(max ( L, Q ))\n - It takes O(L) to initialize lamps\n - It takes O(Q) to process queries \n\n- Space complexity: O(Q)\n - We store all on nodes in self.on \n - We store 4 pieces of location information for each of those \n - We thus store 4V information in self.on and self.locations\n - We store Q items in illumination status by query\n - So total is O(V) as O(Q) is either as large as V or smaller by problem statement \n\n# Code\n```\nclass Solution:\n def __init__(self) : \n # set of on lights \n self.on = set()\n # set of default dicts representing the lights on \n # in the current row, col, diagonal going up and to the right \n # and diagonal going down and to the left \n self.locations = [collections.defaultdict(int) for _ in range(4)]\n\n def get_location_entries(self, row_index, col_index) : \n # this gets the location entries for locations for any update needed \n return [row_index, col_index, (row_index+col_index), (row_index-col_index)]\n\n def is_illuminated(self, row_index, col_index) : \n # get the location entries for this spot\n location_entries = self.get_location_entries(row_index, col_index)\n # enumerate location entries \n for index, position in enumerate(location_entries) : \n # if any are good return 1 \n if self.locations[index][position] > 0 : \n return 1\n # otherwise return 0 \n return 0\n\n def increment_location_status(self, row_index, col_index, increment) : \n # get the location entries needed\n location_entries = self.get_location_entries(row_index, col_index)\n # go to those spots and apply increment \n for index, position in enumerate(location_entries) : \n self.locations[index][position] += increment\n\n def get_neighborhood(self, row_index, col_index) : \n # get neighborhood around point \n neighborhood = []\n # if edge bound can put a check on neighborhood to be in bounds or not \n for dr in [-1, 0, 1] : \n for dc in [-1, 0, 1] : \n neighborhood.append((row_index+dr, col_index+dc))\n return neighborhood\n\n def turn_off_neighborhood(self, row_index, col_index) : \n # get neighborhood \n for neighbor in self.get_neighborhood(row_index, col_index) : \n # if neighbor is in on \n if (neighbor) in self.on : \n # turn them off and increment locations by -1 \n self.on.remove(neighbor)\n self.increment_location_status(neighbor[0], neighbor[1], -1)\n\n def initialize_illumination(self, lamps) : \n # initialize lamps that are on \n for lamp in lamps : \n # get the specific row and col\n row, col = lamp\n # but only once! \n if (row, col) not in self.on : \n self.on.add((row, col))\n self.increment_location_status(row, col, 1)\n\n def process_queries(self, queries) : \n # set up illumination status by query index \n illumination_status_by_query_index = [0 for _ in range(len(queries))]\n # loop over queries \n for index, query in enumerate(queries) : \n # get row and col of query\n row, col = query\n # mark appropriately \n illumination_status_by_query_index[index] = self.is_illuminated(row, col)\n # turn off as needed \n self.turn_off_neighborhood(row, col)\n # return processed queries \n return illumination_status_by_query_index\n\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n # initialize lamps\n self.initialize_illumination(lamps)\n # return processing of queries\n return self.process_queries(queries)\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
SOLID Principles Practice | Commented and Explained | Set and Dictionaries | grid-illumination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI wanted to solve this in as object oriented a process as possible and try to really focus on my solid principles, so I decided to work this a bit of a long way around. The goal of this was to increase software engineering capability, not just solve the problem. \n\nIn this problem, we need a way to quickly access and update linear spaces of a grid quickly and efficiently. One way of doing that is by splitting this up into the eight orthogonals as 4 directionals. To those that that was gibberish, we want to split North, South, East, West, and NorthEast, NorthWest, SouthEast, SouthWest into 4 sector lines. So we\'d have lines that ran NorthSouth and EastWest, and so on. \n\nTo do this we need to realize a scheme for notating what is where. For ease of reference and relation to the process of diagonal grids, we do this with rows, cols, rows+cols, rows-cols as the four lines to represent West->East, North->South, SouthWest->NorthEast, NorthWest->SouthEast respectively. \n\nThese are set up in the object initiation function as they are needed by all instances of such an object. \n\nThen, we can get location entries for such a state by passing in a row and column index (note, we make no guarantees about spatial awareness, so anything that is physically out of bounds could be present. To limit this, we\'d want to know actual grid size) This will return respectively row index, column index, row index + column index, row index - column index as a list\n\nWe make an is illuminated function that will be given a row and column index. We start by getting the location entries for this row and column index using the prior function described. We then check each by enumerating these location entries. Of those, if any of our location maps at index and position are greater than 0, we are illuminated, so return 1. Otherwise, return 0. \n\nWe make an increment location status function that takes a row, col, and increment. We get the location entries as described above, enumerate over positional relationships, and increment by the passed increment\n\nWe make a get neighborhood function that, when given a row index and column index, returns the N8 neighborhood. A more useful form should allow user to specify type of neighborhood to return and then based on that return a pass to the actual sub function necessary\n\nWe make a turn off neighborhood function that when given a row and column index first gets the neighborhood needed, then for each neighbor in the neighborhood, if that neighbor is in on, it removes them from there, and then increments the location status using the appropriate function with a passed increment of -1. \n\nWe make an initialize illumination function that is given a list of lamps and then iterates over each lamp in the list of lamps. It extracts row and col from lamp, then if not already processed, turns them on and increments location status appropriately \n\nWe make a process queries function that given a set of queries sets up an illumination status by query index of 0 for each query in queries\nWe then enumerate our queries, getting row and col out of the specific query current, then setting the appropriate index of our illumination status array to the result of our call to is illuminated. We then turn off the neighborhood after processing. When done with all queries we return the illumination status by query. \n\nWe then finalize our gridIllumination function as requested by initializing the lamps with the initialize illumination function and then returning the result of a call to process queries. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach to the problem was to design an object oriented system representation that could quickly access the assignments in optimized directionality locations appropriately. \n\n# Complexity\n- Time complexity: O(max ( L, Q ))\n - It takes O(L) to initialize lamps\n - It takes O(Q) to process queries \n\n- Space complexity: O(Q)\n - We store all on nodes in self.on \n - We store 4 pieces of location information for each of those \n - We thus store 4V information in self.on and self.locations\n - We store Q items in illumination status by query\n - So total is O(V) as O(Q) is either as large as V or smaller by problem statement \n\n# Code\n```\nclass Solution:\n def __init__(self) : \n # set of on lights \n self.on = set()\n # set of default dicts representing the lights on \n # in the current row, col, diagonal going up and to the right \n # and diagonal going down and to the left \n self.locations = [collections.defaultdict(int) for _ in range(4)]\n\n def get_location_entries(self, row_index, col_index) : \n # this gets the location entries for locations for any update needed \n return [row_index, col_index, (row_index+col_index), (row_index-col_index)]\n\n def is_illuminated(self, row_index, col_index) : \n # get the location entries for this spot\n location_entries = self.get_location_entries(row_index, col_index)\n # enumerate location entries \n for index, position in enumerate(location_entries) : \n # if any are good return 1 \n if self.locations[index][position] > 0 : \n return 1\n # otherwise return 0 \n return 0\n\n def increment_location_status(self, row_index, col_index, increment) : \n # get the location entries needed\n location_entries = self.get_location_entries(row_index, col_index)\n # go to those spots and apply increment \n for index, position in enumerate(location_entries) : \n self.locations[index][position] += increment\n\n def get_neighborhood(self, row_index, col_index) : \n # get neighborhood around point \n neighborhood = []\n # if edge bound can put a check on neighborhood to be in bounds or not \n for dr in [-1, 0, 1] : \n for dc in [-1, 0, 1] : \n neighborhood.append((row_index+dr, col_index+dc))\n return neighborhood\n\n def turn_off_neighborhood(self, row_index, col_index) : \n # get neighborhood \n for neighbor in self.get_neighborhood(row_index, col_index) : \n # if neighbor is in on \n if (neighbor) in self.on : \n # turn them off and increment locations by -1 \n self.on.remove(neighbor)\n self.increment_location_status(neighbor[0], neighbor[1], -1)\n\n def initialize_illumination(self, lamps) : \n # initialize lamps that are on \n for lamp in lamps : \n # get the specific row and col\n row, col = lamp\n # but only once! \n if (row, col) not in self.on : \n self.on.add((row, col))\n self.increment_location_status(row, col, 1)\n\n def process_queries(self, queries) : \n # set up illumination status by query index \n illumination_status_by_query_index = [0 for _ in range(len(queries))]\n # loop over queries \n for index, query in enumerate(queries) : \n # get row and col of query\n row, col = query\n # mark appropriately \n illumination_status_by_query_index[index] = self.is_illuminated(row, col)\n # turn off as needed \n self.turn_off_neighborhood(row, col)\n # return processed queries \n return illumination_status_by_query_index\n\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n # initialize lamps\n self.initialize_illumination(lamps)\n # return processing of queries\n return self.process_queries(queries)\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Python3: Hashmap O(N) | grid-illumination | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(L + Q), L = lamps.length(); Q = queries.length()$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(L + Q)$$\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n\n rowLights = collections.Counter() #key: row, val = counts\n colLights = collections.Counter() #key: row, val = counts\n diagNegLights = collections.Counter() #key: (row,col), val=counts\n diagPosLights = collections.Counter() #key: (row,col), val=counts\n\n def get_diagonal_edges( row=0, col=0):\n #returns the illuminated diagonal edges (tuples).\n nonlocal rowLights, colLights\n nonlocal diagNegLights, diagPosLights\n\n posDelta = min( row, col)\n diagPos = (row-posDelta, col-posDelta)\n\n negDelta = min( col, n-1-row)\n diagNeg = (row+negDelta, col-negDelta)\n \n return (diagPos), (diagNeg)\n \n def update_light( row, col, isOn = True):\n nonlocal rowLights, colLights\n nonlocal diagNegLights, diagPosLights\n nonlocal lamps\n\n adder = 1 if isOn else -1\n if (row, col) in lamps: \n diagPosPt, diagNegPt = get_diagonal_edges( row, col)\n rowLights[row] += adder\n colLights[col] += adder\n diagPosLights[diagPosPt] += adder\n diagNegLights[diagNegPt] += adder\n return\n\n lamps = set( map( tuple, lamps))\n for row, col in lamps:\n update_light( row, col) \n\n result = list()\n for row, col in queries:\n ## check if pos (row, col) is illuminated.\n diagPosPt, diagNegPt = get_diagonal_edges( row, col)\n isIlluminated = rowLights[row] |\\\n colLights[col] |\\\n diagPosLights[diagPosPt] |\\\n diagNegLights[diagNegPt]\n result.append( min(1, isIlluminated)) #append 1 if illuminated, else 0.\n\n ## turn off light + 8-neighbors.\n for dRow in range(-1, 2):\n for dCol in range(-1, 2):\n update_light( row + dRow, col + dCol, isOn = False)\n lamps.discard( (row + dRow, col + dCol)) \n\n # clean mem. spaces. \n del rowLights, colLights,\\\n diagNegLights, diagPosLights,\\\n lamps\n return result\n``` | 0 | There is a 2D `grid` of size `n x n` where each cell of this grid has a lamp that is initially **turned off**.
You are given a 2D array of lamp positions `lamps`, where `lamps[i] = [rowi, coli]` indicates that the lamp at `grid[rowi][coli]` is **turned on**. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it **illuminates its cell** and **all other cells** in the same **row, column, or diagonal**.
You are also given another 2D array `queries`, where `queries[j] = [rowj, colj]`. For the `jth` query, determine whether `grid[rowj][colj]` is illuminated or not. After answering the `jth` query, **turn off** the lamp at `grid[rowj][colj]` and its **8 adjacent lamps** if they exist. A lamp is adjacent if its cell shares either a side or corner with `grid[rowj][colj]`.
Return _an array of integers_ `ans`_,_ _where_ `ans[j]` _should be_ `1` _if the cell in the_ `jth` _query was illuminated, or_ `0` _if the lamp was not._
**Example 1:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,0\]\]
**Output:** \[1,0\]
**Explanation:** We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid\[0\]\[0\] then turning on the lamp at grid\[4\]\[4\].
The 0th query asks if the lamp at grid\[1\]\[1\] is illuminated or not (the blue square). It is illuminated, so set ans\[0\] = 1. Then, we turn off all lamps in the red square.
The 1st query asks if the lamp at grid\[1\]\[0\] is illuminated or not (the blue square). It is not illuminated, so set ans\[1\] = 0. Then, we turn off all lamps in the red rectangle.
**Example 2:**
**Input:** n = 5, lamps = \[\[0,0\],\[4,4\]\], queries = \[\[1,1\],\[1,1\]\]
**Output:** \[1,1\]
**Example 3:**
**Input:** n = 5, lamps = \[\[0,0\],\[0,4\]\], queries = \[\[0,4\],\[0,1\],\[1,4\]\]
**Output:** \[1,1,0\]
**Constraints:**
* `1 <= n <= 109`
* `0 <= lamps.length <= 20000`
* `0 <= queries.length <= 20000`
* `lamps[i].length == 2`
* `0 <= rowi, coli < n`
* `queries[j].length == 2`
* `0 <= rowj, colj < n` | null |
Python3: Hashmap O(N) | grid-illumination | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(L + Q), L = lamps.length(); Q = queries.length()$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(L + Q)$$\n\n# Code\n```\nclass Solution:\n def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:\n\n rowLights = collections.Counter() #key: row, val = counts\n colLights = collections.Counter() #key: row, val = counts\n diagNegLights = collections.Counter() #key: (row,col), val=counts\n diagPosLights = collections.Counter() #key: (row,col), val=counts\n\n def get_diagonal_edges( row=0, col=0):\n #returns the illuminated diagonal edges (tuples).\n nonlocal rowLights, colLights\n nonlocal diagNegLights, diagPosLights\n\n posDelta = min( row, col)\n diagPos = (row-posDelta, col-posDelta)\n\n negDelta = min( col, n-1-row)\n diagNeg = (row+negDelta, col-negDelta)\n \n return (diagPos), (diagNeg)\n \n def update_light( row, col, isOn = True):\n nonlocal rowLights, colLights\n nonlocal diagNegLights, diagPosLights\n nonlocal lamps\n\n adder = 1 if isOn else -1\n if (row, col) in lamps: \n diagPosPt, diagNegPt = get_diagonal_edges( row, col)\n rowLights[row] += adder\n colLights[col] += adder\n diagPosLights[diagPosPt] += adder\n diagNegLights[diagNegPt] += adder\n return\n\n lamps = set( map( tuple, lamps))\n for row, col in lamps:\n update_light( row, col) \n\n result = list()\n for row, col in queries:\n ## check if pos (row, col) is illuminated.\n diagPosPt, diagNegPt = get_diagonal_edges( row, col)\n isIlluminated = rowLights[row] |\\\n colLights[col] |\\\n diagPosLights[diagPosPt] |\\\n diagNegLights[diagNegPt]\n result.append( min(1, isIlluminated)) #append 1 if illuminated, else 0.\n\n ## turn off light + 8-neighbors.\n for dRow in range(-1, 2):\n for dCol in range(-1, 2):\n update_light( row + dRow, col + dCol, isOn = False)\n lamps.discard( (row + dRow, col + dCol)) \n\n # clean mem. spaces. \n del rowLights, colLights,\\\n diagNegLights, diagPosLights,\\\n lamps\n return result\n``` | 0 | Given an integer array `arr`, partition the array into (contiguous) subarrays of length **at most** `k`. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return _the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a **32-bit** integer._
**Example 1:**
**Input:** arr = \[1,15,7,9,2,5,10\], k = 3
**Output:** 84
**Explanation:** arr becomes \[15,15,15,9,10,10,10\]
**Example 2:**
**Input:** arr = \[1,4,1,5,7,3,6,1,9,9,3\], k = 4
**Output:** 83
**Example 3:**
**Input:** arr = \[1\], k = 1
**Output:** 1
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 109`
* `1 <= k <= arr.length` | null |
Solution | find-common-characters | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<string> commonChars(vector<string>& words) {\n vector<string> res;\n \n sort(words.begin(), words.end());\n \n for (char c : words[0]) {\n bool common = true;\n \n for (int i = 1; i < words.size(); i++) {\n if (words[i].find(c) == string::npos) {\n common = false;\n break;\n } else {\n words[i].erase(words[i].find(c), 1);\n }\n }\n if (common) {\n res.push_back(string(1, c));\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n if len(words) < 2:\n return words\n res = []\n word1 = set(words[0])\n for char in word1:\n frequency = min([word.count(char) for word in words])\n res += [char] * frequency\n return res\n```\n\n```Java []\nclass Solution {\n public List<String> commonChars(String[] A) {\n int[] last = count(A[0]);\n for (int i = 1; i < A.length; i++) {\n last = intersection(last, count(A[i]));\n }\n List<String> arr = new ArrayList<>();\n for (int i = 0; i < 26; i++) {\n if (last[i] != 0) {\n char a = \'a\';\n a += i;\n String s = String.valueOf(a);\n while (last[i] > 0) {\n arr.add(s);\n last[i]--;\n }\n }\n }\n return arr;\n }\n int[] intersection(int[] a, int[] b) {\n int[] t = new int[26];\n for (int i = 0; i < 26; i++) {\n t[i] = Math.min(a[i], b[i]);\n }\n return t;\n }\n int[] count(String str) {\n int[] t = new int[26];\n for (char c : str.toCharArray()) t[c - \'a\']++;\n return t;\n }\n}\n``` | 450 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
Solution | find-common-characters | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<string> commonChars(vector<string>& words) {\n vector<string> res;\n \n sort(words.begin(), words.end());\n \n for (char c : words[0]) {\n bool common = true;\n \n for (int i = 1; i < words.size(); i++) {\n if (words[i].find(c) == string::npos) {\n common = false;\n break;\n } else {\n words[i].erase(words[i].find(c), 1);\n }\n }\n if (common) {\n res.push_back(string(1, c));\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n if len(words) < 2:\n return words\n res = []\n word1 = set(words[0])\n for char in word1:\n frequency = min([word.count(char) for word in words])\n res += [char] * frequency\n return res\n```\n\n```Java []\nclass Solution {\n public List<String> commonChars(String[] A) {\n int[] last = count(A[0]);\n for (int i = 1; i < A.length; i++) {\n last = intersection(last, count(A[i]));\n }\n List<String> arr = new ArrayList<>();\n for (int i = 0; i < 26; i++) {\n if (last[i] != 0) {\n char a = \'a\';\n a += i;\n String s = String.valueOf(a);\n while (last[i] > 0) {\n arr.add(s);\n last[i]--;\n }\n }\n }\n return arr;\n }\n int[] intersection(int[] a, int[] b) {\n int[] t = new int[26];\n for (int i = 0; i < 26; i++) {\n t[i] = Math.min(a[i], b[i]);\n }\n return t;\n }\n int[] count(String str) {\n int[] t = new int[26];\n for (char c : str.toCharArray()) t[c - \'a\']++;\n return t;\n }\n}\n``` | 450 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
For Beginners & more simplified :-) | find-common-characters | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n res = Counter(words[0])\n for i in words:\n res &= Counter(i)\n return list(res.elements())\n \n```\n\n# Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \'&=\'\nThe &= operator in Python is a compound assignment operator that performs a bitwise AND operation between two operands and assigns the result back to the left operand.\n\nThe & operator is a bitwise AND operator that performs a bitwise AND operation between corresponding bits of two integers. It returns a new integer with bits set to 1 only where both corresponding bits of the operands are 1.\n\nThe &= operator combines the bitwise AND operation and assignment operation. It updates the left operand with the result of the bitwise AND operation between the left operand and the right operand.\n\nHere\'s an example to illustrate the usage of &=:\n\npython\n\na = 5\nb = 3\na &= b # Equivalent to: a = a & b\nprint(a) # Output: 1\n\nIn this example, a initially holds the value 5 (binary: 0101) and b holds the value 3 (binary: 0011). After performing a &= b, the value of a is updated to 1 (binary: 0001) because it performs a bitwise AND operation between the two values.\n\nThe &= operator can be used with different types, such as integers, booleans, sets, or custom objects, depending on how it is defined for each type. The specific behavior of &= may vary depending on the data type being used.\n\nIt\'s important to note that the &= operator is not universally defined for all data types. Its availability and behavior depend on the specific implementation and behavior defined for each type.\n\n\n# credits : https://leetcode.com/rioran/ | 4 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
For Beginners & more simplified :-) | find-common-characters | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n res = Counter(words[0])\n for i in words:\n res &= Counter(i)\n return list(res.elements())\n \n```\n\n# Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# \'&=\'\nThe &= operator in Python is a compound assignment operator that performs a bitwise AND operation between two operands and assigns the result back to the left operand.\n\nThe & operator is a bitwise AND operator that performs a bitwise AND operation between corresponding bits of two integers. It returns a new integer with bits set to 1 only where both corresponding bits of the operands are 1.\n\nThe &= operator combines the bitwise AND operation and assignment operation. It updates the left operand with the result of the bitwise AND operation between the left operand and the right operand.\n\nHere\'s an example to illustrate the usage of &=:\n\npython\n\na = 5\nb = 3\na &= b # Equivalent to: a = a & b\nprint(a) # Output: 1\n\nIn this example, a initially holds the value 5 (binary: 0101) and b holds the value 3 (binary: 0011). After performing a &= b, the value of a is updated to 1 (binary: 0001) because it performs a bitwise AND operation between the two values.\n\nThe &= operator can be used with different types, such as integers, booleans, sets, or custom objects, depending on how it is defined for each type. The specific behavior of &= may vary depending on the data type being used.\n\nIt\'s important to note that the &= operator is not universally defined for all data types. Its availability and behavior depend on the specific implementation and behavior defined for each type.\n\n\n# credits : https://leetcode.com/rioran/ | 4 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
C++ O(n) | O(1), two vectors | find-common-characters | 0 | 1 | **Python 3**\nThe `&` operation for counters results in minumum counters for each element. \n```python\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n return reduce(lambda a, b: a & b, map(Counter, words)).elements()\n```\n**C++**\nFor each string, we count characters in ```cnt1```. Then, we track the minimum count for each character in ```cnt```.\n\n```cpp\nvector<string> commonChars(vector<string>& A) {\n vector<int> cnt(26, INT_MAX);\n vector<string> res;\n for (auto s : A) {\n vector<int> cnt1(26, 0);\n for (auto c : s) ++cnt1[c - \'a\'];\n for (auto i = 0; i < 26; ++i) cnt[i] = min(cnt[i], cnt1[i]);\n }\n for (auto i = 0; i < 26; ++i)\n for (auto j = 0; j < cnt[i]; ++j) res.push_back(string(1, i + \'a\'));\n return res;\n}\n```\n## Complexity Analysis\nRuntime: *O(n)*, where *n* is the total number of characters.\nMemory: *O(1)* (we use two fixed-size vectors). | 262 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
C++ O(n) | O(1), two vectors | find-common-characters | 0 | 1 | **Python 3**\nThe `&` operation for counters results in minumum counters for each element. \n```python\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n return reduce(lambda a, b: a & b, map(Counter, words)).elements()\n```\n**C++**\nFor each string, we count characters in ```cnt1```. Then, we track the minimum count for each character in ```cnt```.\n\n```cpp\nvector<string> commonChars(vector<string>& A) {\n vector<int> cnt(26, INT_MAX);\n vector<string> res;\n for (auto s : A) {\n vector<int> cnt1(26, 0);\n for (auto c : s) ++cnt1[c - \'a\'];\n for (auto i = 0; i < 26; ++i) cnt[i] = min(cnt[i], cnt1[i]);\n }\n for (auto i = 0; i < 26; ++i)\n for (auto j = 0; j < cnt[i]; ++j) res.push_back(string(1, i + \'a\'));\n return res;\n}\n```\n## Complexity Analysis\nRuntime: *O(n)*, where *n* is the total number of characters.\nMemory: *O(1)* (we use two fixed-size vectors). | 262 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
✅ [PYTHON] Nested for-in loops [Beats 100.00%] | find-common-characters | 0 | 1 | # Intuition\nI decided to take the shortest word ("min_word") and compare it to the others\n\n# Approach\nI loop through the shortest word, then loop through the remaining words inside. \nIf a character is not in the word, I delete it from "min_word".\nElse, I delete it from the comparable word.\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n min_word = min(words)\n words.remove(min_word)\n for char in min_word[:]: # shallow copy by slice\n for idx_w, word in enumerate(words):\n if char not in word and (idx_w == len(words) or char in min_word):\n min_word = min_word.replace(char, "", 1)\n break\n else:\n words[idx_w] = words[idx_w].replace(char, "", 1)\n return min_word\n```\n\n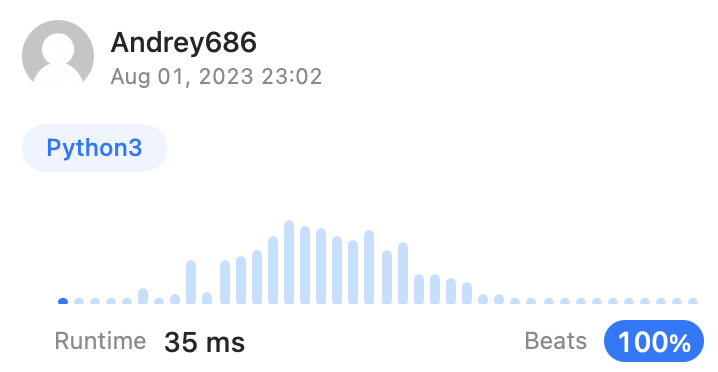 | 2 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
✅ [PYTHON] Nested for-in loops [Beats 100.00%] | find-common-characters | 0 | 1 | # Intuition\nI decided to take the shortest word ("min_word") and compare it to the others\n\n# Approach\nI loop through the shortest word, then loop through the remaining words inside. \nIf a character is not in the word, I delete it from "min_word".\nElse, I delete it from the comparable word.\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n min_word = min(words)\n words.remove(min_word)\n for char in min_word[:]: # shallow copy by slice\n for idx_w, word in enumerate(words):\n if char not in word and (idx_w == len(words) or char in min_word):\n min_word = min_word.replace(char, "", 1)\n break\n else:\n words[idx_w] = words[idx_w].replace(char, "", 1)\n return min_word\n```\n\n | 2 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
Python solution with collections | find-common-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n from collections import Counter\n from typing import List\n\n # Initialize a Counter object with the characters of the first word\n common = Counter(words[0])\n\n # Iterate over the remaining words and update the common Counter object\n for word in words[1:]:\n # Initialize a Counter object for the current word\n word_count = Counter(word)\n # Update the common Counter object to only include characters present in both\n common &= word_count\n\n # Convert the common Counter object to a list of characters\n result = []\n for char, count in common.items():\n result += [char] * count\n\n return result\n``` | 2 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
Python solution with collections | find-common-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n from collections import Counter\n from typing import List\n\n # Initialize a Counter object with the characters of the first word\n common = Counter(words[0])\n\n # Iterate over the remaining words and update the common Counter object\n for word in words[1:]:\n # Initialize a Counter object for the current word\n word_count = Counter(word)\n # Update the common Counter object to only include characters present in both\n common &= word_count\n\n # Convert the common Counter object to a list of characters\n result = []\n for char, count in common.items():\n result += [char] * count\n\n return result\n``` | 2 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
Nice & short collections.Counter - 65 ms - 16.4 MB | find-common-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI recalled a nice tool fit for the job - the Counter class from the collections built-in module. Aside from other solutions - mine is more readable, though slightly less optimized: redundunt 1-st element conversion and Counter-ization of every word.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCounter class creates a dictionary-like object with chars as keys and amounts as values. What is more - we can get intersections of Counters with the "&" operation (and mechanic).\n\n# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nI read every char of the input and perform word by word comparison. If to be more presize - it is O(x*n), where x is an average word length.\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nI store only a small portion of the data, representing at most 2 words at a time.\n\n# Code\n```\nfrom collections import Counter\n\n\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n counter = Counter(words[0])\n for word in words:\n counter &= Counter(word)\n return list(counter.elements())\n``` | 2 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
Nice & short collections.Counter - 65 ms - 16.4 MB | find-common-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI recalled a nice tool fit for the job - the Counter class from the collections built-in module. Aside from other solutions - mine is more readable, though slightly less optimized: redundunt 1-st element conversion and Counter-ization of every word.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCounter class creates a dictionary-like object with chars as keys and amounts as values. What is more - we can get intersections of Counters with the "&" operation (and mechanic).\n\n# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nI read every char of the input and perform word by word comparison. If to be more presize - it is O(x*n), where x is an average word length.\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nI store only a small portion of the data, representing at most 2 words at a time.\n\n# Code\n```\nfrom collections import Counter\n\n\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n counter = Counter(words[0])\n for word in words:\n counter &= Counter(word)\n return list(counter.elements())\n``` | 2 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
Python - Readable/No shortcuts - WITH EXPLANATION | find-common-characters | 0 | 1 | # Approach\nThe idea of this approach is to first start with the counts of every character in the first word and store these `character : character count` pairs in `res_counts`. Then we iterate through every other word in the words list. For each word, we use its own `char_counts` hash map to store `character : character count` pairs. Then we iterate through `res_counts`, and reassign each character\'s count to the min of what it is currently and what we found in this current word. It is important to understand that we have to iterate through `res_counts` characters, not the `char_counts` characters. This is because we want to only update the characters that have been seen previously. If we iterate through every character in the current word, we might not have a character that was in the previous words, so we would skip characters that should actually be updated to have a count of 0 due to them not being present in the current word.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n res_counts = defaultdict(int)\n for char in words[0]:\n res_counts[char] += 1\n\n for i in range(1, len(words)):\n word = words[i]\n char_counts = defaultdict(int)\n for char in word:\n char_counts[char] += 1\n for char in res_counts:\n res_counts[char] = min(res_counts[char], char_counts[char])\n \n res = []\n for char, char_count in res_counts.items():\n if char_count != 0:\n for i in range(char_count):\n res.append(char)\n return res\n``` | 2 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
Python - Readable/No shortcuts - WITH EXPLANATION | find-common-characters | 0 | 1 | # Approach\nThe idea of this approach is to first start with the counts of every character in the first word and store these `character : character count` pairs in `res_counts`. Then we iterate through every other word in the words list. For each word, we use its own `char_counts` hash map to store `character : character count` pairs. Then we iterate through `res_counts`, and reassign each character\'s count to the min of what it is currently and what we found in this current word. It is important to understand that we have to iterate through `res_counts` characters, not the `char_counts` characters. This is because we want to only update the characters that have been seen previously. If we iterate through every character in the current word, we might not have a character that was in the previous words, so we would skip characters that should actually be updated to have a count of 0 due to them not being present in the current word.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n res_counts = defaultdict(int)\n for char in words[0]:\n res_counts[char] += 1\n\n for i in range(1, len(words)):\n word = words[i]\n char_counts = defaultdict(int)\n for char in word:\n char_counts[char] += 1\n for char in res_counts:\n res_counts[char] = min(res_counts[char], char_counts[char])\n \n res = []\n for char, char_count in res_counts.items():\n if char_count != 0:\n for i in range(char_count):\n res.append(char)\n return res\n``` | 2 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
My Solution using hash table -o(n) time and o (1) space | find-common-characters | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n return self.sol1(words)\n\n def sol1(self, words):\n # INIT\n\n # ALGO\n\n # --Build a freq graph of letters\n # --Each letter has an array mapped to it containing the frequency of char in a specific word\n # -- Populate the result array by checking for chars that appear in all strings \n # -- The number if times to add a char is the min \n\n freq_graph = {}\n result = []\n\n for idx, word in enumerate(words):\n for char in word:\n if char not in freq_graph:\n freq_graph[char] = [0] * len(words)\n freq_graph[char][idx] = 1\n else:\n freq_graph[char][idx] += 1\n\n\n for char in freq_graph:\n for i in range(0, min(freq_graph[char])):\n result.append(char)\n\n return result\n\n \n\n \n\n\n\n\n \n``` | 3 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
My Solution using hash table -o(n) time and o (1) space | find-common-characters | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n return self.sol1(words)\n\n def sol1(self, words):\n # INIT\n\n # ALGO\n\n # --Build a freq graph of letters\n # --Each letter has an array mapped to it containing the frequency of char in a specific word\n # -- Populate the result array by checking for chars that appear in all strings \n # -- The number if times to add a char is the min \n\n freq_graph = {}\n result = []\n\n for idx, word in enumerate(words):\n for char in word:\n if char not in freq_graph:\n freq_graph[char] = [0] * len(words)\n freq_graph[char][idx] = 1\n else:\n freq_graph[char][idx] += 1\n\n\n for char in freq_graph:\n for i in range(0, min(freq_graph[char])):\n result.append(char)\n\n return result\n\n \n\n \n\n\n\n\n \n``` | 3 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
two dictionaries python | find-common-characters | 0 | 1 | we create 2 dictionaries \ndictionary d1 stores the value of the minimum occurrence of a letter in a word \ndictionary d2 stores the count of letters of the current word\nwe put the minimum value of a letter after each word \nthe return list will contain the elements in d1 d1[letter] number of times .\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n d1=defaultdict(int)\n for l in range(len(words[0])):\n z =words[0][l]\n d1[z]+=1\n \n for i in range(1,len(words)):\n d2=defaultdict(int)\n z=words[i]\n for l in z:\n d2[l]+=1 \n for k in d1:\n d1[k]=min(d1[k],d2[k])\n ret=[]\n for k in sorted(d1):\n while(d1[k]>0):\n ret.append(k)\n d1[k]-=1 \n return ret\n```\n | 1 | Given a string array `words`, return _an array of all characters that show up in all strings within the_ `words` _(including duplicates)_. You may return the answer in **any order**.
**Example 1:**
**Input:** words = \["bella","label","roller"\]
**Output:** \["e","l","l"\]
**Example 2:**
**Input:** words = \["cool","lock","cook"\]
**Output:** \["c","o"\]
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists of lowercase English letters. | null |
two dictionaries python | find-common-characters | 0 | 1 | we create 2 dictionaries \ndictionary d1 stores the value of the minimum occurrence of a letter in a word \ndictionary d2 stores the count of letters of the current word\nwe put the minimum value of a letter after each word \nthe return list will contain the elements in d1 d1[letter] number of times .\n```\nclass Solution:\n def commonChars(self, words: List[str]) -> List[str]:\n d1=defaultdict(int)\n for l in range(len(words[0])):\n z =words[0][l]\n d1[z]+=1\n \n for i in range(1,len(words)):\n d2=defaultdict(int)\n z=words[i]\n for l in z:\n d2[l]+=1 \n for k in d1:\n d1[k]=min(d1[k],d2[k])\n ret=[]\n for k in sorted(d1):\n while(d1[k]>0):\n ret.append(k)\n d1[k]-=1 \n return ret\n```\n | 1 | Given a string `s`, consider all _duplicated substrings_: (contiguous) substrings of s that occur 2 or more times. The occurrences may overlap.
Return **any** duplicated substring that has the longest possible length. If `s` does not have a duplicated substring, the answer is `" "`.
**Example 1:**
**Input:** s = "banana"
**Output:** "ana"
**Example 2:**
**Input:** s = "abcd"
**Output:** ""
**Constraints:**
* `2 <= s.length <= 3 * 104`
* `s` consists of lowercase English letters. | null |
Solution | check-if-word-is-valid-after-substitutions | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isValid(string s) {\n\n if(s.size()%3!=0) return false;\n stack<char> st;\n\n for(char c:s){\n if(st.empty()) st.push(c);\n else if(c==\'c\'){\n char b=st.top();st.pop();\n if(st.empty()) return false;\n char a = st.top(); st.pop();\n if(b!=\'b\' || a!=\'a\') return false;\n }\n else st.push(c);\n }\n return st.empty();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isValid(self, s: str) -> bool:\n prev = None\n while s != "" and s != prev:\n prev = s\n s = s.replace("abc", "")\n return s == ""\n```\n\n```Java []\nclass Solution {\n public boolean isValid(String s) {\n char[] cs = s.toCharArray();\n int i = 0;\n for (char c : cs) {\n if (c != \'a\' && (i == 0 || c != cs[--i] + 1)) {\n return false;\n }\n if (c != \'c\') {\n cs[i++] = c;\n }\n }\n return i == 0;\n }\n}\n``` | 1 | Given a string `s`, determine if it is **valid**.
A string `s` is **valid** if, starting with an empty string `t = " "`, you can **transform** `t` **into** `s` after performing the following operation **any number of times**:
* Insert string `"abc "` into any position in `t`. More formally, `t` becomes `tleft + "abc " + tright`, where `t == tleft + tright`. Note that `tleft` and `tright` may be **empty**.
Return `true` _if_ `s` _is a **valid** string, otherwise, return_ `false`.
**Example 1:**
**Input:** s = "aabcbc "
**Output:** true
**Explanation:**
" " -> "abc " -> "aabcbc "
Thus, "aabcbc " is valid.
**Example 2:**
**Input:** s = "abcabcababcc "
**Output:** true
**Explanation:**
" " -> "abc " -> "abcabc " -> "abcabcabc " -> "abcabcababcc "
Thus, "abcabcababcc " is valid.
**Example 3:**
**Input:** s = "abccba "
**Output:** false
**Explanation:** It is impossible to get "abccba " using the operation.
**Constraints:**
* `1 <= s.length <= 2 * 104`
* `s` consists of letters `'a'`, `'b'`, and `'c'` | null |
[Easy]Simple Stack And String Replace Approaches | check-if-word-is-valid-after-substitutions | 0 | 1 | ### Without Stack Approach\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n incomplete = True\n \n while incomplete:\n if \'abc\' in s:\n s= s.replace(\'abc\',\'\')\n else:\n incomplete = False\n \n return s == \'\'\n```\n\n### With Stack Approach\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n stack = []\n \n for i in s:\n if i == \'c\' and len(stack) >= 2 and stack[-1] == \'b\' and stack[-2] == \'a\':\n stack.pop()\n stack.pop()\n else:\n stack.append(i)\n \n if \'\'.join(stack) == \'abc\': stack = []\n \n return stack == []\n``` \n**Please upvote if this helped! :)**\n\t\t\n\t\t | 2 | Given a string `s`, determine if it is **valid**.
A string `s` is **valid** if, starting with an empty string `t = " "`, you can **transform** `t` **into** `s` after performing the following operation **any number of times**:
* Insert string `"abc "` into any position in `t`. More formally, `t` becomes `tleft + "abc " + tright`, where `t == tleft + tright`. Note that `tleft` and `tright` may be **empty**.
Return `true` _if_ `s` _is a **valid** string, otherwise, return_ `false`.
**Example 1:**
**Input:** s = "aabcbc "
**Output:** true
**Explanation:**
" " -> "abc " -> "aabcbc "
Thus, "aabcbc " is valid.
**Example 2:**
**Input:** s = "abcabcababcc "
**Output:** true
**Explanation:**
" " -> "abc " -> "abcabc " -> "abcabcabc " -> "abcabcababcc "
Thus, "abcabcababcc " is valid.
**Example 3:**
**Input:** s = "abccba "
**Output:** false
**Explanation:** It is impossible to get "abccba " using the operation.
**Constraints:**
* `1 <= s.length <= 2 * 104`
* `s` consists of letters `'a'`, `'b'`, and `'c'` | null |
[Python3] Good enough | check-if-word-is-valid-after-substitutions | 0 | 1 | ``` Python3 []\nclass Solution:\n def isValid(self, s: str) -> bool:\n while s:\n for i in range(len(s)-2):\n if s[i:i+3]==\'abc\':\n s = s[:i]+s[i+3:]\n break\n else:\n return False\n \n return True\n``` | 0 | Given a string `s`, determine if it is **valid**.
A string `s` is **valid** if, starting with an empty string `t = " "`, you can **transform** `t` **into** `s` after performing the following operation **any number of times**:
* Insert string `"abc "` into any position in `t`. More formally, `t` becomes `tleft + "abc " + tright`, where `t == tleft + tright`. Note that `tleft` and `tright` may be **empty**.
Return `true` _if_ `s` _is a **valid** string, otherwise, return_ `false`.
**Example 1:**
**Input:** s = "aabcbc "
**Output:** true
**Explanation:**
" " -> "abc " -> "aabcbc "
Thus, "aabcbc " is valid.
**Example 2:**
**Input:** s = "abcabcababcc "
**Output:** true
**Explanation:**
" " -> "abc " -> "abcabc " -> "abcabcabc " -> "abcabcababcc "
Thus, "abcabcababcc " is valid.
**Example 3:**
**Input:** s = "abccba "
**Output:** false
**Explanation:** It is impossible to get "abccba " using the operation.
**Constraints:**
* `1 <= s.length <= 2 * 104`
* `s` consists of letters `'a'`, `'b'`, and `'c'` | null |
Simple python3 solution | Stack + Greedy | check-if-word-is-valid-after-substitutions | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def isValid(self, s: str) -> bool:\n stack = []\n for elem in s:\n if (\n elem == \'c\'\n and len(stack) >= 2\n and stack[-2] == \'a\'\n and stack[-1] == \'b\'\n ):\n stack.pop()\n stack.pop()\n else:\n stack.append(elem)\n return len(stack) == 0\n\n``` | 0 | Given a string `s`, determine if it is **valid**.
A string `s` is **valid** if, starting with an empty string `t = " "`, you can **transform** `t` **into** `s` after performing the following operation **any number of times**:
* Insert string `"abc "` into any position in `t`. More formally, `t` becomes `tleft + "abc " + tright`, where `t == tleft + tright`. Note that `tleft` and `tright` may be **empty**.
Return `true` _if_ `s` _is a **valid** string, otherwise, return_ `false`.
**Example 1:**
**Input:** s = "aabcbc "
**Output:** true
**Explanation:**
" " -> "abc " -> "aabcbc "
Thus, "aabcbc " is valid.
**Example 2:**
**Input:** s = "abcabcababcc "
**Output:** true
**Explanation:**
" " -> "abc " -> "abcabc " -> "abcabcabc " -> "abcabcababcc "
Thus, "abcabcababcc " is valid.
**Example 3:**
**Input:** s = "abccba "
**Output:** false
**Explanation:** It is impossible to get "abccba " using the operation.
**Constraints:**
* `1 <= s.length <= 2 * 104`
* `s` consists of letters `'a'`, `'b'`, and `'c'` | null |
Solution | max-consecutive-ones-iii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestOnes(vector<int>& nums, int k) {\n int i=0,j=0;\n while(j<nums.size()){\n if(nums[j]==0){\n k--;\n }\n if(k<0){\n if(nums[i]==0){\n k++;\n }\n i++;\n }\n j++;\n }\n return j-i;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n l=r=0 \n for r in range(len(nums)):\n if nums[r] == 0:\n k-=1\n if k<0:\n if nums[l] == 0:\n k+=1\n l+=1\n return r-l+1\n```\n\n```Java []\nclass Solution {\n public int longestOnes(int[] nums, int k) {\n int start=0;\n int end=0;\n int zeros=0;\n\n while(end<nums.length){\n if(nums[end] == 0){\n zeros++;\n }\n end++;\n if(zeros>k){\n if(nums[start] == 0){\n zeros--;\n }\n start++;\n }\n }\n return end-start;\n }\n}\n``` | 480 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Solution | max-consecutive-ones-iii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestOnes(vector<int>& nums, int k) {\n int i=0,j=0;\n while(j<nums.size()){\n if(nums[j]==0){\n k--;\n }\n if(k<0){\n if(nums[i]==0){\n k++;\n }\n i++;\n }\n j++;\n }\n return j-i;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n l=r=0 \n for r in range(len(nums)):\n if nums[r] == 0:\n k-=1\n if k<0:\n if nums[l] == 0:\n k+=1\n l+=1\n return r-l+1\n```\n\n```Java []\nclass Solution {\n public int longestOnes(int[] nums, int k) {\n int start=0;\n int end=0;\n int zeros=0;\n\n while(end<nums.length){\n if(nums[end] == 0){\n zeros++;\n }\n end++;\n if(zeros>k){\n if(nums[start] == 0){\n zeros--;\n }\n start++;\n }\n }\n return end-start;\n }\n}\n``` | 480 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Easy Python3 Solution using Sliding Window | max-consecutive-ones-iii | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n Used Sliding Window Technique\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n\n start=0\n end=0\n for i in range(len(nums)):\n if(nums[i]==0):\n k-=1\n while(k<0):\n k+=1-nums[start]\n start+=1\n end=max(end,i-start+1)\n return end\n``` | 0 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Easy Python3 Solution using Sliding Window | max-consecutive-ones-iii | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n Used Sliding Window Technique\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n\n start=0\n end=0\n for i in range(len(nums)):\n if(nums[i]==0):\n k-=1\n while(k<0):\n k+=1-nums[start]\n start+=1\n end=max(end,i-start+1)\n return end\n``` | 0 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Python3 sliding window with clear example - explains why the soln works | max-consecutive-ones-iii | 0 | 1 | The solution was confusing for me.\nHere let me try to explain it more clearly with the example below. Hope it helps.\n\n\nHere is what the implementation looks like. I used explicit checks for K to make it clearer to follow.\n\n```\nclass Solution:\n def longestOnes(self, A: List[int], K: int) -> int:\n left = right = 0\n \n for right in range(len(A)):\n # if we encounter a 0 the we decrement K\n if A[right] == 0:\n K -= 1\n # else no impact to K\n \n # if K < 0 then we need to move the left part of the window forward\n # to try and remove the extra 0\'s\n if K < 0:\n # if the left one was zero then we adjust K\n if A[left] == 0:\n K += 1\n # regardless of whether we had a 1 or a 0 we can move left side by 1\n # if we keep seeing 1\'s the window still keeps moving as-is\n left += 1\n \n return right - left + 1\n``` | 351 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Python3 sliding window with clear example - explains why the soln works | max-consecutive-ones-iii | 0 | 1 | The solution was confusing for me.\nHere let me try to explain it more clearly with the example below. Hope it helps.\n\n\nHere is what the implementation looks like. I used explicit checks for K to make it clearer to follow.\n\n```\nclass Solution:\n def longestOnes(self, A: List[int], K: int) -> int:\n left = right = 0\n \n for right in range(len(A)):\n # if we encounter a 0 the we decrement K\n if A[right] == 0:\n K -= 1\n # else no impact to K\n \n # if K < 0 then we need to move the left part of the window forward\n # to try and remove the extra 0\'s\n if K < 0:\n # if the left one was zero then we adjust K\n if A[left] == 0:\n K += 1\n # regardless of whether we had a 1 or a 0 we can move left side by 1\n # if we keep seeing 1\'s the window still keeps moving as-is\n left += 1\n \n return right - left + 1\n``` | 351 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Python || Sliding Windows | max-consecutive-ones-iii | 0 | 1 | # Approach\ni is a pointer that marks the beginning of the current subarray.\n\nmaxi is a variable that stores the length of the longest subarray with at most k replacements of 0s.\n\nj is another pointer that moves through the list to the right.\n\nzero is a counter that keeps track of the number of 0s in the current subarray.\n\nIterating through the list:\n\nFor each element in the list:\nIf the element is a 0, increment the zero counter as we\'ve encountered another 0 in the current subarray.\nCheck if the zero count exceeds the allowed replacements k. If it does, we need to move the i pointer to the right and reduce the zero count until it is less than or equal to k. This is done in a while loop.\nIn the while loop, we essentially shorten the current subarray by moving the start pointer i to the right and decrementing the zero count by removing 0s from the subarray.\nUpdate the maxi variable with the maximum subarray length encountered so far while ensuring that zero is less than or equal to `k.\nContinue moving the j pointer to the right, extending the subarray and updating maxi whenever a longer valid subarray is found.\n\nFinally, return the maxi value, which represents the length of the longest subarray of 1s with at most k replacements of 0s.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n i=0\n maxi=0\n j=0 \n zero=0\n while j<len(nums):\n if nums[j]==0:\n zero+=1 \n if zero>k:\n if nums[i]==0:\n zero-=1 \n i+=1 \n if zero<=k:\n maxi=max(maxi,j-i+1)\n j+=1\n return maxi\n\n\n\n return maxi\n``` | 4 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Python || Sliding Windows | max-consecutive-ones-iii | 0 | 1 | # Approach\ni is a pointer that marks the beginning of the current subarray.\n\nmaxi is a variable that stores the length of the longest subarray with at most k replacements of 0s.\n\nj is another pointer that moves through the list to the right.\n\nzero is a counter that keeps track of the number of 0s in the current subarray.\n\nIterating through the list:\n\nFor each element in the list:\nIf the element is a 0, increment the zero counter as we\'ve encountered another 0 in the current subarray.\nCheck if the zero count exceeds the allowed replacements k. If it does, we need to move the i pointer to the right and reduce the zero count until it is less than or equal to k. This is done in a while loop.\nIn the while loop, we essentially shorten the current subarray by moving the start pointer i to the right and decrementing the zero count by removing 0s from the subarray.\nUpdate the maxi variable with the maximum subarray length encountered so far while ensuring that zero is less than or equal to `k.\nContinue moving the j pointer to the right, extending the subarray and updating maxi whenever a longer valid subarray is found.\n\nFinally, return the maxi value, which represents the length of the longest subarray of 1s with at most k replacements of 0s.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n i=0\n maxi=0\n j=0 \n zero=0\n while j<len(nums):\n if nums[j]==0:\n zero+=1 \n if zero>k:\n if nums[i]==0:\n zero-=1 \n i+=1 \n if zero<=k:\n maxi=max(maxi,j-i+1)\n j+=1\n return maxi\n\n\n\n return maxi\n``` | 4 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
✔️ 5 Ways to Solving Max Consecutive Ones III 🪔 | max-consecutive-ones-iii | 0 | 1 | \nThis is cool right?~~~\n# Solution 1: Sliding Window (Best Performance)\n\n# Intuition\nMaintain a sliding window.\nDecrease k when encountering 0 and increase it when an element is removed from the window.\nEffectively count the number of elements in the middle to find the maximum length of the window.\n# Approach\nInitialize start to 0 and iterate end over the list.\nIf nums[end] is 0, decrement k.\nIf k becomes negative, increment start until k is non-negative again.\nKeep track of the maximum window length.\n# Complexity\n- Time complexity:O(n), where n is the length of the input list.\n\n- Space complexity:O(1).\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n start = 0\n for end in range(len(nums)):\n if nums[end] == 0:\n k -= 1\n if k < 0:\n if nums[start] == 0:\n k += 1\n start += 1\n return end - start + 1\n\n```\n# Solution 2: Hash Map Approach\n\n# Intuition\nUse a hashmap to count the frequency of each element.\nAdjust the window based on the counts of elements, ensuring that the number of 0s doesn\'t exceed k.\n# Approach\nInitialize start, count, and max.\nIterate over the list with end and Right.\nUpdate the count of Right in the hashmap.\nAdjust the window by decreasing the count of 0s when needed.\nKeep track of the maximum window length.\n# Complexity\nTime complexity: O(n), where n is the length of the input list.\nSpace complexity: O(n).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n count = {}\n max_len = 0\n start = 0\n for end, Right in enumerate(nums):\n count[Right] = 1 + count.get(Right, 0)\n if 0 not in count:\n count[0] = 0\n if count[0] > k:\n count[nums[start]] -= 1\n start += 1\n max_len = max(max_len, end - start + 1)\n return max_len\n\n```\n# Solution 3: Hash Map Approach with Reduced Space Complexity\n\n# Intuition\nSimilar to Solution 2 but with reduced space complexity.\n\n# Approach\nInitialize start and count.\nIterate over the list and update the count of elements in the hashmap.\nAdjust the window based on the counts of elements, ensuring that the number of 0s doesn\'t exceed k.\nReturn the maximum window length.\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(n).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n count = {}\n start = 0\n for end, Right in enumerate(nums):\n count[Right] = 1 + count.get(Right, 0)\n if 0 not in count:\n count[0] = 0\n if count[0] > k:\n count[nums[start]] -= 1\n start += 1\n return end - start + 1\n\n```\n# Solution 4: Count Zeros Directly\n\n# Intuition\nCount the number of zeros in the given list by iterating through it.\nMaintain a sliding window to ensure the number of zeros doesn\'t exceed k.\n# Approach\nInitialize start, mx, and zeros.\nIterate over the list with right and n.\nUpdate zeros when encountering zeros and adjust the window when zeros exceeds k.\nKeep track of the maximum window length.\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(1).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n mx = 0\n start = 0\n zeros = 0\n for right, n in enumerate(nums):\n if n == 0:\n zeros += 1\n while zeros > k:\n if nums[start] == 0:\n zeros -= 1\n start += 1\n mx = max(mx, right - start + 1)\n return mx\n\n```\n# Solution 5: Count Ones and Subtract\n\n\n# Intuition\nCount the number of ones in the window and subtract this count from the window length.\nCheck if the remaining zeros in the window exceed k.\nAdjust the window accordingly.\n\n# Approach\nInitialize start, mx, and ones.\nIterate over the list with end.\nUpdate the count of ones (ones) in the window.\nCalculate the number of zeros by subtracting ones from the window length.\nAdjust the window based on the count of zeros and ones.\nKeep track of the maximum window length.\n\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(1).\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n start, mx, ones = 0,0,0\n for end in range(len(nums)):\n if nums[end] == 1:\n ones+=1\n windowLength = end-start+1 \n noOfZeros = windowLength - ones \n if (noOfZeros) > k:\n if nums[start] == 1:\n ones-=1\n start += 1\n mx= max(mx, end-start+1)\n return mx\n \n```\n | 3 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
✔️ 5 Ways to Solving Max Consecutive Ones III 🪔 | max-consecutive-ones-iii | 0 | 1 | \nThis is cool right?~~~\n# Solution 1: Sliding Window (Best Performance)\n\n# Intuition\nMaintain a sliding window.\nDecrease k when encountering 0 and increase it when an element is removed from the window.\nEffectively count the number of elements in the middle to find the maximum length of the window.\n# Approach\nInitialize start to 0 and iterate end over the list.\nIf nums[end] is 0, decrement k.\nIf k becomes negative, increment start until k is non-negative again.\nKeep track of the maximum window length.\n# Complexity\n- Time complexity:O(n), where n is the length of the input list.\n\n- Space complexity:O(1).\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n start = 0\n for end in range(len(nums)):\n if nums[end] == 0:\n k -= 1\n if k < 0:\n if nums[start] == 0:\n k += 1\n start += 1\n return end - start + 1\n\n```\n# Solution 2: Hash Map Approach\n\n# Intuition\nUse a hashmap to count the frequency of each element.\nAdjust the window based on the counts of elements, ensuring that the number of 0s doesn\'t exceed k.\n# Approach\nInitialize start, count, and max.\nIterate over the list with end and Right.\nUpdate the count of Right in the hashmap.\nAdjust the window by decreasing the count of 0s when needed.\nKeep track of the maximum window length.\n# Complexity\nTime complexity: O(n), where n is the length of the input list.\nSpace complexity: O(n).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n count = {}\n max_len = 0\n start = 0\n for end, Right in enumerate(nums):\n count[Right] = 1 + count.get(Right, 0)\n if 0 not in count:\n count[0] = 0\n if count[0] > k:\n count[nums[start]] -= 1\n start += 1\n max_len = max(max_len, end - start + 1)\n return max_len\n\n```\n# Solution 3: Hash Map Approach with Reduced Space Complexity\n\n# Intuition\nSimilar to Solution 2 but with reduced space complexity.\n\n# Approach\nInitialize start and count.\nIterate over the list and update the count of elements in the hashmap.\nAdjust the window based on the counts of elements, ensuring that the number of 0s doesn\'t exceed k.\nReturn the maximum window length.\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(n).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n count = {}\n start = 0\n for end, Right in enumerate(nums):\n count[Right] = 1 + count.get(Right, 0)\n if 0 not in count:\n count[0] = 0\n if count[0] > k:\n count[nums[start]] -= 1\n start += 1\n return end - start + 1\n\n```\n# Solution 4: Count Zeros Directly\n\n# Intuition\nCount the number of zeros in the given list by iterating through it.\nMaintain a sliding window to ensure the number of zeros doesn\'t exceed k.\n# Approach\nInitialize start, mx, and zeros.\nIterate over the list with right and n.\nUpdate zeros when encountering zeros and adjust the window when zeros exceeds k.\nKeep track of the maximum window length.\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(1).\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n mx = 0\n start = 0\n zeros = 0\n for right, n in enumerate(nums):\n if n == 0:\n zeros += 1\n while zeros > k:\n if nums[start] == 0:\n zeros -= 1\n start += 1\n mx = max(mx, right - start + 1)\n return mx\n\n```\n# Solution 5: Count Ones and Subtract\n\n\n# Intuition\nCount the number of ones in the window and subtract this count from the window length.\nCheck if the remaining zeros in the window exceed k.\nAdjust the window accordingly.\n\n# Approach\nInitialize start, mx, and ones.\nIterate over the list with end.\nUpdate the count of ones (ones) in the window.\nCalculate the number of zeros by subtracting ones from the window length.\nAdjust the window based on the count of zeros and ones.\nKeep track of the maximum window length.\n\n# Complexity\nTime complexity: O(n).\nSpace complexity: O(1).\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n start, mx, ones = 0,0,0\n for end in range(len(nums)):\n if nums[end] == 1:\n ones+=1\n windowLength = end-start+1 \n noOfZeros = windowLength - ones \n if (noOfZeros) > k:\n if nums[start] == 1:\n ones-=1\n start += 1\n mx= max(mx, end-start+1)\n return mx\n \n```\n | 3 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Standard Sliding Window Template | max-consecutive-ones-iii | 0 | 1 | # Intuition\nSliding Window template for questions like [424. Longest Repeating Character Replacement](https://leetcode.com/problems/longest-repeating-character-replacement/description/)\n\n# Approach\nKeep increasing the window till count of `zeros > k`, remove left character from window till `zeros <= k`.\n\nP.S. `right - left + 1` is the length of current window.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n left = 0\n zeros = 0\n res = -math.inf\n\n for right in range(len(nums)):\n if nums[right] == 0:\n zeros += 1\n\n while zeros > k:\n if nums[left] == 0:\n zeros -= 1\n left += 1\n res = max(res, right - left + 1)\n\n return res\n``` | 1 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Standard Sliding Window Template | max-consecutive-ones-iii | 0 | 1 | # Intuition\nSliding Window template for questions like [424. Longest Repeating Character Replacement](https://leetcode.com/problems/longest-repeating-character-replacement/description/)\n\n# Approach\nKeep increasing the window till count of `zeros > k`, remove left character from window till `zeros <= k`.\n\nP.S. `right - left + 1` is the length of current window.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n left = 0\n zeros = 0\n res = -math.inf\n\n for right in range(len(nums)):\n if nums[right] == 0:\n zeros += 1\n\n while zeros > k:\n if nums[left] == 0:\n zeros -= 1\n left += 1\n res = max(res, right - left + 1)\n\n return res\n``` | 1 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Easiest solution | max-consecutive-ones-iii | 0 | 1 | # Intuition\nWe use 2 pointers left and right to keep track of sliding window.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n left=0\n count_zero=0\n max_array=0\n\n for right in range(len(nums)):\n if nums[right] == 0:\n count_zero+=1\n \n while count_zero > k:\n if nums[left] == 0:\n count_zero-=1\n left+=1\n \n max_array=max(max_array,right-left+1)\n\n return max_array\n\n\n \n```\n# **PLEASE DO UPVOTE!!!** | 7 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Easiest solution | max-consecutive-ones-iii | 0 | 1 | # Intuition\nWe use 2 pointers left and right to keep track of sliding window.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n left=0\n count_zero=0\n max_array=0\n\n for right in range(len(nums)):\n if nums[right] == 0:\n count_zero+=1\n \n while count_zero > k:\n if nums[left] == 0:\n count_zero-=1\n left+=1\n \n max_array=max(max_array,right-left+1)\n\n return max_array\n\n\n \n```\n# **PLEASE DO UPVOTE!!!** | 7 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
[Python 3] Sliding window + bonus (similar question) || beats 97% | max-consecutive-ones-iii | 0 | 1 | ```python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n zeros, l = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > k:\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n\n```\n\n[485. Max Consecutive Ones](https://leetcode.com/problems/max-consecutive-ones/solutions/4261252/python3-1-line-using-groupby-3-solutions-277ms-beats-99/)\nThe logic almost same, but k = 0\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n zeros, l = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > 0: # the difference is only here\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n```\n\n | 15 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
[Python 3] Sliding window + bonus (similar question) || beats 97% | max-consecutive-ones-iii | 0 | 1 | ```python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n zeros, l = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > k:\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n\n```\n\n[485. Max Consecutive Ones](https://leetcode.com/problems/max-consecutive-ones/solutions/4261252/python3-1-line-using-groupby-3-solutions-277ms-beats-99/)\nThe logic almost same, but k = 0\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n zeros, l = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > 0: # the difference is only here\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n```\n\n | 15 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Sliding Window Problems | max-consecutive-ones-iii | 0 | 1 | # Sliding Window Logic\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n res=[0]*2\n ans=left=0\n for right in range(len(nums)):\n res[nums[right]]+=1\n ans=max(ans,res[nums[right]])\n if (right-left+1)-ans>k:\n res[nums[left]]-=1\n left+=1\n return len(nums)-left\n```\n# please upvote me it would encourage me alot\n# connected Problems:\n1.longest repeating character replacement----->([https://leetcode.com/problems/longest-repeating-character-replacement/])\n2.Find the Longest Equal Subarray----->https://leetcode.com/problems/find-the-longest-equal-subarray/\n3.Maximize the Confusion of an Exam----->https://leetcode.com/problems/maximize-the-confusion-of-an-exam/\n4.Maximum Beauty of an Array After Applying Operation----->https://leetcode.com/problems/maximum-beauty-of-an-array-after-applying-operation/\n | 5 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Sliding Window Problems | max-consecutive-ones-iii | 0 | 1 | # Sliding Window Logic\n```\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n res=[0]*2\n ans=left=0\n for right in range(len(nums)):\n res[nums[right]]+=1\n ans=max(ans,res[nums[right]])\n if (right-left+1)-ans>k:\n res[nums[left]]-=1\n left+=1\n return len(nums)-left\n```\n# please upvote me it would encourage me alot\n# connected Problems:\n1.longest repeating character replacement----->([https://leetcode.com/problems/longest-repeating-character-replacement/])\n2.Find the Longest Equal Subarray----->https://leetcode.com/problems/find-the-longest-equal-subarray/\n3.Maximize the Confusion of an Exam----->https://leetcode.com/problems/maximize-the-confusion-of-an-exam/\n4.Maximum Beauty of an Array After Applying Operation----->https://leetcode.com/problems/maximum-beauty-of-an-array-after-applying-operation/\n | 5 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Binary Search + Sliding Window | max-consecutive-ones-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIn this problem we know the highest and the lowest possible answers which are `0` or `len(nums)`\n\nTherefore, there may be a possible solution for this problem using binary search\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nso using binary search we are checking if a guessed answer can be correct answer\nthat means lets say we have guessed an answer `mid` then it means that we can find the most consequtive `1`\'s of length `mid` after alterting at most `k` zeros\n\nif our guess is correct then we will go for a higher value of `mid` by applying `lo=mid+1` as we need to find the maximum possible correct answer\n\nor if our guessed answer is not a correct answer we are guessing a smaller value to be our `mid`\n\n```\nlo = 0\nhi = len(nums)\nans = 0\nwhile lo <= hi:\n mid = (lo + hi) // 2\n\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n\n lo = mid + 1\n else:\n hi = mid - 1\n\n```\n\nnow how do we check if a guessed `mid` can be a possible correct answer?\n\nwe will use the sliding window approach for this\n\n```\ndef check(self, nums, guess, k):\n start = 0\n end = start + guess\n s = sum(nums[start:end])\n \n while end < len(nums):\n \n \n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n \n s-=nums[start]\n start += 1\n s+=nums[end]\n end += 1\n\n \n s = sum(nums[start:end])\n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n\n return False\n```\n\n# Complexity\n- Time complexity: O(n*log(n)) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# from ast import List\n\n\nclass Solution:\n def check(self, nums, guess, k):\n start = 0\n end = start + guess\n s = sum(nums[start:end])\n \n\n while end < len(nums):\n \n \n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n \n s-=nums[start]\n start += 1\n s+=nums[end]\n end += 1\n\n \n s = sum(nums[start:end])\n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n\n return False\n\n \n\n def longestOnes(self, nums: list[int], k: int) -> int:\n lo = 0\n hi = len(nums)\n ans = 0\n while lo <= hi:\n mid = (lo + hi) // 2\n # print(mid)\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n # print(mid)\n lo = mid + 1\n else:\n hi = mid - 1\n\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n # ans = max(ans,mid)\n\n return ans\n\n\nnums = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1]\nk = 0\nsol = Solution()\nans = sol.longestOnes(nums, k)\nprint(ans)\n\n``` | 2 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
Binary Search + Sliding Window | max-consecutive-ones-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIn this problem we know the highest and the lowest possible answers which are `0` or `len(nums)`\n\nTherefore, there may be a possible solution for this problem using binary search\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nso using binary search we are checking if a guessed answer can be correct answer\nthat means lets say we have guessed an answer `mid` then it means that we can find the most consequtive `1`\'s of length `mid` after alterting at most `k` zeros\n\nif our guess is correct then we will go for a higher value of `mid` by applying `lo=mid+1` as we need to find the maximum possible correct answer\n\nor if our guessed answer is not a correct answer we are guessing a smaller value to be our `mid`\n\n```\nlo = 0\nhi = len(nums)\nans = 0\nwhile lo <= hi:\n mid = (lo + hi) // 2\n\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n\n lo = mid + 1\n else:\n hi = mid - 1\n\n```\n\nnow how do we check if a guessed `mid` can be a possible correct answer?\n\nwe will use the sliding window approach for this\n\n```\ndef check(self, nums, guess, k):\n start = 0\n end = start + guess\n s = sum(nums[start:end])\n \n while end < len(nums):\n \n \n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n \n s-=nums[start]\n start += 1\n s+=nums[end]\n end += 1\n\n \n s = sum(nums[start:end])\n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n\n return False\n```\n\n# Complexity\n- Time complexity: O(n*log(n)) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# from ast import List\n\n\nclass Solution:\n def check(self, nums, guess, k):\n start = 0\n end = start + guess\n s = sum(nums[start:end])\n \n\n while end < len(nums):\n \n \n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n \n s-=nums[start]\n start += 1\n s+=nums[end]\n end += 1\n\n \n s = sum(nums[start:end])\n rem = (end - start) - s\n rem = min(rem, k)\n temp = s + rem\n \n if temp == guess:\n \n return True\n\n return False\n\n \n\n def longestOnes(self, nums: list[int], k: int) -> int:\n lo = 0\n hi = len(nums)\n ans = 0\n while lo <= hi:\n mid = (lo + hi) // 2\n # print(mid)\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n # print(mid)\n lo = mid + 1\n else:\n hi = mid - 1\n\n possible = self.check(nums, mid, k)\n if possible == True:\n ans = max(ans, mid)\n # ans = max(ans,mid)\n\n return ans\n\n\nnums = [1, 1, 1, 0, 0, 0, 1, 1, 1, 1]\nk = 0\nsol = Solution()\nans = sol.longestOnes(nums, k)\nprint(ans)\n\n``` | 2 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
💡Intuitive| ⏳0ms 🥇Beats 95% | ✅ Beginner's Friendly Explanation | max-consecutive-ones-iii | 0 | 1 | 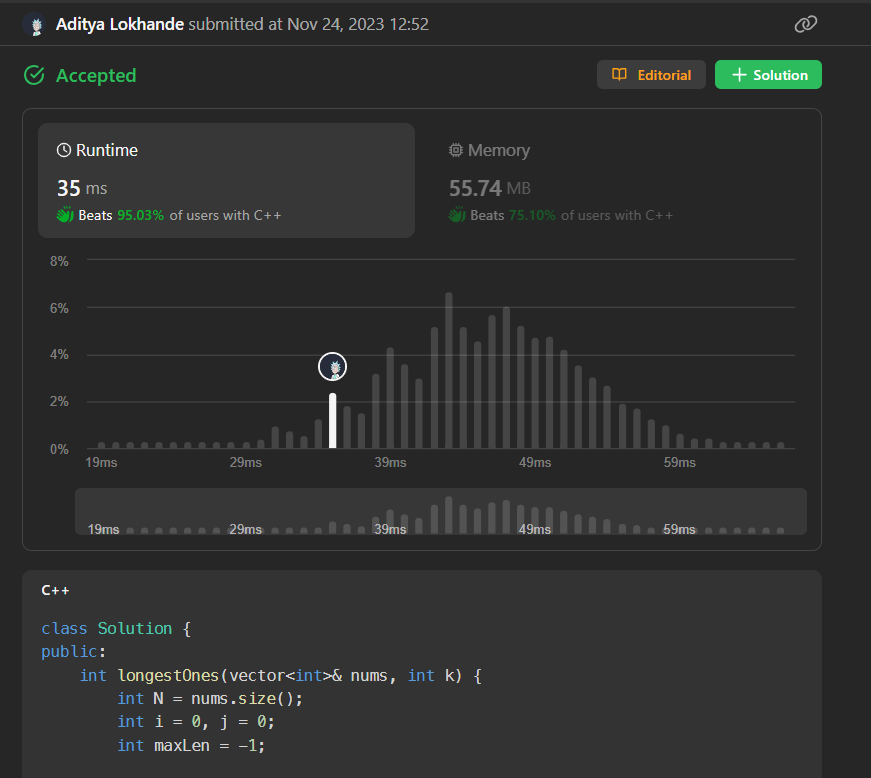\n\n# Intuition\nThe dynamic sliding window approach efficiently explores a binary array to find the longest subarray with at most k zeros. Two pointers define a window that expands on encountering 1s and selectively on encountering 0s (while k is available). The window contracts when k is exhausted. Throughout this process, the algorithm tracks and updates the length of the subarray. This approach ensures optimal exploration with O(n) time complexity and constant O(1) space complexity.\n\n# Approach\nThe dynamic sliding window approach is a common strategy for solving problems related to binary arrays where you need to find the longest subarray with at most k zeros.\n\n1. **Define the Window:**\n - Initialize two pointers, `start` and `end`, both pointing to the zero index of the array.\n - These pointers represent the window, and the goal is to find the longest subarray within this window that satisfies the given condition.\n\n2. **Traverse the Array:**\n - While traversing the array, if you encounter a 1, increase the size of the window by moving the `end` pointer to the right by 1.\n\n3. **Encounter 0:**\n - If you encounter a 0 and `k` is greater than 0, you can still increase the size of the window by moving the `end` pointer to the right by 1.\n - Decrease `k` by 1 to account for the fact that you encountered a 0 and are allowing for at most `k` zeros in the subarray.\n\n4. **Update Window (k becomes 0):**\n - If `k` becomes 0 in the process, it means you\'ve encountered `k` zeros in the window.\n - Now, you need to remove the earliest zero in the window to maintain the condition of at most `k` zeros. Move the `start` pointer to the index of the earliest zero + 1.\n\n5. **Keep Track of Length:**\n - Throughout this process, keep track of the length of the sequence by updating it whenever the window expands.\n\nBy following these steps, you ensure that the window always contains at most `k` zeros, and you continuously update the window to find the longest subarray that satisfies the given condition.\n\n\n# Complexity\n\n### Time Complexity:\nThe time complexity of this algorithm is O(n), where n is the length of the input array. This is because each element is visited at most twice (once by the end pointer and once by the start pointer).\n\n### Space Complexity:\nThe space complexity is O(1), constant space. The space used by the algorithm does not grow with the input size, as it only uses a fixed number of pointers and variables. The sliding window approach is efficient in terms of space usage because it doesn\'t require additional data structures proportional to the input size.\n\nIn summary:\n- Time Complexity: O(n)\n- Space Complexity: O(1)\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int longestOnes(vector<int>& nums, int k) {\n int N = nums.size();\n int i = 0, j = 0;\n int maxLen = -1;\n \n while (j < N) {\n if (nums[j] == 1) {\n j++;\n } \n else {\n k--;\n j++;\n if (k < 0) {\n while (nums[i] != 0) {\n i++;\n }\n i++;\n k++;\n }\n }\n maxLen = max(maxLen, j - i);\n }\n return maxLen;\n }\n};\n```\n```Python []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n N = len(nums)\n i = 0\n j = 0\n maxLen = -1\n while j<N:\n if nums[j]==1:\n j+=1\n else:\n k-=1\n j+=1\n if k<0:\n while nums[i]!=0:\n i+=1\n i+=1\n k+=1\n maxLen = max(maxLen,j-i)\n return (maxLen)\n \n``` | 1 | Given a binary array `nums` and an integer `k`, return _the maximum number of consecutive_ `1`_'s in the array if you can flip at most_ `k` `0`'s.
**Example 1:**
**Input:** nums = \[1,1,1,0,0,0,1,1,1,1,0\], k = 2
**Output:** 6
**Explanation:** \[1,1,1,0,0,**1**,1,1,1,1,**1**\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Example 2:**
**Input:** nums = \[0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1\], k = 3
**Output:** 10
**Explanation:** \[0,0,1,1,**1**,**1**,1,1,1,**1**,1,1,0,0,0,1,1,1,1\]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`.
* `0 <= k <= nums.length` | null |
💡Intuitive| ⏳0ms 🥇Beats 95% | ✅ Beginner's Friendly Explanation | max-consecutive-ones-iii | 0 | 1 | \n\n# Intuition\nThe dynamic sliding window approach efficiently explores a binary array to find the longest subarray with at most k zeros. Two pointers define a window that expands on encountering 1s and selectively on encountering 0s (while k is available). The window contracts when k is exhausted. Throughout this process, the algorithm tracks and updates the length of the subarray. This approach ensures optimal exploration with O(n) time complexity and constant O(1) space complexity.\n\n# Approach\nThe dynamic sliding window approach is a common strategy for solving problems related to binary arrays where you need to find the longest subarray with at most k zeros.\n\n1. **Define the Window:**\n - Initialize two pointers, `start` and `end`, both pointing to the zero index of the array.\n - These pointers represent the window, and the goal is to find the longest subarray within this window that satisfies the given condition.\n\n2. **Traverse the Array:**\n - While traversing the array, if you encounter a 1, increase the size of the window by moving the `end` pointer to the right by 1.\n\n3. **Encounter 0:**\n - If you encounter a 0 and `k` is greater than 0, you can still increase the size of the window by moving the `end` pointer to the right by 1.\n - Decrease `k` by 1 to account for the fact that you encountered a 0 and are allowing for at most `k` zeros in the subarray.\n\n4. **Update Window (k becomes 0):**\n - If `k` becomes 0 in the process, it means you\'ve encountered `k` zeros in the window.\n - Now, you need to remove the earliest zero in the window to maintain the condition of at most `k` zeros. Move the `start` pointer to the index of the earliest zero + 1.\n\n5. **Keep Track of Length:**\n - Throughout this process, keep track of the length of the sequence by updating it whenever the window expands.\n\nBy following these steps, you ensure that the window always contains at most `k` zeros, and you continuously update the window to find the longest subarray that satisfies the given condition.\n\n\n# Complexity\n\n### Time Complexity:\nThe time complexity of this algorithm is O(n), where n is the length of the input array. This is because each element is visited at most twice (once by the end pointer and once by the start pointer).\n\n### Space Complexity:\nThe space complexity is O(1), constant space. The space used by the algorithm does not grow with the input size, as it only uses a fixed number of pointers and variables. The sliding window approach is efficient in terms of space usage because it doesn\'t require additional data structures proportional to the input size.\n\nIn summary:\n- Time Complexity: O(n)\n- Space Complexity: O(1)\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int longestOnes(vector<int>& nums, int k) {\n int N = nums.size();\n int i = 0, j = 0;\n int maxLen = -1;\n \n while (j < N) {\n if (nums[j] == 1) {\n j++;\n } \n else {\n k--;\n j++;\n if (k < 0) {\n while (nums[i] != 0) {\n i++;\n }\n i++;\n k++;\n }\n }\n maxLen = max(maxLen, j - i);\n }\n return maxLen;\n }\n};\n```\n```Python []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n N = len(nums)\n i = 0\n j = 0\n maxLen = -1\n while j<N:\n if nums[j]==1:\n j+=1\n else:\n k-=1\n j+=1\n if k<0:\n while nums[i]!=0:\n i+=1\n i+=1\n k+=1\n maxLen = max(maxLen,j-i)\n return (maxLen)\n \n``` | 1 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the weight of the last remaining stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We combine 7 and 8 to get 1 so the array converts to \[2,4,1,1,1\] then,
we combine 2 and 4 to get 2 so the array converts to \[2,1,1,1\] then,
we combine 2 and 1 to get 1 so the array converts to \[1,1,1\] then,
we combine 1 and 1 to get 0 so the array converts to \[1\] then that's the value of the last stone.
**Example 2:**
**Input:** stones = \[1\]
**Output:** 1
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 1000` | One thing's for sure, we will only flip a zero if it extends an existing window of 1s. Otherwise, there's no point in doing it, right? Think Sliding Window! Since we know this problem can be solved using the sliding window construct, we might as well focus in that direction for hints. Basically, in a given window, we can never have > K zeros, right? We don't have a fixed size window in this case. The window size can grow and shrink depending upon the number of zeros we have (we don't actually have to flip the zeros here!). The way to shrink or expand a window would be based on the number of zeros that can still be flipped and so on. |
Solution | maximize-sum-of-array-after-k-negations | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nlong long getSum(vector<int> negate, vector<int>positive)\n{\n long long sum =0;\n for(int i=0;i<negate.size();i++)\n {\n sum+=negate[i];\n }\n for(int i=0;i<positive.size();i++)\n {\n sum+=positive[i];\n }\n return sum;\n}\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n vector<int>negate;\n vector<int>positive;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]>=0)\n {\n positive.push_back(nums[i]);\n }\n else{\n negate.push_back(nums[i]);\n }\n }\n if(negate.size()>k)\n {\n sort(negate.begin(), negate.end());\n for(int i=0;i<k;i++)\n {\n negate[i] = abs(negate[i]);\n }\n return getSum(negate, positive);\n } else {\n for(int i=0;i<negate.size();i++)\n {\n negate[i] = abs(negate[i]);\n }\n int remainingcount = k-negate.size();\n if(remainingcount%2==0)\n {\n return getSum(negate, positive);\n } else {\n int mini = INT_MAX;\n for(int i=0;i<negate.size();i++)\n {\n mini = min(mini, negate[i]);\n }\n for(int i=0;i<positive.size();i++)\n {\n mini = min(mini, positive[i]);\n }\ncout<<mini<<endl;\ncout<<getSum(negate, positive)<<endl;\n return (getSum(negate, positive) - 2*mini);\n }\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums = sorted(nums)\n for i in range(len(nums)):\n if nums[i] < 0 and k > 0:\n nums[i] = -nums[i]\n k -= 1\n nums = sorted(nums)\n if k > 0 and k % 2 != 0: \n nums[0] = -nums[0]\n return sum(nums)\n```\n\n```Java []\nclass Solution {\n public int largestSumAfterKNegations(int[] nums, int k) {\n int[] numbers = new int[201];\n int sum = 0;\n int maxAbs = 0;\n for (int n: nums) {\n maxAbs = Math.max(maxAbs, Math.abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n if (maxAbs == 0) {\n return 0;\n }\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n return sum;\n }\n}\n``` | 447 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Solution | maximize-sum-of-array-after-k-negations | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nlong long getSum(vector<int> negate, vector<int>positive)\n{\n long long sum =0;\n for(int i=0;i<negate.size();i++)\n {\n sum+=negate[i];\n }\n for(int i=0;i<positive.size();i++)\n {\n sum+=positive[i];\n }\n return sum;\n}\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n vector<int>negate;\n vector<int>positive;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]>=0)\n {\n positive.push_back(nums[i]);\n }\n else{\n negate.push_back(nums[i]);\n }\n }\n if(negate.size()>k)\n {\n sort(negate.begin(), negate.end());\n for(int i=0;i<k;i++)\n {\n negate[i] = abs(negate[i]);\n }\n return getSum(negate, positive);\n } else {\n for(int i=0;i<negate.size();i++)\n {\n negate[i] = abs(negate[i]);\n }\n int remainingcount = k-negate.size();\n if(remainingcount%2==0)\n {\n return getSum(negate, positive);\n } else {\n int mini = INT_MAX;\n for(int i=0;i<negate.size();i++)\n {\n mini = min(mini, negate[i]);\n }\n for(int i=0;i<positive.size();i++)\n {\n mini = min(mini, positive[i]);\n }\ncout<<mini<<endl;\ncout<<getSum(negate, positive)<<endl;\n return (getSum(negate, positive) - 2*mini);\n }\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums = sorted(nums)\n for i in range(len(nums)):\n if nums[i] < 0 and k > 0:\n nums[i] = -nums[i]\n k -= 1\n nums = sorted(nums)\n if k > 0 and k % 2 != 0: \n nums[0] = -nums[0]\n return sum(nums)\n```\n\n```Java []\nclass Solution {\n public int largestSumAfterKNegations(int[] nums, int k) {\n int[] numbers = new int[201];\n int sum = 0;\n int maxAbs = 0;\n for (int n: nums) {\n maxAbs = Math.max(maxAbs, Math.abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n if (maxAbs == 0) {\n return 0;\n }\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n return sum;\n }\n}\n``` | 447 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Python 3 solution beats 98% - simple if else statements | maximize-sum-of-array-after-k-negations | 0 | 1 | This solution is easy but quite tasking to come up with all the edge cases. I did see shorter solutions using heaps which I dont fully understand yet but hope to learn how to apply it in the near future.\n# Code\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int: \n nums.sort()\n negative = sorted(x for x in nums if x < 0)\n len_neg = len(negative)\n positive = sorted(x for x in nums if x > 0)\n if 0 in nums:\n if not negative:\n return sum(positive)\n else:\n if k >= len_neg:\n return sum(positive) - sum(negative)\n return sum(positive) - sum(negative[:k]) + sum(negative[k:])\n else: \n if not negative:\n if k % 2:\n return sum(nums) - 2 * nums[0]\n return sum(nums)\n else:\n if k >= len_neg:\n if (k - len_neg) % 2:\n return sum(positive) - sum(negative) - 2 * min(-negative[-1], positive[0] if positive else float(\'inf\'))\n return sum(positive) - sum(negative)\n if k < len_neg:\n return sum(positive) - sum(negative[:k]) + sum(negative[k:])\n \n``` | 1 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Python 3 solution beats 98% - simple if else statements | maximize-sum-of-array-after-k-negations | 0 | 1 | This solution is easy but quite tasking to come up with all the edge cases. I did see shorter solutions using heaps which I dont fully understand yet but hope to learn how to apply it in the near future.\n# Code\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int: \n nums.sort()\n negative = sorted(x for x in nums if x < 0)\n len_neg = len(negative)\n positive = sorted(x for x in nums if x > 0)\n if 0 in nums:\n if not negative:\n return sum(positive)\n else:\n if k >= len_neg:\n return sum(positive) - sum(negative)\n return sum(positive) - sum(negative[:k]) + sum(negative[k:])\n else: \n if not negative:\n if k % 2:\n return sum(nums) - 2 * nums[0]\n return sum(nums)\n else:\n if k >= len_neg:\n if (k - len_neg) % 2:\n return sum(positive) - sum(negative) - 2 * min(-negative[-1], positive[0] if positive else float(\'inf\'))\n return sum(positive) - sum(negative)\n if k < len_neg:\n return sum(positive) - sum(negative[:k]) + sum(negative[k:])\n \n``` | 1 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
🚀 Beats 100% | Java, C++, Python | Non queue solution | maximize-sum-of-array-after-k-negations | 1 | 1 | > \u26A0\uFE0F **Disclaimer**: The original solution was crafted in Java. Thus, when we mention "Beats 100%" it applies specifically to Java submissions. The performance may vary for other languages.\n\nDont forget to upvote if you like the content below. \uD83D\uDE43\n\n# Intuition\nGiven the problem, we should always aim to negate the smallest number in the array in each iteration to maximize the final sum. However, we can use a micro-optimization by calculating the sum once at the beginning and then adjusting it after each negation.\n\n# Approach\nWe start by creating a frequency array, $$numbers$$, with the index representing the number in the original array + $$100$$. This allows us to handle negative numbers seamlessly.\n\nNext, we iterate through the $$nums$$ array, count the frequencies, and calculate the sum. Simultaneously, we keep track of the maximum absolute value in the array ($$maxAbs$$), which we will use later to determine the start index for the negation process.\n\nIf $$maxAbs$$ is zero after the first pass, it means all elements in the array are zero, and we return $$0$$, as negating zero doesn\'t change the sum.\n\nThen, we perform $$k$$ negations. For each negation, we start at the index $$i$$ equal to $$100 - maxAbs$$, which represents the smallest possible number in the array. We find the first index with a non-zero frequency, decrement its frequency, increment the frequency of its negation $$(200 - i)$$, and adjust the sum by subtracting twice the current number (since we have negated it).\n\n# Complexity\n- Time complexity:\nThe time complexity is $$O(n + k)$$, where $$n$$ is the length of the array and $$k$$ is the number of negations. $$n$$ is for the initial iteration through the nums array, and $$k$$ is for the negations.\n\n- Space complexity:\nThe space complexity is $$O(1)$$, as we only use a constant amount of extra space. The numbers array\'s size is a constant $$201$$, accommodating all possible values from $$-100$$ to $$100$$.\n\nThis solution is optimal for the problem constraints. While a PriorityQueue-based solution could also work, it might not be as fast due to overheads associated with creating and managing the PriorityQueue. Our solution avoids these overheads by using a simple frequency count array and a single pass through the array. The index calculation $$(number + 100)$$ and the negation index calculation $$(200 - index)$$ are straightforward and efficient, making this solution particularly suitable for the given constraints.\n\n# Code\n```java []\nclass Solution {\n public int largestSumAfterKNegations(int[] nums, int k) {\n int[] numbers = new int[201];\n int sum = 0;\n int maxAbs = 0;\n for (int n: nums) {\n maxAbs = Math.max(maxAbs, Math.abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n\n if (maxAbs == 0) {\n return 0;\n }\n\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n\n return sum;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n vector<int> numbers(201, 0);\n int sum = 0;\n int maxAbs = 0;\n for (int n : nums) {\n maxAbs = max(maxAbs, abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n\n if (maxAbs == 0) {\n return 0;\n }\n\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n\n return sum;\n }\n};\n```\n```python []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n numbers = [0] * 201\n total_sum = 0\n max_abs = 0\n \n for n in nums:\n max_abs = max(max_abs, abs(n))\n numbers[100 + n] += 1\n total_sum += n\n\n if max_abs == 0:\n return 0\n\n while k > 0:\n k -= 1\n i = 100 - max_abs\n while numbers[i] == 0:\n i += 1\n numbers[i] -= 1\n numbers[200 - i] += 1\n total_sum -= 2 * (i - 100)\n\n return total_sum\n\n``` | 2 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
🚀 Beats 100% | Java, C++, Python | Non queue solution | maximize-sum-of-array-after-k-negations | 1 | 1 | > \u26A0\uFE0F **Disclaimer**: The original solution was crafted in Java. Thus, when we mention "Beats 100%" it applies specifically to Java submissions. The performance may vary for other languages.\n\nDont forget to upvote if you like the content below. \uD83D\uDE43\n\n# Intuition\nGiven the problem, we should always aim to negate the smallest number in the array in each iteration to maximize the final sum. However, we can use a micro-optimization by calculating the sum once at the beginning and then adjusting it after each negation.\n\n# Approach\nWe start by creating a frequency array, $$numbers$$, with the index representing the number in the original array + $$100$$. This allows us to handle negative numbers seamlessly.\n\nNext, we iterate through the $$nums$$ array, count the frequencies, and calculate the sum. Simultaneously, we keep track of the maximum absolute value in the array ($$maxAbs$$), which we will use later to determine the start index for the negation process.\n\nIf $$maxAbs$$ is zero after the first pass, it means all elements in the array are zero, and we return $$0$$, as negating zero doesn\'t change the sum.\n\nThen, we perform $$k$$ negations. For each negation, we start at the index $$i$$ equal to $$100 - maxAbs$$, which represents the smallest possible number in the array. We find the first index with a non-zero frequency, decrement its frequency, increment the frequency of its negation $$(200 - i)$$, and adjust the sum by subtracting twice the current number (since we have negated it).\n\n# Complexity\n- Time complexity:\nThe time complexity is $$O(n + k)$$, where $$n$$ is the length of the array and $$k$$ is the number of negations. $$n$$ is for the initial iteration through the nums array, and $$k$$ is for the negations.\n\n- Space complexity:\nThe space complexity is $$O(1)$$, as we only use a constant amount of extra space. The numbers array\'s size is a constant $$201$$, accommodating all possible values from $$-100$$ to $$100$$.\n\nThis solution is optimal for the problem constraints. While a PriorityQueue-based solution could also work, it might not be as fast due to overheads associated with creating and managing the PriorityQueue. Our solution avoids these overheads by using a simple frequency count array and a single pass through the array. The index calculation $$(number + 100)$$ and the negation index calculation $$(200 - index)$$ are straightforward and efficient, making this solution particularly suitable for the given constraints.\n\n# Code\n```java []\nclass Solution {\n public int largestSumAfterKNegations(int[] nums, int k) {\n int[] numbers = new int[201];\n int sum = 0;\n int maxAbs = 0;\n for (int n: nums) {\n maxAbs = Math.max(maxAbs, Math.abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n\n if (maxAbs == 0) {\n return 0;\n }\n\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n\n return sum;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n vector<int> numbers(201, 0);\n int sum = 0;\n int maxAbs = 0;\n for (int n : nums) {\n maxAbs = max(maxAbs, abs(n));\n numbers[100 + n]++;\n sum += n;\n }\n\n if (maxAbs == 0) {\n return 0;\n }\n\n while (k-- != 0) {\n int i = 100 - maxAbs;\n while (numbers[i] == 0) {\n i++;\n }\n numbers[i]--;\n numbers[200 - i]++;\n sum -= 2 * (i - 100);\n }\n\n return sum;\n }\n};\n```\n```python []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n numbers = [0] * 201\n total_sum = 0\n max_abs = 0\n \n for n in nums:\n max_abs = max(max_abs, abs(n))\n numbers[100 + n] += 1\n total_sum += n\n\n if max_abs == 0:\n return 0\n\n while k > 0:\n k -= 1\n i = 100 - max_abs\n while numbers[i] == 0:\n i += 1\n numbers[i] -= 1\n numbers[200 - i] += 1\n total_sum -= 2 * (i - 100)\n\n return total_sum\n\n``` | 2 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
1005. Simple solution | Beats 91% | maximize-sum-of-array-after-k-negations | 0 | 1 | # Code\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums.sort()\n last_negative, last_ind = nums[0], 0\n for x, item in enumerate(nums):\n if k <= 0 or item == 0: break\n if item < 0:\n last_negative = -item\n last_ind = x\n nums[x] = -1 * item\n k -= 1\n elif item > 0:\n if k % 2 == 0: break\n else:\n if item > last_negative:\n nums[last_ind] = -1* last_negative\n break\n else:\n nums[x] = -item\n break\n else:\n nums[last_ind] = (-1**k)* last_negative\n return sum(nums)\n\n\n``` | 2 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
1005. Simple solution | Beats 91% | maximize-sum-of-array-after-k-negations | 0 | 1 | # Code\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums.sort()\n last_negative, last_ind = nums[0], 0\n for x, item in enumerate(nums):\n if k <= 0 or item == 0: break\n if item < 0:\n last_negative = -item\n last_ind = x\n nums[x] = -1 * item\n k -= 1\n elif item > 0:\n if k % 2 == 0: break\n else:\n if item > last_negative:\n nums[last_ind] = -1* last_negative\n break\n else:\n nums[x] = -item\n break\n else:\n nums[last_ind] = (-1**k)* last_negative\n return sum(nums)\n\n\n``` | 2 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
🔥 [Python 3] Min Heap for negative values with comments, beats 80% 🥷🏼 | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n # if k <= n(count of negative numbers )=> need make highest negative values positive (here using heap for this)\n # if k > n(count of negative numbers) and k-n is odd => need make all negative numbers positive and minVal make negative\n heap, res, minVal = [], 0, 101\n\n for n in nums:\n if n > 0: res += n\n elif n < 0: heappush(heap, n)\n minVal = min(minVal, abs(n))\n\n # make highest negative values positive while k opertions available\n while heap and k > 0:\n res += -heappop(heap) #add negative value\n k -= 1\n # if still exists negative value, just add them to final sum\n if heap:\n res += sum(heap)\n # if k > 0 and it\'s odd need make minVal negative (if 0 exists it will be smalles value)\n if k % 2:\n res = res - 2 * minVal\n \n return res\n\n``` | 5 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
🔥 [Python 3] Min Heap for negative values with comments, beats 80% 🥷🏼 | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n # if k <= n(count of negative numbers )=> need make highest negative values positive (here using heap for this)\n # if k > n(count of negative numbers) and k-n is odd => need make all negative numbers positive and minVal make negative\n heap, res, minVal = [], 0, 101\n\n for n in nums:\n if n > 0: res += n\n elif n < 0: heappush(heap, n)\n minVal = min(minVal, abs(n))\n\n # make highest negative values positive while k opertions available\n while heap and k > 0:\n res += -heappop(heap) #add negative value\n k -= 1\n # if still exists negative value, just add them to final sum\n if heap:\n res += sum(heap)\n # if k > 0 and it\'s odd need make minVal negative (if 0 exists it will be smalles value)\n if k % 2:\n res = res - 2 * minVal\n \n return res\n\n``` | 5 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Min Heap (O(n + k * log (n)) time / O(1) space) | maximize-sum-of-array-after-k-negations | 0 | 1 | Hi LeetCoders \uD83D\uDC4B\nHere is my simple and clean solution to this problem with use of min-heap.\n\n**Code:**\n```\nfrom heapq import heapify, heapreplace\n\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n heapify(nums)\n while k and nums[0] < 0:\n heapreplace(nums, -nums[0])\n k -= 1\n if k % 2:\n heapreplace(nums, -nums[0])\n return sum(nums)\n```\n\n**Idea explanation:**\n* negate negative numbers as many as you can\n* if ```k % 2 == 1``` negate the smallest element in the heap\n\n**Notes:**\nAvoid using ```heappush + heappop``` because it takes ```O(2 * log (n))``` time, use ```heapreplace``` instead and pay just ```O(log (n))```. Isn\'t that a great deal?\n\n**Algorithm complexity:**\n*n = len(nums)*\n*Time complexity: O(n + k * log (n))*\n*Space complexity: O(1)*\n\nIf you like my solution, I will really appreciate your upvoting. It will help other python-developers to find it faster. And as always, I hope you learned something and wish you an enjoyable time on LeetCode. \uD83D\uDE0A | 28 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Min Heap (O(n + k * log (n)) time / O(1) space) | maximize-sum-of-array-after-k-negations | 0 | 1 | Hi LeetCoders \uD83D\uDC4B\nHere is my simple and clean solution to this problem with use of min-heap.\n\n**Code:**\n```\nfrom heapq import heapify, heapreplace\n\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n heapify(nums)\n while k and nums[0] < 0:\n heapreplace(nums, -nums[0])\n k -= 1\n if k % 2:\n heapreplace(nums, -nums[0])\n return sum(nums)\n```\n\n**Idea explanation:**\n* negate negative numbers as many as you can\n* if ```k % 2 == 1``` negate the smallest element in the heap\n\n**Notes:**\nAvoid using ```heappush + heappop``` because it takes ```O(2 * log (n))``` time, use ```heapreplace``` instead and pay just ```O(log (n))```. Isn\'t that a great deal?\n\n**Algorithm complexity:**\n*n = len(nums)*\n*Time complexity: O(n + k * log (n))*\n*Space complexity: O(1)*\n\nIf you like my solution, I will really appreciate your upvoting. It will help other python-developers to find it faster. And as always, I hope you learned something and wish you an enjoyable time on LeetCode. \uD83D\uDE0A | 28 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Explanation of the whole idea | maximize-sum-of-array-after-k-negations | 0 | 1 | ## Explanation\n```\nAssume nums = [8,-1,8,-3,2,-2], k = 2\n\nTo get the LARGEST SUM we will make positive -3 and -2 as they are the SMALLEST NEGATIVE\nNUMBERS. This finding process would be easier if we sort first:\n\n -3,-2,-1,2,8,8 \n\nIf k were 5, first we would turn all the negative numbers to positive numbers, right?\nCause the Q asked us LARGEST SUM!\n\n 3,2,1,2,8,8 and now k = 5 - 3 = 2\n\nAs we can choose the same index multiple times SO AFTER TURNING NEGATIVE NUMBERS\nTO POSITIVE NUMBERS, OBVIOUSLY WE WILL NOW PICK THE SMALLEST NUMBER TO CHANGE IT\'S SIGN\nTO REMAINING K TIMES TO GET THE LARGEST SUM.\n\nHere the smallest number now is 1 and k = 2, so -1,1 which is same as 1 cause \n if k is even, sign won\'t change, but if k is odd, sign will change 100%.\n```\n\n```CPP []\nclass Solution {\npublic:\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n sort(begin(nums),end(nums));\n for(int i=0; i<nums.size() && nums[i]<0 && k>0; i++, k--)\n nums[i] = -nums[i]; \n\n nums[min_element(begin(nums),end(nums))-begin(nums)] *= ((k&1) == 1? -1 : 1);\n return accumulate(begin(nums),end(nums),0); \n }\n};\n```\n```python []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int :\n nums.sort()\n i = 0\n while i<len(nums) and k>0 and nums[i]<0 :\n nums[i] = -nums[i]\n i, k = i+1, k-1\n nums[nums.index(min(nums))] *= -1 if k&1 else 1\n return sum(nums) \n```\n```\nTime complexity : O(nlogn)\nSpace complexity : O(sort)\n```\n | 2 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Explanation of the whole idea | maximize-sum-of-array-after-k-negations | 0 | 1 | ## Explanation\n```\nAssume nums = [8,-1,8,-3,2,-2], k = 2\n\nTo get the LARGEST SUM we will make positive -3 and -2 as they are the SMALLEST NEGATIVE\nNUMBERS. This finding process would be easier if we sort first:\n\n -3,-2,-1,2,8,8 \n\nIf k were 5, first we would turn all the negative numbers to positive numbers, right?\nCause the Q asked us LARGEST SUM!\n\n 3,2,1,2,8,8 and now k = 5 - 3 = 2\n\nAs we can choose the same index multiple times SO AFTER TURNING NEGATIVE NUMBERS\nTO POSITIVE NUMBERS, OBVIOUSLY WE WILL NOW PICK THE SMALLEST NUMBER TO CHANGE IT\'S SIGN\nTO REMAINING K TIMES TO GET THE LARGEST SUM.\n\nHere the smallest number now is 1 and k = 2, so -1,1 which is same as 1 cause \n if k is even, sign won\'t change, but if k is odd, sign will change 100%.\n```\n\n```CPP []\nclass Solution {\npublic:\n int largestSumAfterKNegations(vector<int>& nums, int k) {\n sort(begin(nums),end(nums));\n for(int i=0; i<nums.size() && nums[i]<0 && k>0; i++, k--)\n nums[i] = -nums[i]; \n\n nums[min_element(begin(nums),end(nums))-begin(nums)] *= ((k&1) == 1? -1 : 1);\n return accumulate(begin(nums),end(nums),0); \n }\n};\n```\n```python []\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int :\n nums.sort()\n i = 0\n while i<len(nums) and k>0 and nums[i]<0 :\n nums[i] = -nums[i]\n i, k = i+1, k-1\n nums[nums.index(min(nums))] *= -1 if k&1 else 1\n return sum(nums) \n```\n```\nTime complexity : O(nlogn)\nSpace complexity : O(sort)\n```\n | 2 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
WEEB EXPLAINS PYTHON SOLUTION | maximize-sum-of-array-after-k-negations | 0 | 1 | 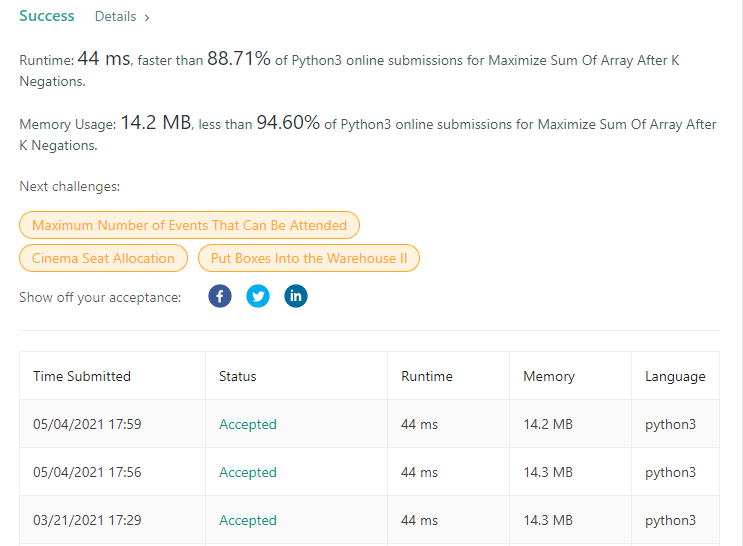\n\n\t\n\tclass Solution:\n\t\tdef largestSumAfterKNegations(self, A: List[int], K: int) -> int:\n\t\t\tA.sort()\n\t\t\ti = 0\n\t\t\twhile i < len(A) and K>0:\n\t\t\t\tif A[i] < 0: # negative value\n\t\t\t\t\tA[i] = A[i] * -1 # update the list, change negative to positive\n\t\t\t\t\tK-=1\n\n\t\t\t\telif A[i] > 0: # positive value\n\t\t\t\t\tif K % 2 == 0: # let K==2(must be even value), this means -1*-1==1 so it has no effect on sum\n\t\t\t\t\t\treturn sum(A)\n\t\t\t\t\telse: return sum(A) - 2 * min(A) # let A==[1,2,3],K=1, so equation is 6-2(1)==4, same as -1+2+3=4 after taking the minimum in the list to give the largest possible sum required in the question\n\n\t\t\t\telse: return sum(A) # if A[i]==0,just sum cuz 0 is neutral: 1-0==1 or 1+0==1 thus no change just sum\n\n\t\t\t\ti+=1\n\n\t\t\tif K > len(A): # that means we have changed all values to positive\n\t\t\t\tA.sort() # cuz now its the opposite let A = [-4,-2,-3], K = 8, now flipping all negatives to positives, we have a new minimum which is 2\n\t\t\t\tif K % 2 == 0: # Here onwards is basically the same thing from before\n\t\t\t\t\treturn sum(A)\n\t\t\t\telse: return sum(A) - 2 * min(A)\n\n\t\t\treturn sum(A)\n\nAight, time for some anime recommendations\n# try watching ***Uzaki-chan Wants to Hang Out!***\n# Genres: Romantic comedy, Slice of life\n# Episodes: 12\n\nOverall, this anime is quite fun to watch. Although i have to warn you, this anime does contain some ecchi(perverted) elements in it, but its not extreme.\n\nNow go take a break and watch some anime.\n | 6 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
WEEB EXPLAINS PYTHON SOLUTION | maximize-sum-of-array-after-k-negations | 0 | 1 | \n\n\t\n\tclass Solution:\n\t\tdef largestSumAfterKNegations(self, A: List[int], K: int) -> int:\n\t\t\tA.sort()\n\t\t\ti = 0\n\t\t\twhile i < len(A) and K>0:\n\t\t\t\tif A[i] < 0: # negative value\n\t\t\t\t\tA[i] = A[i] * -1 # update the list, change negative to positive\n\t\t\t\t\tK-=1\n\n\t\t\t\telif A[i] > 0: # positive value\n\t\t\t\t\tif K % 2 == 0: # let K==2(must be even value), this means -1*-1==1 so it has no effect on sum\n\t\t\t\t\t\treturn sum(A)\n\t\t\t\t\telse: return sum(A) - 2 * min(A) # let A==[1,2,3],K=1, so equation is 6-2(1)==4, same as -1+2+3=4 after taking the minimum in the list to give the largest possible sum required in the question\n\n\t\t\t\telse: return sum(A) # if A[i]==0,just sum cuz 0 is neutral: 1-0==1 or 1+0==1 thus no change just sum\n\n\t\t\t\ti+=1\n\n\t\t\tif K > len(A): # that means we have changed all values to positive\n\t\t\t\tA.sort() # cuz now its the opposite let A = [-4,-2,-3], K = 8, now flipping all negatives to positives, we have a new minimum which is 2\n\t\t\t\tif K % 2 == 0: # Here onwards is basically the same thing from before\n\t\t\t\t\treturn sum(A)\n\t\t\t\telse: return sum(A) - 2 * min(A)\n\n\t\t\treturn sum(A)\n\nAight, time for some anime recommendations\n# try watching ***Uzaki-chan Wants to Hang Out!***\n# Genres: Romantic comedy, Slice of life\n# Episodes: 12\n\nOverall, this anime is quite fun to watch. Although i have to warn you, this anime does contain some ecchi(perverted) elements in it, but its not extreme.\n\nNow go take a break and watch some anime.\n | 6 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Easy Python3 Intuition Approach | maximize-sum-of-array-after-k-negations | 0 | 1 | # Code1\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n for i in range(k):\n n=nums.index(min(nums))\n nums[n]=-1*nums[n]\n return sum(nums)\n```\n\n# Code2\n\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n for i in range(k,0,-1):\n if min(nums)>=0 and i%2==0:return sum(nums)\n n=nums.index(min(nums))\n nums[n]=-1*nums[n] \n return sum(nums)\n``` | 2 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Easy Python3 Intuition Approach | maximize-sum-of-array-after-k-negations | 0 | 1 | # Code1\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n for i in range(k):\n n=nums.index(min(nums))\n nums[n]=-1*nums[n]\n return sum(nums)\n```\n\n# Code2\n\n```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n for i in range(k,0,-1):\n if min(nums)>=0 and i%2==0:return sum(nums)\n n=nums.index(min(nums))\n nums[n]=-1*nums[n] \n return sum(nums)\n``` | 2 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Greedy approach - python | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums.sort(key=abs, reverse=True)\n for i in range(len(nums)):\n if nums[i] < 0 and k > 0:\n nums[i] *= -1\n k -= 1\n if k == 0:\n break\n if k % 2 != 0:\n nums[-1] *= -1\n return sum(nums)\n\t\t``` | 2 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
Greedy approach - python | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:\n nums.sort(key=abs, reverse=True)\n for i in range(len(nums)):\n if nums[i] < 0 and k > 0:\n nums[i] *= -1\n k -= 1\n if k == 0:\n break\n if k % 2 != 0:\n nums[-1] *= -1\n return sum(nums)\n\t\t``` | 2 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
[PYTHON 3] Min Heap | Few - Lines | Easy to Read Solution | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, min_heap: List[int], K: int) -> int:\n heapify(min_heap)\n while K > 0:\n heappush(min_heap , - (heappop(min_heap))) \n K -= 1\n return sum(min_heap)\n``` | 10 | Given an integer array `nums` and an integer `k`, modify the array in the following way:
* choose an index `i` and replace `nums[i]` with `-nums[i]`.
You should apply this process exactly `k` times. You may choose the same index `i` multiple times.
Return _the largest possible sum of the array after modifying it in this way_.
**Example 1:**
**Input:** nums = \[4,2,3\], k = 1
**Output:** 5
**Explanation:** Choose index 1 and nums becomes \[4,-2,3\].
**Example 2:**
**Input:** nums = \[3,-1,0,2\], k = 3
**Output:** 6
**Explanation:** Choose indices (1, 2, 2) and nums becomes \[3,1,0,2\].
**Example 3:**
**Input:** nums = \[2,-3,-1,5,-4\], k = 2
**Output:** 13
**Explanation:** Choose indices (1, 4) and nums becomes \[2,3,-1,5,4\].
**Constraints:**
* `1 <= nums.length <= 104`
* `-100 <= nums[i] <= 100`
* `1 <= k <= 104` | null |
[PYTHON 3] Min Heap | Few - Lines | Easy to Read Solution | maximize-sum-of-array-after-k-negations | 0 | 1 | ```\nclass Solution:\n def largestSumAfterKNegations(self, min_heap: List[int], K: int) -> int:\n heapify(min_heap)\n while K > 0:\n heappush(min_heap , - (heappop(min_heap))) \n K -= 1\n return sum(min_heap)\n``` | 10 | You are given a string `s` consisting of lowercase English letters. A **duplicate removal** consists of choosing two **adjacent** and **equal** letters and removing them.
We repeatedly make **duplicate removals** on `s` until we no longer can.
Return _the final string after all such duplicate removals have been made_. It can be proven that the answer is **unique**.
**Example 1:**
**Input:** s = "abbaca "
**Output:** "ca "
**Explanation:**
For example, in "abbaca " we could remove "bb " since the letters are adjacent and equal, and this is the only possible move. The result of this move is that the string is "aaca ", of which only "aa " is possible, so the final string is "ca ".
**Example 2:**
**Input:** s = "azxxzy "
**Output:** "ay "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | null |
Solution | clumsy-factorial | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int clumsy(int N) {\n if (N == 1)\n return 1;\n if (N == 2)\n return 2;\n if (N == 3)\n return 6;\n if (N == 4)\n return 7;\n if (N % 4 == 1)\n return N + 2;\n if (N % 4 == 2)\n return N + 2;\n if (N % 4 == 3)\n return N - 1;\n return N + 1;\n }\n};\n```\n\n```Python3 []\nclass Solution(object):\n def clumsy(self, n):\n if n == 1:\n return 1\n elif n == 2:\n return 2\n elif n == 3:\n return 6\n elif n == 4:\n return 7\n else:\n if n % 4 == 0:\n return n + 1\n elif n % 4 <= 2:\n return n + 2\n else:\n return n - 1\n```\n\n```Java []\nclass Solution {\n public int clumsy(int n) {\n int ans = 1;\n if(n <= 4){\n if(n <= 2) return n;\n else if(n == 3) return 6;\n else if(n == 4) return 7;\n } else {\n if(n%4 == 1 || n%4 == 2) ans = n+2;\n else if(n%4 == 3) ans = n-1;\n else ans = n+1;\n }\n return ans;\n }\n}\n``` | 443 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
Solution | clumsy-factorial | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int clumsy(int N) {\n if (N == 1)\n return 1;\n if (N == 2)\n return 2;\n if (N == 3)\n return 6;\n if (N == 4)\n return 7;\n if (N % 4 == 1)\n return N + 2;\n if (N % 4 == 2)\n return N + 2;\n if (N % 4 == 3)\n return N - 1;\n return N + 1;\n }\n};\n```\n\n```Python3 []\nclass Solution(object):\n def clumsy(self, n):\n if n == 1:\n return 1\n elif n == 2:\n return 2\n elif n == 3:\n return 6\n elif n == 4:\n return 7\n else:\n if n % 4 == 0:\n return n + 1\n elif n % 4 <= 2:\n return n + 2\n else:\n return n - 1\n```\n\n```Java []\nclass Solution {\n public int clumsy(int n) {\n int ans = 1;\n if(n <= 4){\n if(n <= 2) return n;\n else if(n == 3) return 6;\n else if(n == 4) return 7;\n } else {\n if(n%4 == 1 || n%4 == 2) ans = n+2;\n else if(n%4 == 3) ans = n-1;\n else ans = n+1;\n }\n return ans;\n }\n}\n``` | 443 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
Simplest Solution with Python Conditional Statements | clumsy-factorial | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere I\'m using the basic conditional statements.\nThe \'while loop\' along with some \'if\' conditions are used.\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n l = []\n itr = 0\n while n > 0:\n l.append(str(n))\n if itr%4 == 0:\n l.append(\'*\')\n elif itr%4 == 1:\n l.append(\'//\')\n elif itr%4 == 2:\n l.append(\'+\')\n elif itr%4 == 3:\n l.append(\'-\')\n itr += 1\n n -= 1\n l.pop()\n l = "".join(l)\n return eval(l)\n\n``` | 1 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
Simplest Solution with Python Conditional Statements | clumsy-factorial | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nHere I\'m using the basic conditional statements.\nThe \'while loop\' along with some \'if\' conditions are used.\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n l = []\n itr = 0\n while n > 0:\n l.append(str(n))\n if itr%4 == 0:\n l.append(\'*\')\n elif itr%4 == 1:\n l.append(\'//\')\n elif itr%4 == 2:\n l.append(\'+\')\n elif itr%4 == 3:\n l.append(\'-\')\n itr += 1\n n -= 1\n l.pop()\n l = "".join(l)\n return eval(l)\n\n``` | 1 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
O(n) Stack Python3 Solution | clumsy-factorial | 0 | 1 | ```\nclass Solution:\n \n # O(n) time,\n # O(n) space,\n # Approach: stack, \n def clumsy(self, n: int) -> int:\n stack = [n]\n \n turn = 0\n # multiplicaiton and division\n for num in range(n-1, 0, -1):\n if turn % 4 == 0:\n num1 = stack.pop()\n stack.append(num1*num)\n elif turn % 4 == 1:\n num1 = stack.pop()\n stack.append(num1//num)\n else:\n stack.append(num)\n turn += 1\n \n # addition and substraction\n turn = 0\n for i in range(1, len(stack)):\n if turn % 2 == 0:\n stack[i] += stack[i-1]\n else:\n stack[i] = stack[i-1]-stack[i]\n turn += 1\n \n return stack[-1]\n``` | 1 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
O(n) Stack Python3 Solution | clumsy-factorial | 0 | 1 | ```\nclass Solution:\n \n # O(n) time,\n # O(n) space,\n # Approach: stack, \n def clumsy(self, n: int) -> int:\n stack = [n]\n \n turn = 0\n # multiplicaiton and division\n for num in range(n-1, 0, -1):\n if turn % 4 == 0:\n num1 = stack.pop()\n stack.append(num1*num)\n elif turn % 4 == 1:\n num1 = stack.pop()\n stack.append(num1//num)\n else:\n stack.append(num)\n turn += 1\n \n # addition and substraction\n turn = 0\n for i in range(1, len(stack)):\n if turn % 2 == 0:\n stack[i] += stack[i-1]\n else:\n stack[i] = stack[i-1]-stack[i]\n turn += 1\n \n return stack[-1]\n``` | 1 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
Clumsy factorial Python3 | clumsy-factorial | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIve used stack and implemented it in a for loop and used mod 4 to find the operation to be used in any particular number of the input range.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n \n if n == 1:\n return 1\n \n stack = [n]\n ops = 0 \n \n for i in range(n-1, 0, -1):\n if ops % 4 == 0:\n stack[-1] *= i\n elif ops % 4 == 1:\n stack[-1] = int(stack[-1] / i)\n elif ops % 4 == 2:\n stack.append(i)\n elif ops % 4 == 3:\n stack.append(-i)\n \n ops += 1\n \n return sum(stack)\n\n\n``` | 0 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
Clumsy factorial Python3 | clumsy-factorial | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIve used stack and implemented it in a for loop and used mod 4 to find the operation to be used in any particular number of the input range.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n \n if n == 1:\n return 1\n \n stack = [n]\n ops = 0 \n \n for i in range(n-1, 0, -1):\n if ops % 4 == 0:\n stack[-1] *= i\n elif ops % 4 == 1:\n stack[-1] = int(stack[-1] / i)\n elif ops % 4 == 2:\n stack.append(i)\n elif ops % 4 == 3:\n stack.append(-i)\n \n ops += 1\n \n return sum(stack)\n\n\n``` | 0 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
Two Lines with eval() | clumsy-factorial | 0 | 1 | using an infinite iterator (```cycle```)\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n ops = cycle( [ "*", "//", "+", "-" ] )\n return eval("".join(str(i) + next(ops) for i in range(n, 1, -1)) + "1")``` | 0 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
Two Lines with eval() | clumsy-factorial | 0 | 1 | using an infinite iterator (```cycle```)\n```\nclass Solution:\n def clumsy(self, n: int) -> int:\n ops = cycle( [ "*", "//", "+", "-" ] )\n return eval("".join(str(i) + next(ops) for i in range(n, 1, -1)) + "1")``` | 0 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
Reslove this in clumsy way | clumsy-factorial | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first 4 numbers are positive, then the following numbers are regular (-n*(n-1)/(n-2)+(n-3)), and last will reamin less than 4 numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMany IFs, even nest IFs. It\'s stupid but relizable.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import floor\nclass Solution:\n def clumsy(self, n: int) -> int:\n i=n\n ans=0\n if n>=4:\n ans=floor(i*(i-1)/(i-2))+(i-3)\n i-=4\n if n<4:\n if n==1:\n ans=1\n if n==2:\n ans=2*1\n if n==3:\n ans=floor(3*2/1)\n i=0\n while i>=4:\n ans-=floor(i*(i-1)/(i-2))\n ans+=(i-3)\n i-=4\n if i>0:\n if i==1:\n ans-=i\n if i==2:\n ans-=i*(i-1)\n if i==3:\n ans-=floor(i*(i-1)/(i-2))\n return ans\n\n\n \n``` | 0 | The **factorial** of a positive integer `n` is the product of all positive integers less than or equal to `n`.
* For example, `factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1`.
We make a **clumsy factorial** using the integers in decreasing order by swapping out the multiply operations for a fixed rotation of operations with multiply `'*'`, divide `'/'`, add `'+'`, and subtract `'-'` in this order.
* For example, `clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1`.
However, these operations are still applied using the usual order of operations of arithmetic. We do all multiplication and division steps before any addition or subtraction steps, and multiplication and division steps are processed left to right.
Additionally, the division that we use is floor division such that `10 * 9 / 8 = 90 / 8 = 11`.
Given an integer `n`, return _the clumsy factorial of_ `n`.
**Example 1:**
**Input:** n = 4
**Output:** 7
**Explanation:** 7 = 4 \* 3 / 2 + 1
**Example 2:**
**Input:** n = 10
**Output:** 12
**Explanation:** 12 = 10 \* 9 / 8 + 7 - 6 \* 5 / 4 + 3 - 2 \* 1
**Constraints:**
* `1 <= n <= 104` | null |
Reslove this in clumsy way | clumsy-factorial | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first 4 numbers are positive, then the following numbers are regular (-n*(n-1)/(n-2)+(n-3)), and last will reamin less than 4 numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMany IFs, even nest IFs. It\'s stupid but relizable.\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import floor\nclass Solution:\n def clumsy(self, n: int) -> int:\n i=n\n ans=0\n if n>=4:\n ans=floor(i*(i-1)/(i-2))+(i-3)\n i-=4\n if n<4:\n if n==1:\n ans=1\n if n==2:\n ans=2*1\n if n==3:\n ans=floor(3*2/1)\n i=0\n while i>=4:\n ans-=floor(i*(i-1)/(i-2))\n ans+=(i-3)\n i-=4\n if i>0:\n if i==1:\n ans-=i\n if i==2:\n ans-=i*(i-1)\n if i==3:\n ans-=floor(i*(i-1)/(i-2))\n return ans\n\n\n \n``` | 0 | You are given an array of `words` where each word consists of lowercase English letters.
`wordA` is a **predecessor** of `wordB` if and only if we can insert **exactly one** letter anywhere in `wordA` **without changing the order of the other characters** to make it equal to `wordB`.
* For example, `"abc "` is a **predecessor** of `"abac "`, while `"cba "` is not a **predecessor** of `"bcad "`.
A **word chain** is a sequence of words `[word1, word2, ..., wordk]` with `k >= 1`, where `word1` is a **predecessor** of `word2`, `word2` is a **predecessor** of `word3`, and so on. A single word is trivially a **word chain** with `k == 1`.
Return _the **length** of the **longest possible word chain** with words chosen from the given list of_ `words`.
**Example 1:**
**Input:** words = \[ "a ", "b ", "ba ", "bca ", "bda ", "bdca "\]
**Output:** 4
**Explanation**: One of the longest word chains is \[ "a ", "ba ", "bda ", "bdca "\].
**Example 2:**
**Input:** words = \[ "xbc ", "pcxbcf ", "xb ", "cxbc ", "pcxbc "\]
**Output:** 5
**Explanation:** All the words can be put in a word chain \[ "xb ", "xbc ", "cxbc ", "pcxbc ", "pcxbcf "\].
**Example 3:**
**Input:** words = \[ "abcd ", "dbqca "\]
**Output:** 1
**Explanation:** The trivial word chain \[ "abcd "\] is one of the longest word chains.
\[ "abcd ", "dbqca "\] is not a valid word chain because the ordering of the letters is changed.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 16`
* `words[i]` only consists of lowercase English letters. | null |
Solution | minimum-domino-rotations-for-equal-row | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {\n int flips = 0;\n\n const int num = tops.size();\n\n int top = tops[0];\n int bottom = bottoms[0];\n\n int symmetricals = (top == bottom) ? 1 : 0;\n\n for (int i = 1; i < num; i++) {\n int currTop = tops[i];\n int currBottom = bottoms[i];\n\n if (currTop == currBottom) {\n symmetricals++;\n }\n if (currTop == top || currBottom == bottom) {\n if (currTop != top) {\n top = -1;\n }\n else if (currBottom != bottom) {\n bottom = -1;\n }\n }\n else if (currTop == bottom && currBottom == top) {\n flips++;\n } else if (currBottom == top) {\n flips++;\n bottom = -1;\n } else if (currTop == bottom) {\n flips++;\n top = -1;\n }\n else {\n return -1;\n }\n }\n if (top == -1 && bottom == -1) {\n return -1;\n }\n if (flips * 2 > num - symmetricals) {\n flips = (num - flips) - symmetricals;\n }\n return flips;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:\n n = len(tops)\n ans = float("inf")\n if len(tops)!=len(bottoms):\n return -1\n def get_ans(num):\n ans = float("inf")\n \n ntop = 0\n nbottom = 0\n for t,b in zip(tops, bottoms):\n if t!=num and b!=num:\n return -1\n elif t!=num:\n ntop +=1\n elif b!=num:\n nbottom +=1\n return min(ntop, nbottom)\n \n ts = get_ans(tops[0]) \n if (ts == -1):\n return get_ans(bottoms[0])\n else:\n return ts\n```\n\n```Java []\nclass Solution {\n public int minDominoRotations(int[] A, int[] B) {\n int ans = -1; \n for (int val = 1; val <= 6; val++) {\n int currAns = helper(A, B, val);\n \n if (currAns != -1 && (ans == -1 || ans > currAns)) {\n ans = currAns;\n }\n }\n return ans;\n }\n private int helper(int[] A, int[] B, int val) {\n int ansTop = 0, ansBottom = 0;\n \n for (int i = 0; i < A.length; i++) {\n if (A[i] != val && B[i] != val) {\n return -1;\n } else if (A[i] != val) {\n ansTop++;\n } else if (B[i] != val) {\n ansBottom++;\n }\n }\n return Math.min(ansTop, ansBottom);\n }\n}\n``` | 1 | In a row of dominoes, `tops[i]` and `bottoms[i]` represent the top and bottom halves of the `ith` domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the `ith` domino, so that `tops[i]` and `bottoms[i]` swap values.
Return the minimum number of rotations so that all the values in `tops` are the same, or all the values in `bottoms` are the same.
If it cannot be done, return `-1`.
**Example 1:**
**Input:** tops = \[2,1,2,4,2,2\], bottoms = \[5,2,6,2,3,2\]
**Output:** 2
**Explanation:**
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
**Example 2:**
**Input:** tops = \[3,5,1,2,3\], bottoms = \[3,6,3,3,4\]
**Output:** -1
**Explanation:**
In this case, it is not possible to rotate the dominoes to make one row of values equal.
**Constraints:**
* `2 <= tops.length <= 2 * 104`
* `bottoms.length == tops.length`
* `1 <= tops[i], bottoms[i] <= 6` | null |
Solution | minimum-domino-rotations-for-equal-row | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {\n int flips = 0;\n\n const int num = tops.size();\n\n int top = tops[0];\n int bottom = bottoms[0];\n\n int symmetricals = (top == bottom) ? 1 : 0;\n\n for (int i = 1; i < num; i++) {\n int currTop = tops[i];\n int currBottom = bottoms[i];\n\n if (currTop == currBottom) {\n symmetricals++;\n }\n if (currTop == top || currBottom == bottom) {\n if (currTop != top) {\n top = -1;\n }\n else if (currBottom != bottom) {\n bottom = -1;\n }\n }\n else if (currTop == bottom && currBottom == top) {\n flips++;\n } else if (currBottom == top) {\n flips++;\n bottom = -1;\n } else if (currTop == bottom) {\n flips++;\n top = -1;\n }\n else {\n return -1;\n }\n }\n if (top == -1 && bottom == -1) {\n return -1;\n }\n if (flips * 2 > num - symmetricals) {\n flips = (num - flips) - symmetricals;\n }\n return flips;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:\n n = len(tops)\n ans = float("inf")\n if len(tops)!=len(bottoms):\n return -1\n def get_ans(num):\n ans = float("inf")\n \n ntop = 0\n nbottom = 0\n for t,b in zip(tops, bottoms):\n if t!=num and b!=num:\n return -1\n elif t!=num:\n ntop +=1\n elif b!=num:\n nbottom +=1\n return min(ntop, nbottom)\n \n ts = get_ans(tops[0]) \n if (ts == -1):\n return get_ans(bottoms[0])\n else:\n return ts\n```\n\n```Java []\nclass Solution {\n public int minDominoRotations(int[] A, int[] B) {\n int ans = -1; \n for (int val = 1; val <= 6; val++) {\n int currAns = helper(A, B, val);\n \n if (currAns != -1 && (ans == -1 || ans > currAns)) {\n ans = currAns;\n }\n }\n return ans;\n }\n private int helper(int[] A, int[] B, int val) {\n int ansTop = 0, ansBottom = 0;\n \n for (int i = 0; i < A.length; i++) {\n if (A[i] != val && B[i] != val) {\n return -1;\n } else if (A[i] != val) {\n ansTop++;\n } else if (B[i] != val) {\n ansBottom++;\n }\n }\n return Math.min(ansTop, ansBottom);\n }\n}\n``` | 1 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights `x` and `y` with `x <= y`. The result of this smash is:
* If `x == y`, both stones are destroyed, and
* If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
At the end of the game, there is **at most one** stone left.
Return _the smallest possible weight of the left stone_. If there are no stones left, return `0`.
**Example 1:**
**Input:** stones = \[2,7,4,1,8,1\]
**Output:** 1
**Explanation:**
We can combine 2 and 4 to get 2, so the array converts to \[2,7,1,8,1\] then,
we can combine 7 and 8 to get 1, so the array converts to \[2,1,1,1\] then,
we can combine 2 and 1 to get 1, so the array converts to \[1,1,1\] then,
we can combine 1 and 1 to get 0, so the array converts to \[1\], then that's the optimal value.
**Example 2:**
**Input:** stones = \[31,26,33,21,40\]
**Output:** 5
**Constraints:**
* `1 <= stones.length <= 30`
* `1 <= stones[i] <= 100` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.