text
stringlengths 59
500k
| subset
stringclasses 6
values |
|---|---|
Poverty, vulnerability, and the middle class in Latin America
Marco Stampini1,
Marcos Robles2,
Mayra Sáenz2,
Pablo Ibarrarán1 &
Nadin Medellín1
Between 2000 and 2013, Latin America has considerably reduced poverty (from 46.3 to 29.7 % of the population). In this paper, we use synthetic panels to show that, despite progress, the region remains characterized by substantial vulnerability that also affects the rising middle class. More specifically, we find that 65 % of those with daily income between $4 and 10, and 14 % of those in the middle class experience poverty at least once over a 10-year period. Furthermore, chronic poverty remains widespread (representing 91 and 50 % of extreme and moderate poverty, respectively). Differences between rural and urban areas are substantial. Urban areas, which are now home to most moderate poor and vulnerable, are characterized by higher income mobility, particularly upward mobility. These findings have important implications for the design of effective social safety nets. These need to mix long-term interventions for the chronic poor, especially in rural areas, with flexible short-term support to a large group of transient poor and vulnerable, particularly in urban areas.
In recent years, Latin America has made remarkable progress in the reduction of poverty and inequality. Between 2000 and 2013, the percentage of the population living on less than $2.5 per capita per day decreased from 28.8 to 15.9 %, while the share of the population living on less than $4 dropped from 46.3 to 29.7 %. Over the same period, the region has also managed to reduce its unfortunately distinctive inequality: the Gini coefficient of the income distribution fell from 0.57 to 0.51.
These improvements were largely driven by sustained economic growth, which led to an expansion of the middle class.Footnote 1 However, despite these positive trends, the region is still home to 92 million extreme poor and 77 million moderate poor. In addition, most of those that exited poverty joined the vulnerable class and are still at substantial risk of falling into poverty (Fig. 1).
Income distribution in Latin America (2000–2013), region aggregate
The trends in the incidence and depth of poverty, however, do not fully capture poverty dynamics, i.e., its duration and how often families enter and exit poverty. This information is very important for the design of effective social safety nets, particularly as far as targeting and recertification are concerned.Footnote 2 Frequent movements in and out of poverty imply the need for flexible safety net entry and exit rules.
The analysis of poverty dynamics and income mobility in developing countries has received relatively limited attention, largely due to the lack of adequate longitudinal data.Footnote 3 Recently, Ferreira et al. (2013) and Vakis et al. (2015) have analyzed intra-generational mobility in Latin America, with a focus, respectively, on the middle class and the chronic poor. Their analysis is based on the synthetic panel methodology developed by Dang et al. (2014), which is the same we employ in this paper. The two works construct two-period transition matrices [1995–2010 in Ferreira et al. (2013), 2004–2012 in Vakis et al. (2015)] and define the chronic poor as those that were poor in both years. The analysis only captures mobility from the first period to the last period, and not yearly mobility in between the two. Consequently, it depicts the vulnerable and the middle class as consolidated in their position (with a low probability of experiencing poverty).
In this paper, we generate 10-year synthetic panels for a large sample of Latin American countries, and use them to estimate yearly movements in and out of poverty from 2003 to 2013. We provide a novel classification of households based on poverty duration, which distinguishes chronic poor, transient poor, future poor, and never poor. The future poor include those that initially belonged to the vulnerable, middle, and high-income classes, and experienced poverty at any time over the following decade.
We find that 65 % of the vulnerable (i.e., those with daily income between $4 and 10), and 14 % of those in the middle class (with daily income between $10 and 50) of 2003, experienced poverty at least once during the period 2004–13. At the same time, chronic poverty remains widespread, accounting for 91 and 50 % of extreme and moderate poverty, respectively. Differences between rural and urban areas are substantial. Urban areas, which are now home to most moderate poor and vulnerable, are characterized by higher (particularly upward) income mobility.
The remainder of the paper is organized as follows. Section 2 defines poverty and vulnerability, and describes the data and the methodology employed for constructing synthetic panels and forecasting poverty dynamics. Section 3 presents the trends in poverty reduction and shows that the Latin American region is highly heterogeneous in the stage and speed of the socioeconomic transition towards the middle class. Section 4 analyzes poverty dynamics, including transition matrices and poverty duration, and discusses household characteristics of chronic and transient poor. Section 5 highlights the main differences between urban and rural poverty. Section 6 concludes summarizing key findings and policy implications. Along the paper, we discuss the policy implications of the findings for the design and implementation of the social safety nets, with a particular focus on the targeting and recertification processes.Footnote 4
Six annexes provide additional information on data, methods, sensitivity analyses, and country results. Annex 1 lists the data sources. Annex 2 summarizes the existing literature comparing results from genuine panel data with non-parametric, parametric, and point estimate synthetic-panel methods. Annex 3 shows the bounds of selected estimates, providing a visual representation of the quality of our results. Annex 4 presents sensitivity analyses of key chronic poverty results to the adoption of alternative poverty lines. Annex 5 shows that the variation in the share of urban population is limited between 2003 and 2013, which is necessary for the validity of the rural/urban breakdown of the dynamic analyses based on the pseudo panel methodology. Finally, Annex 6 presents country-specific poverty profiles.
Data and methodology
Non-technical readers can skip this section with no prejudice to their ability to understand the rest of the paper.
We look at poverty through two lenses, one that focuses on depth and the other on duration. The former is static, and analyzes a picture of poverty through the value of daily per-capita income (expressed in 2005 dollars adjusted to reflect purchasing power parity). It divides the population in five groups: (i) the extreme poor, with income below $2.5; (ii) the moderate poor, between $2.5 and 4; (iii) the vulnerable, between $4 and 10; (iv) the middle class, between $10 and 50 [as in López-Calva and Ortiz-Juárez (2011)]; and (v) the high-income class, above $50.
The $2.5 line corresponds to the median of the official extreme poverty lines in Latin American countries (CEDLAS and World Bank 2012), and has already been used in regional studies (World Bank 2014). It is higher than the international extreme poverty line of $1.25 used by Ravallion et al. (2008), which corresponds to the mean of the official extreme poverty lines of the 15 poorest countries in the world. The use of a higher line reflects the relatively more advanced stage of socioeconomic development (and the higher price levels) of the Latin American region. Similar considerations hold for the $4 poverty line. The vulnerable class is defined by López-Calva and Ortiz-Juárez (2011), as having a per capita daily income between $4 and 10, which is empirically observed to imply a probability greater than 10 % of falling into poverty.
The second lens is dynamic and focuses on the duration of poverty. It divides the population in four groups: (i) the chronic poor, that are poor (either extreme or moderate) in the first year of analysis, and in five or more years over the following decade;Footnote 5 (ii) the transient poor, that are poor in the first year, and again in four or less years over the following decade; (iii) the future poor, that are either vulnerable, middle class, or high income in the first year of analysis, but experience poverty in at least 1 year during the following 10 years; (iv) the never poor, who are always above the $4 poverty line.
Conditioning the definition of chronic and transient poverty on being poor in the first year guarantees that the sum of extreme and moderate poverty equals the sum of chronic and transient poverty. In other words, the incidence of poverty does not change, no matter if one looks at it through the lenses of depth or through those of duration.
The analysis focusing on the static definition of poverty is based on observed micro-data from 216 cross-sectional household surveys collected between 2000 and 2013 in 18 Latin American countries (see Annex 1).Footnote 6 These data are from IDB's Harmonized Data Bank of Household Surveys from Latin America and the Caribbean (also known as IDB's Sociometro). Regional estimates of the incidence of poverty are obtained by imputing missing values for years with no survey, then calculating population-weighted averages of country estimates.
The data are representative both at the national level and at the urban–rural level, with the exception of Argentina, Uruguay, and Venezuela. In Argentina, the household survey is only urban. In Uruguay, rural areas have been surveyed only since 2006; we restrict the analysis to urban areas to ensure comparability over the period 2000–2013. In Venezuela, since 2004, the survey does not contain a variable that allows separating rural and urban areas.
Given the unavailability of real-panel data sets, in which the same households are surveyed across time, the analysis of poverty duration is based on the construction of synthetic panels a la Dang et al. (2014).Footnote 7 This method was originally designed to analyze transitions in and out of poverty based on two (or more) rounds of cross-sectional data. In addition, the literature, so far, has focused on proving the reliability of the methodology (Cruces et al. 2011; Fields and Viollaz 2013; Haynes et al. 2013). Our objective is slightly different, as we aim to investigate poverty duration, or more specifically in how many years a family has been poor over a decade. For this purpose, we calculate yearly point estimates of per-capita income based on yearly cross-sectional data.Footnote 8
The sample is made of families surveyed in the first year (t = 0). For each of the following 10 years (s = 1,10), we estimate per-capita income using time-invariant variables observed in t = 0, coefficients estimated in t = s, and empirical residuals.Footnote 9 The methodology assumes a linear structure of the income equation, and is based on the following two assumptions: (i) households do not change, which ensures that time-invariant variables observed in t = 0 can be used to estimate income in t = s, and (ii) the correlation of the error terms across time (\(\varepsilon_{t = 0}\) and ɛ t=s ) is not negative. This is a reasonable assumption given that income shocks show persistence over time, and factors leading to a negative correlation of income over time are unlikely to apply to all households at the same time. The methodology requires estimating the following equations:
$$y_{i,t} = \beta^{\prime}_{t} x_{i,t} + \varepsilon_{i,t} \quad {\text{for }}t = 0,10$$
i.e., for the first period and for the following 10 years, where y i,t is the logarithm of household i's per-capita income at time t, and x i,t is a vector of variables measuring household i's characteristics at time t. Our specification of the model includes variables typically employed in the literature (Dang et al. 2014; Cruces et al. 2011), plus statistically significant variables at the regional level. The vector x contains the following variables:
Household head characteristics: sex, age, age squared, years of schooling, years of schooling squared, and agricultural work;
Region (first-level administrative country subdivision) characteristics: average years of schooling of the household heads, and proportion of workers in agriculture;
Geographic controls: rural–urban residence;
Retrospective regressors at regional level in the initial year (2003): inequality (standard deviation of log income), extreme poverty headcount ($2.5 a day), average per capita income, average household size, and average years of schooling of the household heads.
The regressions produce 11 estimates of vectors β and ε (\(\hat{\beta }_{t}\) and \(\hat{\varepsilon }_{t}\), one for each time period). They also produce 11 estimates of the error term variance (\(\hat{\sigma }_{{\varepsilon_{t} }}\)). These parameters are used to produce the synthetic-panel estimates of yearly per-capita income.
Following Cruces et al. (2011), Fields and Viollaz (2013), and Haynes et al. (2013), we use the "non-parametric" version of the method, i.e., we make no assumptions on the structural form of the joint distribution of the errors terms. Two extreme assumptions on the non-parametric time correlation of the error terms lead to a lower and upper bound estimate of per-capita income mobility. At one extreme, one can assume zero correlation between \(\varepsilon_{t = 0}\) and ɛ t=s , i.e., that the two error terms are independent from each other. The logarithm of per capita income of household i in t = s (\(\hat{y}_{i,t = s}^{U}\)) is estimated as follows:
$$\hat{y}_{i,t = s}^{U} = \hat{\beta }_{t = s}^{'} x_{i,t = 0} + \hat{\tilde{\varepsilon }}_{i,t = s}$$
where the apex U indicates uncorrelated error terms, and \(\hat{\tilde{\varepsilon }}_{i,t = s}\) is the mean of 50 random draws (with replacement) from the vector of estimated residuals in t = s. At the other extreme, one can assume perfect correlation between \(\varepsilon_{t = 0}\) and ɛ t=s . Under this assumption, the logarithm of per capita income of household i in t = s (\(\hat{y}_{i,t = s}^{C}\)) is estimated as follows:
$$\hat{y}_{i,t = s}^{C} = \hat{\beta }_{t = s}^{'} x_{i,t = 0} + \gamma \hat{\varepsilon }_{i,t = 0}$$
where the apex C indicates correlated error terms, \(\hat{\varepsilon }_{i,t = 0}\) is (the time-invariant) household i's empirical error term estimated in t = 0, and \(\gamma = \hat{\sigma }_{{\varepsilon_{t = 0} }} /\hat{\sigma }_{{\varepsilon_{t = s} }}\). is a scale factor.
Dang et al. (2014) and Cruces et al. (2011) show that: (i) Eq. (2) produces upper-bound estimates of income mobility, due to the high variation in the error term, and overestimates people's movements in and out of poverty; (ii) Eq. (3) produces lower-bound estimates of income mobility, due to the constant error term, and underestimates poverty transitions; and (iii) the average of (2) and (3) approximates well the observed income mobility, providing a satisfactory estimation of movements in and out of poverty. This last point is proved empirically by comparing synthetic-panel estimates of mobility with those observed in genuine panel data. We, therefore, calculate point estimates of per-capita income of the households in the synthetic-panel as follows:Footnote 10Recently, Dang and Lanjouw (2013) have developed a point estimate synthetic panel approach, which generalizes the use of non-parametric and parametric methods to produce point estimates of poverty transitions. This could have been used, as alternative to Eq. (4), to produce the estimates of poverty duration presented in this paper. We preferred to rely on Eq. (4), because the two methods have been shown to be empirically equivalent in terms of accuracy, and because Dang and Lanjouw (2013) indicate that the point-estimate methodology is most accurate when short time periods are analyzed. The existing literature comparing results from genuine panel data with non-parametric, parametric, and point estimate synthetic-panel methods is summarized in Annex 2.
$$\hat{y}_{i,t = s} = \hat{\beta }_{t = s}^{'} x_{i,t = 0} + \frac{{\left( {\hat{\tilde{\varepsilon }}_{i,t = s} + \gamma \hat{\varepsilon }_{i,t = 0} } \right)}}{2}.$$
As a result, our analysis of income mobility is based on income observed in 2003 along with income estimated for the years between 2004 and 2013. The quality of the predictions is essential to guarantee that results are credible. As is usual practice, we carefully ensured the quality of the fit (value of R-squared, significance of coefficients, over-fitting). In Annex 3, we show for selected countries that the upper and lower bounds of predicted incomes produce poverty rates that are very close to the rates directly observed from household surveys. We also show the bounds for the estimates of chronic poverty, transient poverty, and future poverty in selected countries.
Our methodology can only be applied to 12 countries that have household survey data for each year between 2003 and 2013 (Argentina, Brazil, Colombia, Costa Rica, Dominican Republic, Ecuador, Honduras, Panama, Paraguay, Peru, El Salvador, and Uruguay). Regional numbers were obtained pooling micro-data from the 12 countries and using survey weights.Footnote 11
Static analysis: an heterogeneous and still vulnerable region
Latin America is a very heterogeneous region in terms of the stage of socioeconomic transition, defined as the process of transition out of poverty towards the middle class. Countries such as Argentina, Chile, and Uruguay, are at an advanced stage, being mainly made of middle and high-income class (with the incidence of poverty around 10 %). On the other hand, countries such as Guatemala and Honduras, are at the earliest stages: almost half of their population still lives in extreme poverty, and the incidence of overall poverty exceeds 65 % (Table 1).
Table 1 Income distribution in Latin American countries (2000–2013).
One feature, however, is common to all countries: the large size of the vulnerable class. This represents in most cases 30–40 % of the population, suggesting that an important share of the population remains at substantial risk of falling into poverty. Countries with low poverty rates and large middle classes are no exception. In these countries, the vulnerable class is the back end of the socioeconomic transition; while in the poorest countries, the vulnerable class leads the way.
Country heterogeneity is also high in the speed of the socio-economic transition. For example, Colombia and Ecuador reduced the incidence of poverty by more than 25 percentage points (pp), and expanded their middle and upper classes by more than 15 pp (Table 1). In contrast, progress was sluggish in Mexico and Dominican Republic, despite the fact that these countries started from poverty headcounts around 40 %.
Table 2 summarizes the region's heterogeneity by classifying the Latin American countries based on the stage and speed of their socioeconomic transition. In the countries in the upper-left cell, for example, Nicaragua and El Salvador, the poor still represents the largest share of the population, and poverty reduction has been relatively slow (less than 25 % between 2000 and 2013). These are the countries with the highest need for reforming and/or expanding the social safety net, as poverty is widespread and resilient. These are also the countries with less financial resources for its implementation, so efficiency should be at the top of their policy agenda.
Table 2 Categorization of Latin American countries, by income distribution and poverty reduction (2000–2013).
Dynamic analysis: poverty is still largely chronic
Income mobility between 2003 and 2013 was considerable. Poverty reduction was the net effect of many exiting poverty, while fewer were falling back. Upward mobility was particularly high for those that started in moderate poverty.
Most of the moderate poor rose to the vulnerable class, and a few (6 %) made it to the middle class (Table 3).Footnote 12 In contrast, 73 % of those that were initially extreme poor were still poor after a decade, although many enjoyed less severe poverty and another quarter rose to the vulnerable class. As may be expected (as they started from higher initial living standards), also the vulnerable enjoyed less upper mobility. Only 28 % of them rose to the middle class, while 62 % remained in the initial income category and 10 % fell into poverty.
Table 3 Poverty transition matrix in Latin America (2003–2013), region aggregate.
Chronic poverty was widespread among both the extreme and the moderate poor. Many of those that were initially moderate poor, despite enjoying a high likelihood of rising to the vulnerable class in 2013, were poor in at least 5 years over the period 2004–2013. This may be explained by an ascending trajectory that only rose above the poverty line in the last part of the period of analysis.
On average, 91 % of extreme poverty were chronic (Table 4), with very little country heterogeneity (Fig. 2). In almost all countries with available data, about 90 % or more of the extreme poor in 2003 remained poor in at least five of the following 10 years. The only exceptions were Argentina and Uruguay, for which data are urban only.
Table 4 Poverty duration in Latin America (2003–2013), region aggregate.
Chronic poverty in Latin American countries (2003–2013)
More surprisingly, also half of the moderate poor in 2003 was chronically poor.Footnote 13 This has important implications for the design and implementation of the social safety nets. In particular, it implies that long-term interventions are not only needed for the extreme poor, but also for an important share of those in moderate poverty. In this respect, however, country heterogeneity was substantial (Fig. 2). For example, while extreme poverty was equally chronic in Ecuador and Colombia, in the former moderate poverty was much more transient than in the latter.
An important share of the vulnerable and, more surprisingly, of the middle class experienced poverty over the period 2004–13. More precisely, 65 % of the vulnerable group and 14 % of the middle class of 2003 were poor at least once over the following decade. We call these families "future poor", a group whose share ranged from 10 % of the population in Argentina to 38 % in Costa Rica (Fig. 3). Finally, the share of the population that was never poor ranged from 8 % in Honduras to 57 % in Uruguay (Fig. 3).
Poverty dynamics in Latin American countries (2003–2013)
The identification of the chronic and transient poor in the samples of 2003 allows investigating the household characteristics that are associated with different poverty durations. In other words, it allows studying who are the chronic poor, how they differ from the transient poor and, for comparison, from the non-poor. We address these questions by looking at Paraguay and Honduras, two countries at different stages of the socio-economic transition.
Household characteristics of the chronic poor broadly mimic those that, in the literature, are commonly associated with extreme poverty. They include larger household size, more children, lower levels of education, more engagement in self-employment, less wage employment, and residence in rural areas. Table 5 reports average household characteristics by dynamic poverty status in Paraguay and Honduras. Despite a few differences between the two countries, most patterns are common and the similarities are striking. In both countries, for example, chronically poor households had no member with complete tertiary education. In Honduras, they did not even have any member with complete secondary education; while in Paraguay, only one in six chronically poor households had one member with this level of schooling. Their likelihood to live in rural areas was ten times higher than among the non-poor. Self-employment decreased and wage employment grew as one moved from chronic poverty to non-poverty. The low level of human capital and the remote location suggest that, at least among the chronic poor, the graduation strategies with which many Latin American countries are attempting to complement the social safety nets have low probability of being successful.
Table 5 Household Characteristics in Paraguay and Honduras (2003), by Poverty Status.
Differences between urban and rural areas
The region has undergone a process of urbanization, which has been slowing down in recent years. The urban share of the population has been growing from 49 % in 1960 to 80 % in 2013, and is expected to reach 83 % in 2025 (ECLAC 2013). In our sample of countries, this figure has increased from 72 % in 2000 to 74 % in 2013 (Table 6, panel B). In this context, it is extremely important to understand the different urban–rural trends in poverty reduction, as when it comes to poverty, cities and countryside remain two worlds apart.Footnote 14
Table 6 Geographic profile of poverty in Latin America (2000–2013), region aggregate.
Extreme and overall poverty have decreased substantially in both urban and rural areas. Yet, in the latter, one-third of the population still lives in extreme poverty, and the incidence of total poverty exceeds 50 % (Table 6, panel A).
The growth of a middle class is an eminently urban phenomenon. In rural areas, poverty reduction has been accompanied by an expansion of the vulnerable class, and only 13 % of the population had per-capita income above $10 in 2013. In contrast, the size of the vulnerable class remained fairly constant in urban areas. This is where the middle class expanded more rapidly (by over 10 pp).
As a result, the rural nature of poverty has intensified, with a substantial increase of the share of poor living in rural areas. While in 2000 the rural areas were home to 54 % of the extreme poor and 30 % of the moderate poor, these figures increased to 58 and 38 %, respectively, in 2013. In addition, the rural share of vulnerable expanded, and only the high-income class became more urban during the period of analysis.
In 2013, the majority of the extreme poor lived in urban areas only in four countries (Brazil, Chile, Colombia and Dominican Republic). In contrast, with few exceptions, moderate poverty was fairly equally distributed between urban and rural areas (Fig. 4). This suggests that long-term social safety net programs are best suited for rural areas, while short-term interventions are equally needed in urban and rural areas.
Rural percentage of poverty and population in Latin American countries (2013)
In the near future, in urban areas, poverty is expected to leave way to a rising middle class (Fig. 5). This forecast is obtained by combining economic growth and demographic projections with the estimated growth elasticity of poverty. While the size of the vulnerable class will remain fairly stable (at around 40 % of the urban population), by 2025 the incidence of urban poverty is expected to fall to 13 %. The middle class will rise to represent 42 % of the urban population.
Poverty, vulnerability, and middle class in Latin America (2000–2025), region aggregate
In contrast, the growth of the middle class will be slow in rural areas. Poverty will be mostly replaced by vulnerability. The vulnerable class is expected to become the single largest group in 2021, and grow to 47 % of the rural population in 2025.
Failing to account for substantial rural to urban migration may bias the results of the poverty dynamic analysis based on the pseudo-panel methodology (which assumes that household characteristics, including residence in rural or urban areas, are constant over time). For example, one may overestimate the number of poverty episodes in rural areas, if some rural families have migrated to urban areas and have managed, through migration, to transition to the vulnerable class. The direction of the bias will depend on who migrates (usually not the poorest) and how migration affects their income.
In Annex 5, we analyze the variation in the proportion of urban population over the period 2003–2013. We show that its magnitude is small, and does not threaten the validity of our findings. This result is consistent with the slowdown in the process of urbanization documented in CELADE—Population Division of ECLAC (2015).
The urban and rural poverty dynamics analyses confirm that most of the mobility out of poverty took place in urban areas. In the cities, 35 % of the extreme poor and 73 % of the moderate poor in 2003 had exited poverty after 10 years, against only 15 and 53 % in rural areas (Table 7). A similar pattern can be observed for upward mobility from the vulnerable class. Symmetrically, the risk of falling from the middle class to the vulnerable class or into poverty was more than double in rural than in urban areas (44 versus 21 %). This may also be due to the differential urban–rural impacts of the world recession in the second part of the period of analysis.
Table 7 Urban and rural poverty transition matrices in Latin America (2003–2013), region aggregate.
Rural areas are characterized by high incidence of chronic poverty and future poverty. 99 % of the extreme poor and 78 % of those that were moderate poor in 2003 experienced chronic poverty between 2004 and 2013. Furthermore, 86 % of the vulnerable and 37 % of the middle class were poor at least once during the period of analysis. The picture is relatively rosier in urban areas, where "only" 86 % of extreme poverty and 42 % of moderate poverty were chronic, and where "only" 62 % of the vulnerable experienced at least one episode of poverty (Fig. 6).
Urban and rural poverty dynamics in Latin America (2003–2013), region aggregate
Cross-country analysis shows that Ecuador and Panama present the widest gap between rural and urban areas, a result that is driven by the highly transient nature of urban moderate poverty. Variability is limited in the percentage of extreme poor that are chronic poor, both in rural and urban areas. More differences emerge when looking at the percentage of moderate poor that experience chronic poverty. This is, particularly, the case in urban areas. While in El Salvador 71 % of urban moderate poor experience chronic poverty over the following decade, the same happens to only one every five urban moderate poor in Ecuador and Panama. This indicates that in these countries, urban moderate poverty is particularly transient (Fig. 7). Complete data by country is presented in Annex 6, for the 12 countries for which we can construct synthetic panels.
Urban and rural chronic poverty in Latin American countries (2003–2013)
Conclusions and implication for the design and implementation of social safety nets
In the absence of information on poverty dynamics, development practitioners frequently assume that extreme poverty is chronic and rural, while moderate poverty is transient and urban. Similarly, they tend to expect that the vulnerable are at risk of falling into poverty, while the middle class has reached a safe place and no longer needs a social safety net.
In this paper, we construct synthetic panels and analyze poverty dynamics for a large sample of Latin American countries, with the aim to provide policy makers and development practitioners (engaged in project design) with estimates of the duration of poverty. While the availability of real long panel data would allow refining and deepening the analysis, we believe that our results constitute a useful proxy and hope they will stimulate further data collection and research. Our analysis contributes to debunking a few common assumptions.
First, we show that chronic poverty is widespread also among the moderate poor. This type of poverty, characterized by long duration, accounts for 91 % of extreme poverty and, surprisingly, 50 % of moderate poverty. As expected, chronic poverty is more frequent in rural areas, where 99 % of the extreme poor and as many as 78 % of the moderate poor are chronic poor.
Second, we show that also the middle class is still exposed to a substantial risk of falling back into poverty. More specifically, we find that 14 % of those that belonged to the middle class in 2003 experienced at least one poverty episode during the following decade.
Our results differ from those of Ferreira et al. (2013) and Vakis et al. (2015), although they are based on the application of a similar synthetic panel methodology. These authors analyze mobility between two periods only, and find that the vulnerable and the middle class are more consolidated in their status. For example, Ferreira et al. (2013, Table 4.1) estimate that only 2.7 % of the vulnerable and 0.5 % of the middle class fall back into poverty.
Our findings have important implications for the design and implementation of social safety nets. First, they suggest that interventions that target the rural poor and the urban extreme poor need to adopt a long-term perspective. The frequent recertification of the beneficiaries might not be needed and, probably, represents a loss of administrative and financial resources.
Second, our findings suggest that interventions that target the urban moderate poor need to adopt flexible entry and exit rules in response to this group's high income mobility. Targeting mechanisms based on proxy means tests are unlikely to perform satisfactorily. The Brazilian model based on declared income may represent a better alternative, if it can be coupled with frequent recertification and electronic audits of eligibility based on crossing information from the roster of beneficiaries with other sources of administrative data (e.g., social security contributions, ownership of assets).
Third, we show that the chronic poor have extremely low levels of human capital and live in rural areas with limited opportunity of wage employment. These are key factors for escaping poverty. Consequently, our findings suggest that, at least for this group, graduation strategies aimed at increasing income-generation capacity have low probabilities of success.Footnote 15
Finally, the finding that both the vulnerable and the middle class are likely to experience poverty in the future implies that the social safety nets remain relevant for many that are currently out of poverty.Footnote 16
A caveat is worth mentioning. Our dynamic analysis is based on 12 countries for which data are available. Further work is needed to incorporate results for more countries and increase the representativeness of our findings.
For an analysis of the key drivers of poverty reduction in Peru, see Robles and Robles (2014).
Targeting is the process of identification of poor and vulnerable beneficiaries, as opposed to universal entitlement to benefits. Recertification is the periodic verification of beneficiaries' living standards, to assess whether they still qualify for receiving the benefits.
See Jalan and Ravallion (1998), Baulch and Hoddinott (2000), Davis and Stampini (2002), Hulme and Shepherd (2003), Dercon and Shapiro (2007), Fields et al. (2007), Stampini and Davis (2009), Ferreira et al. (2013), Vakis et al. (2015). What is missing in this literature is the analysis of poverty or income dynamics with long panels made of consecutive years. Robles and Saenz (2015) have started to fill this gap; using synthetic panels (similar to those employed in this paper) and a discrete-time hazard model, they identify the factors associated with long-term poverty and exit from poverty in a sample of Latin American countries.
We refer to social safety nets as the systems of social protection for the poor and vulnerable. In the Inter-American Development Bank Strategic Framework Document on Social Protection and Poverty, this is defined as "(i) efficient redistributive programs that contribute to human capital development; and (ii) delivery of services for social inclusion, in particular those aimed at early childhood development and at-risk youth" (IDB 2014). The findings of this paper are particularly relevant for the design and implementation of redistributive programs, such as conditional cash transfers (CCTs), whose duration and level of benefits should depend on poverty duration and depth.
The 5-year threshold, like any alternative threshold, is somehow arbitrary. However, the results presented in this paper are generally robust to the adoption of alternative values.
These are the 18 countries that regularly execute household surveys and share their databases with the IDB. We lament not being able to include Caribbean countries, for which such data is not available.
Other synthetic or pseudo-panel approaches are those that track cohorts of individuals or households over repeated cross-sectional surveys (Deaton 1985), and those that recover the stochastic process from cross sectional data and generate individual income dynamics (Bourguignon et al. 2004).
We follow Canavire and Robles (2013), who, using this kind of panels and non-parametric duration models, analyze the sequencing and duration of the episodes of poverty.
Dang et al. (2014) and Cruces et al. (2011) show that the method performs well irrespective of the forecasting direction, i.e. that estimates of mobility are very similar if one predicts per-capita income in each year based on the sample of families that are surveyed in the last year.
Dang et al. (2014) suggest that standard errors for the bounds can be estimated by bootstrapping. This involves bootstrap resampling from the original cross-sections while accounting for survey weights (footnote 14). Similarly, we could obtain standard errors for our point estimates by complementing Dang et al.'s suggested procedure with the application of the delta method.
Brazil does not have a household survey for 2010. In order to include it in the dynamic analysis, we considered mobility over the period 2002–2013. It is important to highlight the caveat that our dynamic analysis is based on twelve countries with available data. Among the excluded countries is Mexico, which accounts for an important share of the population of the region. The exclusion of Mexico is due to the fact that the Encuesta Nacional sobre Ingresos y Gastos de los Hogares is carried out every two years, while the Encuesta Nacional de Ocupación y Empleo is yearly but has been nationally representative only since 2005.
Table 3 presents the two-point transition matrix, similar to Table 4.1 of Ferreira et al. (2013) and Table 1 of Vakis et al. (2015), using a larger number of income groups and extending the time period to 2013.
In Annex 4, we perform sensitivity analysis and show that these key results are robust to the adoption of alternative poverty lines.
It is relevant to acknowledge that the term urban refers to very different sizes of human settlements (Satterthwaite 2010), that may range from as few as 2500 to as many as several million inhabitants. Despite this heterogeneity, in this paper we use the terms urban areas and cities as synonims.
For a review of the experience with recertification and graduation in Latin American conditional cash transfer programs, see Medellín et al. (2015).
For an estimate of the demand for social safety nets in Latin American countries, see Ibarraran et al. (2016).
Given our definition of the income variables, our poverty estimates may differ from the official ones and from those calculated by other institutions that use the same household surveys.
Baulch B, Hoddinott J (eds) (2000) Economic mobility and poverty dynamics in developing countries. Frank Cass, London
Bourguignon F, Goh, C, Kim D (2004) Estimating Individual Vulnerability to Poverty with Pseudo-Panel Data. World Bank Policy Research Working Paper No. 3375
CELADE—Population Division of ECLAC (2015). Latin America: Long term population estimates and projections 1950–2100. The 2015 Revision. http://www.cepal.org/es/estimaciones-proyecciones-poblacion-largo-plazo-1950-2100
Canavire G, Robles M (2013) Non-parametric analysis of poverty duration using repeated cross-section data. An application for Peru. The Inter-American Development Bank, Mimeo
Center for Distributional, Labor and Social Studies (CEDLAS) and World Bank. 2012. A guide to the SEDLAC: Socioeconomic Database for Latin America and the Caribbean. La Plata. http://sedlac.econo.unlp.edu.ar/eng/methodology.php
Cohen J (1988) Statistical power analysis for the behavioral sciences, 2nd edn. Lawrence Erlbaum, Hillsdale
Cruces G, Lanjouw P, Lucchetti L, Perova E, Vakis R, Viollaz M (2011) Intra-generational mobility and repeated cross-sections. A three-country validation exercise. World Bank Policy Research Working Paper No. 5916
Dang H, Lanjouw P, Luoto J, McKenzie D (2014) Using repeated cross-sections to explore movements into and out of poverty. J Dev Econ 107:112–128
Dang HA, Lanjouw P (2013) Measuring poverty dynamics with synthetic panels based on cross-sections. World Bank Policy Research Working Paper No. 6504
Davis B, Stampini M (2002) Pathways towards prosperity in Nicaragua: an analysis of panel households in the 1998 and 2001 LSMS Surveys. United Nations Food and Agriculture Organization, ESA Working Paper 02-10
Deaton A (1985) Panel data from time series of cross-sections. J Econom 30:109–216
Dercon S, Shapiro JS (2007) Moving on, staying behind, getting lost: lessons on poverty mobility from longitudinal data. In: Narayan D, Petesch P (eds) Moving out of poverty. World Bank
Ferreira FHG, Messina J, Rigolini J, López-Calva LF, Lugo MA, Vakis R (2013) Economic mobility and the rise of the latin american middle class. World Bank, Washington, DC
Fields G, Viollaz M (2013) Can the limitations of panel datasets be overcome by using pseudo-panels to estimate income mobility? http://www.iza.org/conference_files/worldb2013/fields_g370.pdf
Fields G, Duval-Hernandez R, Freije-Rodriguez S, Sanchez-Puerta ML (2007) Intergenerational income mobility in Latin America. Journal of LACEA. Latin American and Caribbean Economic Association
Haynes M, Martinez A, Tomaszewski W, Western M (2013) Measuring income mobility using pseudo-panel data. Philipp Stat 62(2):71–99
Hulme D, Shepherd A (2003) Conceptualizing chronic poverty. World Dev 3(3):403–423
Ibarraran P, Medellín N, Perez B, Jara P, Parsons J, Stampini M (2016) Más inclusión social: lecciones de Europa y perspectivas para América Latina. Monograph n. 359. Inter-American Development Bank, Washington DC. https://publications.iadb.org/handle/11319/7486
Inter-American Development Bank. 2014. Strategic Framework Document on Social Protection and Health. http://www.iadb.org/document.cfm?id=39211762
Jalan J, Ravallion M (1998) Transient poverty in postreform rural China. J Comp Econ 26:338–357
López-Calva LF, Ortiz-Juarez E (2011) A vulnerability approach to the definition of the middle class. Policy Research Working Paper Series 5902, The World Bank. Later published as López-Calva, L.F. and Ortiz-Juarez, E. 2014. A vulnerability approach to the definition of the middle class. J Econ Inequal 12(1):23–47
Medellín N, Villa Lora JM, Ibarraran P, Stampini M (2015) Moving ahead: recertification and exit strategies in conditional cash transfer programs. Monograph n. 348. Inter-American Development Bank, Washington DC. http://publications.iadb.org/handle/11319/7359
Ravallion M, Chen S, Sangraula P (2008) Dollar a day revisited. World Bank Policy Research Working Paper No. 4620
Robles A, Robles M (2014) Workforce heterogeneity and decomposing welfare changes. The Inter-American Development Bank, Mimeo
Robles M, Saenz M (2015) The dynamics of poverty spells in Latin America. Mimeo, The Inter-American Development Bank
Satterthwaite D (2010) Urban myths and the mis-use of data that underpin them. In: Beall J, Guha-khasnobis B, Kanbur R (eds) Urbanization and development: multidisciplinary perspectives. Oxford Scholarship Online. doi:10.1093/acprof
Stampini M, Davis B (2009) Discerning transient from chronic poverty in Nicaragua: measurement with a two-period panel data set. Eur J Dev Res 18(1):105–130
The United Nations Economic Commission for Latin America and the Caribbean (ECLAC). 2013. Long term population estimates and projections 1950–2100. 2013 Revision. CELADE-Population Division of ECLAC. http://www.cepal.org/celade/proyecciones/basedatos_BD.htm
Vakis R, Rigolini J, Lucchetti L (2015) Left behind: chronic poverty in Latin America and the Caribbean, overview. World Bank, Washington, DC
World Bank (2014) Social gains in the balance: a fiscal policy challenge for Latin America and the Caribbean. Washington DC
This report has been prepared with funds from the IDB economic and sector work "Social Protection beyond Conditional Cash Transfers: Challenges and Alternatives" (RG-K1374). We thank Ferdinando Regalia, Norbert Schady, Susan Parker, and two anonymous referees for useful comments and suggestions. Remaining errors are ours only. The content and findings of this paper reflect the opinions of the authors and not those of the IDB, its Board of Directors or the countries they represent.
Social Protection and Health Division of the Inter-American Development Bank (IDB), Washington, DC, USA
Marco Stampini
, Pablo Ibarrarán
& Nadin Medellín
Front Office of the Social Sector of the IDB, Washington, DC, USA
Marcos Robles
& Mayra Sáenz
Search for Marco Stampini in:
Search for Marcos Robles in:
Search for Mayra Sáenz in:
Search for Pablo Ibarrarán in:
Search for Nadin Medellín in:
Correspondence to Marco Stampini.
Annex 1: Data sources
IDB's Harmonized Data Bank of Household Surveys from Latin America and the Caribbean (also known as IDB's Sociometro) contains harmonized household data sets for Latin American and Caribbean countries starting from the late 1980s. Variable names, definitions, and contents are kept constant across countries and time. Table 8 shows the number of data sets used for the preparation of this paper.
Table 8 Data sets used in this paper, by Country, 2000–2013
Although it is well known that per-capita consumption is a better proxy for well-being, we use per-capita income, because few countries in the region routinely conduct surveys with a consumption module, while all of them include questions on income. We calculate per-capita income by dividing total household income by the number of household members, without using any adult equivalence scale.
Income components are reported after-tax whenever possible. Extraordinary income sources are not considered. Similarly, we do not include the implicit rent from owned or occupied housing, because not all countries capture the information that allows estimating it.Footnote 17 As is common practice in academic and official studies, we do not make any imputation for missing, null or outlying values in addition to those already contained in the data sets provided by the national statistical offices. Finally, we do not make adjustments for differences in urban–rural prices.
Annex 2: Synthetic-panel methodology
Table 9 summarizes the existing literature comparing results from genuine panel data with non-parametric, parametric, and point estimate synthetic-panel methods. All results reported are based on the use of household time-invariant characteristics, sub-national controls, and region fixed effects, consistently with the definition of our own model. They show that the estimates based on the average of the bounds (Eq. (4)) approximate well the estimates based on genuine panel data, irrespective of the length of the period analyzed (2 years in Peru, versus 10 in Chile), the width of the bounds, the type of poverty transition, and the number of replications used to obtain the upper bound (50, 100, 500). These estimates are found to be as accurate as those obtained with either the parametric approach (for Indonesia and Vietnam) or the point estimate approach (Bosnia-Herzegovina).
Table 9 Summary of the literature comparing estimates from synthetic and genuine panel data
Annex 3: Estimate bounds
See Figs. 8, 9, 10.
Observed versus predicted extreme poverty headcounts in selected countries
Observed versus predicted poverty headcounts in selected countries
Bounds for the estimates of transient poverty, chronic poverty and future poverty in selected LAC countries
Annex 4: Sensitivity analysis of the percentage of chronic poverty to the adoption of alternative poverty lines
Poverty lines are defined with a degree of arbitrariness. To show that our findings are robust to the adoption of alternative poverty lines, we perform sensitivity analysis of our key chronic poverty results. In Sect. 4, we showed that chronic poverty accounted for 91 % of extreme poverty and 50 % of moderate poverty. This occurs when using a 2.5$ extreme poverty line and a 4$ moderate poverty line. In Figs. 11 and 12, we verify how these findings change when considering poverty lines that are 20 % lower or higher.
Percentage of extreme poor that are chronic poor, sensitivity analysis to the adoption of alternative poverty lines
Percentage of moderate poor that are chronic poor, sensitivity analysis to the adoption of alternative poverty lines
With lower poverty lines, i.e., using a 2$ extreme poverty line and a 3.2$ moderate poverty line, we find that chronic poverty accounted for 87 % of extreme poverty and 41 % of moderate poverty. With higher poverty lines, i.e., using a 3$ extreme poverty line and a 4.8$ moderate poverty line, chronic poverty accounted for 94 % of extreme poverty and 58 % of moderate poverty.
Overall, the higher the poverty lines, the higher are the percentages of both extreme and moderate poverty that are found to be chronic. The result is less sensitive for extreme than for moderate poverty. Finally, different poverty lines do not alter the order of magnitude of our key results, nor country rankings.
Annex 5: Variation in the percentage of urban population
As a proxy for rural to urban migration, we test whether the percentage of urban population has changed significantly over the period 2003–2013, which is the timeframe of our poverty dynamics analysis. Given the large size of our samples, the standard error of each sample mean tends to be very close to zero. As a consequence, the t test is likely to reject the null hypothesis of means equality even when the difference is trivial (producing type I–false positive–errors).
We, therefore, adopt an alternative hypothesis testing framework by conducting an effect size type analysis, in which the measure of statistical difference is the standard deviation (which is not shrunk by definition by the size of the sample). Specifically, we use the Cohen's d indicator (Cohen 1988), which is equal to the difference between the two sample means, divided by the standard deviation of the pooled samples. Cohen explains that absolute values of d around 0.2 reflect a small effect size, while 0.5 is a medium effect size and 0.8 indicates a large effect size. The last column of Table 10 shows that the absolute values of Cohen's d are all smaller than 0.2 in our sample of countries, suggesting that rural-to-urban migration is not likely to threaten the validity of our poverty dynamic results.
Table 10 Effect size analysis of the variation in the percentage of urban population.
Annex 6: Country profiles
Country profiles—Argentina.
Extreme poverty
Moderate poverty
Vulnerable class
High income
Incidence in 2000—total – – – – – –
Urban 14.9 15.4 36.5 31.3 2.0 100.0
Rural – – – – – –
Urban 4.0 6.9 34.4 52.5 2.2 100.0
Share rural in 2000 – – – – – –
Transition probabilities—total
Extreme poverty – – – – – –
Moderate poverty – – – – – –
Vulnerable class – – – – – –
Middle class – – – – – –
High income – – – – – –
Transition probabilities—urban
Extreme poverty 5.9 20.5 63.7 7.3 2.7 100.0
Moderate poverty 0.5 2.0 65.2 31.2 1.2 100.0
Vulnerable class 0.1 0.6 27.2 71.1 1.0 100.0
Middle class 0.0 0.1 2.6 90.7 6.7 100.0
High income 0.0 0.0 0.0 33.3 66.7 100.0
Transition probabilities—rural
% of chronic poverty—total – – –
Urban 45.7 1.2 27.7
Rural – – –
% future poor—total – – – –
Urban 25.6 2.5 0.0 16.3
Rural – – – –
– Not available
Chronic poor
Transient poor
Future poor
Never poor
% of population 11.1 29.0 9.8 50.1 100.0
Male household head 0.476 0.483 0.507 0.476 0.481
Household size 6.222 5.294 4.389 3.577 4.448
Number of children (aged 0–5) 1.096 0.709 0.524 0.284 0.521
Adult members
Self-employed 0.348 0.342 0.349 0.309 0.327
Salaried 1.060 1.147 1.372 1.233 1.202
Unemployed 0.538 0.388 0.205 0.178 0.282
Inactive 0.851 0.980 0.854 0.825 0.876
Primary education or less 0.527 0.355 0.321 0.144 0.265
Incomplete secondary educ. 0.759 0.725 0.632 0.386 0.550
Complete secondary educ. 0.298 0.495 0.537 0.582 0.521
Incomplete tertiary educ. 0.136 0.250 0.263 0.514 0.371
Complete tertiary educ. 0.025 0.122 0.113 0.512 0.306
Rural (share) – – – – –
Country Profiles—Brazil.
Incidence in 2001—total 27.1 16.8 32.5 21.3 2.3 100.0
Rural 54.3 18.3 21.9 5.3 0.3 100.0
Rural 26.5 17.5 37.6 17.8 0.6 100.0
Share rural in 2001 32.4 17.6 10.9 4.0 2.1 16.2
Extreme poverty 36.2 37.0 26.0 0.7 0.0 100.0
Moderate poverty 5.9 23.7 65.9 4.5 0.0 100.0
Middle class 0.1 0.8 22.1 75.6 1.4 100.0
% of chronic poverty—total 94.6 51.3 77.8
Urban 92.8 48.2 73.4
Rural 98.4 65.6 89.8
% future poor—total 65.2 11.5 0.3 42.1
Urban 63.5 11.0 0.3 40.0
Rural 79.1 23.0 0.0 67.5
% of population 27.5 10.0 25.0 37.5 100.0
Rural (share) 0.310 0.123 0.125 0.044 0.145
Country Profiles—Colombia. Source: authors' calculations based on household survey data from IDB's Sociometro
Moderate poverty 12.6 29.9 53.4 3.3 0.8 100.0
Vulnerable class 3.5 12.6 59.1 23.7 1.0 100.0
Extreme poverty 67.6 21.6 9.2 0.1 1.5 100.0
Vulnerable class 9.6 27.1 56.6 6.4 0.2 100.0
High income 0.0 0.0 0.0 3.9 96.1 100.0
Country Profiles—Costa Rica.
Urban 8.7 11.6 40.0 37.9 1.9 100.0
Incidence in 2013—total 8.5 10.6 37.7 39.2 4.0 100.0
Share rural in 2000 66.5 54.0 42.1 21.0 11.8 41.3
Moderate poverty 26.8 19.2 40.9 11.9 1.3 100.0
Vulnerable class 10.0 13.8 42.2 33.1 0.8 100.0
% of population 21.6 7.4 37.7 33.3 100.0
Country Profiles—Dominican Republic.
Share rural in 2013 45.1 39.0 29.9 15.8 1.4 32.6
Extreme poverty 57.6 31.9 10.4 0.1 100.0
Moderate poverty 21.5 40.7 37.2 0.6 100.0
Vulnerable class 4.3 22.5 67.6 5.6 100.0
Middle class 0.0 2.0 55.2 42.7 100.0
High income 0.0 0.0 56.3 43.7 100.0
Country Profiles—Ecuador.
Country Profiles—Honduras.
Incidence in 2013—total 49.5 17.0 24.9 8.5 0.2 100.0
Extreme poverty 89.0 8.0 2.6 0.0 0.4 100.0
Vulnerable class 21.1 25.7 48.2 4.6 0.4 100.0
Middle class 9.5 23.4 52.6 14.5 0.0 100.0
% of population 64.3 4.1 23.6 8.0 100.0
Country Profiles—Panama.
Moderate poverty 2.2 13.3 72.6 11.9 0.0 100.0
Country Profiles—Peru.
High income 0.0 0.0 20.1 70.5 9.4 100.0
Country Profiles—Paraguay.
% future poor—total 84.3 40.6 13.8 67.6
Rural 97.8 80.1 26.0 91.3
Country Profiles—El Salvador.
High income 0.0 0.9 3.3 90.7 5.0 100.0
Country Profiles—Uruguay.
% of chronic poverty—total –
Urban 31.4 2.3 – 19.2
% of population 7.3 21.7 13.6 57.3 100.0
Stampini, M., Robles, M., Sáenz, M. et al. Poverty, vulnerability, and the middle class in Latin America. Lat Am Econ Rev 25, 4 (2016) doi:10.1007/s40503-016-0034-1
Poverty dynamics
Transitory and chronic poverty
Panel data
Synthetic panels | CommonCrawl |
\begin{definition}[Definition:Integral Element of Algebra/Definition 4]
Let $A$ be a commutative ring with unity.
Let $f : A \to B$ be a commutative $A$-algebra.
Let $b\in B$.
The element $b$ is '''integral''' over $A$ {{iff}} there exists a faithful $A \sqbrk b$-module whose restriction of scalars to $A$ is finitely generated.
\end{definition} | ProofWiki |
\begin{document}
\title{A non-overlapping domain decomposition method for incompressible Stokes equations with continuous pressure} \pagestyle{myheadings} \thispagestyle{plain} \markboth{JING LI AND XUEMIN TU}{DOMAIN DECOMPOSITION FOR INCOMPRESSIBLE STOKES}
\begin{abstract} A non-overlapping domain decomposition algorithm is proposed to solve the linear system arising from mixed finite element approximation of incompressible Stokes equations. A continuous finite element space for the pressure is used. In the proposed algorithm, Lagrange multipliers are used to enforce continuity of the velocity component across the subdomain domain boundary. The continuity of the pressure component is enforced in the primal form, i.e., neighboring subdomains share the same pressure degrees of freedom on the subdomain interface and no Lagrange multipliers are needed. After eliminating all velocity variables and the independent subdomain interior parts of the pressures, a symmetric positive semi-definite linear system for the subdomain boundary pressures and the Lagrange multipliers is formed and solved by a preconditioned conjugate gradient method. A lumped preconditioner is studied and the condition number bound of the preconditioned operator is proved to be independent of the number of subdomains for fixed subdomain problem size. Numerical experiments demonstrate the convergence rate of the proposed algorithm. \end{abstract}
{\bf keywords} domain decomposition, incompressible Stokes, FETI-DP, BDDC
{\bf AMS} 65F10, 65N30, 65N55
\section{Introduction}
Domain decomposition methods have been studied well for solving incompressible Stokes equations and similar saddle-point problems; see, e.g., \cite{Kla98, 8pavwid, li05, paulo2003, Doh04, li06, kim06, Tu:2005:BPP, Tu:2005:BPD, LucaOlofStef}. In many of those work, special care need be taken to deal with the divergence-free constraints across subdomain boundaries, which often lead to large coarse level problems. The large coarse level problem will be a bottleneck in large scale parallel computations, and additional efforts in the algorithm are needed to reduce its impact, cf.~\cite{Tu:2004:TLB,Tu:2005:TLB,Tudd16,Klawonn:2005:IFM,Dohrmann:2005:ABP,KimTu,Tu:2011:TLBS}. Some recent progress has been made by Dohrmann and Widlund~\cite{Doh09, Doh10} for the almost incompressible elasticity, where the coarse level space is built from discrete subdomain saddle-point harmonic extensions of certain subdomain interface cut-off functions and its dimension is much smaller than those in the previous studies. Kim and Lee~\cite[with Park]{kim11, kim102, kim10} studied both the FETI-DP and BDDC algorithms for incompressible Stokes equations where a lumped preconditioner is used and reduction in the dimension of the coarse level space is also achieved.
In most above mentioned applications and analysis of domain decomposition methods for incompressible Stokes equations, the mixed finite element space contains discontinuous pressures. Application of discontinuous pressures in domain decomposition methods is natural. The decomposing of the pressure components to independent subdomains can be handled conveniently and no continuity of pressures across the subdomain boundary need be enforced. However, a big class of mixed finite elements used for solving incompressible Stokes and Navier-Stokes equations have continuous pressures, e.g., the well known Taylor-Hood type~\cite{Taylor}. There have been a variety of approaches using continuous pressures in domain decomposition methods for solving incompressible Stokes equations, e.g., by Goldfeld \cite{pauloPhD}, by \v{S}\'istek {\em et. al.} \cite{sis11}, and by Benhassine and Bendali \cite{ben10}. In their work, an indefinite system of linear equations need be solved, either by a generalized minimal residual method or simply by a conjugate gradient method. To the best of our knowledge, no scalable convergence rate has been proved analytically for any of those approaches using continuous pressures.
In this paper, we propose a non-overlapping domain decomposition algorithm for solving incompressible Stokes equations with continuous pressure finite element space. The scalability of its convergence rate is proved. In this algorithm, the subdomain boundary velocities are dealt with in the same way as in the FETI-DP method: a few for each subdomain are selected as the coarse level primal variables, which are shared by neighboring subdomains; the others are subdomain independent and Lagrange multipliers are used to enforce their continuity. The subdomain boundary pressure degrees of freedom are all in the primal form. They are shared by neighboring subdomains and no Lagrange multipliers are needed for their continuity. After eliminating all velocity variables and the independent subdomain interior parts of the pressures, the system for the subdomain boundary pressures and the Lagrange multipliers is shown to be symmetric positive semi-definite. A preconditioned conjugate gradient method with a lumped preconditioner is studied. As strong condition number bounds as for the scalar elliptic case are established. In the proposed algorithm and in the estimate of its condition number bound, no additional coarse level variables, except those necessary for solving scalar elliptic problems, are required for incompressible Stokes problems. The resulting coarse level problem is also symmetric positive definite.
To stay focused on the purpose of this paper, the discussion of the proposed algorithm and its analysis are based on two-dimensional problems, even though the same approach can be extended to the three-dimensional case without substantial obstacles. It is also worth pointing out that the domain decomposition algorithm and its analysis presented in this paper apply equally well, with only minor modifications, to the case where discontinuous pressures are used in the mixed finite element space.
The remainder of this paper is organized as follows. The finite element discretization of the incompressible Stokes equation is introduced in Section \ref{section:FEM}. A domain decomposition approach is described in Section~\ref{section:DDM}. The system for the subdomain boundary pressures and the Lagrange multipliers is derived in Section~\ref{section:Gmatrix}. Section \ref{section:techniques} provides some techniques used in the condition number bound estimate. In Section~\ref{section:lumped}, a lumped preconditioner is proposed and a scalable condition number bound of the preconditioned operator is established. At the end, in Section~\ref{section:numerics}, numerical results for solving a two-dimensional incompressible Stokes problem are shown to demonstrate the convergence rate of the proposed algorithm.
\section{Finite element discretization} \label{section:FEM}
We consider solving the following incompressible Stokes problem on a bounded, two-dimensional polygonal domain $\Omega$ with a Dirichlet boundary condition, \begin{equation} \label{equation:Stokes} \left\{ \begin{array}{rcll} -\Delta {\bf u} + \nabla p & = & {\bf f}, & \mbox{ in } \Omega \mbox{ , } \\ -\nabla \cdot {\bf u} & = & 0, & \mbox{ in } \Omega \mbox{ , } \\ {\bf u} & = & {\bf u}_{\partial \Omega}, & \mbox{ on } \partial \Omega \mbox{ , }\\ \end{array}\right. \end{equation} where the boundary data ${\bf u}_{\partial \Omega}$ satisfies the compatibility condition $\int_{\partial \Omega} {\bf u}_{\partial \Omega} \cdot {\bf n} = 0$. For simplicity, we assume that ${\bf u}_{\partial \Omega} = {\bf 0}$ without losing any generality.
The weak solution of \EQ{Stokes} is given by: find $\vvec{u} \in \left(H^1_0(\Omega)\right)^2 = \{ \vvec{v} \in (H^1(\Omega))^2 ~
\big| ~ \vvec{v} = \vvec{0} \mbox{ on } \partial \Omega \}$ and $p \in L^2(\Omega)$, such that \begin{equation} \label{equation:bilinear} \left\{ \begin{array}{lcll} a(\vvec{u}, \vvec{v}) + b(\vvec{v}, p) & = & (\vvec{f}, \vvec{v}), & \forall \vvec{v}\in \left(H^1_0(\Omega)\right)^2 , \\ [0.5ex] b(\vvec{u}, q) & = & 0, & \forall q \in L^2(\Omega) \mbox{ , } \\ \end{array} \right. \end{equation} where \[ a(\vvec{u}, \vvec{v})= \int_{\Omega} \nabla{\bf u} \cdot \nabla{\bf v}, \quad b(\vvec{u},q) = -\int_{\Omega} (\nabla \cdot \vvec{u}) q, \quad (\vvec{f}, \vvec{v}) = \int_{\Omega} \vvec{f} \cdot \vvec{v}. \] We note that the solution of \EQ{bilinear} is not unique, with the pressure $p$ different up to an additive constant.
A modified Taylor-Hood mixed finite element is used in this paper to solve \EQ{bilinear}. The domain $\Omega$ is triangulated into shape-regular elements of characteristic size $h$. The pressure finite element space, $Q \subset L^2(\Omega)$, is taken as the space of continuous piecewise linear functions on the triangulation. The velocity finite element space, $\vvec{W} \in \left(H^1_0(\Omega)\right)^2$, is formed by the continuous piecewise linear functions on the finer triangulation obtained by dividing each triangle into four subtriangles by connecting the middle points of its edges. A demonstration of this mixed finite element on a triangulation of a square domain is shown in Figure \ref{figure:TaylorHood}.
\begin{figure}
\caption{ A modified Taylor-Hood mixed finite element}
\label{figure:TaylorHood}
\end{figure}
The finite element solution $(\vvec{u}, p) \in \vvec{W} \bigoplus Q$ of \EQ{bilinear} satisfies \begin{equation} \label{equation:matrix} \left[ \begin{array}{cccc} A & B^T \\ B & 0 \\ \end{array} \right] \left[ \begin{array}{c} {\bf u} \\ p \\ \end{array} \right] = \left[ \begin{array}{l} {\bf f} \\ 0 \\ \end{array} \right] , \end{equation} where $A$, $B$, and $\vvec{f}$ represent respectively the restrictions of $a( \cdot , \cdot )$, $b(\cdot, \cdot )$ and $(\vvec{f} , \cdot)$ to the finite-dimensional spaces $\vvec{W}$ and $Q$. We use the same notation in this paper to represent both a finite element function and the vector of its nodal values.
The coefficient matrix in \EQ{matrix} is rank deficient. $A$ is symmetric positive definite. The kernel of $B^T$, denoted by $Ker(B^T)$, is the space of all constant pressures in $Q$. The range of $B$, denoted by $Im(B)$, is orthogonal to $Ker(B^T)$ and is the subspace of $Q$ consisting of all vectors with zero average. The solution of \EQ{matrix} always exists and is uniquely determined when the pressure is considered in the quotient space $Q/Ker(B^T)$. In this paper, when $q \in Q/Ker(B^T)$, $q$ always has zero average. For a more general right-hand side vector $({\bf f}, ~ g)$ given in \EQ{matrix}, the existence of its solution requires that $g \in Im(B)$, i.e., $g$ has zero average.
The modified Taylor-Hood mixed finite element space $\vvec{W} \times Q$, as shown in Figure \ref{figure:TaylorHood}, is inf-sup stable in the sense that there exists a positive constant $\beta$, independent of $h$, such that \begin{equation} \label{equation:infsup} \sup_{\vvec{w} \in \vvec{W}}
\frac{b(\vvec{w},q)}{|\vvec{w}|_{H^1}} \geq \beta \|q\|_{L^2}, \hspace{0.5cm} \forall q \in Q/Ker(B^T), \end{equation} cf.~\cite[Chapter III, \S 7]{braess}, or equivalently in matrix/vector form, \begin{equation} \label{equation:infsupMatrix} \sup_{{\bf w} \in {\bf W}} \frac{\left< q, B \vvec{w} \right>^2}{\left< \vvec{w}, A \vvec{w} \right>} \geq \beta^2 \left< q, Z q \right>, \hspace{0.5cm} \forall q \in Q/Ker(B^T). \end{equation}
Here, as always in this paper, $\left< \cdot, \cdot \right>$ represents the inner product of two vectors. The matrix $Z$ represents the mass matrix defined on the pressure finite element space $Q$, i.e., for any $q \in Q$, $\|q\|_{L^2}^2 = \left< q, Z q \right>$. It is easy to see, cf.~\cite[Lemma B.31]{Toselli:2004:DDM}, that $Z$ is spectrally equivalent to $h^2 I$ for two-dimensional problems, where $I$ represents the identity matrix of the same dimension, i.e., there exist positive constants $c$ and $C$, such that \begin{equation} \label{equation:massmatrix} c h^2 I \leq Z \leq C h^2 I. \end{equation} Here, as in other places of this paper, $c$ and $C$ represent generic positive constants which are independent of the mesh size $h$ and the subdomain diameter $H$ (discussed in the following section).
\section{A non-overlapping domain decomposition approach} \label{section:DDM}
The domain $\Omega$ is decomposed into $N$ non-overlapping polygonal subdomains $\Omega_i$, $i = 1, 2, ..., N$. Each subdomain is the union of a bounded number of elements, with the diameter of the subdomain in the order of $H$. The nodes on the interface of neighboring subdomains match across the subdomain boundaries $\Gamma = {(\cup\partial\Omega_i)} \backslash \partial\Omega$. $\Gamma$ is composed of subdomain edges, which are regarded as open subsets of $\Gamma$, and of the subdomain vertices, which are end points of edges.
The velocity and pressure finite element spaces ${\bf W}$ and $Q$ are decomposed into \[ {\bf W} = {\bf W}_I \bigoplus {\bf W}_{\Gamma}, \quad Q = Q_I \bigoplus Q_\Gamma, \] where ${\bf W}_I$ and $Q_I$ are direct sums of independent subdomain interior velocity spaces ${\bf W}^{(i)}_I$, and interior pressure spaces $Q^{(i)}_I$, respectively, i.e., $$ {\bf W}_I = \bigoplus_{i=1}^{N}{\bf W}^{(i)}_I, \quad Q_I = \bigoplus_{i=1}^{N}Q^{(i)}_I. $$ ${\bf W}_{\Gamma}$ and $Q_\Gamma$ are subdomain boundary velocity and pressure spaces, respectively. All functions in ${\bf W}_{\Gamma}$ and $Q_\Gamma$ are continuous across the subdomain boundaries $\Gamma$; their degrees of freedom are shared by neighboring subdomains.
To formulate our domain decomposition algorithm, we introduce a partially sub-assembled subdomain boundary velocity space $\vvec{{\widetilde{W}}}_{\Gamma}$, \[ \vvec{{\widetilde{W}}}_{\Gamma} = \vvec{W}_{\Pi} \bigoplus \vvec{W}_{\Delta} = \vvec{W}_{\Pi} \bigoplus \left( \bigoplus_{i=1}^N \vvec{W}^{(i)}_\Delta \right). \] Here, $\vvec{W}_{\Pi}$ is the continuous, coarse level, primal velocity space which is typically spanned by subdomain vertex nodal basis functions, and/or by interface edge basis functions with constant values, or with values of positive weights on these edges. The primal, coarse level velocity degrees of freedom are shared by neighboring subdomains. The complimentary space $\vvec{W}_{\Delta}$ is the direct sum of independent subdomain dual interface velocity spaces $\vvec{W}_{\Delta}^{(i)}$, which correspond to the remaining subdomain boundary velocity degrees of freedom and are spanned by basis functions which vanish at the primal degrees of freedom. Thus, an element in the space $\vvec{{\widetilde{W}}}_{\Gamma}$ typically has a continuous primal velocity component and a discontinuous dual velocity component.
The functions ${\bf w}_{\Delta}$ in ${\bf W}_{\Delta}$ are in general not continuous across $\Gamma$. To enforce their continuity, we define a boolean matrix $B_\Delta$ constructed from $\{0,1,-1\}$. On each row of $B_\Delta$, there are only two non-zero entries, $1$ and $-1$, corresponding to the same velocity degree of freedom on each subdomain boundary node, but attributed to two neighboring subdomains, such that for any ${\bf w}_{\Delta}$ in ${\bf W}_{\Delta}$, each row of $B_\Delta {\bf w}_{\Delta} = 0$ implies that these two degrees of freedom from the two neighboring subdomains be the same. When non-redundant continuity constraints are enforced, $B_\Delta$ has full row rank. We denote the range of $B_\Delta$ applied on ${\bf W}_{\Delta}$ by $\Lambda$, the vector space of the Lagrange multipliers.
In order to define a certain subdomain boundary scaling operator, we introduce a positive scaling factor $\delta^{\dagger}(x)$ for each node $x$ on the subdomain boundary $\Gamma$. Let ${\cal N}_x$ be the number of subdomains sharing $x$, and we simply take $\delta^{\dagger}(x) = 1/{\cal N}_x$. In applications, these scaling factors will depend on the heat conduction coefficient and the first of the Lam\'{e} parameters for scalar elliptic problems and the equations of linear elasticity, respectively; see \cite{kla02,kla06}. Given such scaling factors at the subdomain boundary nodes, we can define a scaled operator $B_{\Delta, D}$. We note that each row of $B_\Delta$ has only two nonzero entries, $1$ and $-1$, corresponding to the same subdomain boundary node $x$. Multiplying each entry by the scaling factor $\delta^{\dagger}(x)$ gives us $B_{\Delta, D}$.
Solving the original fully assembled linear system~\EQ{matrix} is then equivalent to: find $\left( {\bf u}_I, ~p_I, ~{\bf u}_{\Delta}, ~{\bf u}_{\Pi}, ~p_{\Gamma}, ~\lambda \right) \in {\bf W}_I \bigoplus Q_I \bigoplus {\bf W}_{\Delta} \bigoplus {\bf W}_\Pi \bigoplus Q_\Gamma \bigoplus \Lambda$, such that \begin{equation} \label{equation:bigeq} \left[ \begin{array}{cccccc} A_{II} & B_{II}^T & A_{I \Delta} & A_{I \Pi} & B_{\Gamma I}^T & 0 \\[0.8ex] B_{II} & 0 & B_{I \Delta} & B_{I \Pi} & 0 & 0 \\[0.8ex] A_{\Delta I}& B_{I \Delta} ^T& A_{\Delta\Delta} & A_{\Delta \Pi} & B_{\Gamma \Delta}^T& B_{\Delta}^T\\[0.8ex] A_{\Pi I} & B_{I \Pi}^T & A_{\Pi \Delta} & A_{\Pi \Pi} & B_{\Gamma \Pi}^T & 0 \\[0.8ex] B_{\Gamma I}& 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} & 0 & 0 \\[0.8ex] 0 & 0 & B_{\Delta} & 0 & 0 & 0 \end{array} \right] \left[ \begin{array}{c} {\bf u}_I \\[0.8ex] p_I \\[0.8ex] {\bf u}_{\Delta} \\[0.8ex] {\bf u}_{\Pi} \\[0.8ex] p_{\Gamma} \\[0.8ex] \lambda \end{array} \right] = \left[ \begin{array}{l} {\bf f}_I \\[0.8ex] 0 \\[0.8ex] {\bf f}_{\Delta} \\[0.8ex] {\bf f}_\Pi \\[0.8ex] 0 \\[0.8ex] 0 \end{array} \right] \mbox{ , } \end{equation} where the sub-blocks in the coefficient matrix represent the restrictions of $A$ and $B$ in~\EQ{matrix} to appropriate subspaces. The leading three-by-three block can be made block diagonal with each diagonal block representing one independent subdomain problem.
Corresponding to the one-dimensional null space of~\EQ{matrix}, we consider a vector of the form $\left( {\bf u}_I,~p_I, ~{\bf u}_\Delta, ~ {\bf u}_\Pi, ~p_\Gamma, ~\lambda \right) = \left( {\bf 0},~1_{p_I},~{\bf 0}, ~{\bf 0}, ~1_{p_\Gamma}, \lambda \right)$, where $1_{p_I} \in Q_I$ and $1_{p_\Gamma} \in Q_\Gamma$ represent vectors with value $1$ on each entry. Substituting it into \EQ{bigeq} gives zero blocks on the right-hand side, except at the third block \begin{equation} \label{equation:fdelta} {\bf f}_{\Delta} = [B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\ 1_{p_\Gamma}\end{array}\right]+B^T_\Delta \lambda. \end{equation} The first term on the right-hand side represents the line integral of the normal component of the velocity finite element basis functions across the subdomain boundary on neighboring subdomains. Corresponding to the same subdomain boundary velocity degree of freedom, their values on the two neighboring subdomains are negative of each other. Therefore \[ [B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\ 1_{p_\Gamma}\end{array}\right] = B^T_\Delta B_{\Delta,D}[B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\ 1_{p_\Gamma}\end{array}\right], \] from which we know that $\vvec{f}_\Delta = {\bf 0}$, for \[ \lambda =-B_{\Delta,D}[B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\
1_{p_\Gamma}\end{array}\right]. \] Therefore, a basis of the one-dimensional null space of \EQ{bigeq} is \begin{equation} \label{equation:bignull} \left( \begin{array}{cccccc} 0, & 1_{p_I}, & 0, & 0, & 1_{p_\Gamma}, & -B_{\Delta,D}[B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\ 1_{p_\Gamma}\end{array}\right] \end{array} \right). \end{equation}
\section{A reduced symmetric positive semi-definite system} \label{section:Gmatrix}
The system \EQ{bigeq} can be reduced to a Schur complement problem for the variables $\left(p_{\Gamma}, ~\lambda \right)$. Since the leading four-by-four block of the coefficient matrix in \EQ{bigeq} is invertible, the variables $\left( {\bf u}_I, ~p_I, ~{\bf u}_{\Delta}, ~{\bf u}_{\Pi} \right)$ can be eliminated and we obtain \begin{equation} \label{equation:spd} G \left[ \begin{array}{c} p_\Gamma \\[0.8ex] \lambda \end{array} \right] ~ = ~ g, \end{equation} where \begin{equation} \label{equation:Gmatrix} G = \left[ \begin{array}{cccc} B_{\Gamma I} & 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} \\[0.8ex] 0 & 0 & B_{\Delta} & 0 \end{array} \right] \left[ \begin{array}{cccc} A_{II} & B_{II}^T & A_{I \Delta} & A_{I \Pi} \\[0.8ex] B_{II} & 0 & B_{I \Delta} & B_{I \Pi} \\[0.8ex] A_{\Delta I} & B_{I \Delta} ^T & A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex] A_{\Pi I} & B_{I \Pi}^T & A_{\Pi \Delta} & A_{\Pi \Pi} \end{array} \right]^{-1} \left[ \begin{array}{cc} B_{\Gamma I}^T & 0 \\[0.8ex] 0 & 0 \\[0.8ex] B_{\Gamma \Delta}^T & B_{\Delta}^T \\[0.8ex] B_{\Gamma \Pi}^T & 0 \end{array} \right], \end{equation} and \begin{equation} \label{equation:gvec} g = \left[ \begin{array}{cccc} B_{\Gamma I} & 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} \\[0.8ex] 0 & 0 & B_{\Delta} & 0 \end{array} \right] \left[ \begin{array}{cccc} A_{II} & B_{II}^T & A_{I \Delta} & A_{I \Pi} \\[0.8ex] B_{II} & 0 & B_{I \Delta} & B_{I \Pi} \\[0.8ex] A_{\Delta I} & B_{I \Delta} ^T & A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex] A_{\Pi I} & B_{I \Pi}^T & A_{\Pi \Delta} & A_{\Pi \Pi} \end{array} \right]^{-1} \left[ \begin{array}{l} {\bf f}_I \\[0.8ex] 0 \\[0.8ex] {\bf f}_{\Delta} \\[0.8ex] {\bf f}_\Pi \end{array} \right]. \end{equation}
We denote \begin{equation} \label{equation:AtildeBc} \widetilde{A} = \left[ \begin{array}{cccc} A_{II} & B_{II}^T & A_{I \Delta} & A_{I \Pi} \\[0.8ex] B_{II} & 0 & B_{I \Delta} & B_{I \Pi} \\[0.8ex] A_{\Delta I}& B_{I \Delta} ^T& A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex] A_{\Pi I} & B_{I \Pi}^T & A_{\Pi \Delta} & A_{\Pi \Pi} \end{array} \right] \quad \mbox{and}\quad B_C=\left[ \begin{array}{cccc} B_{\Gamma I} & 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} \\[0.8ex] 0 & 0 & B_{\Delta} & 0 \end{array} \right]. \end{equation} We can see that $-G$ is the Schur complement of the coefficient matrix of \EQ{bigeq} with respect to the last two row blocks, i.e., \[ \left[ \begin{array}{cc} I & 0 \\[0.8ex] -B_C \widetilde{A}^{-1} & I \end{array} \right] \left[ \begin{array}{cc} \widetilde{A} & B_C^T \\[0.8ex] B_C & 0 \end{array} \right] \left[ \begin{array}{cc} I & - \widetilde{A}^{-1} B_C^T \\[0.8ex] 0 & I \end{array} \right] = \left[ \begin{array}{cc} \widetilde{A} & 0 \\[0.8ex] 0 & -G \end{array} \right]. \] From the Sylvester's law of inertia, namely, the number of positive, negative, and zero eigenvalues of a symmetric matrix is invariant under a change of coordinates, we can see that the number of zero eigenvalues of $G$ is the same as the number of zero eigenvalues (with multiplicity counted) of the original coefficient matrix of \EQ{bigeq}, which is one, and all other eigenvalues of $G$ are positive. Therefore $G$ is symmetric positive semi-definite. The null space of $G$ is derived from the null space of the original coefficient matrix of \EQ{bigeq}, and its basis is given by, cf.~\EQ{bignull}, \[ \left( \begin{array}{cc} 1_{p_\Gamma}, & - B_{\Delta,D}[B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{p_I}\\ 1_{p_\Gamma} \end{array} \right] \end{array} \right). \]
We denote $X = Q_\Gamma \bigoplus \Lambda$. The range of $G$, denoted by $R_G$, is the subspace of $X$ orthogonal to the null space of $G$, and has the form \begin{equation} \label{equation:Grange} R_G=\left\{ \left[ \begin{array}{c} g_{p_\Gamma} \\[0.8ex] g_{\lambda}
\end{array} \right] \in X ~ {\Big|} ~ g_{p_\Gamma}^T 1_{{p_\Gamma}} - g_{\lambda}^T \left(B_{\Delta,D}[B_{I\Delta}^T ~~ B_{\Gamma\Delta}^T]\left[\begin{array}{c}1_{{p_I}}\\ 1_{{p_\Gamma}}\end{array}\right]\right)=0\right\}. \end{equation}
The restriction of $G$ to its range $R_G$ is positive definite. The fact that the solution of \EQ{bigeq} always exists for any given $\left( {\bf f}_I, ~{\bf f}_{\Delta}, ~{\bf f}_{\Pi} \right)$ on the right-hand side implies that the solution of~\EQ{spd} exits for any $g$ defined by \EQ{gvec}. Therefore $g \in R_G$. When the conjugate gradient method (CG) is applied to solve \EQ{spd} with zero initial guess, all the iterates are in the Krylov subspace generated by $G$ and $g$, which is also a subspace of $R_G$, and where the CG cannot break down. After obtaining $\left( p_{\Gamma}, ~\lambda \right)$ from solving \EQ{spd}, the other components $\left( {\bf u}_I, ~p_I, ~{\bf u}_{\Delta}, ~{\bf u}_{\Pi} \right)$ in \EQ{bigeq} are obtained by back substitution.
In the rest of this section, we discuss the implementation of multiplying $G$ by a vector. The main operation is the product of ${\widetilde{A}}^{-1}$ with a vector, cf. \EQ{Gmatrix} and \EQ{gvec}. We denote \[ A_{rr} = \left[ \begin{array}{ccc} A_{II} & B_{II}^T & A_{I \Delta} \\[0.8ex] B_{II} & 0 & B_{I \Delta} \\[0.8ex] A_{\Delta I} & B_{I \Delta} ^T & A_{\Delta\Delta} \end{array} \right] , \quad A_{\Pi r} = A_{r \Pi}^T = \left[ A_{\Pi I} \quad B_{I \Pi}^T \quad A_{\Pi \Delta} \right], \quad f_r = \left[ \begin{array}{l} {\bf f}_I \\[0.8ex] 0 \\[0.8ex] {\bf f}_{\Delta} \end{array} \right], \] and define the Schur complement \[ S_{\Pi} = A_{\Pi \Pi} - A_{\Pi r} A_{rr}^{-1} A_{r \Pi}, \] which is symmetric positive definite from the Sylvester's law of inertia. $S_\Pi$ defines the coarse level problem in the algorithm. The product \[
\left[
\begin{array}{cccc}
A_{II} & B_{II}^T & A_{I \Delta} & A_{I \Pi} \\[0.8ex]
B_{II} & 0 & B_{I \Delta} & B_{I \Pi} \\[0.8ex]
A_{\Delta I} & B_{I \Delta} ^T & A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex]
A_{\Pi I} & B_{I \Pi}^T & A_{\Pi \Delta} & A_{\Pi \Pi}
\end{array}
\right]^{-1} \left[
\begin{array}{l}
{\bf f}_I \\[0.8ex]
0 \\[0.8ex]
{\bf f}_{\Delta} \\[0.8ex]
{\bf f}_\Pi
\end{array}
\right] \] can then be represented by \[ \left[ \begin{array}{c} A_{rr}^{-1} f_r \\[0.8ex] \vvec{0} \end{array} \right] ~ + ~ \left[ \begin{array}{c} -A_{rr}^{-1} A_{r \Pi} \\[0.8ex] I_\Pi \end{array} \right] ~ S_{\Pi}^{-1} ~ \left({\bf f}_\Pi - A_{\Pi r} A_{rr}^{-1} f_r \right), \] which requires solving the coarse level problem once and independent subdomain Stokes problems with Neumann type boundary conditions twice.
\section{Some techniques} \label{section:techniques}
We first define certain norms for several vector/function spaces. We denote \begin{equation} \label{equation:Wtilde} \vvec{{\widetilde{W}}} = {\bf W}_I \bigoplus \vvec{{\widetilde{W}}}_{\Gamma}. \end{equation} For any $\vvec{w}$ in $\vvec{{\widetilde{W}}}$, we denote its restriction to subdomain $\Omega_i$ by ${\bf w}^{(i)}$. A subdomain-wise $H^1$-seminorm can be defined for functions in $\vvec{{\widetilde{W}}}$ by \[
|\vvec{w}|^2_{H^1} = \sum_{i=1}^N |\vvec{w}^{(i)}|^2_{H^1(\Omega_i)}. \]
We also define \[ {\widetilde{W}} = {\bf W}_I \bigoplus Q_I \bigoplus {\bf W}_{\Delta} \bigoplus {\bf W}_\Pi, \] and its subspace \begin{equation} \label{equation:W0}
{\widetilde{W}}_0 = \left\{ w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}} ~ \big| ~ B_{I I} \vvec{w}_I + B_{I\Delta} \vvec{w}_\Delta + B_{I\Pi} \vvec{w}_\Pi = 0 \right\}. \end{equation} For any $w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}_0$, let $\vvec{w} = \left( {\bf w}_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in \vvec{{\widetilde{W}}}$. Then \begin{eqnarray} \left< w, w \right>_{\widetilde{A}} & = & \left[ \begin{array}{l} {\bf w}_I \\[0.8ex] {\bf w}_{\Delta} \\[0.8ex] {\bf w}_\Pi \end{array} \right]^T \left[ \begin{array}{ccc} A_{II} & A_{I \Delta} & A_{I \Pi} \\[0.8ex] A_{\Delta I} & A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex] A_{\Pi I} & A_{\Pi \Delta} & A_{\Pi \Pi} \end{array} \right] \left[ \begin{array}{l} {\bf w}_I \\[0.8ex] {\bf w}_{\Delta} \\[0.8ex] {\bf w}_\Pi \end{array} \right] \nonumber \\[0.8ex] & = & \sum_{i=1}^N \left[ \begin{array}{c} {\bf w}_I^{(i)} \\ {\bf w}_{\Delta}^{(i)} \\ {\bf w}_{\Pi}^{(i)} \end{array} \right]^T \left[ \begin{array}{cccc} A_{II}^{(i)} & A_{I \Delta}^{(i)} & A_{I \Pi}^{(i)} \\[0.8ex] A_{\Delta I}^{(i)} & A_{\Delta\Delta}^{(i)} & A_{\Delta \Pi}^{(i)} \\[0.8ex] A_{\Pi I}^{(i)} & A_{\Pi \Delta}^{(i)} & A_{\Pi \Pi}^{(i)} \end{array} \right] \left[ \begin{array}{c} {\bf w}_I^{(i)} \\ {\bf w}_{\Delta}^{(i)} \\ {\bf w}_{\Pi}^{(i)} \end{array} \right]
= \sum_{i=1}^N \left| \left[ \begin{array}{c} {\bf w}_I^{(i)} \\ {\bf w}_{\Delta}^{(i)} \\ {\bf w}_{\Pi}^{(i)} \end{array} \right] \right|_{H^1(\Omega_i)}^2 \label{equation:W0n} \\[0.8ex]
& = & |\vvec{w}|^2_{H^1}, \nonumber \end{eqnarray} i.e., $\left< \cdot , \cdot \right>_{{\widetilde{A}}}$ defines an inner product on ${\widetilde{W}}_0$. In \EQ{W0n}, the superscript ${}^{(i)}$ is used to represent the restrictions of corresponding vectors and matrices to subdomain $\Omega_i$.
Since $\vvec{W}$ is essentially the subspace of $\vvec{{\widetilde{W}}}$ with continuous subdomain boundary velocities, the inf-sup condition \EQ{infsup} and \EQ{infsupMatrix} also holds for the mixed space $\vvec{{\widetilde{W}}} \times Q$. Denote \begin{equation}\label{equation:Btilde} \widetilde{B} = \left[ \begin{array}{ccc} B_{II} & B_{I \Delta} & B_{I \Pi} \\[0.8ex] B_{\Gamma I}& B_{\Gamma \Delta} & B_{\Gamma \Pi} \end{array} \right], \qquad \overline{\widetilde{A}} = \left[ \begin{array}{ccc} A_{II} & A_{I \Delta} & A_{I \Pi} \\[0.8ex] A_{\Delta I}& A_{\Delta\Delta} & A_{\Delta \Pi} \\[0.8ex] A_{\Pi I} & A_{\Pi \Delta} & A_{\Pi \Pi} \end{array} \right], \end{equation} as in \EQ{bigeq}, then \begin{equation} \label{equation:infsupMatrixtilde} \sup_{{\bf w} \in \vvec{{\widetilde{W}}}} \frac{\left< q, \widetilde{B} \vvec{w} \right>^2}{\left< \vvec{w}, \overline{\widetilde{A}} \vvec{w} \right>} \geq \beta^2 \left< q, Z q \right>, \hspace{0.5cm} \forall q \in Q/Ker(B^T), \end{equation} where $\beta$ is the same as in \EQ{infsup} and \EQ{infsupMatrix}.
We also have the following lemma on the stability of the operator $\widetilde{B}$.
\begin{mylemma} \label{lemma:BtildeStability}
For any $\vvec{w} \in \vvec{{\widetilde{W}}}$ and $q \in Q$, $\left< {\widetilde{B}} {\bf w}, q \right> \leq | \vvec{w} |_{H^1} \| q \|_{L^2}$. \end{mylemma}
\indent {\it Proof:~} \begin{eqnarray*}
\left<{\widetilde{B}} {\bf w}, q \right>^2 & = & \left( \sum_{i=1}^N \int_{\Omega_i} \nabla\cdot {\bf w}^{(i)} q \right)^2\leq \left( \sum_{i=1}^N \sqrt{\int_{\Omega_i} | \nabla {\bf w}^{(i)} |^2} \sqrt{\int_{\Omega_i} q^2} \right)^2 \\[0.8ex]
& \le & \left( \sum_{i=1}^N \int_{\Omega_i} | \nabla {\bf w}^{(i)} |^2 \right) \left( \sum_{i=1}^N \int_{\Omega_i} q^2 \right) = | \vvec{w} |^2_{H^1} \| q \|^2_{L^2}. \qquad \Box \end{eqnarray*}
The finite element space for subdomain boundary pressures, $Q_\Gamma$, is a subspace of $L^2(\Gamma)$. For each $p_\Gamma \in Q_\Gamma$, its finite element extension by zero to the interior of subdomains is denoted by $p_\Gamma^E$, which equals $p_\Gamma$ on all subdomain boundary nodes and equals zero on all subdomain interior nodes. We can see that $p_\Gamma^E \in Q \subset L^2(\Omega)$, and $\| p_\Gamma^E \|_{L^2(\Omega)}^2 = \left< p^E_\Gamma, p^E_\Gamma \right>_Z$, from the definition of $Z$ in Section~\ref{section:FEM}.
From \EQ{Gmatrix} and \EQ{AtildeBc}, we can see that \[ G = B_C {\widetilde{A}}^{-1} B_C^T. \] In particular, we denote the first row of $B_C$ by \[ \widetilde{B}_{\Gamma} = \left[ B_{\Gamma I} \quad 0 \quad B_{\Gamma \Delta} \quad B_{\Gamma \Pi} \right]; \] for the second row, we denote the restriction operator from ${\widetilde{W}}$ onto ${\bf W}_{\Delta}$ by $\widetilde{R}_\Delta$, such that for any $w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}$, $\widetilde{R}_\Delta w = {\bf w}_{\Delta}$. Then $G$ can be represented by the following two-by-two block structure \begin{equation} \label{equation:Gtwo} G = \left[ \begin{array}{cc} G_{p_\Gamma p_\Gamma} & G_{p_\Gamma \lambda} \\[0.8ex] G_{\lambda p_\Gamma} & G_{\lambda \lambda} \end{array} \right], \end{equation} where \begin{eqnarray*} & G_{p_\Gamma p_\Gamma} = \widetilde{B}_{\Gamma} \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T, \qquad G_{p_\Gamma \lambda} = \widetilde{B}_{\Gamma} \widetilde{A}^{-1} \widetilde{R}_{\Delta}^T B_{\Delta}^T, & \\ [0.8ex] & G_{\lambda p_\Gamma} = B_{\Delta} \widetilde{R}_\Delta \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T, \qquad G_{\lambda \lambda} = B_{\Delta} \widetilde{R}_\Delta \widetilde{A}^{-1} \widetilde{R}_{\Delta}^T B_{\Delta}^T. & \end{eqnarray*}
The pressure components of all vectors in $R_G$ with $g_\lambda = 0$, cf. \EQ{Grange}, form a subspace of $Q_\Gamma$ and we denote this subspace by $R_{G|Q_\Gamma}$. From the definition of $R_G$, we can see that for any vector $p_\Gamma \in R_{G|Q_\Gamma}$, $p_\Gamma^T 1_{p_\Gamma} = 0$, and then its extension by zero to the interior of subdomains, $p_\Gamma^E$, also has zero average.
The following lemma follows essentially from \cite[Lemma 9.1]{Toselli:2004:DDM}. \begin{mylemma} \label{lemma:mass}
For all $p_\Gamma \in R_{G|Q_\Gamma}$, \[
\beta^2 \| p_\Gamma^E \|_{L^2(\Omega)}^2 ~ \leq ~ \left<p_\Gamma, G_{p_\Gamma p_\Gamma} p_\Gamma \right> ~ \leq ~
\| p_\Gamma^E \|_{L^2(\Omega)}^2, \] where $p_\Gamma^E$ represents the extension by zero of $p_\Gamma$ to the interior of subdomains, and $\beta$ is the same as in \EQ{infsup} and \EQ{infsupMatrix}. \end{mylemma}
\indent {\it Proof:~} Note that even though $\widetilde{A}^{-1}$ is indefinite in ${\widetilde{W}}$, it is positive definite when restricted to a subspace of ${\widetilde{W}}$, where the pressure component equals zero, and the norm $\| \cdot \|_{\widetilde{A}^{-1}}$ is well defined.
To prove the left side inequality, denote for any ${\bf v} = \left( {\bf v}_I, ~{\bf v}_{\Delta}, ~{\bf v}_{\Pi} \right) \in \vvec{{\widetilde{W}}}$, ${\bf v}^\dagger = \left( {\bf v}_I, ~ 0, ~{\bf v}_{\Delta}, ~{\bf v}_{\Pi} \right) \in {\widetilde{W}}$. We have \begin{eqnarray*}
\left<p_\Gamma, \widetilde{B}_{\Gamma} \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma \right> = \| \widetilde{B}_{\Gamma}^T p_\Gamma \|_{\widetilde{A}^{-1}}^2 = \sup_{{\bf v} \in \vvec{{\widetilde{W}}}}
\frac{\left< {\bf v}^\dagger, \widetilde{B}_{\Gamma}^T p_\Gamma \right>^2_{\widetilde{A}^{-1}}}{\| {\bf v}^\dagger \|^2_{\widetilde{A}^{-1}}} = \sup_{{\bf v} \in \vvec{{\widetilde{W}}}} \frac{\left( p_\Gamma^T \widetilde{B}_{\Gamma} \widetilde{A}^{-1} {\bf v}^\dagger \right)^2}{{\bf v}^{\dagger^T} {\widetilde{A}^{-1}} {\bf v}^\dagger} \\ = \sup_{{\bf w} \in \vvec{{\widetilde{W}}}} \frac{\left( p_\Gamma^{T} \widetilde{B}_\Gamma {\bf w}^\dagger \right)^2}{{\bf w}^{\dagger^T} \widetilde{A} {\bf w}^\dagger} = \sup_{{\bf w} \in \vvec{{\widetilde{W}}}}
\frac{\left( p_\Gamma^{E^T} \widetilde{B} {\bf w} \right)^2}{{\bf w}^T \overline{\widetilde{A}} {\bf w}} \geq \beta^2 \left< p_\Gamma^E, p_\Gamma^E \right>_Z = \beta^2 \| p_\Gamma^E \|_{L^2(\Omega)}^2 , \end{eqnarray*} where we have used the inf-sup condition \EQ{infsupMatrixtilde} for the inequality in the middle.
To prove the right side inequality, for any given $p_\Gamma \in R_{G|Q_\Gamma}$, denote ${\bf v}^\dagger = \left( {\bf v}_I, ~ p_I, ~{\bf v}_{\Delta}, ~{\bf v}_{\Pi} \right) = \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma$, and the shorter vector ${\bf v} = \left( {\bf v}_I, ~{\bf v}_{\Delta}, ~{\bf v}_{\Pi} \right)$. From the continuity of ${\widetilde{B}}$ in Lemma \LA{BtildeStability} and \EQ{W0n}, we have \begin{eqnarray*}
& & \left<p_\Gamma, \widetilde{B}_{\Gamma} \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma \right> = \left<p_\Gamma, \widetilde{B}_{\Gamma} {\bf v}^\dagger \right> = \left<p_\Gamma^E, \widetilde{B} \vvec{v} \right> \leq \| p_\Gamma^E \|_{L^2} ~ | \vvec{v} |_{H^1} \\
& = & \| p_\Gamma^E \|_{L^2} ~ \sqrt{\left< \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma, \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma \right>_{{\widetilde{A}}}} = \| p_\Gamma^E \|_{L^2} ~ \left<p_\Gamma, \widetilde{B}_{\Gamma} \widetilde{A}^{-1} \widetilde{B}_{\Gamma}^T p_\Gamma \right>^{1/2}. \qquad \Box \end{eqnarray*}
The following corollary of Lemma~\ref{lemma:mass} is an immediate result from \EQ{massmatrix} and the facts that $\| p_\Gamma^E \|_{L^2(\Omega)}^2 = \left< p_\Gamma^E, p_\Gamma^E \right>_Z$, $\left<p_\Gamma^E, p_\Gamma^E \right> = \left<p_\Gamma, p_\Gamma \right>$. \begin{mycorollary} \label{coro:mass} There exist positive constants $c$ and $C$, such that \[ c h^2 \beta^2 I_{p_\Gamma} ~ \leq ~ G_{p_\Gamma p_\Gamma} ~ \leq ~ C h^2 I_{p_\Gamma} \] where $I_{p_\Gamma}$ is the identity matrix of the same dimension as $G_{p_\Gamma p_\Gamma}$, and $\beta$ is the same as in \EQ{infsup} and \EQ{infsupMatrix}. \end{mycorollary}
\begin{myremark} Lemma \ref{lemma:mass} and Corollary \ref{coro:mass} are not used in our proof of the condition number bound in Section~\ref{section:lumped}. However, it is intuitive to see from Corollary~\ref{coro:mass} that the first diagonal block $G_{p_\Gamma p_\Gamma}$ in matrix $G$ can be approximated spectrally equivalently by the identity matrix multiplied by $h^2$, which is what is being done in our block diagonal preconditioner discussed in Section~\ref{section:lumped}. \end{myremark}
We also need define a certain jump operator across the subdomain boundaries $\Gamma$. Let $P_D: {\widetilde{W}} \rightarrow {\widetilde{W}}$, be defined by, cf.~\cite{li06A}, \[ P_D = \widetilde{R}_{\Delta}^T B_{\Delta, D}^T B_{\Delta} \widetilde{R}_\Delta. \] We can see that application of $P_D$ to a vector essentially computes the difference (jump) of the dual velocity component across the subdomain boundaries and then distributes the jump to neighboring subdomains according to the scaling factor $\delta^\dagger(x)$. In fact, the dual velocity component is the only part of the vector involved in the application of $P_D$; all other components are kept zero and are added into the definition to make $P_D$ more convenient to use in the presentation of the algorithm. We also have, for any $w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}$, \[ \left< P_D w, P_D w \right>_{\widetilde{A}} = \left< B_{\Delta, D}^T B_{\Delta} {\bf w}_{\Delta}, B_{\Delta, D}^T B_{\Delta} {\bf w}_{\Delta} \right>_{A_{\Delta \Delta}}. \] The following lemma can be found essentially from \cite[Section 6]{li07}; see also \EQ{W0n}. \begin{mylemma} \label{lemma:jump} There exists a function $\Phi(H/h)$, such that for all $w \in {\widetilde{W}}_0$, \[ \left< P_D w, P_D w \right>_{\widetilde{A}} \leq \Phi(H/h) \left< w, w \right>_{\widetilde{A}}. \] \end{mylemma}
\begin{myremark} \label{remark:Phi} Just as for the positive definite elliptic problems discussed in \cite[Section~6]{li07}, for two-dimensional problems, when only subdomain corner velocities are chosen as coarse level primal variables, $\Phi(H/h) = C (H/h) (1 + \log{(H/h)})$; when both subdomain corner and edge-average velocity degrees of freedom are chosen as primal variables, $\Phi(H/h) = C H/h$. \end{myremark}
The following lemma is also used and can be found at \cite[Lemma~2.3]{paulo2003}. \begin{mylemma} \label{lemma:paul} Consider the saddle point problem: find $(\vvec{u}, p) \in \vvec{W} \bigoplus Q$, such that \begin{equation} \left[ \begin{array}{cc} A & B^T \\[0.8ex] B & 0 \end{array} \right] \left[ \begin{array}{l} \vvec{u} \\[0.8ex] p \end{array} \right] =\left[ \begin{array}{l} \vvec{f} \\[0.8ex] g \end{array} \right], \end{equation} where $A$ and $B$ are as in \EQ{matrix}, $\vvec{f} \in \vvec{W}$, and $g \in Im(B) \subset Q$. Let $\beta$ be the inf-sup constant specified in \EQ{infsupMatrix}. Then \[
\| \vvec{u} \|_A \le \| \vvec{f} \|_{A^{-1}} + \frac{1}{\beta} \| g \|_{Z^{-1}}, \] where $Z$ is the mass matrix defined in Section \ref{section:FEM}. \end{mylemma}
\section{A lumped preconditioner} \label{section:lumped}
The lumped preconditioner was first used in the FETI algorithm \cite{FETI2} for solving positive definite elliptic problems. Compared with the Dirichlet preconditioner, also used for the FETI algorithm \cite{FETI4}, the lumped preconditioner is less effective in the improvement of convergence rate, but it is also less expensive in the computational costs. The main operation in the lumped preconditioner is subdomain matrix and vector products, while the implementation of the Dirichlet preconditioner requires solving subdomain systems of equations. In this paper, we discuss only the lumped preconditioner in our algorithm for solving the incompressible Stokes equation; study of the Dirichlet preconditioner will be addressed in forthcoming work.
We consider a block diagonal preconditioner for \EQ{spd}. From Corollary~\ref{coro:mass}, the inverse of the first diagonal block $G_{p_\Gamma p_\Gamma}$ of $G$ can be effectively approximated by $1/h^2$ times the identity matrix. The inverse of the second diagonal block $B_{\Delta} \widetilde{R}_\Delta \widetilde{A}^{-1} \widetilde{R}_{\Delta}^T B_{\Delta}^T$, can be approximated by the following lumped block \[ M^{-1}_\lambda = B_{\Delta, D} \widetilde{R}_\Delta \widetilde{A} \widetilde{R}_{\Delta}^T B_{\Delta, D}^T. \] This leads to the lumped preconditioner \[ M^{-1} = \left[ \begin{array}{cc} \frac{1}{h^2} I_{p_\Gamma} & \\[0.8ex] & M^{-1}_\lambda \end{array} \right], \] for solving \EQ{spd}.
\begin{myremark} The mesh size $h$ is used in the above preconditioner. For applications where the mesh size is not explicitly provided and only the coefficient matrix in~\EQ{matrix} is given, an estimate of $h$ can be obtained by comparing the nonzero entries in $A$ and $B$ blocks. From the definition of $A$ and $B$ for the incompressible Stokes problem \EQ{bilinear}, entries in $A$ and entries in $B$ have a difference of factor $h$ in general. \end{myremark}
$M^{-1}$ is symmetric positive definite. Multiplication of $M^{-1}$ by a vector requires mainly the product of $\widetilde{A}$ with a vector. When the CG iteration is applied to solve the preconditioned system \begin{equation} \label{equation:Mspd} M^{-1} G \left[ \begin{array}{c} p_\Gamma \\[0.8ex] \lambda \end{array} \right] ~ = ~ M^{-1} g, \end{equation} with zero initial guess, all the iterates belong to the Krylov subspace generated by the operator $M^{-1} G$ and the vector $M^{-1} g$, which is also a subspace of the range of $M^{-1} G$. We denote the range of $M^{-1} G$ by $R_{M^{-1} G}$. The following lemma shows that the CG iteration applied to solving \EQ{Mspd} cannot break down.
\begin{mylemma} \label{lemma:CG} Let the preconditioner $M^{-1}$ be symmetric positive definite. The CG iteration applied to solving \EQ{Mspd} with zero initial guess cannot break down. \end{mylemma}
\indent {\it Proof:~} We just need to show that for any $0 \neq x \in R_{M^{-1} G}$, $G x \neq 0$. Let $0 \neq x = M^{-1} G y$, for a certain $y \in X$ and $y \neq 0$. $G x = G M^{-1} G y$, which cannot be zero since $G y \neq 0$ and $y^T G M^{-1} G y \neq 0$. $\qquad \Box$
\begin{mylemma} \label{lemma:m1RG} Let $M^{-1}$ be symmetric positive definite. For any $x = (p_{\Gamma}, ~\lambda) \in R_{M^{-1} G}$, \[ \left<Mx,x \right> = \max_{y \in R_G, y \neq 0} \frac{\left<y,x\right>^2}{\left<M^{-1}y,y\right>}. \] \end{mylemma}
\indent {\it Proof:~} Denote the range of $M^{-\frac12}G$ by $R_{M^{-1/2} G}$. For any $x \in R_{M^{-1} G}$, \begin{eqnarray*} \left<Mx,x \right> & = & \left<M^{\frac12} x, M^{\frac12} x \right> = \max_{z \in R_{M^{-1/2} G}, z \neq 0} \frac{\left<M^{\frac12} x, z\right>^2}{\left<z, z\right>} \\ & = & \max_{y \in R_G, y \neq 0} \frac{\left<M^{\frac12} x, M^{-\frac12} y\right>^2}{\left<M^{-\frac12} y, M^{-\frac12} y\right>} = \max_{y \in R_G, y \neq 0} \frac{\left<y,x\right>^2}{\left<M^{-1}y,y\right>} ~ . \qquad \Box \end{eqnarray*}
In the following, we establish a condition number bound of the preconditioned operator $M^{-1} G$. We first have the following lemma.
\begin{mylemma}\label{lemma:upper} For any $w\in {\widetilde{W}}_0$, \[ \left<M^{-1}B_Cw,B_Cw\right>\le \Phi(H/h)\left<{\widetilde{A}} w, w\right>, \] where $\Phi(H/h)$ is as defined in Lemma \LA{jump}. \end{mylemma}
\indent {\it Proof:~} Given $w = \left( {\bf w}_I, ~q_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}_0$, let $g_{p_\Gamma} = B_{\Gamma I} {\bf w}_I + B_{\Gamma \Delta} {\bf w}_\Delta + B_{\Gamma\Pi} {\bf w}_\Pi$. We have \begin{eqnarray} \label{equation:MBW} \left<M^{-1}B_Cw,B_Cw\right> & = & \frac{1}{h^2}\left<g_{p_\Gamma}, g_{p_\Gamma} \right>+ \left(B_\Delta{\widetilde{R}}_\Delta w\right)^T M^{-1}_\lambda B_\Delta{\widetilde{R}}_\Delta w\nonumber\\ &=&\frac{1}{h^2}\left<g_{p_\Gamma}, g_{p_\Gamma} \right>+\left(B_\Delta{\widetilde{R}}_\Delta w\right)^T B_{\Delta,D}{\widetilde{R}}_{\Delta}{\widetilde{A}}{\widetilde{R}}_{\Delta}^TB_{\Delta,D}^T \left(B_\Delta{\widetilde{R}}_\Delta w\right)\nonumber\\ &=&\frac{1}{h^2}\left< g_{p_\Gamma}, g_{p_\Gamma} \right>+\left<P_D w,P_D w\right>_{\widetilde{A}}\nonumber\\ &\le&\frac{1}{h^2}\left< g_{p_\Gamma}, g_{p_\Gamma} \right>+\Phi(H/h)\left<w,w\right>_{\widetilde{A}}, \end{eqnarray} where we used Lemma \LA{jump} for the last inequality. It is sufficient to bound the first term of the right-hand side in the above inequality.
We denote $\vvec{w} = \left( {\bf w}_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in \vvec{{\widetilde{W}}}$. Since $B_{I I} \vvec{w}_I + B_{I\Delta} \vvec{w}_\Delta + B_{I\Pi} \vvec{w}_\Pi = 0$, cf.~\EQ{W0}, we have \begin{eqnarray*} \left<g_{p_\Gamma}, g_{p_\Gamma}\right> & = & \left[ \begin{array}{c} B_{I I} \vvec{w}_I + B_{I\Delta} \vvec{w}_\Delta + B_{I\Pi} \vvec{w}_\Pi \\ B_{\Gamma I} {\bf w}_I + B_{\Gamma \Delta} {\bf w}_\Delta + B_{\Gamma\Pi} {\bf w}_\Pi \end{array} \right]^T \left[ \begin{array}{c} B_{I I} \vvec{w}_I + B_{I\Delta} \vvec{w}_\Delta + B_{I\Pi} \vvec{w}_\Pi \\ B_{\Gamma I} {\bf w}_I + B_{\Gamma \Delta} {\bf w}_\Delta + B_{\Gamma\Pi} {\bf w}_\Pi \end{array} \right] \\ & = & \left<{\widetilde{B}} {\bf w}, {\widetilde{B}} {\bf w} \right>, \end{eqnarray*} where ${\widetilde{B}}$ is defined in \EQ{Btilde}. From \EQ{massmatrix} and the stability of ${\widetilde{B}}$, cf. Lemma \LA{BtildeStability}, we have \begin{eqnarray} \frac{1}{h^2}\left<g_{p_\Gamma}, g_{p_\Gamma}\right> & = & \frac{1}{h^2} \left<{\widetilde{B}} {\bf w}, {\widetilde{B}} {\bf w} \right> \leq C \left<{\widetilde{B}} {\bf w}, {\widetilde{B}} {\bf w} \right>_{Z^{-1}} = C \max_{q \in Q} \frac{\left<{\widetilde{B}} {\bf w}, q \right>^2}{\left<q, q\right>_Z} \label{equation:boundBu}\\
& \le & C \max_{q \in Q} \frac{| \vvec{w} |^2_{H^1} \| q \|^2_{L^2}}{\| q \|^2_{L^2}} = C | \vvec{w} |^2_{H^1} = C \left<w,w\right>_{\widetilde{A}}, \nonumber \end{eqnarray} where for the last equality, we used the fact that $B_{I I} \vvec{w}_I + B_{I\Delta} \vvec{w}_\Delta + B_{I\Pi} \vvec{w}_\Pi = 0$, and~\EQ{W0n}. $\quad \Box$
\begin{mylemma} \label{lemma:lower} For any given $y = (g_{p_{\Gamma}}, g_\lambda) \in R_G$, there exits $w \in {\widetilde{W}}_0$, such that $B_C w = y$, and $\left <{\widetilde{A}} w, w\right> \le \frac{C}{\beta^2} \left< M^{-1}y, y \right>$. \end{mylemma}
\indent {\it Proof:~} Given $y = (g_{p_{\Gamma}}, g_\lambda) \in R_G$, take ${\bf w}_{\Delta}^{(I)} = B_{\Delta, D}^T g_\lambda$. Let ${\bf w}^{(I)} = ({\bf 0}, ~{\bf w}_{\Delta}^{(I)}, {\bf 0}) \in {\bf W}_I \bigoplus {\bf W}_{\Delta} \bigoplus {\bf W}_\Pi$ and $w^{(I)} = ( {\bf 0}, ~0, ~{\bf w}_{\Delta}^{(I)}, ~ {\bf 0} ) \in {\bf W}_I \bigoplus Q_I \bigoplus {\bf W}_{\Delta} \bigoplus {\bf W}_\Pi$. We have \begin{equation} \label{equation:uOne}
| {\bf w}^{(I)} |^2_{H^1} = \left< A_{\Delta\Delta}{\bf w}^{(I)}_\Delta,{\bf w}^{(I)}_\Delta\right>, \end{equation} and \begin{equation} \label{equation:bcWone} B_c w^{(I)} = \left[ \begin{array}{cccc} B_{\Gamma I} & 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} \\[0.8ex] 0 & 0 & B_{\Delta} & 0 \end{array} \right] \left[ \begin{array}{c} {\bf 0} \\[0.8ex] 0 \\[0.8ex] B_{\Delta, D}^T g_\lambda \\[0.8ex] {\bf 0} \end{array} \right] = \left[ \begin{array}{c} B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] g_\lambda \end{array} \right], \end{equation} where we used the fact that $B_\Delta B_{\Delta, D}^T = I$.
We consider the solution to the following fully assembled system of linear equations of the form~\EQ{matrix}: find $({\bf w}_I^{(II)}, ~q_I^{(II)}, ~{\bf w}_{\Gamma}^{(II)}, ~q_\Gamma^{(II)}) \in {\bf W}_I \bigoplus Q_I \bigoplus {\bf W}_{\Gamma} \bigoplus Q_\Gamma$, such that \begin{equation} \label{equation:uTwo} \left[ \begin{array}{cccc} A_{II} & B_{II}^T & A_{I \Gamma} & B_{\Gamma I}^T \\[0.8ex] B_{II} & 0 & B_{I \Gamma} & 0 \\[0.8ex] A_{\Gamma I}& B_{I \Gamma} ^T& A_{\Gamma\Gamma} & B_{\Gamma \Gamma}^T \\[0.8ex] B_{\Gamma I}& 0 & B_{\Gamma \Gamma} & 0 \end{array} \right] \left[ \begin{array}{c} {\bf w}_I^{(II)} \\[0.8ex] q_I^{(II)} \\[0.8ex] {\bf w}_{\Gamma}^{(II)} \\[0.8ex] q_{\Gamma}^{(II)} \end{array} \right] = \left[ \begin{array}{l} {\bf 0} \\[0.8ex] -B_{I\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] {\bf 0} \\[0.8ex] g_{p_{\Gamma}}-B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \end{array} \right] \mbox{ , } \end{equation} where a particular right-hand side is chosen. We first note that, since $(g_{p_{\Gamma}}, g_\lambda) \in R_G$, the right-hand side vector of the above system satisfies, cf. \EQ{Grange}, \[ ( -B_{I\Delta}{\bf w}^{(I)}_\Delta )^T 1_{p_I} + ( g_{p_{\Gamma}}-B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta )^T 1_{p_\Gamma} = g_{p_{\Gamma}}^T 1_{p_\Gamma} - g_\lambda^T B_{\Delta, D} \left( B_{I\Delta}^T 1_{p_I} + B_{\Gamma\Delta}^T 1_{p_\Gamma} \right) = 0, \] i.e., it has zero average, which implies existence of the solution to \EQ{uTwo}.
Denote ${\bf w}^{(II)} = ( {\bf w}_I^{(II)}, ~{\bf w}_{\Gamma}^{(II)} ) \in {\bf W}$. From the inf-sup stability of the original problem \EQ{matrix} and Lemma \ref{lemma:paul}, we have \begin{equation} \label{equation:uIbound}
| {\bf w}^{(II)} |^2_{H^1} \leq \frac{1}{\beta^2} \left\| \left[ \begin{array}{l}
-B_{I\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] g_{p_\Gamma}-B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \end{array} \right] \right\|^2_{Z^{-1}} \le \frac{1}{\beta^2} \left\| \left[ \begin{array}{l} B_{I\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \end{array} \right] \right\|^2_{Z^{-1}} + \frac{1}{\beta^2} \left\|\left[ \begin{array}{l} 0 \\[0.8ex] g_{p_\Gamma} \end{array} \right] \right\|^2_{Z^{-1}}. \end{equation}
The first term on the right-hand side of \EQ{uIbound} can be bounded in the same way as done in \EQ{boundBu}, and we have \begin{equation} \label{equation:uuOne}
\left\| \left[ \begin{array}{l} B_{I\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \end{array} \right] \right\|^2_{Z^{-1}} \leq C \left< A_{\Delta\Delta}{\bf w}^{(I)}_\Delta,{\bf w}^{(I)}_\Delta\right>; \end{equation} the second term can be bounded by, using \EQ{massmatrix}, \begin{equation} \label{equation:uuTwo}
\left\| \left[ \begin{array}{l} 0 \\[0.8ex] g_{p_\Gamma} \end{array} \right] \right\|^2_{Z^{-1}} \le \frac{C}{h^2} \left<g_{p_\Gamma},g_{p_\Gamma}\right>. \end{equation}
Split the continuous subdomain boundary velocity ${\bf w}_{\Gamma}^{(II)}$ into the dual part ${\bf w}_{\Delta}^{(II)} \in {\bf W}_{\Delta}$ and the primal part ${\bf w}_{\Pi}^{(II)} \in {\bf W}_{\Pi}$, and denote $w^{(II)} = ({\bf w}_I^{(II)}, ~q_I^{(II)}, ~{\bf w}_{\Delta}^{(II)}, ~{\bf w}_{\Pi}^{(II)})$. We have, from \EQ{uTwo}, \begin{equation} \label{equation:biWtwo} \left[ \begin{array}{cccc} B_{II} & 0 & B_{I \Delta} & B_{I \Pi} \end{array} \right] \left[ \begin{array}{c} {\bf w}_I^{(II)} \\[0.8ex] q_I^{(II)} \\[0.8ex] {\bf w}_{\Delta}^{(II)} \\[0.8ex] {\bf w}_{\Pi}^{(II)} \end{array} \right] = -B_{I\Delta}{\bf w}^{(I)}_\Delta, \end{equation} and \begin{equation} \label{equation:bcWtwo} B_c w^{(II)} = \left[ \begin{array}{cccc} B_{\Gamma I} & 0 & B_{\Gamma \Delta} & B_{\Gamma \Pi} \\[0.8ex] 0 & 0 & B_{\Delta} & 0 \end{array} \right] \left[ \begin{array}{c} {\bf w}_I^{(II)} \\[0.8ex] q_I^{(II)} \\[0.8ex] {\bf w}_{\Delta}^{(II)} \\[0.8ex] {\bf w}_{\Pi}^{(II)} \end{array} \right] = \left[ \begin{array}{c} g_{p_\Gamma} -B_{\Gamma\Delta}{\bf w}^{(I)}_\Delta \\[0.8ex] 0 \end{array} \right]. \end{equation}
Let $w = w^{(I)} + w^{(II)}$. We can see from \EQ{biWtwo} that $w \in {\widetilde{W}}_0$, cf.~\EQ{W0}. We can also see from \EQ{bcWone} and \EQ{bcWtwo} that $B_C w= y$. Furthermore, by \EQ{W0n}, \[
| w |^2_{\widetilde{A}}=| {\bf w}^{(I)}+ {\bf w}^{(II)}|^2_{H^1} \le | {\bf w}^{(I)} |^2_{H^1}+| {\bf w}^{(II)} |^2_{H^1} \leq \frac{C}{\beta^2} \left< A_{\Delta\Delta}{\bf w}^{(I)}_\Delta,{\bf w}^{(I)}_\Delta\right> + \frac{C}{\beta^2 h^2}\left<g_{p_\Gamma},g_{p_\Gamma}\right>, \] where we used \EQ{uOne}, \EQ{uIbound}, \EQ{uuOne}, and \EQ{uuTwo} for the last inequality.
On the other hand, we have \begin{eqnarray*} \left< M^{-1}y,y \right> & = & \frac{1}{h^2}\left<g_{p_\Gamma}, g_{p_\Gamma}\right>+ g_\lambda^T M^{-1}_{1,\lambda}g_\lambda = \frac{1}{h^2}\left<g_{p_\Gamma},g_{p_\Gamma}\right>+g_{\lambda}^T B_{\Delta,D}{\widetilde{R}}_{\Delta}{\widetilde{A}}{\widetilde{R}}_{\Delta}^TB_{\Delta,D}^Tg_{\lambda}\\ & = & \frac{1}{h^2}\left<g_{p_\Gamma},g_{p_\Gamma}\right> + \left<A_{\Delta\Delta} \vvec{w}^{(I)}_\Delta, \vvec{w}^{(I)}_\Delta\right>. \qquad \Box \end{eqnarray*}
We also need the following lemma. \begin{mylemma} \label{lemma:BcW0} For any $w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}_0$, $B_C w \in R_G$. \end{mylemma}
\indent {\it Proof:~} We know for any $\left( {\bf f}_I, ~{\bf f}_{\Delta}, ~{\bf f}_{\Pi} \right) \in \vvec{W}_I \bigoplus \vvec{W}_\Delta \bigoplus \vvec{W}_\Pi$, $g$ defined by \EQ{gvec} is in $R_G$. For any $w = \left( {\bf w}_I, ~p_I, ~{\bf w}_{\Delta}, ~{\bf w}_{\Pi} \right) \in {\widetilde{W}}_0$, from the definition of ${\widetilde{A}}$ in \EQ{AtildeBc}, there always exists $\left( {\bf f}_I, ~{\bf f}_{\Delta}, ~{\bf f}_{\Pi} \right) \in \vvec{W}_I \bigoplus \vvec{W}_\Delta \bigoplus \vvec{W}_\Pi$, such that \[ {\widetilde{A}} w = \left[ \begin{array}{l} {\bf f}_I \\[0.8ex] 0 \\[0.8ex] {\bf f}_{\Delta} \\[0.8ex] {\bf f}_\Pi \end{array} \right], \quad \mbox{i.e.,} \quad w = {\widetilde{A}}^{-1} \left[ \begin{array}{l} {\bf f}_I \\[0.8ex] 0 \\[0.8ex] {\bf f}_{\Delta} \\[0.8ex] {\bf f}_\Pi \end{array} \right]. \] Taking such $\left( {\bf f}_I, ~{\bf f}_{\Delta}, ~{\bf f}_{\Pi} \right)$, $g$ defined in \EQ{gvec} is $B_C w$. $\qquad \Box$
The following lemma is an immediate result of Lemmas \LA{lower} and \LA{BcW0}.
\begin{mylemma} \label{lemma:RGBcW0} The space $R_G$ is the same as the range of $B_C$ applied on ${\widetilde{W}}_0$. \end{mylemma}
The condition number bound of the preconditioned operator $M^{-1} G$ is given in the following theorem. \begin{mytheorem} \label{theorem:tcond} For all $x = (p_{\Gamma}, ~\lambda) \in R_{M^{-1} G}$, \[ C \beta^2 \left<Mx,x \right>\leq \left< G x,x \right> \leq \Phi(H/h) \left< Mx,x \right>, \] where $\Phi(H/h)$ is as defined in Lemma \LA{jump}, $\beta$ as in \EQ{infsupMatrix}. \end{mytheorem}
\indent {\it Proof:~} \[ \left< Gx,x\right> = x^T B_C{\widetilde{A}}^{-1}B_C^Tx= x^T B_C {\widetilde{A}}^{-1} {\widetilde{A}} {\widetilde{A}}^{-1} B_C^Tx = \left< {\widetilde{A}}^{-1} B_C^Tx, {\widetilde{A}}^{-1} B_C^Tx\right>_{{\widetilde{A}}}. \] Since ${\widetilde{A}}^{-1} B_C^Tx \in {\widetilde{W}}_0$ and $\left< \cdot, \cdot \right>_{{\widetilde{A}}}$ defines an inner product on ${\widetilde{W}}_0$, we have \begin{equation} \label{equation:Gnorm} \left< Gx,x\right> = \max_{v \in {\widetilde{W}}_0, v \neq 0} \frac{\left<v, {\widetilde{A}}^{-1} B_C^Tx \right>^2_{\widetilde{A}}}{\left<v, v \right>_{\widetilde{A}}} =\max_{v \in {\widetilde{W}}_0, v \neq 0} \frac{\left<B_Cv,x\right>^2}{\left<{\widetilde{A}} v,v\right>} . \end{equation}
{\it Lower bound:} From Lemma \ref{lemma:lower}, we know that for any given $y = (g_{p_{\Gamma}}, g_\lambda) \in R_G$, there exits $w \in {\widetilde{W}}_0$, such that $B_C w = y$ and $\left <{\widetilde{A}} w, w\right> \le \frac{C}{\beta^2} \left< M^{-1}y, y \right>$. From \EQ{Gnorm}, we have $$ \left< Gx,x\right> \ge\frac{\left<B_Cw,x\right>^2}{\left<{\widetilde{A}} w,w\right>} \ge C \beta^2 \frac{\left<y,x\right>^2}{\left<M^{-1}y,y\right>}. $$ Since $y$ is arbitrary, using Lemma \ref{lemma:m1RG}, we have $$\left< Gx,x\right> \ge C \beta^2 \max_{y \in R_G, y \neq 0} \frac{\left<y,x\right>^2}{\left<M^{-1}y,y\right>} = C \beta^2 \left<Mx,x \right>.$$
{\it Upper bound:} From \EQ{Gnorm}, Lemmas \LA{upper}, \LA{RGBcW0}, and \LA{m1RG}, we have \begin{eqnarray*} \left< Gx,x\right> & \le & \Phi(H/h)\max_{v\in {\widetilde{W}}_0, v \neq 0} \frac{\left<B_Cv,x\right>^2}{\left<M^{-1} B_Cv,B_Cv\right>} \\ & = & \Phi(H/h) \max_{y\in R_G, y \neq 0} \frac{\left<y,x\right>^2}{\left<M^{-1} y,y\right>} = \Phi(H/h) \left<Mx,x\right>. \qquad \Box \end{eqnarray*}
\begin{myremark} \label{remark:rates} From Theorem \ref{theorem:tcond} and Remark \ref{remark:Phi}, we can see that the condition number bound of the preconditioned operator $M^{-1} G$ is independent of the number of subdomains when $H/h$ is fixed. If only subdomain corner velocities are chosen as coarse level primal variables in the algorithm, the upper eigenvalue bound of the preconditioned operator depends on $H/h$ in terms of $(H/h) (1 + \log{(H/h)})$; if both subdomain corner and edge-average velocity degrees of freedom are chosen as primal variables, the upper eigenvalue bound grows as $H/h$. \end{myremark}
\begin{myremark} \label{remark:discon} With only minor modifications, the algorithm proposed in this paper and its analysis apply equally well to the discontinuous pressure case. In that situation, $p_\Gamma$ and the blocks related to it in \EQ{bigeq} can simply be replaced by the vector containing subdomain constant pressures and its corresponding blocks, respectively. The formulation of the algorithm then follows the same way as presented in Section \ref{section:Gmatrix}, and the same condition number bounds as in Theorem \ref{theorem:tcond} will be obtained. Numerical experiments of our algorithm for the discontinuous pressure case will also be reported in the next section. \end{myremark}
\begin{myremark} \label{remark:kim} The same condition number bound has been proved by Kim and Lee~\cite[with Park]{kim102, kim10} for their FETI-DP algorithms for solving incompressible Stokes equations. In their algorithms, discontinuous pressure is considered and their approaches do not apply to the continuous pressure case. \end{myremark}
\begin{myremark} \label{remark:coarse} We also note that, no additional coarse level degrees of freedom, except those necessary for solving positive definite elliptic problems, are required in our algorithm to achieve a scalable convergence rate. For example, for two-dimensional problems, it is sufficient to include only the subdomain corner velocity degrees of freedom in the coarse level problem. This represents a progress compared with earlier work, e.g., \cite{li05, li06}, where additional continuity constraints enforcing the divergence-free conditions on subdomain boundaries are required in the coarse level problem. Reduction in the coarse level problem size has also been achieved for algorithms discussed in \cite{Doh09, Doh10, kim11, kim102, kim10}, even though discontinuous pressures are considered there. \end{myremark}
\section{Numerical experiments} \label{section:numerics}
We consider solving the incompressible Stokes problem \EQ{Stokes} in the square domain $\Omega=[0,1]\times [0,1]$. Zero Dirichlet boundary condition is used. The right-hand side function $\vvec{f}$ is chosen such that the exact solution is $${\bf u}=\left[\begin{array}{c} \sin^3(\pi x)\sin^2(\pi y)\cos(\pi y)\\[0.8ex] -\sin^2(\pi x)\sin^3(\pi y)\cos(\pi x) \end{array}\right] \quad \mbox{and}\quad p=x^2-y^2. $$
The modified Taylor-Hood mixed finite element, as shown in Figure~\ref{figure:TaylorHood}, is used for the finite element solution. The preconditioned system \EQ{Mspd} is solved by the CG iteration; the iteration is stopped when the $L^2-$norm of the residual is reduced by a factor of $10^{-6}$.
Table \ref{table:M1} shows the minimum and maximum eigenvalues of the iteration matrix $M^{-1} G$, and the iteration counts. The coarse level variable space in this experiment is spanned by the subdomain corner velocities. We can see from Table \ref{table:M1} that the minimum eigenvalue is independent of the mesh size. The maximum eigenvalue is independent of the number of subdomains for fixed $H/h$; for fixed number of subdomains, it depends on $H/h$, presumably in the order of $(H/h) (1 + \log{(H/h)})$ as predicted in Remark \ref{remark:rates}.
\begin{table}[t] \caption{\label{table:M1} Solving \EQ{Mspd}, with only subdomain corner velocities in coarse space.} \centering \begin{tabular}{ccccc} \quad $H/h$ (fixed) \quad & \quad \#sub \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ 8 & $4 \times 4$ & 0.35 & 8.92 & 21 \\[1.2ex]
& $8 \times 8$ & 0.35 & 10.07 & 28 \\[1.2ex]
& $16 \times 16$ & 0.35 & 10.23 & 29 \\[1.2ex]
& $24 \times 24$ & 0.35 & 10.30 & 29 \\[1.2ex]
& $32 \times 32$ & 0.35 & 10.33 & 29 \\ \hline \\[1.2ex] \quad \#sub (fixed) \quad & \quad $H/h$ \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ $8 \times 8$ & 4 & 0.30 & 4.22 & 21 \\[1.2ex]
& 8 & 0.35 & 10.07 & 28 \\[1.2ex]
& 16 & 0.35 & 24.22 & 36 \\[1.2ex]
& 24 & 0.35 & 40.12 & 43 \\[1.2ex]
& 32 & 0.35 & 57.15 & 50 \\ \hline \\ & & & & \\ \end{tabular} \end{table}
\begin{table}[t] \caption{\label{table:M2} Solving \EQ{Mspd}, with both subdomain corner and edge-average velocities in coarse space.} \centering \begin{tabular}{ccccc} \quad $H/h$ (fixed) \quad & \quad \#sub \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ 8 & $4 \times 4$ & 0.36 & 4.29 & 17 \\[1.2ex]
& $8 \times 8$ & 0.36 & 5.29 & 21 \\[1.2ex]
& $16 \times 16$ & 0.36 & 5.56 & 21 \\[1.2ex]
& $24 \times 24$ & 0.36 & 5.61 & 21 \\[1.2ex]
& $32 \times 32$ & 0.36 & 5.64 & 21 \\ \hline \\[1.2ex] \quad \#sub (fixed) \quad & \quad $H/h$ \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ $8 \times 8$ & 4 & 0.33 & 4.00 & 18 \\[1.2ex]
& 8 & 0.36 & 5.29 & 21\\[1.2ex]
& 16 & 0.36 & 11.63 & 26 \\[1.2ex]
& 24 & 0.36 & 18.67 & 31 \\[1.2ex]
& 32 & 0.36 & 26.12 & 36 \\ \hline \end{tabular} \end{table}
For the experiment reported in Table \ref{table:M2}, the coarse level variable space is spanned by both the subdomain corner velocities and the subdomain edge-average velocity components. Even though the edge-average velocity components are not necessary for the analysis, including them in the coarse level problem improves the convergence rate, for which the maximum eigenvalue in Table \ref{table:M2} grows in the order of $H/h$, as discussed in Remark \ref{remark:rates}.
Tables \ref{table:GDM1D} and \ref{table:GDM12D} show the performance of our algorithm for solving the same problem, but using a mixed finite element with discontinuous pressure. We use a uniform mesh of triangles, shown on the left in Figure~\ref{fig:2dfem}; the velocity finite element space contains the piecewise linear functions on the mesh and the pressure is a constant on each union of four triangles as shown on the right in the figure. The same mixed finite element has also been used in \cite{li06}.
\begin{figure}
\caption{The mesh and the mixed finite element.}
\label{fig:2dfem}
\end{figure}
Comparing Tables \ref{table:M1} and \ref{table:M2} with Tables \ref{table:GDM1D} and \ref{table:GDM12D}, we can see that the convergence rates of our algorithm, using either continuous or discontinuous pressure, are quite similar.
\begin{table}[t] \caption{\label{table:GDM1D} Solving \EQ{Mspd} (using discontinuous pressure), with only corner constraints.} \centering \begin{tabular}{ccccc} \quad $H/h$ (fixed) \quad & \quad \#sub \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ 8 & $4 \times 4$ & 0.48 & 7.93 & 22 \\[1.2ex]
& $8 \times 8$ & 0.48 & 9.00 & 25 \\[1.2ex]
& $16 \times 16$ & 0.48 & 9.20 & 25 \\[1.2ex]
& $24 \times 24$ & 0.48 & 9.20 & 25 \\[1.2ex]
& $32 \times 32$ & 0.48 & 9.21 & 25 \\ \hline \\[1.2ex] \quad \#sub (fixed) \quad & \quad $H/h$ \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ $8 \times 8$ & 4 & 0.41 & 3.91 & 19 \\[1.2ex]
& 8 & 0.48 & 9.00 & 25 \\[1.2ex]
& 16 & 0.49 & 21.39 & 36 \\[1.2ex]
& 24 & 0.50 & 35.56 & 43 \\[1.2ex]
& 32 & 0.50 & 50.87 & 50 \\ \hline \end{tabular} \end{table}
\begin{table}[h] \caption{\label{table:GDM12D} Solving \EQ{Mspd} (using discontinuous pressure), with both corner and edge-average constraints.} \centering \begin{tabular}{ccccc} \quad $H/h$ (fixed) \quad & \quad \#sub \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ 8 & $4 \times 4$ & 0.48 & 3.78 & 17 \\[1.2ex]
& $8 \times 8$ & 0.49 & 4.47 & 18 \\[1.2ex]
& $16 \times 16$ & 0.49 &4.68& 19 \\[1.2ex]
& $24 \times 24$ & 0.50 & 4.77 & 19 \\[1.2ex]
& $32 \times 32$ & 0.50 & 4.80 & 19\\ \hline \\[1.2ex] \quad \#sub (fixed) \quad & \quad $H/h$ \quad & \quad $\lambda_{min}$ & \quad $\lambda_{max}$ \quad & \quad iteration \quad \\[1.2ex] \hline \\ $8 \times 8$ & 4 & 0.43 & 2.80 & 16 \\[1.2ex]
& 8 & 0.49 & 4.47 & 18\\[1.2ex]
& 16 & 0.50 & 9.85 & 26 \\[1.2ex]
& 24 & 0.50 & 16.05 & 32 \\[1.2ex]
& 32 & 0.50 & 22.67 & 37 \\ \hline \end{tabular} \end{table}
\section*{Acknowledgment} The authors are very grateful to Olof Widlund and Clark Dohrmann for their suggestion of this problem.
\end{document} | arXiv |
\begin{document}
\title{A planar calculus for infinite index subfactors} \author{ David Penneys } \date{\today} \maketitle \begin{abstract} We develop an analog of Jones' planar calculus for $II_1$-factor bimodules with arbitrary left and right von Neumann dimension. We generalize to bimodules Burns' results on rotations and extremality for infinite index subfactors. These results are obtained without Jones' basic construction and the resulting Jones projections. \end{abstract} \tableofcontents
\section{Introduction}
Jones initiated the modern theory of subfactors in \cite{MR696688}. Given a finite index $II_1$-subfactor $A_0\subseteq A_1$, he used the \underline{basic construction} to obtain the Jones tower $(A_n)_{n\geq 0}$, obtained iteratively by adding the Jones projections $(e_n)_{n\geq 1}$ which satisfy the Temperley-Lieb relations. Jones used this structure to show the index lies in the range $\set{4\cos^2(\pi/n)}{n\geq 3}\cup [4,\infty)$, and he found an example for each value.
Much initial subfactor research classified hyperfinite subfactors of small index ($[A_1\colon A_0] \leq 4$) by studying the \underline{standard invariant}, i.e., the two towers of higher relative commutants $(A_i'\cap A_j)_{i=0,1;j\geq 0}$ \cite{MR996454,MR999799,MR1145672,MR1278111}. This combinatorial data was axiomatized in three slightly different structures: paragroups \cite{MR996454}, $\lambda$-lattices \cite{MR1334479}, and planar algebras \cite{math/9909027}. When combined, these viewpoints produce strong results, e.g., standard invariants with index in $(4,5)$ are completely classified, excluding the $A_\infty$ standard invariant at each index value \cite{MR1198815} (see \cite{1007.1730,1007.2240,1109.3190,1010.3797} for more details).
Some finite index results generalize to infinite index subfactors, such as discrete, irreducible, ``depth $2$" subfactors correspond to outer (cocylce) actions of Kac algebras \cite{MR1055223,MR1387518}, and the classical Galois correspondence still holds for outer actions of infinite discrete groups and minimal actions of compact groups \cite{MR1622812}.
In his Ph.D. thesis \cite{burns}, Burns studied rotations and extremality for infinite index, since the key to isotopy invariance of Jones' planar calculus in \cite{math/9909027} is the rotation operator (also known to Ocneanu). Burns' essential observation for finite index was that the centralizer algebras $A_0'\cap A_n$ coincide with the central $L^2$-vectors: $$ A_0'\cap L^2(A_n)=\set{\zeta\in L^2(A_n)}{a\zeta=\zeta a \text{ for all }a\in A_0}. $$ Burns found an elegant formula for the rotation on $P_{n,+}=A_0'\cap \bigotimes^n_{A_0} L^2(A_1)$: $$ \rho = \sum_{\beta} L_\beta R_\beta^* $$ where $\{\beta\}$ is a Pimsner-Popa basis for $A_1$ over $A_0$, $L_\beta$ is the left creation operator, and $R_\beta^*$ is the right annihilation operator (see Definition \ref{defn:RelativeTensorProduct}). This approach was generalized in \cite{1007.3173} to define a canonical planar $*$-algebra associated to a strongly Markov inclusion of finite von Neumann algebras. Burns adapted his formula to infinite index, and he showed existence of the rotation on the central $L^2$-vectors is equivalent to approximate extremality of the subfactor.
In infinite index, $A_0'\cap A_n$ and $A_0'\cap L^2(A_n)$ do not coincide. One naturally asks:
\begin{quest}\label{quest:StandardInvariant} What is a suitable standard invariant for infinite index subfactors? \end{quest}
A definitive answer to Question \ref{quest:StandardInvariant} is not yet known. On one hand, we have the two towers of centralizer algebras $(A_i'\cap A_j)_{i=0,1;j\geq 0}$ in which we can multiply (the shift isomorphisms $A_i'\cap A_j\cong A_{i+2}'\cap A_{j+2}$ still hold by \cite{MR1387518}). On the other hand, we have the central $L^2$-vectors on which we have Burns' rotation (in the approximately extremal case) and graded multiplication in the sense of \cite{MR2732052} (tensoring of central vectors). However, the operator valued weights which replace the conditional expectations do not preserve these spaces and may not be well-defined. All this structure is necessary for a good planar calculus. We ask:
\begin{quest}\label{quest:PlanarCalculus} What is the strongest planar calculus we can define for infinite index subfactors? \end{quest}
In this paper, we propose an answer to Question \ref{quest:PlanarCalculus} using both centralizer algebras and central $L^2$-vectors. We do so in more generality, starting with a bimodule $\sb{A}H_A$ over a $II_1$-factor $A$ (one recovers the subfactor case when $A=A_0$ and $H=L^2(A_1)$). First, we set $H^n=\bigotimes_A^n H$, $Q_n=A'\cap (A^{\OP})'\cap B(H^n)$ (the centralizer algebras), and $P_n = A'\cap H^n = \set{\zeta\in H^n}{a\zeta=\zeta a\text{ for all }a\in A}$ (the central $L^2$-vectors). As mentioned above, the $P_n$'s naturally form a graded algebra $P_\bullet$ in the sense of \cite{MR2732052} under relative tensor product. We represent central vectors in $P_n$ as in \cite{MR2732052} by boxes with $n$ strings emanating from the top, and we denote graded multiplication (relative tensor product) of $\zeta_m\in P_m$ and $\zeta_n\in P_n$ by $$ \zeta_m\otimes \zeta_n = \TensorPn{m}{\zeta_m}{n}{\zeta_n}\in P_{m+n}. $$ We represent elements of $Q_n$ as boxes with strings emanating from top and bottom. For $\zeta\in P_n$, note that the creation-annihilation operator $L(\zeta)L(\zeta)^*=R(\zeta)R(\zeta)^*$ lies in $Q_n$, which we represent as $$ L(\zeta)L(\zeta)^* = \CentralVectorOperator{n}{\zeta}{\zeta}\in Q_n. $$
\begin{thm} The extended positive cones $\widehat{Q_n^+}$ (in the sense of \cite{MR534673}) naturally form an algebra $\widehat{Q_\bullet^+}$ over the operad $\mathbb{B}\mathbb{P}$ generated by the oriented tangles $$ \idn{n},\, \OperatorValuedWeight{n}{},\,\OperatorValuedWeightOp{n}{},\,\TraceOfTwo{n}{}{},\,\TraceOfTwoOp{n}{}{},\text{ and }\tensor{m}{}{n}{} $$ for $m,n\geq 0$ up to planar isotopy. (We suppress external disks, draw one thick string labelled $n$ for $n$ individual strings, and orient all strings upward unless otherwise specified.)
Moreover, the $\mathbb{B}\mathbb{P}$-algebra $\widehat{Q_\bullet^+}$ and graded algebra $P_\bullet$ are compatible: if $z\in \widehat{Q_n^+}$ and $\zeta\in P_n$, then $$
z(\omega_\zeta)=\TripleInnerProduct{\zeta}{z}{\zeta}= \TraceOfTwoBig{\zeta}{\zeta}{z} =\Tr_n(L(\zeta)L(\zeta)^*\cdot z) $$ where $\Tr_n$ is the canonical trace on $Q_n$ coming from the right $A$-action on $H^n$. (Note that the multiplication tangle only makes sense once we take the trace by \cite{MR534673}. See Theorem \ref{thm:BilinearExtension} for more details.) \end{thm}
We generalize to bimodules Burns' work on rotations: an operator $\rho$ on the central $L^2$-vectors $P_n$ is a \underline{Burns rotation} if for all left and right bounded vectors $b_1,\dots,b_n\in H$, (omitting the subscript $A$ on the tensors,) $$ \langle \rho(\zeta),b_1\otimes\cdots\otimes b_n\rangle = \langle \zeta, b_2\otimes\cdots\otimes b_n\otimes b_1\rangle. $$ Note this equation implies the uniqueness and periodicity of $\rho$ if it exists. We generalize Burns' notion of (approximate) extremality, and we prove the following theorem:
\begin{thm}\label{thm:MainTheorem} Consider the following statements (include all or none of the parenthetical statements): \item[(1)] $H^n$ is (approximately) extremal for some $n\geq 1$, \item[(2)] $H^n$ is (approximately) extremal for all $n\geq 1$, \item[(3)] The (possibly non-)unitary $\rho$ exists on $P_{2n}$ for all $n\geq 1$, and \item[(4)] The (possibly non-)unitary $\rho$ exists on $P_{2n}$ for some $n\geq 1$. \item Then $(1)\Rightarrow(2)\Rightarrow(3)\Rightarrow (4)$. If $H$ is symmetric, then $(4)\Rightarrow (1)$.
When $\rho$ exists, we represent it diagrammatically by $$ \rho^m(\zeta)=\Rotation{m}{n}{\zeta} \text{ for } \zeta\in P_{m+n}, $$ (well-defined by Corollary \ref{cor:POperad}) and these diagrams are compatible with the diagrams above in the sense of Theorem \ref{thm:MoveAround}. \end{thm}
Interestingly, we find our planar structure without the use of Jones' basic construction and resulting Jones projections!
\paragraph{Outline:\\} \hspace{.03in} In Section \ref{sec:preliminaries}, we give a brief introduction to modules, the relative tensor product, extended positive cones, and operator valued weights. Subsections \ref{sec:FactsAboutRelativeTensorProduct} and \ref{sec:LemmataPositiveCones} provide some helpful, well-known results for the convenience of the reader.
In Subsection \ref{sec:TowersOfBimodules}, starting with our $A-A$ bimodule $H$, we introduce $H^n$ along with two towers of algebras $C_n,C_n^{\OP}$, a tower of centralizer algebras $Q_n=C_n\cap C_n^{\OP}$, and the central $L^2$-vectors $P_n$. We then compute formulas for the various canonical maps associated with these towers. In Subsection \ref{sec:PAoverPositiveCones}, we show the extended positive cones (in the sense of \cite{MR534673}) of the centralizer algebras $\widehat{Q_n^+}$ naturally form an algebra over an operad $\mathbb{B}\mathbb{P}$ (we use positive cones so we can ``conditionally expect" using operator valued weights). In Subsection \ref{sec:CentralVectors}, we show that the vectors in $P_\bullet$ are left and right $A$-bounded and form a graded algebra in the sense of \cite{MR2732052}. We then show the compatibility of $\widehat{Q_\bullet^+}$ and $P_\bullet$ in Subsection \ref{sec:compatible}.
Subsection \ref{sec:Extremality} defines extremality for bimodules and Burns rotations. In Subsection \ref{sec:DiagramsOfRotation}, we show how the Burns rotation fits in our planar calculus, and in Subsection \ref{sec:ExtremalityImpliesRotations}, we show that (approximate) extremality implies the existence of the Burns rotation (Theorem \ref{thm:rotation}). A converse of this theorem for symmetric bimodules is obtained in Subsection \ref{sec:symmetric}, which finishes the proof of Theorem \ref{thm:MainTheorem}.
In Section \ref{sec:Examples}, we discuss the centralizer algebras $Q_n$ and central $L^2$-vectors $P_n$ for some basic examples. In particular, in Corollaries \ref{cor:FiniteDimensional} and \ref{cor:InfiniteSymmetric}, we find an infinite index subfactor for which $\dim(Q_n)<\infty$ and $\dim(P_n)=1$ for all $n\in\mathbb{N}$. This example contrasts Burns' example of an infinite index subfactor with a type $III$ summand in a higher relative commutant \cite{burns}.
Throughout the paper, we need some technical results which have been included in a few appendices. Appendix \ref{sec:TensorUnbounded} shows that the relative tensor product of extended positive cones is well-defined and associative, which is necessary for our planar calculus. Appendix \ref{sec:BP} discusses the operad $\mathbb{B}\mathbb{P}$ which acts on the positive cones $\widehat{Q_n^+}$, including results on generating sets of tangles, standard form of tangles, and well-definition of the action. In Appendix \ref{sec:cones}, we axiomatize the notion of \underline{extended positive cone} to make rigorous the idea of a planar algebra over such objects. The main intricacy is that we must make multiplication by $\infty_\mathbb{R}$ well-defined.
\paragraph{Future research:\\} \hspace{.01in} The annular Temperley-Lieb category, especially the rotation, played an important role in the construction of certain exotic finite index subfactors \cite{0902.1294,0909.4099}. In a future paper with Jones, we will incorporate the odd Jones projections for infinite index (see \cite{burns}) into the planar calculus, and we will give the analog of the annular Tempeley-Lieb category for infinite index. We hope this viewpoint will be as fruitful as in the finite index case.
The results of this paper should generalize to bimodules over an arbitrary finite von Neumann algebra. As it requires substantial calculations while obscuring the main new ideas presented here, this generalization will appear in a future paper.
Finally, it would be interesting to try to connect Connes' results on self-dual positive cones \cite{MR0377533} to the extended positive cones axiomatized in Appendix \ref{sec:cones}.
\paragraph{Acknowledgements:\\} \hspace{.09in}The author would like to thank Stephen Curran, Steven Deprez, Michael Hartglass, Vaughan Jones, Scott Morrison, Jean-Luc Sauvageot, J. Owen Sizemore, and Makoto Yamashita for many helpful conversations. The author would like to thank Vaughan Jones again for giving him this project and for his supervision while completing his Ph.D. at the University of California, Berkeley.
This majority of this work was completed at the Institut Henri Poincar\'{e} during the trimester on von Neumann algebras and ergodic theory of groups actions. The author would like to thank the organizers Damien Gaboriau, Sorin Popa, and Stefaan Vaes for their support during this time. The author was also supported by DOD-DARPA grant HR0011-11-1-0001.
\section{Preliminaries}\label{sec:preliminaries}
\begin{nota} \item[$\bullet$] Throughout this paper, a \underline{trace} on a finite von Neumann algebra means a faithful, normal, tracial state unless otherwise specified. \item[$\bullet$] $A$ will always denote a finite von Neumann algebra with trace $\tr_A$. \item[$\bullet$] We use the notation $\widehat{a}$ to denote the image of $a\in A$ in $L^2(A,\tr_A)$. \item[$\bullet$] For a semifinite von Neumann algebra $M$ with normal, faithful, semifinite (n.f.s.) trace $\Tr_M$, we write \begin{align*} \mathfrak{n}_{\Tr_M}&=\set{x\in M}{\Tr_M(x^*x)<\infty}\text{ and}\\ \mathfrak{m}_{\Tr_M}&= \mathfrak{n}_{\Tr_M}^*\mathfrak{n}_{\Tr_M} = \spann\set{x^* y}{x,y\in \mathfrak{n}_{\Tr_M}}. \end{align*} \end{nota}
\subsection{Modules and the relative tensor product}\label{sec:RelativeTensorProduct} This exposition follows \cite{MR561983,MR703809,MR1278111,MR1387518,MR1424954,MR1753177,burns}.
\begin{defn}[Left modules]\label{defn:LeftModule} If $\sb{A}K$ is a left Hilbert A-module, then the set of left $A$-bounded vectors is given by
$$D(\sb{A}K)=\set{\eta\in K}{\|a\eta\|_2\leq \lambda \|a\|_2 \text{ for some }\lambda\geq 0},$$ and each $\eta\in D(\sb{A}K)$ gives a bounded map $R(\eta)\colon L^2(A)\to H$ by the extension of $\widehat{a}\mapsto a\eta$.
For $\eta_1,\eta_2\in D(\sb{A}K)$, we have an $A$-valued inner product given by $\sb{A}\langle \eta_1,\eta_2\rangle = JR(\eta_1)^*R(\eta_2)J\in A$ satisfying \begin{enumerate} \item[(1)] ${\sb{A}\langle} a\eta_1 + \eta_2,\eta_3\rangle= a {\sb{A}\langle}\eta_1,\eta_3\rangle+{\sb{A}\langle}\eta_2,\eta_3\rangle$, \item[(2)] ${\sb{A}\langle} \eta_1, \eta_2\rangle^* = {\sb{A}\langle} \eta_2,\eta_1\rangle$, and \item[(3)] ${\sb{A}\langle} x \eta_1, \eta_2\rangle={\sb{A}\langle} \eta_,x^* \eta_2\rangle$ \end{enumerate} for all $a\in A$, $x\in A'\cap B(K)$, and $\eta_1,\eta_2,\eta_3\in D(\sb{A}K)$ (note $x\eta_i\in D(\sb{A}K)$).
An $\sb{A}K$-basis is a set of vectors $\{\alpha\}\subset D(\sb{A}K)$ such that $$ \sum\limits_\alpha R(\alpha)R(\alpha)^* = 1_K \Longleftrightarrow \sum_\alpha {\sb{A}\langle}\eta ,\alpha\rangle\alpha = \eta\text{ for all }\eta\in D(\sb{A}K). $$ $\sb{A}K$-bases exist by \cite{MR561983}.
The canonical trace on $A'\cap B(K)$ is given by $\Tr_{A'\cap B(K)}(x)= \sum_\alpha \langle x \alpha,\alpha\rangle$ where $\{\alpha\}$ is any $\sb{A}K$ basis.
If $\eta\in D(\sb{A}K)$, then $\Tr_{A'\cap B(K)}(R(\eta)R(\eta)^*)=\tr_A(\sb{A}{\langle} \eta,\eta\rangle)=\|\eta\|^2_2$. \end{defn}
\begin{defn}[Right modules]\label{defn:RightModule} A right Hilbert $A$-module is the same as a left Hilbert $A^{\OP}$-module. If $H_A$ is a right Hilbert $A$-module, we write $\xi a$ for $a^{\OP} \xi$ for all $a^{\OP}\in A^{\OP}$. We get parallel definitions:
The set of right $A$-bounded vectors is given by
$$D(H_A)=\set{\xi\in H}{\|\xi a\|_2\leq \lambda \|a\|_2 \text{ for some }\lambda\geq 0}.$$ Each $\xi \in D(H_A)$ defines a bounded map $L(\xi)\colon L^2(A)\to H$ by the extension of $\widehat{a}\mapsto \xi a$.
For $\xi_1,\xi_2\in D(H_A)$, we have an $A$-valued inner product given by $\langle \xi_1|\xi_2\rangle_A = L(\xi_1)^*L(\xi_2)\in A$ satisfying \begin{enumerate}
\item[(1)] $\langle \xi_1 | \xi_2 a + \xi_3\rangle_A=\langle \xi_1 | \xi_2\rangle_A a+\langle \xi_1 |\xi_3\rangle_A$,
\item[(2)] $\langle \xi_1 | \xi_2\rangle_A^* = \langle \xi_2 | \xi_1\rangle_A$, and
\item[(3)] $\langle x\xi_1 | \xi_2\rangle_A=\langle \xi_1 | x^*\xi_2\rangle_A$ \end{enumerate} for all $a\in A$, $x\in (A^{\OP})'\cap B(H)$, and $\xi_1,\xi_2,\xi_3\in D(H_A)$ (note $x\xi_i\in D(H_A)$).
An $H_A$-basis is a set of vectors $\{\beta\}\subset D(H_A)$ such that $$
\sum\limits_\beta L(\beta)L(\beta)^* = 1_H\Longleftrightarrow \sum_\beta \beta \langle \beta|\xi\rangle_A = \xi \text{ for all } \xi\in D(H_A). $$ $H_A$-bases exist by \cite{MR561983}.
The canonical trace on on $(A^{\OP})'\cap B(H)$ is given by $\Tr_{(A^{\OP})'\cap B(H)}(x)= \sum_\beta \langle x \beta,\beta\rangle$ where $\{\beta\}$ is any $H_A$ basis.
If $\xi\in D(H_A)$, then $\Tr_{(A^{\OP})'\cap B(H)}(L(\xi)L(\xi)^*)=\tr_A(\langle \xi|\xi\rangle_A)=\|\xi\|^2_2$. \end{defn}
\begin{defn}[Relative tensor product]\label{defn:RelativeTensorProduct} The relative tensor product $H\otimes_A K$ is given by one of the three equivalent definitions:
\item[(1)] the completion of the algebraic tensor product $D(H_A)\odot_A K$ under the pseudo-norm induced by the sesquilinear form $\langle \xi\odot \eta, \xi'\odot \eta'\rangle = \langle \langle \xi'|\xi\rangle_A \eta,\eta'\rangle$, \item[(2)] the completion of the algebraic tensor product $H \odot_A D(\sb{A} K)$ under the pseudo-norm induced by the sesquilinear form $\langle \xi\odot \eta, \xi'\odot \eta'\rangle = \langle \xi_1{\sb{A}\langle} \eta_1,\eta_2\rangle, \xi_2\rangle_H$, or \item[(3)] the completion of the algebraic tensor product $D(H_A)\odot_A D(\sb{A} K)$ under the pseudo-norm induced by the sesquilinear form $$
\langle \xi_1\odot \eta_1,\xi_2\odot \eta_2\rangle = \langle \xi_1{\sb{A}\langle} \eta_1,\eta_2\rangle, \xi_2\rangle_H= \langle \langle \xi_2|\xi_1\rangle_A \eta_1,\eta_2\rangle_K . $$ The image of $\xi\odot \eta$ in $H\otimes_A K$ is denoted $\xi\otimes \eta$. (This notation avoids confusion with the operators $x\otimes_A y$ as in Lemma \ref{lem:binormal}.)
Given $\xi\in D(H_A)$ and $\eta\in D(\sb{A} K)$, we get bounded creation operators $L_\xi \colon K\to H\otimes_A K$ by $\eta'\mapsto \xi\otimes \eta'$ and $R_\eta \colon H\to H\otimes_A K$ by $\xi'\mapsto \xi'\otimes \eta$, whose adjoints are the annihilation operators given by
$L_\xi^*(\xi'\otimes\eta')=\langle \xi|\xi'\rangle_A \eta'$ and $R_\eta^*(\xi'\otimes \eta')=\xi'{\sb{A}\langle} \eta',\eta\rangle$. \end{defn}
\begin{defn}[Fiber product, \cite{MR799587,MR1753177}]\label{defn:FiberProduct} Suppose $A^{\OP}\subset M_1\subset B(H)$ and $A\subset M_2\subset B(K)$. Then we define $$ M_1'\otimes_A M_2' = \set{x\otimes_A y}{x\in M_1'\text{ and } y\in M_2'}\subset B(H\otimes_A K) $$ (see Appendix \ref{sec:TensorUnbounded} and Lemma \ref{lem:binormal}), and the fiber product of $M_1$ and $M_2$ over $A$ is given by $M_1 \star_A M_2 = (M_1' \otimes_A M_2')'$. The fiber product satisfies: \item[$\bullet$] $(M_1 \star_A M_2) \cap (N_1 \star_A N_2) = (M_1\cap N_1)\star_A (M_2\cap N_2)$ and \item[$\bullet$] $M_1 \star_A A = ((A^{\OP})'\cap M_1) \otimes_A 1_K$ and $A^{\OP}\star_A M_2 = 1_H \otimes_A (A'\cap M_2)$. \item In particular, $$ (B(H)\star_A A)'=((A^{\OP})'\otimes_A 1_K)'=A^{\OP} \star_A B(K)=1_H \otimes_A A'. $$ \end{defn}
\subsection{Some easy facts about the relative tensor product}\label{sec:FactsAboutRelativeTensorProduct} The following are well-known to experts, but we reproduce them here for the sake of completeness and the reader's convenience. For this subsection, $H_A$ is a right Hilbert $A$-module, and $\sb{A}K$ is a left Hilbert $A$-module unless otherwise stated.
\begin{lem}\label{lem:UnitaryBases} Suppose $\{\beta\}$ is an $H_A$-basis. Then if $u\in U((A^{\OP})'\cap B(H))$, $\{u\beta\}$ is another $H_A$-basis. If $v\in U(A)$, then $\{\beta v\}$ is also an $H_A$-basis. A similar result holds for left modules. \end{lem} \begin{proof} For $u\in (A^{\OP})'\cap B(H)$, $L( u \beta)L(u\beta)^*=uL(\beta) L(\beta)^* u^*$. Thus $$ \sum_{u\beta}L(u\beta)L(u\beta)^*=u\left(\sum_{\beta} L(\beta)L(\beta)^*\right) u^* = 1_H. $$ If $v\in U(A)$, then $L(\beta v) L(\beta v^*)=L(\beta) v v^*L(\beta)^*=L(\beta)L(\beta)^*$, and the result follows. \end{proof}
\begin{lem}\label{lem:remove}
Let $\xi_1,\xi_2\in D(H_A)$ and $\eta_1,\eta_2\in D(\sb{A}K)$. Then $L_{\xi_1}^*L_{\xi_2}\in B(K)$ is left multiplication by $\langle \xi_1|\xi_2\rangle_A$ and $R_{\eta_1}^*R_{\eta_2}\in B(H)$ is right multiplication by $\sb{A}{\langle} \eta_1,\eta_2\rangle$. \end{lem} \begin{proof} $\langle L_{\xi_1}^* L_{\xi_2} \eta_1,\eta_2\rangle = \langle \xi_2\otimes \eta_1, \xi_1\otimes \eta_2\rangle
= \langle \langle \xi_1 | \xi_2\rangle_A \eta_1, \eta_2\rangle $. The other is as trivial. \end{proof}
\begin{lem} If $\{\beta\}$ is an $H_A$-basis, then $\sum_\beta L_\beta L_\beta^* = 1_{H\otimes_A K}$. Similarly, if $\{\alpha\}$ is an $\sb{A}H$-basis, then $\sum_\alpha R_\alpha R_\alpha^*=1_{H\otimes_A K}$. \end{lem} \begin{proof} We prove the first statement. Suppose $\xi\in D(H_A)$ and $\eta\in D(\sb{A}K)$. Then $$
\sum_\beta L_\beta L_\beta^*( \xi\otimes \eta )= \sum_\beta L_\beta (L_\beta^* L_\xi) \eta=\sum_\beta\beta \langle \beta|\xi\rangle_A \otimes \eta=\xi\otimes \eta. $$ \end{proof}
\begin{lem}\label{lem:RN} Suppose $\eta\in {\sb{A}K}$ and $\eta'\in D(\sb{A}K)$. Then there is a unique $\sb{A}\langle \eta',\eta\rangle\in L^2(A)\subset L^1(A)$ such that $\langle a \eta,\eta'\rangle_K = \langle a, {\sb{A}\langle} \eta',\eta\rangle\rangle_{L^2(A)}$ for all $a\in A$. A similar result holds for right modules. \end{lem} \begin{proof} If $\xi\in D(\sb{A}K)$, this is just the usual Radon-Nikodym derivative, and \begin{align*}
\|{\sb{A}\langle} \eta',\eta \rangle\|_2
& =\sup_{a\in A, \|\widehat{a}\|_2\leq 1} |\langle \widehat{a}, {\sb{A}\langle}\eta',\eta\rangle^{\widehat{\hspace{.07in}}}\rangle_{L^2(A)}|
= \sup_{a\in A, \|\widehat{a}\|_2\leq 1} \tr ({\sb{A}\langle}\eta,\eta'\rangle a) \\
& = \sup_{a\in A, \|\widehat{a}\|_2\leq 1} |\langle a \eta,\eta'\rangle_K|
\leq \left(\sup_{a\in A, \|\widehat{a}\|_2\leq 1} \|a^* \eta'\|_2 \right)\|\eta\|_2
\leq \lambda \|\eta\|_2 \end{align*}
for some $\lambda>0$ depending only on $\eta'$ as $\eta'\in D(\sb{A}K)$. Now if $\eta\notin D(\sb{A}K)$, take $\eta_n\in D(\sb{A}K)$ with $\eta_n\to \eta$ in $\|\cdot\|_2$, and define $$ \sb{A}\langle \eta' ,\eta\rangle = \lim_n {\sb{A}\langle} \eta',\eta_n\rangle $$ which exists by the above estimate. Now $\langle a \eta,\eta'\rangle_K = \langle \widehat{a}, {\sb{A}\langle} \eta',\eta\rangle\rangle_{L^2(A)}$ for all $a\in A$ by construction. \end{proof}
\begin{cor} Each $\eta \in {\sb{A}K}$ gives a closable operator $R(\eta)^0\colon \widehat{A}\to {\sb{A}K}$ by $\widehat{a}\mapsto a\eta$. A similar result holds for right modules. \end{cor} \begin{proof} We need only show its adjoint is densely defined. If $\eta'\in D(\sb{A}K)$, then $$ \langle R(\eta)^0 \widehat{a} , \eta'\rangle_K = \langle a\eta,\eta'\rangle_K = \langle \widehat{A} , {\sb{A}\langle} \eta',\eta\rangle \rangle_{L^2(A)} $$ by Lemma \ref{lem:RN}, and the result follows as $D(\sb{A}K)$ is dense in $K$. \end{proof}
\begin{cor}\label{cor:UnboundedLR} Each $\eta\in {\sb{A}K}$ gives a closable unbounded operator $R_\eta^0\colon D(H_A)\to H\otimes_A K$ by $\xi\mapsto \xi\otimes \eta$. A similar result holds for each $\xi'\in H_A$. \end{cor} \begin{proof} Once again, we show its adjoint is densely defined. If $\xi'\in D(H_A)$ and $\eta'\in D(\sb{A}K)$, then by Lemma \ref{lem:RN}, \begin{align*} \langle R_\eta^0 \xi , \xi'\otimes \eta' \rangle_{H\otimes_A K} & = \langle \xi\otimes \eta, \xi'\otimes \eta'\rangle_{H\otimes_A K}
= \langle \langle \xi'|\xi\rangle_A \eta,\eta'\rangle_K
= \langle \langle \xi'|\xi\rangle_A^{\widehat{\hspace{.07in}}}, {\sb{A}\langle} \eta',\eta\rangle^{\widehat{\hspace{.07in}}} \rangle_{L^2(A)}\\ & = \langle L(\xi')^* \xi, {\sb{A}\langle} \eta',\eta\rangle^{\widehat{\hspace{.07in}}} \rangle_{L^2(A)} = \langle \xi, L(\xi'){\sb{A}\langle} \eta',\eta\rangle^{\widehat{\hspace{.07in}}} \rangle_{H}. \end{align*} The result now follows as $D(H_A)\otimes_A D(\sb{A}K)$ is dense in $H\otimes_A K$. \end{proof}
\subsection{Haagerup's extended positive cones and operator valued weights}\label{sec:MR534673}
For this subsection, $M$ is a von Neumann algebra acting on a Hilbert space $H$.
\begin{defn}[Section 1 of \cite{MR534673}] The extended positive cone of $M$, denoted $\widehat{M^+}$, is the set of weights on the predual of $M$, i.e., maps $m\colon M_*^+\to [0,\infty]$ such that \item[(1)] $m(\lambda \phi+\psi) = \lambda m(\phi)+m(\psi)$ for all $\lambda\geq 0$ and $\phi,\psi\in M_*^+$, and \item[(2)] $m$ is lower semicontinuous. \item The extended positive cone has additional structure: \item[$\bullet$] There is a natural inclusion $M^+\to\widehat{M^+}$ by $m\mapsto (\phi\mapsto \phi(m))$. \item[$\bullet$] For $m\in \widehat{M^+}$ and $a\in M$, we define $a^*ma\in \widehat{M^+}$ by $$a^*ma(\phi)=m(a\phi a^*)=m(\phi(a^*\, \cdot\,a)).$$ We write $\lambda m$ for $\lambda^{1/2}m\lambda^{1/2}$ for $\lambda\geq 0$. \item[$\bullet$] There is a natural partial ordering on $\widehat{M^+}$ given by $m_1\leq m_2$ if $m_1(\phi)\leq m_2(\phi)$ for all $\phi\in M_*^+$. \item[$\bullet$] If $I$ is a directed set, we say $(m_i)_{i\in I}\subset\widehat{M^+}$ \underline{increases} to $m\in\widehat{M^+}$ if $i\leq j$ implies $m_i\leq m_j$ and $\sup_{i} m_i(\phi)= m(\phi)$ for all $\phi\in M_*^+$. Hence we can define the sum of elements of $\widehat{M^+}$ pointwise. \item[$\bullet$] Each $\phi\in M_*^+$ extends uniquely to a map $\widehat{M^+}\to[0,\infty]$ by $\phi(m)=m(\phi)$. \end{defn}
\begin{rem}[Section 1 of \cite{MR534673}] There are equivalent definitions of $\widehat{M^+}$: \item[$\bullet$] Given a projection $p\in P(M)$ and a densely-defined positive, self-adjoint operator $S$ in $K=pH$ affiliated with $M$, we can define \begin{equation}\label{eq:KS} m_{(K,S)}(\omega_\xi) = \begin{cases}
\|S^{1/2}\xi\| & \text{ if }\xi\in D(S^{1/2})\\ \infty & \text{ else} \end{cases} \end{equation} where $\omega_\xi = \langle \cdot\, \xi,\xi\rangle$. Conversely, given $m\in \widehat{M^+}$, there are unique $(K,S)$ such that Equation \eqref{eq:KS} holds. In the sequel, we will write $m=(K,S)$ when we use this bijective correspondence. \item[$\bullet$] Each $m\in \widehat{M^+}$ has a unique spectral resolution $$ m(\phi) = \int_0^\infty \lambda d \phi(e_\lambda) + \infty \phi(p) $$ where $\{e_\lambda\}_{\lambda\in [0,\infty)}$ are increasing family of projections in $M$ such that: \begin{enumerate} \item[(1)] $\lambda\mapsto e_\lambda$ is strongly continuous from the right, and \item[(2)] $p=1-\lim_{\lambda\to\infty} e_\lambda$ \end{enumerate} Moreover, \begin{align*} e_0 = 0 &\Longleftrightarrow m(\phi)>0 \text{ for all } \phi \in M_*^+\setminus\{0\}\\ p=0 &\Longleftrightarrow \set{\phi\in M_*^+}{m(\phi)<\infty} \text{ is dense in } M_*^+. \end{align*} \item[$\bullet$] Every $m\in \widehat{M^+}$ is a pointwise limit of an increasing sequence of operators in $M^+$. \item[$\bullet$] $\widehat{M^+}$ is the set of all $m\in \widehat{B(H)^+}$ affiliated to $M$ ($umu^*=m$ for all $u\in U(M')$). \end{rem}
\begin{thm}[\cite{MR534673}, Proposition 1.11, Theorem 1.12]\label{thm:BilinearExtension} Suppose $M$ is a semifinite von Neumann algebra with n.f.s. trace $\Tr_M$. For $x,y\in M^+$, let $\Tr_M(x\cdot y) =\Tr_M(x^{1/2}yx^{1/2})$. Then the map $(x,y)\mapsto \Tr_M(x\cdot y)$ has a unique extension to $\widehat{M^+}\times\widehat{M^+}$ such that \item[$\bullet$] $\Tr_M(x\cdot y) = \Tr_M(y\cdot x)$ for all $x,y\in \widehat{M^+}$, \item[$\bullet$] $\Tr_M$ is additive and homogeneous in both variables, \item[$\bullet$] if $(x_i),(y_j)\subset \widehat{M^+}$ with $x_i\nearrow x$ and $y_j\nearrow y$, then $\Tr_M(x_i\cdot y_j)\nearrow \Tr_M(x\cdot y)$, and \item[$\bullet$] $\Tr_M((a^*xa)\cdot y) = \Tr_M(x\cdot(aya^*))$ for all $x,y\in \widehat{M^+}$ and $a\in M$. \item Moreover \item[$\bullet$] The map $x\mapsto \Tr(x\,\cdot\,)$ is a homogeneous, additive bijection from $\widehat{M^+}$ onto the set of normal weights of $M$, \item[$\bullet$] $x\leq y\Longleftrightarrow \Tr(x\,\cdot\,)\leq \Tr(y\,\cdot\,)$ and $x_i\nearrow x\Longleftrightarrow \Tr(x_i\,\cdot\,)\nearrow \Tr(x\,\cdot\,)$, and \item[$\bullet$] If $x = \int_0^\infty \lambda \, de_\lambda+\infty p$, then $\Tr(x\,\cdot\,)$ is faithful if and only if $e_0=0$ and semifinite if and only if $p=0$. \end{thm}
\begin{defn}[\cite{MR534673}, Definitions 2.1 and 2.2] Let $M$ and $N$ be von Neumann algebras $N\subseteq M$. An operator valued weight from $M\to N$ is a map $T\colon M^+\to \widehat{N^+}$ which satisfies the following conditions: \item[(1)] $T(\lambda x+ y) = \lambda T(x)+T(y)$ for all $\lambda \geq 0$ and $x,y\in M^+$, and \item[(2)] $T(a^*xa)=a^*T(x)a$ for all $x\in M^+$ and $a\in N$. \item As in the case of ordinary weights, we set \begin{align*} \mathfrak{n}_T &= \set{x\in M}{T(x^*x)\in N^+}\text{ and }\\ \mathfrak{m}_T &=\mathfrak{n}_T^*\mathfrak{n}_T=\spann\set{x^*y}{x,y\in\mathfrak{n}_T}. \end{align*} \item Moreover, we say $T$ is: \item[$\bullet$] \underline{normal} if $x_i\nearrow x \Rightarrow T(x_i)\nearrow T(x)$ for all $x_i,x\in M^+$, \item[$\bullet$] \underline{faithful} if $T(x^*x)=0 \Rightarrow x=0$ for all $x\in M^+$, and \item[$\bullet$] \underline{semifinite} if $\mathfrak{n}_T$ is $\sigma$-weakly dense in $M$. \item We will abbreviate normal, faithful, semifinite by the acronym n.f.s. \end{defn}
\begin{rems} \item[(1)] $T$ is a conditional expectation if and only if $T(1)=1$. \item[(2)] If $T$ is normal, it has a unique extension to $\widehat{M^+}$ satisfying (1) and (2). \item[(3)] $\mathfrak{n}_T$ is a left-ideal and $\mathfrak{n}_T,\mathfrak{m}_T$ are algebraic $N-N$ bimodules. By polarization, $T$ extends to a map $T\colon\mathfrak{m}_T\to N$, and $T(axb)=aT(x)b$ for all $x\in \mathfrak{m}_T$ and $a,b\in N$. \end{rems}
\begin{thm}[\cite{MR534673}, Theorem 2.7]\label{thm:Texists} Given an inclusion $N\subseteq M$ of semifinite von Neumann algebras with n.f.s. traces $\Tr_N,\Tr_M$ respectively. Then there is a unique n.f.s. trace-preserving operator valued weight $T\colon M^+\to \widehat{N^+}$. Moreover, if $x\in M^+$, $T(x)$ is the unique element of $\widehat{N^+}$ such that \begin{equation}\label{eq:ovwCondition} \Tr_M(y\cdot x)=\Tr_N(y\cdot T(x))\text{ for all }y\in N^+ \end{equation} (where we also write $\Tr_N$ for the unique extension of $\Tr_N$ to $\widehat{N^+}$). \end{thm}
\begin{defn} For $N\subseteq M$ an inclusion of von Neumann algebras, we write \item[$\bullet$] $\mathcal{P}(M,N)$ for the set of n.f.s. operator valued weights $M^+\to \widehat{N^+}$, and \item[$\bullet$] $\mathcal{P}_0(M,N)\subseteq \mathcal{P}(M,N)$ for the set of operator valued weights whose restriction to $N'\cap M$ is semifinite. \end{defn}
\begin{lem}[\cite{MR1622812}, Lemma 2.5 and Proposition 2.8, \cite{MR1297671}, Corollary 28]\label{lem:SemifiniteRestriction} Let $N\subset M$ be an inclusion of semifinite von Neumann algebras. \item[(1)] There is a unique central projection $z\in N'\cap M$ such that \begin{enumerate} \item[$\bullet$] $\mathcal{P}_0(pMp,pN)=\emptyset$ for all $p\in N'\cap M$, $p\leq (1-z)$ and \item[$\bullet$] $\mathcal{P}_0(zMz,zN)=\mathcal{P}(zMz,zN)$. \end{enumerate} Moreover, for all $T\in\mathcal{P}(M,N)$, \begin{enumerate} \item[$\bullet$] $(1-z)(N'\cap M)\cap \mathfrak{m}_T=\{0\}$, and
\item[$\bullet$] $T|_{z(N'\cap M)}$ is semifinite. \end{enumerate} \item[(2)] If $\mathcal{P}_0(M,N)\neq \emptyset$ and $\mathcal{P}_0(N',M')\neq \emptyset$, then $N'\cap M$ is a direct sum of type $I$ factors, and $pN\subset pMp$ has finite index for every finite rank $p\in N'\cap M$. \end{lem}
\subsection{Useful lemmata on extended positive cones}\label{sec:LemmataPositiveCones}
For this subsection, $M$ is a von Neumann algebra acting on a Hilbert space $H$.
\begin{lem}\label{lem:parallelogram} For $m\in \widehat{M^+}$ and $\eta,\xi\in H$, the parallelogram identity holds: $$ m(\omega_{\eta+\xi})+m(\omega_{\eta-\xi})= 2m(\omega_{\eta})+2m(\omega_{\xi}). $$ \end{lem} \begin{proof} Take $(x_i)\subset M^+$ with $x_i$ increasing to $m$. Then \begin{align*} m(\omega_{\eta+\xi})+m(\omega_{\eta-\xi}) & = \sup_{i,j} \bigg( x_i(\omega_{\eta+\xi})+x_j(\omega_{\eta-\xi}) \bigg)\\ & \leq \sup_{i,j} \bigg(\sup_{k\geq i,j}\bigg(x_k(\omega_{\eta+\xi})+x_k(\omega_{\eta-\xi}) \bigg)\bigg)\\ & = \sup_{i,j} \bigg(\sup_{k\geq i,j}\bigg( 2x_k(\omega_{\eta})+2x_k(\omega_{\xi})\bigg)\bigg)\\ & \leq \sup_{i',j'} \bigg( 2x_{i'}(\omega_{\eta})+2x_{j'}(\omega_{\xi})\bigg) = 2m(\omega_{\eta})+2m(\omega_{\xi}). \end{align*} The other inequality is proved similarly. \end{proof}
\begin{lem}\label{lem:VectorStates} \item[(1)] $m_1\leq m_2$ if and only if $m_1(\omega_\xi)\leq m_2(\omega_\xi)$ for all $\xi\in H$. \item[(2)] $(m_i)_{i\in I}$ increases to $m$ if and only if $i\leq j$ implies $m_i\leq m_j$ and $\sup_i m_i(\omega_\xi) = m(\omega_\xi)$ for all $\xi\in H$. \item[(3)] If $(m_i)_{i\in I}$ increases to $m$ and $a\in M^+$, then $a^*m_i a$ increases to $a^*ma$. \end{lem} \begin{proof} First, note every $\phi\in M_*^+$ is a sum of functionals $\omega_{\xi_k} = \langle \cdot\, \xi_k,\xi_k\rangle$ for $\xi_i\in H$. \item[(1)] Follows immediately by lower semicontinuity of $m\in \widehat{M^+}$. \item[(2)] Suppose $\phi = \sum_k \omega_{\xi_k}$. By lower semicontinuity, \begin{align*} m(\phi) & = \sum_{k} m(\omega_{\xi_k}) = \sum_k \sup_i m_i(\omega_{\xi_k})\\ & \geq \sup_i \sum_km_i(\omega_{\xi_k}) = \sup_i m_i\left(\sum_k \omega_k\right) = \sup_i m_i(\phi). \end{align*} There are two cases: \itt{Case 1} Suppose $m(\phi)=\infty$. Then there is a $\varepsilon>0$ such that $\sup_i m_i(\omega_{\xi_k})>\varepsilon$ for infinitely many $k$, say $(k_n)$. Let $N>0$, and let $M>0$ such that $M\varepsilon>N$. Choose $j_1\in I$ such that $i\geq j_1$ implies $m_i(\omega_{k_1})>\varepsilon$. For $n=2,\dots,M$, inductively choose $j_n> j_{n-1}$ such that $i\geq j_n$ implies $m_i(\omega_{k_n})>\varepsilon$. Then for all $i>j_M$, $$ \sum_k m_i(\omega_{\xi_k}) \geq \sum_{n=1}^M m_i(\omega_{\xi_{k_n}}) \geq \sum_{n=1}^M \varepsilon = M\varepsilon>N. $$ Since $N$ was arbitrary, we must have $$\sup_i m_i(\phi)=\sup_i m_i \left( \omega_k\right)=\sup_i \sum_k m_i(\omega_k)=\infty.$$ \itt{Case 2} Suppose $m(\phi)<\infty$. Let $\varepsilon>0$. Then there is an $N\in\mathbb{N}$ such that $\sum_{k>N} m(\omega_{\xi_k})<\varepsilon$. Now as in the proof of Lemma \ref{lem:parallelogram}, $$ m(\phi)-\varepsilon < \sum_{k=1}^N \sup_i m_i(\omega_{\xi_k})= \sup_i \sum_{k=1}^N m_i(\omega_{\xi_k})\leq \sup_i \sum_k m_i(\omega_k) =\sup_i m_i(\phi), $$ and the result follows as $\varepsilon$ was arbitrary. \item[(3)] We use (2). Let $\xi\in H$. \begin{align*} a^*m_i a (\omega_\xi) &= m_i(\omega_{a\xi})\leq m_j(\omega_{a\xi})= a^* m_j a (\omega_\xi)\text{ for all } i\leq j \text{ and}\\ \sup_i a^*m_ia(\omega_\xi) &= \sup_i m_i(\omega_{a\xi})=m(\omega_{a\xi}) = a^* m a (\omega_\xi). \end{align*} \end{proof}
\begin{rem}\label{rem:sup} Suppose $(x_i)_{i\in I},(y_i)_{i\in I}\subset M^+$ are directed families and $\lambda\geq 0$. Then by Lemma \ref{lem:VectorStates} and techniques similar to those used in the proof of Lemma \ref{lem:parallelogram}, $$ \sup_{i} (\lambda x_i+y_i) = \lambda \sup_i x_i + \sup_j y_j. $$ \end{rem}
\begin{lem}\label{lem:QuadraticForm} Suppose $F\subset \widehat{M^+}$ is a directed family, i.e., if $x,y\in F$, then there is a $z\in F$ with $z\geq x$ and $z\geq y$. Then there is a unique $m_F=(K_F,S_F)\in \widehat{M^+}$ with $K_F=\overline{\Dom(S_F^{1/2})}$ such that \begin{align*} m_F(\omega_\xi)=\langle S_F^{1/2}\xi,S_F^{1/2}\xi\rangle =\sup_{x\in F} x(\omega_\xi) \text{ for all }\\ \xi \in \Dom(S_F^{1/2})=\set{\xi \in H}{ \sup_{x\in F} x(\omega_\xi)<\infty}. \end{align*} We denote $m_F$ by $\sup_{x\in F} x$. \end{lem} \begin{proof} As in \cite{MR534673, MR561983,MR1943006}, one checks that the extended quadratic form $s_F\colon H\to [0_\mathbb{R},\infty_\mathbb{R}]$ given by $s_F(\xi) = \sup_{x\in F}x(\omega_\xi)$ satisfies \begin{enumerate}
\item[(1)] $s_F(\lambda \xi)= |\lambda|^2 s_F(\xi)$, \item[(2)] $s_F(\eta+\xi)+s_F(\eta-\xi) = 2s_F(\eta)+2s_F(\xi)$, \item[(3)] $s_F$ is lower semicontinuous, and \item[(4)] $s_F(u\xi)=s_F(\xi)$ for all $u\in M'$. \end{enumerate} (1) and (4) are trivial. (3) follows as sups of lower semicontinuous maps are lower semicontinuous. (2) is similar to the proof of Lemma \ref{lem:parallelogram}. \end{proof}
\begin{defn}\label{defn:UnboundedRN} Suppose $M$ is a semifinite von Neumann algebra with n.f.s. trace $\Tr_M$ acting on the right of $H$. Let $\xi\in D(H_M)$, and suppose $(x_i)\in (M'\cap B(H))^+$ with $x_i\nearrow x\in \widehat{(M'\cap B(H))^+}$. Then each $L(\xi)^*x_iL(\xi)\in M^+$ as it commutes with the right $M$-action on $L^2(M,\Tr_M)$, so we define $$ L(\xi)^*xL(\xi)\ = \sup_i L(\xi)^*x_iL(\xi)\in \widehat{M^+}. $$ Note that if $\kappa\in L^2(M,\Tr_M)$, then $$ \bigg(L(\xi)^*xL(\xi)\bigg)(\omega_\kappa)=\sup_i \bigg(L(\xi)^*x_iL(\xi)\bigg)(\omega_\kappa) = \sup_i x_i(\omega_{\xi\otimes \kappa})=x(\omega_{\xi\otimes \kappa}), $$ which is independent of the choice of $(x_i)$. Hence $L(\xi)^*xL(\xi)$ is well-defined by Lemma \ref{lem:VectorStates}. Similarly, we may define operators of the form $R(\eta)^*yR(\eta)$, $L_\xi^*xL_\xi$, and $R_\eta^*yR_\eta$. \end{defn}
\section{Planar calculus for bimodules} For this section, let $A$ be a $II_1$-factor, and let $\sb{A}H_A$ be an $A-A$ Hilbert bimodule, i.e., $H$ has commuting actions of $A$ and $A^{\OP}$.
\subsection{Centralizer algebras, central $L^2$-vectors, and canonical maps}\label{sec:TowersOfBimodules}
\begin{defn} For an $A-A$ bimodule $K$ (algebraic or Hilbert), we define $$A'\cap K=\set{\xi\in K}{a\xi = \xi a\text{ for all }a\in A}.$$ \end{defn}
\begin{nota} For $n\geq 0$, let \item[$\bullet$] $H^n = \bigotimes^n_A H$, with the convention that $H^0=L^2(A)$, \item[$\bullet$] $B^n=D(\sb{A}H^n)\cap D(H^n_A)$, which is dense in $H^n$ by Lemma 1.2.2 of \cite{correspondences}. We also use the convention $B=B^1$. Note $B^0=A$. \item[$\bullet$] $\{\alpha\}\subset B$ be an $\sb{A}H$ basis (possible due to the density of $B$ in $H$), with $$\{\alpha^n\}=\set{\alpha_{1}\otimes\cdots\otimes\alpha_{n} }{\alpha_{i}\in\{\alpha\}\text{ for all } i=1,\dots,n}\subset B^n$$ the corresponding $\sb{A}H^n$ basis (as $R_{\alpha_{1}\otimes\cdots\otimes \alpha_{n}} =R_{\alpha_{1}}\cdots R_{\alpha_{n}}$). We let $\{\beta\}\subset B$ be an $H_A$ basis, with $\{{\beta}^n\}\subset B^n$ the corresponding $H_A^n$ basis. \item[$\bullet$] (central $L^2$-vectors) $P_n = A'\cap H^n$. Note $P_0=A'\cap L^2(A) = \mathbb{C}\widehat{1}$. \item[$\bullet$] $C_n = (A^{\OP})'\cap B(H^n)$ (the commutant of the right $A$-action on $H^n$) with canonical trace $\Tr_n=\sum_{{\beta}^n} \langle \, \cdot \, {\beta}^n,{\beta}^n\rangle$, \item[$\bullet$] $C_n^{\OP} = A'\cap B(H^n)$ with canonical trace $\Tr_n^{\OP}=\sum_{{\alpha}^n} \langle \, \cdot \, {\alpha}^n,{\alpha}^n\rangle$, \item[$\bullet$] (centralizer algebras) $Q_n = C_n\cap C_n^{\OP}$. \end{nota}
\begin{rem}\label{rem:central} Note that $A\subset C_n$ and $A^{\OP}\subset C_n^{\OP}$. \end{rem}
\begin{defn}\label{defn:symmetric} $H$ is called \underline{symmetric} if there is a conjugate-linear isomorphism $J\colon H\to H$ such that $J(a\xi b)= b^* (J\xi) a^*$ for all $a,b\in A$ and $\xi\in H$. \end{defn}
\begin{rem}\label{rem:symmetric} If $H$ is symmetric, then for $n\geq 1$, $H^n$ is symmetric with conjugate-linear isomorphism $J_n\colon H^n\to H^n$ given by the extension of $$ J_n( \xi_1\otimes \cdots \otimes \xi_n)=(J\xi_1)\otimes\cdots \otimes (J\xi_n). $$ for $\xi_i\in B$ for all $i$. Note that $J_nAJ_n=A^{\OP}$, $J_n C_nJ_n=C_n^{\OP}$, and $J_n B^n=B^n$. On $B(H^n)$, we define $j_n$ by $j_n(x)=J_nx^*J_n$. Note that $j_n^2=\id$ and $\Tr_n=\Tr_n^{\OP}\circ j_n$.
If $H$ is not symmetric, then in general, $C_n^{\OP}$ is not the opposite algebra of $C_n$, e.g. $\sb{R\otimes 1} L^2(R\otimes R)_{R\otimes R}$ where $R$ is the hyperfinite $II_1$-factor. \end{rem}
\begin{rem}\label{rem:StayBounded} It is clear that $B^n$ is an $A-A$ bimodule. If $\eta\in B^n$ and $c\in C_n$, then $c\xi\in D(H^n_A)$, but in general, $c\xi\notin D(\sb{A}H^n)$. However, if $c\in Q_n$, then clearly $c\xi\in B^n$. \end{rem}
\begin{prop} \label{prop:include} We have natural inclusions: \begin{align*} &i_n\colon C_n\to C_{n+1} \text{ by } x\mapsto x \otimes_A \id_H = (\eta\otimes \xi\mapsto (x\eta)\otimes \xi \text{ for } \eta\in B^n \text{ and }\xi\in B)\text{ and}\\ &i_n^{\OP}\colon C_n^{\OP}\to C_{n+1}^{\OP} \text{ by } y\mapsto \id_H \otimes_A y = (\xi\otimes \eta\mapsto \xi\otimes (y \eta) \text{ for } \xi\in B \text{ and }\eta\in B^{n}). \end{align*} Both maps include $Q_n\to Q_{n+1}$. \end{prop} \begin{proof} If $z\in Q_n$, then $i_n(z)\in Q_{n+1}$ as for all $a,b\in A$, $$ (z\otimes_A \id_H)[a(\xi\otimes \eta)b] = (z(a\xi))\otimes (\eta b)=(a(z\xi))\otimes (\eta b)=a[(z\eta)\otimes \xi]b. $$ The result is similar for $i_n^{\OP}$. \end{proof}
\begin{prop}\label{prop:iFormula} If $x\in C_n$, then $i_n(x)=\sum_\alpha R_\alpha x R_\alpha^*$. If $y\in C_n^{\OP}$, then $i_n^{\OP}(y)=\sum_\beta L_\beta y L_\beta^*$. \end{prop} \begin{proof} We prove the first statement. If $\xi_1,\dots,\xi_{n+1}\in B$, we have \begin{align*} \left(\sum_\alpha R_\alpha x R_\alpha^*\right) \xi_1\otimes\cdots \otimes\xi_n & = \sum_\alpha R_\alpha x( \xi_1\otimes\cdots \otimes \xi_{n-1} {\sb{A}\langle} \xi_n,\alpha\rangle)\\ & = \sum_\alpha \big(x(\xi_1\otimes\cdots \otimes \xi_{n-1}{\sb{A}\langle} \xi_n,\alpha\rangle)\otimes \alpha \big)\\ & = \sum_\alpha \big(x(\xi_1\otimes\cdots \otimes \xi_{n-1})\big)\otimes{\sb{A}\langle} \xi_n,\alpha\rangle \alpha\\ & = [x(\xi_1\otimes\cdots \otimes \xi_{n-1})]\otimes \xi_n = i_n(x) (\xi_1\otimes\cdots\otimes \xi_n). \end{align*} \end{proof}
\begin{rem}\label{rem:FiberProduct} By Definition \ref{defn:FiberProduct}, $(C_k\otimes_A \id_{n-k})'\cap B(H^n)=\id_k\otimes_A C_{n-k}^{\OP}$. \end{rem}
\begin{lem}\label{lem:AlsoClosable} Suppose $\xi\in H^n$ and $y\in (C_{n+1}^{\OP})^+$. Recall the operator $R_\xi^0\colon B\to H^{n+1}$ by $\eta\mapsto \eta\otimes\xi$ is closable by Corollary \ref{cor:UnboundedLR}. Then $y^{1/2}R_\xi^0\colon B\to H^{n+1}$ is also closable. \end{lem} \begin{proof} Let $p$ be the range/kernel perp projection of $y^{1/2}$. By the spectral theorem, there are projections $p_k\in C_{n+1}^{\OP}$ such that $y^{1/2}p_k=p_ky^{1/2}$ is invertible on $p_kH^{n+1}$ and $p_k\nearrow p$ (strongly). Fix $k\geq 0$. Vectors of the form $\zeta=\sum_{i=1}^j \sigma_i \otimes \kappa_i \in p_kH^{n+1}$ where $\sigma_1,\dots,\sigma_j\in B$ and $\kappa_1,\dots,\kappa_j\in B^n$ are dense in $p_k H^{n+1}$ by the density of $B\otimes_A B^n \subset H^{n+1}$. Then for such $\zeta$ and all $\eta\in B$, $$ \langle y^{1/2}R_\xi^0 \eta, y^{-1/2}p_k \zeta\rangle=\sum_{i=1}^j \langle \eta\otimes \xi, \sigma_i\otimes\kappa_i\rangle = \sum_{i=1}^j \langle \eta, L_{\sigma_i} ({\sb{A}\langle} \kappa_i,\xi\rangle) \rangle=\left\langle \eta , \sum_{i=1}^j L_{\sigma_i} ({\sb{A}\langle} \kappa_i,\xi\rangle)\right\rangle $$ (see Corollary \ref{cor:UnboundedLR}). Finally, the span of vectors of the form $y^{-1/2}p_k \zeta$ where $\zeta$ is as above and $k\geq 0$ is dense in $pH^{n+1}$. \end{proof}
The following proposition and its proof are similar to Theorem 3.2.26 and Proposition 3.2.27 of \cite{burns}.
\begin{prop}\label{prop:T} Recall from Proposition \ref{prop:include} that $i_n(C_n)\subset C_{n+1}$ and $i_n^{\OP} (C_n^{\OP})\subset C_{n+1}^{\OP}$. The unique trace-preserving operator valued weight $$T_{n+1}\colon (C_{n+1}^+,\Tr_{n+1})\to (\widehat{C_n^+} ,\Tr_n)\text{ is given by }x\mapsto \sum_\beta R_\beta^* x R_\beta.$$ The unique trace-preserving operator valued weight $$T_{n+1}^{\OP}\colon \left((C_{n+1}^{\OP})^+,\Tr_{n+1}^{\OP}\right) \to \left(\widehat{(C_{n}^{\OP})^+},\Tr_n^{\OP}\right)\text{ is given by }y\mapsto \sum_\alpha L_\alpha^* y L_\alpha.$$ In particular, $T_{n+1}$ and $T_{n+1}^{\OP}$ are independent of the choice of basis. \end{prop} \begin{proof} We prove the result for the second statement.
Suppose $y\in (C_{n+1}^{\OP})^+$ and $\xi\in H^{n}$. By Lemma \ref{lem:AlsoClosable}, $y^{1/2}R_\xi^0$ is closable, so we set $S=(y^{1/2}R_\xi^0)^*\overline{y^{1/2} R_\xi^0}$, which is affiliated with $C_{1}^{\OP}$, and define $m_{S}\in \widehat{(C_{1}^{\OP})^+}$ as in Equation \eqref{eq:KS} by $$ m_{S}(\omega_\eta) = \begin{cases}
\| S^{1/2} \eta \| &\text{ if } \eta \in D(S^{1/2})\supset B\\ \infty & \text{ else.} \end{cases} $$
Now we calculate that \begin{align*} \Tr_{1}^{\OP} (m_{S}) & = \sum_{\alpha} m_{S}(\omega_\alpha)
= \sum_\alpha \|S^{1/2} \alpha\|^2_2
= \sum_\alpha \|y^{1/2} R_\xi^0 \alpha\|^2_2\\ & = \sum_\alpha \langle y (\alpha\otimes \xi) , (\alpha\otimes \xi)\rangle_{H^{n+1}} = \left\langle \left( \sum_\alpha L_\alpha^* y L_\alpha\right) \xi,\xi\right\rangle_{H^n} = T_{n+1}^{\OP}(y)(\omega_\xi). \end{align*} As all elements of $B(H)^+_*$ are sums $\sum_{i} \omega_{\xi_i}$, $T_{n+1}^{\OP}$ is well-defined and independent of the choice of $\{\alpha\}$.
Note that $T_{n+1}^{\OP}((C_{n+1}^{\OP})^+)\subset \widehat{(C_{n}^{\OP})^+}$ as if $y\in (C_{n+1}^{\OP})^+$, $\xi\in H^{n}$, and $u\in U(A)$, then \begin{align*} \sum_\alpha L_\alpha^* y L_\alpha (\omega_{u\xi}) & = \sum_\alpha \langle y (\alpha\otimes u\xi), \alpha \otimes u\xi \rangle
= \sum_\alpha \langle y (\alpha u\otimes \xi), \alpha u\otimes \xi \rangle \\ & = \sum_\alpha L_{\alpha u}^* y L_{\alpha u} (\omega_{\xi}) = \sum_\alpha L_\alpha^* y L_\alpha (\omega_{\xi }) \end{align*} as $\{\alpha u\}$ is another $\sb{A}H$ basis by Lemma \ref{lem:UnitaryBases}.
Finally, if $x\in (C_n^{\OP})^+$ and $y\in (C_{n+1}^{\OP})^+$, then \begin{align*} \Tr_{n+1}^{\OP} \left( [i_n^{\OP}(x^{1/2})] y [i_n^{\OP}(x^{1/2})]\right) & = \sum_{{\alpha}^{n+1}} \left\langle [i_n^{\OP}(x^{1/2})] y [i_n^{\OP}(x^{1/2})]{\alpha}^{n+1},{\alpha}^{n+1}\right\rangle\\ & = \sum_{\alpha,{\alpha}^{n}} \left\langle y (\alpha\otimes (x^{1/2}{\alpha}^{n})),(\alpha\otimes (x^{1/2}{\alpha}^{n}))\right\rangle \\ & = \sum_{{\alpha}^{n}} \left\langle \sum_\alpha L_\alpha^* yL_\alpha (x^{1/2}{\alpha}^{n}), (x^{1/2}{\alpha}^{n})\right\rangle \\ & = \Tr_n^{\OP}\left(x^{1/2} T_{n+1}^{\OP}(y) x^{1/2} \right), \end{align*} so $T_{n+1}^{\OP}$ is the unique trace-preserving operator valued weight by Equation \eqref{eq:ovwCondition} in Theorem \ref{thm:Texists}. \end{proof}
\begin{rem}\label{rem:TForZ} If $z\in Q_{n+1}^+$, then $T_{n+1}^{\OP}(z)\in \widehat{Q_{n}^+}$ as if $\xi\in H^{n}$ and $u\in U(A)$, $$ \sum_\alpha L_\alpha^* z L_\alpha (\omega_{\xi u}) = \sum_\alpha \langle z (\alpha\otimes \xi u), \alpha \otimes \xi u \rangle = \sum_\alpha \langle (z(\alpha \otimes\xi))uu^*, \alpha \otimes \xi\rangle = \sum_\alpha L_{\alpha}^* z L_{\alpha} (\omega_{\xi}). $$ A similar result holds for $T_{n+1}$. \end{rem}
\begin{cor}\label{cor:Z1Traces} If $z\in Q_1^+$, then $\sum_\alpha L(\alpha)^* z L(\alpha) = \Tr_1^{\OP}(z) 1_{L^2(A)}$. Similarly, $\sum_\alpha R(\beta)^* z R(\beta) = \Tr_1(z) 1_{L^2(A)}$. \end{cor} \begin{proof} We prove the first formula. First, $\sum_\alpha L(\alpha)^* z L(\alpha) \in \widehat{Q_0^+}=[0,\infty]$. Now $$ \left(\sum_\alpha L(\alpha)^* z L(\alpha)\right) (\omega_{\widehat{1}}) = \sum_\alpha\langle L(\alpha)^* z L(\alpha) \widehat{1}, \widehat{1} \rangle = \sum_\alpha \langle z \alpha, \alpha \rangle = \Tr_1^{\OP}(z). $$ \end{proof}
\begin{prop}\label{prop:CrossT} The unique trace-preserving operator valued weight $$\widetilde{T_{n+1}}\colon (Q_{n+1}^+,\Tr_{n+1})\to (i_n^{\OP}(\widehat{Q_n^+}) ,\Tr_n)\text{ is given by }x\mapsto \sum_\beta L_\beta^* x L_\beta.$$ The unique trace-preserving operator valued weight $$\widetilde{T_{n+1}^{\OP}}\colon \left(Q_n^+,\Tr_{n+1}^{\OP}\right) \to \left(i_n(\widehat{Q_{n}^+}),\Tr_n^{\OP}\right)\text{ is given by }y\mapsto \sum_\alpha R_\alpha^* y R_\alpha.$$ In particular, $\widetilde{T_{n+1}}$ and $\widetilde{T_{n+1}^{\OP}}$ are independent of the choice of basis. \end{prop} \begin{proof} Similar to the proof of Proposition \ref{prop:T} using Remark \ref{rem:TForZ}. Note that if $u\in U(A)$, then $\{u\alpha\},\{\beta u\}$ are also $\sb{A}H,H_A$-bases respectively by Lemma \ref{lem:UnitaryBases}. \end{proof}
\subsection{Planar algebra over extended positive cones of centralizer algebras}\label{sec:PAoverPositiveCones}
The following theorem is necessary to show the planar calculus is well-defined.
\begin{thm}\label{thm:BPRelations} The following relations hold among the maps $T_n, T_n^{\OP}, \otimes_A,\Tr_n,\Tr_n^{\OP}$ for $m,n\geq 1$ (compare with Theorem \ref{thm:relations}): \item[(1)] $T_n T_{n+1}^{\OP} (z) = T_{n}^{\OP} T_{n+1}(z)$ for all $z\in \widehat{Q_{n+1}^+}$, \item[(2)] $z_1\otimes_A( z_2\otimes_A z_3) = (z_1\otimes_A z_2)\otimes_A z_3$ for all $z_i\in \widehat{Q_{n_i}^+}$, $i=1,2,3$, \item[(3)] $z_1\otimes_A (T_n z_2) = T_{m+n}(z_1\otimes z_2)$ and $(T_m^{\OP} z_1)\otimes_A z_2 = T_{m+n}^{\OP} (z_1\otimes z_2)$ for all $z_1\in \widehat{Q_{m}^+}$ and $z_2\in \widehat{Q_{n}^+}$, and \item[(4)] $\Tr_n(z_1\cdot z_2)=\Tr_n(z_2\cdot z_1)$ and $\Tr_n^{\OP}(z_1\cdot z_2)=\Tr_n^{\OP}(z_2\cdot z_1)$ for all $z_1,z_2\in \widehat{Q_n^+}$. \end{thm} \begin{proof} \item[(1)] For all $\xi \in H^{n}$ and $z\in \widehat{Q_{n+1}^+}$, \begin{align*} \big(T_n T_{n+1}^{\OP} (z) \big)(\omega_\xi) & = \left(\sum_{\beta} R_\beta^*\left(\sum_\alpha L_\alpha^* z L_\alpha \right)R_\beta\right)(\omega_\xi) = \sum_{\alpha,\beta} (R_\beta^* L_\alpha^* z L_\alpha R_\beta )(\omega_\xi) \\ & = \sum_{\alpha,\beta} z(\omega_{\alpha \otimes \xi\otimes\beta}) = \left(\sum_{\alpha} L_\alpha^*\left(\sum_\beta R_\beta^* z R_\beta \right)L_\alpha \right) (\omega_\xi)\\ & = \big(T_{n}^{\OP} T_{n+1}(z)\big)(\omega_\xi). \end{align*} \item[(2)] This is Corollary \ref{cor:associative}. \item[(3)] Suppose $z_{1,j}\in Q_m^+$ increases to $z_1$ and $z_{2,k}\in Q_{n}^+$ increases to $z_2$. Then \begin{align*} T_{m+n} ( z_{1,j}\otimes_A z_{2,k} ) & = \sum_\beta R_\beta^* ( z_{1,j}\otimes_A z_{2,k} ) R_\beta = \sum_\beta z_{1,j}\otimes_A \left(R_\beta^* z_{2,k} R_\beta\right)\\ & = z_{1,j}\otimes_A \left(\sum_\beta R_\beta^* z_{2,k} R_\beta\right) = z_{1,j} \otimes_A (T_nz_{2,k}) \end{align*} Now $T_nz_{2,k}$ increases to $T_n z_2$, and we are finished by Theorem \ref{thm:UnboundedIncrease}. The other equality is similar. \item[(4)] This is Theorem \ref{thm:BilinearExtension}. \end{proof}
\begin{cor}\label{cor:BPRelationsCor} The following relations also hold: \item[(1)] $i_{n+1}i_{n}^{\OP}(z)=i_{n+1}^{\OP} i_{n}(z)$ for all $z\in \widehat{Q_n^+}$. \item[(2)] $i_{m+n} (z_1\otimes_A z_n) = z_1 \otimes_A i_n(z_2)$ and $i_{m+n}^{\OP}(z_1\otimes_A z_2) = i_m^{\OP}(z_1)\otimes_A z_2$ for all $z_1\in \widehat{Q_m^+}$ and $z_2\in \widehat{Q_n^+}$, \item[(3)] $i_{n-1}^{\OP} T_n (z)= T_{n+1} i_{n}^{\OP} (z)$ and $i_{n-1} T_n^{\OP} (z)= T_{n+1}^{\OP} i_n (z)$ for all $z\in \widehat{Q_n^+}$, and \item[(4)] for all $z_1\in \widehat{Q_m^+}$ and $z_2\in \widehat{Q_n^+}$, \begin{align*} (T_{n+1}\circ\cdots\circ T_{m+n})(z_1\otimes_A z_2)&=\Tr_n(z_2)z_1\text{ and}\\ (T_{m+1}\circ\cdots\circ T_{m+n})(z_1\otimes_A z_2)&=\Tr_m^{\OP}(z_1)z_2. \end{align*} In particular, $\Tr_{m+n}(z_1\otimes z_2)=\Tr_m(z_1)\Tr_n(z_2)$ and $\Tr_{m+n}^{\OP}(z_1\otimes z_2)=\Tr_m^{\OP}(z_1)\Tr_n^{\OP}(z_2)$. \end{cor}
\begin{defn} The \underline{bimodule planar operad $\mathbb{B}\mathbb{P}$} is the operad of oriented, unshaded planar tangles (up to planar isotopy) generated by $$ \idn{n},\, \OperatorValuedWeight{n}{},\,\OperatorValuedWeightOp{n}{},\,\TraceOfTwo{n}{}{},\,\TraceOfTwoOp{n}{}{},\text{ and }\tensor{m}{}{n}{} $$ for $m,n\geq 0$ up to planar isotopy. (We draw all disks as boxes, suppress external disks, draw one thick string labelled $n$ for $n$ individual strings, and orient all strings upward unless otherwise specified.) Some topological properties of tangles in $\mathbb{B}\mathbb{P}$ are given in Appendix \ref{sec:BP}.
A \underline{$\mathbb{B}\mathbb{P}$-algebra (of extended positive cones)} $V_\bullet$ is a sequence $\{V_n\}_{n\geq 0}$ of extended positive cones (see Appendix \ref{sec:cones}) and an action by multilinear maps $$Z\colon \mathbb{B}\mathbb{P} \to ML\{V_n\}$$ ($Z$ is the \underline{partition function}) which is well-behaved under composition. \item A $\mathbb{B}\mathbb{P}$-algebra is called: \item[$\bullet$] \underline{connected} if $V_0=[0_\mathbb{R},\infty_\mathbb{R}]$, \item[$\bullet$] \underline{normal} if $Z(\mathcal{T})$ is normal for all $\mathcal{T}\in\mathbb{B}\mathbb{P}$, and \item[$\bullet$] \underline{self-dual} if $V_n$ is self-dual for all $n$, and for all annular tangles $\mathcal{T}\in\mathbb{B}\mathbb{P}$, flipping it inside out gives the adjoint map (see Definition \ref{defn:ExtendedConeAdjoint}). \end{defn}
\begin{thm}\label{thm:ConePA} Given an $A-A$ bimodule $H$, the extended positive cones $\widehat{Q_n^+}$ form a unique connected, normal, self-dual $\mathbb{B}\mathbb{P}$-algebra $\widehat{Q_\bullet^+}$ such that: \item[(1)] $\id_{H^n}=\id_n=\idn{n}$\,, \item[(2)] $T_{n+1}(z)=\OperatorValuedWeight{n}{z}$\, and $T_{n+1}^{\OP}(z)=\OperatorValuedWeightOp{n}{z}$ for all $z\in \widehat{Q_{n+1}^+}$ \item[(3)] $z_1\otimes_A z_2 = \tensor{m}{z_1}{n}{z_2}$ (defined in Appendix \ref{sec:TensorUnbounded}) for all $z_1\in \widehat{Q_m^+}$ and $z_2\in \widehat{Q_n^+}$, and \item[(4)] $\Tr_n(z_1\cdot z_2) = \TraceOfTwo{n}{z_1}{z_2}$ and $\Tr_n^{\OP}(z_1\cdot z_2) = \TraceOfTwoOp{n}{z_1}{z_2}$ for all $z_1,z_2\in \widehat{Q_n^+}$. \item Moreover, the following hold: \item[(5)] $i_n(z) = \include{n}{z}$\, and $i_n^{\OP}(z) = \includeop{n}{z}$ for all $z\in \widehat{Q_n^+}$ and \item[(6)] $\dim_{-A}(H)=T_1(1)=\ClosedLoop{1}$\, and $\dim_{A-}(H)=T_1^{\OP}(1)=\ClosedLoopOp{1}$. \item Note that the well-definition of the partition function $Z$ means that any closed diagram counts for a multiplicative factor in $\widehat{Q_0^+}=\widehat{Z(A)^+}=[0_\mathbb{R},\infty_\mathbb{R}].$ \item We call $\widehat{Q_\bullet^+}$ the canonical $\mathbb{B}\mathbb{P}$-algebra associated to $H$. \end{thm} \begin{proof} It suffices to show (1)-(4) uniquely determine the action of any tangle in $\mathbb{B}\mathbb{P}$. This follows from Theorem \ref{thm:BPRelations} and Appendix \ref{sec:BP}. Note that $\widehat{Q_\bullet^+}$ is connected since $\widehat{Q_0^+}=\widehat{Z(A)^+}=[0_\mathbb{R},\infty_\mathbb{R}]$, normal by Theorem \ref{thm:BilinearExtension} and Remark \ref{rem:normal}, and self-dual by Proposition \ref{prop:adjoint}. \end{proof}
\begin{rem} Given some operad $\mathbb{P}$ of (shaded, unshaded, oriented, disoriented, etc.) planar tangles, it is not always possible to define an (extended) positive cone planar algebra over $\mathbb{P}$. For example, the rotation does not always map positive elements to positive elements in a subfactor planar algebra. \end{rem}
\subsection{Graded algebra of central $L^2$-vectors}\label{sec:CentralVectors}
\begin{lem}\label{lem:CentralBounded} Suppose $K$ is a Hilbert $A-A$ bimodule. Then $A'\cap K \subseteq D(\sb{A}K)\cap D(K_A)$. \end{lem} \begin{proof} Suppose $\zeta\in A'\cap K$, $\zeta\neq 0$. Define $\varphi\colon A_+\to \mathbb{C}$ by $a\mapsto \langle a\zeta,\zeta\rangle$. Note that $\varphi$ is traicial as $$ \varphi(a^*a)=\langle a^*a\zeta,\zeta\rangle = \langle a^* \zeta a,\zeta\rangle = \langle a^* \zeta ,\zeta a^*\rangle = \langle a^* \zeta ,a^* \zeta\rangle= \langle aa^* \zeta ,\zeta\rangle=\varphi(aa^*). $$ Hence there is a $\lambda\geq 0$ such that $\varphi=\lambda \tr_A$ by the uniqueness of the trace on a $II_1$-factor. Now for all $a\in A$, $$
\| a \zeta\|^2_2 =\|\zeta a\|^2_2= \varphi(a^*a)= \lambda \tr_A(a^*a)=\lambda \|a\|^2_2, $$ and $\zeta$ is left and right $A$-bounded. \end{proof}
\begin{rem} In the sequel, we will confuse elements $\zeta\in P_n$ and the operators $L(\zeta)=R(\zeta)\colon L^2(A)\to H^n$. We will omit $R(\zeta)$ and only write $L(\zeta)$. \end{rem}
\begin{thm} Representing elements $\zeta\in P_n$ by boxes with $n$ strings emanating from the top, $$ \zeta,L(\zeta)=\Pn{n}{\zeta}, $$ the $P_n$'s form a graded algebra $P_\bullet$ in the sense of \cite{MR2732052} where the graded multiplication is given by relative tensor product (over $A$) of central vectors. We denote the product of $\zeta_m\in P_m$ and $\zeta_n\in P_n$ by $$ \zeta_m\otimes \zeta_n = \TensorPn{m}{\zeta_m}{n}{\zeta_n}\in P_{m+n}. $$ \end{thm}
\begin{rem} If $z\in Q_n$ and $\zeta\in P_n$, then $z\zeta\in P_n$, which we denote as: $$ z\zeta,L(z\zeta)=\ActOnPn{z}{\zeta}. $$ The dual version of these diagrams denotes the functionals $\langle \,\cdot\,,\zeta\rangle,L(\zeta)^*=\PnStar{n}{\zeta}$. The inner product $\langle \,\cdot\,,\,\cdot\,\rangle\colon P_n\times P_n^*\to \mathbb{C}$ is given by $\langle \xi,\zeta\rangle = \InnerProduct{\zeta}{\xi}$. \end{rem}
\subsection{Compatibility}\label{sec:compatible}
We now show how $\widehat{Q_\bullet^+}$ and $P_\bullet$ are compatible.
\begin{lem}\label{lem:ZetaRelations}
\item[(1)] If $\zeta\in P_n$ and $\xi\in B^n$, then $\sb{A}\langle \zeta,\xi\rangle=\langle \xi|\zeta\rangle_A$.
\item[(2)] If $\zeta,\xi\in P_n$, $\sb{A}\langle \zeta,\xi\rangle=\langle \xi|\zeta\rangle_A=\langle \zeta,\xi\rangle 1_{L^2(A)}\in \mathbb{C} 1_{L^2(A)}$. \item[(3)] For $\zeta\in P_n$, $L(\zeta)L(\zeta)^*=R(\zeta)R(\zeta)^*\in Q_n^+$. We denote the common operator as: $$ \CentralVectorOperator{n}{\zeta}{\zeta}\in Q_n^+. $$
\item[(4)] If $\zeta\in P_n$ and $\|\zeta\|_2=1$, $L(\zeta)L(\zeta)^*|_{P_n}=p_\zeta$, the projection onto $\mathbb{C}\zeta$. \end{lem} \begin{proof} \item[(1)] Suppose $a_1,a_2\in A$. Then \begin{align*} \langle \sb{A}\langle \zeta,\xi\rangle \widehat{a_1},\widehat{a_2}\rangle &=\langle J R(\zeta)^*R(\xi)J \widehat{a_1}, \widehat{a_2}\rangle =\langle \widehat{a_2^*}, R(\zeta)^*R(\xi) \widehat{a_1^*}\rangle =\langle a_2^*\zeta,a_1^*\xi\rangle\\ &=\langle \zeta a_2^*, a_1^*\xi\rangle =\langle a_1\zeta, \xi a_2\rangle =\langle \zeta a_1,\xi a_2\rangle =\langle L(\zeta)\widehat{a_1},L(\xi)\widehat{a_2}\rangle\\
&=\langle \langle \xi|\zeta\rangle_A \widehat{a_1},\widehat{a_2}\rangle. \end{align*} \item[(2)] Since $\zeta,\xi \in P_n$, for all $a,b,a_1,a_2\in A$, \begin{align*}
\langle \langle \xi|\zeta\rangle_A (a\widehat{a_1}b),\widehat{a_2}\rangle & = \langle \zeta aa_1b,\xi a_2\rangle = \langle \zeta a_1, \xi a^* a_2 b^*\rangle\\
& =\langle \langle \xi|\zeta\rangle_A \widehat{a_1}, a^* \widehat{a_2} b^*\rangle
=\langle a(\langle \xi|\zeta\rangle_A \widehat{a_1})b, \widehat{a_2} \rangle, \end{align*}
so $\langle \xi|\zeta\rangle_A \in Z(A)=\mathbb{C} 1_{A}$. Now setting $a=b=a_1=a_2=1_A$ gives the result. \item[(3)] For $\xi\in B^n$, by (1), $$ L(\zeta)L(\zeta)^*\xi
= \zeta \langle \zeta|\xi\rangle_A
= \langle \zeta|\xi\rangle_A \zeta = {\sb{A}\langle} \xi,\zeta\rangle \zeta = R(\zeta)R(\zeta)^* \xi, $$ so the two are equal on $H^n$. We have $C_n\ni L(\zeta)L(\zeta)^* = R(\zeta)R(\zeta)^*\in C_n^{\OP}$, so $L(\zeta)L(\zeta)^*\in Q_n^+$. \item[(4)] Trivial from (2) and (3). \end{proof}
\begin{thm}\label{thm:CloseOffZetas} Suppose $\zeta\in P_n$ and $z\in \widehat{Q_n^+}$. \item[(1)] $L(\zeta)^* z L(\zeta)=z(\omega_\zeta)1_{L^2(A)}=R(\zeta)^*zR(\zeta)$. We denote this diagrammatically as: $$ \TripleInnerProduct{\zeta}{z}{\zeta} $$ \item[(2)] In the notation of Theorem \ref{thm:BilinearExtension}, \begin{align*} z(\omega_\zeta) & = \tr_A(L(\zeta)^* z L(\zeta)) = \Tr_n(L(\zeta)L(\zeta)^*\cdot z)\\ & = \tr_{A^{\OP}}(R(\zeta)^*zR(\zeta)) = \Tr_n^{\OP}(z\cdot R(\zeta)R(\zeta)^*). \end{align*} In diagrams: $$ \TripleInnerProduct{\zeta}{z}{\zeta}= \TraceOfTwoBig{\zeta}{\zeta}{z}= \TraceOfTwoBigOp{\zeta}{\zeta}{z}. $$ \end{thm} \begin{proof} \item[(1)] We show the first equality. If $z\in Q_n^+$, this is just (2) of Lemma \ref{lem:ZetaRelations} with $\zeta_1=\zeta_2=z^{1/2}\zeta$. Now for $z\in \widehat{Q_n^+}$, pick $(z_m)\subset Q_n^+$ with $z_m\nearrow z$ to get $$ L(\zeta)^*zL(\zeta)=\lim_{m\to\infty} L(\zeta)^*z_mL(\zeta)=\lim_{m\to\infty} z_m(\omega_\zeta)1_{L^2(A)}= z(\omega_\zeta)1_{L^2(A)}. $$ The second equality is similar. \item[(2)] We show the second equality. We may assume $z\in Q_n^+$, after which we may take sups to get the full result. Then as $z^{1/2}\zeta\in P_n$, we have \begin{align*} \Tr_n(z\cdot L(\zeta)L(\zeta)^*) & = \Tr_n(z^{1/2} L(\zeta)L(\zeta)^* z^{1/2}) = \Tr_n(L(z^{1/2}\zeta)L(z^{1/2}\zeta)^*)\\ & = \tr_A(L(z^{1/2}\zeta)^*L(z^{1/2}\zeta)) = \tr_A(L(\zeta)^* zL(\zeta)). \end{align*} The other equality is similar. \end{proof}
\begin{rem} If $a\in Q_n$, $z\in \widehat{Q_n^+}$, and $\zeta\in P_n$, $$ \WideTripleInnerProduct{\zeta}{a^*za}{\zeta}=(a^*za)(\omega_\zeta)=z(\omega_{a\zeta})=\TripleInnerProduct{a\zeta}{z}{a\zeta}. $$ \end{rem}
\begin{cor}\label{cor:RemoveSubdiagram} If $\zeta_1\in P_m$, $\zeta_2\in P_n$, $z_1\in Q_m^+$, and $z_2\in Q_n^+$, then $$ \BigInnerProduct{\zeta_1\otimes\zeta_2}{z_1\otimes_A z_2}{\zeta_1\otimes\zeta_2} =\langle (z_1\otimes_A z_2)( \zeta_1\otimes \zeta_2),(\zeta_1\otimes\zeta_2)\rangle =\langle z_1 \zeta_1,\zeta_1\rangle\langle z_2\zeta_2,\zeta_2\rangle =\TripleInnerProduct{\zeta_1}{z_1}{\zeta_1}\TripleInnerProduct{\zeta_2}{z_2}{\zeta_2}. $$ For $z_1\in \widehat{Q_m^+}$, and $z_2\in\widehat{Q_n^+}$, taking sups gives $$ \BigInnerProduct{\zeta_1\otimes\zeta_2}{z_1\otimes_A z_2}{\zeta_1\otimes\zeta_2} =(z_1\otimes_A z_2)(\omega_{\zeta_1\otimes\zeta_2}) =z_1(\omega_{\zeta_1})z_2(\omega_{\zeta_2}) =\TripleInnerProduct{\zeta_1}{z_1}{\zeta_1}\TripleInnerProduct{\zeta_2}{z_2}{\zeta_2}. $$ \end{cor}
\begin{thm}[$P_\bullet$ acts on $\widehat{Q_\bullet^+}$]\label{thm:action} Given a tangle $\mathcal{T}\in \mathbb{B}\mathbb{P}$ with $2n$ boundary points and a $\zeta\in P_n$, we have $$ \TripleInnerProduct{\zeta}{\mathcal{T}}{\zeta}:=\ev_{\omega_\zeta}\circ \mathcal{T} \colon V_{i_1}\times\cdots\times V_{i_k}\to [0_\mathbb{R},\infty_\mathbb{R}]. $$ In this sense, we say $P_\bullet$ \underline{acts as weights} on $\widehat{Q_\bullet^+}$. By Theorems \ref{thm:BPRelations} and \ref{thm:CloseOffZetas} and Corollary \ref{cor:RemoveSubdiagram}, we may remove closed subdiagrams and multiply by the appropriate scalar in $[0,\infty]$. \end{thm}
\begin{rem} If $A\subset (B,\tr_B)$ is an inclusion of $II_1$-factors and $H=L^2(B)$, then one can also define a shaded bimodule planar operad which works similarly to the above construction. This will be explored in a future paper. \end{rem}
\section{Extremality and rotations}\label{sec:ExtremalityRotations} For this section, $A$ is a $II_1$-factor. Assume the notation of the last section.
\subsection{Extremality}\label{sec:Extremality}
\begin{defn} $H$ is \underline{approximately extremal with constant $\lambda>0$} if on $Q_1^+$, $$\lambda^{-1} \Tr_1 \leq \Tr_1^{\OP} \leq \lambda\Tr_1.$$ $H$ is \underline{extremal} if $\Tr_1= \Tr_1^{\OP} $ on $Q_1^+$. \end{defn}
The following proposition is almost identical to Proposition 2.8 in \cite{MR1622812}. \begin{prop}[Structure of $Q_n$] \label{prop:decompose} $Q_n = \mathfrak{a}_{n}\oplus \mathfrak{b}_{n}\oplus \mathfrak{b}_{n}^{\OP}\oplus \mathfrak{c}_{n}$ such that \item[$\bullet$] $\mathfrak{a}_{n}$ is a direct sum of type $I$ factors, and for each finite rank $p\in \mathfrak{a}_{n}$, $pA\subset pC_np$ has finite index.
\item[$\bullet$] $\Tr_n|_{\mathfrak{a}_{n}\oplus\mathfrak{b}_{n}}$ and $\Tr_n^{\OP}|_{\mathfrak{a}_{n}\oplus \mathfrak{b}_{n}^{\OP}}$ are semifinite, \item[$\bullet$] $\mathfrak{b}_{n}^{\OP}\oplus\mathfrak{c}_{n}\cap \mathfrak{m}_{\Tr_n}=\{0\}=\mathfrak{b}_{n}\oplus \mathfrak{c}_{n}\cap \mathfrak{m}_{\Tr_n^{\OP}}$, and \item[$\bullet$] If $H^n$ is symmetric, then $j_n$ fixes $\mathfrak{a}_{n},\mathfrak{c}_{n}$ and $j_n(\mathfrak{b}_{n})=\mathfrak{b}_{n}^{\OP}$. \end{prop} \begin{proof} By Lemma \ref{lem:SemifiniteRestriction}, let $z_{n},z_{n}^{\OP}\in Q_n$ be the unique central projections corresponding to $A\subset C_n$ and $A^{\OP}\subset C_n^{\OP}$. Set \begin{align*} \mathfrak{a}_{n}&= z_{n}z_{n}^{\OP} Q_n & \mathfrak{b}_{n}&= z_{n}(1-z_{n}^{\OP})Q_n\\ \mathfrak{b}_{n}^{\OP} &= (1-z_{n})z_{n}^{\OP} Q_n & \mathfrak{c}_{n} &= (1-z_{n})(1-z_{n}^{\OP}) Q_n, \end{align*} and the rest follows immediately. \end{proof}
\begin{prop} Let $Q_1 = \mathfrak{a}_1\oplus\mathfrak{b}_1\oplus\mathfrak{b}_1^{\OP}\oplus\mathfrak{c}_1$ as in Proposition \ref{prop:decompose}. The following are equivalent: \item[(1)] $H$ is approximately extremal with constant $\lambda>0$, and \item[(2)] $\mathfrak{b}_1=\mathfrak{b}_1^{\OP}=\{0\}$ and there is a $\lambda>0$ such that on $Q_1^+\cap \mathfrak{a}_1$, $$\lambda^{-1} \Tr_1 \leq \Tr_1^{\OP} \leq \lambda\Tr_1.$$ \item A similar result holds for the extremal case. \end{prop} \begin{proof}
\itm{(1)\Rightarrow(2)} Suppose $H$ is approximately extremal. We show $\mathfrak{b}_1=\{0\}$. As $\Tr_1|_{\mathfrak{a}_1\oplus\mathfrak{b}_1}$ is semifinite by Proposition \ref{prop:decompose}, we choose $z\in \mathfrak{b}_1$ such that $z\geq 0$ and $z\in \mathfrak{m}_{\Tr_1}$. Then $z\in \mathfrak{m}_{\Tr_1^{\OP}}$, but $\mathfrak{b}_1\cap \mathfrak{m}_{\Tr_1^{\OP}}=\{0\}$. Similarly $\mathfrak{b}_1^{\OP}=\{0\}$. \itm{(2)\Rightarrow(1)}
$\Tr_1|_{\mathfrak{c}_1\cap Q_1^+}=\Tr_1^{\OP}|_{\mathfrak{c}_1\cap Q_1^+}=\infty$. \end{proof}
\begin{cor} $H$ is extremal if and only if for each Hilbert $A-A$ bimodule $K\subset H$, the left and right von Neumann dimensions agree. \end{cor}
\begin{rem} If $H$ has a two-sided basis $\{\gamma\}$, then $H$ is extremal as $$ \Tr_1 = \sum_\gamma \langle \,\cdot\,\gamma, \gamma\rangle = \Tr_1^{\OP}. $$ \end{rem}
\begin{rem}\label{lem:SwitchBasis} If $H$ is approximately extremal and $z\in \widehat{Q_1^+}$, then there is a $\lambda >0$ such that $$ \lambda^{-1} \sum_\beta z(\omega_\beta) \leq \sum_\alpha z(\omega_\alpha) \leq \lambda \sum_\beta z(\omega_\beta). $$ If $H$ is extremal, then the above holds with $\lambda = 1$. \end{rem}
\begin{thm}\label{thm:extremal} \item[(1)] If $H$ is (approximately) extremal (with constant $\lambda>0$), then $H^n$ is (approximately) extremal for all $n\geq 1$ (with constant $\lambda^n$). \item[(2)] If $H^n$ is (approximately) extremal for some $n\geq 1$, then $H$ is (approximately) extremal. \end{thm} \begin{proof} We prove the extremal case, and the approximately extremal case is similar. \item[(1)] We use strong induction on $n$. Suppose $H^1$ and $H^n$ are extremal. If $z\in Q_{n+1}^+$, $$ \Tr_{n+1}(z)=\TraceEllipse{n+1}{z}=\ExtremalityOne{n}{z}=\ExtremalityTwo{n}{z}=\TraceOpEllipse{n+1}{z}=\Tr_{n+1}^{\OP}(z). $$ Hence $H^{n+1}$ is extremal. \item[(2)] Suppose $H^n$ is extremal and $z\in Q_1^+$. Then $z\otimes_A \cdots \otimes_A z\in Q_n^+$. By the bimodule planar calculus, \begin{align*} \left(\begin{tikzpicture}[rectangular]
\clip (1.25,1.5) --(-.55,1.5) -- (-.55,-1.5) -- (1.25,-1.5);
\draw[] (.8,.5)--(1,.2)--(1.2,.5);
\draw[] (0,.5) arc (180:0:.5cm) --(1,-.5) arc (0:-180:.5cm);
\filldraw[thick, unshaded] (-.5,.5) --(-.5,-.5) -- (.5,-.5) -- (.5,.5)--(-.5,.5);
\node at (0,0) {$z$};
\end{tikzpicture}\right)^n & = \begin{tikzpicture}[rectangular]
\clip (2.5,1.5) --(-3,1.5) -- (-3,-1.5) -- (2.5,-1.5);
\draw[] (1.8,.5)--(2,.2)--(2.2,.5);
\draw[] (-2,.5) .. controls ++(90:1.2cm) and ++(90:1.2cm) ..(2,.5)--(2,-.5) .. controls ++(270:1.2cm) and ++(270:1.2cm) ..(-2,-.5);
\draw[] (.8,.5)--(1,.2)--(1.2,.5);
\draw[] (0,.5) arc (180:0:.5cm) --(1,-.5) arc (0:-180:.5cm);
\filldraw[thick, unshaded] (-2.5,.5) --(-2.5,-.5) -- (-1.5,-.5) -- (-1.5,.5)--(-2.5,.5);
\filldraw[thick, unshaded] (-.5,.5) --(-.5,-.5) -- (.5,-.5) -- (.5,.5)--(-.5,.5);
\node at (0,0) {$z$};
\node at (-2,0) {$z$};
\node at (1.5,0) {{\scriptsize{$\cdots$}}};
\node at (-1,0) {{\scriptsize{$\cdots$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular]
\clip (1.95,1.5) --(-1.5,1.5) -- (-1.5,-1.5) -- (1.95,-1.5);
\draw[ultra thick] (1.5,.5)--(1.7,.2)--(1.9,.5);
\draw[ultra thick] (.2,.5) arc (180:0:.75cm) --(1.7,-.5) arc (0:-180:.75cm);
\filldraw[thick, unshaded] (-1.3,.5) --(-1.3,-.5) -- (1.3,-.5) -- (1.3,.5)--(-1.3,.5);
\node at (0,0) {{\scriptsize{$z\otimes_A\cdots\otimes_A z$}}};
\node at (.4,-1.25) {{\scriptsize{$n$}}}; \end{tikzpicture} \\ & = \begin{tikzpicture}[rectangular]
\clip (-1.95,1.5) --(1.5,1.5) -- (1.5,-1.5) -- (-1.95,-1.5);
\draw[ultra thick] (-1.5,.5)--(-1.7,.2)--(-1.9,.5);
\draw[ultra thick] (-.2,.5) arc (0:180:.75cm) --(-1.7,-.5) arc (-180:0:.75cm);
\filldraw[thick, unshaded] (-1.3,.5) --(-1.3,-.5) -- (1.3,-.5) -- (1.3,.5)--(-1.3,.5);
\node at (0,0) {{\scriptsize{$z\otimes_A\cdots\otimes_A z$}}};
\node at (-.4,-1.25) {{\scriptsize{$n$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular]
\clip (-2.5,1.5) --(3,1.5) -- (3,-1.5) -- (-2.5,-1.5);
\draw[] (-1.8,.5)--(-2,.2)--(-2.2,.5);
\draw[] (2,.5) .. controls ++(90:1.2cm) and ++(90:1.2cm) ..(-2,.5)--(-2,-.5) .. controls ++(270:1.2cm) and ++(270:1.2cm) ..(2,-.5);
\draw[] (-.8,.5)--(-1,.2)--(-1.2,.5);
\draw[] (0,.5) arc (0:180:.5cm) --(-1,-.5) arc (-180:0:.5cm);
\filldraw[thick, unshaded] (2.5,.5) --(2.5,-.5) -- (1.5,-.5) -- (1.5,.5)--(2.5,.5);
\filldraw[thick, unshaded] (-.5,.5) --(-.5,-.5) -- (.5,-.5) -- (.5,.5)--(-.5,.5);
\node at (0,0) {$z$};
\node at (2,0) {$z$};
\node at (-1.5,0) {{\scriptsize{$\cdots$}}};
\node at (1,0) {{\scriptsize{$\cdots$}}}; \end{tikzpicture} = \left(\begin{tikzpicture}[rectangular]
\clip (-1.25,1.5) --(.55,1.5) -- (.55,-1.5) -- (-1.25,-1.5);
\draw[] (-.8,.5)--(-1,.2)--(-1.2,.5);
\draw[] (0,.5) arc (0:180:.5cm) --(-1,-.5) arc (-180:0:.5cm);
\filldraw[thick, unshaded] (-.5,.5) --(-.5,-.5) -- (.5,-.5) -- (.5,.5)--(-.5,.5);
\node at (0,0) {$z$};
\end{tikzpicture}\right)^n. \end{align*} In equations: $$ \Tr_1(z)^n = \Tr_n (z\otimes_A \cdots \otimes_A z) = \Tr_n^{\OP}(z\otimes_A \cdots \otimes_A z)=\Tr_1^{\OP}(z)^n. $$ Taking $n^{\text{th}}$ roots gives the desired result. \end{proof}
\begin{prop} If $H$ is extremal and $z\in \widehat{Q_n^+}$, then $\sum_\beta R_\beta^* z R_\beta=\sum_\alpha R_\alpha^* zR_\alpha$ and $\sum_\alpha L_\alpha^* z L_\alpha = \sum_\beta L_\beta^*zL_\beta$. \end{prop} \begin{proof} Immediate from Propositions \ref{prop:T} and \ref{prop:CrossT}. \end{proof}
\subsection{Rotations}\label{sec:Rotations}
\begin{defn}[Inspired by \cite{burns}]\label{defn:rotation} A \underline{Burns rotation} is a map $\rho\colon P_n\to P_n$ such that for all $\zeta\in P_n$ and $b_1,\dots,b_n\in B$, \begin{equation}\label{eq:rotation} \langle \rho(\zeta),b_1\otimes\cdots\otimes b_n\rangle = \langle \zeta, b_2\otimes\cdots\otimes b_n\otimes b_1\rangle. \end{equation} An \underline{opposite Burns rotation} is defined similarly: $$ \langle \rho^{\OP}(\zeta),b_1\otimes\cdots\otimes b_n\rangle = \langle \zeta, b_n\otimes b_1\otimes\cdots\otimes b_{n-1}\rangle. $$ \end{defn}
\begin{rem}\label{rem:RotationInverse} Note that if such a $\rho$ exists, it is unique, and $\rho^n = \id_{P_n}$. In this case, $\rho^{\OP}=\rho^{-1}$. \end{rem}
\begin{thm}[Essentially due to \cite{burns}] If $\rho=\sum_{\beta} L_\beta R_\beta^*$ converges strongly on $P_n$, then $\rho$ is a Burns rotation. Similarly, if $\rho^{\OP}=\sum_{\alpha} R_\alpha L_\alpha^*$ converges strongly on $P_n$, then $\rho^{\OP}$ is an opposite Burns rotation. \end{thm} \begin{proof} We must show that $\rho$ preserves $P_n$ and that $\rho$ satisfies Equation \eqref{eq:rotation}. The latter follows from: \begin{align*} \langle \rho(\zeta),b_1\otimes\cdots\otimes b_n\rangle &=\sum_{\beta}\langle \zeta, R_\beta L_\beta^* (b_1\otimes \cdots\otimes b_n )\rangle\\
&=\sum_{\beta}\langle \zeta, \langle \beta|b_1\rangle_A b_2\otimes \cdots\otimes b_n\otimes \beta \rangle\\
&=\sum_{\beta}\langle \langle \beta|b_1\rangle_A^*\zeta, b_2\otimes \cdots\otimes b_n\otimes \beta \rangle\\
&=\sum_{\beta}\langle \zeta \langle \beta|b_1\rangle_A^* , b_2\otimes \cdots\otimes b_n\otimes \beta \rangle\\
&=\sum_{\beta}\langle \zeta, b_2\otimes \cdots\otimes b_n\otimes \beta \langle \beta|b_1\rangle_A\rangle\\ &= \langle \zeta, b_2\otimes\cdots\otimes b_n\otimes b_1\rangle. \end{align*} Now $\rho$ is independent of the choice of $\{\beta\}$. In particular, for any $u\in U(A)$, $\{u\beta\}$ is an $H_A$-basis, and $$ u \rho(\zeta) u^* = u \left(\sum_\beta L_\beta R_\beta^* \zeta\right) u^*= \sum_\beta L_{u\beta} R_{u\beta}^* \zeta= \rho(\zeta)\in P_n. $$ \end{proof}
\subsection{Diagrammatic representation of the Burns rotation}\label{sec:DiagramsOfRotation} For this section, we assume the Burns rotation $\rho$ exists on $P_n$ for all $n\geq 0$. Recall for all $k\geq 0$, $\rho^{-k}=(\rho^{\OP})^k$.
\begin{nota} For $\zeta\in P_{m+n}$, we denote $\rho^m(\zeta)=(\rho^{\OP})^n(\zeta)\in P_{m+n}$ by moving $m$ strings around the bottom counterclockwise or by moving $n$ strings around the bottom clockwise: $$ \Rotation{m}{n}{\zeta}=\rho^m(\zeta)=(\rho^{\OP})^n(\zeta)=\RotationOp{n}{m}{\zeta} $$ \end{nota}
\begin{prop}\label{prop:RotateCentral} If $\eta\in P_m$ and $\xi\in P_n$, then $\rho^n (\eta\otimes \xi) = \xi\otimes\eta$: $$ \Switch{n}{\xi}{m}{\eta}=\TensorPn{n}{\xi}{\,\, m}{\eta}. $$ \end{prop} \begin{proof} Suppose $\alpha\in B^m$ and $\beta\in B^n$. Then by (1) of Lemma \ref{lem:ZetaRelations}, $$
\langle \rho^n(\eta\otimes\xi), \beta\otimes\alpha\rangle = \langle \eta\otimes \xi, \alpha\otimes \beta \rangle = \langle \langle \alpha| \eta\rangle_A \xi,\beta\rangle = \langle \xi{\sb{A}\langle} \eta,\alpha\rangle,\beta\rangle =\langle \xi\otimes \eta, \beta\otimes \alpha\rangle. $$ \end{proof}
\begin{defn} For $0\leq j< m$, define $\mu_j\colon P_m\times P_n \to P_{m+n}$ by $\mu_j (\eta,\xi)= \rho^{-j} ( \rho^j(\eta)\otimes \xi)$. We represent $\mu_{j}$ diagrammatically as follows: $$ \mu_j(\eta,\xi)=\Insert{n}{\xi}{m-j}{j}{\eta}\,. $$ Well-definition of this diagram relies on the following proposition. \end{defn}
\begin{prop}\label{prop:insert} The $\mu_i$'s are associative, i.e., if $\sigma\in P_\ell$, $\eta\in P_m$, and $\xi\in P_n$, and $i\leq \ell$, $j\leq m$, then $$ \mu_i(\kappa,\mu_j(\eta,\xi))=\mu_{i+j}(\mu_i(\kappa,\eta),\xi). $$ \end{prop} \begin{proof} Suppose $\alpha\in B^{\ell-i}$, $\beta\in B^{m-j}$, $\gamma\in B^n$, $\delta\in B^j$, and $\varepsilon\in B^i$. Then {\fontsize{10}{10}{ \begin{align*} \langle \mu_i(\kappa,\mu_j(\eta,\xi)), \alpha\otimes\beta\otimes\gamma\otimes \delta\otimes\varepsilon\rangle &=\left\langle \rho^{-i} \big(\rho^i(\kappa) \otimes \rho^{-j}(\rho^j(\eta)\otimes \xi) \big),\alpha\otimes\beta\otimes\gamma\otimes \delta\otimes\varepsilon\right\rangle \\ &=\left\langle \rho^i(\kappa) \otimes \rho^{-j}\big(\rho^j(\eta)\otimes \xi\big), \varepsilon\otimes\alpha\otimes\beta\otimes\gamma\otimes \delta\right\rangle\\
&=\left\langle \rho^{-j}\big(\rho^j(\eta)\otimes \xi\big), \langle \rho^i(\kappa) |\varepsilon\rangle_A\alpha\otimes\beta\otimes\gamma\otimes \delta\right\rangle\\
&=\left\langle \rho^j(\eta)\otimes \xi, \delta\otimes\langle \rho^i(\kappa) |\varepsilon\rangle_A\alpha\otimes\beta\otimes\gamma\right\rangle\\
&=\left\langle \rho^j(\eta), \delta\otimes\langle \rho^i(\kappa) |\varepsilon\rangle_A\alpha\otimes\beta{\sb{A}\langle}\gamma,\xi\rangle\right\rangle\\
&=\left\langle \eta,\langle \rho^i(\kappa) |\varepsilon\rangle_A\alpha\otimes\beta{\sb{A}\langle}\gamma,\xi\rangle\otimes \delta\right\rangle\\ &=\left\langle \rho^i(\kappa)\otimes \eta,\varepsilon\otimes\alpha\otimes\beta{\sb{A}\langle}\gamma,\xi\rangle\otimes \delta\right\rangle\\ &= \left\langle\rho^{j} \big( \rho^i(\kappa)\otimes\eta\big),\delta\otimes\varepsilon\otimes\alpha\otimes\beta{\sb{A}\langle}\gamma,\xi\rangle\right\rangle\\ &= \left\langle\rho^{j} \big( \rho^i(\kappa)\otimes\eta\big)\otimes \xi,\delta\otimes\varepsilon\otimes\alpha\otimes\beta\otimes\gamma\right\rangle\\ &=\left\langle \rho^{-i-j} \big(\rho^{i+j} ( \rho^{-i}(\rho^i(\kappa)\otimes\eta))\otimes \xi\big),\alpha\otimes\beta\otimes\gamma\otimes \delta\otimes\varepsilon\right\rangle\\ &=\langle \mu_{i+j}(\mu_i(\kappa,\eta),\xi), \alpha\otimes\beta\otimes\gamma\otimes \delta\otimes\varepsilon\rangle. \end{align*}}} \end{proof}
\begin{cor}\label{cor:POperad} $P_\bullet$ naturally forms an algebra over the operad generated by the unshaded, oriented tangles $$ \TensorPn{m}{}{n}{},\Rotation{m}{n}{} $$ for $m,n\geq 0$ up to planar isotopy. \end{cor}
The Burns rotation is also compatible with the $\mathbb{B}\mathbb{P}$-algebra $\widehat{Q_\bullet^+}$.
\begin{thm}\label{thm:MoveAround} \item[(1)] For all $\zeta\in P_{m+n}$ and $x\in Q_m$, and $y\in Q_n$, $\rho^n((x\otimes_A y) \zeta) = (y\otimes_A x) \rho^n(\zeta)$: $$ \begin{tikzpicture}[rectangular,baseline=-1cm]
\clip (-1.65,.5) --(2.2,.5) -- (2.2,-3) -- (-1.65,-3);
\draw[ultra thick] (-.6,-1.5) arc (0:180:.4cm) -- (-1.4,-2) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (1.5,-1);
\draw[ultra thick] (0,1)--(0,-2);
\draw[ultra thick] (1.5,1)--(1.5,-1);
\draw[ultra thick] (-1.2,-1.7)--(-1.4,-2)--(-1.6,-1.7);
\filldraw[thick, unshaded] (-.5,0)--(-.5,-1)--(.5,-1)--(.5,0)--(-.5,0);
\filldraw[thick, unshaded] (2,0)--(2,-1)--(1,-1)--(1,0)--(2,0);
\filldraw[thick, unshaded] (.5,-2.5)--(.5,-1.5)--(-1,-1.5)--(-1,-2.5)--(.5,-2.5);
\node at (-.25,-2) {$\zeta$};
\node at (0,-.5) {$y$};
\node at (0.2,.25) {{\scriptsize{$n$}}};
\node at (1.5,-.5) {$x$};
\node at (1.75,.25) {{\scriptsize{$m$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular,baseline=-1cm]
\clip (1.9,.5) --(-1.85,.5) -- (-1.85,-3.2) -- (1.9,-3.2);
\draw[ultra thick] (-1.7,-1)--(-1.5,-1.3)--(-1.3,-1);
\draw[ultra thick] (.7,1)--(.7,-2);
\draw[ultra thick] (-.7,0)--(-.7,-2);
\draw[ultra thick] (-.7,0) arc (0:180:.4cm) -- (-1.5,-2) .. controls ++(270:1.4cm) and ++(270:1.4cm) .. (1.5,-2)--(1.5,1);
\filldraw[thick, unshaded] (-.2,0)--(-.2,-1)--(-1.2,-1)--(-1.2,0)--(-.2,0);
\filldraw[thick, unshaded] (.2,0)--(.2,-1)--(1.2,-1)--(1.2,0)--(.2,0);
\filldraw[thick, unshaded] (1.2,-2.5)--(1.2,-1.5)--(-1.2,-1.5)--(-1.2,-2.5)--(1.2,-2.5);
\node at (0,-2) {$\zeta$};
\node at (.7,-.5) {$y$};
\node at (.9,.25) {{\scriptsize{$n$}}};
\node at (-.7,-.5) {$x$};
\node at (1.75,.25) {{\scriptsize{$m$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular,baseline=-1cm]
\clip (1.85,.5) --(-1.85,.5) -- (-1.85,-3.2) -- (1.85,-3.2);
\draw[ultra thick] (1.7,-1)--(1.5,-1.3)--(1.3,-1);
\draw[ultra thick] (-.7,1)--(-.7,-2);
\draw[ultra thick] (.7,0)--(.7,-2);
\draw[ultra thick] (.7,0) arc (180:0:.4cm) -- (1.5,-2) .. controls ++(270:1.4cm) and ++(270:1.4cm) .. (-1.5,-2)--(-1.5,1);
\filldraw[thick, unshaded] (-.2,0)--(-.2,-1)--(-1.2,-1)--(-1.2,0)--(-.2,0);
\filldraw[thick, unshaded] (.2,0)--(.2,-1)--(1.2,-1)--(1.2,0)--(.2,0);
\filldraw[thick, unshaded] (1.2,-2.5)--(1.2,-1.5)--(-1.2,-1.5)--(-1.2,-2.5)--(1.2,-2.5);
\node at (0,-2) {$\zeta$};
\node at (-.7,-.5) {$x$};
\node at (-.45,.25) {{\scriptsize{$m$}}};
\node at (.7,-.5) {$y$};
\node at (-1.3,.25) {{\scriptsize{$n$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular,baseline=-1cm]
\clip (1.65,.5) --(-2.2,.5) -- (-2.2,-3) -- (1.65,-3);
\draw[ultra thick] (.6,-1.5) arc (180:0:.4cm) -- (1.4,-2) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-1.5,-1);
\draw[ultra thick] (0,1)--(0,-2);
\draw[ultra thick] (-1.5,1)--(-1.5,-1);
\draw[ultra thick] (1.2,-1.7)--(1.4,-2)--(1.6,-1.7);
\filldraw[thick, unshaded] (.5,0)--(.5,-1)--(-.5,-1)--(-.5,0)--(.5,0);
\filldraw[thick, unshaded] (-2,0)--(-2,-1)--(-1,-1)--(-1,0)--(-2,0);
\filldraw[thick, unshaded] (-.5,-2.5)--(-.5,-1.5)--(1,-1.5)--(1,-2.5)--(-.5,-2.5);
\node at (.25,-2) {$\zeta$};
\node at (0,-.5) {$x$};
\node at (.25,.25) {{\scriptsize{$m$}}};
\node at (-1.5,-.5) {$y$};
\node at (-1.3,.25) {{\scriptsize{$n$}}}; \end{tikzpicture}. $$ \item[(2)] If $\rho$ is unitary, then for all $\zeta\in P_{m+n}$ and $x\in \widehat{Q_m^+}$, and $y\in \widehat{Q_n^+}$, $(y\otimes_A x)(\omega_{\rho^n \zeta}) = (x\otimes_A y)(\omega_\zeta)$: $$ \begin{tikzpicture}[rectangular]
\clip (-1.6,2.6) --(2.2,2.6) -- (2.2,-2.6) -- (-1.6,-2.6);
\draw[ultra thick] (-.6,1) arc (0:-180:.4cm) -- (-1.4,1.5) .. controls ++(90:1.4cm) and ++(90:2.2cm) .. (1.5,.5)--(1.5,-.5);
\draw[ultra thick] (-.6,-1) arc (0:180:.4cm) -- (-1.4,-1.5) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (1.5,-.5);
\draw[ultra thick] (0,2)--(0,-2);
\draw[ultra thick] (-1.25,1.5)--(-1.4,1.2)--(-1.55,1.5);
\draw[ultra thick] (-1.25,-1.2)--(-1.4,-1.5)--(-1.55,-1.2);
\filldraw[thick, unshaded] (-.5,.5)--(-.5,-.5)--(.5,-.5)--(.5,.5)--(-.5,.5);
\filldraw[thick, unshaded] (2,.5)--(2,-.5)--(1,-.5)--(1,.5)--(2,.5);
\filldraw[thick, unshaded] (.5,2)--(.5,1)--(-1,1)--(-1,2)--(.5,2);
\filldraw[thick, unshaded] (.5,-2)--(.5,-1)--(-1,-1)--(-1,-2)--(.5,-2);
\node at (-.25,1.5) {$\zeta$};
\node at (-.25,-1.5) {$\zeta$};
\node at (0,0) {$y$};
\node at (0.2,.75) {{\scriptsize{$n$}}};
\node at (0.2,-.75) {{\scriptsize{$n$}}};
\node at (1.5,0) {$x$};
\node at (1.75,.75) {{\scriptsize{$m$}}};
\node at (1.75,-.75) {{\scriptsize{$m$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular]
\clip (1.3,2.6) --(-1.3,2.6) -- (-1.3,-2.6) -- (1.3,-2.6);
\draw[ultra thick] (.7,1.5)--(.7,-1.5);
\draw[ultra thick] (-.7,1.5)--(-.7,-1.5);
\filldraw[thick, unshaded] (-.2,.5)--(-.2,-.5)--(-1.2,-.5)--(-1.2,.5)--(-.2,.5);
\filldraw[thick, unshaded] (.2,.5)--(.2,-.5)--(1.2,-.5)--(1.2,.5)--(.2,.5);
\filldraw[thick, unshaded] (1.2,2)--(1.2,1)--(-1.2,1)--(-1.2,2)--(1.2,2);
\filldraw[thick, unshaded] (1.2,-2)--(1.2,-1)--(-1.2,-1)--(-1.2,-2)--(1.2,-2);
\node at (0,1.5) {$\zeta$};
\node at (0,-1.5) {$\zeta$};
\node at (.7,0) {$y$};
\node at (.9,.75) {{\scriptsize{$n$}}};
\node at (.9,-.75) {{\scriptsize{$n$}}};
\node at (-.7,0) {$x$};
\node at (-.45,.75) {{\scriptsize{$m$}}};
\node at (-.45,-.75) {{\scriptsize{$m$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular]
\clip (1.6,2.6) --(-2.2,2.6) -- (-2.2,-2.6) -- (1.6,-2.6);
\draw[ultra thick] (.6,1) arc (180:360:.4cm) -- (1.4,1.5) .. controls ++(90:1.4cm) and ++(90:2.2cm) .. (-1.5,.5)--(-1.5,-.5);
\draw[ultra thick] (.6,-1) arc (180:0:.4cm) -- (1.4,-1.5) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-1.5,-.5);
\draw[ultra thick] (0,2)--(0,-2);
\draw[ultra thick] (1.25,1.5)--(1.4,1.2)--(1.55,1.5);
\draw[ultra thick] (1.25,-1.2)--(1.4,-1.5)--(1.55,-1.2);
\filldraw[thick, unshaded] (-.5,.5)--(-.5,-.5)--(.5,-.5)--(.5,.5)--(-.5,.5);
\filldraw[thick, unshaded] (-2,.5)--(-2,-.5)--(-1,-.5)--(-1,.5)--(-2,.5);
\filldraw[thick, unshaded] (-.5,2)--(-.5,1)--(1,1)--(1,2)--(-.5,2);
\filldraw[thick, unshaded] (-.5,-2)--(-.5,-1)--(1,-1)--(1,-2)--(-.5,-2);
\node at (.25,1.5) {$\zeta$};
\node at (.25,-1.5) {$\zeta$};
\node at (0,0) {$x$};
\node at (0.25,.75) {{\scriptsize{$m$}}};
\node at (0.25,-.75) {{\scriptsize{$m$}}};
\node at (-1.5,0) {$y$};
\node at (-1.3,.75) {{\scriptsize{$n$}}};
\node at (-1.3,-.75) {{\scriptsize{$n$}}}; \end{tikzpicture}. $$ \end{thm} \begin{proof} \item[(1)] For $\eta\in B^n$ and $\xi\in B^m$, \begin{align*} \langle \rho^n((x\otimes_A y) \zeta) , \eta\otimes\xi \rangle & = \langle (x\otimes_A y) \zeta , \xi\otimes \eta\rangle = \langle \zeta, (x^*\otimes_A y^*)( \xi\otimes \eta) \rangle \\ & = \langle \zeta,(x^*\xi)\otimes (y^*\eta)\rangle = \langle \rho^n (\zeta), (y^*\eta)\otimes (x^*\xi) \rangle \\ & = \langle (y\otimes_A x) \rho^n(\zeta), \eta\otimes\xi\rangle. \end{align*} \item[(2)] Pick $(x_i)\subset Q_m^+$ and $(y_j)\subset Q_n^+$ with $x_i\nearrow x$ and $y_j\nearrow y$. Then by (1), for all $i$, \begin{align*} (y_j\otimes_A x_i)(\omega_{\rho^n \zeta})
& = \| (y_j^{1/2}\otimes_A x_i^{1/2}) \rho^n\zeta\|_2^2
= \|\rho^n((x_i^{1/2}\otimes_A y_j^{1/2})\zeta)\|_2^2 \\
& = \|(x_i^{1/2}\otimes_A y_j^{1/2})\zeta\|_2^2 = (x_i\otimes_A y_j)(\omega_\zeta). \end{align*} We are finished by Theorem \ref{thm:increase}, since $x_i\otimes_A y_j \nearrow x\otimes_A y$ and $y_j\otimes_A x_i\nearrow y\otimes_A x$. \end{proof}
\begin{rem} When the operads for $P_\bullet$ and $\widehat{Q_\bullet^+}$ interact as in Theorem \ref{thm:action}, we may remove closed subdiagrams and multiply by the appropriate scalar in $[0,\infty]$ by Corollary \ref{cor:POperad} and Theorem \ref{thm:MoveAround}. \end{rem}
\subsection{Extremality implies the existence of the Burns rotation}\label{sec:ExtremalityImpliesRotations}
We will show in the next lemma and theorem that (approximate) extremality implies the existence of a Burns rotation. The intuition comes from the bimodule planar calculus. In diagrams, for the extremal case, we have: $$ \begin{tikzpicture}[rectangular,baseline=-.8cm]
\clip (1.6,1) --(-2.2,1) -- (-2.2,-3) -- (1.6,-3);
\draw[] (.6,-.5) arc (180:360:.4cm) -- (1.4,0) .. controls ++(90:1.4cm) and ++(90:2.2cm) .. (-1.5,-1);
\draw[] (.6,-1.5) arc (180:0:.4cm) -- (1.4,-2) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-1.5,-1);
\draw[ultra thick] (0,-2)--(0,0);
\draw[] (1.25,0)--(1.4,-.3)--(1.55,0);
\draw[] (1.25,-1.7)--(1.4,-2)--(1.55,-1.7);
\filldraw[thick, unshaded] (-.5,.5)--(-.5,-.5)--(1,-.5)--(1,.5)--(-.5,.5);
\filldraw[thick, unshaded] (-.5,-2.5)--(-.5,-1.5)--(1,-1.5)--(1,-2.5)--(-.5,-2.5);
\node at (.25,0) {$\zeta$};
\node at (.25,-2) {$\zeta$};
\node at (-.5,-1) {{\scriptsize{$n-1$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular,baseline=1.4cm]
\clip (-2.2,3.7) --(1.45,3.7) -- (1.45,-.2) -- (-2.2,-.2);
\draw[ultra thick] (-1,1.3)--(-1.2,1)--(-1.4,1.3);
\draw[] (1,1.3)--(1.2,1)--(1.4,1.3);
\draw[ultra thick] (-.2,3) arc (0:180:.5cm) --(-1.2,1) arc (-180:0:.5cm);
\draw[] (.2,3) arc (180:0:.5cm) --(1.2,1) arc (0:-180:.5cm);
\filldraw[thick, unshaded] (-.5,1) --(-.5,3) -- (.5,3) -- (.5,1)--(-.5,1);
\draw[thick] (-.5,2)--(.5,2);
\node at (0,2.5) {$\zeta$};
\node at (0,1.5) {$\zeta$};
\node at (-1.75,2.3) {{\scriptsize{$n-1$}}}; \end{tikzpicture} = \begin{tikzpicture}[rectangular,baseline=1.4cm]
\clip (-1,3.7) --(1.35,3.7) -- (1.35,-.2) -- (-1,-.2);
\draw[ultra thick] (.8,1.3)--(1,1)--(1.2,1.3);
\draw[ultra thick] (0,3) arc (180:0:.5cm) --(1,1) arc (0:-180:.5cm);
\filldraw[thick, unshaded] (-.5,1) --(-.5,3) -- (.5,3) -- (.5,1)--(-.5,1);
\draw[thick] (-.5,2)--(.5,2);
\node at (0,2.5) {$\zeta$};
\node at (0,1.5) {$\zeta$};
\node at (1.2,2.3) {{\scriptsize{$n$}}}; \end{tikzpicture} . $$ Although these diagrams are not yet well-defined, they tell us how to proceed. They become well-defined after the Burns rotation exists by Theorems \ref{thm:CloseOffZetas} and \ref{thm:MoveAround}.
\begin{lem}\label{lem:RotationLemma} Let $p_n$ be the projection in $B(H^n)$ with range $P_n$. \item[(1)] If $H$ is approximately extremal with constant $\lambda>0$, then $$\left(\sum_\beta p_nR_\beta R_\beta^*p_n\right)\leq \lambda^{n-1} p_n \text{ and }\left(\sum_\alpha p_nL_\alpha L_\alpha^* p_n\right) \leq \lambda^{n-1} p_n.$$ \item[(2)] If $H$ is extremal, then on $P_n$, $\sum_\beta p_nR_\beta R_\beta^*p_n = p_n=\sum_\alpha p_nL_\alpha L_\alpha^*p_n$. \end{lem} \begin{proof} \item[(1)] We prove the first inequality. Note that $R_{\beta}^*\zeta\in D(\sb{A}H^{n-1})$, and $R(R_\beta^*\zeta)=R_\beta^* R(\zeta)\colon L^2(A)\to H^{n-1}$. Since $H$ is (approximately) extremal, so is $H^{n-1}$ with constant $\lambda^{n-1}$, and \begin{align*} \left\langle\left( \sum_\beta p_nR_\beta R_\beta^*p_n\right) \zeta,\zeta\right\rangle_{P_n}
& = \sum_{\beta} \|R_{\beta}^* \zeta\|_2^2 = \sum_{\beta} \tr_{A}\left({\sb{A}\langle}R_{\beta}^* \zeta,R_{\beta}^* \zeta\rangle \right) \\ & = \sum_{\beta} \Tr_{n-1}^{\OP}\left(R_{\beta}^* R(\zeta)R(\zeta)^*R_{\beta} \right) = \Tr_{n-1}^{\OP} T_{n-1} (R(\zeta)R(\zeta)^*)\\ & \leq \lambda^{n-1} \Tr_{n-1} T_{n-1} (L(\zeta)L(\zeta)^*) = \lambda^{n-1}\Tr_n(L(\zeta)L(\zeta)^*)\\
& = \lambda^{n-1}\|\zeta\|_2^2 = \langle (\lambda^{n-1}p_n) \zeta,\zeta\rangle_{P_n}. \end{align*} \item[(2)] As $\lambda=1$, by (1), $$ \left\langle \left(\sum_\beta p_n R_\beta R_\beta^* p_n\right) \zeta, \zeta\right\rangle = \langle \zeta, \zeta\rangle $$ for all $\zeta\in P_n$, and the result follows from polarization. \end{proof}
\begin{thm}\label{thm:rotation} Suppose $H$ is approximately extremal. Then $\rho=\sum_{\beta} L_\beta R_\beta^* $ converges strongly on $P_n$. Moreover if $H$ is extremal, $\rho$ is unitary. A similar result holds for $\rho^{\OP}=\sum_\alpha R_\alpha L_\alpha^*$. \end{thm} \begin{proof} We begin as in the proof of Proposition 3.3.19 of \cite{burns}, but as we do not have Jones projections, we use Lemma \ref{lem:RotationLemma}.
Suppose $\zeta\in P_n$, and enumerate $\{\beta\}=\{\beta_i\}_{i\in\mathbb{N}}$. We will show $$
\left\|\sum_{i=r}^s L_{\beta_i}R_{\beta_i}^* \zeta\right\|_2^2\to 0 \text{ as } r,s\to \infty. $$ First note that the infinite matrix $(L_{\beta_j}^* L_{\beta_i})$ is a projection, so it is dominated by $1=\delta_{i,j}$. Hence each corner $(L_{\beta_j}^* L_{\beta_i})_{i,j=r}^s$ is dominated by $1=\delta_{i,j}$, and $$
\left\| \sum_{i=r}^s L_{\beta_i} R_{\beta_i}^* \zeta\right\|_2^2
= \sum_{i,j=r}^s\left\langle (L_{\beta_j}^* L_{\beta_i}) R_{\beta_i}^*\zeta, R_{\beta_j}^*\zeta\right\rangle
\leq \sum_{i=r}^s \langle R_{\beta_i}^* \zeta, R_{\beta_i}^* \zeta\rangle. $$
We need to show that the right hand side tends to zero, which is certainly true if the infinite sum $\sum_{\beta} \|R_{\beta}^* \zeta\|_2^2$ converges. But this follows immediately from Lemma \ref{lem:RotationLemma}. Hence $\rho$ converges and $\|\rho\|\leq \sqrt{\lambda^{n-1}}$ (where $\lambda$ is the approximate extremality constant). If $\lambda = 1$, then $\|\rho\|\leq 1$ and $\rho^n=\id_{P_n}$, so $\rho$ is necessarily isometric and thus unitary. \end{proof}
\subsection{Symmetric bimodules and a converse of Theorem \ref{thm:rotation}}\label{sec:symmetric} To prove a converse of Theorem \ref{thm:rotation}, we need additional structure on $H$ due to Example \ref{ex:NoCentralVectors}.
\begin{rem} For the rest of this section, we assume $H$ is symmetric (see Remark \ref{rem:symmetric}). \end{rem}
\begin{lem}\label{lem:switch}
For all $\eta,\xi\in B^n$, $\langle \eta |\xi\rangle_A = {\sb{A}\langle} J\eta, J\xi\rangle$. \end{lem} \begin{proof} Suppose $a_1,a_2\in A$. Then \begin{align*} \big\langle {\sb{A}\langle} J\eta,J\xi\rangle \widehat{a_1},\widehat{a_2}\big\rangle & = \langle J R(J\eta)^* R(J\xi) J \widehat{a_1}, \widehat{a_2}\rangle = \langle \widehat{a_2^*} , R(J\eta)^* R(J\xi) \widehat{a_1^*}\rangle = \langle a_2^* J\eta , a_1^* J\xi\rangle\\ & = \langle J(\eta a_2) , J (\xi a_1)\rangle = \langle \xi a_1, \eta a_2\rangle
= \big\langle \langle \eta| \xi\rangle_A \widehat{a_1} , \widehat{a_2}\big\rangle. \end{align*} \end{proof}
\begin{defn} Using Lemma \ref{lem:switch}, we define an algebra structure on $B^n\otimes_A B^n$ as follows: if $\eta_1,\eta_2,\xi_1,\xi_2\in B^n$, then $$
(\eta_1\otimes \xi_1)( \eta_2\otimes \xi_2) = \eta_1 \langle J\xi_1 | \eta_2\rangle_A \otimes \xi_2 = \eta_1 {\sb{A}\langle} \xi_1,J\eta_2\rangle \otimes \xi_2. $$ \end{defn}
\begin{prop}[\cite{MR703809,MR1055223}]\label{prop:ModuleIso} The map $B^n\otimes_A B^n\to C_n$ by $\eta\otimes J_n\xi \mapsto L(\eta)L(\xi)^*$ gives a $*$-algebra isomorphism onto its image, and it extends to a $C_n-C_n$ bimodule isomorphism $\theta_n\colon H^{2n}\to L^2(C_n,\Tr_n)$. The same result holds swapping $\OP$. \end{prop} \begin{proof} The map is well defined as it is $A$-middle linear: \begin{align*} \eta a \otimes J_n\xi & \mapsto L(\eta a)L(\xi)^* = L(\eta) a L(\xi)^* = L(\eta) L(\xi a^*)^* \text{ and }\\ \eta\otimes a J_n\xi & \mapsto L(\eta) L(J_n(aJ_n\xi))^* = L(\eta)L(\xi a^*)^*. \end{align*} The map clearly preserves the multiplicative structure and is isometric by construction. If $\eta_1,\eta_2,\xi_1,\xi_2\in B^n$, then \begin{align*} \langle L(\eta_1) L(\xi_1)^* , L(\eta_2)L(\xi_2)^* \rangle_{L^2(C_n,\Tr_n)} & = \Tr_n \left(L(\xi_2)L(\eta_2)^*L(\eta_1) L(\xi_1)^*\right)\\
& = \Tr_n \left(L(\xi_2)\langle \eta_2| \eta_1\rangle_A L(\xi_1)^*\right)\\
& = \Tr_n \left(L(\xi_2\langle \eta_2| \eta_1\rangle_A) L(\xi_1)^*\right)\\
& = \langle \xi_2\langle \eta_2| \eta_1\rangle_A,\xi_1\rangle_{H^n} \\
&= \langle J_n\xi_1 , J_n(\xi_2\langle \eta_2| \eta_1\rangle_A)\rangle_{H^n}\\
& = \langle J_n\xi_1 , \langle \eta_1| \eta_2\rangle_AJ_n\xi_2\rangle_{H^n}\\ &= \langle \eta_1\otimes J_n\xi_1 , \eta_2\otimes J_n \xi_2 \rangle_{H^{2n}}. \end{align*} Hence it clearly extends to a $C_n-C_n$ bilinear bimodule isomorphism. \end{proof}
\begin{cor} $C_{n-k}\subseteq C_n\subseteq C_{n+k}$ is standard (isomorphic to the basic construction) for all $n,k\geq 0$. \end{cor} \begin{proof} By Remark \ref{rem:FiberProduct} and Proposition \ref{prop:ModuleIso}, $$ J_{2n}(C_{n-k}\otimes_A \id_{n+k})'J_{2n}=J_{2n}(\id_{n-k}\otimes_A C_{n+k}^{\OP})J_{2n}=C_{n+k}\otimes_A \id_{n-k}. $$ \end{proof}
\begin{lem}[\cite{burns}, Theorem 3.3.13]\label{lem:BurnsL2Lemma} Let $N$ be a von Neumann subalgebra of a semifinite von Neumann algebra $M$ with n.f.s. trace $\Tr_M$. Then
\item[(1)] $N'\cap L^2(M)=\overline{N'\cap \mathfrak{n}_{\Tr_M}}^{\|\cdot\|_2}$
\item[(2)] $(N'\cap L^2(M))^\perp = \overline{[N,\mathfrak{n}_{\Tr_M}]}^{\|\cdot\|_2}$, the closure of the span of the commutators in $L^2(M)$. \end{lem}
\begin{rem} By Proposition \ref{prop:ModuleIso} and Lemma \ref{lem:BurnsL2Lemma}, $\theta_n$ yields an isomorphsim
$$P_{2n} = A'\cap H^{2n}\cong A'\cap L^2(C_n,\Tr_n) = \overline{ A'\cap \mathfrak{n}_{\Tr_n}}^{\|\cdot\|_2}=\overline{C_n^{\OP} \cap \mathfrak{n}_{\Tr_n}}^{\|\cdot\|_2}=L^2(Q_n,\Tr_n)$$ of $Q_n- Q_n$ bimodules. A similar result holds swapping $\OP$. \end{rem}
\begin{thm}\label{thm:RotationConverse} If $\rho$ exists on $P_{2n}$, then $H^n$ is approximately extremal. If $\rho$ is unitary, then $H^n$ is extremal. \end{thm} \begin{proof} The main step is to show the following lemma, whose proof is essentially the same as in \cite{burns}.
\begin{lem}[3.3.21.(ii) of \cite{burns}]\label{lem:BurnsLemma} If $\rho$ exists on $P_{2n}$, then for all $x\in C_n^{\OP}\cap \mathfrak{n}_{\Tr_n}$, $\rho^n(\theta_n^{-1}(\widehat{x}))=\theta_n^{-1}(\widehat{j_n(x)})\in C_n^{\OP}\cap \mathfrak{n}_{\Tr_n}$. In particular, $C_n^{\OP}\cap \mathfrak{n}_{\Tr_n}=\mathfrak{n}_{\Tr_n^{\OP}}\cap \mathfrak{n}_{\Tr_n}$. A similar result holds swapping $\OP$. \end{lem}
Using this lemma, Burns' proof shows $\Tr_n^{\OP}\leq \|\rho^n\| \Tr_n$ on $Q_n^+$. Suppose $z\in Q_n$. If $\Tr_n(z^*z)=\infty$, we are finished. Otherwise, $z\in C_n^{\OP}\cap \mathfrak{n}_{\Tr_n}=\mathfrak{n}_{\Tr_n^{\OP}}\cap \mathfrak{n}_{\Tr_n}$, and \begin{align*} \Tr_n^{\OP} (z^*z) & = \Tr_n\circ j_n (z^*z) = \Tr_n (j_n(z)^* j_n(z)) = \left\langle \widehat{j_n(z)},\widehat{j_n(z)}\right\rangle_{L^2(Q_n,\Tr_n)} \\ & = \left\langle \theta_n^{-1}(\widehat{j_n(z)}),\theta_n^{-1}(\widehat{j_n(z)})\right\rangle_{P_n} = \left\langle \rho^n (\theta_n^{-1}(\widehat{z})), \rho^n (\theta_n^{-1}(\widehat{z}))\right\rangle_{P_n}\\
& = \|\rho^n(\theta_n^{-1}(\widehat{z}))\|^2_{P_n}
\leq \|\rho^n\|^2 \|\theta_n^{-1}(\widehat{z})\|^2_{P_n}
= \|\rho^n\|^2 \|\widehat{z}\|^2_{L^2(Q_n,\Tr_n)} \\
& = \|\rho^n\|^2 \Tr_n(z^*z). \end{align*}
Similarly $\Tr_n \leq \|\rho^n\|^2 \Tr_n^{\OP}$ on $Q_n^+$, and $H^n$ is approximately extremal. In particular, if $\|\rho\|=1$, $H^n$ is extremal. \end{proof}
\begin{rem} Theorem \ref{thm:MainTheorem} now follows immediately from Theorems \ref{thm:extremal}, \ref{thm:rotation}, and \ref{thm:RotationConverse}. \end{rem}
\section{Examples}\label{sec:Examples}
\begin{ex}[Bifinite bimodules] In the case that $H$ is a symmetric, bifinite $A-A$ bimodule, then the $\mathbb{B}\mathbb{P}$-algebra structure encodes the $C^*$-tensor category whose objects are the sub-bimodules of $H^n$ for some $n$ and whose morphisms are intertwiners. \end{ex}
\begin{ex}\label{ex:InfiniteIndex} Suppose $A_0=A\subset B=A_1$ is an infinite index inclusion of $II_1$-factors. Then $H=L^2(B)$ gives an $A-A$ bimodule. In this case, letting $A_{n+1}$ be the $n^{\text{th}}$ iterated basic construction of $A_{n-1}\subset A_n$, we have \item[$\bullet$] $H^n\cong L^2(A_n,\Tr_n)$, \item[$\bullet$] $C_n,C_n^{\OP}$ is the left,right action respectively of $A_{2n}$, and \item[$\bullet$] $Q_n = A_0'\cap A_{2n}$. \item Theorem \ref{thm:MainTheorem} was proven for this case by \cite{burns}. \end{ex}
\begin{ex}\label{ex:NoCentralVectors} Suppose $A$ is a $II_1$-factor, and $\sigma\in \Aut(A)$. Define $H_\sigma = {\sb{A}L^2}(A)_{\sigma(A)}$ by $a\widehat{b}c = \widehat{ab\sigma(c)}$ for all $a,b,c,\in A$. Suppose that $\sigma$ is outer and not periodic, and $\sigma^n$ is outer for all $n\in\mathbb{N}$. Then $H_\sigma^n \cong H_{\sigma^n}$ is extremal and $P_n=(0)$ for all $n\geq 1$. \end{ex}
\begin{ex}[Group actions]\label{ex:GroupActions} Suppose $G$ is a countable i.c.c. group, and $\pi\colon G\to U(K)$ is a unitary representation. We can define two bimodules: \item[(1)] $H=K\otimes_\mathbb{C} \ell^2(G)$ where the left action is given by the diagonal action $\pi\otimes \lambda$ and the right action is given by $1\otimes \rho$ where $\lambda,\rho$ are the left,right regular representation of $G$ on $\ell^2(G)$. Hence $K\otimes_\mathbb{C} \ell^2(G)$ gives an $A-A$ bimodule where $A=LG$. Then we may identify $$ H^n = K^n\otimes_\mathbb{C} \ell^2(G) $$ where we write $K^n=K^{\otimes_\mathbb{C} n}$, and the left action is the diagonal action $\pi^n\otimes \lambda$ and the right action is $1_n\otimes \rho$. It is clear that projections in $Q_n$ correspond to $LG-LG$ invariant subspaces of $H^n$. Every $G$-invariant subspace of $K^n $ yields such a subspace, but in general, they do not exhaust all possible subspaces. \item[(2)] To fix this problem, we use an idea of Richard Burstein and add a copy of the hyperfinite $II_1$-factor $R$. Suppose $\alpha\colon G\to \Aut(R)$ is an outer action, so $A=R\rtimes_\alpha G$ is a $II_1$-factor. Set $H=K\otimes_\mathbb{C} L^2(R) \otimes_\mathbb{C} \ell^2(G)$, and consider the left and right actions where \begin{align*} r_1 (k\otimes \widehat{r_2} \otimes \delta_g) r_3 &= k \otimes \widehat{r_1 r_2 \alpha_{g}^{-1}(r_3)}\otimes \delta_{g} \\ g_1(k\otimes \widehat{r} \otimes \delta_{g_2}) g_3 &= (\pi_{g_1}k)\otimes \widehat{\alpha_{g_1}(r)} \otimes \delta_{g_1g_2g_3} \end{align*} for $r,r_i\in R$ and $g,g_i\in G$ for $i=1,2,3$. Hence $g\in G$ acts on the left by $\pi_g\otimes \alpha_g \otimes \lambda_g$ and on the right by $1\otimes 1\otimes \rho_g$. Then similarly we may identify $$H^n=K^n \otimes_\mathbb{C} L^2(R)\otimes_\mathbb{C} \ell^2(G).$$ \end{ex}
\begin{thm}\label{thm:invariants} For $A=R\rtimes_\alpha G$ and $H^n$ as above, $A-A$ invariant subspaces of $H^n$ correspond to $G$-invariant subspaces of $K^n$. \end{thm} \begin{proof} First, if $L_0\subset K^n$ is a $G$-invariant subspace, then $L_0\otimes L^2(A)$ is an $A-A$ invariant subspace of $H^n$.
Now suppose $L\subset H^n$ is an $A-A$ invariant subspace, and let $p\in Q_n$ be the projection onto $L$. Note that \begin{align*} p&\in \bigg(1_{K^n}\otimes R\bigg)' \cap \bigg(1_{K^n} \otimes A^{\OP}\bigg)' \\ &= \bigg(B(K^n)\otimes (R'\cap B(L^2(A)))\bigg)\cap \bigg(B(K^n)\otimes A\bigg)\\ &=B(K^n)\otimes ( R'\cap A)=B(K^n)\otimes 1_{L^2(A)}. \end{align*} Hence there is a $q\in B(K^n)$ such that $p=q\otimes 1_{L^2(A)}$. But since $q$ commutes with the left $G$-action on $H^n$, we have $q\in \pi(G)'\cap B(K^n)$. \end{proof}
\begin{cor} $A-A$ invariant vectors of $H^n$ correspond to $G$-invariant vectors of $K^n$. \end{cor}
\begin{ex}[Group-subgroup]\label{ex:GroupSubgroup} Suppose $G_0\subseteq G_1$ is an inclusion of countable i.c.c. groups, and let $K=\ell^2(G_1/G_0)$. As in Example \ref{ex:GroupActions}, we consider two cases: \item[(1)] $A_0=LG_0$, $A_1= LG_1$, and $H=K\otimes_\mathbb{C} \ell^2(G_1)$. \item[(2)] $A_0= R\rtimes G_0$, $A_1= R\rtimes G_1$, and $H=K\otimes_\mathbb{C} L^2(R) \otimes \ell^2(G_1)$. \item Note that in either case, $H^n \cong L^2(A_{n+1})$, where $A_{n+1}=J_n A_{n-1}' J_n$ is the basic construction of $A_{n-1}\subset A_{n}$. As in the usual subfactor treatment, we can consider $H^n$ as an $A_i-A_j$ bimodule for $i,j\in \{0,1\}$. \end{ex}
\begin{thm} Let $G_1=S_\infty$, the group of finite permutations of $\mathbb{N}$, and let $G_0=\Stab(1)$ be the permutations which fix $1$. Let $A_0=R\rtimes G_0$ and $A_1=R\rtimes G_1$, and let $H=K\otimes_\mathbb{C} L^2(R)\otimes \ell^2(G_1)$ as in (2) of Example \ref{ex:GroupSubgroup}. Then considering $H^n$ as an $A_0-A_0$ or as an $A_1-A_1$ bimodule, we have that $\dim(Q_n)<\infty$ for all $n\in\mathbb{N}$. \end{thm} \begin{proof} Since $A_i'\cap A_j \cong A_{i+2}'\cap A_{j+2}$ for all $i,j\geq 0$ by \cite{MR1387518}, it suffices to show that $\dim(A_1'\cap A_{2n+1})<\infty$ for all $n\geq 0$. Also by \cite{MR1387518}, $$A_1'\cap A_{2n+1}\cong \End_{A_1-A_1}(L^2(A_{n+1}))\cong \End_{A_1-A_1}(H^n).$$ By Theorem \ref{thm:invariants}, $A_1-A_1$ invariant subspaces of $H^n$ correspond to $G_1$-invariant subspaces of $K^{n}$. The result now follows by \cite{MR0286940}. \end{proof}
\begin{cor}\label{cor:FiniteDimensional} The infinite index $II_1$-subfactor $R\rtimes G_0 \subset R\rtimes G_1$ for $G_0=\Stab(1)\subset S_\infty=G_1$ has finite dimensional higher relative commutants. \end{cor}
\begin{thm} Suppose $G_0\subset G_1$ and $K$ are as in Example \ref{ex:GroupSubgroup} such that $[G_1\colon G_0]=\infty$ and $\#G_0\backslash G_1/G_0=2$. Then \item[(1)] the space of $G_0$-invariant vectors in $K^n$ is one dimensional, and \item[(2)] zero is the only $G_1$-invariant vector in $K^n$. \end{thm} \begin{proof} Let $\{g_i\}_{i\geq 0}$ be a set of coset representatives for $G_1/G_0$ with $g_0=e$. Since $\# G_0\backslash G_1/ G_0 = 2$, for $i,j\geq 1$, there are $h_{i,j}\in G_0$ such that $h_{i,j} g_i G_0 = g_j G_0$. \item[(1)] Suppose $$ \xi = \sum_{i_1,\dots, i_n} \lambda_{i_1,\dots, i_n} \delta_{g_{i_1}G_0}\otimes\cdots \otimes \delta_{g_{i_n}G_0} \in K^n $$ is $G_0$-invariant. Then since $\pi_{h_{i,j}}\xi = \xi$ for all $i,j\geq 1$, we must have $\lambda_{i_1,\dots, i_n}=0$ unless $i_j=0$ for all $j=1,\dots, n$. (Otherwise, there would be infinitely many coefficients which would be nonzero and equal, a contradiction to $\xi\in K^n \cong \ell^2((G_1/G_0)^n)$.) Hence $\xi\in \spann\{ \delta_{G_0}\otimes\cdots \otimes\delta_{G_0}\}$. \item[(2)] Since $\delta_{G_0}\otimes\cdots \otimes\delta_{G_0}$ is not $G_1$-invariant, the result follows from (1). \end{proof}
\begin{cor}\label{cor:InfiniteSymmetric} Let $G_0=\Stab(1)\subset S_\infty= G_1$. Let $A_i= R\rtimes G_i$ for $i=0,1$, and let $K=\ell^2(G_1/G_0)$. \item[(1)] When we consider $H=K\otimes_C L^2(R)\otimes_\mathbb{C} \ell^2(G_1)$ as an $A_1-A_1$ bimodule, $P_n=(0)$. \item[(2)] When we consider $H=L^2(A_1)=L^2(R)\otimes_\mathbb{C} \ell^2(G_1)$ as an $A_0-A_0$ bimodule, $$ H^n\cong L^2(A_n)\cong K^{n-1}\otimes_\mathbb{C} L^2(R)\otimes_\mathbb{C}\ell^2(G_1), $$ and for all $n\geq 0$, $P_n$ is one-dimensional and spanned by $$ \widehat{1}\otimes \cdots \otimes \widehat{1}\in \bigotimes_{A_0}^n L^2(A_1) \cong L^2(A_{n}). $$ \end{cor}
In joint work with Steven Deprez, we have shown an even stronger result: \begin{thm}\label{thm:InfiniteSymmetricGroup} The algebras $Q_n$ for the bimodules in (1) and (2) in Example \ref{ex:GroupSubgroup} are finite dimensional, and the dimensions grow super-factorially. \end{thm}
\begin{cor} The infinite index $II_1$-subfactor $LG_0\subset LG_1$ where $G_0=\Stab(1)\subset S_\infty = G_1$ has finite dimensional higher relative commutants. \end{cor}
\appendix
\section{Relative tensor products of extended positive cones}\label{sec:TensorUnbounded}
\begin{nota} For this section, let $H_A$ be a right Hilbert $A$-module, $\sb{A}K_B$ be a Hilbert $A-B$ bimodule, and $\sb{B}L$ be a left Hilbert $B$-module where $A,B$ are finite von Neumann algebras. We write: \item[$\bullet$] $X=(A^{\OP})'\cap B(H)$, \item[$\bullet$] $\sb{A}K$ when we ignore the right $B$-action, \item[$\bullet$] $Y_0 = A'\cap B(K)$, \item[$\bullet$] $Y=A'\cap (B^{\OP})'\cap B(K)$, \item[$\bullet$] $Z=B'\cap B(L)$, \item[$\bullet$] $X\otimes_A Y_0 = \set{x\otimes_A y}{x\in X\text{ and } y\in Y_0}''$, and \item[$\bullet$] $X\otimes_A Y \otimes_B Z = \set{x\otimes_A y\otimes_B z}{x\in X,\, y\in Y, \text{ and } z\in Z}''$. \end{nota}
The goal of this section is to define the operator $x\otimes_A y \in \widehat{(X\otimes_A Y_0)^+}$ for $x\in \widehat{X^+}$ and $y\in \widehat{Y_0^+}$ such that certain properties, e.g., associativity, are satisfied.
The next three lemmata are straightforward, but we include some proofs for completeness and for the convenience of the reader.
\begin{lem}\label{lem:WeakStrong} Suppose $x\in M^+$ and $(x_i)_{i\in I}\subset M^+$ is a directed net, with $x_i\leq x$ for all $i\in I$. The following are equivalent:
\item[(1)] $x_i\to x$ strongly (if and only if $\sigma$-strongly as $\|x_i\|_\infty\leq \|x\|_\infty$ for all $i$)
\item[(2)] $x_i\to x$ weakly (if and only if $\sigma$-weakly as $\|x_i\|_\infty\leq \|x\|_\infty$ for all $i$) \item[(3)] $x_i\nearrow x$, i.e., $x_i(\omega_\xi)\nearrow x(\omega_\xi)$ for all $\xi\in H$, \item[(4)] $x_i(\omega_\xi)\nearrow x(\omega_\xi)$ for all $\xi$ in a dense subspace $D$ of $H$. \end{lem} \begin{proof} Clearly $(1)\Rightarrow(2)\Rightarrow(3)\Rightarrow(4)$. \itm{(3)\Rightarrow (1)}
Suppose $(x-x_i)(\omega_\xi)\to 0$ for all $\xi \in H$. Then $\|\sqrt{x-x_i}\xi\|_2\to 0$, so $\sqrt{x-x_i}\to 0$ strongly. Hence $x_i\to x$ strongly as multiplication is strongly continuous on bounded sets. \itm{(4)\Rightarrow(3)} Choose an orthonormal basis $\{e_n\}_{n\geq 1}\subset D$ for $H$. Suppose $\xi=\sum_n \lambda_n e_n \in H\setminus\{0\}$, and let $\varepsilon>0$. Then there is an $N>0$ such that $$
\xi_N := \sum_{n>N} \lambda_n e_n \Longrightarrow \|\xi_N\|_2^2 = \sum_{n>N} |\lambda_n|^2 <\frac{\varepsilon^2}{16\|x\|_\infty^2 \|\xi\|_2^2}. $$ For $n=1,\dots,N$, there are $i_n\in I$ such that $i > i_n$ implies $$
|\langle (x-x_i) \lambda_n e_n,\xi\rangle|\leq \|(x-x_i) \lambda_n e_n\|_2\|\xi\|_2< \frac{\varepsilon}{2^{n+1}}. $$ Now choose $i'>i_n$ for all $n=1,\dots,N$. We calculate that for $i>i'$, \begin{align*} (x-x_i)(\omega_\xi) &= \langle (x-x_i) \xi,\xi\rangle
\leq \sum_{n=1}^N |\langle (x-x_i) \lambda_n e_n,\xi\rangle| + \left|\left\langle (x-x_i)\xi_N,\xi\right\rangle\right|\\
& \leq \sum_{n=1}^N \frac{\varepsilon}{2^{n+1}} + \left|\left\langle x\xi_N,\xi\right\rangle\right|+\left|\left\langle x_i\xi_N,\xi\right\rangle\right|
\leq \sum_{n=1}^N \frac{\varepsilon}{2^{n+1}} +2\|x\|_\infty \|\xi_N\|_2 \|\xi\|_2\\
&< \frac{\varepsilon}{2}+2\mu \frac{\varepsilon}{4\|x\|_\infty \|\xi\|_2} \|\xi\|_2 = \varepsilon. \end{align*} As $\varepsilon$ was arbitrary, we are finished. \end{proof}
\begin{lem}\label{lem:CommuteStrong} If $x,y \in M^+$, and $(x_i)_{i\in I},(y_j)_{j\in J}\subset M^+$ are directed nets of increasing operators such that \item[$\bullet$] any two elements in $\{x,y\}\cup \set{x_i}{i\in I}\cup \set{y_j}{j\in J}$ commute and \item[$\bullet$] $x_i\nearrow x$ and $y_j\nearrow y$, \item then $x_iy_j\nearrow xy$ (and Lemma \ref{lem:WeakStrong} applies). \end{lem}
\begin{lem}\label{lem:binormal}
Suppose $x\in X$ and $y\in Y_0$. Then $x\otimes_A y\colon H\otimes_A K\to H\otimes_A K$ given by the unique extension of $\xi\otimes \eta\mapsto (x\xi)\otimes(y\eta)$ where $\xi\in D(H_A)$ and $\eta\in D(\sb{A}K)$ is well-defined and bounded, and $\|x\otimes_A y\|_\infty\leq \|x\|_\infty\|y\|_\infty$. Hence the $*$-algebra map $x\odot_\mathbb{C} y\mapsto x\otimes_A y$ is a binormal representation of $X\odot_\mathbb{C} Y_0$ on $H\otimes_A K$. \end{lem} \begin{proof} \item[(1)] Fix $\xi_1,\dots,\xi_k\in D(H_A)$ and $\eta_1,\dots,\eta_k\in D(\sb{A}K)$, and let $\xi=(\xi_1,\dots,\xi_k)$ and $\eta=(\eta_,\dots,\eta_k)$. Since the matrices $m=({\sb{A}\langle} y\eta_i,y\eta_j\rangle)_{i,j}, n=(\langle \xi_j,\xi_i\rangle_A)_{i,j}\in M_k(A)$ are positive (see Lemma 1.8 of \cite{MR1424954}), we have \begin{align*}
\left\| \sum_{i=1}^k (x\xi_i)\otimes(y\eta_i)\right\|_2^2 & = \sum_{i,j=1}^k \langle (x\xi_i)\otimes(y\eta_i), (x\xi_j)\otimes(y\eta_j)\rangle \\ & = \sum_{i,j=1}^k \langle (x\xi_i){\sb{A}\langle} y\eta_i,y\eta_j\rangle, (x\xi_j)\rangle = \langle (x\xi) n,( x\xi)\rangle
= \|(x\xi)n^{1/2}\|_2^2\\
& =\| x(\xi n^{1/2})\|_2^2\leq \|x\|_\infty^2 \|\xi n^{1/2}\|_2^2
= \|x\|_\infty^2 \sum_{i,j=1}^k \langle \xi_i{\sb{A}\langle} y\eta_i,y\eta_j\rangle, \xi_j\rangle \\
& = \|x\|_\infty^2 \sum_{i,j=1}^k \langle \langle\xi_j,\xi_i\rangle_A ( y\eta_i),(y\eta_j)\rangle
= \|x\|_\infty^2 \|m^{1/2}(y\eta)\|_2^2\\
& = \|x\|_\infty^2 \|y(m^{1/2}\eta)\|_2^2
\leq \|x\|_\infty^2 \|y\|_\infty^2 \|m^{1/2}\eta\|_2^2\\
& = \|x\|_\infty^2\|y\|_\infty^2\left\| \sum_{i=1}^k \xi_i\otimes\eta_i\right\|_2^2. \end{align*} \item[(2)] That $x\mapsto x\otimes_A 1_K$ is a normal representation of $X$ follows from the density of $D(H_A)\otimes_A K$ and (4) of Lemma \ref{lem:WeakStrong}. Similar for $y\mapsto 1_H\otimes_A y$. \end{proof}
\begin{nota}\label{nota:spectral} Let $\mathcal{B}$ be the Borel $\sigma$-algebra of subsets of $[0_\mathbb{R},\infty_\mathbb{R}]$. For a spectral measure $E \colon \mathcal{B}\to P(H)$, we use the conventions $E_\lambda=E([0,\lambda])$, so $E_\infty=1$, and $E^\infty=E(\{\infty\})$ (in general, our spectral measures on $\mathcal{B}$ have non-trivial mass at $\infty$). \end{nota}
\begin{lem}\label{lem:SpectralConvergence} Suppose $E \colon \mathcal{B}\to P(X)\subset B(H_A) $ is a spectral measure. Suppose $f\colon [0,\infty]\to [0,\infty)$ is a bounded Borel-measurable function, and $(\varphi_n)$ is a sequence of positive simple functions increasing pointwise to $f$. Then $$ \int_0^\infty f(\lambda)\, dE_\lambda := \sup_n\int_0^\infty \varphi_n(\lambda) \, dE_\lambda $$ is well defined. \end{lem} \begin{proof} Suppose $\xi\in H$. Then as $\omega_\xi$ is normal, $\omega_\xi \circ E$ is a Borel measure, and $$ \int_0^\infty f(\lambda)\, d(\omega_\xi(E_\lambda))=\sup_n \int_0^\infty \varphi_n(\lambda) \, d(\omega_\xi(E_\lambda)) $$ is independent of the choice of positive simple functions $\varphi_n$ increasing to $f$. \end{proof}
\begin{prop}\label{prop:TensorSpectral} Suppose \begin{align*} E \colon \mathcal{B}&\longrightarrow P(X)\subset B(H_A) \text{ and }\\ F \colon \mathcal{B}&\longrightarrow P(Y_0)\subset B(\sb{A}K) \end{align*} are spectral measures. \item[(1)] The map $E \otimes_A F\colon \mathcal{B}\otimes \mathcal{B}\longrightarrow P(X\otimes_A Y_0)$ by $$ (I_1,I_2)\longmapsto \int_{I_1\times I_2} \, d(E_\lambda\otimes_A F_\mu) := E(I_1)\otimes_A F (I_2) $$ extends uniquely to a spectral measure by countable additivity. \item[(2)] If $\varphi,\psi\colon [0,\infty]\to [0,\infty)$ are positive simple functions, then {\fontsize{10}{10}{ $$ \int_{0}^\infty\int_0^\infty \varphi(\lambda) \psi(\mu) \, d(E_\lambda\otimes_A F_\mu) = \left(\int_0^\infty \varphi(\lambda) \, dE_\lambda\right) \otimes_A \left( \int_0^\infty \psi(\mu) \, dF_\mu \right)\in X\otimes_A Y_0. $$ }} \item[(3)] If $f,g$ are bounded, $\mathcal{B}$-measurable functions and $(\varphi_m),(\psi_n)$ are sequences of positive simple functions increasing to $f,g$, then {\fontsize{10}{10}{ $$ \sup_{m,n} \int_{0}^\infty\int_0^\infty \varphi_m(\lambda) \psi_n(\mu) \, d(E_\lambda\otimes_A F_\mu) = \left(\int_0^\infty f(\lambda) \, dE_\lambda\right) \otimes_A \left( \int_0^\infty g(\mu) \, dF_\mu \right)\in X\otimes_A Y_0. $$ }} \end{prop} \begin{proof} \item[(1)] One simply needs to check countable additivity (pointwise on $H\otimes_A K$), which follows from countably additivity on products of intervals, which is straightforward. \item[(2)] Obvious. \item[(3)] Immediate from (2) together with Lemmas \ref{lem:CommuteStrong} and \ref{lem:SpectralConvergence}. \end{proof}
\begin{lem}\label{lem:TensorSpectralAssociative} The relative tensor product of spectral measures as in Proposition \ref{prop:TensorSpectral} is associative, i.e., if \begin{align*} E \colon \mathcal{B}&\longrightarrow P(X)\subset B(H_A), \\ F\colon \mathcal{B}&\longrightarrow P(Y)\subset B(\sb{A}K_B), \text{ and }\\ G \colon \mathcal{B}&\longrightarrow P(Z)\subset B(\sb{B}L) \end{align*} are spectral measures on $\mathcal{B}$, then $(E\otimes_A F)\otimes_B G=E\otimes_A(F\otimes_B G)$. Moreover, if $f,g,h\colon [0,\infty]\to [0,\infty)$ are bounded $\mathcal{B}$-measurable functions, and $(\varphi_m),(\psi_n),(\gamma_k)$ are positive simple functions increasing to $f,g,h$ respectively, then {\fontsize{10}{10}{ \begin{align*} &\sup_{m,n,k} \int_{0}^\infty\int_0^\infty\int_0^\infty \varphi_m(\lambda) \psi_n(\mu) \gamma_\ell(\nu) \, d(E_\lambda\otimes_A F_\mu\otimes_B G_\nu)=\\ &\hspace{.5in} = \left(\int_0^\infty f(\lambda) \, dE_\lambda\right) \otimes_A \left( \int_0^\infty g(\mu) \, dF_\mu \right)\otimes_B \left( \int_0^\infty h(\nu) \, dG_\nu \right)\in X\otimes_A Y\otimes_B Z. \end{align*} }} \end{lem} \begin{proof} Immediate from associativity of the relative tensor product and Proposition \ref{prop:TensorSpectral}. \end{proof}
\begin{defn}\label{defn:TensorCones} Suppose $x\in \widehat{X^+}$ and $y\in \widehat{Y_0^+}$ have spectral resolutions $$ x = \int_{[0,\infty)} \lambda \, d E_\lambda + \infty E^\infty\text{ and } y = \int_{[0,\infty)} \mu \, dF_\mu+\infty F^\infty $$ (recall Notation \ref{nota:spectral}). Then \begin{align*} E \colon \mathcal{B}&\longrightarrow P(X)\subset B(H_A) \text{ and }\\ F \colon \mathcal{B}&\longrightarrow P(Y_0)\subset B(\sb{A}K) \end{align*} are two spectral measures as in Proposition \ref{prop:TensorSpectral}. For $m,n\in\mathbb{N}$, set $$ x_m = \int_{[0,m]} \lambda \, dE_\lambda +mE^\infty \text{ and } y_n = \int_{[0,n]} \mu \, dF_\mu + nF^\infty. $$ Applying Lemma \ref{lem:QuadraticForm} to the directed set $$ \mathcal{F}=\set{x_m\otimes_A y_n}{m,n\in \mathbb{N}}\subset (X\otimes_A Y_0)^+, $$ we get a positive, self-adjoint operator affiliated to $X\otimes_A Y_0$ and densely-defined in an affiliated subspace of $X\otimes_A Y_0$. We denote this operator as $x\otimes_A y$. \end{defn}
\begin{rem}\label{rem:ThreeProjections} Assume the notation of Definition \ref{defn:TensorCones}. When we work with $x\otimes_A y$, it helps to consider the following $3$ projections: \begin{align*} p_0 & = (E_0\otimes_A 1_K)\vee (1_H\otimes F_0),\\ p_\infty & = \bigg((1-E_0)\otimes_A F^\infty\bigg)+\bigg(E^\infty\otimes_A(1-F_0)\bigg)+E^\infty\otimes_A F^\infty,\text{ and} \\ p_f &= \sup_{\lambda,\mu<\infty} E_\lambda\otimes_A F_\mu = (1-E^\infty)\otimes_A (1-F^\infty), \end{align*} which we should think of as having the following ``supports" given by the shaded areas in $[0_\mathbb{R},\infty_\mathbb{R}]^2$ below: $$ p_0= \begin{tikzpicture}[rectangular,baseline=0cm]
\clip (2.05,2.05) --(-2.6,2.05) -- (-2.6,-2.6) -- (2.05,-2.6);
\filldraw[shaded] (-2,-2)--(-2,2)--(-.8,2)--(-.8,-.8)--(2,-.8)--(2,-2);
\filldraw[shaded] ;
\draw[thick] (-2,-.8)--(2,-.8);
\draw[thick] (-2,.8)--(2,.8);
\draw[thick] (.8,-2)--(.8,2);
\draw[thick] (-.8,-2)--(-.8,2);
\draw[thick] (-2,-2)--(-2,2)--(2,2)--(2,-2)--(-2,-2);
\node at (-2.3,-1.4) {$0$};
\node at (-2.3,-.8) {$\vee$};
\node at (-2.3,0) {$\mu$};
\node at (-2.3,.8) {$\vee$};
\node at (-2.3,1.4) {$\infty$};
\node at (-1.4,-2.3) {$0$};
\node at (-.8,-2.3) {$<$};
\node at (0,-2.3) {$\lambda$};
\node at (.8,-2.3) {$<$};
\node at (1.4,-2.3) {$\infty$}; \end{tikzpicture}, \, p_\infty= \begin{tikzpicture}[rectangular,baseline=0cm]
\clip (2.05,2.05) --(-2.6,2.05) -- (-2.6,-2.6) -- (2.05,-2.6);
\filldraw[shaded] (.8,-.8)--(.8,.8)--(-.8,.8)--(-.8,2)--(2,2)--(2,-.8);
\filldraw[shaded] ;
\draw[thick] (-2,-.8)--(2,-.8);
\draw[thick] (-2,.8)--(2,.8);
\draw[thick] (.8,-2)--(.8,2);
\draw[thick] (-.8,-2)--(-.8,2);
\draw[thick] (-2,-2)--(-2,2)--(2,2)--(2,-2)--(-2,-2);
\node at (-2.3,-1.4) {$0$};
\node at (-2.3,-.8) {$\vee$};
\node at (-2.3,0) {$\mu$};
\node at (-2.3,.8) {$\vee$};
\node at (-2.3,1.4) {$\infty$};
\node at (-1.4,-2.3) {$0$};
\node at (-.8,-2.3) {$<$};
\node at (0,-2.3) {$\lambda$};
\node at (.8,-2.3) {$<$};
\node at (1.4,-2.3) {$\infty$}; \end{tikzpicture},\, p_f= \begin{tikzpicture}[rectangular,baseline=0cm]
\clip (2.05,2.05) --(-2.6,2.05) -- (-2.6,-2.6) -- (2.05,-2.6);
\filldraw[shaded] (-2,-2)--(-2,.8)--(.8,.8)--(.8,-2);
\filldraw[shaded] ;
\draw[thick] (-2,-.8)--(2,-.8);
\draw[thick] (-2,.8)--(2,.8);
\draw[thick] (.8,-2)--(.8,2);
\draw[thick] (-.8,-2)--(-.8,2);
\draw[thick] (-2,-2)--(-2,2)--(2,2)--(2,-2)--(-2,-2);
\node at (-2.3,-1.4) {$0$};
\node at (-2.3,-.8) {$\vee$};
\node at (-2.3,0) {$\mu$};
\node at (-2.3,.8) {$\vee$};
\node at (-2.3,1.4) {$\infty$};
\node at (-1.4,-2.3) {$0$};
\node at (-.8,-2.3) {$<$};
\node at (0,-2.3) {$\lambda$};
\node at (.8,-2.3) {$<$};
\node at (1.4,-2.3) {$\infty$}; \end{tikzpicture} . $$ \item[$\bullet$] These three projections commute with $x\otimes_A y$. \item[$\bullet$] $\Dom((x\otimes_A y)^{1/2})\subset (1-p_\infty)(H\otimes_A K)$, and $(x\otimes_A y)(1-p_\infty)$ is densely defined on $(1-p_\infty)(H\otimes_A K)$. \item[$\bullet$] $(x\otimes_A y)p_f = \sup_{m,n<\infty} \int_{[0,m]}\int_{[0,n]} \lambda \mu \, d(E_\lambda\otimes_A F_\mu)$. \item[$\bullet$]$(x\otimes_A y)p_0=0$. \end{rem}
\begin{lem}\label{lem:LessThan} Let $x\in\widehat{X^+}$ and $y\in\widehat{Y_0^+}$, and assume the notation of Definition \ref{defn:TensorCones} and Remark \ref{rem:ThreeProjections}. Suppose $x'\in X^+$, $y'\in Y_0^+$ with $x'\leq x$ and $y'\leq y$. Then \item[(1)] $(x'\otimes_A y')p_0=p_0(x'\otimes_A y')=0$, \item[(2)] for all $\xi \in H\otimes_A K$, $(x\otimes_A y)(\omega_\xi)=(x\otimes_A y)(\omega_{(1-p_0)\xi})$, and \item[(3)] $x'\otimes_A y'\leq x\otimes_A y$. \end{lem} \begin{proof} \item[(1)] Suppose $\eta\in D((E_0H)_A)$ and $\kappa\in D(\sb{A} K)$ (recall $E_0\in X$ and $F^\infty\in Y_0$). Then since $x'\leq x$, we must have $$
\|(x')^{1/2}\eta\|_H^2=\langle x'\eta,\eta\rangle = x'(\omega_{\eta})\leq x(\omega_\eta)=x(\omega_{E_0\eta})=xE_0(\omega_\eta)=0. $$ But this implies $x'\eta=0$. Hence we have $$ (x'\otimes_A y') (\eta\otimes\kappa) = 0. $$ Similarly, for all $\eta\in D(H_A)$ and $\kappa\in D(\sb{A}(F_0 K))$, $(x'\otimes_A y')(\eta\otimes\kappa)=0$. By density of $D(H_A)\otimes_A D(\sb{A}K)$, we have $(x'\otimes_A y') p_0=0$. Taking adjoints gives $p_0(x'\otimes_A y')=0$. \item[(2)] By (1), for all $m,n>0$, $p_0(x_m\otimes_A y_n)=(x_m\otimes_A y_n)p_0=0$, so \begin{align*} (x\otimes_A y)(\omega_\xi) & = \sup_{m,n} (x_m\otimes_A y_n)(\omega_\xi)\\ & = \sup_{m,n} \bigg( (x_m\otimes_A y_n)(\omega_{(1-p_0)\xi})+\langle (x_m\otimes_A y_n)p_0\xi,p_0\xi\rangle\\ & \hspace{.2in}+\langle (x_m\otimes_A y_n) p_0 \xi,\xi\rangle + \langle (x_m\otimes_A y_n) \xi,p_0\xi\rangle\bigg)\\ & = \sup_{m,n} (x_m\otimes_A y_n )(\omega_{(1-p_0)\xi}) = (x\otimes_A y)(\omega_{(1-p_0)\xi}). \end{align*} \item[(3)] By (2), it suffices to show that for all $\xi \in \Dom((x\otimes_A y)^{1/2})$ with $\xi=p_f\xi$, $$ \bigg(p_f(x'\otimes_A y')p_f\bigg)(\omega_\xi)=(x'\otimes_A y')(\omega_\xi) \leq (x\otimes_A y) (\omega_\xi)=\bigg(p_f(x\otimes_A y)p_f\bigg)(\omega_{\xi}). $$ Fix such a $\xi$, and let $\varepsilon>0$. As $E_\lambda\otimes_A F_\mu \to p_f$ strongly as $\lambda,\mu\to \infty$ from below, there is an $N>0$ such that for all $\lambda,\mu >N$, $$ \bigg(p_f(x'\otimes_A y')p_f - (E_\lambda x' E_{\lambda}\otimes_A F_\mu y' F_{\mu} )\bigg) (\omega_{\xi}) < \varepsilon. $$ Since $x'\leq x$ and $y'\leq y$, we have $E_N x'E_N\leq xE_N$, $F_N y'F_N\leq yF_N$ by Lemma \ref{lem:VectorStates}, so $E_N x' E_N \otimes_A F_N y' F_N\leq xE_N \otimes_A yF_N$ as all these operators mutually commute. Hence \begin{align*} \bigg(p_f(x'\otimes y')p_f\bigg)(\omega_{\xi}) & = \bigg(p_0(x_m\otimes_A y_n)p_0 -(E_Nx' E_{N}\otimes_A F_N y' F_{N} )\bigg)(\omega_{\xi})\\ &\hspace{1in}+(E_N x' E_{N}\otimes_A F_N y' F_{N} )(\omega_\xi) \\ & < \varepsilon +(x E_{N}\otimes_A yF_{N} )(\omega_{\xi}) \leq \varepsilon +(x \otimes_A y )(\omega_{\xi}). \end{align*} Since $\varepsilon$ was arbitrary, the result follows. \end{proof}
\begin{lem}\label{lem:corners} Suppose $(x_j')_{j\in J}\subset \widehat{X^+}$ increases to $x\in \widehat{X^+}$. Suppose $p,q\in P(X)$ are spectral projections of $x$ such that $p+q=1$. Then $\langle x_j' p\xi,q\xi\rangle \to 0$ for all $\xi\in \Dom(x^{1/2})$. \end{lem} \begin{proof} For $k=0,1,2,3$, $p\xi + i^k q\xi \in \Dom(x^{1/2})\subseteq \Dom((x_j')^{1/2})$ for all $j\in J$. Since $x_j'$ increases to $x$, by polarization \begin{align*} \lim_{j\in J} \langle (x_j')^{1/2} p\xi,(x_j')^{1/2}q\xi\rangle &= \lim_{j\in J} \frac{1}{4}\sum_{k=0}^3 i^k x_j'(\omega_{p\xi + i^k q\xi}) = \frac{1}{4} \sum_{k=0}^3 i^k x(\omega_{p\xi + i^k q\xi})\\ & = \langle x^{1/2} p\xi, x^{1/2} q\xi\rangle = 0 \end{align*} as $p,q$ commute with $x^{1/2}$. \end{proof}
\begin{thm}\label{thm:increase} Let $x\in\widehat{X^+}$ and $y\in\widehat{Y_0^+}$, and assume the notation of Definition \ref{defn:TensorCones} and Remark \ref{rem:ThreeProjections}. Suppose there are sequences $(x_m')\subset X^+$, $(y_n')\subset Y_0^+$ which increase to $x, y$ respectively. Then $x_m'\otimes_A y_n'$ increases to $x\otimes_A y$. \end{thm} \begin{proof} \itt{Case 1} Suppose $\xi \notin \Dom((x\otimes_A y)^{1/2})$ and $M>0$. Since $\sup_{m,n} x_m\otimes_A y_n=x\otimes_A y$, there is an $N_0\in\mathbb{N}$ such that for all $m,n\geq N_0$, $(x_m\otimes_A y_n)(\omega_\xi)>M$. Since $p_0\xi\neq \xi$ by Lemma \ref{lem:LessThan}, we must have $$ (1_H\otimes_A (1_K-F_0)) \xi \neq 0 \text{ and } ((1_H-E_0)\otimes_A 1_K)\xi \neq 0. $$ \itt{Claim} There is an $N_1>N_0$ such that $(x_m'\otimes 1_K)\xi\neq 0 \neq (1_H\otimes_A y_n')\xi$ for all $m,n>N_1$. \begin{proof} We prove the second non-equality. Suppose not. Then for each $n>0$, there is an $k>n$ such that $(1\otimes_A y_k')\xi = 0$. But then $$ (1_H\otimes_A y_n')(\omega_\xi)\leq (1_H\otimes_A y_k')(\omega_\xi)=0, $$ so $(1_H\otimes_A y_n')\xi=0$ for all $n\in\mathbb{N}$. Since $(1_H\otimes_A (1-F_0))\xi\neq 0$, and $D(H_A)\otimes_A D(\sb{A}((1-F_0)K))$ is dense in $H\otimes_A ((1_K-F_0)K)$, there is an $\eta\in D(H_A)$ such that $L_\eta^*\xi \in ((1_K-F_0)K)\setminus\{0\}$ and $L_\eta L_\eta^* \leq 1_H\otimes_A 1_K$. Now since $y_n'$ increases to $y$, and $y(\omega_{L_\eta^* \xi})>0$, there is an $N'>0$ such that for all $n>N'$, \begin{align*} 0 &< y_n'(\omega_{L_\eta^* \xi}) = (L_\eta y_n L_\eta^*)(\omega_\xi) = \bigg(L_\eta L_\eta^* (1_H\otimes_A y_n')\bigg)(\omega_\xi) \leq (1_H\otimes_A y_n')(\omega_\xi) =0, \end{align*} a contradiction. \end{proof} Choose $N_1$ as in the claim, and suppose $n>N_1$. Let $\{\alpha_i\}\subset D(\sb{A}K)$ be an $\sb{A}K$-basis, and let $\eta = (1_H\otimes_A (y_{N_1})^{1/2})\xi\neq 0$, and note $(x_{N_1}\otimes_A 1_K)(\omega_\eta)>M$. Then \begin{align*} M & < (x_{N_1}\otimes1_K)(\omega_\eta) = \left((x_{N_1}\otimes_A 1_K) \left( \sum_i R_{\alpha_i} R_{\alpha_i}^*\right)\right)(\omega_\eta) = \sum_i (R_{\alpha_i} (x_{N_1}) R_{\alpha_i}^*)(\omega_\eta), \end{align*} so there is an $N_2>0$ such that $$ M < \sum_{i=1}^{N_2} (R_{\alpha_i} x_{N_1} R_{\alpha_i}^*)(\omega_\eta) = \sum_{i=1}^{N_2} x_{N_1} (\omega_{R_\alpha^* \eta}) \leq \sum_{i=1}^{N_2} x (\omega_{R_\alpha^* \eta}). $$ Now as $x_m'$ increases to $x$, there is an $N_3>N_1$ such that $m>N_3$ implies \begin{align*} M & < \sum_{i=1}^{N_2} x_m' (\omega_{R_\alpha^* \eta}) = \sum_{i=1}^{N_2} (R_{\alpha_i} x_m' R_{\alpha_i}^*)(\omega_\eta) \leq \sum_{i} (R_{\alpha_i} x_m' R_{\alpha_i}^*)(\omega_\eta) \\ & = \left((x_m'\otimes_A 1_K) \left(\sum_i R_{\alpha_i} R_{\alpha_i}^*\right)\right)(\omega_\eta) = (x_m'\otimes y_{N_1})(\omega_\xi). \end{align*} Repeating the above argument for $y_n'$ yields an $N_4$ such that $m,n>N_4$ implies $M < (x_m'\otimes_A y_n') (\omega_\xi)$. \itt{Case 2} Suppose $\xi\in \Dom((x\otimes_A y)^{1/2})$. Then $\xi=(1-p_\infty)\xi$. We want to show $$ \sup_{m,n}( x_m'\otimes_A y_n' )(\omega_\xi) = (x\otimes_A y)(\omega_\xi) =\sup_{m,n} (x_m\otimes_A y_n)(\omega_\xi), $$ so by Lemma \ref{lem:LessThan}, we may assume $\xi=(1-p_0)\xi$, and thus $\xi=p_f\xi$. Let $\varepsilon>0$. Since $$ p_f(x\otimes_A y)p_f = \sup_{\lambda,\mu<\infty} x E_{\lambda}\otimes_A y F_{\mu}, $$ there is an $N_0\in\mathbb{N}$ such that for all $\lambda,\mu\geq N_0$, $$ \bigg((x\otimes_A y) - (x E_{\lambda}\otimes_A y F_{\mu} )\bigg) (\omega_\xi) < \frac{\varepsilon}{4}. $$ By Lemma \ref{lem:LessThan}, $x_m'\otimes_A y_n' \leq x\otimes_A y$ for all $m,n$, so using Lemma \ref{lem:VectorStates}, we have \begin{align*} \bigg((x_m'\otimes_Ay_n') - (E_{N_0} x_m' E_{N_0})\otimes_A (F_{N_0} y_n' F_{N_0})]\bigg) & \leq \bigg((x\otimes_A y) - (x E_{N_0}\otimes_A y F_{N_0} )\bigg) \text{ and }\\ E_{N_0} x_m' E_{N_0}\otimes_A F_{N_0} y_n'F_{N_0} & \leq x E_{N_0}\otimes_A y F_{N_0} \end{align*} by multiplying on either side by $1_{H\otimes_A K}-(E_{N_0}\otimes_A F_{N_0})$ and $E_{N_0}\otimes_A F_{N_0}$ respectively. Now since $x_m',y_n'$ increase to $x,y$ respectively, by Lemma \ref{lem:VectorStates}, $E_{N_0} x_m' E_{N_0}, F_{N_0} y_n' F_{N_0}$ increases to $x E_{N_0}, y F_{N_0}$ respectively. Thus $E_{N_0} x_m' E_{N_0}\otimes_A F_{N_0} y_n' F_{N_0}$ increases to $x E_{N_0}\otimes_A y F_{N_0}$ by Lemma \ref{lem:CommuteStrong}, and there is an $N_1>N_0$ such that for all $m,n\geq N_1$, $$ \bigg((x E_{N_0}\otimes_A y F_{N_0}) - (E_{N_0} x_m' E_{N_0}\otimes_A F_{N_0} y_n' F_{N_0}) \bigg)(\omega_\xi) < \frac{\varepsilon}{4}. $$ By Lemma \ref{lem:corners}, there is an $N_2>N_1$ such that for all $m,n>N_2$, $$
\left|\bigg\langle (x_m'\otimes y_n')(1_{H\otimes_A K}-E_{N_0}\otimes_A F_{N_0}) \xi,(E_{N_0}\otimes_A F_{N_0})\xi\bigg\rangle\right|< \frac{\varepsilon}{4}. $$ Now we calculate that for all $m,n> N_2$, {\fontsize{10}{10}{ \begin{align*} (x\otimes_A y - x_m'\otimes y_n')(\omega_\xi) & = (1-E_{N_0}\otimes_A F_{N_0})(x\otimes_A y - x_m'\otimes y_n')(1-E_{N_0}\otimes_A F_{N_0})(\omega_\xi)\\ &\hspace{.4in} +(1_{H\otimes_A K}-E_{N_0}\otimes_A F_{N_0})(x\otimes_A y - x_m'\otimes y_n')(E_{N_0}\otimes_A F_{N_0})(\omega_\xi)\\ &\hspace{.4in} +(E_{N_0}\otimes_A F_{N_0})(x\otimes_A y - x_m'\otimes y_n')(1_{H\otimes_A K}-E_{N_0}\otimes_A F_{N_0})(\omega_\xi)\\ &\hspace{.4in} +(E_{N_0}\otimes_A F_{N_0})(x\otimes_A y - x_m'\otimes y_n')(E_{N_0}\otimes_A F_{N_0})(\omega_\xi)\\ & \leq \bigg((x\otimes_A y) - (x E_{N_0}\otimes_A y F_{N_0} )\bigg) (\omega_\xi)\\
&\hspace{.4in} +|((1_{H\otimes_A K}-E_{N_0}\otimes_A F_{N_0})(x_m'\otimes_A y_n')(E_{N_0}\otimes_A F_{N_0})(\omega_\xi)|\\
&\hspace{.4in} +|(E_{N_0}\otimes_A F_{N_0})(x_m'\otimes_A y_n')(1-E_{N_0}\otimes_A F_{N_0})(\omega_\xi)|\\ &\hspace{.4in} +\bigg((x E_{N_0}\otimes_A y F_{N_0}) - (E_{N_0} x_m'E_{N_0}\otimes_A F_{N_0} y_n' F_{N_0}) \bigg)(\omega_\xi) \\ & < \frac{\varepsilon}{4}+\frac{\varepsilon}{4}+\frac{\varepsilon}{4}+\frac{\varepsilon}{4} = \varepsilon. \end{align*}}} \end{proof}
\begin{cor}\label{cor:associative} If $x\in \widehat{X^+}$, $y\in \widehat{Y^+}$, and $z\in \widehat{Z^+}$, then $(x\otimes_A y)\otimes_B z = x\otimes_A (y\otimes_B z)$. \end{cor} \begin{proof} Take sequences $(x_m)\subset X^+$, $(y_n)\subset Y^+$, and $(z_\ell)\subset Z^+$ which increase to $x,y,z$ respectively. Then $$ (x\otimes_A y)\otimes_B z =\sup_{m,n,\ell} (x_m\otimes_A y_n) \otimes_B z_\ell=\sup_{m,n,\ell} x_m\otimes_A (y_n \otimes_B z_\ell) = x\otimes_A (y\otimes_B z). $$ \end{proof}
\begin{cor}\label{cor:TensorConeMap} If $x,w \in \widehat{X^+}$, $y\in \widehat{Y_0^+}$, and $\lambda\in [0,\infty]$, then $(\lambda x+w)\otimes_A y = \lambda (x\otimes_A y)+(w\otimes_A y)$. \end{cor} \begin{proof} Choose $X^+ \ni x_m,w_n\nearrow x,w \in \widehat{X^+}$ respectively and $\widehat{Y_0^+}\ni y_\ell \nearrow y\in \widehat{Y_0^+}$. Then $(\lambda x_m+w_n)\otimes_A y_\ell = \lambda (x_m\otimes_A y_\ell)+(w_n\otimes_A y_\ell)$, and the result follows by Remark \ref{rem:sup} and Theorem \ref{thm:increase}. \end{proof}
By taking sups appropriately, and with a little more care, Lemma \ref{lem:LessThan} and Theorem \ref{thm:increase} can be generalized to prove: \begin{thm}\label{thm:UnboundedIncrease} Let $x\in\widehat{X^+}$ and $y\in\widehat{Y_0^+}$. Suppose there are nets $(x_i)_{i\in I}\subset \widehat{X^+}$, $(y_j)_{j\in J}\subset \widehat{Y_0^+}$ which increase to $x, y$ respectively. Then $x_i\otimes_A y_j\nearrow x\otimes_A y$. \end{thm}
\section{The operad $\mathbb{B}\mathbb{P}$}\label{sec:BP} To show the action of $\mathbb{B}\mathbb{P}$ is well-defined in Theorem \ref{thm:ConePA}, we show each connected/internally connected $\mathbb{B}\mathbb{P}$-tangle has a unique standard form that behaves well under composition, analogous to the methods of \cite{0912.1320}. The existence of this standard form is thoroughly sketched, and the behavior under composition is briefly sketched.
\begin{defn} We will again define $\mathbb{B}\mathbb{P}$, an operad of unshaded, oriented tangles up to planar isotopy, but in more detail. First, we require for tangles $\mathcal{T}\in\mathbb{B}\mathbb{P}$ \item[$\bullet$] $\mathcal{T}$ has an external disk $D_0$ and internal disks $D_1,\dots, D_s$, each with an even number $2k_i$ of market boundary points and a distinguished interval marked $*$. \item[$\bullet$] Each boundary point of $\mathcal{T}$ is connected to exactly one oriented string. Each oriented string is either a closed loop, or it is attached to two distinct boundary points. \item[$\bullet$] For $i=1,\dots,s$, reading counter-clockwise from $*$, the strings attached to the first $k_i$ boundary points of $D_i$ are oriented away from $D_i$, and the second $k_i$ strings are oriented toward $D_i$, \item[$\bullet$] Reading counter-clockwise from $*$, the strings attached to the first $k_0$ boundary points of $D_0$ are oriented toward $D_0$, and the second $k_0$ strings are oriented away from $D_0$, \item $\mathbb{B}\mathbb{P}$ is the operad generated by the following tangles: \item[(1)] For $n\geq 0$, the ``Temperley-Lieb" tangle $1_n$ with no inputs and $2n$ boundary points: $$1_n = \idn{n},$$ \item[(2)] For $n\geq 0$, the unique tangles $t_{n+1},t_{n+1}^{\OP}$ with $2n+2$ internal boundary points and $2n$ external boundary points and only one right, left cap respectively: $$ t_{n+1} =\OperatorValuedWeight{n}{}\,\text{ and }t_{n+1}^{\OP}=\OperatorValuedWeightOp{n}{}, $$ \item[(3)] For $m,n\geq 0$, the tangles $\otimes_{m,n}$ with internal disks $D_1,D_2$ with $2m,2n$ internal boundary points and $2(m+n)$ external boundary points as follows: $$\otimes_{m,n}=\tensor{m}{}{n}{}.$$ \item[(4)] For $n\geq 1$, the tangles $\tau_n,\tau_n^{\OP}$ with two input disks, each with $2n$ internal boundary points, and no external boundary points such that boundary point $m$ of input disk $D_1$ is connected to boundary point $2n-m+1$ of input disk $D_2$ for each $m=1,\dots, 2n$ as follows: $$ \tau_n = \TraceOfTwo{n}{}{}\, \text{ and } \tau_n^{\OP} = \TraceOfTwoOp{n}{}{}. $$ \item A tangle $\mathcal{T}\in \mathbb{B}\mathbb{P}$ with disks $\{D_i\}_{i=0}^s$ and strings $\{S_j\}_{j=1}^t$ is called: \item[$\bullet$] \underline{connected} if $\{D_i\}_{i=0}^s\cup\{S_j\}_{j=1}^t$ is a connected in $\mathbb{R}^2$, and \item[$\bullet$] \underline{internally connected} if $\mathcal{T}$ has no external boundary points and $\{D_i\}_{i=1}^s\cup\{S_j\}_{j=1}^t$ is connected in $\mathbb{R}^2$. \end{defn}
\begin{thm}\label{thm:relations} The following relations hold in $\mathbb{B}\mathbb{P}$ for $m,n\geq 0$ (compare with Theorem \ref{thm:BPRelations}): \item[(1)] $t_m t_{m+1}^{\OP} = t_{m}^{\OP} t_{m+1}$, \item[(2)] $\otimes_{\ell,m+n}(-,\otimes_{m,n}(-,-))=\otimes_{\ell+m,n}(\otimes_{\ell,m}(-,-),-)$, \item[(3)] $\otimes_{m,n-1}(-,t_{n}(-))=t_{m+n}(\otimes_{m,n}(-,-))$ and $\otimes_{m-1,n}(t_m^{\OP}(-),-)=t_{m+n}^{\OP}(\otimes_{m,n}(-,-))$, and \item[(4)] $\tau_n(\mathcal{T}_1(-),\mathcal{T}_2(-))=\tau_n(\mathcal{T}_2(-),\mathcal{T}_1(-))$ and $\tau_n^{\OP}(\mathcal{T}_1(-),\mathcal{T}_2(-))=\tau_n^{\OP}(\mathcal{T}_2(-),\mathcal{T}_1(-))$ for all $\mathcal{T}_1,\mathcal{T}_2\in\mathbb{B}\mathbb{P}$ up to reindexing internal disks. \end{thm} \begin{proof} Clear by drawing pictures. \end{proof}
\begin{prop}\label{prop:BPprime} If $\mathcal{T}\in \mathbb{B}\mathbb{P}$ with external disk $D_0$ and internal disks $\{D_i\}_{i=1}^s$, then the strings can only connect the $D_i$'s in the following ways: \item[(1)] If $D_i$ is connected by a string to $D_0$ where $1\leq i\leq s$, then any other string connected to $D_i$ must only be connected to $D_i$ or $D_0$. \item[(2)] If $D_i$ and $D_j$ are connected by a string where $1\leq i,j\leq s$, then no string of $D_i$ or $D_j$ connects to $D_0$. \item[(3)] For each $i=0,\dots,s$, if the string $S$ connects boundary points $m$ and $n$ of $D_i$, then $m=2k_i-n+1$. Such a string is called an \underline{$i$-cap} of $\mathcal{T}$. We call the $i$-cap a \underline{left $i$-cap} if when we connect boundary points $n$ and $2k_i-n+1$ by an imaginary string $S'$ inside $D_i$, the loop $S\cup S'$ contains the distinguished interval of $D_i$. The $i$-cap is a \underline{right $i$-cap} otherwise. \item[(4)] If the string $S$ connects boundary point $m$ of $D_i$ to boundary point $n$ of $D_j$ where $0\leq i<j\leq s$, then there is a string $S'$ connecting boundary point $2k_i-m+1$ of $D_i$ to boundary point $2k_j-n+1$ of $D_j$. If $i>0$, we call $S\cup S'$ an \underline{$i,j$-cap} of $\mathcal{T}$. In this case, if we connect boundary points $m$ and $2k_i-m+1$ of $D_i$ and boundary points $n$ and $2k_j-n+1$ of $D_j$ by imaginary strings $S_i, S_j$ inside $D_i,D_j$ respectively, then if the loop $S\cup S'\cup S_i\cup S_j$ contains the distinguished intervals of $D_i$ and $D_j$, then we call the $i,j$-cap a \underline{left $i,j$-cap}. Otherwise, the distinguished intervals of $D_i,D_j$ must lie outside $S\cup S'\cup S_i\cup S_j$, and we have a \underline{right $i,j$-cap}. \item[(5)] Suppose there is a right (respectively left) $i,j$-cap where $i\neq j$. If $\mathcal{S}$ is the collection of all disks and strings which can be connected to $D_i$ or $D_j$ through other disks and strings, then we may consider $\mathcal{S}$ as an internally connected tangle, and all $k,\ell$-caps in $\mathcal{S}$ ($k\neq \ell$) must form concentric circles. (We will show in Theorem \ref{thm:IJcaps} that all such $k,\ell$-caps are also right (respectively left) caps.) \end{prop} \begin{proof} Clear by drawing pictures. \end{proof}
\begin{ex} The tangle on the left is in $\mathbb{B}\mathbb{P}$ (see the proof of Theorem \ref{thm:IJcaps}), but the tangle on the right is not: $$ \begin{tikzpicture}[scale=.6,baseline=.5cm]
\clip (-2.1,5.2) --(4,5.2) -- (4,-3.1) -- (-2.1,-3.1);
\draw[ultra thick] (-.7,-2)--(-.7,4).. controls ++(90:1.6cm) and ++(90:2.5cm) .. (3.8,3)--(3.8,1.5).. controls ++(270:1.8cm) and ++(270:3cm) .. (-.7,-2);
\draw[ultra thick] (-.2,-2)--(-.2,4).. controls ++(90:1.4cm) and ++(90:2.2cm) .. (3.3,3)--(3.3,1.5).. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-.2,-2);
\draw[ultra thick] (.3,.5)--(.3,3.5).. controls ++(90:1.6cm) and ++(90:1.6cm) .. (3.1,3).. controls ++(270:2.4cm) and ++(270:3.2cm) .. (.3,.5);
\draw[ultra thick] (.8,1.5)--(.8,3).. controls ++(90:1.4cm) and ++(90:1.6cm) .. (2.8,3) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (.8,1.5);
\draw[ultra thick] (1.7,3.5) arc (180:0:.3cm) -- (2.3,2.5) arc (0:-180:.3cm);
\draw[ultra thick] (2.15,3)--(2.3,2.7)--(2.45,3);
\draw[ultra thick] (3.65,2.3)--(3.8,2)--(3.95,2.3);
\draw[ultra thick] (3.15,2)--(3.3,1.7)--(3.45,2);
\draw[ultra thick] (2.4,2.1)--(2.4,1.7)--(2.7,1.9);
\draw[ultra thick] (2.5,1.2)--(2.5,.8)--(2.8,1);
\draw[ultra thick] (-1.3,-1) arc (0:180:.3cm) -- (-1.9,-2) arc (180:360:.3cm);
\draw[ultra thick] (-1.75,-1.2)--(-1.9,-1.5)--(-2.05,-1.2);
\filldraw[thick, unshaded] (.5,-2)--(.5,-1)--(-1.5,-1)--(-1.5,-2)--(.5,-2);
\filldraw[thick, unshaded] (1,-.5)--(1,.5)--(-.5,.5)--(-.5,-.5)--(1,-.5);
\filldraw[thick, unshaded] (1.5,1)--(1.5,2)--(0,2)--(0,1)--(1.5,1);
\filldraw[thick, unshaded] (2,2.5)--(2,3.5)--(.5,3.5)--(.5,2.5)--(2,2.5); \end{tikzpicture} \hspace{.5in} \begin{tikzpicture}[scale=.6,baseline=1.5cm]
\clip (-2.5,5.2) --(3.3,5.2) -- (3.3,-1) -- (-2.5,-1);
\draw[ultra thick] (-.2,1.5)--(-.7,3.5).. controls ++(90:1.4cm) and ++(90:2.2cm) .. (-2.3,3)--(-2.3,1.5).. controls ++(270:1.4cm) and ++(270:1.2cm) .. (-.2,.5);
\draw[ultra thick] (-2.15,2.7)--(-2.3,2.4)--(-2.45,2.7);
\draw[ultra thick] (.3,.5)--(.3,3.5).. controls ++(90:1.6cm) and ++(90:1.6cm) .. (3.1,3)--(3.1,1.5).. controls ++(270:2.4cm) and ++(270:1.2cm) .. (.3,.5);
\draw[ultra thick] (2.55,2.7)--(2.7,2.4)--(2.85,2.7);
\draw[ultra thick] (.8,1.5)--(.8,3).. controls ++(90:1.4cm) and ++(90:1.6cm) .. (2.7,3)--(2.7,1.5) .. controls ++(270:1.4cm) and ++(270:1.2cm) .. (.8,.5);
\draw[ultra thick] (2.95,2.4)--(3.1,2.1)--(3.25,2.4);
\draw[ultra thick] (1.7,3.5) arc (180:0:.3cm) -- (2.3,2.5) arc (0:-180:.3cm);
\draw[ultra thick] (2.15,3)--(2.3,2.7)--(2.45,3);
\draw[ultra thick] (-1.3,3.5) arc (0:180:.3cm) -- (-1.9,2.5) arc (180:360:.3cm);
\draw[ultra thick] (-1.75,3)--(-1.9,2.7)--(-2.05,3);
\filldraw[thick, unshaded] (0,2.5)--(0,3.5)--(-1.5,3.5)--(-1.5,2.5)--(0,2.5);
\filldraw[thick, unshaded] (1,.5)--(1,1.5)--(-.5,1.5)--(-.5,.5)--(1,.5);
\filldraw[thick, unshaded] (2,2.5)--(2,3.5)--(.5,3.5)--(.5,2.5)--(2,2.5); \end{tikzpicture}. $$ \end{ex}
\begin{rems}\label{rem:StandardForm} The following are trivial observations about tangles $\mathcal{T}\in\mathbb{B}\mathbb{P}$: \item[(1)] We may draw $\mathcal{T}$ such that each disk $D_i$ where $i=0,\dots,s$ is a rectangle with $k_i$ points on the top, $k_i$ points on the bottom, and the distinguished interval on the left. When drawing diagrams, we omit the disk $D_0$. \item[(2)] We may draw all strings which are not part of a cap of $\mathcal{T}$ (strings that meet $D_0$) as vertical lines, oriented upward. We will assume this orientation in the sequel. \item[(3)] If $\mathcal{T}\in\mathbb{B}\mathbb{P}$ is connected, then no two internal disks of $\mathcal{T}$ are connected by a string. Hence it is possible to draw $\mathcal{T}$ such that each internal disk $D_i$, $i>0$, is the same vertical size and is on the same horizontal level. Moreover, the ordering of the internal disks from left to right is unique. \end{rems}
\begin{thm}\label{thm:ConnectedStandardForm} Suppose $\mathcal{T}\in\mathbb{B}\mathbb{P}$ is a connected tangle with $s>0$ input disks $D_j$, each with $2k_j$ boundary points. Suppose further that $\mathcal{T}$ is in the form afforded by Remarks \ref{rem:StandardForm}, $\mathcal{T}$ has no strings which connect $D_0$ to $D_0$, and that the $D_j$'s are numbered from left to right in $\mathcal{T}$. Then $\mathcal{T}$ can be written in a unique standard form \begin{align*} &\otimes_{m_1,\sum_{j>1} m_j}( t_{m_1+1}^{\OP}\cdots t_{m_1+v_1}^{\OP} t_{m_1+v_1+1}\cdots t_{m_1+v_1+w_1}(-),\\ &\otimes_{m_2,\sum_{j>2} m_j}(t_{m_2+1}^{\OP}\cdots t_{m_2+v_2}^{\OP} t_{m_2+v_2+1}\cdots t_{m_2+v_2+w_2}(-),\cdots\\ &\otimes_{m_{s-1},m_s}(t_{m_{s-1}+1}^{\OP}\cdots t_{m_{s-1}+v_{s-1}}^{\OP} t_{m_{s-1}+v_{s-1}+1}\cdots t_{m_{s-1}+v_{s-1}+w_{s-1}}(-),\\ &\hspace{1.3in}t_{m_s+1}^{\OP}\cdots t_{m_s+v_s}^{\OP} t_{m_s+v_s+1}\cdots t_{m_s+v_s+w_s}(-))\cdots)) \end{align*} such that for all $j=1,\dots,s$, \item[$\bullet$] $m_j>0$ is half the number of strings connecting $D_j$ to $D_0$, \item[$\bullet$] $v_j\geq 0$ is the number of left caps on $D_j$, \item[$\bullet$] $w_j\geq 0$ is the number of right caps on $D_j$, and \item[$\bullet$] $m_j+v_j+w_j=k_j$. \item Moreover, using the relations in Theorem \ref{thm:relations}, any composite of $t_k, t_\ell^{\OP},\otimes_{m,n}$ for $k,\ell,m,n>0$ can be written uniquely in the above form. \end{thm} \begin{proof} Clearly each tangle/composite can be written in such a form. For uniqueness, note that $m_j,u_j,v_j$ are completely determined by $\mathcal{T}$, and the order of the $\otimes_{m,n}$ is given by ``parenthesizing" the $D_j$'s from right to left (use relation (2) of Theorem \ref{thm:relations}). \end{proof}
\begin{cor}\label{cor:DecomposeTangle} Each connected tangle $\mathcal{T}\in\mathbb{B}\mathbb{P}$ in the form of Remarks \ref{rem:StandardForm} can be written in a similar unique standard form where instead of some of the tangles $$ t_{m_j+1}^{\OP}\cdots t_{m_j+v_j}^{\OP} t_{m_j+v_j+1}\cdots t_{m_j+v_j+w_j}(-), $$ we have tangles $1_{k_j}$ with the condition that we never see two $1_{k_j}$'s in a row, i.e., $$ \otimes_{\ell,m}(1_\ell,\otimes_{m,n}(1_m,\cdots)) \text{ or } \otimes_{s-1,s}(1_{s-1},1_s). $$ This amounts to grouping as many vertical strands connecting $D_0$ to $D_0$ as possible, and treating them as a ``labelled" input disk (as in \cite{math/9909027}). \end{cor}
\begin{thm}\label{thm:IJcaps} Suppose $\mathcal{T}\in\mathbb{B}\mathbb{P}$ is internally connected and has at least two internal disks. Then the $i,j$-caps of $\mathcal{T}$ form concentric circles by (5) in Proposition \ref{prop:BPprime}. Let $C_1$ be the outermost $i,j$-cap of $\mathcal{T}$. There is a unique smallest $n\in\mathbb{N}$ and two unique connected tangles $\mathcal{T}_1,\mathcal{T}_2\in\mathbb{B}\mathbb{P}$ up to swapping such that: \item[(1)] if $C_1$ is a right $i,j$-cap, $\mathcal{T}=\tau_n(\mathcal{T}_1(-),\mathcal{T}_2(-))$, and \item[(2)] if $C_1$ is a left $i,j$-cap, $\mathcal{T}=\tau_n^{\OP}(\mathcal{T}_1(-),\mathcal{T}_2(-))$. \end{thm} \begin{proof} We prove (1). We give an algorithm to build $\mathcal{T}_1$ and $\mathcal{T}_2$ by partitioning the internal disks of $\mathcal{T}$ into two sets $U$ and $L$, standing for ``upper" and ``lower." All $i,j$-caps of $\mathcal{T}$ will be between a $D_i\in U$ and a $D_j\in L$, and we will see they are all right caps. We form $\mathcal{T}_1$ by putting a box around the $D_i\in U$ together with all ``contractible" $i$-caps, and we form $\mathcal{T}_2$ by doing the same to the $D_j\in L$.
Before we describe the algorithm, we give an example: $$ \begin{tikzpicture}[scale=.6,baseline=5]
\clip (-2.1,5.2) --(4,5.2) -- (4,-3.1) -- (-2.1,-3.1);
\draw[ultra thick] (-.7,-2)--(-.7,4).. controls ++(90:1.6cm) and ++(90:2.5cm) .. (3.8,3)--(3.8,1.5).. controls ++(270:1.8cm) and ++(270:3cm) .. (-.7,-2);
\draw[ultra thick] (-.2,-2)--(-.2,4).. controls ++(90:1.4cm) and ++(90:2.2cm) .. (3.3,3)--(3.3,1.5).. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-.2,-2);
\draw[ultra thick] (.3,.5)--(.3,3.5).. controls ++(90:1.6cm) and ++(90:1.6cm) .. (3.1,3).. controls ++(270:2.4cm) and ++(270:3.2cm) .. (.3,.5);;
\draw[ultra thick] (.8,1.5)--(.8,3).. controls ++(90:1.4cm) and ++(90:1.6cm) .. (2.8,3) .. controls ++(270:1.4cm) and ++(270:2.2cm) .. (.8,1.5);
\draw[ultra thick] (1.7,3.5) arc (180:0:.3cm) -- (2.3,2.5) arc (0:-180:.3cm);
\draw[ultra thick] (2.15,3)--(2.3,2.7)--(2.45,3);
\draw[ultra thick] (3.65,2.3)--(3.8,2)--(3.95,2.3);
\draw[ultra thick] (3.15,2)--(3.3,1.7)--(3.45,2);
\draw[ultra thick] (2.4,2.1)--(2.4,1.7)--(2.7,1.9);
\draw[ultra thick] (2.5,1.2)--(2.5,.8)--(2.8,1);
\draw[ultra thick] (-1.3,-1) arc (0:180:.3cm) -- (-1.9,-2) arc (180:360:.3cm);
\draw[ultra thick] (-1.75,-1.2)--(-1.9,-1.5)--(-2.05,-1.2);
\filldraw[thick, unshaded] (.5,-2)--(.5,-1)--(-1.5,-1)--(-1.5,-2)--(.5,-2);
\filldraw[thick, unshaded] (1,-.5)--(1,.5)--(-.5,.5)--(-.5,-.5)--(1,-.5);
\filldraw[thick, unshaded] (1.5,1)--(1.5,2)--(0,2)--(0,1)--(1.5,1);
\filldraw[thick, unshaded] (2,2.5)--(2,3.5)--(.5,3.5)--(.5,2.5)--(2,2.5);
\node at (-.5,-1.5) {$D_2$};
\node at (.25,0) {$D_1$};
\node at (.75,1.5) {$D_3$};
\node at (1.25,3) {$D_4$}; \end{tikzpicture} \longrightarrow \begin{tikzpicture}[scale=.6,baseline=.5]
\clip (-2.3,4) --(5.4,4) -- (5.4,-4) -- (-2.3,-4);
\draw[ultra thick] (-.7,-2)--(-.7,2.2).. controls ++(90:2cm) and ++(90:2cm) .. (5.2,2.2)--(5.2,-2.2).. controls ++(270:1.8cm) and ++(270:2.4cm) .. (-.7,-2);
\draw[ultra thick] (-.2,-2)--(-.2,2).. controls ++(90:1.8cm) and ++(90:1.8cm) .. (4.8,2)--(4.8,-2.2).. controls ++(270:1.4cm) and ++(270:2.2cm) .. (-.2,-2);
\draw[ultra thick] (1.3,-1)--(.3,1)--(.3,2).. controls ++(90:1.6cm) and ++(90:1.2cm) .. (4.4,2)--(4.4,-2.2).. controls ++(270:1cm) and ++(270:1.2cm) .. (1.3,-2);;
\draw[ultra thick] (2,-1)--(2,2).. controls ++(90:1cm) and ++(90:1cm) .. (4,2)--(4,-2) .. controls ++(270:1cm) and ++(270:1cm) .. (2,-2);
\draw[ultra thick] (2.7,2) arc (180:0:.3cm) -- (3.3,1) arc (0:-180:.3cm);
\draw[ultra thick] (3.15,1.5)--(3.3,1.2)--(3.45,1.5);
\draw[ultra thick] (3.85,-.1)--(4,-.4)--(4.15,-.1);
\draw[ultra thick] (4.25,-.4)--(4.4,-.7)--(4.55,-.4);
\draw[ultra thick] (4.65,-.7)--(4.8,-1)--(4.95,-.7);
\draw[ultra thick] (5.05,-1)--(5.2,-1.3)--(5.35,-1);
\draw[ultra thick] (-1.3,-1) arc (0:180:.3cm) -- (-1.9,-2) arc (180:360:.3cm);
\draw[ultra thick] (-1.75,-1.2)--(-1.9,-1.5)--(-2.05,-1.2);
\filldraw[thick, unshaded] (.5,-2)--(.5,-1)--(-1.5,-1)--(-1.5,-2)--(.5,-2);
\filldraw[thick, unshaded] (2.5,-2)--(2.5,-1)--(1,-1)--(1,-2)--(2.5,-2);
\filldraw[thick, unshaded] (1,1)--(1,2)--(-.5,2)--(-.5,1)--(1,1);
\filldraw[thick, unshaded] (3,1)--(3,2)--(1.5,2)--(1.5,1)--(3,1);
\draw[dashed] (-2.2,-2.5)--(-2.2,-.5)--(2.8,-.5)--(2.8,-2.5)--(-2.2,-2.5);
\draw[dashed] (-1,.5)--(-1,2.5)--(3.6,2.5)--(3.6,.5)--(-1,.5);
\node at (-.5,-1.5) {$D_2$};
\node at (1.75,-1.5) {$D_3$};
\node at (.25,1.5) {$D_1$};
\node at (2.25,1.5) {$D_4$}; \end{tikzpicture}. $$
Assume all input disks of $\mathcal{T}$ are rectangles as in Remark \ref{rem:StandardForm}. Reindexing the internal disks, we suppose $C_1$ is a right $1,2$-cap. Set $U=\{D_1\}$ and $L=\{D_2\}$. Isotope the tangle so \item[$\bullet$] $D_1$ appears above $D_2$, \item[$\bullet$] all strings connecting $D_1$ and $D_2$ either go upward from $D_2$ to $D_1$ with no critical points or are large arcs with only two critical points, and \item[$\bullet$] all $1$-caps and $2$-caps which enclose $C_1$ are large arcs with only two critical points, and all $1$-caps and $2$-caps which do not enclose $C_1$ are close to $D_1$ and $D_2$ respectively. \item We work our way inside to the next $i,j$-cap that is not a $1,2$-cap (clearly all the $1,2$-caps are right caps). If there are no other $i,j$-caps, we are finished.
Otherwise, after reindexing, the next innermost $i,j$-cap $C_2$ is either a $1,3$-cap or $2,3$-cap, and all other strings connected to $D_2$ or $D_1$ respectively are $2$-caps or $1$-caps which can be isotoped so they are close to $D_2$ or $D_1$ respectively. We consider the case where $C_2$ is a $1,3$-cap, with the $2,3$-cap case being similar. We set $L=\{D_2,D_3\}$ (in the $2,3$-cap case, $U=\{D_1,D_3\}$), and we note that $C_2$ must also be a right cap as it is contained in $C_1$. We can also isotope the tangle so that \item[$\bullet$] $D_2$ and $D_3$ appear on the same horizontal level by moving $D_3$ around $C_2$, \item[$\bullet$] all strings connecting disks in $U$ and $L$ either go upward from a disk in $L$ to a disk in $U$ with no critical points or are large arcs with only two critical points, and \item[$\bullet$] all $1$-caps which enclose $C_2$ are large arcs with only two critical points (note that no $3$-cap can enclose $C_2$), and all $1$-caps and $2$-caps which do not enclose $C_2$ are close to $D_1$ and $D_2$ respectively. \item We work our way inside to the next $i,j$-cap that is not a $1,3$-cap (clearly all the $1,3$-caps are right caps). If there are no other $i,j$-caps, we are finished.
Otherwise, after reindexing, the next $i,j$-cap $C_3$ is either a $1,4$-cap or a $3,4$-cap, and all other strings connected to $D_3$ or $D_1$ respectively are $3$-caps or $1$-caps which can be isotoped so they are close to $D_3$ or $D_1$ respectively. We consider the case where the next cap is a $3,4$-cap, with the $1,4$-cap case being similar. We set $U=\{D_1,D_4\}$ (in the $1,4$-case, $L=\{D_1,D_3,D_4\}$), and we note that $C_3$ must also be a right cap as it is contained in $C_2$. We can also isotope the tangle so that \item[$\bullet$] all disks in $U$ appear on the same horizontal level by moving $D_4$ around $C_3$, and \item[$\bullet$] all strings connecting disks in $U$ and $L$ either travel upward from a disk in $L$ to a disk in $U$ with no critical points or travel in large arcs with only two critical points. \item[$\bullet$] all $3$-caps which enclose $C_3$ are large arcs with only two critical points (note that no $1$-cap can enclose $C_3$), and all $1$-caps and $3$-caps which do not enclose $C_3$ are close to $D_1$ and $D_3$ respectively. \item We work our way inside once again. Iterating this process until we run out of $i,j$-caps, we see that all $i,j$-caps must be right caps. Moreover, we have partitioned our internal disks into two sets, $U,L$, and we can isotope $\mathcal{T}$ so that: \item[$\bullet$] all disks in $U$ and $L$ appear on the same horizontal levels, \item[$\bullet$] any string connecting a disk $D_i\in U$ to a disk $D_j\in L$ travels upward from $D_j$ to $D_i$ with no critical points, or travels in a large arc from $D_i$ to $D_j$ with only two critical points, and \item[$\bullet$] all $i$-caps for $D_i\in U$ which do not enclose a $k,\ell$-cap are close to $D_i$ and all $j$-caps for $D_j\in L$ which do not enclose a $k,\ell$-cap are close to $D_j$. \item It is now clear that we can put boxes around the disks and caps in $U,L$ as desired, and we are left with $\tau_n(\mathcal{T}_1(-),\mathcal{T}_2(-))$ for some $n\in\mathbb{N}$ and some connected tangles $\mathcal{T}_1,\mathcal{T}_2\in\mathbb{B}\mathbb{P}$. Note that the $n$ is determined by the $i,j$-caps and the $k$-caps which enclose an $i,j$-cap, and this $n$ is minimal when all other $\ell$-caps are contracted so they are close to $D_\ell$. Moreover, the only choice we made was the initial choice $U=\{D_1\}$ and $L=\{D_2\}$, but if we swapped $U$ and $L$, we would have ended up with $\tau_n(\mathcal{T}_2(-),\mathcal{T}_1(-))$. Hence $\mathcal{T}_1,\mathcal{T}_2$ are unique up to swapping. \end{proof}
\begin{cor}\label{cor:subtangles} Each $\mathcal{T}\in\mathbb{B}\mathbb{P}$ with no external boundary points and at least one input disk contains an internally connected subtangle of the standard form: \item[(1)] $t_1^{\OP}\cdots t_{r}^{\OP} t_{r+1} t_{r_i+2}\cdots t_{k}$ for some $0\leq r\leq k$, or \item[(2)] $\tau_{n_1+n_2}(\mathcal{T}_1(-),\mathcal{T}_2(-))$ or $\tau_{n_1+n_2}^{\OP}(\mathcal{T}_1(-),\mathcal{T}_2(-))$ for some connected $\mathcal{T}_1,\mathcal{T}_2\in\mathbb{B}\mathbb{P}$. \end{cor}
\begin{defn}[Action of tangles in $\mathbb{B}\mathbb{P}$]\label{defn:TangleAction} We may now describe the action of a tangle $\mathcal{T}\in \mathbb{B}\mathbb{P}$ on a tuple $$ (z_1,\dots,z_s)\in \prod_{i=1}^s\widehat{Q_{n_i}^+}. $$ If $\mathcal{T}$ is connected, we put $\mathcal{T}$ in the standard form afforded by Corollary \ref{cor:DecomposeTangle}, label the inputs with the $z_i$'s, and replace $1_n$ with $\id_{H_n}$, $t_n,t_n^{\OP}$ with $T_n,T_n^{\OP}$, and $\otimes_{m,n}$ with $\otimes_A$.
If $\mathcal{T}$ is not connected, then there are closed subtangles as in Corollary \ref{cor:subtangles}. These closed subtangles will act as scalars in $\widehat{Q_0^+}=\widehat{Z(A)^+}=[0_\mathbb{R},\infty_R]$, and the order of scalar multiplication does not matter, so it suffices to define the scalar given by a single internally connected subtangle.
First, closed loops count for a multiplicative factor: $$ \dim_{-A}(H)=T_1(1)=\ClosedLoop{1}\, \text{ and } \dim_{A-}(H)=T_1^{\OP}(1)=\ClosedLoopOp{1}. $$ Suppose $\mathcal{S}$ is a closed, internally connected subtangle of $\mathcal{T}$ with only one input disk. Then we put $\mathcal{S}$ in the standard form of (1) in Corollary \ref{cor:subtangles}, label the tangle by $z_i$, and replace $t_n,t_n^{\OP}$ with $T_n,T_n^{\OP}$.
If $\mathcal{S}$ is a closed, internally connected subtangle with more than one input disk. Then there is a right (respectively left) $i,j$-cap, we have unique connected $\mathcal{S}_1,\mathcal{S}_2\in\mathbb{B}\mathbb{P}$ such that $\mathcal{S}=\tau_n(\mathcal{S}_1(-),\mathcal{S}_2(-))$ (respectively $\mathcal{S}=\tau_n^{\OP}(\mathcal{S}_1(-),\mathcal{S}_2(-))$) by Theorem \ref{thm:IJcaps}. Now we replace $\tau_n$ with $\Tr_n$ (respectively $\tau_n^{\OP}$ with $\Tr_n^{\OP}$), and we get the action of $\mathcal{S}_1,\mathcal{S}_2$ as above to get $w_1\in \widehat{Q_{k_1}^+},w_2\in \widehat{Q_{k_2}^+}$, and we use Theorem \ref{thm:BilinearExtension} to get the value $\Tr_n(w_1\cdot w_2)$ (respectively $\Tr_n^{\OP}(w_1\cdot w_2)$).
Hence we have defined the action of any tangle in $\mathbb{B}\mathbb{P}$. To show the action is well-defined (well-behaved under composition of tangles), one uses methods of \cite{0912.1320} to show that the standard forms of connected and internally connected tangles given in Corollaries \ref{cor:DecomposeTangle} and \ref{cor:subtangles} and the maps given in Subsection \ref{sec:TowersOfBimodules} behave the same under composition by Theorems \ref{thm:BPRelations} and \ref{thm:relations}. We briefly sketch such an argument.
First, it suffices to consider the composites $\mathcal{R}\circ_1 \mathcal{T}$, $\mathcal{T}'\circ_i \mathcal{T}$, and $\mathcal{S}\circ_j \mathcal{T}$ of $\mathcal{R},\mathcal{S},\mathcal{T}',\mathcal{T}\in\mathbb{B}\mathbb{P}$ such that $\mathcal{R}$ is internally connected with one input disk (see (1) of Corollary \ref{cor:subtangles}), $\mathcal{S}$ is internally connected with two or more input disks (see (2) of Corollary \ref{cor:subtangles} and Theorem \ref{thm:IJcaps}), and $\mathcal{T},\mathcal{T}'$ are connected. We may assume the respective connectivity properties because if any of $\mathcal{R},\mathcal{S},\mathcal{T}',\mathcal{T}$ had an internally connected subtangle $\mathcal{U}$ which is not involved with the composition, the scalar that $\mathcal{U}$ would contribute when acting remains unchanged by the composition. Note we cannot compose two nontrivial internally connected tangles.
Now if $\mathcal{R}\circ_1 \mathcal{T}, \mathcal{T}'\circ_i \mathcal{T}, \mathcal{S}\circ_j \mathcal{T}$ is still internally connected, internally connected, connected respectively, then we are finished by the existence of the standard forms and Theorems \ref{thm:BPRelations} and \ref{thm:relations}. In the cases of $\mathcal{R}\circ_1 \mathcal{T}$ and $\mathcal{T}'\circ_i\mathcal{T}$, we can only get internally connected tangles of the standard form (1) in Corollary \ref{cor:subtangles}, and once again, Theorems \ref{thm:BPRelations} and \ref{thm:relations} and (4) in Corollary \ref{cor:BPRelationsCor} are sufficient to show the well-definition.
One must treat the case $\mathcal{S}\circ_j \mathcal{T}$ more carefully, as we may create internally connected tangles of the standard form (1) or (2) in Corollary \ref{cor:subtangles}. First, use that there are connected $\mathcal{S}_1,\mathcal{S}_2\in\mathbb{B}\mathbb{P}$ such that $\mathcal{S}=\tau_n(\mathcal{S}_1(-),\mathcal{S}_2(-))$ (or $\OP$) by Theorem \ref{thm:IJcaps}. Then $\mathcal{T}$ is inserted into $S_1$ or $S_2$, so we look at $S_k\circ_\ell \mathcal{T}$. Now Theorems \ref{thm:BPRelations} and \ref{thm:relations} and (4) in Corollary \ref{cor:BPRelationsCor} are once again sufficient. \end{defn}
\section{Extended positive cones}\label{sec:cones} For the bimodule planar calculus, we need to make multiplication by $\infty_\mathbb{R}$ rigorous. We do so by generalizing the notion of an extended positive cone.
\begin{defn}\label{defn:ConeDefn} An \underline{extended positive cone} is a set $V$ together with a partial order $\leq$, an addition $+\colon V\times V\to V$, and a scalar multiplication $\cdot \colon [0_\mathbb{R},\infty_\mathbb{R}] \times V\to V$ such that \itt{Additivity axioms} \item[$\bullet$] (Zero) There is a $0_V\in V$ such that $0_V+v=v+0_V=v$ for all $v\in V$. \item[$\bullet$] (Infinity) There is an $\infty_V\in V\setminus\{0\}$ such that $v+\infty_V = \infty_V+v = \infty_V$ for all $v\in V$. \item[$\bullet$] (Associativity) $v_1+(v_2+v_3)=(v_1+v_2)+v_3$ for all $v_1,v_2,v_3\in V$. \item[$\bullet$] (Commutativity) $v_1+v_2=v_2+v_1$ for all $v_1,v_2\in V$. \itt{Multiplicative axioms} \item[$\bullet$] (Unit) $1_\mathbb{R} v=v$ for all $v\in V$. \item[$\bullet$] (Associativity) $(\lambda\mu) v=\lambda(\mu v)$ for all $\lambda,\mu\in [0_\mathbb{R},\infty_\mathbb{R}]$ and $v\in V$. \item[$\bullet$] (Zero) $0_\mathbb{R} v=0_V$ for all $v\in V$. \item[$\bullet$] (Infinity) $\lambda \infty_V=\infty_V$ for all $\lambda>0_\mathbb{R}$. \itt{Distributivity} \item[$\bullet$] (Scalars distribute)
$\lambda (v_1+v_2)=\lambda v_1+\lambda v_2$ for all $\lambda\in [0_\mathbb{R},\infty_\mathbb{R}]$ and $v_1,v_2\in V$. \item[$\bullet$] ($V$ distributes)
$(\lambda_1+\lambda_2)v = \lambda_1 v + \lambda_2 v$ for all $\lambda_1,\lambda_2\in [0_\mathbb{R},\infty_\mathbb{R}]$ and $v\in V$. \itt{Partial order axioms} \item[$\bullet$] (Non-degeneracy) $0_V\leq x\leq \infty_V$ for all $x\in V$. \item[$\bullet$] (Linearity) if $x_i\leq y_i$ for $i=0,1$ and $\lambda\in [0_\mathbb{R},\infty_\mathbb{R}]$, then $\lambda x_0 +x_1\leq \lambda y_0+y_1$. \end{defn}
\begin{rem} \item[(1)] $0_V,\infty_V\in V$ are unique. \item[(2)] If $\lambda v = 0_V$, then $v=0_V$ or $\lambda=0_\mathbb{R}$. \end{rem}
\begin{exs}\label{ex:EPC} \item[(1)] The set $[0_\mathbb{R},\infty_\mathbb{R}]$ with the usual ordering and the convention that $\lambda \infty_\mathbb{R} = \infty\lambda=\infty_\mathbb{R}$ for all $\lambda\in\mathbb{R}_{>0}$ and $0_\mathbb{R}\infty_\mathbb{R}=\infty_\R0_\mathbb{R}=0_\mathbb{R}$ is an extended positive cone. \item[(2)] Let $X$ be a nonempty set. The space of functions $\{f\colon X\to [0_\mathbb{R},\infty_\mathbb{R}]\}$ is an extended positive cone with pointwise addition and scalar multiplication, where $f\leq g$ if $f(x)\leq g(x)$ for all $x\in X$. Similarly, the space of extended positive measurable functions on a measure space is an extended positive cone. \item[(3)] If $M$ is a von Neumann algebra, $\omega(M)$, the set of normal weights $\omega\colon M^+\to [0_\mathbb{R},\infty_\mathbb{R}]$, is an extended positive cone where $\infty_{\omega(M)}$ is the map which sends $0_M$ to $0_\mathbb{R}$ and all other elements of $M$ to $\infty_\mathbb{R}$, and $\varphi\leq \psi$ if $\varphi(x)\leq \psi(x)$ for all $x\in M^+$. \item[(4)] If $M$ is a von Neumann algebra, $\widehat{M^+}$ is an extended positive cone where $\infty_{\widehat{M^+}}$ is the unbounded operator affiliated to $M$ with domain $(0)$, and $m_1\leq m_2$ if $m_1(\phi)\leq m_2(\phi)$ for all $\phi\in M_*^+$. \item[(5)] If $V,W$ are extended positive cones, then so is $V\times W$ where $(v_1,w_1)+(v_2,w_2)=(v_1+v_2,w_1+w_2)$, $\lambda (v_1,w_1)=(\lambda v_1,\lambda w_1)$, $0_{V\times W} = (0_{V},0_{W})$, $\infty_{V\times W}=(\infty_{V},\infty_{W})$, and $(v_1,w_1)\leq (v_2,w_2)$ if $v_1\leq v_2$ and $w_1\leq w_2$. \end{exs}
\begin{defn} Let $V,W$ be extended positive cones. A function $T\colon V\to W$ is a linear map (of extended positive cones) if \item[$\bullet$] $T(\lambda u+v)=\lambda Tu+Tv$ for all $u,v\in V$ and $\lambda\in [0_\mathbb{R},\infty_\mathbb{R}]$, and \item[$\bullet$] if $u,v\in V$ with $u\leq v$, then $Tu\leq Tv$. \item We define a multi-linear map of extended positive cones $V_1\times \cdots \times V_n\to V_0$ similarly. \end{defn}
\begin{exs}\label{ex:MapExamples} \item[(1)] For a fixed scalar $\lambda\in [0_\mathbb{R},\infty_\mathbb{R}]$, multiplication by $\lambda$ is a map of extended positive cones. \item[(2)] Suppose $\omega\colon M^+\to [0_\mathbb{R},\infty_\mathbb{R}]$ is a normal weight. Then its unique extension to a normal weight $\omega\colon \widehat{M^+}\to [0_\mathbb{R},\infty_\mathbb{R}]$ is a map of extended positive cones. \item[(3)] If $m\in \widehat{M^+}$, then $m\colon \omega(M)\to[0_\mathbb{R},\infty_\mathbb{R}]$ given by$ \varphi\mapsto m(\varphi)$ is a map of extended positive cones. \item[(4)] Suppose $N\subset M$ is an inclusion of von Neumann algebras, $i\colon \widehat{N^+}\to \widehat{M^+}$ is the inclusion (well-defined by Equation \eqref{eq:KS}), and $T\colon \widehat{M^+}\to \widehat{N^+}$ is the unique extension of an operator valued weight $M^+\to \widehat{N^+}$. Then $i,T$ are maps of extended positive cones. \item[(5)] Using the notation of Appendix \ref{sec:TensorUnbounded}, the map $\widehat{X^+} \times \widehat{Y_0^+}\to \widehat{X\otimes_A Y_0^+}$ given by $(x,y)\mapsto x\otimes_A y$ is a multilinear map of extended positive cones by Lemma \ref{cor:TensorConeMap}. \end{exs}
\begin{defn} An increasing net $(x_i)_{i\in I}\subset V$ converges to $x\in V$ if $x$ is the unique least upper bound for $(x_i)_{i\in I}$. We denote this convergence by $\sup_{i\in I} x_i=x$ or $x_i\nearrow x$. \item[$\bullet$] $V$ is \underline{complete} if each increasing net $(x_i)_{i\in I}$ has a unique least upper bound. \item[$\bullet$] A map $T\colon V\to W$ is \underline{normal} if $x_i\nearrow x$ implies $Tx_i \nearrow Tx$. \end{defn}
\begin{rem}\label{rem:normal} The maps in Examples \ref{ex:MapExamples} are all normal. \end{rem}
\begin{defn} The \underline{dual space} of $V$, denoted $V^*$, is the set of all normal maps $V\to [0_\mathbb{R},\infty_\mathbb{R}]$. Note that $V^*$ is a complete extended positive cone with \item[(1)] $(\lambda \varphi+\psi)(v)=\lambda \varphi(v)+\psi(v)$ for all $v\in V$, $\lambda\in [0_\mathbb{R},\infty_\mathbb{R}]$, and $\varphi,\psi\in V^*$, with the convention that $0_\mathbb{R}\cdot \infty_\mathbb{R}=0_\mathbb{R}$, \item[(2)] $0_{V^*}$ is the zero map, \item[(3)] $\displaystyle \infty_{V^*}(v)=\begin{cases} 0 & \text{if } v=0\\ \infty_V & \text{else, and} \end{cases}$ \item[(4)] $(\sup_{i\in I} \varphi_i)(v) := \sup_{i\in I} \varphi_i(v)$. \item[$\bullet$] There is a natural inclusion $V\to V^{**}$ by $x\mapsto (\ev_x\colon \varphi\mapsto \varphi(x))$. \item[$\bullet$] The \underline{completion} of $V$ is the set of sups of increasing nets in the image of $V$ in $V^{**}$. \end{defn}
\begin{thm} Let $M$ be a semifinite von Neumann algebra with n.f.s. trace $\Tr_M$. Let $\omega(M)$ be the set of normal weights on $M^+$. \item[(1)] $\widehat{M^+}$ is the dual extended positive cone of $\omega(M)$ (the ordering on each is given in Examples \ref{ex:EPC}). \item[(2)] The map $\widehat{M^+}\ni x\mapsto \Tr_M(x\,\cdot \, )\in \omega(M)$ is a normal isomorphism of extended positive cones. \end{thm} \begin{proof} This is a rewording of Theorem \ref{thm:BilinearExtension} into the language of this subsection. \end{proof}
\begin{defn}\label{defn:ExtendedConeAdjoint} If $T\colon V\to W$ is a normal map of extended positive cones, we get a map of dual spaces $T^*\colon W^*\to V^*$ by $T^*(\phi)=\phi\circ T$ for all $\phi\in W^*$. We can characterize it as the unique map satisfying $$ \langle T(v), \varphi\rangle_W = \varphi(T(v))=\langle v, T^*(\varphi)\rangle_V $$ for all $v\in V$ and $\varphi\in W$. \end{defn}
\begin{prop}\label{prop:adjoint} Suppose $N\subset M$ is an inclusion of semifinite von Neumann algebras with n.f.s. traces $\Tr_N,\Tr_M$ respectively. Let $i\colon \omega(N)\cong \widehat{N^+}\to \widehat{M^+}\cong \omega(M)$ be the inclusion, and let $T\colon \widehat{M^+}\to \widehat{N^+}$ be the unique extension to $\widehat{M^+}$ of the unique trace-preserving operator valued weight. Then $i,T$ are normal and $T=i^*$, $T^*=i$. \end{prop} \begin{proof} Clearly $i,T$ are normal. Suppose $n\in \widehat{N^+}$ and $m\in (\widehat{M^+})^*=\widehat{M^+}$. Then $$ \langle i(n),m\rangle_{\widehat{M^+}}=\Tr_M(m\cdot n)=\Tr_N(T(m)\cdot n) = \langle n, T(m)\rangle_{\widehat{N^+}}, $$ so $T=i^*$. Since $\Tr_M(m\cdot n) =\Tr_M(n\cdot m)$, $i=T^*$. \end{proof}
\end{document} | arXiv |
Chapters (2)
Materials Research (6)
Symposium - International Astronomical Union (3)
European Psychiatry (2)
Microscopy and Microanalysis (2)
Acta Neuropsychiatrica (1)
Environmental Conservation (1)
European Journal of Anaesthesiology (1)
Journal of Plasma Physics (1)
Materials Research Society Internet Journal of Nitride Semiconductor Research (1)
The European Physical Journal - Applied Physics (1)
Twin Research and Human Genetics (1)
Materials Research Society (7)
International Astronomical Union (3)
European Psychiatric Association (2)
International Soc for Twin Studies (1)
MSA - Microscopy Society of America (1)
Detection and Localization of Eu on Biosilica by Analytical Scanning Electron Microscopy
Ellen Hieckmann, Kaitlin K. K. Kammerlander, Lydia Köhler, Laura Neumann, Stefan Saager, Nico Albanis, Thomas Hutsch, Frank Seifert, Eike Brunner
Journal: Microscopy and Microanalysis / Volume 27 / Issue 6 / December 2021
Print publication: December 2021
Algae like diatoms are widely studied as a means to remediate anthropogenically contaminated sites. In the present study, CL (cathodoluminescence) and EDX (energy-dispersive X-ray) spectroscopy in an SEM (scanning electron microscope) were optimized for the detection of Eu(III) sorbed on diatom biosilica. The required stability of biosilica under a focused electron beam was extensively investigated. Using experimentally determined data of thermal properties, the temperature increase within biosilica exposed to an electron beam was simulated by finite element calculations based on results from Monte Carlo simulations of electron scattering. Complementary thermogravimetric studies substantiated a chemical stability of biosilica in a wide temperature range, confirming its suitability for long-lasting SEM investigations. In subsequent EDX measurements, characteristic Eu lines were detected. Eu was found to preferentially accumulate and aggregate on silica fragments. CL spectra were obtained for the Eu(III) reference material, EuCl3. For Eu-loaded biosilica, even parts without detectable Eu signal in the EDX spectra show significant Eu(III) signals in the CL spectra. This highlights the sensitivity of CL in studying f-element sorption. CL data showed that Eu(III) was distributed on the entire surface. In conclusion, this work demonstrates the merit of CL and EDX methods for sorption studies on biogenic materials.
Overview of the SPARC tokamak
Status of the SPARC Physics Basis
Focus on Fusion
A. J. Creely, M. J. Greenwald, S. B. Ballinger, D. Brunner, J. Canik, J. Doody, T. Fülöp, D. T. Garnier, R. Granetz, T. K. Gray, C. Holland, N. T. Howard, J. W. Hughes, J. H. Irby, V. A. Izzo, G. J. Kramer, A. Q. Kuang, B. LaBombard, Y. Lin, B. Lipschultz, N. C. Logan, J. D. Lore, E. S. Marmar, K. Montes, R. T. Mumgaard, C. Paz-Soldan, C. Rea, M. L. Reinke, P. Rodriguez-Fernandez, K. Särkimäki, F. Sciortino, S. D. Scott, A. Snicker, P. B. Snyder, B. N. Sorbom, R. Sweeney, R. A. Tinguely, E. A. Tolman, M. Umansky, O. Vallhagen, J. Varje, D. G. Whyte, J. C. Wright, S. J. Wukitch, J. Zhu, the SPARC Team
Journal: Journal of Plasma Physics / Volume 86 / Issue 5 / October 2020
Published online by Cambridge University Press: 29 September 2020, 865860502
The SPARC tokamak is a critical next step towards commercial fusion energy. SPARC is designed as a high-field ( $B_0 = 12.2$ T), compact ( $R_0 = 1.85$ m, $a = 0.57$ m), superconducting, D-T tokamak with the goal of producing fusion gain $Q>2$ from a magnetically confined fusion plasma for the first time. Currently under design, SPARC will continue the high-field path of the Alcator series of tokamaks, utilizing new magnets based on rare earth barium copper oxide high-temperature superconductors to achieve high performance in a compact device. The goal of $Q>2$ is achievable with conservative physics assumptions ( $H_{98,y2} = 0.7$) and, with the nominal assumption of $H_{98,y2} = 1$, SPARC is projected to attain $Q \approx 11$ and $P_{\textrm {fusion}} \approx 140$ MW. SPARC will therefore constitute a unique platform for burning plasma physics research with high density ( $\langle n_{e} \rangle \approx 3 \times 10^{20}\ \textrm {m}^{-3}$), high temperature ( $\langle T_e \rangle \approx 7$ keV) and high power density ( $P_{\textrm {fusion}}/V_{\textrm {plasma}} \approx 7\ \textrm {MW}\,\textrm {m}^{-3}$) relevant to fusion power plants. SPARC's place in the path to commercial fusion energy, its parameters and the current status of SPARC design work are presented. This work also describes the basis for global performance projections and summarizes some of the physics analysis that is presented in greater detail in the companion articles of this collection.
P02-249 - Reduced Prefrontal and Orbitofrontal Gray Matter in Female Adolescents with Borderline Personality Disorder: is it Disorder Specific?
R. Henze, R. Brunner, P. Parzer, J. Kramer, N. Feigl, K. Lutz, M. Essig, F. Resch, B. Stieltjes
Journal: European Psychiatry / Volume 25 / Issue S1 / 2010
Published online by Cambridge University Press: 17 April 2020, 25-E875
Neuroimaging studies in adults with borderline personality disorder (BPD) have reported alterations in frontolimbic areas, but cannot differentiate between alterations originating from disease and those occurring as side-effects of medication or other consequences of the disorder.
To provide a clearer picture of the organic origins of BPD, the present study reduced such confounds by examining adolescents in the early stages of the disorder. It also examined the extent to which alterations associated with BPD are specific, or shared more broadly among other psychiatric disorders.
Sixty right-handed, female adolescents (14-18 years) participated. 20 had a DSM-IV diagnosis of BPD, 20 had a different DSM-IV defined psychiatric disorder, and 20 were healthy controls. All groups were matched for age and IQ. Images were analysed using voxel-based morphometry.
No differences were found in limbic or white matter structures. Compared to healthy controls, adolescents with BPD displayed reduced gray matter in dorsolateral prefrontal cortex bilaterally and in left orbitofrontal cortex, but there were no significant differences in gray matter between BPD and other psychiatric patients. Like BPD patients, non-BPD psychiatric patients displayed significantly less gray matter in right dorsolateral prefrontal cortex compared to healthy controls.
These findings indicate that the prefrontal cortex is the earliest affected in the progression of BPD, but this does not distinguish it clearly from other psychiatric disorders. Alterations in limbic areas and white matter structures were not observed, but may play a later role in the progression of the illness.
O-13 - Challenging the Sleep Homeostat in Young Depressed and Healthy Older Women: Sleep in Depression is not Premature Aging
S. Frey, A. Birchler-Pedross, M. Hofstetter, P. Brunner, T. Götz, M. Münch, K. Blatter, V. Knoblauch, A. Wirz-Justice, C. Cajochen
Published online by Cambridge University Press: 15 April 2020, p. 1
Major depression and sleep disturbances are closely related and often occur concomitantly. Many of the observed changes of sleep characteristics in depression are also present in healthy aging, which led to the premise that sleep in depression resembles premature aging.
Here, we aimed at quantifying the homeostatic and circadian sleep-wake regulatory components in young women suffering from major depression disorder and healthy young and older control women during 40 hours of sustained wakefulness.
After an 8-h baseline night 9 depressed women, 8 healthy young and 8 healthy older women underwent a 40-hour sustained wakefulness protocol followed by a recovery night under constant routine conditions. Polysomnographic recordings were carried out continuously. Sleep parameters as well as the time course of EEG slow-wave activity (SWA) (EEG spectra range: 0.75-4.5 Hz), as a marker of homeostatic sleep pressure, was analyzed during the recovery night.
Young depressed women exhibited higher absolute mean SWA levels and a stronger response to sleep deprivation compared to healthy young and healthy older women, particularly in frontal brain regions. In contrast, healthy older women exhibited attenuated SWA values compared to the other two groups and an absence of the frontal predominance of mean SWA during the recovery night.
Our data clearly show that homeostatic sleep regulation as well as sleep architecture in young depressed women is not equal to premature aging. Moreover, our findings demonstrate that young depressed women live on an elevated level of homeostatic sleep pressure.
27 - An Experimental Test of Flexible Combinatorial Spectrum Auction Formats
from Part IV - Experimental Comparisons of Auction Designs
By Christoph Brunner, Alfred-Weber-Institut, University of Heidelberg, Jacob K. Goeree, School of Economics, UNSW Business School, Charles A. Holt, Department of Economics, University of Virginia, John O. Ledyard, Division of the Humanities and Social Sciences, California Institute of Technology
Edited by Martin Bichler, Technische Universität München, Jacob K. Goeree, University of New South Wales, Sydney
Book: Handbook of Spectrum Auction Design
Print publication: 26 October 2017, pp 588-606
View extract
Simultaneous auctions for multiple items are often used when the values of the items are interrelated. An example of such a situation is the sale of spectrum rights by the Federal Communications Commission (FCC). If a telecommunications company is already operating in a certain area, the cost of operating in adjacent areas tends to be lower. In addition, consumers may value larger networks that reduce the cost and inconvenience of "roaming." As a consequence, the value of a collection of spectrum licenses for adjacent areas can be higher than the sum of the values for separate licenses. Value complementarities arise naturally in many other contexts, e.g. aircraft takeoff and landing slots, pollution emissions allowances for consecutive years, and coordinated advertising time slots. This paper reports a series of laboratory experiments to evaluate alternative methods of running multi-unit auctions, in both high and low-complementarities environments.
Various auction formats have been suggested for selling multiple items with interrelated values. The most widely discussed format is the simultaneous multiple round (SMR) auction, first used by the FCC in 1994. In the SMR auction, bidders are only allowed to bid on single licenses in a series of "rounds," and the auction stops when no new bids are submitted on any license. To win a valuable package of licenses in this type of auction, bidders with value complementarities may have to bid more for some licenses than they are worth individually, which may result in losses when only a subset is won. Avoidance of this "exposure problem" may lead to conservative bidding, lower revenue, and inefficient allocations.
The obvious solution to the exposure problem is to allow bidding for packages of items. In such combinatorial auctions, bidders can make sure they either win the entire package or nothing at all. As a result, bids can reflect value complementarities, which should raise efficiency and seller revenue. Combinatorial bidding, however, may introduce new problems. Consider a situation in which a large bidder submits a package bid for several licenses. If other bidders are interested in buying different subsets of licenses contained in the package, they might find it hard to coordinate their actions, even if the sum of their values is higher than the value of the package to the large bidder (the threshold problem). Thus, there is no clear presumption that package bidding will improve auction performance.
The Last Interglacial Ocean
Rose Marie L. Cline, James D. Hays, Warren L. Prell, William F. Ruddiman, Ted C. Moore, Nilva G. Kipp, Barbara E. Molfino, George H. Denton, Terence J. Hughes, William L. Balsam, Charlotte A. Brunner, Jean-Claude Duplessy, Ann G. Esmay, James L. Fastook, John Imbrie, Lloyd D. Keigwin, Thomas B. Kellogg, Andrew McIntyre, Robley K. Matthews, Alan C. Mix, Joseph J. Morley, Nicholas J. Shackleton, S. Stephen Streeter, Peter R. Thompson
Journal: Quaternary Research / Volume 21 / Issue 2 / February 1984
The final effort of the CLIMAP project was a study of the last interglaciation, a time of minimum ice volume some 122,000 yr ago coincident with the Substage 5e oxygen isotopic minimum. Based on detailed oxygen isotope analyses and biotic census counts in 52 cores across the world ocean, last interglacial sea-surface temperatures (SST) were compared with those today. There are small SST departures in the mid-latitude North Atlantic (warmer) and the Gulf of Mexico (cooler). The eastern boundary currents of the South Atlantic and Pacific oceans are marked by large SST anomalies in individual cores, but their interpretations are precluded by no-analog problems and by discordancies among estimates from different biotic groups. In general, the last interglacial ocean was not significantly different from the modern ocean. The relative sequencing of ice decay versus oceanic warming on the Stage 6/5 oxygen isotopic transition and of ice growth versus oceanic cooling on the Stage 5e/5d transition was also studied. In most of the Southern Hemisphere, the oceanic response marked by the biotic census counts preceded (led) the global ice-volume response marked by the oxygen-isotope signal by several thousand years. The reverse pattern is evident in the North Atlantic Ocean and the Gulf of Mexico, where the oceanic response lagged that of global ice volume by several thousand years. As a result, the very warm temperatures associated with the last interglaciation were regionally diachronous by several thousand years. These regional lead-lag relationships agree with those observed on other transitions and in long-term phase relationships; they cannot be explained simply as artifacts of bioturbational translations of the original signals.
Circadian rhythms and sleep regulation in seasonal affective disorder
A. Wirz-Justice, K. Kräuchi, D.P. Brunner, P. Graw, H.-J. Haug, G. Leonhardt, A. Sarrafzadeh, J. English, J. Arendt
Journal: Acta Neuropsychiatrica / Volume 7 / Issue 2 / June 1995
Published online by Cambridge University Press: 18 September 2015, pp. 41-43
Seasonal affective disorder (SAD) is characterised by recurrent episodes in autumn and winter of depression, hypersomnia, augmented appetite with carbohydrate craving, and weight gain, and can be successfully treated with bright light. Circadian rhythm hypotheses (summarized in) have stimulated research into the pathophysiology of SAD, postulating that:
1.The illness is a consequence of delayed phase position,
2.It is correlated with diminished circadian amplitude, or
3.It results from changes in the nocturnal duration between dusk and dawn e.g. of low core body temperature or melatonin secretion. Light is considered to act directly on the circadian pacemaker ('Process C') and not on sleep dependent processes ('Process S'). Thus successful treatment of SAD must act via mechanisms within known retinohypothalamic pathways. Conversely, emergence of SAD symptoms may reflect inappropriate neurobiological response to decreasing daylength.
Heritability of Head Size in Dutch and Australian Twin Families at Ages 0–50 Years
Dirk J. A. Smit, Michelle Luciano, Meike Bartels, Catharine E. M. van Beijsterveldt, Margaret J. Wright, Narelle K. Hansell, Han G. Brunner, G. Frederiek Estourgie-van Burk, Eco J. C. de Geus, Nicholas G. Martin, Dorret I. Boomsma
Journal: Twin Research and Human Genetics / Volume 13 / Issue 4 / 01 August 2010
We assessed the heritability of head circumference, an approximation of brain size, in twin-sib families of different ages. Data from the youngest participants were collected a few weeks after birth and from the oldest participants around age 50 years. In nearly all age groups the largest part of the variation in head circumference was explained by genetic differences. Heritability estimates were 90% in young infants (4 to 5 months), 85–88% in early childhood, 83–87% in adolescence, 75% in young and mid adulthood. In infants younger than 3 months, heritability was very low or absent. Quantitative sex differences in heritability were observed in 15- and 18-year-olds, but there was no evidence for qualitative sex differences, that is, the same genes were expressed in both males and females. Longitudinal analysis of the data between 5, 7, and 18 years of age showed high genetic stability (.78 > RG > .98). These results indicate that head circumference is a highly heritable biometric trait and a valid target for future GWA studies.
Label-Free 3D Imaging of Development of Cell Patterns in Drosophila melanogaster Wing Imaginal Disc
G Rago, F Marty, J Day, R Heeren, K Basler, E Brunner, M Bonn
Journal: Microscopy and Microanalysis / Volume 17 / Issue S2 / July 2011
Published online by Cambridge University Press: 08 April 2017, pp. 228-229
Extended abstract of a paper presented at Microscopy and Microanalysis 2011 in Nashville, Tennessee, USA, August 7–August 11, 2011.
32 - Metastatic Squamous Cell Carcinoma in Organ Transplant Recipients
from Section Eight - Special Scenarios in Transplant Cutaneous Oncology
By Randall K. Roenigk MD, David L. Appert MD, Kelly L. Brunner MD, Jerry D. Brewer MD
Edited by Clark C. Otley, Thomas Stasko, Vanderbilt University, Tennessee
Book: Skin Disease in Organ Transplantation
Published online: 18 January 2010
Print publication: 21 January 2008, pp 217-223
Organ transplant recipients (OTRs) are a special group of patients with important characteristics and unique medical needs. Because squamous cell carcinomas (SCC) in OTRs tend to be common, with more aggressive local invasion, early recurrence, and higher rates of metastases, the recognition and treatment of skin cancer, especially SCC, in these patients is becoming a more important aspect of their overall care. As OTRs live longer with better antirejection regimens, the incidence of metastatic SCC in these patients will most likely increase.
The pathogenesis of malignancies, specifically SCC in OTRs, is multifactorial. The immunosuppression required in OTRs is a well-documented factor in the development of SCC and other malignancies. In fact, cancer of any type is three to four times more likely to develop in OTRs than in the general population. Immunosuppression not only predisposes OTRs to the development of SCC but also increases tumor aggressiveness, the chance of metastatic disease, and the possibility of death. The level and duration of immunosuppression is the single most important factor influencing malignant transformation and metastasis in OTRs. This is well illustrated by cardiac transplant patients, who generally receive higher levels of immunosuppression than recipients of other types of organ transplants and have the highest rate of SCC among OTRs. Moloney et al. postulated that immunosuppression can affect whether a local primary SCC transforms into a tumor with the potential to metastasize.
Immunosuppression may increase the incidence of SCC through at least two mechanisms.
Forest cover change patterns in Myanmar (Burma) 1990–2000
PETER LEIMGRUBER, DANIEL S. KELLY, MARC K. STEININGER, JAKE BRUNNER, THOMAS MÜLLER, MELISSA SONGER
Journal: Environmental Conservation / Volume 32 / Issue 4 / December 2005
Myanmar is one of the most forested countries in mainland South-east Asia. These forests support a large number of important species and endemics and have great value for global efforts in biodiversity conservation. Landsat satellite imagery from the 1990s and 2000s was used to develop a countrywide forest map and estimate deforestation. The country has retained much of its forest cover, but forests have declined by 0.3% annually. Deforestation varied considerably among administrative units, with central and more populated states and divisions showing the highest losses. Ten deforestation hotspots had annual deforestation rates well above the countrywide average. Major reasons for forest losses in these hotspots stemmed from increased agricultural conversion, fuelwood consumption, charcoal production, commercial logging and plantation development. While Myanmar continues to be a stronghold for closed canopy forests, several areas have been experiencing serious deforestation. Most notable are the mangrove forests in the Ayeyarwady delta region and the remaining dry forests at the northern edge of the central dry zone.
Nonequilibrium carrier dynamics in heavily p-doped GaAs
K. Jarasiunas, R. Aleksiejunas, T. Malinauskas, V. Gudelis, M. Sudzius, A. Maaßdorf, F. Brunner, M. Weyers
Journal: The European Physical Journal - Applied Physics / Volume 27 / Issue 1-3 / July 2004
Published online by Cambridge University Press: 15 July 2004, pp. 181-184
A non-degenerate four-wave mixing technique has been applied to investigate carrier transport and recombination in heavily C-doped GaAs embedded in a double-heterostructure. The carriers were injected into the 1 µm-thick p-GaAs layer via the 50 nm-thick barrier of AlGaAs:C or InGaP:Si, using the light interference pattern of two picosecond laser pulses at 532 nm. The dependence of the nonequilibrium carrier grating decay time on the grating period allows the determination of minority carrier diffusion coefficients: D = 35 cm2/s for p-GaAs ($p_0 = 2 \times 10^{19}$ cm−3) with AlGaAs barriers and D = 27 cm2/s for p-GaAs ($p_{0} = 1 \times 10^{19}$ cm−3) with InGaP barriers. This increase of electron mobility at the higher doping level was found to be in agreement with the decreasing role of carrier-carrier scattering in heavily-doped p-GaAs. The fast recombination of nonequilibrium carriers in the vicinity of a front barrier layer was evident and more pronounced for an AlGaAs than for an InGaP barrier.
The effect of remifentanil on the middle latency auditory evoked response and haemodynamic measurements with and without the stimulus of orotracheal intubation
D. R. Wright, C. Thornton, K. Hasan, D. J. A. Vaughan, C. J. Doré, M. D. Brunner
Journal: European Journal of Anaesthesiology / Volume 21 / Issue 7 / July 2004
Background and objective: Changes in the middle latency auditory evoked response following the administration of opioids have been shown. However, it remains unclear as to whether these changes are due to a direct depressant effect of opioids on the middle latency auditory evoked response itself, or an indirect effect on account of their action in attenuating central nervous system arousal associated with noxious stimuli. By comparing changes in the middle latency auditory evoked response in intubated and non-intubated patients, receiving saline or remifentanil in different doses, this study attempts to answer this question.
Methods: Fifty-four patients were anaesthetized with isoflurane and nitrous oxide (0.9 MAC) and randomized to 1–6 groups. Groups 1–3 received a bolus injection of either saline 0.9%, low-dose remifentanil (1 μg kg−1) or high-dose remifentanil (3 μg kg−1) prior to intubation of the trachea. Groups 4–6 were not intubated following the bolus injection.
Results: Pa and Nb amplitudes of the middle latency auditory evoked response increased by 82% and 79% with intubation in the saline group (P < 0.005) and these changes were not seen in the patients given remifentanil. There was a significant linear trend for the reduction in Pa and Nb amplitude with increasing remifentanil dose (P < 0.05). In the absence of endotracheal intubation remifentanil had no effect on either the amplitudes or latencies of the waves Pa and Nb and there was no effect of dose. For the haemodynamic measurements remifentanil attenuated the pressor response to intubation (P < 0.001) and had a significant dose-related effect (P < 0.001) in the absence of intubation.
Conclusions: We demonstrated an effect of remifentanil on both the middle latency auditory evoked response and haemodynamic changes to endotracheal intubation. For the non-intubated patients there was only an effect of remifentanil on the haemodynamic measurements. This suggests that remifentanil has an effect on the middle latency auditory evoked response in attenuating the arousal associated with intubation of the trachea but has no effect in the absence of a stimulus.
Self-assembled Si/Ge quantum dot structures for novel device applications
K. Brunner, D. Bougeard, A. Janotta, M. Herbst, P. H. Tan, H. Riedl, M. Stutzmann, G. Abstreiter
Journal: MRS Online Proceedings Library Archive / Volume 737 / 2002
Published online by Cambridge University Press: 11 February 2011, F2.1
Print publication: 2002
The band structure of self-assembled Si/Ge quantum dot structures deposited by molecular beam epitaxy in the Stranski Krastanov growth mode is characterized by optical and electrical spectroscopy. Interband and intraband absorption, photocurrent, photoluminescence, Raman and admittance spectroscopy of structures with quantum dots of about 20 nm lateral size offer insight into the discrete level scheme within the valence band, the optical transitions and the lifetime of localized hole states. The results are discussed with respect to their possible applications in infrared light detection, storage and quantum-logic devices.
Study of polymer-electrode interfaces in polymer light-emitting diodes using electrical impedance spectroscopy
A. van Dijken, I.N. Hulea, H.B. Brom, K. Brunner
Published online by Cambridge University Press: 11 February 2011, B6.2
Electrical impedance spectroscopy is used to show that time-dependent charge trapping processes occur in double-layer polymer light-emitting diodes based on poly(ethylene-dioxythiophene):poly(styrene sulfonic acid) (PEDOT:PSS) and poly(p-phenylene vinylene) (PPV). No time-dependent charge trapping processes are observed in single-layer devices based on PPV only. Furthermore, in double-layer devices based on poly(2,7-spirofluorene) (PSF) instead of PPV, such processes are also absent. Traps are probably created in the PPV layer close to the PEDOT:PSS interface due to chemical reactions that occur specifically between PEDOT:PSS and PPV.
Lateral Ordering of Self-Assembled Ge Islands
Jian-Hong Zhu, K. Brunner, G. Abstreiter
Published online by Cambridge University Press: 10 February 2011, 165
Two-dimensionally ordered arrays of Ge islands are realized by molecular beam epitaxy on vicinal Si(001) surfaces with regular ripples. Deposition of a 2.5 nm Si0.55Ge0.45/10 nm Si multilayer on vicinal Si(001) surfaces gives rise to the formation of regular ripples with a typical period of 100 nm, due to step-bunching. The ripples lead to the long-range line-up of the Ge islands along their direction, while the strong repulsive interaction between the dense Ge islands determines their relative arrangement on different step bunches of a ripple. The ordering pattern can be controlled by the Ge coverage as well as the direction of the ripples. The Ge islands show a narrow size distribution with the lateral size limited by the ripple period
In contrast, when deposited directly on well-prepared biatomic-stepped vicinal Si(001) surfaces under the same growth conditions, only weak ordering of Ge islands along the step direction is achieved. No ordering of Ge islands has been observed, when a flat Si(001) surface is employed, where no obvious step-bunching occurs.
The results promise efficient control on the position and size of self-assembled and selfordered Ge islands by the steps prepared on vicinal surfaces.
Band Alignment of Si1-xGex And Si1-x-y.GexCy Quantum Wells On Si (001)
N. L. Rowell, R. L. Williams, G. C. Aers, H. Lafontaine, D. C. Houghton, K. Brunner, K. Eberl, O. Schmidt, W. Winter
Recent low-temperature photoluminescence (PL) studies will be discussed for coherent Si1-xGex. and Si1-xGexCy alloy multiple quantum wells on Si (001) substrates grown by either ultra-high vacuum chemical vapour deposition or solid source molecular beam epitaxy. An in-plane applied-stress technique will be described which removes systematically band edge degeneracies revealing the lower, PL-active CB. Applied-stress data taken with this technique at ultra-low excitation intensity proved intrinsic type II CB alignment in SiGe on Si (001). Apparent type I alignment observed at higher intensity will also be discussed. New applied stress PL results are presented for Si1-x-yGexCy quantum wells under various grown-in stress condition
Erbium Doped Si/Sige Waveguide Diodes: Optical And Electrical Characterization
E. Neufeld, A. Luigart, A. Sticht, K. Brunner, G. Abstreiter
We have fabricated erbium- and oxygen-doped Si/SiGe waveguide diodes showing the characteristic 1.54 µm electroluminescence (EL) from incorporated Er+3, ions. All samples were grown by molecular beam epitaxy (MBE). The EL from the polished end facet of the waveguide was measured with a confocal microscope revealing a spatially narrow emission. Additional annealing was not necessary to improve the luminescence characteristics. Only a weak temperature dependence is found for the EL intensity between 4K and room temperature.
AlGaN-Based Bragg Reflectors
O. Ambacher, M. Arzberger, D. Brunner, H. Angerer, F. Freudenberg, N. Esser, T. Wethkamp, K. Wilmers, W. Richter, M. Stutzmann
Journal: Materials Research Society Internet Journal of Nitride Semiconductor Research / Volume 2 / 1997
Published online by Cambridge University Press: 13 June 2014, e22
We have studied the dependence of the absorption edge and the refractive index of wurtzite AlxGa1−xN films on composition using transmission, ellipsometry and photothermal deflection spectroscopy. The Al molar fraction of the AlxGa1−xN films grown by plasma-induced molecular beam epitaxy was varied through the entire range of composition (0 ≤ x ≤ 1). We determined the absorption edges of AlxGa1−xN films and a bowing parameter of 1.3 ± 0.2 eV. The refractive index below the bandgap was deduced from the interference fringes, the dielectric function between 2.5 and 25 eV from ellipsometry measurements. The measured absorption coefficients and refractive indices were used to calculate the design and reflectivity of AlGaN-based Bragg reflectors working in the blue and near-ultraviolet spectral region.
Growth and Characterization of Pseudomorphic Gel-yCy and Si1-yCy Alloy Layers on Si Substrates
K. Brunner, K. Eberl, W. Winter
Published online by Cambridge University Press: 15 February 2011, 87
Pseudomorphic Gel-yCy and Sil-yCy alloy layers have been synthesized by solidsource molecular beam epitaxy on Si (001) substrates. High quality short-period Gel-y Cy/Si superlattice structures with a carbon content up to about 5 % are grown at low substrate temperature. The partial compensation of strain within Ge964C036 layers of 7 Å thickness improves the thermal stability against lattice relaxation, compared to pure Ge layers. Band-edge related photoluminescence is observed from pseudomorphic Sil-yCy/Si multiple quantum well structures at low temperature. The two predominant luminescence lines are attributed to no-phonon transitions and Si-Si TO phonon replicas of bound excitons confined within the Sil-yCy alloy quantum well layers. The tensile strain within the Sil-yCy layers shifts the twofold degenerate Δ(2) conduction band valley down in energy and is mainly responsible for the linear band gap reduction which is observed for increasing C content. | CommonCrawl |
Could PI have a different value in a different universe?
PI is determined by the circumference of a circle.
What bothers me is why is it any particular constant number? What I mean is, would a circle as defined as a perfect circle in any universe lead to a different value of PI?
Would all universes where a circle could be constructed by "people" there also lead to the value of PI?
If its true then it leads to the conclusion that PI is some sort of constant value constant to all universe. What is the meaning of that?
Science fiction references.
In science fiction Pi sometimes has a different value in different universes, for example Greg Bear's "The Way", it says "Gates are capped with cupolas formed from Space-time itself. As distortions in space-time geometry, their nature can be calculated by 21st century instruments laid on their 'surfaces'. The constant Pi, in particular, is most strongly affected.".
A message is found encoded within Pi, in the novel by Carl Sagan, "Contact" "Ellie, acting upon a suggestion by the senders of the message, works on a program which computes the digits of pi to record lengths in different bases. Very far from the decimal point (1020) and in base 11, it finds that a special pattern does exist when the numbers stop varying randomly and start producing 1s and 0s in a very long string.".
PhilPhil
$\begingroup$ [Note: said question is now closed] This question seems like it answers yours (do people want to close as duplicate?). In particular, the main idea in the answers of that question is: $\pi$ is defined in terms of mathematics, not physics. It doesn't "change" depending on "what universe" we are in - math does not depend on reality. $\endgroup$ – Zev Chonoles Jul 22 '11 at 4:22
$\begingroup$ 7 is also a constant value, constant to all universes. So? $\endgroup$ – Gerry Myerson Jul 22 '11 at 4:23
$\begingroup$ I still think there is a "so" here but can't think how to articulate it. $\endgroup$ – Phil Jul 22 '11 at 4:29
$\begingroup$ Imagine a universe where small-scale structure is based on the $p$-adic numbers instead of the real numbers. Perhaps then some number other than pi would be the one attracting the kooks. $\endgroup$ – GEdgar Jul 22 '11 at 14:51
$\begingroup$ @dan: topology won't help you there. Length is not intrinsic to topological spaces. To measure length you need a metric space. To be able to have rigid motion (rotate a curve 360 degrees) you need some sort of symmetry: so you are down to homogeneous spaces essentially. Then if you want the ratio to be independent of the initial length of the segment $AB$ (this is not true in spherical or hyperbolic geometry), then you need scaling invariance. Operations one takes for granted in Euclidean geometry may not be well-defined in other geometries or topologies. $\endgroup$ – Willie Wong Jun 21 '12 at 7:44
Physically, the ratio of a circle's circumference to its diameter $C/d$ is not really $\pi$. General relativity describes gravity in terms of the curvature of spacetime, and roughly speaking, if you take $(C/d-\pi)/A$, where $A$ is the circle's area, what you get is a measure of curvature called the Ricci scalar.
But even if you're doing general relativity, you don't just go around redefining $\pi$. The thing is, $\pi$ occurs in all kinds of contexts, not just as $C/d$. For instance, you could define $\pi$ as $4-4/3+4/5-4/7+\ldots$, which has nothing to do with the curvature of space.
So if you define $\pi$ as $C/d$, you don't even get a consistent value within our own universe, whereas if you define it as $4-4/3+4/5-4/7+\ldots$, you get an answer that is guaranteed to be the same in any other universe.
Another way of looking at it is that $\pi$ is not the $C/d$ ratio of a physical circle, it's the $C/d$ ratio of a mathematically idealized circle that exists in certain axiomatic systems, such as Euclidean geometry. Viewed this way, it doesn't matter that our universe isn't actually Euclidean.
Ben CrowellBen Crowell
$\begingroup$ +1 for mentioning idealised circles. This is probably a more important point to make than saying that $\pi$ can be defined by infinite series or the least positive root of the transcendental function $\sin$ or the square of the integral $\int_{-\infty}^{\infty} \exp(-x^2) \, dx$, etc. $\endgroup$ – Zhen Lin Jul 22 '11 at 7:37
$\begingroup$ +1 for mentioning the mathematically idealized circle vs physical circle. That actually cleared some of my misconceptions about $\pi$ being defined physically. $\endgroup$ – Airdish Mar 15 '16 at 14:55
This is a complement of other answers. One can define a value $\pi_p$ as $\pi$ in $ \ell_p$. $\ell_p$ is two dimensional space with a metric as follows: $$ d\left((x_1,y_1),(x_2,y_2)\right)=\left(|x_1-x_2|^p+|y_1-y_2|^p\right)^{1/p} $$ for $1\leq p \leq \infty$. Then the circle $C_p$ is defined as all points $(x,y)$ such that: $$ \left(|x|^p+|y|^p\right)^{1/p}=1 $$ The diameter of this circle is $2$. And therefore we can define $\pi_p$ as the half of circumference of the circle. It can be seen that $\pi_1=4$, $\pi_2=\pi$ and $\pi_\infty=4$. In following image, you can see the value $\pi_p$ versus p:
Reference: Look at the following article $\pi _{p} $ the Value of π in $\ell _p $.
ArashArash
$\begingroup$ How to be able to read the article mentioned in the reference? Could you explicitly write the formula for pi(p), please. $\endgroup$ – user534397 Nov 9 '18 at 6:52
$\begingroup$ @user534397 Here is another link to the same paper. The formula is the following definite integral: $$\pi_p=4\int_0^{2^{-1/p}}(1+|x^{-p}-1|^{1-p})^{1/p}\,dx.$$ $\endgroup$ – r.e.s. Apr 16 at 13:34
That there will be a number $\pi$ is a mathematical fact. But whether the significant number would be the same is a more interesting question. Some people in our own universe would prefer that the constant had been chosen to be $2\pi$ i.e. $6.28 ...$ instead of $3.14 ... $ as it would reduce the number of factors of 2 in some formulae.
It would also be possible to imagine, in a higher dimensional universe, that the basic round object might be, say, a 3-sphere, with the significant constant would be defined in relation to its geometry rather than the geometry of a circle.
Living in a world which was non-euclidian (e.g. on the surface of a sphere) would make other numbers geometrically significant, but there would still be $\pi$ = $3.14 ...$ sitting in the background.
$\begingroup$ I do live on the surface of a sphere - don't you? $\endgroup$ – Gerry Myerson Jul 22 '11 at 6:45
$\begingroup$ Are there no mountains, valleys, and oceanic trenches on your planet, M. Myerson? ☺ $\endgroup$ – JdeBP Jul 22 '11 at 14:43
$\begingroup$ @Gerry: Indeed, but for practical purposes in ancient times the curvature was not sufficiently evident, and the idealised form of local geometry was/is Euclidean. I'm sure you realise I was thinking about the situation where there was a measurable effect from the curvature of space (so objects within the space would not necessarily be flat). I live on an approximate 2-sphere which is an object in space. But the question would be if 3-dimensional space had a sufficient locally measurable curvature (e.g. a 3-sphere) what would the significant number be? $\endgroup$ – Mark Bennet Jul 22 '11 at 16:33
When I think of different 'universes,' I imagine places that are fundamentally different than our own. Because pi is just the ratio of the circumference to the diameter, that won't change so long as the behavior of the 'metric of the universe' doesn't change.
But suppose that we considered the 'taxi-cab universe,' where the pertinent metric is the taxicab metric (which I have also called the Manhattan Metric, which is nicely alliterative). In such a universe, a circle looks to us to be a square. But within the metric, a circle with radius 4 would have circumference 32. So taxicab-pi would be 4. How nice and even.
I used that as an example, but really it's still just a mathematical creation. One could more or less analyze many different geometries, topologies, manifolds, etc. And to each might be associated some different way of relating a 'circle' (whatever that may mean) to the metric.
davidlowryduda♦davidlowryduda
About Contact: if $\pi$ is normal in base 11 (never proven but almost surely true), the "special pattern [...] of 1s and 0s in a very long string" will appeal an infinite number of times... but also any finite string, long or short.
Martín-Blas Pérez PinillaMartín-Blas Pérez Pinilla
The problem starts with your first sentence .. which most probably coming out of definition Pi=C/D . There is not problem with this definition , problem is in the value of Pi which we use . This value which we use has nothing to do with this definition at first place ,which not many students ever realized . We approximate C by straight line segments and then this approximation is divided by radius ,or diameter. The definition for the value we use should by totally different to not confuse students. Not even calculus is proving Pi , calculus uses Pi as main ingredient . You can't prove Pi by Pi . Another thing is that main formulas like C=DPi , or AC= Pir^2 have not prove . I am not talking about deriving those formulas , but prove of results by those formulas. So your question is a bit misleading, because we don't even know value of number Pi in this universe :) .
$\begingroup$ Yes in other words the question I wrote seems to be like how to derive a axiom of maths, Pi just "is" defined by being Pi, perhaps this is really not a meaningful question but more "interesting" to consider. $\endgroup$ – Phil Apr 16 '17 at 12:40
pi might vary according to the hubble constant. the mathematical shape of a given universe supposedly changes according to the hubble constant the constant is a measurement of the dispersal of mass within the volume of the universe. universes with various hubble constants are in the shapes of planes, saucers, toroids, spheres. calculating a uniform curve which closes in on itself in each of those universes might produce differing values for pi.
if so, pi would be a good way to accurately measure the density (or local density) of the universe.
jspicerjspicer
Not the answer you're looking for? Browse other questions tagged pi or ask your own question.
What will be the shape of circle if it has no pi (π)
Are there any geometries/spaces where pi is a simple (or at least rational) constant?
Patterns in pi in "Contact"
Different "$\pi$s"
Would it be possible to define math based on `π = 1`
Does the number pi have any significance besides being the ratio of a circle's diameter to its circumference?
What is the best numerator and denominator couple to get the value of $\pi$?
How is the value of $\pi$ calculated?
What Gauss *could* have meant?
Different ways of approximation of $\pi$
Could we calculate pi using an iterative series
Is there a difference between the calculated value of Pi and the measured value?
How can pi have infinite number of digits and never repeat them?
Can we ever know the exact value of π
How far would a person have to search through Pi to get a 50% of getting a million consecutive ones? | CommonCrawl |
\begin{document}
\title{Classifying links and spatial graphs with finite $N$-quandles}
\author{Blake Mellor} \address{Loyola Marymount University, 1 LMU Drive, Los Angeles, CA 90045}
\email{[email protected]}
\date{} \maketitle \begin{abstract} The fundamental quandle is a complete invariant for unoriented tame knots \cite{JO, Ma} and non-split links \cite{FR}. The proof involves proving a relationship between the components of the fundamental quandle and the cosets of the peripheral subgroup(s) in the fundamental group of the knot or link. We extend these relationships to spatial graphs, and to $N$-quandles of links and spatial graphs. As an application, we are able to give a complete list of links with finite $N$-quandles, proving a conjecture from \cite{MS}, and a partial list of spatial graphs with finite $N$-quandles. \end{abstract}
\section{Introduction} The fundamental quandle of a link $L$ is an algebraic object that encodes the three Reidemeister moves. For tame knots, Joyce \cite{JO, JO2} and Matveev \cite{Ma} showed that the fundamental quandle is a complete invariant (up to a change of orientation). The proof involves defining a quandle structure on the cosets of the peripheral subgroup of the knot in the fundamental group, and then proving that the resulting quandle is isomorphic to the fundamental quandle. A similar argument proves that the fundamental quandle is a complete invariant for unoriented, tame, non-split links.
While the fundamental quandle of a knot is a powerful invariant, it is often difficult to compute or to compare. Joyce \cite{JO, JO2} also introduced the fundamental $n$-quandle of a knot, which can be thought of as a quotient of the fundamental quandle where every element of the quandle has ``order'' $n$. These are simpler than the fundamental quandle, and in some cases are even finite. Hoste and Shanahan \cite{HS2} extended the relationship between the fundamental quandle and cosets in the fundamental group to $n$-quandles, and used it to give a complete list of links with finite $n$-quandles. In the current paper, we will further generalize this relationship in two ways: first, by extending it to a broader class of quotients of the fundamental quandle, called $N$-quandles \cite{MS}, and second by extending it to spatial graphs. In each case, we will show the fundamental quandle (or $N$-quandle) is isomorphic to a quandle defined on the cosets of a particular subgroup of the fundamental group (or a quotient of the fundamental group). As an application, we are able to give a complete list of links with finite $N$-quandles (verifying the conjecture in \cite{MS}), and, for graphs which are the singular locus of a three-dimensional orbifold, the list of graphs with finite $N$-quandles (proving part of a conjecture in \cite{BM}).
In Section \ref{S:quandles} we review the definitions of quandles and $N$-quandles, ending with a proof that the conjugation group of a finite $N$-quandle is also finite. In Section \ref{S:fundamental} we introduce the fundamental quandles for links and spatial graphs, and provide topological interpretations of these quandles. The topological interpretation for knots and links is due to Fenn and Rourke \cite{FR}; we introduce an extension to spatial graphs. Then, in Section \ref{S:cosets}, we prove our main results about relationships between the fundamental quandle (and $N$-quandle) and the fundamental group. We apply these results in Section \ref{S:finite} to classify links and spatial graphs with finite $N$-quandles (a list is provided in the Appendix). Finally, in Section \ref{S:questions} we pose some questions for further investigation.
\section{Quandles and $N$-quandles} \label{S:quandles}
\subsection{Definitions and notation} \label{SS:definitions}
We begin with the definition of a quandle. We refer the reader to \cite{JO}, \cite{JO2}, \cite{FR}, and \cite{WI} for more detailed information.
A {\it quandle} is a set $Q$ equipped with two binary operations $\rhd$ and $\rhd^{-1}$ that satisfy the following three axioms: \begin{itemize} \item[\bf A1.] $x \rhd x =x$ for all $x \in Q$. \item[\bf A2.] $(x \rhd y) \rhd^{-1} y = x = (x \rhd^{-1} y) \rhd y$ for all $x, y \in Q$. \item[\bf A3.] $(x \rhd y) \rhd z = (x \rhd z) \rhd (y \rhd z)$ for all $x,y,z \in Q$. \end{itemize}
The operation $\rhd$ is, in general, not associative. To clarify the distinction between $(x \rhd y) \rhd z$ and $x \rhd (y \rhd z)$, we adopt the exponential notation introduced by Fenn and Rourke in \cite{FR} and denote $x \rhd y$ as $x^y$ and $x \rhd^{-1} y$ as $x^{\bar y}$. With this notation, $x^{yz}$ will be taken to mean $(x^y)^z=(x \rhd y)\rhd z$ whereas $x^{y^z}$ will mean $x\rhd (y \rhd z)$. We also use $x^{y^n}$ (where $n$ is a positive integer) to denote $x^{yy\cdots y}$, with $n$ copies of $y$ in the exponent.
The following useful lemma from \cite{FR} describes how to re-associate a product in a quandle given by a presentation.
\begin{lemma} \label{leftassoc} If $x^u$ and $y^v$ are elements of a quandle, then $$\left(x^u \right)^{\left(y^v \right)}=x^{u \bar v y v} \ \ \ \ \mbox{and}\ \ \ \ \left(x^u \right)^{\overline{\left(y^v \right)}}=x^{u \bar v \bar y v}.$$ \end{lemma}
Using Lemma~\ref{leftassoc}, elements in a quandle given by a presentation $\langle S \mid R \rangle$ can be represented as equivalence classes of expressions of the form $x^w$ where $x$ is a generator in $S$ and $w$ is a word in the free group on $S$ (with $\bar x$ representing the inverse of $x$).
Two elements $p$ and $q$ of quandle $q$ are in the same {\em component} (or {\em algebraic component}) if $p^w = q$ for some word $w$ in the free group on $Q$. This is an equivalence relations, so the components give a partition of the quandle. A quandle is {\em connected} if it has only one component.
\begin{definition} \label{D:Nquandle} Given a quandle $Q$ with $k$ ordered components, labeled from 1 to $k$, and a $k$-tuple of natural numbers $N = (n_1, \dots, n_k)$, we say $Q$ is an {\em $N$-quandle} if $x^{y^{n_i}} = x$ whenever $x \in Q$ and $y$ is in the $i$th component of $Q$. \end{definition}
In the special case when $n_1=n_2=\cdots = n_k = n$, we have the $n$-quandle introduced by Joyce \cite{JO, JO2}. Note that the ordering of the components in an $N$-quandle is very important; the relations depend intrinsically on knowing which component is associated with which number $n_i$.
Given a presentation $\langle S \,|\, R\rangle$ of $Q$, a presentation of the quotient $N$-quandle $Q_N$ is obtained by adding the relations $x^{y^{n_i}}=x$ for every pair of distinct generators $x$ and $y$, where $y$ is in the $i$th component of $Q$.
\subsection{The conjugation group of a quandle} \label{SS:conj}
In this section we will explain how to naturally associate a group to any quandle or $N$-quandle. For our purposes, it is enough to consider finitely presented quandles. Suppose a quandle $Q$ has a presentation $$Q = \langle q_1, \dots, q_s \mid r_1, \dots, r_m \rangle,$$ where each relation $r_i$ has the form $q_{a_i}^{w_i} = q_{b_i}$, with $a_i, b_i \in \{1, \dots, s\}$ and $w_i$ a word in the $q_j$'s and $\overline{q_j}$'s. Then the conjugation group has the presentation $$Conj(Q) = \langle q_1, \dots, q_s \mid \overline{r_1}, \dots, \overline{r_m} \rangle,$$ where, for any quandle relation $r$ of the form $x^w = y$, $\overline{r}$ is the group relation $w^{-1}xwy^{-1} = 1$ (in the word $w$, $\overline{q_i}$ is interpreted as $q_i^{-1}$). In other words, the quandle operation is replaced by conjugation in the group. This group (under the name {\em Adconj}) was first defined by Joyce \cite{JO, JO2}.
If $Q$ is an $N$-quandle for a $k$-tuple $N = (n_1, \dots, n_k)$ (so $Q$ has $k$ components, denoted $Q_1, \dots, Q_k$), then we can also associate with $Q$ a natural quotient of the conjugation group, denoted $Conj_N(Q)$. Suppose generator $q_i$ is an element of $Q_{j_i}$, then: $$Conj_N(Q) = \langle q_1, \dots, q_s \mid \overline{r_1}, \dots, \overline{r_m}, q_1^{n_{j_1}}, \dots, q_s^{n_{j_s}} \rangle = Conj(Q)/\langle q_1^{n_{j_1}}, \dots, q_s^{n_{j_s}} \rangle,$$ where $\langle q_1^{n_{j_1}}, \dots, q_s^{n_{j_s}} \rangle$ is the normal subgroup generated by $q_1^{n_{j_1}}, \dots, q_s^{n_{j_s}}$.
Our main result in this section is that, if $Q$ is a finite $N$-quandle, then $Conj_N(Q)$ is a finite group. In the special case when $Q$ is an $n$-quandle, this was proved by Joyce in his dissertation \cite{JO2}; our proof is a modified version.
\begin{theorem} \label{T:QtoG} If $Q$ is a finite $(n_1,\dots,n_k)$-quandle with algebraic components $Q_1, \dots, Q_k$, then $Conj_N(Q)$ is a finite group, and $\vert Conj_N(Q) \vert \leq n_1^{\vert Q_1\vert} \cdots n_k^{\vert Q_k\vert}$. \end{theorem} \begin{proof} Let $x_1, x_2, \dots, x_{\vert Q\vert}$ denote the elements of $Q$ and (abusing notation) also the corresponding elements of $Conj_N(Q)$. Suppose $x_i \in Q_j$; then there is a generator $q$ in $Q_j$ such that $q^w = x_i$ in $Q$. In the group $Conj_N(Q)$, we have the relation $q^{n_j} = 1$, and $w^{-1}qw = x_i$. Then $$x_i^{n_j} = (w^{-1}qw)^{n_j} = w^{-1}q^{n_j}w = w^{-1}w = 1.$$ So each element $x_i$ of $Q$ corresponds to an element of finite order in $Cong_N(Q)$, with the order determined by the algebraic component of $Q$ containing $x_i$.
We will prove inductively that any element $z$ of $Conj_N(Q)$ can be written as a product $z = x_1^{a_1}\cdots x_{\vert Q\vert}^{a_{\vert Q\vert}}$. If $x_i$ is in $Q_j$, then $0 \leq a_i < n_j$, so the number of such products is at most $n_1^{\vert Q_1\vert} \cdots n_k^{\vert Q_k\vert}$, giving the desired bound.
Since the generators of $Conj_N(Q)$ correspond to elements of $Q$, every element of $Conj_N(Q)$ can be written as some word in the $x_i$'s and $x_i^{-1}$'s; we will induct on the minimal length of these words. Certainly, if an element $z$ can be written as a single $x_i$ or $x_i^{-1}$, then we're done (note that $x_i^{-1} = x_i^{n_j - 1}$ for some $n_j$).
Now suppose that any element that can be written as a product of $m$ $x_i^{\pm 1}$'s can be rewritten as a product with the subscripts in non-decreasing order from left to right, {\em without} increasing the length of the product. Suppose $z$ has a minimal length of $m+1$ as a product of $x_i^{\pm 1}$'s. Then $z = x_j^\epsilon w$ for some $x_j$ and some word $w$ of length $m$ ($\epsilon = \pm 1$). By our inductive hypothesis, $w$ can be rewritten with the subscripts in non-decreasing order, and still have length at most $m$. Now $w = x_l^\delta w'$ for some $x_l$, so $z = x_j^\epsilon x_l^\delta w'$.
If $j \leq l$, then $z$ is now a product with subscripts in non-decreasing order, and we're done. So suppose $l < j$. In the quandle $Q$, $x_j \rhd^\delta x_l = x_t$ for some $t$. In the group $Conj_N(Q)$, this corresponds to a relation $x_l^{-\delta}x_j x_l^{\delta} = x_t$. Hence $x_l^{-\delta}x_j^\epsilon x_l^{\delta} = x_t^\epsilon$, and so $x_j^\epsilon x_l^{\delta} = x_l^{\delta}x_t^\epsilon$. So we can rewrite $z = x_l^{\delta}x_t^\epsilon w'$, where $l < j$. But now $x_t^\epsilon w'$ is a word of length at most $m$, so it can be rewritten (without increasing its length) so that the subscripts are in non-decreasing order. We can repeat this process, each time reducing the subscript of the first factor of $z$. The process will eventually terminate with all subscripts in non-decreasing order (with the first factor as $x_1^\epsilon$, if not sooner).
So, by induction, every element $z$ can be written as a product of $x_i$'s and $x_i^{-1}$'s with the subscripts in non-decreasing order from left to right, and hence as a product $x_1^{a_1}\cdots x_{\vert Q\vert}^{a_{\vert Q\vert}}$. \end{proof}
\section{Fundamental quandles of Links and Spatial Graphs} \label{S:fundamental}
\subsection{Wirtinger presentations for fundamental quandles} \label{SS:wirtinger}
If $\Gamma$ is an oriented knot, link or spatial graph in $\mathbb{S}^3$, then a presentation of its fundamental quandle, $Q(\Gamma)$, can be derived from a regular diagram $D$ of $\Gamma$ by a process similar to the Wirtinger algorithm. This was developed for links by Joyce \cite{JO}, and extended to spatial graphs by Niebrzydowski \cite{Ni}. We assign a quandle generator $x_1, x_2, \dots , x_n$ to each arc of $D$ (or, if $\Gamma$ is a spatial graph, to each arc of an edge), then at each crossing introduce the relation $x_i=x_k^{ x_j}$ as shown on the left in Figure~\ref{relations}. For spatial graphs, at a vertex with incident edges $x_1, x_2, \dots x_n$, as shown on the right in Figure~\ref{relations}, we introduce the relation $y^{x_1^{{\varepsilon}_1}x_2^{{\varepsilon}_2}\cdots x_n^{{\varepsilon}_n}} = y$ (where ${\varepsilon}_i = 1$ if $a_i$ is directed into the vertex, and ${\varepsilon}_i = -1$ if $a_i$ is directed out from the vertex). Here $y$ can be {\em any} element of the quandle; for a finite presentation it suffices to consider the cases when $y$ is a generator of the quandle. It is easy to check that the Reidemeister moves for links and spatial graphs do not change the quandle given by this presentation so that the quandle is indeed an invariant of $\Gamma$.
\begin{figure}
\caption{The fundamental quandle relations at a crossing and at a vertex.}
\label{relations}
\end{figure}
Fenn and Rourke \cite{FR} observed that, for a link $L$, the components of the quandle $Q(L)$ are in bijective correspondence with the components of $L$, with each component of the quandle containing the generators of the Wirtinger presentation associated to the corresponding link component. Similarly, for a spatial graph $G$, the components of the quandle $Q(G)$ correspond to the edges of the graph. So if we have a link (resp. graph) $\Gamma$ with $k$ components (resp. edges), and label each component (resp. edge) $c_i$ with a natural number $n_i$, we can let $N = (n_1, \dots, n_k)$ and take the quotient $Q_N(\Gamma)$ of the fundamental quandle $Q(\Gamma)$ to obtain the fundamental $N$-quandle of the link or graph (this depends on the ordering of the link components/edges). If $Q(\Gamma)$ has the Wirtinger presentation from a diagram $D$, then we obtain a presentation for $Q_N(\Gamma)$ by adding relations $x^{y^{n_i}} = x$ for each pair of distinct generators $x$ and $y$ where $y$ corresponds to an arc of component (or edge) $c_i$ in the diagram $D$.
If $L$ is a link, then the groups $Conj(Q(L))$ and $Conj_N(Q_N(L))$ have natural interpretations. From the Wirtinger presentation description of the fundamental quandle, it is immediate that $Conj(Q(L))$ is the fundamental group $\pi_1(\mathbb{S}^3 - L)$. If we select a meridian $\mu_i$ for each component, then $Conj_N(Q_N(L)) = \pi_1(\mathbb{S}^3 - L)/\langle \mu_i^{n_i} \rangle$, where $\langle \mu_i^{n_i} \rangle$ is the normal subgroup generated by $\{\mu_i^{n_i}\}$.
If $G$ is a spatial graph, then the quandle relation at the $i$th vertex has the form $x^{w_i} = x$. In $Conj(Q(G))$, this becomes $w_i^{-1}xw_ix^{-1} = 1$, which is a weaker relation than the corresponding vertex relation in $\pi_1(\mathbb{S}^3 - G)$, namely $w_i = 1$. So in this case, we have that $Conj(Q(G))/\langle w_i \rangle = \pi_1(\mathbb{S}^3 - G)$, where $\langle w_i\rangle$ is the normal subgroup generated by $\{w_i\}$. Similarly, if we select a meridian $\mu_i$ for each edge of the graph, then $Conj_N(Q_N(G))/\langle w_i \rangle = \pi_1(\mathbb{S}^3 - G)/\langle \mu_i^{n_i} \rangle$, where $\langle \mu_i^{n_i} \rangle$ is the normal subgroup generated by $\{\mu_i^{n_i}\}$.
This gives us the following Corollary to Theorem \ref{T:QtoG}:
\begin{corollary} \label{C:QtoG} If $\Gamma$ is a link or spatial graph, and $Q_N(\Gamma)$ is a finite quandle, then $\pi_1(\mathbb{S}^3 - \Gamma)/\langle \mu_i^{n_i} \rangle$ is a finite group. \end{corollary}
In Section \ref{S:cosets} we will prove the converse of Corollary \ref{C:QtoG}.
\subsection{A topological interpretation of the fundamental quandle} \label{SS:topological}
Fenn and Rourke \cite{FR} provided a topological interpretation for the fundamental quandle of a knot, and Hoste and Shanahan \cite{HS2} extended it to $n$-quandles of links. In this section, we review this interpretation, and extend it to first to spatial graphs, and then to $N$-quandles for both links and spatial graphs.
For a link $L$, let $X = \mathbb{S}^3 - N(L)$ be the exterior of the link, and choose a basepoint $b$ in $X$. Then $T(L)$ is defined to be the homotopy classes of paths $\alpha: [0,1] \rightarrow X$ such that $\alpha(0) = b$ and $\alpha(1) \in \partial X$. Moreover, the homotopies must be through sequences of paths with one endpoint at $b$ and the other on $\partial X$. We define quandle operations $\rhd$ and $\rhd^{-1}$ on $T(L)$ by $$\alpha \rhd^{\pm 1} \beta = \beta m_{\beta}^{\mp 1} \beta^{-1} \alpha$$ where $m_\beta$ is a meridian of $L$ that begins and ends at $\beta(1)$. In other words, $m_\beta$ is a loop in $\partial N(L)$ which is essential in $\partial N(L)$, null-homotopic in $N(L)$, and has linking number 1 with $L$. So the path $\alpha \rhd \beta$ is formed by following $\beta$ from $b$ to $\partial X$, going around the meridian, following $\beta$ back to $b$, and then traversing the path $\alpha$ (see Figure \ref{F:multiply}). Observe that for each component $L_i$ of the link $L$, the paths which have one endpoint on $\partial N(L_i)$ form an algebraic component of the quandle $T(L)$. Fenn and Rourke \cite{FR} proved that $Q(L)$ and $T(L)$ are isomorphic quandles.
\begin{figure}
\caption{Multiplying paths $\alpha$ and $\beta$ in $T(L)$ to form $\alpha \rhd \beta$.}
\label{F:multiply}
\end{figure}
If $G$ is a spatial graph, we can decompose $N(G)$ into a union of balls (centered at each vertex of the graph) and solid cylinders $N(e_i) = D^2 \times [0,1]$ around each edge of the graph. We choose these so that the portion of the graph inside each ball has a projection with no crossings, and so that the cylinders $N(e_i)$ are all disjoint. Then the meridians of the edge $e_i$ are (homotopic to) the loops $S^1 \times \{t\}$ in $\partial N(e_i)$. We define $T(G)$ in the same way as for links, except that we only consider paths with endpoints in $\partial X \cap \bigcup{\partial N(e_i)}$, and the homotopies are through paths with one endpoint at $b$ and the other in $\partial X \cap \bigcup{\partial N(e_i)}$. In other words, the endpoints of the paths are allowed to wander around the boundary of the cylinder surrounding each edge, but are not allowed to be on the boundaries of the balls around each vertex, and hence cannot move between edges. We define the quandle operation in the same way as for links; the algebraic components of the quandle now correspond to the edges of the graph.
\begin{theorem} \label{T:T=Qgraph} For a spatial graph $G$, the quandles $T(G)$ and $Q(G)$ are isomorphic. \end{theorem} \begin{proof} The proof that $T(G)$ and $Q(G)$ are isomorphic proceeds exactly as it does for links in \cite{FR}; the only modification is that we need to account for the vertices. Namely, we need to check: \begin{enumerate}
\item In the map from $T(G) \rightarrow Q(G)$, that homotoping a path under a vertex does not change the resulting element of $Q(G)$. This is guaranteed by the vertex relations in $Q(G)$.
\item In the map from $Q(G) \rightarrow T(G)$, the paths resulting from an application of a vertex relation are homotopic. This is easily seen by the same approach used for the crossings. \end{enumerate} \end{proof}
To extend our topological interpretation to $N$-quandles, we generalize the $n$-meridian moves introduced in \cite{HS2}.
\begin{definition} \label{D:n-meridian} Suppose $\Gamma$ is a link (resp. spatial graph) with $k$ components (resp. edges), and $N = (n_1, \dots, n_k)$. Let $c_i$ represent the $i$th component (resp. edge), and $m_i$ be a meridian of $c_i$. Suppose $\alpha$ is a path in $X$ with $\alpha(0) = b$ and $\alpha(1) \in \{b\} \cup \left(\bigcup_i{\partial N(c_i)}\right)$. Suppose further there is a $t_0 \in [0,1]$ such that $\alpha(t_0) \in \partial N(c_j)$. Let $\sigma_1(t) = \alpha(tt_0)$ and $\sigma_2(t) = \alpha((1-t)t_0 + t)$, so $\alpha = \sigma_1\sigma_2$. Then we say the path $\sigma_1m_j^{\pm n_j} \sigma_2$ is obtained from $\alpha$ by a $\pm N$-{\em meridian move}. Two paths are {\em N-meridionally equivalent} if they are related by a sequence of $\pm N$-meridian moves and homotopies. \end{definition}
We now define the $N$-quandle $T_N(\Gamma)$ as the set of $N$-meridional equivalence classes of paths in $T(\Gamma)$, with the same quandle operations as defined for $T(\Gamma)$. As before, the algebraic components of $T_N(\Gamma)$ are the sets of paths which end on the same $\partial N(c_i)$.
\begin{theorem} \label{T:T_N=Q_N} The $N$-quandles $T_N(\Gamma)$ and $Q_N(\Gamma)$ are isomorphic. \end{theorem} \begin{proof} Again, this closely follows the proof in \cite{FR}. The addition of $N$-meridional equivalence among the paths in $T_N(\Gamma)$ exactly corresponds to the addition of the relations $x^{y^{n_i}} = x$ in $Q_N(\Gamma)$ (where $y$ is in the $i$th algebraic component of $Q_N(\Gamma)$). \end{proof}
\section{Relating $Q_N(\Gamma)$ to cosets in $\pi_1(\mathbb{S}^3 - \Gamma)/\langle \mu_i^{n_i} \rangle$} \label{S:cosets}
In \cite{JO}, Joyce defined a quandle structure on the set of cosets of the peripheral subgroup of the fundamental group of a knot $K$, and proved the resulting quandle is isomorphic to the knot quandle. This was a key part of his proof that the knot quandle classifies unoriented tame knots. Hoste and Shanahan \cite{HS2} extended this to the fundamental $n$-quandle of a link. Our goal in this section is to further extend to the fundamental $N$-quandles of links and spatial graphs.
Suppose $\Gamma$ is a link (resp. spatial graph) with $k$ components (resp. edges), and $N = (n_1, \dots, n_k)$. Let $\mu_i$ be a meridian for the $i$th component (resp. edge) in $\pi_1(\mathbb{S}^3-\Gamma)$. For convenience, let $\pi_1^N(\Gamma) = \pi_1(\mathbb{S}^3 - \Gamma)/\langle \mu_i^{n_i} \rangle$. We will define {\em peripheral subgroups} $P_i$ (for $1 \leq i \leq k$) as follows. If $\Gamma$ is a link, and $c_i$ is the $i$th component, let $\lambda_i$ be a longitude for $c_i$, and define $P_i$ as the subgroup of $\pi_1^N(\Gamma)$ generated by $\mu_i$ and $\lambda_i$. If $\Gamma$ is a graph, and $c_i$ is the $i$th edge, then $P_i$ is just the (cyclic) subgroup of $\pi_1^N(\Gamma)$ generated by $\mu_i$. Note that in both cases, $P_i$ is an abelian group (since the meridian and longitude of a torus commute).
We denote the set of cosets of $P_i$ in $\pi_1^N(\Gamma)$ by $P_i\backslash \pi_1^N(\Gamma)$. We define a quandle operation on the cosets by: $$P_i g \rhd^{\pm 1} P_i h = P_i gh^{-1}\mu_i^{\pm 1} h$$ To see this operation is well-defined, suppose $P_i g = P_i r$ and $P_i h = P_i s$. So there are $p, q \in P_i$ such that $pg = r$ and $qh = s$. Then $$P_i r \rhd P_i s = P_i rs^{-1}\mu_i s = P_i pgh^{-1}q^{-1}\mu_i qh = P_i gh^{-1}(q^{-1}\mu_i q) h$$ Since $P_i$ is abelian, $q^{-1}\mu_i q = q^{-1}q\mu_i = \mu_i$, so $P_i r \rhd P_i s = P_i g \rhd P_i h$. Hence the operation is well-defined, and it is straightforward to check that it satisfies the quandle axioms. We denote this quandle by $(P_i\backslash \pi_1^N(\Gamma); \mu_i)$. The following theorem was proved by Hoste and Shanahan \cite{HS2} for the fundamental $n$-quandle of a link; however, since the proof was done for each algebraic component, we can simply replace $n$ with $n_i$ to extend it to the fundamental $N$-quandle.
\begin{theorem} \label{T:GtoQ} \cite{HS2} If $L = \{K_1, \dots, K_k\}$ is a link in $\mathbb{S}^3$, $N = (n_1, \dots, n_k)$ is a $k$-tuple of positive integers, and $P_i$ is the subgroup of $\pi_1^N(L)$ generated by a meridian $\mu_i$ and longitude $\lambda_i$ of $K_i$, then the quandle $(P_i\backslash \pi_1^N(L); \mu_i)$ is isomorphic to the $i$th algebraic component $Q_N^i(L)$ of $Q_N(L)$. \end{theorem}
We will prove the corresponding theorem for spatial graphs.
\begin{theorem} \label{T:GtoQgraph} If $G$ is a spatial graph with $k$ edges $e_1, \dots, e_k$, $N = (n_1, \dots, n_k)$ is a $k$-tuple of positive integers, and $P_i$ is the subgroup of $\pi_1^N(G)$ generated by a meridian $\mu_i$ of $e_i$, then the quandle $(P_i\backslash \pi_1^N(G); \mu_i)$ is isomorphic to the $i$th algebraic component $Q_N^i(G)$ of $Q_N(G)$. Similarly, if $P_i$ is the subgroup of $\pi_1(\mathbb{S}^3-G)$ generated by $\mu_i$, then the quandle $(P_i\backslash \pi_1(\mathbb{S}^3-G); \mu_i)$ is isomorphic to the $i$th algebraic component $Q^i(G)$ of $Q(G)$. \end{theorem} \begin{proof} Without loss of generality, we will consider the subgroup $P_1$ generated by a meridian $\mu_1$ of the edge $e_1$. We begin by fixing an element $\nu \in Q_N^1(G)$ which is a path in $X = \mathbb{S}^3 - N(G)$ from the basepoint $b$ to a point in $\partial N(e_1)$. Then $m_\nu$ is the meridian in $\partial N(e_1)$ that starts and ends at $\nu(1)$. So we let $\mu_1 = \nu m_\nu \nu^{-1} \in \pi_1^N(G)$, and $P_1$ is the subgroup generated by $\mu_1$. We define a map $\tau: (P_i\backslash \pi_1^N(G); \mu_i) \rightarrow Q_N(G)$ by $\tau(P_1 \alpha) = \alpha^{-1}\nu$. We need to show that $\tau$ is (1) well-defined, (2) onto $Q_N^1(G)$, (3) injective and (4) a quandle homomorphism.
\noindent {\bf Well-defined.} Suppose $P_1\alpha = P_1\beta$, so $\beta = \mu_1^j \alpha$ for some $j$. Then $$\tau(P_i \beta) = \beta^{-1}\nu = \alpha^{-1} \mu_1^{-j} \nu = \alpha^{-1} (\nu m_\nu \nu^{-1})^{-j} \nu = \alpha^{-1} \nu m_\nu^{-j} \nu^{-1} \nu = \alpha^{-1} \nu m_\nu^{-j}.$$ But since the endpoint of the path can move around $\partial N(e_1)$, $\nu m_\nu^{-j} \sim \nu$, so $\tau(P_i \beta) \sim \alpha^{-1} \nu = \tau(P_1 \alpha)$. Hence $\tau$ is well-defined.
\noindent {\bf Onto $Q_N^1(G)$.} For any $\alpha \in \pi_1^N(G)$, the endpoint $\alpha^{-1} \nu (1) = \nu(1) \in \partial N(e_1)$, so the image of $\tau$ is a subset of $Q_N^1(G)$. To show $\tau$ is onto $Q_N^1(G)$, consider $\sigma \in Q_N^1(G)$. Then $\alpha = \nu \sigma^{-1} \in \pi_1^N(G)$, and $\tau(P_1 \alpha) = \sigma \nu^{-1} \nu = \sigma$. So the image of $\tau$ is equal to $Q_N^1(G)$.
\noindent {\bf Injective.} Suppose $\tau(P_1\alpha) = \tau(P_1\beta)$. Then $\alpha^{-1}\nu = \beta^{-1}\nu$, so $\alpha\beta^{-1}\nu = \nu$. In other words, there is a sequence of homotopies and $N$-meridian moves which transforms $\alpha\beta^{-1}\nu$ into $\nu$. During these homotopies, the endpoint of the path on $\partial N(e_1)$ traces out a loop from $\nu(1)$ back to $\nu(1)$, which is homotopic to $m_\nu^j$ for some $j$. This means that, fixing both endpoints, we have $\alpha\beta^{-1}\nu m_\nu^j \sim \nu$. Hence the loop $\alpha\beta^{-1}\nu m_\nu^j \nu^{-1}$ is trivial in $\pi_1^N(G)$. This loop is the same as $\alpha\beta^{-1} \mu_1^j$, which means $\alpha\beta^{-1} = \mu_1^{-j} \in P_1$. Hence $P_1 \alpha = P_1 \mu_1^{-j} \beta = P_1 \beta$, so $\tau$ is injective.
\noindent {\bf Quandle homomorphism.} Consider $\alpha, \beta \in \pi_1^N(G)$. \begin{align*} \tau(P_1 \alpha \rhd P_1 \beta) &= \tau(P_1 \alpha \beta^{-1} \mu_1 \beta) \\ &= \beta^{-1} \mu_1^{-1} \beta \alpha^{-1} \nu \\ &= \beta^{-1} \nu m_\nu^{-1} \nu^{-1} \beta \alpha^{-1} \nu \\ &= (\beta^{-1} \nu) m_\nu^{-1} (\beta^{-1} \nu)^{-1} (\alpha^{-1} \nu) \\ &= (\alpha^{-1} \nu) \rhd (\beta^{-1} \nu) \\ &= \tau(\alpha) \rhd \tau(\beta) \end{align*}
Therefore, $\tau$ is a quandle isomorphism between $(P_1\backslash \pi_1^N(G); \mu_1)$ and $Q_N^1(G)$. The same argument can be used for any $i$, $1 \leq i \leq k$. If we leave out the $N$-meridian moves, then the same proof shows $(P_i\backslash \pi_1(\mathbb{S}^3-G); \mu_i)$ is isomorphic to the $i$th algebraic component $Q^i(G)$ of $Q(G)$. \end{proof}
If the group $\pi_1^N(\Gamma)$ is finite, then so is the set of cosets of $P_i$ for each $i$; hence the algebraic components of $Q_N(\Gamma)$ are finite as well. Combining Theorems \ref{T:GtoQ} and \ref{T:GtoQgraph} with Corollary \ref{C:QtoG}, we conclude:
\begin{theorem} \label{T:QiffG} For a link or spatial graph $\Gamma$, the fundamental $N$-quandle $Q_N(\Gamma)$ is finite if and only if the group $\pi_1^N(\Gamma)$ is finite. \end{theorem}
In fact, we can make the relationship between the cardinalities of $Q_N(\Gamma)$ and $\pi_1^N(\Gamma)$ explicit. Observe that, if $\Gamma$ is a spatial graph, then $\vert P_i\vert = \vert \langle \mu_i \rangle \vert = n_i$.
\begin{corollary} \label{C:sizes} Let $\Gamma$ be any link or spatial graph, with $k$ components (or edges). If $\pi_1(\Gamma)$ and $Q_N(\Gamma)$ are finite, and $P_i$ is the peripheral subgroup for the $i$th component (or edge), then $\vert \pi_1^N(\Gamma)\vert = \vert P_i \vert \vert Q_N^i(\Gamma)\vert$, for any $1 \leq i \leq k$. In particular, if $\Gamma$ is a spatial graph, then $\vert \pi_1^N(\Gamma)\vert = n_i \vert Q_N^i(\Gamma)\vert$. \end{corollary}
\begin{example} Consider the knotted tetrahedron $G$ in Figure~\ref{F:K4knot}, with the labeling $N = (3, 3, 2, 2, 2, 2)$. As we will see, $Q_N(G)$ is finite, but attempts to compute it directly using {\it Mathematica} \cite{Me2} proved extremely lengthy. However, $\pi_1^N(G)$ was computed very quickly using Miller's implementation of the Todd-Coxeter algorithm \cite{Mi}, and we found $\vert \pi_1^N(G) \vert = 2880$. Hence $\vert Q_N^1(G)\vert = \vert Q_N^2(G)\vert = 2880/3 = 960$ and $\vert Q_N^3(G) \vert = \vert Q_N^4(G) \vert = \vert Q_N^5(G) \vert = \vert Q_N^6(G) \vert = 2880/2 = 1440$. So $\vert Q_N(G) \vert = 960(2) + 1440(4) = 7680$.
\begin{figure}
\caption{A knotted tetrahedron.}
\label{F:K4knot}
\end{figure}
\end{example}
\begin{example} In \cite{BM}, Mellor and Backer Peral computed the $N$-quandle for the graph $G(k,m,n)$ shown in Figure~\ref{F:Gkmn}, with $N = (2,2,m,n,2,2)$. In particular, $\vert Q_N(G(k,m,n))\vert = 4kmn+2km+2kn$, where $\vert Q_N^1\vert = \vert Q_N^2\vert = \vert Q_N^5\vert = \vert Q_N^6\vert = kmn$, $\vert Q_N^3\vert = 2kn$ and $\vert Q_N^4\vert = 2km$. Therefore $\vert\pi_1^N(G(k,m,n))\vert = n_1\vert Q_N^1\vert = 2kmn$.
\begin{figure}
\caption{The spatial graph $G(k, m, n)$, where $k$ indicates the number of positive half-twists in the block.}
\label{F:Gkmn}
\end{figure}
\end{example}
\section{Links and spatial graphs with finite $N$-quandles} \label{S:finite}
We can use Theorem \ref{T:QiffG} to give a complete list of the links with finite $N$-quandles. This extends the classification of links with finite $n$-quandles given by Hoste and Shanahan \cite{HS2}. Suppose $L$ is a link with $k$ components, $N = (n_1, \dots, n_k)$ is a $k$-tuple of positive integers, and $Q_N(L)$ is finite. By Theorem \ref{T:QiffG}, $\pi_1^N(L)$ is also finite.
Define $\mathcal{O}(L, N)$ to be the 3-orbifold with underlying space $\mathbb{S}^3$ and singular locus $L$, where the $i$th component of $L$ is labeled by $n_i$. (See \cite{CHK} for more information on orbifolds.) $\mathcal{O}(L,N)$ has a universal cover, and the group of covering transformations is the orbifold fundamental group $\pi_i^{orb}(\mathcal{O}(L,N))$. In this case, we have (by \cite[Theorem 2.9 ff.]{CHK}) $$\pi_i^{orb}(\mathcal{O}(L,N)) = \pi_1(\mathbb{S}^3 - L)/\langle \mu_i^{n_i} \rangle = \pi_1^N(L)$$ So the orbifold fundamental group is finite, which means the universal cover is a compact, simply-connected manifold. By Thurston's geometrization theorem, this means the universal cover is a sphere. Hence $\mathcal{O}(L, N)$ is a spherical 3-orbifold. This proves:
\begin{theorem} \label{T:linkclass} A link $L$ with $k$ components has a finite $(n_1,\dots, n_k)$-quandle if and only if there is a spherical orbifold with underlying space $\mathbb{S}^3$ whose singular locus is the link $L$, with component $i$ labeled $n_i$. \end{theorem}
Unlike links, not every spatial graph is the singular locus of a 3-orbifold. For a graph to be a singular locus, it must be trivalent, and the 3 labels at each vertex must be $(2, 2, k)$ (where $k \geq 2$), $(2, 3, 3)$, $(2, 3, 4)$ or $(2, 3, 5)$ \cite[Theorem 2.5]{CHK}. However, by the same argument as for links, we can prove
\begin{theorem} \label{T:graphclass} Suppose a graph $G$ with $k$ edges, with edge $i$ labeled $n_i$, is the singular locus of a 3-orbifold. Then $G$ has a finite $(n_1,\dots, n_k)$-quandle if and only if the orbifold is spherical, with underlying space $\mathbb{S}^3$. \end{theorem}
Dunbar \cite{DU} classified all geometric, non-hyperbolic 3-orbifolds. He provided a list of all spherical 3-orbifolds with underlying space $\mathbb{S}^3$ and singular locus a link or spatial graph $L$; hence, it is also the list of all links, and all graphs which satisfy the conditions to be a singular locus of an orbifold, in $\mathbb{S}^3$ with finite $N$-quandle for some $N$. The sizes and structures of the $n$- and $N$-quandles of many of these links and graphs have been determined \cite{BM, CHMS, HS1, Me, MS}. The list is provided in the Appendix.
\section{Questions for further investigation} \label{S:questions}
Finally, we pose a few questions for future study. While we have completely classified the links with finite $N$-quandles, we have not done the same for spatial graphs.
\begin{question} Are there spatial graphs with finite $N$-quandles which are {\em not} the singular locus of a spherical 3-orbifold? \end{question}
One approach might be to explore how various operations on spatial graphs affect the fundamental quandle. We know that deleting edges from a graph with a finite $N$-quandle, or splitting an edge with a vertex of valence two, yield a new graph with a finite $N$-quandle \cite{BM}. But there are many other graph operations (such as contracting edges) that could be explored.
Even among the links and spatial graphs that are known to have finite $N$-quandles, the precise size and structure are not all known. In particular, in Table \ref{linktable} in the Appendix, the 2-quandles of the links in the last row, and the $N$-quandles for the graphs created by adding struts to the rational tangles of the links in the last two rows, have not been completely described.
\begin{question} What are the sizes and structures for the finite $N$-quandles that are not described in \cite{BM, CHMS, HS1, Me, MS}? \end{question}
Finally, the fundamental quandle is a complete invariant for (unoriented) knots and (unoriented, non-split) links; but it is not known how powerful it is for spatial graphs. As we saw in Section \ref{S:fundamental}, the fundamental quandle of a knot or link immediately determines the fundamental group. For a spatial graph, on the other hand, to recover the fundamental group from the fundamental quandle you also need to know the vertex relations, which depend on the particular diagram. So the fundamental quandle on its own is likely not a complete invariant; but what other information is needed to construct a complete invariant?
\begin{question} To what extent does the fundamental quandle of a spatial graph determine the spatial graph? What other information is needed to give a complete invariant for unoriented, connected spatial graphs? \end{question}
\section*{Appendix: Links and graphs with finite $N$-quandles} \label{S:Appendix}
\begin{table}[htbp]
{$ \begin{array}{cccc} \includegraphics[width=1.25in,trim=0 0 0 0,clip]{11.pdf} & \includegraphics[width=1.25in,trim=0 0 0 0,clip]{12.pdf} & \includegraphics[width=1.0in,trim=0 0 0 0,clip]{13.pdf} \\ \scriptstyle n > 1 & \scriptstyle k \neq 0,\ n=2& \scriptstyle n=3, 4, 5 \\ \\ \includegraphics[width=1.0in,trim=0 0 0 0,clip]{21.pdf} & \includegraphics[width=1.0in,trim=0 0 0 0,clip]{22.pdf} & \includegraphics[width=1.0in,trim=0 0 0 0,clip]{23.pdf} \\ \scriptstyle n =3 & \scriptstyle n=2& \scriptstyle n=2 \\ \\ \includegraphics[width=1.0in,trim=0 0 0 0,clip]{31.pdf} & \includegraphics[width=1.0in,trim=0 0 0 0,clip]{32.pdf} & \includegraphics[width=1.25in,trim=0 0 0 0,clip]{33.pdf} \\ \scriptstyle n =3 & \scriptstyle n=2& \scriptstyle k\neq0,\ n=2 \\ \\ \includegraphics[width=1.25in,trim=0 0 0 0,clip]{41.pdf} & \includegraphics[width=1.15in,trim=0 5pt 0 0,clip]{42.pdf} & \includegraphics[width=1.65in,trim=0 0 0 0,clip]{43.pdf} \\ \scriptstyle k+p_1/q+p_2/q \neq 0,\ n =2 &\scriptstyle n=2& \scriptstyle k+p_1/2+p_2/2+p_3/q_3 \neq 0,\ n =2 \\ \\ \includegraphics[width=1.65in,trim=0pt 0pt 0pt 0pt,clip]{51.pdf} & \includegraphics[width=1.65in,trim=0pt 0pt 0pt 0pt,clip]{52.pdf} & \includegraphics[width=1.65in,trim=0pt 0pt 0pt 0pt,clip]{53.pdf}\\ \scriptstyle k+p_1/2+p_2/3+p_3/3 \neq 0,\ n =2 & \scriptstyle k+p_1/2+p_2/3+p_3/4 \neq 0,\ n =2 & \scriptstyle k+p_1/2+p_2/3+p_3/5 \neq 0,\ n =2 \end{array} $}
\caption{\parbox{3.75in}{Links $L \in \mathbb{S}^3$ with finite $Q_n(L)$. Here \fbox{$k$} represents $k$ right-handed half-twists, and \fbox{$p/q$} represents a rational tangle. If $p$ and $q$ are not relatively prime, the tangle contains a ``strut" labeled $\gcd(p,q)$ \cite{DU}, and the resulting spatial graph has a finite $N$-quandle.}} \label{linktable} \end{table}
\begin{table}[htbp]
{$ \begin{array}{ccc} \includegraphics[width=1.5in,trim=0 0 0 0,clip]{link1.pdf} & \hspace{.5in}& \includegraphics[width=1.25in,trim=0 0 0 0,clip]{link2.pdf} \\ \scriptstyle L = T_{3,3};\ N = (2, 3, n);\ n = 3, 4, 5 && \scriptstyle L = T_{2,4}; N = (3, n);\ n=3, 4, 5 \\ \\ \includegraphics[width=1.25in,trim=0 0 0 0,clip]{link3.pdf} && \includegraphics[width=1.5in,trim=0 0 0 0,clip]{link4.pdf} \\ \scriptstyle L = T_{2,4} \cup C; N=(2,2,3) && \scriptstyle L = T_{2,6}; N = (2, n);\ n=3, 4, 5 \\ \\
\includegraphics[width=1.75in,trim=0 0 0 0,clip]{link5.pdf} && \includegraphics[width=2in,trim=0 0 0 0,clip]{link6.pdf} \\ \scriptstyle L = T_{2,8}; N = (2, 3) && \scriptstyle L = T_{2,10}; N = (2, 3) \\ \includegraphics[width=1.5in,trim=0 0 0 0,clip]{link7.pdf} && \includegraphics[width=1.5in,trim=0 0 0 0,clip]{link8.pdf} \\ \scriptstyle L_k = T_{2,k} \cup C; N = (2, n)\ {\rm or}\ (2, 2, n);\ n > 1;\ k \neq 0 && M_k = T_k \cup C; \scriptstyle N = (2, 3) \end{array} $}
\caption{Other links $L \in \mathbb{S}^3$ with finite $Q_N(L)$.} \label{linktable2} \end{table}
\begin{table}[htbp] \begin{center} {$ \begin{array}{ccc} \includegraphics[height=1in,trim=0 0 0 0,clip]{Theta.eps} & \hspace{.5in} & \includegraphics[height=1in,trim=0 0 0 0,clip]{ThetaKnot.eps} \\ \scriptstyle \text{Theta graph } \theta_3 & & \scriptstyle \text{Knotted theta graph } KT \\ \scriptstyle N = (2,2,2), (3,2,2), (n, 3, 2); n = 3, 4, 5 & & \scriptstyle N = (3, 3, 2) \\ && \\ \end{array} $} {$ \begin{array}{ccc} \includegraphics[height=.8in,trim=0 0 0 0,clip]{Handcuff2.eps} & \hspace{.5in} & \includegraphics[height=1in,trim=0 0 0 0,clip]{HandcuffLink.eps} \\ \scriptstyle \text{Hopf Handcuff graph } H_1 & & \scriptstyle \text{2-linked Handcuff graph } H_2 \\ \scriptstyle N = (3, 2, 2), (3, 3, 2) & & \scriptstyle N = (3, 2, 2) \\ && \\ \end{array} $} {$ \begin{array}{ccc} \includegraphics[height=.8in,trim=0 0 0 0,clip]{DoubleHandcuff.eps} & \hspace{.5in} & \includegraphics[height=1in,trim=0 0 0 0,clip]{K4Knot.eps} \\ \scriptstyle \text{Double Handcuff graph } DH & & \scriptstyle \text{Knotted } K_4 \\ \scriptstyle N = (2,2,2,3,2,2), (2,2,3,3,2,2), (2,2,2,3,2,4) & & \scriptstyle N = (3,3,2,2,2,2) \\ && \\ \end{array} $} {$ \begin{array}{ccc} & \includegraphics[height=1in,trim=0 0 0 0,clip]{K4.eps} & \\ & \scriptstyle \text{Planar } K_4 & \\ & \scriptstyle N = (3, n, 2,2,2,2), (3, 3, 2, 2, 2, n); n = 2, 3, 4, 5 & \\ & \scriptstyle N = (3,3,3,2,2,2), (3,4,2,2,2,3) & \\ && \\ \end{array} $} \end{center}
\caption{Other graphs with finite $N$-quandles.} \label{T:exceptional} \end{table}
\end{document} | arXiv |
\begin{document}
\title{The quasineutral limit of the Vlasov-Poisson equation in Wasserstein metric}
\begin{abstract} In this work, we study the quasineutral limit of the one-dimensional Vlasov-Poisson equation for ions with massless thermalized electrons. We prove new weak-strong stability estimates in the Wasserstein metric that allow us to extend and improve previously known convergence results. In particular, we show that given a possibly unstable analytic initial profile, the formal limit holds for sequences of measure initial data converging sufficiently fast in the Wasserstein metric to this profile. This is achieved without assuming uniform analytic regularity. \end{abstract}
{\bf Keywords}: Vlasov-Poisson system, Quasineutral limit, Wasserstein distance.
\section{Introduction}
In this paper we study a Vlasov-Poisson system, which is a model describing the dynamics of ions in a plasma, in the presence of massless thermalized electrons. We shall focus on the one-dimensional case and consider that the equations are set on the phase space $\mathbb{T} \times \mathbb{R}$ (we will sometimes identify $\mathbb{T}$ to $[-1/2,1/2)$ with periodic boundary conditions). The system, which we shall refer to as the Vlasov-Poisson system with \emph{massless electrons}, encodes the fact that electrons move very fast and quasi-instantaneously reach their local thermodynamic equilibrium. It reads as follows: \begin{equation} \label{vpme} (VPME):= \left\{ \begin{array}{ccc}\partial_t f+v\cdot \partial_x f+ E\cdot \partial_v f=0, \\ E=-U', \\ U''=e^U- \int_{\mathbb{R}} f\, dv=:e^U- \rho,\\ f\vert_{t=0}= f_0\ge0,\ \ \int_{\mathbb{T} \times \mathbb{R}} f_0\,dx\,dv=1. \end{array} \right. \end{equation} Here, as usual, $f(t,x,v)$ stands for the distribution function of the ions in the phase space $\mathbb{T} \times \mathbb{R}$ at time $t \in \mathbb{R}^+$, while $U(t,x)$ and $E(t,x)$ represent the electric potential and field respectively, and $U'$ (resp. $U''$) denotes the first (resp. second) spatial derivative of $U$. In the Poisson equation, the semi-linear term $e^U$ stands for the density of electrons, which therefore are assumed to follow a Maxwell-Boltzmann law. We refer for instance to \cite{HK} for a physical discussion on this system.
We are interested in the behavior of solutions to the (VPME) system in the so-called \emph{quasineutral limit}, i.e., when the Debye length of the plasma vanishes. Loosely speaking, the Debye length can be interpreted as the typical scale of variations of the electric potential. It turns out that it is always very small compared to the typical observation length, so that the quasineutral limit is relevant from the physical point of view. As a result, the approximation which consists in considering a Debye length equal to zero is widely used in plasma physics, see for instance \cite{Chen}. This leads to the study of the limit as $\varepsilon\to0$ of the scaled system: \begin{equation} \label{vpme-quasi} (VPME)_\varepsilon:= \left\{ \begin{array}{ccc}\partial_t f_\varepsilon+v\cdot \partial_x f_\varepsilon+ E_\varepsilon\cdot \partial_v f_\varepsilon=0, \\ E_\varepsilon=-U_\varepsilon', \\ \varepsilon^2 U_\varepsilon''=e^{U_\varepsilon}- \int_{\mathbb{R}} f_\varepsilon\, dv=:e^{U_\varepsilon}- \rho_\varepsilon,\\ f_\varepsilon\vert_{t=0}=f_{0,\varepsilon}\ge0,\ \ \int_{\mathbb{T} \times \mathbb{R}} f_{0,\varepsilon}\,dx\,dv=1. \end{array} \right. \end{equation} The formal limit is obtained in a straightforward way by taking $\varepsilon=0$ (which corresponds to a Debye length equal to $0$): \begin{equation} \label{formal} (KIE):= \left\{ \begin{array}{ccc}\partial_t f+v\cdot \partial_x f+ E\cdot \partial_v f=0, \\ E=-U', \\ U= \log \rho,\\ f_0\ge0,\ \ \int_{\mathbb{T} \times \mathbb{R}} f_0\,dx\,dv=1, \end{array} \right. \end{equation} a system we shall call the \emph{kinetic isothermal Euler system}.
We point out that there are variants of the (VPME) system which are also worth studying, such as the linearized (VPME), in which semi-linear term in the Poisson equation is linearized (this turns out to be a standard approximation in plasma physics, see also \cite{HK10,HK,HK13,HKH}), $$ U''= U +1 - \rho, $$ and the Vlasov-Poisson system for electrons with fixed ions (the most studied model in the mathematical literature), in which the Poisson equation reads as follows $$ U''= 1-\rho, $$ which we shall refer to as the \emph{classical} Vlasov-Poisson system. As a matter of fact, our results concerning the (VPME) system have analogous statements for the linearized (VPME) or the classical Vlasov-Poisson system. We have made the choice to study the (VPME) system since the semi-linear term in the Poisson equation creates additional interesting difficulties. As we shall mention in Remark \ref{rmk:VP}, our analysis applies as well, \emph{mutatis mutandis}, to these models, and actually provides a stronger result in terms of the class of data that we are allowed to consider.
The justification of the limit $\varepsilon \to 0$ from \eqref{vpme-quasi} to \eqref{formal} is far from trivial. Indeed, this is known to be true only in few cases (see also \cite{Br89,Gr95,HKH} for further insights): when the sequence of initial data $f_{0,\varepsilon}$ enjoys uniform analytic regularity with respect to the space variable (as we shall describe later in Section \ref{subsec:grenier}, this is just an adaptation of a work of Grenier \cite{Gr96} on the classical Vlasov-Poisson system); when $f_{0,\varepsilon}$ converge to a Dirac measure in velocity $f_0(x,v) = \rho_0(x) \delta_{v= v_0(x)}$ (see \cite{HK} and \cite{Br00,Mas,GSR}); and, following \cite{HKH}, when $f_{0,\varepsilon}$ converge to a homogeneous initial condition $\mu(v)$ which is symmetric with respect to some $\overline{v} \in \mathbb{R}$ and which is first increasing then decreasing. Also, it is conjectured (see \cite{Gr99}) that this result should hold when the sequence of initial data $f_{0,\varepsilon}$ converges to some $f_0$ such that, for all $x \in \mathbb{T}$, $v \mapsto f_{0}(x,v)$ satisfies a stability condition \emph{a la Penrose} \cite{Pen} (typically when $v \mapsto f_{0}(x,v)$ is increasing then decreasing). On the other hand, the limit is known to be false in general, as we will explain later.
In this work, we shall study this convergence issue in a Wasserstein metric. More precisely, we consider the distance between finite (possibly signed) measures given by $$
W_1(\mu,\nu):=\sup_{\|\varphi\|_{\text{Lip}} \leq 1}\biggl( \int \varphi\, d\mu - \int \varphi \,d\nu\biggr), $$
where $\|\cdot\|_{\text{Lip}}$ stand for the usual Lipschitz semi-norm and which is referred to as the $1$-Wasserstein distance (see for instance \cite{Vil03}). We recall that $W_1$ induces the weak topology on the space of Borel probability measures with finite first moment, that we denote by $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$. Notice that, since $\mathbb{T}$ is compact, this corresponds to measures $\mu$ with finite first moment in velocity.
As it will also be clear from our arguments, $W_1$ is particularly suited to estimate the distance between solutions to kinetic equations. Indeed, for Vlasov-Poisson equations, it is very natural to consider atomic solutions (that it, measures concentrated on finitely many points) and $W_1$ is able to control the distance between the supports, while other classical distances (as for instance the total-variation) are too rough for this (recall that the total-variation distance between two Dirac masses is always $2$ unless they coincide).
Before stating our convergence results, we first deal with the existence of global weak solutions in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$.
\begin{thm} \label{thm-exi} Let $f_0$ be a probability measure in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$, that is, \begin{equation} \label{eq:moment}
\int |v|\,df_0(x,v)<\infty. \end{equation} Then there exists a global weak solution to \eqref{vpme-quasi} with initial datum $f_0$. \end{thm} The analogous result for the classical Vlasov-Poisson equation was proved by Zheng and Majda \cite{ZM}, and more recently by Hauray \cite{HauX} with a new proof.
We shall prove Theorem~\ref{thm-exi} by combining the method introduced by Hauray (see \cite{HauX}) with new stability estimates for the massless electron system.
Roughly speaking, the main results of this paper are the following: if we consider initial data for \eqref{vpme-quasi} of the form $f_{0,\varepsilon} = g_{0,\varepsilon} + h_{0,\varepsilon}$ with $g_{0,\varepsilon}$ analytic (or equal to a finite sum of Dirac masses in velocity, with analytic moments) and $h_{0,\varepsilon}$ converging very fast to $0$ in the $W_1$ distance, then the solution starting from $f_{0,\varepsilon}$ converges to the solution of \eqref{formal} with initial condition $g_0 := \lim_{\varepsilon \to 0} g_{0,\varepsilon}$. This means that small perturbations in the $W_1$ distance do not affect the quasineutral limit. Notice that the fact that the size of the perturbation has to be small only in $W_1$ means that $h_{0,\varepsilon}$ could be arbitrarily large in any $L^p$ norm.
To state our main results, we first introduce some notation. The following analytic norm has been used by Grenier \cite{Gr96} to show convergence results for the quasineutral limit in the context of the classical Vlasov-Poisson system.
Such a norm is useful to study the quasineutral limit since the formal limit is false in general in Sobolev regularity (see Proposition \ref{thm3} and the discussion below); one can also see that the formal limit equation exhibits a loss of derivative (in the force term), which can be overcome with analytic regularity.
\begin{defi} \label{def:norm} Given $\delta>0$ and a function $g:\mathbb{T} \to \mathbb R$, we define $$
\| g \|_{B_\delta} := \sum_{k \in \mathbb{Z}} | \widehat{g}(k) | \delta^{|k|}, $$
where $\widehat{g}(k)$ is the $k$-th Fourier coefficient of $g$. We also define $B_\delta$ as the space of functions $g$ such that $\| g \|_{B_\delta}<+\infty$. \end{defi}
\begin{thm} \label{thm1} Consider a sequence of non-negative initial data in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$ for \eqref{vpme-quasi} of the form $$ f_{0,\varepsilon} = g_{0,\varepsilon} + h_{0,\varepsilon}, $$ where $(g_{0,\varepsilon})$ is a sequence of continuous functions satisfying $$
\sup_{\varepsilon\in (0,1)}\sup_{v \in \mathbb{R}} \, (1+v^2) \| g_{0,\varepsilon} (\cdot,v)\|_{B_{\delta_0}} \leq C, $$ $$
\sup_{\varepsilon\in (0,1)} \left\| \int_\mathbb{R} g_{0,\varepsilon}(\cdot,v) \, dv -1 \right\|_{B_{\delta_0}} < \eta,
$$ for some $\delta_0,C,\eta>0$, with $\eta$ small enough, and admitting a limit $g_0$ in the sense of distributions.
There exists a function $\varphi: \mathbb{R}^+ \to \mathbb{R}^+$, with $\lim_{\varepsilon \to 0^+} \varphi(\varepsilon) =0$, such that the following holds.
Assume that $(h_{0,\varepsilon})$ is a sequence of measures with finite first moment, satisfying $$ \forall \varepsilon>0, \quad W_1(h_{0,\varepsilon},0) \leq \varphi(\varepsilon). $$
Then there exist $T>0$ and $g(t)$ a weak solution on $[0,T]$ of \eqref{formal} with initial condition $g_0 = \lim_{\varepsilon \to 0} g_{0,\varepsilon}$, such that, for any global weak solution $f_\varepsilon(t)$ of \eqref{vpme-quasi} with initial condition $f_{0,\varepsilon}$, $$ \sup_{t \in [0,T]} W_1(f_\varepsilon(t), g(t)) \to_{\varepsilon \to 0} 0. $$
We can explicitly take $\varphi(\varepsilon)= \frac{1}{\varepsilon} \exp \left( \frac{\lambda}{\varepsilon^3} \exp \frac{15}{2 \varepsilon^2}\right)$ for some $\lambda<0$.
\end{thm}
We now state an analogous result for initial data consisting of a finite sum of Dirac masses in velocity: \begin{thm} \label{thm2} Let $N\geq 1$ and consider a sequence of non-negative initial data in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$ for \eqref{vpme-quasi} of the form \begin{align*} f_{0,\varepsilon} &= g_{0,\varepsilon} + h_{0,\varepsilon}, \\ g_{0,\varepsilon}(x,v) &= \sum_{i=1}^N \rho_{0,\varepsilon}^i(x) \delta_{v=v_{0,\varepsilon}^i(x)}, \end{align*} where the $(\rho_{0,\varepsilon}^i, \, v_{0,\varepsilon}^i)$ is a sequence of analytic functions satisfying $$
\sup_{\varepsilon\in (0,1)}\sup_{i \in \{ 1, \cdots , N\}} \| \rho^i_{0,\varepsilon}\|_{B_{\delta_0}} + \| v^i_{0,\varepsilon}\|_{B_{\delta_0}} \leq C, $$ $$
\sup_{\varepsilon\in (0,1)} \left\| \sum_{i=1}^N \rho^i_{0,\varepsilon} -1 \right\|_{B_{\delta_0}} < \eta
$$ for some $\delta_0,C,\eta>0$, with $\eta$ small enough,
and admitting limits $(\rho_0^i, v_0^i)$ in the sense of distributions.
There exists a function $\varphi: \mathbb{R}^+ \to \mathbb{R}^+$, with $\lim_{\varepsilon \to 0^+} \varphi(\varepsilon) =0$, such that the following holds.
Assume that $(h_{0,\varepsilon})$ is a sequence of measures with finite first moment, satisfying $$ \forall \varepsilon>0, \quad W_1(h_{0,\varepsilon},0) \leq \varphi(\varepsilon). $$
Then there exist $T>0$, such that, for any global weak solution $f_\varepsilon(t)$ of \eqref{vpme-quasi} with initial condition $f_{0,\varepsilon}$, $$ \sup_{t \in [0,T]} W_1(f_\varepsilon(t), g(t)) \to_{\varepsilon \to 0} 0, $$ where $$ g(t,x,v) = \sum_{i=1}^N \rho^i(t,x) \delta_{v=v^i(t,x)}, $$ and $(\rho^i, v^i)$ satisfy the multi fluid isothermal system on $[0,T]$ \begin{equation} \left\{ \begin{array}{ccc}\partial_t \rho^i+ \partial_x (\rho^i v^i)=0, \\ \partial_t v^i + v^i \partial_x v^i = E, \\ E=-U', \\ U= \log\left( \sum_{i=1}^N \rho^i \right),\\ \rho^i\vert_{t=0}= \rho_{0}^i, v^i\vert_{t=0}= v_{0}^i. \end{array} \right. \end{equation}
We can explicitly take $\varphi(\varepsilon)= \frac{1}{\varepsilon} \exp \left( \frac{\lambda}{\varepsilon^3} \exp \frac{15}{2 \varepsilon^2}\right)$ for some $\lambda<0$.
\end{thm}
\begin{remark} \label{rmk:VP} It is worth mentioning that the previous convergence results can be slightly improved when dealing with the classical Vlasov-Poisson equation. Indeed, thanks to Remark \ref{rmk:VP ws}, the analogue of Theorems \ref{thm1} and \ref{thm2} holds for a larger class of initial data. In fact, it is possible to take $$\varphi(\varepsilon) = \frac{1}{\varepsilon} \exp \left( \frac{\lambda}{\varepsilon}\right)$$ for some $\lambda<0$. \end{remark}
In the following, we shall say that a function $\varphi$ is admissible if it can be chosen in the statements of Theorems \ref{thm1} and \ref{thm2}.
The interest of these results is the following: they prove that it is possible to justify the quasineutral limit without making analytic regularity or stability assumption. The price to pay is that the constants involved in the explicit functions $\varphi$ above are extremely small, so that we are very close to the analytic regime. We see the ``double exponential'' as an {upper bound} on all admissible $\varphi$,\footnote{Notice that, as observed in Remark \ref{rmk:VP}, the upper bound on $\varphi$ for the classical Vlasov-Poisson system is only exponential.} and hope our study will be a first step towards refined bounds.
On the other hand one should have in mind the following negative result, which roughly means that the functions $\varphi(\varepsilon)= \varepsilon^s$, for any $s>0$ are not admissible (this therefore yields a {lower bound} on admissible functions); this is the consequence of \emph{instability} mechanisms described in \cite{Gr99} and \cite{HKH}.
\begin{prop} \label{thm3} There exist smooth homogeneous equilibria $\mu(v)$ such that the following holds. For any $N>0$ and $s>0$, there exists a sequence of non-negative initial data $(f_{0,\varepsilon})$ such that $$
\| f_{\varepsilon,0}- \mu\|_{W^{s,1}_{x,v}} \leq \varepsilon^N, $$ and denoting by $(f_\varepsilon)$ the sequence of solutions to \eqref{vpme-quasi} with initial data $(f_{0,\varepsilon})$, for $\alpha \in [0,1)$, the following holds: $$ \liminf_{\varepsilon \rightarrow 0} \sup_{t \in [0,\varepsilon^\alpha]} W_1(f_\varepsilon(t), \mu) >0. $$
\end{prop}
We can make the following observations.
\begin{itemize} \item In Proposition \ref{thm3}, one can take some equilibrium $\mu$ satisfying the same regularity as in Theorem \ref{thm1}. However, there is no contradiction with our convergence results since in Theorem \ref{thm1} we assume that $g_{0,\varepsilon}$ approximates in an analytic way $g_0$ and that $h_{0,\varepsilon}$ converges faster than any polynomial in $\varepsilon$. Therefore, the quantification of the ``fast'' convergence in Theorem \ref{thm1} is important.
\item Note that we can have $W_1(h_{0,\varepsilon},0) = o_{\varepsilon \to 0} \left(\frac{1}{\varepsilon} \exp \left( \frac{\lambda}{\varepsilon^3} \exp \frac{15}{2\varepsilon^2}\right) \right)$, but $$
\| h_{0,\varepsilon} \|_{L^p} \sim 1\qquad \text{for any $p \in [1,\infty]$}, $$ as fast convergence to $0$ in the $W_1$ distance can be achieved for sequences exhibiting fast oscillations. \end{itemize}
Theorem \ref{thm2} can also be compared to the following result in the \emph{stable} case, that corresponds to initial data consisting of one single Dirac mass (see \cite{HK}). In this case, the analogue of Theorem \ref{thm2} can be proved with weak assumptions on the initial data.
\begin{prop} \label{thm3-2} Consider $$ g_{0}(x,v) = \rho_{0}(x) \delta_{v=u_{0}(x)}. $$ where $\rho_0 >0$ and $\rho_0, u_0 \in H^s(\mathbb{T})$, for $s\geq 2$. Consider a sequence $(f_{0,\varepsilon})$ of non-negative initial data in $L^1\cap L^\infty$ for \eqref{vpme-quasi} such that, for all $\varepsilon>0$, $$
\frac{1}{2}\int f_{0,\varepsilon}\vert v \vert ^2 dv dx
+ \int \left(e^{U_{0,\varepsilon}} \log e^{U_{0,\varepsilon}} - e^{U_{0,\varepsilon}} +1\right)\,dx + \frac{\varepsilon^2}{2} \int \vert U'_{0,\varepsilon} \vert^2 dx \leq C $$ for some $C>0$, and $U_{0,\varepsilon}$ is the solution to the Poisson equation
$$
\varepsilon^2U_{0,\varepsilon}''=e^{U_{0,\varepsilon}}- \int f_{0,\varepsilon} \, dv.
$$ Also, assume that
\begin{multline*} \frac{1}{2}\int g_{0,\varepsilon}\vert v - u_0\vert ^2 dv dx + \int \left(e^{U_{0,\varepsilon}} \log \left( e^{U_{0,\varepsilon}}/ \rho_0 \right) - e^{U_{0,\varepsilon}} +\rho_0\right)\,dx + \frac{\varepsilon^2}{2} \int \vert U'_{0,\varepsilon} \vert^2 dx \to_{\varepsilon \to 0} 0, \end{multline*} Then there exists $T>0$ such that for any global weak solution $f_\varepsilon(t)$ of \eqref{vpme-quasi} with initial condition $f_{0,\varepsilon}$, $$ \sup_{t \in [0,T]} W_1(f_\varepsilon(t), g(t)) \to_{\varepsilon \to 0} 0, $$ where $$ g(t,x,v) = \rho(t,x) \delta_{v=u(t,x)}, $$ and $(\rho, u)$ satisfy the isothermal Euler system on $[0,T]$ \begin{equation} \left\{ \begin{array}{ccc}\partial_t \rho+ \partial_x (\rho u)=0, \\ \partial_t u + u \partial_x u = E, \\ E=-U', \\ U= \log \rho,\\ \rho\vert_{t=0}= \rho_{0}, u\vert_{t=0}= u_{0}. \end{array} \right. \end{equation} \end{prop}
\begin{remark} We could also have stated another similar result using the estimates around \emph{stable symmetric homogeneous equilibria} of \cite{HKH}, but will not do so for the sake of conciseness. \end{remark}
In what follows, we study the quasineutral limit by using Wasserstein stability estimates for the Vlasov-Poisson system. Such stability estimates were proved for the classical Vlasov-Poisson system by Loeper \cite{Loe}, in dimension three. In the one-dimensional case, they can be improved, as recently shown by Hauray in the note \cite{HauX}.
The key estimate is a weak-strong stability result for the (VPME)$_\varepsilon$ system, which basically consists in an adaptation of Hauray's proof, and which we believe is of independent interest.
\begin{thm} \label{thm4} Let $T>0$. Let $f_\varepsilon^1,f_\varepsilon^2$ be two measure solutions of \eqref{vpme-quasi} on $[0,T]$, and assume that $\rho_\varepsilon^1(t,x):=\int f_\varepsilon^1(t,x,v)\,dv$ is bounded in $L^\infty$ on $[0,T]\times \mathbb T$. Then, for all $\varepsilon \in (0,1]$, for all $t \in [0,T]$, $$ W_1(f_\varepsilon^1(t),f_\varepsilon^2(t))
\leq \frac{1}{\varepsilon} e^{\frac1\varepsilon \left[(1 +3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\|\rho_\varepsilon^1(\tau)\|_\infty\,d\tau\right]}W_1(f_\varepsilon^1(0),f_\varepsilon^2(0)). $$ \end{thm}
The proofs of Theorems \ref{thm1} and \ref{thm2} rely on this stability estimate and on a method introduced by Grenier \cite{Gr96} to justify the quasineutral limit for initial data with uniform analytic regularity.
This paper is organized as follows. In Section \ref{sec:wasserstein}, we start by proving Theorem \ref{thm4}. We then turn to the global weak existence theory in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$: in Section \ref{sec:exi}, we prove Theorem~\ref{thm-exi}, using some estimates exhibited in the previous section. Section \ref{sec:proofs} is then dedicated to the proof of the main Theorems \ref{thm1} and \ref{thm2}. We conclude the paper with the study of auxiliary results: in Section \ref{sec:insta} we prove Proposition \ref{thm3}, while in Section \ref{sec:sta} we prove Proposition \ref{thm3-2}.
\section{Weak-strong stability for the VP system with massless electrons: proof of Theorem \ref{thm4}} \label{sec:wasserstein} In this section we prove Theorem \ref{thm4}, i.e., the weak-strong stability estimate for solutions of the (VPME)$_\varepsilon$ system. Notice that our weak-strong stability estimate encloses in particular the case \eqref{vpme} by taking $\varepsilon=1$.
Let us introduce the setup of the problem. We follow the same notations as in \cite{HauX}. In particular, we will use a Lagrangian formulation of the problem.
As a preliminary step, it will be convenient to split the electric field in a singular part behaving as the electric field in Vlasov-Poisson and a regular term. More precisely, let us decompose $E_\varepsilon$ as $\bar E_\varepsilon+\widehat E_\varepsilon$ where $$ \bar E_\varepsilon=-\bar U_\varepsilon',\qquad \widehat E_\varepsilon=-\widehat U_\varepsilon', $$ and $\bar U_\varepsilon$ and $\widehat U_\varepsilon$ solve respectively $$ \varepsilon^2\bar U_\varepsilon''=1-\rho_\varepsilon ,\qquad \varepsilon^2\widehat U_\varepsilon''=e^{\bar U_\varepsilon+\widehat U_\varepsilon} - 1. $$ Notice that in this way $U_\varepsilon:=\bar U_\varepsilon+\widehat U_\varepsilon$ solves $$ \varepsilon^2U_\varepsilon''=e^{U_\varepsilon}-\rho_\varepsilon. $$ Then we can rewrite \eqref{vpme-quasi} as $$ (VPME)_\varepsilon:= \left\{ \begin{array}{ccc}\partial_t f_\varepsilon+v\cdot \partial_x f_\varepsilon+ (\bar E_\varepsilon+\widehat E_\varepsilon)\cdot \partial_v f_\varepsilon=0, \\ \bar E_\varepsilon=-\bar U_\varepsilon',\qquad \widehat E_\varepsilon=-\widehat U_\varepsilon', \\ \varepsilon^2\bar U_\varepsilon''=1-\rho_\varepsilon,\\ \varepsilon^2\widehat U_\varepsilon''=e^{\bar U_\varepsilon+\widehat U_\varepsilon} - 1,\\ f_\varepsilon(x,v,0)\ge0,\ \ \int f_\varepsilon(x,v,0)\,dx\,dv=1. \end{array} \right. $$
To prove Theorem \ref{thm4}, we shall first show a weak-strong stability estimate for a rescaled system (see (VPME)$_{\varepsilon,2}$ below), and then obtain our result by a further scaling argument.
\subsection{A scaling argument} Let us define $$ {\mathcal{F}}_\varepsilon(t,x,v):=\frac{1}{\varepsilon} f_\varepsilon\biggl(\varepsilon t,x,\frac{v}{\varepsilon}\biggr). $$ Then a direct computation gives $$ (VPME)_{\varepsilon,2}:= \left\{ \begin{array}{ccc}\partial_t {\mathcal{F}}_\varepsilon+v\cdot \partial_x {\mathcal{F}}_\varepsilon+ (\bar {\mathcal E}_\varepsilon+\widehat {\mathcal E}_\varepsilon)\cdot \partial_v {\mathcal{F}}_\varepsilon=0, \\ \bar {\mathcal E}_\varepsilon=-\bar {\mathcal U}_\varepsilon',\qquad \widehat {\mathcal E}_\varepsilon=-\widehat {\mathcal U}_\varepsilon', \\ \bar {\mathcal U}_\varepsilon''=1-{\varrho}_\varepsilon,\\ \widehat {\mathcal U}_\varepsilon''=e^{(\bar {\mathcal U}_\varepsilon+\widehat {\mathcal U}_\varepsilon)/ \varepsilon^2 \color{black}} - 1,\\ {\mathcal{F}}_\varepsilon(x,v,0)\ge0,\ \ \int {\mathcal{F}}_\varepsilon(x,v,0)\,dx\,dv=1, \end{array} \right. $$ where $$ {\varrho}_\varepsilon(t,x):=\int {\mathcal{F}}_\varepsilon(t,x,v)\,dv. $$ We remark that $\bar {\mathcal U}_\varepsilon$ is just the classical Vlasov-Poisson potential so, as in \cite{HauX}, $$ \bar {\mathcal E}_\varepsilon(t,x)=-\int_{\mathbb T} W'(x-y){\varrho}_\varepsilon(t,y)\,dy, $$ where $$
W(x):=\frac{x^2-|x|}{2} $$
(recall that we are identifying $\mathbb T$ with $[-1/2,1/2)$ with periodic boundary conditions). In addition, since $W$ is $1$-Lipschitz and $|W|\leq 1$, recalling that \begin{equation} \label{eq:U} \bar {\mathcal U}_\varepsilon(t,x)=\int_{\mathbb T} W(x-y){\varrho}_\varepsilon(t,y)\,dy \end{equation} we see that
$\bar {\mathcal U}_\varepsilon$ is $1$-Lipschitz and $|\bar {\mathcal U}_\varepsilon|\leq 1$.\\
\subsection{Weak-strong estimate for the rescaled system} The goal of this section is to prove a quantitative weak-strong convergence for the rescaled system (VPME)$_{\varepsilon,2}$. In order to simplify the notation, we omit the subscript $\varepsilon$. In the sequel we will need the following elementary result: \begin{lem} \label{lem:media nulla} Let $h: [-1/2,1/2] \to \mathbb{R}$ be a continuous function such that $\int_{-1/2}^{1/2} h=0.$ Then $$
\|h\|_{\infty}\le \int_{-1/2}^{1/2} |h'|. $$ \end{lem}
\begin{proof} Since $\int_{-1/2}^{1/2} h=0$ there exists a point $\bar x$ such that $h(\bar{x})=0.$ Then, by the Fundamental Theorem of Calculus,
$$
|h(x)|= \Big|\int_{\bar{x}}^x h' \Big|\le \int_{-1/2}^{1/2} |h'| \qquad \forall\, x \in [-1/2,1/2]. $$
\end{proof} We can now prove existence of solutions to the equation for $\widehat {\mathcal U}$. \begin{lem} \label{lem:hatU} There exists a unique solution of \begin{equation} \label{eq-lem-Poisson} \widehat {\mathcal U}''=e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} - 1\qquad \text{on }\mathbb T \end{equation} and this solution satisfies $$
\|\widehat {\mathcal U}\|_\infty \leq 3,\quad \|\widehat {\mathcal U}'\|_\infty \leq 2,\quad \|\widehat {\mathcal U}''\|_\infty \leq \frac{3}{\varepsilon^2}. $$ \end{lem}
\begin{proof} We prove existence of $\widehat U$ by finding a minimizer for $$ h \mapsto E[h]:= \int_{\mathbb T} \left(\frac12 (h')^2 + \varepsilon^2e^{(\bar {\mathcal U}+h)/\varepsilon^2} - h \right) \, dx $$ among all periodic functions $h :[-1/2,1/2]\to \mathbb{R}$. Indeed, as we shall see later, the Poisson equation we intend to solve is nothing but the Euler-Lagrange equation of the above functional.
Notice that since $E[h]$ is a strictly convex functional, solutions of the Euler-Lagrange equation are minimizers and the minimizer is unique. Let us now prove the existence of such a minimizer.
Take $h_k$ a minimizing sequence, that is $$ E[h_k] \to \inf_{h}E[h]=:\alpha. $$
Notice that by choosing $h=-\bar{\mathcal U}$ we get (recall that $|\bar{\mathcal U}|, |\bar{\mathcal U}'|\leq 1$, see \eqref{eq:U}) $$ \alpha \leq E[-\bar{\mathcal U}] =\int_{\mathbb T} \left( \frac12 (\bar{\mathcal U}')^2 +\bar{\mathcal U} \right) \, dx \leq 2, $$ hence $$ E[h_k] \leq 3 \qquad \text{for $k$ large enough.} $$ We first want to prove that $h_k$ is uniformly bounded in $H^1$.
We observe that, since $\bar {\mathcal U}\geq -1$, for any $s \in \mathbb{R}$ $$ \varepsilon^2e^{(\bar {\mathcal U}(x)+s)/\varepsilon^2} -s \geq \varepsilon^2e^{(s-1)/\varepsilon^2}-s. $$ Now, for $s \geq 2$ (and $\varepsilon \in (0,1]$) \color{black} we have $$ \varepsilon^2e^{(s-1)/\varepsilon^2}-s \geq e^{s-1}-s \geq s - 2\log 2 \geq s -3, $$ while for $s\leq 2$ we have $$
\varepsilon^2e^{(s-1)/\varepsilon^2}-s \geq -s \geq |s|-4, $$ thus $$
e^{(s-1)/\varepsilon^2}-s \geq |s|- 4 \qquad \forall\,s \in \mathbb{R}. $$
Therefore \begin{equation} \label{eq:energy}
3 \geq E[h_k] \geq \int_{\mathbb T} \frac12 (h_k')^2 +|h_k| - 4, \end{equation} which gives $$
\int_{\mathbb T} \frac12 (h_k')^2 \leq 8. $$ In particular, by the Cauchy-Schwarz inequality this implies \begin{equation} \label{eq:holder} \begin{split}
|h_k(x)-h_k(z)|& \leq \biggl|\int_z^x|h_k'(y)|\,dy \biggr|\leq \sqrt{|x-z|} \sqrt{\int_{\mathbb T}|h_k'(y)|^2\,dy}\\
&\leq 4\,\sqrt{|x-z|}. \end{split} \end{equation} Up to now we have proved that $h_k'$ are uniformly bounded in $L^2$. We now want to control $h_k$ in $L^\infty$.
Let $M_k$ denote the maximum of $|h_k|$ over $\mathbb{T}$. Then by \eqref{eq:holder} we deduce that $$ h_k(x) \geq M_k - 4 \qquad \forall\,x \in \mathbb{T}, $$ hence, recalling \eqref{eq:energy}, \begin{align*}
3 &\geq E[h_k] \geq \int_{\mathbb T}( |h_k(x)| - 4) \,dx \geq M_k -8, \end{align*}
which implies $M_k \leq 11$. Thus, we proved that $|h_k|\leq 11$ for all $k$ large enough, which implies in particular that $h_k$ are uniformly bounded in $L^{2}$.
In conclusion, we have proved that $h_k$ are uniformly bounded in $H^1$ (both $h_k$ and $h_k'$
are uniformly bounded in $L^2$) and in addition they are uniformly bounded and uniformly continuous (as a consequence of \eqref{eq:holder}).
Hence, up to a subsequence, they converge weakly in $H^1$ (by weak compactness of balls in $H^1$) and uniformly (by the Ascoli-Arzel\`a theorem) to a function $\widehat {\mathcal U}$.
We claim that $\widehat {\mathcal U}$ is a minimizer.
Indeed, by the lower semicontinuity of the $L^2$ norm under weak convergence,
$$
\int_{\mathbb T}|\widehat {\mathcal U}'(x)|^2\,dx \leq \liminf_k \int_{\mathbb T}|h_k'(x)|^2\,dx.
$$ On the other hand, by uniform convergence,
$$ \int_{\mathbb T}\left(\varepsilon^2 e^{(\bar {\mathcal U}(x)+h_k(x))/\varepsilon^2} - h_k(x)\right)\,dx \to \int_{\mathbb T}\left( \varepsilon^2 e^{(\bar {\mathcal U}(x)+\widehat {\mathcal U}(x))/\varepsilon^2} - \widehat {\mathcal U}(x) \right)\,dx.
$$
In conclusion
$$
E[\widehat {\mathcal U}] \leq \liminf_k E[h_k]=\alpha,
$$
which proves that $\widehat {\mathcal U}$ is a minimizer.
By the minimality,
$$
0=\frac{d}{d\eta}\bigg|_{\eta=0}E[\widehat{\mathcal U}+\eta h]=\int_{\mathbb T} \left( \widehat {\mathcal U}'\,h' + e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}h-h \right) \, dx
=\int_{\mathbb T}[-\widehat {\mathcal U}''+e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} - 1]h \, dx,
$$
which proves that $\widehat {\mathcal U}$ solves \eqref{eq-lem-Poisson} by the arbitrariness of $h$.
We now prove the desired estimates on $\widehat {\mathcal U}$. Since $\widehat {\mathcal U}'$ is a periodic continuous function we have $$ 0=\int_{\mathbb T} \widehat {\mathcal U}'' \, dx =\int_{\mathbb T} \(e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}-1 \) \, dx. $$ Thus we get $$
\int_{\mathbb T} \big| \widehat {\mathcal U}''\big| \, dx \leq \int_{\mathbb T}\Big| \(e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}-1 \) \Big| \, dx\leq \int_{\mathbb T} e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}\, dx +1=2, $$ and so, by Lemma \ref{lem:media nulla}, we deduce $$
\|\widehat {\mathcal U}'\|_\infty \le \int_{\mathbb T} |\widehat {\mathcal U}''| \, dx \le 2. $$
Since $\|\widehat {\mathcal U}'\|_\infty \le 2,$ $\|\bar {\mathcal U}\|_\infty\le 1$, and $\int_{\mathbb T} e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} \, dx =1$ we claim that $\|\widehat {\mathcal U} \|_\infty \le 3.$
Indeed, suppose that there exists $\bar x$ such that $\widehat {\mathcal U} (\bar x) \ge M.$ Then, recalling that $\|\widehat {\mathcal U}'\|_\infty \le 2,$ we have $\widehat {\mathcal U} (x) \ge M-2$ for all $x$. Using that $\|\bar {\mathcal U}\|_\infty\le 1$ we get $\widehat {\mathcal U}(x)+\bar {\mathcal U}(x) \ge M-3.$ Then, $$ 1= \int_{\mathbb T} e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} \, dx \ge \int_{\mathbb T} e^{(M-3)/\varepsilon^2} \, dx = e^{(M-3)/\varepsilon^2} \Rightarrow M \le 3. $$ On the other hand, if there exists $\bar x$ such that $\widehat {\mathcal U} (\bar x) \le -M,$ then an analogous argument gives $$ 1= \int_{\mathbb T} e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} \, dx \le \int_{\mathbb T} e^{{-(M-3)/\varepsilon^2}} \, dx = e^{{-(M-3)/\varepsilon^2}} \Rightarrow M \le 3. $$
Hence we have that $\|\widehat {\mathcal U} \|_\infty \le 3.$ Finally, to estimate $\widehat {\mathcal U}''$ we differentiate the equation $$ \widehat {\mathcal U}''= \(e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}-1\), $$
recall that $\|\bar {\mathcal U}'\|_\infty\le 1,$ $\|\widehat {\mathcal U}'\|_\infty\le 2$, and $\int_{\mathbb T}e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}=1,$ to obtain $$
\int_{\mathbb T}|\widehat {\mathcal U}'''| = \int_{\mathbb T} \Big|e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2}\biggl(\frac{\bar {\mathcal U}'+\widehat {\mathcal U}'}{\varepsilon^2} \biggr)\Big| \le \frac{\|\bar {\mathcal U}'\|_\infty+\|\widehat {\mathcal U}'\|_\infty}{\varepsilon^2}\int_{\mathbb T}e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} \le \frac{3}{\varepsilon^2}, $$ so, by Lemma \ref{lem:media nulla} again, we get $$
\|\widehat {\mathcal U}''\|_\infty\le \int_{\mathbb T}|\widehat {\mathcal U}'''|\le \frac{3}{\varepsilon^2}, $$ as desired. \end{proof}
To prove the weak-strong stability result for (VPME)$_{\varepsilon,2}$, following the strategy used in \cite{HauX} for the classical Vlasol-Poisson system, we will represent solutions in Lagrangian variables instead of using the Eulerian formulation. In this setting, the phase space is $\mathbb{T}\times\mathbb{R}$ and particles in the phase-space are represented by $Z=(X,V)$, where the random variables $X:[0,1]\to \mathbb{T}$ and $V:[0,1]\to \mathbb{R}$ are maps from the probability space $([0,1],ds)$ to the physical space. The idea is that elements in $[0,1]$ do not have any physical meaning but they just label the particles $\{(X(s),V(s))\}_{s \in [0,1]}\subset \mathbb{T}\times\mathbb{R}$.
We mention that this ``probabilistic'' point of view was already introduced for ODEs by Ambrosio in his study of linear transport equations \cite{amb} and generalized later by Figalli to the case of SDEs \cite{fig}.
To any random variable as above, one associates the mass distribution of particles in the phase space as follows:\footnote{Note that the law of $(X,V)$ may not be absolutely continuous, we just wrote the formula to explain the heuristic. } $$ {\mathcal{F}}(x,v)\,dx\,dv= (X,V)_\# ds, $$ that is ${\mathcal{F}}$ is the law of $(X,V)$. So, instead of looking for the evolution of ${\mathcal{F}}$, we rather let $Z_t:=(X_t,V_t)$ evolve accordingly to the following Lagrangian system (recall that, to simplify the notation, we are omitting the subscript $\varepsilon$) \begin{equation} \label{eq:VPLEL} (VPME)_{L,2}:= \left\{ \begin{array}{cc} \dot X_t=V_t,\\ \dot V_t=\bar {\mathcal E}(X_t) + \widehat {\mathcal E}(X_t),\\ \bar {\mathcal E}=-\bar {\mathcal U}',\qquad \widehat {\mathcal E}=-\widehat {\mathcal U}', \\ \bar {\mathcal U}''=1-\rho,\\ \widehat {\mathcal U}''=e^{(\bar {\mathcal U}+\widehat {\mathcal U})/\varepsilon^2} - 1,\\ \rho(t)=(X_t)_\# ds. \end{array} \right. \end{equation} (Such a formulation is rather intuitive if one thinks of the evolution of finitely many particles.) Notice that the fact that $\rho(t)$ is the law of $X_t$ is a consequence of the fact that ${\mathcal{F}}$ is the law of $Z_t$.
As initial condition we impose that at time zero $Z_t$ is distributed accordingly to ${\mathcal{F}}_0$, that is $$ (Z_0)_\#ds={\mathcal{F}}_0(x,v)\,dx\,dv. $$
We recall the following characterization of the $1$-Wasserstein distance, used also by Hauray in \cite{HauX}: $$
W_1(\mu,\nu)=\min_{X_\#ds=\mu,\,Y_\#ds=\nu} \int_0^1|X(s)-Y(s)|\,ds. $$ Hence, if ${\mathcal{F}}_1,{\mathcal{F}}_2$ are two solutions of (VPME)$_{\varepsilon,2}$, in order to control $W_1({\mathcal{F}}_1(t),{\mathcal{F}}_2(t))$, it is sufficient to do the following: choose $Z_0^1$ and $Z_0^2$ such that $$ (Z_0^i)_\#ds=d f^i(0,x,v),\qquad i=1,2 $$ and $$
W_1(f^1(0),f^2(0))= \int_0^1|Z_0^1(s)-Z_0^2(s)|\,ds, $$
and prove a bound on $ \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds$ for $t \geq 0$. In this way we automatically get a control on $$
W_1({\mathcal{F}}^1(t),{\mathcal{F}}^2(t))\leq \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds. $$
So, our goal is to estimate $ \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds$. For this, as in \cite{HauX} we consider $$
\frac{d}{dt} \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds. $$ Using \eqref{eq:VPLEL}, this is bounded by \begin{align*}
&\int_0^1|V_t^1(s)-V_t^2(s)|\,ds+ \int_0^1|{\mathcal E}_t^1(X_t^1)-{\mathcal E}_t^2(X_t^2)|\,ds\\
& \leq \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds+ \int_0^1|\bar {\mathcal E}_t^1(X_t^1)-\bar {\mathcal E}_t^2(X_t^2)|\,ds
+ \int_0^1|\widehat {\mathcal E}_t^1(X_t^1)-\widehat {\mathcal E}_t^2(X_t^2)|\,ds\\
& \leq \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds+ 8\|{\varrho}^1(t)\|_\infty \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds\\
&+\int_0^1|\widehat {\mathcal E}_t^1(X_t^1)-\widehat {\mathcal E}_t^2(X_t^1)|\,ds+\int_0^1|\widehat {\mathcal E}_t^2(X_t^1)-\widehat {\mathcal E}_t^2(X_t^2)|\,ds, \end{align*} where we split ${\mathcal E}_t^1$ and ${\mathcal E}_t^2$ as a sum of $\bar {\mathcal E}_t^1+\widehat {\mathcal E}_t^1$ and
$\bar {\mathcal E}_t^2+\widehat {\mathcal E}_t^2$, and
we applied the estimate in \cite[Proof of Theorem 1.8]{HauX}
to control
$$
\int_0^1|\bar {\mathcal E}_t^1(X_t^1)-\bar {\mathcal E}_t^2(X_t^2)|\,ds
$$
by
$$
8\|{\varrho}^1(t)\|_\infty \int_0^1|Z_t^1(s)-Z_t^2(s)|\,ds.
$$ To estimate the last two terms, we argue as follows: for the second one we recall that $\widehat {\mathcal E}_t^2$ is $(3/\varepsilon^2)$-Lipschitz (see Lemma \ref{lem:hatU}), hence $$
\int_0^1|\widehat {\mathcal E}_t^2(X_t^1)-\widehat {\mathcal E}_t^2(X_t^2)|\,ds \leq \frac{3}{\varepsilon^2}
\int_0^1|X_t^1-X_t^2|\,ds \leq \frac{3}{\varepsilon^2}\int_0^1|Z_t^1-Z_t^2|\,ds. $$ For the first term, we first observe the following fact: recalling \eqref{eq:U} and that $W$ is 1-Lipschitz, we have \begin{equation} \label{eq:bound U} \begin{split}
|\bar {\mathcal U}_t^1-\bar {\mathcal U}_t^2|(x)&=
\biggl|\int_0^1 W(x-X_t^1) - W(x-X_t^2)\,ds \biggr|\\
& \leq \int_0^1 |X_t^1-X_t^2|\,ds\leq \int_0^1|Z_t^1-Z_t^2|\,ds \end{split} \end{equation} for all $x$. Now we want to estimate $\widehat {\mathcal E}_t^1-\widehat {\mathcal E}_t^2$ in $L^2$: for this we start from the equation $$ (\widehat {\mathcal U}_t^1)'' - (\widehat {\mathcal U}_t^2)''=e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^1)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^2 +\widehat {\mathcal U}_t^2)/\varepsilon^2}. $$ Multiplying by $\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2$ and integrating by parts, we get \begin{align*} 0&=\int_{\mathbb T} \Bigl((\widehat {\mathcal U}_t^1)' - (\widehat {\mathcal U}_t^2)'\Bigr)^2\,dx +\int_{\mathbb T} \left[e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^1)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^2 +\widehat {\mathcal U}_t^2)/\varepsilon^2}\right] [\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2]\,dx\\ &=\int_{\mathbb T} \Bigl((\widehat {\mathcal U}_t^1)' - (\widehat {\mathcal U}_t^2)'\Bigr)^2\,dx +\int_{\mathbb T} \left[e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^1)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^2)/\varepsilon^2}\right] [\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2]\,dx\\ &\qquad + \int_{\mathbb T} \left[e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^2)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^2 +\widehat {\mathcal U}_t^2)/\varepsilon^2}\right] [\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2]\,dx. \end{align*} For the second term we observe that, by the Fundamental Theorem of Calculus, $$ e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^1)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^2)/\varepsilon^2} = \frac{1}{\varepsilon^2} \color{black} \biggl(\int_0^1 e^{[\bar {\mathcal U}_t^1 +\lambda \widehat {\mathcal U}_t^1+(1-\lambda)\widehat {\mathcal U}_t^2]/\varepsilon^2}\,d\lambda\biggr)\,[\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2]. $$ Hence, \begin{align*} &\int_{\mathbb T} \left[e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^1)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^2)/\varepsilon^2}\right] [\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2]\,dx\\ & =\int_{\mathbb T} \frac{1}{\varepsilon^2} \color{black} \biggl(\int_0^1 e^{[\bar {\mathcal U}_t^1 +\lambda \widehat {\mathcal U}_t^1+(1-\lambda)\widehat {\mathcal U}_t^2]/\varepsilon^2}\,d\lambda\biggr)\,(\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2)^2dx\\ &\geq \frac{1}{\varepsilon^2} e^{-5/\varepsilon^2} \color{black} \int_{\mathbb T}(\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2)^2dx \end{align*} where we used that $\bar {\mathcal U}$ and $\widehat {\mathcal U}$ are bounded by $1$ and $4$, respectively.
For the third term, we simply estimate $$
|e^{(\bar {\mathcal U}_t^1 +\widehat {\mathcal U}_t^2)/\varepsilon^2} - e^{(\bar {\mathcal U}_t^2 +\widehat {\mathcal U}_t^2)/\varepsilon^2}| \leq \frac{1}{\varepsilon^2} e^{5/\varepsilon^2} \color{black} |\bar {\mathcal U}_t^1 -\bar {\mathcal U}_t^2|, $$ hence, combining all together, \begin{align*} &\int_{\mathbb T} \Bigl((\widehat {\mathcal U}_t^1)' - (\widehat {\mathcal U}_t^2)'\Bigr)^2\,dx + e^{-5/\varepsilon^2} \color{black} \int_{\mathbb T}(\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2)^2dx\\
&\leq \frac{1}{\varepsilon^2} e^{5/\varepsilon^2} \color{black} \int_{\mathbb T} |\bar {\mathcal U}_t^1 -\bar {\mathcal U}_t^2|\,|\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2|\,dx \\
&\leq \frac{1}{\varepsilon^2} e^{5/\varepsilon^2} \color{black}\delta \int_{\mathbb T} |\widehat {\mathcal U}_t^1 - \widehat {\mathcal U}_t^2|^2\,dx
+ \frac{1}{\varepsilon^2} \frac{e^{5/\varepsilon^2}}{\delta} \color{black} \int_{\mathbb T} |\bar {\mathcal U}_t^1 -\bar {\mathcal U}_t^2|^2\,dx. \end{align*} Thus, choosing $\delta:=\varepsilon^2 e^{-10/\varepsilon^2}$ \color{black} , we finally obtain $$
\int_{\mathbb T} \Bigl((\widehat {\mathcal U}_t^1)' - (\widehat {\mathcal U}_t^2)'\Bigr)^2\,dx \leq \frac{1}{\varepsilon^4} e^{15/\varepsilon^2} \color{black} \int_{\mathbb T} |\bar {\mathcal U}_t^1 -\bar {\mathcal U}_t^2|^2\,dx $$
Observing now that $(\widehat {\mathcal U}_t^i)'=-\widehat {\mathcal E}_t^1$ and recalling \eqref{eq:bound U}, we obtain \begin{equation} \label{eq:continuity E}
\sqrt{\int_{\mathbb T} \Bigl(\widehat {\mathcal E}_t^1 - \widehat {\mathcal E}_t^2\Bigr)^2\,dx} \leq \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black} \int_0^1|Z_t^1-Z_t^2|\,ds. \end{equation}
Thanks to this estimate, we conclude that \begin{align*}
\int_0^1|\widehat {\mathcal E}_t^1(X_t^1)-\widehat {\mathcal E}_t^2(X_t^1)|\,ds&
=\int_{\mathbb T}|\widehat {\mathcal E}_t^1(x)-\widehat {\mathcal E}_t^2(x)|\,{\varrho}^1(t,x)\,dx\\
&\leq \|{\varrho}^1(t)\|_\infty\int_{\mathbb T}|\widehat {\mathcal E}_t^1-\widehat {\mathcal E}_t^2|\,dx\\
&\leq \|{\varrho}^1(t)\|_\infty\sqrt{\int_{\mathbb T}|\widehat {\mathcal E}_t^1-\widehat {\mathcal E}_t^2|^2\,dx}\\
&\leq \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black} \|{\varrho}^1(t)\|_\infty \int_0^1|Z_t^1-Z_t^2|\,ds. \end{align*} Hence, combining all together we proved that $$
\frac{d}{dt} \int_0^1|Z_t^1-Z_t^2|\,ds
\leq \Bigl(1+8\|{\varrho}^1(t)\|_\infty+\frac{3}{\varepsilon^2} + \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}\|{\varrho}^1(t)\|_\infty \Bigr) \int_0^1|Z_t^1-Z_t^2|\,ds, $$ so that, by Gronwall inequality, $$
\int_0^1|Z_t^1-Z_t^2|\,ds
\leq e^{(1 +3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\|{\varrho}^1(\tau)\|_\infty\,d\tau}\int_0^1|Z_0^1-Z_0^2|\,ds, $$ which implies (recalling the discussion at the beginning of this computation) \begin{equation} \label{eq:ws rescaled} W_1({\mathcal{F}}^1(t),{\mathcal{F}}^2(t))
\leq e^{(1 +3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\|{\varrho}^1(\tau)\|_\infty\,d\tau}W_1({\mathcal{F}}^1(0),{\mathcal{F}}^2(0)). \end{equation} This proves the desired weak-strong stability for the rescaled system.
\subsection{Back to the original system and conclusion of the proof} To obtain the weak-strong stability estimate for our original system, we simply use \eqref{eq:ws rescaled} together with the definition of $W_1$. More precisely, given two densities $f_1(x,v)$ and $f_2(x,v)$, consider $$ {\mathcal{F}}_i(x,v):=\frac1\varepsilon f_i(x,v/\varepsilon),\qquad i=1,2. $$ Then \begin{align*}
W_1({\mathcal{F}}_1,{\mathcal{F}}_2)&=\sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int \varphi(x,v) [{\mathcal{F}}_1(x,v) - {\mathcal{F}}_2(x,v)]\,dx\,dv\\
&=\sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int \varphi(x,v) \frac{1}{\varepsilon}[f_1(x,v/\varepsilon) - f_2(x,v/\varepsilon)]\,dx\,dv\\
&=\sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int \varphi(x,\varepsilon w) [f_1(x,w) - f_2(x,w)]\,dx\,dw. \end{align*} We now observe that if $\varphi$ is $1$-Lipschitz so is $\varphi(x,\varepsilon w)$ for $\varepsilon \leq 1$, hence \begin{multline*}
\sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int \varphi(x,\varepsilon w) [f_1(x,w) - f_2(x,w)]\,dx\,dw\\
\leq \sup_{\|\psi\|_{\text{Lip}} \leq 1} \int \psi(x,w) [f_1(x,w) - f_2(x,w)]\,dx\,dw=W_1(f_1,f_2). \end{multline*} Reciprocally, given any 1-Lipschitz function $\psi(x,w)$, the function $\varphi(x,w):=\varepsilon \psi(x,w/\varepsilon)$ is still 1-Lipschitz, hence \begin{multline*}
W_1(f_1,f_2)= \sup_{\|\psi\|_{\text{Lip}} \leq 1} \int \psi(x,w) [f_1(x,w) - f_2(x,w)]\,dx\,dw\\
\leq \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int \frac{1}{\varepsilon}\varphi(x,\varepsilon w) [f_1(x,w) - f_2(x,w)]\,dx\,dw = \frac{1}{\varepsilon} W_1({\mathcal{F}}_1,{\mathcal{F}}_2). \end{multline*} Hence, in conclusion, we have $$ \varepsilon W_1(f_1,f_2) \leq W_1({\mathcal{F}}_1,{\mathcal{F}}_2) \leq W_1(f_1,f_2). $$ In particular, when applied to solutions of (VPME), we deduce that \begin{equation} \label{eq:eps W1} \varepsilon W_1(f_1(\varepsilon t),f_2(\varepsilon t)) \leq W_1({\mathcal{F}}_1(t),{\mathcal{F}}_2(t)) \leq W_1(f_1(\varepsilon t),f_2(\varepsilon t)). \end{equation} Observing that $$
\int_0^t \|{\varrho}^1(\tau)\|_\infty\,d\tau = \int_0^t \|\rho^1(\varepsilon \tau)\|_\infty\,d\tau
= \frac{1}{\varepsilon} \int_0^{\varepsilon t} \|\rho^1(\tau)\|_\infty\,d\tau, $$ \eqref{eq:eps W1} together with \eqref{eq:ws rescaled} gives $$ W_1(f^1(t),f^2(t))
\leq \frac{1}{\varepsilon} e^{\frac1\varepsilon \left[(1+3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\|\rho^1(\tau)\|_\infty\,d\tau\right]}W_1(f^1(0),f^2(0)), $$ which concludes the proof of Theorem \ref{thm4}.
\begin{remark} \label{rmk:VP ws} Notice that, if we were working with the classical Vlasov-Poisson system, the stability estimate would have simply been $$ W_1({\mathcal{F}}^1(t),{\mathcal{F}}^2(t))
\leq e^{t +8 \int_0^t\|{\varrho}^1(\tau)\|_\infty\,d\tau}W_1({\mathcal{F}}^1(0),{\mathcal{F}}^2(0)), $$ (compare with \cite{HauX}), so in terms of $f$ $$ W_1(f^1(t),f^2(t))
\leq \frac{1}{\varepsilon} e^{\frac1\varepsilon \left[t +8 \int_0^t\|\rho^1(\tau)\|_\infty\,d\tau\right]}W_1(f^1(0),f^2(0)), $$ \end{remark}
\section{Proof of Theorem~\ref{thm-exi}} \label{sec:exi}
In this section, we prove the existence of global weak solutions in $\mathcal{P}_1(\mathbb{T} \times \mathbb{R})$ for the (VPME) system. Without loss of generality we prove the existence of solutions when $\varepsilon=1$ (that is, for \eqref{vpme}).
To prove existence of weak solutions we follow \cite[Proposition 1.2 and Theorem 1.7]{HauX}. For this, we take a random variable $(X_0,V_0):[0,1]\to \mathbb T \times \mathbb{R} $ whose law is $f_0$, that is $(X_0,V_0)_\# ds=f_0$, and we solve \begin{equation} \label{eq:VPLELappendix} (VPME)_{L,2}:= \left\{ \begin{array}{cc} \dot X_t=V_t,\\ \dot V_t=\bar {\mathcal E}(X_t) + \widehat {\mathcal E}(X_t),\\ \bar {\mathcal E}=-\bar {\mathcal U}',\qquad \widehat {\mathcal E}=-\widehat {\mathcal U}', \\ \bar {\mathcal U}''=1-\rho,\\ \widehat {\mathcal U}''=e^{(\bar {\mathcal U}+\widehat {\mathcal U})} - 1,\\ \rho(t)=(X_t)_\# ds. \end{array} \right. \end{equation} Indeed, once we have $(X_t,V_t)$, $f_t:=(X_t,V_t)_\# ds$ will be a solution to \eqref{vpme}. We split the argument in several steps.\\
{\it Step 1: Solution of the $N$ particle system (compare with \cite[Proof of Proposition 1.2]{HauX}).} We start from the $N$ particle systems of ODEs, $i=1,\ldots,N$, $$ \left\{ \begin{array}{cc} \dot X^i_t=V_t^i,\\ \dot V_t^i=\bar E(X_t^i) + \widehat E(X_t^i),\\ \bar E=-\bar U',\qquad \widehat E=-\widehat U', \\ \bar U''=\frac{1}{N}\sum_{i=1}^N \delta_{X^i} -1,\\ \widehat U''=e^{\bar U+\widehat U} - 1,\\ \end{array} \right. $$ Because the electric field $\bar E(X^i)=-\frac{1}{N}\sum_{j\neq i} W'(X^i-X^j)$ is singular when $X^i=X^j$ for some $i \neq j$, to prove existence we want to rewrite the above system as a differential inclusion $$ \dot {\mathcal Z}^N(t) \in \mathcal B^N(\mathcal Z^N(t)), $$ where $\mathcal B^N$ is a multivalued map from $\mathbb{R}^{2N}$ into the set of parts of $\mathbb{R}^{2N}$. For this, we write $$ \dot {\mathcal Z}^N(t) \in \mathcal B^N(\mathcal Z^N(t)) \quad \Leftrightarrow \quad \dot X^i=V^i, \quad \dot V^i \in \frac{1}{N}\sum_{j=1}^N F_{ij} $$ where $$ F_{ij}=-F_{ji}=-W'(X^i-X^j)+\widehat E(X^i) \quad \text{when $X^i \neq X^j$}, $$ $$ F_{ij}=-F_{ji} \in [\widehat E(X^i)-1/2, \widehat E(X^i)+1/2] \quad \text{when $X^i = X^j$}. $$ As in \cite{HauX}, this equation is solved by Filippov's Theorem (see \cite{Fil}) which provides existence of a solution, and as shown in \cite[Step 2 of proof of Proposition 1.2]{HauX} the solution of the differential inclusion is a solution to the $N$ particle problem.\\
{\it Step 2: Approximation argument.} To solve $(VPME)_{L,2}$ we approximate $f_0$ with a family of empirical measures $$ f_0^N:=\frac{1}{N}\sum_{i=1}^N \delta_{(x^i,v^i)}, $$ that we can assume to satisfy (thanks to \eqref{eq:moment}) \begin{equation} \label{eq:moment N}
\int |v|\,df_0^N(x,v)\leq C\qquad \forall\,N, \end{equation} and we apply Step 1 to solve the ODE system and find solutions $(X_t^N,V_t^N) \in \mathbb T\times \mathbb{R}$ of $(VPME)_{L,2}$ starting from an initial condition $(X^N_0,V^N_0)$ whose law is $f_0^N$.
Next, we notice that in \cite[Step 2, Proof of Theorem 1.7]{HauX} the only property on the vector field used in the proof is the fact that $F_{ij}$ are bounded by $1/2$, and it is used to show that $$
\sup_{u,s \in [0,t]} \frac{|Z^N(u)-Z^N(u)|}{|s-u|} \leq |V_0^N|+ \frac{1}{2}(1+t), $$ which, combined with \eqref{eq:moment N}, is enough to ensure tightness (see \cite[Step 2, Proof of Theorem 1.7]{HauX} for more details). Since in our case the $F_{ij}$ are also bounded (as we are simply adding a bounded term $\widehat E$), we deduce that for some $C>0$, $$
\sup_{u,s \in [0,t]} \frac{|Z^N(u)-Z^N(u)|}{|s-u|} \leq |V_0^N|+ C(1+t), $$ so the sequence $Z^N:=(X^N,V^N)$ is still tight and (up to a subsequence) converge to a process $Z=(X,V)$: it holds \begin{equation} \label{eq:tightness}
\int_0^1 \sup_{t \in [0,T]} \bigl|Z^N_t(s) - Z_t(s)\bigr| \,ds \to 0 \qquad \text{as $N \to \infty$} \end{equation} for any $T>0$.\\
{\it Step 3: Characterization of the limit process}. We now want to prove that the limit process $Z_t=(X_t,V_t)$ is a solution of $(VPME)_{L,2}$.
Let us denote by $\bar E^N$ and $\widehat E^N$ the electric fields associated to the solution $(X^N,V^N)$. Recall that $(X^N,V^N)$ solve $$ \dot X^N=V^N,\qquad \dot V^N=\bar E^N(X^N)+\widehat E^N(X^N), $$ or equivalently $$ X^N_t=\int_0^t V^N_\tau\,d\tau,\qquad V^N_t=\int_0^t\bar E^N_\tau(X^N_\tau)+\widehat E^N_\tau(X^N_\tau)\,d\tau. $$ In \cite[Step 3, Proof of Theorem 1.7]{HauX}, using \eqref{eq:tightness}, it is proved that $$\int_0^t \bar E^N_\tau(X^N_\tau)\rightarrow \int_0^t \bar E_\tau(X_\tau) \quad \text{ in } L^1([0,1], \,ds),$$ so, to ensure that $(X,V)$ solves $$ X_t=\int_0^t V_\tau\,d\tau,\qquad V_t=\int_0^t\bar E_\tau(X_\tau)+\widehat E_\tau(X_\tau)\,d\tau, $$ it suffices to show that, for any $\tau \geq 0$, $$
\int_0^1 |\widehat E^N_\tau(X^N_\tau(s))-\widehat E_\tau(X_\tau(s))|\,ds \to 0 \qquad \text{as $N \to \infty$.} $$ To show this we see that \begin{align*}
\int_0^1 |\widehat E^N_\tau(X^N_\tau(s))-\widehat E_\tau(X_\tau(s))|\,ds& \leq
\int_0^1 |\widehat E^N_\tau(X^N_\tau(s))-\widehat E_\tau(X_\tau^N(s))|\,ds\\
&+\int_0^1 |\widehat E_\tau(X^N_\tau(s))-\widehat E_\tau(X_\tau(s))|\,ds\\ &=:I_1+I_2 \end{align*} For $I_2$ we use that $\widehat E_\tau$ is $M$-Lipschitz (recall Lemma \ref{lem:hatU}) to estimate $$
I_2\leq M \int_0^1 |X^N_\tau(s)-X_\tau(s)|\,ds $$ that goes to $0$ thanks to \eqref{eq:tightness}.
For $I_1$, we notice that the Cauchy-Schwarz inequality, \eqref{eq:continuity E}, and \eqref{eq:tightness} imply that, as $N \to \infty$, \begin{align*}
\int_{\mathbb T} |\widehat E^N_\tau(x)-\widehat E_\tau(x)|\,dx& \leq
\sqrt{\int_{\mathbb T} |\widehat E^N_\tau(x)-\widehat E_\tau(x)|^2\,dx}\\ &\leq
\bar C\int_0^1|Z_\tau^N(s)-Z_\tau(s)|\,ds \to 0. \end{align*} Hence, we know that $\widehat E^N_\tau$ converge to $\widehat E_\tau$ in $L^1(\mathbb T)$. We now recall that $\{\widehat E^N_\tau\}_{N \geq 1}$ are $M$-Lipschitz, which implies by Ascoli-Arzel\`a that, up to subsequences, they converge uniformly to some limit, but by uniqueness of the limit they have to converge uniformly to $\widehat E_\tau$. Thanks to this fact we finally obtain $$
I_1 \leq \sup_{x \in \mathbb T}|\widehat E^N_\tau(x)-\widehat E_\tau(x)| \to 0, $$ which concludes the proof.
\section{Proofs of Theorems \ref{thm1} and \ref{thm2}} \label{sec:proofs}
Our aim is now to prove Theorems \ref{thm1} and \ref{thm2}. The principle is first to adapt some results from \cite{Gr96} for the (VPME) system in terms of the $W_1$ distance, which allows us to settle the case where $h_{\varepsilon,0}=0$. In a second time, we apply the stability estimate of Theorem \ref{thm4}.
\subsection{The fluid point of view and convergence for uniformly analytic initial data} \label{subsec:grenier} We describe in this section the approach introduced by Grenier in \cite{Gr96} for the study of the quasineutral limit for the classical Vlasov-Poisson system. As we shall see, this can be adapted without difficulty to (VPME)$_\varepsilon$.
We assume that, for all $\varepsilon \in (0,1)$, $g_{0,\varepsilon}(x,v)$ is a \emph{continuous} function; following Grenier \cite{Gr96}, we write each initial condition as a ``superposition of Dirac masses in velocity'': $$ g_{0, \varepsilon}(x,v) = \int_{\mathcal M} \rho_{0,\varepsilon}^\theta(x) \delta_{v= v_{0,\varepsilon}^\theta(x)} \, d\mu(\theta) $$ with ${\mathcal M}:= \mathbb{R}$, $d\mu(\theta) = \frac{1}{\pi} \frac{d\theta}{1+\theta^2}$, $$\rho_{0, \varepsilon}^\theta= \pi (1+ \theta^2) g_{0,\varepsilon}(x,\theta), \quad v_{0,\varepsilon}^\theta = \theta.$$ This leads to the study of the behavior as $\varepsilon\to0$ for solutions to the multi-fluid pressureless Euler-Poisson system \begin{equation} \label{fluid}
\left\{ \begin{array}{ccc}\partial_t \rho_\varepsilon^\theta+ \partial_x (\rho_\varepsilon^\theta v_\varepsilon^\theta)=0, \\ \partial_t v_\varepsilon^\theta + v_\varepsilon^\theta \partial_x v_\varepsilon^\theta = E_\varepsilon, \\ E_\varepsilon=-U_\varepsilon', \\ \varepsilon^2 U_\varepsilon''=e^{U_\varepsilon}- \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta),\\ \rho_\varepsilon^\theta\vert_{t=0}= \rho_{0,\varepsilon}^\theta, v_\varepsilon^\theta\vert_{t=0}= v_{0,\varepsilon}^\theta. \end{array} \right. \end{equation} One then checks that defining $$g_\varepsilon(t,x,v) = \int_{\mathcal M} \rho_\varepsilon^\theta(t,x) \delta_{v= v_\varepsilon^\theta(t,x)} \, d\mu(\theta)$$ gives a weak solution to \eqref{vpme-quasi} (as an application of Theorem~\ref{thm4} and of the subsequent estimates, this is actually \emph{the unique} weak solution to \eqref{vpme-quasi} with initial datum $g_{0,\varepsilon}$).
The formal limit system, which is associated to the kinetic isothermal Euler system, is the following multi fluid isothermal Euler system: \begin{equation} \label{limit-fluid} \left\{ \begin{array}{ccc}\partial_t \rho^\theta+ \partial_x (\rho^\theta v^\theta)=0, \\ \partial_t v^\theta + v^\theta \partial_x v^\theta = E, \\ E=-U', \\ U= \log\left( \int_{\mathcal M} \rho^\theta \, d\mu(\theta)\right),\\ \rho^\theta\vert_{t=0}= \rho_{0}^\theta, v^\theta\vert_{t=0}= v_{0}^\theta, \end{array} \right. \end{equation} where the $\rho_0^\theta$ are defined as the limits of $\rho_{0,\varepsilon}^\theta$ (which are thus supposed to exist) and $v_0^\theta=\theta$.
As before, one checks that defining $$g(t,x,v) = \int_{\mathcal M} \rho^\theta(t,x) \delta_{v= v^\theta(t,x)} \, d\mu(\theta)$$ gives a weak solution to the kinetic Euler isothermal system.
Recalling the analytic norms used by Grenier in \cite{Gr96} (see Definition \ref{def:norm}), we can adapt the results of \cite[Theorems 1.1.2, 1.1.3 and Remark 1 p. 369]{Gr96} to get the following proposition.
\begin{prop} \label{grenier} Assume that there exist $\delta_0,C,\eta>0$, with $\eta$ small enough, such that $$
\sup_{\varepsilon\in (0,1)}\sup_{v \in \mathbb{R}} (1+v^2) \| g_{0,\varepsilon} (\cdot,v)\|_{B_{\delta_0}} \leq C, $$ and that $$
\sup_{\varepsilon\in (0,1)} \left\| \int_\mathbb{R} g_{0,\varepsilon}(\cdot,v) \, dv -1 \right\|_{B_{\delta_0}} < \eta.
$$
Denote for all $\theta \in \mathbb{R}$, $$\rho_{0, \varepsilon}^\theta= \pi (1+ \theta^2) g_{0,\varepsilon}(x,\theta), \quad v_{0,\varepsilon}^\theta = v^\theta= \theta.$$ Assume that for all $\theta \in \mathbb{R}$, $\rho_{0,\varepsilon}^\theta$ has a limit in the sense of distributions and denote $$ \rho_0^\theta= \lim_{\varepsilon \to 0} \rho_{0,\varepsilon}^\theta. $$ Then there exist $\delta_1>0$ and $T>0$ such that: \begin{itemize} \item for all $\varepsilon \in (0,1)$, there is a unique solution $(\rho_\varepsilon^\theta, v_\varepsilon^\theta)_{\theta \in M}$ of \eqref{fluid} with initial data $(\rho_{0,\varepsilon}^\theta, v_{0,\varepsilon}^\theta)_{\theta \in M}$, such that $\rho_\varepsilon^\theta, v_\varepsilon^\theta \in C([0,T]; B_{\delta_1})$ for all $\theta \in M$ and $\varepsilon \in (0,1)$, with bounds that are uniform in $\varepsilon$; \item there is a unique solution $(\rho^\theta, v^\theta)_{\theta \in M}$ of \eqref{limit-fluid} with initial data $(\rho_{0}^\theta, v_{0}^\theta)_{\theta \in M}$, such that $\rho^\theta, v^\theta \in C([0,T]; B_{\delta_1})$
for all $\theta \in M$; \item for all $s \in \mathbb{N}$, we have \begin{equation} \label{eq:conv}
\sup_{\theta \in M} \sup_{t \in [0,T]} \left[ \| \rho_\varepsilon^\theta - \rho^\theta\|_{H^s (\mathbb{T})} + \| v_\varepsilon^\theta - v^\theta\|_{H^s (\mathbb{T})} \right] \to_{\varepsilon \to 0 } 0. \end{equation}
\end{itemize}
\end{prop}
Remark that analyticity is actually needed only in the position variable, and not in the velocity variable. This allows us, for instance, to consider initial data which are compactly supported in velocity.
We shall not give a complete proof of this result (which is of Cauchy-Kovalevski type), since it is very close to the one given by Grenier in \cite{Gr96} for the classical Vlasov-Poisson system, but we just emphasize the main differences.
First of all we begin by noticing that one difficulty in the classical case comes from the fact the one can not directly use the Poisson equation $$-\varepsilon^2 U''_\varepsilon = \rho_\varepsilon - 1$$ if one wants some useful uniform analytic estimates for the electric field. Because of this issue, a combination of the Vlasov and Poisson equation is used in \cite{Gr96}, which allows one to get a kind of wave equation solved by $U_\varepsilon$. This shows in particular that the electric field has a highly oscillatory behavior in time (the fast oscillations in time correspond to the so-called plasma waves) which have to be filtered in order to obtain convergence. For this reason, Grenier needs to introduce some correctors in order to get convergence of the velocity fields (these oscillations and correctors vanish only if the initial conditions are well-prepared, \emph{i.e.} verify some compatibility conditions).
For the (VPME) system, that is when one adds the exponential term in the Poisson equation, such a problem does not occur. To explain this, consider first the linearized Poisson equation $$-\varepsilon^2 U''_\varepsilon + U_\varepsilon = \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta) - 1$$ and observe that this equation is appropriate to get uniform analytic estimates. Indeed, writing $$ U_\varepsilon = (Id - \varepsilon^2 \partial_{xx})^{-1} \left( \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta)- 1\right), $$ this shows that if $\rho_\varepsilon$ is analytic then also $U_\varepsilon$ (and so $E_\varepsilon$) is analytic, which implies that there are no fast oscillations in time, contrary to the classical case. In particular, our convergence result holds without the need of adding any correctors.
A second difference concerns the existence of analytic solutions on an interval of time $[0,T]$ independent of $\varepsilon$: the construction of Grenier of analytic solutions is based on a Cauchy-Kovalevski type proof based on an iteration procedure in a scale of Banach spaces (see \cite[Section 2.1]{Gr96}). Most of the estimates used to prove that such iteration converge use the Fourier transform, that is unavailable in our case since the Poisson equation $$-\varepsilon^2 U''_\varepsilon + e^{U_\varepsilon} = \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta)$$ is nonlinear. However, since we deal with analytic functions, we can express everything in power series to use the Fourier transform and obtain some a priori estimates in the analytic norm. Furthermore, one can write the Poisson equation as $$-\varepsilon^2 U''_\varepsilon + U_\varepsilon = \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta) - 1 - (e^{U_\varepsilon} - U_\varepsilon -1)$$
and rely on the fact that the ``error term'' $(e^{U_\varepsilon} - U_\varepsilon -1)$ is quadratic in $U_\varepsilon$ (which is expected to be small in the regime where $\sup_{\varepsilon\in (0,1)} \left\| \int_{\mathcal M} \rho_\varepsilon^\theta \, d\mu(\theta) -1 \right\|_{B_{\delta_0}} \ll 1$), and thus can be handled in the approximation scheme used in \cite{Gr96}.
We deduce the next corollary. \begin{cor} \label{cor:1} With the same assumptions and notation as in Proposition \ref{grenier}, we have \begin{equation} \label{W1-0} \sup_{t \in [0,T]} W_1(g_\varepsilon (t), g(t)) \to_{\varepsilon\to0} 0, \end{equation} where \begin{equation} \label{g1} g_\varepsilon(t,x,v) = \int_{\mathcal M} \rho_\varepsilon^\theta(t,x) \delta_{v= v_\varepsilon^\theta(t,x)} \, d\mu(\theta), \qquad g(t,x,v) = \int_{\mathcal M} \rho^\theta(t,x) \delta_{v= v^\theta(t,x)} \, d\mu(\theta). \end{equation} \end{cor}
\begin{proof} The convergence \eqref{W1-0} follows from \eqref{eq:conv}, and the Sobolev embedding theorem. We have indeed for all $t\in [0,T]$: \begin{align*}
&W_1(g_\varepsilon (t), g(t)) = \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \langle g_\varepsilon -g, \, \varphi \rangle \\%\left\{ \int_{\mathbb{T} \times \mathbb{R}} (g_\varepsilon(t,x,v) - g(t,x,v)) \varphi(x,v) \, dv dx \right\} \\
&= \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \left\{ \int_{\mathbb{T} } \int_{\mathcal M} (\rho_\varepsilon^\theta(t,x)\varphi(x,v_\varepsilon^\theta(t,x)) - \rho^\theta(t,x)\varphi(x,v^\theta(t,x))) \, d\mu(\theta) \, dx \right\} \\
&=\sup_{\|\varphi\|_{\text{Lip}} \leq 1} \left\{ \int_{\mathbb{T} } \int_{\mathcal M} \rho_\varepsilon^\theta(t,x)(\varphi(x,v_\varepsilon^\theta(t,x))-\varphi(x,v^\theta(t,x)) \, d\mu(\theta) \, dx \right\} \\
&+ \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \left\{ \int_{\mathbb{T}} \int_{\mathcal M} (\rho_\varepsilon^\theta(t,x) - \rho^\theta(t,x))\varphi(x,v^\theta(t,x)) \, d\mu(\theta) \, dx \right\}. \end{align*} Thus, we deduce the estimate \begin{align*} W_1(g_\varepsilon (t), g(t))
&\leq \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \sup_{\varepsilon \in (0,1), \, \theta \in M} \|\rho_\varepsilon^\theta\|_{\infty} \|\varphi\|_{\text{Lip}} \int_{\mathcal M} \| v_\varepsilon^\theta(t,x)-v^\theta(t,x)\|_\infty \, d\mu(\theta) \\
&+ \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \int_{\mathcal M} \|\rho_\varepsilon^\theta- \rho_\theta\|_{\infty} \, d\mu(\theta) \|\varphi\|_{\text{Lip}} \left(1/2+ \sup_{\theta \in M} \|v^\theta(t,x)\|_\infty\right) \\
&+ \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \left\{ \int_{\mathbb{T} \times \mathbb{R}} \int_{\mathcal M} (\rho_\varepsilon^\theta(t,x) - \rho^\theta(t,x))\varphi(0,0) \, d\mu(\theta) \, dx \right\}. \end{align*} We notice that the last term is equal to $0$ since for all $t \geq 0$, $$ \int_\mathbb{T} \int_{\mathcal M} \rho_\varepsilon^\theta(t,x) \, d\mu(\theta) \, dx =\int_\mathbb{T} \int_{\mathcal M} \rho_\varepsilon^\theta(t,x) \, d\mu(\theta) \, dx =1, $$ by conservation of the total mass. After taking the supremum in time, we also see that the other two terms converge to $0$, using the $L^\infty$ convergence of $(\rho_\varepsilon^\theta, v_\varepsilon^\theta)$ to $(\rho_{0}^\theta, v_{0}^\theta)$. This concludes the proof. \end{proof}
This approach is also relevant for singular initial data such as the sum of Dirac masses in velocity: $$ g_{0,\varepsilon}(x,v) = \sum_{i=1}^N \rho_{0,\varepsilon}^i(x) \delta_{v=v_{0,\varepsilon}^i(x)}. $$ and we have a similar theorem assuming that $(\rho_{0,\varepsilon}^i, v_{0,\varepsilon}^i)$ is uniformly analytic.
In this case ${\mathcal M}= \{1,\cdots,N\}$ and $d\mu$ is the counting measure. This leads to the study of the behavior as $\varepsilon \to 0$ of the system (for $i \in \{1,\cdots,N\}$) \begin{equation} \label{eq:Ndirac} \left\{ \begin{array}{ccc}\partial_t \rho^i_\varepsilon+ \partial_x (\rho^i_\varepsilon v^i_\varepsilon)=0, \\ \partial_t v^i_\varepsilon+ v^i_\varepsilon \partial_x v^i_\varepsilon = E_\varepsilon, \\ E_\varepsilon=-U'_\varepsilon, \\ \varepsilon^2 U''_\varepsilon = e^{U_\varepsilon}- \left( \sum_{i=1}^N \rho^i_\varepsilon \right),\\ \rho^i_\varepsilon\vert_{t=0}= \rho_{0,\varepsilon}^i, v^i_\varepsilon\vert_{t=0}= v_{0,\varepsilon}^i. \end{array} \right. \end{equation} and the formal limit is the following multi fluid isothermal system \begin{equation} \label{eq:Ndiraclimit} \left\{ \begin{array}{ccc}\partial_t \rho^i+ \partial_x (\rho^i v^i)=0, \\ \partial_t v^i + v^i \partial_x v^i = E, \\ E=-U', \\ U= \log\left( \sum_{i=1}^N \rho^i \right),\\ \rho^i\vert_{t=0}= \rho_{0}^i, v^i\vert_{t=0}= v_{0}^i. \end{array} \right. \end{equation}
As before, adapting the arguments in \cite{Gr96}, we obtain the following proposition and its corollary. \begin{prop} \label{grenier2} Assume that there exist $\delta_0,C,\eta>0$, with $\eta$ small enough, such that $$
\sup_{\varepsilon\in (0,1)}\sup_{i \in \{ 1, \cdots , N\}} \| \rho^i_{0,\varepsilon}\|_{B_{\delta_0}} + \| v^i_{0,\varepsilon}\|_{B_{\delta_0}} \leq C, $$ and that $$
\sup_{\varepsilon\in (0,1)} \left\| \sum_{i=1}^N \rho^i_{0,\varepsilon} -1 \right\|_{B_{\delta_0}} < \eta.
$$
Assume that for all $i=1,\cdots, N$, $\rho^i_{0,\varepsilon}, v^i_{0,\varepsilon}$ admit a limit in the sense of distributions and denote $$ \rho^i_{0} =\lim_{\varepsilon \to 0} \rho^i_{0,\varepsilon}, \quad v^i_{0} = \lim_{\varepsilon \to 0} v^i_{0,\varepsilon}. $$ Then there exist $\delta_1>0$ and $T>0$ such that: \begin{itemize} \item for all $\varepsilon \in (0,1)$, there is a unique solution $(\rho_\varepsilon^i, v_\varepsilon^i)_{i \in \{ 1, \cdots , N\}}$ of \eqref{eq:Ndirac} with initial data $(\rho_{0,\varepsilon}^i, v_{0,\varepsilon}^i)_{i \in \{ 1, \cdots , N\}}$, such that $\rho_\varepsilon^i, v_\varepsilon^i \in C([0,T]; B_{\delta_1})$ for all $i \in \{ 1, \cdots , N\}$ and $\varepsilon \in (0,1)$, with bounds that are uniform in $\varepsilon$; \item there is a unique solution $(\rho^i, v^i)_{i \in \{ 1, \cdots , N\}}$ of \eqref{eq:Ndiraclimit} with initial data $(\rho_{0}^i, v_{0}^i)_{i \in \{ 1, \cdots , N\}}$, such that $\rho^i, v^i \in C([0,T]; B_{\delta_1})$ for all $i \in \{ 1, \cdots , N\}$; \item for all $s \in \mathbb{N}$, we have $$
\sup_{i \in \{ 1, \cdots , N\}} \sup_{t \in [0,T]} \left[ \| \rho_\varepsilon^i - \rho^i\|_{H^s (\mathbb{T})} + \| v_\varepsilon^i - v^i\|_{H^s (\mathbb{T})} \right] \to_{\varepsilon \to 0 } 0. $$ \end{itemize}
\end{prop}
\begin{cor} \label{cor:2.1} With the same assumptions and notation as in the Proposition \ref{grenier2}, for all $t \in [0,T]$ we have \begin{equation} \label{W1-0-again} W_1(g_\varepsilon (t), g(t)) \to_{\varepsilon\to0} 0, \end{equation} where \begin{equation} \label{g2} g_\varepsilon(t,x,v) = \sum _{i \in \{ 1, \cdots , N\}} \rho_\varepsilon^i(t,x) \delta_{v= v_\varepsilon^i(t,x)}, \quad g(t,x,v) = \sum_{i \in \{ 1, \cdots , N\}} \rho^i(t,x) \delta_{v= v^i(t,x)}. \end{equation} \end{cor}
\subsection{End of the proof of Theorem \ref{thm1} and Theorem \ref{thm2}}
We are now in position to conclude. Let $(f_\varepsilon)$ a sequence of global weak solutions to \eqref{vpme-quasi} with initial conditions $(f_{0,\varepsilon})$ (obtained thanks to Theorem~\ref{thm-exi}).
We denote by $(g_\varepsilon)$ the sequence of weak solutions to \eqref{vpme-quasi} with initial conditions $(g_{0,\varepsilon})$, defined by \eqref{g1} for the case of Theorem~\ref{thm1} and \eqref{g2} for the case of Theorem~\ref{thm2}. Using the triangle inequality, we have \begin{equation*} W_1(f_\varepsilon(t), g(t)) \leq W_1(f_\varepsilon(t), g_\varepsilon (t)) + W_1(g_\varepsilon(t), g(t)), \end{equation*} where $g$ is defined by \eqref{g1} for the case of Theorem~\ref{thm1} and \eqref{g2} for the case of Theorem~\ref{thm2}.
For the first term, we use Theorem \ref{thm4} to get \begin{align*}
W_1(f_\varepsilon(t), g_\varepsilon (t)) &\leq W_1(g_{0,\varepsilon} + h_{0,\varepsilon}, g_{0,\varepsilon} ) \frac{1}{\varepsilon} e^{\frac1\varepsilon \left[(1 +3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\| \rho_\varepsilon(\tau)\|_\infty\,d\tau\right]} \\
&= W_1(h_{0,\varepsilon}, 0) \frac{1}{\varepsilon} e^{\frac1\varepsilon \left[(1 +3/\varepsilon^2 )t +(8+ \frac{1}{\varepsilon^2} e^{15/(2\varepsilon^2)} \color{black}) \int_0^t\| \rho_\varepsilon(\tau)\|_\infty\,d\tau\right]},
\end{align*} where $\rho_\varepsilon$ is here the local density associated to $g_\varepsilon$. By Proposition \ref{grenier} (for the case of Theorem \ref{thm1}) and Proposition \ref{grenier2} (for the case of Theorem \ref{thm2}), there exists $C_0>0$ such that for all $\varepsilon \in (0,1)$, $$
\sup_{\tau \in [0,T]} \| \rho_\varepsilon(\tau)\|_\infty \leq C_0. $$ Consequently, we observe that taking $$ \varphi(\varepsilon)= \frac{1}{\varepsilon} \exp \left( \frac{\lambda}{\varepsilon^3} \exp \frac{15}{2 \varepsilon^2}\right), $$ with $\lambda<0$, we have, by assumption on $h_{0,\varepsilon}$ (take a smaller $T$ if necessary) that $$ \sup_{t \in [0,T]} W_1(f_\varepsilon(t), g_\varepsilon (t)) \to_{\varepsilon \to 0} 0. $$ We also get that $W_1(g_\varepsilon(t), g(t))$ converges to $0$, applying Corollary \ref{cor:1} for the case of Theorem \ref{thm1}, and Corollary \ref{cor:2.1} for the case of Theorem \ref{thm2}.
This concludes the proofs of Theorems \ref{thm1} and \ref{thm2}.
\section{Proof of Proposition \ref{thm3}} \label{sec:insta}
We now discuss a non-derivation result which was first stated by Grenier in the note \cite{Gr99}, and then studied in more details by the first author and Hauray in \cite{HKH} (the latter was stated for a general class of homogeneous data, i.e., independent of the position). In \cite{HKH} such results are given either for the classical Vlasov-Poisson system or for the linearized (VPME) system, but the proofs can be adapted to (VPME).
We first recall two definitions from \cite{HKH}.
\begin{defi} \label{def:Penmod} We say that a homogeneous profile $\mu(v)$ with $\int \mu \, dv=1$ satisfies the Penrose instability criterion if there exists a local minimum point $\bar v$ of $\mu$ such that the following inequality holds: \begin{equation} \label{def:Pen-first-mod} \int_{\mathbb{R}} \frac{ \mu(v) - \mu(\bar v)} {(v-\bar v)^2} \, dv > 1. \end{equation} If the local minimum is flat, i.e., is reached on an interval $[\bar v_1, \bar v_2]$, then~\eqref{def:Pen-first-mod} has to be satisfied for all $\bar v \in [\bar v_1, \bar v_2]$. \end{defi}
\begin{defi} \label{cond-pos}
We say that a positive and $C^1$ profile $\mu(v)$ satisfies the $\delta$-condition\footnote{The appellation is taken from \cite{HKH}. } if \begin{equation} \label{cond:alpha}
\sup_{v \in \mathbb{R}} \, \frac{|\mu'(v)|}{(1+ |v|)\mu(v)} < + \infty. \end{equation} \end{defi}
We can now state the theorem taken from \cite{HKH}. \begin{thm} \label{thmGrenier-revisited} Let $\mu(v)$ be a smooth profile satisfying the Penrose instability criterion. Assume that $\mu$ is positive and satisfies the $\delta$-condition\footnote{It is also possible to consider a non-negative $\mu$ but the relevant condition is rather involved, we refer to \cite{HKH} for details.}. For any $N>0$ and $s>0$, there exists a sequence of non-negative initial data $(f_{0,\varepsilon})$ such that $$
\| f_{\varepsilon,0}- \mu\|_{W^{s,1}_{x,v}} \leq \varepsilon^N, $$ and denoting by $(f_\varepsilon)$ the sequence of solutions to \eqref{vpme-quasi} with initial data $(f_{0,\varepsilon})$, the following holds:
\begin{enumerate} \item {\bf $L^1$ instability for the macroscopic observables:} consider the density $\rho_\varepsilon := \int f_\varepsilon \, dv$ and the electric field $E_\varepsilon = - \partial_x U_\varepsilon$. For all $\alpha\in [0,1)$, we have \begin{equation} \label{insta:macro}
\liminf_{\varepsilon \rightarrow 0} \sup_{t \in [0,\varepsilon^\alpha]} \left\| \rho_\varepsilon(t) - 1 \right\|_{L^1_{x}} >0, \qquad
\liminf_{\varepsilon \rightarrow 0} \sup_{t \in [0,\varepsilon^\alpha]} {\varepsilon}\left\| E_\varepsilon \right\|_{L^1_x} >0. \end{equation}
\item {\bf Full instability for the distribution function:} for any $r \in \mathbb{Z}$, we have \begin{equation} \label{insta:full}
\liminf_{\varepsilon \rightarrow 0} \sup_{t \in [0,\varepsilon^\alpha]} \left\| f_\varepsilon(t) - \mu \right\|_{W^{r,1}_{x,v}} >0. \end{equation} \end{enumerate} \end{thm}
We deduce a proof of Proposition \ref{thm3} from this result. Indeed, take a smooth $\mu$ satisfying the assumptions of Theorem \ref{thmGrenier-revisited}, and consider the sequence of initial conditions $(f_{0,\varepsilon})$ given by this theorem.
By the Sobolev imbedding theorem in dimension $1$, the space $W^{2,1}(\mathbb{T} \times \mathbb{R})$ is continuously imbedded in the space $W^{1,\infty}(\mathbb{T} \times \mathbb{R})$ (i.e., bounded Lipschitz functions), hence there exists a constant $C>0$ such that, for all $\varepsilon \in (0,1)$, \begin{align*}
W_1(f_\varepsilon, \mu) &= \sup_{\|\varphi\|_{\text{Lip}} \leq 1} \langle f_\varepsilon -\mu, \, \varphi \rangle \\
&\geq \sup_{\|\varphi\|_{W^{2,1}} \leq C} \langle f_\varepsilon -\mu, \, \varphi \rangle \\
&= C \|f_\varepsilon - \mu\|_{W^{-2,1}}. \end{align*} Therefore, by \eqref{insta:full} with $r=-2$, we deduce that $$ \liminf_{\varepsilon \rightarrow 0} \sup_{t \in [0,\varepsilon^\alpha]} W_1(f_\varepsilon, \mu) >0, $$ which proves the claimed result.
\section{Proof of Proposition \ref{thm3-2}} \label{sec:sta}
As we already mentioned in the introduction, in the case of one single Dirac mass in velocity, the situation is much more favorable. This was first shown by Brenier in \cite{Br00} for the quasineutral limit of the classical Vlasov-Poisson system, using the so-called relative entropy (or modulated energy) method. It was then adapted by the first author in \cite{HK} for the quasineutral limit of (VPME).
In this case, the expected limit is the Dirac mass in velocity $$ f(t,x,v)= \rho(t,x,v) \delta_{v= u(t,x)} $$ which is a weak solution of \eqref{formal} whenever $(\rho, u)$ is a strong solution to the isothermal Euler system \begin{equation} \label{IE} \left\{ \begin{array}{ccc}\partial_t \rho+ \partial_x (\rho u)=0, \\ \partial_t u + u \partial_x u + \frac{\partial_x \rho}{\rho} = 0, \\ \rho\vert_{t=0}= \rho_{0}, v\vert_{t=0}= u_{0}. \end{array} \right. \end{equation} This is a hyperbolic and symmetric system, that admits local smooth solutions for smooth initial data (in this section, smooth means $H^s$ with $s$ larger than $2$). From \cite{HK} we deduce the following stability result\footnote{In \cite{HK}, computations are done for the model posed on $\mathbb{R}^3$, but the same holds for the model set on $\mathbb{T}$.}. \begin{thm} \label{relative} Let $\rho_0>0, u_0$ be some smooth initial conditions for \eqref{IE}, and $\rho, u$ the associated strong solutions of \eqref{IE} defined on some interval of time $[0,T]$, where $T>0$. Let $f_\varepsilon$ be a non-negative global weak solution of~\eqref{vpme-quasi} such that $f_\varepsilon \in L^1 \cap L^\infty$, $\int f_\varepsilon \, dx dv=1$, and with uniformly bounded energy, i.e., there exists $A>0$, such that for all $\varepsilon \in (0,1)$, $$ \mathcal{E}_\varepsilon(t):= \frac{1}{2}\int f_\varepsilon\vert v\vert ^2 dv \,dx + \int \left(e^{U_\varepsilon} \log e^{U_\varepsilon} - e^{U_\varepsilon} +1\right)\,dx + \frac{\varepsilon^2}{2} \int \vert U'_\varepsilon \vert^2 dx \leq A. $$ For all $\varepsilon \in (0,1)$, define the relative entropy $$ \mathcal{H}_\varepsilon(t):=\frac{1}{2}\int f_\varepsilon\vert v - u\vert ^2 dv \,dx + \int \left(e^{U_\varepsilon} \log \left( e^{U_\varepsilon}/ \rho \right) - e^{U_\varepsilon} +\rho\right)\,dx + \frac{\varepsilon^2}{2} \int \vert U'_\varepsilon \vert^2 dx. $$
Then there exists $C>0$ and a function $G_\varepsilon(t)$ satisfying $\| G_\varepsilon\|_{L^\infty([0,T])} \leq C \varepsilon$ such that, for all $t \in [0,T]$, $$ {\mathcal{H}}_\varepsilon(t) \leq {\mathcal{H}}_\varepsilon(0) + G_\varepsilon(t) + C\int_0^t \Vert \partial_x u \Vert_{L^\infty} \mathcal{H}_\varepsilon(s) ds. $$ In particular, if $ {\mathcal{H}}_\varepsilon(0) \to_{\varepsilon \to 0} 0$, then $ {\mathcal{H}}_\varepsilon(t) \to_{\varepsilon \to 0} 0$
for all $t \in [0,T]$.
In addition, if there is $C_0>0$ such that ${\mathcal{H}}_\varepsilon(0) \leq C_0 \varepsilon$, then there is $C_T>0$ such that $ {\mathcal{H}}_\varepsilon(t) \leq C_T \varepsilon$ for all $t \in [0,T]$ and $\varepsilon \in (0,1)$. \end{thm}
Notice that, by a convexity argument, one also deduces that $\rho_\varepsilon= \int f_\varepsilon \, dv \rightharpoonup \rho$ (and $e^{U_\varepsilon} \rightharpoonup \rho$ as well) and $j_\varepsilon = \int f_\varepsilon v \, dv\rightharpoonup \rho u$ in a weak-$\star$ sense (see \cite{HK}).
We can actually deduce the following corollary, which is a precise version of Proposition \ref{thm3-2}. \begin{cor} \label{cor:2.2} With the same assumptions and notation as in the previous theorem, the following convergence results hold: \begin{enumerate} \item If $ {\mathcal{H}}_\varepsilon(0) \to_{\varepsilon \to 0} 0$, then $$ \sup_{t \in [0,T]} W_1(f_\varepsilon, \rho\, \delta_{v= u}) \to_{\varepsilon \to 0} 0. $$ \item If ${\mathcal{H}}_\varepsilon(0) \leq C_0 \varepsilon$, then there is $C_T'>0$ such that, for all $\varepsilon \in (0,1)$, $$ \sup_{t \in [0,T]} W_1(f_\varepsilon, \rho \,\delta_{v= u}) \leq C'_T \sqrt{\varepsilon}. $$ \end{enumerate} \end{cor}
\begin{proof}
Recall that we denote $\rho_\varepsilon = \int f_\varepsilon \, dv$. Let $\varphi$ such that $\|\varphi\|_{\text{Lip}} \leq 1$ and compute \begin{align*} \langle f_\varepsilon - \rho\, \delta_{v= u}, \, \varphi \rangle &= \langle f_\varepsilon - \rho_\varepsilon\, \delta_{v= u}, \, \varphi \rangle + \langle (\rho_\varepsilon - \rho )\,\delta_{v= u}, \, \varphi \rangle \\ &=: A_1 + A_2. \end{align*}
Using the bound $\|\varphi\|_{\text{Lip}} \leq 1$, the Cauchy-Schwarz inequality, the fact that $f_\varepsilon$ is non-negative and of total mass $1$, and the definition of $\mathcal{H}_\varepsilon(t)$, we have \begin{align*}
|A_1| &= \left|\int_{\mathbb{T}\times\mathbb{R}} f_\varepsilon(t,x,v) (\varphi(t,x,v)- \varphi(t,x,u(t,x)) \, dv dx \right|\\
&\leq \int_{\mathbb{T}\times\mathbb{R}} f_\varepsilon(t,x,v) |\varphi(t,x,v)- \varphi(t,x,u(t,x))| \, dv dx \\
&\leq \int_{\mathbb{T}\times\mathbb{R}} f_\varepsilon(t,x,v) |v- u(t,x)| \, dv dx \\
&\leq \left(\int_{\mathbb{T}\times\mathbb{R}} f_\varepsilon(t,x,v) |v- u(t,x)|^2 \, dv dx\right)^{1/2} \left(\int_{\mathbb{T}\times\mathbb{R}} f_\varepsilon(t,x,v) \, dv dx\right)^{1/2} \\ &\leq \sqrt{2} \sqrt{\mathcal{H}_\varepsilon(t)}. \end{align*} Considering $A_2$, we first have \begin{align*} A_2 &= \int_{\mathbb{T}} (\rho_\varepsilon(t,x)- \rho(t,x)) \varphi(x,u(t,x)) \, dx \\ &= \int_{\mathbb{T}} (\rho_\varepsilon(t,x)- \rho(t,x)) \big(\varphi(x,u(t,x)) - \varphi(0,0) \big) \, dx \end{align*} since the total mass is preserved (and equal to $1$). Furthermore, we use the Poisson equation $$
\rho_\varepsilon = e^{U_\varepsilon}- \varepsilon^2 U_\varepsilon'', $$
to rewrite $A_2$ as
\begin{align*} A_2 &= \int_{\mathbb{T}} (e^{U_\varepsilon}- \rho(t,x)) \left(\varphi(x,u(t,x)) - \varphi(0,0) \right) \, dx \\ &\qquad- \varepsilon^2 \int U_\varepsilon'' \left(\varphi(x,u(t,x)) - \varphi(0,0) \right) \, dx \\ &=: A_2^1 + A_2^2. \end{align*}
Let us start with $A_2^2$. By integration by parts, the Cauchy-Schwarz inequality, and the bound $\|\varphi\|_{\text{Lip}} \leq 1$, we have \begin{align*}
|A_2^2| &= \varepsilon^2 \left| \int_{\mathbb{T}} U_\varepsilon' [\partial_x \varphi(x,u(t,x)) + \partial_x u(t,x) \partial_ v \varphi(x,u(t,x))] \, dx \right| \\
&\leq \varepsilon [1+ \| \partial_x u\|_{\infty}] \left( \varepsilon^2 \int_{\mathbb{T}} |U_\varepsilon'|^2 \, dx \right)^{1/2} \\
&\leq \varepsilon [1+ \| \partial_x u\|_{\infty}] \sqrt{\mathcal{E}_\varepsilon(t)} \\
&\leq \sqrt{A} [1+ \| \partial_x u\|_{\infty}] \varepsilon. \end{align*} For $A_2^1$, we shall use the classical inequality $$ (\sqrt{y}- \sqrt{x})^2 \leq x \log (x/y) -x +y, $$ for $x,y >0$, and proceed as follows: \begin{align*}
|A_2^1| &= \left| \int_{\mathbb{T}} \left(e^{U_\varepsilon}- \rho(t,x)\right) \left(\varphi(x,u(t,x)) - \varphi(0,0) \right) \, dx \right| \\
&= \left| \int_{\mathbb{T}}\left(e^{\frac{1}{2} U_\varepsilon}- \sqrt{\rho(t,x)}\right)\left(e^{\frac{1}{2} U_\varepsilon}+ \sqrt{\rho(t,x)}\right) \left(\varphi(x,u(t,x)) - \varphi(0,0) \right) \, dx \right| \\
&\leq \left( \int_{\mathbb{T}} \left(e^{\frac{1}{2} U_\varepsilon}- \sqrt{\rho(t,x)}\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \right)^{1/2} \\
&\qquad \times \left( \int_{\mathbb{T}} \left(e^{\frac{1}{2} U_\varepsilon}+ \sqrt{\rho(t,x)}\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \right)^{1/2}. \end{align*} We have \begin{align*}
&\left( \int_{\mathbb{T}} \left(e^{\frac{1}{2} U_\varepsilon}- \sqrt{\rho(t,x)}\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \right)\\
&\qquad \leq (1+ \|u\|_\infty) \int \left(e^{U_\varepsilon} \log \left( e^{U_\varepsilon}/ \rho \right) - e^{U_\varepsilon} +\rho\right)\,dx \\
&\qquad \leq (1+ \|u\|_\infty) \mathcal{H}_\varepsilon(t), \end{align*} and likewise we obtain the rough bound \begin{align*}
&\left( \int_{\mathbb{T}} \left(e^{\frac{1}{2} U_\varepsilon}+ \sqrt{\rho(t,x)}\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \right) \\
&\qquad \leq 2 \int_{\mathbb{T}} \left(e^{\frac{1}{2} U_\varepsilon}- 1\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \\
&\qquad + 2 \int_{\mathbb{T}} \left(\sqrt{\rho(t,x)}+1\right)^2\left|\varphi(x,u(t,x)) - \varphi(0,0) \right| \, dx \\
&\qquad \leq 2 (1+ \|u\|_\infty)\left( \mathcal{E}_\varepsilon(t) + \int_{\mathbb{T}} \left(\sqrt{\rho(t,x)}+1\right)^2 \, dx\right) \\
&\qquad \leq 2 (1+ \|u\|_\infty)\left( A + \int_{\mathbb{T}} \left(\sqrt{\rho(t,x)}+1\right)^2 \, dx\right). \end{align*} As a consequence, we get \begin{equation*}
|A_2^2| \leq \sqrt{2} (1+\|u\|_\infty)\left( A + \int_{\mathbb{T}} \left(\sqrt{\rho(t,x)}-1\right)^2 \, dx\right)^{1/2} \sqrt{\mathcal{H}_\varepsilon(t)}. \end{equation*} Gathering all pieces together, we have shown \begin{multline*} \langle f_\varepsilon - \rho \delta_{v= u}, \, \varphi \rangle \\ \leq
\sqrt{2} \left[1+ (1+\|u\|_\infty)\left( A + \int_{\mathbb{T}} \left(\sqrt{\rho(t,x)}+1\right)^2 \, dx\right)^{1/2}\right] \sqrt{\mathcal{H}_\varepsilon(t)}
+ \sqrt{A} [1+ \| \partial_x u\|_{\infty}] \varepsilon, \end{multline*} which allows us to conclude the proof applying Theorem \ref{relative}. \end{proof}
{\bf Acknowledgements.} The authors would like to thank Maxime Hauray for some helpful discussions about his paper \cite{HauX}. We are also grateful to the anonymous referees for their remarks about this work, and for helping us to correct several typos.
\end{document} | arXiv |
\begin{definition}[Definition:Analysis/Complex]
'''Complex analysis''' is a branch of mathematics that studies complex functions.
\end{definition} | ProofWiki |
Diffie-Hellman key exchange works by agreeing on two publicly shared values: a large prime number $q$ and a primitive root $g$. Alice and Bob each generate a secret key—a large random number—$x_a$ and $x_b$ respectively, and each raise the primitive root to the power of the secret key, modulo the large prime number.
The results are sent to each other and the shared key is computed by raising the received value to the secret key modulo the primitive root.
Given a prime number $q$, a primitive root $g$ is a number such that every number from 1 up to $q - 1$ can be computed by raising the primitive root to some number $k$.
A common analogy is that of mixing paint. | CommonCrawl |
Evaluate $\lfloor\sqrt{63}\rfloor$.
Observe that $7<\sqrt{63}<8$, since $\sqrt{49}<\sqrt{63}<\sqrt{64}$. Therefore, the largest integer that is less than $\sqrt{63}$ is $\boxed{7}$. | Math Dataset |
Journal of Biosocial Science (5)
British Journal of Nutrition (1)
Canadian Journal of Mathematics (1)
Nagoya Mathematical Journal (1)
Canadian Mathematical Society (1)
Nestle Foundation - enLINK (1)
Two general series identities involving modified Bessel functions and a class of arithmetical functions
Zeta and $L$-functions: analytic theory
Multiplicative number theory
Bruce C. Berndt, Atul Dixit, Rajat Gupta, Alexandru Zaharescu
Journal: Canadian Journal of Mathematics , First View
Published online by Cambridge University Press: 10 October 2022, pp. 1-31
We consider two sequences $a(n)$ and $b(n)$, $1\leq n<\infty $, generated by Dirichlet series
$$ \begin{align*}\sum_{n=1}^{\infty}\frac{a(n)}{\lambda_n^{s}}\qquad\text{and}\qquad \sum_{n=1}^{\infty}\frac{b(n)}{\mu_n^{s}},\end{align*} $$
satisfying a familiar functional equation involving the gamma function $\Gamma (s)$. Two general identities are established. The first involves the modified Bessel function $K_{\mu }(z)$, and can be thought of as a 'modular' or 'theta' relation wherein modified Bessel functions, instead of exponential functions, appear. Appearing in the second identity are $K_{\mu }(z)$, the Bessel functions of imaginary argument $I_{\mu }(z)$, and ordinary hypergeometric functions ${_2F_1}(a,b;c;z)$. Although certain special cases appear in the literature, the general identities are new. The arithmetical functions appearing in the identities include Ramanujan's arithmetical function $\tau (n)$, the number of representations of n as a sum of k squares $r_k(n)$, and primitive Dirichlet characters $\chi (n)$.
Determinants of hypertension in Nepal using odds ratios and prevalence ratios: an analysis of the Demographic and Health Survey 2016
Rajat Das Gupta, Animesh Talukder, Shams Shabab Haider, Gulam Muhammed Al Kibria
Journal: Journal of Biosocial Science / Volume 53 / Issue 4 / July 2021
This cross-sectional study investigated the factors associated with hypertension among Nepalese adults aged 18 years or above using data from the Nepal Demographic and Health Survey 2016. Prevalence ratios (PRs) and odds ratios (ORs) were obtained using log-binomial regression and logistic regression, respectively. Initially, unadjusted PRs and ORs were obtained. The variables that yielded a significance level below 0.2 in unadjusted analyses were included in the multivariable analysis. The overall prevalence of hypertension among the 13,393 participants (58% male and 61.2% urban) was 21.1% (n = 2827). In the adjusted analysis, those aged 30–49 years (adjusted PR [APR]: 3.1, 95% Confidence Interval (CI): 2.6, 3.7; adjusted OR [AOR]: 3.6, 95% CI: 2.9, 4.5), 50–69 years (APR: 5.3, 95% CI: 4.4, 6.6; AOR: 8.2, 95% CI: 6.4, 10.4) and ≥70 years (APR: 7.3, 95% CI: 5.8, 9.2; AOR: 13.6, 95% CI: 10.1, 18.3) were more likely to be hypertensive than younger participants aged 18–29 years. Males (APR: 1.3, 95% CI: 1.2, 1.4; AOR: 1.5, 95% CI: 1.3, 1.7), overweight/obese participants (APR: 1.8, 95% CI: 1.7, 2.0; AOR: 2.4, 95% CI: 2.2, 2.8) and those in the richest wealth quintile (APR: 1.3, 95% CI: 1.1, 1.5; AOR: 1.5, 95% CI: 1.1, 1.9) had higher prevalences and odds of hypertension than their female, normal weight/underweight and poorest wealth quintile counterparts, respectively. Those residing in Province 4 (APR: 1.2, 95% CI: 1.0, 1.5; AOR: 1.4, 95% CI: 1.1, 1.8) and Province 5 (APR: 1.2, 95% CI: 1.0, 1.4; AOR: 1.3, 95% CI: 1.1, 1.7) were more likely to be hypertensive than those residing in Province 1. The point estimate was inflated more in magnitude by ORs than by PRs, but the direction of association remained the same. Public health programmes in Nepal aimed at preventing hypertension should raise awareness among the elderly, males, individuals in the richest wealth quintile and the residents of Provinces 4 and 5.
Nationally representative surveys show gradual shifting of overweight and obesity towards poor and less-educated women of reproductive age in Nepal
Ipsita Sutradhar, Tahmina Akter, Mehedi Hasan, Rajat Das Gupta, Hemraj Joshi, Mohammad Rifat Haider, Malabika Sarker
Journal: Journal of Biosocial Science / Volume 53 / Issue 2 / March 2021
Overweight and obesity are considered major public health concerns all over the world. They have the potential to increase the risk of developing non-communicable diseases in reproductive age women, increasing their risk of pregnancy related complications and adverse birth outcome. This study was carried out to identify the trend of prevalence of overweight and obesity, along with their determinants, among reproductive age women (15–49 years) in Nepal. Data were taken from the nationally representative 2006, 2011 and 2016 Nepal Demographic and Health Surveys (NDHSs). Women were considered to be overweight or obese when their BMI was 23.0–27.5 kg/m2 or ≥27.5 kg/m2, respectively. Univariate, bivariate and multivariate analyses were performed, with significance taken at p<0.05. The prevalences of overweight and obesity both showed rising trends in women of reproductive age in Nepal from 2006 to 2016, particularly among those with no education, only primary education and poor women. The presence of overweight and obesity was found to be significantly associated with the sample women's age, educational status, wealth index, place of residence, ecological zone, developmental region, number of household members, marital status and ethnicity. In 2016 one in every three women of reproductive age in Nepal was either overweight or obese. As overweight and obesity have detrimental effects on women's health, the Government of Nepal, in collaboration with other government and non-government organizations, should take action to halt the rising trends in overweight and obesity in the country.
Determinants of diabetes in Bangladesh using two approaches: an analysis of the Demographic and Health Survey 2011
Krystal K. Swasey, Rajat Das Gupta, Jannatun Nayeem, Gulam Muhammed Al Kibria
This cross-sectional study analysed data from the Bangladesh Demographic and Health Survey 2011 to investigate factors associated with diabetes in Bangladesh. Data were analysed using logistic and log-binomial regressions to estimate odds ratios (ORs) and prevalence ratios (PRs), respectively. Among the 7544 respondents aged ≥35 years, the estimated prevalence of diabetes was 11.0%. In the adjusted analysis, survey participants in the age group 55–64 years (adjusted PR [APR]: 1.8, 95% Confidence Interval (CI): 1.4, 2.2; adjusted OR [AOR]: 1.9, 95% CI: 1.5, 2.5) and those with at least secondary education level (APR: 1.3, 95% CI: 1.0, 1.6; AOR: 1.3, 95% CI: 1.0, 1.7) were more likely to have diabetes than those in the age group 35–44 years and those with no education. Furthermore, respondents living in Khulna (APR: 0.5, 95% CI: 0.4, 0.6; AOR: 0.4, 95% CI: 0.3, 0.6) were less likely to have diabetes than people living in Barisal. While adjusted estimates of PR and OR were similar in terms of significance of association, the magnitude of the point estimate was attenuated in PR compared with the OR. Nevertheless, the measured factors still had a significant association with diabetes in Bangladesh. The results of this study suggest that Bangladeshi adults would benefit from increased education on, and awareness of, the risk factors for diabetes. Focused public health intervention should target these high-risk populations.
Gender differences in hypertension awareness, antihypertensive use and blood pressure control in Nepalese adults: findings from a nationwide cross-sectional survey
Rajat Das Gupta, Shams Shabab Haider, Ipsita Sutradhar, Mehedi Hasan, Hemraj Joshi, Mohammad Rifat Haider, Malabika Sarker
Journal: Journal of Biosocial Science / Volume 52 / Issue 3 / May 2020
The objective of this cross-sectional study was to determine the gender differences in hypertension awareness, antihypertensive use and blood pressure (BP) control among the adult Nepalese population (≥18 years) using data from the nationally representative Nepal Demographic and Health Survey 2016. A weighted sample of 13,393 adults (5620 males and 7773 females) was included in the final analysis. After conducting descriptive analyses with the selective explanatory variable, multivariable logistic regression analysis was performed to assess the association between the outcome variable and the explanatory variables. The strength of the association was expressed in adjusted odds with 95% confidence intervals. A higher proportion of women had their BP checked (87.7% females vs 73.0% males, p<0.001) and were aware of their raised BP (43.9% females vs 37.1% males, p<0.001) compared with men. Although female hypertensive individuals had a higher prevalence of antihypertensive medication use than their male counterparts (50.1% females vs 47.5% males), a higher proportion of male hypertensive participants had their BP controlled (49.2% females vs 53.5% males). Women with the poorest wealth index had a lower prevalence of antihypertensive use than their male counterparts. The odds of having their own BP measured increased with age among men but decreased with age among women. The household wealth index was positively associated with the odds of BP measurement, awareness of own BP and antihypertensive use. This study revealed that although women had a higher prevalence of hypertension awareness and antihypertensive medication use, the practice did not translate into better BP control. Inequality in antihypertensive medication use was observed among the poorest wealth quintiles. Public health programmes in Nepal should focus on reducing these inequalities. Further research is needed to learn why females have poorer control of BP, despite having higher antihypertensive medication use.
Differences in prevalence and determinants of hypertension according to rural–urban place of residence among adults in Bangladesh
Gulam Muhammed Al Kibria, Krystal Swasey, Rajat Das Gupta, Allysha Choudhury, Jannatun Nayeem, Atia Sharmeen, Vanessa Burrowes
Published online by Cambridge University Press: 19 December 2018, pp. 578-590
This cross-sectional study analysed Bangladesh Demographic and Health Survey 2011 data with the aim of investigating the prevalence of, and risk factors for, hypertension in individuals aged over 35 by rural–urban place of residence. After estimation of the stratified prevalence of hypertension by background characteristics, multivariable logistic regression analysis was conducted to calculate the adjusted odds (AORs) and 95% confidence intervals (CIs) for selected factors. Of the 7839 participants, 1830 were from urban areas and 6009 from rural areas. The overall prevalence of hypertension was 32.6% (95% CI: 30.5–34.8) in urban areas and 23.6% (95% CI: 22.5–24.7) in rural areas. The prevalence and odds of hypertension increased with increasing age, female sex, concomitant diabetes and overweight/obesity and richer wealth status in both urban and rural regions. Although residence in Khulna and Rangpur divisions and higher education level were associated with increased odds of hypertension in urban regions, this was not the case in rural regions (p>0.05). Residence in Sylhet and Chittagong divisions had lower odds of hypertension in rural regions. Furthermore, the proportions of overweight/obese, diabetic and higher wealth status participants were higher in urban than in rural regions. The prevalence and odds of hypertension were found to be associated with several common factors after stratifying by place of residence. Some of these factors are more concentrated in urban regions, so urban residents with these risk factors need to be made more aware of these in order to control hypertension in Bangladesh. Public health programmes also need to be tailored differently for urban and rural regions, based on the different distribution of these significant factors in the two areas.
GENERALIZED LAMBERT SERIES, RAABE'S COSINE TRANSFORM AND A GENERALIZATION OF RAMANUJAN'S FORMULA FOR $\unicode[STIX]{x1D701}(2m+1)$
Diophantine approximation, transcendental number theory
ATUL DIXIT, RAJAT GUPTA, RAHUL KUMAR, BIBEKANANDA MAJI
Journal: Nagoya Mathematical Journal / Volume 239 / September 2020
Print publication: September 2020
A comprehensive study of the generalized Lambert series $\sum _{n=1}^{\infty }\frac{n^{N-2h}\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)},0<a\leqslant 1,~x>0$, $N\in \mathbb{N}$ and $h\in \mathbb{Z}$, is undertaken. Several new transformations of this series are derived using a deep result on Raabe's cosine transform that we obtain here. Three of these transformations lead to two-parameter generalizations of Ramanujan's famous formula for $\unicode[STIX]{x1D701}(2m+1)$ for $m>0$, the transformation formula for the logarithm of the Dedekind eta function and Wigert's formula for $\unicode[STIX]{x1D701}(1/N),N$ even. Numerous important special cases of our transformations are derived, for example, a result generalizing the modular relation between the Eisenstein series $E_{2}(z)$ and $E_{2}(-1/z)$. An identity relating $\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$ is obtained for $N$ odd and $m\in \mathbb{N}$. In particular, this gives a beautiful relation between $\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and $\unicode[STIX]{x1D701}(11)$. New results involving infinite series of hyperbolic functions with $n^{2}$ in their arguments, which are analogous to those of Ramanujan and Klusch, are obtained.
Independent and interactive effects of plant sterols and fish oil n-3 long-chain polyunsaturated fatty acids on the plasma lipid profile of mildly hyperlipidaemic Indian adults
Shweta Khandelwal, Isabelle Demonty, Panniyammakal Jeemon, Ramakrishnan Lakshmy, Rajat Mukherjee, Ruby Gupta, Uma Snehi, Devasenapathy Niveditha, Yogendra Singh, Henk C. M. van der Knaap, Santosh J. Passi, Dorairaj Prabhakaran, K. Srinath Reddy
Journal: British Journal of Nutrition / Volume 102 / Issue 5 / 14 September 2009
Published online by Cambridge University Press: 14 September 2009, pp. 722-732
Print publication: 14 September 2009
The present study was designed to evaluate the independent and interactive effects of a once-a-day yoghurt drink providing 2 g plant sterols/d and capsules providing 2 g fish oil n-3 long-chain (LC) PUFA/d on plasma lipids, apolipoproteins and LDL particle size. Following a 2-week run-in period, 200 mildly hypercholesterolaemic Indian adults aged 35–55 years were randomised into one of four groups of a 2 × 2 factorial, double-blind controlled trial. The 4-week treatments consisted of (1) control yoghurt drink and control capsules, (2) control yoghurt drink and fish oil capsules, (3) plant sterol-enriched yoghurt drink and control capsules, or (4) plant sterol-enriched yoghurt drink and fish oil capsules. Blood was drawn before and after the 4-week intervention. Changes in health status, lifestyle and dietary habits, and daily compliance were recorded. The main effects of plant sterols were a 4·5 % reduction in LDL-cholesterol and a 15 % reduction in TAG without a significant change in HDL-cholesterol. Overall, fish oil n-3 LC-PUFA did not significantly affect cholesterol concentrations but reduced TAG by 15 % and increased HDL-cholesterol by 5·4 %. The combination significantly lowered TAG by 15 % v. control. No significant interaction between plant sterols and n-3 LC-PUFA was observed on plasma cholesterol concentrations. In conclusion, once-a-day intake of 2 g plant sterols/d in a yoghurt drink, 2 g fish oil n-3 LC-PUFA/d in capsules, and their combination had beneficial effects on the lipid profile of mildly hypercholesterolaemic Indian adults. The potent hypotriacylglycerolaemic effect of plant sterols observed in the present study and this population warrants additional investigation. | CommonCrawl |
\begin{document}
\title[On the nullity distribution of a submanifold of a space form] {On the nullity distribution
of a submanifold of a space form} \author[Francisco Vittone]{Francisco Vittone}
\begin{abstract}If $M$ is a submanifold of a space form, the nullity distribution $\mathcal{N}$ of its second fundamental form is (when defined) the common kernel of its shape operators. In this paper we will give a local description of any submanifold of the Euclidean space by means of its nullity distribution. We will also show the following global result: if $M$ is a complete, irreducible submanifold of the Euclidean space or the sphere then its complementary distribution $\mathcal{N}^{\bot}$ is completely non integrable. This means that any two points in $M$ can be joined by a curve everywhere perpendicular to $\mathcal{N}$. We will finally show that this statement is false for a submanifold of the hyperbolic space.
\end{abstract}
\maketitle
\section{Introduction} Let $M^{n}$ be a submanifold of a space form $Q^{n+k}$. The nullity distribution $\mathcal{N}$ of the second fundamental form of $M$ is defined as the common kernel of the shape operators of $M$. The index of nullity (or relative nullity) of $M$ at $p$ is the dimension of $\mathcal{N}_{p}$. It is well known, from Codazzi equation, that $\mathcal{N}$ is an autoparallel distribution restricted to the open and dense subset of $M$ where the index of nullity is locally constant. Moreover, its integral manifolds are totally geodesic submanifolds of the ambient space $Q^{n+k}$. If $M$ is complete, and one restricts to the open subset $U$ of points of $M$ where the index of nullity is minimal, then the integral manifolds of $\mathcal{N}$ through points of $U$ are also complete (see for instance \cite[Ch. 5]{daj} or \cite{ferus}).
Observe that for an Euclidean submanifold, the nullity distribution arises naturally in many problems since $\mathcal{N}=\ker(dG)$, where $G:M\to G_{k}(\mathbb{R}^{n+k})$ is the Gauss map. Moreover, there are many examples of complete submanifolds of the Euclidean space with constant index of nullity and some of them can be obtained from the so called Gauss parametrizations, which involve the Gauss map (see \cite{dajgrom}).
In this paper we will study the perpendicular distribution $\mathcal{H}:=(\mathcal{N})^{\bot}$.
For a general distribution $\mathcal{D}$ on a Riemannian manifold, it is an interesting problem to decide whether it is completely non integrable, in the sense that any two points can be joined by a curve always tangent to $\mathcal{D}$ (this means that the Carnot-Caratheodory distance, associated to $\mathcal{D}$, is finite \cite{gromov}). For the case of submanifolds, a very important result about completely non-integrability, is the so called \textit{Homogeneous Slice Theorem} \cite{hot}, which has many important applications (see \cite{obc}, \cite{tho}). It states, in particular, that for an irreducible complete (connected) isoparametric submanifold of the sphere, one can join any two points by a curve always perpendicular to any given eigendistribution of its shape operator.
Our main goal is to prove a general global result about the non-integrability of the distribution $\mathcal{H}$ for submanifolds of the Euclidean space or the sphere. Namely,
\begin{theor} Let M be an immersed, complete, irreducible submanifold of the Euclidean space or the sphere with constant index of nullity. Then any two points of $M$ can be joined by a curve always perpendicular to the nullity distribution. \label{globalthm} \end{theor} Observe that, in general, the canonical projection $\mathbf{pr}:M\to M/\mathcal{N}$, where $M/\mathcal{N}$ is the set of all maximal integral manifolds of $\mathcal{N}$, is not a Riemannian submersion.
If we drop the assumption that the index of nullity is constant, then Theorem \ref{globalthm} still holds on any connected component of the open subset where this index is minimal. On the other hand, the assumption of completeness can not be removed. In fact, there are abundant many local counter-examples of the above theorem obtained as the union of suitable parallel manifolds. Moreover, Theorem \ref{localth} shows that any local counter-example arises in this way.
Theorem \ref{globalthm} is not true for submanifolds of the hyperbolic space (see remark \ref{hyp}).
For infinite dimensional isoparametric Hilbert submanifolds of codimension at least two, a similar result to Theorem \ref{globalthm} was proved by Heinzte and Liu in \cite{Heintze}, using strongly the isoparamatricity condition. This was a crucial step in the proof of the homogeneity of this type of submanifolds \cite{Heintze}. Theorem \ref{globalthm} shows that, in finite dimension, the non-integrability of the distribution $\mathcal{N}^{\bot}$ is a very general global fact, that does not depend on any extra property of the submanifold.
\section{Basic definitions and general properties}
\subsection{The nullity distribution} Let $M$ be an $n$-dimensional (immersed) Riemannian submanifold of a (simply connected) space form, i.e., the Euclidean space $\mathbb{R}^{n+k}$, the sphere $\mathbb{S}^{n+k}$ or the hyperbolic space $\mathbb{H}^{n+k}$. We denote by $\nabla$ the Levi-Civita connection of $M$ and by $\widetilde{\nabla}$ the Levi-Civita connection of the ambient space form. We will always denote by $\nu M:=TM^{\bot}$ the normal bundle of $M$ endowed with the normal connection $\nabla^{\bot}$. The second fundamental form of $M$ will be denoted by $\alpha$ and the shape operator by $A$. These two tensors are related by the well known formula $$\left\langle\alpha(X,Y),\xi\right\rangle=\left\langle A_{\xi}X,Y\right\rangle,$$ which is symmetric in $X$ and $Y$, for any $X,Y$ tangent fields and $\xi$ normal field.
The connection $\nabla\oplus\nabla^{\bot}$ in $TM\oplus\nu M$ will be denoted by $\overline{\nabla}$. The Codazzi equation states that $\left\langle (\overline{\nabla}_{X}A)_{\xi}Y,Z\right\rangle$, or equivalently $(\overline{\nabla}_{X}\alpha)(Y,Z)$, is symmetric in $X,Y,Z$.
The \textsl{nullity subspace} of $M$ at $p$ is the subspace $\mathcal{N}_{p}$ of $T_{p}M$ defined by $$\mathcal{N}_{p}:=\{x\in T_{p}M:\alpha(x,\cdot)\equiv 0\}=\bigcap_{\xi\in\nu_{p}M}\ker(A_{\xi}).$$ If $M\subset \mathbb{R}^{n+k}$ then $\mathcal{N}_{p}$ coincides with $\ker(d \mathbf{G}_{p})$ where $\mathbf{G}:M\to G_{k}(\mathbb{R}^{n+k})$ is the Gauss map that assigns to each point $p\in M$ its normal space $\nu_{p}M$.
Let $\mu(p):=\dim(\mathcal{N}_{p})$, which is called the \textsl{index of nullity} of $M$ at $p$. Let $\mathcal{C}$ be the set of points $p\in M$ such that $\mu$ is constant in a neighborhood of $p$. Then it is standard to prove, since $\mu$ can not increase locally, that $\mathcal{C}$ is an open and dense subset of $M$ and so $\mu$ is constant on each connected component of $\mathcal{C}$. Moreover, from Codazzi equation, it follows that $\mathcal{N}:p\to\mathcal{N}_{p}$ defines a $C^{\infty}$ autoparallel distribution (and hence with totally geodesic integral manifolds) on each connected component of $\mathcal{C}$. It is not difficult to see that its integral manifolds are also totally geodesic in the ambient space form. If $M$ is complete, then any (maximal) integral manifold of $\mathcal{N}$ through a point with minimal index of nullity is complete (see \cite{ferus}). Then
\begin{lemma} Let $M$ be a complete Riemannian submanifold of a space form with constant index of nullity. Then $\mathcal{N}$ is a $C^{\infty}$ autoparallel distribution of $M$ whose integral manifolds are complete and totally geodesic in the ambient space. \label{null} \end{lemma}
Under the assumptions of Lemma \ref{null}, denote by $M/\mathcal{N}$ the set of maximal connected integral manifolds of $\mathcal{N}$ and let $\mathbf{pr}:M\to M/\mathcal{N}$ be the projection to the quotient.
Recall that a coordinate chart $(U,\varphi=(x^{1},\cdots,x^{n}))$ of $M$ is called \textsl{plane} for the distribution $\mathcal{N}$ if for each $a=(a^{1},\cdots,a^{n})\in \varphi(U)$, the slice $$S_{a}=\{q\in U:x^{l+1}(q)=a^{l+1},\cdots,x^{n}(q)=a^{n}\}$$ is an integral manifold of $\mathcal{N}$, where $l$ is the constant index of nullity of $M$.
From Frobenius theorem, there exists a plane chart $(U,\varphi)$ around each point that intersects each integral manifold of $\mathcal{N}$ in a disjoint countable union of slices of $(U,\varphi)$. Since the integral manifolds of $\mathcal{N}$ are totally geodesic in the ambient space form, it is not difficult to see that there is a plane chart around each point, that intersects each integral manifold of $\mathcal{N}$ in at most one slice. Then the distribution $\mathcal{N}$ is regular.
We give $M/\mathcal{N}$ the quotient topology and so $\mathbf{pr}$ is open (see \cite{palais}). From the fact that the integral manifolds of $\mathcal{N}$ are totally geodesic in $M$ one has, as it is not difficult to show, that $\mathcal{R}=\{(x,y)\in M\times M: \mathbf{pr}(x)=\mathbf{pr}(y)\}$ is closed in $M\times M$. This implies that $M/\mathcal{N}$ is a Hausdorff space (see \cite{kelley}) and therefore it is a differentiable manifold (see \cite[ThmVIII,ChI]{palais}).
\subsection{Fiber bundle structure.} \label{fibrado}
All throughout this section, $M$ will be a submanifold of the Euclidean space or the sphere.
Recall that given three differentiable manifolds $E, N$ and $F$ we say that $\pi:E\to N$ is a \textit{fiber bundle with standard fiber} $F$, if
\begin{itemize}
\item[i)] $\pi$ is a $C^{\infty}$ suryective map;
\item[ii)] there is an open covering $\mathcal{U}$ of $N$ such that for every $U\in\mathcal{U}$ there exists a differentiable map $\Psi:\pi^{-1}(U)\to F$ such that the function $$\overline{\Psi}:=(\pi,\Psi):\pi^{-1}(U)\to U\times F$$ is a diffeomorphism.
\end{itemize}
The map $\overline{\Psi}$ is called a \textsl{local trivialization} for the fiber bundle.
The projection $\pi$ is a submersion and for every $p\in N$, the fiber $E_{p}=\pi^{-1}(p)$ is an embedded submanifold of $E$ diffeomorphic to $F$. Moreover, if $(U,\overline{\Psi})$ is a local trivialization such that $p\in U$, then the diffeomorphism is given by $\Psi_{|E_{p}}$.
Consider now the group $Diff(F)$ of diffeomorphisms of $F$ and let $(\pi,\Theta)$, $(\pi,\Psi)$ be local trivializations over open sets $U$ and $V$ on $N$. Then the function $f_{\Theta,\Psi}:U\cap V\to Diff(F)$ given by $f_{\Theta,\Psi}(p)=\Theta\circ\Psi^{-1}_{|E_{p}}$ is called the \textsl{transition function} between both trivializations. The fiber bundle $\pi:E\to N$ is said to have \textsl{structure group} $G$ if any transition function takes values in a subgroup $G$ of $Diff(G)$.
Denote by $\mathbb{A}^{n}$ the space $\mathbb{R}^{n}$ with its natural affine structure. A fiber bundle $\pi:E\to N$ with standard fiber $\mathbb{A}^{n}$ is an \textsl{affine bundle} if each fiber $E_{p}$ has an affine space structure such that for every local trivialization $(\pi,\Psi)$, $\Psi_{|E_{p}}:E_{p}\to\mathbb{A}^{n}$ is an affine isomorphism. Equivalently, $\pi:E\to N$ is an affine bundle if it has structure group $Aff(n):=GL(n)\ltimes \mathbb{R}^{n}$, the group of affine transformations of $\mathbb{A}^{n}$ (analogous to \cite[Prop. 1.14]{poor}).
A fiber bundle with standard fiber $\mathbb{S}^{n}$ is called a \textsl{sphere bundle}. Then:
\begin{lemma} Let $M$ be a complete submanifold of the Euclidean space or the sphere with constant index of nullity $l$ and let $\mathcal{N}$ be its nullity distribution. Then $\mathbf{pr}:M\to M/\mathcal{N}$ is an affine bundle if $M$ is a Euclidean submanifold and it is a sphere bundle with structure group $O(l+1)$ if $M$ is a submanifold of the sphere. \end{lemma} \begin{proof} The proof is standard, but we include it since it is difficult to find in the bliography and we will need some of the notation introduced here.
In order to simplify the notation, we will assume that $M$ is a $1-1$ immersed submanifold. Let $(U, \varphi=(x^{1},\cdots,x^{n}))$ be a plane regular chart of $M$ with respect to $\mathcal{N}$, such that $0\in\varphi(U)$. Let $l$ be the constant index of nullity of $M$. Then there exists a unique $(n-l)$-dimensional chart $\overline{\varphi}$ in $M/\mathcal{N}$ with domain $\overline{U}=\mathbf{pr}(U)$ such that $\overline{\varphi}\circ\mathbf{pr}=(x^{l+1},\cdots,x^{n})$ (see \cite{palais}). Define the local section $\sigma:\overline{U}\to \mathbf{pr}^{-1}(\overline{U})$ by $\sigma(r)=\varphi^{-1}(j_{0}(\overline{\varphi}(r)))$, where $j_{0}:\mathbb{R}^{n-l}\to \mathbb{R}^{n}$ is the inclusion $j_{0}(x^{l+1},\cdots,x^{n})=(0,\cdots,0,x^{l+1},\cdots,x^{n})$.
Let us begin with the case $M\subset\mathbb{R}^{n+k}$. Set $M_{r}:=\mathbf{pr}^{-1}(r)$. From Lemma \ref{null}, $M_{r}=p+T_{p}M_{r}$ for any $p\in M_{r}$ (identifying $M_{r}$ with the corresponding subspace of $\mathbb{R}^{n+k}$). Set $X_{i}(r)=(\partial/\partial x^{i})_{\sigma(r)}\in \mathbb{R}^{n+k}$ via this identification. So, if $r\in\overline{U}$ then any element $x$ of $M_{r}$ is of the form $$x=\sigma(r)+\sum_{i=1}^{l}v^{i}X_{i}(r).$$
For $(r,(v^{1},\cdots,v^{l}))\in\overline{U}\times\mathbb{A}^{l}$, define $\rho(r,(v^{1},\cdots,v^{l}))=\sigma(r)+\sum_{i=1}^{l}v^{i}X_{i}(r)$. Then it is not difficult to see that $\rho$ is a diffeormorphism from $\overline{U}\times \mathbb{A}^{l}$ into $\mathbf{pr}^{-1}(\overline{U})$ and so $\Psi=\rho^{-1}$ is a local trivialization for $\mathbf{pr}:M\to M/\mathcal{N}$. It is clear from this construction that transition functions are affine.
If $M\subset\mathbb{S}^{n+k}$. Then $M_{r}$ is the $l$-sphere in the ($l+1$)-dimensional linear subspace \begin{equation} L_{r}:=T_{\sigma(r)}M_{r}\oplus \mathbb{R}\sigma(r) \label{Lr} \end{equation} of $\mathbb{R}^{n+k+1}$ (regarding $M$ as a submanifold of $\mathbb{R}^{n+k+1}$ and identifying $T_{\sigma(r)}M_{r}$ with the corresponding subspace of $\mathbb{R}^{n+k+1}$). Let $\{E_{i}\}$ be the (local) orthonormal frame of $TM$ obtained by applying the Gram-Schmidt orthogonalization process to $\{(\partial/\partial x^{i})\}$. Set $\rho:\overline{U}\times\mathbb{S}^{l}\to \mathbf{pr}^{-1}(\overline{U})$ as $$(r,(v^{1},\cdots,v^{l+1}))\mapsto \sum_{i=1}^{l}v^{i}E_{i}(\sigma(r))+v^{l+1}\sigma(r).$$ Then it is not difficult to see that $\rho$ is a diffeormophism and $\Psi=\rho^{-1}$ is a local trivialization for $\mathbf{pr}:M\to M/\mathcal{N}$. It is clear from construction that the transition functions are in $O(l+1)$. \end{proof}
Given a piece-wise differentiable curve $\widetilde{c}:I\to M$ we say that $\widetilde{c}$ is \textsl{horizontal with respect to $\mathcal{N}$} if $\widetilde{c}\;'(t)\;\bot\;\mathcal{N}_{\widetilde{c}\;(t)}$, for every $t\in I$. Given a curve $c:I\to M/\mathcal{N}$ we say that $\widetilde{c}:I\to M$ is a \textsl{horizontal lift} of $c$ if $\widetilde{c}$ is horizontal and $\mathbf{pr}(\widetilde{c}(t))=c(t)$ for every $t\in I$.
As for the case of a vector bundle with a linear connection, one has that any curve in $M/\mathcal{N}$ can be globally lifted. Namely,
\begin{lemma} Let $c:I\to M/\mathcal{N}$ be a (piece-wise differentiable) curve and let $p$ be any point in $\mathbf{pr}^{-1}(c(0))$. Then there is one and only one horizontal lift $\widetilde{c}$ of $c$ to $M$ such that $\widetilde{c}(0)=p$ (called the \emph{horizontal lift} of $c$ through $p$). \label{horlift} \end{lemma} \begin{proof} Let $c:I\to M/\mathcal{N}$ be any curve in $M/\mathcal{N}$. It is standard to see, from basic ordinary differential equation theory, that it suffices to prove the following: for every $b\in I$ there exists an open interval $J_{b}\subset I$ such that $b\in J_{b}$ and such that for every initial condition $z\in \mathbf{pr}^{-1}(c(b))$, there exists a horizontal curve $\widetilde{c}_{b,z}:J_{b}\to M$ which projects down to $c$ and such that $c_{b,z}(b)=z$.
As for any submersion, we have that for every $z_{0}\in\mathbf{pr}^{-1}(c(b))$ there exists a horizontal lift $\widetilde{c}_{z}$ of $c$ with maximal domain $J_{z_{0}}$ such that $\widetilde{c}_{z}(b)=z$, for every $z$ in a neighborhood of $z_{0}$.
So, if $M\subset \mathbb{S}^{n+k}$, the result follows from the fact that the fibers are compact.
If $M\subset\mathbb{R}^{n+k}$, let $q_{0},q_{1},\cdots,q_{n}$ form an affine frame on $\mathbf{pr}^{-1}(\gamma(b))$. Set $J_{b}=\cap_{i=0}^{n}J_{q_{i}}$. Then if $z\in pr^{-1}(b)$, $z=q_{0}+\sum_{i=1}^{n}v^{i}(q_{i}-q_{0})$ and it is not difficult to see that $c_{b,z}(t)=c_{q_{0}}(t)+\sum_{i=0}^{n}v^{i}(c_{q_{0}}(t)-c_{q_{i}}(t))$ is the curve we were looking for. \end{proof}
We can now define a parallel displacement in $\mathbf{pr}:M\to M\mathcal{N}$. For $r\in M/\mathcal{N}$, set $M_{r}:=\mathbf{pr}^{-1}(r)$. Given a (piece-wise differentiable) curve $c:[0,1]\to M/\mathcal{N}$ we define the $\mathcal{N}$-\textsl{parallel displacement} $\tau^{\mathcal{N}}_{c}:M_{c(0)}\to M_{c(1)}$ as $$\tau^{\mathcal{N}}_{c}(p):=\widetilde{c}_{p}(1)$$ where $\widetilde{c}_{p}$ is the horizontal lift of $c$ through $p$.
Since every horizontal lift $\widetilde{c}(t)$ of $c$ is perpendicular to the family of totally geodesic submanifolds $M_{c(t)}$, one has (see e.g. \cite[Lemma 2.8]{olberger})
\begin{lemma} Let $c:I\to M/\mathcal{N}$ be a curve in $M/\mathcal{N}$. Then the parallel displacement $\tau^{\mathcal{N}}_{c}:M_{c(0)}\to M_{c(1)}$ is an isometry \qed \end{lemma} If $r\in M/\mathcal{N}$, we denote by $\Omega(r)$ (resp. $\Omega^{0}(r)$) the set of (piece-wise smooth) loops (resp. null-homotopic loops) in $M/\mathcal{N}$ based at $r$. The \textsl{holonomy group} (associated to $\mathcal{N}$) based at $r\in M/\mathcal{N}$ is $$\Phi_{r}:=\{\tau^{\mathcal{N}}_{c}:c\in\Omega(r)\}\subset \text{Iso}(M_{r})$$ and the \textsl{restricted holonomy group} (associated to $\mathcal{N}$) based at $r$ is the connected subgroup $$\Phi^{0}_{r}:=\{\tau^{\mathcal{N}}_{c}:c\in\Omega^{0}(r)\}\subset \text{Iso}_{0}(M_{r}).$$ It is standard to prove, as in the case of a linear connection (see \cite[Teor. 2.25]{poor} or \cite{kn}) that $\Phi_{r}$ and $\Phi^{0}_{r}$ are Lie groups and that $\Phi^{0}_{r}$ is the connected component of the identity in $\Phi_{r}$.
The \textsl{local holonomy group} (associated to $\mathcal{N}$) based at $r\in M/\mathcal{N}$ is defined by $$\Phi^{loc}_{r}=\bigcap\Phi^{0}(r,\overline{U})$$ varying $\overline{U}$ among all open neighborhoods of $r$, where $\Phi^{0}(r,\overline{U})=\{\tau^{\mathcal{N}}_{c}\in\Phi^{0}_{r}:c\subset\overline{U}\}$. One has that there is an open neighborhood $\overline{U}$ of $r$ such that $\Phi^{loc}_{r}=\Phi^{0}(r,\overline{V})$ for every neighborhood $\overline{V}$ of $r$ contained in $\overline{U}$ (see \cite[Prop. 10.1]{kn}). Let $$(\tau^{\mathcal{N}}_{c})^{*}(\Phi^{loc}_{r}):=\{(\tau^{\mathcal{N}}_{c})^{-1}\circ\tau^{\mathcal{N}}_{\alpha}\circ\tau^{\mathcal{N}}_{c}:\tau^{\mathcal{N}}_{\alpha}\in\Phi^{loc}_{r}\}.$$ Then one has the following Ambrose-Singer type theorem, which will be very useful to prove our main global result.
\begin{lemma} Let $\mathcal{C}$ be a dense subset of $M/\mathcal{N}$. Then the restricted holonomy group $\Phi^{0}_{r}$ is generated by the groups $\tau^{\mathcal{N}}_{c}(\Phi^{loc}_{c(1)})$ varying $c$ among all piece-wise differentiable curves in $M/\mathcal{N}$ such that $c(0)=r$ and $c(1)\in \mathcal{C}$. \label{ambrose} \end{lemma}
\begin{proof} The proof is similar to the case of a linear connection and we shall indicate its main steps.
For each $r\in M/\mathcal{N}$, set $M_{r}=\mathbf{pr}^{-1}(r)$.
We will start assuming that $M\subset\mathbb{R}^{n+k}$. Let $A(M_{r})$ denote the set of affine isomorphisms $h:\mathbb{A}^{l}\to M_{r}$, and set $A(M):=\bigcup_{r\in M/\mathcal{N}}A(M_{r})$. Let $\pi:A(M)\to M/\mathcal{N}$ be the canonical projection (i.e, $\pi(h)=r$ if $h\in A(M_{r})$). Then $A(M)$ is a principal fiber bundle with structure group $Aff(l)$ (see \cite[Ch. III, sec. 3]{kn}).
As for the case of the connection on the frame bundle defined by a vector bundle with a linear connection, one can prove that there is a unique connection $\Gamma$ on $A(M)$ such that the corresponding parallel displacement $\widetilde{\tau}$ is related to $\tau^{\mathcal{N}}$ in the following way (see \cite{poor}). If $h\in A(M_{r})$, then $\{h(0),h(e_{1}),\cdots,h(e_{l})\}$ is an affine frame on $M_{r}$, where $e_{i}$ are the canonical versors in $\mathbb{R}^{l}$. Let $c:I\to M/\mathcal{N}$ be a differentiable curve such that $c(0)=r$ and let $q_{0}=\tau^{\mathcal{N}}_{c}(h(0))$, $q_{i}=\tau^{\mathcal{N}}_{c}(h(e_{i}))$, then $\widetilde{\tau}_{c}(h)$ is the affine isomorphism from $\mathbb{A}^{l}$ to $M_{c(1)}$ that maps $0$ into $q_{0}$ and $e_{i}$ into $q_{i}$, $i=1,\cdots, l$.
Given $h\in A(M)$, let $\widetilde{\Phi}^{0}_{h}$ and $\widetilde{\Phi}^{loc}_{h}$ denote the restricted and local holonomy groups of $\Gamma$ based at $h$, respectively (recall that $\widetilde{\Phi}^{0}_{h}$ is the set of elements $g\in Aff(l)$ such that $\widetilde{\tau}_{c}(h)=h\circ g$ for some curve $c\in\Omega^{0}(\pi(h))$). If $\pi(h)=r$ then the map $T_{h}(g)=h\circ g\circ h^{-1}$ defines an isomorphism from $\widetilde{\Phi}^{0}_{h}$ to $\Phi^{0}_{r}$ and from $\widetilde{\Phi}^{loc}_{h}$ to $\Phi^{loc}_{r}$.
Now, without almost any modification of the proof of Ambrose-Singer holonomy theorem \cite[Thm. 8.1]{kn} and its consequence \cite[Thm. 10.2]{kn} we can prove that the restricted holonomy group $\widetilde{\Phi}^{0}_{h}$ is generated by the local holonomy groups $\widetilde{\Phi}^{loc}_{f}$ varying $f$ in any dense subset $\mathcal{U}$ of the holonomy bundle $P(h)$ (i.e, the set of elements that can be joined to $h$ by a horizontal curve). So $\Phi^{0}_{\pi(h)}$ is generated by the groups $T_{h}(\widetilde{\Phi}^{loc}_{f})$ varying $f$ as before. Now let $\mathcal{U}=\pi^{-1}(\mathcal{C})\cap P(h)$. If $f\in \mathcal{U}$, then $f=\widetilde{\tau}_{c}(h)$ for some $c:I\to M/\mathcal{N}$ such that $c(0)=\pi(h)$ and $c(1)=\pi(f)\in\mathcal{C}$. From the way $\widetilde{\tau}$ and $\tau^{\mathcal{N}}$ are related it is not difficult to prove that if $g\in \widetilde{\Phi}^{loc}_{f}$ then $g=f^{-1}\circ\tau^{\mathcal{N}}_{\alpha}\circ f$ for some $\tau^{\mathcal{N}}_{\alpha}\in\Phi^{loc}_{\pi(f)}$ and $T_{h}(g)=(\tau^{\mathcal{N}}_{c})^{-1}\circ \tau^{\mathcal{N}}_{\alpha}\circ\tau^{\mathcal{N}}_{c}$. So $T_{h}(\widetilde{\Phi}^{loc}_{f})=\tau^{\mathcal{N}}_{c}(\Phi^{loc}_{c(1)})$ as we wanted to prove.
If $M\subset \mathbb{S}^{n+k}$, consider the principal fiber bundle $A(M):=\bigcup_{r\in M/\mathcal{N}}A(M_{r})$ with structure group $O(l+1)$ such that $A(M_{r})$ is the set of isometries from $\mathbb{S}^{l}$ to $M_{r}$. Observe that the elements of $A(M)$ are in a $1-1$ correspondence with the set of orthonormal basis of the subspace $L_{r}$ defined by (\ref{Lr}). The proof follows in the same way as for a submanifold of the Euclidean space. \end{proof}
\subsection{Foliating a spherical tube by holonomy tubes}\label{tuboesferico} The technics of this section are mainly inspired on \cite{ocds}.
Let $M$ be a submanifold of $\mathbb{R}^{n}$.
Assume that there exists a positive real number $\varepsilon$ such that the spherical tube $$N:=S_{\varepsilon}(M)=\{q+\xi_{q}:q\in M, \xi_{q}\in\nu_{q}M, \left\|\xi_{q}\right\|=\varepsilon\}$$ is a well defined hypersurface of $\mathbb{R}^{n}$ (locally this is always true). Consider the canonical projection $$ \pi: N\to M,\ \ \
q+\xi_{q} \stackrel{\pi}{\mapsto} q $$ and the (radial) parallel normal vector field $\Psi$ on $N$ given by $$\Psi(x)=\pi(x)-x.$$ Then $M$ is the parallel focal manifold $N_{\Psi}$ to $N$ and $\pi$ is the usual parallel focal map. Since we will work locally, both in $M$ and in $N$, we may also assume that $N$ has constant index of nullity.
Let $E_{0}=\ker(\hat{A}_{\Psi})$, where by $\hat{A}$ we denote the shape operator of $N$. Then $E_{0}$ is the nullity distribution of $N$, since $N$ is a hypersurface.
For each $x\in N$, set $$S(x)=\pi^{-1}(\pi(x)).$$ Let $E_{1}=\ker(Id-\hat{A}_{\Psi})=\ker(d\pi)$. Then $E_{1}(x)=T_{x}S(x)$ for every $x\in N$.
Regard $N$ and $M$ as submanifolds of the ($n+2$)-Lorentzian space $\mathbb{L}^{n+2}$, identifying $\mathbb{R}^{n}$ with an $n$-dimensional horosphere of the hyperbolic space $\mathbb{H}^{n+1}$. Denote by $\eta$ the radial normal vector field $\eta(x)=-x$ to $\mathbb{H}^{n+1}$ and set $\widetilde{\Psi}:=\delta\Psi+\eta$, for some small $\delta$ such that $\widetilde{\Psi}$ is timelike. Then $$\ker(Id-\hat{A}_{\widetilde{\Psi}})=E_{0}.$$ We can foliate $N$ by the holonomy tubes $$H(x)=(N_{\widetilde{\Psi}})_{-\widetilde{\Psi}(x)}\subset N$$ (locally, see \cite{obc}). We shall further assume that these holonomy tubes have all the same dimension, since we work locally.
If $x,y\in N$, we will denote $x\sim y$ if $x$ and $y$ can be joined by a differential curve in $N$ everywhere normal to $E_{0}$. Then $H(x)$ is locally given by $$H(x)=\{y\in N:x\sim y\}$$ (see \cite{ocds}, cf. \cite{hot}). Since for every $x\in N$, $TS(x)\;\bot\; E_{0}$ we get that $$S(x)\subset H(x).$$
We now consider the distribution $\widetilde{\nu}$ on $N$ given by the normal spaces in $N$ to the holonomy tubes $H(x)$. We will need the following result from \cite[Prop. 2]{ocds} \begin{lemma} \cite{ocds} With the above notations, \begin{enumerate} \item the distribution $\widetilde{\nu}$ is autoparallel, invariant under the shape operator of $N$ and contained in the nullity of $N$. Moreover, if $\widetilde{\Sigma}(x)$ is the integral manifold of $\widetilde{\nu}$ through $x$, then $$\widetilde{\Sigma}(x)=(x+\nu_{x}H(x))\cap N.$$
\item The restriction of $\widetilde{\nu}$ to any $H(x)$ is a parallel and flat sub-bundle of $\nu_{0}H(x)$, the maximal parallel flat sub-bundle of $\nu H(x)$. Moreover $\widetilde{\Sigma}(y)$ moves parallel in the normal connection of the holonomy tube $H(x)$. \label{ellema1} \item If $x\in\widetilde{\Sigma}(q)$, then there is a parallel normal field $\varsigma$ to $H(q)$ such that $\varsigma(q)=x-q$ and such that $H(x)=H(q)_{\varsigma}$. \label{ellema2} \end{enumerate} \label{ellema} \qed \end{lemma}
We aim to prove that $\widetilde{\Sigma}$, and hence $\widetilde{\nu}$, are constant along the fibers of $\pi$.
Note that $H(x)$ has flat normal bundle, since $$\nu H(x)=\widetilde{\nu}_{|H(x)}\oplus\nu N_{|H(x)}=\widetilde{\nu}_{|H(x)}\oplus\mathbb{R}\Psi_{|H(x)}.$$
Observe that $\Psi$ can be regarded as the curvature normal associated to the eigenvalue $1$ of the shape operator $\hat{A}_{\Psi}$ of the hypersurface $N$.
On the other hand, $TN_{|H(x)}=\widetilde{\nu}_{|H(x)}\oplus TH(x)$ with $\widetilde{\nu}$ $\hat{A}$-invariant. Then $H(x)$ is $\hat{A}$-invariant. Finally, since $S(x)\subset H(x)$ we get that $(E_{1})_{|H(x)}\subset TH(x)$. It then follows that $\overline{\Psi}:=\Psi_{|H(x)}$ is a parallel curvature normal of $H(x)$ for every $x\in N$ (see Lemma $1$ in \cite{ocds}).
Let us consider $\widetilde{\Sigma}(x)$, the totally geodesic integral manifold of $\widetilde{\nu}$ through $x$. Since $\widetilde{\nu}\subset E_{0}$, then $T\widetilde{\Sigma}(x)$ is contained in the nullity distribution of $N$ and therefore $\widetilde{\Sigma}(x)$ is totally geodesic as a submanifold of $\mathbb{R}^{n}$ (recall that the integral manifolds of the nullity distribution are totally geodesic in the ambient space).
Fix $x\in N$ and let $y\in \widetilde{\Sigma}(x)$. Let $\varsigma$ be the parallel normal vector field to $H(x)$ such that $\varsigma(x)=y-x$ given by Lemma \ref{ellema}, (\ref{ellema1}). Let now $z\in H(x)$. We shall see that $\varsigma$ is constant in the ambient space along $S(z)\subset H(x)$.
In fact, since $\overline{\Psi}$ and $\varsigma$ are both parallel and $\varsigma$ is tangent to the totally geodesic submanifolds $\widetilde{\Sigma}$, we get that $\left\langle \overline{\Psi}, \varsigma\right\rangle\equiv 0$. On the other hand, given an arbitrary curve $c(t)\subset S(z)$, since $T\widetilde{\Sigma}$ is contained in the nullity of $N$, one has $$\frac{d}{dt}\varsigma(c(t))=A^{H(x)}_{\varsigma}c'(t)=\left\langle \varsigma,\overline{\Psi} \right\rangle c'(t)\equiv 0.$$ So $\varsigma$ is constant along $c$ in the Euclidean ambient space.
It now follows from Lemma \ref{ellema}, (\ref{ellema1}) that
if $z\in H(x)$ and $w\in S(z)$, then \begin{equation} \widetilde{\Sigma}(z)=\widetilde{\Sigma}(w)+(z-w). \label{sigma} \end{equation} Observe also that, since $\widetilde{\Sigma}(x)$ is contained in an integral manifold of the nullity distribution of $N$, then the parallel normal field $\Psi$ is constant in the ambient space along $\widetilde{\Sigma}(x)$. So, if $z\in H(x)$, since $z+\varsigma(z)\in \widetilde{\Sigma}(z)$, then \begin{equation} \Psi(z)=\Psi(z+\varsigma(z)). \label{proj} \end{equation}
Equation (\ref{sigma}) implies that $\widetilde{\Sigma}$, and hence $\widetilde{\nu}$, are constant along the fibers of $\pi$. And equation (\ref{proj}) implies that $\widetilde{\nu}$ projects down to a well defined distribution on $M$. Therefore we get the following lemma which is standard to prove (cf. \cite[Section 2.5]{ocds}). \begin{lemma} The distribution $\widetilde{\nu}$ projects down to a $C^{\infty}$ integrable distribution $\nu^{*}=\pi_{*}(\widetilde{\nu})$ in $M$ which is autoparallel and contained in the nullity distribution of $M$. If $p\in M$ then $\Sigma^{*}(p)$, the integral manifold of $\nu^{*}$ through $p$, is a totally geodesic submanifold of the Euclidean ambient space and for any $x\in \pi^{-1}(p)$ $$\Sigma^{*}(p)=\widetilde{\Sigma}(x)+\Psi(x).$$ The orthogonal complementary distribution $\mathcal{H}^{*}$ to $\nu^{*}$ in $M$ is integrable, invariant under the shape operators of $M$ and the integral manifold through $p\in M$ locally coincides with $\pi(H(x))$, for any $x\in\pi^{-1}(p)$. Moreover, the restriction of $\nu^{*}$ to $\pi(H(x))$ is a parallel and flat sub-bundle of the normal space $\nu(\pi(H(x)))$ in the ambient space. \label{lema1} \qed \end{lemma}
\begin{rem} \emph{ As a consecuence of the previous lemma, one gets that any parallel normal vector field to $H(x)$ (tangent to $N$) projects down to a parallel normal vector field to $\pi(H(x))$.} \label{rem1} \end{rem} \begin{rem} \emph{Observe that since $\nu^{*}\subset \mathcal{N}$, then $\mathcal{N}^{\bot}$ is contained in $\mathcal{H}^{*}$, which is integrable (unlike $\mathcal{N}^{\bot}$). This will be a key point to prove both the local and the global results. } \end{rem}
\subsection{Some remarks on polar actions} Let $Q$ be a space form. A Lie group $G\subset Iso(Q)$ is said to act polarly on $Q$ if there exists a complete, embedded and close submanifold $\Sigma$ that intersects each orbit of $G$ and is perpendicular to orbits at intersection points. The submanifold $\Sigma$ is called a section and it must be totally geodesic. The major property of polar actions is that maximal dimensional orbits are isoparametric submanifolds (see \cite{palaisterng}, \cite{obc}). A point $p$ such that the orbit $G\cdot p$ is maximal dimensional is called a \textsl{principal point}.
The following property is very simple to prove and will be very useful in the following sections.
\begin{lemma} Let $Q$ be a space form and let $G\subset Iso(Q)$ be a Lie group such that its Lie algebra $\mathfrak{g}$ is linearly spanned by the Lie algebras $\mathfrak{g}_{i}$, $i\in I$. Let $G_{i}\subset Iso(Q)$, $i\in I$ be the Lie group associated to the Lie algebra $\mathfrak{g}_{i}$. If each $G_{i}$ acts polarly on $Q$, then the action of $G$ is polar (a section for the $G$-action through a point $p$ is obtained by intersecting the sections for the $G_{i}$-actions through $p$)\qed
\label{gen} \end{lemma}
The action of $G$ is said to be \textsl{locally polar} if the distribution given by the normal spaces to maximal dimensional orbits is integrable (and hence with totally geodesic integral manifolds). The group $G$ may not be closed but the maximal dimensional orbits of an action that is locally polar form a parallel family of isoparametric submanifolds, and so the closure of $G$ acts polarly on $Q$ and has the same orbits as $G$ (see \cite{palaisterng}, \cite{obc}, \cite{heinliuol}). Therefore we shall make no difference between a polar action and a locally polar action. The following lemma is standard to prove.
\begin{lemma} Let $G$ be a Lie subgroup of $Iso(Q)$. Assume there is an open subset $U$ of $Q$ such that the normal spaces of the orbits through points of $U$ define an integrable distribution on $U$. Then the action of $G$ is polar. \label{polar} \end{lemma}
\section{The Local Theorem} \label{localsection}
\begin{thm} \label{localth}Let $M$ be a submanifold of the Euclidean space $\mathbb{R}^{n}$ or the sphere $\mathbb{S}^{n}$ and let $\mathcal{N}_{p}$ be the nullity subspace of $M$ at $p\in M$. If $U$ is an open subset of $M$ and $p,q\in U$, denote by $p\sim_{U} q$ if $p$ and $q$ can be joined by a curve $c$ contained in $U$ such that $c'(t)\; \bot\; \mathcal{N}_{c(t)}$ for every $t$. Let $[p]_{U}$ be the equivalent class $\{q\in U: p\sim_{U} q\}$, for $p\in U$.
There is an open and dense subset$\ \mathcal{C}$ of $M$ such that for every $p\in \mathcal{C}\ $ one and only one of the following statements holds: \begin{enumerate} \item $[p]_{U}$ contains a neighborhood of $p$, for any open neighborhood $U$ of $p$. \item There exists an open neighborhood $U$ of $p$ and a proper submanifold $S$ of $U$ such that $p\in S$ and $U$ is the union of parallel manifolds to $S$ over a parallel flat sub-bundle $\nu^{*}$ of $\nu(S)$ contained in $\mathcal{N}_{U}$. Furthermore, the leaves of this parallel foliation are, locally, equivalent classes.
\end{enumerate}
\end{thm} \begin{proof} We will keep the notations introduced in section \ref{tuboesferico}. Assume first that $M$ is a submanifold of the Euclidean space. Let $\widetilde{\mathcal{C}}$ be the open and dense subset of $M$ of points $p$ such that the index of nullity $\mu$ is constant around $p$. Let $p\in \widetilde{\mathcal{C}}$ and let $U$ be an open neighborhood of $p$ such that there is a well defined spherical tube around $U$. We say that $p$ is a generic point of $\widetilde{\mathcal{C}}$ if $p$ is in the image (via the radial projection) of an open subset of the spherical tube where the index of nullity of the tube is constant and the holonomy tubes $H(x)$ have constan dimension (cf. section \ref{tuboesferico}). It is not difficult to see that the set $\mathcal{C}$ of general points of $\widetilde{\mathcal{C}}$ is open and dense in $M$.
Let $p\in \mathcal{C}$ and assume condition (1) does not hold. Let $U$ be an open neighboorhod of $p$, let $N$ be a spherical tube around $U$ and let $\pi:V\to \pi(V)$ be the radial projection. Let $V$ be an open part of $N$ with constant index of nullity such that $p\in\pi(V)$. let $\Psi$ be the radial normal vector field defined on $V$ and consider the holonomy tubes $$H(x)=(N_{\widetilde{\Psi}})_{-\widetilde{\Psi}(x)}$$ (cf. section \ref{tuboesferico}), which have constant dimension on $V$.
Then, from Lemma \ref{lema1}, $U$ is foliated (locally around $p$) by the submanifolds $\pi(H(x))$, which from statemen (3) of Lemma \ref{ellema}, are parallel manifolds over the parallel and flat sub-bundle $\nu^{*}$ of $\nu \pi(H(x))$.
We shall see that if $q=\pi(x)$, then \begin{equation} [q]_{U}=\pi(H(x))\ \text(locally\ around\ q). \label{eqloc} \end{equation}
If $y\in H(x)$ near $x$, then there is a curve $\widetilde{c}$ in $V$ joining $x$ and $y$ everywhere perpendicular to $E_{0}=\ker\hat{A}_{\Psi}$, where $\hat{A}$ is the shape operator of $N$. Set $c(t)=\pi(\widetilde{c}(t))=\widetilde{c}(t)+\Psi(\widetilde{c}(t))$. It is not hard to see that $c$ is perpendicular to $(\pi)_{*}(E_{0})$.
From the tube formula relating the shape operators of $M$ and $N$ (see \cite{obc}), one gets $\mathcal{N}\subset(\pi)_{*}(E_{0})$. Then $c(t)$ is a horizontal curve (with respect to $\mathcal{N}$) in $U$ joining $q$ and $\pi(y)$. We conclude that $\pi(H(x))\subset [q]_{U}$ (locally around $q$).
The other inclusion follows from the fact that the distribution $\mathcal{H}^{*}$ defined in Lemma \ref{lema1} is integrable and its integral manifolds are the sets $\pi(H(x))$. In fact, if $q'\in [q]_{U}$ there is a horizontal curve (with respect to $\mathcal{N}$) $c(t)$ joining $q$ and $q'$ contained in $U$. But from lemma \ref{lema1}, $\nu^{*}\subset\mathcal{N}$. Hence $c'(t)\;\bot\;\nu^{*}(c(t))$, that is, $c'(t)\in (\mathcal{H}^{*})_{c(t)}$, for all $t$. Then $q'$ is in the same integral manifold of $\mathcal{H}^{*}$ than $q$, so $q'\in\pi(H(x))$.
Suppose now that $M$ is a submanifold of the sphere. Consider the position vector field on $\mathbb{S}^{n}$ given by $\eta(p)=-p$. We can chose a real positive number $\delta$ small enough such that $$\overline{M}:=\bigcup_{-\delta<\varepsilon<\delta}M_{\varepsilon\eta}$$ is a well defined submanifold of $\mathbb{R}^{n+1}$, where $M_{\varepsilon\eta}$ is the parallel manifold to $M$ defined by the parallel normal vector field $\varepsilon\eta$. Observe that $M_{\varepsilon\eta}$ is contained in the sphere $\mathbb{S}_{(1-\varepsilon)}^{n}$ of radius $1-\varepsilon$.
Denote by $\pi_{\varepsilon}:M\to M_{\varepsilon\eta}$ the usual parallel map (observe that $\pi_{0}=Id_{M}$). Let $\overline{\mathcal{N}}$ be the nullity distribution of $\overline{M}$. Then it is not difficult to see that $$\overline{\mathcal{N}}_{\pi_{\varepsilon}(p)}=(d\pi_{\varepsilon})_{p}(\mathcal{N}_{p})\oplus \mathbb{R}\eta(p)$$
Let $\overline{U}$ be an open set in $\overline{M}$ such that $U:=\overline{U}\cap M$ is open in $M$. Denote by $[q]_{\overline{U}}^{*}$ the set of points in $\overline{M}$ that can be joined to $q$ by a curve perpendicular to $\overline{\mathcal{N}}$ contained in $\overline{U}$. If $q\in M_{\varepsilon\eta}$, then $[q]^{*}\subset M_{\varepsilon\eta}$ and in particular if $p\in M$, then $[p]_{\overline{U}}^{*}=[p]_{U}$, the set of point of $M$ that can be joined to $p$ by a curve perpendicular to $\mathcal{N}$ contained in $U$. The theorem for $M$ then follows by applying to $\overline{M}$ the result for submanifolds of the Euclidean space. \end{proof}
\section{The Global Theorem} \label{global} If $f:M\to\mathbb{R}^{n}$ is an immersed submanifold, we say that $M$ is \emph{irreducible} if there is no non trivial, $A$-invariant, autoparallel distribution $\mathcal{D}$ on $M$ such that $\mathcal{D}^{\bot}$ is also autoparallel. This means that $M$ can not be expressed, locally, as the product of submanifolds of the Euclidean space. If $M$ is complete and simply connected, this is equivalent to the fact that $f$ is not a product of immersions (see \cite{obc}). If $M$ is a submanifold of the sphere, we say that $M$ is irreducible if it is irreducible as a submanifold of the Euclidean space.
In this section we will prove Theorem \ref{globalthm}.
Consider the fiber bundle $\mathbf{pr}:M\to M/\mathcal{N}$ defined in section \ref{fibrado}. We will denote, as in the previous sections, $M_{r}:=\mathbf{pr}^{-1}(r)$ for $r\in M/\mathcal{N}$.
\begin{lemma} For any $r\in M/\mathcal{N}$, the restricted holonomy group $\Phi_{r}^{0}$ acts either transitively or polarly on $M_{r}$. \label{accionpolar} \end{lemma}
\begin{proof} We will keep the notations of Theorem \ref{localth}.
Assume first that $M$ is a submanifold of the Euclidean Space. In order to simplify the exposition, we will treat $M$ as an embedded submanifold identifying $i(M)$ with $M$.
First of all, observe that if $\Phi_{r}^{0}$ acts transitively on $M_{r}$ for some $r$, then $\Phi^{0}_{s}$ acts transitively on $M_{s}$ for each $s\in M/\mathcal{N}$. So let us assume that this action is not transitive.
Let $\mathcal{C}$ be the open dense subset of $M$ given by Theorem \ref{localth}. If condition (1) holds for some $p$, then $p$ can be joined by a horizontal curve with respect to $\mathcal{N}$ to any other point in an open neighborhood of $p$ in $M_{r}$ (with $r=\mathbf{pr}(p)$). Then it is not difficult to see that $p$ can be joined to any other point of $M_{r}$ by a horizontal curve, and so the action of $\Phi_{r}^{0}$ on $M$ is transitive. Hence statement (2) on Theorem \ref{localth} must hold for every point of $\mathcal{C}$.
So let $p\in\mathcal{C}$ and let $U$ be the open neighborhood of $p$ given by theorem \ref{localth}. Set $r=\mathbf{pr}(p)$. We shall see that $$\Phi^{loc}_{r}\cdot q= [q]_{U}\cap M_{r}\ (\text{locally around }q)$$
We can assume (possibly by taking a smaller $U$) that $\Phi^{loc}_{r}=\Phi^{0}(r,\mathbf{pr}(U))$. Then $[q]_{U}\cap M_{r}\subset\Phi^{loc}_{r}\cdot q$.
Now fix a Riemannian metric on $M/\mathcal{N}$ and define a Riemannian metric on $M$ such that the vertical and horizontal distributions defined by $\mathbf{pr}$ (i.e.,\,$\mathcal{N}$ and its orthogonal complement) are orthogonal and $\mathbf{pr}$ is a Riemannian submersion.
For a fixed $\delta>0$ let $P_{\delta}$ be the subset of $\Phi^{loc}_{r}$ consisting of the parallel transport transformations determined by curves in $\mathbf{pr}(U)$ of length less than $\delta$. Then, following the same ideas of \cite[Appendix]{olmosesch} we obtain that $P_{\delta}$ contains an open neighborhood $\mathcal{U}(r)$ of the identity in $\Phi^{loc}_{r}$. We may take $\delta$ small enough such that $B_{\delta}(q)$ (an open ball for the new metric) is contained in $U$. Then if $c$ is a loop based at $r$ of length less than $\delta$, its horizontal lift is contained in $U$. So $\mathcal{U}(r)\cdot q$ is an open neighborhood of $q$ in $\Phi^{loc}_{r}\cdot q$ contained in $[q]_{U}$. This proves the other inclusion.
From statement (2) in Theorem \ref{localth} and Lemma \ref{polar} we conclude that the action of $\Phi_{r}^{loc}$ on $M_{r}$ is polar.
Let $\widetilde{\mathcal{C}}:=\mathbf{pr}^{-1}(\mathbf{pr}(\mathcal{C}))$. Then for every $p\in \widetilde{\mathcal{C}}$, the local holonomy group $\Phi^{loc}_{\mathbf{pr}(p)}$ acts polarly on $M_{\mathbf{pr}(p)}$. The lemma now follows from Lemma \ref{ambrose} and Lemma \ref{gen}
For the case of a submanifold of the sphere, the proof follows in the same way.
\end{proof}
\begin{proof}[Proof of Theorem \ref{globalthm}] Since we are working in the cathegory of immersed submanifolds, we may assume that $M$ is simply connected (eventually by passing to the universal cover).
For $p\in M$ denote by $[p]$ the set of points of $M$ that can be joined to $p$ by a curve horizontal with respect to $\mathcal{N}$. Let $V$ be the open and dense subset of principal points of $M$ for the action of the restricted holonomy groups $\Phi^{0}_{r}$. Observe that $V\cap M_{r}$ is also open dense on each fiber $M_{r}$.
Assume first that $M$ is a submanifold of the Euclidean space. If $p\in V$ and $r=\mathbf{pr}(p)$, since the action of $\Phi^{0}_{r}$ is polar by Lemma \ref{accionpolar}, then $\Phi^{0}_{r}\cdot p$ is a complete embedded isoparametric submanifold of the Euclidean space $M_{r}$. Therefore $$\Phi^{0}_{r}\cdot p=E_{0}(p)\times S(p)$$ where $E_{0}$ is the nullity subspace of $\Phi^{0}_{r}\cdot p$ at $p$ and $S(p)$ is a compact isoparametric submanifold of a sphere (see \cite{palaisterng} or \cite[Theor. 5.2.11]{obc}).
Let $\mathcal{D}(p)$ be the nullity subspace of $[p]$ at $p$, regarding $[p]$ as a submanifold of $M$ (and not of $\mathbb{R}^{n+k}$). Set $\mathcal{H}_{p}:=\mathcal{N}^{\bot}_{p}\subset T_{p}M$. We shall see that $$\mathcal{D}(p)=\mathcal{H}_{p}\oplus E_{0}(p).$$ Fix $p\in V$, $r=\mathbf{pr}(p)$ and let $\xi_{p}\in \nu_{p}(\Phi^{0}_{r}\cdot p)\subset \mathcal{N}_{p}$. If $q\in[p]$ and $c$ is a curve in $M/\mathcal{N}$ such that $q=\tau^{\mathcal{N}}_{c}(p)$, set $\xi(q):=(d\tau^{\mathcal{N}}_{c})_{p}(\xi_{p})$. Since $\Phi^{0}_{r}\cdot p\subset M_{r}$ is a principal orbit, $\xi$ is a well defined normal vector field to $[p]$ . Moreover, since the action is polar, $\xi$ is parallel in the directions of the orbits of the holonomy groups (cf. \cite{hot} or \cite[Cor. 3.2.5]{obc}). It is also parallel in the directions of $\mathcal{H}=\mathcal{N}^{\bot}$. In fact, let $\sigma(t)$ be any horizontal curve contained in $[p]$. Set $p'=\sigma(0)$, $p''=p'+\xi(\sigma(0))$. Observe that the horizontal spaces $\mathcal{H}$ are constant along any fiber of $\mathbf{pr}:M\to M/\mathcal{N}$ (since we move along the nullity of $M$). If $\delta(t)$ is the horizontal lift of $\mathbf{pr}(\sigma)$ through $p''$, then it is not difficult to see that $\xi(\sigma(t))=\delta(t)-\sigma(t)$ and so $\frac{d}{dt}\xi(\sigma(t))=\delta'(t)-\sigma'(t)$, which is horizontal and, in particular, tangent to $[p]$. So $\xi$ is parallel with respect to the normal connection of $[p]$.
This also proves that $[p+\xi_{p}]$ is the parallel (possibly focal) manifold $[p]_{\xi}$ to $[p]$.
Let $q=p+\xi_{p}$ and so $\mathcal{H}_{q}$ and $\mathcal{H}_{p}$ coincide (as subspaces of $\mathbb{R}^{n+k}$). Since they are both isomorphic to $T_{\mathbf{pr}(p)}M/\mathcal{N}$ via $d\mathbf{pr}$, one has the isomorphism $$\varphi:=d\mathbf{pr}_{q}^{-1}\circ (d\mathbf{pr}_{p})_{|\mathcal{H}_{p}}:\mathcal{H}_{p}\to\mathcal{H}_{q}\simeq\mathcal{H}_{p}.$$ Let $X\in T_{\mathbf{pr}(p)} M/\mathcal{N}$ and $c(t)$ a curve in $M/\mathcal{N}$ such that $c(0)=\mathbf{pr}(p)$ and $c'(0)=X$. Let $\sigma(t)$ and $\beta(t)$ be the horizontal lifts of $c$ through $p$ and $q$ respectively. We have seen that $\beta(t)=\sigma(t)+\xi(\sigma(t))$. So $$\beta'(0)=\sigma'(0)+\frac{d}{dt}\xi(\sigma(t))=(Id-\widehat{A}_{\xi_{p}})\sigma'(0)$$ where $\widehat{A}_{\xi_{p}}$ is the shape operator of $[p]$ as a submanifold of $M$ (which coincides with the shape operator as a submanifold of $\mathbb{R}^{n+k}$).
Hence $\varphi=(Id-\widehat{A}_{\xi_{p}})$ is an isomorphism from $\mathcal{H}_{p}$ to $\mathcal{H}_{q}\simeq\mathcal{H}_{p}$ for each $\xi_{p}\in\nu_{p}(\Phi^{0}_{r}\cdot p)$. Suppose now that there exists a normal vector $\xi_{p}$ to the orbit $\Phi^{0}_{r}\cdot p$ such that $\widehat{A}_{\xi_{p}|\mathcal{H}_{p}}\neq0$. Then there is an eigenvector $v\in\mathcal{H}_{p}$ associated to a real eigenvalue $\lambda\neq 0$ of $\hat{A}$. Then $(Id-\widehat{A}_{\xi_{p}/\lambda})v=0$, which can not occur. So $\mathcal{H}_{p}$ is contained in the nullity subspace of $[p]$ at $p$. We conclude that $\mathcal{D}(p)=E_{0}(p)\oplus \mathcal{H}_{p}$ as we wanted to show.
Recall that $\mathcal{D}(p)$ is defined only on the dense subset $V$.
Now observe that since any two maximal dimensional orbits on the same fiber $M_{r}$ are parallel manifolds, they have the same extrinsic Euclidean factor (regarded as submanifolds of $M_{r}$). Therefore, the subspaces $E_{0}(p)$ can be all identified on $V\cap M_{r}$ for every fiber $M_{r}$. We can hence extend the distribution $E_{0}$ to the hole $M_{r}$ define $E_{0}(q)$ for $q\in M_{r}$ as the common subspace $E_{0}(p)$ for any $p\in M_{r}\cap V$. If $p$ and $q$ are in different integral manifolds, then there is a point $q'\in M_{\mathbf{pr}(q)}$ such that $\Phi^{0}_{r}\cdot q'$ is the parallel translated of $\Phi^{0}_{r}\cdot p$ (along an appropriate curve in $M/\mathcal{N}$) and is therefore isometric to it. So $dim(E_{0}(q))=dim(E_{0}(q'))=dim(E_{0}(p))$ and $\mathcal{D}$ is a well defined differential distribution on $M$.
We will prove that $\mathcal{D}$ and $\mathcal{D}^{\bot}$ are autoparallel and invariant under the shape operators $A$ of $M$.
Observe that $\mathcal{D}^{\bot}(p)$ in $M$ is the orthogonal complement of $E_{0}(p)$ in $M_{\mathbf{pr}(p)}$ and so $\mathcal{D}^{\bot}$ is an autoparallel distribution on $M$, which is parallel when restricted to any fiber $M_{r}$. Since $\mathcal{H}$ is $A$-invariant and $A_{|E_{0}}\equiv 0$, we get that $\mathcal{D}$ is $A$-invariant. Denote by $\nu^{M}[p]$ and by $\nu^{\mathbb{R}^{n+k}}[p]$ the normal bundles of $[p]$ as a submanifold of $M$ or $\mathbb{R}^{n+k}$ respectively. Since $[p]$ is $A$-invariant, then $\nu^{M}[p]$ is a parallel sub-bundle of $\nu^{\mathbb{R}^{n+k}}[p]$. From Codazzi equation, the distribution $\mathcal{D}$ (which is the nullity of $[p]$ associated to a parallel sub-bundle of $\nu^{\mathbb{R}^{n+k}}[p]$) is autoparallel in $\mathcal{V}$.
Since $V$ is dense in $M$, we get that $\mathcal{D}$ is autoparallel.
Since $M$ is irreducible, $\mathcal{D}^{\bot}$ must be trivial. So any orbit $\Phi^{0}_{r}\cdot p$ coincides with the whole integral manifold $M_{\mathbf{pr}(p)}$.
Assume now that $M$ is a submanifold of the sphere $\mathbb{S}^{n+k}$. As in the proof of Theorem \ref{localth}, let $\eta(p)=-p$ be the position normal vector field and set $N:=\bigcup_{-\delta<\varepsilon<\delta}M_{\varepsilon\eta}$.
If $r\in M/\mathcal{N}$, let $L_{r}:=T_{p}M_{r}\oplus \mathbb{R}\eta_{p}$. $L_{p}$ is the smallest linear subspace of $\mathbb{R}^{n+k+1}$ that contains the sphere $M_{r}$.
Let $p\in V$, where $V$ is as in the Euclidean case. Suppose there exists a normal vector $0\neq\xi_{p}\in \nu_{p}[p]$, where $\nu_{p}[p]$ is the normal space of $[p]$ as a submanifold of $M$. Then $\xi_{p}\in L_{\mathbf{pr}(p)}$ is normal to the isoparametric orbit $\Phi^{0}_{r}\cdot p$. We can extend $\xi_{p}$ to a normal parallel vector field $\xi$ to $[p]$ (as in the Euclidean case).
Consider in $\mathbb{R}^{n+k+1}$ the parallel manifold $\widetilde{[p]}:=[p]_{\xi}$ and then consider the projection $\widetilde{[p]}_{\lambda\eta}$ of this submanifold to the sphere, where $\lambda\neq 1$ is a suitable real number. Then $[p]$ and $\widetilde{[p]}_{\lambda\eta}$ are parallel manifolds on the sphere $\mathbb{S}^{n+k}$. Let $\pi_{\xi}:[p]\to \widetilde{[p]}$ and $\pi_{\lambda\eta}:\widetilde{[p]}\to \widetilde{[p]}_{\lambda\eta}$ be the corresponding focal maps. Then $\pi_{\lambda\eta}\circ\pi_{\xi}(p)\in M_{\mathbf{pr}(p)}$.
Observe that the orthogonal complement $\mathcal{H}_{p}$ to $\mathcal{N}_{p}$ in $T_{p}M$ is constant along $M_{\mathbf{pr}(p)}$. In fact, if we consider the nullity $\overline{\mathcal{N}}$ of $N$, then $\mathcal{H}$ is also the horizontal space associated to $\overline{\mathcal{N}}$ and therefore constant along $L_{\mathbf{pr}(p)}$.
Then it is not difficult to see that the isomorphism $d\mathbf{pr}_{q}^{-1}\circ d\mathbf{pr}_{p}$ from $\mathcal{H}_{p}$ to $\mathcal{H}_{q}\simeq\mathcal{H}_{p}$ is given by $d\pi_{\lambda\eta}\circ (Id-\hat{A}_{\xi})_{|\mathcal{H}_{p}}$, where $\hat{A}$ is the shape operator of $[p]$. In the same way as in the Euclidean case, we conclude that $\hat{A}_{\xi|\mathcal{H}_{p}}\equiv 0$.
Let $\mathcal{D}(p)$ be the nullity subspace of $[p]$ at $p$ as a submanifold of $M$. Then $\mathcal{H}_{p}\subset\mathcal{D}(p)$. Since the orbits of $\Phi^{0}_{r}$ through points in $V$ are isoparametric submanifolds of a sphere we may assume that they have no nullity in the sphere (eventually by passing to a nearby parallel orbit).
Then $\mathcal{H}_{|V}=\mathcal{D}$ is an autoparallel distribution on $V$, and since $V$ is dense, $\mathcal{H}$ is autoparallel in $M$. Since $M$ is irreducible, and both $\mathcal{H}$ and $\mathcal{N}$ are non trivial, the normal space to any orbit $\Phi^{0}_{\mathbf{pr}(p)}\cdot p$ is trivial, or equivalently the orbit coincides with $M_{r}$. \end{proof}
\begin{rem} \emph{It is possible to show with a simple example, that the global theorem is false for submanifolds of the hyperbolic space. We will construct a $2$-dimensional $1-1$ immersed complete submanifold of the hyperbolic space $\mathbb{H}^{3}$ with constant index of nullity $1$ (and such that the perpendicular distribution to the nullity is hence integrable). This submanifold is given as a union of orbits of points in a geodesic by a $1$-parameter subgroup of isometries.}
\noindent \emph{Regard $\mathbb{H}^{3}$ as the connected component through $e_{4}=(0,0,0,1)$ of $\{x\in\mathbb{L}^{4}: \left\langle x,x\right\rangle=-1\}$ where $\mathbb{L}^{4}$ is the space $\mathbb{R}^{4}$ with the Lorentz metric $\left\langle x,y\right\rangle=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}$. Let $\sigma$ be the geodesic trough $e_{4}$ in $\mathbb{H}^{3}$ such that $\sigma'(0)=v$, that is, $\sigma(s)=\sinh(s)v+\cosh(s)e_{4}$, and let $w\in T_{e_{4}}\mathbb{H}^{3}$ such that $w\; \bot\; v$. Consider a matrix $B\in \mathfrak{so}(3)$ such that $Bv=0$ and $Bw\neq0$, and such that $A=\left( \begin{array}{cc} B& w\\ w^{\mathbf{t}}& 0\\ \end{array}\right)$ verifies $A^{3}=0$ (it is not difficult to see that it is always possible). Observe that $A\in\mathfrak{so}_{1}(4)$, the Lie algebra of the group of isometries of $\mathbb{H}^{3}$. Let $X$ be the Killing vector field on $\mathbb{H}^{3}$ defined by $A$ and let $\{\varphi_{t}\}$ the one parameter subgroup associated to it.
Define the function $$f:\mathbb{R}^{2}\to\mathbb{H}^{3}\; /\; (t,s)\mapsto f(t,s)=\varphi_{t}(\sigma(s))=e^{tA}\sigma(s).$$
Then it is not hard to see that $f$ is a $1-1$ immersion. Let $M=f(\mathbb{R}^{2})\subset\mathbb{H}^{3}$. Then it is not difficult to prove that
\begin{enumerate}
\item[i)] The nullity subspace of $M$ at $p=f(s,t)$ is generated by the tangent vector $(d\varphi_{t})_{\sigma(s)}\sigma'(s)$. Therefore $M$ has constant index of nullity $1$.
\item[ii)] If $M$ were an extrinsic product in the Lorentz space $\mathbb{L}^{4}$, it would have constant sectional curvature equal to $0$. But since it is a surface in $\mathbb{H}^{3}$ with nullity, it has constant curvature $-1$. Therefore $M$ is irreducible.
\item[iii)] Since $A^{3}=0$, $\varphi_{t}=\text{e}^{tA}=I+tA+\frac{t^{2}}{2}A^{2}$. Then it is not difficult to show that any Cauchy sequence on $M$ is convergent, and therefore $M$ is complete
\end{enumerate} \label{hyp} This procedure can be generalized to higher dimensions, by asking further properties to the matrix $A$. }
\end{rem}
\textbf{Acknowledgement}: This work is part of the author's Ph.D. thesis, written in FCEIA, UNR, directed of Prof. Carlos Olmos.
\end{document} | arXiv |
Farmer John is attempting to sort his $N$ cows ($1 \leq N \leq 100$), conveniently numbered $1 \dots N$, before they head out to the pastures for breakfast.
The cows are a bit sleepy today, so at any point in time the only cow who is paying attention to Farmer John's instructions is the cow directly facing Farmer John. In one time step, he can instruct this cow to move $k$ paces down the line, for any $k$ in the range $1 \ldots N-1$. The $k$ cows whom she passes will amble forward, making room for her to insert herself in the line after them.
Farmer John is eager to complete the sorting, so he can go back to the farmhouse for his own breakfast. Help him find the minimum number of time steps required to sort the cows.
The first line of input contains $N$.
The second line contains $N$ space-separated integers, $p_1, p_2, p_3, \dots, p_N$, indicating the starting order of the cows.
A single integer: the number of time steps before the $N$ cows are in sorted order, if Farmer John acts optimally. | CommonCrawl |
HomeTextbook AnswersMathCalculusCalculus (3rd Edition)Chapter 11 - Infinite Series - 11.7 Taylor Series - Exercises - Page 58810
Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Appendix A Appendix C Infinite Series - 11.1 Sequences - Preliminary Questions Infinite Series - 11.1 Sequences - Exercises Infinite Series - 11.1 Sequences - Exercises Infinite Series - 11.1 Sequences - Exercises Infinite Series - 11.2 Summing and Infinite Series - Preliminary Questions Infinite Series - 11.2 Summing and Infinite Series - Preliminary Questions Infinite Series - 11.2 Summing and Infinite Series - Exercises Infinite Series - 11.2 Summing and Infinite Series - Exercises Infinite Series - 11.2 Summing and Infinite Series - Exercises Infinite Series - 11.2 Summing and Infinite Series - Exercises Infinite Series - 11.3 Convergence of Series with Positive Terms - Preliminary Questions Infinite Series - 11.3 Convergence of Series with Positive Terms - Exercises Infinite Series - 11.3 Convergence of Series with Positive Terms - Exercises Infinite Series - 11.3 Convergence of Series with Positive Terms - Exercises Infinite Series - 11.4 Absolute and Conditional Convergence - Preliminary Questions Infinite Series - 11.4 Absolute and Conditional Convergence - Exercises Infinite Series - 11.4 Absolute and Conditional Convergence - Exercises Infinite Series - 11.4 Absolute and Conditional Convergence - Exercises Infinite Series - 11.5 The Ratio and Root Tests and Strategies for Choosing Tests - Preliminary Questions Infinite Series - 11.5 The Ratio and Root Tests and Strategies for Choosing Tests - Exercises Infinite Series - 11.5 The Ratio and Root Tests and Strategies for Choosing Tests - Exercises Infinite Series - 11.6 Power Series - Preliminary Questions Infinite Series - 11.6 Power Series - Exercises Infinite Series - 11.6 Power Series - Exercises Infinite Series - 11.6 Power Series - Exercises Infinite Series - 11.7 Taylor Series - Preliminary Questions Infinite Series - 11.7 Taylor Series - Exercises Infinite Series - 11.7 Taylor Series - Exercises Infinite Series - 11.7 Taylor Series - Exercises Infinite Series - Chapter Review Exercises Infinite Series - Chapter Review Exercises Infinite Series - Chapter Review Exercises 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
Chapter 11 - Infinite Series - 11.7 Taylor Series - Exercises - Page 588: 10
$$f(x)=(1-x)^{-1/2}=1+\frac{1}{2}x+\frac{3}{2^2}\frac{x^2}{2!}+\frac{3*5}{2^3}\frac{x^3}{3!}+...$$ Convergent for $|x|\lt 1$
By making use of Table 2, we have the Maclaurin series for $f(x)=(1+x)^a$ as follows $$f(x)=(1+x)^a=1+ax+\frac{a(a-1)x^2}{2!}+\frac{a(a-1)(a-2)x^3}{3!}+...$$ Now by the comparison with the function $f(x)=(1-x)^{-1/2}$, we have the Maclaurin series as follows $$f(x)=(1-x)^{-1/2}=1+\frac{1}{2}x+\frac{3}{2^2}\frac{x^2}{2!}+\frac{3*5}{2^3}\frac{x^3}{3!}+...$$ Moreover, again from Table 2, the Maclaurin series for $f(x)=(1+x)^a$ is convergent for the values $|x|\lt 1$. Hence, the Maclaurin series for $f(x)=(1-x)^{-1/2}$ is convergent for the values $|-x^2|=x^2\lt 1$ or $|x|\lt 1$.
Next Answer Chapter 11 - Infinite Series - 11.7 Taylor Series - Exercises - Page 588: 11 Previous Answer Chapter 11 - Infinite Series - 11.7 Taylor Series - Exercises - Page 588: 9 | CommonCrawl |
Learning to learn via Self-Critique
Antoniou, Antreas and Storkey, Amos J.
[link] Summary by Mikhail Meskhi 1 month ago
### Key points
- Instead of just focusing on supervised learning, a self-critique and adapt network provides a unsupervised learning approach in improving the overall generalization. It does this via transductive learning by learning a label-free loss function from the validation set to improve the base model.
- The SCA framework helps a learning algorithm be more robust by learning more relevant features and improve during the training phase.
### Ideas
1. Combine deep learning models with SCA that help improve genearlization when we data is fed into these large networks.
2. Build a SCA that focuses not on learning a label-free loss function but on learning quality of a concept.
### Review
Overall, the paper present a novel idea that offers a unsupervised learning method to assist a supervised learning model to improve its performance. Implementation of this SCA framework is straightforward and demonstrates promising results. This approach is finally contributing to the actual theory of meta-learning and learning to learn research field. SCA framework is a new step towards self-adaptive learning systems. Unfortunately, the experimentation is insufficient and provided little insight into how this framework can help in cases where task domains vary in distribution or in concept.
Exploring the Origins and Prevalence of Texture Bias in Convolutional Neural Networks
Hermann, Katherine L. and Kornblith, Simon
When humans classify images, we tend to use high-level information about the shape and position of the object. However, when convolutional neural networks classify images,, they tend to use low-level, or textural, information more than high-level shape information. This paper tries to understand what factors lead to higher shape bias or texture bias.
To investigate this, the authors look at three datasets with disagreeing shape and texture labels. The first is GST, or Geirhos Style Transfer. In this dataset, style transfer is used to render the content of one class in the style of another (for example, a cat shape in the texture of an elephant). In the Navon dataset, a large-scale letter is rendered by tiling smaller letters. And, in the ImageNet-C dataset, a given class is rendered with a particular kind of distortion; here the distortion is considered to be the "texture label". In the rest of the paper, "shape bias" refers to the extent to which a model trained on normal images will predict the shape label rather than the texture label associated with a GST image. The other datasets are used in experiments where a model explicitly tries to learn either shape or texture.
https://i.imgur.com/aw1MThL.png
To start off, the authors try to understand whether CNNs are inherently more capable of learning texture information rather than shape information. To do this, they train models on either the shape or the textural label on each of the three aforementioned datasets. On GST and Navon, shape labels can be learned faster and more efficiently than texture ones. On ImageNet-C (i.e. distorted ImageNet), it seems to be easier to learn texture than texture, but recall here that texture corresponds to the type of noise, and I imagine that the cardinality of noise types is far smaller than that of ImageNet images, so I'm not sure how informative this comparison is. Overall, this experiment suggests that CNNs are able to learn from shape alone without low-level texture as a clue, in cases where the two sources of information disagree
The paper moves on to try to understand what factors about a normal ImageNet model give it higher or lower shape bias - that is, a higher or lower likelihood of classifying a GST image according to its shape rather than texture. Predictably, data augmentations have an effect here. When data is augmented with aggressive random cropping, this increases texture bias relative to shape bias, presumably because when large chunks of an object are cropped away, its overall shape becomes a less useful feature. Center cropping is better for shape bias, probably because objects are likely to be at the center of the image, so center cropping has less of a chance of distorting them. On the other hand, more "naturalistic" augmentations like adding Gaussian noise or distorting colors lead to a higher shape bias in the resulting networks, up to 60% with all the modifications. However, the authors also find that pushing the shape bias up has the result of dropping final test accuracy.
https://i.imgur.com/Lb6RMJy.png
Interestingly, while the techniques that increase shape bias seem to also harm performance, the authors also find that higher-performing models tend to have higher shape bias (though with texture bias still outweighing shape) suggesting that stronger models learn how to use shape more effectively, but also that handicapping models' ability to use texture in order to incentivize them to use shape tends to hurt performance overall.
Overall, my take from this paper is that texture-level data is actually statistically informative and useful for classification - even in terms of generalization - even if is too high-resolution to be useful as a visual feature for humans. CNNs don't seem inherently incapable of learning from shape, but removing their ability to rely on texture seems to lead to a notable drop in accuracy, suggesting there was real signal there that we're losing out on.
Better-than-Demonstrator Imitation Learning via Automatically-Ranked Demonstrations
Daniel S. Brown and Wonjoon Goo and Scott Niekum
Keywords: cs.LG, stat.ML
First published: 2019/07/09 (1 year ago)
Abstract: The performance of imitation learning is typically upper-bounded by the performance of the demonstrator. While recent empirical results demonstrate that ranked demonstrations allow for better-than-demonstrator performance, preferences over demonstrations may be difficult to obtain, and little is known theoretically about when such methods can be expected to successfully extrapolate beyond the performance of the demonstrator. To address these issues, we first contribute a sufficient condition for better-than-demonstrator imitation learning and provide theoretical results showing why preferences over demonstrations can better reduce reward function ambiguity when performing inverse reinforcement learning. Building on this theory, we introduce Disturbance-based Reward Extrapolation (D-REX), a ranking-based imitation learning method that injects noise into a policy learned through behavioral cloning to automatically generate ranked demonstrations. These ranked demonstrations are used to efficiently learn a reward function that can then be optimized using reinforcement learning. We empirically validate our approach on simulated robot and Atari imitation learning benchmarks and show that D-REX outperforms standard imitation learning approaches and can significantly surpass the performance of the demonstrator. D-REX is the first imitation learning approach to achieve significant extrapolation beyond the demonstrator's performance without additional side-information or supervision, such as rewards or human preferences. By generating rankings automatically, we show that preference-based inverse reinforcement learning can be applied in traditional imitation learning settings where only unlabeled demonstrations are available.
[link] Summary by Paul Barde 5 months ago
## General Framework
Extends T-REX (see [summary](https://www.shortscience.org/paper?bibtexKey=journals/corr/1904.06387&a=muntermulehitch)) so that preferences (rankings) over demonstrations are generated automatically (back to the common IL/IRL setting where we only have access to a set of unlabeled demonstrations). Also derives some theoretical requirements and guarantees for better-than-demonstrator performance.
## Motivations
* Preferences over demonstrations may be difficult to obtain in practice.
* There is no theoretical understanding of the requirements that lead to outperforming demonstrator.
## Contributions
* Theoretical results (with linear reward function) on when better-than-demonstrator performance is possible: 1- the demonstrator must be suboptimal (room for improvement, obviously), 2- the learned reward must be close enough to the reward that the demonstrator is suboptimally optimizing for (be able to accurately capture the intent of the demonstrator), 3- the learned policy (optimal wrt the learned reward) must be close enough to the optimal policy (wrt to the ground truth reward). Obviously if we have 2- and a good enough RL algorithm we should have 3-, so it might be interesting to see if one can derive a requirement from only 1- and 2- (and possibly a good enough RL algo).
* Theoretical results (with linear reward function) showing that pairwise preferences over demonstrations reduce the error and ambiguity of the reward learning. They show that without rankings two policies might have equal performance under a learned reward (that makes expert's demonstrations optimal) but very different performance under the true reward (that makes the expert optimal everywhere). Indeed, the expert's demonstration may reveal very little information about the reward of (suboptimal or not) unseen regions which may hurt very much the generalizations (even with RL as it would try to generalize to new states under a totally wrong reward). They also show that pairwise preferences over trajectories effectively give half-space constraints on the feasible reward function domain and thus may decrease exponentially the reward function ambiguity.
* Propose a practical way to generate as many ranked demos as desired.
## Additional Assumption
Very mild, assumes that a Behavioral Cloning (BC) policy trained on the provided demonstrations is better than a uniform random policy.
## Disturbance-based Reward Extrapolation (D-REX)


They also show that the more noise added to the BC policy the lower the performance of the generated trajs.
Pretty much like T-REX.
Extrapolating Beyond Suboptimal Demonstrations via Inverse Reinforcement Learning from Observations
Daniel S. Brown and Wonjoon Goo and Prabhat Nagarajan and Scott Niekum
Abstract: A critical flaw of existing inverse reinforcement learning (IRL) methods is their inability to significantly outperform the demonstrator. This is because IRL typically seeks a reward function that makes the demonstrator appear near-optimal, rather than inferring the underlying intentions of the demonstrator that may have been poorly executed in practice. In this paper, we introduce a novel reward-learning-from-observation algorithm, Trajectory-ranked Reward EXtrapolation (T-REX), that extrapolates beyond a set of (approximately) ranked demonstrations in order to infer high-quality reward functions from a set of potentially poor demonstrations. When combined with deep reinforcement learning, T-REX outperforms state-of-the-art imitation learning and IRL methods on multiple Atari and MuJoCo benchmark tasks and achieves performance that is often more than twice the performance of the best demonstration. We also demonstrate that T-REX is robust to ranking noise and can accurately extrapolate intention by simply watching a learner noisily improve at a task over time.
Only access to a finite set of **ranked demonstrations**. The demonstrations only contains **observations** and **do not need to be optimal** but must be (approximately) ranked from worst to best.
The **reward learning part is off-line** but not the policy learning part (requires interactions with the environment).
In a nutshell: learns a reward models that looks at observations. The reward model is trained to predict if a demonstration's ranking is greater than another one's. Then, once the reward model is learned, one simply uses RL to learn a policy. This latter outperform the demonstrations' performance.
Current IRL methods cannot outperform the demonstrations because they seek a reward function that makes the demonstrator optimal and thus do not infer the underlying intentions of the demonstrator that may have been poorly executed.
In practice, high quality demonstrations may be difficult to provide and it is often easier to provide demonstrations with a ranking of their relative performance (desirableness).
## Trajectory-ranked Reward EXtrapolation (T-REX)

Uses ranked demonstrations to extrapolate a user's underlying intent beyond the best demonstrations by learning a reward that assigns greater return to higher-ranked trajectories. While standard IRL seeks a reward that **justifies** the demonstrations, T-REX tries learns a reward that **explains** the ranking over demonstrations.

Having rankings over demonstrations may remove the reward ambiguity problem (always 0 reward cannot explain the ranking) as well as provide some "data-augmentation" since from a few ranked demonstrations you can define many pair-wise comparisons. Additionally, suboptimal demonstrations may provide more diverse data by exploring a larger area of the state space (but may miss the parts relevant to solving the task...)
## Tricks and Tips
Authors used ground truth reward to rank trajectories, but they also show that approximate ranking does not hurt the performance much.
To avoid overfitting they used an ensemble of 5 Neural Networks to predict the reward.
For episodic tasks, they compare subtrajectories that correspond to similar timestep (better trajectory is a bit later in the episode than the one it is compared against so that reward increases as the episode progresses).
At RL training time, the learned reward goes through a sigmoid to avoid large changes in the reward scale across time-steps.



Results are quite positive and performance can be good even when the learned reward is not really correlated with the ground truth (cf. HalfCheetah).
They also show that T-REX is robust to different ranking-noises: random-swapping of pair-wise ranking, ranking by humans that only have access to a description of the task and not the ground truth reward. **They also automatically rank the demonstrations using the number of learning steps of a learning expert: therefore T-REX could be used as an intrinsic reward alongside the ground-truth to accelerate training.**

**Limitations**
They do not show than T-REX can match an optimal expert, maybe ranking demonstrations hurt when all the demos are close to optimality?
Regularizing Trajectory Optimization with Denoising Autoencoders
Boney, Rinu and Palo, Norman Di and Berglund, Mathias and Ilin, Alexander and Kannala, Juho and Rasmus, Antti and Valpola, Harri
[link] Summary by Robert Müller 8 months ago
The typical model based reinforcement learning (RL) loop consists of collecting data, training a model of the environment, using the model to do model predictive control (MPC). If however the model is wrong, for example for state-action pairs that have been barely visited, the dynamics model might be very wrong and the MPC fails as the imagined model and the reality align to longer. Boney et a. propose to tackle this with a denoising autoencoder for trajectory regularization according to the familiarity of a trajectory.
MPC uses at each time t the learned model $s_{t+1} = f_{\theta}(s_t, a_t)$ to select a plan of actions, that is maximizing the sum of expected future reward:
G(a_t, \dots, a_{t+h}) = \mathbb{E}[\sum_{k=t}^{t+H}r(o_t, a_t)] ,$
where $r(o_t, a_t)$ is the observation and action dependent reward. The plan obtained by trajectory optimization is subsequently unrolled for H steps.
Boney et al. propose to regularize trajectories by the familiarity of the visited states leading to the regularized objective:
$G_{reg} = G + \alpha \log p(o_k, a_k, \dots, o_{t+H}, a_{t+H})
Instead of regularizing over the whole trajectory they propose to regularize over marginal probabilities of windows of length w:
$G_{reg} = G + \alpha \sum_{k = t}^{t+H-w} \log p(x_k), \text{ where } x_k = (o_k, a_k, \dots, o_{t+w}, a_{t+w}).$
Instead of explicitly learning a generative model of the familiarity $p(x_k)$ a denoising auto-encoder is used that approximates instead the derivative of the log probability density $\frac{\delta}{\delta x} \log p(x)$. This allows the following back-propagation rule:
$ \frac{\delta G_{reg}}{\delta_i} = \frac{\delta G}{\delta a_i} + \alpha \sum_{k = i}^{i+w} \frac{\delta x_k}{\delta a_i} \frac{\delta}{\delta x} \log p(x).$
The experiments show that the proposed method has competitive sample-efficiency. For example on Halfcheetah the asymptotic performance of PETS is not matched.
This is due to the biggest limitation of this approach, the hindering of exploration. Penalizing the unfamiliarity of states is in contrast to approaches like optimism in the face of uncertainty, which is a core principle of exploration. Aiming to avoid states of high unfamiliarity, the proposed method is the precise opposite of curiosity driven exploration. The appendix proposes preliminary experiments to account for exploration. I would expect, that the pure penalization of unfamiliarity works best in a batch RL setting, which would be an interesting extension of this work.
What Can Learned Intrinsic Rewards Capture?
Zheng, Zeyu and Oh, Junhyuk and Hessel, Matteo and Xu, Zhongwen and Kroiss, Manuel and van Hasselt, Hado and Silver, David and Singh, Satinder
This paper out of DeepMind is an interesting synthesis of ideas out of the research areas of meta learning and intrinsic rewards. The hope for intrinsic reward structures in reinforcement learning - things like uncertainty reduction or curiosity - is that they can incentivize behavior like information-gathering and exploration, which aren't incentivized by the explicit reward in the short run, but which can lead to higher total reward in the long run. So far, intrinsic rewards have mostly been hand-designed, based on heuristics or analogies from human intelligence and learning.
This paper argues that we should use meta learning to learn a parametrized intrinsic reward function that more directly succeeds our goal of facilitating long run reward. They do this by:
- Creating agents that have multiple episodes within a lifetime, and learn a policy network to optimize Eta, a neural network mapping from the agent's life history to scalars, that serves as an intrinsic reward. The learnt policy is carried over from episode to episode.
- The meta learner then optimizes the Eta network to achieve higher lifetime reward according to the *true* extrinsic reward, which the agent itself didn't have access to
- The learned intrinsic reward function is then passed onto the next "newborn" agent, so that, even though its policy is reinitialized, it has access to past information in the form of the reward function
This neatly mimics some of the dynamics of human evolution, where our long term goals of survival and reproduction are distilled into effective short term, intrinsic rewards through chemical signals. The idea is, those chemical signals were evolved over millennia of human evolution to be ones that, if followed locally, would result in the most chance of survival.
The authors find that they're able to learn intrinsic rewards that "know" that they agent they're attached to will be dropped in an environment with a goal, but doesn't know the location, and so learns to incentivize searching until a goal is found, and then subsequently moving towards it. This smooth tradeoff between exploration and exploitation is something that can be difficult to balance between intrinsic exploration-focused reward and extrinsic reward.
While the idea is an interesting one, an uncertainty I have with the paper is whether it'd be likely to scale beyond the simple environments it was trained on. To really learn a useful reward function in complex environments would require huge numbers of timesteps, and it seems like it'd be difficult to effectively assign credit through long lifetimes of learning, even with the lifetime value function used in the paper to avoid needing to mechanically backpropogate through entire lifetimes. It's also worth saying that the idea seems quite similar to a 2017 paper written by Singh et al; having not read that one in detail, I can't comment on the extent to which this work may just build incrementally on that one.
Augmenting Genetic Algorithms with Deep Neural Networks for Exploring the Chemical Space
Nigam, AkshatKumar and Friederich, Pascal and Krenn, Mario and Aspuru-Guzik, Alán
I found this paper a bit difficult to fully understand. Its premise, as far as I can follow, is that we may want to use genetic algorithms (GA), where we make modifications to elements in a population, and keep elements around at a rate proportional to some set of their desirable properties. In particular we might want to use this approach for constructing molecules that have properties (or predicted properties) we want. However, a downside of GA is that its easy to end up in local minima, where a single molecule, or small modifications to that molecule, end up dominating your population, because everything else gets removed for having less-high reward. The authors proposed fix for this is by training a discriminator to tell the difference between molecules from the GA population and those from a reference dataset, and then using that discriminator loss, GAN-style, as part of the "fitness" term that's used to determine if elements stay in the population. The rest of the "fitness" term is made up of chemical desiderata - solubility, how easy a molecule is to synthesize, binding efficacy, etc. I think the intuition here is that if the GA produces the same molecule (or similar ones) over and over again, the discriminator will have an easy time telling the difference between the GA molecules and the reference ones.
One confusion I had with this paper is that it only really seems to have one experiment supporting its idea of using a discriminator as part of the loss - where the discriminator wasn't used at all unless the chemical fitness terms plateaued for some defined period (shown below).
https://i.imgur.com/sTO0Asc.png
The other constrained optimization experiments in section 4.4 (generating a molecule with specific properties, improving a desired property while staying similar to a reference molecule, and drug discovery). They also specifically say that they'd like to be the case that the beta parameter - which controls the weight of the discriminator relative to the chemical fitness properties - lets you smoothly interpolate between prioritizing properties and prioritizing diversity/realness of images, but they find that's not the case, and that, in fact, there's a point at which you move beta a small amount and switch sharply to a regime where chemical fitness values are a lot lower. Plots of eventual chemical fitness found over time seem to be the highest for models with beta set to 0, which isn't what you'd expect if the discriminator was in fact useful for getting you out of plateaus and into long-term better solutions.
Overall, I found this paper an interesting idea, but, especially since it was accepted into ICLR, found it had confusingly little empirical support behind it.
Behavior Regularized Offline Reinforcement Learning
Wu, Yifan and Tucker, George and Nachum, Ofir
Wu et al. provide a framework (behavior regularized actor critic (BRAC)) which they use to empirically study the impact of different design choices in batch reinforcement learning (RL). Specific instantiations of the framework include BCQ, KL-Control and BEAR.
Pure off-policy rl describes the problem of learning a policy purely from a batch $B$ of one step transitions collected with a behavior policy $\pi_b$. The setting allows for no further interactions with the environment. This learning regime is for example in high stake scenarios, like education or heath care, desirable.
The core principle of batch RL-algorithms in to stay in some sense close to the behavior policy. The paper proposes to incorporate this firstly via a regularization term in the value function, which is denoted as **value penalty**. In this case the value function of BRAC takes the following form:
V_D^{\pi}(s) = \sum_{t=0}^{\infty} \gamma ^t \mathbb{E}_{s_t \sim P_t^{\pi}(s)}[R^{pi}(s_t)- \alpha D(\pi(\cdot\vert s_t) \Vert \pi_b(\cdot \vert s_t)))],
where $\pi_b$ is the maximum likelihood estimate of the behavior policy based upon $B$.
This results in a Q-function objective:
$\min_{Q} = \mathbb{E}_{\substack{(s,a,r,s') \sim D \\ a' \sim \pi_{\theta}(\cdot \vert s)}}\left[(r + \gamma \left(\bar{Q}(s',a')-\alpha D(\pi(\cdot\vert s) \Vert \pi_b(\cdot \vert s) \right) - Q(s,a) \right]
and the corresponding policy update:
\max_{\pi_{\theta}} \mathbb{E}_{(s,a,r,s') \sim D} \left[ \mathbb{E}_{a^{''} \sim \pi_{\theta}(\cdot \vert s)}[Q(s,a^{''})] - \alpha D(\pi(\cdot\vert s) \Vert \pi_b(\cdot \vert s) \right]
The second approach is **policy regularization** . Here the regularization weight $\alpha$ is set for value-objectives (V- and Q) to zero and is non-zero for the policy objective.
It is possible to instantiate for example the following batch RL algorithms in this setting:
- BEAR: policy regularization with sample-based kernel MMD as D and min-max mixture of the two ensemble elements for $\bar{Q}$
- BCQ: no regularization but policy optimization over restricted space
Extensive Experiments over the four Mujoco tasks Ant, HalfCheetah,Hopper Walker show:
1. for a BEAR like instantiation there is a modest advantage of keeping $\alpha$ fixed
2. using a mixture of a two or four Q-networks ensemble as target value yields better returns that using one Q-network
3. taking the minimum of ensemble Q-functions is slightly better than taking a mixture (for Ant, HalfCeetah & Walker, but not for Hooper
4. the use of value-penalty yields higher return than the policy-penalty
5. no choice for D (MMD, KL (primal), KL(dual) or Wasserstein (dual)) significantly outperforms the other (note that his contradicts the BEAR paper where MMD was better than KL)
6. the value penalty version consistently outperforms BEAR which in turn outperforms BCQ with improves upon a partially trained baseline.
This large scale study of different design choices helps in developing new methods. It is however surprising to see, that most design choices in current methods are shown empirically to be non crucial. This points to the importance of agreeing upon common test scenarios within a community to prevent over-fitting new algorithms to a particular setting.
Self-Attention Based Molecule Representation for Predicting Drug-Target Interaction
Shin, Bonggun and Park, Sungsoo and Kang, Keunsoo and Ho, Joyce C.
In the last three years, Transformers, or models based entirely on attention for aggregating information from across multiple places in a sequence, have taken over the world of NLP. In this paper, the authors propose using a Transformer to learn a molecular representation, and then building a model to predict drug/target interaction on top of that learned representation. A drug/target interaction model takes in two inputs - a protein involved in a disease pathway, and a (typically small) molecule being considered as a candidate drug - and predicts the binding affinity they'll have for one another. If binding takes place between the two, that protein will be prevented from playing its role in the chain of disease progression, and the drug will be effective.
The mechanics of the proposed Molecular Transformer DTI (or MT-DTI) model work as follows:
https://i.imgur.com/ehfjMK3.png
- Molecules are represented as SMILES strings, a character-based representation of atoms and their structural connections. Proteins are represented as sequences of amino acids.
- A Transformer network is constructed over the characters in the SMILES string, where, at each level, the representation of each character comes from taking an attention-weighted average of the representations at other positions in the character string at that layer. At the final layer, the aggregated molecular representation is taken from a special "REP" token.
- The molecular transformer is pre-trained in BERT-like way: by taking a large corpus (97M molecules) of unsupervised molecular representations, masking or randomizing tokens within the strings, and training the model to predict the true correct token at each point. The hope is that this task will force the representations to encode information relevant to the global structures and chemical constraints of the molecule in question
- This pre-trained Transformer is then plugged into the DTI model, alongside a protein representation model in the form of multiple layers convolutions acting on embedded representations of amino acids. The authors noted that they considered a similar pretrained transformer architecture for the protein representation side of the model, but that they chose not to because (1) the calculations involved in attention are N^2 in the length of the sequence, and proteins are meaningfully longer than the small molecules being studied, and (2) there's no comparably large dataset of protein sequences that could be effectively used for pretraining
- The protein and molecule representations are combined with multiple dense layers, and then produce a final affinity score. Although the molecular representation model starts with a set of pretrained weights, it also fine tunes on top of them.
https://i.imgur.com/qybLKvf.png
When evaluated empirically on two DTI datasets, this attention based model outperforms the prior SOTA, using a convolutional architecture, by a small but consistent amount across all metrics. Interestingly, their model is reasonably competitive even if they don't fine-tune the molecular representation for the DTI task, but only pretraining and fine-tuning together get the MT-DTI model over the threshold of prior work.
Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables
Rakelly, Kate and Zhou, Aurick and Quillen, Deirdre and Finn, Chelsea and Levine, Sergey
Rakelly et al. propose a method to do off-policy meta reinforcement learning (rl). The method achieves a 20-100x improvement on sample efficiency compared to on-policy meta rl like MAML+TRPO.
The key difficulty for offline meta rl arises from the meta-learning assumption, that meta-training and meta-test time match. However during test time the policy has to explore and sees as such on-policy data which is in contrast to the off-policy data that should be used at meta-training. The key contribution of PEARL is an algorithm that allows for online task inference in a latent variable at train and test time, which is used to train a Soft Actor Critic, a very sample efficient off-policy algorithm, with additional dependence of the latent variable.
The implementation of Rakelly et al. proposes to capture knowledge about the current task in a latent stochastic variable Z. A inference network $q_{\Phi}(z \vert c)$ is used to predict the posterior over latents given context c of the current task in from of transition tuples $(s,a,r,s')$ and trained with an information bottleneck. Note that the task inference is done on samples according to a sampling strategy sampling more recent transitions. The latent z is used as an additional input to policy $\pi(a \vert s, z)$ and Q-function $Q(a,s,z)$ of a soft actor critic algorithm which is trained with offline data of the full replay buffer.
https://i.imgur.com/wzlmlxU.png
So the challenge of differing conditions at test and train times is resolved by sampling the content for the latent context variable at train time only from very recent transitions (which is almost on-policy) and at test time by construction on-policy. Sampling $z \sim q(z \vert c)$ at test time allows for posterior sampling of the latent variable, yielding efficient exploration.
The experiments are performed across 6 Mujoco tasks with ProMP, MAML+TRPO and $RL^2$ with PPO as baselines. They show:
- PEARL is 20-100x more sample-efficient
- the posterior sampling of the latent context variable enables deep exploration that is crucial for sparse reward settings
- the inference network could be also a RNN, however it is crucial to train it with uncorrelated transitions instead of trajectories that have high correlated transitions
- using a deterministic latent variable, i.e. reducing $q_{\Phi}(z \vert c)$ to a point estimate, leaves the algorithm unable to solve sparse reward navigation tasks which is attributed to the lack of temporally extended exploration.
The paper introduces an algorithm that allows to combine meta learning with an off-policy algorithm that dramatically increases the sample-efficiency compared to on-policy meta learning approaches. This increases the chance of seeing meta rl in any sort of real world applications.
Meta-Learning via Learned Loss
Sarah Bechtle and Artem Molchanov and Yevgen Chebotar and Edward Grefenstette and Ludovic Righetti and Gaurav Sukhatme and Franziska Meier
Keywords: cs.LG, cs.AI, cs.RO, stat.ML
Abstract: Typically, loss functions, regularization mechanisms and other important aspects of training parametric models are chosen heuristically from a limited set of options. In this paper, we take the first step towards automating this process, with the view of producing models which train faster and more robustly. Concretely, we present a meta-learning method for learning parametric loss functions that can generalize across different tasks and model architectures. We develop a pipeline for meta-training such loss functions, targeted at maximizing the performance of the model trained under them. The loss landscape produced by our learned losses significantly improves upon the original task-specific losses in both supervised and reinforcement learning tasks. Furthermore, we show that our meta-learning framework is flexible enough to incorporate additional information at meta-train time. This information shapes the learned loss function such that the environment does not need to provide this information during meta-test time.
Bechtle et al. propose meta learning via learned loss ($ML^3$) and derive and empirically evaluate the framework on classification, regression, model-based and model-free reinforcement learning tasks.
The problem is formalized as learning parameters $\Phi$ of a meta loss function $M_\phi$ that computes loss values $L_{learned} = M_{\Phi}(y, f_{\theta}(x))$. Following the outer-inner loop meta algorithm design the learned loss $L_{learned}$ is used to update the parameters of the learner in the inner loop via gradient descent:
$\theta_{new} = \theta - \alpha \nabla_{\theta}L_{learned} $. The key contribution of the paper is the way to construct a differentiable learning signal for the loss parameters $\Phi$.
The framework requires to specify a task loss $L_T$ during meta train time, which can be for example the mean squared error for regression tasks. After updating the model parameters to $\theta_{new}$ the task loss is used to measure how much learning progress has been made with loss parameters $\Phi$. The key insight is the decomposition via chain-rule of $\nabla_{\Phi} L_T(y, f_{\theta_{new}})$:
$\nabla_{\Phi} L_T(y, f_{\theta_{new}}) = \nabla_f L_t \nabla_{\theta_{new}}f_{\theta_{new}} \nabla_{\Phi} \theta_{new} = \nabla_f L_t \nabla_{\theta_{new}}f_{\theta_{new}} [\theta - \alpha \nabla_{\theta} \mathbb{E}[M_{\Phi}(y, f_{\theta}(x))]]$.
This allows to update the loss parameters with gradient descent as: $\Phi_{new} = \Phi - \eta \nabla_{\Phi} L_T(y, f_{\theta_{new}})$.
This update rules yield the following $ML^3$ algorithm for supervised learning tasks:
https://i.imgur.com/tSaTbg8.png
For reinforcement learning the task loss is the expected future reward of policies induced by the policy $\pi_{\theta}$, for model-based rl with respect to the approximate dynamics model and for the model free case a system independent surrogate: $L_T(\pi_{\theta_{new}}) = -\mathbb{E}_{\pi_{\theta_{new}}} \left[ R(\tau_{\theta_{new}}) \log \pi_{\theta_{new}}(\tau_{new})\right] $.
The allows further to incorporate extra information via an additional loss term $L_{extra}$ and to consider the augmented task loss $\beta L_T + \gamma L_{extra} $, with weights $\beta, \gamma$ at train time. Possible extra loss terms are used to add physics priors, encouragement of exploratory behavior or to incorporate expert demonstrations. The experiments show that this, at test time unavailable information, is retained in the shape of the loss landscape.
The paper is packed with insightful experiments and shows that the learned loss function:
- yields in regression and classification better accuracies at train and test tasks
- generalizes well and speeds up learning in model based rl tasks
- yields better generalization and faster learning in model free rl
- is agnostic across a bunch of evaluated architectures (2,3,4,5 layers)
- with incorporated extra knowledge yields better performance than without and is superior to alternative approaches like iLQR in a MountainCar task.
The paper introduces a promising alternative, by learning the loss parameters, to MAML like approaches that learn the model parameters. It would be interesting to see if the learned loss function generalizes better than learned model parameters to a broader distribution of tasks like the meta-world tasks.
Once for All: Train One Network and Specialize it for Efficient Deployment
Cai, Han and Gan, Chuang and Han, Song
[link] Summary by ameroyer 9 months ago
**Summary**: The goal of this work is to propose a "Once-for-all" (OFA) network: a large network which is trained such that its subnetworks (subsets of the network with smaller width, convolutional kernel sizes, shallower units) are also trained towards the target task. This allows to adapt the architecture to a given budget at inference time while preserving performance.
**Elastic Parameters.**
The goal is to train a large architecture that contains several well-trained subnetworks with different architecture configurations (in terms of depth, width, kernel size, and resolution). One of the key difficulties is to ensure that each subnetwork reaches high-accuracy even though it is not trained independently but as part of a larger architecture.
This work considers standard CNN architectures (decreasing spatial resolution and increasing number of feature maps), which can be decomposed into units (A unit is a block of layers such that the first layer has stride 2, and the remaining ones have stride 1). The parameters of these units (depth, kernel size, input resolution, width) are denoted as *elastic parameters* in the sense that they can take different values, which defines different subnetworks, which still share the convolutional parameters.
**Progressive Shrinking.**
Additionally, the authors consider a curriculum-style training process which they call *progressive shrinking*. First, they train the model with the maximum depth, $D$, kernel size, $K$, and width, $W$, which yields convolutional parameters . Then they progressively fine-tune this weight, with an additional distillation term from the largest network, while considering different values for the elastic parameters, in the following order:
* Elastic kernel size: Training for a kernel size $k < K$ is done by taking a linear transformation the center $k \times k$ patch in the full $K \times K$ kernels that are in . The linear transformation is useful to model the fact that different scales might be useful for different tasks.
* Elastic depth: To train for depth $d < D$, simply skip the last $D-d$ layers of the unit (rather than looking at every subset of dlayers)
* Elastic width: For a width $w < W$. First, the channels are reorganized by importance (decreasing order of the $L1$-norm of their weights), then use only the top wchannels
* Elastic resolution: Simply train with different image resolutions / resizing: This is actually used for all training processes.
**Experiments.**
Having trained the Once-for-all (OFA) network, the goal is now to find the adequate architecture configuration, given a specific task/budget constraints. To do this automatically, they propose to train a small performance predictive model. They randomly sample 16K subnetworks from OFA, evaluate their accuracy on a validation set, and learn to predict accuracy based on architecture and input image resolution. (Note: It seems that this predictor is then used to perform a cheap evolutionary search, given latency constraints, to find the best architecture config but the whole process is not entirely clear to me. Compared to a proper neural architecture search, however it should be inexpensive).
The main experiments are on ImageNet, using MobileNetv3 as the base full architecture, with the goal of applying the model across different platforms with different inference budget constraints. Overall, the proposed model achieves comparable or higher accuracies for reduced search time, compared to neural architecture search baselines. More precisely their model has a fixed training cost (the OFA network) and a small search cost (find best config based on target latency), which is still lower than doing exhaustive neural architecture search. Furthermore, progressive shrinking does have a significant positive impact on the subnetworks accuracy (+4%).
Combining docking pose rank and structure with deep learning improves protein-ligand binding mode prediction
Joseph A. Morrone and Jeffrey K. Weber and Tien Huynh and Heng Luo and Wendy D. Cornell
Keywords: q-bio.BM, physics.bio-ph, stat.ML
Abstract: We present a simple, modular graph-based convolutional neural network that takes structural information from protein-ligand complexes as input to generate models for activity and binding mode prediction. Complex structures are generated by a standard docking procedure and fed into a dual-graph architecture that includes separate sub-networks for the ligand bonded topology and the ligand-protein contact map. This network division allows contributions from ligand identity to be distinguished from effects of protein-ligand interactions on classification. We show, in agreement with recent literature, that dataset bias drives many of the promising results on virtual screening that have previously been reported. However, we also show that our neural network is capable of learning from protein structural information when, as in the case of binding mode prediction, an unbiased dataset is constructed. We develop a deep learning model for binding mode prediction that uses docking ranking as input in combination with docking structures. This strategy mirrors past consensus models and outperforms the baseline docking program in a variety of tests, including on cross-docking datasets that mimic real-world docking use cases. Furthermore, the magnitudes of network predictions serve as reliable measures of model confidence
This paper focuses on the application of deep learning to the docking problem within rational drug design. The overall objective of drug design or discovery is to build predictive models of how well a candidate compound (or "ligand") will bind with a target protein, to help inform the decision of what compounds are promising enough to be worth testing in a wet lab. Protein binding prediction is important because many small-molecule drugs, which are designed to be small enough to get through cell membranes, act by binding to a specific protein within a disease pathway, and thus blocking that protein's mechanism.
The formulation of the docking problem, as best I understand it, is:
1. A "docking program," which is generally some model based on physical and chemical interactions, takes in a (ligand, target protein) pair, searches over a space of ways the ligand could orient itself within the binding pocket of the protein (which way is it facing, where is it twisted, where does it interact with the protein, etc), and ranks them according to plausibility
2. A scoring function takes in the binding poses (otherwise known as binding modes) ranked the highest, and tries to predict the affinity strength of the resulting bond, or the binary of whether a bond is "active".
The goal of this paper was to interpose modern machine learning into the second step, as alternative scoring functions to be applied after the pose generation . Given the complex data structure that is a highly-ranked binding pose, the hope was that deep learning would facilitate learning from such a complicated raw data structure, rather than requiring hand-summarized features. They also tested a similar model structure on the problem of predicting whether a highly ranked binding pose was actually the empirically correct one, as determined by some epsilon ball around the spatial coordinates of the true binding pose. Both of these were binary tasks, which I understand to be
1. Does this ranked binding pose in this protein have sufficiently high binding affinity to be "active"? This is known as the "virtual screening" task, because it's the relevant task if you want to screen compounds in silico, or virtually, before doing wet lab testing.
2. Is this ranked binding pose the one that would actually be empirically observed? This is known as the "binding mode prediction" task
The goal of this second task was to better understand biases the researchers suspected existed in the underlying dataset, which I'll explain later in this post.
The researchers used a graph convolution architecture. At a (very) high level, graph convolution works in a way similar to normal convolution - in that it captures hierarchies of local patterns, in ways that gradually expand to have visibility over larger areas of the input data. The distinction is that normal convolution defines kernels over a fixed set of nearby spatial coordinates, in a context where direction (the pixel on top vs the pixel on bottom, etc) is meaningful, because photos have meaningful direction and orientation. By contrast, in a graph, there is no "up" or "down", and a given node doesn't have a fixed number of neighbors (whereas a fixed pixel in 2D space does), so neighbor-summarization kernels have to be defined in ways that allow you to aggregate information from 1) an arbitrary number of neighbors, in 2) a manner that is agnostic to orientation. Graph convolutions are useful in this problem because both the summary of the ligand itself, and the summary of the interaction of the posed ligand with the protein, can be summarized in terms of graphs of chemical bonds or interaction sites.
Using this as an architectural foundation, the authors test both solo versions and ensembles of networks:
https://i.imgur.com/Oc2LACW.png
1. "L" - A network that uses graph convolution to summarize the ligand itself, with no reference to the protein it's being tested for binding affinity with
2. "LP" - A network that uses graph convolution on the interaction points between the ligand and protein under the binding pose currently being scored or predicted
3. "R" - A simple network that takes into account the rank assigned to the binding pose by the original docking program (generally used in combination with one of the above).
The authors came to a few interesting findings by trying different combinations of the above model modules. First, they found evidence supporting an earlier claim that, in the dataset being used for training, there was a bias in the positive and negative samples chosen such that you could predict activity of a ligand/protein binding using *ligand information alone.* This shouldn't be possible if we were sampling in an unbiased way over possible ligand/protein pairs, since even ligands that are quite effective with one protein will fail to bind with another, and it shouldn't be informationally possible to distinguish the two cases without protein information. Furthermore, a random forest on hand-designed features was able to perform comparably to deep learning, suggesting that only simple features are necessary to perform the task on this (bias and thus over-simplified)
Specifically, they found that L+LP models did no better than models of L alone on the virtual screening task. However, the binding mode prediction task offered an interesting contrast, in that, on this task, it's impossible to predict the output from ligand information alone, because by construction each ligand will have some set of binding modes that are not the empirically correct one, and one that is, and you can't distinguish between these based on ligand information alone, without looking at the actual protein relationship under consideration. In this case, the LP network did quite well, suggesting that deep learning is able to learn from ligand-protein interactions when it's incentivized to do so. Interestingly, the authors were only able to improve on the baseline model by incorporating the rank output by the original docking program, which you can think of an ensemble of sorts between the docking program and the machine learning model.
Overall, the authors' takeaways from this paper were that (1) we need to be more careful about constructing datasets, so as to not leak information through biases, and (2) that graph convolutional models are able to perform well, but (3) seem to be capturing different things than physics-based models, since ensembling the two together provides marginal value.
Benchmarking Batch Deep Reinforcement Learning Algorithms
Scott Fujimoto and Edoardo Conti and Mohammad Ghavamzadeh and Joelle Pineau
Keywords: cs.LG, cs.AI, stat.ML
Abstract: Widely-used deep reinforcement learning algorithms have been shown to fail in the batch setting--learning from a fixed data set without interaction with the environment. Following this result, there have been several papers showing reasonable performances under a variety of environments and batch settings. In this paper, we benchmark the performance of recent off-policy and batch reinforcement learning algorithms under unified settings on the Atari domain, with data generated by a single partially-trained behavioral policy. We find that under these conditions, many of these algorithms underperform DQN trained online with the same amount of data, as well as the partially-trained behavioral policy. To introduce a strong baseline, we adapt the Batch-Constrained Q-learning algorithm to a discrete-action setting, and show it outperforms all existing algorithms at this task.
The authors propose a unified setting to evaluate the performance of batch reinforcement learning algorithms. The proposed benchmark is discrete and based on the popular Atari Domain. The authors review and benchmark several current batch RL algorithms against a newly introduced version of BCQ (Batch Constrained Deep Q Learning) for discrete environments.
https://i.imgur.com/zrCZ173.png
Note in line 5 that the policy chooses actions with a restricted argmax operation, eliminating actions that have not enough support in the batch.
One of the key difficulties in batch-RL is the divergence of value estimates. In this paper the authors use Double DQN, which means actions are selected with a value net $Q_{\theta}$ and the policy evaluation is done with a target network $Q_{\theta'}$ (line 6).
**How is the batch created?**
A partially trained DQN-agent (trained online for 10mio steps, aka 40mio frames) is used as behavioral policy to collect a batch $B$ containing 10mio transitions. The DQN agent uses either with probability 0.8 an $\epsilon=0.2$ and with probability 0.2 an $\epsilon = 0.001$. The batch RL agents are trained on this batch for 10mio steps and evaluated every 50k time steps for 10 episodes. This process of batch creation differs from the settings used in other papers in i) having only a single behavioral policy, ii) the batch size and iii) the proficiency level of the batch policy.
The experiments, performed on the arcade learning environment include DQN, REM, QR-DQN, KL-Control, BCQ, OnlineDQN and Behavioral Cloning and show that:
- for conventional RL algorithms distributional algorithms (QR-DQN) outperform the plain algorithms (DQN)
- batch RL algorithms perform better than conventional algorithms with BCQ outperforming every other algorithm in every tested game
In addition to the return the authors plot the value estimates for the Q-networks. A drop in performance corresponds in all cases to a divergence (up or down) in value estimates.
The paper is an important contribution to the debate about what is the right setting to evaluate batch RL algorithms. It remains however to be seen if the proposed choice of i) a single behavior policy, ii) the batch size and iii) quality level of the behavior policy will be accepted as standard. Further work is in any case required to decide upon a benchmark for continuous domains.
Limitations of the Empirical Fisher Approximation for Natural Gradient Descent
Frederik Kunstner and Lukas Balles and Philipp Hennig
Abstract: Natural gradient descent, which preconditions a gradient descent update with the Fisher information matrix of the underlying statistical model, is a way to capture partial second-order information. Several highly visible works have advocated an approximation known as the empirical Fisher, drawing connections between approximate second-order methods and heuristics like Adam. We dispute this argument by showing that the empirical Fisher---unlike the Fisher---does not generally capture second-order information. We further argue that the conditions under which the empirical Fisher approaches the Fisher (and the Hessian) are unlikely to be met in practice, and that, even on simple optimization problems, the pathologies of the empirical Fisher can have undesirable effects.
The authors analyse in the very well written paper the relation between Fisher $F(\theta) = \sum_n \mathbb{E}_{p_{\theta}(y \vert x)}[\nabla_{\theta} \log(p_{\theta}(y \vert x_n))\nabla_{\theta} \log(p_{\theta}(y \vert x_n))^T] $ and empirical Fisher $\bar{F}(\theta) = \sum_n [\nabla_{\theta} \log(p_{\theta}(y_n \vert x_n))\nabla_{\theta} \log(p_{\theta}(y_n \vert x_n))^T] $, which has recently seen a surge in interest. . The definitions differ in that $y_n$ is a training label instead of a sample of the model $p_{\theta}(y \vert x_n)$, thus even so the name suggests otherwise $\bar{F}$ is not a empirical, for example Monte Carlo, estimate of the Fisher. The authors rebuff common arguments used to justify the use of the empirical fisher by an amendment to the generalized Gauss-Newton, give conditions when the empirical Fisher does indeed approach the Fisher and give an argument why the empirical fisher might work in practice nonetheless.
The Fisher, capturing the curvature of the parameter space, provides information about the geometry of the parameters pace, the empirical Fisher might however fail so capture the curvature as the striking plot from the paper shows:
https://i.imgur.com/c5iCqXW.png
The authors rebuff the two major justifications for the use of empirical Fisher:
1. "the empirical Fisher matches the construction of a generalized Gauss-Newton"
* for the log-likelihood $log(p(y \vert f) = \log \exp(-\frac{1}{2}(y-f)^2))$ the generalized Gauss-Newton intuition that small residuals $f(x_n, \theta) - y_n$ lead to a good approximation of the Hessian is not satisfied. Whereas the Fisher approaches the Hessian, the empirical Fisher approaches 0
2. "the empirical Fisher converges to the true Fisher when the model is a good fit for the data"
* the authors sharpen the argument to "the empirical Fisher converges at the minimum to the Fisher as the number of samples grows", which is unlikely to be satisfied in practice.
The authors provide an alternative perspective on why the empirical Fisher might be successful, namely to adapt the gradient to the gradient noise in stochastic optimization. The empirical Fisher coincides with the second moment of the stochastic gradient estimate and encodes as such covariance information about the gradient noise. This allows to reduce the effects of gradient noise by scaling back the updates in high variance aka noise directions.
Adversarial camera stickers: A physical camera-based attack on deep learning systems
Li, Juncheng and Schmidt, Frank R. and Kolter, J. Zico
[link] Summary by David Stutz 10 months ago
Li et al. propose camera stickers that when computed adversarially and physically attached to the camera leads to mis-classification. As illustrated in Figure 1, these stickers are realized using circular patches of uniform color. These individual circular stickers are computed in a gradient-descent fashion by optimizing their location, color and radius. The influence of the camera on these stickers is modeled realistically in order to guarantee success.
https://i.imgur.com/xHrqCNy.jpg
Figure 1: Illustration of adversarial stickers on the camera (left) and the effect on the taken photo (right).
CapsAttacks: Robust and Imperceptible Adversarial Attacks on Capsule Networks
Marchisio, Alberto and Nanfa, Giorgio and Khalid, Faiq and Hanif, Muhammad Abdullah and Martina, Maurizio and Shafique, Muhammad
Marchisio et al. propose a black-box adversarial attack on Capsule Networks. The main idea of the attack is to select pixels based on their local standard deviation. Given a window of allowed pixels to be manipulated, these are sorted based on standard deviation and possible impact on the predicted probability (i.e., gap between target class probability and maximum other class probability). A subset of these pixels is then manipulated by a fixed noise value $\delta$. In experiments, the attack is shown to be effective for CapsuleNetworks and other networks.
Efficient Evaluation-Time Uncertainty Estimation by Improved Distillation
Englesson, Erik and Azizpour, Hossein
Englesson and Azizpour propose an adapted knowledge distillation version to improve confidence calibration on out-of-distribution examples including adversarial examples. In contrast to vanilla distillation, they make the following changes: First, high capacity student networks are used, for example, by increasing depth or with. Then, the target distribution is "sharpened" using the true label by reducing the distributions overall entropy. Finally, for wrong predictions of the teacher model, they propose an alternative distribution with maximum mass on the correct class, while not losing the information provided on the incorrect label.
On Norm-Agnostic Robustness of Adversarial Training
Li, Bai and Chen, Changyou and Wang, Wenlin and Carin, Lawrence
Li et al. evaluate adversarial training using both $L_2$ and $L_\infty$ attacks and proposes a second-order attack. The main motivation of the paper is to show that adversarial training cannot increase robustness against both $L_2$ and $L_\infty$ attacks. To this end, they propose a second-order adversarial attack and experimentally show that ensemble adversarial training can partly solve the problem.
Improving Robustness Without Sacrificing Accuracy with Patch Gaussian Augmentation
Lopes, Raphael Gontijo and Yin, Dong and Poole, Ben and Gilmer, Justin and Cubuk, Ekin D.
Lopes et al. propose patch-based Gaussian data augmentation to improve accuracy and robustness against common corruptions. Their approach is intended to be an interpolation between Gaussian noise data augmentation and CutOut. During training, random patches on images are selected and random Gaussian noise is added to these patches. With increasing noise level (i.e., its standard deviation) this results in CutOut; with increasing patch size, this results in regular Gaussian noise data augmentation. On ImageNet-C and Cifar-C, the authors show that this approach improves robustness against common corruptions while also improving accuracy slightly.
MNIST-C: A Robustness Benchmark for Computer Vision
Mu, Norman and Gilmer, Justin
Mu and Gilmer introduce MNIST-C, an MNIST-based corruption benchmark for out-of-distribution evaluation. The benchmark includes various corruption types including random noise (shot and impulse noise), blur (glass and motion blur), (affine) transformations, "striping" or occluding parts of the image, using Canny images or simulating fog. These corruptions are also shown in Figure 1. The transformations have been chosen to be semantically invariant, meaning that the true class of the image does not change. This is important for evaluation as model's can easily be tested whether they still predict the correct labels on the corrupted images.
https://i.imgur.com/Y6LgAM4.jpg
Figure 1: Examples of the used corruption types included in MNIST-C.
A Research Agenda: Dynamic Models to Defend Against Correlated Attacks
Goodfellow, Ian J.
Goodfellow motivates the use of dynamical models as "defense" against adversarial attacks that violate both the identical and independent assumptions in machine learning. Specifically, he argues that machine learning is mostly based on the assumption that the data is samples identically and independently from a data distribution. Evasion attacks, meaning adversarial examples, mainly violate the assumption that they come from the same distribution. Adversarial examples computed within an $\epsilon$-ball around test examples basically correspond to an adversarial distribution the is larger (but entails) the original data distribution. In this article, Goodfellow argues that we should also consider attacks violating the independence assumption. This means, as a simple example, that the attacker can also use the same attack over and over again. This yields the idea of correlated attacks as mentioned in the paper's title. Against this more general threat model, Goodfellow argues that dynamic models are required; meaning the model needs to change (or evolve) – be a moving target that is harder to attack.
Adversarial Examples Are a Natural Consequence of Test Error in Noise
Ford, Nic and Gilmer, Justin and Carlini, Nicholas and Cubuk, Ekin Dogus
Ford et al. show that the existence of adversarial examples can directly linked to test error on noise and other types of random corruption. Additionally, obtaining model robust against random corruptions is difficult, and even adversarially robust models might not be entirely robust against these corruptions. Furthermore, many "defenses" against adversarial examples show poor performance on random corruption – showing that some defenses do not result in robust models, but make attacking the model using gradient-based attacks more difficult (gradient masking).
Adversarially Robust Distillation
Goldblum, Micah and Fowl, Liam and Feizi, Soheil and Goldstein, Tom
Goldblum et al. show that distilling robustness is possible, however, depends on the teacher model and the considered dataset. Specifically, while classical knowledge distillation does not convey robustness against adversarial examples, distillation with a robust teacher model might increase robustness of the student model – even if trained on clean examples only. However, this seems to depend on both the dataset as well as the teacher model, as pointed out in experiments on Cifar100. Unfortunately, from the paper, it does not become clear in which cases robustness distillation does not work. To overcome this limitation, the authors propose to combine adversarial training and distillation and show that this recovers robustness; the student model's robustness might even exceed the teacher model's robustness. This, however, might be due to the additional adversarial examples used during distillation.
When to use parametric models in reinforcement learning?
van Hasselt, Hado and Hessel, Matteo and Aslanides, John
[link] Summary by CodyWild 1 year ago
This paper is a bit provocative (especially in the light of the recent DeepMind MuZero paper), and poses some interesting questions about the value of model-based planning. I'm not sure I agree with the overall argument it's making, but I think the experience of reading it made me hone my intuitions around why and when model-based planning should be useful.
The overall argument of the paper is: rather than learning a dynamics model of the environment and then using that model to plan and learn a value/policy function from, we could instead just keep a large replay buffer of actual past transitions, and use that in lieu of model-sampled transitions to further update our reward estimators without having to acquire more actual experience. In this paper's framing, the central value of having a learned model is this ability to update our policy without needing more actual experience, and it argues that actual real transitions from the environment are more reliable and less likely to diverge than transitions from a learned parametric model. It basically sees a big buffer of transitions as an empirical environment model that it can sample from, in a roughly equivalent way to being able to sample transitions from a learnt model.
An obvious counter-argument to this is the value of models in being able to simulate particular arbitrary trajectories (for example, potential actions you could take from your current point, as is needed for Monte Carlo Tree Search). Simply keeping around a big stock of historical transitions doesn't serve the use case of being able to get a probable next state *for a particular transition*, both because we might not have that state in our data, and because we don't have any way, just given a replay buffer, of knowing that an available state comes after an action if we haven't seen that exact combination before. (And, even if we had, we'd have to have some indexing/lookup mechanism atop the data). I didn't feel like the paper's response to this was all that convincing. It basically just argues that planning with model transitions can theoretically diverge (though acknowledges it empirically often doesn't), and that it's dangerous to update off of "fictional" modeled transitions that aren't grounded in real data. While it's obviously definitionally true that model transitions are in some sense fictional, that's just the basic trade-off of how modeling works: some ability to extrapolate, but a realization that there's a risk you extrapolate poorly.
https://i.imgur.com/8jp22M3.png
The paper's empirical contribution to its argument was to argue that in a low-data setting, model-free RL (in the form of the "everything but the kitchen sink" Rainbow RL algorithm) with experience replay can outperform a model-based SimPLe system on Atari. This strikes me as fairly weak support for the paper's overall claim, especially since historically Atari has been difficult to learn good models of when they're learnt in actual-observation pixel space. Nonetheless, I think this push against the utility of model-based learning is a useful thing to consider if you do think models are useful, because it will help clarify the reasons why you think that's the case.
Are Disentangled Representations Helpful for Abstract Visual Reasoning?
van Steenkiste, Sjoerd and Locatello, Francesco and Schmidhuber, Jürgen and Bachem, Olivier
Arguably, the central achievement of the deep learning era is multi-layer neural networks' ability to learn useful intermediate feature representations using a supervised learning signal. In a supervised task, it's easy to define what makes a feature representation useful: the fact that's easier for a subsequent layer to use to make the final class prediction. When we want to learn features in an unsupervised way, things get a bit trickier. There's the obvious problem of what kinds of problem structures and architectures work to extract representations at all. But there's also a deeper problem: when we ask for a good feature representation, outside of the context of any given task, what are we asking for? Are there some inherent aspects of a representation that can be analyzed without ground truth labels to tell you whether the representations you've learned are good are not?
The notion of "disentangled" features is one answer to that question: it suggests that a representation is good when the underlying "factors of variation" (things that are independently variable in the underlying generative process of the data) are captured in independent dimensions of the feature representation. That is, if your representation is a ten-dimensional vector, and it just so happens that there are ten independent factors along which datapoints differ (color, shape, rotation, etc), you'd ideally want each dimension to correspond to each factor.
This criteria has an elegance to it, and it's previously been shown useful in predicting when the representations learned by a model will be useful in predicting the values of the factors of variation. This paper goes one step further, and tests the value representations for solving a visual reasoning task that involves the factors of variation, but doesn't just involve predicting them. In particular, the authors use learned representations to solve a task patterned on a human IQ test, where some factors stay fixed across a row in a grid, and some vary, and the model needs to generate the image that "fits the pattern".
https://i.imgur.com/O1aZzcN.png
To test the value of disentanglement, they looked at a few canonical metrics of disentanglement, including scores that represent "how many factors are captured in each dimension" and "how many dimensions is a factor spread across". They measured the correlation of these metrics with task performance, and compared that with the correlation between simple autoencoder reconstruction error and performance.
They found that at early stages of training on top of the representations, the disentanglement metrics were more predictive of performance than reconstruction accuracy. This distinction went away as the model learning on top of the representations had more time to train. It makes reasonable sense that you'd mostly see value for disentangled features in a low-data regime, since after long enough the fine-tuning network can learn its own features regardless. But, this paper does appear to contribute to evidence that disentangled features are predictive of task performance, at least when that task directly involves manipulation of specific, known, underlying factors of variation.
Playing the lottery with rewards and multiple languages: lottery tickets in RL and NLP
Yu, Haonan and Edunov, Sergey and Tian, Yuandong and Morcos, Ari S.
Summary: An odd thing about machine learning these days is how far you can get in a line of research while only ever testing your method on image classification and image datasets in general. This leads one occasionally to wonder whether a given phenomenon or advance is a discovery of the field generally, or whether it's just a fact about the informatics and learning dynamics inherent in image data.
This paper, part of a set of recent papers released by Facebook centering around the Lottery Ticket Hypothesis, exists in the noble tradition of "lets try <thing> on some non-image datasets, and see if it still works". This can feel a bit silly in the cases where the ideas or approaches do transfer, but I think it's still an important impulse for the field to have, lest we become too captured by ImageNet and its various descendants.
This paper test the Lottery Ticket Hypothesis - the idea that there are a small subset of weights in a trained network whose lucky initializations promoted learning, such that if you reset those weights to their initializations and train only them you get comparable or near-comparable performance to the full network - on reinforcement learning and NLP datasets. In particular, within RL, they tested on both simple continuous control (where the observation state is a vector of meaningful numbers) and Atari from pixels (where the observation is a full from-pixels image). In NLP, they trained on language modeling and translation, with both a LSTM and a Transformer respectively. (Prior work had found that Transformers didn't exhibit lottery ticket like phenomenon, but this paper found a circumstance where they appear to. )
Some high level interesting results:
https://i.imgur.com/kd03bQ4.png
https://i.imgur.com/rZTH7FJ.png
- So as to not bury the lede: by and large, "winning" tickets retrained at their original initializations outperform random initializations of the same size and configuration on both NLP and Reinforcement Learning problems
- There is wide variability in how much pruning in general (a necessary prerequisite operation) impacts reinforcement learning. On some games, pruning at all crashes performance, on others, it actually improves it. This leads to some inherent variability in results
https://i.imgur.com/4o71XPt.png
- One thing that prior researchers in this area have found is that pruning weights all at once at the end of training tends to crash performance for complex models, and that in order to find pruned models that have Lottery Ticket-esque high-performing properties, you need to do "iterative pruning". This works by training a model for a period, then pruning some proportion of weights, then training again from the beginning, and then pruning again, and so on, until you prune down to the full percentage you want to prune. The idea is that this lets the model adapt gradually to a drop in weights, and "train around" the capacity reduction, rather than it just happening all at once. In this paper, the authors find that this is strongly necessary for Lottery Tickets to be found for either Transformers or many RL problems. On a surface level, this makes sense, since Reinforcement Learning is a notoriously tricky and non-stationary learning problem, and Transformers are complex models with lots of parameters, and so dramatically reducing parameters can handicap the model. A weird wrinkle, though, is that the authors find that lottery tickets found without iterative pruning actually perform worse than "random tickets" (i.e. initialized subnetworks with random topology and weights). This is pretty interesting, since it implies that the topology and weights you get if you prune all at once are actually counterproductive to learning. I don't have a good intuition as to why, but would love to hear if anyone does.
https://i.imgur.com/9LnJe6j.png
- For the Transformer specifically, there was an interesting divergence in the impact of weight pruning between the weights of the embedding matrix and the weights of the rest of the network machinery. If you include embeddings in the set of weights being pruned, there's essentially no difference in performance between random and winning tickets, whereas if you exclude them, winning tickets exhibit the more typical pattern of outperforming random ones. This implies that whatever phenomenon that makes winning tickets better is more strongly (or perhaps only) present in weights for feature calculation on top of embeddings, and not very present for the embeddings themselves
Uncertainty-guided Continual Learning with Bayesian Neural Networks
Ebrahimi, Sayna and Elhoseiny, Mohamed and Darrell, Trevor and Rohrbach, Marcus
[link] Summary by Massimo Caccia 1 year ago
Bayesian Neural Networks (BNN): intrinsic importance model based on weight uncertainty; variational inference can approximate posterior distributions using Monte Carlo sampling for gradient estimation; acts like an ensemble method in that they reduce the prediction variance but only uses 2x the number of parameters.
The idea is to use BNN's uncertainty to guide gradient descent to not update the important weight when learning new tasks.
## Bayes by Backprop (BBB):
https://i.imgur.com/7o4gQMI.png
Where $q(w|\theta)$ is our approximation of the posterior $p(w|x)$. $q$ is most probably gaussian with diagonal covariance. We can optimize this via the ELBO:
https://i.imgur.com/OwGm20b.png
## Uncertainty-guided CL with BNN (UCB):
UCB the regularizing is performed with the learning rate such that the learning rate of each parameter and hence its gradient update becomes a function of its importance. They set the importance to be inversely proportional to the standard deviation $\sigma$ of $q(w|\theta)$
Simply put, the more confident the posterior is about a certain weight, the less is this weight going to be updated.
You can also use the importance for weight pruning (sort of a hard version of the first idea)
## Cartoon
https://i.imgur.com/6Ld79BS.png
One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers
Morcos, Ari S. and Yu, Haonan and Paganini, Michela and Tian, Yuandong
In my view, the Lottery Ticket Hypothesis is one of the weirder and more mysterious phenomena of the last few years of Machine Learning. We've known for awhile that we can take trained networks and prune them down to a small fraction of their weights (keeping those weights with the highest magnitudes) and maintain test performance using only those learned weights. That seemed somewhat surprising, in that there were a lot of weights that weren't actually necessary to encoding the learned function, but, the thinking went, possibly having many times more weights than that was helpful for training, even if not necessary once a model is trained. The authors of the original Lottery Ticket paper came to the surprising realization that they could take the weights that were pruned to exist in the final network, re-initialize them (and only them) to the values they had during initial training, and perform almost as well as the final pruned model that had all weights active during training. And, performance using the specific weights and their particular initialization values is much higher than training a comparable topology of weights with random initial values.
This paper out of Facebook AI adds another fascinating experiment to the pile of off evidence around lottery tickets: they test whether lottery tickets transfer *between datasets*, and they find that they often do (at least when the dataset on which the lottery ticket is found is more complex (in terms of in size, input complexity, or number of classes) than the dataset the ticket is being transferred to. Even more interestingly, they find that for sufficiently simple datasets, the "ticket" initialization pattern learned on a more complex dataset actually does *better* than ones learned on the simple dataset itself. They also find that tickets by and large transfer between SGD and Adam, so whatever kind of inductive bias or value they provide is general across optimizers in addition to at least partially general across datasets.
https://i.imgur.com/H0aPjRN.png
I find this result fun to think about through a few frames. The first is to remember that figuring out heuristics for initializing networks (as a function of their topology) was an important step in getting them to train at all, so while this result may at first seem strange and arcane, in that context it feels less surprising that there are still-better initialization heuristics out there, possibly with some kind of interesting theoretical justification to them, that humans simply haven't been clever enough to formalize yet, and have only discovered empirically through methods like this.
This result is also interesting in terms of transfer: we've known for awhile that the representations learned on more complex datasets can convey general information back to smaller ones, but it's less easy to think about what information is conveyed by the topology and connectivity of a network. This paper suggests that the information is there, and has prompted me to think more about the slightly mind-bending question of how training models could lead to information compressed in this form, and how this information could be better understood.
Generating Diverse High-Fidelity Images with VQ-VAE-2
Razavi, Ali and van den Oord, Aäron and Vinyals, Oriol
VQ-VAE is a Variational AutoEncoder that uses as its information bottleneck a discrete set of codes, rather than a continuous vector. That is: the encoder creates a downsampled spatial representation of the image, where in each grid cell of the downsampled image, the cell is represented by a vector. But, before that vector is passed to the decoder, it's discretized, by (effectively) clustering the vectors the network has historically seen, and substituting each vector with the center of the vector it's closest to. This has the effect of reducing the capacity of your information bottleneck, but without just pushing your encoded representation closer to an uninformed prior. (If you're wondering how the gradient survives this very much not continuous operation, the answer is: we just pretend that operation didn't exist, and imagine that the encoder produced the cluster-center "codebook" vector that the decoder sees).
The part of the model that got a (small) upgrade in this paper is the prior distribution model that's learned on top of these latent representations. The goal of this prior is to be able to just sample images, unprompted, from the distribution of latent codes. Once we have a trained decoder, if we give it a grid of such codes, it can produce an image. But these codes aren't one-per-image, but rather a grid of many codes representing features in different part of the image. In order to generate a set of codes corresponding to a reasonable image, we can either generate them all at once, or else (as this paper does) use an autoregressive approach, where some parts of the code grid are generated, and then subsequent ones conditioned on those. In the original version of the paper, the autoregressive model used was a PixelCNN (don't have the space to fully explain that here, but, at a high level: a model that uses convolutions over previously generated regions to generate a new region). In this paper, the authors took inspiration from the huge rise of self-attention in recent years, and swapped that operation in in lieu of the convolutions. Self-attention has the nice benefit that you can easily have a global receptive range (each region being generated can see all other regions) which you'd otherwise need multiple layers of convolutions to accomplish.
In addition, the authors add an additional layer of granularity: generating both a 32x32 and 64x64 grid, and using both to generate the decoded reconstruction. They argue that this allows one representation to focus on more global details, and the other on more precise ones.
https://i.imgur.com/zD78Pp4.png
The final result is the ability to generate quite realistic looking images, that at least are being claimed to be more diverse than those generated by GANs (examples above). I'm always a bit cautious of claims of better performance in the image-generation area, because it's all squinting at pixels and making up somewhat-reasonable but still arbitrary metrics. That said, it seems interesting and useful to be aware of the current relative capabilities of two of the main forms of generative modeling, and so I'd recommend this paper on that front, even if it's hard for me personally to confidently assess the improvements on prior art.
Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model
Julian Schrittwieser and Ioannis Antonoglou and Thomas Hubert and Karen Simonyan and Laurent Sifre and Simon Schmitt and Arthur Guez and Edward Lockhart and Demis Hassabis and Thore Graepel and Timothy Lillicrap and David Silver
Abstract: Constructing agents with planning capabilities has long been one of the main challenges in the pursuit of artificial intelligence. Tree-based planning methods have enjoyed huge success in challenging domains, such as chess and Go, where a perfect simulator is available. However, in real-world problems the dynamics governing the environment are often complex and unknown. In this work we present the MuZero algorithm which, by combining a tree-based search with a learned model, achieves superhuman performance in a range of challenging and visually complex domains, without any knowledge of their underlying dynamics. MuZero learns a model that, when applied iteratively, predicts the quantities most directly relevant to planning: the reward, the action-selection policy, and the value function. When evaluated on 57 different Atari games - the canonical video game environment for testing AI techniques, in which model-based planning approaches have historically struggled - our new algorithm achieved a new state of the art. When evaluated on Go, chess and shogi, without any knowledge of the game rules, MuZero matched the superhuman performance of the AlphaZero algorithm that was supplied with the game rules.
The successes of deep learning on complex strategic games like Chess and Go have been largely driven by the ability to do tree search: that is, simulating sequences of actions in the environment, and then training policy and value functions to more speedily approximate the results that more exhaustive search reveals. However, this relies on having a good simulator that can predict the next state of the world, given your action. In some games, with straightforward rules, this is easy to explicitly code, but in many RL tasks like Atari, and in many contexts in the real world, having a good model of how the world responds to your actions is in fact a major part of the difficulty of RL.
A response to this within the literature has been systems that learn models of the world from trajectories, and then use those models to do this kind of simulated planning. Historically these have been done by designing models that predict the next observation, given past observations and a passed-in action. This lets you "roll out" observations from actions in a way similar to how a simulator could. However, in high-dimensional observation spaces it takes a lot of model capacity to accurately model the full observation, and many parts of a given observation space will often be irrelevant.
https://i.imgur.com/wKK8cnj.png
To address this difficulty, the MuZero architecture uses an approach from Value Prediction Networks, and learns an internal model that can predict transitions between abstract states (which don't need to match the actual observation state of the world) and then predict a policy, value, and next-step reward from the abstract state. So, we can plan in latent space, by simulating transitions from state to state through actions, and the training signal for that space representation and transition model comes from being able to accurately predict the reward, the empirical future value at a state (discovered through Monte Carlo rollouts) and the policy action that the rollout search would have taken at that point. If two observations are identical in terms of their implications for these quantities, the transition model doesn't need to differentiate them, making it more straightforward to learn. (Apologies for the long caption in above screenshot; I feel like it's quite useful to gain intuition, especially if you're less recently familiar with the MCTS deep learning architectures DeepMind typically uses)
https://i.imgur.com/4nepG6o.png
The most impressive empirical aspect of this paper is the fact that it claims (from what I can tell credibly) to be able to perform as well as planning algorithms with access to a real simulator in games like Chess and Go, and as well as model-free models in games like Atari where MFRL has typically been the state of the art (because world models have been difficult to learn). I feel like I've read a lot recently that suggests to me that the distinction between model-free and model-based RL is becoming increasingly blurred, and I'm really curious to see how that trajectory evolves in future.
Way Off-Policy Batch Deep Reinforcement Learning of Implicit Human Preferences in Dialog
Jaques, Natasha and Ghandeharioun, Asma and Shen, Judy Hanwen and Ferguson, Craig and Lapedriza, Àgata and Jones, Noah and Gu, Shixiang and Picard, Rosalind W.
Given the tasks that RL is typically used to perform, it can be easy to equate the problem of reinforcement learning with "learning dynamically, online, as you take actions in an environment". And while this does represent most RL problems in the literature, it is possible to learn a reinforcement learning system in an off-policy way (read: trained off of data that the policy itself didn't collect), and there can be compelling reasons to prefer this approach. In this paper, which seeks to train a chatbot to learn from implicit human feedback in text interactions, the authors note prior bad experiences with Microsoft's Tay bot, and highlight the value of being able to test and validate a learned model offline, rather than have it continue to learn in a deployment setting. This problem, of learning a RL model off of pre-collected data, is known as batch RL. In this setting, the batch is collected by simply using a pretrained language model to generate interactions with a human, and then extracting reward from these interactions to train a Q learning system once the data has been collected.
If naively applied, Q learning (a good approach for off-policy problems, since it directly estimates the value of states and actions rather than of a policy) can lead to some undesirable results in a batch setting. An interesting one, that hadn't occurred to me, was the fact that Q learning translates its (state, action) reward model into a policy by taking the action associated with the highest reward. This is a generally sensible thing to do if you've been able to gather data on all or most of a state space, but it can also bias the model to taking actions that it has less data for, because high-variance estimates will tend make up a disproportionate amount of maximum values of any estimated distribution. One approach to this is to learn two separate Q functions, and take the minimum over them, and then take the max of that across actions (in this case: words in a sentence being generated). The idea here is that low-data, high-variance parts of state space might have one estimate be high, but might have the other be low, because high variance. However, it's costly to train and run two separate models. Instead, the authors here propose the simpler solution of training a single model with dropout, and using multiple "draws" from that model to simulate a distribution over Q value estimates. This will have a similar effect of penalizing actions whose estimate varies across different dropout masks (which can be hand-wavily thought of as different models).
The authors also add a term to their RL training that penalizes divergence from the initial language model that they used to collect the data, and also that is the initialization point for the parameters of the model. This is done via KL-divergence control: the model is penalized for outputting a distribution over words that is different in distributional-metric terms from what the language model would have output. This makes it costlier for the model to diverge from the pretrained model, and should lead to it only happening in cases of convincing high reward.
Out of these two approaches, it seems like the former is more convincing to me as a general-purpose method to use in batch RL settings. The latter is definitely something I would have expected to work well (and, indeed, KL-controlled models performed much better in empirical tests in the paper!), but more simply because language modeling is hard, and I would expect it to be good to constrain a model to be close to realistic outputs, since the sentiment-based reward signal won't reward realism directly. This seems more like something generally useful for avoiding catastrophic forgetting when switching from an old task to a new one (language modeling to sentiment modeling), rather than a particularly batch-RL-centric innovation.
https://i.imgur.com/EmInxOJ.png
An interesting empirical observation of this paper is that models without language-model control end up drifting away from realism, and repeatedly exploit part of the reward function that, in addition to sentiment, gave points for asking questions. By contrast, the KL-controlled models appear to have avoided falling into this local minimum, and instead generated realistic language that was polite and empathetic. (Obviously this is still a simplified approximation of what makes a good chat bot, but it's at least a higher degree of complexity in its response to reward).
Overall, I quite enjoyed this paper, both for its thoughtfulness and its clever application of engineering to use RL for a problem well outside of its more typical domain.
Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer
Raffel, Colin and Shazeer, Noam and Roberts, Adam and Lee, Katherine and Narang, Sharan and Matena, Michael and Zhou, Yanqi and Li, Wei and Liu, Peter J.
At a high level, this paper is a massive (34 pgs!) and highly-resourced study of many nuanced variations of language pretraining tasks, to see which of those variants produce models that transfer the best to new tasks. As a result, it doesn't lend itself *that* well to being summarized into a central kernel of understanding. So, I'm going to do my best to pull out some high-level insights, and recommend you read the paper in more depth if you're working particularly in language pretraining and want to get the details.
The goals here are simple: create a standardized task structure and a big dataset, so that you can use the same architecture across a wide range of objectives and subsequent transfer tasks, and thus actually compare tasks on equal footing. To that end, the authors created a huge dataset by scraping internet text, and filtering it according to a few common sense criteria. This is an important and laudable task, but not one with a ton of conceptual nuance to it.
https://i.imgur.com/5z6bN8d.png
A more interesting structural choice was to adopt a unified text to text framework for all of the tasks they might want their pretrained model to transfer to. This means that the input to the model is always a sequence of tokens, and so is the output. If the task is translation, the input sequence might be "translate english to german: build a bed" and the the desired output would be that sentence in German. This gets particularly interesting as a change when it comes to tasks where you're predicting relationships of words within sentences, and would typically have a categorical classification loss, which is changed here to predicting the word of the correct class. This restructuring doesn't seem to hurt performance, and has the nice side effect that you can directly use the same model as a transfer starting point for all tasks, without having to add additional layers. Some of the transfer tasks include: translation, sentiment analysis, summarization, grammatical checking of a sentence, and checking the logical relationship between claims.
All tested models followed a transformer (i.e. fully attentional) architecture. The authors tested performance along many different axes. A structural variation was the difference between an encoder-decoder architecture and a language model one.
https://i.imgur.com/x4AOkLz.png
In both cases, you take in text and predict text, but in an encoder-decoder, you have separate models that operate on the input and output, whereas in a language model, it's all seen as part of a single continuous sequence. They also tested variations in what pretraining objective is used. The most common is simple language modeling, where you predict words in a sentence given prior or surrounding ones, but, inspired by the success of BERT, they also tried a number of denoising objectives, where an original sentence was corrupted in some way (by dropping tokens and replacing them with either masks, nothing, or random tokens, dropping individual words vs contiguous spans of words) and then the model had to predict the actual original sentence.
https://i.imgur.com/b5Eowl0.png
Finally, they performed testing as to the effect of dataset size and number of training steps. Some interesting takeaways:
- In almost all tests, the encoder-decoder architecture, where you separately build representations of your input and output text, performs better than a language model structure. This is still generally (though not as consistently) true if you halve the number of parameters in the encoder-decoder, suggesting that there's some structural advantage there beyond just additional parameter count.
- A denoising, BERT-style objective works consistently better than a language modeling one. Within the set of different kinds of corruption, none work obviously and consistently better across tasks, though some have a particular advantage at a given task, and some are faster to train with due to different lengths of output text.
- Unsurprisingly, more data and bigger models both lead to better performance. Somewhat interestingly, training with less data but the same number of training iterations (such that you see the same data multiple times) seems to be fine up to a point. This potentially gestures at an ability to train over a dataset a higher number of times without being as worried about overfitting.
- Also somewhat unsurprisingly, training on a dataset that filters out HTML, random lorem-ipsum web text, and bad words performs meaningfully better than training on one that doesn't
Generalization in Reinforcement Learning with Selective Noise Injection and Information Bottleneck
Igl, Maximilian and Ciosek, Kamil and Li, Yingzhen and Tschiatschek, Sebastian and Zhang, Cheng and Devlin, Sam and Hofmann, Katja
Keywords: approximate, readings, generalization, optimization, information, compression, theory
Coming from the perspective of the rest of machine learning, a somewhat odd thing about reinforcement learning that often goes unnoticed is the fact that, in basically all reinforcement learning, performance of an algorithm is judged by its performance on the same environment it was trained on. In the parlance of ML writ large: training on the test set. In RL, most of the focus has historically been on whether automatic systems would be able to learn a policy from the state distribution of a single environment, already a fairly hard task. But, now that RL has had more success in the single-environment case, there comes the question: how can we train reinforcement algorithms that don't just perform well on a single environment, but over a range of environments. One lens onto this question is that of meta-learning, but this paper takes a different approach, and looks at how straightforward regularization techniques pulled from the land of supervised learning can (or can't straightforwardly) be applied to reinforcement learning.
In general, the regularization techniques discussed here are all ways of reducing the capacity of the model, and preventing it from overfitting. Some ways to reduce capacity are:
- Apply L2 weight penalization
- Apply dropout, which handicaps the model by randomly zeroing out neurons
- Use Batch Norm, which uses noisy batch statistics, and increases randomness in a way that, similar to above, deteriorates performance
- Use an information bottleneck: similar to a VAE, this approach works by learning some compressed representation of your input, p(z|x), and then predicting your output off of that z, in a way that incentivizes your z to be informative (because you want to be able to predict y well) but also penalizes too much information being put in it (because you penalize differences between your learned p(z|x) distribution and an unconditional prior p(z) ). This pushes your model to use its conditional-on-x capacity wisely, and only learn features if they're quite valuable in predicting y
However, the paper points out that there are some complications in straightforwardly applying these techniques to RL. The central one is the fact that in (most) RL, the distribution of transitions you train on comes from prior iterations of your policy. This means that a noisier and less competent policy will also leave you with less data to train on. Additionally, using a noisy policy can increase variance, both by making your trained policy more different than your rollout policy (in an off-policy setting) and by making your estimate of the value function higher-variance, which is problematic because that's what you're using as a target training signal in a temporal difference framework.
The paper is a bit disconnected in its connection between justification and theory, and makes two broad, mostly distinct proposals:
1. The most successful (though also the one least directly justified by the earlier-discussed theoretical difficulties of applying regularization in RL) is an information bottleneck ported into a RL setting. It works almost the same as the classification-model one, except that you're trying to increase the value of your actions given compressed-from-state representation z, rather than trying to increase your ability to correctly predict y. The justification given here is that it's good to incentivize RL algorithms in particular to learn simpler, more compressible features, because they often have such poor data and also training signal earlier in training
2. SNI (Selective Noise Injection) works by only applying stochastic aspects of regularization (sampling from z in an information bottleneck, applying different dropout masks, etc) to certain parts of the training procedure. In particular, the rollout used to collect data is non-stochastic, removing the issue of noisiness impacting the data that's collected. They then do an interesting thing where they calculate a weighted mixture of the policy update with a deterministic model, and the update with a stochastic one. The best performing of these that they tested seems to have been a 50/50 split. This is essentially just a knob you can turn on stochasticity, to trade off between the regularizing effect of noise and the variance-increasing-negative effect of it.
https://i.imgur.com/fi0dHgf.png
https://i.imgur.com/LLbDaRw.png
Based on my read of the experiments in the paper, the most impressive thing here is how well their information bottleneck mechanism works as a way to improve generalization, compared to both the baseline and other regularization approaches. It does look like there's some additional benefit to SNI, particularly in the CoinRun setting, but very little in the MultiRoom setting, and in general the difference is less dramatic than the difference from using the information bottleneck.
Adversarial Self-Defense for Cycle-Consistent GANs
Bashkirova, Dina and Usman, Ben and Saenko, Kate
Domain translation - for example, mapping from a summer to a winter scene, or from a photorealistic image to an object segmentation map - is often performed by GANs through something called cycle consistency loss. This model works by having, for each domain, a generator to map domain A into domain B, and a discriminator to differentiate between real images from domain B, and those that were constructed through the cross-domain generator. With a given image in domain A, training happens by using the A→B generator to map it into domain B, and then then B→ A generator to map it back the original domain. These generators are then trained using two losses: one based on the B-domain discriminator, to push the generated image to look like it belongs from that domain, and another based on the L2 loss between the original domain A image, and the image you get on the other end when you translate it into B and back again.
This paper addresses an effect (identified originally in an earlier paper) where in domains with a many to one mapping between domains (for example, mapping a realistic scene into a domain segmentation map, where information is inherently lost by translating pixels to object outlines), the cycle loss incentivizes the model to operate in a strange, steganographic way, where it saves information about the that would otherwise be lost in the form of low-amplitude random noise in the translated image. This low-amplitude information can't be isolated, but can be detected in a few ways. First, we can simply examine images and notice that information that could not have been captured in the lower-information domain is being perfectly reconstructed. Second, if you add noise to the translation in the lower-information domain, in such a way as to not perceptibly change the translation to human eyes, this can cause the predicted image off of that translation to deteriorate considerably, suggesting that the model was using information that could be modified by such small additions of noise to do its reconstruction.
https://i.imgur.com/08i1j0J.png
The authors of this paper ask whether it's possible to train models that don't perform this steganographic information-storing (which they call "self adversarial examples"). A typical approach to such a problem would be to train generators to perform translations with and without the steganographic information, but even though we can prove the existence of the information, we can't isolate it in a way that would allow us to remove it, and thus create these kinds of training pairs. The two tactics the paper uses are:
1) Simply training the generators to be able to translate a domain-mapped image with noise as well as one without noise, in the hope that this would train it not use information that can be interfered with by the application of such noise.
2) In addition to a L2 cycle loss, adding a discriminator to differentiate between the back-translated image and the original one. I believe the idea here is that if both of the encoders are adding in noise as a kind of secret signal, this would be a way for the discriminator to distinguish between the original and reconstructed image, and would thus be penalized.
They find that both of these methods reduce the use of steganographic information, as determined both by sensitivity to noise (where less sensitivity of reconstruction to noise means less use of coded information) and reconstruction honesty (which constrains accuracy of reconstruction in many to one domains to be no greater than the prediction that a supervised predictor could make given the image from the compressed domain
CATER: A diagnostic dataset for Compositional Actions and TEmporal Reasoning
Girdhar, Rohit and Ramanan, Deva
In Machine Learning, our models are lazy: they're only ever as good as the datasets we train them on. If a task doesn't require a given capability in order for a model to solve it, then the model won't gain that capability. This fact motivates a desire on the part of researchers to construct new datasets, to provide both a source of signal and a not-yet-met standard against which models can be measured. This paper focuses on the domain of reasoning about videos and the objects within them across frames. It observes that, on many tasks that ostensibly require a model to follow what's happening in a video, models that simply aggregate some set of features across frames can do as well as models that actually track and account for temporal evolution from one frame for another. They argue that this shows that, on these tasks, which often involve real-world scenes, the model can predict what's happening within a frame simply based on expectations of the world that can be gleaned from single frames - for example, if you see a swimming pool, you can guess that swimming is likely to take place there. As an example of the kind of task they'd like to get a model to solve, they showed a scene from the Godfather where a character leaves the room, puts a gun in his pocket, and returns to the room. Any human viewer could infer that the gun is in his pocket when it returns, but there doesn't exist any single individual frame that could give evidence of that, so it requires reasoning across frames.
https://i.imgur.com/F2Ngsgw.png
To get around this inherent layer of bias in real-world scenes, the authors decide to artificially construct their own dataset, where objects are moved, and some objects are moved to be contained and obscured within others, in an entirely neutral environment, where the model can't generally get useful information from single frames. This is done using the same animation environment as is used in CLEVR, which contains simple objects that have color, texture, and shape, and that can be moved around a scene. Within this environment, called CATER, the benchmark is made up of three tasks:
- Simply predicting what action ("slide cone" or "pick up and place box") is happening in a given frame. For actions like sliding, where in a given frame a sliding cone is indistinguishable from a static one, this requires a model to actually track prior position in order to correctly predict an action taking place
- Being able to correctly identify the order in which a given pair of actions occurs
- Watching a single golden object that can be moved and contained within other objects (entertainingly enough, for Harry Potter fans, called the snitch), and guessing what frame it's in at the end of the scene. This is basically just the "put a ball in a cup and move it around" party trick, but as a learning task
https://i.imgur.com/bBhPnFZ.png
The authors do show that the "frame aggregation/pooling" methods that worked well on previous datasets don't work well on this dataset - which accords with both expectations and the authors goals. Obviously, it's still a fairly simplified environment, but they hope CATER can still be a useful shared benchmark for people working in the space to solve a task that is known to require more explicit spatiotemporal reasoning.
Can You Trust Your Model's Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift
Ovadia, Yaniv and Fertig, Emily and Ren, Jie and Nado, Zachary and Sculley, David and Nowozin, Sebastian and Dillon, Joshua V. and Lakshminarayanan, Balaji and Snoek, Jasper
A common critique of deep learning is its brittleness off-distribution, combined with its tendency to give confident predictions for off-distribution inputs, as is seen in the case of adversarial examples. In response to this critique, a number of different methods have cropped up in recent years, that try to capture a model's uncertainty as well as its overall prediction. This paper tries to do a broad evaluation of uncertainty methods, and, particularly, to test how they perform on out of distribution data, including both data that is perturbed from its original values, and fully OOD data from ground-truth categories never seen during training. Ideally, we would want an uncertainty method that is less confident in its predictions as data is made more dissimilar from the distribution that the model is trained on. Some metrics the paper uses for capturing this are:
- Brier Score (The difference between predicted score and ground truth 0/1 label, averaged over all examples)
- Negative Log Likelihood
- Expected Calibration Error (Within a given bucket, this is calculated as the difference between accuracy to ground truth labels, and the average predicted score in that bucket, capturing that you'd ideally want to have a lower predicted score in cases where you have low accuracy, and vice versa)
- Entropy - For labels that are fully out of distribution, and don't map to any of the model's categories, you can't directly calculate ground truth accuracy, but you can ideally ask for a model that has high entropy (close to uniform) probabilities over the classes it knows about when the image is drawn from an entirely different class
The authors test over image datasets small (MNIST) and large (ImageNet and CIFAR10), as well as a categorical ad-click-prediction dataset. They came up with some interesting findings.
https://i.imgur.com/EVnjS1R.png
1. More fully principled Bayesian estimation of posteriors over parameters, in the form of Stochastic Variational Inference, works well on MNIST, but quite poorly on either categorical data or higher dimensional image datasets
https://i.imgur.com/3emTYNP.png
2. Temperature scaling, which basically performs a second supervised calibration using a hold-out set to push your probabilities towards true probabilities, performs well in-distribution but collapses fairly quickly off-distribution (which sort of makes sense given that it too is just another supervised method that can do poorly when off-distribution)
3. In general, ensemble methods, where you train different models on different subsets of the data and take their variance as uncertainty, perform the best across the bigger image models as well as the ad click model, likely because SVI (along with many other Bayesian methods) is too computationally intensive to get to work well on higher-dimensional data
4. Overall, none of the methods worked particularly well, and even the best-performing ones were often confidently wrong off-distribution
I think it's fair to say that we're far from where we wish we were when it comes to models that "know when they don't know," and this paper does a good job of highlighting that in specific fashion.
Goal-conditioned Imitation Learning
Ding, Yiming and Florensa, Carlos and Phielipp, Mariano and Abbeel, Pieter
This paper combines imitation learning algorithm GAIL with recent advances in goal-conditioned reinforcement learning, to create a combined approach that can make efficient use of demonstrations, but can also learn information about a reward that can allow the agent to outperform the demonstrator.
Goal-conditioned learning is a form of reward-driven reinforcement learning where the reward is a defined to be 1 when an agent reaches a particular state, and 0 otherwise. This can be a particularly useful form of learning for navigation tasks, where, instead of only training your agent to reach a single hardcoded goal (as you would with a reward function) you teach it to reach arbitrary goals when information about the goal is passed in as input. A typical difficulty with this kind of learning is that its reward is sparse: for any given goal, if an agent never reaches it, it won't ever get reward signal it can use to learn to find it again. A clever solution to this, proposed by earlier method HER (Hindsight Experience Replay), is to perform rollouts of the agent trajectory, and then train your model to reach all the states it actually reached along that trajectory. Said another way, even if your agent did a random, useless thing with respect to one goal, if you retroactively decided that the goal was where it ended up, then it'd be able to receive reward signal after all. In a learning scenario with a fixed reward, this trick wouldn't make any sense, since you don't want to train your model to only go wherever it happened to initially end up. But because the policy here is goal-conditioned, we're not giving our policy wrong information about how to go to the place we want, we're incentivizing it to remember ways it got to where it ended up, in the hopes that it can learn generalizable things about how to reach new places.
The other technique being combined in this paper is imitation learning, or learning from demonstrations. Demonstrations can be highly useful for showing the agent how to get to regions of state space it might not find on its own. The authors of this paper advocate creating a goal-conditioned version of one particular imitation learning algorithm (Generative Adversarial Imitation Learning, or GAIL), and combining that with an off-policy version of Hindsight Experience Replay. In their model, a discriminator tries to tell the behavior of the demonstrator from that of the agent, given some input goal, and uses that as loss, combined with the loss of a more normal Q learning loss with a reward set to 1 when a goal is achieved. Importantly, they amplify both of these methods using the relabeling trick mentioned before: for both the demonstrators and the actual agent trajectories, they take tuples of (state, next state, goal) and replace the intended goal with another state reached later in the trajectory. For the Q learner, this performs its normal role as a way to get reward in otherwise sparse settings, and for the imitation learner, it is a form of data amplification, where a single trajectory + goal can be turned into multiple trajectories "successfully" reaching all of the intermediate points along the observed trajectory. The authors show that their method learns more quickly (as a result of the demonstrations), but also is able to outperform demonstrators, which it wouldn't generally be able to do without an independent, non-demonstrator reward signal
FreeLB: Enhanced Adversarial Training for Language Understanding
Zhu, Chen and Cheng, Yu and Gan, Zhe and Sun, Siqi and Goldstein, Tom and Liu, Jingjing
Adversarial examples and defenses to prevent them are often presented as a case of inherent model fragility, where the model is making a clear and identifiable mistake, by misclassifying a label humans would classify correctly. But, another frame on the adversarial examples research is that they're a way of imposing a certain kind of prior requirement on our models: that they be sensitive to certain scales of perturbation to their inputs. One reason to want to do this is because you believe the model might reasonably need to interact with such perturbed inputs in future. But, another is that smoothness of model outputs, in the sense of an output that doesn't change sharply in the immediate vicinity of an example, can be a useful inductive bias that improves generalization. In images, this is often not the case, as training on adversarial examples empirically worsens performance on normal examples. In text, however, it seems like you can get more benefit out of training on adversarial examples, and this paper proposes a specific way of doing that.
An interesting up-front distinction is the one between generating adversarial examples in embeddings vs raw text. Raw text is generally harder: it's unclear how to permute sentences in ways that leave them grammatically and meaningfully unchanged, and thus mean that the same label is the "correct" one as before, without human input. So the paper instead works in embedding space: adding a delta vectors of adversarial noise to the learned word embeddings used in a text model. One salient downside of generating adversarial examples to train on is that doing so is generally costly: it requires calculating the gradients with respect to the input to calculate the direction of the delta vector, which requires another backwards pass through the network, in addition to the ones needed to calculate the parameter gradients to update those. It happens to be the case that once you've calculated gradients w.r.t inputs, doing so for parameters is basically done for you for free, so one possible solution to this problem is to do a step of parameter gradient calculation/model training every time you take a step of perturbation generation. However, if you're generating your adversarial examples via multi-step Projected Gradient Descent, doing a step of model training at each of the K steps in multi-step PGD means that by the time you finish all K steps and are ready to train on the example, your perturbation vector is out of sync with with your model parameters, and so isn't optimally adversarial. To fix this, the authors propose actually training on the adversarial example generated by each step in the multi-step generation process, not just the example produced at the end. So, instead of training your model on perturbations of a given size, you train them on every perturbation up to and including that size. This also solves the problem of your perturbation being out of sync with your parameters, since you "apply" your perturbation in training at the same step where you calculate it.
The authors sole purpose in this was to make models that generalize better, and they show reasonably convincing evidence that this method works slightly better than competing alternatives on language modeling tasks. More saliently, in my view, they come up with a straightforward and clever solution to a problem, which could potentially be used in other domains.
Ease-of-Teaching and Language Structure from Emergent Communication
Li, Fushan and Bowling, Michael
An interesting category of machine learning papers - to which this paper belongs - are papers which use learning systems as a way to explore the incentive structures of problems that are difficult to intuitively reason about the equilibrium properties of. In this paper, the authors are trying to better understand how different dynamics of a cooperative communication game between agents, where the speaking agent is trying to describe an object such that the listening agent picks the one the speaker is being shown, influence the communication protocol (or, to slightly anthropomorphize, the language) that the agents end up using.
In particular, the authors experiment with what happens when the listening agent is frequently replaced during training with a untrained listener who has no prior experience with the agent. The idea of this experiment is that if the speaker is in a scenario where listeners need to frequently "re-learn" the mapping between communication symbols and objects, this will provide an incentive for that mapping to be easier to quickly learn.
https://i.imgur.com/8csqWsY.png
The metric of ease of learning that the paper focuses on is "topographic similarity", which is a measure of how compositional the communication protocol is. The objects they're working with have two properties, and the agents use a pair of two discrete symbols (two letters) to communicate about them. A perfectly compositional language would use one of the symbols to represent each of the properties. To mathematically measure this property, the authors calculate (cosine) similarity between the two objects property vectors, and the (edit) distance between the two objects descriptions under the emergent language, and calculate the correlation between these quantities. In this experimental setup, if a language is perfectly compositional, the correlation will be perfect, because every time a property is the same, the same symbol will be used, so two objects that share that property will always share that symbol in their linguistic representation.
https://i.imgur.com/t5VxEoX.png
The premise and the experimental setup of this paper are interesting, but I found the experimental results difficult to gain intuition and confidence from. The authors do show that, in a regime where listeners are reset, topographic similarity rises from a beginning-of-training value of .54 to an end of training value of .59, whereas in the baseline, no-reset regime, the value drops to .51. So there definitely is some amount of support for their claim that listener resets lead to higher compositionality. But given that their central quality is just a correlation between similarities, it's hard to gain intuition for whether the difference is a meaningful. It doesn't naively seem particularly dramatic, and it's hard to tell otherwise without more references for how topographic similarity would change under a wider range of different training scenarios.
Plan Arithmetic: Compositional Plan Vectors for Multi-Task Control
Devin, Coline and Geng, Daniel and Abbeel, Pieter and Darrell, Trevor and Levine, Sergey
If you've been at all aware of machine learning in the past five years, you've almost certainly seen the canonical word2vec example demonstrating additive properties of word embeddings: "king - man + woman = queen". This paper has a goal of designing embeddings for agent plans or trajectories that follow similar principles, such that a task composed of multiple subtasks can be represented by adding the vectors corresponding to the subtasks. For example, if a task involved getting an ax and then going to a tree, you'd want to be able to generate an embedding that corresponded to a policy to execute that task by summing the embeddings for "go to ax" and "go to tree".
https://i.imgur.com/AHlCt76.png
The authors don't assume that they know the discrete boundaries between subtasks in multiple-task trajectories, and instead use a relatively simple and clever training structure in order to induce the behavior described above. They construct some network g(x) that takes in information describing a trajectory (in this case, start and end state, but presumably could be more specific transitions), and produces an embedding. Then, they train a model on an imitation learning problem, where, given one demonstration of performing a particular task (typically generated by the authors to be composed of multiple subtasks), the agent needs to predict what action will be taken next in a second trajectory of the same composite task. At each point in the sequence of predicting the next action, the agent calculates the embedding of the full reference trajectory, and the embedding of the actions they have so far performed in the current stage in the predicted trajectory, and calculates the difference between these two values. This embedding difference is used to condition the policy function that predicts next action. At each point, you enforce this constraint, that the embedding of what is remaining to be done in the trajectory be close to the embedding of (full trajectory) - (what has so far been completed), by making the policy that corresponds with that embedding map to the remaining part of the trajectory. In addition to this core loss, they also have a few regularization losses, including:
1. A loss that goes through different temporal subdivisions of reference, and pushes the summed embedding of the two parts to be close to the embedding of the whole
2. A loss that simply pushes the embeddings of the two paired trajectories performing the same task closer together
The authors test mostly on relatively simple tasks - picking up and moving sequences of objects with a robotic arm, moving around and picking up objects in a simplified Minecraft world - but do find that their central partial-conditioning-based loss gives them better performance on demonstration tasks that are made up of many subtasks.
Overall, this is an interesting and clever paper: it definitely targeted additive composition much more directly, rather than situations like the original word2vec where additivity came as a side effect of other properties, but it's still an idea that I could imagine having interesting properties, and one I'd be interested to see applied to a wider variety of tasks.
RTFM: Generalising to Novel Environment Dynamics via Reading
Zhong, Victor and Rocktäschel, Tim and Grefenstette, Edward
Reinforcement learning is notoriously sample-inefficient, and one reason why is that agents learn about the world entirely through experience, and it takes lots of experience to learn useful things. One solution you might imagine to this problem is the ones humans by and large use in encountering new environments: instead of learning everything through first-person exploration, acquiring lots of your knowledge by hearing or reading condensed descriptions of the world that can help you take more sensible actions within it. This paper and others like it have the goal of learning RL agents that can take in information about the world in the form of text, and use that information to solve a task. This paper is not the first to propose a solution in this general domain, but it claims to be unique by dint of having both the dynamics of the environment and the goal of the agent change on a per-environment basis, and be described in text.
The precise details of the architecture used are very much the result of particular engineering done to solve this problem, and as such, it's a bit hard to abstract away generalizable principles that this paper showed, other than the proof of concept fact that tasks of the form they describe - where an agent has to learn which objects can kill which enemies, and pursue the goal of killing certain ones - can be solved.
Arguably the most central design principle of the paper is aggressive and repeated use of different forms of conditioning architectures, to fully mix the information contained in the textual and visual data streams. This was done in two main ways:
- Multiple different attention summaries were created, using the document embedding as input, but with queries conditioned on different things (the task, the inventory, a summarized form of the visual features). This is a natural but clever extension of the fact that attention is an easy way to generate conditional aggregated versions of some input
https://i.imgur.com/xIsRu2M.png
- The architecture uses FiLM (Featurewise Linear Modulation), which is essentially a many-generations-generalized version of conditional batch normalization in which the gamma and lambda used to globally shift and scale a feature vector are learned, taking some other data as input. The canonical version of this would be taking in text input, summarizing it into a vector, and then using that vector as input in a MLP that generates gamma and lambda parameters for all of the convolutional layers in a vision system. The interesting innovation of this paper is essentially to argue that this conditioning operation is quite neutral, and that there's no essential way in which the vision input is the "true" data, and the text simply the auxiliary conditioning data: it's more accurate to say that each form of data should conditioning the process of the other one. And so they use Bidirectional FiLM, which does just that, conditioning vision features on text summaries, but also conditioning text features on vision summaries.
https://i.imgur.com/qFaH1k3.png
- The model overall is composed of multiple layers that perform both this mixing FiLM operation, and also visually-conditioned attention. The authors did show, not super surprisingly, that these additional forms of conditioning added performance value to the model relative to the cases where they were ablated
openaccess.thecvf.com
Deep High-Resolution Representation Learning for Human Pose Estimation
Sun, Ke and Xiao, Bin and Liu, Dong and Wang, Jingdong
[link] Summary by Oleksandr Bailo 1 year ago
This paper is a top-down (i.e. requires person detection separately) pose estimation method with a focus on improving high-resolution representations (features) to make keypoint detection easier.
During the training stage, this method utilizes annotated bounding boxes of person class to extract ground truth images and keypoints. The data augmentations include random rotation, random scale, flipping, and [half body augmentations](http://presentations.cocodataset.org/ECCV18/COCO18-Keypoints-Megvii.pdf) (feeding upper or lower part of the body separately). Heatmap learning is performed in a typical for this task approach of applying L2 loss between predicted keypoint locations and ground truth locations (generated by applying 2D Gaussian with std = 1).
During the inference stage, pre-trained object detector is used to provide bounding boxes. The final heatmap is obtained by averaging heatmaps obtained from the original and flipped images. The pixel location of the keypoint is determined by $argmax$ heatmap value with a quarter offset in the direction to the second-highest heatmap value.
While the pipeline described in this paper is a common practice for pose estimation methods, this method can achieve better results by proposing a network design to extract better representations. This is done through having several parallel sub-networks of different resolutions (next one is half the size of the previous one) while repeatedly fusing branches between each other:
https://raw.githubusercontent.com/leoxiaobin/deep-high-resolution-net.pytorch/master/figures/hrnet.png
The fusion process varies depending on the scale of the sub-network and its location in relation to others:
https://i.imgur.com/mGDn7pT.png
Learning to Predict Without Looking Ahead: World Models Without Forward Prediction
Freeman, C. Daniel and Metz, Luke and Ha, David
Reinforcement Learning is often broadly separated into two categories of approaches: model-free and model-based. In the former category, networks simply take observations and input and produce predicted best-actions (or predicted values of available actions) as output. In order to perform well, the model obviously needs to gain an understanding of how its actions influence the world, but it doesn't explicitly make predictions about what the state of the world will be after an action is taken. In model-based approaches, the agent explicitly builds a dynamics model, or a model in which it takes in (past state, action) and predicts next state. In theory, learning such a model can lead to both interpretability (because you can "see" what the model thinks the world is like) and robustness to different reward functions (because you're learning about the world in a way not explicitly tied up with the reward).
This paper proposes an interesting melding of these two paradigms, where an agent learns a model of the world as part of an end-to-end policy learning. This works through something the authors call "observational dropout": the internal model predicts the next state of the world given the prior one and the action, and then with some probability, the state of the world that both the policy and the next iteration of the dynamics model sees is replaced with the model's prediction. This incentivizes the network to learn an effective dynamics model, because the farther the predictions of the model are from the true state of the world, the worse the performance of the learned policy will be on the iterations where the only observation it can see is the predicted one. So, this architecture is model-free in the sense that the gradient used to train the system is based on applying policy gradients to the reward, but model-based in the sense that it does have an internal world representation.
https://i.imgur.com/H0TNfTh.png
The authors find that, at a simple task, Swing Up Cartpole, very low probabilities of seeing the true world (and thus very high probabilities of the policy only seeing the dynamics model output) lead to world models good enough that a policy trained only on trajectories sampled from that model can perform relatively well. This suggests that at higher probabilities of the true world, there was less value in the dynamics model being accurate, and consequently less training signal for it. (Of course, policies that often could only see the predicted world performed worse during their original training iteration compared to policies that could see the real world more frequently).
On a more complex task of CarRacing, the authors looked at how well a policy trained using the representations of the world model as input could perform, to examine whether it was learning useful things about the world.
https://i.imgur.com/v9etll0.png
They found an interesting trade-off, where at high probabilities (like before) the dynamics model had little incentive to be good, but at low probabilities it didn't have enough contact with the real dynamics of the world to learn a sensible policy.
Are Sixteen Heads Really Better than One?
Michel, Paul and Levy, Omer and Neubig, Graham
In the last two years, the Transformer architecture has taken over the worlds of language modeling and machine translation. The central idea of Transformers is to use self-attention to aggregate information from variable-length sequences, a task for which Recurrent Neural Networks had previously been the most common choice. Beyond that central structural change, one more nuanced change was from having a single attention mechanism on a given layer (with a single set of query, key, and value weights) to having multiple attention heads, each with their own set of weights. The change was framed as being conceptually analogous to the value of having multiple feature dimensions, each of which focuses on a different aspect of input; these multiple heads could now specialize and perform different weighted sums over input based on their specialized function. This paper performs an experimental probe into the value of the various attention heads at test time, and tries a number of different pruning tests across both machine translation and language modeling architectures to see their impact on performance.
In their first ablation experiment, they test the effect of removing (that is, zero-masking the contribution of) a single head from a single attention layer, and find that in almost all cases (88 out of 96) there's no statistically significant drop in performance. Pushing beyond this, they ask what happens if, in a given layer, they remove all heads but the one that was seen to be most important in the single head tests (the head that, if masked, caused the largest performance drop). This definitely leads to more performance degradation than the removal of single heads, but the degradation is less than might be intuitively expected, and is often also not statistically significant.
https://i.imgur.com/Qqh9fFG.png
This also shows an interesting distribution over where performance drops: in machine translation, it seems like decoder-decoder attention is the least sensitive to heads being pruned, and encoder-decoder attention is the most sensitive, with a very dramatic performance dropoff observed if particularly the last layer of encoder-decoder attention is stripped to a single head. This is interesting to me insofar as it shows the intuitive roots of attention in these architectures; attention was originally used in encoder-decoder parts of models to solve problems of pulling out information in a source sentence at the time it's needed in the target sentence, and this result suggests that a lot of the value of multiple heads in translation came from making that mechanism more expressive.
Finally, the authors performed an iterative pruning test, where they ordered all the heads in the network according to their single-head importance, and pruned starting with the least important. Similar to the results above, they find that drops in performance at high rates of pruning happen eventually to all parts of the model, but that encoder-decoder attention suffers more quickly and more dramatically if heads are removed.
https://i.imgur.com/oS5H1BU.png
Overall, this is a clean and straightforward empirical paper that asks a fairly narrow question and generates some interesting findings through that question. These results seem reminiscent to me of the Lottery Ticket Hypothesis line of work, where it seems that having a network with a lot of weights is useful for training insofar as it gives you more chances at an initialization that allows for learning, but that at test time, only a small percentage of the weights have ultimately become important, and the rest can be pruned. In order to make the comparison more robust, I'd be interested to see work that does more specific testing of the number of heads required for good performance during training and also during testing, divided out by different areas of the network. (Also, possibly this work exists and I haven't found it!)
Wasserstein Dependency Measure for Representation Learning
Ozair, Sherjil and Lynch, Corey and Bengio, Yoshua and van den Oord, Aäron and Levine, Sergey and Sermanet, Pierre
Self-Supervised Learning is a broad category of approaches whose goal is to learn useful representations by asking networks to perform constructed tasks that only use the content of a dataset itself, and not external labels. The idea with these tasks is to design tasks such that solving them requires the network to have learned useful Some examples of this approach include predicting the rotation of rotated images, reconstructing color from greyscale, and, the topic of this paper, maximizing mutual information between different areas of the image. The hope behind this last approach is that if two areas of an image are generated by the same set of underlying factors (in the case of a human face: they're parts of the same person's face), then a representation that correctly captures those factors for one area will give you a lot of information about the representation of the other area. Historically, this conceptual desire for representations that are mutually informative has been captured by mutual information. If we define the representation distribution over the data of area 1 as p(x) and area 2 as q(x), the mutual information is the KL divergence between the joint distribution of these two distributions and the product of their marginals. This is an old statistical intuition: the closer the joint is to the product of marginals, the closer the variables are to independent; the farther away, the closer they are to informationally identical.
https://i.imgur.com/2SzD5d5.png
This paper argues that the presence of the KL divergence in this mutual information formulation impedes the ability of networks to learn useful representations. This argument is theoretically based on a result from a recent paper (which for the moment I'll just take as foundation, without reading it myself) that empirical lower-bound measurements of mutual information, of the kind used in these settings, are upper bounded by log(n) where n is datapoints. Our hope in maximizing a lower bound to any quantity is that the bound is fairly tight, since that means that optimizing a network to push upward a lower bound actually has the effect of pushing the actual value up as well. If the lower bound we can estimate is constrained to be far below the actual lower bound in the data, then pushing it upward doesn't actually require the value to move upward. The authors identify this as a particular problem in areas where the underlying mutual information of the data is high, such as in videos where one frame is very predictive of the next, since in those cases the constraint imposed by the dataset size will be small relative to the actual possible maximum mutual information you could push your network to achieve.
https://i.imgur.com/wm39mQ8.png
Taking a leaf out of the GAN literature, the authors suggest keeping replacing the KL divergence component of mutual information and replacing it with the Wasserstein Distance; otherwise known as the "earth-mover distance", the Wasserstein distance measures the cost of the least costly way to move probability mass from one distribution to another, assuming you're moving that mass along some metric space. A nice property of the Wasserstein distance, in both GANs and in this application) is that they don't saturate quite as quickly: the value of a KL divergence can shoot up if the distributions are even somewhat different, making it unable to differentiate between distributions that are somewhat and very far away, whereas a Wasserstein distance continues to have more meaningful signal in that regime. In the context of the swap for mutual information, the authors come up with the "Wasserstein Dependency Measure", which is just the Wasserstein Distance between the joint distributions and the product of the marginals.
https://i.imgur.com/3s2QRRz.png
In practice, they use the dual formulation of the Wasserstein distance, which amounts to applying a (neural network) function f(x) to values from both distributions, optimizing f(x) so that the values are far apart, and using that distance as your training signal. Crucially, this function has to be relatively smooth in order for the dual formulation to work: in particular it has to have a small Lipschitz value (meaning its derivatives are bounded by some value). Intuitively, this has the effect of restricting the capacity of the network, which is hoped to incentivize it to use its limited capacity to represent true factors of variation, which are assumed to be the most compact way to represent the data. Empirically, the authors found that their proposed Wasserstein Dependency Measure (with a slight variation applied to reduce variance) does have the predicted property of performing better for situations where the native mutual information between two areas is high.
I found the theoretical points of this paper interesting, and liked the generalization of the idea of Wasserstein distances from GANs to a new area. That said, I wish I had a better mechanical sense for how it ground out in actual neural network losses: this is partially just my own lack of familiarity with how e.g. mutual information losses are actually formulated as network objectives, but I would have appreciated an appendix that did a bit more of that mapping between mathematical intuition and practical network reality.
Explanations can be manipulated and geometry is to blame
Dombrowski, Ann-Kathrin and Alber, Maximilian and Anders, Christopher J. and Ackermann, Marcel and Müller, Klaus-Robert and Kessel, Pan
In response to increasing calls for ways to explain and interpret the predictions of neural networks, one major genre of explanation has been the construction of salience maps for image-based tasks. These maps assign a relevance or saliency score to every pixel in the image, according to various criteria by which the value of a pixel can be said to have influenced the final prediction of the network. This paper is an interesting blend of ideas from the saliency mapping literature with ones from adversarial examples: it essentially shows that you can create adversarial examples whose goal isn't to change the output of a classifier, but instead to keep the output of the classifier fixed, but radically change the explanation (their term for the previously-described pixel saliency map that results from various explanation-finding methods) to resemble some desired target explanation. This is basically a targeted adversarial example, but targeting a different property of the network (the calculated explanation) while keeping an additional one fixed (keeping the output of the original network close to the original output, as well as keeping the input image itself in a norm ball around the original image. This is done in a pretty standard way: by just defining a loss function incentivizing closeness to the original output and also closeness of the explanation to the desired target, and performing gradient descent to modify pixels until this loss was low.
https://i.imgur.com/N9uReoJ.png
The authors do a decent job of showing such targeted perturbations are possible: by my assessment of their results their strongest successes at inducing an actual targeted explanation are with Layerwise Relevance Propogation and Pattern Attribution (two of the 6 tested explanation methods). With the other methods, I definitely buy that they're able to induce an explanation that's very unlike the true/original explanation, but it's not as clear they can reach an arbitrary target. This is a bit of squinting, but it seems like they have more success in influencing propogation methods (where the effect size of the output is propogated backwards through the network, accounting for ReLus) than they do with gradient ones (where you're simply looking at the gradient of the output class w.r.t each pixel.
In the theory section of the paper, the authors do a bit of differential geometry that I'll be up front and say I did not have the niche knowledge to follow, but which essentially argues that the manipulability of an explanation has to do with the curvature of the output manifold for a constant output. That is to say: how much can you induce a large change in the gradient of the output, while moving a small distance along the manifold of a constant output value. They then go on to argue that ReLU activations, because they are by definition discontinuous, induce sharp changes in gradient for points nearby one another, and this increase the ability for networks to be manipulated. They propose a softplus activation instead, where instead of a sharp discontinuity, the ReLU shape becomes more curved, and show relatively convincingly that at low values of Beta (more curved) you can mostly eliminate the ability of a perturbation to induce an adversarially targeted explanation.
https://i.imgur.com/Fwu3PXi.png
For all that I didn't have a completely solid grasp of some of the theory sections here, I think this is a neat proof of concept paper in showing that neural networks can be small-perturbation fragile on a lot of different axes: we've known this for a while in the area of adversarial examples, but this is a neat generalization of that fact to a new area.
Saccader: Improving Accuracy of Hard Attention Models for Vision
Elsayed, Gamaleldin F. and Kornblith, Simon and Le, Quoc V.
If your goal is to interpret the predictions of neural networks on images, there are a few different ways you can focus your attention. One approach is to try to understand and attach conceptual tags to learnt features, to form a vocabulary with which models can be understood. However, techniques in this family have to content with a number of challenges, from the difficulty in attaching clear concepts to the sheer number of neurons to interpret. An alternate approach, and the one pursued by this paper, is to frame interpretability as a matter of introspecting on *where in an image* the model is pulling information from to make its decision.
This is the question for which hard attention provides an answer: identify where in an image a model is making a decision by learning a meta-model that selects small patches of an image, and then makes a classification decision by applying a network to only those patches which were selected. By definition, if only a discrete set of patches were used for prediction, those were the ones that could be driving the model's decision. This central fact of the model only choosing a discrete set of patches is a key complexity, since the choice to use a patch or not is a binary, discontinuous action, and not something through which one can back-propogate gradients. Saccader, the approach put forward by this paper, proposes an architecture which extracts features from locations within an image, and uses those spatially located features to inform a stochastic policy that selects each patch with some probability. Because reinforcement learning by construction is structured to allow discrete actions, the system as a whole can be trained via policy gradient methods.
https://i.imgur.com/SPK0SLI.png
Diving into a bit more detail: while I don't have a deep familiarity with prior work in this area, my impression is that the notion of using policy gradient to learn a hard attention policy isn't a novel contribution of this work, but rather than its novelty comes from clever engineering done to make that policy easier to learn. The authors cite the problem of sparse reward in learning the policy, which I presume to mean that if you start in more traditional RL fashion by just sampling random patches, most patches will be unclear or useless in providing classification signal, so it will be hard to train well. The Saccader architecture works by extracting localized features in an architecture inspired by the 2019 BagNet paper, which essentially applies very tall and narrow convolutional stacks to spatially small areas of the image. This makes it the case that feature vectors for different overlapping patches can be computed efficiently: instead of rerunning the network again for each patch, it just combined the features from the "tops" of all of the small column networks inside the patch, and used that aggregation as a patch-level feature. These features from the "representation network" were then used in an "attention network," which uses larger receptive field convolutions to create patch-level features that integrated the context of things around them. Once these two sets of features were created, they were fed into the "Saccader cell", which uses them to calculate a distribution over patches which the policy then samples over. The Saccader cell is a simplified memory cell, which sets a value to 1 when a patch has been sampled, and applies a very strong penalization on that patch being sampled on future "glimpses" from the policy (in general, classification is performed by making a number of draws and averaging the logits produced for each patch).
https://i.imgur.com/5pSL0oc.png
I found this paper fairly conceptually clever - I hadn't thought much about using a reinforcement learning setup for classification before - though a bit difficult to follow in its terminology and notation. It's able to perform relatively well on ImageNet, though I'm not steeped enough in that as a benchmark to have an intuitive sense for the paper's claim that their accuracy is meaningfully in the same ballpark as full-image models. One interesting point the paper made was that their system, while limited to small receptive fields for the patch features, can use an entirely different model for mapping patches to logits once the patches are selected, and so can benefit from more powerful generic classification models being tacked onto the end.
Meta-Learning with Implicit Gradients
Aravind Rajeswaran and Chelsea Finn and Sham Kakade and Sergey Levine
Keywords: cs.LG, cs.AI, math.OC, stat.ML
Abstract: A core capability of intelligent systems is the ability to quickly learn new tasks by drawing on prior experience. Gradient (or optimization) based meta-learning has recently emerged as an effective approach for few-shot learning. In this formulation, meta-parameters are learned in the outer loop, while task-specific models are learned in the inner-loop, by using only a small amount of data from the current task. A key challenge in scaling these approaches is the need to differentiate through the inner loop learning process, which can impose considerable computational and memory burdens. By drawing upon implicit differentiation, we develop the implicit MAML algorithm, which depends only on the solution to the inner level optimization and not the path taken by the inner loop optimizer. This effectively decouples the meta-gradient computation from the choice of inner loop optimizer. As a result, our approach is agnostic to the choice of inner loop optimizer and can gracefully handle many gradient steps without vanishing gradients or memory constraints. Theoretically, we prove that implicit MAML can compute accurate meta-gradients with a memory footprint that is, up to small constant factors, no more than that which is required to compute a single inner loop gradient and at no overall increase in the total computational cost. Experimentally, we show that these benefits of implicit MAML translate into empirical gains on few-shot image recognition benchmarks.
[link] Summary by Prateek Gupta 1 year ago
This paper builds upon the previous work in gradient-based meta-learning methods.
The objective of meta-learning is to find meta-parameters ($\theta$) which can be "adapted" to yield "task-specific" ($\phi$) parameters.
Thus, $\theta$ and $\phi$ lie in the same hyperspace.
A meta-learning problem deals with several tasks, where each task is specified by its respective training and test datasets.
At the inference time of gradient-based meta-learning methods, before the start of each task, one needs to perform some gradient-descent (GD) steps initialized from the meta-parameters to obtain these task-specific parameters.
The objective of meta-learning is to find $\theta$, such that GD on each task's training data yields parameters that generalize well on its test data.
Thus, the objective function of meta-learning is the average loss on the training dataset of each task ($\mathcal{L}_{i}(\phi)$), where the parameters of that task ($\phi$) are obtained by performing GD initialized from the meta-parameters ($\theta$).
F(\theta) = \frac{1}{M}\sum_{i=1}^{M} \mathcal{L}_i(\phi)
In order to backpropagate the gradients for this task-specific loss function back to the meta-parameters, one needs to backpropagate through task-specific loss function ($\mathcal{L}_{i}$) and the GD steps (or any other optimization algorithm that was used), which were performed to yield $\phi$.
As GD is a series of steps, a whole sequence of changes done on $\theta$ need to be considered for backpropagation.
Thus, the past approaches have focused on RNN + BPTT or Truncated BPTT.
However, the author shows that with the use of the proximal term in the task-specific optimization (also called inner optimization), one can obtain the gradients without having to consider the entire trajectory of the parameters.
The authors call these implicit gradients.
The idea is to constrain the $\phi$ to lie closer to $\theta$ with the help of proximal term which is similar to L2-regularization penalty term.
Due to this constraint, one obtains an implicit equation of $\phi$ in terms of $\theta$ as
\phi = \theta - \frac{1}{\lambda}\nabla\mathcal{L}_i(\phi)
This is then differentiated to obtain the implicit gradients as
\frac{d\phi}{d\theta} = \big( \mathbf{I} + \frac{1}{\lambda}\nabla^{2} \mathcal{L}_i(\phi) \big)^{-1}
and the contribution of gradients from $\mathcal{L}_i$ is thus,
\big( \mathbf{I} + \frac{1}{\lambda}\nabla^{2} \mathcal{L}_i(\phi) \big)^{-1} \nabla \mathcal{L}_i(\phi)
The hessian in the above gradients are memory expensive computations, which become infeasible in deep neural networks.
Thus, the authors approximate the above term by minimizing the quadratic formulation using conjugate gradient method which only requires Hessian-vector products (cheaply available via reverse backpropagation).
\min_{\mathbf{w}} \mathbf{w}^\intercal \big( I + \frac{1}{\lambda}\nabla^{2} \mathcal{L}_i(\phi) \big) \mathbf{w} - \mathbf{w}^\intercal \nabla \mathcal{L}_i(\phi)
Thus, the paper introduces computationally cheap and constant memory gradient computation for meta-learning.
Temporal Cycle-Consistency Learning
Dwibedi, Debidatta and Aytar, Yusuf and Tompson, Jonathan and Sermanet, Pierre and Zisserman, Andrew
[link] Summary by jerpint 1 year ago
# Overview
This paper presents a novel way to align frames in videos of similar actions temporally in a self-supervised setting. To do so, they leverage the concept of cycle-consistency. They introduce two formulations of cycle-consistency which are differentiable and solvable using standard gradient descent approaches. They name their method Temporal Cycle Consistency (TCC). They introduce a dataset that they use to evaluate their approach and show that their learned embeddings allow for few shot classification of actions from videos.
Figure 1 shows the basic idea of what the paper aims to achieve. Given two video sequences, they wish to map the frames that are closest to each other in both sequences. The beauty here is that this "closeness" measure is defined by nearest neighbors in an embedding space, so the network has to figure out for itself what being close to another frame means. The cycle-consistency is what makes the network converge towards meaningful "closeness".

# Cycle Consistency
Intuitively, the concept of cycle-consistency can be thought of like this: suppose you have an application that allows you to take the photo of a user X and increase their apparent age via some transformation F and decrease their age via some transformation G. The process is cycle-consistent if you can age your image, then using the aged image, "de-age" it and obtain something close to the original image you took; i.e. F(G(X)) ~= X.
In this paper, cycle-consistency is defined in the context of nearest-neighbors in the embedding space. Suppose you have two video sequences, U and V. Take a frame embedding from U, u_i, and find its nearest neighbor in V's embedding space, v_j. Now take the frame embedding v_j and find its closest frame embedding in U, u_k, using a nearest-neighbors approach. If k=i, the frames are cycle consistent. Otherwise, they are not. The authors seek to maximize cycle consistency across frames.
# Differentiable Cycle Consistency
The authors present two differentiable methods for cycle-consistency; cycle-back classification and cycle-back regression.
In order to make their cycle-consistency formulation differentiable, the authors use the concept of soft nearest neighbor:
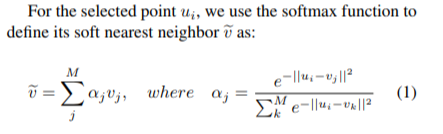
## cycle-back classification
Once the soft nearest neighbor v~ is computed, the euclidean distance between v~ and all u_k is computed for a total of N frames (assume N frames in U) in a logit vector x_k and softmaxed to a prediction ŷ = softmax(x):
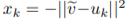.
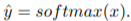
Note the clever use of the negative, which will ensure the softmax selects for the highest distance. The ground truth label is a one-hot vector of size 1xN where position i is set to 1 and all others are set to 0. Cross-entropy is then used to compute the loss.
## cycle-back regression
The concept is very similar to cycle-back classification up to the soft nearest neighbor calculation. However the similarity metric of v~ back to u_k is not computed using euclidean distance but instead soft nearest neighbor again:
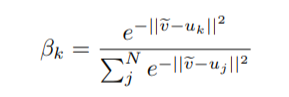
The idea is that they want to penalize the network less for "close enough" guesses. This is done by imposing a gaussian prior on beta centered around the actual closest neighbor i.
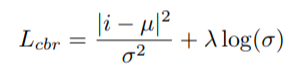
The following figure summarizes the pipeline:
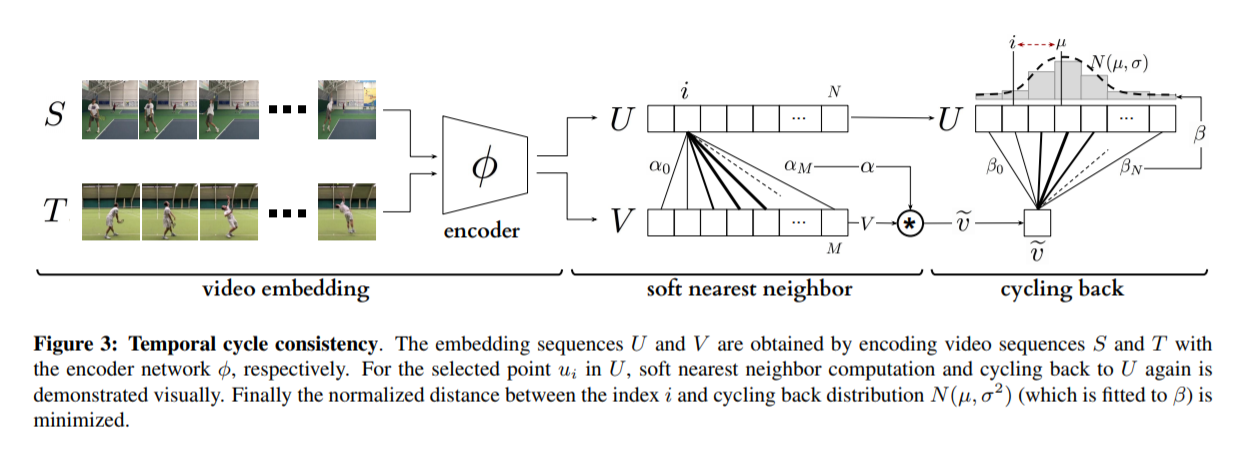
# Datasets
All training is done in a self-supervised fashion. To evaluate their methods, they annotate the Pouring dataset, which they introduce and the Penn Action dataset. To annotate the datasets, they limit labels to specific events and phases between phases

# Model
The network consists of two parts: an encoder network and an embedder network.
## Encoder
They experiment with two encoders:
* ResNet-50 pretrained on imagenet. They use conv_4 layer's output which is 14x14x1024 as the encoder scheme.
* A Vgg-like model from scratch whose encoder output is 14x14x512.
## Embedder
They then fuse the k following frame encodings along the time dimension, and feed it to an embedder network which uses 3D Convolutions and 3D pooling to reduce it to a 1x128 feature vector. They find that k=2 works pretty well.
Benchmarking Model-Based Reinforcement Learning
Wang, Tingwu and Bao, Xuchan and Clavera, Ignasi and Hoang, Jerrick and Wen, Yeming and Langlois, Eric and Zhang, Shunshi and Zhang, Guodong and Abbeel, Pieter and Ba, Jimmy
[link] Summary by dav1309 1 year ago
This is not a detailed summary, just general notes:
Authors make a excellent and extensive comparison of Model Free, Model based methods in 18 environments. In general, the authors compare 3 classes of Model Based Reinforcement Learning (MBRL) algorithms using as metric for comparison the total return in the environment after 200K steps (reporting the mean and std by taking windows of 5000 steps throughout the whole training - and averaging across 4 seeds for each algorithm). They compare MBRL classes:
- **Dyna style:** using a policy to gather data, training a transition function model on this data(i.e. dynamics function / "world model"), and using data predicted by the model (i.e. "imaginary" data) to train the policy)
- **Policy Search with Backpropagation through Time (BPTT):** starting at some state $s_0$ the policy rolls out an episode using the model. Then given the trajectory and its sum of rewards (or any other objective function to maximize) one can differentiate this expression with respect to the policies parameters $\theta$
to obtain the gradient. The training process iterates between collecting data using the current policy and improving the policy via computing the BPTT gradient ... Some version include dynamic programming approaches where the ground -truth dynamics need to be known
- **Model Predictive Control (MPC) / Shooting methods:** There is in general no explicit policy to choose actions, rather the actions sequence is chosen by: starting with a set of candidates of actions sequences $a_{t:t+\tau}$ , propagating this actions sequences in the dynamics model, and then choosing the action sequence which achieved the highest return through out the propagated episode. Then, the agent only applies the first action from the optimal sequence and re-plans at every time-step.
They also compare this to Model Free (MF) methods such as SAC and TD3.
**Brief conclusions which I noticed from MB and MF comparisons:** (note the $>$
indicates better than )
- **MF:** SAC & TD3 $>$ PPO & TRPO
- **Performance:** MPC (shooting, robust performance except for complex env.) $>$ Dyna (bad for long H) $>$ BPTT (SVG very good for complex env.)
- **State and Action Noise:** MPC (shooting, re-planning compensates for noise) $>$ Dyna (lots of Model predictive errors … although meta learning actually benefits from noisy do to lack of exploration)
- **MB dynamics error accumulation:** MB performance plateaus, more data $\neq$ better performance $\rightarrow$ 1. prediction error accumulates through time 2. As we the policy and model improvement are closely link, we can (early) fall into local minima
- **Early Termination (ET):** including ET always negatively affects MB methods. Different ways of incorporating ET into planning horizon (see appendix G for details) work better for some environment but worst for more complex envs. - so, tbh theres no conclusion to be made about early termination schemes (same as for there entire paper :D, but it's not the authors fault, is just the (sad) direction in which most RL / DL research is moving in)
**Some stuff which seems counterintuitive:**
- Why can't we see a significant sample efficiency of MB w.r.t to MF ?
- Why does PILCO suck at almost everything ? original authors/ implementation seems to excel at several tasks
- When using ensembles (e.g. PETS), why is predicting the next state as the Expectation over the ensemble (PE-E: $\boldsymbol{s}_{t+1}=\mathbb{E}\left[\widetilde{f}_{\boldsymbol{\theta}}\left(\boldsymbol{s}_{t}, \boldsymbol{a}_{t}\right)\right]$) better or at least highly comparable to propagating a particle by leveraging the ensemble of models (PE-TS: given $P$ initial states $\boldsymbol{s}_{t=0}^{p}=\boldsymbol{s}_{0} \forall \boldsymbol{p}$, propagate each state / particle $p$ using *one* model $b(p)$ from the entire ensemble ($B$), such that $\boldsymbol{s}_{t+1}^{p} \sim \tilde{f}_{\boldsymbol{\theta}_{b(p)}}\left(\boldsymbol{s}_{t}^{\boldsymbol{p}}, \boldsymbol{a}_{t}\right)$ ), which should in theory better capture uncertainty / multimodality of the State space ??
Online Continual Learning with Maximally Interfered Retrieval
Rahaf Aljundi and Lucas Caccia and Eugene Belilovsky and Massimo Caccia and Laurent Charlin and Tinne Tuytelaars
Abstract: Continual learning, the setting where a learning agent is faced with a never ending stream of data, continues to be a great challenge for modern machine learning systems. In particular the online or "single-pass through the data" setting has gained attention recently as a natural setting that is difficult to tackle. Methods based on replay, either generative or from a stored memory, have been shown to be effective approaches for continual learning, matching or exceeding the state of the art in a number of standard benchmarks. These approaches typically rely on randomly selecting samples from the replay memory or from a generative model, which is suboptimal. In this work we consider a controlled sampling of memories for replay. We retrieve the samples which are most interfered, i.e. whose prediction will be most negatively impacted by the foreseen parameters update. We show a formulation for this sampling criterion in both the generative replay and the experience replay setting, producing consistent gains in performance and greatly reduced forgetting.
Disclaimer: I am an author
# Intro
Experience replay (ER) and generative replay (GEN) are two effective continual learning strategies. In the former, samples from a stored memory are replayed to the continual learner to reduce forgetting. In the latter, old data is compressed with a generative model and generated data is replayed to the continual learner. Both of these strategies assume a random sampling of the memories. But learning a new task doesn't cause **equal** interference (forgetting) on the previous tasks!
In this work, we propose a controlled sampling of the replays. Specifically, we retrieve the samples which are most interfered, i.e. whose prediction will be most negatively impacted by the foreseen parameters update. The method is called Maximally Interfered Retrieval (MIR).
## Cartoon for explanation
https://i.imgur.com/5F3jT36.png
Learning about dogs and horses might cause more interference on lions and zebras than on cars and oranges. Thus, replaying lions and zebras would be a more efficient strategy.
# Method
1) incoming data: $(X_t,Y_t)$
2) foreseen parameter update: $\theta^v= \theta-\alpha\nabla\mathcal{L}(f_\theta(X_t),Y_t)$
### applied to ER (ER-MIR)
3) Search for the top-$k$ values $x$ in the stored memories using the criterion $$s_{MI}(x) = \mathcal{L}(f_{\theta^v}(x),y) -\mathcal{L}(f_{\theta}(x),y)$$
### or applied to GEN (GEN-MIR)
\underset{Z}{\max} \, \mathcal{L}\big(f_{\theta^v}(g_\gamma(Z)),Y^*\big) -\mathcal{L}\big(f_{\theta}(g_\gamma(Z)),Y^*\big)
\text{s.t.} \quad ||z_i-z_j||_2^2 > \epsilon \forall z_i,z_j \in Z \,\text{with} \, z_i\neq z_j
i.e. search in the latent space of a generative model $g_\gamma$ for samples that are the most forgotten given the foreseen update.
4) Then add theses memories to incoming data $X_t$ and train $f_\theta$
# Results
### qualitative
https://i.imgur.com/ZRNTWXe.png
Whilst learning 8s and 9s (first row), GEN-MIR mainly retrieves 3s and 4s (bottom two rows) which are similar to 8s and 9s respectively.
### quantitative
GEN-MIR was tested on MNIST SPLIT and Permuted MNIST, outperforming the baselines in both cases.
ER-MIR was tested on MNIST SPLIT, Permuted MNIST and Split CIFAR-10, outperforming the baselines in all cases.
# Other stuff
### (for avid readers)
We propose a hybrid method (AE-MIR) in which the generative model is replaced with an autoencoder to facilitate the compression of harder dataset like e.g. CIFAR-10.
Explainable AI for Trees: From Local Explanations to Global Understanding
Lundberg, Scott M. and Erion, Gabriel and Chen, Hugh and DeGrave, Alex and Prutkin, Jordan M. and Nair, Bala and Katz, Ronit and Himmelfarb, Jonathan and Bansal, Nisha and Lee, Su-In
Keywords: interpretable
[link] Summary by Apoorva Shetty 1 year ago
Tree-based ML models are becoming increasingly popular, but in the explanation space for these type of models is woefully lacking explanations on a local level. Local level explanations can give a clearer picture on specific use-cases and help pin point exact areas where the ML model maybe lacking in accuracy.
**Idea**: We need a local explanation system for trees, that is not based on simple decision path, but rather weighs each feature in comparison to every other feature to gain better insight on the model's inner workings.
**Solution**: This paper outlines a new methodology using SHAP relative values, to weigh pairs of features to get a better local explanation of a tree-based model. The paper also outlines how we can garner global level explanations from several local explanations, using the relative score for a large sample space. The paper also walks us through existing methodologies for local explanation, and why these are biased toward tree depth as opposed to actual feature importance.
The proposed explanation model titled TreeExplainer exposes methods to compute optimal local explanation, garner global understanding from local explanations, and capture feature interaction within a tree based model.
This method assigns Shapley interaction values to pairs of features essentially ranking the features so as to understand which features have a higher impact on overall outcomes, and analyze feature interaction.
Approximating CNNs with Bag-of-local-Features models works surprisingly well on ImageNet
Brendel, Wieland and Bethge, Matthias
Brendel and Bethge show empirically that state-of-the-art deep neural networks on ImageNet rely to a large extent on local features, without any notion of interaction between them. To this end, they propose a bag-of-local-features model by applying a ResNet-like architecture on small patches of ImageNet images. The predictions of these local features are then averaged and a linear classifier is trained on top. Due to the locality, this model allows to inspect which areas in an image contribute to the model's decision, as shown in Figure 1. Furthermore, these local features are sufficient for good performance on ImageNet. Finally, they show, on scrambled ImageNet images, that regular deep neural networks also rely heavily on local features, without any notion of spatial interaction between them.
https://i.imgur.com/8NO1w0d.png
Figure 1: Illustration of the heap maps obtained using BagNets, the bag-of-local-features model proposed in the paper. Here, different sizes for the local patches are used.
Towards Stable and Efficient Training of Verifiably Robust Neural Networks
Zhang, Huan and Chen, Hongge and Xiao, Chaowei and Li, Bo and Boning, Duane S. and Hsieh, Cho-Jui
Zhang et al. combine interval bound propagation and CROWN, both approaches to obtain bounds on a network's output, to efficiently train robust networks. Both interval bound propagation (IBP) and CROWN allow to bound a network's output for a specific set of allowed perturbations around clean input examples. These bounds can be used for adversarial training. The motivation to combine BROWN and IBP stems from the fact that training using IBP bounds usually results in instabilities, while training with CROWN bounds usually leads to over-regularization.
Generalization in Deep Networks: The Role of Distance from Initialization
Nagarajan, Vaishnavh and Kolter, J. Zico
Nagarajan and Kolter show that neural networks are implicitly regularized by stochastic gradient descent to have small distance from their initialization. This implicit regularization may explain the good generalization performance of over-parameterized neural networks; specifically, more complex models usually generalize better, which contradicts the general trade-off between expressivity and generalization in machine learning. On MNIST, the authors show that the distance of the network's parameters to the original initialization (as measured using the $L_2$ norm on the flattened parameters) reduces with increasing width, and increases with increasing sample size. Additionally, the distance increases significantly when fitting corrupted labels, which may indicate that memorization requires to travel a larger distance in parameter space.
Batch Normalization is a Cause of Adversarial Vulnerability
Galloway, Angus and Golubeva, Anna and Tanay, Thomas and Moussa, Medhat and Taylor, Graham W.
Galloway et al. argue that batch normalization reduces robustness against noise and adversarial examples. On various vision datasets, including SVHN and ImageNet, with popular self-trained and pre-trained models they empirically demonstrate that networks with batch normalization show reduced accuracy on noise and adversarial examples. As noise, they consider Gaussian additive noise as well as different noise types included in the Cifar-C dataset. Similarly, for adversarial examples, they consider $L_\infty$ and $L_2$ PGD and BIM attacks; I refer to the paper for details and hyper parameters. On noise, all networks perform worse with batch normalization, even though batch normalization increases clean accuracy slightly. Against PGD attacks, the provided experiments also suggest that batch normalization reduces robustness; however, the attacks only include 20 iterations and do not manage to reduce the adversarial accuracy to near zero, as is commonly reported. Thus, it is questionable whether batch normalization makes indeed a significant difference regarding adversarial robustness. Finally, the authors argue that replacing batch normalization by weight decay can recover some of the advantage in terms of accuracy and robustness.
How Can We Be So Dense? The Benefits of Using Highly Sparse Representations
Ahmad, Subutai and Scheinkman, Luiz
Ahmad and Scheinkman propose a simple sparse layer in order to improve robustness against random noise. Specifically, considering a general linear network layer, i.e.
$\hat{y}^l = W^l y^{l-1} + b^l$ and $y^l = f(\hat{y}^l$
where $f$ is an activation function, the weights are first initialized using a sparse distribution; then, the activation function (commonly ReLU) is replaced by a top-$k$ ReLU version where only the top-$k$ activations are propagated. In experiments, this is shown to improve robustness against random noise on MNIST.
Adversarial Examples Are Not Bugs, They Are Features
Ilyas, Andrew and Santurkar, Shibani and Tsipras, Dimitris and Engstrom, Logan and Tran, Brandon and Madry, Aleksander
Keywords: adversarial
Ilyas et al. present a follow-up work to their paper on the trade-off between accuracy and robustness. Specifically, given a feature $f(x)$ computed from input $x$, the feature is considered predictive if
$\mathbb{E}_{(x,y) \sim \mathcal{D}}[y f(x)] \geq \rho$;
similarly, a predictive feature is robust if
$\mathbb{E}_{(x,y) \sim \mathcal{D}}\left[\inf_{\delta \in \Delta(x)} yf(x + \delta)\right] \geq \gamma$.
This means, a feature is considered robust if the worst-case correlation with the label exceeds some threshold $\gamma$; here the worst-case is considered within a pre-defined set of allowed perturbations $\Delta(x)$ relative to the input $x$. Obviously, there also exist predictive features, which are however not robust according to the above definition. In the paper, Ilyas et al. present two simple algorithms for obtaining adapted datasets which contain only robust or only non-robust features. The main idea of these algorithms is that an adversarially trained model only utilizes robust features, while a standard model utilizes both robust and non-robust features. Based on these datasets, they show that non-robust, predictive features are sufficient to obtain high accuracy; similarly training a normal model on a robust dataset also leads to reasonable accuracy but also increases robustness. Experiments were done on Cifar10. These observations are supported by a theoretical toy dataset consisting of two overlapping Gaussians; I refer to the paper for details.
Bit-Flip Attack: Crushing Neural Network withProgressive Bit Search
Rakin, Adnan Siraj and He, Zhezhi and Fan, Deliang
Rakin et al. introduce the bit-flip attack aimed to degrade a network's performance by flipping a few weight bits. On Cifar10 and ImageNet, common architectures such as ResNets or AlexNet are quantized into 8 bits per weight value (or fewer). Then, on a subset of the validation set, gradients with respect to the training loss are computed and in each layer, bits are selected based on their gradient value. Afterwards, the layer which incurs the maximum increase in training loss is selected. This way, a network's performance can be degraded to chance level with as few as 17 flipped bits (on ImageNet, using AlexNet).
Benchmarking Deep Learning Hardware and Frameworks: Qualitative Metrics
Wei Dai and Daniel Berleant
Keywords: cs.DC, cs.LG, cs.PF
Abstract: Previous survey papers offer knowledge of deep learning hardware devices and software frameworks. This paper introduces benchmarking principles, surveys machine learning devices including GPUs, FPGAs, and ASICs, and reviews deep learning software frameworks. It also reviews these technologies with respect to benchmarking from the angles of our 7-metric approach to frameworks and 12-metric approach to hardware platforms. After reading the paper, the audience will understand seven benchmarking principles, generally know that differential characteristics of mainstream AI devices, qualitatively compare deep learning hardware through our 12-metric approach for benchmarking hardware, and read benchmarking results of 16 deep learning frameworks via our 7-metric set for benchmarking frameworks.
[link] Summary by Wei Dai 1 year ago
Previous papers on benchmarking deep neural networks offer knowledge of deep learning hardware devices and software frameworks. This paper introduces benchmarking principles, surveys machine learning devices including GPUs, FPGAs, and ASICs, and reviews deep learning software frameworks. It also qualitatively compares these technologies with respect to benchmarking from the angles of our 7-metric approach to deep learning frameworks and 12-metric approach to machine learning hardware platforms.
After reading the paper, the audience will understand seven benchmarking principles, generally know that differential characteristics of mainstream artificial intelligence devices, qualitatively compare deep learning hardware through the 12-metric approach for benchmarking neural network hardware, and read benchmarking results of 16 deep learning frameworks via our 7-metric set for benchmarking frameworks.
The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
Jonathan Frankle and Michael Carbin
Keywords: cs.LG, cs.AI, cs.NE
Abstract: Neural network pruning techniques can reduce the parameter counts of trained networks by over 90%, decreasing storage requirements and improving computational performance of inference without compromising accuracy. However, contemporary experience is that the sparse architectures produced by pruning are difficult to train from the start, which would similarly improve training performance. We find that a standard pruning technique naturally uncovers subnetworks whose initializations made them capable of training effectively. Based on these results, we articulate the "lottery ticket hypothesis:" dense, randomly-initialized, feed-forward networks contain subnetworks ("winning tickets") that - when trained in isolation - reach test accuracy comparable to the original network in a similar number of iterations. The winning tickets we find have won the initialization lottery: their connections have initial weights that make training particularly effective. We present an algorithm to identify winning tickets and a series of experiments that support the lottery ticket hypothesis and the importance of these fortuitous initializations. We consistently find winning tickets that are less than 10-20% of the size of several fully-connected and convolutional feed-forward architectures for MNIST and CIFAR10. Above this size, the winning tickets that we find learn faster than the original network and reach higher test accuracy.
Frankle and Carbin discover so-called winning tickets, subset of weights of a neural network that are sufficient to obtain state-of-the-art accuracy. The lottery hypothesis states that dense networks contain subnetworks – the winning tickets – that can reach the same accuracy when trained in isolation, from scratch. The key insight is that these subnetworks seem to have received optimal initialization. Then, given a complex trained network for, e.g., Cifar, weights are pruned based on their absolute value – i.e., weights with small absolute value are pruned first. The remaining network is trained from scratch using the original initialization and reaches competitive performance using less than 10% of the original weights. As soon as the subnetwork is re-initialized, these results cannot be reproduced though. This suggests that these subnetworks obtained some sort of "optimal" initialization for learning.
Certified Adversarial Robustness via Randomized Smoothing
Jeremy M Cohen and Elan Rosenfeld and J. Zico Kolter
Abstract: We show how to turn any classifier that classifies well under Gaussian noise into a new classifier that is certifiably robust to adversarial perturbations under the $\ell_2$ norm. This "randomized smoothing" technique has been proposed recently in the literature, but existing guarantees are loose. We prove a tight robustness guarantee in $\ell_2$ norm for smoothing with Gaussian noise. We use randomized smoothing to obtain an ImageNet classifier with e.g. a certified top-1 accuracy of 49% under adversarial perturbations with $\ell_2$ norm less than 0.5 (=127/255). No certified defense has been shown feasible on ImageNet except for smoothing. On smaller-scale datasets where competing approaches to certified $\ell_2$ robustness are viable, smoothing delivers higher certified accuracies. Our strong empirical results suggest that randomized smoothing is a promising direction for future research into adversarially robust classification. Code and models are available at http://github.com/locuslab/smoothing.
Cohen et al. study robustness bounds of randomized smoothing, a region-based classification scheme where the prediction is averaged over Gaussian samples around the test input. Specifically, given a test input, the predicted class is the class whose decision region has the largest overlap with a normal distribution of pre-defined variance. The intuition of this approach is that, for small perturbations, the decision regions of classes can't vary too much. In practice, randomized smoothing is applied using samples. In the paper, Cohen et al. show that this approach conveys robustness against radii R depending on the confidence difference between the actual class and the "runner-up" class. In practice, the radii also depend on the number of samples used.
The Limitations of Adversarial Training and the Blind-Spot Attack
Zhang, Huan and Chen, Hongge and Song, Zhao and Boning, Duane S. and Dhillon, Inderjit S. and Hsieh, Cho-Jui
Zhang et al. search for "blind spots" in the data distribution and show that blind spot test examples can be used to find adversarial examples easily. On MNIST, the data distribution is approximated using kernel density estimation were the distance metric is computed in dimensionality-reduced feature space (of an adversarially trained model). For dimensionality reduction, t-SNE is used. Blind spots are found by slightly shifting pixels or changing the gray value of the background. Based on these blind spots, adversarial examples can easily be found for MNIST and Fashion-MNIST.
Towards Interpretable Deep Neural Networks by Leveraging Adversarial Examples
Dong, Yinpeng and Bao, Fan and Su, Hang and Zhu, Jun
Dong et al. study interpretability in the context of adversarial examples and propose a variant of adversarial training to improve interpretability. First the authors argue that neurons do not preserve their interpretability on adversarial examples; e.g., neurons corresponding to high-level concepts such as "bird" or "dog" do not fire consistently on adversarial examples. This result is also validated experimentally, by considering deep representations at different layers. To improve interpretability, the authors propose adversarial training with an additional regularizer enforcing similar features on true and adversarial training examples.
Adversarial Initialization - when your network performs the way I want
Grosse, Kathrin and Trost, Thomas Alexander and Mosbach, Marius and Backes, Michael and Klakow, Dietrich
Grosse et al. propose an adversarial attack on a deep neural network's weight initialization in order to damage accuracy or convergence. An attacker with access to the used deep learning library is assumed. The attack has no knowledge about the training data or the addressed task; however, the attacker has knowledge (through the library's API) about the network architecture and its initialization. The goal of the attacker is to permutate the initialized weights, without being detected, in order to hinder training. In particular, as illustrated in Figure 1 for two fully connected layers described by
$y(x) = \text{ReLU}(B \text{ReLU}(Ax + a) + b)$,
the attack tries to force a large part of neurons to have zero activation from the very beginning. This attack assumes non-negative input, e.g., images in $[0,1]$ as well as ReLU activations in order to zero-out the selected neurons. In Figure 1, this is achieved by permutating the weights in order to concentrate its negative values in a specific part of the weight matrix. Consecutive application of both weight matrices results in most activations to be zero. This will hinder training significantly as no gradients are available, while keeping the statistics of the weights (e.g., mean and variance) unchanged. A similar strategy can be applied to consecutive convolutional layers, as discussed in detail in the paper. Additionally, by slightly shifting the weights in each weight matrix allows to control the rough number of neurons that receives zero activations; this is intended to have control over the "degree" of damage, i.e. whether the network should diverge or just achieve lower accuracy. In experiments, the authors show that the proposed attacks on weight initialization allow to force training to diverge or reach lower accuracy. However, in the majority of cases, training diverges, which makes the attack less stealthy, i.e., easier to detect by the attacked user.
https://i.imgur.com/wqwhYFL.png
https://i.imgur.com/2zZMOYW.png
Figure 1: Illustration of the idea of the proposd attacks on two fully connected layers as described in the text. The color coding illustrates large, usually positive, weight values in black and small, often negative, weight values in light gray.
Robustness of Generalized Learning Vector Quantization Models against Adversarial Attacks
Sascha Saralajew and Lars Holdijk and Maike Rees and Thomas Villmann
Keywords: cs.LG, cs.AI, cs.CV, stat.ML
Abstract: Adversarial attacks and the development of (deep) neural networks robust against them are currently two widely researched topics. The robustness of Learning Vector Quantization (LVQ) models against adversarial attacks has however not yet been studied to the same extent. We therefore present an extensive evaluation of three LVQ models: Generalized LVQ, Generalized Matrix LVQ and Generalized Tangent LVQ. The evaluation suggests that both Generalized LVQ and Generalized Tangent LVQ have a high base robustness, on par with the current state-of-the-art in robust neural network methods. In contrast to this, Generalized Matrix LVQ shows a high susceptibility to adversarial attacks, scoring consistently behind all other models. Additionally, our numerical evaluation indicates that increasing the number of prototypes per class improves the robustness of the models.
Saralajew et al. evaluate learning vector quantization (LVQ) approaches regarding their robustness against adversarial examples. In particular, they consider generalized LVQ where examples are classified based on their distance to the closest prototype of the same class and the closest prototype of another class. The prototypes are learned during training; I refer to the paper for details. Robustness is compared to adversarial training and evaluated against several attacks, including FGSM, DeepFool and Boundary – both white-box and black-box attacks. Regarding $L_\infty$, LVQ usually demonstrates poorer performance than adversarial training. Still, robustness seems to be higher than normally trained deep neural networks. One of the main explanations of the authors is that LVQ follows a max-margin approach; this max-margin idea seems to favor robust models.
Large-Batch Training for LSTM and Beyond
You, Yang and Hseu, Jonathan and Ying, Chris and Demmel, James and Keutzer, Kurt and Hsieh, Cho-Jui
[link] Summary by sudharsansai 1 year ago
Often the best learning rate for a DNN is sensitive to batch size and hence need significant tuning while scaling batch sizes to large scale training. Theory suggests that when you scale the batch size by a factor of $k$ (in the case of multi-GPU training), the learning rate should be scaled by $\sqrt{k}$ to keep the variance of the gradient estimator constant (remember the variance of an estimator is inversely proportional to the sample size?). But in practice, often linear learning rate scaling works better (i.e. scale learning rate by $k$), with a gradual warmup scheme.
This paper proposes a slight modification to the existing learning rate scheduling scheme called LEGW (Linear Epoch Gradual Warmup) which helps us in bridging the gap between theory and practice of large batch training.
The authors notice that in order to make square root scaling work well in practice, one should also scale the warmup period (in terms of epochs) by a factor of $k$. In other words, if you consider learning rate as a function of time period in terms of epochs, scale the periodicity of the function by $k$, while scaling the amplitude of the function by $\sqrt{k}$, when the batch size is scaled by $k$. The authors consider various learning rate scheduling schemes like exponential decay, polynomial decay and multi-step LR decay and find that square root scaling with LEGW scheme often leads to little to no loss in performance while scaling the batch sizes. In fact, one can use SGD with LEGW with no tuning and make it work as good as Adam.
Thus with this approach, one can tune the learning rate for a small batch size and extrapolate it to larger batch sizes while making use of parallel hardwares.
A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms
Yoshua Bengio and Tristan Deleu and Nasim Rahaman and Rosemary Ke and Sébastien Lachapelle and Olexa Bilaniuk and Anirudh Goyal and Christopher Pal
Abstract: We propose to meta-learn causal structures based on how fast a learner adapts to new distributions arising from sparse distributional changes, e.g. due to interventions, actions of agents and other sources of non-stationarities. We show that under this assumption, the correct causal structural choices lead to faster adaptation to modified distributions because the changes are concentrated in one or just a few mechanisms when the learned knowledge is modularized appropriately. This leads to sparse expected gradients and a lower effective number of degrees of freedom needing to be relearned while adapting to the change. It motivates using the speed of adaptation to a modified distribution as a meta-learning objective. We demonstrate how this can be used to determine the cause-effect relationship between two observed variables. The distributional changes do not need to correspond to standard interventions (clamping a variable), and the learner has no direct knowledge of these interventions. We show that causal structures can be parameterized via continuous variables and learned end-to-end. We then explore how these ideas could be used to also learn an encoder that would map low-level observed variables to unobserved causal variables leading to faster adaptation out-of-distribution, learning a representation space where one can satisfy the assumptions of independent mechanisms and of small and sparse changes in these mechanisms due to actions and non-stationarities.
[link] Summary by Joseph Paul Cohen 1 year ago
How can we learn causal relationships that explain data? We can learn from non-stationary distributions. If we experiment with different factorizations of relationships between variables we can observe which ones provide better sample complexity when adapting to distributional shift and therefore are likely to be causal.
If we consider the variables A and B we can factor them in two ways:
$P(A,B) = P(A)P(B|A)$ representing a causal graph like $A\rightarrow B$
$P(A,B) = P(A|B)P(B)$ representing a causal graph like $A \leftarrow B$
The idea is if we train a model with one of these structures; when adapting to a new shifted distribution of data it will take longer to adapt if the model does not have the correct inductive bias. For example let's say that the true relationship is $A$=Raining causes $B$=Open Umbrella (and not vice-versa). Changing the marginal probability of Raining (say because the weather changed) does not change the mechanism that relates $A$ and $B$ (captured by $P(B|A)$), but will have an impact on the marginal $P(B)$.
So after this distributional shift the function that modeled $P(B|A)$ will not need to change because the relationship is the same. Only the function that modeled $P(A)$ will need to change. Under the incorrect factorization $P(B)P(A|B)$, adaptation to the change will be slow because both $P(B)$ and $P(A|B)$ need to be modified to account for the change in $P(A)$ (due to Bayes rule).
Here a difference in sample complexity can be observed when modeling the joint of the shifted distribution. $B\rightarrow A$ takes longer to adapt:
https://i.imgur.com/B9FEmA7.png
Here the idea is that sample complexity when adapting to a new distribution of data is a heuristic to inform us which causal graph inductive bias is correct.
Experimentally this works and they also observe that when models have more capacity it seems that the difference between the models grows.
This summary was written with the help of Yoshua Bengio.
Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
Yunpeng Chen and Haoqi Fan and Bing Xu and Zhicheng Yan and Yannis Kalantidis and Marcus Rohrbach and Shuicheng Yan and Jiashi Feng
Abstract: In natural images, information is conveyed at different frequencies where higher frequencies are usually encoded with fine details and lower frequencies are usually encoded with global structures. Similarly, the output feature maps of a convolution layer can also be seen as a mixture of information at different frequencies. In this work, we propose to factorize the mixed feature maps by their frequencies and design a novel Octave Convolution (OctConv) operation to store and process feature maps that vary spatially "slower" at a lower spatial resolution reducing both memory and computation cost. Unlike existing multi-scale meth-ods, OctConv is formulated as a single, generic, plug-and-play convolutional unit that can be used as a direct replacement of (vanilla) convolutions without any adjustments in the network architecture. It is also orthogonal and complementary to methods that suggest better topologies or reduce channel-wise redundancy like group or depth-wise convolutions. We experimentally show that by simply replacing con-volutions with OctConv, we can consistently boost accuracy for both image and video recognition tasks, while reducing memory and computational cost. An OctConv-equipped ResNet-152 can achieve 82.9% top-1 classification accuracy on ImageNet with merely 22.2 GFLOPs.
[link] Summary by Hadrien Bertrand 1 year ago
Natural images can be decomposed in frequencies, higher frequencies contain small changes and details, while lower frequencies contain the global structure. We can see an example in this image:

Each filter of a convolutional layer focuses on different frequencies of the image. This paper proposes a way to group them explicitly into high and low frequency filters.
To do that, the low frequency group is reduced spatially by 2 in all dimensions (which they define as an octave), before applying the convolution. The spatial reduction, which is a pooling operation, makes sense as it is a low pass filter, small details are discarded but the global structure is kept.
More concretely, the layer takes as input two groups of feature maps, one with a higher resolution than the other. The output is also two groups of feature maps, separated as high/low frequencies. Information is exchanged between the two groups by pooling or upsampling as needed, and as is shown on this image:

The proportion of high and low frequency feature maps is controlled through a single parameter, and through testing the authors found that having around 25% of low frequency features gives the best performance.
One important fact about this layer is that it can simply be used as replacement for a standard convolutional layer, and thus does not require other changes to the architecture. They test on various ResNets, DenseNets and MobileNets.
In terms of tasks, they get performance near state-of-the-art on [ImageNet top-1](https://paperswithcode.com/sota/image-classification-on-imagenet) and top-5. So why use this octave convolution? Because it reduces the amount of memory and computation required by the network.
# Comments
- I would have liked to see more groups of varying frequencies. Since an octave is a spatial reduction of 2^n, the authors could do the same with n > 1. I expect this will be addressed in future work.
- While the results are not quite SOTA, octave convolutions seem compatible with EfficientNet, and I expect this would improve the performance of both.
- Since each octave convolution layer outputs a multi-scale representation of the input, doesn't that mean that pooling becomes less necessary in a network? If so, octave convolutions would give better performances on a new architecture optimized for them.
Code: [Official](https://github.com/facebookresearch/OctConv), [all implementations](https://paperswithcode.com/paper/drop-an-octave-reducing-spatial-redundancy-in)
Hierarchical Autoregressive Image Models with Auxiliary Decoders
Fauw, Jeffrey De and Dieleman, Sander and Simonyan, Karen
Current work in image generation (and generative models more broadly) can be split into two broad categories: implicit models, and likelihood-based models. Implicit models is a categorically that predominantly creates GANs, and which learns how to put pixels in the right places without actually learning a joint probability model over pixels. This is a detriment for applications where you do actually want to be able to calculate probabilities for particular images, in addition to simply sampling new images from your model. Within the class of explicit probability models, the auto-encoder and the autoregressive model are the two most central and well-established.
An auto-encoder works by compressing information about an image into a central lower-dimensional "bottleneck" code, and then trying to reconstruct the original image using the information contained in the code. This structure works well for capturing global structure, but is generally weaker at local structure, because by convention images are generated through stacked convolutional layers, where each pixel in the image is sampled separately, albeit conditioned on the same latent state (the value of the layer below). This is in contrast to an auto-regressive decoder, where you apply some ordering to the pixels, and then sample them in sequence: starting the prior over the first pixel, and then the second conditional on the first, and so on. In this setup, instead of simply expecting your neighboring pixels to coordinate with you because you share latent state, the model actually has visibility into the particular pixel sampled at the prior step, and has the ability to condition on that. This leads to higher-precision generation of local pixel structure with these models .
If you want a model that can get the best of all of these worlds - high-local precision, good global structure, and the ability to calculate probabilities - a sensible approach might be to combine the two: to learn a global-compressed code using an autoencoder, and then, conditioning on that autoencoder code as well as the last sampled values, generate pixels using an autoregressive decoder. However, in practice, this has proved tricky. At a high level, this is because the two systems are hard to balance with one another, and different kinds of imbalance lead to different failure modes. If you try to constrain the expression power of your global code too much, your model will just give up on having global information, and just condition pixels on surrounding (past-sampled) pixels. But, by contrast, if you don't limit the capacity of the code, then the model puts even very local information into the code and ignores the autoregressive part of the model, which brings it away from playing our desired role as global specifier of content.
This paper suggests a new combination approach, whereby we jointly train an encoder and autoregressive decoder, but instead of training the encoder on the training signal produced by that decoder, we train it on the training signal we would have gotten from decoding the code into pixels using a simpler decoder, like a feedforward network. The autoregressive network trains on the codes from the encoder as the encoder trains, but it doesn't actually pass any signal back to it. Basically, we're training our global code to believe it's working with a less competent decoder, and then substituting our autoregressive decoder in during testing.
https://i.imgur.com/d2vF2IQ.png
Some additional technical notes:
- Instead of using a more traditional continuous-valued bottleneck code, this paper uses the VQ-VAE tactic of discretizing code values, to be able to more easily control code capacity. This essentially amounts to generating code vectors as normal, clustering them, passing their cluster medians forward, and then ignoring the fact that none of this is differentiable and passing back gradients with respect to the median
- For their auxiliary decoders, the authors use both a simple feedforward network, and also a more complicated network, where the model needs to guess a pixel, using only the pixel values outside of a window of size of that pixel. The goal of the latter variant is to experiment with a decoder that can't use local information, and could only use global
Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned
Elena Voita and David Talbot and Fedor Moiseev and Rico Sennrich and Ivan Titov
Keywords: cs.CL
Abstract: Multi-head self-attention is a key component of the Transformer, a state-of-the-art architecture for neural machine translation. In this work we evaluate the contribution made by individual attention heads in the encoder to the overall performance of the model and analyze the roles played by them. We find that the most important and confident heads play consistent and often linguistically-interpretable roles. When pruning heads using a method based on stochastic gates and a differentiable relaxation of the L0 penalty, we observe that specialized heads are last to be pruned. Our novel pruning method removes the vast majority of heads without seriously affecting performance. For example, on the English-Russian WMT dataset, pruning 38 out of 48 encoder heads results in a drop of only 0.15 BLEU.
In the two years since it's been introduced, the Transformer architecture, which uses multi-headed self-attention in lieu of recurrent models to consolidate information about input and output sequences, has more or less taken the world of language processing and understanding by storm. It has become the default choice for language for problems like translation and questioning answering, and was the foundation of OpenAI's massive language-model-trained GPT. In this context, I really appreciate this paper's work to try to build our collective intuitions about the structure, specifically by trying to understand how the multiple heads that make up the aforementioned multi-head attention divide up importance and specialize function.
As a quick orientation, attention works by projecting each value in the sequence into query, key, and value vectors. Then, each element in the sequence creates its next-layer value by calculating a function of query and key (typically dot product) and putting that in a softmax against the query results with every other element. This weighting distribution is then used as the weights of a weighted average, combining the values together. By default this is a single operation, with a single set of projection matrices, but in the Transformer approach, they use multi-headed attention, which simply means that they learn independent parameters for multiple independent attention "filters", each of which can then notionally specialize to pull in and prioritize a certain kind of information.
https://i.imgur.com/yuC91Ja.png
The high level theses of this paper are:
- Among attention heads, there's a core of the most crucial and important ones, and then a long tail of heads that can be pruned (or, have their weight in the concatenation of all attention heads brought to nearly zero) and have a small effect on performance
- It's possible and useful to divide up the heads according to the kinds of other tokens that it is most consistently pulling information from. The authors identify three: positional, syntactic, and rare. Positional heads consistently (>90% of the time) put their maximum attention weight on the same position relative to the query word. Syntactic heads are those that recurringly in the same grammatical relation to the query, the subject to its verb, or the adjective to its noun, for example. Rare words is not a frequently used head pattern, but it is a very valuable head within the first layer, and will consistently put its highest weight on the lowest-frequency word in a given sentence.
An interesting side note here is that the authors tried at multiple stages in pruning to retrain a network using only the connections between unpruned heads, and restarting from scratch. However, in a effect reminiscent of the Lottery Ticket Thesis, retraining from scratch cannot get quite the same performance.
Few-Shot Adversarial Learning of Realistic Neural Talking Head Models
Egor Zakharov and Aliaksandra Shysheya and Egor Burkov and Victor Lempitsky
Keywords: cs.CV, cs.GR, cs.LG
Abstract: Several recent works have shown how highly realistic human head images can be obtained by training convolutional neural networks to generate them. In order to create a personalized talking head model, these works require training on a large dataset of images of a single person. However, in many practical scenarios, such personalized talking head models need to be learned from a few image views of a person, potentially even a single image. Here, we present a system with such few-shot capability. It performs lengthy meta-learning on a large dataset of videos, and after that is able to frame few- and one-shot learning of neural talking head models of previously unseen people as adversarial training problems with high capacity generators and discriminators. Crucially, the system is able to initialize the parameters of both the generator and the discriminator in a person-specific way, so that training can be based on just a few images and done quickly, despite the need to tune tens of millions of parameters. We show that such an approach is able to learn highly realistic and personalized talking head models of new people and even portrait paintings.
https://i.imgur.com/JJFljWo.png
This paper follows in a recent tradition of results out of Samsung: in the wake of StyleGAN's very impressive generated images, it uses a lot of similar architectural elements, combined with meta-learning and a new discriminator framework, to generate convincing "talking head" animations based on a small number of frames of a person's face. Previously, models that generated artificial face videos could only do so by training by a large number of frames of each individual speaker that they wanted to simulate. This system instead is able to generate video in a few-shot way: where they only need one or two frames of a new speaker to do convincing generation.
The structure of talking head video generation as a problem relies on the idea of "landmarks," explicit parametrization of where the nose, the eyes, the lips, the head, are oriented in a given shot. The model is trained to be able to generate frames of a specified person (based on an input frame), and in a specific pose (based on an input landmark set).
While the visual quality of the simulated video generated here is quite stunning, the most centrally impressive fact about this paper is that generation was only conditioned on a few frames of each target person. This is accomplished through a combination of meta-learning (as an overall training procedure/regime) and adaptive instance normalization, a way of dynamically parametrizing models that was earlier used in a StyleGAN paper (also out of the Samsung lab). Meta-learning works by doing simulated few-shot training iterations, where a model is trained for a small number of steps on a given "task" (where here a task is a given target face), and then optimized on the meta-level to be able to get good test set error rates across many such target faces.
https://i.imgur.com/RIkO1am.png
The mechanics of how this meta-learning approach actually work are quite interesting: largely a new application of existing techniques, but with some extensions and innovations worked in.
- A convolutional model produces an embedding given an input image and a pose. An average embedding is calculated by averaging over different frames, with the hopes of capturing information about the video, in a pose-independent way. This embedding, along with a goal set of landmarks (i.e. the desired facial expression of your simulation) is used to parametrize the generator, which is then asked to determine whether the generated image looks like it came from the sequence belonging to the target face, and looks like it corresponds to the target pose
- Adaptive instance normalization works by having certain parameters of the network (typically, per the name, post-normalization rescaling values) that are dependent on the properties of some input data instance. This works by training a network to produce an embedding vector of the image, and then multiplying that embedding by per-layer, per-filter projection matrices to obtain new parameters. This is in particular a reasonable thing to do in the context of conditional GANs, where you want to have parameters of your generator be conditioned on the content of the image you're trying to simulate
- This model structure gives you a natural way to do few-shot generation: you can train your embedding network, your generator, and your projection matrices over a large dataset, where they've hopefully learned how to compress information from any given target image, and generate convincing frames based on it, so that you can just pass in your new target image, have it transformed into an embedding, and have it contain information the rest of the network can work with
- This model uses a relatively new (~mid 2018) formulation of a conditional GAN, called the projection discriminator. I don't have time to fully explain this here, but at a high level, it frames the problem of a discriminator determining whether a generated image corresponds to a given conditioning class by projecting both the class and the image into vectors, and calculating a similarity-esque dot product.
- During few-shot application of this model, it can get impressively good performance without even training on the new target face at all, simply by projecting the target face into an embedding, and updating the target-specific network parameters that way. However, they do get better performance if they fine-tune to a specific person, which they do by treating the embedding-projection parameters as an initialization, and then taking a few steps of gradient descent from there
HellaSwag: Can a Machine Really Finish Your Sentence?
Rowan Zellers and Ari Holtzman and Yonatan Bisk and Ali Farhadi and Yejin Choi
Abstract: Recent work by Zellers et al. (2018) introduced a new task of commonsense natural language inference: given an event description such as "A woman sits at a piano," a machine must select the most likely followup: "She sets her fingers on the keys." With the introduction of BERT, near human-level performance was reached. Does this mean that machines can perform human level commonsense inference? In this paper, we show that commonsense inference still proves difficult for even state-of-the-art models, by presenting HellaSwag, a new challenge dataset. Though its questions are trivial for humans (>95% accuracy), state-of-the-art models struggle (<48%). We achieve this via Adversarial Filtering (AF), a data collection paradigm wherein a series of discriminators iteratively select an adversarial set of machine-generated wrong answers. AF proves to be surprisingly robust. The key insight is to scale up the length and complexity of the dataset examples towards a critical 'Goldilocks' zone wherein generated text is ridiculous to humans, yet often misclassified by state-of-the-art models. Our construction of HellaSwag, and its resulting difficulty, sheds light on the inner workings of deep pretrained models. More broadly, it suggests a new path forward for NLP research, in which benchmarks co-evolve with the evolving state-of-the-art in an adversarial way, so as to present ever-harder challenges.
[Machine learning is a nuanced, complicated, intellectually serious topic...but sometimes it's refreshing to let ourselves be a bit less serious, especially when it's accompanied by clear, cogent writing on a topic. This particular is a particularly delightful example of good-natured silliness - from the dataset name HellaSwag to figures containing cartoons of BERT and ELMO representing language models - combined with interesting science.]
https://i.imgur.com/CoSeh51.png
This paper tackles the problem of natural language comprehension, which asks: okay, our models can generate plausible looking text, but do they actually exhibit what we would consider true understanding of language? One natural structure of task for this is to take questions or "contexts", and, given a set of possible endings or completion, pick the correct one. Positive examples are relatively easy to come by: adjacent video captions and question/answer pairs from WikiHow are two datasets used in this paper. However, it's more difficult to come up with *negative* examples. Even though our incorrect endings won't be a meaningful continuation of the sentence, we want them to be "close enough" that we can feel comfortable attributing a model's ability to pick the correct answer as evidence of some meaningful kind of comprehension. As an obvious failure mode, if the alternative multiple choice options were all the same word repeated ten times, that would be recognizable as being not real language, and it would be easy for a model to select the answer with the distributional statistics of real language, but it wouldn't prove much. Typically failure modes aren't this egregious, but the overall intuition still holds, and will inform the rest of the paper: your ability to test comprehension on a given dataset is a function of how contextually-relevant and realistic your negative examples are.
Previous work (by many of the same authors as are on this paper), proposed a technique called Adversarial Filtering to try to solve this problem. In Adversarial Filtering, a generative language model is used to generate possible many endings conditioned on the input context, to be used as negative examples. Then, a discriminator is trained to predict the correct ending given the context. The generated samples that the discriminator had the highest confidence classifying as negative are deemed to be not challenging enough comparisons, and they're thrown out and replaced with others from our pool of initially-generated samples. Eventually, once we've iterated through this process, we have a dataset with hopefully realistic negative examples. The negative examples are then given to humans to ensure none of them are conceptually meaningful actual endings to the sentence. The dataset released by the earlier paper, which used as it's generator a relatively simple LSTM model, was called Swag.
However, the authors came to notice that the performance of new language models (most centrally BERT) on this dataset might not be quite what it appears: its success rate of 86% only goes down to 76% if you don't give the classifier access to the input context, which means it can get 76% (off of a random baseline of 25%, with 4 options) simply by evaluating which endings are coherent as standalone bits of natural language, without actually having to understand or even see the context. Also, shuffling the words in the words in the possible endings had a similarly small effect: the authors are able to get BERT to perform at 60% accuracy on the SWAG dataset with no context, and with shuffled words in the possible answers, meaning it's purely selecting based on the distribution of words in the answer, rather than on the meaningfully-ordered sequence of words.
https://i.imgur.com/f6vqJWT.png
The authors overall conclusion with this is: this adversarial filtering method is only as good as the generator, and, more specifically, the training dynamic between the generator that produces candidate endings, and the discriminator that filters them. If the generator is too weak, the negative examples can be easily detected as fake by a stronger model, but if the generator is too strong, then the discriminator can't get good enough to usefully contribute by weeding samples out. They demonstrate this by creating a new version of Swag, which they call HellaSwag (for the expected acronym-optimization reasons), with a GPT generator rather than the simpler one used before: on this new dataset, all existing models get relatively poor results (30-40% performance). However, the authors' overall point wasn't "we've solved it, this new dataset is the end of the line," but rather a call in the future to be wary, and generally aware that with benchmarks like these, especially with generated negative examples, it's going to be a constantly moving target as generation systems get better.
Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask
Zhou, Hattie and Lan, Janice and Liu, Rosanne and Yosinski, Jason
Keywords: pruning, nas
The Lottery Ticket Hypothesis is the idea that you can train a deep network, set all but a small percentage of its high-magnitude weights to zero, and retrain the network using the connection topology of the remaining weights, but only if you re-initialize the unpruned weights to the the values they had at the beginning of the first training. This suggests that part of the value of training such big networks is not that we need that many parameters to use their expressive capacity, but that we need many "draws" from the weight and topology distribution to find initial weight patterns that are well-disposed for learning.
This paper out of Uber is a refreshingly exploratory experimental work that tries to understand the contours and contingencies of this effect. Their findings included:
- The pruning criteria used in the original paper, where weights are kept according to which have highest final magnitude, works well. However, an alternate criteria, where you keep the weights that have increased the most in magnitude, works just as well and sometimes better. This makes a decent amount of sense, since it seems like we're using magnitude as a signal of "did this weight come to play a meaningful role during training," and so weights whose influence increased during training fall in that category, regardless of their starting point
https://i.imgur.com/wTkNBod.png
- The authors' next question was: other than just re-initialize weights to their initial values, are there other things we can do that can capture all or part of the performance effect? The answer seems to be yes; they found that the most important thing seems to be keeping the sign of the weights aligned with what it was at its starting point. As long as you do that, redrawing initial weights (but giving them the right sign), or re-setting weights to a correctly signed constant value, both work nearly as well as the actual starting values
https://i.imgur.com/JeujUr3.png
- Turning instead to the weights on the pruning chopping block, the authors find that, instead of just zero-ing out all pruned weights, they can get even better performance if they zero the weights that moved towards zero during training, and re-initialize (but freeze) the weights that moved away from zero during training. The logic of the paper is "if the weight was trying to move to zero, bring it to zero, otherwise reinitialize it". This performance remains high at even lower levels of training than does the initial zero-masking result
- Finally, the authors found that just by performing the masking (i.e. keeping only weights with large final values), bringing those back to their values, and zeroing out the rest, *and not training at all*, they were able to get 40% test accuracy on MNIST, much better than chance. If they masked according to "large weights that kept the same sign during training," they could get a pretty incredible 80% test accuracy on MNIST. Way below even simple trained models, but, again, this model wasn't *trained*, and the only information about the data came in the form of a binary weight mask
This paper doesn't really try to come up with explanations that wrap all of these results up neatly with a bow, and I really respect that. I think it's good for ML research culture for people to feel an affordance to just run a lot of targeted experiments aimed at explanation, and publish the results even if they don't quite make sense yet. I feel like on this problem (and to some extent in machine learning generally), we're the blind men each grabbing at one part of an elephant, trying to describe the whole. Hopefully, papers like this can bring us closer to understanding strange quirks of optimization like this one
Meta-learners' learning dynamics are unlike learners'
Neil C. Rabinowitz
Abstract: Meta-learning is a tool that allows us to build sample-efficient learning systems. Here we show that, once meta-trained, LSTM Meta-Learners aren't just faster learners than their sample-inefficient deep learning (DL) and reinforcement learning (RL) brethren, but that they actually pursue fundamentally different learning trajectories. We study their learning dynamics on three sets of structured tasks for which the corresponding learning dynamics of DL and RL systems have been previously described: linear regression (Saxe et al., 2013), nonlinear regression (Rahaman et al., 2018; Xu et al., 2018), and contextual bandits (Schaul et al., 2019). In each case, while sample-inefficient DL and RL Learners uncover the task structure in a staggered manner, meta-trained LSTM Meta-Learners uncover almost all task structure concurrently, congruent with the patterns expected from Bayes-optimal inference algorithms. This has implications for research areas wherever the learning behaviour itself is of interest, such as safety, curriculum design, and human-in-the-loop machine learning.
Meta learning, or, the idea of training models on some distribution of tasks, with the hope that they can then learn more quickly on new tasks because they have "learned how to learn" similar tasks, has become a more central and popular research field in recent years. Although there is a veritable zoo of different techniques (to an amusingly literal degree; there's an emergent fad of naming new methods after animals), the general idea is: have your inner loop consist of training a model on some task drawn from a distribution over tasks (be that maze learning with different wall configurations, letter identification from different languages, etc), and have the outer loop that updates some structural part of your model be based on improving generalization error on each task within the distribution. It's been demonstrated that meta-learned systems can in fact learn more quickly (at least when their tasks are "in distribution" relative to the distribution they were trained on, which is an important point to be cognizant of), but this paper is less interested with how much better or faster they're learning, and more interested in whether there are qualitative differences in the way normal learning systems and meta-trained learning systems go about learning a new task.
The author (oddly for DeepMind, which typically goes in for super long author lists, there's only the one on this paper) goes about this by studying simple learning tasks where it's easier for us to introspect into what each model is learning over time.
https://i.imgur.com/ceycq46.png
In the first test, he looks at linear regression in a simple setting: where for each individual "task" data is generated according a known true weight matrix (sampled from a prior over weight matrices), with some noise added in. Given this weight matrix, he takes the singular value decomposition (think: PCA), and so ends up with a factorized representation of the weights, where higher eigenvalues on the factors, or "modes", represent that those factors represent larger-scale patterns that explain more variance, and lower eigenvalues are smaller scale refinements on top of that. He can apply this same procedure to the weights the network has learned at any given point in training, and compare, to see how close the network is to having correctly captured each of these different modes. When normal learners (starting from a raw initialization) approach the task, they start by matching the large scale (higher eigenvalue) factors of variation, and then over the course of training improve performance on the higher-precision factors. By contrast, meta learners, in addition to learning faster, also learn large scale and small scale modes at the same rate. Similar analysis was performed and similar results found for nonlinear regression, where instead of PCA-style components, the function generating data were decomposed into different Fourier frequencies, and the normal learner learned the broad, low-frequency patterns first, where the meta learner learned them all at the same rate.
The paper finds intuition for this by showing that the behavior of the meta learners matches quite well against how a Bayes-optimal learner would update on new data points, in the world where that learner had a prior over the data-generating weights that matched the true generating process. So, under this framing, the process of meta learning is roughly equivalent to your model learning a prior correspondant with the task distribution it was trained on. This is, at a high level, what I think we all sort of thought was happening with meta learning, but it's pretty neat to see it laid out in a small enough problem where we can actually validate against an analytic model.
A bit of a meta (heh) point: I wish this paper had more explanation of why the author chose to use the specific eigenvalue-focused metrics of progression on task learning that he did. They seem reasonable, but I'd have been curious to see an explication of what is captured by these, and what might be captured by alternative metrics of task progress.
(A side note: the paper also contained a reinforcement learning experiment, but I both understood that one less well and also feel like it wasn't really that analogous to the other tests)
Multitask Soft Option Learning
Igl, Maximilian and Gambardella, Andrew and Nardelli, Nantas and Siddharth, N. and Böhmer, Wendelin and Whiteson, Shimon
This paper blends concepts from variational inference and hierarchical reinforcement learning, learning skills or "options" out of which master policies can be constructed, in a way that allows for both information transfer across tasks and specialization on any given task.
The idea of hierarchical reinforcement learning is that instead of maintaining one single policy distribution (a learned mapping between world-states and actions), a learning system will maintain multiple simpler policies, and then learn a meta-policy for transitioning between these object-level policies. The hope is that this setup leads to both greater transparency and compactness (because skills are compartmentalized), and also greater ability to transfer across tasks (because if skills are granular enough, different combinations of the same skills can be used to solve quite different tasks).
The differentiating proposal of this paper is that, instead of learning skills that will be fixed with respect to the master, task-specific policy, we instead learning cross-task priors over different skills, which can then be fine-tuned for a given specific task. Mathematically, this looks like a reward function that is a combination of (1) actual rewards on a trajectory, and (2) the difference in the log probability of a given trajectory under the task-specific posterior and under the prior.
https://i.imgur.com/OCvmGSQ.png
This framing works in two directions: it allows a general prior to be pulled towards task-specific rewards, to get more specialized value, but it also pulls the per-task skill towards the global prior. This is both a source of transfer knowledge and general regularization, and also an incentive for skills to be relatively consistent across tasks, because consistent posteriors will be more locally clustered around their prior. The paper argues that one advantage of this is a symmetry-breaking effect, avoiding a local minimum where two skills are both being used to solve subtask A, and it would be better for one of them to specialize on subtask B, but in order to do so the local effect would be worse performance of that skill on subtask A, which would be to the overall policy's detriment because that skill was being actively used to solve that task. Under a prior-driven system, the model would have an incentive to pick one or the other of the options and use that for a given subtask, based on whichever's prior was closest in trajectory-space.
https://i.imgur.com/CeFQ9PZ.png
On a mechanical level, this set of priors is divided into a few structural parts:
1) A termination distribution, which chooses whether to keep drawing actions from the skill/subpolicy you're currently on, or trade it in for a new one. This one has a prior set at a Bernoulli distribution with some learned alpha
2) A skill transition distribution, which chooses, conditional on sampling a "terminate", which skill to switch to next. This has a prior of a uniform distribution over skills, which incentivizes the learning system to not put all its sampling focus on one policy too early
3) A distribution of actions given a skill choice, which, as mentioned before, has both a cross-task prior and a per-task learned posterior
Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks
Shen, Yikang and Tan, Shawn and Sordoni, Alessandro and Courville, Aaron C.
This paper came on my radar after winning Best Paper recently at ICLR, and all in all I found it a clever way of engineering a somewhat complicated inductive bias into a differentiable structure. The empirical results weren't compelling enough to suggest that this structural shift made a regime-change difference in performing, but it does seem to have some consistently stronger ability to do syntactic evaluation across large gaps in sentences.
The core premise of this paper is that, while language is to some extent sequence-like, it is in a more fundamental sense tree-like: a recursive structure of modified words, phrases, and clauses, aggregating up to a fully complete sentence. In practical terms, this cashes out to parse trees, labels akin to the sentence diagrams that you or I perhaps did once upon a time in grade school.
https://i.imgur.com/GAJP7ji.png
Given this, if you want to effectively model language, it might be useful to have a neural network structure explicitly designed to track where you are in the tree. To do this, the authors of this paper use a clever activation function scheme based on the intuition that you can think of jumping between levels of the tree as adding information to the stack of local context, and then removing that information from the stack when you've reached the end of some local phrase. In the framework of a LSTM, which has explicit gating mechanisms for both "forgetting" (removing information from cell memory) and input (adding information to the representation within cell memory) this can be understood as forcing a certain structure of input and forgetting, where you have to sequentially "close out" or add nodes as you move up or down the tree.
To represent this mathematically, the authors use a new activation function they developed, termed cumulative max or cumax. In the same way that the softmax is a differentiable (i.e. "soft") version of an argmax, the cumulative max is a softened version of a vector that has zeros up to some switch point k, and ones thereafter. If you had such a vector as your forget mask, then "closing out" a layer in your tree would be equivalent to shifting the index where you switch from 0 to 1 up by one, so that a layer that previously had a "remember" value of 1.0 now is removing its content from the stack. However, since we need to differentiate, this notional 0/1 vector is instead represented as a cumulative sum of a softmax, which can be thought of as the continuous-valued probability that you've reached that switch-point by any given point in the vector. Outside of the abstractions of what we're imagining this cumax function to represent, in a practical sense, it does strictly enforce that you monotonically remember or input more as you move along the vector. This has the practical fact that the network will be biased towards remembering information at one end of the representation vector for longer, meaning it could be a useful inductive bias around storing information that has a more long-term usefulness to it. One advantage that this system has over a previous system that, for example, had each layer of the LSTM operate on a different forgetting-decay timescale, is that this is a soft approximation, so, up to the number of neurons in the representation, the model can dynamically approximate whatever number of tree nodes it likes, rather than being explicitly correspondent with the number of layers.
Beyond being a mathematically clever idea, the question of whether it improves performance is a little mixed. It does consistently worse at tasks that require keeping track of short term dependency information, but seems to do better at more long-term tasks, although not in a perfectly consistent or overly dramatic way. My overall read is that this is a neat idea, and I'm interested to see if it gets built on, as well as interested to see later papers that do some introspective work to validate whether the model is actually using this inductive bias in the tree-like way that we're hoping and imagining it will.
Xiaohua Zhai and Avital Oliver and Alexander Kolesnikov and Lucas Beyer
Abstract: This work tackles the problem of semi-supervised learning of image classifiers. Our main insight is that the field of semi-supervised learning can benefit from the quickly advancing field of self-supervised visual representation learning. Unifying these two approaches, we propose the framework of self-supervised semi-supervised learning ($S^4L$) and use it to derive two novel semi-supervised image classification methods. We demonstrate the effectiveness of these methods in comparison to both carefully tuned baselines, and existing semi-supervised learning methods. We then show that $S^4L$ and existing semi-supervised methods can be jointly trained, yielding a new state-of-the-art result on semi-supervised ILSVRC-2012 with 10% of labels.
It's possible I'm missing something here, but my primary response to reading this paper is just a sense of confusion: that there is an implicit presenting of an approach as novel, when there doesn't seem to me to be a clear mechanism that is changed from prior work. The premise of this paper is that self-supervised learning techniques (a subcategory of unsupervised learning, where losses are constructed based on reconstruction or perturbation of the original image) should be made into supervised learning by learning on a loss that is a weighted combination of the self-supervised loss and the supervised loss, making the overall method a semi-supervised one.
The self-supervision techniques that they identify integrating into their semi-supervised framework are:
- Rotation prediction, where an image is rotated to one of four rotation angles, and then a classifier is applied to guess what angle
- Exemplar representation invariance, where an imagenet is cropped, mirrored, and color-randomized in order to provide inputs, whose representations are then pushed to be closer to the representation for the unmodified image
My confusion is due to the fact that the I know that I've read several semi-supervised learning papers that do things of this ilk (insofar as combining unsupervised and supervised losses together) and it seems strange to identify it as a novel contribution. That said, this paper does give an interesting overview of self-supervisation techniques, I found it valuable to read for that purpose.
On the Pitfalls of Measuring Emergent Communication
Lowe, Ryan and Foerster, Jakob and Boureau, Y.-Lan and Pineau, Joelle and Dauphin, Yann
Language seems obviously useful to humans in coordinating on complicated tasks, and, the logic goes, you might expect that if you gave agents in a multi-agent RL system some amount of shared interest, and the capacity to communicate, that they would use that communication channel to coordinate actions. This is particularly true in cases where some part of the environment is only visible to one of the agents. A number of papers in the field have set up such scenarios, and argued that meaningful communication strategies developed, mostly in the form of one agent sending a message to signal its planned action to the other agent before both act. This paper tries to tease apart the various quantitative metrics used to evaluate whether informative message are being sent, and tries to explain why they can diverge from each other in unintuitive ways. The experiments in the paper are done in quite simple environments, where there are simple one-shot actions and a payoff matrix, as well as an ability for the agents to send messages before acting.
Some metrics identified by the paper are:
- Speaker Consistency: There's high mutual information shown between the message a speaker sends, and what action it takes. Said another way, you could use a speaker's message to predict their action at a rate higher than random, because it contains information about the action
- Heightened reward/task completion under communication: Fairly straightforward, this metric argues that informative communication happened when pairs of agents do better in the presence of communication channels than when they aren't available
- Instantaneous coordination: Measures the mutual information between the message sent by agent A and the action of agent B, in a similar way to Speaker Consistency.
This work agrees that it's important to measure the causal impact of messages on other-agent actions, but argues that instantaneous communication is flawed because the mutual information metric between messages and response actions doesn't properly condition on the state of the game under whcih the message is being sent. Even if you successfully communicate your planned action to me, the action I actually take in response will be conditioned on my personal payoff matrix, and may average out to seeming unrelated or random if you take an expectation over every possible state the message could be recieved in. Instead, they suggest doing an explicit causal causal approach, where for each configuration of the game (different payoff matrix), they sample different messages, and calculate whether you see messages driving more consistent actions when you condition on other factors in the game.
An interesting finding of this paper is that, at least in these simple environments, you're able to find cases where there is Speaker Consistency (SC; messages that contain information about the speaker's next action), but no substantial Causal Influence of Communication (CIC). This may seem counterintuitive, since, why would you as an agent send a message containing information about your action, if not because you're incentivized to communicate with the other agent? It seems like the answer is that it's possible to have this kind of shared information *on accident,* as a result of the shared infrastructure between the action network and the messaging network. Because both use a shared set of early-layer representations, you end up having one contain information about the other as an incidental fact; if the networks are fully separated with no shared weights, the Speaker Consistency values drop.
An important caveat to make here is that this paper isn't, or at least shouldn't be, arguing that agents in multi-agent systems don't actually learn communication. The environments used here are quite simple, and just might not plausibly be difficult enough to incentivize communication. However, it is a fair point that it's valuable to be precise in what exactly we're measuring, and test how that squares with what we actually care about in a system, to try to avoid cases like these where we may be liable to be led astray by our belief about how the system *should* be learning, rather than how it actually is
The Lottery Ticket Hypothesis at Scale
Frankle, Jonathan and Dziugaite, Gintare Karolina and Roy, Daniel M. and Carbin, Michael
In 2018, a group including many of the authors of this updated paper argued for a theory of deep neural network optimization that they called the "Lottery Ticket Hypothesis". It framed itself as a solution to what was otherwise a confusing seeming-contradiction: that you could prune or compress trained networks to contain a small percentage of their trained weights without loss of performance, but also that if you tried to train a comparably small network (comparable to the post-training pruned network) from initialization, you wouldn't be able to achieve similar performance. They showed that, at least for some set of tasks, you could in fact train a smaller network to equivalent performance, but only if you kept the same connectivity patterns as in the pruned network, and if you re-initialized those neurons to the same values they were initialized at during the initial training. These lucky initialization patterns are the lottery tickets being referred to in the eponymous hypothesis: small subnetworks of well-initialized weights that are set up to be able to train well. This paper assesses whether and under what conditions the LTH holds on larger problems, and does a bit of a meta-analysis over different alternate theories in this space.
One such alternate theory, from Liu et al, proposes that, in fact, there is no value in re-initializing to the specific initial values, and that you can actually get away with random initialization if you keep the connectivity patterns of the pruned weights. The "At Scale" paper compares the two methods over a wide range of pruning percentages, and convincingly shows that while random initialization with the same connectivity can perform well up to 80% of the weights being removed, after 80%, the performance of the random initialization drops, whereas the performance of the "winning ticket" approach remains comparable with full network training up to 99% of the weights being pruned. This seems to provide support for the theory that there is value in re-initializing the weights to how they were, especially when you prune to very small subnetworks.
https://i.imgur.com/9O2aAIT.png
The core of the current paper focuses on a difficulty in the original LTH paper: that the procedure of iterative pruning (train, then prune some weights, then train again) wasn't able to reliably find "winning tickets" for deep networks of the type needed to solve ImageNet or CIFAR. To be precise, re-initializing pruned networks to their original values did no better than initializing them randomly in these networks. In order to actually get these winning tickets to perform well, the original authors had to do a somewhat arcane process of of starting the learning rate very small and scaling it up, called "warmup". Neither paper gave a clear intuition as to why this would be the case, but the updated paper found that they could avoid the need for this approach if, instead of re-initializing weights to their original value, they set them to the values they were at after some small number of iterations into training. They justify this by showing that performance under this new initialization is related to something they call "stability to pruning," which measures how close the learned weights after re-initialization are to the original learned weights in the full model training. And, while the weights of deeper networks are unstable (by this metric) when first initialized, they become stable fairly early on. I was a little confused by this framing, since it seemed fairly tautological to me, since you're using "how stably close are the weights to the original weights" as a way to explain "when can you recover performance comparable to original performance." This was framed as being a mechanistic explanation of why you can see a lottery ticket phenomenon to some extent, but only if you do a "late reset" to several iterations after initialization, but it didn't feel quite mechanistically satisfying enough to me.
That said, I think this is overall an intriguing idea, and I'd love to see more papers discuss it. In particular, I'd love to read more qualitative analysis about whether there are any notable patterns shared by "winning tickets".
Generating Long Sequences with Sparse Transformers
Child, Rewon and Gray, Scott and Radford, Alec and Sutskever, Ilya
The Transformer, a somewhat confusingly-named model structure that uses attention mechanisms to aggregate information for understanding or generating data, has been having a real moment in the last year or so, with GPT-2 being only the most well-publicized tip of that iceberg. It has lots of advantages: the obvious attractions of strong performance, as well as the ability to train in parallel across parts of a sequence, which RNNs can't do because of the need to build up and maintain state. However, a problematic fact about the Transformer approach is how it scales to large sequences of input data. Because attention is based on performing pairwise queries between each point in the data sequence and each other point, to allow for aggregation of information from places throughout the sequence, it scales as O(N^2), because every new element in the sequence needs to be queried by N other ones. This makes it resource-intensive to run transformer models on large architectures.
The Sparse Transformer design proposed in this OpenAI paper tries to cut down on this resource cost by loosening the requirement that, in every attention operation, each element directly pulls information from every other element. In this new system, each point doesn't get information about each other point in a single operation, but, having two operations such limited operations being chained in a row provides that global visibility. This is done in one of two ways.
(1) The first, called the "strided" version, performs two operations in a row, one masked attention that only looks at the last k timesteps (for example, the last 7), and then a second masked attention that only looks at every kth timestep. So, at the end of the second operation, each point has pulled information from points at checkpoints 7, 14, 21 steps ago, and each of these has pulled information from the window between it and its preceding checkpoint, giving visibility into a full global receptive frame in the course of two operations
(2) The second, called the "fixed" version, uses a similar sort of logic, but instead of having the "window accumulation points" be defined in reference to the point doing the querying, you instead have fixed accumulation points responsible for gathering information from the windows around them. So, using the example given in the paper, if you imagine a window of size 128, and an "accumulation points per window" of 8, then the points in indices 120-128 (say) would have visibility into points 0-128. That represents the first operation, and in the second one, all other points in the sequence pull in information by querying the designated accumulation points for all the windows that aren't masked for it.
The paper argues that, between these two systems, the Strided system should work best when the data has some inherent periodicity, but I don't know that I particularly follow that intuition. I have some sense that the important distinction here is that in the strided case you have many points of accumulation, each with not much context, whereas in the fixed case you have very few accumulation points each with a larger window, but I don't know what performance differences exactly I'd expect these mechanical differences to predict.
This whole project of reducing access to global information seems initially a little counterintuitive, since the whole point of a transformer design, in some sense, was its ability to gain global context in a single layer, as opposed to a convnet needing multiple layers to build receptive field, or a RNN needing to maintain state throughout the sequence. However, I think this paper makes the most sense as a way of interpolating the space between something like a CNN and a full attention design, for the sake of efficiency. With a CNN, you have a fixed kernel, and so as your sequence gets longer, you need to add more and more layers in order for any given point to be able to incorporate into its representation information from the complete other side of the sequence. With a RNN, as your sequence gets longers, you pay the cost of needing to backpropogate state farther. So, by contrast, even though the Sparse Transformer seems to be giving up its signal advantage, it's instead just trading one constant number of steps to achieve global visibility (1), for another (2, in this paper, but conceptually could be more), but still in a way that's constant with respect to the length of the data. And, in exchange for this trade, they get very sparse, very masked operations, where many of the multiplications involved in these big query calculations can be ignored, making for faster computation speeds.
On the datasets tried, the Sparse Transformer increased speed, and in fact in I think all cases increased performance - not by much, the performance gain by itself isn't that dramatic, but in the context of expecting if anything worse performance as a result of limiting model structure, it's encouraging and interesting that it either stays about the same or possible improves. | CommonCrawl |
Journal of Cotton Research
GbAt11 gene cloned from Gossypium barbadense mediates resistance to Verticillium wilt in Gossypium hirsutum
Tingting QIU1 na1,
Yanjun WANG1 na1,
Juan JIANG1,
Jia ZHAO1,
Yanqing WANG1 &
Junsheng QI1
Journal of Cotton Research volume 3, Article number: 9 (2020) Cite this article
Gossypium hirsutum is highly susceptible to Verticillium wilt, and once infected Verticillium wilt, its yield is greatly reduced. But G. barbadense is highly resistant to Verticillium wilt. It is possible that transferring some disease-resistant genes from G. barbadense to G. hirsutum may contribute to G. hirsutum resistance to Verticillium wilt.
Here, we described a new gene in G. barbadense encoding AXMN Toxin Induced Protein-11, GbAt11, which is specifically induced by Verticillium dahliae in G. barbadense and enhances Verticillium wilt resistance in G. hirsutum. Overexpression in G. hirsutum not only significantly improves resistance to Verticillium wilt, but also increases the boll number per plant. Transcriptome analysis and real-time polymerase chain reaction showed that GbAt11 overexpression can simultaneously activate FLS2, BAK1 and other genes, which are involved in ETI and PTI pathways in G. hirsutum.
These data suggest that GbAt11 plays a very important role in resistance to Verticillium wilt in cotton. And it is significant for improving resistance to Verticillium wilt and breeding high-yield cotton cultivars.
Verticillium wilt is a highly destructive soil-borne fungal disease of plants that affects an extensive range of host species, including many agricultural crops (Burpee and Bloom 1978; Fradin et al. 2011; Qi et al. 2016). Verticillium wilt of cotton is caused by Verticillium dahliae, but how the pathogen causes the disease of plants remains to be clarified (Gao et al. 2011). However, there is an accumulative evidence to show that the toxin produced by V. dahliae is the main pathogenic factor, for example, a protein or glycoprotein is mainly responsible for the wilt symptoms. Studies on the resistance mechanisms of plants to Verticillium wilt found two genetic loci, Ve1 and Ve2 in tomato. The expression of both Ve1 and Ve2 in potato can enhance resistance to V. dahliae (Kawchuk et al. 2001; Simko et al. 2004). Although it has been shown that Ve1 gene is functional only in tomato (Fradin et al. 2011; Fradin et al. 2009), GbVe1, which is a homolog of the tomato Vel cloned from Gossypium barbadense, is highly resistant to Verticillium wilt, and its overexpression in Arabidopsis thaliana has confirmed the disease resistance function of this gene (Zhang et al. 2011; Zhang et al. 2013). Based on the genetic principle of immune response induction, we treated G. barbadense with purified V. dahliae filtrate protein, extracted RNA, and cloned 11 full-length cDNAs of specific genes (GbAt1 - GbAt11) using suppression subtractive hybridization (SSH). The objective of this study was to analyze the molecular role of GbAt11 gene in resistance of cotton to Verticillium wilt.
Recently, considerable progress has been made in understanding the immune mechanisms underlying the response of plants to pathogen infection. Studies have shown that plants identify pathogenic microorganisms by the presence of specific molecular motifs, known as pathogen-associated molecular patterns (PAMP)(Ozinsky et al. 2000), for example, the flagellin protein Flag22 on the surface of Pseudomonas syringae, the bacterial elongation factor EF-Tu, and chitin (Asai et al. 2002; Wan et al. 2008). When plants contact Flag22, the receptor protein FLS2 is activated on the surface of plant cells and is up-regulated through MAPK kinase signal transduction and transcription factor WRKY29 expression (Asai et al. 2002; Gomez-Gomez and Boller 2000; Adachi et al. 2015), therefore causing the production of reactive oxygen species (ROS) and the accumulation of callose at the infected site, thus protecting against the pathogen invasion (Nurnberger et al. 2004). FLS2-mediated disease resistance pathways are also involved in the BAK1 element in the brassinosteroids (BR) pathway, which is the co-receptor of both BR and FLS2 (Albrecht et al. 2008; Lin et al. 2013). After FLS2 is activated by Flag22, BAK1 is recruited to form a complex, and then transfers the resistance signal to downstream by a process called PAMP-Triggered-Immunity (PTI)(Albrecht et al. 2012). Some bacterial pathogens have evolved effectors to inhibit PTI; however, plants have evolved proteins to counteract these effectors, which can relieve the inhibition of effectors on PTI through a process called effector-triggered-immunity (ETI). Thus, host plants and their pathogens co-evolve during this mutually antagonistic process.
Since GbAt11 was induced in G. barbadense with high resistance to Verticillium wilt, we studied the function of GbAt11 in resistance to Verticillium wilt, and the GbAt11-G. hirsutum lines significantly increased resistance to Verticillium wilt. Similarly, we found that overexpression of GbAt11 can up-regulate the expression of FLS2, BAK1 and other related disease resistance genes. Therefore, we speculate that GbAt11 plays an important role in the process of resistance to Verticillium wilt and is beneficial for improving resistance to Verticillium wilt and breeding high-yield cotton cultivars. And it also has reference value for the study of the mechanism of plant antifungal diseases.
G. barbadense variety H7124 seeds were purchased from the National Cotton Seeds Repository (China). Seeds of G. hirsutum variety JM169 were provided by the Institute of Cotton, Hebei Academy of Agriculture and Forestry Sciences (Shijiazhuang, Hebei). G. barbadense and G. hirsutum were grown in greenhouse at 25 °C with a 12 h/12 h (day/night) cycle, and G. hirsutum JM169 was used as the wild type (WT) control. All transgenic plants used in this study are in JM169 background.
GbAt11 gene cloning and sequencing
The G. barbadense seedlings were divided into two groups, and one was soaked in a solution of V. dahliae toxin, while the other was soaked in water as the control. Three plants were sampled at 6, 12, 18, and 24 h of treatment, respectively, while their total RNA was extracted, and mRNA was purified, then used as SSH (Diatchenko et al. 1996). A total of 11 specific gene fragments were obtained, cloned into T-vector and sequenced by Sangon Biotech Co. Ltd. From the sequencing results, they were named GbAt1 to GbAt11. This study focused on exploring the role of GbAt11 gene. Basic local alignment search tool (Blast) searches were performed against GenBank to find the full-length cDNA sequence. The chromosomal location of the GbAt11 gene was obtained from an analysis at the website.
Specific real-time PCR detection of GbAt11 expression in G. barbadense and G. hirsutum
Seedlings of G. barbadense and G. hirsutum were grown in a greenhouse. Leaves were collected at the adult-plant stage from the same parts of the plants, soaked in Vd991 spore suspension (1 × 106 per mL), sampled after 0 h, 4 h, 8 h, 12 h, and 24 h, respectively, and total RNA was extracted from 100 mg of powder. Then we used real-time polymerase chain reaction (RT-PCR) (Salin et al. 2005) to quantify the level of GhAt11-specific mRNA at different times. RNA was extracted with the EASYspin plant RNA rapid extraction kit (Beijing Aidlab biotechnologiesCo. Ltd), quantified, and the relative expression of GbAt11 mRNA was measured using RT-PCR after cDNA synthesis by reverse transcription. PCR primer sequences were designed as follows: forward primer 5′-AGGGTTTCGTCGTCTACT-3′, and reverse primer 5′-GATGCTTCTCCTCATAGG-3′. Amplification reactions (20 μL) contained 10 μL SYBR Premix Ex Taq, 0.6 μL of each primer (F + R), 0.4 μL ROX, 1–2 μL cDNA, and ddH2O to 20 μL.
Construction of the GbAt11 overexpression binary vector (the concentration of primary proteinsis quantified with spectrophotometer)
We replaced the HygR gene with the tfdA gene in the pCAMBIA1300 binary vector to make a vector called pSPT. We designed primers containing Sal1/KpnI restriction enzyme sites on both ends of the GbAt11 open reading frame (ORF); AT11–2-SalI-F: 5′-CGGTCGACATG TCGATCGCGTTGGAACG-3′, and AT11–2-KpnI-R: 5′-CGGGTACCGTTATATTCAC GTACATCAGCC-3′, and obtained the target gene by reverse transcription of G. barbadense AXMN mRNA. The pSPT vector was digested with SalI and KpnI, then ligated with the target gene fragment using T4 DNA ligase to construct the recombinant binary vector containing the GbAt11 gene.
Verticillium dahliae inoculations
V. dahliae inoculations was conducted according to Fradin etc. (2009). The 2~ 3-week-old cotton plants were uprooted, and then the roots and (or) adult-stage cotton leaves were rinsed in water. Subsequently, the roots or petioles were dipped for 24–72 h in a suspension of 106conidia per mL of Czapek's medium dextrose broth (Difco) and harvested from 2-week-old Verticillium cultures on Czapek's medium dextrose agar (Oxoid). Control plants were treated similarly, but their roots were dipped in Czapek's medium without conidiospores. After dipping, the disease phenotype was recorded and photographed from 1 h to 72 h.
Screening of transgenic positive cotton lines
Transformation of G. hirsutum was performed using the pistil drip method (Zhang and Chen 2012). Transgenic seeds were sown in the field, sprayed with 2,4-D at 30 mg·kg− 1 after sprouting, and the plants with a completely unfolded true leaf were screened. DNA was extracted and plants were screened for the tfdA gene and the target gene. Primers for tfdA amplification were tfdA-F:5′-ATGAGATCCATGGGTGAGCG-3′, and tfdA-R:5′-AGAACGCAGCGGTTGTCC-3′. PCR was used to identify single copy transgenic plants based on the segregation ratio of the T2 generation against 2,4-D. We first identified disease resistance in the single copy lines in the disease nursery (cotton stalks inoculated with Vd991 were crushed and evenly spreaded in the field every year, to ensure the uniformity of V. dahliae in the disease nursery), and then we selected lines L-213, L-214, and L-235 with good field resistance, treated with a V. dahliae spore suspension (concentration of 1 × 106 per mL) for resistance identification in a disease assay. We next extracted total proteins from L-214 leaves, concentrated the GbAT11-Flag protein fusion using the Flag tag, fractionated the proteins on a denaturing polyacrylamide gel, and then detected the anti-Flag antibody by western hybridization.
Transcriptome analysis
Transcriptome analysis was performed by Beijing Biomarker Technologies Co. Ltd.
Subcellular localization of the GbAT11-GFP fusion protein
We constructed the pCAMBIA:GbAT11-GFP recombinant expression vector and used it to transform Arabidopsis thaliana. T2 generation transgenic seeds were sown on murashige and skoog basal medium (MS) medium, and after the GbAT11-GFP-expressing seedlings grew for 1 week, GFP fluoresence was observed with a laser scanning confocal microscope. The excitation and emitting wavelengths for GFP were 488 and 525 nm, respectively. This allowed us to see whether GbAT11 was localized to the cell wall after treated with V. dahliae toxin. We treated the roots of transgenic Arabidopsis with 20% sucrose solution to plasmolyze the cells in order to observe the membrane localization of GbAT11.
Field disease resistance identification and examination of yield traits
The test on Verticillium wilt resistance of plants carrying the endogenous At11 gene, transgenic plants overexpressing GbAt11, and G. hirsutum carrying a TALENT knockout of GhAt11 was carried out in a field disease nursery inoculated with the Vd991 in Shandong province. There were two lines of each variety, a total of 60 plants. Plants were examined for symptoms of Verticillium wilt on June 20 and August 20, and were classified into five levels based on the degree of morbidity (ratings of 0 to 4). We calculated the Verticillium wilt disease index according to the formula (1), for every line, and counted the average number of bolls per plant on September 10. And the same test was carried out at the test base of China Agricultural University (Hebei province, in north-central China).
Screening of Gossypium barbadense-response genes induced by Verticillium wilt using suppressive subtraction hybridization
Gossypium barbadense possesses the highest level of resistance to verticillium wilt among the four cotton species, while the widely cultivated G. hirsutum is highly susceptible. We soaked seedlings of G. barbadense and G. hirsutum in a solution of purified proteins secreted by V. dahliae, and necrotic lesions were found present on the leaves of G. barbadense after 72 h, while the entire leaves of G. hirsutum were withered (data not shown). We induced the verticillium wilt-resistant G. barbadense with a solution of purified V. dahliae proteins, and obtained 11 specific genes (GbAt1-GbAt11) using SSH.
We initially focused on GbAt11 because its expression appeared to be strongest in G. barbadense induced by V. dahliae. The full-length GbAt11 cDNA is 768 bp, and the predicted molecular mass of the protein is about 27 kd. The N-terminal ORF from G. barbadense has an additional 17 amino acids than the predicted protein from G. hirsutum. In addition, BLAST searches confirmed that no GbAt11-like gene was present in A. thaliana. Further DNA sequence comparison and amino acid sequence analysis predicted that GbAT11 has 49.08% and 48.76% amino acid sequence homology with MTD1 (Methylene-tetrahydrofolate dehydrogenase [NAD(+)]) and Jatropha curcas serine/arginine repetitive matrix protein 2-like (SRRM2-like), respectively. But the strange thing is that the primary amino acid sequence of GbAT11 is closely similar to Damaged DNA-binding 2, putative isoform 1 (DDB2), but the gene has not yet been reported, and the most similar homolog gene is related with the uncharacterized protein LOC105800652 in NCBI (National Center for Biotechnology Information). A further search of the COTTONGEN (http://www.cottondb.org) indicated that the GbAt11 gene is located on Chromosome 9 in G. raimondii, so GbAt11 is a new gene which may be located on chromosome 9 in G. hirsutum.
GbAt11 gene expression is specifically induced by Verticillium dahliae in Gossypium barbadense
In order to investigate the relationship between GbAt11 and V. dahliae, and to explore transcriptional difference between G. barbadense and G. hirsutum, we collected young leaves at the adult-plant stage from the same parts of wild G. barbadense and wild G. hirsutum. Leaves were dipped in filtration of Vd991 (spore concentration of 1 × 106per mL). Total RNA was extracted from samples at different induction times, then reversely transcribed into cDNA to determine the relative level of GbAt11 transcription by RT-PCR. Results showed that: (1) transcription of GbAt11 increased 10-fold in seedlings treated with Vd991 for 4 h in G. barbadense, and then declined to the initial level. Transcription of GbAt11 increased significantly when induced for 8 h, and peaked at 24 h at more than 70-fold. These results indicated that the GbAt11 gene is specifically induced by V. dahliae in G. barbadense. (2) Transcription of GhAt11 increased slightly in G. hirsutum, but the leaves were heavily wilted at 12 h, and RNA were failed to be extrated. These results showed that expression of GbAt11 is specifically induced by V. dahliae, and is closely related to the host resistance response to pathogenic bacteria. In response to inducing by V. dahliae, GbAt11 is specifically overexpressed in Verticillium wilt-resistant G. barbadense, but the homolog of this gene was not specifically induced in G. hirsutum which is susceptible to Verticillium wilt, and its leaves appeared serious wilting within 12 h (Fig. 1).
GbAt11 expression is specifically induced by Verticillium dahliae toxin in Gossypium barbadense.a The representative G. barbadense and G. hirsutum leaves after treated with V. dahliae spore suspension (1 × 106 per mL) for indicated times. b-c Transcription changes of GbAt11 gene in G. barbadense (b) and G. hirsutum (c) after treated with V. dahliae spores (1 × 106/mL) for indicated times
GbAt11 overexpression enhances resistance to Verticillium wilt in Gossypium hirsutum
Because GbAt11 is specifically induced in highly Verticillium wilt-resistant G. barbadense, we speculated that overexpression of GbAt11 could improve the resistance to Verticillium wilt in susceptible G. hirsutum. To test this hypothesis, we transformed the wilt-susceptible G. hirsutum variety JM169 (WT) with GbAt11 and obtained 52 transgenic plants. Verticillium wilt-resistance ratings of field and greenhouse in a disease nursery were performed on the T2 generation plants of 17 transgenic lines. L-214 is a high-yielding line with good disease resistance. As shown in Fig. 2a, compared with the parental line (WT), L-214 showed the highest disease resistance, followed by L-213, but L-235 showed poor disease resistance.
The correspondence between the expression of GbAt11 and disease resistance. a Leaf phenotypes of three transgenic plants overexpressing GbAt11 and the wild type (WT, G. hirsutum JM169) after treated with Vd991 spore suspension (1 × 106 per mL) for 24 h. b Flag tagged GbAT11 protein were detected by Western blot with an anti-flag antibody. c Relative expression of GbAt11 gene in indicated plants after treated with Vd991 spore suspension (1 × 106 per mL) for 24 h. d Quantitative statistics of disease index in three GbAt11 overexpression lines and JM169 line treated with Vd991 spore suspension (1 × 106 per mL) for 24 h
In order to further confirm the role of GbAt11 gene in disease resistance, we extracted total proteins from leaves of transgenic L-214 (the flag tag fused to the C-terminal end of GbAT11) and the parental line WT (No flag tag). Anti-flag antibody-coated magnetic beads were incubated with the total protein to capture the flag tagged GbAT11 (IP). Then we used anti-flag antibody for Western blot detection, which showed that transgenic L-214 had one hybridizing band between 25 and 35 kd, which was absent in JM169, confirming the presence of GbAT11 protein in L-214 (Fig. 2b). To shed light on the relationship between the level of GbAt11 transcription and disease resistance, we quantified GbAt11 expression in transgenic lines L-213, L-214, and L-235 using real-time PCR. The results showed that GbAt11 expression was the highest in L-214 with the best Verticillium wilt resistance, and successively decreased in lines L-213 and L-235 (Fig. 2c), corresponding to the relative levels of Verticillium wilt resistance in the two lines (Fig. 2c and d). In subsequent experiments, L-214 was selected as its excellent disease resistance.
The disease index was calculated as formula (1):
$$ \mathrm{Index}=\frac{\sum \mathrm{disease}\kern0.34em \mathrm{rating}\kern0.28em c\times \mathrm{plant}\kern0.34em \mathrm{number}\kern0.28em c}{4\times \mathrm{total}\kern0.34em \mathrm{plant}\kern0.34em \mathrm{number}}\times 100. $$
Here, disease rating c was scored in five grades (0 to 4) based on the severity of Verticillium wilt symptoms in cotton. Grade 0, health, no disease symptom of leaves; grade 1, leaves have slight disease symptoms; grade 2, leaves have disease symptoms in moderate degree; grade 3, leaves have remarkable disease symptoms; And grade 4, leaves have severe disease symptoms. Plant number c was the number of plants corresponding to the rating of disease severity. The '4' was grade 4 which was the highest grade.
GbAt11 overexpression in Gossypium hirsutum up-regulates transcription of several key genes in the immunity pathways
Given that GbAt11 overexpression can improve disease resistance in plants, further transcriptome analyses (Wang et al. 2009) were performed in L-214 line and WT line. Clustering differentially expressed genes showed that gene transcription was significantly altered in the transgenic GbAt11-expressing line compared with the parent line. A total of 472 genes showed significant expression differences (FDR < 0.01)(Fig. 3a). Further transcriptome analysis showed that many genes involved in "plant-pathogen interactions" (KEGG Pathway) were up-regulated in transgenic plants of GbAt11, including FLS2 and the calcium dependent protein kinase CDPK (Harmon et al. 1994; Rigo et al. 2013); RPS2, RIN4 (Rigo et al. 2013) and PBS1 (Joys 1965), which are disease-resistance genes in ETI; and HSP90, the downstream gene in ETI. Therefore, it is reasonable to speculate that the transgenic GbAt11 line can activate ETI by affecting post-translational modifications, protein transporting and folding, relieving the inhibition of the pathogen on PTI-based immunity and improving resistance to Verticillium wilt in cotton. To confirm the result of transcriptome, real-time PCR was conducted in three lines, and the data showed that FLS2 in L214 and L213 is extremely significant higher than WT (Fig. 3b). Nextly, 7 genes involved in ETI and PTI process were assayed via real-time PCR in L214. The results confirmed that FLS2, BAK1, MKK2, FRK1, RIN4, RPS2 genes were significantly up-regulated in transgenic line L-214, and the FLS2 gene showed the highest up-regulation (Fig. 3c).
GbAt11 overexpression in G. hirsutum up-regulates expression of multiple key genes in the PTI and ETI pathways a Heat map clustering of differentially expressed genes; T1 is the parental line JM169, and T2 is the transgenic line L-214. Colors represent the relative gene expression level in each sample; blue indicates low level of expression, and red indicates high level of expression. b The relative expression of FLS2 gene in indicated G. hirsutum lines. c The relative expression of indicated genes related to PTI and ETI pathway in L-214 line and the parental line JM169
Subcellular localization of GbAT11 in Arabidopsis thaliana
We used Arabidopsis thaliana to explore the functional site of GbAT11 at the cellular level. We first produced transgenic plants of Arabidopsis thaliana expressing GbAt11-gfp, and then observed the subcellular localization of the GbAT11-GFP fusion protein in the root tip by laser scanning confocal microscopy. The results showed that GbAT11 is mainly localized to the nucleus (Fig. 4a), and a small amount presents on the cell wall (Fig. 4b). To clarify whether GbAT11 is also located on the cell membrane in addition to the nucleus, we treated Arabidopsis root tips with a 20% sucrose solution to separate cytoplasm from the cell wall, and then observed them under a fluorescence microscope. We found that the GbAT11-GFP protein was indeed located on the cell membrane (Fig. 4c). We also observed that the fluorescence intensity of the cell membrane was enhanced in Fig. 4c, which could be caused by shrinkage of the cell membrane, or the transfer of the GbAT11-GFP fusion protein from the nucleus to the membrane under osmotic stress.
Subcellular localization of GbAT11 in roots of transgenic Arabidopsis thaliana. a This image shows the localization of GFP-GbAT11 fusion protein in Arabidopsis cells, and green fluorescence appears under laser scanning confocal microscopy. b Laser scanning confocal microscopy showing the GbAT11 protein was localized in the nucleus after PI treatment. c Laser scanning confocal microscopy observed that GbAT11 protein was localized in the nucleus, and localized on the cell membrane after plasmolysis with 20% sucrose solution treatment of transgenic Arabidopsis thaliana roots
GbAt11 overexpression increase cotton yield
A common misconception is that it is difficult to have both disease resistance and high yield in the same plant. However, our results showed that overexpression of GbAt11 not only improved disease resistance, but also increased boll-setting, which is the most important factor in cotton production. To identify the high yielding transgenic lines that overexpress GbAt11, we investigated disease severity of the transgenic lines in a V. dahliae nursery and also analyzed the basic yield traits, such as boll number per plant, boll opening phenotype in the field (Fig. 5a). The disease indexes of Verticillium wilt were 6.52, 7.35, and 9.09 in L-214, L-213, and L-235, respectively, and 69.44, 60.23, 6.25, and 61.36 in the wild type control (WT), the susceptible control (SCK), the disease resistant control (RCK), and the high yield control (YCK), respectively. Through analysis, it was found that the disease indexes of all transgenic lines were lower than the WT, YCK, and SCK, moreover, L-214 was extremely close to the RCK (Fig. 5b). The results showed that the bolls per plant of L-214, L-213 and L-235 were 14.9, 17.6 and 20.0, respectively, and 12.5, 8.9, 11.2, and 11.7 in WT, SCK, RCK, and YCK, respectively. Boll-setting in all three transgenic lines was higher than the parent lines and other controls. Other than these three lines, the bolls per plant in many other different lines were also better than YCK (Fig. 5c). In conclusion, overexpression of the GbAt11 gene in G. hirsutum not only improved its resistance to disease caused by V. dahliae, but also increased the number of bolls per plant in a field that was severely infested with Verticillium wilt.
Disease resistance and yield performance of GbAt11-overexpressing cotton lines and statistical results. a Boll opening phenotype of transgenic line L-214 and WT in a V. dahliae nursery at the boll opening stage (Shandong, 2013.09). b Morbidity of Verticillium wilt at the flowering and boll-forming stages. The disease index come from the results of August 20. The indexes of L-214 and other lines were significantly lower than those of WT, YCK, and SCK, but similar to RCK. c Bolls per plant at the late flowering and boll-forming stages; several lines, including L-214, were better than JM169 and YCK
In this study, GbAt11 gene expression experiments showed that GbAt11 up-regulation started at 4 h after induction in G. barbadense, then decreased at 8 h, and increased to 70-fold at 24 h. This result is a normal response of plants to pathogen infection: the expression of genes associated with disease resistance will increase, followed by a process of adaptation, and then expression increases again as the infection becomes severe (Denance et al. 2013). This pattern of GbAt11 expression was observed in the response of G. barbadense to infection by V. dahliae. As for the highly susceptible G. hirsutum, expression of genes relevant to disease resistance are not induced, but occurs systemic infection and results in leaf wilt. Thus it appears that GbAt11 plays an important role in determining Verticillium wilt resistance in G. barbadense.
Previous studies have shown that after low temperature treatment, dehydrated protein WZY2 will leave the dehydration point and disperse into the cytoplasm, indicating that low temperature will affect the distribution of wheat dehydrated protein WZY2 in cells (Lv 2014). Observing the localization of GbAT11, we can find that the cell membrane leaves the cytoplasm after the plasma wall separation occurs, and the fluorescence is localized in the cell membrane.The fluorescence brightness of the cell membrane in Fig. 4c is enhanced, which may be caused by shrinkage of the cell membrane, or when the cell is stressed, the GbAt11-GFP fusion protein localized in the nucleus is transferred to the cell membrane.
Typically, overexpression of transcription factors, such as DRE, can improve stress tolerance or disease resistance in plants, but it may also cause dwarfing and yield reduction, etc. (Narusaka et al. 2003). We found that the cotton strain transferred to GbAt11 had a significant effect against Verticillium wilt. In addition, later production of cotton showed that the yield of transgenic cotton was higher than wild type. Although we demonstrated that the transgenic lines overexpressing GbAt11 had better resistance to Verticillium wilt, the mutant strain was failed to be constructed. Because cotton is a heterotetraploid plant, and AT11 has two copies in G. barbadense, it is difficult to knock them out together with the same vector. In addition, because of the limitation of cotton growth cycle, it is impossible to obtain double mutant in a short time. So next we will use the virus induced gene silencing system to silence the GbAt11 gene, and then further investigate the cotton resistance to Verticillium wilt. Unfortunately, we were unable to identify any proteins that directly interact with GbAT11 by co-immunoprecipitation and yeast two hybrid assays, so this remains to be further investigated in the future. Although its function needs to be further researched, the effect of increasing yield and resistance to Verticillium wilt has guiding significance to cotton production practice.
GbAt11 has been identified as a new gene which is specifically induced by V. dahliae. Its overexpression in G. hirsutum not only significantly improves resistance to Verticillium wilt, but also up-regulates transcription of several key genes in the immunity pathways. These results show that GbAt11 plays a role in disease resistance. Furthermore, overexpression of the GbAt11 gene in G. hirsutum can also increase the number of bolls per plant to increase cotton yield.
The source data underlying Figs.1, 2, 3, 4 and 5 are provided as a Source Data file. All other data that support the findings of this study are available from the corresponding author upon request.
Adachi H, Nakano T, Miyagawa N, et al. WRKY transcription factors phosphorylated by MAPK regulate a plant immune NADPH oxidase in Nicotiana benthamiana. Plant Cell. 2015;27(9):2645–63. https://doi.org/10.1105/tpc.15.00213.
Albrecht C, Boutrot F, Segonzac C, et al. Brassinosteroids inhibit pathogen-associated molecular pattern-triggered immune signaling independent of the receptor kinase BAK1. PNAS. 2012;109(1):303–8. https://doi.org/10.1073/pnas.1109921108.
Albrecht C, Russinova E, Kemmerling B, et al. Arabidopsis SOMATIC EMBRYOGENESIS RECEPTOR KINASE proteins serve brassinosteroid-dependent and -independent signaling pathways. Plant Physiol. 2008;148(1):611–9. https://doi.org/10.1104/pp.108.123216.
Asai T, Tena G, Plotnikova J, et al. MAP kinase signalling cascade in Arabidopsis innate immunity. Nature. 2002;415(6875):977–83. https://doi.org/10.1038/415977a.
Burpee LL, Bloom JR. The influence of Pratylenchus penetrans on the incidence and severity of Verticillium wilt of potato. J Nematol. 1978;10(1):95–9.
Denance N, Sanchez-Vallet A, Goffner D, Molina A. Disease resistance or growth: the role of plant hormones in balancing immune responses and fitness costs. Front Plant Sci. 2013;4:155. https://doi.org/10.3389/fpls.2013.00155.
Diatchenko L, Lau Y, Campbell AP, et al. Suppression subtractive hybridization: a method for generating differentially regulated or tissue-specific cDNA probes and libraries. PNAS. 1996;93(12):6025–30. https://doi.org/10.1073/pnas.93.12.6025.
Fradin EF, Abd-El-Haliem A, Masini L, et al. Interfamily transfer of tomato Ve1 mediates Verticillium resistance in Arabidopsis. Plant Physiol. 2011;156(4):2255–65. https://doi.org/10.1104/pp.111.180067.
Fradin EF, Zhang Z, Ayala JCJ, et al. Genetic dissection of Verticillium wilt resistance mediated by tomato Ve1. Plant Physiol. 2009;150(1):320–32. https://doi.org/10.1104/pp.109.136762.
Gao X, Wheeler T, Li Z, et al. Silencing GhNDR1 and GhMKK2 compromises cotton resistance to Verticillium wilt. Plant J. 2011;66(2):293–305. https://doi.org/10.1111/j.1365-313X.2011.04491.x.
Gomez-Gomez L, Boller T. FLS2: an LRR receptor-like kinase involved in the perception of the bacterial elicitor flagellin in Arabidopsis. Mol Cell. 2000;5(6):1003–11. https://doi.org/10.1016/s1097-2765(00)80265-8.
Harmon AC, Yoo BC, Mccaffery C. Pseudosubstrate inhibition of CDPK, a protein kinase with a calmodulin-like domain. Biochemistry. 1994;33(23):7278–87. https://doi.org/10.1021/bi00189a032.
Joys TM. Correlation between susceptibility to bacteriophage PBS1 and motility in Bacillus subtilis. J Bacteriol. 1965;90(6):1575–7.
Kawchuk LM, Hachey J, Lynch DR, et al. Tomato Ve disease resistance genes encode cell surface-like receptors. PNAS. 2001;98(11):6511–5. https://doi.org/10.1073/pnas.091114198.
Lin W, Lu D, Gao X, et al. Inverse modulation of plant immune and brassinosteroid signaling pathways by the receptor-like cytoplasmic kinase BIK1. PNAS. 2013;110(29):12114–9. https://doi.org/10.1073/pnas.1302154110.
Lv D. The effect of cold stress on subcellular localization of wheat Dehydrin WZY2. Yangling: North West Agriculture and Forestry University; 2014. p. 1–56.
Narusaka Y, Nakashima K, Shinwari ZK, et al. Interaction between two cis-acting elements ABRE and DRE in ABA-dependent expression of Arabidopsis rd29A gene in response to dehydration and high-salinity stresses. Plant J. 2003;34(2):137–48. https://doi.org/10.1046/j.1365-313x.2003.01708.x.
Nurnberger T, Brunner F, Kemmerling B, Piater L. Innate immunity in plants and animals: striking similarities and obvious differences. Immunol Rev. 2004;198:249–66. https://doi.org/10.1111/j.0105-2896.2004.0119.x.
Ozinsky A, Underhill DM, Fontenot JD, et al. The repertoire for pattern recognition of pathogens by the innate immune system is defined by cooperation between toll-like receptors. PNAS. 2000;97(25):13766–71. https://doi.org/10.1073/pnas.250476497.
Qi X, Su X, Guo H, et al. VdThit, a thiamine transport protein, is required for pathogenicity of the vascular pathogen Verticillium dahliae. Mol Plant-microbe In. 2016;29(7):545–59. https://doi.org/10.1094/MPMI-03-16-0057-R.
Rigo G, Ayaydin F, Tietz O, et al. Inactivation of plasma membrane-localized CDPK-related kinase5 decelerates PIN2 exocytosis and root gravitropic response in Arabidopsis. Plant Cell. 2013;25(5):1592–608. https://doi.org/10.1105/tpc.113.110452.
Salin C, Sunchai P, Apiradee T. Dengue typing assay based on real-time PCR using SYBR green I. J Virol Methods. 2005;129(1):8–15. https://doi.org/10.1016/j.jviromet.2005.05.006.
Simko I, Costanzo S, Haynes KG, et al. Linkage disequilibrium mapping of a Verticillium dahliae resistance quantitative trait locus in tetraploid potato (Solanum tuberosum) through a candidate gene approach. Theor Appl Genet. 2004;108(2):217–24. https://doi.org/10.1007/s00122-003-1431-9.
Wan J, Zhang XC, Stacey G. Chitin signaling and plant disease resistance. Plant Signal Behav. 2008;3(10):831–3. https://doi.org/10.4161/psb.3.10.5916.
Wang Z, Gerstein M, Snyder M. RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet. 2009;10(1):57–63. https://doi.org/10.1038/nrg2484.
Zhang T, Chen T. Cotton pistil drip transformation method. Methods Mol Biol. 2012;847:237–43. https://doi.org/10.1007/978-1-61779-558-9_20.
Zhang Y, Wang XF, Li YY, et al. Ectopic expression of a novel Ser/Thr protein kinase from cotton (Gossypium barbadense), enhances resistance to Verticillium dahliae infection and oxidative stress in Arabidopsis. Plant Cell Rep. 2013;32(11):1703–13. https://doi.org/10.1007/s00299-013-1481-7.
Zhang Y, Wang XF, Yang S, et al. Cloning and characterization of a Verticillium wilt resistance gene from Gossypium barbadense and functional analysis in Arabidopsis thaliana. Plant Cell Rep. 2011;30(11):2085–96. https://doi.org/10.1007/s00299-011-1115-x.
We thank Prof. GONG Zhizhong and Prof. LI Jigang of the Department of Plant Science, College of Biological Sciences of China Agricultural University for their assistance. We gratefully acknowledge the State Key Laboratory of Plant Physiology and Biochemistry for allowing this work to take places in their laboratory.
This research was financially supported by the National Key Research and Development Program of China (2016YFD0101904).
Qiu TT and Wang YJ contributed equally to this work.
State Key Laboratory of Plant Physiology and Biochemistry, Department of Plant Science, College of Biology Science, China Agricultural University, Beijing, 100193, China
Tingting QIU, Yanjun WANG, Juan JIANG, Jia ZHAO, Yanqing WANG & Junsheng QI
Tingting QIU
Yanjun WANG
Juan JIANG
Jia ZHAO
Yanqing WANG
Junsheng QI
Qi JS conceived and initiated the research. Qi JS, Qiu TT, Wang YJ and Jiang J performed the experiments. Qi JS, Qiu TT, Wang YJ and Zhao J analyzed the data. Qi JS, Qiu TT, Wang YJ and Jiang J wrote the article. The authors read and approved the final manuscript.
Correspondence to Junsheng QI.
This study was approved by the local ethics committee.
We accept publication.
Additional file 1.
(XLS 215535 kb)
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
QIU, T., WANG, Y., JIANG, J. et al. GbAt11 gene cloned from Gossypium barbadense mediates resistance to Verticillium wilt in Gossypium hirsutum. J Cotton Res 3, 9 (2020). https://doi.org/10.1186/s42397-020-00047-3
Gossypium barbadense, GbAt11, Verticillium wilt, resistance
Physiology and Pathology
Submission enquiries: [email protected] | CommonCrawl |
\begin{document}
\title{Stochastic electrodynamics and the interpretatiion of quantum theory} \author{Emilio Santos} \maketitle \tableofcontents
\begin{abstract} I propose that quantum mechanics is a stochastic theory and quantum phenomena derive from the existence of real vacuum stochastic fields filling space. I revisit stochastic electrodynamics (SED), a theory that studies classical systems of electrically charged particles immersed in an electromagnetic (zeropoint) radiation field with spectral density proportional to the cube of the frequency, Planck's constant appearing as the parameter fixing the scale. Asides from briefly reviewing known results, I make a detailed comparison between SED and quantum mechanics. Both theories make the same predictions when the stochastic equations of motion are of first order in Planck constant, but not in general. I propose that SED provides a clue for a realistic interpretation of quantum theory. \end{abstract}
\section{Introduction}
\subsection{Charges immersed in a random (vacuum) radiation field}
The basic assumption in this article is that the quantum vacuum fields are real stochastic fields. For the sake of clarity let us consider the best known vacuum field, the electromagnetic zeropoint radiation. The spectrum, that here I define as the energy per unit volume and unit frequency interval, is given by eq.$\left( \ref{roZPF}\right) $ below. The parameter fixing the scale of the field is Planck constant. Therefore it is interesting to see whether the reality of the vacuum electromagnetic field, combined with classical physics, allows to explain some phenomena believed as typically quantal, thus providing a hint for the realistic interpretation of quantum theory. With that purpose I shall study a restricted domain of phenomena with a theory defined by:
1) Just one of the interactions of nature, that is electromagnetic, a choice that we expect should lead to an approximation of quantum electrodynamics (QED). Actually QED includes two (quantum) vacuum fields, namely electromagnetic and electron-positron.
2) Nonrelativistic energies. Thus we shall exclude positrons and study only electrons ignoring spin, or more generally charged particles without structure, in given electromagnetic fields and/or interacting with other charges.
3) Planck constant $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
$ appears exclusively in the vacuum electromagnetic radiation. Consequently for the evolution we shall use the laws of classical electrodynamics throughout, but taking the additional force of the vacuum field into account.
\subsection{Stochastic electrodynamics}
The theory defined with these constraints is already known with the name stochastic (or random) electrodynamics (SED in the following). It has been developed by a small number of people during the last sixty years. Actually SED may be defined in several slightly different forms, for instance as classical electrodynamics modified by the assumption that the vacuum is not empty but there is a random electromagnetic field (or zeropoint field, ZPF) with spectrum eq.$\left( \ref{roZPF}\right) $ filling the whole space. With the precise definition here proposed SED is an approximation to quantum electrodynamics to lowest nontrivial order in the Planck constant, the zeroth order being purely classical electrodynamics. A review of the work made until 1995 is the book by L. de la Pe\~{n}a and A. M. Cetto\cite{dice} and new results are included in more recent reviews \cite{dice2}, \cite {Boyer19}. The application of similar ideas to optics will be reviewed in Chapter 6.
The origin of SED may be traced back to Walter Nernst, who extended to the electromagnetic field the zeropoint fluctuations of oscillators assumed by Planck in his second radiation theory of 1912. Nernst also suggested that the zeropoint fluctuations might explain some empirical facts, like the stability of atoms and the chemical bond. The proposal was soon forgotten due to the success of Bohr\'{}s model of 1913 and the subsequent development of the (old) quantum theory. Many years later the idea has been put forward again several times (e. g. by Braffort et al. in 1954\cite{Braffort} and by Marshall in 1963\cite{Marshall}).
SED studies the motion of charged particles immersed in ZPF, but the back actions of the charged particles on the ZPF are neglected (indeed the effects would be of higher order in Planck constant), so that the random field of free space is used. Assuming that the field is Lorentz invariant (at not too high frequencies) determines the spectrum, that is the energy per unit volume and unit frequency interval\cite{Milonni}, \cite{dice}. It is given by \begin{equation} \rho _{ZPF}\left( \omega \right) =\frac{1}{2\pi ^{2}c^{3}}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega ^{3}, \label{roZPF} \end{equation} that corresponds to an average energy $\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega $ per normal mode. Planck constant $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
$ enters the theory via fixing the scale of the assumed universal random radiation. Of course the spectrum eq.$\left( \ref{roZPF}\right) $ implies a divergent energy density and any cutoff would break Lorentz invariance. However we may assume that it is valid for low enough frequencies, the behaviour at high frequencies requiring the inclusion of other vacuum fields and general relativity theory. The spectrum eq.$\left( \ref{roZPF}\right) $ is appropriate for systems at zero Kelvin, but SED may be also studied at a finite tempereture, where we should add to eq. $\left( \ref{roZPF}\right) $ the thermal Planck spectrum. In addition SED may provide an interpretation of phenomena where the free spectrum is modified by boundary conditions derived from macroscopic bodies, but the average energy $\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega $ per normal mode still holds true. These phenomena will be revisited in Chapter 6.
The SED\ study of some simple systems provides an intuitive picture of several phenomena usually considered as purely quantum, like \textit{the stability of the classical (Rutherford) atom, Heisenberg uncertainty relations, entanglement, specific heats of solids, behaviour of atoms in cavities, etc.} For this reason I propose that SED may be considered as a clue in the search for a realistic interpretation of quantum theory.
\subsection{Scope of stochastic electrodynamics}
Not all predictions that have been claimed to follow from SED derive from the theory as defined above. In some cases additional assumptions are introduced in order to agree with the quantum predictions. In this form most of nonrelativistic quantum mechanics might be derived from SED\cite{dice2}. However with extra assumptions not resting upon deep arguments the physical bases of the theory become unclear and a realistic interpretation problematic.
In this paper we will study SED strictly as defined in Section 1.1. With that definition there are many examples where SED predicts results in contradiction with quantum mechanics and with experiments, as discussed in Section 6 below. In particular SED deals only with charged particles whilst QM laws are valid for both charged and neutral particles. It has been claimed that the restriction may be avoided taking into account that neutral particles may contain charged parts (e. g. the neutron possesses a magnetic moment). I think this is flawed, the application to those neutral particles might be valid in order to explain the stationary equilibrium state, which is effectively defined over an infinite time and it results independent on the total charge, as seen for instance in eqs.$\left( \ref{Wx}\right) $ and $ \left( \ref{Wv}\right) $ below. However this is not the case for time dependent properties like eq.$\left( \ref{general}\right) $ where the value of the charge is relevant.
With the definition of Section 1.1 SED is an approximation to QED at the lowest nontrivial order in Planck constant. A different approach is to consider that SED is ``the closest classical approximation to quantum theory'' \cite{Boyer19}. This suggests that there are two different theories, namely classical and quantum, but it is assumed that the validity of classical theory may be extended if we include the hypothesis of a radiation field with a Lorentz invariant spectrum in free space. It seems that this approach would increase, rather than solve, the problem of the ``infamous boundary'' between classical and quantum theories. Indeed in the standard wisdom (i. e. ignoring SED) the boundary is defined (roughly) by the relative value of Planck constant as compared with the typical magnitude of the action variable for the system. That is, classical theories are an approximation of quantum theories when Planck constant may be negleted. An argument for the need of distinguishing between quantum theory and generalizations of SED is the fact that there are peculiarities of quantum theory, like discrete spectra, that cannot be achieved by generalized SED. However there are numerical calculation providing hints that this problem might be solved, as we will comment on Section 2.5. In any case a generalization of SED (or equivalently a realistic interpretation of quantum theory) needs to agree with quantum theory \textit{exclusively} in the predictions of results of actual experiments, either performed or at least possible. But it is not required that predictions for ideal (not realistic) experiments or for unobservable facts should agree.
In this book it is supported the view that the whole of quantum theory should admit a realistic (classical-like) interpretation. That interpretation might be obtained via a generalization of SED taking into account not only the effect of the electromagnetic field on the motion of charged particles, but also the back action of the particles on the field and also all other vacuum fields, including metric fluctuations of spacetime. Attempts in that direction have been made elsewhere\cite{metric}. In summary SED may be taken as an approximation to quantum electrodynanics in some limited domain. In particular when the equations of motion are linear.
\subsection{Plan of the article}
In the following a short review of SED is presented and the analogies and differences between SED and nonrelativistic quantum mechanics (QM in the following) for some simple systems are studied. Most of the results have been reviewed in more detail elsewhere\cite{dice}. The novelty here is a more careful comparison of SED with QM and the emphasis on those quantum phenomena that might be better understood via the analogy with the picture provided by SED.
In the second and third sections the harmonic oscillator is revisited, with an application to oscillators in several dimensions in section 4. In sections 5 and 6 SED is applied to other linear systems, namely the free particle and the particle in a homogeneous magnetic field. Section 7 is devoted to the application of SED to some nonlinear systems, showing that in this case some disagreements with QM and with the experiments usualy appear. Section 8 presents the conclusions. This chapter includes many calculations and, in order that the reader does not loss the essential points, I will write in italics the relevant aspects for the comparison between SED and QM.
\section{The harmonic oscillator. Stationary state}
\subsection{Equation of motion}
The harmonic oscillator in one dimension is the most simple system to be treated within SED (the free particle requires a more careful study in order to avoid divergences). It is not strange that it was the first system studied. In this and the following sections we revisit a well known treatment of the oscillator in SED\cite{S74},\cite{dice}, but the study of the aspects that may provide a clue for the interpretation of quantum mechanics is original.
If a charged particle moves in one dimension in a potential well and it is also immersed in electromagnetic noise, it may arrive at a dynamical equilibrium between absorption and emission of radiation. In order to study the equilibrium I shall write the differential equation for the one-dimensional motion of the particle in the non-relativistic approximation. The passage to more dimensions is straightforward. We will neglect magnetic effects of the ZPF and the dependence of the field on the position coordinate, which corresponds to the common electric dipole approximation, plausible in a non-relativistic treatment. Thus the differential equation of motion of the particle in a harmonic oscillator potential is \begin{equation} m\stackrel{..}{x}=-m\omega _{0}^{2}x+m\tau \stackrel{...}{x}+eE\left( t\right) , \label{ode} \end{equation} where $m(e)$ is the particle mass (charge) and $E\left( t\right) $ is the $x$ component of the electric field of the radiation (the zeropoint field, ZPF). The equation of the mechanical (classical) oscillator is modified by the two latter terms. The second term on the right side of eq.$\left( \ref{ode} \right) ,$ is the damping force due to emission of radiation. It should appear also in the classical electrodynamical treatment. Only the third term is specific of SED because it involves Planck constant (it is of order O$ \left(
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
^{1/2}\right) ).$ The parameter $\tau $ given by \begin{equation} \tau =\frac{2e^{2}}{3mc^{3}}\Rightarrow \tau \omega _{0}=\frac{2}{3}\frac{ e^{2}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
c}\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}{mc^{2}}<<1. \label{gamma} \end{equation} so that the dimensionless quantity $\tau \omega _{0}$ is very small, it being the product of two small numbers namely the fine structure constant, $ \alpha \equiv e^{2}/
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
c\sim 1/137,$ and the nonrelativistic ratio $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}/mc^{2}\simeq $ $v^{2}/c^{2}<<1.$ Thus the two latter terms of eq. $\left( \ref{ode}\right) $ may be taken as small, which allows some useful approximations. Eq.$\left( \ref{ode}\right) $ is a stochastic differential equation of Langevin\'{}s type with coloured (non-white) noise. It has been named Braffort-Marshall equation by the early workers on SED\cite{Braffort} , \cite{Marshall}. Solving an equation of this kind usually means finding the evolution of the probability distribution of the relevant quantities as a function of time, starting from given initial conditions. When the time goes to infinity the probability distributions become independent of the initial conditions, giving rise to the stationary or equilibrium distribution.
\subsection{Average values of the potential and kinetic energies}
Several solutions of the eq.$\left( \ref{ode}\right) $ have been published \cite{S74}, \cite{dice}. The most simple is the stationary solution, which may be found by Fourier transform of eq.$\left( \ref{ode}\right) $ as follows. Firstly we define the Fourier transform of the stationary process $ E(t)$ in a finite time interval by \begin{equation} \widetilde{E}\left( \omega ,T\right) \equiv \frac{1}{\sqrt{4\pi T}} \int_{-T}^{T}E(t)\exp \left( -i\omega t\right) dt. \label{spectrum0} \end{equation}
Hence it may be shown that$\left| \widetilde{E}\left( \omega ,T\right)
\right| ^{2}/8\pi $ is the mean (in the time interval $\left( -T,T\right) )$ energy density per unit frequency interval associated to one electric field component. Thus the total energy density per unit frequency interval, $\rho \left( \omega \right) $ eq.$\left( \ref{roZPF}\right) ,$ should be $6$ times that quantity (6 because in the ZPF there are 3 components of the electric field and another 3 of the magnetic field all contributing equally on the average). Consequently we define the spectral density, $S_{E}\left( \omega \right) ,$ of the field $E(t)$ as follows \begin{equation}
S_{E}\left( \omega \right) \equiv \lim_{T\rightarrow \infty }\left|
\widetilde{E}\left( \omega ,T\right) \right| ^{2}=\frac{4\pi }{3}\rho \left( \omega \right) =\frac{2}{3\pi c^{3}}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega ^{3},
\label{Espectrum} \end{equation} the equality giving the relation between the spectral density and the energy density of the ZPF, eq.$\left( \ref{roZPF}\right) .$ For short the spectral density will be named spectrum in the following.
A Fourier transform similar to eq.$\left( \ref{spectrum0}\right) $ of all terms of eq.$\left( \ref{ode}\right) $ provides a relation between the spectrum of the field component and the spectrum of the coordinate, $x(t)$, namely \begin{equation} m(\omega _{0}^{2}-\omega ^{2}+i\tau \omega ^{3})\widetilde{x}\left( \omega \right) =e\widetilde{E}\left( \omega \right) , \label{Fourier} \end{equation} where $\widetilde{x}\left( \omega \right) $ and $\widetilde{E}\left( \omega \right) $ are the Fourier transforms of $x(t)$ and $E(t)$ respectively. Hence the spectrum of $x\left( t\right) $ is easily got in terms of the spectrum of $E\left( t\right) $ that is \begin{equation}
S_{x}\left( \omega \right) =\lim_{T\rightarrow \infty }\left| \widetilde{E}
\left( \omega ,T\right) \right| ^{2}=\frac{3c^{3}\tau }{2m\left[ \left( \omega _{0}^{2}-\omega ^{2}\right) ^{2}+\tau ^{2}\omega ^{6}\right] } S_{E}\left( \omega \right) , \label{spectrum} \end{equation} whence we obtain, taking eq.$\left( \ref{Espectrum}\right) $ into account, \begin{equation} S_{x}\left( \omega \right) =\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega ^{3}}{\pi m\left[ \left( \omega _{0}^{2}-\omega ^{2}\right) ^{2}+\tau ^{2}\omega ^{6}\right] }. \label{oscilspectrum} \end{equation}
From the spectrum it is trivial to get the quadratic means of the relevant variables namely \begin{equation} \left\langle x^{2}\right\rangle =\int_{0}^{\infty }S_{x}\left( \omega \right) d\omega ,\left\langle v^{2}\right\rangle =\int_{0}^{\infty }\omega ^{2}S_{x}\left( \omega \right) d\omega ,
\label{mean} \end{equation} where $\left\langle {}\right\rangle $ means time average, and the quantities in eq.$\left( \ref{mean}\right) $ are the coordinate of the oscillator and its velocity, respectively. The spectrum of the velocity is $\omega ^{2}$ times the spectrum of the coordinate because the time derivative leads to multiplication of the Fourier transform times $i\omega $. In our treatment of stationary states in SED an ergodic hypothesis is made, that is ensemble averages are assumed equal to time averages for the stationary stochastic processes involved.
Calculating the integral of $S_{x}\left( \omega \right) $ is lengthy but it becomes trivial in the limit $\tau \rightarrow 0$ where the integrand is highly peaked at $\omega \simeq \omega _{0}.$ If $\tau $ is small the contribution to the integral comes only from values of $\omega $ close to $ \omega _{0}$ and we may put $\omega \rightarrow \omega _{0},$ except in the difference $\omega -\omega _{0}$, and then to extend the integral to the whole real line. With this substitution the integrand becomes a Dirac\'{}s delta in the limit $\tau \rightarrow 0$ and the integral becomes trivial$,$ that is
\begin{eqnarray} \left\langle x^{2}\right\rangle &=&\int_{0}^{\infty }S_{x}\left( \omega \right) d\omega \simeq \int_{-\infty }^{\infty }\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega _{0}^{3}}{\pi m\left[ 4\omega _{0}^{2}\left( \omega _{0}-\omega \right) ^{2}+\tau ^{2}\omega _{0}^{6}\right] }d\omega \nonumber \\ &\simeq &\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2m\omega _{0}}\int_{-\infty }^{\infty }\delta \left( \omega -\omega _{0}\right) d\omega =\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2m\omega _{0}}, \label{2.3} \end{eqnarray} whence the mean potential energy is \[ \left\langle V\right\rangle =\frac{1}{2}m\omega _{0}^{2}\left\langle x^{2}\right\rangle =\frac{1}{4}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}. \] The contribution of the high frequencies, $\left\langle x^{2}\right\rangle _{hf},$ may be approximated by the integral of the spectrum eq.$\left( \ref {oscilspectrum}\right) $ with zero substituted for $\omega _{0}.$ However, in order to exclude the low frequency part, calculated in eq.$\left( \ref {2.3}\right) ,$ we shall put $2\omega _{0}$ as lower limit of the integral, that is \begin{eqnarray} \left\langle x^{2}\right\rangle _{hf} &\simeq &\int_{2\omega _{0}}^{\infty } \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega ^{3}}{\pi m\left[ \omega ^{4}+\tau ^{2}\omega ^{6}\right] } d\omega \nonumber \\ &\simeq &-\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi m}\log \left( \tau \omega _{0}\right) , \label{2.3a} \end{eqnarray} which is positive (see eq.$\left( \ref{gamma}\right) ).$ We see that the result depends but slightly on the lower limit of the integral (provided it is of order $2\omega _{0}).$
A similar procedure might be used for the quadratic mean velocity, by performing the integral of the velocity spectrum. However that integral is divergent and we shall assume that there is some frequency cut-off, $\omega _{c}$. The result of the integral is the sum of two terms. One of them comes from frequencies near $\omega _{0}$ and it is independent of the cut-off in the limit $\tau \rightarrow 0$ giving \begin{equation} \left\langle v^{2}\right\rangle =\int_{0}^{\omega _{c}}\omega ^{2}S_{x}\left( \omega \right) d\omega \simeq \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}{2m}\Rightarrow \frac{1}{2}m\left\langle v^{2}\right\rangle = \frac{1}{4}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}. \label{2.4} \end{equation} The other term comes from the high frequency region and it is divergent when the cut-off goes to infinity. It may be approximated as in the case of $ \left\langle x^{2}\right\rangle ,$ although here we may put zero as lower limit of the integral, that is \begin{equation} \left\langle v^{2}\right\rangle _{hf}\simeq \int_{0}^{\omega _{c}}\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega ^{5}}{\pi m\left[ \omega ^{4}+\tau ^{2}\omega ^{6}\right] } d\omega =\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2\pi m\tau }\log \left( 1+\tau ^{2}\omega _{c}^{2}\right) . \label{vhf} \end{equation} However that term is not very relevant because for those frequencies the non-relativistic approximation breaks down (see below the discussion of the velocity dispersion in the free particle case). Adding eqs.$\left( \ref{2.3} \right) $ and $\left( \ref{2.4}\right) $ gives the total mean energy to zeroth order in the small quantity $\tau \omega _{0}$, namely \begin{equation} \left\langle U\right\rangle =\left\langle \frac{1}{2}m\omega _{0}^{2}x^{2}+ \frac{1}{2}mv^{2}\right\rangle =\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}. \label{energy} \end{equation}
An alternative definition of the energy is possible in terms of the canonical momentum, $p,$ which avoids problems of divergence. The momentum is defined by \begin{equation} p\equiv mv-\frac{e}{c}A\mathbf{,}U\equiv \frac{p^{2}}{2m}+\frac{1}{2}m\omega _{0}^{2}x^{2}. \label{momentum} \end{equation} Now we take into account that the potential vector, whose $x$ component we label $A,$ contains two parts one coming from the ZPF and the other one from the particle self-field, the latter producing the radiation reaction. These two terms give rise to the latter two terms of eq.$\left( \ref{ode}\right) .$ Taking this relation into account it is straightforward to get the spectrum of the canonical momentum, that is \begin{eqnarray} \frac{d}{dt}p &=&-m\omega _{0}^{2}x\Rightarrow S_{p}\left( \omega \right) = \frac{m^{2}\omega _{0}^{4}}{\omega ^{2}}S_{x}\left( \omega \right) \label{canonmom} \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
m\tau \omega _{0}^{4}\omega }{\pi \left[ \left( \omega _{0}^{2}-\omega ^{2}\right) ^{2}+\tau ^{2}\omega ^{6}\right] }. \nonumber \end{eqnarray} Hence we get \begin{equation} \left\langle p^{2}\right\rangle =m^{2}\omega _{0}^{4}\int_{0}^{\infty }\omega ^{-2}S_{x}\left( \omega \right) d\omega =\frac{m
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}{2}\Rightarrow \frac{\left\langle p^{2}\right\rangle }{2m}=\frac{ 1}{4}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}, \label{2.4a} \end{equation} in the limit $\tau \rightarrow 0.$ We see that the energy defined from the velocity is divergent (a cut-off was needed), whilst the one derived from the canonical momentum is finite. Thus the use of the canonical momentum in the definition of the energy seems more convenient. We may expect that in a more correct relativistic treatment the former would be also convergent and not too different from the latter.
\subsection{Probability distributions of position, momentum and energy}
In order to fully define the stationary state of the oscillator immersed in ZPF it is necessary to get the probability distributions, not just the mean values. Before doing that we need to clarify the meaning of the probability distributions involved. Up to now we have considered averages over infinite time intervals, see eq.$\left( \ref{Espectrum}\right) .$ However we assume that the time dependent quantities are stochastic processes, that is probability distributions of functions of time. Thus we should write $ x(t,\lambda )$ (as is standard it the mathematical theory of stochastic processes) rather than just $x(t)$, where $\lambda \in \Lambda $ and there is a probability distribution on the set $\Lambda .$ For a fixed value of $t$ this provides a probabiltity distribution of the random variable $x(t)$. We assume that the probability distribution of each component, $E(t,\lambda )$, of the ZPF (in free space) is Gaussian with zero mean and also that it is a stationary ergodic process, that is any time average (over an infinite time interval) equals the ensemble average over the probability distribution of $ \Lambda $ at any single time.
Eq.$\left( \ref{ode}\right) $ is linear, whence the Gaussian character of $ E(t,\lambda )$ gives rise to Gaussian distributions (with zero mean) for both positions and velocities. Thus eq.$\left( \ref{2,3}\right) $ fixes completely the normalized probability distribution of the positions to be
\begin{equation} W\left( x\right) dx=\sqrt{\frac{m\omega _{0}}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}}\exp \left[ -\frac{m\omega _{0}x^{2}}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\right] dx. \label{Wx} \end{equation} Similarly eq.$\left( \ref{2.4a}\right) $ fixes the distribution of momenta, that is \begin{equation} W\left( p\right) dp=\sqrt{\frac{m}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}}\exp \left[ -\frac{p^{2}}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
m\omega _{0}}\right] dp, \label{Wv} \end{equation} which is also normalized. The distribution of velocities is similar to that one, with $mv$ substituted for $p$ (modulo ignoring the part due to high frequencies).
In order to get the distribution of energy, $U$, to lowest order in Planck constant $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
$ we take into account that, as eqs.$\left( \ref{Wx}\right) $ and $\left( \ref{Wv}\right) $ already contain $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
$, the relation between $x,v$ and $U$ should be written to zeroth order in $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
,$ that is using the classical relation. Then we get the following exponential distribution of energies, $U$, \begin{eqnarray} W\left( U\right) dU &=&\int W\left( x\right) dx\int W\left( p\right) dp\delta \left( U-\frac{1}{2}m\omega _{0}^{2}x^{2}-\frac{1}{2m}p^{2}\right) dU \nonumber \\ &=&\frac{2}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}\exp \left( -\frac{2U}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}}\right) dU,U\geq 0.
\label{WE} \end{eqnarray} where $\delta \left( {}\right) $ is Dirac\'{}s delta. Hence the fluctuation of the energy is \begin{equation} \sqrt{\left\langle U^{2}\right\rangle -\left\langle U\right\rangle ^{2}} =\left\langle U\right\rangle =\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}. \label{fluctE} \end{equation} The distributions of positions and momenta, eqs.$\left( \ref{Wx}\right) $ and $\left( \ref{Wv}\right) $ agree with the QM predictions, but this is not the case for the energy because QM predicts a sharp energy, in disagreement with the SED eq.$\left( \ref{WE}\right) .$ Below we shall study this discrepancy, that is very relevant for our realistic interpretation of quantum theory.
Eqs.$\left( \ref{Wx}\right) $ and $\left( \ref{Wv}\right) $ show that the Heisenberg uncertainty relations, \begin{equation} \Delta x\Delta p\geq
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
/2, \label{Heisineq} \end{equation} appear in a natural way in SED. Indeed the probability distributions eqs.$ \left( \ref{Wx}\right) $ and $\left( \ref{Wv}\right) $ correspond to what in quantum language is called a ``minimum uncertainty wavepacket'', that is the quantum state where the Heisenberg inequality, eq.$\left( \ref{Heisineq} \right) ,$ saturates i. e. it becomes an equality.
Calculating the corrections due to the finite value of the parameter $\tau $ in eqs.$\left( \ref{2.3}\right) $ to $\left( \ref{energy}\right) $ is straightforward although lenghty\cite{S74},\cite{dice} and it will not be reproduced here. A relevant point is that the correction is not analytical in $\tau $ (or in the fine structure constant $\alpha ),$ but the leading term agrees with the radiative corrections of quantum electrodynamics (Lamb shift). An advantage of the SED calculation is that the radiative corrections (to the nonrelativistic treatment) may be got exactly whilst in quantum electrodynamics the required perturbative techniques allow only an expansion in powers of $\tau $ (or $\alpha ),$ once a ultraviolet cut-off is introduced. In any case the radiative corrections depend on the high frequency region of integrals like eq.$\left( \ref{oscilspectrum}\right) ,$ where the non-relativistic approximation breaks down. Therefore the calculation of these corrections has a purely academic interest.
\subsection{Comparison between the stationary state in SED and the ground state in QM}
A conclusion of the study of the stationary state of the oscillator in SED is that it is rather similar to the ground state of the oscillator en QM. Indeed the probability distribution of positions and momenta in the stationary state of SED agree with the predictions of QM for the ground state, in the limit $\tau \rightarrow 0$, eqs.$\left( \ref{Wx}\right) $ and $ \left( \ref{Wv}\right) ,$ whilst the corrections for finite $\tau $, that depend on the small quantity $\tau \omega _{0},$ correspond to the radiative corrections of quantum electrodynamics. However the probability distribution of the energy does not agree with QM. In the following I study more carefully this discrepancy.
\subsubsection{John von Neumann\'{}s theorem against hidden variables}
Firstly I should mention that the conflict between the QM prediction and the SED eq.$\left( \ref{WE}\right) $ is an example of the general argument used by von Neumann\cite{von Neumann4} in his celebrated theorem of 1932 proving that hidden variable theories are incompatible with QM. That theorem prevented research in hidden variables theories until Bell\'{}s rebuttal in 1966\cite{BellRMP4}. J. von Neumann starts with the assumption that any linear relation between quantum observables should correspond to a similar linear relation between the possible (dispersion free) values in a hypothetical hidden variables theory. In our case the energy $U$ is a linear combination of $v^{2}$ and $x^{2}.$ Thus as the energy predicted by quantum mechanics, $U=
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}/2,$ is sharp, any pair of values of $v^{2}$ and $x^{2}$ in the hidden variables theory should fulfil, according to von Neumann\'{}s hypothesis, \begin{equation} m(v^{2}+\omega _{0}^{2}x^{2})=
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}, \label{linear} \end{equation} which is not compatible with the distributions eqs.$\left( \ref{Wx}\right) $ and $\left( \ref{Wv}\right) $ (for instance the possible value $v^{2}=2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0}/m$ is incompatible with eq.$\left( \ref{linear}\right) $ because it would imply $x^{2}\geq 0).$ Bell's rebutted von Neumann pointing out that the contradiction only arises when two of the quantum obervables involved do not commute and in this case the measurement of the three observables should be made in, at least, two different experiments. Thus a contextual hidden variables theory is possible, that is a theory where it is assumed that the value obtained in the measurement depends on both the state of the observed system and the full experimental context.
\subsubsection{The apparent contradiction between QM and SED}
In our case the apparent contradiction between SED eq.$\left( \ref{WE} \right) $ and the QM prediction of a sharp energy dissapears if we take into account how\emph{\ }the energy of a state is defined \emph{operationally } (i. e. how it may be measured.) In SED the stationary state corresponds to a dynamical equilibrium between the oscillator and the ZPF. Checking empirically whether a dynamical equilibrium exists requires a long time, ideally infinite time. If we define the energy of the oscillator in equilibrium as the average over an infinite time, it would be obviously sharp. In fact the probability distribution of the ``mean energies over time intervals of size $\Delta t$ $"$ has a smaller dispersion as greater is $ \Delta t,$ and will be dispersion free in the limit $\Delta t\rightarrow \infty .$ Thus it is natural to assume that the ground state energy as defined by QM actually corresponds to measurements made over infinitely long times. This fits fairly well with the quantum energy-time uncertainty relation \begin{equation} \Delta U\Delta t\geq
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
/2, \label{energytime} \end{equation} which predicts that the measured energy does possess a dispersion $\Delta U$ if the measurement involves a finite time $\Delta t$. Thus no contradiction exists between SED and QM for the energy in the ground state.
It is remarkable that QM and SED lead to the same result via rather different paths. In fact in QM the state vector of the ground state of a system is an eigenstate of the Hamiltionian, which implies a nil dispersion of the state energy, but the uncertainty relation gives rise to some uncertainty for any actual measurement. This leads us to propose that \emph{ the ground state of a physical system in QM corresponds to a dynamical equilibrium between emission of radidation to the vacuum fields and absorption from them.} The instantaneous energy is a badly defined concept. Indeed the SED distribution eq.$\left( \ref{WE}\right) $ derives from the (classical) definition of total energy in terms of positions and momenta, but it does not possesses any operational (measurable) meaning.
\subsection{Spectrum of the light emitted or absorbed by the SED oscillator}
There is another trivial agreement between the SED and QM predictions for the oscillator, namely the spectrum of emitted or absorbed light. In fact the standard quantum method to derive the spectrum of a system starts solving the stationary Schr\"{o}dinger equation and then calculating the frequencies using the rule \[ \omega _{jk}=\frac{E_{j}-E_{k}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}=(j-k)\omega _{0}, \] where the eigenvalues of the oscillator Hamiltonian, $E_{n}=n
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{0},$ have been taken into account. However in the oscillator there is a selection rule that, within the electric dipole approximation, forbids transitions except if $j-k=\pm 1,$ whence the spectrum has a single frequency that agrees with the classical one. Actually the spectrum contains also the frequencies $n\omega _{0}$, that correspond to electric multipole transitions, although these transitions have low probability. The multipoles of the fundamental frequency may be found also in SED calculations if the electric dipole approximation is not made, that is if the following Lorentz force is substituted for the last term of eq.$\left( \ref{ode}\right) $ \[ F_{x}=e\left[ \mathbf{E+}\frac{\mathbf{\dot{r}}}{c}\times \mathbf{B}\right] _{x}, \] $\mathbf{E}$ and $\mathbf{B}$ being the electric and magnetic fields of the ZPF. To be consistent the other terms of eq.$\left( \ref{ode}\right) $ should be also changed to become relativistic in order to be consistent. Then the differential equation of motion becomes nonlinear and it is far more difficult to solve, but this may be achieved numerically and good agreement with quantum predictions is obtained for the spectrum of emitted or absorbed light\cite{Huang}.
SED may also offer intuitive pictures for cavity quantum electrodynamics, a well established experimental field of research\cite{dice}. An atom in a cavity get modified its properties, in particular its lifetime. In fact the atom does not decay if the modes having the frequency of the emitted radiation are not possible inside the cavity. In the quantum treatment the intriguing question is how the atom ``knows'' in advance that it should not decay in these conditions. In SED the explanation is trivial: spontaneous decay is actually stimulated by appropriate modes of the ZPF, and the modes required for the stimulation do not exist inside the cavity. For instance in an early experiment by Haroche et al.\ref{Haroche} the excited atoms propagates between two metallic mirrors separated by 1.1 $\mu m$\ for about 13 natural lifetimes without appreciable decay. The experiment involved a small applied magnetic field in order to demonstrate the anisotropy of spontaneous emission between mirrors. This experiment has been studied within SED via modelling the atom by a harmonic oscillator whence the empirical results have been reproduced quantitatively, but I will not review that work here\cite{Humba2}, \cite{Humba}.
\subsection{Lessons for a realistic interpretation of quantum theory}
\textit{Our study of a particle in a potential well shows that inclusion of the vacuum random electromagnetic field leads to predictions resembling those of quantum electrodynamics. }
\textit{The quantum ground state of a particle in a potential well corresponds to a stationary state of a particle performing a highly irregular (stochastic) motion driven by vacuum fields.}
\textit{The spectrum of the field (or the energy per unit volume and unit frequency interval) determines the spectrum for the motion of the particle. It is such that the quadratic mean coordinate position and the quadratic mean momentum agree with quantum predictions and fulfil the Heisenberg uncertainty relations. These are here interpreted as a consequence of the (unavoidable) random motion of the particles. }
\textit{No contradiction arises between the exponential distribution of energy in SED and the sharp energy in QM. They are different operational definitions. The former refers to the instantaneous energy }(\textit{or the mean in a small time interval) but the latter to the mean over an infinite (or very large) time interval. This difference is a good illustration for the flaw in the celebrated von Neumann theorem against hidden variables in quantum mechanics.}
\textit{Radiative corrections (e. g. Lamb shift) appear naturally in SED with a transparent interpretation, i. e. as a consequence of the interaction between the charged particle and the real vacuum fields.}
\section{Time-dependent properties of oscillators and free particles}
\subsection{Evolution of the dynamical variables}
In Newtonian mechanics the study of the evolution consists of finding the position as a function of time for given initial conditions, that is initial positions and velocities of the particles involved. Thus the evolution describes a curve in phase space parametrized by time. If there are forces not fully known, which we represent as noise, all we may get is the evolution of the probability distribution in phase space with given initial conditions, i. e. either a point or a probability distribution in phase space. This is the case for the oscillator in SED that we study in the following. In order to calculate the evolution of the oscillator it is convenient to start anew from the equation of motion, eq.$\left( \ref{ode} \right) $. We shall work to lowest nontrivial order in the small parameter $ \tau $ (see eq.$\left( \ref{gamma}\right) )$ Thus we may approximate the third order eq.$\left( \ref{ode}\right) $ by another one of second order substituting $-m\tau \omega _{0}^{2}\dot{x}$ for $m\tau \stackrel{...}{x}$ on its right side. That is writing \begin{equation} m\stackrel{..}{x}=-m\omega _{0}^{2}x-m\tau \omega _{0}^{2}\dot{x}+eE\left( t\right) , \label{ode1} \end{equation} which agrees with eq.$\left( \ref{ode}\right) $ to first order in $\tau .$ This second order equation in $x(t)$ is equivalent to two coupled stochastic differential equations of Langevin type, in the variables $x(t)$ and $\dot{x} (t).$ We used eq.$\left( \ref{ode}\right) ,$ rather than $\left( \ref{ode1} \right) $ because the former was more appropriate for the study of radiative corrections than the latter.
A convenient vay to study the motion of the oscillator in SED consists of introducing new variables, $a(t)$\ and $b(t),$ as follows \begin{eqnarray} x\left( t\right) &=&a(t)\cos \left( \omega _{0}t\right) +b(t)\sin \left( \omega _{0}t\right) +\xi (t), \label{xab} \\ \dot{x}\left( t\right) &=&-a(t)\omega _{0}\sin \left( \omega _{0}t\right) +b(t)\omega _{0}\cos \left( \omega _{0}t\right) +\dot{\xi}(t). \nonumber \end{eqnarray} The rapidly fluctuating quantity $\xi (t)$\ is related to the high frequency part of the spectrum $S_{x}\left( \omega \right) $\ (see comment after eq.$ \left( \ref{2.4}\right) $) and it will be ignored in the following. The variables $a$ and $b$ are constants of the motion in the classical mechanical oscillator and they are slowly varying functions of time, with typical variation time $1/(\tau \omega _{0}^{2})>>\omega _{0}^{-1},$ see below. An alternative to eq.$\left( \ref{xab}\right) $ would be to write the coordinate in terms of the amplitude, $c(t),$ and the phase, $\phi \left( t\right) ,$ both slowly varying with time, that is \[ x\left( t\right) =c(t)\cos \left[ \omega _{0}t+\phi \left( t\right) \right] +\xi (t), \] but the choise eq.$\left( \ref{xab}\right) $ is more easy to solve. At the initial time, $t=0$, the parameters $a(t)$\ and $b(t)$ are easily related to the initial position, $x_{0},$ and momentum, $p_{0}$, that is \begin{equation} a\left( t_{0}\right) =x_{0},b\left( t_{0}\right) =\frac{\dot{x}_{0}}{\omega _{0}}=\frac{p_{0}}{m\omega _{0}}. \label{xpab} \end{equation}
Calculating the evolution of the variables $a(t)$\ and $b(t)$ simplifies if we introduce a complex function $z\left( t\right) $ such that \begin{eqnarray} x(t) &=&\func{Re}\left[ z(t)\exp (-i\omega _{0}t)\right] , \label{z} \\ \func{Re}z(t) &=&a(t),\func{Im}z(t)=b(t). \nonumber \end{eqnarray} The function $z(t)$ is slowly varying and therefore we may neglect its second (first) derivative in the term of order $0$ (order $\tau $) in the equation that results from inserting eq.$\left( \ref{z}\right) $ into eq.$ \left( \ref{ode1}\right) .$ This gives \begin{equation} -2im\omega _{0}\dot{z}\left( t\right) =im\tau \omega _{0}^{3}z\left( t\right) +eE\left( t\right) \exp \left( i\omega _{0}t\right) . \label{z1} \end{equation} The solution of this equation is trivial and we get \[ z\left( t\right) =\exp \left( -\frac{1}{2}\tau \omega _{0}^{3}t\right) \left[ z(0)+\frac{ie}{2m\omega _{0}}\int_{0}^{t}E(t^{\prime })\exp \left( \frac{1}{2}\tau \omega _{0}^{2}t^{\prime }+i\omega _{0}t^{\prime }\right) dt^{\prime }\right] . \] Hence it is easy to get the ensemble average, or expectation, of $z\left( t\right) $ taking into account that $E(t)$ is a stochastic process with zero mean. We get \begin{equation} \left\langle z\left( t\right) \right\rangle =\exp \left( -\frac{1}{2}\tau \omega _{0}^{2}t\right) \left\langle z\left( 0\right) \right\rangle . \label{z0} \end{equation} Also we may obtain the following quadratic mean \begin{equation}
\left\langle \left| z\left( t\right) -\exp \left( -\frac{1}{2}\tau \omega _{0}^{3}t\right) z\left( 0\right) \right| ^{2}\right\rangle =\frac{e^{2}}{ 4m^{2}\omega _{0}^{2}}\exp \left( -\tau \omega _{0}^{3}t\right) F, \label{z2} \end{equation} where \begin{equation} F\equiv \int_{0}^{t}dt^{\prime }\int_{0}^{t}dt^{\prime \prime }\left\langle E(t^{\prime })E(t^{\prime \prime })\right\rangle \exp \left[ \left( \frac{1}{ 2}\tau \omega _{0}^{2}+i\omega _{0}\right) t^{\prime }+\left( \frac{1}{2} \tau \omega _{0}^{2}-i\omega _{0}\right) t^{\prime \prime }\right] . \label{F} \end{equation} The selfcorrelation of the process $E(t)$ is the Fourier transform of the spectral density, that is \begin{equation} \left\langle E(t^{\prime })E(t^{\prime \prime })\right\rangle =\frac{1}{2} \int_{-\infty }^{\infty }\frac{2}{3\pi c^{3}}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega ^{3}\exp \left[ i\omega \left( t^{\prime \prime }-t^{\prime }\right) \right] d\omega , \label{EE} \end{equation} where eq.$\left( \ref{Espectrum}\right) $ has been taken into account. I stress that the process $E(t)$ is stationary and assumed ergodic, whence time average (over an infinite time) and ensemble average agree. However here we do not assume that $x(t)$ is stationary but we are investigating its time dependence. If eq.$\left( \ref{EE}\right) $ is put in eq.$\left( \ref{F} \right) $ and the integrals in $t^{\prime }$ and $t^{\prime \prime }$ performed we get \begin{eqnarray*} F &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{3\pi c^{3}}\int_{-\infty }^{\infty }\omega ^{3}d\omega \frac{4}{\tau
^{2}\omega _{0}^{4}+4\left( \omega -\omega _{0}\right) ^{2}}\left| \exp \left( \frac{1}{2}\tau \omega _{0}^{2}+i\omega _{0}-i\omega \right)
t-1\right| ^{2} \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{3\pi c^{3}}\int_{-\infty }^{\infty }\frac{4\omega ^{3}}{\tau ^{2}\omega _{0}^{4}+4\left( \omega -\omega _{0}\right) ^{2}}\times \\ &&\times \left[ \exp (\tau \omega _{0}^{2}t)+1-2\exp (\frac{1}{2}\tau \omega _{0}^{2}t)\cos \left( \omega t-\omega _{0}t\right) \right] d\omega . \end{eqnarray*} The integral in $\omega $ is ultraviolet divergent but the contribution of the high frequencies will be ignored here (see comment after eq.$\left( \ref {xab}\right) ).$ Thus taking into account that $\tau \omega _{0}<<1,$ the overwhelming contribution to the integral comes from frequencies $\omega \simeq \omega _{0}$ and the integral may be approximated putting $\omega ^{3}=\omega _{0}^{3}$ whence we obtain \begin{equation}
\left\langle \left| z\left( t\right) -\exp \left( -\frac{1}{2}\tau \omega _{0}^{3}t\right) z\left( 0\right) \right| ^{2}\right\rangle \simeq \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2m\omega _{0}^{2}}\left[ 1-\exp \left( -\tau \omega _{0}^{2}t\right) \right] . \label{zz} \end{equation} Taking eq.$\left( \ref{z}\right) $ into account we may separate the real and the imaginary parts in eqs.$\left( \ref{z0}\right) $ and $\left( \ref{zz} \right) .$ Thus we obtain information about the evolution of the classical constants of the motion $a=Re$ $z$ and $b=Im$ $z$, that is \begin{eqnarray} \left\langle a\left( t\right) \right\rangle &=&\exp \left( -\frac{1}{2}\tau \omega _{0}^{2}t\right) \left\langle a\left( 0\right) \right\rangle , \label{a12} \\ \left\langle \left[ a(t)-\left\langle a\left( t\right) \right\rangle \right] ^{2}\right\rangle &=&\left\langle \left[ a(t)-\exp \left( -\frac{1}{2}\tau \omega _{0}^{3}t\right) a(0)\right] ^{2}\right\rangle \nonumber \\ &\simeq &\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{4m\omega _{0}^{2}}\left[ 1-\exp \left( -\tau \omega _{0}^{2}t\right) \right] , \nonumber \end{eqnarray} and similar for $b(t)$ because both variables, $a(t)$\ and $b(t),$ have similar contributions to eq.$\left( \ref{zz}\right) ,$ which follows from their roles in eqs.$\left( \ref{xab}\right) .$ Eqs.$\left( \ref{a12}\right) $ and the similar ones for $b(t)$ mean that for any initial distribution of positions and momenta, the oscillator will arrive at a distribution corresponding to the stationary state (corresponding to the quantum ground state).
\subsection{Diffusion of the probability density in phase space}
It is possible to derive differential equations for the probability densities of $a$ and $b.$ They have the form of Fokker-Planck (or diffusion ) equation like \[ \frac{\partial \rho (a,t)}{\partial t}=\frac{\partial }{\partial a}(A\rho )+ \frac{\partial ^{2}}{\partial a^{2}}(D\rho ). \] The coefficients of drift, $A,$ and diffusion, $D,$ may be calculated from eqs.$\left( \ref{a12}\right) $ as follows \[ A=\lim_{t\rightarrow \infty }\frac{\left\langle a(t)\right\rangle }{t}=- \frac{1}{2}\tau \omega _{0}^{2},D=\lim_{t\rightarrow \infty }\frac{ \left\langle \left[ a(t)-\left\langle a\left( t\right) \right\rangle \right] ^{2}\right\rangle }{t}=\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{4m}. \] whence the Fokker-Planck equation reads \begin{equation} \frac{\partial \rho (a,t)}{\partial t}=\frac{1}{2}\tau \omega _{0}^{2}\frac{ \partial }{\partial a}(a\rho )+\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{4m}\frac{\partial ^{2}\rho }{\partial a^{2}}, \label{FP} \end{equation} and a similar one with $b$ substituted for $a$. I must point out that the stochastic processes $a(t)$ and $b(t)$ are correlated. In fact their crosscorrelation may be easily obtained as follows \begin{eqnarray*} \left\langle a(t)b(t^{\prime })\right\rangle &=&\left\langle \left[ x\left( t\right) \cos \left( \omega _{0}t\right) -\frac{p(t)}{m\omega _{0}}\sin \left( \omega _{0}t\right) \right] \left[ x(t^{\prime })\cos \left( \omega _{0}t^{\prime }\right) +\frac{p(t^{\prime })}{m\omega _{0}}\sin \left( \omega _{0}t^{\prime }\right) \right] \right\rangle \\ &=&-\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\sin \left[ \omega _{0}\left( t^{\prime }-t\right) \right] \exp (-\tau
\omega _{0}^{2}\left| t^{\prime }-t\right| )=-\left\langle b(t)a(t^{\prime })\right\rangle , \end{eqnarray*} where we have taken into account eqs.$\left( \ref{xab}\right) .$ Due to this correlation a joint probability density $\rho (a,$ $b,t)$ cannot be got as a product of the individual densities. Consequently deriving the differential equation for $\rho (a,$ $b,t)$ is involved and it will be not made here.
The conclusion of our calculation is that the classical constants of the motion, like the parameters $a$ and $b$ or the energy, $U$, perform a slow random motion with typical relaxation time $1/\left( \tau \omega _{0}^{2}\right) .$ In particular the energy is related to these parameters as follows\textrm{\ } \begin{equation} U(t)=\frac{1}{2}m\omega _{0}^{2}x(t)^{2}+\frac{1}{2}m\dot{x}(t)^{2}=\frac{1}{ 2}m\omega _{0}^{2}\left[ a(t)^{2}+b(t)^{2}\right] , \label{Uab} \end{equation} where eqs.$\left( \ref{xab}\right) $ have been taken into account. The change of the classical constants of the motion of the oscillator in SED is obviously due to the two latter terms of eq.$\left( \ref{ode}\right) .$\ The term involving the vacuum field produces diffusion, characterized by $D$, and the radiation reaction term gives rise to drift, characterized by $A$. The diffusion rate is independent of the particle\'{}s velocity whence $D$ is a constant, but the drift increases with the velocity with the result that $A$ is proportional to $a.$ The effect of the diffusion is reduced to some extent by the drift, with the consequence that the probability densities remain localized. In fact, when time increases indefinitely the densities approach the stationary solution studied in section 2. In particular the stationary solution of eq.$\left( \ref{FP}\right) $ (with normalized $\rho ,$\ which implies that $\rho $\ vanishes for $a\rightarrow \pm \infty )$\ is \[ \rho =\sqrt{\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{\pi m\omega _{0}^{2}}}\exp \left( -\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{m\omega _{0}^{2}}a^{2}\right) , \] and similar for $b$. The energy tends to the density given by eq.$\left( \ref {WE}\right) .$
\subsection{States of the oscillator in stochastic electrodynamics and in quantum mechanics}
Every nonnegative definite function in phase space may be taken as an initial probability density and thus be considered a state of the SED oscillator. We see that the set of states in SED is quite different from the set of states in QM (given by a density operator each). In particular the pure states in SED are those whose initial conditions correspond to points in phase space, whilst the pure states in QM correspond to state vectors (or wave functions). The comparison between SED and QED becomes more clear if we define the quantum states by means of functions in phase space, which might be achieved via the Wigner function formalism, to be revisited in Chapter 5. Thus in the case of pure quantum states it is obvious that only a small fraction of them correspond to states in SED. Actually, asides from the ground state there are only two interesting pure quantum states that correspond precisely to SED states, namely coherent states and squeezed states. The latter are relevant in case of radiation (squeezed states of light), but not so much for matter oscillators and they will not be studied here.
Coherent states in SED appear as solutions of the oscillator eq.$\left( \ref {ode}\right) $ obtained by combining the stationary solution of the equation with the general solution of the homogenous equation, that is \[ \stackrel{..}{x}+\omega _{0}^{2}x+\tau \omega _{0}^{2}\stackrel{.}{x} =0\Rightarrow x\simeq A\cos \left( \omega _{0}t+\phi \right) \exp \left( -\tau \omega _{0}t\right) , \] where I have approximated $\stackrel{...}{x}\simeq -\omega _{0}^{2}\stackrel{ .}{x}$ and neglected a small shift, of order $\tau ,$ in the frequency $ \omega _{0}.$ Hence, taking eq.$\left( \ref{Wx}\right) $ into account, we see that the solution of eq.$\left( \ref{ode}\right) $ leads to the following time dependent probability distribution of positions
\begin{equation} W\left( x,t\right) \simeq \sqrt{\frac{m\omega _{0}}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}}\exp \left[ -\frac{m\omega _{0}}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\left[ x-A\cos \left( \omega _{0}t+\phi \right) \exp \left( -\tau \omega _{0}^{2}t\right) \right] ^{2}\right] , \label{general} \end{equation} which contains two integration constants, $A$ and $\phi .$ It must be stressed that this expression for the probability density derives from eq.$ \left( \ref{ode}\right) $ and the ZPF spectrum eq.$\left( \ref{Espectrum} \right) $ with the approximation of putting $\tau \rightarrow 0$ except in the exponential decay. It may be seen that when $\tau =0$ the evolution of the position probability density eq.$\left( \ref{general}\right) $ fully agrees with the one of the coherent states of quantum mechanics, whilst the expression for finite $\tau $ contains the most relevant contribution of the radiative corrections of quantum electrodynamics to these states (a decay towards the stationary state with relaxation time $\left( \tau \omega _{0}^{2}\right) ^{-1}$)\cite{S74}.
\textit{In summary we see that a few states of the oscillator in SED correspond to pure quantum states in a phase-space representation. But no pure state of SED corresponds to a state of QM. Also most of the pure states of QM do not correspond to states of SED. However for mixed states the agreement is greater, and actually all (mixed) quantum states possessing a positive Wigner function closely correspond to mixed states of SED with the same phase-space distribution. }
\textit{In spite of these differences the quantum theory of the harmonic oscillator admits a realistic interpretation via SED, provided that the same predictions may be obtained for actual experiments. In particular the quantum states, solutions of Schr\"{o}dinger equation, might be just mathematical auxiliary functions used in the QM formalism but not required in the SED approach for the prediction of the same results. }
\subsection{The free particle}
For a free particle the differential equation of motion is like the oscillator's eq.$\left( \ref{ode}\right) $ with $\omega _{0}=0,$ that is \begin{equation} m\stackrel{..}{x}=m\tau \stackrel{...}{x}+eE\left( t\right) . \label{odefree} \end{equation} This fact may suggest studying the free particle as the limit of an oscillator whose characteristic frequency decreases to zero. However this method is not appropriate because there is a qualitative difference between the two systems. In fact the motion in the oscillator is always bound which is not the case for the free particle. Thus we shall study the motion of the free particle starting from eq.$\left( \ref{odefree}\right) .$ It is a third order equation and therefore has three independent solutions, but one of them is \textit{runaway }that is the energy increases without limit, which is physically nonsense. The reason is that the radiation reaction term, the former term on the right side of eq.$\left( \ref{odefree}\right) $, is a linearized approximation not valid for a free particle (in the oscillator the runaway solution is effectively cut-off by the potential and the approximation of eq.$\left( \ref{ode}\right) $ is good enough). Thus we shall substitute the following integro-differential equation for eq.$\left( \ref{odefree}\right) $ \[ \stackrel{..}{x}=-\frac{e}{m\tau }\exp \left( \frac{t}{\tau }\right) \int_{t}^{\infty }E\left( t^{\prime }\right) \exp \left( -\frac{t^{\prime }}{ \tau }\right) dt^{\prime }. \] It has the same solutions as eq.$\left( \ref{odefree}\right) $ except the runaway ones. Hence, it is trivial to get the following equations of evolution for the velocity and the coordinate, respectively, that is \begin{eqnarray} v(t) &=&v_{0}-\frac{e}{m\tau }\int_{0}^{t}\exp \left( \frac{s}{\tau }\right) ds\int_{s}^{\infty }E\left( u\right) \exp \left( -\frac{u}{\tau }\right) du, \label{dispv} \\ x(t) &=&x_{0}+v_{0}t-\frac{e}{m\tau }\int_{0}^{t}ds\int_{0}^{s}\exp \left( \frac{u}{\tau }\right) du\int_{u}^{\infty }E\left( w\right) \exp \left( - \frac{w}{\tau }\right) dw, \nonumber \end{eqnarray} where $x_{0}$ is the initial position and $v_{0}$ the initial velocity at time $t=0$. Hence, taking into account that the ensemble average of $E\left( t\right) $ is zero, it is trivial to get the mean position and velocity of a particle, that is \begin{equation} \left\langle x\left( t\right) \right\rangle =x_{0}+v_{0}t. \label{xvt} \end{equation}
The most interesting quantities are the dispersions of velocity and position with time. The velocity dispersion may be got from the first eq.$\left( \ref {dispv}\right) $ putting $v_{0}=0.$ We obtain, taking eq.$\left( \ref{gamma} \right) $ into account, \begin{eqnarray} \left\langle v\left( t\right) ^{2}\right\rangle &=&\frac{3c^{3}}{2m\tau } \int_{0}^{t}\exp \left( \frac{s}{\tau }\right) ds\int_{s}^{\infty }\exp \left( -\frac{u}{\tau }\right) du \label{vv} \\ &&\times \int_{0}^{t}\exp \left( \frac{s^{\prime }}{\tau }\right) ds^{\prime }\int_{s}^{\infty }\exp \left( -\frac{u^{\prime }}{\tau }\right) du^{\prime }\left\langle E\left( u\right) E\left( u^{\prime }\right) \right\rangle . \nonumber \end{eqnarray} The $E(t)$ selfcorrelation is the Fourier transform of the spectrum (see eq.$ \left( \ref{deltaxx}\right) ),$ that is \begin{eqnarray} \left\langle E\left( u\right) E\left( u^{\prime }\right) \right\rangle &=&\int_{0}^{\infty }S_{x}\left( \omega \right) \cos \left[ \omega \left( u-u^{\prime }\right) \right] d\omega \nonumber \\
&=&\frac{1}{2}\int_{-\infty }^{\infty }\left| S_{x}\left( \omega \right)
\right| \exp \left[ i\omega \left( u-u^{\prime }\right) \right] d\omega . \label{Ess} \end{eqnarray} I point out that this relation is correct because $E(t)$ is a stationary process, but it is not possible to get eq.$\left( \ref{vv}\right) $ from the spectrum of $v\left( t\right) $ because in the free particle case we cannot get the spectrum of $v(t)$ from that of $E(t)$ (as we made in the derivation of eq.$\left( \ref{oscilspectrum}\right) $ for the equilibrium state of oscillator, where both $x(t)$ and $v(t)$ are stationary processes). Inserting eq.$\left( \ref{Ess}\right) $ in eq.$\left( \ref{vv}\right) $ we get, after changing the order of the integrations, \begin{eqnarray*} \Delta v^{2} &\equiv &\left\langle v\left( t\right) ^{2}\right\rangle =\frac{
e^{2}}{2m^{2}\tau ^{2}}\int_{-\infty }^{\infty }\left| S_{x}\left( \omega
\right) \right| d\omega \left| \int_{0}^{t}\exp \left( \frac{s}{\tau } \right) ds\int_{s}^{\infty }\exp \left( -\frac{u}{\tau }+i\omega u\right)
du\right| ^{2} \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2\pi m\tau }\int_{-\infty }^{\infty }\frac{\left| \omega \right| d\omega }{
\omega ^{2}+\tau ^{-2}}\left| 1-\exp (i\omega t)\right| ^{2}=\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi m}\int_{0}^{\infty }\frac{\omega d\omega }{1+\tau ^{2}\omega ^{2}}
\left| 1-\cos (\omega t)\right| . \end{eqnarray*} Thus the velocity dispersion gives an ultraviolet divergent integral that may be made convergent by introducing a cut-off frequency $\omega _{c}$. Thus we get \begin{eqnarray} \Delta v^{2} &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi m}\int_{0}^{\omega _{c}}\frac{\omega d\omega }{1+\tau ^{2}\omega ^{2}}\left[ 1-\cos (\omega t)\right] \label{4.10} \\ &\sim &\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2\pi m\tau }\left[ \log (1+\omega _{c}^{2}\tau ^{2})+\frac{\tau ^{2}}{t^{2} }\right] ,\text{ for }t>>\tau . \nonumber \end{eqnarray} The dispersion $\Delta v$ becomes rapidly independent of $t$, but greater than the velocity of light. In order that $\Delta v<c$ we must have \[ \omega _{c}<\sqrt{\frac{3\pi }{\alpha }}\frac{mc^{2}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\approx 0.2\frac{c}{\lambda _{C}}<<\frac{1}{\tau }, \] $\lambda _{C}$ being the Compton wavelength. This implies that eq.$\left( \ref{4.10}\right) $ may be rewritten \begin{equation} \Delta v^{2}\sim \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega _{c}^{2}}{2\pi m}+\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2\pi m\tau t^{2}},\text{ for }t>>\tau . \label{4.10a} \end{equation} A correct calculation would require a relativistic theory, which will not be attempted here. Nevertheless the result obtained shows that the particle performs a random motion with relativistic speed although the mean velocity remains a constant (see eq.$\left( \ref{xvt}\right) ).$ Also the result suggests that in a relativistic calculation the most relevant wavelengths would be those not too far from the Compton one. The increase of the velocity of a free charged particle by the action of the ZPF has been proposed as possible origen of the observed ultrahigh-energy X rays coming to Earth from outside the Solar System\cite{Rueda}.
It is interesting to compare the velocity dispersion of the free particle in SED with the particle immersed in Rayleigh-Jeans (classical) radiation. Taking into account that the ZPF and the Rayleigh-Jeans radiation correspond to $\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega $ and $kT$ per normal mode, respectively, the replacement $\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega $ $\rightarrow $ $kT$ in eq.$\left( \ref{4.10}\right) $ leads to \begin{eqnarray*} \Delta v^{2} &=&\frac{\tau kT}{\pi m}\int_{0}^{\omega _{c}}\frac{d\omega }{ 1+\tau ^{2}\omega ^{2}}\left[ 1-\cos (\omega t)\right] \\ &\sim &\frac{kT}{m}\text{ for }t>>\tau . \end{eqnarray*} We see that the velocity dispersion of the charged free particle does not increase indefinitely but becomes, after a long enough time, a constant corresponding to the kinetic energy $kT/2$ (which is the equipartition of the energy of classical statistical mechanics.)
The dispersion of position oa the free particle according to SED may be obtained by a similar method, that is inserting the latter eq.$\left( \ref {Ess}\right) $ in eq.$\left( \ref{dispv}\right) .$ We obtain \begin{eqnarray} \Delta x^{2} &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{2\pi m}\int_{-\infty }^{\infty }\frac{\left| \omega \right| d\omega }{
1+\tau ^{2}\omega ^{2}}\left| \int_{0}^{t}\left[ 1-\exp (i\omega s)\right]
ds\right| ^{2} \nonumber \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi m}\int_{0}^{\infty }\frac{\omega d\omega }{1+\tau ^{2}\omega ^{2}} \left[ t^{2}-\frac{2t\sin \left( \omega t\right) }{\omega }+\frac{2-2\cos (\omega t)}{\omega ^{2}}\right] \nonumber \\ &\simeq &\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega _{c}^{2}}{2\pi m}t^{2}+\frac{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi m}\left[ \log \left( \frac{t}{\tau }\right) -C-1\right] ,\text{ } t>>\tau , \label{4.10b} \end{eqnarray} where C=0.577... is the Euler constant.
The former term, which dominates at long times, is a consequence of the velocity dispersion, as may be easily seen by a comparison with eq.$\left( \ref{4.10}\right) .$ The (canonical) momentum has no dispersion as shown by the former eq.$\left( \ref{canonmom}\right) $ when we put $\omega _{0}=0.$ This agrees with the quantum prediction that the momentum of a free particle is a constant. For a particle with zero canonical momentum, the typical distance from the original position increases with about one tenth the velocity of light so that a relativistic treatment would give a quite different picture.
\textit{The picture that emerges, and gives hints for the interpretation of the free particle in QM, is as follows. The free particle possesses a conserved canonical momentum with an associated inertial motion but, superimposed to this, it has a random motion with a velocity close to that of light. This produces an apparently contradictory behaviour that derives from the spectrum,} $S_{E}\left( \omega \right) \varpropto \omega ^{3},$ \textit{\ of the zeropoint field: At short times the motion is governed by the high frequencies where} $S_{E}\left( \omega \right) $ \textit{is large thus inducing a rapid erratic motion, at long times it is governed by the low frequencies where} $S_{E}\left( \omega \right) $ \textit{is small whence the memory of the initial velocity is lost very slowly. This fact contrast with what happens in Brownian motion and what our intuition may suggest, namely that memory of the initial conditions should be quickly lost. The special behaviour of diffusion in SED is a consequence of the fact that the spectrum }$S_{E}\left( \omega \right) $ \textit{is very different from the popular (Brownian) white noise}, $S_{white}\left( \omega \right) $\textit{\ } $\simeq constant.$
\subsection{Commutation rules}
Stochastic electrodynamics also provides a clue for the interpretation of commutation rules, that is the essential ingredient in the canonical formulation of quantum mechanics. In fact I will define the commutator at two times, $t,t^{\prime }$, of a stationary stochastic process, $x\left( t\right) ,$ via the \textit{sinus} Fourier transform of the spectrum. Then I shall show that this stochastic commutator applied to the SED oscillator closely resembles the quantum commutator in the Heisenberg picture of QM.
The introduction of the stochastic commutator is suggested by the Fourier transform of the spectrum, $S_{x}\left( \omega \right) .$ It consists of two terms, that is \begin{eqnarray} \int_{0}^{\infty }S_{x}\left( \omega \right) \exp \left[ i\omega \left( t^{\prime }-t\right) \right] d\omega &=&\left\langle x\left( t\right) x\left( t^{\prime }\right) \right\rangle +\frac{1}{2}\left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] , \nonumber \\ \left\langle x\left( t\right) x\left( t^{\prime }\right) \right\rangle &=&\int_{0}^{\infty }S_{x}\left( \omega \right) \cos \left[ \omega \left( t^{\prime }-t\right) \right] d\omega , \nonumber \\ \left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] &=&2i\int_{0}^{\infty }S_{x}\left( \omega \right) \sin \left[ \omega \left( t^{\prime }-t\right) \right] d\omega , \label{comm} \end{eqnarray} where the spectrum is defined to be zero for negative frequencies, that is $ S_{x}\left( \omega \right) =0$ if $\omega <0.$ The real part, $\left\langle x\left( t\right) x\left( t^{\prime }\right) \right\rangle ,$ is the selfcorrelation function of the stochastic process so that it is plausible that the imaginary part, $\left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] ,$\ is also relevant and we define it as the commutator. The factor 2 is chosen in order to be similar to the quantum commutator. I point out that the cosinus Fourier transform of the spectrum is the selfcorrelation only for stationary processes that are ergodic, as is proved by the Wiener-Khinchine theorem.
The relation between spectrum and stochastic commutator is also suggested by the fact that in QM there is a similar relation between the spectrum and the two-times commutator of the coordinate operator in the Heisenberg picture. That relation is fulfilled for the ground state of a particle in any potential well. For the proof here I consider a one-dimensional (quantum) problem defining the spectrum, $S_{x}\left( \omega \right) ,$ as follows \begin{equation}
S_{x}\left( \omega \right) \equiv \sum_{n}\left| \left\langle \psi _{0}\left| \hat{x}\left( 0\right) \right| \psi _{n}\right\rangle \right| ^{2}\delta \left( \omega -\omega _{0n}\right) , \label{sumrule} \end{equation} where $\hat{x}$ is the quantum position operator of the particle. The coefficients of the Dirac's deltas are proportional to the transition probabilities in QM from the ground state to all possible excited states. (Although I stress that in QED the deltas are approximations of highly peaked functions with a finite width when radiative corrections are takent into account). The analogy with the latter eq.$\left( \ref{comm}\right) $ is shown as follows. From the Heisenberg equation of motion \[ \hat{x}\left( t\right) =\exp (i\hat{H}t/
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
)\hat{x}\left( 0\right) \exp (-i\hat{H}t/
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
). \] we may obtain the expectation value of the commutator in the ground state,
\[ \left\langle \left[ \hat{x}\left( 0\right) ,\hat{x}\left( t\right) \right]
\right\rangle =\left\langle \psi _{0}\left| \hat{x}\left( 0\right) \hat{x}
\left( t\right) \right| \psi _{0}\right\rangle -\left\langle \psi _{0}\left|
\hat{x}\left( t\right) \hat{x}\left( 0\right) \right| \psi _{0}\right\rangle . \] After introducing the resolution of the identity between $\hat{x}\left( 0\right) $ and $\hat{x}\left( t\right) $ and between $\hat{x}\left( t\right) $ and $\hat{x}\left( 0\right) $ in terms of eigenvectors of the Hamiltonian $ \hat{H},$ this gives \[ \left\langle \left[ \hat{x}\left( 0\right) ,\hat{x}\left( t\right) \right]
\right\rangle =2i\sum_{n}\left| \left\langle \psi _{0}\left| \hat{x}\left(
0\right) \right| \psi _{n}\right\rangle \right| ^{2}\sin \left( \omega _{0n}t\right) =2i\int S_{x}\left( \omega \right) \sin \left( \omega t\right) d\omega , \] where in the latter equality we have taken eq.$\left( \ref{sumrule}\right) $ into account. This equality, similar to the stochastic latter eq.$\left( \ref {comm}\right) ,$ played an important role in the origin of quantum mechanics. In fact the derivative with respect to $t$ leads to \[
2im\sum_{n}\omega _{0n}\left| \left\langle \psi _{0}\left| \hat{x}\left(
0\right) \right| \psi _{n}\right\rangle \right| ^{2}\cos \left( \omega _{0n}t\right) =\left[ \hat{x}\left( 0\right) ,\hat{p}\left( t\right) \right] , \] that in the limit $t\rightarrow 0$ becomes an example of the well known Thomas-Reiche-Kuhn sum rule. The rule is usually applied to atoms where a sum over the three coordinates of the Z electrons is performed, so that it reads \[
2m\sum_{n}\omega _{0n}\left| \left\langle \psi _{0}\left| \sum_{j=1}^{Z}
\mathbf{r}_{j}\right| \psi _{n}\right\rangle \right| ^{2}=-i\sum_{k=1}^{3Z}\left[ \hat{x}_{k}\left( 0\right) ,\hat{p}_{k}\left( 0\right) \right] =3Z
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
. \]
For a stationary process both the selfcorrelation and the commutator depend only on the time difference $\left( t-t^{\prime }\right) .$ In this case the latter eq.$\left( \ref{comm}\right) $ may be easily inverted via a time integral. In fact we get \begin{eqnarray*} &&\int_{-\infty }^{\infty }\sin \left[ \nu \left( t-t^{\prime }\right) \right] \left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] dt \\ &=&\int_{-\infty }^{\infty }\sin \left[ \nu \left( t-t^{\prime }\right) \right] dt2i\int_{0}^{\infty }S_{x}\left( \omega \right) \sin \left[ \omega \left( t^{\prime }-t\right) \right] d\omega \\ &=&-2i\int_{0}^{\infty }S_{x}\left( \omega \right) d\omega \int_{-\infty }^{\infty }\sin \left[ \nu \left( t-t^{\prime }\right) \sin \left[ \omega \left( t-t^{\prime }\right) \right] \right] dt=-i\pi S_{x}\left( \nu \right) , \end{eqnarray*} where in the latter equality we take into account that $S_{x}\left( v\right) =0$ for $v<0.$
All stationary properties of the SED oscillator studied in Section 2 may be equally well obtained either from the spectrum eq.$\left( \ref{oscilspectrum} \right) ,$ from the selfcorrelation or from the commutator, the latter being \begin{eqnarray} \left[ x\left( 0\right) ,x\left( t\right) \right] &=&2i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\int_{0}^{\infty }\frac{\tau \omega ^{3}\sin \left[ \omega t\right] d\omega }{\pi m\left[ \left( \omega _{0}^{2}-\omega ^{2}\right) ^{2}+\tau ^{2}\omega ^{6}\right] } \nonumber \\ &=&i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\int_{-\infty }^{\infty }\frac{\tau \omega ^{3}\exp \left[ i\omega t\right] d\omega }{\pi m\left[ \left( \omega _{0}^{2}-\omega ^{2}\right) ^{2}+\tau ^{2}\omega ^{6}\right] }. \label{com1} \end{eqnarray} This equality shows the advantage of the commutator with respect to the selfcorrelation in the stochastic process associated to the SED oscillator. In fact the latter integral may be performed analytically via the method of residues, whilst getting the selfcorrelation requires approximations. \textit{Thus I propose that the reason for the use of commutators in QM is the fact that the basic stochastic processes involved have spectra that are odd with respect to the change }$\omega \rightarrow -\omega .$
Performing the integral eq.$\left( \ref{com1}\right) $ is now straightforward. For $t>0$ we shall take into account the three simple poles in the upper half plane of the complex variable $\omega $, that is \[ \omega =\pm \omega _{0}+\frac{1}{2}i\tau \omega _{0}^{2}+O\left( \tau ^{2}\omega _{0}^{3}\right) ,\omega =\pm i\left( \frac{1}{\tau }+\tau \omega _{0}^{2}\right) +O\left( \tau ^{2}\omega _{0}^{3}\right) . \]
For $t<0$ we shall use the poles in the lower half plane. The contribution of the poles in the imaginary axis should be neglected because it contains an exponential of the form $\exp \left( -\left| t\right| /\tau \right) $ that is zero except for extremely small values of time. (Actually the term derives from the high-frequency part of the spectrum and should be cut-off, as discussed in Section 1.4.) Thus the result may be written, to order $ O\left( \tau \omega _{0}^{2}\right) ,$ \begin{equation} \left[ x\left( 0\right) ,x\left( t\right) \right] =\frac{i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{m\omega _{0}}\left\{ \sin \left( \omega _{0}t\right) +\tau \omega _{0}
\frac{t}{\left| t\right| }\cos \left( \omega _{0}t\right) \right\} \exp
\left( -\frac{1}{2}\tau \omega _{0}^{2}\left| t\right| \right) , \label{xx} \end{equation} Similarly, taking eqs. $\left( \ref{comm}\right) $ and $\left( \ref{canonmom} \right) $ into account we may obtain the commutator of the canonical momentum, that is \begin{equation} \left[ p\left( 0\right) ,p\left( t\right) \right] =i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
m\omega _{0}\sin \left( \omega _{0}t\right) \exp \left( -\frac{1}{2}\tau
\omega _{0}^{2}\left| t\right| \right) . \label{pp} \end{equation} In the limit $\tau \rightarrow 0$ the commutator eq.$\left( \ref{xx}\right) $ agrees with the one derived from elementary quantum mechanics for the corresponding (time dependent) operators in the Heisenberg picture.
The commutator of the particle coordinate in the SED oscillator may be derived from the commutator of the electric field of the zeropoint radiation taking eqs.$\left( \ref{Espectrum}\right) $ and $\left( \ref{comm}\right) $ into account. Actually the relation between the commutator of the vacuum field and the commutator of a charged particle immersed in the field may be obtained in the context of quantum mechanics without passing through the spectrum. Indeed this was made long ago by Schiller for quantum commutators \cite{dice},\cite{Milonni}.
Our definition of commutator may be generalized to two different stationary stochastic processes as follows:
\begin{definition} Given two stationary stochastic process, $x(t)$\ and $y(t),$\ I define the (stochastic) commutator of these processes, $\left[ x\left( t\right) ,y\left( t^{\prime }\right) \right] ,$\ as $2i$\ times the Hilbert transform of the crosscorrelation, $\left\langle x\left( t\right) y\left( t^{\prime }\right) \right\rangle .$ \end{definition}
The Hilbert transform, $g(u),$ of a function $f(t),t\in \left( -\infty ,\infty \right) $ is defined by \[ g(u)=\frac{1}{\pi }P\int_{-\infty }^{\infty }f(t)\frac{1}{u-t}dt,f\left( t\right) =\frac{1}{\pi }P\int_{-\infty }^{\infty }g\left( u\right) \frac{1}{ u-t}du, \] where $P$\ means principal part and the second equality corresponds to the inverse transform. However the inverse transform does not always recovers the original. For instance the Hilbert transform of a constant is zero and the inverse of zero is also zero. The relevant property for us is that the Hilbert transforms changes sin$\left( \omega t\right) $ into cos$\left( \omega u\right) $ and cos$\left( \omega t\right) $ into -sin$\left( \omega u\right) ,$ provided that $\omega \neq 0$.
After that it is possible to define the derivative of a commutator with respect to time, that is \begin{eqnarray*} \frac{d}{dt}\left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] &=&\lim_{t^{\prime \prime }\rightarrow t^{\prime }}\frac{\left[ x\left( t\right) ,x\left( t^{\prime \prime }\right) \right] -\left[ x\left( t\right) ,x\left( t^{\prime }\right) \right] }{t^{\prime \prime }-t^{\prime }} \\ &=&\lim_{t^{\prime \prime }\rightarrow t^{\prime }}\frac{\left[ x\left( t\right) ,x\left( t^{\prime \prime }\right) -x\left( t^{\prime }\right) \right] }{t^{\prime \prime }-t^{\prime }}=\left[ x\left( t\right) ,\frac{ dx\left( t^{\prime }\right) }{dt^{\prime }}\right] , \end{eqnarray*} where the linearity of the commutator has been used. Hence taking eq.$\left( \ref{xx}\right) $ into account we get to zeroth order in $\tau $ \[ \left[ x\left( 0\right) ,p\left( t\right) \right] =i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\cos \left( \omega _{0}t\right) \Rightarrow \left[ x\left( 0\right) ,p\left( 0\right) \right] =i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
, \] the latter being the fundamental commutation rule of quantum mechanics.
\textit{The stochastic commutator provides a hint for a realistic interpretation of the quantum commutation rules as a disguised form of stablishing the properties of some peculiar stochastic processes. The main peculiarity is the fact that the spectra of the processes are usually odd with respect to a change }$\omega \rightarrow -\omega $ \textit{of the frequency}.
\section{Coupled oscillators in SED}
The generalization of the harmonic oscillator in SED to many dimensions is straightforward using the appropriate extension of eq.$\left( \ref{ode} \right) .$ In the following I will study two simple examples of coupled oscillators. Firstly a system of two one-dimensional oscillators at a long distance as an example of van der Waals force. The system is interesting because it shows that a phenomenon similar to quantum entanglement appears also in SED. The second example is an array of coupled three-dimensional oscillators at a finite temperature, that reproduces Debye theory of the specific heat of solids.
\subsection{A model for quantum entanglement}
Entanglement is a quantum property of systems with several degrees of freedom, which appears when the total state vector cannot be written as a product of vectors associated to one degree of freedom each. In formal terms a typical entangled state fulfils \begin{equation} \mid \psi \left( 1,2\right) \rangle =\sum_{m,n}c_{mn}\mid \psi _{m}\left( 1\right) \rangle \mid \psi _{n}\left( 2\right) \rangle , \label{entangled} \end{equation} where $1$ and $2$ correspond to two different degrees of freedom, usually belonging to different subsystems. The essential condition is that the state eq.$\left( \ref{entangled}\right) $ cannot be written as a product, that is the sum cannot be reduced to just one term via a change of basis in the Hilbert space. Entanglement appears as a specifically quantum form of correlation, which is claimed to be dramatically different from the correlations of classical physics. The latter may be usually written in the form \begin{equation} \rho \left( 1,2\right) =\sum_{m,n}w_{mn}\rho _{m}\left( 1\right) \rho _{n}\left( 2\right) , \label{ro12} \end{equation} where the quantities $\rho \gtrsim 0$ are probability densities and the coefficients play the role of weights fulfilling $w_{mn}\gtrsim 0$, in sharp contrast with eq.$\left( \ref{entangled}\right) $ where $\mid \psi \rangle $ are vectors in a Hilbert space and $c_{mn}$ are complex numbers.
In the last decades entanglement has been the subject of intense study, and a resource for many applications, specially in the domain of quantum information. In this case the relevant entanglement usually involves spin or polarization. Entanglement is quite common in nonrelativistic quantum mechanics of many-particle systems, e.g. for electrons in atoms or molecules. However it is most relevant when the state-vectors $\mid \psi _{m}\left( 1\right) \rangle $ and $\mid \psi _{n}\left( 2\right) \rangle $ of eq.$\left( \ref{entangled}\right) $ belong to different systems placed far from each other. A study of entanglement and its relation with ``local realism'' will be made in Chapter 4 and examples of photon entanglement will be provided in Chapter 6. Here I will illustrate, with a simple example, that entanglement might be understood as a correlation induced by quantum vacuum fluctuations acting in two different places.
\subsection{London-van der Waals forces}
I shall study the London theory of the van der Waals forces in a simple model of two one-dimensional oscillating electric dipoles. Each dipole consists of a particle at rest and another particle (which we will name electron) with mass $m$ and charge $e$. In the model it is assumed that every electron moves in a harmonic oscillator potential and there is an additional interaction between the electrons. Thus the Hamiltonian is \begin{equation} H=\frac{p_{1}^{2}}{2m}+\frac{1}{2}m\omega _{0}^{2}x_{1}^{2}+\frac{p_{2}^{2}}{ 2m}+\frac{1}{2}m\omega _{0}^{2}x_{2}^{2}-Kx_{1}x_{2}, \label{dip} \end{equation} where $x_{1}(x_{2})$ is the position of the electron of the first (second) dipole with respect to the equilibrium position. The positive parameter $ K<m\omega _{0}^{2}$ depends on the distance bewteen the dipoles, but the dependence is irrelevant for our purposes. (For a more complete study of this problem within SED see Refs.\cite{dice}, \cite{dice2}). We shall work both the QM and the SED calculations.
\subsection{Quantum theory of the model}
An exact quantum calculation is not difficult. We take $x_{j},p_{j}$ and $H$ as operators in the Hilbert space of the full system, fulfilling the standard commutation relations \begin{equation} \left[ \hat{x}_{j},\hat{x}_{l}\right] =\left[ \hat{p}_{j},\hat{p}_{l}\right] =0,\left[ \hat{x}_{j},\hat{p}_{l}\right] =i
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\delta _{jl}. \label{7.10} \end{equation} Now we introduce the new operators \begin{eqnarray} \hat{x}_{+}\left( t\right) &=&\frac{1}{\sqrt{2}}\left[ \hat{x}_{1}\left( t\right) +\hat{x}_{2}\left( t\right) \right] ,\hat{x}_{-}\left( t\right) = \frac{1}{\sqrt{2}}\left[ \hat{x}_{1}\left( t\right) -\hat{x}_{2}\left( t\right) \right] , \nonumber \\ p_{+}\left( t\right) &=&\frac{1}{\sqrt{2}}\left[ \hat{p}_{1}\left( t\right) + \hat{p}_{2}\left( t\right) \right] ,\hat{p}_{-}\left( t\right) =\frac{1}{ \sqrt{2}}\left[ \hat{p}_{1}\left( t\right) -\hat{p}_{2}\left( t\right) \right] . \label{7.11} \end{eqnarray} It is easy to derive the commutation relations of the new operators, that are similar to eqs.$\left( \ref{7.10}\right) $ with the subindices $+,-$ susbstituted for $1,2$. The Hamiltonian eq.$\left( \ref{dip}\right) $ in terms of the new operatos is \[ \hat{H}=\frac{\hat{p}_{+}^{2}}{2m}+\frac{1}{2}\left( m\omega _{0}^{2}+K\right) \hat{x}_{+}^{2}+\frac{\hat{p}_{-}^{2}}{2m}+\frac{1}{2} \left( m\omega _{0}^{2}-K\right) \hat{x}_{-}^{2}. \] This is equivalent to two uncoupled harmonic oscillators with the same mass, $m$, and frequencies \[ \omega _{+}=\sqrt{\omega _{0}^{2}+K/m},\omega _{-}=\sqrt{\omega _{0}^{2}-K/m} ,\left( K<m\omega _{0}^{2}\right) \] respectively$.$ Thus the wavefunction of the two-electron system is \begin{eqnarray} \psi &=&\psi \left( x_{+}\right) \psi \left( x_{-}\right) =\sqrt{\frac{m}{ \pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\sqrt{\omega _{+}\omega _{-}}}}\exp \left[ -\frac{m}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\left( \omega _{+}x_{+}^{2}+\omega _{-}x_{-}^{2}\right) \right] \label{7.12} \\ &=&\sqrt{\frac{m}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\sqrt{\omega _{+}\omega _{-}}}}\exp \left\{ -\frac{m}{4
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\left[ (\omega _{+}+\omega _{-})\left( x_{1}^{2}+x_{2}^{2}\right) +2(\omega _{+}-\omega _{-})\left( x_{1}x_{2}\right) \right] \right\} , \nonumber \end{eqnarray} and the interaction energy of the system is \[ \Delta E=\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2}\left( \sqrt{\omega _{0}^{2}-K/m}+\sqrt{\omega _{0}^{2}-K/m}-2\omega _{0}\right) =-\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
K^{2}}{4m^{2}\omega _{0}^{3}}+O\left( K^{4}\right) , \] that to lowest nontrivial order in the coupling constant $K$ gives \begin{equation} \psi =\sqrt{\frac{m\omega _{0}}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}}\left( 1+\frac{2Kx_{1}x_{2}}{m\omega _{0}}\right) \exp \left[ -\frac{ m\omega _{0}}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\left( x_{1}^{2}+x_{2}^{2}\right) \right] , \label{7.12a} \end{equation} which may be written in terms of the wavefunctions of the ground state, $ \psi _{0}\left( x\right) ,$ and the first excited state, $\psi _{1}\left( x\right) ,$ of the simple oscillator as follows \[ \psi =\psi _{0}\left( x_{1}\right) \psi _{0}\left( x_{2}\right) +\frac{K}{ m\omega _{0}^{2}}\psi _{1}\left( x_{1}\right) \psi _{1}\left( x_{2}\right) . \] (The function is not normalized because the normalization was lost when we truncated at first order the expansion in powers of $K$). In quantum language this wavefunction $\psi $ may be interpreted saying that the two-system state is a sum of two amplitudes, one of them corresponds to both oscillators being in the ground state and the other one to both being in the first excited state. It is true that eq.$\left( \ref{7.12}\right) $ is not an irreducible sum of products like eq.$\left( \ref{entangled}\right) .$ However, in cannot be factorized in terms of wavefunctions of individual electrons and therefore it is not a classical correlation that might be represented as eq.$\left( \ref{ro12}\right) $. Therefore it may by considered an entangled state involving two distant systems.
Although quantum mechanics usually does not offer intuitive pictures of the phenomena, in this case it is difficult to refrain from interpreting the entanglement in this example as a correlation of the (random) motions of the electrons. Indeed the modulus squared of the wavefunction eq.$\left( \ref {7.12}\right) $ gives the probability density for the positions of the electrons, which is larger when the electrons are far from each other so that their mutual repulsion energy is smaller. Then the correlation (entanglement) lowers the energy giving rise to an attractive force between the oscillators. Of course this explanation departs from the Copenhagen interpretation (see Chapter 3), that should not speak about the probability that \emph{one electron is} in the region $x_{1}>0$ and the \emph{other one} \emph{is} in the region $x_{2}>0$. Instead it compels us to say something like ``if we perform a measurement of the simultaneous positions of the electrons \emph{the probability that we get} one of them in the region $ x_{1}>0$ and the other one is in the region $x_{2}>0$ is given by the modulus squared of eq.$\left( \ref{7.12}\right) "$. (Simultaneous measurements are possible because the observables commute.) In any case the origin of the correlation is not clear in quantum mechanics.
\subsection{The model in stochastic electrodynamics}
In sharp contrast with QM the interpretation offered by SED is transparent: the random motion of the electrons is induced by the ZPF, and the correlation is produced by the interaction. The SED calculation is as follows. The differential equations of motion may be obtained from eq.$ \left( \ref{dip}\right) $. I shall write them including the forces due to the random ZPF and the radiation reaction, see eq.$\left( \ref{ode}\right) ,$ that is \begin{eqnarray} m\stackrel{..}{x_{1}} &=&-m\omega _{0}^{2}x_{1}-Kx_{2}+\frac{2e^{2}}{3c^{3}} \stackrel{...}{x_{1}}+eE_{1}\left( t\right) , \nonumber \\ m\stackrel{..}{x}_{2} &=&-m\omega _{0}^{2}x_{2}-Kx_{1}+\frac{2e^{2}}{3c^{3}} \stackrel{...}{x_{2}}+eE_{2}\left( t\right) . \label{ode2} \end{eqnarray} The approximation of neglecting the $x$ dependence of the field, $E(\mathbf{ x,}t)$, is not good if the dipoles are at a long distance (on the other hand the Hamiltonian eq.$\left( \ref{dip}\right) $ is not valid for short distances). However we may neglect the $x$ dependence within each dipole, that is we will approximate $E\left( \mathbf{x}_{1,}t\right) \simeq $ $ E\left( \mathbf{a},t\right) ,E\left( \mathbf{x}_{2},t\right) \simeq $ $ E\left( \mathbf{b,}t\right) ,$ where $\mathbf{a}$ and $\mathbf{b}$ are the positions of the first and second dipole, respectively. Also we will simplify the notation writing $E_{1}\left( t\right) $ for $E\left( \mathbf{a, }t\right) $ and $E_{2}\left( t\right) $ for $E\left( \mathbf{a,}t\right) .$ Furthermore, as we assume that the distance between dipoles is large, we shall take the stochastic processes $E_{1}\left( t\right) $ and $E_{2}\left( t\right) $ as uncorrelated.
The coupled eqs.$\left( \ref{ode2}\right) $ may be decoupled via writing new equations which are the sum and the difference of the former, and introducing the new position variables \begin{equation} x_{+}\left( t\right) =\frac{1}{\sqrt{2}}\left[ x_{1}\left( t\right) +x_{2}\left( t\right) \right] ,x_{-}\left( t\right) =\frac{1}{\sqrt{2}} \left[ x_{1}\left( t\right) -x_{2}\left( t\right) \right] , \label{ode5} \end{equation} and similarly definitions for $E_{+}\left( t\right) $ and $E_{-}\left( t\right) .$ We get \begin{eqnarray} m\stackrel{..}{x_{+}} &=&-(m\omega _{0}^{2}-K)x_{+}+\frac{2e^{2}}{3c^{3}} \stackrel{...}{x_{+}}+eE_{+}\left( t\right) , \nonumber \\ m\stackrel{..}{x}_{-} &=&-(m\omega _{0}^{2}+K)x_{-}+\frac{2e^{2}}{3c^{3}} \stackrel{...}{x_{-}}+eE_{-}\left( t\right) , \label{ode3} \end{eqnarray} where the stochastic processes $E_{+}\left( t\right) $ and $E_{-}\left( t\right) $ are statistically independent as a consequence of $E_{1}\left( t\right) $ and $E_{2}\left( t\right) $ being uncorrelated. With the method used to solve eqs.$\left( \ref{2.3}\right) $ and $\left( \ref{2.4}\right) $ we get \begin{equation} \left\langle x_{\pm }^{2}\right\rangle =\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{2m\sqrt{\omega _{0}^{2}\mp K/m}},\left\langle v_{\pm }^{2}\right\rangle = \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\sqrt{\omega _{0}^{2}\mp K/m}}{2m}. \label{xv} \end{equation} The Hamiltonian eq.$\left( \ref{dip}\right) $ may be written in terms of $ x_{+}\left( t\right) $, $x_{-}\left( t\right) $ leading to \[ H=\frac{p_{+}^{2}}{2m}+\frac{1}{2}m\omega _{0}^{2}x_{+}^{2}+\frac{p_{-}^{2}}{ 2m}+\frac{1}{2}m\omega _{0}^{2}x_{-}^{2}-\frac{1}{2}K\left( x_{+}^{2}-x_{-}^{2}\right) . \] Hence, defining $p_{\pm }=mv_{\pm },$ it is easy to get the total energy, $ \left\langle H\right\rangle ,$ taking eqs.$\left( \ref{xv}\right) $ into account. The result is in agreement with the quantum eq.$\left( \ref{7.13} \right) .$ The joint probability distribution of positions is Gaussian and factorizes because eqs.$\left( \ref{ode3}\right) $ are decoupled. That is \[ \rho \left( x_{+},x_{-}\right) dx_{+}dx_{-}=\rho _{+}\left( x_{+}\right) \rho _{-}\left( x_{-}\right) dx_{+}dx_{-}. \] The densities $\rho _{\pm }$ should be normalized whence we get \[ \rho _{\pm }\left( x\right) =\sqrt{\frac{2m}{\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}}\left( \omega _{0}^{2}\mp K/m\right) ^{-1/4}\exp \left[ -\frac{m}{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\sqrt{\omega _{0}^{2}\mp K/m}x_{\pm }^{2}\right] . \] Hence it is easy to get the joint probability in terms of the variables $ x_{1}$ and $x_{2}$ taking eqs.$\left( \ref{ode5}\right) $ into account. The result is in agreement with the quantum prediction, eq.$\left( \ref{7.12} \right) .$
In the equation of motion$\left( \ref{ode2}\right) $ I have assumed that the ZPF components, $E_{1}\left( t\right) $ and $E_{2}\left( t\right) $, acting upon the two particles are uncorrelated. This is a good approximation if the particles are at a distance which is large in comparison with wave lenght, $ \lambda \simeq c/\omega _{0}$, corresponding to the typical frequencies involved. However if the distance is of that order or smaller, the ZPF components will be correlated, which would cause a much stronger correlation between the particle$\acute{}$s motions. We might speculate that correlations induced by the ZPF are related to quantum statistics, that is behaviour of particles as either bosons or fermions. But this possibility will not be further discussed in this book.
\textit{The conclusion of our study of the two coupled oscillators in SED is the suggestion that quantum entanglement is a correlation between the quantum fluctuations of different systems, mediated by the vacuum fields, these fields not being apparent in the quantum formalism.}
\subsection{Specific heats of solids}
An application of SED at a finite temperature is the calculation of the specific heat of solids, which we summarize in the following\cite{Blanco2}. We shall consider a solid as a set of positive ions immersed in an electron gas. As is well known the electrons contribute but slightly to the specific heat at not too high temperatures. In SED we shall study the motion of the ions under the action of three forces. The first one derives from the interaction with the neighbour ions and the electron gas, that may be modelled by an oscillator potential which increases when the distance between neighbour ions departs from the equilibrium configuration. The second is the random background radiation with Planck spectrum (including the ZPF) and the third one is the radiation reaction. This gives rise to a discrete set of coupled third order differential equations that may be decoupled by the introduction of normal mode coordinates. After that, every equation is similar to eq.$\left( \ref{ode}\right) $ and may be solved in anologous form. The net result is that the mean (potential plus kinetic) energy in equilibrium becomes \begin{equation} E(\omega )=\frac{1}{2}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega \coth \left( \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega }{2kT}\right) , \label{solids} \end{equation} where $\omega $ is the frequency of the mode. With an appropriate distribution, $\rho \left( \omega \right) ,$ of modes this leads to the quantum result derived by Debye\cite{Debye12}, the specific heat being the derivative of the total energy with respect to the temperature.
There are other interesting results of SED at a finite temperature, in particular about magnetic properties. They may be seen in the books of de la Pe\~{n}a et al.\cite{dice}, \cite{dice2} and references therein.
\textit{The SED calculation of the specific heat of solids provides another argument for the continuity (as opposed to discreteness) of the energies of quantum oscillators. If it is hard to accept that electromagnetic radiation consists of particles (photons) in a realistic interpretation of quantum physics, it is still harder to assume that quantized oscillations of the ions in a solid ( phonons) are particles. It is more plausible to assume that the energies of the normal modes of the set of ions have a continuous, although random, distribution of energies such that the average for a mode is given by eq.}$\left( \ref{solids}\right) .$\textit{\ Also it is plausible that the mean energy of a vibration mode of every ion is the same as the mean energy of the radiation mode having the same frequency, that is the result here obtained.}
\section{The particle in a homogeneous magnetic field}
Another linear problem that has been extensively studied within SED is the motion of a charged particle in a homogeneous magnetic field\cite{dice}. The most relevant result is the prediction of diamagnetic properties of a free charge (without magnetic moment), which departs from classical physics and agrees with QM. Here I shall revisit the SED calculation of the free charged particle in a homogeneous field of magnitude $B$.
\subsection{Classical theory}
The classical motion may be got from Newton\'{}s law\textbf{\ }with the Lorentz force, that is \begin{equation} m\stackrel{..}{\mathbf{r}}=\mathbf{-}\left( e/c\right) \stackrel{\cdot }{ \mathbf{r}}\times \mathbf{B}. \label{Lorentzforce} \end{equation} \textbf{\ }If we choose the Z axis in the direction of the $\mathbf{B}$ the motion in that direction is uniform and in the perpendicular plane it is given by \begin{eqnarray} x &=&R\cos \left[ 2\omega _{0}\left( t-t_{0}\right) \right] +x_{0}, \nonumber \\ y &=&R\sin \left[ 2\omega _{0}\left( t-t_{0}\right) \right] +y_{0},
\omega _{0}\equiv \frac{eB}{2mc}, \label{classmag} \end{eqnarray} with four integration constants, namely $\{R,t_{0},x_{0},x_{0}\}.$ The motion is circular with radius $R$ and constant (Larmor) angular frequency $ \omega _{0}.$ The total energy $E$ may be identified with the Hamiltonian, that is \begin{equation} H=\frac{p_{x}^{2}}{2m}+\frac{p_{y}^{2}}{2m}-\omega _{0}\left( xp_{y}-yp_{x}\right) +\frac{1}{2}m\omega _{0}^{2}\left( x^{2}+y^{2}\right) . \label{Hmag} \end{equation} Taking Hamilton equations into account we get \begin{equation} E=\frac{1}{2}m\left( \stackrel{\cdot }{x}^{2}+\stackrel{\cdot }{y} ^{2}\right) =2mR^{2}\omega _{0}^{2}. \label{magenergy} \end{equation}
Actually in a classical electrodynamical calculation we should include the radiation reaction (similar to the second term of the right side in the oscillator eq.$\left( \ref{ode}\right) ).$ This term would give rise to a loss of energy by radiation whence the system will eventually arrive at the state of minimal energy, that is zero (when $R=0$). This shows that no diamagnetic effects can be expected to occur in classical physics.
\subsection{Quantum theory}
The QM treatment starts from a quantum Hamiltonian operator which may be got from eq.$\left( \ref{Hmag}\right) $ by promoting the classical coordinates and momenta to operators in a Hilbert space (for a detailed study see\cite {Dicke}). The Z component of the angular momentum operator and the Hamiltonian commute and we may search for simultaneous eigenvectors having eigenvalues \begin{eqnarray} L_{z} &\equiv &xp_{y}-yp_{x}\rightarrow m_{l}
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
,m_{l}=0,\pm 1,\pm 2,..., \nonumber \\ H &\rightarrow &E_{r}=\left( 2r+1\right)
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\left| \omega _{0}\right| ,r=0,1,2,... \label{Qmag} \end{eqnarray} We see that the quantum ground state, given by $r=0$ and $E_{r}=
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\left| \omega _{0}\right| $, has an infinite degeneracy because this energy is shared by states with all possible values of $m_{l}.$ For this reason it is common to add to the Hamiltonian a two-dimensional oscillator potential with characteristic frequency $\omega _{1}(>0.)$ Then the energy eigenvalues have an additional term $\left( 2n+1\right)
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\omega _{1}$ with $n=2r-m_{l}\geq 0,$which breaks the degeneracy, the ground state now corresponding to $r=n=m_{l}=0.$ From eq.$\left( \ref{Qmag}\right) $ we may get the most relevant parameter, that is the magnetic moment. In the ground state it is \begin{equation} \mathbf{M}=-\nabla _{\mathbf{B}}E=-
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\nabla _{\mathbf{B}}\left| \omega _{0}\right| =-M_{B}\frac{\mathbf{B}}{B} ,M_{B}=\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\left| e\right| }{2mc} \label{magmom} \end{equation} where $M_{B}$ is the Bohr magneton. This (or the ground state energy, second eq.$\left( \ref{Qmag}\right) )$ is the result that we may expect to reproduce in SED.
\subsection{SED treatment}
In SED we should add the action of the ZPF (plus the radiation reaction) to the force derived from the homogeneous magnetic field, see eq.$\left( \ref {Lorentzforce}\right) $. We will study only the motion in the $XY$ plane. If $u\equiv $ $\stackrel{\cdot }{x}$ and $v$ $\equiv $ $\stackrel{\cdot }{y}$ are the components of the velocity vector the equations of motion are \begin{equation} m\stackrel{\cdot }{u}=\frac{e}{c}vB+m\tau \ddot{u}+eE_{u},\text{ }m\stackrel{ \cdot }{v}=-\frac{e}{c}uB+m\tau \stackrel{\cdot \cdot }{v}+eE_{v}, \label{magn} \end{equation} where the first term is the component of the Lorentz force, the second is the radiation reaction and the third one the action of the ZPF (in the long wavelength approximation, see eq.$\left( \ref{ode}\right) ).$ The components of the electric ZPF, $E_{u}\left( t\right) $ and $E_{v}\left( t\right) ,$ are assumed statistically independent stochastic processes.
The small value of $\tau <<1/\omega _{0}$ allows an approximation similar to the one made in the free particle case, Section 3.4. We may substitute $ evB/(cm\tau )$ for $\ddot{u}$ and similar for $\stackrel{\cdot \cdot }{v},$ thus obtaining two first order equations from eqs.$\left( \ref{magn}\right) . $ Then the solution is straightforward and we get, with steps similar to those involved in the solution of eq.$\left( \ref{ode}\right) $ lead to \begin{equation} \left\langle u^{2}\right\rangle =\int_{0}^{\infty }\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega ^{3}\left( 4\omega _{0}^{2}+\omega ^{2}\right) }{\pi m\left[ \left( 4\omega _{0}^{2}-\omega ^{2}\right) ^{2}+4\tau ^{2}\omega ^{6}\right] }d\omega \simeq \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\left| \omega _{0}\right| }{m}, \label{mag2} \end{equation} and the same result for $\left\langle v^{2}\right\rangle .$ Actually the integral in eq.$\left( \ref{mag2}\right) $ is ultraviolet divergent so that a a high frequency cutoff, $\omega _{c}$, should be included. It may be seen that for small $\tau $, i. e. $\tau \omega _{0}<<1,$ the main contributions to the integral eq.$\left( \ref{mag2}\right) $ come either from frequencies $ \omega $ close to $2\omega _{0}$ or for high frequencies $\omega >>2\omega _{0}$ (a similar case happens in the oscillator, see eqs.$\left( \ref{2.3} \right) $ and $\left( \ref{2.4}\right) $). The former contribution, given by eq.$\left( \ref{mag2}\right) ,$ is independent of both the cut-off frequency and the precise value of $\tau .$ The latter, high frequencies, contribution may be obtained neglecting $\omega _{0}$ in comparison with $\omega ,$ and putting $4\omega _{0}$ as lower limit of the integral in order to exclude the frequency region around $2\omega _{0}$ calculated in eq.$\left( \ref {mag2}\right) .$ Thus we get \begin{eqnarray*} \left\langle u^{2}\right\rangle _{hf} &\simeq &\int_{4\omega _{0}}^{\omega _{c}}\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau \omega ^{5}d\omega }{\pi m\left( \omega ^{4}+4\tau ^{2}\omega ^{6}\right) } \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{8\pi m\tau }\log \left( 1+4\tau ^{2}\omega _{c}^{2}\right) \simeq \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{2\pi m}\omega _{c}^{2}, \end{eqnarray*} where we have assumed $2\tau \omega _{c}<<1$. A comparison with eq.$\left( \ref{4.10a}\right) $ shows that this contribution is the same for a free particle. Indeed it is independent of the magnetic field (which does appear in eq.$\left( \ref{mag2}\right) .$
The mean energy in SED is obtained inserting eq.$\left( \ref{mag2}\right) $ in the expression of the energy (see eq.$\left( \ref{magenergy}\right) )$ giving \begin{equation} \left\langle E\right\rangle =\frac{1}{2}m\left\langle u^{2}+v^{2}\right\rangle =
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\left| \omega _{0}\right| , \label{7.0} \end{equation} in agreement with the quantum result. Hence there is also agreement for the magnetic moment, eq.$\left( \ref{magmom}\right) $\textrm{.}
Another interesting result from SED is the mean value of the angular momentum that is \begin{equation} \left\langle L_{z}\right\rangle =\left\langle xp_{y}-yp_{x}\right\rangle
=m\left\langle xv-yu\right\rangle =-\frac{e}{\left| e\right| }
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
, \label{7.1a} \end{equation} independently of the magnitude of the magnetic field and the mass of the particle. I omit the proof that is straightforward. Thus the angular momentum is parallel to the magnetic field if the charge is negative and antiparallel if it is positive. We saw that the magnetic moment is always antiparallel to the magnetic field. The results eqs.$\left( \ref{7.0}\right) $ and $\left( \ref{7.1a}\right) $ correspond to the limit $\tau \rightarrow 0.$ In both cases there are corrections for finite $\tau $ which would requiere a relativistic treatment. If an appropriate cutoff is introduced, say $\omega _{c}=mc^{2}/
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
,$ the high frequencies contribution is small.
There is however a disagreement between QM and SED for the angular momentum in the stationary state. SED predicts a finite value given by eq.$\left( \ref {7.1a}\right) $ but in QM there are many possible angular momenta in the ground state as shown in eq.$\left( \ref{Qmag}\right) .$ On the other hand if we include an additional oscillator potential with characteristic frequency $\omega _{1}$, then the quantum prediction for the ground state angular momentum is zero that also disagrees with the SED result. Thus in QM there are two features whose realistic interpretation is difficult. Firstly eq.$\left( \ref{magmom}\right) $ that strongly suggests that the angular momentum in the ground state is the same of the SED prediction, eq.$\left( \ref{7.1a}\right) $ rather than the degeneracy eq.$\left( \ref{Qmag}\right) . $ Secondly that an additional oscillator potential no matter how small breaks the degeneracy, but leading to zero angular momentum, rather than the most intuitive value eq.$\left( \ref{7.1a}\right) .$ These facts show that a realistic interpretation of the angular momentum in quantum mechanics is difficult. A possible solution is proposed in Section 6.4.
\textit{In summary the SED treatment of the particle in a homogeneous magnetic field reproduces the most relevant results of QM and provides a realistic interpretation for the QM prediction of a diamagnetic behaviour of the charged particle in the presence of an homogeneous magnetic field. However there is disagreement for the angular momentum.}
\section{SED application to nonlinear systems}
Several nonlinear systems have been studied in stochastic electrodynamics that provide some results in semiquantitative agreement with quantum mechanics, but badly fail in other cases. Actually SED reproduces quantum results, and agrees with experiments, in a limited domain, namely for systems of charged particles that may be treated linearly and within a nonrelativistic approximation. In sharp contrast the treatment of nonlinear systems gives results that frequently disagree with quantum predictions. The explanation of this fact is that SED, as defined in the introduction section, is an approximation to QED to lowest order in Planck constant $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
,$ but quantum mechanics gives predictions for nonlinear systems that involve $
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
$ to higher order. Therefore to be valid for all physical systems, SED should be generalized, likely including all vacuum fields and taking into account the back action of the particles on the fields. I propose that this would lead to quantum theory, but the steps needed are not known. There is here a paradox, namely we might foresee that the final theory should be rather cumbersome due to the large number of fields involved and the nonlinearity of equations, but it is the case that quantum theory has a relatively simple formalism. This is the magic of quantum theory and one of the reasons for the difficulty of getting a realistic interpretation of it.
In the following I comment on some calculations for nonliner systems . The best method for the SED study in these cases is to get the evolution of the classical mechanical `constants of the motion', one of them being the total energy. These parameters are no longer constant due to the interaction with the ZPF and the radiation reaction, but may be slowly varying. The method was used in Section 3 for the oscillator and it will be illustrated in the following for a nonlinear system, the rigid planar rotor. After that I will comment on the hydrogen atom in SED and the problem of equilibrium between radiation and matter.
\subsection{The planar rigid rotator}
The planar rigid rotor is the most simple nonlinear system studied in SED \cite{Boyerrotor}. A model of the rotor is a particle of mass $m$ and charge $e$ constrained to move in the $XY$ plane always at a distance $R$ of a fixed point. Thus the problem has a single degree of freedom and the SED equation of motion may be written in terms of the polar angle $\phi $ as follows \begin{eqnarray*} mR\stackrel{..}{\phi } &=&-m\tau R\stackrel{\cdot }{\phi }^{3}+m\tau \stackrel{...}{\phi }+eE, \\ E &=&-\cos \phi E_{x}\left( t\right) +\sin \phi E_{y}\left( t\right) . \end{eqnarray*} The former two terms of the right side give the tangential component of the radiation reaction force, $m\tau \stackrel{...}{\mathbf{r}},$ and the tangential component of the force due to the ZPF, respectively. In terms of the angular velocity, $\omega =\stackrel{\cdot }{\phi },$ the equation becomes \begin{mathletters} \begin{equation} \stackrel{\cdot }{\omega }=-\tau \omega ^{3}+\tau \stackrel{..}{\omega }+ \frac{e}{mR}E. \label{rotor} \end{equation} Eq.$\left( \ref{rotor}\right) $ may be solved perturbatively in two steps. In the first step we solve the classical equation of motion $\stackrel{\cdot }{\omega }=0,$ which trivially gives $\omega =\omega _{0}=$constant. That constant becomes slowly varying when we take into account the radiation raction and the action of the ZPF. In order to get that variation eq.$\left( \ref{rotor}\right) $ may be solved substituting $\omega _{0}$ for $\omega $ in the perturbation, that is in all terms of the right side. The solution with initial condition $\omega \left( 0\right) =\omega _{0}$ becomes \end{mathletters} \[ \omega (t)=\omega _{0}+\int_{0}^{t}dt^{\prime }\left[ -\tau \omega _{0}^{3}+ \frac{e}{mR}\left( -\cos \left( \omega _{0}t^{\prime }\right) E_{x}\left( t\right) +\sin \left( \omega _{0}t^{\prime }\right) E_{y}\left( t^{\prime }\right) \right) \right] \] The former term within the integral sign represents drift and the latter term diffusion. The diffusion constant may be calculated via the limit \begin{eqnarray} D &=&\lim_{t\rightarrow \infty }\frac{1}{t}\left\langle \left[ \int_{0}^{t}dt^{\prime }\frac{e}{mR}\left( -\cos \left( \omega _{0}t^{\prime }\right) E_{x}\left( t^{\prime }\right) +\sin \left( \omega _{0}t^{\prime }\right) E_{y}\left( t^{\prime }\right) \right) \right] ^{2}\right\rangle \nonumber \\ &=&\left( \frac{e}{mR}\right) ^{2}\lim_{t\rightarrow \infty }\frac{1}{t} \int_{0}^{t}dt^{\prime }\int_{0}^{t}dt^{^{\prime \prime }}\cos \left[ \omega _{0}\left( t^{\prime }-t^{\prime \prime }\right) \right] \left\langle E_{x}\left( t^{\prime }\right) E_{x}\left( t^{\prime \prime }\right) \right\rangle , \label{diffusion} \end{eqnarray} where I have taken into account that $\left\langle E_{x}\left( t^{\prime }\right) E_{x}\left( t^{\prime \prime }\right) \right\rangle =\left\langle E_{y}\left( t^{\prime }\right) E_{y}\left( t^{\prime \prime }\right) \right\rangle $ and that $\left\langle E_{x}\left( t^{\prime }\right) E_{y}\left( t^{\prime \prime }\right) \right\rangle =0.$ The field correlation may be easily got from the spectrum, eq.$\left( \ref{Espectrum} \right) $ as follows \[ \left\langle E_{x}\left( t^{\prime }\right) E_{x}\left( t^{\prime \prime }\right) \right\rangle =\frac{2
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}{3\pi c^{3}}\int_{0}^{\infty }u^{3}\cos \left[ u\left( t^{\prime }-t^{\prime \prime }\right) \right] du. \] When this is inserted in eq.$\left( \ref{diffusion}\right) $ the variables $ t^{\prime }$ and $t^{\prime \prime }$ may be changed to $w\equiv \left( t^{\prime }+t^{\prime \prime }\right) /2$ and $t^{\prime }-t^{\prime \prime }\equiv s$ . With good approximation the integration may be performed from $ 0 $ to $t$ for the $w$ integral and for the whole real line for the variable $s $. Then the limit $t\rightarrow \infty $ in eq.$\left( \ref{diffusion} \right) $ is trivial and we get, taking the definition of $\tau ,$ eq.$ \left( \ref{gamma}\right) ,$ into account, \begin{eqnarray*} D &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi mR^{2}}\int_{0}^{\infty }u^{3}du\int_{-\infty }^{\infty }\cos \left( us\right) \cos \left( \omega _{0}s\right) ds \\ &=&\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{\pi mR^{2}}\int_{0}^{\infty }u^{3}du\pi \left[ \delta \left( \omega _{0}+u\right) +\delta \left( \omega _{0}-u\right) \right] =\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{mR^{2}}\omega _{0}^{3}. \end{eqnarray*}
From the diffusion constant and the damping it is possible to obtain the following Fokker-Planck equation for the probability density, $\rho \left( \omega _{0}\right) ,$ of frequencies of the rotor \[ \frac{\partial \rho }{\partial t}=\frac{\partial }{\partial \omega _{0}} \left( \tau \omega _{0}^{3}\rho \right) +\frac{1}{2}\frac{\partial ^{2}}{ \partial \omega _{0}^{2}}\left( \frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
\tau }{mR^{2}}\omega _{0}^{3}\rho \right) , \] whose (regular) stationary solution is \[ \rho =\frac{2mR^{2}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\exp \left( -\frac{2mR^{2}\omega _{0}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\right) . \]
A similar method may be used for the three-dimensional rotor\cite{Boyerrotor} and the result is \begin{equation} \rho =\left( \frac{2mR^{2}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\right) ^{2}\omega _{0}\exp \left( -\frac{2mR^{2}\omega _{0}}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\right) . \label{3drotor} \end{equation}
\subsection{Comparison between SED and QM}
The predictions of SED for the rigid rotor disagree with those of QM at least in four respects, that will be illustrated in the following for the particular case of the three-dimensional rigid rotor:
1. \emph{The distribution of positions or momenta in the minimal energy state. }In quantum mechanics the eigenstates of the angular momentum squared and the Hamiltonian of the rotor are, respectively, \begin{equation} \mathbf{L}^{2}=
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
^{2}l(l+1),E_{l}=\frac{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
^{2}}{2I}l(l+1),l=0,1,2... \label{qrotor} \end{equation} so that the ground state corresponds to $\mathbf{L}^{2}=E=0.$ In contrast the stationary solution in SED is given by eq.$\left( \ref{3drotor}\right) $ where there is a spherical distribution of angular momenta given by \begin{equation} W(L)LdL=\frac{4}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
^{2}}\exp \left( -\frac{2L}{
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
}\right) LdL. \label{srotor} \end{equation}
2. \emph{The set of states}. As in the oscillator studied in section 3.3 the set of possible states is quite different in QM and SED.
3. \emph{The spectrum}$.$ In QM the spectrum consists of the set of frequencies \begin{equation} \omega _{lj}=\left(
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
/2I\right) \left[ j(j+1)-l(l+1)\right] \rightarrow \left(
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
/I\right) \left( l+1\right) , \label{freqrotor} \end{equation} the latter frequencies corresponding to the transitions allowed in the atomic dipole approximation. In sharp contrast SED predicts a continuous spectrum, although the most intense absorption from the stationary state eq.$ \left( \ref{qrotor}\right) $ corresponds to the maximum absorption, that may be shown to be $\omega =
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h
/I$ \cite{dice}, in agreement with the QM result for the transition from the ground to the first excited state, see eq.$\left( \ref{freqrotor}\right) .$ However QM predicts a sharp frequency whilst the SED prediction corresponds to a wide band. In experiments the frequency is not sharp, but it is less wide than the SED prediction. The disagreement between the QM prediction and experiments is usually explained because the rigid rotator is not a realistic model of a molecule. For instance molecules are not completely rigid. The disagreement with experiments is greater in SED and it cannot be explained as easily as in QM.
4. \emph{The specific heat. }There is also a discrepancy as shown in the comparison between quantum and SED treatments \cite{Boyerrotor}. This point will not be discussed here.
\subsection{A difficulty with the angular momentum}
The disagreement between the quantum prediction, eq.$\left( \ref{qrotor} \right) ,$ and the SED prediction, eq.$\left( \ref{srotor}\right) ,$ for the rigid rotor is actually general and it puts a problem for any realistic model of the rotation in quantum physics. For instance if we want to get a picture of a rotating molecule. The quantum ground state of the rigid rotor possesses \emph{zero angular momentum} and \emph{spherical symmetry, }but these two properties are contradictory for any realistic interpretation. For the sake of clarity let us consider a more realistic example, for instance the molecule of carbon oxide, $CO,$ which may be modelled by a three-dimensional rigid rotor. It consists of an oxigen atom and a carbon atom at a distance which is very well known empirically. The ground state of this molecule possesses zero angular momentum and \emph{therefore} (according to the quantum formalism) spherical symmetry. Discarding explanations which are bizarre for any realistic interpretation, like saying that ``the form of the molecule emerges during the act of measurement'', the meaning of spherical symmetry is unclear. The unique meaning compatible with a physical picture is that the molecule is rotating randomly in such a way that the probability distribution of the orientations of the axis in space possesses spherical symmetry. However this is in conflict with the quantum prediction that the total angular momentum is zero, \emph{dispersion-free}. Therefore the mean square angular momentum is also zero. The situation is quite common, it involves many molecules, atoms or nuclei. It seems that either the standard quantum prediction is wrong (e. g. the ground state is not physically achievable) or a \emph{realistic} physical model is not possible.
A possible solution to the dilemma is that the quantum formalism actually provides the total angular momentum of the molecule \textit{plus} the vacuum fields that interact with it. If the ground state correspond to an equilibrium of the system (e. g. the molecule) with the vacuum fields it is plausible to assume that there is a continuous exchange of angular momentum between the system and the vacuum fields so that the total angular momentum (a conserved quantity) remains always zero. This is the case in the SED treatment of the planar rigid rotor of the previous section. In fact, eq.$ \left( \ref{rotor}\right) $ may be interpreted as the equation for the balance of angular momentum. In fact the equation may be rewritten as the Z component of the angular momentum vector, that is \[ \frac{d}{dt}(I\omega )=-\tau I\omega ^{3}+\tau I\stackrel{..}{\omega } +e\left( \mathbf{R}\times \mathbf{E}\right) _{z}, \] where the change of the rotor angular momentum equals the radiated momentum (the first two terms) minus the momentum absorbed from the ZPF. In summary there is no real contradiction between the fact that the SED predicts a distribution of angular momenta of \emph{the rotor alone} and our interpretation of the QM prediction that the angular momentum of \emph{rotor plus field} is stricly zero. I do not believe that SED is the correct reinterpretation of QM, but I think that it illustrates adequately the possible solution to the problem.
A similar solution may be given to the strange, if not paradoxical, quantum prediction that a charged particle in a homogeneous magnetic field has zero component of the angular momentum in the direction of the field, but the energy is precisely the product of the field times the Bohr magneton. The SED results are more intuitive, namely the energy of the equilibrium state, eq.$\left( \ref{7.0}\right) ,$ agrees with the quantum ground energy, but there is a component of the angular momentum in the direction of the field, see eq.$\left( \ref{7.1a}\right) .$
\subsection{The hydrogen atom}
The hydrogen atoms is the most relevant nonlinear system within elementary quantum mechanics, therefore a crucial test for the validity of SED. Once the stationary state of the harmonic oscillator had been solved with success, several authors devoted a big effort during the 1960's to study the hydrogen atom in SED. Several approximation methods were proposed for calculating the stationary state of the atom (modelled as two particles with opposite charge, one of them at rest). The most successfull method devised for the study of a charged particle in a potential well rests upon the assumption that the classical constants of the motion change slowly. That is the motion is close to the classical one, the action of the ZPF and the radiation reaction giving rise to a slow diffusion in the space of classical orbits. As every classical orbit is determined by the initial position and velocity, $\left\{ \mathbf{r}_{0},\mathbf{v}_{0}\right\} ,$ the final result of the calculation is a probability distribution in the phase space of positions and velocities, $\left\{ \mathbf{r},\mathbf{v}\right\} ,$ that is the same as the distribution of initial positions and velocities, $\left\{ \mathbf{r}_{0},\mathbf{v}_{0}\right\} ,$ if the state is stationary. This is similar to what happens in the planar rigid rotator.
In the case of the hydrogen atom the result of the calculation did not provide a stationary solution. In fact the prediction was that the atom is not stable but ionizes spontaneously due to the orbits passing close to the nucleus\cite{Claverie}.
That work has been criticized because such orbits cannot be treated with a non-relativistic approximation, and a relativistic treatment could produce an important change in the results. Actually the prediction of spontaneous ionization made by SED analytical calculation is not a too strong argument against the SED prediction. In fact the result depends crucially on the electron orbits passing close to the nucleus, that would requiere a relativistic treatment. Also quantum theory predicts that the free atom is unstable against ionization at any finite temperature, no matter how small. This trivially follows from the fact that the quantum partition function is divergent, that is \[ Z=\sum_{n=1}^{\infty }\sum_{l=0}^{n-1}(2l+1)\exp \left( -\frac{E_{0}}{n^{2}} \right) \rightarrow \infty . \] Therefore it is not too relevant if an approximation method used in SED has an effect (spontaneous ionization) similar to the effect of a thermal radiation in QM.
Furthermore numerical solutions of the hydrogen atom in SED have been made \cite{Cole} since 2003 that explain the stability of the atom. They led to stationary distribution fairly close to the quantum prediction for the position distribution in the ground sate. However more powerful calculations made in 2015\cite{Nieu} predict a ionization of the atom. Numerical calculations have the advantage that do not require approximations in the differential equations, like the neglect of the dependence on position of the ZPF (the electric dipole approximation). However the numerical methods have uncertainties that may explain the discrepancy as commented above for the early analytical treatment. See also \cite{Cole18}.
\subsection{Thermal equilibrium between radiation and matter. SED derivation of Planck Law.}
Several authors have claimed that Planck's law may be derived from classical postulates, usually within the framework of SED\cite{dice2},\cite{Boyer12}. A derivation of the thermal radiation should follow from the study of the thermal equilibrium between radiation and matter. In the framework of standard quantum theory it leads to Planck's law, but here we are considering the question whether it may be obtained from classical electrodynamics. The difficulty is related to the fact that the equilibrium radiation-matter should involve nonlinear systems. In particular the study of equilibrium requires a balance between absorption of energy from the radiation at a frequency and emission at a different frequency. Only in these conditions it is possible to study the distribution of energy amongst the different frequencies that is the essential purpose of a radiation law. If we deal only with linear (harmonic) oscillators both the absorption and emission of radiation take place at the same frequency.
The problem of thermal equilibrium was extensively studied in the first decades of the 20th century and the conclusion was uncontroversial in my opinion: If one assumes classical dynamics then thermal equilibrium is achieved when the particles have the Maxwell-Boltzmann distribution and the radiation the Rayleigh-Jeans spectrum\cite{vanVleck}. Thus there is a contradiction between the derivation reported by van Vleck and the derivations claiming that the classical equilibrium spectrum is given by Planck\'{}s law. It was suggested that early derivations\cite{vanVleck} involved Newtonian dynamics and that a study with relativistic dynamics might led to Planck\'{}s law. However it has been shown that thermal equilibrium of relativistic particles also leads to the Rayleigh-Jeans law \cite{Blanco}. A different question is whether Planck law may be derived for systems of charged particles immersed in the ZPF field plus additional radiation and we assume thermal equilibrium of that radiation with the particles. In these conditions Planck spectrum is obtained\cite{Boyer12}, \cite{Boyer18}.
A related result is the classical derivation of the Davies-Unruh effect initially derived from quantum electrodynamics\cite{Davies}, \cite{Unruh}. It is interpreted in quantum theory as the production of photons with Planck distribution of frequencies when a detector moves in the vacuum with accelerated motion. The result may be got in SED with the interpretation that the spectrum of the ZPF appears as thermal when seen from an accelerated reference frame\cite{Boyer13}, \cite{Milonni}.
\section{SED as a clue for a realistic interpretation of quantum mechanics}
We have seen that calculations of several linear systems within SED provide a remarkable agreement with the predictions of QM. On the other hand the realistic interpretation of SED is rather obvious. Thus the question arises, offers SED the realistic interpretation of QM which we are searching for?. Unfortunately the answer is in the negative, the difficulties of SED for the interpretation of phenomena associated to nonlinear systems seem unsourmontable.
I propose that geting a realistic interpretation of QM would be possible accepting the general ideas of SED but rejecting many of the particular assumptions. The general ideas to be retained are the following: 1) Nuclei, atoms or molecules (but maybe not elementary particles like electrons) are bodies with well defined size and form following definite, but highly irregular, trajectories. (If the bodies are composite, like atoms, they may suffer deformations). 2) The motion is strongly influenced by the fluctuations of the vacuum fields.
A summary of the clues provided by SED for a realistic interpretation of (non-relativistic) quantum mechanics follows.
\textit{The attempt to interpret the quantum mechanics of particles alone is misleading if quantum fields, in particular vacuum fields, are not included. }
\textit{The quantum ground state of a particle in a potential well corresponds to a stationary state of the particle performing a highly irregular (stochastic) motion driven by vacuum fields. There is a dynamical equilibrium between absorption from and emission of radiation to the vacuum fields. The interaction gives rise to probability distributions of coordinates and momenta of the particle that agree with quantum predictions for linear systems, but for nonlinear ones there is disagreement. Radiative corrections (e, g. Lamb shift) have a transparent interpretation. }
\textit{The study of coupled oscillators at zero Kelvin provides an intuitive picture of entanglement as a correlation between quantum fluctuations mediated by the vacuum fiels. At a finite temperature it gives a simple realistic interpretation of the Debye theory of specific heats of solids.}
\textit{\ The motion of particles is highly irregular due to the interaction with the vacuum fields. In particular the free particle possesses a conserved canonical momentum with an associated inertial motion but, superimposed to this, it has a random motion with high velocity that cannot be studied adequately in the nonrelativistic approximation. This derives from the spectrum,} $S_{E}\left( \omega \right) \varpropto \omega ^{3},$ \textit{\ of the vacuum radiation fields: At short times the motion is governed by the high frequencies where} $S_{E}\left( \omega \right) $ \textit{is large thus inducing a rapid erratic motion, at long time it is governed by the low frequencies where} $S_{E}\left( \omega \right) $ \textit{ is small, whence the memory of the initial velocity is lost slowly. This behaviour is very different from Brownian motion.}
\textit{The spectrum of the radiation absorbed or emitted by a particle in a potential well badly fails to reproduce the quantum spectrum, except in the trivial case of the harmonic oscillator whose spectrum consists of a single frequency. This fact suggests that the back action of the particles on the vacuum radiation field and/or the inclusion of many fields would be essential for the prediction of spectra, e. g. of atoms.}
\textit{The stochastic commutator provides a hint for a realistic interpretation of the quantum commutation rules as a disguised form of stablishing the properties of some peculiar stochastic processes. The main peculiarity is the fact that the spectra of the processes is usually odd with respect to a change }$\omega \rightarrow -\omega $ \textit{of the frequency}. \textit{Thus I propose that the reason for the success of formulating QM with noncommuting mathematical objects is the fact that the basic stochastic processes involved have spectra that are odd with respect to the change }$\omega \rightarrow -\omega .$\textit{\ }
\textit{The SED calculation of the specific heat of solids provides an argument for the continuity of the energies of ions. Quantized oscillations of the ions in a solid (phonons) are not particles, the energies of the normal modes of the set of ions having a continuous distribution of energies. The mean energy of a vibration mode of the ions is the same as the mean energy of a radiation mode with the same frequency.}
\textit{The prediction that the angular momentum is zero, dispersion-free, in some cases is possibly the most paradoxical prediction of QM. In fact a molecule, or the electron in the ground state of a hydrogen atom, are predicted to be in a state with spherical symetry. A realistic interpretation is possible only if we assume that there is a random rotation having zero angular momentun on the average, but the mean squared angular momentum being diffeent from zero. Our study suggests a ralistic interpretation assuming that the dispersion-free momentum refers to the addition of two highly correlated random angular momenta, namely those of the material system plus the vacuum fields, these modified by the presence of matter.}
\section{Bibliography}
\end{document} | arXiv |
Math Forum/Help
Adding and subtracting up to 10
Comparing numbers up to 10
Addition and Subtraction within 20
Adding and Subtracting up to 100
Addition and Subtraction within 1000
Multiplication up to 5
Addition, Multiplication, Division
Adding and Subtracting
Equivalent Fractions
Divisibility by 2, 3, 4, 5, 9
Area of Squares and Rectangles
Fraction Multiplication and Division
Mixed Numbers
Signed Numbers
The Coordinate Plane
Symplifying Expressions
Polynomial Vocabulary
Polynomial Expressions
Linear Functions
Congurence of Triangles
Systems of equations
Parametric Linear Equations
Quadratic Inequalities
Rational Inequalities
Vieta's Formulas
Arithmetic Progressions
Number Sequences
Reciprocal Equations
Logarithms
Logarithmic Expressions
Logarithmic Equations
Trigonometric Inequalities
Extremal value problems
Numbers Classification
Intercept Theorem
Law of Sines
Limits of Functions
Properties of Triangles
Inverse Trigonometric Functions
Conic sections
Integration by Parts
Trigonometric Substitutions
Polynomial Vocabulary: Problems with Solutions
Polinomial: $a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2} + ... + a_1x^1+a_0$
Terms: $a_nx^n, a_{n-1}x^{n-1}, a_{n-2}x^{n-2}, a_1x^1, a_0$
Coefficients: $a_n, a_{n-1}, a_{n-2}, ... ,a_1, a_0$
Main Coefficient: $a_n$
Grade: $n$
Variable: $x$
Independent term: $a_0$
What is the grade of this polynomial?
$5x^{2}-3x^{5}+2x-5$
We order the exponents from the largest exponent to the smallest.
$-3x^{5}+5x^{2}+2x-5$
Grade $5$
How many terms does the polynomial have?
$2y^{6}-\frac{3}{2}y^{2}+1$
Number of terms 3.
$\frac{5}{2}-x+5x^{4}-3x^{2}+\frac{1}{2}$
$5x^{4}-3x^{2} -x+\left( \frac{1}{2}+\frac{5}{2}\right)$
Sum the constants.
$5x^{4}-3x^{2} -x+3$
This polynomial has 4 terms and its grade is 3.
$4x^{3}-4x^{5}+4x+4$
Certainly, the polynomial has 4 terms, but its grade is 5.
We observe it better if we order its terms.
$-4x^{5}+ 4x^{3}+4x+4$
A polynomial that has grade 3, independent term 3 and main coefficient 3, is called a trinomial.
A trinomial is a polynomial that has 3 terms.
The following polynomial is a trinomial, it has grade 4, the variable is x and it has an independent term -2.
$5x^{2}-x^{4}+(3-5)$
We order and simplify: $5x^{2}-x^{4}+(3-5)= -x^{4}+5x^{2}-2$
Write a polynomial of grade 1, main coefficient 1, that has an independent term 0, and its variable is y.
$y$ is the only one polynomial of grade 1, main coefficient 1, that has an independent term 0, and its variable is y.
How many terms must a binomial have?
A binomial has 2 terms, for example,
$x^{2}-4$
Which of the following algebraic expressions is a polynomial?
$\sqrt{x}+7x^{3}-5$
$\sqrt{2}x^{3}-\sqrt[3]{7}x+\frac{3}{2}$
$\frac{2}{x^{2}-5x+3}+1$
$x-2x^{-3}+8$
Answer: $\sqrt{2}x^{3}-\sqrt[3]{7}x+\frac{3}{2}$
This is the only expression that is a polynomial, its coefficient can be any real number. Here the coefficients are
$\sqrt{2};-\sqrt[3]{7};\frac{3}{2}$
Grade $3$,
Independent term $\frac{3}{2}$
$\frac{1}{2}x^{3}+x^{2}-\pi $
$\sqrt{5}x^{5}+2$
$\pi y^{4}-ey^{3}+(\sqrt{2}-\sqrt{3})y+1$
All of the these are polynomials.
Correct answer: All of these are polynomials.
Variable $x$,
Number of terms $3$
Variable $y$,
Submit a problem on this page.
Problem text:
Your name(if you would like to be published):
E-mail(you will be notified when the problem is published)
Notes: use [tex][/tex] (as in the forum if you would like to use latex).
Unsolved problems:
Follow us on Twitter Facebook | CommonCrawl |
Ergodic Theory and Dynamical Systems
Regions of instability for non-twist maps
JOHN FRANKS and
PATRICE LE CALVEZ
Department of Mathematics, Northwestern University, Evanston, IL 60208-2730 (e-mail: [email protected])
Laboratoire Analyse, Géometrie et Applications, UMR CNRS 7539, Institut Galilée, Université Paris 13, 93430 Villetaneuse, France
In this paper we consider an analog of the regions of instability for twist maps in the context of area preserving diffeomorphisms which are not twist maps. Several properties analogous to those of classical regions of instability are proved.
Ergodic Theory and Dynamical Systems , Volume 23 , Issue 1 , February 2003 , pp. 111 - 141
2003 Cambridge University Press
Total number of PDF views: 56 *
Gaidashev, Denis and Koch, Hans 2004. Renormalization and shearless invariant tori: numerical results. Nonlinearity, Vol. 17, Issue. 5, p. 1713.
Apte, A Llave, Rafael de la and Petrov, Nikola P 2005. Regularity of critical invariant circles of the standard nontwist map. Nonlinearity, Vol. 18, Issue. 3, p. 1173.
Xia, Zhihong 2006. Area-Preserving Surface Diffeomorphisms. Communications in Mathematical Physics, Vol. 263, Issue. 3, p. 723.
Xia, Zhihong and Zhang, Hua 2006. ACrclosing lemma for a class of symplectic diffeomorphisms. Nonlinearity, Vol. 19, Issue. 2, p. 511.
Lerman, L. 2010. Breaking hyperbolicity for smooth symplectic toral diffeomorphisms. Regular and Chaotic Dynamics, Vol. 15, Issue. 2-3, p. 194.
Koropecki, Andres 2010. Aperiodic invariant continua for surface homeomorphisms. Mathematische Zeitschrift, Vol. 266, Issue. 1, p. 229.
Contreras, Gonzalo 2010. Geodesic flows with positive topological entropy, twist maps and hyperbolicity. Annals of Mathematics, Vol. 172, Issue. 2, p. 761.
Koropecki, Andres and Nassiri, Meysam 2011. Erratum to: Transitivity of generic semigroups of area-preserving surface diffeomorphisms. Mathematische Zeitschrift, Vol. 268, Issue. 1-2, p. 601.
Addas-Zanata, Salvador and Tal, Fábio Armando 2011. Boyland's Conjecture for Rotationless Homeomorphisms of the Annulus with Two Fixed Points. Qualitative Theory of Dynamical Systems, Vol. 10, Issue. 1, p. 23.
Mann, Kathryn 2012. Bounded orbits and global fixed points for groups acting on the plane. Algebraic & Geometric Topology, Vol. 12, Issue. 1, p. 421.
Jäger, T. Kwakkel, F. and Passeggi, A. 2013. A classification of minimal sets of torus homeomorphisms. Mathematische Zeitschrift, Vol. 274, Issue. 1-2, p. 405.
Gelfreich, Vassili and Gelfreikh, Natalia 2014. Unique normal forms near a degenerate elliptic fixed point in two-parametric families of area-preserving maps. Nonlinearity, Vol. 27, Issue. 7, p. 1645.
Passeggi, Alejandro and Xavier, Juliana 2014. A classification of minimal sets for surface homeomorphisms. Mathematische Zeitschrift, Vol. 278, Issue. 3-4, p. 1153.
Xia, Zhihong and Zhang, Pengfei 2014. Homoclinic points for convex billiards. Nonlinearity, Vol. 27, Issue. 6, p. 1181.
ADDAS-ZANATA, SALVADOR 2015. Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior. Ergodic Theory and Dynamical Systems, Vol. 35, Issue. 1, p. 1.
Asaoka, Masayuki and Irie, Kei 2016. A $${C^\infty}$$ C ∞ closing lemma for Hamiltonian diffeomorphisms of closed surfaces. Geometric and Functional Analysis, Vol. 26, Issue. 5, p. 1245.
Zhang, Pengfei 2017. Convex billiards on convex spheres. Annales de l'Institut Henri Poincare (C) Non Linear Analysis, Vol. 34, Issue. 4, p. 793.
JÄGER, T. and TAL, F. 2017. Irrational rotation factors for conservative torus homeomorphisms. Ergodic Theory and Dynamical Systems, Vol. 37, Issue. 5, p. 1537.
Koropecki, Andres 2017. Realizing rotation numbers on annular continua. Mathematische Zeitschrift, Vol. 285, Issue. 1-2, p. 549.
Jäger, Tobias and Koropecki, Andres 2017. Poincaré Theory for Decomposable Cofrontiers. Annales Henri Poincaré, Vol. 18, Issue. 1, p. 85.
JOHN FRANKS (a1) and PATRICE LE CALVEZ (a2) | CommonCrawl |
viXra.org > Geophysics
2012 - 1202(1) - 1209(2) - 1210(2) - 1211(5) - 1212(5)
2014 - 1401(2) - 1402(2) - 1403(1) - 1406(3) - 1407(2) - 1408(1) - 1410(1) - 1411(2) - 1412(1)
2015 - 1501(4) - 1502(1) - 1503(3) - 1504(4) - 1506(6) - 1507(2) - 1510(1) - 1511(11) - 1512(20)
2016 - 1601(3) - 1602(4) - 1603(1) - 1604(2) - 1605(2) - 1606(1) - 1607(2) - 1608(2) - 1610(3) - 1611(1)
The 3-rd Prognosis of Large Earthquakes and Volcanic Eruptions According Daily Indexes of Solar Activity
Authors: A.M.Eigenson, I.B.Bazylevych, M.S.Shevchenko
Recently we have done two prognosis of earthquakes (EQ) and volcanic eruptions (VE) on daily indexes of solar activity [1,2]. Both these forecasting's are just confirmed, and here we represent the next one. All these predictions have the basis in the investigation of the first as the authors [3,4]. These was shown that when solar activity curve begins go down, then in the vicinity of its minimum the EQ and VE occur with large probability. So, knowing the behavior of solar curve, one could make the corresponding prognosis. Our previous prognosis deals in the period of Spring 2019, and now we present the prediction for Summer, 2019. In Fig.1 we see that the evident minimum of W Number was on July, 27. So we prognose the new dangerous area would be between this date and July,11 (may be, even later). (Remark: earthquakes 6+ are noted as circle's, earthquakes 7+ as ellipses)
Category: Geophysics
Geochronology and Movement of the Sun Around the Galaxy Center
Authors: V.F. Chekalev, E.V. Chekalev
The motion of Solar system round the Galaxy center is considered in this article. Joint use of geochronological and astronomical data allowed to determine parameters of galactic orbits of Solar system in the Phanerozoe. As a result of the analysis the duration of some geological periods are modified and the new geological period is entered. The future duration of the Quaternary period is calculated also and is defined more exactly duration of the first period of the Phanerozoe - Vendian.
How does Geomagnetic Field form
Authors: Jianfei Chen
Geomagnetic field is important to every life, forming of which has not been explained well. This paper linked lodestone on earth and distance from earth to sun to explain forming of the geomagnetic field. Finally found that key to forming the geomagnetic field is distance from earth to sun. Affected by this distance, the matter earth gets from sun is special magnetic energy particles, which promotes to form lodestone, magnetic energy from which is stored in lodestone. Much lodestone on earth makes up a huge magnet, which release unified magnetic energy to make up the geomagnetic field. Email: [email protected] / [email protected]
Invisibility Cloaks for Stress Waves
Despite casting deep doubt on dozens of theoretical papers on "elastodynamic" cloaking, the new study's authors from the Georgia Institute of Technology don't think civil engineers should completely give up on it, just on the idea of an ideal cloak. [19] University of Southern Denmark researchers have conducted simulations of dark matter particles hitting the Earth. [18] A global team of scientists, including two University of Mississippi physicists, has found that the same instruments used in the historic discovery of gravitational waves caused by colliding black holes could help unlock the secrets of dark matter, a mysterious and as-yet-unobserved component of the universe. [17] The lack of so-called "dark photons" in electron-positron collision data rules out scenarios in which these hypothetical particles explain the muon's magnetic moment. [16]
Proposal for Definition and Implementation of a Unified Geodetic Referential for North Africa
Authors: Abdelmajid Ben Hadj Salem; Magtouf Rezgui
Comments: 6 Pages. It is a numerical version of the original paper. In French.
In this paper, we present the details of the proposal for definition and implementation of a unified geodetic referential for the countries of North Africa as : - the choice of the system of the referential, - the steps of the realization of the project, - the training of the geodesists working on the project.
A Solution of the Laplacian Using Geodetic Coordinates
Authors: Abdelmajid Ben Hadj Salem
Using the geodetic coordinates $(\varphi,\lambda,h)$, we give the expression of the laplacian $\Delta V=\ds \frac{\partial^2 V}{\partial x ^2}+\frac{\partial^2 V}{\partial y ^2}+\frac{\partial^2 V}{\partial z ^2}$ in these coordinates. A solution of $\Delta V=0$ of type $V=f(\lambda).g(\varphi,h)$ is given. The partial differential equation satisfied by $g(\varphi,h)$ is transformed in an ordinary differential equation of a new variable $u=u(\varphi,h)$.
New Short-Term Prognosis of Strong Earthquakes and Volcanic Eruptions According to Daily Indexis of Solar Activity
Recently we have made the prognosis of such terrestrial events for the period between April 22 and May 2, 2019. This forecasting is confirmed. Now we do the same prognosis for the next 2 weeks, from May 19 until June 2, 2019. During this period new great catastrophes are expected to occur on our Earth. In our days, we see from Fig. 1 that the dangerous area lies between May 19 and June 2, 2019. (Addition: earthquakes 6+ are noted as circle's, earthquakes 7+ as ellipsis and volcanic eruptions as crosses). So, the people of seismic zones: BE CAREFUL!
Le Découpage Cartographique International
Comments: 7 Pages. In French.
This note concerns the international cartographic division. It gives how is organized the numbering of sheets at different scales ranging from 1/500 to 1/50000 and their sizes and surfaces.
Systèmes de Référence Systèmes Projectifs
Authors: Henri Marcel Dufour, Abdemajid Ben Hadj Salem
Comments: 27 Pages. In French. It is an-update version of a paper dated 1979 with comments of the second author.
Many geodetic works currently exist on the surface of the globe, which have developed through regional networks, usually each having a fundamental point, where the astronomical data (\phi= latitude,\lambda= longitude,Az= azimuth) of a reference are confused with the counterparts geodetic data. The comparison of 2 networks, and, step by step, of all the connectable networks, can be done by the analysis of the coordinates of their common points. To this end, we can use 3 types of coordinates: - Geographical coordinates = simple method, but not very convenient for different ellipsoids. - Three-dimensional cartesian coordinates, the most rigorous method in the case where the so-called geoid correction has been made. - Coordinates in conformal projection. An analysis of the main formulas that can be used is studied by the author in this article.
A Note About Dufour-Fezzani Formula
In this note, we review the Dufour-Fezzani formula concerning the comparison of two geodetic networks. This formula is developed for ellipsoidal models.
Collection of Exercises and Problems of Topography, Astronomy, Geodesy and Least Squares Theory
Comments: 70 Pages. In French.
I have often received students in geomatic requests asking me to provide them with exercises or problems of geodesy, topography, astronomy or the application of the theory of least squares. The paper is a collection of exercises and problems that comes to fill the need of the students in this matter.
Short-Term Prognosis of Strong Earthquakes and Volcanic Eruptions According to Daily Indexis of Solar Activity
Recently one of the authors [1-6] has shown that when solar activity curve begins to go down, then in the vicinity of it's minimum earthquakes and volcanic eruptions occur. Analysis of data during the period 2010-2018 shows that the probability of false prognosis is no more 2 %. This feature could be used for forecasting these terrestrial events several days in advance. The "opposite" Forbush effect is proposed as possible reason for explanation of this phenomena. In our days, we see from Fig. 1 that the dangerous area lies between April 22 and May 2, 2019. (Addition: earthquakes 6+ are noted as circle's, earthquakes 7+ as ellipsis and volcanic eruptions as crosses).
Numerical Solution of Master Equation Corresponding to Schumann Waves
Comments: 7 Pages. This paper has not been submitted to a journal. Comments are welcome
Following a hypothesis by Marciak-Kozlowska, 2011, we consider one dimensional Schumann wave transfer phenomena. Numerical solution of that equation was obtained by the help of Mathematica.
Attractions of the Sun and the Moon on The Earth
This note gives the elements on the attraction of the sun and the moon. It was inspired by the reading of the book by Helmut Moritz and Ivan I. Muller entitled Earth Rotation: Theory and Observation which can be a tidal introductory course. \\ It includes the following chapters: - The lunar-solar tidal potential. - Zonal, sectoral and tesseral terms
Report of Spatial Geodesy on the Rapid Implementation of a Unified Geodetic System in Africa
Authors: Fezzani Chedly, Ben Hadj Salem Abdelmajid
Comments: 13 Pages. It is a numerical edition of the original paper dedicated to the memory of the first author who passed away on March 09, 2019. In French.
Having a unified reference system, established on a universally accepted and utilitarian basis, is an important contribution to the judicious use of geographic information to promote Africa's economic development at the national level, regional and continental. To do so, it is important today to make the best use of space technologies and to assimilate them, especially through Cartographic National Institutions. This paper: - is written for small African mapping institutions, - defines the organizational prerequisites for rapidly implementing the Unified Reference System at the continental level. - serves as a framework to guide the debate on the real questions to be asked in this area.
Nullspace and Mitigation in Seismic Imaging and Seismic Inversion
Authors: August Lau, Alfonso Gonzalez
Seismic inversion is the inverse problem in seismic data processing. Seismic inversion is normally used to recover the medium properties or reflectivity series given the input seismic traces. Nullspace is common in linearized inversion where many vectors could be mapped into the one vector. It is an indication that many models could fit the same data, regardless of the inversion method. Inversion could give odd geometric shapes that are not physical or geological. We will discuss mitigation of nullspace to yield results that are meaningful for interpretation of geologic layers for oil and gas exploration.
Proven Methods for Filtering SG Data
Authors: Herbert Weidner
Subject are different methods for noise-free data reduction of low-frequency geophysical data and identification of interference sources. The most important method is the selective compensation of strong spectral lines.
Non-Parametric Wavelet Functional Analysis for Horizontal and Vertical Displacements Derived from GPS Stations in Western Alaska During the Year 2012
Authors: Homayoon Zahmatkesh, Abbas Abedini
Comments: 19 Pages. Earth Science Research; Vol. 6, No. 2; 2017
In order to analyze the dynamic processes of the Earth interior and the effect of the propagation of the seismic waves to the surface, a comprehensive study of the Earth crust kinematics is necessary. Although the Global Positing System (GPS) is a powerful method to measure ground displacements and velocities both horizontally and vertically as well as to infer the tectonic stress regime generated by the subsurface processes (from local fault systems to huge tectonic plate movements and active volcanoes), the complexity of the deformation pattern generated during such movements is not always easy to be interpreted. Therefore, it is necessary to work on new methodologies and modifying the previous approaches in order to improve the current methods and better understand the crustal movements. In this paper, we focus on western Alaska area, where many complex faults and active volcanoes exist. In particular, we analyze the data acquired each 30 seconds by three GPS stations located in western Alaska (AC31, AB09 d AB11) from January 1, 2012 to December 31, 2012 in order to compute their displacements in horizontal and vertical components by vectorial summation of the average daily and annual velocities components. Furthermore, we design non-parametric DMeyer and Haar wavelets for horizontal and vertical velocities directions in order to identify significant and homogenous displacements during the year 2012. Finally, the non-parametric decomposition of total horizontal and vertical normalized velocities based on level 1 and level 2 coefficients have been applied to compute normal and cumulative probability histograms related to the accuracy and statistical evolution of each applied wavelet. The results present a very good agreement between the designed non-parametric wavelets and their decomposition functions for each of the three above mentioned GPS stations displacements and velocities during the year 2012.
A Peculiar Natural Resonance of the Earth at 46.265 µHz
By carefully choosing the filter methods, the noise level of geophysical data could be reduced sufficiently to detect a hitherto unknown spectral line whose modulation is phase-locked to the duration of the year. The origin is enigmatic.
On the True Shape of the Earth
Authors: Royan Rosche
I show why the Earth does not have a geometric shape
Completing the Slichter Triplet
Following the discovery of a spectral line with an unusually high quality factor, exactly two other lines with comparable characteristics were found in the frequency range 45 to 130 μHz. Maybe it is the desired Slichter triplett.
Weak Signal Detection in Geophysical Data using Vector-FFT
The gravimeter in CB measures at 50.65 μHz a hitherto unknown, amplitude-modulated and very weakly damped natural vibration of the earth, the cause of which is not recognizable. It could be a member of the famous "Slichter Triplet".
Frequency Measurements in Noisy Records using Vector-FFT
The search for weak spectral lines with SNR ≈ 1 in noisy gravitational data is difficult, since the analysis methods used so far do not exploit all available information. The vector FFT presented here reduces the noise level and narrows the FWHM of all spectral lines by taking advantage of the phase information of the FFT.
Black Carbon Shuts Out Daylight in Soil
Authors: Magnus Carlsson, Olof Andrén
We tested the effects of charcoal addition on growth of Lepidium Sativum in soil.
Exploration Geophysics at Home: Search for Minerals.
Authors: Giuliano Bettini
Exploration geophysics is an applied branch of geophysics, which uses physical methods, such as seismic, gravitational, magnetic, electromagnetic etc, to measure the physical properties of the subsurface. It is most often used to detect or infer the presence and position of economically useful geological deposits, such as ore minerals. The paper shows the results of a mineral search at a feldspar mine with contact rocks wich are rich in peculiar minerals. Nickel and silver mineral were analyzed in this locality, some of them yet unidentified.
Två Markvetare
Authors: Magnus Carlsson
Two prominent soil scientists and their deeds are described.
Эффекта Джанибекова, "кувырок" Земли и глобальные катастрофы. (Ru) /// Janibekov Effect," Somersault " of the Earth and Global Catastrophes.
Authors: A.V. Antipin
Comments: 15 Pages. language: Ru
В статье рассматривается вопрос о возможности для Земли совершать «кувырки» в силу «эффекта Джанибекова». Показано, что Эффект Джанибекова ПОЛНОСТЬЮ объясняется классической механикой. Этот эффект является одним из допустимых режимов вращения свободного ассиметричного волчка вокруг средней по величине из трёх главных осей инерции. Представлены аргументы в пользу того, что такие кувырки не могли происходить в исторический период, т.е. в последние 500 – 1000 лет и, тем более, неоднократно. \\\ The article discusses the possibility for the Earth to make " somersaults "because of the" Janibekov effect". It is shown that the Janibekov Effect is fully explained by classical mechanics. This effect is one of the permissible modes of rotation of the free asymmetric gyroscope around the average of the three main axes of inertia Arguments are presented in favor of the fact that such somersaults could not occur in the historical period, i.e. in the last 500 – 1000 years and, especially, repeatedly.
The Effect of Geological Structures on Groundwater in Sedimentary Formation of Abuja. Nigeria.
Authors: Adaji John Desmond
Comments: 22 Pages. The work is on Groundwater development
Abuja sedimentary formation is located within the southern part of the federal capital territory which house Abaji and Kwali area councils. This area was investigated for ground water potential using the effect of the rock structures to determine the hydrology components of the studied area. Geophysical method and geological method of exploration involving the vertical electrical sounding was employed to prospect for groundwater in the Abuja sedimentary Formations. Vertical electrical sounding using the Schlumberger electrode array configuration were deployed along traverses within the area. The soundings were conducted at seven locations .The qualitative analysis of the resistivity data identified relatively high conductive regions indicating possible aquifer zones. The quantitative interpretation of the modelled sounding curves delineated between five and seven subsurface layers at different location within the Formation. These layers were inferred to be the top soil, sandy-clay/clayey-sand, laterite and coarse sandstone. The modelled VES curves characterized the topsoil/weathered basement with resistivity range of 4 to 10Ωm with an estimated depth to basement ranging from 45 m to 120m. The results of the study confirm that the VES methods are very suitable for development of groundwater in these communities within Abuja sedimentary formation. Geophysical method combined with geological logging should hence, form an integral part of groundwater exploration programmes in solving problems associated with groundwater prospecting to locate potential aquifers for the supply of potable water to communities within this Formation.
Crustal Diameter vs. Total Diameter in Stellar Metamorphosis
Comments: 4 Pages. handwritten notes included
A paper is written to show that during stellar evolution according to stellar metamorphosis, the crustal diameter and the total diameter change in ways not predicted by the nebular hypothesis or plate tectonics. Explanation is provided.
Fast Sublithospheric Currents an Overlooked Cause of Biospheric Extinctions?
Authors: Edgars Alksnis
In vortical world, direct exposure to "torsion" radiation from turbulent melted rocks should be dangerous
Phase Inversion of the 3S2 Oscillation of the Earth
The analysis of the gravitational data from 2004 and 2011 consistently shows regular phase reversal at intervals of around 50 hours. The four-leaf directional pattern rotates in 200 hours westwards around the N-S axis of the earth. The supposed "anomalous splitting" of 3S2 is a measurement error, caused by wrongly chosen parameters of the Fourier transformation.
Co2 Flush Rates After Soil Crumbling as Related to Soil Carbon Pools and Soil Fragmentation Characteristics
Authors: Magnus Carlsson, Olof Andrén, Vera Kainiemi, Thomas Kätterer
Sensible use of tillage requires knowledge about different aspects of soil crumbling. Decisions of best management practices must be based on complex considerations regarding e.g. effective tractor use, long-term soil health, etc. Research on soil carbon fluxes in tilled soils is an area of investigation which has received much attention recently, but ideally it should be approached in a combined bio-physical manner. We conducted studies on respiration from freshly fragmented clay soil in different aggregate size fractions with help of a multi-channel respirometer. The fragmented soil was characterized in terms of different soil carbon pools. The physical fragmentation itself was characterized in a manner that should be relevant to the three existing ways of relating use of a specific tool configuration to physical outcome of the operation, namely soil mechanical tillage experiments in situ, tests in soil bins and computational soil mechanics. Linear regressions showed that higher specific aggregate surface area, more free organic C per dry soil and more occluded C per dry soil led to higher soil respiration rates.
Ball Lightning as a Hot, Highly Charged, Sphere of Air.
Authors: Chris Allen Broka
Comments: 13 Pages. The Supplementary material may be accessed by emailing the author.
An exceptionally simple model of ball lightning is proposed that describes it as a highly charged sphere of hot, conductive, air surrounded by colder air. This conductive sphere possesses a net excess of charge. This charge will create a corona discharge that will heat the surrounding air thus maintaining the temperature of the ball itself. Numerical simulations are presented which give results that would appear to agree with what many witnesses have reported. It is argued that such spheres are likely positively charged.
Reading Professor Dmitriev
Treasure-house of unexplained and uncomfortable facts in fascinating books of famous Siberian astrogeophysicist allows me to comment on wide range of cosmogeophysical problems, opposing mainstream "explanations". More data in favour of liquid Earth's mantle concept. Possibility to ease climatic and seismic stresses by manipulation of "smart energies" from Earth's surface get some observational support and theoretic background.
An Open Correction to James Hutton's Famous Quote Concerning Uniformitarianism as First Principle
A quote is taken from the father of modern Geology and given correction, so that deeper fundamentals can have the flood gates opened concerning deep time. In effect, it is one of the ideals, deep time, that is supported while another conflicting belief is removed. Explanation is provided.
Comprehensive Presentation and Analysis of All Flat Earth Evidence and Proof
Authors: Grothos Malachias
In this study I will attempt to provide all evidence and proofs related to our true realm the magnificent Flat Earth.
Quake Tomato: Strange Electrical Signals from a Tomato Plant in Taiwan Five Days Before the 2008 Sichuan M8.0 Earthquake
Authors: Dyson Lin
I observed strange electrical signals from a tomato plant in Taiwan five days before the 2008 Sichuan M8.0 Earthquake. That opened my door to quake forecast. Since then, I observed electrical signals of plants, tofu, soil, water or air to predict earthquakes. I successfully predicted a lot of quakes. Now I have about 30 quake forecast stations all over the world. I will publish a series of papers to describe my discoveries in the past 10 years. This paper is the start of the series. I am Founder and CEO of Taiwan Quake Forecast Institute.
Global "geomagnetic" Field Without Iron
Global "geomagnetic" field could be effect of bosonic field from fast Earth's mantle turbulence
Geysers on Enceladus and Europa Prompt Water Rich Earth's Interior Idea
Waterless Earth's interior concept is connected with one of large piece of iron in Earth's centre. Since latter concept is disproved, water rich Earth sounds logical.
The Earth-Moon Collisions, Presenting Three Collisions in Detail
Authors: R. Winnubst
To verify the likelihood of a new solar system formation hypothesis, research was conducted into a possible low speed, shallow angled Earth-Moon collision at 4.1 billion years ago. Via a tailored set of indicators, not just one but three collisions were identified beyond a reasonable doubt. All are presented in great photographic and topographic detail in this paper. On the Moon, the three impact areas are: Aitkin basin (4.1Ga), a double string of major maria (3.9Ga) and wider Oceanus Procellarum (450Ma?). On Earth, the respective corresponding impact areas are identifed as: The Arctic, the Canadian shield and equatorial Gondwana (centred at current Antarctica). As a result, many issues in geology can now be explained, from the 'faint young Sun paradox' to Hadean geology and continental drift.
Water Content of Earth Underestimated
Next step for reform of geophysics after conclusion, that Earth's density is overestimated, should be- reestimation of terrestrial internal water content. This could prompt new look to earthquakes phenomena, Expanding Earth theory and other geophysical oddities.
Probability Density Functions as Mathematical Tools to Probe Computational Aspects of Petroleum Sciences in the Context of Computational Fluid Dynamics & Petroleum Microbiology – A Novel Suggestion Using Higher Order Logic(HOL)/Scala/Scalalab/JikesRVM.
Comments: 4 Pages. Short Communication
As stated in our TITLE we intend to focus on PDF based computational aspects of Petroleum Sciences and Engineering using HOL-Scala-Scalalab-JikesRVM.To the best of our knowledge we believe this is one of the pioneering short communications in this domain.
Stormy 2018 from Perspective of Vortical Astrogeophysics
One level of acting forces of astrogeophysics are deciphered here in examples of July/August and September/October ephemerides.
Expansion Tectonics – Is It All Wet?
Authors: Raymond HV Gallucci
Expansion Tectonics postulates that the Earth has grown from a much smaller orb over its history, the size once being as low as 1/4 of today's radius at the extreme (more common estimates are around 60% of today's radius). Scientists have also long speculated as to the source of Earth's water, estimated today to be anywhere from 1.5 to 11 times the current volume of the oceans, with a rough agreement around three times today's ocean volume (implying 2/3 today is "within" the Earth). This paper examines some of the implications of Expansion Tectonics in conjunction with a total water volume three times today's ocean volume, with neither an increase in Earth's mass or water volume over time. Speculation at two extremes range from an early "saturated sponge" Earth, where all this water was retained within the Earth, with essentially none at the surface (the more common postulate of Expansion Tectonics) to a complete "waterworld," where all of the water was atop the surface, i.e., none within.
Earth's Mass Overestimated
As method of calculation of Earth's mass by analysis of movement of the Moon is disproved, mainstream hardly has other method to calculate Earth's mass. Raw estimate of Earth's density is possible, using data from vortical celestial mechanics.
The Geocentric Testimony of the Tides
Authors: Robert Bennett
Static gravity alone accounts for the observation of the double tides on opposite sides of the earth and the different range of the lunar and solar tides. When the centrifugal acceleration of the Earth's orbital speed is added to the gravitational accelerations, the HelioC theory is exposed as fictitious. There is no evidence of a centrifugal acceleration ...or force... in the tidal behavior. This agrees with other GC tests, like Newton's Bucket, Sagnac's rotor and R. Wang's linear Sagnac version. Conversely, there are no proofs by scientific method testing or realistic interpretation that the Earth orbits the Sun. The rise and fall of the tides around the world is a semi-diurnal repetitive demonstration of the Earth's central position in the universe.
Global Atmospheric Circulation in the Light of Liquid Turbulent Earth's Interior Idea
Initial thoughts about possibility of Earth's liquid turbulent interior and its influence to climate affairs are presented
Earth Interior Theory Could be Wrong Completely
Alternative explanation for differences of propagation of seismic waves in Earth interior is presented in short.
Tunguska Explosion Revisited
Authors: M. Kovalyov
A few aspects of the Tunguska explosion unnoticed until now are reviewed
Wave and Tide Essay
Authors: Cres Huang
Wave is a fundamental action of the universe. Water waves when it is disturbed by internal or external force. And, there be higher water level when waves meet the shore. This study examines the driving forces of waving gas, liquid, and solid anew when gravity is not force of attraction.
Driving Force of Tectonic Plate
Gravity is the inward force of keeping it's spherical shape. Force of tectonic motion has to fight against gravity to push the crust from the ocean floor to the top of mountain ranges. The only force that is persistently counteracting and can be stronger then gravity is the centrifugal force. It is likely the centrifugal acceleration made Earth oblate spheroid, and the main driving force of waving mantle along with crust, water and atmosphere.
This preliminary is only an open proposal for further study from the view of mantle/crust waves. Additionally, the added mass and energy of Solar particles and momentum could impact the crust. Like kneading Earth dough, the magnitude could be larger than we think by far. Further study is also recommended.
Cours de Géodésie Pour Les élèves Ingénieurs Option Géomatique
Comments: 306 Pages. In French.
It a course notes of geodesy for the students of Geomatics Option of ESAT school.
Examination of MAXLOW'S Model for Expansion Tectonics – an Astronomical Perspective
While not drawing any conclusion regarding the validity of the theory that Earth has undergone volumetric (and mass) expansion over the course of its geologic history, this paper examines one of the leading contenders' models for just such growth, that of James Maxlow ("Global Tectonic Data Modeling," Terella Press, Australia [2017]). Maxlow's extensive analysis of (paleo-)geology, paleomagnetics, space geodetics, paleogeography, paleoclimatology, paleobiology, fossil fuels, past extinctions and metallogenics suggest that Earth's radius has grown exponentially over the past 1.6 x 109 years by a factor of 3.75, with sufficient increase in mass to ensure that surface gravity has not decreased, and quite possibly has increased. A much more cursory examination of this assumption from the perspective of astronomical physics, particularly conservation of Earth's orbital and rotational angular momentum, suggests a much more "modest" rate of increase, not necessarily exponential. And, while quite limited in comparison to Maxlow's analysis, this simplified one still raises apparently valid discrepancies that should be addressed. Hopefully, further research and analysis, or validation of different assumptions, can bring these two competing arenas into closer agreement.
The Gravity Theory of Mass Extinction
Authors: John Stojanowski
The cause of mass extinctions is a subject that has been debated for well over a hundred years. Currently, the two prime suspects are bolide impact and volcanism, specifically flood basalt eruptions referred to as Large Igneous Provinces (LIPs). Bolide impact has only been associated with one of the Big Five mass extinctions at the end of the Cretaceous Period whereas four of the Big Five mass extinctions have unquestionably been associated with LIPs as is the case for other major extinctions. Based upon the above, volcanic association with mass extinction is hypothesized to have had its lethal effect via global warming, global cooling, anoxia and hypoxia. However, the problem with the volcanogenic extinction hypothesis is that the onset of eruptions in the mid-Phanerozoic eon slightly postdates the main phase of extinctions.09,14 This paper introduces a third theory to explain the mass extinctions, the Gravity Theory of Mass Extinction (GTME)01, which is able to explain the primary cause of the extinctions, which is not volcanogenic and not the result of bolide impact. It is also able to explain why LIPs are associated with most of the extinctions as well as geomagnetic reversals and massive changes in sea level. In addition, it offers a reason why a bolide impact occurred near the end of the Cretaceous Period.
Possible Source of The Earth's Geomagnetic Field
Authors: Yuanjie Huang
The earth's geomagnetic field provides a safe environment for the earth's biology against solar wind. However, revealing source of geomagnetic field is very challenging and it has puzzled people for several hundred years. Here, based on the previously proposed Yuheng Zhang effect, I show a simple theory to account for generation of geomagnetic field. This theory only has two requisites, one is metallic core, the other is self-rotation of the earth. Based on this theory, several interesting points are concluded: 1) negative charges accumulate at a metallic thin layer (MTL) at core-mantle boundaries (CMB) and positive charges distribute within the earth's core; 2) rotation of the separated charges would yield geomagnetic field and gives field strength for the Earth, Ganymede and Mercury, which are in agreement with measurement values; 3) misalignment of MTL rotation axis with the earth's rotation axis causes geomagnetic declination and a quadrupole field; 4) for a planet, a solid metallic core will generate a geomagnetic field without magnetic declination and geomagnetic reversal, and geomagnetic declination suggests a liquid metallic core; 5) dynamic evolution processes of MTL dominate long-term geomagnetic variations and reversals, e.g., a slower MTL rotation causing a geomagnetic reversal and recovery of MTL rotation eliminating geomagnetic reversal; 6) at center of the earth's inner core, the geomagnetic field would show a reversal at a critical radius, and geomagnetic fields point from the earth's south pole to north pole; 7) the earth's geomagnetic pole and some quadrupoles would exhibit the same angular velocity of westward drift; 8) even if geomagnetic dipole vanished, quadrupole fields would continue to sustain and protect biology from harmful ultraviolet radiation and the solar wind; 9) absence of internal magnetic field for the Venus, Moon and Mars implies non-existence of metallic core in these planets and moons. In all, this theory provide people a new sight to understand the source of the earth's geomagnetic field.
On the Relationship of Lunar Events to Seismic Activity and Its Seasonality
Authors: Kovalyov, M.
A number of authors have proved the existence of a correlation between lunar phases and perigees on one hand and seismic activity on the other hand. A similar number have authors have disproved the existence of such a correlation. We show that such a correlation exists but only "seasonally".
Plausibility of Earth Once Having a Thick Atmosphere – Examining the Rate of Impact Cratering
Authors: Raymond H.V. Gallucci
Theories abound as to how dinosaurs and other prehistoric creatures could have grown to such immense sizes, inconsistent with the spectrum of sizes for today's creatures and Earth's living conditions. Some focus directly on changes in the governing physics of the universe, such as a different gravitational constant. Some postulate that, rather than this difference, the earlier Earth experienced lower gravity due to differences in its size and mass. The majority focus on biological and aerodynamical anomalies that may have prevailed to explain these gargantuan sizes. This paper focuses on the latter group, offering an independent means by which to test the hypothesis that a (much) thicker atmosphere provided the buoyancy needed by these creatures to exist on land. This means is astronomical, an examination of possible differences in the rate of impact cratering on Earth due to atmospheric differences. With the Earth's atmosphere allegedly experiencing eras of much greater thickness than current, and alternating between these "thick" and "thin" atmospheric eras, it is postulated that, in addition to the biological and aerodynamical anomalies, a difference in the cratering rate from meteor impacts on Earth should be evident. Thicker atmosphere would "burn up" more meteors, reducing the cratering rate when compared to that during thinner atmospheric eras. This paper explores this, using the cratering rate from meteor impacts on the Moon as a "control" since it has no atmosphere to attenuate meteors but also is in Earth's orbital vicinity and should have experienced a nearly equivalent rate of meteor influx per unit surface area.
Early Smoothness and Expansion/Contraction of the Earth
Comments: 1 Page. 1 illustration
In Earth's earlier history when it had an extremely thick atmosphere, on par with atmospheres thicker than Jupiter's, the central core was very, very pressurized and essentially liquid. This means it was extremely comparatively smooth to Earth as it currently is with mountains and ocean trenches. A short explanation for how the transition to its varying surface from being at an initial smooth state is provided.
The Rock Cycle Versus Stellar Metamorphosis
All phases of matter exist in stars as they cool and evolve. This means the rock cycle has a closed loop between solid/liquid material and does not give the complete picture of stellar evolution (planet formation), nor does it explain the structures found on the Earth such as a giant iron nickel/core, which comprises a much larger portion of the Earth than just a thin lithosphere.
Correlation Between Solar and Seismic Activity: Prognosis of Earthquakes and Volcanic Eruptions Based on Daily Solar Indexes
Authors: A. M. Eigenson
Large earthquakes and volcanic eruptions are compared with the epochs of minima of 11-year cycles of solar activity. We use the data from 405 earthquakes with magnitude 7 and more and 71 volcanic eruption during 260 years. Close correlation between years of these terrestrial events and years of minima of solar activity is shown. We also use also daily solar indexes SSp and compare them with terrestrial events, constituting the main novelty of this work. Here we use the data of earthquakes between December 856 and January 2016, as well as data of volcanic eruptions in the same period. We subsequently compare daily indexes SSp during 2016 and 4 months of 2017 with earthquakes and volcanic eruptions. An important results is demonstrated: as soon as solar activity curve begins to go down, on the same day or some days after the earthquakes and volcanic eruptions occur. Evidently, this circumstance could be used for prognosis of these terrestrial events for several days in advance. In all cases considered our prognosis is confirmed. This is the main result of this article.
Comment on "Estimating the Extent of Antarctic Summer Sea Ice During the Heroic Age of Antarctic Exploration" by Tom Edinburgh and Jonathan J. Day, the Cryosphere, 10, 2721–2730, 2016.
Authors: Krzysztof Sienicki
No Abstrect
Close Correlation Between Solar and Seismic Activities
Large earthquakes in the last 260 years are compared with the epochs of minima of 11-year cycles of Solar activity. We use the data from 352 earthquakes of magnitude 7 and larger. Close correlation between earthquakes and the minima of solar cycles is shown, with the correlation coefficient of 0.9998. Maximal number of earthquakes shows 11-year periodicity. The number of earthquakes increases with time and reaches its currently largest number in the last Solar cycles, corresponding to the decrease of Solar activity in cycle 23. Furthermore, we analyse the data of large volcanic eruptions in the last 400 years. Similarly to earthquakes, the volcanic eruptions show the correlation with the minima of Solar activity, with the correlation coefficient of 0.9994. The volcanic eruptions also tend to increase with time, corresponding to the decrease of Solar activity. The found correlation between solar and seismic activities opens the possibility of prognosis because the Solar activity may be predicted for many years forward.
Threat of Emergence of Accidents of Nuclear and Other Power Plants Because of Deep Underground Explosions
Authors: Korniienko V
Comments: 15 Pages. In Russian
In article it is shown that property of generators of power plants to develop S-radiations, cause formation of underground tunnels on which under power units hydrocarbons migrate and there is a synthesis of explosives from them. Their deep explosions cause severe accidents of power units about which reasons experts have no consensus. The provided schemes confirm this hypothesis, and growth of volumes of migration of hydrocarbons on tunnels which happens in recent years, increases probability of explosions under power units, increases probability of severe accidents, up to education on the place of reactors of huge holes in the earth. Measures which are capable to prevent such explosions are proposed.
The Prognostics Equation for Biogeochemical Tracers Has no Unique Solution.
Authors: Han Geurdes
In this paper a tracer prognostic differential equation related to the marine chemistry HAMOC model is studied. Recently, the present author found that the Navier Stokes equation has no exact solution. The following question can therefore be justified. Do numerical solutions from prognostic equations provide unique information about the distribution of nutrients in the ocean.
A Tide Loading Driving for Plate Motion
Authors: Yongfeng Yang
Comments: 18 Pages. Please see the following version for a detailed description of this work.
A significant progress in the geophysics field in the last century is the confirmation of plate motion. But the force behind this motion remains unknown so far, regardless of the continuous efforts by scientific community. Here we propose, the daily tide loading yields a liquid pressure onto continental slope via ocean water, this pressure further contributes a horizontal force to push continent's side and thus move continent and the plate it sites on. The resultant horizontal force based on ideal parameters determines a motion of 39.72, 48.98, and 53.26 mm/year respectively for African, Indian, and Australian plate, and a rotation of 6.84*10-9 rad/year for American plate.
Earthquake Theory
Authors: Wan-Chung Hu
Earthquake is thought to be due to plate tectonic movement. However, this theory has several fetal defects which fail to lead successful earthquake prediction. First, sudden outset of earthquake in a certain point cannot be due to chronic continental drift in large scale. Second, continental drift is only proved between South America and Africa which cannot explain all the mechanisms of earthquakes. Third, plate movement theory cannot explain huge intraplate earthquakes. Fourth, the old crusts sunk into toughs after the generation of new crusts in mid-ocean ridge. Thus, it cannot be the driving crusting force for earthquakes. Fifth, we experience a first longitudinal P wave followed by a transverse S wave during earthquakes. If plate movement causes earthquakes, we should experience a transverse S wave first and majorly. Here, I propose that earthquakes are actually the abrupt release of electromagnetic radiation from the faults. There is high temperature which can generate radiation from inside earth, especially accumulation for several decades. This new theory can explain why earthquakes likely happen in hotspots such as Hawaii or in peri-pacific bands because of crust fissures and toughs. This new theory can explain possible huge intra-plate earthquakes. It can also explain the sunquakes or moonquakes which cannot be explained by plate movement theory. It will also explain why super-moon trends to induce earthquakes. The mechanism of earthquake is the gravity acceleration produced by outward light because light is electromagnetic wave as well as gravity wave. This mechanism can also explain earthquake light and ionosphere anomaly as well as EM field anomaly during earthquakes. This new theory will lead a successful earthquake prediction.
Decrease in Disaster Risks from Earthquakes and Explosions of Volcanoes by Extraction of the Hydrocarbons Coming to Them
Authors: V.Korniienko
The analysis of space pictures in a range of S-radiations has allowed us to find global network of breaks tunnels of crust on which from global Polar fields huge volumes of hydrocarbons (HC) migrate to the equator. On the way these tunnels cross all known fields of HC, and also zone of earthquakes, active volcanoes and huge holes in the earth. In these parts porous and jointed rocks in which there is a leak from HC tunnels that creates conditions for synthesis from them explosive substances which explosions cause these cataclysms prevail. We also have developed a method of search of places for drilling in tunnels of search wells that allows to get them unlimited volumes of HC that will cause decrease in number of earthquakes and explosions of volcanoes. It is offered to force production of UV from a tunnel which energy will save the population from the volcanic winter caused by explosion of the Yellowstone volcano.
Way of Ten Times Increase Efficiency of Geological Branch and Row Stok Safety of Mankind
Authors: Feliks Royzenman
Because of exhaustion of stocks of deposits on the Earth's surface, new deposits can be discovered mainly in depth. But confidence of deep earth prognosis of industrial deposits in the modern geology is for most of the minerals just 5-10% (90-95% error!). It threatens the world economy and development of the mankind. To solve this crucial issue, the author developed and successfully used for 40 year a new system of high-precision deep earth prognosis of deposits [3]. This system of prognosis makes the mining and geological industry more than 10-fold efficient, provides mineral and raw-stock supply security and creates the basis for efficient development of civilization. Key words: deposits, deep earth prognosis, high confidence of prognosis, discovery of deposits.
Van Allen Radiation Belts
Authors: Yibing Qiu
Abstract: shows a viewpoint with regards to Van Allen Radiation Belts.
Point de Laplace & Exemple de Calcul Géodésique et Analyse Des Résultats en Géodésie Tridimensionnelle
It is my thesis to obtain the diploma of Engineer from the French National School of Geographic Sciences(ENSG, IGN France), presented in October 1981. The first part of the thesis is concerned with the determination of the equation of the observation of Laplace point in the option of 3D geodesy. The second part is about a study of a 3D model of deformation of geodetic networks that was presented by the Senior Geodesist H.M. Dufour in two dimensions.
Why Don't Clouds Fall?
Authors: Solomon I. Khmelnik
Based on gravitomagnetism theory, a mathematical model of cloud is suggested. It allows answering the question put in the header.
Why do Clouds not Fall Down? \\ Почему облака не падают?
Comments: 3 Pages. in Russian
Based gravitoelectromagnetism theory, described by the mathematical model of the cloud , that allows you to answer the question posed in the title. \\ На основе теории гравитомагнетизма предлагается математическая модель облака, которая позволяет ответить на вопрос, поставленный в заглавии.
The Geometry of Non-Linear Adjustment of the Trisection Problem in the the Option of the 3-Dimensional Geodesy
In an article, E. Grafarend and B. Schaffrin studied the geometry of non-linear adjustment of the planar trisection problem using the Gauss Markov model and the method of the least squares. This paper develops the same method working on an example of the determination of a point by trilateration in the three-dimensional geodetic option for determining the coordinates (x, y, z) of an unknown point from measurements known distances to n points.
Geometric Theory of Inversion and Seismic Imaging II: Inversion + Datuming + Static + Enhancement
Authors: August Lau, Chuan Yin
Comments: 8 pages, 11 figures
The goal of seismic processing is to convert input data collected in the field into a meaningful image based on signal processing and wave equation processing and other algorithms. It is normally a global approach like tomography or FWI (full waveform inversion). Seismic imaging or inversion methods fail partly due to the thin-lens effect or rough surfaces. These interfaces are non-invertible. To mitigate the problem, we propose a more stable method for seismic imaging in 4 steps as layer stripping approach of INVERSION + DATUMING + STATIC + ENHANCEMENT.
Coherent Detection of Signals below Noise Level
The search for a phase coherent signal near 50.93 µHz in the data set of the superconducting gravimeter H1 indicates a weakly damped signal 14 dB below noise. It might belong to the long-sought Slichter triplet.
Time to Dismantle the Megaliths?
Part of ~ 11 500 year old megaliths can be built with purpose- to influence astrogeophysics.
Pore-Scale Modeling of Non-Newtonian Flow in Porous Media
Authors: Taha Sochi
Comments: 190 Pages.
The thesis investigates the flow of non-Newtonian fluids in porous media using pore-scale network modeling. Non-Newtonian fluids show very complex time and strain dependent behavior and may have initial yield stress. Their common feature is that they do not obey the simple Newtonian relation of proportionality between stress and rate of deformation. They are generally classified into three main categories: time-independent, time-dependent and viscoelastic. Two three-dimensional networks representing a sand pack and Berea sandstone were used. An iterative numerical technique is used to solve the pressure field and obtain the flow rate and apparent viscosity. The time-independent category is investigated using two fluid models: Ellis and Herschel-Bulkley. The analysis confirmed the reliability of the non-Newtonian network model used in this study. Good results are obtained, especially for the Ellis model, when comparing the network model results to experimental data sets found in the literature. The yield-stress phenomenon is also investigated and several numerical algorithms were developed and implemented to predict threshold yield pressure of the network. An extensive literature survey and investigation were carried out to understand the phenomenon of viscoelasticity with special attention to the flow in porous media. The extensional flow and viscosity and converging-diverging geometry were thoroughly examined as the basis of the peculiar viscoelastic behavior in porous media. The modified Bautista-Manero model was identified as a promising candidate for modeling the flow of viscoelastic materials which also show thixotropic attributes. An algorithm that employs this model was implemented in the non-Newtonian code and the initial results were analyzed. The time-dependent category was examined and several problems in modeling and simulating the flow of these fluids were identified.
The Aqueous Geochemistry Principle
Comments: 3 Pages. 1 screenshot, 1 illustrative graph
A central tenant to stellar metamorphosis theory is the fact that the stages of the evolution of a star include aqueous material, and this aqueous material facilitates the chemical reactions that occur as the star evolves, cools and dies becoming the remnant or "planet/exoplanet" used in popular circles. This paper outlines a simple fact of geochemistry.
A possible correlation between earthquake, electric fields and ionosphere
Candidates for the Slichter Triplet II
The systematic search for coincident signals with a software-defined receiver in the data sets of fifteen superconducting gravimeters yields six striking signals in the frequency range 35 µHz to 100 µHz that can not be assigned to a known geophysical causes. Some might belong to the long-sought Slichter triplet.
Gravitational Collapse Versus Plate Tectonics to Explain Earthquakes
It is presented sound reasoning that earthquakes are caused by buildup and release of huge amounts of pressure in rocks due to gravitational collapse of the Earth, and not moving plates.
Gravity Waves and Mercury Revise Geodynamo
Most people have a rough idea of the cause of Earth's magnetic field, don't they? It's the geodynamo, also called the magnetic dynamo theory. The heat from the solid inner core puts the liquid outer core in motion, and the movements of the outer core's electrically conducting fluids (such as molten iron) generate the planet's magnetic field. Electrically conducting fluids occur in the Sun, other stars and most planets – and are the scientifically accepted mechanism for magnetic fields. However, the planet Mercury suggests this process is wrong. Is it possible to propose a plausible alternative? The proposal here has both Earthly and Space components - it is still linked to the nature of, and motions in, the core plus it refers to the phenomenon of zero electrical resistance known as superconductivity as well as the recent discovery of gravitational waves. It also refers to the Moon's attraction on Earth's oceans, binary stars, the Sun's coronal heating and mass ejections, sunspots and mini ice ages, and black holes. A proposal that has support from only one or two sources may indeed prove to be correct. But surely support from several additional sources must greatly improve that proposal's chances of success. It's the goal of this article to be comprehensive in presenting its approach to the geodynamo. It's important to properly understand our planet's magnetic field because it protects us from the charged particles of the solar wind and cosmic rays. Without this protection from the magnetosphere, Earth would be stripped of its ozone layer that keeps excess ultraviolet radiation from harming life. And no magnetic field also means no atmospheric light displays called auroras, as well as no direction-finding compasses.
Candidates for the Slichter Triplet
During the last 55 years, there have been many attempts to measure the three frequencies of the 1S1 self-resonance, the vibration of the Earth's core. One reason for this failure could be the insufficient reduction of the background noise, caused by the earthquakes. This is just another attempt to solve the ancient mystery. This time, perhaps with more success ;-)
SG Gravimeters Measure Toroidal Modes of the Earth
In contrast to previous assumptions, gravimeters can measure not only radial movements of the earth's surface, but also horizontal movements. This is first shown on the mode 0T4.
Tidal Asymmetry
Comments: 16 Pages. Also published in the Proceedings of the John Chappell Natural Philosophy Society, Second Annual Conference, July 2016, University of Maryland
The Earth's diametrically opposed, presumably symmetric, tides are due to the Moon's differential gravitational force varying across the Earth. This is not intuitively obvious, but becomes clear when the physics is examined mathematically. The presumed symmetry is due to an approximation that holds when the radius of the affected body (e.g., The Earth) is much less than its center-to-center distance from the affecting body (e.g., the Moon). The exact solution indicates an asymmetry, which becomes more pronounced as the assumption loses its applicability.
More About the Nature of the Earth's Magnetism
A hypothesis of the Earth magnetism nature is presented and debated.
More About the Nature of the Earth's Magnetism \\ Еще о природе Земного магнетизма
A hypothesis of the Earth magnetism nature is presented and debated. \\ Предлагается и обсуждается гипотеза о природе Земного магнетизма.
Analyzing the 13S1, 13S2 and 13S3 Normal Modes
The use of specialized filtering techniques allows the identification of three eigenresonances of the earth near 4800 µHz, which are sensitive to the inner core. Careful programming prevents the formation of interfering intermodulation products and lowers the noise level. The accurately measured frequencies differ by about 1.1% from the PREM predictions.
Time Dependent Analysis of the 2S3 Normal Mode
The time dependent analysis of the normal mode 2S3 near 1244 µHz allows a precise determination of phase and frequency and reveals a phase modulation with a strong geographical dependence. All measurements are performed by a phase-locked loop.
The time dependent analysis of the normal mode 3S2 near 1102.8 µHz allows a precise determination of the frequency and reveals a surprising phase modulation. This phase flip was first observed with the 10S2 normal mode and, by careless use of FFT, it may be misinterpreted as a frequency splitting. The correct demodulation requires the very robust method of homodyn conversion.
Time Dependent Analysis of the 10S2 Quintet
The time dependent analysis of the normal mode 10S2 near 4040 µHz allows a precise determination of the frequencies of the five singlets and reveals a frequency modulation by 23 µHz, probably generated by the moon. The results of the data from 18 stations distributed worldwide deliver very good matching results and may help to figure out some properties of the isotropic layer at the top of the inner core.
Evolutionary Earth Vs. Uniformitarianism
An alternative worldview of Earth's history is presented to replace outdated uniformitarianism philosophy.
The Electromagnetic Signatures Produced by Earthquakes
Comments: 6 Pages. The effects created by the electromagnetic signatures produced by earthquakes need extensive additional study.
For centuries, there was no reliable way to know whether an earthquake was eminent, even though strange animal behavior and odd lights in the sky had been observed before earthquakes. It was noted that long range radio skip was interrupted before the 1960 Valdavia, Chile earthquake and the same interruption occurred before the 1964 Alaska earthquake. Scientists took notice, primarily outside of the seismology community, and began inquiring what mechanism could cause such an interruption. In the 1960s, it was already known that certain types of sunspot activity could cause the same type of radio skip alteration. It is now known there is a prodigious amount of electromagnetic activity proceeding and during an earthquake. It has been demonstrated in the laboratory that certain types of rock act like semiconductors when subjected to stress and produce an electric current that fluctuates. It is not known how many other earthquake related issues remain outside of our knowledge, especially the odd coincidence of human health problems just before and coincident to an earthquake.
Random Dynamics of Dikes
Comments: 19 Pages. Na
Inthis paper, random dynamic systems theory is applied to time series ($\Delta t=5$ minutes) of measurement of water level, $W$, temperature, $T$, and barometric pressure, $P$, in sea dikes. The time series were obtained from DDSC and are part of DMC systems dike maintenance program of the Ommelanderzeedijk in northern Netherlands. The result of numerical analysis of dike $(W,T,P)$ time series is that after the onset of a more or less monotone increase in barometric pressure, an unexpected relatively sharp increase or decrease in water level can occur. The direction of change is related to random factors shortly before the onset of the increase. From numerical study of the time series, we found that $\Delta W_{max}\approx \pm 0.5$ mNAP\footnote{NAP indicates New Amsterdam water level which is a zero determining water level well known in the Netherlands.}. The randomness in the direction of change is most likely explained by the random outcome of two competitive processes shortly before the onset of a continuous barometric pressure increase. The two processes are pore pressure compaction and expulsion of water by air molecules. An important cause of growing barometric pressure increase can be found in pressure subsidence following a decrease in atmospheric temperature. In addition, there is a diurnal atmospheric tide caused by UV radiation fluctuations. This can give an additional $\Delta P_{tide}\approx\pm 0.1$ kPa barometric fluctuation\footnote{1Pa=1Pascal=$1Nm^{-2} \approx 10kg s^{-2}m^{-1}$.} in the mid latitudes ($30^{\circ}N-60^{\circ}N$).
[99] viXra:1601.0248 [pdf] submitted on 2016-01-23 04:06:55
Note sur les Représentations Planes UTM et Gauss-Krüger
In this paper,we present the definitions and the mathematical formulas of the two cartographic mappings UTM and Gauss-Krüger.
Terraforming in Stellar Metamorphosis
Terraforming happens naturally as an end-product of stellar evolution as is covered via the General Theory of Stellar Metamorphosis.
Interconnectedness and Geo-Compatibility: A Paradigm Shift in the Perception of Planet Earth
Nonlinear Science has witnessed exponential growth in recent years, due to the enhanced ability it offers in understanding intricate patterns of system evolution. The present work purports to the application of such nonlinear analysis tools to obtain an enhanced perspective of the home planet earth. Specifically, nonlinear analyses of latitudinal and longitudinal altitude profiles reveal the presence of underlying chaotic dynamics and patterns. Interpretations of these results lead to the concept of interconnectedness of every location on earth to every other location, through space and time, where man and his evolutions and developments are seen as an integral part of nature's transformation. Taking cue from this, the concept of "Geo-Compatibility" is introduced, given by the covariance of their chaotic signatures. Following this, Geo-Compatibilities of assorted location pairs are computed. From the results, it is seen that geographical similarities across and within continents show low and high Geo-Compatibilities respectively. However, the most interesting results are the high values of Geo-Compatibility obtained for pairings between Holy Sites suggesting that the development of civilizations and cultures, which are a result of man-nature interactions over hundreds of years, too possess intricate patterns. The entire work is thus a testimony to the concept of interconnectedness.
A Note on the Errors in the Reduction of Distances
The papers presents the errors during the reduction of ellipsoid distances with the use of the radius of the earth.
Geodetic Calculations
Ii is a powerpoint presentation of the geodetic calculations presented to the seminar "Intensif Calculations Week",27 november -1st december 2006, held at the ENIT school, Tunis.
The Application of Spatial Positioning at the OTC (1982-2004)
The paper is a review of the use of the spatial positioning technology during the years 1982-2004 at the OTC the Tunisian Institute of Surveying and Mapping.
The Polynomial Transformations
We present the polynomial transformations between geodetic systems. Then we study the case of Conformal Polynomial transformations of order 1,2 and 3.
A Note On The Unification of The Tunisian Geodetic Terrestrial Systems
It is a note about the unification of the Tunisian geodetic terrestrial systems used in Tunisia.This note was presented to the International Conference on the Cadastre, 25-26 october 2002, Tunis, Tunisia.
The Otc Contribution to the North African Reference Project Nafref
It the OTC contribution to the NORTH AFRICAN REFERENCE PROJECT - NAFREF - presented at the Second North African Geodetic Workshop On the Unification of the Geodetic References, held in Algiers, 26 - 27 May 2001.
Note Sur la Possibilité de L'Intégration Des Points Ados Dans le Projet Afref
It is a paper presented at the Second North African Geodetic Workshop On the Unification of the Geodetic References, held in Algiers, 26 - 27 May 2001. The paper concerns the integration of the geodetic points determined in ADOS Project in NAFREF Project.
The Model of Bursa-Wolf
The paper explains how we obtain the formulas of the transformation of Bursa-Wolf between two geodetic systems.
The Geometry of the Non-Linear Adjustment- Example of the Problem of Spatial Intersection
The paper concerns the adjustment of the non-linear method by the least squares method with the example of the spatial intersection.
Lecture: Introduction to GPS
Comments: 63 Pages. 63 Slides in French.
It is an introduction to GPS.
The Determination of the Heights of the Geoïd Using the Method of Astro-Geodetic Levelling
Comments: 5 Pages. In French
The determination of the heights of the geoïd by the method of astro-geodetic levelling is described.
The Evolution of the Tunisian Geodesy: from Laplace Points to GPS Stations
This paper concerns the evolution of the Tunisian geodesy from the Laplace geodetic points to the installation of GPS permanant stations in the new Tunisian geodetic network. The paper was prepared for the 120th anniversary of the creation of the Tunisian Topographic Service.
The Unification of the Tunisian GeodeticTerrestrial Systems
Comments: 15 Pages. In French with an abstract.
It is the paper proposed to be presented at the FIG Working Week 2012 "Knowing to manage the territory, protect the environment, evaluate the cultural heritage" Rome, Italy, 6-10 May 2012. The paper descried the unification of the Tunisian terrestrial geodetic systems.
A Memoir of Mathematical Cartography
It is a memoir of mathematical cartography concerning the traduction of the paper '' A Conformal Mapping Projection With Minimum Scale Error" de W.I. Reilly, published in Survey Review, Volume XXII, n°168, april 1973.
A Course of Mathematical Cartography
This is a the numerical version of the manuscript of a course of mathematical cartography given by the General Geographe Engineer A. Commiot in the 1980's, at the ENSG, IGN France. The author has brought some developpment.
Unification the Terrestrial Geodetic Systems by GPS
The paper presents a method to unify many terrestrial geodetic systems using GPS observations.
Selected Papers de L'Ingénieur Abdelmajid Ben Hadj Salem Tome II
Comments: 261 Pages. Key words: Geodesy, Mapping, Differential geometry of the ellipsoïde, Geostatistique. In French.
It is the second part of the selected papers of the Senior Geodesist Abdelmajid Ben Hadj Salem.
Note on Quasi-Conformal Mappings
We give the definition of a quasi-conformal mapping and we present one example.
Selected Papers DE L'ingenieur Abdelmajid Ben Hadj Salem
Comments: 297 Pages. In French. Geodesy, Mapping, Theory of Errors, Differential Geometry of the Ellipsoïd, Geophysics.
This the first part of the Selected Papers of the Senior Engineer Abdelmajid Ben Hadj Salem
Homogeneous Nucleation of Iron/Nickel Vapor During Early Stellar Evolution and the Principle of Differentiation
Comments: 1 Page. 1 diagram, 1 video reference
It is hypothesized that stars undergo homogeneous nucleation (crystal growth in similar patterns) of iron/nickel vapor during early stellar evolution. The evidence is provided in meteorites and inside of all ancient stars which possess these iron/nickel crystal cores.
The Stereographic Projection
The paper concerns the streographic projection or mapping. Its proprieties are described.
Détermination D'un Géoide de Haute Précision Par L'approche D'a. Ardalan I: Rappels de la Théorie de Pizzetti-Somigliana
This paper gives a rappel of the theory of Pizzetti-Somigliana for the determination of a geoid. It is the first part of an investigation to use the approch of A. Ardalan for the calcul of a regional géoid of high resolution to determine a tunisian geoid.
Combinaison of Doppler and Terrestrial Observations in the Adjustment of Geodetic Networks
Comments: 129 Pages. It is my graduate thesis(numerical version) submitted in October 1986 to obtain the Diploma of "Ingénieur Civil Géographe", ENSG, IGN France. In French.
The investigation concerns the combination of Doppler data and terrestrial classical observations for the adjustment of geodetic networks and the determination of the 7 parameters (translation, rotation and scale) between terrestrial geodetic and Doppler networks. Models of adjustment are presented. They are part of two groups : 1- a combined adjustment, 2- a commun adjustment. Bursa-Wolf's model and Molodensky formulas are used to determine the parameters. Systematic errors in orientation and scale of geodetic terrestrial networks are studied.
The Second Structure of Constant Current
Here we explore the structure of DC and the flow of electromagnetic energy in a wire. We show that the flow of electromagnetic energy is spreading inside the wire along a spiral. For a constant current value the density of spiral trajectory decreases with decreasing remaining load resistivity.
Analyse de Structure D'un Réseau Géodésique de Base:aspect Tridimensionnel
Cette étude permettra d'analyser les fondements d'un réseau géodésique de base ou primordial et de comparer les déformations que subit le réseau en des points séparés par de longues distances.
Cours de Cartographie Mathématique et Les Transformations de Passage Entre Les Systèmes Géodésiques
Comments: 86 Pages. in French, with an index.
A course of mathematical cartography and transformations between geodetic systems, given to the students of Geomatic department of the ESAT school, the first semester of 2015.
Note Sur la Méthode Des Référentiels Inverses Régionaux en Géodésie
In this paper, a review of the regional inverse referential is presented with application on geodesy for the determination of the parameters of the passage from a geodetic system to another. An numerical exemple is also given.
Eléments de Géodésie et de la Théorie Des Moindres Carrés
It is a preliminary version of a book on " Geodesy and the Theory of Least Squares". The book contains two parts. The first part is about geomtric and spatial geodesy. The second part concerns the theory of errors of least squares, we give an idea of the theory when we use non-linear models.
Replacements of recent Submissions
[48] viXra:1906.0045 [pdf] replaced on 2019-06-14 13:25:32
Authors: Abdelmajid Ben Hadj Salem, Magtouf Rezgui
Comments: 6 Pages. In French. It is a numerical version of the original paper.
Systèmes de Référence, Systèmes Projectifs
Authors: Henri Marcel Dufour, Abdelmajid Ben Hadj Salem
Many geodetic works currently exist on the surface of the globe, which have developed through regional networks, usually each having a fundamental point, where the astronomical data (\phi= latitude,\lambda=longitude,Az=azimuth) of a reference are confused with the counterparts geodetic data. The comparison of 2 networks, and, step by step, of all the connectable networks, can be done by the analysis of the coordinates of their common points. To this end, we can use 3 types of coordinates: - Geographical coordinates = simple method, but not very convenient for different ellipsoids. - Three-dimensional cartesian coordinates, the most rigorous method in the case where the so-called geoid correction has been made. - Coordinates in conformal projection. An analysis of the main formulas that can be used is studied by the first author in this article.
Authors: Fezzani Chedly, Abdelmajid Ben Hadj Salem
From Hilbert to Dilbert: a Non-Orthodox Approach to Gravitation, Psychosynthesis, Economics, Cosmology and Other Issues
Authors: Victor Christianto, Florentin Smarandache, Robert Neil Boyd, Yunita Umniyati, Daniel Chandra
Comments: 208 Pages. This book has been published by Divine Publisher. Your comments are welcome
This book took an unconventional theme because we submit an unorthodox theme too. Karl Popper's epistemology suggests that when the theory is refuted by observation, then it is time to look for a set of new approaches. In the first chapter, it is shown that Hilbert's axiomatic program has failed not only by experiment (Mie theory does not agree with experiment) but also in terms of logic (Gödel theorem). Therefore we set out a new approach, starting from an old theory of Isaac Newton. Dilbert cartoon series often offer surprising for old problems, especially in this era of corporatocracy. Now we would call such an out-of-the-box solution to the old Hilbert axiomatic program as Dilbert way (or Dilbertian, if you wish). Readers may ask : but what can physicists learn from Dilbert cartoons? While it seems not obvious at first glance, yes we believe there is a great character of Dilbert cartoon, i.e. to put it in one phrase: "out-of-the box and brutally honest." We do think that such a brutal honesty is also needed in many fields of physics: from theoretical physics to applied physics, as will be discussed throughout this book.
Comments: 5 Pages. I fixed two English grammar errors. Now I think the paper is in its final form.
Five days before the 2008 Sichuan M8.0 Earthquake, I observed strange electrical signals from a tomato plant in Yilan, Taiwan. That opened my door to quake forecast. Since then, I observed electrical signals of plants, tofu, soil, water or air to predict earthquakes. I successfully predicted a lot of quakes. Now I have about 30 quake forecast stations all over the world. I will publish a series of papers for my discoveries in the past 10 years. This paper is the start of the series. I am Founder and CEO of Taiwan Quake Forecast Institute.
Comments: 5 Pages. I added Chinese translation to my original English paper. Now the paper is in English and Chinese.
The Earth Moon Collisions: Presenting Three Collisions in Detail
To verify the likelihood of a new solar system formation hypothesis, research was conducted into a possible low speed, shallow angled collision between an ice-covered Earth and Moon, 4.1 billion years ago. Via a tailored set of indicators, not just one but three collisions were identified beyond a reasonable doubt. All are presented in great photographic and topographic detail in this paper. On the Moon, the three impact areas are: Aitkin basin, a double string of major maria and wider Oceanus Procellarum. On Earth, the respective corresponding impact areas are: The Arctic, the Canadian Shield and equatorial Gondwana (centred at current Antarctica). As a result, many issues in geology can now be explained, from the 'faint young Sun paradox' to Hadean geology and continental drift.
Authors: Mikhail Kovalyov
In this paper we discuss the previously unnoticed connection of the Tunguska explosion to natural events decades or even centuries long: 1) the third geomagnetic maximum appeared not too far from the epicenter of the Tunguska explosion in the 19th century and has been moving towards the epicenter of the Tunguska explosion along a straight line since 1908; 2) the magnetic North Pole is moving along the path leading to the epicenter of the Tunguska explosion, 3) all magnitude > or = 7.6 earthquakes sufficiently far from the ocean form an arrow pointing towards the epicenter of the Tunguska explosion; 4) the Tunguska explosion occurred at the end of the twisted portion in the path of the magnetic North Pole and at the time when magnitude > or =8.2 earthquakes and VEI > or = 5 volcanic eruptions recovered correlation with syzygies.
Comments: 23 Pages. the articles replaces the previous versions which had an arithmetical mistake
The effect of lunar syzygies on powerful seismic events is studied.
On the Relationship of Seismic Activity to Lunar Motion.
We discuss the correlation of seismic activity on Earth with the closest/2nd closest perigees and New/Full Moon. We show that the time and nature of correlation depend on the type of earthquakes and on the time interval considered.
Authors: Raymond H Gallucci
Comments: 20 Pages. Now includes presentation.
The Rock Cycle Versus Stellar Metamorphosis: The Rock Cycle is Outdated
Comments: 3 Pages. 3 pictures
What Drives Plate Motions ?
Plate motion is an amazing feature on the Earth and is widely ascribed to several driving forces like ridge push, slab pull, and basal drag. However, an in-depth investigation shows these forces incomplete. Here we propose, the deep oceans are generating pressures everywhere, the application of these pressures over the walls of ocean basins, which consists of the sides of continents, may yield enormous horizontal forces (i.e., the ocean-generating forces), the net effect of these forces provides lateral push to the continents and may cause them to move horizontally, further, the moving continents drag the crusts that they connect to move, these totally give birth to plate motion. A roughly estimation shows that the ocean-generating forces may give South American, African, Indian, and Australian continents a movement of respectively 2.8, 4.2, 5.7, and 6.3 cm/yr, and give Pacific Plate a movement of 8.9 cm/yr.
Comments: 40 Pages. Significant improvements are made in this version.
What Drives Plate Motion?
Plate motion was widely thought to be a manifestation of mantle dynamics. However, an in-depth investigation shows this understanding incompetent. Here we propose, the tide-related oceans yield varying pressures between them, the application of these pressures to the continent's sides forms enormously unequal horizontal forces (i.e., the ocean-generating forces), the net effect of these forces provides lateral push to the continent and may cause it to move horizontally, further, the travelling continent works its adjacent crusts to move, these totally form plate motion. A roughly estimation shows that the ocean-generating force may give South American, African, Indian, and Australian continents a movement of respectively 2.8, 4.2, 5.7, and 6.3 cm/yr, and give Pacific Plate a movement of 8.9 cm/yr. Some torque effects of the ocean-generating force contributes to rotate North American and Eurasian continents.
Comments: 27 Pages. Significant improvement was made in this present version.
Plate motion was widely thought to be a manifestation of mantle dynamics. However, an in-depth investigation shows this understanding incompetent. Here we propose, the daily tides yield varying pressures between oceans, the application of these pressures to the continent's sides forms enormously unequal horizontal forces, the net effect of these forces provides lateral push to the continent and may cause it to move horizontally, further, the moving continent by basal drag entrains its adjacent crust to move, these totally give birth to plate motion. A roughly estimation shows that the oceanic tide-generating force may independently give South American, African, Indian, and Australian continents a movement of respectively 2.8, 4.2, 5.6, and 6.3 cm/yr. Some torque effects may rotate North American and Eurasian continents, and a combination of two lateral pushes offers Pacific Plate unusual motion (nearly orthogonal to Australian plate's motion).
What Drives Plate Motions?
Plate motion was widely thought to be a manifestation of mantle dynamics. However, an in-depth investigation shows this understanding incompetent. Here we propose, the daily tides yield varying pressures between oceans, the application of these pressures to the continent's sides forms enormously unequal horizontal forces, the net effect of these forces provides lateral push to the continent and may cause it to move horizontally, further, the moving continent by basal drag entrains its lower lithosphere to move, these totally form plate motion. Quantitatively estimation shows that the tide generating force give South American, African, Indian, and Australian continents a movement of respectively 2.8, 4.2, 5.6, and 6.3 cm/yr. A torque effect may independently rotate North American and Eurasian continents, and the combination of two lateral pushes offers Pacific Plate unusual motion (nearly orthogonal to Australian plate's motion).
Comments: 24 Pages. Significant improvement is made in this version.
Plate tectonics that principally describes earth's plate motion and terrestrial features was long thought to be a manifestation of mantle dynamics. However, an in-depth investigation finds the convection currents incompetent in explaining plate motion. Here we propose, the daily tide loadings around the margins of continents yield unequal pressures onto continental slopes, the net effect of these pressures is to push continents to horizontally move. The travelling continents, by means of basal friction, moderately entrain the continental crusts beneath them and adjoining oceanic crusts, creating weaker motions and terrestrial features for the latter. Quantitatively estimation shows that the pressures yielded due to tide loadings provide South American, African, Indian, and Australian continents respectively a motion of 33, 20, 64, and 71 mm/year. A torque effect likely contributes rotation to North American and Eurasian continents, while the combination of two lateral push forces respectively from North American Plate and from Australian Plate gives Pacific Plate unusual motion (nearly orthogonal to the Australian Plate's).
What Drives the Earth's Plates ?
Comments: 20 Pages. Significant revision in this version.
Plate tectonic theory that comprehensively describes the earth's plate motion and terrestrial features represents one of the most significantly achievements in the past 100 years. However, an indisputable fact around this theory is the force behind plate motion is still unknown. Here we propose, the daily tide loadings around continents yield pressures onto continental slopes, the net effect combined from these pressures pushes the continents to globally move. These moving continents, representing the upper parts of the continental crusts, by means of basal friction, moderately entrain the crusts beneath them and the adjoining oceanic crusts, creating various terrestrial features. Quantitatively estimation shows that tide loadings provide South American, African, Indian, and Australian continents respectively a nearly straight motion of 28.44, 41.11, 55.63, and 61.60 mm/year. A torque effect likely contributes rotation to North American and Eurasian continents.
Comments: 4 Pages. 3 illustrations, 1 link
The stages of the evolution of a star include aqueous material, and this aqueous material facilitates the chemical reactions that occur as the star evolves, cools and dies becoming the remnant or "planet/exoplanet" used in popular circles. This paper outlines a simple fact of geochemistry.
Gravitational Waves Explain Planetary Magnetic Fields
The cause of Earth's magnetic field is said to be the geodynamo, also called the magnetic dynamo theory. The heat from the solid inner core puts the liquid outer core in motion, and the movements of the outer core's electrically conducting fluids (such as molten iron) generate the planet's magnetic field. Electrically conducting fluids occur in the Sun, other stars and most planets – and are the scientifically accepted mechanism for magnetic fields. However, the planets Mercury and Venus suggest this process is only partly correct.
During the last 55 years, there have been many unsuccessful attempts to measure the three frequencies of the 1S1 self-resonance, the vibration of the Earth's core. One reason for this failure could be the insufficient reduction of the background noise, caused by the earthquakes. This is just another attempt to solve the ancient mystery. This time, perhaps with more success ;-)
The Unification of the Tunisian Terrestrial Geodetic Systems
Comments: 15 Pages. In French with an abstract
It is the paper proposed to be presented at the FIG Working Week 2012 "Knowing to manage the territory, protect the environment, evaluate the cultural heritage" Rome, Italy, 6-10 May 2012. The paper described the unification of the Tunisian terrestrial geodetic systems.
Selected Papers de L'Ingénieur Abdelmajid Ben Hadj Salem Tome I
Comments: 297 Pages. In French. Key words: Geodesy, Mapping, Theory of Errors, Differential Geometry of the ellipsoïd, Geophysics.
This is the first part of the Selected Papers of the Senior Engineer Abdelmajid Ben Hadj Salem.
[9] viXra:1511.0231 [pdf] replaced on 2016-01-28 11:33:59
Contact - Disclaimer - Privacy - Funding | CommonCrawl |
\begin{document}
\title{ extbf{Quantum Machine and SR Approach: a Unified Model} \begin{abstract} \noindent The Geneva--Brussels approach to quantum mechanics (QM) and the semantic realism (SR) nonstandard interpretation of QM exhibit some common features and some deep conceptual differences. We discuss in this paper two elementary models provided in the two approaches as intuitive supports to general reasonings and as a proof of consistency of general assumptions, and show that Aerts' \emph{quantum machine} can be embodied into a macroscopic version of the \emph{microscopic SR model}, overcoming the seeming incompatibility between the two models. This result provides some hints for the construction of a unified perspective in which the two approaches can be properly placed.
\noindent \textbf{Key Words}. quantum mechanics; quantum machine; semantic realism. \end{abstract} \section{Introduction} The \emph{Geneva--Brussels} (\emph{GB}) \emph{approach} to quantum mechanics (QM) is well known. It was started by Jauch and Piron in Geneva \cite{j68}, \cite{p76} and then continued by Aerts and his collaborators in Brussels \cite{a82}--\cite{a04}. It can be classified in the field of ``quantum structures research'' \cite{a99b}, aiming both at basing QM on fundamental concepts that can be operationally defined and at providing a physical justification of the relations established by QM among these concepts. In its latest version it also proposes, however, some fundamental changes of the standard theory in order to avoid a number of quantum problems and paradoxes and overcome the limits of the QM description of the physical world (with special attention to compound quantum systems).
The GB approach exhibits two relevant features. Firstly, quantum probabilities are interpreted as \emph{epistemic} (they express our ignorance about \emph{hidden measurements} rather than about hidden states of the physical system), at variance with the standard interpretation, where quantum probabilities are (mostly) ontologic. Secondly, the mathematical structure of the set of \emph{empirical propositions} called quantum logic (QL) is interpreted as a consequence of our ``possibilities of active experimenting'' on physical systems, not as a new logic formalizing some ``process of our reflection'', so that QL does not characterize the microscopic world (indeed, when our possibilities of active experimenting on a \emph{macroscopic} entity are suitably limited, one can find quantum logical structures associated with this entity).
The above features also appear within the \emph{semantic realism} (\emph{SR}) \emph{interpretation} of QM propounded by the Lecce research group on the foundations of QM as an alternative to the standard interpretation \cite{gs96a}--\cite{ga02}, aiming to avoid the same problems and paradoxes considered by the GB approach. Moreover, the SR interpretation also implies that a broader theory embodying QM is, at least in principle, possible. This suggests that a comparison between the two perspectives could be interesting, and that an attempt at extablishing links between them could be fruitful. Yet, whenever one starts this job, one immediately meets a serious difficulty. Indeed, the GB approach is highly contextual, following in this sense the standard QM tradition. On the contrary, the SR interpretation mantains that contextuality is the root of most quantum paradoxes and elaborates a strategy (based on some epistemological criticisms to the standard interpretation) to avoid it without conflicting with the mathematical apparatus and the predictions of QM. Thus the two approaches seem conceptually incompatible at first sight. However, a deeper insight shows that this is not necessarily the case. We cannot yet prove this by providing a general perspective in which both approaches find a proper place, but we can show that an integration is possible in the case of the models introduced in the GB and SR approaches as intuitive supports to general reasonings (and also as a demonstration of consistency of some abstract assumptions, especially within the SR interpretation). To be precise, we intend to show in the present paper that a macroscopic version of the intuitive picture for the SR model provided in some previous papers \cite{ga03}, \cite{gp04} (briefly, \emph{microscopic SR model} in the following) can be constructed which embodies Aerts' \emph{quantum machine} (which plays an important role in Aerts' approach since it provides a macroscopic model for spin measurements on spin--$\frac{1}{2}$ quantum systems). This \emph{unified} (\emph{SR}) \emph{model} provides the same predictions as Aerts' quantum machine whenever one takes into account those and only those samples of the physical system under investigation that are actually detected if a measurement is performed. In this sense we can say that the two models are formally equivalent (the equivalence is attained, however, by means of a rather artificial and complicate construction, which does not aim to represent any physical reality but only to illustrate a logical possibility).
It must still be stressed that our unified model applies to quantum systems described by two dimensional Hilbert spaces, just as the quantum machine. The GB approach provides, however, more general models which apply to higher dimensional quantum cases. Embodying these models within a generalized unified (SR) model seems possible in principle (the microscopic SR model makes no reference to the dimensionality of the Hilbert space of the system) but it may raise some problems. In particular, it could be difficult in this case to reconciliate the contextuality of the GB models with the noncontextuality of the SR model. We do not discuss this problem in the present paper and limit ourselves to note that the remarks in Sec. 4.1 on the different notions of contextuality introduced in the literature may help in solving it.
Finally, let us briefly resume the content of the various sections of our paper. Firstly, we sketch the guidelines of the microscopic SR model and quantum machine in Secs. 2 and 3, respectively. This leads us, in particular, to complete the microscopic SR model by means of some equations which do not appear in the original draft. Then, our unified model is introduced in Sec. 4, it is discussed in the case of pure states in Sec. 4.1, and it is generalized to the case of mixed states in Sec. 4.2.
\section{The microscopic SR model} As we have anticipated in the Introduction, the consistency of the SR approach has recently been demonstrated by means of a set--theoretical model, the microscopic SR model, that shows, circumventing known no--go theorems, how a local and noncontextual (hence objective) picture of the microworld can be constructed without altering the formalism and the (statistical) interpretation of QM. We report the essentials of it here.
To begin with, let us accept the standard notion of state of a physical system $\Omega$ as a class of physically equivalent preparing devices \cite{l83}. Furthermore, let us call \emph{physical object} any individual sample $x$ of $\Omega$ obtained by activating a preparing device, and say that \emph{x is in the state $S$} if the device $\pi $ preparing $x$ belongs to $S$. Whenever $\Omega$ is a microscopic physical system, let us introduce a set $\mathcal{E}$ of \emph{microscopic} physical properties that characterize $\Omega$ and play the role of theoretical entities. For every physical object $x$, every property $f \in \mathcal{E}$ is associated with $x$ in a dichotomic way, so that one briefly says that every $f \in \mathcal{E}$ either is possessed or it is not possessed by $x$. This is the main difference between the SR interpretation and the ortodox interpretation of QM, in which it is assumed that microphysical objects generally do not possess a property until it is measured \cite{me93}. The set $\mathcal{F}_{0}$ of all \emph{macroscopic} properties is then introduced as in standard QM, that is, it is defined as the set of all pairs of the form $({\mathcal A}_{0},\Delta)$, where ${\mathcal A}_{0}$ is an observable (that is, a class of physically equivalent measuring apparatuses) with spectrum $\Lambda _{0}$, and $\Delta $ a Borel set on the real line $\Re$ (for every observable ${\mathcal A}_{0}$, different Borel sets containing the same subset of $\Lambda _{0}$ obviously define physically equivalent properties; we note explicitly that, whenever we speak about macroscopic properties in the following, we actually understand such classes of physically equivalent macroscopic properties). Yet, every observable ${\mathcal A}_{0}$ is obtained from a suitable observable $\mathcal{A}$ of standard QM by adding to the spectrum $\Lambda $ of $\mathcal{A}$ a further outcome $a_{0}$ that does not belong to $\Lambda$, called the \emph{no--registration} outcome of $\mathcal{A}_{0}$ (note that such an outcome is introduced also within the standard quantum theory of measurement, but it plays here a different theoretical role), so that $\Lambda _{0}=\Lambda\cup \left\{ a_{0} \right\}$. The set $\mathcal{E}$ of all microscopic properties is then assumed to be in one--to--one correspondence with the subset ${\mathcal F} \subseteq {\mathcal F}_{0}$\ of all macroscopic properties of the form $F=({\mathcal A}_{0},\Delta)$, where ${\mathcal A}_{0}$ is an observable and $a_{0}\notin \Delta$.
Basing on the above definitions and assumptions, one can provide the following description of the measurement process. Whenever a physical object $x$ is prepared in a state $S$ by a given device $\pi $, and ${\mathcal A}_{0}$ is measured by means of a suitable apparatus, the set of microscopic properties possessed by $x$ produces a probability (which is either 0 or 1 if the model is \emph{deterministic}) that the apparatus does not react, so that the outcome $a_{0}$ may be obtained. In this case, $x$ is not detected and one cannot get any explicit information about the microscopic physical properties possessed by $x$. If, on the contrary, the apparatus reacts, an outcome different from $a_{0}$, say $a$, is obtained, and one is informed that $x$ possesses all microscopic properties associated with macroscopic properties of the form $F=({\mathcal A}_{0},\Delta)$, where $\Delta $ is a Borel set such that $a_{0}\notin \Delta $ and $a \in \Delta $ (for the sake of brevity we also say that $x$ \textit{possesses} all macroscopic properties as $F$ in this case).
In order to place properly quantum probability within the above picture, let us consider a preparing device $\pi \in S$ that is activated repeatedly. In this case a (finite) set $\mathscr{S}$ of physical objects in the state $S$ is prepared. Then, let us partition $\mathscr{S}$ into subsets ${\mathscr S}^{1}$, ${\mathscr S}^{2}$, ..., ${\mathscr S}^{n}$, such that in each subset all objects possess the same \emph{microscopic} properties (we can briefly say that the objects in ${\mathscr S}^{i}$, possessing the same microscopic properties, are in the same \emph{microstate} $S^{i}$), and assume that a measurement of an observable ${\mathcal A}_{0}$ is done on every object. Finally, let us introduce the following symbols (see \textbf{Fig. 1}).
\begin{center}
\begin{tabular}{|c|c|c|c|c|c|c|} \hline ${\mathscr S}^{1}$ & \ldots & ${\mathscr S}^{i}$ & \ldots & ${\mathscr S}^{j}$ & \ldots & ${\mathscr S}^{n}$ \\ $(g,f,h,..)^{1}$ & \ldots & $(g,f,\neg h..)^{i}$ & \ldots & $(g,\neg f,h,..)^{j}$ & \ldots & $(\neg g,\neg f,h,..)^{n}$ \\ $N^{1}$ & \ldots & $N^{i}$ & \ldots & $N^{j}$ & \ldots & $N^{n}$ \\ \hline \hline
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\ $N_F^{1}=$ & & $N_{F}^{i}=$ & & $N_F^{j}=0$ & & $N_F^{n}=0$ \\ $N^{1}-N_0^{1}$ & & $N^{i}-N_0^{i}$ & & & & \\
& & & & & & \\
& & & & & & \\ \cline{6-6} & & & & & & \\ \cline{3-3} & & & & & & \\ \cline{1-1} & & & & & & \\ \cline{7-7} & & & & & & \\ \cline{5-5} & & & & & & \\ \cline{4-4} \cline{2-2} & & & & & & \\ $N_0^{1}$ & & $N_0^{i}$ & & $N_0^{j}$ & & $N_0^{n}$ \\
& & & & & & \\ \hline \end{tabular} \end{center}
\noindent \textbf{Fig. 1}. \emph{Set--theoretical representation of the general SR model. The property $F$ is the macroscopic property corresponding to the microscopic property $f$.}
(i) The number $N$ of physical objects in ${\mathscr S}$.
(ii) The number $N_{0}$ of physical objects in ${\mathscr S}$ that are not detected.
(iii) The number $N^{i}$ of physical objects in ${\mathscr S}^{i}$.
(iv) The number $N_{0}^{i}$ of physical objects in ${\mathscr S}^{i}$ that are not detected.
(v) The number $N_{F}^{i}$ of physical objects in ${\mathscr S}^{i}$ that possess the macroscopic property $F=({\mathcal A}_{0},\Delta)$, with $a_0 \notin \Delta$, corresponding to the microscopic property $f$.
It is apparent that the number $N_{F}^{i}$ either coincides with $N^{i}-N_{0}^{i}$ or with $0$. The former case occurs whenever $f$ is possessed by the objects in ${\mathscr S}^{i}$, since all objects that are detected then yield outcome in $\Delta$. The latter case occurs whenever $f$ is not possessed by the objects in ${\mathscr S}^{i}$, since all objects that are detected then yield outcome different from $a_{0}$ but outside $\Delta $ (note that the microscopic property $\neg f$ corresponding to $F^{\perp}=({\mathcal A}_{0}, \Re \setminus (\Delta \cup \{ a_0 \}))$ is possessed by the objects in ${\mathscr S}^{i}$ in this case). In both cases one can assume that $N^{i}-N_{0}^{i}\neq 0$\footnote{Note that in a deterministic model either $N_0^i=0$ or $N_0^i=N^i$, hence either $N^i-N_0^{i}=N^{i}$ or $N^i-N_0^{i}=0$, so that the assumption $N^{i}-N_{0}^{i}\neq 0$ does not hold. However, $N^{i}-N_{0}^{i}=0$ implies $N_F^{i}=0$, and eq. (\ref{macro2}) can be recovered by modifying our reasonings in an obvious way.}, so that the following equation holds. \begin{equation} \label{micro1} \frac{N_{F}^{i}}{N^{i}}=\frac{N^{i}-N_{0}^{i}}{N^{i}}\frac{N_{F}^{i}}{N^{i}-N_{0}^{i}}. \end{equation} The term on the left in eq. (\ref{micro1}) represents the fraction of objects possessing the property $F$ in $\mathscr{S}^{i}$, the first term on the right the fraction of objects in ${\mathscr S}^{i}$ that are detected, the second term (which is either $0$ or $1$) indicates whether the objects in ${\mathscr S}^{i}$ that are detected possess the property $F$ or not.
The fraction of objects in ${\mathscr S}$ that possess the property $F$ is given by \begin{equation} \label{macro1} \frac{1}{N}\sum_{i}N_{F}^{i}=\frac{N-N_{0}}{N} \Big (\sum_{i}\frac{N_{F}^{i}}{N-N_{0}} \Big ). \end{equation} Let us assume now that all fractions of objects converge in the large number limit, so that they can be substituted by probabilities, and that these probabilities do not depend on the choice of the preparing device $\pi$ in $S$. Hence, if one considers the large number limit of eq. (\ref{micro1}), one gets \begin{equation} \label{micro2} {\mathscr P}_{S}^{i,t}(F)={\mathscr P}_{S}^{i,d}(F) {\mathscr P}_{S}^{i}(F), \end{equation} where ${\mathscr P}_{S}^{i,t}(F)$ is the total probability that a physical object $x$ which possesses the microscopic properties that characterize ${\mathscr S}^{i}$, \emph{i.e.}, which is in the state $S^{i}$, also possesses the property $F$, ${\mathscr P}_{S}^{i,d}(F)$ is the probability that $x$ is detected when $F$ is measured on it, ${\mathscr P}_{S}^{i}(F)$ (which is either $0$ or $1$) is the probability that $x$ possesses the property $F$ when detected. Analogously, the large number limit of eq. (\ref{macro1}) yields \begin{equation} \label{macro2} {\mathscr P}_{S}^{t}(F)={\mathscr P}_{S}^{d}(F) {\mathscr P}_{S}(F), \end{equation} where ${\mathscr P}_{S}^{t}(F)$ is the total probability that a physical object $x$ in a state $S$ possesses the property $F$, ${\mathscr P}_{S}^{d}(F)$ is the probability that $x$ is detected when $F$ is measured on it, ${\mathscr P}_{S}(F)$ is the probability that $x$ possesses the property $F$ when detected.
If we identify the previous probabilities with the corresponding fractions of objects in the large number limit, it is possible to express the macroscopic probabilities in eq. (\ref{macro2}) in terms of the microscopic probabilities in eq. (\ref{micro2}). Indeed, \begin{displaymath} {\mathscr P}_{S}^{d}(F)=\frac{N-N_0}{N}=\frac{1}{N}\sum_{i} (N^{i}-N_{0}^{i})=\sum_{i} \Big ( \frac{N^{i}}{N}\frac{N^{i}-N_{0}^{i}}{N^{i}} \Big )= \end{displaymath} \begin{equation} \label{newprobability-d}
=\sum_{i} {\mathscr P}(S^{i}|S) {\mathscr P}_{S}^{i,d}(F), \end{equation}
where we have identified the fraction of objects in the microstate $S^{i}$ with respect to the objects in the state $S$ with the conditional probability ${\mathscr P}(S^{i}|S)$ that an object $x$ in the state $S$ actually is in the microstate $S^{i}$. Analogously, we get \begin{displaymath} {\mathscr P}_{S}^{t}(F)=\frac{1}{N}\sum_{i}N_{F}^{i}=\sum_{i}\Big ( \frac{N^{i}}{N}\frac{N^i-N_0^i}{N^{i}}\frac{N_{F}^{i}}{N^i-N_0^i} \Big )= \end{displaymath} \begin{equation} \label{newprobability-t}
=\sum_{i} {\mathscr P}(S^{i}|S) {\mathscr P}_{S}^{i,d}(F){\mathscr P}_{S}^{i}(F). \end{equation}
The interpretation of ${\mathscr P}_{S}(F)$ makes it reasonable to identify this probability with the quantum probability that a physical object in the state $S$ possesses the property $F$. Hence, standard QM can be recovered within the model as the theory that allows one to evaluate ${\mathscr P}_{S}(F)$ (and its evolution in time) for every system $\Omega$, state $S$, and property $F=({\mathcal A}_{0},\Delta)$ such that $a_{0}\notin \Delta $. In this perspective, no change of the formalism and the statistical interpretation of standard QM is required. In particular, any state $S$ can be represented, as usual, by means of a trace class operator $\rho _{S}$ on a Hilbert space $\mathscr {H}$ associated with $\Omega$ and any macroscopic property $F$ that corresponds to a microscopic property can be represented by means of a projection operator $P_{F}$ on $\mathscr{H}$, so that ${\mathscr P}_{S}(F)=Tr \{\rho_{S}P_{F} \}$. Thus, the model provides a picture of the microworld which embodies standard QM. This picture is objective, in the sense that for every physical object $x$ in the state $S$, every macroscopic property of the form $F=(\mathcal{A}_{0},\Delta)$ (where $a_{0}$ may now belong or not to $\Delta$) either is possessed or is not possessed by $x$, and the probability that it is possessed/not possessed is determined by the microscopic properties possessed by $x$, which do not depend on the measuring apparatus (hence microscopic properties play in the model a role similar to states in objective local theories \cite{ch74}).
Objectivity has some relevant consequences. We list here some of them.
(i) The probabilities that appear in the microscopic SR model are epistemic, since they can be interpreted as due to a lack of knowledge about microscopic properties.
(ii) The local and noncontextual picture of the microworld provided by the microscopic SR model is inconsistent with the Bell and the Bell--Kocken--Specker theorems. One it can show that it violates an assumption underlying those theorems, which is usually left implicit. Whenever this assumption is stated explicitly, it proves to be physically problematical \cite{gs96b}, \cite{ga99}, \cite{ga00}, \cite{ga02}, \cite{gp04}, which makes its violation admissible.
(iii) From the viewpoint of the model, QM is a theory that is incomplete in several senses (it does not provide the probabilities ${\mathscr P}_{S}^{t}(F)$ and ${\mathscr P}_{S}^{d}(F)$ and it does not say anything about the distribuition of microscopic properties on physical objects in a given state whenever the objects are not detected). From this viewpoint, a broader theory embodying QM can be envisaged, according to which the quantum probability ${\mathscr P}_{S}(F)$ is considered as a conditional rather than an absolute probability.
(iv) The microscopic properties that appear in the model are hidden parameters, but are not hidden variables in the standard sense. Indeed, it can be proved \cite{ga02}, \cite{gp04}, \cite{ga05} that they are not bound to satisfy in every physical situation the condition introduced by Kocken and Specker as a basic requirement ``for the successful introduction of hidden variables'' \cite{ks67}, \cite{me93}. This explains why microscopic properties are noncontextual.
(v) The no--registration outcome does not occur because of flaws of the measuring apparatus, but it is determined by the microscopic properties of the physical object. Hence, ${\mathscr P}_{S}^{d}(F)$ may be less than $1$ also in the case of ideal apparatuses.
\section{The quantum machine} By introducing the entity called \emph{quantum machine} \cite{a86}--\cite{a94b} one can produce a macroscopic model for measurements on a quantum system described by a two--dimensional Hilbert space (\emph{e.g.}, a spin--$\frac{1}{2}$ quantum particle whenever only spin observables are taken into account), which suggests that quantum probabilities can be reinterpreted as epistemic rather than ontologic.
The quantum machine consists of a classical point particle bound to stay on the surface of a spherical ball with radius $1$. Hence each pure state of the machine is represented by a point $P$ of this surface, or, equivalently, by a position vector $\vec v$ belonging to the unitary \emph{Aerts sphere}. Furthermore, each possible experiment connected to the quantum machine can be described as follows. Consider two diametrically opposite points on the Aerts sphere, briefly identified with the (unitary) position vectors $\vec u$ and $-\vec u$ respectively, and install an elastic strip of $2$ units of length, fixed with one of its end--points in $\vec u$ and the other end--point in $-\vec u$ (\textbf{Fig. 2 (a)}). Whenever the experiment is performed, the particle falls from its original place orthogonally onto the elastic, and sticks to it (\textbf{Fig. 2 (b)}). Then, the elastic breaks at some arbitrary point. Consequently the particle, attached to one of the two pieces of the elastic (\textbf{Fig. 2 (c)}), is pulled to one of the two end--points $\vec u$ or $-\vec u$ (\textbf{Fig. 2 (d)}). Now, depending on whether the particle arrives in $\vec u$ or in $-\vec u$, we give the outcome $o_1$ or $o_2$ to the experiment.
Let us now calculate the probabilities of the two outcomes. If we demand that the elastic, installed between $\vec u$ and $-\vec u$, can break at any point of this interval with the same probability, the probability $\mu(\vec u, \vec v, o_1)$ that the particle ends up in point $\vec u$, so that the experiment gives outcome $o_1$, when the quantum machine is in the state represented by the vector $\vec v$, is given by the length of the piece of elastic $L_1$ divided by the total length of the elastic (\textbf{Fig. 3}). The probability $\mu(\vec u, \vec v, o_2)$ that the particle ends up in point $-\vec u$, so that the experiment gives outcome $o_2$, when the quantum machine is in the state represented by the vector $\vec v$, is given by the length of the piece of elastic $L_2$ divided by the total length of the elastic. Thus we get \begin{equation} \label{Aerts1} \mu(\vec {u},\vec {v},o_{1})=\frac{L_{1}}{2}=\frac{1+\cos {\gamma}}{2}=\cos^{2}{\frac{\gamma}{2}}, \end{equation} \begin{equation} \label{Aerts2} \mu(\vec {u},\vec {v},o_{2})=\frac{L_{2}}{2}=\frac{1-\cos {\gamma}}{2}=\sin^{2}{\frac{\gamma}{2}}, \end{equation} where $\gamma$ is the angle between $\vec u$ and $\vec v$.
It is well known that the above probabilities coincide with the probabilities that appear in spin measurements on a spin--$\frac{1}{2}$ quantum particle. Indeed, a pure (spin) state of such a particle is represented by the vector \begin{equation} \label{bloch}
|\psi\rangle=\cos\frac{\theta}{2}e^{-i\frac{\phi}{2}}|+\rangle+\sin\frac{\theta}{2}e^{i\frac{\phi}{2}}|-\rangle \end{equation}
which is an eigenvector corresponding to the eigenvalue $+\frac{1}{2}\hbar$ of the self--adjoint operator $A=\frac{1}{2}\hbar \vec{\sigma} \cdot \vec{v}$, representing the observable \emph{spin along the direction} $\vec v=\hat{x}\sin\theta\cos\phi+\hat{y}\sin\theta\sin\phi+\hat{z}\cos\theta$. This establishes a correspondence $\omega$ between vectors representing pure states of the spin--$\frac{1}{2}$ quantum particle and points of the surface of a sphere with radius $1$ centered in the origin of $\Re^3$ (\emph{Bloch sphere representation}). This correspondence is one--to--one (up to a phase factor) and obviously induces a bijective mapping of the set of states of the spin--$\frac{1}{2}$ quantum particle on the set of states of the classical point particle considered above. Then, let us consider a measurement of the observable $\mathcal A$ represented by the operator $A=\frac{1}{2}\hbar \vec{\sigma} \cdot \vec{u}$, with $\vec u=\hat{x}\sin\alpha\cos\beta+\hat{y}\sin\alpha\sin\beta+\hat{z}\cos\beta$, on the spin--$\frac{1}{2}$ quantum particle in a state represented by the vector $|\psi\rangle$, and let us denote by $\gamma$ the angle between the two vectors $\vec u$ and $\vec v=\omega(|\psi\rangle)$. It is easy to prove that the probabilities ${\mathscr P}_{\psi}^{A,QM}(+\frac{1}{2}\hbar)$ and ${\mathscr P}_{\psi}^{A,QM}(-\frac{1}{2}\hbar)$ that the measurement yields results $+\frac{1}{2}\hbar$ and $-\frac{1}{2}\hbar$, respectively, are given by \begin{equation} \label{QM1} {\mathscr P}_{\psi}^{A,QM}(+\frac{1}{2}\hbar)=\cos^{2}\frac{\gamma}{2}, \end{equation} \begin{equation} \label{QM2} {\mathscr P}_{\psi}^{A,QM}(-\frac{1}{2}\hbar)=\sin^{2}\frac{\gamma}{2}, \end{equation}
which coincide with the probabilities $\mu(\vec u, \vec v, o_1)$ and $\mu(\vec u, \vec v, o_2)$ in eqs. (\ref{Aerts1}) and (\ref{Aerts2}), respectively. Hence, our measurement is equivalent to performing an experiment with the quantum machine in the state represented by the vector $\vec v=\omega(|\psi\rangle)$ and the elastic installed between $\vec u$ and $-\vec u$. It follows that the quantum machine provides a macroscopic model for measures of the spin of a spin--$\frac{1}{2}$ quantum particle or, more generally, for any quantum system associated with a two--dimensional complex Hilbert space.
\section{A unified model} The models described in the previous sections have different features and have been constructed with different aims. The microscopic SR model is a noncontextual general model for measurements on any kind of quantum system, aiming to demonstrate the consistency of the SR interpretation of QM. The quantum machine provides a macroscopic model for measurements on quantum systems described by two dimensional Hilbert spaces, aiming in particular to suggest some enlargements of QM which would allow us to go beyond its present limits, which is classified by the authors as \emph{highly contextual}\cite{a04} (in the sense that the result of a measurement depends also on the measuring apparatus and not only on the state of the particle that is measured).
There are however some remarkable analogies between the two models. Let us point out some of them.
First of all, in both models probabilities are epistemic, which follows from the adoption of two ``nonstandard'' hidden variables theories. An measurement on the quantum machine is an example of \emph{hidden measurement}, in the sense that probabilities appear because of lack of knowledge about the specific measurement that is actually performed on the entity (namely, one does not know the specific point in which the elastic breaks), not because of lack of knowledge about states of a quantum object, as in a standard hidden variables theory. The epistemicity of probabilities in the microscopic SR model follows instead both from lack of knowledge about the microstates (as in a standard hidden variables theory) and about the measurement (unknown probability of the $a_0$ outcome in a microstate); this lack of knowledge disappears, however, in a deterministic model, see footnote 1). Hence, the microscopic SR model (which is noncontextual and local) can also be considered a nonstandard hidden variables theory.
Secondly, both models reproduce quantum probabilities by introducing suitable conditions. Within the quantum machine model only elastic measurements are permitted. Within the microscopic SR model quantum probabilities follow whenever one considers only objects that are actually detected.
Bearing in mind the above similarities, one may wonder whether a macroscopic version of the microscopic SR model can be constructed which embodies Aerts' quantum machine. At first sight this task seems impossible because of the opposite features of the two models with respect to contextuality. We show in the next sections that the problem can be overcome and construct the desired model.
\subsection{Description of the model for pure states} Bearing in mind the microscopic SR model discussed in Sec. 2, we modify Aerts' quantum machine as illustrated in \textbf{Fig. 4}. To be precise, let us suppose that the classical point particle that is in the point $P$, hence in the state $S$ represented by the vector $\vec v$ according to Aerts' model, is actually in one of the points on the surface of the second sphere (\emph{detection sphere}), which is identical to Aerts' sphere and tangent to it in the point $P$. Let us install an elastic of $2$ units of length in the direction determined by the vector $\vec v$. Whenever a measurement is performed, the particle falls orthogonally onto the elastic, then the elastic breaks in some arbitrary point and the particle ends up in one of the two extremal points of the elastic. If the particle ends up in the contact point $P$ with Aerts sphere, then we say that the particle is \emph{detected} and, in this case, the experimental process can give one of two outcomes, $o_1$ or $o_2$, with the probabilities predicted by Aerts' model. On the contrary, if the particle ends up in the other extreme, we say that it is \emph{not detected} and, in this case, the outcome $a_0$ is obtained.
Let us remind that in the microscopic SR model every pure state $S$ of the physical system can be split into microstates $S^{i}$, and let us identify these \emph{hidden} states in our model with the points on the surface of the detection sphere. Furthermore, let us note that the macroscopic property $F$ in Sec. 2 can be identified now either (i) with the pair $(\vec u, o_1)$, or (ii) with the pair $(\vec u,o_2)$. The measurements of both properties are performed in the same way, hence we can assume that the detection probability ${\mathscr P}_{S}^{i,d}(F)$ in eq. (\ref{newprobability-d}) does not depend on $o_1$ and $o_2$ but only on $\vec u$, and write it ${\mathscr P}_{S}^{i,d}(\vec u)$ in our particular case. Therefore the detection probability ${\mathscr P}_{S}^{d}(F)$ will be written ${\mathscr P}_{S}^{d}(\vec u)$ in our case and eq. (\ref{newprobability-d}) becomes \begin{equation}
{\mathscr P}_{S}^{d}({\vec u})=\sum_{i}{\mathscr P}(S^{i}|S) {\mathscr P}_{S}^{i,d}({\vec u}). \end{equation} Let $(\theta_i,\phi_i)$ be the spherical coordinates of the point of the detection sphere which correspond to the microstate $S^i$ when the polar axis is chosen parallel to $\vec v$. Let us reason as in Sec. 3, yet assuming that the probability that the elastic in the detection sphere breaks at some arbitrary point is not the same for every point, but is described by a probability distribution depending on $\gamma$. Hence, we put \begin{equation} {\mathscr P}_{S}^{i,d}({\vec u})=p(\gamma,\theta_i), \end{equation} whence \begin{equation}
{\mathscr P}_{S}^{d}({\vec u})=\sum_{i}{\mathscr P}(S^{i}|S)p(\gamma,\theta_i). \end{equation}
The conditional probabilities ${\mathscr P}(S^{i}|S)$ are not predetermined and it is possible to make assumptions on them. For example, by considering the continuum limit, we can substitute $S^{i}$ with $S(\theta,\phi)$ and introduce the following assumptions, based on symmetry arguments.
(i) The conditional probability density is independent of the spherical coordinate $\phi$, hence ${\mathscr P}(S^{i}|S) \longrightarrow {\mathscr P}(S(\theta,\phi)|S)=f(\theta)$.
(ii) Only the hidden states belonging to the surface of a spherical cap $\mathscr C$ centered in $P$ have a conditional probability density $f(\theta)$ different from $0$, and the limit angle $\theta_0$ of the cap depends on the vector $\vec v$, hence we write $\theta_0=\theta_0({\vec v})$.
Because of the above assumptions, the probability ${\mathscr P}_{S}^{d}({\vec u})$ is given by \begin{equation} {\mathscr P}_{S}^{d}({\vec u})=\int_{0}^{2\pi}d\phi\int_{\theta_0(\vec v)}^{{\pi}} f(\theta) p(\gamma,\theta) \sin\theta d\theta. \end{equation}
One can make the model more specific by adding suitable assumptions on $p(\gamma,\theta)$ and $f(\theta)$. In any case, if we require that the particle has to be in a definite state, $f(\theta)$ must be such that \begin{equation} \int_{{\mathscr C}}f(\theta) d\sigma=\int_{0}^{2\pi}d\phi\int_{\theta_0({\vec v})}^{\pi} f(\theta) \sin\theta d\theta=1. \end{equation}
Let us consider now eq. (\ref{macro2}) and the two possibilities (i) $F=(\vec u, o_1)$ and (ii) $F=(\vec u, o_2)$. It is apparent that in case (i) ${\mathscr P}_{S}(F)$ coincides with the probability $\mu(\vec u,\vec v,o_1)$ in eq. (\ref{Aerts1}), while in case (ii) it coincides with $\mu(\vec u,\vec v,o_2)$ in eq. (\ref{Aerts2}). Hence, we get \begin{equation} \label{goodform_1} {\mathscr P}_{S}^{t}\Big ( ({\vec u},o_1) \Big ) ={\mathscr P}_{S}^{d}({\vec u})\mu(\vec u,\vec v,o_1)={\mathscr P}_{S}^{d}(\vec u) \cos^{2}\frac{\gamma}{2}, \end{equation} \begin{equation} \label{goodform_2} {\mathscr P}_{S}^{t} \Big ( ({\vec u},o_2) \Big ) ={\mathscr P}_{S}^{d}(\vec u)\mu(\vec u,\vec v,o_2)={\mathscr P}_{S}^{d}(\vec u)\sin^{2}\frac{\gamma}{2}. \end{equation}
In order to complete the model from an SR viewpoint, we must still point out two properties $f_{+}$ and $f_{-}$ of the classical point particle which correspond to $(\vec u,o_1)$ and $(\vec u,o_2)$, respectively, and state a criterion for establishing whether $f_{+}$ or $f_{-}$ is possessed by the particle in a given hidden state $S^i$. This can be done as follows. Firstly, partition the spherical cap $\mathscr C$ considered above into a inner spherical cap ${\mathscr C}_{+}$ centered in $P$ and an outer spherical crown ${\mathscr C}_{-}$. Then assume that $\int_{{\mathscr C}_{+}}f(\theta)d\sigma=\cos^{2}\frac{\gamma}{2}$ and $\int_{{\mathscr C}_{-}}f(\theta)d\sigma=\sin^{2}\frac{\gamma}{2}$. Finally, assume that a particle in a hidden state belonging to ${\mathscr C}_{+}$ (${\mathscr C}_{-}$) produces a breakdown of the elastic in the segment $L_1$ ($L_2$) of \textbf{Fig. 3}, hence outcome $o_1$ ($o_2$). The properties $f_{+}$ and $f_{-}$ are then characterized by the set of hidden states in ${\mathscr C}_{+}$ and ${\mathscr C}_{-}$, respectively, and the factors $\cos^{2}\frac{\gamma}{2}$ and $\sin^{2}\frac{\gamma}{2}$ in eqs. (\ref{goodform_1}) and (\ref{goodform_2}), respectively, are explained in terms of microstates.
The construction of our unified model is thus concluded. However, this opens a new problem. Indeed, the new model is a macroscopic version of the microscopic SR model, which we classified as noncontextual at the beginning of this section. One may then wonder how it was possible to embody in it the quantum machine, which provides a model which was classified instead as highly contextual by the authors themselves. The answer to this question is not trivial, and requires a brief preliminary analysis of the concept of contextuality.
According to a standard viewpoint, a physical theory is contextual whenever the value of an observable $\mathcal A$ in a given state of a physical system depends on the set of (compatible) measurements that are simultaneously performed on the system \cite{me93}. We call this kind of contextuality here \emph{contextuality$_1$}, and note that no reference is made in its definition to individual differences between apparatuses measuring $\mathcal A$, which are thus implicitly considered ideal and identical. On the contrary, according to the GB approach the contextuality of the quantum machine follows from the fact that each individual experiment introduces a different set of hidden variables of the measuring apparatus, so that different measurements of the same observable may yield different results \cite{a04}. This provides implicitly a different definition of contextuality, that we call here \emph{contextuality$_2$}, which makes reference to the differences that unavoidably exist between individual apparatuses measuring $\mathcal A$.
Let us come now to the microscopic SR model and to the quantum machine. The former can be classified as noncontextual when contextuality$_1$ is understood (indeed, the result of a measurement depends only on the microscopic properties possessed by the physical object that one is considering, that is, on the microscopic state $S^i$ of the object)\footnote{We remind that the price for noncontextuality$_{1}$ of the microscopic SR model is accepting that the laws of QM cannot be applied to those physical situations that are unaccessible, \emph{in principle}, to empirical control \cite{gs96b}--\cite{ga02}. Such situations actually occur in QM because of the existence of incompatible observables. We stress that this feature of the SR model allows one to avoid a number of paradoxes without conflicting with the theoretical description and the predictions of QM (which refer to detected physical objects only).}. If, on the contrary, contextuality$_2$ is understood and the detection probability ${\mathscr P}_{S}^{i,d}(F)$ in eq. (\ref{newprobability-d}) is interpreted as expressing lack of knowledge on the interaction between the measurement and the physical object, the microscopic SR model can be classified as contextual (but also this kind of contextuality disappears if the SR model is deterministic). Analogously, it is apparent that the measurements on the quantum machine are noncontextual if contextuality$_{1}$ is understood (indeed, measurements with the elastic strip in different directions are never compatible). On the contrary, they are highly contextual, as stated in the GB approach, if contextuality$_{2}$ is understood. Our problem above is thus solved.
It is still interesting to observe that our unified model reduces in some sense the contextuality$_{2}$ of the measurements on the quantum machine because of the final part of our construction above. Indeed, it is apparent that the unknown features of an experiment on the quantum machine (the point in which the elastic breaks), which affect the result of the measurement, are explained within our unified model in terms of the hidden states $S^i$, hence only the contextuality$_{2}$ following from the unknown probability of the $a_0$ outcome is left in the model.
It remains to ``close the circle'' by showing that the above macroscopic model mimics a spin measurement of a spin--$\frac{1}{2}$ quantum particle according to the microscopic SR model. To this end, let us consider the observable $\mathcal A$ represented by the operator $A=\frac{1}{2}\hbar \vec{\sigma} \cdot \vec{u}$ in standard QM (Sec. 3). According to the microscopic SR model, this observable must actually contain in its spectrum, besides the values $+\frac{1}{2}\hbar$ and $-\frac{1}{2}\hbar$, a further value $a_0$ that is considered as the outcome of a measurement when the physical object is not detected, hence it must be substituted by an observable ${\mathcal A}_0$ (we remind that the lack of detection is not interpreted as an inefficiency of the measuring apparatus, but as a consequence of the microscopic properties of the measured object, see Sec. 2). Let ${\mathscr P}_{\psi}^{A}(+\frac{1}{2}\hbar)$ and ${\mathscr P}_{\psi}^{A}(-\frac{1}{2}\hbar)$ be the probabilities of finding the outcomes $+\frac{1}{2}\hbar$ and $-\frac{1}{2}\hbar$, respectively, in a measurement of the observable ${\mathcal A}_0$ on a quantum particle in the state represented by the vector $|\psi\rangle$ in eq. (\ref{bloch}). By setting (i) $F=({\mathcal A}_0, \{ +\frac{\hbar}{2} \})$ and (ii) $F=({\mathcal A}_0, \{ -\frac{\hbar}{2} \})$, these probabilities particularize in two different cases the probability ${\mathscr P}_{S}^{t}(F)$ in eq. (\ref{macro2}). Both in (i) and (ii) the measurement of $F$ is performed by measuring ${\mathcal A}_0$, hence the detection probability ${\mathscr P}_{S}^{d}(F)$ that appears in (\ref{macro2}) is the same in both cases and we briefly denote it by ${\mathscr P}_{\psi}^{d}(A)$. Finally, ${\mathscr P}_{S}(F)$ in eq. (\ref{macro2}) obviously coincides with ${\mathscr P}_{\psi}^{A,QM}(+\frac{1}{2}\hbar)$ (see eq. (\ref{QM1})) in case (i) and with ${\mathscr P}_{\psi}^{A,QM}(-\frac{1}{2}\hbar)$ (see eq. (\ref{QM2})) in case (ii). Thus, we get from eq. (\ref{macro2}), \begin{equation} \label{unifiedform_1} {\mathscr P}_{\psi}^{A}(+\frac{1}{2}\hbar)={\mathscr P}_{\psi}^{d}(A){\mathscr P}_{\psi}^{A,QM}(+\frac{1}{2}\hbar)={\mathscr P}_{\psi}^{d}(A){\cos}^{2}\frac{\gamma}{2}, \end{equation} \begin{equation} \label{unifiedform_2} {\mathscr P}_{\psi}^{A}(-\frac{1}{2}\hbar)={\mathscr P}_{\psi}^{d}(A){\mathscr P}_{\psi}^{A,QM}(-\frac{1}{2}\hbar)={\mathscr P}_{\psi}^{d}(A){\sin}^{2}\frac{\gamma}{2}. \end{equation} These equations coincide with eqs. (\ref{goodform_1}) and (\ref{goodform_2}), respectively, if one puts ${\mathscr P}_{\psi}^{d}(A)={\mathscr P}_{S}^{d}({\vec u})$.
We would like to stress that our unified model aims to provide a macroscopic analogue of a quantum measurement, but does not claim in any way to explain what actually occurs at a microscopic level. Nevertheless, the unspecified factor ${\mathscr P}_{S}^{d}({\vec u})$ reminds us that, according to the SR interpretation, QM is an incomplete theory which could be embedded, at least in principle, into a broader theory (which is excluded by the standard interpretation).
\subsection{Description of the model for mixed states} The unified model proposed in the previous section can be generalized to the case of nonpure (mixed) states or \emph{mixtures}. Let us shortly describe this generalization.
Let us broaden the set of states of the quantum machine by adding the inner points of the Aerts sphere to the points on the surface as possible locations of the classical point particle. Then, let us note that the state $D$ characterized by the vector $\vec w$ such that $|\vec w| < 1$ can be written as a convex combination of the vectors $\vec v=\frac{\vec w}{|\vec w|}$ and $-\vec v=-\frac{\vec w}{|\vec w|}$ representing the pure states $S_1$ and $S_2$, respectively. Indeed, $\vec w=\lambda_1 \vec v+\lambda_2(-\vec v)$, with $\lambda_1=\frac{1+|\vec w|}{2}$ and $\lambda_2=\frac{1-|\vec w|}{2}$ (hence $0 \le \lambda_1,\lambda_2 \le 1$ and $\lambda_1+\lambda_2=1$). If we then perform a measurement of the kind considered in Sec. 3 whenever the quantum machine is in the state $D$ (see \textbf{Fig. 3} with $\vec w$ in place of $\vec v$), the probabilities of obtaining outcomes $o_1$ or $o_2$ are given by \begin{equation} \label{QM_mixed1}
\mu(\vec u,\vec w,o_1)=\frac{L_1}{2}=\frac{1+|\vec w|\cos\gamma}{2}=\lambda_1 \cos^{2}\frac{\gamma}{2}+\lambda_2 \sin^{2}\frac{\gamma}{2}, \end{equation} and \begin{equation} \label{QM_mixed2}
\mu(\vec u, \vec w, o_2)=\frac{L_2}{2}=\frac{1-|\vec w|\cos\gamma}{2}=\lambda_1 \sin^{2}\frac{\gamma}{2}+\lambda_2 \cos^{2}\frac{\gamma}{2}, \end{equation} respectively.
Let us now remind that not only pure states, but also mixed states of spin--$\frac{1}{2}$ quantum particles can be represented on the Bloch sphere. In fact, a mixed state represented in standard QM by the density operator $W=\lambda_1|\psi_1\rangle\langle\psi_1|+\lambda_2|\psi_2\rangle\langle\psi_2|$ (where $|\psi_1\rangle$ and $|\psi_2\rangle$ are normalized and orthogonal vectors in the Hilbert space of the system, $0 \le \lambda_1, \lambda_2 \le 1$, $\lambda_1+\lambda_2=1$) corresponds to the inner point of the Bloch sphere characterized by the vector $\vec w=\lambda_1 \vec v+\lambda_2 (-\vec v)$ (where $\vec v$ and $-\vec v$ are the vectors corresponding to $|\psi_1\rangle$ and $|\psi_2\rangle$, respectively, in the Bloch representation discussed in Sec. 3), with $|\vec w|=|\lambda_1-\lambda_2|$. It is then immediate to see that the probabilities ${\mathscr P}_{W}^{A,QM}(+\frac{1}{2}\hbar)$ and ${\mathscr P}_{W}^{A,QM}(-\frac{1}{2}\hbar)$ predicted by QM for a spin measurement in direction $\vec u$ on a spin--$\frac{1}{2}$ quantum particle in the state represented by $W$ coincide with the probabilities in eqs. (\ref{QM_mixed1}) and (\ref{QM_mixed2}), respectively. Hence, the quantum machine provides a macroscopic model for this kind of measurements also in the case of mixed states. It must be stressed, however, that, according to Aerts, $D$ is not interpreted as a mixed state of the quantum machine, which is highly relevant in Aerts' perspective \cite{a99b}.
Let us evaluate the probabilities ${\mathscr P}_{D}^{t}\Big (({\vec u},o_1) \Big )$ and ${\mathscr P}_{D}^{t}\Big ( ({\vec u},o_2) \Big )$ of finding the outcomes $o_1$ and $o_2$, respectively, in a measurement of the kind described in Sec. 4.1 whenever the quantum machine is in the state $D$ within our unified model. If we consider (contrary to Aerts) the state $D$ as a mixture of the states $S_1$ and $S_2$, the coefficients $\lambda_1$ and $\lambda_2$ can be interpreted as the probabilities that the quantum machine in the state $D$ is actually in the state $S_1$ or in the state $S_2$, respectively. Hence, we get \begin{equation} \label{SR_mixed1} {\mathscr P}_{D}^{t} \Big (({\vec u},o_1) \Big )=\lambda_1{\mathscr P}_{S_1}^{t}\Big ( ({\vec u},o_1)\Big )+\lambda_2 {\mathscr P}_{S_2}^{t}\Big (({\vec u},o_1) \Big ), \end{equation} \begin{equation} \label{SR_mixed2} {\mathscr P}_{D}^{t} \Big (({\vec u},o_2) \Big )=\lambda_1{\mathscr P}_{S_1}^{t}\Big ( ({\vec u},o_2) \Big )+\lambda_2 {\mathscr P}_{S_2}^{t}\Big ( ({\vec u},o_2) \Big ). \end{equation} The probabilities ${\mathscr P}_{S_1}^{t} \Big (({\vec u},o_1)\Big )$, ${\mathscr P}_{S_2}^{t}\Big (({\vec u},o_2)\Big )$, etc., can be calculated by using eqs. (\ref{goodform_1}) and (\ref{goodform_2}). One gets, with $\gamma_1$ and $\gamma_2$ as in \textbf{Fig. 5}, ${\mathscr P}_{S_1}^{t} \Big (({\vec u}, o_1) \Big )={\mathscr P}_{S_1}^{d}(\vec u) \cos^{2}\frac{\gamma_1}{2}$, ${\mathscr P}_{S_2}^{t} \Big (({\vec u}, o_1) \Big )={\mathscr P}_{S_2}^{d}(\vec u) \cos^{2}\frac{\gamma_2}{2}$, etc. Since, now, $S_1$ and $S_2$ are represented by the opposite vectors $\vec v$ and $-\vec v$, respectively, and $\gamma_2=\pi-\gamma_1$, the symmetries of the particular physical system at issue suggest to assume that ${\mathscr P}_{S_1}^{d}(\vec u)={\mathscr P}_{S_2}^{d}(\vec u)$. By setting ${\mathscr P}_{S_1}^{d}(\vec u)={\mathscr P}_{S_2}^{d}(\vec u)={\mathscr P}_{D}^{d}(\vec u)$ and $\gamma_1=\gamma$, we get
\begin{equation} \label{SR_mixed1f} {\mathscr P}_{D}^{t}\Big (({\vec u}, o_1)\Big )={\mathscr P}_{D}^{d}(\vec u)(\lambda_1 \cos^{2}\frac{\gamma}{2}+\lambda_2\sin^{2}\frac{\gamma}{2}), \end{equation} \begin{equation} \label{SR_mixed2f} {\mathscr P}_{D}^{t} \Big (({\vec u}, o_2)\Big )={\mathscr P}_{D}^{d}(\vec u)(\lambda_1 \sin^{2}\frac{\gamma}{2}+\lambda_2\cos^{2}\frac{\gamma}{2}). \end{equation} Proceeding as in Sec. 4.1, the above probabilities can then be identified with the probabilities ${\mathscr P}_{W}^{A}(+\frac{1}{2}\hbar)$ and ${\mathscr P}_{W}^{A}(-\frac{1}{2}\hbar)$, respectively, that a measurement of the observable ${\mathscr A}_0$ on a spin--$\frac{1}{2}$ quantum particle in the state represented by $W$ yields outcome $+\frac{1}{2}\hbar$ and $-\frac{1}{2}\hbar$, respectively, according to the microscopic SR model.
Our unified model has thus been generalized to the case of mixtures, as desired. It must be stressed, however, that this has been done at the expense of betraying Aerts' original idea of not considering the state $D$ of the quantum machine as a mixture.
\section{Conclusions} The construction in Sec. 4 shows that Aerts' quantum machine can be used as a basis for producing a more complex model for quantum measurements on spin--$\frac{1}{2}$ particles. The new model constitutes a macroscopic version of the microscopic model for quantum measurements introduced within the SR interpretation, hence it establishes a first formal link between the GB approach and the SR interpretation of QM. Moreover, some relevant differences between the two approaches, which seemingly make them incompatible, are bypassed in the model. This suggests that they can be bypassed in general by using similar procedures, even if some difficulties could arise when considering models for quantum systems described by Hilbert spaces whose dimension is greater that 2. In any case, the model presented in this paper may serve as an intuitive basis for the attempt at linking together the GB approach and the SR intepretation, aiming to construct a broader theory going beyond the present limits of QM.
\end{document} | arXiv |
Search all SpringerOpen articles
Robotics and Biomimetics
Route bundling in polygonal domains using Differential Evolution
Victor Parque ORCID: orcid.org/0000-0001-7329-14681,2,
Satoshi Miura1 &
Tomoyuki Miyashita1
Robotics and Biomimetics volume 4, Article number: 22 (2017) Cite this article
Route bundling implies compounding multiple routes in a way that anchoring points at intermediate locations minimize a global distance metric to obtain a tree-like structure where the roots of the tree (anchoring points) serve as coordinating locus for the joint transport of information, goods and people. Route bundling is a relevant conceptual construct in a number of path-planning scenarios where the resources and means of transport are scarce/expensive, or where the environments are inherently hard to navigate due to limited space. In this paper we propose a method for searching optimal route bundles based on a self-adaptive class of Differential Evolution using a convex representation. Rigorous computational experiments in scenarios with and without convex obstacles show the feasibility and efficiency of our approach.
In this paper we tackle the route bundling problem which consists of compounding multiple routes in a way that intermediate points minimize a global distance metric of multiple origin–destinations pairs. In this context, the ultimate goal in route bundling is to construct tree-like graph structures where the anchoring points, being roots of the tree structure, serve as coordinating locus for the joint transport of information, goods and people.
A fundamental problem behind the construction of route bundles lies in deciding the locations of roots and intermediate nodes to form the optimal tree structures. Also, the presence of obstacles makes the problem non-trivial due to the non-convexity of the search space, thus being hard to deal with analytical and statistical methods. In order to exemplify the conceptual framework involved in route bundling, Fig. 1a shows a bipartite graph which denotes transport needs between origin–destination pairs (which is normally known a priori). Here, nodes of the bipartite graph denote locations for origin and destination, while edges denote needs for transport/communication. Figure 1b shows the bundled route which represents the tree structure aiming at minimizing the global distance metric while avoiding obstacle collision. Here, note that anchoring points are located at some intermediate region of the origin–destination pairs.
Basic idea of route bundling. Given a polygonal map and edges representing desirable origin–destination pairs, the goal is to find optimal anchoring points minimizing the global distance metric of the bundled route. a Bipartite graph and obstacles, b route bundling
Application background
Compared to the path-planning problem with single origin–destination nodes, the route bundling problem is a generalized formulation in the sense that the latter considers multiple origin–destination pairs. Naturally, in path planning with single origin–destination pairs, the anchoring point (root of minimal tree) coincides with the origin–destination nodes. In the literature, the path planning is a well-studied topic [1,2,3,4,5,6]; yet, the route bundling problem is an emergent research topic having potential applications in problem scenarios involving compounded path planning with multiple origin–destination pairs. Here, designing the optimal network is relevant for the efficient use of resources while integrating and coordinating transport/communication needs.
Concretely speaking, route bundling has specific applications in environments where resources or means of transport/communication are scarce or expensive. For instance, consider the design of a network for transporting goods from/to multiple areas in an environment covered with obstacles; naturally, since one-to-one transport would cause unwanted traffic or excessive cost in network construction, one is interested in designing a network where intermediate nodes serve as coordinating locus for source/destination locations.
Also, consider the design of optimal wire harness topologies for machines (e.g., cars and ships). Here, free space for electrical wiring is scarce and one-to-one links are rather undesirable; thus, wire harness becomes essential to build tree-like structures aiming to minimize global connectivity while ensuring minimal use of space.
Furthermore, consider the deployment of sensor networks for many-to-many robots in the presence of attenuating obstacles (e.g., disaster areas). Here, attenuating obstacles induce in data loss or deterioration of the ability to communicate (e.g., concrete floors, steel reinforced floors, ceilings, elevators, walls, rock, and reinforced materials). Thus, it becomes imperative to design networks allowing to get the sensor signal around the obstructing materials. In disaster areas, route bundling becomes the building block to enable energy-efficient networks.
Generally speaking, the presence of obstacles and holes in the environment induces on limited space and navigability, thus making route bundling relevant when either transport and communication means are scarce and expensive, or when optimal networking is a goal in many-to-many origin–destination settings.
Basically, the algorithmic foundations of the route bundling have been laid out in two different fields: wireless sensor networks and network visualization.
In one hand, the study of wireless sensor networks [7] has rendered methodologies for network protocol and topology construction. Examples include the construction of a connected network to ensure complete coverage of an area of interest with the minimum number of nodes as possible [8], the degree-constrained minimum-weight connected dominated set for energy-efficient topology control in wireless sensor networks [9], the topological optimization for consensus-based clock synchronization protocols [10], the tree topology construction for heterogeneous wireless sensor networks [11], the self-stabilizing algorithms to construct rooted trees under the assumption of node disconnection [12] and a number of topology optimization for network coverage, connectivity, energy savings, delay minimization, optimal routing and broadcasting [13,14,15,16,17].
In other domains, the route bundling problem has its closest foundations in edge bundling for network visualization field. Here, the basic aim is to compound edges in complex networks to ease the visualization or rendering of large-scale networks. In particular, the conventional works have focused on the geometry-based edge clustering, in which the edges in the graph are forced to pass through points in a control mesh [18]. Also, the force-based edge bundling where edges are modeled as springs being able to attract to each other [19, 20]. Furthermore, hierarchical clustering approaches have emerged. Here, in [21], the authors describe an approach based on attraction to the skeleton of the adjacent edges. And, in [22], the authors describe a kd-tree-based optimization of the centroid points of close edges in the graph.
Although the above described algorithms for topology optimization in wireless sensor networks aim at finding an optimal hierarchy given a number of nodes, the existing algorithms are irrelevant to our scope since route bundling does not require centralized communication and compliance with network coverage (e.g., hoping diameter).
On the other hand, existing algorithms for edge bundling have a different scope: network bundles aim at rendering aesthetically pleasing and topologically compact drawings; yet, the existing algorithms do not necessarily aim at minimizing a global distance metric. Furthermore, it is non-trivial for the existing edge bundling algorithms to obtain minimal-length networks in the presence of obstacles and holes in the environment.
Thus, in order to fill the above gaps, and having a different scope, we focus on the problem of designing optimal route bundles. In order to tackle this problem, we use Differential Evolution embedded with a convex representation of the search space (free region) to optimize route planning and bundling in polygonal domains. The basic idea of our approach is to search over the space of a convex representation of a polygonal map by sampling with self-adaptive interpolation vectors. Here, the unique point of our approach is to balance the explorative and exploitative sampling of anchoring points while explicitly avoiding the computations of point inside polygons. Our contributions are summarized as follows:
We propose a nature-inspired algorithm for searching tree bundles aiming at minimizing global length in a polygonal domain. In our approach, we use Differential Evolution and study the performance of our proposed algorithmic variants including the following:
DENC, Differential Evolution with Neighborhood and Convex Representation.
DEN, Differential Evolution with Neighborhood.
DEC, Differential Evolution with Convex Representation.
DE, Differential Evolution without Neighborhood nor Convex Representation.
We perform more than 12,000 experimental evaluations to confirm the feasibility, efficiency and robustness of our approach by considering diverse number of edges in the input bipartite network, diverse complexity configurations of polygonal obstacles with convex and non-convex geometry (number of edges in polygon up to 10), and parametric comparisons considering population size and neighborhood size. Furthermore, we compare the convergence performance of the above described algorithmic variants. Based on these computational experiments, we provide insights on how to design optimal tree bundles by using our nature-inspired approach.
In the rest of the paper, we describe our framework in "Methods" section, and then we describe our results and provide insights from our computational experiments in "Computational experiments" section, and finally conclude our paper in "Conclusions" section.
Basic steps in the proposed approach. Inputs consist of a polygonal map and a bipartite network, wherein edges of the bipartite network represent desirable source–destination pairs. The output is a tree-like network with anchoring points at intermediate points optimizing a global distance metric
This section describes the basic ideas as well as the algorithmic foundations in our proposed approach for route bundling.
Basic framework
The basic concept of our proposed approach is depicted by the following equation:
$$\begin{aligned} &\underset{x}{{\mathbf{Minimize }}}&F(x) \\&\text {{subject to}}&x \in {{\mathbf {T}}}\end{aligned}$$
where x is the encoding (representation) of the route bundle, F(x) is the distance metric which is used to evaluate the quality/fitness of the bundled routes, and \({\mathbf {T}}\) is the search space of feasible route bundles.
In the above definition, the encoding implicitly represents a tree structure whose edges are free of overlaps with obstacles.
Also, note that the constraint \(x \in {\mathbf {T}}\) makes explicit the requirement that optimization is realized within the space \({\mathbf {T}}\) of feasible route bundles. In latter sections, we describe the representation which allows sampling of feasible route bundles.
Then, in order to solve the above problem, a set of explicit a priori knowledge is considered fundamental. In our study, we assume to have knowledge of the following elements (as shown by Fig. 2):
Definition of a bipartite graph \(G = (V,E)\) wherein the edge \(e \in E\) represents the origin–destination pair (implying needs for communication/transportation between two points). Here, the number of edges and the locations of the source–destination pairs in the graph G are defined by the characteristics of the environment and/or by the needs of the user or network designer.
Definition of locations and geometry of the obstacles in the environment (which denote unfeasible areas for navigation/transportation). For simplicity and without loss of generality, we use polygonal obstacles with/without convexity properties which are reminiscent of indoor environments.
In order to give a glimpse of the algorithmic flow in our proposed approach, Fig. 2 and Algorithm 1 show the basic steps for route bundling. Basically, our approach consists as follows:
First, the geometry of the free space is computed given information of the set of obstacles (map) and bipartite network.
Then, the free space is triangulated using the Delaunay approach.
Finally, the locations of the anchoring points are optimized within the triangulated free space. Here, during optimization, fitness is defined by the distance metric F(x).
In the following, we describe the fundamental concepts involved in our approach: (1) the encoding (representation) of bundled routes, (2) the distance metric, as well as (3) the optimization method to solve Eq. (1).
Representation of bundled routes
This subsection describes the mechanism used to represent bundled routes.
Given a bipartite graph \(G = (V, E)\) with edges representing origin–destination pairs, the reader may note that a bundled route can be easily represented by the coordinates of a pair of anchoring points connecting all origins and destinations, as Fig. 1 shows. By using this concept, whenever the coordinates of the vertices \(v \in V\) of the bipartite graph G are presented in \(\mathbb {R}^2\), then the route bundling can be easily represented by the following 4-element tuple:
$$\begin{aligned} x = (P_x, P_y, Q_x, Q_y) \end{aligned}$$
where \(P_x\) and \(P_y\) are the coordinates in the x-axis and y-axis, respectively, in which the anchoring point nearest to the origins is located at \((P_x, P_y)\), and the anchoring point nearest to the destination is located at \((Q_x, Q_y)\). The reader may easily note that \(x \in \mathbb {R}^4\) holds.
The above representation is simple; yet, it has a fundamental problem: it is unable to encode feasible route bundles since the condition \(P,Q \in \mathbb {R}^2\), implying \(P = (P_x, P_y)\) and \(Q = (Q_x, Q_y)\), does not ensure that coordinates are outside the non-navigable space (overlapping with obstacles).
In order to tackle the above problem, we propose representing the coordinates of the anchoring points by using only the navigable free space. The basic concept is as follows.
The free space of the polygonal map is triangulated using the Delaunay approach [23], as Fig. 2 exemplifies, in which a set \(T = \{t_1, t_2, \ldots , t_i, \ldots , t_n\}\) of n triangles are obtained.
Then, the anchoring points can be represented by 3-element tuples, as follows:
$$\begin{aligned} P = {(i, r_1, r_2) } \end{aligned}$$
where \(i \in [n]\) and \(r_1, r_2 \in [0,1]\). In the above encoding, i is the index of the i-th triangle \(t_i \in T\), and \(r_1, r_2\) are real numbers in the interval [0, 1].
The unique feature of the above encoding lies in the ability to represent arbitrary points in \(\mathbb {R}^2\) which guarantee to be inside the (free) navigable space. Note that the following relation holds:
$$\begin{aligned} P \in {\mathbb {N}^{[n]}} \times \mathbb {R}^{[0,1]} \times \mathbb {R}^{[0,1]} \end{aligned}$$
Furthermore, for a polygonal map in 2-D, the equivalent cartesian coordinates can be computed by using the following relation [24]:
$$\begin{aligned} (P_x, P_y) = (1-r_1)A_i + \sqrt{r_1}(1-r_2)B_i + \sqrt{r_1}r_2C_i \end{aligned}$$
where \(A_i, B_i, C_i\) are the 2-dimensional coordinates of the vertices of the i-th triangle \(t_i \in T\). Intuitively, \(r_1\) represents the percentage from vertex \(A_i\) to the opposing edge in the triangle \(t_i \in T\). The square root of \(r_1\) has the role of considering a uniform random point with respect to the triangle area. Although it is possible to use the simple barycentric interpolation, the above representation has the added benefit of enabling the uniform sampling of arbitrary points.
Then, for a route bundle with two connected anchoring points P and Q, in which P connects to the origin nodes, and Q connects to the destination nodes (see Fig. 2 for a basic reference), it is possible to use Eq. 3, to deduce an encoding for route bundles by using a 6-element tuple, as follows:
$$\begin{aligned} x = (i^P, r^P_1, r^P_2, i^Q, r^Q_1, r^Q_2) \end{aligned}$$
where \(i^P, i^Q\) are natural numbers in the interval [n], and \(r^P_1, r^P_2, r^Q_1, r^Q_2\) are real numbers in the interval [0, 1]. Basically, the above expression has the role of representing two coordinates in the plane, and for simplicity, we denote the search space \(x \in {\mathbf {T}}\), wherein the following holds:
$$\begin{aligned} {\mathbf {T}}\,\equiv & {}\, {\mathbb {N}^{[n]}} \times \mathbb {R}^{[0,1]} \times \mathbb {R}^{[0,1]} \times {\mathbb {N}^{[n]}} \times \mathbb {R}^{[0,1]} \times \mathbb {R}^{[0,1]} \end{aligned}$$
Thus, by using a triangulation of the free space and the relations of Eqs. (3)–(5), it becomes possible to sample arbitrary points uniformly in the convex search space \({\mathbf {T}}\). Intuitively, the above representation allows to render feasible route bundles efficiently since,
Bijection to Cartesian coordinates is possible in O(1) by using Eq. 4.
Route bundles are guaranteed to avoid overlaps with obstacles, and
Explicit computation of point inside polygon is avoided, implying the efficiency in scalability while sampling a very large number of points in the free navigable space.
In this subsection, we describe the distance metric used to measure the quality/fitness of route bundles.
Once the search space \(x \in {\mathbf {T}}\) is constructed, our next goal is to find anchoring points P and Q (as shown by Fig. 2) which minimize a distance metric. For simplicity and without loss of generality, we use the following metric:
$$\begin{aligned} F(x) = \sum _{e \in E}d(e_o,P) + d(P,Q) + \sum _{e \in E}d(Q,e_d) \end{aligned}$$
where d(a, b) is the Euclidean obstacle-free shortest distance metric between points a and b, \(e_o\) is the coordinate of the origin node of the edge \(e \in E\), \(e_d\) is the coordinate of the destination node of the edge \(e \in E\), and P and Q are anchoring points being closer to the origin \(e_o\) and destination \(e_d\), respectively.
Intuitively, the above cost function represents the euclidean distance between three different groups:
the distance of the shortest paths between origin nodes to anchoring point P,
the distance of the shortest paths between the anchoring points P and Q, and
the distance of the shortest paths between the anchoring points and the destination nodes.
The shortest paths are computed by using A* search [3] and the visibility trace, which is pre-computed from the Delaunay triangulation.
Note that the 2-dimensional coordinates of the anchoring points P and Q can be computed by combining Eqs. (3)–(5), as follows:
$$\begin{aligned} (P_x, P_y) = (1-r^P_1)A^P_i + \sqrt{r^P_1}(1-r^P_2)B^P_i + \sqrt{r^P_1}r^P_2C^P_i \end{aligned}$$
$$\begin{aligned} (Q_x, Q_y) = (1-r^Q_1)A^Q_i + \sqrt{r^Q_1}(1-r^Q_2)B^Q_i + \sqrt{r^Q_1}r^Q_2C^Q_i \end{aligned}$$
where \(A^P_i, B^P_i, C^P_i\) are the 2-dimensional coordinates of the vertices of the i-th triangle \(t_i \in T\) where point P lies in.
Further extensions are possible. For example, instead of using the above euclidean metric, it is possible to use Manhattan distance (useful for designing networks for integrated circuits and tubular networks inside buildings). Also, it is possible to include weights in the above metric to balance the relevance of the distance to the origins compared to the distance to destinations.
Differential Evolution
This subsection describes the optimization algorithm used to compute the optimal route bundles.
We use Differential Evolution [25, 26] considering global and local interpolation vectors in order to tackle the problem of dealing with multimodal search space (the reader may note that Eq. 6 is multimodal in the case of polygonal maps with non-convex obstacles).
Concretely speaking, the method for sampling in the above mechanism is described by the following equations:
$$\begin{aligned} x_{t+1} = {\left\{ \begin{array}{ll} u_t &\quad{} { F(u_t) \le F(x_t)}\\ x_t &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$
\(x_t\) represents Eq. 5 at iteration t, in other words \(x_t\) is the individual (route bundle),
F(.) is the objective function at Eq. (6) (minimization), and
\(u_t\) is the trial route bundle solution at iteration t.
In the above definition, sampling of new points is realized when the trial vector \(u_t\) minimizes or achieves equal performance compared to the current state.
The trial vector \(u_t\) is computed from the interpolation of two vectors, as follows:
$$\begin{aligned} u_t=\,& {} x^c_t + m_t \circ (v_t - x^c_t ) \end{aligned}$$
$$\begin{aligned} m_t=\,& {} [m_{t,1}, m_{t,2}, m_{t,3}, \ldots , m_{t,D}] \end{aligned}$$
\(\circ\) is the Hadamard product (element-wise).
\(x^c\) is the crossover individual at iteration t.
\(v_t\) is the mutant individual at iteration t.
\(m_t\) is a vector of masks containing zeros and ones.
The mask \(m_t\) is computed as follows:
$$\begin{aligned} m_{t, j}= & {} {\left\{ \begin{array}{ll} 1, &{}{\mathbf {r}}_{t,j} \le CR \text { or } j = jrand\\ 0, &{}\text {otherwise} \end{array}\right. } \end{aligned}$$
$$\begin{aligned} v_t= & {} w^{x_t}.g_t + (1-w^{x_t}).l_t \end{aligned}$$
\({\mathbf {r}}_{t,j}\) and jrand are random numbers uniformly distributed in \(\mathbb {R}^{[0,1]}\) and \(\mathbb {N}^{[D]}\) respectively.
CR is the probability of crossover.
\(D = 6\) is the dimensionality of the route bundling problem, Eq. (5).
In the above definitions, the user may note that high values of the crossover rate CR incite higher number of ones in the mask vector \(m_t\), thus a highly explorative behavior of the search space.
The global and local interpolation vectors are computed as follows:
$$\begin{aligned} g_t=\, & {} x_t + \alpha ({x_{gbest}} - x_t) + \beta (x^{1} - x^{2}) \end{aligned}$$
$$\begin{aligned} l_t= \,& {} x_t + \alpha ({x_{nbest_x}} - x_t) + \beta (x^{p} - x^{q}) \end{aligned}$$
$$\begin{aligned} w^{x_t}= \,& {} w^{x_t} + \alpha (w_{gbest} - w^{x_t}) + \beta (w^{1} - w^{2}) \end{aligned}$$
Neighborhood of \(x_t\) for \(\rho =2\) in a ring topology. Spheres denote individuals
\(g_t\) is the global donor individual.
\(l_t\) is the local donor individual.
\(\{x^1_t, x^2_t\} \subset {\mathbf P}\), are random individuals sampled from \({\mathbf P}\) for \(x^1 \ne x^2 \ne x_t\).
\(x_{gbest}\) is the global best in the population at iteration t.
\(x_{nbest_x}\) is the local best in the neighborhood \({\mathbf N} (x_t)\) of individual \(x_t\) at iteration t.
the neighborhood \({\mathbf N} (x_t)\) of vector \(x_t\) is the set of individuals contiguous to \(x_t\) by radius \(\rho = \frac{|{\mathbf P} |.\eta }{2}\) in a ring topology (see Fig. 3 for a ring topology with radius \(\rho = 2\)).
\(\{x^p, x^q\} \subset {\mathbf N} (x_t)\), are random individuals for \(x^p \ne x^q \ne x_t\).
\(w^{x_t}\) denotes the coefficient of individual \(x_t\), in which any coefficient \(w^{x_t} \in U[0,1]\) is set randomly at initial iteration.
\(w_{gbest}\) is the coefficient associated to \(x_{gbest}\),
\(w^{1}, w^{2}\) are the coefficients associated to the vectors \(x^{1}, x^{2}\) respectively.
Note that in the above definitions, Differential Evolution uses global and local interpolation vectors \(g_t\) and \(l_t\), respectively; in which the mutant vector \(v_t\) is a linear interpolation between \(g_t\) and \(l_t\).
The global (local) interpolation vector \(g_t\) (\(l_t\)) represents the position to which the direction of the trial vector should aim at in the 6-dimensional search space, considering information from the population (neighborhood). Thus, the global (local) interpolation vector is the result of the current solution being translated by a sum of two directional vectors, one vector representing the direction to the best solution in the population (neighborhood) and another vector representing an arbitrary direction computed from the difference of two solutions within the population (neighborhood).
The first perturbation vector (the one multiplying \(\alpha\)) is an arithmetical recombination operator, while the second perturbation vector (the one multiplying \(\beta\)) is a differential mutation. The parameters \(\alpha\) and \(\beta\) have a scaling role toward best and arbitrary directions, respectively. A priori knowledge of problem convexity, uni-modality or multi-modality eases the selection of good values of \(\alpha\) and \(\beta\). Unimodal and convex (multimodal and non-convex) fitness landscapes would favor values of \(\alpha\) (\(\beta\)) being larger than \(\beta\) (\(\alpha\)) to induce in an exploitative (explorative) behavior in both the global and local neighborhood, and to ease the faster convergence. Without a-prior knowledge of the fitness landscape, it is recommendable to use \(\alpha , \beta \in (0, 2)\) to avoid overshooting while sampling in the search space [25, 26]. Furthermore, note that when \(\alpha = \beta\) and \(w = 1\), the above Differential Evolution is equivalent to the conventional DE/target-to-best/1 strategy [26]; thus, the above algorithm is a generalization in which it considers not only the global population, but also the local neighborhood.
In computing the local neighborhood we use the ring topology to ensure speciation of individuals while preserving efficiency in the computation of best individuals in the neighborhood. An alternative approach is to use a clustering approach in which the neighborhood is defined as a local cluster. Yet, compared to the clustering approach, the ring topology is more efficient since computing the best individuals in the neighborhood takes \(O({\mathbf P} )\), while the clustering approach takes \(O({\mathbf P} ^2)\) for \({\mathbf P}\) being the population size.
Finally, the use of Differential Evolution with global and local interpolation vectors is advantageous to balance both exploration and exploitation over the entire search space \(x \in {\mathbf {T}}\), wherein the trade-off between the global and the local search is self-adapted throughout the iterations.
Computational experiments
This section discusses our experimental results as well as obtained insights after evaluating the performance of our proposed method by using exhaustive computational experiments in diverse polygonal maps with both convex and non-convex topology.
Our computing environment was Intel i7-4930K @ 3.4GHz, MATLAB 2016a.
Table 1 shows the key parameters of Differential Evolution such as the probability of crossover CR and the scaling factors \(\alpha\) and \(\beta\).
The reason of using a crossover probability \(CR = 0.5\) is to give equal importance to the search directions obtained from historical search, and those obtained considering local and global interpolations.
Also, without a priori knowledge of problem convexity, uni-modality or multi-modality of the route bundling problem, we choose conservative values of \(\alpha\) and \(\beta\) to induce smooth balance of exploitation and exploration in both the global and local neighborhood; thus, the scaling factor, \(\displaystyle \alpha = \beta = \Big |\frac{ln(U(0,1))}{2} \Big |\), allows to search in small steps when computing the global, the local and the self-adaptive directions.
Table 1 Parameters in Differential Evolution
Experimental scenarios
In order to enable a meaningful evaluation of our proposed approach, we consider the following environmental scenarios:
Table 2 Experimental scenarios
In order to give a glimpse of the type of polygonal maps used in our study, Figs. 4 and 5 show the topology of the bipartite network and the polygonal maps. Note that these domains are organized in a grid in which the horizontal (vertical) axis portrays, in ascending order from left (bottom) to right (top), the number of routes (polygons) involved in route bundling.
The main reason of using values of the number of edges |E| up to 25 is due to our interest in evaluating the performance in scenarios reminiscent to indoor environments, where the complexity of the environment is controlled by the following elements:
the number of obstacles in the polygonal map, and/or
the number of sides for each obstacle.
Thus, complex polygonal domains induce in large number of triangles, edges and vertices in the visibility graph, thus representing a challenging search space for any path-planning algorithm. Our future work aims at using configurations considering large scenarios and being close to outdoor environments.
Furthermore, we considered the following:
For each combination of the above, 15 independent experiments were performed to solve Eq. 1 by using the optimization algorithm in Eq. 9, and
For each independent experiment, the maximum number of functions evaluations is set as \(10^4\) with initial solutions of route bundles \(x_o \in {\mathbf {T}}\) being initialized randomly and independently.
The above is due to our interest in avoiding random bias/luck, and evaluating the efficiency of the proposed method under restrictive computational budget.
As a result of the above considerations, 12,000 experimental conditions were evaluated,Footnote 1 and 11,250,000,000 function evaluations were performed.Footnote 2
Bipartite network and polygonal map with 5 sides
Bipartite network and polygonal map with 10 sides
Route bundles in polygonal domains of S = 5 sides
Route bundles in polygonal domains of S = 10 sides
Convergence in polygonal domains of S = 5 sides
Convergence in polygonal domains of S = 10 sides
Number of evaluations required to achieve convergence in route bundling, in which darker colors imply large number of evaluations. The x-axis of each heatmap denotes the population size |P|, whereas the y-axis of each heatmap denotes the neighborhood scaling factor \(\eta\). Heatmaps are arranged in a 2-dimensional grid, in which the horizontal axis of the grid denotes the number of edges |E| in the bipartite network and the vertical axis of the grid denotes the number of obstacles in the map. In this arrangement, heatmaps located at bottom/left (top/right) of the grid imply simple (complex) route bundling scenarios
Number of evaluations required to achieve convergence in route bundling, in which darker colors imply large number of evaluations. The x-axis of each heatmap denotes the population size |P|, whereas the y-axis of each heatmap denotes the neighborhood scaling factor \(\eta\). Heatmaps are arranged in a 2-dimensional grid, in which the horizontal axis of the grid denotes the number of edges |E| in the bipartite network, and the vertical axis of the grid denotes the number of obstacles in the map. In this arrangement, heatmaps located at bottom/left (top/right) of the grid imply simple (complex) route bundling scenarios
In order to show the kind of tree structures obtained in the route bundling process, Figs. 6 and 7 show the obtained route bundles in polygonal domains with obstacles of 5 and 10 sides, respectively. In order to show the efficiency of the proposed method, Figs. 8 and 9 show the convergence characteristics. Note that these figures are arranged in a grid in which the horizontal axis shows the number of edges |E| in the bipartite graph, and the vertical axis shows the number of obstacles in the polygonal map. In these figures, for the sake of simplicity, the values of \({\mathbf P} = 25\) and \(\eta = 0.2\) are used; other values as denoted in Table 2 are discussed in subsequent sections.
In regard to the obtained route bundles, we can confirm the following facts:
Regardless of the configuration of the polygonal map and the structure of the bipartite graph, it is possible to generate tree structures representing the bundled routes which aim at minimizing the global distance metric.
The location of the anchoring points of the bundled routes is close to, but not necessarily at, the center of the origin and destination pairs of the bipartite graph.
The route between the anchoring points of the bundled routes is not necessarily a straight line, and, regardless of increasing the number of edges in the bipartite graph, the routes between the anchoring points and the topologies of route bundles are structurally similar, but not equivalent. This is due to the fact of having edges with close origin–destination pairs.
The above observations has important implications to extend our proposed method in the following ways:
instead of using arbitrary initial solutions in the optimization algorithm, it may be possible to compute the initial solutions of x which are close to the center/centroid of the origin and destination pairs, and
it may be possible to use pre-computed routes between the anchoring points as initial solutions whenever the number of edges is expected to increase, since these routes are expected to be structurally similar.
The above are foundational insights to enable even faster convergence to the optimal solutions.
Furthermore, in regard to the convergence behavior of the Differential Evolution algorithm, Figs. 8 and 9 show the convergence behavior of the optimization algorithm over 15 independent runs. By observing these figures, it is possible to confirm the following facts:
Regardless of the configuration of the polygonal maps and the structure of bipartite graphs, it is possible to converge to the bundled routes minimizing a global distance metric within 1000 function evaluations and 15 independent runs.
Increasing the number of edges has a natural effect on increasing the distance metric by some small factor smaller than 1. This observation is in line with our above insights on the structural similarity of route bundles when increasing the number of edges.
The convergence behavior of each simulation is different due to the heuristic nature of solution sampling in Differential Evolution, and the independent arbitrary initialization at each independent run. Note that it is imperative to use different arbitrary initializations in order to evaluate our approach exhaustively under diverse initialization conditions.
The above results imply the feasibility and efficiency to obtain optimal route bundles in polygonal maps with both convex and non-convex obstacles.
It is important to note that since obtaining a mathematical proof of convergence is unfeasible due to the heuristic nature of Differential Evolution, we argue that our converged results are approximations to the true global optima. Yet, our study is able to provide insights when Differential Evolution is used to tackle the route bundling problem under complex environments and diverse initialization conditions. Studying the theoretical convergence under non-heuristic algorithmic schemes is in our future agenda.
Histogram of \((|{\mathbf P} |, \eta )\) representing the best population size \(|{\mathbf P} |\) and the best neighborhood scaling factor \(\eta\) for all scenarios. Here, the meaning of best implies the tuple \((|{\mathbf P} |, \eta )\) which achieves the smallest number of evaluations to converge given a tolerance value. a The case when convergence is evaluated using \(\hbox {Tol }= 1\). b The case when convergence is evaluated using \(\hbox {Tol }= 10^{-1}\). c The case when convergence is evaluated using \(\hbox {Tol }= 10^{-2}\). d The case when convergence is evaluated using \(\hbox {Tol }= 10^{-3}\)
Furthermore, in order to show the convergence at finer scale under different number of obstacles, routes, complexity of map, population size and neighborhood ratio, Figs. 10 and 11 show the required number of evaluations to achieve convergence. In these figures, the achievement of convergence is computed from the comparison of (1) the average difference of the cost function within 5 units of the convergence time series, to (2) the tolerance for convergence, which is a user-defined value rather than an optimization variable since it depends on the granularity of the polygonal map (maps requiring higher granularity imply finer and lower values of convergence tolerance).
In Figs. 10 and 11, for each number of routes and number of obstacles in the map, the heatmaps represent the number of evaluations required to achieve convergence for route bundling. Here, for each heatmap, darker colors imply large number of evaluations (max. number of evaluations is provided in the right side of each heatmap). Also, the x-axis of each heatmap represents the population size \(|{\mathbf P} | = \{25, 50, 100, 200\}\) in Differential Evolution, whereas the y-axis of each heatmap denotes the neighborhood scaling factor \(\eta \in \{0.1, 0.2, 0.4, 0.8\}\). Heatmaps are arranged in a 2-dimensional grid, in which the horizontal axis of the grid denotes the number of edges \(|E| \in \{5, 10, 15, 20, 25\}\) in the input bipartite network, and the vertical axis of the grid denotes the number of obstacles in the map \(\in \{1, 2, 3, 4, 5\}\). By this arrangement, heatmaps located at bottom/left grid imply simple route bundling scenarios, while heatmaps located at the top/right imply complex scenarios.
Then, by looking the results of Figs. 10 and 11, we observe that our proposed approach achieves faster convergence when using smaller populations (\(|{\mathbf P} | = 25\)) in most of the cases. We believe this is due to the fact of using a convex representation and a ring topology in Differential Evolution: whereas the convex representation helps sampling and evaluating unique solutions in the search space, the ring topology helps exploring the search space in areas close to the sampled solution. Thus, large populations or large neighborhood size has a detriment effect in widening the sampling space, which implies increasing the computational budget, and thus the required number of function evaluations to achieve convergence.
Population and neighborhood size
Based on the above observations, the reader may wonder: what are good values of population size \(|{\mathbf P} |\) and neighborhood scaling factor \(\eta\)? In order to answer this question, Fig. 12 shows the histogram of (\(|{\mathbf P} |\), \(\eta\)) for the fastest converged values. In this figure, the x-axis of the histogram denotes the population size \(|{\mathbf P} |\) and the y-axis of the histogram denotes the neighborhood ratio \(\eta\). The histograms are based on the number of times in which the tuple (\(|{\mathbf P} |\), \(\eta\)) achieved the smallest number of evaluations to achieve convergence. By observing Fig. 12, and in line of the above observations, for any value of evaluated tolerance for convergence in \(\{1, 10^{-1}, 10^{-2}, 10^{-3}\}\) , smaller populations are always beneficial. In regard to the neighborhood size, for convergence tolerances being \(10^{-1}\) or \(10^{-2}\), the neighborhood scaling factor \(\eta = 0.2\) is always beneficial, whereas for convergence tolerances being \(10^{-3}\), the neighborhood scaling factor \(\eta = 0.8\) is beneficial. These observations occur due to the fact of smaller tolerances implying the need to explore the search space at finer scale, thus higher neighborhood scaling factor \(\eta\) enables the effective sampling of the search space without the need to increase population size (which would induce in unwanted space memory overhead). These results show that our proposed approach performs the heuristic search efficiently by using small populations.
Algorithmic variants
The use of neighborhood and convex representation in Differential Evolution are relevant components in our proposed approach. Thus, in order to study the performance of these components in our proposed heuristic algorithm, we compared the following four variants:
DENC: Differential Evolution with Neighborhood and Convex Encoding. In this scheme, we use a neighborhood with \(\eta = 0.2\), based on our above observations, and the Convex Encoding denoted by the 6-dimensional tuple in Eq. 5 (described by "Representation of bundled routes" section).
DEN: Differential Evolution with Neighborhood Only. In this scheme, we use a neighborhood with \(\eta = 0.2\), based on our above observations, and the encoding denoted by the 4-dimensional tuple in Eq. 2, which is a simple representation yet computationally more expensive due to the fact of requiring checks of point inside polygon per every sampled solution to ensure feasible route bundles (coordinates are to be outside of obstacles). In this scenario, the cost function is computed as follows:
$$\begin{aligned} F(x)= & {} {\left\{ \begin{array}{ll} G(x) &{}\, P, Q \in {\mathrm{free\,space}}\\ \infty &{} {\mathrm{otherwise}} \end{array}\right. } \end{aligned}$$
$$\begin{aligned} G(x)= & {} \sum _{e \in E}d(e_o,P) + d(P,Q) + \sum _{e \in E}d(Q,e_d) \end{aligned}$$
where d(a, b) is the Euclidean obstacle-free shortest distance metric between points a and b, \(e_o\) is the Cartesian coordinate of the origin node of the edge \(e \in E\), \(e_d\) is the Cartesian coordinate of the destination node of the edge \(e \in E\), and P and Q are the Cartesian coordinates of anchoring points being closer to the origin \(e_o\) and destination \(e_d\), respectively. The condition \(P, Q \in\) free space satisfies that both P and Q are outside of the polygonal obstacles. Note that in this scheme, the Delaunay triangulation is not a requirement since all points are in \(\mathbb {R}^2\).
DEC, Differential Evolution with Convex Encoding Only. In this scheme, we use the Convex Encoding denoted by the 6-dimensional tuple in Eq. 5 (described by "Representation of bundled routes" section); yet, we avoid using neighborhood concepts, and thus the mutant vector \(v_t\) (denoted by Eq. 13) is computed without the local interpolation vector, as follows:
$$\begin{aligned} v_t = w^{x_t}.g_t \end{aligned}$$
In the above, we keep the weight to be multiplying the global interpolation vector in order to enable individual self-adaptation.
DE: Differential Evolution without Neighborhood nor Convex Encoding. In this scheme, we avoid using neighborhood concepts as well as the Convex Encoding. Therefore, the mutant vector \(v_t\) is computed by Eq. 19, the encoding is depicted by the 4-dimensional tuple in Eq. 2, and the cost function is computed by Eq. 18.
Comparison of convergence in polygonal domains of S = 5 sides
Comparison of convergence in polygonal domains of S = 10 sides
In the above described variants, we used the population size as \(|{\mathbf P} | = 25\), based on our above observations describing the superiority of smaller populations. All other parameters in Differential Evolution are kept constant as described by Table 2.
In order to evaluate and compare the performance of the above described variants, Figs. 13 and 14 show the comparison of the average convergence behavior over 15 independent runs up to 2000 evaluations. The convergence figures are arranged in a 2-dimensional grid in which the x-axis portrays the number of edges in the input bipartite graph, and the y-axis portrays the number obstacles in the map. Thus, by looking at Figs. 13 and 14 we can observe the following facts:
In all cases, DENC and DEC have better solutions during the initialization phase (when the number of evaluations is up to \(|{\mathbf P} | = 25\)) and the first number of evaluations (up to 200 in all cases). This occurs due to that fact of DENC and DEC using the convex representation which ensures sampling feasible points, always. Conversely, DE and DEN require additional number of evaluations (and checks of point inside polygon) in order to sample and evaluate feasible solutions.
In all cases, either DENC or DEN has better convergence performance compared to DE. And in 26 out of 50 cases, DE has issues in stagnation. These observations imply that Differential Evolution using the interpolation vectors in the global and local neighborhood alone, or embedded with the convex representation, is useful not only to allow faster convergence, but also to allow escaping from stagnation. This occurs due to the fact of generating feasible solutions (by the convex representation), and due to the fact of self-balancing between directions toward the best in the population, and directions toward the best in the local neighborhood.
Furthermore, in 10 out of 50 cases, DEC has issues of stagnation, which is in line with the above insights. Since DEC uses no information of the local neighborhood, sampled solutions will stagnate in directions close to the global best. Then, without any explorative factor, DEC is likely to stagnate. Thus, as the above observations indicate, the use of neighborhood enables to add an explorative factor to avoid stagnation.
Further computational experiments using large number of edges and diverse obstacle configurations reminiscent of outdoor environments are in our agenda. Also, although the main focus of this paper is environments in 2D, the extension of 3D is straightforward since:
Delaunay triangulation in 3D takes in the worst case \(O(n^2)\), and in the expected case can be even O(n).
Differential Evolution can sample in an 8-dimensional tuple (for a convex representation) or 6-dimensional tuple (for a non-convex representation).
Path planning in 3D is possible by either geometric or point cloud approaches.
Also, we aim at dealing with dynamic environments in our future work. A simple extension would consider the following principles:
Obstacle geometry have minor changes over small time intervals, thus, to obtain the next optimal bundle, instead of using arbitrary initialization over the entire search space, it is possible to initialize candidate solutions with small perturbations to the current converged solutions and run Differential Evolution over a small number of evaluations. In this way, it becomes possible to quickly update the topology of the route bundles when changes in obstacle geometry are expected occur.
The same strategy can be used whenever the locations of origin and destination in the bipartite graph are expected to occur.
In order to realize a fast response time, it is possible to use multi-core computing since Differential Evolution supports parallelization inherently.
Also, in our agenda remains the use of undirected and directed graphs [27, 28], modularity by combinatorial groupings of nodes and edges [29, 30] to build trees with increased depth (to improve scalability) and its application to network design [31, 32]. Furthermore, it remains in our agenda the study of changing structures during network optimization, and the use of concurrent exploration and exploitation. Last but no least, the extension to generate curved and collision-free navigation bundles in cluttered environments [33,34,35] is left for future work. Our results offer building blocks to further advance toward developing global network optimization with convex, flexible and scalable representations.
In this paper, we have proposed a method for searching optimal route bundles based on a self-adaptive class of Differential Evolution and a convex representation. The basic idea of our approach is to sample over a triangulated search space by using self-adaptive interpolation vectors. And the unique point of our proposed method is the possibility to balance exploration and exploitation while sampling arbitrary points in a convex search space of route bundles. Then, it becomes possible the rendering of feasible route bundles efficiently since: (1) absence of overlaps with obstacles is guaranteed, and (2) computation of point inside polygon is explicitly avoided. Computational experiments involving more than 12,000 route bundling cases and 11,250,000,000 evaluations of path planning in a diverse class of polygonal domains show that (1) it is possible to obtain bundled routes with an optimized global distance metric via a reasonable number of sample evaluations, (2) the convergence towards the optimal solutions is possible over independent runs, (3) smaller populations are always beneficial, and (4) the interpolation vectors in the global and local neighborhood and the convex representation are useful not only to allow faster convergence, but also to allow escaping from stagnation.
In our future work, we aim at using polygonal environments reminiscent of outdoor configurations in which the number of edges of the bipartite network is allowed to increase. Also, in our future endeavors, we aim at exploring the generalization ability in dynamic environments, where both the input bipartite graph and the polygonal obstacles are allowed to change. We believe our approach opens new frontiers to further develop compounded and global path-planning algorithms via gradient-free optimization algorithms and convex representations of the search space.
\(5\times 5\times 2\times 4\times 4\times 15.\)
considering population size, number of independent runs, number of max. evaluations for all experimental conditions.
Dijkstra EW. A note on two problems in connexion with graphs. Numer Math. 1959;1:269–71.
MathSciNet Article MATH Google Scholar
Cormen T, Leiserson C, Rivest R. Introduction to algorithms. Cambridge: MIT Press; 1993.
Hart PE, Nilsson NJ, Raphael B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans Syst Sci Cybern. 1968;4(2):100–7.
Kallmann M. Path planning in triangulations. In: Proceedings of the workshop on reasoning, representation, and learning in computer games, IJCAI, 2005. p 49–54
Chazelle B. A Theorem on polygon cutting with applications. In: Proceedings of the 23rd IEEE symposium on foundations of computer science, 1982. p. 339–49
Lee DT, Preparata FP. Euclidean shortest paths in the presence of rectilinear barriers. Networks. 1984;14(3):393–410.
Faludi R. Building Wireless Sensor Networks, O'Reilly Media. 2014
Wightman P, Labardor M. A family of simple distributed minimum connected dominating set-based topology construction algorithms. J Netw Comput Appl. 2011;34:1997–2010.
Torkestani JA. An energy-efficient topology construction algorithm for wireless sensor networks. Comput Netw. 2013;57:1714–25.
Panigrahi N, Khilar PM. An evolutionary based topological optimization strategy for consensus based clock synchronization protocols in wireless sensor network. Swarm Evol Comput. 2015;22:66–85.
Szurley J, Bertrand A, Moonen M. Distributed adaptive node-specific signal estimation in heterogeneous and mixed-topology wireless sensor networks. Signal Process. 2015;117:44–60.
Christian G, Nicolas H, David I, Colette J. Disconnected components detection and rooted shortest-path tree maintenance in networks. In: The 16th international symposium on stabilization. safety, and security of distributed systems, Springer LNCS. 2014; 8736(SSS14): p. 120–34.
He J, Ji S, Pan Y, Cai Z. Approximation algorithms for load-balanced virtual backbone construction in wireless sensor networks. Theor Comput Sci. 2013;507:2–16.
Chu S, Wei P, Zhong X, Wang X, Zhou Y. Deployment of a connected reinforced backbone network with a limited number of backbone nodes. IEEE Trans Mob Comput. 2013;12(6):1188–200.
Zou Y, Chakrabarty K. A distributed coverage- and connectivity-centric technique for selecting active nodes in wireless sensor networks. IEEE Trans Comput. 2005;54(8):978–91.
Zhou H, Liang T, Xu C, Xie J. Multiobjective coverage control strategy for energy-efficient wireless sensor networks. Int J Distrib Sensor Netw. 2012;2012:1–10.
Park YK, Lee MG, Jung KK, Yoo JJ, Lee SH, Kim HS. Optimum sensor nodes deployment using fuzzy c-means algorithm. In: International symposium on computer science and society (ISCCS), 2011. p. 389-92
Cui W, Zhou H, Qu H, Wong PC, Li X. Geometry-based edge clustering for graph visualization. IEEE Trans Vis Comput Graph. 2008;14:1277–84.
Selassie D, Heller B, Heer J. Divided edge bundling for directional network data. IEEE Trans Vis Comput Graph. 2011;17(12):2354–63.
Holten D, van Wijk JJ. Force-directed edge bundling for graph visualization. In: IEEE-VGTC symposium on visualization: eurographics; 2009.
Ersoy O, Hurther C, Paulovich F, Cabtareiro G, Telea A. Skeleton-based edge bundling for graph visualization. IEEE Trans Vis Comput Graph. 2011;17(12):2364–73.
Gansner ER, Hu Y, North S, Scheidegger C. Multilevel agglomerative edge bundling for visualizing large graphs. In: Pacific visualization symposium, 2011. p. 187–94
Chew LP. Constrained Delaunay triangulations In: Proceedings of the annual symposium on computational geometry. ACM; 1987. p. 215–22
Osada R, Funkhouser T, Chazelle B, Dobki D. Shape distributions. ACM Trans Graph Euro-graphics. 2002;21(4):807–32.
Das S, Abraham A, Chakraborty UK, Konar A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans Evol Comput. 2009;13(3):526–53.
Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11:341–59.
Parque V, Kobayashi M, Higashi M. Bijections for the numeric representation of labeled graphs. In: IEEE international conference on systems, man and cybernetics, 2014. p. 447–52
Parque V, Miyashita T. On succinct representation of directed graphs. In: IEEE international conference on big data and smart computing, 2017. p. 199–205
Parque V, Miyashita T. On k-subset sum using enumerative encoding. In: International symposium on signal processing and information technology, 2016. p. 81–6
Parque V, Kobayashi M, Higashi M. Searching for machine modularity using explorit. In: IEEE international conference on systems, man and cybernetics, 2014. p. 2599–604
Parque V, Kobayashi M, Higashi M. Neural computing with concurrent synchrony. In: International conference on neural information processing, 2014. p. 304–11
Parque V, Kobayashi M, Higashi M. Reinforced explorit on optimizing vehicle powertrains. In: International conference on neural information processing, 2013. p. 579–86
Liu S, Watterson M, Mohta K, Sun K, Bhattacharya S, Taylor CJ, Kumar V. Planning dynamically feasible trajectories for quadrotors using safe flight corridors in 3-D complex environments. IEEE Robot Autom Lett. 2017;2(3):1688–95.
Deits R, Tedrake R. Computing large convex regions of obstacle-free space through semidefinite programming. In: Akin H, Amato N, Isler V, van der Stappen A, editors. Algorithmic foundations of robotics XI, vol 107. Cham: Springer; 2015. p. 109–24.
Deits R, Tedrake R. Efficient mixed-integer planning for UAVs in cluttered environments. In: IEEE international conference on robotics and automation, 2015. p. 42–9
VP contributed to the ideas, the programming work, and the writing of the paper. SM and TM help to revise the manuscript. All authors read and approved the final manuscript.
Authors' information
Victor Parque is Assistant Professor at the Department of Modern Mechanical Engineering, Waseda University, as well as Associate Professor at Egypt-Japan University of Science and Technology. He obtained the MBA degree from Esan University in 2009 and obtained the Doctoral degree from Waseda University in 2011. He was a Postdoctoral Fellow at Toyota Technological Institute from 2012 to 2014. His research interests include Learning and Intelligent Systems and its applications to Design Engineering and Control. Satoshi Miura is Research Associate at the Department of Modern Mechanical Engineering, Waseda University. He obtained the Master Degree in 2013, and the Doctoral degree in 2016 from Waseda University. His research interests span the intuitive operability in hand–eye coordination of master–slave robot using brain activity measurement, development of intuitive interface for locomotion robot, driving assist technology of automobile, sports training by real-time visual feedback, typing support device and development of interface for automatic driving of car. Tomoyuki Miyashita is Professor at the Department of Modern Mechanical Engineering, Waseda University. After joining Nippon Steel Co. Ltd. in 1992, he obtained the doctoral degree from Waseda University in 2000. He was Research Associate at Waseda University and Ibaraki University since 200 and 2002, respectively. He became Associate Professor and Professor at Waseda University in 2005 and 2007, respectively. His research interests are Design Process, Design Optimization, Organ Deformation.
Acknowlegements
The generous support from Waseda University to fund the publication in open-access format is highly appreciated.
The dataset supporting the conclusions of this article is available in the GitHub repository: https://github.com/vparque/DEBundling.
Fund from Waseda University for Open-Access Publications.
Department of Modern Mechanical Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo, 169-8555, Japan
Victor Parque, Satoshi Miura & Tomoyuki Miyashita
Department of Mechatronics and Robotics, Egypt-Japan University of Science and Technology, Qesm Borg Al Arab, Alexandria, 21934, Egypt
Victor Parque
Satoshi Miura
Tomoyuki Miyashita
Correspondence to Victor Parque.
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Parque, V., Miura, S. & Miyashita, T. Route bundling in polygonal domains using Differential Evolution. Robot. Biomim. 4, 22 (2017). https://doi.org/10.1186/s40638-017-0079-x
Accepted: 25 November 2017
DOI: https://doi.org/10.1186/s40638-017-0079-x
Route bundling
Real-time Computing and Robotics
Follow SpringerOpen
SpringerOpen Twitter page
SpringerOpen Facebook page | CommonCrawl |
\begin{document}
\title {$E_{2}$ Structures and Derived Koszul Duality in String Topology}
\author{Andrew J. Blumberg} \address{Department of Mathematics, The University of Texas, Austin, TX \ 78712} \email{[email protected]} \thanks{The first author was supported in part by NSF grant DMS-1151577} \author{Michael A. Mandell} \address{Department of Mathematics, Indiana University, Bloomington, IN \ 47405} \thanks{The second author was supported in part by NSF grant DMS-1505579} \email{[email protected]}
\date{January 10, 2017} \subjclass[2010]{Primary 55P50, 16E40, 16D90.} \keywords{}
\begin{abstract} We construct an equivalence of $E_{2}$ algebras between two models for the Thom spectrum of the free loop space that are related by derived Koszul duality. To do this, we describe the functoriality and invariance properties of topological Hochschild cohomology. \end{abstract}
\maketitle
\section*{Introduction}
Chas and Sullivan started the subject of string topology with their observation that the homology of the free loop space $LM$ of a closed oriented manifold $M$ admits a Gerstenhaber structure that can be defined geometrically in terms of natural operations on loops and intersection of chains on the manifold. Contemporaneously, the solution to Deligne's Hochschild cohomology conjecture (by Kontsevich-Soibelman~\cite{Kontsevich-Deligne}, McClure-Smith~\cite{McClureSmith-Deligne}, Tamarkin~\cite{Tamarkin-Deligne}, Voronov~\cite{Voronov-Deligne}, Berger-Fresse~\cite{BergerFresse-Deligne}, and perhaps others) established a Gerstenhaber algebra structure on the Hochschild cohomology of a ring or differential graded algebra or even $A_{\infty}$ ring spectrum. Cohen-Jones~\cite{CohenJones-THC}, in the course of giving a homotopical interpretation of the string topology product, connected these two ideas by relating a certain Thom spectrum of $LM$ with the topological Hochschild cohomology $THC(DM)$ of the Spanier-Whitehead dual $DM$. The homology of $THC(DM)$ is canonically isomorphic to the Hochschild cohomology of the cochain algebra $C^{*}(M)$; Cohen-Jones~\cite{CohenJones-THC} in particular produces a shifted isomorphism from the homology of the free loop space to the homology of $THC(DM)$ that takes the string topology product to the cup product in Hochschild cohomology. Later work of Malm~\cite{Malm-Thesis} and Felix-Menichi-Thomas~\cite{FelixMenichiThomas} give an isomorphism of Gerstenhaber algebras.
The Felix-Menichi-Thomas work derives from work of Keller~\cite{Keller-Picard} (see also~\cite{Keller-DIH}) building on unpublished work of Buchweitz. Keller~\cite{Keller-DIH} shows that (under mild hypotheses) the Hochschild cochains of Koszul dual dg algebras are equivalent as $E_{2}$ algebras (or, more specifically, $B_{\infty}$ algebras, cf.~\cite{GerstenhaberVoronov,Young-Thesis}). When $M$ is simply connected, the derived Koszul dual of $C^{*}M$ is the cobar construction $\bar\Omega C_{*}M$, which is the Adams-Hilton model for the chains on the based loop space $C_{*}(\Omega M)$; Felix-Menichi-Thomas~\cite{FelixMenichiThomas} constructs an isomorphism of Gerstenhaber algebras \[ HH^{*}(C^{*}M)\iso HH^{*}(\bar\Omega C_{*}M). \] Since $HH^{*}(\bar\Omega C_{*}M)$ is isomorphic to the homology of $THC(\Sigma^{\infty}_+ \Omega M)$, in spectral models, we should look for an equivalence of $E_{2}$ ring spectra between $THC(DM)$ and $THC(\Sigma^{\infty}_+ \Omega M)$. Our main result is the following theorem, proved in Section~\ref{sec:pfstring}.
\begin{main}\label{main:string} Let $X$ be a simply connected finite cell complex; then $THC(DX)$ and $THC(\Sigma^{\infty}_+ \Omega X)$ are weakly equivalent as $E_{2}$ ring spectra. \end{main}
Beyond the technical role of $HH^{*}(\bar\Omega C_{*}M)$ in the comparison of Gerstenhaber algebra structures, the spectral analogue $THC(\Sigma^{\infty}_+ \Omega M)$ in the previous theorem also provides a connection between string topology and topological field theory, as explained in~\cite{BCT}. Furthermore, \cite{BCT} sketches a relationship between $THC(\Sigma^{\infty}_+ \Omega M)$ and the wrapped Fukaya category of $T^{*}M$, motivated by the work of Abbondandolo-Schwarz~\cite{AbbondandoloSchwarz} and Abouzaid~\cite{Abouzaid}. (See also~\cite{SeidelICM} for discussion of the significance of Hochschild cohomology of Fukaya categories.) Indeed, the previous theorem (and the machinery we develop to prove it) fills in results stated in~\cite{BCT} but deferred to a future paper.
In the discussion above and in the statement of Theorem~\ref{main:string}, we are using $THC$ to denote a derived version of the topological Hochschild cohomology spectrum. What this means is slightly complicated by the fact the standard cosimplicial construction is not functorial. In the setting of differential graded categories, Keller~\cite{Keller-Picard,Keller-DIH} made sense of this for Hochschild cochains and proved limited functoriality and invariance results for Hochschild cohomology. Part of the purpose of this paper is to provide a spectral version of this theory.
For the $E_{2}$ structure, we use the McClure-Smith theory of~\cite{McClureSmith-Deligne,McClureSmith-CosimplicialCubes}, which establishes the action of a specific $E_{2}$ operad $\mathcal{D}_{2}$ on totalization ($\Tot$) of the topological Hochschild cosimplicial construction of a strictly associative ring spectrum in any modern category of spectra (such as symmetric spectra, orthogonal spectra, or EKMM $S$-modules). We denote this point-set topological Hochschild cohomology construction as $CC$ in the following theorem, proved in Section~\ref{sec:pfwefunct}.
\begin{main}\label{main:wefunct} Let ${\catsymbfont{S}}$ denote either symmetric spectra, orthogonal spectra, or EKMM $S$-modules; let ${\catsymbfont{S}}[\mathop{\oA\mathrm{ss}}\nolimits]$ be the category of associative ring spectra (in ${\catsymbfont{S}}$); and let $\Ho{\catsymbfont{S}}[\mathop{\oA\mathrm{ss}}\nolimits]$ denote its homotopy category. Let $\Ho{\catsymbfont{S}}[\mathop{\oA\mathrm{ss}}\nolimits]^{\simeq}$ denote the subcategory of $\Ho{\catsymbfont{S}}[\mathop{\oA\mathrm{ss}}\nolimits]$ where the maps are isomorphisms. There is a contravariant functor $THC$ from $\Ho{\catsymbfont{S}}[\mathop{\oA\mathrm{ss}}\nolimits]^{\simeq}$ to the homotopy category of $E_{2}$ ring spectra together with canonical isomorphisms $THC(R)\to CC(R)$ for those $R$ whose underlying objects of ${\catsymbfont{S}}$ are fibrant and cofibrant relative to the unit. \end{main}
\iffalse The correct generality for $THC$ is the setting of small spectral categories, which generalize associative ring spectra. In section~\ref{sec:MS}, we explain that the McClure-Smith theory extends to construct an $E_{2}$ structure on the $\Tot$ of the topological Hochshild-Mitchell cosimplicial construction $CC({\catsymbfont{C}})$ for a small spectral category ${\catsymbfont{C}}$. The natural weak equivalences for spectral categories are the \term{Dwyer-Kan} equivalences, or DK-equivalences. Given a spectral category ${\catsymbfont{C}}$, the homotopy groups of the mapping spectra define a category $\pi_{*}{\catsymbfont{C}}$ enriched in graded abelian groups and a spectral functor $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ defines an enriched functor $\pi_{*}\phi \colon \pi_{*}{\catsymbfont{D}}\to \pi_{*}{\catsymbfont{C}}$. The functor $\phi$ is a DK-equivalence when $\pi_{*}\phi$ is an equivalence; equivalently, $\phi$ is a DK-equivalence if $\phi$ induces a weak equivalence ${\catsymbfont{D}}(a,b)\to {\catsymbfont{C}}(F(a),F(b))$ for all objects $a,b$ of ${\catsymbfont{D}}$ and induces an equivalence of \term{homotopy categories} $\pi_{0}{\catsymbfont{D}}\to \pi_{0}{\catsymbfont{C}}$. Separating out the pointwise condition, we say that $\phi$ is a DK-embedding when $\pi_{*}\phi$ is fully faithful, or equivalently, when $\phi$ induces a weak equivalence ${\catsymbfont{D}}(a,b)\to {\catsymbfont{C}}(\phi(a),\phi(b))$ for all objects $a,b$ of ${\catsymbfont{D}}$. The following is the natural generalization of Theorem~\ref{main:wefunct} to this setting. \fi
The correct generality for $THC$ is the setting of small spectral categories, which generalize associative ring spectra. In Section~\ref{sec:MS}, we explain that the McClure-Smith theory extends to construct an $E_{2}$ structure on the $\Tot$ of the topological Hochshild-Mitchell cosimplicial construction $CC({\catsymbfont{C}})$ for a small spectral category ${\catsymbfont{C}}$. The natural weak equivalences for spectral categories are the \term{Dwyer-Kan} equivalences, or DK-equivalences. A spectral functor $\phi\colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ is a \term{DK-embedding} if it induces a weak equivalence ${\catsymbfont{D}}(a,b)\to {\catsymbfont{C}}(\phi(a),\phi(b))$ for all objects $a,b$ of ${\catsymbfont{D}}$; a DK-equivalence is a DK-embedding that induces an equivalence of \term{homotopy categories} $\pi_{0}{\catsymbfont{D}}\to \pi_{0}{\catsymbfont{C}}$.
The following theorem, proved in Section~\ref{sec:pfdkfunct}, is the natural generalization of Theorem~\ref{main:wefunct} to this setting; the theorem roughly says that $THC$ is functorial in DK-embeddings. In it, we use the condition for small spectral categories analogous to the condition we used for associative ring spectra in Theorem~\ref{main:wefunct}: We say that a small spectral category ${\catsymbfont{C}}$ is pointwise relatively cofibrant if the mapping spectra ${\catsymbfont{C}}(c,c)$ are cofibrant relative to the unit for all objects $c$ in ${\catsymbfont{C}}$ and the mapping spectra ${\catsymbfont{C}}(c,d)$ are cofibrant for all pairs of objects $c\neq d$ in ${\catsymbfont{C}}$. Similarly, we say a small spectral category is pointwise fibrant if each mapping spectrum ${\catsymbfont{C}}(c,d)$ is fibrant.
\begin{main}\label{main:dkfunct} Let ${\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits$ denote the category of small spectral categories and\break $\Ho({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits)$ the category obtained by formally inverting the DK-equivalences. Let $\Ho({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits)^{DK}$ be the subcategory of $\Ho({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits)$ generated by the DK-embeddings. There is a contravariant functor $THC$ from $\Ho({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits)^{DK}$ to the homotopy category of $E_{2}$ ring spectra together with canonical isomorphisms $THC({\catsymbfont{C}})\to CC({\catsymbfont{C}})$ for those ${\catsymbfont{C}}$ which are pointwise relatively cofibrant and pointwise fibrant. \end{main}
For any small spectral category ${\catsymbfont{C}}$, we can construct a functorial ``thick closure'' ${\mathrm{Perf}}({\catsymbfont{C}})$~\cite[\S 5]{BM-tc} (after fixing a cardinal bound); roughly speaking, this is the full subcategory of spectral presheaves on ${\catsymbfont{C}}$ generated under finite homotopy colimits and retracts by ${\catsymbfont{C}}$. A spectral functor $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ is a Morita equivalence when the induced functor ${\mathrm{Perf}}({\catsymbfont{C}}) \to {\mathrm{Perf}}({\catsymbfont{D}})$ is a DK-equivalence. One reason for interest in the Morita equivalences is that the Bousfield localization of the category of small spectral categories at the Morita equivalences is a model for the $\infty$-category of small stable idempotent-complete $\infty$-categories~\cite[4.23]{BGT}. The following theorem, proved in Section~\ref{sec:pfme}, shows that $THC$ descends to a functor on a subcategory of this localization.
\begin{main}\label{main:me} If $\phi\colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ is a Morita equivalence, then $THC(\phi)\colon THC({\catsymbfont{C}})\to THC({\catsymbfont{D}})$ is an isomorphism in the homotopy category of $E_{2}$ ring spectra. \end{main}
Theorems~\ref{main:wefunct} and~\ref{main:me} describe invariance properties of $THC$ analogous to the well-established invariance properties of $THH$. However, $THC$ in fact has more general invariance properties. For example, if ${\catsymbfont{D}}$ is a small spectral subcategory of the category of cofibrant-fibrant right ${\catsymbfont{C}}$-modules that factors the Yoneda embedding, then $THC({\catsymbfont{C}})\to THC({\catsymbfont{D}})$ is an isomorphism in the homotopy category of $E_{2}$ ring spectra (see Example~\ref{ex:perf} below). The most general expression of this invariance we know can be expressed in terms of the double centralizer condition, which is also a generalization of derived Koszul duality.
Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and let ${\catsymbfont{M}}$ be a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule (a commuting left ${\catsymbfont{C}}$-module and right ${\catsymbfont{D}}$-module structure; see Definition~\ref{defn:bibimod} or~\ref{defn:sbimod} below). Then there are canonical maps in the categories of homotopical $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodules and homotopical $({\catsymbfont{D}},{\catsymbfont{D}})$-bimodules, respectively, \[ {\catsymbfont{C}}\to \mathbf{R}\Hom_{{\catsymbfont{D}}^{\op}}({\catsymbfont{M}},{\catsymbfont{M}}),\qquad {\catsymbfont{D}}\to \mathbf{R}\Hom_{{\catsymbfont{C}}}({\catsymbfont{M}},{\catsymbfont{M}}). \] A standard definition is that ${\catsymbfont{M}}$ satisfies the \term{double centralizer condition} when both these maps are weak equivalences. Working backward from this terminology, we say that ${\catsymbfont{M}}$ satisfies the \term{single centralizer condition for ${\catsymbfont{C}}$} when the first map (out of ${\catsymbfont{C}}$) is a weak equivalence and the \term{single centralizer condition for ${\catsymbfont{D}}$} when the second map (out of ${\catsymbfont{D}}$) is a weak equivalence. The following is the spectral version of the main theorem of Keller~\cite{Keller-DIH}; we prove it in Section~\ref{sec:pfdcc}.
\begin{main}\label{main:dcc} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and ${\catsymbfont{M}}$ a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule that satisfies the single centralizer condition for ${\catsymbfont{D}}$; then there is a canonical map in the homotopy category of $E_{2}$ ring spectra $THC({\catsymbfont{C}})\toTHC({\catsymbfont{D}})$. If ${\catsymbfont{M}}$ satisfies the double centralizer condition, then $THC({\catsymbfont{C}})\toTHC({\catsymbfont{D}})$ is an isomorphism in the homotopy category of $E_{2}$ ring spectra. \end{main}
We deduce Theorem~\ref{main:string} in Section~\ref{sec:pfstring} as an immediate corollary of the previous theorem. Dwyer-Greenlees-Iyengar~\cite[4.22]{DwyerGreenleesIyengar-Duality} relates the double centralizer condition for the sphere spectrum ${\mathbb{S}}$ as a $(\Sigma^{\infty}_+ \Omega X,DX)$-bimodule to the Eilenberg-Moore spectral sequence; Section~3 of~\cite{BM-Koszul} describes nice models of $DX$ and $\Sigma^{\infty}_+ \Omega X$ and explicitly proves the double centralizer condition when $X$ is a simply connected finite cell complex for a bimodule whose underlying spectrum is equivalent to ${\mathbb{S}}$.
Theorems~\ref{main:dkfunct} and~\ref{main:me} have an $\infty$-categorical extension. Specifically, we prove the following theorem in Section~\ref{sec:inftyfunct}.
\begin{main}\label{main:inf} Let $\mathop{\aC\!\mathrm{at}}\nolimits^{\ex}$ denote the $\infty$-category of small stable idempotent-complete $\infty$-categories and exact functors. Then $THC$ extends to a functor from the subcategory of $\mathop{\aC\!\mathrm{at}}\nolimits^{\ex}$ where the morphisms are fully-faithful inclusions to the $\infty$-category of $E_2$ ring spectra. \end{main}
\iffalse which allow us to describe $THC$ as a functor from a subcategory of the $\infty$-category of small stable idempotent-complete $\infty$-categories to the $\infty$-category of $E_{2}$ ring spectra. \fi
\subsection*{Conventions}
In this paper, ${\catsymbfont{S}}$ denotes either the category of symmetric spectra (of topological spaces), or the category of orthogonal spectra, or the category of EKMM $S$-modules. For brevity we call ${\catsymbfont{S}}$ the \term{category of spectra} and objects of ${\catsymbfont{S}}$ \term{spectra}. We regard the \term{stable category} as the homotopy category obtained from ${\catsymbfont{S}}$ be formally inverting the weak equivalences. (The words ``spectrum'' and ``spectra'' when used in this paper should not be construed as refering to any other notion or category.)
\subsection*{Acknowledgments} The authors thank Ralph Cohen, Zachery Lindsey, and Constantin Teleman for useful conversations; we additionally thank Ralph Cohen for suggesting this project.
\iffalse
Menichi (BV algebra structures on Hoch coh) shows that HH^* (C^* M) has a BV algebra structure extending the Gerstenhaber structure
Menichi (Van den Bergh) shows that HH^* of C_* \Omega M is isomorphic to HH_* of C_* \Omega M (via Poincare duality) and conjectures that the associated BV structure is the same as the string topology one under the identification of HH_*(C_* \Omega M) with H_* (LM).
Malm constructs a BV algebra structure on HH^* of C_* \Omega M in the same way as Menichi (but maybe upgraded to chains rather than on homology) again via PD and shows that actually is the same as the string topology one. (But maybe this paper isn't quite correct.)
Felix and Thomas produce a BV algebra isomorphism between H_* (LM) and HH^*(C^* M); Malm conjectures this isomorphism is the same as his up to a sign.
FMT: GA iso HH^{*}(C^{*}M) and HH^{*}(C_{*}\Omega M) Malm: BV iso H_{*}LM and HH^{*}(C_{*}\Omega M) FT: BV iso H_{*}LM and HH^*(C^* M) over Q \fi
\section{Bi-indexed spectra and the tensor-Hom adjunctions} \label{sec:bis}
The purpose of this section is to establish technical foundations for proving tensor-$\Hom$ adjunctions for modules over small spectral categories. To do this, we work here with the theory of ``bi-indexed'' spectra, which are like spectrally enriched directed graphs but where the source and target vertices can be in different sets.
\begin{defn}\label{defn:bis} For sets $A$ and $B$, an $(A,B)$-spectrum ${\catsymbfont{X}}$ consists of a choice of spectrum ${\catsymbfont{X}}(a,b)$ for each object $(a,b)$ of $A\times B$; we call $(a,b)$ a \term{bi-index}. A morphism of $(A,B)$-spectra ${\catsymbfont{X}}\to {\catsymbfont{Y}}$ consists of a map of spectra ${\catsymbfont{X}}(a,b)\to Y(a,b)$ for all bi-indexes $(a,b)\in A\times B$. A bi-indexed spectrum ${\catsymbfont{X}}$ is an $(A,B)$-spectrum for some $A,B$; we define the \term{source} of ${\catsymbfont{X}}$ (denoted $S({\catsymbfont{X}})$) to be $B$ and the \term{target} of ${\catsymbfont{X}}$ to be $A$ (denoted $T({\catsymbfont{X}})$). If $S(X)=S(Y)$ and $T(X)=T(Y)$, then the set of maps of bi-indexed spectra from ${\catsymbfont{X}}$ to ${\catsymbfont{Y}}$ is the set of maps of $(T({\catsymbfont{X}}),S({\catsymbfont{X}}))$-spectra from ${\catsymbfont{X}}$ to ${\catsymbfont{Y}}$; otherwise, it is empty.
For a bi-indexed spectrum ${\catsymbfont{X}}$, let ${\catsymbfont{X}}^{\op}$ denote the bi-indexed spectrum with \begin{itemize} \item $S({\catsymbfont{X}}^{\op})=T({\catsymbfont{X}})$, \item $T({\catsymbfont{X}}^{\op})=S({\catsymbfont{X}})$, and \item ${\catsymbfont{X}}^{op}(s,t)={\catsymbfont{X}}(t,s)$ for all $(t,s)\in T({\catsymbfont{X}})\times S({\catsymbfont{X}})$. \end{itemize} \end{defn}
We have written and typically write generic bi-indexed spectra with the target variable first and the source variable second; we refer to this as the $TS$-indexing convention. For the bi-indexed spectra associated to small spectral categories (see Definition~\ref{defn:scat} below), it is more usual to use the $ST$-indexing convention, writing the source variable first and the target variable second, and we follow this convention for spectral categories and their bimodules. When it is unclear from the context which indexing is used, we add a superscript $st$ or $ts$, so \[ {\catsymbfont{X}}^{st}(a,b)={\catsymbfont{X}}^{ts}(b,a). \] We emphasize the distinction between $(-)^{st}$ and $(-)^{\op}$: $(-)^{st}$ just reverses the notation of source and target, while $(-)^{\op}$ reverses the notion of source and target.
As defined above, the category of bi-indexed spectra only admits maps between objects whose source sets agree and target sets agree and so it is sometimes useful to alter these sets.
\begin{defn}\label{defn:restriction} Given functions $f\colon A'\to A$, $g\colon B'\to B$ and an $(A,B)$-spectrum ${\catsymbfont{X}}$, define the \term{restriction of ${\catsymbfont{X}}$ along $(f,g)$} to be the $(A',B')$-spectrum $R_{f,g}{\catsymbfont{X}}$ where \[ (R_{f,g}{\catsymbfont{X}})(a',b')={\catsymbfont{X}}(f(a'),g(b')) \] for all $(a',b')\in A'\times B'$. We define the \term{target restriction of ${\catsymbfont{X}}$ along $f$} and the \term{source restriction of ${\catsymbfont{X}}$ along $g$} to be the $(A',B)$-spectrum $T_{f}{\catsymbfont{X}}$ and $(A,B')$-spectrum $S_{g}{\catsymbfont{X}}$ where \[ (T_{f}{\catsymbfont{X}})(a',b)={\catsymbfont{X}}(f(a'),b),\qquad (S_{g}{\catsymbfont{X}})(a,b')={\catsymbfont{X}}(a,g(b')) \] for all $(a',b)\in A'\times B$, $(a,b')\in A\times B'$. \end{defn}
Since bi-indexed spectra are determined by their constituent spectra on each bi-index, we have \[ T_{g}S_{f} = R_{f,g} = S_{f}T_{g} \] and for $f'\colon A''\to A'$ and $g'\colon B''\to B'$, \[ S_{f'}S_{f} = S_{f\circ f'}, \qquad R_{(f',g')}R_{f,g} = R_{f\circ f',g\circ g'}, \qquad T_{g'}T_{g} = T_{g\circ g'}. \] We could use the preceding definition to define a more sophisticated category of bi-indexed sets incorporating non-identity maps on source and target sets, but the advantage of the current approach is that this category of bi-indexed spectra has a partial monoidal structure, constructed as follows.
\begin{cons}\label{cons:tensor} For ${\catsymbfont{X}}$ an $(A,B)$-spectrum and ${\catsymbfont{Y}}$ a $(B,C)$-spectrum, define ${\catsymbfont{X}}\otimes {\catsymbfont{Y}}$ to be the $(A,C)$-spectrum \[ ({\catsymbfont{X}}\otimes {\catsymbfont{Y}})(a,c) = \bigvee_{b\in B}{\catsymbfont{X}}(a,b)\sma {\catsymbfont{Y}}(b,c). \] For ${\catsymbfont{Z}}$ a $(C,D)$-spectrum, the associativity isomorphism for the smash product and the universal property of coproduct induce an associativity isomorphism \[ \alpha_{{\catsymbfont{X}},{\catsymbfont{Y}},{\catsymbfont{Z}}}\colon ({\catsymbfont{X}}\otimes {\catsymbfont{Y}})\otimes {\catsymbfont{Z}}\iso {\catsymbfont{X}}\otimes ({\catsymbfont{Y}}\otimes {\catsymbfont{Z}}). \] For a set $A$, let ${\mathbb{S}}_{A}$ be the $(A,A)$-spectrum where \[ {\mathbb{S}}(a_{1},a_{2})=\begin{cases} *&a_{1}\neq a_{2}\\ {\mathbb{S}}&a_{1}=a_{2}. \end{cases} \] The left and right unit isomorphism for the smash product induce left and right unit isomorphisms \[ \eta^{\ell}_{{\catsymbfont{X}}}\colon {\mathbb{S}}_{A}\otimes {\catsymbfont{X}}\iso {\catsymbfont{X}}\qquad \text{and}\qquad \eta^{r}_{{\catsymbfont{X}}}\colon {\catsymbfont{X}}\otimes {\mathbb{S}}_{B}\iso {\catsymbfont{X}}. \] \end{cons}
The coherence of associativity and unit isomorphisms for spectra then imply the following proposition.
\begin{prop}\label{prop:pmc} The category of bi-indexed spectra is a partial monoidal category under $\otimes$: The object ${\catsymbfont{X}}\otimes {\catsymbfont{Y}}$ is defined when $T({\catsymbfont{Y}})=S({\catsymbfont{X}})$, and whenever defined, the following associativity \[ \[email protected]{ &&({\catsymbfont{W}}\otimes {\catsymbfont{X}})\otimes ({\catsymbfont{Y}}\otimes {\catsymbfont{Z}}) \ar[drr]^-{\quad\alpha_{{\catsymbfont{W}},{\catsymbfont{X}},{\catsymbfont{Y}}\otimes {\catsymbfont{Z}}}}\\ (({\catsymbfont{W}}\otimes {\catsymbfont{X}})\otimes {\catsymbfont{Y}})\otimes {\catsymbfont{Z}} \ar[urr]^-{\alpha_{{\catsymbfont{W}}\otimes {\catsymbfont{X}},{\catsymbfont{Y}},{\catsymbfont{Z}}}\quad} \ar[dr]_-{\alpha_{{\catsymbfont{W}},{\catsymbfont{X}},{\catsymbfont{Y}}}\otimes \id_{{\catsymbfont{Z}}}\quad} &&&& {\catsymbfont{W}}\otimes ({\catsymbfont{X}}\otimes ({\catsymbfont{Y}}\otimes {\catsymbfont{Z}}))\\ &({\catsymbfont{W}}\otimes ({\catsymbfont{X}}\otimes {\catsymbfont{Y}}))\otimes {\catsymbfont{Z}} \ar[rr]_-{\alpha_{{\catsymbfont{W}},{\catsymbfont{X}}\otimes {\catsymbfont{Y}},{\catsymbfont{Z}}} \vrule height1em width0pt depth0pt} && {\catsymbfont{W}}\otimes (({\catsymbfont{X}}\otimes {\catsymbfont{Y}})\otimes {\catsymbfont{Z}}) \ar[ur]_-{\quad\id_{{\catsymbfont{W}}}\otimes \alpha_{{\catsymbfont{X}},{\catsymbfont{Y}},{\catsymbfont{Z}}}} } \] and unit \[ \[email protected]{ ({\catsymbfont{X}}\otimes {\mathbb{S}}_{B})\otimes {\catsymbfont{Y}} \ar[rr]^{\alpha_{{\catsymbfont{X}},{\mathbb{S}}_{B},{\catsymbfont{Y}}}} \ar[dr]_{\eta^{r}_{{\catsymbfont{X}}}}&& {\catsymbfont{X}}\otimes ({\mathbb{S}}_{B}\otimes {\catsymbfont{Y}}) \ar[dl]^{\eta^{\ell}_{{\catsymbfont{Y}}}}&& \\ &{\catsymbfont{X}}\otimes {\catsymbfont{Y}} } \] diagrams commute. \end{prop}
The tensor product has two partially defined right adjoints and we also construct a third closely related functor.
\begin{cons}\label{cons:homlrb} If ${\catsymbfont{X}}$ is an $(A,B)$-spectrum, ${\catsymbfont{Y}}$ is an $(A,C)$-spectrum, and ${\catsymbfont{Z}}$ is a $(D,B)$-spectrum, we define the $(B,C)$-spectrum $\Hom^{\ell}({\catsymbfont{X}},{\catsymbfont{Y}})$ as \[ (\Hom^{\ell}({\catsymbfont{X}},{\catsymbfont{Y}}))(b,c)=\prod_{a\in A} F({\catsymbfont{X}}(a,b),{\catsymbfont{Y}}(a,c)) \] and the $(D,A)$-spectrum $\Hom^{r}({\catsymbfont{X}},{\catsymbfont{Z}})$ as \[ (\Hom^{r}({\catsymbfont{X}},{\catsymbfont{Z}}))(d,a)=\prod_{b\in B} F({\catsymbfont{X}}(a,b),{\catsymbfont{Z}}(d,b)) \] (where $F$ denotes the function spectrum construction, adjoint to the smash product). For ${\catsymbfont{X}}'$ an $(A,B)$-spectrum, we define the spectrum $\Hom^{b}({\catsymbfont{X}},{\catsymbfont{X}}')$ as \[ \Hom^{b}({\catsymbfont{X}},{\catsymbfont{X}}')=\prod_{(a,b)\in A\times B}F({\catsymbfont{X}}(a,b),{\catsymbfont{X}}'(a,b)). \] \end{cons}
We note that $\Hom^{b}$ provides a \term{partial spectral enrichment} of bi-indexed spectra: when $\Hom^{b}({\catsymbfont{X}},{\catsymbfont{X}}')$ is defined, maps of spectra from ${\mathbb{S}}$ into $\Hom^{b}({\catsymbfont{X}},{\catsymbfont{X}}')$ are canonically in one-to-one correspondence with maps of bi-indexed spectra from ${\catsymbfont{X}}$ to ${\catsymbfont{X}}'$, and when $\Hom^{b}({\catsymbfont{X}},{\catsymbfont{X}}')$ is not defined, the set of maps of bi-indexed spectra from ${\catsymbfont{X}}$ to ${\catsymbfont{X}}'$ is empty. An easy check of definitions shows the following adjunction property.
\begin{prop}\label{prop:bisadj} Let ${\catsymbfont{X}}$ be an $(A,B)$-spectrum, ${\catsymbfont{Y}}$ a $(B,C)$-spectrum, and ${\catsymbfont{Z}}$ an $(A,C)$-spectrum. Then there are canonical isomorphisms of spectra \[ \Hom^{b}({\catsymbfont{X}},\Hom^{r}({\catsymbfont{Y}},{\catsymbfont{Z}}))\iso \Hom^{b}({\catsymbfont{X}}\otimes {\catsymbfont{Y}},{\catsymbfont{Z}})\iso \Hom^{b}({\catsymbfont{Y}},\Hom^{\ell}({\catsymbfont{X}},{\catsymbfont{Z}})). \] \end{prop}
When $S({\catsymbfont{X}})=T({\catsymbfont{X}})=O$ for some set $O$, ${\catsymbfont{X}}$ is precisely a small spectral $O$-graph (with the reverse convention on the order of variables, i.e., with the $TS$-indexing convention); the tensor product above restricts to a monoidal product on $O$-graphs and it is well known that the category of small spectral $O$-categories is isomorphic to the category of monoids for this monoidal product (see~\cite[\S6.2]{SSMonoidalEq}; compare~\cite[\S II.7]{MacLane-Categories}). We say more about this below in Section~\ref{sec:rewrite}. Partly to avoid confusion with the indexing conventions, we will call the monoids under this convention bi-indexed ring spectra.
\begin{defn}\label{defn:birs} A \term{bi-indexed ring spectrum} is a monoid for $\otimes$ in bi-indexed spectra. For a bi-indexed ring spectrum ${\catsymbfont{X}}$, the \term{object set} $O({\catsymbfont{X}})$ is $S({\catsymbfont{X}})=T({\catsymbfont{X}})$. \end{defn}
Note that with the above definition, the natural morphisms for bi-indexed ring spectra only allow maps between small spectral categories with the same object sets. Instead of defining the analogue of spectral functors directly, it is more convenient to work with bimodules.
\begin{defn}\label{defn:bibimod} Let ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$ be bi-indexed ring spectra. An $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule consists of a bi-indexed spectrum ${\catsymbfont{M}}$ together with a left ${\catsymbfont{X}}$-object structure (for $\otimes$) and a commuting right ${\catsymbfont{Y}}$-object structure. We write $\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{X}},{\catsymbfont{Y}}}$ for the category of $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules. \end{defn}
Commuting here means that for the left-object structure $\xi\colon {\catsymbfont{X}}\otimes {\catsymbfont{M}}\to {\catsymbfont{M}}$ and the right object structure $\upsilon\colon {\catsymbfont{M}}\otimes {\catsymbfont{Y}}\to {\catsymbfont{M}}$, the diagram \[ \xymatrix@C-1pc{ ({\catsymbfont{X}}\otimes {\catsymbfont{M}})\otimes {\catsymbfont{Y}}\ar[rr]^{\alpha_{{\catsymbfont{X}},{\catsymbfont{M}},{\catsymbfont{Y}}}} \ar[d]_{\xi\otimes \id_{{\catsymbfont{Y}}}} &&{\catsymbfont{X}}\otimes ({\catsymbfont{M}}\otimes {\catsymbfont{Y}}) \ar[d]^{\id_{{\catsymbfont{X}}}\otimes \upsilon}\\ {\catsymbfont{M}}\otimes {\catsymbfont{Y}}\ar[dr]_{\upsilon}&&{\catsymbfont{X}}\otimes {\catsymbfont{M}}\ar[dl]^{\xi}\\ &{\catsymbfont{M}} } \] commutes. The left and right object structures require (and are defined by the requirement that) the associativity \[ \xymatrix@R-1pc@C+.75pc{ ({\catsymbfont{X}}\otimes {\catsymbfont{X}})\otimes {\catsymbfont{M}}\ar[r]^-{\alpha_{{\catsymbfont{X}},{\catsymbfont{X}},{\catsymbfont{M}}}}\ar[d]_-{\mu_{{\catsymbfont{X}}}\otimes \id_{{\catsymbfont{M}}}} &{\catsymbfont{X}}\otimes ({\catsymbfont{X}}\otimes {\catsymbfont{M}})\ar[r]^-{\id_{{\catsymbfont{X}}}\otimes \xi} &{\catsymbfont{X}}\otimes {\catsymbfont{M}}\ar[d]^-{\xi}\\ {\catsymbfont{X}}\otimes {\catsymbfont{M}}\ar[rr]_-{\xi}&&{\catsymbfont{M}}\\ ({\catsymbfont{M}}\otimes {\catsymbfont{Y}})\otimes {\catsymbfont{Y}}\ar[r]^-{\alpha_{{\catsymbfont{M}},{\catsymbfont{Y}},{\catsymbfont{Y}}}}\ar[d]_-{\upsilon\otimes \id_{{\catsymbfont{Y}}}} &{\catsymbfont{M}}\otimes ({\catsymbfont{Y}}\otimes {\catsymbfont{Y}})\ar[r]^-{\id_{{\catsymbfont{M}}}\mu_{{\catsymbfont{Y}}}} &{\catsymbfont{M}}\otimes {\catsymbfont{Y}}\ar[d]^-{\upsilon}\\ {\catsymbfont{M}}\otimes {\catsymbfont{Y}}\ar[rr]_-{\upsilon}&&{\catsymbfont{M}} } \] and unit \[ \xymatrix@R-1pc@C+.75pc{ {\mathbb{S}}_{O({\catsymbfont{X}})}\otimes {\catsymbfont{M}}\ar[r]^-{\eta_{{\catsymbfont{X}}}\otimes \id_{{\catsymbfont{M}}}}\ar[dr]_-{\eta^{\ell}} &{\catsymbfont{X}}\otimes {\catsymbfont{M}}\ar[d]^-{\xi} & {\catsymbfont{M}}\otimes {\mathbb{S}}_{O({\catsymbfont{Y}})}\ar[r]^-{\id_{{\catsymbfont{M}}}\otimes \eta_{{\catsymbfont{Y}}}}\ar[dr]_-{\eta^{r}} &{\catsymbfont{M}}\otimes {\catsymbfont{Y}}\ar[d]^-{\upsilon} \\ &{\catsymbfont{M}}&&{\catsymbfont{M}} } \] diagrams commute, where $\mu_{{\catsymbfont{X}}},\mu_{{\catsymbfont{Y}}}$ denote the multiplications and $\eta_{{\catsymbfont{X}}},\eta_{{\catsymbfont{Y}}}$ denote the units for the monoid structures on ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$.
Given a function $\phi \colon O({\catsymbfont{Y}})\to O({\catsymbfont{X}})$, we obtain an $(O({\catsymbfont{X}}),O({\catsymbfont{Y}}))$-spectrum $S_{\phi}{\catsymbfont{X}}={\catsymbfont{X}}(-,\phi(-))$, which has a canonical left ${\catsymbfont{X}}$-object structure, given by the monoid structure of ${\catsymbfont{X}}$. We explain in Section~\ref{sec:rewrite} why the following definition captures the correct notion of spectral functor.
\begin{defn}\label{defn:bifunc} Let ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$ be bi-indexed ring spectra. A \term{spectral functor} $\phi\colon {\catsymbfont{Y}}\to {\catsymbfont{X}}$ consists of a function $\phi\colon O({\catsymbfont{Y}})\to O({\catsymbfont{X}})$ and an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule structure on the left ${\catsymbfont{X}}$-object $S_{\phi}{\catsymbfont{X}}={\catsymbfont{X}}(-,\phi(-))$. \end{defn}
The Hochshild-Mitchell construction requires a version of $\Hom^{b}$ ``over'' a pair of small spectral categories and the adjunction of Proposition~\ref{prop:bisadj} suggests the utility of analogues of $\otimes$, $\Hom^{\ell}$, and $\Hom^{r}$ over small spectral categories.
\begin{cons} Let ${\catsymbfont{X}}$, ${\catsymbfont{Y}}$, and ${\catsymbfont{Z}}$ be bi-indexed ring spectra. If ${\catsymbfont{M}}$ is an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule and ${\catsymbfont{N}}$ is a $({\catsymbfont{Y}},{\catsymbfont{Z}})$-bimodule, then we define the $({\catsymbfont{X}},{\catsymbfont{Z}})$-bimodule ${\catsymbfont{M}}\otimes_{{\catsymbfont{Y}}}{\catsymbfont{N}}$ to be the usual coequalizer \[ \xymatrix@C-1pc{ {\catsymbfont{M}}\otimes {\catsymbfont{Y}}\otimes {\catsymbfont{N}} \ar@<-.5ex>[r]\ar@<.5ex>[r] &{\catsymbfont{M}}\otimes {\catsymbfont{N}}\ar[r] &{\catsymbfont{M}}\otimes_{{\catsymbfont{Y}}}{\catsymbfont{N}} } \] of the left and right ${\catsymbfont{Y}}$-actions. If ${\catsymbfont{M}}$ is an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule and ${\catsymbfont{P}}$ is an $({\catsymbfont{X}},{\catsymbfont{Z}})$-bimodule, we define the $({\catsymbfont{Y}},{\catsymbfont{Z}})$-bimodule $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{P}})$ to be the usual equalizer \[ \xymatrix@C-1pc{ \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{P}})\ar[r] &\Hom^{\ell}({\catsymbfont{M}},{\catsymbfont{P}})\ar@<.5ex>[r]\ar@<-.5ex>[r] &\Hom^{\ell}({\catsymbfont{X}}\otimes {\catsymbfont{M}},{\catsymbfont{P}}) } \] where one map is induced by the left ${\catsymbfont{X}}$-action on ${\catsymbfont{M}}$ and the other map is composite of the left ${\catsymbfont{X}}$-action on ${\catsymbfont{P}}$ and the map \[ \Hom^{\ell}({\catsymbfont{M}},{\catsymbfont{P}}) \to \Hom^{\ell}({\catsymbfont{X}}\otimes {\catsymbfont{M}},{\catsymbfont{X}}\otimes {\catsymbfont{P}}) \] adjoint to the map \[ {\catsymbfont{X}}\otimes {\catsymbfont{M}} \otimes \Hom^{\ell}({\catsymbfont{M}},{\catsymbfont{P}})\to {\catsymbfont{X}}\otimes {\catsymbfont{P}} \] that applies the counit of the ${\catsymbfont{M}}\otimes (-)$, $\Hom({\catsymbfont{M}},-)$ adjunction. If ${\catsymbfont{M}}$ is an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule and ${\catsymbfont{Q}}$ is a $({\catsymbfont{Z}},{\catsymbfont{Y}})$-bimodule, we define the $({\catsymbfont{Z}},{\catsymbfont{X}})$-bimodule $\Hom^{r}_{{\catsymbfont{Y}}}({\catsymbfont{M}},{\catsymbfont{Q}})$ to be the usual equalizer \[ \xymatrix@C-1pc{ \Hom^{r}_{{\catsymbfont{Y}}}({\catsymbfont{M}},{\catsymbfont{Q}})\ar[r] &\Hom^{r}({\catsymbfont{M}},{\catsymbfont{Q}})\ar@<.5ex>[r]\ar@<-.5ex>[r] &\Hom^{r}({\catsymbfont{M}}\otimes {\catsymbfont{Y}},{\catsymbfont{Q}}) } \] using the analogous pair of maps for $\Hom^{r}$. If ${\catsymbfont{M}}$ is an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule and ${\catsymbfont{M}}'$ is an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule, we define the spectrum $\Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},{\catsymbfont{M}}')$ to be the usual equalizer \[ \xymatrix@C-1pc{ \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},{\catsymbfont{M}}')\ar[r] &\Hom^{b}({\catsymbfont{M}},{\catsymbfont{M}}')\ar@<.5ex>[r]\ar@<-.5ex>[r] &\Hom^{b}({\catsymbfont{X}}\otimes {\catsymbfont{M}}\otimes {\catsymbfont{Y}},{\catsymbfont{M}}') } \] with the analogous pair of maps for $\Hom^{b}$. \end{cons}
An easy check shows that the spectrum of maps $\Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}$ provides a spectral enrichment of the category of $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules.
Proposition~\ref{prop:bisadj} now generalizes to the following proposition. The proof is again purely formal.
\begin{prop}\label{prop:bimadj} Let ${\catsymbfont{X}}$, ${\catsymbfont{Y}}$, and ${\catsymbfont{Z}}$ be bi-indexed ring spectra. Let ${\catsymbfont{M}}$ be an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule, let ${\catsymbfont{N}}$ be a $({\catsymbfont{Y}},{\catsymbfont{Z}})$-bimodule, and let ${\catsymbfont{P}}$ be an $({\catsymbfont{X}},{\catsymbfont{Z}})$ bimodule. Then there are canonical isomorphisms of spectra \iffalse \begin{multline*} \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},\Hom^{r}_{{\catsymbfont{Z}}}({\catsymbfont{N}},{\catsymbfont{P}}))\iso \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Z}}}({\catsymbfont{M}}\otimes_{{\catsymbfont{Y}}} {\catsymbfont{N}},{\catsymbfont{P}})\\\iso \Hom^{b}_{{\catsymbfont{Y}},{\catsymbfont{Z}}}({\catsymbfont{N}},\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{P}})) \end{multline*} \fi \begin{align*} &\hspace{-3em}\Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Z}}}({\catsymbfont{M}}\otimes_{{\catsymbfont{Y}}} {\catsymbfont{N}},{\catsymbfont{P}})\hspace{-3em}\\ \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},\Hom^{r}_{{\catsymbfont{Z}}}({\catsymbfont{N}},{\catsymbfont{P}}))\iso&& \iso\Hom^{b}_{{\catsymbfont{Y}},{\catsymbfont{Z}}}({\catsymbfont{N}},\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{P}})). \end{align*} \end{prop}
We note that $\otimes$ and $\otimes_{{\catsymbfont{Y}}}$ commute with target restriction (Definition~\ref{defn:restriction}) on the first variable and source restriction on the second variable; $\Hom^{\ell}$ and $\Hom^{\ell}_{{\catsymbfont{X}}}$ convert source restriction on the first variable to target restriction and preserves source restriction on the second variable. Likewise, $\Hom^{r}$ and $\Hom^{r}_{{\catsymbfont{Y}}}$ convert target restriction on the first variable to source restriction and preserve target restriction on the second variable.
The balanced tensor product produces the composition of spectral functors for the definition of spectral functors (Definition~\ref{defn:bifunc}) above. Given a spectral functor $\phi$ from ${\catsymbfont{Y}}$ to ${\catsymbfont{X}}$ and a spectral functor $\theta$ from ${\catsymbfont{Z}}$ to ${\catsymbfont{Y}}$, using the $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule structure on $S_{\phi}{\catsymbfont{X}}$ inherent in $\phi$, we can make sense of the tensor product over ${\catsymbfont{Y}}$ on the right and construct a map of left ${\catsymbfont{X}}$-objects \[ S_{\phi}{\catsymbfont{X}}\otimes_{{\catsymbfont{Y}}}S_{\theta}{\catsymbfont{Y}} \to S_{\phi\circ \theta}{\catsymbfont{X}}. \] This map is an isomorphism because $\otimes_{{\catsymbfont{Y}}}$ commutes with source restriction in the second variable; intrinsically, for every fixed $x\in O({\catsymbfont{X}})$ and $z\in O({\catsymbfont{Z}})$, the diagram \[ \xymatrix@C-1pc@R-2pc{ \coprod\limits_{y_{0},y_{1}\in O({\catsymbfont{Y}})}\hspace{-2ex} {\catsymbfont{X}}(x,\phi(y_{0}))\sma {\catsymbfont{Y}}(y_{0},y_{1})\sma {\catsymbfont{Y}}(y_{1},\theta(z)) \ar@<-.5ex>[r]\ar@<.5ex>[r] &\coprod\limits_{y\in O({\catsymbfont{Y}})}\hspace{-1ex} {\catsymbfont{X}}(x,\phi(y))\sma {\catsymbfont{Y}}(y,\theta (z))\\ &\longrightarrow{\catsymbfont{X}}(x,\phi(\theta(z))) } \] is a split coequalizer. Using the isomorphism to give $S_{\phi\circ\theta}{\catsymbfont{X}}$ a right ${\catsymbfont{Z}}$-action makes it an $({\catsymbfont{X}},{\catsymbfont{Z}})$-bimodule. We define the composite of the spectral functors $\phi \circ \theta$ to consist of the object function $\phi \circ \theta$ and this bimodule structure on $S_{\phi \circ \theta}{\catsymbfont{X}}$.
\section{Small spectral categories and the tensor-Hom adjunctions} \label{sec:rewrite}
This section translates the work from the previous section to the framework of small spectral categories. When working in this framework, we use the $ST$-indexing convention as this is standard in this context. We begin by reviewing the definitions.
\begin{defn}\label{defn:scat} A \term{small spectral category} is a small category enriched over spectra. It consists of: \begin{enumerate} \item a set of objects $O({\catsymbfont{C}})$, \item a spectrum ${\catsymbfont{C}}(a,b)$ for each pair of objects $a,b\in O({\catsymbfont{C}})$, \item a unit map ${\mathbb{S}}\to {\catsymbfont{C}}(a,a)$ for each object $a \in O({\catsymbfont{C}})$, and \item a composition map ${\catsymbfont{C}}(b,c)\sma {\catsymbfont{C}}(a,b)\to {\catsymbfont{C}}(a,c)$ for each triple of objects $a,b,c\in O({\catsymbfont{C}})$, \end{enumerate} satisfying the usual associativity and unit properties. A \term{strict morphism} ${\catsymbfont{C}}\to {\catsymbfont{C}}'$ of small spectral categories with the same object set consists of a map of spectra ${\catsymbfont{C}}(a,b)\to {\catsymbfont{C}}'(a,b)$ for every pair of objects $a,b\in O({\catsymbfont{C}})=O({\catsymbfont{C}}')$ that commutes with the unit and composition maps; there are no strict morphisms between small spectral categories with different object sets. \end{defn}
We have inverse functors between the category of bi-indexed ring spectra and small spectral categories (with strict morphisms) defined as follows. For a bi-indexed ring spectrum ${\catsymbfont{X}}$, let $C_{{\catsymbfont{X}}}$ be the small spectral category defined by setting \begin{enumerate} \item the object set $O(C_{{\catsymbfont{X}}})=O({\catsymbfont{X}})$, \item the mapping spectra $C_{{\catsymbfont{X}}}(a,b)={\catsymbfont{X}}^{st}(a,b)={\catsymbfont{X}}^{ts}(b,a)$ for all $a,b\in O(C_{{\catsymbfont{X}}})$, \item the unit ${\mathbb{S}}\to C_{{\catsymbfont{X}}}(a,a)$ to be the map induced by the monoid structure unit ${\mathbb{S}}_{O({\catsymbfont{X}})}\to {\catsymbfont{X}}$ for all $a\in O(C_{{\catsymbfont{X}}})$, and \item the composition $C_{{\catsymbfont{X}}}(b,c)\sma C_{{\catsymbfont{X}}}(a,b)\to C_{{\catsymbfont{X}}}(a,c)$ to be the map ${\catsymbfont{X}}(c,b)\sma {\catsymbfont{X}}(b,a)\to {\catsymbfont{X}}(c,a)$ that appears as a wedge summand in the monoid structure multiplication ${\catsymbfont{X}}\otimes {\catsymbfont{X}}\to {\catsymbfont{X}}$. \end{enumerate} Similarly, for a small spectral category ${\catsymbfont{C}}$, we define a bi-indexed ring spectrum $B_{{\catsymbfont{C}}}$ with the same object set by taking $B_{{\catsymbfont{C}}}(a,b)={\catsymbfont{C}}(b,a)$ and the obvious unit and multiplication. These assignments are evidently functorial.
\begin{prop}\label{prop:iso} The functors $C$ and $B$ above are inverse isomorphisms of categories between the category of bi-indexed ring spectra and the category of small spectral categories (with strict morphisms). \end{prop}
The more usual category of small spectral categories has morphisms given by \term{spectral functors}, which are simply the spectrally enriched functors. The following theorem relates this notion to Definition~\ref{defn:bifunc}. We prove it at the end of the section after reviewing more of the theory of small spectral categories and their modules.
\begin{thm}\label{thm:functor} There is a canonical bijection between the set of spectral functors of small spectral categories ${\catsymbfont{D}}\to {\catsymbfont{C}}$ and the set of spectral functors of the corresponding bi-indexed ring spectra. This bijection is compatible with composition. \end{thm}
Left and right modules are basic notions for small spectral categories that do not precisely correspond to left and right objects for bi-indexed ring spectra.
\begin{defn} Let ${\catsymbfont{C}}$ be a small spectral category. The (spectrally enriched) category $\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}}}$ of \term{left ${\catsymbfont{C}}$-modules} is the (spectrally enriched) category of spectrally enriched functors from ${\catsymbfont{C}}$ to spectra; the (spectrally enriched) category $\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}}^{\op}}$ of \term{right ${\catsymbfont{C}}$-modules} is the (spectrally enriched) category of spectrally enriched contravariant functors from ${\catsymbfont{C}}$ to spectra. \end{defn}
For any one-point set $\{a\}$, the category of left ${\catsymbfont{C}}$-modules is isomorphic to the full subcategory category of left $B_{{\catsymbfont{C}}}$-objects with source set $\{a\}$ and is isomorphic as a spectrally enriched category to the category of $(B_{{\catsymbfont{C}}},{\mathbb{S}}_{\{a\}})$-bimodules. Likewise, the category of right ${\catsymbfont{C}}$-modules is isomorphic to the full subcategory category of right $B_{{\catsymbfont{C}}}$-objects with target set $\{a\}$ and is isomorphic as a spectrally enriched category to the category of $({\mathbb{S}}_{\{a\}},B_{{\catsymbfont{C}}})$-bimodules. The category of left $B_{{\catsymbfont{C}}}$-objects is essentially the category of (singly) indexed left $B_{{\catsymbfont{C}}}$-modules: a left $B_{{\catsymbfont{C}}}$-object ${\catsymbfont{M}}$ consists of a left ${\catsymbfont{C}}$-module ${\catsymbfont{M}}^{st}(a,-)$ for each $a$ in $S({\catsymbfont{M}})$.
Bimodules for small spectral categories do correspond precisely with bimodules for bi-indexed ring spectra. In the context of bimodules of small spectral categories, just as in the context of bi-indexed spectra, we take the convention that the category on the left has the left action and the category on the right has the right action. However, as always in the context of small spectral category concepts, we follow the $ST$-indexing convention implicit in the definition below that the righthand variable is the covariant one while the lefthand variable is the contravariant one.
\begin{defn}\label{defn:sbimod} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories. Let ${\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}}$ be the small spectral category with objects $O({\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}})=O({\catsymbfont{D}})\times O({\catsymbfont{C}})$, mapping spectra \[ ({\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}})((d,c),(d',c'))={\catsymbfont{D}}(d',d)\sma {\catsymbfont{C}}(c,c'), \] unit induced by the units of ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ (and the canonical isomorphism ${\mathbb{S}}\sma {\mathbb{S}}\iso{\mathbb{S}}$), and composition induced by the composition on ${\catsymbfont{D}}$ (performed backwards) and the composition on ${\catsymbfont{C}}$: \begin{multline*} ({\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}})((d',c'),(d'',c''))\sma ({\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}})((d,c),(d',c'))\\ =({\catsymbfont{D}}(d'',d')\sma {\catsymbfont{C}}(c',c''))\sma ({\catsymbfont{D}}(d',d)\sma {\catsymbfont{C}}(c,c'))\\ \iso ({\catsymbfont{D}}(d',d)\sma{\catsymbfont{D}}(d'',d'))\sma ({\catsymbfont{C}}(c',c'')\sma {\catsymbfont{C}}(c,c'))\\ \to {\catsymbfont{D}}(d'',d)\sma {\catsymbfont{C}}(c,c'') =({\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}})((d,c),(d'',c'')). \end{multline*} The (spectrally enriched) category $\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}},{\catsymbfont{D}}}$ of \term{$({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules} is the (spectrally enriched) category of spectrally enriched functors from ${\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}}$ to spectra. \end{defn}
Given a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule ${\catsymbfont{F}}$, we write $B_{{\catsymbfont{F}}}$ for the $(O({\catsymbfont{C}}),O({\catsymbfont{D}}))$-spectrum \[ B_{{\catsymbfont{F}}}(c,d)=B^{st}_{{\catsymbfont{F}}}(d,c)={\catsymbfont{F}}(d,c) \] for $(c,d)\in O({\catsymbfont{C}})\times O({\catsymbfont{D}})$. This has a canonical $(B_{{\catsymbfont{C}}},B_{{\catsymbfont{D}}})$-bimodule structure with action maps induced by \[ B_{{\catsymbfont{C}}}(c,c')\sma B_{{\catsymbfont{F}}}(c',d)= {\catsymbfont{C}}(c',c)\sma {\catsymbfont{F}}(d,c')\to {\catsymbfont{F}}(d,c)=B_{{\catsymbfont{F}}}(c,d) \] and \[ B_{{\catsymbfont{F}}}(c,d)\sma B_{{\catsymbfont{D}}}(d,d') ={\catsymbfont{F}}(d,c)\sma {\catsymbfont{D}}(d',d)\to {\catsymbfont{F}}(d',c)=B_{{\catsymbfont{F}}}(c,d'). \] This is evidently functorial, and indeed extends canonically to a spectrally enriched functor from the category of $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules to the category of $(B_{{\catsymbfont{C}}},B_{{\catsymbfont{D}}})$-bimodules (in bi-indexed spectra).
\begin{prop} The spectrally enriched functor $B$ from $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules to $(B_{{\catsymbfont{C}}},B_{{\catsymbfont{D}}})$-bimodules (in bi-indexed spectra) is an isomorphism of spectrally enriched categories. \end{prop}
We write the inverse isomorphism as $C$; evidently, $C_{{\catsymbfont{M}}}(c,d)={\catsymbfont{M}}(d,c)$ for all $(c,d)\in O({\catsymbfont{C}})\times O({\catsymbfont{D}})$.
In light of the previous proposition, for $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules ${\catsymbfont{F}}$ and ${\catsymbfont{G}}$, we write $\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{G}})$ for the spectrum of bimodule maps from ${\catsymbfont{F}}$ to ${\catsymbfont{G}}$ and we more generally define $\otimes$, $\otimes_{{\catsymbfont{D}}}$, $\Hom^{\ell}$, $\Hom^{\ell}_{{\catsymbfont{C}}}$, $\Hom^{r}$, and $\Hom^{r}_{{\catsymbfont{D}}}$ in terms of the inverse isomorphisms $B$ and $C$ (for spectral categories / bi-indexed ring spectra and bimodules). In explicit terms, we have:
\begin{prop}\label{prop:formulas} Let ${\catsymbfont{A}}$, ${\catsymbfont{B}}$, and ${\catsymbfont{C}}$ be small spectral categories. \begin{enumerate} \item\label{i:tensor} For an $({\catsymbfont{A}},{\catsymbfont{B}})$-bimodule ${\catsymbfont{F}}$ and a $({\catsymbfont{B}},{\catsymbfont{C}})$-bimodule ${\catsymbfont{G}}$, the $({\catsymbfont{A}},{\catsymbfont{C}})$-bimodule ${\catsymbfont{F}}\otimes {\catsymbfont{G}}=C_{B_{{\catsymbfont{F}}}\otimes B_{{\catsymbfont{G}}}}$ satisfies \[ ({\catsymbfont{F}}\otimes {\catsymbfont{G}})(c,a)=\bigvee_{b\in O({\catsymbfont{B}})}{\catsymbfont{F}}(b,a)\sma {\catsymbfont{G}}(c,b) \] and ${\catsymbfont{F}}\otimes_{{\catsymbfont{B}}} {\catsymbfont{G}}=C_{B_{{\catsymbfont{F}}}\otimes_{B_{{\catsymbfont{B}}}} B_{{\catsymbfont{G}}}}$ is the coequalizer \[ \xymatrix@C-1pc{ {\catsymbfont{F}}\otimes {\catsymbfont{B}}\otimes {\catsymbfont{G}} \ar@<.5ex>[r]\ar@<-.5ex>[r] &{\catsymbfont{F}}\otimes {\catsymbfont{G}}\ar[r] &{\catsymbfont{F}}\otimes_{{\catsymbfont{B}}}{\catsymbfont{G}}. } \] \item\label{i:Homl} For an $({\catsymbfont{A}},{\catsymbfont{B}})$-bimodule ${\catsymbfont{F}}$ and an $({\catsymbfont{A}},{\catsymbfont{C}})$-bimodule ${\catsymbfont{G}}$, the $({\catsymbfont{B}},{\catsymbfont{C}})$-bimodule $\Hom^{\ell}({\catsymbfont{F}},{\catsymbfont{G}})=C_{\Hom^{\ell}(B_{{\catsymbfont{F}}},B_{{\catsymbfont{G}}})}$ satisfies \[ (\Hom^{\ell}({\catsymbfont{F}},{\catsymbfont{G}}))(c,b)=\prod_{a\in O({\catsymbfont{A}})}F({\catsymbfont{F}}(b,a),{\catsymbfont{G}}(c,a)) \] and $\Hom^{\ell}_{{\catsymbfont{A}}}({\catsymbfont{F}},{\catsymbfont{G}})=C_{\Hom^{\ell}_{B_{{\catsymbfont{A}}}}(B_{{\catsymbfont{F}}},B_{{\catsymbfont{G}}})}$ is the equalizer \[ \xymatrix@C-1pc{ \Hom^{\ell}_{{\catsymbfont{A}}}({\catsymbfont{F}},{\catsymbfont{G}})\ar[r] &\Hom^{\ell}({\catsymbfont{F}},{\catsymbfont{G}}) \ar@<.5ex>[r]\ar@<-.5ex>[r] &\Hom^{\ell}({\catsymbfont{A}}\otimes {\catsymbfont{F}},{\catsymbfont{G}}). } \] \item\label{i:Homr} For an $({\catsymbfont{A}},{\catsymbfont{B}})$-bimodule ${\catsymbfont{F}}$ and a $({\catsymbfont{C}},{\catsymbfont{B}})$-bimodule ${\catsymbfont{G}}$, the $({\catsymbfont{C}},{\catsymbfont{A}})$-bimodule $\Hom^{r}({\catsymbfont{F}},{\catsymbfont{G}})=C_{\Hom^{r}(B_{{\catsymbfont{F}}},B_{{\catsymbfont{G}}})}$ satisfies \[ (\Hom^{r}({\catsymbfont{F}},{\catsymbfont{G}}))(a,c)=\prod_{b\in O({\catsymbfont{B}})}F({\catsymbfont{F}}(b,a),{\catsymbfont{G}}(b,c)) \] and $\Hom^{r}_{{\catsymbfont{B}}}({\catsymbfont{F}},{\catsymbfont{G}})=C_{\Hom^{r}_{B_{{\catsymbfont{B}}}}(B_{{\catsymbfont{F}}},B_{{\catsymbfont{G}}})}$ is the equalizer \[ \xymatrix@C-1pc{ \Hom^{r}_{{\catsymbfont{B}}}({\catsymbfont{F}},{\catsymbfont{G}})\ar[r] &\Hom^{r}({\catsymbfont{F}},{\catsymbfont{G}}) \ar@<.5ex>[r]\ar@<-.5ex>[r] &\Hom^{r}({\catsymbfont{F}}\otimes {\catsymbfont{B}},{\catsymbfont{G}}). } \] \end{enumerate} \end{prop}
As an immediate consequence of Proposition~\ref{prop:bimadj}, we obtain the corresponding adjunction in the context of small spectral categories.
\begin{prop}\label{prop:scbimadj} Let ${\catsymbfont{A}}$, ${\catsymbfont{B}}$, and ${\catsymbfont{C}}$ be small spectral categories. Let ${\catsymbfont{F}}$ be an $({\catsymbfont{A}},{\catsymbfont{B}})$-bimodule, ${\catsymbfont{G}}$ be a $({\catsymbfont{B}},{\catsymbfont{C}})$-bimodule, and let ${\catsymbfont{H}}$ be an $({\catsymbfont{A}},{\catsymbfont{C}})$ bimodule. Then there are canonical isomorphisms of spectra \begin{align*} &\hspace{-3em}\Hom^{b}_{{\catsymbfont{A}},{\catsymbfont{C}}}({\catsymbfont{F}}\otimes_{{\catsymbfont{B}}} {\catsymbfont{G}},{\catsymbfont{H}})\hspace{-3em}\\ \Hom^{b}_{{\catsymbfont{A}},{\catsymbfont{B}}}({\catsymbfont{F}},\Hom^{r}_{{\catsymbfont{C}}}({\catsymbfont{G}},{\catsymbfont{H}}))\iso&& \iso\Hom^{b}_{{\catsymbfont{B}},{\catsymbfont{C}}}({\catsymbfont{G}},\Hom^{\ell}_{{\catsymbfont{A}}}({\catsymbfont{F}},{\catsymbfont{H}})). \end{align*} \end{prop}
Comparing the formulas in Proposition~\ref{prop:formulas} with the intrinsic definition of the spectral enrichment of a category of spectral functors reveals the following relationship between $\Hom^{\ell}_{{\catsymbfont{C}}}$ and the spectral enrichment on the category of left ${\catsymbfont{C}}$-modules, which is essentially a special case of the observation on $\Hom^{\ell}_{{\catsymbfont{X}}}$ and source restriction in the previous section. An analogous result holds for $\Hom^{r}_{{\catsymbfont{C}}}$ and the spectral enrichment on the category of right ${\catsymbfont{C}}$-modules.
\begin{prop}\label{prop:homover} In the notation of Proposition~\ref{prop:formulas}.(\ref{i:Homl}), \[ (\Hom^{\ell}_{{\catsymbfont{A}}}({\catsymbfont{F}},{\catsymbfont{G}}))^{st}(c,b) \iso \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{A}}}({\catsymbfont{F}}(b,-),{\catsymbfont{G}}(c,-)) \] for all $b\in O({\catsymbfont{B}})$, $c\in O({\catsymbfont{C}})$. \end{prop}
Finally, we return to Theorem~\ref{thm:functor}.
\begin{proof}[Proof of Theorem~\ref{thm:functor}] Let ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$ be bi-indexed ring spectra and let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ denote the corresponding small spectral categories.
Given a spectral functor $\psi\colon {\catsymbfont{D}}\to {\catsymbfont{C}}$, let ${\catsymbfont{F}}_{\psi}$ denote the $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule with component spectra ${\catsymbfont{F}}^{st}_{\psi}(d,c)={\catsymbfont{C}}(\psi(d),c)$ and the evident bimodule structure. Then the underlying left ${\catsymbfont{X}}$-object of the $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule $B_{{\catsymbfont{F}}_{\psi}}$ is $S_{\psi}{\catsymbfont{X}}$. Let $B_{\psi}$ be the spectral functor ${\catsymbfont{X}} \to {\catsymbfont{Y}}$ that uses the underlying object function of $\psi$ as the function on object sets and $B_{{\catsymbfont{F}}_{\psi}}$ as specifying the bimodule structure on $S_{\psi}{\catsymbfont{X}}$.
Given a spectral functor $\phi\colon {\catsymbfont{Y}} \to {\catsymbfont{X}}$, we obtain a spectral functor $C_{\phi}$ from ${\catsymbfont{D}}$ to ${\catsymbfont{C}}$ using the same object function and the map on morphism spectra defined as follows. The map of left ${\catsymbfont{X}}$-objects $S_{\phi}{\catsymbfont{X}}\otimes {\catsymbfont{Y}}\to S_{\phi}{\catsymbfont{X}}$ is adjoint to a map of bi-indexed spectra ${\catsymbfont{Y}}\to \Hom^{\ell}_{{\catsymbfont{X}}}(S_{\phi}{\catsymbfont{X}},S_{\phi}{\catsymbfont{X}})$. Because $\Hom^{\ell}$ converts source restriction in the first variable and preserves source restriction in the second variable, we have a canonical isomorphism \[ \Hom^{\ell}_{{\catsymbfont{X}}}(S_{\phi}{\catsymbfont{X}},S_{\phi}{\catsymbfont{X}})\iso R_{\phi,\phi}\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{X}},{\catsymbfont{X}}) \iso R_{\phi,\phi}{\catsymbfont{X}}. \] The map of bi-indexed spectra ${\catsymbfont{Y}}\to R_{\phi,\phi}{\catsymbfont{X}}$ then specifies a map ${\catsymbfont{D}}(a,b)\to {\catsymbfont{C}}(\phi(a),\phi(b))$ for all $a,b\in O({\catsymbfont{D}})$. In light of Proposition~\ref{prop:homover}, this map is the composite \[ {\catsymbfont{D}}(a,b)\to F_{{\catsymbfont{C}}}({\catsymbfont{C}}(\phi(b),-),{\catsymbfont{C}}(\phi(a),-))\iso {\catsymbfont{C}}(\phi(a),\phi(b)) \] of the adjoint of ${\catsymbfont{C}}(\phi(b),-)\sma {\catsymbfont{D}}(a,b)\to {\catsymbfont{C}}(\phi(a),-)$ and the enriched Yoneda lemma isomorphism. From here it follows easily that the constructed map on morphism spectra preserves units and composition.
It is clear that $B_{C_{\phi}}=\phi$, $C_{B_{\psi}}=\psi$, and moreover that $B$ preserves composition of spectral functors. \end{proof}
Using the enriched form of the Yoneda lemma, it is straightforward to check that natural transformations of spectral functors between small spectral categories correspond to maps of bimodules for spectral functors between bi-indexed ring spectra; we do not use this result.
\iffalse From here on, we will typically drop notation for conversion between small spectral category concepts and bi-indexed spectra concepts except when needed for clarity. \fi
\section{Hochschild-Mitchell and McClure-Smith constructions}\label{sec:MS}
In this section, we review the point-set construction of topological Hochschild cohomology of a small spectral category in terms of the Hochschild-Mitchell complex $CC$. We then observe that this fits into the framework of the McClure-Smith approach to the Deligne conjecture; in particular, there is a natural $E_{2}$ ring spectrum structure on $CC$.
\begin{cons}[Topological Hochschild-Mitchell construction]\label{cons:HM} Let ${\catsymbfont{C}}$ be a\break small spectral category and ${\catsymbfont{M}}$ a $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodule. Let $CC^{\bullet}({\catsymbfont{C}};{\catsymbfont{M}})$ be the cosimplicial spectrum $\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{C}}}(B_{\bullet}({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}}),{\catsymbfont{M}})$, where $B_{\bullet}$ denotes the two-sided bar construction for the monoidal product $\otimes$. More concretely, $CC^{\bullet}({\catsymbfont{C}};{\catsymbfont{M}})$ is the cosimplicial spectrum which in cosimplicial degree $n$ is \[ \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{C}}}({\catsymbfont{C}}\otimes \underbrace{{\catsymbfont{C}}\otimes \cdots \otimes {\catsymbfont{C}}}_{n\text{ factors}} \otimes {\catsymbfont{C}},{\catsymbfont{M}}) \] with coface map $\delta^{i}$ induced by the product ${\catsymbfont{C}}\otimes {\catsymbfont{C}}\to {\catsymbfont{C}}$ (q.v.~Proposition~\ref{prop:iso}, Definition~\ref{defn:birs}) on the $i$th, $(i+1)$th factors (starting the count from zero outside the braces) and codegeneracy $\sigma^{i}$ maps the unit map $C_{{\mathbb{S}}_{O({\catsymbfont{C}})}}\to {\catsymbfont{C}}$ (q.v.~Proposition~\ref{prop:pmc}) inserting the ${\catsymbfont{C}}$ as the $i$th factor. We write $CC^{\bullet}({\catsymbfont{C}})$ for $CC^{\bullet}({\catsymbfont{C}};{\catsymbfont{C}})$ in the case ${\catsymbfont{M}} = {\catsymbfont{C}}$. Let $CC({\catsymbfont{C}};{\catsymbfont{M}})$ and $CC({\catsymbfont{C}})$ denote the spectra obtained by applying $\Tot$. \end{cons}
Construction~\ref{cons:HM} is evidently covariantly functorial in maps of the bimodule ${\catsymbfont{M}}$ and contravariantly functorial in spectral functors of the small spectral category ${\catsymbfont{C}}$ (pulling back the bimodule structure along the spectral functor). Without hypotheses on ${\catsymbfont{C}}$ and ${\catsymbfont{M}}$, the topological Hochschild-Mitchell construction may not preserve weak equivalences. However, when ${\catsymbfont{C}}$ is pointwise relatively cofibrant (see Definition~\ref{defn:relcof}) and ${\catsymbfont{M}}$ is pointwise fibrant, $CC$ preserves weak equivalences in each variable; see Proposition~\ref{prop:hypreedy} and Theorem~\ref{thm:inv}.
The free, forgetful adjunction arising from the interpretation of small spectral categories as monoids for $\otimes$ (Proposition~\ref{prop:iso}) allows us to rewrite the cosimplicial object in Construction~\ref{cons:HM} more explicitly as \[ CC^{0}({\catsymbfont{C}},{\catsymbfont{M}})=\prod_{c}{\catsymbfont{M}}(c,c) \] and \begin{equation}\label{eq:HM} \begin{aligned} CC^{n}({\catsymbfont{C}};{\catsymbfont{M}})&\iso\Hom^{b}(\underbrace{{\catsymbfont{C}}\otimes \cdots \otimes {\catsymbfont{C}}}_{n\text{ factors}},{\catsymbfont{M}})\\ &\iso \prod_{c_{0},\ldots,c_{n}}F({\catsymbfont{C}}(c_{1},c_{0})\sma \cdots \sma{\catsymbfont{C}}(c_{n},c_{n-1}),{\catsymbfont{M}}(c_{n},c_{0})). \end{aligned} \end{equation} In this form, the faces $\delta^{1},\ldots,\delta^{n-1}\colon CC^{n-1}\to CC^{n}$ are induced by the composition in the category with $\delta^{0},\delta^{n}$ induced by the bimodule structure on ${\catsymbfont{M}}$; the degeneracies $\sigma^{i}\colon CC^{n}\to CC^{n+1}$ are induced by ${\mathbb{S}}\to {\catsymbfont{C}}(c_{i},c_{i})$, inserting the identity map in the $i$th position. This is the usual explicit description of the Hochschild-Mitchell construction for an enriched category.
Thinking in terms of the partial monoidal category of bi-indexed spectra (Section~\ref{sec:bis}), the description of $CC^{\bullet}({\catsymbfont{C}})$ as $\Hom^{b}({\catsymbfont{C}}\otimes \cdots \otimes {\catsymbfont{C}},{\catsymbfont{C}})$ identifies $CC^{\bullet}({\catsymbfont{C}})$ as the (non-symmetric) endomorphism operad $\mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})$ of the corresponding bi-indexed spectrum $B_{{\catsymbfont{C}}}$. Because $B_{{\catsymbfont{C}}}$ is a monoid for the monoidal product, there is a canonical map ${\mathbb{S}}\to \mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})(n)$ for all $n$ induced by the iterated multiplication \[ B_{{\catsymbfont{C}}}\otimes \cdots \otimes B_{{\catsymbfont{C}}}\to B_{{\catsymbfont{C}}}. \] These assemble to a map of non-symmetric operads $\mathop{\oA\mathrm{ss}}\nolimits\to \mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})$, where $\mathop{\oA\mathrm{ss}}\nolimits$ denotes the non-symmetric associative operad in spectra $\mathop{\oA\mathrm{ss}}\nolimits(n)={\mathbb{S}}$. This is precisely a ``operad with multiplication'' in the terminology of McClure-Smith~\cite[10.1]{McClureSmith-CosimplicialCubes}. The point of identifying this structure is that it is the data required in the McClure-Smith theory to induce an $E_{2}$ ring structure on $\Tot$. Specifically, as a consequence of~\cite[9.1,10.3]{McClureSmith-CosimplicialCubes}, we can immediately deduce the following proposition.
\begin{prop} The topological Hochschild-Mitchell construction $CC({\catsymbfont{C}}))$ has a canonical structure of a $\mathcal{D}_{2}$-algebra ($E_{2}$ ring spectrum) where ${\catsymbfont{D}}_{2}$ is the $E_{2}$ operad of McClure-Smith~\cite[\S9]{McClureSmith-CosimplicialCubes}. \end{prop}
\begin{proof} In terms of the maps $e\colon {\mathbb{S}}\to \mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})(0)$ and $\mu\colon {\mathbb{S}}\to \mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})(2)$, under the isomorphism of $\mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})(n)$ with $CC^{n}({\catsymbfont{C}})$, the face and degeneracy maps for $CC({\catsymbfont{C}})$ above coincide with the ones described on p.~1136 of~\cite{McClureSmith-CosimplicialCubes} in the proof of Theorem~10.3: for $f\in \mathop{\oE\mathrm{nd}^{b}}\nolimits(B_{{\catsymbfont{C}}})$ \[ \sigma^{i}f=f\circ_{i+1}e, \qquad \qquad \delta^{i}f=\begin{cases} \mu\circ_{2}f&i=0\\ f\circ_{i}\mu&i=1,\ldots,n\\ \mu \circ_{1}f&i=n+1. \end{cases} \qedhere \] \end{proof}
There is no naturality statement in the preceding proposition because $CC({\catsymbfont{C}})$ is not functorial in ${\catsymbfont{C}}$ (on the point-set level) in any reasonable way. It does have a very limited functoriality for spectral functors that induce isomorphisms on mapping spectra; we refer to these as \term{strictly fully faithful} spectral functors. For a strictly fully faithful spectral functor $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$, there is a restriction map $\phi^{*}\colon \mathop{\oE\mathrm{nd}^{b}}\nolimits({\catsymbfont{C}})\to \mathop{\oE\mathrm{nd}^{b}}\nolimits({\catsymbfont{D}})$, which is a map of operads with multiplication, constructed as follows.
On arity $n$, the map takes the form \begin{multline*} \mathop{\oE\mathrm{nd}^{b}}\nolimits({\catsymbfont{C}})(n)=\prod_{c_{0},\ldots,c_{n}}F({\catsymbfont{C}}(c_{1},c_{0})\sma \cdots \sma{\catsymbfont{D}}(c_{n},c_{n-1}),{\catsymbfont{D}}(c_{n},c_{0})) \\ \to\prod_{d_{0},\ldots,d_{n}}F({\catsymbfont{D}}(d_{1},d_{0})\sma \cdots \sma{\catsymbfont{D}}(d_{n},d_{n-1}),{\catsymbfont{D}}(d_{n},d_{0})) =\mathop{\oE\mathrm{nd}^{b}}\nolimits({\catsymbfont{D}})(n) \end{multline*} where on the $d_{0},\ldots,d_{n}$ factor of the target, we use projection onto the $c_{i}=\phi(d_{i})$ factor of the source and the isomorphism ${\catsymbfont{C}}(\phi(d_{i}),\phi(d_{j}))\iso {\catsymbfont{D}}(d_{i},d_{j})$ of the strictly fully faithful spectral functor $\phi$.
It is straightforward to verify that this map is compatible with the operad structures and commutes with the inclusion of $\mathop{\oA\mathrm{ss}}\nolimits$.
\begin{prop}\label{prop:limitednaturality} The topological Hochschild-Mitchell construction $CC$ extends to a functor from the category of small spectral categories and strictly fully faithful spectral functors to $\mathcal{D}_{2}$-algebras ($E_{2}$ ring spectra). \end{prop}
\section{Homotopy theory of objects and bimodules over small spectral categories}
Proposition~\ref{prop:limitednaturality} established a very limited naturality for the functor $CC$. To extend this functoriality to the more general derived statement of Theorems~\ref{main:dkfunct} and~\ref{main:dcc}, we need to introduce in the next section some conditions on bimodules that we call centralizer conditions. These are phrased in terms of the derived functors of $\Hom^{\ell}_{{\catsymbfont{C}}}$ and $\Hom^{r}_{{\catsymbfont{D}}}$; the purpose of this section is to set up the homotopical algebra and review some conditions that ensure that the point-set functors represent the derived functors.
Before beginning the discussion of model category structures, it is convenient to introduce terminology for extending conditions and properties on spectra and maps of spectra to small spectral categories, left and right objects, and bimodules.
\begin{defnsch} For any property or condition on spectra or maps of spectra, we say the property holds \term{pointwise} on a bi-indexed spectrum, bi-indexed spectrum with extra structure, or a map of bi-indexed spectra with extra structure when it holds at every bi-index. We say that such a property holds \term{pointwise} for a small spectral category, bimodule, strict morphism of small spectral categories, or map of bimodules when it holds for the underlying bi-indexed spectrum or map of bi-indexed spectra. \end{defnsch}
For the model structures on the category of bi-indexed spectra and for bi-indexed ring spectra ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$, the categories of left ${\catsymbfont{X}}$-objects, right ${\catsymbfont{Y}}$-objects, and $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules, we take the weak equivalences to be the pointwise weak equivalences and the fibrations to be the pointwise fibrations. To describe the cofibrations, let $I$ denote the standard set of generating cofibrations for the model category of spectra. Then given sets $A,B$, elements $a\in A$, $b\in B$ and element $i\colon C\to D$ in $I$, let $C_{A,B;a,b;i}$ and $D_{A,B;a,b;i}$ be the $(A,B)$-spectra that are $C$ and $D$ (respectively) on $(a,b)$ and $*$ elsewhere, and let $f_{A,B;a,b;i}\colon C_{A,B;a,b;i}\to D_{A,B;a,b;i}$ be the map of bi-indexed spectra that does $i\colon C\to D$ on $(a,b)$. Although the collection $BI$ of such maps does not form a small set, for any given bi-indexed spectrum ${\catsymbfont{Z}}$, the collection of maps from the domains of the elements of $BI$ does form a small set (or is isomorphic to one) since only those $C_{A,B;a,b;i}$ with $A=T({\catsymbfont{Z}})$ and $B=S({\catsymbfont{Z}})$ admit a map to ${\catsymbfont{Z}}$. This allows the small object argument to be applied with the collection $BI$. The cofibrations of bi-indexed spectra are exactly the pointwise cofibrations (maps that are cofibrations at each bi-index $(a,b)$) and these are exactly the maps that are retracts of relative cell complexes built by attaching cells from $BI$ (in the sense of \cite[5.4]{MMSS}). The cofibrations in the category of left ${\catsymbfont{X}}$-objects, right ${\catsymbfont{Y}}$-objects, and $({\catsymbfont{X}},{\catsymbfont{Y}})$ bimodules are the retracts of relative cell complexes (in the sense of \cite[5.4]{MMSS}) built by attaching cells of the form ${\catsymbfont{X}}\otimes f_{O({\catsymbfont{X}}),B;a,b;i}$, $f_{A,O({\catsymbfont{Y}});a,b;i}\otimes {\catsymbfont{Y}}$, and ${\catsymbfont{X}}\otimes f_{O({\catsymbfont{X}}),O({\catsymbfont{Y}});a,b;i}$, respectively. The usual arguments (e.g., \cite[\S5]{MMSS}) prove the following proposition.
\begin{prop} The category of bi-indexed spectra and for bi-indexed ring spectra ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$, the categories of left ${\catsymbfont{X}}$-objects, right ${\catsymbfont{Y}}$-objects, and $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules are topologically enriched closed model categories with fibrations and weak equivalences the pointwise fibrations and pointwise weak equivalences, and cofibrations the retracts of relative cell complexes. The category of $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules is a spectrally enriched closed model category. \end{prop}
\begin{prop} For small spectral categories ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$, the category of $({\catsymbfont{C}},{\catsymbfont{D}})$ bimodules is a spectrally enriched closed model category with fibrations and weak equivalences the pointwise fibrations and pointwise weak equivalences and cofibrations the retracts of relative cell complexes. \end{prop}
In the statement ``topologically enriched'' or ``spectrally enriched'' means that the categories satisfy the topological or spectral version of Quillen's Axiom SM7, which is called the ``Enrichment Axiom'' in \cite[\S3]{LewisMandell2}.
For identifying cofibrant resolutions in Section~\ref{sec:pfcatzigzag}, we need to know when cofibrant bimodules are pointwise cofibrant; a sufficient condition is for the small spectral categories in question to be pointwise ``semicofibrant'': Recall from Lewis-Mandell~\cite[1.2,6.4]{LewisMandell2} that a spectrum $X$ is \term{semicofibrant} when $X\sma(-)$ preserves cofibrations and acyclic cofibrations, or equivalently, $F(X,-)$ preserves fibrations and acyclic fibrations. Cofibrant spectra are in particular semicofibrant; in the standard model structure on symmetric spectra and orthogonal spectra, the sphere spectrum is cofibrant and all semicofibrant objects are cofibrant. In the positive stable model category and in EKMM $S$-modules, the sphere spectrum is not cofibrant but is only semicofibrant. It follows formally that a weak equivalence of semicofibrant spectra $X\to X'$ induces a weak equivalence $X\sma Y\to X'\sma Y$ for any spectrum $Y$ (to see this, smash with a cofibrant approximation of ${\mathbb{S}}$) and a weak equivalence $F(X',Z)\to F(X,Z)$ for any fibrant spectrum $Z$ \cite[6.2]{LewisMandell2}. The explicit description of cofibrations in the bimodule model structures implies the following proposition.
\begin{prop} A cofibrant bi-indexed spectrum is pointwise cofibrant. If ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$ are pointwise semicofibrant bi-indexed ring spectra then the cofibrant objects in left ${\catsymbfont{X}}$-objects, right ${\catsymbfont{Y}}$-objects, and $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules are pointwise cofibrant. In particular if ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ are pointwise semicofibrant small spectral categories then cofibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules are pointwise cofibrant. \end{prop}
In later work, we use the following slightly stronger hypothesis on the small spectral categories.
\begin{defn}\label{defn:relcof} A small spectral category ${\catsymbfont{C}}$ is pointwise relatively cofibrant when for every object $c$ in $O({\catsymbfont{C}})$, the unit map ${\mathbb{S}}\to{\catsymbfont{C}}(c,c)$ is a cofibration of spectra, and for every pair of distinct objects $c,d$ in $O({\catsymbfont{C}})$, the mapping spectrum ${\catsymbfont{C}}(c,d)$ is cofibrant as a spectrum. \end{defn}
Pointwise relatively cofibrant small spectral categories are in particular pointwise semicofibrant~\cite[1.3(c)]{LewisMandell2}. The following proposition produces sufficient examples of such small spectral categories. We made the following observation in~\cite[2.6--7]{BM-tc} based on the earlier work of Schwede-Shipley~\cite[6.3]{SSMonoidalEq}, extending functoriality in strict morphisms to functoriality in arbitrary spectral functors. Although stated there in the context of symmetric spectra of simplicial sets, the same arguments prove it for the other modern categories of spectra.
\begin{prop}\label{prop:replace} Let ${\catsymbfont{C}}$ be a small spectral category. There are functorial spectral categories ${\catsymbfont{C}}^{\Cell}$ and ${\catsymbfont{C}}^{\Cell,\Omega}$ and natural DK-equivalences that are isomorphisms on object sets (or, equivalently, strict morphisms that are pointwise weak equivalences) \[ {\catsymbfont{C}}\from {\catsymbfont{C}}^{\Cell}\to {\catsymbfont{C}}^{\Cell,\Omega} \] such that ${\catsymbfont{C}}^{\Cell}$ is pointwise relatively cofibrant and ${\catsymbfont{C}}^{\Cell,\Omega}$ is pointwise relatively cofibrant and pointwise fibrant. Moreover, if ${\catsymbfont{C}}$ is pointwise fibrant, then so is ${\catsymbfont{C}}^{\Cell}$. \end{prop}
Next we move on to derived functors. We concentrate on the case of \[ \Hom^{\ell}_{{\catsymbfont{X}}}(-,-)\colon (\aO\mathrm{bj}^{\ell}_{{\catsymbfont{X}}})^{\op}\times \aO\mathrm{bj}^{\ell}_{{\catsymbfont{X}}}\to \aB\aS \] which takes a pair of left ${\catsymbfont{X}}$-objects to a bi-indexed spectrum, where ${\catsymbfont{X}}$ is an arbitrary bi-indexed ring spectrum. The discussion for $\Hom^{r}$ has an exact parallel for $\Hom^{\ell}$, switching left/right and source/target, with all corresponding results holding. In essence, Section~5 of~\cite{LewisMandell2} discusses this kind of derived functor, although the story here is complicated because bi-indexed spectra and categories of left objects are not enriched over spectra, but are only partially enriched: once we fix a source set $A$, the full subcategory of left ${\catsymbfont{X}}$-objects with source set $A$ is isomorphic to the category of $({\catsymbfont{X}},{\mathbb{S}}_{A})$-bimodules and then is enriched, while there are no maps between left ${\catsymbfont{X}}$-objects with different source sets. Therefore, constructing ``partially enriched'' derived functors of two variables for the entire category of left ${\catsymbfont{X}}$-objects is equivalent to constructing enriched derived functors of two variables on each pair of these categories of bimodules. Applying \cite[5.8]{LewisMandell2}, we have the following result.
\begin{thm}\label{thm:derhom} Let ${\catsymbfont{X}}$ be a bi-indexed ring spectrum. For the functor \[ \Hom^{\ell}_{{\catsymbfont{X}}}(-,-)\colon (\aO\mathrm{bj}^{\ell}_{{\catsymbfont{X}}})^{\op}\times \aO\mathrm{bj}^{\ell}_{{\catsymbfont{X}}}\to \aB\aS \] the partially enriched right derived functor ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}}(-,-)$ exists and is constructed by cofibrant replacement of the first variable and fibrant replacement of the second variable. \end{thm}
\begin{proof} As indicated above, we restrict the source set to $A$ for the first variable (the contravariant variable) and the source set to $B$ for the second variable (the covariant variable) to apply \cite[5.8]{LewisMandell2} directly. In the statement of \cite[5.8]{LewisMandell2}, to reach this conclusion, we need to observe that (1) $\Hom^{\ell}_{{\catsymbfont{X}}}$ fits into an enriched parametrized adjunction, (2) that each adjunction of one variable is a Quillen adjunction when the parametrizing variable is cofibrant, and (3) that the left adjoint preserves weak equivalences between cofibrant objects in the parametrizing variable when the adjunction variable is cofibrant (or, equivalently, the analogous condition for fibrant objects on the right adjoint). In this case, the enriched parametrized left adjoint is given by the functor $\otimes$ that takes a left ${\catsymbfont{X}}$-object with source set $A$ and an $(A,B)$-spectrum to a left ${\catsymbfont{X}}$-object with source set $B$. (Here the $(A,B)$-spectrum is the adjunction variable and the left ${\catsymbfont{X}}$-object with source set $A$ is the parametrizing variable.) From the explicit description of cofibrations, it is clear that $\otimes$ preserves cofibrations in each variable when the other is cofibrant. Since smash product of spectra preserves acyclic cofibrations of spectra and the smash product with a cofibrant spectrum preserves arbitrary weak equivalences, it is clear from the formula for $\otimes$ that it preserves acyclic cofibrations in each variable when the other variable is cofibrant. This then verifies the hypotheses of~\cite[5.8]{LewisMandell2}. \end{proof}
When ${\catsymbfont{X}}\to {\catsymbfont{X}}'$ is a map of bi-indexed ring spectra, we obtain a canonical forgetful or pullback functor from left ${\catsymbfont{X}}'$-objects to left ${\catsymbfont{X}}$-objects, which induces a natural transformation $\Hom^{\ell}_{{\catsymbfont{X}}'}\to \Hom^{\ell}_{{\catsymbfont{X}}}$ and a natural transformation of derived functors ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}'}\to {\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}}$. The argument for~\cite[8.3]{LewisMandell2} then implies the following result.
\begin{prop}\label{prop:change} If ${\catsymbfont{X}}\to {\catsymbfont{X}}'$ is a weak equivalence of bi-indexed ring spectra, then the forget functor from left ${\catsymbfont{X}}'$-objects to left ${\catsymbfont{X}}$-objects is the right adjoint of a Quillen equivalence and the natural map ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}'}\to {\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}}$ is a natural isomorphism in the homotopy category of bi-indexed spectra. \end{prop}
We prefer to phrase the centralizer conditions in the next section in terms of small spectral categories and bimodules over small spectral categories. One technical wrinkle that arises (and indeed is the main issued studied by \cite{LewisMandell2} as a whole) is that when we plug bimodules into $\Hom^{\ell}_{{\catsymbfont{X}}}$ and consider functors of the form \begin{equation}\label{eq:bimodhom} \Hom^{\ell}_{{\catsymbfont{X}}}\colon (\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{X}},{\catsymbfont{Y}}})^{\op}\times \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{X}},{\catsymbfont{Z}}}, \to \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{Y}},{\catsymbfont{Z}}} \end{equation} even when the enriched right derived functor exists, it may not agree with the derived functor ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}}$ of Theorem~\ref{thm:derhom} without hypotheses on ${\catsymbfont{Y}}$. We return to this question below.
The technical issue just mentioned causes some awkwardness in trying to state a version of Theorem~\ref{thm:derhom} for small spectral categories. We dealt with this in the introduction by phrasing the centralizer conditions in terms of homotopical bimodules, which are defined as follows. By neglect of structure, small spectral categories become small categories enriched over the stable category; in the definition below ${\catsymbfont{D}}^{\op}\sma^{{\mathbb{L}}}{\catsymbfont{C}}$ denotes the small category enriched over the stable category that is defined analogously to ${\catsymbfont{D}}^{\op}\sma {\catsymbfont{C}}$ in the Definition~\ref{defn:sbimod}, but using the smash product in the stable category.
\begin{defn} A homotopical $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule is an enriched functor from ${\catsymbfont{D}}^{\op}\sma^{{\mathbb{L}}}{\catsymbfont{C}}$ to the stable category. More generally, for a category $\Cat$ (partially) enriched over spectra or over the stable category, homotopical left ${\catsymbfont{C}}$-modules in $\Cat$, homotopical right ${\catsymbfont{D}}$-modules in $\Cat$, and homotopical $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules in $\Cat$ are functors enriched over the stable category from ${\catsymbfont{C}}$, ${\catsymbfont{D}}^{\op}$, and ${\catsymbfont{D}}^{\op}\sma^{{\mathbb{L}}}{\catsymbfont{C}}$ into $\Cat$, respectively. \end{defn}
When ${\catsymbfont{M}}$ is a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule, by neglect of structure it is a homotopical right ${\catsymbfont{D}}$-module in the homotopy category of left ${\catsymbfont{C}}$-objects and any cofibrant approximation in the category of left ${\catsymbfont{C}}$-modules inherits the canonical structure of a homotopical right ${\catsymbfont{D}}$-module. Similar observations apply to the fibrant approximation of a $({\catsymbfont{C}},{\catsymbfont{E}})$-bimodule, giving \begin{equation}\label{eq:derhom} {\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{M}},{\catsymbfont{N}})={\mathbb{R}}\Hom^{\ell}_{B_{{\catsymbfont{C}}}}(B_{{\catsymbfont{M}}},B_{{\catsymbfont{N}}}) \end{equation} the canonical structure of a homotopical $({\catsymbfont{D}},{\catsymbfont{E}})$-bimodule, for ${\mathbb{R}}\Hom^{\ell}_{B_{{\catsymbfont{C}}}}$ the right derived functor in Theorem~\ref{thm:derhom}.
We now return to the question of when the right derived functor of~\eqref{eq:bimodhom} exists and is compatible with the right derived functor in Theorem~\ref{thm:derhom}. Although written in the context of symmetric monoidal categories, Theorems~1.7(a) and~1.11(a) of~\cite{LewisMandell2} show that both of these hold when the underlying bi-indexed spectrum of ${\catsymbfont{Y}}$ is pointwise semicofibrant. In our context, the following gives the most convenient statement; as always, the analogous result for $\Hom^{r}_{{\catsymbfont{D}}}$ also holds.
\begin{thm}\label{thm:LMmain} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and assume that ${\catsymbfont{D}}$ is pointwise semicofibrant. \begin{enumerate} \item The forgetful functor from $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules to left ${\catsymbfont{C}}$-objects preserves cofibrations (and all weak equivalences). \item The enriched right derived functor of \[ \Hom^{\ell}_{{\catsymbfont{C}}}\colon (\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}},{\catsymbfont{D}}})^{\op}\times \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}},{\catsymbfont{D}}}\to \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{D}},{\catsymbfont{D}}} \] exists and is constructed by cofibrant replacement of the contravariant variable and fibrant replacement of the covariant variable. \item Moreover, the underlying functor to homotopical $({\catsymbfont{D}},{\catsymbfont{D}})$-bimodules of the right derived functor of~(ii) agrees with the derived functor of~\eqref{eq:derhom}. \end{enumerate} \end{thm}
\begin{proof} The explicit description of the cofibrations shows that when ${\catsymbfont{D}}$ is pointwise semicofibrant, a cofibration of $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules forgets to a cofibration of left ${\catsymbfont{C}}$-objects. From here it is straightforward to check the conditions of~\cite[5.4]{LewisMandell2} that ensure the existence of the enriched right derived functor, and the comparison with the derived functor of~\eqref{eq:derhom} is immediate. \end{proof}
\iffalse \begin{thm}\label{thm:LMmain} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and assume that ${\catsymbfont{D}}$ is pointwise semicofibrant. Then the enriched right derived functor of \[ \Hom^{\ell}_{{\catsymbfont{C}}}\colon (\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}},{\catsymbfont{D}}})^{\op}\times \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{C}},{\catsymbfont{D}}}\to \mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{D}},{\catsymbfont{D}}} \] exists and can be calculated as $\Hom^{\ell}_{{\catsymbfont{C}}}$ with a semicofibrant object in the contravariant variable and a fibrant object in the covariant variable. Moreover, the underlying functor to homotopical $({\catsymbfont{D}},{\catsymbfont{D}})$-bimodules agrees with the derived functor of~\eqref{eq:derhom}. \end{thm}
For convenience, we use the rest of the section to prove Theorem~\ref{thm:LMmain}, essentially rewriting the proof of~\cite{LewisMandell2} in the current context, but taking advantage of the special features of the category of spectra that simplify the argument when possible.
The first step it to identify a convenient condition on the contavariant variable sufficient to ensure that $\Hom^{\ell}_{{\catsymbfont{D}}}$ represents the derived functor when the covariant variable is fibrant. As a spectrally enriched model category, the category of $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules has a notion of semicofibrant object: An $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule ${\catsymbfont{M}}$ is semicofibrant when $\Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},-)$ takes fibrations and acyclic fibrations of $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodules to fibrations and acyclic fibrations of spectra. Extending the definition of semicofibrant to the category of left ${\catsymbfont{X}}$-objects, we say that a left ${\catsymbfont{X}}$-object ${\catsymbfont{R}}$ is semicofibrant when $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{R}},-)$ takes fibrations and acyclic fibrations of right ${\catsymbfont{X}}$-objects to fibrations and acyclic fibrations of bi-indexed spectra. When ${\catsymbfont{C}}=C_{{\catsymbfont{X}}}$, applying Proposition~\ref{prop:homover} we see that in terms of the category of left ${\catsymbfont{C}}$-modules, ${\catsymbfont{R}}$ is semicofibrant precisely when the left ${\catsymbfont{C}}$-modules ${\catsymbfont{R}}^{ts}(-,d)$ are semicofibrant for all $d\in S({\catsymbfont{R}})$.
\begin{defn} For ${\catsymbfont{X}}$ and ${\catsymbfont{Y}}$ be bi-indexed ring spectra, an $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule ${\catsymbfont{M}}$ is \term{target semicofibrant} (resp., \term{target cofibrant}) if its underlying left ${\catsymbfont{Y}}$-object is semicofibrant (resp., cofibrant). For ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories, a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule ${\catsymbfont{F}}$ is \term{target cofibrant} if the corresponding $(B_{{\catsymbfont{C}}},B_{{\catsymbfont{D}}})$-bimodule $B_{{\catsymbfont{F}}}$ is target semicofibrant. \end{defn}
By way of terminology, we note that in our conventions (Definition~\ref{defn:bifunc}, Theorem~\ref{thm:functor}) a spectral functor $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ corresponds to a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule; the left module structure specifies the target small spectral category.
The following example indicates that target semicofibrant bimodules actually arise naturally in the current context.
\begin{example} Let $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ be a spectral functor. Then the $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule ${\catsymbfont{F}}_{\phi}={\catsymbfont{C}}(\phi(-),-)$ is target semicofibrant. \end{example}
The following proposition (the analogue of~\cite[6.6]{LewisMandell2}) gives additional examples of target semicofibrant objects and is the first key step in the proof of Theorem~\ref{thm:LMmain}.
\begin{prop}\label{prop:sctsc} If ${\catsymbfont{C}}$ is any small spectral category and ${\catsymbfont{D}}$ is a pointwise semicofibrant small spectral category, then semicofibrant (resp., cofibrant) $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules are target semicofibrant (resp., target cofibrant). \end{prop}
\begin{proof} The cofibrant case is clear from the explicit description of cofibrations. For the semicofibrant case, let ${\catsymbfont{X}}=B_{{\catsymbfont{C}}}$, ${\catsymbfont{Y}}=B_{{\catsymbfont{D}}}$, and let ${\catsymbfont{M}}$ be a target semicofibrant $({\catsymbfont{X}},{\catsymbfont{Y}})$-bimodule. Let $f\colon {\catsymbfont{N}}\to {\catsymbfont{N}}'$ be a fibration (resp., acyclic fibration) of left ${\catsymbfont{X}}$-objects. Fix $B=S({\catsymbfont{N}})=S({\catsymbfont{N}}')$, $A=O({\catsymbfont{Y}})$; then $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})$ and $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}')$ are left ${\catsymbfont{Y}}$-objects but in particular $(A,B)$-indexed spectra. For $(a,b)\in A\times B$, let ${\mathbb{S}}_{A,B;a,b}$ denote the $(A,B)$-indexed spectrum that is ${\mathbb{S}}$ at index $(a,b)$ and $*$ at all other indices. Then when ${\catsymbfont{P}}$ is an $(A,B)$-indexed spectrum \[ \Hom^{b}({\mathbb{S}}_{A,B;a,b},{\catsymbfont{P}})\iso{\catsymbfont{P}}(a,b) \] and when in addition ${\catsymbfont{P}}$ is a left ${\catsymbfont{Y}}$-module, the isomorphism $\Hom^{\ell}_{{\catsymbfont{Y}}}({\catsymbfont{Y}},{\catsymbfont{P}})\iso {\catsymbfont{P}}$ and the adjunction of Proposition~\ref{prop:bimadj} give an extension of scalars isomorphism \begin{align*} \Hom^{b}({\mathbb{S}}_{A,B;a,b},{\catsymbfont{P}})&\iso \Hom^{b}_{{\mathbb{S}}_{A},{\mathbb{S}}_{B}}({\mathbb{S}}_{A,B;a,b},{\catsymbfont{P}})\\ &\iso \Hom^{b}_{{\mathbb{S}}_{A},{\mathbb{S}}_{B}}({\mathbb{S}}_{A,B;a,b},\Hom^{\ell}_{{\catsymbfont{Y}}}({\catsymbfont{Y}},{\catsymbfont{P}}))\\ &\iso \Hom^{b}_{{\catsymbfont{Y}},{\mathbb{S}}_{B}}({\catsymbfont{Y}}\otimes {\mathbb{S}}_{A,B;a,b},{\catsymbfont{P}}). \end{align*} Now taking ${\catsymbfont{P}}=\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})$ and applying the adjunction of Proposition~\ref{prop:bimadj} again, we get an isomorphism \begin{align*} (\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}))(a,b)&\iso \Hom^{b}_{{\catsymbfont{Y}},{\mathbb{S}}_{B}}({\catsymbfont{Y}}\otimes {\mathbb{S}}_{A,B;a,b},\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}))\\ &\iso \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},\Hom^{r}_{{\mathbb{S}}_{B}}({\catsymbfont{Y}}\otimes {\mathbb{S}}_{A,B;a,b},{\catsymbfont{N}}))\\ &\iso \Hom^{b}_{{\catsymbfont{X}},{\catsymbfont{Y}}}({\catsymbfont{M}},\Hom^{r}({\catsymbfont{Y}}\otimes {\mathbb{S}}_{A,B;a,b},{\catsymbfont{N}})). \end{align*} The analogous formulas likewise hold replacing ${\catsymbfont{N}}$ by ${\catsymbfont{N}}'$ or by the map induced by $f\colon {\catsymbfont{N}}\to {\catsymbfont{N}}'$. From the formula in Construction~\ref{cons:homlrb}, we have \[ (\Hom^{r}({\catsymbfont{Y}}\otimes {\mathbb{S}}_{A,B;a,b},{\catsymbfont{N}}))(x,y)\iso F({\catsymbfont{Y}}(y,a),{\catsymbfont{N}}(x,b)) \] for all $x\in O({\catsymbfont{X}})$ and $y\in O({\catsymbfont{Y}})$. Since ${\catsymbfont{Y}}$ is pointwise semicofibrant, we have that \[ F({\catsymbfont{Y}}(y,a),{\catsymbfont{N}}(x,b))\to F({\catsymbfont{Y}}(y,a),{\catsymbfont{N}}'(x,b)) \] is a fibration (resp., acyclic fibration) of for all $a,b,x,y$ and it follows that \[ \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},f)\colon \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})\to \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}') \] is a fibration (resp., acyclic fibration) of bi-indexed spectra. \end{proof}
As indicated in Theorem~\ref{thm:derhom}, the right derived functor is constructed by cofibrant replacement of the contravariant variable and fibrant replacement of the covariant variable; the following proposition indicates that it suffices to use a semicofibrant object in the contravariant variable.
\begin{prop}\label{prop:LM62} Let ${\catsymbfont{X}}$ be a bi-indexed ring spectrum. If ${\catsymbfont{N}}$ is a (pointwise) fibrant left ${\catsymbfont{X}}$-object then $\Hom^{\ell}_{{\catsymbfont{X}}}(-,{\catsymbfont{N}})$ preserves weak equivalences between semicofibrant left ${\catsymbfont{X}}$-objects. In particular if ${\catsymbfont{M}}$ is a semicofibrant left ${\catsymbfont{X}}$-object then $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})$ represents the right derived functor ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})$. \end{prop}
\begin{proof} This is the analogue of \cite[6.2]{LewisMandell2} but the argument simplifies enormously because smashing with cofibrant objects in the category of spectra preserves weak equivalences. Let ${\mathbb{S}}_{c}\to {\mathbb{S}}$ be a cofibrant replacement. The Lemma~\ref{lem:smacof} below argues that when ${\catsymbfont{M}}$ is a semicofibrant left ${\catsymbfont{X}}$-module, then ${\catsymbfont{M}}\sma {\mathbb{S}}_{c}$ (the left ${\catsymbfont{X}}$-module which is ${\catsymbfont{M}}(a,b)\sma {\mathbb{S}}_{c}$ in each bi-index) is a cofibrant left ${\catsymbfont{X}}$-module. Since $(-)\sma {\mathbb{S}}_{c}$ preserves weak equivalences between any bi-indexed spectra and $\Hom^{\ell}_{{\catsymbfont{X}}}(-,{\catsymbfont{N}})$ preserves weak equivalences between cofibrant left ${\catsymbfont{X}}$-modules, it suffices to see that \[ \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})\to \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}} \sma {\mathbb{S}}_{c},{\catsymbfont{N}}) \] is a weak equivalence. The composite of the map above and the isomorphism \[ \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}}\sma {\mathbb{S}}_{c},{\catsymbfont{N}})\iso \Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},F({\mathbb{S}}_{c},{\catsymbfont{N}})) \] is the map on $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},-)$ induced by the weak equivalence of fibrant objects ${\catsymbfont{N}}\to F({\mathbb{S}}_{c},{\catsymbfont{N}})$. Since $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},-)$ preserves fibrations and acyclic fibrations, it preserves weak equivalences between all fibrant objects, and we see that the map is a weak equivalence. \end{proof}
We used the following lemma in the proof of Proposition~\ref{prop:LM62}.
\begin{lem}\label{lem:smacof} If ${\catsymbfont{M}}$ is a semicofibrant left ${\catsymbfont{X}}$-object and $Z$ is a cofibrant spectrum, then ${\catsymbfont{M}}\sma Z$ is a cofibrant left ${\catsymbfont{X}}$-object. \end{lem}
\begin{proof} It suffices to show that for an acyclic fibration of left ${\catsymbfont{X}}$-objects $f\colon {\catsymbfont{N}}\to {\catsymbfont{N}}'$ and a map of left ${\catsymbfont{X}}$-objects ${\catsymbfont{M}}\sma Z\to {\catsymbfont{N}}'$, there exists a lift ${\catsymbfont{M}}\sma Z\to {\catsymbfont{N}}$. In this situation, we have $S({\catsymbfont{M}})=S({\catsymbfont{N}})=S({\catsymbfont{N}}')$, which we abbreviate to $A$. Since the category of $({\catsymbfont{X}},{\mathbb{S}}_{A})$ is isomorphic to the full subcategory of left ${\catsymbfont{X}}$-objects with source $A$, $\Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}$ provides a spectral enrichment. Since \[ \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}}\sma Z,-)\iso F(X,\Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}}\sma Z,-)) \] the space of maps of left ${\catsymbfont{X}}$-objects from ${\catsymbfont{M}}\sma Z$ to ${\catsymbfont{N}}$ is isomorphic to the space of maps of spectra from $X$ to $\Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}})$ and likewise for ${\catsymbfont{N}}'$. This reduces to showing that the map \[ \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}})\to \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}}') \] is an acyclic fibration of spectra. The adjunction of Proposition~\ref{prop:bimadj} then gives adjunctions \begin{multline*} \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}}) \iso \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}}\otimes {\mathbb{S}}_{A},{\catsymbfont{N}})\\ \iso \Hom^{b}({\mathbb{S}}_{A},\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}})) =\prod_{a\in A}(\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}))(a,a) \end{multline*} and likewise for ${\catsymbfont{N}}'$. Since $\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},-)$ preserves acyclic fibrations, it follows that each map map \[ (\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}))(a,a)\to (\Hom^{\ell}_{{\catsymbfont{X}}}({\catsymbfont{M}},{\catsymbfont{N}}'))(a,a) \] is an acyclic fibration of spectra for all $a$ and so the map \[ \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}})\to \Hom^{b}_{{\catsymbfont{X}},{\mathbb{S}}_{A}}({\catsymbfont{M}},{\catsymbfont{N}}') \] is an acyclic fibration of spectra. \end{proof}
Finally, we prove Theorem~\ref{thm:LMmain}.
\begin{proof}[Proof of Theorem~\ref{thm:LMmain}] The existence of the enriched right derived functor and the rule for calculating it follows from~\cite[5.4]{LewisMandell2} using the definition of target semicofibrant (and K.~Brown's lemma) and Propositions~\ref{prop:sctsc} and~\ref{prop:LM62} to check the conditions. Proposition~\ref{prop:sctsc} then shows the compatibility between this right derived functor and the right derived functor of~\eqref{eq:derhom}. \end{proof} \fi
\section{Centralizer conditions, maps of $CC$, and the proof of the main theorem}\label{sec:pfstring}\label{sec:pfme}\label{sec:pfdcc}
In this section we begin the process of extending the functoriality of $CC$ by constructing zigzags associated to bimodules that satisfy centralizer conditions that we review below. We do enough work that we can prove the main theorem of the introduction, Theorem~\ref{main:string}, that gives an equivalence of $E_{2}$ ring spectra for the two $THC$ constructions commonly studied in string topology. We also prove Theorems~\ref{main:me} and~\ref{main:dcc}.
We begin with the centralizer conditions.
\begin{defn}\label{defn:dcc} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and let ${\catsymbfont{F}}$ be a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule. The \term{centralizer map for ${\catsymbfont{D}}$} is the map in the category of homotopical ${\catsymbfont{D}}$-modules \[ {\catsymbfont{D}}\to{\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}}) \] adjoint to the map ${\catsymbfont{F}}\otimes{\catsymbfont{D}}\to {\catsymbfont{F}}$ where ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}$ is as in~\eqref{eq:derhom} (that is, the right derived functor in Theorem~\ref{thm:derhom}). The \term{centralizer map for ${\catsymbfont{C}}$} is the analogous map \[ {\catsymbfont{C}}\to {\mathbb{R}}\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}}). \] We say that: \begin{enumerate} \item ${\catsymbfont{F}}$ satisfies the \term{double centralizer condition} when both centralizer maps are weak equivalences. \item ${\catsymbfont{F}}$ satisfies the \term{single centralizer condition} for ${\catsymbfont{C}}$ or ${\catsymbfont{D}}$ when the centralizer map for ${\catsymbfont{C}}$ or ${\catsymbfont{D}}$ (resp.) is a weak equivalence. \end{enumerate} \end{defn}
We have the following motivating examples.
\begin{example}[DK-embeddings]\label{ex:dke} If $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$ is a spectral functor and ${\catsymbfont{F}}$ is the bimodule ${\catsymbfont{F}}_{\phi}={\catsymbfont{C}}(\phi(-),-)$ then the enriched form of the Yoneda lemma shows that $\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}})$ is canonically isomorphic to ${\catsymbfont{C}}(\phi(-),\phi(-))$ and the centralizer map ${\catsymbfont{D}}\to \Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}})$ is the map $\phi\colon {\catsymbfont{D}}(-,-)\to {\catsymbfont{C}}(\phi(-),\phi(-))$; moreover, ${\catsymbfont{C}}(\phi(-),\phi(-))$ also represents the derived functor ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}})$. It follows that ${\catsymbfont{F}}$ satisfies the single centralizer condition for ${\catsymbfont{D}}$ if and only if $\phi$ is a DK-embedding. Moreover, if $\phi$ is a DK-equivalence then the enriched Yoneda lemma in the homotopy category shows that ${\catsymbfont{C}}\to {\mathbb{R}}\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}})$ is a weak equivalence and ${\catsymbfont{F}}$ satisfies the double centralizer condition. \end{example}
\begin{example}[${\catsymbfont{D}}$ and ${\mathrm{Perf}}({\catsymbfont{D}})$]\label{ex:perf} Let ${\catsymbfont{D}}$ be a pointwise fibrant small spectral category, and ${\catsymbfont{C}}$ be a small full spectral subcategory of the category of right ${\catsymbfont{D}}$-modules consisting of only cofibrant-fibrant objects. Assume the Yoneda embedding factors $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$, and let ${\catsymbfont{F}}={\catsymbfont{F}}_{\phi}$. For example, ${\catsymbfont{C}}={\mathrm{Perf}}({\catsymbfont{D}})$ (for any large enough cardinality) fits into this context. Then the bimodule ${\catsymbfont{F}}$ satisfies the double centralizer condition. Since $\phi$ is a DK-embedding, as per the previous example, ${\catsymbfont{F}}$ satisfies the single centralizer condition for ${\catsymbfont{D}}$. To see that the centralizer map for ${\catsymbfont{C}}$ is a weak equivalence, we consider the map \[ {\catsymbfont{C}}(x,y)\to {\mathbb{R}}\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}(-,x),{\catsymbfont{F}}(-,y)) \] for fixed $x,y$. Recalling that $x$ and $y$ are ${\catsymbfont{D}}$-modules, the enriched Yoneda lemma gives isomorphisms $x(d)\iso{\catsymbfont{F}}(d,x)$ and $y(d)\iso{\catsymbfont{F}}(d,y)$ for all $d$ in ${\catsymbfont{D}}$, and hence an isomorphism \[ \Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}(-,x),{\catsymbfont{F}}(-,y))\iso \Hom^{r}_{{\catsymbfont{D}}}(x(-),y(-))\iso\mathop {\aM\mathrm{od}}\nolimits_{{\catsymbfont{D}}^{\op}}(x,y)={\catsymbfont{C}}(x,y) \] (see Proposition~\ref{prop:homover}). Since we have assumed that $x$ and $y$ are cofibrant-fibrant right ${\catsymbfont{D}}$-modules, the point-set functor represents the right derived functor, and we see that ${\catsymbfont{F}}$ also satisfies the single centralizer condition for ${\catsymbfont{C}}$. \end{example}
\begin{example}[Morita contexts]\label{ex:mc} Let ${\catsymbfont{M}}$ be a cofibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule (and we assume without loss of generality that ${\catsymbfont{C}}$ and ${\catsymbfont{C}}$ are pointwise semicofibrant). Then the left derived functor of ${\catsymbfont{M}}\otimes_{{\catsymbfont{D}}}(-)$ from the derived category of ${\catsymbfont{D}}$-modules to the derived category of ${\catsymbfont{C}}$-modules is an equivalence of homotopy categories if and only if ${\catsymbfont{M}}\otimes_{{\catsymbfont{D}}}(-)$ restricts to a DK-equivalence ${\mathrm{Perf}}({\catsymbfont{D}})\to {\mathrm{Perf}}({\catsymbfont{C}})$ (for models of large enough cardinality). When this holds, the derived functor of the right adjoint $\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{M}},-)$ induces the inverse equivalence and represents the right derived functor ${\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{M}},-)$ in Definition~\ref{defn:dcc}. In particular, the unit of the derived adjunction for ${\catsymbfont{D}}$ is the centralizer map ${\catsymbfont{D}}\to {\mathbb{R}}\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{M}},{\catsymbfont{M}})$ and so ${\catsymbfont{M}}$ satisfies the single centralizer condition for ${\catsymbfont{D}}$. Although written in the context of associative ring spectra, the proof of Theorem~4.1.2 of~\cite{SSStable} implies that there exists a cofibrant $({\catsymbfont{D}},{\catsymbfont{C}})$-bimodule ${\catsymbfont{N}}$ such that ${\catsymbfont{M}}\otimes_{{\catsymbfont{D}}}{\catsymbfont{N}}$ is weakly equivalent to ${\catsymbfont{C}}$ as a $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodule and ${\catsymbfont{N}}\otimes_{{\catsymbfont{C}}}{\catsymbfont{N}}$ is weakly equivalent to ${\catsymbfont{D}}$ as a $({\catsymbfont{D}},{\catsymbfont{D}})$-bimodule. It then follows that the left derived functor of $(-)\otimes_{{\catsymbfont{C}}}{\catsymbfont{M}}$ from the derived category of right ${\catsymbfont{C}}$-modules to the derived category of right ${\catsymbfont{D}}$-modules is an equivalence of categories, which implies that ${\catsymbfont{M}}$ satisfies the single centralizer condition for ${\catsymbfont{C}}$. Thus, ${\catsymbfont{M}}$ satisfies the double centralizer condition. \end{example}
\begin{example}[$DX$ and $\Omega X$]\label{ex:dxloop} Let $X$ be a simply connected finite cell complex, or equivalently (up to homotopy) the geometric realization of a reduced finite simplicial set. In~\cite[\S3]{BM-Koszul}, we consider the Kan loop group model $GX$ for $\Omega X$ and describe an explicit $(\Sigma^{\infty}_+ GX,DX)$-bimodule $SP$ (whose underlying spectrum is equivalent to ${\mathbb{S}}$) that we show satisfies the double centralizer condition. (This example is originally due Dwyer-Greenlees-Iyengar~\cite[4.22]{DwyerGreenleesIyengar-Duality}, at least after extension of scalars to a field.) \end{example}
To construct the zigzag, we use the following construction of Keller~\cite[\S 4.5]{Keller-DIH}.
\begin{cons} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and ${\catsymbfont{F}}$ a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule. Let $\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}}$ be the small spectral category with objects $O({\catsymbfont{C}})\amalg O({\catsymbfont{D}})$, mapping spectra \[ \mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}}(a,b)=\begin{cases} {\catsymbfont{C}}(a,b)&a,b\in O({\catsymbfont{C}})\\ *&a\in O({\catsymbfont{C}}), b\in O({\catsymbfont{D}})\\ {\catsymbfont{F}}(a,b)&a\in O({\catsymbfont{D}}), b\in O({\catsymbfont{C}})\\ {\catsymbfont{D}}(a,b)&a,b\in O({\catsymbfont{D}})\\ \end{cases} \] with units coming from the units of ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$, and composition coming from the composition in ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ and the bimodule structure of ${\catsymbfont{F}}$. \end{cons}
The construction comes with canonical strictly fully faithful spectral functors ${\catsymbfont{C}}\to \mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}}$ and ${\catsymbfont{D}}\to \mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}}$, which by Proposition~\ref{prop:limitednaturality} induce maps of $\mathcal{D}_{2}$-algebras \[ CC({\catsymbfont{D}})\from CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to CC({\catsymbfont{C}}). \] The following theorem ties in the double centralizer condition. We prove it in Section~\ref{sec:pfcatzigzag}.
\begin{thm}\label{thm:catzigzag} Assume ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ are pointwise relatively cofibrant and pointwise fibrant small spectral categories and let ${\catsymbfont{F}}$ be a pointwise semicofibrant-fibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule. \begin{enumerate} \item If ${\catsymbfont{F}}$ satisfies the single centralizer condition for ${\catsymbfont{D}}$, then the map\break $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to CC({\catsymbfont{C}})$ is a weak equivalence. \item If ${\catsymbfont{F}}$ satisfies the single centralizer condition for ${\catsymbfont{C}}$, then the map\break $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to CC({\catsymbfont{D}})$ is a weak equivalence. \end{enumerate} \end{thm}
If we take for granted that a functor $THC$ exists as in Theorem~\ref{main:wefunct}, then the previous theorem combined with the examples above gives just what we need to prove Theorems~\ref{main:string}, \ref{main:me}, and~\ref{main:dcc}.
\begin{proof}[Proof of Theorem~\ref{main:string}] As per the statement of Theorem~\ref{main:wefunct}, for any associative ring spectrum $A$, $THC(A)$ may be constructed as $CC(A')$ for an associative ring spectrum $A'$ whose underlying spectrum is fibrant and for which the inclusion of the unit ${\mathbb{S}}\to A$ is a cofibration of spectra (e.g., applying cofibrant and fibrant replacement functors in category of associative ring spectra). Indeed, in all previous literature discussing $THC(DX)$ and $THC(\Sigma^{\infty}_+ \Omega X)$, this was always done tacitly. Using such a model $DX'$ for $DX$ and $R$ for $\Sigma^{\infty}_+ \Omega X$ (or $GX$ as in Example~\ref{ex:dxloop}), we have a cofibrant bimodule $SP$ satisfying the double centralizer condition, as in the example. The required chain of weak equivalences of $E_{2}$ ring spectra is then given by the zigzag \[ CC(DX')\from CC(\mathop{\aC\!\mathrm{at}}\nolimits_{SP})\to CC(R) \] of weak equivalences of $\mathcal{D}_{2}$-algebras. \end{proof}
\begin{proof}[Proof of Theorems~\ref{main:me} and~\ref{main:dcc}] By Examples~\ref{ex:dke} and ~\ref{ex:perf}, Theorem~\ref{main:me} is a special case of Theorem~\ref{main:dcc}. The proof of Theorem~\ref{main:dcc} is identical to the special case given by Theorem~\ref{main:string}: Apply both parts of Theorem~\ref{thm:catzigzag} to appropriate pointwise relatively cofibrant-fibrant replacements as in Proposition~\ref{prop:replace}. \end{proof}
\section{The construction of $THC$ (Proof of Theorems~\ref{main:wefunct} and~\ref{main:dkfunct})} \label{sec:pfwefunct}\label{sec:pfdkfunct}\label{sec:inftyfunct}
The purpose of this section is to construct topological Hochschild cohomology as a homotopical functor. We begin by constructing $THC$ as a functor on the homotopy category level from a subcategory of the homotopy category of small spectral categories to the homotopy category of $E_{2}$ ring spectra. Using work of Lindsey~\cite{Lindsey-XYZ}, we then show that essentially the same argument actually constructs $THC$ as a functor from a subcategory of the $(\infty,1)$-category $\mathop{\aC\!\mathrm{at}}\nolimits^{\ex}$ of small stable idempotent-complete $(\infty,1)$-categories to the $(\infty,1)$-category of $E_{2}$ ring spectra. Throughout, we work with quasicategories as a model for $(\infty,1)$-categories and rely on the foundational setup of Joyal and Lurie~\cite{Lurie-HTT, Lurie-HA}.
\begin{defn}\label{defn:THCobj} For a small spectral category ${\catsymbfont{C}}$, let $THC({\catsymbfont{C}})=CC({\catsymbfont{C}}^{\Cell,\Omega})$ where ${\catsymbfont{C}}^{\Cell,\Omega}$ is the functorial pointwise relatively cofibrant-fibrant replacement of Proposition~\ref{prop:replace}. \end{defn}
Given a DK-embedding $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$, by functoriality we get a DK-embedding $\tilde\phi\colon {\catsymbfont{D}}^{\Cell,\Omega}\to {\catsymbfont{C}}^{\Cell,\Omega}$ and the bimodule ${\catsymbfont{F}}_{\tilde\phi}$ representing this functor (see Definition~\ref{defn:bifunc}, Theorem~\ref{thm:functor}) satisfies the single centralizer condition for ${\catsymbfont{C}}^{\Cell,\Omega}$ (q.v.~Example~\ref{ex:dke}). Writing $\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi}$ as an abbreviation for $\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}_{\tilde\phi}}$, Theorem~\ref{thm:catzigzag} then gives us a zigzag of maps of $\mathcal{D}_{2}$-algebras \begin{equation}\label{eq:1simp} CC({\catsymbfont{C}}^{\Cell,\Omega})\overfrom{\simeq}CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi})\to CC({\catsymbfont{D}}), \end{equation} which we interpret as a map in the homotopy category of $E_{2}$ ring spectra \[ THC({\catsymbfont{C}})\to THC({\catsymbfont{D}}). \] This gives the next step in the construction of $THC$ as a functor, the definition on maps.
\begin{defn}\label{defn:THCmorph} For a DK-embedding $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$, define $THC(\phi)$ to be the map $THC({\catsymbfont{C}})\to THC({\catsymbfont{D}})$ in the homotopy category of $E_{2}$-ring spectra arising from the zigzag of~\eqref{eq:1simp}. \end{defn}
To check that this definition respects composition and unit maps, we use the following construction.
\begin{defn}\label{defn:nsimp} Let $\phi_{1}\colon {\catsymbfont{C}}_{0}\to {\catsymbfont{C}}_{1}$,\dots, $\phi_{n}\colon {\catsymbfont{C}}_{n-1}\to {\catsymbfont{C}}_{n}$ be a composable sequence of spectral functors. Define $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}}$ to be the small spectral category with objects the disjoint union of the objects of ${\catsymbfont{C}}_{i}$ for all $i$ and with mapping spectra \[ \mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}}(a,b) = \begin{cases} {\catsymbfont{C}}_{j}(\phi_{i,j}(a),b)&i\leq j\\ *&i>j \end{cases} \] for $a\in O({\catsymbfont{C}}_{i})$ and $b\in O({\catsymbfont{C}}_{j})$, where $\phi_{i,j}=\id$ if $i=j$ and $\phi_{i,j}=\phi_{j-1}\circ \cdots \circ \phi_{i}$ for $i<j$. Composition is induced by composition in ${\catsymbfont{C}}_{0}$,\dots, ${\catsymbfont{C}}_{n}$ and the functors $\phi_{i}$, and units come from the units in ${\catsymbfont{C}}_{0}$,\dots, ${\catsymbfont{C}}_{n}$. \end{defn}
We note that for a single morphism, $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi}$ is $\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}_{\phi}}$ for the bimodule ${\catsymbfont{F}}_{\phi}$ associated to $\phi$, which is consistent with the notation we used in~\eqref{eq:1simp}. We deduce from Theorem~\ref{thm:catzigzag} the following corollary.
\begin{cor}\label{cor:nsimp} With notation as in Definition~\ref{defn:nsimp}, assume each ${\catsymbfont{C}}_{i}$ is pointwise relatively cofibrant-fibrant and that $\phi_{1}$ is a DK-embedding. Then the inclusion of ${\catsymbfont{C}}_{0}$ in $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}}$ induces a weak equivalence $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}})\to CC({\catsymbfont{C}}_{0})$. \end{cor}
\begin{proof} Let $\psi\colon {\catsymbfont{C}}_{0}\to \mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{2},\ldots,\phi_{n}}$ be the composite of $\phi_{1}$ with the inclusion of ${\catsymbfont{C}}_{1}$ in $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{2},\ldots,\phi_{n}}$. We then have a canonical isomorphism of small spectral categories from $\mathop{\aC\!\mathrm{at}}\nolimits_{\psi}$ to $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}}$. Since $\phi_{1}$ is a DK-embedding, so is $\psi$, and Theorem~\ref{thm:catzigzag} implies that the induced map $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\psi})\to CC({\catsymbfont{C}}_{0})$ is a weak equivalence. \end{proof}
We can now prove Theorems~\ref{main:wefunct} and~\ref{main:dkfunct}.
\begin{proof}[Proof of Theorems~\ref{main:wefunct} and~\ref{main:dkfunct}] The proofs of the two theorems are essentially the same; for the proof of Theorem~\ref{main:wefunct}, simply restrict to the subcategory of small spectral categories consisting of the associative ring spectra. (Note that even in the case of Theorem~\ref{main:wefunct}, the argument still requires use of $CC$ of small spectral categories, namely, the small spectral categories $\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}_{\phi}}$.)
We have defined $THC$ on objects and morphisms in Definitions~\ref{defn:THCobj} and~\ref{defn:THCmorph}; we need to show that $THC$ preserves composition and units. Given $\phi_{1}\colon {\catsymbfont{C}}_{0}\to {\catsymbfont{C}}_{1}$ and $\phi_{2}\colon {\catsymbfont{C}}_{1}\to {\catsymbfont{C}}_{2}$, let $\tilde\phi_{1}$ and $\tilde\phi_{2}$ denote the induced functors on ${\catsymbfont{C}}_{i}^{\Cell,\Omega}$. We then have the following strictly commuting diagram of strictly fully faithful morphisms \[ \[email protected]{ &&{\catsymbfont{C}}^{\Cell,\Omega}_{2}\ar[dl]\ar[dr]\\ &\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{2}\circ \tilde\phi_{1}}\ar[r] &\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{1},\tilde\phi_{2}} &\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{2}}\ar[l]\\ {\catsymbfont{C}}^{\Cell,\Omega}_{0}\ar[rr]\ar[ur]&&\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{1}}\ar[u]&&{\catsymbfont{C}}^{\Cell,\Omega}_{1}\ar[ll]\ar[ul] } \] from which we get the following commutative diagram of $\mathcal{D}_{2}$-algebras. \[ \[email protected]{ &&CC({\catsymbfont{C}}^{\Cell,\Omega}_{2})\\ &CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{2}\circ \tilde\phi_{1}})\ar[ur]\ar[dl]_{\sim} &CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{1},\tilde\phi_{2}})\ar[l]_{\sim}\ar[r]\ar[d]_{\sim} &CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{2}})\ar[ul]\ar[dr]^{\sim}\\ CC({\catsymbfont{C}}^{\Cell,\Omega}_{0}) &&CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\tilde\phi_{1}})\ar[ll]^{\sim}\ar[rr] &&CC({\catsymbfont{C}}^{\Cell,\Omega}_{1}) } \] The arrows marked with ``$\sim$'' are weak equivalences by Theorem~\ref{thm:catzigzag}, Corollary~\ref{cor:nsimp}, and the 2-out-of-3 property. Since $THC(\phi_{1})$, $THC(\phi_{2})$, and $THC(\phi_{2}\circ \phi_{1})$ are defined by the outer zigzags in the diagram above, we see that \[ THC(\phi_{2}\circ \phi_{1})=THC(\phi_{1})\circ THC(\phi_{2}). \] Although $THC(\id_{{\catsymbfont{C}}})$ is not defined to be the identity map, part~(ii) of Theorem~\ref{thm:catzigzag} shows that $THC(\id_{{\catsymbfont{C}}})$ is an isomorphism (in the homotopy category), which together with the fact just shown that $THC(\id_{{\catsymbfont{C}}})=THC(\id_{{\catsymbfont{C}}})\circ THC(\id_{{\catsymbfont{C}}})$, proves that $THC(\id_{{\catsymbfont{C}}})$ is the identity map for any small spectral category ${\catsymbfont{C}}$. \end{proof}
Finally, we prove Theorem~\ref{main:inf} by explaining how to refine $THC$ into an functor of $\infty$-categories. For the source, for simplicity, we take the nerve of the category of small spectral categories and DK-embeddings, ${\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK}$; the functor will take DK-equivalences (and indeed Morita equivalences) to equivalences in the target, and so one can from there factor through an $\infty$-categorical Bousfield localization. For the target category, we will use the homotopy coherent nerve of a pointwise fibrant replacement of the Dwyer-Kan hammock localization of the category of $\mathcal{D}_{2}$-algebras, $N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}]$. We do not get a point-set map of quasicategories, however, because although our construction above takes morphisms of small spectral categories to zigzags of $\mathcal{D}_{2}$-algebras, which are honest morphisms in the hammock localization, it does not preserve composition strictly. If we think in terms of zigzags in the original category of $\mathcal{D}_{2}$-algebras, the construction $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}})$ gives $n$-simplex zigzags associated to a sequence of composable morphisms. Zachery Lindsey studied this kind of $\infty$-functoriality in his 2018 Indiana University thesis~\cite{Lindsey-XYZ}; in the notation there, we construct a map \[ N({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK})\to \Zig(N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}],N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}]^{\simeq}) \] as follows. \begin{enumerate} \setcounter{enumi}{-1} \item A $0$-simplex of $N({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK})$ is a small spectral category ${\catsymbfont{C}}$; it maps to $CC({\catsymbfont{C}}^{\Cell,\Omega})$. \item A $1$-simplex of $N({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK})$ is a DK-embedding $\phi \colon {\catsymbfont{C}}_{0}\to {\catsymbfont{C}}_{1}$; it maps to the zigzag~\eqref{eq:1simp}. \item In general, an $n$-simplex consists of $n$-composable DK-embeddings\break $\phi_{i}\colon {\catsymbfont{C}}_{i-1}\to {\catsymbfont{C}}_{i}$; it maps to the $n$-simplex zigzag for $\mathop{\aC\!\mathrm{at}}\nolimits_{\phi_{1},\ldots,\phi_{n}}$ generalizing the $2$-simplex zigzag pictured in the proof of Theorem~\ref{main:dkfunct}. \end{enumerate}
Although both the source and target simplicial sets are quasicategories, this is not a map of quasicategories because it only preserves face maps and not degeneracy maps. The work of Steimle~\cite{Steimle-Degeneracies} (see Theorems~1.2 and~1.4) allows us to correct this to construct a functor from $N({\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK})$ to $\Zig(N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}],N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}]^{\simeq})$.
Lindsey~\cite{Lindsey-XYZ} shows that the inclusion of a quasicategory ${\catsymbfont{Q}}$ in the quasicategory $\Zig({\catsymbfont{Q}},{\catsymbfont{Q}}^{\simeq})$ is a categorical equivalence. This then proves the following theorem.
\begin{thm} The preceding construction constructs a zigzag of maps of quasicategories from $N{\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK}$ to $N^{hc}L{\catsymbfont{S}}[\mathcal{D}_{2}]$, providing a functor $THC$ from the category of small spectral categories and DK-embeddings to the category of $E_{2}$ ring spectra that sends Morita equivalences to weak equivalences. \end{thm}
Since $THC$ sends Morita equivalences to weak equivalences, it factors through the Bousfield localization of $N{\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits^{DK}$ at the Morita equivalences; using the equivalence of~\cite[4.23]{BGT} between the localization of $N{\catsymbfont{S}}\mathop{\aC\!\mathrm{at}}\nolimits$ at the Morita equivalences and $\mathop{\aC\!\mathrm{at}}\nolimits^{\ex}$ then proves Theorem~\ref{main:inf}.
\section{Proof of Theorem~\ref{thm:catzigzag}}\label{sec:pfcatzigzag}
This section is devoted to the proof of Theorem~\ref{thm:catzigzag}. The basic idea is to compare $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})$ to a construction of the form $\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}},{\catsymbfont{F}})$, where ${\catsymbfont{R}}$ is a certain simplicial object resolving ${\catsymbfont{F}}$. We start with the following simplicial construction.
\begin{cons} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and let ${\catsymbfont{G}}$ be a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule. The simplicial $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule ${\catsymbfont{R}}_{\bullet}({\catsymbfont{C}};{\catsymbfont{G}};{\catsymbfont{D}})$ is defined by \[ {\catsymbfont{R}}_{n}({\catsymbfont{C}};{\catsymbfont{G}};{\catsymbfont{D}})=\bigvee_{j=0,\ldots,n+1} \underbrace{{\catsymbfont{C}}\otimes \cdots \otimes {\catsymbfont{C}}}_{j\text{ factors}} \otimes {\catsymbfont{G}}\otimes \underbrace{{\catsymbfont{D}}\otimes \cdots \otimes {\catsymbfont{D}}}_{n+1-j\text{ factors}} \] (a total of $n+2$ summands each with $n+2$ factors) where the face map $d_{i}$ multiplies the $i$th and $(i+1)$st factors using the multiplication of ${\catsymbfont{C}}$ or ${\catsymbfont{D}}$ or action on ${\catsymbfont{G}}$ and the degeneracy map $s_{i}$ is induced by the map ${\mathbb{S}}_{O({\catsymbfont{C}})}\to {\catsymbfont{C}}$ in the $(i+1)$st factor on the $j$th summand for $i<j$ and induced by the map ${\mathbb{S}}_{O({\catsymbfont{D}})}\to {\catsymbfont{D}}$ in the $(i+1)$st factor on the $j$th summand for $i\geq j$. We write ${\catsymbfont{R}}_{\bullet}({\catsymbfont{G}})$ when ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ are clear, and we write ${\catsymbfont{R}}({\catsymbfont{G}})$ for the geometric realization. \end{cons}
For example, ${\catsymbfont{R}}_{0}({\catsymbfont{G}})={\catsymbfont{G}}\otimes {\catsymbfont{D}}\vee {\catsymbfont{C}}\otimes {\catsymbfont{G}}$ and the degeneracy map $s_{0}$ is \[ {\catsymbfont{G}}\otimes {\catsymbfont{D}}\iso {\catsymbfont{G}}\otimes {\mathbb{S}}_{O({\catsymbfont{D}})}\otimes {\catsymbfont{D}}\to {\catsymbfont{G}}\otimes {\catsymbfont{D}}\otimes {\catsymbfont{D}} \] on the $0$th summand and \[ {\catsymbfont{C}}\otimes {\catsymbfont{G}}\iso {\catsymbfont{C}}\otimes {\mathbb{S}}_{O({\catsymbfont{C}})}\otimes {\catsymbfont{G}}\to {\catsymbfont{C}}\otimes {\catsymbfont{C}}\otimes {\catsymbfont{G}} \] on the $1$st summand.
We have an augmentation map of $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules $\epsilon \colon {\catsymbfont{R}}_{\bullet}({\catsymbfont{G}})\to {\catsymbfont{G}}$ induced by multiplying all the ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ factors through.
\begin{prop}\label{prop:epsilon} The augmentation $\epsilon \colon {\catsymbfont{R}}_{\bullet}({\catsymbfont{G}})\to {\catsymbfont{G}}$ is a homotopy equivalence of simplicial bi-indexed spectra. \end{prop}
\begin{proof} In the category of bi-indexed spectra, the simplicial object ${\catsymbfont{R}}_{\bullet}({\catsymbfont{G}})$ has an ``extra degeneracy'' in the sense of \cite[\S4.5]{Riehl-CategoricalBook}: Define $s_{-1}\colon {\catsymbfont{R}}_{n}({\catsymbfont{G}})\to {\catsymbfont{R}}_{n+1}{\catsymbfont{G}}$ to be the map \[ {\catsymbfont{R}}_{n}({\catsymbfont{G}})\iso {\mathbb{S}}_{O({\catsymbfont{C}})}\otimes {\catsymbfont{R}}_{n}({\catsymbfont{G}})\to {\catsymbfont{C}}\otimes {\catsymbfont{R}}_{n}({\catsymbfont{G}})\subset {\catsymbfont{R}}_{n+1}({\catsymbfont{G}}). \] These maps satisfy \begin{align*} s_{-1}s_{i}&=s_{i+1}s_{-1} &s_{-1}d_{i}&=d_{i+1}s_{-1}\\ s_{0}s_{-1}&=s_{-1}s_{-1} &d_{0}s_{-1}&=\id. \end{align*} The map $s\colon {\catsymbfont{G}}\to {\catsymbfont{R}}_{0}({\catsymbfont{G}})$ given by \[ {\catsymbfont{G}}\iso {\mathbb{S}}_{O({\catsymbfont{C}})}\otimes {\catsymbfont{G}}\to {\catsymbfont{C}}\otimes {\catsymbfont{G}}\subset {\catsymbfont{R}}_{0}({\catsymbfont{G}}) \] splits the map $\epsilon$ and (with $s_{-1}$) exhibits $\epsilon$ as the split coequalizer of $d_{0},d_{1}\colon {\catsymbfont{R}}_{1}({\catsymbfont{G}})\to {\catsymbfont{R}}_{0}({\catsymbfont{G}})$. Meyer's theorem~\cite[4.5.1]{Riehl-CategoricalBook} now gives the result. \end{proof}
The Reedy model structures on simplicial and cosimplicial spectra are convenient for identifying when maps of simplicial spectra realize to cofibrations and when maps of cosimplicial spectra $\Tot$ to fibrations. The following proposition follows the usual outline of similar results, which are proved from the pushout-product property of the smash product of spectra and the construction of the latching object of a simplicial spectrum as a sequence of pushouts.
\begin{prop} If ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ are pointwise relatively cofibrant small spectral categories and ${\catsymbfont{G}}$ is a cofibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule then the geometric realization of ${\catsymbfont{R}}_{\bullet}({\catsymbfont{G}})$ is a cofibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule and for every fibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule, the cosimplicial spectrum $\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}}_{\bullet}({\catsymbfont{G}}),{\catsymbfont{F}})$ is Reedy fibrant. \end{prop}
The same kind of observation applied to the two-sided bar construction $B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}})$ in the construction of $CC$ proves the following proposition.
\begin{prop}\label{prop:hypreedy} If ${\catsymbfont{C}}$ is a pointwise relatively cofibrant small spectral category and ${\catsymbfont{M}}$ is a fibrant $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodule, then the cosimplicial spectrum $CC^{\bullet}({\catsymbfont{C}},{\catsymbfont{M}})$ is Reedy fibrant. \end{prop}
The previous proposition together with the formula for $CC({\catsymbfont{C}};{\catsymbfont{M}})$ in~\eqref{eq:HM} proves invariance under weak equivalences of fibrant ${\catsymbfont{M}}$ for ${\catsymbfont{C}}$ satisfying the hypothesis. Although this is all we need for the proof of Theorem~\ref{thm:catzigzag} below, we state a more general invariance theorem for convenience of future reference.
\begin{thm}\label{thm:inv} Let ${\catsymbfont{C}}$ be a pointwise relatively cofibrant small spectral category and let ${\catsymbfont{M}}$ be a a fibrant $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodule. \begin{enumerate} \item $CC({\catsymbfont{C}};{\catsymbfont{M}})$ represents the derived functor ${\mathbb{R}}\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{C}}}({\catsymbfont{C}},{\catsymbfont{M}})$. In particular, $CC({\catsymbfont{C}};-)$ preserves weak equivalences between fibrant $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodules. \item Assume ${\catsymbfont{C}}'$ is a pointwise relatively cofibrant small spectral category. If $\phi \colon {\catsymbfont{C}}'\to {\catsymbfont{C}}$ be a DK-equivalence, then the induced map $CC({\catsymbfont{C}};{\catsymbfont{M}})\to CC({\catsymbfont{C}}';\phi^{*}M)$ is a weak equivalence. \end{enumerate} \end{thm}
\begin{proof} The hypothesis on ${\catsymbfont{C}}$ implies that the inclusion of the degree zero part of bar construction \[ {\catsymbfont{C}}\otimes {\catsymbfont{C}}\to B_{\bullet}({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}}) \] is a Reedy cofibration of $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodules, and it follows that $B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}})$ is a semicofibrant $({\catsymbfont{C}},{\catsymbfont{C}})$-bimodule. Part~(i) is then~\cite[6.3]{LewisMandell2}. Part~(ii) follows immediately from part~(i). \end{proof}
Proposition~\ref{prop:hypreedy} does not apply directly to $\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}}$ under the hypotheses of Theorem~\ref{thm:catzigzag} unless we further require ${\catsymbfont{F}}$ to be pointwise cofibrant (which is not the case in the main example of interest, ${\catsymbfont{F}}={\catsymbfont{F}}_{\phi}$ for a DK-embedding $\phi \colon {\catsymbfont{D}}\to {\catsymbfont{C}}$). Nevertheless, the same argument applies to prove the following proposition.
\begin{prop} If ${\catsymbfont{C}}$, ${\catsymbfont{D}}$, and ${\catsymbfont{F}}$ satisfy the hypotheses of Theorem~\ref{thm:catzigzag}, then the cosimplicial spectrum $CC^{\bullet}(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})$ is Reedy fibrant. \end{prop}
\begin{cons} Let ${\catsymbfont{C}}$ and ${\catsymbfont{D}}$ be small spectral categories and ${\catsymbfont{F}}$ a $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodule. We construct a map of cosimplicial spectra \[ \gamma^{\bullet} \colon CC^{\bullet}(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}}_{\bullet}({\catsymbfont{F}}),{\catsymbfont{F}}) \] as follows. In cosimplicial degree $0$, we have \[ CC^{0}(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\iso \prod_{d\in O({\catsymbfont{D}})}{\catsymbfont{D}}(d,d)\times \prod_{c\in O({\catsymbfont{C}})}{\catsymbfont{C}}(c,c) \] while \begin{align*} \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}&({\catsymbfont{R}}_{0}({\catsymbfont{F}}),{\catsymbfont{F}})=\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{F}}\otimes {\catsymbfont{D}}\vee {\catsymbfont{C}}\otimes {\catsymbfont{F}},{\catsymbfont{F}})\\ &\iso \Hom^{b}_{{\mathbb{S}}_{O({\catsymbfont{D}})},{\catsymbfont{D}}}({\catsymbfont{D}},\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}}))
\times \Hom^{b}_{{\catsymbfont{C}},{\mathbb{S}}_{O({\catsymbfont{C}})}}({\catsymbfont{C}},\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}}))\\ &\iso \prod_{d\in O({\catsymbfont{D}})}(\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}}))(d,d)\times \prod_{c\in O({\catsymbfont{C}})}(\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}}))(c,c) \end{align*} and we define $\gamma^{0}$ to be the product of the centralizer maps. For $n>0$, for any $j=1,\ldots,n$, given $c_{0},\ldots,c_{j-1}\in O({\catsymbfont{C}})$ and $d_{j},\ldots,d_{n}\in O({\catsymbfont{D}})$ let \begin{multline*} ({\catsymbfont{C}},{\catsymbfont{F}},{\catsymbfont{D}})_{n,j}(c_{0},\ldots,c_{j-1},d_{j},\ldots,d_{n})=\\ \qquad\quad {\catsymbfont{C}}(c_{1},c_{0})\sma \cdots \sma {\catsymbfont{C}}(c_{j-1},c_{j-2})\sma
{\catsymbfont{F}}(d_{j},c_{j-1})\sma {\catsymbfont{D}}(d_{j+1},d_{j})\sma\cdots\sma {\catsymbfont{D}}(d_{n},d_{n-1}), \end{multline*} where we understand this formula as \begin{align*} &{\catsymbfont{F}}(d_{1},c_{0})\sma {\catsymbfont{D}}(d_{2},d_{1})\sma\cdots\sma {\catsymbfont{D}}(d_{n},d_{n-1}), \qquad \text{and}\\ &{\catsymbfont{C}}(c_{1},c_{0})\sma \cdots \sma {\catsymbfont{C}}(c_{n-1},c_{n-2})\sma
{\catsymbfont{F}}(d_{n},c_{n-1}) \end{align*} when $j=1$ and $j=n$, respectively. Then in this notation, \begin{align*} CC^{n}&(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\iso \prod_{d_{0},\ldots,d_{n}\in O({\catsymbfont{D}})}F({\catsymbfont{D}}(d_{1},d_{0})\sma\cdots\sma {\catsymbfont{D}}(d_{n},d_{n-1}),{\catsymbfont{D}}(d_{n},d_{0}))\\ &\times \prod_{j=1}^{n}\ \prod_{\putatop{c_{0},\ldots,c_{j-1}\in O({\catsymbfont{C}})}{d_{j},\ldots,d_{n}\in O({\catsymbfont{D}})}}
F(({\catsymbfont{C}},{\catsymbfont{F}},{\catsymbfont{D}})_{n,j}(c_{0},\ldots,c_{j-1},d_{j},\ldots,d_{n}),{\catsymbfont{F}}(d_{n},c_{0}))\\ &\times \prod_{c_{0},\ldots,c_{n}\in O({\catsymbfont{C}})}F({\catsymbfont{C}}(c_{1},c_{0})\sma\cdots\sma {\catsymbfont{C}}(c_{n},c_{n-1}),{\catsymbfont{C}}(c_{n},c_{0})) \end{align*} while \begin{align*} \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}&({\catsymbfont{R}}_{n}({\catsymbfont{F}}),{\catsymbfont{F}})\iso\\ &\prod_{d_{0},\ldots,d_{n}\in O({\catsymbfont{D}})}F({\catsymbfont{D}}(d_{1},d_{0})\sma\cdots\sma {\catsymbfont{D}}(d_{n},d_{n-1}),(\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}}))(d_{n},d_{0}))\\ &\times \prod_{j=1}^{n}\ \prod_{\putatop{c_{0},\ldots,c_{j-1}\in O({\catsymbfont{C}})}{d_{j},\ldots,d_{n}\in O({\catsymbfont{D}})}}
F(({\catsymbfont{C}},{\catsymbfont{F}},{\catsymbfont{D}})_{n,j}(c_{0},\ldots,c_{j-1},d_{j},\ldots,d_{n}),{\catsymbfont{F}}(d_{n},c_{0}))\\ &\times \prod_{c_{0},\ldots,c_{n}\in O({\catsymbfont{C}})}F({\catsymbfont{C}}(c_{1},c_{0})\sma\cdots\sma {\catsymbfont{C}}(c_{n},c_{n-1}),(\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}}))(c_{n},c_{0})) \end{align*} and we define $\gamma^{n}$ to be the map induced by the centralizer maps ${\catsymbfont{D}}\to \Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}},{\catsymbfont{F}})$ and ${\catsymbfont{C}}\to \Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}},{\catsymbfont{F}})$ on the outer factors and the identity on the inner factors. The maps $\gamma^{\bullet}$ clearly commute with the degeneracy maps and all but the zeroth and last face maps. A tedious but straightforward check of the definitions verifies that the $\gamma^{\bullet}$ also commutes with the zeroth and last face maps. Let $\gamma$ denote the map on $\Tot$ induced by $\gamma^{\bullet}$. \end{cons}
\begin{proof}[Proof of Theorem~\ref{thm:catzigzag}] Fix ${\catsymbfont{C}}$, ${\catsymbfont{D}}$, and ${\catsymbfont{F}}$ as in the statement. Let ${\catsymbfont{F}}'\to {\catsymbfont{F}}$ be a cofibrant replacement in the category of $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules, and consider the composite map \[ \gamma'\colon CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\overto{\gamma}\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}}({\catsymbfont{F}}),{\catsymbfont{F}})\to \Hom^{b}({\catsymbfont{R}}({\catsymbfont{F}}'),{\catsymbfont{F}}). \] We note that $\gamma'$ can be described in terms of the $\Tot$ of a cosimplicial map with formula analogous to $\gamma$. The inclusion of the summands \[ {\catsymbfont{F}}'\otimes {\catsymbfont{D}} \otimes \cdots \otimes {\catsymbfont{D}}\qquad \text{and}\qquad {\catsymbfont{C}}\otimes \cdots \otimes {\catsymbfont{C}}\otimes {\catsymbfont{F}}' \] in ${\catsymbfont{R}}_{\bullet}({\catsymbfont{F}}')$ assemble to a map of simplicial $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules \[ B_{\bullet}({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}})\vee B_{\bullet}({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}) \to {\catsymbfont{R}}_{\bullet}({\catsymbfont{C}};{\catsymbfont{F}}';{\catsymbfont{D}}) \] where $B$ denotes the two-sided bar construction for $\otimes$. The hypotheses on ${\catsymbfont{C}}$, ${\catsymbfont{D}}$, and ${\catsymbfont{F}}'$ are sufficient for this map to be a Reedy cofibration, and so it induces a fibration \[ \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}}({\catsymbfont{F}}'),{\catsymbfont{F}})\to \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}})\vee B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}'),{\catsymbfont{F}}) \] since ${\catsymbfont{F}}$ is fibrant. We then have a canonical isomorphism \begin{align*} &\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}})\vee B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}'),{\catsymbfont{F}})\\ &\ \ \iso\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}}),{\catsymbfont{F}})\times \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}'),{\catsymbfont{F}})\\ &\ \ \iso\Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{F}}'\otimes_{{\catsymbfont{D}}}B({\catsymbfont{D}};{\catsymbfont{D}};{\catsymbfont{D}}),{\catsymbfont{F}})\times \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}})\otimes_{{\catsymbfont{C}}}{\catsymbfont{F}}',{\catsymbfont{F}})\\ &\ \ \iso\Hom^{b}_{{\catsymbfont{D}},{\catsymbfont{D}}}(B({\catsymbfont{D}};{\catsymbfont{D}};{\catsymbfont{D}}),\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}}))\times \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{C}}}(B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{C}}),\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}}))\\ &\ \ \isoCC({\catsymbfont{D}};\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}}))\times CC({\catsymbfont{C}};\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})) \end{align*} Opening up the construction of $\gamma$, we see that the following diagram commutes \[ \xymatrix{ CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\ar[r]\ar[d]_{\gamma'}&CC({\catsymbfont{D}})\otimes CC({\catsymbfont{C}})\ar[d]\\ \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}({\catsymbfont{R}}({\catsymbfont{F}}'),{\catsymbfont{F}})\ar[r]&CC({\catsymbfont{D}};\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}}))\times CC({\catsymbfont{C}};\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})) } \] where the right vertical map is induced by the double centralizer maps on the bimodule variables of $CC$. We have observed that bottom horizontal map is a fibration and in particular the $\Tot$ of a Reedy fibration of cosimplicial spectra; the top horizontal map is also a fibration and the $\Tot$ of a Reedy fibration of cosimplicial spectra. The map on horizontal fibers is the $\Tot$ of the cosimplical map that in each degree is the weak equivalence \begin{multline*} \prod_{j=1}^{n}\ \prod_{\putatop{c_{0},\ldots,c_{j-1}\in O({\catsymbfont{C}})}{d_{j},\ldots,d_{n}\in O({\catsymbfont{D}})}}
F(({\catsymbfont{C}},{\catsymbfont{F}},{\catsymbfont{D}})_{n,j}(c_{0},\ldots,c_{j-1},d_{j},\ldots,d_{n}),{\catsymbfont{F}}(d_{n},c_{0}))\\ \to \prod_{j=1}^{n}\ \prod_{\putatop{c_{0},\ldots,c_{j-1}\in O({\catsymbfont{C}})}{d_{j},\ldots,d_{n}\in O({\catsymbfont{D}})}}
F(({\catsymbfont{C}},{\catsymbfont{F}}',{\catsymbfont{D}})_{n,j}(c_{0},\ldots,c_{j-1},d_{j},\ldots,d_{n}),{\catsymbfont{F}}(d_{n},c_{0})). \end{multline*} $\Tot$ takes this degreewise weak equivalence of Reedy fibrant objects to a weak equivalence of spectra. It follows that the square above is homotopy cartesian. Both maps \begin{gather*} \Hom^{b}({\catsymbfont{R}}({\catsymbfont{F}}'),{\catsymbfont{F}})\to \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}}),{\catsymbfont{F}}) \iso CC({\catsymbfont{D}};\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}}))\\ \Hom^{b}({\catsymbfont{R}}({\catsymbfont{F}}'),{\catsymbfont{F}})\to \Hom^{b}_{{\catsymbfont{C}},{\catsymbfont{D}}}(B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}'),{\catsymbfont{F}}) \iso CC({\catsymbfont{C}};\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})) \end{gather*} are weak equivalences since the maps $B({\catsymbfont{F}}';{\catsymbfont{D}};{\catsymbfont{D}})\to {\catsymbfont{R}}({\catsymbfont{F}})$ and $B({\catsymbfont{C}};{\catsymbfont{C}};{\catsymbfont{F}}')\to {\catsymbfont{R}}({\catsymbfont{F}})$ are weak equivalences of cofibrant $({\catsymbfont{C}},{\catsymbfont{D}})$-bimodules. Since ${\catsymbfont{F}}'$ is cofibrant as both a left ${\catsymbfont{C}}$-object and right ${\catsymbfont{D}}$-object (Theorem~\ref{thm:LMmain}.(i) and the right object version), $\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ and $\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ are pointwise fibrant. It follows that when ${\catsymbfont{D}}\to \Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ is a weak equivalence, so is the map $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to CC({\catsymbfont{C}})$; likewise, when ${\catsymbfont{C}}\to \Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ is a weak equivalence, so is the map $CC(\mathop{\aC\!\mathrm{at}}\nolimits_{{\catsymbfont{F}}})\to CC({\catsymbfont{D}})$. By Theorem~\ref{thm:LMmain}.(iii) (and its analogue for $\Hom^{r}_{{\catsymbfont{D}}}$), both $\Hom^{\ell}_{{\catsymbfont{C}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ and $\Hom^{r}_{{\catsymbfont{D}}}({\catsymbfont{F}}',{\catsymbfont{F}})$ represent the derived functors in the statement of the centralizer conditions. The theorem now follows. \end{proof}
\end{document} | arXiv |
linearity, continuity, $F(x)=x$, and the Cauchy field automorphism equations and transcendental values
Where $F: [0,1] \to [0,1]$; along with $F(1)=1$. Do the field auto-morphism equations
$F(x+y)=F(x)+F(y) \quad\forall x\in\, [0,1]$
$F(xy)=F(x)F(y)\quad \forall x\in\, [0,1]$
Uniquely specify that $F(x)=x$, and that $F$ is an involution $F(F(x))=x$
I find that hard to completely believe, do these equations say anything precise about the value $F(x)$ where $x$ is transcendental number,? $\in [0,1]$.
Transcendental values, that is $\in [0,1]$ compatible with the probability calculus Which are presumably, all or, almost all such transcendental values in $[0,1]$.
Which would be entailed by $F(x)=x$) without any further regularity requirements and conversely as well except only monotonicity, (not even strict)mono-tonicity and not even $F(1)=1$.
If, so What about,along with
$$F:[0,1]→[0,1]$$;
$$F(1)=1$$
$$(1) \forall (x,y) \in [0,1];\, F(x+y)=F(x)+F(y)$$
Please see the comment by below.
Where merely (1) holds, without any further continuity, or regularity conditions explicitly added. Also note, that the domain is restricted to $[0,1]$ so when $x+y>1$ but $(x,y)\in dom(F)$ but $x+y \notin dom(F)$. Does this result still under this restriction. Its presumably implicit. The function is not defined for values of x+y>1 (it will nonetheless restrict these function sums, at least if x+y is rational $F(60)+F(70)=1.3$ nonetheless
Note Please see comment below by Mohsen Shahriari
Please see the Azcel (1989) quotation (eq)18 and (2) corollary 9 ;
$$\text{eq}(2)\, \forall(x,y) \in \mathbb{R_{2}^{+}};\,G(x+y)=G(x)+G(y)$$
Where if $G:_\mathbb{R^{+}} \to R$ satisfies $(2)$ and is continuous at a point, or monotonic, or Lebesgue measurable, or bounded from one side on a set of positive measure, then there exists constants, c, such that $$(18): 'G(x)=cx\, \forall x\, \geq 0$$
"in particular if $(2)$ holds with '$g(x) \geq 0$'; then "$(18)$" holds, with $c\geq 0$ (Azcel 1989, page 18)
I presumed that the last sentence was meant to read that given:
'the regularity conditions(in bold) of corollary $(9)$ are satisfied (continuity at a point etc), and $G:_R+ \to \mathbb{R}$ satisfies $(2)$, then if, in addition $g(x) \geq 0$ holds, the general solution is the same, except that $c$ is restricted to be non-negative.
(18)'$$ \forall x \geq 0;\, G(x)=cx ,\quad\text{and} c \geq 0$$
In contrast, to $(19)$ id '$G:_R+\to R$' satisfies '$(2) \, {\&} g(x) \geq 0$' then '$x\geq 0\,;\,G(x)=cx; \,;c \geq 0$' holds full stop.
And that the continuity/regularity conditions are immediately satisfied.
Although, $(2)$ suggests that it needs to hold for all non-negative reals, I am not sure, but I presume that this remain valid if the Function is only defined on a particular non negative interval ie $[0,1]$ and that with relation to that relevant interval $(2)$ holds, ie here $[0,1]$.
If so, that would mean that any function $F:[0,1]→[0,1]$; would already satisfy $F(x)\geq 0$ as its co-domain is $[0,1]$?
Then, as its domain, is a non-negative real interval $[0,1]$ as well,ie $$(A)F:[0,1]→[0,1]$$
Then if $(1)$ and $(A)$ below hold; $(A)$ being Cauchy' equation over the entire domain then $F(x)=x$ immediately, with no further regularity or continuity requirements; not even mono-tonicity having being presumed for the irrational values: $$(1)F(1)=1$$
$$(2) \forall (x,y)\, \in [0,1]; F(x+y)=F(x)+F(y)$$.
Which are all for all elements of the non-negative real valued domain.
I think I must be missing something here, as this would appear to reduce $$F(x)=ax .;\,a \geq 0$$;
From being the unique continuous solution for a function, $F$ that satisfies Cauchy's equation, over its entire domain, whose domain is $[0,1]$ and co-domain is $[0,1]$, if in addition $F(1)=1$,. to the unique solution full stop.
As continuity is automatic, $F(x)=x$ over $[0,1]$changes to only solution (not merely the only unique solution ) solution>
Thus in the context of an infinite modal probability (canoncal simplex vector space) probability function representation.
That is, infinitely many probability spaces (the entirety of $\triangle^{2}$. The canonical probability 2-simplex)the entire convex hull of its three vertices, as a euclidean triangle $\in \mathcal{R}^{3}$ with vertices #(0,0,1), (1,0,0), (0,1,0)# etc) .
The set of all and only three outcome probability triples.
all ,and only all triples $\in [0,1]^3$, whose elements are $3$ non negative reals $\in [0,1]$ which sum to 1,$ \sum_{t=1}^{t=3}=1$ .
$\langle x_{v_{i}},y_{v_{i}},z_{v_{i}},\emptyset_{v_{i}}=0, \Omega_{v_{i}}=1 \rangle_{v_{i}};\quad \forall (v_{i} \in \mathcal([0,1]^{3}\cap \triangle^{2}):$.
$\forall(v_{i}\in [0,1]^3): x_{v_{i}}+ y_{v_{i}}+z_{v_{i}}=1$. $\forall(v_{i}\in [0,1]^3): x_{v_{i}},y_{v_{i}},z_{v_{i}}\in [0,1]$.
which gives $\triangle^{2}$.
and the function $F$ being such that: $\forall(v_{i}\in triangle^{2}):F(x_{v_{i}})+F(y_{v_{i}})+F(z_{v_{i}})=1$.
$\forall(v_{i}\in triangle^{2}): F(x_{v_{i}}),F(y_{z_{i}}),F(z_{v_{i}})\in [0,1]$.
$$\forall(v_{i} \in \triangle^{2}):\text {in the entire 2-probability canonical simplex} :F(\Omega_{v_{i}})=1 \land F(\emptyset_{v_{i}})=0$$.
$$\forall (v_{i}\in \triangle^{2}):\, \forall(e^{j}_{i} \in v_{i}): 0<e^{j}_{i}<1 \iff 0<F(e^{j}_{i})<1 $$.
$$ \land \text{ on vertices,e.g}:.$$
$v_{b1}=\langle0,0,1\,\rangle_{v_{b1}}=$. $\langle\,e^{1}_{v_{b1}}=0,e^{2}_{v_{b1}}=0,e^{3}_{v_{b1}}=1\,\rangle_{v_{b1}}$.
$v_{b3}=\langle0,0,1\,\rangle_{v_{b3}}=$. $\langle\,e^{1}_{v_{b3}}=0,e^{2}_{v_{b3}}=0,e^{3}_{v_{b3}}= 1\,\rangle_{v_{b3}}$. $v_{b2}=\langle0,1,0\,\rangle_{v_{b2}}=$. $\langle\,e^{1}_{v_{b2}}=0,e^{2}_{v_{b2}}=1,e^{3}_{v_{b2}}=0\,\rangle_{v_{b2}}$ :
$F(e^{2}_{v_{b2}}=1)=F(e^{1}_{v_{b3}}=1)=F(e^{3}_{v_{b1}})=1)=1$ .
$\land F(0)=0\text{for the other 6dom value=0 basis elements/events}$ .
whose individual events, are globally ordered, vector independent(everywhere). mo-dally (between vector), locally (within a vector), vector regardless of whether $x_{v_{j}} , x_{v_{k}} ,\, y_{v_{i}},\,z_{v_{m}}$ are elements of the same vector or not.
And event independent,regardless of whether the events are both are not both $x$'s etc $( x,y,z)$ connected.
And a probability function $F$ whose domain is the probability simplex.
Or numerical elements /coordinates,in the vectors in the simplex) and is strictly totally ordered numerically by the equivalence classes and domain values of each event in each vector and between each vector, probability vectors $v_{i}$. where the events are denoted by their point wise numerical domain value in the simplex .
The function only has sum to unity within a vector (vector dependent_) for all vectors) but the rank is context free, (basis independent) which will lead to :.
$\forall(v_{i},v_{j})\in\,\triangle^{2}:\forall(e^{t}_{j})\in \,v_{i}\,,t=[1..5]:\,\forall(e^{t}_{j})\in\,v_{j}\,,t\in [1..5]:$.
$$ \text{all probability vectors in simplex}.$$
$$\text{each element, in each vector denoted/defined by their probability/numerical coordinate value}.$$
$$e^{t_{[1..5]}}_{j}<e^{t_{[1..5]}}_{i}\,\iff\,F(e^{t_{[1..5]}}_{j}) < F(e^{t_{[1..5]}}_{i}).$$ $$e^{t_{[1..5]}}_{j} > e^{t_{[1..5]}}_{i}\,\iff\,F(e^{t_{[1..5]}}_{j}) < F(e^{t_{[1..5]}}_{i}).$$ $$e^{t_{[1..5]}}_{j}=e^{t_{[1..5]}}_{i}\,\iff F(e^{t_{[1..5]}}_{j}) = F(e^{t_{[1..5]}}_{i}).$$
$$\text{ie}$$. $x_{v_{i}}=e^{1}_{i},x_{v_{j}}=e^{1}_{j}$ $y_{v_{j}}=e^{2}_{i}, y_{v_{i}}=e^{2}_{j}\,,z_{v_{i}}=e^{3}_{i}$ $\,z_{v_{j}=e^{3}_{j}},\emptyset_{v_{i}}=e^{4}_{i}=0\,,$ $\emptyset_{v_{j}}=e^{4}_{j}=0$, $\Omega_{v_{i}}=e^{5}_{i}=1, \Omega_{v_{i}}=e^{5}_{j}=1).$
$$\text{ elements, atomic events + unit, and empty set)}.$$
$$\text{st. function is globally ordered by these values,regardless of whether those number/event, are members of the same vector} i=j\or \text{or not},\, i\neqj \text{or the same type of event super-scripts equal or not}$$.
Where'= '(means elements with the same numerical values s must have the same function value .
The elements can be distinct, but their domain value \in [0,1] is the same real number (these may be be a different event, and may be on a different vector but have the same simplex domain probability value and thus function range probability value).
$\if F(x)<F(y) $ are globally, locally and modall-y ranked point-wise, by the values in the canonical probability simplex, somewhat like QM ,event and vector independent.
but which are locally finite $dim\geq3 $ where $\text{dim=the same finite number of atomic events in each vector}.
Where the natural unit and bottom element on each space and on the vertices is:
$$\forall(v):F(\Omega_v)=1 \,\land F(\emptyset_{v})=0$$.
$$ \text{on vertices eg} \,, \langle1,0,0\rangle\,,F(1)=1,\land\, F(0)=0$$ .
And the domain and range of $F$ is $[0,1]$ a derivation of Cauchy's equation would grant linearity. Due to rank equalites disjoint nomramlization of both entities and global rank equalites vector independtnnoramlization of $F$ for disjoint events on the same vectors becomes bvector independent normalization between events $(1)$above becomes global and (to any arbitary three events, same vector or not)) $$(1)F(1-x-y)+F(x)+F(y)=1$$ $$F^{-1}(1-x-y)+F^{-1}(x)+F^{-1}(y)=1$$ $$x+y=z+m\iff F(x)+F(y)=F(z)+F(m)$$ $x+y>z+m\iff F(x)+F(y)>F(z)+F(m)$$ $$x+y1\iff F(x)+F(y)+F(z)>1$$
$$x+y = \frac{2}{3} \iff F(x)+F(y)=\frac{2}{3}$$ $$F(\frac{1}{3})=\frac{1}{3}$$ $$F(\frac{1}{2})<\frac{13}{24}$$ $${2}{3}>x>\frac{1}{3}\iff \frac{2}{3}<F(x)<\frac{1}{3}$$ $$\frac{1}{3}>x\geq\frac{1}{4} \iff frac{1}{3}>F(x)\geq\frac{11}{48}$$ \frac{2}{3}\geq x \iff frac{1}{3}\leq F(x)<\frac{1}{6}$$ etc
rational homogeneity and Cauchy's equation (deriving , and continuity (complete linearity) in one move, without further ado?
See Chapter 2 section 1 corollary 9,eq (18 on page(18) in
Aczel, Janos, Dhombres, J, Functional equations in several variables with applications to mathematics, information theory and to the natural and social sciences, Encyclopedia of Mathematics and its Applications 31. Cambridge: Cambridge University Press (ISBN 978-0-521-06389-0). xiii, 462 p. (2008). ZBL1139.39043.
probability functional-analysis linear-transformations functional-equations
William Balthes
William BalthesWilliam Balthes
In fact the first equation is enough. First use induction and prove that $ F \left( \frac 1 n \right) = \frac { F ( 1 ) } n $ and then note that since the value of $ F $ is always nonnegative, hence by the first equation, it's increasing which proves what was desired.
Mohsen ShahriariMohsen Shahriari
$\begingroup$ Thanks for this; so just be just be sure that I am reading this correctly 1.F(1) 2.F(x+y)=F(x)+F(y); F:[0,1]→[0,1];specify F(x)=x on that interval. I know that one show non-negativity and F(1/n)=F(1)/n (and thus F(1/n)=1/n. $\endgroup$ – William Balthes Apr 21 '17 at 1:39
$\begingroup$ So I suspect that, F(1)=1 is required, as well, to ensure that F is strictly monotone increasing, or increasing/bounded/continuous, with (and not just) along with F:[0,1]to [0,1] and to ensure that F(x)=Ax, with A a positive constnat and thus F(x)=x, (which I think gives the continuity- like, result,F(x)=F(1)x (in this F(x)=x). I think $\endgroup$ – William Balthes Apr 21 '17 at 2:32
Is this the case for a Jensen's function where $(1)$ is replaced with Jensen's equation and $F(0)=0$ For example
$$(A)F:[0,1]→[0,1]$$ $$(1) F(0)=0,\, F(1)=1$$ $$(2)\forall (x,y)\, \in [0,1]; F(\frac{x}{2}+\frac{y}{2})=\frac{F(x)}{2}+\frac{F(y)}{2}$$
If 'Jensen's equation when combined with $F(0)=0$ where $0$ is an element of the domain and co-domain', over $F:[0,1]\to[0,1]$, is literally identical to 'Cauchy's equation' before continuity is applied, then one would presume that continuity and $F(x)=x$ would be likewise automatic, as above without any further requirement.Is it?
By this I mean not just indirectly (or for all extents and purposes) but that continuity should be automatic, $F(x)=x$ automatic, without so much as mentioning monoton-icity?. Due to the non-negative domain and range, and $F(1)=1$ bounding the function.
I believe that monotonic increasing-ness, however, is required to get to continuity for Jensen's equation in the form expressed above. Is that correct?
whilst both functional equations, (Cauchy and Jensen's equation) are expressed in their non-continuous form. (that is not, via '1-point homo-geineity', or the 'linearity superposition principle', or 'concavity plus convexity for Jensen's equation' without the restriction that $\sum \lambda=1$ due to $F(0)=0$ or the restriction that $\lambda \in \mathbb{Q}$
Whilst 'Jensens equation with $F(0)=0$', and 'Cauchy's equation' both can only, and only express 'rational homogeneity'.
Cauchy's equation applies additivity to all reals or at least to an appropriate subset of reals, in the domain of interest, nonetheless.
so is Cauchy's equation, even in the restricted form above, restricted as( $x+y>1; x+y \notin text{dom}(F)=[0,1]$ and Cauchy' equation cannot be directly applied?. Nonetheless is it stronger than Jensen's function described above.
Where remember that with $F(0)=0$; $0\in text{dom}(F)$, in some sense or not? (before continuity, being applied)
Unless that was the error, that the result above does not hold for cauchy as stated, because it only applies when one can extend the function; its unclear as I stated it, whether Cauch'ys equation applies to $x+y>1 $ (it says for all elements of the domain $(x,y)$ with no mention of$ x+y$, one one hand, and restricted the domain to $[0,1]$ f
its nonetheless real valued additive (for all, $(x,y)$ in the domain) whether $x$, $y$ are irrationals, that sum to an irrational, or a rational, or whether or not they are rational multiples of their sum or each other. $$\forall \lambda \in \mathbb{Q^{+}\cup 0}, \forall(x)\in dom(F)=[0,1]:F(\lambda x)=\lambda F(x)$$ so long that $\lambda \times x\in [0,1]$
Is Jensen's equation "real valued additive" in the same way? That is, before continuity is applied, and if not, what this explain the difference.
that Cauchy' equation bounds the irrationals values, in a stronger sense, to between the closest two rational function values, to abuse terminology. That is Cauchy equation above' essentially' implies strict monotonic increasing-ness even for irrational values?
That is, in the above context, which is over above non-negativity, as it ensure that their values will be approximately correct already.? perhaps, due to the interconnections with other rational values, and irrational values 'vis a vis' additivity, and rational homogeneity over even irrational domain values?
$$x>y \leftrightarrow F(x)>F(y), (x,y)\in \mathbb{IR} \land (x,y)\text{ are NOT rational multiples of each other}$$
Which is generally implied by Cauchy's equation.
that is via real valued additivity, which may connect the function values of irrational elements of the domain of the function indirectly to each other and some the rational values which are clearly strictly monotonic increasing?.
$F(x)=x$ clearly for all rational values in both cases I think before continuity is applied
(which apparently it already is, above for Cauchy's equation).
That is when Jensen's equation applies to all elements of a real valued domain, then if $F(0)=0$ does Cauchy's equation apply as to real reals in the domain, so long that $x+y \in dom(F)$.?
Apparently Jensen's equation only implies restricted rational convexity and concavity.
$$(A)\text{(restricted convexity and concavity, jensens generalized, without F(0)=0)}:\forall t \,\in\, \{\mathbb{Q} \cap [0,1]\}\,;\,\forall (x,y)\in \text{dom}(F)\,;\, F(tx +(1-t)y)=tF(x) + (1-t)F(y)$$
$$(B)\text{(convexity and concavity, Jensen's generalized, with F(0)=0)}:\forall (t_1,t_2)\,\in\, \{\mathbb{Q} \cap [0,1]\}\,;\,\forall (x,y)\in \text{dom}(F)\,;\, F(t_1x +t_2y)= t_1F(x) + t_2F(y)$$
where $t_1 +t_2$ need sum equal $1$ in $(B)$; that is,the requirement that $\sum_i t_i=1$ in $(A)$ is removed in $(B)$ given $F(0)=0$.
Are these generalizations of Jensen's equation correct?
That is before continuity is applied, but when $F$ is real valued or applies whose domain and co-domain, are real valued intervals such $[0,1]$
When it holds over the entire domain or only over the real line or open intervals.
But does Jensen's equation really imply real valued Cauchy add-itivity, in the non-continuous case, as does Cauchy's equation?
I know that midpoint convexity may have issues with rational convexity as opposed to dyadic rational convexity on closed intervals, which is somewhat related to the issue of continuity of the endpoint.
presume that jen-sen equation would not have this issue because its an equality equation.
And I presume that the 'convexity and concavity ' combined equation can made less restrictive when $F(0)=0$ . That is so that $F(x+y)=F(x)+F(y)$ the rational superposition principle and $F(0)=0$ can be recovered from it, via lifting the restricting that $\sum \lambda =1$
midpoint convexity- implies $$\forall t\,\in\, \{\mathbb{Q} \cap [0,1]\}\,;\,\forall (x,y)\in \text{dom}(F)\,;\, F(\sigma x +(1-\sigma)y) \leq \sigma F(x) + (1-\sigma)F(y)$$.
Ff $F$ is real valued on an open interval
Does it imply this, without continuity on a closed interval. Or only
$$\forall t\,\in\, \{\ \mathbb{D_{Q}} \cap [0,1]\}\,;\,\forall (x,y)\in \text{dom}(F)\,;\, F( \sigma x +(1- \sigma) y) \leq [\sigma F(x) + (1- \sigma)F(y)]$$.
where \mathbb{D_{Q}} stands for the dyadic rationals; with $F(0)=0$ and $F(1)=1$, and strictly monotonic, ?
It can express convexity for $$ \sigma \in\mathbb{Q_D} \in [0,1],\ \sum\sigma=1$$
$$ F( \frac{a}{2^{n}} x) \leq \frac{a}{2^{n}}F(x)$$ with $F(0)=0$where $n \in \{\mathbb{N}\cup 0\};\forall(a) \in \mathbb{N};1 \leq a \leq 2^{n}$
$$F( \frac{a}{2^{n}}x) \leq \frac{a}{2^{n}}F(x)$$ with $F(0)=0$
$$F( \frac{2^{n}}{a}x) \geq \frac{2^{n}}{a}F(x)$$ with $F(0)=0$ where $a>1$\in where $n \in \{\mathbb{N} \cup 0\};\forall(a);1 \leq a \leq 2^{n}$
or dyadic rational super-additivity (otherwise sub-linear functions would be linear full stop) with $F(0)=0$ and maybe not even that that.
Some of this, has to do with its mid-point convexity being an inequality-case which makes things difficult.One often uses $F(2x)=2F(x)$ on midpoint convexity to get sub-additivity AND $F(2x)=2F(x)$ on midpoint concavity to get superaddivity (despite convexity being most often associated with super-additivity).
Is the same nonetheless the case with Jensen's equation? That the equations $(A)$ , $(B)$ above only hold for dyadic $t, t_1,t_2$ over closed intervals?
I presume not, as the equality just as it makes it make it easier to get to derived real valued additivity (even in the non continuous case).
It makes it much easier to progress from mid-2pt-to dyadic and all all the way rational homogeoneeity/rational convexity concavity?.
I know that one can trivially 'derive Cauchy's equation' from jensens equation with $F(0)=0$, buts it unclear to me that this is derivation in full generality or just a pairwise result
I note that its unclear, in the formulation of my question above, whether Cauchy's equation applies when $x+y>1$?
$$(1)\forall ((x,y)\in \text{Dom(F)=[0,1]};x+y>1): F(x+y)=x+y$$.
I presume not, as above I said that;
$$\forall ( (x,y)\in \text{Dom(F)=[0,1]}): F(x+y)=F(x)+F(y)$$.
Whilst, there is no explicit mention of a restriction to only those domain elements,$\,(x,y);\,\,(x,y)\in \, \text{Dom(F)}=[0,1]$, whose sum: $x+y;\,\, x+y \in \, \text{Dom(F)}=[0,1]$ in the question above. Clearly, Cauchy' equation, as I used it, is restricted to domain elements: $(x,y)\in [0,1]=\text{Dom(F)}$, whose sum: $x+y;\,\, x+y\in [0,1]$ s.t $x+y\,\leq1$ ?
I presume that:$(A):\, \forall (x \in [0,1]):\,F(x)=x$, still holds, regardless of this restriction? Is that correct?
This being, due to non-negativity of $F:\, F(x)\geq 0\,,\,\text{CoDom(F)=Dom(F)}=[0,1]$,which gives, from Cauchy' equation above, that $F$ is monotonic increasing over $[0,1]$.
And, $F(1)=1$,which gives:
$$\forall(x\in [0,1]\cap \mathcal Q): F(x)=x$$.
And these collectively give $(A)$?
So I presume that restricted Cauchy function $F$ still preserves rational sums $x+y>1$ in the sense of: $(1)$, $(2.1$), or $(2.2)$ below?
$$(1):\forall ((x,y)\in \{\text{Dom(F)=[0,1]}\cap \mathcal Q\};x+y>1): F(x+y)=x+y$$.
$$\forall ((x,y,z)\in \text{Dom(F)=[0,1]};\forall (x_1, y_1,z_1)\in \text{Dom(F)=[0,1]};\,x+y+z>1):$$ $$(2.1): \, x+y+z=x_1+y_1+z_1 \iff F(x)+F(y)+F(z) =F(x_1)+F(y_1)+F(z_1)$$.
$$(2.2):\, F(x+y+z)=F(x_1+y_1+z_1) \iff F(x)+F(y)+F(z) =F(x_1)+F(y_1)+F(z_1)$$.
Is that correct?
Not the answer you're looking for? Browse other questions tagged probability functional-analysis linear-transformations functional-equations or ask your own question.
Finding smallest and largest possible values for the probability of the union of 3 events
The inner product spaces and linearity in probability
Is the following construction a measure?
Probability that two drawn cards values are the same after an interchange
What probability measure is used in the definition of an unbiased estimator?
Strictly Monotonic increasing, Symmetric ,doubling Function $F:[0,1]\to [0,1]$
Is 1 point homogeinety (essentially) , with F(1)=1; F:[0,1]\to[0,1], equivalent to, Cauchy's equation and continuity, by itself?
valid values of p for a probabilty function
Law of total probability and absolute value paradox
Independence of random variables and events | CommonCrawl |
\begin{document}
\title{Supplementary Materials for ``Quantum Neuronal Sensing of Quantum Many-Body States on a 61-Qubit Programmable Superconducting Processor''}
\author{Ming Gong$^{1,2,3}$} \thanks{These authors contributed equally to this work.} \author{He-Liang Huang$^{1,2,3}$} \thanks{These authors contributed equally to this work.} \author{Shiyu Wang$^{1,2,3}$} \thanks{These authors contributed equally to this work.} \author{Chu Guo$^{1,2,3}$} \author{Shaowei Li$^{1,2,3}$} \author{Yulin Wu$^{1,2,3}$} \author{Qingling Zhu$^{1,2,3}$} \author{Youwei Zhao$^{1,2,3}$} \author{Shaojun Guo$^{1,2,3}$} \author{Haoran Qian$^{1,2,3}$} \author{Yangsen Ye$^{1,2,3}$} \author{Chen Zha$^{1,2,3}$} \author{Fusheng Chen$^{1,2,3}$} \author{Chong Ying$^{1,2,3}$} \author{Jiale Yu$^{1,2,3}$} \author{Daojin Fan$^{1,2,3}$} \author{Dachao Wu$^{1,2,3}$} \author{Hong Su$^{1,2,3}$} \author{Hui Deng$^{1,2,3}$} \author{Hao Rong$^{1,2,3}$} \author{Kaili Zhang$^{1,2,3}$} \author{Sirui Cao$^{1,2,3}$} \author{Jin Lin$^{1,2,3}$} \author{Yu Xu$^{1,2,3}$} \author{Lihua Sun$^{1,2,3}$} \author{Cheng Guo$^{1,2,3}$} \author{Na Li$^{1,2,3}$} \author{Futian Liang$^{1,2,3}$} \author{Akitada Sakurai$^{4,6}$} \author{Kae Nemoto$^{6,7,4}$} \author{W. J. Munro$^{5,6}$} \email{[email protected]} \author{Yong-Heng Huo$^{1,2,3}$} \author{Chao-Yang Lu$^{1,2,3}$} \author{Cheng-Zhi Peng$^{1,2,3}$} \author{Xiaobo Zhu$^{1,2,3}$} \email{[email protected]} \author{Jian-Wei Pan$^{1,2,3}$} \email{[email protected]}
\affiliation{$^1$ Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China} \affiliation{$^2$ Shanghai Branch, CAS Center for Excellence in Quantum Information and Quantum Physics, University of Science and Technology of China, Shanghai 201315, China} \affiliation{$^3$ Shanghai Research Center for Quantum Sciences, Shanghai 201315, China} \affiliation{$^4$ School of Multidisciplinary Science, Department of Informatics, SOKENDAI (the Graduate University for Advanced Studies), 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan} \affiliation{$^5$ NTT Basic Research Laboratories and Research Center for Theoretical Quantum Physics, 3-1 Morinosato-Wakamiya, Atsugi, Kanagawa 243-0198, Japan} \affiliation{$^6$ National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan} \affiliation{$^7$ Okinawa Institute of Science and Technology Graduate University, Onna-son, Okinawa 904-0495, Japan}
\maketitle \tableofcontents
\beginsupplement \section{Quantum processor performance} The experiment is performed on a superconducting quantum computing platform as in [Science 372, 948-952 (2021)]~\cite{Gong2021}. The quantum processor, namely ``\textit{Zuchongzhi} 1.0'', contains 64 transmon qubits arranged in an 8-by-8 array, among them two qubits are not functional, and one qubit that is not frequency fast-tunable (Fig.~\ref{figS0}). Between neighboring qubits, a coplanar waveguide resonator couples both qubits. Through the virtual photon interaction via the quantum bus, an effective coupling between neighboring qubits is realized.
\begin{figure*}\label{figS0}
\end{figure*}
\blue{In realizing the high-fidelity continuous time Hamiltonian evolution, where $H_d=\hbar \sum g_{i,j}(\sigma_x^i\sigma_x^j+\sigma_y^i\sigma_y^j)/2+\hbar \sum d_i\sigma_z^i$, we need to realize a high-precision control of qubit frequency. In this work, we utilize two technologies to realize the requirement: the Z pulse distortion correction, and the alignment of qubit frequency.}
\blue{The Z pulse distortion correction is to remove the unwanted distortion of the control pulse applied on the flux bias of the qubit. The goal of the correction is to obtain a constant frequency $d_i$ for the time-independent evolution of the system. We utilized the calibration and correction discussed in Ref.~\cite{yan2019strongly}. We show the results before and after the correction in Fig.\ref{pulsecorrection}. After correcting the Z pulse distortion, we utilized the calibration of the qubit-frequency alignment with multi-qubit swapping at different qubit sites as discussed in Ref.~\cite{Gong2021}. Examples of the calibrations are shown in Fig.~\ref{qqswap}, where disorders have been corrected, and coherent oscillations can be observed for at least 500 ns.}
There are two qubit frequencies in this experiment: the idle points and the interacting points. The qubits are biased at their idle points to perform the single-qubit and readout operations. For each qubit, the idle points are designed to be away from their neighbors to avoid the unnecessary microwave crosstalk. Meanwhile, we optimize the idle points to maximize the single-qubit operation fidelity and readout performances following the procedures listed in Ref.~\cite{Gong2021}. The interacting point is set at 5.192 GHz for 3 by 3 instances, and 5.09 GHz for the 4 by 4 to 8 by 8 instances, respectively. Using the interacting point as the reference, we detune the qubits to the corresponding frequencies to utilize disorders. At the interacting point, the average effective coupling strength for all nearest-neighboring qubit pairs is 2.185 MHz for 3 by 3 instances, and 2.75 MHz for 4 by 4 to 8 by 8 instances.
For state readout, we utilize the second-excited state readout technology \cite{Wang2021} to reduce the impact of state relaxation. The readout fidelity is 0.971 (0.937) for $\ket{0}$ ($\ket{1}$) state for all qubits in average. We benchmark the single-qubit gate error using cross-entropy benchmarking (XEB)~\cite{arute2019quantum}. The average XEB Pauli error is 0.65$\%$, among which 0.47$\%$ is the speckle purity benchmarking (SPB)~\cite{Aaronson2017} error and 0.18$\%$ is the control error. We summarize the performances of the quantum processor in Tab.~\ref{tableSa} and Fig.~\ref{figS1}.
\blue{Now let’s discuss the effect of ramping up and ramping down time. In our experiment, we need to tune all qubits to the chosen detuning or interacting frequency for state preparation and quantum neural network, respectively. In the tuning operation, there are a ramping up stage, a constant amplitude stage, and a ramping down stage. The ramping up and down time are extremely short in comparing with the coupling strength. In our experiment, the ramping up and down time is only 4 ns. We numerically simulated the process with 0 to 100 ns as the ramping up and down time. As shown in Fig.~\ref{rampingtime}, we use the squared statistical overlap as a quantification of fidelity defined by $F=(\sum\sqrt{p_{(i,j)}q_{(i,j)}})^2/\sum p_{i,j}\sum q_{i,j}$, and find that the fidelity keeps in a high level for the ramping time short than 10 ns. The ramping up and down in such a short time mostly contribute to the single qubit phase. In our experiment, in the state preparation, such local single qubit phase will not affect the property of the state whether it is an ergodic or localized state. In the quantum neural network, such single qubit phase can also be regarded as part of the parameters of the QNN, thus will not introduce error. }
\begin{figure*}
\caption{\textbf{The wave sequence and results for pulse distortion correction.} }
\label{pulsecorrection}
\end{figure*}
\begin{figure*}
\caption{\textbf{The coherent oscillation for different number of qubits from 2 to 5 qubits.} In the experiment, the qubit marked in orange is excited, then all qubits are detuned to the same interaction frequency, and the population of all involved qubits are measured. The solid lines correspond to numerical simulations with no disorders and the dots correspond to the experimental data. We fit the experimental data with simulations with disorder considered to extract the disorders. In these examples, the disorders are mostly negligible.}
\label{qqswap}
\end{figure*}
\begin{figure*}
\caption{\textbf{System parameters for our quantum processor.} }
\label{figS1}
\end{figure*}
\begin{figure*}
\caption{\textbf{The simulated fidelity as a function of the ramping up and down time.} We use the squared statistical overlap as a quantification of fidelity. The system contains 9 qubits arranged in 3 by 3, with coupling strength defined as 2 MHz. The evolution time for the constant amplitude stage is 200 ns. }
\label{rampingtime}
\end{figure*}
\begin{table*}[htb] \centering \begin{tabular}{cccc} \hline Parameters& Median& Mean& Stdev.\\ \hline Qubit idle frequency (GHz)& 5.204& 5.202& 0.196\\ $T_1$ at idle frequency ($\mu$s)& 12.94& 13.50& 5.54\\ $T_1$ at working point ($\mu$s)& 11.05& 12.13& 5.55\\ $T_2^*$ at idle frequency ($\mu$s)& 1.34& 1.41& 0.56\\ Effective coupling strength $g/2\pi$ between neighboring qubits (MHz)& 2.174& 2.185& 0.070\\ \hline Readout fidelity of $\ket{0}$ $f_{00}$& 0.975& 0.971& 0.016 \\ Readout fidelity of $\ket{1}$ $f_{11}$& 0.940& 0.937& 0.023 \\ Effective qubit temperature (mK)& 65& 66& 11\\ \hline Single-qubit SPB Pauli error& 0.0042& 0.0047& 0.0029\\ Single-qubit XEB Pauli error& 0.0050& 0.0065& 0.0046\\ Single-qubit control error& 0.0007& 0.0018& 0.0026\\ \hline \end{tabular} \caption{\textbf{Performance parameter of the ``Zuchongzhi 1.0'' quantum processor.}} \label{tableSa} \end{table*}
\section{level statistics} The quantum system can be in distinct regimes~\cite{Kuhn_2007,Escalante2018,Zhang2021,abanin2019colloquium}, ergodic and localized regimes, depending on the disorder strength $h/g$. The system thermalizes under the dynamics and follows the eigenstate thermalization hypothesis~\cite{mori2018thermalization} for low disorder strengths, and would be in the localized phase for large disorder strengths~\cite{Kuhn_2007,Escalante2018,Zhang2021,abanin2019colloquium}.
Level statistics is one of the standard approach to distinguish the different phases~\cite{Manai2015,White2020,sierant2019level,sierant2020model,atas2013distribution}. The gap ratio of consecutive spacings between energy levels
\begin{equation} {r_n} = \min \{ {\delta _n},{\delta _{n - 1}}\} /\max\{ {\delta _n},{\delta _{n - 1}}\} \end{equation} is introduced as a simple probe of the level statistics in Ref.~\cite{oganesyan2007localization}, where ${\delta _n} = {E_{n + 1}} - {E_n}$ is an energy difference between two consequtive levels. The average gap ratio, $\bar r$, is different for ergodic systems ($\bar r \approx 0.527$) and for localized systems ($\bar r \approx 0.386$), as analyzed in Ref.~\cite{atas2013distribution}.
We perform numerical simulation to analyze the level statistics of the $3\times3$ system. Figure~\ref{level_statistic} shows the average gap ratio $\bar r$ as a function of disorder strength $h/g$ and captures the phase transition from the ergodic to the localized phase. We note that although level statistics can be used to probe these two phases, the calculation of level statistic is very expensive for large system, since the complexity of calculating the eigenvalues of a $N$-qubit system is O($2^{3N}$), which grows exponentially over the number of qubits.
\begin{figure*}
\caption{\textbf{Level statistics of the $3\times 3$ system.} Average level spacing $\bar r$ as a function of the disorder strength $h/g$. }
\label{level_statistic}
\end{figure*}
\section{Imbalance dynamics}
\begin{figure*}
\caption{\textbf{Evolution of the imbalance.} (a) Time evolutions of the system imbalance at different disorder strengths and system sizes. Each data point is averaged over 50 disorder realizations. (b) The quasi-steady-state imbalance taken at 200 ns as functions of disorder strengths for different system sizes. The shadow is the error estimated via the standard deviation in the 50 disorder realizations.
}
\label{figS2}
\end{figure*}
In our experiment, the ergodic states and localized states are generated by the system's evolution in the absence and presence of disorder, respectively. Here, we apply the order parameter of imbalance, defined as $\mathcal{I}=(N_e-N_o)/(N_e+N_o)$, to monitor the evolution of the system, where $N_e$ ($N_o$) is the total number of excitation quanta on the even (odd) number sites. Imbalance is an effective order parameter that reflects the preservation of the local magnetizations of the initial state. The evolution of the imbalance of the quantum system with different system sizes and different disorder strengths is depicted in Fig.~\ref{figS2}A. We found that at long times above 150~ns, the imbalance reaches a steady state. The imbalance of the steady-state approaches 0 for $h/g\approx 0$, where $h$ is the disorder strength and $g\approx 2.185~\text{MHz}$ the effective average coupling strength between neighboring qubits. However, if the disorder strength increases, the steady-state imbalance becomes larger, signaling the breakdown of the ergodicity. Meanwhile, we also provide the results of imbalance at time $t=200~\text{ns}$ as a function of the disorder strength for different system sizes (see Fig.~\ref{figS2}B). We can observe that as the system size increases, the slope of the curve becomes smaller, indicating that more disorder is required to enter the localized phase for a larger system. It is worth noting that these experimental results have gone beyond the classical simulatable area and have never been produced in theory or experiment to the best of our knowledge, which can provide good guidance for future research.
\section{Numerical simulations}
Here we provide the numerical simulation results of applying the quantum neuronal sensing to the small-scale $3\times3$ quantum system (see Fig.~\ref{3_3_simulation}). The setting of the parameters in our simulation is consistent with the experiment. The training (testing) data has 20 (50) individual states, respectively, of which half are ergodic states and the remaining localized states. In Fig.~\ref{3_3_simulation}A,B we plot the loss and accuracy values of 25 epochs during the training of the QNN, where each point is the average of 10 independent training instances of the QNN with initial parameters and dataset randomly generated. In Fig.~\ref{3_3_simulation}C, we show the measurement results of the readout qubit when the QNN of the last training epochs is applied to the testing data. The testing data are clearly distinguished into two groups at the end of the last epoch. By comparing with Figure 2 in the main text, we can find that the experiment is in good agreement with the numerical simulation, indicating the high quality of our experiment.
\hhl{ Besides, we note that the QNN with single-qubit measurement is sufficient for the classification task on $3\times3$ quantum systems. This brings great convenience to the scalability of QNN, mainly due to the following two factors:
1) As proven in Ref.~\cite{cerezo2021cost}, cost function with global observables leads to exponentially vanishing gradients (i.e., barren plateaus), while cost function with local observables leads to at worst a polynomially vanishing gradient.
2) Experimentally, the noise introduced by single-qubit measurement is obviously much smaller multi-qubit measurements, and single-qubit measurements are immune to correlated measurement noise.
Since we need to scale the system to 61 qubits, we chose local observables to alleviate the problems of barren plateau and measurement noise as it scales up. Fortunately, the results of our large-scale experiments (see Fig.3 in the main text) show that our employed architecture works for the given problem, indicating that this architecture has the expressive power to solve this specific problem.}
\begin{figure*}
\caption{\textbf{Numerical simulation of Quantum Neuronal Sensing for the 3x3 system size.} (a) The loss and accuracy at every epoch during the training, respectively, where each point is the average of 10 independent training instances of the QNN. (b) Results of applying the QNN at the last epochs to the testing data set containing 50 quantum states. The two different groups are well separated after 25 epochs of training. The solid lines represent the Gaussian fitting to the distributions of data. }
\label{3_3_simulation}
\end{figure*}
\section{Extended data}
In our experiment, the evolution time of the analog circuit part in the QNN is set to 200~ns. These settings can also be regarded as hyperparameters of our QNN.
\subsection{The hyperparameter of evolution time in the analog circuit part}
\begin{figure*}
\caption{\textbf{Classification accuracy of the QNN with different evolution times $t_d$ in the analog circuit part.} For the $3\times 3$ system, the classification accuracy of the trained QNN model for various evolution times $t_d=100~\text{ns}, 200~\text{ns}, 300~\text{ns},~\text{and}~400~\text{ns}$ used in the analog circuit part on the testing data, where each point is the average of 5 individual trainings of the QNN. }
\label{fig_td}
\end{figure*}
We also experimentally tested the performance of the QNNs with different evolution times $t_d$ in the analog circuit part. Figure~\ref{fig_td} shows the classification accuracy of the QNNs for various times $t_d=100~\text{ns}, 200~\text{ns}, 300~\text{ns},~\text{and}~400~\text{ns}$ used in the analog circuit part, respectively. In all four cases, the trained models can achieve high classification accuracy on the testing data. And the stability of the results and the classification accuracy are relatively higher when $t_d = 200~\text{ns}$. Thus, we finally set the default evolution time of the analog circuit part in the QNN as $t_d=200~\text{ns}$.
\begin{figure*}
\caption{\textbf{Classification accuracy of the QNN at different evolution time $t_0$.} Presented are the classification accuracy of the QNN on the testing data for the $3\times 3$ system at different evolution time $t_0=100~\text{ns}, 200~\text{ns}, 300~\text{ns},~\text{and}~400~\text{ns}$, where each point is the average of 5 individual trainings of the QNN. \blue{The solid line and the shadow correspond to the numerical simulations.} }
\label{fig_t0}
\end{figure*}
\subsection{Classification of quantum states at other evolution times} As analyzed in Section 2, at long times around 200 ns or above, the system reaches a steady-state. In our experiments, after the system has evolved for 200 ns, we then distinguish whether the system's state at this time is ergodic or localized. As a general quantum neuronal sensing, our approach, in principle, can be used to distinguish the quantum states with different properties. Figure~\ref{fig_t0} shows the results of applying the quantum neuronal sensing to distinguish the quantum states generated from the system in the absence and presence of disorder, after system has evolved for different times $t_0=100~\text{ns}, 200~\text{ns}, 300~\text{ns},~\text{and}~400~\text{ns}$. For quantum states at different evolutionary moments, our approach can distinguish the quantum state from a system with or without a disorder with a high success rate, showing the universality and scalability of our approach.
\begin{figure*}\label{fig4}
\end{figure*}
\begin{figure*}\label{fig_predvsls}
\end{figure*}
\subsection{\hhl{Generalization of the trained QNN}}
\hhl{The above results demonstrate that our approach has the ability to discriminate each quantum state produced by the given two types of systems with high accuracy. We further investigate more potential applications of the trained QNN by applying it to identify the statistics of quantum systems with different settings than the training set. In Fig.\ref{fig4}\textbf(a), we show that the trained QNN can be used to monitor the dynamical evolution of quantum states with large and small disorder strength, and statistically the localized and ergodic states can be clearly distinguished by QNN when the evolution time is higher than about 40 ns. In Fig.\ref{fig4}\textbf(b), we show that the trained QNN can be used to predict the probability of the localized quantum states with different disorders. We select 20 values equally spaced in between $h_{erg}$ and $h_{loc}$. For each selected $h$, we randomly generate 50 sets of disorders uniformly distributed in $[-h, h]$. We count the probability that the quantum state in each data set being classified as a localized state. This probability reflects the closeness of the quantum states generated under a given disorder to the trained localized state. Then, with the well-trained QNN for different system size, we also predicted the probability of the localized quantum states with different disorders. As shown in Fig.\ref{fig4}\textbf(b), it is observed that the probability of the quantum states in localization increases together with the increment of the disorder as expected, which shows highly consistent with the prediction by level statistics~\cite{luitz2015many,sierant2020model} (see Section D for more discussion), suggesting that our protocol can provide us a different perspective to the study of quantum phases such as ergodic and localized states. These observations clearly demonstrate the strong generalization of QNN, providing us a positive signal that our quantum enhanced processing technique might have a wide range of applications in the study of many-body physics.}
\hhl{ \subsection{\hhl{Correlation between QNN and level statistics}}
We have shown in Fig.~\ref{fig4}(b) that the trained QNN can be utilized to predict the probability of the localized quantum states with different disorders. The level statistics can be also utilized for comparable tasks, as shown in section II. Figure~\ref{fig_predvsls} shows the experimental result of trained QNN and the numerical result of level statistics for the $3\times 3$ system with various disorders. We calculate the correlation coefficient $R$ of the covariance matrix of these two arrays of results in Fig~\ref{fig_predvsls}. The correlation coefficient $R$ of two arrays is defined as
\[R = \frac{{{C_{12}}}}{{\sqrt {{C_{11}}{C_{22}}} }}\] where $C$ is the covariance matrix of two arrays. The value of $R$ range from -1 to +1, and the larger the absolute value of $R$, the larger is the correlation value. If the correlation coefficient $R$ is less than 0 then it negatively correlated. And if it’s greater than 0 then it’s positively correlated. The calculated correlation between the two arrays of results is $-0.936 \pm0.044$. It shows that these two arrays of results are highly negatively correlated, indicating the trained QNN has the potential to be an order parameter like the level statistics for many-body quantum physics. Moreover, the computational cost of level statistic grows exponentially over the number of qubits, as shown in section II. However, our QNN is very efficient, it only requires a shallow parametered quantum circuit and only single-qubit measurement. }
\begin{figure*}\label{fig9}
\end{figure*}
\hhl{ \subsection{\hhl{Classification of quantum states using an ancilla qubit}}
We particularly designed an experiment to further demonstrate that our quantum neuronal sensing approach can be utilized as a probe to learn the properties of the quantum system. In this experiment, the qubit measured, which is called ancilla or probe qubit, after running the quantum neural network were not among those involved in the many-body quantum state. Specifically, our experiment uses the middle qubit, marked as Q5 in Fig.~\ref{fig9}(a) in the $3\times3$ grid for this role, and the 8 outer qubits for preparing the many-body state. The equivalent quantum circuit is shown on the right side of Fig.~\ref{fig9}(a). The experimental results are shown in Fig.~\ref{fig9}(b,c). During the training procedure, the parameter initialization strategy introduced in the main text is employed to determine a good initial parameters. As can be seen from the curves of loss and accuracy (see Fig.~\ref{fig9}(b)), the training procedure can further improve the performance of QNN. And finally, the two classes of ergodic and localized states can be distinguished by detecting the probe qubit (see Fig.~\ref{fig9}(c)). After the QNN, there appears to be a minor class imbalance; however, by simply adjusting the threshold to around 0.41, we can get classification accuracy as high as 0.960$\pm$0.018, which is averaged over five instances.
We note that the probe qubit is completely unaware of the quantum system's state prior to QNN processing because it is not involved in the quantum system's evolution. However, following QNN processing, the probe qubit can be used to distinguish whether the system is local or ergodic. Such an experiment shows clearly that the distinguishability could credibly be attributed to a non-trivial behavior of the QNN.}
\end{document} | arXiv |
\begin{document}
\newtheorem*{theorem*}{Theorem} \newtheorem{theorem}{Theorem} \newtheorem{lemma}[theorem]{Lemma} \newtheorem{algol}{Algorithm} \newtheorem{cor}[theorem]{Corollary} \newtheorem{prop}[theorem]{Proposition}
\newtheorem{proposition}[theorem]{Proposition} \newtheorem{corollary}[theorem]{Corollary} \newtheorem*{conjecture*}{Conjecture} \newtheorem{conjecture}[theorem]{Conjecture} \newtheorem{definition}[theorem]{Definition} \newtheorem{remark}[theorem]{Remark} \renewcommand{\empty{}}{\empty{}}
\numberwithin{equation}{section}
\numberwithin{theorem}{section}
\newcommand{\comm}[1]{\marginpar{ \vskip-\baselineskip \raggedright\footnotesize \itshape\hrule
#1\par
\hrule}}
\def\mathop{\sum\!\sum\!\sum}{\mathop{\sum\!\sum\!\sum}} \def\mathop{\sum\ldots \sum}{\mathop{\sum\ldots \sum}} \def\mathop{\int\ldots \int}{\mathop{\int\ldots \int}} \newcommand{\twolinesum}[2]{\sum_{\substack{{\scriptstyle #1}\\ {\scriptstyle #2}}}}
\def{\mathcal A}{{\mathcal A}} \def{\mathcal B}{{\mathcal B}} \def{\mathcal C}{{\mathcal C}} \def{\mathcal D}{{\mathcal D}} \def{\mathcal E}{{\mathcal E}} \def{\mathcal F}{{\mathcal F}} \def{\mathcal G}{{\mathcal G}} \def{\mathcal H}{{\mathcal H}} \def{\mathcal I}{{\mathcal I}} \def{\mathcal J}{{\mathcal J}} \def{\mathcal K}{{\mathcal K}} \def{\mathcal L}{{\mathcal L}} \def{\mathcal M}{{\mathcal M}} \def{\mathcal N}{{\mathcal N}} \def{\mathcal O}{{\mathcal O}} \def{\mathcal P}{{\mathcal P}} \def{\mathcal Q}{{\mathcal Q}} \def{\mathcal R}{{\mathcal R}} \def{\mathcal S}{{\mathcal S}} \def{\mathcal T}{{\mathcal T}} \def{\mathcal U}{{\mathcal U}} \def{\mathcal V}{{\mathcal V}} \def{\mathcal W}{{\mathcal W}} \def{\mathcal X}{{\mathcal X}} \def{\mathcal Y}{{\mathcal Y}} \def{\mathcal Z}{{\mathcal Z}}
\def\mathbb{C}{\mathbb{C}} \def\mathbb{F}{\mathbb{F}} \def\mathbb{K}{\mathbb{K}} \def\mathbb{Z}{\mathbb{Z}} \def\mathbb{R}{\mathbb{R}} \def\mathbb{Q}{\mathbb{Q}} \def\mathbb{N}{\mathbb{N}} \def\textsf{M}{\textsf{M}}
\def\({\left(} \def\){\right)} \def\[{\left[} \def\right]{\right]} \def\langle{\langle} \def\rangle{\rangle}
\title[The maximum size of short character sums.] {\bf The maximum size of short character sums.}
\author{Marc Munsch} \address{5010 Institut f\"{u}r Analysis und Zahlentheorie 8010 Graz, Steyrergasse 30, Graz} \email{[email protected]}
\date{\today}
\subjclass[2010]{11L40, 11N25} \keywords{Dirichlet characters, large values, friable numbers, multiplicative functions.}
\begin{abstract}
In the present note, we prove new lower bounds on large values of character sums $\Delta(x,q):=\max_{\chi \neq \chi_0} \vert \sum_{n\leq x} \chi(n)\vert$ in certain ranges of $x$. Employing an implementation of the resonance method developed in a work involving the author in order to exhibit large values of $L$- functions, we improve some results of Hough in the range $\log x = o(\sqrt{\log q})$. Our results are expressed using the counting function of $y$- friable integers less than $x$ where we improve the level of smoothness $y$ for short intervals. \end{abstract}
\maketitle
\section{Introduction}
The behavior of character sums $S_{\chi}(x):=\sum_{n\leq x}\chi(n)$ where $\chi$ is a non-principal Dirichlet character modulo $q$ is of great importance in many number theoretical problems such as the distribution of non-quadratic residues or primitive roots. Showing some cancellation in such character sums has been an intensive topic of study for many decades, originating from the unconditional bound of P\'{o}lya and Vinogradov $S(\chi) \ll \sqrt{q}\log q$. In the present note, we are interested in the opposite problem which consists of bounding from below the quantity \begin{equation}\label{max} \Delta(x,q):= \max_{\chi \neq \chi_0}\left\vert \sum_{n \leq x} \chi(n)\right\vert.\end{equation} Here and throughout this paper we write $\log_j$ for the $j$-th iterated logarithm, for example $\log_2 q = \log \log q$. Assuming the Generalized Riemann Hypothesis, Montgomery and Vaughan showed $\Delta(x,q) \ll \sqrt{q} \log_2 q$ (strenghtening the work of P\'{o}lya and Vinogradov) which matches the omega results obtained earlier by Paley \cite{Paley}. Nonetheless, the situation for shorter intervals remains in certain cases open. An intensive study of this quantity through the computation of high moments was carried out by Granville and Soundararajan \cite{largeGS} giving very precise results for short intervals. Few years later, Soundararajan developed the so-called resonance method \cite{sound} in order to show the existence of large values of $L$- functions at the central point. In the intermediate range $\sqrt{\log q}<\log x<(1-\epsilon) \log q$, even though the situation remains widely open, recent progress have been made using this method (see the results obtained by Hough \cite{Hough} reinforcing the previous results of Granville and Soundararajan \cite{largeGS}). It is worth noticing that de la Bret\`{e}che and Tenenbaum \cite{Gal} recently obtained the following result improving earlier bounds of Hough for very large $x$, precisely as soon as $\log x \geq (\log q)^{1/2+\epsilon}$,
$$\Delta(x,q) \geq \sqrt{x} \exp\left((\sqrt{2}+o(1))\sqrt{\frac{\log (q/x) \log_3 (q/x)}{\log_2 (q/x)}} \right).$$ \\
In this paper, we will give new bounds in the range $\log x < \sqrt{\log q}$.
Originating from ideas going back to Montgomery and Vaughan \cite{expmulti}, we expect, in that case, the behavior of the character sum to be closely linked to the behavior of the character sum over friable numbers. In particular, it emphases the fact that character sums can only be large because of a special bias for small primes. This fruitful idea can be traced back to Littlewood \cite{Littlewood} which showed the existence of large real character sums by prescribing the values of the first $\log q$ primes. \\
In order to state our results, let us define by $\mathcal{S}(x,y)$ the set of $y$- friable numbers less than $x$ and denote by $\Psi(x,y)$ the cardinal of this set. More generally, for any arithmetic function $f$, we write
$$\Psi(x,y;f)=\sum_{n\in \mathcal{S}(x,y)}f(n).$$ Granville and Soundararajan \cite{largeGS} made the following conjecture
\begin{conjecture*} There exists a constant $A>0$ such that for any non-principal character $\chi (\bmod q)$ and for any $1\leq x\leq q$ we have, uniformly,
$$\sum_{n\leq x} \chi(n) = \Psi(x,y;\chi) + o(\Psi(x,y;\chi_0)),$$ where $y=(\log q + \log^2 x)(\log \log q)^A$.
\end{conjecture*}
This would directly imply the upper bound
$$\Delta(x,q) \ll \Psi(x,(\log q + \log^2 x)\log_2^A q).$$
On the other hand, this can hold only with $A\geq 1$. Indeed, Hough using the resonance method proved the following estimate in the transition range $\log x=(\log q)^{1/2-\epsilon}$,
\begin{equation}\label{Hough} \Delta(x,q) \geq \Psi(x,\log q \log_2^{1-o(1)} q).\end{equation}
In this article, we prove that such a lower bound can be obtained relatively easily in some ranges of $x$. Our argument relies on the recent variant of the long resonance method introduced in \cite{AMM} and \cite{AMMP}. In few words, the method consists of bounding from below the following quotient \begin{equation}\label{quotient}
\frac{\left|\sum_{\chi \bmod q} S_{\chi}(x) |R(\chi)^2| \right|}{\sum_{\chi \bmod q} |R(\chi)|^2}, \end{equation} where $R(\chi)$ is a well-chosen ``resonator''. As explained in \cite{AMM} and \cite{AMMP}, it is possible to define the function $R(\chi)$ as a truncated Euler product of size $\approx \log q\log_2 q$. The main advantage of this method is the complete multiplicative structure of the resonator defined as a short Euler product leading naturally to sums over friable integers. A well suited choice of the weights for every prime allows us to relate the lower bound of the quotient (\ref{quotient}) to the counting function of friable integers with some relatively large level of smoothness. \\
Precisely, we prove
\begin{theorem}\label{lowfriable} For $q$ a sufficiently large prime, under the condition $\log q< x\leq \exp(\sqrt{\log q})$, we have
$$ \Delta(x,q)=\max_{\chi \neq \chi_0} \vert S_{\chi}(x) \vert \geq \Psi \left(x,\left(\frac{1}{4}+o(1)\right)\frac{(\log q)(\log_2 q)}{\max\{(\log_2 x -\log_3 q),\log_3 q\}}\right). $$
\end{theorem}
In some ranges of $x$, the lower bound can be rewritten in a more compact way.
\begin{cor}\label{ranges} Suppose that $\log x= (\log q)^{\sigma}$ for a fixed $0<\sigma<1/2$. Then $$ \Delta(x,q) \geq \Psi\left(x,\frac{1}{2\sigma}(1+o(1))\log q\right).$$
\end{cor}
When $\log x$ is a small power of $\log q$, our result improves the result of Hough which proved (see \cite[Corollary $3.3$]{Hough}) that $\Delta(x,q) \geq \Psi(x,(8/e^3+o(1)) \log q)$. Previously, results of the same quality were proved for real characters. Let us define $\Delta_{\mathbb{R}}(x,q)= \max_{D \in \mathcal{F}, q < \vert D\vert \leq 2q} \vert S_{\chi_D}\vert$ where $\mathcal{F}$ is the set of fundamental discriminants. In the same spirit as Littlewood original argument, Granville and Soundararajan \cite{largeGS} showed $$ \Delta_{\mathbb{R}}(x,q) \geq \Psi\left(x,\frac{1}{3} \log q\right).$$ As pointed out by Hough \cite{Hough}, breaking the natural barrier $\log q$ using this method seems to be a very difficult problem. Corollary \ref{ranges} enables us to do so in the full range $\log x= (\log q)^{\sigma}, 0<\sigma<1/2$. Let us though stretch that our argument can not be adapted to the case of real characters due to the more subtle orthogonality relations. Furthermore, the bound of \cite{Hough} overcomes our result when $\log x$ approaches $\sqrt{\log q}$. \\
For even smaller ranges of $x$, namely as soon as $\log_2 x = o(\log_ 2 q)$, a lower bound of the same precision as in the inequality (\ref{Hough}) follows directly from Theorem \ref{lowfriable}. To illustrate this, we deduce the following consequence
\begin{cor}\label{smallrange} Let $A>1$ and set $x=\log^A q$. Then $$\Delta(x,q) \geq \Psi\left(x,\frac{1}{2}(1+o(1))\frac{(\log q)(\log_2 q)}{\log_3 q}\right).$$
\end{cor}
To have a better insight on the lower bounds of Theorem \ref{lowfriable}, Corollaries \ref{ranges} and \ref{smallrange}, we could write it down in a more pleasant way. Indeed (see \cite{HildTensurvey} for the details), in the range $\log q\leq x \leq \exp(\sqrt{\log q})$, the following approximation $$\Psi(x,k\log q)=x\exp(-u\log u- u \log_2(u+2)+u+o(u))$$ holds uniformly for $1\leq k\ll x/\log q$ where $u=\frac{\log x}{\log y}$.\\
For the sake of simplicity, we first stated our results for $q$ prime. Howewer, we can obtain similar results for more general moduli $q$ under certain additional restrictions. In order to describe the result, we define for any integer $m\geq 1$
$$\Psi_m(x,y)=\sum_{n\in \mathcal{S}(x,y) \atop (n,m)=1} 1.$$
Denote by $\omega(q)$ the number of distinct prime divisors of $q$. Tenenbaum \cite{Tencrible} proved that $\Psi_q(x,y) \approx \frac{\phi(q)}{q} \Psi(x,y)$ whenever $\log y \gg (\log 2\omega(q))(\log_2 x)$. Since we have $q/\phi(q)\ll \log(\omega(q))$, we observe that a close argument (setting the resonator with an extra factor $1/(\log(\omega(q))$) leads to the following result
\begin{theorem}\label{lowfriablemod} For $q$ sufficiently large and $\log q \leq x\leq \exp(\sqrt{\log q})$. Under the supplementary condition $\log_2 q \gg \log (1+\omega(q))(\log_2 x - \log_3 q)$, we have
$$ \Delta(x,q) \geq \Psi_q \left(x,\left(\frac{1}{6}+o(1)\right)\frac{(\log q)(\log_2 q)}{\max\{(\log_2 x-\log_3 q),\log_3 q \}}\right). $$
\end{theorem}
\begin{remark}For almost all modulus $q$, $\omega(q)\sim \log_2 q$ and the restriction on $x$ of Theorem \ref{lowfriablemod} is therefore not so restrictive. It is for instance trivially fulfilled for $x$ being any power of $\log q$. \end{remark} For information, precise estimates of the quantity $\Psi_q(x,y)$ in various ranges of the parameters can be found in \cite{dlBTstat}. \\
In the next section, we give some results concerning averages over friable numbers necessary to control error terms coming from the choice of the resonator. In the last section, we give the proof of the Main Theorem \ref{lowfriable} and sketch the few necessary modifications needed to deduce Corollaries \ref{ranges}, \ref{smallrange} as well as to demonstrate Theorem \ref{lowfriablemod}.
\section{Some results about friables numbers}
As usual, for $x \geq y \geq 2$, we set $u=\frac{\log x}{\log y}$. We denote by $\Omega(n)$ the number of prime factors of $n$ counted with multiplicity. We easily have the individual bound $\Omega(n) \ll \log n$. In fact, for small values of the parameter $u$, $\Omega(n)$ displays more cancellation when averaged over friable integers.
\begin{lemma}\label{averageomega}
We have, uniformly for $x \geq y \geq 2$,
$$\sum_{n \in \mathcal{S}(x,y)} \Omega(n) \ll \Psi(x,y) (u + \log_2 y). $$
\end{lemma}
\begin{proof}
Applying Theorem $2.9$ of \cite{dlBTstat} to the additive function $f=\Omega$ leads to
\begin{equation}\label{diviseurs}\sum_{n \in \mathcal{S}(x,y)} \Omega(n) \ll \Psi(x,y) \sum_{p \leq y}\frac{1}{p^{\alpha}-1}\end{equation} where as usual $\alpha:=\alpha(x,y)$ is defined as the unique positive solution of the equation
$$\sum_{p\leq y} \frac{\log p}{p^{\alpha}-1}= \log x.$$ A precise evaluation of the saddle point $\alpha$ as in \cite[Lemma $3.1$]{dlbTKublius} combined with an application of the Prime Number Theorem
gives uniformly
$$\sum_{p\leq y} \frac{1}{p^{\alpha}-1} \ll u + \log_2 y$$which concludes the proof.
\end{proof}
It is worth noticing that precise asymptotical estimates can be obtain in some ranges of $u$ for averages of general additive functions \cite{dlBTstat}. Moreover, the normal order of additive functions over the set of friable integers $\mathcal{S}(x,y)$ can be determined using the friable Tur\'{a}n-Kubilius inequality
originally considered by Alladi \cite{AlladiKubilius} and proved by de la Bret\`{e}che and Tenenbaum \cite{dlbtkubentier} in the full range of parameters $x\geq y \geq 2$. \\
The following lemma gives information on $\Psi(x,y)$ for small variations of $y$.
\begin{lemma}\label{comparaison}\cite[Corollary $5.6$]{Hough} Assume $u < \sqrt{y}$, then for
$|\kappa| < 1$ we have \begin{equation}\label{constante}\log \frac{\Psi(x, e^\kappa y)}{\Psi(x,y)} = \left(\frac{\kappa+ O(\log^{-1}u)}{\log y}\right) u (\log u + \log_2(u+2)).\end{equation} \end{lemma}
\section{Resonance method and large values of character sums}
\subsection{Proof of Theorem \ref{lowfriable}} Denote by $X_q$ the group of characters modulo $q$. For every $\chi \in X_q$ and real $x\geq 2$, we recall the definition $$ S_{\chi}(x) = \sum_{n=1}^{x} \chi(n). $$
In order to exhibit large values of character sums, we apply the resonance method in a similar manner as performed in \cite{AMM} and \cite{AMMP}. Let us first define our ``resonator" as a short Euler product. For a constant $c<1/4$, we take $$y=c\frac{(\log q)(\log_2 q)}{\max\{(\log_2 x-\log_3 q),\log_3 q\}}$$ and set $q_1=1$ and $q_p=0$ for $p>y$. Setting as before $u=\frac{\log x}{\log y}$, we define further $q_p=\left(1-\frac{1}{u(\log_2 q)^{1+\epsilon}}\right)$ for small primes $p\leq y$. We extend it in a completely multiplicative way to obtain weights $q_n$ for all $n\geq 1$. We now define for $\chi\in X_q$ $$R(\chi)=\prod_{p\leq y} \left(1-q_p\chi(p)\right)^{-1}.$$ We can write $R(\chi)$ as a Dirichlet series in the form \begin{equation} \label{rdi} R(\chi) = \sum_{a=1}^\infty q_a \chi(a). \end{equation}
Let us consider the following sums
$$S_1 = \sum_{\chi \in X_q} S_{\chi}(x)\vert R(\chi)\vert^2 $$ and
$$S_2 =\sum_{\chi \in X_q} \vert R(\chi)\vert^2.$$ The heart of the resonance method is contained in the simple inequality
\begin{equation}\label{resonance} \frac{ \vert S_1 \vert}{S_2 } \leq \max_{\chi \in X_q} \vert S_{\chi}(x)\vert. \end{equation} Therefore we would like to prove that the quotient in the left hand side of (\ref{resonance}) grows sufficiently quickly with $q$. Moreover, we need to show that the contribution of the trivial character to $S_1$ and $S_2$ is in some sense inoffensive. A similar estimation as in \cite{AMMP} leads to \begin{equation}\label{ulogq}
\log (|R(\chi)|^2) \leq 2\sum_{p \leq y} \left( \log u + \log_3 q \right)
= 2\frac{y}{\log y}(\log u + \log_3 q+o(1)). \end{equation}Hence, by our choice of $y$, we have \begin{equation}\label{Rmaj}
|R(\chi)|^2 \leq \exp((4c+o(1)) \log q) \leq q^{4c + o(1)}. \end{equation}
In the other hand, we have trivially, \begin{equation}\label{S2tout} \sum_{\chi \in X_q} \vert R(\chi)\vert^2 =\sum_{\chi\in X_q} q_a q_b \chi(a)\overline{\chi}(b)=\phi(q) \left(\sum_{a=b \bmod q} q_a q_b\right) \geq q^{1-o(1)}\end{equation} where we used the classical inequality $\phi(q) \geq q/\log_2 q$. Similarly, we can disregard the contribution of the trivial character to $S_1$. Indeed, by hypothesis, we have
\begin{equation}\label{trivial} S_{\chi_0}(x) \leq x = q^{o(1)}.\end{equation} Expanding $|R(\chi)|^2 $ and switching the summation, we have \begin{eqnarray*} S_1 & = & \sum_{\chi \in X_q}\vert R(\chi)\vert^2 S_{\chi}(x)\\ & = & \sum_{n=1}^{x} \left\{ \sum_{a,b = 1}^\infty q_a q_b
\sum_{\chi \in X_q}\chi(a)\overline{\chi}(b)\chi(n)\right\} \end{eqnarray*} where the inner sum is positive due to the orthogonality relations on $X_q$. Thus,
\begin{equation}\label{quotientdev} S_{1} = \sum_{n=1}^{x}\left\{\phi(q)\sum_{a,b \atop na=b \bmod q} q_a q_b \right\}.\end{equation} Assume $n$ to be fixed such that $(n,q)=1$. Then, using the positivity and the completely multiplicative property of the coefficients $q_n$ we get
\begin{eqnarray*}
\phi(q)\sum_{a,b\atop na=b \bmod q} q_a q_b &\geq& \phi(q)\ \sum_{a,b, n | b \atop na=b \bmod q} q_a q_b \\ & = &\phi(q) \sum_{a,b' \atop na=nb' \bmod q} q_a \underbrace{q_{nb'}}_{=q_n q_{b'}} = q_n \phi(q) \left(\sum_{a=b' \bmod q} q_a q_{b'}\right) \\ &=& q_n S_2. \\ \end{eqnarray*} Noticing that $q_p=0$ for primes $p>y$, we deduce from (\ref{quotientdev})
\begin{eqnarray}\label{quotientfinal}\frac{S_1}{S_2} &\geq & \sum_{n=1\atop (n,q)=1}^{x} q_n = \sum_{n=1 \atop n\, y- \textrm{friable}}^{x} q_n = \sum_{n\in \mathcal{S}(x,y)} q_n \end{eqnarray} where we used the fact that $q$ is prime. Our particular choice of the weights $q_n$ helps us to relate this sum to the counting function of $y$- friable numbers using results of Section $2$. Indeed, we first remark that for $n\in \mathcal{S}(x,y)$, we have trivially $$q_n \geq \left(1-\frac{1}{u(\log_2 q)^{1+\epsilon}}\right)^{\Omega(n)} \geq 1- \frac{\Omega(n)}{u (\log_2 q)^{1+\epsilon}}.$$ Summing over $n$, we get
\begin{equation}\label{minoration}\sum_{n \in \mathcal{S}(x,y)} q_n \geq \Psi(x,y) + O\left(\frac{1}{u(\log_2 q)^{1+\epsilon}} \sum_{n \in \mathcal{S}(x,y)} \Omega(n) \right).\end{equation}
Using Lemma \ref{averageomega}, we have that
$$\sum_{n \in \mathcal{S}(x,y)} \Omega(n) \ll \Psi(x,y)(u + \log_2 y).$$
Inserting it in (\ref{minoration}) and combining with (\ref{quotientfinal}), we obtain
\begin{equation}\label{minofinale}\max_{\chi \in X_q} S_{\chi}(x) \geq \Psi(x,y)\left(1+O\left(\frac{\log_3 q}{(\log_2 q)^{1+\epsilon}}\right)\right).\end{equation} Applying Lemma \ref{comparaison}, we deduce after easy computations that the right hand side of (\ref{minofinale}) is bounded from below by $\Psi(x,y(1-\delta)) $ for any $\delta>0$. Recalling (\ref{Rmaj}), (\ref{S2tout}) and (\ref{trivial}), the inequality (\ref{quotientfinal}) remains true when we sum over non trivial characters yielding to
$$ \max_{\chi \neq \chi_0} S_{\chi}(x) \geq \Psi(x,y(1+o(1))) .$$
\subsection{Proof of Corollaries \ref{ranges} and \ref{smallrange}} In the proof of Theorem \ref{lowfriable}, we can in fact in the appropriate ranges define $y$ in a similar way with $c<1/2$. Indeed in these cases one of the two terms $\log u$ or $\log_3 q$ dominates the other one in Equation (\ref{ulogq}) and thus we can replace $4c$ by $2c+o(1)$ in Equation (\ref{Rmaj}).
\subsection{Proof of Theorem \ref{lowfriablemod}} Denoting as before $u=\frac{\log x}{\log y}$, Tenenbaum \cite{Tencrible} proved that $\Psi_q(x,y) \approx \frac{\phi(q)}{q} \Psi(x,y)$ whenever $\log y \gg \log (1+\omega(q))\log (1+u)$. Since we have $q/\phi(q)\ll \log_2 q$, it is sufficient to pertubate slightly the weights in the definition of the resonator. Precisely, for a constant $c<1/6$, we set $$y=c\frac{(\log q)(\log_2 q)}{\max\{(\log_2 x-\log_3 q),\log_3 q\}}$$ and set $q_1=1$ and $q_p=0$ for $p>y$. We define analogously with an extra factor $q_p=\left(1-\frac{1}{u(\log_2 q)^{2+\epsilon}}\right)$ for small primes $p\leq y$. Similarly as in the proof of Theorem \ref{lowfriable}, we get $$\vert R(\chi_0)\vert \ll q^{6c+o(1)}.$$ After observing that $\displaystyle{\Psi_q(x,y)=\sum_{n\in \mathcal{S}(x,y)} \chi_0(n)}$ where $\chi_0$ denotes the trivial character modulo $q$, the rest of the proof follows exactly the same lines as that of Theorem \ref{lowfriable} using again Lemma \ref{comparaison} to conclude.
\end{document} | arXiv |
Pólya conjecture
In number theory, the Pólya conjecture (or Pólya's conjecture) stated that "most" (i.e., 50% or more) of the natural numbers less than any given number have an odd number of prime factors. The conjecture was set forth by the Hungarian mathematician George Pólya in 1919,[1] and proved false in 1958 by C. Brian Haselgrove. Though mathematicians typically refer to this statement as the Pólya conjecture, Pólya never actually conjectured that the statement was true; rather, he showed that the truth of the statement would imply the Riemann hypothesis. For this reason, it is more accurately called "Pólya's problem".
The size of the smallest counterexample is often used to demonstrate the fact that a conjecture can be true for many cases and still fail to hold in general,[2] providing an illustration of the strong law of small numbers.
Statement
The Pólya conjecture states that for any n > 1, if the natural numbers less than or equal to n (excluding 0) are partitioned into those with an odd number of prime factors and those with an even number of prime factors, then the former set has at least as many members as the latter set. Repeated prime factors are counted repeatedly; for instance, we say that 18 = 2 × 3 × 3 has an odd number of prime factors, while 60 = 2 × 2 × 3 × 5 has an even number of prime factors.
Equivalently, it can be stated in terms of the summatory Liouville function, with the conjecture being that
$L(n)=\sum _{k=1}^{n}\lambda (k)\leq 0$
for all n > 1. Here, λ(k) = (−1)Ω(k) is positive if the number of prime factors of the integer k is even, and is negative if it is odd. The big Omega function counts the total number of prime factors of an integer.
Disproof
The Pólya conjecture was disproved by C. Brian Haselgrove in 1958. He showed that the conjecture has a counterexample, which he estimated to be around 1.845 × 10361.[3]
An explicit counterexample, of n = 906,180,359 was given by R. Sherman Lehman in 1960;[4] the smallest counterexample is n = 906,150,257, found by Minoru Tanaka in 1980.[5]
The conjecture fails to hold for most values of n in the region of 906,150,257 ≤ n ≤ 906,488,079. In this region, the summatory Liouville function reaches a maximum value of 829 at n = 906,316,571.
References
1. Pólya, G. (1919). "Verschiedene Bemerkungen zur Zahlentheorie". Jahresbericht der Deutschen Mathematiker-Vereinigung (in German). 28: 31–40. JFM 47.0882.06.
2. Stein, Sherman K. (2010). Mathematics: The Man-Made Universe. Courier Dover Publications. p. 483. ISBN 9780486404509..
3. Haselgrove, C. B. (1958). "A disproof of a conjecture of Pólya". Mathematika. 5 (2): 141–145. doi:10.1112/S0025579300001480. ISSN 0025-5793. MR 0104638. Zbl 0085.27102.
4. Lehman, R. S. (1960). "On Liouville's function". Mathematics of Computation. 14 (72): 311–320. doi:10.1090/S0025-5718-1960-0120198-5. JSTOR 2003890. MR 0120198.
5. Tanaka, M. (1980). "A Numerical Investigation on Cumulative Sum of the Liouville Function". Tokyo Journal of Mathematics. 3 (1): 187–189. doi:10.3836/tjm/1270216093. MR 0584557.
External links
• Weisstein, Eric W. "Pólya Conjecture". MathWorld.
Disproved conjectures
• Borsuk's
• Chinese hypothesis
• Connes
• Euler's sum of powers
• Ganea
• Hedetniemi's
• Hauptvermutung
• Hirsch
• Kalman's
• Keller's
• Mertens
• Ono's inequality
• Pólya
• Ragsdale
• Schoen–Yau
• Seifert
• Tait's
• Von Neumann
• Weyl–Berry
• Williamson
Prime number conjectures
• Hardy–Littlewood
• 1st
• 2nd
• Agoh–Giuga
• Andrica's
• Artin's
• Bateman–Horn
• Brocard's
• Bunyakovsky
• Chinese hypothesis
• Cramér's
• Dickson's
• Elliott–Halberstam
• Firoozbakht's
• Gilbreath's
• Grimm's
• Landau's problems
• Goldbach's
• weak
• Legendre's
• Twin prime
• Legendre's constant
• Lemoine's
• Mersenne
• Oppermann's
• Polignac's
• Pólya
• Schinzel's hypothesis H
• Waring's prime number
| Wikipedia |
\begin{document}
\title{Representations of quantum groups defined over commutative rings III.
} \begin{abstract} We survey some of our old results given in \cite{MR1327136} and \cite{MR2586983} and present some new ones in the last three sections. \end{abstract}
\section{Introduction and Summary of Results.}
\subsection{}
For the convenience of the reader we survey below material that was developed in \cite{MR1327136} and \cite{MR2586983}.
Let $v$ be an indeterminate and $\mathbb k$ a field of characteristic zero. Let $\mathbf U$ be the quantized enveloping algebra defined over $\mathbb k(v)$ with generators $K^{\pm 1},E,F$ and relations $$ [E,F]=\frac{K-K^{-1}}{ v-v^{-1}} , \quad KEK^{-1}=v^2E\quad \text{and} \quad KFK^{-1}=v^{-2}F. $$ Let $\mathbf U^0$ be the subalgebra generated by $K^{\pm 1}$ and let $B$ be the subalgebra generated by $\mathbf U^0$ and $E$. More precisely we are following the notation given in \cite{MR2586983} where we take $I=\{i\}$, $i\cdot i=2$, $Y=\mathbb Z[I]\cong \mathbb Z$, $X=\hom(\mathbb Z[I], \mathbb Z)\cong \mathbb Z$, $F=F_i$, $E=E_i$, and $K=K_i$.
Let $R$ be the power series ring in $T-1$ with coefficients in $\mathbb k(v)$ i.e. \begin{equation} R=k(v)[[T-1]]:=\lim_\leftarrow \frac{\mathbb k(v)[T,T^{-1}]}{ (T-1)^i}. \end{equation} Set $\mathcal K$ equal to the field of fractions of $R$. Let $s$ be the involution of $R$ induced by $T\to T^{-1}$, i.e. the involution that sends $T$ to $T^{-1}=1/(1+(T-1))=\sum_{i\geq 0}(-1)^i(T-1)^i$. Let the subscript $R$ denote the extension of scalars from $\mathbb k(v)$ to $R$ , e.g. $\mathbf U_R = R\otimes_{\mathbb k(v)} \mathbf U$. For any representation $(\pi,A)$ of $\mathbf U_R$ we can twist the representation in two ways by composing with automorphisms of $\mathbf U_R$. The first is $\pi \circ (s\otimes 1)$ while the second is $\pi \circ (1\otimes \Theta)$ for any automorphsim $\Theta$ of $\mathbf U$. We designate the corresponding $\mathbf U_R$-modules by $A^s$ and $A^{\Theta}$. Twisting the action by both $s$ and $\Theta$ we obtain the composite $(A^s)^{\Theta}=(A^{\Theta})^s$ which we denote by $A^{s\Theta}$.
Let $m$ denote the homomorphism of $\mathbf U_R^0$ onto $R$ with $m(K)=T$. For $\lambda \in \mathbb Z$ let $m+\lambda$ denote the homomorphism of $\mathbf U^0$ to $R$ with $(m+\lambda )(K)=Tv^\lambda$. We use the additive notation $m+\lambda$ to indicate that this map originated in the classical setting from an addition of two algebra homomorphisms. It however is not a sum of two homomorphisms but rather a product. Let $R_{m+\lambda}$ be the corresponding $_RB$-module and define the Verma module
\begin{equation} _RM(m+\lambda )=\mathbf U_R\otimes_{_RB} R_{m+\lambda-1} . \end{equation}
Let $\rho_1:\mathbf U\to \mathbf U$ be the algebra isomorphism determined by the assignment \begin{equation} \rho_1(E)=-vF,\quad \rho_1(F)=-v^{-1}E,\quad \rho_1(K)=K^{-1} \end{equation} for all $i\in I$ and $\mu\in Y$. Define also an algebra anti-automorphism $\mathbf \rho:\mathbf U\to \mathbf U$ by \begin{equation} \mathbf \rho(E)=vKF,\quad \mathbf \rho(F)=vK^{-1}E,\quad \mathbf \rho(K_\mu)=K_\mu. \end{equation} These maps are related through the antipode $S$ of $\mathbf U$ by $\mathbf \rho=\mathbf \rho_1S$.
For $\mathbf U_R$-modules $M,N$ and $\mathcal F$, let $\mathbb P(M,N)$ and $\mathbb P(M,N,\mathcal F)$ denote the space of $R$-bilinear maps of $M\times N$ to $R$ and $\mathcal F$ respectively, with the following invariance condition: \begin{equation} \sum x_{(1)}*\phi(Sx_{(3)}\cdot a,\varrho(x_{(2)})b)=\mathbf e(x) \phi(a,b) \end{equation} where $\Delta\otimes 1\circ \Delta (x)=\sum x_{(1)}\otimes x_{(2)}\otimes x_{(3)}$ and $\mathbf e:\mathbf U\to k(v)$ is the counit. If we let $\hom_{\mathbf U_R}(A,B)$ denote the set of module $\mathbf U_R$-module homomorphisms, then one can check on generators of $\mathbf U_R$ that $\mathbb P(M,N,\mathcal F)\cong \hom_{\mathbf U_R} (M\otimes_R N^{\rho_1},{_R\mathcal F}^\mathbf \rho)$ (see \cite[3.10.6]{MR1359532}). Let $\mathbb P(N)=\mathbb P(N,N)$ denote the $R$-module of invariant forms on $N$.
For the rest of the introduction we let $M$ denote the $\mathbf U_R$ Verma module with highest weight $Tv^{-1}$ i.e. $M=M(m)$ and let $\mathcal F$ be any finite dimensional $\mathbf U$-module. A natural parameterization for $\mathbb P(M\otimes {_R\mathcal F})$ was given in \cite{MR1327136}. Fix an invariant form $\phi_M$ on $M$ normalized as in \eqnref{}. For each $\mathbf U_R$-module homomorphism $\beta:{_R\mathcal F}\otimes_R\mathcal F^{\rho_1}\to\mathbf U_R$ define what we call the induced form $\chi_{\beta,\phi_M}$ by the formula, for $e,f\in _R\mathcal F, \ m,n\in M$, \begin{equation} \chi_{\beta,\phi_M}(m\otimes e,n\otimes f)=\phi_M( m,\beta(e\otimes f)*n). \end{equation} \begin{prop}[\cite{MR2586983}] Suppose $\beta:{_R\mathcal F}\otimes {_R\mathcal F^{\rho_1}}\to \mathbf U_R$ is a module homomorphism with $\mathbf U_R$ having the adjoint action. Then $M\otimes {_R\mathcal F}$ decomposes as the $\chi_{\beta,\phi_M}$-orthogonal sum of indecomposible $\mathbf U_R$-modules. \end{prop}
This last result has a number of intriguing consequences which are formulated in the context of induced filtrations. For any $R$-module $B$ set $\overline B=B/(T-1)\cdot B$ and for any filtration $B=B_0\supset B_1\supset ...\supset B_r$, let $\overline B=\overline B_0\supset \overline B_1\supset ...\supset \overline B_r$ be the induced filtration of $\overline B$, with $\overline B_i=(\overline B_i+(T-1)\cdot B)/ (T-1)\cdot B$.
Now an invariant form $\chi$ on an $\mathbf U_R$-module $B$ gives a filtration on $B$ by setting \begin{equation}\label{filtration}
B_i=\{v\in B | \chi(v,B)\subset (T-1)^i\cdot R\}. \end{equation} \begin{prop}[\cite{MR2586983}] Suppose $\mathcal F$ is a finite dimensional $\mathbf U$-module and $\phi$ is an invariant form on $M\otimes {_R\mathcal F}$. Let $M\otimes {_R\mathcal F}=B_0\supset B_1\supset ...\supset B_r$ be the filtration \eqnref{filtration} and $\overline B_0\supset \overline B_1\supset ...\supset \overline B_r$ the induced filtration on $\overline{M\otimes {_R\mathcal F}}$. Then \begin{enumerate} \item The $\mathbf U$-module $\overline{B_i}/\overline{B_{i+1}}$ is finite dimensional for $i$ odd. \item The $\mathbf U$-module $\overline B_i/\overline B_{i+1}$ is both free and cofree as a $\mathbb k(v)[F]$-module, for $i$ even. \end{enumerate} \end{prop}
A final result is cast in the language of hereditary filtrations which we now describe. Let $\mathcal E$ denote the simple two dimensional $\mathbf U$-module with highest weight $v$ and set $P=M\otimes {_R\mathcal E}$. Then $P$ is isomorphic to the basic module $P_1=P(m+1)$ as defined through the equations \eqnref{P_iF}. Set $M_\pm=M(m\pm 1)$. The construction of $P$ gives inclusions and a short exact sequence: \begin{equation}\label{ses-inclusions} (T-1)M_+\oplus (T-1)M_- \subset P\subset M_+\oplus M_- ,\quad 0\to (T-1) M_+\to P\to M_- \to 0. \end{equation}
Let $\mathcal F$ be any finite dimensional $\mathbf U$-module and set \begin{equation}\label{mathbbABDP} \mathbb A=(T-1)\cdot M_+\otimes _R\mathcal F ,\quad \mathbb B=(T-1)\cdot M_- \otimes _R\mathcal F ,\quad \mathbb D= M_- \otimes_R\mathcal F ,\quad \mathbb P=P\otimes_R\mathcal F. \end{equation}
Then \eqnref{ses-inclusions}, gives inclusions and the short exact sequence: \begin{equation} \mathbb A\oplus \mathbb B\subset \mathbb P \subset (T-1)^{-1}(\mathbb A\oplus \mathbb B),\quad\quad 0\to \mathbb A\to \mathbb P\ { \overset \Pi\to}\ \mathbb D\to 0 . \end{equation}
Now fix an induced invariant form $\chi=\chi_{\beta,\phi_P}$ on $\mathbb P$ where $\beta$ is a homomorphism of $_R\mathcal F\otimes_R \mathcal F^{\rho_1}$ into $\mathbf U_R$ and $\phi_P$ is an invariant form on $P$. Filter $\mathbb A,\mathbb B$ and $\mathbb P$ using \eqnref{filtration} and \eqnref{mathbbABDP}. Then we say that $\chi$ gives a {\it hereditary filtration} if, for all i, \begin{equation} \mathbb A_i\cap \mathbb B=\mathbb B_i. \end{equation} For any weight module $N$ for $\mathbf U$, let $N_{\le h}$ denote the span of the weight spaces with weights $t\le h$. We say that $\chi$ gives a {\it weakly hereditary filtration} if, for some $h$ and for all $i$, $\mathbb A_{i,\le h}\cap \mathbb B=\mathbb B_{i,\le h}$.
There is an action of the Weyl $\{1,s\}$ group of $\mathfrak{sl}_2$ on the space of forms $\chi_{\beta,\phi}$ where the lifted form $\chi_{\beta,\phi}^\sharp$ satisfies $\chi_{\beta,\phi}^\sharp=\chi_{s\beta,\phi}$ (see \cite[Theorem 38]{MR2586983}). We say that $\chi$ is even if $\chi_{\beta,\phi}^\sharp=\chi_{\beta,\phi}$ and odd if $\chi_{\beta,\phi}^\sharp=-\chi_{\beta,\phi}$. Our aim is to prove our conjecture that \begin{conj} Suppose $\chi$ is either even or odd. Then $\chi$ gives a weakly hereditary filtration. \end{conj}
\section{$q$-Calculus.} \subsection{Definitions} As many before us have done, we define \begin{align*} [m]&:=\frac{v^m-v^{-m}}{v-v^{-1}}, \\ [m]!&:=[m]\cdot [m-1]\cdots [1] \\ [0]!&:=1 \\ \qbinom{m}{ n}&=\frac{[m]!}{[n]![m-n]!}\quad \text{for} \quad n\leq m \\ \\ \qbinom{m}{ n}&=\begin{cases}0 &\quad {\rm if}\quad m<n\quad{\rm or}\quad n<0 , \\ 1 &\quad {\rm if}\quad n=m\quad{\rm or}\quad m=0. \end{cases} \end{align*}
For $r\in Z$ define \begin{gather} [T;r]:=\frac{v^{r}T- v^{-r}T^{-1}}{ v-v^{-1}}, \\ \\ [T;r]_{(j)}:=[T;r][T;r-1]\cdots [T;r-j+1], \quad\quad [T;r]^{(j)}:=[T;r+1]\cdots [T;r+j] \quad\text{if}\quad j>0,\notag\\ [T;r]_{(0)}:= [T;r]^{(0)}:=1, \notag \\ \notag \\ \qbinom{T;r}{ j}:=\begin{cases}[T;r]_{(j)}/[j]! & \text{if}\quad j\geq 0 \\ 0& \text{if}\quad j<0.\end{cases} \end{gather} Observe that \begin{equation}\label{r1} [T;r]^{(j)} = [T;r+j]_{(j)}. \end{equation} and \begin{equation}\label{r2} (-1)^j[T;r]^{(j)}=[T^{-1};-r-1]\cdots [T^{-1};-r-1-j+1] = [T^{-1};-r-1]_{(j)}. \end{equation} Moreover note that $[T;\lambda]^{(k)}$ is invertable in $R$ for $\lambda\geq 0$ and $[T;\lambda+1]_{(k)}$ is invertible provided and $\lambda+1> k$ or $\lambda<0$ ($k\geq 0$). In fact \begin{equation}\label{cong1} [r]![T;r]_{(r)}^{-1}\cong T^r\mod (T-1). \end{equation} Indeed the map sending $T\mapsto 1$ defines a surjection of $R$ onto $\mathbb k(v)$ and under this map $[T;r]_{(r)}\mapsto [r]!$. Moreover for $k\neq 0$, \begin{align*} [T;k]^{-1} &=T[k]^{-1}\left( \frac{1}{1-(T-1)\frac{v^{k}}{1-v^k}}\right)\left( \frac{1}{1+(T-1)\frac{v^{k}}{1+v^k}}\right) \end{align*} and the two fractions on the right can be written as power series in $T-1$ with $1$ as their leading coefficient. \color{black}
\subsection{Identities} Two useful formulae for us will be
\begin{equation}\label{Ma1} \qbinom{s-u}{ r}=\sum_p (-1)^pv^{\pm (p(s-u-r+1)+ru)}\qbinom{u}{ p}\qbinom{s-p}{ r-p} \end{equation} \begin{equation}\label{Ma2} \qbinom{u+v+r-1}{ r}=\sum_p v^{\pm (p(u+v)-ru)}\qbinom{u+p-1}{ p}\qbinom{v+r-p-1}{r-p} \end{equation} which come from \cite{MR1337274}, equations 1.160a and 1.161a respectively.
\section{$\mathbf U_i$ Automorphisms and Intertwining Maps.} \label{automorphism} \subsection{} Following Lusztig, \cite[Chapter 5]{MR1227098}, we let $\mathcal C'$ denote the category whose objects are $\mathbb Z$- graded $\mathbf U$-modules $M=\oplus _{n\in\mathbb Z}M^n$ such that
\begin{enumerate}[(i)] \item $E,F$ act locally nilpotently on $M$, \item $Km=v^nm$ for all $m\in M^n$. \end{enumerate}
Fix $e=\pm 1$ and let $M\in \mathcal C'$. Define Lusztig's automorphisms $ T_i', T_i'':M\to M$ by \begin{equation}
T_i'(m):=\sum_{a,b,c;a-b+c=n}(-1)^bv^{e(-ac+b)}F^{(a)}E^{(b)}F^{(c)}m, \end{equation} and \begin{equation}
T_i''(m):=\sum_{a,b,c;-a+b-c=n}(-1)^bv^{e(-ac+b)}E^{(a)}F^{(b)}E^{(c)}m
\end{equation} for $m\in M^n$. In the above $E^{(a)}:=E^a/[a]!$ is the $a$-th {\it divided power of $E$}.
Lusztig defined automorphisms $T''_{i,e}$ and $ T'_{i,e}$ on $\mathbf U$ by $$ T'_e(E^{(p)})=(-1)^pv^{ep(p-1)}K^{ep}F^{(p)},\quad \quad T'_e(F^{(p)})=(-1)^pv^{-ep(p-1)}E^{(p)}K^{-ep} $$ and $$ T''_{-e}(E^{(p)})=(-1)^pv^{ep(p-1)}F^{(p)}K^{-ep},\quad \quad T''_{-e}(F^{(p)})=(-1)^pv^{-ep(p-1)}K^{ep}E^{(p)}. $$
One can check on generators that $\rho_1\circ T_{-1}'=T_{-1}'\circ \rho_1$.
In order to distinguish the algebra homomorphisms above from their module homomorphism counterparts we will sometimes use the notation $T_{e,\rm{mod}}'$ and $T_{e,\rm{mod}}''$to denote the later. If $M$ is in $\mathcal C'$, $x\in \mathbf U$ and $m\in M$, then we have
\begin{equation} \Theta (x\cdot m) =\Theta(x) \Theta m \end{equation} for $\Theta=T_{i,e}'$ or $\Theta=T_{i,e}''$ (see \cite[37.1.2]{MR1227098}). The last identity can be interpreted to say that $\Theta$ and $\Theta\otimes s$ are intertwining maps;
\begin{equation} \Theta:M \to M^\Theta\quad \quad \quad \quad \Theta\otimes s\ :{_R}M\to {_R}M^{\Theta\otimes s}. \end{equation}
To simplify notation we shall sometimes write $s\Theta$ in place of $\Theta\otimes s$.
We now describe the explicit action of $\Theta$ on $M$. \begin{lem}(\cite[Prop.5.2.2]{MR954661}). \label{symmetries} Let $m\geq 0$ and $j,h\in [0,m]$ be such that $j+h=m$. \begin{enumerate}[(a)] \item If $\eta\in M^m$ is such that $E\eta=0$, then $T_{i,e}'(F^{(j)}\eta)=(-1)^jv^{e(jh+j)}F^{(h)}\eta$. \item If $\zeta\in M^{-m}$ is such that $F\zeta=0$, then $T_{i,e}''(E^{(j)}\zeta) =(-1)^jv^{e(jh+j)}E^{(h)}\zeta$. \end{enumerate} \end{lem}
Let $F(\mathbf U)$ denote the ad-locally finite submodule of $\mathbf U$. We know from \cite{MR1198203} that $F(\mathbf U)$ is tensor product of harmonic elements $\mathcal H$ and the center $Z(\mathbf U)$. Here $\mathcal H=\oplus_{m\in\mathbb Z} \mathcal H_{2m}$ and $\mathcal H_{2m}=\text{ad}\, \mathbf U (EK^{-1})$.
There is another category that we will need and it is defined as follows: Let $M$ be a $\mathbf U_R$-module. One says that $M$ is {\it $_R\mathbf U^0$-semisimple} if $M$ is the direct sum of $R$-modules $M^{\mu}$ where $K$ acts by $T \ v^\mu$, $\mu\in\mathbb Z$; i.e. by weight $m+\mu$. Then $\mathcal C_{R}$ denotes the category of $\mathbf U_R$-modules $M$ for which $E$ acts locally nilpotently and $M$ is $_R\mathbf U^0$-semisimple.
For $M$ and $N$ two objects in $\mathcal C'$ or one of them is in $_R\mathcal C$, Lusztig defined the linear map $L:M\otimes N\to M\otimes N$ given by \begin{equation}\label{L} L(x\otimes y)=\sum_n(-1)^nv^{-n(n-1)/2}\{n\}F^{(n)}x\otimes E^{(n)}y \end{equation}
where $\{n\}:=\prod_{a=1}^n(v^a-v^{-a})$ and $\{0\}:=1$.
One can show $$ L^{-1}(x\otimes y)=\sum_nv^{n(n-1)/2}\{n\}F^{(n)}x\otimes E^{(n)}y. $$
\begin{lem}\label{LLemma1}(\cite{MR1227098}). Let $M$ and $N$ be two objects in $\mathcal C'$. Then $ T_{1}'' L(z)=(T_{1}''\otimes T_{1}'')(z)$ for all $z\in M\otimes N$. \end{lem}
\begin{lem}\label{LLemma2} Let $M$ be a module in $\mathcal C_R$ and $N$ a module in $\mathcal C'$. Then for $x\in M^t$ and $y\in N^s$ we have \begin{align*}
FL(x\otimes y) &=L(x\otimes Fy+v^sFx\otimes y) \\ EL(x\otimes y) &=L(Ex\otimes y+v^{-t}T^{-1}x\otimes Ey) . \end{align*} \end{lem}
\begin{cor}\label{Lisomorphism} Let $M$ be a module in $\mathcal C_R$ and $\mathcal E$ a module in $\mathcal C'$. Then $L$ defines an isomorphism of the $\mathbf U$-module $M^{T_{-1}'}\otimes \mathcal E^{T_{-1}'}$ onto $(M\otimes\mathcal E)^{T_{-1}'}$. \end{cor}
\corref{Lisomorphism} through the use of \lemref{LLemma1}, however one must take into account that $T_e'$ may not be defined on $M$.
Set \begin{equation}\label{mathcalLinv} \mathcal L^{-1}=\sum_p(-1)^pv^{3\frac{p(p-1)}{ 2}}\{p\}E^{(p)}K^pF^{(p)}, \end{equation} and \begin{align}\label{mathcalL} \mathcal L
&=\sum_p
v^{-3\frac{p(p-1)}{2}}\{p\}E^{(p)}K^{-p}F^{(p)}. \end{align} and note that $\mathcal L$ and $\mathcal L^{-1}$ are well defined operators on lowest weight modules.
\begin{lem} Suppose that $M$ and $N$ be highest weight modules with $\psi_M:M^{sT'_{-1}}_\pi\to M$, $\psi_N:N^{sT'_{-1}}_\pi\to N$ homomorphisms and $\phi$ a $\rho$-invariant form on $M\times N$. Then
\begin{equation}\label{Ll} \phi\circ(\psi_M\otimes \psi_N)\circ L^{-1}=\phi\circ (\psi_M\otimes \psi_N) \circ (\mathcal L^{-1}\otimes 1). \end{equation}
\end{lem}
\begin{lem} $T'_{-1}(u)\mathcal L^{-1}=\mathcal L^{-1}T_1'(u)$ as operators on $M_\pi$ for all $u\in{_R\mathbf U}$. \end{lem}
\section{Invariant Forms and Liftings}
\subsection{} Elements of $\mathbb P(M,N)$ are called {\it invariant pairings} and for $M=N $, set $\mathbb P(M) =\mathbb P(M,M)$ and call the elements {\it invariant forms} on $M$.
\begin{lem} Let $M$ and $N$ be finite dimensional $\mathbf U_R$-modules in $\mathcal C'$ and $\phi$ an invariant pairing. Then, for $m\in M,n\in N$, $ \phi(T_{i,e}'' m,T_{i,e}'' n)=\phi(m,n)$. \end{lem}
Note that if $\phi(\eta,\eta)=1$, then for $0\leq j\leq \nu$, the proof above shows that \begin{equation}\label{normalizedforms} \phi(F^{(j)}\eta,F^{(j)}\eta)=v^{j^2-\nu j}{\qbinom \nu j} \end{equation}
For the proof of some future results we must be explicit about the definition of $_f\mathcal R$. Recall a $\mathbf U$-module $M$ is said to be {\it integrable} if for any $m\in M$ and all $i\in I$, there exists a positive integer $N$ such that $E^{(n)}_im=0=F^{(n)}_im$ for all $n\geq N$ , and $M=\oplus _{\lambda\in X}M^\lambda$ where for any $\mu\in Y, \lambda\in X$ and $m\in M^\lambda$ one has $K_\mu m=v^{\angles{\mu ,\lambda}m}$. Let $\mathbf U_0^\times$ denote the set of units of $\mathbf U_0$ and let $f:X\times X\to \mathbf U_0^\times$ be a function such that
\begin{equation} f(\zeta+\nu,\zeta'+\nu')=f(\zeta,\zeta')v^{ -\sum \nu_i\angles{i,\zeta'}(i\cdot i/2)-\sum \nu'_i\angles{i,\zeta}(i\cdot i/2) -\nu\cdot \nu'}\tilde K_\nu \end{equation} for all $\zeta,\zeta'\in X$ and all $\nu,\nu'\in X$ (see \cite[32.1.3]{MR1227098}). Here $\tilde K_\nu=\prod_iK_{(i\cdot i/2)\nu_ii}$.
\begin{thm}(\cite[32.1.5]{MR1227098}). If $\mathcal E$ is an integrable $\mathbf U_R $ module and $A\in \mathcal C_{R}$, then for each $f$ satisfying (3.1.1), there exists an isomorphism $_f\mathcal R:A\otimes \mathcal E\to \mathcal E\otimes A$. \end{thm}
The map $\tau:A\otimes B\to B\otimes A$ for any two modules $A$ and $B$ denotes the twist map $\tau(a\otimes b)=b\otimes a$. Define $\prod _f:\in\mathop{\mathrm{End}}\nolimits_R({_R\mathcal E}\otimes{_R\mathcal F}\otimes_R M)$ by $\prod_f(e\otimes e'\otimes m)= f(\lambda,\lambda')e\otimes e' \otimes m$ for $m\in M^{\lambda'}$ and $e\otimes e'\in (\mathcal E\otimes{_R\mathcal F})^{\lambda}$. Lastly we define $\chi\in \mathop{\mathrm{End}}\nolimits_R({_R\mathcal E\otimes{_R\mathcal F}}\otimes_R M)$ by $$ \chi(e\otimes e'\otimes m)= \sum_\nu\sum_{b,b'\in \mathbf B_\nu}p_{b,b'}b^-(e\otimes e')\otimes {b'}^+m $$ where $p_{b,b'}=p_{b',b}\in R$, and $\mathbf B_\nu$ is a subset of $\mathfrak f$. Then $_f\mathcal R$ is defined to be equal to $\chi\circ \prod_f\circ \tau$. The proof that it is an $\mathbf U$-module homomorphism is almost exactly the same as in \cite{MR1227098}, 32.1.5, or \cite{MR1359532}, 3.14], which the exception that one must take into account that $M$ is in the category $\mathcal C_R$ instead of $_R\mathcal C'$.
Let $\mathcal E$ and $\mathcal F$ be finite dimensional $\mathbf U$-modules and $\tau: _R\mathcal E\otimes _R\mathcal F^{\rho_1} \rightarrow \mathbf U$, a $\mathbf U$-module homomorphism into $\mathbf U$, where $\mathbf U$ is a module under the adjoint action. Suppose $\phi$ is a pairing of $M$ and $N$. Define $\psi_{\tau,\phi}$ to be the invariant pairing of $ M\otimes _R\mathcal E$ and $N\otimes _R\mathcal F$ defined by the formula, for $e\in \mathcal E ,f\in \mathcal F,m\in M,$ and $n\in N$, \begin{equation}\label{inducedpairing} \psi_{\tau,\phi} (m\otimes e,n \otimes f)= \phi( m,\tau(e\otimes f)*n)\ , \end{equation}
Here ${\mathcal F}^{\rho_1}$ is a twist of the representation $\mathcal F$ by $\rho_1$. We call the pairing $\psi_{\tau,\phi}$ the {\it pairing induced} by $\tau$ and $\phi$. In the cases when $M,N$ and $\phi$ are fixed we write $\psi_\tau$ in place of $\psi_{\tau,\phi}$ and say this pairing is induced by $\tau$.
Let us check that $\psi_{\tau,\phi}$ indeed is a $\mathbf \rho$-invariant pairing: For $x\in\mathbf U$ \begin{align*} \sum \psi_{\tau,\phi} (S(x_{(2)})(m\otimes e),&\mathbf \rho(x_{(1)})(n \otimes f)) \\ &=\sum \psi_{\tau,\phi} (S(x_{(4)})m\otimes S(x_{(3)})e),\mathbf \rho(x_{(1)})n \otimes \mathbf \rho(x_{(2)})f)) \\ &=\sum \phi(S(x_{(4)})m, \tau(S(x_{(3)})e\otimes \mathbf \rho(x_{(2)})f)*(\mathbf \rho(x_{(1)})n)) \\ &=\sum \phi(S(x_{(4)})m, \sum \mathbf \rho(x_{(3)})\rho_1(\tau(e\otimes f))\mathbf \rho(x_{(1)}S(x_{(2)}))n) \\ &=\sum \phi(S(x_{(2)})m, \mathbf \rho(x_{(1)})(\tau(e\otimes f)*n))) \\ &=\mathbf e(x)\phi( m,\tau(e\otimes f)*n)\ , \end{align*} The first equality is due to the act that \begin{equation}\label{diagonalS} S\otimes S\circ \Delta =\tau \circ \Delta \circ S \end{equation} where $\tau:\mathbf U\otimes \mathbf U\to \mathbf U\otimes \mathbf U$ is the twist map and the fact that $\mathbf \rho\otimes \mathbf \rho\circ \Delta=\Delta\circ\mathbf \rho$. The second equality follows from the definition of $\psi_{\tau,\phi}$. The third equality is obtained from \eqnref{diagonalS} and the fact that $\mathbf \rho$ is an anti-automorphism. The last equality is due to the assumption that $\phi$ is $\mathbf \rho$-invariant.
\subsection{} A result from \cite{MR1327136} shows that in the setting of Verma modules the collection of maps $\tau$ is a natural set of parameters for invariant forms.
\begin{prop}[\cite{MR1327136}] Suppose $\mathbf U$ is of finite type and $\mathcal E$ and $\mathcal F$ are finite dimensional $\mathbf U$-modules. Let $M$ be an $_R\mathbf U$-Verma module and $\phi$ the Shapovalov form on $M$. Suppose the Shapovalov form on $M$ is nondegenerate. Then every invariant pairing of $M\otimes _R\mathcal E$ and $M\otimes _R\mathcal F$ is induced by $\phi$. \end{prop}
\subsection{}
\begin{thm}(\cite[Lifting Theorem]{MR1327136}). Let $A$ and $B$ be modules in $\mathcal C_{R}$ and $\phi\in {\mathbb P}_{\mathbf \rho }(A,B)$. Then $\phi$ uniquely determines an invariant form $\phi_F\in {\mathbb P}_{\mathbf \rho}(A_F,B_F)$ which is determined by the following properties: \begin{enumerate} \item $\phi_F$ vanishes on the subspaces $\iota A\times B_F$ and $A_F\times \iota B$ . \item For each $\mu \in \mathbb Z$ with $\mu+1= r\in \mathbb N$, and any vectors $a\in A$ and $b\in B$ both of weight $m+\epsilon\mu$ with $\epsilon\in \{1,s\}$ and $E\ a=E\ b=0$ , \begin{equation}
\phi_F(F^{-1}a ,F^{-1} b)= v^{-r+1}\frac{\iota\epsilon[T;0]}{ \i \epsilon[T;r-1]\ }\ \ \phi(a,b). \end{equation} \end{enumerate} \end{thm}
\begin{prop} The form $\phi_F$ induces an $\mathbf \rho$-invariant bilinear map on $A_\pi \times B_\pi$ which we denote by $\phi_\pi$. \end{prop}
\subsection{} At times the subscript notation for lifted forms will be inconvenient and so we shall also use the symbol $loc$ for the localization of both forms and modules. We write $loc(\phi)$ and $loc(A)$ in place of $\phi_F$ and $A_F$.
For invariant forms we find that induction and localization commute in the following sense.
\section{Quantum Clebsch-Gordan decomposition}
\subsection{Basis and Symmetries} \label{basisandsymmetries} For $m\in\mathbb Z$, let $\mathcal F_m$ denote the finite dimenisonal irreducible module of highest weight $v^m$ with highest weight vector $u^{(m)}$. For $k$ any non-negative integer set $u^{(m)}_k=F^{(k)}u^{(m)}$ and $u^{(m)}_{-1}=0$.
In particular $$ \theta^{-1}(u^{(m)}_j)=T_1''(u^{(m)}_j)=(-1)^{m-j}v^{(m-j)(j+1)}u^{(m)}_{m-j} $$ and \begin{equation}\label{irred} K^pu^{(m)}_j=v^{p(m-2j)}u^{(m)}_j,\quad \quad F^{(p)}u^{(m)}_j= {\qbinom {p+j} j}u^{(m)}_{j+p},\quad\quad
E^{(p)}u^{(m)}_j=\qbinom{m+p-j}{ p} u^{(m)}_{j-p}. \end{equation}
\begin{lem} \label{CG}[Clebsch-Gordan, \cite{MR2586983}] For any two non-negative integers $m\geq n$, there is an isomorphism of $\mathbf U$-modules $$ \mathcal F_{m+n}\oplus \mathcal F_{m+n-2}\oplus \cdots \oplus \mathcal F_{m-n}\cong\mathcal F_m\otimes \mathcal F_n. $$ Moreover the isomorphism is defined on highest weight vectors by $$ \varPhi(u^{(m+n-2p)})=\sum_{k=0}^p(-1)^k \frac{[n-p+k]![m-k]!}{[n-p]![m]!} v^{(k-p)(m-p-k+1)}u_k^{(m)}\otimes u_{p-k}^{(n)}. $$ \end{lem} \begin{lem} The map $\varphi:\mathcal F_m^{\rho_1}\to \mathcal F_m$ given by $\varphi(u^{(m)}_k)=(-v)^{-k}u^{(m)}_{m-k}$ is an isomorphism. \end{lem}
\begin{cor}\label{CG2} Let $m\geq n$ be two non-negative integers. Then there is an isomorphism of $\mathbf U$-modules $$ \mathcal F_{m+n}\oplus \mathcal F_{m+n-2}\oplus \cdots \oplus \mathcal F_{m-n}\cong\mathcal F_m\otimes \mathcal F_n^{\rho_1}. $$ Moreover the isomorphism is defined on highest weight vectors by \begin{align*} \Phi(u^{(m+n-2p)})&=\sum_{k=0}^p(-1)^{n-p}\frac{[n-p+k]![m-k]!}{[n-p]![m]!} v^{k\,\left( 2 + m -k\right) + n - 2\,p - m\,p + p^2}u_k^{(m)}\otimes u_{n-p+k}^{(n)} \\ \color{red} &=(-1)^{n-p}v^{ n +p(p- 2 - m)}\sum_{k=0}^p
v^{k\,\left( 2 + m -k\right)} \qbinom{n-p+k}{ k}
\qbinom{m}{ k}^{-1} u_k^{(m)}\otimes u_{n-p+k}^{(n)}. \end{align*} \color{black}
(the action on the second factor $u^{(n)}_l$ is twisted by the automorphism $\rho_1$). \end{cor}
\begin{lem}\label{CGspecialcase}\cite{MR2586983}. For $0\leq k\leq \min\{n-p,m+n-2p\}$, \begin{align*} &\left[\begin{matrix} m & n & m+n-2p
\\ 0 & p+k & k \end{matrix}\right]= v^{-p(m-p+1)}{\qbinom {p+k} {p}}\\
\notag \end{align*} and for $\max\{0,m-p\}\leq k\leq m+n-2p$ \begin{align*} &\left[\begin{matrix} m & n & m+n-2p
\\ m & p+k-m & k \end{matrix}\right] \\ &\quad \quad =v^{p(p-1)-m(m +n -p - k)}
\sum_{l=0}^{\min\{p,m\}} (-1)^lv^{l\,\left( 1 + m + n - 2\,p - k \right)} {\qbinom {n-p+l} l} {\qbinom {p+k-m} {p-l}} \notag \\ &\quad \quad=(-1)^pv^{(p-m)(m +n) +m k}
{\qbinom {m+n-p-k} {p}},\quad \text{if }\quad n\leq m. \notag \end{align*} \end{lem}
Consider now the $\rho$-invariant forms \eqnref{normalizedforms} on $\mathcal F_m$ and $\mathcal F_n$, both denoted by $(,)$, normalized so that their highest weight vectors have norm $1$. Define the symmetric invariant bilinear form on $\mathcal F_m\otimes \mathcal F_n$ given by the tensor product of the two forms (the resulting pairing is $\rho$-invariant). In this case
\begin{align*} (u^{(m+n-2p)},u^{(m+n-2p)})&= \sum_{k=0}^p\left(\frac{[n-p+k]![m-k]!}{[n-p]![m]!} v^{(k-p)(m-p-k+1)}\right)^2(u_k^{(m)},u_k^{(m)})(u_{p-k}^{(n)},u_{p-k}^{(n)}) \\ &= \sum_{k=0}^p\left(\frac{[n-p+k]![m-k]!}{[n-p]![m]!}\right)^2 v^{2(k-p)(m-p-k+1)+k^2-m k+(p-k)^2-n(p- k)} {\qbinom m k} {\qbinom n {p-k}} \\ &= \sum_{k=0}^p\frac{[n]![n-p+k]![m-k]!}{[n-p]!^2[p-k]![k]![m]!} v^{k\,\left( 2 + m + n - 2\,p \right) +
p\,\left(3\,p -2 - 2\,m - n \right)} \\ &= v^{p\,\left(3\,p -2 - 2\,m - n \right)}\frac{[n]!}{[n-p]!^2[m]!} \sum_{k=0}^p\frac{[n-p+k]![m-p+(p-k)]!}{[k]![p-k]!} v^{k\,\left( 2 + m + n - 2\,p \right)} \\ &= v^{p\,\left(2\,p - 2\,m -1\right)}\frac{[n]![m+n-p+1]![m-p]!}{[m]![p]![m+n-2p+1]![n-p]!}. \end{align*}
where we have used formula \eqnref{Ma2}.
The same proof that gave us \eqnref{normalizedforms} now implies \begin{equation*} (u^{(m+n-2p)}_k,u^{(m+n-2p)}_k)= v^{p\,\left(2\,p - 2\,m -1\right)-(m+n-2p-k) k} \left[\begin{matrix} n \\ p \end{matrix}\right]\left[\begin{matrix} m+n-p+1
\\ p \end{matrix}\right]{\qbinom {m+n-2p} k}\left[\begin{matrix} m \\ p \end{matrix}\right]^{-1}. \end{equation*} \begin{prop}[\cite{MR2586983}] \begin{enumerate}[(i).] \item The basis $\{u_k^{(m+n-2p)}\}$ of \hbox{$\mathcal F_m\otimes{\mathcal F_n}$} is orthogonal. \item For $0\leq i\leq m$, and $0\leq j\leq n$, \begin{align*} u_i^{(m)}\otimes u_j^{(n)}
&=v^{in +jm -2ij}
\sum_p v^{(1 + m - n - p) p}
\frac{
\left[\begin{matrix} m \\ i
\end{matrix}\right]\left[\begin{matrix} n \\
j\end{matrix}\right]
\left[\begin{matrix} m
\\ p \end{matrix}\right]\left[\begin{matrix} m & n & m+n-2p
\\ i & j & {i+j-p} \end{matrix}\right]}
{\left[\begin{matrix} n
\\ p \end{matrix}\right]
\left[\begin{matrix} m+n-p+1
\\ p \end{matrix}\right]\left[\begin{matrix} m+n-2p
\\ {i+j-p} \end{matrix}\right]}u_{i+j-p}^{(m+n-2p)}. \end{align*} \end{enumerate} \end{prop}
In \hbox{$\mathcal F_m\otimes{\mathcal F_n}^{\rho_1}$} (recall $\phi(u^{(n)}_j)=(-v)^{-j} u^{(n)}_{n-j}$ ) \begin{align} u^{(m)}_i\otimes u_j^{(n)} &=(-1)^{j} v^{i( 2j - n ) + mn-j(1 +m) } \\
&\quad \times \sum_p v^{(1+m-n-p)p}
\frac{\left[\begin{matrix} m \\ i
\end{matrix}\right]\left[\begin{matrix} n \\
j\end{matrix}\right]
\left[\begin{matrix} m \\ p\end{matrix}\right]
\left[\begin{matrix} m & n & m+n-2p
\\ i & n-j & i+n-j-p \end{matrix}\right]}{
\left[\begin{matrix} m+n-p+1 \\ p \end{matrix}\right]
\left[\begin{matrix} n \\ p \end{matrix}\right]
\left[\begin{matrix} m+n-2p
\\ i+n-j-p \end{matrix}\right]}u_{i+n-j-p}^{(m+n-2p)}.\notag \end{align}
In particular \begin{align}\label{CGdecomp} u^{(m)}\otimes u_j^{(n)}&=(-1)^{j} v^{ m n-j(1 +m)} \sum_{p=0}^{\min\{n-j,m+j\}} v^{-np}
\frac{\left[\begin{matrix} n \\ j \end{matrix}\right]
\left[\begin{matrix} m \\ p\end{matrix}\right]
\left[\begin{matrix}{n-j} \\ {p}\end{matrix}\right]}{
\left[\begin{matrix} m+n-p+1 \\ p \end{matrix}\right]
\left[\begin{matrix} n \\ p \end{matrix}\right]
\left[\begin{matrix} m+n-2p
\\ n-j-p \end{matrix}\right]}u_{n-j-p}^{(m+n-2p)} . \end{align} as \begin{equation*} \left[\begin{matrix} m & n & m+n-2p \\ 0 & p+r & r \end{matrix}\right] =v^{(-p)(m-p+1)}{\qbinom {p+r} {p}}. \end{equation*} for $0\leq n-j-p\leq m+n-2p$, i.e. for $p\leq \{n-j,m+j\}$ \begin{align} u^{(m)}_m\otimes u_j^{(n)} &=(-1)^{j} v^{ m(m+j - n) -j} \\
&\quad \times \sum_p v^{(1+m-n-p)p}
\frac{\left[\begin{matrix} n \\
j\end{matrix}\right]
\left[\begin{matrix} m \\ p\end{matrix}\right]
\left[\begin{matrix} m & n & m+n-2p
\\ m & n-j & m+n-j-p \end{matrix}\right]}{
\left[\begin{matrix} m+n-p+1 \\ p \end{matrix}\right]
\left[\begin{matrix} n \\ p \end{matrix}\right]
\left[\begin{matrix} m+n-2p
\\ m+n-j-p \end{matrix}\right]}u_{m+n-j-p}^{(m+n-2p)}\\ &=(-1)^{j} v^{-j} \\
&\quad \times \sum_p (-1)^pv^{(1+m-p)p}
\frac{\left[\begin{matrix} n \\
j\end{matrix}\right]
\left[\begin{matrix} m \\ p\end{matrix}\right]
\left[\begin{matrix} j \\ p \end{matrix}\right]}{
\left[\begin{matrix} m+n-p+1 \\ p \end{matrix}\right]
\left[\begin{matrix} n \\ p \end{matrix}\right]
\left[\begin{matrix} m+n-2p
\\ m+n-j-p \end{matrix}\right]}u_{m+n-j-p}^{(m+n-2p)},\notag \end{align} if $m\geq n$, as \begin{align*} &\left[\begin{matrix} m & n & m+n-2p
\\ m & p+k-m & k \end{matrix}\right] =(-1)^pv^{(p-m)(m +n) +mk}
{\qbinom {m+n-p-k} {p}}. \notag \end{align*}
\section{Basis and the Intertwining map $\mathcal L$} \subsection{A Basis} For $s\geq 1$, and any lowest weight vector $\eta$ of weight $Tv^{\lambda+\rho}$, set \begin{equation}\label{defofFinv} F^{(-k)}\eta:=T'_{-1}(F^{(k)})\eta =v^{k(k-1)}F^{-k}K^{k}[K;-1]^{(k)}\eta =v^{k(\lambda+k)}T^k[T;\lambda]^{(k)}F^{-k}\eta \end{equation} as $$ T'_{-1}(E^{(k)})=(-1)^kv^{-k(k-1)}K^{-k}F^{(k)},\quad \quad T'_{-1}(F^{(k)})=(-1)^kv^{k(k-1)}E^{(k)}K^{k}. $$
\begin{lem}[\cite{MR2586983}] \label{binomiallemma} Suppose $r,s\in\mathbb Z$, $s> r\geq 0$, $\zeta$ is a highest weight vector of weight $Tv^{\lambda-\rho}$ and $\eta$ is a lowest weight vector of weight $Tv^{\lambda+\rho}$. Then \begin{equation}\label{hw1} E^{(r)}F^{(s)}\zeta =\qbinom{T;\lambda-1+r-s}{ r}F^{(s-r)}\zeta, \quad F^{(r)}F^{(s)}\zeta =\qbinom{r+s}{ r}F^{(s-r)}\zeta, \end{equation} and \begin{align} F^{(r)}F^{(-s)}\eta &=v^{r(\lambda+2s-r)}T^r
\qbinom{T;\lambda+s}{ r} F^{(r-s)}\eta, \\ E^{(r)}F^{(-s)}\eta &=(-1)^rv^{-r(\lambda+r+2s)}T^{-r}
\qbinom{r+s}{ r}
F^{(-r-s)}\eta, \end{align} \end{lem} Define indexing sets $ I_\lambda$ and $ I_{-\lambda}$ by $ I_\lambda = \lbrace n-2,n-4,...\rbrace$, $ I_{-\lambda} = \lbrace -n,-n-2,...\rbrace. $ One should compare the previous result with \begin{lem}\label{locstructure}\cite[2.2]{MR2586983} Now for integers $j \in I_\lambda$ (resp. $ I_{-\lambda}$) set $ k_j = {\frac{n-2-j}{ 2}}$ and $l_j = {\frac{-n-j}{2}} $ and define basis vectors for $M(m+\l)$ and $M(m-\l)$ by $\mathbf v_j= F ^{k_j} \otimes 1_{m+\lambda}$ and $\mathbf v_{j,s}= F ^{l_j}\otimes 1_{m-\lambda -\rho}$. The action of $\mathbf U_R$ is given by
\begin{align} K\mathbf v_j&= Tv^{\lambda-1-2k_j}\mathbf v_j, \quad F \mathbf w_{\lambda,j} = \mathbf w_{\lambda,j-2} \\ K\mathbf v_{j,s}&=Tv^{-\lambda-1-2l_j}\mathbf v_{j,s}\quad F\mathbf w_{\lambda,j} =\mathbf w_{\lambda,j-2} \\ E\mathbf v_j&= [k_j][T; -l_j] \mathbf w_{\lambda,j+2}\quad ,\quad E\mathbf v_j = [l_j][T; -k_j] \mathbf w_{-\lambda,j+2}. \end{align} \end{lem}
\begin{cor}\label{Lonbasis} For $k\geq 0$ and $0\leq j\leq n$ we have \begin{align*} \mathcal L&(F^{(-k)}\eta \otimes u_j^{(n)}) \\
&= \sum_{q=j-n}^{j}
\sum_{p=0}^{n-j+k}\sum_{t=q}^k\,
(-1)^{t-q} v^{-\frac{3p(p-1)}{2}+p( 2j+ 2p- n ) }\{p\} \\ &\quad \times
v^{t( -1 + 2j - 2k - n - \lambda) +
q(1 + 4k - p - 2q + 2\lambda )} \\ &\quad \times
T^{2q-t}{\qbinom {p-t+j} j}\qbinom{T;\lambda+k}{ t}
\qbinom{k-q}{ t-q}\qbinom{n+q-j }{ p+q-t}
F^{(q-k)}
\eta\otimes u^{(n)}_{j-q}. \end{align*} \end{cor}
\subsection{} The articles \cite{MR1327136} and \cite{MR2586983} study noncommutative localization of highest weight modules. This article may be viewed as an extension of what was begun there. For any $\mathbf U$-module $A$ let $A_F$ denote the localization of $A$ with respect to the multiplicative set in $\mathbf U$ generated by $F$. If $F$ acts without torsion on $A$ (we shall assume this throughout) then $A$ injects into $A_F$ and we have the short exact sequence of $\mathbf U$-modules: $0\to A\to A_F\to A_\pi \to 0$.
\section{Maps into the Harmonics.} \subsection{Harmonics} We know from \cite{MR1198203} that $F(\mathbf U)\cong \mathcal H\otimes Z(\mathbf U)$ where $\mathcal H=\oplus_{n\in\mathbb N}\mathcal L_{2n}$ is the space of {\it harmonics}, and $\mathcal L_{2n}\cong \mathcal F_{2n}$. We would now like to give an explicit basis of $\mathcal L_{2n}$.
\begin{lem} For $n\in\mathbb N$, we can take \begin{equation} \mathcal H_{2n}=\oplus_{p=0}^{n}k(v)\text{ad}\,F^{(p)}(E^{(n)}K^{-n}), \end{equation} where \begin{align} \text{ad}\,F^{(p)}(E^{(n)}K^{-n}) =\sum_{i=0}^n
F^{(p-i)}\sum_{m=0}^{p-i}
(-1)^{m+i}v^{( 1-p+2n )(m+i) }
\qbinom{ p-i }{ m} \qbinom{K; i-m-n}{ i}E^{(n-i)}K^{p-n} \end{align} \end{lem}
For $m$, $n$, $r$ integers with $m+n$ even, $0\leq 2r\leq m+n$, we let $\beta^{m,n}_{2r}:\mathcal F_m\otimes\mathcal F_n^{\rho_1}\to \mathcal H$, be the $\mathbf U$-module homomorphism determined by \begin{equation} \beta^{m,n}_{2r}(u^{(m+n-2q)})=\delta_{2r,m+n-2q}E^{(r)} K^{-r}. \end{equation} so that $\text{im}\enspace\beta^{m,n}_{2r}=\mathcal L_{2r}$.
\begin{prop}\label{betaonabasis}Suppose $\eta$ is a lowest weight vector of weight $Tv^{\lambda+\rho}$. Then \begin{align*} \rho_1&\Big(\beta^{m,n}_{2r}(u^{(m)}_i\otimes u^{(n)}_{j})
\Big) F^{(-c)}\eta\\ &=(-1)^jv^{i(2j - n)+ mn-j(1 +m) +(1+ \frac{m-3n}{2}+r) (\frac{m+n}{2}-r)} \\ \\ &\quad \times
\frac{\left[\begin{matrix} m \\ i \end{matrix}\right]
\left[\begin{matrix} m \\ \frac{m+n}{2}-r \end{matrix}\right]
\left[\begin{matrix} n \\ j \end{matrix}\right]
\left[\begin{matrix} m & n & 2r
\\ i & {n-j} & {i-j+\frac{n-m}{2}+r} \end{matrix}\right]}
{\left[\begin{matrix} n
\\ \frac{m+n}{2}-r \end{matrix}\right]
\left[\begin{matrix} \frac{m+n}{2}+r+1
\\ \frac{m+n}{2}-r \end{matrix}\right]\left[\begin{matrix} 2r
\\ {i-j+\frac{n-m}{2}+r} \end{matrix}\right]} \\ \\ &\quad \times (v^{2\lambda+2+i-j+\frac{n-m}{2}+4c}T^2)^{j-i+\frac{m-n}{2}}\\ \\ &\quad \times
\sum_{l=0}^{i-j+\frac{n-m}{2}+r} (-1)^{r-l}
v^{l\left(r+j-i+\frac{m-n}{2}+1 \right) }
\qbinom{i-j+\frac{n-m}{2}+c}{ i-j+\frac{n-m}{2}+r-l}
\qbinom{T;\lambda+l+c}{ r}
\qbinom{l+c}{ l}
F^{(j-i+\frac{m-n}{2}-c)}\eta \end{align*} and\begin{align*} \rho_1&\Big(T_{-1}'\beta^{m,n}_{2r}(u^{(m)}_i\otimes u^{(n)}_{j})
\Big) F^{(-c)}\eta\\ &=(-1)^jv^{i(2j - n)+ mn-j(1 +m) +(1+ \frac{m-3n}{2}+r) (\frac{m+n}{2}-r)} \\ \\ &\quad \times
\frac{\left[\begin{matrix} m \\ i \end{matrix}\right]
\left[\begin{matrix} m \\ \frac{m+n}{2}-r \end{matrix}\right]
\left[\begin{matrix} n \\ j \end{matrix}\right]
\left[\begin{matrix} m & n & 2r
\\ i & {n-j} & {i-j+\frac{n-m}{2}+r} \end{matrix}\right]}
{\left[\begin{matrix} n
\\ \frac{m+n}{2}-r \end{matrix}\right]
\left[\begin{matrix} \frac{m+n}{2}+r+1
\\ \frac{m+n}{2}-r \end{matrix}\right]\left[\begin{matrix} 2r
\\ {i-j+\frac{n-m}{2}+r} \end{matrix}\right]} (v^{ 2\,c +\lambda}T)^{i-j+\frac{n-m}{2}}\\ \\ &\quad\times \sum_{l=0}^{i-j+\frac{n-m}{2}+r}(-1)^{r-l}
v^{ l (r +j-i+\frac{m-n}{2}+1) }
\left[\begin{matrix}T;\lambda+c \\ l \end{matrix}\right]
\left[\begin{matrix}T;\lambda+r+c-l \\ i-j+\frac{n-m}{2}+r-l \end{matrix}\right]
\left[\begin{matrix}r+c-l \\ r \end{matrix}\right]
F^{(i-j+\frac{n-m}{2}-c)}\eta \end{align*}
\end{prop}
\section{Symmetry Properties of Induced Forms}
\subsection{Twisted action of $R$.} We shall twist by an automorphism of $\mathbf U_R$ in the setting of $\mathbf U_R$-modules. Let $\Theta$ be an automorphism of $\mathbf U_R$. Then for any $\mathbf U_R$-module ${_R\mathcal E}$ define a new $\mathbf U_R $-module ${_R\mathcal E}$ with set equal to that of ${_R\mathcal E}$ and action given by: for $e\in {_R\mathcal E}$ and $x\in\mathbf U_R $ the action of $x$ on $e$ equals $\Theta(x)e$. For any $\mathbf U_R$-module $A$, let $A^{s\Theta}$ denote the module with action $\delta_i $ on $A^{s\Theta}$ defined as follows: For $a\in A$ and $x\in\mathbf U_R$, $$ x\delta_i a= s\Theta(x)\ a. $$
\begin{lem} Suppose $\phi$ is a $\mathbf \rho$-invariant $R$-valued pairing of $\mathbf U_R $-modules $A$ and $B$. Then $s\circ \phi$ is a $\mathbf \rho$-invariant pairing of $A^s$ and $B^s$ as well as $A^{sT_{i,e}''}$ and $B^{sT_{-e}''}$. Also $\phi$ itself is $\mathbf \rho$-invariant pairing of these two pairs taking values in the $R$-module $R^s$. \end{lem}
{\begin{lem} Let $m$ be a lowest weight vector in $M_\pi$ of weight $Tv$ and $\Psi(m)$ a highest weight vector in $M$ of weight $Tv^{-1}$. The map $\Psi:(M_\pi)^{s\Theta}\to M$ given by $$ \Psi(F^{-k}m)=\frac{(-1)^kv^{-k^2}T^k}{[k]![T;-1]_{(k)}}F^{k}\Psi(m) $$ for $k\geq 0$ is an isomorphism. \end{lem}} The above can be rewritten as $$ \Psi(F^{(-k)}m)=F^{(k)}\Psi(m). $$
Set
\begin{equation} \bar \Psi:=\Psi \otimes s\Theta\circ L^{-1}:(M_\pi\otimes \mathcal E)^{s\Theta}\to M\otimes \mathcal E. \end{equation} Define $t\in \mathop{\mathrm{End}}\nolimits(\mathbb P(M\otimes \mathcal E, N\otimes \mathcal F))$ by \begin{equation}\label{twistedpairing} t(\chi)(\bar\Psi(a),\bar\Psi(b)):= s\circ\chi_\pi\circ L(a\otimes b) \end{equation} for $a\in (M\otimes \mathcal E)_\pi$, $b\in (N\otimes \mathcal F)_\pi$ and $\chi\in\mathbb P(M\otimes \mathcal E,N\otimes \mathcal F)$. On the left hand side one is to consider $a\in(M\otimes \mathcal E)_\pi^{s\theta}$, and $b\in (N\otimes\mathcal F)^{s \theta}_\pi$ and on the right hand side $a\in (M\otimes \mathcal E)_\pi$, $b\in (N\otimes \mathcal F)_\pi^{\rho_1}$. We can view $L:(M\otimes \mathcal E)_\pi^{s\theta}\otimes (N\otimes \mathcal F)_\pi^{ s\theta\rho_1}\to ((M\otimes \mathcal E)_\pi\otimes (N\otimes \mathcal F)^{\rho_1}_\pi)^{s\theta}$ as a module isomorphism (see \lemref{Tandrho} and \corref{Lisomorphism}) Then $s\circ \chi_\pi\circ L:(M\otimes \mathcal E)_\pi^{s\theta}\otimes (N\otimes \mathcal F)_\pi^{s\theta\rho_1}\to R$ is a module homorphism. More explicitly we can show that $t(\chi)\in \mathbb P(M\otimes \mathcal E, N\otimes \mathcal F)$ by the following calculation for $x\in \mathbf U$:
\begin{align*} \sum\chi^\#(S(x_{(2)})\bar\Psi(a),\mathbf \rho(x_{(1)})\bar\Psi(b))&= \sum\chi^\#(\bar\Psi(\theta S(x_{(2)})a),\bar\Psi( \theta \mathbf \rho(x_{(1)})b)) \\
&=\sum s\circ\chi_\pi\circ L(\theta S(x_{(2)})a\otimes \theta \mathbf \rho(x_{(1)})b) \\
&= s\circ\chi_\pi(\theta S(x)L(a\otimes b)) \\
&= \mathbf e(x)s\circ\chi_\pi\circ L(a\otimes b) \\
&=\mathbf e(x)\chi^\#(\bar\Psi(a),\bar\Psi(b))\\ \end{align*} where the third equality is from \corref{Lisomorphism}, and the fourth equality is due to the fact that $\chi_\pi$ is $\rho$-invariant Note that as a linear map $L\in\text{End}\,((M\otimes \mathcal E)_\pi\otimes(N\otimes \mathcal F)_\pi)$ is well defined as $F$ acts locally nilpotently on $ (M\otimes \mathcal E)_\pi$.
\subsection{} For any homomorphism $\beta$ of $_R\mathcal E^{s\Theta}\otimes _R(\mathcal F^{s\Theta})^{\mathbf \rho_1}$ into $F(\mathbf U)$, define another such $t(\beta)$ by the formula \begin{equation} t(\beta) = s \Theta^{-1}\circ \beta \circ L\circ (s\Theta_{_R\mathcal E}\otimes s\Theta_{_R\mathcal F}) \end{equation} where the $\Theta^{-1}$ on the left is assumed to be the module homomorphism defined on $F(\mathbf U)$.
\begin{thm} Let $\lambda=0$. Suppose $\chi$ is the induced pairing $\chi_{\beta,\phi}$ as defined in \eqnref{inducedpairing}, $\mathcal F_m$ and $\mathcal F_n$ are the $X$-graded finite dimensional $\mathbf U$-modules given in \secref{CG} and $\phi$ is a $\mathbf U$-invariant pairing satisfying $s\circ \phi_{\pi}\circ L=\phi\circ (\Psi\otimes \Psi)$. Then \begin{equation}\label{hardprop} t(\chi _{\beta,\phi}) = \chi_{\beta ,\phi}\ . \end{equation} \end{thm}
\subsection{} Fix a finite dimensional $\mathbf U$-module $\mathcal F$ with highest weight $v^n$ and let $M$ be the Verma module of highest weight $Tv^{-1}$. Recall from \cite[\S 2]{MR1327136}, the modules $P(m+\lambda):=P_{m+\lambda}$. Then we have the decomposition $M\otimes\mathcal F =\sum_iP(m+i)$ where the sum is over the nonnegative weights of $\mathcal F$ and by convention we set $P(m)=M(m)$. Set $P_i=P(m+i)$ and following the notation of [E,3.6] let $\mathbb Z_i$ equal the set of integers with the opposite parity to $i$. For $j\in \mathbb Z_\iota$ , set $z^i_j = \mathbf v_j + \mathbf v_{j,s}$. Then for $i\in \mathbb N^*$, the set $\{ [T;0] \mathbf v_j :j\in \mathbb Z_\iota\} \cup \{ z^i_j : j\in \mathbb Z_\iota\}$ is an $R$ basis for the localization $P_{i,F}$. Also the action of ${_R}\mathbf U_i$ is given by the formulas in \lemref{locstructure} as well as the formulas : for all indices $j\in \mathbb Z_\lambda $, \begin{align}
K_\mu \mathbf z_j&= T\, v^{\angles {\mu}{s\lambda-\rho-l_ji'}}\mathbf z_j ,\quad F \mathbf z_j = \mathbf z_{j-2}\label{eqn1} \\ E \mathbf z_j &= [l_j][T;-k_j] \mathbf z_{j+2} +[k_j-l_j][T;0]\mathbf w_{\lambda ,j+2}.\label{eqn2} \end{align}
The corresponding picture for $P_n$ of weight vectors for $P_n$ is given by
\[ \xymatrix{ & {\overbrace{\mathbf z_{n+1}}} \ar[d]\\ & \mathbf z_{n-1} \ar@/^/[u] \ar[d]\\ & {\vdots} \ar@/^/[u] \ar[d]\\ & \mathbf z_{-n-1}\ar@/^/[u] \ar[d]\\ \mathbf w_{-n-3,-n-1}\ar@/^/[ur] \ar[d] & {\overbrace{\mathbf z_{-n-3}}} \ar[d]\\ \mathbf w_{-n-5,-n-1} \ar@/^/[ur] \ar@/^/[u] \ar[d] & \mathbf z_{-n-5} \ar@/^/[u] \ar[d]\\ {\vdots} \ar@/^/[ur] \ar@/^/[u] & {\vdots} \ar@/^/[u] } \]
Fix a positive weight $v^r$ of $\mathcal F$ and let $P=P_r$. Set $\mathfrak L$ equal to the $m-r$th weight space of $P$. Then $\mathfrak L$ is a free rank two $R$-module with basis $\{\mathbf z^r_{-r-1},[T;0] \mathbf w_{r,-r-1}\}$. Define an $s$-linear map $\Gamma$ on $\mathfrak L$ and constants $a_{\pm r}$ by the formula: \begin{equation} \Gamma ([T;0] \mathbf w_{\epsilon r,-r-1}) = \Psi_F([T;0] \mathbf w_{\epsilon r,r+1}) = a_{\epsilon r}\ [T;0] \mathbf w_{-\epsilon r,-r-1}. \end{equation}
\def\overline{\overline}
This s-linear map $\Gamma$ is the mechanism by which we analyze the symmetries which arise through the exchange of $\mathfrak L\cap ([T;0]\cdot M(m+r))$ and $\mathfrak L\cap ([T;0]\cdot M(m-r))$. The following is a fundamental calculation for all which follows. Set $\overline{\Gamma}=[r]!\ \Gamma$.
\begin{lem} Let $\epsilon=\pm 1$. For $a,b\in \mathfrak L\cap M(m+\epsilon r)$, we have: $$ \chi^\sharp(\Gamma a,\Gamma b)=\frac{1}{ T^r [r]![T^{-\epsilon};r]_{(r)}}\ s\chi(a,b)\quad and \quad \chi^\sharp(\overline\Gamma a,\overline\Gamma b)=u_\epsilon\ s\chi(a,b), $$ where $u_\epsilon$ is a unit and $u_\epsilon\equiv 1 \mod (T-1)$.
\end{lem}
\subsection{} Now we recall to the delicate calculation of the constants $a_{\pm r}$.
\begin{lem}[\cite{MR2586983}] We may choose a basis for $P_r$ satisfying the relations \eqnref{eqn1} and \eqnref{eqn2}, dependent only on the cycle $\Psi$, and such that the constants $a_{\pm r}$ are uniquely determined by the three relations: \begin{align}
a_{-r}=s\ a_r, \quad a_r^2=\frac{1}{ [r]![T^{-1};r]_{(r)}} \quad \text{and} \quad a_r\equiv \frac{-1}{ [r]!} \mod T-1. \end{align}
\end{lem} \begin{cor} For $\epsilon=\pm$, $$ \overline\Gamma ([T;0] \mathbf w_{\epsilon r,-r-1}] = w_{r,\epsilon} [T;0] \mathbf w_{-\epsilon r,-r-1}\ , $$ where $w_{r,\epsilon}$ is the unit determined by conditions: \begin{equation} w_{r,\epsilon}^2=\frac{[r]!}{ [T^{-\epsilon};r]_{(r)}}\quad \text{and} \quad w_{r,\epsilon}\equiv -1-\epsilon\alpha (r)(T-1)\ \mod\ (T-1)^2\ . \end{equation}
Moreover $\overline\Gamma$ induces a $\mathbb C$-linear map on $\mathfrak L/ \ (T-1)\cdot \mathfrak L$ given by the matrix \begin{equation} \begin{pmatrix}
1&-\frac{\alpha (r)T(v-v^{-1})}{ (1+T)} \\ 0&1 \end{pmatrix} \end{equation} where $\alpha(r)=-\sum_{s=1}^r \frac{v^s+v^{-s}}{ v^s-v^{-s}}$. Moreover, if $x_\epsilon\in M(m+\epsilon r)$ and $[T;0]\cdot x_\epsilon$ is an $R$-basis vector for $\mathfrak L\cap M(m+\epsilon r)$ then $\{[T;0]\cdot x_\epsilon,x_\epsilon +\overline \Gamma x_ \epsilon\}$ is an $R$-basis for $\mathfrak L$ and $x_\epsilon+\overline \Gamma x_\epsilon$ generates the $\mathbf U_R $-submodule $P_r$. \end{cor}
\subsection{} To verify the correct choice of sign for the third identity we shall need some preliminary lemmas. Let $M^\prime$ denote the span of all the weight subspaces of $M$ other than the highest weight space. Let $\delta$ denote the projection of $M\otimes_R \mathcal F$ onto $w_{0,-1}\otimes \mathcal F$ with kernel $M'\otimes_R \mathcal F$. Define constants $c_\pm$ by the relations:
$\delta(w_{r,r-1})\equiv c_+ w_{0,-1}\otimes F^{(k)}f_n\mod \ M'\otimes _R\mathcal F$ and $\delta(w_{ -r,-r-1})\equiv c_- w_{0,-1}\otimes F^{(l)}f_n \mod \ M'\otimes_R\mathcal F$ where $n-2k-1=r-1$ and $n-2l-1=-r-1$. For any integer $t$ set $z_t=w_{0,-1}\otimes F^{(t)} f_n$. In a similar fashion define the projection $\delta^\vee$ of $M_F\otimes _R\mathcal F$ onto $w_{0,1}\otimes _R\mathcal F$ with kernel $M^\vee\otimes _R\mathcal F$ and $M^\vee$ equal to the span of all weight subspaces in $M_F$ for weights other than $m+1$.
\begin{lem} [\cite{MR2586983}] Set $$ A_t=\frac{[n-k+t]_{(t)}T^tv^{-t^2}}{ [t]!\ [T^{-1};t]_{(t)}} $$ then $$ w_{r,r-1}=c_+\sum_{0\le t\le k}A_t w_{0,-1-2t}\otimes F^{(k-t)}f_n. $$ \end{lem} \begin{proof} Note that $0=E\cdot w_{r,r-1}$ and solve the recursion relations in $A_t$. \end{proof}
\begin{lem} [\cite{MR2586983}] \begin{align} \delta^\vee(w_{r,r+1})=c_+\ \frac{v^{(n-k)(k+1)} [T^{-1};2k-n-1]_{(k)}}{ [T^{-1};k]_{(k)}} \ w_{0,1} \otimes F^{(k)} f_n, \\
-\frac{c_-}{ [l]!}\equiv \frac{c_+}{ [k]!}\mod T-1 \ \ \ \text{and} \quad \delta(\Psi w_{r,r+1})\equiv -c_-\ \frac{1}{ [r-1]!}\ z_l\mod\ \ (T-1)\cdot P_r. \end{align} \end{lem}
We now return to the proof of the congruence. Since $\Psi(w_{r,r-1})=-a_r w_{-r,-r-1}$ we can calculate the constant $a_r$ as the ratio of $\delta(\Psi(w_{r,r-1}))$ and $\delta( w_{-r,-r-1})$. From (4.4) we find the ratio is congruent to $\frac{-1}{ [r-1]}\mod T-1$. This completes the proof of Lemma 4.5.
\subsection{} Recall from \secref{automorphism} the category $_R\mathcal C_i$ and note that any module $N$ in the category is the direct sum of generalized eigenspaces for the Casimir element \cite{MR2586983} in the sense that $N=\sum N^{(\pm r)}$ where the sum is over $\mathbb N$ and $N^{(\pm r)}$ contains all highest weight vectors in $N$ with weights $m+r-1$ and $m-r-1$. Note that $N^{(\pm r)} $ need not be generated by its highest weight vectors. The decomposition in (4.2), $M\otimes_R\mathcal F\equiv \sum P_i$ where the sum is over the nonnegative weights of $\mathcal F_R$ is such a decomposition. In this case $(M\otimes _R\mathcal F)^{(\pm i)}= P_i$. The Casimir element $\Omega_0$ of $_R\mathbf U$ by \begin{equation}\label{quantumCasimir} \Omega_0 =F E + \frac{v\tilde K_i-2+v^{-1}\tilde K^{-1} }{( v-v^{-1})^2}. \end{equation}
Let $N^{(r)}$ (resp. $N^{(-r)}$) denote the submodule of $N$ where the Casimir element acts by the scalar \begin{align} c(\lambda)&=\frac{v^{r-1}T-2+v^{-r+1}T^{-1}}{( v-v^{-1})^2 }=[\sqrt{T};(r-1)/2]^2\ \\ c(s\lambda)&= \frac{v^{-r+1}T-2+v^{r-1} T^{-1}}{ ( v-v^{-1})^2}=[\sqrt{T};(-r+1)/2]^2 . \end{align}
\subsection{} We now turn to the general case where $\mathcal F$ is a finite dimensional ${_R}\mathbf U_i$-module but not necessarily irreducible. We extend the definition of the $s$-linear maps $\Gamma$ and $\overline \Gamma$ defined in \eqnref{} as follows. Decompose $M\otimes_R \mathcal F$ into generalized eigenspaces for the Casimir $(M\otimes_R \mathcal F)^{(\pm r)}$ and let $\mathfrak L^r$ denote the $m-r-1$ weight subspace of $(M\otimes_R \mathcal F)^{(\pm r)}$. Then set $\mathbb L=\sum \mathfrak L^r$. Decompose $\mathcal F=\sum \mathcal F_j$ into irreducible ${_R}\mathbf U_i$ modules. Then $M\otimes_R \mathcal F=\sum M\otimes_R \mathcal F_j$ and so we obtain $s$-linear extensions also denoted $\Gamma$ and $\overline \Gamma$ from $\mathbb L\cap (M\otimes_R \mathcal F_j)$ to all of $\mathfrak L$.
\begin{prop} [\cite{MR2586983}] Suppose $\phi$ is any invariant form on $M\otimes_R \mathcal F$ with $\phi = \pm \phi^\sharp$. Let $\{w_j, j\in J\}$ be an $R$-basis for the
highest weight space of $(M\otimes_R \mathcal F)^{(0)}$ and $\{u_i, i\in I\}$ a basis of weight vectors for the $E$-invariant weight spaces of weight $m+t$ for $t<-1$. Set $M_j$ equal to the ${_R}\mathbf U_i$-module generated by $w_j$ and $Q_l$ the ${_R}\mathbf U_i$-module generated by $(T-1)^{-1}(u_l+ \Gamma(u_l))$. Then $M\otimes_R \mathcal F=\sum_jM_j\oplus \sum_lQ_l$ where each $M_j\cong M(m)$ and if $U_l$ has weight $m-t$, then $Q_l\cong P(m+t)$. Moreover, if the basis vectors $w_j$ and $u_l$ are $\phi$-orthogonal then the sum is an orthogonal sum of ${_R}\mathbf U_i$-modules.
\end{prop}
\begin{prop}[\cite{MR2586983}] Suppose $\phi$ is any invariant form on $M\otimes_R \mathcal F$ with $\phi = \pm \phi^\sharp$. Then $M\otimes_R \mathcal F$ admits an orthogonal decomposition with each summand an indecomposible $\mathfrak a$-module and isomorphic to $M$ or some $P(m+t)$ for $t\in\mathbb N^*$. \end{prop}
\begin{proof} Since $R$ is a discrete valuation ring we may choose an orthogonal $R$-basis for the free $R$-module $\mathfrak L\cap (F_R\otimes M)^{(+)}$. \end{proof}
\section{Filtrations}
\subsection{} We continue with the notation of the previous section. So $\phi$ is an invariant form on $M\otimes_R \mathcal F=\sum_iP_i$. For any $R$-module $B$ set $\overline B=B/(T-1)\cdot B$ and for any filtration $B=B_0\supset B_1\supset ...\supset B_r$, let $\overline B=\overline B_0\supset \overline B_1\supset ...\supset \overline B_r$ be the induced filtration of $\overline B$, with $\overline B_i=(\overline B_i+(T-1)\cdot B)/ (T-1)\cdot B$.
Now $\phi$ induces a filtration on $F_R\otimes M$ by \begin{equation}
(M\otimes_R \mathcal F)^i=\{v\in M\otimes_R \mathcal F| \phi(v,M\otimes_R \mathcal F)\subset (T-1)^i\cdot R\}. \end{equation}
\subsection{}
Let $P=P_r$ and $\mathfrak L$ equal to the $m-r$th weight subspace of $P$. Suppose $P=P_0\supset P_1\supset ...\supset P_t=0$ is a filtration. Then choose constants $a,b$ and $c$ so that $a$ is maximal with $\overline P=\overline P_a$ , $b\ge a$ maximal with $\overline P_{a+1}/\overline P_b$ finite dimensional if such exist and otherwise set $b=a$and $c$ maximal with $\overline P_c\neq 0$. We say that the filtration is of type $(a,b,c)$.
\begin{lem} Set $\phi(w_{r,-r-1},w_{r,-r-1})=p$ and $\phi(w_{-r,-r-1},w_{-r,-r-1})=q$. Then on $\mathfrak L$, $\phi$ is represented with respect to the basis $\{w_{r,-r-1},(T-1)^{-1}(w_{r,-r-1}+w_{-r,-r-1})\}$ by the matrix:
$$ \begin{pmatrix} p&(T-1)^{-1}p\\ (T-1)^{-1}p& (T-1)^{-2}(p+q) \end{pmatrix} $$ with determinant $(T-1)^{-2}pq$. Suppose $p$ has order $d$ (i.e. $(T-1)^d$ divides $p$ and $(T-1)^{d+1}$ does not) and $q$ has order $d^\prime$. Then if $d\neq d^\prime$, the filtration is of type $(min\{d,d^\prime\}-2,d-1,max\{d,d^\prime\})$ and if $d=d^\prime$, the filtration is either of type $(d-1,d-1,d-1)$ or type $(d-2,d-1,d)$ depending as $p+q\equiv 0\ mod \ (T-1)^{d+1}$ or not. \end{lem}
\subsection{} Suppose $\phi^\sharp = \phi$ (resp. $-\phi$). In the first case we say $\phi$ is $\mathbb Z_2$-invariant and in the second skew invariant.
\begin{cor} Suppose $\phi^\sharp = \phi$ (resp. $-\phi$). and other notation is as in (5.2). Then if $d$ is even, $(P_r,\phi)$ has a filtration of type $(d-2,d-1,d)$ (resp. $(d-1,d-1,d-1)$ ) and if $d$ is odd $(P_r,\phi)$ has a filtration of type $(d-1,d-1,d-1)$ (resp. $(d-2,d-1,d)$).
\def\overline{\overline} \end{cor}
\subsection{} \begin{cor}
Suppose $\mathcal F$ is a finite dimensional $\mathbf U_i$-module and $\phi$ is an invariant form on $M\otimes_R \mathcal F$. Assume $\phi^\sharp = \phi$ (resp. $-\phi$) and let $M\otimes_R \mathcal F=B_0\supset B_1\supset ...\supset B_r$ be the filtration (5.1.1) and $\overline B_0\supset \overline B_1\supset ...\supset \overline B_r$ the induced filtration on $\overline{M\otimes_R \mathcal F}$. Then \begin{enumerate} \item {(i)} The $\mathbf U_i$-module $\overline B^i/\overline B^{i+1}$ is finite dimensional for $i$ odd (resp. even). \item {(ii)} The $\mathbf U_i$-module $\overline B^i/\overline B^{i+1}$ is both free and cofree as a $ k(v)[F]$-module, for $i$ even (resp. odd). \end{enumerate} \end{cor}
\subsection{} The symmetry of $\mathbb Z_2$-invariant and skew forms can be expressed in another form. Define the Jantzen sum of a filtration to be $\sum_i character(\overline B_i)$.
\begin{cor} Let notation and assumptions be as in (5.4). Then in both cases the Jantzen sum of the filtration is invariant by the Weyl group action on the characters which exchanges the characters of Verma modules $M(t)$ and $M(-t)$ for all $t\in \mathbb Z$.
\end{cor} \def(T-1)^{-1}\cdot{(T-1)^{-1}\cdot} \def\mathbb A{\mathbb A} \def\mathbb B{\mathbb B} \def\mathbb P{\mathbb P} \def\mathbb L{\mathbb L} \def\mathbb D{\mathbb D} \def\overline{\mathbb A}{\overline{\mathbb A}} \def\overline{\mathbb B}{\overline{\mathbb B}} \def\overline{\mathbb P}{\overline{\mathbb P}} \def\overline{\mathbb L}{\overline{\mathbb L}} \def\overline{\mathbb D}{\overline{\mathbb D}} \def\hookrightarrow{\hookrightarrow} \section{ Filtrations and Wall-crossing }
\subsection{}\label{P} Here we begin the study of the relationships of wall-crossing and the theory of induced and $\mathbb Z_2$-invariant forms. As in section four set $M$ equal to the Verma module with highest weight $Tv^{-1}$:i.e. $M=M(m)$. Then $M_\pi^{s\Theta}$ is isomorphic to $M$ itself and so we may choose a cycle $\Psi : M_F\to M$ which induces the isomorphism. For $a\in M, x\in \mathbf U_R, \ \Psi(sT_{i,-1}'(x)\cdot a)=x\cdot \Psi(a).$ Recall that $\Psi$ is not $R$ linear due to the role of $s$ in the previous formula. Let $\mathcal E$ denote the simple two dimensional $\mathbf U_i$-module and set $P=M\otimes_R\mathcal E$. Then $P$ is isomorphic to the basis module $P_1=P(m+1)$ as defined in \eqnref{eqn1} and \eqnref{eqn2}. Set $M_\pm=M(m\pm 1)$. Then the construction of $P$ gives inclusions and a short exact sequence: \begin{equation} (T-1)\cdot M_+\oplus (T-1)\cdot M_- \subset P\subset M_+\oplus M_- , \quad 0\to (T-1)\cdot M_+\to P\to M_- \to 0. \end{equation}
Let $\mathcal F$ be a finite dimensional $\mathbf U_i$-module and set $\mathbb A= (T-1)\cdot M_+\otimes _R\mathcal F\ , \quad \mathbb B=(T-1)\cdot M_- \otimes _R\mathcal F \ ,\quad \mathbb D=M_- \otimes _R\mathcal F\ ,\quad \mathbb P=P\otimes _R\mathcal F $. Then (6.1.1) gives:
\begin{equation}\label{ses3} \mathbb A\oplus \mathbb B\subset \mathbb P \subset (T-1)^{-1}(\mathbb A\oplus \mathbb B),\quad 0\to \mathbb A\to \mathbb P\ { \overset \Pi\to}\ \mathbb D\ra0 \end{equation}
\subsection{} We now turn to the study of the $s$-linear map $\Gamma$ defined in (4.2.2) and derived from the cycle $\Psi_\mathbb P=\Theta_{\mathcal F}\otimes \Theta_{\mathcal E}\otimes \Psi$. Decompose $\mathbb P$ into generalized eigenspaces for the Casimir $\mathbb P^{(\pm r)}$ and let $\mathfrak L^r$ denote the $Tv^{-r-1}$ weight subspace of $\mathbb P^{(\pm r)}$. Recall $\mathbb L=\sum \mathfrak L^r$. From (4.2.2) we obtain an $s$-linear map $\Gamma:\mathbb L\to \mathbb L$. \begin{lem} We have the following \begin{enumerate}[i).] \item $\Gamma$ restricts to an $s$-linear involutive isomorphism $\Gamma\ :\mathbb L\cap\mathbb A\cong \mathbb L\cap\mathbb B$. \item $\Gamma$ induces the identity map mod $T-1$; i.e. $\Gamma(e)\equiv e$ mod $(T-1)\cdot \mathbb L$. \item Suppose $\phi$ is any $\mathbb Z_2$-invariant (resp. skew invariant) form on $\mathbb P$. Then for all $e\in \mathbb L$, $\ \phi(\Gamma e, \Gamma e)=s\phi(e,e)$ (resp. $\ \phi(\Gamma e, \Gamma e)=-s\phi(e,e)$). \end{enumerate} \end{lem} \subsection{} As before for any ${_R}\mathbf U_i$-module $N$ we let $\overline N$ equal the quotient $N/T\cdot N$. From \eqnref{ses3} we obtain inclusions and a short exact sequence:
\begin{equation} \overline{\mathbb A} \subset \overline{\mathbb P},\quad\overline{\mathbb B} \subset \overline{\mathbb P},\quad 0\to \overline{\mathbb A}\to\overline{\mathbb P}\ \overset\Pi\to \overline{\mathbb D}\to 0\ . \end{equation} Now fix an invariant form $\phi$ on $\mathbb P$ and let superscripts denote the filtrations on $\mathbb P$,$\mathbb A ,\mathbb B$ and $\mathbb D$ induced by $\phi$ and the restrictions of $\phi$ to $\mathbb A\times \mathbb A$ , $\mathbb B\times \mathbb B$ and $\mathbb D\times \mathbb D$ respectively. Let superscripts on $\overline{\mathbb A},\overline{\mathbb B}$, $\overline{\mathbb D}$ and $\overline{\mathbb P}$ give the filtrations obtained by projecting. So $\overline{\mathbb A}^i=\mathbb A^i/(T-1)\cdot \mathbb A\cap \mathbb A^i$,etc.
The ${_R}\mathbf U_i$-module $\overline P$ is of course also an $\mathbf U_i$-module and it has simple socle $M(-1)$. So we find that the inclusions $M_\pm\hookrightarrow P$ induce an inclusion $\overline M_-\hookrightarrow \overline M_+$. In turn we obtain the inclusion $\overline{\mathbb B}\hookrightarrow \overline{\mathbb A}$. \begin{prop} Let $\pi$ denote the natural map $\pi:\mathbb P\to\overline{\mathbb P}$ and suppose $\phi$ is any $\mathbb Z_2$-invariant (resp. skew invariant) form on $\mathbb P$. Then $\pi(\mathbb L\cap\mathbb A)=\pi(\mathbb L\cap\mathbb B)$ and for each $i$, $\Gamma$ induces an $s$-isometry (resp. skew $s$-isometry)of $\mathbb L\cap \mathbb A^i$ onto $\mathbb L\cap \mathbb B^i$.
\end{prop} \begin{cor} For all $i$, $\overline{\mathbb A}^i\cap \pi(\mathbb L) =\overline{\mathbb B}^i\cap \pi(\mathbb L)$. \end{cor}
For any form $\phi$ on $\mathbb P$ we say $\phi$ is {\it weakly hereditary} whenever the identity of the corollary holds. We say $\phi$ is {\it hereditary} if for all $i$, $\overline{\mathbb A}^i\cap \mathbb B=\overline{\mathbb B}^i$.
\subsection{} The relationship between the filtrations of $\mathbb A$ and $\mathbb P$ is more delicate than that between $\mathbb A$ and $\mathbb B$. \begin{lem}
Assume that $\phi$ is induced from an invariant form on $P$. Then $\mathbb A$ and $\mathbb B$ are orthogonal submodules,and $\mathbb A^i\subset \mathbb P^{i-1}$ , $\mathbb B^i\subset \mathbb P^{i-1}$, and $ \Pi(\mathbb P^i)\subset \mathbb D^{i-1}$. Also $\mathbb D^i=(T-1)^{-1}\mathbb B^{i+2}$. \end{lem}
\begin{lem} Assume that $\phi$ is induced from an invariant form on $P$ and is $\mathbb Z_2$-invariant or skew invariant. Then $$ \mathbb L\cap\mathbb D^i\subset\Pi(\mathbb P^i)\quad \text{ and }\quad \overline{\mathbb L}\cap \overline{\mathbb P}^i\cap\overline{\mathbb A}\subset \overline{\mathbb A}^i\ . $$ \end{lem}
\section{Equivalence Classes of Forms}
\subsection{} In this section we describe explicitly all the equivalence classes of invariant forms on $B\otimes \mathcal E_R$ where $\mathcal E$ is the irreducible two dimensional ${_R}\mathbf U_i$-module and $B$ is one of the indecomposible modules $M(\mathbf U_R,m+b),\ b\in \mathbb Z$ or $P(\mathbf U_R,m+b),\ b\in \mathbb N^*$. Two invariant forms $\chi$ and $\chi^\rho$ on a $\mathbf U_R$-module $A$ are equivalent if there exists an $\mathbf U_R$-module automorphism $\kappa:A\to A$ with $\chi(a,b)=\chi^\rho(\kappa a,\kappa b)$.
For $n\in \mathbb N$ let $\phi_{\pm n}$ denote the Shapovalov form on $M({_R}\mathbf U_i,m\pm n)$ normalized by the identities: \begin{equation}\label{normalization} \phi_n(\mathbf v_{n,-n-1},\mathbf v_{n,-n-1})=1=\phi_{-n}(\mathbf v_{-n,-n-1},\mathbf v_{-n,-n-1}) \ . \end{equation}
{\bf Caution}: This is not the obvious normalization. But we will find it to be the most convenient. \begin{lem} The equivalence classes of invariant forms on $M(\mathbf U_R,m+n)$ (resp. $M(\mathbf U_R, m-n)$ are represented by the forms $\ \ T^r\cdot \phi_n,\ r\in \mathbb N^*$ (resp. $T^r\cdot \phi_{-n},\ r\in \mathbb N$).
\end{lem}
\subsection{} The indecomposible module $P_n=P(\mathbf U_R,m+n)$ was constructed as a submodule $P_n\subset M_n\oplus M_{-n}$ where we set $M_n=M(\mathbf U_R,m+n)$ and $M_{-n}=M(\mathbf U_R,m-n)$. Therefore any invariant form on $P$ is the restriction of the orthogonal sum of a form on $M_n$ and one on $M_{-n}$. For scalars $q$ and $r$ let $\phi_{n,q,r}=q\phi_n\oplus r\phi_{-n}$ denote such an orthogonal sum of forms. \begin{lem} \label{lemma1.1} The equivalence classes of invarant forms on $P_n$ are represented by the degenerate forms: $\phi_{_{n,T^b,0}}$ and $ \phi_{_{n,0,T^b}},\ b\in \mathbb N$ and the nondegenerate forms: $\phi_{_{n,T^l,uT^k}}$ where $u$ is nonzero complex number and $k,l\in \mathbb N$.
\end{lem} \begin{proof} Recall the automorphism $\kappa$ of $P_n$ determined by the units $u$ and $v$ with $u\equiv v$ mod $T$, as in the proof of
\lemref{lemma1.1}. Then by $\kappa$, we see that $\phi_{n,q,r}$ and $\phi_{n,u^2q,v^2r}$ are equivalent. Choose integers $k$ and $l$ and units $u_0$ and $v_0$ with $q=u_0t^k$ and $r=v_0T^l$. Let $c$ be the complex number which is the ratio of the constant term of $v_0$ by that of $u_0$. Then $r=v_1cT^l$ with $v_1$ a unit and $U_0\equiv v_1$ mod $T$. Choose square roots $u$ and $v$ with $u^2=u_0$,$v^2=v_1$ and $U\equiv v$ mod $T$. Then with $\kappa$ defined as above, we find that $ \phi_{n,q,r}$ is equivalent to $\phi_{n,T^k,cT^l}$. \end{proof} \subsection{} Suppose $\Psi$ is a cycle on $P_n$ and the basis is chosen as in Lemma and Corollary 4.3. Set $v_\pm=v_{\pm n,-n-1}$. Then $\overline\Gamma v_\pm=v_\mp$. \begin{lem} Suppose $\chi$ is an invariant form on $P_n$ which is also $\mathbb Z_2$-invariant. Then, for some $q\in R$, $\chi=\phi_{n,q,sq}$ and $\chi$ is equivalent to one of the $\mathbb Z_2$-invariant forms $\phi_{n,T^d,(-1)^dT^d}$, for $d\in \mathbb N$. \end{lem} \begin{proof} Choose $q$ and $r$ with $\chi=\phi_{n,q,r}$. Then $\mathbb Z_2$-invariance gives $r=sq$. Write $q=uT^d$ with $u$ a unit. Then $r=(-1)^dsu\ T^d$. Let $\kappa$ be the automorphism of $P_n$ which equals $u_1$ on $M(\mathbf U_R,m+n)$ and $su_1$ on $M(\mathbf U_R,m-n)$ where $u_1^2=u$. Then via $\kappa$, $\phi_{n,q,r}$ is equivalent to $\phi_{n,T^d,(-1)^dT^d}$. \end{proof}
Let us consider the identity
\begin{equation} \Theta\circ \beta(a\otimes b)=\beta(L (\Theta_{\mathcal E}a\otimes \Theta_{\mathcal E}b))\ . \end{equation} Here $\Theta$ on the left is assumed to be the module homomorphism. The motivation for this comes from \cite[5.3.4]{MR1227098}. Let $v\in (\mathcal E\otimes \mathcal F)^m$ be a highest weight vector, then $\beta(v)\in F(\mathbf U)^m$ is a highest weight vector. Then \begin{align*} \beta(L \circ(\Theta_{\mathcal E}\otimes \Theta_{\mathcal F})(F^{(j)}v))
& =\beta(\Theta_{\mathcal E\otimes \mathcal F}(F^{(j)}v)) =\beta((-1)^jv^{e(jh+j)}F^{(h)}v) \\
&=(-1)^jv^{e(jh+j)}F^{(h)}\beta(v) =T_{-1}'\beta(v) \end{align*} where $h+j=m$.
\begin{proof} Fix $m\in \mathbb N^*$ and let $D$ denote the $T+b-2m$ weight space in $\mathcal E_R\otimes M(\mathbf U_R,m+b)$. Set $\overline {\mathbf v}=\mathbf v_{b,b-1-2m}$. Then $D$ has basis $\{d_+,d_-\}$ where $d_+=E\otimes F\overline{\mathbf v},b_-=FK\otimes \overline{\mathbf v}$ and the form $\delta\otimes \phi_b$ on $D$ is given by: \begin{equation} \begin{pmatrix}
-1&0\\0&-m(T+b-m) \end{pmatrix} \phi_b(\overline v,\overline v). \end{equation}
Suppose $b\ne 0$. Then $\mathcal E_R\otimes M_b\equiv M_{b-1}\oplus M_{b+1}$ and if we look at the weight space $D$ for $m\ne b$ we conclude: $\delta\otimes \phi_b=q\phi_{b-1}+r\phi_{b+1}$ where both $q$ and $r$ equal $\phi_b(\overline {\mathbf v},\overline{\mathbf v})$ times a unit. Inturn this gives the formula for $b\ne 0$. For $b=0$ note that $\delta\otimes \phi_b$ is $\mathbb Z^2$-invariant and since $\mathcal E_R\otimes M_0\equiv P(\mathbf U_R,m+1)$, $\delta\otimes \phi_0=\phi_{1,q,sq}$ for some $q\in R$. Write $q=uT^d$ for some unit $u$. To determine the integer $d$ we need only compare the values of the forms on an $R$-basis vector for the highest weight space. But $\delta\otimes \phi_0(e_+\otimes\mathbf v_{0,-1}, e_+\otimes \mathbf v_{0,-1})=-\phi_0(\mathbf v_{0,-1},\mathbf v_{0,-1})=-1$. \end{proof}
\section{Change of Coordinates for Induced Forms}
\subsection{} We continue with the notation from the earlier sections.. Set $M$ (resp. $M_\pm$) equal to the $\mathbf U_R$-Verma module with highest weight $T-1$ (resp. $T,T-2$). Let $\phi$ and $\phi_\pm$ be the canonical invariant forms on these Verma modules. Let $\mathcal E $ (resp. $\mathcal F$) be an irreducible $\mathbf U_i$-module of dimension $d+1$ (resp. $d+2$). Then as $\mathbf B$-modules we have the short exact sequence: \begin{equation}\label{nonsplit} 0\to \mathcal E \otimes R_{T}\to \mathcal F\otimes R_{T-1}\to R_{T-d-1}\to 0\ . \end{equation} Inducing up to $\mathbf U_R$ we obtain: \begin{equation} 0\to \mathcal E_R \otimes M_+\to \mathcal F_R\otimes M\to M(\mathbf U_R,T-d)\to 0\ . \end{equation} From \cite{} we know that restriction from $\mathcal E_R\otimes M(\mathbf U_R,T+b)$ to $\mathcal E_R \otimes R_{T+b-1}$ gives an isomorphism of $\mathbf U_R$-invariant forms on $\mathcal E_R \otimes M(\mathbf U_R,T+b)$ to $\mathbf U_0$-invariant forms on $\mathcal E_R\otimes R_{T+b-1}$. Since \eqnref{nonsplit} splits as an $\mathbf U_0$-module, each $\mathbf U_0$-invariant form on $\mathcal E_R \otimes R_{T}$ can be extended uniquely to $\mathcal F_R\otimes R_{T-1}$ with it equaling zero on the weight space for $T-d-1$. With this convention we obtain a map $\phi _{\mathcal E}$ from invariant forms on $\mathcal E _R\otimes M_+$ to those on $ \mathcal F_R\otimes M$.
\subsection{} Fix a nonnegative integer $d$ and suppose $\beta$ is an $\mathbf U_R$-module homomorphism $\beta:\mathcal E _R^\Theta \otimes \mathcal E _R\to\mathbf U_R$ with image equal to the irreducible with highest weight vector $E^{(d)}$ and normalized so that $\beta(f_d \otimes f_{-d})=\text{ad}(F^{(d)})(E^{(d)})$. Normalize the basis of $\mathcal E _R$ by setting $\overline f_{d-2j}= \frac{1}{ j!} f_{d-2j}$. Then $\Theta_{\mathcal E}(\overline f_{d-2j})=(-1)^d \overline f_{-d+2j}.$
\begin{lem}\label{lastlemma} Let $\gamma$ be the invariant form on $M_b=M(\mathbf U_R,T+b+1)$ normalized by $\gamma(v_{b-1,b},v_{b-1,b})=1$ and $\chi_{\beta,\gamma}$ the induced form on ${\mathcal E}_R\otimes M_b$. For $0\le j\le d$, define complex constants by $\beta(\Theta_{\mathcal E} f_{d-2j}\otimes f_{d-2j})=c_j\ \beta(f_d \otimes f_{-d})$ and define $p_d\in \mathbf U_0$ by $p_d(T)= \prod_{1\le t\le d} \qbinom{T;d-2t}{2t}$. Then with respect to the basis $\overline f_{d,d-2j}\otimes 1$, the restriction of the induced form $\chi_{\beta,\phi}$ to $\mathcal E_R\otimes R_{T+b}$ is given by the diagonal matrix \begin{equation}\label{matrixexp} \begin{pmatrix} c_0& & \\ &\ddots & \\ & & c_d \end{pmatrix} p_c(T+b). \end{equation}
Moreover, the constants have the symmetry: $c_{d-j}=(-1)^dc_j,\ 0\le j\le d$.
\end{lem} \begin{proof} Let $\pi$ be the projection of ${_R}\mathbf U_i$ onto $\mathbf U_0$ which is zero on $F\cdot \mathbf U_i+\mathbf U_i\cdot E$. First we evaluate $\pi \beta(f_d\otimes f_{-d})$. Since \begin{equation} \text{ad} F^{(p)}(E^{(d)}_j)=E^{(d)}_{j+p},\end{equation} by \eqnref{irred}, we conclude using \eqnref{hw1} \begin{equation} \text{ad}(F^{(d-2j)})E^{(d-2j)} =\qbinom{T;d-2j}{ d}E^{(d-2j)}, \end{equation} that \begin{align} \beta\pi(\text{ad}(F^{(d-2j)})(E^{(d-2j)}))= \qbinom{T;d-2j}{ d-2j} \end{align}
Now to obtain the matrix expression in \eqnref{matrixexp} we observe \begin{align*} \chi_{\beta,\gamma}(\overline f_{d-2j}\otimes 1,\overline f_{d-2j}\otimes 1)= \beta(\Theta_{\mathcal E}\overline f_{d-2j}\otimes \overline f_{d-2j})\cdot 1_{T+b} &=c_j \prod_{1\le t\le d} \qbinom{T;d-2t}{2t}. \end{align*}
Finally regarding the symmetry, $\beta\circ (\Theta_{\mathcal E}\otimes \Theta_{\mathcal E})=\Theta \circ \beta$. So by the basis given in \secref{basisandsymmetries}, gives us \begin{align*} (-1)^dc_j\beta(\overline f_d\otimes \overline f_{-d})&= \Theta\beta(\Theta_{\mathcal E} \overline f_{d-2j}\otimes \overline f_{d-2j})= \beta(\Theta_{\mathcal E}^2\overline f_{d-2j}\otimes \Theta_{\mathcal E} \overline f_{d-2j}) \\ &=\beta(\Theta_{\mathcal E}\overline f_{-d+2j}\otimes \overline f_{-d+2j})=c_{d-j} \beta(\overline f_d\otimes \overline f_{-d}).\notag \end{align*} This gives the symmetry of the constants and completes the proof. \end{proof}
Let $\mathbb D$ denote the diagonal matrix with constants $c_j$ on the diagonal. Then \lemref{lastlemma} asserts that the induced form $\chi_{\beta,\gamma}$ is determined by the matrix $\mathbb D\cdot p_d(T+b)$. We shall call $\mathbb D$ the coefficient matrix associated to $\beta$ and $\mathbb D\cdot p_d(T+b)$ the full matrix associated to the form $\chi_{\beta,\gamma}$.
We plan on describing the coefficient matrix for particular cases in a future publication.
\section{Aknowledgements} The first author has been supported in part by a Simons Collaboration Grant \#319261. The second author has been supported in part by NSF Grant DMS92-06941.
\def$'${$'$}
\end{document} | arXiv |
Filters: Author is Gimzewski, JK [Clear All Filters]
Naranjo, B., Gimzewski, J. K. & Putterman, S. E. T. H. Observation of nuclear fusion driven by a pyroelectric crystal. Nature 434, 1115–1117 (2005).
Gimzewski, J. K., Berndt, R. & Schlittler, R. R. Observation of the temporal evolution of the (1 times 2) reconstructed Au (110) surface using scanning tunneling microscopy. Journal of Vacuum Science and Technology. B, Microelectronics Processing and Phenomena;(United States) 9, (Submitted).
Gimzewski, J. K., Berndt, R. & Schlittler, R. R. Observation of the temporal evolution of the (1$\times$ 2) reconstructed Au (110) surface using scanning tunneling microscopy. Journal of Vacuum Science & Technology B 9, 897–901 (1991).
Jung, T., Schlittler, R., Gimzewski, J. K. & Himpsel, F. J. One-dimensional metal structures at decorated steps. Applied Physics A 61, 467–474 (1995).
Gimzewski, J. K., Affrossman, S., Gibson, M. T., Watson, L. M. & Fabian, D. J. Oxidation of scandium by oxygen and water studied by XPS. Surface Science 80, 298–305 (1979).
Schmit, J., Reed, J., Novak, E. & Gimzewski, J. K. Performance advances in interferometric optical profilers for imaging and testing. Journal of Optics A: Pure and Applied Optics 10, 064001 (2008).
Gimzewski, J. K., VATEL, O. & Hallimaoui, A. Ph. DUMAS*, M. GU*, C. SYRYKH*, F. SALVAN*,* GPEC, URA CNRS 783, Fac. de Luminy, 13288, Marseille Cedex 9, France. Optical Properties of Low Dimensional Silicon Structures: Proceedings of the NATO Advanced Research Workshop, Meylan, France, March 1-3, 1993 244, 157 (1993).
Berndt, R. R. J. K. B. R. R. W. D. M. et al. Photon emission at molecular resolution induced by a scanning tunneling microscope. Science 262, 1425–1427 (1993).
Coombs, J. H., Gimzewski, J. K., Reihl, B., Sass, J. K. & Schlittler, R. R. Photon emission experiments with the scanning tunnelling microscope. Journal of Microscopy 152, 325–336 (1988).
Berndt, R. et al. Photon emission from adsorbed C60 molecules with sub-nanometer lateral resolution. Applied Physics A 57, 513–516 (1993).
Berndt, R., Gimzewski, J. K. & Schlittler, R. R. Photon emission from nanostructures in an STM. Nanostructured Materials 3, 345–348 (1993).
Berndt, R., Gimzewski, J. K. & Schlittler, R. R. Photon emission from small particles in an STM. Zeitschrift für Physik D Atoms, Molecules and Clusters 26, 87–88 (1993).
Berndt, R., Schlittler, R. R. & Gimzewski, J. K. Photon emission processes in STM. AIP Conf Proceedings 241, 328–336 (1992).
Berndt, R., Schlittler, R. R. & Gimzewski, J. K. Photon emission scanning tunneling microscope. Journal of Vacuum Science & Technology B 9, 573–577 (1991).
Gimzewski, J. K., Reihl, B., Coombs, J. H. & Schlittler, R. R. Photon emission with the scanning tunneling microscope. Zeitschrift für Physik B Condensed Matter 72, 497–501 (1988).
Dumas, P. et al. Photon spectroscopy, mapping, and topography of 85% porous silicon. Journal of Vacuum Science & Technology B 12, 2064–2066 (1994).
Dumaks, P. et al. Photon Spectroscopy, Mapping, and Topography of 85-Percent Porous Silicon. Journal of Vacuum Science & Technology B 12, 2064–2066 (1994).
McKinnon, A. W., Welland, M. E., Wong, T. M. H. & Gimzewski, J. K. Photon-emission scanning tunneling microscopy of silver films in ultrahigh vacuum: A spectroscopic method. Physical Review B 48, 15250 (1993).
Joachim, C., Gimzewski, J. K. & Tang, H. Physical principles of the single-C 60 transistor effect. Physical Review B 58, 16407 (1998).
Humbert, A., Gimzewski, J. K. & Reihl, B. Postannealing of coldly condensed Ag films: Influence of pyridine preadsorption. Physical Review B 32, 4252 (1985).
Welland, M. E., Miles, M. J. & Gimzewski, J. K. Probe Microscopy: Editorial. Probe Microscopy 1, 1–1 (1997).
Veprek, S. et al. Properties of microcrystalline silicon. IV. Electrical conductivity, electron spin resonance and the effect of gas adsorption. Journal of Physics C: Solid State Physics 16, 6241 (1983).
Sass, J. K. & Gimzewski, J. K. Proposal for the simulation of electrochemical charge transfer in the scanning tunneling microscope. Journal of electroanalytical chemistry and interfacial electrochemistry 251, 241–245 (1988).
Gimzewski, J. K., Padalia, B. D., Affrossman, S., Watson, L. M. & Fabian, D. J. The reaction of oxygen and water with iron films studied by X-Ray photoelectron spectroscopy. Surface Science 62, 386–396 (1977).
Padalia, B. D. et al. The reactions of oxygen and water with the rare-earth metals terbium to lutetium studied by x-ray photoelectron spectroscopy. Surface Science 61, 468–482 (1976).
Cuberes, M. T., Schlittler, R. R. & Gimzewski, J. K. Room temperature supramolecular repositioning at molecular interfaces using a scanning tunneling microscope. Surface science 371, L231–L234 (1997).
Gimzewski, J. K. Scanning tunneling and local probe studies of fullerenes. NATO ASI Series E Applied Sciences-Advanced Study Institute 316, 117–138 (1996).
Gimzewski, J. K., Humbert, A., Pohl, D. W. & Vepfek, S. A SCANNING TUNNELING MICROSCOPIC (STM) STUDY OF THE SURFACE TOPOGRAPHY OF PLASMA-DEPOSITED NANOCRYSTALLINE SILICON. (1985).
Gimzewski, J. K. Scanning tunneling microscopy. Le Journal de Physique IV 3, C7–41 (1993).
Cuberes, M. T., Schlittler, R. R., Jung, T. A., Schaumburg, K. & Gimzewski, J. K. A scanning tunneling microscopy investigation of 4, 4′-dimethylbianthrone molecules adsorbed on Cu (111). Surface science 383, 37–49 (1997).
Gimzewski, J. K., Jung, T. A., Cuberes, M. T. & Schlittler, R. R. Scanning tunneling microscopy of individual molecules: beyond imaging. Surface science 386, 101–114 (1997).
Gimzewski, J. K., Stoll, E. & Schlittler, R. R. Scanning tunneling microscopy of individual molecules of copper phthalocyanine adsorbed on polycrystalline silver surfaces. Surface Science 181, 267–277 (1987).
Gimzewski, J. K., Humbert, A., Pohl, D. W. & Veprek, S. Scanning tunneling microscopy of nanocrystalline silicon surfaces. Surface Science 168, 795–800 (1986).
Gimzewski, J. K., Modesti, S., David, T. & Schlittler, R. R. Scanning tunneling microscopy of ordered C60 and C70 layers on Au (111), Cu (111), Ag (110), and Au (110) surfaces. Journal of Vacuum Science & Technology B 12, 1942–1946 (1994).
Gimzewski, J. K. & Humbert, A. Scanning tunneling microscopy of surface microstructure on rough surfaces. SPIE MILESTONE SERIES MS 107, 249–249 (1995).
Gimzewski, J. K. & Humbert, A. Scanning tunneling microscopy of surface microstructure on rough surfaces. IBM journal of research and development 30, 472–477 (1986).
Gimzewski, J. K., Berndt, R. & Schlittler, R. R. Scanning-tunneling-microscope study of antiphase domain boundaries, dislocations, and local mass transport on Au (110) surfaces. Physical Review B 45, 6844 (1992).
Hofmann, F. et al. Scrape-off measurements during Alfvén wave heating in the TCA tokamak. Journal of Nuclear Materials 121, 22–28 (1984).
Gimzewski, J. K., Humbert, A., Bednorz, J. G. & Reihl, B. Silver films condensed at 300 and 90 K: scanning tunneling microscopy of their surface topography. Physical review letters 55, 951 (1985).
Schlittler, R. R. et al. Single crystals of single-walled carbon nanotubes formed by self-assembly. Science 292, 1136–1139 (2001).
Schaffner, M. - H. et al. Size-dependent light emission from mass-selected clusters. The European Physical Journal D-Atomic, Molecular, Optical and Plasma Physics 2, 79–82 (1998).
Sass, J. K. & Gimzewski, J. K. Solvent dynamical effects in scanning tunneling microscopy with a polar liquid in the gap. Journal of electroanalytical chemistry and interfacial electrochemistry 308, 333–337 (1991).
Langlais, V. J. et al. Spatially resolved tunneling along a molecular wire. Physical review letters 83, 2809 (1999).
Modesti, S., Gimzewski, J. K. & Schlittler, R. R. Stable and metastable reconstructions at the C sub 60/Au (110) interface. Surf. Sci.(The Netherlands) 331, 1129–1135 (1994).
Modesti, S., Gimzewski, J. K. & Schlittler, R. R. Stable and metastable reconstructions at the C< sub> 60/Au (110) interface. Surface science 331, 1129–1135 (1995).
Cuberes, M. T., Schlittler, R. R. & Gimzewski, J. K. Supramolecular assembly of individual C 60 molecules on a monolayer of 4, 4′-dimethylbianthrone molecules. Applied Physics A: Materials Science & Processing 66, S745–S748 (1998). | CommonCrawl |
What are the derivatives of common functions?
trigonometric
asked Sep 12, 2022 in Mathematics by ♦Gauss Diamond (71,587 points) | 59 views
1. Constant Rule: \(\frac{d}{d x}(c)=0\), where \(c\) is a constant.
2. Power Rule: \(\frac{d}{d x}\left(x^n\right)=n x^{n-1}\), where \(n\) is an integer, \(n>0\).
3. \(\frac{d}{d x}(\sin x)=\cos x\)
4. \(\frac{d}{d x}(\cos x)=-\sin x\)
5. \(\frac{d}{d x}\left(e^x\right)=e^x\)
6. \(\frac{d}{d x}(\ln x)=\frac{1}{x}\)
answered Sep 12, 2022 by ♦Gauss Diamond (71,587 points)
post related question
What are the derivatives of sine and cosine functions?
What are the derivatives of common trigonometric functions?
What are the derivatives of some of the trigonometric functions?
\(\mathrm{T} / \mathrm{F}\) : The derivatives of the trigonometric functions that start with "c" have minus signs in them.
Prove these trig expressions
asked Jan 24 in Mathematics by ♦Gauss Diamond (71,587 points) | 7 views
Solve for \(x\) if \(\sin \left(x+30^{\circ}\right)=-0,2\) where \(x \in\left(-180^{\circ} ; 0^{\circ}\right)\)
Solve the equation \[ \sin 9^{\circ} \sin 21^{\circ} \sin \left(102^{\circ}+x\right)=\sin 30^{\circ} \sin 42^{\circ} \sin x \]
asked Dec 8, 2022 in Mathematics by ♦MathsGee Platinum (163,814 points) | 13 views
\(\dfrac{\cos \theta-\cos 2 \theta+2}{3 \sin \theta-\sin 2 \theta}=\dfrac{1+\cos \theta}{\sin \theta}\)
asked Aug 15, 2022 in Mathematics by ♦Gauss Diamond (71,587 points) | 59 views
derive
If \(\sin ^{6} \theta+\cos ^{6} \theta=\frac{1}{4}\) then \(\frac{1}{\sin ^{6} \theta}+\frac{1}{\cos ^{6} \theta}=?\)
asked Jul 25, 2022 in Mathematics by ♦MathsGee Platinum (163,814 points) | 79 views
Solve \(\cos \left(2^{\circ}\right) \sin \left(8^{\circ}\right) \cos \left(14^{\circ}\right) \sin \left(20^{\circ}\right) \ldots \sin \left(80^{\circ}\right) \cos \left(86^{\circ}\right)\)
asked Jul 22, 2022 in Mathematics by ♦Gauss Diamond (71,587 points) | 80 views
If \(\sin ^{2} \theta+\sin \theta=1\), then find \(\cos ^{4} \theta+\cos ^{2} \theta\)
Solve the trigonometric equation \(\sin \left(x-30^{\circ}\right)=\cos 2 x\)
asked Jun 16, 2022 in Mathematics by ♦Gauss Diamond (71,587 points) | 62 views
Solve the following equation: $2^{3^{x}}=10$
asked May 10, 2021 in Mathematics by ♦MathsGee Platinum (163,814 points) | 137 views
Solve $2^{x} \cdot 3^{x+1}=10$
asked May 6, 2021 in Mathematics by Student SIlver Status (11,376 points) | 98 views
Solve the trigonometric equation $2\cos{(\dfrac{3}{10}x)} - 3\sin{(\dfrac{1}{2}x)}=0$
asked Apr 12, 2021 in Mathematics by ♦MathsGee Platinum (163,814 points) | 233 views | CommonCrawl |
Detailed methodology information
Concepts, sources and methods
Australian System of National Accounts: Concepts, Sources and Methods
2020-21 financial year
Chapter 19 Productivity measures
Annex C Measurement of the income tax parameter
Print current page
Print all pages
Australian System of National Accounts: Concepts, Sources and Methods, 2020-21 financial year
Chapter 2 Overview of the conceptual framework
Chapter 3 Stocks, flows, and accounting rules
Chapter 4 Institutional units and sectors
Chapter 5 Producing units, products and industries
Chapter 6 Price and volume measures
Chapter 7 Annual benchmarks and quarterly estimates
Chapter 8 Gross Domestic Product
Chapter 9 Gross Domestic Product - Production approach (GDP(P))
Chapter 10 Gross Domestic Product – Expenditure approach (GDP(E))
Chapter 11 Gross Domestic Product - Income approach (GDP(I))
Chapter 12 The production account
Chapter 13 The income account
Chapter 14 The capital account
Chapter 15 The financial accounts
Chapter 16 The other changes in the volume of assets account
Chapter 17 The balance sheet
Chapter 18 External account
Data sources and methods
Accuracy, quality and reliability of productivity measures
Annex A Growth accounting framework
Annex B Compiling quality-adjusted labour input indexes
Chapter 20 Analytical measures
Chapter 21 State accounts
Chapter 22 Input output tables
Chapter 23 Satellite accounts
Chapter 24 Quality of the National Accounts
Appendix 1 Classifications
Appendix 2 Differences between ASNA and 2008 SNA
Appendix 3 Links between business accounts and national accounts
Appendix 4 Changes in this addition
Australian System of National Accounts: Concepts, Sources and Methods Archive release Reference Period 2015
19C.1 The income tax parameter,\(T_{ijt}\) allows for the variation of income tax allowances according to different industries, asset types, and variations in allowances over time. Changes in corporate profit taxes over time are also allowed for. Corporate taxes aside, these provisions increase the after-tax returns on investment and lower the rental price of capital. For each industry \(i\), and asset type \(j\), \(T_{ijt}\) is expressed as:
\(\large {T_{ijt}} = \frac{{1 - {u_t}{z_{ijt}} - {u_t}{a_{ijt}}}}{{1 - {u_t}}}\)
\(u_t\) = the corporate profit tax rate;
\(Z_{ijt}\) = the present discounted value of one dollar of depreciation allowances; and
\(a_{ijt}\) = the additional allowance rate.
19C.2 The tax parameter reflects the differing tax circumstances that owners of capital face. The method adopted by ABS follows Jorgenson\(¹⁰²\) and Hall and Jorgenson¹⁰³ ¹⁰⁴ and reflects changes to:
tax concessions;
write off periods (i.e. tax lives);
deductions allowable;
allowable capital expenditure;
special allowances; and
amortisation of capital.
19C.3 For example, allowance is made for the differing depreciation and additional allowances available to specific industries and asset types over time. These allowances tended to be more generous in the Agriculture, forestry and fishing, Mining, and Manufacturing industries, especially for certain types of equipment. In addition, the Australian Taxation Office (ATO) allowed for faster depreciation rates over time through shorter effective tax lives. Since 1985, various research and development (R&D) tax concessions have been introduced to encourage increased investment in R&D by Australian companies. These concessions have had the effect of reducing rental prices on R&D considerably.
19C.4 The Corporate Profit Tax Rates (\(u\)) are obtained from the ATO website.
19C.5 The depreciation allowance (\(z\)) is the present discounted value (PDV) of the stream of deductions multiplied by the marginal tax rate applicable in that year. Asset lives and a nominal discount rate are used to determine the present discounted value of depreciation allowances. Prior to 1980, the average asset lives used to calculate capital stock for each asset type are used. After 1980, the asset life consistent with the shortest life within broad asset life bands specified by the ATO is used. Broad banding reduces the effective life of the asset. The nominal discount rate is based on the business overdraft rate published in the Reserve Bank Bulletin. It assumes that the business overdraft rate applies to all borrowers for investment in equipment or structures and contains a risk premium (over and above government bonds).
19C.6 Specific rulings on eligible depreciation allowances are obtained from the Master Tax Guides (MTG), ATO rulings published online, and Commonwealth Budget Papers. Of the two depreciation schedules permitted, the diminishing value method has been chosen. Prior to 10 May 2006, it allowed software and machinery and equipment assets to be geometrically depreciated at 150 per cent of the straight-line rate (the other schedule permitted). From 10 May 2006, the government introduced a 200 per cent diminishing balance rate for eligible new plant and equipment assets.
19C.7 From 1980, broad banded depreciation rates were introduced, allowing assets with effective lives over a particular band of years to depreciate at a certain rate. In 1996, for example, assets with a life of 0-3 years could be depreciated immediately, and assets with a life of 3 to 5 years could be depreciated at a prime cost rate of 40 per cent of its purchase price.
19C.8 In addition to broad banding, the Commonwealth Government allowed a loading factor of between 18 per cent and 20 per cent from 1990, depreciating some assets more quickly. Most equipment except motor vehicles was permitted to use loading factors.
19C.9 Double depreciation allowances were permitted for most assets for the period in 1974-76. Between 1 July 1974 and 30 June 1976, companies were allowed to depreciate new investment excluding motor vehicles at twice the stated rates. Once purchased, the asset continued to be depreciated at these accelerated rates until completely depreciated. We treat this by doubling the loading factor which has the effect of doubling the depreciation rate.
19C.10 In 1980, the Commonwealth Government permitted a separate allowance for buildings. Depending on the year, a straight-line allowance of 2.5 per cent or 4 per cent was permitted. This allowance is treated in the same way as depreciation allowance in the tax parameter.
19C.11 On 1 July 2001, the government introduced the 'uniform capital allowances regime'. This regime replaced the special capital allowance provisions for the Mining industry. The regime applied to all depreciable assets except where specific provisions apply to R&D activities, investments in Australian films, or cars.
19C.12 In 2002, statutory effective life caps were introduced, allowing an accelerated depreciation for certain types of equipment. Specifically, statutory life caps halved the effective tax lives of aircraft (to 10 years) and buses and trucks (larger than 3.5 tonnes) to 7.5 years.
19C.13 Depreciation rates are applied to purchased (packaged) software, customised, and in-house software combined. MTG defines in-house software as: computer software, or a right to use such software, that is acquired, developed or commissioned, and that is mainly for the taxpayer to use in performing the functions for which the software was developed (i.e. not for resale). From May 1998, acquiring, developing or commissioning software is depreciable at 40 per cent per annum, so that the asset life is 2.5 years.
Non-dwelling construction
19C.14 The effective lives of 'industrial' buildings and 'non-industrial' buildings are 25 years and 40 years respectively.
Non-depreciable assets
19C.15 For land and inventories, the effective life does not apply to these capital assets as they are not subjected to depreciation resulting from production.
Additional allowance rate
19C.16 The additional allowance rate (\(a\)) is an immediate write-off which results in tax savings (i.e. discounting is not required). The value of an allowance is the tax savings which is the product of the tax rate and the rate of the allowance. For example, if the allowance rate is 50 per cent and the profit tax rate is 30 per cent, then the company effectively saves 15 per cent of the purchase price of the asset in tax savings (\(30\%×50\% =u×a\)). Most equipment types have attracted an allowance of some kind.
19C.17 There are general allowances across all industries and special allowances. Special allowances vary widely according to asset type and time period. In 1996, for example, purchasers of machinery and equipment (other than motor vehicles) were permitted to deduct an additional ten per cent in the purchase year.
19C.18 Pro rata adjustments are made to align the dates of the tax law with the financial year, assuming that investment occurred evenly over the tax year. This leads to determining pro rata depreciation rates based on the portion of the year covered.
19C.19 Some allowances may have not been taken into consideration because of the assets eligible may be at a finer detail than assets classes to which tax parameters can be assigned (i.e. the asset classification in the Perpetual Inventory Model), or because further research was needed. The ABS welcomes comments which may assist in improving the accuracy and fitness-for-purpose of tax parameters.
Film tax concessions
19C.20 According to the MTG 2011, three types of film concession were available in 2010-11. Since a film's eligibility for tax concessions is limited to one of the concession types, the 'additional allowance rate' for film has been set at 15 per cent, which is the lowest available concession rate.
19C.21 Since 1985, tax incentives have been available to encourage increased investment in research and development (R&D) by Australian companies. Up until 2010-11, the 'R&D Tax Concession' program was in place. The most recent elements of the R&D Tax Concession included:
An enhanced rate of tax deduction at 125 per cent of eligible expenditure incurred on Australian R&D activities of at least $20,000. Eligible R&D expenditures included salaries and wages to company employees associated with the R&D activities, along with expenditure on materials used and an allowance for the decline in value of capital equipment used in R&D.
A premium 175 per cent rate of tax deduction applied to the amount of R&D expenditure that exceeds a given company's average expenditure over the previous 3 years.
19C.22 This tax concession scheme had been treated as a general allowance for all industries. Between 1985 and 2011, the allowance in (a) ranged from 125 to 150 per cent.
19C.23 From July 1, 2011, the 'R&D Tax Concession' was replaced by the 'R&D Tax Incentive'. The R&D Tax Incentive aims to encourage companies to engage in R&D activities where the knowledge gained is likely to benefit the wider Australian economy. The two key components of the R&D tax incentive are:
A 45 per cent refundable tax offset (equivalent to a 150 per cent deduction at a 30 per cent company income tax rate) on Australian R&D activities of at least $20,000 for companies with an aggregated turnover of less than $20 million per annum. Companies can receive a cash refund for income years where a tax loss is recorded.
A non-refundable 40 per cent tax offset (equivalent to a 133 per cent deduction at a 30 per cent company income tax rate) to all other companies, allowing for unused offset amounts to be carried forward for use in future income years.
19C.24 Effectively, the treatment of the tax parameter is the same for both schemes. The ABS estimates that most R&D spending will fall into (d), attracting the 40 per cent tax offset.
Jorgenson, D. W. (1963). Capital theory and investment behavior. The American Economic Review, 53(2), 247-259.
Hall, R. E., & Jorgenson, D. W. (1967). Tax policy and investment behavior. The American Economic Review, 57(3), 391-414.
Jorgenson, D., Hall, R. E. (1971). Application of the theory of optimum capital accumulation. In G. Fromm (Ed.), Tax incentives and capital spending (pp. 9-60). Washington: The Brookings Institution
Book traversal links for Annex C Measurement of the income tax parameter
Previous page Annex B Compiling quality-adjusted labour input indexes
Next page Chapter 20 Analytical measures | CommonCrawl |
Direct observation of one-dimensional disordered diffusion channel in a chain-like thermoelectric with ultralow thermal conductivity
Jiawei Zhang ORCID: orcid.org/0000-0003-0740-08511,
Nikolaj Roth1,
Kasper Tolborg ORCID: orcid.org/0000-0002-0278-115X1,
Seiya Takahashi2,
Lirong Song1,
Martin Bondesgaard1,
Eiji Nishibori ORCID: orcid.org/0000-0002-4192-65772 &
Bo B. Iversen ORCID: orcid.org/0000-0002-4632-10241
Nature Communications volume 12, Article number: 6709 (2021) Cite this article
Structure of solids and liquids
Structural disorder, highly effective in reducing thermal conductivity, is important in technological applications such as thermal barrier coatings and thermoelectrics. In particular, interstitial, disordered, diffusive atoms are common in complex crystal structures with ultralow thermal conductivity, but are rarely found in simple crystalline solids. Combining single-crystal synchrotron X-ray diffraction, the maximum entropy method, diffuse scattering, and theoretical calculations, here we report the direct observation of one-dimensional disordered In1+ chains in a simple chain-like thermoelectric InTe, which contains a significant In1+ vacancy along with interstitial indium sites. Intriguingly, the disordered In1+ chains undergo a static-dynamic transition with increasing temperature to form a one-dimensional diffusion channel, which is attributed to a low In1+-ion migration energy barrier along the c direction, a general feature in many other TlSe-type compounds. Our work provides a basis towards understanding ultralow thermal conductivity with weak temperature dependence in TlSe-type chain-like materials.
Structural disorder plays a crucial role in understanding the physical properties of a material1. Disorder and defects usually act as scattering centers for quasiparticles, such as electrons and phonons, influencing and governing the transport properties. In particular, the structural disorder is well known to scatter phonons and results in a lower thermal conductivity2,3, an essential property that is fundamentally important in technological applications such as thermal barrier coatings and thermoelectric (TE) energy conversion. For the TE technology directly interconverting heat and electricity, reducing thermal conductivity is an essential strategy to improve the figure of merit zT = α2σT/κ of a TE material, where α, σ, T, and κ represent the Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively. Structural disorder with great potential in reducing thermal conductivity can be achieved in various ways. In addition to the substitutional disorder commonly used in alloys3,4, the disorder can be realized intrinsically through vacancies, interstitial sites, off-center displacements, rattling atoms, or fast ionic diffusion within the unit cell in many state-of-the-art TE materials5,6,7,8,9.
Understanding, characterizing, and modeling the structural disorder is of significant interest in TE materials with ultralow glass-like thermal conductivity, which poses great challenges to both theorists and experimentalists. Ultralow thermal conductivity is common in large complex crystal structures, whereas it is rare in simple crystal structures. However, in recent years many simple inorganic crystalline solids such as SnSe10, Tl3VSe411, and BaTiS312 have been discovered to show ultralow thermal conductivity approaching or even lower than the glass limit13 for the amorphous and highly disordered solids. Theoretical models11,14 recently developed have been quite successful in modeling ultralow, weak temperature-dependent thermal conductivities of crystalline solids through introducing a wave-like tunneling term for describing the disorder. However, very few detailed experimental characterizations on atomic disorder are available in these simple crystalline solids typically because of great challenges for experimentalists to probe subtle structural disorders. One class of such crystalline solids is the TlSe-type compounds. The TlSe structure type covers a rich variety of binary and ternary compositions, among which TlInTe2, TlGaTe2, TlSe, and InTe have been discovered as promising TE materials with ultralow thermal conductivity15,16,17,18. Ultralow thermal conductivity was typically attributed to strong anharmonic rattling induced by weakly bonded In1+ or Tl1+ atoms with lone pair electrons16,17. On the other hand, the atomic disorder, prone to appear for rattling atoms in oversize cages, should not be overlooked as it may also contribute to low thermal conductivity. In particular, the superionic conductivity19,20 widely observed in this type of materials was suggested to be induced by the structural disorder and ion diffusion. However, no direct experimental evidence of the structural disorder or ion diffusion has been reported so far in any TlSe-type compound.
Here we combine multitemperature single-crystal synchrotron X-ray diffraction (SCSXRD) and the maximum entropy method (MEM) to obtain the electron density distribution for probing structural disorder in an archetypal TlSe-type compound InTe. A detailed structural analysis reveals a significant deficiency on the In1+ site as the dominant intrinsic defect for understanding intrinsic p-type behavior, consistent with the theoretical defect calculations. Moreover, the structure contains two interstitial indium sites between the In1+ sites, forming a one-dimensional (1D) disordered In1+ chain along the c axis. Interestingly, the MEM electron density at elevated temperatures and ab initio molecular dynamics simulations clearly show a static-dynamic transition of interstitial, disordered In1+ ions, suggesting a 1D In1+-ion diffusion/hopping pathway. We attribute such a diffusion pathway to a very low In1+-ion migration energy barrier along the c direction, which is found to be a general feature in many other TlSe-type compounds. The local correlations in the 1D In1+ chains are examined through single-crystal diffuse X-ray scattering, and it is found that the static-dynamic transition is related to the degree of local order in the chains. The direct visualization of a 1D disordered diffusion channel not only accounts for the reported superionic conductivity but also provides a basis for understanding ultralow thermal conductivity and its peculiar, weak temperature dependence in InTe and other TlSe-type compounds.
Ideal crystal structure and thermal conductivity
Despite simple crystal structure with relatively light mass, InTe has been reported to show ultralow thermal conductivity values of ~0.7–0.4 W m−1 K−1 at 300–700 K16, much lower than those in many well-known binary tellurides such as PbTe and Bi2Te33. InTe, crystallizing in the TlSe-type structure with the space group I4/mcm21, is generally described by the formula \({{{{{{\rm{In}}}}}}}^{1+}{{{{{{\rm{In}}}}}}}^{3+}{{{{{{\rm{Te}}}}}}}_{2}^{2-}\). The In3+ ions are tetrahedrally coordinated to Te2− ions forming (InTe2)− chains along the c axis, while the In1+ ions with 5s2 lone pair electrons are weakly bound to a cage-like system of eight Te atoms with the square antiprismatic arrangement (Fig. 1a, b). Thermal displacement parameters of In1+ ions were found by Hogg and Sutherland21 to be very large and anisotropic with the maximum vibration along the c axis. In this study, we synthesized large InTe single crystals using the vertical Bridgman method. Energy-dispersive spectroscopy (EDS) mapping was conducted using scanning transmission electron microscopy (STEM) and the result confirmed a uniform distribution of In and Te in the crystal (Supplementary Fig. 1). The chemical composition of the single crystal was determined to be x = 0.98 ± 0.01 in InxTe by inductively coupled plasma optical emission spectrometry (ICP-OES) (Supplementary Table 1). Due to the weak interactions between (InTe2)− chains, the crystal tends to cleave along the (hh0) planes (Fig. 1c). The intersection line of two perpendicular cleavage planes (hh0) of A and B was used to determine the crystallographic c direction (Supplementary Fig. 2). With the identified crystal orientation, we then measured the thermal conductivity from 2 to 723 K for the InTe crystals along the c direction (see Fig. 1d). The measured low-temperature thermal conductivity data along the c direction show a very good agreement with those reported in ref. 22. By comparing with the reported data along the [110] direction in ref. 23, it is found that the thermal conductivity of InTe single crystal is clearly anisotropic at room temperature but becomes less anisotropic or even nearly isotropic at high temperatures. A peculiar feature of the thermal conductivity is found with a nearly temperature-independent behavior (~T−0.1) at low temperatures of ~25–80 K, where the extrinsic scattering should be more important. Even with increasing temperature well above the Debye temperature (~120 K, Supplementary Table 2), where the intrinsic phonon-phonon scattering is expected to be dominant, the temperature dependence of thermal conductivity (~T−0.69) still deviates from T−1. Such abnormal behavior, also observed in ref. 22, is typically an indication of the extrinsic scattering induced by structural disorder. In this work, we focus on a proper description of the crystal structure as a basis for a profound understanding of the atomic disorder in thermoelectric InTe.
Fig. 1: Ideal crystal structure and thermal conductivity of InTe single crystal.
a, b Illustration of the reported ideal crystal structure of InTe along the c axis (a) and the [110] direction (b). c XRD patterns of the cleavage surfaces of InTe single crystal for the determination of the crystallographic directions. The intersection line of the two perpendicular cleavage planes (hh0) determines the c axis. The inset photo shows the cleaved crystal with two perpendicular cleavage surfaces of A and B. d Measured temperature-dependent thermal conductivity of InTe single crystal along the [001] direction. The reported thermal conductivity data along [001] and [110] directions of InTe single crystal from refs. 22,23 are plotted for comparison. The PPMS and LFA denote the Physical Property Measurement System and Laser Flash Apparatus for the low- and high-temperature thermal conductivity data measurements, respectively.
Disordered In1+ atoms and intrinsic defects
High-resolution SCSXRD data were used for the detailed crystal structure determination of InTe. We conducted the SCSXRD measurements at the BL02B1 beamline24 from SPring-8 using a high photon energy of 50.00 keV. The data at 25 K were measured with a high resolution of sinθ/λ < 1.67 Å–1 on a small high-quality single-crystal extracted from the as-grown large crystal. A total of 89,683 reflections were collected and reduced to 2723 unique reflections with a high redundancy of 32.9 and Rmerge = 4.13% (Supplementary Table 3). The structure at 25 K was solved with lattice parameters of a = 8.3685(3) and c = 7.1212(2) Å in I4/mcm space group. Accurate structure factors obtained from the SCSXRD data were used for MEM calculations. The MEM can provide a non-biased reconstruction of the most probable electron density from scaled and phased structure factors25,26, making it a powerful tool to study the location of atoms27, structural disorder5,28, and migration pathways of ions29,30.
Combining the MEM electron density and structure refinements, a precise structure model can be derived for understanding the atomic disorder (Fig. 2a, b). A three-dimensional (3D) MEM electron density map of InTe at 25 K (Fig. 2a) clearly reveals two small, nonequivalent additional regions of electron density between the In1+ atoms along the c direction. The two-dimensional (2D) slice and 1D profile of the MEM density further confirm two small electron density maxima between the In1+ atoms (Fig. 2c, d, and Supplementary Figs. 3–5), suggesting two interstitial sites with low occupancy in addition to the three main atomic sites. The localized nature of the extra electron density with distinct peaks along the c direction demonstrates a clear 1D static disordered feature. By analyzing the peak positions with crystal symmetry, two interstitial sites were determined to be 8 f (0.5 0.5 0.5463(4)) and 8 f (0.5 0.5 0.6369(4)). If interstitial indium atoms of Ini(1) and Ini(2) are allocated to the two additional sites, a two interstitial model can be obtained (see Fig. 2b and Supplementary Table 4).
Fig. 2: Disordered indium atoms and intrinsic defects in InTe revealed by the MEM electron density at 25 K.
a 3D electron density surface of InTe calculated by the MEM using high-resolution SCSXRD data at 25 K. The isosurface value is 15 e Å-3. b Two interstitial structure model based on the MEM electron density for InTe. c 2D MEM electron density map on the (100) plane at x = 0.5 for InTe. d 1D MEM electron density profile through the In1+ atoms along the [001] direction. The origin of the line plot is placed at (x = 0.5, y = 0.5, z = 0). e Theoretical formation energies of native defects in InTe.
To better elaborate the structure determination, we conducted and compared the refinements of different structure models with intermediate steps towards the two interstitial model (see Table 1 and Supplementary Tables 5–7). We started with the reported simple full occupancy model21 with three main atomic sites fully occupied, then moved to the vacancy model with the indium vacancy allowed, and finally explored the two interstitial model with two interstitial indium atoms added. Notably, we found that each intermediate step greatly improves the agreement with the experimental SCSXRD data as the RF value drops remarkably from 2.54% to 2.06% to 1.33%, the wRF value from 5.54% to 4.14% to 2.15%, and the goodness-of-fit (GoF) from 3.02 to 2.26 to 1.37. In addition to the significantly improved fit to the experimental diffraction data, only the two interstitial model shows a composition of In0.98Te consistent with the experimental value measured by ICP-OES.
Table 1 Comparison of different structure models for InTe with intermediate steps to the two interstitial model at 25 K.
The new structure determination paves the way to understand the dominant intrinsic defects and persistent p-type behavior of InTe. In contrast to the nearly fully occupied In3+ site, our structure refinements clearly show a significant vacancy on the In1+ site with only ~90% occupancy (Table 1). Moreover, the distances between In1+ and In-interstitial sites are generally too small (<2.2 Å) so that it is unlikely for indium atoms to occupy these sites at the same time, suggesting the formation of Frenkel pairs. The dominant In1+ vacancy along with small proportions of the Frenkel pairs thereby reasonably describes the observed structural disorder. To further elucidate the experimental observation, we conducted formation energy calculations of native defects in InTe using density functional theory. As depicted in Fig. 2e, the vacancy on the In1+ site is the dominant native defect showing a much lower formation energy than other intrinsic defects including the In3+ vacancy, Te vacancy, and antisite defects. The easier formation of the In1+ vacancy may be attributed to very weak adjacent bonds of In1+ atoms, showing large nearest-neighbor distances of 3.56 and 3.54 Å, respectively with In1+ and Te atoms. The dominant native defect of the In1+ vacancy, normally negatively charged, is known to pin the Fermi level close to the valence band maximum, which therefore explains the persistent p-type behavior of InTe reported in previous studies16,23.
In comparison with the In1+ vacancy, the formation of Frenkel pairs including the experimental indium-interstitials alone is energetically unfavorable owing to a bit higher formation energies (Fig. 2e), which is expected due to the resulting small In-In distances. However, on the basis of the In1+ vacancy, the formation of Frenkel pairs becomes more favorable with lower formation energy, indicating that the formation of Frenkel pairs in InTe is vacancy-mediated, consistent with the experimental observation. This may typically be ascribed to the vacancy-induced void space that helps avoid small In-In distances during the formation of Frenkel pairs.
Temperature-driven 1D diffusive In1+ channel
To explore the temperature dependence of the disordered indium in InTe, we further conducted MEM calculations based on the SCSXRD data at 100–700 K (Supplementary Table 8 and Supplementary Figs. 6–10). Similarly, the SCSXRD data at 100–700 K were collected with high resolutions of (sinθ/λ)max = 0.97–1.83, as well as high redundancy of 28.8-88.0 (Supplementary Table 3). The 3D and 2D MEM electron density maps at various temperatures of 25–700 K are plotted in Fig. 3a, b for comparison. Strikingly, with increasing temperature, electron densities on the In1+ and interstitial In sites become delocalized and eventually form a smooth, continuous 1D diffusion channel through In1+ atoms along the c direction. In Fig. 3c we compare the normalized 1D MEM electron density profile through In1+ atoms along the [001] direction at 25–700 K (see also Supplementary Figs. 11 and 12). At 25 and 100 K, the electron densities with distinct peaks on the two interstitial In sites are generally well separated, though the electron densities of the In1+ and the nearest interstitial Ini(2) are partially connected. With increasing temperature from 100 to 200 K, there are two notable changes in the 1D electron density profile. One is that the In1+ density expands and merges with the electron density of the Ini(2), resulting in the disappearance of the peak on the interstitial site Ini(2). The other is the onset of the electron density connection between the In1+, Ini(1), and Ini(2) through the c direction (see also Supplementary Fig. 13). The two clear changes in electron density are likely the origin of the kink observed on the resistivity versus temperature curve between 100 and 200 K (Supplementary Fig. 14). The kink in resistivity data has been consistently observed in both single-crystalline22 and polycrystalline31 InTe at low temperatures and is thus not due to a measurement artifact. Finally, as the temperature increases further (≥300 K) the electron density maxima of the Ini(1) are smeared out and flattened, forming a continuous 1D channel connecting In1+ atoms along the c direction.
Fig. 3: Temperature-driven 1D diffusive, disordered In1+ channel in InTe.
a 3D MEM electron density maps at 25-700 K. The isosurface values are set at 1.45% and 2.35% of the peak electron density values of the In1+ sites for the 25-600 K and 700 K MEM maps, respectively. b 2D MEM electron density maps at 25-700 K on the (100) plane at x = 0.5. The 2D MEM density maps at 25-600 K and 700 K are normalized, respectively, with one times and 1.58 times of the maximum values at the In1+ sites. The ED denotes the electron density. c 1D MEM electron density profile through the In1+ ions along the [001] direction at 25–700 K. The EDs at different temperatures are normalized for better comparison. d The RF, wRF, and GoF values for the constrained structure refinements with one interstitial indium moving along the c axis between In1+ sites. Two light gray vertical lines represent the locations of the two interstitial indium sites. e Anisotropic atomic displacement parameters (ADPs) of InTe refined with the two interstitial model. f Enlarged 3D MEM electron density map of InTe at 700 K with an isosurface value of 1.01 e Å-3.
In Fig. 3d we show the temperature-dependent constrained structure refinements with one interstitial indium manually moving along the 1D channel between the In1+ main sites. At temperatures of 25–200 K, the RF, wRF, and GoF values all show two distinct local minima, the location of which exactly correspond to the two indium interstitial sites. This signifies the generally static feature of the two interstitial indium sites. In contrast, at elevated temperatures of 300–700 K the RF, wRF, and GoF values generally become nearly constant with moving the interstitial indium between the In1+ sites along the c direction, suggesting nearly equal probability for the occupation of the interstitial indium. This result along with the MEM densities indicates a static-dynamic transition of the interstitial indium positions. The dynamic behavior of the interstitial indiums makes the structure refinements with the two interstitial model only feasible up to 200 K (Supplementary Table 7). A sudden increase in the thermal vibration along the c axis (U33) of the interstitial indiums between 100 and 200 K shown in Fig. 3e suggests the onset of the dynamic motion along the c axis, consistent with the MEM density at 200 K (Fig. 3c and Supplementary Fig. 13). It should be noted that we are not able to determine whether this dynamic behavior is induced by the thermal disorder or the dynamically positional disorder since the time-space averaged MEM density is not deconvoluted with the thermal smearing effect. Nevertheless, the continuous 1D MEM density channel above 200 K clearly reveals the probability for In1+ to diffuse or hop between the In1+ sites, indicating the 1D In1+-ion hopping/diffusion pathway along the c direction (Fig. 3a, f). The In1+-ion diffusion/hopping probability increases with increasing temperatures, but is generally not very high as the MEM electron density value of the diffusion channel even at 700 K is about 5.3% of the maximum peak value of the main In1+ site (Fig. 3c, f). The ion diffusion/hopping in InTe is clearly weaker than those in conventional superionic conductors5,9,29, which might pose a challenge to probe the signature of superionic conductivity in InTe. An external driving force such as a higher temperature, a large electric field20, or the increased In1+ vacancy may be required to enhance the diffusion/hopping probability. The In1+ diffusion/hopping may be associated with very large thermal motions of the In1+ and interstitial indiums along the c direction (Fig. 3e and Supplementary Fig. 15). In particular, exceptionally large U33 values of the In1+ atom at elevated temperatures do not extrapolate to zero at 0 K, another clear indication of atomic disorder along the c direction32.
The local structural ordering of vacancies and interstitial sites in the 1D chains was investigated through diffuse X-ray scattering, shown in Fig. 4a (see also Supplementary Fig. 16). At 25 K the diffuse scattering forms 2D planes for even values of L, seen as lines in the figure, indicative of strong correlations along the c direction, and weak correlations in other directions33. At 300 K the planes have disappeared and been replaced by more 3D features with strong maxima at the Bragg peak positions, a typical indication of thermal diffuse scattering from correlated vibrations. This is seen in more detail using the three-dimensional difference pair distribution function (3D-ΔPDF), shown in Fig. 4b (see also Supplementary Fig. 17). The 3D-ΔPDF shows the local correlations in disordered crystals34,35,36,37. It is a map showing which interatomic vectors are more or less present in the real structure compared to the average crystal structure. Positive features show vectors, which separate atoms more frequently in reality and negative features show vectors separating fewer atoms. The 3D-ΔPDF at 25 K shows strong correlations along z, which become weaker at 300 K, showing the vacancies and interstitials to be strongly correlated along the 1D chains at low temperatures, but less so at higher temperatures. This is shown in more detail along the z direction in Fig. 4c. At x, y, z = 0 there is noise due to Fourier ripples. For vectors equal to ½c and 1c (z equal to 3.56 and 7.1 Å), there are positive peaks, indicating that In atoms will most often be separated by these vectors, as they would in the ideal structure. Around these positive peaks, there are negative signals, indicating vectors that do not separate In atoms in the real structure. At low temperature the negative signal around positive peaks is asymmetric, a typical indication of local relaxations from atoms moving slightly towards neighboring vacancies34,37. At 25 K a positive peak is found at 5.8 Å, corresponding to a vector separating an Ini(1) and an Ini(2) interstitial, as illustrated in Fig. 4d, suggesting that the interstitial Frenkel pairs tend to be separated by this distance. At 300 K the asymmetry in the negative signal and the Frenkel pair peak have disappeared, indicating that the positions of vacancies and interstitials are less correlated at high temperatures consistent with the 1D In1+-ion diffusion/hopping behavior.
Fig. 4: Local ordering in 1D In1+ chains.
a Measured diffuse X-ray scattering in the HHL plane at 25 and 300 K. b 3D-ΔPDF in the x0z plane at 25 and 300 K. c Zoom on features in the 3D-ΔPDF along z at 25, 100 and 300 K. d Illustration of the 1D chain with the characteristic distance between interstitial sites marked, corresponding to the positive peak marked in (c) by a black arrow.
The experimental observation of the 1D In1+-ion diffusion pathway is further confirmed by the ab initio molecular dynamics simulation. As illustrated in Fig. 5a, b, and Supplementary Fig. 18, the trajectories of the In1+ ions for the simulation at 700 K show a clear hopping/diffusion behavior along the c direction. We note that only a limited number of In1+ ions show 1D diffusion/hopping behavior in the simulated supercell, indicating that the probability of the In1+-ion diffusion is not very significant consistent with the experimental MEM electron density. To understand the 1D diffusion/hopping pathway of the In1+ in InTe, we further conducted nudged elastic band calculations to estimate the energy barriers for the vacancy-mediated In1+-ion migration. Three possible indium ion migration pathways along the [001], [110], and [100] directions were considered (Fig. 5c). Notably, the In1+ migration barrier along the [001] direction is significantly lower than those along the other two directions (Fig. 5d), which reasonably explains the 1D diffusion channel along the c direction in the MEM electron density. The flat energy landscape with a very low energy barrier may be attributed to the weak atomic interaction along the c direction.
Fig. 5: 1D In1+-ion migration pathways and energy barriers in InTe and several other ABX2 compounds with the TlSe-type structure.
a, b Illustration of the 700 K molecular dynamics simulation trajectories of indium atoms in the In1+-deficient supercell In63Te64 (In0.984Te) projected along the [110] (a) and [001] (b) directions. c, d The vacancy-mediated In1+-ion migration pathways (c) and calculated energy barriers (d) along the [001], [110], and [100] directions in InTe. e The activation energies of the vacancy-mediated A1+-ion migration along the [001] direction in several ABX2 compounds with the TlSe-type structure, in comparison with that in InTe.
Interstitial, disordered, diffusive atoms with large thermal motions are known to be a highly effective mechanism for reducing thermal conductivity. One remarkable example is Zn4Sb3, which shows extremely low thermal conductivity due to multiple disordered Zn interstitials that substantially reduce the phonon mean-free path5. Interstitial, disordered atomic positions are commonly observed in large complex crystal structures such as Zn4Sb35 and oxide-ion conductors30, whereas they are rarely found in small simple crystal structures. The 1D interstitial, disordered, diffusive In1+ ions discovered in InTe are quite noteworthy, given the simple structure with merely 8 atoms in primitive cell. The lattice thermal conductivity in both single-crystalline and polycrystalline InTe is unexpectedly low at high temperatures16,23, which has been shown to reach the theoretical glass limit (~0.3 W m−1 K−1) proposed by Cahill13 for the amorphous and disordered solids.
The interstitial, disordered, diffusive In1+ ions could be considered as an important origin of the ultralow, weak temperature-dependent lattice thermal conductivity in InTe. The correlated disorder is known to lead to the broadening of phonon linewidth that is inversely proportional to lattice thermal conductivity38. Correlated disorder of indium vacancies and interstitials in 1D In1+ chains could potentially broaden the phonon linewidth for the low-energy In1+ vibration modes, resulting in the suppression of phonon lifetime, phonon mean-free path, and thereby lattice thermal conductivity. In particular, the structural disorder of In1+ ions was suggested by Misra et al.22 to be a key origin of the broadening of In1+-weighted low-energy optical modes and the limited energy range of heat-carrying acoustic phonons, lowering the lattice thermal conductivity. Moreover, the plateau with nearly temperature-independent behavior (~T−0.1) in thermal conductivity at ~25–80 K may be attributed to the correlated static disorder in 1D In1+ chains revealed by the MEM density and 3D-ΔPDF, similar to those observed in strongly disordered materials39,40,41. With increasing temperature above the Debye temperature of ~120 K, as the intrinsic phonon-phonon scattering begins to be dominant thermal conductivity shows a clear decreasing trend but its temperature dependence is still a bit weaker than T−1, which is likely induced by the wavelike tunneling11,14 contribution from interstitial, disordered, diffusive In1+ ions. However, the exact impact of the structural disorder with interstitial, disordered, diffusive In1+ ions comparing with the anharmonic phonon-phonon scattering on lattice thermal conductivity in InTe still requires further systematic theoretical and experimental investigations.
We expect the 1D disordered diffusion channel to be transferable to many other ABX2 compounds with the TlSe-type structure. In Fig. 5e we show the calculated A1+-ion migration energy barrier along the [001] direction in ten other ABX2 compounds with the TlSe-type structure in comparison with that in InTe. Notably, nearly all these compounds show comparable or lower migration energy barriers than that of InTe. This suggests that the 1D disordered diffusion channel of the A1+-ions along the c direction is very likely to appear in many other TlSe-type compounds, given commonly observed large thermal displacements and low migration energy barriers of the A1+-ions along the c direction. The intrinsic p-type transport behavior in nearly all other TlSe-type compounds may be understood by the dominant A1+ cationic vacancy as described in this work. Considering the A1+-ion diffusion has been widely mentioned in previous studies19,20 without any experimental evidence to date, the direct observation of the 1D hopping/diffusion cationic channel in our work thereby provides long-awaited experimental evidence for understanding the electric-field enhanced superionic conductivity19,20 observed in many TlSe-type compounds. Moreover, the proper description and fine details of the atomic disorder and hopping/diffusion in this work could be helpful for theory in developing models to understand ultralow thermal conductivity with weak temperature-dependent behavior in InTe and other TlSe-type chain-like materials.
Single crystal growth and characterization
Large InTe single crystal was synthesized with the vertical Bridgman method. Indium shots (99.999%, ChemPUR) and tellurium pieces (99.999%, ChemPUR) were combined in stoichiometric ratio and placed into a carbon-coated quartz ampoule. The ampoule was flame-sealed after being evacuated to a pressure below 10−4 mbar. The sealed ampoule was then put into a box furnace, heated to 1023 K in 10 h with a dwell time of 24 h, and then slowly cooled to room temperature in 10 h. The obtained polycrystalline ingot was crushed into small pieces and loaded into a carbon-coated quartz ampoule with a conical tip, which was subsequently evacuated and sealed. For the crystal growth, the sample was kept at 1030 K for 24 h for homogenizing the melt and then slowly cooled directionally from the melt with a temperature gradient of ~6 K cm-1 and a sample moving rate of 2 mm h-1. To determine the c axis of the single crystal, X-ray diffraction data of cleavage surfaces were measured on a Rigaku Smartlab in the Bragg-Brentano geometry using a Cu Kα1 source. The intersection line of the two perpendicular cleavage planes (hh0) defines the c axis. The chemical composition of the InTe single crystal was determined using the inductively coupled plasma optical emission spectrometry (ICP-OES). The sample was dissolved with PlasmaPure aqua regia and diluted to 1% acid concentration with MilliQ-water. The ICP-OES measurement was carried out on a Spectro ARCOS ICP-OES equipped with a Burgener Nebulizer and Cyclonic Spray Chamber with an ASX-520 Auto sampler. For quantification of the elements, the standard curves series was measured. The standard series consists of concentrations for each element with 0, 0.01, 0.05, 0.1, 0.5, 1, 5, 10, 20, and 50 ppm. The homogeneous elemental distribution of the InTe single crystal was confirmed with the Scanning Transmission Electron Microscopy Energy Dispersive Spectroscopy (STEM-EDS) by elemental mapping analysis using an FEI Talos F200X microscope operated at 200 kV. The microscope is equipped with an X-FEG electron source and Super-X EDS detector system. Small single crystals were extracted from the as-grown big crystal and screened with a Bruker Kappa Apex II diffractometer equipped with a Mo source (λ = 0.71073 Å). A small high-quality needle-shaped single crystal (~20 × 20 × 200 μm3) was selected for the single-crystal synchrotron X-ray diffraction.
Single-crystal synchrotron X-ray diffraction
High-resolution single-crystal synchrotron X-ray diffraction data of InTe were collected at the BL02B1 beamline24 from SPring-8 using a photon energy of 50.00 keV with a Pilatus3 X 1 M CdTe (P3) detector, which recently has been found capable of achieving extremely high quality for the electron density data42. The low-temperature data at 25, 100, 200, 300, and 400 K and the high-temperature data at 500, 600, and 700 K were collected with two different wavelengths of 0.2480 Å and 0.2509 Å on two different beam times, respectively. The collected frames were converted to the Bruker.sfrm format42, which were integrated using SAINT-Plus43. After the integration, the data were scaled and corrected for absorption and other random errors using SADABS44. Subsequently, the data averaging and the uncertainty estimation were conducted using SORTAV45. The structure was solved with SHELXT46, and the detailed structure refinement was conducted using JANA200647 (Supplementary Note 1 and Supplementary Tables 5–7). Details of the single-crystal diffraction data collection and reduction are summarized in Supplementary Table 3. The high-quality single-crystal synchrotron data here ensure accurate structure factors for obtaining high-quality, smooth MEM electron density.
MEM density analysis
Structure factors extracted from the structure refinement of high-resolution single-crystal synchrotron X-ray diffraction data were used for the calculations of MEM electron densities. The Sakato-Sato algorithm implemented in the BayMEM software48 was used to conduct the MEM calculations. The unit cell of InTe was divided into \({N}_{pix}=168\times 168\times 144\) pixels along the a, b, and c directions with a fine grid size of ~0.05 Å. Using scaled, phased, "error-free" structure factors as input, MEM calculations reconstruct and determine the electron density of the pixel i (\({\rho }_{i}\)) that maximizes the information entropy, defined as
$$S=-{\sum }_{i=1}^{{N}_{pix}}{\rho }_{i}\,{{{{\mathrm{ln}}}}}\left(\frac{{\rho }_{i}}{{\rho }_{i}^{prior}}\right),$$
under the constraints based on the observed structure factors
$${\chi }^{2}=\frac{1}{{N}_{F}}{\sum }_{i=1}^{{N}_{F}}{\left(\frac{|{F}_{obs}-{F}_{MEM}|}{\sigma ({F}_{obs})}\right)}^{2}.$$
Here \({N}_{F}\) is the number of the observed structure factors, \({F}_{obs}\) is the observed experimental structure factors with standard uncertainties \(\sigma ({F}_{obs})\), \({F}_{MEM}\) is the structure factors corresponding to the final calculated electron density, and \({\rho }_{i}^{prior}\) is the prior density that introduces prior information available for the system. Either a uniform prior density or a non-uniform prior density based on the independent spherical atom model may be used for the MEM calculations. In this study, the tests of MEM calculations with both a uniform (flat) prior and a nonuniform prior were conducted and the corresponding results were confirmed to be virtually identical (see Supplementary Fig. 4). For simplicity, the results of MEM calculations with uniform prior density were adopted for discussion in the main text. To ensure the optimal MEM density, the optimal stopping criterion χ2 of the MEM calculation was determined with the fractal dimension analysis of the residual density49 (Supplementary Note 2 and Supplementary Figs. 9 and 10). The MEM electron density is independent of different structural models, which is elucidated by virtually the same results using different structure models as input (Supplementary Fig. 3). For consistency, here we use the MEM electron density calculated with the structure factors from the full occupancy model for discussion in the main text. The 3D MEM electron density maps and crystal structures were visualized by VESTA50.
Diffuse scattering and 3D-ΔPDF
In addition to the normal Bragg diffraction data for structural analysis and MEM calculations, X-ray diffuse scattering data of InTe single crystal at 25, 100, and 300 K were collected on the same setup at the BL02B1 beamline. Here 4 runs were measured, each a 180° Ω rotation with 900 frames, for χ = 0° and χ = 40°, with the detector at 2θ = 0° and 2θ = 20°. An exposure time of 2 s per frame was used. Background and air-scattering were measured using the same exposure time and detector positions as for the crystal. For each combination of these, 200 frames of air scattering were measured and averaged. The data were converted to reciprocal space using a custom Matlab script. During this process the data were corrected for Lorentz and polarization factors, the background scattering from air was subtracted, and a solid angle correction was applied as the detector is flat. The resulting scattering data were reconstructed on a 901 × 901 × 901 point grid with each axis spanning ± 28.3 Å−1. The resulting data were symmetrized using the 4/mmm point symmetry of the Laue group, and outlier rejection was used in the symmetrization, such that symmetry equivalent voxels were compared and rejected if they deviated by more than two standard deviations from the median of the equivalents45. The Bragg peaks were punched and filled. Because a large degree of diffuse scattering is observed at the positions of the Bragg peaks, care has to be taken to remove all Bragg scattering while leaving as much of the diffuse scattering as possible. To accomplish this, the Bragg peaks were masked in the raw data frames before conversion using a Python script which masks sharp and strong peaks in the data. This is possible as the diffuse scattering here is slowly-varying compared to Bragg peaks. The script compares the measured pixels to all neighboring pixels, and if a pixel is relatively much stronger (a factor of 2.5 was used here) than its neighbors, it is marked as part of a Bragg peak. To avoid weak noise from being marked as peaks, a lower bound for the absolute intensity needed for a peak is also used. A high-intensity cutoff is also used, for which pixels larger than this value are automatically marked as peaks. Once peak pixels have been marked this way, the pixels neighboring these are also marked as being part of peaks. This approach effectively masks most Bragg peaks, but leaves some of the almost-zero-intensity Bragg peaks at large scattering vectors. To fill in the masked regions and remove remaining weak peaks, a small punch was applied to the allowed Bragg positions after conversion to reciprocal space and linear interpolation was used to fill. A constant value was also filled into the regions where no data has been measured to minimize Fourier ripples. The 3D-ΔPDF is obtained as the inverse Fourier transform of the diffuse scattering intensity, Id, and is given by the autocorrelation of the deviations in electron density from the average crystal structure34:
$${{{{{\rm{3D}}}}}}\mbox{-}\Delta {{{{{\rm{PDF}}}}}}={ {\mathcal F} }^{-1}[{I}_{d}]=\langle\delta \rho \otimes \delta \rho \,\rangle.$$
Here \(\delta \rho ({{{\bf{r}}}},t)=\,\rho ({{{\bf{r}}}},t)-{\rho}_{periodic}({{\bf{r}}})\) is the difference between the total electron density of the crystal and the periodic average electron density. The brackets \(\langle \ldots \rangle\) indicate time averaging, \(\otimes\) denotes cross correlation, and \({\mathcal F}\) is the Fourier transform.
Thermal conductivity measurements
A small bar-shaped sample obtained by cutting the large single crystal along the c axis was used for low-temperature thermal conductivity measurement. Low-temperature thermal conductivities from 2 to 300 K were measured with a Physical Property Measurement System (PPMS, Quantum Design, US) using the Thermal Transport Option (TTO) under high vacuum. A flat sample (~ 6 × 6 × 1.9 mm3) with the surface normal along the c axis was extracted from the large single crystal and used for high-temperature thermal diffusivity measurement. The thermal diffusivity (D) measurement from 300 to 723 K was carried out on a Netzsch LFA457 setup using the laser flash method. High-temperature thermal conductivity was then determined using \(\kappa \,=\,{{{\it{dD}}}}{C}_{{{\rm{P}}}}\), where the heat capacity \({C}_{{{\rm{P}}}}\) was estimated using the Dulong-Petit law \({C}_{{{\rm{P}}}}=3{k}_{{{\rm{B}}}}\) per atom and the sample density d was measured with the Archimedes method.
All density functional theory calculations were conducted with the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation51 based on the projector-augmented wave method52 (PAW) as implemented in the Vienna ab initio simulation package53 (VASP). Defect calculations were conducted in a supercell of 2 × 2 × 2 conventional unit cells. A Γ-centered 4 × 4 × 4 k-point mesh was used for the structure optimization as well as the total energy calculation. A plane wave cutoff energy of 400 eV and an energy convergence criterion of 10−4 eV were applied. For the structural optimization of defect supercells, all atomic positions were relaxed into their equilibrium positions until the Hellmann-Feynman force was converged to be smaller than 0.01 eV Å−1 while the lattice parameters were fixed at the optimized values from the perfect supercell. For the defect supercells with interstitial indiums (Ini(1) and Ini(2)), the positions of interstitial indiums were fixed at the experimental values while the atomic positions of other atoms were fully relaxed. The formation energy of a native point defect was simply calculated using54:
$$\varDelta {E}_{f}^{d}={E}_{tot}^{d}-{E}_{tot}^{bulk}-{\sum }_{i}{n}_{i}{\mu }_{i},$$
where \(\varDelta {E}_{f}^{d}\) is the total energy of the defect supercell, \({E}_{tot}^{bulk}\) is the total energy of the bulk supercell without any defects, \({n}_{i}\) denotes the number of atoms of type i that is added to (nі > 0) or removed from (\({n}_{i}\) < 0) the bulk supercell, and \({\mu }_{i}\) represents the atomic chemical potential. The chemical potentials of In and Te in InTe should fulfill the thermodynamic condition:\(\,\varDelta {\mu }_{{{{{{\rm{In}}}}}}}+\varDelta {\mu }_{{{{{{\rm{Te}}}}}}}=2\varDelta {H}_{f}({{{{{\rm{InTe}}}}}})\). Under the In-rich condition, the chemical potentials are limited by the formation energy of the secondary phase In4Te3 (\(4\varDelta {\mu }_{{{{{{\rm{In}}}}}}}+3\varDelta {\mu }_{{{{{{\rm{Te}}}}}}}\le 7\varDelta {H}_{f}({{{{{{\rm{In}}}}}}}_{4}{{{{{{\rm{Te}}}}}}}_{3})\)). Under the In-poor condition, the chemical potentials are limited by the formation energy of the competing phase In3Te4 (\(3\varDelta {\mu }_{{{{{{\rm{In}}}}}}}+4\varDelta {\mu }_{{{{{{\rm{Te}}}}}}}\le 7\varDelta {H}_{f}({{{{{{\rm{In}}}}}}}_{3}{{{{{{\rm{Te}}}}}}}_{4})\)).
The calculations of minimum-energy diffusion pathways and migration barriers of In1+ ions in InTe were performed with the climbing image nudged elastic band (CI-NEB) method55. The calculations were conducted in a 2 × 2 × 2 supercell of the conventional unit cell, where one vacancy was introduced on the In1+ sites. We calculated the diffusion energy barriers for a single nearest indium ion diffusing to the created vacancy. The atomic positions were relaxed until the residual forces were within 10 meV Å−1. A total energy convergence criterion of 10−6 eV and a Γ-centered 2 × 2 × 2 k-point mesh were used for the CI-NEB calculations. The same calculation procedure was applied to calculate the migration barriers of the A1+ ion along the [001] direction in several other ABX2 compounds (including InGaTe2, TlGaTe2, TlInTe2, InGaSe2, TlAlSe2, TlGaSe2, TlInSe2, TlInS2, TlSe, and TlS) with the TlSe-type structure.
Ab initio molecular dynamics (MD) calculations were performed using the PBE functional as implemented in the VASP code. The MD simulations at 700 K were conducted with the NVT ensemble using a Nosé thermostat with the default Nosé mass. A supercell with 127 atoms (2 × 2 × 2 conventional cells) containing one In1+ vacancy was used so that the simulated composition In63Te64 (In0.984Te) is close to the experimental observation. A 300 eV cutoff energy and an energy convergence criterion of 10−5 eV along with the Γ-point sampling were adopted for the simulations. The simulations were run for 130 ps for statistical analysis with a time step of 2 fs, and the first 10 ps was disregarded for equilibrium. The trajectories of the MD simulations were visualized by VMD56.
The data supporting the findings of this study are available within the paper and its Supplementary Information files and are available from the corresponding authors upon reasonable request.
Code availability
Custom computer codes used in this work are available from the corresponding authors upon reasonable request.
Simonov, A. & Goodwin, A. L. Designing disorder into crystalline materials. Nat. Rev. Chem. 4, 657–673 (2020).
Chiritescu, C. et al. Ultralow thermal conductivity in disordered, layered WSe2 crystals. Science 315, 351–353 (2007).
ADS CAS PubMed Google Scholar
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Gascoin, F., Ottensmann, S., Stark, D., Haïle, S. M. & Snyder, G. J. Zintl phases as thermoelectric materials: tuned transport properties of the compounds CaxYb1-xZn2Sb2. Adv. Funct. Mater. 15, 1860–1864 (2005).
Snyder, G. J., Christensen, M., Nishibori, E., Caillat, T. & Iversen, B. B. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nat. Mater. 3, 458–463 (2004).
Biswas, K. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Sales, B. C., Mandrus, D. & Williams, R. K. Filled skutterudite antimonides: a new class of thermoelectric materials. Science 272, 1325–1328 (1996).
Christensen, M. et al. Avoided crossing of rattler modes in thermoelectric materials. Nat. Mater. 7, 811–815 (2008).
Liu, H. et al. Copper ion liquid-like thermoelectrics. Nat. Mater. 11, 422–425 (2012).
ADS PubMed Google Scholar
Zhao, L.-D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377 (2014).
Mukhopadhyay, S. et al. Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4. Science 360, 1455–1458 (2018).
Sun, B. et al. High frequency atomic tunneling yields ultralow and glass-like thermal conductivity in chalcogenide single crystals. Nat. Commun. 11, 6039 (2020).
Cahill, D. G., Watson, S. K. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131–6140 (1992).
ADS CAS Google Scholar
Simoncelli, M., Marzari, N. & Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809–813 (2019).
Matsumoto, H., Kurosaki, K., Muta, H. & Yamanaka, S. Systematic investigation of the thermoelectric properties of TlMTe2 (M=Ga, In, or Tl). J. Appl. Phys. 104, 073705 (2008).
ADS Google Scholar
Jana, M. K., Pal, K., Waghmare, U. V. & Biswas, K. The origin of ultralow thermal conductivity in InTe: Lone-pair-induced anharmonic rattling. Angew. Chem. Int. Ed. 55, 7792–7796 (2016).
Jana, M. K. et al. Intrinsic rattler-induced low thermal conductivity in Zintl type TlInTe2. J. Am. Chem. Soc. 139, 4350–4353 (2017).
Dutta, M. et al. Ultralow thermal conductivity in chain-like TlSe due to inherent Tl+ rattling. J. Am. Chem. Soc. 141, 20293–20299 (2019).
Sardarly, R. et al. Superionic conductivity in one-dimensional nanofibrous TlGaTe2 crystals. Jpn. J. Appl. Phys. 50, 05FC09 (2011).
Sardarly, R. M. et al. Superionic conductivity and switching effect with memory in TlInSe2 and TlInTe2 crystals. Semiconductors 45, 1387–1390 (2011).
Hogg, J. H. C. & Sutherland, H. H. Indium telluride. Acta Crystallogr. B 32, 2689–2690 (1976).
Misra, S. et al. Reduced phase space of heat-carrying acoustic phonons in single-crystalline InTe. Phys. Rev. Res. 2, 043371 (2020).
Misra, S. et al. Synthesis and physical properties of single-crystalline InTe: towards high thermoelectric performance. J. Mater. Chem. C. 9, 5250–5260 (2021).
Sugimoto, K. et al. Extremely high resolution single crystal diffractometory for orbital resolution using high energy synchrotron radiation at SPring-8. AIP Conf. Proc. 1234, 887–890 (2010).
Collins, D. M. Electron density images from imperfect data by iterative entropy maximization. Nature 298, 49–51 (1982).
Iversen, B. B., Larsen, F. K., Souhassou, M. & Takata, M. Experimental evidence for the existence of non-nuclear maxima in the electron-density distribution of metallic beryllium. A comparative study of the maximum entropy method and the multipole refinement method. Acta Crystallogr. B 51, 580–591 (1995).
Takata, M. et al. Confirmation by X-ray diffraction of the endohedral nature of the metallofullerene Y@C82. Nature 377, 46–49 (1995).
Kastbjerg, S. et al. Direct evidence of cation disorder in thermoelectric lead chalcogenides PbTe and PbS. Adv. Funct. Mater. 23, 5477–5483 (2013).
Nishimura, S.-i et al. Experimental visualization of lithium diffusion in LixFePO4. Nat. Mater. 7, 707–711 (2008).
Kuang, X. et al. Interstitial oxide ion conductivity in the layered tetrahedral network melilite structure. Nat. Mater. 7, 498–504 (2008).
Back, S. Y. et al. Temperature-induced Lifshitz transition and charge density wave in InTe1−δ thermoelectric materials. ACS Appl. Energy Mater. 3, 3628–3636 (2020).
Sales, B. C., Mandrus, D. G. & Chakoumakos, B. C. in Recent Trends in Thermoelectric Materials Research II (ed. Tritt, T.) 1-36 (Semiconductors and Semimetals Series 70, Elsevier, 2001).
Welberry, T. R. Diffuse x-ray scattering and models of disorder. Rep. Prog. Phys. 48, 1543–1594 (1985).
Weber, T. & Simonov, A. The three-dimensional pair distribution function analysis of disordered single crystals: basic concepts. Z. Kristallogr. 227, 238–247 (2012).
Roth, N. & Iversen, B. B. Solving the disordered structure of β-Cu2−xSe using the three-dimensional difference pair distribution function. Acta Crystallogr. A 75, 465–473 (2019).
Krogstad, M. J. et al. Reciprocal space imaging of ionic correlations in intercalation compounds. Nat. Mater. 19, 63–68 (2020).
Roth, N. et al. Tuneable local order in thermoelectric crystals. IUCrJ 8, 695–702 (2021).
Overy, A. R., Simonov, A., Chater, P. A., Tucker, M. G. & Goodwin, A. L. Phonon broadening from supercell lattice dynamics: Random and correlated disorder. Phys. Status Solidi B 254, 1600586 (2017).
Zeller, R. C. & Pohl, R. O. Thermal conductivity and specific heat of noncrystalline solids. Phys. Rev. B 4, 2029–2041 (1971).
Beekman, M. & Cahill, D. G. Inorganic crystals with glass-like and ultralow thermal conductivities. Cryst. Res. Technol. 52, 1700114 (2017).
Christensen, S. et al. "Glass-like" thermal conductivity gradually induced in thermoelectric Sr8Ga16Ge30 clathrate by off-centered guest atoms. J. Appl. Phys. 119, 185102 (2016).
Krause, L. et al. Accurate high-resolution single-crystal diffraction data from a Pilatus3 X CdTe detector. J. Appl. Crystallogr. 53, 635–649 (2020).
Bruker. SAINT-Plus Integration Engine, version 8.38A. (Bruker AXS Inc., Madison, Wisconsin, USA, 2013).
Krause, L., Herbst-Irmer, R. & Stalke, D. An empirical correction for the influence of low-energy contamination. J. Appl. Crystallogr. 48, 1907–1913 (2015).
Blessing, R. H. Outlier treatment in data merging. J. Appl. Crystallogr. 30, 421–426 (1997).
Sheldrick, G. SHELXT - Integrated space-group and crystal-structure determination. Acta Crystallogr. A 71, 3–8 (2015).
MATH Google Scholar
Petricek, V., Dusek, M. & Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr 229, 345 (2014).
van Smaalen, S., Palatinus, L. & Schneider, M. The maximum-entropy method in superspace. Acta Cryst. A 59, 459–469 (2003).
Bindzus, N. & Iversen, B. B. Maximum-entropy-method charge densities based on structure-factor extraction with the commonly used Rietveld refinement programs GSAS, FullProf and Jana2006. Acta Crystallogr. A 68, 750–762 (2012).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Walle, C. G. V. D. & Neugebauer, J. First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 95, 3851–3879 (2004).
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Humphrey, W., Dalke, A. & Schulten, K. VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
Aref Mamakhel is acknowledged for the STEM-EDS measurement. Mads R. V. Jørgensen is thanked for fruitful discussions. This work was supported by the Villum Foundation and the Danish Agency for Science, Technology and Innovation (DanScatt). Affiliation with the Aarhus University Center for Integrated Materials Research (iMAT) is gratefully acknowledged. This work was partly supported by the Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) Grant Number JP19KK0132 and JP20H4656. The synchrotron experiments were performed at SPring-8 BL02B1 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) as a Partner User (Proposals No. 2017B0078, No. 2018A0078, No. 2018B0078, and No. 2019A0159). Beamline scientist K. Sugimoto is acknowledged for support during synchrotron experiments. The theoretical calculations in this work were conducted at the Center for Scientific Computing in Aarhus (CSCAA).
Center for Materials Crystallography, Department of Chemistry and iNANO, Aarhus University, DK-8000, Aarhus, Denmark
Jiawei Zhang, Nikolaj Roth, Kasper Tolborg, Lirong Song, Martin Bondesgaard & Bo B. Iversen
Faculty of Pure and Applied Sciences and Tsukuba Research Center for Energy Materials Science (TREMS), University of Tsukuba, Tsukuba, 305-8571, Japan
Seiya Takahashi & Eiji Nishibori
Jiawei Zhang
Nikolaj Roth
Kasper Tolborg
Seiya Takahashi
Lirong Song
Martin Bondesgaard
Eiji Nishibori
Bo B. Iversen
J.Z. designed the project under the supervision of B.B.I. J.Z. prepared and characterized the single crystals. J.Z. carried out the data analysis, structure refinement, and MEM density analysis. N.R. analyzed the diffuse scattering data and 3D-ΔPDF. K.T. provided guidance on the analysis of synchrotron data and MEM density. S.T. and E.N. collected single-crystal synchrotron X-ray diffraction data. J.Z. conducted theoretical calculations. J.Z. and L.S. conducted thermal conductivity measurements. M.B. conducted the ICP-OES measurement. J.Z., N.R., K.T., L.S., and B.B.I. contributed to the discussion of the results. J.Z., N.R., and B.B.I. wrote the manuscript. All other authors read and edited the manuscript.
Correspondence to Jiawei Zhang or Bo B. Iversen.
The authors declare no competing interests.
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer Review File
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
Zhang, J., Roth, N., Tolborg, K. et al. Direct observation of one-dimensional disordered diffusion channel in a chain-like thermoelectric with ultralow thermal conductivity. Nat Commun 12, 6709 (2021). https://doi.org/10.1038/s41467-021-27007-y
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Editors' Highlights
Nature Communications (Nat Commun) ISSN 2041-1723 (online) | CommonCrawl |
\begin{document}
\title{Quantum states characterization for the zero-error capacity}
\author{Rex A C Medeiros$^{\dag,\ddag,1,2}$ Romain Alléaume$^{\dag,2}$, Gérard Cohen$^{\dag,3}$ and Francisco M. de Assis$^{\ddag,4}$ }
\address{ ~\\ $^\dag$ Département Informatique et Réseaux,\\
École Nationale Supérieure des Télécommunications \\
46 rue Barrault, F-75634, Paris Cedex 13, France\\
~ }
\address{ $^\ddag$ Departamento de En\-ge\-nha\-ria Elétrica \\
Universidade Federal de Campina Grande \\
Av. Apr\'{i}gio Veloso, 882, Bodocong\'{o}\\ Campina Grande-PB, 58109-970, Brazil \\ ~ }
\ead{$^1$ [email protected]} \ead{$^2$ [email protected]} \ead{$^3$ [email protected]} \ead{$^4$ [email protected]}
\begin{abstract} The zero-error capacity of quantum channels was defined as the least upper bound of rates at which classical information can be transmitted through a quantum channel with probability of error equal to zero. This paper investigates some properties of input states and measurements used to attain the quantum zero-error capacity. We start by reformulating the problem of finding the zero-error capacity in the language of graph theory. This alternative definition is used to prove that the zero-error capacity of any quantum channel can be reached by using tensor products of pure states as channel inputs, and projective measurements in the channel output. We conclude by presenting an example that illustrates our results. \end{abstract}
\pacs{03.67.-a, 03.67.Hk}
\submitto{\JPA}
\maketitle
\section{Introduction}
Classical and quantum information theory~\cite{Cover:91,BS:98} usually look for asymptotic solutions to information treatment and transmission problems. For example, the Shannon's coding theorem guarantees the existence of a channel capacity $C$ such that for any rate $R$ approaching $C$ there exist a sequence of codes for which the probability of error goes asymptotically to zero. A zero-error probability approach for information transmission through noisy channel was introduced by Shannon in 1956~\cite{Sha:56}. Given a discrete memoryless channel, it was defined a capacity for transmitting information with an error probability equal to zero. The so called zero-error information theory~\cite{KoOr:98} found applications in areas like graph theory, combinatorics, and computer science.
More recently, the zero-error capacity of quantum channels was defined as the least upper bound of rates at which classical information can be transmitted through a quantum channel with error probability equal to zero~\cite{MeAs:05a}. Some results followed the definition. For example, it was shown that the zero-error capacity of any quantum channel is upper bounded by the HSW capacity~\cite{MeAs:04d}.
Because of the direct relation with graph theory, the quantum zero-error capacity should have connections with several areas of quantum information and computation, like quantum error-correction codes~\cite{ZR97c}, quantum noiseless subsystems~\cite{Zan01,CK:05}, faut-tolerant quantum computation~\cite{KBLW01a}, graph states~\cite{HEB04}, and quantum computation complexity.
In this paper we give an alternative definition for the zero-error capacity of quantum channels in terms of graph theory. Also, we present new results concerning quantum states attaining the quantum channel capacity. Particulary, we show that non-adjacent states live into orthogonal Hilbert subspaces, and that non-adjacent states are orthogonal. Our main result asserts that the quantum zero-error capacity can be reached by using only pure states. In addition, we prove that general POVM measurements are not required: for a given quantum channel, it is always possible to find a von Neumann measurement attaining the quantum zero-error capacity. A mathematically motivated example is given to illustrate our results.
The rest of this paper is structured as follows. Section~\ref{sec:back} recalls some definitions concerning the zero-error capacity of a quantum channel. Section 3 reformulates the problem of finding the quantum zero-error capacity into the graph language. This alternative definition is used in Sec.~\ref{sec:charact} to study the behavior of input states. Section~\ref{sec:measurements} discusses about measurements reaching the quantum zero-error capacity, and Sec.~\ref{sec:ex} illustrates the results with an example. Finally, Sec.~\ref{sec:conclu} presents the conclusions and discusses further works.
\section{Background\label{sec:back}}
We review some important definitions. Consider a $d-$dimensional quantum channel ${\mathcal{E}} \equiv \{E_a\}$ and a subset $\ensuremath{{\cal{S}}}$ of input states, and let $\rho_i \in \ensuremath{{\cal{S}}}$. We denote $\sigma_i = \ensuremath{{\cal{E}}}(\rho_i)$ the received quantum state when $\rho_i$ is transmitted through the quantum channel. Define a POVM $\{M_j\}$, where $\sum_j M_j =\one$. For convenience, we call Alice the sender and Bob the recipient. If $p(j|i)$ denotes the probability of Bob gets the outcome $j$ given that Alice sent the state $\rho_i$, then, $ p(j|i) = \tra{\sigma_{i} M_{j}}$.
By analogy with classical information theory~\cite{Sha:56}, the zero-error capacity of a quantum channel is defined for product states. A product of any $n$ input states will be called an input quantum codeword, $\ensuremath{\overline{\rho}}_i = \rho_{i_1} \otimes \dots \otimes \rho_{i_n}$, belonging to a $d^n$-dimensional Hilbert space $\ensuremath{{\cal{H}}}^n$. A mapping of $K$ classical messages (which we may take to be the integers $1,\dots,K$) into a subset of input quantum codewords will be called a quantum block code of length $n$. Thus, $\frac{1}{n}\log K$ will be the rate for this code. A piece of $n$ output indices obtained from measurements performed by means of a POVM $\{M_1,\dots,M_m\}$ will be called an output word, $w \in \{1,\dots,m\}^n$.
A decoding scheme for a quantum block code of length $n$ is a function that univocally associates each output word with integers 1 to $K$ representing classical messages. The probability of error for this code is greater than zero if the decoding system identifies a different message from the message sent.
Figure~\ref{fig:system} illustrates a system that makes use of a quantum channel to transmit classical information with a probability of error equal to zero. Initially, Alice chooses a message $i$ from a set of $K$ classical messages. Based on the message $i$ and on the structure of a quantum block code of length $n$, the quantum encoder prepares a $n$-tensor product of quantum states which is sent through the quantum channel $\ensuremath{{\cal{E}}}(\cdot)$. In the reception, Bob performs a POVM measurement in order to obtain an output word $w$. The decision system, called decoder, should associate the output word $w$ with a message $\tilde{\imath}$. In a zero-error context it is required $\tilde{\imath} = i$ with probability one.
\begin{figure}
\caption{ General representation of a quantum zero-error communication system.}
\label{fig:system}
\end{figure} \normalsize
\begin{definition} \label{def:qzec} Let $\ensuremath{{\cal{E}}}(\cdot)$ be a trace-preserving quantum map representing a noisy quantum channel. The zero-error capacity of~$\ensuremath{{\cal{E}}}(\cdot)$, denoted by $C^{(0)}(\ensuremath{{\cal{E}}})$, is the least upper bound of achievable rates with probability of error equal to zero. That is, \begin{equation} \label{eq:qzec}
C^{(0)}({\ensuremath{{\cal{E}}}}) = \sup_{n} \frac{1}{n}\log K(n), \end{equation} where $K(n)$ stands for the maximum number of classical messages that the system can transmit without error, when a quantum block code of length $n$ is used. \end{definition}
A canonical method for calculating the supremum in the Eq.~(\ref{eq:qzec}) involves a search on all possible input state subsets $\ensuremath{{\cal{S}}}$ and POVMs ${\mathcal{P}}$. Given a particular $(\ensuremath{{\cal{S}}},{\mathcal{P}})$, $\ensuremath{{\cal{S}}} = \{\rho_{1},\dots,\rho_{l}\}$, ${\mathcal{P}} = \{M_{1},\dots,M_{m}\}$, and supposing a memoryless quantum channel, one may define a classical discrete memoryless channel (DMC) as follows. Take indexes $j$ of $\rho_{j}$ and $k$ of $M_{k}$ as input and output alphabets, respectively. The transition matrix will be a $||\ensuremath{{\cal{S}}}||\times||{\mathcal{P}}||$ matrix given by $T=[p(k|j)]$, where \begin{equation} \label{eq:transitionmatrix}
p(k|j)=\tra{{\mathcal{E}}(\rho_{j})M_{j}}. \end{equation} Clearly, this classical equivalent channel has a zero-error capacity. Then, the zero-error error capacity of the quantum channel will be the maximum of these capacities over all possibles $(\ensuremath{{\cal{S}}},{\mathcal{P}})$.
\begin{definition} \label{def:optimum} An optimum $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}})$ for a quantum channel $\ensuremath{{\cal{C}}}$ is composed of a set $\ensuremath{{\cal{S}}} = \{\rho_i\}$ and a POVM $\ensuremath{{\cal{P}}} = \{M_j\}$ for which the zero-error capacity is reached. \end{definition}
Next we recall the definition of non-adjacent states.
\begin{definition} Two quantum states $\rho_1$ and $\rho_2$ are said to be non-adjacent with relation to a POVM $\ensuremath{{\cal{P}}} = \{M_j\}_{j=1}^{m}$ if $A_1 \cap A_2 =\oslash$, where $$ A_k = \{ j \in \{1,\dots,m\}; \; \tra{\ensuremath{{\cal{E}}}(\rho_k)M_{j}} > 0\}; \; k = 1,2. $$ \end{definition}
We proved a necessary and sufficient condition for which a quantum channel has zero-error capacity greater than zero:
\begin{proposition}[\cite{MeAs:05a}] \label{pro:cond} The zero-error capacity of a quantum channel is greater than zero if and only if there exist a subset $\ensuremath{{\cal{S}}}=\{\rho_i\}_{i=1}^{l}$ and a POVM $\ensuremath{{\cal{P}}} = \{M_j\}_{j=1}^{m}$ for which at least two states in $\ensuremath{{\cal{S}}}$ are non-adjacents with relation to the POVM ${\mathcal{P}}$. \end{proposition}
\section{Relation with graph theory}
Given a classical discrete memoryless channel, two input symbols are adjacent if there is an output symbol which can be caused by either of these two. From such channels, we may construct a graph $G$ by taking as many vertices as the number of input symbols, and connecting two vertices if the corresponding input symbols are non-adjacent. Shannon~\cite{Sha:56} showed that the zero-error capacity of the DMC is given by $$
C = \sup_n \frac{1}{n} \log \omega\left(G^n\right) , $$ where $\omega (G)$ is the clique number of the graph $G$ and $G^n$ is the $n-$product graph of $G$.
The problem of finding the zero-error capacity of a quantum channel is straightforwardly reformulated in the language of graph theory. Given a subset of input states $\ensuremath{{\cal{S}}}_{(i)}$ and a POVM ${\mathcal{P}}_{(i)}$, we can construct a characteristic graph ${\mathcal{G}}_{(i)}$ as follows. Take as many vertices as $||\ensuremath{{\cal{S}}}_{(i)}||$ and connect two vertices if the corresponding input states in $\ensuremath{{\cal{S}}}_{(i)}$ are non-adjacents for the POVM ${\mathcal{P}}_{(i)}$.
\begin{definition}[Alternative definition] \label{def:equiv} The zero-error capacity of the quantum channel is given by \begin{equation} \label{eq:clique} C^{(0)}({\ensuremath{{\cal{E}}}}) = \sup_{(\ensuremath{{\cal{S}}}_{(i)},{\mathcal{P}}_{(i)})} \sup_n \frac{1}{n} \log \omega\left({\mathcal{G}}_{(i)}^n\right), \end{equation} where $\omega ({\mathcal{G}})$ is the clique number of the graph ${\mathcal{G}}$ and ${\mathcal{G}}_{(i)}^n$ is the $n-$product graph of ${\mathcal{G}}_{(i)}$. \end{definition}
It is easy to see that the supremum in Eq.~(\ref{eq:clique}) is achieved for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$. Moreover, the characteristic graph we construct from the transition matrix defined by Eq.~(\ref{eq:transitionmatrix}) is identical to ${\mathcal{G}}_{(i)}$. We use this alternative definition to prove further results.
\section{Characterizing input states\label{sec:charact}}
It is known that finding the clique number of a graph (and consequently que zero-error capacity) is a NP-complete problem~\cite{Bollo:98}. One might expect that calculating the zero error-capacity of quantum channels is a more difficult task. For such channels, this process involves a search for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$. For example, a priori the subset $\ensuremath{{\cal{S}}}$ may contain any kind of quantum states. The results presented in this section aim to reduce the search space of operators in $\ensuremath{{\cal{S}}}$. Particularly, we show that it is only needed to consider pure states to attain the supremum in~Eq.(\ref{eq:clique}).
Proposition below relates orthogonality of output states and adjacency.
\begin{proposition}\label{teo:orto} For a quantum channel ${\mathcal{E}} \equiv \{E_a\}$, two input states $\rho_1,\rho_2 \in \ensuremath{{\cal{S}}}$ are non-adjacent for a given POVM $\ensuremath{{\cal{P}}} = \{M_1,\dots,M_m\}$ if and only if ${\mathcal{E}}(\cdot)$ takes $\rho_1$ and $\rho_2$ into orthogonal subspaces. \end{proposition}
More specifically, Proposition~\ref{teo:orto} asserts that if $\rho_1$ and $\rho_2$ are non-adjacent, then their images ${\mathcal{E}}(\rho_1)$ and ${\mathcal{E}}(\rho_2)$ are entirely inside orthogonal Hilbert subspaces. At first glance this seems to be an obvious result. However, remember that ${\mathcal{E}}(\rho_i)$ may be mixed states and it is important to know in which subspace each of them lives.
\begin{proof} Given a complete set of POVM operators $\ensuremath{{\cal{P}}} = \{M_1,\dots,M_m\}$, a POVM measurement apparatus can be viewed as a black box that outputs a number from $1$ to $m$ when an unknown quantum state is measured.
Suppose that $\rho_1$ and $\rho_2$ are non-adjacent quantum input states. For integers $k,l$ satisfying $k+l\leq m$, we can always reorder the POVM indexes so that $\ensuremath{{\cal{P}}} = \{M_1,\dots,M_k,\dots,M_{k+l},\dots,M_m\}$and $$
\textrm{Prob } [ i \; | \; \rho_1 \textrm{ was sent }] \begin{cases} > 0 \; \forall \; i=1,\dots,k\\ = 0 \; \textrm { otherwise} \end{cases} $$ and $$
\textrm{Prob } [ i \; | \; \rho_2 \textrm{ was sent }] \begin{cases} > 0 \; \forall \; i=k+1,\dots,k+l \\ = 0 \; \textrm{ otherwise}. \end{cases} $$
This scenario is explained in Fig.~\ref{fig:povm}. On the left side we put the states $\rho_i$, and all POVM elements on the right side. Next we draw a line from $\rho_i$ to $M_j$ if $\textrm{Prob } [ \textrm{get output } j \; | \; \rho_i \textrm{ was sent }] = \tra{{\mathcal{E}}(\rho_i)M_j}> 0$.
\begin{figure}\label{fig:povm}
\end{figure}
It is possible to build a new POVM containing only two elements $\{M^{(1)},M^{(2)}\}$ as
\begin{equation} M^{(1)} = \sum_{i=1}^{k} M_i \qquad \textrm{and} \qquad M^{(2)} = \sum_{i=k+1}^{m} M_i \end{equation} for which \begin{eqnarray*}
\textrm{Prob } [ \textrm{get output } (1) \; | \; \rho_1 \textrm{ was sent }] &=& 1 \\
\textrm{Prob } [ \textrm{get output } (2) \; | \; \rho_2 \textrm{ was sent }] &=& 1, \end{eqnarray*} or equivalently, \begin{eqnarray*} \tra{{\mathcal{E}}(\rho_1)M^{(1)}} &=& 1 \\ \tra{{\mathcal{E}}(\rho_2)M^{(2)}} &=& 1. \end{eqnarray*}
For the ``if'' part it is sufficient to demonstrate that $M^{(1)}$ and $M^{(2)}$ are orthogonal projectors. Note that $M^{(1)} + M^{(2)} = \one$. Hence, if $M^{(1)}$ is a projector, then $M^{(2)}$ is its orthogonal complement.
Let ${\mathcal{E}}(\rho_1) = \sum_a E_a \rho_1 E_a^\dagger$ be the output state when $\rho_1$ is sent through the quantum channel. The spectral decomposition of ${\mathcal{E}}(\rho_1)$ gives us $$
{\mathcal{E}}(\rho_1) = \sum_i \alpha_i^{(1)} \op{a_i}, $$ for an orthonormal base $\qu{a_i}$ and positive numbers $\alpha_i^{(1)}$, $\sum_i \alpha_i^{(1)} = 1$. Then, verifying $\tra{{\mathcal{E}}(\rho_1)M_1^{(1)}} = 1 $ implies \begin{eqnarray*}
\tra{M^{(1)}\sum_i \alpha_i^{(1)} \op{a_i}} &=& \sum_i \alpha_i^{(1)} \ip{a_i}{M^{(1)}|a_i} \\ &=& \sum_i \alpha_i^{(1)} \\ &=& 1. \end{eqnarray*}
Notice that $M^{(1)}$ is a positive matrix satisfying $M^{(1)} \leq \one$. From this we conclude that $\ip{a_i}{M^{(1)}|a_i} = 1 \; \forall \; i $ such that $\qu{a_i}$ is in the support of $ {{\mathcal{E}}(\rho_1)}$. Finally, we can write $M^{(1)}$ as $$
M^{(1)} = \sum_{\{i:\qu{a_i} \in \sup {{\mathcal{E}}(\rho_1)} \} }\op{a_i}, $$ which is a projector on the subspace spanned by the eigenvectors of ${\mathcal{E}}(\rho_1)$ with nonzero eigenvalues.
Conversely, let ${\mathcal{E}}$ be a quantum channel that take $\rho_1$ and $\rho_2$ into orthogonal subspaces. If $M^{(1)}$ and $M^{(2)}$ are projectors over these subspaces, then $$
\tra{{\mathcal{E}}(\rho_1)M^{(1)}} = 1 \quad \Rightarrow \quad \tra{{\mathcal{E}}(\rho_1)M^{(2)}} = 0 $$ and $$
\tra{{\mathcal{E}}(\rho_2)M^{(2)}} = 1 \quad \Rightarrow \quad \tra{{\mathcal{E}}(\rho_2)M^{(1)}} = 0, $$ and the result follows. \end{proof}
We recall the definition of the Holevo-Schumacher-Westmoreland's classical capacity for a quantum channel~\cite{Hol:98,SW:97}: {\small $$
C_{1,\infty}(\ensuremath{{\cal{E}}}) \equiv \max_{\{p_i,\rho_i\}} \left[ S\left(\ensuremath{{\cal{E}}}\left(\sum_i p_i\rho_i\right)\right) - \sum_i p_i S(\ensuremath{{\cal{E}}}(\rho_i))\right]. $$ } A very interesting result about this capacity claims that the maximum is reached by using only pure states, i.e., we need only consider states like $\rho_i = \op{v_i}$ in the input of the channel.
For the quantum zero-error capacity (QZEC), we have an analogous result:
\begin{proposition}\label{teo:puros} The QZEC of quantum channels is calculated by using an optimum map $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}})$, where the set $\ensuremath{{\cal{S}}}$ is composed only by pure quantum states, i.e., $\ensuremath{{\cal{S}}} = \{\rho_i = \op{v_i}\}$. \end{proposition}
\begin{proof} Consider a quantum channel represented by a trace-preserving linear map, $\ensuremath{{\cal{E}}}(\cdot)$, with operation elements $\{E_a\}$. Suppose $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}})$ is an optimum map, with $\ensuremath{{\cal{S}}} = \{\rho_1,\dots,\rho_l\}$ and $\ensuremath{{\cal{P}}} = \{M_1,\dots,M_m\}$, and each state $\rho_i$ may be a mixed state. We call ${\mathcal{G}} $ the characteristic graph associated with $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}})$. To demonstrate the proposition, we show that it is always possible to obtain a subset $\ensuremath{{\cal{S}}}'$ from $\ensuremath{{\cal{S}}}$, such that $\ensuremath{{\cal{S}}}'$ contains only pure states and $(\ensuremath{{\cal{S}}}',\ensuremath{{\cal{P}}}'=\ensuremath{{\cal{P}}})$ is also optimum.
Let $\rho_i \in \ensuremath{{\cal{S}}}$, $\rho_i = \sum_v \lambda_{v_i} \op{v_i}$ be an input quantum state. Then, the output of the channel when $\rho_i$ is transmitted is given by
\begin{eqnarray}
\ensuremath{{\cal{E}}}(\rho_i) &=& \sum_a E_a \rho_i E_a^\dagger \nonumber\\
&=& \sum_a E_a \left[ \sum_v \lambda_{v_i} \op{v_i} \right] E_a^\dagger \nonumber\\
&=& \sum_a \sum_v E_a \lambda_{v_i} \op{v_i} E_a^\dagger. \end{eqnarray}
By using the POVM $\ensuremath{{\cal{P}}}$, the probability of measuring $j$ given that the quantum state $\rho_i$ was sent is
\begin{eqnarray}
p(j|i) &=& \tra{\ensuremath{{\cal{E}}}(\rho_i) M_j} \nonumber \\
&=& \tra{\left(\sum_a \sum_v E_a \lambda_{v_i} \op{v_i} E_a^\dagger \right) M_j} \nonumber \\
&=& \sum_v \lambda_{v_i} \tra{\left( \sum_a E_a \op{v_i} E_a \right) M_j}. \label{eq:traco} \end{eqnarray}
Note that in the equation above, $\tra{\cdot}$ is always greater than or equal to zero and $0< \lambda_{v_i}\leq 1$. It represents the probability of getting output $j$ given that the pure state $\qu{v_i}$ was sent through the quantum channel. If we replace the mixed states $\rho_i$ by any pure state $\qu{v_i}$ in the support of $\rho_i$, the cardinality of the subset $A_i$ (see Def. 3) never increases. To see this, let $M_k$ be an POVM element so that $\tra{{\mathcal{E}}(\rho_i)M_k} = 0$. From Eq.~(\ref{eq:traco}), \begin{eqnarray} \tra{{\mathcal{E}}(\rho_i)M_k} &=& \sum_v \lambda_{v_i} \tra{\left( \sum_a E_a \op{v_i} E_a \right) M_k} \nonumber\\ &=& 0 \end{eqnarray} implies $ \tra{\left( \sum_a E_a \op{v_i} E_a \right) M_k} = 0$ for all pure states $\qu{v_i}$ in the support of $\rho_i$. Now define a new set $\ensuremath{{\cal{S}}}'$ by replacing each mixed state $\rho_i \in \ensuremath{{\cal{S}}}$ with a pure state $\qu{v_i} \in \sup \rho_i$. The number of non-adjacent states in $\ensuremath{{\cal{S}}}'$ is at least that of $\ensuremath{{\cal{S}}}$. A larger number of non-adjacency leads to a more connected characteristic graph. For any graph $G$, and in particular for the characteristic graph, it is well known that adding edges never decreases (and may increase) the clique number~\cite{Bollo:98}, and according to Eq.~(\ref{eq:clique}) this may not reduce the zero-error capacity of the quantum channel.
Finally, we may always find a set $\ensuremath{{\cal{S}}}' = \{\rho'_1,\dots,\rho'_l\}$, where $\rho'_i = \op{v_i} \in \sup \rho_i$ and $(\ensuremath{{\cal{S}}}',\ensuremath{{\cal{P}}})$ is also optimum.
\end{proof}
The proposition~\ref{teo:puros} allow us to prove the next result considering only pure states:
\begin{proposition} Let $\qu{v_1}$ e $\qu{v_2}$ be two non-adjacent states. Then, $\ip{v_1}{v_2}=0$. \end{proposition}
~ \begin{proof} To prove the proposition, we make use of a distance measure for quantum states called trace distance. The trace distance between $\sigma_1$ and $\sigma_2$ is given by $$
D(\sigma_1,\sigma_2) = \frac{1}{2} \textrm{tr }\left|\sigma_1 - \sigma_2 \right|. $$ Note that the trace distance is maximum and equal to one if, and only if, $ \sigma_1$ and $\sigma_2$ have orthogonal supports.
Proposition~\ref{teo:orto} guarantees that if $\qu{v_1}$ and $\qu{v_2}$ are non-adjacent, then ${\mathcal{E}}(\qu{v_1})$ and ${\mathcal{E}}(\qu{v_2})$ have orthogonal supports. Because we assumed $\qu{v_1}$ and $\qu{v_2}$ non-adjacent, we have $$ D({\mathcal{E}}(\qu{v_1}),{\mathcal{E}}(\qu{v_2})) = 1. $$ It is easy to show that quantum channels ${\mathcal{E}} \equiv \{E_a\}$ are contractive~\cite[pp. 406]{NC:2000}, i.e., $D(\qu{v_1},\qu{v_2}) \ge D({\mathcal{E}}(\qu{v_1}),{\mathcal{E}}(\qu{v_2}))$. The result now follows: \begin{equation} 1 \ge D(\qu{v_1},\qu{v_2}) \ge D({\mathcal{E}}(\qu{v_1}),{\mathcal{E}}(\qu{v_2})) =1, \\ \end{equation} which means that $D(\qu{v_1},\qu{v_2}) = 1$ and $\qu{v_1}$ are orthogonal to $\qu{v_2}$ . \end{proof}
Consider a qubit channel and an orthonormal basis for the 2-dimensional Hilbert space. Our results allow for the analysis of such channels in a zero-error context: either the zero-error capacity is equal to one bit per use or to zero. This is because these channels have at most two non-adjacent input states. If we take any subset $\ensuremath{{\cal{S}}}$ containing $n$ states, $n-2$ states will be adjacent with at least one of the others two.
For a quantum channel in a $d-$dimensional Hilbert space, the canonical method presented in Sec.~\ref{sec:back} can be improved. The search for the subset $\ensuremath{{\cal{S}}}$ should start by taking sets of orthogonal pure states. Evidently, adjacent states can be added to the initial set if they contribute to increase the clique number in Eq.~(\ref{eq:clique}).
\section{POVM measurements attaining the zero-error capacity\label{sec:measurements}}
As pointed in the Sec.~\ref{sec:charact}, the problem of calculating the quantum zero-error capacity should be, in general, more difficult than finding the classical zero-error capacity. This fact can be understood by analyzing Eq.~(\ref{eq:clique}). Each choice of $(\ensuremath{{\cal{S}}}_{(i)},{\mathcal{P}}_{(i)})$ gives rise to a classical channel. Therefore, the quantum zero-error capacity can be interpreted as the supremum of the classical zero-error capacity of such equivalent channels over all possible $(\ensuremath{{\cal{S}}}_{(i)},{\mathcal{P}}_{(i)})$. Hence, a major issue is to restrict the global search space of operators in $\ensuremath{{\cal{S}}}$ and measurements ${\mathcal{P}}$. The main result in Sec.~\ref{sec:charact} claims that we only need to consider pure states in $\ensuremath{{\cal{S}}}$ to attain the zero-error capacity of a quantum channel.
Concerning the measurements, We have proven that we can restrict ${\mathcal{P}}$ to a projective measurement in order to attain the supremum in Eq.~(\ref{eq:clique}).
\begin{proposition}\label{teo:povm} The QZEC can be calculated by using an optimum map $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}})$, where ${\mathcal{P}}$ stands for a set of von Neumann operators $M_i$ with $\sum_i M_i = \one$. \end{proposition}
\begin{proof} First consider an optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$, where $\ensuremath{{\cal{S}}} = \{\qu{v_i}\}$, ${\mathcal{P}} = \{M_i\}$, and $M_i$ are positive operators satisfying $\sum_i M_i = \one$. Let ${\mathcal{H}}_i$ be the Hilbert space spanned by the states in the support of ${\mathcal{E}}(\qu{v_i})$. It is known that $\qu{v_i}$ and $ \qu{v_j}$ are non-adjacent if and only if ${\mathcal{H}}_i \bot {\mathcal{H}}_j$.
Let ${\mathcal{G}}$ be the characteristic graph for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$. To demonstrate the result, it is only need to show the existence of a Von Neumann measurement giving rise to the same characteristic graph.
Consider ${\mathcal{V}}_i$ an orthonormal basis of ${\mathcal{H}}_i$, and ${\mathcal{V}}$ an orthonormal basis of ${\mathcal{H}}$, the whole Hilbert space of dimension $d$. From ${\mathcal{G}}$, it \emph{ should} exist at least one orthonormal basis ${\mathcal{V}}$ of ${\mathcal{H}}$ , say ${\mathcal{V}} = \{\qu{\varphi_1},\dots,\qu{\varphi_d}\}$, with ${\mathcal{V}}_i \subset {\mathcal{V}}$, for which all (non-)adjacency relations in ${\mathcal{G}}$ are satisfied.
Now define a POVM ${\mathcal{P}}' = \{\op{\varphi_i}\}$. It is easy to see that $(\ensuremath{{\cal{S}}},\ensuremath{{\cal{P}}}')$ gives rise to the same characteristic graph ${\mathcal{G}}$. \end{proof}
Note that each ${\mathcal{V}}_i$ is not necessarily composed by the vectors on the support of ${\mathcal{E}}(v_i)$. This is only true if all quantum states ${\mathcal{E}}(v_i)$ are mutually orthogonal.
\section{A non-trivial example: the pentagon\label{sec:ex}}
We discuss in this section an example of a quantum channel which has a non-trivial zero-error capacity. By non-trivial we mean a channel whose characteristic graph for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$ is neither a complete nor a empty graph, \emph{and} for which the supremum in Eq.~(\ref{eq:clique}) is attained for $n>1$. Trivial examples of the quantum zero-error capacity can be found in~\cite{MeAs:05a}. The following example is mathematically motivated, and has not a physical meaning. However, it is interesting because the quantum channel we constructed gives rise to the pentagon as the characteristic graph for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$. Historically, the zero-error capacity of the pentagon was studied by Shannon~\cite{Sha:56} in 1956, that gives lower and upper bounds for it. Only in 1979, Lovász~\cite{Lov:79} gave an exact solution for this problem.
Let ${\mathcal{E}}(\cdot)$ be a quantum channel with Kraus operators $\{E_1,E_2,E_3\}$ given by $$ E_1 = \left( \begin{array}{ccccc}
\alpha & 0 & 0 & 0 & \beta \\
\alpha & \beta & 0 & 0 & 0 \\
0 & \alpha & \beta & 0 & 0 \\
0 & 0 & \alpha & \beta & 0 \\
0 & 0 & 0 & \alpha & \beta \end{array} \right), \qquad E_2 = \left( \begin{array}{ccccc}
\alpha & 0 & 0 & 0 & -\beta \\
\alpha & -\beta & 0 & 0 & 0 \\
0 & \alpha & -\beta & 0 & 0 \\
0 & 0 & \alpha & -\beta & 0 \\
0 & 0 & 0 & \alpha & -\beta \end{array} \right), $$ $$ E_3 = \left( \begin{array}{ccccc}
\sqrt{1-4\alpha^2} & 0 & 0 & 0 & 0 \\
0 & \sqrt{1-2\alpha^2-2\beta^2}& 0 & 0 & 0 \\
0 & 0 & \sqrt{1-2\alpha^2-2\beta^2} & 0 & 0 \\
0 & 0 & 0 & \sqrt{1-2\alpha^2-2\beta^2} & 0 \\
0 & 0 & 0 & 0 & \sqrt{1-4\beta^2} \end{array} \right), $$ where $0\leq \alpha,\beta \leq 0,5$. It is easy to see that $\sum_a E_a^\dagger E_a = \one$, and ${\mathcal{E}}(\cdot)$ is a linear trace-preserving quantum map that represents a physical process.
The channel model was proposed in a way that the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$ is given by: $$
\ensuremath{{\cal{S}}} = \{\qu{v_1},\dots,\qu{v_5}\} \qquad {\mathcal{P}} = \{\op{v_i}\}_{i=1}^5, $$ where $\qu{v_i}$ is the computation basis of the Hilbert space of dimension five. Once we have the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$, the adjacency relationships are easily obtained by taking \begin{equation}
\mathrm{Prob ~}(\mathrm{get~output ~ } j| \; \qu{\psi_i} \mathrm{ ~was~ sent}) = \tr{{\mathcal{E}}(\op{v_i})M_j}; \quad i,j=1,\dots,5. \end{equation} The characteristic graph for the optimum $(\ensuremath{{\cal{S}}},{\mathcal{P}})$ is illustrated in Fig.~\ref{fig:pentagono}.
\begin{figure}\label{fig:pentagono}
\end{figure}
The Shannon capacity of this graph was calculated by Lovázs~\cite{Lov:79}, and it is attained for $n=2$: $$
C^{(0)}(\mathrm{pentagon}) = \frac{1}{2} \log 5. $$ Therefore, $ C^{(0)}(\mathrm{pentagon})$ is the maximum rate for which classical information can be transmitted through the quantum channel with a probability of error equal to zero. A quantum block code of length two reaching the capacity is \begin{eqnarray} \ensuremath{\overline{\rho}}_1 = \qu{v_0}\qu{v_0}, \quad \ensuremath{\overline{\rho}}_2 = \qu{v_1}\qu{v_2}, \quad \ensuremath{\overline{\rho}}_3 = \qu{v_2}\qu{v_4}\nonumber\\ \ensuremath{\overline{\rho}}_4 = \qu{v_3}\qu{v_1}, \qquad \ensuremath{\overline{\rho}}_5 = \qu{v_4}\qu{v_3}. \end{eqnarray}
\section{Conclusions\label{sec:conclu}} We have presented in this paper some results concerning the characterization of input states for the calculation of the zero-error capacity of quantum channels.
We initially showed that calculating the zero-error capacity of such channels is equivalent to finding the clique number of graph products. This first result is used to prove the main result of this paper: we have shown that the quantum zero-error capacity can be reached by using only pure input states. In the literature, it was demonstrated an analogous result for the HSW capacity~\cite[pp. 555]{NC:2000}.
We have also proven that general POVM measurements are not needed to attain the zero-error capacity of quantum channels, and that projective measurements are sufficient. These results were illustrated with an example of a quantum channel having a pentagon as characteristic graph.
Further work will include the study of relations with others areas of quantum information theory and quantum computation. More specifically, we think the theory of quantum zero-error is closely connected with quantum noiseless subsystems and the theory of graph states.
\section*{References}
\end{document} | arXiv |
\begin{document}
\title{Nash equilibria in games over graphs equipped
with a communication mechanism}
\begin{abstract}
We study pure Nash equilibria in infinite-duration games on graphs,
with partial visibility of actions but communication (based on a
graph) among the players. We show that a simple communication
mechanism consisting in reporting the deviator when seeing it and
propagating this information is sufficient for characterizing Nash
equilibria.
We propose an epistemic game construction, which conveniently
records important information about the knowledge of the
players. With this abstraction, we are able to characterize Nash
equilibria which follow the simple communication pattern via winning
strategies. We finally discuss the size of the construction, which
would allow efficient algorithmic solutions to compute Nash
equilibria in the original game. \end{abstract}
\section{Introduction}
Multiplayer concurrent games over graphs allow to model rich interactions between players. Those games are played as follows. In a state, each player chooses privately and independently an action, defining globally a move (one action per player); the next state of the game is then defined as the successor (on the graph) of the current state using that move; players continue playing from that new state, and form a(n infinite) play. Each player then gets a reward given by a payoff function (one function per player). In particular, objectives of the players may not be contradictory: those games are non-zero-sum games, contrary to two-player games used for controllers or reactive synthesis~\cite{thomas02,henzinger05}.
Using solution concepts borrowed from game theory, one can describe interactions among the players, and in particular rational behaviours of selfish players. One of the most basic and classically studied solution concepts is that of Nash equilibria~\cite{nash50}. A Nash equilibrium is a strategy profile where no player can improve her payoff by unilaterally changing her strategy. The outcome of a Nash equilibrium can therefore be seen as a rational behaviour of the system.
While very much studied by game theorists, e.g. over (repeated) matrix games, such a concept (and variants thereof) has been only rather recently studied over infinite-duration games on graphs. Probably the first works in that direction are~\cite{CMJ04,CHJ06,ummels06,ummels08}. Several series of works have followed. To roughly give an idea of the existing results, pure Nash equilibria always exist in turn-based games for $\omega$-regular objectives~\cite{UW11} but not in concurrent games, even with simple objectives; they can nevertheless be computed~\cite{UW11,BBMU15,brenguier16,bouyer18} for large classes of objectives. The problem becomes harder with mixed (that is, stochastic) Nash equilibria, for which we often cannot decide the existence~\cite{UW11a,BMS14}.
Computing Nash equilibria requires to (i) find a good behaviour of the system; (ii) detect deviations from that behaviour, and identify deviating players; (iii) punish them. This simple characterization of Nash equilibria is made explicit in~\cite{CFGR16}. Variants of Nash equilibria require slightly different ingredients, but they are mostly of a similar vein.
Many of those results are proven using the construction of a two-player game, in which winning strategies correspond (in some precise sense) to Nash equilibria in the original game. This two-player game basically records the knowledge of the various players about everything which can be uncertain: (a) the possible deviators in~\cite{BBMU15}, and (b) the possible states the game can be in~\cite{bouyer18}. Extensions of this construction can be used for other solution concepts like robust equilibria~\cite{brenguier16} or rational synthesis~\cite{COT18}.
In this work, we consider infinite-duration games on graphs, in which the game arena is perfectly known by all the players, but players have only a partial information on the actions played by the other players.
The partial-information setting of this work is inspired by~\cite{RT98}: it considers repeated games played on matrices, where players only see actions of their neighbours. Neighbours are specified by a communication graph. To ensure a correct detection of deviators, the solution is to propagate the identity of the deviator along the communication graph. A fingerprint (finite sequence of actions) of every player is agreed at the beginning, and the propagation can be made properly if and only if the communication graph is 2-connected, ensuring large sets of Nash equilibria (formalized as a folk theorem). Fingerprints are not adapted to the setting of graphs, since they may delay the time at which a player will learn the identity of the deviator, which may be prohibitive if a bad component of a graph is then reached.
We therefore propose to add real communication among players. Similarly to~\cite{RT98}, a player can communicate only with her neighbours (also specified by a communication graph), but can send arbitrary messages (modelled as arbitrary words over alphabet $\{0,1\}$).
We assume that visited states are known by the players, hence only the deviator (if any) may be unknown to the players. In this setting, we show the following results: \begin{itemize} \item We show that a very simple epidemic-like communication mechanism
is sufficient for defining Nash equilibria. It consists in (a)
reporting the deviator (for the neighbours of the deviator) as soon
as it is detected, and (b) propagating this information (for the
other players). \item We build an epistemic game, which tracks those strategy profiles
which follow the above simple communication pattern. This is a
two-player turn-based game, in which \Eve (the first player) suggest
moves, and \Adam (the second player) complies (to generate the main
outcome), or not (to mimic single-player deviations). The
correctness of the construction is formulated as
follows: there is a Nash equilibrium in the original game of payoff
$p$ if and only if there is a strategy for \Eve in the epistemic
game which is winning for $p$. \item We analyze the complexity of this construction. \end{itemize}
Note that we do not assume connectedness of the communication graph, hence the particular case of a graph with no edges allows to recover the setting of~\cite{BBMU15} while a complete graph allows to recover the settings of~\cite{UW11,brenguier16}.
In Section~\ref{sec:defs}, we define our model and give an example to illustrate the role of the communication graph. In Section~\ref{sec:reducs}, we prove the simple communication pattern. In Section~\ref{sec:epistemic}, we construct the epistemic game and discuss its correctness.
In Section~\ref{sec:complexity}, we discuss complexity issues. All proofs are postponed to the technical appendix.
\section{Definitions} \label{sec:defs}
We use the standard notations $\bbR$ (resp. $\bbQ$, $\bbN$) for the set of real (resp. rational, natural) numbers. If $S$ is a subset of $\bbR$, we write $\overline{S}$ for $S \cup \{-\infty,+\infty\}$.
Let $S$ be a finite set and $R \subseteq S$. If $m$ is an $S$-vector over some set $\Sigma$, we write $m(R)$ (resp. $m(-R)$) for the vector composed of the $R$-components of $m$ (resp. all but the $R$-components). We also use abusively the notations $m(i)$ (resp. $m(-i)$) when $i$ is a single element of $S$, and may sometimes even use $m_i$ if this is clear in the context. Also, if $s \in S$ and $a \in \Sigma$, then $m[s/a]$ is the vector where the value $m(s)$ is replaced by $a$.
If $S$ is a finite set, we write $S^*$ (resp. $S^+$, $S^\omega$) for the set of words (resp. non-empty word, infinite words) defined on alphabet $S$.
\subsection{Concurrent games and communication graphs}
We use the model of concurrent multi-player games~\cite{BBMU15}, based on the two-player model of~\cite{AHK02}.
\begin{definition}
A \emph{concurrent multiplayer game} is a tuple $\calG =
\tuple{V,v_\init,\Act,\Agt,\Sigma,\Allow,\Tab, (\payoff_a)_{a \in
\Agt}}$, where $V$ is a finite set of vertices, $v_\init \in V$
is the initial vertex, $\Act$ is a finite set of actions, $\Agt$ is
a finite set of players, $\Sigma$ is a finite alphabet,
$\Allow\colon V \times \Agt \to 2^\Act\setminus\{\emptyset\}$ is a
mapping indicating the actions available to a given player in a
given vertex,\footnote{This condition ensures that the game is
non-blocking.} $\Tab\colon V \times \Act^{\Agt} \to V$ associates,
with a given vertex and a given action tuple the target vertex, for
every $a \in \Agt$, $\payoff_a \colon V^\omega \to \bbD$ is a payoff
function with values in a domain $\bbD \subseteq \overline{\bbR}$. \end{definition}
An element of $\Act^\Agt$ is called a \emph{move}. Standardly (see~\cite{AHK02} for two-player games and~\cite{BBMU15} for the multiplayer extension), concurrent games are played as follows: from a given vertex $v$, each player selects independently an action (allowed by $\Allow$), which altogether form a move $m$; then, the game proceeds to the next vertex, given by $\Tab(v,m)$; the game continues from that new vertex.
Our setting will refine this model, in that at each round, each player will also broadcast a message, which will be received by some of the players. The players that can receive a message will be specified using a communication graph that we will introduce later. The role of the messages will remain unclear until we commit to the definition of a strategy.
Formally, a \emph{full history} $h$ in $\calG$ is a finite sequence \[ v_0 \cdot (m_0,\mes_0) \cdot v_1 \cdot (m_1,\mes_1) \cdot v_2 \ldots (m_{s-1},\mes_{s-1}) \cdot v_s \in V \cdot \left(\left(\Act^\Agt
\times (\{0,1\}^*)^\Agt\right)\cdot V\right)^* \] such that for every $0 \le r < s$, for every $a \in \Agt$, $m_r(a) \in \Allow(v_r,a)$, and $v_{r+1} = \Tab(v_r,m_r)$. For every $0 \le r < s$, for every $a \in \Agt$, the set $\mes_r(a)$ is the message appended to action $m_r(a)$ at step $r+1$, which will be broadcast to some other players. For readability we will also write $h$ as \[
v_0 \xrightarrow{m_0,\mes_0} v_1 \xrightarrow{m_1,\mes_1} v_2 \ldots
\xrightarrow{m_{s-1},\mes_{s-1}} v_s \] We write $\vertices(h) = v_0 \cdot v_1 \cdots v_s$, and $\last(h)$ for the last vertex of $h$ (that is, $v_s$). If $r \le s$, we also write $h_{\ge r}$ (resp. $h_{\le r}$) for the suffix $v_r \cdot (m_r,\mes_r) \cdot v_{r+1} \cdot (m_{r+1},\mes_{r+1}) \ldots (m_{s-1},\mes_{s-1}) \cdot v_s$ (resp. prefix $v_0 \cdot (m_0,\mes_0) \cdot v_1 \cdot (m_1,\mes_1) \ldots (m_{r-1},\mes_{r-1}) \cdot v_r$). We write $\Hist_\calG(v_0)$ (or simply $\Hist(v_0)$ if $\calG$ is clear in the context) for the set of full histories in $\calG$ that start at $v_0$. If $h \in \Hist(v_0)$ and $h' \in \Hist(\last(h))$, then we write $h \cdot h'$ for the obvious concatenation of histories (it then belongs to $\Hist(v_0)$).
We add a \emph{communication (directed) graph} $G = (\Agt,E)$ to the context. The set of vertices of $G$ is the set of players, and edges define a neighbourhood relation. An edge $(a,b) \in E$ (with $a \ne b$) means that player $b$ can see which actions are played by player $a$ together with the messages broadcast by player $a$.
Later we write $a \fleche b$ whenever $(a,b) \in E$ or $a = b$, and $\Vois(b) = \{a \in \Agt \mid a \fleche b\}$ for the so-called \emph{neighbourhood} of $b$ (that is, the set of players about which player $b$ has information).
If $a,b \in \Agt$, we write $\dist_G(a,b)$ for the distance in $G$ from $a$ to $b$ ($+\infty$ if there is no path from $a$ to $b$).
Let $a \in \Agt$ be a player.
The projection of $h$ for $a$ is denoted $\pi_a(h)$ and is defined by \begin{multline*}
v_0 \cdot (m_0(\Vois(a)),\mes_0(\Vois(a))) \cdot v_1 \cdot
(m_1(\Vois(a)),\mes_1(\Vois(a))) \cdot v_2 \ldots \\
\ldots (m_{s-1}(\Vois(a)),\mes_{s-1}(\Vois(a))) \cdot v_s \in V
\cdot \left(\left(\Act^{\Vois(a)} \times
(\{0,1\}^*)^{\Vois(a)}\right) \cdot V \right)^* \end{multline*} This will be the information available to player $a$. In particular, messages broadcast by the players are part of this information. Note that we assume perfect recall, that is, while playing, player $a$ will remember all her past knowledge, that is, all of $\pi_a(h)$ if $h$ has been played so far. We define the \emph{undistinguishability relation
$\sim_a$} as the equivalence relation over full histories induced by $\pi_a$: for two histories $h$ and $h'$, $h \sim_a h'$ iff $\pi_a(h) = \pi_a(h')$. While playing, if $h \sim_a h'$, $a$ will not be able to know whether $h$ or $h'$ has been played. We write $\Hist_{\calG,a}(v_0)$ for the set of histories for player $a$ (also called $a$-histories) from $v_0$.
We extend all the above notions to infinite sequences in a straightforward way and to the notion of \emph{full play}. We write $\Plays_\calG(v_0)$ (or simply $\Plays(v_0)$ if $\calG$ is clear in the context) for the set of full plays in $\calG$ that start at $v_0$.
A \emph{strategy} for a player $a \in \Agt$ from vertex $v_0$ is a mapping $\sigma_a \colon \Hist_{\calG}(v_0) \to \Act \times \{0,1\}^*$ such that for every history $h \in \Hist_{\calG}(v_0)$, $\sigma_a(h)[1] \in \Allow(\last(h),a)$, where the notation $\sigma_a(h)[1]$ denotes the first component of the pair $\sigma(h)$. The value $\sigma_a(h)[1]$ represents the action that player $a$ will do after $h$, while $\sigma_a(h)[2]$ is the message that she will append to her action and broadcast to all players $b$ such that $a \fleche b$. The strategy $\sigma_a$ is said \emph{$G$-compatible} if furthermore, for all histories $h,h' \in \Hist(v_0)$, $h \sim_a h'$ implies $\sigma_a(h) = \sigma_a(h')$. In that case, $\sigma_a$ can equivalently be seen as a mapping $\Hist_{\calG,a}(v_0) \to \Act \times \{0,1\}^*$. An \emph{outcome} of $\sigma_a$ is a(n infinite) play $\rho = v_0 \cdot (m_0,\mes_0) \cdot v_1 \cdot (m_1,\mes_1) \ldots$ such that for every $r \ge 0$, $\sigma_a(\rho_{\le r}) = (m_r(a),\mes_r(a))$. We write $\out(\sigma_a,v_0)$ for the set of outcomes of $\sigma_a$ from $v_0$.
A \emph{strategy profile} is a tuple $\sigma_\Agt=(\sigma_a)_{a \in \Agt}$, where, for every player $a \in \Agt$, $\sigma_a$ is a strategy for player $a$. The strategy profile is said \emph{$G$-compatible} whenever each $\sigma_a$ is $G$-compatible. We write $\out(\sigma_\Agt,v_0)$ for the unique full play from $v_0$, which is an outcome of all strategies part of $\sigma_\Agt$.
When $\sigma_\Agt$ is a strategy profile and $\sigma'_d$ a player-$d$ $G$-compatible strategy, we write $\sigma_\Agt[d/\sigma'_d]$ for the profile where player $d$ plays according to $\sigma'_d$, and each other player $a$ ($\ne d$) plays according to $\sigma_a$. The strategy $\sigma'_d$ is a \emph{deviation} of player $d$, or a \emph{$d$-deviation} w.r.t. $\sigma_\Agt$. Such a $d$-deviation is said \emph{profitable} w.r.t. $\sigma_\Agt$ whenever $\payoff_d \Big(\vertices(\out(\sigma_\Agt,v_0))\Big) < \payoff_d\Big(\vertices(\out(\sigma_\Agt[d/\sigma'_d],v_0))\Big)$.
\begin{definition}
A \emph{Nash equilibrium} from $v_0$ is a $G$-compatible strategy
profile $\sigma_\Agt$ such that for every $d \in \Agt$, there is no
profitable $d$-deviation w.r.t. $\sigma_\Agt$. \end{definition} In this definition, deviation $\sigma'_d$ needs not really to be $G$-compatible, since the only meaningful part of $\sigma'_d$ is along $\out(\sigma[d/\sigma'_d],v_0)$, where there are no $\sim_d$-equivalent histories: any deviation can be made $G$-compatible without affecting the profitability of the resulting outcome.
\begin{remark}
Before pursuing our study, let us make clear what information
players have: a player knows the full arena of the game and the
whole communication graph; when playing the game, a player sees
the states which are visited, and see actions of and messages from
her neighbours (in the communication graph). When playing the
profile of a Nash equilibrium, all players know all strategies,
hence a player knows precisely what is expected to be the main
outcome; in particular, when the play leaves the main outcome,
each player knows that a deviation has occurred, even though she
didn't see the deviator or received any message. Note that
deviations which do not leave the main outcome may occur; in this
case, only the neighbours of the deviator will know that such a
deviation occurred; we will see that it is useless to take care of
such deviations. \end{remark}
\subsection{An example} \label{subsec:ex}
\begin{figure}
\caption{A five-player game (left) and three communication graphs
(right); self-loops $a \fleche a$ omitted from the picture. The
action alphabet is $\{\alpha,\beta\}$. The transition function is
represented as arrows from one vertex to another labeled with the
action profile(s) allowing to go from the origin vertex to the
destination one. We write action profiles with length-5
words. Convention: no label means complementary labels (e.g. one
goes from $v_0$ to $v'_0$ using any action profile that is not in
$\alpha^5+(\alpha\beta+\beta\beta+\beta\alpha)\Act^3+\alpha^2(\beta\alpha^2+\alpha\beta\alpha+\alpha^2\beta))$.}
\label{gameex}
\end{figure}
We consider the five-player game described in Figure~\ref{gameex} in which we denote the players $\Agt = \{0,1,2,3,4\}$. The action alphabet is $\Act=\{\alpha,\beta\}$, and the initial vertex is assumed to be $v_0$. We suppose the payoff function vector is defined as (to be read as the list of payoffs of the players): \[ \payoff(\rho)= \left\{\begin{array}{ll}
(0,0,1,1,1) & \text{if}\ \rho\ \text{visits}\ v_1\ \text{infinitely
often}\\
(0,0,2,2,2) & \text{if}\ \rho\ \text{visits}\ v_1\ \text{finitely
often and}\ v'_1\ \text{infinitely
often} \\
(0,0,0,2,2) & \text{if}\ \rho\ \text{ends
up in}\ v_2\\
(0,0,2,0,2) & \text{if}\ \rho\ \text{ends
up in}\ v_3\\
(0,0,2,2,0) & \text{if}\ \rho\ \text{ends
up in}\ v_4\\
(0,0,3,3,3) & \text{if}\ \rho\ \text{ends
up in}\ v'_0 \end{array}\right. \]
We consider a (partial) strategy profile $\sigma$ whose main outcome is: \[ \rho = \big(v_0 \cdot (\alpha^5,\mes_\epsilon) \cdot v_1 \cdot (\alpha^5,\mes_\epsilon) \big)^\omega \] where $\mes_\epsilon(a) = \epsilon$ for every $a \in \Agt$. Note that players $0$ and $1$ cannot benefit from any deviation since their payoffs is uniformly $0$. Then notice that no one alone can deviate from $\rho$ to $v'_0$. Now, the three players $2$, $3$ and $4$ can alone deviate to $v'_1$ and (try to) do so infinitely often. We examine those deviations. If players $0$ and $1$ manage to learn who is the deviator, then, together, they can punish the deviator: if they learn that player $2$ (resp. $3$, $4$) is the deviator, then they will enforce vertex $v_2$ (resp. $v_3$, $v_4$). If they do not manage to learn who is the deviator, then they will not know what to do, and therefore, in any completion of the strategy profile, there will be some profitable deviation for at least one of the players (hence there will not be any Nash equilibrium whose main outcome is $\rho$).
We examine now the three communication graphs $G_1$, $G_2$ and $G_3$ depicted in Figure~\ref{gameex}. Using communication based on graph $G_1$, if player $4$ deviates, then player $0$ will see this immediately and will be able to communicate this fact to player $1$; if player $3$ deviates, then player $4$ will see this immediately and will be able to communicate this fact to player $0$, which will transmit to player $1$; if player $2$ deviates, then no one will see anything, hence they will deduce the identity of the deviator in all the cases.
Using communication based on graph $G_2$, if either player $3$ or player $4$ deviates, then player $0$ will see this immediately and will be able to communicate this fact to player $1$ using the richness of the communication scheme (words over $\{0,1\}$). Like before, the identity of deviator $2$ will be guessed after a while.
Using communication based on graph $G_3$, if player $4$ deviates, then player $0$ will see this immediately and will be able to communicate this fact to player $1$ (as before); now, no one (except players $2$ and $3$) will be able to learn who is deviating, if player $2$ or player $3$ deviates.
We can conclude that there is a Nash equilibrium with graph $G_1$ or $G_2$ whose main outcome is $\rho$, but not with graph $G_3$.
\subsection{Two-player turn-based game structures}
Two-player turn-based game structures are specific cases of the previous model, where at each vertex, at most one player has more than one action in her set of allowed actions. But for convenience, we will give a simplified definition, with only objects that will be useful.
{ \emergencystretch 2cm A two-player turn-based game structure is a tuple $G = \tuple{S,S_\Eve,S_\Adam,s_\init,A,\Allow,\Tab}$, where $S = S_\Eve \sqcup S_\Adam$ is a finite set of states (states in $S_\Eve$ belong to player \Eve whereas states in $S_\Adam$ belong to player \Adam), $s_\init \in S$ is the initial state, $A$ is a finite alphabet, $\Allow \colon S \to 2^A \setminus \{\emptyset\}$ gives the set of available actions, and $\Tab \colon S \times A \to S$ is the next-state function. If $s \in S_\Eve$ (resp. $S_\Adam$), $\Allow(s)$ is the set of actions allowed to \Eve (resp. \Adam) in state $s$.}
In this context, strategies will use sequences of states.
That is, if $a$ denotes \Eve or \Adam, an $a$-strategy is a partial function $\sigma_a: S^* \cdot S_a \to A$ such that for every $H \in S^* \cdot S_a$ such that $\sigma_a(H)$ is defined, $\sigma_a(H) \in \Allow(\last(H))$. Note that we do not include any winning condition or payoff function in the tuple, hence the name structure.
\subsection{The problems we are looking at}
We are interested in the constrained existence of a Nash equilibrium. For simplicity, we define rectangular threshold constraints, but could well impose more complex constraints, like Boolean combinations of linear constraints.
\begin{problem}[Constrained existence problem]
\emergencystretch 1.5cm Given a concurrent game $\calG = \langle
V,v_\init,\Agt,\Act,\Sigma,\Allow,\Tab, (\payoff_a)_{a \in \Agt}
\rangle$, a communication graph $G$ for $\Agt$, a predicate $P$ over
$\mathbb{R}^{|\Agt|}$, can we decide whether there exists a Nash
equilibrium $\sigma_\Agt$ from $v_\init$ such that
$\payoff(\vertices(\out(\sigma_\Agt,v_\init))) \in P$? If so,
compute one.
If the predicate $P$ is trivial, we simply speak of the existence
problem. \end{problem}
The case where the communication graph has no edge was studied in depth in~\cite{BBMU15}, with a generic two-player construction called the suspect construction, allowing to decide the constrained existence problem for many kinds of payoff functions. The case where the communication graph is a clique was the subject of the work~\cite{brenguier16}. The general case of a communication graph has not been investigated so far, but induces interesting developments. In the next section, we show that we can restrict the search of Nash equilibria to the search of so-called normed strategy profiles, where the communication via messages follows a very simple pattern. We also argue that deviations which do not impact the visited vertices should not be considered in the analysis. Given those reductions, we then propose the construction of a two-player game, which will track those normed profiles. This construction is inspired by the suspect-game construction of~\cite{BBMU15} and of the epistemic game of~\cite{bouyer18}.
\section{Reduction to profiles following a simple communication mechanism} \label{sec:reducs}
We fix a concurrent game $\calG = \tuple{V,v_\init,\Act,\Agt,\Sigma,\Allow,\Tab, (\payoff_a)_{a
\in \Agt}}$ and a communication graph $G$. We assume that $v_\init = v_0$. We will reduce the search for Nash equilibria to the search for strategy profiles with a very specific shape. In particular, we will show that the richness of the communication offered by the setting is somehow useless, and that a very simple communication pattern will be sufficient for characterizing Nash equilibria.
In the following, we write $\mes_\epsilon$ for the vector assigning the empty word $\epsilon$ to every player $a \in \Agt$. Furthermore, for every $d \in \Agt$, we pick some word $\id_d \in \{0,1\}^+$ which are all distinct (and different from $\epsilon$).
We first define restrictions for deviations. Let $\sigma_\Agt$ be a strategy profile. A player-$d$ deviation $\sigma'_d$ is said \emph{immediately visible} whenever, writing $h$ for the longest common prefix of $\out(\sigma_\Agt,v_0)$ and $\out(\sigma_\Agt[d/\sigma'_d],v_0)$, $\Tab(\last(h),m) \ne \Tab(\last(h),m')$, where $m = \sigma_\Agt(h)[1]$ and $m' = \big(\sigma_\Agt[d/\sigma'_d](h)\big)[1]$ are the next moves according to $\sigma_\Agt$ and $\sigma_\Agt[d/\sigma'_d]$. That is, at the first position where player $d$ changes her strategy, it becomes public information that a deviation has occurred (even though some players know who deviated~---all the players $a$ with $d \fleche a$---, and some other don't know). It is furthermore called \emph{honest} whenever for every $h' \in \out(\sigma_\Agt[d/\sigma'_d],v_0)$ such that $h$ is a (non-strict) prefix of $h'$, $\sigma'_d(h')[2] = \id_d$. Somehow, player $d$ admits she deviated, and does so immediately and forever.
The simple communication mechanism that we will design consists in reporting the deviator (role of the direct neighbours of the deviator), and propagating this information along the communication graph (for all the other players). Formally, let $\sigma_\Agt$ be a strategy profile, and let $\rho$ be its main outcome. The profile $\sigma_\Agt$ will be said \emph{normed} whenever the following conditions hold: \begin{enumerate} \item for every
$h \in \out(\sigma_\Agt) \cup \bigcup_{d \in \Agt,\ \sigma'_d}
\out(\sigma_\Agt[d/\sigma'_d],v_0)$, if $\vertices(h)$ is a prefix
of $\vertices(\rho)$, then for every $a \in \Agt$,
$\sigma_a(h)[2] = \epsilon$; \item for every $d \in \Agt$, for every $d$-strategy $\sigma'_d$,
if $h \cdot (m,\mes) \cdot v \in \out(\sigma_\Agt[d/\sigma'_d],v_0)$
is the first step out of $\vertices(\rho)$, then for every $d
\fleche a$,
$\sigma_a(h \cdot (m,\mes) \cdot v)[2] = \id_d$; \item for every $d \in \Agt$, for every $d$-strategy $\sigma'_d$, if
$h \cdot (m,\mes) \cdot v \in \out(\sigma_\Agt[d/\sigma'_d],v_0)$
has left the main outcome for more than one step, then for every $a
\in \Agt$, $\sigma_a(h \cdot (m,\mes) \cdot v)[2] = \epsilon$ if for
all $b \fleche a$, $\mes(b) = \epsilon$ and $\sigma_a(h \cdot
(m,\mes) \cdot v)[2] = \id_d$ if there is $b \fleche a$ such that
$\mes(b) = \id_d$; note that this is well defined since at most one
id can be transmitted. \end{enumerate} The first condition says that, as long as a deviation is not visible, then no message needs to be sent;
the second condition says that as soon as a deviation becomes visible, then messages denouncing the deviator should be sent by ``those who know'', that is, the (immediate) neighbours of the deviator; the third condition says that the name (actually, the id) of the deviator should propagate according to the communication graph in an epidemic way.
Note that the profiles discussed in Section~\ref{subsec:ex}
were actually normed.
\begin{restatable}{theorem}{coro}
\label{coro}
The existence of a Nash equilibrium $\sigma_\Agt$ with payoff $p$ is
equivalent to the existence of a normed strategy profile
$\sigma'_\Agt$ with payoff $p$, which is resistant to immediately
visible and honest single-player deviations. \end{restatable}
The proof of this theorem is rather technical, hence postponed to Appendix~\ref{app:reducs}, page~\pageref{app:reducs}. We only give some intuition here. First, we explain why being resistant to immediately visible and honest deviations is enough. Notice that as long as the sequence of vertices follows the main outcome, then one can simply ignore the deviation and act only when the deviation becomes visible, in a way as if the deviator had started deviating only at this moment. This will be enough to punish the deviator. The ``honest'' part comes from the fact that one should simply ignore the messages sent by the deviator as it can be only in her interest to not ignore them (if it was not, then why would she send any message at all?).
Second, we show why no one should communicate as long as the sequence of vertices follows the main outcome. The reason is that if no one has deviated then any message is essentially useless, and if a deviation has happened, as explained earlier it can just be ignored as long as it has not become visible.
Finally, we demonstrate why the richness of the communication mechanism is in a way useless. Intuitively, one can understand that the only factors that should matter when playing are the sequence of the vertices that have been visited (because payoff functions only take into account the visited vertices) and the identity of the deviator. Thus the messages should only be used so that players can know of the identity of the deviator in the fastest possible way, and we show that nothing is faster than a sort of epidemic mechanism where one simply broadcasts the identity of the deviator whenever one received the information.
\section{The epistemic game abstraction} \label{sec:epistemic}
We fix a concurrent game $\calG = \tuple{V,v_\init,\Act,\Agt,\Sigma,\Allow,\Tab, (\payoff_a)_{a
\in \Agt}}$ for the rest of the section, and $G$ be a communication graph for $\Agt$. We will implement an epistemic abstraction, which will track normed strategy profiles, and check that there is no profitable immediately visible and honest single-player deviations.
\subsection{Description of the epistemic game}
A \emph{situation} is a triple $(d,I,K)$ in $\Agt \times 2^\Agt \times \Big(2^{\Agt}\Big)^\Agt$, which consists of a deviator $d \in \Agt$, a list of players $I$ having received the information that $d$ is the deviator, and a knowledge function $K$ that associates to every player $a$ a list of suspects $K(a)$; in particular, it should be the case that $d\in I$ and for every $a \in I$, $K(a) = \{d\}$. We write $\Ssit$ for the set of situations.
The epistemic game $\calE_\calG^G$ of $\calG$ and $G$ is defined as a two-player game structure $\tuple{S,S_\Eve,S_\Adam,s_\init,\Sigma',\Allow',\Tab'}$. We describe the states and the transitions leaving those states; in particular, components $\Sigma'$, $\Allow'$, $\Tab'$ of the above tuple will only be implicitely defined.
\Eve's states $S_\Eve$ consist of elements of $V \times 2^\Ssit$ such that if $(v,X)$ is a state then for all $a \in \Agt$ the set $\{(d,I,K)\in X \mid d=a\}$ is either a singleton or empty (there is at most one situation associated with a given player $a$). We write $\dev(X)$ the set $\{d \in \Agt \mid \exists (d,I,K) \in X\}$ of agents which are a deviator in one situation of $X$. If $d \in \dev(X)$, we write $(d,I^X_d,K^X_d)$ for the unique triple belonging to $X$ having deviator $d$. Hence, $X = \{(d,I^X_d,K^X_d) \mid d \in \dev(X)\}$. Intuitively, an \Eve's state $(v,X)$ will correspond to a situation where the game has proceeded to vertex $v$, but, if $\dev(X) \ne \emptyset$, several players may have deviated. Each player $d \in \dev(X)$ may be responsible for the deviation; some people will have received a message denouncing $d$ (those are in the set $I^X_d$), and some will deduce things from what they observe (this is given by $K^X_d$). Note that the (un)distinguishability relation of a player $a$ will be deduced from $X$: if $d$ deviated and $a \in I^X_d$, then $a$ will know $d$ deviated; if $a$ is neither in $I^X_d$ nor in $I^X_{d'}$, then $a$ will not be able to know whether $d$ or $d'$ deviated (as we will prove later, in Lemma~\ref{lma}).
First let us consider the case where $X=\emptyset$, which is to be understood as the case where no deviation has arisen yet. In state $(v,\emptyset)$, \Eve's actions are moves in $\calG$ enabled in $v$. When she plays move $m \in \Act^\Agt$, the game progresses to \Adam's state $((v,\emptyset),m) \in S_\Adam$ where \Adam's actions are vertices $v' \in V$ such that there exists a player $d \in \Agt$ and an action $\delta \in \Act$ such that $\Tab(v,(m[d/\delta]))=v'$. When \Adam plays $v'$, either $v'=\Tab(v,m)$ and the game progresses to \Eve's state $(v',\emptyset)$ or $v'\neq \Tab(v,m)$ and the game progresses to \Eve's state $(v',X')$ where: \begin{itemize} \item $d \in \dev(X')$ if and only if there is $\delta \in \Act$ such
that $\Tab(v,(m[d/\delta]))=v'$. It means that given the next state
$v'$, $d$ is a possible deviator; \item if $d \in \dev(X')$, then:
\begin{itemize}
\item $I^{X'}_d = \{a \in \Agt \mid d\fleche a\}$;
\item for every $a \in I_d^{X'}$, $K_d^{X'}(a) = \{d\}$;
\item for every $a \notin I^{X'}_d$, $K^{X'}_d(a) = \{b\in \Agt \mid
\exists \beta \in \Act\ \text{s.t.}\ \Tab(v,(m[b/\beta])) = v'\}
\setminus \{b\in \Agt \mid b \fleche a\}$.
Those are all the players that can be suspected by $a$, given the
vertex $v'$, and the absence of messages so far.
\end{itemize} \end{itemize} We write $X' = \update((v,\emptyset),m,v')$. Note that $X' = \emptyset$ whenever (and only when) $\Tab(v,m) = v'$.
In a state $(v,X) \in S_\Eve$ where $X\neq \emptyset$, \Eve's actions consist of functions from $\dev(X)$ to $\Act^\Agt$ that are compatible with players' knowledge, that is: $f: \dev(X) \to \Act^\Agt$ is an action enabled in $(v,X)$ if and only if (i) for all $d \in \dev(X)$, for each $a \in \Agt$, $f(d)(a) \in \Allow(v,a)$, (ii) for all $d,d' \in \dev(X)$, for all $a \in \Agt$, if $a \notin I^X_d \cup I^X_{d'}$ and $K^X_d(a)=K^X_{d'}(a)$ then $f(d)(a) = f(d')(a)$;\footnote{Note in particular that ``$K^X_d(a)$ singleton''
does not imply $a \in I_d^X$, those are two distinguishable
situations: the message with the identity of the deviator may not
have been received in the first case, while it has been received in
the second case.} that is, if a player has not received any message so far but has the same knowledge about the possible deviators in two situations, then \Eve's suggestion for that player's action must be the same in both situations. When \Eve plays action $f$ in $(v,X)$, the next state is $((v,X),f) \in S_\Adam$, where \Adam's actions correspond to states of the game that are compatible with $(v,X)$ and $f$, that is states $v'$ such that there exists $d \in \dev(X)$ and $\delta\in \Act$ such that $\Tab(v,f(d)[d/\delta])=v'$.
When \Adam chooses the action $v'$ in $((v,X),f)$, the game progresses to \Eve's state $(v',X')$, where: \begin{itemize} \item $d \in \dev(X')$ if and only if $d\in \dev(X)$ and there exists
$\delta \in \Act$ such that $\Tab(v,f(d)[d/\delta])=v'$. It
corresponds to a case where $d$ was already a possible deviator and
can continue deviating so that the game goes to $v'$;
\item if $d \in \dev(X')$, then:
\begin{itemize}
\item $I_d^{X'} = I_d^X \cup \{a \in \Agt \mid \exists b \in I_d^X\
\text{s.t.}\ b \fleche a\}$. New players receive a message with
the deviator id;
\item for every $a \in I_d^{X'}$, $K_d^{X'}(a) = \{d\}$;
\item for every $a \notin I_d^{X'}$, $K_d^{X'}(a) = \{b \in K_d^X(a)
\mid \exists \beta \in \Act\ \text{s.t.}\
\Tab(v,f(b)[b/\beta])=v'\} \setminus \{c \in \Agt \mid
\dist_G(c,a) \le \max \{\dist_G(c,c') \mid c' \in I_c^X\} +1\}$.
Those are the players that could have deviated but for which
player $a$ would not have received the signal yet.
\end{itemize} \end{itemize} We write $X' = \update((v,X),f,v')$. Note that $X' \ne \emptyset$ and that $\dev(X') \subseteq \dev(X)$.
We let $R = (v_0,X_0) \cdot ((v_0,X_0),f_0) \cdot (v_1,X_1) \dots$ be an infinite play from $(v_0,X_0) = (v_\init,\emptyset)$. We write $\visited(R)$ for $ v_0 v_1 \dots \in V^\omega$ the sequence of vertices visited along $R$. We also define $\dev(R) = \emptyset$ if $X_r = \emptyset$ for every $r$, and $\dev(R) =\lim_{r \to +\infty} \dev(X_r)$ otherwise. This is the set of possible deviators along $R$.
\subsubsection{Winning condition of \Eve.}
A zero-sum game will be played on the game structure $\calE_\calG^G$, and the winning condition of \Eve will be given on the branching structure of the set of outcomes of a strategy for \Eve, and not individually on each outcome, as standardly in two-player zero-sum games. We write $s_\init = (v_\init,\emptyset)$ for the initial state. Let $p = (p_a)_{a \in \Agt} \in \bbR^\Agt$, and $\zeta$ be a strategy for \Eve in $\calE_\calG^G$; it is said winning for $p$ from $s_\init$ whenever $\payoff(\visited(R)) = p$, where $R$ is the unique outcome of $\zeta$ from $s_\init$ where \Adam complies to \Eve's suggestions, and for every other outcome $R'$ of $\zeta$, for every $d \in \dev(R')$, $\payoff_d(\visited(R')) \le p_d$.
\subsection{An example}
\begin{figure}
\caption{Part of the epistemic game corresponding to the game
described in Figure \ref{gameex} (with graph $G_1$). This does not
represent the whole epistemic game and a lot of actions accessible
in the states we show here are not written. In situations
$(d,I,K)$ we describe $K$ by the list of its values for players
$a\notin I$, as for all $a$ in $I$ we have $K(a)=\{d\}$ by
definition.}
\label{epistemicex}
\end{figure}
In Figure~\ref{epistemicex} we present a part of the epistemic game corresponding to the game we described in Figure \ref{gameex} with graph $G_1$. In state $(v_0,\emptyset)$, \Eve can play the action profile $\alpha^5$ and make the game go to $((v_0,\emptyset),\alpha^5)$ where \Adam can either play $v_1 = \Tab(v_0,\alpha^5)$ (we say that \Adam complies with \Eve) or choose a different state accessible from $v_0$ and an action profile that consists in a single-player deviation from $\alpha$, for instance $v'_1=\Tab(v_0,\alpha^2\beta\alpha^2) = \Tab(v_0,\alpha^3\beta\alpha) =\Tab(v_0,\alpha^4\beta) $. If \Adam chooses $v'_1$, then three players are possible deviators: $2$, $3$ and $4$. We write $X$ for the corresponding set of situations, and we already know that $\dev(X) = \{2,3,4\}$ . \begin{itemize} \item If player $2$ is the deviator, then no one (except himself)
directly receives this information. Player $0$ knows that player $4$
did not deviate (since $4 \fleche 0$ in $G_1$), hence
$K_2^X(0)=\{2,3\}$; Player $1$ has no information hence $K_2^X(1) =
\{2,3,4\}$; Player $3$ knows that he is not the deviator but cannot
know more, hence $K_2^X(3)=\{2,4\}$; Finally, player $4$ can deduce
many things: he knows he is not the deviator, and he saw that player
$3$ is not the deviator (since $3 \fleche 4$ in $G_1$), hence
$K_2^X(4) = \{2\}$. \item If player $3$ is the deviator, then both players $3$ and $4$ get
the information, hence $I^X_3=\{3,4\}$. Other players can guess some
things, for instance player $0$ sees that player $4$ cannot be the
deviator, this is why $K^X_3(0) = \{2,3\}$. Etc. \item The reasoning for player $4$ is similar. \end{itemize} In the situation we have just described, when the game will proceed to $v'_1$, then either player $0$ knows that player $4$ has deviated, or he knows that player $4$ didn't deviate but he suspects both $2$ and $3$. On the other hand, player $4$ will precisely know who deviated. And player $3$ knows whether he deviated or not, but if he didn't, then he cannot know whether it was player $2$ or player $4$ who deviated. This knowledge is stored in situation $X$ we have described, and which is fully given in Figure~\ref{epistemicex}.
Let us now illustrate how actions of \Eve are defined
in states with a non-empty set of situations. Assume we are in
\Eve's state $(v_0,X)$, with $X$ as previously defined. From that
state, an action for \Eve is a mapping
$f : \{2,3,4\} \to \Act^\Agt$ such that:
\[
f(2)(0) = f(3)(0) \quad f(2)(1) = f(3)(1) = f(4)(1) \quad f(3)(2) =
f(4)(2) \quad f(2)(3) = f(4)(3)
\]
The intuition behind these constraints is the following: Player $0$
knows whether Player $4$ deviated or not, but in the case she did not
cannot know whether Player $2$ or Player $3$ deviated; Player $1$ does
not know who deviated, hence should play the same action in the three
cases (that she cannot distinguish); Player $2$ does only know whether
she deviated hence in the case she did not cannot know whether Player $3$
or Player $4$ deviated; the case for Player $3$ is similar;
finally Player $4$ knows for sure who deviated: she saw if Player $3$
deviated and knows whether she herself deviated, thus can distinguish
between the three cases.
\subsection{Correctness of the epistemic game construction}
When constructing the epistemic game, we mentioned that \Eve's states will allow to properly define the undistinguishability relation for all the players. Towards that goal, we show by an immediate induction the following result:
\begin{restatable}{lemma}{lma}\label{lma}
If $(v,X)$ is an \Eve's state reachable from some $(v_0,\emptyset)$ in
$\calE_\calG^G$, then for all $d \in \dev(X)$:
\begin{itemize}
\item for all $a \in I^X_d$, $K^X_d(a) = \{d\}$;
\item for all $a \notin I^X_d$,
$K^X_d(a) = \dev(X) \setminus \{d' \in\dev(X) \mid a \in I^X_{d'}\}$.
\end{itemize}
In particular, for all $d,d' \in \dev(X)$, for all
$a \notin I^X_d \cup I^X_{d'}$, $K^X_d(a) = K^X_{d'}(a)$. \end{restatable} So, either a player $a$ will have received from a neighbour the identity of the deviator, or she will not have received any deviator identity yet, and she will have a set of suspected deviators that she will not be able to distinguish.
This allows to deduce the following correspondence between $\calG$ and $\calE_\calG^G$:
\begin{proposition}
There is a winning strategy for \Eve in $\calE_\calG^G$ for payoff
$p$ if and only if there is a normed strategy profile in $\calG$,
whose main outcome has payoff $p$ and which is resistant to
single-player immediately visible and honest deviations. \end{proposition}
The proof of correctness of the epistemic game then goes through the following steps, which are detailed in Appendix~\ref{sec:correctness}, page~\pageref{sec:correctness}. First, given an $\Eve$'s strategy $\zeta$, we build a function $E_\zeta$ associating with $a$-histories (for every $a \in \Agt$) in the original game $\Eve$'s histories in the epistemic game such that $\Eve$ plays according to $\zeta$ along $E_\zeta$.
Then we use this function to create a strategy profile $\Omega(\zeta)$ for the original game where the action prescribed by this profile to player $a$ after history $h$ corresponds in some sense to $\zeta(E_\zeta(h))(d)(a)$, where $d$ is a suspected deviator according to player~$a$. This works because, thanks to Lemma~\ref{lma}, we know that either player $a$ knows who the deviator is, or player $a$ has a subset of suspect deviators and $\Eve$'s suggestion for $a$ (by construction of $\calE_\calG^G$) is the same for all those possible deviators.
Finally we prove that if $\zeta$ is a winning strategy for $\Eve$ then $\Omega(\zeta)$ is both normed and resistant to single-player immediately visible and honest deviations in $\calG$.
To prove the converse proposition we build a function $\Lambda$ associating with $\Eve$'s histories in the epistemic game families of single-player histories in the original game. We then use this correspondence to build a function $\Upsilon$ associating with normed strategy profiles $\Eve$'s strategies in a natural way.
Finally we prove that if $\sigma$ is normed and resistant to single-player immediately visible honest deviations, then $\Upsilon(\sigma)$ is a winning strategy for $\Eve$.
Gathering results of Theorem~\ref{coro} and of this proposition, we get the following theorem:
\begin{restatable}{theorem}{main}
\label{theo:main}
There is a Nash equilibrium with payoff $p$ in $\calG$ if and only
if there is a winning strategy for \Eve in $\calE_\calG^G$ for
payoff $p$. \end{restatable}
\begin{remark}
Note that all the results are constructive, hence if one can
synthesize a winning strategy for \Eve in $\calE_\calG^G$, then one
can synthesize a correponding Nash equilibrium in $\calG$. \end{remark}
\section{Complexity analysis} \label{sec:complexity}
We borrow all notations of previous sections. A rough analysis of the size of the epistemic game $\calE_\calG^G$ gives an exponential bound. We will give a more precise bound, pinpointing the part with an exponential blowup.
We write $\diam(G)$ for the diameter of $G$, that is $\diam(G) = \max \{\dist_G(a,b) \mid \dist_G(a,b) <+\infty\}$.
\begin{restatable}{lemma}{size}
Assuming that $\Tab$ is given explicitely in $\calG$, the number of
states in the reachable part of $\calE_\calG^G$ from $s_\init =
(v_\init,\emptyset)$ is bounded by
\[
|S_\Eve| \le |V| + |V| \cdot |\Tab|^2 \cdot (\diam(G)+2)\qquad
\text{and} \qquad |S_\Adam| \le |S_\Eve| \cdot |\Act|^{|\Agt|^2}
\]
The number of edges is bounded by $|S_\Adam| + |S_\Adam| \cdot
|S_\Eve|$.
If $|\Agt|$ is assumed to be a constant of the problem, then the
size of $\calE_\calG^G$ is polynomial in the size of $\calG$.
\end{restatable}
We will not detail algorithmics issues, but the winning condition of \Eve in $\calE_\calG^G$ is very similar to the winning condition of \Eve in the suspect-game construction of~\cite{BBMU15} (for Boolean or ordered objectives), or in the deviator-game construction of~\cite{brenguier16} (for mean-payoff), or in a closer context to the epistemic-game construction of~\cite{bouyer18}. Hence, when the size of the epistemic game is polynomial, rather efficient algorithms can be designed to compute Nash equilibria. For instance, in a setting where the size of $\calE_\calG^G$ is polynomial, using a bottom-up labelling algorithm similar to that of~\cite[Sect. 4.3]{bouyer17}, one obtains a polynomial space algorithm for deciding the (constrained) existence of a Nash equilibrium when payoffs are Boolean payoffs corresponding to parity conditions.
\section{Conclusion} \label{sec:conclusion}
In this paper, we have studied multiplayer infinite-duration games over graphs, and focused on games where players can communicate with neighbours, given by a directed graph. We have shown that a very simple communication mechanism was sufficient to describe Nash equilibria. This mechanism is sort of epidemic, in that if a player deviates, then his neighbours will see it and transmit the information to their own neighbours; the information then propagates along the communication graph. This framework encompasses two standard existing frameworks, one where the actions are invisible (represented with a graph with no edges), and one where all actions are visible (represented by the complete graph). We know from previous works that in both frameworks, one can compute Nash equilibria for many kinds of payoff functions. In this paper, we also show that we can compute Nash equilibria in this generalized framework, by providing a reduction to a two-player game, the so-called epistemic game construction. Winning condition in this two-player game is very similar to winning conditions encountered in the past, yielding algorithmic solution to the computation of Nash equilibria. We have also analyzed the size of the abstraction, which is polynomial when the number of players is considered as a constant of the problem.
The current framework assumes messages can be appended to actions by players, allowing a rich communication between players. The original framework of~\cite{RT98} did not allow additional messages, but did encode identities of deviators by sequences of actions. This was possible in~\cite{RT98} since games were repeated matrix games, but it is harder to see how we could extend this approach and how we could encode identities of players with actions, taking into account the graph structure. For instance, due to the graph, having too long identifiers might be prohibitive to transmit in a short delay the identity of the deviator. Nevertheless, that could be interesting to see if something can be done in this framework.
\begin{thebibliography}{10}
\bibitem{AHK02} Rajeev Alur, {\relax Th}omas~A. Henzinger, and Orna Kupferman. \newblock Alternating-time temporal logic. \newblock {\em Journal of the ACM}, 49:672--713, 2002.
\bibitem{bouyer17} Patricia Bouyer. \newblock Games on graphs with a public signal monitoring. \newblock Research Report \url{https://arxiv.org/abs/1710.07163}, arXiv, 2017.
\bibitem{bouyer18} Patricia Bouyer. \newblock Games on graphs with a public signal monitoring. \newblock In {\em Proc. 21st International Conference on Foundations of
Software Science and Computation Structures (FoSSaCS'18)}, volume 10803 of
{\em Lecture Notes in Computer Science}, pages 530--547. Springer, 2018.
\bibitem{BBMU15} Patricia Bouyer, Romain Brenguier, Nicolas Markey, and Michael Ummels. \newblock Pure {N}ash equilibria in concurrent games. \newblock {\em Logical Methods in Computer Science}, 11(2:9), 2015.
\bibitem{BMS14} Patricia Bouyer, Nicolas Markey, and Daniel Stan. \newblock Mixed {N}ash equilibria in concurrent games. \newblock In {\em Proc. 33rd Conference on Foundations of Software Technology
and Theoretical Computer Science (FSTTCS'14)}, volume~29 of {\em LIPIcs},
pages 351--363. Leibniz-Zentrum f{\"u}r Informatik, 2014.
\bibitem{BT19-rr} Patricia Bouyer and Nathan Thomasset. \newblock Nash equilibria in games over graphs equipped with a communication
mechanism. \newblock Research Report \url{https://arxiv.org/abs/1906.07753}, arXiv, 2019.
\bibitem{brenguier16} Romain Brenguier. \newblock Robust equilibria in mean-payoff games. \newblock In {\em Proc. 19th International Conference on Foundations of
Software Science and Computation Structures (FoSSaCS'16)}, volume 9634 of
{\em Lecture Notes in Computer Science}, pages 217--233. Springer, 2016.
\bibitem{CHJ06} Krishnendu Chatterjee, {\relax Th}omas~A. Henzinger, and Marcin Jurdzi{\'n}ski. \newblock Games with secure equilibria. \newblock {\em Theoretical Computer Science}, 365(1-2):67--82, 2006.
\bibitem{CMJ04} Krishnendu Chatterjee, Rupak Majumdar, and Marcin Jurdzi{\'n}ski. \newblock On {N}ash equilibria in stochastic games. \newblock In {\em Proc. 18th International Workshop on Computer Science Logic
(CSL'04)}, volume 3210 of {\em Lecture Notes in Computer Science}, pages
26--40. Springer, 2004.
\bibitem{CFGR16} Rodica Condurache, Emmanuel Filiot, Raffaella Gentilini, and Jean-Fran\c{c}ois
Raskin. \newblock The complexity of rational synthesis. \newblock In {\em Proc. 43rd International Colloquium on Automata, Languages
and Programming (ICALP'16)}, volume~55 of {\em LIPIcs}, pages 121:1--121:15.
Leibniz-Zentrum f{\"u}r Informatik, 2016.
\bibitem{COT18} Rodica Condurache, Youssouf Oualhadj, and Nicolas Troquard. \newblock The complexity of rational synthesis for concurrent games. \newblock In {\em Proc. 29th International Conference on Concurrency Theory
(CONCUR'18)}, volume 118 of {\em LIPIcs}, pages 38:1--38:15. Leibniz-Zentrum
f{\"u}r Informatik, 2018.
\bibitem{henzinger05} Thomas~A. Henzinger. \newblock Games in system design and verification. \newblock In {\em Proc. 10th Conference on Theoretical Aspects of Rationality
and Knowledge (TARK'05)}, pages 1--4, 2005.
\bibitem{nash50} John~F. Nash. \newblock Equilibrium points in $n$-person games. \newblock {\em Proceedings of the National Academy of Sciences of the United
States of America}, 36(1):48--49, 1950.
\bibitem{nava16} Francesco Nava. \newblock {\em Repeated Games and Networks}. \newblock The Oxford Handbook of the Economics of Networks. Oxford University
Press, 2016.
\bibitem{RT98} J{\'e}r{\^o}me Renault and Tristant Tomala. \newblock Repeated proximity games. \newblock {\em International Journal of Game Theory}, 27(4):539--559, 1998.
\bibitem{thomas02} Wolfgang {\relax Th}omas. \newblock Infinite games and verification. \newblock In {\em Proc. 14th International Conference on Computer Aided
Verification (CAV'02)}, volume 2404 of {\em Lecture Notes in Computer
Science}, pages 58--64. Springer, 2002. \newblock Invited Tutorial.
\bibitem{ummels06} Michael Ummels. \newblock Rational behaviour and strategy construction in infinite multiplayer
games. \newblock In {\em Proc. 26th Conference on Foundations of Software Technology
and Theoretical Computer Science (FSTTCS'06)}, volume 4337 of {\em Lecture
Notes in Computer Science}, pages 212--223. Springer, 2006.
\bibitem{ummels08} Michael Ummels. \newblock The complexity of {N}ash equilibria in infinite multiplayer games. \newblock In {\em Proc. 11th International Conference on Foundations of
Software Science and Computation Structures (FoSSaCS'08)}, volume 4962 of
{\em Lecture Notes in Computer Science}, pages 20--34. Springer, 2008.
\bibitem{UW11a} Michael Ummels and Dominik Wojtczak. \newblock The complexity of {N}ash equilibria in limit-average games. \newblock In {\em Proc. 22nd International Conference on Concurrency Theory
(CONCUR'11)}, volume 6901 of {\em Lecture Notes in Computer Science}, pages
482--496. Springer, 2011.
\bibitem{UW11} Michael Ummels and Dominik Wojtczak. \newblock The complexity of {N}ash equilibria in stochastic multiplayer games. \newblock {\em Logical Methods in Computer Science}, 7(3), 2011.
\end{thebibliography}
\appendix
\section{Proof of Section~\ref{sec:reducs}} \label{app:reducs}
\coro*
We will divide the proof of this theorem into several parts and prove several intermediary results.
\subsection{Reduction to immediately visible and honest deviations}
\begin{restatable}{lemma}{lemmaun}
\label{lemma1}
Assume $\sigma_\Agt$ is a strategy profile from $v_0$ such that
there is no profitable single-player immediately visible honest
deviation w.r.t. $\sigma_\Agt$, then one can construct a Nash
equilibrium $\widetilde\sigma_\Agt$ from $v_0$ such that (i)
$\vertices(\out(\sigma_\Agt,v_0)) =
\vertices(\out(\widetilde\sigma_\Agt,v_0))$; (ii) for every
$h \in \Hist(v_0)$ such that $\vertices(h)$ is a prefix of
$\vertices(\out(\widetilde\sigma_\Agt,v_0))$, for every
$a \in \Agt$, $\widetilde\sigma_a(h)[2] = \epsilon$. \end{restatable} Condition (ii) in the statement means somehow that no message is required along the main outcome and along deviations that are not visible yet (in the sense that they follow the same sequence of vertices as the main outcome).
\begin{proof}
From $\sigma_\Agt$, we will build a profile $\widetilde\sigma_\Agt$
such that:
\begin{itemize}
\item $\widetilde\sigma_\Agt$'s and $\sigma_\Agt$'s main outcomes
visit the same sequence of vertices;
\item no message is broadcast by $\widetilde\sigma_\Agt$ as long as
the sequence of vertices of the main outcome is followed;
\item any single-player $d$-deviation of $\widetilde\sigma_\Agt$
will correspond to an immediately visible single-player honest
$d$-deviation of $\sigma_\Agt$.
\end{itemize}
Let $\rho=\out(\sigma_\Agt,v_o)$. For every $h \in \Hist(v_0)$ such
that $\vertices(h) = \vertices(\rho_{\le r})$ for some $r$, for
every $a \in \Agt$, we define
$\widetilde{\sigma}_a(h) = \big(\sigma_a(\rho_{\le
r})[1],\epsilon\big)$. As a consequence of this definition, the
main outcome $\widetilde\rho$ of $\widetilde\sigma_\Agt$ visits the
same sequence of vertices (and even follows the same moves) as the
main outcome $\rho$ of $\sigma$; only messages which are broadcast
may differ. Thereafter, we write:
\[
\rho = v_0 \cdot (m_0,\mes_0) \cdot v_1 \cdot (m_1,\mes_1) \cdot
v_2 \ldots (m_{r-1},\mes_{r-1}) \cdot v_r \ldots
\]
and, by definition of $\widetilde\sigma_\Agt$:
\[
\widetilde\rho = v_0 \cdot (m_0,\mes_\epsilon) \cdot v_1 \cdot
(m_1, \mes_\epsilon) \cdot v_2 \ldots (m_{r-1}, \mes_\epsilon)
\cdot v_r \ldots
\]
where $\widetilde\rho=\out(\widetilde\sigma_\Agt,v_0)$. Note also
that the above definition takes care of single-player deviations
w.r.t. $\widetilde\sigma_\Agt$ which do not `leave' the main outcome
(that is, which visit the same sequence of vertices): against such
deviations, simply doing nothing and going on as if no one deviated
will be enough to punish the deviator.
We will now extend the definition ot profile
$\widetilde\sigma_\Agt$ to histories generated by single-player
deviations. We will do so by induction, by considering histories
that can be derived by single-player deviations of the
so-far-defined profile, and which have become visible.
Let $h$ be a history resulting from a single-player (named $d$)
deviation w.r.t. $\widetilde\sigma_\Agt$, which has become visible.
It can be decomposed as:
\[
h = v_0 \cdot (\bar{m}_0,\bar\mes_0) \cdot v_1 \cdot
(\bar{m}_1,\bar\mes_1) \ldots v_r \cdot (\bar{m}_r,\bar\mes_r)
\cdot h_1
\]
where $\textit{first}(h_1) \ne v_{r+1}$ (that is, the deviation
becomes visible at that point!). Note however that it may be the
case that player $d$ started deviating earlier, but this will not be
taken into account.
We remark that, by definition of $\widetilde\sigma_\Agt$ along the
main outcome or for invisible deviations, it is the case that for
every $0 \le s \le r$, $\bar{m}_s(-d) = m_s(-d)$ and
$\bar\mes_s(-d) = \mes_\epsilon(-d)$.
With these notations, we can set:
\[
\widetilde\sigma_a(h) = \sigma_a\big(h_{\le r} \cdot
(\bar{m}_r,\mes_r^{+d}) \cdot h_1^{+d}\big)
\]
where $\mes_r^{+d}(d) = \id_d$,
$\mes_r^{+d}(-d) = \mes_r(-d) = \epsilon$, and $h_1^{+d}$ is the
same as $h_1$, but each message of player $d$ is set to $\id_d$.
In some sense, we tell the players to ignore any deviation as long
as it has not become visible and then treat it as if it were an
immediately visible and honest deviation.
Indeed, $h_{\le r} \cdot (m'_r,\mes_r^{+d}) \cdot h_1^{+d}$ is the
history resulting from playing an immediately visible and honest
deviation visiting the same vertices as $h$.
We argue why this is well-defined. Pick two such deviations, for
players $d$ and $d'$ respectively, which generate histories
$h = h_{\le r} \cdot (\bar{m}_r,\bar\mes_r) \cdot
h_1$ and $h' = h'_{\le r} \cdot (\bar{m}'_r,\bar\mes'_r) \cdot
h'_1$ respectively.
We assume $a \ne d,d'$. It is the case
that $a$ cannot distinguish between $h$ and $h'$ if and only if
$\pi_a(h) = \pi_a(h')$. By considering the players in the
neighbourhood of $d$, it is not difficult to get that
$\pi_a(h) = \pi_a(h')$ implies
$\pi_a(h_{\le r} \cdot (\bar{m}_r,\mes_r^{+d}) \cdot h_1^{+d}) =
\pi_a(h'_{\le r} \cdot (\bar{m}'_r,{\mes'_r}^{+d}) \cdot
{h'_1}^{+d})$. Hence, this is well-defined.
Now, let $\rho'$ be the outcome of a $d$-deviation
w.r.t. $\widetilde\sigma_\Agt$. It can be written as
$v_0 \cdot (\bar{m}_0,\bar\mes_0) \cdot v_1 \cdot
(\bar{m}_1,\bar\mes_1) \ldots v_r \cdot (\bar{m}_r,\bar\mes_r) \cdot
\rho_1$ (as before). We have that
$\rho_{\le r} \cdot (\bar{m}_r,\mes_r^{+d}) \cdot \rho_1^{+d}$ is
the outcome of an immediately visible and honest $d$-deviation of
$\sigma_\Agt$ (since one can check all players but $d$ play
according to $\sigma_\Agt$ along the play). Hence, it cannot be
profitable to the deviator (by hypothesis on $\sigma_\Agt$). Since
the two sequences $\vertices(\rho')$ and
$\vertices(\rho_{\le r} \cdot (\bar{m}_r,\mes_r^{+d}) \cdot
\rho_1^{+d})$ coincide, we conclude that $\rho'$ is not a profitable
deviation, and therefore that $\widetilde\sigma_\Agt$ is a Nash
equilibrium. \end{proof}
\subsection{A simple communication pattern is sufficient! Reduction to
normed strategy profiles}
In this part, we will show that the richness of the communication offered by the setting is somehow useless, in that we will show that a very simple communication pattern will be sufficient for generating Nash equilibria. This pattern consists in reporting the deviator (role of the direct neighbours of the deviator), and propagating this information (for all the other players, following the communication graph).
We recall the notion of a normed profile. Let $\sigma_\Agt$ be a strategy profile. Let $\rho$ be its main outcome. The profile $\sigma_\Agt$ is said \emph{normed} whenever the following conditions hold: \begin{enumerate} \item for every
$h \in \out(\sigma_\Agt) \cup \bigcup_{d \in \Agt,\ \sigma'_d}
\out(\sigma_\Agt[d/\sigma'_d],v_0)$, if $\vertices(h)$ is a prefix
of $\vertices(\rho)$, then for every $a \in \Agt$,
$\sigma_a(h)[2] = \epsilon$; \item for every $d \in \Agt$, for every $d$-strategy $\sigma'_d$,
if $h \cdot (m,\mes) \cdot v \in \out(\sigma_\Agt[d/\sigma'_d],v_0)$
is the first step out of $\vertices(\rho)$, then for every $d
\fleche a$,
$\sigma_a(h \cdot (m,\mes) \cdot v)[2] = \id_d$; \item for every $d \in \Agt$, for every $d$-strategy $\sigma'_d$, if
$h \cdot (m,\mes) \cdot v \in \out(\sigma_\Agt[d/\sigma'_d],v_0)$
has left the main outcome for more than one step, then for every $a
\in \Agt$, $\sigma_a(h \cdot (m,\mes) \cdot v)[2] = \epsilon$ if for
all $b \fleche a$, $\mes(b) = \epsilon$ and $\sigma_a(h \cdot
(m,\mes) \cdot v)[2] = \id_d$ if there is $b \fleche a$ such that
$\mes(b) = \id_d$; note that this is well defined since at most one
id can be transmitted. \end{enumerate} The first condition says that, as long as a deviation is not visible, then no message needs to be sent;
the second condition says that as soon as a deviation becomes visible, then messages denouncing the deviator should be sent by ``those who know'', that is, the (immediate) neighbours of the deviator; the third condition says that the name (actually, the id) of the deviator should propagate according to the communication graph.
Our first issue is that it can be the case that the deviator can deviate in two distinct ways (two different actions or messages) but leading to the same sequence of vertices. Those two deviations should be treated in the same way by the other players. This might in general not the case, hence we provide a construction to ensure it.
First, let us introduce a new equivalence relation on histories. Given a strategy profile $\sigma_\Agt$ we say that $h \equiv_{\sigma_\Agt} h'$ if either $h=h'$ or writing $h=v_0\cdot(m_0,\mes_0)\cdot v_1...\cdot v_{s-1} \cdot (m_{s-1},\mes_{s-1})\cdot v_s$ and $h'=v_0\cdot(m'_0,\mes'_0)\cdot v'_1...\cdot v'_{s-1} \cdot (m'_{s-1},\mes'_{s-1})\cdot v'_s$, we have:
\begin{itemize}
\item $\vertices(h)=\vertices(h')$;
\item there is $d\in \Agt$ such that $h$ and $h'$ are both
$d$-deviations w.r.t. $\sigma_\Agt$, and
$\min\{l \mid (m_l,\mes_l)\neq\sigma_\Agt(h_{\le l})\} = \min\{l
\mid (m'_l,\mes'_l)\neq\sigma_\Agt(h'_{\le l})\}$. \end{itemize}
Essentially both $h$ and $h'$ leave the main outcome of $\sigma_\Agt$ due to a single-player deviation from the same player, and follow the same sequence of vertices.
\begin{lemma}
\label{lmaequiv}
Let $\sigma_\Agt$ be a strategy profile which is resistant to
immediately visible single-player honest deviations
w.r.t. $\sigma_\Agt$. For every history $h$ we define a canonical
representative of the equivalence class of $h$ under
$\equiv_{\sigma_\Agt}$ which we denote by $\overline h$, with the
constraint that whenever possible $\overline h$ will be generated by
playing $\sigma_\Agt$ against a single-player deviation (there exists
$d$, $\tau_d$ and $k$ such that
$\overline h = \out(\sigma_\Agt[d/\tau_d],v_0)_{\leq k}$).
We define the strategy profile $\sigma'_\Agt$ inductively by
\begin{itemize}
\item if $h = \out(\sigma_\Agt,v_0)_{\leq k}$ for some $k$, then
$\sigma'_\Agt(h)=\sigma_\Agt(h)$;
\item otherwise, if $h = \out(\sigma'_\Agt[d/\tau_d],v_0)_{\leq k}$
for some $k$, some player $d\in \Agt$ and some $d$-deviation $\tau_d$,
then:
\begin{itemize}
\item if $d \fleche a$, then $\sigma'_a(h)=\sigma_a(\overline h)$;
\item else $\sigma'_a(h)=\sigma_a(h)$.
\end{itemize}
\end{itemize}
Then, $\sigma'_\Agt$ is a strategy profile which is resistant to
immediately visible single-player honest deviations
w.r.t. $\sigma'_\Agt$, with the same outcome as $\sigma_\Agt$ and
satisfies if $h\equiv_{\sigma'_\Agt} h'$ then $\sigma'_\Agt(h)=\sigma'_\Agt(h')$. \end{lemma}
\begin{proof}
First we argue why $\sigma'_\Agt$ is well-defined. Consider two
histories $h$ and $h'$ generated by playing $\sigma'_\Agt$ against
single-player deviations with deviators $d$ and $d'$ respectively,
and a player $a$ such that $h \sim_a h'$. If $d \fleche a$ or $d'
\fleche a$, then, since $h\sim_a h'$, we deduce that $d=d'$. Thus,
by hypothesis, $\overline{h} = \overline{h'}$, which implies
$\sigma'_a(h)=\sigma'_a(h') = \sigma_a(\overline{h})$. If $d
\notfleche a$ and $d' \notfleche a$, then
$\sigma'_a(h)=\sigma_a(h)=\sigma_a(h')=\sigma'_a(h')$.
It is fairly easy to show by induction that if $h\equiv_{\sigma'_\Agt} h'$
then $\sigma'_\Agt(h)=\sigma'_\Agt(h')$.
Finally, we explain why $\sigma'_\Agt$ is resistant to immediately
visible single-player deviations. We show by induction that for
every $k\in\mathbb{N}$, for every deviator $d$ and every
$d$-deviation $\tau_d$ w.r.t. $\sigma'_\Agt$ there exists a
$d$-deviation $\tau'_d$ w.r.t. $\sigma_\Agt$ such that
$\vertices(\out(\sigma'_\Agt[d/\tau_d],v_0)_{\leq k})=
\vertices(\out(\sigma_\Agt[d/\tau'_d],v_0)_{\leq k})$.
Hence, since $\sigma_\Agt$ is resistant to immediately visible
single-player deviations, then so is $\sigma'_\Agt$. \end{proof}
Let us now use this to prove the following result.
\begin{restatable}{lemma}{lemmadeux}
\label{lemma2}
Assume $\sigma_\Agt$ is a strategy profile which is resistant to
immediately visible single-player honest deviations
w.r.t. $\sigma_\Agt$ and such that, if $\vertices(h)$ is a prefix of
$\vertices(\out(\sigma_\Agt,v_0))$, then
$\sigma_\Agt(h)[2] = \epsilon$. Then one can construct a normed
strategy profile $\widehat\sigma$ which is resistant to immediately
visible honest single-player deviations, and such that
$\vertices(\out(\sigma_\Agt,v_0)) =
\vertices(\out(\widehat\sigma_\Agt,v_0))$. \end{restatable}
\begin{proof}
Let $\sigma_\Agt$ be a strategy profile which is resistant to
immediately visible single-player honest deviations, with no
communication along the main outcome. Furthermore, by usage of
Lemma~\ref{lmaequiv}, we can suppose that for all histories $h$ and
$h'$ such that $h\equiv_{\sigma_\Agt} h'$, we have that
$\sigma_\Agt(h)=\sigma_\Agt(h')$. We will build a profile
$\widehat\sigma_\Agt$ which will be normed and will coincide in some
sense to $\sigma_\Agt$. Let $\rho$ be the main outcome of
$\sigma_\Agt$. We analyse immediately visible deviations from
$\sigma_\Agt$ at some given step of $\rho$, say after prefix
$h_0 = \rho_{\le r}$, and show that the undistinguishability
relation of deviations from that point is then very simple.
\begin{lemma}
\label{lemma2}
Let $a$ be a player, and assume $d$ and $d'$ are two players such
that $\dist_G(d,a) > n$ and $\dist_G(d',a)>n$. Then, for each
length-$(r+n)$ immediately visible $d$-deviation $h$
w.r.t. $\sigma_\Agt$, after $h_0$, for each length-$(r+n)$
immediately visible $d'$-deviation $h'$ w.r.t. $\sigma_\Agt$,
after $h_0$, if the projection over vertices of $h$ and $h'$
coincide, then $h \sim_a h'$.
\end{lemma}
\begin{proof}
We do the proof by induction on $n$.
\textit{Case $n=1$:} We look at one-step deviations after
$h_0$, say $h = h_0 \cdot (m,\mes) \cdot v$ and
$h' = h_0 \cdot (m',\mes') \cdot v$ (the final vertex $v$ is
assumed to be the same, otherwise those two deviations will for
sure be distinguished by every player). Then, the following holds:
\begin{itemize}
\item $m(-d) = \sigma_\Agt(h_0)(-d)[1]$ and
$\mes(-d) = \mes_\epsilon(-d)$;
\item $m'(-d') = \sigma_\Agt(h_0)(-d')[1]$ and
$\mes'(-d') = \mes_\epsilon(-d')$.
\end{itemize}
The fact that $\dist_G(d,a) > n$ and $\dist_G(d',a)>n$ means that
$d \notfleche a$ and $d' \notfleche a$.
Hence, for every $b \fleche a$, $m(b) = \sigma_b(h_0)[1] = m'(b)$
and $\mes(b) = \epsilon = \mes'(b)$. This implies that $\pi_a(h_0
\cdot (m,\mes) \cdot v) = \pi_a(h_0 \cdot (m',\mes') \cdot v)$,
which means that $h \sim_a h'$. This concludes the case $n=1$.
\textit{Inductive step:} assume that $\dist_G(d,a) > n+1$ and
$\dist_G(d',a)>n+1$, and that $h \cdot (m,\mes) \cdot v$ and
$h' \cdot (m',\mes') \cdot v$ are respectively length-$(r+n+1)$
immediately visible $d$- (resp. $d'$-)deviations after $h_0$
w.r.t. $\sigma_\Agt$, which project on the same sequences of
vertices. For every $b \fleche a$, $\dist_G(d,b)>n$, hence, by
induction hypothesis, $h \sim_b h'$. It implies that
$\sigma_b(h) = \sigma_b(h')$, hence $m(b) = m'(b)$ and
$\mes(b) = \mes'(b)$. We deduce that
$h \cdot (m,\mes) \cdot v \sim_a h' \cdot (m',\mes') \cdot
v$. This concludes the proof of the inductive step.
\end{proof}
We will now see that this simple undistinguishability relation can
be defined using the message propagation mechanism of normed
profiles: a player doesn't send any message, unless she receives the
id of the deviator from (at least) one neighbour.
We first define normalized versions of immediately visible
single-player deviations, and for this we set
$\eta(\rho_{\le r}) = \rho_{\le r}$ for every integer $r$. Let now
$h$ be an immediately visible and honest $d$-deviation
w.r.t. $\sigma_\Agt$, which becomes visible right after
$\rho_{\le r}$. We define $\eta(h)$ inductively as follows:
\begin{itemize}
\item If $h = \rho_{\le r} \cdot (m,\mes) \cdot v$, we set
$\eta(h) = (\rho_{\le r} \cdot (m,\mes_d) \cdot v)$ where
$\mes_d(d) = \id_d$ and $\mes_d(-d) = \mes_\epsilon(-d)$;
\item if $h$ already extends $\rho_{\le r}$, then $\eta(h \cdot
(m,\mes) \cdot v) = (\eta(h) \cdot (m,\mes') \cdot v)$ where, for
every $a \in \Agt$, $\mes'(a) = \epsilon$ if for every $b \fleche
a$, $\bar\mes(b) = \epsilon$ and $\mes'(a) = \id_d$ if there is
some $b \fleche a$ such that $\bar\mes(b) = \id_d$, where
$\bar\mes$ is the last message along $\eta(h)$.
\end{itemize}
Somehow, $\eta$ propagates properly messages after a deviation has
happened.
Now define profile $\widehat\sigma_\Agt$ as follows: for every $r$,
set $\widehat\sigma_\Agt(\rho_{\le r}) = \sigma_\Agt(\rho_{\le
r})$. In particular, the main outcome of $\widehat\sigma_\Agt$ is
$\rho$. Let now $h$ be an immediately visible and honest
$d$-deviation w.r.t. $\sigma_\Agt$, after $\rho_{\le r}$; we set for
every $a \in \Agt$:
\begin{itemize}
\item if $|h| \ge \dist_G(d,a)-r$, we set
$\widehat\sigma_a(\eta(h)) = (\sigma_a(h)[1],\id_d)$;
\item if $|h| < \dist_G(d,a)-r$, we set
$\widehat\sigma_a(\eta(h)) = (\sigma_a(h)[1],\epsilon)$.
\end{itemize}
We argue why $\widehat\sigma_\Agt$ is defined everywhere it should
be defined. For that we show that every immediately visible
single-player deviation of $\widehat\sigma_\Agt$ is the image by
$\eta$ of some immediately visible single-player deviation of
$\sigma_\Agt$. This can easily be done by induction on the length of
the deviation.
We then notice that, by construction, $\widehat\sigma_\Agt$
propagates messages properly. We finally argue below why
$\widehat\sigma_\Agt$ is well-defined.
Assume that $h$ and $h'$ are two histories generated by immediately visible $d$-
(resp. $d'$-)deviations w.r.t. $\widehat\sigma_\Agt$ such that
$\eta(h) \sim_a \eta(h')$ but such that $h \not\sim_a h'$. From
Lemma~\ref{lemma2}, we deduce that $\dist_G(d,a)<r+n$ or
$\dist_G(d',a)<r+n$ where $h$ and $h'$ become visible at step $r+1$
and are of length $r+n$ (we know they are of the same length, become
visible on the same step and that $\vertices(h)=\vertices(h')$ from
$\eta(h)\sim_a \eta(h')$). This means in turns thanks to the
construction of $\widehat\sigma_\Agt$ that player $a$ received
message $\id_d$ at some step along $\eta(h)$ or signal $\id_{d'}$ at
some step along $\eta(h')$. Hence we have $d=d'$ and player $a$
received message $\id_d$ at the same step along both $\eta(h)$ and
$\eta(h')$ since otherwise, she would be able to tell the difference
between them. Thus, $h$ and $h'$ are generated by playing two $d$-deviations
visiting the same vertices and deviating from the main outcome at the same time.
Hence, we have that $h \equiv_{\sigma_\Agt} h'$,
which means from our hypothesis on $\sigma_\Agt$ that
$\sigma_\Agt(h)=\sigma_\Agt(h')$, thus $\widehat\sigma_\Agt$ is
well-defined.
Now we prove that $\widehat\sigma_\Agt$ is resistant to immediately
visible single-player deviations. Toward a contradiction, assume
there is a profitable immediately visible $d$-deviation. As noticed
above, this deviation is the image by $\eta$ of some immediately
visible $d$-deviation w.r.t. $\sigma_\Agt$. Since $\eta$ preserves
the sequences of vertices, this deviation is profitable as
well. This is not possible, by assumption on $\sigma_\Agt$, hence
$\widehat\sigma_\Agt$ is resistant to immediately visible
single-player deviations. \end{proof}
\subsection{Proof of Theorem~\ref{coro}}
\coro*
\begin{proof}
Assume $\sigma_\Agt$ is a Nash equilibrium with payoff $p$. It is
in particular resistant to immediately visible single-player honest
single-player deviations. Applying Lemma~\ref{lemma1}, $\sigma_\Agt$
can be turned to a profile $\widetilde\sigma_\Agt$ satisfying the
hypotheses of Lemma~\ref{lemma2}, and having payoff $p$. Applying
Lemma~\ref{lemma2}, there is another profile $\widehat\sigma_\Agt$,
which is normed and resistant to immediately visible single-player
deviations, and such that its main outcome visits the same sequence
of vertices as the main outcome of $\sigma_\Agt$. In particular, it
has payoff $p$.
Assume that $\sigma_\Agt$ is a normed strategy profile, which is
resistant to immediately visible and honest single-player
deviations, and which has payoff $p$. Thanks to Lemma~\ref{lemma1},
one can construct a Nash equilibrium $\widetilde\sigma_\Agt$, whose
main outcome visits the same sequence of vertices as the main
outcome of $\sigma_\Agt$, hence its payoff is $p$ as well. \end{proof}
\section{Correctness of the epistemic game construction} \label{sec:correctness}
In this section, we let $\calG$ be a concurrent game, $G$ be a communication graph for the players of $\calG$, and we let $\calE_\calG^G$ be the corresponding epistemic game. We assume all previous notations.
We write $\ID = \{\id_d \mid d\in \Agt\}$ and $\ID_\epsilon = \ID \cup \{\epsilon\}$.
\subsection{Basic properties of the epistemic game}
Considering an $\calE_{\calG}^G$-history $H = (v_0,X_0),(v_0,X_0,f_0)...(v_k,X_k)$ (notice we always have perfect alternation between \Eve's states and \Adam's state), we write $\visited(H)$ for $v_0...v_k \in V^*$. We denote by $\Hist_{\calE_\calG^G}(v_0,X_0)$ the set of such histories. An important result that will be useful later is the following:
\lma*
\begin{proof}
A proof by induction follows immediately from the structure of the
epistemic game. \end{proof}
\subsection{From \Eve's strategies in $\calE_\calG^G$ to normed profiles in
$\calG$}
We fix a strategy $\zeta$ for \Eve, associating to every possible $\calE_{\calG}^G$-history a certain \Eve's action. From $\zeta$, one defines inductively (on the size of histories) a partial function $E_\zeta: \bigcup_{a\in \Agt} \Hist_{\calG,a}(v_0) \to \Hist_{\calE_\calG^G}(v_0,\emptyset)$ associating a $\calE_{\calG}^G$-history to some $a$-history $h$ in the original game such that if $(m,\mes) \cdot v$ is a suffix of $h$, then
\begin{itemize} \item (i) for every $b \in \Vois(a)$, $\mes(b) \in \ID_\epsilon$; \item (ii) for every $b,c \in \Vois(a)$, $\mes(b) \ne \mes(c)$ implies
$\mes(b) = \epsilon$ or $\mes(c) = \epsilon$; for every
$b \in \Vois(a)$, if the message sent by $b$ earlier along $h$ is
$\id_d$ for some $d \in \Agt$, then $\mes(b) = \id_d$;
\item (iii) $\last(E_\zeta(h)) = (v,X)$, with the following additional properties: \label{ddag}
\begin{itemize}
\item $X = \emptyset$ implies for each $b \in \Vois(a)$, $\mes(b) =
\epsilon$;
\item if there is $b \in \Vois(a)$ with $\mes(b) = \id_d$, then $d
\in \dev(X)$ and $a \in I^X_d$;
\item if $X \ne \emptyset$ and for every $b \in \Vois(a)$,
$\mes(b) = \epsilon$, then there exists $c \in \dev(X)$ such that
$a \notin I^X_c$;
\end{itemize} \end{itemize}
We write $(\ddag)$ those conditions.
Together with this partial function $E_\zeta$, we define a strategy profile $\sigma_\Agt$ in $\calG$, which will in some sense (that we will explicit later) correspond to $\zeta$.
For history $v_0 \in \Hist_{\calG,a}(v_0)$, we abusively assume that the last message (denoted $\mes$) assigns $\epsilon$ to every player in $\Vois(a)$ (that is, $\mes(\Vois(a)) = \mes_\epsilon(\Vois(a))$). All conditions $(\ddag)$ are then immediately satisfied and we define $E_\zeta(v_0) = (v_0,\emptyset)$.
Pick now a history $h \in \Hist_{\calG,a}(v_0)$, ending with $(m,\mes) \cdot v$, such that $E_\zeta(h)$ is well-defined (induction hypothesis). Notice this implies that $h$ satisfies all conditions $(\ddag)$. Writing $\last(E_\zeta(h)) = (v,X)$, we will define $\sigma_a(h)$, and extend $E_\zeta$ to several extensions of $h$. We distinguish several cases: \begin{itemize} \item Assume first that $X=\emptyset$. Then,
$\zeta(E_\zeta(h)) \in \Act^\Agt$. We set
$\sigma_a(h) = \big(\zeta(E_\zeta(h))(a), \epsilon \big)$.
We extend $E_\zeta$ as follows.
\begin{itemize}
\item First, if all players follow the suggestion of \Eve (that is,
do not deviate), then the next state will be
$v' = \Tab\big(v, \zeta(E_\zeta(h))\big)$. In this case, no
message should be broadcast, and in $\calE_\calG^G$ (under
$E_\zeta$), \Adam complies with the suggestion of \Eve and goes to
$(v',\emptyset)$:
\[
E_\zeta\big(h \cdot \pi_a\big(\zeta(E_\zeta(h)), \mes_\epsilon
\big) \cdot v'\big) = E_\zeta(h) \cdot ((v,\emptyset),
\zeta(E_\zeta(h))) \cdot (v',\emptyset)
\]
\item Else, for every $d \in \Agt$ and $\delta \in \Act$, writing
$v' = \Tab\big(v,\zeta(E_\zeta(h))[d/\delta]\big)$ and assuming
that $v' = \Tab\big(v, \zeta(E_\zeta(h))\big)$ (which means it is
an invisible deviation), no message should be broadcast as well
since the deviation is somehow harmless, and in $\calE_\calG^G$
(under $E_\zeta$), \Adam complies with the suggestion of \Eve and
goes to $(v',\emptyset)$:
\[
E_\zeta\big(h \cdot \pi_a\big(\zeta(E_\zeta(h))[d/\delta],
\mes_d \big) \cdot v'\big) = E_\zeta(h) \cdot
((v,\emptyset), \zeta(E_\zeta(h))) \cdot (v',\emptyset)
\]
where $\mes_d(d) = \id_d$ and $\mes_d(-d) = \mes_\epsilon(-d)$.
\item Finally, for every $d \in \Agt$ and $\delta \in \Act$, writing
$v' = \Tab\big(v,\zeta(E_\zeta(h))[d/\delta]\big)$ and assuming
that $v' \ne \Tab\big(v, \zeta(E_\zeta(h))\big)$ (which means it
is a visible deviation), and $X' =
\update((v,\emptyset),\zeta(E_\zeta(h)),v')$ (which is then
defined and nonempty):
\[
E_\zeta\big(h \cdot \pi_a\big(
\zeta(E_\zeta(h))[d/\delta],\mes_d \big) \cdot v'\big) =
E_\zeta(h) \cdot ((v,\emptyset), \zeta(E_\zeta(h))) \cdot
(v',X')
\]
where $\mes_d(d) = \id_d$ and $\mes_d(-d) = \mes_\epsilon(-d)$.
\end{itemize}
Note that in all cases, the expected conditions are satisfied. \item Assume that $X \ne \emptyset$. If there is $b \in \Vois(a)$
such that $\mes(b) \ne \epsilon$, then pick $d \in \dev(X)$ such
that $\mes(b) = \id_d$; otherwise pick any $d \in \dev(X)$ such that
$a \notin I^X_d$ (it must exist as well by induction
hypothesis). We let $m = \zeta(E_\zeta(h))(d)$, and we set:
\[
\sigma_a(h) = \left\{\begin{array}{ll} (m(a),\id_d) &
\text{if there is}\ b \in \Vois(a)\ \text{s.t.}\ \mes(b) = \id_d, \\
(m(a),\epsilon) & \text{otherwise.}
\end{array}\right.
\]
In the first case, player $a$ has received the message blaming
player $d$, the deviator, while in the second case player $a$
has received no message.
This is well-defined for two different reasons: (i) those two cases
can be distinguished in $h$ thanks to the messages
$\pi_a(\mes) = \mes(\Vois(a))$; (ii) in the second case, thanks to
Lemma~\ref{lma} and to the definition of actions in the epistemic
game, the value $\zeta(E_\zeta(h))(d)(a)$ is independent of the
choice of $d \in \dev(X)$ satisfying $a \notin I^X_d$.
We furthermore extend $E_\zeta$ as follows.
\begin{itemize}
\item For every $\delta \in \Act$, writing
$v' = \Tab(v,m[d/\delta])$, and
$X' = \update((v,X),\zeta(E_\zeta(h)),v')$ (which is then
defined and nonempty):
\[
E_\zeta\big(h \cdot \pi_a(m[d/\delta],\mes') \cdot v'\big) =
E_\zeta(h) \cdot ((v,X), \zeta(E_\zeta(h))) \cdot (v',X')
\]
with $\mes'(b) = \id_d$ if $b \in I^X_d$ and
$\mes'(b) = \epsilon$ otherwise.
\end{itemize}
Note that all conditions of the induction hypothesis are satisfied. \end{itemize} Note that $(\ddag)$ are satisfied by every $h$ such that $E_\zeta(h)$ is defined.
This allows to define a function $\Omega$ associating a strategy profile in the original game to every \Eve's strategy in the epistemic game.
Pick $\zeta$ an \Eve's strategy in the epistemic game. Let $\sigma = \Omega(\zeta)$ be the strategy profile in the original game we have just constructed, together with the partial function $E_\zeta$. We show the following lemma: \begin{lemma}
\label{lemma5}
\begin{itemize}
\item Profile $\sigma$ is normed.
\item Let $\rho$ be the main outcome of profile $\sigma$. Then,
taking $E_\zeta$ at the limit, for every player $a \in \Agt$,
$E_\zeta(\pi_a(\rho))$ is well-defined, and equal to $R$, the
unique outcome of $\zeta$ where \Adam complies to \Eve's
suggestions. In particular, $E_\zeta(\pi_a(\rho))$ is independent
of the choice of player $a \in \Agt$.
\item Consider a honest and immediately visible single-player
deviation, and let $\rho'$ be the corresponding outcome. Then,
taking $E_\zeta$ at the limit, for every $a \in \Agt$,
$E_\zeta(\pi_a(\rho'))$ is well-defined, and equal to $R'$, an
outcome of $\zeta$, where \Adam does not comply to \Eve's
suggestions. In particular, $R' \ne R$.
\end{itemize} \end{lemma}
\begin{proof}
Let
$R = (v_0,\emptyset) \cdot ((v_0,\emptyset),f_0) \cdot
(v_1,\emptyset) \dots (v_s,\emptyset) \dots$ be the outcome of
$\zeta$, where \Adam complies to \Eve's suggestion. For every
$r \ge 0$, $f_r \in \Act^\Agt$. We let
$\rho = v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \dots
(f_{s-1},\mes_\epsilon) \cdot v_s \dots$. We can show (but omit it,
since it is obvious) by induction on $s$ that (i) for every $a$,
$E_\zeta(\pi_a(v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \dots
(f_{s-1},\mes_\epsilon) \cdot v_s))$ is defined, and is equal to
$(v_0,\emptyset) \cdot ((v_0,\emptyset),f_0) \cdot (v_1,\emptyset)
\dots (v_s,\emptyset)$, the prefix of length $s$ of $R$; and (ii)
$\sigma_a(v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \dots
(f_{s-1},\mes_\epsilon) \cdot v_s) = ((f_s)_a,\epsilon)$. In
particular, the unique outcome of profile $\sigma$ is $\rho$, and
messages are handled correctly by $\sigma$ on that part.
Then, notice that single-player deviations that do follow the
sequence of vertices of the main outcome of $\sigma$ are considered
as non-deviations by $\sigma$ (by construction, second item of the
case $X = \emptyset$).
Pick a `honest and visible' deviation $\sigma'_d$ for player $d$. We
show that messages propagate properly, and that the outcome of
$\sigma[d/\sigma'_d]$ corresponds to an outcome of $\zeta$, distinct
from the main outcome, where \Adam complies to \Eve's
suggestions. We write
$\rho' = v'_0 \cdot (f'_0,\mes'_0) \cdot v'_1 \dots
(f'_{s-1},\mes'_{s-1}) \cdot v'_s \dots$ for the outcome of
$\sigma[d/\sigma'_d]$. There exists $s$ such that
$v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \dots
(f_{s-1},\mes_\epsilon) \cdot v_s = v'_0 \cdot (f'_0,\mes'_0) \cdot
v'_1 \dots (f'_{s-1},\mes'_{s-1}) \cdot v'_s$,
$v'_{s+1} \ne v_{s+1}$ and $f'_s = f_s[d/\delta]$ for some action
$\delta$, while $\mes'_s(d) = \id_d$ and $\mes'_s(a) = \epsilon$ if
$a \ne d$ (this is by definition of a honest and visible
deviation). So far, the message propagation system is working
well. For every $r \ge s+1$, we write $h'_r$ for the prefix of
length $r$ of $\rho'$. We show by induction on $r \ge s+1$ that for
every $a$, $E_\zeta(\pi_a(h'_r))$ is well-defined and equal to
$R'_r$, with $\last(R'_r) = (v'_r,X'_r)$ ($X'_r \ne \emptyset$),
$R'_r$ is an outcome of $\zeta$, and the message propagation system
has been working properly along $h'_r$.
\begin{itemize}
\item By construction of partial function $E_\zeta$, for every $a$,
$E_\zeta(\pi_a(h'_{s+1}))$ is well-defined, and is equal to
$R'_{s+1} = (v_0,\emptyset) \cdot ((v_0,\emptyset),f_0) \cdot
(v_1,\emptyset) \dots (v_s,\emptyset) \cdot
((v_s,\emptyset),f_{s+1}) \cdot (v'_{s+1},X'_{s+1})$, where
$X'_{s+1} = \update((v_s,\emptyset),f_{s+1},v'_{s+1})$ (with
$X'_{s+1} \ne \emptyset$). Obviously, $R'_{s+1}$ is a prefix of an
outcome of $\zeta$. So far, the message propagating system has
worked well along $h'_{s+1}$.
\item We assume that for every $a$, $E_\zeta(\pi_a(h'_r))$ (with
$r \ge s+1$) is well-defined and equal to $R'_r$, with
$\last(R'_r) = (v'_r,X'_r)$ ($X'_r \ne \emptyset$). We also assume
that $R'_r$ is (a prefix of) an outcome of $\zeta$. Finally we
assume that the message propagation system has worked properly
along $h'_r$.
We show that the same properties hold for $h'_{r+1}$. We fix a
player $a$.
Since $E_\zeta(\pi_a(h'_r)) = R'_r$, we have that $X'_r$ and
$\mes'_{r-1}$ satisfy the conditions $(\ddag)$ given on
page~\pageref{ddag}.
To do the inductive step, we first look at
$\sigma_a(h'_r)$:
\[
\sigma_a(h'_r) = \left\{\begin{array}{ll}
\Big(\big(\zeta(E_\zeta(\pi_a(h'_r)))(d)\big)_a,\id_d\Big) &
\text{if there is}\ b \in \Vois(a)\ \text{s.t.}\
\mes'_{r-1}(b)
\ne
\epsilon \\
\Big(\big(\zeta(E_\zeta(\pi_a(h'_r)))(d)\big)_a,\epsilon\Big)
&
\text{otherwise}
\end{array}\right.
\]
Hence, in all cases, we have
$\sigma_a(h'_r)[1] = \big(\zeta(E_\zeta(\pi_a(h'_r)))(d)\big)_a =
\big(\zeta(R'_r)(d)\big)_a$, and messages are properly propagated
by player $a$. We write $m' = \zeta(R'_r)(d)$, and define the
message $\mes'_r$ by $\mes'_r(a) = \id_d$ if there is
$b \in \Vois(a)$ such that $\mes'_{r-1}(b) = \id_d$, and
$\mes'_r(a) = \epsilon$ otherwise. Now, there is an action
$\delta \in \Act$ such that
\[
h'_{r+1} = h'_r \cdot (m'[d/\delta],\mes'_r) \cdot v'_{r+1}
\]
We define
\[
R'_{r+1} = R'_r \cdot ((v'_r,X'_r),\zeta(R'_r)) \cdot
(v'_{r+1},X'_{r+1})
\]
with $X'_{r+1} = \update((v'_r,X),\zeta(R'_r),v'_{r+1})$. Note
that $X'_{r+1}$ is well-defined and nonempty since this is
witnessed by
$\Tab(v'_r,\big(\zeta(R'_r)(d)\big)[d/a]) = v'_{r+1}$. By
construction of $E_\zeta$, we have that $E_\zeta(\pi_a(h'_{r+1}))$
is well-defined and equal to $R'_{r+1}$. Finally, along
$h'_{r+1}$, the communication system has been working properly,
and $R'_{r+1}$ is obviously (a prefix of) an outcome of $\zeta$
(distinct from $R$). This concludes the proof of the inductive
step, and of the lemma.
\end{itemize} \end{proof}
The following statement is an obvious consequence of the construction of $E_\zeta$:
\begin{lemma}
\label{sens1}
If $\zeta$ is a winning strategy for \Eve in $\calE_\calG^G$, then
$\sigma=\Omega(\zeta)$ is a normed strategy profile, which is
resistant to single-player visible and honest deviations, and whose
payoff is equal to the payoff of the outcome of $\zeta$ where \Adam
complies to \Eve's suggestions. \end{lemma}
\begin{proof}
We assume that $\zeta$ is a winning strategy for \Eve, and that the
payoff of the main outcome $R$ of $\zeta$ is $p = (p_a)_{a \in
\Agt}$. Then, for each other outcome of $\zeta$, the payoff is
bounded by $p$.
Applying Lemma~\ref{lemma5}, the main outcome $\rho$ of $\sigma$ is
such that $E_\zeta(\rho) = R$, yielding payoff $p$ for $\rho$. Pick
a honest and visible $d$-deviation $\sigma'_d$, and let $\rho'$ be
the outcome of $\sigma[d/\sigma'_d]$. Then, $E_\zeta(\rho')$ is
defined and is an outcome of $\zeta$ (again by application of
Lemma~\ref{lemma5}), which payoff is therefore bounded by $p$. Hence,
$\sigma$ satisfies the expected conditions. \end{proof}
\subsection{From normed profiles in $\calG$ to \Eve's strategies in
$\calE_\calG^G$}
We assume an arbitrary total order $<$ on the set $\Act$. This will be used to define unique corresponding (local) histories in $\calG$.
We first define a mapping assigning families of (local) histories in $\calG$ to histories in $\calE_\calG^G$. Consider an $\Eve$'s history $H = (v_0,X_0) \cdot (v_0,X_0,f_0) \dots (v_s,X_s)$ in $\calE_\calG^G$. \begin{itemize} \item If $X_s = \emptyset$, then for every $r < s$,
$X_r = \emptyset$ as well, and therefore $f_r \in \Act^\Agt$. We
then associate with $H$ the single full history, which is easily
seen to be well-defined:
\[
h=v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \cdot
(f_1,\mes_\epsilon) \cdot v_2 \dots (f_{s-1},\mes_\epsilon) \cdot
v_s
\] \item If $X_s \ne \emptyset$, then there is a smallest index $0<r_0
\le s$ such that $X_{r_0} \ne \emptyset$, and for every $r_0 \le r
\le s$, $X_r \ne \emptyset$. Note also that for every $r_0 \le r_1
\le r_2 \le s$, $\dev(X_{r_2}) \subseteq \dev(X_{r_1})$. We then
associate with $H$ and with every deviator $d \in \dev(X_s)$, the
(unique) full history:
\[
h_d = v_0 \cdot (m_0,\mes_0) \cdot v_1 \dots (m_{s-1},\mes_{s_1})
\cdot v_s
\]
such that:
\begin{itemize}
\item $l < r_0$ implies $m_l = f_l$ and $\mes_l = \mes_\epsilon$;
\item Let $l \ge r_0$. For every $a \in \Agt$, $\mes_l(a) = \id_d$
if $a \in I^{X_l}_d$, otherwise $\mes_l(a) = \epsilon$. Then,
$m_l(-d) = f_l(d)(-d)$, and $m_l(d)$ is the $<$-smallest
action $\delta \in \Act$ such that $v_{l+1} = \Tab(v_l,
f_l(d)[d/\delta])$.
\end{itemize} \end{itemize} We denote by $\Lambda$ the function that associates with every $\Eve$'s history $H$ in $\calE_\calG^G$, either the single full history $h$ (first case), or the family of full histories $(h_d)_{d \in \dev(X_s)}$ (second case).
Let $\sigma$ be a normed strategy profile in the original game. We define the \Eve's strategy $\zeta$ as follows: \begin{itemize} \item if $H$ is such that $\last(H) = (v,\emptyset)$, then $\zeta(H)
\in \Act^\Agt$ and $\zeta(H)(a) = \sigma_a(\Lambda(H))[1]$; \item if $H$ is such that $\last(H) =(v,X)$ with $X \ne \emptyset$,
then $\zeta(H) : \dev(X) \to \Act^\Agt$ is such that
$\zeta(H)(d)(a)= \sigma_a(\Lambda(H)(d))[1]$ for all $d \in
\dev(X)$. \end{itemize} This allows to define a function $\Upsilon$ associating a strategy in the epistemic game to every normed profile in the original game.
Pick $\sigma$ a normed strategy profile in $\calG$, and write $\zeta = \Upsilon(\sigma)$ for the corresponding strategy in $\calE_\calG^G$.
\begin{lemma}
\label{lemma7}
\begin{itemize}
\item Let $R$ be the unique outcome of $\zeta$ where \Adam complies
to \Eve's suggestions. Then, at the limit, $\Lambda(R)$ is the
unique outcome $\rho$ of profile $\sigma$.
\item Let $R'$ be an outcome of $\zeta$ along which \Adam does not
always comply to \Eve's suggestions. Then, for every $d \in
\lim_{s \to +\infty} \dev(X'_s)$, there exists some honest and
visible deviation $\sigma'_d$ such that $\Lambda(R')(d) =
\out(\sigma[d/\sigma'_d],v_0)$.
\end{itemize} \end{lemma}
\begin{proof}
Write
$R = (v_0,\emptyset) \cdot ((v_0,\emptyset),f_0) \cdot
(v_1,\emptyset) \cdot ((v_1,\emptyset),f_1) \cdot (v_2,\emptyset)
\dots$ for the outcome of $\zeta$, along which \Adam complies to
\Eve's suggestions. Then it is easy to argue that the outcome of
$\sigma$ is
$\rho = v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \cdot
(f_1,\mes_\epsilon) \cdot v_2 \dots$, and $\rho$ coincides with
$\Lambda(R)$ (at the limit).
Let $R' = (v'_0,X'_0) \cdot ((v'_0,X'_0),f'_0) \cdot (v'_1,X'_1)
\dots$ such that there is some (the first) $r$ such that $X'_r \ne
\emptyset$. We show by induction on $s \ge r$ that for every $d \in
\dev(X'_s)$, there is a honest $d$-deviation $\sigma'_d$ such that
the length-$s$ outcome of $\sigma[d/\sigma'_d]$ is
\[
v'_0 \cdot (f'_0,\mes_0) \cdot v'_1 \cdot (f'_1,\mes_1) \cdot v'_2
\dots (f'_{s-1},\mes_{s-1}) \cdot v'_s = \Lambda(R'_{\le s})(d)
\]
In the same induction, we will prove that
$I^{X'_s}_d = \{a \in \Agt \mid \exists b \in \Vois(a)\ \text{s.t.}\
\mes_{s-1}(b) = \id_d\}$.
Before proving the induction, notice that
$v'_0 \cdot (f'_0,\mes_0) \cdot v'_1 \cdot (f'_1,\mes_1) \dots
v'_{r-1} = v_0 \cdot (f_0,\mes_\epsilon) \cdot v_1 \cdot
(f_1,\mes_\epsilon) \dots v_{r-1}$ (that is, it follows the main
outcome), and $v'_r \ne v_r$.
\begin{itemize}
\item Assume $s=r$. Then,
$X'_r = \update((v_{r-1},\emptyset),\zeta(R_{\le r-1}),v'_r)$
(defined and nonempty), with
$\zeta(R_{\le r-1})(a) = \sigma_a(\rho_{\le r-1})[1]$. By
construction, for every $d \in \dev(X'_r)$, there is
$\delta \in \Act$ such that
$v'_r = \Tab(v_{r-1},\sigma(\rho_{\le r-1})[d/\delta])$, where
$\sigma(\rho_{\le r-1})$ denotes abusively the tuple
$(\sigma_a(\rho_{\le r-1})[1])_{a \in \Agt}$. We define
$\sigma'_d(\rho_{\le r-1}) = (\delta,\id_d)$ (this is a honest and
visible deviation). Then,
$\rho_{\le r} \in \out(\sigma[d/\sigma'_d],v_0)$. Also, since the
system of message propagation under $\sigma$ is behaving well, it
is the case that for every $a$, $\mes_{s-1}(a) = \epsilon$ if
$a \ne d$, and $\mes_{s-1}(d) = \id_d$ (as given by
$\sigma'_d(\rho_{\le r-1})$). It is an easy check to prove the
property on messages.
\item Assume we have proven the result at rank $s$, and consider
$R'_{\le s+1} = R'_{\le s} \cdot ((v'_s,X'_s),f'_s) \cdot
(v'_{s+1},X'_{s+1})$. Pick $d \in \dev(X'_{s+1})$. Since then,
$d \in \dev(X'_s)$ as well, we can apply the induction hypothesis
to $R'_{\le s}$, and we have a deviation $\sigma'_d$ such that the
length-$s$ outcome of $\sigma[d/\sigma'_d]$ is
$\Lambda(R'_{\le s})(d)$.
By definition, $X'_{s+1} = \update((v'_s,X'_s),f'_s,v'_{s+1})$,
hence there exists $\delta \in \Act$ such that
$\Tab(v'_s,f'_s(d)[d/\delta]) = v'_{s+1}$. We then define
$\sigma'_d(\Lambda(R'_{\le s})_d) = (\delta,\id_d)$. The
length-$(s+1)$ outcome of $\sigma[d/\sigma'_d]$ is
\[
\Lambda(R'_{\le s})(d) \cdot (m[d/\delta],\mes) \cdot v'
\]
where:
\begin{itemize}
\item for every $a \in \Agt$, $m(a) = \sigma_a(\Lambda(R'_{\le
s})(d))[1]$
\item for every $a \in \Agt$,
$\mes(a)= \sigma_a(\Lambda(R'_{\le s})(d))[2]$
\item $v' = \Tab(v'_s,m[d/\delta])$
\end{itemize}
Now, we show $m[d/\delta] = f'_s(d)$: $f'_s(d)(a) = (\zeta(R'_{\le
s})(d))(a) = \sigma_a(\Lambda(R'_{\le s})(d)[1] = m(a)$. Hence,
$v' = v'_{s+1}$. We conclude that the length-$(s+1)$ outcome of
$\sigma[d/\sigma'_d]$ is
\[
\Lambda(R'_{\le s})(d) \cdot (\zeta(R'_{\le
s})(d)[d/\delta],\mes) \cdot v'_{s+1} = \Lambda(R'_{\le
s+1})(d)
\]
Concerning the messages:
$I^{X'_{s+1}}_d = \{a \in \Agt \mid \exists b \in I^{X'_s}_d\
\text{s.t.}\ \dist_G(a,b) \le 1\}$. Since $d$ is the deviator and
the deviation is honest, $\mes_{s-1}(d) = \mes_s(d) = \id_d$, and
for every $a \ne d$,
$\mes_s(a) = \mes(a) = \sigma_a(\Lambda(R'_{\le s})(d))[2]$. Since
$\sigma$ is normed, messages are propagated correctly by all players
$a \ne d$. Hence the expected equality holds.
\end{itemize} \end{proof}
\begin{lemma}
\label{sens2}
If $\sigma$ is a normed strategy profile in $\calG$, which is
resistant to single-player immediately visible and honest
deviations, then $\zeta = \Upsilon(\sigma)$ is a winning strategy in
$\calE_\calG^G$. \end{lemma}
\begin{proof}
Let $p$ be the payoff associated with $\rho = \out(\sigma,v_0)$. The
outcome of $\zeta$ when \Adam complies to \Eve's suggestions is $R$
such that $\rho = \Lambda(R)$. In particular, $R$ has the same
payoff as $\rho$, that is, $p$.
Assume now that $R' = (v_0,X_0) \cdot ((v_0,X_0),f_0) \cdot
(v_1,X_1) \dots$ is a play in the epistemic game such that from some
point on, $X_i \ne \emptyset$. Then, from Lemma~\ref{lemma7}, for
every $d \in \lim_{s \to +\infty} \dev(X'_s)$, there exists
$\sigma'_d$ such that
\[
\rho' = \out(\sigma[d/\sigma'_d],v_0) = \Lambda(R')(d)
\]
The payoff of $\rho'$ and $R'$ therefore coincide (and are equal to
$p'$). Since $\sigma$ is a Nash equilibrium, $p'_d \le p_d$. Hence
for every $d \in \lim_{s \to +\infty} \dev(X'_s)$, the payoff of
player $d$ along $R'$ is bounded by $p_d$. Hence $\zeta$ is
winning. \end{proof}
\subsection{Conclusion}
As a consequence of Theorem~\ref{coro}, Lemmas~\ref{sens1} and~\ref{sens2}, we get Theorem~\ref{theo:main}:
\main*
Note that all the results are constructive, hence if one can synthesize a winning strategy for \Eve in $\calE_\calG^G$, then we can synthesize a correponding Nash equilibrium in $\calG$.
\section{Complexity analysis}
By application of Lemma~\ref{lma}, we get:
\begin{lemma}
\label{coro:small}
Let $(v,\emptyset) \cdot ((v,\emptyset),f_0) \cdot (v_1,X_1) \cdot
((v_1,X_1),f_1) \cdot (v_2,X_2) \dots$ with $X_1 \ne \emptyset$ be a
history in $\calE_\calG^G$. Then for every $r \ge 1$:
\begin{itemize}
\item $\dev(X_r) \subseteq \dev(X_1)$;
\item for every $d \in \dev(X_r)$, for every $a \in \Agt$,
$\dist_G(d,a) \le r$ iff $a \in I_d^{X_r}$.
\item If $d \in \dev(X_r)$ and $\dist_G(d,a) \le r$, then
$K_d^{X_r}(a) = \{d\}$.
\item If $d \in \dev(X_r)$ and $\dist_G(d,a) > r$, then
$K_d^{X_r}(a) = \dev(X_r) \setminus \{d' \in \dev(X_r) \mid
\dist_G(d',a) \le r\}$.
\end{itemize} \end{lemma}
\size*
\begin{proof}
We start by evaluating the number of \Eve's states.
First, the number of \Eve's states $(v,\emptyset)$ is obviously
$|V|$.
Then, pick an \Eve state $(v',X')$ with $X' \ne \emptyset$, such
that there is a transition $((v,\emptyset),f) \to (v',X')$ in
$\calE_\calG^G$ (those are immediate visible deviations). Then,
following an argument used in~\cite[Prop.~4.8]{BBMU15}, we can show
that $|\Tab| \ge 2^{|\dev(X')|}$: indeed, each player in $\dev(X')$
has been able to deviate, hence can at least do two actions from the
current state, yielding the claimed bound.
We will now analyze the part which is reachable from
$(v',X')$. Applying Lemma~\ref{coro:small}, any \Eve's state
$(v'',X'')$ reachable from $(v',X')$ is such that $\dev(X'')
\subseteq \dev(X')$, and is fully characterized by
$(v',\dev(X''),r)$ where $\dev(X'') \subseteq \dev(X')$ and $r$ is
the distance from $(v',X')$. Hence, this number of states is bounded
by $|V| \cdot 2^{|\dev(X')|} \cdot (\diam(G)+2)$, where $\diam(G)$
is the maximal diameter of the connected components of $G$ (the $+2$
term is for ``distance $+\infty$'' and for ``distance larger than
the diameter''). Hence it is bounded by $|V| \cdot |\Tab| \cdot
(\diam(G)+2)$.
Since there are at most $|\Tab|$ possible deviation starting points
$(v',X')$, the number of \Eve's states is bounded by $|V| + |V| \cdot
|\Tab|^2 \cdot (\diam(G)+2)$.
Now we evaluate the number of \Adam's states. There are at most
$|\Tab|$ states of the form $((v,\emptyset),f)$. Now, from an
\Eve's state $(v,X)$ with $X \ne \emptyset$, there are \Adam's states
$((v,X),f)$ with $f : \dev(X) \to \Act^\Agt$. It is a priori
difficult to reduce the number of such $f$, which is bounded by
$|\Act|^{|\dev(X)| \cdot |\Agt|}$, hence by~$|\Act|^{|\Agt|^2}$.
\end{proof}
\end{document} | arXiv |
Cost of electricity by source | Wikipedia audio article
In electrical power generation, the distinct ways of generating electricity incur significantly different costs. Calculations of these costs can be made at the point of connection to a load or to the electricity grid. The cost is typically given per kilowatt-hour or megawatt-hour It includes the initial capital, discount rate, as well as the costs of continuous operation, fuel, and maintenance. This type of calculation assists policymakers, researchers and others to guide discussions and decision making The levelized cost of energy (LCOE) is a measure of a power source that allows comparison of different methods of electricity generation on a consistent basis. It is an economic assessment of the average total cost to build and operate a power-generating asset over its lifetime divided by the total energy output of the asset over that lifetime. The LCOE can also be regarded as the average minimum price at which electricity must be sold in order to break-even over the lifetime of the project == Cost factors == While calculating costs, several internal cost factors have to be considered. Note the use of "costs," which is not the actual selling price, since this can be affected by a variety of factors such as subsidies and taxes: Capital costs (including waste disposal and decommissioning costs for nuclear energy) – tend to be low for fossil fuel power stations; high for wind turbines, solar PV (photovoltaics); very high for waste to energy, wave and tidal, solar thermal, and nuclear Fuel costs – high for fossil fuel and biomass sources, low for nuclear, and zero for many renewables. Fuel costs can vary somewhat unpredictably over the life of the generating equipment, due to political and other factors Factors such as the costs of waste (and associated issues) and different insurance costs are not included in the following: Works power, own use or parasitic load – that is, the portion of generated power actually used to run the station's pumps and fans has to be allowed for.To evaluate the total cost of production of electricity, the streams of costs are converted to a net present value using the time value of money. These costs are all brought together using discounted cash flow === Levelized cost of electricity === The levelized cost of electricity (LCOE), also known as Levelized Energy Cost (LEC), is the net present value of the unit-cost of electricity over the lifetime of a generating asset. It is often taken as a proxy for the average price that the generating asset must receive in a market to break even over its lifetime. It is a first-order economic assessment of the cost competitiveness of an electricity-generating system that incorporates all costs over its lifetime: initial investment, operations and maintenance, cost of fuel, cost of capital The levelized cost is that value for which an equal-valued fixed revenue delivered over the life of the asset's generating profile would cause the project to break even. This can be roughly calculated as the net present value of all costs over the lifetime of the asset divided by the total electrical energy output of the asset.The levelized cost of electricity (LCOE) is given by: L C O E = sum of costs over lifetime sum of electrical energy produced over lifetime = ∑ t = 1 n I t + M t + F t ( 1 + r ) t ∑
t = 1 n E t ( 1 + r ) t {\displaystyle \mathrm {LCOE} ={\frac {\text{sum of costs over lifetime}}{\text{sum of electrical energy produced over lifetime}}}={\frac {\sum _{t=1}^{n}{\frac {I_{t}+M_{t}+F_{t}}{\left({1+r}\right)^{t}}}}{\sum _{t=1}^{n}{\frac {E_{t}}{\left({1+r}\right)^{t}}}}}} Typically the LCOE is calculated over the design lifetime of a plant, which is usually 20 to 40 years, and given in the units of currency per kilowatt-hour or megawatt-day, for example AUD/kWh or EUR/kWh or per megawatt-hour, for example AUD/MWh (as tabulated below) However, care should be taken in comparing different LCOE studies and the sources of the information as the LCOE for a given energy source is highly dependent on the assumptions, financing terms and technological deployment analyzed. In particular, assumption of capacity factor has significant impact on the calculation of LCOE. Thus, a key requirement for the analysis is a clear statement of the applicability of the analysis based on justified assumptions.Many scholars, such as Paul Joskow, have described limits to the "levelized cost of electricity" metric for comparing new generating sources In particular, LCOE ignores time effects associated with matching production to demand. This happens at two levels: Dispatchability, the ability of a generating system to come online, go offline, or ramp up or down, quickly as demand swings The extent to which the availability profile matches or conflicts with the market demand profile.Thermally lethargic technologies like coal and nuclear are physically incapable of fast ramping. Capital intensive technologies such as wind, solar, and nuclear are economically disadvantaged unless generating at maximum availability since the LCOE is nearly all sunk-cost capital investment. Intermittent power sources, such as wind and solar, may incur extra costs associated with needing to have storage or backup generation available At the same time, intermittent sources can be competitive if they are available to produce when demand and prices are highest, such as solar during summertime mid-day peaks seen in hot countries where air conditioning is a major consumer. Despite these time limitations, leveling costs is often a necessary prerequisite for making comparisons on an equal footing before demand profiles are considered, and the levelized-cost metric is widely used for comparing technologies at the margin, where grid implications of new generation can be neglected Another limitation of the LCOE metric is the influence of energy efficiency and conservation (EEC) EEC has caused the electricity demand of many countries to remain flat or decline. Considering only the LCOE for utility scale plants will tend to maximise generation and risks overestimating required generation due to efficiency, thus "lowballing" their LCOE. For solar systems installed at the point of end use, it is more economical to invest in EEC first, then solar (resulting in a smaller required solar system than what would be needed without the EEC measures). However, designing a solar system on the basis of LCOE would cause the smaller system LCOE to increase (as the energy generation [measured in kWh] drops faster than the system cost [$]). The whole of system life cycle cost should be considered, not just the LCOE of the energy source. LCOE is not as relevant to end-users than other financial considerations such as income, cashflow, mortgage, leases,
rent, and electricity bills. Comparing solar investments in relation to these can make it easier for end-users to make a decision, or using cost-benefit calculations "and/or an asset's capacity value or contribution to peak on a system or circuit level" === Avoided cost === The US Energy Information Administration has recommended that levelized costs of non-dispatchable sources such as wind or solar may be better compared to the avoided energy cost rather than to the LCOE of dispatchable sources such as fossil fuels or geothermal. This is because introduction of fluctuating power sources may or may not avoid capital and maintenance costs of backup dispatchable sources. Levelized Avoided Cost of Energy (LACE) is the avoided costs from other sources divided by the annual yearly output of the non-dispatchable source However, the avoided cost is much harder to calculate accurately === Marginal cost of electricity === A more accurate economic assessment might be the marginal cost of electricity. This value works by comparing the added system cost of increasing electricity generation from one source versus that from other sources of electricity generation (see Merit Order) === External costs of energy sources === Typically pricing of electricity from various energy sources may not include all external costs – that is, the costs indirectly borne by society as a whole as a consequence of using that energy source. These may include enabling costs, environmental impacts, usage lifespans, energy storage, recycling costs, or beyond-insurance accident effects The US Energy Information Administration predicts that coal and gas are set to be continually used to deliver the majority of the world's electricity. This is expected to result in the evacuation of millions of homes in low-lying areas, and an annual cost of hundreds of billions of dollars' worth of property damage.Furthermore, with a number of island nations becoming slowly submerged underwater due to rising sea levels, massive international climate litigation lawsuits against fossil fuel users are currently beginning in the International Court of Justice.An EU funded research study known as ExternE, or Externalities of Energy, undertaken over the period of 1995 to 2005 found that the cost of producing electricity from coal or oil would double over its present value, and the cost of electricity production from gas would increase by 30% if external costs such as damage to the environment and to human health, from the particulate matter, nitrogen oxides, chromium VI, river water alkalinity, mercury poisoning and arsenic emissions produced by these sources, were taken into account. It was estimated in the study that these external, downstream, fossil fuel costs amount up to 1%–2% of the EU's entire Gross Domestic Product (GDP), and this was before the external cost of global warming from these sources was even included. Coal has the highest external cost in the EU, and global warming is the largest part of that cost.A means to address a part of the external costs of fossil fuel generation is carbon pricing — the method most favored by economics for reducing global-warming emissions. Carbon pricing charges those who emit carbon dioxide (CO2) for their emissions That charge, called a 'carbon price', is the amount that must be paid for the right to emit one tonne of CO2 into the atmosphere Carbon pricing usually takes the form of a carbon tax or a requirement to purchase permits to emit (also called "allowances") Depending on the assumptions of possible accidents and their probabilites external costs for nuclear power vary significantly and can reach between 0.2 and 200 ct/kWh. Furthermore, nuclear power is working under an insurance framework
that limits or structures accident liabilities in accordance with the Paris convention on nuclear third-party liability, the Brussels supplementary convention, and the Vienna convention on civil liability for nuclear damage and in the U.S. the Price-Anderson Act. It is often argued that this potential shortfall in liability represents an external cost not included in the cost of nuclear electricity; but the cost is small, amounting to about 0.1% of the levelized cost of electricity, according to a CBO study.These beyond-insurance costs for worst-case scenarios are not unique to nuclear power, as hydroelectric power plants are similarly not fully insured against a catastrophic event such as the Banqiao Dam disaster, where 11 million people lost their homes and from 30,000 to 200,000 people died, or large dam failures in general. As private insurers base dam insurance premiums on limited scenarios, major disaster insurance in this sector is likewise provided by the state.Because externalities are diffuse in their effect, external costs can not be measured directly, but must be estimated. One approach estimate external costs of environmental impact of electricity is the Methodological Convention of Federal Environment Agency of Germany That method arrives at external costs of electricity from lignite at 10.75 Eurocent/kWh, from hard coal 8.94 Eurocent/kWh, from natural gas 4.91 Eurocent/kWh, from photovoltaic 1.18 Eurocent/kWh, from wind 0.26 Eurocent/kWh and from hydro 0.18 Eurocent/kWh. For nuclear the Federal Environment Agency indicates no value, as different studies have results that vary by a factor of 1,000. It recommends the nuclear given the huge uncertainty, with the cost of the next inferior energy source to evaluate Based on this recommendation the Federal Environment Agency, and with their own method, the Forum Ecological-social market economy, arrive at external environmental costs of nuclear energy at 10.7 to 34 ct/kWh === Additional cost factors === Calculations often do not include wider system costs associated with each type of plant, such as long distance transmission connections to grids, or balancing and reserve costs Calculations do not include externalities such as health damage by coal plants, nor the effect of CO2 emissions on the climate change, ocean acidification and eutrophication, ocean current shifts. Decommissioning costs of nuclear plants are usually not included (The USA is an exception, because the cost of decommissioning is included in the price of electricity, per the Nuclear Waste Policy Act), is therefore not full cost accounting These types of items can be explicitly added as necessary depending on the purpose of the calculation. It has little relation to actual price of power, but assists policy makers and others to guide discussions and decision making.These are not minor factors but very significantly affect all responsible power decisions: Comparisons of life-cycle greenhouse gas emissions show coal, for instance, to be radically higher in terms of GHGs than any alternative. Accordingly, in the analysis below, carbon captured coal is generally treated as a separate source rather than being averaged in with other coal Other environmental concerns with electricity generation include acid rain, ocean acidification and effect of coal extraction on watersheds Various human health concerns with electricity generation, including asthma and smog, now dominate decisions in developed nations that incur health care costs publicly. A Harvard University Medical School study estimates the US health costs of coal alone at between 300 and 500 billion US dollars annually
While cost per kWh of transmission varies drastically with distance, the long complex projects required to clear or even upgrade transmission routes make even attractive new supplies often uncompetitive with conservation measures (see below), because the timing of payoff must take the transmission upgrade into account == Current global studies == === Lazard (2018) === In November, 2018, Lazard found that not only are utility-scale solar and wind cheaper than fossil fuels, "[i]n some scenarios, alternative energy costs have decreased to the point that they are now at or below the marginal cost of conventional generation." Overall, Lazard found "The low end levelized cost of onshore wind-generated energy is $29/MWh, compared to an average illustrative marginal cost of $36/MWh for coal. The levelized cost of utility-scale solar is nearly identical to the illustrative marginal cost of coal, at $36/MWh. This comparison is accentuated when subsidizing onshore wind and solar, which results in levelized costs of energy of $14/MWh and $32/MWh, respectively. … The mean levelized cost of energy of utility-scale PV technologies is down approximately 13% from last year and the mean levelized cost of energy of onshore wind has declined almost 7%." === Bloomberg (2018) === Bloomberg New Energy Finance estimates a "global LCOE for onshore wind [of] $55 per megawatt-hour, down 18% from the first six months of [2017], while the equivalent for solar PV without tracking systems is $70 per MWh, also down 18%." Bloomberg does not provide its global public LCOEs for fossil fuels, but it notes in India they are significantly more expensive: "BNEF is now showing benchmark LCOEs for onshore wind of just $39 per MWh, down 46% on a year ago, and for solar PV at $41, down 45%. By comparison, coal comes in at $68 per MWh, and combined-cycle gas at $93." === IRENA (2018) === The International Renewable Energy Agency (IRENA) released a study based on comprehensive international datasets in January 2018 which projects the fall by 2020 of the kilowatt cost of electricity from utility scale renewable projects such as onshore wind farms to a point equal or below that of electricity from conventional sources === Banks (2018) === The European Bank for Reconstruction and Development (EBRD) says that "renewables are now cheapest energy source", elaborating: "the Bank believes that renewable energy markets in many of the countries where it invests have reached a stage where the introduction of competitive auctions will lead both to a steep drop in electricity prices and an increase in investment." The World Bank (World Bank) President Jim Yong Kim agreed on 10 October 2018: "We are required by our by-laws to go with the lowest cost option, and renewables have now come below the cost of [fossil fuels]." == Regional and historical studies == === Australia ===
According to various studies, the cost for wind and solar has dramatically reduced since 2006. For example, the Australian Climate Council states that over the 5 years between 2009–2014 solar costs fell by 75% making them comparable to coal, and are expected to continue dropping over the next 5 years by another 45% from 2014 prices. They also found that wind has been cheaper than coal since 2013, and that coal and gas will become less viable as subsidies are withdrawn and there is the expectation that they will eventually have to pay the costs of pollution.A CO2CRC report, printed on the 27th of November 2015, titled "Wind, solar, coal and gas to reach similar costs by 2030:", provides the following updated situation in Australia. "The updated LCOE analysis finds that in 2015 natural gas combined cycle and supercritical pulverised coal (both black and brown) plants have the lowest LCOEs of the technologies covered in the study. Wind is the lowest cost large-scale renewable energy source, while rooftop solar panels are competitive with retail electricity prices. By 2030 the LCOE ranges of both conventional coal and gas technologies as well as wind and large-scale solar converge to a common range of A$50 to A$100 per megawatt hour." An updated report, posted on the 27th of September 2017, titled "Renewables will be cheaper than coal in the future. Here are the numbers", indicated that a 100% renewables system is competitive with new-build supercritical (ultrasupercritical) coal, which, according to the Jacobs calculations in the report link above, would come in at around A$75(80) per MWh between 2020 and 2050 This projection for supercritical coal is consistent with other studies by the CO2CRC in 2015 (A$80 per MWh) and used by CSIRO in 2017 (A$65-80 per MWh) === France === The International Energy Agency and EDF have estimated for 2011 the following costs. For nuclear power, they include the costs due to new safety investments to upgrade the French nuclear plant after the Fukushima Daiichi nuclear disaster; the cost for those investments is estimated at 4 €/MWh. Concerning solar power, the estimate of 293 €/MWh is for a large plant capable of producing in the range of 50–100 GWh/year located in a favorable location (such as in Southern Europe). For a small household plant that can produce around 3 MWh/year, the cost is between 400 and 700 €/MWh, depending on location. Solar power was by far the most expensive renewable source of electricity among the technologies studied, although increasing efficiency and longer lifespan of photovoltaic panels together with reduced production costs have made this source of energy more competitive since 2011. By 2017, the cost of photovoltaic solar power had decreased to less than 50 €/MWh === Germany === In November 2013, the Fraunhofer Institute for Solar Energy Systems ISE assessed the levelised generation costs for newly built power plants in the German electricity sector PV systems reached LCOE between 0.078 and 0.142 Euro/kWh in the third quarter of 2013,
depending on the type of power plant (ground-mounted utility-scale or small rooftop solar PV) and average German insolation of 1000 to 1200 kWh/m² per year (GHI). There are no LCOE-figures available for electricity generated by recently built German nuclear power plants as none have been constructed since the late 1980s An update of the ISE study was published in March 2018 === Japan === A 2010 study by the Japanese government (pre-Fukushima disaster), called the Energy White Paper, concluded the cost for kilowatt hour was ¥49 for solar, ¥10 to ¥14 for wind, and ¥5 or ¥6 for nuclear power. Masayoshi Son, an advocate for renewable energy, however, has pointed out that the government estimates for nuclear power did not include the costs for reprocessing the fuel or disaster insurance liability. Son estimated that if these costs were included, the cost of nuclear power was about the same as wind power === United Kingdom === The Institution of Engineers and Shipbuilders in Scotland commissioned a former Director of Operations of the British National Grid, Colin Gibson, to produce a report on generation levelised costs that for the first time would include some of the transmission costs as well as the generation costs. This was published in December 2011. The institution seeks to encourage debate of the issue, and has taken the unusual step among compilers of such studies of publishing a spreadsheet.On 27 February 2015 Vattenfall Vindkraft AS agreed to build the Horns Rev 3 offshore wind farm at a price of 10.31 Eurocent per kWh. This has been quoted as below £100 per MWh In 2013 in the United Kingdom for a new-to-build nuclear power plant (Hinkley Point C: completion 2023), a feed-in tariff of £92.50/MWh (around 142 USD/MWh) plus compensation for inflation with a running time of 35 years was agreed.The Department for Business, Energy and Industrial Strategy (BEIS) publishes regular estimates of the costs of different electricity generation sources, following on the estimates of the merged Department of Energy and Climate Change (DECC). Levelised cost estimates for new generation projects begun in 2015 are listed in the table below === United States === ==== Energy Information Administration ==== The following data are from the Energy Information Administration's (EIA) Annual Energy Outlook released in 2015 (AEO2015). They are in dollars per megawatt-hour (2013 USD/MWh). These figures are estimates for plants going into service in 2020. The LCOE below is calculated based off a 30-year recovery period using a real after tax weighted average cost of capital (WACC) of 6.1%. For carbon intensive technologies 3 percentage points are added to the WACC (This is approximately equivalent fee of $15 per metric ton of carbon dioxide CO2) Since 2010, the US Energy Information Administration (EIA) has published the Annual Energy Outlook (AEO), with yearly LCOE-projections for future utility-scale facilities to be commissioned in about five years' time. In 2015, EIA has been criticized by the Advanced Energy Economy (AEE) Institute after its release of the AEO 2015-report to "consistently underestimate
the growth rate of renewable energy, leading to 'misperceptions' about the performance of these resources in the marketplace". AEE points out that the average power purchase agreement (PPA) for wind power was already at $24/MWh in 2013. Likewise, PPA for utility-scale solar PV are seen at current levels of $50–$75/MWh These figures contrast strongly with EIA's estimated LCOE of $125/MWh (or $114/MWh including subsidies) for solar PV in 2020 The electricity sources which had the most decrease in estimated costs over the period 2010 to 2017 were solar photovoltaic (down 81%), onshore wind (down 63%) and advanced natural gas combined cycle (down 32%) For utility-scale generation put into service in 2040, the EIA estimated in 2015 that there would be further reductions in the constant-dollar cost of concentrated solar power (CSP) (down 18%), solar photovoltaic (down 15%), offshore wind (down 11%), and advanced nuclear (down 7%). The cost of onshore wind was expected to rise slightly (up 2%) by 2040, while natural gas combined cycle electricity was expected to increase 9% to 10% over the period ==== NREL OpenEI (2015) ==== OpenEI, sponsored jointly by the US DOE and the National Renewable Energy Laboratory (NREL), has compiled a historical cost-of-generation database covering a wide variety of generation sources. Because the data is open source it may be subject to frequent revision Note: Only Median value = only one data point Only Max + Min value = Only two data points ==== California Energy Commission (2014) ==== LCOE data from the California Energy Commission report titled "Estimated Cost of New Renewable and Fossil Generation in California". The model data was calculated for all three classes of developers: merchant, investor-owned utility (IOU), and publicly owned utility (POU) ==== Lazard (2015) ==== In November 2015, the investment bank Lazard headquartered in New York, published its ninth annual study on the current electricity production costs of photovoltaics in the US compared to conventional power generators. The best large-scale photovoltaic power plants can produce electricity at 50 USD per MWh. The upper limit at 60 USD per MWh. In comparison, coal-fired plants are between 65 USD and $150 per MWh, nuclear power at 97 USD per MWh Small photovoltaic power plants on roofs of houses are still at 184–300 USD per MWh, but which can do without electricity transport costs. Onshore wind turbines are 32–77 USD per MWh. One drawback is the intermittency of solar and wind power. The study suggests a solution in batteries as a storage, but these are still expensive so far.Lazard's long standing Levelized Cost of Energy (LCOE) report is widely considered and industry benchmark In 2015 Lazard published its inaugural Levelized Cost of Storage (LCOS) report, which was developed by the investment bank Lazard in collaboration
with the energy consulting firm, Enovation.Below is the complete list of LCOEs by source from the investment bank Lazard NOTE: ** Battery Storage is no longer include in this report (2015). It has been rolled into its own separate report LCOS 1.0, developed in consultation with Enovation Partners (See charts below) Below are the LCOSs for different battery technologies. This category has traditionally been filled by Diesel Engines. These are "Behind the meter" applications Below are the LCOSs for different battery technologies. This category has traditionally been filled by Natural Gas Engines. These are "In front of the meter" applications ==== Lazard (2016) ==== On December 15, 2016 Lazard released version 10 of their LCOE report and version 2 of their LCOS report ==== Lazard (2017) ==== On November 2, 2017 the investment bank Lazard released version 11 of their LCOE report and version 3 of their LCOS report Below are the unsubsidized LCOSs for different battery technologies for "Behind the Meter" (BTM) applications Below are the Unsubsidized LCOSs for different battery technologies "Front of the Meter" (FTM) applications Note: Flow battery value range estimates === Global === ==== IEA and NEA (2015) ==== The International Energy Agency and the Nuclear Energy Agency published a joint study in 2015 on LCOE data internationally === Other studies and analysis === ==== Buffett Contract (2015) ==== In a power purchase agreement in the United States in July 2015 for a period of 20 years of solar power will be paid 3.87 UScent per kilowatt hour (38.7 USD/MWh). The solar system, which produces this solar power, is in Nevada (USA) and has 100 MW capacity ==== Sheikh Mohammed Bin Rashid solar farm (2016) ==== In the spring of 2016 a winning bid of 2.99 US cents per kilowatt-hour of photovoltaic solar energy was achieved for the next (800MW capacity) phase of the Sheikh Mohammed Bin Rashid solar farm in Dubai ==== Brookings Institution (2014) ==== In 2014, the Brookings Institution published The Net Benefits of Low and No-Carbon Electricity Technologies which states, after performing an energy and emissions cost analysis, that "The net benefits of new nuclear, hydro, and natural gas combined cycle plants far outweigh the net benefits of new wind or solar plants", with the most cost effective low carbon power technology being determined to be nuclear power ==== Brazilian electricity mix: the Renewable and Non-renewable Exergetic Cost (2014) ====
As long as exergy stands for the useful energy required for an economic activity to be accomplished, it is reasonable to evaluate the cost of the energy on the basis of its exergy content Besides, as exergy can be considered as measure of the departure of the environmental conditions, it also serves as an indicator of environmental impact, taking into account both the efficiency of supply chain (from primary exergy inputs) and the efficiency of the production processes In this way, exergoeconomy can be used to rationally distribute the exergy costs and CO2 emission cost among the products and by-products of a highly integrated Brazilian electricity mix. Based on the thermoeconomy methodologies, some authors have shown that exergoeconomy provides an opportunity to quantify the renewable and non-renewable specific exergy consumption; to properly allocate the associated CO2 emissions among the streams of a given production route; as well as to determine the overall exergy conversion efficiency of the production processes Accordingly, the non-renewable unit exergy cost (cNR) [kJ/kJ] is defined as the rate of non-renewable exergy necessary to produce one unit of exergy rate/flow rate of a substance, fuel, electricity, work or heat flow, whereas the Total Unit Exergy Cost (cT) includes the Renewable (cR) and Non-Renewable Unit Exergy Costs. Analogously, the CO2 emission cost (cCO2) [gCO2/kJ] is defined as the rate of CO2 emitted to obtain one unit of exergy rate/flow rate == Renewables == === Photovoltaics === Photovoltaic prices have fallen from $76.67 per watt in 1977 to nearly $0.23 per watt in August 2017, for crystalline silicon solar cells. This is seen as evidence supporting Swanson's law, which states that solar cell prices fall 20% for every doubling of cumulative shipments. The famous Moore's law calls for a doubling of transistor count every two years By 2011, the price of PV modules per MW had fallen by 60% since 2008, according to Bloomberg New Energy Finance estimates, putting solar power for the first time on a competitive footing with the retail price of electricity in some sunny countries; an alternative and consistent price decline figure of 75% from 2007 to 2012 has also been published, though it is unclear whether these figures are specific to the United States or generally global The levelised cost of electricity (LCOE) from PV is competitive with conventional electricity sources in an expanding list of geographic regions, particularly when the time of generation is included, as electricity is worth more during the day than at night. There has been fierce competition in the supply chain, and further improvements in the levelised cost of energy for solar lie ahead, posing a growing threat to the dominance of fossil fuel generation sources in the next few years. As time progresses, renewable energy technologies generally get cheaper, while fossil fuels generally get more expensive: The less solar power costs, the more favorably it compares to conventional power, and the more attractive it becomes to utilities and energy users around the globe. Utility-scale solar power [could in 2011] be delivered in California at prices well below $100/MWh ($0.10/kWh) less than most other peak generators, even those running on low-cost natural gas. Lower solar module costs also stimulate demand from consumer markets where the cost of solar compares very favourably to retail electric rates In the year 2015, First Solar agreed to supply solar power at 3.87 cents/kWh levelised price from its 100 MW Playa Solar 2 project which
is far cheaper than the electricity sale price from conventional electricity generation plants From January 2015 through May 2016, records have continued to fall quickly, and solar electricity prices, which have reached levels below 3 cents/kWh, continue to fall. In August 2016, Chile announced a new record low contract price to provide solar power for $29.10 per megawatt-hour (MWh). In September 2016, Abu Dhabi announced a new record breaking bid price, promising to provide solar power for $24.2 per MWh In October 2017, Saudi Arabia announced a further low contract price to provide solar power for $17.90 per MWh.With a carbon price of $50/ton (which would raise the price of coal-fired power by 5c/kWh), solar PV is cost-competitive in most locations The declining price of PV has been reflected in rapidly growing installations, totaling a worldwide cumulative capacity of 297 GW by end 2016. According to some estimates total investment in renewables for 2011 exceeded investment in carbon-based electricity generation.In the case of self consumption, payback time is calculated based on how much electricity is not brought from the grid. Additionally, using PV solar power to charge DC batteries, as used in Plug-in Hybrid Electric Vehicles and Electric Vehicles, leads to greater efficiencies, but higher costs. Traditionally, DC generated electricity from solar PV must be converted to AC for buildings, at an average 10% loss during the conversion. Inverter technology is rapidly improving and current equipment has reached 99% efficiency for small scale residential, while commercial scale three-phase equipment can reach well above 98% efficiency However, an additional efficiency loss occurs in the transition back to DC for battery driven devices and vehicles, and using various interest rates and energy price changes were calculated to find present values that range from $2,057.13 to $8,213.64 (analysis from 2009).It is also possible to combine solar PV with other technologies to make hybrid systems, which enable more stand alone systems. The calculation of LCOEs becomes more complex, but can be done by aggregating the costs and the energy produced by each component. As for example, PV and cogen and batteries while reducing energy- and electricity-related greenhouse gas emissions as compared to conventional sources === Solar thermal === LCOE of solar thermal power with energy storage which can operate round the clock on demand, has fallen to AU$78/MWh (US$61/MWh) in August 2017. Though solar thermal plants with energy storage can work as stand alone systems, combination with solar PV power can deliver further cheaper power. Cheaper and dispatchable solar thermal storage power need not depend on costly or polluting coal/gas/oil/nuclear based power generation for ensuring stable grid operation.When a solar thermal storage plant is forced to idle due to lack of sunlight locally during cloudy days, it is possible to consume the cheap excess infirm power from solar PV, wind and hydro power plants (similar to a lesser efficient, huge capacity and low cost battery storage system) by heating the hot molten salt to higher temperature for converting the stored thermal energy in to electricity during the peak demand hours when the electricity sale price is profitable === Wind power === Current land-based windIn the windy great plains expanse of the central United States
new-construction wind power costs in 2017 are compellingly below costs of continued use of existing coal burning plants. Wind power can be contracted via a power purchase agreement at two cents per kilowatt hour while the operating costs for power generation in existing coal-burning plants remain above three cents Current offshore windIn 2016 the Norwegian Wind Energy Association (NORWEA) estimated the LCoE of a typical Norwegian wind farm at 44 €/MWh, assuming a weighted average cost of capital of 8% and an annual 3,500 full load hours, i.e. a capacity factor of 40%. NORWEA went on to estimate the LCoE of the 1 GW Fosen Vind onshore wind farm which is expected to be operational by 2020 to be as low as 35 €/MWh to 40 €/MWh. In November 2016, Vattenfall won a tender to develop the Kriegers Flak windpark in the Baltic Sea for 49.9 €/MWh, and similar levels were agreed for the Borssele offshore wind farms. As of 2016, this is the lowest projected price for electricity produced using offshore wind Historic levelsIn 2004, wind energy cost a fifth of what it did in the 1980s, and some expected that downward trend to continue as larger multi-megawatt turbines were mass-produced As of 2012 capital costs for wind turbines are substantially lower than 2008–2010 but are still above 2002 levels. A 2011 report from the American Wind Energy Association stated, "Wind's costs have dropped over the past two years, in the range of 5 to 6 cents per kilowatt-hour recently…. about 2 cents cheaper than coal-fired electricity, and more projects were financed through debt arrangements than tax equity structures last year…. winning more mainstream acceptance from Wall Street's banks…. Equipment makers can also deliver products in the same year that they are ordered instead of waiting up to three years as was the case in previous cycles…. 5,600 MW of new installed capacity is under construction in the United States, more than double the number at this point in 2010. 35% of all new power generation built in the United States since 2005 has come from wind, more than new gas and coal plants combined, as power providers are increasingly enticed to wind as a convenient hedge against unpredictable commodity price moves."This cost has additionally reduced as wind turbine technology has improved. There are now longer and lighter wind turbine blades, improvements in turbine performance and increased power generation efficiency. Also, wind project capital and maintenance costs have continued to decline. For example, the wind industry in the USA in 2014 was able to produce more power at lower cost by using taller wind turbines with longer blades, capturing the faster winds at higher elevations. This opened up new opportunities in Indiana, Michigan, and Ohio. The price of power from wind turbines built 300 to 400 ft (91 to 122 m) above the ground can now compete with conventional fossil fuels like coal. Prices have fallen to about 4 cents per kilowatt-hour in some cases and utilities have been increasing the amount of wind energy in their portfolio, saying it is their cheapest option == See also == == Further reading == Economic Value of U.S. Fossil Fuel Electricity Health Impacts. United States Environmental Protection Agency The Hidden Costs of Electricity: Comparing
the Hidden Costs of Power Generation Fuels Civil Society Institute Lazard's Levelized Cost of Energy Analysis – Version 11.0 (Nov. 2017 | CommonCrawl |
\begin{document}
\vglue20pt
\begin{center}
{\huge \bf Robust analysis of preferential\\[.2cm] attachment models with fitness} \end{center}
\centerline{{\Large{\sc Steffen Dereich$^{1}$} and {\sc Marcel Ortgiese$^2$}}}
\begin{center}\it \parbox[c][3cm][t]{0.5\textwidth}{ \begin{center} $^1$Institut f\"ur Mathematische Statistik\\ Westf.\ Wilhelms-Universit\"at M\"unster\\ Einsteinstra\ss{}e 62\\ 48149 M\"unster\\ Germany \\[2mm] \end{center} }
\parbox[c][3cm][t]{0.5\textwidth}{ \begin{center} $^2$Institut f\"ur Mathematik\\ Technische Universit\"at Berlin\\ Str.\ des 17.\ Juni 136\\ 10623 Berlin\\ Germany\\ \end{center} }
{\rm 14 February 2013}\\ \end{center}
{\leftskip=1truecm \rightskip=1truecm \baselineskip=15pt \small
\noindent{\slshape\bfseries Abstract.} The preferential attachment network with fitness is a dynamic random graph model. New vertices are introduced consecutively and a new vertex is attached to an old vertex with probability proportional to the degree of the old one multiplied by a random fitness. We concentrate on the typical behaviour of the graph by calculating the fitness distribution of a vertex chosen proportional to its degree. For a particular variant of the model, this analysis was first carried out by Borgs, Chayes, Daskalakis and Roch. However, we present a new method, which is robust in the sense that it does not depend on the exact specification of the attachment law. In particular, we show that a peculiar phenomenon, referred to as Bose-Einstein condensation, can be observed in a wide variety of models. Finally, we also compute the joint degree and fitness distribution of a uniformly chosen vertex.
\noindent{\slshape\bfseries Keywords.} Barab\'asi-Albert model,
power law, scale-free network, nonlinear preferential attachment, nonlinearity, dynamic random graph, condensation.
\noindent {\slshape\bfseries 2010 Mathematics Subject Classification.} Primary 05C80 Secondary 60G42, 90B15
}
\section{Introduction}
Preferential attachment models were popularized by~\cite{BarabasiAlbert_1999} as a possible model for complex networks such as the world-wide-web. The authors observed that a simple mechanism can explain the occurrence of power law degree distributions in real world networks. Often networks are the result of a continuous dynamic process: new members enter social networks or new web pages are created and linked to popular old ones. In this process new vertices prefer to establish links to old vertices that are well connected. Mathematically, one considers a sequence of random graphs (\emph{random dynamic network}), where new vertices are introduced consecutively and then connected to each old vertex with a probability proportional to the degree of the old vertex. This rather simple mechanism leads to networks with power law degree distributions and thus offers an explanation for their occurrence, see e.g.~\cite{BRST} for a mathematical account.
There are many variations of the classic model to address different shortcomings, see e.g.~\cite{RemcoNotes} for an overview. For example, a more careful analysis of the classical model
shows that one can observe a ``first to market''-advantage, where from a certain point onwards the vertex with maximal degree will always remain maximal, see e.g.~\cite{DereichMoertes09}. Clearly, this is not the only possible scenario observed in real networks. One possible improvement is to model the fact that vertices have an intrinsic quality or fitness, which would allow even younger vertices to overtake old vertices in popularity.
Introducing fitness has a significant effect on the network formation. In particular, it may provoke condensation effects as indicated in~\cite{BB_2001}.
A first mathematically rigorous analysis was carried out in~\cite{BCDR07} for the following variant of the model:
First every (potential) vertex $i\in\mathbb{N}$ is assigned an independent identically distributed (say $\mu$-distributed) fitness~$\mathcal{F}_i$. Starting with the network $\mathcal{G}_1$ consisting of the single vertex $1$ with a self-loop, the network is formed as follows. Suppose we have constructed the graph $\mathcal{G}_n$ with vertices~$\{1,\dots,n\}$, then we obtain $\mathcal{G}_{n+1}$ by \begin{itemize} \item insertion of the vertex $n+1$ and \item insertion of a single edge linking up the new vertex to the old vertex $i\in\{1,\dots,n\}$ with probability proportional to \begin{align}\label{eq:1710-1} \mathcal{F}_i\,\deg_{\mathcal{G}_n}(i), \end{align} \end{itemize} where $\deg_\mathcal{G}(i)$ denotes the degree of vertex $i$ in a graph $\mathcal{G}$.
In~\cite{BCDR07}, the authors compute the asymptotic fitness distribution of a vertex chosen proportional to its degree. This limit distribution is either absolutely continuous with respect to $\mu$ (``\emph{fit-get-richer phase}'') or has a singular component that puts mass on the essential supremum of $\mu$ (``\emph{condensation phase}'' or ``\emph{Bose-Einstein phase}''). In the condensation phase a positive fraction of mass is shifted towards the essential supremum of~$\mu$.
The analysis in~\cite{BCDR07} uses a coupling argument with a generalized urn model, which was investigated by~\cite{Janson_2004} using in turn a coupling with a multitype branching process. A more direct approach was presented in~\cite{Bhamidi}, who explicitly couples the random graph model with a multitype branching process and then uses classical results, see e.g.~\cite{JagersNerman_1996}, to complete the analysis. Both results rely very much on the particularities of the model specification. This is in strong contrast to the physicists' intuition which suggests that explicit details of the model specification do not have an impact.
The aim of the article is to close or at least reduce this gap significantly. We present a new approach to calculating fitness distributions, which is robust in the sense that it does not rely on the exact details of the attachment rule. In particular, we show that the condensation phenomenon can be observed in a wide range of variations of the model.
What makes the preferential attachment model with fitness more difficult to analyse than classic preferential attachment models is that the normalisation, obtained by summing the weights in~(\ref{eq:1710-1}) over all vertices $i$, is neither deterministic nor is it linear in the degrees.
In the framework of the classical preferential attachment model, there are several approaches to specify the model fairly robustly. A rather general approach to calculate degree distributions
in the case of a constant normalisation is presented in~\cite{HagbergWiuf_2006}, where only a (linear) recursion for the degree sequence is assumed. However, the approach is restricted to a deterministic out-degree. For a linear model, the requirement of a deterministic normalisation can be relaxed. For example in~\cite{CooperFrieze_2003}, apart from more complicated update rules, the out-degree of a new vertex is also allowed to be random (albeit of bounded degree). Similarly, in~\cite{Jordan_2006} it is only assumed that the out-degree distribution has exponential moments. However, in these cases even though the normalisation is random, it is rather well concentrated around its mean. A particular interesting variant is when the out-degree is heavy-tailed as analysed in~\cite{Deijfenetal_2009}. Here, the fluctuations of the normalisation around its mean start interfering and alter the degree distributions significantly.
For non-linear preferential attachment models, a particular elegant way of dealing with a random normalisation
is to establish a coupling with a branching process, which implicitly takes care of the problem, see for example the survey~\cite{Bhamidi}. This also includes models with sublinear preferential attachment rules, see e.g.~\cite{RTV_07}. A generalisation of the model with fitness is presented in~\cite{jordan_geometric_2012}, where the attractiveness of a vertex is a function of a random location in some metric space. However, in that setting the full analysis is only carried out when the metric space is finite, which corresponds to only finitely many different values for the random fitness in our model.
Our approach shows a new way of dealing with the normalisation constant using a bootstrapping argument. The idea is to start with a bound $\theta$ on the normalisation, from which we deduce a new bound $T(\theta)$. Then, by a continuity argument, we deduce that the correct limit of the normalisation is a fixed point of $T$. We stress that the mapping $T$ is new and has not appeared in the physics literature on complex networks with fitness yet.
In particular, our proofs show that the condensation effect can be observed irrespectively of the fine details of the model. The phenomenon of Bose-Einstein condensation seems to have a universal character, for an overview of further models see~\cite{DM_emer_2012}. The precise analysis of the dynamics in a closely related model are carried out in~\cite{Dereich_13}.
\section{Definitions and main results}
We consider a dynamic graph model with fitness. Each vertex $i\in\mathbb{N}$ is assigned an independent $\mu$-distributed fitness~$\mathcal{F}_i$, where $\mu$ is a compactly supported distribution on the Borel sets of $(0,\infty)$ that is not a Dirac-distribution. We call $\mu$ the \emph{fitness distribution}.
We measure the importance of a vertex $i$ in a directed graph $\mathcal{G}$ by its \emph{impact} $$\mathrm{imp}_{\mathcal{G}}(i):= 1+\text{ indegree of $i$ in $\mathcal{G}$}.$$ For technical reasons, we set $\mathrm{imp}_{\mathcal{G}}(i)=0$, if $i$ is not a vertex of $\mathcal{G}$.
The complex network is represented by a sequence $(\mathcal{G}_n)_{n\in\IN}$ of random directed multigraphs without loops that is built according to the following rules. Each graph $\mathcal{G}_n$ consists of $n$ vertices labeled by $1,\dots,n$. The first graph consists of the single vertex~$1$ and no edges. Further, given $\mathcal{G}_n$, the network $\mathcal{G}_{n+1}$ is formed by carrying out the following two steps: \begin{itemize}\item Insertion of the vertex $n+1$. \item Insertion of directed edges $n+1\to i$ for each old vertex $i\in\{1,\dots,n\}$ with intensity proportional to \begin{align}\label{connect} \mathcal{F}_i \cdot \mathrm{imp} _{\mathcal{G}_n} (i). \end{align}
\end{itemize}
Note that this is not a unique description of the network formation. We still need to clarify the explicit rule how new vertices connect to old ones. We will do this in terms of the \emph{impact evolutions}: for each $i\in\mathbb{N}$, we consider the process $\mathcal{Z}(i)=(\mathcal{Z}_n(i))_{n\in\mathbb{N}}$ defined by $$ \mathcal{Z}_n(i):=\mathrm{imp}_{\mathcal{G}_n}(i). $$ Since all edges point from younger to older vertices and since in each step all new edges attach to the new vertex, the sequence $(\mathcal{G}_n)_{n\in\mathbb{N}}$ can be recovered from the impact evolutions $(\mathcal{Z}(i):i\in\mathbb{N})$. Indeed, for any $i,j,n\in\mathbb{N}$ with $i<j\leq n$ there are exactly $$ \Delta \mathcal{Z}_{j-1}(i):= \mathcal{Z}_j(i)-\mathcal{Z}_{j-1}(i) $$ links pointing from $j$ to $i$ in $\mathcal{G}_n$. Note that each impact evolution $\mathcal{Z}(i)$ is monotonically increasing, $\mathbb{N}_0$-valued and satisfies $\mathcal{Z}_n(i)=\1_{\{n=i\}}$ for $n\leq i$, and any choice for the impact evolutions with these three properties describes uniquely a dynamic graph model. We state the assumptions in terms of the impact evolutions. For a discussion of relevant examples, we refer the reader to the discussion below.
{\bf Assumptions.} Let $\lambda > 0$ be a parameter and define $$ \bar\mathcal{F}_n=\frac 1 {\lambda n} \sum_{j=1}^n \mathcal{F}_j\,\mathrm{imp}_{\mathcal{G}_n}(j)=\frac1{\lambda n}\langle \mathcal{F}, \mathcal{Z}_n\rangle, $$ where $\mathcal{Z}_n:=(\mathcal{Z}_n(i))_{i\in\mathbb{N}}$.
We assume that the following three conditions are satisfied:
\begin{tabularx}{\textwidth}{ p{.8cm} >{\raggedright\arraybackslash}X}
{\bf (A1)}
& \[ \mathbb{E} [ \Delta \mathcal{Z}_{n}(i) | \mathcal{G}_n] = \frac {\mathcal{F}_i \,\mathcal{Z}_n(i)}{n \bar \mathcal{F}_n} .\] \\
{\bf (A2)} & There exists a constant $C^{\rm var}$ such that
\[ \mathrm{Var} ( \Delta \mathcal{Z}_{n}(i) | \mathcal{G}_n ) \leq C^{\rm var} \mathbb{E} [ \Delta \mathcal{Z}_{n}(i) | \mathcal{G}_n] . \]
\\
{\bf (A3)} & Conditionally on $\mathcal{G}_n$, for $i \neq j$, we assume that $\Delta \mathcal{Z}_{n}(i)$ and $\Delta \mathcal{Z}_{n}(j)$ are negatively correlated. \end{tabularx}
By assumption the essential supremum of $\mu$ is finite and strictly positive, say $s$. Since the model will still satisfy assumptions (A1) - (A3), if we replace $\mathcal{F}_i$ by $\mathcal{F}_i'=\mathcal{F}_i/s$, we can and will assume without loss of generality that
\begin{tabularx}{\textwidth}{ p{.8cm} >{\raggedright\arraybackslash}X} {\bf (A0)} &
\[ \mathrm{ess\,sup}(\mu)=1 . \] \end{tabularx}
\begin{remark}\label{re:outdeg} Assumptions (A1)-(A3) guarantee that
the total number of edges in the system is of order $\lambda n$, see Lemma~\ref{le:outdeg}. \end{remark}
Let us give two examples that satisfy our assumptions.
\begin{example}\label{ex:Pois} \emph{Poisson outdegree (M1).} The definition depends on a parameter $\lambda >0$. In model (M1), given $\mathcal{G}_n$, the new vertex $n+1$ establishes for each old vertex $i\in\{1,\dots,n\}$ an independent Poisson-distributed number of links $n+1\rightarrow i$ with parameter $$ \frac {\mathcal{F}_i\, \mathcal{Z}_{n}(i)}{n\, \bar\mathcal{F}_n}. $$ Note that the conditional outdegree of a new vertex $n+1$, given~$\mathcal{G}_n$, is Poisson-distributed with parameter~$\lambda$. \end{example}
\begin{example}\label{ex:multi} \emph{Fixed outdegree (M2).} The definition relies on a parameter $\lambda\in\IN$ denoting the deterministic outdegree of new vertices. Given $\mathcal{G}_n$, the number of edges connecting $n+1$ to the individual old vertices $1,\dots,n$ forms a multinomial random variable with parameters $\lambda$ and $$ \Bigl( \frac {\mathcal{F}_i\, \mathcal{Z}_{n}(i)}{\lambda n\, \bar\mathcal{F}_n}\Bigr)_{i=1,\dots,n}, \text{ where }\bar\mathcal{F}_n=\frac 1 {\lambda n} \sum_{i=1}^n \mathcal{F}_i\,\mathcal{Z}_n(i). $$ The model (M2) with $\lambda=1$ is the one analysed in \cite{BCDR07}.
\end{example}
We analyse a sequence of random measures $(\Gamma_n)_{n\in\IN}$ on $[0,1]$ given by $$ \Gamma_n= \frac 1n \sum_{i=1}^n \mathcal{Z}_n(i)\, \delta_{\mathcal{F}_i} $$ the \emph{impact distributions}. These measures describe the relative impact of fitnesses. Note also that, up to normalisation, $\Gamma_n$ is the distribution of the fitness of a vertex chosen proportional to its impact.
\begin{thm}\label{thm:main} Suppose that Assumptions (A0)-(A3) are satisfied. If $\int \frac{f}{1-f}\,\mu(df)\geq \lambda$, we denote by $\theta^*\geq 1$ the unique value with $$ \int \frac f{\theta^*-f}\,\mu(df)=\lambda $$ and set otherwise $\theta^*=1$. One has $$ \lim_{n\to\infty} \bar\mathcal{F}_n=\theta^*, \text{ almost surely} $$ and we distinguish two regimes: \begin{itemize} \item[(i)] {\bf Fit-get-richer phase.} Suppose that $\int \frac{f}{1-f}\,\mu(df)\geq \lambda$. $(\Gamma_n)$ converges, almost surely, in the weak$^*$ topology to $\Gamma$, where $$ \Gamma(df)= \frac{\theta^*}{\theta^*-f} \,\mu(df) $$
\item[(ii)] {\bf Bose-Einstein phase.} Suppose that $\int \frac{f}{1-f}\,\mu(df)< \lambda$. $(\Gamma_n)$ converges, almost surely, in the weak$^*$ topology to $\Gamma$, where $$ \Gamma(df) = \frac{1}{1- f}\, \mu(df) + \Big(1 + \lambda - \int_{[0,1)} \frac{1}{1-f} \mu(df)\Big) \, \delta_1. $$ \end{itemize} \end{thm}
\begin{remark} In particular, the two phases can be characterized as follows. In the \emph{Fit-get-richer phase}, i.e.\@\xspace if $\int\frac {f}{1-f}\,\mu(dx)\geq \lambda$, then the limit of $(\Gamma_n)$ is absolutely continuous with respect to $\mu$. However, in the \emph{Bose-Einstein-phase}, i.e.\@\xspace if $\int\frac {f}{1-f}\,\mu(dx)<\lambda$, then the limit of $(\Gamma_n)$ is not absolutely continuous with respect to $\mu$, but has an atom in~$1$. The explanation for this phenomenon is that a positive fraction of newly incoming edges connects to vertices with fitness that is closer and closer to the essential supremum of the fitness distribution $\mu$, which in the limit amounts to an atom at the essential supremum. \end{remark}
Next, we restrict attention to vertices with a fixed impact $k\in\mathbb{N}$. For $n\in\mathbb{N}$ we consider the random measure \[ \Gamma^\ssup{k}_n := \frac 1n \sum_{i=1}^n \1_{\{\mathcal{Z}_n(i)=k\}} \delta_{\mathcal{F}_i} , \] representing -- up to normalisation -- the random fitness of a uniformly chosen vertex with impact $k$.
To prove convergence of $(\Gamma_n^\ssup {k})$, we need additional assumptions. Indeed, so far our assumptions admit models for which vertices are always connected by multiple edges in which case there would be no vertices with impact $2$.
We will work with the following assumptions:
\begin{tabularx}{\textwidth}{ p{.8cm} >{\raggedright\arraybackslash}X}
{\bf (A4)} & $\forall k\in\mathbb{N}$: $\sup_{i=1,\dots,n} \1_{\{Z_n(i)= k\}}\, n \,\mathbb{P}(\Delta \mathcal{Z}_n(i)\geq 2|\mathcal{G}_n)\to0$, \ a.s. \\[.3cm]
{\bf (A4')} & $\forall k\in\mathbb{N}$: $\sup_{i=1,\dots,n} \1_{\{Z_n(i)= k\}}\, n \bigl|\,\mathbb{P}(\Delta \mathcal{Z}_n(i)=1|\mathcal{G}_n)- \frac {\mathcal{F}_i Z_n(i)}{n\,\bar\mathcal{F}_n}\bigr|\to 0$, \ a.s.\\[.35cm]
\end{tabularx} Further we impose an additional assumption on the correlation structure:
\begin{tabularx}{\textwidth}{ p{.8cm} >{\raggedright\arraybackslash}X} {\bf (A5)} & Given $\mathcal{G}_n$, the collection $\{ \Delta \mathcal{Z}_n(i) \}_{i = 1}^n$ is negatively quadrant dependent in the sense that for any $i \neq j$, and any $k,l \in \mathbb{N}$
\[ \mathbb{P} \{ \Delta \mathcal{Z}_n(i) \leq k ; \Delta \mathcal{Z}_n(j) \leq \ell | \mathcal{G}_n\}
\leq \mathbb{P} \{ \Delta \mathcal{Z}_n(i) \leq k | \mathcal{G}_n \} \mathbb{P} \{ \Delta \mathcal{Z}_n(j) \leq \ell | \mathcal{G}_n\} \] \end{tabularx}
\begin{remark} Note that both Examples~\ref{ex:Pois} and~\ref{ex:multi} also satisfy these additional assumptions. Moreover, under Assumption (A1), Assumptions (A4) and (A4') are equivalent to
\begin{tabularx}{\textwidth}{ p{.85cm} >{\raggedright\arraybackslash}X} {\bf (A4'')} & $\forall k\in\mathbb{N}$: $\sup_{i=1,\dots,n} \1_{\{Z_n(i)= k\}}\, n \,
\mathbb{E}[ \Delta Z_n(i) 1\hspace{-0.098cm}\mathrm{l}_{\{ \Delta Z_n(i) \geq 2 \}} | \mathcal{G}_n] \to0$, \ a.s.\\[.4cm] \end{tabularx} \end{remark}
\begin{thm}\label{thm:2} Suppose that Assumptions (A0), (A4), (A4') and (A5) are satisfied and that for some $\theta^*\in[1,\infty)$ $$ \lim_{n\to\infty} \bar\mathcal{F}_n=\theta^*, \ \text{ almost surely.} $$ Then one has that, almost surely, $(\Gamma_n^\ssup{k})$ converges in the weak$^*$ topology to $\Gamma^\ssup{k}$, where \begin{equation}\label{eq:2811-1} \Gamma^\ssup{k} (df) = \frac{1}{k+ \frac{\theta^*}{f}} \frac{\theta^*}{f} \prod_{i=1}^{k-1} \frac{i}{i+ \frac{\theta^*}{f}}
\mu(df) \end{equation} \end{thm}
The theorem immediately allows to control the number of vertices with impact $k\in\mathbb{N}$. Let $$ p_n(k):=\frac 1n \sum_{i=1}^n \1_{\{\mathcal{Z}_n(i)=k\}} = \Gamma_n^\ssup{k}([0,1]). $$
\begin{corollary}Under the assumptions of Theorem~\ref{thm:2}, one has that \[ \lim_{n\to\infty} p_n(k) = \int_{(0,1]} \frac{1}{k+ \frac{\theta^*}{f}} \frac{\theta^*}{f} \prod_{i=1}^{k-1} \frac{i}{i+ \frac{\theta^*}{f}}
\mu(df), \ \text{ almost surely.}\] \end{corollary}
\subsubsection*{Outline of the article}
Section~\ref{se:prelim} starts with preliminary considerations. In particular, it introduces a stochastic approximation argument which among other applications also appeared in the context of generalized urn models, see e.g.\ the survey~\cite{PemantleSurvey}. In preferential attachment models, these techniques only seem to have been used directly in~\cite{jordan_geometric_2012}. Roughly speaking, key quantities are expressed as approximations to stochastically perturbed differential equations. The perturbation is asymptotically negligible and one obtains descriptions by differential equations that are typically referred to as \emph{master equations}.
Section~\ref{se:bootstrap} is concerned with the proof of Theorem~\ref{thm:main}. Here the main task is to prove convergence of the random normalisation $(\bar\mathcal{F}_n)$. This goal is achieved via a bootstrapping argument. Starting with an upper bound on $(\bar \mathcal{F}_n)$ of the form $$ \limsup_{n\to\infty} \bar\mathcal{F}_n\leq \theta, \ \text{ almost surely}, $$ we show that this statement remains true when replacing $\theta$ by \begin{equation}\label{eq:T} T(\theta)= 1+ \frac 1\lambda \int \frac {\theta-1}{\theta-f}\,f \,\mu(df).\end{equation} Iterating the argument yields convergence to a fixed point. The mapping $T$ always has the fixed point $\theta = 1$. Moreover, it has a second fixed point $\theta^* > 1$ if and only if $\int \frac{x}{\theta-x}\mu(dx) >\lambda$, which corresponds to the fit-get-richer phase. In this case, one can check that only the larger fixed point $\theta^*$ is stable.
However, in the condensation phase, $T$ has only a single fixed point, which is also stable. See also Figure~\ref{fig:T} for an illustration.
\begin{figure}
\caption{The figure on the left shows the schematic graph of $T$ in the case that $\theta^* > 1$, while the one on the right is for the case $\theta^* = 1$.}
\label{fig:T}
\end{figure}
Section~\ref{se:deg_dist} is concerned with the proof of Theorem~\ref{thm:2}. The proof is based on stochastic approximation techniques introduced in Section~\ref{se:prelim}. In our setting these differential equations are non-linear because of the normalisation $\bar \mathcal{F}_n$. However, since we can control the normalisation by Theorem~\ref{thm:main}, in the analysis of the joint fitness and degree distribution, we arrive at linear equations (or more precisely inequalities) for the stochastic approximation. The latter then yield Theorem~\ref{thm:2} via an approximation argument.
\section{Preliminaries}\label{se:prelim}
We first recall the general idea of stochastic approximation, which goes back to~\cite{RobbinsMonro_1951} and can be stated for example for a stochastic process ${\bf X}_n$ taking values in $\mathbb{R}^d$. Then, ${\bf X}_n$ is known as a stochastic approximation process, if it satisfies a recursion of the type \begin{equation}\label{eq:2401-1} {\bf X}_{n+1} - {\bf X}_n = \frac{1}{n+1} F({\bf X}_n) + {\bf R}_{n+1} - {\bf R}_n,\end{equation} where $F$ is a suitable vector field and the increment of ${\bf R}$ corresponds to an (often stochastic) error. In our setting, we could for example restrict to the case when $\mu$ is supported on finitely many values $\{ f_1, \ldots, f_d\}\subset (0,1]$ and denote by \[ X_n(k) = \frac{1}{n} \sum_{i=1}^n \mathcal{Z}_n(i) 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{F}_i = f_k \}} , \] the proportion of vertices that have fitness $f_k$ weighted by their impact. Then, one can easily calculate the conditional expectation of $X_{n+1}(k)$ given the graph $\mathcal{G}_n$ up to time $n$. Indeed, as we will see in the proof of Proposition~\ref{prop:lower_emp}, under our assumptions we obtain that
\[ \mathbb{E}[ X_{n+1}(k) - X_n(k)\, |\,\mathcal{G}_n ]
= \frac{1}{n+1} \Big( \mu(\{ f_k\}) + \frac{f_k}{\bar \mathcal{F}_n} X_n(k)- X_n(k) \Big) \] Therefore, we note that ${\bf X_n} = (X_n(k))_{k=1}^d$ satisfies \[ X_{n+1}(k) - X_n(k)
= \frac{1}{n+1} \Big( \mu(\{ f_k\}) + \frac{f_k}{\bar \mathcal{F}_n} X_n(k)- X_n(k) \Big) + R_{n+1}(k) - R_n(k) , \] so that ${\bf X}_n = (X_n(k))_{k=1}^d$
satisfies an equation of type~\ref{eq:2401-1}, provided we take $R_{n+1}(k) - R_n(k) = X_{n+1}(k) - \mathbb{E}[ X_{n+1}(k) | \mathcal{G}_n]$, which defines a martingale, for which we can employ the standard techniques to show convergence.
Provided that the random perturbations are asymptotically negligible, it is possible to analyse the random dynamical system by the corresponding master equation $$ \dot{\bf x}_t =F({\bf x}_t). $$ There are many articles exploiting such connections and an overview is provided by~\cite{BenaimSurvey}. The connection to general urn models is further explained in~\cite{PemantleSurvey}. In random graphs, the resulting differential equation is closely related to what is known as the master equation in heuristic derivations, see e.g.~\cite[Ch. 14]{newman_networks_2010}.
However, in our setting, this method is not directly applicable. First of all, we would like to consider arbitrary fitness distributions (i.e.\ not restricted to finitely many values) and secondly the resulting equation is not linear, because of the appearance of the normalization $\bar \mathcal{F}_n$. The latter problem is addressed by using a bootstrapping method (as described in the introduction). However, this leads to an inequality on the increment, rather than an equality as in~(\ref{eq:2401-1}). Fortunately, the resulting vector field $F$ has a very simple structure and so we can deduce the long-term behaviour of $\mathbf{X}_n$ by elementary means, the corresponding technical result is Lemma~\ref{le:stApp}. By using inequalities, we also gain the flexibility to approximate arbitrary fitness distribution by discretization.
In order to keep our proofs self-contained, we will first state and prove an easy special case of the technique adapted to our setting.
\begin{lemma}\label{le:stApp}
Let $(X_n)_{n \geq 0}$ be a non-negative stochastic process. We suppose that the following estimate holds \begin{equation}\label{eq:2911-1} X_{n+1} - X_n \leq \frac{1}{n+1} (A_n - B_n X_n) + R_{n+1}-R_{n}, \end{equation} where \begin{enumerate} \item $(A_n)$ and $(B_n)$ are almost surely convergent stochastic processes with deterministic limits $A,B>0$, \item $(R_n)$ is an almost surely convergent stochastic process. \end{enumerate} Then one has that, almost surely, \[ \limsup_{n \rightarrow\infty} X_n \leq \frac{A}{B} . \] Similarly, if instead under the same conditions (i) and (ii) \[ X_{n+1} - X_n \geq \frac{1}{n+1} (A_n - B_n X_n) + R_{n+1} -R_n, \] then almost surely \[ \liminf_{n \rightarrow \infty} X_n \geq \frac{A}{B}. \] \end{lemma}
\begin{proof} This is a slight adaptation of Lemma~2.6 in~\cite{PemantleSurvey}. Fix $\delta \in (0,1)$. By our assumptions, almost surely, we can find $n_0$ such that for all $m,n \geq n_0$,
\[ A_n \leq (1+\delta)A, \quad B_n \geq (1-\delta)B, \quad |R_m - R_n| \leq \delta . \] Then, by~(\ref{eq:2911-1}), we have that for any $m > n \geq n_0$, \begin{equation}\label{eq:2911-2} \begin{aligned} X_m - X_n & \leq \sum_{j=n}^{m-1} \frac{1}{j+1} ( A_j - B_j X_j)
+ |R_m-R_n| \\ & \leq \sum_{j = n}^{m-1} \underbrace{\frac{1}{j+1}((1+\delta)A - (1-\delta)B X_j))}_{=:Y_j} + \delta . \end{aligned} \end{equation} Let $C = \frac{(1+\delta)A}{(1-\delta)B}$. For each index $j\geq n_0$ with $X_j\geq C+\delta$, one has that $$Y_j\leq -B (1-\delta) \delta /(j+1).$$ Since the harmonic series diverges, by~(\ref{eq:2911-1}) there exists $m_0\geq n_0$ with $X_{m_0}\leq C+\delta$.
Next, we prove that for any $m\geq m_0$ one has $X_m\leq C+3\delta$ provided that $n_0$ is chosen sufficiently large (i.e. $\frac{1}{n_0 + 1}(1+\delta) A \leq \delta$). Suppose that $X_m> C+\delta$. We choose~$m_1$ as largest index smaller than $m$ with $X_{m_1}\leq C+\delta$. Clearly, $m_1\geq m_0$ and an application of estimate~(\ref{eq:2911-2}) gives $$ X_m\leq X_{m_1}+ Y_{m_1}+ \delta \leq C+2\delta +\frac {1}{m+1} (1+\delta)A \leq C+3\delta = \frac {(1+\delta) A}{(1-\delta)B}+3\delta. $$ Since $\delta\in(0,1)$ is arbitrary, we get that, almost surely, $$ \limsup_{n\to\infty} X_n\leq \frac AB. $$ The argument for the reverse inequality works analogously. \end{proof}
As a first application of Lemma~\ref{le:stApp}, we can show that the total number of edges converges if properly normalized.
\begin{lemma}\label{le:outdeg} Almost surely, we have that \[ \lim_{n \rightarrow \infty} \frac{1}{n}\sum_{i =1}^n \mathcal{Z}_n(i) = 1 + \lambda .\] \end{lemma}
\begin{proof} Define $Y_n = \frac{1}{n} \sum_{i=1}^n \mathcal{Z}_n(i)$. Then, we calculate the conditional expectation of $Y_{n+1}$ given $\mathcal{G}_n$ using that $\mathcal{Z}_{n+1}(n+1) = 1$ by definition as
\[ \begin{aligned} \mathbb{E}[ Y_{n+1} | \mathcal{G}_n] & =
\frac{1}{n+1} \big( \sum_{i=1}^n \mathbb{E}[ \mathcal{Z}_{n+1}(i) | \mathcal{G}_n ] + 1\big) \\
& = Y_n + \frac{1}{n+1} \big(1+ \sum_{i=1}^n\mathbb{E}[ \Delta Z_n(i) | \mathcal{G}_n] - Y_n \big) \\
& = Y_n + \frac{1}{n+1} (1+ \lambda
- Y_n ) ,\\ \end{aligned} \] where we used assumption (A1) on the conditional mean of $\Delta Z_n(i)$ and the definition of $\bar \mathcal{F}_n$. Thus, we can write \begin{equation}\label{eq:2401-3} Y_{n+1} - Y_n = \frac{1}{n+1} ( 1 + \lambda - Y_n) + R_{n+1} - R_n , \end{equation} where we define $R_0 = 0$ and
\[ \Delta R_n := R_{n+1} - R_n = Y_{n+1} - \mathbb{E}[ Y_{n+1} | \mathcal{G}_n] . \] Therefore, $R_n$ is a martingale and $R_n$ converges almost surely, if we can show that $\mathbb{E}[ (\Delta R_n)^2 ]$ is summable. Indeed, first using (A3) which states that impact evolutions of distinct vertices are negatively correlated, we can deduce that
\[\begin{aligned} \mathbb{E}[ (\Delta R_n)^2 | \mathcal{G}_n ]
& \leq \frac{1}{(n+1)^2} \bigl(\sum_{i =1}^n \mathbb{E} [ (\Delta \mathcal{Z}_n(i) - \mathbb{E}[ \Delta \mathcal{Z}_n(i) | \mathcal{G}_n])^2 | \mathcal{G}_n ] + 1\bigr) \\
& \leq \frac{1}{(n + 1)^2} \bigl( C^{\rm var} \sum_{i=1}^n \mathbb{E}[ \Delta \mathcal{Z}_n(i) | \mathcal{G}_n] + 1\bigr) \\ & \leq \frac{1}{(n+1)^2} ( C^{\rm var} \,\lambda + 1) , \end{aligned} \] which is summable.
Hence, we can apply both parts of Lemma~\ref{le:stApp} together with the convergence of $(R_n)$ to obtain the almost surely convergence $\lim_{n \rightarrow \infty} Y_n = 1 + \lambda$. \end{proof}
Later on, we will need some a priori bounds on the normalisation sequence.
\begin{lemma}\label{le:triv_bound} Almost surely, we have that
\begin{align*} \int x\, \mu(dx) \leq \liminf_{n\rightarrow\infty} \tfrac{1}{n} \bar\mathcal{F}_n \leq
\limsup_{n\rightarrow\infty} \tfrac{1}{n} \bar \mathcal{F}_n & \leq 1+ \lambda.
\end{align*} \end{lemma}
\begin{proof} For the lower bound, notice that by definition $\mathcal{Z}_n(i) \geq 1$, and therefore
\[ \liminf_{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^n \mathcal{F}_i \mathcal{Z}_n(i) \geq \liminf_{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^n \mathcal{F}_i
= \int x\, \mu(dx) .
\] Conversely, one can use that the $\mathcal{F}_i \leq 1$ and combine with $\lim_{n \rightarrow\infty} \frac{1}{n} \sum_{i=1}^n \mathcal{Z}_n(i) = 1+ \lambda$, see also Lemma~\ref{le:outdeg}. \end{proof}
\section{Proof of Theorem~\ref{thm:main}}\label{se:bootstrap}
The central bootstrap argument is carried out at the end of this section. It is based on Lemma~\ref{lemma:from_measure_to_normalisation}. Before we state and prove Lemma~\ref{lemma:from_measure_to_normalisation}, we prove a technical proposition which will be crucial in the proof of the lemma.
\begin{prop} \begin{itemize} \item[(i)]\label{prop:lower_emp} Let $\theta \geq 1$. If \[ \limsup_{n\rightarrow\infty} \bar {\mathcal{F}}_n \leq \theta , \text{ almost surely}, \] then for any $0\leq a< b\leq 1$, one has \[ \liminf_{n\rightarrow\infty} \frac{1}{n} \sum_{i = 1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in(a,b]\}} \mathrm{imp}_{n}(i) \geq \int_{(a,b]} \frac \theta{\theta-f} \, \mu(df) , \] almost surely. \item[(ii)]\label{prop:up_emp} Let $\theta > 0$. If
\[ \liminf_{n \rightarrow \infty} \bar \mathcal{F}_n \geq \theta , \] then for any $0\leq a < b < \theta\wedge 1$, \[ \limsup_{n\rightarrow\infty} \frac{1}{n}\sum_{i=1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in (a,b]\}} \mathcal{Z}_n(i)
\leq \int_{(a,b]} \frac \theta{\theta-f} \, \mu(df). \] \end{itemize} \end{prop}
\begin{proof} (i) First we prove that under the assumptions of $(i)$, one has for $0\leq f<f'\leq 1$, that \begin{align}\label{eq:2401-2} \liminf_{n\rightarrow\infty} \frac{1}{n} \sum_{i = 1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in(f,f']\}}\,\mathcal{Z}_n(i)\geq \frac \theta{\theta-f} \, \mu((f,f']), \text{ almost surely.} \end{align} Let $0\leq f < f' \leq 1$ and denote by \[ X_n = \Gamma_n((f,f']) = \frac{1}{n} \sum_{i \in \mathbb{I}_n} \mathcal{Z}_n(i), \] where we denote by $\mathbb{I}_n = \{ i \in \{1, \ldots,n\}\, : \, \mathcal{F}_i \in (f,f']\}$.
We will show~(\ref{eq:2401-2}) with the help of the stochastic approximation argument explained in Section~\ref{se:prelim}, see Lemma~\ref{le:stApp}. We need to provide a lower bound for the increment $X_{n+1} - X_n$. Using assumption (A1), we can calculate the conditional expectation of $X_{n+1}$:
\[ \begin{aligned} \mathbb{E}[ X_{n+1} | \mathcal{G}_n ]
& = \frac{1}{n+1} \sum_{i \in \mathbb{I}_n} \mathbb{E}[\mathcal{Z}_{n+1}(i) | \mathcal{G}_n ] + \frac{1}{n+1} \mathbb{P} ( \mathcal{F}_{n+1} \in (f,f']) \\
& = X_n + \frac{1}{n+1} \Big( \sum_{i \in \mathbb{I}_n} \mathbb{E}[ \Delta \mathcal{Z}_n(i) | \mathcal{G}_n] - X_n + \mu((f,f']) \Big) \\ & = X_n + \frac{1}{n+1} \Big( \sum_{i \in \mathbb{I}_n} \frac{\mathcal{F}_i \mathcal{Z}_n(i)}{n \bar \mathcal{F}_n} - X_n + \mu((f,f']) \Big) .\\ \end{aligned} \] Hence, rearranging yields
\[ \mathbb{E}[ X_{n+1} |\mathcal{G}_n] - X_n
\geq \frac{1}{n+1} \Big( \mu(f,f'] - \big( 1 - \frac{f}{\sup_{m \geq n} \bar \mathcal{F}_m} \big) X_n \big) \] Thus, we can write \[ X_{n+1} - X_n \geq \frac{1}{n+1} \Big( \mu(f,f'] - \big( 1 - \frac{f}{\sup_{m \geq n} \bar \mathcal{F}_m} \big) X_n \big) + R_{n+1} - R_n, \] where $R_n$ is a martingale defined via $R_0 =0$ and
\[ \Delta R_n := R_{n+1} - R_n = X_{n+1} - \mathbb{E}[ X_{n+1} | \mathcal{G}_n ] . \] If we can show that $R_n$ converges almost surely, then Lemma~\ref{le:stApp} together with the assumption that $\limsup_{n \rightarrow \infty} \bar \mathcal{F}_n \leq \theta$ shows that \[ \liminf_{ n \rightarrow \infty} X_n \geq \frac{\theta}{\theta - f}\mu((f,f']) , \] which is the required bound~(\ref{eq:2401-2}).
The martingale convergence follows if we show that $\mathbb{E} [ (\Delta R_n)^2 | \mathcal{G}_n]$ is summable. Indeed,
\[ \Delta R_n = \frac{1}{n+1} \sum_{i \in \mathbb{I}_n} ( \mathcal{Z}_{n+1}(i) - \mathbb{E}[\mathcal{Z}_{n+1}(i) | \mathcal{G}_n])
+ \frac{1}{n+1} ( 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{F}_{n+1} \in (f,f']\}} - \mu((f,f']) . \] The second moment of the last expression is clearly bounded by $\frac{1}{(n+1)^2} \mu((f,f'])$ which is summable, so we can concentrate on the first term. Now, we can use (A3), the negative correlation of $\Delta Z_n(i)$, and then (A1) and (A2) to estimate the variance to deduce that
\[ \begin{aligned} \frac{1}{(n+1)^2} & \mathbb{E}\Big[ \big.\Big( \sum_{i \in \mathbb{I}_n} ( \mathcal{Z}_{n+1}(i) - \mathbb{E}[\mathcal{Z}_{n+1}(i) | \mathcal{G}_n]) \Big)^2
\big| \mathcal{G}_n \Big]\\
& \leq \frac{1}{(n+1)^2} \mathbb{E}\Big[ \big. \Big( \sum_{i \in \mathbb{I}_n} ( \Delta \mathcal{Z}_n(i) - \mathbb{E}[\Delta \mathcal{Z}_n(i) | \mathcal{G}_n]) \Big)^2
\big|\mathcal{G}_n \Big] \\
& \leq \frac{1}{(n+1)^2} \sum_{i \in \mathbb{I}_n} \mathrm{Var} ( \Delta \mathcal{Z}_n(i) | \mathcal{G}_n ) \\
& \leq \frac{1}{(n+1)^2} C^{\rm var} \sum_{i \in \mathbb{I}_n} \frac{\mathcal{F}_i \mathcal{Z}_n}{n \bar \mathcal{F}_n} \leq \frac{1}{(n+1)^2} C^{\rm var} \lambda , \end{aligned} \] where we used the definition of $\bar \mathcal{F}_n$ in the last step. The latter is obviously summable, so that $R_n$ converges almost surely.
Note that the assertion (i) follows by a Riemann approximation. One partitions $(a,b]$ via $a=f_0<\dots<f_\ell=b$ with an arbitrary $\ell\in\IN$. Then it follows that $$ \liminf_{n\to\infty} \frac 1n \sum_{i = 1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in(a,b]\}} \mathrm{imp}_{n}(i) \geq \sum_{k=0}^{\ell-1} \frac \theta{\theta-f_k} \, \mu((f_k,f_{k+1}]), \text{ almost surely}, $$ and the right hand side approximates the integral up to an arbitrary small constant.
(ii) It suffices to prove that for $0\leq f<f'<\theta\wedge 1$ one has \begin{align}\label{eq0502-1} \limsup_{n\rightarrow\infty} \frac{1}{n} \sum_{i = 1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in(f,f']\}}\,\mathcal{Z}_n(i)\leq \frac \theta{\theta-f'} \, \mu((f,f']), \text{ almost surely.} \end{align} This follows completely analogous to part (i) using Lemma~\ref{le:stApp}. Then the statement (ii) follows as above by a Riemann approximation. \end{proof}
The next lemma takes the lower bound on the fitness distribution obtained in Proposition~\ref{prop:lower_emp} to produce a new upper bound on the normalisation. We set for $\theta\geq 1$ \begin{align}\label{eq0602-1} T(\theta)= 1+ \frac 1\lambda \int \frac {\theta-1}{\theta-f}\,f \,\mu(df) \end{align}
\begin{lemma}\label{lemma:from_measure_to_normalisation} \begin{enumerate}\item[(i)] Let $\theta>1$. If $$\limsup_{n\to\infty} \bar \mathcal{F}_n\leq \theta, \text{ almost surely,}$$ then $$\limsup_{n\to\infty} \bar \mathcal{F}_n\leq T(\theta), \text{ almost surely,}$$ \item[(ii)] Let $\theta> 0$ and suppose that $$\liminf_{n\to\infty} \bar \mathcal{F}_n\geq \theta, \text{ almost surely.}$$ One has, almost surely, $$\liminf_{n\to\infty} \bar \mathcal{F}_n \geq \left\{ \begin{array}{ll} T(\theta) & \mbox{if } \theta \geq 1, \\
\theta+\frac \theta\lambda (1-\mu[0,\theta)) & \mbox{if } \theta \in (0,1). \end{array} \right. $$
\end{enumerate} \end{lemma}
\begin{proof} (i) Define a measure $\nu$ on $[0,1)$ via $$ \nu(df)= \frac {\theta}{\theta-f}\,\mu(df). $$ Further, set $\nu'= \nu+ ((1+\lambda)-\nu[0,1))\delta_1$. Since by Lemma~\ref{le:outdeg}, $\lim_{n\to\infty} \frac1n \sum_{i=1}^n \mathcal{Z}_n(i)=1+\lambda$, almost surely, we get with Proposition~\ref{prop:lower_emp} that, for every $t\in(0,1)$, $$ \limsup_{n\to\infty} \frac{1}{n} \sum_{i=1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i \in [t,1) \}}\mathcal{Z}_n(i) \leq 1+\lambda - \nu([0,t)) =\nu'([t,1]), \text{ almost surely.} $$ This allows us to compute a new asymptotic upper bound for $(\bar\mathcal{F}_n)$: let $m\in\IN$, observe that, almost surely, \begin{align*} \bar \mathcal{F}_n&=\frac 1{\lambda n} \sum_{i=1}^n \mathcal{F}_i \,\mathcal{Z}_n(i) \leq \frac 1{\lambda n} \sum_{i=1}^n \frac 1m \sum_{j=0}^{m-1} 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i\geq j/m\}} \,\mathcal{Z}_n(i)\\ &= \frac 1{\lambda m} \sum_{j=0}^{m-1} \frac 1n \sum_{i=1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i\geq j/m\}} \,\mathcal{Z}_n(i), \end{align*} so that $$ \limsup_{n\to\infty} \bar\mathcal{F}_n\leq \frac 1{\lambda m} \sum_{j=0}^{m-1} \nu'([j/m,1]), \ \text{ almost surely}. $$ The latter expression tends with $m\to \infty$ to the integral $\frac 1\lambda \int x\,\nu'(dx)$ and we finally get that, almost surely, $$ \limsup_{n\to\infty} \bar\mathcal{F}_n \leq\frac 1\lambda \int f\,\nu'(df) = T(\theta). $$
(ii) Let $\theta'\in(0,\theta\wedge 1)$ and consider the (signed) measures $\nu=\nu(\theta')$ and $\nu'=\nu'(\theta')$ defined by $$ \nu(df)=\frac {\theta}{\theta-f} 1\hspace{-0.098cm}\mathrm{l}_{[0,\theta']}(f) \, \mu(df) $$ and $$ \nu'= \nu +(1+\lambda-\nu[0,1])\delta_{\theta'}. $$ As above we conclude with Proposition~\ref{prop:lower_emp} that for $t<\theta'$, almost surely, $$ \liminf_{n\to\infty} \sum_{i=1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{\mathcal{F}_i\in(t,1]\}} \mathcal{Z}_n(i) \geq 1+\lambda -\nu((0,t]) = \nu'((t,1]). $$ We proceed as above and note that for any $m \in \mathbb{N}$, \[ \begin{aligned} \bar \mathcal{F}_n & = \frac{1}{\lambda n} \sum_{i=1}^n \mathcal{F}_i \mathcal{Z}_n(i) \geq \frac{1}{\lambda n} \sum_{i=1}^n \frac{\theta'}{m}\sum_{i=1}^{m-1} 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{F}_i \geq \frac{j}{m}\theta' \}} \mathcal{Z}_n(i) \\ & = \frac{\theta'}{\lambda m}\sum_{j=1}^{m-1} \frac{1}{n} \sum_{i=1}^n 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{F}_i \geq \frac{j}{m}\theta' \}} \mathcal{Z}_n(i) \end{aligned} \] which yields that, almost surely, $$ \liminf_{n\to\infty} \bar\mathcal{F}_n\geq \frac{\theta'}{\lambda m } \sum_{j=1}^m \nu'( ( \tfrac{j}{m}\theta' ,1]). $$ Since $m\in\mathbb{N}$ is arbitrary, we get that, almost surely, $$ \liminf_{n\to\infty} \bar \mathcal{F}_n\geq \frac 1\lambda \int f \,\nu'(df)= \frac 1{\lambda} \Bigl(\theta'(1+\lambda) -\theta \int_{[0,\theta']} \frac{\theta'-f}{\theta-f} \mu(df)\Bigr). $$ We distinguish two cases. If $\theta<1$, we use that the latter integral is dominated by $\mu([0,\theta'])$ and let $\theta'\uparrow \theta$ to deduce that $$ \liminf_{n\to\infty} \bar \mathcal{F}_n\geq \theta+\frac \theta\lambda (1-\mu[0,\theta)), \text{ almost surely}. $$ If $\theta\geq 1$, we let $\theta'\uparrow 1$ and get $$ \liminf_{n\to\infty} \bar \mathcal{F}_n\geq \frac 1\lambda \int f \,\nu'(df)= \frac 1{\lambda} \Bigl(1+\lambda -\theta \int \frac{1-f}{\theta-f} \mu(df)\Bigr)=T(\theta). $$ \end{proof}
Finally, we can prove Theorem~\ref{thm:main}, where we first show the normalisation converges using a bootstrap argument based on Lemma~\ref{lemma:from_measure_to_normalisation}. Finally we use the bound on the fitness distribution obtained in Proposition~\ref{prop:lower_emp} to show convergence of fitness distributions.
\begin{proof}[Proof of Theorem~\ref{thm:main}] \emph{(i) Fit-get-richer phase.} Suppose that $\theta^{**}$ is the smallest value in $[\theta^*,\infty)$ with \begin{align}\label{eq0812-2} \limsup_{n\to\infty} \bar \mathcal{F}_n \leq \theta^{**}, \text{ almost surely}. \end{align} Such a value exists due to Lemma~\ref{le:triv_bound}. We prove that $\theta^{**}=\theta^*$ by contradiction. Suppose that $\theta^{**}>\theta^*$. We apply Lemma~\ref{lemma:from_measure_to_normalisation} and get that $$ \limsup_{n\to\infty} \bar\mathcal{F}_n\leq T(\theta^{**}), \text{ almost surely}. $$ Now note that $T$ is continuous on $[\theta^*,\theta^{**}]$ and differentiable on $(\theta^*,\theta^{**})$ with $$ T'(\theta)=\frac 1\lambda\int \frac{f(1-f)}{(\theta-f)^2}\,\mu(df)\leq \frac 1\lambda \int \frac f{(\theta-f)} \,\mu(df)<1. $$ Further $\theta^*$ is a fixed point of $T$. Therefore, by the mean value theorem, $$ T(\theta^{**})= T(\theta^*)+ T'(\theta) (\theta^{**}-\theta^*) <\theta^{**} $$ for an appropriate $\theta\in(\theta^*,\theta^{**})$. This contradicts the minimality of $\theta^{**}$.
We now turn to the convergence of the measures $\Gamma_n$. Note that the measure $\Gamma$ defined by $$ \Gamma(df)= \frac {\theta^*}{\theta^*-f}\,\mu(df) $$ has total mass $1+\lambda$. Since $\Gamma_n(0,1)=\frac 1n\sum_{i=1}^n \mathcal{Z}_n(i)$ tends to $1+\lambda$, almost surely, one can apply the Portmanteau theorem to prove convergence of $(\Gamma_n)$. Let $\mathcal{D}=\bigcup_{n\in\IN} 2^{-n}\mathbb{Z}\cap[0,1]$ denote the dyadic numbers on $[0,1]$. We remark that the number of dyadic intervals $(a,b]$ with endpoints $a,b\in\mathcal{D}$ is countable so that, by Proposition~\ref{prop:lower_emp}, there exists an almost sure event $\Omega_0$, such that for all dyadic intervals $(a,b]$ $$ \liminf_{n\to\infty} \Gamma_n(a,b]\geq \Gamma(a,b] \ \text{ on } \ \Omega_0. $$ Let now $U\subset (0,1)$ be an arbitrary open set. We approximate $U$ monotonically from within by a sequence of sets $(U_m)_{m\in\IN}$ with each $U_m$ being a union of finitely many pairwise disjoint dyadic intervals as above. Then, for any $m\in\IN$, one has $$ \liminf_{n\to\infty} \Gamma_n(U) \geq \liminf_{n\to\infty} \Gamma_n(U_m) \geq\Gamma(U_m) \ \text{ on } \ \Omega_0 $$ and by monotone convergence, it follows that $\liminf_{n\to\infty} \Gamma_n(U) \geq\Gamma(U)$ on $\Omega_0$. This proves convergence $$ \Gamma_n \Rightarrow \Gamma, \ \text{ almost surely.} $$ Since $\bar \mathcal{F}_n=\frac 1\lambda \int f \,\Gamma_n(df)$, we conclude that, almost surely, $$ \lim_{n\to\infty} \bar\mathcal{F}_n =\frac 1\lambda \int f \,\Gamma(df)= \theta^*. $$
\emph{(ii) Bose-Einstein phase.} Let $\theta^*=1$. We start as in (i). Let $\theta^{**}$ denote the smallest value in $[1,\infty)$ with $$ \limsup_{n\to\infty} \bar\mathcal{F}_n \leq \theta^{**}, \text{ almost surely.} $$ As above a proof by contradiction proves that $\theta^{**}=1$. Next, let $\theta^{**}$ denote the largest real in $(0,1]$ with \begin{align}\label{eq0602-3} \liminf_{n\to\infty} \bar\mathcal{F}_n \geq \theta^{**}, \text{ almost surely.} \end{align} By Lemma~\ref{le:triv_bound}, such a $\theta^{**}$ exists and we assume that $\theta^{**}<1$. By Lemma~\ref{lemma:from_measure_to_normalisation}, the inequality (\ref{eq0602-3}) remains valid for $$ \theta^{**}+\frac {\theta^{**}}{\lambda}(1-\mu[0,\theta^{**}))>\theta^{**} $$ contradicting the maximality of $\theta^{**}$. Hence, $$ \lim_{n\to\infty} \bar\mathcal{F}_n=1,\text{ almost surely}. $$ By Proposition~\ref{prop:lower_emp}, one has, for $0\leq a<b<1$, $$ \liminf_{n\to\infty} \Gamma_n(a,b] \geq \int_{(a,b]} \frac {1}{1-f}\,\mu(df) =\Gamma(a,b], \text{ almost surely}, $$ and, for $0\leq a <b=1$, $$ \liminf_{n\to\infty} \Gamma_n(a,1] = 1+\lambda -\limsup_{n\to\infty} \Gamma_n(0,a] =\Gamma(a,1], \text{ almost surely.} $$ The rest of the proof is in line with the proof of (i). \end{proof}
\section{Proof of Theorem~\ref{thm:2}}\label{se:deg_dist}
The proof is achieved via a stochastic approximation technique as discussed in Section~\ref{se:prelim}.
\begin{proof}[Proof of Theorem \ref{thm:2}] We prove the statement via induction over $k=1,2,\dots$. The proof of the initial statement ($k=1$) is similar to the proof of the induction step and we will mainly focus on the latter task.
Let $k\in\{2,3,\dots\}$ and suppose that the statement is true when replacing $k$ by a value in $1,\dots,k-1$. We fix $f,f'\in[0,1]$ with $\mu(\{f,f'\})=0$, $\mu((f,f']) > 0$ and consider the random variables $$ X_n :=\Gamma^\ssup{k}_n((f,f']) $$ for $n\in\mathbb{N}$. In the first step we derive a lower bound for the increments of $(X_n)$ that is suitable for the application of Lemma~\ref{le:stApp}.
We restrict attention to vertices with fitness in $(f,f']$ and denote $\mathbb{I}_n:=\{i\in\{1,\dots ,n\}: \mathcal{F}_i\in(f,f']\}$. Note that \begin{align}\begin{split}\label{eq0401-1}
\mathbb{E}[X_{n+1}|\mathcal{G}_n]&= \frac{1}{n+1}\sum_{i\in\mathbb{I}_n} \sum_{l=1}^k \1_{\{\mathcal{Z}_{n}(i)=l\}}\mathbb{P}(\Delta \mathcal{Z}_{n}(i)=k-l|\mathcal{G}_n)\\
&=X_n+\frac{1}{n+1}\sum_{i\in\mathbb{I}_n}\Bigl( \sum_{l=1}^{k-1} \1_{\{\mathcal{Z}_{n}(i)=l\}} \mathbb{P}(\Delta \mathcal{Z}_{n}(i)=k-l|\mathcal{G}_n)\\
& \ \ \ \ \ \ \ \ \ \ \qquad \qquad - \1_{\{\mathcal{Z}_{n}(i)=k\}} \mathbb{P}(\Delta \mathcal{Z}_{n}(i)\not =0|\mathcal{G}_n)\Bigr)- \frac{X_n}{n+1}. \end{split}\end{align} An application of the induction hypothesis gives that for fixed $l\in\{1,\dots,k-1\}$ $$
\lim_{n\to\infty} \sum_{i\in\mathbb{I}_n} \1_{\{\mathcal{Z}_{n}(i)=l\}}\mathbb{P}(\Delta \mathcal{Z}_{n}(i)=k-l|\mathcal{G}_n) = \1_{\{l=k-1\}} \, \frac {k-1}{\theta^*} \int_{(f,f']} x\,\mathrm{d} \Gamma^\ssup{k-1}(dx), $$ almost surely. Indeed, for $l=k-1$ \begin{align*}
\Bigl| \sum_{i\in\mathbb{I}_n}& \1_{\{\mathcal{Z}_{n}(i)=k-1\}}\mathbb{P}(\Delta \mathcal{Z}_{n}(i)=1|\mathcal{G}_n) - \frac {k-1}{\bar\mathcal{F}_n} \int_{(f,f']} x\,\mathrm{d} \Gamma^\ssup{k-1}(dx)\Bigr| \\
&\leq \sup_{i=1,\dots,n} \1_{\{\mathcal{Z}_{n}(i)=k-1\}} n \Bigl| \mathbb{P}(\Delta \mathcal{Z}_{n}(i)=1|\mathcal{G}_n)- \frac{(k-1)\mathcal{F}_i}{n\,\bar\mathcal{F}_n}\Bigr| \\
& \quad + \frac{k-1}{\bar \mathcal{F}_n}\Bigl| \int_{(f,f']} x\,\mathrm{d} \Gamma_n^\ssup{k-1}(dx)-\int_{(f,f']} x\,\mathrm{d} \Gamma^\ssup{k-1}(dx)\Bigr| \end{align*} and the former term tends to zero due to assumption (A4') and the latter term tends to zero by the induction hypothesis (and the fact hat $\Gamma^{(k-1)}$ puts no mass on $f$ and $f'$). Analogously, one verifies the statement for the remaining $l$'s invoking assumption (A4). Further one has that \[ \begin{aligned} \sum_{i \in \mathbb{I}_n} & 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{Z}_n(i) = k \}} \mathbb{P} ( \Delta \mathcal{Z}_n(i) \neq 0 ) - \frac{f' k}{ \bar \mathcal{F}_n} X_n \\
& \leq \sum_{i \in \mathbb{I}_n} 1\hspace{-0.098cm}\mathrm{l}_{\{ \mathcal{Z}_n(i) = k \}} \Big( \mathbb{P} ( \Delta \mathcal{Z}_n(i) =1 | \mathcal{G}_n )- \frac{\mathcal{F}_i k}{n \bar \mathcal{F}_n} \Big) +
\sup_{i=1,\ldots,n} n \mathbb{P} (\Delta \mathcal{Z}_n(i) \geq 2 | \mathcal{G}_n) \end{aligned} \] where the two terms on the right hand side converge to $0$ by assumptions (A4) and (A4').
Consequently, there exist stochastic processes $(A_n)$ and $(B_n)$ such that $$
\mathbb{E}[X_{n+1}|\mathcal{G}_n]-X_n\geq \frac 1{n+1} (A_n-B_n X_n) $$ with $A_n\to \frac {k-1}{\theta^*} \int_{(f,f']} x\,\mathrm{d} \Gamma^\ssup{k-1}(x)$ and $B_n\to 1+\frac{k \, f'}{\theta^*}$, almost surely (where the former limit is positive since $\mu((f,f']) > 0$). We now choose $(R_n)$ as the martingale with $$
R_n=\sum_{k=1}^{n} (X_k-\mathbb{E}[X_k|\mathcal{G}_{k-1}]) , $$ where we define $\mathcal{G}_0$ as the empty graph and observe that \begin{equation}\label{eq:1801-1} X_{n+1}-X_n \geq \frac1{n+1}(A_n-B_n X_n)+R_{n+1}-R_n. \end{equation}
\emph{Convergence of the remainder term.} Next, we prove that $(R_n)$ converges almost surely. An elementary calculation shows that the process $(R_n)$ is the difference of two martingales, namely $$
M^\ssup{1}_{n+1}=M^{\ssup 1}_n+\frac1{n+1}\Bigl(\sum_{i\in\mathbb{I}_n} \1_{\{\mathcal{Z}_{n}(i)<k,\mathcal{Z}_{n+1}(i) \geq k\}} -\mathbb{E}\big[\sum_{i\in\mathbb{I}_n} \1_{\{\mathcal{Z}_{n}(i)<k,\mathcal{Z}_{n+1}(i) \geq k\}}|\mathcal{G}_n\big]\Bigr), $$ and \begin{equation}\label{eq:1801-2}
M^\ssup{2}_{n+1}=M^{\ssup 2}_n+\frac1{n+1}\Bigl(\sum_{i\in\mathbb{I}_n} \1_{\{\mathcal{Z}_{n}(i)\leq k,\mathcal{Z}_{n+1}(i) > k\}} -\mathbb{E}\big[\sum_{i\in\mathbb{I}_n} \1_{\{\mathcal{Z}_{n}(i) \leq k,\mathcal{Z}_{n+1}(i)>k\}}|\mathcal{G}_n\big]\Bigr)
\end{equation} both starting in $0$. Since both martingales are the same up to a shift of parameter $k$, we only have to show that either converges almost surely for fixed $k \in \mathbb{N}$. We will show that $M^\ssup{2}$ converges by showing that its quadratic variation process converges almost surely. Indeed we will show that
$\mathbb{E} [ ( \Delta M_n^\ssup{2} )^2 |\mathcal{G}_n]$ is almost surely summable, where $\Delta M_n^\ssup{2} = M_{n+1}^\ssup{2} - M_n^\ssup{2}$.
First using assumption (A5), i.e.\ the conditional negative quadrant dependence of $\Delta Z_n(i)$, we find that
\[ \begin{aligned} \mathbb{E} [ & (\Delta M_n^\ssup{2} ) ^2 | \mathcal{G}_n ] \\ & \leq \frac{1}{(n+1)^2} \sum_{i \in \mathbb{I}_n} \mathbb{E} \Big[ \Big. \Big(
\1_{\{\mathcal{Z}_{n}(i)\leq k,\mathcal{Z}_{n+1}(i) > k\}} -\mathbb{P} \big( \mathcal{Z}_{n}(i) \leq k,\mathcal{Z}_{n+1}(i)>k\} | \mathcal{G}_n \big) \Big)^2 \Big| \mathcal{G}_n \Big] \\ & \leq \frac{1}{(n+1)^2} \sum_{i \in \mathbb{I}_n} 1\hspace{-0.098cm}\mathrm{l}_{\{ Z_n(i) \leq k \}}
\mathbb{P} ( \Delta Z_n(i) \geq 1 | \mathcal{G}_n ) \\ & \leq \frac{1}{(n+1)^2} \sup_{i =1, \ldots,n} n
1\hspace{-0.098cm}\mathrm{l}_{\{ Z_n(i) \leq k \}} \Big| \mathbb{P} ( \Delta Z_n(i) \geq 1 | \mathcal{G}_n )
- \frac{\mathcal{F}_i Z_n(i)}{ n \bar \mathcal{F}_n} \Big| + \frac{\lambda}{(n+1)^2} , \end{aligned} \] where we used the definition of $\bar \mathcal{F}_n$ in the last step. By assumptions (A4) and (A4') the latter expression is indeed almost surely summable.
\emph{Completing the induction step.} Combining the convergence of the remainder term $R_n$ with the recursion in~(\ref{eq:1801-1}), it follows with Lemma~\ref{le:stApp} that \begin{align}\label{eq0601-1} \liminf_{n\to\infty} \Gamma_n^\ssup{k}((f,f'])\geq \frac{(k-1) \int_{(f,f']} x \,d\Gamma^\ssup{k-1}(x)}{\theta^*+ k f'} \end{align} Recall that $f,f'\in[0,1]$ were chosen arbitrarily with $f<f'$ and $\mu(\{f,f'\})=0$, where we can drop the assumption that $\mu((f,f']) > 0$, since the statement holds trivially in that case. We now pick a countable subset $\mathbb{F}\subset [0,1]$ that is dense such that for each of its entries $f$ one has $\mu(\{f\})=0$. The above theorem shows that there exists an almost sure set $\Omega_0$ on which ~(\ref{eq0601-1}) holds for any pair $f,f'\in\mathbb{F}$ with $f<f'$. Suppose now that $U$ is an arbitrary open set. By approximating the set $U$ from below by unions of small disjoints intervals $(f,f']$ with $f,f'\in\mathbb{F}$ it is straight-forward to verify that $$ \liminf_{n\to\infty} \Gamma_n^\ssup{k}(U)\geq (k-1) \int_{(f,f']} \frac{x}{\theta^*+ k x} \,d\Gamma^\ssup{k-1}(x) $$ on $\Omega_0$. The proof of the converse inequality, namely that almost surely, for any closed $A$, one has $$ \limsup_{n\to\infty} \Gamma_n^\ssup{k}(A)\leq (k-1) \int_{(f,f']} \frac{x}{\theta^*+ k x} \,d\Gamma^\ssup{k-1}(x) $$ is established in complete analogy. We thus obtain that $\Gamma_n^\ssup{k}$ converges almost surely, in the weak$^*$-topology to $\Gamma^\ssup{k}$ given by $$ \Gamma^\ssup{k}(dx)= \frac {(k-1)x}{ k x + \theta^*} \,\Gamma^\ssup{k-1}(dx)=\prod_{l=2}^{k} \frac{(l-1)x}{lx + \theta^*}\, \Gamma^\ssup{1}(dx). $$
\emph{Initialising the induction.} To complete the argument, we still need to verify the statement for the initial choice $k=1$. We again define $X_n = \Gamma_n^\ssup{1}((f,f'])$ for $f,f' \in [0,f]$ with $\mu(\{ f,f'\}) = 0$, $\mu(f,f'] > 0$ and we define $\mathbb{I}_n = \{ i \in \{1,\ldots,n\}: \mathcal{F}_i \in (f,f']\}$. Then, it follows that since $\mathcal{Z}_{n+1}(n+1) = 1$ by definition,
\[\begin{aligned} \mathbb{E}[ X_{n+1} | \mathcal{G}_n] & = \frac{1}{n+1}
\sum_{i \in \mathbb{I}_n} \mathbb{P} ( Z_{n+1} = 1 | \mathcal{G}_n) + \frac{1}{n+1}\mathbb{P} ( \mathcal{F}_{n+1} \in (f,f']) \\ & = X_n + \frac{1}{n+1} \Big[ \sum_{i \in \mathbb{I}_n} 1\hspace{-0.098cm}\mathrm{l}_{\{ Z_n(i) = 1\}}
\mathbb{P} ( \Delta Z_{n+1} \geq 1 | \mathcal{G}_n) - X_n + \mu((f,f']) \Big] . \end{aligned} \] Thus, in complete analogy with the induction step, one can show that \[ X_{n+1} - X_n \geq \frac{1}{n+1} ( A_n - B_n X_n) + R_{n+1} - R_n , \] where $A_n \rightarrow \mu((f,f'])$ and $B_n \rightarrow 1 + \frac{f'}{\theta^*}$
and $R_{n+1} - R_n = X_{n+1} - \mathbb{E} [ X_{n+1} | \mathcal{G}_n]$. The remainder term $R_n$ can then be decomposed as $M^\ssup{1}_n - M^\ssup{2}_n + I_n$ as above with $M^\ssup{1}_n = 0$, $M^\ssup{2}_n$ defined as in~(\ref{eq:1801-2}) and the additional term defined as \[ I_n = \frac{1}{n} \big( 1\hspace{-0.098cm}\mathrm{l}_{ \{ \mathcal{F}_n \in (f,f'] \}} - \mathbb{P} ( \mathcal{F}_n \in (f,f'] )\big) . \] We have already seen that $M^\ssup{2}$ converges. Moreover, an elementary martingale argument (for i.i.d.\ random variables) shows that $\sum_{n \in \mathbb{N}} I_n$ also converges almost surely. Therefore, by Lemma~\ref{le:stApp} we can deduce that \[ \liminf_{n \rightarrow\infty} X_n \geq \frac{\theta^*}{\theta^* + f'} \mu((f,f']) . \] Repeating the same approximation arguments as before, we obtain that $\Gamma^\ssup{1}$ converges almost surely in the weak* topology to $\Gamma^\ssup{1}$ given by \[ \Gamma^\ssup{1}(dx) = \frac{ \theta^* } {\theta^* + x} \mu( dx) , \] which completes the proof by induction. \end{proof}
\end{document} | arXiv |
Works by Paul Howard
( view other items matching `Paul Howard`, view all matches )
Disambiguations Disambiguations:
Paul Howard [34] Paul E. Howard [13] Paul Isaac Howard [1]
Limitations on the Fraenkel-Mostowski method of independence proofs.Paul E. Howard - 1973 - Journal of Symbolic Logic 38 (3):416-422.details
The Fraenkel-Mostowski method has been widely used to prove independence results among weak versions of the axiom of choice. In this paper it is shown that certain statements cannot be proved by this method. More specifically it is shown that in all Fraenkel-Mostowski models the following hold: 1. The axiom of choice for sets of finite sets implies the axiom of choice for sets of well-orderable sets. 2. The Boolean prime ideal theorem implies a weakened form of Sikorski's theorem.
Axioms of Set Theory in Philosophy of Mathematics
Polish Philosophy in European Philosophy
Direct download (7 more)
Compactness in Countable Tychonoff Products and Choice.Paul Howard, K. Keremedis & J. E. Rubin - 2000 - Mathematical Logic Quarterly 46 (1):3-16.details
We study the relationship between the countable axiom of choice and the Tychonoff product theorem for countable families of topological spaces.
The Fraenkel-Mostowski Method for Independence Proofs in Set Theory.J. W. Addison, Leon Henkin, Alfred Tarski & Paul E. Howard - 1975 - Journal of Symbolic Logic 40 (4):631-631.details
Model Theory in Logic and Philosophy of Logic
On infinite-dimensional Banach spaces and weak forms of the axiom of choice.Paul Howard & Eleftherios Tachtsis - 2017 - Mathematical Logic Quarterly 63 (6):509-535.details
Independence results for class forms of the axiom of choice.Paul E. Howard, Arthur L. Rubin & Jean E. Rubin - 1978 - Journal of Symbolic Logic 43 (4):673-684.details
Let NBG be von Neumann-Bernays-Gödel set theory without the axiom of choice and let NBGA be the modification which allows atoms. In this paper we consider some of the well-known class or global forms of the wellordering theorem, the axiom of choice, and maximal principles which are known to be equivalent in NBG and show they are not equivalent in NBGA.
Independence Results in Set Theory in Philosophy of Mathematics
The Axiom of Choice in Philosophy of Mathematics
Rado's selection lemma does not imply the Boolean prime ideal theorem.Paul E. Howard - 1984 - Zeitschrift fur mathematische Logik und Grundlagen der Mathematik 30 (9-11):129-132.details
Areas of Mathematics in Philosophy of Mathematics
Non-constructive Properties of the Real Numbers.J. E. Rubin, K. Keremedis & Paul Howard - 2001 - Mathematical Logic Quarterly 47 (3):423-431.details
We study the relationship between various properties of the real numbers and weak choice principles.
No decreasing sequence of cardinals.Paul Howard & Eleftherios Tachtsis - 2016 - Archive for Mathematical Logic 55 (3-4):415-429.details
In set theory without the Axiom of Choice, we investigate the set-theoretic strength of the principle NDS which states that there is no function f on the set ω of natural numbers such that for everyn ∈ ω, f ≺ f, where for sets x and y, x ≺ y means that there is a one-to-one map g : x → y, but no one-to-one map h : y → x. It is a long standing open problem whether NDS implies (...) AC. In this paper, among other results, we show that NDS is a strong axiom by establishing that ACLO ↛ NDS in ZFA set theory. The latter result provides a strongly negative answer to the question of whether "every Dedekind-finite set is finite" implies NDS addressed in G. H. Moore "Zermelo's Axiom of Choice. Its Origins, Development, and Influence" and in P. Howard–J. E. Rubin "Consequences of the Axiom of Choice". We also prove that ACWO ↛ NDS in ZF and that "for all infinite cardinals m, m + m = m" ↛ NDS in ZFA. (shrink)
Cardinals and Ordinals in Philosophy of Mathematics
Subgroups of a free group and the axiom of choice.Paul E. Howard - 1985 - Journal of Symbolic Logic 50 (2):458-467.details
Rado's selection lemma does not imply the Boolean prime ideal theorem.Paul E. Howard - 1984 - Mathematical Logic Quarterly 30 (9‐11):129-132.details
Products of compact spaces and the axiom of choice II.Omar De la Cruz, Eric Hall, Paul Howard, Kyriakos Keremedis & Jean E. Rubin - 2003 - Mathematical Logic Quarterly 49 (1):57-71.details
This is a continuation of [2]. We study the Tychonoff Compactness Theorem for various definitions of compactness and for various types of spaces . We also study well ordered Tychonoff products and the effect that the multiple choice axiom has on such products.
Products of Compact Spaces and the Axiom of Choice.O. De la Cruz, Paul Howard & E. Hall - 2002 - Mathematical Logic Quarterly 48 (4):508-516.details
We study the Tychonoff Compactness Theorem for several different definitions of a compact space.
Definitions of compactness and the axiom of choice.Omar De la Cruz, Eric Hall, Paul Howard, Jean E. Rubin & Adrienne Stanley - 2002 - Journal of Symbolic Logic 67 (1):143-161.details
We study the relationships between definitions of compactness in topological spaces and the roll the axiom of choice plays in these relationships.
The strength of the $\Delta$-system lemma.Paul Howard & Jeffrey Solski - 1992 - Notre Dame Journal of Formal Logic 34 (1):100-106.details
Logic and Philosophy of Logic, Miscellaneous in Logic and Philosophy of Logic
Logics in Logic and Philosophy of Logic
The axiom of choice for countable collections of countable sets does not imply the countable union theorem.Paul E. Howard - 1992 - Notre Dame Journal of Formal Logic 33 (2):236-243.details
Divisibility of dedekind finite sets.David Blair, Andreas Blass & Paul Howard - 2005 - Journal of Mathematical Logic 5 (1):49-85.details
A Dedekind-finite set is said to be divisible by a natural number n if it can be partitioned into pieces of size n. We study several aspects of this notion, as well as the stronger notion of being partitionable into n pieces of equal size. Among our results are that the divisors of a Dedekind-finite set can consistently be any set of natural numbers, that a Dedekind-finite power of 2 cannot be divisible by 3, and that a Dedekind-finite set can (...) be congruent modulo 3, to all of 0, 1, and 2 simultaneously. (shrink)
On vector spaces over specific fields without choice.Paul Howard & Eleftherios Tachtsis - 2013 - Mathematical Logic Quarterly 59 (3):128-146.details
The axiom of choice for well-ordered families and for families of well- orderable sets.Paul Howard & Jean E. Rubin - 1995 - Journal of Symbolic Logic 60 (4):1115-1117.details
We show that it is not possible to construct a Fraenkel-Mostowski model in which the axiom of choice for well-ordered families of sets and the axiom of choice for sets are both true, but the axiom of choice is false.
Unions and the axiom of choice.Omar De la Cruz, Eric J. Hall, Paul Howard, Kyriakos Keremedis & Jean E. Rubin - 2008 - Mathematical Logic Quarterly 54 (6):652-665.details
We study statements about countable and well-ordered unions and their relation to each other and to countable and well-ordered forms of the axiom of choice. Using WO as an abbreviation for "well-orderable", here are two typical results: The assertion that every WO family of countable sets has a WO union does not imply that every countable family of WO sets has a WO union; the axiom of choice for WO families of WO sets does not imply that the countable union (...) of countable sets is WO. (shrink)
Russell's alternative to the axiom of choice.Norbert Brunner & Paul Howard - 1992 - Zeitschrift fur mathematische Logik und Grundlagen der Mathematik 38 (1):529-534.details
Russell's alternative to the axiom of choice.Norbert Brunner & Paul Howard - 1992 - Mathematical Logic Quarterly 38 (1):529-534.details
We prove the independence of some weakenings of the axiom of choice related to the question if the unions of wellorderable families of wellordered sets are wellorderable.
Versions of Normality and Some Weak Forms of the Axiom of Choice.Paul Howard, Kyriakos Keremedis, Herman Rubin & Jean E. Rubin - 1998 - Mathematical Logic Quarterly 44 (3):367-382.details
We investigate the set theoretical strength of some properties of normality, including Urysohn's Lemma, Tietze-Urysohn Extension Theorem, normality of disjoint unions of normal spaces, and normality of Fσ subsets of normal spaces.
Maximal $p$-subgroups and the axiom of choice.Paul E. Howard & Mary Yorke - 1987 - Notre Dame Journal of Formal Logic 28 (2):276-283.details
Definitions of compact.Paul E. Howard - 1990 - Journal of Symbolic Logic 55 (2):645-655.details
Von Rimscha's Transitivity Conditions.Paul Howard, Jean E. Rubin & Adrienne Stanley - 2000 - Mathematical Logic Quarterly 46 (4):549-554.details
In Zermelo-Fraenkel set theory with the axiom of choice every set has the same cardinal number as some ordinal. Von Rimscha has weakened this condition to "Every set has the same cardinal number as some transitive set". In set theory without the axiom of choice, we study the deductive strength of this and similar statements introduced by von Rimscha.
A Proof of a Theorem of Tennenbaum.Paul E. Howard - 1972 - Zeitschrift fur mathematische Logik und Grundlagen der Mathematik 18 (7):111-112.details
Properties of the real line and weak forms of the Axiom of Choice.Omar De la Cruz, Eric Hall, Paul Howard, Kyriakos Keremedis & Eleftherios Tachtsis - 2005 - Mathematical Logic Quarterly 51 (6):598-609.details
We investigate, within the framework of Zermelo-Fraenkel set theory ZF, the interrelations between weak forms of the Axiom of Choice AC restricted to sets of reals.
A Proof of a Theorem of Tennenbaum.Paul E. Howard - 1972 - Mathematical Logic Quarterly 18 (7):111-112.details
Bases, spanning sets, and the axiom of choice.Paul Howard - 2007 - Mathematical Logic Quarterly 53 (3):247-254.details
Two theorems are proved: First that the statement"there exists a field F such that for every vector space over F, every generating set contains a basis"implies the axiom of choice. This generalizes theorems of Halpern, Blass, and Keremedis. Secondly, we prove that the assertion that every vector space over ℤ2 has a basis implies that every well-ordered collection of two-element sets has a choice function.
On a variant of Rado's selection lemma and its equivalence with the Boolean prime ideal theorem.Paul Howard & Eleftherios Tachtsis - 2014 - Archive for Mathematical Logic 53 (7-8):825-833.details
We establish that, in ZF, the statementRLT: Given a setIand a non-empty setF\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathcal{F}}$$\end{document}of non-empty elementary closed subsets of 2Isatisfying the fip, ifF\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathcal{F}}$$\end{document}has a choice function, then⋂F≠∅\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\bigcap\mathcal{F} \ne \emptyset}$$\end{document},which was introduced in Morillon :739–749, 2012), is equivalent to the Boolean Prime Ideal Theorem. The result provides, on one hand, an affirmative answer to Morillon's corresponding (...) question in Morillon and, on the other hand, a negative answer—in the setting of ZFA —to the question in Morillon of whether RLT is equivalent to Rado's selection lemma. (shrink)
Paracompactness of Metric Spaces and the Axiom of Multiple Choice.Paul Howard, K. Keremedis & J. E. Rubin - 2000 - Mathematical Logic Quarterly 46 (2):219-232.details
The axiom of multiple choice implies that metric spaces are paracompact but the reverse implication cannot be proved in set theory without the axiom of choice.
The finiteness of compact Boolean algebras.Paul Howard - 2011 - Mathematical Logic Quarterly 57 (1):14-18.details
We show that it consistent with Zermelo-Fraenkel set theory that there is an infinite, compact Boolean algebra.
The Boolean Prime Ideal Theorem Plus Countable Choice Do Not Imply Dependent Choice.Paul Howard & Jean E. Rubin - 1996 - Mathematical Logic Quarterly 42 (1):410-420.details
Two Fraenkel-Mostowski models are constructed in which the Boolean Prime Ideal Theorem is true. In both models, AC for countable sets is true, but AC for sets of cardinality 2math image and the 2m = m principle are both false. The Principle of Dependent Choices is true in the first model, but false in the second.
Variations of Rado's lemma.Paul Howard - 1993 - Mathematical Logic Quarterly 39 (1):353-356.details
The deductive strengths of three variations of Rado's selection lemma are studied in set theory without the axiom of choice. Two are shown to be equivalent to Rado's lemma and the third to the Boolean prime ideal theorem. MSC: 03E25, 04A25, 06E05.
Metric spaces and the axiom of choice.Omar De la Cruz, Eric Hall, Paul Howard, Kyriakos Keremedis & Jean E. Rubin - 2003 - Mathematical Logic Quarterly 49 (5):455-466.details
We study conditions for a topological space to be metrizable, properties of metrizable spaces, and the role the axiom of choice plays in these matters.
Finiteness Classes and Small Violations of Choice.Horst Herrlich, Paul Howard & Eleftherios Tachtsis - 2016 - Notre Dame Journal of Formal Logic 57 (3):375-388.details
We study properties of certain subclasses of the Dedekind finite sets in set theory without the axiom of choice with respect to the comparability of their elements and to the boundedness of such classes, and we answer related open problems from Herrlich's "The Finite and the Infinite." The main results are as follows: 1. It is relatively consistent with ZF that the class of all finite sets is not the only finiteness class such that any two of its elements are (...) comparable. 2. The principle "Small Violations of Choice" —introduced by A. Blass—implies that the class of all Dedekind finite sets is bounded above. 3. "The class of all Dedekind finite sets is bounded above" is true in every permutation model of ZFA in which the class of atoms is a set, and in every symmetric model of ZF. 4. There exists a model of ZFA set theory in which the class of all atoms is a proper class and in which the class of all infinite Dedekind finite sets is not bounded above. 5. There exists a model of ZF in which the class of all infinite Dedekind finite sets is not bounded above. (shrink)
The Existence of Level Sets in a Free Group Implies the Axiom of Choice.Paul E. Howard - 1987 - Zeitschrift fur mathematische Logik und Grundlagen der Mathematik 33 (4):315-316.details
Disjoint Unions of Topological Spaces and Choice.Paul Howard, Kyriakos Keremedis, Herman Rubin & Jean E. Rubin - 1998 - Mathematical Logic Quarterly 44 (4):493-508.details
We find properties of topological spaces which are not shared by disjoint unions in the absence of some form of the Axiom of Choice.
Well Ordered Subsets of Linearly Ordered Sets.Hartmut Höft & Paul Howard - 1994 - Notre Dame Journal of Formal Logic 35 (3):413-425.details
The deductive relationships between six statements are examined in set theory without the axiom of choice. Each of these statements follows from the axiom of choice and involves linear orderings in some way.
A graph theoretic equivalent to the axiom of choice.Hartmut Höft & Paul Howard - 1973 - Mathematical Logic Quarterly 19 (11‐12):191-191.details
If vector spaces are projective modules then multiple choice holds.Paul Howard - 2005 - Mathematical Logic Quarterly 51 (2):187.details
We show that the assertion that every vector space is a projective module implies the axiom of multiple choice and that the reverse implication does not hold in set theory weakened to permit the existence of atoms.
The Existence of Level Sets in a Free Group Implies the Axiom of Choice.Paul E. Howard - 1987 - Mathematical Logic Quarterly 33 (4):315-316.details
Using PhilPapers from home?
General Editors:
David Bourget (Western Ontario)
David Chalmers (ANU, NYU)
Area Editors:
David Bourget
Gwen Bradford
Berit Brogaard
Margaret Cameron
James Chase
Rafael De Clercq
Ezio Di Nucci
Esa Diaz-Leon
Barry Hallen
Hans Halvorson
Michelle Kosch
Øystein Linnebo
JeeLoo Liu
Paul Livingston
Brandon Look
Manolo Martínez
Matthew McGrath
Michiru Nagatsu
Susana Nuccetelli
Giuseppe Primiero
Jack Alan Reynolds
Darrell P. Rowbottom
Aleksandra Samonek
Constantine Sandis
Howard Sankey
Thomas Senor
Robin Smith
Daniel Star
Jussi Suikkanen
Aness Kim Webster
Other editors
Learn more about PhilPapers | CommonCrawl |
\begin{document}
\title{A note on panchromatic colorings}
\begin{abstract} This paper studies the quantity $p(n,r)$, that is the minimal number of edges of an $n$-uniform hypergraph without panchromatic coloring (it means that every edge meets every color) in $r$ colors. If $r \leq c \frac{n}{\ln n}$ then all bounds have a type $A_1(n, \ln n, r)(\frac{r}{r-1})^n \leq p(n, r) \leq A_2(n, r, \ln r) (\frac{r}{r-1})^n$, where $A_1$, $A_2$ are some algebraic fractions. The main result is a new lower bound on $p(n,r)$ when $r$ is at least $c \sqrt n$; we improve an upper bound on $p(n,r)$ if $n = o(r^{3/2})$.
Also we show that $p(n,r)$ has upper and lower bounds depend only on $n/r$ when the ratio $n/r$ is small, which can not be reached by the previous probabilistic machinery.
Finally we construct an explicit example of a hypergraph without panchromatic coloring and with $(\frac{r}{r-1} + o(1))^n$ edges for $r = o(\sqrt{\frac{n}{\ln n}})$. \end{abstract}
\section {Introduction}
A hypergraph is a pair $(V, E)$, where $V$ is a finite set whose elements are called vertices and $E$ is a family of subsets of $V$, called edges. A hypergraph is $n$-uniform if every edge has size $n$. A vertex $r$-coloring of a hypergraph $(V , E)$ is a map $c : V \rightarrow \{1, \dots ,r\}$.
An $r$-coloring of vertices of a hypergraph is called \textit{panchromatic} if every edge contains a vertex of every color. The problem of the existence of a panchromatic coloring of a hypergraph was stated in the local form by P.~Erd\H{o}s and L.~Lov{\'a}sz in~\cite{EL}. They proved that if every edge of an $n$-uniform hyperhraph intersects at most $r^{n-1}/4(r-1)^n$ other edges then the hypergraph has a panchromatic $r$-coloring. Then A.~Kostochka in~\cite{Kost} stated the problem in the present form and linked it with the $r$-choosability problem using ideas by P.~Erd\H{o}s, A.~L.~Rubin and H.~Taylor from~\cite{ErdRubTay}. Also A.~Kostochka and D.~R.~Woodall~\cite{KostWood} found some sufficient conditions on a hypergraph to have a panchromatic coloring in terms of Hall ratio. Reader can find a survey on history and results on the related problems in~\cite{Kost3, RaiSh}.
\subsection{Upper bounds}
Using the results from~\cite{Noga} A.~Kostochka proved~\cite{Kost} that for some constants $c_1$, $c_2 > 0$ \begin{equation} \frac{1}{r} e^{c_1 \frac{n}{r}} \leq p(n,r) \leq r e^{c_2\frac{n}{r}}. \label{1} \end{equation}
\noindent In works~\cite{shaba1,shaba2} D.~Shabanov gives the following upper bounds:
$$p (n,r) \leq c \frac{n^2 \ln r }{r^2} \left (\frac{r}{r-1}\right)^n, \mbox{ if } 3 \leq r = o(\sqrt n), n > n_0;$$ \begin{equation} p (n,r) \leq c \frac{n^{3/2} \ln r }{r} \left (\frac{r}{r-1}\right)^n, \mbox{ if } r = O(n^{2/3}) \mbox{ and } n_0 < n = O(r^2); \label{2} \end{equation} $$p (n,r) \leq c \max \left (\frac{n^2}{r}, n^{3/2} \right) \ln r \left (\frac{r}{r-1}\right)^n \mbox{ for all } n, r \geq 2.$$
Let us introduce the quantity $p'(n,r)$ that is the minimal number of edges in an $n$-uniform hypergraph $H = (V,E)$ such that any subset of vertices $V' \subset V$ with
$|V'| \geq \left\lceil \frac{r-1}{r}|V| \right\rceil$ contains an edge. In fact $p'(n,r)$ coincides with $T(|V|, \frac{r-1}{r}|V|, n)$, where $T(a,b,c)$ stands for \textit{Tur{\'a}n number} (see~\cite{sidor} for a survey).
Note that by pigeonhole principle every vertex $r$-coloring contains a color of size at most $\left\lfloor \frac{1}{r}|V| \right\rfloor$. So the complement to this color has size at least
$|V| - \left\lfloor \frac{1}{r}|V| \right\rfloor = \left\lceil \frac{r-1}{r}|V| \right\rceil$. Hence, $p(n,r) \leq p'(n,r)$. This argument is in spirit of the standard estimation of the chromatic number via the independence number.
The following theorem gives better upper bound in the case when $n = o(r^{3/2})$.
\begin{theorem} The following inequality holds for every $n \geq 2$, $r \geq 2$ $$p' (n,r) \leq c \frac{n^2 \ln r}{r} \left (\frac{r}{r-1}\right)^n.$$ It immediately implies $$p (n,r) \leq c \frac{n^2 \ln r}{r} \left (\frac{r}{r-1}\right)^n.$$ \label{theo1} \end{theorem}
\subsection{Lower bounds}
We start by noting that an evident probabilistic argument gives $p(n,r) \geq \frac{1}{r} (\frac{r}{r-1})^n$. This gives lower bound~(\ref{1}) with $c_1 = 1$. This was essentially improved by D.~Shabanov in~\cite{shaba1}: $$p(n,r) \geq c\frac{1}{r^2} \left ( \frac{n}{\ln n} \right ) ^{1/3} \left (\frac{r}{r-1}\right)^n \mbox { for } n, r \geq 2, r < n.$$
\noindent Next, A.~Rozovskaya and D.~Shabanov~\cite{roz} showed that $$p(n,r) \geq c\frac{1}{r^2} \sqrt {\frac{n}{\ln n}}\left (\frac{r}{r-1}\right)^n \mbox { for } n, r \geq 2, r \leq \frac{n}{2\ln n}.$$
\noindent Using the Alterations method (see Section 3 of~\cite{alon2016probabilistic}) we can get the following lower bound for all the range of $n$, $r$. It gives better results when $r \geq c\sqrt{n}$.
\begin{theorem} For $n \geq r \geq 2$ holds $$p(n,r) \geq e^{-1}\frac{r-1}{n-1}e^{\frac{n-1}{r-1}}.$$ \label{theo2} \end{theorem}
\noindent There is a completely another way to get almost the same bound. First, we need to prove intermediate bound. It is based on the geometric rethinking of A.~Pluh{\' a}r's ideas~\cite{Pl}.
\begin{theorem} For $n \geq r \geq 2$ such that $r \leq c\frac{n}{\ln n}$ holds $$p(n,r) \geq c \max \left(\frac{n^{1/4}}{r\sqrt{r}}, \frac{1}{\sqrt n}\right) \left (\frac{r}{r-1}\right)^n.$$ \label{theo2'} \end{theorem}
\noindent Combining Theorems~\ref{theo2} and~\ref{theo2'} we prove the following theorem.
\begin{theorem} For $n \geq r \geq 2$ such that $\sqrt{n} \leq r \leq c'\frac{n}{\ln n}$ holds $$p(n,r) \geq c \frac{r}{n}e^{\frac{n}{r}}.$$ \label{theo2''} \end{theorem}
\begin{remark} Theorem~\ref{theo2'}, unlike Theorem~\ref{theo2} and Theorem~\ref{theo2''}, admits a local version. \end{remark}
\subsection{Small $n/r$}
Consider the case when the ratio $n/r$ is small; $n/r = const$ is a good model case. In the case $\frac{n}{r} \leq c \ln n$ the best upper bound was $r e^{cn/r}$~\cite{Kost}, where $c \geq 4$ is a constant. Using the following theorem we give a bound depending only on $n/r$.
\begin{theorem} The following inequality holds for every integer triple $m, n, r$ $$p (mn, mr) \leq p' (n, r).$$ \label{theo3} \end{theorem}
\noindent As a corollary of Theorem~\ref{theo3} and an evident inequality $\max(p(n, r), p(n+1, r+1)) \leq p(n+1, r)$ we get a better upper bound, for the case of small $n/r$.
\begin{corollary} The following inequality holds for every integer $k \leq r$ $$p (n, r) \leq p' \left (\left\lceil \frac{n}{r - k + 1} \right\rceil k, k \right).$$ In particular, if $n < r^2$ one can put $k := \alpha \frac{n}{r}$ and get $p (n,r) \leq c (\frac{n}{r})^2 \ln \frac{n}{r} \cdot e^{\frac{n}{r}}$. \label{col} \end{corollary}
\noindent There was no known lower bound in this case (all the previous methods give something less than $1$). Theorem~\ref{theo2} covers this gap, but note also that there exists a very simple greedy algorithm.
\begin{proposition} The following inequality holds for every integer $n \geq r$ $$p (n,r) \geq \left\lfloor \frac{n}{r} \right\rfloor.$$ \label{theo4} \end{proposition}
\begin{proof}[Proof of Proposition~\ref{theo4}]
Consider a hypergraph $H = (V,E)$ with $|E| \leq \left\lfloor n/r \right\rfloor$. Let us pick an edge $e \in E$ and color its arbitrary $r$ vertices in different colors. Then let us delete $e$ and all colored vertices from $H$. The remaining hypergraph has $|E| - 1$ edge, and the size of every edge is at least $n - r$. So we can do this procedure $\left\lfloor n/r \right\rfloor$ times showing the claim. \end{proof}
\subsection{Explicit constructions}
Recently, H.~Gebauer~\cite{GeB} gave an explicit example of an $n$-uniform hypergraph with chromatic number $r+1$ and with $(r + o(1))^n$ edges for a constant $r$. We generalize this example to the case of panchromatic colorings.
\begin{theorem} Let $r = o(\sqrt{\frac{n}{\ln n}})$. There is an explicit consruction of an $n$-uniform hypergraph $H = (V,E)$ without panchromatic coloring and such that
$$|E(H)| = \left( \frac{r}{r-1} + o(1)\right)^n.$$ \label{theo5} \end{theorem}
\section {Proofs}
The following proof is just a rephrasing of the proof by P.~Erd\H{o}s~\cite{Erdos2}.
\begin{proof}[Proof of Theorem~\ref{theo1}]
Consider a vertex set $V$ of size $|V| = n^2$. Let us construct a hypergraph $H = (V, E)$ by random (uniformly and indepentently) choosing an edge $m := c\frac{n^2\ln r}{r} (\frac{r}{r-1} )^n$ times.
We can choose an edge multiple times during this process, but in this case the total number of egdes can only decrease, i.~e.~$|E| \leq m$.
Let us fix a subset of vertices $V' \subset V$ of size $|V'| = \left\lceil \frac{r-1}{r} |V| \right\rceil$. Denote the probability that a random edge is a subset of $V'$ by $p$. Obviously,
$$p = \frac{\binom{|V'|}{n}}{\binom{|V|}{n}} = \prod_{i=0}^{n-1} \frac{\left\lceil \frac{r-1}{r}n^2 \right\rceil - i}{n^2 - i} \geq \left (\frac{\left\lceil \frac{r-1}{r}n^2 \right\rceil - n}{n^2 - n} \right )^n$$ $$\geq \left (\frac{\left\lceil \frac{r-1}{r} n^2 \right\rceil - 2\left\lceil \frac{r-1}{r}n \right\rceil}{n(n-1)}\right )^n = e \left(\frac{r-1}{r}\right)^n (1+o(1)).$$
\noindent The probability that $V'$ does not contain an edge is equal to $(1-p)^m$. The total number of such sets $V'$ is $\binom{n^2}{\left\lceil (r-1)n^2/r \right\rceil} = \binom{n^2}{\left\lfloor n^2/r \right\rfloor}$. If $\binom{n^2}{\left\lceil (r-1)n^2/r \right\rceil} (1-p)^m < 1$ then a hypergraph realizing the inequality $p'(n,r) \leq m$ exists with positive probability. One can see that $$\binom{n^2}{\left\lfloor n^2/r \right\rfloor} (1-p)^m \leq \frac{n^{2 \left\lfloor n^2/r \right\rfloor}}{\left\lfloor n^2/r \right\rfloor!} e^{-pm} = e^{c\ln r \left\lfloor n^2/r \right\rfloor - e \left(\frac{r-1}{r}\right)^n m}.$$ So for $m = c\frac{n^2\ln r}{r} (\frac{r}{r-1} )^n$ the claim is proved. \end{proof}
\begin{proof}[Proof of Theorem~\ref{theo2}] Let $H = (V, E)$ be a given hypergraph with
$$|E| \leq e^{-1}\frac{r-1}{n-1}e^{\frac{n-1}{r-1}}.$$ We should show that $H$ has a panchromatic coloring.
Consider an uniform independent coloring of the vertex set into $a > r$ colors. The expectation of the number of such pairs $(e, q)$ that edge $e \in E$ has no color $q$ is $|E| a (\frac{a-1}{a})^n$.
So, if $|E| a (\frac{a-1}{a})^n < a-r$, then with positive probability there are $r$ colors such that they are contained in every edge. Substituting $a = \frac{(n-1)}{n-r}r$ one has that for $$|E| \leq \frac{r-1}{n-1} \left(\frac{nr-r}{nr-n} \right)^n \leq e^{-1} \frac{r-1}{n-1} e^{\frac{r-1}{n-1}}$$ a panchromatic coloring exists. \end{proof}
\begin{proof}[Proof of Theorem~\ref{theo2'}] Let $H = (V, E)$ be a given hypergraph with
$$|E| \leq c \max \left(\frac{n^{1/4}}{r\sqrt{r}}, \frac{1}{\sqrt n}\right) \left (\frac{r}{r-1}\right)^n.$$ We should show that $H$ has a panchromatic coloring.
Consider an $(r-1)$-dimensional unit simplex, and let us map every vertex of $H$ to the 1-face skeleton (edges of the simplex) according to the uniform measure and independently. Then let us fix a bijection $f$ between colors and vertices of the simplex. We are going to color the hypergraph in the following way: for every edge $e$ of the hypergraph and every color $i$, we give color $i$ to the nearest (with respect to the induced metric) vertex of edge $e$ (with probability $1$ it is unique; let us call it $v_i(e)$) to the vertex of the simplex $f(i)$. If the coloring is not self-contradictory then it is obviously panchromatic.
Let us evaluate the probability of such contradiction. We are going to show that such probability is less than 1 showing the claim. Let us call a \textit{bad event of the first type}, the event that for some edge $e\in E$ and some color $i$ the vertex $v_i(e)$ does not lie on the adjacent to $f(i)$ edge of the simplex. The probability of this event is $\left( \frac{r-2}{r} \right)^n$. Summing up over all edges and colors we get $Poly (r, n) \left( \frac{r}{r-1} \right)^n \left( \frac{r-2}{r} \right)^n = Poly (r, n) \left( \frac{r-2}{r-1} \right)^n$ which tends to zero if $r \leq c\frac{n}{\ln n}$.
Now let us go to \textit{bad events of the second type}, i.\ e. the events that there is a vertex $x$ such that it should have color $i$ and $j$ simultaneously (let us call $x$ a \textit{conflict vertex}).
Consider a pair of edges $(e_1, e_2) \in E^2$; denote the size of their intersection by $t := |e_1 \cap e_2|$. We will estimate the probability (denote it by $q$) that $e_1$ and $e_2$ demand to color a conflict vertex $x \in e_1 \cap e_2$ in different colors, and then sum up over all pairs of edges. The case $e_1 = e_2$ (i.\ e. $t = n$) corresponds to the event that the coloring is contradictory even on one edge $e_1$.
First, we should choose a conflict vertex $x$ (there are $t$ ways to do it) and a conflict pair of colors $(i,j)$ (there are $r(r-1)/2$ ways). Note that $x$ should lie on the edge $(f(i), f(j))$ of the simplex (this event has the probability $\frac{2}{(r-1)r}$), otherwise we have already counted them in the previous step. If $\mbox {dist} (x, f(i)) = a$, then $\mbox {dist} (x, f(j)) = 1-a$. Since $x$ is the nearest vertex to $f(i)$ in the edge $e_1$ any vertex $y \in e_1$ cannot lie in the union of $r-1$ segments of length $a$ with endpoint $f(i)$. Analogously, any vertex $z \in e_2$ cannot lie in the union of $r-1$ segments of length $1-a$ with endpoint $f(j)$. So any vertex $w \in e_1 \cap e_2$ cannot lie in both forbidden sets (note that the forbidden sets have empty intersection). So for fixed $a$ the probability is $$\left (\frac{r-2}{r} \right)^{t-1} \left(1 - \frac{2a}{r}\right)^{n-t} \left(1 - \frac{2-2a}{r}\right)^{n-t}.$$ Summing up, we have $$q = t \frac{(r-1)r}{2} \frac{2}{(r-1)r} \left (\frac{r-2}{r} \right)^{t-1} \int^1_0 \left(1 - \frac{2a}{r}\right)^{n-t} \left(1 - \frac{2-2a}{r}\right)^{n-t} da$$ $$= t \left (1-\frac{1}{(r-1)^2} \right )^{t-1} \left (\frac{r-1}{r}\right )^{2(t - 1)}\int^1_0 \left(1 - \frac{2a}{r}\right)^{n-t} \left(1 - \frac{2-2a}{r}\right)^{n-t} da.$$ Put $A := t e^{-tr^{-2}} > t e^{-t(r-1)^{-2}} \geq t \left (1-\frac{1}{(r-1)^2} \right )^{t} \geq \frac{1}{2} t \left (1-\frac{1}{(r-1)^2} \right )^{t-1}$. Let us show that $A \leq c \min (r^2, n)$. Indeed, $A = r^2 \frac{t}{r^2} e^{-tr^{-2}} \leq cr^2$ and $A \leq t \leq n$, so $A \leq c \min (r^2, n)$. Put also $$B := \left (\frac{r-1}{r}\right )^{2(t - 1)}\int^1_0 \left(1 - \frac{2a}{r}\right)^{n-t} \left(1 - \frac{2-2a}{r}\right)^{n-t} da.$$ Obviously, $(1 - \frac{2a}{r})(1 - \frac{2 - 2a}{r}) \leq (1 - \frac{1}{r})^2$, thus $B \leq \left (\frac{r-1}{r}\right )^{2n - 2}.$ Exchange $x = 1-\frac{2a}{r}$ gives $$B = \left (\frac{r-1}{r}\right )^{2(t - 1)} \frac{r}{2} \int^1_{1 - 2/r} x^{n-t} \left(2 - \frac{2}{r} - x \right)^{n-t} dx.$$ After exchange $y = \frac{1}{2}\frac{r}{r-1}x$ we have $$B = \left (\frac{r-1}{r}\right )^{2(n - 1)} 2^{2(n-t)} \frac{r}{2} \int^{\frac{r}{2(r-1)}}_{\frac{r-2}{2(r-1)}} y^{n-t} (1-y)^{n-t} dx,$$ but this integral is not bigger than beta function $$B(n-t+1,n-t+1) = \frac{1}{2(n-t)+1} \frac{1}{\binom{2(n-t)}{n-t}} \leq c \frac{1}{\sqrt{n-t}} 2^{2(t-n)}.$$ Summing up, we have $B \leq c\frac{r}{\sqrt{n-t}} \left (\frac{r-1}{r} \right)^{2n}$ which implies $B \leq c \min \left(1, \frac{r}{\sqrt{n}}\right) \left( \frac{r-1}{r} \right)^{2n}$. Finally, $$q \leq AB \leq c \min (r^2, n) \min \left(1, \frac{r}{\sqrt{n}} \right) \left (\frac{r-1}{r} \right)^{2n} = c \min \left(n, \frac{r^3}{\sqrt{n}} \right) \left (\frac{r-1}{r} \right)^{2n}.$$
The total number of such pairs $(e_1, e_2)$ is $|E|^2$, so $q|E|^2 \leq AB|E|^2 \leq \frac{1}{2}$ for a corresponding value of $c$. Recall that the probability of bad events of the first type tends to zero, so the union bound shows the claim.
\end{proof}
\begin{proof}[Proof of Theorem~\ref{theo2''}] Let $H = (V, E)$ be a given hypergraph with
$$|E| \leq c \frac{r}{n}e^{\frac{n}{r}}.$$ We should show that $H$ has a panchromatic coloring.
Put $a := r + \frac{r^2}{n}$. Since $r \leq c'\frac{n}{\ln n}$, we have $a \leq 2r \leq \frac{c}{2} \frac{n}{\ln n}$, where $c$ is from Theorem~\ref{theo2'}. So we can repeat the proof of Theorem~\ref{theo2}.
The probability of the union of the events of the first type still tends to zero very fast. Now let us note that for $r \geq \sqrt{n}$ we have $\min \left(n, \frac{r^3}{\sqrt{n}} \right) = n$. Hence the expectation of the number of such triples $(e_1,e_2,q)$ that edges $e_1$, $e_2 \in E$ conflict on color $q$ is less than
$$|E|^2cn \left (\frac{a-1}{a} \right)^{2n} = c \frac{r^2}{n}e^{\frac{2n}{r}} \left (1 - \frac{1}{r + \frac{r^2}{n}} \right)^{2n} \leq c \frac{r^2}{n}.$$ Summing up, $$\mathbb{E}(\# \mbox{bad triples}) \leq c \frac{r^2}{n} = \frac{a-r}{2}.$$ So by Markov inequality we have $$\mathbb{P} (\# \mbox{bad triples} > {a-r}) \leq \frac{1}{2}.$$ It means that with positive probability there are $r$ colors such that they are contained in every edge.
\end{proof}
\begin{proof}[Proof of Theorem~\ref{theo3}]
Let $H = (V, E)$ be a hypergraph realizing the quantity $p'(n, r)$. Put $J = (W, F)$, where $W := \{(v,i) | v\in V, 1\leq i \leq m\}$, $F := \{\cup_{v \in e, 1\leq i \leq m} (v, i) | e \in E \}$. Obviously, $J$ is $mn$-uniform and $|F| = |E|$. A subset $A_v := \{(v, i) \in W | 1\leq i \leq m\}$ is called a \textit{block} (note that blocks are disjoint).
Consider an arbitrary coloring of $|W|$ in $mr$ colors. By pigeonhole principle there is a color $i$ such that it appears in at most $\left\lfloor \frac{|W|}{mr} \right\rfloor = \left\lfloor \frac{|V|}{r} \right\rfloor$ vertices. Hence there are at most $\left\lfloor \frac{|V|}{r} \right\rfloor$ blocks with a vertex of color $i$.
Let $V' \subset V$ be a set of such vertices $v \in V$ that the block $A_v$ does not contain color $i$. It has the size at least $|V| - \left\lfloor \frac{|V|}{r} \right\rfloor = \left\lceil \frac{r-1}{r}|V| \right\rceil$, which implies the existence of an edge $e \in E$ such that $e \subset V'$.
So the corresponding edge of $J$ does not contain color $i$, hence $p(mn, mr) \leq |F| = p'(n,r)$. \end{proof}
\begin{proof}[Proof of Corollary~\ref{col}]
Obviously, $$p(n,r) \leq p \left (n, \left\lfloor \frac{r}{k} \right\rfloor k \right) \leq p \left (\left\lceil \frac{n}{\left\lfloor r/k \right\rfloor k} \right\rceil \left\lfloor \frac{r}{k} \right\rfloor k , \left\lfloor \frac{r}{k} \right\rfloor k \right),$$ so by Theorem~\ref{theo3} $p (n, r) \leq p' \left (\left\lceil \frac{n}{\left\lfloor r/k \right\rfloor k} \right\rceil k, k \right) \leq p' \left (\left\lceil \frac{n}{r - k + 1} \right\rceil k, k \right)$.
In fact, estimate (\ref{2}) is proved for $p'(n,r)$ (see~\cite{shaba1}). So let us put $k := \alpha \frac{n}{r}$ and apply (\ref{2}). It gives $p\left(\frac{k^2}{\alpha},k \right) \leq c \frac{k^3\ln k}{k} \left (\frac{k}{k-1} \right)^{\frac{k^2}{\alpha}} = c k^2 \ln k \cdot e^{\frac{k}{\alpha}}$ showing the claim.
\end{proof}
\begin{proof} [Proof of Theorem~\ref{theo5}]
Let us construct a hypergraph $H_1 = (V_1, E_1)$ in the following way. Fix an integer $t | n$ and put $k := \left\lceil \left (\frac{r}{r-1} \right)^t \right\rceil \frac{n}{t}$,
then $V := \{ (i, j) | 1 \leq i \leq k, 1 \leq j \leq rt \} = [k] \times [rt]$. Let the set of edges be
$$E := \bigcup_{A \subset [rt]} \bigcup_{\substack{0 \leq i_{\alpha} < k \\ \alpha \in A}} \bigcup_{\substack{B \subset [k] \\ |B| = \frac{n}{t}}} \left \{ \left ( (\beta + i_\alpha)\mbox{ mod } k, \alpha \right ) | \alpha \in A, \beta \in B \right \}.$$ Note that
$$|E| \leq \binom{rt}{t} k^t \binom{k}{n/t} \leq (rt)^t \left( \left (\frac{r}{r-1} \right)^t \frac{n}{t}\right)^t \left (e \left (\frac{r}{r-1} \right)^t\right)^{n/t} \leq (rn)^t \left (\frac{r}{r-1}\right)^{t^2} e^{n/t} \left (\frac{r}{r-1}\right)^n.$$
Put $t := \sqrt{\frac{n}{\ln n}}$. Since $r = o(\sqrt{\frac{n}{\ln n}})$, one can give an estimate $(rn)^t \leq n^{2t} = e^{2t\ln n} = e^{o(n/r)}$. Also, $\left (\frac{r}{r-1}\right)^{t^2} = \left(\frac{r}{r-1}\right)^{o(n)}$ and $e^{n/t} = e^{o(n/r)}$. Summing up, $|E(H)| = \left( \frac{r}{r-1} + o(1)\right)^n$.
Let us show that $H$ has no panchromatic coloring. Suppose the contrary and consider a panchromatic coloring. Let us call a color $q$ a \textit{minor color} for a line $[k] \times \{i\}$ if it has at most $\left\lfloor \frac{k}{r} \right\rfloor$ vertices. By pigeonhole principle every line $[k] \times \{i\}$ has a minor color.
Again, by pigeonhole principle there is a set $A \subset [rt]$ of lines with the same minor color $q$ such that $|A| \geq t$.
Next, for any fixed $\beta$ the proportion of such $\{ i_\alpha \}_{\alpha\in A}$ that $\left \{ \left ( (\beta + i_\alpha)\mbox{ mod } k, \alpha \right ) | \alpha \in A \right \}$
has no color $q$, is at least $\left (\frac{r-1}{r} \right)^t$. By the linearity of expectation there is a choice of $\{ i_\alpha \}_{\alpha\in A}$ such that at least $k \left (\frac{r-1}{r} \right)^t = \frac{n}{t}$ indices $\beta \in B$ give $q$-free sets $\left \{ \left ( (\beta + i_\alpha)\mbox{ mod } k, \alpha \right ) | \alpha \in A \right \}$. So there is an edge without color $q$, which gives a contradiction.
\end{proof}
\end{document} | arXiv |
Noncrossing partition
In combinatorial mathematics, the topic of noncrossing partitions has assumed some importance because of (among other things) its application to the theory of free probability. The number of noncrossing partitions of a set of n elements is the nth Catalan number. The number of noncrossing partitions of an n-element set with k blocks is found in the Narayana number triangle.
Definition
A partition of a set S is a set of non-empty, pairwise disjoint subsets of S, called "parts" or "blocks", whose union is all of S. Consider a finite set that is linearly ordered, or (equivalently, for purposes of this definition) arranged in a cyclic order like the vertices of a regular n-gon. No generality is lost by taking this set to be S = { 1, ..., n }. A noncrossing partition of S is a partition in which no two blocks "cross" each other, i.e., if a and b belong to one block and x and y to another, they are not arranged in the order a x b y. If one draws an arch based at a and b, and another arch based at x and y, then the two arches cross each other if the order is a x b y but not if it is a x y b or a b x y. In the latter two orders the partition { { a, b }, { x, y } } is noncrossing.
Crossing: a x b y
Noncrossing: a x y b
Noncrossing: a b x y
Equivalently, if we label the vertices of a regular n-gon with the numbers 1 through n, the convex hulls of different blocks of the partition are disjoint from each other, i.e., they also do not "cross" each other. The set of all non-crossing partitions of S is denoted ${\text{NC}}(S)$. There is an obvious order isomorphism between ${\text{NC}}(S_{1})$ and ${\text{NC}}(S_{2})$ for two finite sets $S_{1},S_{2}$ with the same size. That is, ${\text{NC}}(S)$ depends essentially only on the size of $S$ and we denote by ${\text{NC}}(n)$ the non-crossing partitions on any set of size n.
Lattice structure
Like the set of all partitions of the set { 1, ..., n }, the set of all noncrossing partitions is a lattice when partially ordered by saying that a finer partition is "less than" a coarser partition. However, although it is a subset of the lattice of all partitions, it is not a sublattice of the lattice of all partitions, because the join operations do not agree. In other words, the finest partition that is coarser than both of two noncrossing partitions is not always the finest noncrossing partition that is coarser than both of them.
Unlike the lattice of all partitions of the set, the lattice of all noncrossing partitions of a set is self-dual, i.e., it is order-isomorphic to the lattice that results from inverting the partial order ("turning it upside-down"). This can be seen by observing that each noncrossing partition has a complement. Indeed, every interval within this lattice is self-dual.
Role in free probability theory
The lattice of noncrossing partitions plays the same role in defining free cumulants in free probability theory that is played by the lattice of all partitions in defining joint cumulants in classical probability theory. To be more precise, let $({\mathcal {A}},\phi )$ be a non-commutative probability space (See free probability for terminology.), $a\in {\mathcal {A}}$ a non-commutative random variable with free cumulants $(k_{n})_{n\in \mathbb {N} }$. Then
$\phi (a^{n})=\sum _{\pi \in {\text{NC}}(n)}\prod _{j}k_{j}^{N_{j}(\pi )}$
where $N_{j}(\pi )$ denotes the number of blocks of length $j$ in the non-crossing partition $\pi $. That is, the moments of a non-commutative random variable can be expressed as a sum of free cumulants over the sum non-crossing partitions. This is the free analogue of the moment-cumulant formula in classical probability. See also Wigner semicircle distribution.
References
• Germain Kreweras, "Sur les partitions non croisées d'un cycle", Discrete Mathematics, volume 1, number 4, pages 333–350, 1972.
• Rodica Simion, "Noncrossing partitions", Discrete Mathematics, volume 217, numbers 1–3, pages 367–409, April 2000.
• Roland Speicher, "Free probability and noncrossing partitions", Séminaire Lotharingien de Combinatoire, B39c (1997), 38 pages, 1997
| Wikipedia |
A general framework for validated continuation of periodic orbits in systems of polynomial ODEs
JCD Home
A self-consistent dynamical system with multiple absolutely continuous invariant measures
January 2021, 8(1): 33-58. doi: 10.3934/jcd.2021003
The geometry of convergence in numerical analysis
George W. Patrick
Department of Mathematics and Statistics, University of Saskatchewan, Saskatoon, SK S7N5E6, Canada
Received September 2019 Revised June 2020 Published August 2020
The domains of mesh functions are strict subsets of the underlying space of continuous independent variables. Spaces of partial maps between topological spaces admit topologies which do not depend on any metric. Such topologies geometrically generalize the usual numerical analysis definitions of convergence.
Keywords: Numerical method, convergence, covariance, geometric integration, hypertopology.
Mathematics Subject Classification: Primary: 65LXX; Secondary: 54B20.
Citation: George W. Patrick. The geometry of convergence in numerical analysis. Journal of Computational Dynamics, 2021, 8 (1) : 33-58. doi: 10.3934/jcd.2021003
R. Abraham and J. E. Marsden, Foundations of Mechanics, 2nd edition, Addison-Wesley, 1978. Google Scholar
U. M. Ascher and L. R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-algebraic Equations, SIAM, 1998. doi: 10.1137/1.9781611971392. Google Scholar
K. Back, Concepts of similarity for utility functions, J. Math. Econom., 15 (1986), 129-142. doi: 10.1016/0304-4068(86)90004-2. Google Scholar
G. Beer, On the Fell topology, Set-valued Analysis, 1 (1993), 69-80. doi: 10.1007/BF01039292. Google Scholar
G. Beer, Topologies on Closed and Closed Convex Sets, Kluwer Academic Publishers Group, Dordrecht, 1993. doi: 10.1007/978-94-015-8149-3. Google Scholar
G. Beer, A. Caserta, G. D. Maio and R. Lucchetti, Convergence of partial maps, J. Math. Anal. Appl., 419 (2014), 1274-1289. doi: 10.1016/j.jmaa.2014.05.040. Google Scholar
R. D. Canary, D. B. A. Epstein and P. L. Green, Notes on notes of Thurston, in Fundamentals of Hyperbolic Geometry: Selected Expositions, London Math. Soc. Lecture Note Ser., 328, Cambridge Univ. Press, Cambridge, 2006. Google Scholar
C. Chabauty, Limite dénsembles et géométrie des nombres, Bull. Soc. Math. France, 78 (1950), 143-151. Google Scholar
C. Cuell and G. W. Patrick, Geometric discrete analogues of tangent bundles and constrained Lagrangian systems, J. Geom. Phys., 59 (2009), 976-997. doi: 10.1016/j.geomphys.2009.04.005. Google Scholar
P. de la Harpe, Spaces of closed subgroups of locally compact groups, preprint, arXiv: 0807.2030. Google Scholar
J. M. G. Fell, A Hausdorff topology for the closed subsets of a locally compact non-Hausdorff space, Proc. Amer. Math. Soc., 13 (1962), 472-476. doi: 10.1090/S0002-9939-1962-0139135-6. Google Scholar
A. C. Hansen, A theoretical framework for backward error analysis on manifolds, J. Geom. Mech., 3 (2011), 81-111. doi: 10.3934/jgm.2011.3.81. Google Scholar
A. Illanes and S. B. Nadler, Hyperspaces. Fundamentals and Recent Advances., Marcel Dekker, Inc., New York, 1999. Google Scholar
A. Iserles, A First Course in the Numerical Analysis of Differential Equations, 2nd edition, Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge, 2009. Google Scholar
A. Iserles, H. Z. Munthe-Kass, S. P. Norsett and A. Zanna, Lie-group methods, Acta Numerica, 9 (2000), 215-365. doi: 10.1017/S0962492900002154. Google Scholar
K. Kuratowski, Sur l'espace des fonctions partielles, Ann. Mat. Pura Appl. (4), 40 (1955), 61–67. doi: 10.1007/BF02416522. Google Scholar
K. Kuratowski, Topology. Vol. I, Academic Press, New York-London; Państwowe Wydawnictwo Naukowe, Warsaw, 1966. Google Scholar
K. Kuratowski, Topology. Vol. II, Academic Press, New York-London; Pańtwowe Wydawnictwo Naukowe Polish Scientific Publishers, Warsaw, 1968. Google Scholar
R. Lucchetti and A. Pasquale, A new approach to hyperspace theory, J. Convex Anal., 1 (1994), 173-193. Google Scholar
J. E. Marsden, G. W. Patrick and S. Shkoller, Multisymplectic geometry, variational integrators, and nonlinear PDEs, Comm. Math. Phys., 199 (1998), 351-395. doi: 10.1007/s002200050505. Google Scholar
J. E. Marsden and M. West, Discrete mechanics and variational integrators, Acta Numerica, 10 (2001), 357-514. doi: 10.1017/S096249290100006X. Google Scholar
K. Matsuzaki, The Chabauty and the Thurston topologies on the hyperspace of closed subsets, J. Math. Soc. Japan, 69 (2017), 263-292. doi: 10.2969/jmsj/06910263. Google Scholar
E. Michael, Topologies on spaces of subsets, Trans. Amer. Math. Soc., 71 (1951), 152-182. doi: 10.1090/S0002-9947-1951-0042109-4. Google Scholar
J. R. Munkres, Topology, Prentice Hall, 2000. Google Scholar
S. B. Nadler, Hyperspaces of Sets. A Text with Research Questions, Marcel Dekker, Inc., New York-Basel, 1978. Google Scholar
R. S. Palais, When proper maps are closed, Proc. Amer. Math. Soc., 24 (1970), 835-836. doi: 10.2307/2037337. Google Scholar
G. W. Patrick and C. Cuell, Error analysis of variational integrators of unconstrained Lagrangian systems, Numerische Mathematik, 113 (2009), 243-264. doi: 10.1007/s00211-009-0245-3. Google Scholar
W. Rudin, Functional Analysis, McGraw-Hill, 1973. Google Scholar
V. Runde, A Taste of Topology, Universitext, Springer, New York, 2005. Google Scholar
[30] M. Schatzman, Numerical Analysis: A Mathematical Introduction, Clarendon Press, Oxford, 2002. Google Scholar
[31] E. Süli and D. F. Mayer, An Introduction to Numerical Analysis, Cambridge University Press, Cambridge, 2003. doi: 10.1017/CBO9780511801181. Google Scholar
S. Willard, General Topology, Addison-Wesley, 1970. Google Scholar
Figure 1. Illustrating convergence in the lower and upper Vietoris topologies. Right: a subbasic neighbourhood of a subset $ A $, in the upper Vietoris topology, is defined by an open set $ U $. $ A $ is contained in $ U $ and the green sets are in the subbasic neighbourhood are contained in $ U $. As $ U $ shrinks, every point in the green sets in drawn to some point in $ A $—everything approximable is in $ {\rm cl}A $. At left, in the lower Vietoris topology, the green sets only have to intersect $ U $, and shrinking $ U $ around a single point of $ A $ generates approximations when the green sets also meet $ U $—everything in $ A $ is approximable
Figure 2. Left: a neighbourhood of the geometric topology is defined by an open set $ U $, a compact set $ K $, and open sets $ V_i $. Containment within $ U $ has to occur only inside the compact set $ K $, with effect that a convergent sequence of subsets $ \langle A_i\rangle $ has $ K\cap A_i $ finally contained in $ U $, say for some $ i\ge N $, but larger $ K $ require larger $ N $. As shown the set $ A $ is inside the neighbourhood because its intersection with $ K $ is contained in $ U $ and contacts each $ V_i $. Smaller $ U $, and larger $ K $, and more and smaller $ V_i $, correspond to a smaller more restrictive neighbourhood. Right: a basic neighbourhood of a compact set $ B $ in the geometric topology. A subset of $ X $ is inside such a neighbourhood if it is contained in $ U $ and contacts each $ V_i $
Figure 3. Left: the discrete approximations $ y_i $, $ i = 1, 2, 3\ldots $ (circles) are limiting to a continuous $ y $. Shown (squares on red curves) are three selections of subsequences from the graphs of $ y_i $. Every such subsequence converges to the graph of $ y $, and that graph is the limit of such subsequences. Right: an open neighbourhood of the red graph is defined by a compact set $ K $, an open set $ U $, and open sets $ V_i $. $ K $, which may be restricted to a product of compact sets, may be thought of as a frame within which proximity to the graph is controlled by $ U $. The other black curves are in the neighbourhood because they also contact the $ V_i $. Larger $ K $, smaller $ U $, and more and smaller $ V_i $, correspond to smaller neighbourhoods
Luca Dieci, Cinzia Elia. Smooth to discontinuous systems: A geometric and numerical method for slow-fast dynamics. Discrete & Continuous Dynamical Systems - B, 2018, 23 (7) : 2935-2950. doi: 10.3934/dcdsb.2018112
Enrico Gerlach, Charlampos Skokos. Comparing the efficiency of numerical techniques for the integration of variational equations. Conference Publications, 2011, 2011 (Special) : 475-484. doi: 10.3934/proc.2011.2011.475
Cheng Wang. Convergence analysis of the numerical method for the primitive equations formulated in mean vorticity on a Cartesian grid. Discrete & Continuous Dynamical Systems - B, 2004, 4 (4) : 1143-1172. doi: 10.3934/dcdsb.2004.4.1143
Hongguang Xiao, Wen Tan, Dehua Xiang, Lifu Chen, Ning Li. A study of numerical integration based on Legendre polynomial and RLS algorithm. Numerical Algebra, Control & Optimization, 2017, 7 (4) : 457-464. doi: 10.3934/naco.2017028
Sanjit Kumar Mohanty, Rajani Ballav Dash. A quadrature rule of Lobatto-Gaussian for numerical integration of analytic functions. Numerical Algebra, Control & Optimization, 2021 doi: 10.3934/naco.2021031
Sergio Blanes, Fernando Casas, Alejandro Escorihuela-Tomàs. Applying splitting methods with complex coefficients to the numerical integration of unitary problems. Journal of Computational Dynamics, 2021 doi: 10.3934/jcd.2021022
Sebastián J. Ferraro, David Iglesias-Ponte, D. Martín de Diego. Numerical and geometric aspects of the nonholonomic SHAKE and RATTLE methods. Conference Publications, 2009, 2009 (Special) : 220-229. doi: 10.3934/proc.2009.2009.220
Ruijun Zhao, Yong-Tao Zhang, Shanqin Chen. Krylov implicit integration factor WENO method for SIR model with directed diffusion. Discrete & Continuous Dynamical Systems - B, 2019, 24 (9) : 4983-5001. doi: 10.3934/dcdsb.2019041
Hao-Chun Lu. An efficient convexification method for solving generalized geometric problems. Journal of Industrial & Management Optimization, 2012, 8 (2) : 429-455. doi: 10.3934/jimo.2012.8.429
Zhanyuan Hou. Geometric method for global stability of discrete population models. Discrete & Continuous Dynamical Systems - B, 2020, 25 (9) : 3305-3334. doi: 10.3934/dcdsb.2020063
Wen Li, Song Wang, Volker Rehbock. A 2nd-order one-point numerical integration scheme for fractional ordinary differential equations. Numerical Algebra, Control & Optimization, 2017, 7 (3) : 273-287. doi: 10.3934/naco.2017018
Michael Anderson, Atsushi Katsuda, Yaroslav Kurylev, Matti Lassas and Michael Taylor. Metric tensor estimates, geometric convergence, and inverse boundary problems. Electronic Research Announcements, 2003, 9: 69-79.
Aurore Back, Emmanuel Frénod. Geometric two-scale convergence on manifold and applications to the Vlasov equation. Discrete & Continuous Dynamical Systems - S, 2015, 8 (1) : 223-241. doi: 10.3934/dcdss.2015.8.223
Annalisa Cesaroni, Valerio Pagliari. Convergence of nonlocal geometric flows to anisotropic mean curvature motion. Discrete & Continuous Dynamical Systems, 2021, 41 (10) : 4987-5008. doi: 10.3934/dcds.2021065
Shuang Liu, Xinfeng Liu. Krylov implicit integration factor method for a class of stiff reaction-diffusion systems with moving boundaries. Discrete & Continuous Dynamical Systems - B, 2020, 25 (1) : 141-159. doi: 10.3934/dcdsb.2019176
Antonia Katzouraki, Tania Stathaki. Intelligent traffic control on internet-like topologies - integration of graph principles to the classic Runge--Kutta method. Conference Publications, 2009, 2009 (Special) : 404-415. doi: 10.3934/proc.2009.2009.404
Lekbir Afraites, Chorouk Masnaoui, Mourad Nachaoui. Shape optimization method for an inverse geometric source problem and stability at critical shape. Discrete & Continuous Dynamical Systems - S, 2022, 15 (1) : 1-21. doi: 10.3934/dcdss.2021006
Jahnabi Chakravarty, Ashiho Athikho, Manideepa Saha. Convergence of interval AOR method for linear interval equations. Numerical Algebra, Control & Optimization, 2021 doi: 10.3934/naco.2021006
Jinyan Fan, Jianyu Pan. On the convergence rate of the inexact Levenberg-Marquardt method. Journal of Industrial & Management Optimization, 2011, 7 (1) : 199-210. doi: 10.3934/jimo.2011.7.199
Stefan Kindermann. Convergence of the gradient method for ill-posed problems. Inverse Problems & Imaging, 2017, 11 (4) : 703-720. doi: 10.3934/ipi.2017033
Impact Factor: | CommonCrawl |
Economics Meta
Economics Stack Exchange is a question and answer site for those who study, teach, research and apply economics and econometrics. It only takes a minute to sign up.
Proper definition of extensive form game
Consider the following game: Let $N := \{1,2,3,4\}$ denote a set of agents. Going from 1 to 4 each agent can decide how many of the remaining agents he wants to integrate into a coalition. The strategy sets are given by $S_1 := \{1,2,3,4\}$, $S_2 := \{1,2,3\}$, $S_3 := \{(1,1),(1,2),(2,1),(2,2)\}$ and $S_4 := \{(1,1,1)\}$. I want to generalize the game for $|N| = n$. So basically agent 1 picks a number $s_1 \in N$. Then agent $1 + s_1$ picks a number $s_{1+s_1} \in \{1,\ldots,n-s_1\}$ and so forth. Eventually there exists an agent who integrates all the remaining agents $\exists j \in N : s_j = 1+n-j$.
What's a proper definition of this simple game? What are the strategy sets?
game-theory extensive-games
cluelessclueless
$\begingroup$ What do you mean by 'proper definition'? Also, aren't your strategy sets already given? Are you looking for a closed formula for the strategy sets? $\endgroup$
– Giskard
$\begingroup$ Well, by proper I orginally meant a tuple of nodes, edges, histories etc. But that's probably overkill anyway. For my purpose it would suffice to have a closed formula of strategy sets $S_i$ for $i \in \{1,\ldots,n\}$, where $A_i = \{1,\ldots,n+1-i\}$ denote the action sets. $\endgroup$
– clueless
Let the set of players be $N=\{1,\dots,n\}$.
According to my understand your description of the game, I take the following statements to be true:
Each player chooses a number of players to integrate, not players with specific identities. As a result, the player making the choice may or may not be included in the coalition.
Each player has to choose at least 1 player, if still available.
Each player moves exactly once.
The game is with perfect information.
Under the above interpretation, player $i$'s ($i\ge2$) action space would be $A_i=\{0,1,\dots,n+1-i\}$, as, in principle, $i$ could choose at most $n+1-i$ other players (when all players $j<i$ chose $1$) and at least $0$ (when all previous players have exhausted the player list). An exception applies to the first player, where the option $0$ is not feasible. Thus $A_1=\{1,\dots,n\}$.
Player 1's strategy space would be $S_1=\{1,\dots,n\}$. Player 2's would be $S_2=\{1,\dots,n-s_1\}$, since after $s_1$ players are picked by player 1, there are only $n-s_1$ players left to be picked by player 2. Carrying this argument forward, player $i$'s strategy space would be $S_i=\{1,\dots,n-s_1-\cdots-s_{i-1}\}$.
Generalizing from the above reasoning and taking into account boundary cases, let history at stage $i$ be $h^i=(s_0,s_1,\dots,s_{i-1})$, where we set $s_0=0$. (In general, though, stages should be indexed by a parameter different from the player index. But in your game, since each player moves exactly once, we can use the same index for stages as well as players to economize notation.) The history dependent strategy space for player $i$ would thus be \begin{equation} S_i(h^i)= \begin{cases} \{1,\dots,n-\sum_{j=0}^{i-1}s_j\} & \text{if } n-\sum_{j=0}^{i-1}s_j\ge 1 \\ \{0\} & \text{otherwise}. \end{cases} \end{equation}
Herr K.Herr K.
I was carefully rereading the underlying paper (Bloch, 1996) and found what I was looking for. Let $N = \{1,\ldots,n\}$ denote the set of agents and let $\Pi_{\{1, \ldots, i-1\}}$ denote the set of coalition structures of $\{1, \ldots, i-1\}$ for all $i \in \{2,\ldots,n\}$. A strategy in the game of coalition size is a mapping $s_i : \Pi_{\{1, \ldots, i-1\}} \to \{1, \ldots, n-(i-1)\}$ for all $i \in \{2,\ldots,n\}$. Further $s_1 \in N$.
Example with $n=4$. With some abuse of notation (saving curly brackets) we get \begin{align} &s_1 \in \{1,2,3,4\}\\ &s_2:\{1\} \to \{1,2,3\}\\ &s_3:\{\{1,2\},\{12\}\} \to \{1,2\}\\ &s_4:\{\{1,2,3\},\{12,3\},\{1,23\},\{123\}\} \to \{1\} \end{align}
Bloch (1996): "Sequential Formation of Coalitions in Games with Externalities and Fixed Payoff Division", GEB
$\begingroup$ This does not answer your own question. Which part of it is the closed formula? $\endgroup$
$\begingroup$ What do you mean by closed formula then? In my opinion it is the mapping $s_i : \Pi_{\{1,\ldots,i-1\}} \to \{1,\ldots,n-(i-1)\} =: S_i$. That's precisely the $S_i$ of Herr K., no? You're right that now we don't get the same $S_i$'s as in the question, though. $\endgroup$
$\begingroup$ I would not call a definition of $S_i$ that says all elements of the set are mapping such that... a closed form. I was also a bit frustrated that you did not reveal the underlying paper in your original question and that in your answer you used none of the elements that you gave in your clarifying comment. I did some reading though and I realize now that there is no exact definition for closed form solutions. If you edit your answer I will remove the downvote. (The system does not let me change the vote without edits.) $\endgroup$
$\begingroup$ It was not my intention to hide the paper. I was just confused. I'm not too familiar with extensive form games and was just thinking that a strategy set contains all potential moves at every node. Which is obviously not the case here. So I thought of reframing the game without the set of partitions, because you don't need them to define the game. $\endgroup$
Thanks for contributing an answer to Economics Stack Exchange!
Not the answer you're looking for? Browse other questions tagged game-theory extensive-games or ask your own question.
Identifying Nash equilibria in extensive form game
Terminology for "part" of extensive form game
Extensive Form Games
Extensive form of multiplayer games
Sequential Game is Extensive form game?
Bayes Correlated Equilibrium with complete information
Extensive Form Representation
Understanding the properties of extensive form games | CommonCrawl |
\begin{definition}[Definition:Directed Subset]
Let $\struct {S, \precsim}$ be a preordered set.
Let $H$ be a non-empty subset of $S$.
Then $H$ is a '''directed subset''' of $S$ {{iff}}:
:$\forall x, y \in H: \exists z \in H: x \precsim z$ and $y \precsim z$
\end{definition} | ProofWiki |
Let $r$ be a complex number such that $r^5 = 1$ and $r \neq 1.$ Compute
\[(r - 1)(r^2 - 1)(r^3 - 1)(r^4 - 1).\]
We can write $r^5 - 1 = 0,$ which factors as
\[(r - 1)(r^4 + r^3 + r^2 + r + 1) = 0.\]Since $r \neq 1,$ $r^4 + r^3 + r^2 + r + 1 = 0.$
To compute the product, we can arrange the factors in pairs:
\begin{align*}
(r - 1)(r^2 - 1)(r^3 - 1)(r^4 - 1) &= [(r - 1)(r^4 - 1)][(r^2 - 1)(r^3 - 1)] \\
&= (r^5 - r - r^4 + 1)(r^5 - r^2 - r^3 + 1) \\
&= (1 - r - r^4 + 1)(1 - r^2 - r^3 + 1) \\
&= (2 - r - r^4)(2 - r^2 - r^3) \\
&= 4 - 2r^2 - 2r^3 - 2r + r^3 + r^4 - 2r^4 + r^6 + r^7 \\
&= 4 - 2r^2 - 2r^3 - 2r + r^3 + r^4 - 2r^4 + r + r^2 \\
&= 4 - r - r^2 - r^3 - r^4 \\
&= 5 - (1 + r + r^2 + r^3 + r^4) = \boxed{5}.
\end{align*} | Math Dataset |
\begin{document}
\thispagestyle{empty}
\
\
\
\begin{center}
{\Large{\bf{Twist maps for non-standard quantum algebras }}}
{\Large{\bf{and discrete Schr\"odinger symmetries}}}
\end{center}
\begin{center} A. Ballesteros$\dagger$, F.J. Herranz$\dagger$, J. Negro$\ddagger$ and L.M. Nieto$\ddagger$ \end{center}
\begin{center} {\it ${\dagger}$ Departamento de F\1sica\\ Universidad de Burgos, E-09001 Burgos, Spain} \end{center}
\begin{center} {\it ${\ddagger}$ Departamento de F\1sica Te\'orica\\ Universidad de Valladolid, E-47011 Valladolid, Spain} \end{center}
\begin{abstract}
The minimal twist map introduced by Abdesselam {\em et al} \cite{Abde} for the non-standard (Jordanian) quantum $sl(2,{\mathbb R})$ algebra is used to construct the twist maps for two different non-standard quantum deformations of the (1+1) Schr\"odinger algebra. Such deformations are, respectively, the symmetry algebras of a space and a time uniform lattice discretization of the $(1+1)$ free Schr\"odinger equation. It is shown that the corresponding twist maps connect the usual Lie symmetry approach to these discrete equations with non-standard quantum deformations. This relationship leads to a clear interpretation of the deformation parameter as the step of the uniform (space or time) lattice.
\end{abstract}
\sect{Introduction}
The non-standard quantum deformation of the $sl(2,{\mathbb R})$ algebra (also known as Jordanian or $h$-deformation) \cite{Demidov,Zakr,Ohn,nonsb,Ogi,nonsc,nonsd} has induced the construction of several non-standard quantum algebras which are naturally related with $sl(2,{\mathbb R})$ by means of either a central extension ($gl(2)$) or contraction (the $(1+1)$-dimensional Poincar\'e algebra ${\cal P}$). The contraction of the quantum $gl(2)$ algebra leads to a quantum harmonic oscillator $h_4$ algebra which, in turn, can be interpreted as a central extension of the Poincar\'e algebra ${\cal P}$. These relationships have been studied in \cite{boson} within the context of boson representations and are displayed in the l.h.s.\ of the following diagram: $$ \begin{CD} U_z(sl(2,{\mathbb R}))@>>{\mbox{\footnotesize{central extension}}}> U_z(gl(2))@>>{\mbox{\footnotesize{Hopf subalgebra}}}> U_\tau({\cal S})\longrightarrow \mbox{\footnotesize{Discrete time SE}}\\ @VV{\varepsilon \to 0}V @VV{\varepsilon \to 0}V\\ U_z({\cal P})@>>{\mbox{\footnotesize{central extension}}}> U_z(h_4)@>>{\mbox{\footnotesize{Hopf subalgebra}}}> U_\sigma({\cal S})\longrightarrow \mbox{\footnotesize{Discrete space SE}} \end{CD} $$ The cornerstone of the above four quantum algebras is the triangular Hopf algebra with generators $J_3,J_+$ verifying $[J_3,J_+]=2 J_+$, and with classical $r$-matrix \cite{Drinfelda,Drinfeldb} \begin{equation} r=z J_3\wedge J_+ . \label{aaa} \end{equation}
The deformed commutator, coproduct and universal quantum $R$-matrix are: \begin{equation}
[J_3,J_+]=\frac{e^{2 z J_+}-1}{z}\qquad
\Delta(J_+)=1\otimes J_+ + J_+ \otimes 1\qquad \Delta(J_3)=1\otimes J_3 + J_3 \otimes e^{2 z J_+} \label{aa} \end{equation} \begin{equation} {\cal R}=\exp\{-z J_+\otimes J_3\}\exp\{z J_3\otimes J_+\}. \label{ab} \end{equation} This structure is a Hopf (Borel) subalgebra of all the quantum algebras that we have previously mentioned. We recall that the Jordanian twisting element for the Borel algebra was given in \cite{Ogi}, the expression for the $R$-matrix (\ref{ab}) was deduced in \cite{nonsd} and another construction for ${\cal R}$ can be found in \cite{nonsc}. The quantum algebra (\ref{aa}) underlies the approach to physics at the Planck scale introduced in \cite{Majida, Majidb}.
The triangular nature of a quantum deformation (like (\ref{aa})) ensures the existence of a twist operator (as the one given in \cite{Ogi}) which relates the (classical) cocommutative coproduct with the (deformed) non-cocommutative one \cite{Drinfeldb}. This means that there should exist an invertible twist map which turns the deformed commutation rules into usual Lie commutators. In this respect, a class of twist maps for the non-standard quantum $sl(2,{\mathbb R})$ algebra has been explicitly constructed by Abdesselam {\em et al} \cite{Abde}; amongst these maps we will consider the simplest one, which is called the `minimal twist map'. A first aim of this paper is to implement the minimal twist map in the quantum algebras $U_z(gl(2))$, $U_z({\cal P})$ and $U_z(h_4)$, showing their relationships with $U_z(sl(2,{\mathbb R}))$ through either contraction or central extension; this task is carried out in the section 2. In relation with this kind of twists, we recall that a different deformation map for $U_z({\cal P})$ was introduced in \cite{Khorrami} and a similar construction for $U_z(e(3))$ was given in \cite{e3}. Jordanian twists for $sl(n)$ and for some inhomogeneous Lie algebras have been also studied in \cite{Kulisha}, and a general construction of a chain of Jordanian twists has been introduced in \cite{Kulishb} and applied to the semisimple Lie algebras of the Cartan series $A_n$, $B_n$ and $D_n$.
On the other hand, $gl(2)$ and $h_4$ are Lie subalgebras of the centrally extended $(1+1)$-dimensional Schr\"odinger algebra ${\cal S}$ \cite{Hagen,Nied}. These Lie subalgebra embeddings have been implemented at a quantum algebra level and two non-standard quantum Schr\"odinger algebras have been obtained from them by imposing that either $U_z(gl(2))$ or $U_z(h_4)$ remains as a Hopf subalgebra. The former \cite{twotime}, $U_\tau({\cal S})\supset U_z(gl(2))$, has been shown to be the symmetry algebra of a time discretization of the heat or (time imaginary) Schr\"odinger equation (SE) on a uniform lattice. Likewise,
as we shall show in this paper, the latter \cite{twospace}, $U_\sigma({\cal S})\supset U_z(h_4)$, can be related with a space discretization of the SE also on a uniform lattice. These connections are displayed in the r.h.s.\ of the above diagram. Obviously, when the deformation parameters $z,\tau,\sigma$ go to zero we recover the usual Lie algebra picture and the continuous SE.
In this context of discrete symmetries, we recall that quantum algebras have been connected with different versions of spacetime lattices through several algebraic constructions that have no direct relationship with the usual Lie symmetry theory \cite{LRN,FS,null}. Recent works \cite{Winternitz} have also developed new techniques for dealing with the symmetries of difference or differential-difference equations and have tried to adapt in this field the standard methods that have been so successful when applied to differential equations. An exhaustive study for the discretization on $q$-lattices of classical linear differential equations has shown that their symmetries obeyed to $q$-deformed commutation relations with respect to the Lie algebra structure of the continuous symmetries \cite{FVa,FVb,Dobrev}. However, Hopf algebra structures underlying these $q$-symmetry algebras have been not found. When the discretization of linear equations is made on uniform lattices it seems that the relevant symmetries preserve the Lie algebra structure \cite{Luismi,Javier}. Perhaps, this is the reason why the symmetry approach to these equations has not been directly related to quantum algebras.
The second and main objective of this paper is to relate the discrete SE's and their associated differential-difference symmetry operators provided by the quantum Schr\"odinger algebras $U_\sigma({\cal S})$, $U_\tau({\cal S})$ with the results concerning a discrete SE and operators obtained in \cite{Luismi} by following a Lie symmetry approach. Since the latter operators close the Schr\"odinger Lie algebra ${\cal S}$, the crucial point in our procedure is to find out the twist maps for the Hopf algebras $U_\sigma({\cal S})$, $U_\tau({\cal S})$; these are straightforwardly obtained from the maps corresponding to their Hopf subalgebras $U_z(h_4)$ and $U_z(gl(2))$. These nonlinear changes of basis allow us to write explicitly the Hopf Schr\"odinger algebras with classical commutators and non-cocommutative coproduct, so that the connection with the results of \cite{Luismi} can be established. The two quantum algebras $U_\sigma({\cal S})$, $U_\tau({\cal S})$ are analyzed separately in the sections 3 and 4, respectively. Finally, some remarks close the paper.
\sect{Twist maps for non-standard quantum algebras}
\subsect{Non-standard quantum $sl(2,{\mathbb R})$ algebra}
The commutation rules and coproduct of the Hopf algebra $U_z(sl(2,{\mathbb R}))$ in the original form deduced in \cite{Ohn} are given by \begin{eqnarray} &&[H,X]=2\,\frac{\sinh (zX)}{z}\qquad [H,Y]=-Y\cosh (z X) - \cosh(z X)\, Y \qquad [X,Y]=H\cr &&\Delta(X)=1\otimes X+X\otimes 1 \qquad \Delta(Y)=e^{-zX}\otimes Y +Y\otimes e^{zX}\cr &&\Delta(H)=e^{-zX}\otimes H +H\otimes e^{zX} . \label{ba} \end{eqnarray} The nonlinear invertible map defined by \cite{Negro} \begin{equation} J_+=X\qquad J_3=e^{zX}H\qquad J_-=e^{zX}\left(Y- z \sinh(zX) /4 \right) \label{bb} \end{equation} allows us to write the former structure of $U_z(sl(2,{\mathbb R}))$ as follows: \begin{eqnarray} &&[J_3,J_+ ]= \frac{e^{2 z J_+} -1 } z \qquad [J_3,J_-]=-2 J_- +z J_3^2 \qquad [J_+ ,J_-]= J_3 \cr \label{eb} && \Delta (J_+) =1 \otimes J_+ + J_+ \otimes 1 \qquad \Delta (J_-) = 1 \otimes J_- + J_-\otimes e^{2 z J_+ } \cr && \Delta (J_3) =1 \otimes J_3 + J_3\otimes e^{2z J_+ } . \label{bc} \end{eqnarray} We remark that in this basis the universal quantum $R$-matrix of $U_z(sl(2,{\mathbb R}))$ adopts the factorized expression (\ref{ab}) and the classical $r$-matrix is (\ref{aaa}).
Now if we apply to (\ref{bc}) a second invertible map given by \begin{equation} {\cal J}_+=\frac{1-e^{-2 z J_+}}{2z}\qquad {\cal J}_3=J_3 \qquad {\cal J}_-= J_- -\frac z2 J_3^2 \label{bd} \end{equation} then we find the classical commutators of $sl(2,{\mathbb R})$ \begin{equation} [{\cal J}_3,{\cal J}_+]=2{\cal J}_+\qquad [{\cal J}_3,{\cal J}_-]=-2{\cal J}_-\qquad [{\cal J}_+,{\cal J}_-]={\cal J}_3 \label{be} \end{equation} while the coproduct turns out to be \begin{eqnarray} &&\Delta({\cal J}_+)=1\otimes {\cal J}_+ + {\cal J}_+\otimes 1 - 2 z {\cal J}_+ \otimes {\cal J}_+\cr &&\Delta({\cal J}_3)=1\otimes {\cal J}_3 + {\cal J}_3\otimes \frac{1}{1- 2z{\cal J}_+}\cr &&\Delta({\cal J}_-)=1\otimes {\cal J}_- + {\cal J}_-\otimes \frac{1}{1- 2z{\cal J}_+} - z {\cal J}_3 \otimes \frac{1}{1- 2z{\cal J}_+}{\cal J}_3\cr &&\qquad\qquad -z^2 ({\cal J}_3^2+2{\cal J}_3)\otimes \frac{{\cal J}_+}{(1- 2z{\cal J}_+)^2} . \label{bf} \end{eqnarray} Note that although the new generator ${\cal J}_+$ is non-primitive, its coproduct satisfies \begin{equation} \Delta((1-2z{\cal J}_+)^a)=(1-2z{\cal J}_+)^a\otimes (1-2z{\cal J}_+)^a \label{bg} \end{equation} since the old generator $J_+$ fulfils $\Delta(e^{a z J_+})=e^{a z J_+}\otimes e^{a z J_+}$ for any real number $a$.
The composition of both maps, (\ref{bb}) and (\ref{bd}), gives rise to \begin{equation} {\cal J}_+=\frac{1-T^{-2}}{2z}\qquad {\cal J}_3=TH\qquad {\cal J}_-=TY-\frac{z}{2} (TH)^2-\frac{z}{8}(T^2-1) \label{bh} \end{equation}
where $T=e^{zX}$. This (invertible) twist map carries the former Hopf structure of $U_z(sl(2,{\mathbb R}))$ (\ref{ba}) to the last one characterized by (\ref{be}) and (\ref{bf}) and is the so called minimal twist map obtained by Abdesselam {\em et al} \cite{Abde}.
We emphasize that the coproduct (\ref{bf}) has been explicitly obtained in a `closed' form which is worth to be compared with the previous literature on nonlinear maps for the non-standard quantum $sl(2,{\mathbb R})$ algebra \cite{Abde,Abdea,Abdeb,Aizawa,vander} since, in general, the transformed coproduct has a very complicated form. In this respect see \cite{Aizawa} where the corresponding map is used to construct the representation theory of $U_z(sl(2,{\mathbb R}))$ and also \cite{vander} where the Clebsch--Gordan coefficients are computed.
\subsect{Non-standard quantum $gl(2)$ algebra}
A non-standard quantum deformation of $gl(2)$ whose underlying Lie bialgebra is again generated by the classical $r$-matrix (\ref{aaa}) was constructed in \cite{boson}. The Hopf algebra $U_z(gl(2))$ reads \begin{eqnarray} &&[J_3,J_+ ]= \frac{e^{2 z J_+} -1 } z \qquad [J_3,J_-]=-2 J_- +z J_3^2 \cr &&[J_+ ,J_- ]= J_3 - I\,e^{2z J_+} \qquad [I,\,\cdot\,]=0 \label{ca} \end{eqnarray} \begin{equation} \begin{array}{l} \Delta (J_+) =1 \otimes J_+ + J_+ \otimes 1 \qquad \Delta (J_3) =1 \otimes J_3 + J_3\otimes e^{2z J_+ } \cr \Delta (I) =1 \otimes I + I \otimes 1 \qquad
\Delta (J_-) = 1 \otimes J_- + J_-\otimes e^{2 z J_+ } + z J_3\otimes I\, e^{2 z J_+ } . \end{array} \label{cb} \end{equation} The universal quantum $R$-matrix of $U_z(gl(2))$ is also given by (\ref{ab}).
The twist map which turns (\ref{ca}) into classical commutation rules is exactly the same as for $U_z(sl(2,{\mathbb R}))$ given in (\ref{bd}) together with ${\cal I}=I$. The resulting Hopf structure is \begin{equation} [{\cal J}_3,{\cal J}_+]=2{\cal J}_+\qquad [{\cal J}_3,{\cal J}_-]=-2{\cal J}_-\qquad [{\cal J}_+,{\cal J}_-]={\cal J}_3-{\cal I}\qquad [{\cal I},\,\cdot\,]=0 \label{cc} \end{equation} \begin{eqnarray} &&\Delta({\cal J}_+)=1\otimes {\cal J}_+ + {\cal J}_+\otimes 1 - 2 z {\cal J}_+ \otimes {\cal J}_+\cr &&\Delta({\cal J}_3)=1\otimes {\cal J}_3 + {\cal J}_3\otimes \frac{1}{1- 2z{\cal J}_+} \cr &&\Delta({\cal J}_-)=1\otimes {\cal J}_- + {\cal J}_-\otimes \frac{1}{1- 2z{\cal J}_+} - z {\cal J}_3 \otimes \frac{1}{1- 2z{\cal J}_+}({\cal J}_3-{\cal I})\cr &&\qquad\qquad -z^2 \left( {\cal J}_3^2+2 {\cal J}_3\right)\otimes \frac{{\cal J}_+}{(1- 2z{\cal J}_+)^2} \cr &&\Delta({\cal I})=1\otimes {\cal I} + {\cal I}\otimes 1. \label{cd} \end{eqnarray}
It is clear that $U_z(gl(2))$ can be seen as an extended $U_z(sl(2,{\mathbb R}))$ by ${\cal I}$ which is a central and primitive generator; if we take ${\cal I}=0$ we recover the results of the above subsection.
In relation with this construction we recall that a two-parameter quantum $gl(2)$ algebra, $U_{g,h}(gl(2))$, was introduced in \cite{Aneva}; it includes $U_{z}(gl(2))$ as a particular case (when both deformation parameters are identified with $z$). The Drinfeld twist operator and map for $U_{g,h}(gl(2))$ were analyzed in \cite{Aizawab}.
\subsect{Non-standard quantum Poincar\'e algebra}
The Hopf algebra $U_z(sl(2,{\mathbb R}))$ can be contracted to the non-standard (1+1) Poincar\'e algebra by means of the following transformation of the generators and deformation parameter \cite{boson}: \begin{equation} P_+=\varepsilon J_+ \qquad P_-=\varepsilon J_- \qquad K=\frac 12 J_3 \qquad z\to 2\frac {z}{\varepsilon} . \label{da} \end{equation} The limit $\varepsilon\to 0$ gives rise to the Hopf algebra
$U_z({\cal P})$ (written in a null-plane basis): \begin{equation} \begin{array}{l} \displaystyle{[K,P_+ ]= \frac{e^{ z P_+} -1 } {z} }\qquad [K,P_-]=- P_- \qquad [P_+ ,P_- ]=0\cr
\Delta (P_+) =1 \otimes P_+ + P_+ \otimes 1 \qquad \Delta (P_-) = 1 \otimes P_- + P_-\otimes e^{ z P_+ } \cr \Delta (K) =1 \otimes K + K\otimes e^{z P_+ } \end{array} \label{db} \end{equation}
and the corresponding classical $r$-matrix is $r= z
K\wedge P_+$ while the universal $R$-matrix is similar to (\ref{ab}).
The contraction (\ref{da}) allows us to obtain straightforwardly the twist map for $U_z({\cal P})$ and its resulting Hopf algebra; they are \begin{equation}
{\cal P}_+=\frac{1-e^{- z P_+}}{z}\qquad
{\cal K}=K \qquad {\cal P}_-= P_- \label{dc} \end{equation} \begin{equation} [{\cal K},{\cal P}_+]= {\cal P}_+\qquad [{\cal K},{\cal P}_-]=- {\cal P}_-\qquad [{\cal P}_+,{\cal P}_-]=0 \label{dd} \end{equation} \begin{eqnarray} &&\Delta({\cal P}_+)=1\otimes {\cal P}_+ + {\cal P}_+\otimes 1 - z {\cal P}_+ \otimes {\cal P}_+\cr &&\Delta({\cal K})=1\otimes {\cal K} + {\cal K}\otimes \frac{1}{1- z{\cal P}_+}\cr &&\Delta({\cal P}_-)=1\otimes {\cal P}_- + {\cal P}_-\otimes \frac{1}{1- z{\cal P}_+} . \label{de} \end{eqnarray}
\subsect{Non-standard quantum harmonic oscillator algebra}
The Jordanian quantum oscillator algebra
$U_z( h_4)$ can be obtained by applying the following contraction \cite{boson} to the Hopf algebra $U_z(gl(2))$ given in (\ref{ca}) and (\ref{cb}): \begin{equation} A_+ = \varepsilon J_+ \qquad A_- = \varepsilon J_- \qquad N = \frac 12 J_3 \qquad M = \varepsilon^2 I \qquad z\to 2\frac {z}{\varepsilon} \label{fa} \end{equation} together with the limit $\varepsilon \to 0$. Thus we find
the Hopf structure of $U_z(h_4)$: \begin{equation} \begin{array}{l} \displaystyle{ [N,A_+]=\frac{e^{z A_+}-1}{z}} \qquad [N,A_- ]=-A_- \qquad [A_- ,A_+]=M e^{z A_+} \qquad [M,\cdot\,]=0 \cr \Delta(A_+)=1\otimes A_+ + A_+ \otimes 1 \qquad
\Delta(N)=1\otimes N +N \otimes e^{z A_+} \cr \Delta(M)=1\otimes M +M \otimes 1\qquad \Delta(A_-)=1\otimes A_- +A_- \otimes e^{z A_+}+zN\otimes M\, e^{z A_+} \cr \end{array} \label{fb} \end{equation} whose classical $r$-matrix is $r=z N\wedge A_+$.
The above contraction gives also the twist map and the corresponding Hopf algebra: \begin{equation}
{\cal A}_+=\frac{1-e^{- z A_+}}{z}\qquad
{\cal N}=N \qquad
{\cal A}_-= A_- \qquad {\cal M}=M \label{fc} \end{equation} \begin{equation} [{\cal N},{\cal A}_+]= {\cal A}_+\qquad [{\cal N},{\cal A}_-]=- {\cal A}_-\qquad [{\cal A}_-,{\cal A}_+]={\cal M}\qquad [{\cal M},\,\cdot\,]=0 \label{fe} \end{equation} \begin{eqnarray} &&\Delta({\cal A}_+)=1\otimes {\cal A}_+ + {\cal A}_+\otimes 1 - z {\cal A}_+ \otimes {\cal A}_+\cr &&\Delta({\cal N})=1\otimes {\cal N} + {\cal N}\otimes \frac{1}{1- z{\cal A_+}}\cr &&\Delta({\cal A}_-)=1\otimes {\cal A}_- + {\cal A}_-\otimes \frac{1}{1- z{\cal A}_+} + z {\cal N} \otimes \frac{{\cal M}}{1- z{\cal A}_+} \cr
&&\Delta({\cal M})=1\otimes {\cal M} + {\cal M}\otimes 1 . \label{fg} \end{eqnarray}
If we set the central generator ${\cal M}=0$ and denote ${\cal N}={\cal K}$, ${\cal A_+}={\cal P_+}$ and ${\cal A_-}={\cal P_-}$, then we find the results concerning
the non-standard (1+1) Poincar\'e algebra of section 2.3. Therefore we have completed the first part of the diagram of the Introduction at the level of (minimal) twist maps.
\sect{Discrete space Schr\"odinger symmetries}
Let us consider the discrete version of the SE on a two-dimensional uniform lattice introduced in \cite{Luismi} \begin{equation} (\Delta_x^2- 2 m \Delta_t)\phi(x,t)=0 \label{ac} \end{equation} where the difference operators $\Delta_x$ and $\Delta_t$
can be expressed in terms of shift operators $T_x= e^{\sigma \partial_x}$ and $T_t=e^{\tau \partial_t}$ as \begin{equation} \Delta_x=\frac{T_x-1}{\sigma} \qquad \Delta_t=\frac{T_t-1}{\tau}. \label{ad} \end{equation} The parameters $\sigma$ and $\tau$ are the lattice constants in the space $x$ and time $t$ directions, respectively. The action of $\Delta_x$ (resp.\ $\Delta_t$) on a function $\phi(x,t)$ consists in a discrete derivative, which in the limit $\sigma\to 0$ (resp.\ $\tau\to 0$) comes into $\partial_x$ (resp.\ $\partial_t$). We shall say that an operator ${\cal O}$ is a symmetry of the linear equation $E \phi(x,t)=0$ if ${\cal O}$ transforms solutions into solutions, that is, if ${\cal O}$ is such that \begin{equation}
E\, {\cal O} = \Lambda\, E \label{ae} \end{equation}
where $\Lambda$ is another operator. In this way, the symmetries of the equation (\ref{ac}) were computed in \cite{Luismi} showing that they spanned the Schr\"odinger Lie algebra ${\cal S}$, which is exactly the same result as for the continuous case \cite{Hagen,Nied}.
\subsect{Quantum Schr\"odinger algebra $U_\sigma({\cal S})$ and discrete space Schr\"odinger equation}
We consider the Schr\"odinger generators of time translation $H$, space translation $P$, Galilean boost $K$, dilation $D$, conformal transformation $C$, and central generator $M$ \cite{Hagen,Nied}. Let $U_\sigma({\cal S})$ be the quantum Schr\"odinger algebra \cite{twospace} whose underlying Lie bialgebra is generated by the non-standard classical $r$-matrix \begin{equation} r =\sigma D' \wedge P \label{ga} \end{equation} where $D'=D+\frac 12 M$; hereafter we shall use this notation in order to simplify some expressions. The coproduct of $U_\sigma({\cal S})$ has two primitive generators: the central one $M$ and the space translation $P$; it reads \cite{twospace} \begin{equation} \begin{array}{l} \Delta(M)=1\otimes M + M \otimes 1 \qquad \Delta(P)=1\otimes P + P \otimes 1 \\ [2pt] \Delta(H)=1\otimes H + H\otimes e^{2\sigma P} \\ [2pt] \Delta(K)=1\otimes K + K\otimes e^{-\sigma P}+\sigma D'\otimes e^{-\sigma P}M \\ [4pt] \Delta(D)=1\otimes D + D\otimes e^{-\sigma P} + \frac 12 M\otimes(e^{-\sigma P}-1) \\ [4pt] \Delta(C)=1\otimes C + C\otimes e^{-2\sigma P} -\frac \sigma 2 K\otimes e^{-\sigma P} D' +\frac \sigma 2 D'\otimes e^{-\sigma P}(K-\sigma D' M) \end{array} \label{gb} \end{equation} while the deformed commutation rules are given by \begin{equation} \begin{array}{l} [D,P]=\frac 1{\sigma} (e^{-\sigma P}-1) \qquad [D,K]=K \qquad [K,P]=M e^{-\sigma P }\qquad [M,\,\cdot\,]=0 \\ [4pt] [D,H]= - 2 H \qquad\qquad [D,C]=2 C +\frac {\sigma}2 K D' \qquad\qquad [H,P]=0 \\ [4pt] [H,C]= \frac 12(1+ e^{\sigma P}) D' -\frac 12 M -\sigma K H \qquad\qquad [K,C]= \frac {\sigma}2 K^2 \\ [4pt] [P,C]=-\frac 12 (1+ e^{-\sigma P}) K + \frac {\sigma}2 e^{-\sigma P} M D' \qquad\qquad [K,H]=\frac 1{\sigma}({ e^{\sigma P}-1}) . \end{array} \label{gc} \end{equation}
The relationship between $U_\sigma({\cal S})$ and a space discretization of the SE can be established by means of the following differential-difference realization of (\ref{gc}) in terms of the space and time coordinates $(x,t)$: \begin{eqnarray} && P=\partial_x \qquad\qquad H=\partial_t \qquad \qquad M= m \cr && K=- t \left(\frac {{ e^{\sigma \partial_x}-1}}{\sigma}\right) - m x e^{-\sigma \partial_x} \qquad D=2 t \partial_t
+ x\left( \frac {{ 1-e^{-\sigma \partial_x}}}{\sigma}\right) +\frac 12 \cr && C= t^2 \partial_t e^{\sigma \partial_x} + t x \left( \frac {\sinh \sigma\partial_x}{\sigma} +\sigma m \partial_t e^{-\sigma \partial_x}\right) +\frac 12 m x^2 e^{-\sigma \partial_x}\cr && \qquad\qquad -\frac 14 t \left\{ 1- 3 e^{\sigma \partial_x} +
m (1-e^{\sigma \partial_x})\right\} -\frac 14 \sigma m (1- m) x e^{-\sigma \partial_x} . \label{gd} \end{eqnarray} The limit $\sigma\to 0$ gives the classical Schr\"odinger vector field representation. The Galilei generators $\{K,H,P,M\}$ close a deformed subalgebra (but not a Hopf subalgebra) whose Casimir is \begin{equation} E_{\sigma} = \left(\frac { e^{\sigma P}-1}{\sigma} \right)^2 - 2 M H. \label{ge} \end{equation} The action of $E_{\sigma}$ on a function $\phi(x,t)$ through (\ref{gd})
provides a space discretization of the SE by choosing for $E_{\sigma}$ the zero eigenvalue: \begin{equation} E_{\sigma}\phi(x,t)=0\quad\Longrightarrow\quad \left( \left(\frac { e^{\sigma \partial_x}-1 } {\sigma}\right)^2 - 2 m \partial_t\right) \phi(x,t)=0 . \label{gf} \end{equation} Furthermore, according to the definition of a symmetry operator (\ref{ae}) we find that the quantum algebra $U_\sigma({\cal S})$ is a symmetry algebra of (\ref{gf}) since their operators (\ref{gd}) verify \begin{equation} \begin{array}{l} [E_{\sigma},X]=0\quad \mbox{for}\quad X\in\{K,H,P,M\}\qquad [E_{\sigma},D]= 2 E_{\sigma} \cr
[E_{\sigma},C]=\left\{ t (e^{\sigma \partial_x} +1) +\sigma m x e^{-\sigma \partial_x} \right\} E_{\sigma} . \end{array} \label{gg} \end{equation}
\subsect{Twist map for $U_\sigma({\cal S})$}
The quantum $h_4$ algebra described in the section 2.4 arises as a Hopf subalgebra of $U_\sigma({\cal S})$ once we rename the generators and deformation parameter of $U_z(h_4)$ as \begin{equation} \begin{array}{l} A_+=P\qquad A_-=K\qquad N=-D- \frac 12 M \equiv -D'\qquad z=-\sigma \end{array} \label{ha} \end{equation}
keeping $M$ as the same central generator. Notice that under this identification the classical $r$-matrices of both quantum algebras coincide: $r=zN\wedge A_+=\sigma D'\wedge P$. The embedding $U_z(h_4)\subset U_\sigma({\cal S})$ allows us to deduce straightforwardly the (minimal) twist map for $U_\sigma({\cal S})$. The map associated to $U_z(h_4)$ (\ref{fc}) written in the Schr\"odinger basis (\ref{ha}) reads \begin{equation} {\cal P}=\frac {e^{\sigma P}-1}{\sigma} \qquad {\cal D}=D \qquad {\cal K}=K \qquad {\cal M}=M . \label{hb} \end{equation} The change of basis for $U_\sigma({\cal S})$ is completed with the transformation of the two remaining generators that turns out to be \begin{equation} {\cal H}=H\qquad {\cal C}=C+\frac {\sigma}2 K D' . \label{hc} \end{equation}
In this new basis the commutation rules (\ref{gc}) of the Hopf algebra $U_\sigma({\cal S})$ come into the Schr\"odinger Lie algebra: \begin{equation} \begin{array}{llll}
[{\cal D},{\cal P}]=-{\cal P} \quad &[{\cal D},{\cal K}]={\cal K} \quad &[{\cal K},{\cal P}]= {\cal M} \quad &[{\cal M},\,\cdot\,]=0\cr
[{\cal D},{\cal H}]=-2{\cal H} \quad &[{\cal D},{\cal C}]=2{\cal C} \quad &[{\cal H},{\cal C}]={\cal D} \quad &[{\cal H},{\cal P}]=0 \cr
[{\cal P},{\cal C}]= - {\cal K} \quad &
[{\cal K},{\cal H}]= {\cal P}\quad &[{\cal K},{\cal C}]=0
\quad & \end{array} \label{hd} \end{equation} and the coproduct is now given by \begin{eqnarray} &&\Delta({\cal M})=1\otimes {\cal M} + {\cal M}\otimes 1\cr &&\Delta({\cal P})=1\otimes {\cal P} + {\cal P}\otimes 1 + \sigma {\cal P}\otimes {\cal P}\cr &&\Delta({\cal H})=1\otimes {\cal H} + {\cal H}\otimes (1 + \sigma {\cal P})^2\cr &&\Delta({\cal K})=1\otimes {\cal K} + {\cal K}\otimes \frac{1}{1 + \sigma {\cal P}} +\sigma {\cal D}'\otimes \frac{{\cal M}}{1 + \sigma {\cal P}}\cr &&\Delta({\cal D})=1\otimes {\cal D} + {\cal D}\otimes \frac{1}{1 + \sigma {\cal P}} - \frac{1}2 {\cal M}\otimes \frac{\sigma {\cal P}}{1 + \sigma {\cal P}}\cr &&\Delta({\cal C})=1\otimes {\cal C} + {\cal C}\otimes \frac{1}{(1 + \sigma {\cal P})^2} + \sigma {\cal D}'\otimes \frac{1}{1 + \sigma {\cal P}}\,{\cal K} \cr &&\qquad\qquad+ \frac{\sigma^2}{2}{\cal D}'({\cal D}'-1)\otimes \frac{{\cal M}}{(1 + \sigma {\cal P})^2} \label{he} \end{eqnarray} where we have used again the shorthand notation ${\cal D}'={\cal D}+\frac 12 {\cal M}$. Note that the new generator ${\cal P}$ is non-primitive but satisfies a property similar to (\ref{bg}).
The mapping defined by (\ref{hb}) and (\ref{hc}) transforms the differential-difference realization (\ref{gd}) into \begin{eqnarray} &&{\cal P}=\Delta_x \qquad \qquad {\cal H}=\partial_t \qquad \qquad {\cal M}= m \cr &&{\cal K}=- t \Delta_x - m x T_x^{-1} \qquad {\cal D}=2 t \partial_t + x \Delta_x T_x^{-1} + \frac 12 \cr &&{\cal C}= t^2 \partial_t + t x \Delta_x T_x^{-1}
+\frac 12 m (x^2 -\sigma x) T_x^{-2} +\frac 12 t \label{hf} \end{eqnarray} where $\Delta_x$ and $T_x$ are the difference and shift operators defined by (\ref{ad}). Obviously, the Casimir of the Galilei subalgebra $E_\sigma$ (\ref{ge}) leads to the classical one \begin{equation} E={\cal P}^2 -2 {\cal M}{\cal H} \label{hg} \end{equation} so that the discretized SE obtained as the realization (\ref{hf}) of $E\phi(x,t)=0$ is \begin{equation} (\Delta_x^2- 2 m \partial_t)\phi(x,t)=0 \label{hi} \end{equation} which coincides with (\ref{gf}); the operators (\ref{hf}) are symmetries of this equation satisfying \begin{equation} [E,X]=0\quad X\in\{{\cal K},{\cal H},{\cal P},{\cal M}\}\qquad [E,{\cal D}]= 2 E\qquad
[E,{\cal C}]= 2 t E . \label{hk} \end{equation}
\subsect{Relation of $U_\sigma({\cal S})$ with the Lie symmetry approach}
The discrete space SE (\ref{hi}) is just the limit $\tau\to 0$ of the equation (\ref{ac}) considered in \cite{Luismi}. Hence it is rather natural to expect a connection between the differential-difference symmetries obtained in \cite{Luismi} which close the Lie Schr\"odinger algebra (\ref{hd}) and our realization of $U_\sigma({\cal S})$. Although the operators (\ref{hf}) do not coincide with those given in \cite{Luismi} we will show that indeed both realizations are related by means of a similarity transformation (see \cite{Abde} for $U_z(sl(2,{\mathbb R}))$).
The twist map defined by \begin{eqnarray} && {\cal P}=\frac { e^{\sigma P}-1}{\sigma} \qquad {\cal D}=D+\frac 12 (1-e^{-\sigma P}) \qquad {\cal K}= K -\frac{\sigma}{2} M e^{-\sigma P} \cr &&{\cal M}=M \qquad {\cal H}=H \qquad {\cal C}=C+\frac{\sigma}{2} K D' -\frac{\sigma}{2} K e^{-\sigma P}-\frac{\sigma^2}8 M e^{-2 \sigma P} \label{ia} \end{eqnarray} is equivalent to the one defined by (\ref{hb}) and (\ref{hc}) since it gives rise to the {\it same} Schr\"odinger Lie algebra (\ref{hd}) and non-cocommutative coproduct (\ref{he}). However, the new map applied to the realization (\ref{gd}) leads to \begin{eqnarray} && {\cal P}=\Delta_x \qquad \qquad {\cal H}=\partial_t \qquad \qquad {\cal M}= m \cr && {\cal K}=- t \Delta_x - m x T_x^{-1} -\frac{m\sigma}{2}
T_x^{-1} \qquad {\cal D}=2 t \partial_t + x \Delta_x T_x^{-1} - \frac 12 T_x^{-1} +1 \cr && {\cal C}= t^2 \partial_t + t x \Delta_x T_x^{-1}
+\frac 12 m x^2 T_x^{-2}
+ t \left( 1- \frac 12 T_x^{-1} \right) -\frac {m \sigma^2}{8} T_x^{-2} \label{ib} \end{eqnarray} which are just the symmetry operators of the equation (\ref{ac}) obtained in \cite{Luismi}, provided the continuous time limit $\tau\rightarrow 0$ is performed, $m=\frac 12$ and ${\cal K}\to -2{\cal K}$. In other words, we have shown that the space differential-difference SE introduced in \cite{Luismi} has $U_\sigma({\cal S})$ as its Hopf symmetry algebra; the operators (\ref{ib}) fulfil the same relations (\ref{hk}). The deformation parameter $\sigma$ is interpreted as the lattice step in the $x$ coordinate, meanwhile the time $t$ remains a continuous variable. We also remark that, by using (\ref{ib}), the solutions of (\ref{hi}) have been obtained in \cite{Luismi} for $m=\frac 12$.
\sect{Discrete time Schr\"odinger symmetries}
\subsect{Quantum Schr\"odinger algebra $U_\tau({\cal S})$ and discrete time Schr\"odinger equation}
A similar procedure can be applied to the quantum Schr\"odinger algebra $U_\tau({\cal S})$ \cite{twotime} coming from the non-standard classical $r$-matrix \begin{equation} \begin{array}{l} r= \frac{\tau}{2} D'\wedge H . \end{array} \label{ja} \end{equation} The coproduct of $U_\tau({\cal S})$ has two primitive generators: the central one $M$ and the time translation $H$ (instead of $P$); it is given by \cite{twotime} \begin{equation} \begin{array}{l} \Delta(M)=1\otimes M + M \otimes 1\qquad \Delta(H)=1\otimes H + H \otimes 1 \\ [2pt] \Delta(P)=1\otimes P + P\otimes e^{\tau H/2}\\ [2pt] \Delta(K)=1\otimes K + K\otimes e^{-\tau H/2}+\frac{\tau}{2} D'\otimes e^{-\tau H}P\\ [2pt] \Delta(D)=1\otimes D + D\otimes e^{-\tau H} + \frac 12 M\otimes (e^{-\tau H}-1)\\ [2pt] \Delta(C)=1\otimes C + C\otimes e^{-\tau H}+\frac{\tau}{4} D'\otimes e^{-\tau H} M \end{array} \label{jb} \end{equation} and the compatible commutation rules are \begin{equation} \begin{array}{l} [D,P]=-P \qquad [D,K]=K\qquad [K,P]=M \qquad [M,\,\cdot\,]=0\\ [2pt] [D,H]= \frac 2{\tau} (e^{-\tau H}-1) \qquad [D,C]=2 C -\frac{\tau}{2} (D')^2\qquad [H,P]=0\\ [2pt] [H,C]= D' -\frac 12 M e^{-\tau H}\qquad [K,C]=-\frac{\tau}{4}(D'K+KD') \\ [2pt] [P,C]=-K+\frac{\tau}{4} (D'P+PD') \qquad [K,H]= e^{-\tau H}P. \end{array} \label{jc} \end{equation} A differential-difference realization of (\ref{jc}) reads \cite{twotime} \begin{eqnarray} &&H=\partial_t \qquad \qquad P=\partial_x\qquad\qquad M=m \nonumber\\ [2pt] &&K=- (t -\tau) e^{-\tau \partial_t} \partial_x - m x \qquad
D=2 (t-\tau) \left(\frac{1-e^{-\tau \partial_t} }{\tau}\right) + x\partial_x + \frac 12\nonumber\\ [2pt] &&C=(t^2 +\tau b t) \left(\frac{1-e^{-\tau \partial_t}}{\tau}\right) + t x \partial_x + \frac 12 t + \frac 12 m x^2 +\tau (b +1) e^{-\tau \partial_t} \nonumber \\ [4pt] &&\qquad\qquad +\frac{\tau}{4} x^2 \partial_{x}^2 +\frac{\tau}{2} (b+1) x \partial_x +\frac{\tau}{4}(b+1/2)^2 \label{jd} \end{eqnarray} where $b= \frac m2 -2$. A time discretization of the SE is obtained by considering the deformed Casimir of the Galilei subalgebra \begin{equation} E_{\tau}=P^2- 2 M \left( \frac{e^{\tau H}-1}{\tau}\right) \label{je} \end{equation} written in terms of the realization (\ref{jd}): \begin{equation} E_{\tau}\phi(x,t)=0\quad\Longrightarrow\quad \left(\partial_x^2 - 2 m \left(\frac { e^{\tau\partial_t}-1}{\tau}\right)\right) \phi(x,t)=0 . \label{jf} \end{equation} Under the realization (\ref{jd}) the generators of $U_\tau({\cal S})$ are symmetry operators of this equation as they satisfy \begin{equation} \begin{array}{l} [E_{\tau},X]=0\quad X\in\{K,H,P,M\}\qquad [E_{\tau},D]= 2 E_{\tau} \cr
[E_{\tau},C]=2\left\{ t -\frac{\tau}{4} (1 - m - 2 x \partial_x)\right\} E_{\tau} . \end{array} \label{jg} \end{equation}
\subsect{Twist map for $U_\tau({\cal S})$}
The quantum $gl(2)$ algebra studied in the section 2.2 arises as a Hopf subalgebra of $U_\tau({\cal S})$ under the following identification: \begin{equation} \begin{array}{l} J_+=H\quad J_-=-C\quad J_3=-D- \frac 12 M \equiv -D'\quad I=- \frac 12 M \quad z=-\frac 12 \tau . \end{array} \label{ka} \end{equation} In the Schr\"odinger basis the twist map for $U_z(gl(2))$ (\ref{bd}) (which is the same as for $U_z(sl(2,{\mathbb R}))$) is given by \begin{equation} {\cal H}=\frac {e^{\tau H}-1}{\tau} \qquad {\cal D}=D \qquad {\cal C}=C-\frac{\tau}{4}(D')^2 \qquad {\cal M}=M . \label{kb} \end{equation} The twist map for $U_\tau({\cal S})\supset U_z(gl(2))$ is completed with the transformation of the two generators out of $U_z(gl(2))$ which is simply \begin{equation} {\cal P}=P\qquad {\cal K}=K . \label{kc} \end{equation} If we apply (\ref{kb}) and (\ref{kc}) to (\ref{jb}) and (\ref{jc}), we find again the classical commutation rules of the Schr\"odinger algebra (\ref{hd}) while the coproduct reads now \begin{eqnarray} &&\Delta({\cal M})=1\otimes {\cal M} + {\cal M}\otimes 1\cr &&\Delta({\cal H})=1\otimes {\cal H} + {\cal H}\otimes 1 + \tau {\cal H}\otimes {\cal H}\cr &&\Delta({\cal P})=1\otimes {\cal P} + {\cal P}\otimes (1 + \tau {\cal H})^{1/2}\cr &&\Delta({\cal K})=1\otimes {\cal K} + {\cal K}\otimes \frac{1}{(1 + \tau {\cal H})^{1/2}} +\frac{\tau}{2} {\cal D}'\otimes \frac{{\cal P}}{1 + \tau {\cal H}}\cr &&\Delta({\cal D})=1\otimes {\cal D}
+ {\cal D}\otimes \frac{1}{1 + \tau {\cal H}}
- \frac{1}2 {\cal M}\otimes \frac{\tau {\cal H}}{1 + \tau {\cal H}}\cr &&\Delta({\cal C})= 1\otimes {\cal C} + {\cal C}\otimes \frac{1}{1 + \tau {\cal H}} - \frac {\tau}{2} {\cal D}'\otimes
\frac{1}{1 + \tau {\cal H}} {\cal D} \cr &&\qquad\qquad + \frac{\tau}4 {\cal D}'({\cal D}' - 2 )\otimes \frac{\tau {\cal H}}{(1 + \tau {\cal H})^2} . \label{kd} \end{eqnarray} In this new basis the realization (\ref{jd}) turns out to be \begin{eqnarray} && {\cal H}=\Delta_t \qquad {\cal P}=\partial_x \qquad {\cal M}= m \cr && {\cal K}=-( t-\tau) \partial_x T_t^{-1} - m x \qquad {\cal D}=2 ( t-\tau) \Delta_t T_t^{-1} + x \partial_x + \frac 12 \label{ke}\\ && {\cal C}= t^2 \Delta_t T_t^{-2} + x(t-\tau) \partial_x T_t^{-1}
+\frac 12 m x^2+3 t T_t^{-2} -\frac 5 2 t T_t^{-1} - 2 \tau T_t^{-2} +\frac {3\tau}{2} T_t^{-1} . \nonumber \end{eqnarray} The corresponding discretized SE is provided by the (non-deformed) Casimir $E$ of the Galilei subalgebra (\ref{hg}) written through (\ref{ke}) leading again to (\ref{jf}): \begin{equation} (\partial^2_x- 2 m \Delta_t)\phi(x,t)=0 . \label{kf} \end{equation} The new operators (\ref{ke}) are symmetries of this equation satisfying \begin{equation} [E,X]=0\quad X\in\{{\cal K},{\cal H},{\cal P},{\cal M}\}\qquad [E,{\cal D}]= 2 E \qquad [E,{\cal C}]= 2 (t-\tau) T_t^{-1} E . \label{kg} \end{equation}
\subsect{Relation of $U_\tau({\cal S})$ with the Lie symmetry approach}
The connection with the time discretization of the SE analyzed in \cite{Luismi} is provided by the twist map defined by \begin{eqnarray} && {\cal H}=\frac {e^{\tau H}-1}{\tau} \qquad {\cal D}=D+ 2(1-e^{-\tau H}) \qquad {\cal C}=C-\frac{\tau}{4} (D')^2 +\tau D e^{-\tau H} \cr &&{\cal M}=M\qquad {\cal P}= P \qquad {\cal K}= K -\tau P e^{-\tau H} . \label{la} \end{eqnarray} This nonlinear map is a similarity transformation of the former change of basis defined by (\ref{kb}) and (\ref{kc}) since it leads to the same Lie Schr\"odinger commutators (\ref{hd}) and non-cocommutative coproduct (\ref{kd}). Under this map the realization (\ref{jd}) becomes \begin{eqnarray} && {\cal H}=\Delta_t \qquad {\cal P}=\partial_x \qquad {\cal M}= m \cr && {\cal K}=- t \partial_x T_t^{-1} - m x \qquad {\cal D}=2 t \Delta_t T_t^{-1} + x \partial_x + \frac 12 \cr && {\cal C}= t^2 \Delta_t T_t^{-2} + t x \partial_x T_t^{-1}
+\frac 12 m x^2 + t \left( T_t^{-2}
- \frac 12 T_t^{-1} \right) . \label{lb} \end{eqnarray} These difference-differential operators are the limit $\sigma\rightarrow 0$ of the symmetry operators obtained in \cite{Luismi} once we set $m=\frac 12$ and ${\cal K}\to -2{\cal K}$. The corresponding discretized SE is again (\ref{kf}) and the new operators are symmetries of this equation satisfying \begin{equation} [E,X]=0\quad X\in\{{\cal K},{\cal H},{\cal P},{\cal M}\}\qquad [E,{\cal D}]= 2 E \qquad [E,{\cal C}]= 2 t T_t^{-1} E . \label{lc} \end{equation} Henceforth we have explicitly shown that the space discretization of the SE on a uniform lattice formerly studied in \cite{Luismi} within a pure Lie algebra approach has actually a quantum algebra symmetry associated to the Hopf algebra $U_\tau({\cal S})$. Consequently the deformation parameter $\tau$ is the time lattice step on this discrete time SE (the space coordinate $x$ remains as a continuous variable). In this way, the relationships displayed in the r.h.s. of the diagram of the Introduction have been studied at the level of twist maps.
\sect{Concluding remarks}
We have explicitly shown that the symmetry algebra \cite{Luismi} of the space discretization of the SE obtained from (\ref{ac}) by taking the limit $\tau\to 0$ is just the quantum Schr\"odinger algebra $U_\sigma({\cal S})$ \cite{twospace} and the deformation parameter $\sigma$ is exactly the space lattice constant. Likewise, we have also shown that the time discretization of the SE obtained from (\ref{ac}) by means of the limit $\sigma\to 0$ has the quantum Schr\"odinger algebra $U_\tau({\cal S})$ \cite{twotime} as its symmetry algebra; in this case, the time lattice step $\tau$ plays the role of the deformation parameter. Consequently, a direct relationship between non-standard (or Jordanian) deformations and regular lattice discretizations has been established.
We wish to point out that the existence of a Hopf algebra structure for the symmetries of a given equation associated to an elementary system allows us to write equations of composed systems keeping the same symmetry algebra \cite{EnricoA,EnricoB}. In order to use this property for the two discrete SE's here discussed, we see that only the last commutator in either (\ref{hk}) or (\ref{kg}) involving the conformal generator ${\cal C}$ is not algebraic, but depends explicitly on the chosen representation (the same happens at the continuous level). Therefore the composed systems characterized by the equation $\Delta(E) \phi = 0$ will have, by construction, $\Delta({\cal H}),\Delta({\cal P}), \Delta({\cal K}), \Delta({\cal D})$, and $\Delta({\cal M})$ as symmetry operators (moreover they close a Hopf subalgebra!). However, in general, this will not be the case for $\Delta({\cal C})$, and a further study on the behaviour of this operator is needed in order to construct coupled equations with full quantum Schr\"odinger algebra symmetry.
Finally, we stress that the applicability of the constructive approach presented here is not limited to the cases analyzed before, since it could be directly extended to other quantum algebras by means of their corresponding differential-difference realizations. In particular, the results of this paper indicate that there should exist an analogous relationship between the discrete symmetries of the $(1+1)$ wave equation on a uniform lattice obtained in \cite{Javier} and some non-standard quantum deformation of the algebra $so(2,2)$. Work on this line is in progress.
\noindent {\section*{Acknowledgments}}
\noindent This work was partially supported by DGES (Project PB98--0370) from the Ministerio de Educaci\'on y Cultura de Espa\~na and by Junta de Castilla y Le\'on (Projects CO2/197
and CO2/399).
\end{document} | arXiv |
Fundamental group of real $3\times 3$ matrices with rank $1$
In "Manetti - Topologia" there is the following exercise:
Compute the fundamental group of real $3\times 3$ matrices with rank $1$.
He suggests to show that there is a covering map of degree $2$ between the total space $E=S^{2} \times (\mathbb{R}^{3}\smallsetminus \{0\})$ and the base space $X=\mathcal{M}(3,\mathbb{R})$ with rank $1$.
I think $p: E \mapsto X$ sends a vector and its unit vector into a matrix which columns are multiples of this vector, but I can't show that this map has degree $2$.
How can I solve this exercise?
general-topology fundamental-groups
Stefan Hamcke
TheWandererTheWanderer
I solved this exercise: we know that $X=\mathfrak{M}(3,\mathbb{R})$ with rank $1$ is of the form $\{uv^{T}, u,v \in \mathbb{R}^3, u,v \ne 0\}.$ We also note that choosing $\lambda \in \mathbb{R}^{*}$, we have $$ uv^T=\lambda u \frac{1}{\lambda}v^T, $$ so we can take $u \in S^2$ and $v \in \mathbb{R}^3 \setminus \{0\}$. In this way, we can define the covering map $p: E \mapsto X$ as the hint of the book.
Not the answer you're looking for? Browse other questions tagged general-topology fundamental-groups or ask your own question.
helix and covering space of the unit circle
Prove that the fundamental group of $X$ is Abelian
Why is the fundamental group of a topological group independent of the basepoint?
Calculation of fundamental group using Van Kampen
Fundamental Group of Torus Covering Map
Fundamental group of unit sphere with three diameters
Find fundamental group of space $X=(S^1\times S^1)/(S^1\times \{s_0\})$ | CommonCrawl |
Proportionality of significance and effect size
Is it true that, given a fixed sample size N, it can be said that some measure of effect size and the measure of statitical significance (e.g., 1-p) are proportional? In other words, that, when keeping sample size constant, in order to reach significance you need to be trying to prove an effect that is large enough.
And is it correct to (simplistically) summarise the relationship between the three concepts (effect size, sample size, and statistical significance) with the following graph, which essentially describes the old adage "with large sample sizes, small effects become significant"
statistical-significance sample effect-size power
whuber♦
z8080z8080
$\begingroup$ Very closely related: stats.stackexchange.com/questions/91561, stats.stackexchange.com/questions/85878, and stats.stackexchange.com/a/80960. Looking at the power curves in the answers may be helpful. $\endgroup$ – whuber♦ May 5 '14 at 19:28
$\begingroup$ proportional? No; the relationship isn't even linear. However, I'd never call $1-p$ "significance", since that term already has a well established meaning that is different from that (you have significance when $p<\alpha$; it's a 0-1 step function in $p$, not a smooth thing like $1-p$). $\endgroup$ – Glen_b -Reinstate Monica May 6 '14 at 0:00
As an example, look at the relationship between t, p and d in the t-test.
p is defined as the probability of obtaining a test statistic this or more extreme, if the hypothesis under test is true. It is inversely related to both the sample size and the test statistic - in this case, t. Conversely, t ~ 1-p and n ~ 1-p.
For correlated samples, $d_{z} = \frac{t}{\sqrt{n}}$. Then, $d_{z}\sqrt{n} = t$; then, if n is held constant, as $d_{z}$ increases, t increases; and since t ~ 1-p, $d_{z}$ ~ 1-p. Also, if $d_{z}$ is held constant, as n increases, t increases, and n ~ 1-p. Colloquially speaking, since both 1-p and the measures of effect size depend on how extreme the test statistic is, they are correlated.
This will apply to other measures of effect size as well, such as the relationship between F, n and $\eta^2$ - trivially for those cases where the F-test converges with the t-test; or for correlation coefficients, which can also converge with the t-test. (I'd be very interested to learn if there are any measures of effect size which do not behave in this way, and by which justification they could be associated with other standardised measures of effect size.)
in order to reach significance you need to be trying to prove an effect that is large enough
Note that an effect size (such as r) is a descriptive statistic, a property of the sample. It is not inferential. To support a claim about the population, confidence intervals over effect sizes can be used.
jonajona
Not the answer you're looking for? Browse other questions tagged statistical-significance sample effect-size power or ask your own question.
Interpretation of power and detectable difference
If the level of a test is decreased, would the power of the test be expected to increase?
How to calculate power of different normality tests such as Shapiro-Wilk, Ryan test etc
How to interpret and report eta squared / partial eta squared in statistically significant and non-significant analyses?
(Inverse) proportionality between significance and effect size, for a fixed sample size?
When testing for a difference between effect sizes, is test power affected by their respective magnitude?
2X2 ANOVA: low power, statistical significance for only 1 IV, medium-low effect size
Relationship between effect size and statistical significance
Is the Shapiro Wilk test W an effect size?
Effect size for Wilcoxon signed rank test that incorporates the possible range of the attribute
Estimation statistics vs NHST, or: CIs and interval- vs point-estimates of effect size
Practical significance and effect size | CommonCrawl |
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T•(V), is the algebra of tensors on V (of any rank) with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property (see below).
The tensor algebra is important because many other algebras arise as quotient algebras of T(V). These include the exterior algebra, the symmetric algebra, Clifford algebras, the Weyl algebra and universal enveloping algebras.
The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, but does lead to the concept of a cofree coalgebra, and a more complicated one, which yields a bialgebra, and can be extended by giving an antipode to create a Hopf algebra structure.
Note: In this article, all algebras are assumed to be unital and associative. The unit is explicitly required to define the coproduct.
Construction
Let V be a vector space over a field K. For any nonnegative integer k, we define the kth tensor power of V to be the tensor product of V with itself k times:
$T^{k}V=V^{\otimes k}=V\otimes V\otimes \cdots \otimes V.$
That is, TkV consists of all tensors on V of order k. By convention T0V is the ground field K (as a one-dimensional vector space over itself).
We then construct T(V) as the direct sum of TkV for k = 0,1,2,…
$T(V)=\bigoplus _{k=0}^{\infty }T^{k}V=K\oplus V\oplus (V\otimes V)\oplus (V\otimes V\otimes V)\oplus \cdots .$
The multiplication in T(V) is determined by the canonical isomorphism
$T^{k}V\otimes T^{\ell }V\to T^{k+\ell }V$
given by the tensor product, which is then extended by linearity to all of T(V). This multiplication rule implies that the tensor algebra T(V) is naturally a graded algebra with TkV serving as the grade-k subspace. This grading can be extended to a Z grading by appending subspaces $T^{k}V=\{0\}$ for negative integers k.
The construction generalizes in a straightforward manner to the tensor algebra of any module M over a commutative ring. If R is a non-commutative ring, one can still perform the construction for any R-R bimodule M. (It does not work for ordinary R-modules because the iterated tensor products cannot be formed.)
Adjunction and universal property
The tensor algebra T(V) is also called the free algebra on the vector space V, and is functorial; this means that the map $V\mapsto T(V)$ extends to linear maps for forming a functor from the category of K-vector spaces to the category of associative algebra. Similarly with other free constructions, the functor T is left adjoint to the forgetful functor that sends each associative K-algebra to its underlying vector space.
Explicitly, the tensor algebra satisfies the following universal property, which formally expresses the statement that it is the most general algebra containing V:
Any linear map $f:V\to A$ from V to an associative algebra A over K can be uniquely extended to an algebra homomorphism from T(V) to A as indicated by the following commutative diagram:
Here i is the canonical inclusion of V into T(V). As for other universal properties, the tensor algebra T(V) can be defined as the unique algebra satisfying this property (specifically, it is unique up to a unique isomorphism), but this definition requires to prove that an object satisfying this property exists.
The above universal property implies that T is a functor from the category of vector spaces over K, to the category of K-algebras. This means that any linear map between K-vector spaces U and W extends uniquely to a K-algebra homomorphism from T(U) to T(W).
Non-commutative polynomials
If V has finite dimension n, another way of looking at the tensor algebra is as the "algebra of polynomials over K in n non-commuting variables". If we take basis vectors for V, those become non-commuting variables (or indeterminates) in T(V), subject to no constraints beyond associativity, the distributive law and K-linearity.
Note that the algebra of polynomials on V is not $T(V)$, but rather $T(V^{*})$: a (homogeneous) linear function on V is an element of $V^{*},$ for example coordinates $x^{1},\dots ,x^{n}$ on a vector space are covectors, as they take in a vector and give out a scalar (the given coordinate of the vector).
Quotients
Because of the generality of the tensor algebra, many other algebras of interest can be constructed by starting with the tensor algebra and then imposing certain relations on the generators, i.e. by constructing certain quotient algebras of T(V). Examples of this are the exterior algebra, the symmetric algebra, Clifford algebras, the Weyl algebra and universal enveloping algebras.
Coalgebra
The tensor algebra has two different coalgebra structures. One is compatible with the tensor product, and thus can be extended to a bialgebra, and can be further be extended with an antipode to a Hopf algebra structure. The other structure, although simpler, cannot be extended to a bialgebra. The first structure is developed immediately below; the second structure is given in the section on the cofree coalgebra, further down.
The development provided below can be equally well applied to the exterior algebra, using the wedge symbol $\wedge $ in place of the tensor symbol $\otimes $; a sign must also be kept track of, when permuting elements of the exterior algebra. This correspondence also lasts through the definition of the bialgebra, and on to the definition of a Hopf algebra. That is, the exterior algebra can also be given a Hopf algebra structure.
Similarly, the symmetric algebra can also be given the structure of a Hopf algebra, in exactly the same fashion, by replacing everywhere the tensor product $\otimes $ by the symmetrized tensor product $\otimes _{\mathrm {Sym} }$, i.e. that product where $v\otimes _{\mathrm {Sym} }w=w\otimes _{\mathrm {Sym} }v.$
In each case, this is possible because the alternating product $\wedge $ and the symmetric product $\otimes _{\mathrm {Sym} }$ obey the required consistency conditions for the definition of a bialgebra and Hopf algebra; this can be explicitly checked in the manner below. Whenever one has a product obeying these consistency conditions, the construction goes through; insofar as such a product gave rise to a quotient space, the quotient space inherits the Hopf algebra structure.
In the language of category theory, one says that there is a functor T from the category of K-vector spaces to the category of K-associative algebras. But there is also a functor Λ taking vector spaces to the category of exterior algebras, and a functor Sym taking vector spaces to symmetric algebras. There is a natural map from T to each of these. Verifying that quotienting preserves the Hopf algebra structure is the same as verifying that the maps are indeed natural.
Coproduct
The coalgebra is obtained by defining a coproduct or diagonal operator
$\Delta :TV\to TV\boxtimes TV$
Here, $TV$ is used as a short-hand for $T(V)$ to avoid an explosion of parentheses. The $\boxtimes $ symbol is used to denote the "external" tensor product, needed for the definition of a coalgebra. It is being used to distinguish it from the "internal" tensor product $\otimes $, which is already being used to denote multiplication in the tensor algebra (see the section Multiplication, below, for further clarification on this issue). In order to avoid confusion between these two symbols, most texts will replace $\otimes $ by a plain dot, or even drop it altogether, with the understanding that it is implied from context. This then allows the $\otimes $ symbol to be used in place of the $\boxtimes $ symbol. This is not done below, and the two symbols are used independently and explicitly, so as to show the proper location of each. The result is a bit more verbose, but should be easier to comprehend.
The definition of the operator $\Delta $ is most easily built up in stages, first by defining it for elements $v\in V\subset TV$ and then by homomorphically extending it to the whole algebra. A suitable choice for the coproduct is then
$\Delta :v\mapsto v\boxtimes 1+1\boxtimes v$
and
$\Delta :1\mapsto 1\boxtimes 1$
where $1\in K=T^{0}V\subset TV$ is the unit of the field $K$. By linearity, one obviously has
$\Delta (k)=k(1\boxtimes 1)=k\boxtimes 1=1\boxtimes k$
for all $k\in K.$ It is straightforward to verify that this definition satisfies the axioms of a coalgebra: that is, that
$(\mathrm {id} _{TV}\boxtimes \Delta )\circ \Delta =(\Delta \boxtimes \mathrm {id} _{TV})\circ \Delta $
where $\mathrm {id} _{TV}:x\mapsto x$ is the identity map on $TV$. Indeed, one gets
$((\mathrm {id} _{TV}\boxtimes \Delta )\circ \Delta )(v)=v\boxtimes 1\boxtimes 1+1\boxtimes v\boxtimes 1+1\boxtimes 1\boxtimes v$
and likewise for the other side. At this point, one could invoke a lemma, and say that $\Delta $ extends trivially, by linearity, to all of $TV$, because $TV$ is a free object and $V$ is a generator of the free algebra, and $\Delta $ is a homomorphism. However, it is insightful to provide explicit expressions. So, for $v\otimes w\in T^{2}V$, one has (by definition) the homomorphism
$\Delta :v\otimes w\mapsto \Delta (v)\otimes \Delta (w)$
Expanding, one has
${\begin{aligned}\Delta (v\otimes w)&=(v\boxtimes 1+1\boxtimes v)\otimes (w\boxtimes 1+1\boxtimes w)\\&=(v\otimes w)\boxtimes 1+v\boxtimes w+w\boxtimes v+1\boxtimes (v\otimes w)\end{aligned}}$
In the above expansion, there is no need to ever write $1\otimes v$ as this is just plain-old scalar multiplication in the algebra; that is, one trivially has that $1\otimes v=1\cdot v=v.$
The extension above preserves the algebra grading. That is,
$\Delta :T^{2}V\to \bigoplus _{k=0}^{2}T^{k}V\boxtimes T^{2-k}V$
Continuing in this fashion, one can obtain an explicit expression for the coproduct acting on a homogenous element of order m:
${\begin{aligned}\Delta (v_{1}\otimes \cdots \otimes v_{m})&=\Delta (v_{1})\otimes \cdots \otimes \Delta (v_{m})\\&=\sum _{p=0}^{m}\left(v_{1}\otimes \cdots \otimes v_{p}\right)\;\omega \;\left(v_{p+1}\otimes \cdots \otimes v_{m}\right)\\&=\sum _{p=0}^{m}\;\sum _{\sigma \in \mathrm {Sh} (p,m-p)}\;\left(v_{\sigma (1)}\otimes \dots \otimes v_{\sigma (p)}\right)\boxtimes \left(v_{\sigma (p+1)}\otimes \dots \otimes v_{\sigma (m)}\right)\end{aligned}}$
where the $\omega $ symbol, which should appear as ш, the sha, denotes the shuffle product. This is expressed in the second summation, which is taken over all (p, m − p)-shuffles. The shuffle is
${\begin{aligned}\operatorname {Sh} (p,q)=\{\sigma :\{1,\dots ,p+q\}\to \{1,\dots ,p+q\}\;\mid \;&\sigma {\text{ is bijective}},\;\sigma (1)<\sigma (2)<\cdots <\sigma (p),\\&{\text{and }}\;\sigma (p+1)<\sigma (p+2)<\cdots <\sigma (m)\}.\end{aligned}}$ :\{1,\dots ,p+q\}\to \{1,\dots ,p+q\}\;\mid \;&\sigma {\text{ is bijective}},\;\sigma (1)<\sigma (2)<\cdots <\sigma (p),\\&{\text{and }}\;\sigma (p+1)<\sigma (p+2)<\cdots <\sigma (m)\}.\end{aligned}}}
By convention, one takes that Sh(m,0) and Sh(0,m) equals {id: {1, ..., m} → {1, ..., m}}. It is also convenient to take the pure tensor products $v_{\sigma (1)}\otimes \dots \otimes v_{\sigma (p)}$ and $v_{\sigma (p+1)}\otimes \dots \otimes v_{\sigma (m)}$ to equal 1 for p = 0 and p = m, respectively (the empty product in $TV$). The shuffle follows directly from the first axiom of a co-algebra: the relative order of the elements $v_{k}$ is preserved in the riffle shuffle: the riffle shuffle merely splits the ordered sequence into two ordered sequences, one on the left, and one on the right.
Equivalently,
$\Delta (v_{1}\otimes \cdots \otimes v_{n})=\sum _{S\subseteq \{1,\dots ,n\}}\left(\prod _{k=1 \atop k\in S}^{n}v_{k}\right)\boxtimes \left(\prod _{k=1 \atop k\notin S}^{n}v_{k}\right)\!,$
where the products are in $TV$, and where the sum is over all subsets of $\{1,\dots ,n\}$.
As before, the algebra grading is preserved:
$\Delta :T^{m}V\to \bigoplus _{k=0}^{m}T^{k}V\boxtimes T^{(m-k)}V$
Counit
The counit $\epsilon :TV\to K$ is given by the projection of the field component out from the algebra. This can be written as $\epsilon :v\mapsto 0$ for $v\in V$ and $\epsilon :k\mapsto k$ for $k\in K=T^{0}V$. By homomorphism under the tensor product $\otimes $, this extends to
$\epsilon :x\mapsto 0$
for all $x\in T^{1}V\oplus T^{2}V\oplus \cdots $ It is a straightforward matter to verify that this counit satisfies the needed axiom for the coalgebra:
$(\mathrm {id} \boxtimes \epsilon )\circ \Delta =\mathrm {id} =(\epsilon \boxtimes \mathrm {id} )\circ \Delta .$
Working this explicitly, one has
${\begin{aligned}((\mathrm {id} \boxtimes \epsilon )\circ \Delta )(x)&=(\mathrm {id} \boxtimes \epsilon )(1\boxtimes x+x\boxtimes 1)\\&=1\boxtimes \epsilon (x)+x\boxtimes \epsilon (1)\\&=0+x\boxtimes 1\\&\cong x\end{aligned}}$
where, for the last step, one has made use of the isomorphism $TV\boxtimes K\cong TV$, as is appropriate for the defining axiom of the counit.
Bialgebra
A bialgebra defines both multiplication, and comultiplication, and requires them to be compatible.
Multiplication
Multiplication is given by an operator
$\nabla :TV\boxtimes TV\to TV$
which, in this case, was already given as the "internal" tensor product. That is,
$\nabla :x\boxtimes y\mapsto x\otimes y$
That is, $\nabla (x\boxtimes y)=x\otimes y.$ The above should make it clear why the $\boxtimes $ symbol needs to be used: the $\otimes $ was actually one and the same thing as $\nabla $; and notational sloppiness here would lead to utter chaos. To strengthen this: the tensor product $\otimes $ of the tensor algebra corresponds to the multiplication $\nabla $ used in the definition of an algebra, whereas the tensor product $\boxtimes $ is the one required in the definition of comultiplication in a coalgebra. These two tensor products are not the same thing!
Unit
The unit for the algebra
$\eta :K\to TV$
is just the embedding, so that
$\eta :k\mapsto k$
That the unit is compatible with the tensor product $\otimes $ is "trivial": it is just part of the standard definition of the tensor product of vector spaces. That is, $k\otimes x=kx$ for field element k and any $x\in TV.$ More verbosely, the axioms for an associative algebra require the two homomorphisms (or commuting diagrams):
$\nabla \circ (\eta \boxtimes \mathrm {id} _{TV})=\eta \otimes \mathrm {id} _{TV}=\eta \cdot \mathrm {id} _{TV}$
on $K\boxtimes TV$, and that symmetrically, on $TV\boxtimes K$, that
$\nabla \circ (\mathrm {id} _{TV}\boxtimes \eta )=\mathrm {id} _{TV}\otimes \eta =\mathrm {id} _{TV}\cdot \eta $
where the right-hand side of these equations should be understood as the scalar product.
Compatibility
The unit and counit, and multiplication and comultiplication, all have to satisfy compatibility conditions. It is straightforward to see that
$\epsilon \circ \eta =\mathrm {id} _{K}.$
Similarly, the unit is compatible with comultiplication:
$\Delta \circ \eta =\eta \boxtimes \eta \cong \eta $
The above requires the use of the isomorphism $K\boxtimes K\cong K$ in order to work; without this, one loses linearity. Component-wise,
$(\Delta \circ \eta )(k)=\Delta (k)=k(1\boxtimes 1)\cong k$
with the right-hand side making use of the isomorphism.
Multiplication and the counit are compatible:
$(\epsilon \circ \nabla )(x\boxtimes y)=\epsilon (x\otimes y)=0$
whenever x or y are not elements of $K$, and otherwise, one has scalar multiplication on the field: $k_{1}\otimes k_{2}=k_{1}k_{2}.$ The most difficult to verify is the compatibility of multiplication and comultiplication:
$\Delta \circ \nabla =(\nabla \boxtimes \nabla )\circ (\mathrm {id} \boxtimes \tau \boxtimes \mathrm {id} )\circ (\Delta \boxtimes \Delta )$
where $\tau (x\boxtimes y)=y\boxtimes x$ exchanges elements. The compatibility condition only needs to be verified on $V\subset TV$; the full compatibility follows as a homomorphic extension to all of $TV.$ The verification is verbose but straightforward; it is not given here, except for the final result:
$(\Delta \circ \nabla )(v\boxtimes w)=\Delta (v\otimes w)$
For $v,w\in V,$ an explicit expression for this was given in the coalgebra section, above.
Hopf algebra
The Hopf algebra adds an antipode to the bialgebra axioms. The antipode $S$ on $k\in K=T^{0}V$ is given by
$S(k)=k$
This is sometimes called the "anti-identity". The antipode on $v\in V=T^{1}V$ is given by
$S(v)=-v$
and on $v\otimes w\in T^{2}V$ by
$S(v\otimes w)=S(w)\otimes S(v)=w\otimes v$
This extends homomorphically to
${\begin{aligned}S(v_{1}\otimes \cdots \otimes v_{m})&=S(v_{m})\otimes \cdots \otimes S(v_{1})\\&=(-1)^{m}v_{m}\otimes \cdots \otimes v_{1}\end{aligned}}$
Compatibility
Compatibility of the antipode with multiplication and comultiplication requires that
$\nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta =\eta \circ \epsilon =\nabla \circ (\mathrm {id} \boxtimes S)\circ \Delta $
This is straightforward to verify componentwise on $k\in K$:
${\begin{aligned}(\nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta )(k)&=(\nabla \circ (S\boxtimes \mathrm {id} ))(1\boxtimes k)\\&=\nabla (1\boxtimes k)\\&=1\otimes k\\&=k\end{aligned}}$
Similarly, on $v\in V$:
${\begin{aligned}(\nabla \circ (S\boxtimes \mathrm {id} )\circ \Delta )(v)&=(\nabla \circ (S\boxtimes \mathrm {id} ))(v\boxtimes 1+1\boxtimes v)\\&=\nabla (-v\boxtimes 1+1\boxtimes v)\\&=-v\otimes 1+1\otimes v\\&=-v+v\\&=0\end{aligned}}$
Recall that
$(\eta \circ \epsilon )(k)=\eta (k)=k$
and that
$(\eta \circ \epsilon )(x)=\eta (0)=0$
for any $x\in TV$ that is not in $K.$
One may proceed in a similar manner, by homomorphism, verifying that the antipode inserts the appropriate cancellative signs in the shuffle, starting with the compatibility condition on $T^{2}V$ and proceeding by induction.
Cofree cocomplete coalgebra
Main article: Cofree coalgebra
One may define a different coproduct on the tensor algebra, simpler than the one given above. It is given by
$\Delta (v_{1}\otimes \dots \otimes v_{k}):=\sum _{j=0}^{k}(v_{0}\otimes \dots \otimes v_{j})\boxtimes (v_{j+1}\otimes \dots \otimes v_{k+1})$
Here, as before, one uses the notational trick $v_{0}=v_{k+1}=1\in K$ (recalling that $v\otimes 1=v$ trivially).
This coproduct gives rise to a coalgebra. It describes a coalgebra that is dual to the algebra structure on T(V∗), where V∗ denotes the dual vector space of linear maps V → F. In the same way that the tensor algebra is a free algebra, the corresponding coalgebra is termed cocomplete co-free. With the usual product this is not a bialgebra. It can be turned into a bialgebra with the product $v_{i}\cdot v_{j}=(i,j)v_{i+j}$ where (i,j) denotes the binomial coefficient for ${\tbinom {i+j}{i}}$. This bialgebra is known as the divided power Hopf algebra.
The difference between this, and the other coalgebra is most easily seen in the $T^{2}V$ term. Here, one has that
$\Delta (v\otimes w)=1\boxtimes (v\otimes w)+v\boxtimes w+(v\otimes w)\boxtimes 1$
for $v,w\in V$, which is clearly missing a shuffled term, as compared to before.
See also
• Braided vector space
• Braided Hopf algebra
• Monoidal category
• Multilinear algebra
• Stanisław Lem's Love and Tensor Algebra
• Fock space
References
• Bourbaki, Nicolas (1989). Algebra I. Chapters 1-3. Elements of Mathematics. Springer-Verlag. ISBN 3-540-64243-9. (See Chapter 3 §5)
• Serge Lang (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (3rd ed.), Springer Verlag, ISBN 978-0-387-95385-4
Algebra
• Outline
• History
Areas
• Abstract algebra
• Algebraic geometry
• Algebraic number theory
• Category theory
• Commutative algebra
• Elementary algebra
• Homological algebra
• K-theory
• Linear algebra
• Multilinear algebra
• Noncommutative algebra
• Order theory
• Representation theory
• Universal algebra
Basic concepts
• Algebraic expression
• Equation (Linear equation, Quadratic equation)
• Function (Polynomial function)
• Inequality (Linear inequality)
• Operation (Addition, Multiplication)
• Relation (Equivalence relation)
• Variable
Algebraic structures
• Field (theory)
• Group (theory)
• Module (theory)
• Ring (theory)
• Vector space (Vector)
Linear and
multilinear algebra
• Basis
• Determinant
• Eigenvalues and eigenvectors
• Inner product space (Dot product)
• Hilbert space
• Linear map (Matrix)
• Linear subspace (Affine space)
• Norm (Euclidean norm)
• Orthogonality (Orthogonal complement)
• Rank
• Trace
Algebraic constructions
• Composition algebra
• Exterior algebra
• Free object (Free group, ...)
• Geometric algebra (Multivector)
• Polynomial ring (Polynomial)
• Quotient object (Quotient group, ...)
• Symmetric algebra
• Tensor algebra
Topic lists
• Algebraic structures
• Abstract algebra topics
• Linear algebra topics
Glossaries
• Field theory
• Linear algebra
• Order theory
• Ring theory
• Category
• Mathematics portal
• Wikibooks
• Linear
• Abstract
• Wikiversity
• Linear
• Abstract
Tensors
Glossary of tensor theory
Scope
Mathematics
• Coordinate system
• Differential geometry
• Dyadic algebra
• Euclidean geometry
• Exterior calculus
• Multilinear algebra
• Tensor algebra
• Tensor calculus
• Physics
• Engineering
• Computer vision
• Continuum mechanics
• Electromagnetism
• General relativity
• Transport phenomena
Notation
• Abstract index notation
• Einstein notation
• Index notation
• Multi-index notation
• Penrose graphical notation
• Ricci calculus
• Tetrad (index notation)
• Van der Waerden notation
• Voigt notation
Tensor
definitions
• Tensor (intrinsic definition)
• Tensor field
• Tensor density
• Tensors in curvilinear coordinates
• Mixed tensor
• Antisymmetric tensor
• Symmetric tensor
• Tensor operator
• Tensor bundle
• Two-point tensor
Operations
• Covariant derivative
• Exterior covariant derivative
• Exterior derivative
• Exterior product
• Hodge star operator
• Lie derivative
• Raising and lowering indices
• Symmetrization
• Tensor contraction
• Tensor product
• Transpose (2nd-order tensors)
Related
abstractions
• Affine connection
• Basis
• Cartan formalism (physics)
• Connection form
• Covariance and contravariance of vectors
• Differential form
• Dimension
• Exterior form
• Fiber bundle
• Geodesic
• Levi-Civita connection
• Linear map
• Manifold
• Matrix
• Multivector
• Pseudotensor
• Spinor
• Vector
• Vector space
Notable tensors
Mathematics
• Kronecker delta
• Levi-Civita symbol
• Metric tensor
• Nonmetricity tensor
• Ricci curvature
• Riemann curvature tensor
• Torsion tensor
• Weyl tensor
Physics
• Moment of inertia
• Angular momentum tensor
• Spin tensor
• Cauchy stress tensor
• stress–energy tensor
• Einstein tensor
• EM tensor
• Gluon field strength tensor
• Metric tensor (GR)
Mathematicians
• Élie Cartan
• Augustin-Louis Cauchy
• Elwin Bruno Christoffel
• Albert Einstein
• Leonhard Euler
• Carl Friedrich Gauss
• Hermann Grassmann
• Tullio Levi-Civita
• Gregorio Ricci-Curbastro
• Bernhard Riemann
• Jan Arnoldus Schouten
• Woldemar Voigt
• Hermann Weyl
| Wikipedia |
Radial stability of periodic solutions of the Gylden-Meshcherskii-type problem
DCDS Home
Global bounded solutions of the higher-dimensional Keller-Segel system under smallness conditions in optimal spaces
May 2015, 35(5): 1905-1920. doi: 10.3934/dcds.2015.35.1905
$L^q$-Extensions of $L^p$-spaces by fractional diffusion equations
Der-Chen Chang 1, and Jie Xiao 2,
Department of Mathematics and Department of Computer Science, Georgetown University, Washington D.C. 20057
Department of Mathematics and Statistics, Memorial University of Newfoundland, St. John's, NL A1C 5S7, Canada
Received May 2014 Revised September 2014 Published December 2014
Based on the geometric-measure-theoretic analysis of a new $L^p$-type capacity defined in the upper-half Euclidean space, this note characterizes a nonnegative Randon measure $\mu$ on $\mathbb R^{1+n}_+$ such that the extension $R_\alpha L^p(\mathbb R^n)\subseteq L^q(\mathbb R^{1+n}_+,\mu)$ holds for $(\alpha,p,q)\in (0,1)\times(1,\infty)\times(1,\infty)$ where $u=R_\alpha f$ is the weak solution of the fractional diffusion equation $(\partial_t + (-\Delta_x)^\alpha)u(t, x) = 0$ in $\mathbb R^{1+n}_+$ subject to $u(0,x)=f(x)$ in $\mathbb R^n$.
Keywords: $L^p$-type capacities, fractional diffusion equations, heat kernel., $L^q$-extensions.
Mathematics Subject Classification: Primary: 31C15, 35K08, 35K9.
Citation: Der-Chen Chang, Jie Xiao. $L^q$-Extensions of $L^p$-spaces by fractional diffusion equations. Discrete & Continuous Dynamical Systems, 2015, 35 (5) : 1905-1920. doi: 10.3934/dcds.2015.35.1905
D. R. Adams, On the existence of capacitary strong type estimates in $\mathbf R^n$, Ark. Mat., 14 (1976), 125-140. doi: 10.1007/BF02385830. Google Scholar
D. R. Adams, Capacity and blow-up for the $3+1$ dimensional wave opartor, Forum Math. 20 (2008), 341-357. doi: 10.1515/FORUM.2008.017. Google Scholar
D. R. Adams and L. I. Hedberg, Function Spaces and Potential Theory, A Series of Comprehensive Studies in Mathematics, Springer, Berlin, 1996. doi: 10.1007/978-3-662-03282-4. Google Scholar
D. R. Adams and J. Xiao, Strong type estimates for homogeneous Besov capacities, Math. Ann. 325 (2003), 695-709. doi: 10.1007/s00208-002-0396-3. Google Scholar
J. Bisquert, Interpretation of a fractional diffusion equation with nonconserved probability density in terms of experimental systems with trapping or recombination, Physical Review E, 72 (2005), 011109. doi: 10.1103/PhysRevE.72.011109. Google Scholar
R. M. Blumenthal and R. K. Getoor, Some theorems on stable processes, Trans. Amer. Math. Soc., 95 (1960), 263-273. doi: 10.1090/S0002-9947-1960-0119247-6. Google Scholar
L. Caffarelli and L. Silvestre, An extension problem related to the fractional Laplacian, Comm. Partial Diff. Equ., 32 (2007), 1245-1260. doi: 10.1080/03605300600987306. Google Scholar
L. Caffarelli and L. Silvestre, Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian, Invent. Math., 171 (2008), 425-461. doi: 10.1007/s00222-007-0086-6. Google Scholar
D. Chamorro, Remarks on a Fractional Diffusion Transport Equation with Applications to the Dissipative Quasi-Geostrophic Equation, hal-00505027, version 4 - 12 Apr 2011. Google Scholar
J. Chen, Q. Deng, Y. Ding and D. Fan, Estimates on fractional power dissipatve equations in function spaces, Nonlinear Anal., 75 (2012), 2959-2974. doi: 10.1016/j.na.2011.11.039. Google Scholar
Z.-Q. Chen and R. Song, Estimates on Green functions and Poisson kernels for symmetric stable processes, Math. Ann., 312 (1998), 465-501. doi: 10.1007/s002080050232. Google Scholar
P. Constantin and J. Wu, Behavior of solutions of 2D quasi-geostrophic equations, SIAM J. Math. Anal., 30 (1999), 937-948. doi: 10.1137/S0036141098337333. Google Scholar
A. Córdoba and D. Córdoba, A maximum principle applied to quasi-geostrophic equations, Commmun. Math. Phys., 249 (2004), 511-528. doi: 10.1007/s00220-004-1055-1. Google Scholar
E. B. Fabes, B. F. Jones and N. M. Riviere, The initial value problem for the Navier-Stokes equations, Arch. Rational Mech. Anal., 45 (1972), 222-240. doi: 10.1007/BF00281533. Google Scholar
H. Federer, Geometric Measure Theory, Springer-Verlag, New York, 1969. Google Scholar
R. Jiang, J. Xiao, D. Yang and Z. Zhai, Regularity and capacity for the fractional dissipative operator,, , (). Google Scholar
D. Li, On a frequency localized Bernstein inequality and some generalized Poincare-type inequalities, Math. Res. Lett., 20 (2013), 933-945. arXiv:1212.0183v1 [math.AP]2Dec2012. doi: 10.4310/MRL.2013.v20.n5.a9. Google Scholar
V. G. Maz'ya and Yu. V. Netrusov, Some counterexamples for the theory of Sobolev spaces on bad domains, Potential Anal., 4 (1995), 47-65. doi: 10.1007/BF01048966. Google Scholar
C. Miao, B. Yuan and B. Zhang, Well-posedness of the Cauchy problem for the fractional power dissipative equations, Nonlinear Anal., 68 (2008), 461-484. doi: 10.1016/j.na.2006.11.011. Google Scholar
M. Nishio, K. Shimomura and N. Suzuki, $\alpha$-parabolic Bergman spaces, Osaka J. Math., 42 (2005), 133-162. Google Scholar
M. Nishio, N. Suzuki and M. Yamada, Toeplitz operators and Carleson type measures on parabolic Bergman spaces, Hokkaido Math. J., 36 (2007), 563-583. doi: 10.14492/hokmj/1277472867. Google Scholar
M. Nishio, N. Suzuki and M. Yamada, Compact Toeplitz operators on parabolic Bergman spaces, Hiroshima Math. J., 38 (2008), 177-192. Google Scholar
M. Nishio, N. Suzuki and M. Yamada, Carleson inequalities on parabolic Bergman spaces, Tohoku Math. J., 62 (2010), 269-286. doi: 10.2748/tmj/1277298649. Google Scholar
M. Nishio and M. Yamada, Carleson type measures on parabolic Bergman spaces, J. Math. Soc. Japan, 58 (2006), 83-96. doi: 10.2969/jmsj/1145287094. Google Scholar
L. Vázquez, J. J. Trujillo and M. P. Velasco, Fractional heat equation and the second law of thermodynamics, Frac. Calc. Appl. Anal., 14 (2011), 334-342. doi: 10.2478/s13540-011-0021-9. Google Scholar
G. Wu and J. Yuan, Well-posedness of the Cauchy problem for the fractional power dissipative equation in critical Besov spaces, J. Math. Anal. Appl., 340 (2008), 1326-1335. doi: 10.1016/j.jmaa.2007.09.060. Google Scholar
J. Wu, Dissipative quasi-geostrophic equations with $L^p$ data, Electron. J. Differential Equations, 2001 (2001), 1-13. Google Scholar
J. Wu, Lower Bounds for an integral involving fractional Laplacians and the generalized Navier-Stokes equations in Besov spaces, Commun. Math. Phys., 263 (2006), 803-831. doi: 10.1007/s00220-005-1483-6. Google Scholar
J. Xiao, Carleson embeddings for Sobolev spaces via heat equation, J. Diff. Equ., 224 (2006), 277-295. doi: 10.1016/j.jde.2005.07.014. Google Scholar
J. Xiao, Homogeneous endpoint Besov space embeddings by Hausdorff capacity and heat equation, Adv. Math., 207 (2006), 828-846. doi: 10.1016/j.aim.2006.01.010. Google Scholar
L. Xie and X. Zhang, Heat kernel estimates for critical fractional diffusion operator,, , (). Google Scholar
Z. Zhai, Strichartz type estimates for fractional heat equations, J. Math. Anal. Appl., 356 (2009), 642-658. doi: 10.1016/j.jmaa.2009.03.051. Google Scholar
Z. Zhai, Carleson measure problems for parabolic Bergman spaces and homogeneous Sobolev spaces, Nonlinear Anal., 73 (2010), 2611-2630. doi: 10.1016/j.na.2010.06.040. Google Scholar
Samer Dweik. $ L^{p, q} $ estimates on the transport density. Communications on Pure & Applied Analysis, 2019, 18 (6) : 3001-3009. doi: 10.3934/cpaa.2019134
Damiano Foschi. Some remarks on the $L^p-L^q$ boundedness of trigonometric sums and oscillatory integrals. Communications on Pure & Applied Analysis, 2005, 4 (3) : 569-588. doi: 10.3934/cpaa.2005.4.569
Karen Yagdjian, Anahit Galstian. Fundamental solutions for wave equation in Robertson-Walker model of universe and $L^p-L^q$ -decay estimates. Discrete & Continuous Dynamical Systems - S, 2009, 2 (3) : 483-502. doi: 10.3934/dcdss.2009.2.483
Masahiro Ikeda, Takahisa Inui, Mamoru Okamoto, Yuta Wakasugi. $ L^p $-$ L^q $ estimates for the damped wave equation and the critical exponent for the nonlinear problem with slowly decaying data. Communications on Pure & Applied Analysis, 2019, 18 (4) : 1967-2008. doi: 10.3934/cpaa.2019090
Markus Riedle, Jianliang Zhai. Large deviations for stochastic heat equations with memory driven by Lévy-type noise. Discrete & Continuous Dynamical Systems, 2018, 38 (4) : 1983-2005. doi: 10.3934/dcds.2018080
Ming Wang, Yanbin Tang. Attractors in $H^2$ and $L^{2p-2}$ for reaction diffusion equations on unbounded domains. Communications on Pure & Applied Analysis, 2013, 12 (2) : 1111-1121. doi: 10.3934/cpaa.2013.12.1111
Tadeusz Iwaniec, Gaven Martin, Carlo Sbordone. $L^p$-integrability & weak type $L^{2}$-estimates for the gradient of harmonic mappings of $\mathbb D$. Discrete & Continuous Dynamical Systems - B, 2009, 11 (1) : 145-152. doi: 10.3934/dcdsb.2009.11.145
L. Cherfils, Y. Il'yasov. On the stationary solutions of generalized reaction diffusion equations with $p\& q$-Laplacian. Communications on Pure & Applied Analysis, 2005, 4 (1) : 9-22. doi: 10.3934/cpaa.2005.4.9
Lucas C. F. Ferreira, Elder J. Villamizar-Roa. On the heat equation with concave-convex nonlinearity and initial data in weak-$L^p$ spaces. Communications on Pure & Applied Analysis, 2011, 10 (6) : 1715-1732. doi: 10.3934/cpaa.2011.10.1715
Lucas C. F. Ferreira, Elder J. Villamizar-Roa. On the stability problem for the Boussinesq equations in weak-$L^p$ spaces. Communications on Pure & Applied Analysis, 2010, 9 (3) : 667-684. doi: 10.3934/cpaa.2010.9.667
Chérif Amrouche, Nour El Houda Seloula. $L^p$-theory for the Navier-Stokes equations with pressure boundary conditions. Discrete & Continuous Dynamical Systems - S, 2013, 6 (5) : 1113-1137. doi: 10.3934/dcdss.2013.6.1113
Angelo Favini, Alfredo Lorenzi, Hiroki Tanabe, Atsushi Yagi. An $L^p$-approach to singular linear parabolic equations with lower order terms. Discrete & Continuous Dynamical Systems, 2008, 22 (4) : 989-1008. doi: 10.3934/dcds.2008.22.989
Fabio Cipriani, Gabriele Grillo. On the $l^p$ -agmon's theory. Conference Publications, 1998, 1998 (Special) : 167-176. doi: 10.3934/proc.1998.1998.167
Yong Xia, Yu-Jun Gong, Sheng-Nan Han. A new semidefinite relaxation for $L_{1}$-constrained quadratic optimization and extensions. Numerical Algebra, Control & Optimization, 2015, 5 (2) : 185-195. doi: 10.3934/naco.2015.5.185
C. García Vázquez, Francisco Ortegón Gallego. On certain nonlinear parabolic equations with singular diffusion and data in $L^1$. Communications on Pure & Applied Analysis, 2005, 4 (3) : 589-612. doi: 10.3934/cpaa.2005.4.589
Alexandre N. Carvalho, Jan W. Cholewa. Strongly damped wave equations in $W^(1,p)_0 (\Omega) \times L^p(\Omega)$. Conference Publications, 2007, 2007 (Special) : 230-239. doi: 10.3934/proc.2007.2007.230
Patrizia Pucci, Mingqi Xiang, Binlin Zhang. A diffusion problem of Kirchhoff type involving the nonlocal fractional p-Laplacian. Discrete & Continuous Dynamical Systems, 2017, 37 (7) : 4035-4051. doi: 10.3934/dcds.2017171
Leszek Gasiński, Nikolaos S. Papageorgiou. Dirichlet $(p,q)$-equations at resonance. Discrete & Continuous Dynamical Systems, 2014, 34 (5) : 2037-2060. doi: 10.3934/dcds.2014.34.2037
Ismail Kombe, Abdullah Yener. A general approach to weighted $L^{p}$ Rellich type inequalities related to Greiner operator. Communications on Pure & Applied Analysis, 2019, 18 (2) : 869-886. doi: 10.3934/cpaa.2019042
Qunyi Bie, Haibo Cui, Qiru Wang, Zheng-An Yao. Incompressible limit for the compressible flow of liquid crystals in $ L^p$ type critical Besov spaces. Discrete & Continuous Dynamical Systems, 2018, 38 (6) : 2879-2910. doi: 10.3934/dcds.2018124
Der-Chen Chang Jie Xiao | CommonCrawl |
\begin{document} \maketitle
\begin{abstract}. It is proved that, for every infinite field ${\ensuremath{\mathbf F}}$, the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ has Krull dimension $n$. The proof uses only ``high school algebra'' and the rudiments of undergraduate ``abstract algebra.'' \end{abstract}
\section{Prime ideals and Krull dimension}
In this paper, a \emph{ring} is a commutative ring with a multiplicative identity. A \emph{prime ideal} in a ring $R$ is an ideal $\ensuremath{ \mathfrak P} \neq R$ such that, if $a,b \in R$ and $ab \in \ensuremath{ \mathfrak P}$, then $a \in \ensuremath{ \mathfrak P}$ or $b \in \ensuremath{ \mathfrak P}$. The ring $R$ is an integral domain if and only if $\{ 0\}$ is a prime ideal in $R$. In a unique factorization domain, a nonzero principal ideal \ensuremath{ \mathfrak P}\ is prime if and only if $\ensuremath{ \mathfrak P} \neq R$ and \ensuremath{ \mathfrak P}\ is generated by an irreducible element. For example, in the ring \ensuremath{\mathbf Z}, an ideal \ensuremath{ \mathfrak P}\ is prime if and only if $\ensuremath{ \mathfrak P} = \{ 0\}$ or $\ensuremath{ \mathfrak P} = p\ensuremath{\mathbf Z}$ for some prime number $p$.
An \emph{ideal chain of length $n$}\index{chain!ideal}\index{ideal chain} in the ring $R$ is a strictly increasing sequence of $n+1$ ideals of $R$. A \emph{prime ideal chain of length $n$}\index{chain!prime ideal}\index{prime ideal chain} in $R$ is a strictly increasing sequence of $n+1$ prime ideals of $R$. The \emph{Krull dimension}\index{Krull dimension} of $R$ is the supremum of the lengths of prime ideal chains in $R$. Eisenbud~\cite[page 215]{eise95} wrote, \begin{quotation} ``Arguably the most fundamental notion in geometry and topology is dimension\ldots. [Its] \ldots algebraic analogue plays an equally fundamental role in commutative algebra and algebraic geometry.'' \end{quotation} We shall prove that, for every infinite field ${\ensuremath{\mathbf F}}$, the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ has Krull dimension $n$.
Krull dimension has many applications. In algebraic geometry, if $S$ is a nonempty set of polynomials in ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$, then the \emph{ variety}\index{variety} (also called the \emph{algebraic set}) $V$ determined by $S$ is the set of points in ${\ensuremath{\mathbf F}}^n$ that are common zeros of the polynomials in $S$: \[ V = V(S) = \left\{ (x_1 , \ldots, x_n ) \in {\ensuremath{\mathbf F}}^n: f(x_1,\ldots, x_n) = 0 \text{ for all } f \in S \right\}. \] The \emph{vanishing ideal}\index{vanishing ideal} ${\ensuremath{ \mathfrak I}}(V)$ is the set of polynomials that vanish on the variety $V$: \[ {\ensuremath{ \mathfrak I}}(V) = \left\{ f \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_n] : f(x_1,\ldots, x_n) = 0 \text{ for all } (x_1 , \ldots, x_n ) \in V \right\}. \] The quotient ring \[ {\ensuremath{\mathbf F}}[V] ={\ensuremath{\mathbf F}}[t_1,\ldots, t_n]/{\ensuremath{ \mathfrak I}}(V) \] is called the \emph{coordinate ring}\index{coordinate ring} of $V$. One definition of the dimension of the variety $V$ is the Krull dimension of its coordinate ring ${\ensuremath{\mathbf F}}[V]$. For example, if $S = \{0\} \subseteq \ensuremath{\mathbf F}[t_1,\ldots, t_n]$ is the set whose only element is the zero polynomial, then $V = V( \{0\} ) = \ensuremath{\mathbf F}^n$, and the vanishing ideal of $V$ is $\ensuremath{ \mathcal I}(V) = \ensuremath{ \mathcal I}(\ensuremath{\mathbf F}^n) = \{0\}$. We obtain the coordinate ring \[ \ensuremath{\mathbf F}[V]= {\ensuremath{\mathbf F}}[t_1,\ldots, t_n]/{\ensuremath{ \mathfrak I}}(V) \cong {\ensuremath{\mathbf F}}[t_1,\ldots, t_n] \] and so the variety $\ensuremath{\mathbf F}^n$ has dimension $n$. Nathanson~\cite{nath16} explicitly computes the dimensions of some varieties generated by monomials.
The proof that the Krull dimension of the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ is $n$ uses only high school algebra and the rudiments of undergraduate abstract algebra. ``High school algebra'' means formal manipulations of polynomials. Results from high school algebra are collected and proved in Sections~\ref{Krull:section:LowerBound} and~\ref{Krull:section:HighSchool}. ``Rudimentary abstract algebra'' means results whose proofs use only material found in standard undergraduate algebra texts. Section~\ref{Krull:section:algebra} contains results from abstract algebra.
For other proofs, see Atiyah and Macdonald~\cite[Chapter 11]{atiy-macd69}, Cox, Little, and O'Shea~\cite[Chapter 9]{cox-litt-oshe07}, and Kunz~\cite[Chapter 2]{kunz13}.
\section{A lower bound for the Krull dimension} \label{Krull:section:LowerBound}
A polynomial in one variable $f = \sum_{i =0}^d c_i t^i \in R[t]$ has degree $d$ if $c_d \neq 0$. The \emph{leading term}\index{leading term} of $f$ is $c_dt^d$, and the \emph{leading coefficient}\index{leading coefficient} of $f$ is $c_d$. The polynomial $f$ is \emph{monic}\index{monic polynomial} if its leading coefficient is 1.
Let $\ensuremath{ \mathbf N }_0$ denote the set of nonnegative integers. For variables $t_1,\ldots, t_n$ and for the $n$-tuple $I = (i_1, i_2, \ldots, i_n) \in \ensuremath{ \mathbf N }_0^n$, we define the monomial \[ t^I = t_1^{i_1}t_2^{i_2}\cdots t_n^{i_n}. \] The \emph{degree of the monomial}\index{degree!monomial} $t^I$ is
$|I| = i_1+i_2+\cdots + i_n$. The \emph{degree of the variable}\index{degree!variable} $t_j$ in the monomial $t^I$ is $i_j$.
Let ${\ensuremath{\mathbf F}}$ be a field. The polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ is a vector space over ${\ensuremath{\mathbf F}}$. A basis for this vector space is the set of monomials $\left\{ t^I: I \in \ensuremath{ \mathbf N }_0^n \right\}$. Every nonzero polynomial $f \in \ensuremath{\mathbf F}[t_1,\ldots, t_n]$ has a unique representation in the form \begin{equation} \label{Krull:UniquePolyRep} f = \sum_{I \in \ensuremath{ \mathcal I}} c_It^I \end{equation} where $\ensuremath{ \mathcal I}$ is a nonempty finite subset of $\ensuremath{ \mathbf N }_0^n$ and $c_I \in {\ensuremath{\mathbf F}}\setminus \{ 0\}$ for every $n$-tuple $I \in \ensuremath{ \mathcal I}$. The \emph{degree of the polynomial}\index{degree!polynomial}
$f$ is $\max( |I|: I \in \ensuremath{ \mathcal I})$, and the degree of the variable $t_j$ in $f$ is $\max( i_j: I \in \ensuremath{ \mathcal I})$. The degree of the zero polynomial is undefined.
We write $S \subseteq T$ is $S$ is a subset of $T$, and $S \subset T$ if $S$ is a proper subset of $T$.
\begin{theorem} \label{Krull:theorem:polynomial-n} Let ${\ensuremath{\mathbf F}}$ be a field and let $R = {\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ be the polynomial ring in $n$ variables with coefficients in \ensuremath{\mathbf F}. Let $\ensuremath{ \mathfrak P}_0 = \{ 0\}$, and, for $k = 1,2, \ldots, n$, let $\ensuremath{ \mathfrak P}_k$ be the ideal of $R$ generated by $\{t_1,t_2,\ldots, t_k\}$. Then \begin{equation} \label{Krull:polynomial-n} \ensuremath{ \mathfrak P}_0 \subset \ensuremath{ \mathfrak P}_1 \subset \ensuremath{ \mathfrak P}_2 \subset \cdots \subset \ensuremath{ \mathfrak P}_n \end{equation} is a strictly increasing chain of prime ideals in $R$, and so the Krull dimension of $R$ is at least $n$. \end{theorem}
\begin{proof} The ideal $\ensuremath{ \mathfrak P}_0 = \{ 0\}$ is prime because $R$ is an integral domain. For $k \in \{1,\ldots, n\}$, every monomial in every nonzero polynomial in the ideal \[ \ensuremath{ \mathfrak P}_k = \left\{ \sum_{j=1}^k t_j f_j: f_j \in R \text{ for } j \in \{1,\ldots, n\} \right\} \] is divisible by $t_j$ for some $j \in \{1,\ldots, k\}$. For $k \in \{0,1,\ldots, n-1\}$, we have $t_{k+1} \in \ensuremath{ \mathfrak P}_{k+1}$ but $t_{k+1} \notin \ensuremath{ \mathfrak P}_k$, and so~\eqref{Krull:polynomial-n} is a strictly increasing sequence of ideals. Moreover, $1 \notin \ensuremath{ \mathfrak P}_n$, and so $\ensuremath{ \mathfrak P}_n$ is a proper ideal in $R$. We shall prove that each ideal $\ensuremath{ \mathfrak P}_k$ is prime.
Let $k \in \{1,\ldots, n\}$. Consider the polynomial $f \in R$ of the form~\eqref{Krull:UniquePolyRep}. If \[ \ensuremath{ \mathcal I}_1 = \{ (i_1,\ldots, i_n)\in \ensuremath{ \mathcal I}: i_j \geq 1 \text{ for some } j \in \{1,\ldots, k \} \} \] and \[ \ensuremath{ \mathcal I}_2 = \{ (i_1,\ldots, i_n)\in \ensuremath{ \mathcal I}: i_j = 0 \text{ for all } j \in \{1,\ldots, k\} \} \] then $f= f_1 + f_2$, where \[ f_1 = \sum_{I \in \ensuremath{ \mathcal I}_1} c_I t^I \in \ensuremath{ \mathfrak P}_k \qqand f_2 = \sum_{I \in \ensuremath{ \mathcal I}_2} c_I t^I \in R. \] We have $f \in \ensuremath{ \mathfrak P}_k$ if and only if $f_2 = 0$.
For example, let $n = 2$ and \begin{equation} \label{Krull:f-example} f = t_1^3 + 2t_1^2t_2 + 4t_2^3 \in R = \ensuremath{\mathbf F}[t_1,t_2]. \end{equation} Choosing $k = 1$, we obtain $\ensuremath{ \mathcal I}_1 = \{ (3,0), (2,1)\}$ and $\ensuremath{ \mathcal I}_2 = \{ (0,3) \}$, and so $f_1 = t_1^3 + 2t_1^2t_2 \in \ensuremath{ \mathfrak P}_1$ and $f_2 = 4 t_2^3 \in R\setminus \ensuremath{ \mathfrak P}_1$. It follows that $f \notin \ensuremath{ \mathfrak P}_1$.
Let $f \in \ensuremath{ \mathfrak P}_k$, and let $g$ and $h$ be polynomials in $R$ such that $f = gh$. We write $g = g_1+g_2$ and $h = h_1 + h_2$, where $g_1$ and $h_1$ are polynomials in $\ensuremath{ \mathfrak P}_k$, and $g_2$ and $h_2$ are polynomials in $R$ that are sums of monomials not divisible by $t_j$ for any $j \in \{1,\ldots, k\}$. Note that $g_2 h_2 \in \ensuremath{ \mathfrak P}_k$ if and only if $g_2h_2=0$ if and only if $g_2 = 0$ or $h_2 = 0$. We have \[ f = gh = (g_1+g_2) ( h_1 + h_2) = (g_1h_1+g_1h_2+g_2h_1) + g_2h_2. \] Because $\ensuremath{ \mathfrak P}_k$ is an ideal, \[ g_1h_1+g_1h_2+g_2h_1\in \ensuremath{ \mathfrak P}_k \] and so \[ g_2 h_2 = f - (g_1h_1+g_1h_2+g_2h_1) \in \ensuremath{ \mathfrak P}_k. \] It follows that either $g_2 = 0$ and $g \in \ensuremath{ \mathfrak P}_k$, or $h_2 = 0$ and $h \in \ensuremath{ \mathfrak P}_k$. Therefore, $\ensuremath{ \mathfrak P}_k$ is a prime ideal. \end{proof}
The main result of this paper (Theorem~\ref{Krull:theorem:KrullDimension}) is that the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ has Krull dimension $n$. Although this implies the maximality of the prime ideal chain~\eqref{Krull:polynomial-n}, there is a nice direct proof of this result.
\begin{theorem} \label{Krull:theorem:polynomial-max} The prime ideal chain~\eqref{Krull:polynomial-n} is maximal. \end{theorem}
\begin{proof} The first step is to prove that $\ensuremath{ \mathfrak P}_n$ is a maximal ideal. The ideal $\ensuremath{ \mathfrak P}_n$ consists of all polynomials with constant term 0. Let $g \in R\setminus \ensuremath{ \mathfrak P}_n$, and let \ensuremath{ \mathfrak I}\ be the ideal of $R$ generated by the set $\{ t_1,\ldots, t_n, g \}$. The polynomial $g$ has constant term $c \neq 0$, and $g-c \in \ensuremath{ \mathfrak P}_n \subseteq \ensuremath{ \mathfrak I}$. The equation $c^{-1} (g - (g-c) ) = 1$ implies that $1$ is in \ensuremath{ \mathfrak I}, and so $R = \ensuremath{ \mathfrak I}$. Thus, the ideal $\ensuremath{ \mathfrak P}_n$ is maximal.
We shall prove that, for every integer $k \in \{1,2,\ldots, n\}$, if $\ensuremath{ \mathfrak P}'$ is a prime ideal of $R$ such that \begin{equation} \label{Krull:Krull-q} \ensuremath{ \mathfrak P}_{k-1} \subset \ensuremath{ \mathfrak P}' \subseteq \ensuremath{ \mathfrak P}_k \end{equation} then $\ensuremath{ \mathfrak P}' = \ensuremath{ \mathfrak P}_k$. This implies that~\eqref{Krull:polynomial-n} is a maximal prime ideal chain.
Let $k \geq 1$, and let \ensuremath{ \mathfrak P}'\ be an ideal of $R$ satisfying~\eqref{Krull:Krull-q}. It follows that $\ensuremath{ \mathfrak P}' \setminus \ensuremath{ \mathfrak P}_{k-1} \neq \emptyset$. Because $\ensuremath{ \mathfrak P}' \subseteq \ensuremath{ \mathfrak P}_k$, every polynomial in $\ensuremath{ \mathfrak P}' \setminus \ensuremath{ \mathfrak P}_{k-1} $ contains at least one monomial of the form \begin{equation} \label{Krull:KrullDim} t_k^{i_k} t_{k+1}^{i_{k+1}} \cdots t_n^{i_n} \end{equation} with $i_k \geq 1$. Let ${\ell}_k$ be the smallest positive integer $i_k$ such that a monomial of the form~\eqref{Krull:KrullDim} occurs with a nonzero coefficient in some polynomial in $\ensuremath{ \mathfrak P}' \setminus \ensuremath{ \mathfrak P}_{k-1} $. There exists a polynomial $f$ in $\ensuremath{ \mathfrak P}' \setminus \ensuremath{ \mathfrak P}_{k-1} $ that contains a monomial of the form ~\eqref{Krull:KrullDim} with $i_k = \ell_k$. \begin{equation} \label{Krull:KrullDim-2} t_k^{\ell_k} t_{k+1}^{i_{k+1}} \cdots t_n^{i_n} \end{equation} We write $f=f_1 + f_2$, where \[ f_1 = \sum_{\substack{I = (i_1,\ldots, i_n) \in \ensuremath{ \mathbf N }_0^k \\ i_j \geq 1 \text{ for some } j \in \{1,\ldots, k-1\} }} c_I t^I \in \ensuremath{ \mathfrak P}_{k-1} \] and \[ f_2 = \sum_{\substack{I = (i_1,\ldots, i_n) \in \ensuremath{ \mathbf N }_0^k \\ i_j = 0 \text{ for all } j \in \{1,\ldots, k-1\} \\ \text{ and } i_k \geq \ell_k}} c_I t^I = t_k^{{\ell}_k} h \] for some nonzero polynomial $h \in R$. Because $f_2$ contains the monomial~\eqref{Krull:KrullDim-2} in which the variable $t_k$ occurs with degree exactly $\ell_k$, the polynomial $h$ must contain a monomial not divisible by $t_i$ for all $i \in \{1,\ldots, k-1, k\}$, and so $h \notin \ensuremath{ \mathfrak P}_k$. It follows that $ t_k^{{\ell}_k -1} h \notin \ensuremath{ \mathfrak P}'$.
We have $f_2 = f - f_1 \in \ensuremath{ \mathfrak P}'$ because $f \in \ensuremath{ \mathfrak P}'$ and $f_1 \in \ensuremath{ \mathfrak P}_{k-1} \subseteq \ensuremath{ \mathfrak P}'$. We factor $f_2$ as follows: \[ f_2 = t_k^{{\ell}_k} h = t_k \left( t_k^{{\ell}_k -1} h \right). \] Because $ t_k^{{\ell}_k -1} h \notin \ensuremath{ \mathfrak P}'$ and \ensuremath{ \mathfrak P}'\ is a prime ideal, it follows that $t_k \in \ensuremath{ \mathfrak P}'$. Therefore, $\ensuremath{ \mathfrak P}'$ contains $\{t_1,\ldots, t_{k-1}, t_k \}$, and so $\ensuremath{ \mathfrak P}' = \ensuremath{ \mathfrak P}_k$. This completes the proof. \end{proof}
\section{Results from high school algebra} \label{Krull:section:HighSchool}
Let $d$ be a nonnegative integer. A polynomial $f = \sum_{I \in \ensuremath{ \mathcal I}} c_It^I \in \ensuremath{\mathbf F}[t_1,\ldots, t_n]$ is \emph{homogeneous of degree $d$}\index{homogeneous polynomial}\index{polynomial!homogeneous} if all of its monomials have degree $d$. Let $\lambda \in \ensuremath{\mathbf F}$ and $a = (a_1,\ldots, a_n) \in \ensuremath{\mathbf F}^n$. If $t^I = t_1^{i_1}\cdots t_n^{i_n}$ is a monomial of degree $d$, then \[ (\lambda a)^I = (\lambda a_1)^{i_1}\cdots (\lambda a_n)^{i_n} = \lambda^{\sum_{j=1}^n i_j} a_1^{i_1}\cdots a_n^{i_n} = \lambda^d a^I. \] If $f = \sum_{I \in \ensuremath{ \mathcal I}} c_It^I$ is homogeneous of degree $d$, then \begin{equation} \label{Krull:homogeneous} f(\lambda a_1,\ldots, \lambda a_n) = \sum_{I \in \ensuremath{ \mathcal I}} c_I (\lambda a)^I = \lambda^d \sum_{I \in \ensuremath{ \mathcal I}} c_I a^I = \lambda^df( a_1,\ldots, a_n). \end{equation} For example, the polynomial $f$ defined by~\eqref{Krull:f-example} is homogeneous of degree 3, and \begin{align*} f(\lambda a_1, \lambda a_2) & = (\lambda a_1)^3 + 2(\lambda a_1)^2 (\lambda a_2) + 4(\lambda a_2)^3 \\ & = \lambda^3 \left( a_1^3 + 2 a_1^2 a_2 + 4 a_2^3 \right) = \lambda^3 f( a_1, a_2). \end{align*}
Let $ f = \sum_{I \in \ensuremath{ \mathcal I}} c_It^I$ be a nonzero polynomial of degree $d$, and let \[
\ensuremath{ \mathcal I}_d = \{ I = (i_1,\ldots, i_n) \in \ensuremath{ \mathcal I} : |I| = \sum_{j=1}^n i_j = d \}. \] Then $\ensuremath{ \mathcal I}_d \neq \emptyset$ and \[ f_d = \sum_{ I \in \ensuremath{ \mathcal I}_d} c_It^I \in {\ensuremath{\mathbf F}}[t_1,\ldots, t_n] \] is a homogeneous polynomial of degree $d$.
The real numbers \ensuremath{\mathbf R}, the complex numbers \ensuremath{\mathbf C }, and the rational functions with real coefficients or with complex coefficients are infinite fields. An example of a finite field is ${\ensuremath{\mathbf F}}_2 = \{ 0, 1\}$, with addition defined by $0+0=1+1=0$ and $1+0 = 0+1 = 1$, and with multiplication defined by $0\cdot 0 = 0\cdot 1 = 1 \cdot 0 = 0$ and $1 \cdot 1 = 1$.
In the ring of polynomials $\ensuremath{\mathbf F}_2[t_1,t_2]$ with coefficients in $\ensuremath{\mathbf F}_2$, the homogeneous polynomial $f(t_1,t_2) = t_1^2 + t_1t_2$ has the property that \[ f(a_1,1) = a_1^2 + a_1 = 0 \] for all $a_1 \in \ensuremath{\mathbf F}_2$. The following Lemma shows that this behavior is impossible for polynomials with coefficients in an infinite field.
\begin{lemma} \label{Krull:lemma:NoetherNorm1} Let ${\ensuremath{\mathbf F}}$ be an infinite field, and let $f$ be a nonzero polynomial in ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$. There exist infinitely many points $(a_1,\ldots, a_{n-1},a_n) \in \left( \ensuremath{\mathbf F}\setminus \{ 0\} \right)^n$ such that \[ f(a_1,\ldots, a_{n-1},a_n) \neq 0. \] If $f$ is homogeneous, then there exist infinitely many points $(a_1,\ldots, a_{n-1}) \in \left( \ensuremath{\mathbf F}\setminus \{ 0\} \right)^{n-1}$ such that \[ f(a_1,\ldots, a_{n-1},1) \neq 0. \] \end{lemma}
\begin{proof} By induction on the number $n$ of variables. If $n = 1$, then $f(t_1)$ has only finitely many zeros. Because the field \ensuremath{\mathbf F}\ is infinite, there exist infinitely many $a_1\in \ensuremath{\mathbf F}\setminus \{ 0\}$ with $f(a_1) \neq 0$. If $f$ is homogeneous, then $f(t_1) = c_dt_1^d$ for some $d \in \ensuremath{ \mathbf N }_0$ and $c_d \in \ensuremath{\mathbf F}\setminus \{ 0\}$, and $f(1) = c_d \neq 0$.
Let $n \geq 2$, and assume that the Lemma holds for polynomials in $n-1$ variables. A polynomial $f \in {\ensuremath{\mathbf F}}[t_1, \ldots, t_{n-1}, t_n]$ can also be represented as a polynomial in the variable $t_n$ with coefficients in the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}]$. Thus, there exist polynomials $f_0, f_1,\ldots, f_d \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}]$ such that $f_d \neq 0$ and \begin{equation} \label{Krull:NoetherNorm} f(t_1, \ldots, t_{n-1}, t_n) = \sum_{j=0}^d f_j(t_1,\ldots, t_{n-1}) t_n^j. \end{equation}
By the induction hypothesis, there exist infinitely many points $(a_1,\ldots, a_{n-1}) \in \left( \ensuremath{\mathbf F}\setminus \{ 0\} \right)^{n-1}$ such that \begin{equation} \label{Krull:NoetherNorm-2} f_d(a_1,\ldots, a_{n-1}) \neq 0. \end{equation} By~\eqref{Krull:NoetherNorm} and~\eqref{Krull:NoetherNorm-2}, the polynomial \[ f(a_1, a_2,\ldots, a_{n-1}, t_n) = \sum_{j=0}^d f_j(a_1,\ldots, a_{n-1}) t_n^j \in{\ensuremath{\mathbf F}}[t_n] \] has degree $d$. Because a nonzero polynomial of degree $d$ has at most $d$ roots in ${\ensuremath{\mathbf F}}$, and because the field ${\ensuremath{\mathbf F}}$ is infinite, there exist infinitely many elements $a_n \in{\ensuremath{\mathbf F}} \setminus \{0\}$ such that \[ f(a_1, a_2,\ldots, a_{n-1}, a_n) \neq 0. \]
Let $f \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}, t_n]$ be a homogeneous polynomial of degree $d$, and let $(a_1,\ldots, a_{n-1},a_n) \in \left( \ensuremath{\mathbf F}\setminus \{ 0\} \right)^n$ satisfy $f(a_1,\ldots, a_{n-1},a_n) \neq 0$. Applying the homogeneity identity~\eqref{Krull:homogeneous} with $\lambda = a_n^{-1}$, we obtain \[ f(a_n^{-1} a_1,\ldots, a_n^{-1} a_{n-1}, 1) = a_n^{-d} f(a_1,\ldots, a_{n-1},a_n) \neq 0 \] This completes the proof. \end{proof}
We shall apply Lemma~\ref{Krull:lemma:NoetherNorm1} to prove an important result (Lemma~\ref{Krull:lemma:NoetherNorm2}) that may appear ``complicated'' and ``technical,'' but is essential in Section~\ref{Krull:section:UpperBound} in the proof of the fundamental theorem about Krull dimension.
Let $t_1,\ldots, t_n, x_1,\ldots, x_n$ be variables, and let $I = (i_1,\ldots, i_n) \in \ensuremath{ \mathbf N }_0^n$. We consider the polynomials \[ (t_j+x_jt_n)^{i_j} \in \ensuremath{\mathbf F}[x_1,\ldots, x_n,t_1,\ldots, t_n] = \ensuremath{\mathbf F}[x_1,\ldots, x_n,t_1,\ldots, t_{n-1}] [ t_n] \] for $j = 1, \ldots, n$. As a polynomial in $t_n$, the leading term of $(t_j+x_jt_n)^{i_j}$ is $x_j^{i_j} t_n^{i_j}$ and the leading term of \[ (t_1+x_1t_n)^{i_1} (t_2+x_2t_n)^{i_2}\cdots (t_{n-1}+x_{n-1}t_n)^{i_{n-1}} (x_nt_n)^{i_n} \] is \begin{equation} \label{Krull:LeadingTerm} \prod_{j=1}^n (x_jt_n)^{i_j} = \left( \prod_{j=1}^nx_j^{i_j} \right) t_n^{\sum_{j=1}^n i_j}
= x^I t_n^{ |I| }. \end{equation}
Let $g$ be a nonzero polynomial in ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$. If $g$ has degree $d$ in $t_n$, then there exist unique polynomials $g_0,\ldots, g_d \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}]$ with $g_d \neq 0$ such that \[ g(t_1,\ldots, t_{n-1}, t_n) = \sum_{j =0}^d g_j(t_1,\ldots, t_{n-1}) t_n^j. \] The polynomial $g$ is \emph{monic in $t_n$}\index{monic in $t_n$} if $g_d =1$, that is, if \[ g(t_1,\ldots, t_{n-1}, t_n) = t_n^d + \sum_{j =0}^{d-1} g_j(t_1,\ldots, t_{n-1}) t_n^j. \]
\begin{lemma} \label{Krull:lemma:NoetherNorm2} Let ${\ensuremath{\mathbf F}}$ be an infinite field, and let $f = \sum_{I \in \ensuremath{ \mathcal I}} c_It^I \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ be a nonzero polynomial. There exist $a_1,\ldots, a_{n-1}, \lambda \in{\ensuremath{\mathbf F}}$ with $\lambda \neq 0$ and a polynomial $g \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ such that $g$ is monic in $t_n$ and \[ g(t_1,\ldots, t_{n-1}, t_n) = \lambda^{-1} f(t_1+a_1t_n, t_2+a_2t_n, \ldots, t_{n-1}+a_{n-1}t_n, t_n). \] \end{lemma}
\begin{proof} If $f$ has degree $d$, then \[
\ensuremath{ \mathcal I}_d = \{ I = (i_1,\ldots, i_n) \in \ensuremath{ \mathcal I} : |I| = \sum_{j=1}^n i_j = d \} \neq \emptyset \] and \[ f_d = \sum_{ I \in \ensuremath{ \mathcal I}_d} c_It^I \in{\ensuremath{\mathbf F}}[t_1,\ldots, t_n] \] is a nonzero homogeneous polynomial of degree $d$.
We introduce additional variables $x_1,\ldots, x_n$, and consider \[ f_d(t_1+ x_1t_n, t_2+x_2t_n, \ldots, t_{n-1}+x_{n-1}t_n, x_nt_n) \] as a polynomial in $t_n$ with coefficients in the ring ${\ensuremath{\mathbf F}}[x_1,\ldots, x_n, t_1,\ldots, t_{n-1}]$. Applying~\eqref{Krull:LeadingTerm}, we have \begin{align*} f_d(t_1+ & x_1t_n, t_2+x_2t_n, \ldots, t_{n-1}+x_{n-1}t_n, x_nt_n) \\ & = \sum_{I = (i_1,\ldots, i_n) \in \ensuremath{ \mathcal I}_d } c_I \prod_{j=1}^{n-1} (t_j+x_jt_n)^{i_j} \ (x_nt_n)^{i_n} \\ & = \sum_{ I= (i_1,\ldots, i_n) \in \ensuremath{ \mathcal I}_d } c_I \prod_{j=1}^n (x_j t_n)^{i_j} + \text{ lower order terms in $t_n$} \\ & = \left( \sum_{ I \in \ensuremath{ \mathcal I}_d } c_I x^I \right) t_n^d + \text{ lower order terms in $t_n$} \\ & = f_d(x_1,\ldots, x_{n-1}, x_n) t_n^d + \text{ lower order terms in $t_n$}. \end{align*} By Lemma~\ref{Krull:lemma:NoetherNorm1}, there exist $a_1,\ldots, a_{n-1} \in{\ensuremath{\mathbf F}}$ such that \[ \lambda = f_d(a_1,\ldots, a_{n-1},1) \neq 0. \] It follows that \begin{align*} \lambda^{-1}f_d(t_1+ & a_1t_n, t_2+a_2t_n, \ldots, t_{n-1}+a_{n-1}t_n, t_n) \\ & = \lambda^{-1}f_d(a_1,\ldots, a_{n-1}, 1) t_n^d + \text{ lower order terms in $t_n$} \\ & = t_n^d + \text{ lower order terms in $t_n$} \end{align*} and so the polynomial \begin{align*} g(t_1, & \ldots, t_{n-1}, t_n) \\ & = \lambda^{-1}f(t_1+ a_1t_n, t_2+a_2t_n, \ldots, t_{n-1}+a_{n-1}t_n, t_n) \\ & = \lambda^{-1} f_d(t_1+ a_1t_n, \ldots, t_{n-1}+a_{n-1}t_n, t_n) + \text{ lower order terms in $t_n$} \\ & = \lambda^{-1} f_d(a_1,\ldots, a_{n-1}, 1) t_n^d + \text{ lower order terms in $t_n$} \\ & = t_n^d + \text{ lower order terms in $t_n$} \end{align*} is monic in $t_n$. This completes the proof. \end{proof}
\section{Results from undergraduate algebra}\label{Krull:section:algebra}
To obtain an upper bound for the Krull dimension of the polynomial ring, we need to study the image of a chain of ideals in a quotient ring.
\begin{lemma} \label{Krull:lemma:PQRideals} If \[ \ensuremath{ \mathfrak I} \subset \ensuremath{ \mathfrak I}' \subset \ensuremath{ \mathfrak I}'' \] is an ideal chain in the ring $R$, then \[ \{ \ensuremath{ \mathfrak I} \} \subset \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I} \subset \ensuremath{ \mathfrak I}'' /\ensuremath{ \mathfrak I} \] is an ideal chain in the quotient ring $R/\ensuremath{ \mathfrak I} $. If $\ensuremath{ \mathfrak I}'$ is a prime ideal in $R$, then $\ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I}$ is a prime ideal in $R/\ensuremath{ \mathfrak I}$. \end{lemma}
\begin{proof} In the quotient ring $R/\ensuremath{ \mathfrak I}$, the set containing only the coset $0+\ensuremath{ \mathfrak I} = \ensuremath{ \mathfrak I}$ is $\{ \ensuremath{ \mathfrak I} \} $. The sets $\ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I} = \{a +\ensuremath{ \mathfrak I}: a \in \ensuremath{ \mathfrak I}' \}$ and $\ensuremath{ \mathfrak I}''/\ensuremath{ \mathfrak I} = \{b+\ensuremath{ \mathfrak I}: b \in \ensuremath{ \mathfrak I}''\}$ are ideals in $R/\ensuremath{ \mathfrak I}$.
We have $\ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I} \neq \{ \ensuremath{ \mathfrak I} \} $ because $\ensuremath{ \mathfrak I}' \neq \ensuremath{ \mathfrak I}$. Because $\ensuremath{ \mathfrak I}'$ is a proper subset of $\ensuremath{ \mathfrak I}''$, there exists $b \in \ensuremath{ \mathfrak I}''$ with $b \notin \ensuremath{ \mathfrak I}'$, and $b + \ensuremath{ \mathfrak I} \in \ensuremath{ \mathfrak I}''/\ensuremath{ \mathfrak I}$. If $b + \ensuremath{ \mathfrak I} \in \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I}$, then there exists $a \in \ensuremath{ \mathfrak I}'$ such that $b+ \ensuremath{ \mathfrak I} = a+\ensuremath{ \mathfrak I}$, and so $b-a \in \ensuremath{ \mathfrak I} \subseteq \ensuremath{ \mathfrak I}'$. It follows that $b = (b-a)+a \in \ensuremath{ \mathfrak I}'$, which is absurd. Therefore, $b + \ensuremath{ \mathfrak I} \notin \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I}$ and $\ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I} \neq \ensuremath{ \mathfrak I}''/\ensuremath{ \mathfrak I}$.
Let $\ensuremath{ \mathfrak I}'$ be a prime ideal in $R$. If $a,b \in R$ and \[ (a+ \ensuremath{ \mathfrak I} )(b+ \ensuremath{ \mathfrak I} ) \in \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I} \] then there exists $c \in \ensuremath{ \mathfrak I}'$ such that $ab+ \ensuremath{ \mathfrak I} = c + \ensuremath{ \mathfrak I}$ and so $ab = c + x$ for some $x \in \ensuremath{ \mathfrak I} \subseteq \ensuremath{ \mathfrak I}'$. Therefore, $ab \in \ensuremath{ \mathfrak I}'$. Because $\ensuremath{ \mathfrak I}'$ is a prime ideal, we have $a \in \ensuremath{ \mathfrak I}'$ or $b \in \ensuremath{ \mathfrak I}'$, and so $a+ \ensuremath{ \mathfrak I} \in \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I}$ or $b+ \ensuremath{ \mathfrak I} \in \ensuremath{ \mathfrak I}'/\ensuremath{ \mathfrak I}$. This completes the proof. \end{proof}
\begin{theorem} \label{Krull:theorem:strictPQRideals} If \[ \ensuremath{ \mathfrak P}_1 \subset \ensuremath{ \mathfrak P}_2 \subset \cdots \subset \ensuremath{ \mathfrak P}_m \] is a prime ideal chain in the ring $R$, then \begin{equation} \label{Krull:strictPQRideals} \{ \ensuremath{ \mathfrak P}_1 \} \subset \ensuremath{ \mathfrak P}_2 /\ensuremath{ \mathfrak P}_1 \subset \cdots \subset \ensuremath{ \mathfrak P}_m /\ensuremath{ \mathfrak P}_1 \end{equation} is a prime ideal chain in the quotient ring $R/\ensuremath{ \mathfrak P}_1$. \end{theorem}
\begin{proof} This follows immediately from Lemma~\ref{Krull:lemma:PQRideals}. \end{proof}
We also need some results about integral extensions of a ring. The ring $S$ is an \emph{extension ring}\index{extension ring} of $R$ and the ring $R$ is a \emph{subing}\index{subring} of $S$ if $R \subseteq S$ and the multiplicative identity in $R$ is the multiplicative identity in $S$. An element $a \in S$ is \emph{integral} over $R$\index{integral element} if there is a monic polynomial $f \in R[t]$ of degree $d \geq 1$ such that $f(a) = 0$.
The ring $S$ is an \emph{integral extension}\index{integral extension ring} of $R$ if $S$ is an extension ring of $R$ and every element of $S$ is integral over $R$. For example, the ring of Gaussian integers $\ensuremath{\mathbf Z}[i] = \{a+bi:a,b \in \ensuremath{\mathbf Z}\}$ is an integral extension of \ensuremath{\mathbf Z}\ because $a+bi \in \ensuremath{\mathbf Z}[i] $ is a root of the monic quadratic polynomial $t^2 -2at + a^2+b^2 \in \ensuremath{\mathbf Z}[t]$. The ring $R$ is an integral extension of itself because every element $a \in R$ is a root of the monic linear polynomial $t-a \in R[t]$.
\begin{lemma} \label{Krull:lemma:extend-1} Let $S$ be an extension ring of $R$. \begin{enumerate} \item[(i)] If $\ensuremath{ \mathfrak P}$ is a prime ideal in $S$, then $\ensuremath{ \mathfrak P} \cap R$ is a prime ideal in $R$. \item[(ii)]
Let $S$ be an integral domain that is an integral extension of the ring $R$. If $\ensuremath{ \mathfrak I}$ is a nonzero ideal in $S$, then $\ensuremath{ \mathfrak I} \cap R$ is a nonzero ideal in $R$. \end{enumerate} \end{lemma}
\begin{proof} (i) If $\ensuremath{ \mathfrak I}$ is an ideal in $S$, then $\ensuremath{ \mathfrak I} \cap R$ is an ideal in $R$. Let $\ensuremath{ \mathfrak P}$ be a prime ideal in $S$, and let $\ensuremath{ \mathfrak p} = \ensuremath{ \mathfrak P} \cap R$. If $a,b \in R$ and $ab \in \ensuremath{ \mathfrak p}$, then $ab \in \ensuremath{ \mathfrak P}$ and so $a \in \ensuremath{ \mathfrak P}$ or $b \in \ensuremath{ \mathfrak P}$. It follows that $a \in \ensuremath{ \mathfrak p}$ or $b \in \ensuremath{ \mathfrak p}$, and so \ensuremath{ \mathfrak p}\ is a prime ideal in $R$.
(ii) Let $S$ be an integral domain that is an integral extension of the ring $R$, and let $\ensuremath{ \mathfrak I}$ be a nonzero ideal in $S$. Let $a \in \ensuremath{ \mathfrak I}$, $a \neq 0$. Because $S$ is integral over $R$, there is a monic polynomial $f$ of minimum degree $d$ \[ f = t^d + c_{d-1}t^{d-1} + \cdots + c_1t + c_0 \in R[t] \] such that \[ f(a) = a^d + c_{d-1}a^{d-1} + \cdots + c_1a + c_0 = 0. \] If $c_0 = 0$, then \[ \left( a^{d-1} + c_{d-1}a^{d-2} + \cdots + c_1\right) a = 0. \] Because $S$ is an integral domain and $a \neq 0$, we obtain \[ a^{d-1} + c_{d-1}a^{d-2} + \cdots + c_1 = 0 \] and so $a$ is a root of a monic polynomial of degree $d-1$. This contradicts the minimality of $d$. Therefore, $c_0 \neq 0$. Because $a \in \ensuremath{ \mathfrak I}$ and $\ensuremath{ \mathfrak I}$ is an ideal, we have \[ a^d + c_{d-1}a^{d-1} + \cdots + c_1a = \left( a^{d-1} + c_{d-1}a^{d-2} + \cdots + c_1\right) a \in \ensuremath{ \mathfrak I} \] and so \[ c_0 = -\left( a^d + c_{d-1}a^{d-1} + \cdots + c_1a \right) \in \ensuremath{ \mathfrak I} \cap R. \] Thus, $\ensuremath{ \mathfrak I} \cap R \neq \{ 0\}$. This completes the proof. \end{proof}
\begin{lemma} \label{Krull:lemma:extend-2} Let $S$ be a ring, and let $R$ be a subring of $S$ such that $S$ is integral over $R$. If $\ensuremath{ \mathfrak P}$ and $\ensuremath{ \mathfrak I}$ are ideals in $S$ such that
$\ensuremath{ \mathfrak P} \subset \ensuremath{ \mathfrak I}$ and \ensuremath{ \mathfrak P}\ is prime, then $\ensuremath{ \mathfrak P} \cap R \neq \ensuremath{ \mathfrak I} \cap R$. \end{lemma}
\begin{proof} The quotient ring $S/\ensuremath{ \mathfrak P}$ is an integral domain because the ideal \ensuremath{ \mathfrak P}\ is prime. The ring $R/\ensuremath{ \mathfrak P}$ is a subring of $S/\ensuremath{ \mathfrak P}$, and $(\ensuremath{ \mathfrak P} \cap R)/\ensuremath{ \mathfrak P} = \{\ensuremath{ \mathfrak P}\}$. Thus, to prove that $\ensuremath{ \mathfrak P} \cap R \neq \ensuremath{ \mathfrak I} \cap R$, it suffices to prove that $(\ensuremath{ \mathfrak I} \cap R)/\ensuremath{ \mathfrak P} \neq \{\ensuremath{ \mathfrak P}\}$.
We prove first that $S/\ensuremath{ \mathfrak P}$ is an integral extension of $R/\ensuremath{ \mathfrak P}$. Let $a \in S$, and consider the coset $a + \ensuremath{ \mathfrak P}$. Because $a$ is integral over $R$, there is a monic polynomial \[ f = t^d + \sum_{i=0}^{d-1} c_i t^i \in R[t] \] such that \[ f(a) = a^d + \sum_{i=0}^{d-1} c_i a^i = 0. \] Defining the monic polynomial \[ \tilde{f}= t^d + \sum_{i=0}^{d-1} (c_i + \ensuremath{ \mathfrak P}) t^i \in (R/\ensuremath{ \mathfrak P}) [t] \] we obtain \begin{align*} \tilde{f}( a + \ensuremath{ \mathfrak P} ) & = ( a + \ensuremath{ \mathfrak P} )^d + \sum_{i=0}^{d-1} (c_i + \ensuremath{ \mathfrak P})(a+ \ensuremath{ \mathfrak P})^i \\ & = \left( a^d + \sum_{i=0}^{d-1} c_i a^i \right) + \ensuremath{ \mathfrak P} \\ & = f(a)+\ensuremath{ \mathfrak P} = \ensuremath{ \mathfrak P} \end{align*} and so $a + \ensuremath{ \mathfrak P}$ is integral over the ring $R/\ensuremath{ \mathfrak P}$. Thus, $S/\ensuremath{ \mathfrak P}$ is an integral extension of $R/\ensuremath{ \mathfrak P}$.
The ideal $\ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}$ is nonzero in $S/\ensuremath{ \mathfrak P}$ because $\ensuremath{ \mathfrak P}$ is a proper subset of \ensuremath{ \mathfrak I}. It follows from Lemma~\ref{Krull:lemma:extend-1} that $( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) $ is a nonzero ideal in $R/\ensuremath{ \mathfrak P}$, that is, $( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) \neq \{\ensuremath{ \mathfrak P}\}$.
We shall prove that $(\ensuremath{ \mathfrak I} \cap R)/\ensuremath{ \mathfrak P} = ( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) $. The inclusion $(\ensuremath{ \mathfrak I} \cap R)/\ensuremath{ \mathfrak P} \subseteq( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) $ is immediate. To prove the opposite inclusion, let $r+\ensuremath{ \mathfrak P} \in ( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) $ for some $r \in R$. There exists $a \in \ensuremath{ \mathfrak I}$ such that $r+\ensuremath{ \mathfrak P} = a+\ensuremath{ \mathfrak P}$, and so
$r -a = b \in \ensuremath{ \mathfrak P} \subset \ensuremath{ \mathfrak I}$. It follows that $r = a+ b \in \ensuremath{ \mathfrak I}$ and so $r \in \ensuremath{ \mathfrak I} \cap R$. Therefore, $( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) \subseteq (\ensuremath{ \mathfrak I} \cap R)/\ensuremath{ \mathfrak P}$.
We conclude that $( \ensuremath{ \mathfrak I} \cap R) /\ensuremath{ \mathfrak P} = ( \ensuremath{ \mathfrak I}/\ensuremath{ \mathfrak P}) \cap (R/ \ensuremath{ \mathfrak P}) \neq \{\ensuremath{ \mathfrak P}\}$, and so $\ensuremath{ \mathfrak P} \cap R \neq \ensuremath{ \mathfrak I} \cap R$. This completes the proof. \end{proof}
\begin{theorem} \label{Krull:theorem:extend-4} Let $S$ be an integral domain, and let $R$ be a subring of $S$ such that $S$ is integral over $R$. If \[ \ensuremath{ \mathfrak P}_0 \subset \ensuremath{ \mathfrak P}_1 \subset \cdots \subset \ensuremath{ \mathfrak P}_m \] is a prime ideal chain in $S$, then \begin{equation} \label{Krull:extend-4} \ensuremath{ \mathfrak P}_0 \cap R \ \subset \ \ensuremath{ \mathfrak P}_1 \cap R \ \subset \cdots \subset \ \ensuremath{ \mathfrak P}_m \cap R \end{equation} is a prime ideal chain in $R$. \end{theorem}
\begin{proof} This follows immediately from Lemmas~\ref{Krull:lemma:extend-1} and~\ref{Krull:lemma:extend-2}. \end{proof}
A \emph{minimal prime ideal}\index{minimal prime ideal}\index{prime ideal!minimal} in a ring $R$ is a nonzero prime ideal \ensuremath{ \mathfrak P}\ such that, if $\ensuremath{ \mathfrak P}' $ is a prime ideal and $\{ 0 \} \subseteq \ensuremath{ \mathfrak P}' \subseteq \ensuremath{ \mathfrak P}$, then $\ensuremath{ \mathfrak P}' = \{ 0 \}$ or $\ensuremath{ \mathfrak P}' = \ensuremath{ \mathfrak P}$. In a field, the only prime ideal is $\{0\}$ and there is no minimal prime ideal.
\begin{lemma} \label{Krull:lemma:UFD-minimalPrime} In a unique factorization domain $R$, a prime ideal is minimal if and only if it is a principal ideal generated by an irreducible element. \end{lemma}
\begin{proof} In a unique factorization domain, the principal ideal generated by an irreducible element is a nonzero prime ideal.
Let $\ensuremath{ \mathfrak P}$ be a minimal prime ideal in $R$. Because $\ensuremath{ \mathfrak P} \neq \{0\}$ and $\ensuremath{ \mathfrak P} \neq R$, the ideal $\ensuremath{ \mathfrak P}$ contains a nonzero element that is not a unit. This element is a product of irreducible elements. Because $\ensuremath{ \mathfrak P}$ is a prime ideal, it contains at least one of these irreducible factors. If $a \in \ensuremath{ \mathfrak P}$ and $a$ is irreducible, then $\ensuremath{ \mathfrak P}$ contains the principal ideal $\langle a \rangle$, which is a nonzero prime ideal. The minimality of $\ensuremath{ \mathfrak P}$ implies that $\ensuremath{ \mathfrak P} = \langle a \rangle$. Thus, every minimal prime ideal is a principal ideal generated by an irreducible.
Conversely, let $a$ be an irreducible element in $R$, and consider the nonzero prime ideal $\langle a \rangle$. If $\ensuremath{ \mathfrak P}$ is a nonzero prime ideal contained in $\langle a \rangle$, then $\ensuremath{ \mathfrak P}$ contains a nonzero element that is not a unit. This element is a product of irreducibles, and, because the ideal $\ensuremath{ \mathfrak P}$ is prime, it must contain at least one of these irreducible elements. Let $b$ be an irreducible element in \ensuremath{ \mathfrak P}, and let $\langle b \rangle$ be the principal ideal generated by $b$. We have \[ \langle b \rangle \subseteq \ensuremath{ \mathfrak P} \subseteq \langle a \rangle \] and so $a$ divides $b$. Because $a$ and $b$ are irreducible elements in $R$, it follows that $a$ and $b$ are associates and so $\langle a \rangle = \ensuremath{ \mathfrak P} = \langle b \rangle$. Therefore, $ \langle a \rangle$ is a minimal prime ideal. This completes the proof. \end{proof}
\begin{lemma} \label{Krull:lemma:determinant} Let $S_0$ be an extension ring of $R$. If there is a finite set $\{x_1,\ldots, x_d\} \subseteq S_0$ such that every element of $S_0$ is an $R$-linear combination of elements of $\{x_1,\ldots, x_d\} $, that is, if \[ S_0 = \left\{ \sum_{j=1}^d r_j x_j:r_j \in R \text{ for } j = 1,\ldots, d \right\} \] then $S_0$ is an integral extension of $R$. \end{lemma}
\begin{proof} Note that $S_0 \neq \{ 0\}$ because $1 \in S_0$, and so $ \{x_1,\ldots, x_d\} \neq \{0\}$.
The \emph{Kronecker delta}\index{Kronecker delta} $\delta_{i,j} $ is defined by $\delta_{i,j} = 1$ if $i=j$, and $\delta_{i,j} = 0$ if $i \neq j$.
Let $s \in S_0$. Because $S_0$ is a ring and $ \{x_1,\ldots, x_d\} \subseteq S_0$, for all $i \in \{1,\ldots, d \}$ we have $sx_i \in S_0$, and so there exist $r_{i,j} \in R$ such that \[ sx_i = \sum_{j=1}^d r_{i,j} x_j. \] Equivalently, \[ \sum_{j=1}^d (\delta_{i,j}s - r_{i,j} )x_j = 0 \] and so the homogeneous system of linear equations \[ \sum_{j=1}^d (\delta_{i,j}s - r_{i,j} )t_j = 0 \qquad\text{for $i=1,\ldots, d$.} \] has the nonzero solution $ \{x_1,\ldots, x_d\}$. This implies that the determinant of the matrix of coefficients of this system of linear equations is 0. This $d \times d$ matrix is \[ \left(\begin{matrix} s - a_{1,1} & -a_{1,2} & \cdots & -a_{1,d} \\ -a_{2,1} & s - a_{2,2} & \cdots & -a_{2,d} \\ \vdots & & & \\ -a_{n,1} & -a_{n,2} & \cdots & s - a_{d,d} \end{matrix}\right). \] and its determinant is a monic polynomial of degree $d$ in $s$ with coefficients in $R$. Therefore, $s$ is integral over $R$. This completes the proof. \end{proof}
\begin{lemma} \label{Krull:lemma:R[a]} Let $S$ be an integral domain, let $R$ be a subring of $S$, and let $a \in S$. Let $R[a]$ be the smallest subring of $S$ that contains $R$ and $a$. If $a$ is integral over $R$, then the ring $R[a]$ is an integral extension of $R$. \end{lemma}
\begin{proof} Every element of $R[a]$ is a polynomial in $a$ with coefficients in $R$, that is, an $R$-linear combination of elements in the infinite set $\{a^i:i=0,1,2,\ldots \}$. Because $a$ is integral over $R$, there is a monic polynomial $f \in R[t]$ of degree $d$ such that $f(a) = 0$. Rearranging this equation, we obtain \[ a^d = \sum_{j=0}^{d-1} c_{d,j} a^j \] with $c_{d,j} \in R$ for $j = 0,1,\ldots, d-1$. If $i \geq d$ and \[ a^i = \sum_{j=0}^{d-1} c_{i,j} a^j \] with $c_{i,j} \in R$ for $j = 0,1,\ldots, d-1$, then \begin{align*} a^{i+1} & = a \cdot a^i = a \sum_{j=0}^{d-1} c_{i,j} a^j = \sum_{j=0}^{d-2} c_{i,j} a^{j+1}+ c_{i,d-1} a^d \\ & = \sum_{j=1}^{d-1} c_{i,j-1} a^{j}+ c_{i,d-1} \sum_{j=0}^{d-1} c_{i,j} a^j \\ & = c_{i,d-1} c_{i,0} + \sum_{j=1}^{d-1} ( c_{i,j-1} + c_{i,d-1} c_{i,j} ) a^j\\ & = \sum_{j=0}^{d-1} c_{i+1,j} a^j \end{align*} where $c_{i+1,0} = c_{i,d-1} c_{i,0}$ and $c_{i+1,j} = c_{i,j-1} + c_{i,d-1} c_{i,j} \in R$ for $j=1,\ldots, d-1$. It follows by induction that every nonnegative power of $a$ can be written as an $R$-linear combination of elements in the finite set $\{1,a,a^2,\ldots, a^{d-1} \}$, and so every element in $R[a]$ is also an $R$-linear combination of elements in the finite set $\{1,a,a^2,\ldots, a^{d-1} \}$. By Lemma~\ref{Krull:lemma:determinant}, the ring $R[a]$ is an integral extension of $R$. \end{proof}
\section{An upper bound for the Krull dimension} \label{Krull:section:UpperBound}
\begin{theorem} \label{Krull:theorem:KrullDimension} Let ${\ensuremath{\mathbf F}}$ be an infinite field. For every nonnegative integer $n$, the Krull dimension of the polynomial ring ${\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$ is $n$. \end{theorem}
\begin{proof} Let $m$ be the Krull dimension of the ring $R = {\ensuremath{\mathbf F}}[t_1,\ldots, t_n]$. We have $m \geq n$ by Theorem~\ref{Krull:theorem:polynomial-n}. We must prove that $m \leq n$. The proof is by induction on $n$.
If $n = 0$, then $R$ is the field ${\ensuremath{\mathbf F}}$, the only prime ideal in a field is $\{ 0\}$, there is no minimal prime ideal, and $R$ has Krull dimension 0.
If $n = 1$, then $R ={\ensuremath{\mathbf F}}[t_1]$ is a principal ideal domain, and, consequently, a unique factorization domain. By Lemma~\ref{Krull:lemma:UFD-minimalPrime}, the nonzero prime ideals in $R$ are the principal ideals generated by irreducible polynomials, and every nonzero prime ideal in $R$ is minimal. Therefore, ${\ensuremath{\mathbf F}}[t_1]$ has Krull dimension 1.
Let $n \geq 2$, and let $R = {\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}, t_n] = R'[t_n]$, where $R' ={\ensuremath{\mathbf F}}[t_1,\ldots, t_{n-1}]$. By the induction hypothesis, $R'$ has Krull dimension at most $n-1$. Let \begin{equation} \label{Krull:MaxChain-1} \{ 0\} = \ensuremath{ \mathfrak P}_0 \subset \ensuremath{ \mathfrak P}_1 \subset \cdots \subset \ensuremath{ \mathfrak P}_m \end{equation} be a maximal chain of prime ideals in $R$. The polynomial ring $R $ is a unique factorization domain, and the ideal $\ensuremath{ \mathfrak P}_1$ is a minimal prime ideal in $R$. By Lemma~\ref{Krull:lemma:UFD-minimalPrime}, $\ensuremath{ \mathfrak P}_1$ is a principal ideal generated by an irreducible polynomial $f = f(t_1,\ldots, t_n)$.
Here is the critical application of Lemma~\ref{Krull:lemma:NoetherNorm2}: There exist $a_1,\ldots, a_{n-1}, \lambda \in{\ensuremath{\mathbf F}}$ with $\lambda \neq 0$ such that \[ g = g(t_1,\ldots, t_{n-1}, t_n) = \lambda^{-1} f(t_1+a_1t_n, t_2+a_2t_n, \ldots, t_{n-1}+a_{n-1}t_n, t_n) \] is a polynomial that is monic in the variable $t_n$ with coefficients in $R'$. We can represent $g$ in the form \begin{equation} \label{Krull:tilde-g} g = \tilde{g}(t_n) = t_n^d + \sum_{i=0}^{d-1} c_i t_n^i \in R'[t_n] \end{equation} for some positive integer $d$ and polynomials $c_0,c_1,\ldots, c_{d-1} \in R'$.
The function $\varphi: R \rightarrow R$ defined by $\varphi(a) = a$ for $a \in \ensuremath{\mathbf F}$ and \[ \varphi(t_j) = \begin{cases} t_j + a_j t_n & \text{ if $j = 1, \ldots, n-1$} \\ t_n & \text{ if $j=n$} \end{cases} \] is a ring isomorphism. Because a ring isomorphism sends prime ideals to prime ideals, \[ \{ 0\} = \varphi(\ensuremath{ \mathfrak P}_0) \subset \varphi(\ensuremath{ \mathfrak P}_1) \subset \cdots \subset \varphi( \ensuremath{ \mathfrak P}_m ) \] is also a maximal chain of prime ideals in $R$. We have \begin{align*} \varphi(f(t_1,\ldots, t_n) ) & = f(t_1+a_1t_n, t_2 + a_2 t_n, \ldots, t_{n-1} + a_{n-1} t_n, t_n) \\ & = \lambda g(t_1,\ldots, t_n) \end{align*} and so $\varphi(\ensuremath{ \mathfrak P}_1)$ is the principal ideal generated by $\lambda g(t_1,\ldots, t_n)$. Because $\lambda \in \ensuremath{\mathbf F} \setminus \{0\}$ is a unit in $R$, the principal ideal $\varphi(\ensuremath{ \mathfrak P}_1)$ is also generated by $g(t_1,\ldots, t_n)$. Thus, we can assume that the minimal ideal $\ensuremath{ \mathfrak P}_1$ in the prime ideal chain~\eqref{Krull:MaxChain-1} is a principal ideal generated by a monic polynomial $g \in R'[t_n]$.
The quotient ring $R/\ensuremath{ \mathfrak P}_1$ is an integral domain because $\ensuremath{ \mathfrak P}_1$ is a prime ideal. By Theorem~\ref{Krull:theorem:strictPQRideals}, \begin{equation} \label{Krull:MaxChain-2} \{ \ensuremath{ \mathfrak P}_1 \} \subset \ensuremath{ \mathfrak P}_2/\ensuremath{ \mathfrak P}_1 \subset \cdots \subset \ensuremath{ \mathfrak P}_m/\ensuremath{ \mathfrak P}_1 \end{equation} is a prime ideal chain in $R/\ensuremath{ \mathfrak P}_1$. Every coset in the quotient ring $R / \ensuremath{ \mathfrak P}_1$ is of the form $f + \ensuremath{ \mathfrak P}_1$, where \[ f = \sum_{i=0}^k f_i t_n^i \in R'[t_n] \] and $f_i \in R'$ for $i = 0,1,\ldots, k$. It follows that $f_i + \ensuremath{ \mathfrak P}_1 \in R'/\ensuremath{ \mathfrak P}_1$, and so \[ f + \ensuremath{ \mathfrak P}_1 = \left( \sum_{i=0}^k f_i t_n^i \right) + \ensuremath{ \mathfrak P}_1 = \sum_{i=0}^k (f_i + \ensuremath{ \mathfrak P}_1) (t_n + \ensuremath{ \mathfrak P}_1)^i \in \left( R'/ \ensuremath{ \mathfrak P}_1 \right) [t_n + \ensuremath{ \mathfrak P}_1]. \] This proves that $R / \ensuremath{ \mathfrak P}_1 \subseteq \left( R'/ \ensuremath{ \mathfrak P}_1 \right) [t_n + \ensuremath{ \mathfrak P}_1]$. Conversely, $ \left( R'/ \ensuremath{ \mathfrak P}_1 \right) [t_n + \ensuremath{ \mathfrak P}_1] \subseteq R / \ensuremath{ \mathfrak P}_1$ and so
$\left( R'/ \ensuremath{ \mathfrak P}_1 \right) [t_n + \ensuremath{ \mathfrak P}_1]= R / \ensuremath{ \mathfrak P}_1$.
Thus, we see that the quotient ring $R / \ensuremath{ \mathfrak P}_1$ is also the extension ring of $R' / \ensuremath{ \mathfrak P}_1$ that is generated by the coset $t_n + \ensuremath{ \mathfrak P}_1$. From~\eqref{Krull:tilde-g}, we have \begin{align*} (t_n + \ensuremath{ \mathfrak P}_1)^d & + \sum_{i=0}^{d-1} (c_i+ \ensuremath{ \mathfrak P}_1) (t_n + \ensuremath{ \mathfrak P}_1)^i \\ & = \left( t_n^d + \sum_{i=0}^{d-1} c_i t_n^i \right) + \ensuremath{ \mathfrak P}_1 \\ & = \tilde{g}(t_n) + \ensuremath{ \mathfrak P}_1 = g + \ensuremath{ \mathfrak P}_1= \ensuremath{ \mathfrak P}_1 \end{align*} and so $t_n + \ensuremath{ \mathfrak P}_1$ is integral over $R' / \ensuremath{ \mathfrak P}_1$. By Lemma~\ref{Krull:lemma:R[a]}, $R/\ensuremath{ \mathfrak P}_1 = (R'/\ensuremath{ \mathfrak P}_1) [ t_n + \ensuremath{ \mathfrak P}_1] $ is an integral extension of $R'/\ensuremath{ \mathfrak P}_1$. By Theorem~\ref{Krull:theorem:extend-4}, \begin{equation} \label{Krull:MaxChain-3} \{ \ensuremath{ \mathfrak P}_1 \} \cap R'/\ensuremath{ \mathfrak P}_1 \subset \left( \ensuremath{ \mathfrak P}_2/\ensuremath{ \mathfrak P}_1 \right) \cap R'/\ensuremath{ \mathfrak P}_1
\subset \cdots \subset \left( \ensuremath{ \mathfrak P}_m/\ensuremath{ \mathfrak P}_1 \right) \cap R'/\ensuremath{ \mathfrak P}_1 \end{equation} is a prime ideal chain of length $m-1$ in the ring $R'/\ensuremath{ \mathfrak P}_1$.
The degree of $t_n$ in the polynomial $g$ is positive, and so the degree of $t_n$ in every nonzero polynomial in the principal ideal $\ensuremath{ \mathfrak P}_1 = \langle g \rangle$ is positive. The degree of $t_n$ in every polynomial in $R' = \ensuremath{\mathbf F}[t_1,\ldots, t_{n-1}]$ is 0, and so \[ R' \cap \ensuremath{ \mathfrak P}_1 = \{0\}. \] This implies that the homomorphism $\psi:R' \rightarrow R/\ensuremath{ \mathfrak P}_1$ defined by $\psi(f) = f+\ensuremath{ \mathfrak P}_1$ is one-to-one, and so \[ R' \cong \psi(R') = R'/\ensuremath{ \mathfrak P}_1. \] Applying the isomorphism $\psi^{-1}: R'/ \ensuremath{ \mathfrak P}_1 \rightarrow R'$ to the maximal prime ideal chain~\eqref{Krull:MaxChain-3} in $R'/ \ensuremath{ \mathfrak P}_1$ gives a prime ideal chain of length $m-1$ in $R'$. The induction hypothesis implies that $m-1 \leq n-1$. This completes the proof. \end{proof}
\def$'$} \def\cprime{$'${$'$} \def$'$} \def\cprime{$'${$'$} \providecommand{\bysame}{\leavevmode\hbox to3em{\hrulefill}\thinspace} \providecommand{\MR}{\relax\ifhmode\unskip\space\fi MR }
\providecommand{\MRhref}[2]{
\href{http://www.ams.org/mathscinet-getitem?mr=#1}{#2} } \providecommand{\href}[2]{#2}
\end{document} | arXiv |
Google matrix
Leonardo Ermann et al. (2016), Scholarpedia, 11(11):30944. doi:10.4249/scholarpedia.30944 revision #187113 [link to/cite this article]
Curator: Dima Shepelyansky
Nick Orbeck
Klaus Frahm
Leonardo Ermann
Michelle L. Jones
Thomas Guhr
Dr. Leonardo Ermann, Laboratorio Tandar, Comision Nacional de Energia Atomica, Buenos Aires, Buenos Aires, Argentina
Prof. Klaus Frahm, Laboratoire de Physique Theorique du CNRS, Universite Paul Sabatier, Toulouse
Dima Shepelyansky, Laboratoire de Physique Théorique, CNRS, Université Paul Sabatier, Toulouse
The Google matrix \(G\) of a directed network is a stochastic square matrix with non-negative matrix elements and the sum of elements in each column being equal to unity. This matrix describes a Markov chain (Markov, 1906-a) of transitions of a random surfer performing jumps on a network of nodes connected by directed links. The network is characterized by an adjacency matrix \(A_{ij}\) with elements \(A_{ij}=1\) if node \(j\) points to node \(i\) and zero otherwise. The matrix of Markov transitions \(S_{ij}\) is constructed from the adjacency matrix \(A_{ij}\) by normalization of the sum of column elements to unity and replacing columns with only zero elements (dangling nodes) with equal elements \(1/N\) where \(N\) is the matrix size (number of nodes). Then the elements of the Google matrix are defined as \[ \tag{1} \displaystyle G_{ij} = \alpha S_{ij} + (1-\alpha)/N \ , \]
Figure 1: Google matrix \(G\) of the network Wikipedia English articles for Aug 2009 in the basis of nodes ordered by PageRank index \(K\); matrix indexes are \(K,K'\) in \(x,y\) axes with top values for \(K=K'=1\) in the top left corner (see text for definition of indexes \(K, K'\)) . Left panel shows first \(200 \times 200 \) matrix elements, right panel shows density of all matrix elements coarse-grained on $500\times 500$ cells. Color shows the density of matrix elements changing from black for minimum value (\((1-\alpha)/N\)) to white for maximum value via green and yellow; here the damping factor is \(\alpha = 0.85\), the matrix size is \(N=3282257\). (from Ermann, 2015-b)
where the damping factor \(0< \alpha < 1\) is the probability that a random surfer follows a link according to the stochastic matrix \(S\) while with probability \(1-\alpha\) he may jump to any network node. In this form the Google matrix was introduced by Brin and Page in 1998 (Brin, 1998-a) for the description of the World Wide Web (WWW). The right eigenvector of \(G\) with the largest (by modulus) unit eigenvalue is the PageRank vector whose non-negative elements correspond to the stationary probability to find a random surfer on a given node. The product of two Google matrices is also a Google matrix. The above construction of \(S\) can be directly generalized to the case of weighted transitions with the sum of elements in each column of \(S\) equal to unity. The general spectral properties of \(G\) matrix are described below with concrete examples of various real networks. An example image of \(G\) is shown in Figure 1 for the Wikipedia network. The Google matrix belongs to the class of Perron-Frobenius operators which appear in the description of dynamical chaotic systems (Brin, 2002-b) and related Ulam networks (Ulam, 1960-b,Ermann, 2010-a).
Figure 2: (a) Example of simple network with directed links between 5 nodes. (b) Distribution of 5 nodes from (a) on the PageRank-CheiRank plane \((K,K^*)\), where the size of node is proportional to PageRank probability \(P(K)\) and color of node is proportional to CheiRank probability \(P^*(K^*)\), with maximum at red and minimum at blue; the location of nodes of panel (a) on PageRank-CheiRank plane is: (2,4), (1,3),(3,1), (4,2), (5,5) for original nodes \(i=\)1,2,3,4,5 respectively; PageRank and CheiRank vectors are computed from the Google matrices \(G\) and \(G^*\) shown in Figure 3 at a damping factor \(\alpha=0.85\). (from Ermann, 2015-b)
1 Simple network example
2 PageRank and CheiRank eigenvectors
3 Numerical methods for \(G\) matrix
4 Spectrum of \(G\) matrix
5 Fractal Weyl law
6 Ulam networks
7 Linux Kernel networks
8 WWW networks of UK universities
9 Wikipedia networks
9.1 Top 100 historical figures of Wikipedia
9.2 Wikipedia ranking of world universities
10 Multiproduct world trade network
11 Other networks
12 Outlook
12.1 Random matrix theory for G ?
12.2 Anderson localization for Google matrix eigenstates
12.3 Reduced Google matrix
13 Historical notes
14 Lectures about Google matrix
15 Research articles
16 Books and reviews
17 External links to data sets
18 Video lectures
Simple network example
An example of simple directed network with 5 nodes is shown in Figure 2(a), here nodes are numbered from 1 to 5. The distribution of nodes on the PageRank-CheiRank plane of indexes \((K,K^*)\) is shown in Figure 2(b) (see definition of \((K,K^*)\) in next Section). The corresponding adjacency matrix \(A\) and matrices \(S, G\) are given in Figure 3(a,c,e). In addition it is useful to consider the network with inverted link directions. The corresponding adjacency matrix \(A^*\) and related matrices \(S^*, G^*\) are shown for this case in Figure 3(b,d,f).
Figure 3: (a) Adjacency matrix \(A\) of network of (a) with indexes used there, (b) adjacency matrix \(A^*\) for the network with inverted links; matrices \(S\) (c) and \(S^*\) (d) corresponding to the matrices \(A, A^*\); the Google matrices \(G\) (e) and \(G^*\) (f) corresponding to matrices \(S\) and \(S^*\) for \(\alpha=0.85\) (only 3 digits of matrix elements are shown. (from Ermann, 2015-b)
PageRank and CheiRank eigenvectors
According to the Perron-Frobenius theorem all eigenvalues \(\lambda_i\) of \(G\) are distributed inside the unitary circle \(|\lambda_i| \leq 1\). The right eigenvectors \( \psi_i(j)\) are defined by the equation \( \sum_{j'} G_{jj'} \psi_i(j') = \lambda_i \psi_i(j)\). In the following we will also use the notation eigenstates for such eigenvectors in analogy to eigenstates in quantum Hamiltonian systems. It can be shown that for \(\alpha<1\) the eigenvalue \(\lambda_0=1\) is not degenerate with only one right eigenvector called the PageRank vector \(P\). The positive elements \( P(j)\) of the PageRank vector, when the sum of them is normalized to unity, give the probability to find a random surfer on a node \(j\) in the stationary limit of long times. Only the eigenvectors of \(S\) for \(\lambda_0=1\) (which may be degenerate) are affected by the damping factor while other eigenvectors of \(S\) (with eigenvalues \(\lambda_i\neq 1\)) are also eigenvectors of \(G\) independent of \( \alpha\) due to their orthogonality to the left eigenvector (with identical unit entries) at \(\lambda_0=1\) but with rescaled eigenvalues \(\alpha\lambda_i\) for \(G\) (Langville, 2006-b,Gantmacher, 2000-b). The variation of \( \alpha\) in the range \( 0.5 \leq \alpha \leq 0.95 \) does not significantly affect the PageRank probabilities so that the results are usually presented for a typical value \( \alpha =0.85\) (Langville, 2006-b, Ermann, 2015-b).
The network with inverted link directions is described by the matrix \(G^*\), the PageRank eigenvector of \(G^*\) is called the CheiRank vector. The statistical properties of the CheiRank vector \( P^*\) have been first studied in (Chepelianskii, 2010-a) for the Linux Kernel network and later extended to the Wikipedia network (Zhirov, 2010-a).
All network nodes can be ordered by monotonically decreasing probabilities of PageRank or CheiRank vectors providing indexes \(K\) and \(K^*\) with the maximal probability at \(K=K^*=1\), and minimum probability at \(K=K^*=N\). The PageRank index \(K\) is used for the presentation of \(G\) in Figure 1: here all nodes are ordered by the PageRank index \(K\) and the strength of matrix elements $G_{KK'}$ is shown by color on a small scale (left panel) and on the whole matrix scale with coarse-graining (right panel).
The distribution of nodes on the PageRank-CheiRank plane for the simple network example is shown in Figure 2(b).
It is known that on average the PageRank probability is proportional to the number of ingoing links, characterizing how popular or known a given node is (Langville, 2006-b). Real networks are often characterized by power law distributions for the number of ingoing and outgoing links per node \( w_{in,out} \propto 1/k^{\mu_{in,out}}\) with typical exponents \(\mu_{in} \approx 2.1\) and \(\mu_{out} \approx 2.7\) for the WWW (Donato, 2004-a,Dorogovtsev, 2010-b,Newman, 2010-b). Assuming that the PageRank probability decays algebraically as \( P(i) \sim 1/{K(i)}^\beta\) we obtain that the number of nodes \(N_P\) with PageRank probability \( P\) scales as \(N_P \sim 1/P^{\mu_{in}}\) with \( \mu_{in} =1 +1/\beta\). Thus for the typical above values of \( \mu_{in}\) we have \(\beta =1/(\mu_{in,out}-1) \approx 0.9\) for PageRank \(P\) and \(\beta \approx 0.6\) for CheiRank \( P^*\) which is proportional to the number of outgoing links due to the inversion of direction. Examples of the probability decay of \( P, P^*\) are shown in Figure 4 for networks of Wikipedia and University of Cambridge. It should be noted that the decay is only approximately described by a power law. WWW networks of larger sizes (about 3.5 billions) also only approximately described by an algebraic decay (Meusel, 2015-a).
Figure 4: Dependence of probabilities of PageRank \(P\) (red curve) and CheiRank \(P^*\) (blue curve) vectors on the corresponding rank indexes \(K\) and \(K^*\) for networks of Wikipedia Aug 2009 (top curves) and University of Cambridge (bottom curves, moved down by a factor 100). The straight dashed lines show the power law fits for PageRank and CheiRank with the slopes \(\beta=0.92; 0.58\) respectively, corresponding to \(\beta=1/(\mu_{\rm in,out}-1)\) for Wikipedia, and \(\beta = 0.75, 0.61\) for Cambridge. (from Ermann, 2015-b)
For the case of the simple network visible in (a) the distribution of nodes on the PageRank-CheiRank plane is shown in (b). The distributions for Wikipedia and Linux Kernel networks are shown in Figure 5. It is convenient to characterize the network by the PageRank-CheiRank correlator \(\kappa =N \sum^N_{i=1} P(K(i)) P^*(K^*(i)) - 1\) (Chepelianskii, 2010-a) which takes different values depending on internal network properties even if the decay of PageRank and CheiRank probabilities is approximately the same in these networks. Thus we have \( \kappa = 4.08; -0.034\) for panels (a;b) of Figure 5. At small correlators the density is homogeneous along the line \( \ln K \approx - \ln K^*\) while for large positive values it is more concentrated along the line \( \ln K \approx \ln K^*\). More correlator values for different networks are given in (Ermann, 2015-b)]]).
It is also useful to rank network nodes by a 2DRank using a combination of PageRank and CheiRank: for this one considers a sequence of squares on the PageRank-CheiRank plane with the left bottom corner at \(K=K^*=1\) and increasing size placing nodes in 2DRank \(K_2\) in order of their appearance on square sides (see more detail at (Zhirov, 2010-a)).
Figure 5: Density distribution of network nodes \( W (K,K^*) = d^2 N_i/dK dK^* \) shown on the plane of PageRank and CheiRank indexes in log-scale \((\log_N K,\log_N K^*)\) for all \(1 \leq K,K^* \leq N\), density is computed over equidistant grid in plane \((\log_N K, \log_N K^*)\) with \(100 \times 100\) cells; color shows average value of \(W\) in each cell for the unit normalization condition for all nodes. Density \(W(K,K^*)\) is shown by color with blue for minimum in (a),(b) and white (a) and yellow (b) for maximum (black for zero). Panel (a): data for Wikipedia Aug (2009), \( N=3282257 \), green/red points show top 100 persons from PageRank/CheiRank, yellow pluses show top 100 persons from (Hart, 1992-b). Panel (b): density distribution for Linux Kernel V2.4 network with \( N = 85757\). (from Ermann, 2015-b)
The characterization of a directed network by both PageRank and CheiRank probabilities allows to characterized in a better way the information flow on the network taking into account ingoing flows, related to PageRank, and outgoing flows, related to CheiRank (see more detail in Ermann, 2015-b).
The density distribution of nodes on the PageRank-CheiRank plane is shown in Figure 5 for Wikipedia (a) and Linux (b) networks. The density \( W (K,K^*) = d^2 N_i/dK dK^* \) is computed on logarithmic-equidistant greed (cells) so that \( W (K,K^*) \) is given by the number \(N_i\) of network nodes appearing in a given cell divided by the cell area on \((K,K^*)\) plane.
Numerical methods for \(G\) matrix
Usually scale-free networks have algebraic distributions of ingoing and outgoing links with a relatively small average number of links \( N_\ell/N\) per node (see e.g. Dorogovtsev, 2010-b,Newman, 2010-b) corresponding to a very sparse adjacency matrix. For example for the networks of Figure 1, Figure 4, Figure 5 we have \( N_\ell/N \approx 22, 10, 2.3\). Therefore the PageRank vector can be efficiently computed by the power method which consists of multiplying repeatedly the matrix G to a random initial (sum normalized) vector. Each such matrix vector multiplication can be implemented by a loop over the link index and has therefore a complexity \(N_\ell\) which is much smaller than the matrix size \(N^2\). The particular contributions due to the dangling nodes or the damping factor in the Google matrix correspond to a complexity \(N\) and do not increase the overall complexity. Due to the presence of a gap between \( \lambda=1\) and the next eigenvalue with \( |\lambda| \leq 1-\alpha\) the convergence of the PageRank vector is exponential (e.g. after about 150 iterations the variation of the vector norm becomes less than \(10^{-12}\) for the Wikipedia network of Figure 1).
For typical networks the whole set of nodes can be decomposed in invariant subspace nodes and fully connected core space nodes leading to a block structure of the matrix \(S\) (Frahm, 2011-a): \[ \displaystyle S=\left(\begin{array}{cc} S_{ss} & S_{sc} \\ 0 & S_{cc} \\ \end{array}\right) \ . \] The core space block \(S_{cc}\) contains links between core space nodes and the coupling block \(S_{sc}\) may contain links from certain core space nodes to certain invariant subspace nodes. In contrast there are no links from subspace nodes to the nodes of core space (block with zero elements). By construction there are no links from nodes of invariant subspaces to the nodes of the core space. The subspace-subspace block \(S_{ss}\) is actually composed of many diagonal blocks for different invariant subspaces whose number can generally be rather large. Each of these blocks corresponds to a column sum normalized matrix with positive elements of the same type as $G$ and has therefore at least one unit eigenvalue. This leads to a high degeneracy \(N_1\) of the eigenvalue \(\lambda_0=1\) of \(S\), for example \(N_1\sim 10^3\) for the case of UK universities (see below). For each initial node one can iteratively determine a limit set of nodes that can be reached by a chain of non-zero matrix elements of \(S\) from the initial node. This set extends either over (nearly) the full network or it is limited, e.g. less than 10% of all network nodes. In the first case the initial node is attributed to the core space and in the second case the limit set defines an invariant subspace. For example for the WWW networks of UK universities, all invariant subspaces typically represent about \(20-30\%\) of the whole network.
The largest eigenvalues of \(S_{cc}\) (taken by their modulus) can be efficiently obtained by the powerful Arnoldi method [1] (see also Stewart, 2001-b,Ermann, 2015-b). The main idea of this method is to construct, by an iterative scheme of matrix vector multiplication and orthogonalization, an orthonormal basis on a subspace of modest dimension \(n_A\), called Krylov space, and to diagonalize the representation matrix of G on this subspace which provides typically good approximations for the largest eigenvalues of G (taken by their modulus). Also the corresponding eigenvectors are available by this method.
For the particular case of networks with a nearly triangular adjacency matrix the effects of numerical and round-off errors on the precision of eigenvalues may become very important and require high precision computations for the Arnoldi method or other particular special methods (Frahm, 2014-a,Ermann, 2015-b).
Figure 6: Panels (a) and (b) show the complex eigenvalue spectrum \(\lambda\) of the matrix \(S\) for the University of Cambridge 2006 and Oxford 2006 respectively.The spectrum \(\lambda\) of the matrix \(S^*\) for Cambridge 2006 and Oxford 2006 are shown in panels (c) and (d). Eigenvalues \(\lambda\) of the core space are shown by red points, eigenvalues of isolated subspaces are shown by blue points and the green curve (when shown) is the unit circle. Panels (e) and (f) show the fraction \(j/N\) of eigenvalues with \(|\lambda| > |\lambda_j|\) for the core space eigenvalues (red bottom curve) and all eigenvalues (blue top curve)from top row data for Cambridge 2006 and Oxford 2006. (from Ermann, 2015-b)
Spectrum of \(G\) matrix
Typical complex eigenvalue spectra of \(G, G^*\) are shown in Figs.6,7 for examples of UK universities and Wikipedia networks.
The spectra of \(S, S^*\) of universities of Cambridge and Oxford in 2006 are shown in Figure 6. These networks have a size \(N \approx 2 \times 10^5\). All subspace eigenvalues and \(n_A=20000\) core eigenvalues with maximal \(|\lambda|\) are shown. There is a strong degeneracy of the unit eigenvalue (about \(2\%\) of all eigenvectors). The global spectral structure has visible similarities with the spectra of random orthostochastic matrices of small size \(N=3,4\) analyzed numerically and analytically in (Zyczkowski, 2003a). The spikes visible at certain angles \(2\pi/p\) for \(p=2, 3, 4, 6\) correspond to approximate cycles of length \(p\) for the links between particular nodes ("close friends") that appear in top rank positions of the corresponding eigenstates of such eigenvalues.
The spectrum of the core space of \( S\) for the Wikipedia network (Aug 2009) is shown in Figure 7. The eigenstates with maximal values of \(|\lambda|\) correspond to certain quasi-isolated communities, they are marked by the most frequent words appearing in largest amplitudes of the corresponding eigenvectors. The results show that the eigenvectors of \(G\) clearly identify interesting specific communities of the network.
Figure 7: Complex eigenvalue spectrum of the matrices \(S\) for English Wikipedia Aug 2009. Highlighted eigenvalues represent different communities of Wikipedia and are labeled by the most repeated and important words following word counting of first 1000 nodes. Panel (a) shows complex plane for positive imaginary part of eigenvalues, while panels (b) and (c) zoom in the negative and positive real parts. (from Ermann, 2015-b)
Fractal Weyl law
In quantum mechanics the Weyl law (1912) gives a fundamental relation between the number of states and the phase volume of a Hamiltonian closed system of dimension \(d\). The generalization to operators of open quantum systems, appearing in the problems of quantum chaotic scattering with complex eigenenergies (Gaspard, 2014b), has been done relatively recently by (Sjostrand,1990a). The spectrum of corresponding operators has a complex spectrum \(\lambda\). The spread width \(\gamma=-2\ln|\lambda|\) of eigenvalues \(\lambda\) determines the life time of a corresponding eigenstate.
According to the fractal Weyl law the number of eigenvalues \(N_\gamma\), which have escape rates \(\gamma\) in a finite band width $0 \leq \gamma \leq \gamma_b$, scales as \[ \displaystyle N_\gamma \propto \hbar^{-d/2} \propto N^{\nu} \; , \;\; \nu = d/2 \ , \] where \(d\) is a fractal dimension of a classical strange repeller formed by classical orbits nonescaping in future and past times, \(\hbar\) is the Planck constant. In the context of eigenvalues \(\lambda\) of the Google matrix we have \(\gamma=-2 \ln|\lambda|\). As usual the Planck constant is inversely proportional to the number of states, which is determined by the matrix size, so that \(\hbar \propto 1/N\).
The fractal Weyl law of open systems with a fractal dimension \(d<2\) leads to a striking consequence: only a relatively small fraction of eigenvalues \(\mu_W \sim N_\gamma/N \propto \hbar^{(2-d)/2} \propto N^{(d-2)/2} \ll 1\) has finite values of \(|\lambda|\) while almost all eigenstates of the matrix operator of size \(N \propto 1/\hbar\) have \(\lambda \rightarrow 0\). The eigenstates with finite \(|\lambda| >0\) are related to the classical fractal sets of orbits non-escaping neither in the future neither in the past. The fractal Weyl law for the Ulam networks is discussed in next Section. This law has been shown to be valid for the Linux Kernel network with \(d \approx 1.3\) (see Figure 8 and related Section). For the Physical Review network it is found that \(d \approx 1\) Frahm, 2014-a).
There is an expectation that the eigenstates with large \(|\lambda|\), forming the fractal Weyl law, capture certain hidden interesting communities. It is qualitatevely confirmed by the analysis of eigenvectors of Wikipedia matrix \(G\) (see Figure 7 and Frahm, 2014-a).
Mathematical aspects of the fractal Weyl law are reviewed in (Nonnenmacher, 2014b).
Figure 8: Panel (a) shows distribution of eigenvalues \(\lambda\) in the complex plane for the Google matrix \(G\) of the Linux Kernel version 2.6.32 with \(N=285509\) and \(\alpha=0.85\); the solid curves represent the unit circle and the lowest limit of computed eigenvalues. Panel (b) shows dependence of the integrated number of eigenvalues \(N_\lambda\) with \(\vert\lambda\vert>0.25\) (red squares) and \(\vert\lambda\vert>0.1\) (black circles) as a function of the total number of processes \(N\) for versions of Linux Kernels. The values of \(N\) correspond (in increasing order) to Linux Kernel versions \(1.0, 1.1, 1.2, 1.3, 2.0, 2.1, 2.2, 2.3, 2.4, 2.6\). The power law \(N_\lambda\propto N^{\nu}\) has fitted values \(\nu_{\vert\lambda\vert>0.25}=0.622 \pm 0.010\) and \(\nu_{\vert\lambda\vert>0.1}=0.630 \pm 0.015\). Inset shows data for the Google matrix \(G^*\) with inverse link directions, the corresponding exponents are \(\nu^*_{\vert\lambda\vert>0.25}=0.696 \pm 0.010\) and \(\nu^*_{\vert\lambda\vert>0.1}=0.652 \pm 0.007\). (from Ermann, 2015-b)
Ulam networks
By construction the Google matrix belongs to the class of Perron-Frobenius operators which naturally appear in ergodic theory and dynamical systems with Hamiltonian or dissipative dynamics (Brin, 2002-b). In 1960 Ulam (Ulam, 1960-b) proposed a method, now known as the Ulam method, for a construction of finite size approximants for the Perron-Frobenius operators of dynamical maps. The method is based on discretization of the phase space and construction of a Markov chain based on probability transitions between such discrete cells given by the dynamics. Using as an example a simple chaotic map Ulam made a conjecture that the finite size approximation converges to the continuous limit when the cell size goes to zero. Indeed, it has been proven that for hyperbolic maps in one and higher dimensions the Ulam method converges to the spectrum of the continuous system. The probability flows in dynamical systems have rich and nontrivial features of general importance, like simple and strange attractors with localized and delocalized dynamics governed by simple dynamical rules. Such objects are generic for nonlinear dissipative dynamics and therefore they can have relevance for actual WWW structure. The analysis of Ulam networks, generated by the Ulam method, allows to obtain a better intuition about the spectral properties of Google matrix.
Figure 9: Phase space representation of eigenstates of the Ulam approximate of the Perron-Frobenius operator (UPFO) \(S\) for \(N = 110 \times 110\) cells (color is proportional to absolute value \(|\psi_i|\) with red for maximum and blue for zero). Panel (a) shows an eigenstate with maximum eigenvalue \(\lambda_1 = 0.756\) for the Chirikov standard map with absorption at \(K_s = 7, a=2, \eta=1\), the space region is (\(-aK_s/4\pi \leq y \leq aK_s/4\pi\), \(0 \leq x \leq 1\)), the fractal dimension of the strange repeller set nonescaping in future is \(d_e=1+d/2 = 1.769\). Panel (b) shows an eigenstate at \(\lambda = 1\) of the UPFO of the map without absorption at \(K_s = 7, \eta = 0.3\), the shown space region is (\(-1/\pi \leq y \leq 1/\pi, 0 \leq x \leq 1\)) and the fractal dimension of the strange attractor is \(d = 1.532\). (from Ermann, 2015-b)
The Ulam method works as following: the phase space of a dynamical map is divided in equal cells and a number of trajectories $N_c$ is propagated by a map iteration. Thus a number of trajectories \(N_{ij}\) arriving from cell \(j\) to cell \(i\) is determined. Then the matrix of Markov transition is defined as \(S_{ij}=N_{ij}/N_c\). By construction this matrix belongs to the class of Perron-Frobenius operators which includes the Google matrix. The physical meaning of the coarse grain description by a finite number of cells is that it introduces in the system a noise of cell size amplitude. More details can be found at (Ermann, 2015-b).
Examples of eigenstates of the Ulam approximate of Perron-Frobenius operators (UPFO) of two Ulam networks are shown in Figure 9. The networks are generated by the Ulam method applied to the dynamical map \[ \displaystyle {\bar y} = \eta y + \frac{K_s}{2\pi} \sin (2\pi x) \; , \;\; {\bar x} = x + {\bar y} \;\; ({\rm mod} \; 1) \; \ . \] Here bars mark the variables after one map iteration and we consider the dynamics to be periodic on a torus so that \(0 \leq x \leq 1, -1/2 \leq y \leq 1/2\); \(K_s\) is a dimensionless parameter of chaos. At \(\eta=1\) we have the area-preserving symplectic map, known as the Chirikov standard map (Chirikov, 2008-b), for \(0< \eta <1\) we have a dissipative dynamics with a strange attractor. At \( \eta = 1 \) the absorption is introduced so that all orbits leaving the interval $-aK_s/4\pi \leq y \leq aK_s/4\pi$ are absorbed after one iteration. Thus the UPFO has the maximal eigenvalue \(\lambda <1 \) with a strange repeller of orbits remaining in the system after many map iterations. For the dissipative case at \( \eta < 1 \) the orbits drop on a strange attractor (see Figure 9). The fractal dimension \(d\) of these strange sets depends on the system parameters that allows to vary it in a large range \( 0<d<2\). The spectral analysis of UPFO in these systems confirms the validity of the fractal Weyl law for variation of the exponent \( \nu \) in the interval \( 0 < \nu <1\) (Ermann, 2010-a).
Linux Kernel networks
Modern software codes represent now complex large scale structures and analysis and optimization of their architecture become a challenge. An interesting approach to this problem was proposed in (Chepelianskii, 2010-a) on the basis of directed network analysis. Thus the Procedure Call Networks (PCN) are constructed for the open source programs of Linux Kernel written in the C programming language. In this language the code is structured as a sequence of procedures calling each other. Due to that feature the organization of a code can be naturally represented as a PCN, where each node represents a procedure and each directed link corresponds to a procedure call. For the Linux source code such a directed network is built by its lexical scanning with the identification of all the defined procedures. For each of them a list keeps track of the procedures calls inside their definition.
It is found that the PageRank and CheiRank probabilities in this network decay as a power law with the approximate exponent values \(\beta \approx 1; 0.5\) respectively. For V2.6.32 the top three procedures of PageRank are printk, memset, kfree, while at the top of CheiRank we have start_kernel, btrfs_ioctl, menu_finalize. These procedures perform rather different tasks with printk reporting messages and start_kernel initializing the Kernel and managing the repartition of tasks. This gives an idea that both PageRank and CheiRank order can be useful to highlight different aspects of directed and inverted flows on our network. Of course, in the context of WWW ingoing links related to PageRank are less vulnerable as compared to outgoing links related to CheiRank, which can be modified by a user rather easily.
For the Linux Kernel network the correlator \(\kappa\) between PageRank and CheiRank vectors is close to zero. This confirms the statistical independence of these two vectors. The density distribution of nodes of the Linux Kernel network, shown in Figure 5(b), has a homogeneous distribution along \(\ln K + \ln K^*=const\) lines demonstrating once more absence of correlations between \(P(K(i))\) and \(P^*({K^*(i)})\). Indeed, such homogeneous distributions appear if nodes are generated randomly with factorized probabilities \(P(i) , P^*(i) \).
The physical reasons for absence of correlations between \(P(K), P^*(K^*)\) have been explained (Chepelianskii, 2010-a) on the basis of the concept of separation of concerns in software architecture. It is argued that a good code should decrease the number of procedures that have high values of both PageRank and CheiRank since such procedures will play a critical role in error propagation since they are both popular and highly communicative at the same time. For example in the Linux Kernel, do_fork, that creates new processes, belongs to this class. Such critical procedures may introduce subtle errors because they entangle otherwise independent segments of code. The above observations suggest that the independence between popular procedures, which have high \(P(K(i))\) and fulfill important but well defined tasks, and communicative procedures, which have high \(P^*({K^*(i)})\) and organize and assign tasks in the code, is an important ingredient of well structured software.
The different Linux versions from V1.0 to V2.6 provide a network size variation in a range \( 2752 \leq N \leq 285510\) allowing to demonstrate the validity of the fractal Weyl law with the fractal dimension \( d \approx 1.3\) (see Figure 8). Linux network data sets are available at (FETNADINE, 2015-e).
WWW networks of UK universities
The WWW networks of certain UK universities for the years between 2002 and 2006 are publicly available at (UK universities, 2006-e; selected networks are given at EU-FET-NADINE site FETNADINE, 2015-e). The universal emergence of PageRank, properties of PageRank and CheiRank vectors and the spectral properties of \( G, G^*\) are analyzed in detail at (Frahm, 2011-a, see also Figs.4,6). It is established that the rescaled distribution of sizes \(d_i\) of invariant subspaces of university networks is described by a universal function \(F(x)=1/(1+2x)^{3/2}\) with \( x= d_i/<d> \), where \( <d> \) is an average subspace dimension computed for a WWW of a given university. This is related with a universal power law decay of PageRank probability \( P \propto 1/K^{2/3}\) emerging at \( \alpha \rightarrow 0\). It is shown that for certain universities the maximal eigenvalue \(\lambda_c\)of the core space is enormously close to unity (e.g \( 1-\lambda_c < 10^{-16}\)); the corresponding eigenstates are localized on a small node subset. More results are available at (Frahm, 2011-a,Ermann, 2015-b).
Wikipedia networks
The free online encyclopedia Wikipedia is a huge repository of human knowledge. Its size is growing permanently accumulating a enormous amount of information. The hyperlink citations between Wikipedia articles provide an important example of directed networks evolving in time for many different languages.
The decay of probabilities of PageRank and CheiRank are shown in Figure 4 for English Wikipedia edition of August 2009 (Zhirov, 2010-a). They are satisfactory described by a power law decay with exponents \(\beta_{PR,CR} =1/(\mu_{\rm in,out}-1) = 0.92; 0.58\).
The density distribution of articles over the PageRank-CheiRank plane \((\log_N K, \log_N K^*)\) is shown in Figure 5(a). The density is very different from those generated by the product of independent probabilities of \(P\) and \(P^*\) which gives the distribution similar to the case of the Linux Kernel network shown in Figure 5(b) where the correlator \(\kappa\) between PageRank and CheiRank vectors is almost zero (while for Wikipedia \(\kappa = 4.08\)).
The difference between PageRank and CheiRank is clearly seen from the names of articles with highest ranks. At the top of PageRank there are 1. United States, 2. United Kingdom, 3. France while for CheiRank one finds 1. Portal:Contents/Outline of knowledge/Geography and places, 2. List of state leaders by year, 3. Portal:Contents/Index/Geography and places. Clearly the PageRank selects first articles on a broadly known subject with a large number of ingoing links while the CheiRank selects first highly communicative articles with many outgoing links. The 2DRank combines these two characteristics of information flow on directed network. At the top of 2DRank \(K_2\) one has 1. India, 2. Singapore, 3. Pakistan. Thus, these articles are most known/popular and most communicative at the same time. Results of ranking of the Wikipedia Aug 2009 edition for various categories are available at (Wiki2009, 2010-e).
The complex spectrum of eigenvalues of $G$ for this Wikipedia network is shown in Figure 7 (due to symmetry of eigenvalues \(\lambda = \lambda^*\) only the upper plane of \(\lambda\) is shown). As for university networks, the spectrum also has some invariant subspaces resulting in degeneracies of the leading eigenvalue \(\lambda=1\) of \(S, S^*\). However, due to the stronger connectivity of the Wikipedia network these subspaces are significantly smaller compared to university networks.
It is expected that the eigenstates with large values of \(|\lambda|\) select certain specific communities. If \(|\lambda|\) is close to unity then the relaxation of probability from such nodes is rather slow and we can expect that such eigenstates highlight some new interesting information even if these nodes are located in the tail of the PageRank. The important advantage of the Wikipedia network is that its nodes are Wikipedia articles with a relatively clear meaning allowing to understand the origins of appearance of certain nodes in one community. The frequency analysis of words appearing at the largest amplitudes of eigenvectors with large modulus of \(|\lambda|\) confirms this expectation (see Figure 7 and Ermann, 2015-b).
Top 100 historical figures of Wikipedia
There is always significant public interest to know who are the most significant historical figures, or persons, of humanity. The Hart list of the top 100 people who, according to him, most influenced human history is available at (Hart, 1992-b). Hart "ranked these 100 persons in order of importance: that is, according to the total amount of influence that each of them had on human history and on the everyday lives of other human beings." Of course, a human ranking can always be objected arguing that an investigator has his or her own preferences. Also investigators from different cultures can have different viewpoints on the same historical figure. Thus it is important to perform a ranking of historical figures on purely mathematical and statistical grounds which exclude any cultural and personal preferences of investigators.
A detailed two-dimensional ranking of persons of the English Wikipedia August 2009 was done by (Zhirov, 2010-a). Earlier studies had been done in a non-systematic way without any comparison with established top 100 lists. The distribution of the top 100 PageRank, CheiRank, and Hart's persons on PageRank-CheiRank plane is shown in Figure 5(a). For the PageRank top 100 list the overlap with the Hart list is at 35% (PageRank), 10% (2DRank), and almost zero for CheiRank. This is attributed to a very broad distribution of historical figures on the 2D plane, as shown in Figure 5(a), and a large variety of human activities. The distribution of the top 100 persons of the Wikipedia August 2009 remains stable and compact for PageRank and 2DRank for the period 2007–2011 while for CheiRank the fluctuations of positions are large (Ermann, 2015-b). This is due to the fact that outgoing links are easily modified and fluctuating.
However, it is important to take into account not only the view point of English Wikipedia but also to consider viewpoints of other language editions of Wikipedia representing other cultures. Thus the ranking of world historical figures was done on the basis of 24 editions (Eom, 2015-a). In 2014 these 24 languages cover 59 percent of world population, and the corresponding 24 editions cover 68 percent of the total number of Wikipedia articles in all 287 available languages. Also the selection of people from the rank list of each edition is now done in an automatic computerized way. For this a list of about 1.1 million biographical articles about people with their English names is generated. From this list of persons, with their biographical article title in the English Wikipedia, the corresponding titles in other language editions are determined using the inter-language links provided by Wikipedia. The rank score of each persons is averaged over all 24 editions thus equally taking into account the opinions of these 24 cultures.
For PageRank the top global three historical figures are Carl Linnaeus, Jesus, and Aristotle. All other ranks are available at (TopWikiPeople, 2014-e). The overlap of top 100 PageRank and Hart's lists have 43 common persons. The fact that Carl Linnaeus is the top historical figure of the Wikipedia PageRank list came as a surprise for media and the broad public (see Refs. in Ermann, 2015-b). This ranking is due to the fact that Carl Linnaeus created a classification of world species including animals, insects, herbs, trees, etc. Thus all articles of these species point to the article Carl Linnaeus in various languages. As a result Carl Linnaeus appears on almost all top positions in all 24 languages. Hence, even if a politician, like Barack Obama, takes the second position in his country language EN (Napoleon is at the first position in EN) he is usually placed at a low ranking in other language editions. As a result Carl Linnaeus takes the first global PageRank position. More details, including the distribution of historical figures over world countries and 35 centuries of human history, can be found at (Eom, 2015-a,Ermann, 2015-b,TopWikiPeople, 2014-e). The results of other research groups for ranking of historical figures of Wikipedia are referenced in (PantheonMIT, 2015-e, StonyBrookranking, 2015-e, see more Refs. in Eom, 2015-a, Ermann, 2015-b).
Wikipedia ranking of world universities
Figure 10: Geographical distribution of universities appearing in the top 100 universities of all 24 Wikipedia editions given by PageRank algorithm. The total number of universities is 1025. Colors range from dark blue (small number of universities) to dark red (maximum number of universities, here 118 for US). Countries filled by dashed lines pattern have no university in the top 100 lists of 24 editions. (from Lages, 2016-a)
The ranking of universities for the English Wikipedia edition Aug 2009 was done in (Zhirov, 2010-a) giving at the top of PageRank list: University of Harvard, University of Oxford, University of Cambridge with the overlap of 70% for the top 100 list of Academic ranking of world universities of Shanghai in 2009 (Shanghai, 2015-e). All results of ranking of universities are available at (Wiki2009, 2010-e). However, it is important also to take into account the opinions of other cultures and not only of the English edition to determine the university ranking.
Thus, the above approach for ranking of historical figures is also used for the Wikipedia ranking of world universities, using the same datasets of 24 Wikipedia editions. The combined results (Lages, 2016-a) obtained from top 100 universities of each edition give total global lists of 1025, 1379, 1560 universities for PageRank, CheiRank, and 2DRank algorithms respectively. All these results are available at (TopWikiUniversities, 2015-e). The distribution of 1025 PageRank universities over the world countries is shown in Figure 10. For the global PageRank list the top three positions are taken by University of Cambridge, University of Oxford, Harvard University. The overlap of top 100 PageRank list with top 100 of Academic ranking of world universities of Shanghai (Shanghai, 2015-e) is equal to 62 universities (English, French, German editions have overlaps of 65, 41, 35 universities respectively; the comparison is done for the year 2013).
The time evolution of the geographical distribution of leading world universities over 10 centuries is given in (TopWikiUniversities, 2015-e). Before the 19th century universities of Germany dominate this ranking (thus among the top universities of PageRank list with 139 universities, founded before year 1800, the main part of 25 universities is located in Germany, see Fig.10 in (Lages, 2016-a)). However, already for the universities founded before the 20th century (before year 1900) the lead is taken by the USA (see Fig.9 in (Lages, 2016-a)). The analysis of the university ranking evolution through ten centuries shows that Wikipedia highlights significantly stronger historically important universities whose role is reduced in the Shanghai ranking. Nowadays the PageRank algorithm gives the top 5 countries: USA, UK, Germany, Sweden, and France, while the Shanghai ranking gives USA, UK, Canada, Switzerland, and Japan.
The Wikipedia ranking provides a sound mathematical statistical evaluation of world universities which can be viewed as a new independent ranking being complementary to already existing approaches. A comparison of various web-based rankings of world universities is reported in (Pagell, 2016-a). In the view of the importance of university ranking for higher education (Hazelkorn, 2015-b) it is possible to expect that the Wikipedia ranking of world universities will also find a broad usage together with other rankings.
Multiproduct world trade network
Figure 11: Country positions in PageRank-CheiRank plane \((K,K^*)\) for the world trade in all commodities in 2008. Each country is shown by circle with its own flag. (from Ermann, 2015-b)
The Google matrix of the world trade network was constructed in (WTN, 2011-e) on the basis of the United Nations Commodity Trade Statistics Database (UNCOMTRADE, 2015-e) for all UN countries and various trade commodities for all available years from 1962 to 2009. The trade flows on this network are classified with the help of the PageRank and CheiRank algorithms and the distribution of countries on the PageRank-CheiRank plane is shown in for the trade in all commodities (or all products). This ranking treats all countries on equal democratic grounds independent of country richness but this method still puts at the top a group of industrially developed countries, reproducing about 75% of G20 members. The matrix \(S\) is obtained by column normalization of the monetary trade flow matrix \(M_{cc'p}\) available for each year at (UNCOMTRADE, 2015-e) for countries \(c, c'\) and product \(p\) (\(c \neq c' \)). Then the matrix \(G\) is obtained by the general rule (1).
The case, when the trade is considered for all commodities, gives a typical distribution visible in with concentration of countries in a vicinity of the diagonal \(K=K^*\). This is due to the economic trade balance which each country tries to equilibrate roughly. In a certain sense the PageRank corresponds to country import (ingoing links) and CheiRank to export (outgoing links). However, the import and export take into account only one link trade between countries while the Google matrix analysis takes into account multiple links and significance of nodes. In general the country distribution on the PageRank-CheiRank plane is quite similar to the distribution on the Import-Export plane (see WTN, 2011-e). However, there are also some exceptions with noticeable differences such as Singapore (it improves its position from 15 in export rank to \(K^*=11\) in CheiRank) showing the stability and broadness of its export trade in 2008. On the other hand Canada and Mexico have a lower ("better") position in export rank than in CheiRank due to a too strong orientation of their export to the USA.
The time evolution of PageRank and CheiRank indexes captures correctly known crises at certain years for certain countries (e.g Russia in 1998, Argentina in 2001) which typically lead to a strong increase of the country's PageRank index \(K\) related to the drop of its import during a crisis.
The aproach developed in (WTN, 2011-e) allows to perform the Google matrix analysis for one specific product or for all commodities counted together. In this way the matrix size is always restricted to the number of countries \(N_c\) being significantly smaller than the total number of nodes \(N=N_c N_p\) for a trade with \(N_p\) products.
Figure 12: Geographical distribution of the derivative of probabilities balance \(dB_c/d \delta_{33}\) of world countries over petroleum price \(\delta_{33}\) for the year 2008. The country balance is determined from CheiRank and PageRank vectors as \(B_c= ({P^*}_c-P_c)/({P^*}_c+P_c)\). (from Ermann, 2015-a)
The Google matrix of the multiproduct world trade was constructed in (Ermann, 2015-a). This construction treats all countries on equal democratic grounds independently of their richness and at the same time it considers the contributions of trade products proportionally to their trade volume. This is achieved by the introduction of a personalized vector in the term of \(G\) with \((1-\alpha)\), that makes the contribution of products being proportional to their trade volume, while all countries are treated on equal grounds. This analysis was done for \(M_p=61\) products and up to \(N_c=227\) countries. The obtained results show that the trade contribution of products is asymmetric: some of them are export oriented while others are import oriented even if the ranking by their trade volume is symmetric in respect to export and import after averaging over all world countries. The construction of the multiproduct Google matrix allows to investigate the sensitivity of the trade balance with respect to price variations of products, e.g. petroleum and gas, taking into account the world connectivity of trade links. An example of the country sensitivity to the petroleum price increase \(\delta_{33}\) is shown in Figure 12. It shows that the dimensionless trade balance \(B_c= ({P^*}_c-P_c)/({P^*}_c+P_c)\) is increased for petroleum producing countries like Russia and Saudi Arabia while the trade balance of China drops significantly (\( P_c, {P^*}_c\) are PageRank and CheiRank probabilities of a country \(c\) after summation over all products).
The Google matrix analysis of multiproduct world trade allows to establish hidden dependencies between various products and countries and opens new prospects for further studies of this interesting complex system of world importance.
This approach was successfully extended to the analysis of the world network of economic activities from the OECD-WTO TiVA database (Kandiah, 2015-a). This network describes the exchange of 37 activity sectors of 58 countries in years 1995 - 2008. In contrast to the UN COMTRADE these datasets contain also exchange between different sectors. The exchange balance \(B_c\) allows to determine economically rising countries with a robust network of economic relations. The sensitivity of \(B_c\) to price variations and labor cost in various countries determines the hidden relations between world economies being not visible for the usual export-import exchange analysis. The analysis of financial network transactions between various bank units can be also well suited for the Google matrix approach.
The Google matrix analysis can be considered as a further extension of the matrix analysis of Input-Output transactions broadly used in economy (Miller, 2009-b), starting from the fundamental works of Leontief (Leontief, 1953-a, Leontief, 1986-b).
The Google matrix approach allows to obtain interesting and useful results for a variety of directed networks: network of integers and citation network of Physical Review with nilpotent (triangular or nearly triangular) adjacency matrices, networks of game go (Kandiah, 2014-a) , the entire Twitter network of 41 million size in 2009, network of business process management, neural network of a large-scale thalamocortical model (Izhikevich, 2008-a), neural network of C.elegans, networks of word transitions in DNA sequences, gene regulation networks (see Refs. in Ermann, 2015-b).
In physics, the Random matrix theory was introduced by Wigner (Wigner, 1967-b) to explain spectral properties of complex nuclei, atoms and molecules. This theory, developed for Hermitian and unitary matrices, captures universal spectral properties and find numerous applications in atomic, mesoscopic and nuclear systems (Guhr, 1998-b, Mehta, 2004-b, Fyodorov, 2011-b). This approach also describes the spectral properties of quantum chaotic systems which are characterized by matrices of a relatively simple structure (Haake, 2001-b). It is interesting to note that the quantum algorithm for computations with the Google matrix on a quantum computer has been also analyzed recently (Paparo, 2014-a). The development of a random matrix theory for Markov chains and Google matrix ensembles still remains a challenge. Some attempts in this direction are described below. It is
Random matrix theory for G ?
On a first glance there are various preferential attachment models generating complex scale-free networks (Dorogovtsev, 2010-b, Newman, 2010-b). A well known example is the Albert-Barabasi procedure (AB) which builds networks by an iterative process. Such a procedure has been generalized to generate directed networks with an expectation that such networks can generate spectra of Google matrices being close to real cases (see Refs. in Ermann, 2015-b). However, it has been found that the spectrum of \(G\) of the AB model has all \(|\lambda_i|<0.4\) (except one unit eigenvalue). Thus, even if the decay of PageRank probability is well described by the relation \(P \sim 1/K\), the spectrum of \(G\) for the AB model is drastically different from real cases of WWW and other networks described above.
A class of random matrix models of \(G\) has been analyzed in (Frahm, 2014-a). These models have \(Q\) positive random elements at random positions per column whose sum is normalized to unity. For this case it was shown that all eigenvalues (except the unit one) are concentrated inside a circle around zero with radius \( R \sim 1/\sqrt{Q} \). Therefore these models are not suitable as well to reproduce spectral features of real networks.
The class of orthostochastic matrices of size \(N=3; 4\) (Zyczkowski, 2003-a) approximately reproduces triplet and cross structures well visible for real networks (see Figs.6,7,8), but their size is too small to be used for real systems.
Anderson localization for Google matrix eigenstates
The phenomenon of Anderson localization appears in a variety of quantum physical systems including electron transport in disordered solids and waves in random media (see Refs. in Guhr, 1998-b, Ermann, 2015-b, Zhirov, 2015-a). It is usually analyzed in the framework of Hermitian or unitary matrices. The possibilities of Anderson like localization and delocalization for matrices belonging to the class of Markov chains and Google matrices are considered in (Ermann, 2015-b, Zhirov, 2015-a). It was shown that certain matrix models, composed of blocks of orthostochastic matrices of size \( N=3; 4\) (Zyczkowski, 2003-a), can have an algebraic decay of PageRank probability with the exponent \( \beta \sim 0.5 \) (for the case \(\alpha=1\)) which is related to the existence of an Anderson transition of eigenstates and a mobility edge in the complex \(\lambda-\)plane. A further development of such models can allow to establish a closer link between the Anderson delocalization phenomenon in disordered solids and of delocalization of eigenstates for the Google matrix of directed networks.
Reduced Google matrix
In many cases the real directed networks can be very large. However, in certain cases one may be interested in the particular interactions among a small reduced subset of \(N_r\) nodes with \(N_r \ll N\) instead of the interactions of the entire network. The interactions between these \(N_r\) nodes should be correctly determined taking into account that there are many indirect links between the \(N_r\) nodes via all other \(N_s=N-N_r\) nodes of the network. This leads to the problem of the reduced Google matrix \(G_{\rm R}\) with \(N_r\) nodes which describes the interactions of a subset of \(N_r\) nodes. The matrix \(G_{\rm R}\) has the form (Frahm, 2016-a): \[ \displaystyle G_{\rm R}P_r=P_r\quad,\quad G_{\rm R}=G_{rr}+G_{rs}({\bf 1}-G_{ss})^{-1} G_{sr} \; \ , \] where \(G_{rr}, G_{rs}\) and \(G_{sr}, G_{ss}\) are sub blocks of the matrix \(G\) with respect to the decomposition of nodes in the reduced and the complementary subset of nodes: \[ \displaystyle G=\left(\begin{array}{cc} G_{rr} & G_{rs} \\ G_{sr} & G_{ss} \\ \end{array}\right) \ . \] The matrix \(G_{\rm R}\) takes into account effective interactions between subset nodes by all their indirect links via the whole network. It belongs to the class of Google matrices and its PageRank vector has the same probabilities as the \(N_r\) nodes of matrix \(G\) (after rescaling due to normalization). The numerical methods of computation of \(G_{\rm R}\) are described in (Frahm, 2016-a). This approach provides new possibilities to analyze effective interactions in a group of nodes embedded in large directed networks. An example of application of this approach to recovery of hidden links between political leaders is given in (Frahm, 2016b-a).
Starting from the work of Markov (Markov, 1906-a) many scientists contributed to the development of spectral ranking of Markov chains. Research of Perron (1907) and Frobenius (1912) led to the Perron-Frobenius theorem for square matrices with positive entries (see e.g. Brin, 2002-b). A detailed historical description of spectral ranking research is reviewed by (Franceschet, 2011-a and Vigna, 2015-a). As described there, important steps have been done by researchers in psychology, sociology and mathematics including J.R.Seeley (1949), T.-H.Wei (1952), L.Katz (1953), C.H.Hubbell (1965). In the WWW context, the Google matrix in the form (1), with regularization of dangling nodes and damping factor \(\alpha\), was introduced by (Brin, 1998-a).
The PageRank vector of a Google matrix \(G^*\) with inverted directions of links has been considered by (Fogaras, 2003-a, Hrisitidis, 2008-a), but no systematic statistical analysis of 2DRanking was presented there. An important step was done by (Chepelianskii, 2010-a) who analyzed \(\lambda=1\) eigenvectors of \(G\) for directed network and of \(G^*\) for network with inverted links. The comparative analysis of the Linux Kernel network and WWW of the University of Cambridge demonstrated a significant difference in the correlator \(\kappa\) for these networks and different functions of top nodes in \(K\) and \(K^*\). The term CheiRank was coined in (Zhirov, 2010-a) to have a clear distinction between eigenvectors of \(G\) and \(G^*\). We note that top PageRank and CheiRank nodes have certain similarities with authorities and hubs appearing in the HITS algorithm (Kleinberg, 1999-a). However, the HITS is query dependent while the rank probabilities \(P(K(i))\) and \(P^*({K(i)}^*)\) classify all nodes of the network.
Lectures about Google matrix
Video lectures about Google matrix are available at (Frahm, 2014-v,Georgeot, 2014-v,Shepelyansky, 2014-v,IHES, 2018-v).
(cited as "first_author, year-a")
Brin S., and Page L. (1998). The anatomy of a large scale hypertextual web search engine, Computer Networks and ISDN Systems 30, 107.
Chepelianskii A.D. (2010). Towards physical laws for software architecture, arXiv:1003.5455 [cs.SE].
Donato D., Laura L., Leonardi S., and Millozzi S. (2004). Large scale properties of the webgraph, Eur. Phys. J. B 38, 239.
Eom Y.-H., Aragon P., Laniano D., Kaltenbrunner A., Vigna S., and Shepelyansky D.L. (2015). Interactions of cultures and top people of Wikipedia from ranking of 24 language editions, PLoS ONE 10(3), e0114825.
Ermann L., and Shepelyansky D.L. (2010). Ulam method and fractal Weyl law for Perron-Frobenius operators, Eur. Phys. J. B 75, 299.
Ermann L., and Shepelyansky D.L. (2015). Google matrix analysis of the multiproduct world trade network, Eur. Phys. J. B 88, 84.
Fogaras D. (2003). Where to start browsing the Web?, Lect. Notes Comp. Sci. (Springer) 2877, 95.
Frahm K.M., Eom Y.-H., and Shepelyansky D.L. (2014). Google matrix of the citation network of Physical Review, Phys. Rev. E 88, 052814.
Frahm K.M., Georgeot B., and Shepelyansky D.L. (2011). Universal emergence of PageRank, J. Phys. A: Math. Theor. 44, 465101.
Frahm K.M., and Shepelyansky D.L. (2016). Reduced Google matrix, arXiv:1602.02394 [physics.soc-ph ].
Frahm K.M., Jaffres-Runser K., and Shepelyansky D.L. (2016)b. Wikipedia mining of hidden links between political leaders, arXiv:1609.01948 [cs.SI ].
Franceschet M. (2011). PageRank: standing on the shoulders of giants, Comm. ACM 54(6), 92.
Hristidis V., Hwang H., and Papakonstantinou Y. (2008). Authority-based keyword search in databases, ACM Trans. Database Systems 33(1), 1.
Izhikevich E.M., and Edelman G.M. (2008). Large-scale model of mammalian thalamocortical systems, Proc. Nat. Acad. Sci. USA 105, 3593.
Kandiah V., Georgeot B., and Giraud O. (2014). Move ordering and communities in complex networks describing the game of go, Eur. Phys. J. B 87, 246.
Kandiah V., Escaith H., and Shepelyansky D.L. (2015). Google matrix of the world network of economic activities, Eur. Phys. J. B 88, 186.
Kleinberg J.M. M. (1999). Authoritative sources in a hyperlinked environment, Jour. ACM 46(5), 604.
Lages J., Patt A., and Shepelyansky D.L. (2016). Wikipedia ranking of world universities, Eur. Phys. J. B 89, 69.
Leontief W. (1953). Domestic production and foreign trade; the American capital position re-examined, Proc. Am. Phios. Soc.97, 332.
Markov A.A. (1906). Rasprostranenie zakona bol'shih chisel na velichiny, zavisyaschie drug ot druga, Izvestiya Fiziko-matematicheskogo obschestva pri Kazanskom universitete, 2-ya seriya, 15, 135 (in Russia); English trans.: Extension of the limit theorems of probability theory to a sum of variables connected in a chain, reprinted in Appendix B of Howard B.A. Dynamic Probabilistic Systems, volume 1 Markov models, Dover Publ. (2007).
Meusel R., Vigna S., Lehmberg O., and Bizer C. (2015). The graph structure in the web – analyzed on different aggregation levels, J. Web Sci. 1, 33.
Pagell R.A. (2016). Wikipedia and Google Scholar as Sources for University Rankings – Influence and popularity and open bibliometrics.
Paparo G.D., Muller M., Comellas F., and Martin-Delgado M.A. (2014). Quantum Google algorithm, construction and application to complex networks, Eur. Phys. J. Plus 129, 150.
Sjostrand J. (1990). Geometry bounds on the density of resonances of quasi-bound states in open quantum systems, Duke Math. J. 60, 1.
Vigna S. (2015). Spectral ranking, arXiv:0912.0238v14.
Zhirov A.O., Zhirov O.V., and Shepelyansky D.L. (2010). Two-dimensional ranking of Wikipedia articles, Eur. Phys. J. B 77, 523.
Zhirov O.V., and Shepelyansky D.L. (2015). Anderson transition for Google matrix eigenstates, Annalen der Physik (Berlin) 527, 713.
Zyczkovski K., Kus M., Slomczynski W., and Sommers H.-J. (2003). Random unistochastic matrices, J. Phys. A: Math. Gen. 36, 3425.
(cited as "first_author, year-b")
Brin M., and Stuck G. (2002). Introduction to dynamical systems, Cambridge University Press, Cambridge UK.
Chirikov B., and Shepelyansky D. (2008). Chirikov standard map, Scholarpedia 3(3), 3550.
Dorogovtsev S. (2010), "Lectures on complex networks", Oxford University Press, Oxford UK.
Ermann L., Frahm K.M., and Shepelyansky D.L. (2015). Google matrix analysis of directed networks, Rev. Mod. Phys. 87, 1261.
Fyodorov Y. (2011). Random matrix theory, Scholarpedia 6(3), 9886.
Gantmacher F.R. (2000), "The theory of matrices, Vol.2", AMS Chelsa Publ., New York.
Gaspard P. (2014). Quantum chaotic scattering, Scholarpedia 9(6), 9806.
Guhr T., Muller-Groeling A., and Weidenmuller H.A. (1998). Random matrix theories in quantum physics: common concepts, Phys. Reports 299, 189.
Haake F. (2001), "Quantum signatures of chaos", Springer, Berlin.
Hart M.H. (1992), "The 100: ranking the most influential persons in history", Citadel Press, New York.
Hazelkorn E. (2015), "Rankings and the reshaping of higher education: the battle for world-class excellence", Palgrave Macmillan, New York.
Langville A.M., and Meyer C.D. (2006), "Google's PageRank and beyond: the science of search engine rankings", Princeton University Press, Princeton NJ.
Leontief W.W. (1986), "Input-Output economics", Oxford University Press, New York.
Mehta M.L. (2004), "Random matrices (3rd edition)", Elsevier Academic Press, Amsterdam.
Miller R.E., and Blair P.D. C.D. (2009), "Input-output analysis: foundations and extensions", Cambridge University Press, Cambridge UK.
Newman M.E.J. (2010), "Networks: an introduction", Oxford University Press, Oxford UK.
Nonnenmacher S., Sjostrand J., and Zworski M. (2014). Fractal Weyl law for open chaotic maps, Ann. Mathematics 179, 179.
Stewart G.W.. (2001). Matrix algorithms v.II: Eigensystems, SIAM, Philadelphia PA.
Ulam S. (1960). A collection of mathematical problems, Interscience Tracts in Pure and Applied Mathematics, Interscience New York.
Wigner E. (1967). Random matrices in physics, SIAM Reviews 9(1), 1.
External links to data sets
(cited as "name, year-e")
Network data sets of EU FET NADINE project (2015)
Pantheon MIT Wikipedia project (2015)
Shanghai Academic ranking of world universities (2015)
Stony-Brook Wikipedia ranking (2015)
Top 100 historical figures of Wikipedia (2014)
Top 100 world universities of Wikipedia (2015)
WWW of UK universities (2002-2006)
UN Comtrade Database (2015)
Wikipedia Aug 2009 ranking results (2010)
World trade network data (2011)
(cited as "name, year-v")
Frahm K.M. (2014) Spectral properties of Google matrix Lectures at ecole de Luchon (slides+videos, 1+1+1 hours at 23,24,25 June)
Georgeot B. (2014) Game of GO as a complex network Lectures at ecole de Luchon (slides+video, 1 hour at 3 July)
Shepelyansky D.L. (2014) Google matrix analysis of world trade network Lectures at ecole de Luchon (slides+video, 1 hour at 4 July)
IHES Workshop "Google matrix: fundamentals, applications and beyond", 15 - 18 October 2018, Bures-sur-Yvette, France Video talks and slides
Reviewed by: Prof. Thomas Guhr, Faculty of Physics, University of Duisburg-Essen, Germany
Reviewed by: Anonymous (via Dr. Michelle L. Jones, Jones Biomediting, Gouda, Netherlands)
Retrieved from "http://www.scholarpedia.org/w/index.php?title=Google_matrix&oldid=187113"
Quantum Chaos
"Google matrix" by Leonardo Ermann, Klaus Frahm and Dima Shepelyansky is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. Permissions beyond the scope of this license are described in the Terms of Use | CommonCrawl |
\begin{definition}[Definition:Cancellable/Also known as]
An object that is '''cancellable''' can also be referred to as '''cancellative'''.
Hence the property of '''being cancellable''' is also referred to on {{ProofWiki}} as '''cancellativity'''.
Some authors use '''regular''' to mean '''cancellable''', but this usage can be ambiguous so is not generally endorsed.
Category:Definitions/Cancellability
\end{definition} | ProofWiki |
\begin{document}
\title{A Pair Measurement Surface Code on Pentagons}
\date{\today} \author{Craig Gidney} \email{[email protected]} \affiliation{Google Quantum AI, Santa Barbara, California 93117, USA}
\begin{abstract} In this paper, I present a way to compile the surface code into two-body parity measurements ("pair measurements"), where the pair measurements run along the edges of a Cairo pentagonal tiling. The resulting circuit improves on prior work by Chao et al. by using fewer pair measurements per four-body stabilizer measurement (5 instead of 6) and fewer time steps per round of stabilizer measurement (6 instead of 10). Using Monte Carlo sampling, I show that these improvements increase the threshold of the surface code when compiling into pair measurements from $\approx 0.2\%$ to $\approx 0.4\%$, and also that they improve the teraquop footprint at a $0.1\%$ physical gate error rate from $\approx6000$ qubits to $\approx3000$ qubits. However, I also show that Chao et al's construction will have a smaller teraquop footprint for physical gate error rates below $\approx 0.03\%$ (due to bidirectional hook errors in my construction). I also compare to the planar honeycomb code, showing that although this work does noticeably reduce the gap between the surface code and the honeycomb code (when compiling into pair measurements), the honeycomb code is still more efficient (threshold $\approx 0.8\%$, teraquop footprint at $0.1\%$ of $\approx 1000$). \end{abstract}
\maketitle
\emph{The source code that was written, the exact noisy circuits that were sampled, and the statistics that were collected as part of this paper are available at \href{https://doi.org/10.5281/zenodo.6626417}{doi.org/10.5281/zenodo.6626417}~\cite{craig_gidney_2022_6626417}.}
\section{Introduction} \label{sec:introduction}
Last year, Hastings and Haah introduced a class of quantum error correcting codes now called "floquet codes"~\cite{hastings2021dynamically}. Floquet codes are interesting for a lot of reasons, but from a practical perspective they're interesting because they're extremely efficient when implemented using two-body parity measurements (hereafter "pair measurements"). For example, the very first floquet code was the honeycomb code. When using pair measurements, the honeycomb code has a threshold around $1\%$ and a teraquop footprint of around 1000 qubits at a $0.1\%$ physical gate error rate~\cite{gidney2022planarhoneycomb,paetznick2022floquetmajoranaperformance,chao2020optimization}. (The teraquop footprint is the number of physical qubits required to create a logical qubit reliable enough to survive one trillion operations.)
From the perspective of hardware designed around pair measurements~\cite{paetznick2022floquetmajoranaperformance}, a notable problem comes up when attempting to compare floquet codes to previous work: most previous work wasn't done in terms of pair measurements. It's far more common to see circuits compiled into unitary interactions, like CNOTs or CZs. Hardware designed around pair measurements may not even be able to execute those circuits. So, ideally, we'd prefer to compare to previous work that also used pair measurements.
An example of previous work using pair measurements is Chao et al.~\cite{chao2020optimization}. They compiled the surface code into pair measurements. The surface code is well known as one of the most promising quantum error correcting codes for building a scalable fault tolerant quantum computer, because of its high threshold and planar connectivity requirements~\cite{fowler2012surfacecodereview}. This suggests that compiling the surface code into pair measurements should set a solid baseline that other codes can compare against. However, ignoring the problems with comparing across gate sets for the moment, Chao et al. found that the surface code performed much worse when using pair measurements. Their pair measurement surface code's threshold was roughly $0.2\%$ (as opposed to roughly $0.8\%$ when using unitary interactions). For comparison, the honeycomb code has a threshold around $1\%$ when using pair measurements~\cite{gidney2022planarhoneycomb,paetznick2022floquetmajoranaperformance}.
This paper is my attempt to improve on Chao et al's result. There are three reasons I thought it would be possible to do better. First, Chao et al's work conceptualizes the problem as a quantum circuit problem. In my experience, the ZX calculus~\cite{coecke2011introducezx} is a better tool for reasoning about and optimizing measurement based constructions~\cite{de2017zxlattice}. I suspected that if I modelled the problem as a ZX graph, I could find a better solution. Second, Chao et al. used a union find decoder with unweighted edges~\cite{delfosse2021almost}. By contrast, estimates of the cost of the honeycomb code have been based on correlated minimum weight perfect matching~\cite{gidney2021honeycombmemory,gidney2022planarhoneycomb}, which is slower but more accurate. Using the same decoder for the surface code would make the comparison fairer. Third, Chao et al. only estimated the threshold. I wanted to check if the loss in threshold was actually matched by an increase in the teraquop footprint.
The paper is divided as follows. In \sec{construction}, I present the more compact construction that I found by using the ZX calculus. In \sec{results}, I present the simulation data obtained using a correlated minimum weight perfect matching decoder. In \sec{conclusion}, I discuss conclusions, including the ironic fact that although my construction has a better threshold, its teraquop footprint eventually becomes larger than Chao et al.'s as physical error rate decreases. The paper also includes \app{uncertainty}, which specifies how I computed line fits, \app{noise_model}, which specifies the noise model I used, \app{example_circuit}, which includes an example circuit showing my construction, and \app{other_plots}, which includes additional data plots.
\begin{figure}
\caption{
Different ZX graphs implementing a four-body parity measurement.
(a) The ZX graph for the well known decomposition into four CNOT operations.
(b) The ZX graph produced by replacing each CNOT with a lattice surgery CNOT~\cite{horsman2012latticesurgery}.
(c) The smallest possible ZX graph implementing a four-body parity measurement.
(d) The construction found by Chao et al. using brute force search~\cite{chao2020optimization}.
(e) The construction presented by this paper.
The graphs are all equal because, when spider fusion is repeatedly applied, they reduce to (c).
White circles are X type nodes.
Black circles are Z type nodes.
Assuming time moves from left to right, leaf nodes correspond to single qubit initializations and demolition measurements while vertical edges correspond to CNOT operations (if the linked nodes have opposite type) or pair measurements (if the linked nodes have the same type).
}
\label{fig:zx_identities}
\end{figure}
\section{Construction} \label{sec:construction}
This paper is not intended to be an introduction to the ZX calculus. I'll cover barely enough detail to convey that an efficient graph that implements a four-body X basis parity measurement is going to look like a Z type core surrounded by X type limbs leading to the data qubits. I recommend any of \cite{backens2016simplifiedzx,de2017zx,coecke2017picturing} as starting points for learning the ZX calculus.
In the ZX calculus, an X basis parity measurement can be added to a graph by placing an X type node on each involved qubit and linking all of the nodes to a central Z type node (see graph (c) of \fig{zx_identities}). To create other implementations of this parity measurement, rewrite rules can be applied to the graph~\cite{backens2016simplifiedzx}. For example, the "spider fusion" rule (called "S1" in \cite{backens2016simplifiedzx}) allows any edge to be contracted if it's between nodes of the same type. As another example, the "redundant node" rule (called "S3" in \cite{backens2016simplifiedzx}) allows nodes to be added to the middle of edges.
Consider the following circuit decomposition of an X basis parity measurement. First, init an ancilla in the X basis producing a $|+\rangle$. Then, for each involved data qubit, apply a CNOT controlled by the ancilla and targeting the data qubit. Finally, demolition measure the ancilla in the X basis. In the ZX calculus, a CNOT is represented by a Z type node on the control linked to an X type node on the target. X basis init and demolition measurement are both represented by Z type leaf nodes (note: it's intentional that the leaf node's type is not the same as the init/measure basis). So, after converting into a ZX graph, the circuit construction would look like a Z type leaf (the init) leading into a series of Z type nodes linked to X type nodes on the data qubits (the CNOTs), leading into a Z type leaf (the measurement). This graph is graph (a) in \fig{zx_identities}. By repeatedly applying the spider fusion rule, you can contract all of the Z type nodes into a single node, producing graph (c) in \fig{zx_identities}, proving the circuit decomposition is correct.
Now consider the second circuit shown in Figure 6 of Chao et al's paper~\cite{chao2020optimization}. This circuit involves single-qubit non-demolition measurements, X pair measurements, Z pair measurements, and Pauli feedback. The Pauli feedback is irrelevant in the ZX calculus, and can be added in again later, so the first step to converting the circuit into a ZX graph is to delete all of the feedback. Each X basis pair measurement becomes a pair of linked X type nodes (normally an X parity measurement would link the qubits to a central Z type node but, in the specific case of a pair measurement, that node can be omitted because of the "redundant node" rule). Similarly, Z basis pair measurements become a pair of linked Z type nodes. Each single qubit measurement ends up being a leaf node, via rule B1 from \cite{backens2016simplifiedzx}, with some of the leaf nodes corresponding to demolition measurements and some corresponding to inits. The final converted graph is graph (d) in \fig{zx_identities}. You can verify that it's correct by repeatedly applying the spider fusion rule.
\begin{figure}
\caption{
Decomposition of a four-body parity measurement into five pair measurements.
This circuit was derived from graph (e) in \fig{zx_identities}.
Dashed operations are classical Pauli feedback, which can be removed by folding its effects into the definitions of detectors and observables used by the surrounding surface code (see \fig{detector}).
\href{https://algassert.com/quirk\#circuit=\%7B\%22cols\%22\%3A\%5B\%5B\%22~evn6\%22\%2C\%22~evn6\%22\%2C1\%2C1\%2C\%22~evn6\%22\%2C\%22~evn6\%22\%5D\%2C\%5B1\%2C1\%2C\%22~jqn9\%22\%2C\%22~jqn9\%22\%2C1\%2C1\%2C\%22~7jvd\%22\%2C\%22~7jvd\%22\%5D\%2C\%5B\%22X\%22\%2C1\%2C\%22X\%22\%2C1\%2C1\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C\%22X\%22\%2C1\%2C\%22X\%22\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22Measure\%22\%2C\%22Measure\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22~7jvd\%22\%5D\%2C\%5B1\%2C1\%2C\%22Z\%22\%2C\%22Z\%22\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22Measure\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22~7jvd\%22\%2C\%22~7jvd\%22\%5D\%2C\%5B1\%2C\%22X\%22\%2C\%22X\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C\%22X\%22\%2C\%22X\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22Measure\%22\%2C\%22Measure\%22\%5D\%2C\%5B1\%2C1\%2C\%22Measure\%22\%2C\%22Measure\%22\%5D\%2C\%5B1\%2C\%22X\%22\%2C\%22\%E2\%80\%A2\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%2C\%22X\%22\%5D\%2C\%5B\%22X\%22\%2C\%22X\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%2C1\%2C1\%2C1\%2C\%22X\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%2C1\%2C1\%2C\%22X\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%2C\%22X\%22\%5D\%2C\%5B\%22~jcpu\%22\%2C\%22~jcpu\%22\%2C1\%2C1\%2C\%22~jcpu\%22\%2C\%22~jcpu\%22\%2C1\%2C1\%2C1\%2C1\%2C\%22~s93v\%22\%5D\%2C\%5B\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%2C\%22~jjav\%22\%5D\%2C\%5B1\%2C1\%2C\%22\%3C\%3C3\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C\%22\%3C\%3C3\%22\%5D\%2C\%5B\%22Amps4\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%97\%A6\%22\%5D\%2C\%5B\%5D\%2C\%5B\%5D\%2C\%5B\%5D\%2C\%5B\%22Amps4\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%5D\%2C\%5B\%5D\%2C\%5B\%5D\%2C\%5B\%5D\%2C\%5B\%22X\%22\%2C\%22X\%22\%2C\%22X\%22\%2C\%22X\%22\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%8A\%96\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22\%E2\%80\%A2\%22\%2C\%22X\%22\%5D\%2C\%5B1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C1\%2C\%22Chance\%22\%5D\%5D\%2C\%22gates\%22\%3A\%5B\%7B\%22id\%22\%3A\%22~evn6\%22\%2C\%22name\%22\%3A\%22in\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%2C\%7B\%22id\%22\%3A\%22~jjav\%22\%2C\%22name\%22\%3A\%22check\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%2C\%7B\%22id\%22\%3A\%22~jcpu\%22\%2C\%22name\%22\%3A\%22out\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%2C\%7B\%22id\%22\%3A\%22~s93v\%22\%2C\%22name\%22\%3A\%22result\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%2C\%7B\%22id\%22\%3A\%22~7jvd\%22\%2C\%22name\%22\%3A\%22store\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%2C\%7B\%22id\%22\%3A\%22~jqn9\%22\%2C\%22name\%22\%3A\%22\%7C0\%3E\%22\%2C\%22matrix\%22\%3A\%22\%7B\%7B1\%2C0\%7D\%2C\%7B0\%2C1\%7D\%7D\%22\%7D\%5D\%7D}{(Click here to open an equivalent circuit in Quirk.)}
}
\label{fig:xxxx_circuit}
\end{figure}
So far, all of these constructions look like a Z type core with X type limbs leading to each data qubit. This is not technically required to be true, but because we're trying to find an efficient construction it's unlikely that there's space to do anything else. So let's explicitly assume that the optimal construction will have this form. Notice that this implies the graph must have four core-to-limb transitions, where there is an edge between a Z type node (from the core) and an X type node (from a limb). Since pair measurements don't link nodes of opposite type, and the only interactions we're using are pair measurements, the core-to-limb transitions have to occur along timelike edges (edges that correspond to the worldline of a qubit). Supposing the core was a single Z type pair measurement, there would be exactly four timelike edges coming out of this pair measurement (two inputs and two outputs). That's exactly enough to get the four transitions that must appear in the graph. Surrounding this central pair measurement with four X type pair measurements, one leading to each data qubit, is then exactly enough connections to have each limb reach a data qubit and connect the whole system together. This construction is graph (e) of \fig{zx_identities}. By spider fusion, it implements the desired four-body parity measurement. The corresponding circuit (with feedback restored) is shown in \fig{xxxx_circuit}.
A different way to prove that this construction is correct is to show that it has all of the stabilizer generators of a four-body $X$ basis parity measurement. These generators are $X_1 \rightarrow X_1$, $X_2 \rightarrow X_2$, $X_3 \rightarrow X_3$, $X_4 \rightarrow X_4$, $Z_1Z_2 \rightarrow Z_1Z_2$, $Z_2Z_3 \rightarrow Z_2Z_3$, $Z_3Z_4 \rightarrow Z_3Z_4$, and $X_1 X_2 X_3 X_4 \rightarrow 1$. \fig{zx_stabilizer_examples} gives example visual proofs for three out of these eight rules. \fig{zx_detector_example} then shows how these rules can be chained together to form detectors.
\begin{figure}
\caption{
Pair measurement layout for a 5x5 surface code.
White circles are data qubits.
Black circles are measurement qubits.
Red shapes are the X stabilizers of the surface code.
Blue shapes are the Z stabilizers of the surface code.
Red edges are XX pair measurements performed by the circuit.
Blue edges are ZZ pair measurements performed by the circuit.
The red and blue edges form a planar graph with pentagonal faces.
}
\label{fig:tiling}
\end{figure}
The four body parity measurement construction that I've described uses five pair measurements. This is fewer than the six pair measurement construction reported by Chao et al. This is surprising, because Chao et al. ran a brute force search of the solution space. I see two plausible reasons that Chao et al. could have missed the five pair measurement solution, or decided not to report it. First, this solution involves the data qubits directly interacting with \emph{both} measurement qubits. Chao et al. may have been looking for solutions that only directly interacted the data qubits with one of the measurement qubits (because this has consequences for the topology required of the hardware). The second reason Chao et al. may not have reported this solution is because it has bidirectional hook errors.
A hook error is a single physical error that affects multiple data qubits due to the details of how abstract operations required by an error correcting code are decomposed into an explicit circuit. Look closely at \fig{xxxx_circuit}. A hook error equivalent to the data errors $Z_a Z_b$ occurs if the result of the central measurement (labelled $z_1$) is flipped. A hook error equivalent to the data errors $Z_b Z_c$ occurs if the two qubit depolarizing noise during the central measurement applies $X \otimes X$ to the two measurement qubits. These two different hook errors are equivalent to pairs of data errors. These pairs overlap on one data qubit. Therefore, when laid out in 2d, these hook errors will move in different directions. This is a problem because error chains will be able to use these hook errors to grow at double speed both vertically and horizontally, regardless of the orientation and ordering used when interleaving parity measurements. This cuts the code distance of the construction in half.
I'd normally consider halving the code distance to be a showstopping problem. In fact, if I'd realized early on that my construction had bidirectional hook errors, I'd have dropped the whole project and moved on to something else. But I actually only caught the problem later, when trying to understand my initial results, and the initial results were promising enough that I decided to continue despite the problem.
When mapping the circuit shown in \fig{xxxx_circuit} into 2d, it's natural to place the respective measurement qubits close to the two data qubits they each interact with. The connections required by the circuit then form a ``puckered H" shape. Although there are hook errors in both directions, it's still the case that one hook error is more likely than the other. So, it's still beneficial to orient the puckered H layouts one way for the Z basis measurements and the other way for the X basis measurements (because the X and Z boundaries are in different directions). \fig{tiling} shows the result of applying this to each of the stabilizers of the surface code. Pleasingly, the resulting set of connections form a pentagonal tiling of the plane known as the Cairo pentagonal tiling~\cite{wiki:Cairo_pentagonal_tiling}.
I tried a few possible ways of interleaving the stabilizer measurements. The best interleaving that I found was to do all of the X basis stabilizer measurements then all of the Z basis stabilizer measurements. If these two steps are partially pipelined, then only six additional layers of circuit are needed per round of stabilizer measurements. The exact circuit interleaving, and the resulting structure of a detector, are shown in \fig{detector}.
\begin{figure}
\caption{
Examples of stabilizer generators satisfied by a ZX graph implementing a four-body parity measurement.
Red highlight represents X sensitivity.
Blue highlight represents Z sensitivity.
For highlights to be valid they must satisfy two rules.
First, sensitivity \emph{crosses} nodes of the same type.
All white (black) nodes must have red (blue) highlight on an even number of adjacent edges.
Second, sensitivity \emph{broadcasts} over nodes of the opposite type.
All black (white) nodes must have red (blue) highlight on all adjacent edges or on no adjacent edges.
}
\label{fig:zx_stabilizer_examples}
\end{figure}
\begin{figure}
\caption{
Example of a detector (an internal tautology) in a ZX graph built from four-body parity measurements.
This graph is a simplified version of what occurs in a surface code (in particular, the detector crosses two parity measurements in the opposite basis instead of four).
When converting into a circuit, the measurements that define the detector will correspond to the highlighted pair measurements in the same basis (vertical edges between white nodes) combined with the highlighted single qubit measurements in the opposite basis (black leaf nodes pointing rightward).
}
\label{fig:zx_detector_example}
\end{figure}
\begin{figure}
\caption{
Order of operations used by my construction, and the resulting structure of a detector in the bulk.
In the circuit diagram, the parity of the 14 measurements colored black is always the same under noiseless execution, forming a detector.
Red highlights show where a Z or Y error would cause the detector to produce a detection event.
Gray boxes with dots always correspond to an $M_{XX}$ measurement with a qubit not shown in the circuit diagram.
The top right panel shows the 2d layout of the circuit with layer order annotations.
The top axis indicates the layers of the circuit diagram, corresponding to the layer annotations in the top right panel.
The overlapping layers ("6,0" and "7,1") are due to partial pipelining of the rounds of stabilizer measurements.
The bottom right panel shows where the measurements included in the detector are, in space, with bold lines for included pair measurements and bold circles for included single qubit measurements.
}
\label{fig:detector}
\end{figure}
\section{Simulation} \label{sec:results}
To quantify how well my construction works I used Stim, Sinter, and an internal correlated minimum weight perfect matching decoder written by Austin Fowler. Stim is a tool for fast simulation and analysis of stabilizer circuits~\cite{gidney2021stim}. Sinter is a tool for bulk sampling and decoding of Stim circuits using python multiprocessing~\cite{sinter-source}.
I wrote python code to generate Stim circuits representing my construction, for various error rates and patch sizes. I also implemented python code to generate Stim circuits reproducing the best construction described by Chao et al.~\cite{chao2020optimization}. I also generated honeycomb code circuits for comparison, by using the python code attached to \cite{gidney2022planarhoneycomb}. I added noise to these circuits using a noise model described in detail in \app{noise_model}. I then sampled the logical error rate of each noisy circuit, targeting a hundred million shots or ten thousand errors (whichever came first). Using a 96 core machine, the sampling process took approximately four days.
\fig{error_rate_plot} shows the sampled logical error rate from each construction for various code distances and physical error rates. It shows that the threshold of my construction is roughly double the threshold of Chao et al.'s construction. However, if you look closely at the slopes of the curves, you can see the effects of the bidirectional hook errors: my construction is improving slower than Chao et al's as the physical error rate decreases.
\fig{extrapolation_plot} shows essentially the same data as \fig{error_rate_plot}, but accompanied by line fits that project the number of qubits required to achieve a given logical error rate. The line fits were computed using a Bayesian method, with a truncation step to represent systemic uncertainty (see \app{uncertainty} for details).
\fig{footprint_plot} highlights the intercepts of the line fits from \fig{extrapolation_plot} with a target logical error rate of one in a trillion. In other words, it estimates the number of physical qubits per logical qubit needed to reach algorithmically relevant logical error rates. In this plot you can clearly see the effect where my construction is initially better than Chao et al's construction, but will eventually become worse as the physical error rate decreases. You can also clearly see that, although my construction closes some of the gap between the surface code and the honeycomb code when compiling into pair measurements, the honeycomb code is still more efficient. At a physical error rate of 0.1\%, the honeycomb code has a teraquop footprint of around 1000 qubits, compared to 3000 qubits for my construction and 6000 qubits for Chao et al's construction.
\begin{figure}
\caption{
Physical error rate vs logical error rate for various patch widths.
Based on X basis memory experiments; see \app{other_plots} for Z basis.
Note that the honeycomb code uses a qubit patch with a 2:3 aspect ratio (costs an extra factor of 1.5 in qubit count relative to the surface code constructions) but has no measurement ancillae (saves a factor of 1.5 in qubit count relative to the surface code constructions), so ultimately all the constructions have similar qubit counts at a given width.
Decoding was done using correlated minimum weight perfect matching.
Shading shows the range of hypothesis probabilities with a likelihood within a factor of 1000 of the max likelihood hypothesis, given the sampled data.
}
\label{fig:error_rate_plot}
\end{figure}
\begin{figure}
\caption{
Linear extrapolation of log logical error rate versus square root qubit count, for various physical error rates.
Based on X basis memory experiments; see \app{other_plots} for Z basis.
The vertical bar attached to each point shows the range of hypothesis probabilities with a likelihood within a factor of 1000 of the max likelihood hypothesis, given the sampled data.
See \app{uncertainty} for a discussion of how the line fits were computed.
}
\label{fig:extrapolation_plot}
\end{figure}
\begin{figure}
\caption{
Estimated teraquop footprints for error correcting codes compiled into pair measurements.
Based on X basis memory experiments; see \app{other_plots} for Z basis.
Derived from the X intercepts at $Y=10^{-12}$ in \fig{extrapolation_plot}.
The teraquop footprint is the number of physical qubits needed to create a logical qubit large enough to reliably to execute one trillion code distance blocks, which is enough blocks to build classically intractable instances of textbook algorithms like Shor's algorithm.
See \app{uncertainty} for a discussion of how the line fits used for these data points were computed.
}
\label{fig:footprint_plot}
\end{figure}
\section{Conclusion} \label{sec:conclusion}
In this paper, I presented a new way to compile the surface code into pair measurements, found by using the ZX calculus. Although the resulting construction isn't as efficient as the honeycomb code, and although it has bidirectional hook errors that cut its code distance in half, my construction doubled the threshold and halved the teraquop footprint (at a physical error rate of 0.1\%) compared to previous work compiling the surface code into pair measurements.
One of the striking things I noticed, after compiling the surface code into pair measurements, is how the compiled circuit looks a lot like the circuit for a floquet code. The circuit doesn't really know about the stabilizers that it came from, it only knows about the pair measurements running along the pentagonal faces. Detectors are formed from the edge measurements by combining them in surprising ways that narrowly avoid anti-commuting with intermediate measurements (see \fig{detector}). That's also what detectors look like in floquet codes. Particularly notable is that the compiled circuit is constantly moving the logical observable (for example, see the stim circuit shown in \app{example_circuit} and note the OBSERVABLE\_INCLUDE instruction inside the REPEAT block). Having to constantly move the observable is normally thought of as \emph{the} defining aspect of a floquet code~\cite{hastings2021dynamically}, but here the same property is occurring in a compiled surface code circuit.
Another fact about the circuit that surprised me was how well it performs, despite having half code distance. In the past, I've tried very hard to make sure I didn't accidentally cut the code distance of a construction in half. In this paper, I instead just accepted the halved code distance, moved forward, and found that the results were still competitive. This suggests that (at least for physical error rates above $0.1\%$), whether the code distance was cut in half isn't a reliable predictor of performance.
\appendix
\section{Line Fits} \label{app:uncertainty}
The line fits shown in \fig{extrapolation_plot} and used for the data points in \fig{footprint_plot} were computed by using a Bayesian method, with a truncation step to represent systemic uncertainty.
The line $Y = mX + b$ was defined to be the hypothesis that, for a qubit count $q$ satisfying $\sqrt{q} = X$, sampling whether or not a shot had a logical error was equivalent to sampling from a Bernoulli distribution with parameter $p=\exp(Y)=\exp(m \sqrt{q} + b)$.
Given a hypothesis, and the data that was actually sampled, you can compute the probability that the hypothesis assigned to seeing that data. This is the hypothesis' likelihood. Note that the probability of any one specific thing happening is always tiny, well below the smallest finite values that can be presented by floating point numbers, so likelihood computations have to be done in log space.
The dashed lines shown in \fig{extrapolation_plot} are the max likelihood hypotheses. They are the lines whose hypotheses assigned the highest probability to the data. The shaded regions are the union of all the lines whose likelihoods were within a factor of 1000 of the likelihood of the max likelihood hypothesis.
The benefit of this fitting method, over just performing a typical least squares error line fit to the points shown in \fig{extrapolation_plot} are (1) it doesn't require discarding data when no errors are observed, (2) it gives a good sense of the shape of nearby hypotheses, and (3) it naturally accounts for varying statistical uncertainty in the locations of points being used for the fit.
Unfortunately, although this fitting method is essentially optimal at quantifying which hypotheses are more likely, it doesn't deal well with systemic error where the true hypothesis is not one of the hypotheses being considered. For example, by adding more data, you can make the line fits qualitatively worse. If you keep collecting more and more samples for two points with high logical error rates, which is cheap to do, you'll force the line fit to exactly predict those two specific points. But the true system doesn't have logical error rates that lie exactly on a line, so this sacrifices the correspondence to reality of the fit for points at low logical error rates. And our goal is to predict the behavior at low logical error rates.
To mitigate this problem, I used a hack: I clamped how many errors a point could claim it had. Any point with $s$ shots and $e$ errors, with $e > 10$, was instead presented to the fitting function as a point with $\lceil s \cdot 10/e \rceil$ shots and $10$ errors. The truncation is supposed to represent the fact that there is unavoidable uncertainty in how closely the line can estimate the true curve.
Anecdotally, using truncation appears to significantly improve the fits. It's better than treating all the points equally, which gives low sample count points too much pull (lone "unlucky" errors, which do appear in the data, shift the prediction too drastically). It's also better than not clamping, which gives high sample count points too much pull and produces obviously overconfident predictions.
Note that \fig{extrapolation_plot} doesn't show data points that had 0 observed errors because, although the points themselves wouldn't be visible, their error bars would all overlap and obscure the data points with less than 5 sampled errors. Although these data points aren't shown, they were still included when fitting. The samples they represented correctly affected the likelihoods computed for each hypothesis.
Note that, before line fitting begins, points with sampled logical error rates above 40\% are discarded (to avoid working with points above threshold).
\section{Noise Model} \label{app:noise_model}
The noise model used by this paper treats all measurements the same: single qubit measurements are treated the same as pair measurements, and demolition measurements are treated the same as non-demolition measurements. The noise model applies anti-commuting Pauli errors after resets, depolarization after any other operation (including idling), and it probabilistically flips measurement results. See \tbl{noise_model}.
Note that the model asserts that classically controlled Pauli gates are completely free. Classically controlled Paulis introduce no noise, they consume no time, they do not prevent other operations from being applied to the target qubit, they don't affect whether the target qubit is idling, and they incur no reaction delay from waiting for measurement results. This is because, in stabilizer circuits, classically controlled Paulis can always be applied entirely within the control system and can be deferred until later by conjugating them by upcoming Clifford operations.
\begin{table}[h]
\centering
\begin{tabular}{|r|l|}
\hline
Noise channel & Probability distribution of effects
\\
\hline
$\text{MERR}(p)$ & $\begin{aligned}
1-p &\rightarrow \text{(report previous measurement correctly)}
\\
p &\rightarrow \text{(report previous measurement incorrectly; flip its result)}
\end{aligned}$
\\
\hline
$\text{XERR}(p)$ & $\begin{aligned}
1-p &\rightarrow I
\\
p &\rightarrow X
\end{aligned}$
\\
\hline
$\text{ZERR}(p)$ & $\begin{aligned}
1-p &\rightarrow I
\\
p &\rightarrow Z
\end{aligned}$
\\
\hline
$\text{DEP1}(p)$ & $\begin{aligned}
1-p &\rightarrow I
\\
p/3 &\rightarrow X
\\
p/3 &\rightarrow Y
\\
p/3 &\rightarrow Z
\end{aligned}$
\\
\hline
$\text{DEP2}(p)$ & $\begin{aligned}
1-p &\rightarrow I \otimes I
&\;\;
p/15 &\rightarrow I \otimes X
&\;\;
p/15 &\rightarrow I \otimes Y
&\;\;
p/15 &\rightarrow I \otimes Z
\\
p/15 &\rightarrow X \otimes I
&\;\;
p/15 &\rightarrow X \otimes X
&\;\;
p/15 &\rightarrow X \otimes Y
&\;\;
p/15 &\rightarrow X \otimes Z
\\
p/15 &\rightarrow Y \otimes I
&\;\;
p/15 &\rightarrow Y \otimes X
&\;\;
p/15 &\rightarrow Y \otimes Y
&\;\;
p/15 &\rightarrow Y \otimes Z
\\
p/15 &\rightarrow Z \otimes I
&\;\;
p/15 &\rightarrow Z \otimes X
&\;\;
p/15 &\rightarrow Z \otimes Y
&\;\;
p/15 &\rightarrow Z \otimes Z
\end{aligned}$
\\
\hline
\end{tabular}
\caption{
Definitions of various noise channels.
Used by \tbl{noise_model}.
}
\label{tbl:noise_channels} \end{table}
\begin{table}[h!]
\centering
\begin{tabular}{|r|l|}
\hline
Ideal gate & Noisy gate
\\
\hline
(Idling) & $\text{DEP1}(p)$
\\
(Single qubit gate) $U_1$ & $U_1 \circ \text{DEP1}(p)$
\\
\hline
$R_X$ & $R_X \circ \text{ZERR}(p)$
\\
$R_Y$ & $R_Y \circ \text{XERR}(p)$
\\
$R_Z$ & $R_Z \circ \text{XERR}(p)$
\\
\hline
$M_X$ & $M_X \circ \text{MERR}(p) \circ \text{DEP1}(p)$
\\
$M_Y$ & $M_Y \circ \text{MERR}(p) \circ \text{DEP1}(p)$
\\
$M_Z$ & $M_Z \circ \text{MERR}(p) \circ \text{DEP1}(p)$
\\
\hline
$M_{XX}$ & $M_{XX} \circ \text{MERR}(p) \circ \text{DEP2}(p)$
\\
$M_{YY}$ & $M_{YY} \circ \text{MERR}(p) \circ \text{DEP2}(p)$
\\
$M_{ZZ}$ & $M_{ZZ} \circ \text{MERR}(p) \circ \text{DEP2}(p)$
\\
\hline
(classically controlled Pauli) $P^m$ & (Done in classical control system.)
\\
\hline
\end{tabular}
\caption{
How to turn ideal gates into noisy gates under the "pair measurement depolarizing noise" model used by this paper.
The model is defined by a single parameter $p$.
Note $A \circ B = B \cdot A$ meaning $B$ is applied after $A$.
Noise channels are defined in \tbl{noise_channels}.
}
\label{tbl:noise_model} \end{table}
\section{Example Circuit} \label{app:example_circuit}
This \href{https://github.com/quantumlib/Stim/blob/main/doc/file_format_stim_circuit.md}{stim circuit} is a noisy 10-round X-basis $d=3$ pentagonal-surface-code memory experiment.
\begin{lstlisting}[style=stimcircuit] QUBIT_COORDS(-1, 6) 0 QUBIT_COORDS(0, 0) 1 QUBIT_COORDS(0, 4) 2 QUBIT_COORDS(0, 8) 3 QUBIT_COORDS(1, 2) 4 QUBIT_COORDS(2, -1) 5 QUBIT_COORDS(2, 5) 6 QUBIT_COORDS(2, 7) 7 QUBIT_COORDS(3, 2) 8 QUBIT_COORDS(4, 0) 9 QUBIT_COORDS(4, 4) 10 QUBIT_COORDS(4, 8) 11 QUBIT_COORDS(5, 6) 12 QUBIT_COORDS(6, 1) 13 QUBIT_COORDS(6, 3) 14 QUBIT_COORDS(6, 9) 15 QUBIT_COORDS(7, 6) 16 QUBIT_COORDS(8, 0) 17 QUBIT_COORDS(8, 4) 18 QUBIT_COORDS(8, 8) 19 QUBIT_COORDS(9, 2) 20 RX 1 2 3 9 10 11 17 18 19 R 0 4 8 12 16 20 X_ERROR(0.001) 0 4 8 12 16 20 Z_ERROR(0.001) 1 2 3 9 10 11 17 18 19 DEPOLARIZE1(0.001) 5 6 7 13 14 15 TICK MPP(0.001) X0*X2 X1*X4 X8*X9 X10*X12 X16*X18 X17*X20 DEPOLARIZE2(0.001) 0 2 1 4 8 9 10 12 16 18 17 20 DEPOLARIZE1(0.001) 3 5 6 7 11 13 14 15 19 TICK MPP(0.001) Z4*Z8 Z12*Z16 DEPOLARIZE2(0.001) 4 8 12 16 DEPOLARIZE1(0.001) 0 1 2 3 5 6 7 9 10 11 13 14 15 17 18 19 20 TICK RX 5 6 7 13 14 15 MPP(0.001) X0*X3 X2*X4 X8*X10 X11*X12 X16*X19 X18*X20 DEPOLARIZE2(0.001) 0 3 2 4 8 10 11 12 16 19 18 20 Z_ERROR(0.001) 5 6 7 13 14 15 DEPOLARIZE1(0.001) 1 9 17 TICK M(0.001) 0 4 8 12 16 20 MPP(0.001) Z1*Z5 Z2*Z6 Z3*Z7 Z9*Z13 Z10*Z14 Z11*Z15 DEPOLARIZE1(0.001) 0 4 8 12 16 20 DEPOLARIZE2(0.001) 1 5 2 6 3 7 9 13 10 14 11 15 DEPOLARIZE1(0.001) 17 18 19 TICK MPP(0.001) X6*X7 X13*X14 DEPOLARIZE2(0.001) 6 7 13 14 DEPOLARIZE1(0.001) 0 1 2 3 4 5 8 9 10 11 12 15 16 17 18 19 20 TICK R 0 4 8 12 16 20 MPP(0.001) Z5*Z9 Z6*Z10 Z7*Z11 Z13*Z17 Z14*Z18 Z15*Z19 DEPOLARIZE2(0.001) 5 9 6 10 7 11 13 17 14 18 15 19 X_ERROR(0.001) 0 4 8 12 16 20 DEPOLARIZE1(0.001) 1 2 3 TICK MX(0.001) 5 6 7 13 14 15 MPP(0.001) X0*X2 X1*X4 X8*X9 X10*X12 X16*X18 X17*X20 DETECTOR(-2, 6, 0) rec[-46] rec[-38] DETECTOR(2, 2, 0) rec[-45] rec[-44] rec[-37] rec[-36] DETECTOR(6, 6, 0) rec[-43] rec[-42] rec[-35] rec[-34] DETECTOR(10, 2, 0) rec[-41] rec[-33] OBSERVABLE_INCLUDE(0) rec[-12] rec[-9] SHIFT_COORDS(0, 0, 1) DEPOLARIZE1(0.001) 5 6 7 13 14 15 DEPOLARIZE2(0.001) 0 2 1 4 8 9 10 12 16 18 17 20 DEPOLARIZE1(0.001) 3 11 19 TICK REPEAT 8 {
MPP(0.001) Z4*Z8 Z12*Z16
DEPOLARIZE2(0.001) 4 8 12 16
DEPOLARIZE1(0.001) 0 1 2 3 5 6 7 9 10 11 13 14 15 17 18 19 20
TICK
RX 5 6 7 13 14 15
MPP(0.001) X0*X3 X2*X4 X8*X10 X11*X12 X16*X19 X18*X20
DEPOLARIZE2(0.001) 0 3 2 4 8 10 11 12 16 19 18 20
Z_ERROR(0.001) 5 6 7 13 14 15
DEPOLARIZE1(0.001) 1 9 17
TICK
M(0.001) 0 4 8 12 16 20
MPP(0.001) Z1*Z5 Z2*Z6 Z3*Z7 Z9*Z13 Z10*Z14 Z11*Z15
DEPOLARIZE1(0.001) 0 4 8 12 16 20
DEPOLARIZE2(0.001) 1 5 2 6 3 7 9 13 10 14 11 15
DEPOLARIZE1(0.001) 17 18 19
TICK
MPP(0.001) X6*X7 X13*X14
DEPOLARIZE2(0.001) 6 7 13 14
DEPOLARIZE1(0.001) 0 1 2 3 4 5 8 9 10 11 12 15 16 17 18 19 20
TICK
R 0 4 8 12 16 20
MPP(0.001) Z5*Z9 Z6*Z10 Z7*Z11 Z13*Z17 Z14*Z18 Z15*Z19
DEPOLARIZE2(0.001) 5 9 6 10 7 11 13 17 14 18 15 19
X_ERROR(0.001) 0 4 8 12 16 20
DEPOLARIZE1(0.001) 1 2 3
TICK
MX(0.001) 5 6 7 13 14 15
MPP(0.001) X0*X2 X1*X4 X8*X9 X10*X12 X16*X18 X17*X20
DETECTOR(-2, 6, 0) rec[-86] rec[-78] rec[-60] rec[-46] rec[-38]
DETECTOR(2, -2, 0) rec[-66] rec[-58] rec[-40] rec[-26] rec[-18]
DETECTOR(2, 2, 0) rec[-85] rec[-84] rec[-77] rec[-76] rec[-59] rec[-52] rec[-51] rec[-45] rec[-44] rec[-37] rec[-36]
DETECTOR(2, 6, 0) rec[-65] rec[-64] rec[-57] rec[-56] rec[-40] rec[-32] rec[-31] rec[-30] rec[-29] rec[-25] rec[-24] rec[-17] rec[-16]
DETECTOR(6, 2, 0) rec[-63] rec[-62] rec[-55] rec[-54] rec[-39] rec[-30] rec[-27] rec[-23] rec[-22] rec[-15] rec[-14]
DETECTOR(6, 6, 0) rec[-83] rec[-82] rec[-75] rec[-74] rec[-60] rec[-51] rec[-50] rec[-48] rec[-47] rec[-43] rec[-42] rec[-35] rec[-34]
DETECTOR(6, 10, 0) rec[-61] rec[-53] rec[-39] rec[-29] rec[-28] rec[-21] rec[-13]
DETECTOR(10, 2, 0) rec[-81] rec[-73] rec[-59] rec[-49] rec[-48] rec[-41] rec[-33]
OBSERVABLE_INCLUDE(0) rec[-12] rec[-9]
SHIFT_COORDS(0, 0, 1)
DEPOLARIZE1(0.001) 5 6 7 13 14 15
DEPOLARIZE2(0.001) 0 2 1 4 8 9 10 12 16 18 17 20
DEPOLARIZE1(0.001) 3 11 19
TICK } MPP(0.001) Z4*Z8 Z12*Z16 DEPOLARIZE2(0.001) 4 8 12 16 DEPOLARIZE1(0.001) 0 1 2 3 5 6 7 9 10 11 13 14 15 17 18 19 20 TICK RX 5 6 7 13 14 15 MPP(0.001) X0*X3 X2*X4 X8*X10 X11*X12 X16*X19 X18*X20 DEPOLARIZE2(0.001) 0 3 2 4 8 10 11 12 16 19 18 20 Z_ERROR(0.001) 5 6 7 13 14 15 DEPOLARIZE1(0.001) 1 9 17 TICK M(0.001) 0 4 8 12 16 20 MPP(0.001) Z1*Z5 Z2*Z6 Z3*Z7 Z9*Z13 Z10*Z14 Z11*Z15 DEPOLARIZE1(0.001) 0 4 8 12 16 20 DEPOLARIZE2(0.001) 1 5 2 6 3 7 9 13 10 14 11 15 DEPOLARIZE1(0.001) 17 18 19 TICK MPP(0.001) X6*X7 X13*X14 DEPOLARIZE2(0.001) 6 7 13 14 DEPOLARIZE1(0.001) 0 1 2 3 4 5 8 9 10 11 12 15 16 17 18 19 20 TICK MPP(0.001) Z5*Z9 Z6*Z10 Z7*Z11 Z13*Z17 Z14*Z18 Z15*Z19 DEPOLARIZE2(0.001) 5 9 6 10 7 11 13 17 14 18 15 19 DEPOLARIZE1(0.001) 0 1 2 3 4 8 12 16 20 TICK MX(0.001) 5 6 7 13 14 15 OBSERVABLE_INCLUDE(0) rec[-6] rec[-3] MX(0.001) 1 2 3 9 10 11 17 18 19 DETECTOR(-2, 6, 0) rec[-89] rec[-81] rec[-63] rec[-49] rec[-41] DETECTOR(2, -2, 0) rec[-69] rec[-61] rec[-43] rec[-29] rec[-21] DETECTOR(2, 2, 0) rec[-88] rec[-87] rec[-80] rec[-79] rec[-62] rec[-55] rec[-54] rec[-48] rec[-47] rec[-40] rec[-39] DETECTOR(2, 6, 0) rec[-68] rec[-67] rec[-60] rec[-59] rec[-43] rec[-35] rec[-34] rec[-33] rec[-32] rec[-28] rec[-27] rec[-20] rec[-19] DETECTOR(6, 2, 0) rec[-66] rec[-65] rec[-58] rec[-57] rec[-42] rec[-33] rec[-30] rec[-26] rec[-25] rec[-18] rec[-17] DETECTOR(6, 6, 0) rec[-86] rec[-85] rec[-78] rec[-77] rec[-63] rec[-54] rec[-53] rec[-51] rec[-50] rec[-46] rec[-45] rec[-38] rec[-37] DETECTOR(6, 10, 0) rec[-64] rec[-56] rec[-42] rec[-32] rec[-31] rec[-24] rec[-16] DETECTOR(10, 2, 0) rec[-84] rec[-76] rec[-62] rec[-52] rec[-51] rec[-44] rec[-36] SHIFT_COORDS(0, 0, 1) DETECTOR(-2, 6, 0) rec[-49] rec[-41] rec[-23] rec[-8] rec[-7] DETECTOR(2, 2, 0) rec[-48] rec[-47] rec[-40] rec[-39] rec[-22] rec[-15] rec[-14] rec[-9] rec[-8] rec[-6] rec[-5] DETECTOR(6, 6, 0) rec[-46] rec[-45] rec[-38] rec[-37] rec[-23] rec[-14] rec[-13] rec[-11] rec[-10] rec[-5] rec[-4] rec[-2] rec[-1] DETECTOR(10, 2, 0) rec[-44] rec[-36] rec[-22] rec[-12] rec[-11] rec[-3] rec[-2] OBSERVABLE_INCLUDE(0) rec[-9] rec[-6] rec[-3] DEPOLARIZE1(0.001) 5 6 7 13 14 15 1 2 3 9 10 11 17 18 19 0 4 8 12 16 20 \end{lstlisting}
\section{Additional Data} \label{app:other_plots}
\begin{figure}
\caption{
Physical error rate vs logical error rate for various patch widths, based on Z basis memory experiments.
See \fig{error_rate_plot} for X basis.
The X and Z basis results are not exactly identical (due to differences in the layout of each observable, and due to statistical noise) but are qualitatively identical.
}
\label{fig:error_rate_plot_z}
\end{figure}
\begin{figure}
\caption{
Linear extrapolation of log logical error rate versus square root qubit count, for various physical error rates.
Based on Z basis memory experiments; see \fig{extrapolation_plot} for X basis.
The X and Z basis results are not exactly identical (due to differences in the layout of each observable, and due to statistical noise) but are qualitatively identical.
}
\label{fig:extrapolation_plot_other_z}
\end{figure}
\begin{figure}
\caption{
Estimated teraquop footprints for error correcting codes compiled into pair measurements.
Based on Z basis memory experiments; see \fig{footprint_plot} for X basis.
The X and Z basis results are not exactly identical (due to differences in the layout of each observable, and due to statistical noise) but are qualitatively identical.
}
\label{fig:footprint_plot_z}
\end{figure}
\end{document} | arXiv |
Simultaneous measurement of nitrous acid, nitric acid, and nitrogen dioxide by means of a novel multipollutant diffusive sampler in libraries and archives
Francesca Vichi1,
Ludmila Mašková2Email author,
Massimiliano Frattoni1,
Andrea Imperiali1 and
Jiří Smolík2
Heritage Science20164:4
© Vichi et al. 2016
Accepted: 11 February 2016
A novel multipollutant diffusive sampler for HONO, HNO3, and NO2 was used and tested at four different libraries/archives in different seasons. Two were located in Switzerland in Bern (Swiss National Library) and Geneve (Bibliotheque de Geneve), both with HVAC system equipped with filters for pollutants removal, and the other two in the Czech Republic in Teplice (Regional Library) and in Prague (National Archives), where in this case the former is naturally ventilated and whereas the latter is equipped with HVAC system with filtration.
The ratios between indoor and outdoor concentrations of NO2 showed a greater penetration of pollutants indoors in the naturally ventilated library than in the filtrated archives. The indoor concentrations of HNO3 were very low probably due to the high deposition velocity of nitric acid on available surfaces. HONO concentration values were usually lower outdoors, which indicated that HONO was produced by reactions on indoor surfaces.
The results revealed that the reproducibility of the new multipollutant sampler measurements was reasonable (according to EU directives) for NO2 and HNO3 and that the newly developed multipollutant sampler can be used in archives and libraries, allowing to map the pollutants distribution indoors. Due to high efficiency of insulating systems normally employed and of filtration systems, the values recorded for the pollutants indoors are often lower than the detection limits.
Diffusive sampling
Nitrous acid
Indoor/outdoor ratio
Nitrogen oxides penetrate from the outdoor to the indoor environment and can be transformed, through complex reaction pathways, into gaseous nitric (HNO3) and nitrous acids (HONO) [1]. HNO3 is a very aggressive acid in contrast with HONO. The latter is not particularly active by itself, even if it is an important source of OH radicals, one of the most important air oxidants [2]. This air pollution cause oxidation and hydrolytic degradation of archive materials such as colour changes and reduction of degree of polymerisation of paper [3], decomposition of leather [4], corrosion of metals [5, 6], and damage of colorants [7–10].
Several works report measurements of nitrous and nitric acid in various indoor environments [11–13] and recent works highlight the importance of the former species as an emerging indoor pollutant [14], but studies in cultural heritage buildings are scarce [15, 16]. A well established and known technique to collect these trace gases is represented by denuder sequence based systems [17–19], but this technique is time consuming and labour intensive. Diffusive sampling can overcome these problems since it represents an easy to use technique which exploits the spontaneous diffusion of species collected by specific absorbing media. Diffusive samplers have been used for air quality monitoring of single gases in cultural heritage buildings [20–23]. Nevertheless, when conditions which promote the formation of HONO are present (high air moisture content and surface to volume ratio), especially indoors, monitoring of NO2 by diffusive sampling can result in overestimation since the interference of the former pollutant is not negligible [24]. Therefore to overcome this problem and to account correctly for the different species a novel multipollutant diffusive sampler was designed for simultaneous sampling of three different pollutants (nitric acid, nitrous acid, and nitrogen dioxide) collected at separate sampling stages [25]. After the laboratory development, these devices were used indoors in different dwellings, as reported in [25]. The campaigns described in the following were the first applications to places of interest for cultural heritage conservation, as libraries and archives, where a certain kind of control on environmental parameters is commonly present. The aim of this study was, indeed, to test the newly developed multipollutant sampler for evaluating the air quality inside different libraries with or without HVAC (heating and ventilating and air conditioning systems). The exposure period, after these first sampling trials, could then be adjusted according to the typical range of values found for the different pollutants in the indoors of interest. These preliminary trials were necessary to avoid the saturation of the absorbing pads and the collection of insufficient analyte to be determined after the exposure period. Furthermore the sampler was also exposed outdoors to compare the pollutants concentration values and calculate indoor/outdoor ratios.
Sampling locations
Over the last 4 years the multipollutant sampler was used in different periods inside archives and libraries. Two seasonal campaigns were carried out at four different libraries: two libraries in Switzerland (the Swiss National Library in Bern and the Bibliotheque de Geneve in Geneva) and two libraries in the Czech Republic (the National Archives in Prague and the Regional Library in Teplice). All the indoor activities in the libraries are very limited.
The library in Bern is a modern building composed of a ground floor and four underground levels (1UG-4UG), the building is equipped with a heating, ventilation, and air conditioning (HVAC) system providing air filtered through a particulate filter and active carbon. An additional Purafil purification system is installed at the floor 3UG where newspaper collection is stored. Five indoor sites were selected at the different levels and an outdoor site (OUT) was chosen as well. One site was placed at the ground floor (A26) and the other four monitoring sites were placed both at the entrance, just outside of the double door insulation (WA2UG and WA3UG), and inside the second and third underground level (2UG and 3UG) in the area insulated by the double door system. The overall volume of the building in Bern is of approximately 4500 m3.
The library in Geneva is a historical building with a HVAC system equipped with particulate filters. Three indoor sampling sites were selected: the first in a compactor (number 51 in the following), the second at "La Reserve" and the third in a corridor. An outdoor site was chosen also in Geneva where the diffusive samplers were placed in a balcony (OUT). The library in Geneva has a volume of approximately 200 m3.
The archive in Prague is located in a modern building. The indoor measurements were carried out in a depository of "Bohemian tables (BT)" and in a depository of "Archives of the Czech Kingdom (ACK)". The BT and ACK depositories have volumes of approximately 550 and 220 m3, respectively. Each depository is equipped with its own HVAC system with air recirculation. The HVAC systems in both depositories contain HEPA filters for removing airborne particles. In addition the AKC depository is equipped with filters for removing NO2 and SO2. The outdoor measurements were performed on a balcony of the building orientated toward a busy street (OUT).
The library in Teplice is equipped with double glassed windows and an electrical heating system, i.e., the only ventilation is through cracks and small openings in the building, windows and doors. The measurements were performed inside the library (IN) and just outside of the window oriented to the chateau park (OUT). The depository has a volume of approximately 450 m3.
One monitoring location in each indoor and outdoor site was selected, because other measurements confirmed that the indoor air is well mixed [26].
Measurement campaigns
Seasonal campaigns were conducted in Switzerland during the spring/summer period of 2011 (S1) and during winter and spring/summer 2012 (W, S2). Later other measurements were performed in the Czech Republic during three campaigns in spring/summer 2013 (S1, S2) and winter 2014 (W) (Table 1).
Monitoring scheme
Exposition period
Other pollutants measured
Swiss National Library (SNL)
1 level: site A26
2 level: sites 2UG; WA2UG
Outdoor: Balcony
NO2; NOx (Analyst)
Bibliotheque de Geneve (BdG)
Site 1: Compactor 51
Site 2: La Reserve
Site 3: Corridor
Site 1: BT
Site 2: ACK
Outdoor: Window
8.4.2013–10.5.1013
HNO3, SO2, O3 and NH3 (Analyst)
Acetic acid; formic acid (IVL)
10.5.2013–11.6.2013
6.1.2014–6.2.2014
Regional library
Spring/
Three multipollutant samplers were exposed indoors and three outdoors for during each campaign at every location.
In parallel the exposure of single stage Analyst diffusive samplers (Marbaglass, Italy) provided measurements of NO2 and NOx during the campaigns in Switzerland. Other species (HNO3, SO2, O3 and NH3) were also monitored by the Analyst samplers in the campaigns carried out in the Czech Republic, where in addition IVL diffusive samplers (Swedish Environmental Research Institute, Sweden) for monitoring formic and acetic acids were employed.
In both cases at least 10 % of the total number of samplers was used for each campaign as field blanks. The blanks were prepared and handled along with other samplers except for the exposition to pollutants. Additionally, basic meteorological parameters including ambient temperature and relative humidity were measured at both locations in Czech Republic, both indoors and outdoors, by Tiny Tag data loggers (Gemini, UK).
Multipollutant diffusive sampler
The body of the multipollutant diffusive sampler is similar to the Analyst [27]. The internal design of the sampler, on the other hand, was changed to collect HNO3, on the first filter and NO2 and HONO in the successive absorbing pads.
A correct speciation of these compounds, intertwined through the hydrolysis mechanism according to the known pathway [28–30]:
$$2 {\text{NO}}_{ 2} + {\text{ H}}_{ 2} {\text{O }} \to {\text{ HONO }} + {\text{ HNO}}_{ 3}$$
could, indeed, only be achieved by the subsequent collection of the two species on successive reactive substrates.
Most frequently NO2, which is the predominant species in the atmosphere also due to the photolysis of HONO in the outdoor ambient air, can affect the measurements of the less abundant HONO. On the other hand, particularly indoors, when moisture and an elevated surface/volume ratio is present, NO2 measurements can be overestimated as reported in [24]. Therefore there is a mutual interference on the measurement of these two species. In this case, since nitrite is the species collected and analytically determined to get to the atmospheric concentration of these pollutants, the selectivity in the sampling phase was achieved through the implementation of successive sampling stages. After the first filter used to collect HNO3, other two successive pads were used to collect these species, assuming that HONO and part of the NO2 would both react on the second, whereas only NO2, normally the most abundant, is collected on the successive filter. During the development of this diffusive sampler trials, aimed at quantifying the relative amounts of nitrite collected on the second and third filter at different HONO/NO2 concentration ratios, were performed. The ratio of the amounts of analyte collected on the two filters at RH = 0 was determined and used in the calibration of the device.
Hence three polyethylene discs housing three active glass microfiber filters were placed along the same diffusive path of the former sampler. The first two filters perform the sequential collection of the two acidic species and the third filter is used to estimate the interference of NO2 on the HONO measurement and vice versa.
Before impregnation with the reactive solution, a washing procedure of the microfiber filters with sodium carbonate (5 %) and successive rinse (for three times) with deionized water was implemented to improve the quality of the blanks. The filters (Whatman GF/A) inside the first polyethylene disc were then coated by using a 0.1 % (w/v) aqueous solution of sodium chloride then dried in an oven at 80 °C.
The following other two glass microfiber filters, used to collect HONO and to account for the interference of NO2, were impregnated by using a 1.8 % (w/v) aqueous solution of sodium carbonate containing 1.8 % (w/v) of glycerine, they were then dried in an oven at 80 °C. Filters are placed along the diffusive path in front of the alkaline carbon filter prepared according to the procedure already described [27] and positioned at the bottom of the device for the sole NO2 sampling. An enlarged scheme of the sampler is reported in Fig. 1.
Exploded scheme of the multipollutant sampler. 1 Plastic cap (before and after exposition) or air barrier (during exposition), 2 Ring, 3 Polyethylene holder of absorbing pad impregnated with NaCl (HNO3 sampling), 4 Polyethylene holder of absorbing pad impregnated with Na2CO3 (HONO sampling), 5 Polyethylene holder of absorbing pad impregnated with Na2CO3 (interference of HONO and NO2), 6 Carbon Filter (NO2 sampling), 7, 8, 9 Plastic spacer, 10 Body of the sampler, 11 Absorbing pad (containing Na2CO3 or NaCl). Geometric features A cross sectional area (330 mm2), R maximum length of the plastic support (10 mm), r plastic support radius (6.5 mm), a diffusive path to NaCl impregnated filter (4.5 mm), b diffusive path to first Na2CO3 impregnated filter (11.3 mm), c diffusive path to second Na2CO3 impregnated filter (17.1 mm), d diffusive path to impregnated carbon filter (24.0 mm)
Chemical analysis procedure
As for the other diffusive samplers, the multipollutant samplers at the end of collection time were sealed and successively analysed according to a procedure similar to the one reported elsewhere for NO2 [27]. In this case the filters were removed from the sampler, then they were extracted by adding a solution of sodium bicarbonate and carbonate, 0.3 mM NaHCO3 and 2.7 mM Na2CO3 in a plastic vial. The solution obtained was stirred with VIBROMIX 203 EVT (from Tehtnica, Železniki, Poland) and analysed through ion chromatography (IC) (Dionex ICS 1000 equipped with AS12A column. The concentrations of analytes such as nitrate and nitrite were determined referring to calibration curves constructed with water solutions prepared by opportune dilution of stock standards (Certipur from Merck, Milan, Italy) containing 1000 mg/L of each analyte.
Multipollutant diffusive sampler calibration
Some information will be given concerning the calibration of the new device performed during the laboratory trials in the development phase. The prototypes of the new sampler were exposed to standard atmospheres containing the pollutants of interest in a smog chamber. The experimental setup was equipped with reference technique for the measurement of each species, the data were used to calibrate the new device. The calibration was achieved through comparison with denuder data: NaCl coated denuders were the reference for HNO3, whereas two Na2CO3 coated denuders [31] accounted for nitrous acid.
Successively the comparison between the two different techniques gave good results also in field trials (for HNO3 R2 = 0.97; for HONO R2 = 0.96). The chemiluminescent analyser, used as a reference for NO2, was also in agreement with the newly developed diffusive sampler (R2 = 0.97).
A paired t test was performed to compare the data obtained by denuder technique and diffusive sampling [HONO: t(10) = 0.31 p = 0.75; HNO3: t(10) = 2.18 p = 0.053], and by chemiluminescent analyzer and diffusive sampling [NO2: t(10) = 1.59 p = 0.14]. At a p value of 0.05, in all cases the results are consistent with the null hypothesis that there is no difference between techniques would be accepted, and certainly for HONO there is very good agreement; for HNO3 more measurements might in retrospect have been appropriate to form a more considered view.
A comparison with the Analyst sampler for NO2 was also performed. The Analyst differs from the multipollutant sampler for the geometry, since it is basically a cylinder open on one end, whereas the multipollutant has a rather complex structure (Fig. 1). The uptake rate (Ur), which is defined as:
$$Ur = \frac{D \cdot A}{L}$$
where D is the diffusion coefficient (cm2/s) of the gaseous species, A is the cross-sectional area (cm2) and L the diffusive path (cm), is quite different for the two samplers. The ratio between the uptake rate for NO2 for the Analyst and the multipollutant is 3, being the Ur Analyst about 12 cm3/min and Ur Multipollutant about 4 cm3/min (measured at RH = 0 %, in a dry atmosphere containing NO2 without HONO). This feature of the newly developed diffusive sampler can explain the lower sensitivity to NO2 if compared to the Analyst, since in the same lapse of time the latter can collect a higher amount of analyte (nitrite), on the other hand the selectivity of multipollutant sampling is increased as already explained.
In field use of Analyst and multipollutant sampler
As a first approach, the agreement of the measurements of NO2 obtained by the Analyst sampler and by the multipollutant sampler was checked (Fig. 2). The correlation coefficient was quite good (R2 = 0.87), taking into account the whole set of measurements (both Swiss and Czech libraries and archives).
Regression between the multipollutant and the analyst sampler results of NO2 measurements
The new multipollutant samplers and standard Analyst samplers were also compared by estimation of sensitivity given as limits of detection (LODs) and uncertainty given as relative standard deviations. The LODs were calculated as three times the standard deviation of blank samples [32]. The sensitivity of multipollutant and Analyst samplers was comparable for HNO3, but the Analyst samplers were more sensitive to low concentrations of NO2. The lowest detectable concentrations for the multipollutant samplers after one month exposure were found to be 1.4 µg/m3 for NO2, 0.2 µg/m3 for HNO3, and 0.5 µg/m3 for HONO, and for the Analyst samplers 1.0 µg/m3 for NO2 and 1.0 µg/m3 for HNO3.
To assess the reproducibility [33] relative standard deviations were considered. Standard deviations were calculated for each set of replicates during the different campaigns. The standard deviations for multipollutant samples were found to be 4 % for NO2 and 20 % for HNO3 and for Analyst samplers 5 % for NO2 and 26 % for HNO3. These results were in agreement with the variations found by other studies [34, 35] and also fulfil the ±25 % uncertainty requirement of the European Directive for indicative monitoring with diffusion samplers [36]. Higher values of the standard deviations were found for HONO measured by the multipollutant samplers (approximately 68 %). HONO measurements reproducibility was likely affected by the really low values found indoors, which in many cases were below the detection limit, therefore the dataset was eventually composed by a narrow number of data.
NO2 and HNO3 concentrations values at the different locations in Swiss libraries, in particular at the SNL where abatement of the pollutants was achieved through the combination of different filters, were often lower than the detection limit.
Nitric acid concentrations were very low probably due to the very high deposition velocity on available surfaces [1, 37].
The extension of the exposure period was implemented to increase the amounts of analyte collected, optimizing the sampling length according to the sensitivity of the technique. Therefore the duration of the campaigns in Switzerland was of about 20 days, whereas the later campaigns in Czech Republic were extended to about a month.
Indoor and outdoor concentrations
Indoor pollutant concentrations are influenced by indoor sources and sinks and penetration from the outdoor environment. As it can be seen from a comparison of the different environments I/O (indoor/outdoor) ratios (Tables 2, 3, 4, 5), the efficiency of the filtration systems (turned off at Bern during the second and third campaign) in removing the pollutants does not seem to produce large differences in the environmental parameters measured. For HONO, when it was possible to perform the calculation, these ratios were always higher than 1 indicating that the formation of the pollutant happens indoors. In this case the filtration systems removing NO2 should avoid the formation of this pollutant, rather than removing it from infiltrating air.
The Swiss National Library in Bern campaigns results (µg/m3), bdl—below detection limit
IN Average
3UG
WA3UG
A26-Coll
HONO
HNO3
The Bibliotheque de Geneve campaigns results (µg/m3), bdl—below detection limit
Depot 51
The National Archives in Prague campaigns results (µg/m3), bdl—below detection limit
I/O OUT
The library of Regional Museum in Teplice campaigns results (µg/m3), bdl—below detection limit
The reaction (1) is negligible in the gas phase but occurs in the presence of surfaces, where produced HNO3 remains in the surface water film, whereas HONO forms an equilibrium shifted towards the gaseous phase [38].
According to (1) the equilibrium concentration of HONO should depend on NO2 concentration and relative humidity RH.
The surface/volume ratio is also known [30] to affect both the formation of HONO and NO at different concentrations of NO2 and for different values of relative humidity.
It is in agreement with higher NO2 and HONO outdoor concentration in Prague than in Teplice. Indoor concentrations of HONO were found in the BT depository and the Teplice library, with similar indoor conditions: indoor NO2 concentrations (Tables 4, 5), RH (Table 6), and a surface/volume ratio 2.6/m and 2.9/m in Teplice and BT, respectively.
Temperature and relative humidity
Moreover, HONO was not detected in the ACK depository, where NO2 concentrations were lower than the detection limit of both types of dosimeters. These results are in agreement with the production of HONO indoors from NO2 by reactions on exposed surfaces which include books and manuscripts, giving rise to acid deposition of HNO3.
The outdoor concentrations of the pollutants measured in the four cities reflect the seasonal trend, being higher everywhere during wintertime due to low atmospheric layers mixing. The cities of Geneva and Prague showed the highest values (about 40 µg/m3).
The concentration values of NO2 were always lower indoors than outdoors, which indicates that there were no indoor sources. Higher indoor values of NO2 were measured at WA3UG and WA2UG, the two rooms at the library in Bern where the insulation from double doors is not provided. In these two rooms the HONO levels were also higher than in the others. The A26 Collection, where a window is sometimes opened, the concentrations of the pollutants monitored were the highest at the library in Bern. The same can be observed for the corridor at the library in Geneva.
Relatively constant values of NO2 were observed at the first indoor site in Prague (BT) during all sampling periods. Concentrations measured inside the second indoor site (ACK) were always below detection limit. The difference in NO2 concentrations was probably caused by the efficiency of filters for NO2 in the HVAC system of the AKC depository compared to the BT depository equipped only with filters for particles. Indoor NO2 concentrations measured at Teplice were comparable to concentrations in BT though outdoor concentrations were lower. This was probably due to the higher natural ventilation in this library as compared to the isolated archives.
The results revealed that the reproducibility of the new multipollutant sampler measurements was reasonable (according to EU directives) for NO2 and HNO3. The measured data were comparable with the standard Analyst sampler results, but differ for lower NO2 concentrations, probably due to differences in sampling and analytical procedure.
The results showed that the newly developed multipollutant sampler can be used in archives and libraries, allowing to map the pollutants distribution indoors. Due to high efficiency of insulating systems normally employed (such as double doors etc.) and filtration systems, the values recorded for the pollutants indoors are often lower than the detection limits. Hence HONO and HNO3 measurements were carried out in very "clean" environments, and the dataset eventually available was likely not wide enough to truly assess the reproducibility of the measurements, especially for the former pollutant.
FV design of the monitoring project and discussion of the results. LM samplings organization and revision of the manuscript. MF technical support in the laboratory. AI analytical activity. JS revision of the manuscript. All authors read and approved the final manuscript.
The measurements in Switzerland were made possible by the kind help of Carmen Effner and Giovanna Di Pietro della Hochschule der Künste (Bern).
The monitoring project organization in Czech Republic was supported by CAS/CNR Bilateral Agreement Exchange Programme, which funded the exchange of visits between the Italian and the Czech research groups.
Institute of Atmospheric Pollution Research, Italian National Research Council, Via Salaria Km. 29,300, Monterotondo Stazione, 00016 Rome, Italy
Institute of Chemical Process Fundamentals of the CAS, Rozvojová 135, 165 02 Prague, Czech Republic
Spicer CW, Kenny DV, Ward GF, Billick IH. Transformations, lifetimes, and sources of NO2, HONO, and HNO3 in indoor environments. J Air Waste Manage. 1993;43:1479–85.View ArticleGoogle Scholar
Jenkin ME, Cox RA, Williams DJ. Laboratory studies of the kinetics of formation of nitrous acid from the thermal reaction of the nitrogen dioxide and water vapour. Atmos Environ. 1988;22(3):487–98.View ArticleGoogle Scholar
Menart E, De Bruin G, Strlič M. Dose–response functions for historic paper. Polymer Deg Stability. 2011;96(12):2029–39.View ArticleGoogle Scholar
Larsen R. Experiments and observations in the study of environmental impact on historical vegetable tanned leathers. Thermochim Acta. 2000;365:85–99.View ArticleGoogle Scholar
Samie F, Tidblad J, Kucera V, Leygraf C. Atmospheric corrosion effects of HNO3—Influence of concentration and air velocity on laboratory-exposed copper. Atmos Environ. 2006;40(20):3631–9.View ArticleGoogle Scholar
Samie F, Tidblad J, Kucera V, Leygraf C. Atmospheric corrosion effects of HNO3—Comparison of laboratory-exposed copper, zinc and carbon steel. Atmos Environ. 2007;41(23):4888–96.View ArticleGoogle Scholar
Grosjean D, Salmon LG, Cass GR. Fading of organic artists' colorants by atmospheric nitric acid: reaction products and mechanisms. Environ Sci Technol. 1992;26:952–9.View ArticleGoogle Scholar
Grosjean D, Grosjean E, Williams EL. Fading of Artists' Colorants by a Mixture of Photochemical Oxidants. Atmos Environ. 1993;27A(5):765–72.View ArticleGoogle Scholar
Katsanos NA, De Santis F, Cordoba A, Roubani-Kalantzopoulou F, Pasella D. Corrosive effects from the deposition of gaseous pollutants on surfaces of cultural and artistic value inside museums. J Hazard Mater. 1999;64:21–36.View ArticleGoogle Scholar
Whitmore PM, Cass GR. The Fading of Artists' Colorants by Exposure to Atmospheric Nitrogen Dioxide. Stud Conser. 1989;34(2):85–97.View ArticleGoogle Scholar
Brauer M, Ryan PB, Suh HH, Koutrakis P, Spengler JP. Measurements of nitrous acid inside two research houses. Environ Sci Technol. 1990;24:1521–7.View ArticleGoogle Scholar
Park SS, Hong JH, Lee JH, Kim YJ, Cho SY, Seung JK. Investigation of nitrous acid concentration in an indoor environment using an in situ monitoring system. Atmos Environ. 2008;42:6586–96.View ArticleGoogle Scholar
Khoder MI. Nitrous acid concentrations in homes and offices in residential areas in Greater Cairo. J Environ Monit. 2002;4:573–8.View ArticleGoogle Scholar
Gligorovski S. Nitrous acid (HONO) An emerging indoor pollutant. J Photochem Photobiol, A Chemistry. 2016;314:1–5.View ArticleGoogle Scholar
Chianese E, Riccio A, Duro I, Trifuoggi M, Iovino P, Capasso S, Barone G. Measurements for indoor air quality assessment at the Capodimonte Museum in Naples (Italy). Int J Environ Res. 2012;6(2):509–18.Google Scholar
De Santis F, Di Palo V, Allegrini I. Determination of some atmospheric pollutants inside a museum: relationship with the concentration outside. Sci Total Environ. 1992;127(3):211–23.View ArticleGoogle Scholar
Benner CL, Eatough NL, Lewis EA, Eatough DJ. Diffusion coefficients for ambient nitric and nitrous acids from Denuder experiments in the 1985 nitrogen species methods comparison study. Atmos Environ. 1988;22(8):1669–72.View ArticleGoogle Scholar
Genfa Z, Slanina S, Boring CB, Jongejan PAC, Dasgupta PK. Continuous wet denuder measurements of atmospheric nitric and nitrous acids during the 1999 Atlanta Supersite. Atmos Environ. 2003;37(9–10):1351–64.View ArticleGoogle Scholar
Febo A, Perrino C, Cortiello M. A denuder technique for the measurement of nitrous acid in urban atmospheres. Atmos Environ. 1993;27(11):1721–8.View ArticleGoogle Scholar
López-Aparicio S, Smolík J, Mašková L, Součková M, Grøntoft T, Ondráčková L, Stankiewicz J. Relationship of indoor and outdoor air pollutants in a naturally ventilated historical building envelope. Build Environ. 2011;46:1460–8.View ArticleGoogle Scholar
Godoi RHM, Carneiro BHB, Paralovo SL, Campos VP, Tavares TM, Evangelista H, Van Grieken R, Godoi AFL. Indoor air quality of a museum in a subtropical climate: the Oscar Niemeyer museum in Curitiba, Brazil. Sci Total Environ. 2013;452:314–20.View ArticleGoogle Scholar
Krupinska B, Van Grieken R, De Wael K. Air quality monitoring in a museum for preventive conservation: results of a three-year study in the Plantin-Moretus Museum in Antwerp, Belgium. Microchem J. 2013;110:350–60.View ArticleGoogle Scholar
Grøntoft T, Odlyha M, Mottner P, Dahlin E, López-Aparicio S, Jakiela S, Scharff M, Andrade G, Obarzanowski M, Ryhl-Svendsen M, Thickett D, Hackney S, Wadum J. Pollution monitoring by dosimetry and passive diffusion sampling for evaluation of environmental conditions for paintings in microclimate frames. J Cult Heritage. 2010;11(4):411–9.View ArticleGoogle Scholar
Spicer CW, Billick IH, Yanagisawa Y. Nitrous acid interference with passive NO2 measurement methods and the impact on indoor NO2 data. Indoor Air. 2001;11:156–61.View ArticleGoogle Scholar
Vichi F. Development of a diffusive sampler for the simultaneous measurement of nitrogen dioxide, nitrous acid and nitric acid by means of a novel, multipollutant diffusive sampler. Ph.D. Dissertation 2013. University of Rome La Sapienza, 89 pp, http://padis.uniroma1.it/handle/10805/29/browse?type=author&order=ASC&rpp=20&value=VICHI%2C+FRANCESCA.
Mašková L. Characterization of Aerosol Particles in the Indoor Environment of Different Types of Libraries and Archives. Ph.D. Dissertation 2015. Charles University in Prague, 124 pp, https://is.cuni.cz/webapps/zzp/detail/83446/.
De Santis F, Dogeroglu T, Fino A, Menichelli S, Vazzana C, Allegrini I. Laboratory development and field evaluation of a new diffusive sampler to collect nitrogen oxides in the ambient air. Anal Bioanal Chem. 2002;373:901–7.View ArticleGoogle Scholar
Svensson R, Ljungström E, Lindqvist O. Kinetics of the reaction between nitrogen dioxide and water vapour. Atmos Environ. 1987;21:1529–39.View ArticleGoogle Scholar
Kleffmann J, Becker KH, Wiesen P. Heterogeneous NO2 conversion processes on acid surfaces: possible atmospheric implications. Atmos Environ. 1998;32:2721–9.View ArticleGoogle Scholar
Finlayson-Pitts BJ, Wingen LM, Sumner AL, Syomin D, Ramazan KA. The heterogeneous hydrolysis of NO2 in laboratory systems and in outdoor and indoor atmospheres: an integrated mechanism. Phys Chem Chem Phys. 2003;5:223–42.View ArticleGoogle Scholar
Perrino C, DeSantis F, Febo A. Criteria for the choice of a denuder sampling technique devoted to the measurement of atmospheric nitrous and nitric acids. Atmos Environ. 1990;24:617–26.View ArticleGoogle Scholar
MacDougall D, Crummett WBB, et al. Guidelines for data acquisition and data quality evaluation in environmental chemistry. Anal Chem. 1980;52:2242–9.View ArticleGoogle Scholar
ISO 5725–1:1994. Accuracy (trueness and precision) of measurement methods and results—Part 1: General principles and definitions. Ed. 1.Google Scholar
Stevenson K, Bush T, Mooney D. Five years of nitrogen dioxide measurement with diffusion tube samplers at over 1000 sites in the UK. Atmos Environ. 2001;35:281–7.View ArticleGoogle Scholar
Gerboles M, Buzica D, Amantini L, Lagler F. Laboratory and field comparison of measurements obtained using the available diffusive samplers for ozone and nitrogen dioxide in ambient air. J Environ Monit. 2006;8:112–9.View ArticleGoogle Scholar
EU. Council directive 1999/30/EC relating to limit values for sulphur dioxide, nitrogen dioxide and oxides of nitrogen, particulate matter and lead in ambient air. Off J Eur Communities Legis. 1999; L163/41.Google Scholar
Walcek CJ, Brost RA, Chang JS. SO2, sulfate and HNO3 deposition velocities computed using regional landuse and meteorological data. Atmos Environ. 1986;20(5):949–64.View ArticleGoogle Scholar
Febo A, Perrino C. Prediction and experimental evidence for high air concentration of nitrous acid in indoor environments. Atmos Environ. 1991;25A:1055–61.View ArticleGoogle Scholar
In these collections
11th International Conference on Indoor Air Quality in Heritage and Hist... | CommonCrawl |
A synthetic derivative of Piracetam, aniracetam is believed to be the second most widely used nootropic in the Racetam family, popular for its stimulatory effects because it enters the bloodstream quickly. Initially developed for memory and learning, many anecdotal reports also claim that it increases creativity. However, clinical studies show no effect on the cognitive functioning of healthy adult mice.
Tuesday: I went to bed at 1am, and first woke up at 6am, and I wrote down a dream; the lucid dreaming book I was reading advised that waking up in the morning and then going back for a short nap often causes lucid dreams, so I tried that - and wound up waking up at 10am with no dreams at all. Oops. I take a pill, but the whole day I don't feel so hot, although my conversation and arguments seem as cogent as ever. I'm also having a terrible time focusing on any actual work. At 8 I take another; I'm behind on too many things, and it looks like I need an all-nighter to catch up. The dose is no good; at 11, I still feel like at 8, possibly worse, and I take another along with the choline+piracetam (which makes a total of 600mg for the day). Come 12:30, and I disconsolately note that I don't seem any better, although I still seem to understand the IQ essays I am reading. I wonder if this is tolerance to modafinil, or perhaps sleep catching up to me? Possibly it's just that I don't remember what the quasi-light-headedness of modafinil felt like. I feel this sort of zombie-like state without change to 4am, so it must be doing something, when I give up and go to bed, getting up at 7:30 without too much trouble. Some N-backing at 9am gives me some low scores but also some pretty high scores (38/43/66/40/24/67/60/71/54 or ▂▂▆▂▁▆▅▇▄), which suggests I can perform normally if I concentrate. I take another pill and am fine the rest of the day, going to bed at 1am as usual.
…It is without activity in man! Certainly not for the lack of trying, as some of the dosage trials that are tucked away in the literature (as abstracted in the Qualitative Comments given above) are pretty heavy duty. Actually, I truly doubt that all of the experimenters used exactly that phrase, No effects, but it is patently obvious that no effects were found. It happened to be the phrase I had used in my own notes.
I'm wary of others, though. The trouble with using a blanket term like "nootropics" is that you lump all kinds of substances in together. Technically, you could argue that caffeine and cocaine are both nootropics, but they're hardly equal. With so many ways to enhance your brain function, many of which have significant risks, it's most valuable to look at nootropics on a case-by-case basis. Here's a list of 9 nootropics, along with my thoughts on each.
The abuse liability of caffeine has been evaluated.147,148 Tolerance development to the subjective effects of caffeine was shown in a study in which caffeine was administered at 300 mg twice each day for 18 days.148 Tolerance to the daytime alerting effects of caffeine, as measured by the MSLT, was shown over 2 days on which 250 g of caffeine was given twice each day48 and to the sleep-disruptive effects (but not REM percentage) over 7 days of 400 mg of caffeine given 3 times each day.7 In humans, placebo-controlled caffeine-discontinuation studies have shown physical dependence on caffeine, as evidenced by a withdrawal syndrome.147 The most frequently observed withdrawal symptom is headache, but daytime sleepiness and fatigue are also often reported. The withdrawal-syndrome severity is a function of the dose and duration of prior caffeine use…At higher doses, negative effects such as dysphoria, anxiety, and nervousness are experienced. The subjective-effect profile of caffeine is similar to that of amphetamine,147 with the exception that dysphoria/anxiety is more likely to occur with higher caffeine doses than with higher amphetamine doses. Caffeine can be discriminated from placebo by the majority of participants, and correct caffeine identification increases with dose.147 Caffeine is self-administered by about 50% of normal subjects who report moderate to heavy caffeine use. In post-hoc analyses of the subjective effects reported by caffeine choosers versus nonchoosers, the choosers report positive effects and the nonchoosers report negative effects. Interestingly, choosers also report negative effects such as headache and fatigue with placebo, and this suggests that caffeine-withdrawal syndrome, secondary to placebo choice, contributes to the likelihood of caffeine self-administration. This implies that physical dependence potentiates behavioral dependence to caffeine.
Many people find that they experience increased "brain fog" as they age, some of which could be attributed to early degeneration of synapses and neural pathways. Some drugs have been found to be useful for providing cognitive improvements in these individuals. It's possible that these supplements could provide value by improving brain plasticity and supporting the regeneration of cells.10
Medication can be ineffective if the drug payload is not delivered at its intended place and time. Since an oral medication travels through a broad pH spectrum, the pill encapsulation could dissolve at the wrong time. However, a smart pill with environmental sensors, a feedback algorithm and a drug release mechanism can give rise to smart drug delivery systems. This can ensure optimal drug delivery and prevent accidental overdose.
Neuroplasticity, or the brain's ability to change and reorganize itself in response to intrinsic and extrinsic factors, indicates great potential for us to enhance brain function by medical or other interventions. Psychotherapy has been shown to induce structural changes in the brain. Other interventions that positively influence neuroplasticity include meditation, mindfulness , and compassion.
The methodology would be essentially the same as the vitamin D in the morning experiment: put a multiple of 7 placebos in one container, the same number of actives in another identical container, hide & randomly pick one of them, use container for 7 days then the other for 7 days, look inside them for the label to determine which period was active and which was placebo, refill them, and start again.
Like caffeine, nicotine tolerates rapidly and addiction can develop, after which the apparent performance boosts may only represent a return to baseline after withdrawal; so nicotine as a stimulant should be used judiciously, perhaps roughly as frequent as modafinil. Another problem is that nicotine has a half-life of merely 1-2 hours, making regular dosing a requirement. There is also some elevated heart-rate/blood-pressure often associated with nicotine, which may be a concern. (Possible alternatives to nicotine include cytisine, 2'-methylnicotine, GTS-21, galantamine, Varenicline, WAY-317,538, EVP-6124, and Wellbutrin, but none have emerged as clearly superior.)
As I am not any of the latter, I didn't really expect a mental benefit. As it happens, I observed nothing. What surprised me was something I had forgotten about: its physical benefits. My performance in Taekwondo classes suddenly improved - specifically, my endurance increased substantially. Before, classes had left me nearly prostrate at the end, but after, I was weary yet fairly alert and happy. (I have done Taekwondo since I was 7, and I have a pretty good sense of what is and is not normal performance for my body. This was not anything as simple as failing to notice increasing fitness or something.) This was driven home to me one day when in a flurry before class, I prepared my customary tea with piracetam, choline & creatine; by the middle of the class, I was feeling faint & tired, had to take a break, and suddenly, thunderstruck, realized that I had absentmindedly forgot to actually drink it! This made me a believer.
The majority of smart pills target a limited number of cognitive functions, which is why a group of experts gathered to discover a formula which will empower the entire brain and satisfy the needs of students, athletes, and professionals. Mind Lab Pro® combines 11 natural nootropics to affect all 4 areas of mental performance, unlocking the full potential of your brain. Its carefully designed formula will provide an instant boost, while also delivering long-term benefits.
That is, perhaps light of the right wavelength can indeed save the brain some energy by making it easier to generate ATP. Would 15 minutes of LLLT create enough ATP to make any meaningful difference, which could possibly cause the claimed benefits? The problem here is like that of the famous blood-glucose theory of willpower - while the brain does indeed use up more glucose while active, high activity uses up very small quantities of glucose/energy which doesn't seem like enough to justify a mental mechanism like weak willpower.↩
It is a known fact that cognitive decline is often linked to aging. It may not be as visible as skin aging, but the brain does in fact age. Often, cognitive decline is not noticeable because it could be as mild as forgetting names of people. However, research has shown that even in healthy adults, cognitive decline can start as early as in the late twenties or early thirties.
In my last post, I talked about the idea that there is a resource that is necessary for self-control…I want to talk a little bit about the candidate for this resource, glucose. Could willpower fail because the brain is low on sugar? Let's look at the numbers. A well-known statistic is that the brain, while only 2% of body weight, consumes 20% of the body's energy. That sounds like the brain consumes a lot of calories, but if we assume a 2,400 calorie/day diet - only to make the division really easy - that's 100 calories per hour on average, 20 of which, then, are being used by the brain. Every three minutes, then, the brain - which includes memory systems, the visual system, working memory, then emotion systems, and so on - consumes one (1) calorie. One. Yes, the brain is a greedy organ, but it's important to keep its greediness in perspective… Suppose, for instance, that a brain in a person exerting their willpower - resisting eating brownies or what have you - used twice as many calories as a person not exerting willpower. That person would need an extra one third of a calorie per minute to make up the difference compared to someone not exerting willpower. Does exerting self control burn more calories?
A total of 14 studies surveyed reasons for using prescription stimulants nonmedically, all but one study confined to student respondents. The most common reasons were related to cognitive enhancement. Different studies worded the multiple-choice alternatives differently, but all of the following appeared among the top reasons for using the drugs: "concentration" or "attention" (Boyd et al., 2006; DeSantis et al., 2008, 2009; Rabiner et al., 2009; Teter et al., 2003, 2006; Teter, McCabe, Cranford, Boyd, & Guthrie, 2005; White et al., 2006); "help memorize," "study," "study habits," or "academic assignments" (Arria et al., 2008; Barrett et al., 2005; Boyd et al., 2006; DeSantis et al., 2008, 2009; DuPont et al., 2008; Low & Gendaszek, 2002; Rabiner et al., 2009; Teter et al., 2005, 2006; White et al., 2006); "grades" or "intellectual performance" (Low & Gendaszek, 2002; White et al., 2006); "before tests" or "finals week" (Hall et al., 2005); "alertness" (Boyd et al., 2006; Hall et al., 2005; Teter et al., 2003, 2005, 2006); or "performance" (Novak et al., 2007). However, every survey found other motives mentioned as well. The pills were also taken to "stay awake," "get high," "be able to drink and party longer without feeling drunk," "lose weight," "experiment," and for "recreational purposes."
Studies show that B vitamin supplements can protect the brain from cognitive decline. These natural nootropics can also reduce the likelihood of developing neurodegenerative diseases. The prevention of Alzheimer's and even dementia are among the many benefits. Due to their effects on mental health, B vitamins make an excellent addition to any smart drug stack.
The flanker task is designed to tax cognitive control by requiring subjects to respond based on the identity of a target stimulus (H or S) and not the more numerous and visually salient stimuli that flank the target (as in a display such as HHHSHHH). Servan-Schreiber, Carter, Bruno, and Cohen (1998) administered the flanker task to subjects on placebo and d-AMP. They found an overall speeding of responses but, more importantly, an increase in accuracy that was disproportionate for the incongruent conditions, that is, the conditions in which the target and flankers did not match and cognitive control was needed.
Manually mixing powders is too annoying, and pre-mixed pills are expensive in bulk. So if I'm not actively experimenting with something, and not yet rich, the best thing is to make my own pills, and if I'm making my own pills, I might as well make a custom formulation using the ones I've found personally effective. And since making pills is tedious, I want to not have to do it again for years. 3 years seems like a good interval - 1095 days. Since one is often busy and mayn't take that day's pills (there are enough ingredients it has to be multiple pills), it's safe to round it down to a nice even 1000 days. What sort of hypothetical stack could I make? What do the prices come out to be, and what might we omit in the interests of protecting our pocketbook?
Fatty acids are well-studied natural smart drugs that support many cognitive abilities. They play an essential role in providing structural support to cell membranes. Fatty acids also contribute to the growth and repair of neurons. Both functions are crucial for maintaining peak mental acuity as you age. Among the most prestigious fatty acids known to support cognitive health are:
Bacopa is a supplement herb often used for memory or stress adaptation. Its chronic effects reportedly take many weeks to manifest, with no important acute effects. Out of curiosity, I bought 2 bottles of Bacognize Bacopa pills and ran a non-randomized non-blinded ABABA quasi-self-experiment from June 2014 to September 2015, measuring effects on my memory performance, sleep, and daily self-ratings of mood/productivity. Because of the very slow onset, small effective sample size, definite temporal trends probably unrelated to Bacopa, and noise in the variables, the results were as expected, ambiguous, and do not strongly support any correlation between Bacopa and memory/sleep/self-rating (+/-/- respectively).
Some supplement blends, meanwhile, claim to work by combining ingredients – bacopa, cat's claw, huperzia serrata and oat straw in the case of Alpha Brain, for example – that have some support for boosting cognition and other areas of nervous system health. One 2014 study in Frontiers in Aging Neuroscience, suggested that huperzia serrata, which is used in China to fight Alzheimer's disease, may help slow cell death and protect against (or slow the progression of) neurodegenerative diseases. The Alpha Brain product itself has also been studied in a company-funded small randomized controlled trial, which found Alpha Brain significantly improved verbal memory when compared to adults who took a placebo.
We included studies of the effects of these drugs on cognitive processes including learning, memory, and a variety of executive functions, including working memory and cognitive control. These studies are listed in Table 2, along with each study's sample size, gender, age and tasks administered. Given our focus on cognition enhancement, we excluded studies whose measures were confined to perceptual or motor abilities. Studies of attention are included when the term attention refers to an executive function but not when it refers to the kind of perceptual process taxed by, for example, visual search or dichotic listening or when it refers to a simple vigilance task. Vigilance may affect cognitive performance, especially under conditions of fatigue or boredom, but a more vigilant person is not generally thought of as a smarter person, and therefore, vigilance is outside of the focus of the present review. The search and selection process is summarized in Figure 2.
Productivity is the most cited reason for using nootropics. With all else being equal, smart drugs are expected to give you that mental edge over other and advance your career. Nootropics can also be used for a host of other reasons. From studying to socialising. And from exercise and health to general well-being. Different nootropics cater to different audiences.
The absence of a suitable home for this needed research on the current research funding landscape exemplifies a more general problem emerging now, as applications of neuroscience begin to reach out of the clinical setting and into classrooms, offices, courtrooms, nurseries, marketplaces, and battlefields (Farah, 2011). Most of the longstanding sources of public support for neuroscience research are dedicated to basic research or medical applications. As neuroscience is increasingly applied to solving problems outside the medical realm, it loses access to public funding. The result is products and systems reaching the public with less than adequate information about effectiveness and/or safety. Examples include cognitive enhancement with prescription stimulants, event-related potential and fMRI-based lie detection, neuroscience-based educational software, and anti-brain-aging computer programs. Research and development in nonmedical neuroscience are now primarily the responsibility of private corporations, which have an interest in promoting their products. Greater public support of nonmedical neuroscience research, including methods of cognitive enhancement, will encourage greater knowledge and transparency concerning the efficacy and safety of these products and will encourage the development of products based on social value rather than profit value.
(People aged <=18 shouldn't be using any of this except harmless stuff - where one may have nutritional deficits - like fish oil & vitamin D; melatonin may be especially useful, thanks to the effects of screwed-up school schedules & electronics use on teenagers' sleep. Changes in effects with age are real - amphetamines' stimulant effects and modafinil's histamine-like side-effects come to mind as examples.)
Vitamin B12 is also known as Cobalamin and is a water-soluble essential vitamin. A (large) deficiency of Vitamin B12 will ultimately lead to cognitive impairment [52]. Older people and people who don't eat meat are at a higher risk than young people who eat more meat. And people with depression have less Vitamin B12 than the average population [53].
And in his followup work, An opportunity cost model of subjective effort and task performance (discussion). Kurzban seems to have successfully refuted the blood-glucose theory, with few dissenters from commenting researchers. The more recent opinion seems to be that the sugar interventions serve more as a reward-signal indicating more effort is a good idea, not refueling the engine of the brain (which would seem to fit well with research on procrastination).↩
One symptom of Alzheimer's disease is a reduced brain level of the neurotransmitter called acetylcholine. It is thought that an effective treatment for Alzheimer's disease might be to increase brain levels of acetylcholine. Another possible treatment would be to slow the death of neurons that contain acetylcholine. Two drugs, Tacrine and Donepezil, are both inhibitors of the enzyme (acetylcholinesterase) that breaks down acetylcholine. These drugs are approved in the US for treatment of Alzheimer's disease.
There is much to be appreciated in a brain supplement like BrainPill (never mind the confusion that may stem from the generic-sounding name) that combines tried-and-tested ingredients in a single one-a-day formulation. The consistency in claims and what users see in real life is an exemplary one, which convinces us to rate this powerhouse as the second on this review list. Feeding one's brain with nootropics and related supplements entails due diligence in research and seeking the highest quality, and we think BrainPill is up to task. Learn More...
Intrigued by old scientific results & many positive anecdotes since, I experimented with microdosing LSD - taking doses ~10μg, far below the level at which it causes its famous effects. At this level, the anecdotes claim the usual broad spectrum of positive effects on mood, depression, ability to do work, etc. After researching the matter a bit, I discovered that as far as I could tell, since the original experiment in the 1960s, no one had ever done a blind or even a randomized self-experiment on it.
There are also premade 'stacks' (or formulas) of cognitive enhancing superfoods, herbals or proteins, which pre-package several beneficial extracts for a greater impact. These types of cognitive enhancers are more 'subtle' than the pharmaceutical alternative with regards to effects, but they work all the same. In fact, for many people, they work better than smart drugs as they are gentler on the brain and produce fewer side-effects.
Or in other words, since the standard deviation of my previous self-ratings is 0.75 (see the Weather and my productivity data), a mean rating increase of >0.39 on the self-rating. This is, unfortunately, implying an extreme shift in my self-assessments (for example, 3s are ~50% of the self-ratings and 4s ~25%; to cause an increase of 0.25 while leaving 2s alone in a sample of 23 days, one would have to push 3s down to ~25% and 4s up to ~47%). So in advance, we can see that the weak plausible effects for Noopept are not going to be detected here at our usual statistical levels with just the sample I have (a more plausible experiment might use 178 pairs over a year, detecting down to d>=0.18). But if the sign is right, it might make Noopept worthwhile to investigate further. And the hardest part of this was just making the pills, so it's not a waste of effort.
Still, the scientific backing and ingredient sourcing of nootropics on the market varies widely, and even those based in some research won't necessarily immediately, always or ever translate to better grades or an ability to finally crank out that novel. Nor are supplements of any kind risk-free, says Jocelyn Kerl, a pharmacist in Madison, Wisconsin.
COGNITUNE is for informational purposes only, and should not be considered medical advice, diagnosis or treatment recommendations. Always consult with your doctor or primary care physician before using any nutraceuticals, dietary supplements, or prescription medications. Seeking a proper diagnosis from a certified medical professional is vital for your health.
The main area of the brain effected by smart pills is the prefrontal cortex, where representations of our goals for the future are created. Namely, the prefrontal cortex consists of pyramidal cells that keep each other firing. However in some instances they can become disconnected due to chemical imbalances, or due to being tired, stressed, and overworked.
Furthermore, there is no certain way to know whether you'll have an adverse reaction to a particular substance, even if it's natural. This risk is heightened when stacking multiple substances because substances can have synergistic effects, meaning one substance can heighten the effects of another. However, using nootropic stacks that are known to have been frequently used can reduce the chances of any negative side effects.
11:30 AM. By 2:30 PM, my hunger is quite strong and I don't feel especially focused - it's difficult to get through the tab-explosion of the morning, although one particularly stupid poster on the DNB ML makes me feel irritated like I might on Adderall. I initially figure the probability at perhaps 60% for Adderall, but when I wake up at 2 AM and am completely unable to get back to sleep, eventually racking up a Zeo score of 73 (compared to the usual 100s), there's no doubt in my mind (95%) that the pill was Adderall. And it was the last Adderall pill indeed.
As with any thesis, there are exceptions to this general practice. For example, theanine for dogs is sold under the brand Anxitane is sold at almost a dollar a pill, and apparently a month's supply costs $50+ vs $13 for human-branded theanine; on the other hand, this thesis predicts downgrading if the market priced pet versions higher than human versions, and that Reddit poster appears to be doing just that with her dog.↩
My worry about the MP variable is that, plausible or not, it does seem relatively weak against manipulation; other variables I could look at, like arbtt window-tracking of how I spend my computer time, # or size of edits to my files, or spaced repetition performance, would be harder to manipulate. If it's all due to MP, then if I remove the MP and LLLT variables, and summarize all the other variables with factor analysis into 2 or 3 variables, then I should see no increases in them when I put LLLT back in and look for a correlation between the factors & LLLT with a multivariate regression.
A key ingredient of Noehr's chemical "stack" is a stronger racetam called Phenylpiracetam. He adds a handful of other compounds considered to be mild cognitive enhancers. One supplement, L-theanine, a natural constituent in green tea, is claimed to neutralise the jittery side-effects of caffeine. Another supplement, choline, is said to be important for experiencing the full effects of racetams. Each nootropic is distinct and there can be a lot of variation in effect from person to person, says Lawler. Users semi-annonymously compare stacks and get advice from forums on sites such as Reddit. Noehr, who buys his powder in bulk and makes his own capsules, has been tweaking chemicals and quantities for about five years accumulating more than two dozens of jars of substances along the way. He says he meticulously researches anything he tries, buys only from trusted suppliers and even blind-tests the effects (he gets his fiancée to hand him either a real or inactive capsule).
At dose #9, I've decided to give up on kratom. It is possible that it is helping me in some way that careful testing (eg. dual n-back over weeks) would reveal, but I don't have a strong belief that kratom would help me (I seem to benefit more from stimulants, and I'm not clear on how an opiate-bearer like kratom could stimulate me). So I have no reason to do careful testing. Oh well.
The infinite promise of stacking is why, whatever weight you attribute to the evidence of their efficacy, nootropics will never go away: With millions of potential iterations of brain-enhancing regimens out there, there is always the tantalizing possibility that seekers haven't found the elusive optimal combination of pills and powders for them—yet. Each "failure" is but another step in the process-of-elimination journey to biological self-actualization, which may be just a few hundred dollars and a few more weeks of amateur alchemy away.
Nootropics are a great way to boost your productivity. Nootropics have been around for more than 40 years and today they are entering the mainstream. If you want to become the best you, nootropics are a way to level up your life. Nootropics are always personal and what works for others might not work for you. But no matter the individual outcomes, nootropics are here to make an impact!
A large review published in 2011 found that the drug aids with the type of memory that allows us to explicitly remember past events (called long-term conscious memory), as opposed to the type that helps us remember how to do things like riding a bicycle without thinking about it (known as procedural or implicit memory.) The evidence is mixed on its effect on other types of executive function, such as planning or ability on fluency tests, which measure a person's ability to generate sets of data—for example, words that begin with the same letter.
Several new medications are on the market and in development for Alzheimer's disease, a progressive neurological disease leading to memory loss, language deterioration, and confusion that afflicts about 4.5 million Americans and is expected to strike millions more as the baby boom generation ages. Yet the burning question for those who aren't staring directly into the face of Alzheimer's is whether these medications might make us smarter.
In 3, you're considering adding a new supplement, not stopping a supplement you already use. The I don't try Adderall case has value $0, the Adderall fails case is worth -$40 (assuming you only bought 10 pills, and this number should be increased by your analysis time and a weighted cost for potential permanent side effects), and the Adderall succeeds case is worth $X-40-4099, where $X is the discounted lifetime value of the increased productivity due to Adderall, minus any discounted long-term side effect costs. If you estimate Adderall will work with p=.5, then you should try out Adderall if you estimate that 0.5 \times (X-4179) > 0 ~> $X>4179$. (Adderall working or not isn't binary, and so you might be more comfortable breaking down the various how effective Adderall is cases when eliciting X, by coming up with different levels it could work at, their values, and then using a weighted sum to get X. This can also give you a better target with your experiment- this needs to show a benefit of at least Y from Adderall for it to be worth the cost, and I've designed it so it has a reasonable chance of showing that.)
A LessWronger found that it worked well for him as far as motivation and getting things done went, as did another LessWronger who sells it online (terming it a reasonable productivity enhancer) as did one of his customers, a pickup artist oddly enough. The former was curious whether it would work for me too and sent me Speciosa Pro's Starter Pack: Test Drive (a sampler of 14 packets of powder and a cute little wooden spoon). In SE Asia, kratom's apparently chewed, but the powders are brewed as a tea.
Jesper Noehr, 30, reels off the ingredients in the chemical cocktail he's been taking every day before work for the past six months. It's a mixture of exotic dietary supplements and research chemicals that he says gives him an edge in his job without ill effects: better memory, more clarity and focus and enhanced problem-solving abilities. "I can keep a lot of things on my mind at once," says Noehr, who is chief technology officer for a San Francisco startup.
But, if we find in 10 or 20 years that the drugs don't do damage, what are the benefits? These are stimulants that help with concentration. College students take such drugs to pass tests; graduates take them to gain professional licenses. They are akin to using a calculator to solve an equation. Do you really want a doctor who passed his boards as a result of taking speed — and continues to depend on that for his practice? | CommonCrawl |
\begin{document}
\title{Most Powerful Test Sequences with Early Stopping Options}
\titlerunning{mpact of Early Stopping Options}
\author{Sergey Tarima \and
Nancy Flournoy }
\authorrunning{Flournoy and Flournoy}
\institute{Institute for Health and Society, Medical College of Wisconsin, 8701 Watertown Plank Rd, Wauwatosa, WI, 53226
\and Department of Statistics, University of Missouri, 600 S State St., Apt. 408 Bellingham, WA 98225}
\date{Received: date / Accepted: date}
\maketitle
\begin{abstract}
Sequential likelihood ratio testing is found to be most powerful in sequential studies with early stopping rules when grouped data come from the one-parameter exponential family. First, to obtain this elusive result, the probability measure of a group sequential design is constructed with support for all possible outcome events, as is useful for designing an experiment prior to having data. This construction identifies impossible events that are not part of the support. The overall probability distribution is dissected into stage specific components. These components are sub-densities of interim test statistics first described by Armitage, McPherson and Rowe (1969) that are commonly used to create stopping boundaries given an $\alpha$-spending function and a set of interim analysis times. Likelihood expressions conditional on reaching a stage are given to connect pieces of the probability anatomy together.
The reduction of the support caused by the adoption of an early stopping rule induces sequential truncation (not nesting) in the probability distributions of possible events.
Multiple testing induces mixtures on the adapted support. Even asymptotic distributions of inferential statistics are mixtures of truncated distributions. In contrast to the classical result on local asymptotic normality (Le Cam 1960), statistics that are asymptotically normal without stopping options have asymptotic distributions that are mixtures of truncated normal distributions under local alternatives with stopping options; under fixed alternatives, asymptotic distributions of test statistics are degenerate.
\keywords{Adaptive designs \and adapted support \and group sequential designs \and local asymptotics \and interim hypothesis testing \and likelihood ratio tests}
\end{abstract}
\section{Introduction} \label{Introduction} We define a \emph{sequential experiment} to be one in which the decision to stop collecting data is based on data collected previously in the study.
\citet{wetherill1986} emphasize that "\emph{two aspects of a sequential procedure must be clearly distinguished, the stopping rule, and the manner in which inferences are made once observations are stopped. $\ldots$ in the design problem, it is important to know how probable are various possible results."} We distinguish the probability framework underpinning these two activities, and also a third - the probability framework underlying interim hypothesis tests.
\citet{dodge1929} proposed the first known sequential test procedure in which a decision to stop or continue collecting data was based on prior data, recognizing that decisions to stop or continue a trial made based on prior observations could substantially reduce the expected numbers of required subjects; it was a two-stage design. \citet{bartky1943} devised a multiple sequential testing procedure for binomial data based on \citet{neyman1933}'s likelihood ratio test that \citet{wald1947} cites as a "forerunner" to his more general \emph{sequential probability ratio test} (SPRT) procedure in which the probabilities of type I and II errors are controlled. Extensions with stopping decisions based on groups of subjects [\emph{Group Sequential Designs (GSDs)}] are given in \citet{jennison1999}.
\citet{neyman1933} show that likelihood ratio tests are most powerful for testing a simple null versus a simple alternative hypotheses. In \citet{ferguson2014mathematical}, the Karlin-Rubin theorem is viewed as an extension of Neyman-Pearson approach to most powerful testing of composite hypotheses. The Karlin-Rubin theorem applies to the one-dimensional exponential family. With sequential stopping options, some elements of the sample space become impossible, which changes the distributions of statistics. Sufficient statistics become dependent on the random sample size; see \citet{blackwell1947}. If statistics belong to the exponential family without early stopping options, then they belong to a curved exponential family when exposed to early stopping options (\citet{efron1975, liu1999,liu2006}). Section \ref{mostpower} shows that despite being from a curved exponential family, the sequential tests based on likelihood ratios continue to be most powerful for any $\alpha$-spending function.
\subsection{Notation and A Simple Example}\label{sec:ex_simple} This example demonstrates a couple important repercussions of sequential stopping rules: \begin{itemize} \setlength\itemsep{.0em}
\item The support is reduced,
\item Bivariate normal random variables become non-observable; the observable bivariate random variable is a mixture of truncated normal random variables,
\end{itemize} Let $X_1$ and $X_2$ be $N(\theta,1)$ random variables with an unknown location parameter $\theta$.
\subsubsection{Non-sequential experiments}
If $X_1=x_1$ alone is observed, the log-likelihood $$l(\theta|X_1=x_1)=-2\log \sqrt{2\pi} -0.5 (x_1-\theta)^2$$ is maximized at $\widehat\theta_1=x_1$.
If both $X_1=x_1$ and $X_2=x_2$ are
observed independently,
the random variable $(X_1,X_2)$ is defined on the probability space $\left(R^2,{\cal{B}}, P\right)$, where $R^2$ is the sample space [$R=\left(-\infty,\infty\right)$], ${\cal{B}}$ is the Borel $\sigma$-algebra on $R^2$ and $P$ is a bivariate normal distribution with mean vector $(\theta,\theta)$, units variances and zero correlation.
The log-likelihood function is
$$l(\theta|X_1=x_1, X_2=x_2) = -2 \log \sqrt{2\pi} -0.5 (x_1-\theta)^2 -0.5 (x_2-\theta)^2$$ and the maximum likelihood estimator (MLE) of $\theta$ is $\widehat\theta_2=(x_1+x_2)/2$.
\subsubsection{Sequential experiments: likelihood, support and probability measures }\label{sec:seq_exp} What happens in \textit{sequential settings} when $X_2$ is only observed if $X_1<2.18$? Let $D$ denote the random stopping stage. Then $D = 1+I(X_1< 2.18)$, where $I(\cdot)$ is an indicator function. In this simple example, $D$ is also the random sample size.
The joint distribution of (\textbf{X},D) and the marginal distribution of \textbf{X} are the same: \begin{align}\label{eq:jtden}
f_{\textbf{X}}\left(\textbf{x}|\theta \right)=f_{\textbf{X},D}\left(\textbf{x},d|\theta \right) &= \phi(x_1-\theta) \left[\phi(x_2-\theta)\right]^{I\left(d=2\right)}\\&= [\phi(x_1-\theta)]^{I(d=1)} \left[\phi(x_1-\theta)\phi(x_2-\theta)\right]^{I\left(d=2\right)},\notag \end{align}
where $\phi(\cdot)$ is the standard normal density. The representation of $f_{\textbf{X}}\left(\textbf{x}|\theta \right)$ in the first line of \eqref{eq:jtden} partitions the density according to data collection stages, while the representation in the second line partitions the density according to stopping stages. In canonical form,
\begin{eqnarray}f_{\textbf{X},D}\left(\textbf{x},d|\theta \right) &=& h(\mathbf{x})\exp \Big(\left[x_1 + I(d=2)x_2\right]\theta - \left[1+I(d=2)\right]\frac{\theta^2}{2}\Big), \label{marginal_density} \end{eqnarray} where $h(\mathbf{x}) = \exp \Big( -\frac{1}{2} \left[x_1^2 + I(d=2)x_2^2 + I(d=2) \log \left(\sqrt{\pi}\right) +\log \left(\sqrt{\pi} \right)\right] \Big)$. Thus, the density (\ref{marginal_density}) belongs to the curved exponential family with a sufficient statistic $$\left(\sum_{k=1}^d x_i, d\right) = \left[x_1 + I(d=2)x_2,\, 1+I(d=2)\right].$$ Curved exponential families were defined by \citet{efron1975} and the sufficient statistic with a random number of summands $\sum_{k=1}^Dx_k$ was derived by \citet{blackwell1947}. Probability distribution (\ref{marginal_density}) is a special case of the exponential family derived in \citet{liu2006} [see their formula (2.6)]. A more general probability distribution of $\mathbf{X}$ is presented in Section \ref{sec:densities}.
The log-likelihood function \begin{align*}
l(\theta|X_1=x_1, X_2=x_2, D=d) &= \begin{cases} [\phi(x_1-\theta)]^{I(d=1)} &\textrm{ if } D=1, \\ \left[\phi(x_1-\theta)\phi(x_2-\theta)\right]^{I\left(d=2\right)} & \textrm{ if } D=2 \end{cases} \end{align*}
is maximized at $\widehat\theta = I(d=1)x_1 + I(d=2)(x_1+x_2)/2.$
Consequently, the score function, the MLE and the observed information are the same as for the non-sequential experiment. What changes?
The joint support of $X_1$ and $X_2$ changes because $X_2$ becomes impossible (not just missing) when $X_1\ge 2.18$. The random variable $(X_1,X_2)$ is non-observable when $X_1\ge 2.18$ and the joint distribution of $X_1$ and $X_2$ is therefore truncated and not normal. Formally, the support for joint density can be decomposed into support for the experiment stopping with $X_1$ and support for the experiment continuing to observe $X_2$: $${\cal{T}}=\{x_1 \ge 2.18 \}\ \cup \ \{ \{x_1 < 2.18\} \cap \{x_2 \in R\} \}\ \subset R^2.$$ This ${\cal{T}}$ is a special case of the support formalized in \citet{liu2006}.
If $A \in {\cal{T}}$, then \begin{eqnarray}
P_{(D)} = \text{Pr}((X_1,X_2) \in A) &=& \text{Pr}(X_1 \ge 2.18)\text{Pr}(X_1 \in A|X_1 \ge 2.18) \notag \\ &+&
\text{Pr}(X_1 < 2.18)\text{Pr}((X_1, X_2) \in A|X_1 < 2.18) \end{eqnarray} is a probability measure on the $\sigma$-algebra $\sigma({\cal{T}})$. Thus, the observable random variable \begin{align*}
\mathbf{X}_{{\cal{T}}} = \begin{cases} X_1 &\textrm{ if } $D=1$ \\ (X_1,X_2) & \textrm{ if } $D=2$. \end{cases} \end{align*}
is defined on the probability space $\left({\cal{T}}, \sigma({\cal{T}}), P_{(D)}\right).$
In contrast to $(X_1,X_2)$, $\mathbf{X}_{{\cal{T}}}$ is observable for this sequential experiment. The MLE, is a random variable defined on $\left({\cal{T}}, \sigma({\cal{T}}), P_{(D)}\right)$ and its probability distribution is a mixture of the left truncated normal random variable $\{X_1|D=1\}$ and an average of the right truncated normal random variable $\{X_1|D=2\}$ and the normal random variable $X_2$.
Thus, in this sequential experiment, MLEs are not normal random variables as illustrated in Figure~\ref{pic:ex_simple}. The first column shows the distribution of the MLE if the experiment stopped at stage 1, which is left truncated normal. The seconds of histograms shows the distribution of the MLE if the experiment proceeded to stage 2. This distribution is a mixture of right truncated data from stage 1 and untruncated normal data from stage 2. The final column shows unconditional distribution of the MLE.
\begin{figure}
\caption{ Distribution of MLEs from the experiment described in Section~\ref{sec:ex_simple}. $n_1=n_2=1$; $10^6$ Monte-Carlo simulations.}
\label{MLEcpic}
\label{pic:ex_simple}
\end{figure}
\subsection{The Scope of this Paper} We consider sequential experiments having a small finite number of interim decision points, that is, experimental set-ups for which Martingale central limit theorems and Brownian theory are not suitable.
Our interest is in experiments that aim primarily on a hypothesis test of effect size. We focus on characterizing the effect of sequential stopping rules on probability distributions of test statistics.
In this manuscript, Section~\ref{sec:densities} introduces notation for GSDs with stopping rules dependent on a parameter of interest [through the distributions of the test statistics]. This section also presents distributions of cumulative test statistics conditional on reaching a stage, conditional on stopping at a stage, and unconditional defined on the probability space with truncation-adapted support. All of these probability distributions are truncated or truncated-mixtures. Section~\ref{Sec:likelihood} presents likelihood-based inference on the truncation-adapted probability space. In section \ref{LSP} a local asymptotic distribution of the MLEs is found to be non-degenerate; it is a mixture of truncated normal distributions. Section \ref{mostpower} shows that the possibility of early stopping does not change the monotonicity of likelihood ratios in the one-parameter exponential family. Thus, stage-specific tests continue to be uniformly most powerful by the Karlin-Rubin theorem, which makes sequential tests based on monotone likelihood ratio uniformly most powerful. Throughout Sections \ref{sec:densities} and \ref{Sec:likelihood} theoretical results are illustrated by a two stage example, \citet{Pocock1977}. Finally, Section \ref{Conclusion} concludes this article with a summary and a discussion of impact within the contemporary research environment.
\section{Probability Distributions with Early Stopping}\label{sec:densities}
Let $X$ denote subjects' outcome variable and assume that, when observed in isolation, it has a probability distribution function or a probability mass function $f_X=f_X\left(x|\theta\right)$. To simplify the material, the term \textit{density} is used to refer to probability measures without formally distinguishing between them. Let a sequence of $X$s be observed with the primary objective of testing the null hypothesis $H_0:\theta=0$ with overall $\alpha$-level type~1 error and $1-\beta$ power at an alternative $H_1: \theta=\theta_1$.
It is convenient to group the random sample into \emph{stages} separated by the interim analysis times: $\mathbf{X}_{1}, \mathbf{X}_{2}, \ldots$, where $\mathbf{X}_{k} = (X_{n_{(k-1)}+1}, \ldots,X_{n_{(k)}})$; $n_{(k)}=\sum_{j=1}^kn_j$; here for simplicity $n_j$ is a pre-specified number of observations in stage $j$, $1\le k\le K$; $n_{(0)}=0$ and $K-1$ is the maximum number of interim analyses permitted. Every stage is assumed to be ``reachable'', that is, there is a positive probability of reaching each stage. Data collection at each stage is followed by a hypothesis test that results in a decision to stop the study or to enroll a new group of patients; except that if stage $K$ is reached, the experiment stops after $n_{(K)}$ observations regardless of the last $n_{K}$ observations' values.
\subsection{Stopping Decisions}
Let $T_{(k)}$ be a function of observations $\mathbf{X}_{(k)} = (X_1,\ldots,X_{n_{(k)}})$ that is compared against a cutoff value $c_k$ to determine whether to stop at stage $k$ or continue through stage~$k+1$, $1\le k < K-1$. These decisions are defined by the events $\left\{\cap_{j=1}^{k-1}\left\{T_{(j)}\le c_j\right\}\right\}\cap \left\{T_{(k)}>c_k\right\}$ and $\cap_{j=1}^{K-1}\left\{T_{(j)}\le c_k\right\}$, respectively, and are conveniently summarized by a random variable denoting the stopping stage: $$D = K \cdot I\left(\cap_{j=1}^{K-1}\left\{T_{(j)}\le c_j\right\}\right) + \sum_{k=1}^{K-1} k \cdot I\left(\left(\cap_{j=1}^{k-1}\left\{T_{(j)}\le c_j\right\}\right)\cap \left\{T_{(k)}>c_k\right\}\right);$$ $D\in \{1,\ldots,K\}$ will appear as random index such as in $\mathbf{X}_{(D)}$ to emphasize that the stopping stage is unknown and is described probabilistically though the random variable $D$. $\mathbf{X}_{(d)}$ is the random variable $\mathbf{X}_{(D)}$ conditioned on stopping with stage $D=d, d=1,\ldots,K$.
It is important to account for $D$ in probability statements about $T_{(d)}$ because $D$ determines the observations' probability support as illustrated in Section~\ref{sec:ex_simple}.
\subsection{After deciding to stop} \begin{figure}
\caption{ Support associated with different stopping decisions when $K=3$;
$c_k$ is the critical value for stopping at stage $k$.}
\label{support_white}
\label{pic:support_D=3}
\end{figure}
If study stops at stage $D=d<K$, $H_0$ is rejected. If $d=K$, the final hypothesis test determines acceptance or rejection of $H_0$. At the time of the final analysis, the density of observations conditional on stopping at stage $d$ (i.e., the density of $\mathbf{X}_{(d)}=\mathbf{X}_{(D)}\vert \{D=d\}$)
is \begin{align}\label{densK} f_{\mathbf{X}_{(d)}}^C=f_{\mathbf{X}_{(D)}} \left(\textbf{\textit{x}}_{(D)}\vert D=d, \theta \right) = \frac{I\left(D=d\right)}{\text{Pr}_{\theta}\left(D=d\right)} f_{\mathbf{X}_{(d)}} \left(\textbf{\textit{x}}_{(d)}\vert \theta \right) = \frac{f_{\mathbf{X}_{(d)}}^{sub}}{\text{Pr}_{\theta}\left(D=d\right)},\end{align} where
$f_{\mathbf{X}_{(d)}}^{sub}=[f_{\mathbf{X}_{(d)}}(\textbf{\textit{x}}_{(d)}|\theta)]^{I\left(D=d\right)}$ denotes the \textit{sub-density} with support defined by $D=d$ (see the exemplary sketches in Figure~\ref{support_white}). Similarly, for a statistic $T_{(d)} = T(\mathbf{X}_{(d)})$, the conditional on $D=d$ density is $f_{T_{(d)}}^C$.
In contrast, if the stopping rule is not random and the experiment stops with $n_{(d)}$ observations, $\text{Pr}_{\theta}(D=d)\equiv 1$ and the observations have density $f_{\mathbf{X}_{(d)}}$.
\subsection{At the Time of Experimental Design }
Prior to data collection, both $D$ and $X_{(D)}$ are unknown and the \textit{joint} density of $X_{(D)}$ can be written in several ways:
\begin{eqnarray} \label{densjoint} f_{\mathbf{X}_{(D)}}\left(\textbf{\textit{x}}_{(D)}\vert \theta \right) &=&
\sum_{d=1}^{K} [f_{\mathbf{X}_{(d)}}(\textbf{\textit{x}}_{(d)}|\theta)]^{I\left(D=d\right)}\notag \\ &=&\sum_{d=1}^{K}f_{\mathbf{X}_{(d)}}^{sub} = \sum_{d=1}^{K} \text{Pr}_{\theta}\left(D=d\right) f_{\mathbf{X}_{(d)}}^C.\end{eqnarray} The joint density is a mixture of densities corresponding to possible outcome vectors; i.e., these densities are defined on non-overlapping regions of the density's support.
When a test statistic $T_d$ summarizes $d$th stage data, the density of $T_{(D)}$ can be written analogous to Equation (\ref{densjoint}) as \begin{eqnarray} \label{dens_cond1} f_{T_{(D)}}\left({\textit{t}}_{(D)}\vert \theta \right) &=&
\sum_{d=1}^{K} [f_{{T}_{(d)}}({\textit{t}}_{(d)}|\theta)]^{I\left(D=d\right)}\notag \\ &=&\sum_{d=1}^{K}f_{{T}_{(d)}}^{sub} = \sum_{d=1}^{K} \text{Pr}_{\theta}\left(D=d\right) f_{{T}_{(d)}}^{C}.\end{eqnarray} Even if every stage-specific test statistic $T_d$ is normally distributed, the distribution of $T_{(D)}$ is not.
\subsection{At Interim Hypothesis Testing} Suppose at stage $d-1$, the decision was made to continue sampling, the support for the $d$th test statistic is characterized by $D \ge d$. The density of $T_{(D)}$ conditional on $D \ge d$ is \begin{eqnarray} \label{densjoint2} f_{T_{(D)}}\left(t_{(D)}\vert D \ge d, \theta\right) &=& \frac{\sum_{k=d}^{K}f_{T_{(k)}}^{sub} }{\text{Pr}_{\theta}\left(D\ge d\right)} = \sum_{k=d}^{K} \frac{\text{Pr}_{\theta}\left(D=k\right)}{\text{Pr}_{\theta}\left(D\ge d\right)} f_{T_{(k)}}^{C}.\end{eqnarray} Again, even if each $T_k$ is normal, the distributions of $T_{(D)}\vert D \ge d$ are not.
\subsubsection{Connection with Armitage's algorithm}\label{connectArmitage} SAS's popular SEQDESIGN procedure, R's gsDesign package, Cytel's EAST and others assess type I and power properties using a recursive sub-density formula (\citet{Armitage1969}) to evaluate the distribution of $T_{(D)}\vert D \ge d$. Armitage's subdensity is $f_{T_{(D)}\vert D \ge d}^{sub} = \sum_{k=d}^K f_{T_{(k)}}^{sub}$ and \begin{eqnarray} \label{densjoint2_} f_{T_{(D)}}\left(t_{(D)}\vert D \ge d, \theta\right) &=& \frac{f_{T_{(D)}\vert D \ge d}^{sub}}{\text{Pr}_{\theta}\left(D\ge d\right)}.\end{eqnarray}
For example, at $K=2$, the sub-density of $T_{(D)}\vert D \ge d$ is \begin{equation} \label{arm_subdens}
f^{sub}_{T_{(D)}\vert D \ge 2}(t|\theta) = \int_{-\infty}^{c_1} f_{T_{(D\ge 2)}|T_{(1)}} (t|t_1,\theta) f_{T_{(1)}}(t_1|\theta) dt_1 \end{equation} and its density is
$f_{T_{(D)}\vert D \ge 2}(t|\theta) = f^{sub}_{T_{(D)}\vert D \ge d}(t|\theta)\left(\int_{-\infty}^{c_1} f_{T_{(1)}}(t_1|\theta)dt_1\right)^{-1}$. Recursively, the density conditional on reaching the $d$th interim analysis is \begin{equation}\label{arm_dens}
f_{T_{(D)}}(t|D\ge d,\theta) = \frac{\int_{-\infty}^{c_{d-1}} f_{T_{(D \ge d)}|T_{(d-1)}}(t|t_{d-1},\theta) f_{T_{(d-1)}}(t_{d-1}|\theta) dt_{d-1}}{\int_{-\infty}^{c_{d-1}} f_{T_{(d-1)}}(t_{d-1}|\theta)dt_{d-1}}. \end{equation}
\subsection{$\sigma-$fields and support defined by a set of critical values} \label{subspace}
At the time of $d$th hypothesis test, given $D \ge d$, the values $\{x_j:j > n_{(d)}\}$ are not observable and hence do not contribute to the density; indeed, they do not belong to the adaptation-rule driven sample space, and consequently, they do not belong to a $\sigma$-field of the random process being monitored: hence, they do not belong to the sequential experiment as a whole. In this paper, by analogy with structural zeroes in contingency tables, these values are excluded from the sample space.
The $d$th stage-specific test statistic $T_{d}=T\left(\textbf{X}_d\right)$ is defined on a probability space $\left({\cal{T}}_d, \sigma\left({\cal{T}}_d\right), P_d\right)$, where ${\cal{T}}_d$ is typically a real line (${\cal{R}}$), $\sigma\left({\cal{T}}_d\right)$ is Borel $\sigma-$field and $P_d$ is a probability measure on the measurable space $\left({\cal{T}}_d,\sigma\left({\cal{T}}_d\right)\right)$. A sequence of nested $\sigma$-fields ${\cal{F}}_{(d)} := \sigma\left({\cal{T}}_1\right) \times \cdots \times \sigma\left({\cal{T}}_d\right),$ $d=1,\ldots,K$, creates a filtration $\textbf{F}=\left({\cal{F}}_{(d)}\right)_{d\le K}$ on the product probability space $\left({\cal{T}}, {\cal{F}}_{(K)}, P\right)$, where ${\cal{T}} = {\cal{T}}_1 \times \cdots \times {\cal{T}}_K$ and $P = P_1 \times \cdots \times P_K$. But in the presence of possible stopping, not all combinations of $(T_1,\ldots,T_K)$ are possible. The cumulative test statistics $T_{(d)} = T_{(d)}(T_1,\ldots,T_d)$ are defined only on a subspace of the sample space ${\cal{T}}_1 \times \cdots \times {\cal{T}}_d$. Thus, probability environment substantially changes.
\subsubsection{Interim hypothesis testing} The statistic $T_{(1)}=T_1$ conditional on reaching stage $1$ $(D\ge1)$ is defined on the sample space ${\cal{T}}_{(1)} = {\cal{T}}_1$; so
$\sigma\left({\cal{T}}_{(1)}\right) = {\cal{F}}_{(1)}$. The statistic $T_{(2)}$ conditional on $D\ge 2$ is defined on $${\cal{T}}_{(2)} = \left[(t_1,t_2): \{t_1 \le c_1\}\right],$$ and $\sigma\left({\cal{T}}_{(2)}\right) \subset {\cal{F}}_{(2)}$. Further, for $d\in\{3,\ldots,K\}$, $T_{(d)}$ conditional on $D\ge d$ is defined on $$ {\cal{T}}_{(d)} = \left((t_1,\ldots,t_d): \left\{t_{(j)} \le c_j \right\}, j=1,\ldots,d-1 \right). $$
For all $d$, the support ${\cal{T}}_{(d)}$ and the $\sigma$-field $\sigma\left({\cal{T}}_{(d)}\right)$ is reduced by the possibility of early stopping: $\sigma\left({\cal{T}}_{(d)}\right) \subset {\cal{F}}_{(d)}$. This creates new measurable spaces $\left({\cal{T}}_{(d)}, \sigma\left({\cal{T}}_{(d)}\right)\right)$ for interim tests at every possible stage $1,\ldots,K$. Armitage's recursive sub-density formula [\citet{Armitage1969}] is defined on this measurable space; see Equation (\ref{arm_subdens}) for $K=2$. Re-scaling yields a density function [see Equation (\ref{arm_dens})] which defines a probability measure to complete the probability space $\left({\cal{T}}_{(d)}, \sigma\left({\cal{T}}_{(d)}\right), P_{(d)}\right)$, where the probability measure $P_{(d)}$ is determined by density (\ref{arm_dens}): $P_{(d)}(A) = \int_A f_{T_{(D)}}(t|D\ge d,\theta) dt$, $A \in \sigma\left({\cal{T}}_{(d)}\right)$.
\subsubsection{After the stop decision is made} At each interim stage $d=1,\ldots,K-1$, the decision to reject or accept $H_0$ splits ${\cal{T}}_{(d)}$ into two non-overlapping regions denoted ${\cal{T}}_{(d)}^{stop}$ and ${\cal{T}}_{(d)}^{cont}$, respectively. Since ${\cal{T}}_{(d)}^{stop} \cap {\cal{T}}_{(d+1)} = \emptyset$ and ${\cal{T}}_{(d)}^{cont} \subset {\cal{T}}_{(d+1)}$, then the sets ${\cal{T}}_{(1)}^{stop},\ldots,{\cal{T}}_{(K-1)}^{stop},$ and ${\cal{T}}_{(K)}$ make a partition of the sample space of $T_{(D)}$:
$${\cal{T}}_{(K)} + \sum_{k=1}^{K-1}{\cal{T}}_{(k)}^{stop} = \left(\cup_{d=1}^{K-1}{\cal{T}}_{(d)}^{stop}\right) \cup {\cal{T}}_{(K)} = \cup_{d=1}^K{\cal{T}}_{(d)} \subset {\cal{T}}.$$ We define a probability space for the observable random variable ${T}_{(d)}$ using the probability measures $P_{(d)}$ defined by $f_{T_{(d)}}^C$ on the measurable space $\left({\cal{T}}_{(d)}^{stop}, \sigma\left({\cal{T}}_{(d)}^{stop}\right)\right)$. At $D=K$, the probability measure $P_{(K)}$ defined by $f_{T_{(K)}}^C$ completes the probability space for a measurable space $\left({\cal{T}}_{(K)}, \sigma\left({\cal{T}}_{(K)}\right)\right)$.
Thus, at the end of the study, at $D=d$, the researcher operates with an \emph{observable} random variable $T_{(d)}$.
\subsubsection{At the design stage} The conditional random variables, $T_{(d)}$, defined on non-overlapping $\sigma$-fields are combined together into the unconditional random variable $T_{(D)} \sim f_{T_{(D)}}$ defined on the sample space $\left(\cup_{d=1}^{K-1}{\cal{T}}_{(d)}^{stop}\right) \cup {\cal{T}}_{(K)}$. The probability distribution defined on the $\sigma$-field on this sample space is $P_{(D)} = \sum_{d=1}^K\text{Pr}\left(D=d\right) P_{(d)}$.
\subsubsection{Impossible events} The set ${\cal{T}}_0 = {\cal{T}} \setminus \cup_{d=1}^K{\cal{T}}_{(d)}$ contains all impossible combinations of $(t_1,\ldots,t_K) $ under a chosen stopping rule. If $K=2$, for example, then ${\cal{T}} \setminus \cup_{d=1}^2{\cal{T}}_{(d)} = \left\{(t_1,t_2): t_1>c_1\right\}$. Without the possibility of early stopping, all combinations of $(t_1,\ldots,t_K)\in{\cal{T}}$ would be possible.
\subsection{Pocock's Example: One-Sided Two-Group Sequential Z-test}\label{Pocock_example}
\citet{Pocock1977} proposed a simple two-stage procedure for testing $H_0: \theta = 0$ with a pre-determined power at $H_1: \theta = \theta_1$ on normal data. With $n_1=n_2$, $c_1=c_2=2.18$ is used to secure the overall type~1 error rate $\alpha=0.025$ with a one-sided $z$ test. Let $n_0=0$ and $$Z_k = \frac{1}{\sqrt{n_{k}}}\sum_{i=n_{(k-1)}+1}^{n_{(k)}} X_{i} = \sqrt{n_{k}} \cdot \bar X_k \overset{d}{=} \mathcal{N}(\theta,1),\quad k=1,2.$$
The study is stopped for efficacy at stage 1 if $Z_1\ge 2.18$ and proceeds to stage 2 when $Z_1 < 2.18$. If the study is stopped at stage~1, the support for $\bar X_1|Z_1\ge 2.18$ starts at $2.18/\sqrt{n_1} $ and stretches to $+\infty$. If the study continues through stage~2, support for $\bar X_1|Z_1<2.18$ ranges from $-\infty$ to $2.18/\sqrt{n_1}$ .
The test statistic for the second stage, under $Z_1<2.18$, $$Z_{(2)}=\frac{\sqrt{n_1}}{\sqrt{n_1+n_2}}Z_1 + \frac{\sqrt{n_2}}{\sqrt{n_1+n_2}}Z_2 = \frac{1}{\sqrt{n_1+n_2}}\sum_{i=1}^{n_1+n_2}X_i.$$
The distribution of $Z_{(2)}$ is a mixture of a right-truncated normal $Z_1 |Z_1 < 2.18$ and the normal $Z_2$.
Figure~\ref{Z_example} shows histograms of $Z_1 |Z_1 \ge 2.18$, $Z_{(2)} |Z_1 < 2.18$, and $Z_{(D)}$ estimated from $100,000$ Monte-Carlo samples assuming $\theta=2.18$. These histograms based on $n_1=n_2=100$ are almost identical to the histograms in Figure \ref{MLEcpic} based on $n_1=n_2=1$. This highlights on the important message that non-normality continues to be present even asymptotically \cite{Tarima2019}.
\begin{figure}\label{Z_example}
\end{figure}
\section{Likelihood-based Inference with Early Stopping } \label{Sec:likelihood} If the stopping rule is not random and the experiment stopped with $n_{(d)}$ observations, $\text{Pr}_{\theta}(D=d)\equiv 1$, the likelihood is \begin{eqnarray} \label{Lfix} {\mathcal{L}}^{fix}\left(\theta \vert k,\textbf{\textit{x}}_{(d)} \right) = f_{\mathbf{X}_{(d)}}.\end{eqnarray}
Considering the joint density \eqref{densjoint} conditional on the data $\left(d,\textbf{\textit{x}}_{(d)}\right)$ observed at the end of a sequential experiment, the likelihood is \begin{eqnarray} \label{LKjoint} {\mathcal{L}}\left(\theta \vert d,\textbf{\textit{x}}_{(d)} \right) = f_{\mathbf{X}_{(d)}}^{sub}.\end{eqnarray}
The indicator in \eqref{densK} emphasizes that support for the random variables is reduced by the conditioning; see this illustrated in Figure~\ref{support_white}. Note also in Figure~\ref{support_white} that the support conditional on stopping at one stage is disjoint from the support conditional on stopping at another stage.
${\cal{L}}$ is a function of $\theta$ and the observed data $(d, \textbf{\textit{x}}_{(d)})$, but ${\cal{L}}$ is a continuous function only of $\theta$, as discontinuities in $(d, \textbf{\textit{x}}_{(d)})$ arise from the mixture distribution of $\mathbf{X}_{(D)}$. These discontinuities are inherited by MLEs and other statistics derived from them. Conditional on $(d, \textbf{\textit{x}}_{(d)})$, MLEs maximizing ${\mathcal{L}}$
are
\begin{align*} \widehat\theta &= \arg \max_{\theta} f_{\mathbf{X}_{(d)}}^{sub}. \end{align*}
For every $\left(d,\textbf{\textit{x}}_{(d)}\right)$, $f_{\mathbf{X}_{(d)}}^{sub} =f_{\mathbf{X}_{(d)}}$ for all $\theta$; consequently, $$\widehat\theta^{fix} := \arg \max_{\theta} f_{\mathbf{X}_{(d)}} = \arg \max_{\theta} f_{\mathbf{X}_{(d)}}^{sub} = \widehat\theta,$$ that is, as is well known, making stopping decisions does not alter maximum likelihood point estimates; they are the same whether obtained by maximizing ${\mathcal{L}}$ or ${\mathcal{L}}^{fix}$ and
other observed statistics derived from the likelihood (e.g., the score function and the observed information) are unaffected as well.
The following example extends the simple one in Section~\ref{sec:ex_simple} with $n_1=n_2=1$ to arbitrary $n_1$ and $n_2$ to illustrate (as is proven later) that, although maximum likelihood point estimates and test statistics are unaffected by early stopping decisions, their probability distribution does not tend to normality even with larger sample sizes.
\subsection{Large Sample Properties}\label{LSP} The $d$th stage-specific MLEs $\widehat\theta_d$ of $\theta$ and their statistical models are called \emph{regular} if, without the possibility of early stopping, \begin{equation} \label{ctlholds} \xi_d= \sqrt{n_d}\left(\widehat\theta_d - \theta\right) \overset{d}{\to} {\cal{N}}(0,\sigma^2), \end{equation} where $0<\sigma < \infty$. Assumption \eqref{ctlholds} was described in \citet{Tarima2019} to include the more specific assumptions for \begin{itemize} \item independent, identically distributed observations by Cram\'er [e.g., for example, \citet{Ferguson1996}], \item independent not identically distributed observations [e.g., \citet{philippou1973asymptotic}], \item dependent observations [e.g., \citet{crowder1976maximum}], \item and densities whose support depends on parameters [e.g., \citet{Wang14}]. \end{itemize} All these specific sets of assumptions include assumptions of the existence and consistency of the MLE.
With large samples, the MLE at the stage $d$ analysis can be approximated recursively by \begin{align} \widehat\theta_{(d)} &\approx \frac{n_{(d-1)}}{n_{(d)}}\widehat\theta_{(d-1)} +
\frac{n_d}{n_{(d)}}\widehat\theta_d \label{MLE_d} \approx \sum_{j=1}^d \frac{n_j}{n_{(d)}} \widehat\theta_d, \end{align}\label{eq:MLE} where $\widehat\theta_{(d-1)}$ is an MLE based on cumulative data from stages $1$ to $d-1$ and $\widehat\theta_{d}$ is the $d$th stage-specific MLE. The standardized $d$th stage-specific MLE is so, $$T_{(d)} = \sqrt{n_{(d)}} \sum_{j=1}^d \frac{n_j}{n_{(d)}} \left(\frac{\widehat\theta_j-\theta}{\sigma}\right) =
\sum_{j=1}^d
\sqrt{\frac{n_j}{n_{(d)}}}\ \xi_j \approx \sqrt{n_{(d)}} \left(\frac{\widehat\theta_{(d)}-\theta}{\sigma}\right),$$ that is, $T_{(d)}$ is (approximately) the standardized $d$th stage-specific MLE. The asymptotic properties of $T_{(D)}$
depend on the existence and distribution of a limiting random variable $r_{(D)}$ defined by \begin{equation}\label{tau_n} \sum_{d=1}^K I(D=d)\frac{n_{(d)}}{n_{d}} \overset{d}{\to} \sum_{d=1}^K I(D=d)r_{(d)} = r_{(D)}, \end{equation} where $r_{(d)}=\lim_{n_{d}\to\infty} n_{(d)}/n_{d}$ is the asymptotic ratio of the $d$th cumulative-stage and stage-specific sample sizes
[Theorem 1 in \citet{Tarima2019}];
$r_{(D)}$ is a multinomial random variable with support on $r_{(d)}$.
Assume the limits $n_{(d)}/n_j \to r_{(d)j} \in (0,\infty)$, $j\le d$ exist with $r_{(d)d} = r_{(d)}$. Then given $D = d$, $$T_{(d)} \to \sum_{j=1}^d \frac{\xi_j}{\sqrt{r_{(d)j}}}.$$ While $\xi_j \overset{d}{\to} {\cal{N}}(0,1)$, the distributions used for the final analysis, the interim analysis and experimental design, respectively, are mixtures of truncated distributions:
\begin{eqnarray*}{\text{Pr}_{\theta}}\left(T_{(D)} < v|D=d \right) &\to& \text{Pr}_{\theta}\left(\sum_{j=1}^d \frac{\xi_j}{\sqrt{r_{(d)j}}} < v \Big\vert D=d \right),\\
{\text{Pr}_{\theta}}\left(T_{(D)} < v | D\ge d\right) &\to& \sum_{k=d}^K {\text{Pr}_{\theta}}\left(D=k\right){\text{Pr}_{\theta}}\left(\sum_{j=1}^k \frac{\xi_j}{\sqrt{r_{(k)j}}} < v \Big\vert D=k \right),\\ \text{Pr}_{\theta}\left(T_{(D)} < v \right) &\to& \sum_{k=1}^K {\text{Pr}_{\theta}}\left(D=k\right){\text{Pr}_{\theta}}\left(\sum_{j=1}^k \frac{\xi_j}{\sqrt{r_{(k)j}}} < v \Big\vert D=k \right). \end{eqnarray*}
\subsection*{Pocock's Example: Large Sample Properties}\label{sec:example} Under assumption \eqref{ctlholds} with large sample sizes, $\widehat\theta_{(D)} = I(D=1)\widehat\theta_{(1)} + I(D=2)\widehat\theta_{(2)}$ are standardized as \begin{align} T_{(D)} &= \sqrt{n_{(D)}}\left(\widehat\theta_{(D)} - \theta\right)/\sigma \notag \\ &= I(D=1)\sqrt{n_1}\left(\widehat\theta_{(1)} - \theta\right)/\sigma + I(D=2)\sqrt{n_1+n_2}\left(\widehat\theta_{(2)} - \theta\right)/\sigma.\end{align}
Assume the limit $I(D=1) + I(D=2)\frac{n_1+n_2}{n_2} \overset{d}{\to} r_{(D)}$ exists as $n_1\to\infty$,
Then, adopting the local
alternative hypothesis $\theta = h / \sqrt{n_1}$ yields a non-degenerate limiting distribution of $T_{(D)}$ that models both stages of the experiment: \begin{eqnarray}\text{Pr}_{\theta}\left(T_{(D)} < v \right) &\to& p_1 \Phi\left(\left. v\right\vert D=1\right) \notag \\ &+& (1-p_1) \int_{-\infty}^{c_1} \Phi\left(
\sqrt{r_{(D)}} v - \sqrt{r_{(D)}-1} y\right) \phi\left(y|D=2\right) dy, \end{eqnarray} where $p_1 = \lim_{n_1\to\infty}{\text{Pr}_{\theta}}\left(D=1\right)$ is the limiting stage 1 stopping probability; $\phi$ and $\Phi$ denote the standard normal density and cumulative distribution function, respectively. With a fixed alternative $\theta$, $\text{Pr}_{\theta}\left(T_{(D)} < v \right) \to \Phi(v)$ because $p_1\to 1$ with probability 1, and modeling related to stage~2 data is lost.
In Pocock's example, $T_{(D)} = I(D=1)Z_1 + I(D=2)\left(Z_1 + Z_2\right)/\sqrt{2}$ and \begin{eqnarray} \text{Pr}_{\theta}\left(T_{(D)} < v \right) &\to& \text{Pr}_{\theta}\left(Z_1>c_1\right) \Phi\left(\left. v\right\vert Z_1>c_1 \right) \notag \\ &+& \text{Pr}_{\theta}\left(Z_1\le c_1\right) \int_{-\infty}^{c_1} \Phi\left( \sqrt{2} v - y\right) \frac{\phi\left(y\right)}{\text{Pr}\left(y \le c_1\right)}dy \end{eqnarray} Note if $Z_1\le c_1$, then $$\text{Pr}_{\theta}\left(\frac{Z_1+Z_2}{\sqrt{2}} < v \vert Z_1\le c_1\right) = \int_{-\infty}^{c_1} \Phi\left( \sqrt{2} v - y\right) \frac{\phi\left(y\right)}{\text{Pr}\left(y \le c_1\right)} dy,$$ which is a continuous mixture of distributions.
\subsection{Most Powerful Group Sequential Tests} \label{mostpower} Let $X\sim f_X(\theta)$, where $f$ belongs to the one-parameter exponential family. Without a possibility of early stopping, the likelihood for a realization $\textbf{\textit{x}}=\left(x_1,\ldots,x_n\right)$ of a random sample $\textbf{X}=\left(X_1,\ldots,X_n\right)$ is \begin{align*}
{\cal{L}}\left(\theta|\textbf{\textit{x}}\right) = \prod_{i=1}^n f_X\left(\textbf{\textit{x}}\right) &=
h\left(\textbf{\textit{x}}\right) g \left(T\left(\textbf{\textit{x}}\right) |\theta \right) = h\left(\textbf{\textit{x}}\right) e^{\eta(\theta)T\left(\textbf{\textit{x}}\right) + A\left(\theta\right)} \end{align*} where all relevant information about $\theta$ is absorbed by a sufficient statistic $T\left(\textbf{\textit{x}}\right)$. Assume the test statistic $Z$ is a one-to-one transformation of $T$.
If $LR(t)=g(t|\theta)/g(t|\theta_0)$ has monotone likelihood ratio (MLR) in $t$, then the Karlin-Rubin theorem provides uniformly most powerful (UMP) tests.
In sequential testing settings, when $d$th stage is reached $\left(D\ge d\right)$, the interim likelihood \begin{eqnarray}
{\cal{L}}\left(\theta|D\ge d,\textbf{\textit{x}}_{(d)}\right) &=& I\left(D\ge d\right) h\left(\textbf{\textit{x}}_{(d)}\right) e^{\eta(\theta)T\left(\textbf{\textit{x}}_{(d)}\right) + A_d\left(\theta\right)} \label{Lu} \end{eqnarray} has the associated interim likelihood ratio \begin{eqnarray}
LR(t|D\ge d) = \frac{{\cal{L}}\left(\theta|D\ge d,\textbf{\textit{x}}_{(d)}\right)}{{\cal{L}}\left(\theta_0|D\ge d,\textbf{\textit{x}}_{(d)}\right)}. \notag \end{eqnarray} For every $d$th stage hypothesis test, $D\ge d$ and $$
LR(t|D\ge d)= \exp \left[\left(\eta(\theta_1)-\eta(\theta_0)\right) T_{(d)} + \left(A_d(\theta_1)-A_d(\theta_0)\right)\right]$$ which means that \textit{the MLR property is preserved with early stopping}.
\textbf{Definition:} A sequence of $\alpha_d$-level interim tests $\{T_{(1)} > c_1\},\ldots,\{T_{(D)} > c_D\}$ will be called the sequential test.
\begin{theorem} \label{theorem1} For any fixed $(\alpha_1,\ldots,\alpha_K)$ and $\left(n_1,\ldots,n_K\right)$ $(1)$ the interim LR test $\{T_{(d)} > c_d\}$ is a UMP $\alpha_d$-level test and $(2)$ no sequential test is more powerful than the sequential test based interim LRs. \end{theorem}
\begin{table}[bt!]
\centering
\begin{tabular}{|c|c|}
\hline
Feature & Mathematical Definition \\
\hline
\textit{overall type $1$ error} & $\alpha = \sum_{k=1}^K \alpha_k \prod_{j=1}^{k-1}\text{Pr}_{0}\left(Z_{(j)}\le u_{j}\right)$\\
\textit{stage-specific type 1 error} & $\alpha_d = \text{Pr}_{0}\left( Z_{(d)} > u_d \big| \cap_{j=1}^{d-1} \left\{Z_{(j)}\le u_{j} \right\}\right)$ \\
\textit{$\alpha$-spending function} & $\alpha_{(d)} = \sum_{j=1}^d\alpha_j \prod_{i=1}^{j-1}\text{Pr}_{0}\left(Z_{(j)}\le u_{j}\right)$\\
\hline
\textit{overall type 2 error} & $\beta(\theta)=\sum_{j=1}^K\beta_j(\theta) \prod_{i=1}^{j-1}\text{Pr}_{\theta}\left( Z_{(j)}\le u_{j}\right)$\\
\textit{stage-specific type 2 error} & $\beta_d(\theta) = \text{Pr}_{\theta}\left( Z_{(d)} > u_d \big| \cap_{j=1}^{d-1} \left\{Z_{(j)}\le u_{j} \right\} \right)$\\
\textit{$\beta$-spending function} & $\beta_{(d)}\left(\theta\right) = \sum_{j=1}^d\beta_j(\theta) \prod_{i=1}^{j-1}\text{Pr}_{\theta}\left(Z_{(j)}\le u_{j}\right)$\\
\hline
\textit{overall power} & $1-\beta(\theta)$\\
\textit{stage-specific power} & $ 1-\beta_d(\theta)$\\
\textit{cumulative power} & $1-\beta_{(d)}\left(\theta\right)$\\
\hline \end{tabular}
\caption{Definitions of Operational Characteristics for Sequential Tests $d=1,\ldots,K$; $\prod_{i=1}^0[\cdot] = 1$.}
\label{Definitions} \end{table}
\textbf{Proof.} $(1)$ As shown above, conditional on reaching stage $d$, $(D\ge d)$, $T_{(d)}$ continues to be sufficient in exponential families and the MLR property is preserved. By the Karlin-Rubin theorem, the test based on $T_{(d)}$ is uniformly most powerful at $d^{th}$ stage. \\ $(2)$ Using Table \ref{Definitions} notation, $$1-\beta(\theta) = \sum_{k=1}^K \left(\prod_{j=1}^{k-1}\left[\beta_j(\theta)\right] \right) [1-\beta_k(\theta)]= 1 - \prod_{k=1}^{K}\beta_k(\theta).$$
At $K=1$, $\alpha_1$ and $n_1$ uniquely define $c_1$ and $\left\{T_{(1)} > c_{1}\right\}$ is a UMP by part 1 with a stage-specific power curve $1-\beta_1(\theta)$. At an arbitrary stage $d$, $\alpha_d$ and $n_d$ uniquely define $c_d$ and, by part 1 of the theorem, the stage-specific power $1-\beta_d(\theta)$, is the highest. Thus, for any choice of $(\alpha_1,\ldots,\alpha_K)$ and $\left(n_1,\ldots,n_K\right)$, and consequently $\{T_{(d)} > c_d\}$, the power of the sequential test based on LRs is $1-\beta(\theta) = 1-\prod_{k=1}^K\beta_k(\theta)$. This power is the highest for any given $\theta$, because the stage specific type 2 errors $\beta_d(\theta)$ are the lowest for each $d$ at any $\theta$. \textbf{Q.E.D.}
\subsection*{Pocock's Example: Likelihood Ratio} For $X_i\sim {\cal{N}}(\theta,1)$, $i=1,\ldots,n$, the likelihood ratio for testing $H_0:\theta=\theta_0$ vs $H_A:\theta=\theta_1>\theta_0$ is $$\log LR(t) = -n\left(\log \theta_0 - \log \theta_1\right) - t/\theta_1,$$ which has rejection region $\left\{t>c\right\}$, where $t = \sum_{i=1}^n X_i$ is a sufficient statistic. Using $Z=t/\sqrt{n} \sim f_{Z} = {\cal{N}}(\theta_1,1)$, the likelihood ratio test is $\left\{Z>c/\sqrt{n}\right\}$.
With Pocock's example, under $D \ge 1$, $Z_1$ is a normal random variable used for stage 1 hypothesis testing, and
$$\log LR(Z_1|D\ge 1) = -n_1\left(\log \theta_0 - \log \theta_1\right) - \sqrt{n_1}Z_1/\theta_1.$$
Then,
$$\log LR(Z_{(2)}|D\ge 2) = -(n_1+n_2)\left(\log \theta_0 - \log \theta_1\right) - \sqrt{n_1+n_2}Z_{(2)}/\theta_1 + C,$$
where $C = \log \text{Pr}\left(Z_1<c_1|\theta_0\right) -
\log \text{Pr}\left(Z_1<c_1|\theta_1\right)$ is independent of data given $D \ge 2$. By Theorem \ref{theorem1}, $\{Z_{(d)} \ge c_d\}$ is the UMP test at stage $d$ given $\alpha_d$ and $n_d$, and no other sequential test is more powerful overall.
\section{Impact and Summary} \label{Conclusion}
To establish that a sequence of likelihood ratio tests are most powerful, we began by constructing the joint probability distribution over the set of \textit{possible} events. The use of an early stopping criterion eliminates the possibility of some realizations of cumulative test statistics $\mathbf{Z}=\left(Z_{(1)},\ldots,Z_{(K)}\right)$. This makes an otherwise normal random process $\mathbf{Z}$ unobservable. On its true \textit{stopping rule adapted support}, the distribution of $\mathbf{Z}$ is a mixture of truncated distributions at each stage. Thus, unadapted distributional assumptions should be modified to take into account the planned adaptation scheme. \citet{liu1999} and \citet{liu2006} recognized change in support in the one-parameter exponential family and investigated bias estimation. \citet{schou2013meta} recognized presence of truncation in the joint distribution of stage-specific test statistics, but they mostly focused on bias in meta-analytic studies. The adapted support is critical for derivation MLEs' and test statistics' distributions in Section \ref{sec:densities}.
In Section \ref{sec:densities}, distinct probability measures are derived for design [unconditional], interim hypothesis testing [conditional on collecting data up to the time of interim testing] and when the study is completed [conditional on deciding to stop at a particular stage]. These probability distributions formalized a new probabilistic framework (Section \ref{sec:densities}) which is used in Section \ref{mostpower} to show no testing sequence is more powerful than sequential likelihood ratio tests.
Likelihood ratio tests are most powerful for testing simple hypotheses and, under monotone likelihood ratio, for testing composite hypotheses; see \citet{neyman1933} and Karlin-Rubin theorem in \citet{ferguson2014mathematical}. The Karlin-Rubin theorem works with the one-parameter exponential family and Section \ref{mostpower} shows that most powerful testing continues to hold for sequential tests. Even though distributions of sample-size-dependent sufficient statistics (\citet{blackwell1947}) belong to a curved exponential family (\citet{efron1975, liu1999,liu2006}), the distributions conditional on the sample size still belong to one-parameter exponential family. This fact is used in Section \ref{mostpower} to show that likelihood ratio sequential tests are most powerful tests with any pre-determined $\alpha$-spending function. This result is applicable to many common group sequential designs.
Treatment-effect-dependent (non-ancillary) stopping rules are part of many common GSDs including Pocock \cite{Pocock1977}, O'Brien \& Fleming \cite{Brien1979}, and Haybittle-Peto designs \cite{haybittle1971,peto1976}. If the data follow a normal distribution with known variance (without possibility of early stopping), then these designs are most powerful for their $\alpha$-spending functions. Similarly, application of Simes test (see \citet{simes1986improved}) and its recently proposed modification for sequential testing (see \citet{Tamhane2020}) cannot have higher power than group sequential tests from \citet{jennison1999} with the same $\alpha$-spending function.
Historically, many researchers have relied, and currently rely, on joint normality (e.g., \citet{jennison1999}, \citet{Proschan2006}, \citet{Kunz2020}). Critical adjustments ate often done with recursive sub-density estimation; see \citet{Armitage1969}. Section \ref{connectArmitage} places Armitage's sub-density formula in the broader probability framework of possible events and confirms, from the prospective of this $\sigma$-algebra, that the common current practice of using Armitage's formula for calculating distributions of interim test statistics is appropriate.
There is plenty of evidence that adaptive designs make statistics non-normally distributed. \citet{Demets1994} point out that the distribution of stage-specific test statistics is not normal and should be estimated recursively. \citet{jennison1999} plot the density of a normal test statistic used in GSD settings [pages 174-177], where discontinuity points clearly show non-normality. \citet{Li2002} find the joint density of stage 1 and stage 2 standardized test statistics not to be bivariate normal. Local asymptotic non-normality was established following sample size recalculations (SSRs) that depend on an interim observed treatment effect (\citet{Tarima2019,Tarima2020}); and a GSD with a single interim analysis can be viewed as a special case of an SSR. MLEs converging to random mixtures of normal variables have been found in other adaptive designs (\citet{Ivanova2000}, \citet{Ivanova2001}, \citet{May2010}, \citet{Lane2012}, \citet{flournoy2018effects}).
\citet{milanzi2015} developed a likelihood approach that applies when the early stopping rule does not depend on the parameter of interest. In this case, sample size adaptation is ancillary to the treatment effect and asymptotic normality of MLEs holds. \citet{gnedenko1996, Bening2012, christoph2020second, korolev2019asymptotic} assume that the distribution of the random sample size does not depend on previosly collected data; \citet{molengerghs2012} assumes this asymptotically.
Nevertheless, convergence of sample means to non-normal random variables was shown even for ancillary random sample sizes. In \cite{gnedenko1996}, Gnedenko and Korolev show convergence of standardized sums with random number of summands of infinitely divisible random variables to mixtures of stationary distributions. They give conditions for convergence to a mixture of normal distributions. Bening et al. \cite{Bening2012} and Christoph et al. \cite{christoph2020second} explore convergence to mixtures of normal distributions and to Student's limit distribution. When convergence is \emph{mixed} (see, for example \citet{hausler2015stable}), \citet{lin2020random} shows how norming with the observed information can result in a normal limit. However, the requirement for mixed convergence appears strong, and it does not cover the limiting mixtures obtained in this paper.
The impact of early stopping is pervasive. It affects the probabilistic characterisation of the tests (e.g., type I error and Fisher Information) as well as the distributions of MLEs and test statistics. Its effect on Fisher information, when stopped at different stages, is not widely recognized.
During the design phase, before observations are taken, the full form of the joint density (\ref{densjoint}), accounting for all possible events, is appropriate. This contrasts with the current practice of using the density assuming the experiment will continue through stage $K$. More details on the differences resulting from these two design approaches will be the subject of another paper.
However, normality and asymptotic normality assumptions continue to be directly used with non-normally distributed statistics. We identify two main reasons for this. \begin{enumerate}
\item
Many researchers consider large sample properties against a fixed treatment effect independent of the sample size. From one point of view, a treatment effect is a population quantity which does not change with sample size. But if one develops an asymptotic approximation to the testing environment using a fixed treatment effect, the statistical experiment stops at the first interim analysis with probability one for any consistent test; test statistics degenerate to a point mass; see Section 7.4 in \citet{Fleming1991}. Under a fixed treatment effect, the power converges to one and cannot be used to compare different testing procedures. This issue triggered development of various descriptions of asymptotic relative efficiency. The most popular approach is Pitman asymptotic relative efficiency \cite{pitman1948}, where asymptotic power is evaluated under local alternatives; see \citet{nikitin1995asymptotic}. In addition, local alternatives clearly reflect actual practice for experiment planning. Experiments are never planned for a statistical power = 1. Small sample size studies (pre-clinical, animal studies) are planned to detect large effect sizes, moderate sample sizes (typical phase 3 studies) are used to detect moderate effect sizes, and large sample sizes (epidemiological studies, like vaccine studies) are used to detect small differences.
\citet{koopmeiners2012} explored MLEs conditional on stopping, but assumed asymptotic normality to evaluate their uncertainty. \citet{martens2018} relied on asymptotic normality for evaluating regression coefficients under the Fine--Gray model in GSD settings. \citet{Asendorf2018} evaluated asymptotic properties with SSR under a fixed alternative for negative binomial random variables. \item Some researchers investigate \textit{local} asymptotic properties when early stopping is not possible or is ancillary to the treatment effect. This also leads to asymptotic normality. \citet{Scharfstein1997} show that without possibility of early stopping ``time-sequential joint distributions of many statistics $\ldots$ are multivariate normal with an independent increments covariance structure'' under local alternatives. These results are generally consistent with the classical results on local asymptotic normality of \citet{lecam1960}, where both mean and variance of the limiting normal distribution depend on the parameter of interest; see Chapter 7 of \citet{vandervaart1998}. However, Section \ref{LSP} shows that the possibility of early stopping destroys local asymptotic normality: the limiting distribution of standardized test statistics is a mixture of truncated normal distributions. Similar findings were previously proved for non-ancillary sample size recalculations; see \citet{Tarima2019}. \end{enumerate} \citet{gao2013} is a rare exception in not making a normality assumption; these authors mostly deal with set operations and probabilities and, using stage-wise ordering of events, they calculate P-values, confidence intervals, and a median unbiased estimate of the parameter of interest.
It is recommended that the full form of the joint density (\ref{densjoint}), accounting for all possible events, be used for study design before observations are taken. This contrasts with the current practice of using the density assuming the experiment will continue through stage $K$.
\section*{Conflict of interest}
The authors declare that they have no conflict of interest.
\end{document} | arXiv |
Using data from 1944 through 2000, the histogram shows the number of years that had a particular number of hurricanes reaching the East Coast of the U.S. For example, in 14 of those years there was exactly one hurricane each year that reached the East Coast of the U.S. What is the median number of hurricanes per year reaching the East Coast from 1944 through 2000?
[asy]
size(150);
real textsize = 10*pt;
real w = 1;
draw((0,17)--(0,0)--(18,0),linewidth(w));
for(int i = 1; i <= 17; ++i)
if(i != 5 && i != 10 && i != 15)
draw(shift(i*up)*((0,0)--(18,0)));
else
draw(shift(i*up)*((0,0)--(18,0)),linewidth(w));
for(int i = 0; i < 17; ++i)
draw(shift(i*up)*((-.3,1)--(.3,1)),linewidth(w));
label(rotate(90)*"\textbf{Number of Years}",(-3.5,17/2),fontsize(textsize));
for(int i = 1; i<4; ++i)
label("\textbf{"+string(5i)+"}",(0,5i),left,fontsize(textsize));
for(int i = 0; i<4; ++i)
label("\textbf{"+string(2i)+"}",(4i+2,0),S,fontsize(textsize));
label("\textbf{Number of Hurricanes}",(9,-3),fontsize(textsize));
void bar(int barnumber,int height)
{filldraw((2barnumber -1 ,0)--(2barnumber-1,height)--(2barnumber + 1,height)--(2barnumber + 1,0)--cycle,gray(.6),black+linewidth(w));
}
bar(1,5); bar(2,14); bar(3,17); bar(4,12); bar(5,2); bar(6,4); bar(7,2); bar(8,1);
[/asy]
Based on the histogram, we can make an educated guess that the median number of hurricanes per year reaching the east coast will be around $2$ or $3$ (simply because there are a large number of years for which no hurricanes or only one hurricane reached the east coast). To this end, we begin by calculating the number of years in which three to seven hurricanes reached the east coast: $12 + 2 + 4 + 2 + 1 = 21$. There are $5 + 14 = 19$ years in which zero or one hurricanes reached the east coast. Thus, the median number of hurricanes per year reaching the east coast is $\boxed{2}$. | Math Dataset |
Notre Dame Journal of Formal Logic
Notre Dame J. Formal Logic
On Sequentially Compact Subspaces of without the Axiom of Choice
Kyriakos Keremedis and Eleftherios Tachtsis
More by Kyriakos Keremedis
More by Eleftherios Tachtsis
Enhanced PDF (149 KB) PDF File (116 KB)
We show that the property of sequential compactness for subspaces of is countably productive in ZF. Also, in the language of weak choice principles, we give a list of characterizations of the topological statement 'sequentially compact subspaces of are compact'. Furthermore, we show that forms 152 (= every non-well-orderable set is the union of a pairwise disjoint well-orderable family of denumerable sets) and 214 (= for every family A of infinite sets there is a function f such that for all y∊ A, f(y) is a nonempty subset of y and ∣ f(y) ∣ = א₀) of Howard and Rubin are equivalent.
Notre Dame J. Formal Logic, Volume 44, Number 3 (2003), 175-184.
First available in Project Euclid: 28 July 2004
https://projecteuclid.org/euclid.ndjfl/1091030855
doi:10.1305/ndjfl/1091030855
Primary: 54D30: Compactness 54D55: Sequential spaces 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.)
weak forms of the axiom of choice compactness sequential compactness Tychonoff product
Keremedis, Kyriakos; Tachtsis, Eleftherios. On Sequentially Compact Subspaces of without the Axiom of Choice. Notre Dame J. Formal Logic 44 (2003), no. 3, 175--184. doi:10.1305/ndjfl/1091030855. https://projecteuclid.org/euclid.ndjfl/1091030855
[1] Church, A., "Alternatives to Zermelo's assumption", Transactions of the American Mathematical Society, vol. 29 (1927), pp. 178--208.
Mathematical Reviews (MathSciNet): MR1501383
Zentralblatt MATH: 53.0170.05
[2] De la Cruz, O., E. Hall, P. Howard, K. Keremedis, and J. E. Rubin, "Products of compact spaces and the axiom of choice. II", Mathematical Logic Quarterly, vol. 49 (2003), pp. 57--71.
Mathematical Reviews (MathSciNet): MR2004b:03074
Zentralblatt MATH: 1018.03040
Digital Object Identifier: doi:10.1002/malq.200310004
[3] Feferman, S., and A. Lévy, "Independence results in set theory by Cohen's method. II", Notices of the American Mathematical Society, vol. 10 (1963), p. 593.
[4] Gutierres, G., "Sequential topological conditions in $\mathbb R$" in the absence of the axiom of choice, Mathematical Logic Quarterly, vol. 49 (2003), pp. 293--98.
Mathematical Reviews (MathSciNet): MR2004c:03066
[5] Herrlich, H., "Products of Lindelöf $T\sb 2$"-spaces are Lindelöf---in some models of ZF, Commentationes Mathematicae Universitatis Carolinae, vol. 43 (2002), pp. 319--33.
Mathematical Reviews (MathSciNet): MR2003f:54049
[6] Herrlich, H., and G. E. Strecker, ``When is N Lindelöf?'' Commentationes Mathematicae Universitatis Carolinae, vol. 38 (1997), pp. 553--56.
Mathematical Reviews (MathSciNet): MR99c:03070
[7] Howard, P., K. Keremedis, J. E. Rubin, and A. Stanley, "Compactness in countable Tychonoff products and choice", Mathematical Logic Quarterly, vol. 46 (2000), pp. 3--16.
Digital Object Identifier: doi:10.1002/(SICI)1521-3870(200001)46:1<3::AID-MALQ3>3.0.CO;2-E
[8] Howard, P., K. Keremedis, J. E. Rubin, A. Stanley, and E. Tatchtsis, "Non-constructive properties of the real numbers", Mathematical Logic Quarterly, vol. 47 (2001), pp. 423--31.
Digital Object Identifier: doi:10.1002/1521-3870(200108)47:3<423::AID-MALQ423>3.0.CO;2-0
[9] Howard, P., and J. E. Rubin, Consequences of the Axiom of Choice, vol. 59 of Mathematical Surveys and Monographs, American Mathematical Society, Providence, 1998.
Mathematical Reviews (MathSciNet): MR99h:03026
[10] Jech, T. J., The Axiom of Choice, vol. 75 of Studies in Logic and the Foundations of Mathematics, North-Holland Publishing Co., Amsterdam, 1973.
Mathematical Reviews (MathSciNet): MR53:139
[11] Kelley, J. L., "The Tychonoff product theorem implies the axiom of choice", Fundamenta Mathematicae, vol. 37 (1950), pp. 75--76.
Mathematical Reviews (MathSciNet): MR12,626d
[12] Keremedis, K., "Disasters in topology without the axiom of choice", Archive for Mathematical Logic, vol. 40 (2001), pp. 569--80.
Mathematical Reviews (MathSciNet): MR2002m:54005
Digital Object Identifier: doi:10.1007/s001530100094
[13] Keremedis, K., "The failure of the axiom of choice implies unrest in the theory of Lindelöf metric spaces", Mathematical Logic Quarterly, vol. 49 (2003), pp. 179--86.
Mathematical Reviews (MathSciNet): MR2004a:03054
[14] Keremedis, K., and E. Tachtsis, "On Loeb and weakly Loeb Hausdorff spaces", Scientiae Mathematicae Japonicae, vol. 53 (2001), pp. 247--51.
[15] Keremedis, K., and E. Tachtsis, "Some weak forms of the axiom of choice restricted to the real line", Mathematical Logic Quarterly, vol. 47 (2001), pp. 413--22.
Mathematical Reviews (MathSciNet): MR2002e:03077
[16] Loeb, P. A., "A new proof of the Tychonoff theorem", American Mathematical Monthly, vol. 72 (1965), pp. 711--17.
Mathematical Reviews (MathSciNet): MR32:8306
Digital Object Identifier: doi:10.2307/2314411
[17] Truss, J., "Models of set theory containing many perfect sets", Annals of Mathematical Logic, vol. 7 (1974), pp. 197--219.
Digital Object Identifier: doi:10.1016/0003-4843(74)90015-1
Note on Volumes 35-40
Products of some special compact spaces and restricted forms of AC
Keremedis, Kyriakos and Tachtsis, Eleftherios, Journal of Symbolic Logic, 2010
Notions of compactness for special subsets of ℝI and some weak forms of the axiom of choice
Morillon, Marianne, Journal of Symbolic Logic, 2010
The Axiom of Choice for Well-Ordered Families and for Families of Well- Orderable Sets
Howard, Paul and Rubin, Jean E., Journal of Symbolic Logic, 1995
The Decidability of the $ \forall^*\exists$ Class and the Axiom of Foundation
Bellè, Dorella and Parlamento, Franco, Notre Dame Journal of Formal Logic, 2001
Almost Disjoint Sets and Martin's Axiom
Wage, Michael L., Journal of Symbolic Logic, 1979
Nonconstructive Properties of Well-Ordered T2 topological Spaces
Keremedis, Kyriakos and Tachtsis, Eleftherios, Notre Dame Journal of Formal Logic, 1999
The completeness of Heyting first-order logic
Tait, W. W., Journal of Symbolic Logic, 2003
A Single Axiom for Set Theory
Bennett, David, Notre Dame Journal of Formal Logic, 2000
The ground axiom
Reitz, Jonas, Journal of Symbolic Logic, 2007
On Generic Extensions Without the Axiom of Choice
Monro, G. P., Journal of Symbolic Logic, 1983
euclid.ndjfl/1091030855 | CommonCrawl |
Polycube
A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes.[1]
"Tetracube" redirects here. For the four-dimensional object, see tesseract.
Enumerating polycubes
Like polyominoes, polycubes can be enumerated in two ways, depending on whether chiral pairs of polycubes are counted as one polycube or two. For example, 6 tetracubes have mirror symmetry and one is chiral, giving a count of 7 or 8 tetracubes respectively.[2] Unlike polyominoes, polycubes are usually counted with mirror pairs distinguished, because one cannot turn a polycube over to reflect it as one can a polyomino given three dimensions. In particular, the Soma cube uses both forms of the chiral tetracube.
Polycubes are classified according to how many cubical cells they have:[3]
n Name of n-polycube Number of one-sided n-polycubes
(reflections counted as distinct)
(sequence A000162 in the OEIS)
Number of free n-polycubes
(reflections counted together)
(sequence A038119 in the OEIS)
1 monocube 1 1
2 dicube 1 1
3 tricube 2 2
4 tetracube 8 7
5 pentacube 29 23
6 hexacube 166 112
7 heptacube 1023 607
8 octacube 6922 3811
Polycubes have been enumerated up to n=18.[4][5] More recently, specific families of polycubes have been investigated.[6][7]
Symmetries of polycubes
As with polyominoes, polycubes may be classified according to how many symmetries they have. Polycube symmetries (conjugacy classes of subgroups of the achiral octahedral group) were first enumerated by W. F. Lunnon in 1972. Most polycubes are asymmetric, but many have more complex symmetry groups, all the way up to the full symmetry group of the cube with 48 elements. Numerous other symmetries are possible; for example, there are seven possible forms of 8-fold symmetry [2]
Properties of pentacubes
12 pentacubes are flat and correspond to the pentominoes. 5 of the remaining 17 have mirror symmetry, and the other 12 form 6 chiral pairs.
The bounding boxes of the pentacubes have sizes 5×1×1, 4×2×1, 3×3×1, 3×2×1, 4×2×2, 3×2×2, and 2×2×2.[8]
A polycube may have up to 24 orientations in the cubic lattice, or 48, if reflection is allowed. Of the pentacubes, 2 flats (5-1-1 and the cross) have mirror symmetry in all three axes; these have only three orientations. 10 have one mirror symmetry; these have 12 orientations. Each of the remaining 17 pentacubes has 24 orientations.
Octacube and hypercube unfoldings
The tesseract (four-dimensional hypercube) has eight cubes as its facets, and just as the cube can be unfolded into a hexomino, the tesseract can be unfolded into an octacube. One unfolding, in particular, mimics the well-known unfolding of a cube into a Latin cross: it consists of four cubes stacked one on top of each other, with another four cubes attached to the exposed square faces of the second-from-top cube of the stack, to form a three-dimensional double cross shape. Salvador Dalí used this shape in his 1954 painting Crucifixion (Corpus Hypercubus)[9] and it is described in Robert A. Heinlein's 1940 short story "And He Built a Crooked House".[10] In honor of Dalí, this octacube has been called the Dalí cross.[11][12] It can tile space.[11]
More generally (answering a question posed by Martin Gardner in 1966), out of all 3811 different free octacubes, 261 are unfoldings of the tesseract.[11][13]
Boundary connectivity
Although the cubes of a polycube are required to be connected square-to-square, the squares of its boundary are not required to be connected edge-to-edge. For instance, the 26-cube formed by making a 3×3×3 grid of cubes and then removing the center cube is a valid polycube, in which the boundary of the interior void is not connected to the exterior boundary. It is also not required that the boundary of a polycube form a manifold. For instance, one of the pentacubes has two cubes that meet edge-to-edge, so that the edge between them is the side of four boundary squares.
If a polycube has the additional property that its complement (the set of integer cubes that do not belong to the polycube) is connected by paths of cubes meeting square-to-square, then the boundary squares of the polycube are necessarily also connected by paths of squares meeting edge-to-edge.[14] That is, in this case the boundary forms a polyominoid.
Unsolved problem in mathematics:
Can every polycube with a connected boundary be unfolded to a polyomino? If so, can every such polycube be unfolded to a polyomino that tiles the plane?
(more unsolved problems in mathematics)
Every k-cube with k < 7 as well as the Dalí cross (with k = 8) can be unfolded to a polyomino that tiles the plane. It is an open problem whether every polycube with a connected boundary can be unfolded to a polyomino, or whether this can always be done with the additional condition that the polyomino tiles the plane.[12]
Dual graph
The structure of a polycube can be visualized by means of a "dual graph" that has a vertex for each cube and an edge for each two cubes that share a square.[15] This is different from the similarly-named notions of a dual polyhedron, and of the dual graph of a surface-embedded graph.
Dual graphs have also been used to define and study special subclasses of the polycubes, such as the ones whose dual graph is a tree.[16]
See also
• Tripod packing
References
1. Weisstein, Eric W. "Polycube." From MathWorld
2. Lunnon, W. F. (1972), "Symmetry of Cubical and General Polyominoes", in Read, Ronald C. (ed.), Graph Theory and Computing, New York: Academic Press, pp. 101–108, ISBN 978-1-48325-512-5
3. Polycubes, at The Poly Pages
4. Kevin Gong's enumeration of polycubes
5. Aleksandrowicz, Gadi; Barequet, Gill (2006). Chen, Danny Z.; Lee, D. T. (eds.). "Counting d-Dimensional Polycubes and Nonrectangular Planar Polyominoes". Computing and Combinatorics. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer: 418–427. doi:10.1007/11809678_44. ISBN 978-3-540-36926-4.
6. "Enumeration of Specific Classes of Polycubes", Jean-Marc Champarnaud et al, Université de Rouen, France PDF
7. "Dirichlet convolution and enumeration of pyramid polycubes", C. Carré, N. Debroux, M. Deneufchâtel, J. Dubernard, C. Hillairet, J. Luque, O. Mallet; November 19, 2013 PDF
8. Aarts, Ronald M. "Pentacube". From MathWorld.
9. Kemp, Martin (1 January 1998), "Dali's dimensions", Nature, 391 (27): 27, Bibcode:1998Natur.391...27K, doi:10.1038/34063
10. Fowler, David (2010), "Mathematics in Science Fiction: Mathematics as Science Fiction", World Literature Today, 84 (3): 48–52, doi:10.1353/wlt.2010.0188, JSTOR 27871086, S2CID 115769478, Robert Heinlein's "And He Built a Crooked House," published in 1940, and Martin Gardner's "The No-Sided Professor," published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle, and the hypercube (tesseract)..
11. Diaz, Giovanna; O'Rourke, Joseph (2015), Hypercube unfoldings that tile $\mathbb {R} ^{3}$ and $\mathbb {R} ^{2}$, arXiv:1512.02086, Bibcode:2015arXiv151202086D.
12. Langerman, Stefan; Winslow, Andrew (2016), "Polycube unfoldings satisfying Conway's criterion" (PDF), 19th Japan Conference on Discrete and Computational Geometry, Graphs, and Games (JCDCG^3 2016).
13. Turney, Peter (1984), "Unfolding the tesseract", Journal of Recreational Mathematics, 17 (1): 1–16, MR 0765344.
14. Bagchi, Amitabha; Bhargava, Ankur; Chaudhary, Amitabh; Eppstein, David; Scheideler, Christian (2006), "The effect of faults on network expansion", Theory of Computing Systems, 39 (6): 903–928, arXiv:cs/0404029, doi:10.1007/s00224-006-1349-0, MR 2279081, S2CID 9332443. See in particular Lemma 3.9, p. 924, which states a generalization of this boundary connectivity property to higher-dimensional polycubes.
15. Barequet, Ronnie; Barequet, Gill; Rote, Günter (2010), "Formulae and growth rates of high-dimensional polycubes", Combinatorica, 30 (3): 257–275, doi:10.1007/s00493-010-2448-8, MR 2728490, S2CID 18571788.
16. Aloupis, Greg; Bose, Prosenjit K.; Collette, Sébastien; Demaine, Erik D.; Demaine, Martin L.; Douïeb, Karim; Dujmović, Vida; Iacono, John; Langerman, Stefan; Morin, Pat (2011), "Common unfoldings of polyominoes and polycubes", Computational geometry, graphs and applications (PDF), Lecture Notes in Comput. Sci., vol. 7033, Springer, Heidelberg, pp. 44–54, doi:10.1007/978-3-642-24983-9_5, MR 2927309.
External links
• Wooden hexacube puzzle by Kadon
• Polycube Symmetries
• Polycube solver Program (with Lua source code) to fill boxes with polycubes using Algorithm X.
Polyforms
Polyominoes
• Domino
• Tromino
• Tetromino
• Pentomino
• Hexomino
• Heptomino
• Octomino
• Nonomino
• Decomino
Higher dimensions
• Polyominoid
• Polycube
Others
• Polyabolo
• Polydrafter
• Polyhex
• Polyiamond
• Pseudo-polyomino
• Polystick
Games and puzzles
• Blokus
• Soma cube
• Snake cube
• Tangram
• Hexastix
• Tantrix
• Tetris
WikiProject Portal
| Wikipedia |
Rectified truncated icosahedron
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.
Rectified truncated icosahedron
TypeNear-miss Johnson solid
Faces92:
60 isosceles triangles
12 pentagons
20 hexagons
Edges180
Vertices90
Vertex configuration3.6.3.6
3.5.3.6
Schläfli symbolrt{3,5}
Conway notationatI[1]
Symmetry groupIh, [5,3], (*532) order 120
Rotation groupI, [5,3]+, (532), order 60
Dual polyhedronRhombic enneacontahedron
Propertiesconvex
Net
As a near-miss Johnson solid, under icosahedral symmetry, the pentagons are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the pentagons, having slightly different but alternating angles, causing the triangles to be isosceles instead. The shape is a symmetrohedron with notation I(1,2,*,[2])
Images
Dual
By Conway polyhedron notation, the dual polyhedron can be called a joined truncated icosahedron, jtI, but it is topologically equivalent to the rhombic enneacontahedron with all rhombic faces.
Related polyhedra
The rectified truncated icosahedron can be seen in sequence of rectification and truncation operations from the truncated icosahedron. Further truncation, and alternation operations creates two more polyhedra:
Name Truncated
icosahedron
Truncated
truncated
icosahedron
Rectified
truncated
icosahedron
Expanded
truncated
icosahedron
Truncated
rectified
truncated
icosahedron
Snub
rectified
truncated
icosahedron
Coxeter tI ttI rtI rrtI trtI srtI
Conway atI etI btI stI
Image
Net
Conway dtI = kD kD kdtI jtI jtI otI mtI gtI
Dual
Net
See also
• Near-miss Johnson solid
• Rectified truncated tetrahedron
• Rectified truncated octahedron
• Rectified truncated cube
• Rectified truncated dodecahedron
References
1. "PolyHédronisme".
• Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
• George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
Near-miss Johnson solids
Truncated forms
• Truncated triakis tetrahedron
• Chamfered cube (Truncated rhombic dodecahedron)
• Chamfered dodecahedron (Truncated rhombic triacontahedron)
Other forms
• Tetrated dodecahedron
• Rectified truncated icosahedron
• Pentahexagonal pyritoheptacontatetrahedron
| Wikipedia |
\begin{definition}[Definition:Zero Complement]
Let $\struct {S, \circ, \preceq}$ be a naturally ordered semigroup.
Let $0$ be the zero of $S$.
Let $S^* := \relcomp S {\set 0} = S \setminus \set 0$ be the complement of $\set 0$ in $S$.
Then $S^*$ is called the '''zero complement''' of $S$.
\end{definition} | ProofWiki |
\begin{definition}[Definition:Cotangent/Definition from Circle/Fourth Quadrant]
Consider a unit circle $C$ whose center is at the origin of a cartesian plane.
:500px
Let $P$ be the point on $C$ in the fourth quadrant such that $\theta$ is the angle made by $OP$ with the $x$-axis.
Let a tangent line be drawn to touch $C$ at $A = \tuple {0, 1}$.
Let $OP$ be produced to meet this tangent line at $B$.
Then the '''cotangent''' of $\theta$ is defined as the length of $AB$.
Category:Definitions/Cotangent Function
\end{definition} | ProofWiki |
Methodology and data
Full paper
Performance of uniform and heterogeneous slip distributions for the modeling of the November 2016 off Fukushima earthquake and tsunami, Japan
Kenji Nakata1Email authorView ORCID ID profile,
Yutaka Hayashi2,
Hiroaki Tsushima3,
Kenichi Fujita1,
Yasuhiro Yoshida4 and
Akio Katsumata1
Earth, Planets and Space201971:30
Accepted: 1 March 2019
The Mw 6.9 earthquake off Fukushima Prefecture, Japan, of 22 November 2016 was followed by a tsunami that struck the Japanese coast from Hokkaido in northern Japan to Wakayama Prefecture in western Japan. We compared the performance of a seismologically deduced single-fault model, a seismologically deduced finite fault slip model (FFM), an optimized single-fault model based on tsunami data, the FFM with horizontal shift, and the tsunami waveform inversion models of the previous studies considered for this earthquake regarding reproduction of tsunami waves by tsunami computations. It is important to discuss how these models work well because it is sometimes desirable to obtain an earthquake source model to estimate tsunami waves with a simple process obtained with limited data from the viewpoint of tsunami prediction. The seismologically deduced FFM has an advantage in terms of the information of slip regions of fault plane and was superior to the seismologically deduced single-fault model, especially in predicting amplitudes of tsunami waves. This means that when only with seismic data, the FFM could narrow the range of forecast of tsunami amplitude. In the comparison of models optimized with tsunami data, the single-fault model showed the almost equivalent performance of the tsunami waveform inversion models of previous studies regarding the waveform coincidence with observations and the horizontal location at the negative peak of the initial sea surface displacement. In case the main generation region of the tsunami is concentrated in one place, the tsunamis can be expressed by a single-fault model by conducting the detailed grid search. We also confirmed that the centroid location of centroid moment tensor (CMT) solution and the absolute location of the FFM were not necessarily suitable to express tsunamis, while the moment magnitude, the focal mechanism, the centroid depth of CMT solution, and the relative slip distribution of the FFM were effective to represent tsunamis. Since this event occurred at the shallow depth, the speed of tsunami wave is particularly slow. Therefore, it would be advisable to pay attention to the horizontal uncertainty to apply seismologically obtained solution to tsunami forecast, especially when a tsunami occurs in shallow water.
2016 off Fukushima earthquake
Tsunami computation
Uniform single-fault model
Seismologically deduced finite fault slip model
After an earthquake of moment magnitude (Mw) 6.9 occurred beneath the Pacific Ocean off Fukushima Prefecture, Japan, on 22 November 2016 at 05:59 JST (UTC + 09:00), tsunamis were observed from Hokkaido in northern Japan to Wakayama Prefecture in western Japan. The maximum amplitude of the tsunami was 1.4 m at Sendai Port in Miyagi Prefecture (JMA 2016a). According to the Japan Meteorological Agency (JMA), this was a normal faulting event that occurred in the crust of the North American plate above its boundary with the Pacific plate (JMA 2016a). Its epicenter was about 50 km off the coast. Direct waves as well as reflected waves from the coast of Fukushima Prefecture were observed along the coast of Miyagi Prefecture (JMA 2017a). The distribution of aftershocks from this event defined an east-dipping fault plane (Headquarters for Earthquake Research Promotion 2016; Toda and Goto 2016).
Fujii and Satake (2016) and Gusman et al. (2017a) simulated the tsunami from this event using a single-fault model with a size of 20 × 10 km. Gusman et al. (2017a) and Adriano et al. (2018) estimated the tsunami source by inversion of the tsunami waveforms. Suppasri et al. (2017) conducted tsunami computations using 15-m-resolution topographic data and compared their results with data from field surveys. While the previous studies specified various wave source models, the question remains whether how the models obtained from the data limited to seismic waves could work, and how much performance a simple uniform single-fault model can have for a complicated model, which have heterogeneous slip distribution, in this event. It is important to discuss such models' performances because it is sometimes desirable to obtain an earthquake source model to estimate tsunami waves with a simple process obtained with limited data from the viewpoint of tsunami prediction.
JMA utilizes an immediate centroid moment tensor (CMT) solution for an immediate tsunami forecast (Kamigaichi 2015). In that case, a uniform single-fault model is used since the slip distribution on the fault plane is unavailable in short duration soon after occurrence of the earthquake. Gusman et al. (2017a) pointed out that it was difficult to represent tsunami observation waveforms at all stations used for the tsunami source estimation with the single-fault model even if the size of the slip region of the model is adjusted. However, the optimum horizontal position of the model was not discussed in Gusman et al. (2017a). The distribution of slip on the fault plane, which is directly related to the area of tsunami generation, can be obtained as a finite fault slip model (FFM) estimated only with seismic waveforms (e.g., Yoshida et al. 2011; Iwakiri et al. 2014) as well as tsunami waveform inversion. Even though this event was relatively small, of magnitude 7 class, the FFM was obtained (JMA 2017b). So far, there have been studies on the use of FFM models for magnitude 8 class earthquakes to predict tsunami (e.g., Heidarzadeh et al. 2017; Gusman et al. 2017b). In those cases, the coastal grid intervals used for the tsunami computation were not so fine probably because of the long wavelength of tsunami waves considered. For the magnitude 7 class earthquakes, there have been few studies on the performance of the FFM by the comparison of tsunami waveforms.
In this study, we compared the performance of five models: the seismologically deduced single-fault model, the seismologically deduced FFM, the optimized single-fault model with tsunami waveform data, the FFM with horizontal shift, and the tsunami waveform inversion models of the previous studies. First, tsunami prediction by a single-fault model by CMT solution was compared with that by a seismologically deduced FFM. Next, an optimum single-fault model and the optimum FFM with horizontal shift were obtained using tsunami waveform data. Finally, the performances of models in this study were compared with that of the tsunami waveform inversion models of previous studies.
Single-fault model
The single-fault model is parameterized by fault length, fault width, fault depth, slip amount, horizontal location, strike, dip, and rake. When the fault length and width are unknown, as is often the case in an immediate analysis soon after an earthquake occurrence, they are determined by a scaling law from the earthquake magnitude (e.g., Tanioka et al. 2017). In this study, we used the scaling law proposed by Utsu (2001):
$${ \log }_{10} S = M_{w} - 4.0 ,$$
where S = LW is the fault area (km2), based on fault length L and fault width W, and Mw is the moment magnitude. Given M and assuming W = L/2, this equation yields S, L, and W. This relation predicts the aftershock area well (Utsu 2001) and is used to calculate a synoptic image of the rupture zone under the assumption of a constant stress drop of 3 MPa (Kikuchi 2003). When the slip distribution can be derived from other information such as tsunami data, L and W can be determined directly from it.
The average slip amount is obtained from the seismic moment and fault area according to Aki (1966):
$$M_{0} = \mu DS,$$
where M0 is the seismic moment, μ is the shear modulus of the rocks, and D is the average slip amount. The moment magnitude Mw (Kanamori 1977) is
$$M_{w} = \frac{{{ \log }M_{0} - 9.1}}{1.5}.$$
D is commonly calculated by assuming a certain value of μ. In this study, μ is assumed to be 30 GPa at a depth of about 10 km on the basis of the Preliminary Reference Earth Model (Dziewonski and Anderson 1981).
The strike, dip, slip angle, and midpoint depth of the fault were taken from the CMT solutions released by various institutions (Table 1). The horizontal location was determined from the distribution of aftershocks that occurred during the first hour after the earthquake.
East-dipping CMT solutions for the 22 November 2016 event from various institutions
Latitude (°N)
Longitude (°E)
NIED (2016)
– 90°
JMA (2016b)
JMA (2016c)
USGS (2016)
– 101°
GCMT (2016)
Seismologically deduced FFM (finite fault slip model)
The seismologically deduced FFM models an earthquake fault as a set of small sub-faults, each with its own slip amount and slip history. The FFM used in this study is based on analysis of teleseismic body waves. The analysis starts by assuming a fault plane (often specified from the CMT solution) and an initial rupture starting point (typically the hypocenter). The parameters are estimated from the time-series waveform at seismic observation stations at teleseismic distances of 30°–100°. In this study, which assumed that a high-quality FFM is obtained in real time, we used the FFM released by the JMA (JMA 2017b) about 1 month after the earthquake. (The FFM gave Mw 7.2, which was larger than the Mw 6.9–7.0 given by CMT analyses.) The horizontal location of the FFM was not adjusted in use for the tsunami computation.
Tsunami observation data
The computed tsunami waveforms were compared with waveforms observed at the 13 coastal tide gauge stations and offshore GPS buoys (Kato et al. 2000; Kawai et al. 2012) shown in Fig. 1. The tidal component was removed from the observations by subtracting the theoretical values calculated by superposition of trigonometric functions (e.g., Murakami 1981).
Locations of the 22 November 2016 event epicenter, tide gauge stations, and GPS buoys. Stations Kuji, Ishinomaki, Sendai Shinko, Kashima, and both GPS buoys are operated by the Port Authority of the Ministry of Land, Infrastructure, Transport and Tourism; station Soma is operated by the Geographical Survey Institute; and stations Miyako, Ofunato, Ayukawa, Onahama, Oarai, and Choshi are operated by the Japan Meteorological Agency
Tsunami computation and bathymetry data
The tsunami computation relies on solving nonlinear long-wave equations with a staggered leapfrog finite-difference scheme. The TUNAMI code (e.g., Imamura 1995; Goto et al. 1997) was used, with input/output modifications by the Meteorological Research Institute. Crustal deformation at the seafloor is calculated by the method of Mansinha and Smylie (1971) on the basis of fault parameters set by a single-fault model or an FFM. The tsunami computation assumes that the seafloor deformation instantaneously displaces the sea surface to the same extent.
For the bathymetry data, we used the gridded data set of the Cabinet Office Central Disaster Management Council of Japan (Cabinet Office 2003). The nested grid system was used as well as Gusman et al. (2017a) and Adriano et al. (2018). The computation proceeded from the coarsest to the finest grid interval (1350 m, 450 m, 150 m, 50 m) for successively smaller domains, from the ocean to the vicinity of tide gauge stations (Fig. 2). The waveform at each tide gauge station was computed with a 50 m grid interval. While the construction works have been done since 2003 when the data set was made, the noticeable change in coastal structures near the tide gauge stations blocking the arrival of the tsunami was not seen at the bathymetry of 50 m grid interval, compared with the images from the Google Earth (https://www.google.co.jp/earth/). Coastal structures in this data set, such as levees, are defined in terms of the boundaries of 50 m grid cells. For convenience, if a coastal structure was indicated on either the north or east side of a cell, the elevation of the cell was replaced by the elevation of the coastal structure.
The nested grid system used in this study. Red square frame indicates the computation area at 450 m grid intervals, blue 150 m, green 50 m
Measurement of amplitude and period
The amplitude and period of the first wave cycle were used to compare the computed and observed waveforms. Because the main effect of this normal faulting event was subsidence of the seafloor, we measured the pulling wave as the first wave cycle, ignoring the weak push wave that preceded it.
Waveform coincidence score
To quantify the degree of coincidence between the computed and observed waveforms, we relied on the variance reduction (VR) score. This score is often used for quality control of CMT solutions (e.g., Usui et al. 2010) and for evaluating tsunami waveform predictions (Tsushima et al. 2009). It is defined as:
$${\text{VR}} = 1 - \frac{{\mathop \smallint \nolimits_{0}^{T} \left[ {o_{i} \left( t \right) - s_{i} \left( t \right)} \right]^{2} {\text{d}}t}}{{\mathop \smallint \nolimits_{0}^{T} o_{i} \left( t \right)^{2} {\text{d}}t}},$$
where oi(t) and si(t) are the ith observed and theoretical waveforms, respectively, and T is the data length of the waveform used for analysis. VR has a value of 1 if the waveforms are perfectly matched and decreases as the difference between the waveforms increases.
We determined VR on the basis of two different data lengths. In one (VR1), only the first wave cycle was compared, and in the other (VR2), the full waveform from the first wave cycle to 9:00 JST on 22 November 2016 was compared.
Tsunami computation by seismologically deduced single-fault model and FFM
We compared the observations of the 22 November 2016 tsunami to the waveforms computed by the single-fault model from the earthquake scaling law (model A) and the FFM based on seismic data (model B), as described in the "Methodology and data" section. Model A used the CMT solution from the National Research Institute for Earth Science and Disaster Resilience (NIED 2016), Mw 6.9 (Table 1), and the fault parameters are listed in Table 2. Figure 3 shows the initial sea surface displacement of the tsunami under both models, and Fig. 4 shows the observed and computed waveforms at each station.
Model fault parameters
Source model
Lat. (°N)
Long. (°E)
Length (km)
Width (km)
Slip (m)
A (single-fault)
B FFM
Multiple faults (JMA 2017b)
C (optimized single-fault)
D (optimized FFM)
Model B shifted horizontally
Initial sea surface displacement of model A, B, C, and D. The red rectangle represents the surface projection of the fault plane onto the horizontal plane. The mainshock and the locations of the first hour of aftershocks were also shown. The mainshock was derived by JMA (2016a), and the aftershocks are by the Seismological Bulletin of Japan (http://www.data.jma.go.jp/svd/eqev/data/bulletin/index_e.html)
Comparison of waveforms at 13 stations from observations, model A, and model B. Tsunami waveforms at tide gauge stations and GPS buoys (locations in Fig. 1). Black curves are the observed waveforms, blue curves are waveforms from model A, and red curves are waveforms from model B. Data lengths for calculating VR1 and VR2 at each station are indicated by purple lines
Model B contains a region of strong local subsidence that does not appear in model A, which reflects a region of large slip on the fault plane (Fig. 3). A comparison of computed and observed waveforms shows that model B more closely approximated the observed amplitudes than model A (Fig. 4).
Values of VR1 for model A were consistently positive for all stations (Fig. 5). This means that defining the horizontal fault location from the area of immediate aftershocks that occurred during the first hour after the earthquake led to good phase matching of tsunami waves. VR1 values for model B were higher than those for model A at stations near the epicenter, but much lower at more distant stations. The main reason for this pattern is that the waveform phases (arrival times) did not match between the observations and computations.
Comparison of models A, B, C, and D at 13 stations. a Absolute amplitudes of the first pulling tsunami wave cycle. b Difference between the absolute amplitude of the computation and that of the observation. c Periods of the first wave cycle. d VR1. The dotted lines in b represent approximate best-fit curves
Optimization of single-fault model based on tsunami data
We performed a grid search to find an optimal single-fault model based on tsunami data. To obtain an optimal single-fault model as a tsunami source, we examined various values of fault length L, fault width W, slip amount D, moment magnitude Mw, horizontal location, and focal depth. Candidate values were 30, 25, and 20 km for L; 20, 15, and 10 km for W; 6.8–7.1 for Mw; and 37.24–37.29°N and 141.42–141.47°E for the fault midpoint. Here, D determined from Mw was restricted to less than 10 m so as to be consistent with the maximum slip of the small fault segments in the FFM. Other parameters were the same as in model A. The parameters that maximized the value of VR1 for all 13 stations (0.82 median, 0.76 mean) were as follows: location 37.28°N, 141.50°E, L = 20 km, W = 10 km, and Mw = 6.95. These were adopted in the optimized single-fault model (model C). The determined location was about 20 km away from the centroid location of used CMT solution. Figure 6 shows details of this optimization for the horizontal fault location (Fig. 6a); L, W, and Mw (Fig. 6b); and fault depth (Fig. 6c). In particular, the depth was optimal around 10 km, showing that the assumed depth for the initial model (given with reference to centroid depth of CMT solution) was reasonable. The initial sea surface displacement and the computed tsunami waveforms from model C are shown in Figs. 3 and 7, and the parameters are listed in Table 2. VR1 values showed that the computed and observed waveforms agreed well (Fig. 5). As a result of the relocation, it produced wave periods closer to the observations than those from models A and B, and the VR1 values became acceptable for all stations, including the distant ones. The region of slip on the fault plane from model C was about half the size estimated from the earthquake scaling law of Utsu (2001).
Mean values of VR for model C after various parameters were changed from model A. a Changes in VR from shifting the horizontal location of model A (red star). The area within the dashed rectangle was searched in horizontal increments of 0.01° to find the optimal location (red square). b VR1 versus Mw for various combinations of L (km) and W (km) in model C. c VR for various fault depths between 5 and 50 km in model C
Comparison of waveforms at 13 stations from observations, model C, and model D. Black curves are the observed waveforms, green curves are waveforms from model C, and orange curves are waveforms from model D. Data lengths for calculating VR1 and VR2 at each station are indicated by purple lines
FFM with horizontal shift
We improved the horizontal fault location produced by the FFM to fit the observed tsunami waveforms through a grid search that first shifted model B horizontally at intervals of 0.05° and then refined the grid search at 0.01° intervals while keeping the slip distribution unchanged. The number of computations was 30 (6 × 5) for 0.05° and 80 (8 × 10) for 0.01°.
In the resulting model, model D, the VR1 value was positive for all but one station (Fig. 5) when the original FFM was shifted 0.02° to the north and 0.06° to the west (Fig. 8). The VR2 values show the same tendency as the VR1 values. The computed waveform is compared with observations in Fig. 7. The mean VR1 value for all 13 stations improved from a median of 0.30 and a mean of 0.04 with the original FFM to a median of 0.61 and a mean of 0.42 with model D. It thus was more advantageous to use a horizontally shifted FFM to compute this tsunami. The 0.06° (about 6 km) shift is within the range of sub-fault size of 10 km.
Spatial distribution of mean values of VR for model D, the horizontally shifted version of model B. The color scale indicates the values of VR, and the spatial scale indicates the difference from the initial position. The initial shift from the location of model B (red star) was 0.05°; then the dashed rectangle was searched at increments of 0.01° to find the optimal location (red square)
Comparison of single-fault models and FFMs
In the comparison with the single-fault model by scaling law (model A), the FFM (model B) is advantageous because it has the information of the slip distribution of the fault plane. In fact, the model B better represented the amplitude than model A (Fig. 5b). Tsunami amplitude is the most important factor for tsunami forecast. When only with seismic data, the FFM could narrow the range of forecast of the tsunami amplitude.
In the comparison between the optimum single-fault model (model C) and the FFM with horizontal shift (model D), the model C was superior to the model D with the smaller amplitude differences (Fig. 5b) and the VR values (Fig. 5d). The first reason for this is that the main slip region was concentrated in one place that the single-fault model could express. The second reason is that the slip distribution and slip amount of the FFM may have not been strictly represented due to estimation errors in the seismological analysis, while there was no limitation on fault parameters of the optimum single-fault model to fit the observed tsunami waveforms.
Uncertainty of horizontal location from seismic data
The optimum single-fault model (model C) located about 10–20 km west from the centroid location of various institutions (Fig. 9). The FFM with horizontal shift (model D) also located 0.02° to the north and 0.06° to the west from the original FFM (model B). Both results show that the horizontal location was determined relatively poorly only from the seismic data. This may be related to the propagation speed difference between seismic and tsunami waves. Since this event occurred at the shallow depth, the speed of tsunami wave is particularly slow. While such location difference would not significantly affect the comparison of seismic waveforms, the same amount of location difference would cause recognizable tsunami waveform misfits.
Comparison of horizontal locations. Red triangles show the horizontal locations of the negative peak of the initial sea surface displacement for each model. The horizontal locations were measured by the figure of Gusman et al. (2017a), Adriano et al. (2018) and this study. The centroid locations of each institution are also shown with blue squares
Comparison of models in this study and models from previous studies
We compared the results of the optimum single-fault model (model C) and the FFM with horizontal shift (model D) and the tsunami inversion models of previous studies (Gusman et al. 2017a; the GCMT model of Adriano et al. 2018). The Mw of the model C (Mw 6.95 [μ = 30 GPa]; Mw 6.92 [μ = 27 GPa]) almost agrees with Mw 7.0 (μ = 27 GPa) of Gusman et al. (2017a) and Mw 6.95 (μ = 27 GPa) of Adriano et al. (2018). It is also consistent with the Mw 6.9–7.0 from the CMT solutions. The normalized root-mean-square misfit (Heidarzadeh et al. 2016) for the model C was 0.75 for the same data period as the calculation of VR2, which is lower (better) than 0.85 in the prototype single-fault model (GCMT NP1) of Gusman et al. (2017a). The value only for Sendai Shinko was 0.47, which was also lower (better) than 0.686 in the tsunami inversion model of Adriano et al. (2018). From the comparison with the figures shown in the papers, the single-fault model in this study has almost equivalent performance with Gusman et al. (2017a) and Adriano et al. (2018). This means that a simple model has the almost same performance as a complicated model in this event. The first reason for this is that the main slip region on the fault plane was concentrated in one place in this event; therefore, the single-fault model could express it. The second reason may be that the horizontal position of small sub-faults is fixed beforehand in the tsunami waveform inversion, while the horizontal position of the single-fault model can be freely moved at 0.01° interval in this study.
Figure 9 shows the horizontal locations of the negative peak of the initial sea surface displacement for various models. The location of the model D in this study is close to that of Gusman et al. (2017a); and the location of the model C is close to that of Adriano et al. (2018). The location of the model C is located about 10 km south–southwest of that of the model D. The location of the model C would be more plausible since it can express the tsunami waveforms better than the model D (Fig. 5d). The location difference between the Gusman et al. (2017a) and the Adriano et al. (2018) may be due to the difference of the number of sub-faults and locations.
We compared the performance of five models: the seismologically deduced single-fault model based on the CMT solution, the seismologically deduced FFM, the optimum single-fault model with tsunami data, the FFM with horizontal shift, and the tsunami waveform inversion models of the previous study for the earthquake off Fukushima Prefecture on 22 November 2016, Japan. We compared the models with the amplitudes, the period, and the VR, and obtained results as:
The seismologically deduced FFM has an advantage in terms of the information of slip regions of fault plane and was superior to the seismologically deduced single-fault model, especially in predicting amplitudes of tsunami. When only with seismic data, the FFM could narrow the range of forecast of tsunami amplitude.
The optimized single-fault model with tsunami data has performance to represent the observed tsunami waveforms at 13 stations well. It is better than the prototype single-fault model of Gusman et al. (2017a) and has the almost equivalent performance with the tsunami waveform inversion models of Adriano et al. (2018). The horizontal location of its negative peak of the initial sea surface displacement located close to that of Adriano et al. (2018) rather than that by the centroid location of CMT solution. In case the main generation region of the tsunami is concentrated in one place like this event, the tsunami wave can be expressed by a single-fault model by conducting the detailed grid search.
The centroid location of CMT solution and the absolute location of the FFM were not necessarily proper enough to get good agreement between observed and computed tsunami waves, while the Mw, the focal mechanism, the centroid depth of CMT solution, and the relative slip distribution of a seismologically deduced FFM were effective to represent tsunami wave reproduction. This may be due to difference in the propagation speeds between seismic wave and tsunami wave. Since this event occurred at the shallow depth, the speed of tsunami wave is particularly slow. To utilize the analysis of seismic waves in tsunami forecasting, careful attention should be paid to its horizontal uncertainty, especially when a tsunami occurs in shallow water.
FFM:
finite fault slip model
GCMT:
the Global Centroid Moment Tensor Project
the Japan Meteorological Agency
NIED:
the National Research Institute for Earth Science and Disaster Resilience
USGS:
the US Geological Survey
variance reduction
VR1:
VR for the first wave cycle
VR for the data period from the first wave arrival to 9:00 JST on 22 November 2016
KN proposed the initial idea of this study, conducted the analyses and drafted the manuscript. YH made suggestions about the organization and method of the article. HT supported the tsunami computation and the evaluation of the results. KF gave advice on using the FFM. YY gave advice on using the FFM and supported the manuscript preparation. AK made suggestions about the organization of the article and supported the manuscript preparation. All authors read and approved the final manuscript.
Records from tide gauge stations and GPS buoys were provided by the Port Authority of the Ministry of Land, Infrastructure, Transport and Tourism, the Geospatial Information Authority of Japan website (http://tide.gsi.go.jp/main.php?number=18), and the Japan Meteorological Agency. We used the TUNAMI code developed by Tohoku University as a tsunami computing simulation code, with input/output modifications by the Meteorological Research Institute. Topographical data were provided by the Cabinet Office Central Disaster Management Council, which are also available on the website (http://www.bousai.go.jp/kaigirep/chuobou/senmon/nihonkaiko_chisimajishin/index.html). Parts of the figures were created with Generic Mapping Tools (Wessel and Smith 1998). We thank Editor Stephen Bannister and two anonymous reviewers for their thorough reviews and valuable suggestions on improving the quality of this article.
Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Meteorological Research Institute, Japan Meteorological Agency, 1-1 Nagamine, Tsukuba Ibaraki, 305-0052, Japan
Ministry of Education, Culture, Sports, Science and Technology, 3-2-2 Kasumigaseki, Chiyoda-ku, Tokyo 100-8959, Japan
Seismology and Volcanology Department, Japan Meteorological Agency, 1-3-4 Otemachi, Chiyoda-ku, Tokyo 100-8122, Japan
Meteorological College, Japan Meteorological Agency, 7-4-81 Asahi, Kashiwa Chiba, 277-0852, Japan
Adriano B, Fujii Y, Koshimura S (2018) Tsunami source and inundation features around Sendai Coast, Japan, due to the November 22, 2016 Mw 6.9 Fukushima earthquake. Geosci Lett 5:2. https://doi.org/10.1186/s40562-017-0100-9 View ArticleGoogle Scholar
Aki K (1966) Generation and propagation of G waves from the Niigata Earthquake of June 16, 1964: part 2. Estimation of earthquake moment, released energy, and stress-strain drop from the G wave spectrum. Bull Earthq Res Inst 44:73–88Google Scholar
Cabinet Office (2003) Expert study group on subduction zone earthquake around Japan trench and Chishima trench. http://www.bousai.go.jp/kaigirep/chuobou/senmon/nihonkaiko_chisimajishin/index.html. Accessed 17 July 2018 (in Japanese)
Dziewonski AM, Anderson DL (1981) Preliminary reference Earth model. Phys Earth Planet Inter 25:297–356. https://doi.org/10.1016/0031-9201(81)90046-7 View ArticleGoogle Scholar
Fujii Y, Satake K (2016) Off-Fukushima Tsunami on Nov. 21, 2016. http://iisee.kenken.go.jp/staff/fujii/Fukushima2016/tsunami.html. Accessed 17 July 2018
Global Centroid-Moment-Tensor Project (2016) http://www.globalcmt.org/. Accessed 27 Dec 2016
Goto C, Ogawa Y, Shuto N, Imamura F (1997) Numerical method of tsunami simulation with the leap-frog scheme in IUGG/IOC TIME Project IOC Manual and Guides. UNESCO, ParisGoogle Scholar
Gusman AR, Satake K, Shinohara M, Sakai S, Tanioka Y (2017a) Fault slip distribution of the 2016 Fukushima earthquake estimated from tsunami waveforms. Pure Appl Geophys 174:2925–2943. https://doi.org/10.1007/s00024-017-1590-2 View ArticleGoogle Scholar
Gusman AR, Satake K, Harada T (2017b) Rupture process of the 2016 Wharton Basin strike-slip faulting earthquake estimated from joint inversion of teleseismic and tsunami waveforms. Geophys Res Lett 44:4082–4089. https://doi.org/10.1002/2017GL073611 View ArticleGoogle Scholar
Headquarters For Earthquake Research Promotion, Ministry of Education, Culture, Sports, Science and Technology (2016) Monthly Reports on Evaluation of Seismic Activities in Japan. https://www.static.jishin.go.jp/resource/monthly/2016/2016_11.pdf. Accessed 17 July 2018 (in Japanese)
Heidarzadeh M, Murotani S, Satake K, Ishibe T, Gusman AR (2016) Source model of the 16 September 2015 Illapel, Chile, Mw 8.4 earthquake based on teleseismic and tsunami data. Geophys Res Lett 43:643–650. https://doi.org/10.1002/2015GL067297 View ArticleGoogle Scholar
Heidarzadeh M, Murotani S, Satake K, Takagawa T, Saito T (2017) Fault size and depth extent of the Ecuador earthquake (Mw 7.8) of 16 April 2016 from teleseismic and tsunami data. Geophys Res Lett 44:2211–2219. https://doi.org/10.1002/2017GL072545 View ArticleGoogle Scholar
Imamura F (1995) Review of tsunami simulation with a finite difference method. In: Yeh H, Liu P, Synolakis C (eds) Long-wave runup models. World Scientific, Singapore, pp 25–42Google Scholar
Iwakiri K, Kawazoe Y, Hasegawa Y (2014) Source process analysis performed by Japan Meteorological Agency using seismic waveforms—analysis method and scaling relationships derived from fault slip distributions. Q J Seismol 78:65–91 (in Japanese with English abstract and figure captions) Google Scholar
Japan Meteorological Agency (2016a) Monthly report on earthquakes and volcanoes in Japan November 2016. http://www.data.jma.go.jp/svd/eqev/data/gaikyo/monthly/201611/201611index.html. Accessed 17 July 2018 (in Japanese)
Japan Meteorological Agency (2016b) Focal mechanism solution of major earthquakes (preliminary report). http://www.data.jma.go.jp/svd/eew/data/mech/top.html. Accessed 23 Nov 2016 (in Japanese)
Japan Meteorological Agency (2016c) CMT solutions for earthquakes in November, 2016. http://www.data.jma.go.jp/svd/eqev/data/mech/pdf/cmt201611.pdf. Accessed 17 July 2018
Japan Meteorological Agency (2017a) Evaluation of tsunami warning etc. on the earthquake off Fukushima Prefecture on 22 November 2016, study session on tsunami prediction technology. http://www.data.jma.go.jp/svd/eqev/data/study-panel/tsunami/benkyokai14/shiryou2-2.pdf. Accessed 17 July 2018 (in Japanese)
Japan Meteorological Agency (2017b) Results of source process analysis of remarkable earthquakes occurring in Japan. http://www.data.jma.go.jp/svd/eqev/data/sourceprocess/index.html. Accessed 5 Jan 2018 (in Japanese)
Kamigaichi O (2015) Tsunami forecasting and warning. In: Meyers R (ed) Encyclopedia of complexity and systems science. Springer, Heidelberg, pp 1–38. https://doi.org/10.1007/978-3-642-27737-5_568-3 View ArticleGoogle Scholar
Kanamori H (1977) The energy release in great earthquakes. J Geophys Res 82:2981–2987View ArticleGoogle Scholar
Kato T, Terada Y, Kinoshita M, Kakimoto H, Isshiki H, Matsuishi M, Yokoyama A, Tanno T (2000) Real-time observation of tsunami by RTK-GPS. Earth Planets Space 52:841–845. https://doi.org/10.1186/BF03352292 View ArticleGoogle Scholar
Kawai H, Satoh M, Kawaguchi K, Seki K (2012) Recent tsunamis observed by GPS buoys off the Pacific coast of Japan. In: Proceedings of the 33rd Conference on Coastal Engineering, ASCE, pp 47–61Google Scholar
Kikuchi M (2003) Real-time seismology. University of Tokyo Press, Tokyo (in Japanese) Google Scholar
Mansinha L, Smylie DE (1971) The displacement field of inclined faults. Bull Seismol Soc Am 61:1433–1440Google Scholar
Murakami K (1981) The harmonic analysis of tides and tidal currents by least square method and its accuracy. Technical note of the port and harbor research institute Ministry of transport Japan 369 (in Japanese with English abstract) Google Scholar
National Research Institute for Earth Science and Disaster Resilience (2016) Earthquake mechanism information. http://www.fnet.bosai.go.jp/event/tdmt.php?_id=20161121205800.NO1&LANG=en Accessed 17 July 2018
Suppasri A, Yamashita K, Latcharote P, Roeber V, Hayashi A, Ohira H, Fukui K, Hisamatsu A, Imamura F (2017) Numerical analysis and field survey of the 2016 Fukushima earthquake and tsunami. J Jpn Soc Civ Eng Ser B2 Coast Eng 73(2):1597–1602. https://doi.org/10.2208/kaigan.73.i_1597 (in Japanese with English abstract) View ArticleGoogle Scholar
Tanioka Y, Miranda GJA, Gusman AR, Fujii Y (2017) Method to determine appropriate source models of large earthquakes including tsunami earthquakes for tsunami early warning in Central America. Pure Appl Geophys 174:3237–3248. https://doi.org/10.1007/s00024-017-1630-y View ArticleGoogle Scholar
Toda and Goto (2016) Identification of the active fault that caused the earthquake off Fukushima Prefecture (M7.4) on November 22. http://irides.tohoku.ac.jp/media/files/earthquake/eq/2016_fukushima_eq/20161122_fukushima_eq_activefault_toda.pdf. Accessed 30 Nov 2016 (in Japanese)
Tsushima H, Hino R, Fujimoto H, Tanioka Y, Imamura F (2009) Near-field tsunami forecasting from cabled ocean bottom pressure data. J Geophys Res 114:B06309. https://doi.org/10.1029/2008JB005988 View ArticleGoogle Scholar
U.S. Geological Survey (2016) M 6.9—35 km ESE of Namie, Japan. https://earthquake.usgs.gov/earthquakes/eventpage/us10007b88#moment-tensor. Accessed 17 July 2018
Usui Y, Aoki S, Hayashimoto N, Shimoyama T, Nozaka D, Yoshida T (2010) Description of and advances in automatic CMT inversion analysis. Q J Seismol 73:169–184 (in Japanese with English abstract and figure captions) Google Scholar
Utsu T (2001) Seismology, 3rd edn. Kyoritsu Shuppan, Tokyo (in Japanese) Google Scholar
Wessel P, Smith WHF (1998) New, improved version of the Generic Mapping Tools released. EOS Trans AGU 79:579View ArticleGoogle Scholar
Yoshida Y, Ueno H, Muto D, Aoki S (2011) Source process of the 2011 off the Pacific coast of Tohoku Earthquake with the combination of teleseismic and strong motion data. Earth Planets Space 63:10. https://doi.org/10.5047/eps.2011.05.011 View ArticleGoogle Scholar
4. Seismology | CommonCrawl |
\begin{document}
\title{Geometry and Curvature of Spin Networks} \author{\IEEEauthorblockN{E Jonckheere\IEEEauthorrefmark{1},
S G Schirmer\IEEEauthorrefmark{2} and
F C Langbein\IEEEauthorrefmark{3}} \IEEEauthorblockA{\IEEEauthorrefmark{1}
Ming Hsieh Department of Electrical Engineering,
University of Southern California, Los Angeles, CA 90089-2563\\
Email: [email protected]} \IEEEauthorblockA{\IEEEauthorrefmark{2}
Dept of Applied Maths \& Theoretical Physics,
Univ. of Cambridge, Cambridge, CB3 0WA, United Kingdom\\
Email: [email protected]} \IEEEauthorblockA{\IEEEauthorrefmark{3}
School of Computer Science \& Informatics,
Cardiff University, 5 The Parade, Cardiff, CF24 3AA, United Kingdom\\
Email: [email protected]}
} \maketitle \begin{abstract} A measure for the maximum quantum information transfer capacity (ITC) between nodes of a spin network is defined, and shown to induce a metric on a space of equivalence classes of nodes for homogeneous chains with XX and Heisenberg couplings. The geometry and curvature of spin chains with respect of this metric are studied and compared to the physical network geometry. For general networks hierarchical clustering is used to elucidate the proximity of nodes with regard to the maximum ITC. Finally, it is shown how minimal control can be used to overcome intrinsic limitations and speed up information transfer. \end{abstract}
\section{Introduction}
Networks of interacting quantum particles --- so-called spin-networks --- are important for transferring and distributing quantum information between different parts of a larger system such as different quantum components on a chip~\cite{Bose-review}. Spin chains, linear arrangements of spins, for example, can play the role of classical wires connecting two parts, and branched networks allow the distribution of quantum information to different nodes. The way quantum information propagates through spin networks, however, is quite different from classical information flow due to quantum inference effects. In particular, quantum state transfer between the nodes of the network is limited by fundamental physical principles and perfect quantum state transfer is usually possible only in very special cases. Quantifying state transfer fidelities for spin networks is not easy in general, but for certain types of networks such as spin-$\frac{1}{2}$ particles with interactions of so-called XXZ type, for example, this problem can be reduced to the maximum probability for a single excitation to propagate from one node to another, which can be computed efficiently numerically, and in some cases analytically. Thus, for the respective spin networks, the latter is a basic measure for the maximum information transfer capacity (ITC) between different nodes. For certain types of simple networks such as homogeneous chains the maximum ITC is shown to induce a metric on a set of equivalence classes. We study the topology of simple networks with regard to this metric, showing that it differs substantially from the physical geometry. Networks with trivial physical geometry such as linear chains can have a surprisingly rich geometric structure including curvature. Analysis of the latter shows that spin chains appear to be Gromov-hyperbolic with regard to this maximum ITC metric but unlike classical hyperbolic networks their Gromov boundary appears to be a single point. For more complex networks the maximum ITC does not induce a metric but we can use hierarchical clustering to assess the proximity of nodes with regard to information transfer capacity. Again, the resulting cluster structures differ substantially from the neighborhood relations induced by the physical geometry of the network, showing that the latter is not very useful in assessing the maximum ITC between nodes in a network, unlike in the classical case. Finally, we consider how minimal control of a single node in the network allows us to change information flow in the network, effectively changing the information transfer capacities (and network ``topology''), allowing us to achieve higher state transfer fidelities as well as generally speeding up the rate of information transfer.
\section{Information Transfer Capacity}
The Hilbert space of spin networks with XXZ interactions can be decomposed into so-called excitation subspaces $\mathcal{H}=\oplus_{n=0}^N \mathcal{H}_n$, where $n$ is the number of excitations in the network, ranging from $0$ to $N$. If we denote the spin basis states by $\ket{{\uparrow}}$ and $\ket{{\downarrow}}$, taking the latter to denote the ground state, then the $0$-excitation subspace consists of a single state $\ket{0} := \ket{{\downarrow}}\otimes \cdots \otimes\ket{{\downarrow}}$, while the one-excitation subspace consists of $N$ states $\ket{n}:=\ket{{\downarrow}}\otimes\cdots\otimes \ket{{\uparrow}} \otimes \cdots \otimes \ket{{\downarrow}}$, where the excitation $\ket{{\uparrow}}$ is in the $n$th position. Thus transferring a quantum state $\ket{\psi}=\cos(\theta)\ket{{\downarrow}}+e^{i\phi}\sin(\theta)\ket{{\uparrow}}$ from spin $m$ to $n$ is equivalent to transferring an excitation $\ket{{\uparrow}}$ from spin $m$ to $n$: \begin{align*}
\ket{\psi}_m
&= \cos(\theta) \ket{0} + e^{i\phi}\sin(\theta)\ket{m} \\
&\mapsto \cos(\theta) \ket{0} + e^{i\phi}\sin(\theta)\ket{n} = \ket{\psi}_n, \end{align*} where we used the shorthand $\ket{\psi}_n$ to denote a product state $\ket{{\downarrow}} \otimes \ket{\psi} \otimes \ket{{\downarrow}}$, whose $n$th factor is $\ket{\psi}$, all others being $\ket{{\downarrow}}$.
\begin{table*} \[\begin{array}{llll} \hline N & \mbox{vertices/equivalence classes}
& \mbox{geometry} & \mbox{Distances}\\\hline 3 & a=\{1,3\}, b=\{2\}
& \mbox{single edge}
& \overline{ab}=0.81 \\ 4 & a=\{1,4\}, b=\{2,3\}
& \mbox{single edge} & \overline{ab}=0.32 \\ 5 & a=\{1,5\}, b=\{2,4\}, c=\{3\}
& \mbox{triangle}
& 0.33 = \overline{ac}=\overline{bc} > \overline{ab} = 0.87\\ 6 & a=\{1,6\}, b = \{2,5\}, c=\{3,4\}
& \mbox{triangle}
& 0.48 = \overline{ab}=\overline{cb} > \overline{ac} = 0.36\\ 7 & a = \{1,7\}, b= \{2,6\}, c=\{3,5\}, d=\{4\}
& \mbox{triangular pyramid}
& \overline{ad}=\overline{bc}=\overline{cd} \gg
\overline{ab}=\overline{bc}=\overline{ac} \\ 8 & a = \{1,8\}, b= \{2,7\}, c=\{3,6\}, d=\{4,5\}
& \mbox{triangular pyramid}
& \overline{ad}=\overline{bc}=\overline{cd} >
\overline{ab}=\overline{bc}=\overline{ac} \\ 9 & a = \{1,9\}, b=\{3,7\}, c=\{4,6\}, d=\{2,8\}, e=\{5\}
& \mbox{4-simplex}
& \overline{ab}=\overline{ac}=\overline{bc}<
\overline{ad}=\overline{bd}=\overline{cd} \ll
\overline{ae}=\overline{be}=\overline{ce} \\ 10& a = \{1,10\}, b=\{2,9\}, c=\{4,7\}, d=\{5,6\}, e=\{3,8\}
& \mbox{4-simplex}
& \overline{ab}=\overline{ac}=\overline{bc} <
\overline{ad}=\overline{bd}=\overline{cd} <
\overline{ae}=\overline{be}=\overline{ce}\\\hline \end{array}\] \caption{ITC geometry of linear Heisenberg chains.} \label{table1} \end{table*}
\begin{figure*}
\caption{Chain length versus 4-point Gromov $\delta$ (left) and scaled 4-point Gromov $\delta$ (right). Scaled-Gromov $\delta$ remains below the upper bound singled out in~\cite{4point_Fariba}, 4-point Gromov $\delta$ saturates at large chain length, revealing Gromov hyperbolic property. $G=L+M+S$ where $L$, $M$ and $S$ are the pairs of opposite diagonals of a quadrangle corresponding to the largest, medium and smallest length.}
\label{f:Gromov-plot}
\end{figure*}
The probability that an excitation created at site $\ket{i}$ has propagated to site $\ket{j}$ after some time $t$ is given by \begin{equation}
p(\ket{i},\ket{j},t) = |\bra{j}e^{-\imath H t}\ket{i}|^2 \end{equation} in the system of units where $\hbar=1$. The maximum of this probability $p(i,j)=\max_{t\ge 0} p(i,j,t)$, or a monotonic function thereof such as \begin{equation}
\label{eq:dist}
d(i,j) = -\log p(i,j) \end{equation} gives a measure for the maximum state transfer fidelity between two nodes in a spin network without control, quantifying the intrinsic capacity of a spin network for quantum state transfer tasks. It can be shown that \begin{align*}
p(i,j)
&= \left| \bra{i} e^{-\imath H t} \ket{j} \right|
= \left| \sum_k \ip{i}{v_k} \ip{v_k}{j} e^{-\imath\lambda_k t}\right| \\
&\leq \sum_k \left| \ip{i}{v_k}\ip{v_k}{j} \right|, \end{align*} where $H=\sum_{k=1}^N \lambda_k \ket{v_k}\bra{v_k}$ is the eigendecomposition of the Hamiltonian operator $H$ of the network in the first excitation subspace $\mathcal{H}_1$. If the rescaled eigenvalues $\frac{\lambda_1}{\pi}, \ldots, \frac{\lambda_N}{\pi}$ are rationally independent~\cite[Proposition 1.4.1]{KatokHasselblatt} then it can be shown that for any $\epsilon>0$ there exists a $t_\epsilon>0$ such that $p_{\max}(i,j)-p(i,j,t_\epsilon))<\epsilon$, i.e., the maximum ITC is a tight bound and attainable in the limit.
\section{ITC Geometry \& Curvature of Chains}
\begin{figure*}
\caption{Inertia ($\alpha=2$) versus chain length plots for Heisenberg chains. For $N$ odd (left) the central node is a strong anti-gravity center. For $N$ even (right) there are weaker anti-gravity centers between end spins and middle (right). The inertia is symmetric about the central node as antipodal spins belong to the same equivalence class.}
\label{f:InertiaPlot-H}
\end{figure*}
\begin{figure*}
\caption{Inertia ($\alpha=2$) versus chain length plots for XX chains. For $N$ odd (left) the central node is a strong anti-gravity center and weaker anti-gravity centers exist for intermediate nodes. For $N$ (even) the anti-gravity centers are located between end and central spins. Again, the inertia is symmetric about the central node as antipodal spins belong to the same equivalence class.}
\label{f:InertiaPlot-XX}
\end{figure*}
Inspired by~\cite{eurasip_clustering} we may hope that the maximum ITC measure $d(i,j)$ defined above can be shown to be a distance. $d(i,j)$ clearly satisfies $d(i,i)=0$ as $p(i,i)=1$, and we also have symmetry as obviously $p(i,j)=p(j,i)$. However, $d(i,j)$ can vanish for $i\neq j$ if $p(i,j)=1$, and in general we cannot expect the triangle inequality to hold. In special cases, however, such as for homogeneous chains with either XX or Heisenberg coupling, numerical exploration for systems up to 500 spins shows that the triangle inequality \begin{equation}
D_{ijk} = d(i,k) + d(j,k)) - d(i,j) \ge 0. \end{equation} seems to be universally satisfied. This renders $d(i,j)$ a semi-distance, which induces a proper distance on a set of equivalence classes defined by identifying nodes with $d(i,j)=0$. Specifically, for Heisenberg or XX chain with uniform coupling the $N$ spins can be shown to form $\lceil\tfrac{N}{2}\rceil$ equivalence classes comprised of spins $n$ and $N+1-n$, which we shall denote by $n$ for $n=1,\ldots,\lceil N/2 \rceil$ in a slight abuse of notation. On this set of equivalence classes the ITC measure $d(i,j)$ is a metric, and it is interesting to study the induced geometry of a spin chain with respect to the ITC metric, and how it differs from the physical network geometry. Table~\ref{table1} gives the ITC geometry for Heisenberg chains up to $N=10$, showing that it is very different from the (trivial) physical geometry. A Heisenberg chain of length $N=7$, for instance, appears as a pyramid structure with an equilateral triangle as its base formed by the vertices $a=\{1,7\}$, $b=\{2,6\}$, $c=\{3,5\}$ and $d=\{4\}$ as its apex, where $n$ refers to the index of the spin in the chain. Chains up to length $N=8$ can be embedded in $\mathbb{R}^3$ but for longer chains higher-dimensional spaces are required. By Schoenberg's theorem~\cite{Schoenberg1935} the distances $d(i,j)$ can be realized in $\mathbb{R}^d$ if and only if the Gram matrix $G=(G_{ij})$ is positive semi-definite of rank $d$, where \begin{equation}
G_{ij} = \tfrac{1}{2} \left(d(i,N)^2 + d(j,N)^2 - d(i,j)^2 \right). \end{equation} (This is equivalent to the Cayley-Menger matrix criterion of~\cite{Blumenthal1953}.) We numerically verified that the Gram matrix for both Heisenberg and XX chains is positive semi-definite for spins up to $N=500$. Analysis of the rank of the Gram matrix furthermore suggests that the dimension $d$ required to embed a chain of length $N$ is $\lceil\tfrac{N-2}{2}\rceil$ for both Heisenberg and XX chains. Note that Schoenberg's theorem also applies to the geometric realisability of general spin networks and whether our ITC measure fulfills the triangle inequality.
To better understand the geometry for very long chains we analyze its curvature \`a la Gromov. From both the Gromov and the scaled-Gromov point of view~\cite{scaled_gromov} spin chain of both Heisenberg and XX coupling type appear hyperbolic. The strict Gromov point of view is displayed in Fig.~\ref{f:Gromov-plot}(a) and the scaled-Gromov point of view is shown in Fig.~\ref{f:Gromov-plot}(b). The Gromov property might appear to conflict with the Euclidean embeddability of the metric space made up by the clusters with the ITC metric, as the Bonk-Schramm~\cite{bonk_schramm} theorem says that Gromov negatively curved spaces are embeddable in hyperbolic space. However, some metric spaces are embeddable in {\it both} Euclidean and hyperbolic spaces, the most striking example being that of a complete graph with uniform edge weight, and spin chains with uniform couplings appear to fall into this category.
Classical communication networks, both wired~\cite{scaled_gromov, internet_mathematics} and wireless~\cite{eurasip_clustering}, have been shown to be Gromov hyperbolic. Gromov hyperbolic spaces have a unique vertex that achieves the minimum inertia~\cite{Jost1997}, the so-called \semph{gravity center} \begin{equation}
g = \arg \min_{i} I(i)
= \arg \min_{i} \sum_{j} d^\alpha(i,j), \quad \alpha \geq 1. \end{equation} Classical networks indeed show a point of minimum inertia, which can be interpreted as a congestion point~\cite{IJCCC}. Classical networks also have the property that their Gromov boundary in the asymptotic limit is a Cantor set~\cite{JonckheerLouHespanhaBarooahSep07}. Quite surprisingly, quantum networks differ from their classical counterparts in that they have points of maximum inertia, or \semph{anti-gravity centers}, as shown in Figs~\ref{f:InertiaPlot-H} and \ref{f:InertiaPlot-XX} for Heisenberg and XX chains, respectively, and their Gromov boundary is a single point. The interpretation of the antigravity center is that the information flow in the network avoids this node, making it difficult to transfer excitation to and from it. It is interesting to note in this context that the distance between antipodal nodes is $0$, meaning that we can achieve state transfer fidelities arbitrarily close to $1$, i.e., near perfect state transfer between the ends of the chain of any length given sufficient time, while near perfect state transfer is never possible between any pair of nodes with $d(i,j)>0$, no matter how long we wait.
\section{ITC ``Topology'' Of General Networks}
The maximum transfer probability is also a useful measure for the maximum fidelity of quantum state transfer in general spin networks. Although it is in general no longer a metric, it can still be used as a similarity measure to define a hierarchical clustering. We use the pairwise clustering algorithm introduced in~\cite{Mills2001a}. Pairs of nodes are grouped hierarchically into clusters in order of their similarity, and only those clusters whose elements are closer to each other than any element outside the cluster are preserved. If we define a relation \begin{equation}
\ket{a} =_\epsilon \ket{b} :\Leftrightarrow
d(\ket{a},\ket{b}) < \epsilon \end{equation} for nodes $\ket{a}$, $\ket{b}$, then these clusters are the equivalence classes of $=_\epsilon$ for a certain $\epsilon$. The cluster hierarchy reveals the closeness of the nodes in terms of information transfer.
For example, consider a network of 10 spins distributed in a square forming a general spin network as shown in Fig.~\ref{f:Cluster-network}. The positions of the spins are indicated by the blue dots. Taking the coupling strength $J(i,j)$ between spins $i$ and $j$ to be inversely proportional to the cube of the physical distance between the nodes, we compute the Hamiltonian of the network, assuming XX-coupling. We then diagonalize this Hamiltonian and compute the maximum transfer probabilities $p(i,j)$ and the associated $d(i,j)$, which are used as input for our clustering algorithm. The resulting hierarchical clustering structure is shown in Fig.~\ref{f:Cluster-network}. Different colours indicate clusters for different similarity levels; i.e. for clusters marked in the same colour there exists an $\epsilon$ for which these are the equivalence classes of $=_\epsilon$. Again, the example shows that the physical distance of the spins is not a good measure of their proximity in an quantum information transfer fidelity sense. For instance, spin $9$ is physically closer to $3$ than any of the other nodes, yet the clustering indices that $9$ and $3$ are several levels removed with regard to the maximum ITC.
\begin{figure}
\caption{Clustering induced by maximum transfer probability measure for a general spin network shows that clustering differs from what would be expected if we clustered according to physical distance.}
\label{f:Cluster-network}
\end{figure}
\section{Control of Information Transfer}
To overcome intrinsic limitations on quantum state transfer or speed up transfer, one can either try to engineer spin chains or networks with non-uniform couplings or introduce dynamic control to change the network topology. The idea of engineered couplings was originally proposed to achieve perfect state transfer between the end spin in spin chain quantum wires~\cite{perfect-state-transfer}. The analysis above shows that engineering the couplings is not strictly necessary. As the distance between the end spins with regard to the ITC metric defined above is zero for uniform XX and Heisenberg chains, we can achieve arbitrary high fidelities state transfer between the end spins if we wait long enough. Engineering the couplings, however, can speed up certain state transfer tasks such as state transfer between the end spins at the expense of others.
A more flexible alternative to fixed engineered couplings is to apply control. For instance, suppose we would like to transfer an excitation from node $1$ to $4$ for an XX chain of length $N=7$. Node $4$ being the anti-gravity center, the maximum transfer probability without control is low regardless how long we are prepared to wait. If we are able to change the Hamiltonian of the network by applying some control perturbtation so that $H=H_0+u(t)H_1$ we can change the situation even if the control is restricted to $u(t)=0,1$, and $H_1$ is a local perturbation, e.g., of a single spin induced by a magnetic field, e.g., $H_1=\op{\sigma}_z^{(1)}$. Switching the control on/off at times $t_n$ induces the evolution \begin{equation}
U_{u}(t_n,0) = U_{n-1\!\!\!\mod 2}(t_n,t_{n-1})
\cdots U_1(t_2,t_1)U_{0}(t_1,t_0) \end{equation} where $U_0(t_k,t_{k-1})=e^{-\imath (t_k-t_{k-1})H_0}$ and $U_1(t_k,t_{k-1})= e^{-\imath (t_k-t_{k-1})(H_0+H_1)}$. By optimizing the control sequence, i.e., in this restricted case the switching times $\{t_k\}$, we can change the dynamics to achieve near perfect transfer of an excitation or quantum state to a desired target node. In \cite{sophie_spin_network} it was shown that applying a simple bang-bang control sequence to a single spin can significantly speed up quantum state transfer between the ends of a chain, but control also allows us to overcome fundamental limits imposed the maximum ITC, enabling us to achieve near perfect excitation transfer to the anti-gravity center in very short time, as shown in Fig.~\ref{f:ControlEvol}, for example. We can think of the control sequence as implementing an effective Hamiltonian $H_{\rm eff}$ defined by $e^{-i H_{\rm eff} t_n} = U_{u}(t_n,0)$ at time $t_n$. This effective Hamiltonian differs from the system Hamiltonian $H_0$, as do the transition probabilities. For comparison, we diagonalize the effective Hamiltonian, compute the associated maximum transition probabilities $p_{\rm eff}(i,j)$, and use hierarchical clustering to elucitate the proximity relations between spins under the original and effective Hamiltonian. Fig.~\ref{f:Control} shows that the results for a particular control example.
\begin{figure}
\caption{Population of $\ket{4}$ for a uniform chain XX chain of length $N=7$ under free and controlled evolution. Under free evolution (dashed) the population cannot exceed $0.4268$ (dash-dot line) but control can overcome this restriction resulting in near perfect excitation transfer.}
\label{f:ControlEvol}
\end{figure}
\begin{figure}
\caption{Clustering induced by maximum transfer probability for a uniform chain XX chain of length $N=7$ without control (a) and clustering induced by controlled transition probability (b) for a bang-bang control sequence designed to achieve perfect state transfer from spin $1$ to $4$.}
\label{f:Control}
\end{figure}
\section{Conclusions}
Following the recent trend of {\it geometrization} of classical communication networks, we have here developed the geometry of spin networks using an Information Transfer Capacity metric. Classical and quantum networks bear the similarity that they are both Gromov hyperbolic, with the difference that classical networks have a Cantor Gromov boundary while spin chains have their Gromov boundary reduced to a point. This probably accounts for yet another discrepancy: classical networks have a gravity center (a congestion point) while quantum networks have an anti-gravity center, a spin difficult to communicate with. The broader implication of this geometrization is that it specifies {\it where} control is necessary to overcome such limitations of the physics.
\section{Acknowledgments}
Edmond Jonckheere acknowledges funding from US National Science Foundation under Grant CNS-NetSE-1017881. Sophie G Schirmer acknowledges funding from EPSRC ARF Grant EP/D07192X/1 and Hitachi. Frank C Langbein acknowledges funding for RIVIC One Wales National Research Centre from WAG.
\appendix
\subsection{proof of attainability}
\begin{theorem} \label{t:attainability} If the numbers $\frac{\lambda_1}{\pi},\ldots,\frac{\lambda_N}{\pi}$ are rationally independent~\cite[Proposition 1.4.1]{KatokHasselblatt}, then $\forall \epsilon>0$ there exists a $t>0$ large enough such that $p(i,j)-p(i,j,t)<\epsilon$. \end{theorem}
\begin{IEEEproof} Set the system of units such that $\hbar=1$. In order to reach the maximum probability {\it exactly}, one must find a $t$ such that \begin{align*} -\lambda_k t = (2m+1)\pi &\mbox{ if } \operatorname{Sgn}(v_{ik} v_{jk}) =-1\\ -\lambda_k t = (2m)\pi &\mbox{ if } \operatorname{Sgn}(v_{ik} v_{jk}) =+1 \end{align*} where $v_{ik}=\ip{i}{v_k}$ is the projection of the eigenstate $\vec{v_k}$ onto the basis state $\ket{i}$, etc, and $v_{ik}^*=v_{ik}$ as the eigenstates are real for real-symmetric Hamiltonians. In other words, the state of the $N$-dimensional dynamical system \begin{equation*}
\dot{\tilde{x}}(t) =
-\mbox{diag}\left\{\lambda_1,...,\lambda_N\right\}, \quad \tilde{x}(0)=0 \end{equation*} must hit a point whose coordinates are integer multiples of $\pi$, with the correct parity. As the pariety is not affected by the modulo $2\pi$ operation the problem reduces to whether the state of the system \begin{equation} \dot{x}(t) = -\mbox{diag}\left\{\lambda_1,...,\lambda_N\right\} \mod
2\pi, \quad x(0)=0 \end{equation} hits a point $x^*$ with coordinates $0$ or $\pi$, depending on the signs of the various $v_{ik}v_{jk}$. This dynamical system is the {\it linear flow} on the $N$-torus, $\mathbb{T}^N$ and by~\cite[Proposition 1.5.1]{KatokHasselblatt} it is minimal~\cite[Definition 1.3.2]{KatokHasselblatt}, that is, the orbit of {\it every point} is dense. (Observe that minimality is stronger than topological transitivity~\cite[Definition 1.3.1]{KatokHasselblatt}!) Hence we can get arbitrarily close to the point with desired coordinates provided we allow $t$ to be large enough. \end{IEEEproof}
To get a quantitative estimate of how close the state $x(t)$ has to be to the target point $x^*$ with coordinates $0,\pi$ so that $p(i,j)-p(i,j,t) \leq \epsilon$ note that \begin{align*} \sqrt{p(i,j)}
=& \left| \sum_k (\pm 1) v_{ik}v_{jk} \right| \\
=& \left| \sum_k v_{ik}v_{jk} e^{-\imath \lambda_k t}
+ v_{ik}v_{jk}\left(\pm 1-e^{-\imath \lambda_k t} \right) \right|\\
\leq & \sqrt{p(i,j)} + \sum_k \left| v_{ij}v_{jk}
\left(\pm 1 -e^{-\imath \lambda_k t} \right) \right|\\ \leq & \sqrt{p(i,j)}
+ \sum_k \left| \pm 1 -e^{-\imath \lambda_k t} \right|. \end{align*} Thus we have $\sqrt{p(i,j)}-\sqrt{p(i,j,t)} \leq
\sum_k \left| \pm 1 -e^{-\imath \lambda_k t} \right|$.
From physical considerations we know that $0\le p(i,j,t)\le 1$. \[
p_{\max}-p = \left(\sqrt{p_{\max}} -\sqrt{p} \right)
\left(\sqrt{p_{\max}} +\sqrt{p} \right) \] thus shows that to secure $p_{\max}-p\leq \epsilon$, it suffices to make
$\left|\pm 1 -e^{-\imath \lambda_k t}\right|\leq \frac{\epsilon}{2N}$. If we set $x_k(t)=-\lambda_kt$ and denote the dynamical target state as
$x^*_k:= 0 \mbox{ or } \pi$, it suffices that the target state and the actual state are within the specification $|x^*_k-x_k(t)|\leq \sin^{-1}\left(\frac{\epsilon}{2N}\right)$. Since the topology induced by hypercubes is equivalent to the usual topology induced by balls, the latter specification can be achieved by the density of the orbit of $0$.
\subsection{Estimate of time to attain maximum probability}
The preceding material only tells us that one can reach arbitrarily closely the maximum probability, but it does not tell us how much time it takes. A conservative estimate can be derived, conservative in the sense that it assumes that the dynamical evolution in $x$ has been discretized as the {\it translation on the torus}~\cite[Sec. 1.4]{KatokHasselblatt}, \[
x(n+1)= x(n)-\mbox{diag}\{\lambda_1,...,\lambda_N\}
\quad \bmod 2\pi, \quad x(0)=0 \] The key result is that, under the condition that $\frac{\lambda_1}{\pi},...,\frac{\lambda_N}{\pi},1$ are rationally independent, the {\it translation} on the torus is also minimal~\cite[Prop. 1.4.1]{KatokHasselblatt}. In this case, the problem consists in finding $n \in \mathbb{N}$ such that \begin{align*} -\lambda_k n = (2m+1)\pi &\mbox{ if } \operatorname{Sgn} (v_{ik}v_{jk})=-1\\ -\lambda_k n = (2m)\pi &\mbox{ if } \operatorname{Sgn} (v_{ik}v_{ij})=+1 \end{align*} is satisfied with arbitrary accuracy, which can be derived from:
\begin{theorem}[Nowak\cite{Novak84}] For any $\frac{\lambda_k}{\pi} \in \mathbb{R} \setminus \mathbb{Z}$, $k=1,...,N$, there exist infinitely many $((p_1,...,p_N),q) \in \mathbb{Z}^N \times \mathbb{N}$ such that \begin{equation}
\sum_{k=1}^N \left| -\frac{\lambda_k}{\pi} - \frac{p_k}{q}\right| \leq
\frac{c_N^{-1/N}}{q^{1+1/N}} \end{equation} where the supremum, $\bar{c}_N$, of all $c_N$'s satisfying the above is known as $\bar{c}_1=\sqrt{5}$, $\bar{c}_2=\sqrt{23}/2$, and for larger $N$ estimated as $\bar{c}_3 \geq 1.7739$, and, for $N \geq 4$, $\bar{c}_N \geq (N+1)^{(N+1)/2} N^{-N/2}(\pi/2)^{(N+1)/2}/\Gamma((N+5)/2)$. \end{theorem}
We already know by the minimality of the discrete flow, except for the error bound. Therefore, the set of $((p_1,...,p_N),q) \in \mathbb{Z}^N \times \mathbb{N}$ of the above theorem and the set of those that satisfy the parity condition have a nonempty intersection. Take a $((p_1,...,p_N),q)$ in this intersection; thus the $p_k$ are consistent with the parity condition. Hence \begin{equation*}
\sum_{k=1}^N \left| -\frac{\lambda_k n}{\pi} - \frac{p_k}{q}n \right|
< \frac{c_N^{-1/N}}{q^{1+1/N}} n \end{equation*} Taking $n = q$ yields an $\ell^1$ error bound of $c_N^{-1/N}/q^{1/N}$ on the $(x/\pi)$-dynamics and furthermore an error bound of $\frac{\pi c_N^{-1/N}}{q^{1/N}} =: \epsilon$ on the $x$-dynamics. Thus the time it takes to be within an $\ell^1$-ball of ``radius'' $\epsilon$ around one of the desired points is estimated as $n = q \approx \frac{\pi^N c_N^{-1}}{\epsilon^N}$.
\end{document} | arXiv |
The Value of Information
The Value of Information pp 91-141 | Cite as
The Informative Role of Advertising and Experience in Dynamic Brand Choice: An Application to the Ready-to-Eat Cereal Market
Yan Chen
Ginger Zhe Jin
We study how consumers make brand choices when they have limited information. In a market of experience goods with frequent product entry and exit, consumers face two types of information problems: first, they have limited information about a product's existence; second, even if they know a product exists, they do not have full information about its quality until they purchase and consume it. In this chapter, we incorporate purchase experience and brand advertising as two sources of information and examine how consumers use them in a dynamic process. The model is estimated using the Nielsen Homescan data in Los Angeles, which consist of grocery shopping history for 1,402 households over 6 years. Taking ready-to-eat cereal as an example, we find that consumers learn about new products quickly and form strong habits. More specifically, advertising has a significant effect in informing consumers of a product's existence and signaling product quality. However, advertising's prestige effect is not significant. We also find that incorporating limited information about a product's existence leads to larger estimates of the price elasticity. Based on the structural estimates, we simulate consumer choices under three counterfactual experiments to evaluate brand marketing strategies and a policy on banning children-oriented cereal advertising. Simulation suggests that the advertising ban encourages consumers to consume less sugar and more fiber, but their expenditures are also higher because they switch to family and adult brands, which are more expensive.
Consumer choice Experience goods Informative and prestige advertising Ready-to-eat cereal market Child-oriented advertising Childhood obesity
This paper is based on Yan Chen's dissertation, "Information, Consumer Choice and Firm Strategy in an Experience Good Market" (August 2008). We are deeply grateful to Mark Denbaly and Ephraim Leibtag at the U.S. Department of Agriculture's Economic Research Service for providing access to the Nielsen Homescan data. We have also benefited from the insightful comments of John Rust, Roger Betancourt, Erkut Ozbay, Pallassana Kannan, and seminars participants at the University of Maryland and the Economic Research Service. All errors are ours.
5. Appendixes
5.1.Controlling for Unobserved Consumer Heterogeneity
We introduce consumer-brand random effects to capture the unobserved consumer heterogeneity in brand preferences. Specifically, the utility function can be written as
$$ {U_{ijt}} = {Z_{ijt}} \bullet \Phi + {\nu_{ij}} + {\varepsilon_{ijt}} $$
where Z ijt represents the vector of explanatory variables, Φ represents the vector of coefficients corresponding to Z ijt , and \( {\nu_{ij}} \)represents consumer i's unobserved preference for brand j, which is independent from \( {Z_{ijt}} \) and\( {\varepsilon_{ijt}} \).
Let \( {\nu_{ij}} = {\mu_{ij}} + {\omega_j} \). \( {\mu_{ij}} : N(0,\varsigma_{ij}^2) \), and \( {\omega_j} = E({\nu_{ij}}) \) is a constant. Assuming \( {\varepsilon_{ijt}} \) has a generalized extreme value distribution, then we can write the probability that consumer i will choose j conditional on\( {\mu_{i1}},\;{\mu_{i2}}, \ldots {\mu_{i51}} \), and choice set \( {C_{it}} \)as
$$ \begin{array}{llll} P(j|{\mu_{i1}},{\mu_{i2}},...,{\mu_{i51}},{C_{it}}) = & \frac{{\exp (({Z_{ijt}} - {Z_{i51t}}) \bullet \Phi + {\mu_{ij}} + {\omega_j} - {\omega_{51}})}}{{\sum\limits_{l = 1}^{51} {\exp (({Z_{ilt}} - {Z_{i51t}}) \bullet \Phi + {\mu_{il}} + {\omega_l} - {\omega_{51}})} }} \\= & \frac{{\exp ({z_{ijt}} \bullet \Phi + {\mu_{ij}} + {\xi_j})}}{\sum\limits_{l = 1}^{51} {\exp ({z_{ilt}} \bullet \Phi + {\mu_{il}} + {\xi_l})}} \end{array} $$
where for the second equal sign we use \( {z_{ijt}} = {Z_{ijt}} - {Z_{i51t}} \) and \( {\xi_j} = {\omega_j} - {\omega_{51}} \).
\( p(j|{C_{it}}) \)is equal to \( P(j|{\mu_{i1}},{\mu_{i2}}, \ldots, {\mu_{i51}},{C_{it}}) \)integrated over the marginal distribution of the \( {\mu_{ij}} \)'s. Specifically, it is equal to
$$ \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {...\int_{ - \infty }^\infty {\frac{{\exp ({z_{ijt}} \bullet \Phi + {\mu_{ij}} + {\xi_j})}}{{\sum\limits_{l = 1}^{51} {\exp (} {z_{ilt}} \bullet \Phi + {\mu_{il}} + {\xi_l})}}f(} } } {\mu_{i1}})f({\mu_{i2}}) \ldots f({\mu_{i51}})d{\mu_{i1}}d{\mu_{i2}} \ldots d{\mu_{i51}} $$
It is hard to compute \( p(j|{C_{it}}) \) analytically, and we simulate it by taking S draws from the distribution of \( {\mu_{ij}} \), for all j. The simulator for\( p(j|{C_{it}}) \) is
$$ \hat{p}(j|{C_{it}}) = \frac{1}{S}\sum\limits_{s = 1}^S {\frac{{\exp ({z_{ijt}} \bullet \Phi + \mu_{ij}^s + {\xi_j})}}{{\sum\limits_{l = 1}^{51} {\exp ({z_{ilt}} \bullet \Phi + \mu_{il}^s + {\xi_l})} }}} $$
To reduce the number of parameters to be estimated, we allow \( {\omega_j} \) to vary across brand segment, and \( \varsigma_{ij}^2 \) to vary across both brand segment and whether the household has children. There are a total of eight parameters to estimate for unobserved consumer-brand preferences, of which six are scale parameters: \( \varsigma_{FK}^2,\varsigma_{FN}^2,\varsigma_{AK}^2,\varsigma_{AN}^2,\varsigma_{KK}^2,\varsigma_{KN}^2 \), where the first subscript denotes whether the brand belongs to the family, adult, or kid segment, and the second subscript denotes whether there are any children in the household; two are location parameters: \( {\omega_A} \) and \( {\omega_K} \), where the subscript denotes whether the brand belongs to the adult or kid segment. \( {\omega_F} \) is normalized to zero.
5.2.Choice Set Simulation Details
In the simulation, we assume that choice set is a function of brand advertising and purchase experience, as shown in Eqs. (5.1) and (5.2). The specific choice set simulation process is outlined as follows.
Step 1. Calculate \( {q_{ijt}} \)(ϕ) for each consumer, each brand, and each time, where ϕ = (ϕ0, ϕ1, ϕ2).
Step 2. For each consumer-time-brand combination, draw a random number \( u_{ijt}^r \)from the uniform distribution between 0 and 1.
Step 3. If \( u_{ijt}^r < {q_{ijt}} \), then brand j is included in consumer i's choice set at time t; otherwise it is not. This defines the choice set in the rth simulation \( C_{it}^r \). After simulating the choice set, we can calculate simulated brand choice probabilities for each consumer.
Step 4. Calculate \( {P^r}(j|{C_{it}}) \), consumer i's probability of choosing brand j conditional on \( C_{it}^r \) . (The formula for calculating \( {P^r}(j|{C_{it}}) \) depends on the distributional assumption on the error term in the utility function).
Step 5. Calculate \( p_{ijt}^r = \prod\limits_{j \in C_{it}^r} {{q_{ijt}}\prod\limits_{k \notin C_{it}^r} {(1 - {q_{ikt}})} } \times {P^r}(j|{C_{it}}) \), consumer i's unconditional probability of choosing brand j at time t in the rth simulation.
Step 6. Draw the random numbers \( u_{ijt}^r \) repeatedly for R times, and each time repeat steps 2–5.
Step 7. Calculate the simulated choice probability \( {\hat{p}_{ijt}} = \frac{1}{R}\sum\limits_{r = 1}^R {p_{ijt}^r} . \).
5.3.Contraction Mapping Details
In the instrumental variable estimation, we need to find the δ that makes predicted market shares based on the model equal to the observed market shares. Given an initial guess of δ, \( \Pi \), and \( \Sigma \), the predicted market share for brand j, \( {\sigma_j}(\delta^h,\Pi, \Sigma, \kappa, \lambda, \gamma ) \), is calculated as follows.
First, based on advertising data and household characteristics, simulate choice sets for each consumer on each shopping occasion.
Second, given δ, \( \Pi \),\( \Sigma \), κ, λ, and γ, a consumer compares the utility levels of all brands in his choice set on the shopping occasion and chooses the one that yields the highest utility.
Third, sum the consumer brand choices in a year to get predicted brand market shares.
To obtain the values of δ that solve \( {\sigma_j}(\delta^h,\Pi, \Sigma, \kappa, \lambda, \gamma ) = {S_j} \), we use the iteration
\( \delta_j^{h + 1} = \delta_j^h + \ln ({S_j}) - \ln ({\sigma_j}(\delta^h,\Pi, \Sigma, \kappa, \lambda, \gamma )) \). The proof that the iteration is a contraction mapping follows Goeree (2008).
Define \( f({\delta_j}) = {\delta_j} + \ln ({S_j}) - \ln ({\sigma_j}(\delta^h,\Pi, \Sigma, \kappa, \lambda, \gamma )) \). To show that f is a contraction mapping, we need to show that \( \forall \)j and m, \( \partial f({\delta_j})/\partial {\delta_m} \ge 0 \), and \( \sum\limits_{m = 1}^J {\partial f({\delta_j}} )/\partial {\delta_m} < 1 \).
We can write\( {\sigma_j} = \int {\sum\limits_{{C_i} \in {\Omega_j}} {\prod\limits_{l \in {C_i}} {{q_{ilt}}} \prod\limits_{k \not in {C_i}} {(1 - {q_{ikt}}} )} } P(j|{C_i})f(v)dv \),where, and Ωj denotes the set of choice sets that include j.
$$ \partial f({\delta_j})/\partial {\delta_m} = \frac{1}{{{\sigma_j}}}\int {\sum\limits_{{C_i} \in {\Omega_j}} {\prod\limits_{l \in {C_i}} {{q_{ilt}}} \prod\limits_{k \notin {C_i}} {(1 - {q_{ikt}}} )} } P(j|{C_i})Q_j^mf(v)dv, $$
$$ p(j|{C_i}) = \int\limits_v {\frac{{\exp ({\delta_j} + {\chi_j}\bullet \Pi \bullet {D_i} + {\chi_j}\bullet \Sigma \bullet v + \kappa \cdot unuse{d_{ij}} + {\lambda_i} \cdot unuse{d_{ij}} \cdot ad{v_j} + pastchoic{e_{ij}} \bullet \gamma )}}{{\sum\limits_{k = 1}^{51} {\exp ({\delta_k} + {\chi_k}\bullet \Pi \bullet {D_i} + {\chi_k}\bullet \Sigma \bullet v\kappa \cdot unuse{d_{ij}} + {\lambda_i} \cdot unuse{d_{ij}} \cdot ad{v_j} + pastchoic{e_{ij}} \bullet \gamma )} }}} f(v)d(v)$$
$$ \begin{array}{llll} Q_j^m = \frac{{\exp ({\delta_m} + {\chi_m}\bullet \Pi \bullet {D_i} + {\chi_m}\bullet \Sigma \bullet v + \kappa \cdot unuse{d_{im}} + {\lambda_i} \cdot unuse{d_{im}} \cdot ad{v_m} + pastchoic{e_{im}} \bullet \gamma )}}{{\sum\limits_{l \in {C_i}} {\exp ({\delta_l} + {\chi_l}\bullet \Pi \bullet {D_i} + {\chi_l}\bullet \Sigma \bullet v + \kappa \cdot unuse{d_{il}} + {\lambda_i} \cdot unuse{d_{il}} \cdot ad{v_l} + pastchoic{e_{il}} \bullet \gamma )} }},if\begin{array}{*{20}{c}} {m \in {\Omega_j}} & {} \\ \end{array} \hfill \\ \begin{array}{*{20}{c}} {} & { = 0,if\begin{array}{*{20}{c}} {m \notin {\Omega_j}} & {} \\ \end{array} } \\ \end{array} \hfill \\ \end{array} $$
Note that for m = j, \( Q_j^m = P(j|{C_i}) \)
Since all elements in the integral are nonnegative, we have \( \partial f({\delta_j})/\partial {\delta_m} \ge 0 \).
Moreover, \( \sum\limits_{m \in {\Omega_j},m \ne 51} {Q_j^m} < 1 \), therefore \( \sum\limits_{m \in {\Omega_j},m \ne 51} {\partial f({\delta_j}} )/\partial {\delta_m} \,< \,1 \) is satisfied.
5.4.Price Elasticity Calculation
Suppressing the time subscript, we can write the consumer utility function as
$$ {U_{ij}} = {\alpha_i}{p_j} + {\Upsilon_j}g {\beta_\Upsilon }_i + {\varepsilon_{ij}} $$
where \( {\alpha_i} = \alpha + {\Pi_3}g {D_i} + {\Sigma_{33}} \cdot {v_3} \), \( {\Upsilon_j} \) represents the vector of variables other than price, and \( {\beta_{\Upsilon i}} \) the vector of coefficients for \( {\Upsilon_j} \).
The formula for price elasticity is given by
$$ {\rho_{jk}} = \frac{{\partial {s_j}}}{{\partial {p_k}}} \cdot \frac{{{p_k}}}{{{s_j}}} = \left\{ {\begin{array}{ll} {\frac{{{p_j}}}{{{s_j}}}\frac{1}{N}\sum\limits_{i = 1}^N {\int {{\alpha_i}{{\hat{p}}_{ij}}(1 - {{\hat{p}}_{ij}})f(v)dv,\begin{array}{ll} {j = k} & {} \\\end{array} } } } \\{ - \frac{{{p_k}}}{{{s_j}}}\frac{1}{N}\sum\limits_{i = 1}^N {\int {{\alpha_i}{{\hat{p}}_{ij}}{{\hat{p}}_{ik}}f(v)dv,\begin{array}{ll} {j \ne k} & {} \\\end{array} } } } \\\end{array} } \right. $$
where p ij represents the probability that consumer i will choose brand j.
In the estimation, we take NR random draws of v from f(v) to get αi and compute ρ jk using the formula
$$ {\hat{\rho }_{jk}} = \left\{ {\begin{array}{lll} {\frac{{{p_j}}}{{{s_j}}}\frac{1}{{N*NR}}\sum\limits_{i = 1}^N {\sum\limits_{nr = 1}^{NR} {\alpha_{_i}^{nr}{{\hat{p}}_{ij}}(1 - {{\hat{p}}_{ij}})} }, j = k} \\{ - \frac{{{p_k}}}{{{s_j}}}\frac{1}{{N*NR}}\sum\limits_{i = 1}^N {\sum\limits_{nr = 1}^{NR} {\alpha_{_i}^{nr}{{\hat{p}}_{ij}}{{\hat{p}}_{ik}},j \ne k} } } \\\end{array} } \right. $$
5. Commentary: Explaining Market Dynamics: Information Versus Prestige
Mead Over
Information is valuable to cereal manufacturers, who pay for advertising. Information is valuable to consumers, who reveal by their expenditure response that they attend to advertising. Information is valuable to nutrition activists, as a policy instrument to manipulate in the paternalistic hope that consumers deprived of advertising for sugary cereals will feed their children less sugar. And finally, information is valuable to the authors of the chapter, because using more of it enables them to explain more of the variation in market shares across the cereal brands and to predict more plausibly the reaction of consumers to price or advertising interventions for an individual brand or by a government consumer protection agency
Advertising is one of the industries whose business model involves the packaging and delivery of information. In contrast to the commercial publishing industry, wherein the author and originator of the information profits when the consumer values the information enough to buy the book, profits of the advertising industry derive from the advertiser's willingness to pay to subsidize information provision to the consumer. The distinction is due to the fact that consumers of books value them for their own sake, whereas consumers of information about advertised products use that information to inform their expenditures on those products. In an imperfectly competitive market for ready-to-eat cereals, cereal manufacturers are willing to subsidize consumers' information acquisition in order to differentiate brands from one another and reduce consumers' price elasticity of demand for their own brands.
The chapter deploys a variety of interesting microeconomic modeling and computationally intense econometric techniques to exploit a large data set on consumer purchases of ready-to-eat cereals and estimate the potential effect of a specific type of government intervention in this market: a ban on the advertising of children's cereal. The authors conclude that such a ban would indeed be effective in reallocating consumer expenditure away from the least healthful types of cereals and toward more healthful, more expensive brands, but it would induce consumers to spend more on cereal than they would without the ban. But one wonders whether the extraordinarily complex econometric paraphernalia the authors would really be required to show these impacts of advertising.
Since the authors generously provide the market shares of the top 50 brands as well as their average prices, brand-specific monthly advertising expenses, and market segment (in Table 5.2), one can calculate a descriptive ordinary least squares regression of (the logit of) market share on this grouped data. The results of this "naïve" regression are presented here in Table 5.C.1.
Table 5.C.1
Ordinary least squares regression of logit of average market share on log price and advertising expenditures, by market segment
Number of obs = 50 F(8, 41) = 10.73 Prob > F = 0.0000 R-squared = 0.6768 Adj R-squared = 0.6137 Root MSE = .55338
Logit of (marketshare)
Coef.
P > |t|
[95%]
Log(price):
−.88
.00086
Constants:
−13.43
Source: This reviewer's estimates using the grouped data from Table 5.2
Although requiring very little effort beyond the tabulation of the average market shares, prices, and advertising expenditures for the 50 top brands, these results seem somewhat informative. The point estimates of the three estimated price coefficients, one for each of the three market segments, are all negative, as expected, with the one for family cereals being large (>2 in absolute magnitude) and statistically significant. Furthermore, all three advertising coefficients are highly statistically significant, suggesting that an extra million dollars of advertising increases market share by 0.86% for adult cereals, 0.92% for family cereals, and 1.05% for kid cereals. The category of kid cereals seems to respond more to advertising expenditures than the other two.
So why do more? What have the authors' prodigious efforts added to our knowledge of the ready-to-eat cereal market?
This chapter supports the proposition that "information is valuable to economic researchers" in three ways. First, by exploiting detailed information on the thousands of individual consumer transactions summarized in Table 5.2, the authors are able to relax several of the assumptions that are maintained by the above naïve analysis. In so doing, they demonstrate the value of that detailed information to the understanding of this complex market. Second, by bringing to bear an economic theory of decision making, the authors demonstrate that this theory itself has information content—because it helps explain the market data. Third, by combining the unusually detailed and granular data with this powerful theory, the authors are able to distinguish the two channels by which advertising hypothetically affects consumer behavior, the "information" channel and the "prestige" channel, and to demonstrate that it's the information that influences the consumer's behavior—not the prestige. Fourth, by using information from the supply side of the cereal market, the authors are able to reject some types of endogeneity that would cast doubt not only on my naïve model, but also on their three principal models.
Consider the estimated price elasticities. Figure 5.C.1 displays for each of the three market segments the confidence intervals for my naively estimated price elasticities from Table 5.C.1 and the range of estimated elasticities for the top 10 cereal brands presented by the authors in their Table 5.8. There are two adult cereal brands in the top 10, six family brands and two kid brands. Note the extremely wide confidence intervals from my naïve estimates. Next to those confidence intervals (in green), my Fig. 5.C.1 displays the range of estimated price elasticities for each of the authors' three estimated models. Although the authors do not report confidence intervals, the point estimates of the brand-specific coefficient estimates from which these elasticities are derived (the first row of Table 5.5) are from 3 to 50 times larger than their estimated standard errors, suggesting tight confidence intervals for the elasticities. And the range of these reported estimates is also relatively tight within each market segment. Thus, one benefit of the information in the granular data appears to be tighter estimates of the brand-specific price elasticities.
Fig. 5.C.1
Adding information either with more granular data or more theory-constrained economic structure increases both the precision and heterogeneity of estimated price elasticities across brands
The authors' basic model is a random-coefficients logit model (RCL) structured to assume that the choice sets for all consumers include all 50 brands (plus a 51st composite of all other brands) and characteristics of all brands are known. Figure 5.C.1 shows that the estimated elasticities for this model are roughly the same across the three market segments. (See the orange boxes in Fig. 5.C.1.) The authors' second model, whose elasticity estimates are represented by the blue boxes labeled "RCL + Learning," relaxes the assumption that all consumers know the characteristics of all brands. In this model the consumers again choose among all brands but only know the qualities of brands previously purchased. Advertising directly influences a brands market share. Thus, the impact of the economic theory on the estimated elasticities is to differentiate the three theoretically distinct markets, information that is useful to students of this ready-to-eat cereal market. Finally when the authors use an elaborate simulation model to require advertising to inform consumers of an unused brand's existence before it can affect their purchases (the assumption of heterogeneous choice sets), the estimated elasticities diverge even more across the three market segments (pink boxes) and also increase substantially in absolute magnitude. In the words of the authors, "[t]he estimated price elasticities in the … specification [allowing a heterogeneous choice set] are more plausible, since their absolute values are all bigger than 1, which is consistent with the fact that profit-maximizing firms should be operating at the elastic part of the demand curve." Once more, economic theory has improved the fit of the model and contributed insight on the cereal market.
Variation in observed market shares, the naïve model contains substantial information. Its prediction error (defined by the authors as the square root of the sum of squared differences between the actual market share of Table 5.6 and the predicted share) equals 6.5, which is actually less than the 7.26 scored by the authors' random-coefficients model (bottom row of Table 5.6). However, both of the authors' more sophisticated models do better than my naïve model, scoring 5.28 and 3.81 respectively, and thus can be said to contain more valuable information.
Because they are able to simulate the consumers' choice sets each time on each visit to the grocery store, the authors can distinguish the two possible channels by which advertising might induce people to spend more on cereal—the information channel and the prestige channel. It's interesting that for this market, the authors find no support for the hypothesis that advertising persuades consumers to increase their consumption of ready-to-eat cereals that are familiar to them—which would be a prestige effect of advertising. Instead, advertising's role seems to be to induce consumers to try cereals that are unfamiliar. When they model this effect, the authors estimate much larger price elasticities (the pink boxes in Fig. 5.C.1). Since consumers have many choices in the cereal market, evidence that price elasticities are large in the children's cereal market and small in the adult cereal market suggests that the adults who purchase cereal for children see them as highly substitutable for one another, whereas they are loath to substitute one adult cereal for another. Adult cereal brands thus have more market power than children's brands.30
The authors' simulations of a ban on advertising for children's cereal and of a "pulsed" advertising strategy both raise the issue of the potential value to the public of government use of advertising. Using their third model, which incorporates consumer learning and heterogeneous choice sets, and assuming that affected cereal manufacturers hold constant the prices of their brands, the authors simulate a ban on advertising and conclude that "the total market share of kid brands goes down by about 6%, of which 2% goes to the adult brands and 4% goes to the family brands." It's possible to perform this same experiment with the naïve model, by first computing the fitted market shares from the OLS regression in the children's market and then computing them a second time after the value of advertising has been set to zero. The result from the naïve model is that the total market share of children's brands would decline from 17.7 to 9.5% of the market, a reduction of about 8.2%. Under the assumption of the independence of irrelevant alternatives (the well-known IIA assumption typically maintained in multinomial logit models), about 2.2 percentage points of this decline would be reflected by an increase in the adult segment and about 5.8% age points would go to the family segment. Despite the simplicity of the naïve model, these results are remarkably similar to those obtained by the authors.
In contrast to the ban on advertising of children's cereals, the possible effects on the market of pulsed advertising could not be analyzed with the naïve model. The authors have used their heterogeneous choice set model to show that spreading the same advertising dollars smoothly is less effective at increasing market share than would be a strategy of bunching the advertising in specific months. The superior effectiveness of pulsing seems to be due to the lack of a prestige effect of advertising in this market. The implication is that government public awareness campaigns that intend to improve people's awareness of alternatives—and subsequently depend on their good experience with these alternatives to motivate behavior—could also benefit from pulse advertising. Whether the reverse is true for public awareness campaigns that intend to enhance the prestige of certain behavior remains to be determined.
The authors allude in passing to monopolistic pricing strategies when they point out that a monopolist operates in the elastic portion of its demand curve. Under certain conditions one could go further and assert that a profit-maximizing firm in a monopolistic or monopolistically competitive market will set its price-cost margin equal to the inverse of the elasticity of demand. According to the authors' heterogeneous choice set model, the median elasticities in the adult, family, and children's market segments are about −1.5, −2.3, and −2.8, respectively. This suggests that typical markups of price over marginal cost in these three segments are 65, 49, and 38 % of marginal costs, respectively. Furthermore, markups on individual brands vary from 34 to 72% of marginal costs. This information is of only academic interest in the market for ready-to-eat cereals, imagine if a similar analysis of the pharmaceutical market revealed such information about the prices of pharmaceutical brands. Views on pharmaceutical pricing range from the idea that monopoly profits in the pharmaceutical market are unproductive "rent" gained from branding products that largely result from government-subsidized research to the position that these profits are a just return on pharmaceutical firms' own research investments and motivate their future research. An objective observer would grant that both views have some legitimacy in various parts of the market. But policy intervention on the prices of individual drugs is hampered by the secrecy with which pharmaceutical firms guard their cost information. To the extent that the techniques employed in this chapter could be used to reveal the apparent markups of pharmaceutical prices over costs, regulators would value this information as an input to the regulation of the monopoly prices of individual pharmaceutical products.
Ackerberg, D. (2001). Empirically distinguishing informative and prestige effects of advertising. The RAND Journal of Economics, 32(2), 316–333.CrossRefGoogle Scholar
Ackerberg, D. (2003). Advertising, learning, and consumer choice in experience good markets: A structural empirical examination. International Economic Review, 44(3), 1007–1040.CrossRefGoogle Scholar
Allenby, G., & Ginter, J. (1995). The effects of in-store display and feature advertising on consideration sets. International Journal of Research in Marketing, 12, 67–80.CrossRefGoogle Scholar
Anand, BN., & Shachar, R. (2011). Advertising, the Matchmaker. The RAND Journal of Economics, 42(2), 205–245.Google Scholar
Andrews, R., & Srinivasan, T. (1995, Feburary). Studying consideration effects in empirical choice models using scanner panel data. Journal of Marketing Research, 32, 30–41.CrossRefGoogle Scholar
Becker, G., & Murphy, K. (1993). A simple theory of advertising as a good or bad. Quarterly Journal of Economics, 108, 942–964.CrossRefGoogle Scholar
Berry, S. (1994). Estimating discrete choice models of product differentiation. The RAND Journal of Economics, 25(2), 242–262.CrossRefGoogle Scholar
Berry, S., Levinsohn, J., & Pakes, A. (1995). Automobile prices in market equilibrium. Econometrica, 63(4), 841–890.CrossRefGoogle Scholar
Berry, S., Levinsohn, J., & Pakes, A. (2004). Differentiated products demand systems from a combination of micro and macro data: The new car market. Journal of Political Economy, 112(1), 68–105.CrossRefGoogle Scholar
Berry, S., Linton, O., & Pakes, A. (2004). Limit theorems for estimating the parameters of differentiated product demand systems. Review of Economics Studies, 71(3), 613 –654.CrossRefGoogle Scholar
Betancourt, R., & Clague, C. (1981). Capital utilization: A theoretical and empirical analysis. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Butters, G. (1977). Equilibrium distribution of prices and advertising. The Review of Economic Studies, 44, 465–492.CrossRefGoogle Scholar
Chen, Y., & Kuan, C. (2002). The pseudo-true score encompassing test for non-nested hypotheses. Journal of Econometrics, 106, 271–295.CrossRefGoogle Scholar
Chintagunta, P., Jiang, R., & Jin, G. (2009). Information, learning, and drug diffusion: The case of Cox-2 inhibitors. Quantitative Marketing and Economics, 7(4), 399–443.CrossRefGoogle Scholar
Costantino, C. (2004). Three essays on vertical product differentiation: Exclusivity, non-exclusivity and advertising. Ph.D. dissertation, University of Maryland, College Park.Google Scholar
Crawford, G., & Shum, M. (2005). Uncertainty and learning in pharmaceutical demand. Econometrica, 73, 1137–1174.CrossRefGoogle Scholar
Dubé, J. (2004). Multiple discreteness and product differentiation: Demand of carbonated soft drinks. Marketing Science, 23(1), 66–81.CrossRefGoogle Scholar
Dubé, J., Hitsch, G., & Manchanda, P. (2005). An empirical model of advertising dynamics. Quantitative Marketing and Economics, 3(2), 107–144.CrossRefGoogle Scholar
Einav, L., Leibtag, E., & Nevo, A. (2010, June). Recording discrepancies in Nielsen Homescan data: Are they present and do they matter? Quantitative Marketing and Economics, 8(2), 207–239.CrossRefGoogle Scholar
Eliaz, K., & Spiegler, R. (2011). Consideration sets and competitive marketing, Review of Economic Studies, 78(1), 235–262.Google Scholar
Erdem, T., & Keane, M. (1996). Decision-making under uncertainty: Capturing dynamic brand choices in turbulent consumer goods markets. Marketing Science, 15, 1–20.CrossRefGoogle Scholar
Geweke, J., Keane, M., & Runkle, D. (1994). Alternative computational approaches to inferences in the multinomial probit model. The Review of Economics and Statistics, 76(4), 609–632.CrossRefGoogle Scholar
Goeree, M. S. (2008). Limited information and advertising in the US personal computer industry. Econometrica, 76(5), 1017–1074.CrossRefGoogle Scholar
Grossman, G., & Shapiro, C. (1984). Informative advertising with differentiated products. The Review of Economic Studies, 51, 63–81.CrossRefGoogle Scholar
Hausman, J. (1996). Valuation of new goods under perfect and imperfect competition. In The economics of new goods (pp. 209–237). Chicago: University of Chicago Press.Google Scholar
Hendel, I. (1999). Estimating multiple-discrete choice models. The Review of Economic Studies, 66(2), 423–446.CrossRefGoogle Scholar
Hendel, I., & Nevo, A. (2006). Measuring the implications of sales and consumer inventory behavior. Econometrica, 74(6), 1637–1673.CrossRefGoogle Scholar
Hitsch, G. (2006). An empirical model of optimal dynamic product launch and exit under demand uncertainty. Marketing Science, 25(1), 25–50.CrossRefGoogle Scholar
Keane, M. (1994). A computationally practical simulation estimator for panel data. Econometrica, 61(1), 95–116.CrossRefGoogle Scholar
Kihlstrom, R., & Riordan, M. (1984). Advertising as a signal. Journal of Political Economy, 92, 427–450.CrossRefGoogle Scholar
Mehta, N., Rajiv, S., & Srinivasan, K. (2003). Price uncertainty and consumer search: A structural model of consideration set formation. Marketing Science, 22(1), 58–84.CrossRefGoogle Scholar
Milgrom, P., & Roberts, J. (1986). Price and advertising signals of product quality. Journal of Political Economy, 94, 796–821.CrossRefGoogle Scholar
Naik, P., Mantrala, M., & Sawyer, A. (1998). Planning media schedules in the presence of dynamic advertising quality. Marketing Science, 17(3), 214–235.CrossRefGoogle Scholar
Nelson, P. (1970). Information and consumer behavior. Journal of Political Economy, 78(2), 311–329.CrossRefGoogle Scholar
Nelson, P. (1974). Advertising as information. Journal of Political Economy, 82, 729–753.CrossRefGoogle Scholar
Nevo, A. (2001). Measuring market power in the ready-to-eat cereal industry. Econometrica, 69(2), 307–342.CrossRefGoogle Scholar
Nevo, A., & Hendel, I. (2006). Sales and consumer inventory. The RAND Journal of Economics, 37(3), 543–561.Google Scholar
Osborne, M. (2006). Consumer learning and habit formation in packaged goods markets, Ph.D. thesis. Stanford University.Google Scholar
Roberts, J., & Lattin, J. (1997). Consideration: Review of research and prospects for future insights. Journal of Marketing Research, 34(3), 406–410.CrossRefGoogle Scholar
Shum, M. (2004). Does advertising overcome brand loyalty? Evidence from the breakfast-cereals market. Journal of Economics and Management Strategy, 13(2), 241–272.CrossRefGoogle Scholar
Stigler, G., & Becker, G. (1977). De Gustibus Non Est Disputandum. The American Economic Review, 67(2), 76–90.Google Scholar
Swait, J. (2001). Choice set generation within the generalized extreme value family of discrete choice models. Transportation Research Part B: Methodological, 35, 643–666.CrossRefGoogle Scholar
Train, K. (2003). Discrete choice methods with simulation. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Vuong, Q. (1989). Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica, 57, 307–333.CrossRefGoogle Scholar
1.Bates WhiteWashingtonUSA
2.Department of EconomicsUniversity of MarylandCollege ParkUSA
3.National Bureau of Economic ResearchCambridgeUSA
Chen Y., Jin G.Z. (2012) The Informative Role of Advertising and Experience in Dynamic Brand Choice: An Application to the Ready-to-Eat Cereal Market. In: Laxminarayan R., Macauley M. (eds) The Value of Information. Springer, Dordrecht
DOI https://doi.org/10.1007/978-94-007-4839-2_5
eBook Packages Business and Economics | CommonCrawl |
Reliance on model-based and model-free control in obesity
Reduced model-based decision-making in gambling disorder
Florent Wyckmans, A. Ross Otto, … Xavier Noël
Individual differences in sensory and expectation driven interoceptive processes: a novel paradigm with implications for alexithymia, disordered eating and obesity
Hayley A. Young, Chantelle M. Gaylor, … David Benton
Impaired belief updating and devaluation in adult women with bulimia nervosa
Laura A. Berner, Vincenzo G. Fiore, … Sanne de Wit
Goal-directed vs. habitual instrumental behavior during reward processing in anorexia nervosa: an fMRI study
Julius Steding, Ilka Boehm, … Stefan Ehrlich
Inflexible habitual decision-making during choice between cocaine and a nondrug alternative
Youna Vandaele, Caroline Vouillac-Mendoza & Serge H. Ahmed
Trait impulsivity and acute stress interact to influence choice and decision speed during multi-stage decision-making
Candace M. Raio, Anna B. Konova & A. Ross Otto
Baseline impulsivity may moderate L-DOPA effects on value-based decision-making
Johannes Petzold, Annika Kienast, … Michael N. Smolka
Greater mindful eating practice is associated with better reversal learning
Lieneke K. Janssen, Iris Duif, … Esther Aarts
Dorsolateral and medial prefrontal cortex mediate the influence of incidental priming on economic decision making in obesity
Filip Morys, Stefan Bode & Annette Horstmann
Lieneke K. Janssen ORCID: orcid.org/0000-0002-0166-81631,2,
Florian P. Mahner2,
Florian Schlagenhauf2,3,
Lorenz Deserno1,2,4,5,6 na1 &
Annette Horstmann ORCID: orcid.org/0000-0001-6184-84841,2,7 na1
Learning algorithms
An Author Correction to this article was published on 11 February 2021
This article has been updated
Consuming more energy than is expended may reflect a failure of control over eating behaviour in obesity. Behavioural control arises from a balance between two dissociable strategies of reinforcement learning: model-free and model-based. We hypothesized that weight status relates to an imbalance in reliance on model-based and model-free control, and that it may do so in a linear or quadratic manner. To test this, 90 healthy participants in a wide BMI range [normal-weight (n = 31), overweight (n = 29), obese (n = 30)] performed a sequential decision-making task. The primary analysis indicated that obese participants relied less on model-based control than overweight and normal-weight participants, with no difference between overweight and normal-weight participants. In line, secondary continuous analyses revealed a negative linear, but not quadratic, relationship between BMI and model-based control. Computational modelling of choice behaviour suggested that a mixture of both strategies was shifted towards less model-based control in obese participants. Our findings suggest that obesity may indeed be related to an imbalance in behavioural control as expressed in a phenotype of less model-based control potentially resulting from enhanced reliance on model-free computations.
Obesity is the result of systematically consuming more energy than is expended. This can be seen as a failure of control over eating behaviour1,2,3 and could result from altered processing of reward4. As a consequence, appetitive and often high-caloric foods are over-consumed despite negative consequences, such as the uncomfortable feeling of being full, feelings of regret, or long-term health risks. Such failures of behavioural control in obesity may arise from alterations in reinforcement learning5. Indeed, obesity-related impairments in reward- and punishment-based cue-conditioning have been observed in the context of both food and monetary outcomes6, as well as impairments in appetitive conditioning in the context of chocolate rewards7 (but see8). Furthermore, obese participants exhibited impairments in learning from negative outcomes when money or points served as an incentive6,9,10. These studies have focused on forms of learning that mostly resemble retrospective model-free 'trial-and-error' reinforcement learning. However, behavioural control arises from a balance between model-based and model-free control11,12. Model-based control relies on an internal model of the environment to enable forward planning. As a result, this system is flexible (but cognitively costly), allowing us to be goal-directed even when the environment changes, e.g. abrupt change in the current outcome value, changes. In contrast, the model-free system is cognitively inexpensive and fast (but inflexible) and is thought to underlie habitual control. To better understand this balance in obesity, the current study investigates relative reliance on model-based and model-free control of choice behaviour.
Indirect evidence links obesity to reduced model-based, or rather, goal-directed control. Previous outcome devaluation studies tapping into goal-directed and habitual control of food choices in obesity have shown a negative correlation between goal-directed control and degree of obesity in humans13,14. That is, the higher the BMI, the less participants adjusted their food choices after devaluation of one of the two choices. Behavioural adjustment after outcome devaluation of non-food rewards related positively to model-based, but not model-free control, in healthy human participants performing a two-step decision-making task15,16,17 (but see18). Alterations in model-based vs. model-free control have been associated with behavioural inflexibility as observed in clinical populations such as metamphetamine addiction, obsessive compulsive disorder, and binge eating disorder19,20, as well as in a general population sample reporting symptoms of the same disorders and of other eating disorders21. However, Voon et al.19 did not find differences in model-based and model-free control between obese participants without binge eating disorder and non-obese control participants. The absence of an association between obesity and model-based or model-free control seems surprising, given the above-mentioned obesity-related performance differences in simple reinforcement learning tasks and outcome devaluation tasks, resembling more model-free and model-based control, respectively.
We propose two reasons why the study by Voon et al.19 might have lacked power to detect obesity-related group differences in model-based and model-free control. First, rather subtle behavioural alterations are to be expected in obese individuals that are physically healthy. With a relatively low contrast in body mass index (BMI) between the obese and non-obese group (BMI [kg/m2]: obese: M = 31.49, SD = 3.6; non-obese: M = 23.54, SD = 2.9), and an average BMI for the obese group only slightly above the cutoff for obesity (> 30 kg/m2), such behavioural alterations may be difficult to detect. Second, the relationship between BMI and model-based and model-free control may in fact be quadratic in nature, thus masking potential obesity-related differences. A quadratic relationship with degree of obesity has indeed been observed for reward sensitivity22 and cognitive restraint of eating behaviour23. Furthermore, obesity may quadratically relate to alterations in striatal dopamine tone24. This is relevant because there is accumulating evidence that different measures and manipulations of dopamine transmission overall relate positively to model-based control as measured in the two-step task25,26,27,28,29.
In the current study, we aimed to address the two issues raised above by including (1) more highly obese individuals to boost the contrast between groups, and (2) an intermediate overweight group for more sensitivity to detect the existence of potential linear or quadratic relationships between weight status and behavioural control. The original two-step task was implemented to disentangle and directly compare the reliance on model-based and model-free control16,25,30. We hypothesized that weight status relates to the degree to which individuals rely on model-based and model-free learning, and that it may do so in a linear or quadratic manner.
The results reported in this study are based on data from 90 healthy right-handed participants in a wide BMI range (45 women; age [years]: M = 26.9; SD = 3.6; range 21–35; BMI [kg/m2]: M = 27.9, SD = 6.4, range 18.4–47.6). Participants were recruited based on their BMI status, i.e., normal-weight [n(women) = 31(16), BMI [kg/m2] = 18.5–24.9], overweight [n(women) = 29(14), BMI [kg/m2] = 25–29.9] and obese [n(women) = 30(15), BMI > 30] (Table 1). Note that the reported data were acquired in two parts. Fifty-seven datasets were acquired as a part of several studies running in the department between October 2012 and August 2014. Data acquisition of overweight and obese participants was not completed at the time due to logistic reasons. To finally conclude the study, the remaining participants were tested between February and March 2018 (n = 37, for details see Supplemental Figure S1). Part of the reported data have previously been published in a study comparing relative reliance on model-based and model-free control to habit propensity in a slips-of-action task in specifically normal-weight women and men (n = 28)16. Participants were tested at the Department of Neurology of the Max Planck Institute for Human Cognitive and Brain Sciences (Leipzig, Germany) and received monetary compensation on an hourly basis, as well as a bonus based on their task performance (between 3 and 10€; M = 6.5€, SD = 0.82). All participants gave written consent prior to the study. The study was carried out in accordance with the Declaration of Helsinki and approved by the Ethics Committee at the University of Leipzig, Germany.
Table 1 Group characteristics displaying mean (standard deviation) and range if not otherwise stated, followed by the test-statistic and p-value of group comparison for each measure.
After having provided informed consent, weight and height of the participants was measured, followed by the two-step task (for details see "Experimental paradigm"). Participants were then asked to complete a number of self-report questionnaires—validated in German—for characterizing the sample: Beck's Depression Inventory (BDI)31 to assess possible depressive symptoms (cut-off for exclusion > 18, indicating possibility of moderate to severe depression), the Behavioural Inhibition System/Behavioural Activation System questionnaire (BIS/BAS)32,33 to assess punishment and reward sensitivity, the Three-Factor Eating Questionnaire (TFEQ)34,35 to assess eating behaviour in terms of cognitive restraint, disinhibition and hunger, the UPPS Impulsive Behaviour Scale36,37 to assess impulsive behaviour in terms of Urgency, lack of Premeditation, lack of Perseverance, and Sensation seeking, and the Yale Food Addiction Scale (YFAS)38,39 to assess symptoms that could be indicative of food addiction. Finally, participants performed several cognitive tests to examine their potential relation to performance on the task: the Viennese Matrices Test (VMT)40 to assess non-verbal IQ. We also administered a computerized version of the Visual Paired Associates test of the Wechsler Memory Scale (VPA)41,42 to assess visual short term memory. Participants were included if none of the following exclusion criteria applied: estimated non-verbal IQ (< 85 based on the VMT), known metabolic disorders (e.g., diabetes), smoking, (history of) neurological, psychiatric, or eating disorders, symptoms of depression, drug or alcohol dependence, current pregnancy, and psychological treatment. In total 94 participants were tested of which three participants did not complete the experimental paradigm and one participant was excluded from analysis because of an estimated non-verbal IQ below 85.
Experimental paradigm
We administered a sequential decision making task16,25,30, in which participants were asked to make two subsequent decisions on each trial to earn a monetary reward (20 cents) or no reward (Fig. 1a). At the first stage, participants were asked to choose between two grey stimuli, which would bring them to one of two second-stage stimulus pairs (the green or yellow pair). One of the grey first-stage stimuli was connected commonly (70%) to the green and rarely (30%) to the yellow stimulus pair, and vice versa for the other grey stimulus (Fig. 1b). The first-stage stimuli and transition probabilities were fixed throughout the experiment. After selecting one of the two second-stage stimuli, participants either received the monetary reward or not (Fig. 1c). The probability of receiving reward for each of the four second-stage stimuli changed slowly and continuously according to Gaussian random walks to ensure continuous learning. The changes were kept consistent for all participants performing the experiment. Participants completed a total of 201 trials. Prior to the experiment, participants went through elaborate computer-based instructions and were then asked to explain the task including its first-stage transition probabilities to the experimenter. Open questions were addressed by the experimenter. The instructions included a detailed knowledge of common (70%) and rare (30%) transitions after first-stage choices, and the slowly changing probabilities after second-stage choices. After the instructions participants performed 56 training trials with a different set of stimuli. Participants were made aware that the height of their financial bonus depended on the accumulated reward in the task. The bonus was based on a randomly drawn subset of trials.
The two-step task25,30. (a) Trial structure of an example trial with a rare transition, which allows for the dissociation of model-based and model-free control of behaviour. (b) Transition structure showing how each first-stage stimulus (grey) leads to one of the two second-stage stimulus pairs (green or yellow) in 70% of the trials (common, blue arrows) and to the other pair in 30% of the trials (rare, red arrows). (c) Possible outcomes (reward, no reward). Reward probability for the four second-stage stimuli varies throughout the task according to random walks to encourage continuous learning.
Calculation of first-stage stay probabilities on the two-step task, as well as computational modeling of participants' choice behaviour were performed using in-house scripts in Matlab (version 2017b, The MathWorks, Inc.). Statistical analyses of self-reported, behavioural, and computational data were run in R Studio (version 3.4.4., R Core Team, 201843) and SPSS (version 24, IBM Corp., 2018). The R package ggplot2 was used to plot the results44.
Shapiro–Wilk's test of normality and Levene's test of equality of variance were ran for all group characteristics, including scores on self-reported questionnaires and neuropsychological tests, as well as for the accumulated reward (i.e., number of rewarded trials), raw stay probabilities (per condition), reaction times, and for the estimated model parameters.
The alpha level was set to 0.05 (α = 0.05) for all a priori analyses of interest. Note that for post hoc analyses, we did not correct for multiple comparisons as these results are exploratory and should be interpreted as such.
Partial η2 (ηp2) is reported as an effect size for all parametric univariate analyses because it meaningfully describes effects in a design in which multiple measures have been experimentally manipulated (as in the two-step task), and it yields very similar estimates as η2 for analyses that only include a between-group variable45,46. Note that ηp2 does not depend on the number of variables in the model and, thus, can be compared across studies. For non-parametric Kruskal–Wallis tests, η2H was calculated as follows: (H − k + 1)/(n − k), with H reflecting the test statistic, k the number of groups, and n the total sample size47.
To check the robustness of our findings and rule out that any observed effect of group on behaviour could have been driven by age21,48,49 or IQ16,21,50,51 rather than weight status, we reran all models post hoc including age and non-verbal IQ as covariates of no interest.
Characterization of the groups
We tested for group differences in age and sex to confirm that the groups were well-matched. BMI was analysed to confirm the grouping of participants into normal-weight, overweight and obese participants. Group analysis of cognitive tests (including non-verbal IQ) and self-reported questionnaire data were run to further characterize the sample.
For normally distributed data (age, VPA score, BIS/BAS, UPPS), we ran a one-way ANOVA with between-subjects factor weight group for each measure. Upon violation of the assumption of normality or equality of variance (BMI, non-verbal IQ, BDI, TFEQ, YFAS symptom score), the Kruskal–Wallis test by ranks was performed. Sex distribution between groups was analysed using Chi-Square Test. Group differences were followed up by post hoc parametric (independent T-test) or nonparametric (Mann–Whitney U Test) pairwise comparisons.
Raw behaviour according to first-stage stay probabilities
Investigating the likelihood with which participants choose a first-stage stimulus depending on the previous trial type (Rewarded/Unrewarded, Common/Rare), gives an insight into how much they relied on model-based or model-free control. Therefore, we calculated first-stage stay probabilities as the proportion of trials in which participants chose the same first-stage stimulus as in the previous trial (coded as 'stay') for each of the conditions (Rewarded Common, Rewarded Rare, Unrewarded Common, Unrewarded Rare). We then analysed participants' stay probabilities using ANOVA with the between-subject factor Group (Normal-weight, Overweight, Obese), and within-subject factors Reward (Rewarded, Unrewarded) and Transition (Common, Rare). Because the aim was to test for a three-way interaction and the group sizes are well balanced, type III sums of squares were calculated in this analysis.
A purely model-free agent relies on whether or not the previous trial was rewarded, irrespective of transition probability (Common/Rare). If rewarded, the previous first-stage choice should be repeated. If not, it may be better for the model-free agent to switch to the other first-stage stimulus. As a consequence, model-free control is reflected in a main effect of Reward. On the other hand, a purely model-based agent optimally relies both on reward and transition probability of the previous trial. A model-based agent will also stay with a previous first-stage choice when a common trial was rewarded, and switch when a common trial was not rewarded. However, the model-based agent differs in choice behaviour following rare trials. That is, in contrast to a purely model-free agent, a model-based agent can infer that when a rare trial was rewarded, reward probability on the current trial is higher if one chooses the other first-stage stimulus (switch), and vice versa for unrewarded rare trials (stay). Model-based control is therefore reflected in the interaction between Reward and Transition. Here, we were mainly interested in group differences in model-based and model-free control and thus focused on the Group × Reward × Transition interaction and Group × Reward interaction on stay probabilities, respectively.
We hypothesized that the relationship between weight status and model-based or model-free control might be linear or quadratic in nature. To investigate the nature of these relationships, we next performed planned pairwise group comparisons on the Reward × Transition interaction term [i.e., (Rewarded Common − Rewarded Rare) − (Unrewarded Common − Unrewarded Rare)] and on the main effect of Reward [i.e., (Rewarded Common + Rewarded Rare) − (Unrewarded Common + Unrewarded Rare)] on stay probabilities.
Finally, we ran two post hoc linear models (lm() from the R stats package): (1) on the Reward × Transition interaction term, and (2) on the main effect of Reward to investigate the existence of a linear and quadratic relationship with BMI on a continuous scale. Both models included BMI and BMI2 as orthogonal predictors.
To investigate how participants' choices were affected by reward and transition probability throughout the experiment rather than in the previous trial alone, we computationally modeled choice behaviour. We implemented a hybrid of a model-free and model-based reinforcement algorithm as is described in detail in our previous work16,25 and in the original paper30.
In short, the model-free algorithm (SARSA(λ)) included a learning rate for each stage (α1, α2) and a parameter λ, which allows the second stage prediction error to affect the next first-stage values (Q). The model-based algorithm learns values by planning forward and computes first-stage values by multiplying the value of the better second-stage option with the associated transition probabilities. Then, the model-free and model-based first-stage decision values are connected in the hybrid algorithm:
$$Q_{net}\left({s}_{A},{a}_{j}\right)=\omega { Q}_{MB}\left({s}_{A},{a}_{j}\right)+(1- \omega ){ Q}_{MF}\left({s}_{A},{a}_{j}\right)$$
where \(Q_{net}\left({s}_{A},{a}_{j}\right)\) denotes the decision value of the chosen stimulus \({a}_{j}\) from the first stage stimulus pair \({s}_{A}\), and \(\omega\) captures the relative weighting of the model-based (\({Q}_{MB}\left({s}_{A},{a}_{j}\right)\)) and model-free algorithm (\({Q}_{MF}\left({s}_{A},{a}_{j}\right)\)). The weighting parameter \(\omega\) is the main parameter of interest and can take a value between 0 and 1. If \(\omega\) = 1, first-stage choices are purely controlled by model-based control, and if \(\omega\) = 0, they are purely controlled by model-free control. Note that at the second stage \(Q_{net}={ Q}_{MB}\,{=Q}_{MF}\).
Finally, the decision values were transformed into action probabilities using the softmax function for \(Qnet\):
$$P(a_{i,t} = a{|}s_{i,t} {)} = \frac{{exp\left( {\beta_{i} \left[ { Q_{net} \left( {s_{i,t} ,a} \right) + \rho \cdot rep\left( a \right)} \right]} \right)}}{{\sum\limits_{{a^{\prime}}} {{\text{exp}}\left( {\beta_{i} \left[ { Q_{net} \left( {s_{i,t} ,a^{\prime}} \right) + \rho \cdot rep\left( {a^{\prime}} \right)} \right]} \right.} }}$$
where \({\beta }_{i}\) controls the stochasticity of choices at stage \(i\) = 1 or 2, and repetition parameter \(\rho\) reflects choice perseveration at the first stage.
The model had a total of seven parameters that were bounded by transforming them to a logistic \(({\alpha }_{1},{\alpha }_{2}, \lambda , \omega )\) or exponential \(({\beta }_{1},{\beta }_{2})\) distribution. To infer the maximum-a-posteriori estimate of each parameter for each subject, the (empirical) Gaussian prior distribution was set to the maximum-likelihood estimates given the data of all participants and then expectation–maximization was used52. We report the negative log-likelihood (− LL) as a measure of model fit.
We assessed group differences in \(\omega\) using ANOVA with between-group factor weight status. Planned pairwise comparisons were performed as part of the ANOVA or using Mann–Whitney U test as a nonparametric alternative. For each of these analyses, the alpha level was set at 0.05. Finally, we investigated the relationship between \(\omega\) and weight status on a continuous scale by running a post hoc linear regression model including BMI and BMI2 as orthogonal predictors.
After having detected between-group differences on the model parameters' of interest, an important sanity check is whether the inferred parameters actually reproduce the observed behavioural data in terms of stay probabilities. To do so, we re-ran the model based on each individual's inferred parameters to generate data for each individual (1000 simulations per subject) and performed the original ANOVA.
We then ran simulation recovery analyses for the model to assess whether the model parameters captured the observed behavioural data. Based on the estimated parameters, we simulated choice behaviour on the task and investigated stay probabilities. The reported significant Group × Reward × Transition interaction was fully reproduced indicating that the model captured important aspects of the data (Supplemental Figure S2).
Finally, to confirm that the chosen hybrid model including \(\lambda\) was the best-fitting algorithm in this study, we compared the model to less complex models. To avoid inclusion of numerous combinations of parameters, we focus on models that capture distinct behaviour in this task by setting \(\omega\) to 1 or 0, and \(\lambda\) to 0 or fitting it as a free parameter. This gives four additional models: (1) a hybrid model without \(\lambda\) (\(\omega\) = 0), (2) a model only including the model-based learning algorithm (\(\omega\) = 1, \(\lambda\) can not be fitted), (3) a model only including the model-free learning algorithm with \(\lambda\) (\(\omega\) = 0), and (4) the same model-free model without \(\lambda (\omega = 0)\). Integrated Bayesian Information Criterion (BIC) is reported for all models52.
Table 1 summarizes the weight groups [normal-weight (NW), overweight (OW), and obese (OB)] in terms of age, sex and BMI, as well as in terms of their scores on the cognitive tests and self-report questionnaires. The groups were well matched on sex and age, and did not differ in visual short-term memory (VPA), or non-verbal IQ as measured on the Viennese Matrices Test (VMT). However, a trend-level group difference was observed for non-verbal IQ, with numerically higher IQ scores for the normal-weight and overweight relative to the obese group (Table 1). We did observe a group difference in the average number of depressive symptoms (KW(2) = 11.5, p = 0.003, η2H = 0.11) even though the scores are not clinically relevant in the current sample. This difference was driven by the obese participants having a higher symptom score relative to normal-weight, but not overweight, participants (post hoc pairwise comparisons: NW vs. OB, p = 0.004; OW vs. OB, p = 0.137; NW vs OW, p = 0.254). Post hoc covariate analyses of behavioural and computational data controlling for BDI score did not change the primary effects of interest (see "Supplemental Materials" for statistics). The average number of food addiction symptoms also differed between the groups (KW(2) = 17.3, p < 0.001, η2H = 0.18), again, driven by a higher number of symptoms for obese relative to normal-weight, but not overweight, participants (post hoc pairwise comparisons: NW vs. OB, p < 0.001; OW vs. OB, p = 0.159; NW vs OW, p = 0.242). In terms of self-reported eating behaviour (TFEQ) the groups differed in disinhibition (KW(2) = 16.9, p < 0.001, η2H = 0.17) and restraint (KW(2) = 7.2, p = 0.027, η2H = 0.06). Disinhibition scores were higher for obese relative to both normal-weight and overweight participants and somewhat higher for overweight relative to normal-weight participants (post hoc pairwise comparisons: NW vs. OB, p < 0.001; OW vs. OB, p = 0.010; NW vs OW, p = 0.076). Restraint scores were highest for overweight participants and lower for normal-weight, but not obese participants (post hoc pairwise comparisons: NW vs. OB, p < 0.375; OW vs. OB, p = 0.374; NW vs OW, p = 0.013). No other group differences were observed.
Analysis of stay probabilities (Fig. 2a) revealed that participants' first-stage choices were significantly affected by reward (main effect Reward: F(1,87) = 27.2, p < 0.001, ηp2 = 0.238) as well as by the combination of reward and transition probability (interaction Reward × Transition: F(1,87) = 183.4, p < 0.001, ηp2 = 0.678) on the previous trial. This is in line with previous research25,30 and suggests that, across groups, the participants relied on both model-based and model-free choice strategies, respectively. Transition probability alone did not significantly affect participants' first-stage choices (Transition: F(1,87) = 3.4, p = 0.070, ηp2 = 0.037).
Stay probabilities. (a) Average stay probabilities per condition for each group. Error bars represent ± 1 SEM. (b) On the group level, the use of a model-based choice strategy (i.e., the Reward × Transition interaction term) was lower for obese relative to normal-weight and overweight participants, whereas (c) the use of a model-free choice strategy (i.e., the main effect of Reward) did not differ significantly between groups. The box plots in (b) and (c) show the median and interquartile range for each group, with the black dot denoting the mean. (d) On the continuous level, the Reward × Transition interaction term was negatively related to BMI, with no additional significant quadratic relationship. (e) No linear or quadratic relationship was observed between BMI and the main effect of Reward. The scatter plots in (d) and (e) show the model fit (black line) and confidence interval (shaded) of the respective regression models with predictors BMI and BMI2. Individual data points are color-coded based on weight group for illustrative purpose.
The weight groups significantly differed in the use of a model-based choice strategy (Fig. 2b) as reflected by a significant three-way Group × Reward × Transition interaction on stay probabilities (F (2,87) = 4.3, p = 0.017, ηp2 = 0.090), but not in the use of a model-free choice strategy (Group × Reward: F (2,87) = 1.8, p = 0.174, ηp2 = 0.039, Fig. 2c). Planned comparisons of the Reward × Transition interaction between groups showed that the three-way interaction was driven by a significantly higher interaction term for normal-weight relative to obese (p = 0.017) and for overweight relative to obese (p = 0.010) participants, whereas normal-weight and overweight participants did not differ from each other (p = 0.817).
We observed no Group × Transition interaction (F (2,87) = 1.2, p = 0.297, ηp2 = 0.028), nor a main effect of Group (F (2,87) = 1.7, p = 0.187, ηp2 = 0.038) on stay probabilities. These results suggest that choices of obese participants relied relatively less on model-based control than those of normal-weight and overweight participants.
Post hoc simple effects analyses were performed to further investigate the three-way interaction on stay probabilities and revealed a striking difference between the groups. Interestingly, we observed a Group × Reward interaction for rare (F(2,87) = 4.2, p = 0.018), but not common trials (F(2,87) < 1, p = 0.497). This in turn was driven by a simple main effect of Group on stay probabilities following rewarded rare trials (F(2,87) = 4.6, p = 0.012), but not unrewarded rare trials (F(2,87) < 1, p = 0.688). The simple effect of Group was also reflected in a Group × Transition interaction for rewarded (F (2,87) = 3.8, p = 0.026), but not unrewarded trials (F (2,87) = 2.4, p = 0.100). Finally, pairwise group comparisons of rewarded rare trials showed that obese participants were more likely to stay with their previous first-stage choices when a rare trial had been rewarded relative to normal-weight (t(59) = − 2.5, p = 0.014) and overweight participants (t(57) = − 2.9, p = 0.006), with no difference between normal-weight and overweight participants (t(58) = 0.3, p = 0.766). This is of interest because it is participants' behaviour following rare trials that allows us to dissociate model-based from model-free control. Increased staying after a rare rewarded trial hints at more model-free control, even though this effect was not sufficiently strong to come out as a significant interaction between Group and Reward. Nevertheless, it seems that the observed group difference in model-based control may in fact be driven by enhanced reliance on model-free computations (see "Discussion" for more).
Another means of probing the model-based control system in the framework of this task, is to investigate second-stage reaction times25,53. Since a model-based agent uses knowledge of the likelihood of the transition into a second-stage state, encountering an unexpected rare rather than an expected common transition should increase reaction times for choices at the second stage. In a post hoc analysis, we indeed observed a main effect of Transition on second-stage reaction times, which reflected significantly larger reaction times following a rare relative to a common transition (M(SD) rare = 992.3 (137.5) ms > M(SD)common = 731.1 (101.2) ms, F (1,87) = 366.2, p < 0.001, ηp2 = 0.808). We did not, however, observe a significant Group by Transition interaction (F (2,87) < 1, p = 0.411, ηp2 = 0.020), which is in line with the above interpretation that the observed Group × Reward × Transition interaction on stay probabilities may not purely reflect a group difference in model-based control. The absence of the Group by Transition interaction could not be explained by general reaction times differences between the groups, as the groups did not differ in their RTs overall for either stage 1 (M(SD) = 656.7 (8.8) ms, F (2,87) < 1, p = 0.847, ηp2 = 0.004), or stage 2 decisions (M(SD) = 808.3 (9.6) ms, F (2,87) < 1, p = 0.808, ηp2 = 0.005).
Next, we addressed the question if reliance on model-based and model-free control related to obesity in a linear and/or quadratic manner. Because the traditional weight categories of normal-weight, overweight and obese individuals reflect unequal intervals in terms of BMI, we turned to BMI as a continuous variable, even though the study was designed for group-based analyses. We ran two linear regression models including BMI and BMI2 as orthogonal predictors in each, and investigated their relationship with the (1) Reward × Transition interaction term, and (2) the main effect of Reward on stay probabilities. BMI related negatively to the Reward × Transition interaction term (βBMI = − 0.28, p = 0.007), but no additional quadratic relationship was observed (βBMI2 = 0.10, p = 0.319) (Fig. 2d). Together, BMI and BMI2 explained a significant proportion of variance in the effect of Reward and Transition on choice strategy (adjusted R2 = 0.069, F(2,87) = 4.3, p = 0.017). In line with the absence of a Group × Reward effect on stay probabilities, we did not observe a linear or quadratic relationship between BMI and the main effect of Reward on stay probabilities (βBMI = 0.08, p = 0.463; βBMI2 = 0.01, p = 0.892) (Fig. 2e), nor did the model explain a significant proportion of variance (adjusted R2 = − 0.016, F (2,87) = 0.3, p = 0.756). Note that a post hoc analysis results suggest that the linear relationship between BMI and the Reward × Transition interaction term may be moderated by BDI score (see "Supplemental Materials" for statistics).
Accumulated reward
The accumulated reward (i.e., sum of rewarded trials) of participants was analyzed as a measure of overall performance. The groups did not differ in the sum of rewarded trials throughout the experiment (M = 97.2, SD = 7.7, F (2,87) = 1.6, p = 0.209, ηp2 = 0.035). The sum of rewarded trials also did not correlate to participants' tendency to rely on model-based or model-free choice strategies in any of the measures of interest (p's > 0.299).
Computational modeling of choice behaviour
Computational modeling of behaviour allowed us to take into account participants' choices throughout the experiment rather than only considering the effect of the previous trial. For a summary of all parameters and group comparisons, see Table 2.
Table 2 Summary and group comparisons of all model parameters.
The parameter ω was of initial interest because it reflects participants' relative reliance on model-based vs. model-free control. A purely model-based agent has an ω of 1, whereas a purely model-free agent has an ω of 0. As expected, we observed a significant group effect on ω (F (2,87) = 5.3, p = 0.007, ηp2 = 0.109) (Fig. 3a). Planned comparisons showed that the group effect on ω was driven by higher values for normal-weight relative to obese (t(59) = 2.1, p = 0.042) and overweight relative to obese participants (t(57) = 3.1, p = 0.003). Although overweight participants numerically had the highest ω values, there was no statistical difference with normal-weight participants (t(58) = -1.1, p = 0.265).
Relative reliance on model-based and model-free control (omega). (a) On the group level, omega was significantly lower for obese relative to normal-weight and overweight participants. The box plot reflects the median, interquartile range, and mean value (black dot) for each weight group. (b) On the continuous level, omega was negatively related to BMI, with no additional significant quadratic relationship. The scatter plot shows the model fit (black line) and confidence interval (shaded) of the regression model. Individual data points are color-coded based on weight group for illustrative purposes.
To investigate the nature of the relationship between ω and weight on a continuous scale (i.e., BMI), we again ran a post hoc regression model including the linear term BMI and quadratic term BMI2 as predictors. The linear term related negatively to values of ω with lower values in individuals with a higher BMI (βBMI = − 0.23, p = 0.030), whereas the quadratic term did not significantly add to the model (βBMI2 = − 0.005, p = 0.964) (Fig. 3b). In total, the model explained 3.1% of variance in ω (adjusted R2 = 0.031, F (2,87) = 2.4, p = 0.093), which reflects only a small effect of BMI on reliance on model-based vs. model-free control. Similar to post hoc analysis of the relationship between BMI and the interaction effect of Reward × Transition on stay probabilities, the negative relationship between BMI and ω may be moderated by BDI score (see "Supplemental Materials" for statistics).
None of the other model parameters differed significantly between the groups (Table 2). This indicates that the groups did not differ in terms of first or second stage learning rates (α1, α2), stochasticity of first or second stage choices (β1, β2), the tendency to persevere independent of reward or transition (ρ), the eligibility parameter (λ), and importantly, how well the model fit participants' data (− LL).
Finally, to confirm that the chosen hybrid model including \(\lambda\) was the best-fitting algorithm in this study, we compared the model to four less complex models by setting \(\omega\) to 1 or 0, and \(\lambda\) to 0 or fitting it as a free parameter. Comparing the Bayesian Information Criterion (BIC) scores of the five models across the entire sample as well as in each group separately shows clear superiority for the 'full' hybrid model in each case (Table 3).
Table 3 Model comparison.
Correcting for age and IQ
To check the robustness of our findings and rule out that the observed group differences could be explained by age21,48,49 or IQ16,21,50,51 rather than weight status, we reran all models post hoc including age and non-verbal IQ as covariates of no interest. In case of nonparametric tests, the analyses were performed after having regressed out age and non-verbal IQ from the dependent variables using linear regression.
Adding the covariates did not change the results qualitatively—the outcomes were largely in line with the original analyses and suggest that weight status, over and above age and IQ, explains unique variance in the degree to which individuals rely on measures of model-based, and possibly model-free, control (see Supplemental Table S1 for a graphical overview of the outcomes of all analyses of interest). Notably, the reported group differences in model-based control, as observed in stay probabilities, and the relative reliance on model-based and model-free control, as reflected in the model parameter ω, were relatively robust when correcting for age and non-verbal IQ. However, the pairwise comparison in model-based control between normal-weight and obese participants did not reach significance. Furthermore, on the continuous level we observed a similar negative relationship between BMI and model-based control (stay probabilities) (see "Supplemental Materials" for statistics).
The aim of this study was to investigate the relationship between weight status (i.e., normal-weight, overweight, and obese) and reliance on model-based and model-free control in the two-step task16,25,30. Our results indicate that obese participants relied less strongly on model-based control than overweight and—to a lesser extent—normal-weight participants, with no difference in performance between overweight and normal-weight participants. This was observed in group analysis of participants' choice behaviour (i.e., stay probabilities), as well as in the continuous analysis where BMI negatively related to model-based choice behaviour. No quadratic relationship with BMI was observed. Furthermore, computational modeling of participants' choices revealed a similar group difference in the weighting of model-based and model-free control (i.e., ω) that was driven by less model-based control for obese relative to overweight and normal-weight participants. Secondary analyses, however, did not show group differences in the slowing of second-stage reaction times after rare transitions, as would be expected given the observed decrease in model-based choice behaviour in obesity.
Although seemingly contradictory, together these findings may in fact suggest that the observed obesity-related difference in model-based control is driven, in part, by enhanced reliance on model-free computations. This interpretation concurs with our post hoc simple effects analyses of stay probabilities, which revealed that the group difference in model-based control was driven by an increased inclination of obese (relative to normal-weight) to stay with their choice specifically after trials on which a rare transition led to reward. Rare trials are the trials of interest in this task, because performance following rare trials is used to dissociate model-based from model-free choices. Common trials, on the other hand, lead to the same decision in model-based and model-free agents. The group difference was only observed for rewarded, not unrewarded rare trials. We speculate that obese individuals may more easily fall back on model-free control, or in other words be more reactive after having been rewarded than normal-weight participants, whilst relying similarly on model-based control in the case of no reward. This speculative interpretation should be interpreted with care, as it has been shown that model-free control on this task can potentially be due to a misunderstanding of the model of the task54. Furthermore, the current task is not designed to address this subtle effect, which could explain why it was not reflected in a group difference in model-free control in the analysis of stay probabilities.
Our findings are in contrast to those of a previous study by Voon et al.19 using the same paradigm. When comparing non-obese controls and obese participants with and without binge-eating disorder, Voon et al.19 reported no difference in the weighting parameter ω between obese participants without binge-eating disorder and non-obese controls, whereas ω was on average lower for obese participants with binge-eating disorder relative to matched non-obese controls. Interestingly, our findings in healthy obese participants better match the previous findings in obese participants with binge-eating disorder. It should be noted however that ω, and thus the reliance on model-based over model-free control, was much higher in the current study (mean (SD) omega: 0.6 (0.11) vs. 0.3 (0.24), range 0–1). The discrepancy between the studies can be explained by several factors. First, the current study tested a more severely obese group than the Voon-study with a mean BMI of 35.4 kg/m2 (SD 4.5) vs. 31.5 kg/m2 (SD 3.6). In fact, in terms of BMI our sample was closer to the binge-eating group (mean BMI[kg/m2] 35.0, SD 5.6). It may thus be the case that the reported finding of a lower weighting parameter ω in binge-eating disorder in the Voon-study can partially be explained by the severity of obesity. Alternatively, even though no psychiatric conditions were reported, the obese participants in our sample might unbeknownst fulfill criteria for binge-eating disorder or have other co-morbidities, as we did not conduct a full psychiatric screening. We did, however, observe a group difference in self-reported depressive symptom score as assessed by Beck's Depression Inventory (BDI), with higher—but subclinical—scores for the obese relative to the normal-weight and overweight group. Post hoc analyses showed that variation in BDI scores could not explain the observed group difference in reliance on model-based control. On the continuous level, BDI score did seem to moderate the negative relationship between model-based control and BMI, with a stronger negative relationship for higher BDI scores. It should be noted that the results of the post hoc analyses have to be interpreted with caution because BDI score was not systematically sampled and the use of the BDI as a continuous measure of depressive symptoms in obesity is criticized. The BDI includes both non-somatic and somatic items. High scores on the somatic items (e.g., fatigue, sleep disturbance, body image) may either reflect true depressive symptoms or they are instead related to individuals' obesity. Second, we included an intermediate weight group for increased sensitivity to detect group differences and potential quadratic effects that might otherwise remain uncovered. The group difference in model-based control in the current study was indeed mostly driven by the difference between overweight and obese participants. We therefore recommend that cognitive studies of obesity should include a wide BMI range, preferably also sampling severe to morbid obesity to assess for quadratic relationships, and to carefully disentangle between contributions of weight status and compulsive measures such as binge-eating symptoms.
The observed difference in reliance on model-based control in obesity generally concurs with previous outcome devaluation studies in relation to obesity that found reduced goal-directed control13,14. Goal-directed and model-based control are often equated11 and have been found to relate, albeit weakly15,16,17. However, the concepts measured in the two types of tasks do not reflect the exact same constructs. Whereas the two-step task is designed to dissociate model-based and model-free control, it is difficult to disentangle reliance on goal-directed and habitual control in outcome devaluation paradigms in humans. In fact, for the current version of the two-step task—with reliance on model-based vs. model-free choice strategy not affecting overall outcome—one could paradoxically speculate that those who rely more strongly on model-free control are putatively even more efficient. For model-based control to be a more sensible strategy than model-free control, it should pay off to spend the extra cognitive resources associated with it55. That participants indeed follow this strategy was recently confirmed in a similar sequential decision-making task in which the incentive size was manipulated: model-based control indeed increased with larger incentives in a heterogeneous nonpatient population56. Furthermore, goal-directed and habitual control may be organized hierarchically rather than in parallel. That is, the goal-directed system may benefit from habits in goal-pursuit and thus rely on the habit system57, and the habit system may affect what goals are selected and pursued by the goal-directed system58. Empirical evidence for the existence of such hierarchies comes from a new generation of sequential decision-making tasks59,60,61. It will be relevant for future studies to focus on habitual goal-selection in the context of obesity, as has been suggested for addiction and other disorders of compulsivity58, and investigate if it relates more closely to maladaptive eating behaviour in daily life.
The current study has several limitations. First, the dataset was collected in two parts with a sampling bias in terms of group and sex (see Supplemental Figure S1). Due to this bias we could not meaningfully account for sex and sample (2012–2014 vs. 2018) as covariates of no interest, because variance explained by sample and weight group or sample and sex cannot be disentangled in our design62. However, the task was identical in both sampling periods and administered in very similar lab spaces within the department. More importantly, extensive computerized instructions were implemented to minimize variability in performance due to differences in instructions between experimenters. We are therefore fairly confident that the observed group differences are not confounded by sampling period. Second, as emphasized above, the observed group differences are subtle with modest effect sizes and await replication. We speculate that these differences may be more pronounced when taking into account participants' diet rather than obesity. Rodent studies suggest that rather than obesity, the intake of high fat and/or sugar diets may better predict alterations in dopamine-transmission63,64,65,66,67,68. We expect these changes to be at the heart of the maladaptive behavioural control in obesity24 and there is accumulating evidence that different measures and manipulations of dopamine transmission overall related positively to model-based control as measured in the two-step task25,26,27,28,29. Whether diet rather than obesity relates to maladaptive behavioural control needs to be addressed in further studies. A third limitation is that, although the continuous analyses converge with the observed group differences in model-based control and strengthens the conclusion that obesity is indeed associated with altered reliance on model-based vs. model-free control, the design of the current study was not optimal for this type of analysis. BMI was not equidistributed across the complete sample due to the group-based recruitment-strategy. Hence, the current study might have been underpowered to robustly show true effects between BMI and behavioural control strategies on a continuous level. Another reason for interpreting the reported relationship between BMI and behavioural control on a continuous level with care is the low retest reliability of the task, as has recently been shown in a large-scale investigation of self-regulation paradigms69. For the investigation of individual differences in task performance within groups, other variables such as reaction time and latent variables from drift diffusion modeling could give a more reliable estimate of behavioural control70. Following Hedge et al.71, the poor retest reliability that is the result of low between-subject variability does not negate the observed group differences. In fact, low-between subject variability is required to observe reliable group differences in task performance. Despite these limitations, the findings from our two independent analysis approaches did converge. That is, analysis of raw choice behaviour in terms of stay probabilities and of the model parameter ω both point to alterations in the reliance on model-based vs. model-free control in obesity. Simulation recovery analysis of the parameter estimates of the computational models further strengthened our confidence in the observed findings, because it recovered the observed three-way interaction between group, reward and transition probability on stay probabilities.
In conclusion, we found evidence for a relationship between the degree of obesity and reliance on model-based and model-free control relative to overweight and normal-weight participants, which may in fact be linear rather than quadratic in nature. Obesity, on the group-level, was associated with relatively lower model-based control compared to normal-weight and overweight, which was driven by an increased inclination of obese (relative to normal-weight) to stay with their choice specifically after trials on which a rare transition led to reward. Together, our findings suggest that it may be the combination of decreased model-based and increased model-free control in this task that characterizes the obese group. Whether or not the observed effects are dopamine-mediated, as hypothesized, remains an open question that warrants further investigation, for example, by pharmacologically manipulating dopamine transmission, or investigating the interaction between BMI and individual differences in dopamine transmission in terms of genetic or epigenetic variation.
The datasets analysed during the current study are available from the corresponding author on reasonable request.
A Correction to this paper has been published: https://doi.org/10.1038/s41598-021-83028-z
Horstmann, A. It wasn't me; it was my brain—Obesity-associated characteristics of brain circuits governing decision-making. Physiol. Behav. 176, 125–133 (2017).
Volkow, N. D., Wise, R. A. & Baler, R. The dopamine motive system: Implications for drug and food addiction. Nat. Rev. Neurosci. 18, 741 (2017).
Lowe, C. J., Reichelt, A. C. & Hall, P. A. The prefrontal cortex and obesity: A health neuroscience perspective. Trends Cogn. Sci. 23, 349–361 (2019).
García-García, I. et al. Reward processing in obesity, substance addiction and non-substance addiction. Obes. Rev. 15, 853–869 (2014).
Kroemer, N. B. & Small, D. M. Fuel not fun: Reinterpreting attenuated brain responses to reward in obesity. Physiol. Behav. 162, 37–45 (2016).
Coppin, G., Nolan-Poupart, S., Jones-Gotman, M. & Small, D. M. Working memory and reward association learning impairments in obesity. Neuropsychologia 65, 146–155 (2014).
van den Akker, K., Schyns, G. & Jansen, A. Altered appetitive conditioning in overweight and obese women. Behav. Res. Ther. 99, 78–88 (2017).
Meemken, M. T., Kube, J., Wickner, C. & Horstmann, A. Keeping track of promised rewards: Obesity predicts enhanced flexibility when learning from observation. Appetite 131, 117–124 (2018).
Mathar, D., Neumann, J., Villringer, A. & Horstmann, A. Failing to learn from negative prediction errors: Obesity is associated with alterations in a fundamental neural learning mechanism. Cortex 95, 222–237 (2017).
Kube, J. et al. Altered monetary loss processing and reinforcement-based learning in individuals with obesity. Brain Imaging Behav. 12, 1431–1449 (2018).
Dolan, R. J. & Dayan, P. Goals and habits in the brain. Neuron 80, 312–325 (2013).
Daw, N. D., Niv, Y. & Dayan, P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 8, 1704 (2005).
Horstmann, A. et al. Slave to habit? Obesity is associated with decreased behavioural sensitivity to reward devaluation. Appetite 87, 175–183 (2015).
Janssen, L. K. et al. Loss of lateral prefrontal cortex control in food-directed attention and goal-directed food choice in obesity. Neuroimage 146, 148–156 https://doi.org/10.1016/j.neuroimage.2016.11.015 (2017).
Gillan, C. M., Otto, A. R., Phelps, E. A. & Daw, N. D. Model-based learning protects against forming habits. Cogn. Affect. Behav. Neurosci. 15, 523–536 (2015).
Sjoerds, Z. et al. Slips of action and sequential decisions: A cross-validation study of tasks assessing habitual and goal-directed action control. Front. Behav. Neurosci. 10, 234 (2016).
Friedel, E. et al. Devaluation and sequential decisions: Linking goal-directed and model-based behavior. Front. Hum. Neurosci. 8, 587 (2014).
Byrne, K. A., Otto, A. R., Pang, B., Patrick, C. J. & Worthy, D. A. Substance use is associated with reduced devaluation sensitivity. Cogn. Affect. Behav. Neurosci. 19, 40–55 (2019).
Voon, V. et al. Disorders of compulsivity: A common bias towards learning habits. Mol. Psychiatry 20, 345–352 (2015).
Voon, V. et al. Motivation and value influences in the relative balance of goal-directed and habitual behaviours in obsessive-compulsive disorder. Transl. Psychiatry 5, e670 (2015).
Gillan, C. M., Kosinski, M., Whelan, R., Phelps, E. A. & Daw, N. D. Characterizing a psychiatric symptom dimension related to deficits in goal-directed control. Elife 5, e11305 (2016).
Davis, C., Strachan, S. & Berkson, M. Sensitivity to reward: implications for overeating and overweight. Appetite 42, 131–138 (2004).
Dietrich, A., Federbusch, M., Grellmann, C., Villringer, A. & Horstmann, A. Body weight status, eating behavior, sensitivity to reward/punishment, and gender: Relationships and interdependencies. Front. Psychol. 5, 1073 (2014).
Horstmann, A., Fenske, W. K. & Hankir, M. K. Argument for a non-linear relationship between severity of human obesity and dopaminergic tone. Obes. Rev. 16, 821–830 (2015).
Deserno, L. et al. Ventral striatal dopamine reflects behavioral and neural signatures of model-based control during sequential decision making. Proc. Natl. Acad. Sci. 112, 1595 LP – 1600 (2015).
Sharp, M. E., Foerde, K., Daw, N. D. & Shohamy, D. Dopamine selectively remediates 'model-based' reward learning: A computational approach. Brain 139, 355–364 (2016).
Doll, B. B., Bath, K. G., Daw, N. D. & Frank, M. J. Variability in dopamine genes dissociates model-based and model-free reinforcement learning. J. Neurosci. 36, 1211–1222 (2016).
Wunderlich, K., Smittenaar, P. & Dolan, R. J. Dopamine enhances model-based over model-free choice behavior. Neuron 75, 418–424 (2012).
Kroemer, N. B. et al. L-DOPA reduces model-free control of behavior by attenuating the transfer of value to action. Neuroimage 186, 113–125 (2019).
Daw, N. D., Gershman, S. J., Seymour, B., Dayan, P. & Dolan, R. J. Model-based influences on humans' choices and striatal prediction errors. Neuron 69, 1204–1215 (2011).
Kühner, C., Bürger, C., Keller, F. & Hautzinger, M. Reliabilität und Validität des revidierten Beck-Depressionsinventars (BDI-II). Nervenarzt 78, 651–656 (2007).
Carver, C. S. & White, T. L. Behavioral inhibition, behavioral activation, and affective responses to impending reward and punishment: The BIS/BAS Scales. J. Pers. Soc. Psychol. 67, 319–333 (1994).
Strobel, A., Beauducel, A., Debener, S. & Brocke, B. Eine deutschsprachige version des BIS/BAS-Fragebogens von Carver und White. Zeitschrift für Differ. und Diagnostische Psychol. 22, 216–227 (2001).
Stunkard, A. J. & Messick, S. The three-factor eating questionnaire to measure dietary restraint, disinhibition and hunger. J. Psychosom. Res. 29, 71–83 (1985).
Pudel, V. & Westenhöfer, J. Fragebogen zum essverhalten (FEV): handanweisung (Verlag für Psychologie Hogrefe, 1989).
Whiteside, S. P. & Lynam, D. R. The Five Factor Model and impulsivity: Using a structural model of personality to understand impulsivity. Pers. Individ. Dif. 30, 669–689 (2001).
Schmidt, R. E., Gay, P., d'Acremont, M. & Van der Linden, M. A German adaptation of the UPPS impulsive behavior scale: Psychometric properties and factor structure. Swiss J. Psychol. 67, 107–112 (2008).
Gearhardt, A. N., Corbin, W. R. & Brownell, K. D. Preliminary validation of the Yale food addiction scale. Appetite 52, 430–436 (2009).
Meule, A., Vögele, C. & Kübler, A. Deutsche Übersetzung und Validierung der Yale food addiction scale. Diagnostica 58, 115–126 (2012).
Formann, A. K. & Piswanger, K. Wiener Matrizen-Test: WMT; ein Rasch-skalierter sprachfreier Intelligenztest; Manual; mit englisch-und französischsprachigen Instruktionen im Anhang (Beltz Test Ges., Chicago, 1979).
Wechsler, D. Wechsler Memory Scale–revised: Manual (Psychological Corporation, Chicago, 1987).
von Aster, M. N. A. & Horn, R. Wechsler Intelligenztest für Erwachsene WIE. Übersetzung und Adaption der WAIS-III von David Wechsler [German adaption of the WAIS-III] (2006).
Team, R. C. R: A language and environment for statistical computing. (2013).
Wickham, H. ggplot2: elegant graphics for data analysis (Springer, New York, 2016).
Baguley, T. Standardized or simple effect size: What should be reported?. Br. J. Psychol. 100, 603–617 (2011).
Levine, T. R. & Hullett, C. R. Eta squared, partial eta squared, and misreporting of effect size in communication research. Hum. Commun. Res. 28, 612–625 (2002).
Cohen, B. H. Explaining Psychological Statistics (Wiley, New York, 2008).
Eppinger, B., Walter, M., Heekeren, H. R. & Li, S.-C. Of goals and habits: Age-related and individual differences in goal-directed decision-making. Front. Neurosci. 7, 253 (2013).
Eppinger, B., Schuck, N. W., Nystrom, L. E. & Cohen, J. D. Reduced striatal responses to reward prediction errors in older compared with younger adults. J. Neurosci. 33, 9905–9912 (2013).
Otto, A. R., Gershman, S. J., Markman, A. B. & Daw, N. D. The curse of planning: Dissecting Multiple reinforcement-learning systems by taxing the central executive. Psychol. Sci. 24, 751–761 (2013).
Otto, A. R., Skatova, A., Madlon-Kay, S. & Daw, N. D. Cognitive control predicts use of model-based reinforcement learning. J. Cogn. Neurosci. 27, 319–333 (2014).
Huys, Q. J. et al. Disentangling the roles of approach, activation and valence in instrumental and pavlovian responding. PLoS Comput. Biol. 7(4), e1002028 (2011).
MathSciNet CAS PubMed PubMed Central Google Scholar
Decker, J. H., Otto, A. R., Daw, N. D. & Hartley, C. A. From creatures of habit to goal-directed learners: Tracking the developmental emergence of model-based reinforcement learning. Psychol. Sci. 27, 848–858 (2016).
da Silva, C. F. & Hare, T. A. Humans are primarily model-based and not model-free learners in the two-stage task. bioRxiv https://doi.org/10.1101/682922 (2019).
Kool, W., Cushman, F. A. & Gershman, S. J. When does model-based control pay off?. PLOS Comput. Biol. 12, e1005090 (2016).
PubMed PubMed Central ADS Google Scholar
Patzelt, E. H., Kool, W., Millner, A. J. & Gershman, S. J. Incentives boost model-based control across a range of severity on several psychiatric constructs. Biol. Psychiatry 85(5), 425–433 (2019).
Wood, W. & Neal, D. T. A new look at habits and the habit-goal interface. Psychol. Rev. 114, 843–863 (2007).
Daw, N. D. Of goals and habits. Proc. Natl. Acad. Sci. 112, 13749–13750 (2015).
CAS PubMed ADS Google Scholar
Dezfouli, A. & Balleine, B. W. Actions, action sequences and habits: Evidence that goal-directed and habitual action control are hierarchically organized. PLoS Comput. Biol. 9, e1003364 (2013).
Keramati, M., Smittenaar, P., Dolan, R. J. & Dayan, P. Adaptive integration of habits into depth-limited planning defines a habitual-goal-directed spectrum. Proc. Natl. Acad. Sci. https://doi.org/10.1073/pnas.1609094113 (2016).
Cushman, F. & Morris, A. Habitual control of goal selection in humans. Proc. Natl. Acad. Sci. 112, 13817 LP – 13822 (2015).
Miller, G. A. & Chapman, J. P. Misunderstanding analysis of covariance. J. Abnorm. Psychol. 110, 40–48 (2001).
Friend, D. M. et al. Basal ganglia dysfunction contributes to physical inactivity in obesity. Cell Metab. 25, 312–321 (2017).
Alsiö, J. et al. Dopamine D1 receptor gene expression decreases in the nucleus accumbens upon long-term exposure to palatable food and differs depending on diet-induced obesity phenotype in rats. Neuroscience 171, 779–787 (2010).
Cone, J. J., Chartoff, E. H., Potter, D. N., Ebner, S. R. & Roitman, M. F. Prolonged high fat diet reduces dopamine reuptake without altering DAT gene expression. PLoS ONE 8, e58251 (2013).
CAS PubMed PubMed Central ADS Google Scholar
Baladi, M. G., Horton, R. E., Owens, W. A., Daws, L. C. & France, C. P. Eating high fat chow decreases dopamine clearance in adolescent and adult male rats but selectively enhances the locomotor stimulating effects of cocaine in adolescents. Int. J. Neuropsychopharmacol. 18(7) (2015).
Li, Y. et al. High-fat diet decreases tyrosine hydroxylase mRNA expression irrespective of obesity susceptibility in mice. Brain Res. 1268, 181–189 (2009).
Davis, J. F. et al. Exposure to elevated levels of dietary fat attenuates psychostimulant reward and mesolimbic dopamine turnover in the rat. Behav. Neurosci. 122, 1257–1263 (2008).
Enkavi, A. Z. et al. Large-scale analysis of test–retest reliabilities of self-regulation measures. Proc. Natl. Acad. Sci. 116, 5472 LP – 5477 (2019).
Shahar, N. et al. Improving the reliability of model-based decision-making estimates in the two-stage decision task with reaction-times and drift-diffusion modeling. PLOS Comput. Biol. 15, e1006803 (2019).
Hedge, C., Powell, G. & Sumner, P. The reliability paradox: Why robust cognitive tasks do not produce reliable individual differences. Behav. Res. Methods 50, 1166–1186 (2018).
The authors thank Anja Dietrich, Tilmann Wilbertz, and Sarah Kusch for their help with data acquisition, and Zsuzsika Sjoerds for the helpful discussion about the data. The authors are also grateful to Nils Kroemer, Ying Lee, Kathleen Wiencke, and the O'BRAIN Lab for their constructive feedback regarding data-analysis. This work was supported by the Federal Ministry for Education and Research, Germany, FKZ: 01EO1501 (LKJ, LD, AH) and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) (Project number 209933839-SFB 1052), SFB 1052 "Obesity Mechanisms", subproject A05 (AH).
Open Access funding enabled and organized by Projekt DEAL.
These authors contributed equally: Lorenz Deserno and Annette Horstmann.
Integrated Research and Treatment Center Adiposity Diseases, Leipzig University Medical Center, Leipzig, Germany
Lieneke K. Janssen, Lorenz Deserno & Annette Horstmann
Department of Neurology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
Lieneke K. Janssen, Florian P. Mahner, Florian Schlagenhauf, Lorenz Deserno & Annette Horstmann
Department of Psychiatry and Psychotherapy, Charité-Universitätsmedizin Berlin, Campus Charité Mitte, Berlin, Germany
Florian Schlagenhauf
Max Planck UCL Centre for Computational Psychiatry and Ageing Research, University College London, London, UK
Lorenz Deserno
The Wellcome Centre for Human Neuroimaging, University College London, London, UK
Department of Child and Adolescent Psychiatry, Psychotherapy and Psychosomatics, University of Würzburg, Würzburg, Germany
Department of Psychology and Logopedics, Faculty of Medicine, University of Helsinki, Helsinki, Finland
Annette Horstmann
Lieneke K. Janssen
Florian P. Mahner
A.H., L.D., and F.S., designed the experiment. F.M. and L.J. set up the study. F.M. collected data. L.J., L.D., and F.M. analysed the data. L.J., L.D., and A.H. wrote the manuscript. All authors read and approved the manuscript.
Correspondence to Lieneke K. Janssen.
Supplementary Information.
Janssen, L.K., Mahner, F.P., Schlagenhauf, F. et al. Reliance on model-based and model-free control in obesity. Sci Rep 10, 22433 (2020). https://doi.org/10.1038/s41598-020-79929-0 | CommonCrawl |
npg asia materials
High spin mixing conductance and spin interface transparency at the interface of a Co2Fe0.4Mn0.6Si Heusler alloy and Pt
Braj Bhusan Singh1,
Koustuv Roy1,
Pushpendra Gupta1,
Takeshi Seki2,3,
Koki Takanashi2,3,4 &
Subhankar Bedanta ORCID: orcid.org/0000-0002-1044-76451
NPG Asia Materials volume 13, Article number: 9 (2021) Cite this article
Condensed-matter physics
Magnetic properties and materials
Ferromagnetic materials exhibiting low magnetic damping (α) and moderately high-saturation magnetization are required from the viewpoints of generation, transmission, and detection of spin waves. Since spin-to-charge conversion efficiency is another important parameter, high spin mixing conductance \(({g_{r}^{\uparrow \downarrow}})\) is the key for efficient spin-to-charge conversion. Full Heusler alloys, e.g., Co2Fe0.4Mn0.6Si (CFMS), which are predicted to be 100% spin-polarized, exhibit low α. However, \(g_r^{ \uparrow \downarrow }\) at the interface between CFMS and a paramagnet is not fully understood. Here, we report investigations of spin pumping and the inverse spin Hall effect in CFMS/Pt bilayers. Damping analysis indicates the presence of significant spin pumping at the interface of CFMS and Pt, which is also confirmed by the detection of an inverse spin Hall voltage. We show that in CFMS/Pt, \(g_r^{ \uparrow \downarrow }\) (1.70 × 1020 m−2) and the interface transparency (83%) are higher than the values reported for other ferromagnetic/heavy metal systems. We observed a spin Hall angle of ~0.026 for the CFMS/Pt bilayer system.
Spin transport across interfaces in ferromagnetic (FM)/heavy metal (HM) systems is important to develop future spintronic devices1,2. Spin orbital torque3, spin-transfer torque1,2, the spin pumping/inverse spin Hall effect4,5, spin Seebeck effects6, etc. are major phenomena that are predominantly affected by interface spin transport in FM/HM systems. Spin pumping is an efficient method to produce pure spin current (\(\overrightarrow {J_s}\)), which is the flow of spin angular momentum, and investigate spin propagation across FM/HM interfaces. The efficiency of spin transport at FM/HM interfaces is characterized by a factor known as the spin mixing conductance (\(g_r^{ \uparrow \downarrow }\)), which is related to \(\overrightarrow {J_s}\) by the expression2
$$\overrightarrow {J_s} = \frac{\hbar }{{4\pi }}g_r^{ \uparrow \downarrow }\hat m \times \frac{{{\mathrm{d}}\hat m}}{{{\mathrm{d}}t}},$$
where \(\hat m\) is the unit vector of magnetization. \(\overrightarrow {J_s}\) can be converted into the transverse voltage (VISHE) by the inverse spin Hall effect (ISHE)7:
$$V_{{\mathrm{ISHE}}}\propto \,\theta _{{\mathrm{SH}}}\left| {\overrightarrow {J_s} \times \vec \sigma } \right|,$$
where θSH is the spin Hall angle, which defines the conversion efficiency between the charge current (\(\overrightarrow {J_c}\)) and \(\overrightarrow {J_s}\), and \(\vec \sigma\) contains the spin matrices governed by the spin-polarization direction. Therefore, in order to obtain high VISHE and hence \(g_r^{ \uparrow \downarrow }\) in an FM/HM heterostructure, θSH of the HM needs to be large. The value of θSH depends mostly on the spin–orbit interaction (SOI) and conductivity of the HM2,8. Efficient interfacial spin transport critically depends on the type of interfaces and its associated FM and HM materials, and FM materials with low magnetic damping (α) are important to generate large spin currents and hence high \(g_r^{ \uparrow \downarrow }\)2. In this context, various low-damping materials, such as NiFe, CoFeB, and Y3Fe5O12, have been studied. Further, there is another class of half-metallic materials, e.g., Heusler alloys, which have been established as low-damping systems. It is also noted here that spin pumping and the resultant spin current can be described as an accumulation of up and down spins9. Therefore, it is expected that the spin pumping efficiency is larger in Heusler alloys than in other alloys due to the presence of only one type of spin at the Fermi level. In addition, low magnetic damping and expected high spin pumping make Heusler alloys suitable for interface spin transport studies and pure spin current-based spin-torque nano-oscillators10. There have been intense studies of spin dynamics with low-damping materials, e.g., NiFe and CoFeB with various HMs11,12,13,14,15. However, there are only a few reports on the spin dynamics of Heusler alloys with HMs9,16. Co2Fe0.4Mn0.6Si (CFMS) is a Heusler alloy that shows low damping and 100% spin polarization17. Figure 1a shows a typical schematic for the density of states for a half-metallic material. However, \(g_r^{ \uparrow \downarrow }\) in CFMS/HM systems has so far not been evaluated, which would help to understand their use for applications. Here, we report on a spin pumping study in a CFMS/Pt system with varying Pt thickness via (1) measurement of the ISHE, (2) evaluation of \(g_r^{ \uparrow \downarrow }\) and (3) and characterization of the spin interface transparency.
Fig. 1: Structural quality of CFMS and measurement geometry for inverse spin Hall effect.
a A schematic of the density of states (D(E)) for an ideal half metal alloy. b, c are the RHEED patterns for samples S4 and S5, respectively, on the MgO (100) substrate along the [100] and [110] azimuths. d Schematic of the setup for ISHE measurement, where hrf is the rf magnetic field generated in a coplanar waveguide (CPW) perpendicular to the applied magnetic field (H).
The bilayer samples viz. S1♯ CFMS(20 nm)/Pt(3 nm), S2♯ CFMS(20 nm)/Pt(5 nm), S3♯ CFMS(20 nm)/Pt(7 nm), S4♯ CFMS(20 nm)/Pt(10 nm), S5♯ CFMS(20 nm)/Pt(20 nm), and S6♯ CFMS(20 nm) were prepared on MgO(100) substrates using dc magnetron sputtering in a vacuum system with a base pressure of ~1 × 10−9 mbar18. The composition of CFMS was Co2Fe0.4Mn0.6Si. This composition was chosen due to the observation of the lowest α at 60% Mn concentration in a recent study by Pan et al.19. The prepared CFMS thin films were annealed in situ at 600 °C/1 h to improve their crystallinity and surface quality. Reflection high-energy electron diffraction (RHEED) patterns were acquired to characterize the surface and crystalline quality of the CFMS layers. After the preparation of the CFMS layer, the Pt layer was deposited at room temperature by dc magnetron sputtering. The thickness and interface roughness of the films were evaluated using X-ray reflectivity (XRR) as measured by an X-ray diffractometer (Rigaku Smartlab). Ferromagnetic resonance (FMR) measurements have been performed in the frequency range of 5–17 GHz on a coplanar waveguide in the flip-chip manner20,21. ISHE measurements were performed by connecting a nanovoltmeter over two ends of the sample (sample size: 3 × 2 mm). The details of the ISHE setup can be found elsewhere22.
Crystalline quality
Figure 1b, c shows the RHEED patterns for samples S4 and S5, respectively, observed along the MgO[100] and MgO[110] azimuths. From the streaks and spots of the RHEED patterns, it is confirmed that a CFMS layer with a (001) crystalline orientation was epitaxially grown on the MgO (001) substrate. The streak lines that are elongated spots in the vertical direction in the RHEED pattern imply the improvement of flatness at the CFMS surface. Supplementary Fig. A1 in the Supplementary Information shows the XRR data and the corresponding best fits. From the best fits, the values of interface roughness at the CFMS-Pt interface are found to be 0.9 ± 0.02, 1.0 ± 0.02, 1.4 ± 0.03, 1.4 ± 0.03, 1.4 ± 0.03, and 1.5 ± 0.02 nm for samples S1–S5. Figure 1d shows the sample structure and ISHE measurement geometry, which are discussed in the next section.
Magnetic damping
Figure 2a, b shows the plots of resonance frequency (f) versus resonance field (Hr) and linewidth (ΔH) versus f, respectively. Here, the values of Hr and ΔH were evaluated using FMR spectra (see Supplementary Fig. A2a, b for samples S1 and S5, respectively, in the Supplementary Information). To evaluate the gyromagnetic ratio (γ) and effective demagnetization (4πMeff), Fig. 2a was fitted to Kittel's equation23 as:
$$f = \frac{\gamma}{{2\pi}} \sqrt {\left( {H_K + H_r} \right){\left( {H_K + H_r + 4 \pi M_{eff}} \right)}},$$
$$4\pi M_{eff} = 4\pi M_s + \frac{{2K_s}}{{M_st_{FM}}}$$
and HK, KS, Ms, and tFM are the anisotropy field, perpendicular surface magnetic anisotropy constant, saturation magnetization, and thickness of the FM layer, respectively. Here, α was evaluated by fitting the data of Fig. 2b using the following expression24:
$${\Delta} H = {\Delta} H_0 + \frac{{4\pi \alpha f}}{\gamma },$$
where ΔH0 is the inhomogeneous broadening of the linewidth, which depends on the homogeneity of the sample. There are various other effects, such as interface effects, impurities, and magnetic proximity effects (MPEs), which can also enhance the value of α of the system. Hence, the total α can be written as:
$$\alpha = \alpha _{{\mathrm{int}}} + \alpha _{{\mathrm{impurity}}} + \alpha _{{\mathrm{MPE}}} + \alpha _{{\mathrm{sp}}},$$
where αint is the intrinsic damping. Further αimpurity, αMPE, and αsp are the contributions from impurities, MPE, and spin pumping to α, respectively25.
Fig. 2: Evaluation of damping constant.
a f vs Hr and b ΔH vs f plots for samples S1 (open squares) and S5 (open circles). The solid lines are the best fits obtained from Eq. (3) and (5).
The linear behavior of the ΔH vs f plots implies good homogeneity in our samples. It is observed from Table 1 that Sample S2 shows the lowest value of ΔH0, which indicates better homogeneity in the sample. Further, S2 shows the highest spin pumping voltage among all samples, which is discussed later. However, sample S3 shows the highest value of ΔH0 among all samples, which indicates a more disordered structure in S3. We also observed a negative sign of HK for samples S1 and S5. This may be due to the orientation of the sample with respect to the magnetic field direction in the FMR setup. We have observed this change in sign while performing in-plane angle-dependent damping measurements; the sign changes from −ve to +ve after 180° rotation.
Table 1 Parameters extracted by fitting the experimental data to Eqs (3) and (5) of the main text.
From Table 2, it is observed that the values of α for the bilayer samples (S1–S5) are larger than the value for a single layer of CFMS (S6). See Supplementary Fig. A3 a, b in the Supplementary Information showing the frequency-dependent resonance and linewidth, respectively. The best fit to Supplementary Fig. A3b yields an α value for sample S6 of ~0.0048 ± 0.0001, which is consistent with the reported value in the literature18. This enhancement in the values of α is an indication of spin pumping. However, we cannot rule out other effects, e.g., MPE, and any impurities that may contribute to enhancing the value of α (see Eq. (6)). To investigate the MPE or magnetic dead layer formation at the interface, we measured the Ms for all the samples by a SQUID magnetometer (data not shown). The measured values of Ms for all the samples were found to be 861 emu/cc (S1), 842 emu/cc (S2), 792 emu/cc (S3), 845 emu/cc (S4), and 807 emu/cc (S5).
Table 2 The values of α for samples S1–S6.
Inverse spin Hall effect measurement
To confirm the spin pumping in our system, we performed ISHE measurements on all the samples, as shown in schematic Fig. 1d. The measurements are carried out at +15 dBm power and 7 GHz frequency.
The angle \(\varphi\) denotes the angle between the measured voltage direction and the perpendicular direction of the applied DC magnetic field (H). Angle-dependent measurements of the voltage were conducted to identify and remove spin rectification effects, e.g., anisotropic magnetoresistance (AMR) and the anomalous Hall effect (AHE). Figure 3 shows the measured voltage (Vmeas) (open blue symbol) versus H along with the FMR signal (open black symbol) for sample S1 at angles \(\varphi\) = 0° (a), 30° (b), 90° (c), and 180° (d). It should be noted that \(\varphi\) = 0° means that the field was applied along the easy-magnetization axis of the sample. There was a very weak signal observed at \(\varphi\) = 90° (Fig. 3b). This is due to the negligible amount of spin accumulation parallel to the applied magnetic field. It is evident from Fig. 3a, d that the sign of Vmeas is reversed when \(\varphi\) moves from 0° to 180°. This indicates that the voltage is produced primarily by spin pumping. It is well-known that if the sign of Vmeas does not reverse with the angle, then the contribution comes solely from different spin rectification effects.
Fig. 3: Inverse spin Hall effect voltage measurements and FMR spectra for sample S1.
Voltage (Vmeas) measured across the sample with an applied magnetic field along with the FMR signal for sample S1 at φ values of (a) 0°, (b) 30°, (c) 90°, and (d) 180°. Open symbols show the experimental data. Solid lines are the fits to the experimental data using Eq. (7). Short dashed and dotted lines show the symmetric (Vsym) and antisymmetric (Vasym) components of the voltage, respectively.
Figure 4 shows a Vmeas versus H plot for sample S5 measured at \(\varphi\) = 0° (a), 30° (b), 90° (c), 180° (d). A similar kind of ISHE signal was observed for all the samples (data not shown). It is observed that the strength of Vmeas for sample S5 (20-nm-thick Pt) is three times smaller than that of sample S1 (3-nm-thick Pt). This is consistent with the fact that the ISHE voltage is inversely proportional to the conductivity and thickness of the HM layer26.
Vmeas versus H and FMR signal for sample S5 at the φ values of (a) 0°, (b) 30°, (c) 90°, and (d) 180°. Open symbols represent the measured voltage. Experimental data are fitted (solid lines) using Eq. (7). Dashed and dotted lines show the symmetric (Vsym) and antisymmetric (Vasym) voltage components fitted to Eq. (7), respectively.
For the separation of the spin pumping contribution from Vmeas by excluding other spurious effects, Vmeas versus H plots for samples S1 (Fig. 3) and S5 (Fig. 4) were fitted with the Lorentzian equation27, which is given by:
$$V_{{\mathrm{meas}}} = V_{{\mathrm{sym}}}\frac{{\left( {{\Delta} H} \right)^2}}{{\left( {H - H_r} \right)^2 + \left( {{\Delta} H} \right)^2}} + V_{{\mathrm{asym}}}\frac{{2{\Delta} H\left( {H - H_r} \right)}}{{\left( {H - H_r} \right)^2 + \left( {{\Delta} H} \right)^2}},$$
where Vsym and Vasym are the symmetric and antisymmetric components, respectively. Solid lines are the fits to the experimental data. Vsym contains a major contribution from spin pumping and minor contributions from the AHE and AMR effects. The AHE contribution is zero here if the rf field and H are perpendicular to each other, which is the case in our measurement. The AHE and AMR are the major contributions in the Vasym component. Figures 3 and 4 also show the plots of Vsym (dashed line) and Vasym (dotted line) separately for samples S1 and S5, respectively.
In-plane angle-dependent measurements of Vmeas were performed at intervals of 2° to quantify spin pumping and other spin rectification contributions (Fig. 5a, b for sample S1 and Fig. 5c, d for sample S5). This is a well-established method to decouple the individual components from the measured voltage25,28,29. The model given by Harder et al.30 considered the rectification effects, i.e., parallel AMR (\({\mathrm{V}}_{{\mathrm{asym/sym}}}^{{\mathrm{AMR}}\,\parallel }\)) and perpendicular AMR (\({\mathrm{V}}_{{\mathrm{asym/sym}}}^{{\mathrm{AMR}} \bot }\)), to the applied rf field and the AHE contribution due to the FM layer. The relation between the measured voltage and those rectification effects is as follows28:
$$V_{{\mathrm{asym}}} = V_{{\mathrm{AHE}}}{\mathrm{cos}}\left( {\varphi + \varphi _0} \right){\mathrm{sin}}\emptyset + {\mathrm{V}}_{{\mathrm{asym}}}^{{\mathrm{AMR}}\, \bot }{\mathrm{cos2}}\left( {\varphi + \varphi _0} \right){\mathrm{cos}}\left( {\varphi + \varphi _0} \right) + {\mathrm{V}}_{{\mathrm{asym}}}^{{\mathrm{AMR}}\,\parallel }{\mathrm{sin2}}\left( {\varphi + \varphi _0} \right){\mathrm{cos}}\left( {\varphi + \varphi _0} \right),$$
$$\begin{array}{l}V_{{\mathrm{sym}}} = V_{{\mathrm{sp}}}{\it{{\mathrm{cos}}}}^3\left( {\varphi + \varphi _0} \right) + V_{{\mathrm{AHE}}}{\mathrm{cos}}\left( {\varphi + \varphi _0} \right){\mathrm{cos}}\emptyset + {\mathrm{V}}_{{\mathrm{sym}}}^{{\mathrm{AMR}}\, \bot }{\mathrm{cos2}}\left( {\varphi + \varphi _0} \right){\mathrm{cos}}\left( {\varphi + \varphi _0} \right)\\ + {\mathrm{V}}_{{\mathrm{sym}}}^{{\mathrm{AMR}}\,\parallel }{\mathrm{sin2}}\left( {\varphi + \varphi _0} \right){\mathrm{cos}}\left( {\varphi + \varphi _0} \right)\end{array}.$$
Fig. 5: Angle dependent measurements of ISHE.
Angle-dependent (φ) Vsym and Vasym measurements for samples S1 (a and b) and S5 (c and d), respectively.
VAHE and Vsp correspond to the AHE voltage and the spin pumping contributions, respectively. In addition, \(\emptyset\) is the angle between the applied H and the rf magnetic field, which is always perpendicular in the present measurement. The extra factor \(\varphi_0\) is taken to incorporate the misalignment of sample positioning in defining the \(\emptyset\) value during the measurement. The detailed fits with and without incorporation of a small offset in the \(\emptyset\) value are shown in Supplementary Figs. A4 and A5 in the Supplementary Information. Further, the AMR contribution can also be quantified by the following formula28:
$$V_{{\mathrm{AMR}}} = \sqrt {\left( {{\mathrm{V}}_{{\mathrm{Asym}}}^{{\mathrm{AMR}} \bot ,\parallel }} \right)^2 + \left( {{\mathrm{V}}_{{\mathrm{sym}}}^{{\mathrm{AMR}} \bot ,\parallel }} \right)^2}.$$
Here, \({\mathrm{V}}_{{\mathrm{Asym}}}^{{\mathrm{AMR}} \bot ,\parallel }\) and \({\mathrm{V}}_{{\mathrm{sym}}}^{{\mathrm{AMR}} \bot ,\parallel }\) are evaluated from the in-plane angle-dependent Vmeas measurements by fitting those values by Eqs (8) and (9), respectively. The extracted values of the various components are listed in Table 3.
Table 3 Fitted parameters from φ-dependent voltage measurements for all five samples.
It is observed that Vsp dominates over other unwanted spin rectification effects in all the samples (see Supplementary Fig. A6 in Supplementary Information). However, the magnitude of the AHE is comparable to that of spin pumping, which is decreased by one order of magnitude for thicker Pt samples. This may be due to the increase in conduction of the Pt layer caused by the increase in its thickness. It is well-known that the AHE depends primarily on the magnetization of the sample due to the Berry curvature of the FM31. The AHE contribution is an intrinsic property of the FM layer. Co-based FM materials are always a potential candidate for AHE phenomena32,33. The saturation magnetization measurements of all the samples indicated the presence of MPE in the Pt (see Supplementary Fig. A7 and description in Supplementary Information) or dead layer formation at the interface, which may result in a decrease in the VAHE contribution as the Pt thickness increases from 3 to 20 nm. However, the AMR values are of a similar order in all the samples. The finite AMR contribution indicates that the samples are anisotropic in nature. A positive value of Vsp indicates a positive spin Hall angle in Pt, which is consistent with the literature26.
The lowest α in S2 shows the maximum spin pumping voltage (Vsp) because of the smooth interface between CFMS/Pt. Vsp is dominated by the conductivity of Pt for thicker Pt samples. Thus, Vsp decreases with increasing tPt.
Figure 6a shows the relationship between effective spin mixing conductance \(g_{eff}^{ \uparrow \downarrow }\) and Pt thickness, while Fig. 6b represents the Pt thickness dependence of the spin Hall angle. Here, \(g_{eff}^{ \uparrow \downarrow }\) was calculated by the following expression using a damping constant2:
$$g_{eff}^{ \uparrow \downarrow } = \frac{{{\Delta} \alpha 4\pi M_St_{{\mathrm{CFMS}}}}}{{g\mu _B}},$$
where \({\Delta} \alpha ,t_{{\mathrm{CFMS}}}\), μB, and g are the changes in α due to spin pumping, the thickness of the CFMS layer, the Bohr magneton, and the Lande g-factor (2.1), respectively. To calculate \(g_r^{ \uparrow \downarrow }\), we considered two models based on spin memory loss (SML) and spin backflow (SBF). The value of \(g_{r}^{\uparrow \downarrow}\) is found to be negative using the SBF model, which is unphysical. This is discussed in detail later. SML is due mainly to interfacial roughness and disorder34. In this model, the effective spin mixing conductance is given by the following equation34:
$$g_{eff}^{ \uparrow \downarrow } = g_r^{ \uparrow \downarrow }\frac{{r_{sI}{\mathrm{cosh}}\left( \delta \right) + r_{sN}^\infty {\mathrm{coth}}\left( {\frac{{t_{{\mathrm{Pt}}}}}{{\lambda _{{\mathrm{Pt}}}}}} \right){\mathrm{sinh}}\left( \delta \right)}}{{r_{sI}\left[ {1 + 0.5\sqrt {\frac{3}{\varepsilon }} \coth \left( {\frac{{t_{{\mathrm{Pt}}}}}{{\lambda _{{\mathrm{Pt}}}}}} \right)} \right]\cosh \left( \delta \right) + r_{sN}^\infty {\mathrm{coth}}\left( {\frac{{t_{{\mathrm{Pt}}}}}{{\lambda _{{\mathrm{Pt}}}}}} \right) + 0.5\frac{{r_{sI}^2}}{{r_{sN}^\infty }}\sqrt {\frac{3}{\varepsilon }} {\mathrm{sinh}}\left( \delta \right)}},$$
where ε is the ratio of the spin conserved to spin-flip relaxation times. Based on ref. 33, we set ε = 0.1 for the present Pt. In addition, rsI, \(r_{sN}^\infty\), δ, and λPt are the interfacial spin resistance, Pt spin resistance, spin-flip parameter for the CFMS/Pt interface, and spin diffusion length in Pt, respectively. Figure 6a shows the fitting (solid line) of the data of \(g_{eff}^{ \uparrow \downarrow }\) using Eq. (12). The fitting gives the values of λPt = 7.5 ± 0.5 nm, \(g_r^{ \uparrow \downarrow }\)= 1.70 ± 0.03 × 1020 m−2, and δ = 0.1. It is noted here that due to the interdependency of the parameters, we changed each parameter one by one to reach the convergence of the fit. We have varied different values of \(g_r^{ \uparrow \downarrow }\) in order to obtain the best fit (see Supplementary Fig. A8 in Supplementary Information). We observed that only for \(g_r^{ \uparrow \downarrow }\) = 1.7 × 1020 m−2 does the best fit pass through three data points, while the other fits are far from the data points. Therefore, we concluded that this is the best fit.
Fig. 6: Extraction of spin mixing conductance and spin Hall angle.
a \(g_{eff}^{ \uparrow \downarrow }\) and b spin Hall angle as a function of Pt thickness. The solid line in (a) is the best fit using Eq. (12).
The values of \(r_{sI}\) and \(r_{sN}^\infty\) are 0.85 fΩm2 and 0.58 fΩm2, respectively, which are similar to the reported values for Co/Pt systems34. In the CFMS/Pt system, the SML probability (\([1 - exp\left( { - \delta } \right)] \times 100\)) is found to be 9.5%. This implies that the disorder at the interfaces is small since spin depolarization is caused mainly by disorder at the interfaces. The rsI is given by \(\frac{{r_b}}{\delta }\), where rb is the interface resistance. This indicates that most of the spin current flows through the interface compared to the bulk SOC of the Pt if the SML probability is large. However, in our case, the SML probability is very small (9.5%), which means that most of the spin current is dissipated through the bulk SOC of the Pt, which produces a charge current and hence creates VISHE. It is mentioned here that such high values of \(g_r^{ \uparrow \downarrow }\)and \(g_{eff}^{ \uparrow \downarrow }\) can be due to (1) higher interface spin mixing conductance than Sharvin conductance of Pt, (2) SML at the interface and alloying at the interface of the FM/Pt layer, (3) SBF, and (4) overestimation due to two-magnon scattering (TMS). The spin mixing conductance cannot be higher than the Sharvin conductance of Pt. Further, it is observed that the SML probability is very small (9.5%), which normally comes from interface disorder or alloying. Therefore, SML cannot be the primary reason for observing such a high value of \(g_r^{ \uparrow \downarrow }\) and \(g_{eff}^{ \uparrow \downarrow }\). To understand the role of SBF, we considered the SBF model to evaluate spin mixing conductance using the following equation2:
$$g_r^{ \uparrow \downarrow } = \frac{{\frac{{g_{eff}^{ \uparrow \downarrow }}}{{2\rho _{{\mathrm{Pt}}}\lambda _{{\mathrm{Pt}}}}}}}{{\frac{h}{{2e^2\rho _{{\mathrm{Pt}}}\lambda _{{\mathrm{Pt}}}}} - g_{eff}^{ \uparrow \downarrow }\coth \left( {\frac{{t_{{\mathrm{Pt}}}}}{{\lambda _{{{{\mathrm{Pt}}}}}}}} \right)}},$$
where ρPt is the resistivity of the Pt layer, which is 2.3 × 10−7 Ωm. The evaluated values of \({g_{r}^{\uparrow \downarrow}}\)are found to be negative, which is unphysical. Therefore, it can be concluded that the SBF model is not applicable in our samples and cannot be the reason for the high spin mixing conductance. Further, in order to separate the contribution of TMS in our samples, we performed angle-dependent damping constant measurements in the range of 0 to 180° at intervals of 10° for samples S5 and S6. TMS generally comes from the defects and imperfections present in thin films. If thin films are well ordered, the scattering intensity should follow the symmetry present in the thin films. Because our CFMS thin films are epitaxial and have cubic magnetic anisotropy, the damping constant is symmetric with respect to crystallographic directions. Due to the epitaxial nature of our CFMS thin films, angle-dependent damping analysis gives the opportunity to separate TMS contributions. Conca et al.35 used this methodology with epitaxial Fe/Al, Fe/Pt, and Fe/MgO layers. We chose sample S5 since the interface roughness is highest among the samples; if there is any interface contribution, it is expected to be higher in sample S5. Figure 7a, b shows the angle-dependent damping constant for samples S6 and S5, respectively, revealing the anisotropy in the damping constant. We followed the model given by Arias et al.36, which was also used by Conca et al.35. It can be written as
$$\alpha _{2M} = \mathop {\sum}\limits_{x_i} {{\Gamma} _{x_i}f\left( {\varphi - \varphi _{x_i}} \right)},$$
where \({\Gamma} _{x_i}\) is the contribution of TMS along the in-plane crystallographic direction xi. The function \(f(\varphi - \varphi _{x_i})\) is the ansatz and can be written as:
$$f\left( {\varphi - \varphi _{x_i}} \right) = {\it{{\mathrm{cos}}}}^2\left( {4\varphi - \varphi _{\left[ {100} \right]}} \right).$$
Fig. 7: Angle-dependence of damping constant (α) for samples S6 and S5.
Solid symbols and solid lines show the experimental data and best fit to Eq. (16), respectively.
Therefore, the effective damping can be written as
$$\alpha = \alpha _{iso} + \alpha _{2M} = \alpha _{iso} + {\Gamma} _{2M}{\it{{\mathrm{cos}}}}^2\left( {4\varphi - \varphi _{\left[ {100} \right]}} \right),$$
where αiso is the total damping due to Gilbert damping, spin pumping, and magnetic proximity effect. Γ2M represents the strength of the TMS contribution.
We fitted the experimental data (solid symbols) to Eq. (16) (solid line), as shown in Fig. 7a, b, for samples S6 and S5, respectively. The fitting parameters are listed in Table 4. The values of Γ2M are found to be 0.00170 ± 0.00057 and 0.00165 ± 0.00035 for samples S6 and S5, respectively. It is inferred that the strength of the TMS contribution is similar in the single CFMS film (S6) and the bilayer CFMS/Pt sample (S5). Because \(g_{eff}^{ \uparrow \downarrow }\) is directly proportional to Δα, it does not affect the calculations of \(g_{eff}^{ \uparrow \downarrow }\) or \(g_r^{ \uparrow \downarrow }\) For example, the value of Δα is evaluated to be 0.00382 after removing the TMS contribution compared to 0.00386 considering the TMS contribution. The values of \(g_{eff}^{ \uparrow \downarrow }\) are 4.1 × 1019 m−2 and 4.3 × 1019 m−2 for sample S5 without and with TMS contributions, respectively. Hence, we concluded that the TMS contribution comes from the CFMS layer, not from the interface of the CFMS/Pt layer. This means that TMS is not the reason for observing such a high value of spin mixing conductance. Therefore, the effective value of α, as mentioned in Eq. (6), may have TMS but it cannot have any effect on the evaluation of \(g_{eff}^{ \uparrow \downarrow }\) after subtraction of α from a single CFMS layer. From the above, one may infer that the low damping, epitaxial nature, and high spin polarization of the CFMS layer could be the primary sources for observing this high value of \(g_{eff}^{ \uparrow \downarrow }\).
Table 4 Fitting parameters of angle-dependent damping constant data to Eq. (16) for samples S5 and S6.
Further, we compared the \(g_r^{ \uparrow \downarrow }\) and \(g_{eff}^{ \uparrow \downarrow }\) values evaluated in this work to the literature for various FM/HM systems in Table 5. It can be observed that the values of \(g_r^{ \uparrow \downarrow }\) and \(g_{eff}^{ \uparrow \downarrow }\) are higher than the available literature values for systems with Pt. In addition, it should be noted here that the values of \(g_r^{ \uparrow \downarrow }\) and \(g_{eff}^{ \uparrow \downarrow }\) are large compared to those of other reported low-damping systems, viz. Y3Fe5O12/Pt, CoFeB/Pt, and Co2MnSi/Pt37,38. Therefore, the CFMS/Pt system can be a potential system for spin-transfer torque and logic devices. In addition to \(g_r^{ \uparrow \downarrow }\), spin interface transparency (T) is another parameter that is useful for spin–orbit torque-based devices. The value of T is affected by the electronic structure matching of the FM and HM layers. We used the following expression to calculate T39:
$$T = \frac{{g_r^{ \uparrow \downarrow }{\mathrm{tanh}}\left( {\frac{{t_{{\mathrm{Pt}}}}}{{2\lambda _{{\mathrm{Pt}}}}}} \right)}}{{g_r^{ \uparrow \downarrow }\coth \left( {\frac{{t_{{\mathrm{Pt}}}}}{{\lambda _{{\mathrm{Pt}}}}}} \right) + \frac{{h\sigma _{{\mathrm{Pt}}}}}{{2e^2\lambda _{{\mathrm{Pt}}}}}}},$$
where σPt is the conductivity of Pt layer. For tPt = 20 nm, T is calculated to be 0.83 ± 0.02 by Eq. (17), which is much higher than the values reported in the literature for NiFe/Pt and Co/Pt systems39. Further, it is also higher than the recently developed low-damping Co2FeAl/Ta layer system (68%)40. We also calculated θSH for Pt using the following expression2:
$$\mid{\overrightarrow {J_s} }\mid \approx \left( {\frac{{g_{eff}^{ \uparrow \downarrow }\hbar }}{{8\pi }}} \right)\left( {\frac{{\mu _0h_{rf}\gamma }}{\alpha }} \right)^2 \times \left[ {\frac{{\mu _0M_S\gamma + \sqrt {\left( {\mu _0M_S\gamma } \right)^2 + 16\left( {\pi f} \right)^2} }}{{\left( {\mu _0M_S\gamma } \right)^2 + 16\left( {\pi f} \right)^2}}} \right]\left( {\frac{{2e}}{\hbar }} \right),$$
$$V_{{\mathrm{ISHE}}} = \left( {\frac{{w_y}}{{\sigma _{{\mathrm{FM}}}t_{{\mathrm{FM}}} + \sigma _{{\mathrm{Pt}}}t_{{\mathrm{Pt}}}}}} \right) \times \theta _{{\mathrm{SH}}}\lambda _{{\mathrm{Pt}}}\tanh \left( {\frac{{t_{{\mathrm{Pt}}}}}{{2\lambda _{{\mathrm{Pt}}}}}} \right)\left| {\overrightarrow {J_s} } \right|.$$
Table 5 Spin diffusion length (λPt), spin mixing conductance (\(g_r^{ \uparrow \downarrow }\)), and effective mixing conductance (\(g_{eff}^{ \uparrow \downarrow }\)) obtained from the literature and in this work.
The resistivity (ρ) of the samples was measured using the four-probe technique, and ρPt and ρCFMS were found to be 2.3 × 10−7 Ω-m and 1.7 × 10−6 Ω-m, respectively. Here, σ corresponds to the conductivity of the individual layers.
The rf field (μ0hrf) and CPW transmission linewidth (wy) for our setup are 0.5 Oe (at +15 dBm rf power) and 200 μm, respectively. The obtained values of θSH are plotted in Fig. 6b. The values of θSH are comparable to the literature values41. In our case, we observe a higher SHA value for sample S1 than for sample S5. This may be due to the higher resistivity of the 3-nm Pt layers, which is consistent with the results obtained by Liu et al.42.
Further, we also determined the power dependence of the VISHE measurements (Supplementary Fig. A9, Supplementary Information). We observed a linear dependence of VISHE, which confirmed spin pumping at the CFMS/Pt interface.
We observed a strong dependency of the spin pumping voltage on the thickness of Pt. The spin pumping voltage was decreased when the thickness of Pt was increased, which may be due to the increase in conductivity of Pt with increasing thickness. The presence of substantial spin pumping maintains the damping constant values on the order of ~10−3. The \(g_r^{ \uparrow \downarrow }\) was obtained to be 1.70 × 1020 m−2, higher than those for the other reported FM/Pt systems. We also performed angle-dependent damping constant measurements to quantify TMS contributions. We found that TMS in CFMS/Pt is not significant and does not affect the obtained high value of \(g_r^{ \uparrow \downarrow }\). In addition, we observed the highest spin interface transparency (83%) of any FM/Pt system. Low magnetic damping and a large value of \(g_r^{ \uparrow \downarrow }\) with high interface transparency make the CFMS/Pt system a potential candidate for spintronic applications.
Bader, S. D. & Parkin, S. S. P. Spintronics. Annu. Rev. Condens. Matter Phys. 1, 71–88 (2010).
Tserkovnyak, Y., Brataas, A., Bauer, G. E. W. & Halperin, B. I. Nonlocal magnetization dynamics in ferromagnetic heterostructures. Rev. Mod. Phys. 77, 1375–1421 (2005).
Avci, C. O. et al. Unidirectional spin Hall magnetoresistance in ferromagnet/normal metal bilayers. Nat. Phys. 11, 570–575 (2015).
Sánchez, J. C. R. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 4, 2944 (2013).
Tao, X. et al. Self-consistent determination of spin Hall angle and spin diffusion length in Pt and Pd: the role of the interface spin loss. Sci. Adv. 4, eaat1670 (2018).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced Gilbert damping in thin ferromagnetic films. Phys. Rev. Lett. 88, 117601 (2002).
Chudo, H. et al. Spin pumping efficiency from half metallic Co2MnSi. J. Appl. Phys. 109, 073915 (2011).
Demidov, V. E. et al. Magnetization oscillations and waves driven by pure spin currents. Phys. Rep. 673, 1–31 (2017).
Mizukami, S., Ando, Y. & Miyazaki, T. Effect of spin diffusion on Gilbert damping for a very thin permalloy layer in Cu/permalloy/Cu/Pt films. Phys. Rev. B 66, 104413 (2002).
Miao, B. F., Huang, S. Y., Qu, D. & Chien, C. L. Inverse Spin Hall effect in a ferromagnetic metal. Phys. Rev. Lett. 111, 066602 (2013).
Chen, L., Ikeda, S., Matsukura, F. & Ohno, H. DC voltages in Py and Py/Pt under ferromagnetic resonance. Appl. Phys. Express 7, 013002 (2013).
Kim, S.-I., Seo, M.-S., Choi, Y. S. & Park, S.-Y. Irreversible magnetic-field dependence of ferromagnetic resonance and inverse spin Hall effect voltage in CoFeB/Pt bilayer. J. Magn. Magn. Mater. 421, 189–193 (2017).
Cecot, M. et al. Influence of intermixing at the Ta/CoFeB interface on spin Hall angle in Ta/CoFeB/MgO heterostructures. Sci. Rep. 7, 1–11 (2017).
Gościańska, I. & Dubowik, J. Inverse Spin Hall Effect by spin-pumping in Co_2Cr_{0.4}Fe_{0.6}Al/Pt structures. Acta Phys. Polonica A 118, 851–853 (2010).
Hirohata, A. & Takanashi, K. Future perspectives for spintronic devices. J. Phys. D: Appl. Phys. 47, 193001 (2014).
Pan, S., Seki, T., Takanashi, K. & Barman, A. Role of the Cr buffer layer in the thickness-dependent ultrafast magnetization dynamics of Co2Fe0.4Mn0.6 Si Heusler alloy thin films. Phys. Rev. Appl. 7, 064012 (2017).
Pan, S., Seki, T., Takanashi, K. & Barman, A. Ultrafast demagnetization mechanism in half-metallic Heusler alloy thin films controlled by the Fermi level. Phys. Rev. B 101, 224412 (2020).
NanOsc A. B. NanOsc AB http://www.nanosc.se/.
Singh, B. B., Jena, S. K. & Bedanta, S. Study of spin pumping in Co thin film vis-à-vis seed and capping layers using ferromagnetic resonance spectroscopy. J. Phys. D: Appl. Phys. 50, 345001 (2017).
Singh, B. B. et al. Inverse spin Hall effect in electron beam evaporated topological insulator Bi2Se3 thin film. Phys. Status Solidi (RRL) – Rapid Res. Lett. 13, 1800492 (2019).
Kittel, C. On the theory of ferromagnetic resonance absorption. Phys. Rev. 73, 155–161 (1948).
Heinrich, B., Cochran, J. F. & Hasegawa, R. FMR linebroadening in metals due to two‐magnon scattering. J. Appl. Phys. 57, 3690–3692 (1985).
Conca, A. et al. Study of fully epitaxial Fe/Pt bilayers for spin pumping by ferromagnetic resonance spectroscopy. Phys. Rev. B 93, 134405 (2016).
Ando, K. et al. Inverse spin-Hall effect induced by spin pumping in metallic system. J. Appl. Phys. 109, 103913 (2011).
Iguchi, R. & Saitoh, E. Measurement of spin pumping voltage separated from extrinsic microwave effects. J. Phys. Soc. Jpn. 86, 011003 (2016).
Conca, A. et al. Lack of correlation between the spin-mixing conductance and the inverse spin Hall effect generated voltages in CoFeB/Pt and CoFeB/Ta bilayers. Phys. Rev. B 95, 174426 (2017).
Harder, M., Gui, Y. & Hu, C.-M. Electrical detection of magnetization dynamics via spin rectification effects. Phys. Rep. 661, 1–59 (2016).
Harder, M., Cao, Z. X., Gui, Y. S., Fan, X. L. & Hu, C.-M. Analysis of the line shape of electrically detected ferromagnetic resonance. Phys. Rev. B 84, 054423 (2011).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Zhang, W. et al. Determination of the Pt spin diffusion length by spin-pumping and spin Hall effect. Appl. Phys. Lett. 103, 242414 (2013).
Zahnd, G. et al. Spin diffusion length and polarization of ferromagnetic metals measured by the spin-absorption technique in lateral spin valves. Phys. Rev. B 98, 174414 (2018).
Rojas-Sánchez, J.-C. et al. Spin pumping and inverse spin Hall effect in platinum: the essential role of spin-memory loss at metallic interfaces. Phys. Rev. Lett. 112, 106602 (2014).
Conca, A., Keller, S., Schweizer, M. R., Papaioannou, E. T. H. & Hillebrands, B. Separation of the two-magnon scattering contribution to damping for the determination of the spin mixing conductance. Phys. Rev. B 98, 214439 (2018).
Arias, R. & Mills, D. L. Extrinsic contributions to the ferromagnetic resonance response of ultrathin films. Phys. Rev. B 60, 7395–7409 (1999).
Wang, H. Understanding of Pure Spin Transport in a Broad Range of Y3Fe5O12-Based Heterostructures. PhD, The Ohio State Univ. (2015).
Belmeguenai, M. et al. Investigation of the annealing temperature dependence of the spin pumping in Co20Fe60B20/Pt systems. J. Appl. Phys. 123, 113905 (2018).
Zhang, W. et al. Role of transparency of platinum–ferromagnet interfaces in determining the intrinsic magnitude of the spin Hall effect. Nat. Phys. 11, 496–502 (2015).
Akansel, S. et al. Thickness-dependent enhancement of damping in Co2 FeAl/β-Ta thin films. Phy. Rev. B 97, 134421 (2018)..
Nakayama, H. et al. Geometry dependence on inverse spin Hall effect induced by spin pumping in Ni81Fe19/Pt films. Phys. Rev. B 85, 144408 (2012).
Liu, J., Ohkubo, T., Mitani, S., Hono, K. & Hayashi, M. Correlation between the spin Hall angle and the structural phases of early 5d transition metals. Appl. Phys. Lett. 107, 232408 (2015).
The authors acknowledge DAE and DST, Government of India, for financial support of the experimental facilities. B.B.S. acknowledges DST for INSPIRE faculty fellowship. K.R. and P.G. thank CSIR and UGC for their JRF fellowships, respectively. S.B. acknowledges an ICC-IMR fellowship to visit IMR, Tohoku University, for this collaborative work to prepare the thin films.
Laboratory for Nanomagnetism and Magnetic Materials (LNMM), School of Physical Sciences, National Institute of Science Education and Research (NISER), HBNI, Jatni, Odisha, India
Braj Bhusan Singh, Koustuv Roy, Pushpendra Gupta & Subhankar Bedanta
Institute for Materials Research, Tohoku University, Sendai, Japan
Takeshi Seki & Koki Takanashi
Center for Spintronics Research Network, Tohoku University, Sendai, Japan
Center for Science and Innovation in Spintronics, Core Research Cluster, Tohoku University, Sendai, Japan
Koki Takanashi
Braj Bhusan Singh
Koustuv Roy
Pushpendra Gupta
Takeshi Seki
Subhankar Bedanta
S.B. conceived the idea. B.B.S., S.B., and T.S. designed the experiment. Sample preparation and RHEED observation were performed by T.S. and S.B. Spin pumping and ISHE measurements were performed by B.B.S. and K.R. Resistivity measurements were performed by B.B.S., K.R. and P.G. SQUID measurements were performed by P.G. and B.B.S. Data analysis and discussion were conducted by B.B.S., K.R., S.B., and T.S. Spin mixing conductance and spin transparency analysis were performed by B.B.S. This paper was written by B.B.S., K.R., and S.B. All authors contributed to the paper corrections.
Correspondence to Subhankar Bedanta.
Supplementray information
Singh, B.B., Roy, K., Gupta, P. et al. High spin mixing conductance and spin interface transparency at the interface of a Co2Fe0.4Mn0.6Si Heusler alloy and Pt. NPG Asia Mater 13, 9 (2021). https://doi.org/10.1038/s41427-020-00268-7
For Authors & Referees
NPG Asia Materials (NPG Asia Mater) ISSN 1884-4057 (online) ISSN 1884-4049 (print) | CommonCrawl |
Quantum algorithm for linear systems of equations (HHL09): Step 2 - What is $|\Psi_0\rangle$?
This is a sequel to Quantum algorithm for linear systems of equations (HHL09): Step 1 - Confusion regarding the usage of phase estimation algorithm and Quantum algorithm for linear systems of equations (HHL09): Step 1 - Number of qubits needed.
In the paper: Quantum algorithm for linear systems of equations (Harrow, Hassidim & Lloyd, 2009), what's written up to the portion
The next step is to decompose $|b\rangle$ in the eigenvector basis, using phase estimation [5–7]. Denote by $|u_j\rangle$ the eigenvectors of $A$ (or equivalently, of $e^{iAt}$), and by $\lambda_j$ the corresponding eigenvalues.
on page $2$ makes some sense to me (the confusions up till there have been addressed in the previous posts linked above). However, the next portion i.e. the $R(\lambda^{-1})$ rotation seems a bit cryptic.
Let $$|\Psi_0\rangle := \sqrt{\frac{2}{T}}\sum_{\tau =0}^{T-1} \sin \frac{\pi(\tau+\frac{1}{2})}{T}|\tau\rangle$$
for some large $T$. The coefficients of $|\Psi_0\rangle$ are chosen (following [5-7]) to minimize a certain quadratic loss function which appears in our error analysis (see [13] for details).
Next, we apply the conditional Hamiltonian evolution $\sum_{\tau = 0}^{T-1}|\tau\rangle \langle \tau|^{C}\otimes e^{iA\tau t_0/T}$ on $|\Psi_0\rangle^{C}\otimes |b\rangle$, where $t_0 = \mathcal{O}(\kappa/\epsilon)$.
1. What exactly is $|\Psi_0\rangle$? What do $T$ and $\tau$ stand for? I've no idea from where this gigantic expression $$\sqrt{\frac{2}{T}}\sum_{\tau =0}^{T-1} \sin \frac{\pi(\tau+\frac{1}{2})}{T}|\tau\rangle$$ suddenly comes from and what its use is.
2. After the phase estimation step, the state of our system is apparently:
$$\left(\sum_{j=1}^{j=N}\beta_j|u_j\rangle\otimes |\tilde\lambda_j\rangle\right)\otimes |0\rangle_{\text{ancilla}}$$
This surely cannot be written as $$\left(\sum_{j=1}^{j=N}\beta_j|u_j\rangle\right)\otimes \left(\sum_{j=1}^{j=N}|\tilde\lambda_j\rangle\right)\otimes |0\rangle_{\text{ancilla}}$$ i.e.
$$|b\rangle\otimes \left(\sum_{j=1}^{j=N}|\tilde\lambda_j\rangle\right)\otimes |0\rangle_{\text{ancilla}}$$
So, it is clear that $|b\rangle$ is not available separately in the second register. So I've no idea how they're preparing a state like $|\Psi_0\rangle^{C}\otimes |b\rangle$ in the first place! Also, what does that $C$ in the superscript of $|\Psi_0\rangle^{C}$ denote?
3. Where does this expression $\sum_{\tau = 0}^{T-1}|\tau\rangle \langle \tau|^{C}\otimes e^{iA\tau t_0/T}$ suddenly appear from ? What's the use of simulating it? And what is $\kappa$ in $\mathcal{O}(\kappa/\epsilon)$ ?
algorithm hhl-algorithm hamiltonian-simulation
Sanchayan Dutta
Sanchayan DuttaSanchayan Dutta
Names and symbols used in this answer follow the ones defined in Quantum linear systems algorithms: a primer (Dervovic, Herbster, Mountney, Severini, Usher & Wossnig, 2018). A recall is done below.
1.1 Register names
Register names are defined in Figure 5. of Quantum linear systems algorithms: a primer (Dervovic, Herbster, Mountney, Severini, Usher & Wossnig, 2018) (reproduced below):
$S$ (1 qubit) is the ancilla register used to check if the output is valid or not.
$C$ ($n$ qubits) is the clock register, i.e. the register used to estimate the eigenvalues of the hamiltonian with quantum phase estimation (QPE).
$I$ ($m$ qubits) is the register storing the right-hand side of the equation $Ax = b$. It stores $x$, the result of the equation, when $S$ is measured to be $\left|1\right>$ at the end of the algorithm.
2. About $\left|\Psi_0\right>$:
What exactly is $\left|\Psi_0\right>$?
$\left|\Psi_0\right>$ is one possible initial state of the clock register $C$.
What do $T$ and $\tau$ stand for?
$T$ stands for a big positive integer. This $T$ should be as large as possible because the expression of $\left|\Psi_0\right>$ asymptotically minimise a given error for $T$ growing to infinity. In the expression of $\left|\Psi_0\right>$, $T$ will be $2^n$, the number of possible states for the quantum clock $C$.
$\tau$ is just the summation index
Why such a gigantic expression for $\left|\Psi_0\right>$?
See DaftWullie's post for a detailed explanation.
Following the citations in Quantum algorithm for linear systems of equations (Harrow, Hassidim & Lloyd, 2009 v3) we end up with:
The previous version of the same paper Quantum algorithm for linear systems of equations (Harrow, Hassidim & Lloyd, 2009 v2). The authors revised the paper 2 times (there are 3 versions of the original HHL paper) and version n°3 does not include all the informations provided in the previous versions. In the V2 (section A.3. starting at page 17), the authors provide a detailed analysis of the error with this special initial state.
Optimal Quantum Clocks (Buzek, Derka, Massar, 1998) where the expression of $\left|\Psi_0\right>$ is given as $\left|\Psi_{opt}\right>$ in Equation 10. I don't have the knowledge to understand fully this part, but it seems like this expression is "optimal" in some sense.
3. Preparation of $\left|\Psi_0\right>$:
As said in the previous part, $\left|\Psi_0\right>$ is an initial state. They do not prepare $\left|\Psi_0\right>$ after the phase estimation procedure. The sentence ordering is not really optimal in the paper. The phase estimation procedure they use in the paper is a little bit different from the "classic" phase estimation algorithm represented in the quantum circuit linked in part 1, and that is why they explain it in details.
Their phase estimation algorithm is:
Prepare the $\left|\Psi_0\right>$ state in the register $C$.
Apply the conditional Hamiltonian evolution to the registers $C$ and $I$ (which are in the state $\left|\Psi_0\right>\otimes \left|b\right>$).
Apply the quantum Fourier transform to the resulting state.
Finally, the $C$ in $\left| \Psi_0 \right>^C$ means that the state $\left| \Psi_0 \right>$ is stored in the register $C$. This is a short and convenient notation to keep track of the registers used.
4. Hamiltonian simulation:
First of all, $\kappa$ is the condition number (Wikipedia page on "condition number") of the matrix $A$.
$\sum_{\tau = 0}^{T-1}|\tau\rangle \langle \tau|^{C}\otimes e^{iA\tau t_0/T}$ is the mathematical representation of a quantum gate.
The first part in the sum $|\tau\rangle \langle \tau|^{C}$ is a control part. It means that the operation will be controlled by the state of the first quantum register (the register $C$ as the exponent tells us).
The second part is the "Hamiltonian simulation" gate, i.e. a quantum gate that will apply the unitary matrix given by $e^{iA\tau t_0/T}$ to the second register (the register $I$ that is in the initial state $\left|b\right>$).
The whole sum is the mathematical representation of the controlled-U operation in the quantum circuit of "1. Definitions", with $U = e^{iA\tau t_0/T}$.
Adrien SuauAdrien Suau
$\newcommand{\bra}[1]{\left\langle#1\right|}\newcommand{\ket}[1]{\left|#1\right\rangle}\newcommand{\proj}[1]{|#1\rangle\langle#1|}\newcommand{\half}{\frac12}$In answer to your first question, I wrote myself some notes some time ago about my understanding of how it worked. The notation is probably a bit different (I've tried to bring it more into line, but it's easy to miss bits), but attempts to explain that choice of the state $|\Psi_0\rangle$. There also seem to be some factors of $\frac12$ floating around in places.
When we first study phase estimation, we're usually thinking about it in respect to use in some particular algorithm, such as Shor's algorithm. This has a specific goal: getting the best $t$-bit approximation to the eigenvalue. You either do, or you don't, and the description of phase estimation is specifically tuned to give as high a success probability as possible.
In HHL, we are trying to produce some state $$ \ket{\phi}=\sum_j\frac{\beta_j}{\lambda_j}\ket{\lambda_j}, $$ where $\ket{b}=\sum_j\beta_j\ket{\lambda_j}$, making use of phase estimation. The accuracy of the approximation of this will depend far more critically on an accurate estimation of the eigenvalues that are close to 0 rather than those that are far from 0. An obvious step therefore, is to attempt to modify the phase estimation protocol so that rather than using `bins' of fixed width $2\pi/T$ for approximating the phases of $e^{-iAt}$ ($T=2^t$ and $t$ is number of qubits in phase estimation register), we might rather specify a set of $\phi_y$ for $y\in\{0,1\}^t$ to act as the centre of each bin so that we can have vastly increased accuracy close to 0 phase. More generally, you might specify a trade-off function for how tolerant you might be of errors as a function of the phase $\phi$. The precise nature of this function can then be tuned to a given application, and the particular figure of merit which you will use to determine success. In the case of Shor's algorithm, our figure of merit was simply this binning protocol -- we were successful if the answer was in the correct bin, and unsuccessful outside it. This is not going to be the case in HHL, whose success is more reasonably captured by a continuous measure such as the fidelity. So, for the general case, we shall designate a cost function $C(\phi,\phi')$ which specifies a penalty for answers $\phi'$ if the true phase is $\phi$.
Recall that the standard phase estimation protocol worked by producing an input state that was the uniform superposition of all basis states $\ket{x}$ for $x\in\{0,1\}^t$. This state was used to control the sequential application of multiple controlled-$U$ gates, which are followed up by an inverse Fourier transform. Imagine we could replace the input state with some other state $$ \ket{\Psi_0}=\sum_{x\in\{0,1\}^t}\alpha_x\ket{x}, $$ and then the rest of the protocol could work as before. For now, we will ignore the question of how hard it is to produce the new state $\ket{\Psi_0}$, as we are just trying to convey the basic concept. Starting from this state, the use of the controlled-$U$ gates (targeting an eigenvector of $U$ of eigenvalue $\phi$), produces the state $$ \sum_{x\in\{0,1\}^t}\alpha_xe^{i\phi x}\ket{x}. $$ Applying the inverse Fourier transform yields $$ \frac{1}{\sqrt{T}}\sum_{x,y\in\{0,1\}^t}e^{ix\left(\phi-\frac{2\pi y}{M}\right)}\alpha_x\ket{y}. $$ The probability of getting an answer $y$ (i.e. $\phi'=2\pi y/T$) is $$ \frac{1}{T}\left|\sum_{x\in\{0,1\}^t}e^{ix\left(\phi-\frac{2\pi y}{T}\right)}\alpha_x\right|^2 $$ so the expected value of the cost function, assuming a random distribution of the $\phi$, is $$ \bar C=\frac{1}{2\pi T}\int_0^{2\pi}d\phi\sum_{y\in\{0,1\}^t}\left|\sum_{x\in\{0,1\}^t}e^{ix\left(\phi-\frac{2\pi y}{T}\right)}\alpha_x\right|^2C(\phi,2\pi y/T), $$ and our task is to select the amplitudes $\alpha_x$ that minimise this for any specific realisation of $C(\phi,\phi')$. If we make the simplifying assumption that $C(\phi,\phi')$ is only a function of $\phi-\phi'$, then we can make a change of variable in the integration to give $$ \bar C=\frac{1}{2\pi}\int_0^{2\pi}d\phi\left|\sum_{x\in\{0,1\}^t}e^{ix\phi}\alpha_x\right|^2C(\phi), $$ As we noted, the most useful measure is likely to be a fidelity measure. Consider we have a state $\ket{+}$ and we wish to implement the unitary $U_\phi=\proj{0}+e^{i\phi}\proj{1}$, but instead we implement $U_{\phi'}=\proj{0}+e^{i\phi'}\proj{1}$. The fidelity measures how well this achieves the desired task, $$ F=\left|\bra{+}U_{\phi'}^\dagger U\ket{+}\right|^2=\cos^2\left(\frac{\phi-\phi'}{2}\right), $$ so we take $$ C(\phi-\phi')=\sin^2\left(\frac{\phi-\phi'}{2}\right), $$ since in the ideal case $F=1$, so the error, which is what we want to minimise, can be taken as $1-F$. This will certainly be the correct function for evaluating any $U^t$, but for the more general task of modifying the amplitudes, not just the phases, the effects of inaccuracies propagate through the protocol in a less trivial manner, so it is difficult to prove optimality, although the function $C(\phi-\phi')$ will already provide some improvement over the uniform superposition of states. Proceeding with this form, we have $$ \bar C=\frac{1}{2\pi}\int_0^{2\pi}d\phi\left|\sum_{x\in\{0,1\}^t}e^{ix\phi}\alpha_x\right|^2\sin^2\left(\half\phi\right), $$ The integral over $\phi$ can now be performed, so we want to minimise the function $$ \half\sum_{x,y=0}^{T-1}\alpha_x\alpha_y^\star(\delta_{x,y}-\half\delta_{x,y-1}-\half\delta_{x,y+1}). $$ This can be succinctly expressed as $$ \min\bra{\Psi_0}H\ket{\Psi_0} $$ where $$ H=\half\sum_{x,y=0}^{T-1}(\delta_{x,y}-\half\delta_{x,y-1}-\half\delta_{x,y+1})\ket{x}\bra{y}. $$ The optimal choice of $\ket{\Psi_0}$ is the minimum eigenvector of the matrix $H$, $$ \alpha_x=\sqrt{\frac{2}{T+1}}\sin\left(\frac{(x+1)\pi}{T+1}\right), $$ and $\bar C$ is the minimum eigenvalue $$ \bar C=\half-\half\cos\left(\frac{\pi}{T+1}\right). $$ Crucially, for large $T$, $\bar C$ scales as $1/T^2$ rather than the $1/T$ that we would have got from the uniform coupling choice $\alpha_x=1/\sqrt{T}$. This yields a significant benefit for the error analysis.
If you want to get the same $|\Psi_0\rangle$ as reported in the HHL paper, I believe you have to add the terms $-\frac14\left(\ket{0}\bra{T-1}+\ket{T-1}\bra{0}\right)$ to the Hamiltonian. I have no justification for doing so, however, but this is probably my failing.
DaftWullieDaftWullie
Not the answer you're looking for? Browse other questions tagged algorithm hhl-algorithm hamiltonian-simulation or ask your own question.
Quantum algorithm for linear systems of equations (HHL09): Step 1 - Confusion regarding the usage of phase estimation algorithm
Clarification of the "Calculations" section of the (HHL09) paper
Quantum algorithm for linear systems of equations (HHL09): Step 2 - Preparation of the initial states $|\Psi_0\rangle$ and $|b\rangle$
Quantum algorithm for linear systems of equations (HHL09): Step 1 - Number of qubits needed
HHL algorithm, how to decide n qubits to prepare for expressing eigenvalue of A?
HHL algorithm — controlled-by-eigenvalues rotations
HHL algorithm — problem with the outcome of postselection
SWAP gate(s) in the $R(\lambda^{-1})$ step of the HHL circuit for $4\times 4$ systems
Understanding the filter functions in the HHL algorithm
Confusion regarding time complexity in the HHL algorithm | CommonCrawl |
Enhanced speed advice for connected vehicles in the proximity of signalized intersections
Evangelos Mintsis ORCID: orcid.org/0000-0002-2599-86421,
Eleni I. Vlahogianni1,
Evangelos Mitsakis2 &
Seckin Ozkul3
European Transport Research Review volume 13, Article number: 2 (2021) Cite this article
Technological advancements in the field of transportation are gradually enabling cooperative, connected and automated mobility (CCAM). The progress in information and communication technology (ICT) has provided mature solutions for infrastructure-to-vehicle (I2V) communication, which enables the deployment of Cooperative-ITS (C-ITS) services that can foster comfortable, safe, environmentally friendly, and more efficient traffic operations. This study focuses on the enhancement of speed advice comfort and safety in the proximity of signalized intersections, while ensuring energy and traffic efficiency. A detailed microscopic simulation model of an urban network in the city of Thessaloniki, Greece is used as test bed. The performance of dynamic eco-driving is evaluated for different penetration rates of the dynamic eco-driving technology and varying traffic conditions. The simulation analysis indicates that speed advice can be comfortable and safe without adversely impacting energy and traffic efficiency. However, efficient deployment of dynamic eco-driving depends on road design characteristics, activation distance of the service, traffic signal plans, and prevailing traffic conditions.
C-ITS and Advanced Driver Assistance Systems (ADAS) can significantly enhance comfort, safety, traffic efficiency and energy savings via real-time information provision (tailored to the needs of individual vehicles), and cooperative driving [30]. Road safety impact assessment of the latter systems has been conducted through real world experiments [26] and with the use of microscopic traffic simulation tools [31] that utilize surrogate measures of safety to indicate conflict risk for both uninterrupted and interrupted traffic flow [3, 9, 10, 12, 22].
C-ITS applications and ADAS that enable eco-driving and yield environmental benefits have also received significant attention from funding agencies, vehicle manufacturers, road authorities, technology providers, and the research community. Specifically, dynamic eco-driving in the proximity of signalized intersection uses real-time traffic and Signal Phase and Timing (SPaT) information to communicate robust and real-time speed and/or countdown advice to connected vehicles (CVs). Comprehensive reviews discussing different aspects of dynamic eco-driving in a connected (and automated) road environment can be found in [2, 13, 16, 29, 45, 47, 49].
Methodologically, the operation and performance of dynamic eco-driving was previously assessed through microscopic traffic simulation studies, driving simulators, controlled field experiments and real-world experiments [29].
The operation of most dynamic eco-driving models relies on the assumption that traffic signals are pre-timed [5, 20, 27, 40, 41, 50, 55]. However, researchers developed and simulated methodologies that facilitate the implementation of dynamic eco-driving services for actuated and adaptive traffic lights using empirical signal and loop detector data [6, 14, 25, 32, 44, 53]. Erdmann and Liang et al. [11, 23] proposed the combination of adaptive signal control with Green-Light-Optimal-Speed-Advisory (GLOSA) to develop signal plans that exploit vehicle state information.
Efforts were also placed for the development of dynamic eco-driving models that can estimate energy and traffic efficient speed advice for CV platoons in the proximity of signalized intersections [7, 43, 52, 54, 59]. Recently, artificial intelligence has been also used for applying dynamic eco-driving control in the proximity of signalized intersections [33, 58].
The majority of proposed dynamic eco-driving models that were evaluated with the use of microscopic traffic simulation tools considered hypothetical networks with simplified demand scenarios [5, 18, 27, 41, 42, 55, 56]. A few studies focused on real-world isolated signalized intersections [21, 48], and others simulated either single vehicle [15] or multi vehicle [4, 46, 51] scenarios along actual urban arterial corridors (very limited information is provided though regarding the calibration and validation of the respective real-world simulation models). Moreover, deceleration strategies received greater interest, since they provide higher energy savings potential, while some researchers considered the recommendation of acceleration as safety critical [41]. Finally, focus has been also placed in modelling and simulation of human factors related to dynamic eco-driving [24, 38, 40, 57].
The literature review indicates that limited focus was previously placed on the comfort and safety of dynamic eco-driving technologies [29]. Early evidence from field testing of an eco-cruise control system in the vicinity of traffic signalized intersections showed that manual speed adaptation based on countdown advice proved less comfortable, but equally safe and desirable compared to automated eco-cooperative adaptive cruise control (Eco-CACC) [39]. Thus, there is significant potential for enhancing dynamic eco-driving performance via the introduction of novel features that improve comfort, user acceptance and safety.
Undoubtedly, drivers/passengers would be more willing to adopt dynamic eco-driving if it ensured comfortable, safe and intuitive speed advice. According to the profile of existing deceleration strategies, a CV initially decelerates and subsequently cruises at a steady-state speed towards a signalized intersection until the signal status changes to green, when vehicle accelerates back to its desired speed beyond the signalized intersection. This implies that existing dynamic eco-driving services instruct CVs to cruise at significant steady speed while the vehicle approaches the signalized intersection and the signal status remains red. In this case, many drivers/passengers would feel uncomfortable driving/riding a vehicle that cruises in close vicinity to a signalized intersection while the traffic light status is still red. That would be especially true in the early stages of CVs market introduction when mixed traffic conditions are expected to prevail on the streets and drivers/passengers will be less familiar with CV technology.
This study proposes and evaluates enhancements on an existing dynamic eco-driving model (velocity planning algorithm – VPA) that encompass the following novel features:
provision of non-crawling speed advice, and
vehicle acceleration begins prior to CV arrival at signalized intersection after deceleration strategy
The enhanced VPA is examined with the use of microscopic traffic simulation along an actual urban arterial corridor that was thoroughly calibrated against real traffic conditions.
Enhanced speed advice
Enhanced dynamic eco-driving accounts for intuitive speed advice that drivers/passengers can easily and conveniently adapt to, and encompasses comfortable accelerations/decelerations, acceptable cruising speeds, as well as guidance that facilitates safe interactions with surrounding road users and elements (e.g. traffic lights). As mentioned above, existing literature has overlooked specific aspects of speed advice pertaining to comfort and safety which this study aims to address. To this end, we present in the following sections the reference model (VPA) previously developed by [55] and an enhanced VPA version proposed by this study that promotes speed advice comfort and safety without adversely impacting energy and traffic efficiency.
Velocity planning algorithm (VPA)
Xia et al. [55] introduced VPA considering that energy savings can be realized when drivers exhibit the following behavior:
maintain a steady-state speed near the speed limit,
keep a safe headway distance from the leading vehicle, and
avoid idling, or idle the least possible time at the traffic light if this is unavoidable.
Thus, an optimization problem was formulated that minimized a vehicle's tractive force and idling time while accounting for ride comfort and the local speed limit (vlim). To avoid stopping at a traffic light, a vehicle should arrive at the signalized intersection during a green signal status. Based on the current signal status, a green arrival interval can be estimated as:
$$ {t}_{arrival}=\left\{\begin{array}{ll}\left[0,\left.{t}_r\right\}\right.\ \mathrm{or}\ {\left[t\right.}_g,\left.{t}_{r1}\right),& \mathrm{if}\ \mathrm{signal}\ \mathrm{status}=\mathrm{green}\\ {}\left[{t}_g,\left.{t}_r\right),\right.& \mathrm{if}\ \mathrm{signal}\ \mathrm{status}=\mathrm{red}\end{array}\right. $$
where tr is the time to the upcoming red phase, tg represents the time to the next green phase, and tr1 is the time to the second red phase. Thus, if the signal is green, a vehicle can either cruise at current speed or accelerate to a target speed to pass through the intersection during the first green window or decelerate and cross the intersection during the second green window. If the signal is red (yellow time is considered to be red time), the vehicle can cruise at current speed or decelerate to a target speed to cross the intersection during the upcoming green window.
The possible values of tarrival can range between [tl, th], where tl and th are low and high values according to Eq. 1. Given the range [tl, th] and the vehicle's distance to intersection dint, the possible target velocities varrival can be expressed as the range [vl, vh], where vl is the maximum between zero and vlo(vlo = dint/th) and vh is the minimum between vlim and vho(vho = dint/tl). Evidently, dint and signal timing information are key parameters for the estimation of optimal speed trajectories.
When varrival is estimated, the provision of speed advice to CV is determined according to its current speed vc. If vc lies within [vl, vh], then the vehicle can pass the intersection cruising at current speed. Alternatively, it can accelerate or decelerate with respect to vh, which [55] have selected as the target velocity to achieve travel time savings apart from environmental benefits. The energy-efficient speed profiles are estimated according to the following functions:
$$ {v}_{opt}=\left\{\begin{array}{ll}{v}_h-{v}_d\ast \cos \left(\mu t\right),& \mathrm{for}\ 0\le t<\frac{\pi }{2\mu}\\ {}{v}_h-{v}_d\ast \frac{\mu }{\rho}\ast \cos \left(t-\frac{\pi }{2\mu }+\frac{\pi }{2\rho}\right),& \mathrm{for}\ \frac{\pi }{2\mu}\le t<\left(\frac{\pi }{2\rho }+\frac{\pi }{2\mu}\right)\\ {}{v}_h+{v}_d\ast \frac{\mu }{\rho }& \mathrm{for}\ \left(\frac{\pi }{2\rho }+\frac{\pi }{2\mu}\right)\le t\le \frac{d_{int}}{v_h}\ \end{array}\right. $$
where vd is equal to vh − vc. Positive vd values generate acceleration profiles, and negative values generate deceleration profiles. The only unknown parameters in Eq. 2 are μ and ρ, which determine the acceleration/deceleration rate. The higher the value of μ, the higher the acceleration/deceleration rate. The values of μ and ρ can be computed by solving the following three constraints:
$$ \left\{\begin{array}{l}{\int}_0^{\frac{\pi }{2\mu }}\left({v}_h-{v}_d\ast \cos \left(\mu t\right)\right) dt+{\int}_{\frac{\pi }{2\mu}}^{\frac{\pi }{2\rho }+\frac{\pi }{2\mu }}\left({v}_h-{v}_d\ast \frac{\mu }{\rho}\ast \cos \rho \left(t-\frac{\pi }{2\rho }+\frac{\pi }{2\mu}\right)\right) dt\\ {}+\left({v}_h+{v}_d\ast \frac{\mu }{\rho}\right)\ast \left(\frac{d_{int}}{v_h}-\frac{\pi }{2\rho }-\frac{\pi }{2\mu}\right)={d}_{int}\\ {}{jerk}_{\mathrm{m} ax}=\left|{v}_d\ast \mu \ast \rho \right|\le 10\ and\ {a}_{max}\le 2.5\ m/{s}^2\\ {}\mu =\max \left\{\mu \right\}\end{array}\right. $$
The first constraint in Eq. 3 is the distance constraint, which ensures vehicle's arrival at the downstream signalized intersection in the shortest time. The second constraint pertains to ride comfort. The third was set based on the finding of [55], which suggests that minimization of fuel consumption and emissions occurs for the largest possible μ value (i.e. a vehicle accelerates sharply instead of smoothly to vh). Moreover, it has to be noted that VPA can be explicitly implemented at signalized intersections with fixed signal control plans, and it does not consider queue dynamics at signalized intersections. A more detailed description of VPA can be found in [55].
Enhanced velocity planning algorithm (EVPA)
This study introduced enhancements to the control logic of the reference model (VPA) accounting for actual behavioral traits of drivers. The enhanced velocity planning algorithm (EVPA) increases the comfort and safety of the provided speed advice to facilitate acceptance of dynamic eco-driving service from the driver's/passenger's side.
The control logic of the reference model implies that the minimum speed advice is an explicit function of the vehicle's traveling state (approach speed and distance to the signalized intersection) and the signal timing information of the signalized intersection. Thus, vl could acquire rather low values (e.g. 10 km/h), which implies that a vehicle might be advised to cruise towards a signalized intersection at a crawling speed. However, in practice, drivers would refrain from driving below a minimum speed threshold (anxiety reasons), irrespective of the provided speed advice. Thus, the authors propose that varrival is not only bounded on the upper limit by the speed limit, but also on the lower limit by a minimum acceptable speed value (vmin). Therefore, vl would become the maximum between vmin and vlo(vlo = dint/th). It is expected that this enhancement will increase the indirect benefits of dynamic eco-driving, since legacy vehicles (LVs) will overtake CVs less frequently, thus inducing less turbulence to traffic. Additionally, previous research has shown that cruising at low speeds at the end of deceleration strategies might incur higher energy consumption, even compared to a standstill strategy [41].
The second enhancement also pertains to deceleration strategies. According to the control logic of existing dynamic eco-driving models, a CV's arrival at traffic lights after the implementation of a deceleration strategy is concurrent with the onset of the green phase. However, many drivers/passengers would feel uncomfortable riding a vehicle that cruises at high steady speed in close vicinity to a signalized intersection while the signal status is still red. Therefore, this study suggests that the lowest cruising speed vcr of the initially estimated deceleration profile is used for the computation of the CV's practical stopping distance, assuming it had complied with the initial deceleration strategy. In this case, the vehicle's practical stopping distance dstop is given by the following formula:
$$ {d}_{stop}=\frac{v_{cr}^2}{2g\left(\left(\frac{a_d}{g}\right)\pm G\right)} $$
where ad is the deceleration rate, g is the gravitational constant, and G is the roadway grade. Eq. 4 provides an estimate of typical braking distances and is more simplistic and usable than the theoretical stopping distance one. Given the assumption that CVs fully stop and road grades are small, mass factor accounting for moments of inertia during braking (which is considered for the estimation of theoretical stopping distance) can be ignored due to its small effects [28]. Moreover, we assume that friction is always guaranteed in our simulation experiments and anomalous situations such as sudden and strong braking do not occur.
Subsequently, the practical stopping distance is subtracted from dint, and the result (d′ = dint − dstop) is returned to the algorithm for the estimation of an enhanced deceleration profile. According to this updated deceleration profile, the vehicle decelerates to a lower cruising speed \( {v}_{cr}^{\prime } \) compared to the initial one, but the onset of the green phase occurs prior to the vehicle's arrival at the signalized intersection. Moreover, sufficient time and space remain available for the CV to stop in case of red light running from the opposite direction. Since the practical stopping distance is a function of the vehicle's cruising speed, the EVPA is expected to perform efficiently within a wide range of cruising speeds. The enhanced dynamic eco-driving service is expected to be perceived as more intuitive, convenient and safer by drivers, who would thus increase their confidence regarding the system's operation and performance.
Simulation experiment
Microscopic traffic simulation model
A detailed microscopic simulation model of an urban arterial corridor in the city of Thessaloniki, Greece, was developed with the use of the microscopic traffic simulation tool Aimsun. Its total length is 15 km (road grade is nearly zero across the full length of the corridor) and it encompasses 26 signalized intersections (17 equipped with road-side units) which are controlled by pre-timed signal control plans. The reference and the enhanced dynamic eco-driving services were deployed on 23 signalized intersection approaches (IA) (highlighted in yellow) of the examined simulation network (Fig. 1). Side-street parking and seven public transport lines (along with their corresponding time plans) that travesrse the central business district (CBD) of Thessaloniki were simulated as well.
Test site in Thessaloniki, Greece (real world and simulation)
A thorough macroscopic calibration process was conducted to ensure the ability of the microscopic traffic simulation model to replicate actual traffic operations (without dynamic eco-driving service) on the examined road network. Calibration parameters of Aimsun driver models (car-following, lane-changing, and gap-acceptance models) were adjusted for the reconciliation of field and simulated traffic counts. Field traffic data were obtained from several traffic detectors that monitor traffic conditions in the CBD of Thessaloniki. The latter data contain traffic volumes, average time mean speed, and travel time information for selected network routes.
Field and simulated traffic counts were used for the conduct of the appropriate statistical test (GEH) to verify the validity of the simulation model [8]. The estimated GEH values were lower than 5 for more than 85% of the selected detector stations (volume and speed counts). Moreover, GEH index was also lower than 5 when comparing average travel time between field and simulation along the urban arterial corridor shown in Fig. 1. Thus, the calibration procedure demonstrated that the simulation model can credibly replicate traffic operations pertaining to manual driving on the test network.
However, we also deem that our simulation model remains valid for different market penetration rates of dynamic eco-driving technology, since we assumed that CVs are manually driven beyond the service activation zone (cf. Section 3.2) and existing literature [2, 13, 16, 29, 45, 47, 49] addressing the impacts of dynamic eco-driving on traffic operations does not indicate changes to route choice due to speed advice provision in the proximity of signalized intersections.
(E)VPA - Application Programming Interface (API)
VPA and EVPA were simulated in Aimsun with the use of an Application Programming Interface (API) that was directly interfaced with the core Aimsun models. The API estimates a single energy optimal driving strategy for every CV that enters the dynamic eco-driving service activation zone. Then, the CV becomes "tracked" in the simulation and strictly follows the provided speed advice (every simulation time step) until it crosses the signalized intersection. Thus, CVs fully comply with the estimated speed advice within the service activation zone. However, a CV can discard speed advice if it enters car-following state. An empirical formula was used to assess the car-following state of CVs during the simulation [37]. The maximum car-following distance is given as:
$$ {x}_{cf}=T{u}_{k-1}+\beta $$
where T is a time constant, uk − 1 is the speed of the following vehicle, and β is the average distance between two vehicles in standstill. If a CV's distance to the leader becomes shorter than xcf, then it becomes "untracked" in the simulation and its motion is subsequently dictated by the Aimsun driver models. In this case, an updated speed advice is not provided to the CV even though it is still driving within the activation zone. The behavior of CV beyond the activation zone is determined by Aimsun driver models that are parametrized to reflect manual driving conditions.
The length of the activation zone (per signalized IA) is set equal to the total length of the corresponding signalized IA (road section between two consecutive intersections). During the simulation of VPA, the estimated speed advice can range between 5 and 50 km/h. On the other hand, while EVPA is simulated the estimated speed advice can range between the minimum cruising speed after deceleration (20 km/h) and the speed limit (50 km/h). Table 1 provides an elaborate list of the parameter values that affect the operation of the reference and enhanced models in the simulation experiments.
Table 1 Parameter values used in the simulation experiments
Microscopic emission model
To estimate carbon dioxide (CO2) emissions within the simulation loop (second-by-second estimation, 1 Hz.), the Panis microscopic emission model calibrated with real world emission data is used [36]. As this model combines multiple non-linear regression models to estimate emission functions per vehicle type and pollutant (with instantaneous speed and acceleration as explanatory variables) it was considered relevant for the evaluation of the environmental impacts of dynamic eco-driving.
The fleet composition with respect to engine type for Greece was obtained from [1]. To this end, in our simulation experiments taxis, heavy duty vehicles (HDV), and buses run on diesel engines. Passenger cars are divided into the following shares according to their fuel type: 92% petrol, 5% diesel, and 2% LPG. The emission constants used for the estimation of CO2 emissions per combination of vehicle and engine type are presented in Table 2.
Table 2 CO2 emission constants per combination of vehicle and engine type
Simulation scenarios
The performance of the reference (VPA) and the proposed (EVPA) speed advice algorithms was assessed for different traffic demand levels and different penetration rates of the dynamic eco-driving technology (Table 3). In total, 48 scenarios were simulated (38 with service on and 10 with service off). The calibration scenario corresponds to D100 traffic demand level (initial demand input to the microscopic simulation model). The effect of the penetration rate of the CV technology was tested both for uncongested (D50) and congested (D100) traffic conditions. On the other hand, the performance of CV technology for a wide spectrum of traffic conditions (uncongested – near congested – congested/D10 – D100) was evaluated for three different penetration rates (low – moderate – high/P15 – P50 – P100). Speed advice was explicitly provided to passenger cars and taxis among the simulated vehicle types (passenger cars, taxis, trucks, and buses), since the reference model was explicitly developed for light-duty vehicles.
Table 3 Simulated demand levels and penetration rates of the dynamic eco-driving service
Aimsun is a stochastic microscopic traffic simulation tool. Thus, multiple runs of each simulated scenario were executed so that the obtained simulation outputs can be statistically significant. Initially, five runs of the calibration scenario were executed (each corresponding to a different random seed) and statistics of the average network speed were collected. The required number of runs is determined based on the standard deviation of speed for a specific significance level and the tolerable error [35]. In this case, for 95% significance level and tolerable error equal to 0.5 km/h, the required number of runs was determined to be 10.
Simulation results were analyzed for the "do-nothing" (i.e. no dynamic eco-driving), VPA, and EVPA scenarios in three different aggregation levels:
single vehicle performance (along different routes)
average section statistics (along different IAs)
average network-wide statistics (whole simulated network)
To facilitate the description of the results we use the capital letters assigned to different traffic lights of the test site (Fig. 1) to indicate road sections of interest in the context of this analysis. Specifically, the notation {R → Q} connotes the road section between traffic lights R and Q. The arrow symbol determines the direction of traffic along the road section. In the cases of VPA and EVPA scenarios, it is also implied that dynamic eco-driving is deployed on the corresponding road section. The analysis of simulation results is presented in three dedicated subsections (per aggregation level) below.
Single vehicle performance
The analysis of single vehicle performance encompasses four different types of plots: a) speed vs distance, b) speed vs time, c) cumulative CO2 emissions vs distance, and d) acceleration vs speed. These plots reveal the influence of dynamic eco-driving on CV behavior and the corresponding CV performance in terms of CO2 emissions. The CV performance displayed in Figs. 2 and 3 pertains to traffic demand level D50, penetration rate P100 and two different routes of the test site.
Single vehicle performance on IA:{R → Q}
Single vehicle performance on urban arterial corridor {O → A}
Figure 2 shows information about a single CV performance along IA:{R → Q} (one-way multi-lane road segment). While the CV has to stop at the traffic light in the "do-nothing" scenario, it can adopt a deceleration strategy in the VPA and EVPA scenarios to avoid a standstill and generate lesser CO2 emissions. However, it can be seen (in the focus area of the right top plot) that the EVPA algorithm allows the CV to cruise at a marginally lower speed compared to the VPA one, and consequently begin acceleration approximately 10 m upstream of the traffic light (when the signal status changes to green).
As explained in Section 3 of this study, the latter behavior can promote comfort, safety and user acceptance of the system since the CV will not reach the traffic light (in red status) at cruising speed (enhanced speed advice); and increase intersection safety since there will be further available time for intersection clearance or CV tactical maneuvering in case of red light running from vehicles driving along other directions (possible scenario in mixed traffic conditions). Interestingly, the EVPA deceleration strategy does not adversely impact CO2 emissions savings. This is also justified by the same acceleration/deceleration patterns between VPA and EVPA depicted in Fig. 2 (bottom right plot).
The behavior of a single CV with (VPA and EVPA) and without ("do-nothing") dynamic eco-driving technology is examined along the urban arterial corridor {O → A}. Every signalized intersection is equipped with a road-side unit (RSU) along the corridor (one-way four-lane urban arterial corridor with reserved bus lane on the right-most lane and side-street parking on the left-most lane), thus enabling CVs to implement separate acceleration/deceleration strategies per IA.
Figure 3 (top plots) indicates that VPA allows the CV to successfully execute a deceleration strategy thrice, while EVPA only once given road characteristics, prevailing traffic conditions, and deployed traffic signal plan. However, the first two deceleration strategies suggested by VPA lead to rather low cruising speeds (< 20 km/h) that can be non-acceptable by drivers or passengers in the case of fully autonomous vehicles. Moreover, they yield CO2 emissions savings that are not significant compared to the "do-nothing" and EVPA scenarios when the same CV has to fully stop at the traffic light and accelerate back to desired speed from standstill.
Nonetheless, a noteworthy observation is that dynamic eco-driving alters the traffic patterns of CVs even in space and time intervals that energy optimal driving strategies are not applied or possible. This phenomenon can generate unfavorable conditions for the CV due to surrounding traffic (queued vehicles disrupting the adoption of speed advice) or mistimed entrance at an intersection approach. Hence, the cumulative CO2 emissions of the CV (EVPA case) eventually surpass those of the unequipped equivalent (left bottom plot) along the examined path. Finally, results demonstrate that the VPA produces milder acceleration/deceleration rates for the examined CV (right bottom plot), and thus lesser cumulative CO2 emissions along its travelled path {O → A}.
Individual intersection approach statistics
A plethora of information is provided to scrutinize the performance of dynamic eco-driving on two benchmark IAs of the test site and compare the behavior of VPA and EVPA methods. The evaluation of the different algorithms is conducted in terms of CO2 emissions (gr/km), number of stops per vehicle, and mean travel time (seconds). The reported travel time and CO2 emissions results also consider the road sections downstream of the examined IAs where benefits from energy efficient deceleration strategies can be realized. Moreover, a comprehensive analysis of the provided speed advice is presented per IA. Results are analyzed for traffic demand levels D50 (uncongested conditions) and D100 (congested conditions), and penetration rates ranging between P5 – P100.
IA:{R → Q} was selected as benchmark in the context of this study since it is isolated and vehicle arrival patterns are not influenced by implementation of dynamic eco-driving along upstream IAs. Moreover, it is a one-way four-lane road section spanning up to 360 m where there is available space for CVs to adopt dynamic eco-driving maneuvers. SPaT messages are received up to 360 m upstream of signalized intersection Q by CVs, and 65.00 s of the signal cycle (72.22% of the cycle duration) are allocated to the through movement (speed advice is estimated specifically for this movement). The minimum cruising speed is 20 km/h in the case of EPVA, and 5 km/h in the case of VPA. An influence zone calibration parameter of 0.01 indicates that CVs will reach the traffic signal on red light status while driving at cruising speed in the end of a deceleration strategy (VPA scenario). On the other hand, a 0.5 parameter value (EVPA scenario) ensures that CVs' acceleration will commence prior to arrival on red signal status to the intersection stop line.
Despite increased demand in D100, traffic conditions remain uncongested along IA:{R → Q} (Fig. 4). Mean travel time (min/km) is slightly affected by dynamic eco-driving (bottom plots) and mostly for higher penetration rates (> 75%). Both VPA and EVPA manage to significantly reduce idling (number of stops/veh) in mixed traffic, while stop events almost vanish in the case of fully equipped fleet (middle plots). However, it can be noticed that for low to intermediate penetration rates (P15 – P50) and highest demand level (D100) EVPA outperforms VPA in terms of preventing CV stops at traffic light Q. VPA advices lower cruising speeds in the context of deceleration strategies, and thus non-equipped vehicles (which represent the highest share in the fleet mix for low penetration rates of dynamic eco-driving technology) tend to overpass CVs causing more stops at traffic lights compared to the EVPA scenario. Both algorithms generate CO2 emissions savings beyond medium penetration rate (P50) that are maximized for fully equipped fleet (P100). Maximum CO2 emissions savings rise approximately to 7.0% (top plots) and do not occur in the expense of significant travel time costs (bottom plots). Moreover, VPA and EVPA exhibit similar CO2 emissions savings potential in the case of IA:{R → Q}.
Key Performance Indicators (KPIs) of dynamic eco-driving deployment on IA:{R → Q}
The reason IA:{N → M} is selected as benchmark and studied explicitly is multifold. IA:{N → M} is part of urban arterial corridor {O → A} where dynamic eco-driving is deployed on all signalized IAs (Fig. 1). It is one of the few IAs on urban arterial corridor {O → A} that spans 240 m long, thus providing enough space for CVs to execute dynamic eco-driving maneuvers. Additionally, it is fed with traffic by three different IAs (i.e. {O → N}, {P → N}, and {R → N}) where dynamic eco-driving is also applied. Hence, vehicle arrival patterns vary significantly on IA:{N → M} giving the opportunity to test dynamic eco-driving for different CV approach speeds (also influenced upstream by dynamic eco-driving). Furthermore, 62.00 s of the signal cycle (68.89% of the cycle duration) are allocated to the through movement (speed advice is estimated specifically for this movement). Consequently, there is adequate red duration to induce energy efficient deceleration strategies. Algorithmic settings (VPA and EVPA) for IA:{N → M} are similar to that of {R → Q}.
Congested conditions prevail along IA:{N → M} for the highest demand level (D100). Mean travel time increases four times compared to uncongested conditions (D50) for the "do-nothing" scenario (Fig. 5). The deployment of dynamic eco-driving further disrupts traffic flow on IA:{N → M} for higher penetration rates. As explained in Section 3 of this study, both VPA and EVPA do not account for traffic light queues when estimating acceleration/deceleration strategies. Therefore, CVs can receive speed advice upon entrance to the intersection approach but eventually will need to abort it (due to reaching tail of queue), thus escalating travel time and CO2 emissions. Noticeably, EVPA outperforms VPA on the basis of the examined KPIs (left plots – D100) for the majority of the tested penetration rates (most significant difference for higher penetration rates). Due to the higher minimum speed advice threshold in the case of EVPA (i.e. 20 km/h), lesser speed advices are provided to equipped vehicles, hence reducing the intensity of disruption to the traffic flow and CO2 emissions performance incurred by dynamic eco-driving.
KPIs of dynamic eco-driving deployment on IA:{N → M}
On the other hand, traffic conditions are uncongested along IA:{N → M} for the intermediate demand scenario (D50). Queued traffic almost diminishes at traffic light M (Fig. 5 – middle right plot) for higher penetration rates (> 75%). EVPA generates CO2 emissions savings along IA:{N → M}, which approximately rise to 13.0% and 8.5% reduction compared to the "do-nothing" and VPA scenarios respectively (Fig. 5 – top right plot). Notably, EVPA exhibits significantly improved performance compared to VPA with respect to emissions reduction, although it adapts speed advice to improve comfort and safety. Finally, it can be observed that for low to intermediate penetration rates vehicle stops increase with deployment of VPA. This phenomenon occurs due to the behavior of non-equipped vehicles as it was explained in the aforementioned analysis of simulation results for IA:{R → Q} as well.
Network-wide statistics
The effects of dynamic eco-driving (VPA and EVPA) on network performance are assessed in terms of: i) average network speed, b) CO2 emissions per kilometer driven (gr/km), and c) average stop time per kilometer driven (s/km). Network-wide statistics are reported for the full spectrum of examined demand levels (D10 – D100) and two penetration rates (P50 and P100) to identify triggering points for VPA and EVPA activation according to the prevailing traffic conditions on the examined test site.
Figure 6 indicates that both VPA and EVPA can yield CO2 emissions savings when average network speed is over 25 km/h (D10 – D80), but the latter savings are insignificant though. Moreover, network-wide savings diminish as traffic demand shifts from light to moderate (D10 → D80). On the other hand, the tested algorithms exhibit similar performance to the "do-nothing" case for heavy traffic conditions (congestion) when average stop time increases significantly both for 50% and 100% penetration rates. As aforementioned, this is reasonable considering that both algorithms are not designed to account for traffic light queues when estimating energy efficient speed advice. Moreover, it can be seen that lower share of CVs in the fleet mix (P50) results in slightly lesser impacts of dynamic eco-driving on the network scale compared to the case of fully equipped fleet (P100).
Average network KPIs of dynamic eco-driving deployment on Thessaloniki's test site
VPA generates marginally higher CO2 emissions savings compared to EVPA in uncongested conditions when the whole test site is considered. However, these savings are realized in the expense of marginally increased travel times. Longer travel times are expected in the VPA scenarios due to the minimum speed advice threshold (i.e. 5 km/h). Lower CO2 emissions on the network level can be attributed to more energy efficient patterns generated by VPA at areas of the network where speed advice is not implemented successfully or at all as previously highlighted and explained in the analysis of single vehicle performance. Finally, the lower stop times observed for VPA can be also ascribed to crawling speeds that can be advised by the latter algorithm.
Simulation results indicate that EVPA can exhibit similar or even better performance compared to VPA for specific road characteristics, activation distances of dynamic eco-driving service, traffic conditions and traffic signal plans, despite adapting speed advice to improve user acceptance and intersection safety. It is also noteworthy, that improved EVPA performance occurs when VPA advices deceleration strategies that encompass cruising speeds that undercut the minimum cruising speed after deceleration (vmin). For this reason EVPA and VPA performance is similar along IA:{R → Q}, while EVPA significantly outperforms VPA in the case of IA:{N → M}. Moreover, the fact that EVPA suggests vehicle acceleration prior to CV arrival at the signalized intersection after deceleration strategies does not weaken its ability to yield CO2 emissions savings.
On the other hand, the analysis of single vehicle performance and network-wide statistics revealed that VPA slightly outperforms EVPA in terms of environmental benefits on the network level. Nonetheless, this occurs at the cost of marginally higher travel times. Both VPA and EVPA generate different traffic patterns on the examined test site even in areas where speed advice is not feasible due to surrounding traffic or mistimed arrival at intersection approach.
Moreover, both algorithms do not produce significant network-wide emissions savings compared to the "do-nothing" scenario even for low to moderate traffic demand. As it can be seen in Fig. 1, traffic lights are closely spaced beyond traffic light M along the urban arterial corridor {O → A}, where the speed limit is 50 km/h along {O → A}. Thus, dynamic eco-driving benefits diminish due to low approach speeds, confined speed range and space for adapting to speed advice, and VPA/EVPA algorithmic logic that considers single signalized intersections for estimating energy efficient driving strategies instead of multi-intersection corridors controlled by traffic lights. Previous research has also indicated that inappropriate deployment of dynamic eco-driving could even generate environmental disbenefits due to unfavorable factors [39, 40, 46, 55]. Hence, the deployment scheme of dynamic eco-driving that encompasses road design characteristics, activation distance of the service, traffic signal plans and traffic conditions significantly affect its energy efficiency and emissions savings potential.
According to the latter information, it is important to identify the deployment scheme that enables EVPA to perform efficiently (in terms of CO2 emissions reduction) on the network scale. Thus, travel time, user acceptance and safety benefits also provided by EVPA can be realized.
Additionally, we show that VPA and EVPA deteriorate traffic conditions during congestion since they do not consider traffic light queues for speed advice estimation. The corresponding simulation results pose irregular patterns with respect to speed advice efficiency and CO2 emissions. Notably, interactions between CVs and non-equipped vehicles become more complex especially in the case of VPA when crawling speeds can be advised to CVs.
Finally, it is of note that we assumed full diver compliance to speed advice in the context of this simulation study. However, human factors can exert significant impacts on traffic flow performance [34] and intersection safety [17, 19]. Hence, we plan to address partial compliance to speed advice based on real-world data in future research efforts and assess safety implications of human factors with respect to dynamic eco-driving with the use of rigorous mathematical methods such as the Surrogate Safety Assessment Model (SSAM).
CV applications have received significant attention from the research community in the past two decades. Several dynamic eco-driving models were proposed for the estimation of energy efficient speed advice in the vicinity of signalized intersections. This study focused on the enhancement of speed advice comfort and safety without negatively affecting energy and traffic efficiency. A microscopic simulation analysis on an actual urban network is conducted to evaluate the performance of an enhanced velocity planning algorithm (EVPA) for different penetration rates of dynamic eco-driving technology and traffic demand levels.
Simulation results indicated that EVPA can generate CO2 emissions savings on the order of 13% along individual intersection approaches and 2.5% on a network scale, without substantially escalating travel times. Moreover, EVPA ensures increased speed advice comfort and safety due to its inherent control logic. However, it was also identified that EVPA's efficiency is dependent on roadway characteristics, activation distance of the service, traffic signal plans and traffic conditions. Thus, the deployment scheme of dynamic eco-driving on urban networks plays a significant role in warranting environmental benefits and traffic efficiency.
Additionally, it was proven that speed advice estimation should consider signal plans from consecutive traffic lights on urban arterial corridors with closely spaced signalized intersections to increase dynamic eco-driving performance. Finally, this study explicitly assumed connected vehicles that can precisely follow speed advice using automation functions. In future research, the authors plan to utilize actual speed advice data to model the influence of human factors in the adoption of speed advice when CVs are manually driven and meticulously evaluate respective impacts on traffic safety and emissions savings.
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
ACEA. (2017). Vehicles in use – Europe 2017. European Automobile Manufacturers Association. https://www.acea.be/uploads/statistic_documents/ACEA_Report_Vehicles_in_use-Europe_2017.pdf
Alam, M. S., & McNabola, A. (2014). A critical review and assessment of eco-driving policy & technology: Benefits & limitations. Transport Policy, 35, 42–49. https://doi.org/10.1016/j.tranpol.2014.05.016.
Archer, J. (2005). Indicators for traffic safety assessment and prediction and their application in micro-simulation modelling: A study of urban and suburban intersections. Doctoral Thesis, KTH.
Asadi, B., & Vahidi, A. (2011). Predictive cruise control: Utilizing upcoming traffic signal information for improving fuel economy and reducing trip time. IEEE Transactions on Control Systems Technology, 19(3), 707–714. https://doi.org/10.1109/TCST.2010.2047860.
Barth, M., Mandava, S., Boriboonsomsin, K., & Xia, H. (2011). Dynamic ECO-driving for arterial corridors. In In 2011 IEEE Forum on Integrated and Sustainable Transportation Systems (FISTS), (pp. 182–188). https://doi.org/10.1109/FISTS.2011.5973594.
Bodenheimer, R., Brauer, A., Eckhoff, D., & German, R. (2014). Enabling GLOSA for adaptive traffic lights. In 2014 IEEE Vehicular Networking Conference (VNC), (pp. 167–174). https://doi.org/10.1109/VNC.2014.7013336.
Chen, W., Liu, Y., Yang, X., Bai, Y., Gao, Y., & Li, P. (2015). Platoon-based speed control algorithm for Ecodriving at signalized intersection. Transportation Res Rec, 2489(1), 29–38. https://doi.org/10.3141/2489-04.
Chu, L., Liu, H. X., Oh, J. S., & Recker, W. (2003). A calibration procedure for microscopic traffic simulation. In Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems (ITSC), (pp. 1574–1579). https://doi.org/10.1109/ITSC.2003.1252749.
Dalla Chiara, B., Deflorio, F. P., & Cuzzola, S. (2014). A proposal of risk indexes at signalised intersections for ADAS aimed to road safety. In Informatics in Control, Automation and Robotics, (pp. 265–278). Cham: Springer. https://doi.org/10.1007/978-3-319-03500-0_17.
Dalla Chiara, B., Deflorio, F., & Diwan, S. (2009). Assessing the effects of inter-vehicle communication systems on road safety. IET Intelligent Transport Systems, 3(2), 225–235. https://doi.org/10.1049/iet-its:20080059.
Erdmann, J. (2013). Combining adaptive junction control with simultaneous green-light-optimal-speed-advisory. In 2013 IEEE 5th International Symposium on Wireless Vehicular Communications (WiVeC), (pp. 1–5). https://doi.org/10.1109/wivec.2013.6698230.
Gettman, D., & Pu, L. (2006). Theoretical validation of surrogate safety assessment methodology for roundabouts and cross intersections. In Proceedings of the 13th ITS World Congress.
Guanetti, J., Kim, Y., & Borrelli, F. (2018). Control of connected and automated vehicles: State of the art and future challenges. Annual Reviews in Control, 45, 18–40. https://doi.org/10.1016/j.arcontrol.2018.04.011.
Hao, P., Wu, G., Boriboonsomsin, K., & Barth, M. J. (2018). Eco-approach and departure (EAD) application for actuated signals in real-world traffic. IEEE Transactions on Intelligent Transportation Systems, 20(1), 1–11. https://doi.org/10.1109/TITS.2018.2794509.
He, X., Liu, H. X., & Liu, X. (2015). Optimal vehicle speed trajectory on a signalized arterial with consideration of queue. Transportation Research Part C: Emerging Technologies, 61, 106–120. https://doi.org/10.1016/j.trc.2015.11.001.
Huang, Y., Ng, E. C. Y., Zhou, J. L., Surawski, N. C., Chan, E. F. C., & Hong, G. (2018). Eco-driving technology for sustainable road transport: A review. Renewable and Sustainable Energy Reviews, 93, 596–609. https://doi.org/10.1016/j.rser.2018.05.030.
Hurwitz, D. S. (2009). Application of driver behavior and comprehension to dilemma zone definition and evaluation. Doctoral Thesis, University of Massachusetts Amherst. https://doi.org/10.7275/bxwp-8c84.
Jiang, H., Hu, J., An, S., Wang, M., & Park, B. B. (2017). Eco approaching at an isolated signalized intersection under partially connected and automated vehicles environment. Transportation Research Part C: Emerging Technologies, 79, 290–307. https://doi.org/10.1016/j.trc.2017.04.001.
Johansson, G., & Rumar, K. (1971). Drivers' brake reaction times. Human factors, 13(1), 23–27. https://doi.org/10.1177/2F001872087101300104.
Kamalanathsharma, R. K., & Rakha, H. A. (2016). Leveraging connected vehicle technology and telematics to enhance vehicle fuel efficiency in the vicinity of signalized intersections. Journal of Intelligent Transportation Systems, 20(1), 33–44. https://doi.org/10.1080/15472450.2014.889916.
Kamalanathsharma, R. K., Rakha, H. A., & Yang, H. (2015). Networkwide impacts of vehicle Ecospeed control in the vicinity of traffic signalized intersections. Transportation Research Record: Journal of the Transportation Research Board, 2503(1), 91–99. https://doi.org/10.3141/2503-10.
Kim, K. J., & Sul, J. (2009). Development of intersection traffic accident risk assessment model. In 4th IRTAD Conference.
Liang, X., Guler, S. I., & Gayah, V. V. (2019). Joint optimization of signal phasing and timing and vehicle speed guidance in a connected and autonomous vehicle environment. Transportation Research Record: Journal of the Transportation Research Board, 2673(4), 70–83. https://doi.org/10.1177/0361198119841285.
Liao, R., Chen, X., Yu, L., & Sun, X. (2018). Analysis of emission effects related to drivers' compliance rates for cooperative vehicle-infrastructure system at signalized intersections. International Journal of Environmental Research and Public Health, 15(1), 122. https://doi.org/10.3390/ijerph15010122.
Mahler, G., & Vahidi, A. (2012). Reducing idling at red lights based on probabilistic prediction of traffic signal timings. In 2012 American Control Conference (ACC), (pp. 6557–6562). https://doi.org/10.1109/ACC.2012.6314942.
Maile, M., & Delgrossi, L. (2009). Cooperative intersection collision avoidance system for violations (cicas-v) for prevention of violation-based intersection crashes. In Proceedings of International Technical Conference on the Enhanced Safety of Vehicles.
Mandava, S., Boriboonsomsin, K., & Barth, M. (2009). Arterial velocity planning based on traffic signal information under light traffic conditions. In 12th International IEEE Conference on Intelligent Transportation Systems (ITSC 2009), (pp. 1–6). https://doi.org/10.1109/ITSC.2009.5309519.
Mannering, F., Kilareski, W., & Washburn, S. (2007). Principles of highway engineering and traffic analysis. USA: Wiley.
Mintsis, E., Vlahogianni, E. I., & Mitsakis, E. (2020). Dynamic eco-driving near signalized intersections: Systematic review and future research directions. Journal of Transportation Engineering, Part A: Systems, 146(4). https://doi.org/10.1061/JTEPBS.0000318.
Monteil, J., Billot, R., & El Faouzi, N. E. (2011). Towards cooperative traffic management: methodological issues and perspectives. In Proceedings of Australasian Transport Research Forum, (pp. 28–30).
Morsink, P. L., Wismans, L. J., & Dijkstra, A. (2008). Micro-simulation for road safety impact assessment of advanced driver assistance systems. In 7th European Congress and Exhibition on Intelligent Transport Systems and Services.
Mousa, S. R., Ishak, S., Mousa, R. M., & Codjoe, J. (2019). Developing an eco-driving application for semi-actuated signalized intersections and modeling the market penetration rates of eco-driving. Transportation Research Record: Journal of the Transportation Research Board, 2673(5), 466–477. https://doi.org/10.1177/0361198119839960.
Mousa, S. R., Mousa, R., & Ishak, S. (2018). A Deep-Reinforcement Learning Algorithm for Eco-Driving Control at Signalized Intersections with Prioritized Experience Replay, Target Network, and Double Learning. In Transportation Research Board 97th Annual Meeting https://trid.trb.org/view/1497121.
Ni, D., Li, L., Wang, H., & Jia, C. (2017). Observations on the fundamental diagram and their interpretation from the human factors perspective. Transportmetrica B: transport dynamics, 5(2), 159–176. https://doi.org/10.1080/21680566.2016.1190673.
Ott, L., & Longnecker, M. (2004). A first course in statistical methods. Thomson-Brooks/Cole.
Panis, L. I., Broekx, S., & Liu, R. (2006). Modelling instantaneous traffic emission and the influence of traffic speed limits. Science of The Total Environment, 371(1–3), 270–285. https://doi.org/10.1016/j.scitotenv.2006.08.017.
Pipes, L. A. (1953). An operational analysis of traffic dynamics. Journal of Applied Physics, 24(3), 274–281. https://doi.org/10.1063/1.1721265.
Qi, X., Wang, P., Wu, G., Boriboonsomsin, K., & Barth, M. J. (2018). Connected cooperative Ecodriving system considering human driver error. IEEE Transactions on Intelligent Transportation Systems, 19(8), 2721–2733. https://doi.org/10.1109/TITS.2018.2845799.
Rakha, H. A., Chen, H., Almannaa, M., El-Shawarby, I., & Loulizi, A. (2016). Developing and field implementing an Ecocruise control system in the vicinity of traffic signalized intersections (no. NY17–02). TranLIVE. University of Idaho https://rosap.ntl.bts.gov/view/dot/36797.
Rakha, H. A., Kamalanathsharma, R. K., & Ahn, K. (2012). AERIS: Eco-vehicle speed control at signalized intersections using I2V communication (FHWA-JPO-12-063). Virginia Tech Transportation Institute http://ntl.bts.gov/lib/46000/46300/46329/FHWA-JPO-12-063_FINAL_PKG.pdf.
Raubitschek, C., Schutze, N., Kozlov, E., & Baker, B. (2011). Predictive driving strategies under urban conditions for reducing fuel consumption based on vehicle environment information. In 2011 IEEE Forum on Integrated and Sustainable Transportation Systems (FISTS), (pp. 13–19). https://doi.org/10.1109/FISTS.2011.5973609.
Schuricht, P., Michler, O., & Bäker, B. (2011). Efficiency-increasing driver assistance at signalized intersections using predictive traffic state estimation. In 14th International IEEE Conference on Intelligent Transportation Systems (ITSC 2011), (pp. 347–352). https://doi.org/10.1109/ITSC.2011.6083111.
Stebbins, S., Hickman, M., Kim, J., & Vu, H. L. (2017). Characterising green light optimal speed advisory trajectories for platoon-based optimisation. Transportation Research Part C: Emerging Technologies, 82, 43–62. https://doi.org/10.1016/j.trc.2017.06.014.
Sun, C., Guanetti, J., Borrelli, F., & Moura, S. (2018). Robust eco-driving control of autonomous vehicles connected to traffic lights. ArXiv: 1802.05815 [Math]. http://arxiv.org/abs/1802.05815
Taiebat, M., Brown, A. L., Safford, H. R., Qu, S., & Xu, M. (2018). A review on energy, environmental, and sustainability implications of connected and automated vehicles. Environmental Science & Technology, 52(20), 11449–11465. https://doi.org/10.1021/acs.est.8b00127.
Tielert, T., Killat, M., Hartenstein, H., Luz, R., Hausberger, S., & Benz, T. (2010). The impact of traffic-light-to-vehicle communication on fuel consumption and emissions. In 2010 Internet of Things (IOT), (pp. 1–8). https://doi.org/10.1109/IOT.2010.5678454.
Vahidi, A., & Sciarretta, A. (2018). Energy saving potentials of connected and automated vehicles. Transportation Research Part C: Emerging Technologies, 95, 822–843. https://doi.org/10.1016/j.trc.2018.09.001.
Vreeswijk, J. D., Mahmod, M. K. M., & van Arem, B. (2010). Energy efficient traffic management and control – The eCoMove approach and expected benefits. In 13th International IEEE Conference on Intelligent Transportation Systems (ITSC 2010), (pp. 955–961). https://doi.org/10.1109/ITSC.2010.5625122.
Wadud, Z., MacKenzie, D., & Leiby, P. (2016). Help or hindrance? The travel, energy and carbon impacts of highly automated vehicles. Transportation Research Part A: Policy and Practice, 86, 1–18. https://doi.org/10.1016/j.tra.2015.12.001.
Wan, N., Vahidi, A., & Luckow, A. (2016). Optimal speed advisory for connected vehicles in arterial roads and the impact on mixed traffic. Transportation Research Part C: Emerging Technologies, 69, 548–563. https://doi.org/10.1016/j.trc.2016.01.011.
Wang, Z., Wu, G., & Barth, M. J. (2019). Cooperative eco-driving at signalized intersections in a partially connected and automated vehicle environment. In IEEE Transactions on Intelligent Transportation Systems, (pp. 1–10). https://doi.org/10.1109/TITS.2019.2911607.
Wang, Z., Wu, G., Hao, P., & Barth, M. J. (2018). Cluster-wise cooperative eco-approach and departure application for connected and automated vehicles along signalized arterials. IEEE Transactions on Intelligent Vehicles, 3(4), 404–413. https://doi.org/10.1109/TIV.2018.2873912.
Weber, A., & Winckler, A. (2013). Exploratory advanced research project: Advanced traffic signal control. BMW Final Report. https://merritt.cdlib.org/d/ark:%2F13030%2Fm5s4865n/1/producer%2F884614370.pdf
Wu, X., Zhao, X., Xin, Q., Yang, Q., Yu, S., & Sun, K. (2019). Dynamic cooperative speed optimization at signalized arterials with various platoons. Transportation Research Record: Journal of the Transportation Research Board, 2673(5), 528–537. https://doi.org/10.1177/0361198119839964.
Xia, H., Boriboonsomsin, K., & Barth, M. (2013). Dynamic eco-driving for signalized arterial corridors and its indirect network-wide energy/emissions benefits. Journal of Intelligent Transportation Systems, 17(1), 31–41. https://doi.org/10.1080/15472450.2012.712494.
Xia, H., Wu, G., Boriboonsomsin, K., & Barth, M. (2013). Development and evaluation of an enhanced eco-approach traffic signal application for connected vehicles. In 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), (pp. 296–301). https://doi.org/10.1109/ITSC.2013.6728248.
Xiang, X., Zhou, K., Zhang, W.-B., Qin, W., & Mao, Q. (2015). A closed-loop speed advisory model with Driver's behavior adaptability for eco-driving. IEEE Transactions on Intelligent Transportation Systems, 16(6), 3313–3324. https://doi.org/10.1109/TITS.2015.2443980.
Yang, Z., Zeng, H., Yu, Z., Wei, X., Liu, A., & Fan, X. (2019). Research on eco-driving strategy at intersection based on vehicle infrastructure cooperative system. Advances in Mechanical Engineering, 11(4). https://doi.org/10.1177/1687814019843368.
Zhou, F., Li, X., & Ma, J. (2017). Parsimonious shooting heuristic for trajectory design of connected automated traffic part I: Theoretical analysis with generalized time geography. Transportation Research Part B: Methodological, 95, 394–420. https://doi.org/10.1016/j.trb.2016.05.007.
This work was supported by the State Scholarships Foundation (IKY) under the IKY/SIEMENS Research Projects for Excellence Programme [grant number 1516] "Analysis and Upgrade of the Operations of Cooperative Intelligent Transportations Systems in Urban Networks".
Department of Transportation Planning and Engineering, School of Civil Engineering, National Technical University of Athens, 5 Iroon Polytechniou Str., Zografou Campus, 15773, Athens, Greece
Evangelos Mintsis & Eleni I. Vlahogianni
Centre for Research and Technology Hellas, Hellenic Institute of Transport, 6th km Charilaou-Thermi Rd, 57001, Thermi, Greece
Evangelos Mitsakis
MUMA College of Business, University of South Florida, 4202 E. Fowler Ave., BSN 3108, Tampa, FL, 33620, USA
Seckin Ozkul
Evangelos Mintsis
Eleni I. Vlahogianni
The author(s) read and approved the final manuscript.
Correspondence to Evangelos Mintsis.
Mintsis, E., Vlahogianni, E.I., Mitsakis, E. et al. Enhanced speed advice for connected vehicles in the proximity of signalized intersections. Eur. Transp. Res. Rev. 13, 2 (2021). https://doi.org/10.1186/s12544-020-00458-y
Dynamic eco-driving
Microscopic traffic simulation
Signalized intersection | CommonCrawl |
Diagonalize the following matrix. The real eigenvalues are given to the right of the matrix.
\[ \boldsymbol{ \left [ \begin{array}{ c c c } 2 & 5 & 5 \\ 5 & 2 & 5 \\ 5 & 5 & 2 \end{array} \right ] \ ; \ \lambda \ = \ 12 } \]
The aim of this question is to understand the diagonalization process of a given matrix at given eigenvalues.
To solve this question, we first evaluate the expression $ \boldsymbol{ A \ – \ \lambda I } $. Then we solve the system $ \boldsymbol{ ( A \ – \ \lambda I ) \vec{x}\ = 0 } $ to find the eigen vectors.
Given that:
\[ A \ = \ \left [ \begin{array}{ c c c } 2 & 5 & 5 \\ 5 & 2 & 5 \\ 5 & 5 & 2 \end{array} \right ] \]
\[ \lambda \ = \text{ Eigen Values } \]
For $ \lambda \ = \ 12 $:
\[ A \ – \ \lambda I \ = \ \left [ \begin{array}{ c c c } 2 & 5 & 5 \\ 5 & 2 & 5 \\ 5 & 5 & 2 \end{array} \right ] \ – \ 12 \ \left [ \begin{array}{ c c c } 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right ] \]
\[ A \ – \ \lambda I \ = \ \left [ \begin{array}{ c c c } 2 \ – \ 12 & 5 & 5 \\ 5 & 2 \ – \ 12 & 5 \\ 5 & 5 & 2 \ – \ 12 \end{array} \right ] \]
\[ A \ – \ \lambda I \ = \ \left [ \begin{array}{ c c c } -10 & 5 & 5 \\ 5 & -10 & 5 \\ 5 & 5 & -10 \end{array} \right ] \]
Converting to row echelon form through row operations:
\[ \begin{array}{ c } R_2 = 2R_2 + R_1 \\ \longrightarrow \\ R_3 = 2R_3+R_1 \end{array} \left [ \begin{array}{ c c c } -10 & 5 & 5 \\ 0 & -15 & 15 \\ 0 & 15 & -15 \end{array} \right ] \]
\[ \begin{array}{ c } R_1 = R_1 + \frac{ R_2 }{ 3 } \\ \longrightarrow \\ R_3 = R_2 + R_3 \end{array} \left [ \begin{array}{ c c c } -10 & 0 & 10 \\ 0 & -15 & 15 \\ 0 & 0 & 0 \end{array} \right ] \]
\[ \begin{array}{ c } R_1 = \frac{ -R_1 }{ 10 } \\ \longrightarrow \\ R_2 = \frac{ -R_2 }{ 3 } \end{array} \left [ \begin{array}{ c c c } 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right ] \]
\[ A \ – \ \lambda I \ = \ \left [ \begin{array}{ c c c } 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right ] \]
To find the eigenvectors:
\[ ( A \ – \ \lambda I ) \vec{x}\ = 0 \]
Substituting Values:
\[ \left [ \begin{array}{ c c c } 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right ] \ \left [ \begin{array}{ c } x_1 \\ x_2 \\ x_3 \end{array} \right ] \ = \ 0 \]
Solving this simple system yields:
\[ \vec{x} \ = \ \left [ \begin{array}{ c } 1 \\ 1 \\ 1 \end{array} \right ] \]
Diagonalize the same matrix given in the above question for $ lambda \ = \ -3 $:
For $ \lambda \ = \ -3 $:
\[ A \ – \ \lambda I \ = \ \left [ \begin{array}{ c c c } 5 & 5 & 5 \\ 5 & 5 & 5 \\ 5 & 5 & 5 \end{array} \right ] \]
\[ \begin{array}{ c } R_2 = R_2 – R_1 \\ \longrightarrow \\ R_3 = R_3 – R_1 \end{array} \left [ \begin{array}{ c c c } 5 & 5 & 5 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right ] \]
\[ \begin{array}{ c } R_1 = \frac{ R_1 }{ 5 } \\ \longrightarrow \end{array} \left [ \begin{array}{ c c c } 1 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right ] \]
Posted byWilliam Smith November 29, 2022 November 30, 2022 Posted inMatrices Q&A
An iceberg (specific gravity 0.917) floats in the ocean (specific gravity 1.025 ). What percent of the volume of the iceberg is under water?
A rocket is launched at an angle of 53 degrees above the horizontal with an initial speed of 200 m/s. The rocket moves for 2.00 s along its initial line of motion with an acceleration of 20.0 m/s^2. At this time, its engines fail and the rocket proceeds to move as a projectile. Calculate the following quantities. | CommonCrawl |
Dual pairs for matrix groups
Dual pairs and regularization of Kummer shapes in resonances
June 2019, 11(2): 239-254. doi: 10.3934/jgm.2019013
Dispersive Lamb systems
Peter J. Olver , and Natalie E. Sheils
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA
* Corresponding author: Peter J. Olver
Received October 2017 Revised March 2018 Published May 2019
Full Text(HTML)
Under periodic boundary conditions, a one-dimensional dispersive medium driven by a Lamb oscillator exhibits a smooth response when the dispersion relation is asymptotically linear or superlinear at large wave numbers, but unusual fractal solution profiles emerge when the dispersion relation is asymptotically sublinear. Strikingly, this is exactly the opposite of the superlinear asymptotic regime required for fractalization and dispersive quantization, also known as the Talbot effect, of the unforced medium induced by discontinuous initial conditions.
Keywords: Lamb system, periodic boundary conditions, Talbot effect, dispersive quantization.
Mathematics Subject Classification: Primary: 35B99.
Citation: Peter J. Olver, Natalie E. Sheils. Dispersive Lamb systems. Journal of Geometric Mechanics, 2019, 11 (2) : 239-254. doi: 10.3934/jgm.2019013
M. V. Berry, I. Marzoli and W. Schleich, Quantum carpets, carpets of light, Physics World, 14 (2001), 39-44. Google Scholar
G. Chen and P. J. Olver, Dispersion of discontinuous periodic waves, Proc. Roy. Soc. London, 469 (2012), 20120407, 21pp. doi: 10.1098/rspa.2012.0407. Google Scholar
V. Chousionis, M. B. Erdoğan and N. Tzirakis, Fractal solutions of linear and nonlinear dispersive partial differential equations, Proc. London Math. Soc., 110 (2015), 543-564. doi: 10.1112/plms/pdu061. Google Scholar
B. Deconinck, Q. Guo, E. Shlizerman and V. Vasan, Fokas's uniform transform method for linear systems, Quart. Appl. Math., 76 (2018), 463-488, arXiv 1705.00358. doi: 10.1090/qam/1484. Google Scholar
B. Deconinck, B. Pelloni and N. E. Sheils, Non-steady state heat conduction in composite walls, Proc. Roy. Soc. London A, 470 (2014), 20130605. Google Scholar
J. J. Duistermaat, Self-similarity of ``Riemann's nondifferentiable function'', Nieuw Arch. Wisk., 9 (1991), 303-337. Google Scholar
M. B. Erdoğan, personal communication, 2018. Google Scholar
M. B. Erdoğan and G. Shakan, Fractal solutions of dispersive partial differential equations on the torus, Selecta Math., 25 (2019), 11. doi: 10.1007/s00029-019-0455-1. Google Scholar
M. B. Erdoğan and N. Tzirakis, Talbot effect for the cubic nonlinear Schrödinger equation on the torus, Math. Res. Lett., 20 (2013), 1081-1090. doi: 10.4310/MRL.2013.v20.n6.a7. Google Scholar
[10] M. B. Erdoğan and N. Tzirakis, Dispersive Partial Differential Equations: Wellposedness and Applications, London Math. Soc. Student Texts, vol. 86, Cambridge University Press, Cambridge, 2016. doi: 10.1017/CBO9781316563267. Google Scholar
A. S. Fokas, A unified transform method for solving linear and certain nonlinear PDEs, Proc. Roy. Soc. London A, 453 (1997), 1411-1443. doi: 10.1098/rspa.1997.0077. Google Scholar
A. S. Fokas, A Unified Approach to Boundary Value Problems, CBMS-NSF Conference Series in Applied Math., vol. 78, SIAM, Philadelphia, 2008. doi: 10.1137/1.9780898717068. Google Scholar
P. Hagerty, A. M. Bloch and M. I. Weinstein, Radiation induced instability, Siam J. Appl. Math., 64 (2003), 484-524. doi: 10.1137/S0036139902418717. Google Scholar
I. A. Kunin, Elastic Media with Microstructure I, , Springer-Verlag, New York, 1982. Google Scholar
G. L. Lamb, On a peculiarity of the wave-system due to the free vibrations of a nucleus in an extended medium, Proc. London Math. Soc., 32 (1900), 208-211. doi: 10.1112/plms/s1-32.1.208. Google Scholar
P. J. Olver, Dispersive quantization, Amer. Math. Monthly, 117 (2010), 599-610. doi: 10.4169/000298910x496723. Google Scholar
P. J. Olver, Introduction to Partial Differential Equations, Undergraduate Texts in Mathematics, Springer, New York, 2014. doi: 10.1007/978-3-319-02099-0. Google Scholar
K. I. Oskolkov, A class of I.M. Vinogradov's series and its applications in harmonic analysis, Progress in Approximation Theory, Springer Ser. Comput. Math., 19, Springer, New York, 1992,353-402. doi: 10.1007/978-1-4612-2966-7_16. Google Scholar
A. C. Scott, Soliton oscillations in DNA, Phys. Rev. A, 31 (1985), 3518-3519. doi: 10.1103/PhysRevA.31.3518. Google Scholar
N. E. Sheils and B. Deconinck, Heat conduction on the ring: interface problems with periodic boundary conditions, Appl. Math. Lett., 37 (2014), 107-111. doi: 10.1016/j.aml.2014.06.006. Google Scholar
H. F. Talbot, Facts related to optical science. No. Ⅳ, Philos. Mag., 9 (1836), 401-407. Google Scholar
H. F. Weinberger, A First Course in Partial Differential Equations, Dover Publ., New York, 1995. Google Scholar
G. B. Whitham, Linear and Nonlinear Waves, John Wiley & Sons, New York, 1974. Google Scholar
Figure 1. The Lamb Oscillator on the Line.
Figure Options
Download as PowerPoint slide
Figure 2. The Lamb Oscillator on the Line at Large Time.
Figure 3. The Periodic Lamb Oscillator.
Figure 4. The Dispersive Periodic Lamb Oscillator with $ \omega (k) = k^2 $.
Figure 5. The Dispersive Periodic Lamb Oscillator for the Klein-Gordon Model.
Figure 6. The Dispersive Periodic Lamb Oscillator with $ \omega(k) = \sqrt{\left| k \right|} $.
Figure 7. The Dispersive Periodic Lamb Oscillator for the Regularized Boussinesq Model.
Figure 8. The Unidirectional Periodic Lamb Oscillator for the Transport Model.
Figure 9. The Unidirectional Dispersive Periodic Lamb Oscillator for $ \omega(k) = {k^2} $.
Figure 10. The Unidirectional Dispersive Periodic Lamb Oscillator for $ \omega(k) = \sqrt{k} $.
Figure 11. The Unidirectional Dispersive Periodic Lamb Oscillator for $ \omega(k)=k^{2} /\left(1+\frac{1}{3} k^{2}\right) $
Gong Chen, Peter J. Olver. Numerical simulation of nonlinear dispersive quantization. Discrete & Continuous Dynamical Systems, 2014, 34 (3) : 991-1008. doi: 10.3934/dcds.2014.34.991
Qiong Meng, X. H. Tang. Solutions of a second-order Hamiltonian system with periodic boundary conditions. Communications on Pure & Applied Analysis, 2010, 9 (4) : 1053-1067. doi: 10.3934/cpaa.2010.9.1053
Shin-Ichiro Ei, Toshio Ishimoto. Effect of boundary conditions on the dynamics of a pulse solution for reaction-diffusion systems. Networks & Heterogeneous Media, 2013, 8 (1) : 191-209. doi: 10.3934/nhm.2013.8.191
Setsuro Fujiié, Jens Wittsten. Quantization conditions of eigenvalues for semiclassical Zakharov-Shabat systems on the circle. Discrete & Continuous Dynamical Systems, 2018, 38 (8) : 3851-3873. doi: 10.3934/dcds.2018167
Micol Amar. A note on boundary layer effects in periodic homogenization with Dirichlet boundary conditions. Discrete & Continuous Dynamical Systems, 2000, 6 (3) : 537-556. doi: 10.3934/dcds.2000.6.537
Ciprian G. Gal, M. Grasselli. On the asymptotic behavior of the Caginalp system with dynamic boundary conditions. Communications on Pure & Applied Analysis, 2009, 8 (2) : 689-710. doi: 10.3934/cpaa.2009.8.689
Meina Gao, Jianjun Liu. A degenerate KAM theorem for partial differential equations with periodic boundary conditions. Discrete & Continuous Dynamical Systems, 2020, 40 (10) : 5911-5928. doi: 10.3934/dcds.2020252
Satoshi Kosugi, Yoshihisa Morita, Shoji Yotsutani. A complete bifurcation diagram of the Ginzburg-Landau equation with periodic boundary conditions. Communications on Pure & Applied Analysis, 2005, 4 (3) : 665-682. doi: 10.3934/cpaa.2005.4.665
F. Ali Mehmeti, R. Haller-Dintelmann, V. Régnier. Dispersive waves with multiple tunnel effect on a star-shaped network. Discrete & Continuous Dynamical Systems - S, 2013, 6 (3) : 783-791. doi: 10.3934/dcdss.2013.6.783
Matthias Geissert, Horst Heck, Christof Trunk. $H^{\infty}$-calculus for a system of Laplace operators with mixed order boundary conditions. Discrete & Continuous Dynamical Systems - S, 2013, 6 (5) : 1259-1275. doi: 10.3934/dcdss.2013.6.1259
Ammar Khemmoudj, Taklit Hamadouche. General decay of solutions of a Bresse system with viscoelastic boundary conditions. Discrete & Continuous Dynamical Systems, 2017, 37 (9) : 4857-4876. doi: 10.3934/dcds.2017209
Laurence Cherfils, Stefania Gatti, Alain Miranville. Long time behavior of the Caginalp system with singular potentials and dynamic boundary conditions. Communications on Pure & Applied Analysis, 2012, 11 (6) : 2261-2290. doi: 10.3934/cpaa.2012.11.2261
Franck Davhys Reval Langa, Morgan Pierre. A doubly splitting scheme for the Caginalp system with singular potentials and dynamic boundary conditions. Discrete & Continuous Dynamical Systems - S, 2021, 14 (2) : 653-676. doi: 10.3934/dcdss.2020353
Le Thi Phuong Ngoc, Khong Thi Thao Uyen, Nguyen Huu Nhan, Nguyen Thanh Long. On a system of nonlinear pseudoparabolic equations with Robin-Dirichlet boundary conditions. Communications on Pure & Applied Analysis, 2022, 21 (2) : 585-623. doi: 10.3934/cpaa.2021190
Long Hu, Tatsien Li, Bopeng Rao. Exact boundary synchronization for a coupled system of 1-D wave equations with coupled boundary conditions of dissipative type. Communications on Pure & Applied Analysis, 2014, 13 (2) : 881-901. doi: 10.3934/cpaa.2014.13.881
Petr Kučera. The time-periodic solutions of the Navier-Stokes equations with mixed boundary conditions. Discrete & Continuous Dynamical Systems - S, 2010, 3 (2) : 325-337. doi: 10.3934/dcdss.2010.3.325
Anna Kostianko, Sergey Zelik. Inertial manifolds for the 3D Cahn-Hilliard equations with periodic boundary conditions. Communications on Pure & Applied Analysis, 2015, 14 (5) : 2069-2094. doi: 10.3934/cpaa.2015.14.2069
Amru Hussein, Martin Saal, Marc Wrona. Primitive equations with horizontal viscosity: The initial value and The time-periodic problem for physical boundary conditions. Discrete & Continuous Dynamical Systems, 2021, 41 (7) : 3063-3092. doi: 10.3934/dcds.2020398
Anna Kostianko, Sergey Zelik. Inertial manifolds for 1D reaction-diffusion-advection systems. Part Ⅱ: periodic boundary conditions. Communications on Pure & Applied Analysis, 2018, 17 (1) : 285-317. doi: 10.3934/cpaa.2018017
Andreas Henrici. Symmetries of the periodic Toda lattice, with an application to normal forms and perturbations of the lattice with Dirichlet boundary conditions. Discrete & Continuous Dynamical Systems, 2015, 35 (7) : 2949-2977. doi: 10.3934/dcds.2015.35.2949
HTML views (254)
Peter J. Olver Natalie E. Sheils | CommonCrawl |
Endemism-based butterfly conservation: insights from a study in Southern Western Ghats, India
M. Anto ORCID: orcid.org/0000-0001-8179-65971,
C. F. Binoy1 &
Ignatious Anto2
The Western Ghats, a biodiversity hotspot in India harbours a high percentage of endemic species due to its unique and diverse habitats. These species which cannot survive elsewhere due to their specialised habitat requirements are at high risk from climatic and anthropogenic disturbances. The butterfly fauna of the region although well documented has not been investigated intensively at local scales. In this study, we present information on species presence within 10 km × 10 km grid cells (n= 30; area=3000 km2) of 94 butterfly species in the Western Ghats region. The data on the species distribution within these grids which included three wildlife sanctuaries and four forest divisions was mapped. Indicator analysis was performed in R using multipatt function in indispecies package to determine species associated with sites/site combinations. The corrected weighted endemism indices of the study grids were estimated.
The data collected over a 4-year period comprised of 393 records of 60 endemic species belonging to five families observed along 102 transects. Troides minos was the most widespread species occuring in 19 grids. Seventeen species indicative of sites and site combinations were obtained, of which Cirrochroa thais, Papilio paris tamilana, Papilio helenus daksha, Parthenos sylvia virens and Mycalesis patnia were significant. The highest corrected weighted endemism index was observed in grid 25 (14.44) followed by grids 24 (12.06) and 19 (11.86). Areas harbouring unique and range restricted species were Parambikulam WLS/TR: Kuthirakolpathy, Pupara, Kalyanathi, Top slip and Muthalakuzhy; Peechi-Vazhani WLS: Ayyapankadu; Thrissur FD: Chakkapara and Vellakarithadam; Nenmara FD: Karikutty, Pothumala and Nelliampathy estate; Vazhachal FD: Poringalkuthu dam, Meenchal and Vazhachal.
The study area which covers 2.14% of the Western Ghats hotspot harbours almost 63.82% of the region's endemic butterfly species making this particular region crucial for butterfly conservation and management. Studying the phylogenetic endemism of the butterflies, identification of microrefugia and testing the mountain geobiodiversity hypothesis with respect to butterflies are the suggested approaches to be adopted for fine-tuning research and conservation of butterflies in this fragile hotspot.
The forests in the Kerala region of the Western Ghats, a biodiversity hotbed, have recently been the target of unpredictable monsoons (Mishra et al., 2018). Studies show an increasing trend of extreme rainfall (Roxy et al., 2017) as well as increases in minimum temperature in the Western Ghats and peninsular India (Dash, Nair, Kulkarni, & Mohanty, 2011; Mondal, Khare, & Kundu, 2015). Butterfly migrations of several species of Papilionidae, Nymphalidae and Pieridae have been reported to coincide with the monsoonal system in peninsular India (Bhaumik & Kunte, 2018; Kunte, 2005). Apart from decades of anthropogenic disturbances leading to forest fragmentation (Jha, Dutt, & Bawa, 2000; Menon & Bawa, 1998; Nair, 1991), recent studies have highlighted other detrimental activities like mining, road construction and irrigation projects (Bharucha, 2006).
In the backdrop of increasing habitat degradation, formulation of priorities for conservation in the Western Ghats is challenging. Many approaches may be adopted but the simplest and most effective would be focusing our attention and action towards reducing the loss of biodiversity based on a framework of vulnerability and irreplaceability (Margules & Pressey, 2000). Subsequently, areas with exceptionally high concentrations of endemic species were prioritised for conservation and the global 'biodiversity hotspot' concept was developed to address this crucial issue (Mittermeier, Myers, Robles-Gil, & Mittermeier, 1999; Myers, 1988, 1990, 2003; Myers, Mittermeier, Mittermeier, da Fonseca, & Kent, 2000). Although hotspots are designated as areas for priority conservation action, the fauna and flora of many hotspots are poorly studied and relevant data are insufficient for effective conservation planning (Mittermeier et al., 2004; Mittermeier, Turner, Larsen, Brooks, & Gascon, 2011). Moreover, it is also likely that true hotspots may go unrecognised due to lack of organised data, biogeographical biases and regional misconceptions (Noss et al., 2015).
In the hotspot analysis whereby 25 areas were identified, the Western Ghats was among the top eight critical regions in terms of endemism and extent of original primary vegetation (Myers et al., 2000) and later designated as 'hyperhot' for conservation prioritisation (Brooks et al., 2002). The number of global hotspots was later expanded to 35 (Mittermeier et al., 2011). The Western Ghats is a 1600 km mountain chain running almost parallel to India's western coast and spread over six states—Gujarat, Maharastra, Goa, Karnataka, Tamil Nadu and Kerala. It includes two biosphere reserves, the Nilgiris Biosphere Reserve (11,040 km2) and the Agasthyamalai Biosphere Reserve (3500 km2). Kerala lies between 8° 18′ and 12° 48′ N latitude and 74° 54′ and 77° 12′ E longitude in the south-west region of the Indian peninsula between the Arabian sea and the Western Ghats (Fig. 1).
Location of the Western Ghats range in India
Topographic heterogeneity (from sea level to 2695 m at its highest point) and a strong precipitation gradient (annual rainfall of < 50 cm in eastern valleys to > 700 cm along western slopes) has given rise to remarkable diversity in flora and fauna. The forests in the state are classified into wet evergreen, semi-evergreen, moist deciduous, dry deciduous and thorn forest types (Champion & Seth, 1968). Studies by Reddy, Jha, & Dadhwal (2016) on the extent, distribution and changes in forests of the Western Ghats reveal a net loss of 35.3% of forest area from 1920 to 2013. Endemism in butterflies is closely linked to the endemism of their host plants. The Western Ghats harbours 330 species out of Indian butterfly fauna of 1501 species. Of these, 37 species are narrow endemics found only in the Western Ghats and 23 species are endemic to Sri Lanka as well (Gaonkar, 1996). Endemism and species richness are widely used indicators of conservation value and an index combining both has been calculated and mapped at regional, continental and global scales (Crisp, Laffan, Linder, & Monro, 2001; Kier & Barthlott, 2001; Kier et al., 2009; Venevsky & Venevskaia, 2005). However, such studies at local scales (less than 5000 km2) are still scarcely seen. As a result of detailed analyses of Australian flora, Crisp et al. (2001) concluded that the corrected endemism index is a useful method to detect centres of endemism using species-in-grid-cell data.
Studies in the last decade indicate that microrefugia may be formed due to topographic variations at scales of metres (Dobrowski, 2011) as well as local influences (De Frenne, Rodríguez-Sánchez, Coomes, et al., 2013) and that these effects are not reflected in GIS models of climate change (De Frenne et al., 2013; Keppel et al., 2017). However, most of these studies are based on flora (Bátori et al., 2017; Keppel et al., 2017; Noss, 2013) and mammals (Camacho-Sanchez et al., 2018). In a study of bush frogs in the Western Ghats, Vijayakumar, Menezes, Jayarajan, & Shanker (2016) highlighted the evolutionary significance of massifs which harbour unique refugia due to steep topographical and environmental shifts. Thus, protection of refugia resulting from mountain topography and climatic stability which buffers lineages against extinction is the current trend as it assures future protection (Klein et al., 2009; Mosblech, Bush, & van Woesik, 2011; Stewart, Lister, Barnes, & Dalén, 2010). Gaonkar (1996) details the state-wise distribution of the butterflies of the Western Ghats and Kunte (2008) delineated their distribution within the four zones whilst assigning conservation values to species.
In this context of impending challenges both biotic and abiotic to the forest ecosystems in the Western Ghats, we venture to ask the key question—Can endemic butterflies be used as indicators for conservation management at local scales in the Western Ghats hotspot? In this study, we have mapped the distribution of endemic butterfly species in an area of 3000 km2 in the central region of the Kerala part of the Western Ghats and calculated the endemic richness index of various grids of the study area. We expect that the sampling of endemic butterfly species at this microscale level will help detect microrefugia and unique habitats in this fragile hotspot. The indicator species occurring in the study area were identified using the R software.
The study was carried out in the central region of the Kerala part of the Southern Western Ghats which included three wildlife sanctuaries: Peechi-Vazhani wildlife sanctuary (Peechi-Vazhani WLS), Chinmony wildlife sanctuary (Chinmony WLS), Parambikulam wildlife sanctuary/tiger reserve (Parambikulam WLS/TR) and four forest divisions: Nenmara forest division (Nenmara FD), Vazhachal forest division (Vazhachal FD), Thrissur forest division (Thrissur FD) and Chalakudy forest division (Chalakudy FD). The study area was divided into 10 km × 10 km grids and a total of 30 grids were obtained (Fig. 2). In each grid cell, ten transects were covered over the study period and the length of transects in the different grids ranged between 800 m and 1000 m. Butterflies in the study grids were sampled along the transects using the Pollard line transect method (Pollard & Yates, 1993) with slight modifications. Butterflies sighted within 5 m on either side and in front of the observer walking at a constant pace of 1 km/h were recorded. The individuals that could not be identified by sight were either caught with an insect net for close examination or photographed and released. The butterflies were identified using suitable keys (Evans, 1932; Kehimkar, 2008; Wynter-Blyth, 1957). The sanction obtained from the Kerala Forest and Wildlife Department (No. WL 10-36790/15) for sampling in protected areas in the Western Ghats prohibited collection of endemic species. Hence, identification of smaller species belonging to families Lycaenidae and Hesperidae by sight was difficult.
Study area divided into 30 grids of 10 km × 10 km
The sampling was done over a 4-year period from May 2015 to April 2019 and the transect data collected along 102 transects (Table 1) was used to map the distribution of endemic species/subspecies onto the grids of the study area. The species occurrence matrix was prepared by scoring the presence/absence (1/0) of endemic species within the sampling grids. The geographic coordinates of transects were marked using Global Positioning System (GPS; GPSMAP 76Cx) which has good receptivity in forest areas. The GPS readings are plotted over geo-referenced Survey of India (SOI) by using open source Geographic Information System (GIS) software. The base layers such as water bodies, forest and boundaries were digitised from SOI topo sheets and updating of layers from latest satellite imageries done using GIS and remote sensing software. The final distribution map of endemic species whereby each point represents the occurrence of a single individual within the study area was prepared using the GIS software (Environmental Systems Research Institute (ESRI), 2011).
Table 1 Geographic coordinates of transects sampled in 30 grids of study area
Using the sampling data for 4 years, the relationship between the observed species occurrence in the surveyed sites and site groups was analysed and the indicator species determined (De Cáceres & Legendre, 2009; De Cáceres, Legendre, Wiser, & Brotons, 2012; Dufrene & Legendre, 1997). Analyses were implemented in RStudio ver. 3.6.2 (RStudio Team, 2015) and indicative species were identified using multipatt function in package indispecies ver.1.7.9. The total count of species within each grid cell was measured as the species richness. Weighted endemism (WE) is a function of species richness and range size rarity (Crisp et al., 2001; Kier & Barthlott, 2001):
$$ \mathbf{WE}=\boldsymbol{\Sigma}\ \mathbf{1}/\mathbf{C} $$
where C is the number of grids in which each species occurs.
The total WE index of each grid was obtained by summing the WE indices of all species recorded in that particular grid. Finally, the corrected weighted endemism index (CWEI) was calculated for each cell by dividing the weighted endemism index by the total count of species in that particular cell (Linder, 2000). Since the proportion of endemics in a grid cell is measured, this index corrects the species richness effect.
$$ \mathbf{CWEI}=\mathbf{WE}/\mathbf{K} $$
where C is the number of grid cell in which each endemic species occurs, and K is the total number of species in a grid cell.
The data set for sampling comprised of 94 endemic species (Tables 2 and 3) which include 60 species recorded as endemic to Western Ghats and Sri Lanka (Gaonkar, 1996), 1 species endemic to peninsular India and 33 subspecies reported as endemic to the area (Kunte, Nitin, & Basu, 2018).
Table 2 Species recorded as endemic to the Western Ghats, Sri Lanka and peninsular India
Table 3 Subspecies recorded as endemic to the Western Ghats
The number of species occurrence varied from one to thirty-eight and consisted of only presence points. Overall, 393 sightings of endemic species and subspecies were recorded within the 30 grids over the 4 years. The distribution of 60 endemic species/subspecies recorded during the study was mapped onto grids of the study (Figs. 3, 4, 5, 6 and 7).
a-l Distribution maps of endemic butterflies of family Papilionidae within study area. a Troides minos. b Pachliopta pandiyana. c Pachliopta hector. d Papilio liomedon. e Papilio dravidarum. f Papilio polymnestor. g Papilio buddha. h Papilio crino. i Graphium sarpedon teredon. j Graphium antiphates naira. k Papilio helenus daksha. l Papilio paris tamilana
a-i Distribution maps of endemic butterflies of family Pieridae within study area. a Eurema nilgiriensis. b Colias nilagiriensis. c Delias eucharis. d Pareronia ceylanica. e Eurema andersonii shimai. f Appias indra shiva. g Appias lyncida latifasciata. h Pieris canidia canis. i Hebomoia glaucippe australis
a-z Distribution maps of endemic butterflies of family Nymphalidae within study area. a Discophora lepida. b Lethe drypetis. c Mycalesis subdita. d Mycalesis igilia. e Mycalesis patnia. f Zipoetis saitis. g Ypthima ceylonica. h Ypthima chenui. i Ypthima ypthimoides. j Cethosia nietneri. k Cirrochroa thais. l Euthalia nais. m Kallima horsfieldi. n Parantica nilgiriensis. o Idea malabarica. p Rohana parisatis atacinus. q Charaxes schreiber wardii. r Vindula erota saloma. s Dolpha evelina laudabalis. t Athyma selenophora kanara. u Lassipe viraja kanara. v Parthenos sylvia virens. w Vanessa indica pholoe. x Melanitis phedima varaha. y Melanitis zitenius gokala. z Mycalesis anaxias anaxias
a-h Distribution maps of endemic butterflies of family Lycaenidae within study area. a Udara akasa. b Udara singalensis. c Celatoxia albidisca. d Spindasis ictis. e Spindasis abnormis. f Zesius chrysomallus. g Curetis thetis. h Curetis siva
a-e Distribution maps of endemic butterflies of family Hesperidae within study area. a Sarangesa purendra. b Aeromachus pygmaeus. c Sovia hyrtacus. d Pseudocoladenia dan dan. e Oriens concinna
When considering the family-wise distribution of endemics recorded, Papilionidae had the highest number of sightings (194) followed by Nymphalidae (116), Pieridae (54), Hesperidae (17), and Lycenidae (12). Troides minos was the most sighted (38 sightings) and widespread species being recorded in 19 grids (63.3%). Species which were restricted to the montane and upper montane areas of the Karimala peak in Parambikulam WLS/TR and Nelliampathy in the Nenmara FD include Celatoxia albidisca, Udara akasa, U. singalensis, Curetis thetis, Eurema nilgiriensis, E. andersonii shimai, Colias nilagiriensis, Melanitis phedima varaha, Ypthima ceylonica, Y. chenui, Y. ypthimoides, Athyma selenophora kanara, Lassipe viraja kanara and Parantica nilgiriensis. Sovia hyrtacus was recorded only from the Vazhachal FD whilst Kallima horsfieldi was recorded from Vazhzachal FD and Peechi-Vazhani WLS. Widespread endemic species like Troides minos, Pachliopta hector and Delias eucharis were observed along transects which were located near settlements and roads. Rohana parisatis atacinus, Parthenos sylvia virens and Graphium sarpedon teredon were forest edge species whilst Cirrocroa thais and Papilio polymnestor were common at low elevations. Twenty-one out of the 37 Western Ghats endemics (56%); 18 out of the 24 Western Ghats, Sri Lanka and peninsular India endemics (75%) and 21 out of the 33 endemic subspecies (63%) were observed during the 4-year period. Seven endemic species was recorded in family Nymphalidae followed by Papilionidae (5), Hesperidae (4), Lycaenidae (3), and Pieridae (2).
Indicator analysis identified seventeen indicator species of which five, namely Cirrochroa thais, Papilio paris tamilana, Papilio helenus daksha, Parthenos sylvia virens and Mycalesis patnia were significant at p≤0.001 and the remaining twelve species were significant at p≤0.05 (Table 4). In the former group, two were endemic to Western Ghats and Sri Lanka whilst three were endemic to the Western Ghats at subspecies level. An interesting and unexpected trend noticed is that out of the seventeen indicator species, five species were endemic to the Western Ghats, four were endemic to the Western Ghats and Sri Lanka region and eight species were endemic at the subspecies level. Does a greater number of subspecies level endemic indicators hint at subtle speciation events in progress? The five most significant species were indicative of habitats in Chinmony WLS, Peechi-Vazhani WLS, Parambikulam WLS/TR, Nenmara FD and Vazhachal FD. The number of transects in the above locations which had sightings of these species were as follows: Cirrochroa thais (15), Papilio paris tamilana (8), Papilio helenus daksha (19), Parthenos sylvia virens (17) and Mycalesis patnia (15). The endemic species indicative of Chalakudy FD and Thrissur FD were Troides minos and Pachliopta hector which were common and widespread species.
Table 4 Indicator species analysis for all combinations of site categories
Calculating the endemism index of the species helped identify locations having higher conservation implications (Fig. 8). When examining the corrected endemism index (CWEI) values, the highest index was observed in grid 25 (CWEI—14.44) followed by grids 24 (CWEI—12.06) and 19 (CWEI—11.86). Sixteen grids (3, 4, 5, 8, 9, 11, 12, 15, 17, 18, 20, 21, 22, 23, 26, 28) have CWEI values ranging from 4.07 to 7.75 and seven grids (1, 2, 6, 7, 10, 27, 30) have CWEI values between 2.07 and 3.89. In four grids (13, 14, 16, 29), no endemic species were recorded. Grids with the lowest values were those located in areas within towns with high human activities.
Corrected weighted endemism index values of the grids within study area
Out of the 94 endemic species and subspecies reported from the Western Ghats, 60 species were recorded and mapped in this study. The study area which covers 2.14% of the Western Ghats hotspot harbours almost 63.82% of the region's endemic butterfly species making this particular region as important and crucial for conservation and management. Assessment of selected sites with respect to butterflies indicate that locations like Vazhachal Reserve Forest, Nelliampathy Reserve Forest, Parambikulam Wildlife Sanctuary/Tiger Reserve, and Peechi-Vazhani Wildlife Sanctuary harbour endemic species and should be prioritised in biodiversity conservation plans. A simple monitoring protocol using endemic butterflies was developed and the GIS mapping provided information on the distribution of endemic species within the study area. These monitoring studies clearly emphasise the well documented fact that reliable field data along with robust analytic tools will help guide conservation of these fragile endemics in this biodiversity hotspot.
Kessler and Kluge (2008) postulated that distribution patterns of endemic species along tropical elevational gradients usually reach a maximum richness between 500 and 2000 m. In this study, the grids with the highest peaks, Padagiri (1585 m; grid 19) and Karimala (1438 m; grid 25) also showed high endemism indices of 11.89 and 14.14 respectively. Mangattu Kumban (grid 9) at mid elevation of 635 m had an endemism index of 7.78 (Fig. 9). These findings thus support the elevational gradient-species richness relationship proposed above.
Relationship between corrected weighted endemism index and elevation
The main advantage of the CWEI is its non-correlation to species richness and ability to distinguish range-restricted species at a very subtle level. We could identify unique pockets where such species occur within the study area: Parambikulam WLS/TR: Kuthirakolpathy, Pupara, Kalyanathi, Top slip and Muthalakuzhy; Peechi-Vazhani WLS: Ayyapankadu; Thrissur FD: Chakkapara and Vellakarithadam; Nenmara FD: Karikatty, Pothumala and Nelliampathy estate; Vazhachal FD: Poringalkuthu dam, Meenchal and Vazhachal (Fig. 10). The biotic and abiotic factors in these areas should be rigorously studied to determine if they are microrefugial habitats of these rare species.
Locations of range-restricted species within study area
It is a well-established fact that current spatial distribution and diversity patterns are a reflection of a long evolutionary and biogeographical history. In order to elucidate these complex mechanisms we suggest further studies in this vulnerable hotspot by adopting the following three approaches: (1) studying the phylogenetic endemism (Rosauer, Laffan, Crisp, Donnellan, & Cook, 2009) would help uncover the events that have shaped the rich diversity of this region having Gondwanan, Sundaland and recent biogeographical elements with respect to butterflies. The butterfly fauna of this region with over 300 well documented species would an ideal template for such investigations (2) identification of microrefugia which Harrison and Noss (2017) caution will assume greater relevance against the backdrop of climate change would be another area for butterfly research in this hotspot and (3) finally, the Western Ghats with its steep gradients and undulating terrain would be the perfect arena to test the 'Mountain Geobiodiversity Hypothesis' (Mosbrugger, Favre, Muellner-Riehl, Päckert, & Mulch, 2018) with respect to butterflies.
Endemic species are useful indicators of habitat quality and can also act as umbrella species for conservation planning and management. Given the high diversity and endemism among the butterfly communities of the Kerala part of the Western Ghats, implementation of effective conservation actions would require an integrated approach involving: (1) management of vulnerable and unique habitats at microscale level as landscape level management may sometimes fail to recognise truly 'hot' microhabitats (2) conservation-driven research with emphasis on phylogenetic endemism and microrefugia of species (3) continuous monitoring of habitat and populations based on community forest management through stakeholder participation (4) raising conservation awareness in local communities living in close proximity to and highly dependent on forest resources.
The distribution of 60 endemic species/subspecies was recorded and mapped within the 30 study grids over the 4-year study period. Overall, 393 sightings of endemic species and subspecies were recorded and the family Papilionidae had the highest number of sightings (194) followed by Nymphalidae (116), Pieridae (54), Hesperidae (17) and Lycenidae (12). Out of the total of 37 species endemic to the Western Ghats, 21 species (56%); 18 species of the total of 24 (75%) species endemic to Western Ghats, Sri Lanka and peninsular India and 21 species of a total of 33 (63%) endemic subspecies were recorded. The highest number of Western Ghats endemics was recorded in family Nymphalidae (7) followed by Papilionidae (5), Hesperidae (4), Lycaenidae (3) and Pieridae (2).
Indicator analysis identified seventeen indicator species of which five, namely Cirrochroa thais, Papilio paris tamilana, Papilio helenus daksha, Parthenos sylvia virens, and Mycalesis patnia were significant and were indicative of habitats in Chinmony WLS, Peechi Vazhani WLS, Parambikulam WLS/TR, Nenmara FD and Vazhachal FD. The endemic species indicative of Chalakudy FD and Thrissur FD were Troides minos and Pachliopta hector.
The highest corrected weighted endemism index was observed in grid 25 followed by grids 24 and 19. Sixteen grids showed values ranging from 4.07 to 7.75 and seven grids had values between 2.07 and 3.89. The grids with the highest peaks of the study area, Padagiri, Karimala and Mangattu Kumban also showed high endemism indices. Kuthirakolpathy, Pupara, Kalyanathi, Top slip, Muthalakuzhy, Ayyapankadu, Chakkapara Vellakarithadam, Karikatty, Pothumala, Nelliampathy estate, Poringalkuthu dam, Meenchal, and Vazhachal were areas harbouring unique and range restricted species.
This study has shown interesting geographic patterns of the spatial structure of endemism richness in a highly critical hotspot area. Conservation management in the Indian context is expected to benefit if biodiversity can be characterised to more local levels (Bossuyt et al., 2004). This study shows that even within hotspots, endemicity is not uniform and our efforts should be to focus on small areas that represent unique species associations. Even though the addition of more taxa will be useful for a more complete overview, we believe that these are primary areas in the central region of the Kerala part of the Western Ghats that harbour species of conservation value. Moreover, these are also species having a complex evolutionary history and should therefore be monitored and studied in further depth, especially when designing conservation strategies. Thus as we advance into a future wrought with climatic instabilities and increased human impacts, research should be fine-tuned and the delineation of phylogenetic endemism patterns and identification of microrefugia would definitely be a step forward in the right direction for butterfly conservation in this fragile hotspot.
All data generated or analysed during this study are included in this published article.
WLS:
WLS/TR:
Wildlife sanctuary/tiger reserve
FD:
Forest division
SOI:
GIS:
Weighted endemism
CWEI:
Corrected weighted endemism index
Bátori, Z., Vojtkó, A., Farkas, T., Szabó, A., Havadtői, K., Vojtkó, A. E., … Keppel, G. (2017). Large and small-scale environmental factors drive distributions of cool-adapted plants in karstic microrefugia. Annals of Botany, 119(2), 301–309. https://doi.org/10.1093/aob/mcw233.
Bharucha, E. (2006). Protected areas and Land-scape linkages: Case studies from the Maharastra scenario. Journal of Bombay Natural History Society, 103(2), 327.
Bhaumik, V., & Kunte, K. (2018). Female butterflies modulate investment in reproduction and flight in response to monsoon -driven migrations. Oikos, 127(2), 285–296. https://doi.org/10.1111/oik.04593.
Bossuyt, F., Meegaskumbura, M., Beenaerts, N., Gower, D., Pethiyagoda, R., Roelants, K., … Milinkovitch, M. (2004). Local endemism within the Western Ghats-Sri Lanka biodiversity hotspot. Science (New York, N.Y.), 306(5695), 479–481. https://doi.org/10.1126/science.1100167.
Brooks, T. M., Mittermeier, R. A., Mittermeier, C. G., Fonseca, C., Rylands, G., Konstant, A., … Craig (2002). Habitat loss and extinction in the hotspots of biodiversity. Conservation Biology, 16(4), 909–923. https://doi.org/10.1046/j.1523-1739.2002.00530.x.
Camacho-Sanchez, M., Quintanilla, I., Hawkins, M. T. R., Tuh, F. Y. Y., Wells, K., Maldonado, J. E., & Leonard, J. A. (2018). Interglacial refugia on tropical mountains: Novel insights from the summit rat (Rattus baluensis), a Borneo mountain endemic. Diversity and Distributions, 24(9), 1252–1266. https://doi.org/10.1111/ddi.12761.
Champion, H. G., & Seth, S. K. (1968). A revised survey of the forest types of India. Govt. of India Press.
Crisp, M. D., Laffan, S., Linder, H. P., & Monro, A. (2001). Endemism in the Australian flora. Journal of Biogeography, 28(2), 183–198. https://doi.org/10.1046/j.1365-2699.2001.00524.x.
Dash, S., Nair, A. A., Kulkarni, M. A., & Mohanty, U. (2011). Characteristic changes in the long and short spells of different rain intensities in India. Theoretical Applied Climatology, 105. https://doi.org/10.1007/s00704-011-0416-x.
De Cáceres, M., & Legendre, P. (2009). Associations between species and groups of sites: Indices and statistical inference. Ecology, 90(12), 3566–3574. https://doi.org/10.1890/08-1823.1.
De Cáceres, M., Legendre, P., Wiser, S. K., & Brotons, L. (2012). Using species combinations in indicator value analyses. Methods in Ecology and Evolution, 3(6), 973–982. https://doi.org/10.1111/j.2041-210X.2012.00246.x.
De Frenne, P., Rodríguez-Sánchez, F., Coomes, D. A., et al. (2013). Microclimate moderates plant responses to macroclimate warming. Proceedings of the National Academy of Sciences of the United States of America., 110(46), 18561–18565. https://doi.org/10.1073/pnas.1311190110.
Dobrowski, S. Z. (2011). A climatic basis for microrefugia: The influence of terrain on climate. Global Change Biology, 17(2), 1022–1035. https://doi.org/10.1111/j.1365-2486.2010.02263.x.
Dufrene, M., & Legendre, P. (1997). Species assemblages and indicator species: The need for a flexible asymmetrical approach. Ecological Monographs, 67, 345–366.
Environmental Systems Research Institute (ESRI). (2011) Arc GIS Desktop: Release 10.
Evans, W. H. (1932). Identification of Indian butterflies. Bombay Natural History Society.
Gaonkar, H. (1996). Butterflies of the Western Ghats, India, including Sri Lanka: A biodiversity assessment of a threatened mountain system. Centre for Ecological Sciences, Indian Institute of Science & London: Natural History Museum.
Harrison, S., & Noss, R. (2017). Endemism hotspots are linked to stable climatic refugia. Annals of Botany, 119(2), 207–214. https://doi.org/10.1093/aob/mcw248.
Jha, C., Dutt, C., & Bawa, K. (2000). Deforestation and land use changes in Western Ghats, India. Current Science, 79, 231–238.
Kehimkar, I. (2008). The book of Indian butterflies. Bombay Natural History Society.
Keppel, G., Robinson, T. P., Wardell-Johnson, G. W., Yates, C. J., van Niel, K. P., Byrne, M., & Schut, A. G. T. (2017). Low-altitude mountains as refugium for two narrow endemics in the Southwest Australian Floristic Region biodiversity hotspot. Annals of Botany, 119(2), 289–300. https://doi.org/10.1093/aob/mcw182.
Kessler, M., & Kluge, J. (2008). Diversity and endemism in tropical montane forests-from patterns to processes. Biodiversity and Ecology Series, 2, 35–50.
Kier, G., & Barthlott, W. (2001). Measuring and mapping endemism and species richness: A new methodological approach and its application on the flora of Africa. Biodiversity Conservation, 10(9), 1513–1529. https://doi.org/10.1023/A:1011812528849.
Kier, G., Kreft, H., Lee, T. M., Jetz, W., Ibisch, P. L., Nowicki, C., … Barthlott, W. (2009). A global assessment of endemism and species richness across island and mainland regions. PNAS, 106(23), 9322–9327. https://doi.org/10.1073/pnas.0810306106.
Klein, C., Wilson, K., Watts, M., Stein, J., Berry, S., Carwardine, J., … Possingham, H. (2009). Incorporating ecological and evolutionary processes into continental-scale conservation planning. Ecological Applications, 19(1), 206–217. https://doi.org/10.1890/07-1684.1.
Kunte, K. (2005). Species composition, sex-ratio and movement patterns in danaine butterfly migrations in southern India. Journal of the Bombay Natural History Society, 102, 280–286.
Kunte, K. (2008). The Wildlife (Protection) Act and conservation prioritization of butterflies of the Western Ghats, southwestern India. Current Science, 94, 729–735.
Kunte, K., Nitin, R., & Basu, D. N. (2018). A systematic, annotated checklist of the of the butterflies of the Western Ghats. In K. Kunte, S. Sondhi, & P. Roy (Eds.), Butterflies of India, v.2.53. Indian Foundation for Butterflies.
Linder, H. P. (2000). Plant diversity and endemism in sub-Saharan tropical Africa. Journal of Biogeography, 28, 169–182.
Margules, C. R., & Pressey, R. L. (2000). Systematic conservation planning. Nature, 405(6783), 243–253. https://doi.org/10.1038/35012251.
Menon, S., & Bawa, K. S. (1998). Deforestation in the tropics: Reconciling disparities in estimates for India. Ambio, 27, 567–577.
Mishra, V., Aaadhar, S., Shah, H., Kumar, R., Pattanaik, D. R., & Tiwari, A. D. (2018). The Kerala flood of 2018: Combined impact of extreme rainfall and reservoir storage. Hydrology and Earth System Sciences Discussions. https://doi.org/10.5194/hess-2018-480.
Mittermeier, R. A., Myers, N., Robles-Gil, P., & Mittermeier, C. G. (1999). Hotspots: Earth's biologically richest and most endangered terrestrial ecoregions. CEMEX.
Mittermeier, R. A., Robles-Gil, P., Hoffmann, M., Pilgrim, J., Brooks, T., Mittermeier, C. G., … da Fonseca, G. A. B. (2004). Hotspots revisited: Earth's biologically richest and most endangered terrestrial ecoregions. CEMEX.
Mittermeier, R. A., Turner, W. R., Larsen, F. W., Brooks, T. M., & Gascon, C. (2011). Global biodiversity conservation: The critical role of hot spots. In F. E. Zachos, & J. C. Habel (Eds.), Biodiversity hotspots: distribution and protection of conservation priority areas, (pp. 3–22). Springer-Verlag. https://doi.org/10.1007/978-3-642-20992-5_1.
Mondal, A., Khare, D., & Kundu, S. (2015). Spatial and temporal analysis of rainfall and temperature trend of India. Theoretical and Applied Climatology, 122(1-2), 143–158. https://doi.org/10.1007/s00704-014-1283-z.
Mosblech, N. A. S., Bush, M. B., & van Woesik, R. (2011). On metapopulations and microrefugia: Palaeoecological insights. Journal of Biogeography, 38(3), 419–429. https://doi.org/10.1111/j.1365-2699.2010.02436.x.
Mosbrugger, V., Favre, A., Muellner-Riehl, A. N., Päckert, M., & Mulch, A. (2018). Cenozoic evolution of geo-biodiversity in the Tibeto-Himalayan region. In C. Hoorne, A. Perrigio, & A. Atonelli (Eds.), Mountains, climate and biodiversity, (pp. 429–448). Wiley-Blackwell.
Myers, N. (1988). Threatened biotas: "hotspots" in tropical forests. Environmentalist, 1988, 187–208.
Myers, N. (1990). The biodiversity challenge: Expanded hot-spots analysis. Environmentalist, 10(4), 243–256. https://doi.org/10.1007/BF02239720.
Myers, N. (2003). Biodiversity hotspots revisited. Bioscience, 53, 916–917.
Myers, N., Mittermeier, R. A., Mittermeier, C. G., da Fonseca, G. A. B., & Kent, J. (2000). Biodiversity hotspots for conservation priorities. Nature, 403(6772), 853–858. https://doi.org/10.1038/35002501.
Nair, S. C. (1991). The southern western Ghats: A biodiversity conservation plan. Indian National Trust for Art and Cultural Heritage.
Noss, R. F. (2013). Forgotten grasslands of the South: Natural history and conservation. Island Press. https://doi.org/10.5822/978-1-61091-225-9.
Noss, R. F., Platt, W. J., Sorrie, B. A., Weakley, A. S., Means, D. B., Costanza, J., & Peet, R. K. (2015). How global biodiversity hotspots may go unrecognized: Lessons from the North American Coastal Plain. Diversity and Distributions, 21(2), 236–244. https://doi.org/10.1111/ddi.12278.
Pollard, E., & Yates, T. J. (1993). Monitoring butterflies for ecology and conservation. Chapman and Hall.
Reddy, C. S., Jha, C. S., & Dadhwal, V. K. (2016). Assessment and monitoring of long-term forest cover changes (1920–2013) in Western Ghats biodiversity hotspot. Journal of Earth System Science, 125(1), 103–114. https://doi.org/10.1007/s12040-015-0645-y.
Rosauer, D., Laffan, S. W., Crisp, M. D., Donnellan, S. C., & Cook, L. G. (2009). Phylogenetic endemism: A new approach for identifying geographical concentrations of evolutionary history. Molecular Ecology, 18(19), 4061–4072. https://doi.org/10.1111/j.1365-294X.2009.04311.x.
Roxy, M. K., Ghosh, S., Pathak, A., Athulya, R., Mujumdar, M., Murtugudde, R., … Rajeevan, M. (2017). A threefold rise in widespread extreme rain events over central India. Nature Communications, 8(1), 1–11.
RStudio Team (2015). RStudio: Integrated development for R. RStudio Inc.
Stewart, J. R., Lister, A. M., Barnes, D., & Dalén, L. (2010). Refugia revisited: individualistic responses of species in time and space. Proceedings of the Royal Society B: Biological Sciences, 277(1682), 661–671. https://doi.org/10.1098/rspb.2009.1272.
Venevsky, S., & Venevskaia, I. (2005). Hierarchical systematic conservation planning at the national level: Identifying national biodiversity hotspots using abiotic factors in Russia. Biological Conservation, 124(2), 235–251. https://doi.org/10.1016/j.biocon.2005.01.036.
Vijayakumar, S. P., Menezes, R. C., Jayarajan, A., & Shanker, K. (2016). Glaciations, gradients and geography: Multiple drivers of diversification of bush frogs in the Western Ghats Escarpment. Proceedings of the Royal Society B: Biological Sciences, 283(1836), 20161011. https://doi.org/10.1098/rspb.2016.1011.
Wynter-Blyth, M. A. (1957). Butterflies of the Indian region. Bombay Natural History Society.
A.M. acknowledges the University Grants Commission, New Delhi, India, for providing the post-doctoral fellowship. The authors thank Suganthasakthivel R. and Roby T.J. for figures and maps; Sandex V. and Vinod M.B. for assistance rendered during field surveys and the staff of the Kerala Forest Department for logistic support. The authors are also grateful to the anonymous reviewers and editor for their valuable comments/suggestions which have helped us to improve an earlier version of the manuscript.
This work was supported by a postdoctoral research grant (F.15-1/2012-13/PDFWM-2012-13-GE-KER-21937 (SA-II) to the first author from the University Grants Commission, Government of India. The funding was for research purposes, mainly travel and contingency expenses associated with the project.
Research and Post Graduate Department of Zoology, St. Thomas College, Thrissur, Kerala, 680001, India
M. Anto & C. F. Binoy
Quantiphi Analytics, Trifecta Adatto, Whitefield, Bengaluru, Karnataka, 560048, India
Ignatious Anto
M. Anto
C. F. Binoy
A.M. conceived and designed the study, conducted field surveys and data collection and drafted the manuscript. B.C.F. helped coordinate the study and review the manuscript. I.A. performed the data analysis in R. The authors read and approved the final manuscript.
Correspondence to M. Anto.
Sampling in protected areas was conducted under permit (No. WL 10-36790/15) from the Kerala Forest and Wildlife Department, India. No animals were harmed during field sampling. No endemic butterfly or plant species were collected from protected areas during the study.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Anto, M., Binoy, C.F. & Anto, I. Endemism-based butterfly conservation: insights from a study in Southern Western Ghats, India. JoBAZ 82, 22 (2021). https://doi.org/10.1186/s41936-021-00221-2
Distribution mapping
Indicator species
Endemism index
Biodiversity hotspot | CommonCrawl |
Prediction of compressibility parameters of the soils using artificial neural network
T. Fikret Kurnaz1,
Ugur Dagdeviren2,
Murat Yildiz3 &
Ozhan Ozkan3
The compression index and recompression index are one of the important compressibility parameters to determine the settlement calculation for fine-grained soil layers. These parameters can be determined by carrying out laboratory oedometer test on undisturbed samples; however, the test is quite time-consuming and expensive. Therefore, many empirical formulas based on regression analysis have been presented to estimate the compressibility parameters using soil index properties. In this paper, an artificial neural network (ANN) model is suggested for prediction of compressibility parameters from basic soil properties. For this purpose, the input parameters are selected as the natural water content, initial void ratio, liquid limit and plasticity index. In this model, two output parameters, including compression index and recompression index, are predicted in a combined network structure. As the result of the study, proposed ANN model is successful for the prediction of the compression index, however the predicted recompression index values are not satisfying compared to the compression index.
It is necessary to determine the compressibility parameters of soils such as the compression index (Cc) and the recompression index (Cr) for safe and economic design of civil engineering structures. In order to calculate the consolidation settlement of normally consolidated and over-consolidated saturated fine-grained soils, the compressibility parameters are determined by means of laboratory oedometer test on undisturbed samples based on Terzaghi's consolidation theory. These parameters can be influenced from the quality of samples used in the tests. Although the compressibility parameters must be obtained from careful oedometer test measurements based on good quality undisturbed samples, conventional oedometer test comprises major disadvantages such as costliness, unwieldiness and time-consuming. In addition, the other important disadvantage of the estimation of the compressibility parameters is that the graphical method directly depends on the personal experience. Because of these factors, many researchers have been tried to develop practical and fast solutions.
The presence of relationships between the compressibility parameters and the basic soil properties has been investigated from past to present. Many different correlations based on multiple linear regression analysis have been proposed for determination of compression index (Cc) soil by researchers (Skempton 1944; Terzaghi and Peck 1967; Azzouz et al. 1976; Nagaraj and Srinivasa Murthy 1985; Lav and Ansal 2001; Yoon et al. 2004; Solanki et al. 2008; Dipova and Cangir 2010; Bae and Heo 2011; Akayuli and Ofosu 2013; Lee et al. 2015). These studies are generally focused on relationships between the compression index and physical properties of the soils such as the initial void ratio (e0), natural water content (wn), liquid limit (LL), and plasticity index (PI). Besides, the studies on the recompression index (Cr) seem to be quite limited (Nagaraj and Srinivasa Murthy 1985; Nakase et al. 1988; Isik 2009). The researches show that the physical parameters of soils have a significant effect on compressibility parameters of soil. In literature, the given regression equations to predict the compressibility parameters generally divided into two groups; connected with state variables such as void ratio and water content and connected with intrinsic variables such as liquid limit and plasticity index. It is known that the fully disturbed samples losing their memory involved with soil structure or stress history. Therefore, intrinsic properties are generally obtained by using fully disturbed samples. A number of previous researchers have reported that the compressibility of remolded clay has a specific relationship with the intrinsic variable of the clay (Lee et al. 2015). Due to the compression index of natural clay affected by the sedimentation case induced by deposition environments the evaluation using only intrinsic variables seems to be erroneous.
Artificial neural networks (ANNs) have become a commonly used method due to give a more efficient and accurate results according to regression based statistical equations especially in terms of making estimates in nonlinear systems. Recently, ANNs have been successfully applied to many geotechnical engineering problems such as slope stability, liquefaction, settlement behavior, bearing capacity of shallow and deep foundations (Lee and Lee 1996; Sakellariou and Ferentinou 2005; Kim and Kim 2006; Kuo et al. 2009; Kalinli et al. 2011; Sulewska 2011; Chik et al. 2014). Due to the compression index (Cc) and the recompression index (Cr) are affected by multiple parameters, many researchers have been used the soft computing methods to determine these indexes in a much shorter time (Isik 2009; Park and Lee 2011; Kalantary and Kordnaeij 2012; Namdarvand et al. 2013; Demir 2015).
In this paper, an ANN application was performed to determine the compressibility parameters by using the index parameters of fine grained soils as a variable. Thus, it was aimed to get much better results compared to the obtained by the empirical formulas based on the regression analysis in the previous studies. On the other hand, most of the other studies related to predict the compressibility parameters (compression or recompression index) by using ANN models have checked carefully and it was seen that these studies preferred single output models despite using a number of different input parameters. In the presented study, both the compression index and the recompression index were tried to predict by using a two-output combined ANN model based on natural water content (wn), initial void ratio (e0), liquid limit (LL) and plasticity index (PI). Two or more output models provided time saving and reduced the workload and also successful results have been obtained by these models. A total of 246 laboratory oedometer and index tests results of fine-grained soils obtained by the various geotechnical investigations in Turkey were used in this work. The performance of the proposed ANN model was evaluated based on the correlation coefficient (R) and mean squared error (MSE).
Consolidation settlement
The settlement of structures on the fine-grained soil stratums due to the vertical stress increment is one of the most important problems in geotechnical engineering. The total settlement of a structure comprises three parts: (1) immediate (elastic) compression, (2) primary consolidation, (3) secondary consolidation (creep). Elastic settlement occurs immediately due to applied load without any change in the water content. Primary consolidation is a main component of settlement of fine-grained saturated soils having low permeability, because the excess pore water pressure dissipates with time. The secondary consolidation is creep of soils such as peats and soft organic clays under constant effective stress. The primary and secondary consolidation settlements can be several times greater than the elastic settlement in saturated fine-grained soils.
The consolidation settlement of a normally consolidated soil (sc) due to an increase in vertical stress (Δσv) can be determined as;
$$s_{c} = \frac{{H_{0} }}{{1 + e_{0} }} \cdot C_{c} \cdot \log \left( {\frac{{\sigma_{v0}^{\prime } + \Delta \sigma_{v} }}{{\sigma_{v0}^{\prime } }}} \right)$$
where; Cc is the compression index; H0, e0 and \(\sigma_{{{\text{v}}0}}^{{\prime }}\) are initial thickness, initial void ratio and average vertical effective stress of the soil layer, respectively.
If the final effective stress (\(\sigma_{v0}^{\prime } + \Delta \sigma_{v}\)) is less than the preconsolidation stress (\(\sigma_{p}^{{\prime }}\)) of the over-consolidated soil, then recompression index Cr can be used in place of compression index Cc in Eq. 1. When the final effective stress exceeds the preconsolidation stress, the settlement equation consists of two parts and both Cr and Cc must be used to calculate the consolidation settlement of over-consolidated soil as:
$$s_{c} = \frac{{H_{0} }}{{1 + e_{0} }} \cdot C_{r} \cdot \log \left( {\frac{{\sigma_{p}^{\prime } }}{{\sigma_{v0}^{\prime } }}} \right) + \frac{{H_{0} }}{{1 + e_{0} }} \cdot C_{c} \cdot \log \left( {\frac{{\sigma_{v0}^{\prime } + \Delta \sigma_{v} }}{{\sigma_{p}^{\prime } }}} \right)$$
The compressibility parameters such as compression index and recompression index are usually obtained by using the graphical analysis of compression curve in void ratio—effective stress (e − log σ) plots in Fig. 1. The slope of the straight-line portion of the virgin part of the compression curve on a semi-logarithmic plot is the compression index (Cc) and the slope of the recompression or swelling curve is the recompression index (Cr) as shown in Fig. 1.
Definition of Cc and Cr from compression curve
Database compilation
The database used in this study consist of 246 laboratory oedometer and index tests results of fine-grained soils obtained by the various geotechnical investigations in different locations in Turkey which belongs to the public agencies (State Hydraulic Works, General Directorate of Highways, Municipality) and private geotechnical companies. Soil parameters used in the database are the natural water content, liquid limit, plasticity index, initial void ratio, recompression index and compression index. The index and consolidation properties of soil samples were determined based on ASTM standard test methods. Almost all of the soil samples are classified according to USCS as low and high plasticity clay (CL–CH), and all of them are normally consolidated or lightly over-consolidated (OCR < 2.5). Statistical description of the input and output soil parameters in the database are shown in Table 1 and the values of the natural water content, liquid limit and plasticity index are given in percent.
Table 1 Descriptive statistics of parameters
The database that can be used for the development of regression-based new equations and comparison of the performance of existing regression-based empirical equations, involves a wide range of data as seen on the Table 1. However, the database was only created to determine the compression index and the recompression index from physical parameters of fine grained soils by using ANN in this study.
The compressibility parameters of the soils were supposed to be affected mainly by state parameters such as natural water content and initial void ratio, and intrinsic parameters such as liquid limit and plasticity index. The relationships between the compressibility parameters and index parameters of the soils used in this study are shown in Fig. 2. It is shown that the natural water content and the initial void ratio have more relatively linear correlations with the recompression–compression indexes than liquid limit and plasticity index of fine grained soils. In fully disturbed remoulded soil samples, the compressibility has a strong relationship with the intrinsic variables because the samples ideally lose all memory related to soil structure or stress history (Lee et al. 2015). However, the compressibility parameters of natural soils are particularly affected by the in situ state parameters such as sedimentation, deposition environments, stress history and natural soil conditions. The correlations between Cc and wn or e0 in Fig. 2 have supported the idea.
The relationships between compressibility and index parameters of the samples; a natural water content (wn) and Cr or Cc, b liquid limit (LL) and Cr or Cc, c plasticity index (PI) and Cr or Cc, d void ratio (e0) and Cr or Cc
ANNs, created based on the biological neural networks, are calculating or operating systems which consist of large number of interconnected simple processors. Process elements of the ANNs are nonlinear circuits with nth degree named as cell. These circuits are called node too. Every node can have numerous input connections. However, there should be only one connection at their outputs. Output part is calculated depend on a selected mathematical model (Oztemel 2003). On the other hand, ANNs are divided into subsets which include neurons and named as layer. Input layer is a layer, have inputs come from external world to ANN. In this layer, process elements transfer information to the hidden layers as receiving from external world. Hidden layer is the layer where the information comes from the input layer. Incoming information from the input layer are processed in the hidden layer and forwarded to the output layer. The number of hidden layers can be changed according to the network structure. The increase in the number of neurons in the hidden layer boosts the complexity and calculation time. Nevertheless, this structure also enables the use of ANN in solving more complex problems. Output layer is the layer that produces outputs that correspond to the data from the input layer of the network by processing information from the hidden layer. The outputs generated in this layer are sent to the external world. Figure 3 shows a sample network.
A sample structure of ANN
The network is produced by the interconnection of the layers. There are three type of network in ANN. In feed-forward networks, the processor elements are decomposed into layers and flow of the information moves only one direction from the input layer to the output layer in these networks (Sagiroglu et al. 2003). In the ANNs connected in cascade, cells only receive information from the cells in the previous layer (MATLAB 2009). ANN with back propagation is widely used because of being useful and safe. The most important features of this type of ANN are being eligible for estimation, classification and to be useful in contains nonlinear structural models (Demuth et al. 2007). Also both feed forward and back propagation network structures can be described.
Basically learning methods in the ANN are divided into three groups. These are supervised learning which the training data is used for ANN's training, unsupervised learning which is the set of weights of the connection of the mathematical relationship between the data without using any training kit and last one is reinforced learning which is a close method to supervised learning (Oz et al. 2002; MATLAB 2002). ANN model structure, network type and learning method used for the study are specified in the relevant section.
Proposed artificial neural network model
In the ANN models, the available database is generally divided into three subsets: training, validation and testing sets. In this study, 70 % of the 246 samples (172 randomly selected data) for training, 15 % of the total data (37 randomly selected data) for validation and also 15 % of the database (37 randomly selected data) for testing were used to predict the compressibility parameters.
In order to evaluate the performance of the proposed ANN model, the correlation coefficient (R) and mean squared error (MSE) were used as statistical measures for comparison of the measured and predicted values. The correlation coefficient (R) and mean squared error (MSE) are given in Eqs. (3)–(4).
$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {C_{i,m} - \overline{{C_{i,m} }} } \right)\left( {C_{i,p} - \overline{{C_{i,p} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {C_{i,m} - \overline{{C_{i,m} }} } \right)^{2} \times \mathop \sum \nolimits_{i = 1}^{n} \left( {C_{i,p} - \overline{{C_{i,p} }} } \right)^{2} } }}$$
$$MSE = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {C_{i,m} - C_{i,p} } \right)^{2} }}{n}$$
where C i,m and C i,p are the measured and predicted output values; \(\overline{C_{i,m}}\) and \(\overline{C_{i,p}}\) are the averages of the measured and predicted output values, respectively. n is the number of sample.
The multilayer perceptron neural networks consist of three layers: input layer, hidden layer and output layer. Four basic soil parameters such as natural water content, liquid limit, plasticity index and initial void ratio were used as input parameters for the ANN model. The output layer consists of two neurons which are compression index and recompression index. In this model, ANN model using one hidden layer was preferred. A series of trial-and-error with different number of neuron between 8 and 40 were tried to find the optimum number of neurons in the hidden layer. At the end of these processes, MSE values for different number of neurons were obtained for the training and testing sets as shown in Fig. 4. The optimal architecture of the ANN model was determined based on the minimum mean square error and maximum correlation coefficient. The best performance was obtained from the ANN model with 20 neurons in the hidden layer. Therefore, the 20 neurons in the hidden layer can be considered as optimum value for the ANN model.
The optimization of the number of neurons in the hidden layer
The feed-forward with back-propagation algorithm which is the most preferred algorithm (Rumelhart et al. 1986) in neural networks was used during the training stage. Standard Levenberg–Marquardt training function used as a learning algorithm in the developed ANN model. Additionally, a number of multilayer networks with different transfer functions for hidden and output layers were tried to predict the compressibility parameters. The most appropriate results for the network model were obtained from the sigmoid transfer function in the hidden layer and the linear transfer function in the output layer. The selected architecture of the ANN model used to predict the recompression and compression indexes of soil is shown in Fig. 5.
The architecture of the ANN model used for estimating Cc and Cr
An error histogram can be examined for obtaining contrary data points at the ANN performance. Error histogram indicates that significant errors made on which estimated data and thus a neural network model in higher accuracy designing by purging incorrect data. Figure 6 shows that the error histogram of the obtained simulation results while there were 20 neurons in the hidden layer. The blue bars, the green bars and the red bars represent the training data, the validation data and the test data respectively at the error histogram. Considering the error histogram, the majority of the errors between the measured value and the predicted value are seen on between −0.04 and 0.04. The predicted and measured compression index and recompression index values for both training and test data have been shown in Fig. 7. It is seen that there are minor errors in the compression index data while the majority errors are in the recompression index data considering the differences between the measured and predicted values in the training and testing data.
Error histogram
Simulation results; a training results of the Cc values for the proposed ANN model, b test results of the Cc values for the proposed ANN model, c training results of the Cr values for the proposed ANN model, d test results of the Cr values for the proposed ANN model
Figure 8 shows the relationship between measured and predicted values obtained through the training and testing process. The calculated coefficients of determination (R2) for the compression index are 0.8926 and 0.8973 for training and testing stage, respectively. These results show that a quite close relationship between the measured values and the predicted values by ANN model. However, the coefficients of determination (R2) for the recompression index were calculated as 0.6071 and 0.3600 for training and testing, respectively. It is seen that the proposed ANN model obtained well correlation for the compression index compared with the recompression index.
Comparison between the predicted and measured compression index (a) and recompression index (b)
Discussions and conclusions
In this study, a neural network simulation practice has been made to predict the compression index and recompression index based on the geotechnical characteristics of different borehole data collected from Turkey. ANN is a powerful tool in predicting the consolidation parameters and more accurate results than the conventional methods are obtained. The previous studies based on this issue were generally focused on the predicting only compression index or recompression index by ANN. In this study, both the compression index and the recompression index are tried to predict on the combined ANN model structure. In the proposed ANN model, the input parameters are the soil properties such as the initial void ratio, the liquid limit, the natural water content and the plasticity index. The proposed model of the ANN results compared with the experimental values and the predicted compression index values were found close to the experimental values. However, the proposed ANN model did not show the same success for the recompression index data. This can be explained with the poor relationships between the recompression index and the physical properties in this study. The successful recompression index predictions with same input parameters should be difficult for the other data sets in similar ANN models. Nevertheless, the predicted compression index values using proposed ANN model are compatible with the measured compression index values as seen in this research.
Akayuli CFA, Ofosu B (2013) Empirical model for estimating compression index from physical properties of weathered birimian phyllites. Electron J Geotech Eng 18:6135–6144
Azzouz AS, Krizek RJ, Corotis RB (1976) Regression analysis of soil compressibility. Soils Found 16(2):19–29
Bae W, Heo TY (2011) Prediction of compression index using regression analysis of transformed variables method. Mar Georesour Geotechnol 29(1):76–94
Chik Z, Aljanabi QA, Kasa A, Taha MR (2014) Tenfold cross validation artificial neural network modeling of the settlement behavior of a stone column under a highway embankment. Arab J Geosci 7(11):4877–4887
Demir A (2015) New computational network models for better predictions of the soil compression index. Acta Geotech Slov 12(1):59–69
Demuth H, Beale M, Hagan M (2007) Neural network toolbox user's guide for use with matlab. Mathworks Inc, Natick
Dipova N, Cangir B (2010) Lagün kökenli kil-silt zeminde sıkışabilirlik özelliklerinin regresyon ve yapay sinir ağları yöntemleri ile belirlenmesi. İMO Teknik Dergi 21(3):5069–5086 (in Turkish)
Isik SN (2009) Estimation of swell index of fine grained soils using regression equations and artificial neural networks. Sci Res Essays 4(10):1047–1056
Kalantary F, Kordnaeij A (2012) Prediction of compression index using artificial neural network. Sci Res Essays 7(31):2835–2848
Kalinli A, Acar MC, Gunduz Z (2011) New approaches to determine the ultimate bearing capacity of shallow foundations based on artificial neural networks and ant colony optimization. Eng Geol 117(1–2):29–38
Kim YS, Kim BT (2006) Use of artificial neural networks in the prediction of liquefaction resistance of sands. J Geotech Geoenviron Eng 132(11):1502–1504
Kuo YL, Jaksa MB, Lyamin AV, Kaggwa WS (2009) ANN-based model for predicting the bearing capacity of strip footing on multi-layered cohesive soil. Comput Geotech 36(3):503–516
Lav MA, Ansal MA (2001) Regression analysis of soil compressibility. Turk J Environ Sci 25:101–109
Lee I, Lee J (1996) Prediction of pile bearing capacity using artificial neural networks. Comput Geotech 18(3):189–200
Lee C, Hong SJ, Kim D, Lee W (2015) Assessment of compression index of Busan and Incheon clays with sedimentation state. Mar Georesour Geotechnol 33(1):23–32
MATLAB® (2002) Documentation neural network toolbox help version 6.5, release 13. MathWorks Inc, Natick
MATLAB® (2009) Documentation neural network toolbox help, Levenberg–Marquardt algorithm, release 2009. MathWorks Inc, Natick
Nagaraj TS, Srinivasa Murthy BR (1985) Prediction of the preconsolidation pressure and recompression index of soils. Geotech Test J 8(4):199–202
Nakase A, Kamei T, Kusakabe O (1988) Constitute parameters estimated by plasticity index. J Geotech Eng 114(7):844–858
Namdarvand F, Jafarnejadi A, Sayyad G (2013) Estimation of soil compression coefficient using artificial neural network and multiple regressions. Int Res J Appl Basic Sci 4(10):3232–3236
Oz C, Köker R, Cakar S (2002) Yapay sinir ağları ile karakter tabanlı plaka tanıma. Elektrik-Elektronik-Bilgisayar Mühendisliği Sempozyumu (ELECO), Bursa (in Turkish)
Oztemel E (2003) Yapay sinir ağları. Papatya Yayıncılık (in Turkish)
Park HI, Lee SR (2011) Evaluation of the compression index of soils using an artificial neural network. Comput Geotech 38(4):472–481
Rumelhart DE, Hinton GE, Williams RJ (1986) Learning internal representation by error propagation. In: Rumelhart DE, McClelland JL (eds) Parallel distributed processing vol 1, no 8. MIT Press, Cambridge
Sagiroglu S, Besdok E, Erler M (2003) Mühendislikte yapay zeka uygulamaları-I. Ufuk Kitap Kırtasiye Yayıncılık (in Turkish)
Sakellariou MG, Ferentinou M (2005) A study of slope stability prediction using neural networks. Geotech Geol Eng 24(3):419–445
Skempton AW (1944) Notes on the compressibility of clays. Q J Geol Soc Lond 100(1–4):119–135
Solanki CH, Desai MD, Desai JA (2008) Statistical analysis of index and consolidation properties of alluvial deposits and new correlations. Int J Appl Eng Res 3(5):681–688
Sulewska MJ (2011) Applying artificial neural networks for analysis of geotechnical problems. Comput Assist Mech Eng Sci 18:231–241
Terzaghi K, Peck RB (1967) Soil mechanics in engineering practice, 2nd edn. Wiley, New York
Yoon GL, Kim BT, Jeon SS (2004) Empirical correlations of compression index for marine clay from regression analysis. Can Geotech J 41:1213–1221
TFK and UD were deal with the data collection and the theory of the issue. MY and OO were also performed the ANN model for the research topic. All authors read and approved the final manuscript.
Department of Geophysical Engineering, Engineering Faculty, Sakarya University, Serdivan, Sakarya, Turkey
T. Fikret Kurnaz
Department of Civil Engineering, Engineering Faculty, Dumlupinar University, Kutahya, Turkey
Ugur Dagdeviren
Department of Electrical and Electronics Engineering, Engineering Faculty, Sakarya University, Serdivan, Sakarya, Turkey
Murat Yildiz & Ozhan Ozkan
Murat Yildiz
Ozhan Ozkan
Correspondence to T. Fikret Kurnaz.
Kurnaz, T.F., Dagdeviren, U., Yildiz, M. et al. Prediction of compressibility parameters of the soils using artificial neural network. SpringerPlus 5, 1801 (2016). https://doi.org/10.1186/s40064-016-3494-5
Compressibility
Compression index
Recompression index | CommonCrawl |
Food Science and Biotechnology
Korean Society of Food Science and Technology (KOSFOST)
Agriculture, Fishery and Food > Science of Food and Crops
Agriculture, Fishery and Food > Food Science
The Food Science and Biotechnology (Food Sci. Biotechnol.; FSB) was launched in 1992 as the Food Biotechnology and changed to the present name in 1998. It is an international peer-reviewed journal published monthly by the Korean Society of Food Science and Technology (KoSFoST). The FSB journal covers; Food chemistry/food component analysis Food microbiology and biotechnology Food processing and engineering Food hygiene and toxicology Biological activity and nutrition in foods Sensory and consumer science Consumer perception and sensory evaluation on processed foods are accepted only when they are relevant to the laboratory research work. As a general rule, manuscripts dealing with analysis and efficacy of extracts from natural resources prior to the processing or without any related food processing may not be considered within the scope of the journal. The FSB journal does not deal with only local interest and a lack of significant scientific merit. The main scope of our journal is seeking for human health and wellness through constructive works and new findings in food science and biotechnology field.
http://www.fsnb.or.kr/submission/ KSCI KCI SCIE
Advanced Glycation Endproduct-induced Diabetic Complications
Lee, Hyun-Sun;Hong, Chung-Oui;Lee, Kwang-Won 1131
PDF KSCI
Diabetic complications are a leading cause of blindness, renal failure, and nerve damage. Additionally, diabetes-accelerated atherosclerosis leads to increased risk of myocardial infarction, stroke, and limb amputation. At the present time, 4 main molecular mechanisms have been implicated in hyperglyceamia-mediated vascular damage. In particular, advanced glycation endproducts (AGE), which are formed by complex, heterogeneous, sugar-derived protein modifications, have been implicated as a major pathogenic process for diabetic complications. Recently, AGE inhibitors such as aminoguanidin, ALT-946, and pyridoxamine have been reported. Such an integrating paradigm provides a new conceptual framework for future research on diabetes complications and on discovering drugs to prevent the progression of AGE-induced maladies.
Role of Water in Bread Staling: A Review
Choi, Young-Jin;Ahn, Soon-Cheol;Choi, Hyun-Shik;Hwang, Duck-Ki;Kim, Byung-Yong;Baik, Moo-Yeol 1139
Bread is an essential food consumed worldwide. Bread rapidly loses its desirable texture and flavor qualities associated with freshness through a process known as staling. The shelf life of bread is limited by this staling leading to economical losses in the range of one billion dollars per year. There are a number of mechanisms thought to be related to the staling process, such as water migration and redistribution, starch retrogradation, and gluten transformation. In this review, roles of water and water migration on bread staling are summarized and discussed.
$PPAR_{\gamma}$ Ligand-binding Activity of Fragrin A Isolated from Mace (the Aril of Myristica fragrans Houtt.)
Lee, Jae-Young;Kim, Ba-Reum;Oh, Hyun-In;Shen, Lingai;Kim, Naeung-Bae;Hwang, Jae-Kwan 1146
Peroxisome proliferator-activated receptor-gamma ($PPAR_{\gamma}$), a member of the nuclear receptor of ligand-activated transcription factors, plays a key role in lipid and glucose metabolism or adipocytes differentiation. A lignan compound was isolated from mace (the aril of Myristica fragrans Houtt.) as a $PPAR_{\gamma}$ ligand, which was identified as fragrin A or 2-(4-allyl-2,6-dimethoxyphenoxy)-1-(4-hydroxy-3-methoxyphenyl)-propane. To ascertain whether fragrin A has $PPAR_{\gamma}$ ligand-binding activity, it was performed that GAL-4/$PPAR_{\gamma}$ transactivation assay. $PPAR_{\gamma}$ ligand-binding activity of fragrin A increased 4.7, 6.6, and 7.3-fold at 3, 5, and $10{\mu}M$, respectively, when compared with a vehicle control. Fragrin A also enhanced adipocytes differentiation and increased the expression of $PPAR_{\gamma}$ target genes such as adipocytes fatty acid-binding protein (aP2), lipoprotein lipase (LPL), and phosphoenol pyruvate carboxykinase (PEPCK). Furthermore, it significantly increased the expression level of glucose transporter 4 (GLUT4). These results indicate that fragrin A can be developed as a $PPAR_{\gamma}$ agonist for the improvement of insulin resistance associated with type 2 diabetes.
A Mixture of Curcumin, Vitamin C, and E Prolongs the Antioxidant Effect to Beyond That of Each Component Alone in Vivo
Jeon, Hee-Young;Kim, Jeong-Kee;Lee, Ji-Eun;Shin, Hyun-Jung;Lee, Sang-Jun 1151
This study aimed to investigate the alterations in plasma antioxidant activity after the consumption of a single oral dose of curcumin, vitamin C, and E administered individually or in combination to (i) assess possible synergies or antagonism between the antioxidants and (ii) determine the optimal composition of the antioxidant mixture such that the duration of action is prolonged to beyond that of individual antioxidants. Each antioxidant was administered to male Sprague-Dawley rats, and blood samples were drawn at different time points up to 180 min to measure the plasma total antioxidant capacity (TAC). Five antioxidant compositions (M1-M5) were evaluated to assess the possible synergies or antagonisms among them and to determine the optimal composition of the antioxidant mixture. Blood samples were collected up to 360 min post-consumption. A single oral dose of individual antioxidants significantly increased the TAC values; however, the time to reach the peak TAC value varied. Among the 5 antioxidant compositions, M2 exhibited the highest and most prolonged antioxidant effect in plasma; this was greater than the proportional sum of the effects of the individual antioxidants in the composition. This result indicates a synergistic interaction among antioxidants in the optimal composition M2.
Antioxidant Activities of Different Parts of Synurus deltoids Nakai Extracts in Vitro
Jung, Mee-Jung;Heo, Seong-Il;Wang, Myeong-Hyeon 1156
The antioxidant activity of hot water extracts of various parts, the leaf, stem, and root of Synurus deltoides was evaluated by various antioxidant assays, including total phenolic content, 1,1-diphenyl-2-picrylhydrazyl (DPPH) radical scavenging, hydroxyl radical (${\cdot}OH$) scavenging, superoxide dismutase (SOD), and xanthine oxidase (XOI) activities. The various antioxidant activities were compared with the standard antioxidants such as L-ascorbic acid, $\alpha$-tocopherol, and butylated hydroxyanisole (BHA). Among the different plant parts, stem has been found to possess the highest activity in all tested model systems, the activity decreased in the order stems>roots>leaves. These results indicate that stem extract could be used as potential source of natural antioxidant.
Isolation of Alcohol-tolerant Amylolytic Saccharomyces cerevisiae and Its Application to Alcohol Fermentation
Jung, He-Kyoung;Park, Chi-Duck;Bae, Dong-Ho;Hong, Joo-Heon 1160
An novel amylolytic yeast, Saccharomyces cerevisiae HA 27, isolated from nuruk, displayed resistance against high sugar (50% glucose) and alcohol (15%). Maximal production of amylolytic enzyme by S. cerevisiae HA 27 was achieved on 9 days of cultivation at the optimal temperature $20^{\circ}C$ and pH 6.0. The activity of amylolytic enzyme produced by S. cerevisiae HA 27 was stable, even at $70^{\circ}C$, and over a broad pH range (4.0-11.0). Also, the amylolytic enzyme of S. cerevisiae HA 27 showed optimal activity in pH 5.0 at $50^{\circ}C$. S. cerevisiae HA 27 exhibited 6.2%(v/v) alcohol fermentation ability using starch as a carbon source.
Inhibitory Effects of Flavonoids Isolated from Leaves of Petasites japonicus on $\beta$-Secretase (BACE1)
Song, Kyung-Sik;Choi, Sun-Ha;Hur, Jong-Moon;Park, Hyo-Jun;Yang, Eun-Ju;MookJung, In-Hee;Yi, Jung-Hyun;Jun, Mi-Ra 1165
The deposition of the amyloid $\beta}$ ($A{\beta}$)-peptide following proteolytic processing of amyloid precursor protein (APP) by $\beta$-secretase (BACE1) and $\gamma$-secretase is critical feature in the progress of Alzheimer's disease (AD). Consequently, BACE1, a key enzyme in the production of $A{\beta}$, is a prime target for therapeutic intervention in AD. In the course of searching for BACE1 inhibitors from natural sources, the ethyl acetate fraction of Petasites japonicus showed potent inhibitory activity. Two BACE1 inhibitors quercetin (QC) and kaempferol 3-O-(6"-acetyl)-$\beta$-glucopyranoside (KAG) were isolated from P. japonicus by activity-guided purification. QC, in particular, non-competitively attenuated BACE1 activity with $IC_{50}$ value of $2.1{\times}10^{-6}\;M$ and $K_i$ value of $3.7{\times}10^{-6}\;M$. Both compounds exhibited less inhibition of $\alpha$-secreatase (TACE) and other serine proteases including chymotrypsin, trypsin, and elastase, suggesting that they ere relatively specific and selective inhibitors to BACE1. Furthermore, both compounds significantly reduced the extracellular $A{\beta}$ secretion in $APP_{695}$-transfected B103 cells.
Genotyping Based on Polymerase Chain Reaction of Enterobacter sakazakii Isolates from Powdered Infant Foods
Choi, Suk-Ho;Choi, Jae-Won;Lee, Seung-Bae 1171
This study was undertaken to classify Enterobacter sakazakii isolates from 13 powdered infant formula products, 25 powdered weaning diet products, and 33 weaning diet ingredients on polymerse chain reaction (PCR) methods. The numbers of the isolates from 1 powdered infant formula product, 7 powdered weaning diet products, and 6 weaning diet ingredients were 1, 14, and 8, respectively. The contaminated ingredients were 1 rice powder, 2 millet powders, 2 vegetable powders, and 1 fruit and vegetable premix. PCR with the primer of repetitive extragenic palindromic element (REP-PCR) and random amplification of polymorphic DNA(RAPD) were effective in discriminating among the isolates, but tRNA-PCR and PCR with the primer of l6S-23S internal transcribed spacer (ITS-PCR) were not. Some of E. sakazakii isolates from vegetable powders, fruit and vegetable premix, and millets powders were classified into the clonal groups based on the DNA patterns in the REP-PCR and RAPD analysis. A close genetic relationship among the isolates from some of the powdered weaning diet products and the rice powder was also detected in the cluster analysis based on the DNA patterns in RAPD.
Hepatoprotective Effects of Potato Peptide against D-Galactosamine-induced Liver Injury in Rats
Ohba, Kiyoshi;Han, Kyu-Ho;Liyanage, Ruvini;Nirei, Megumi;Hashimoto, Naoto;Shimada, Ken-ichiro;Sekikawa, Mitsuo;Sasaki, Keiko;Lee, Chi-Ho;Fukushima, Michihiro 1178
The effect of some peptides on hepatoprotection and cecal fermentation against D-galactosamine (GalN)-treated rats was studied. In acute hepatic injury tests, serum alanine aminotransferase (ALT), aspartate aminotranferase (AST), and lactic dehydrogenase (LDH) activities were remarkably increased after injection of GalN. However, potato and soybean peptides significantly decreased GalN-induced alterations of serum ALT and AST activities. Hepatic thiobarbituric acid-reactive substance (TBARS) concentration in GalN-treated groups fed potato and soybean peptides was significantly lower than that in GalN-treated control group. Hepatic glutathione level in the GalN-treated group fed potato peptide was significantly higher than that in GalN-treated control group. Furthermore, cecal Lactobacillus level in GalN-treated groups fed potato and soybean peptides was significantly higher than that in GalN-treated control group, and cecal short-chain fatty acid concentrations in GalN-treated group fed potato peptide were significantly higher than in GalN-treated control group. These results indicate that potato peptide may improve the cecal fermentation and prevent the GalN-induced liver damage in rats.
Immunostimulating and Anticancer Activities of Hot-water Extracts from Acanthopanax senticosus and Glycyrrhiza uralensis
Hwang, Jong-Hyun;Suh, Hyung-Joo;Yu, Kwang-Won 1185
When 10 kinds of herbal medicines were fractionated into hexane, MeOH, cold-water, and hot-water extracts, hot-water extracts from Acanthopanax senticosus (AS), Glycyrrhiza uralensis (GU), Cichorium intybus (CI), and Polygonatum odoratum (PO) showed the potent intestinal immune system modulating activity (1.72-, 1.62-, 1.60-, and 1.53-fold of control at $100{\mu}g/mL$, respectively). Especially, hot-water extracts from AS (215% compared with the control) and GU (187%) also had macrophages stimulating activity and mitogenic activity of splenocytes (7.1- and 6.5-fold) at $100{\mu}g/mL$. In addition, the effects of hot-water extracts from herbal medicines on anticancer activities were studied in mice. Hot-water extracts from AS and GU enhanced cytotoxicity of natural killer cell against cancer cell, Yac-1 (37 and 34% cytotoxicity) at E/T ratio 100:1, and colon 26-M3.1 cancer cell lines had significantly inhibited (82.1 and 75.2%) in experimental lung metastasis. These results suggest that hot-water extracts from A. senticosus and G. uralensis can be used as biological response modifiers to stimulate immune system and inhibit tumor.
Functional Characterizations of Extruded White Ginseng Extracts
Norajit, Krittika;Ryu, Gi-Hyung 1191
The antibacterial and antioxidant potentials of extruded ginseng extract (EGE) with 60% ethanol and methanol were investigated. The inhibitory activity of the EGE in Gram-positive bacteria was significantly higher than in Gram-negative bacteria. Higher antibacterial activity was observed with methanol ginseng extract when moisture content and barrel temperature were 20% and $115^{\circ}C$, respectively, that diameter of inhibition zone at 1,500 mg/mL was $15.40{\pm}0.13\;mm$ for Bacillus subtilis and $9.31{\pm}0.05\;mm$ for Salmonella typhimurium. The amount of total phenolics was highest in extruded ginseng at 20% moisture content and $115^{\circ}C$ barrel temperature. Especially, a positive correlation was observed between the total phenolic content and antioxidant activity of the extracts. In the 2,2-diphenyl-1-picryhydrazyl radical (DPPH) system, all tested extract of extruded ginseng at 20% moisture content exhibited very strong antioxidant properties when compared to red ginseng with percent scavenging effect of 23-35% at 20mg/mL. In conclusion, it can be said that the extracts of extruded ginseng could be used as natural antimicrobial and antioxidant agents in the food preservation.
Anti-platelet Activity of Tissue-cultured Mountain Ginseng Adventitious Roots in Human Whole Blood
Jeon, Won-Kyung;Yoo, Bo-Kyung;Kim, Yeong-Eun;Park, Sun-Ok;Hahn, Eun-Joo;Paek, Kee-Yoeup;Ko, Byoung-Seob 1197
Present study investigated the effects of the 70% ethanol extracts of tissue-cultured mountain ginseng (TCMG), Korean red ginseng (KRG), and Panax ginseng (PG) on agonist-induced platelet aggregation and activation in human whole blood. The $IC_{50}$ values for TCMG, KRG, and PG were 1.159, 3.695, and 4.978mg/mL for collagen-induced aggregation, 0.820, 2.030, and 4.743mg/mL for arachidonic acid-induced aggregation, and 1.070, 2.617, and 2.954 mg/mL for ADP-induced aggregation, respectively. Also, this study assessed the effects of the most active extract, TCMG, on markers of platelet activation by determining receptor expression on platelet membranes in healthy subjects, including expression of GPIIb/IIIa-like (PAC-1) and P-selectin (CD62), by flow cytometry. A significant decrease in PAC-l expression (p=0.018) was observed in the presence of TCMG. These results show that TCMG has potent anti-platelet activity.
Preparation of a Silk Fibroin Film Containing Catechin and Its Application
Ku, Kuoung-Ju;Hong, Yun-Hee;Song, Kyung-Bin 1203
Silk fibroin (SF) film containing catechin was prepared and the antimicrobial activity as well as physical property of the film was examined. Tensile strength of the SF film decreased with increasing concentration of catechin, and water vapor permeability of the film decreased. The film's antimicrobial activity against Escherichia coli O157:H7 increased with increasing catechin concentration. Sausage samples were inoculated with E. coli 0157:H7 and Listeria monocytogenes, and the sausage packaged with the SF film containing catechin had a decrease in the populations of E. coli O157:H7 and L. monocytogenes by 0.83 and 0.85 log CFU/g after 12 days of storage, respectively, compared to the control. In addition, the sausage had a better quality than the control regarding lipid oxidation. Our results indicate that sausages can be packed with the SF film containing catechin to extend shelf life.
Effect of Zinc-enriched Yeast FF-10 Strain on the Alcoholic Hepatotoxicity in Alcohol Feeding Rats
Cha, Jae-Young;Heo, Jin-Sun;Cho, Young-Su 1207
The possible protective effects of highly zinc-containing yeast Saccharomyces cerevisiae, FF-10 strain, isolated from tropical fruit rambutan on acute alcoholic liver injury in rats were evaluated. Zinc concentration in this strain was 30.6mg%. The activities of serum alanine aminotransferase (ALT), aspartate aminotransferase (AST), and $\gamma$-glutamyl transpeptidase ($\gamma$-GTP) were highly increased when alcohol was treated, relative to the normal rats. Also, a highly significant increase in the blood alcohol and acetaldehyde levels by alcohol treatment was observed. Administration of FF-10 strain markedly prevented alcohol-induced elevation of the activities of serum ALT, AST, and $\gamma$-GTP, and the levels of blood alcohol and acetaldehyde, and these reduced levels reached to that of normal rats. As compared with alcohol treated control rats, the FF-10 strain supplementation showed highly decreased the triglyceride concentration in serum. Alcohol treatment induced the marked accumulation of small lipid droplets, hepatocytes necrosis, and inflammation, but FF-10 strain administration attenuated to alcohol-induced accumulation of small lipid droplets and hepatocyte necrosis in the liver. Therefore, the current finding suggests that zinc-enriched yeast FF-10 strain isolated from tropical fruit rambutan may have protective effect against alcohol-induced hepatotoxicity.
Phenolic Compounds from the Fruit Body of Phellinus linteus Increase Alkaline Phosphatase (ALP) Activity of Human Osteoblast-like Cells
Lyu, Ha-Na;Lee, Dae-Young;Kim, Dong-Hyun;Yoo, Jong-Su;Lee, Min-Kyung;Kim, In-Ho;Baek, Nam-In 1214
Secondary metabolites from the fruit body of Phellinus linteus were evaluated for their proliferative effect on human osteoblast-like cells. 3-[4,5-Dimethylthiazole-2-y1]-2,5-diphenyl-tetraxolium bromide (MTT) assay and alkaline phosphatase (ALP) activity assay were used to assess the effect those isolates on the human osteoblast-like cell line (Saos-2). Activity-guided fractionation led to the isolation of ALP-activating phenolic compounds through the extraction of P. linteus, solvent partitioning, and repeated silica gel and octadecyl silica gel (ODS) column chromatographic separations. From the result of spectroscopic data including nuclear magnetic resonance (NMR), mass spectrometry (MS), and infrared spectroscopy (IR), the chemical structures of the compounds were determined as 4-(4-hydroxyphenyl)-3-buten-2-one(1), 2-(3',4'-dihydroxyphenyl)-1,3-benzodioxole-5-aldehyde (2), 4-(3,4-dihydroxyphenyl)-3-buten-2-one (3), 3,4-dihydroxybenzaldehyde (4), and protocatechuic acid methyl ester (5), respectively. This study reports the first isolation of compounds 1-3 and 5 from P. linteus. In addition, all phenolic compounds stimulated proliferation of the osteoblast-like cells and increased their ALP activity in a dose-dependent manner ($10^{-8}$ to $10^{-1}\;mg/mL$). The present data demonstrate that phenolic compounds in P. linteus stimulated mineralization in bone formation caused by osteoporosis. The bone-formation effect of P. linteus seems to be mediated, at least partly, by the stimulating effect of the phenolic compounds on the growth of osteoblasts.
Use of the Cellulase Gene as a Selection Marker of Food-grade Integration System in Lactic Acid Bacteria
Lee, Jung-Min;Jeong, Do-Won;Lee, Jong-Hoon;Chung, Dae-Kyun;Lee, Hyong-Joo 1221
The application of the cellulase gene (celA) as a selection marker of food-grade integration system was investigated in Lactobacillus (Lb.) casei, Lactococcus lactis, and Leuconostoc (Leu.) mesenteroides. The 6.0-kb vector pOC13 containing celA from Clostridium thermocellum with an integrase gene and a phage attachment site originating from bacteriophage A2 was used for site-specific recombination into chromosomal DNA of lactic acid bacteria (LAB). pOC13 was also equipped with a broad host range plus replication origin from the lactococcal plasmid pWV01, and a controllable promoter of nisA ($P_{nisA}$) for the production of foreign proteins. pOC13 was integrated successfully into Lb. casei EM116, and pOC13 integrants were easily detectable by the formation of halo zone on plates containing cellulose. Recombinant Lb. casei EM 116::pOC13 maintained these traits in the absence of selection pressure during 100 generations. pOC13 was integrated into the chromosome of L. lactis and Leu. mesenteroides, and celA acted as an efficient selection marker. These results show that celA can be used as a food-grade selection marker, and that the new integrative vector could be used for the production of foreign proteins in LAB.
A Vinegar-processed Ginseng Radix (Ginsam) Ameliorates Hyperglycemia and Dyslipidemia in C57BL/KsJ db/db Mice
Han, Eun-Jung;Park, Keum-Ju;Ko, Sung-Kwon;Chung, Sung-Hyun 1228
Having idea to develop more effective anti-diabetic agent from ginseng root, we comprehensively assessed the anti-diabetic activity and mechanisms of ginsam in C57BL/KsJ db/db mice. The db/db mice were divided into 4 groups; diabetic control (DC), ginsam at a dose of 300 or 500 mg/kg (GS300 or GS500) and metformin at a dose of 300 mg/kg (MT300). Ginsam was orally administered for 8 weeks. GS500 reduced the blood glucose concentration and significantly decreased an insulin resistance index. In addition, GS500 reduced the plasma non-esterified fatty acid, triglyceride, and increased high density lipoprotein-cholesterol as well as decreased the hepatic cholesterol and triglyceride. More interestingly, ginsam increased the plasma adiponectin level by 17% compared to diabetic control group. Microarray, quantitative-polymerase chain reaction and enzyme activity results showed that gene and protein expressions associated with glycolysis, gluconeogenesis, and fatty acid oxidation were changed to the way of reducing hepatic glucose production, insulin resistance and enhancing fatty acid $\beta$-oxidation. Ginsam also increased the phosphorylation of AMP-activated protein kinase and glucose transporter expressions in the liver and skeletal muscle, respectively. These changes in gene expression were considered to be the mechanism by which the ginsam exerted the anti-diabetic and anti-dyslipidemic activities in C57BL/KsJ db/db mice.
Antioxidant and Antiproliferative Activities of Methanolic Extracts from Thirty Korean Medicinal Plants
Choi, Young-Min;Gu, Ja-Bi;Kim, Myung-Hee;Lee, Jun-Soo 1235
To study the health promoting effects of medicinal plants, 30 medicinal plants commonly available in Korea have been evaluated for their antioxidant compounds and antioxidant and antiproliferative activities. Total polyphenolics and flavonoids in the methanolic extracts were measured by spectrophotometric methods and 1,1-diphenyl-2-picrylhydrazyl (DPPH) and 2,2-azino-bis-(3-ethylbenzothiazoline-6-sulfonic acid (ABTS) radical scavenging activities and chelating effects have been determined for antioxidant activities. Moreover, the effects of medicinal plants on cell proliferation of intestinal (Caco-2) and pituitary (GH3) tumor cells were investigated using thiazolyl blue terazolium bromide (MIT) assay. The methanolic extracts of Pueraria thunbergiana and Artemisiae asiatria contained the highest total polyphenolic and flavonoid contents, respectively. P. thunbergiana exhibited the highest antioxidant activities. A. asiatria showed the strongest antiproliferative activity against Caco-2 and Ponciruc trifoliata Rafin and Lophathrum gracile Bronghiart exhibited the highest activities against GH3. Although there was positive correlation between ABTS radical scavenging activity and polyphenolic contents ($R^2=8189$), no relationship was found between antiproliferative and antioxidant activities.
Simultaneous Detection of Food-borne Pathogenic Bacteria in Ready-to-eat Kimbab Using Multiplex PCR Method
Cho, Kye-Man;Kambiranda, Devaiah M;Kim, Seong-Weon;Math, Renukaradhya K;Lim, Woo-Jin;Hong, Su-Young;Yun, Han-Dae 1240
Kimbab is the most popular ready-to-eat (RTE) food in Korea. A rapid detection method based on multiplex PCR technique was developed for detection of major food-borne pathogens like Salmonella spp., Shigella spp., Bacillus cereus, Listeria monocytongenes, and Staphylococcus aureus. Specific bands were obtained as 108 bp (Sau, S. aureus), 284 bp (Sal, S. enterica, S. enteritids, and S. typhmurium), 404 bp (Lmo, L. monocytogenes), 475 bp (Bce, B. cereus), and 600 bp (Shi, S. flexineri and S. sonnei). Visible cell numbers varied from 4.14-5.03, 3.61-4.47, and 4.10-5.11 log CFU/g in randomly collected June, July, and August samples, respectively. Among the 30 kimbab samples obtained 83.3% samples were contaminated and 16.7% samples were free from contamination. The highest rate of contamination was with S. aureus (56.7%) followed by B. cereus (43.3%), Salmonella spp. (36.7%), Shigella spp. (13.3%), and L. monocytogenes (6.7%). The identification of the pathogenic species could be faster using one polymerase chain reaction (PCR) and the ability to test for food-borne pathogenic species in kimbab will save time and increase the ability to assure its quality.
Isolation and Identification of Taxol, an Anticancer Drug from Phyllosticta melochiae Yates, an Endophytic Fungus of Melochia corchorifolia L.
Kumaran, Rangarajulu Senthil;Muthumary, Johnpaul;Hur, Byung-Ki 1246
Phyllosticta melochiae, an endophytic fungus isolated from the healthy leaves of Melochia corchorifolia, was screened for the production of an anticancer drug, taxol on modified liquid medium and potato dextrose broth medium in culture for the first time. The presence of taxol was confirmed by spectroscopic and chromatographic methods of analysis. The amount of taxol produced by this fungus was quantified by high performance liquid chromatography. The maximum amount of fungal taxol production was recorded as $274{\mu}g/L$. The production rate was increased to $5.5{\times}1,000$ fold than that found in the culture broth of earlier reported fungus, Taxomyces andreanae. The fungal taxol extracted also showed a strong cytotoxic activity in the in vitro culture of tested human cancer cells by apoptotic assay. The results designate that the fungal endophyte, P. melochiae is an excellent candidate for an alternate source of taxol supply and can serve as a potential species for genetic engineering to enhance the production of taxol to a higher level.
Enhancement of Immunomodulatory and Anticancer Activity of Fucoidan by Nano Encapsulation
Qadir, Syed Abdul;Kwon, Min-Chul;Han, Jae-Gun;Ha, Ji-Hye;Jin, Ling;Jeong, Hyang-Suk;Kim, Jin-Chul;You, Sang-Guan;Lee, Hyeon-Yong 1254
The aim of the present study was to prepare nanosample of fucoidan using lecithin as encapsulated material and to investigate the anticancer and immunomodulatory activity of nanoparticle in vitro. The nanoparticles have been characterized by dynamic light scattering (DLS) and transmission electron microscopy (TEM). Confocal microscopy confirmed the internalization of the fucoidan conjugates into the immune cells. The uptake of nanoparticles was confirmed with confocal microscopy demonstrating their localization in the cells. The anticancer activity was increased over 5-10% in different cancer cells of fucoidan nanoparticle as compare with fucoidan. The human B and T cells growth and the secretion of interleukin-6 and tumor necrosis factor-a from B cell were also improved by fucoidan nanoparticle because of the rapid absorption of nanoparticle into the cells as compare to fucoidan. At 0.6 mg/mL concentrations, the fucoidan nanoparticle showed better activity than 1.0 mg/mL concentration in T cell growth because the cells reached their saturation capacity. When the fucoidan was encapsulated in lecithin, its anticancer as well as its immunomodulatory activity proved to be superior from that of itself in pure form.
Conjugated Linoleic Acid (CLA) Supplementation for 8 Weeks Reduces Body Weight in Healthy Overweight/Obese Korean Subjects
Park, Eun-Ju;Kim, Jung-Mi;Kim, Kee-Tae;Paik, Hyun-Dong 1261
In the present study, a randomized, double-blind, placebo-controlled trial to determine the effect of conjugated linoleic acid (CLA) supplementation (50:50 ratio of cis-9, trans-11 and trans-10, cis-12 isomers) for 8 weeks on body composition and biochemical parameters in healthy overweight/obese (body mass index, BMI${\geq}23\;kg/m^2$) Korean subjects was performed, Thirty participants (3 males and 27 females) were randomized to receive placebo (2.4 g olive oil/day) or 2.4g/day CLA (mixture containing 36.9% of cis-9, trans-11 and 37.9% of trans-10, cis-12). Eight weeks of CLA supplementation significantly decreased body weight by -0.75kg, BMI by $-0.27\;kg/m^2$, and hip circumference by -1.11 cm. The reduction of body weight was ascribed to the reduction of body fat mass (-0.59 kg) and lean body mass (-0.18 kg), although these changes were not significant. No significant differences in serum lipid profiles, liver function enzyme activities, and protein concentration were observed in either the CLA or placebo groups. These results indicate that short tenn supplementation (8 weeks) with CLA (2.4 g/day) may decrease body weight in Korean overweight/obese subjects.
Anti-tumor and Anti-inflammatory Activity of the Methanol Extracts from Adlay Bran
Lee, Ming-Yi;Tsai, Shu-Hsien;Kuo, Yueh-Hsiung;Chiang, Wenchang 1265
Adlay bran is a waste product previously thought to have no commercial value, Its methanolic extract was fractionated using n-hexane (ABM-Hex), ethyl acetate (ABM-EtOAc), 1-butanol (ABM-BuOH), and water (ABM-$H_2O$). The ABM-EtOAc fraction exhibited a strongest inhibition against growth of human lung cancer cell A549 and human colorectal carcinoma cells HT-29 and COLO 205. Inhibition of cell cycle progression at $G_0/G_1$ transition, increase of cells at the sub-$G_1$ phase, and DNA ladders were observed in cells treated with ABM-EtOAc. The ABM-BuOH fraction showed the strongest inhibition of proinflammatory cytokines tumor necrosis factor (TNF)-$\alpha$ and interlukin (IL)-$1{\beta}$ in stimulated RAW 264.7 macrophages. Further, ABM-EtOAc and ABM-BuOH inhibited cyclooxygenase (COX)-2 expression in A549 and HT-29 carcinoma cells, while COX-l expression was not affected. These results reveal that both ABM-EtOAc and ABM-BuOH may aid the prevention of cancers and the applications in cancer chemotherapy.
Evaluation of the Atopic Dermatitis-mitigating and Anti-inflammatory Effects of Kyung Hee Allergic Disease Herbal Formula (KAHF)
Koh, Duck-Jae;Kim, Yang-Hee;Kim, Deog-Gon;Lee, Jin-Yong;Lee, Kyung-Tae 1272
The purpose of this study was to investigate the effects of Kyung Hee Allergic Disease Herbal Formula (KAHF) on atopic dermatitis (AD) and its mode of action. Our clinical study showed KAHF reduced Severity Scoring of Atopic Dermatitis (SCORAD) indexes and subjective symptom scores. In parallel, the decreased levels of interferon (IFN)-$\gamma$ and interleukin (IL)-5 in serum, which contributed to its AD-mitigating effect was observed. To reveal the underlying mechanisms of KAHF in AD, its anti-inflammatory effect on lipopolysaccharide (LPS)-induced responses in RAW 264.7 cells was examined. KAHF was found to significantly inhibit the productions of nitric oxide (NO), prostaglandin $E_2$ ($PGE_2$), and IL-$1{\beta}$ in LPS-stimulated RAW 264.7 macrophages. Consistently, KAHF potently inhibited protein and mRNA expressions of inducible nitric oxide synthase (iNOS) and cyclooxygenase-2 (COX-2). Furthermore, KAHF inhibited LPS-induced activation of nuclear factor (NF)-$\kappa}B$. Taken together, our data suggest that KAHF has a beneficial effect on several eicosanoid-related skin inflammations, such as atopic dermatitis.
Differences in Manufacturing Process and Quality between Cheonggukjang for Use in the Raw and Cheonggukjang for Stew
Seo, Byoung-Joo;Kim, Young-Ho;Kim, Jong-Kyu 1279
When cheonggukjgang was manufactured using a Bacillus subtilis CH10-1 starter culture, a short-term fermentation for 14-18 hr appeared to be the optimal for the raw cheonggukjang to avoid the formation of a bitter taste and to contain a high concentration of free sugars, whereas a long-term fermentation for more than 4 days was the optimal for the cheonggukjang for stew in order to contain a high concentration of free amino and organic acids, which are responsible for sweet, savory, and bitter tastes present in stewed cheonggukjang, During activation of murine splenic T cells with phytohemagglutinin (PHA), the presence of either poly-$\gamma$-glutamic acid ($\gamma$-PGA) or partially hydrolyzed $\gamma$-PGA resulted in reduction in the level of interferon-$\gamma$ production and enhancement in the level of interleukin-5 production, possibly due to suppression of Th1 activity and augmentation of Th2 activity. Taken together these results indicate that the raw cheonggukjang and the cheonggukjang for stew are different in their quality and taste as well as immunomodulating activity.
Modulatory Activity of CpG Oligonucleotides from Bifidobacterium longum on Immune Cells
Choi, Young-Ok;Seo, Jeong-Min;Ji, Geun-Eog 1285
The purpose of this study was to characterize and investigate the immune activity of CpG oligodeoxynucleotides (ODNs) from Bifidobacterium longum. Bacterial CpG motifs have attracted considerable interests because of their immunomodulatory activities. Genomic DNA from B. longum was prepared and amplified for 4 different 180-188-mer double-stranded ODNs (BLODN1-BLODN4). When immune cells (RAW 264.7 murine macrophages and JAWS II dendritic cells) with these ODNs were treated, BLODN4 induced the highest immune activity. To assess the effectiveness of the CpG sequences within BLODN4, single-stranded 40-mer ODNs containing CpG sequences (sBLODN4-1, sBLODN4-2) were synthesized. sBLODN4-1 induced higher level of cytokines such as interleukin (IL)-12p40 and tumor necrosis factor (TNF)-$\alpha$ by macrophage and IL-6 and TNF-$\alpha$ by dendritic cells than did sBLODN4-2. The results suggest that CpG ODNs-enriched components of B. longum might be useful as an immunomodulatory functional food ingredient.
Functional Properties of Enzymatically Modified Egg Yolk Powder Produced by Phospholipase $A_2$ Treatment
Kim, Mi-Ra;Shim, Jae-Yong;Park, Ki-Hwan;Imm, Jee-Young 1289
Fresh egg yolk (EY) was enzymatically modified using phospholipase $A_2$ ($PLA_2$) to produce an enzymatically modified-egg yolk powder (EM-EYP). The EM-EYP offered significantly higher emulsifying activity, emulsion stability, protein solubility, and mayonnaise stability than the control EYP. By employing $PLA_2$ in the enzymatic modification process, structural changes occurred in the phospholipids and lipoproteins of the yolk, and cleavage of apo-high density lipoprotein (HDL) components (Mw 105 kDa) was detected by sodium dodecyl sulfate-polyaerylamide gel electrophoresis (SDS-PAGE). Based on its functional properties, EM-EYP has great potential as a replacement for fresh EY in the production of processed food products such as mayonnaise.
Guggulsterone Suppresses the Activation of NF-${\kappa}B$ and Expression of COX-2 Induced by Toll-like Receptor 2, 3, and 4 Agonists
Ahn, Sang-Il;Youn, Hyung-Sun 1294
Toll-like receptors (TLRs) induce innate immune responses recognizing conserved microbial structural molecules. All TLR signaling pathways culminate in the activation of nuclear factor-${\kappa}B$ (NF-${\kappa}B$). The activation of NF-${\kappa}B$ leads to the induction of inflammatory gene products such as cyclooxygenase-2 (COX-2). Guggul has been used for centuries to treat a variety of diseases. Guggulstreone, one of the active ingredients in guggul, has been used to treat many chronic diseases. However, the mechanism as to how guggulsterone mediate the health effects is largely unknown. Here, we report biochemical evidence that guggulsterone inhibits the NF-${\kappa}B$ activation and COX-2 expression induced by TLR2, TLR3, and TLR4 agonists. Guggulsterone also inhibits the NF-${\kappa}B$ activation induced by downstream signaling components of TLRs, myeloid differential factor 88 (MyD88), $I{\kappa}B$ kinase ${\beta}$ ($IKK{\beta}$), and p65. These results imply that guggulsterone can modulate the immune responses regulated by TLR signaling pathways.
Antioxidant Activity of Fractions from 70% Methanolic Extract of Sonchus oleraceus L.
Yin, Jie;Heo, Seong-Il;Jung, Mee-Jung;Wang, Myeong-Hyeon 1299
The potential antioxidant activities of different fractions from a 70% methanolic (MeOH) extract of Sonchus oleraceus were assayed in vitro. All of the fractions exception of n-hexane showed a strong antioxidant activity, especially the ethyl acetate (EtOAc) fraction, which showed the highest 1,1-diphenyl-2-picrylhydrazyl (DPPH) free radical scavenging activity ($IC_{50}=19.25{\mu}g/mL$). The results of hydroxyl radical scavenging activity and a reducing power assay showed concentration dependence, the EtOAc fraction demonstrating a better result than the other fractions at the same concentration in the studies. Additionally, the fractions' total phenolic (TP) contents was measured, phenolic compounds such as tannic acid, p-coumatric acid, quercetin, epicathchin, and kaempferol being detected by high performance liquid chromatography (HPLC). Meanwhile, a regression analysis revealed a moderate-to-high correlation coefficient between the antiradical activity and the TP contents, suggesting that fractions obtained from the 70% MeOH extract of S. oleraceus are of potential use as sources of antioxidant material.
Regulation of Caspase Activity During Apoptosis Induced by Baicalein in HL60 Human Leukemia Cell Line
Byun, Boo-Hyeong;Kim, Bu-Yeo 1305
Baicalein, one of the major flavonoid in Scutellaria baicalensis, has been known for its effects on proliferation and apoptosis of many tumor cell lines. Most biological effects of baicalein are thought to be from its antioxidant and prooxidant activities. In this report, baicalein was found to induce apoptosis in HL60 human promyelocytic leukemia cell line. Baicalein treatment induced DNA fragmentation and typical morphological features of apoptosis. To elucidate the mechanism of baicalein-induced apoptosis, the activities of the members of caspase family were measured. Interestingly caspase 2, 3, and 6 were significantly activated whereas caspase 1, 8, and 9 were not activated, suggesting selective involvement of specific caspases. Further, treatment with caspase inhibitors also supports the involvement of caspase 2 in apoptosis process. Although it has been reported that baicalein can induce apoptosis through many caspase pathways, the present study indicates that caspase 2 not caspase 9 pathway may be the important step in apoptosis on HL60 cell line.
Influence of pH on the Antioxidant Activity of Melanoidins Formed from Different Model Systems of Sugar/Lysine Enantiomers
Kim, Ji-Sang;Lee, Young-Soon 1310
This study was to investigate the influence of pH on the antioxidant activity of melanoidins formed from glucose (Glc) and fructose (Fru) with lysine enantiomers in the Maillard reaction. Melanoidins formed from D-isomers were found to be effective antioxidants in different in vitro assays with regard to the ferrous ion chelating activity, 1, l-diphenyl-2-picryl-hydrazil (DPPH) radical scavenging activities, ferric reducing/antioxidant power (FRAP), and 2,2'-azinobis(3-ethylbenothiazoline-6-sulfonic acid) diammonium salt (ABTS) radical scavenging activity. In particular, the chelating activity of these melanoidins at a pH of 7.0 was greater than those with pH of 4.0 and 10.0. The chelating activity and DPPH radical scavenging activity of the melanoidins formed from the Glc systems were higher than those of the melanoidins formed from the Fru systems. However, the FRAP and ABTS radical scavenging activity of these melanoidins were not different according to pH level, with exceptions being the Fru systems.
Prediction of Listeria monocytogenes Growth Kinetics in Sausages Formulated with Antimicrobials as a Function of Temperature and Concentrations
Bang, Woo-Suk;Chung, Hyun-Jung;Jin, Sung-Sik;Ding, Tian;Hwang, In-Gyun;Woo, Gun-Jo;Ha, Sang-Do;Bahk, Gyung-Jin;Oh, Deog-Hwan 1316
This study was conducted to develop a model to describe the effect of antimicrobials [potassium sorbate (PS), potassium lactate (PL), and combined PL and sodium diacetate (SDA, PLSDA)] on the growth parameters of Listeria monocytogenes such as specific growth rate (SGR) and lag phase periods (LT) in air-dried raw sausages as a function of storage temperature (4, 10, 16, and $25^{\circ}C$). Results showed that the SGR of L monocytogenes was dependent on the storage temperature and level of antimicrobials used. The most effective treatment was the 4% PLSDA, followed by the 2% PLSDA and 4% PL and 0.2% PS exhibited the least antimicrobial effect. Increased growth rates were observed with increasing storage temperatures from 4 to $25^{\circ}C$. The growth data were fitted with a Gompertz equation to determine the SGR and LT of the L. monocytogenes. Six polynomial models were developed for the SGR and LT to evaluate the effect of PS (0.1, 0.2%) and PL (2,4%) alone and PLSDA (2, 4%) on the growth kinetics of L. monocytogenes from 4 to $25^{\circ}C$.
Characterization of Lactobacilli with Tannase Activity Isolated from Kimchi
Kwon, Tae-Yeon;Shim, Sang-Min;Lee, Jong-Hoon 1322
Tannase catalyzes the hydrolysis of gallic acid esters and hydrolysable tannins. Twenty-two Lactobacillus strains with tannase activity were isolated from 7 types of kimchi. A polymerase chain reaction-based assay targeting the recA gene assigned all isolates to either Lactobacillus plantarum or Lactobacillus pentosus. The tannase activities of isolates measured in whole cells and cell-free extracts varied even within each species. The activities of the isolates varied with the assay method, but both methods indicated that isolate LT7 (identified as L. pentosus) showed the highest activity. The results of thin layer chromatography and high performance liquid chromatography, respectively, showed that tannic acid and gallic acid degraded to pyrogallol in resting L. pentosus LT7 cells. Therefore, the putative biochemical pathway for the degradation of tannic acid by L. pentosus implies that tannic acid is hydrolyzed to gallic acid and glucose, with the formed gallic acid being decarboxylated to pyrogallol. This study revealed the possible production of pyrogallol from tannic acid by the resting cell reaction with L. pentosus LT7.
Inhibitory Effect of Ethyl Acetate Extract of White Peach Pericarp on Adipogenesis of 3T3-L1 Preadipocyte Cells
Park, Hong-Gyu;Kim, Jin-Moon;Kim, Jung-Mogg;Chung, Won-Yoon;Yoo, Yun-Jung;Cha, Jeong-Heon 1327
In order to determine whether peach contains compounds to regulate adipocyte differentiation, extracts of flesh/pericarp of yellow/white peach were prepared in water, ethyl acetate (EtOAc), or n-butanol solvent and determined for effects on adipocyte differentiation in C3H10T1/2 or 3T3-L1 cells. Interestingly, none of peach extracts has statistically significant stimulatory effect on the adipocyte differentiation in C3H10T1/2. Furthermore, the presence of EtOAc extract of white peach pericarp (WPP) was found to inhibit lipid accumulation in 3T3-L1 cells both by microscopic examination of Oil Red O-stained lipid droplets and by spectrophotometric quantification of extracted stain, indicating a significant inhibitory effect on adipocyte differentiation. The inhibition of lipid accumulation was accompanied by a significant decrease in the expression levels of adipocyte molecular markers-peroxisome proliferator-activated receptor $\gamma$, CAAT enhancer binding protein $\alpha$, and fatty acid-binding protein. Thus, this study determined that WPP EtOAc extract contains the inhibitory compound(s) on adipogenesis.
In Vitro and Cellular Antioxidant Activity of a Water Extract of Saururus chinensis
Kim, Gyo-Nam;Lee, Jung-Sook;Jang, Hae-Dong 1332
The water extract of Saururus chinensis was investigated for oxygen radical absorbance capacity (ORAC), reducing capacity, metal chelating activity, and intracellular antioxidant activity using HepG2 cell. When 2,2'-azobis(2-amidinopropane) dihydrochloride (AAPH) was used for the generation of peroxyl radicals in vitro, S. chinensis extract (SC-E) showed the strong and concentration-dependent scavenging activity through donating protons which could be explained by its reducing property. When hydroxyl radicals were generated in vitro through the addition of $Cu^{2+}$ and $H_2O_2$, SC-E demonstrated the antioxidant activity depending on its concentration. In HepG2 cell model, most of intracellular oxidative stress generated by AAPH was efficiently removed by SC-E. However, when $Cu^{2+}$ without $H_2O_2$ was used as an oxidant in the intracellular assay, SC-E partially reduced the oxidative stress caused by $Cu^{2+}$ in cellular antioxidant activity assay system. These results indicate that SC-E could be utilized for the development of functional foods as antioxidant resource in the near future.
Distribution of Indicator Organisms and Incidence of Pathogenic Bacteria in Raw Beef Used for Korean Beef Jerky
Kim, Hyoun-Wook;Kim, Hye-Jung;Kim, Cheon-Jei;Paik, Hyun-Dong 1337
The objective of this study was to evaluate the microbial safety of raw beef used to produce Korean beef jerky, The raw beef samples harbored large populations of microorganisms. In particular, psychrophilic bacteria were found to be most numerous ($9.2{\times}10^3-1.0{\times}10^5\;CFU/g$) in the samples. Mesophilic bacteria and anaerobic bacteria were present in average numbers ($10^3-10^5\;CFU/g$). Spore-forming bacteria and coliforms were not detected below detection limit. Yeast and molds were detected at $2.2{\times}10^1-7.8{\times}10^2\;CFU/g$ in the raw beef. Ten samples of raw beef were analyzed for the presence of pathogenic bacteria. Bacillus cereus was isolated from sample B, G, and H. The B. cereus isolates from raw beef samples were identified with 99.8% agreement according to the API CHB 50 kit.
Antioxidant Effects of Elsholtzia splendens Extract on DMBA-induced Oxidative Stress in Mice
Choi, Eun-Jeong;Kim, Tae-Hee;Kim, Gun-Hee 1341
The present study was conducted to investigate the effects of flowers ethanol extract of Elsholtzia splendens (ESE) on the antioxidant defence system in mice with 7,12-dimethylbenz(a)anthracene (DMBA)-induced oxidative stress. The ESE was pre-administered orally to 2 groups of mice at 10 and 50mg/kg body weight (BW) for 5 weeks. Subsequently, mice with pretreatment of ESE received DMBA intragastrically at a dose of 34 mg/kg BW twice a week for 2 weeks. In DMBA alone group, biomarkers of oxidative stress (TBARS value, carbonyl content, and serum 8-OH-dG) were significantly increased. Also, the antioxidant enzymes were down-regulated. ESE significantly restored the TBARS value and carbonyl content at both doses, while a decrease in the elevated serum 8-OH-dG content was observed only at the higher dose. The DMBA-induced decreases in catalase and superoxide dismutase (SOD) activities were restored to nearly control levels by ESE. Glutathione peroxidase (GSH-px) and glutathione reductase (GR) activities, as well as the reduced glutathione (GSH)/oxidized GSH (GSSG) ratio, were significantly affected by ESE at the higher dose. These results suggest that ESE possesses antioxidant activity, which plays a protective role against DMBA-induced oxidative stress.
Antibacterial Effect of $TiO_2$ Photocatalytic Reactor against Food-borne Pathogens
Kim, Byung-Hoon;Cho, Dong-Lyun;Ohk, Seung-Ho;Ko, Yeong-Mu 1345
Titanium dioxide ($TiO_2$) shows antibacterial effects when exposed to near ultra violet (UV) light. In this study, $TiO_2$ photocatalytic continuous reactor was designed and applied to food-borne pathogens such as Vibrio parahaemolyticus ATCC 17802, Salmonella choleraesuis ATCC 14028, and Listeria monocytogenes ATCC 15313. $TiO_2$ films were prepared by conventional sol-gel dip-coating method using titanium tetra iso-propoxide (TTIP). The antibacterial activity of photocatalytic reactor with various flow rates and UV-A illumination time showed effective bactericidal activity. As the UV-A illumination time increased, survival rates of those bacteria decreased. After 60 min of UV-A illumination, the survival rates of V. parahaemolyticus and S. choleraesuis were less than 0.1%. However, that of L. monocytogenes was about 5% at that time point. These results present an effective way to exclude pathogenic bacteria from aqueous foods.
Maillard Browning Reaction of D-Psicose as Affected by Reaction Factors
Baek, Seung-Hee;Kwon, So-Young;Lee, Hyeon-Gyu;Baek, Hyung-Hee 1349
This study examined the effects of temperature, D-psicose concentration, pH, and various amino acids on the Maillard browning reaction of D-psicose and glycine mixture and compared browning color intensity with those of other sugars, such as sucrose, D-glucose, D-fructose, and D-tagatose. When D-psicose (0.1 M) and glycine (0.1 M) mixture was heated at $70-100^{\circ}C$ for 5 hr, the absorbance at 420 nm increased with increasing reaction temperature and time. The Hunter a, b values, and color difference (${\Delta}E$) increased with increasing D-psicose concentration and pH within the range of pH 3-7 except at pH 6, while the L value decreased. The rate of Maillard browning reaction was in order of D-tagatose>D-psicose $\fallingdotseq$ D-fructose>D-glucose>sucrose. The browning color intensity of the D-psicose-basic and non-polar amino acids mixtures was higher than that of the D-psicose-acidic amino acids.
Application of Bootstrap Method to Primary Model of Microbial Food Quality Change
Lee, Dong-Sun;Park, Jin-Pyo 1352
Bootstrap method, a computer-intensive statistical technique to estimate the distribution of a statistic was applied to deal with uncertainty and variability of the experimental data in stochastic prediction modeling of microbial growth on a chill-stored food. Three different bootstrapping methods for the curve-fitting to the microbial count data were compared in determining the parameters of Baranyi and Roberts growth model: nonlinear regression to static version function with resampling residuals onto all the experimental microbial count data; static version regression onto mean counts at sampling times; dynamic version fitting of differential equations onto the bootstrapped mean counts. All the methods outputted almost same mean values of the parameters with difference in their distribution. Parameter search according to the dynamic form of differential equations resulted in the largest distribution of the model parameters but produced the confidence interval of the predicted microbial count close to those of nonlinear regression of static equation.
Antibacterial Activity of Panduratin A and Isopanduratin A Isolated from Kaempferia pandurata Roxb. against Acne-causing Microorganisms
Song, Min-Soo;Shim, Jae-Seok;Gwon, Song-Hui;Lee, Chan-Woo;Kim, Han-Sung;Hwang, Jae-Kwan 1357
Propionibacterium acnes is the predominant organism in sebaceous regions of the skin and is thought to play an important role in the pathogenesis of inflamed lesions. Antibacterial compounds against P. acnes were isolated from the ethanol extract of Kaempferia pandurata Roxb. and identified as panduratin A and isopanduratin A. Minimum inhibitory concentration (MIC) and minimum bactericidal concentration (MBC) of panduratin A for P. acnes were 2 and $4{\mu}g/mL$, respectively, while those of isopanduratin A were 4 and $8{\mu}g/mL$, respectively. The time-dependent killing effect showed that panduratin A and isopanduratin A completely inhibited the growth of P. acnes at 4 and $8{\mu}g/mL$ in 48 hr, respectively. Panduratin A and isopanduratin A demonstrated high antibacterial activities not only against P. acnes but also other skin microorganisms. The results suggest that panduratin A and isopanduratin A could be employed as natural antibacterial agents to inhibit the growth of acne and skin disease causing microorganisms.
Inhibitory Effects of Naringenin, Kaempherol, and Apigenin on Cholesterol Biosynthesis in HepG2 and MCF-7 Cells
Kim, Kee-Tae;Yeo, Eun-Ju;Moon, Sun-Hee;Cho, Ssang-Goo;Han, Ye-Sun;Nah, Seung-Yeol;Paik, Hyun-Dong 1361
The inhibitory effects of naringenin, kaempherol, and apigenin on the production of cholesterol in HepG2 KCLB 88065 and MCF-7 KCLB 30022 cells were evaluated. In this study, quercetin was used as a reference reagent. After incubation for 3 days, fat-soluble contents of both cell types were extracted by using the Folch method and the cholesterol contents in both cultured cells were determined by high performance liquid chromatography. The concentration of cholesterol in untreated each tissue cells was $12.2{\pm}0.11$ and $8.83{\pm}0.12\;mg/g$ of lipid, respectively. The total concentration of each flavonoid was adjusted to 0, 35, or $350{\mu}M$ in the culture broth. As the results, the addition of 2% methanol and dimethyl sulfoxide (DMSO) to the media (control for flavonoid solvents) did not significantly affect cell growth; however, DMSO caused an increase in the production of cholesterol. Each flavonoid inhibited the production of cholesterol in both HepG2 and MCF-7 cells at the concentration of $35{\mu}M$ above. In addition, the inhibitory effect of kaempherol on the production of cholesterol in these cells was greater than the other flavonoids tested and HepG2 cells are more sensitive to flavonoids than MCF-7. From the results, the inhibitory effects of flavonoids on cholesterol production are different depending on the cell type.
Effects of Food Components on the Antibacterial Activity of Chitosan against Escherichia coli
Hong, Yi Fan;Moon, Eun-Pyo;Park, Yun-Hee 1365
The antibacterial activity of chitosan against Escherichia coli was investigated in the presence of NaCl, sucrose, and ethanol to assess the potential use of chitosan as a biopreservative in food products containing these components. The inhibitory activity of chitosan decreased slightly upon the addition of NaCl and sucrose, respectively to culture broth containing 100 ppm of chitosan (Mw 3,000), while the addition of ethanol enhanced the inhibitory activity of chitosan on growing cells. The addition of these components to non-growing cells prior to chitosan treatment demonstrated that NaCl protected the cells from the inhibitory activity of chitosan, while sucrose had no effect. Ethanol addition to non-growing cells increased cell death by chitosan treatment. Finally, binding of fluorescein isothiocyanate (FITC)-labeled chitosan to E. coli was measured in the presence of the food components. The FITC-labeled chitosan binding to cells decreased upon NaCl addition, was not affected by sucrose, and increased following treatment with ethanol.
Enterobacteriaceae and Related Microorganisms Isolated from Rump of Raw Beefs
Kwon, Eun-Ah;Kim, Myung-Hee 1368
In this study, 50 rump samples of raw beef obtained from local Korean supermarkets were analyzed to survey microbial distributions. As results, mesophilic microorganisms ranged from $(1.4{\pm}0.01){\times}10^2$ to $(1.6{\pm}0.05){\times}10^5\;CFU/g$, and total coliforms ranged from 0 to $(1.3{\pm}0.04){\times}10^4\;CFU/g$. Major foodborne pathogens, including Listeria monocytogenes, Escherichia coli O157:H7, and Salmonella spp., were not found among the samples. However, Staphylococcus aureus was isolated with 4% frequency. Other isolated microorganisms included Enterobacter amnigenus (4%), Enterobacter cloacae (24%), E. coli (24%), Listeria innocua (8%), Staphylococcus saprophyticus (56%), Staphylococcus xylosus (10%), and Staphylococcus warneri (8%).
Heterologous Gene Expression of aprE2 Encoding a 29 kDa Fibrinolytic Enzyme from Bacillus subtilis in Bacillus licheniformis ATCC 10716
Kwon, Gun-Hee;Jeong, Woo-Ju;Lee, Ae-Ran;Park, Jae-Yong;Cha, Jae-Ho;Song, Young-Sun;Kim, Jeong-Hwan 1372
The aprE2 gene from Bacillus subtilis CH3-5 was expressed in Bacillus licheniformis ATCC 10716 using a Bacillus-Escherichai coli shuttle vector, pHY300PLK. The fibrinolytic activity of transformant (TF) increased significantly compared to B. licheniformis 10716 control cell. During the 100 hr incubation in Luria-Bertaini broth at $37^{\circ}C$, fibrinolytic activity of B. licheniformis TF increased rapidly at the late growth stage, after 52 hr of incubation, which was confirmed by zymography using a fibrin gel. pHY3-5 was stably maintained in B. licheniformis without tetracycline (Tc) in the media, 60.9% of cells still maintained pHY3-5 after 100 hr of cultivation.
Tachioside, an Antioxidative Phenolic Glycoside from Bamboo Species
Li, Ting;Park, Min-Hee;Kim, Mi-Jeong;Ryu, Bog-Mi;Kim, Myo-Jung;Moon, Gap-Soon 1376
Tachioside (4-hydroxy-3-methoxy-phenyl-1-O-glucoside), a known phenolic glycoside, was isolated from various bamboo species. The 1,1-diphenyl-2-picrylhydrazyl (DPPH) radical scavenging activity and Trolox equivalent antioxidant capacity determined a significant antioxidant activity of tachioside which was comparable to L-ascorbic acid. Each culm and leaf extracts were tested and the culm of Phyllostachys bambusoides appeared to contain the highest amount of tachioside.
Analysis of Ginsenoside Composition of Ginseng Berry and Seed
Ko, Sung-Kwon;Bae, Hye-Min;Cho, Ok-Sun;Im, Byung-Ok;Chung, Sung-Hyun;Lee, Boo-Yong 1379
This study was performed to provide basic information that can be used to differentiate Korean ginseng (Panax ginseng CA. Meyer) berry and seed from American ginseng (Panax quinquefolium L.) seed. Total ginsenoside contents of Korean ginseng berry, Korean ginseng seed, and American ginseng seed were 9.09, 3.30, and 4.06%, respectively. Total ginsenoside content of Korean ginseng berry was about 2.2 to 2.7 times higher than those of Korean ginseng seed and American ginseng seed. Particularly ginsenoside Re content of 4-year cultivated Korean ginseng berry (5.99%) was about 3.6 to 5.4 times higher than that of 4-year cultivated Korean ginseng seed (1.65%) and 4-year cultivated American ginseng seed (1.10%). The contents of total ginsenoside and ginsenoside Re of Korean ginseng berry were about 4.8 and 28 times higher, respectively, than those of 4-year cultivated Korean ginseng root. In general the contents of total ginsenoside and ginsenoside Re of Korean ginseng berry were significantly higher than those of Korean ginseng seed and American ginseng seed.
Quality Characteristics of Colored Soybean Curd Containing Paprika (Capsicum annuum L.)
Jeon, Eun-Raye;Jung, Lan-Hee 1383
This study was conducted to examine the quality characteristics of soybean curd containing red paprika juice (RPJ) and green paprika juice (GPJ). The proximate compositions of RPJ showed higher levels of ash, carbohydrate, and vitamin C than GPJ. The yield of soybean curd was not significantly different with the level of RPJ and GPJ. However there was a significant decrease in the pH and an increase in the acidity with the addition of RPJ and GPJ. The L, a, and b values of soybean curd containing RPJ and the L value of soybean curd containing GPJ were significantly different. The hardness and chewiness of soybean curd containing RPJ and GPJ increased significantly with the level of juice.
Changes in Antioxidant Activity of Rehmannia radix Libosch with Heat Treatment
Woo, Koan-Sik;Hwang, In-Guk;Song, Dae-Sik;Lee, Youn-Ri;Lee, Jun-Soo;Jeong, Heon-Sang 1387
This study evaluated the effects of heat treatment on antioxidant activity of Rehmannia radix Libosch (RRL). RRL was heated at various temperatures ($110-150^{\circ}C$) for various times (1-5 hr), and the total polyphenol, flavonoid content, and antioxidant activity were investigated. With increased heating temperature and exposure time, total content of polyphenol, flavonoid, as well as antioxidant activity increased. The highest total polyphenol and flavonoid contents were 21.65 and 3.56 mg/g, respectively, these values were occurred after heating for 3 hr at $150^{\circ}C$ (RRL was 5.09 and 0.83 mg/g, respectively). The 1,1-diphenyl-2-picrylhydrazyl (DPPH) radical scavenging activity was highest value of 83.46% after heating for 3hr at $150^{\circ}C$. The 2,2-azino-bis-3-ethylbenzothiazoline-6-sulfonic acid (ABTS) cation radical scavenging activity was highest value of 20.43mg ascorbic acid (AA) eq/g after heating for 2 hr at $150^{\circ}C$. There were highly significant differences in the total polyphenol, flavonoid content, and antioxidant activity among heating temperatures and times (p<0.001), with heating temperature having the greater effect.
Characterization of Low Temperature-adapted Leuconostoc citreum HJ-P4 and Its Dextransucrase for the Use of Kimchi Starter
Yim, Chang-Youn;Eom, Hyun-Ju;Jin, Qing;Kim, So-Young;Han, Nam-Soo 1391
Leuconostoc citreum HJ-P4 is a strain isolated for kimchi fermentation with its low temperature-adapted growth feature and its high dextransucrase activity. The detailed characteristics of cell growth and dextran sucrase activities were investigated at various environmental conditions such as temperatures, pHs, salts, and raw ingredients. This strain showed almost 2-fold higher maximal cell concentration ($X_{max}$) than that of the type culture Leuconostoc mesenteroides B-512F at $10^{\circ}C$. The $X_{max}$ of the strain was maximum at pH 7 and the cell growth was inhibited by salts in a dose-dependent mode up to 7%. Addition of pepper (<6%), garlic (<10%), and ginger (<2%) in kimchi gave no inhibition effect on the growth of HJ-P4. Dextransucrase synthesized by this strain retained over 80% of its maximum activity at $10^{\circ}C$ showing a comparable cold-adapted feature to its host microbe. This culture can be used as a starter culture in the industrial kimchi production giving desirable functions and predominance at low temperature. | CommonCrawl |
\begin{document}
\pagenumbering{arabic} \setlength{\headheight}{12pt} \pagestyle{myheadings}
\title[Hypergeometric Functions over $\fp$]{Hypergeometric functions over $\fp$ and relations to elliptic curves and modular forms} \subjclass[2000]{Primary: 11F30; Secondary: 11T24, 11G20, 33C99}
\author{Jenny G. Fuselier} \maketitle
\date{} \maketitle
\begin{abstract} For primes $p\equiv 1 \pmod{12}$, we present an explicit relation between the traces of Frobenius on a family of elliptic curves with $j$-invariant $\frac{1728}{t}$ and values of a particular $_2F_1$-hypergeometric function over $\fp$. Additionally, we determine a formula for traces of Hecke operators $\textnormal{T}_k(p)$ on spaces of cusp forms of weight $k$ and level 1 in terms of the same traces of Frobenius. This leads to formulas for Ramanujan's $\tau$-function in terms of hypergeometric functions. \end{abstract}
\section{Introduction and Statement of Main Results}\label{intro}
Let $p$ be a prime and let $\widehat{\mathbb{F}_{p}^{\times}}$ denote the group of all multiplicative characters on $\fpc$. We extend $\chi\in\ \widehat{\mathbb{F}_{p}^{\times}}$ to all of $\fp$ by setting $\chi(0)=0$. For $A,B\in\fphat$, let $J(A,B)$ denote the usual Jacobi symbol and define
\begin{equation}\label{binom coeff} \binom{A}{B}:=\frac{B(-1)}{p}J(A,\overline{B})=\frac{B(-1)}{p} \sum_{x\in \fp} A(x)\overline{B}(1-x). \end{equation}
\noindent In the 1980s, Greene \cite{Gr87} defined \emph{hypergeometric functions over $\fp$} in the following way:
\begin{defn}[\cite{Gr87} Defn. 3.10]\label{hg} If $n$ is a positive integer, $x\in\fp$, and $A_0,A_1,\dots,A_n,$\\$B_1,B_2,\dots,B_n \in \widehat{\mathbb{F}_{p}^{\times}}$, then define $$ _{n+1}F_{n} \left( \begin{matrix} A_0, & A_1, & \dots, & A_n \\
& B_1, & \dots, & B_n \\ \end{matrix} \bigg{\vert} x \right) := \frac{p}{p-1} \sum_{\chi\in\widehat{\mathbb{F}_{p}^{\times}}} \binom{A_0\chi}{\chi} \binom{A_1\chi}{B_1\chi} \dots \binom{A_n\chi}{B_n\chi} \chi(x).$$ \end{defn}
Greene explored the properties of these functions and showed that they satisfy many transformations analogous to those enjoyed by their classical counterparts. The introduction of these hypergeometric functions over $\fp$ generated interest in finding connections they may have with modular forms and elliptic curves. In recent years, many results have been proved in this direction, and the main results given here are similar in nature.
Throughout, we consider a family of elliptic curves having $j$-invariant $\frac{1728}{t}$. Specifically, for $t\in\fp$, $t\neq0,1 $ we let \begin{equation}\label{defn of E} E_t: y^2=4x^3-\frac{27}{1-t}x - \frac{27}{1-t}. \end{equation} Further, we let $a(t,p)$ denote the trace of the Frobenius endomorphism on $E_t$. In particular, for $t\neq0,1$, we have $$a(t,p)=p+1-\#E_t(\fp),$$ where $\#E_t(\fp)$ counts the number of solutions to $y^2 \equiv 4x^3-\frac{27}{1-t}x - \frac{27}{1-t}$ (mod $p$), including the point at infinity.
Henceforth, we let $p$ be a prime number with $p\equiv 1$ (mod 12). With this in mind, we let $\xi\in \widehat{\mathbb{F}_{p}^{\times}}$ have order 12. Also, we denote by $\varepsilon$ and $\phi$ the trivial and quadratic characters, respectively. In this setting, our first main result explicitly relates the above trace of Frobenius and the values of a hypergeometric function over $\fp$.
\begin{theorem}\label{first main theorem} Suppose $p\equiv 1 \pmod{12}$ is prime and $\xi\in \widehat{\mathbb{F}_{p}^{\times}}$ has order $12$. Then, if $t\in\fp\backslash\{0,1\}$ and notation is as above, we have $$p\,\hg{\xi}{\xi^5}{\varepsilon}{t}= \psi(t) a(t,p),$$ where $\psi(t)= -\phi(2)\xi^{-3}(1-t)$. \end{theorem}
After setting up the necessary preliminaries, we give the proof of Theorem \ref{first main theorem} in Section \ref{proof of theorem 1}. The second main result utilizes the same family of elliptic curves, $E_t$, to obtain a trace formula for Hecke operators on spaces of cusp forms in level $1$.
Let $\Gamma=SL_2(\mathbb{Z})$ and let $M_k$ and $S_k$, respectively, denote the spaces of modular forms and cusp forms of weight $k$ for $\Gamma.$ Further, let $\textnormal{Tr}_k(\Gamma,p)$ denote the trace of the Hecke operator $\textnormal{T}_k(p)$ on $S_k$. Then the following completely describes these traces $\textnormal{Tr}_k(\Gamma,p)$, for a certain class of primes $p$:
\begin{theorem}\label{second main theorem} Suppose $p\equiv 1 \pmod{12}$ is prime. Let $a,b\in\mathbb{Z}$ such that $p=a^2+b^2$ and $a+bi \equiv 1 \,(2+2i)$ in $\mathbb{Z}[i]$. Also, let $c,d\in\mathbb{Z}$ such that $p=c^2-cd+d^2$ and $c+d\omega \equiv 2 \,(3)$ in $\mathbb{Z}[\omega]$, where $\omega=e^{2\pi i/3}$. Then for even $k\geq4$, $$ \textnormal{Tr}_k(\Gamma,p)=-1-\lambda(k,p)-\sum_{t=2}^{p-1} G_k(a(t,p),p),$$ where $$\lambda(k,p)=\frac{1}{2}[G_k(2a,p)+G_k(2b,p)]+\frac{1}{3}[G_k(c+d,p)+G_k(2c-d,p)+G_k(c-2d,p)]$$ and $$G_k(s,p)=\sum_{j=0}^{\frac{k}{2}-1} (-1)^j \binom{k-2-j}{j} p^j s^{k-2j-2}.$$ \end{theorem}
Combining Theorems \ref{first main theorem} and \ref{second main theorem} gives a way of writing the traces $\textnormal{Tr}_k(\Gamma,p)$ in terms of hypergeometric functions. Formulas for Ramanujan's $\tau$-function follow by taking $k=12$ in Theorem \ref{second main theorem}.
Finally, Theorem \ref{second main theorem} gives rise to an inductive formula for the traces $\textnormal{Tr}_k(\Gamma,p)$, in terms of hypergeometric functions. To state it, we utilize the notation for $G_k(s,p)$ and $\lambda(k,p)$ given in Theorem \ref{second main theorem}.
\begin{theorem}\label{recursion} Suppose $p\equiv 1 \pmod{12}$ is prime. Let $k\geq 4$ be even and define $m=\frac{k}{2}-1$. Then \begin{align*} \textnormal{Tr}_{2(m+1)}(\Gamma,p)&=-1-\lambda(2m+2,p)+b_0(p-2)-\sum_{t=2}^{p-1}p^{2m}\phi^m(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}^{2m}\\ &\quad\,-\sum_{i=1}^{m-1}b_i(1+\lambda(2i+2,p))-\sum_{i=1}^{m-1}b_i\textnormal{Tr}_{2i+2}(\Gamma,p), \end{align*} where $$b_i=p^{m-i}\left[\binom{2m}{m-i}-\binom{2m}{m-i-1}\right].$$
\end{theorem}
In Section \ref{history hg and ec}, we recall a few recent results that relate counting points on varieties over $\fp$ to hypergeometric functions and make comparisons with classical hypergeometric functions. In Section \ref{preliminaries}, we introduce necessary preliminaries and give the proof of Theorem \ref{first main theorem} in Section \ref{proof of theorem 1}. In Sections \ref{history hg and mf} and \ref{proof of theorem 2}, we focus on Theorem \ref{second main theorem}, beginning with a history of similar results, and building to a proof of the theorem. This is followed by Section \ref{recursion proof}, in which we give a proof of Theorem \ref{recursion}. We close in Section \ref{tau corollaries} with various corollaries relating Ramanujan's $\tau$-function to hypergeometric functions. Specifically, Corollary \ref{tau corollary 2} expresses $\tau(p)$ explicitly in terms of tenth powers of a $_2F_1$-hypergeometric function.
\section{Recent History: Hypergeometric Functions and Elliptic Curves}\label{history hg and ec}
Relationships between hypergeometric functions over $\fp$ and elliptic curves are perhaps not surprising, as classical hypergeometric series have many known connections to elliptic curves. An important example of these classical series is defined for $a,b,c \in \mathbb{C}$ as $$_2F_1[a,b;c;z]:=\sum_{n=1}^{\infty} \frac{(a)_n(b)_n}{(c)_nn!}z^n,$$ where $(w)_n=w(w+1)(w+2)\cdots (w+n-1)$.
The specialization $_2F_1[\frac{1}{2},\frac{1}{2};1;t]$ is related to the Legendre family of elliptic curves, as it is a constant multiple of an elliptic integral which represents a period of the associated lattice. More recently, Beukers \cite{Be93} gave identifications between periods of families of elliptic curves and values of particular hypergeometric series. For example, he related a period of $y^2=x^3+tx+1$ to the values $_2F_1[\frac{1}{12},\frac{7}{12};\frac{2}{3};-\frac{4}{27}t^3]$ and a period of $y^2=x^3-x-t$ to the values $_2F_1[\frac{1}{12},\frac{5}{12};\frac{1}{2};\frac{27}{4}t^2]$. We give finite field analogues of these results at the close of the next section.
Following Greene's introduction of hypergeometric functions over $\fp$ in the 1980s, results emerged linking their values to counting points on varieties over $\fp$. Let $\phi$ and $\varepsilon$ denote the unique quadratic and trivial characters, respectively, on $\fpc$. Further, define two families of elliptic curves over $\fp$ by \begin{align*} _2E_1(t):y^2=x(x-1)(x-t)\\ _3E_2(t):y^2=(x-1)(x^2+t). \end{align*} Then, for odd primes $p$ and $t\in\fp$, define the traces of Frobenius on the above families by \begin{align*} _2A_1(p,t)&=p+1- \#_2E_1(t)(\fp),\quad t\neq0,1\\ _3A_2(p,t)&=p+1- \#_3E_2(t)(\fp),\quad t\neq0,-1. \end{align*} These families of elliptic curves are closely related to particular hypergeometric functions over $\fp$. For example, $\hg{\phi}{\phi}{\varepsilon}{t}$ arises in the formula for Fourier coefficients of a modular form associated to $_2E_1(t)$ (\cite{Ko92,On98}). Further, Koike and Ono, respectively, gave the following explicit relationships:
\begin{theorem}[(a) Koike \cite{Ko92}, (b) Ono \cite{On98}]\label{koike ono} Let $p$ be an odd prime. Then
$(a)\quad p \, \hg{\phi}{\phi}{\varepsilon}{t}=-\phi(-1) _2A_1(p,t), \quad t\neq0,1$
$(b)\quad p^2 \, _{3}F_{2} \left( \begin{matrix} \phi, & \phi, & \phi \\
& \varepsilon, & \varepsilon \\ \end{matrix} \bigg{\vert} 1+\frac{1}{t} \right) = \phi(-t)(_3A_2(p,t)^2-p), \quad t\neq 0,-1.$ \end{theorem}
\section{Preliminaries on Characters and Hypergeometric Functions}\label{preliminaries}
The proof of Theorem \ref{first main theorem} involves two main steps. First, we derive a formula for $a(t,p)$ in terms of Gauss sums, and then we write the hypergeometric function in terms of Gauss sums. The final proof follows from comparing the two. Before doing that, we fix notation and recall some basic facts regarding Gauss sums.
Throughout, let $p\equiv 1 \pmod{12}$ be prime. If $A\in\fphat$, let $$ G(A)=\sum_{x\in\fp}A(x)\zeta^{x}$$ denote the Gauss sum, with $\zeta=e^{2\pi i/p}$.
Since $\fpc$ is cyclic, let $T$ denote a fixed generator of the character group, i.e. $\langle T \rangle= \widehat{\mathbb{F}_{p}^{\times}}$. With this in mind, we often use the notation $G_m:=G(T^m)$. Recall the following elementary properties of Gauss sums, the proofs of which can be found in Chapter 8 of \cite{IR90}:
\begin{lemma}\label{orthog relation} Let $T$ be a generator for $\widehat{\mathbb{F}_{p}^{\times}}$. Then
$(a) \quad \displaystyle{\sum_{x\in\fp}T^n(x)= \begin{cases} p-1 & \textnormal{if} \,\, T^n=\varepsilon\\ 0 & \textnormal{if} \,\, T^n\neq\varepsilon \end{cases}}$
$(b) \quad \displaystyle{\sum_{n=0}^{p-2}T^n(x)= \begin{cases} p-1 & \textnormal{if} \,\, x=1\\ 0 & \textnormal{if} \,\, x \neq 1. \end{cases}}$
\end{lemma}
The next result calculates the values of two particular Gauss sums, $G(\varepsilon)$ and $G(\phi)$.
\begin{lemma}\label{special Gauss sums} $(a) \quad G(\varepsilon)=G_0=-1$ \\ \hspace*{0.9in}$(b) \quad \displaystyle{G(\phi)=G_\frac{p-1}{2}= \begin{cases} \sqrt{p} & \textnormal{if}\,\, p\equiv 1 \pmod{4}\\ i\sqrt{p} & \textnormal{if}\,\,p\equiv 3 \pmod{4}. \end{cases}}$ \end{lemma}
We now define an additive character
\begin{eqnarray*}\label{theta def} \theta:\fp &\rightarrow\mathbb{C} \\ \theta(\alpha)&=\zeta^{\alpha}. \end{eqnarray*}
Notice that we can write Gauss sums in terms of $\theta$, as we have $G(A)=\sum_{x\in\fp} A(x)\theta(x)$. In addition, the following lemma describing $\theta$ in terms of Gauss sums is straightforward to prove via the orthogonality relations given above:
\begin{lemma}\label{theta equality} For all $\alpha\in\fpc$, $$\theta(\alpha)=\frac{1}{p-1} \sum_{m=0}^{p-2} G_{-m}T^m(\alpha).$$ \end{lemma}
We also require a few properties of hypergeometric functions over $\fp$ that Greene proved in \cite{Gr87}. The first provides a formula for the multiplicative inverse of a Gauss sum.
\begin{lemma}[\cite{Gr87} Eqn. 1.12]\label{greene 112} If $k\in\mathbb{Z}$ and $T^k\neq\varepsilon$, then $$G_kG_{-k}=pT^k(-1).$$ \end{lemma}
The following result was given by Greene as the definition of the hypergeometric function when $n=1$. It provides an alternative to Definition \ref{hg}, and in particular, it allows us to write the $_2F_1$ hypergeometric function as a character sum. \begin{theorem}[\cite{Gr87} Defn. 3.5]\label{greene 35} If $A,B,C \in \widehat{\mathbb{F}_{p}^{\times}}$ and $x \in \fp$, then $$\hg{A}{B}{C}{x} = \varepsilon(x) \frac{BC(-1)}{p} \sum_{y=0}^{p-1} B(y)\overline{B}C(1-y)\overline{A}(1-xy).$$ \end{theorem}
In \cite{Gr87}, Greene presented many transformation identities satisfied by the hypergeometric functions he defined. The theorem below allows for the argument $x\in\fp$ to be replaced by $1-x$.
\begin{theorem}[\cite{Gr87} Theorem 4.4]\label{greene 44} If $A,B,C \in \widehat{\mathbb{F}_{p}^{\times}}$ and $x\in\fp \backslash \{0,1\}$, then $$\hg{A}{B}{C}{x}=A(-1)\hg{A}{B}{AB\overline{C}}{1-x}.$$ \end{theorem}
Next,we recall a classical relationship between Gauss and Jacobi sums, but we write it utilizing Greene's definition for the binomial coefficient, given in \eqref{binom coeff}.
\begin{lemma}\label{greene 29} If $T^{m-n}\neq \varepsilon$, then $$ \binom{T^m}{T^n}=\frac{G_mG_{-n}T^n(-1)}{G_{m-n} \cdot p}.$$ \end{lemma}
The final relation on characters that is necessary for our proof is the \emph{Hasse-Davenport relation.} The most general version of this relation involves an arbitrary additive character, and can be found in \cite{La90}. We require only the case when $\theta$ is taken as the additive character:
\begin{theorem}[Hasse-Davenport Relation \cite{La90}]\label{Hasse Davenport} Let $m$ be a positive integer and let $p$ be a prime so that $p\equiv1 \pmod{m}.$ Let $\theta$ be the additive character on $\mathbb{F}_p$ defined by $\theta(\alpha)=\zeta^{\alpha}$, where $\zeta=e^{2\pi i/p}$. For multiplicative characters $\chi,\psi\in \widehat{\mathbb{F}_{p}^{\times}}$, we have $$\prod_{\chi^m=1}G(\chi\psi)=-G(\psi^m)\psi(m^{-m})\prod_{\chi^m=1}G(\chi).$$ \end{theorem}
\begin{proof} See \cite{La90}, page 61. \end{proof}
The proof of Theorem \ref{first main theorem} requires two special cases of the Hasse-Davenport relation, which are easily verified by taking $m=2$ and $m=3$, respectively.
\begin{corollary}\label{HD2} If $p\equiv 1 \pmod{4}$ and $k\in\mathbb{Z}$, $$G_{-k}G_{-\frac{p-1}{2}-k}=\sqrt{p}\,G_{-2k}T^k(4).$$ \end{corollary}
\begin{corollary}\label{HD3} If $k\in\mathbb{Z}$ and $p$ is a prime with $p\equiv 1 \pmod{3}$ then $$G_kG_{k+\frac{p-1}{3}}G_{k+\frac{2(p-1)}{3}}=p\,T^{-k}(27)T^{\frac{p-1}{3}}(-1)G_{3k}.$$ \end{corollary}
\section{Proof of Theorem \ref{first main theorem}}\label{proof of theorem 1}
We begin by deriving a formula for the trace of Frobenius in terms of Gauss sums. Throughout this section, let $s=\frac{p-1}{12}$ and define $P(x,y)= y^2-4x^3+\frac{27}{1-t}x+ \frac{27}{1-t}$.
Recall from the previous section that $\theta$ is the additive character on $\fp$ given by $\theta(\alpha)=\zeta^{\alpha}$, where $\zeta=e^{2\pi i/p}$. Note that if $(x,y)\in\fp^2$, then $$\sum_{z\in\fp}\theta(zP(x,y))=\begin{cases} p & \textnormal{if} \,P(x,y)=0\\ 0 &\textnormal{if}\, P(x,y)\neq 0. \end{cases}$$ So we have \begin{align*} p\cdot(\#E_t(\fp)-1) &= \sum_{z\in\fp} \sum_{x,y \in\fp} \theta(zP(x,y))\\
&= \sum_{x,y,\in\fp} 1 + \sum_{z\in\fpc}\sum_{x,y\in\fp}\theta(zP(x,y)), \end{align*} after breaking apart the $z=0$ contribution. Then, by separating the sums according to whether $x$ and $y$ are $0$ and applying the additivity of $\theta$, we have \begin{align*} p\cdot(\#E_t(\fp)-1)&= p^2+ \sum_{z\in\fpc}\theta\left(z\frac{27}{1-t}\right)+\sum_{z\in\fpc}\sum_{y\in\fpc} \theta(zy^2)\theta\left(z\frac{27}{1-t}\right)\\
&\hspace*{0.2in} + \sum_{z\in\fpc}\sum_{x\in\fpc}\theta(-4zx^3)\theta\left(zx\frac{27}{1-t}\right)\theta\left(z\frac{27}{1-t}\right)\\
&\hspace*{0.2in}+\sum_{x,y,z\in\fpc}\theta(zP(x,y))\\
&:= p^2+A+B+C+D, \end{align*} where $A$, $B$, $C$, and $D$ are set to be the four sums appearing in the previous line. These four sums are computed using Lemmas \ref{orthog relation}, \ref{special Gauss sums} and \ref{theta equality} repeatedly. We provide the computation for $D$ here, which requires the most steps. The other three follow in a similar manner. We begin with four applications of Lemma \ref{theta equality} and find that
\allowdisplaybreaks{ \begin{align*} D &= \frac{1}{(p-1)^4}\sum_{x,y,z \in\fpc}\sum_{j,k,\ell,m=0}^{p-2}G_{-j}G_{-k}G_{-\ell}G_{-m}T^j(zy^2)T^k(-4zx^3)\\&\qquad\qquad\qquad \cdot T^{\ell}\left(zx\frac{27}{1-t}\right)T^m\left(z\frac{27}{1-t}\right)\\
&= \frac{1}{(p-1)^4}\sum_{x,y \in\fpc}\sum_{j,k,\ell,m=0}^{p-2}G_{-j}G_{-k}G_{-\ell}G_{-m}T^j(y^2)T^k(-4x^3)T^{\ell}\left(x\frac{27}{1-t}\right)\\
& \qquad \qquad \qquad \cdot T^m\left(\frac{27}{1-t}\right)\sum_{z\in\fpc}T^{j+k+\ell+m}(z), \end{align*} } \noindent after simplifying to collect all $T(z)$ terms. Now, Lemma \ref{orthog relation} implies the final sum is nonzero only when $m=-j-k-\ell$. Performing this substitution, together with collecting all $T(x)$ terms gives \begin{align*} D &= \frac{1}{(p-1)^3}\sum_{y \in\fpc}\sum_{j,k,\ell=0}^{p-2}G_{-j}G_{-k}G_{-\ell}G_{j+k+\ell}T^j(y^2)T^k(-4)\\ &\qquad \qquad \qquad \cdot T^{-j-k}\left(\frac{27}{1-t}\right)\sum_{x\in\fpc}T^{3k+\ell}(x)\\
&= \frac{1}{(p-1)^2}\sum_{j,k=0}^{p-2}G_{-j}G_{-k}G_{3k}G_{j-2k}T^k(-4)T^{-j-k}\left(\frac{27}{1-t}\right)\sum_{y\in\fpc}T^{2j}(y). \end{align*} The second equality follows by applying the substitution $\ell=-3k$, according to Lemma \ref{orthog relation}, and collecting all $T(y)$ terms. Finally, note that $T^{2j}=\varepsilon$ precisely when $j=0, \frac{p-1}{2}$. Accounting for both of these cases, we arrive at \begin{align*} D &= \frac{1}{p-1}\sum_{k=0}^{p-2}G_{0}G_{-k}G_{3k}G_{-2k}T^k(-4)T^{-k}\left(\frac{27}{1-t}\right)\\
& \qquad \qquad + \frac{1}{p-1}\sum_{k=0}^{p-2}G_{-\frac{p-1}{2}}G_{-k}G_{3k}G_{\frac{p-1}{2}-2k}T^k(-4)T^{-k-\frac{p-1}{2}}\left(\frac{27}{1-t}\right)\\
&= \frac{1}{p-1}\sum_{k=0}^{p-2}G_{-k}G_{3k}T^k(-4)\left[-G_{-2k}T^{-k}\left(\frac{27}{1-t}\right)+ \sqrt{p}\,G_{6s-2k}T^{-k-6s}\left(\frac{27}{1-t}\right)\right]\\
&= \frac{1}{p-1}\sum_{k=0}^{p-2}G_{-k}G_{3k}T^k(-4)T^{-k}\left(\frac{27}{1-t}\right)\left[-G_{-2k}+\sqrt{p}\,G_{6s-2k}\phi\left(\frac{3}{1-t}\right)\right], \end{align*} after collecting like terms and simplifying.
By a similar analysis, one can compute that
\begin{align*} A &= -1\\ B &= 1+p\phi\left(\frac{3}{1-t}\right)\\ C &= \frac{1}{p-1}\sum_{j=0}^{p-2}G_{-j}G_{3j}G_{-2j}T^j(-4)T^{-j}\left(\frac{27}{1-t}\right). \end{align*} Combining our calculations for $A$, $B$, $C$, and $D$, we see that \begin{align*} p\cdot(\#E_t(\fp)-1)&=p^2+A+B+C+D\\
&=p^2+p\phi\left(\frac{3}{1-t}\right)\\ & \,\,\qquad +\frac{\sqrt{p}}{p-1}\phi\left(\frac{3}{1-t}\right)\sum_{k=0}^{p-2}G_{-k}G_{3k}G_{6s-2k}T^k(-4)T^{-k}\left(\frac{27}{1-t}\right). \end{align*}
Now we compute the trace of Frobenius $a(t,p)$. Since $a(t,p)=p+1-\#E_t(\fp)$, we have proved:
\begin{prop}\label{trace calculation}If $p$ is a prime, $p\equiv 1 \pmod{12}$, $s=\frac{p-1}{12}$, and $E_t$ is as in \eqref{defn of E}, then $$a(t,p)=-\phi\left(\frac{3}{1-t}\right)-\frac{\phi\left(\frac{3}{1-t}\right)}{\sqrt{p}\,(p-1)}\sum_{k=0}^{p-2}G_{-k}G_{3k}G_{6s-2k}T^k(-4)T^{-k}\left(\frac{27}{1-t}\right).$$ \end{prop}
Now that we have a formula for the trace of Frobenius on $E_t$ in terms of Gauss sums, we write our specialization of the $_2F_1$ hypergeometric function in similar terms. Recall that $s=\frac{p-1}{12}$ and $T$ generates the character group $\widehat{\mathbb{F}_{p}^{\times}}$. Thus, we may take the character $\xi$ of order 12 in the statement of Theorem \ref{first main theorem} to be $T^s$.
The next result gives an explicit formula for $\hg{\xi}{\xi^5}{\varepsilon}{t}$ in terms of Gauss sums. In its proof, we make use of the specific instances of the Hasse-Davenport relation that were given in Section \ref{preliminaries}.
\begin{prop}\label{2f1 formula}For $t\in\fp\backslash\{0,1\},$ $$\hg{\xi}{\xi^5}{\varepsilon}{t}=\frac{T^{3s}(4(1-t))}{\sqrt{p}(p-1)} \sum_{k=0}^{p-2}G_{6s-2k}G_{3k}\frac{1}{G_{k}}T^k(4)T^{-k}\left(\frac{27}{1-t}\right).$$ \end{prop}
\begin{proof} By Theorem \ref{greene 44},
\begin{align*} \hg{\xi}{\xi^5}{\varepsilon}{t} &= \xi(-1)\hg{\xi}{\xi^5}{\xi^6}{1-t} & \\
&= T^s(-1)\frac{p}{p-1}\sum_{\chi}\binom{\xi \chi}{\chi}\binom{\xi^5 \chi}{\xi^6 \chi}\chi(1-t) & \text{(Definition \ref{hg})}\\
&= T^s(-1)\frac{p}{p-1}\sum_{k=0}^{p-2}\binom{T^{s+k}}{T^k}\binom{T^{5s+k}}{T^{6s+k}}T^k(1-t), & \end{align*}
as $T$ generates the character group. Now we rewrite the product $\binom{T^{s+k}}{T^k}\binom{T^{5s+k}}{T^{6s+k}}$ of binomial coefficients in terms of Gauss sums, by way of Lemma \ref{greene 29}. Since $T^s=\xi$ and $T^{-s}=\xi^{-1}$ are not trivial, we have
\begin{align*} \binom{T^{s+k}}{T^k}\binom{T^{5s+k}}{T^{6s+k}} &= \left[\frac{G_{s+k}G_{-k}T^k(-1)}{pG_{s}}\right] \cdot \left[ \frac{G_{5s+k}G_{-6s-k}T^{6s+k}(-1)}{pG_{-s}} \right]\\
&= \frac{1}{p^3}G_{s+k}G_{-k}G_{5s+k}G_{-6s-k}T^{5s+2k}(-1), \end{align*}
since $G_sG_{-s}=pT^s(-1)$ by Lemma \ref{greene 112}. Thus,
\begin{align*} \hg{\xi}{\xi^5}{\varepsilon}{t} &= \frac{T^s(-1)}{p^2(p-1)} \sum_{k=0}^{p-2} G_{s+k}G_{-k}G_{5s+k}G_{-6s-k}T^{5s+2k}(-1)T^k(1-t)\\
&= \frac{\phi(-1)}{p^2(p-1)} \sum_{k=0}^{p-2} G_{s+k}G_{-k}G_{5s+k}G_{-6s-k}T^k(1-t), \end{align*}
since $T^sT^{5s}=\phi$ and $T^{2k}(-1)=1 \,\,\mbox{for all}\, k.$
Now we apply the Hasse-Davenport relation (Corollary \ref{HD2}) and make a substitution for $G_{-k}G_{-6s-k}$. We obtain $$\hg{\xi}{\xi^5}{\varepsilon}{t}=\frac{\phi(-1)}{p^{\frac{3}{2}}(p-1)} \sum_{k=0}^{p-2} G_{s+k}G_{5s+k}G_{-2k}T^k(4)T^k(1-t).$$
\noindent Next, we let $k \mapsto k+3s$ and find
\begin{align*} \hg{\xi}{\xi^5}{\varepsilon}{t} &= \frac{\phi(-1)}{p^{\frac{3}{2}}(p-1)} \sum_{k=0}^{p-2} G_{4s+k}G_{8s+k}G_{-2k-6s}T^{k+3s}(4)T^{k+3s}(1-t)\\
&= \frac{\phi(-1)T^{4s}(-1)}{\sqrt{p}(p-1)} \sum_{k=0}^{p-2} G_{6s-2k}G_{3k}\frac{1}{G_k}T^{-k}(27)T^{k+3s}(4)T^{k+3s}(1-t), \end{align*}
by applying the Hasse-Davenport relation (Corollary \ref{HD3}) to make a substitution for $G_{4s+k}G_{8s+k}$, and by noting that $G_{-2k-6s}=G_{-2k+6s}$. Then, since $p \equiv 1\pmod{12}$ implies $\phi(-1)T^{4s}(-1)=T^{10s}(-1)=1$, we simplify to obtain \begin{equation*} \hg{\xi}{\xi^5}{\varepsilon}{t} = \frac{T^{3s}(4(1-t))}{\sqrt{p}(p-1)} \sum_{k=0}^{p-2}G_{6s-2k}G_{3k}\frac{1}{G_{k}}T^k(4)T^{-k}\left(\frac{27}{1-t}\right), \end{equation*} as desired. \end{proof}
We now have the necessary tools to complete the proof of Theorem \ref{first main theorem}.
\begin{proof}[Proof of Theorem \ref{first main theorem}] We combine the results of Propositions \ref{trace calculation} and \ref{2f1 formula} with a bit of algebra to complete the proof. We begin by taking the formula for $\hg{\xi}{\xi^5}{\varepsilon}{t}$ given in Proposition \ref{2f1 formula}, splitting off the $k=0$ term in the sum and applying Lemma \ref{greene 112} to the $k\geq1$ terms, to move all Gauss sums to the numerator. We also simplify by noticing that $T^{-k}(-1)=T^k(-1)$ implies $T^{-k}(-1)T^k(4)=T^k(-4)$. We see that \begin{align*} \hg{\xi}{\xi^5}{\varepsilon}{t} &= \frac{T^{3s}(4(1-t))}{\sqrt{p}(p-1)} \Biggl[ \sqrt{p}+ \frac{1}{p}\sum_{k=1}^{p-2} G_{6s-2k}G_{3k}G_{-k}T^{-k}(-1)T^k(4)\Biggr.\\ &\Biggl. \hspace*{0.4in} \cdot T^{-k}\left( \frac{27}{1-t} \right) \Biggr]\\
&= \frac{T^{3s}(4(1-t))}{\sqrt{p}(p-1)} \left[ \sqrt{p} + \frac{1}{p}\sum_{k=1}^{p-2} G_{6s-2k}G_{3k}G_{-k}T^k(-4)T^{-k}\left( \frac{27}{1-t} \right) \right]. \end{align*} Next, we multiply by $\displaystyle{\frac{\phi(3)T^{3s}(1-t)}{\phi(3)T^{3s}(1-t)}}$ and rearrange, while recalling that $\phi=\phi^{-1}$. We obtain \begin{align*} \hg{\xi}{\xi^5}{\varepsilon}{t} &= -\frac{T^{3s}(4)}{\phi(3)T^{3s}(1-t)} \left[ -\frac{1}{p-1}\phi \left( \frac{3}{1-t} \right)\right.\\
& \hspace*{0.2in}\left.- \frac{1}{p^{\frac{3}{2}}(p-1)}\phi \left( \frac{3}{1-t} \right) \sum_{k=1}^{p-2} G_{6s-2k}G_{3k}G_{-k}T^k(-4)T^{-k}\left( \frac{27}{1-t} \right) \right]\\
&= -T^{3s}(4)\phi(3)T^{-3s}(1-t) \left[ -\frac{\phi \left( \frac{3}{1-t} \right)}{p} \right.\\
& \hspace*{0.2in}\left. - \frac{\phi \left( \frac{3}{1-t} \right)}{p^{\frac{3}{2}}(p-1)} \sum_{k=0}^{p-2} G_{6s-2k}G_{3k}G_{-k}T^k(-4)T^{-k}\left( \frac{27}{1-t} \right) \right]. \end{align*} \noindent The last equality follows by noting that the $k=0$ term of the final sum is $-\frac{\phi \left( \frac{3}{1-t} \right)}{p(p-1)}$ and $$ -\frac{\phi \left( \frac{3}{1-t} \right)}{p-1}+ \frac{\phi \left( \frac{3}{1-t} \right)}{p(p-1)}= -\frac{\phi \left( \frac{3}{1-t} \right)}{p}.$$
\noindent Recalling the expression for $a(t,p)$ given by Proposition \ref{trace calculation}, we have that
$$p\,\hg{\xi}{\xi^5}{\varepsilon}{t}=-T^{3s}(4)\phi(3)T^{-3s}(1-t)a(t,p),$$ so the proof is complete if $T^{3s}(4)\phi(3)T^{-3s}(1-t)=\phi(2)\xi^{-3}(1-t)$. Since $T^{3s}=\xi^3$ and $T^{-3s}=\xi^{-3}$, we need only show that \begin{equation}\label{simplify character} \xi^3(4)\phi(3)=\phi(2). \end{equation} By multiplicativity, $\xi^3(4)=\xi^6(2)=\phi(2)$. Further, $\phi(3)=\bigl(\frac{3}{p}\bigr)=\bigl(\frac{p}{3}\bigr)$ by quadratic reciprocity, since $p\equiv1\pmod{4}$. Also, since $p\equiv1\pmod{3}$, we have $\phi(3)=\left(\frac{1}{3}\right)=1$. This verifies (\ref{simplify character}), and hence completes the proof. \end{proof}
We have proved two other results similar to Theorem \ref{first main theorem}, but which apply to different families of elliptic curves. These results are finite field analogues of Beukers results (see \cite{Be93}) relating periods of families of elliptic curves to values of classical hypergeometric functions, as described in Section \ref{history hg and ec}. Note that the characters which appear in our $_2F_1$ bear a striking resemblance to the parameters Beukers used in the classical case.
\begin{prop}\label{prop 2.5} Suppose $p \equiv 1 \pmod{12}$ is prime, and let $\xi\in \widehat{\mathbb{F}_{p}^{\times}}$ have order $12$. Let $E_t:y^2=x^3+tx+1$, and let $a(t,p)=p+1-\#E_t(\fp)$. Then $$p \, \hg{\xi}{\xi^7}{\xi^8}{-\frac{4}{27}t^3}=\chi(t)a(t,p),$$ where $\chi(t)=-\xi^{-1}(-4)\xi^{-4}(\frac{t^3}{27})$. \end{prop}
\begin{prop}\label{prop 2.4} Suppose $p \equiv 1 \pmod{12}$ is prime, and let $\xi\in \widehat{\mathbb{F}_{p}^{\times}}$ have order $12$. Let $E_t:y^2=x^3-x-t$, and let $a(t,p)=p+1-\#E_t(\fp)$. Then $$p \, \hg{\xi}{\xi^5}{\phi}{\frac{27}{4}t^2}=-\xi^3(-27)a(t,p).$$ \end{prop}
It is interesting to note that in Proposition \ref{prop 2.5}, the values of the character $\chi(t)$, which appears as the coefficient of $a(t,p)$, are simply sixth roots of unity, and in Proposition \ref{prop 2.4}, the values of $\xi^3(-27)$ are simply $\pm 1$. A priori, $\xi^3(-27)\in\{\pm1,\pm i\},$ but in fact, we have $(\xi^3(-27))^2=(\xi^3(-1)\xi^3(27))^2=\phi(-1)\phi(27)=\phi(-1)\phi(3)=1$. This follows since $p\equiv 1\pmod{12}$ implies $\phi(-1)=1$ and since $\phi(3)=1$, as shown in the proof of Theorem \ref{first main theorem}.
\section{Recent History: Hypergeometric Functions and Modular Forms}\label{history hg and mf}
As with elliptic curves, classical hypergeometric functions have connections to modular forms. Investigations into these relations began in the early twentieth century. More recently, Stiller \cite{St88} proved an array of results linking the two objects. In fact, the classical hypergeometric series and family of elliptic curves (i.e. one with $j$-invariant $\frac{1728}{t}$) considered by Stiller prompted the choice of family $E_t$ and the $_2F_1$ function used in our main results. For this reason, we now state one of Stiller's results in full. We let
$$E_4(q)=1+204\sum_{n\geq 1} \sigma_3(n)q^n$$ and $$E_6(q)=1-504 \sum_{n\geq 1} \sigma_5(n)q^n$$ be the classical Eisenstein series of weights $4$ and $6$, respectively, for $\Gamma$. Stiller directly related these two modular forms to classical hypergeometric series:
\begin{theorem}[Stiller \cite{St88}, Thm. 5] Let $\mathbb{C}[E_4,E_6]$ be the graded algebra of modular forms for $\Gamma$ and let $\mathbb{C} [ _2F_1[\frac{1}{12},\frac{5}{12};1;t]^4, (1-t)^{1/2} \, _2F_1[\frac{1}{12},\frac{5}{12};1;t]^6]$ be the graded algebra of hypergeometric functions (graded by the power of $_2F_1$). Then these two algebras are canonically isomorphic as graded algebras of power series in $q=e^{2\pi i z}$ and $t$, respectively. Moreover, the isomorphism is the pull-back $\pi^*$, where $\pi(q)=\frac{1728}{j(q)}$ and $j$ is the usual elliptic modular function. \end{theorem}
Following Greene's introduction of hypergeometric functions over finite fields, results emerged relating them to modular forms. Ahlgren, Ono, and others produced formulas for traces of Hecke operators on certain spaces of cusp forms. These formulas were given in terms of traces of Frobenius on related families of elliptic curves.
Specifically, in 2000 and 2002, Ahlgren and Ono \cite{AO00} and Ahlgren \cite{Ah02} exhibited formulas for the traces of Hecke operators on spaces of cusp forms in levels 8 and 4. Let $k\geq2$ be an even integer, and define $$F_k(x,y)=\frac{x^{k-1}-y^{k-1}}{x-y}.$$ Then letting $x+y=s$ and $xy=p$ gives rise to polynomials $G_k(s,p)=F_k(x,y)$. These polynomials can be written alternatively as \begin{equation}\label{defn of G} G_k(s,p)=\sum_{j=0}^{\frac{k}{2}-1} (-1)^j \binom{k-2-j}{j} p^j s^{k-2j-2}. \end{equation} The results given below are given in \cite{AO00} and \cite{Ah02} for the cases of level 4, weight 6 and of level 8, weight 4, respectively. However, the statements hold for all even $k\geq 4$ with the same proofs.
\begin{theorem}[(a) Ahlgren and Ono \cite{AO00}, (b) Ahlgren \cite{Ah02}] Let $p$ be an odd prime and $k\geq4$ be an even integer. Then
$(a) \quad \displaystyle{\,\,\textnormal{Tr}_k(\Gamma_0(8),p)=-4-\sum_{t=2}^{p-2} G_k(_2A_1(p,t^2),p)}$
$(b) \quad \displaystyle{\,\,\textnormal{Tr}_k(\Gamma_0(4),p)=-3-\sum_{t=2}^{p-1} G_k(_2A_1(p,t),p).}$ \end{theorem}
Ahlgren and Ono's methods involved combining the Eichler-Selberg trace formula \cite{Hi89} with a theorem given by Schoof \cite{Sc87}. In the proof of Theorem \ref{second main theorem}, given in the next section, we use similar techniques to exhibit a formula in the level 1 setting. Recently, Frechette, Ono, and Papanikolas expanded the techniques of Ahlgren and Ono and obtained results in the level 2 case:
\begin{theorem}[Frechette, Ono, and Papanikolas \cite{FOP04}] Let $p$ be an odd prime and $k\geq 4$ be even. When $p \equiv 1 \pmod{4}$, write $p=a^2+b^2$, where $a,b$ are nonnegative integers, with $a$ odd. Then $$\textnormal{Tr}_k(\Gamma_0(2),p)=-2-\delta_k(p)-\sum_{t=1}^{p-2} G_k(_3A_2(p,t),p),$$ where \begin{equation*} \delta_k(p)= \begin{cases} \frac{1}{2}G_k(2a,p)+\frac{1}{2}G_k(2b,p) &\textnormal{if}\,\, p\equiv1\pmod{4}\\ (-p)^{k/2-1} &\textnormal{if}\,\, p\equiv3\pmod{4}. \end{cases} \end{equation*} \end{theorem}
In addition, Frechette, Ono, and Papanikolas used relationships between counting points on varieties over $\fp$ and hypergeometric functions over $\fp$ to obtain further results for the traces of Hecke operators on spaces of newforms in level 8. Most recently, Papanikolas \cite{Pa06} used the results in \cite{FOP04} as a starting point to obtain a new formula for Ramanujan's $\tau$ function, as well as a new congruence for $\tau(p) \pmod{11}$.
\section{Proof of Theorem \ref{second main theorem}}\label{proof of theorem 2}
The proof of Theorem \ref{second main theorem} utilizes three important results. First, we use Hasse's classical bound on the number of points on an elliptic curve defined over a finite field. (See, for example, \cite{Si86} page 131 for details.) We also use a theorem of Schoof, together with Hijikata's version of the Eichler-Selberg trace formula, which require some notation. We follow the treatment given in \cite{FOP04}. If $d<0$, $d\equiv 0,1 \pmod{4}$, let $\mathcal{O}(d)$ denote the unique imaginary quadratic order in $\mathbb{Q}(\sqrt{d})$ having discriminant $d$. Let $h(d)=h(\mathcal{O}(d))$ be the order of the class group of $\mathcal{O}(d)$, and let $w(d)=w(\mathcal{O}(d))$ be half the cardinality of the unit group of $\mathcal{O}(d)$. We then let $h^*(d)=h(d)/w(d)$. Further, if $d$ is the discriminant of an imaginary quadratic order $\mathcal{O}$, let \begin{equation}\label{defn of H} H(d):=\sum_{\mathcal{O}\subseteq\mathcal{O}'\subseteq\mathcal{O}_{max}}h(\mathcal{O}'), \end{equation} where the sum is over all orders $\mathcal{O}'$ between $\mathcal{O}$ and $\mathcal{O}_{max}$, the maximal order. A complete treatment of the theory of orders in imaginary quadratic fields can be found in section 7 of \cite{Co89}.
Additionally, if $K$ is a field, we define
$$\emph{Ell}_K:=\{[E]_K | E \,\textnormal{is defined over}\, K\},$$ where $[E]_K$ denotes the isomorphism class of $E$ over $K$ and $[E_1]_K=[E_2]_K$ if there exists an isomorphism $\beta:E_1 \rightarrow E_2$ over $K$. Now if $p$ is an odd prime, define \begin{equation}\label{defn of I}
I(s,p):=\{[E]_{\fp}\in\emph{Ell}_{\fp} | \#E(\fp)=p+1 \pm s\}. \end{equation} Schoof proved the following theorem, connecting the quantities in (\ref{defn of H}) and (\ref{defn of I}).
\begin{theorem}[Schoof \cite{Sc87}, Thm. 4.6]\label{schoof's theorem} If $p$ is an odd prime and $s$ is an integer with $0<s<2\sqrt{p}$, then \[ \#I(s,p)=2H(s^2-4p). \] \end{theorem}
The final key ingredient to the proof of Theorem \ref{second main theorem} is the Eichler-Selberg trace formula, which provides a starting point for calculating the trace of the $p^{th}$ Hecke operator on $S_k$. We use Hijikata's version of this formula, which is found in \cite{Hi89}, but we only require the level 1 formulation.
Let $p\equiv 1 \pmod{12}$ be prime, and recall the definition of polynomials $G_k(s,p)$ given in (\ref{defn of G}), and in the statement of Theorem \ref{second main theorem}. Note that when writing the polynomials $G_k(s,p)$, we take the convention $s^0=1$, so that the constant term of $G_k(s,p)$ is $(-p)^{\frac{k}{2}-1}$, for all values of $s$. Using this notation, the formulation given below is a straightforward reduction of Hijikata's trace formula in the level one case.
\begin{theorem}[Hijikata \cite{Hi89}, Thm. 2.2]\label{hijikata} Let $k\geq 2$ be an even integer, and let $p\equiv 1 \pmod{12}$ be prime. Then
$$\textnormal{Tr}_k(\Gamma,p)=-h^*(-4p)(-p)^{\frac{k}{2}-1}-1-\sum_{0<s<2\sqrt{p}}G_k(s,p)\sum_{f|\ell}h^*\left(\frac{s^2-4p}{f^2}\right)+\delta(k),$$ where $$\delta(k)=\begin{cases} p+1 &\mbox{if}\,\, k=2\\0 & \mbox{otherwise}\end{cases}$$ and where we classify integers $s$ with $s^2-4p<0$ by some positive integer $\ell$ and square-free integer $m$ via $$s^2-4p=\begin{cases}\ell^2m, & 0>m\equiv 1 \pmod{4}\\\ell^24m, & 0>m\equiv 2,3 \pmod{4}.\end{cases}$$
\end{theorem}
Next, we recall a result which relates isomorphism classes in $\emph{Ell}_{\overline{\mathbb{F}}_p}$ and $\emph{Ell}_{\fp}$. Define a map \begin{align*} \eta:\emph{Ell}_{\fp}&\rightarrow \emph{Ell}_{\overline{\mathbb{F}}_p}\\ [E]_{\fp} &\mapsto [E]_{\overline{\mathbb{F}}_p}. \end{align*}
Note that $\eta$ is well defined since two curves which are isomorphic over $\fp$ are necessarily isomorphic over $\overline{\mathbb{F}}_p$.
\begin{lemma}[]\label{fp and fpbar} Let $p\geq5$ be prime. Suppose $[E]_{\overline{\mathbb{F}}_p}\in\emph{Ell}_{\overline{\mathbb{F}}_p}$ and $E$ is defined over $\fp$. Then $$\#\eta^{-1}([E]_{\overline{\mathbb{F}}_p})=\begin{cases} 2 & \textnormal{if} \, j\neq 0, 1728\\ 4 & \textnormal{if} \, j=1728 \\ 6 & \textnormal{if} \, j=0.\end{cases}$$ \end{lemma} \begin{proof} See Section X.5 of \cite{Si86}. \end{proof}
Among isomorphism classes of elliptic curves over $\fp$, two are of particular interest to us: those having $j$-invariant $1728$ and those having $j$-invariant $0$. If $E$ is any elliptic curve defined over $\fp$, we let $a(E)$ be given by $a(E)=p+1-\#E(\fp)$. The following two lemmas compute formulas for the sums of $a(E)^n$ over all curves $E$ over $\fp$ having $j$-invariant $1728$ or $0$, respectively.
\begin{lemma}[\cite{Fu07}, Lemma IV.3.3]\label{j inv 1728} Let $p\equiv 1 \pmod{12}$ and let $a,b\in\mathbb{Z}$ be such that $p=a^2+b^2$ and $a+bi \equiv 1 \,(2+2i)$ in $\mathbb{Z}[i]$. Then for $n\geq2$ even, $$\sum_{\substack{[E]_{\fp}\in Ell_{\fp}\\j(E)=1728}}a(E)^n=2^{n+1}(a^n+b^n).$$ \end{lemma}
\begin{lemma}[\cite{Fu07}, Lemma IV.3.5]\label{j inv 0} Let $p\equiv 1 \pmod{12}$ and let $c,d\in\mathbb{Z}$ such that $p=c^2-cd+d^2$ and $c+d\omega \equiv 2 \,(3)$ in $\mathbb{Z}[\omega]$, where $\omega=e^{2\pi i /3}$. Then for $n\geq2$ even, $$\sum_{\substack{[E]_{\fp}\in Ell_{\fp}\\j(E)=0}}a(E)^n=2[(c+d)^n+(2c-d)^n+(c-2d)^n].$$ \end{lemma}
We omit the proofs of Lemmas \ref{j inv 1728} and \ref{j inv 0}, as they are quite tedious and require checking dozens of cases. However, these proofs are not difficult. The only tools used are the classification of elliptic curves over $\fp$ having $j$-invariant 1728 or 0, together with known formulas for $a(E)$ in these cases. These formulas (see Chapter 18 of \cite{IR90}) are given in terms of $m^{th}$ power residues, whose values must be calculated on a case by case basis for each curve with the given $j$-invariant. Complete details of the proofs of Lemmas \ref{j inv 1728} and \ref{j inv 0} can be found in \cite{Fu07}.
Now we proceed toward the proof of Theorem \ref{second main theorem}. As before, let $p\equiv 1\pmod{12}$ be prime. As in (\ref{defn of E}), we define a family of elliptic curves over $\fp$ by $$E_t:y^2=4x^3-\frac{27}{1-t}x-\frac{27}{1-t}.$$ Further, for $t\in\fp$, $t\neq 0,1$, recall that $$a(t,p)=p+1-\#E_t(\fp).$$ As in Lemmas \ref{j inv 1728} and \ref{j inv 0}, we let integers $a,b,c,$ and $d$ be defined by $p=a^2+b^2=c^2-cd+d^2$, where $a+bi\equiv 1 \, (2+2i)$ in $\mathbb{Z}[i]$ and $c+d\omega\equiv 2 \, (3)$ in $\mathbb{Z}[\omega]$, where $\omega=e^{2\pi i/3}$. Finally, we let $h$, $h^{*}$, $w$, and $H$ be defined as at the start of this section.
\begin{lemma}\label{h to h*} If $p\equiv 1 \pmod{12}$ is prime and notation is as above, then for $n\geq 2$ even, \begin{multline*}
\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h\left(\frac{s^2-4p}{f^2}\right)=\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h^*\left(\frac{s^2-4p}{f^2}\right)\\+\frac{1}{4}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n+\frac{1}{3}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=0}}a(E)^n, \end{multline*} where we classify integers $s$ with $s^2-4p<0$ by some positive integer $\ell$ and square-free integer $m$ via $$s^2-4p=\begin{cases}\ell^2m, & 0>m\equiv 1 \pmod{4}\\\ell^24m, & 0>m\equiv 2,3 \pmod{4}.\end{cases}$$ \end{lemma}
\begin{proof} First, notice that $h$ and $h^*$ agree unless the argument $\frac{s^2-4p}{f^2}=-3$ or $-4$, since in all other cases $w(d)=1$. Thus, we have \begin{multline*}
\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h\left(\frac{s^2-4p}{f^2}\right)=\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}\neq -3,-4}}h^{*}\left(\frac{s^2-4p}{f^2}\right)\\
+\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-4}}h(-4)+\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-3}}h(-3). \end{multline*} When $\frac{s^2-4p}{f^2}=-4$, we have the maximal order $\mathbb{Z}[i]$ and $h^*(-4)=\frac{h(-4)}{w(-4)}=\frac{1}{2}$, so $h(-4)=h^*(-4)+\frac{1}{2}$. On the other hand, when $\frac{s^2-4p}{f^2}=-3$, we have the maximal order $\mathbb{Z}[\omega]$ and $h^*(-3)=\frac{h(-3)}{w(-3)}=\frac{1}{3}$, so $h(-3)=h^*(-3)+\frac{2}{3}$. Making these substitutions, we see that \begin{multline}\label{h* step}
\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h\left(\frac{s^2-4p}{f^2}\right)=\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h^*\left(\frac{s^2-4p}{f^2}\right)\\
+\frac{1}{2}\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-4}}1\,\,+\frac{2}{3}\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-3}}1. \end{multline} To complete the proof, we must verify that \begin{equation}\label{h=-4}
\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-4}}1 = \frac{1}{2}\sum_{\substack{[E]_{\fp}\in\emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n \end{equation} and \begin{equation}\label{h=-3}
\sum_{0<s<2\sqrt{p}}s^n\sum_{\substack{f|\ell\\\frac{s^2-4p}{f^2}=-3}}1 = \frac{1}{2}\sum_{\substack{[E]_{\fp}\in\emph{Ell}_{\fp}\\j(E)=0}}a(E)^n. \end{equation}
First, we consider \eqref{h=-4}. Using known formulas for $a(E)$ in the case of curves with $j$-invariant 1728 (see Chapter 18 of \cite{IR90}), one can show that $a(E)=\pm 2a,\pm 2b$ for all $E$ relevant to \eqref{h=-4} with $j$-invariant $1728$. Also, it is easy to verify that $s=|2a|,|2b|$ satisfy $\frac{s^2-4p}{\ell^2}=-4$ (with $\ell=|b|,|a|$, respectively). Now, suppose $0<s<2\sqrt{p}\,$ satisfies $\frac{s^2-4p}{\ell^2}=-4$. Then $s^2-4p=-4\ell^2$ implies $s$ is even, so we have $\left(\frac{s}{2}\right)^2+\ell^2=p.$ Thus, it must be that $\frac{s}{2}=|a|,|b|$, since $\mathbb{Z}[i]$ is a UFD and $p=a^2+b^2$. Since $n$ is even, $(2a)^n=(-2a)^n$ and $(2b)^n=(-2b)^n$, so \eqref{h=-4} follows.
We prove \eqref{h=-3} in a similar manner. Using known formulas for $a(E)$ in the case of curves with $j$-invariant 0 (see Chapter 18 of \cite{IR90}), one can show that $a(E)=\pm(c+d),\pm(2c-d),\pm(c-2d)$ for all $E$ with $j$-invariant $0$ that appear in \eqref{h=-3}. Also, $s=|c+d|$, $|2c-d|$, and $|c-2d|$ satisfy $\frac{s^2-4p}{\ell^2}=-3$ (by taking $\ell=|c-d|$, $|d|$, and $|c|$, respectively). Now, suppose $\frac{s^2-4p}{\ell^2}=-3$. Then in $\mathbb{Z}[\sqrt{-3}]$, we have $$4p=(s+\sqrt{-3}\,\ell)(s-\sqrt{-3}\,\ell).$$
Since $-3\equiv 5 \pmod{8}$, $2$ is inert in $\mathbb{Z}[\sqrt{-3}]$, so we must have $2|(s\pm \sqrt{-3}\,\ell)$. This implies \begin{equation}\label{factor p} p=\left(\frac{s}{2}+\sqrt{-3}\,\frac{\ell}{2}\right)\left(\frac{s}{2}-\sqrt{-3}\,\frac{\ell}{2}\right) \end{equation} in $\mathbb{Z}[\sqrt{-3}]$. Recall that we have $p=c^2-cd+d^2$. In $\mathbb{Z}[\omega]$, we can write this as \begin{align} p&=c^2-cd+d^2 \notag\\ &=(c+d\omega)(c+d\omega^2) \label{first}\\ &=(d+c\omega)(d+c\omega^2)\label{second}\\ &=(c\omega+d\omega^2)(c\omega^2+d\omega).\label{third} \end{align}
Since $\omega=e^{2\pi i/3}=-\frac{1}{2}+\frac{\sqrt{-3}}{2}$, we can consider each of these factorizations in $\mathbb{Z}[\sqrt{-3}]$, and each must be the same as \eqref{factor p}, since $\mathbb{Z}[\sqrt{-3}]$ is a UFD. Making the substitution for $\omega$ into \eqref{first}, \eqref{second}, and \eqref{third} and comparing to \eqref{factor p} implies that $s=|2c-d|$, $|2d-c|$, and $|c+d|$, respectively. So in fact, $s=|2c-d|$, $|2d-c|$, $|c+d|$ are the only contributing $s$ values to the sum on the left hand side of \eqref{h=-3}. Then since $a(E)=\pm(c+d),\pm(2c-d),\pm(c-2d)$ and $n$ is even, we have proved \eqref{h=-3}.
The lemma is finally proved by making the substitutions from \eqref{h=-4} and \eqref{h=-3} into \eqref{h* step}. \end{proof}
\begin{prop}\label{step 1 of thm 2 proof} Let $p\equiv 1 \pmod{12}$ be prime and notation as above. Then for $n\geq2$ even,
\begin{multline*}\sum_{t=2}^{p-1}a(t,p)^n=\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h^{*} \left(\frac{s^2-4p}{f^2}\right)\\-2^{n-1}(a^n+b^n)-\frac{1}{3}[(c+d)^n+(2c-d)^n+(c-2d)^n],\end{multline*}where we classify integers $s$ with $s^2-4p<0$ by some positive integer $\ell$ and square-free integer $m$ via $$s^2-4p=\begin{cases}\ell^2m, & 0>m\equiv 1 \pmod{4}\\\ell^24m, & 0>m\equiv 2,3 \pmod{4}.\end{cases}$$ \end{prop}
\begin{proof} Notice that for the given family of elliptic curves, $j(E_t)=\frac{1728}{t}$. Thus, as $t$ ranges from $2$ to $p-1$, each $E_t$ represents a distinct isomorphism class of elliptic curves in $\emph{Ell}_{\overline{\mathbb{F}}_p}$. Moreover, since $j(E_t)$ gives an automorphism of $\mathbb{P}^1$, every $j$-invariant other than $0$ and $1728$ is represented precisely once. Thus, for even $n\geq 2$, we have $$\sum_{t=2}^{p-1}a(t,p)^n=\sum_{\substack{[E]_{\overline{\mathbb{F}}_p}\in Ell_{\overline{\mathbb{F}}_p}\\E/\fp\\j(E)\neq 0,1728}}a(E)^n.$$
For elliptic curves with $j$-invariant other than $0$ and $1728$, each class $[E]\in\emph{Ell}_{\overline{\mathbb{F}}_p}$ gives rise to two distinct classes in $\emph{Ell}_{\fp}$ (see Lemma \ref{fp and fpbar}), represented by $E$ and its quadratic twist $E^{tw}$. For such curves, $a(E)$ and $a(E^{tw})$ differ only by a sign, and so $a(E)^n=a(E^{tw})^n$, since $n$ is even. Therefore, we have $$\sum_{t=2}^{p-1}a(t,p)^n=\sum_{\substack{[E]_{\overline{\mathbb{F}}_p}\in Ell_{\overline{\mathbb{F}}_p}\\E/\fp\\j(E)\neq 0,1728}}a(E)^n=\frac{1}{2}\sum_{\substack{[E]_{\fp}\in Ell_{\fp}\\j(E)\neq 0,1728}}a(E)^n.$$ Then, if we add and subtract the contributions from the classes $[E]_{\fp}\in\emph{Ell}_{\fp}$ with $j(E)=0, 1728$, we have \begin{equation}\label{prop step 2} \sum_{t=2}^{p-1}a(t,p)^n=\frac{1}{2}\left[ \sum_{[E]_{\fp}\in Ell_{\fp}}a(E)^n - \sum_{\substack{[E]_{\fp}\in Ell_{\fp}\\j(E)=1728}}a(E)^n-\sum_{\substack{[E]_{\fp}\in Ell_{\fp}\\j(E)=0}}a(E)^n\right]. \end{equation}
Now we look more closely at the sum $\displaystyle{\sum_{[E]_{\fp}\in \emph{Ell}_{\fp}}a(E)^n}$. By Hasse's theorem, $\emph{Ell}_{\fp}$ is the the disjoint union $$\emph{Ell}_{\fp}=\bigcup_{0\leq s<2\sqrt{p}}I(s,p),$$ where $I(s,p)$ is defined as in (\ref{defn of I}). Then since $n\geq2$ is even, we may write \begin{align*} \sum_{[E]_{\fp}\in \emph{Ell}_{\fp}}a(E)^n&=\sum_{0\leq s <2\sqrt{p}}\quad\sum_{[E]_{\fp}\in I(s,p)} s^n\\ &=\sum_{0< s <2\sqrt{p}}\#I(s,p)s^n, \end{align*} since $s=0$ makes no contribution. Substituting this into (\ref{prop step 2}) gives $$\sum_{t=2}^{p-1}a(t,p)^n=\frac{1}{2}\sum_{0<s<2\sqrt{p}}\#I(s,p)s^n-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=0}}a(E)^n.$$ Now we may apply Theorem \ref{schoof's theorem} to obtain $$\sum_{t=2}^{p-1}a(t,p)^n=\sum_{0<s<2\sqrt{p}}H(s^2-4p)s^n-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=0}}a(E)^n.$$ Recall from (\ref{defn of H}) that if $d$ is the discriminant of an imaginary quadratic order $\mathcal{O}$, $$H(d):=\sum_{\mathcal{O}\subseteq\mathcal{O}'\subseteq\mathcal{O}_{max}}h(\mathcal{O}'),$$ where the sum is over all orders between $\mathcal{O}$ and the maximal order. Then taking $\ell$ as defined as in the statement of the Proposition, we have
$$H(s^2-4p)=\sum_{f|\ell} h\left(\frac{s^2-4p}{f^2}\right),$$ which gives \begin{equation}\label{h step}
\sum_{t=2}^{p-1}a(t,p)^n=\sum_{0<s<2\sqrt{p}}s^n\sum_{f|\ell} h\left(\frac{s^2-4p}{f^2}\right)-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n-\frac{1}{2}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=0}}a(E)^n. \end{equation} To complete the proof, we apply Lemma \ref{h to h*} to the right side of \eqref{h step}, to replace $h$ by $h^*$. Then, collecting terms gives \begin{align*}
\sum_{t=2}^{p-1}a(t,p)^n&=\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h^*\left(\frac{s^2-4p}{f^2}\right)-\frac{1}{4}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=1728}}a(E)^n-\frac{1}{6}\sum_{\substack{[E]_{\fp}\in \emph{Ell}_{\fp}\\j(E)=0}}a(E)^n\\
&=\sum_{0<s<2\sqrt{p}}s^n \sum_{f|\ell}h^*\left(\frac{s^2-4p}{f^2}\right)-2^{n-1}(a^n+b^n)\\
&\quad-\frac{1}{3}[(c+d)^n+(2c-d)^n+(c-2d)^n], \end{align*} by Lemmas \ref{j inv 1728} and \ref{j inv 0}. This is the desired result. \end{proof}
Proposition \ref{step 1 of thm 2 proof} and Theorem \ref{hijikata} give us the tools necessary to complete the proof our second main theorem: \begin{proof}[Proof of Theorem \ref{second main theorem}] By Theorem \ref{hijikata}, we have for $k\geq4$ even, \allowdisplaybreaks{ \begin{align*} \textnormal{Tr}_k(\Gamma,p)&=-1-\frac{1}{2}h^*(-4p)(-p)^{\frac{k}{2}-1}-\sum_{0<s<2\sqrt{p}}G_k(s,p)\sum_fh^*\left(\frac{s^2-4p}{f^2}\right)\\
&=-1-\frac{1}{2}h^*(-4p)(-p)^{\frac{k}{2}-1}-\sum_{0<s<2\sqrt{p}}\Biggl[(-p)^{\frac{k}{2}-1}\Biggr.\\
&\hspace*{0.25in}\Biggl.+\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^js^{k-2j-2}\Biggr]\sum_fh^*\left(\frac{s^2-4p}{f^2}\right)\\
&=-1-\frac{1}{2}h^*(-4p)(-p)^{\frac{k}{2}-1}-(-p)^{\frac{k}{2}-1}\sum_{0<s<2\sqrt{p}}1\sum_fh^*\left(\frac{s^2-4p}{f^2}\right)\\
&\hspace*{0.2in}-\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\sum_{0<s<2\sqrt{p}}s^{k-2j-2}\sum_fh^*\left(\frac{s^2-4p}{f^2}\right), \end{align*}}after substituting in the definition of $G_k(s,p)$ and distributing. Now, note that taking $k=2$ in Theorem \ref{hijikata} provides $$0=p-\frac{1}{2}h^*(-4p)-\sum_{0<s<2\sqrt{p}}1\sum_fh^*\left(\frac{s^2-4p}{f^2}\right).$$ We apply this, together with Proposition \ref{step 1 of thm 2 proof} and obtain \begin{align*} \textnormal{Tr}_k(\Gamma,p)&=-1-\frac{1}{2}h^*(-4p)(-p)^{\frac{k}{2}-1}+(-p)^{\frac{k}{2}-1}\left(\frac{1}{2}h^*(-4p)-p\right)\\
&\hspace*{0.2in}-\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\Biggl[\sum_{t=2}^{p-1}a(t,p)^{k-2j-2}+\frac{1}{2}\left[2^{k-2j-2}(a^{k-2j-2}\right. \Biggr.\\
&\left. \hspace*{0.2in} +b^{k-2j-2})\right] \Biggl.+\frac{1}{3}\left[(c+d)^{k-2j-2}+(2c-d)^{k-2j-2}+(c-2d)^{k-2j-2}\right]\Biggr]\\
&=-1+(-p)^{\frac{k}{2}-1}\cdot(-p)-\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\sum_{t=2}^{p-1}a(t,p)^{k-2j-2}\\
&\hspace*{0.2in}-\frac{1}{2}\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\left[(2a)^{k-2j-2}+(2b)^{k-2j-2}\right]\\
&\hspace*{0.2in}-\frac{1}{3}\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\left[(c+d)^{k-2j-2}+(2c-d)^{k-2j-2}\right.\\&\hspace*{0.2in}\left.+(c-2d)^{k-2j-2}\right], \end{align*} after distributing once again. Now, we notice the simple fact that $$(-p)^{\frac{k}{2}-1}\cdot(-p)=-(-p)^{\frac{k}{2}-1}(p-2)-2\left(\frac{1}{2}(-p)^{\frac{k}{2}-1}\right)-3\left(\frac{1}{3}(-p)^{\frac{k}{2}-1}\right).$$ Splitting up the factors of $(-p)^{\frac{k}{2}-1}$ in this way gives that \begin{align*} \textnormal{Tr}_k(\Gamma,p) &=-1-\frac{1}{2}\left[G_k(2a,p)+G_k(2b,p)\right]\\
&\hspace*{0.2in}-\frac{1}{3}\left[G_k(c+d,p)+G_k(2c-d,p)+G_k(c-2d,p)\right]\\
&\hspace{0.2in}-(p-2)(-p)^{\frac{k}{2}-1}-\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^j\sum_{t=2}^{p-1}a(t,p)^{k-2j-2}\\
&=-1-\lambda(k,p)-\sum_{t=2}^{p-1}(-p)^{\frac{k}{2}-1}-\sum_{t=2}^{p-1}\sum_{j=0}^{\frac{k}{2}-2}(-1)^j\binom{k-2-j}{j}p^ja(t,p)^{k-2j-2}\\
&=-1-\lambda(k,p)-\sum_{t=2}^{p-1}G_k(a(t,p),p), \end{align*} according to the definitions of $G_k$ and $\lambda(k,p)$ given in the statement of the theorem. This completes the proof of Theorem \ref{second main theorem}. \end{proof}
\begin{remark}\label{remk} According to Theorem \ref{first main theorem}, we may rewrite $a(t,p)$ in terms of the hypergeometric function $\hg{\xi}{\xi^5}{\varepsilon}{t}$. Thus, Theorem \ref{second main theorem} can be reformulated to give $\textnormal{Tr}_k(\Gamma,p)$ in terms of $\lambda(k,p)$ and $G_k\left(\psi^{-1}(t)p\,\hg{\xi}{\xi^5}{\varepsilon}{t},p\right)$, where $\psi(t)=-\phi(2)\xi^{-3}(1-t).$ \end{remark}
\section{Proof of Theorem \ref{recursion}}\label{recursion proof}
Theorem \ref{recursion} is proved by combining Theorems \ref{first main theorem} and \ref{second main theorem} with an inverse pair given in \cite{Ri68}. First, recall that
$$G_k(s,p)=\sum_{j=0}^{\frac{k}{2}-1} (-1)^j \binom{k-2-j}{j} p^j s^{k-2j-2}.$$ Letting $m=\frac{k}{2}-1$ and $H_m(x) :=\sum_{i=0}^{m}\binom{m+i}{m-i}x^i$, we have that \begin{equation}\label{G and H} G_k(s,p)=(-p)^mH_m\left(\frac{-s^2}{p}\right). \end{equation} Now, we make use of the inverse pair \cite[p. 67]{Ri68} given by \begin{equation}\label{inverse pair} \rho_n(x)=\sum_{k=0}^{n}\binom{n+k}{n-k}x^k, \qquad x^n=\sum_{k=0}^n(-1)^{k+n}\left[\binom{2n}{n-k}-\binom{2n}{n-k-1}\right]\rho_k(x). \end{equation} Applied to the definition of $H_m$, this gives \begin{equation*} x^m=\sum_{i=0}^{m}(-1)^{i+m}\left[\binom{2m}{m-i}-\binom{2m}{m-i-1}\right]H_i(x). \end{equation*} By taking $x=\frac{-s^2}{p}$, together with \eqref{G and H}, we have
\begin{eqnarray}\label{s2m eqn} s^{2m}&=&\sum_{i=0}^{m}p^{m-i}\left[\binom{2m}{m-i}-\binom{2m}{m-i-1}\right]G_{2i+2}(s,p)\notag\\ &=&\sum_{i=0}^{m}b_iG_{2i+2}(s,p), \end{eqnarray} where $b_i$ is as defined in the statement of Theorem \ref{recursion}.
\begin{proof}[Proof of Theorem \ref{recursion}] By \eqref{s2m eqn}, we have \begin{eqnarray}\label{s2m eqn2} s^{2m}&=&\sum_{i=0}^{m}b_iG_{2i+2}(s,p)\notag \\ &=&G_{2m+2}(s,p)+\sum_{i=0}^{m-1}b_iG_{2i+2}(s,p), \end{eqnarray} since $b_m=1$. Now, for $m\geq1$, Theorem \ref{second main theorem} implies \begin{align*} \textnormal{Tr}_{2(m+1)}(\Gamma,p)&= -1-\lambda(2m+2,p)-\sum_{t=2}^{p-1}G_{2m+2}(a(t,p),p)\\ &=-1-\lambda(2m+2,p)-\sum_{t=2}^{p-1}\Biggl( a(t,p)^{2m} \Biggr. \\ &\left. \hspace*{.2in}-\sum_{i=0}^{m-1}b_iG_{2i+2}(a(t,p),p)\right) \qquad (\textnormal{by \eqref{s2m eqn2}})\\
&=-1-\lambda(2m+2,p)-\sum_{t=2}^{p-1}a(t,p)^{2m}+b_0\sum_{t=2}^{p-1}G_2(a(t,p),p)\\ & \hspace*{0.2in}+\sum_{i=1}^{m-1}b_i\sum_{t=2}^{p-1}G_{2i+2}(a(t,p),p)\\ &=-1-\lambda(2m+2,p)-\sum_{t=2}^{p-1}a(t,p)^{2m}+b_0(p-2)\\ &\hspace*{0.2in}-\sum_{i=1}^{m-1}b_i(\textnormal{Tr}_{2i+2}(\Gamma,p)+1+\lambda(2i+2,p)), \end{align*} by Theorem \ref{second main theorem} and since $G_2=1$. The proof is completed by rearranging and noting that Theorem \ref{first main theorem} implies
\begin{align*} a(t,p)^{2m}&=p^{2m}\phi^{2m}(2)\xi^{6m}(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}^{2m}\\ &=p^{2m}\phi^m(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}^{2m}, \end{align*} since $\phi^2=\varepsilon$ and $\xi^6=\phi$. \end{proof}
\section{$\tau(p)$ Corollaries}\label{tau corollaries}
Specializing to various values of $k$ in Theorem \ref{second main theorem}, we arrive at more explicit formulas. In particular, by taking $k=12$ we obtain a formula for Ramanujan's $\tau$-function. Recall that we define $\tau(n)$ by $$(2\pi)^{-12}\Delta(z)=q\prod_{n=1}^{\infty}(1-q^n)^{24}=\sum_{n=1}^{\infty}\tau(n)q^n.$$ Also, recall that $\Delta(z)$ generates the one dimensional space $S_{12}$, and thus $\textnormal{Tr}_{12}(\Gamma,p)=\tau(p)$ for primes $p$. We conclude with results that stem from this specialization to $k=12$.
Throughout, we let $a,b\in\mathbb{Z}$ be such that $p=a^2+b^2$ and $a+bi \equiv 1 \,(2+2i)$ in $\mathbb{Z}[i]$. Further, let $c,d\in\mathbb{Z}$ satisfy $p=c^2-cd+d^2$ and $c+d\omega \equiv 2 \,(3)$ in $\mathbb{Z}[\omega]$, where $\omega=e^{2\pi i /3}$. The first corollary follows from a straightforward application of Theorem \ref{second main theorem}:
\begin{corollary}\label{tau corollary 1} Let $a,b,c,$ and $d$ be defined as above, and set $x=a^2b^2$ and $y=cd$. If $p$ is a prime, $p \equiv 1 (12)$, then $$\tau(p)=-1-8p^5+80p^3x-256px^2+27y^2p^3-27y^3p^2 -\sum_{t=2}^{p-1} G_{12}(a(t,p),p),$$ where $$G_{12}(s,p)=s^{10}-9ps^8+28p^2s^6-35p^3s^4+15p^4s^2-p^5.$$ \end{corollary}
As noted previously, \ref{tau corollary 1} can be reformulated in terms of the hypergeometric function $\hg{\xi}{\xi^5}{\varepsilon}{t}$. In fact, we can inductively arrive at a formula for $\tau(p)$ in terms only of $10^{th}$ powers of this hypergeometric function.
\begin{corollary}\label{tau corollary 2} Let $p\equiv 1 \pmod{12}$ be prime and let $a$, $b$, $c$, and $d$ be defined as above. Let $\xi$ be an element of order $12$ in $\widehat{\mathbb{F}_p^{\times}}$. Then \begin{align*} \tau(p)&=42p^6-90p^4-75p^3-35p^2-9p-1-2^9(a^{10}+b^{10})\\ &\quad -\frac{1}{3}\left( (c+d)^{10}+(2c-d)^{10}+(c-2d)^{10} \right) - \sum_{t=2}^{p-1} p^{10}\phi(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}^{10}. \end{align*} \end{corollary}
\begin{proof} Recall from the statement of Theorem \ref{second main theorem} that we have $$\lambda(k,p)=\frac{1}{2}[G_k(2a,p)+G_k(2b,p)]+\frac{1}{3}[G_k(c+d,p)+G_k(2c-d,p)+G_k(c-2d,p)],$$ where $$G_k(s,p)=\sum_{j=0}^{\frac{k}{2}-1}(-1)^j\binom{k-2-j}{j}p^js^{k-2j-2}.$$ Then, one can check by hand or with Maple that we have the following, recalling the relations $p=a^2+b^2=c^2-cd+d^2$: \begin{align*}\label{lambdas} \lambda(4,p)&=2p\\ \lambda(6,p)&=-4p^2+2^3(a^4+b^4)\\ \lambda(8,p)&=-8p^3+2^5(a^6+b^6)-40p(a^4+b^4)+\frac{1}{3}((c+d)^6+(2c-d)^6+(c-2d)^6)\\ \lambda(10,p)&=52p^4+2^7(a^8+b^8)-224p(a^6+b^6)+120p^2(a^4+b^4)\\ &\quad+\frac{1}{3}((c+d)^8+(2c-d)^8+(c-2d)^8)-\frac{7}{3}p((c+d)^6+(2c-d)^6+(c-2d)^6)\\ \lambda(12,p)&=-152p^5+2^{9}(a^{10}+b^{10})-1152p(a^8+b^8)+896p^2(a^6+b^6)-280p^3(a^4+b^4)\\ &\quad+\frac{1}{3}((c+d)^{10}+(2c-d)^{10}+(c-2d)^{10})\\&\quad-3p((c+d)^8+(2c-d)^8+(c-2d)^8)\\ &\quad+\frac{28}{3}p^2((c+d)^6+(2c-d)^6+(c-2d)^6). \end{align*} By using each successive formula for $G_k(a(t,p),p)$, together with Theorem \ref{second main theorem} and the formulas for $\lambda(k,p)$ given above, we can compute $\sum_{t=2}^{p-1}a(t,p)^{k-2}$, for $k=4,\dots,12$. We exhibit the computations in the cases $k=4$ and $k=6$, to give the idea of the technique. First, notice that $G_4(s,p)=s^2-p$ and recall $\textnormal{Tr}_4(\Gamma,p)=0$, as there are no cusp forms of weight $4$ for $\Gamma$. Thus, Theorem \ref{second main theorem} implies \begin{align*} 0=\textnormal{Tr}_4(\Gamma,p)&=-1-\lambda(4,p)-\sum_{t=2}^{p-1}G_4(a(t,p),p)\\ &=-1-2p-\sum_{t=2}^{p-1}(a(t,p)^2-p)\\ &=-1-2p+p(p-2)-\sum_{t=2}^{p-1}a(t,p)^2. \end{align*} Thus, after simplifying, we see that \begin{equation}\label{power 2} 0=p^2-4p-1-\sum_{t=2}^{p-1}a(t,p)^2. \end{equation} Now, we utilize this computation to derive a formula for the sum of $4^{th}$ powers of $a(t,p)$. For $k=6$, we have $G_6(s,p)=s^4-3ps^2+p^2$ and once again $\textnormal{Tr}_6(\Gamma,p)=0$. Then, by Theorem \ref{second main theorem} and the formula for $\lambda(6,p)$ given at the start of the proof, we see that \begin{align*} 0=\textnormal{Tr}_6(\Gamma,p)&=-1-\lambda(6,p)-\sum_{t=2}^{p-1}G_6(a(t,p),p)\\ &=-1+4p^2-2^3(a^4+b^4)-\sum_{t=2}^{p-1}(a(t,p)^4-3pa(t,p)^2+p^2). \end{align*} We distribute the summation across the polynomial $G_6(a(t,p),p)$ and then make a substitution for $\sum_{t=2}^{p-1}a(t,p)^2$, according to (\ref{power 2}). This gives \begin{align*} 0=\textnormal{Tr}_6(\Gamma,p)&=4p^2-1-2^3(a^4+b^4)-\sum_{t=2}^{p-1}a(t,p)^4+3p\sum_{t=2}^{p-1}a(t,p)^2-p^2(p-2)\\ &=4p^2-1-2^3(a^4+b^4)-\sum_{t=2}^{p-1}a(t,p)^4\\ &\hspace*{0.75in}+3p(-2p-1+p(p-2))-p^2(p-2). \end{align*} After simplifying, we arrive at \begin{equation}\label{power 4} 0=2p^3-6p^2-3p-2^3(a^4+b^4)-1-\sum_{t=2}^{p-1}a(t,p)^4. \end{equation} We continue this process, using successive formulas for $G_k(s,p)$ and $\lambda(k,p)$ and back-substituting previous results such as (\ref{power 2}) and (\ref{power 4}). We omit the tedious details of the next couple of cases, which result in the following: \begin{multline}\label{power 6} \textnormal{Tr}_8(\Gamma,p)=0=5p^4-9p^2-5p-1-2^5(a^6+b^6)\\-\frac{1}{3}((c+d)^6+(2c-d)^6+(c-2d)^6)-\sum_{t=2}^{p-1}a(t,p)^6 \end{multline} \begin{multline}\label{power 8} \textnormal{Tr}_{10}(\Gamma,p)=0=14p^5-28p^3-20p^2-7p-1-2^7(a^8+b^8)\\-\frac{1}{3}((c+d)^8+(2c-d)^8+(c-2d)^8)-\sum_{t=2}^{p-1}a(t,p)^8 \end{multline}
Now, we use (\ref{power 2}),$\dots$,(\ref{power 8}) together with the formula for $\lambda(12,p)$ from the beginning of the proof to compute a formula for $\tau(p)$. Since $G_{12}(s,p)=s^{10}-9ps^8+28p^2s^6-35p^3s^4+15p^4s^2-p^5$ and $\textnormal{Tr}_{12}(\Gamma,p)=\tau(p)$, Theorem \ref{second main theorem} gives \begin{align*} \tau(p)&=-1-\lambda(12,p)-\sum_{t=2}^{p-1}G_{12}(a(t,p),p)\\ &=-1-\lambda(12,p)-\sum_{t=2}^{p-1}a(t,p)^{10}+9p\sum_{t=2}^{p-1}a(t,p)^8-28p^2\sum_{t=2}^{p-1}a(t,p)^6\\ &\hspace*{0.2in}+35p^3\sum_{t=2}^{p-1}a(t,p)^4-15p^4\sum_{t=2}^{p-1}a(t,p)^2+p^5(p-2) \end{align*}
Substitutions via (\ref{power 2}),$\dots$,(\ref{power 8}), together with the formula for $\lambda(12,p)$, give rise to many cancellations, resulting in \begin{multline}\label{power 10} \tau(p)=42p^6-90p^4-75p^3-35p^2-9p-1-2^9(a^{10}+b^{10})\\-\frac{1}{3}((c+d)^{10}+(2c-d)^{10}+(c-2d)^{10})-\sum_{t=2}^{p-1}a(t,p)^{10}.
\end{multline}
Finally, to complete the proof, we recall that Theorem \ref{first main theorem} implies $$p\, \hg{\xi}{\xi^5}{\varepsilon}{t}=-\phi(2)\xi^{-3}(1-t)a(t,p)$$ for $t\in\fp \backslash \{0,1\}$. Thus, $$a(t,p)^{10}=\left(-p\phi(2)\xi^3(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}\right)^{10}=p^{10}\phi(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}^{10},$$ since $\phi^{10}=\varepsilon$ and $\xi^{30}=\xi^6=\phi$. This, together with (\ref{power 10}), confirms the corollary. \end{proof}
The technique used in the proof of Corollary \ref{tau corollary 2} can be extended one step further to arrive at yet another formula for $\tau(p)$: \begin{corollary}\label{tau corollary 3} Let $p\equiv 1 \pmod{12}$ be prime and let $a$, $b$, $c$, and $d$ be defined as above. Let $\xi$ be an element of order $12$ in $\widehat{\mathbb{F}_p^{\times}}$. Then \begin{align*} \tau(p)&=12p^6-27p^4-25p^3-14p^2-\frac{54}{11}p-1-\frac{1}{11p}-\frac{2^{11}}{11p}(a^{12}+b^{12})\\ &\hspace*{0.2in}-\frac{1}{33p}((c+d)^{12}+(2c-d)^{12}+(c-2d)^{12})-\frac{1}{11}\sum_{t=2}^{p-1}p^{11}\,\hg{\xi}{\xi^5}{\varepsilon}{t}^{12}. \end{align*} \end{corollary}
\begin{proof} The proof follows in the same way as for Corollary \ref{tau corollary 2}, but by taking $k=14$, so we give a sketch here. First, one calculates that
\begin{equation*} G_{14}(s,p)=s^{12}-11ps^{10}+45p^2s^8-84p^3s^6+70p^4s^4-21p^5s^2+p^6. \end{equation*} Now, since there are no cusp forms of level $14$ for $\Gamma$, we have $\textnormal{Tr}_{14}(\Gamma,p)=0$. Thus, Theorem \ref{second main theorem} implies \begin{equation*} 0=-1-\lambda(14,p)-\sum_{t=2}^{p-1}G_{14}(a(t,p),p). \end{equation*} Now, by applying (\ref{power 2}),$\dots$,(\ref{power 10}), together with a formula for $\lambda(14,p)$, given by
\begin{align*}
\lambda(14,p)&=338p^6+2^{11}(a^{12}+b^{12})-11\cdot2^9p(a^{10}+b^{10})+45\cdot2^7p^2(a^8+b^8)\\ &\hspace*{0.2in}-84\cdot2^5p^3(a^6+b^6)+70\cdot2^3p^4(a^4+b^4)\\ &\hspace*{0.2in}+\frac{1}{3}((c+d)^{12}+(2c-d)^{12}+(c-2d)^{12})\\ &\hspace*{0.2in}-\frac{11}{3}p((c+d)^{10}+(2c-d)^{10}+(c-2d)^{10})\\ &\hspace*{0.2in}+15p^2((c+d)^8+(2c-d)^8+(c-2d)^8)\\ &\hspace*{0.2in}-28p^3((c+d)^6+(2c-d)^6+(c-2d)^6), \end{align*} one makes cancellations and finds that \begin{multline}\label{power 12} 0=132p^7-297p^5-275p^4-154p^3-54p^2-1-11p-11p\tau(p)-2^{11}(a^{12}+b^{12})\\-\frac{1}{3}((c+d)^{12}+(2c-d)^{12}+(c-2d)^{12})-\sum_{t=2}^{p-1}a(t,p)^{12}. \end{multline} We now recall that Theorem \ref{first main theorem} implies $$p\, \hg{\xi}{\xi^5}{\varepsilon}{t}=-\phi(2)\xi^{-3}(1-t)a(t,p)$$ for $t\in\fp \backslash \{0,1\}$. Therefore, $$a(t,p)^{12}=\left(-p\phi(2)\xi^3(1-t)\hg{\xi}{\xi^5}{\varepsilon}{t}\right)^{12}=p^{12}\, \hg{\xi}{\xi^5}{\varepsilon}{t}^{12},$$ since $\phi$ has order $2$ and $\xi$ has order $12$. Making this substitution into (\ref{power 12}) and then solving for $\tau(p)$ gives the desired result.
\end{proof}
\section*{Acknowledgments} The author thanks her advisor M. Papanikolas for his advice and support during the preparation of this paper. The author also thanks the Department of Mathematics at Texas A$\&$M University, where the majority of this research was conducted.
\end{document} | arXiv |
Help with math
Visual illusions
Cut the knot!
What is what?
Inventor's paradox
Math as language
Outline mathematics
Analogue gadgets
Proofs in mathematics
Things impossible
Index/Glossary
Fast Arithmetic Tips
Stories for young
Make an identity
Elementary geometry
Without Loss of Generality
Without loss of generality - WLOG, for short - is a frequent stratagem in problem solving. It is incredibly powerful, although, at first sight, often appears innocuous. The essence of WLOG is in making a random selection among a number of available ones for the reason of all possible variants being equipotent, i.e., leading to exactly same procedure and result. This is akeen to the arguments by symmetry or analogy, but, perhaps, made more explicitly.
An almost classical example appeared in The Mathematical Gazette (v 98, n 543, Nov 2014, p 487):
Assume $a,b,c\ge 0.$ Prove that
$\begin{align} (b+c-a)(b-c)^{2}+(c+&a-b)(c-a)^{2}\\ &+(a+b-c)(a-b)^{2}\ge 0. \end{align}$
To avoid repetitions, denote the left-hand side of the inequality $f(a,b,c).$ Assume, without loss of generality, that $a\le b\le c.$ (Since the set $\mathbb{R}$ of all real number is totally ordered, the three numbers are bound to come in a certain order. For specific numbers the order may not be known a priori; but it does not matter: we can get one ordering from another by simply renaming the numbers.)
Assuming $a\le b\le c$ leads to a one-step solution. Note that under this assumption $(c-a)^{2}\ge (a-b)^{2}$ which implies
$f(a,b,c)\ge (b+c-a)(b-c)^{2}+2a(a-b)^{2}\ge 0.$
A similar assumption works for another problem:
Find all right triangles all of whose side lengths are Fibonacci numbers.
There are no such triangle. Indeed, take any three Fibonacci numbers, $F_m,$ $F_n,$ $F_p.$ Assume without loss of generality that $m \lt n \lt p.$ Then
$\begin{align} F_m + F_n &\le F_{n-1} + F_n\\ &= F_{n+1}\\ &\le F_p, \end{align}$
But the lengths of the sides of a triangle should satisfy the triangle inequality: $F_{m}+F_{n}\gt F_p.$
Points in the plane are each colored with one of two colors: red or blue. Prove that, for a given distance $d,$ there always exist two points of the same color at the distance $d$ from each other.
Consider the vertices of an arbitrary equilateral triangle $ABC$ of side length $d.$ Without loss of generality, we may assume that one of them, say, $A$ is red. Then one of the two: either both $B$ and $C$ are blue (and solve the problem), or one of them is red and, thus, pairs up with $A$ for a solution.
Here are additional examples; many more could be found by searching this site.
A Curious Property of Numbers 3 and 5
How to write an equation of the union of two sets
Central and Inscribed Angles in Complex Numbers
Four Travelers, Ken Ross' Solution
The Affirmative Action Problem
Pythagorean Theorem, a Proof by David Houston
All antichains
What Is the Extremal Principle?
No Equilateral Triangles, Please
Bottema in Three Rotations
Pigeonhole with Disjoint Intervals
Lines Crossing Circles at Vertices of Equilateral Triangle
Sanchez's Viviani's Area Analogue
Schur's Inequality
Chasing Secant Angles
An Inequality with Constraint VIII
Cyclic Quadrilateral from the USAMO
An Inequality in Integers II
Occasionally, the WLOG reasoning may not be applicable, appearances notwithstanding. Here's one example.
|Contact| |Front page| |Contents| |What is What|
Copyright © 1996-2018 Alexander Bogomolny | CommonCrawl |
Hypercomputation
Hypercomputation or super-Turing computation is a set of models of computation that can provide outputs that are not Turing-computable. For example, a machine that could solve the halting problem would be a hypercomputer; so too would one that can correctly evaluate every statement in Peano arithmetic.
The Church–Turing thesis states that any "computable" function that can be computed by a mathematician with a pen and paper using a finite set of simple algorithms, can be computed by a Turing machine. Hypercomputers compute functions that a Turing machine cannot and which are, hence, not computable in the Church–Turing sense.
Technically, the output of a random Turing machine is uncomputable; however, most hypercomputing literature focuses instead on the computation of deterministic, rather than random, uncomputable functions.
History
A computational model going beyond Turing machines was introduced by Alan Turing in his 1938 PhD dissertation Systems of Logic Based on Ordinals.[1] This paper investigated mathematical systems in which an oracle was available, which could compute a single arbitrary (non-recursive) function from naturals to naturals. He used this device to prove that even in those more powerful systems, undecidability is still present. Turing's oracle machines are mathematical abstractions, and are not physically realizable.[2]
State space
In a sense, most functions are uncomputable: there are $\aleph _{0}$ computable functions, but there are an uncountable number ($2^{\aleph _{0}}$) of possible super-Turing functions.[3]
Models
Hypercomputer models range from useful but probably unrealizable (such as Turing's original oracle machines), to less-useful random-function generators that are more plausibly "realizable" (such as a random Turing machine).
Uncomputable inputs or black-box components
A system granted knowledge of the uncomputable, oracular Chaitin's constant (a number with an infinite sequence of digits that encode the solution to the halting problem) as an input can solve a large number of useful undecidable problems; a system granted an uncomputable random-number generator as an input can create random uncomputable functions, but is generally not believed to be able to meaningfully solve "useful" uncomputable functions such as the halting problem. There are an unlimited number of different types of conceivable hypercomputers, including:
• Turing's original oracle machines, defined by Turing in 1939.
• A real computer (a sort of idealized analog computer) can perform hypercomputation[4] if physics admits general real variables (not just computable reals), and these are in some way "harnessable" for useful (rather than random) computation. This might require quite bizarre laws of physics (for example, a measurable physical constant with an oracular value, such as Chaitin's constant), and would require the ability to measure the real-valued physical value to arbitrary precision, though standard physics makes such arbitrary-precision measurements theoretically infeasible.[5]
• Similarly, a neural net that somehow had Chaitin's constant exactly embedded in its weight function would be able to solve the halting problem,[6] but is subject to the same physical difficulties as other models of hypercomputation based on real computation.
• Certain fuzzy logic-based "fuzzy Turing machines" can, by definition, accidentally solve the halting problem, but only because their ability to solve the halting problem is indirectly assumed in the specification of the machine; this tends to be viewed as a "bug" in the original specification of the machines.[7][8]
• Similarly, a proposed model known as fair nondeterminism can accidentally allow the oracular computation of noncomputable functions, because some such systems, by definition, have the oracular ability to identify reject inputs that would "unfairly" cause a subsystem to run forever.[9][10]
• Dmytro Taranovsky has proposed a finitistic model of traditionally non-finitistic branches of analysis, built around a Turing machine equipped with a rapidly increasing function as its oracle. By this and more complicated models he was able to give an interpretation of second-order arithmetic. These models require an uncomputable input, such as a physical event-generating process where the interval between events grows at an uncomputably large rate.[11]
• Similarly, one unorthodox interpretation of a model of unbounded nondeterminism posits, by definition, that the length of time required for an "Actor" to settle is fundamentally unknowable, and therefore it cannot be proven, within the model, that it does not take an uncomputably long period of time.[12]
"Infinite computational steps" models
In order to work correctly, certain computations by the machines below literally require infinite, rather than merely unlimited but finite, physical space and resources; in contrast, with a Turing machine, any given computation that halts will require only finite physical space and resources.
A Turing machine that can complete infinitely many steps in finite time, a feat known as a supertask. Simply being able to run for an unbounded number of steps does not suffice. One mathematical model is the Zeno machine (inspired by Zeno's paradox). The Zeno machine performs its first computation step in (say) 1 minute, the second step in ½ minute, the third step in ¼ minute, etc. By summing 1 + ½ + ¼ + ... (a geometric series) we see that the machine performs infinitely many steps in a total of 2 minutes. According to Shagrir, Zeno machines introduce physical paradoxes and its state is logically undefined outside of one-side open period of [0, 2), thus undefined exactly at 2 minutes after beginning of the computation.[13]
It seems natural that the possibility of time travel (existence of closed timelike curves (CTCs)) makes hypercomputation possible by itself. However, this is not so since a CTC does not provide (by itself) the unbounded amount of storage that an infinite computation would require. Nevertheless, there are spacetimes in which the CTC region can be used for relativistic hypercomputation.[14] According to a 1992 paper,[15] a computer operating in a Malament–Hogarth spacetime or in orbit around a rotating black hole[16] could theoretically perform non-Turing computations for an observer inside the black hole.[17][18] Access to a CTC may allow the rapid solution to PSPACE-complete problems, a complexity class which, while Turing-decidable, is generally considered computationally intractable.[19][20]
Quantum models
Some scholars conjecture that a quantum mechanical system which somehow uses an infinite superposition of states could compute a non-computable function.[21] This is not possible using the standard qubit-model quantum computer, because it is proven that a regular quantum computer is PSPACE-reducible (a quantum computer running in polynomial time can be simulated by a classical computer running in polynomial space).[22]
"Eventually correct" systems
Some physically realizable systems will always eventually converge to the correct answer, but have the defect that they will often output an incorrect answer and stick with the incorrect answer for an uncomputably large period of time before eventually going back and correcting the mistake.
In mid 1960s, E Mark Gold and Hilary Putnam independently proposed models of inductive inference (the "limiting recursive functionals"[23] and "trial-and-error predicates",[24] respectively). These models enable some nonrecursive sets of numbers or languages (including all recursively enumerable sets of languages) to be "learned in the limit"; whereas, by definition, only recursive sets of numbers or languages could be identified by a Turing machine. While the machine will stabilize to the correct answer on any learnable set in some finite time, it can only identify it as correct if it is recursive; otherwise, the correctness is established only by running the machine forever and noting that it never revises its answer. Putnam identified this new interpretation as the class of "empirical" predicates, stating: "if we always 'posit' that the most recently generated answer is correct, we will make a finite number of mistakes, but we will eventually get the correct answer. (Note, however, that even if we have gotten to the correct answer (the end of the finite sequence) we are never sure that we have the correct answer.)"[24] L. K. Schubert's 1974 paper "Iterated Limiting Recursion and the Program Minimization Problem"[25] studied the effects of iterating the limiting procedure; this allows any arithmetic predicate to be computed. Schubert wrote, "Intuitively, iterated limiting identification might be regarded as higher-order inductive inference performed collectively by an ever-growing community of lower order inductive inference machines."
A symbol sequence is computable in the limit if there is a finite, possibly non-halting program on a universal Turing machine that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π and of every other computable real, but still excludes all noncomputable reals. The 'Monotone Turing machines' traditionally used in description size theory cannot edit their previous outputs; generalized Turing machines, as defined by Jürgen Schmidhuber, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges; that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt Gödel (1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problem could be solved. Schmidhuber ([26][27]) uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everything. Generalized Turing machines can eventually converge to a correct solution of the halting problem by evaluating a Specker sequence.
Analysis of capabilities
Many hypercomputation proposals amount to alternative ways to read an oracle or advice function embedded into an otherwise classical machine. Others allow access to some higher level of the arithmetic hierarchy. For example, supertasking Turing machines, under the usual assumptions, would be able to compute any predicate in the truth-table degree containing $\Sigma _{1}^{0}$ or $\Pi _{1}^{0}$. Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree, which is known to be $\Delta _{2}^{0}$. Gold further showed that limiting partial recursion would allow the computation of precisely the $\Sigma _{2}^{0}$ predicates.
Model Computable predicates Notes Refs
supertasking $\operatorname {tt} \left(\Sigma _{1}^{0},\Pi _{1}^{0}\right)$ dependent on outside observer [28]
limiting/trial-and-error $\Delta _{2}^{0}$ [23]
iterated limiting (k times) $\Delta _{k+1}^{0}$ [25]
Blum–Shub–Smale machine incomparable with traditional computable real functions [29]
Malament–Hogarth spacetime HYP dependent on spacetime structure [30]
analog recurrent neural network $\Delta _{1}^{0}[f]$ f is an advice function giving connection weights; size is bounded by runtime [31][32]
infinite time Turing machine $AQI$ Arithmetical Quasi-Inductive sets [33]
classical fuzzy Turing machine $\Sigma _{1}^{0}\cup \Pi _{1}^{0}$ for any computable t-norm [8]
increasing function oracle $\Delta _{1}^{1}$ for the one-sequence model; $\Pi _{1}^{1}$ are r.e. [11]
Criticism
Martin Davis, in his writings on hypercomputation,[34][35] refers to this subject as "a myth" and offers counter-arguments to the physical realizability of hypercomputation. As for its theory, he argues against the claims that this is a new field founded in the 1990s. This point of view relies on the history of computability theory (degrees of unsolvability, computability over functions, real numbers and ordinals), as also mentioned above. In his argument, he makes a remark that all of hypercomputation is little more than: "if non-computable inputs are permitted, then non-computable outputs are attainable."[36]
See also
• Digital physics
• Limits of computation
References
1. Turing, A. M. (1939). "Systems of Logic Based on Ordinals†". Proceedings of the London Mathematical Society. 45: 161–228. doi:10.1112/plms/s2-45.1.161. hdl:21.11116/0000-0001-91CE-3.
2. "Let us suppose that we are supplied with some unspecified means of solving number-theoretic problems; a kind of oracle as it were. We shall not go any further into the nature of this oracle apart from saying that it cannot be a machine" (Undecidable p. 167, a reprint of Turing's paper Systems of Logic Based On Ordinals)
3. J. Cabessa; H.T. Siegelmann (Apr 2012). "The Computational Power of Interactive Recurrent Neural Networks" (PDF). Neural Computation. 24 (4): 996–1019. CiteSeerX 10.1.1.411.7540. doi:10.1162/neco_a_00263. PMID 22295978. S2CID 5826757.
4. Arnold Schönhage, "On the power of random access machines", in Proc. Intl. Colloquium on Automata, Languages, and Programming (ICALP), pages 520–529, 1979. Source of citation: Scott Aaronson, "NP-complete Problems and Physical Reality" p. 12
5. Andrew Hodges. "The Professors and the Brainstorms". The Alan Turing Home Page. Retrieved 23 September 2011.
6. H.T. Siegelmann; E.D. Sontag (1994). "Analog Computation via Neural Networks". Theoretical Computer Science. 131 (2): 331–360. doi:10.1016/0304-3975(94)90178-3.
7. Biacino, L.; Gerla, G. (2002). "Fuzzy logic, continuity and effectiveness". Archive for Mathematical Logic. 41 (7): 643–667. CiteSeerX 10.1.1.2.8029. doi:10.1007/s001530100128. ISSN 0933-5846. S2CID 12513452.
8. Wiedermann, Jiří (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theoretical Computer Science. 317 (1–3): 61–69. doi:10.1016/j.tcs.2003.12.004. Their (ability to solve the halting problem) is due to their acceptance criterion in which the ability to solve the halting problem is indirectly assumed.
9. Edith Spaan; Leen Torenvliet; Peter van Emde Boas (1989). "Nondeterminism, Fairness and a Fundamental Analogy". EATCS Bulletin. 37: 186–193.
10. Ord, Toby (2006). "The many forms of hypercomputation". Applied Mathematics and Computation. 178: 143–153. doi:10.1016/j.amc.2005.09.076.
11. Dmytro Taranovsky (July 17, 2005). "Finitism and Hypercomputation". Retrieved Apr 26, 2011.
12. Hewitt, Carl. "What Is Commitment." Physical, Organizational, and Social (Revised), Coordination, Organizations, Institutions, and Norms in Agent Systems II: AAMAS (2006).
13. These models have been independently developed by many different authors, including Hermann Weyl (1927). Philosophie der Mathematik und Naturwissenschaft.; the model is discussed in Shagrir, O. (June 2004). "Super-tasks, accelerating Turing machines and uncomputability". Theoretical Computer Science. 317 (1–3): 105–114. doi:10.1016/j.tcs.2003.12.007., Petrus H. Potgieter (July 2006). "Zeno machines and hypercomputation". Theoretical Computer Science. 358 (1): 23–33. arXiv:cs/0412022. doi:10.1016/j.tcs.2005.11.040. S2CID 6749770. and Vincent C. Müller (2011). "On the possibilities of hypercomputing supertasks". Minds and Machines. 21 (1): 83–96. CiteSeerX 10.1.1.225.3696. doi:10.1007/s11023-011-9222-6. S2CID 253434.
14. Andréka, Hajnal; Németi, István; Székely, Gergely (2012). "Closed Timelike Curves in Relativistic Computation". Parallel Processing Letters. 22 (3). arXiv:1105.0047. doi:10.1142/S0129626412400105. S2CID 16816151.
15. Hogarth, Mark L. (1992). "Does general relativity allow an observer to view an eternity in a finite time?". Foundations of Physics Letters. 5 (2): 173–181. Bibcode:1992FoPhL...5..173H. doi:10.1007/BF00682813. S2CID 120917288.
16. István Neméti; Hajnal Andréka (2006). "Can General Relativistic Computers Break the Turing Barrier?". Logical Approaches to Computational Barriers, Second Conference on Computability in Europe, CiE 2006, Swansea, UK, June 30-July 5, 2006. Proceedings. Lecture Notes in Computer Science. Vol. 3988. Springer. doi:10.1007/11780342. ISBN 978-3-540-35466-6.
17. Etesi, Gabor; Nemeti, Istvan (2002). "Non-Turing computations via Malament-Hogarth space-times". International Journal of Theoretical Physics. 41 (2): 341–370. arXiv:gr-qc/0104023. doi:10.1023/A:1014019225365. S2CID 17081866.
18. Earman, John; Norton, John D. (1993). "Forever is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes". Philosophy of Science. 60: 22–42. doi:10.1086/289716. S2CID 122764068.
19. Brun, Todd A. (2003). "Computers with closed timelike curves can solve hard problems". Found. Phys. Lett. 16 (3): 245–253. arXiv:gr-qc/0209061. doi:10.1023/A:1025967225931. S2CID 16136314.
20. S. Aaronson and J. Watrous. Closed Timelike Curves Make Quantum and Classical Computing Equivalent
21. There have been some claims to this effect; see Tien Kieu (2003). "Quantum Algorithm for the Hilbert's Tenth Problem". Int. J. Theor. Phys. 42 (7): 1461–1478. arXiv:quant-ph/0110136. doi:10.1023/A:1025780028846. S2CID 6634980. or M. Ziegler (2005). "Computational Power of Infinite Quantum Parallelism". International Journal of Theoretical Physics. 44 (11): 2059–2071. arXiv:quant-ph/0410141. Bibcode:2005IJTP...44.2059Z. doi:10.1007/s10773-005-8984-0. S2CID 9879859. and the ensuing literature. For a retort see Warren D. Smith (2006). "Three counterexamples refuting Kieu's plan for "quantum adiabatic hypercomputation"; and some uncomputable quantum mechanical tasks". Applied Mathematics and Computation. 178 (1): 184–193. doi:10.1016/j.amc.2005.09.078..
22. Bernstein, Ethan; Vazirani, Umesh (1997). "Quantum Complexity Theory". SIAM Journal on Computing. 26 (5): 1411–1473. doi:10.1137/S0097539796300921.
23. E. M. Gold (1965). "Limiting Recursion". Journal of Symbolic Logic. 30 (1): 28–48. doi:10.2307/2270580. JSTOR 2270580. S2CID 33811657., E. Mark Gold (1967). "Language identification in the limit". Information and Control. 10 (5): 447–474. doi:10.1016/S0019-9958(67)91165-5.
24. Hilary Putnam (1965). "Trial and Error Predicates and the Solution to a Problem of Mostowksi". Journal of Symbolic Logic. 30 (1): 49–57. doi:10.2307/2270581. JSTOR 2270581. S2CID 44655062.
25. L. K. Schubert (July 1974). "Iterated Limiting Recursion and the Program Minimization Problem". Journal of the ACM. 21 (3): 436–445. doi:10.1145/321832.321841. S2CID 2071951.
26. Schmidhuber, Juergen (2000). "Algorithmic Theories of Everything". arXiv:quant-ph/0011122.
27. J. Schmidhuber (2002). "Hierarchies of generalized Kolmogorov complexities and nonenumerable universal measures computable in the limit". International Journal of Foundations of Computer Science. 13 (4): 587–612. arXiv:quant-ph/0011122. Bibcode:2000quant.ph.11122S. doi:10.1142/S0129054102001291.
28. Petrus H. Potgieter (July 2006). "Zeno machines and hypercomputation". Theoretical Computer Science. 358 (1): 23–33. arXiv:cs/0412022. doi:10.1016/j.tcs.2005.11.040. S2CID 6749770.
29. Lenore Blum, Felipe Cucker, Michael Shub, and Stephen Smale (1998). Complexity and Real Computation. Springer. ISBN 978-0-387-98281-6.{{cite book}}: CS1 maint: multiple names: authors list (link)
30. P.D. Welch (2008). "The extent of computation in Malament-Hogarth spacetimes". British Journal for the Philosophy of Science. 59 (4): 659–674. arXiv:gr-qc/0609035. doi:10.1093/bjps/axn031.
31. H.T. Siegelmann (Apr 1995). "Computation Beyond the Turing Limit" (PDF). Science. 268 (5210): 545–548. Bibcode:1995Sci...268..545S. doi:10.1126/science.268.5210.545. PMID 17756722. S2CID 17495161.
32. Hava Siegelmann; Eduardo Sontag (1994). "Analog Computation via Neural Networks". Theoretical Computer Science. 131 (2): 331–360. doi:10.1016/0304-3975(94)90178-3.
33. P.D. Welch (2009). "Characteristics of discrete transfinite time Turing machine models: Halting times, stabilization times, and Normal Form theorems". Theoretical Computer Science. 410 (4–5): 426–442. doi:10.1016/j.tcs.2008.09.050.
34. Davis, Martin (2006). "Why there is no such discipline as hypercomputation". Applied Mathematics and Computation. 178 (1): 4–7. doi:10.1016/j.amc.2005.09.066.
35. Davis, Martin (2004). "The Myth of Hypercomputation". Alan Turing: Life and Legacy of a Great Thinker. Springer.
36. Martin Davis (Jan 2003). "The Myth of Hypercomputation". In Alexandra Shlapentokh (ed.). Miniworkshop: Hilbert's Tenth Problem, Mazur's Conjecture and Divisibility Sequences (PDF). MFO Report. Vol. 3. Mathematisches Forschungsinstitut Oberwolfach. p. 2.
Further reading
• Aoun, Mario Antoine (2016). "Advances in Three Hypercomputation Models" (PDF). Electronic Journal of Theoretical Physics. 13 (36): 169–182.
• Burgin, M. S. (1983). "Inductive Turing Machines". Notices of the Academy of Sciences of the USSR. 270 (6): 1289–1293.
• Burgin, Mark (2005). Super-recursive algorithms. Monographs in computer science. Springer. ISBN 0-387-95569-0.
• Cockshott, P.; Michaelson, G. (2007). "Are there new Models of Computation? Reply to Wegner and Eberbach". The Computer Journal. doi:10.1093/comjnl/bxl062.
• Cooper, S. B.; Odifreddi, P. (2003). "Incomputability in Nature" (PDF). In Cooper, S. B.; Goncharov, S. S. (eds.). Computability and Models: Perspectives East and West. New York, Boston, Dordrecht, London, Moscow: Plenum Publishers. pp. 137–160. Archived from the original (PDF) on 2011-07-24. Retrieved 2011-06-16.
• Cooper, S. B. (2006). "Definability as hypercomputational effect". Applied Mathematics and Computation. 178: 72–82. CiteSeerX 10.1.1.65.4088. doi:10.1016/j.amc.2005.09.072. S2CID 1487739.
• Copeland, J. (2002). "Hypercomputation" (PDF). Minds and Machines. 12 (4): 461–502. doi:10.1023/A:1021105915386. S2CID 218585685. Archived from the original (PDF) on 2016-03-14.
• Hagar, A.; Korolev, A. (2007). "Quantum Hypercomputation—Hype or Computation?*" (PDF). Philosophy of Science. 74 (3): 347–363. doi:10.1086/521969. S2CID 9857468.
• Ord, Toby (2002). "Hypercomputation: Computing more than the Turing machine can compute: A survey article on various forms of hypercomputation". arXiv:math/0209332.
• Piccinini, Gualtiero (June 16, 2021). "Computation in Physical Systems". Stanford Encyclopedia of Philosophy. Retrieved 2023-07-31.
• Sharma, Ashish (2022). "Nature Inspired Algorithms with Randomized Hypercomputational Perspective". Information Sciences. 608: 670–695. doi:10.1016/j.ins.2022.05.020. S2CID 248881264.
• Stannett, Mike (1990). "X-machines and the halting problem: Building a super-Turing machine". Formal Aspects of Computing. 2 (1): 331–341. doi:10.1007/BF01888233. S2CID 7406983.
• Stannett, Mike (2006). "The case for hypercomputation" (PDF). Applied Mathematics and Computation. 178 (1): 8–24. doi:10.1016/j.amc.2005.09.067. Archived from the original (PDF) on 2016-03-04.
• Syropoulos, Apostolos (2008). Hypercomputation: Computing Beyond the Church–Turing Barrier. Springer. ISBN 978-0-387-30886-9.
Authority control: National
• Germany
| Wikipedia |
HMAC and assumptions on the cryptographic hash
According to Wikipedia, a cryptographic hash function has the following properties:
Pre-image resistance: Given $h$, it's difficult to find any message $m$ such that $h = H(m)$.
Second pre-image resistance: Given $m_1$, it's difficult to find another $m_2$ such that $m_1 \ne m_2$ and $H(m_1) = H(m_2)$
Collision Resistance: It's difficult to find two distinct messages $m_1$ and $m_2$ such that $H(m_1) = H(m_2)$
Assuming $H$ is a hash function, the following function $H'$ should — to my understanding — also be a hash function:
$$H'(m) = m_0 || H(m_1||m_2||\dots||m_k)$$
where $m_i$ is the $i$th byte of $m$.
$H'$ leaks the first byte of $m$, but even just leaking one byte, you still can't find a pre-image or any collisions.
When looking at HMAC, Wikipedia says that it takes a hash function (without maker further assumptions on the hash function). Taking my hash function $H'$ (just let it leak $\operatorname{len}(key)$ bytes, but not the long message) for HMAC, HMAC would be insecure, since everybody now sees the key.
So maybe my $H'$ is not a cryptographic hash function after all — in which case my question is: Why not?
Or $H'$ is a cryptographic hash function, but building an HMAC requires additional assumptions. What additional assumptions must be fulfilled by the hash function to be secure in HMAC? Do the three properties above imply some other properties I don't see?
Also PBKDF2 takes a PRF, where HMAC-SHA256 should be secure, but HMAC just given a hash function which has the three properties, won't be a PRF to my understanding. Again the same questions: Are there more assumptions? Even more than on HMAC?
hash hmac
Gilles 'SO- stop being evil'
So MorrSo Morr
$\begingroup$ > In order for a hash function with n bits of output to be collision resistant, it must take at least $2^n$ work and storage to find a collision Don't you just need $2^{\frac{n}{2}}$ due the birthday attack to find a collision? $\endgroup$
– So Morr
$\begingroup$ In order for a hash function with $n$ bits of output to be collision resistant, it must take at least $2^{n/2}$ work and storage to find a collision. Presuming your hash function $H$ is collision resistant, it is not obvious $H′$ also is collision resistant. Finding two different messages that both share the same prefix, and collide in the last $n−8$ bits, requires less work and less storage than finding a collision in all $n$ bits of $H$. $\endgroup$
– Henrick Hellström
Before we jump into this question, you first need to know a bit about the internals of hash functions with the Merkle-Dåmgard construction. Here's a pretty picture from Wikipedia:
In this diagram, you see the compression function $f$ being fed the message blocks along with the output of the state of the previous compression block (or the IV). The final output is the result of the last compression function. (You can ignore the finalization step for our purposes.)
Now, let's focus on the original NMAC/HMAC paper. In it, the authors state:
In the rest of this paper we will concentrate on iterated hash functions, except if stated otherwise.
This should be the first clue that your scheme is not one that will work with NMAC/HMAC: it's not iterated! Not all of it, at least. The fact that the first $n$ bytes are concatenated (leaked, what have you) means that your hash function's output is no longer solely the result from the compression function evaluated on the last block. This changes the construction of the scheme drastically.
In regular circumstances, the (almost implicit) assumption that the underlying hash function is iterated is not an unreasonable one at all: all of the popular hash functions of today are. (SHA3/Keccak is a bit of a special case. It's not clear one even needs the HMAC construction for it. But that's a topic for another question.)
For example, what do you do with the IV (initialization vector, or as Bellare et al call it, "initial variable")? Do you simply pass it along to the $H$ in $H'$? If so, then your scheme doesn't actually leak the key with NMAC, although it does leak $k \oplus \mathtt{opad}$ in HMAC. In case you're unfamiliar with NMAC, the basic idea of the scheme is replace the IVs of the regular hash functions with the keys $k = (k_1, k_2)$. In the case of HMAC, the "new IVs" are (where $f$ is the compression function for the hash in question) $k_1 = f(k \oplus \mathtt{opad})$ and $k_2 = f(k \oplus \mathtt{ipad})$. But note that this, too, carries with it the implicit assumption that the starting state of the next $f$ in the chain is the previous evaluation of $f$.
Trying to discuss $H'$ in the context of HMAC is difficult, though. The primary issue is that your $H'$ doesn't have a clearly available compression function. Sure, $H$ (probably) has a compression function, but for $H'$, things are much less certain. Even if you attempted to define a compression function for $H'$, in order to be an iterated hash function, it would somehow have to leak the first $n$ bytes of the original message while simultaneously evaluating $H$ for the rest of the message.
Here is the problem, though: even if you created such a compression function, it would be insecure, naturally. Namely, it no longer would act as a pseudorandom function (PRF) (or for Wikipedia's less thorough, but perhaps easier, explanation, see here). In this relatively new paper, Bellare proves that HMAC is a PRF itself if the compression function of the underlying hash is a PRF. If $H'$ had a compression function, then it definitely would not be a PRF, since it (quite literally) leaks part of the input.
The prerequisite that the compression function is a PRF is quite a weak requirement, too. Given that $H'$ (even if you did somehow come up with a compression function for it) simply fails this requirement, the security proofs for HMAC do not cover it. Further, pretty much all of the security proofs given in favor of HMAC assume that the attacker doesn't know the key. Those proofs are possibly invalid if this assumption is invalid.
So, to answer your question directly, HMAC requires an iterated hash scheme whose compression function is, as best as we can tell, a PRF. A generic cryptographic hash function, at least using the definition Wikipedia gives, is not strong enough to guarantee a solid MAC. But the PRF requirement is relatively weak, as even MD5 (which is completely broken as far as collisions go) still appears to satisfy it.
ReidReid
Inspired by Henrick Hellström's comment, I think you need to dig a bit deeper into what "difficult" means.
Pre-image resistance means that given $h$, it's difficult to find $m$ such that $h = H(m)$. Intuitively speaking, your only chance is to have started with an $h$ that is in the relatively small set of already-computed hashes.
Now suppose you have $h'$ and are looking for $m'$ such that $h' = H'(m)$. You have a better chance of finding $m'$ than you had of finding $m$, because if you had previously computed $H'(a||m'') = a||H(m'')$ such that $h' = b||H(m'')$, you can take $m' = b||m''$. With an alphabet of size $n$, $H'$ gives you $n$ times better chances to find a pre-image.
This is perhaps more visible if you think of $H'$ consisting of, say, the first 128 bits of the message followed by a 128-bit hash of the rest. Then $H'$ hashes are 256 bits long but the preimage resistance of $H'$ is no more than that of a 128-bit hash, only half as strong as expected.
A natural question at this point is, what if you define $H''(m) = m_0 || H(m)$? (That is, calculate the same hash, but leak a fixed-size prefix of the message.) You do not get a better chance of finding a pre-computed pre-image. However, the amount of work required to find a pre-image by brute-force is clearly less, because you can concentrate your efforts on messages with the prefix $m_0$. This is actually closer to the mathematical definition of difficulty (computational complexity of finding a pre-image) than the informal explanation above.
I'm not fully satisfied with this explanation. What about $H^\circ(m) = \mathbf{0} || H(m)$ where $\mathbf{0}$ is some constant string? This is obviously as good a hash as $H$ since it doesn't leak anything. Yet the amount of work required to find a pre-image is only as good as $H$, despite the longer hash, which is no different from the complaint against $H'$ above.
In any case, as far as I know, the Wikipedia article is a simplification: there is no general result that any hash function can be used to build a HMAC in this way. The security proofs of HMAC only apply to hash functions of a certain form, which includes all Merkle-Damgård hash functions, but not the oddball variants considered in this thread.
Gilles 'SO- stop being evil'Gilles 'SO- stop being evil'
$\begingroup$ The last part of this answer is the crucial bit: HMAC's security proof relies iterated hash functions, specifically MD constructions. The construction in the question fails this criterion. $\endgroup$
– Reid
$\begingroup$ For modern criteria for HMAC security, I recommend New Proofs for NMAC and HMAC: Security without Collision-Resistance, although it is hard reading and some of it goes over my head. $\endgroup$
– fgrieu ♦
$\begingroup$ @Reid I don't find this fully satisfactory: sure, the proof doesn't apply, but what causes the result not to hold? $\endgroup$
$\begingroup$ @Gilles: The structure of the above construction is entirely different from usual hash schemes. How would you define the compression function for $H'$? And note that in order for NMAC's security proof to be relevant, the scheme needs to be iterated, so you somehow have to define the compression function in such a way that the final state will include the first $n$ bytes of the message. Of course, the compression function needs to be a PRF, but leaking even the first byte of the message sounds like a death knell for that idea. $\endgroup$
$\begingroup$ @Reid Please write an answer that expands on this! I'd be very interested. $\endgroup$
Not the answer you're looking for? Browse other questions tagged hash hmac or ask your own question.
Creating a hash of XOR'd blocks
What type of hash functions provides non-malleability of hash digests?
How does Truecrypt change password without the need for a complete re-encryption of volume
Second pre-image resistance vs Collision resistance
Computational requirements for breaking SHA-256?
Use of cryptographic hash for computing previous block hashes in blockchains | CommonCrawl |
Physics And Astronomy (138)
Materials Research (111)
Chemistry (109)
Statistics and Probability (22)
Psychiatry (13)
MRS Online Proceedings Library Archive (99)
Epidemiology & Infection (22)
Proceedings of the International Astronomical Union (19)
The Journal of Agricultural Science (16)
Journal of Materials Research (10)
Psychological Medicine (10)
Microscopy and Microanalysis (7)
The Journal of Laryngology & Otology (6)
The European Physical Journal - Applied Physics (5)
Bulletin of Entomological Research (3)
International Astronomical Union Colloquium (3)
Journal of Helminthology (3)
Publications of the Astronomical Society of Australia (3)
Agricultural and Resource Economics Review (2)
Animal Science (2)
British Journal of Nutrition (2)
Journal of Mechanics (2)
Powder Diffraction (2)
Cambridge University Press (5)
Materials Research Society (109)
International Astronomical Union (23)
BSAS (16)
Brazilian Society for Microscopy and Microanalysis (SBMM) (7)
The Australian Society of Otolaryngology Head and Neck Surgery (6)
Testing Membership Number Upload (3)
Northeastern Agricultural and Resource Economics Association (2)
Nutrition Society (2)
Global Science Press (1)
International Glaciological Society (1)
Mineralogical Society (1)
Nestle Foundation - enLINK (1)
Royal College of Speech and Language Therapists (1)
The Association for Asian Studies (1)
test society (1)
Cambridge Handbooks in Psychology (2)
Cambridge Handbooks (2)
Cambridge Handbooks of Psychology (2)
A COMPREHENSIVE STUDY OF THE 14C SOURCE TERM IN THE 10 MW HIGH-TEMPERATURE GAS-COOLED REACTOR
X Liu, W Peng, L Wei, M Lou, F Xie, J Cao, J Tong, F Li, G Zheng
Journal: Radiocarbon , First View
Published online by Cambridge University Press: 24 June 2019, pp. 1-15
While assessing the environmental impact of nuclear power plants, researchers have focused their attention on radiocarbon (14C) owing to its high mobility in the environment and important radiological impact on human beings. The 10 MW high-temperature gas-cooled reactor (HTR-10) is the first pebble-bed gas-cooled test reactor in China that adopted helium as primary coolant and graphite spheres containing tristructural-isotropic (TRISO) coated particles as fuel elements. A series of experiments on the 14C source terms in HTR-10 was conducted: (1) measurement of the specific activity and distribution of typical nuclides in the irradiated graphite spheres from the core, (2) measurement of the activity concentration of 14C in the primary coolant, and (3) measurement of the amount of 14C discharged in the effluent from the stack. All experimental data on 14C available for HTR-10 were summarized and analyzed using theoretical calculations. A sensitivity study on the total porosity, open porosity, and percentage of closed pores that became open after irradiating the matrix graphite was performed to illustrate their effects on the activity concentration of 14C in the primary coolant and activity amount of 14C in various deduction routes.
Experimental Investigation of 14C in the Primary Coolant of the 10 MW High Temperature Gas-Cooled Reactor
F Xie, W Peng, J Cao, X Feng, L Wei, J Tong, F Li, K Sun
Journal: Radiocarbon / Volume 61 / Issue 3 / June 2019
Print publication: June 2019
The very high temperature reactor (VHTR) is a development of the high-temperature gas-cooled reactors (HTGRs) and one of the six proposed Generation IV reactor concept candidates. The 10 MW high temperature gas-cooled reactor (HTR-10) is the first pebble-bed gas-cooled test reactor in China. A sampling system for the measurement of carbon-14 (14C) was established in the helium purification system of the HTR-10 primary loop, which could sample 14C from the coolant at three locations. The results showed that activity concentration of 14C in the HTR-10 primary coolant was 1.2(1) × 102 Bq/m3 (STP). The production mechanisms, distribution characteristics, reduction routes, and release types of 14C in HTR-10 were analyzed and discussed. A theoretical model was built to calculate the amount of 14C in the core of HTR-10 and its concentration in the primary coolant. The activation reaction of 13C has been identified to be the dominant 14C source in the core, whereas in the primary coolant, it is the activation of 14N. These results can supplement important information for the source term analysis of 14C in HTR-10 and promote the study of 14C in HTGRs.
Consistent improvements in soil biochemical properties and crop yields by organic fertilization for above-ground (rapeseed) and below-ground (sweet potato) crops
X. P. Li, C. L. Liu, H. Zhao, F. Gao, G. N. Ji, F. Hu, H. X. Li
Journal: The Journal of Agricultural Science / Volume 156 / Issue 10 / December 2018
Published online by Cambridge University Press: 19 March 2019, pp. 1186-1195
Although application of organic fertilizers has become a recommended way for developing sustainable agriculture, it is still unclear whether above-ground and below-ground crops have similar responses to chemical fertilizers (CF) and organic manure (OM) under the same farming conditions. The current study investigated soil quality and crop yield response to fertilization of a double-cropping system with rapeseed (above-ground) and sweet potato (below-ground) in an infertile red soil for 2 years (2014–16). Three fertilizer treatments were compared, including CF, OM and organic manure plus chemical fertilizer (MCF). Organic fertilizers (OM and MCF) increased the yield of both above- and below-ground crops and improved soil biochemical properties significantly. The current study also found that soil-chemical properties were the most important and direct factors in increasing crop yields. Also, crop yield was affected indirectly by soil-biological properties, because no significant effects of soil-biological activities on yield were detected after controlling the positive effects of soil-chemical properties. Since organic fertilizers could not only increase crop yield, but also improve soil nutrients and microbial activities efficiently and continuously, OM application is a reliable agricultural practice for both above- and below-ground crops in the red soils of China.
Accuracy of self-reported weight in the Women's Health Initiative
Juhua Luo, Cynthia A Thomson, Michael Hendryx, Lesley F Tinker, JoAnn E Manson, Yueyao Li, Dorothy A Nelson, Mara Z Vitolins, Rebecca A Seguin, Charles B Eaton, Jean Wactawski-Wende, Karen L Margolis
Journal: Public Health Nutrition / Volume 22 / Issue 6 / April 2019
Published online by Cambridge University Press: 19 November 2018, pp. 1019-1028
Print publication: April 2019
To assess the extent of error present in self-reported weight data in the Women's Health Initiative, variables that may be associated with error, and to develop methods to reduce any identified error.
Prospective cohort study.
Forty clinical centres in the USA.
Women (n 75 336) participating in the Women's Health Initiative Observational Study (WHI-OS) and women (n 6236) participating in the WHI Long Life Study (LLS) with self-reported and measured weight collected about 20 years later (2013–2014).
The correlation between self-reported and measured weights was 0·97. On average, women under-reported their weight by about 2 lb (0·91 kg). The discrepancies varied by age, race/ethnicity, education and BMI. Compared with normal-weight women, underweight women over-reported their weight by 3·86 lb (1·75 kg) and obese women under-reported their weight by 4·18 lb (1·90 kg) on average. The higher the degree of excess weight, the greater the under-reporting of weight. Adjusting self-reported weight for an individual's age, race/ethnicity and education yielded an identical average weight to that measured.
Correlations between self-reported and measured weights in the WHI are high. Discrepancies varied by different sociodemographic characteristics, especially an individual's BMI. Correction of self-reported weight for individual characteristics could improve the accuracy of assessment of obesity status in postmenopausal women.
Epidemiological survey and sequence information analysis of swine hepatitis E virus in Sichuan, China
Y. Y. Li, Z. W. Xu, X. J. Li, S. Y. Gong, Y. Cai, Y. Q. Chen, Y. M. Li, Y. F. Xu, X. G. Sun, L. Zhu
Journal: Epidemiology & Infection / Volume 147 / 2019
Published online by Cambridge University Press: 19 November 2018, e49
Hepatitis E is an important zoonosis that is prevalent in China. Hepatitis E virus (HEV) is a pathogen that affects humans and animals and endangers public health in China. In this study, the detection of HEV epidemics in swine in Sichuan Province, China, was carried out by nested real-time PCR. A total of 174 stool samples and 160 bile samples from swine in Sichuan Province were examined. In addition, software was used to analyse the biological evolution of HEV. The results showed that within 2 years of swine HEV (SHEV) infection in China, SHEV was first detected in Sichuan Province. HEV was endemic in Sichuan; the positive rate for pig farms was 11.1%, and the total positive sample rate was 10.5%. The age of swine with the highest positive rate (17.9%) was 5–9 weeks. The examined swine species in order of highest to lowest HEV infection rates were Chenghua pig, Large White, Duroc, Pietrain, Landrace and Hampshire. Nucleotide and amino acid sequence analysis showed that the HEV epidemic in swine in Sichuan Province was related to genotype IV, which had the highest homology to HEV in Beijing. Sichuan strains have greater variation than Chinese representative strains, which may indicate the presence of new HEV strains.
Improving the estimation and partitioning of plant nitrogen in the RiceGrow model
L. Tang, R. J. Chang, B. Basso, T. Li, F. X. Zhen, L. L. Liu, W. X. Cao, Y. Zhu
Journal: The Journal of Agricultural Science / Volume 156 / Issue 8 / October 2018
Published online by Cambridge University Press: 28 November 2018, pp. 959-970
Print publication: October 2018
Plant nitrogen (N) links with many physiological progresses of crop growth and yield formation. Accurate simulation is key to predict crop growth and yield correctly. The aim of the current study was to improve the estimation of N uptake and translocation processes in the whole rice plant as well as within plant organs in the RiceGrow model by using plant and organ maximum, critical and minimum N dilution curves. The maximum and critical N (Nc) demand (obtained from the maximum and critical curves) of shoot and root and Nc demand of organs (leaf, stem and panicle) are calculated by N concentration and biomass. Nitrogen distribution among organs is computed differently pre- and post-anthesis. Pre-anthesis distribution is determined by maximum N demand with no priority among organs. In post-anthesis distribution, panicle demands are met first and then the remaining N is allocated to other organs without priority. The amount of plant N uptake depends on plant N demand and N supplied by the soil. Calibration and validation of the established model were performed on field experiments conducted in China and the Philippines with varied N rates and N split applications; results showed that this improved model can simulate the processes of N uptake and translocation well.
Effect of stocking rate on grazing behaviour and diet selection of goats on cultivated pasture
L. Q. Wan, K. S. Liu, W. Wu, J. S. Li, T. C. Zhao, X. Q. Shao, F. He, H. Lv, X. L. Li
Journal: The Journal of Agricultural Science / Volume 156 / Issue 7 / September 2018
Published online by Cambridge University Press: 17 October 2018, pp. 914-921
Print publication: September 2018
Cultivated pastures in southern China are being used to improve forage productivity and animal performance, but studies on grazing behaviour of goats in these cultivated pastures are still rare. In the current study, the grazing behaviour of Yunling black goats under low (5 goats/ha) and high (15 goats/ha) stocking rates (SRs) was evaluated. Data showed that the proportion of time goats spent on activities was: eating (0.59–0.87), ruminating (0.05–0.35), walking (0.03–0.06) and resting (0.01–0.03). Compared with low SR, goats spent more time eating and walking, and less time ruminating and resting under high SR. Goats had similar diet preferences under both SR and preferred to eat grasses (ryegrass and cocksfoot) more than a legume (white clover). The distribution of eating time on each forage species was more uniform under high v. low SR. Bites/step, bite weight and daily intake were greater under low than high SR. Results suggest that the SR affects grazing behaviour of goats on cultivated pasture, and identifying an optimal SR is critical for increasing bite weight and intake.
The Maia Detector Journey: Development, Capabilities and Applications
C G Ryan, D P Siddons, R Kirkham, A J Kuczewski, P A Dunn, G De Geronimo, A. Dragone, Z Y Li, G F Moorhead, M Jensen, D J Paterson, M D de Jonge, D L Howard, R Dodanwela, G A Carini, R Beuttenmuller, D Pinelli, L Fisher, R M Hough, A Pagès, S A James, P Davey
Journal: Microscopy and Microanalysis / Volume 24 / Issue S1 / August 2018
Published online by Cambridge University Press: 01 August 2018, pp. 720-721
Print publication: August 2018
Experimental platform for the investigation of magnetized-reverse-shock dynamics in the context of POLAR
HPL Laboratory Astrophysics
B. Albertazzi, E. Falize, A. Pelka, F. Brack, F. Kroll, R. Yurchak, E. Brambrink, P. Mabey, N. Ozaki, S. Pikuz, L. Van Box Som, J. M. Bonnet-Bidaud, J. E. Cross, E. Filippov, G. Gregori, R. Kodama, M. Mouchet, T. Morita, Y. Sakawa, R. P. Drake, C. C. Kuranz, M. J.-E. Manuel, C. Li, P. Tzeferacos, D. Lamb, U. Schramm, M. Koenig
Journal: High Power Laser Science and Engineering / Volume 6 / 2018
Published online by Cambridge University Press: 16 July 2018, e43
The influence of a strong external magnetic field on the collimation of a high Mach number plasma flow and its collision with a solid obstacle is investigated experimentally and numerically. The laser irradiation ( $I\sim 2\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$ ) of a multilayer target generates a shock wave that produces a rear side plasma expanding flow. Immersed in a homogeneous 10 T external magnetic field, this plasma flow propagates in vacuum and impacts an obstacle located a few mm from the main target. A reverse shock is then formed with typical velocities of the order of 15–20 $\pm$ 5 km/s. The experimental results are compared with 2D radiative magnetohydrodynamic simulations using the FLASH code. This platform allows investigating the dynamics of reverse shock, mimicking the processes occurring in a cataclysmic variable of polar type.
Rabbit SLC15A1, SLC7A1 and SLC1A1 genes are affected by site of digestion, stage of development and dietary protein content
L. Liu, H. Liu, L. Ning, F. Li
Journal: animal / Volume 13 / Issue 2 / February 2019
Published online by Cambridge University Press: 22 June 2018, pp. 326-332
Print publication: February 2019
Peptide transporter 1 (SLC15A1, PepT1), excitatory amino acid transporter 3 (SLC1A1, EAAT3) and cationic amino acid transporter 1 (SLC7A1, CAT1) were identified as genes responsible for the transport of small peptides and amino acids. The tissue expression pattern of rabbit (SLC15A1, SLC7A1 and SLC1A1) across the digestive tract remains unclear. The present study investigated SLC15A1, SLC7A1 and SLC1A1 gene expression patterns across the digestive tract at different stages of development and in response to dietary protein levels. Real time-PCR results indicated that SLC15A1, SLC7A1 and SLC1A1 genes throughout the rabbits' entire development and were expressed in all tested rabbit digestive sites, including the stomach, duodenum, jejunum, ileum, colon and cecum. Furthermore, SLC7A1 and SLC1A1 mRNA expression occurred in a tissue-specific and time-associated manner, suggesting the distinct transport ability of amino acids in different tissues and at different developmental stages. The most highly expressed levels of all three genes were in the duodenum, ileum and jejunum in all developmental stages. All increased after lactation. With increased dietary protein levels, SLC7A1 mRNA levels in small intestine and SLC1A1 mRNA levels in duodenum and ileum exhibited a significant decreasing trend. Moreover, rabbits fed a normal level of protein had the highest levels of SLC15A1 mRNA in the duodenum and jejunum (P<0.05). In conclusion, gene mRNA differed across sites and with development suggesting time and sites related differences in peptide and amino acid absorption in rabbits. The effects of dietary protein on expression of the three genes were also site specific.
Induction of nuclear factor-κB signal-mediated apoptosis and autophagy by reactive oxygen species is associated with hydrogen peroxide-impaired growth performance of broilers
X. Chen, R. Gu, L. Zhang, J. Li, Y. Jiang, G. Zhou, F. Gao
Journal: animal / Volume 12 / Issue 12 / December 2018
Published online by Cambridge University Press: 03 May 2018, pp. 2561-2570
The oxidative study has always been particularly topical in poultry science. However, little information about the occurrence of cellular apoptosis and autophagy through the reactive oxygen species (ROS) generation in nuclear factor-κB (NF-κB) signal pathway was reported in the liver of broilers exposed to hydrogen peroxide (H2O2). So we investigated the change of growth performance of broilers exposed to H2O2 and further explored the occurrence of apoptosis and autophagy, as well as the expression of NF-κB in these signaling pathways in the liver. A total of 320 1-day-old Arbor Acres male broiler chickens were raised on a basal diet and randomly divided into five treatments which were arranged as non-injected treatment (Control), physiological saline (0.75%) injected treatment (Saline) and H2O2 treatments (H2O2(0.74), H2O2(1.48) and H2O2(2.96)) received an intraperitoneal injection of H2O2 with 0.74, 1.48 and 2.96 mM/kg BW. The results showed that compared to those in the control and saline treatments, 2.96 mM/kg BW H2O2-treated broilers exhibited significantly higher feed/gain ratio at 22 to 42 days and 1 to 42 days, ROS formation, the contents of oxidation products, the mRNA expressions of caspases (3, 6, 8), microtubule-associated protein 1 light chain 3 (LC3)-II/LC3-I, autophagy-related gene 6, Bcl-2 associated X and protein expressions of total caspase-3 and total LC3-II, and significantly lower BW gain at 22 to 42 days and 1 to 42 days, the activities of total superoxide dismutase and glutathione peroxidase, the expression of NF-κB in the liver. Meanwhile, significantly higher feed/gain ratio at 1 to 42 days, ROS formation, the contents of protein carbonyl and malondialdehyde, the mRNA expression of caspase-3 and the protein expressions of total caspase-3 and total LC3-II, as well as significantly lower BW gain at 22 to 42 days and 1 to 42 days were observed in broilers received 1.48 mM/kg BW H2O2 treatment than those in control and saline treatments. These results indicated that oxidative stress induced by H2O2 had a negative effect on histomorphology and redox status in the liver of broilers, which was associated with a decline in growth performance of broilers. This may attribute to apoptosis and autophagy processes triggered by excessive ROS that suppress the NF-κB signaling pathway.
Germination vigour difference of superior and inferior rice grains revealed by physiological and gene expression studies
Y. F. Zhao, H. Z. Sun, H. L. Wen, Y. X. Du, J. Zhang, J. Z. Li, T. Peng, Q. Z. Zhao
Journal: The Journal of Agricultural Science / Volume 156 / Issue 3 / April 2018
Superior and inferior rice grains have different weights and are located on the upper primary branch and lower secondary branches of the panicle, respectively. To study differences in germination vigour of these two types of grain, a number of factors were investigated from 0 to 48 h of germination. The present study demonstrated that in inferior grains the starch granule structure was looser at 0 h, with full water absorption at 48 h, while in superior grains the structure was tight and dense. Relative water content increased, and dry matter decreased, more rapidly in inferior grains than in superior ones. Abscisic acid and gibberellin levels, as well as α-amylase activity, also changed more rapidly in inferior grains, while soluble sugar content and amylase coding gene expression increased more rapidly in inferior than superior grains during early germination. The expression of OsGAMYB was higher in inferior grains at 24 h but higher in superior grains at 48 h. The phenotypic index of seedlings was higher in seedlings from superior grains at the two-leaf stage. However, the thousand-grain weight and yield per plant in superior and inferior plants showed no significant difference at harvest. The present study indicates that inferior grains germinate faster than superior ones in the early germination stage. Although inferior grains produced weaker seedlings, it is worthwhile using them in rice production due to their comparative yield potential over that of superior grains.
Studies of the relationship between rice stem composition and lodging resistance
M. Y. Gui, D. Wang, H. H. Xiao, M. Tu, F. L. Li, W. C. Li, S. D. Ji, T. X. Wang, J. Y. Li
Published online by Cambridge University Press: 25 May 2018, pp. 387-395
Plant height and lodging resistance can affect rice yield significantly, but these traits have always conflicted in crop cultivation and breeding. The current study aimed to establish a rapid and accurate plant type evaluation mechanism to provide a basis for breeding tall but lodging-resistant super rice varieties. A comprehensive approach integrating plant anatomy and histochemistry was used to investigate variations in flexural strength (a material property, defined as the stress in a material just before it yields in a flexure test) of the rice stem and the lodging index of 15 rice accessions at different growth stages to understand trends in these parameters and the potential factors influencing them. Rice stem anatomical structure was observed and the lignin content the cell wall was determined at different developmental stages. Three rice lodging evaluation models were established using correlation analysis, multivariate regression and artificial radial basis function (RBF) neural network analysis, and the results were compared to identify the most suitable model for predicting optimal rice plant types. Among the three evaluation methods, the mean residual and relative prediction errors were lowest using the RBF network, indicating that it was highly accurate and robust and could be used to establish a mathematical model of the morphological characteristics and lodging resistance of rice to identify optimal varieties.
Isolation, purification and identification of the active compound of turmeric and its potential application to control cucumber powdery mildew
W. J. Fu, J. Liu, M. Zhang, J. Q. Li, J. F. Hu, L. R. Xu, G. H. Dai
Cucumber powdery mildew is a destructive foliar disease caused by Podosphaera xanthii (formerly known as Sphaerotheca fuliginea) that substantially damages the yield and quality of crops. The control of this disease primarily involves the use of chemical pesticides that cause serious environmental problems. Currently, numerous studies have indicated that some plant extracts or products potentially have the ability to act as natural pesticides to control plant diseases. It has been reported that turmeric (Curcuma longa L.) and its extract can be used in agriculture due to their insecticidal and fungicidal properties. However, the most effective fungicidal component of this plant is still unknown. In the current study, the crude extract of C. longa L. was found to have a fungicidal effect against P. xanthii. Afterwards, eight fractions (Fr.1–Fr.8) were gradually separated from the crude extract by column chromatography. Fraction 1 had the highest fungicidal effect against this pathogen among the eight fractions. The active compound, (+)-(S)-ar-turmerone, was separated from Fr 1 by semi-preparative high-performance liquid chromatography and identified based on its 1H nuclear magnetic resonance (NMR) and 13C NMR spectrum data. The EC50 value of (+)-(S)-ar-turmerone was found to be 28.7 µg/ml. The compound also proved to have a curative effect. This is the first study to report that the compound (+)-(S)-ar-turmerone has an effect on controlling this disease. These results provide a basis for developing a new phytochemical fungicide from C. longa L. extract.
Effects of tributyrin supplementation on short-chain fatty acid concentration, fibrolytic enzyme activity, nutrient digestibility and methanogenesis in adult Small Tail ewes
Q. C. Ren, J. J. Xuan, Z. Z. Hu, L. K. Wang, Q. W. Zhan, S. F. Dai, S. H. Li, H. J. Yang, W. Zhang, L. S. Jiang
In vivo and in vitro trials were conducted to assess the effects of tributyrin (TB) supplementation on short-chain fatty acid (SFCA) concentrations, fibrolytic enzyme activity, nutrient digestibility and methanogenesis in adult sheep. Nine 12-month-old ruminally cannulated Small Tail ewes (initial body weight 55 ± 5.0 kg) without pregnancy were used for the in vitro trial. In vitro substrate made to offer TB at 0, 2, 4, 6 and 8 g/kg on a dry matter (DM) basis was incubated by ruminal microbes for 72 h at 39°C. Forty-five adult Small Tail ewes used for the in vivo trial were randomly assigned to five treatments with nine animals each for an 18-d period according to body weight (55 ± 5.0 kg). Total mixed ration fed to ewes was also used to offer TB at 0, 2, 4, 6 and 8 g/kg on a DM basis. The in vitro trial showed that TB supplementation linearly increased apparent digestibility of DM, crude protein, neutral detergent fibre and acid detergent fibre, and enhanced gas production and methane emissions. The in vivo trial showed that TB supplementation decreased DM intake, but enhanced ruminal fermentation efficiency. Both in vitro and in vivo trials showed that TB supplementation enhanced total SFCA concentrations and carboxymethyl cellulase activity. The results indicate that TB supplementation might exert advantage effects on rumen microbial metabolism, despite having an enhancing effect on methanogenesis.
Effects of in ovo feeding of l-arginine on breast muscle growth and protein deposition in post-hatch broilers
L. L. Yu, T. Gao, M. M. Zhao, P. A. Lv, L. Zhang, J. L. Li, Y. Jiang, F. Gao, G. H. Zhou
Journal: animal / Volume 12 / Issue 11 / November 2018
Published online by Cambridge University Press: 26 February 2018, pp. 2256-2263
Print publication: November 2018
In ovo feeding (IOF) of l-arginine (Arg) can affect growth performance of broilers, but the response of IOF of Arg on breast muscle growth is unclear, and the mechanism involved in protein deposition remains unknown. Hense, this experiment was conducted to evaluate the effects of IOF of Arg on breast muscle growth and protein-deposited signalling in post-hatch broilers. A total of 720 fertile eggs were collected from 34-week-old Arbor Acres breeder hens and distributed to three treatments: (1) non-injected control group; (2) 7.5 g/l (w/v) NaCl diluent-injected control group; (3) 0.6 mg Arg/egg solution-injected group. At 17.5 days of incubation, fertile eggs were injected 0.6 ml solutions into the amnion of the injected groups. Upon hatching, 80 male chicks were randomly assigned to eight replicates of 10 birds each and fed ad libitum for 21 days. The results indicated that IOF of Arg increased relative breast muscle weight compared with those of control groups at hatch, 3-, 7- and 21-day post-hatch (P<0.05). In the Arg-injected group, the plasma total protein and albumen concentrations were higher at 7- and 21-day post-hatch than those of control groups (P<0.05). The alanine aminotransferase activity in Arg group was higher at hatch than that of control groups (P<0.05). The levels of triiodothyronine at four time points and thyroxine hormones at hatch, 7- and 21-day post-hatch in Arg group were higher than those of control groups (P<0.05). In addition, IOF of Arg increased the amino acid concentrations of breast muscle at hatch, 7- and 21-day post-hatch (P<0.05). In ovo feeding of Arg also enhanced mammalian target of rapamycin, ribosomal protein S6 kinase-1 and eIF4E-bindingprotein-1 messenger RNA expression levels at hatch compared with those of control groups (P<0.05). It was concluded that IOF of Arg treatment improved breast muscle growth, which might be associated with the enhancement of protein deposition.
Follow Up of GW170817 and Its Electromagnetic Counterpart by Australian-Led Observing Programmes
Gravitational Wave Astronomy
I. Andreoni, K. Ackley, J. Cooke, A. Acharyya, J. R. Allison, G. E. Anderson, M. C. B. Ashley, D. Baade, M. Bailes, K. Bannister, A. Beardsley, M. S. Bessell, F. Bian, P. A. Bland, M. Boer, T. Booler, A. Brandeker, I. S. Brown, D. A. H. Buckley, S.-W. Chang, D. M. Coward, S. Crawford, H. Crisp, B. Crosse, A. Cucchiara, M. Cupák, J. S. de Gois, A. Deller, H. A. R. Devillepoix, D. Dobie, E. Elmer, D. Emrich, W. Farah, T. J. Farrell, T. Franzen, B. M. Gaensler, D. K. Galloway, B. Gendre, T. Giblin, A. Goobar, J. Green, P. J. Hancock, B. A. D. Hartig, E. J. Howell, L. Horsley, A. Hotan, R. M. Howie, L. Hu, Y. Hu, C. W. James, S. Johnston, M. Johnston-Hollitt, D. L. Kaplan, M. Kasliwal, E. F. Keane, D. Kenney, A. Klotz, R. Lau, R. Laugier, E. Lenc, X. Li, E. Liang, C. Lidman, L. C. Luvaul, C. Lynch, B. Ma, D. Macpherson, J. Mao, D. E. McClelland, C. McCully, A. Möller, M. F. Morales, D. Morris, T. Murphy, K. Noysena, C. A. Onken, N. B. Orange, S. Osłowski, D. Pallot, J. Paxman, S. B. Potter, T. Pritchard, W. Raja, R. Ridden-Harper, E. Romero-Colmenero, E. M. Sadler, E. K. Sansom, R. A. Scalzo, B. P. Schmidt, S. M. Scott, N. Seghouani, Z. Shang, R. M. Shannon, L. Shao, M. M. Shara, R. Sharp, M. Sokolowski, J. Sollerman, J. Staff, K. Steele, T. Sun, N. B. Suntzeff, C. Tao, S. Tingay, M. C. Towner, P. Thierry, C. Trott, B. E. Tucker, P. Väisänen, V. Venkatraman Krishnan, M. Walker, L. Wang, X. Wang, R. Wayth, M. Whiting, A. Williams, T. Williams, C. Wolf, C. Wu, X. Wu, J. Yang, X. Yuan, H. Zhang, J. Zhou, H. Zovaro
Journal: Publications of the Astronomical Society of Australia / Volume 34 / 2017
Published online by Cambridge University Press: 20 December 2017, e069
The discovery of the first electromagnetic counterpart to a gravitational wave signal has generated follow-up observations by over 50 facilities world-wide, ushering in the new era of multi-messenger astronomy. In this paper, we present follow-up observations of the gravitational wave event GW170817 and its electromagnetic counterpart SSS17a/DLT17ck (IAU label AT2017gfo) by 14 Australian telescopes and partner observatories as part of Australian-based and Australian-led research programs. We report early- to late-time multi-wavelength observations, including optical imaging and spectroscopy, mid-infrared imaging, radio imaging, and searches for fast radio bursts. Our optical spectra reveal that the transient source emission cooled from approximately 6 400 K to 2 100 K over a 7-d period and produced no significant optical emission lines. The spectral profiles, cooling rate, and photometric light curves are consistent with the expected outburst and subsequent processes of a binary neutron star merger. Star formation in the host galaxy probably ceased at least a Gyr ago, although there is evidence for a galaxy merger. Binary pulsars with short (100 Myr) decay times are therefore unlikely progenitors, but pulsars like PSR B1534+12 with its 2.7 Gyr coalescence time could produce such a merger. The displacement (~2.2 kpc) of the binary star system from the centre of the main galaxy is not unusual for stars in the host galaxy or stars originating in the merging galaxy, and therefore any constraints on the kick velocity imparted to the progenitor are poor.
Acetate alters the process of lipid metabolism in rabbits
C. Fu, L. Liu, F. Li
Journal: animal / Volume 12 / Issue 9 / September 2018
Published online by Cambridge University Press: 04 December 2017, pp. 1895-1902
An experiment was conducted to investigate the effect of acetate treatment on lipid metabolism in rabbits. New Zealand Rabbits (30 days, n=80) randomly received a subcutaneous injection (2 ml/injection) of 0, 0.5, 1.0 or 2.0 g/kg per day body mass acetate (dissolved in saline) for 4 days. Our results showed that acetate induced a dose-dependent decrease in shoulder adipose (P<0.05). Although acetate injection did not alter the plasma leptin and glucose concentration (P>0.05), acetate treatment significantly decreased the plasma adiponectin, insulin and triglyceride concentrations (P<0.05). In adipose, acetate injection significantly up-regulated the gene expression of peroxisome proliferator-activated receptor gamma (PPARγ), CCAAT/enhancer-binding protein α (C/EBPα), differentiation-dependent factor 1 (ADD1), adipocyte protein 2 (aP2), carnitine palmitoyltransferase 1 (CPT1), CPT2, hormone-sensitive lipase (HSL), G protein-coupled receptor (GPR41), GPR43, adenosine monophosphate-activated protein kinase α1 (AMPKα1), adiponectin receptor (AdipoR1), AdipoR2 and leptin receptor. In addition, acetate treatment significantly increased the protein levels of phosphorylated AMPKα, extracellular signaling-regulated kinases 1 and 2 (ERK1/2), p38 mitogen-activated protein kinase (P38 MAPK) and c-jun amino-terminal kinase (JNK). In conclusion, acetate up-regulated the adipocyte-specific transcription factors (PPARγ, C/EBPα, aP2 and ADD1), which were associated with the activated GPR41/43 and MAPKs signaling. Meanwhile, acetate decreased fat content via the upregulation of the steatolysis-related factors (HSL, CPT1 and CPT2), and AMPK signaling may be involved in the process.
Impact of an intervention programme on knowledge, attitudes and practices of population regarding severe fever with thrombocytopenia syndrome in endemic areas of Lu'an, China
Y. LYU, C.-Y. HU, L. SUN, W. QIN, P.-P. XU, J. SUN, J.-Y. HU, Y. YANG, F.-L. LI, H.-W. CHANG, X.-D. LI, S.-Y. XIE, K.-C. LI, X.-X. HUANG, F. DING, X.-J. ZHANG
Journal: Epidemiology & Infection / Volume 146 / Issue 1 / January 2018
Knowledge, attitudes and practices (KAP) of the population regarding severe fever with thrombocytopenia syndrome (SFTS) in endemic areas of Lu'an in China were assessed before and after an intervention programme. The pre-intervention phase was conducted using a sample of 425 participants from the 12 selected villages with the highest rates of endemic SFTS infection. A predesigned interview questionnaire was used to assess KAP. Subsequently, an intervention programme was designed and applied in the selected villages. KAP was re-assessed for each population in the selected villages using the same interview questionnaire. Following 2 months of the programme, 339 participants had completed the re-assessed survey. The impact of the intervention programme was evaluated using suitable statistical methods. A significant increase in the KAP and total KAP scores was noted following the intervention programme, whereas the proportion of correct knowledge, the positive attitudes and the effective practices toward SFTS of respondents increased significantly. The intervention programme was effective in improving KAP level of SFTS in populations that were resident in endemic areas. | CommonCrawl |
\begin{definition}[Definition:Pie Graph]
A '''pie graph''' is a form of graph which consists of a circle divided into sectors whose areas represent the proportion of the corresponding statistic relative to the whole.
:500px
\end{definition} | ProofWiki |
$\triangle DEF$ is inscribed inside $\triangle ABC$ such that $D,E,F$ lie on $BC, AC, AB$, respectively. The circumcircles of $\triangle DEC, \triangle BFD, \triangle AFE$ have centers $O_1,O_2,O_3$, respectively. Also, $AB = 23, BC = 25, AC=24$, and $\stackrel{\frown}{BF} = \stackrel{\frown}{EC},\ \stackrel{\frown}{AF} = \stackrel{\frown}{CD},\ \stackrel{\frown}{AE} = \stackrel{\frown}{BD}$. The length of $BD$ can be written in the form $\frac mn$, where $m$ and $n$ are relatively prime integers. Find $m+n$.
[asy] size(150); defaultpen(linewidth(0.8)); import markers; pair B = (0,0), C = (25,0), A = (578/50,19.8838); draw(A--B--C--cycle); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); pair D = (13,0), E = (11*A + 13*C)/24, F = (12*B + 11*A)/23; draw(D--E--F--cycle); label("$D$",D,dir(-90)); label("$E$",E,dir(0)); label("$F$",F,dir(180)); draw(A--E,StickIntervalMarker(1,3,size=6));draw(B--D,StickIntervalMarker(1,3,size=6)); draw(F--B,StickIntervalMarker(1,2,size=6)); draw(E--C,StickIntervalMarker(1,2,size=6)); draw(A--F,StickIntervalMarker(1,1,size=6)); draw(C--D,StickIntervalMarker(1,1,size=6)); label("24",A--C,5*dir(0)); label("25",B--C,5*dir(-90)); label("23",B--A,5*dir(180)); [/asy]
From adjacent sides, the following relationships can be derived:
\begin{align*} DC &= EC + 1\\ AE &= AF + 1\\ BD &= BF + 2 \end{align*}
Since $BF = EC$, and $DC = BF + 1$, $BD = DC + 1$. Thus, $BC = BD + DC = BD + (BD - 1)$. $26 = 2BD$. Thus, $BD = 13/1$. Thus, the answer is $\boxed{14}$. | Math Dataset |
Simplify $\left(\dfrac{-1+i\sqrt{3}}{2}\right)^6+\left(\dfrac{-1-i\sqrt{3}}{2}\right)^6.$
We have that
\[(-1 + i \sqrt{3})^2 = (-1 + i \sqrt{3})(-1 + i \sqrt{3}) = 1 - 2i \sqrt{3} - 3 = -2 - 2i \sqrt{3},\]and
\[(-1 + i \sqrt{3})^3 = (-1 + i \sqrt{3})(-2 - 2i \sqrt{3}) = 2 + 2i \sqrt{3} - 2i \sqrt{3} + 6 = 8,\]so $(-1 + i \sqrt{3})^6 = 64.$ Then
\[\left( \frac{-1 + i \sqrt{3}}{2} \right)^6 = \frac{64}{2^6} = 1.\]Similarly,
\[\left( \frac{-1 - i \sqrt{3}}{2} \right)^6 = \frac{64}{2^6} = 1,\]so the expression is equal to $\boxed{2}.$ | Math Dataset |
OSA Publishing > Biomedical Optics Express > Volume 11 > Issue 9 > Page 5212
Retinal choroidal vessel imaging based on multi-wavelength fundus imaging with the guidance of optical coherence tomography
Zhiyu Huang, Zhe Jiang, Yicheng Hu, Da Zou, Yue Yu, Qiushi Ren, Gangjun Liu, and Yanye Lu
Zhiyu Huang,1 Zhe Jiang,1 Yicheng Hu,1,2 Da Zou,1 Yue Yu,1 Qiushi Ren,1,2,3 Gangjun Liu,2,3,5 and Yanye Lu1,3,4,6
1Department of Biomedical Engineering, College of Engineering, Peking University, Beijing 100871, China
2Institute of Biomedical Engineering, Shenzhen Bay Laboratory, No. 9 Duxue Road, Nanshan District, Shenzhen 518071, China
3Institute of Biomedical Engineering, Peking University Shenzhen Graduate School, Shenzhen 518055, China
4Pattern Recognition Lab, Department of Computer Science, Friedrich-Alexander-University, Erlangen-Nuremberg, Martensstrasse 3, 91058 Erlangen, Germany
[email protected]
[email protected]
Yanye Lu https://orcid.org/0000-0002-3063-8051
Z Huang
Z Jiang
Y Hu
D Zou
Y Yu
Q Ren
G Liu
Y Lu
Zhiyu Huang, Zhe Jiang, Yicheng Hu, Da Zou, Yue Yu, Qiushi Ren, Gangjun Liu, and Yanye Lu, "Retinal choroidal vessel imaging based on multi-wavelength fundus imaging with the guidance of optical coherence tomography," Biomed. Opt. Express 11, 5212-5224 (2020)
Pixel-wise segmentation of severely pathologic retinal pigment epithelium and choroidal stroma using multi-contrast Jones matrix optical coherence tomography (BOE)
Multi-wavelength, en-face photoacoustic microscopy and optical coherence tomography imaging for early and selective detection of laser induced retinal vein occlusion (BOE)
Attenuation correction assisted automatic segmentation for assessing choroidal thickness and vasculature with swept-source OCT (BOE)
Ophthalmic imaging
Three dimensional imaging
Original Manuscript: May 15, 2020
Revised Manuscript: August 12, 2020
Manuscript Accepted: August 17, 2020
Material and method
A multispectral fundus camera (MSFC), as a novel noninvasive technology, uses an extensive range of monochromatic light sources that enable the view of different sectional planes of the retinal and choroidal structures. However, MSFC imaging involves complex processes affected by various factors, and the recognized theory based on light absorption above the choroid is not sufficient. In an attempt to supplement the relevant explanations, in this study, we used optical coherence tomography (OCT), a three-dimensional tomography modality, to analyze MSFC results at the retina and choroid. The swept-source OCT system at 1060 nm wavelength with a 200 kHz A-scan rate and an MSFC with 11 bands at 470 to 845 nm are employed. A quantitative evaluation procedure is proposed to compare MSFC and OCT en face images. The comparative study shows that 1) the MSFC images with the illumination wavelength of less than 605 nm could mainly provide the retinal structure information; 2) Relative choroidal layer thickness information could be inferred from the MSFC images, especially the image acquiring under the wavelength more than 605 nm. According to the results, further investigation revealed the contribution of the perivascular tissue and the sclera scattering in the difference of vascular brightness in MSFC images.
Fundus vessels, known to be associated with a wide range of ophthalmic diseases [1–5], have great significance for being visualized in clinical. Retinal vessels and choroidal vessels are the two main categories of fundus vessels at different axial locations. As a kind of wavelength-resolved fundus camera, MSFC can acquire multi-band fundus images simultaneously or sequentially to provide the structural information from different depths. In addition, it can provide functional information such as blood oxygen. Typically, such depth-resolved capability of the MSFC comes from that each biological tissue type has different optical absorption and reflection coefficients at different wavelengths [6–10]. The wavelength range for imaging is usually among the visible and near-infrared regions [7,11]. With longer illumination wavelengths, more choroidal structures can be revealed using MSFC [12].
MSFC images have been used clinically, but the analysis of choroid via MSFC imaging is not sufficient. Previous studies suggested that the absorption coefficient of the tissue above the choroid, such as the pigment in the retinal pigment epithelium (RPE) layer [11,12], should be the main factors influencing the choroid imaging results in MSFC. However, this mechanism cannot give a clear explanation for the signals from bright vascular structures in MSFC images. Hence, more critical factors, such as optical properties of choroid itself and high scattering coefficients of the sclera, need to be considered, which is important for better understanding and diagnosis of ocular fundus diseases as well as enabling quantitative measurement.
It's worth mentioning that accurate three-dimension spatial analysis can promote a better understanding of MSFC imaging results so that optical coherence tomography (OCT) is a solid choice to investigate fundus structures. As a noninvasive optical imaging modality, OCT performs 3D volumetric imaging of the internal microstructure in biological tissue by measuring the echoes of backscattered light [13]. Benefiting from its extremely high resolution and 3D imaging mode, OCT has been fully used in ophthalmic diagnostics [14–16]. Recently, a few newly designed light sources and systems have been proposed to acquire a larger field of view, making it possible to obtain complete fundus vessel images in a short time [17–21]. The deeper imaging capability of OCT brings the potential to explore the explanation of choroid imaging results via MSFC.
To conduct better investigations of retinal, choroidal vessel imaging, an MSFC with longest illumination wavelength of 840 nm, and a custom-built 200 kHz, 1060 nm resolved swept-source OCT system was employed for deep region imaging reaching sclera in this work. The segmented OCT en face images were generated and compared with the MSFC images from different illumination wavelengths using an introduced quantification method.
The contrastive studies between the MSFC and the OCT revealed that for the wavelengths below 605 nm, the penetration would be limited by RPE, and the MSFC images only show the retinal information. On the other hand, MSFC images with wavelengths longer than 605 nm will demonstrate the information on choroidal and sclera. The choroid thickness plays an essential role in the near-infrared fundus images via MSFC, and thicker choroid would induce a blurred choroidal structure in the MSFC images. We also analyzed the differences between choroidal and retinal perivascular tissue to explain the different brightness performance of blood vessels in different imaging modalities.
2. Material and method
In this paper, eight sets of fundus data were collected from eight healthy volunteers without eye medical history using OCT and MSFC, respectively. In order to compare the two different data sets, OCT images were segmented, and planar intensity projections of each layer were obtained. After the registration, the two types of images were compared by our proposed evaluation method.
The human study protocol was approved by the institutional review boards of the Peking University First Hospital. After explaining the study, all subjects obtained written informed consent. All procedures adhered to the tenets of the Declaration of Helsinki. Eight healthy volunteers with no known history of retinal disease participated in the study.
2.1 OCT system and scanning protocol
Swept-source OCT is a typical swept-source system [18]. Briefly, we used a commercially available swept laser (Axsun 1060, Axsun Technologies, Billerica, MA, USA) with a sweep rate of 200 kHz, a center wavelength of 1044 nm, and a tuning range of 104 nm. Based on the system, a typical raster scanning protocol was used to generate 3D images. In the x (fast-scan) direction, 1024 A-lines were acquired to form a B-frame, determining a frame rate of around 200 frames per second (fps); in the y (slow-scan) direction, 512 scanning steps were sequentially acquired. The total acquisition time and the field of view were ∼ 3.6s and $10 \times 10\; mm$ (30° × 30°), respectively. The measured power on the cornea was 1.8 mW, which is consistent with safe ocular exposure limits set by the American National Standard for Safe Use of Lasers [22].
2.2 Multispectral fundus camera system
A custom-built MSFC imaging system with an angle of view of 45° was employed in this study. The system adopted a set of electronically controlled fast-switching LEDs for illumination. An optical annular fiber bundle was used to deliver the LED light to the system. The cross-sectional area of the fiber bundle showed a donut shape, which formed an annular illumination pattern on the corner of the imaging subject. Twelve representative wavelengths were selected in the system, i.e., 470 nm, 500 nm, 520 nm, 548 nm, 605 nm, 610 nm, 635 nm, 665 nm, 740 nm, 810 nm, 820 nm, and 845 nm, respectively. The unweighted anterior segment visible and infrared radiation irradiance of the system is listed in Table 1 [23]. The maximum optical lateral resolution of the MSFC imaging system is 16μm in the center 30-degree region and 25 μm beyond the central 30-degree region. The depth of field is around 245μm at 845 nm. The spectrum switching and camera exposure are synchronized by an STM32 controller (STM32-F103C8T6, STMicroelectronics, Geneva, Switzerland). The pupil tracking and split-line focus assist system are employed to ensure the focusing accuracy. All twelve band images can be acquired within 0.2 seconds, which makes the system superior to clinical usage.
Table 1. Unweighted anterior segment visible and infrared radiation irradiance of MSFC system.
2.3 Image preprocessing
In order to contrast OCT images with MSFC images, the OCT images were segmented into eight layers using a graph cut based method [24]. For each layer, the mean intensity projection map was calculated to obtain the corresponding en face image. For the choroid layer in OCT images, the attenuation compensation method is employed to enhance the contrast of the result [25]. Then, image registration was performed between the MSFC images and en face images to eliminate the effect of micro-saccades. That is, paired feature points $({x,y} )$ and $({u,v} )$ from two corresponding images were first manually selected using MATLAB's Point Selection Tool. Based on the feature points, affine transformation matrix was estimated between images, which can be denoted as follows:
(1)$$\left[ {\begin{array}{{c}} u\\ v \end{array}} \right] = \left[ {\begin{array}{{ccc}} {{a_2}}&{{a_1}}&{{a_0}}\\ {{b_2}}&{{b_1}}&{{b_0}} \end{array}} \right]\left[ {\begin{array}{{c}} x\\ y\\ 1 \end{array}} \right],$$
where ${a_i}$ and ${b_i}\; $($i \in 0,1,2$) are the parameters of the reflection transformation determined by the least-square method.
2.4 Evaluation process
In order to efficiently conduct the contrastive studies, we have developed an evaluation pipeline, which is illustrated in Fig. 1. As shown in the figure, the vessel structure was first extracted using a hessian filter based algorithm [26]. By parameter modification, the hessian filter is able to distinguish bright and dark tubular structures. In fact, either structure could be contained in OCT en face images of different layers and MSFC images of different wavelengths, respectively. Hence, it is necessary to adapt the parameters of the filter to different scenarios. Next, the area of interest (around 6${\times} $6 mm in the center of the registered images) was selected in the respective group of images being evaluated. Considering that non-rigid distortions caused by the ocular motion along the OCT slow scan direction still exist in the registered images, the images were resized (using bicubic interpolation) to a size of 30${\times} $30 pixels to reduce the effect of image distortion on evaluation. Finally, a Pearson correlation coefficient (R) between the images was calculated. R is defined as:
(2)$$\textrm{R}({y,z} )= \frac{{{\sigma _{yz}}}}{{{\sigma _z}{\sigma _y}}},$$
where ${\delta _{yz}}$ is the covariance between two input images y and z. R represents the degree of correlation between the two images, which is between 0 and 1. A larger R-value reflects a higher relationship.
Fig. 1. Overview of the evaluation pipeline. The images have been registered in preprocessing. Hessian filters with different parameters are used to separate the dark and light vessel structures, respectively. Afterwards, down-sampling is adopted to reduce non-rigid distortions, and a Pearson correlation coefficient (R) between the images is calculated for the quantitative evaluation.
3.1 Fundus imaging results from MSFC and OCT
Generally speaking, longer wavelengths have better penetration capabilities of biological tissue. Within the wavelength range selected in this article (470∼845 nm), MSFC imaging also obeys this rule and shows different tissue in different band images. The MSFC images from a normal eye are shown in Fig. 2. It can be seen that retinal structure is clear with few choroidal information in the MSFC images with short wavelengths less than 605 nm. For the MSFC images with long wavelengths of more than 605 nm, the choroidal structure is much clear, whereas the retinal structure becomes blurred. Figure 2(a)–2(d) (wavelength band centers of 470 nm, 500 nm, 520 nm, and 548 nm, respectively) show significant visual similarity. Figure 2(m) presents the respective R-value calculated between the 470 nm MSFC image and the other band images. It can be seen that R-values tend to decrease as the wavelength increases. Although the R-value is increasing again for wavelengths longer than 740 nm, it still remains a low level. We would recommend paying attention to both the R-value and its standard deviation. It should be noted for the wavelength increase above 740 nm, the R-value is increasing again, but the standard deviation remains large, which means data are unstable. In this study, only the R-value of more than 0.75 with a standard deviation of less than 0.070 could be considered as well correlated results. Note that, the R values are higher than 0.8 for the wavelengths below 605 nm, demonstrating high similarity between the 470 nm MSFC image and these band images. However, Fig. 2(n) poses a high contrast with those below 605 nm, in which the R values calculated with the pictures of longer wavelengths, indicating a broader distribution range that infers various tubular structures being displayed in each image. We speculate that different penetration depths of wavelengths may lead to this result.
Fig. 2. The MSFC images from a healthy eye with (a-I) 12 illumination wavelengths. (m) The respective Pearson correlation coefficient R calculated between 470 nm MSFC and other images in all datasets (the dark structures were enhanced by hessian filter). (n) The respective Pearson correlation coefficient R calculated between 845 nm MSFC and other images in all datasets (the bright structures were enhanced by hessian filter). The "+" means outliers of the datasets. An outlier is a value that is more than 1.5 times the interquartile range away from the top or bottom of the box. Scalebar: 1.2mm.
Different from the cross-sectional B-scan image, en face OCT image provides similar sight to the traditional 2D imaging modality. The en face OCT images from different layers of the same eye in Fig. 2 are shown in Fig. 3. Despite vessel shadowing artifacts exit in some OCT en face images, it can be noticed that the information from the deep layers differs from the images of surficial layers. From Fig. 3(a) and Fig. 3(h), it can be seen that the choroid vessels were shown up as dark signal regions in the images [19]. Recent findings suggest that the fringe washout and the weak scattering of near-infrared light of the blood may affect the weak OCT signals in choroid vessels [27,28]. The sclera layer is also displayed in Fig. 3(i), and the vasculature was marked with arrows. These structures were bright in B-scan [Fig. 3(a) marked with arrows].
Fig. 3. OCT layer segmentation results and the mean intensity en face projection maps of different layers in the macular region. (a) OCT B-scan image and the results of the segmentation being labeled. (a1) OCT Aline profile, averaging Alines in the dotted box. (b-i) en face projection maps of different layers. NFL = nerve fiber layer, GCL = Ganglion cell layer, IPL = inner plexiform layer, INL = inner nuclear layer, OPL = outer plexiform layer, ONL = outer Nuclear layer, RPE = retinal pigment Epithelium. For convenience, in this article, RPE includes Ellipsoid Zone, Outer segments of photoreceptors, and RPE / Bruch 's complex. Scale bars: 200$\mu m$.
3.2 Contrastive study of the MSFC images and the OCT en face images
3.2.1 Comparison on retinal vessels
For the comparison of the two different modalities, the images were first registered with the MSFC image as the baseline image. Figure 4(a),4(b) shows the averaged en face OCT images of the retina (above RPE layer) and RPE layer, respectively. Meanwhile, Fig. 4(c) presents the 470 nm MSFC image. The correlation coefficients R between the retina OCT en face images, and the 470 nm MSFC image is over 0.8. However, it can be seen that the vessels in the en face image of the retina show higher intensity than the other regions. On the contrary, the vessels in the 470 nm MSFC image show lower intensity than the other non-vessel regions, and a similar phenomenon can also be observed in the en face image of the RPE layer in Fig. 4(b). Therefore, it can be considered that the reflected signals from the RPE layer contribute a lot to the MSFC imaging results, as vessels show up as dark in MSFC images but display as bright in en face images from layers above the RPE. Since blood has a higher absorption coefficient than the prevascular tissue, the vessels present lower signals in both 470 nm MSFC images and en face images of the RPE layer. In Fig. 4(d), higher R-values can be observed from layers above the RPE. It's because the layers above the RPE show the ideal vessel signals, and the signals of RPE are from the shadow of the vessel. However, only a little difference exits between images of layers above the RPE and RPE layer, which may occur due to the complex composition of the returning signal in MSFC. The signals from the vascular surface, hemoglobin, and other layers (including RPE) can contribute to the intensity of the vascular signal in MSFC imaging [29–32].
Fig. 4. The mean intensity projection OCT en face images above the RPE layer (including RPE) and the MSFC images at 470 nm. Refer to Fig. 2, the similarity within these images indicates that the images with short wavelengths show mainly retinal information above choroid. These images, including the OCT average intensity en face projection images of (a) layers above RPE, (b) RPE layer, and (c) 470 nm MSFC image, have high similarity in vascular structure. (d) The correlation coefficients R between OCT en face and MSFC images. Scale bars: 800$\mu m$.
3.2.2 Comparison of choroidal vessels
Contrastively studies between en face OCT images below the RPE layer and long-wavelength MSFC images on the same eye were conducted to evaluate the imaging results on choroid. Figure 5(a)–5(d) show the en face OCT image (intensity inverted) of the choroidal layer, the 840 nm MSFC image, the en face OCT image of the sclera layer, and the choroidal layer thickness map from the same eye, respectively. The large choroidal vessels are shown as black regions in the OCT en face image [Fig. 5(a)] [33]. As shown in the enlarged images of selected regions (dashed boxes) in Fig. 5(a) and Fig. 5(b), most structures of the choroidal blood vessels shown in the MSFC image [Fig. 5(b)] can match the en face OCT image [Fig. 5(a)]. Note that vessel structures are blurred on the right side of Fig. 5(b) and Fig. 5(c). One primary reason for such a phenomenon is that the imaging regions have the thicker choroidal layer, which can be verified by the choroidal thickness map presented in Fig. 5(d). It can be found that the choroidal layer is thicker in those regions, resulting in blurred choroidal vessel structure in the images.
Fig. 5. The comparison of OCT en face image and 840 nm MSFC image for the sclera and choroid. OCT en face and MSFC near-infrared results correspond well in those areas with thin choroids. (a) choroidal OCT mean intensity projection en face image (inverse color). (b) 845 nm multispectral imaging results. (c) Scleral OCT en face image. The retinal vessel shows up as dark, and the choroidal vessels show up as bright in (b) and (c). (a1-c1, a2-c2) enlarged images of selected regions, marked with rectangular boxes. (d) Thickness map of the choroid. (e) OCT B scan, corresponding to the position marked with a dotted line in (c). Scale bars: 500$\textrm{\; }\mu m$.
Figure 6 shows the results from another eye with a thicker choroid layer. As presented in Fig. 6(d), the choroid thickness in most areas exceeds 280 microns, and the average choroidal layer thickness is 291.4 $\mu m$. The thinnest area in the map, located in the lower right corner of the image, is about an average value of 100 microns, but the MSFC imaging did not capture such an area. Because the entire choroid is thick, choroidal vessels cannot be imaged in the MSFC image [Fig. 6(a)] and the OCT en face image [Fig. 6(b)]. Since almost no signal from the sclera is observed in the figure, choroidal vascular signals are barely extracted in the scleral en face plane.
Fig. 6. A case of choroidal imaging results, choroidal vessels are hardly observed in subjects with extremely thick choroids. (a) 845 nm multispectral imaging results. The OCT en face images were generated from (b) choroid (inverse color), and (c) sclera. (d) Thickness map of the choroid. (e) OCT B-scan, corresponding to the position marked with a dotted line in (b). Scale bars: 500$\textrm{\; }\mu m$.
In order to verify the association of retinal thickness with MSFC imaging, the choroidal thickness maps were overlaid with the OCT en face image of the choroidal layer and the 840 nm MSFC image, respectively. Three regions were respectively divided in Fig. 7(a) and Fig. 7(b) based on the thickness of the choroid, and pixels in the different areas are listed separately. Subsequently, the correlation coefficients R of the different regions were calculated between the choroidal en face image and the MSFC image. In this work, three different thickness levels were 0∼150$\; \mu m$, 150∼220$\; \mu m$ and >220$\; \mu m$, respectively. At present, the division of the thickness map is based on the experience value and mainly depends on image observation. Statistical results show that the results from different regions indeed present very different correlation coefficients [Fig. 7(c)]. The correlation value R is large for thin choroidal layers regions and is small for thick regions. Generally, the correlation value R tends to decrease as the choroidal thickness increases.
Fig. 7. Correlation coefficients of MSFC and OCT choroid en face images in different regions zoned by choroid thickness. The correlation coefficients of results from different areas are quite different. Parts are shown in the (a) OCT en face and (b) 845 nm images through layers of different colors. (c) Boxplot of correlation coefficients R between OCT en face and MSFC images. Scale bar: 1 mm.
Based on the proposed contrastive studies, we can conclude that the imaging capability of the 840 nm MSFC on choroidal vessel structures is correlated to choroidal thickness. The vessel structure is clearer in the thin choroidal regions and is blurred in thick regions. We believe that sclera, as a tissue with the highest fundus scattering capacity [Fig. 8(a)], plays an important role in explaining such a phenomenon. In thin regions, light is more likely to reach sclera, resulting in more scattered light signals [Fig. 8(b)] of the sclera returning to the detector [marked in Fig. 5(e) by the dashed box]. The intensity of these scattered signals from the sclera will be different, owing to the optical properties of the tissue above the sclera. As shown in Fig. 5(c) and Fig. 5(e), the OCT signal below the choroid vessels is stronger in the thin choroidal areas than in the thick choroidal areas. The choroid contains a large amount of melanin, which has higher absorbing and scattering coefficients than blood vessels [3,34,35]. Because the choroidal vessels themselves do not have a strong scattering signal in OCT B-scan [Fig. 5(e), Fig. 6(e)] and the weak attenuation of blood vessels, it is convincible that the scattered signals from sclera transmitted through choroidal vessels are much stronger than the reflection signals of the vessels [Fig. 8(b)]. Additionally, the perivascular tissue of the choroid has strong attenuation. Building on these findings, we speculate that the majority of the choroidal vessel imaging in MSFC is not from the light reflection on the vessels but the scattered light from sclera transmitted through the vessels. Therefore, it is reasonable that the choroidal vessels were shown as bright structures in the long-wavelength image of MSFC.
Fig. 8. Reflecting retinal layers in the near-infrared. The illuminating beam (red arrows) is reflected by diverse retinal layers for diverse extents. (a) The main reflection is SCL, photoreceptor layer, RPE, ILM, and NFL. The number and length of the blue arrows indicate the degree of near-infrared reflectance (Figure adapted from [36]). (b-c) Influence of the choroid on the scleral reflex signal, where (b) represents the condition at the lower thickness and (c) at higher thickness.
In order to estimate the image similarity, we resized the image to a small size, although details of images will be lost. The method is inspired by the Perceptual hash algorithm (PHA) [37], the difference is that we use Pearson correlation to quantify the relevance of images in the space domain, obtaining results that are suitable for statistical analysis. There are two reasons that we resize the image to a small size. 1) We are interested in the correlation among the different regions instead of a specific pixel. 2) To reduce the effect of the image distortion. The distortion in both MSFC imaging and OCT imaging is mainly caused by eye motion during the imaging acquisition and related to the optical design. The effectiveness of resizing operation in reducing image distortion is presented in Fig. 9. Two affine transforms are applied to a typical enhanced MSFC image [Fig. 9(a)]. One consists of translation with an affine transformation matrix of [1, 0, 6; 0, 1, 6], and the other consists of rotation and scaling with an affine transformation matrix of [1.01, 0.05, 0; -0.01, 1, 0]. The original image is shown in Fig. 9(a). False-color images synthesized by original image and image after transform as the Green and Blue channels are illustrated in Figs. 9(b)–9(c). The resized images are shown in Figs. 9(d)–9(f). In Table 2, the R-values of different size images are listed. From the table, we can find that the R-values between the full-scale images has been greatly affected (0.63 for translation transform and 0.53 for affine transform). By resizing the image to a small size, R-values increases. In general, the method in the manuscript is justified. But, resizing the image to a small size can result in loss of detail and false-positive results. So, the accurate distortion analysis, cross-modal non-rigid registration, faster imaging should be applied in the future.
Fig. 9. Two affine transforms were applied to a typical vessel enhanced MSFC image to verify the effectiveness of the operation of resizing image in reducing image distortion. (a) An original vessel enhanced MSFC image; (b) false-color images synthesized by original image and image after translation transform; (c) false-color images synthesized by original image and image after rotation and scaling transform; (d) resized images of (a) original image; (e) false-color images synthesized by the resized original image and resized image after translation transform; (f) false-color images synthesized by the resized original image and resized image after rotation and scaling transform. Scale bar: 1 mm.
Table 2. R-value of resized images after translation and similarity transform (consisting of rotation and scale transform).
To the best of our knowledge, the obtained fundus images are usually blurred when the fundus camera illuminated with relative long-wavelength (NIR region). This could be seen from typical fundus camera preview images, which usually uses ∼800 nm wavelength. Such a phenomenon could also be seen from the fundus camera with even longer wavelength (see Refs. [11,12]). This blurriness may be due to the following factors. 1) The longer wavelength intrinsically has a lower resolution. 2) The longer wavelength can penetrate more in-depth so that the light will experience many more multiple scattering effects. 3) Fundus images are based on the reflection/scattering signal from all the depth that the light could penetrate. They are generally a summation of information of all depth. The MSFC we used is a fundus camera with pupil tracking and a split-line focus assist system to ensure the focusing accuracy. There are many methods, such as local frequency signal and picture sharpness evaluation, which can quantify the "blurry" level. But in this study, our chief concern is the correlation between the OCT en face images, OCT thickness map, and MSFC images. For this purpose, we employed the Pearson correlation. "Blurry" level is important for fundus imaging, and we do believe that certain retina pathologies, such as retina edema and leakage, may affect the "blurry level" of the vessel structure. So its further impact should be included in our future studies.
Multispectral fundus camera and OCT have been widely used in ophthalmic imaging. It can be expected that with the improvement of system speed, the MSFC functional imaging and large 3D-field SS-OCT imaging will play more important and crucial roles in improving early diagnosis, treatment, social and medical rehabilitation. In this work, a quantification method was employed to compare the imaging characteristics of the two modalities on the blood vessel structure, and the signal sources of the vascular features in MSFC images are analyzed. From the comparison results, we can obtain three significant conclusions:
1) For the retinal vessels above RPE layers, the OCT en face images match well with the short-wavelength (< 605 nm) MSFC images and present a correlation coefficient higher than 0.7, which suggests that the MSFC images with the illumination wavelength of less than 605 nm could mainly provide the retinal structure information. On the other hand, for MSFC images with wavelengths longer than 605 nm, a clear difference exists between the retina and choroidal structure, and more choroidal information will be displayed with the increase of wavelengths.
2) Relative choroidal layer thickness information could be inferred from the MSFC images, especially the image acquiring under the wavelength of more than 605 nm. The areas with a thick choroid show a blurred choroidal structure. In contrast, thinner choroidal regions present a clear structure.
3) The difference in scattering properties between choroidal vessels and retinal vessels were also investigated. In OCT en face images, due to differences in perivascular tissue, it can be concluded that the retinal vessels show a higher signal than the non-vessel regions. In comparison, the choroidal vessels show a lower signal than the non-vessel regions. In the MSFC images, the retinal vessels show a lower signal than the non-vessel regions, while the choroidal vessels show a higher signal than the non-vessel regions.
On the other hand, this study also has several limitations. We resized the image to a small size to eliminate distortion. The loss of detail has, to some extent, affected the result. So, the accurate distortion analysis, cross-modal non-rigid registration, faster imaging should be applied in the future. Our analysis suggested that scleral scattering has a considerable effect on imaging, but proving experiments were not included in this work. As a result, additional phantom experiments and simulations should be studied in the future. On the other hand, considering that choroid thickness is related to axial length, position, age, and myopia [38–40], more imaging data and imaging methods could be introduced to verify the hypothesis further. Finally, clinical imaging studies of retinal disease patients and age-matched healthy people are required to assess the ultimate clinical value of choroidal vessels.
National Key Scientific Instrument and Equipment Development Projects of China (2013YQ030651); National Natural Science Foundation of China (61875123, 81421004); Shenzhen Science and Technology Program (1210318663).
1. S. S. Hayreh and S. S. Hayreh, "In vivo choroidal circulation and its watershed zones," Eye 4(2), 273–289 (1990). [CrossRef]
2. D. L. Nickla and J. Wallman, "The multifunctional choroid," Prog. Retinal Eye Res. 29(2), 144–168 (2010). [CrossRef]
3. Y. Sun and L. E. H. Smith, "Retinal vasculature in development and diseases," Annu. Rev. Vis. Sci. 4(1), 101–122 (2018). [CrossRef]
4. J. T. Cao, D. S. McLeod, C. A. Merges, and G. A. Lutty, "Choriocapillaris degeneration and related pathologic changes in human diabetic eyes," Arch. Ophthalmol. 116(5), 589–597 (1998). [CrossRef]
5. A. W. Fryczkowski, B. L. Hodes, and J. Walker, "Diabetic choroidal and iris vasculature scanning electron-microscopy findings," Int. Ophthalmol. 13(4), 269–279 (1989). [CrossRef]
6. N. L. Everdell, I. B. Styles, A. Calcagni, J. Gibson, J. Hebden, and E. Claridge, "Multispectral imaging of the ocular fundus using light emitting diode illumination," Rev. Sci. Instrum. 81(9), 093706 (2010). [CrossRef]
7. Y. Xu, X. Liu, L. Cheng, L. Su, and X. Xu, "A light-emitting diode (LED)-based multispectral imaging system in evaluating retinal vein occlusion," Lasers Surg. Med. 47(7), 549–558 (2015). [CrossRef]
8. A. Calcagni, J. M. Gibson, I. B. Styles, E. Claridge, and F. Orihuela-Espina, "Multispectral retinal image analysis: a novel non-invasive tool for retinal imaging," Eye 25(12), 1562–1569 (2011). [CrossRef]
9. G. Lu and B. Fei, "Medical hyperspectral imaging: a review," J. Biomed. Opt. 19(1), 010901 (2014). [CrossRef]
10. J. Kaluzny, H. Li, W. Liu, P. Nesper, J. Park, H. F. Zhang, and A. A. Fawzi, "Bayer filter snapshot hyperspectral fundus camera for human retinal imaging," Curr. Eye Res. 42(4), 629–635 (2017). [CrossRef]
11. T. Alterini, F. Díaz-Doutón, F. J. Burgos-Fernández, L. González, C. Mateo, and M. Vilaseca, "Fast visible and extended near-infrared multispectral fundus camera," J. Biomed. Opt. 24(9), 1–9 (2019). [CrossRef]
12. S. Li, L. Huang, Y. Bai, Y. Cheng, J. Tian, S. Wang, Y. Sun, K. Wang, F. Wang, and Q. Zhang, "In vivo study of retinal transmission function in different sections of the choroidal structure using multispectral imaging," Invest. Ophthalmol. Visual Sci. 56(6), 3731–3742 (2015). [CrossRef]
13. W. Drexler, U. Morgner, F. X. Kartner, C. Pitris, S. A. Boppart, X. D. Li, E. P. Ippen, and J. G. Fujimoto, "In vivo ultrahigh-resolution optical coherence tomography," Opt. Lett. 24(17), 1221–1223 (1999). [CrossRef]
14. U. Schmidt-Erfurth, R. A. Leitgeb, S. Michels, B. Povazay, S. Sacu, B. Hermann, C. Ahlers, H. Sattmann, C. Scholda, and A. F. Fercher, "Three-dimensional ultrahigh-resolution optical coherence tomography of macular diseases," Invest. Ophthalmol. Visual Sci. 46(9), 3393–3402 (2005). [CrossRef]
15. A. G. Podoleanu, G. M. Dobre, R. G. Cucu, R. Rosen, P. Garcia, J. Nieto, D. Will, R. Gentile, T. Muldoon, J. Walsh, L. A. Yannuzzi, Y. Fisher, D. Orlock, R. Weitz, J. A. Rogers, S. Dunne, and A. Boxer, "Combined multiplanar optical coherence tomography and confocal scanning ophthalmoscopy," J. Biomed. Opt. 9(1), 86–93 (2004). [CrossRef]
16. I. Gorczynska, V. J. Srinivasan, L. N. Vuong, R. W. S. Chen, J. J. Liu, E. Reichel, M. Wojtkowski, J. S. Schuman, J. S. Duker, and J. G. Fujimoto, "Projection OCT fundus imaging for visualising outer retinal pathology in non-exudative age-related macular degeneration," Br. J. Ophthalmol. 93(5), 603–609 (2009). [CrossRef]
17. C. Blatter, T. Klein, B. Grajciar, T. Schmoll, W. Wieser, R. Andre, R. Huber, and R. A. Leitgeb, "Ultrahigh-speed non-invasive widefield angiography," J. Biomed. Opt. 17(7), 0705051 (2012). [CrossRef]
18. G. Liu, J. Yang, J. Wang, Y. Li, P. Zang, Y. Jia, and D. Huang, "Extended axial imaging range, widefield swept source optical coherence tomography angiography," J. Biophotonics 10(11), 1464–1472 (2017). [CrossRef]
19. B. Povazay, "Wide-field optical coherence tomography of the choroid in vivo," Invest. Ophthalmol. Visual Sci. 50(4), 1856–1863 (2008). [CrossRef]
20. T. Klein, W. Wieser, C. M. Eigenwillig, B. R. Biedermann, and R. Huber, "Megahertz OCT for ultrawide-field retinal imaging with a 1050 nm Fourier domain mode-locked laser," Opt. Express 19(4), 3044–3062 (2011). [CrossRef]
21. J. Yang, R. Chandwani, R. Zhao, Z. Wang, Y. Jia, D. Huang, and G. Liu, "Polarization-multiplexed, dual-beam swept source optical coherence tomography angiography," J. Biophotonics 11(3), e201700303 (2018). [CrossRef]
22. A. Standard, "Z136. 1. American national standard for the safe use of lasers," American National Standards Institute Inc. (1993).
23. I. O. G. Standardization, "Ophthalmic instruments-Fundamental requirements and test methods," in International Standard I 15004-2. Ophthalmic Instruments; Light Hazard protection, (2007).
24. S. J. Chiu, X. T. Li, P. Nicholas, C. A. Toth, J. A. Izatt, and S. Farsiu, "Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation," Opt. Express 18(18), 19413–19428 (2010). [CrossRef]
25. H. Zhou, Z. Chu, Q. Zhang, Y. Dai, G. Gregori, P. J. Rosenfeld, and R. K. Wang, "Attenuation correction assisted automatic segmentation for assessing choroidal thickness and vasculature with swept-source OCT," Biomed. Opt. Express 9(12), 6067–6080 (2018). [CrossRef]
26. A. F. Frangi, W. J. Niessen, K. L. Vincken, and M. A. Viergever, "Multiscale vessel enhancement filtering," in International Conference on Medical Image Computing and Computer-Assisted Intervention, (Springer, 1998), 130–137.
27. M. A. Kirby, C. Li, W. J. Choi, G. Gregori, P. Rosenfeld, and R. Wang, "Why choroid vessels appear dark in clinical OCT images," in 2018.
28. R. Hua and H. Wang, "Dark signals in the choroidal vasculature on optical coherence tomography angiography: an artefact or not?" J. Ophthalmol. 2017, 1–8 (2017). [CrossRef]
29. B. Khoobehi, J. M. Beach, and H. Kawano, "Hyperspectral imaging for measurement of oxygen saturation in the optic nerve head," Invest. Ophthalmol. Visual Sci. 45(5), 1464–1472 (2004). [CrossRef]
30. J. M. Beach, K. J. Schwenzer, S. Srinivas, D. Kim, and J. S. Tiedeman, "Oximetry of retinal vessels by dual-wavelength imaging: calibration and influence of pigmentation," J. Appl. Physiol. 86(2), 748–758 (1999). [CrossRef]
31. S. H. Hardarson, A. Harris, R. A. Karlsson, G. H. Halldorsson, L. Kagemann, E. Rechtman, G. M. Zoega, T. Eysteinsson, J. A. Benediktsson, A. Thorsteinsson, P. K. Jensen, J. Beach, and E. Stefansson, "Automatic retinal oximetry," Invest. Ophthalmol. Visual Sci. 47(11), 5011–5016 (2006). [CrossRef]
32. A. Geirsdottir, O. Palsson, S. H. Hardarson, O. B. Olafsdottir, J. V. Kristjansdottir, and E. Stefánsson, "Retinal vessel oxygen saturation in healthy individuals," Invest. Ophthalmol. Visual Sci. 53(9), 5433 (2012). [CrossRef]
33. T. Fabritius, S. Makita, Y. Hong, R. A. Myllylä, and Y. Yasuno, "Automated retinal shadow compensation of optical coherence tomography images," J. Biomed. Opt. 14(1), 010503 (2009). [CrossRef]
34. H. Hammer, D. Schweitzer, E. Thamm, A. Kolb, and J. Strobel, "Scattering properties of the retina and the choroids determined from OCT-A-scans," Int. Ophthalmol. 23(4/6), 291–295 (2001). [CrossRef]
35. W. Liu and H. F. Zhang, "Photoacoustic imaging of the eye: A mini review," Photoacoustics, S2213597916300180.
36. T. Theelen, C. B. Hoyng, and B. J. Klevering, "Near-infrared subretinal imaging in choroidal neovascularization," in Medical Retina (Springer, 2010), pp. 77–93.
37. C. Zauner, "Implementation and benchmarking of perceptual image hash functions," (2010).
38. I. Flores-Moreno, F. Lugo, J. S. Duker, and J. M. Ruiz-Moreno, "The relationship between axial length and choroidal thickness in eyes with high myopia," Am. J. Ophthalmol. 155(2), 314–319 (2012). [CrossRef]
39. V. Manjunath, M. Taha, J. G. Fujimoto, and J. S. Duker, "Choroidal thickness in normal eyes measured using cirrus HD optical coherence tomography," Am. J. Ophthalmol. 150(3), 325–329 (2010)..= [CrossRef]
40. S. Wang, Y. Wang, X. Gao, N. Qian, and Y. Zhuo, "Choroidal thickness and high myopia: A cross-sectional study and meta-analysis retina," BMC Ophthalmol. 15(1), 70 (2015). [CrossRef]
S. S. Hayreh and S. S. Hayreh, "In vivo choroidal circulation and its watershed zones," Eye 4(2), 273–289 (1990).
D. L. Nickla and J. Wallman, "The multifunctional choroid," Prog. Retinal Eye Res. 29(2), 144–168 (2010).
Y. Sun and L. E. H. Smith, "Retinal vasculature in development and diseases," Annu. Rev. Vis. Sci. 4(1), 101–122 (2018).
J. T. Cao, D. S. McLeod, C. A. Merges, and G. A. Lutty, "Choriocapillaris degeneration and related pathologic changes in human diabetic eyes," Arch. Ophthalmol. 116(5), 589–597 (1998).
A. W. Fryczkowski, B. L. Hodes, and J. Walker, "Diabetic choroidal and iris vasculature scanning electron-microscopy findings," Int. Ophthalmol. 13(4), 269–279 (1989).
N. L. Everdell, I. B. Styles, A. Calcagni, J. Gibson, J. Hebden, and E. Claridge, "Multispectral imaging of the ocular fundus using light emitting diode illumination," Rev. Sci. Instrum. 81(9), 093706 (2010).
Y. Xu, X. Liu, L. Cheng, L. Su, and X. Xu, "A light-emitting diode (LED)-based multispectral imaging system in evaluating retinal vein occlusion," Lasers Surg. Med. 47(7), 549–558 (2015).
A. Calcagni, J. M. Gibson, I. B. Styles, E. Claridge, and F. Orihuela-Espina, "Multispectral retinal image analysis: a novel non-invasive tool for retinal imaging," Eye 25(12), 1562–1569 (2011).
G. Lu and B. Fei, "Medical hyperspectral imaging: a review," J. Biomed. Opt. 19(1), 010901 (2014).
J. Kaluzny, H. Li, W. Liu, P. Nesper, J. Park, H. F. Zhang, and A. A. Fawzi, "Bayer filter snapshot hyperspectral fundus camera for human retinal imaging," Curr. Eye Res. 42(4), 629–635 (2017).
T. Alterini, F. Díaz-Doutón, F. J. Burgos-Fernández, L. González, C. Mateo, and M. Vilaseca, "Fast visible and extended near-infrared multispectral fundus camera," J. Biomed. Opt. 24(9), 1–9 (2019).
S. Li, L. Huang, Y. Bai, Y. Cheng, J. Tian, S. Wang, Y. Sun, K. Wang, F. Wang, and Q. Zhang, "In vivo study of retinal transmission function in different sections of the choroidal structure using multispectral imaging," Invest. Ophthalmol. Visual Sci. 56(6), 3731–3742 (2015).
W. Drexler, U. Morgner, F. X. Kartner, C. Pitris, S. A. Boppart, X. D. Li, E. P. Ippen, and J. G. Fujimoto, "In vivo ultrahigh-resolution optical coherence tomography," Opt. Lett. 24(17), 1221–1223 (1999).
U. Schmidt-Erfurth, R. A. Leitgeb, S. Michels, B. Povazay, S. Sacu, B. Hermann, C. Ahlers, H. Sattmann, C. Scholda, and A. F. Fercher, "Three-dimensional ultrahigh-resolution optical coherence tomography of macular diseases," Invest. Ophthalmol. Visual Sci. 46(9), 3393–3402 (2005).
A. G. Podoleanu, G. M. Dobre, R. G. Cucu, R. Rosen, P. Garcia, J. Nieto, D. Will, R. Gentile, T. Muldoon, J. Walsh, L. A. Yannuzzi, Y. Fisher, D. Orlock, R. Weitz, J. A. Rogers, S. Dunne, and A. Boxer, "Combined multiplanar optical coherence tomography and confocal scanning ophthalmoscopy," J. Biomed. Opt. 9(1), 86–93 (2004).
I. Gorczynska, V. J. Srinivasan, L. N. Vuong, R. W. S. Chen, J. J. Liu, E. Reichel, M. Wojtkowski, J. S. Schuman, J. S. Duker, and J. G. Fujimoto, "Projection OCT fundus imaging for visualising outer retinal pathology in non-exudative age-related macular degeneration," Br. J. Ophthalmol. 93(5), 603–609 (2009).
C. Blatter, T. Klein, B. Grajciar, T. Schmoll, W. Wieser, R. Andre, R. Huber, and R. A. Leitgeb, "Ultrahigh-speed non-invasive widefield angiography," J. Biomed. Opt. 17(7), 0705051 (2012).
G. Liu, J. Yang, J. Wang, Y. Li, P. Zang, Y. Jia, and D. Huang, "Extended axial imaging range, widefield swept source optical coherence tomography angiography," J. Biophotonics 10(11), 1464–1472 (2017).
B. Povazay, "Wide-field optical coherence tomography of the choroid in vivo," Invest. Ophthalmol. Visual Sci. 50(4), 1856–1863 (2008).
T. Klein, W. Wieser, C. M. Eigenwillig, B. R. Biedermann, and R. Huber, "Megahertz OCT for ultrawide-field retinal imaging with a 1050 nm Fourier domain mode-locked laser," Opt. Express 19(4), 3044–3062 (2011).
J. Yang, R. Chandwani, R. Zhao, Z. Wang, Y. Jia, D. Huang, and G. Liu, "Polarization-multiplexed, dual-beam swept source optical coherence tomography angiography," J. Biophotonics 11(3), e201700303 (2018).
A. Standard, "Z136. 1. American national standard for the safe use of lasers," American National Standards Institute Inc. (1993).
I. O. G. Standardization, "Ophthalmic instruments-Fundamental requirements and test methods," in International Standard I 15004-2. Ophthalmic Instruments; Light Hazard protection, (2007).
S. J. Chiu, X. T. Li, P. Nicholas, C. A. Toth, J. A. Izatt, and S. Farsiu, "Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation," Opt. Express 18(18), 19413–19428 (2010).
H. Zhou, Z. Chu, Q. Zhang, Y. Dai, G. Gregori, P. J. Rosenfeld, and R. K. Wang, "Attenuation correction assisted automatic segmentation for assessing choroidal thickness and vasculature with swept-source OCT," Biomed. Opt. Express 9(12), 6067–6080 (2018).
A. F. Frangi, W. J. Niessen, K. L. Vincken, and M. A. Viergever, "Multiscale vessel enhancement filtering," in International Conference on Medical Image Computing and Computer-Assisted Intervention, (Springer, 1998), 130–137.
M. A. Kirby, C. Li, W. J. Choi, G. Gregori, P. Rosenfeld, and R. Wang, "Why choroid vessels appear dark in clinical OCT images," in 2018.
R. Hua and H. Wang, "Dark signals in the choroidal vasculature on optical coherence tomography angiography: an artefact or not?" J. Ophthalmol. 2017, 1–8 (2017).
B. Khoobehi, J. M. Beach, and H. Kawano, "Hyperspectral imaging for measurement of oxygen saturation in the optic nerve head," Invest. Ophthalmol. Visual Sci. 45(5), 1464–1472 (2004).
J. M. Beach, K. J. Schwenzer, S. Srinivas, D. Kim, and J. S. Tiedeman, "Oximetry of retinal vessels by dual-wavelength imaging: calibration and influence of pigmentation," J. Appl. Physiol. 86(2), 748–758 (1999).
S. H. Hardarson, A. Harris, R. A. Karlsson, G. H. Halldorsson, L. Kagemann, E. Rechtman, G. M. Zoega, T. Eysteinsson, J. A. Benediktsson, A. Thorsteinsson, P. K. Jensen, J. Beach, and E. Stefansson, "Automatic retinal oximetry," Invest. Ophthalmol. Visual Sci. 47(11), 5011–5016 (2006).
A. Geirsdottir, O. Palsson, S. H. Hardarson, O. B. Olafsdottir, J. V. Kristjansdottir, and E. Stefánsson, "Retinal vessel oxygen saturation in healthy individuals," Invest. Ophthalmol. Visual Sci. 53(9), 5433 (2012).
T. Fabritius, S. Makita, Y. Hong, R. A. Myllylä, and Y. Yasuno, "Automated retinal shadow compensation of optical coherence tomography images," J. Biomed. Opt. 14(1), 010503 (2009).
H. Hammer, D. Schweitzer, E. Thamm, A. Kolb, and J. Strobel, "Scattering properties of the retina and the choroids determined from OCT-A-scans," Int. Ophthalmol. 23(4/6), 291–295 (2001).
W. Liu and H. F. Zhang, "Photoacoustic imaging of the eye: A mini review," Photoacoustics, S2213597916300180.
T. Theelen, C. B. Hoyng, and B. J. Klevering, "Near-infrared subretinal imaging in choroidal neovascularization," in Medical Retina (Springer, 2010), pp. 77–93.
C. Zauner, "Implementation and benchmarking of perceptual image hash functions," (2010).
I. Flores-Moreno, F. Lugo, J. S. Duker, and J. M. Ruiz-Moreno, "The relationship between axial length and choroidal thickness in eyes with high myopia," Am. J. Ophthalmol. 155(2), 314–319 (2012).
V. Manjunath, M. Taha, J. G. Fujimoto, and J. S. Duker, "Choroidal thickness in normal eyes measured using cirrus HD optical coherence tomography," Am. J. Ophthalmol. 150(3), 325–329 (2010)..=
S. Wang, Y. Wang, X. Gao, N. Qian, and Y. Zhuo, "Choroidal thickness and high myopia: A cross-sectional study and meta-analysis retina," BMC Ophthalmol. 15(1), 70 (2015).
Ahlers, C.
Alterini, T.
Andre, R.
Bai, Y.
Beach, J.
Beach, J. M.
Benediktsson, J. A.
Biedermann, B. R.
Blatter, C.
Boxer, A.
Burgos-Fernández, F. J.
Calcagni, A.
Cao, J. T.
Chandwani, R.
Chen, R. W. S.
Cheng, L.
Cheng, Y.
Chiu, S. J.
Chu, Z.
Claridge, E.
Cucu, R. G.
Dai, Y.
Díaz-Doutón, F.
Dobre, G. M.
Duker, J. S.
Dunne, S.
Eigenwillig, C. M.
Everdell, N. L.
Eysteinsson, T.
Fabritius, T.
Farsiu, S.
Fawzi, A. A.
Fei, B.
Fisher, Y.
Flores-Moreno, I.
Frangi, A. F.
Fryczkowski, A. W.
Garcia, P.
Geirsdottir, A.
Gentile, R.
Gibson, J.
Gibson, J. M.
González, L.
Gorczynska, I.
Grajciar, B.
Gregori, G.
Halldorsson, G. H.
Hammer, H.
Hardarson, S. H.
Harris, A.
Hayreh, S. S.
Hebden, J.
Hermann, B.
Hodes, B. L.
Hong, Y.
Hoyng, C. B.
Hua, R.
Huang, L.
Huber, R.
Ippen, E. P.
Izatt, J. A.
Jensen, P. K.
Jia, Y.
Kagemann, L.
Kaluzny, J.
Karlsson, R. A.
Kartner, F. X.
Kawano, H.
Khoobehi, B.
Kim, D.
Kirby, M. A.
Klein, T.
Klevering, B. J.
Kolb, A.
Kristjansdottir, J. V.
Li, C.
Li, H.
Li, X. D.
Li, X. T.
Liu, G.
Liu, J. J.
Liu, W.
Lu, G.
Lugo, F.
Lutty, G. A.
Makita, S.
Manjunath, V.
Mateo, C.
McLeod, D. S.
Merges, C. A.
Michels, S.
Morgner, U.
Muldoon, T.
Myllylä, R. A.
Nesper, P.
Nicholas, P.
Nickla, D. L.
Niessen, W. J.
Nieto, J.
Olafsdottir, O. B.
Orihuela-Espina, F.
Orlock, D.
Palsson, O.
Park, J.
Pitris, C.
Podoleanu, A. G.
Qian, N.
Rechtman, E.
Reichel, E.
Rogers, J. A.
Rosen, R.
Rosenfeld, P.
Rosenfeld, P. J.
Ruiz-Moreno, J. M.
Sacu, S.
Schmidt-Erfurth, U.
Schmoll, T.
Scholda, C.
Schuman, J. S.
Schweitzer, D.
Schwenzer, K. J.
Smith, L. E. H.
Srinivas, S.
Srinivasan, V. J.
Standard, A.
Standardization, I. O. G.
Stefansson, E.
Stefánsson, E.
Strobel, J.
Styles, I. B.
Su, L.
Sun, Y.
Taha, M.
Thamm, E.
Theelen, T.
Thorsteinsson, A.
Tian, J.
Tiedeman, J. S.
Toth, C. A.
Viergever, M. A.
Vilaseca, M.
Vincken, K. L.
Vuong, L. N.
Walker, J.
Wallman, J.
Walsh, J.
Wang, F.
Wang, K.
Wang, S.
Wang, Z.
Weitz, R.
Wieser, W.
Will, D.
Wojtkowski, M.
Yang, J.
Yannuzzi, L. A.
Yasuno, Y.
Zang, P.
Zauner, C.
Zhang, Q.
Zhao, R.
Zhou, H.
Zhuo, Y.
Zoega, G. M.
Am. J. Ophthalmol. (2)
Annu. Rev. Vis. Sci. (1)
Arch. Ophthalmol. (1)
BMC Ophthalmol. (1)
Br. J. Ophthalmol. (1)
Curr. Eye Res. (1)
Int. Ophthalmol. (2)
Invest. Ophthalmol. Visual Sci. (6)
J. Appl. Physiol. (1)
J. Biomed. Opt. (5)
J. Ophthalmol. (1)
Prog. Retinal Eye Res. (1)
Rev. Sci. Instrum. (1)
(1) [ u v ] = [ a 2 a 1 a 0 b 2 b 1 b 0 ] [ x y 1 ] ,
(2) R ( y , z ) = σ y z σ z σ y ,
Unweighted anterior segment visible and infrared radiation irradiance of MSFC system.
Wavelength(nm) 470 500 520 548 605 615 635 665 740 810 820 845
EIR-CL (10−5mW/cm2) 1.7 1.6 1.3 1.5 1.9 1.6 1.2 3.6 6.7 8.8 1.2 4.9
R-value of resized images after translation and similarity transform (consisting of rotation and scale transform).
Image size(Pixel)
Origin (512×512)
R-Value Translation transform 0.62 0.74 0.79 0.86 0.95
Similarity transform 0.53 0.61 0.66 0.76 0.88 | CommonCrawl |
\begin{document}
\title{{Markov-modulated Ornstein-Uhlenbeck processes}}
\author{G.\ Huang$^\bullet$, H.\ M. Jansen$^{\bullet,\dagger}$, M.\ Mandjes$^{\bullet,\star}$, P.\ Spreij$^\bullet$, \& K.\ De Turck$^\dagger$} \maketitle \begin{abstract} \noindent In this paper we consider an Ornstein-Uhlenbeck ({\sc ou}) process $(M(t))_{t\geqslant 0}$ whose parameters are determined by an external Markov process $(X(t))_{t\geqslant 0}$ on a finite state space $\{1,\ldots,d\}$; this process is usually referred to as {\it Markov-modulated Ornstein-Uhlenbeck} (or: {\sc mmou}). We use stochastic integration theory to determine explicit expressions for the mean and variance of $M(t)$. Then we establish a system of partial differential equations ({\sc pde}\,s) for the Laplace transform of $M(t)$ and the state $X(t)$ of the background process, jointly for time epochs $t=t_1,\ldots,t_K.$ Then we use this {\sc pde} to set up a recursion that yields all moments of $M(t)$ and its stationary counterpart; we also find an expression for the covariance between $M(t)$ and $M(t+u)$. We then establish a functional central limit theorem for $M(t)$ for the situation that certain parameters of the underlying {\sc ou} processes are scaled, in combination with the modulating Markov process being accelerated; interestingly, specific scalings lead to drastically different limiting processes. We conclude the paper by considering the situation of a single Markov process modulating {\it multiple} {\sc ou} processes.
\noindent {\it Keywords.} Ornstein-Uhlenbeck processes $\star$ Markov modulation $\star$ regime switching $\star$ martingale techniques $\star$ central-limit theorems
\noindent {Work partially done while K.\ de Turck was visiting Korteweg-de Vries Institute for Mathematics, University of Amsterdam, the Netherlands, with greatly appreciated financial support from {\it Fonds Wetenschappelijk Onderzoek / Research Foundation -- Flanders}.
\begin{itemize} \item[$^\bullet$] Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, the Netherlands. \item[$^\star$] CWI, P.O. Box 94079, 1090 GB Amsterdam, the Netherlands. \item[$^\dagger$] TELIN, Ghent University, St.-Pietersnieuwstraat 41, B9000 Gent, Belgium. \end{itemize} \noindent M.\ Mandjes is also with E{\sc urandom}, Eindhoven University of Technology, Eindhoven, the Netherlands, and IBIS, Faculty of Economics and Business, University of Amsterdam, Amsterdam, the Netherlands.}
\noindent {\it Email}. {\scriptsize $\{$\tt{g.huang|h.m.jansen|m.r.h.mandjes|p.j.c.spreij}$\}$\tt{@uva.nl},
{\tt [email protected]}} \end{abstract}
\section{Introduction} The Ornstein-Uhlenbeck ({\sc ou}) process is a stationary Markov-Gauss process, with the additional feature that is eventually reverts to its long-term mean; see the seminal paper \cite{OU}, as well as \cite{JAC} for a historic account. Having originated from physics, by now the process has found widespread use in a broad range of other application domains: finance, population dynamics, climate modeling, etc. In addition, it plays an important role in queueing theory, as it can be seen as the limiting process of specific classes of infinite-server queues under a certain scaling \cite{ROBE}. The {\sc ou} process is characterized by three parameters (which we call $\alpha$, $\gamma$, and $\sigma^2$ throughout this paper), which relate to the process' mean, convergence speed towards the mean, and variance, respectively.
The probabilistic properties of the {\sc ou} process have been thoroughly studied. One of the key results is that its value at a given time $t$ has a Normal distribution, with a mean and variance that can be expressed explicitly in terms of the parameters $\alpha$, $\gamma$, and $\sigma^2$ of the underlying {\sc ou} process; see for instance \cite[Eqn.\ (2)]{JAC}. In addition, various other quantities have been analyzed, such as the distribution of first passage times or the maximum value attained in an interval of given length; see e.g.\ \cite{ALI} and references therein.
The concept of {\it regime switching} (or:\ {\it Markov modulation}, as it is usually referred to in the operations research literature) has become increasingly important over the past decades. In regime switching, the parameters of the underlying stochastic process are determined by an external {\it background process} (or: {\it modulating process}), that is typically assumed to evolve independently of the stochastic process under consideration. Often the background process is assumed to be a Markov chain defined on a {\it finite} state space, say $\{1,\ldots,d\}$; in the context of Markov-modulated {\sc ou} ({\sc mmou}) this means that when this Markov chain is in state $i$, the process locally behaves as a {\sc ou} process with parameters $\alpha_i$, $\gamma_i$, and $\sigma^2_i.$
Owing to its various attractive features, regime switching has become an increasingly popular concept. In a broad spectrum of application domains it offers a natural framework for modeling situations in which the stochastic process under study reacts to an autonomously evolving environment. In finance, for instance, one could identify the background process with the `state of the economy', for instance as a two-state process (that is, alternating between a `good' and a `bad' state), to which e.g.\ asset prices react. Likewise, in wireless networks the concept can be used to model the channel conditions that vary in time, and to which users react.
In the operations research literature there is a sizable body of work on Markov-modulated queues, see e.g.\ the textbooks \cite[Ch.\ XI]{ASM} and \cite{NEUTS}, while Markov modulation has been intensively used in insurance and risk theory as well \cite{AA}. In the financial economics literature, the use of regime switching dates back to at least the late 1980s \cite{HAM}; various specific models have been considered since then, see for instance \cite{ANG,EMAM,ESIU}.
In this paper we present a set of new results in the context of the analysis of {\sc mmou}. Here and in the sequel we let $M(t)$ denote the position of the {\sc mmou} process at time $t$, whereas $M$ denotes its stationary counterpart. In the first place we derive explicit formulas for the mean and variance of $M(t)$ and $M$, jointly with the state of the background process, relying on standard machinery from stochastic integration theory. In specific special cases the resulting formulas simplify drastically (for instance when it is assumed that the background process starts off in equilibrium at time 0, or when the parameters $\gamma_i$ are assumed uniform across the states $i\in\{1,\ldots,d\}$).
The second contribution concerns the derivation of a system of partial differential equations for the Laplace transform of $M(t)$; when equating the partial derivative with respect to time to 0, we obtain a system of ordinary differential equations for the Laplace transform of $M$. This result is directly related to \cite[Thm. 3.2]{XING}, with the differences being that there the focus is on just stationary behavior, and that the system considered there has the additional feature of reflection at a lower boundary (to avoid the process attaining negative values). We set up a recursive procedure that generates all moments of $M(t)$; in each iteration a non-homogeneous system of differential equations needs to be solved. This procedure complements the recursion for the moments of the steady-state quantity $M$, as presented in \cite[Corollary 3.1]{XING} (in which each recursion step amounts to solving a system of linear equations). In addition, we also set up a system of partial differential equations for the Laplace transform associated with the joint distribution of $M(t_1),\ldots, M(t_K)$, and determine the covariance ${\mathbb C}{\rm ov}\,(M(t,t+u)).$
A third contribution concerns the behavior of the {\sc mmou} process under certain parameter scalings. \begin{itemize} \item[$\rhd$] A first scaling that we consider concerns speeding up the jumps of the background process by a factor $N$. Using the system of partial differential equations that we derived earlier, it is shown that the limiting process, obtained by sending $N\to\infty$, is an {\it ordinary} (that is, non-modulated) {\sc ou} process, with parameters that are time averages of the individual $\alpha_i$, $\gamma_i$, and $\sigma_i^2$. \item[$\rhd$] A second regime that we consider scales the transition rates of the Markovian background process by $N$, while the $\alpha_i$ and $\sigma_i^2$ are inflated by a factor $N^h$ for some $h>0$; the resulting process we call $M^{[N,h]}(t)$. We then center (subtract the mean, which is roughly proportional to $N^h$) and normalize $M^{[N,h]}(t)$, with the goal to establish a central limit theorem ({\sc clt}). Interestingly, it depends on the value of $h$ what the appropriate normalization is. If $h<1$ the variance of $M^{[N,h]}(t)$ is roughly proportional to the `scale' at which the modulated {\sc ou} process operates, viz.\ $N^h$, and as a consequence the normalization looks like $N^{h/2}$; at an intuitive level, the timescale of the background process is so fast, that the process essentially looks like an {\sc ou} process with time-averaged parameters. If, on the contrary, $h>1$, then the variance of $M^{[N,h]}(t)$ grows like $N^{2h-1}$, which is faster than $N^h$; as a consequence, the proper normalization looks like $N^{h-1/2}$; in this case the variance that appears in the {\sc clt} is directly related to the deviation matrix \cite{CS} associated with the background process. Importantly, we do not just prove Normality for a given value of $t>0$, but rather weak convergence (at the process level, that is) to the solution of a specific limiting stochastic differential equation.
\iffalse The proof of this result is rather involved, and intensively uses the system of (partial) differential equations that we derived earlier; this is a $d$-dimensional system, as it describes the Laplace transform of $M^{(N)}(t)$ jointly with the state of the background process. The idea is to manipulate the differential equations for the time-scaled process (in which step the deviation matrix enters the computations), which is then translated into system of differential equations for the centered and normalized version of $M^{(N)}(t)$ (again jointly with the state of the background process). This eventually results in a single-dimensional differential equation for the Laplace transform of the limiting value ($N\to\infty$) of the centered and normalized version of $M^{(N)}(t)$. This Laplace transform corresponds to a Normal distribution, and with L\'evy's convergence theorem the asymptotic Normality follows. \fi \end{itemize} The last contribution focuses on the situation that a single Markovian background process modulates {\it multiple} {\sc ou} processes. This, for instance, models the situation in which different asset prices react to the same `external circumstances' (i.e., state of the economy), or the situation in which different users of a wireless network react to the same channel conditions. The probabilistic behavior of the system is captured through a system of partial differential equations. It is also pointed out how the corresponding moments can be found.
Importantly, there is a strong similarity between the results presented in the framework of the present paper, and corresponding results for Markov-modulated {\it infinite-server queues}. In these systems the background process modulates an M/M/$\infty$ queue, meaning that we consider an M/M/$\infty$ queue of which the arrival rate and service rate are determined by the state of the background process \cite{DAURIA,FRALIXADAN2009}. For these systems, the counterparts of our {\sc mmou} results have been established: the mean and variance have been computed in e.g.\ \cite{BKMT,OCP}, (partial) differential equations for the Laplace transform of $M(t)$, as well as recursions for higher moments can be found in \cite{BMT,BKMT,OCP}, whereas parameter scaling results are given in \cite{BMT,BKMT} and, for a slightly different model \cite{BMTh}. Roughly speaking, any property that can be handled explicitly for the Markov-modulated infinite-server queue can be explicitly addressed for {\sc mmou} as well, and vice versa.
This paper is organized as follows. Section \ref{MOD} defines the model, and presents preliminary results. Then Section \ref{TB} deals with the system's transient behavior, in terms of a recursive scheme that yields all moments of $M(t)$, with explicit expressions for the mean and variance. Section \ref{TBPDE} presents a system of partial differential equations for the Laplace transform of $M(t)$ (which becomes a system of ordinary differential equations in steady state). In Section \ref{Sec:TS}, the parameter scalings mentioned above are applied (resulting in a process $M^{(N)}(t)$), leading to a functional {\sc clt} for an appropriately centered and normalized version of $M^{(N)}(t)$. The last section considers the setting of a single background process modulating multiple {\sc ou} processes.
\section{Model and preliminaries}\label{MOD} We start by giving a detailed model description of the Markov-modulated Ornstein-Uhlenbeck ({\sc mmou}) process. We are given a probability space $\mathopen{}\mathclose\bgroup\originalleft( \Omega , \mathcal{F} , \mathbb{P} \aftergroup\egroup\originalright)$ on which a random variable $M_0$, a standard Brownian motion $(B(t))_{t \geqslant 0}$ and a continuous-time Markov process $(X(t))_{t \geqslant 0}$ with finite state space are defined. It is assumed that $M_0$, $X$ and $B$ are independent. The process $X$ is the so-called background process; its state space is denoted by $\mathopen{}\mathclose\bgroup\originalleft\lbrace 1 , \ldots , d \aftergroup\egroup\originalright\rbrace$.
The idea behind {\sc mmou} is that the background process $X \mathopen{}\mathclose\bgroup\originalleft( \cdot \aftergroup\egroup\originalright)$ modulates an Ornstein-Uhlenbeck process. Intuitively, this means that while $X \mathopen{}\mathclose\bgroup\originalleft( \cdot \aftergroup\egroup\originalright)$ is in state $i \in \mathopen{}\mathclose\bgroup\originalleft\lbrace 1 , \ldots , d \aftergroup\egroup\originalright\rbrace$, the {\sc mmou} process $\mathopen{}\mathclose\bgroup\originalleft( M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) \aftergroup\egroup\originalright)_{t \geqslant 0}$ behaves as an Ornstein-Uhlenbeck process $U_{i} \mathopen{}\mathclose\bgroup\originalleft( \cdot \aftergroup\egroup\originalright)$ with parameters $\alpha_{i}$, $\gamma_{i}$ and $\sigma_{i}$, which evolves independently of the background process $X \mathopen{}\mathclose\bgroup\originalleft( \cdot \aftergroup\egroup\originalright)$. In mathematical terms, this means that $M \mathopen{}\mathclose\bgroup\originalleft( \cdot \aftergroup\egroup\originalright)$ should obey the stochastic differential equation \begin{align} \label{SDE:MMOU} {\rm d} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \mathopen{}\mathclose\bgroup\originalleft( \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} - \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \, {\rm d} t + \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright). \end{align}
To be more precise, we will call a stochastic process $(M(t))_{t \geqslant 0}$ an {\sc mmou} process with initial condition $M(0) = M_0$ if \begin{align} \label{SIE:intMMOU} M(t) = M_0 + \int_{0}^{t} \mathopen{}\mathclose\bgroup\originalleft( \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} - \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} M \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \, {\rm d} s + \int_{0}^{t} \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright). \end{align} The following theorem provides basic facts about the existence, uniqueness and distribution of an {\sc mmou} process. For proofs and additional details, see Section~\ref{sec:mmouexist}. As mentioned in the introduction, specific aspects of {\sc mmou} have been studied earlier in the literature; see for instance \cite{XING}.
\begin{theorem}\label{PROP} Define $\Gamma (t) := \int_{0}^{t} \gamma_{X (s)} \, {\rm d} s$. Then the stochastic process $(M(t))_{t \geqslant 0}$ given by \begin{align*} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = M_0 e^{ - \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) } + \int_{0}^{t} e^{ - \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} s + \int_{0}^{t} e^{ - \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \end{align*} is the unique {\sc mmou} process with initial condition $M_0$.
Conditional on the process $X$, the random variable $M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)$ has a Normal distribution with random mean \begin{equation} \label{rmu} \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = M _0 \exp \mathopen{}\mathclose\bgroup\originalleft( - \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) + \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} s\end{equation} and random variance \begin{equation}\label{rv} v \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)}^2 \, {\mathrm d} s. \end{equation} \end{theorem}
This result is analogous with the corresponding result for the Markov-modulated infinite-server queue in \cite{BKMT,DAURIA}: there it is shown that the number of jobs in the system has a Poisson distribution with random parameter.
For later use, we now recall some concepts pertaining to the theory of deviation matrices of Markov processes. For an introduction to this topic we refer to standard texts such as \cite{KEIL,KEM,SYS}. For a compact survey, see \cite{CS}.
Let the transition rates corresponding to the continuous-time Markov chain $(X(t))_{t\geqslant 0}$ be given by $q_{ij}\geqslant 0$ for $i\not=j$ and $q_i:=-q_{ii}:=\sum_{j\not=i}q_{ij}$. These transition rates define the {\it intensity matrix} or {\it generator} $Q$. The (unique) invariant distribution corresponding to $Q$ is denoted by (the column vector) ${\boldsymbol \pi}$, i.e., it obeys ${\boldsymbol \pi}Q = {\boldsymbol 0}$ and $ \vec{1}^{\rm T} \vec{\pi}=1$, where $ \vec{1}$ is a $d$-dimensional all-ones vector.
Let $\Pi := \vec{1} \vec{\pi}^{\rm T}$ denote the {\it ergodic matrix.} Then the {\it fundamental matrix} is given by $F := (\Pi - Q)^{-1}$, whereas the {\it deviation matrix} is defined by $D := F - \Pi$. Standard identities are $QF=FQ=\Pi - I$, as well as $\Pi D= D \Pi =0$ (here $0$ is to be read as an all-zeros $d\times d$ matrix) and $F\vec{1}=\vec{1}.$ The $(i,j)$-th entry of the deviation matrix, with $i,j\in\{1,\ldots,d\}$, can be alternatively computed as \[
D_{ij}:= \int_0^\infty({\mathbb P}(X(t)=j\,|\,X(0)=i)-\pi_j){\rm d}t,\] which in matrix form reads \begin{equation}\label{eq:d} D=\int_0^\infty \mathopen{}\mathclose\bgroup\originalleft(\exp(Qt)-\mathbf{1}\vec{\pi}^{\rm T}\aftergroup\egroup\originalright)\,\mathrm{d} t. \end{equation}
\section{Transient behavior: moments}\label{TB} In this section we analyze the moments of $M(t)$. First considering the mean and variance in the general situation, we then concentrate on more specific cases in which the expressions simplify greatly. In particular, we address the situation that all the $\gamma_i$s are equal, the situation that the background process starts off in equilibrium at time $0$, and the steady-state regime. The computations are immediate applications of stochastic integration theory. The section is completed by deriving an expression for the covariance between $M(t)$ and $M(t+u)$ (for $t,u\geqslant 0$), and a procedure that uses It\^o's formula to recursively determine all moments.
\subsection{Mean and variance: general case}\label{section:gc} Let ${\boldsymbol Z}(t)\in\{0,1\}^d$ be the vector of indicator functions associated with the Markov chain $(X(t))_{t\geqslant 0}$, that is, we let $Z_i(t)=1$ if $X(t)=i$ and $0$ else. Let $\vec{p}_t$ denote the vector of transient probabilities of the background process, i.e., $({\mathbb P}(X(t) = 1),\ldots,{\mathbb P}(X(t)=d))^{\rm T}$ (where we have not specified the distribution of the initial state $X(0)$ yet).
We subsequently find expressions for the mean $\mu_t:={\mathbb E}M(t)$ and variance $v_t:={\mathbb V}{\rm ar}\,M(t)$. \begin{itemize} \item[$\rhd$] The mean can be computed as follows. To this end, we consider the mean of $M(t)$ jointly with the state of the background process at time $t$. To this end, we define $\vec{Y}(t):=\vec{Z}(t) M(t),$ and $\vec{\nu}_t:={\mathbb E}\vec{Y}(t).$ \iffalse Directly from the definitions, with $\vec{Y}(t):=\vec{Z}(t) M(t),$ \[{\rm d}\mu_t = {\mathbb E}({\boldsymbol \alpha}^{\rm T}\vec{Z}(t)-\vec{\gamma}^{\rm T}\vec{Y}(t){\rm d}t.\] Let $\vec{\nu}_t:={\mathbb E}\vec{Y}(t).$ From the above we conclude that \begin{equation} \label{MU}\mu_t' = {\boldsymbol \alpha}^{\rm T}\vec{p}_t-\vec{\gamma}^{\rm T}\vec{\nu}_t.\end{equation} Obviously, this differential equation does not lead to an expression for $\mu_t$ yet (as $\mu_t$ appears on the left-hand side, while $\vec{\nu}_t$ appears on the right-hand side). This problem can be overcome as follows. \fi It is clear that \begin{equation}\label{eq:zz} {\rm d}\vec{Z}(t) = Q^{\rm T}\vec{Z}(t)\,{\rm d}t +{\rm d} \vec{K}(t), \end{equation} for a $d$-dimensional martingale $\vec{K}(t).$ With It\^o's rule we get, with $\bar{Q}_{\vec{\gamma}}:=Q^{\rm T}-{\rm diag}\{\vec{\gamma}\}$, \begin{align} {\rm d}\vec{Y}(t) & =M(t)\mathopen{}\mathclose\bgroup\originalleft(Q^{\rm T}\vec{Z}(t)\,{\rm d}t+{\rm d}\vec{K}(t)\aftergroup\egroup\originalright)+\vec{Z}(t)\mathopen{}\mathclose\bgroup\originalleft(\mathopen{}\mathclose\bgroup\originalleft(\vec{\alpha}^{\rm T}\vec{Z}(t)-\vec{\gamma}^{\rm T}\vec{Y}(t)\aftergroup\egroup\originalright){\rm d}t+\vec{\sigma}^{\rm T}\vec{Z}(t){\rm d}B(t)\aftergroup\egroup\originalright) \nonumber\\ & = \mathopen{}\mathclose\bgroup\originalleft(\bar{Q}_{\vec{\gamma}} \vec{Y}(t)+\mathrm{diag}(\alpha)\vec{Z}(t) \aftergroup\egroup\originalright)\,\mathrm{d} t +\mathrm{diag}\{\vec{\sigma}\}\vec{Z}(t){\rm d}B(t)+M(t)\,\mathrm{d} \vec{K}(t).\label{eq:y} \end{align} Taking expectations of both sides, we obtain the system \[\vec{\nu}'_t = \bar{Q}_{\vec{\gamma}}\vec{\nu}_t +{\rm diag}\{\vec{\alpha}\}\vec{p}_t.\] This is a non-homogeneous linear system of differential equations, that is solved by\[\vec{\nu}_t=e^{\bar{Q}_{\vec{\gamma}}t}\vec{\nu}_0+\int_0^t e^{\bar Q_{\vec{\gamma}}(t-s)}{\rm diag}\{\vec{\alpha}\}\vec{p}_s{\rm d}s;\] then $\mu_t=\vec{1}^{\rm T}{\vec{\nu}_t}.$ Realize that $\vec{\nu}_0 =m_0\vec{p}_0$, as we assumed that $M(0)$ equals $m_0.$
The equations simplify drastically if the background process starts off in equilibrium at time $0$; then evidently $\vec{p}_t=\vec{\pi}$ for all $t\ge 0$. As a result, we find $\vec{\nu}_t=e^{\bar{Q}_{\vec{\gamma}}t}\vec{\nu}_0-\bar{Q}_{\vec{\gamma}}^{-1}(I-e^{\bar{Q}_{\vec{\gamma}}t}){\rm diag}\{\vec{\alpha}\}\vec{\pi}.$
We now consider the steady-state regime (i.e., $t\to\infty$). From the above expressions, it immediately follows that $\vec{\nu}_\infty=-\bar{Q}_{\vec{\gamma}}^{-1}{\rm diag}\{\vec{\alpha}\}\vec{\pi}$, and $\mu_\infty =\vec{1}^{\rm T}\vec{\nu}_\infty = -\vec{1}^{\rm T}\bar{Q}_{\vec{\gamma}}^{-1}{\rm diag}\{\vec{\alpha}\}\vec{\pi}$. We further note that $\vec{\gamma}=-(Q-{\rm diag}\{\vec{\gamma}\})\vec{1}$, and hence $\vec{\gamma}^{\rm T}\bar{Q}_{\vec{\gamma}}^{-1}=-\vec{1}^{\rm T}$, so that $\vec{\gamma}^{\rm T}\vec{\nu}_\infty= \vec{\pi}^{\rm T}\vec{\alpha}.$
\item[$\rhd$] The variance can be found in a similar way. Define $\bar{\vec{Y}}(t):=\vec{Z}(t) M^2(t)$, and $\vec{w}_t:={\mathbb E}\bar{\vec{Y}}(t).$ Now our starting point is the relation \[{\rm d}(M(t)-\mu_t)=\mathopen{}\mathclose\bgroup\originalleft(\vec{\alpha}^{\rm T}(\vec{Z}(t)-\vec{p}_t)-\vec{\gamma}^{\rm T}(\vec{Y}(t)-\vec{\nu}_t)\aftergroup\egroup\originalright){\rm d}t +\vec{\sigma}^{\rm T}\vec{Z}(t){\rm d}B(t),\] so that \begin{eqnarray*} {\rm d}(M(t)-\mu_t)^2&=&2(M(t)-\mu_t)\mathopen{}\mathclose\bgroup\originalleft(\vec{\alpha}^{\rm T}(\vec{Z}(t)-\vec{p}_t)-\vec{\gamma}^{\rm T}(\vec{Y}(t)-\vec{\nu}_t)\aftergroup\egroup\originalright){\rm d}t \\ &&+\:2(M(t)-\mu_t) \vec{\sigma}^{\rm T}\vec{Z}(t)\,{\rm d}B(t)\,+\, \vec{\sigma}^{\rm T}{\rm diag}\{\vec{Z}(t)\}\vec{\sigma}\,{\rm d}t. \end{eqnarray*} Taking expectations of both sides, \[v_t'=2\vec{\alpha}^{\rm T}\vec{\nu}_t-2\mu_t\vec{\alpha}^{\rm T}\vec{p}_t -2\vec{\gamma}^{\rm T}\vec{w}_t+2\mu_t\vec{\gamma}^{\rm T}\vec{\nu}_t+\vec{\sigma}^{\rm T}{\rm diag}\{\vec{p}_t\}\vec{\sigma}.\] Clearly, to evaluate this expression, we first need to identify $\vec{w}_t$. To this end, we set up and equation for ${\rm d}\bar{\vec{Y}}(t)$ as before, take expectations, so as to obtain \[\vec{w}'_t =\bar{Q}_{2\vec{\gamma}} \vec{w}_t + 2\,{\rm diag}\{\vec{\alpha}\}\vec{\nu}_t + {\rm diag}\{\vec{\sigma}^2\}\vec{p}_t;\] here $\vec{\sigma}^2$ is the vector $(\sigma_1^2,\ldots,\sigma_d^2)^{\rm T}$. This leads to \begin{equation} \label{WW}\vec{w}_t=e^{\bar{Q}_{2\vec{\gamma}}t} \vec{w}_0+ \int_0^t e^{\bar Q_{\vec{2\gamma}}(t-s)}\mathopen{}\mathclose\bgroup\originalleft( 2\,{\rm diag}\{\vec{\alpha}\}\vec{\nu}_s + {\rm diag}\{\vec{\sigma}^2\}\vec{p}_s\aftergroup\egroup\originalright) {\rm d}s,\end{equation} so that $v_t=\vec{1}^{\rm T}{\vec{w}_t}-\mu_t^2.$ Observe that $\vec{w}_0=m_0^2\vec{p}_0.$
Again simplifications can be made if $\vec{p}_0=\vec{\pi}$ (and hence $\vec{p}_t=\vec{\pi}$ for all $t\geqslant 0$). In that case, we had already found an expression for $\vec{\nu}_s$ above, and as a result (\ref{WW}) can be explicitly evaluated.
For the stationary situation ($t\to\infty$, that is) we obtain \ \[\vec{w}_\infty = -\bar{Q}_{2\vec{\gamma}}^{-1}\mathopen{}\mathclose\bgroup\originalleft(2\,{\rm diag}\{\vec{\alpha}\}\vec{\nu}_\infty + {\rm diag}\{\vec{\sigma}^2\}\vec{\pi}\aftergroup\egroup\originalright),\] and $v_\infty=\vec{1}^{\rm T}{\vec{w}_\infty}-\mu_\infty^2.$ \end{itemize}
We consider now an even more special case: $\gamma_i\equiv\gamma$ for all $i$ (in addition to $\vec{p}_t={\vec{\pi}}$; we let $t\geqslant 0$). It is directly seen that $\mu_\infty= \vec{\pi}^{\rm T}\vec{\alpha}/\gamma.$ Note that $\vec{\gamma}^{\rm T}\bar{Q}_{\vec{\gamma}}^{-1}=-\vec{1}^{\rm T}$ implies $\vec{1}^{\rm T}\bar{Q}_{\delta\vec{1}}^{-1}=-\delta^{-1}\vec{1}^{\rm T}$ for any $\delta>0$, so that \begin{eqnarray*}v_\infty&=&\vec{1}^{\rm T}{\vec{w}_\infty}-\mu_\infty^2=\frac{\vec{1}^{\rm T}{\rm diag}\{\vec{\alpha}\}\vec{\nu}_\infty}{\gamma}+\frac{\vec{\pi}^{\rm T}\vec{\sigma}^2}{2\gamma}-\mathopen{}\mathclose\bgroup\originalleft(\frac{\vec{\pi}^{\rm T}\vec{\alpha}}{\gamma}\aftergroup\egroup\originalright)^2\\ &=&-\frac{\vec{1}^{\rm T}{\rm diag}\{\vec{\alpha}\} \bar{Q}_{\gamma\vec{1}}^{-1}{\rm diag}\{\vec{\alpha}\}\vec{\pi} }{\gamma}+\frac{\vec{\pi}^{\rm T}\vec{\sigma}^2}{2\gamma}-\mathopen{}\mathclose\bgroup\originalleft(\frac{\vec{\pi}^{\rm T}\vec{\alpha}}{\gamma}\aftergroup\egroup\originalright)^2 .\end{eqnarray*} Now observe that, with $\check{D}_{ij}(\gamma):=\int_0^\infty p_{ij}(v)e^{-\gamma v}{\rm d}v$ for $\gamma>0$, integration by parts yields \[Q\check{D}(\gamma)= \int_0^\infty QP(v)e^{-\gamma v}{\rm d}v= \int_0^\infty P'(v)e^{-\gamma v}{\rm d}v= -I+\int_0^\infty \gamma P(v)e^{-\gamma v}{\rm d}v= -I+\gamma \check{D}(\gamma). \] As a consequence, $-(Q-\gamma I)\check{D}(\gamma) = I,$ so that \[v_\infty= \frac{\vec{\pi}^{\rm T}\vec{\sigma}^2}{2\gamma} +\frac{1}{\gamma}\vec{\alpha}^{\rm T}{\rm diag}\{\vec{\pi}\}\check{D}(\gamma)\vec{\alpha} -\mathopen{}\mathclose\bgroup\originalleft(\frac{\vec{\pi}^{\rm T}\vec{\alpha}}{\gamma}\aftergroup\egroup\originalright)^2,\] which, with $D_{ij}(\gamma):=\int_0^\infty (p_{ij}(v)-\pi_j)e^{-\gamma v}{\rm d}v= \check{D}_{ij}(\gamma)-\pi_j/\gamma$, eventually leads to \[v_\infty= \frac{\vec{\pi}^{\rm T}\vec{\sigma}^2}{2\gamma} +\frac{1}{\gamma}\vec{\alpha}^{\rm T}{\rm diag}\{\vec{\pi}\}{D}(\gamma)\vec{\alpha} .\] The next subsection further studies the case in which the $\gamma_i$s are equal, i.e., $\gamma_i\equiv \gamma$, and the background process is in steady state at time $0$, i.e., and $\vec{p}_t=\vec{\pi}$. As it turns out, under these conditions the mean and variance can also be found by an alternative elementary, insightful argumentation.
\subsection{Mean and variance: special case of equal ${\boldsymbol \gamma}$, starting in equilibrium}\label{SPECC} In this subsection we consider the special case $\gamma_i\equiv \gamma$ for all $i$, while the Markov chain $X(t)$ starts off in equilibrium at time $0$ (so that ${\mathbb P}(X(t)=i)={\mathbb P}(X(0)=i)=\pi_i$ for all $t\geqslant 0$). In this special case we can evaluate $\mu_t$ and $v_t$ rather explicitly, particularly when in addition particular scalings are imposed.
We first concentrate on computing the transient mean $\mu_t$. We denote by $X$ the path $(X(s), s\in [0,t]).$
Now using the representation of Thm.\ \ref{PROP}, and recalling the standard fact that $\mu_t$ can be written as ${\mathbb E} \,(\,{\mathbb E}(M(t)\,|\,X))$, it is immediately seen that $\mu_t$ can be written as a convex mixture of $m_0$ and ${\boldsymbol\pi}^{\rm T}{\boldsymbol\alpha}/\gamma$: \[\mu_t = m_0e^{-\gamma t} + e^{-\gamma t}\int_0^t e^{\gamma s}{\rm d}s \mathopen{}\mathclose\bgroup\originalleft(\sum_{i=1}^d \pi_i\alpha_i \aftergroup\egroup\originalright)=m_0e^{-\gamma t} +\frac{ {\boldsymbol\pi}^{\rm T}{\boldsymbol\alpha}}{\gamma}\,(1-e^{-\gamma t});\] use that $(X(t))_{t\geqslant 0}$ started off in equilibrium at time $0$. This expression converges, as $t\to\infty$, to the stationary mean ${\boldsymbol\pi}^{\rm T}{\boldsymbol\alpha}/\gamma$, as expected.
The variance $v_t$ can be computed similarly, relying on the so called {\it law of total variance}, which says that ${\mathbb V}{\rm ar}\,M(t)=
{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft({\mathbb V}{\rm ar}(M(t)\,|\,X)\aftergroup\egroup\originalright)+{\mathbb V}{\rm ar}\mathopen{}\mathclose\bgroup\originalleft({\mathbb E}(M(t)\,|\,X)\aftergroup\egroup\originalright)$. Regarding the first term, it is seen that Thm.\ \ref{PROP} directly yields
\begin{eqnarray*}{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft({\mathbb V}{\rm ar}(M(t)\,|\,X)\aftergroup\egroup\originalright)&=&{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft(\int_0^t e^{-2\gamma(t-s)}\sigma^2_{X(s)}\,{\rm d}s \aftergroup\egroup\originalright)\\ &=&\int_0^t e^{-2\gamma(t-s)}{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft(\sigma^2_{X(s)}\aftergroup\egroup\originalright)\,{\rm d}s=\sum_{i=1}^d \pi_i\sigma_i^2\mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-2\gamma t}}{2\gamma}\aftergroup\egroup\originalright). \end{eqnarray*} Along similar lines,
\begin{eqnarray*}{\mathbb V}{\rm ar}\mathopen{}\mathclose\bgroup\originalleft({\mathbb E}(M(t)\,|\,X)\aftergroup\egroup\originalright)&=& {\mathbb V}{\rm ar}\mathopen{}\mathclose\bgroup\originalleft(\int_0^t e^{-\gamma(t-s)}\alpha_{X(s)}\,{\rm d}s\aftergroup\egroup\originalright)\\&=& \int_0^t\int_0^t {\mathbb C}{\rm ov}\mathopen{}\mathclose\bgroup\originalleft(e^{-\gamma(t-s)}\alpha_{X(s)},
e^{-\gamma(t-u)}\alpha_{X(u)}\aftergroup\egroup\originalright){\rm d}u\,{\rm d}s\\&=& e^{-2\gamma t}\int_0^t\int_0^t e^{\gamma (s+u)}{\mathbb C}{\rm ov}\mathopen{}\mathclose\bgroup\originalleft(\alpha_{X(s)}, \alpha_{X(u)}\aftergroup\egroup\originalright){\rm d}u\,{\rm d}s. \end{eqnarray*} The latter integral expression can be made more explicit. Recalling that $(X(t))_{t\geqslant 0}$ started off in equilibrium at time $0$, it can be evaluated as \begin{eqnarray*}\lefteqn{2e^{-2\gamma t}\int_0^t\int_0^s e^{\gamma (s+u)}{\mathbb C}{\rm ov}\mathopen{}\mathclose\bgroup\originalleft(\alpha_{X(s)}, \alpha_{X(u)}\aftergroup\egroup\originalright){\rm d}u\,{\rm d}s}\\ &=& 2e^{-2\gamma t}\int_0^t\int_0^s e^{\gamma (s+u)}\sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j \pi_i(p_{ij}(s-u)-\pi_j){\rm d}u\,{\rm d}s\\ &=&\frac{1}{\gamma} \sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j \int_0^t \mathopen{}\mathclose\bgroup\originalleft(e^{-\gamma v}-e^{-\gamma(2t-v)}\aftergroup\egroup\originalright)\pi_i(p_{ij}(v)-\pi_j){\rm d}v \end{eqnarray*} (where the last equation follows after changing the order of integration and some elementary calculus). We arrive at the following result. \begin{proposition} \label{PROP2} For $t\ge 0$, \[\mu_t = m_0e^{-\gamma t} +\frac{ {\boldsymbol\pi}^{\rm T}{\boldsymbol\alpha}}{\gamma}\,(1-e^{-\gamma t}),\] and \[v_t =\sum_{i=1}^d \pi_i\sigma_i^2\mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-2\gamma t}}{2\gamma}\aftergroup\egroup\originalright)+
\sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j \int_0^t \mathopen{}\mathclose\bgroup\originalleft(\frac{e^{-\gamma v}-e^{-\gamma(2t-v)}}{\gamma}\aftergroup\egroup\originalright)\pi_i(p_{ij}(v)-\pi_j){\rm d}v.\] \end{proposition}
We conclude this section by considering two specific limiting regimes, to which we return in Section~\ref{Sec:TS} where we will derive limit distributions under parameter scalings. \begin{itemize} \item[$\rhd$] Specializing to the situation that $t\to\infty$, we obtain \[{\mathbb V}{\rm ar}\, M =\frac{ {\boldsymbol\pi}^{\rm T}{\boldsymbol\sigma}^2}{2\gamma}+ \frac{1}{\gamma} \sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j \pi_iD_{ij}(\gamma)= \frac{ {\boldsymbol\pi}^{\rm T}{\boldsymbol\sigma}^2}{2\gamma}+ \frac{1}{\gamma} \vec{\alpha}^{\rm T}{\rm diag}\{\vec{\pi}\}D(\gamma)\vec{\alpha},\] in accordance with the expression we found before. \item[$\rhd$] Scale ${\boldsymbol\alpha}\mapsto N^h{\boldsymbol\alpha}$, ${\boldsymbol\sigma^2}\mapsto N^h{\boldsymbol\sigma^2}$, and $Q\mapsto NQ$ for some $h\ge 0$. We obtain that ${\mathbb V}{\rm ar} \,M(t)$ equals \[ N^h\sum_{i=1}^d \pi_i\sigma_i^2\mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-2\gamma t}}{2\gamma}\aftergroup\egroup\originalright)\hspace{-0.4mm}+{N^{2h}}\sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j\hspace{-0.4mm} \int_0^t \mathopen{}\mathclose\bgroup\originalleft(\frac{e^{-\gamma v}-e^{-\gamma(2t-v)}}{\gamma}\aftergroup\egroup\originalright)\hspace{-0.4mm}\pi_i\hspace{-0.2mm}\mathopen{}\mathclose\bgroup\originalleft(p_{ij}(vN)-\pi_j\aftergroup\egroup\originalright)\hspace{-0.2mm} {\rm d}v,\] which for $N$ large behaves as \begin{eqnarray} \lefteqn{\hspace{-15mm}\mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-2\gamma t}}{2\gamma}\aftergroup\egroup\originalright)\mathopen{}\mathclose\bgroup\originalleft(N^h\sum_{i=1}^d \pi_i\sigma_i^2+2N^{2h-1}\sum_{i=1}^d\sum_{j=1}^d\alpha_i\alpha_j\pi_iD_{ij}\aftergroup\egroup\originalright)}\nonumber\\&=& \mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-2\gamma t}}{2\gamma}\aftergroup\egroup\originalright)\mathopen{}\mathclose\bgroup\originalleft(N^h\vec{\pi}^{\rm T}\vec{\sigma}^2+2N^{2h-1} \vec{\alpha}^{\rm T}{\rm diag}\{\vec{\pi}\}D\vec{\alpha}\aftergroup\egroup\originalright)\label{PD} ,\end{eqnarray} where $D:=D(0)$ is the deviation matrix introduced in Section \ref{MOD}.
We observe an interesting dichotomy: for $h<1$ the variance is essentially linear in the `scale' of the {\sc ou} processes $N^h$, while for $h>1$ it behaves superlinearly in $N^h$ (more specifically, proportionally to $N^{2h-1}$). It is this dichotomy that also featured in earlier work on Markov-modulated infinite-server queues \cite{BMT}.
The intuition behind the dichotomy is the following. If $h<1$, then the timescale of the background process systematically exceeds that of the $d$ underlying {\sc ou} processes (that is, the background process is `faster'). As a result, the system essentially behaves as an {\it ordinary} (that is, non-modulated) {\sc ou} process with `time average' parameters $\alpha_\infty:={\boldsymbol \pi}^{\rm T}{\boldsymbol\alpha}$, $\gamma$, and $\sigma_\infty^2:={\boldsymbol \pi}^{\rm T}{\boldsymbol\sigma^2}$. If $h>1$, on the contrary, the background process jumps at a slow rate, relative to the typical timescale of the {\sc ou} processes; as a result, the process $(M(t))_{t\geqslant 0}$ moves between multiple local limits (where the individual `variance coefficients' $\sigma_i^2$ do not play a role). \iffalse \footnote{\tt {\scriptsize MM: Peter proposed to include: "But note that we don't only upscale the process $M$ in time. We also dampen the mean reversion behavior, effectively by replacing $\gamma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)}$ in \eqref{SDE:MMOU} with $\gamma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)}/n$ if time $t$ is replaced with $nt$ in order to prevent $M_{nt}$ converging to a stationary distribution." The more I read these lines, the less I understand them. Wouldn't the reader interpret them as if we DO impose some scaling on the $\gamma$s too (which we don't)? If $\gamma$ were scaled then "the process doesn't blow up by a factor $n$", which is what we want. I propose to either rephrase Peter's statement, or to leave it out.}\fi \end{itemize}
Note that it follows from (\ref{PD}) that ${\rm diag}\{\vec{\pi}\}D$ is a nonnegative definite matrix, although singular and non-symmetric in general; more precisely, it is a consequence of the fact that (\ref{PD}) is a variance and hence nonnegative, in conjunction with the fact the we can pick ${\boldsymbol\sigma^2}={\boldsymbol 0}$. Below we state and prove the nonnegativity by independent arguments; cf.\ \cite[Prop 3.2]{DAVE}.
\begin{proposition}\label{prop:nnd} The matrix $D^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}+\mathrm{diag}\{\vec{\pi}\}D$ is symmetric and nonnegative definite. \end{proposition}
\begin{proof} First we prove the claim that the matrix $Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}+\mathrm{diag}\{\vec{\pi}\}Q$ is (symmetric and) nonpositive definite. To that end we start from the semimartingale decomposition \eqref{eq:zz} for $\vec{Z}$. By the product rule we obtain, collecting all the martingale terms in $\mathrm{d} M(t)$, \[ \mathrm{d} (\vec{\vec{Z}}(t)\vec{Z}(t)^\mathrm{T})= Q^\mathrm{T} \vec{Z}(t)\vec{Z}(t)^\mathrm{T}\,\mathrm{d} t + \vec{Z}(t)\vec{Z}(t)^\mathrm{T} Q\,\mathrm{d} t +\mathrm{d}\langle \vec{Z}\rangle_t +\mathrm{d} M(t). \] As the predictable quadratic variation of $\vec{Z}$ is absolutely continuous and increasing, we can write $\mathrm{d}\langle \vec{Z}\rangle_t=P_t\,\mathrm{d} t$, where $P_t$ is a nonnegative definite matrix. Next we make the obvious observation that $\vec{Z}(t)\vec{Z}(t)^\mathrm{T}=\mathrm{diag}\{\vec{Z}(t)\}$. Hence we have by combining \eqref{eq:zz} and the above display \[ \mathrm{diag}\{Q^\mathrm{T} \vec{Z}(t)\}=Q^\mathrm{T}\mathrm{diag}\{\vec{Z}(t)\}+\mathrm{diag}\{\vec{Z}(t)\}Q+P_t. \] Taking expectations w.r.t.\ the stationary distribution of $\vec{Z}_t$ and using $Q^\mathrm{T}\pi=0$, we obtain \[ 0=Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}+\mathrm{diag}\{\vec{\pi}\}Q+\mathbb{E} P_t, \] from which it follows that $Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}+\mathrm{diag}\{\vec{\pi}\}Q$ is (symmetric and) nonpositive definite.
This in turn implies that $-D^\mathrm{T}(Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}+\mathrm{diag}\{\vec{\pi}\}Q)D$ is symmetric and nonnegative definite. Recall now that $FQ=\Pi-I$ and hence $DQ=\Pi-I$. Then $D^\mathrm{T} Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}D= -(\mathrm{diag}\{\vec{\pi}\}-\vec{\pi}\vec{\pi}^\mathrm{T})D$. But $\vec{\pi}^\mathrm{T} D=0$, so $D^\mathrm{T} Q^\mathrm{T}\mathrm{diag}\{\vec{\pi}\}D= -\mathrm{diag}\{\vec{\pi}\}D$. The result now follows. \end{proof}
\subsection{Covariances} In this subsection we point out how to compute the covariance \[c(t,u) :={\mathbb C}{\rm ov}\,(M(t), M(t+u)),\] for $t,u\geqslant 0.$ To this end, we observe that by applying a time shift, we first assume in the computations to follow that $t=0$ ,and we consider $c(t):=\cov(M(t),M(0))$. Below we make frequently use of the additional quantities $\vec{C}(t)=\cov(\vec{Y}(t),M(0))$ and $\vec{B}(t)=\cov(\vec{Z}(t),M(0))$. Note that $c(t)=\mathbf{1}^{\rm T} \vec{C}(t)$. Multiplying Equations \eqref{eq:zz} and~\eqref{eq:y} by $M(0)$, we obtain upon taking expectation the following system of {\sc ode}\,s: \[ \begin{pmatrix} \vec{B}'(t) \\ \vec{C}'(t) \end{pmatrix} =R\begin{pmatrix} B(t) \\ C(t) \end{pmatrix},\:\:\:\:\mbox{where}\:\:\:\: R:= \begin{pmatrix} Q^{\rm T} & 0 \\ \mathrm{diag}\{\vec{\alpha}\} & \bar{Q}_{\vec{\gamma}} \end{pmatrix} \begin{pmatrix} \vec{B}(t) \\ \vec{C}(t) \end{pmatrix} \] with initial conditions $\vec{B}(0)=\cov(\vec{Z}(0),M(0))$ and $\vec{C}(0)=\cov(\vec{Y}(0),M(0))$. In a more compact and obvious notation, we have $ \vec{A}'(t)=RA(t), $ and hence $ \vec{A}(t) =\exp(Rt) \vec{A}(0)$.
Likewise we can compute \[ A(t,u) := \begin{pmatrix} \cov(\vec{Z}(t+u),M(t)) \\ \cov(\vec{Y}(t+u),M(t)) \end{pmatrix} =\exp(Ru) \begin{pmatrix} \cov(\vec{Z}(t),M(t)) \\ \cov(\vec{Y}(t),M(t)) \end{pmatrix} . \] It remains to derive an expression for the last covariances. For $\cov(\vec{Z}(t),M(t))$ we need $\mathbb{E} M(t)\vec{Z}(t)=\mathbb{E} \vec{Y}(t)$ and $\mathbb{E} M(t)$, $\mathbb{E}\vec{Z}(t)$. For $\cov(\vec{Y}(t),M(t))$ we need $\mathbb{E} M(t)\vec{Y}(t)=\mathbb{E} M(t)^2\vec{Z}(t)$, $\mathbb{E} \vec{Y}(t)$ and $\mathbb{E} M(t)$. All these quantities have been obtained in Section~\ref{section:gc}.
\subsection{Recursive scheme for higher order moments}\label{ss:rec}
The objective of this section is to set up a recursive scheme to generate all transient moments, that is, the expected value of $M(t)^k$, for any $k\in\{1,2,\ldots\}$, jointly with the indicator function $1\{X(t)=i\}$. To that end we consider the expectation of $(M(t))^k\,\vec{Z}(t)$. First we rewrite Equation~\eqref{SDE:MMOU} as \begin{equation}\label{eq:mmouz} {\rm d} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \mathopen{}\mathclose\bgroup\originalleft( \vec{\alpha}^{\rm T} \vec{Z}(t) - \vec{\gamma}^{\rm T} \vec{Z}(t)X(t)\aftergroup\egroup\originalright) \, {\rm d} t + \vec{\sigma}^{\rm T} \vec{Z}(t) \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright). \end{equation} It\^o's lemma and \eqref{eq:mmouz} directly yield \begin{align*} {\rm d}(M(t))^k & = k(M(t))^{k-1}\mathopen{}\mathclose\bgroup\originalleft( \vec{\alpha}^{\rm T} \vec{Z}(t) - \vec{\gamma}^{\rm T} \vec{Z}(t)X(t)\aftergroup\egroup\originalright) \, {\rm d} t + k(M(t))^{k-1}\vec{\sigma}^{\rm T} \vec{Z}(t) \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) \\ & \qquad +\frac{1}{2}k(k-1)(M(t))^{k-2}\vec{\sigma}^{\rm T}\mathrm{diag}\{\vec{Z}(t)\}\vec{\sigma}\,{\rm d} t. \end{align*} Then we apply the product rule to $M(t)^k\vec{Z}(t)$, together with the just obtained equation and Equation~\eqref{eq:zz}, so as to obtain \begin{eqnarray*} {\rm d}\mathopen{}\mathclose\bgroup\originalleft((M(t))^k\vec{Z}(t)\aftergroup\egroup\originalright) & =& k(M(t))^{k-1}\mathopen{}\mathclose\bgroup\originalleft( \mathrm{diag}\{\vec{\alpha}\}\vec{Z}(t) - \mathrm{diag}\{\vec{\gamma}\} \vec{Z}(t)M(t)\aftergroup\egroup\originalright) \, {\rm d} t \\ &&\hspace{-2mm}+ \:k(M(t))^{k-1}\mathrm{diag}\{\vec{\sigma}\}\vec{Z}(t) \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) +\frac{1}{2}k(k-1)(M(t))^{k-2}\mathrm{diag}\{\vec{\sigma}^2\}\vec{Z}(t)\,{\rm d} t \\&&\hspace{-2mm}+\: (M(t))^k\mathopen{}\mathclose\bgroup\originalleft(Q^{\rm T} \vec{Z}(t)\,{\rm d}t+{\rm d}K(t)\aftergroup\egroup\originalright). \end{eqnarray*} All martingale terms on the right are genuine martingales and thus have expectation zero. Putting $\vec{H}_k(t):=\mathbb{E} M(t)^k\vec{Z}(t)$, we get the following recursion in {\sc ode} form: \begin{eqnarray*} \frac{{\rm d}}{{\rm d}t}\vec{H}_k(t) & =&k\mathrm{diag}\{\vec{\alpha}\}\vec{H}_{k-1}(t)-k\mathrm{diag}\{\vec{\gamma}\}\vec{H}_k(t)+ \frac{1}{2}k(k-1)\mathrm{diag}\{\vec{\sigma}^2\}\vec{H}_{k-2}(t) + Q^{\rm T} \vec{H}_k(t) \\ & =& \bar{Q}_{k\gamma}\vec{H}_k(t) + k\mathrm{diag}\{\vec{\alpha}\}\vec{H}_{k-1}(t)+ \frac{1}{2}k(k-1)\mathrm{diag}\{\vec{\sigma}^2\}\vec{H}_{k-2}(t). \end{eqnarray*} Stacking $\vec{H}_0(t),\ldots,\vec{H}_{n}(t)$ into a single vector $\bar{\vec{H}}_n(t)$, we obtain the differential equation \[ \frac{{\rm d}}{{\rm d}t}\bar{\vec{H}}_n(t)=A_n\bar{\vec{H}}_n(t), \] with $A_n\in\mathbb{R}^{(n+1)d\times (n+1)d}$ denoting a lower block triangular matrix, whose solution is $\vec{H}_n(t)=\exp(A_nt)\vec{H}_n(0)$. Eventually, $h_k(t):=\mathbb{E}M(t)^k$ is given by $h_k(t)=\mathbf{1}^{\rm T} \vec{H}_k(t)$. Note that for $k=1,2$ the results of Section~\ref{TB} can be recovered.
\section{Transient behavior: partial differential equations} \label{TBPDE} The goal of this section is to characterize, for a given vector $\vec{t}\in{\mathbb R}^K$ (with $K\in{\mathbb N}$) such that $0\leqslant t_1\leqslant \cdots\leqslant t_K$, the Laplace transform of $(M(t+t_1), \ldots, M(t+t_K))$ (together with the state of the background process at these time instances). More specifically, we set up a system of {\sc pde}\,s for \[g_{\vec{i}}(\vec{\vartheta},{t}) := {\mathbb E} e^{-(\vartheta_1M(t_1+t)+\cdots+ \vartheta_K M(t_K+t))} 1\{X(t_1+t)=i_1,\ldots, X(t_K+t)=i_K\};\] here $t\geqslant 0$, $\vec{i}\in \{1,\ldots,d\}^K$ and $\vec{\vartheta}\in{\mathbb R}^K.$ The system of {\sc pde}\,s is with respect to $t$ and $\vartheta_1$ up to $\vartheta_K.$ We first point out the line of reasoning for the case $K=1$, and then present the {\sc pde} for $K=2$. The cases $K\in\{3,4,\ldots\}$ can be dealt with fully analogously, but lead to notational inconveniences and are therefore left out.
It is noted that the stationary version of the result below (i.e., $t\to\infty$) for the special case $K=1$ has appeared in \cite{XING} (where we remark that in \cite{XING} the additional issue of reflection at $0$ has been incorporated).
\subsection{Fourier-Laplace transform}\label{FLT}
For $K=1$, the object of interest is \[g_i(\vartheta,t) := {\mathbb E} e^{-\vartheta M(t)} 1\{X(t)=i\},\] for $i=1,\ldots,d$; realize that, without loss of generality, we have taken $t_1=0.$ For a more compact notation we stack the $g_i$ in a single vector ${\boldsymbol g}$, so ${\boldsymbol g}(\vartheta,t) = {\mathbb E} e^{-\vartheta M(t)} \vec{Z}(t)$. Replacing in this expression $\vartheta$ by $-\mathrm{i} u$ for $u\in\mathbb{R}$ gives the characteristic function of $M(t)$ jointly with $\vec{Z}(t)$.
\begin{theorem} \label{PDEth} Consider the case $K=1$ and $t_1=0$. The Laplace transforms ${\boldsymbol g}(\vartheta,t)$ satisfy the following system of \,{\sc pde}\,s:
\begin{equation}\label{eq:cfpde} \frac{\partial}{\partial t}{\boldsymbol g}(\vartheta,t)=Q^{\rm T}{\boldsymbol g}(\vartheta,t)-\mathopen{}\mathclose\bgroup\originalleft(\vartheta\,{\rm diag}\{{\boldsymbol \alpha}\}-\frac{1}{2}\vartheta^2{\rm diag}\{{\boldsymbol \sigma}^2\}\aftergroup\egroup\originalright) {\boldsymbol g}(\vartheta,t) -\vartheta\,{\rm diag}\{{\boldsymbol \gamma}\}\,\frac{\partial}{\partial \vartheta}{\boldsymbol g}(\vartheta,t). \end{equation} The corresponding initial conditions are ${\boldsymbol g}(0,t)={\boldsymbol p}_t$ and ${\boldsymbol g}(\vartheta,0) = e^{-\vartheta m_0}{\boldsymbol p}_0.$ \end{theorem}
\begin{proof} The proof mimics the procedure used in Section \ref{ss:rec} to determine the moments of $M(t).$ Letting $f(\vartheta,t)=e^{-\vartheta M(t)}$, applying It\^o's formula to \eqref{eq:mmouz} yields \[ \mathrm{d} f(\vartheta,t)=-\vartheta f(\vartheta,t)\mathopen{}\mathclose\bgroup\originalleft(\mathopen{}\mathclose\bgroup\originalleft( \vec{\alpha}^{\rm T} \vec{Z}(t) - \vec{\gamma}^{\rm T} \vec{Z}(t)M(t)\aftergroup\egroup\originalright) \, {\rm d} t + \vec{\sigma}^{\rm T} \vec{Z}(t) \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)\aftergroup\egroup\originalright)+\half\vartheta^2f(\vartheta,t)\mathrm{diag}\{\vec{\sigma}^2\}\vec{Z}(t)\mathrm{d} t. \] We then apply the product rule to $f(\vartheta,t)\vec{Z}(t)$, using the just obtained equation in combination with Equation \eqref{eq:zz}. This leads to \begin{align*} \mathrm{d} \mathopen{}\mathclose\bgroup\originalleft(f(\vartheta,t)\vec{Z}(t)\aftergroup\egroup\originalright) & = -\vartheta f(\vartheta,t)\mathopen{}\mathclose\bgroup\originalleft(\mathopen{}\mathclose\bgroup\originalleft( \mathrm{diag}\{\vec{\alpha}\} \vec{Z}(t) - \mathrm{diag}\{\vec{\gamma}\} \vec{Z}(t)M(t)\aftergroup\egroup\originalright) \, {\rm d} t + \mathrm{diag}\{\vec{\sigma}\} \vec{Z}(t) \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)\aftergroup\egroup\originalright) \\\ & \qquad+\half\vartheta^2f(\vartheta,t)\mathrm{diag}\{\vec{\sigma}^2\}\vec{Z}(t)\mathrm{d} t + f(\vartheta,t)\mathopen{}\mathclose\bgroup\originalleft(Q^{\rm T} \vec{Z}(t)\,{\rm d}t+{\rm d}K(t)\aftergroup\egroup\originalright). \end{align*} Taking expectations, and recalling that ${\boldsymbol g}(\vartheta,t)=\mathbb{E} f(\vartheta,t)\vec{Z}(t)$ and that the martingale terms have expectation zero, we obtain \begin{eqnarray*} \frac{\partial}{\partial t} {\boldsymbol g}(\vartheta,t) & = & -\vartheta \mathrm{diag}\{\vec{\alpha}\}{\boldsymbol g}(\vartheta,t)+\vartheta \mathrm{diag}\{\vec{\gamma}\} \mathbb{E}\mathopen{}\mathclose\bgroup\originalleft(f(\vartheta,t)M(t)\vec{Z}(t)\aftergroup\egroup\originalright) \\
&&+\:\half\vartheta^2\mathrm{diag}\{\vec{\sigma}^2\} f(\vartheta,t) + Q^{\rm T} f(\vartheta,t). \end{eqnarray*} Realizing that ${\partial}{\boldsymbol g}/{\partial\vartheta}=-\mathbb{E}\mathopen{}\mathclose\bgroup\originalleft(f(\vartheta,t)M(t)\vec{Z}(t)\aftergroup\egroup\originalright)$, we can rewrite this as \eqref{eq:cfpde}.
\end{proof}
It is remarked that the above system \eqref{eq:cfpde} of {\sc pde}\,s coincides, for $t\to\infty$, with the stationary result of \cite{XING} (where it is mentioned that in \cite{XING} the feature of reflection at 0 has been incorporated). In addition, it is noted that this system can be converted into a system of {\it ordinary} differential equations, as follows. Let $T$ be exponentially distributed with mean $\tau^{-1},$ independent of all other random features involved in the model. Define \[g_i(\vartheta) := {\mathbb E} e^{-\vartheta M(T)} 1\{X(T)=i\}.\] Now multiply the {\sc pde} featuring in Thm.\ \ref{PDEth} by $\tau e^{-\tau t}$, and integrate over $t\in[0,\infty)$, to obtain (use integration by parts for the left-hand side) \[\lambda\mathopen{}\mathclose\bgroup\originalleft({\boldsymbol g}(\vartheta)- e^{-\vartheta m_0}{\boldsymbol p}_0\aftergroup\egroup\originalright) = Q^{\rm T} {\boldsymbol g}(\vartheta) - \mathopen{}\mathclose\bgroup\originalleft(\vartheta\,{\rm diag}\{{\boldsymbol \alpha}\}-\frac{1}{2}\vartheta^2{\rm diag}\{{\boldsymbol \sigma}^2\}\aftergroup\egroup\originalright) {\boldsymbol g}(\vartheta) -\vartheta\,{\rm diag}\{{\boldsymbol \gamma}\}\,\frac{\partial}{\partial \vartheta}{\boldsymbol g}(\vartheta).\]
All above results related to the case $K=1.$ For higher values of $K$ the same procedure can be followed; as announced we now present the result for $K=2$. Let $i,k$ be elements of $\{1,\ldots,d\}$, and $\vec{\vartheta}\equiv(\vartheta_1,\vartheta_2)\in{\mathbb R}^2$. We obtain the following system of {\sc pde}\,s: \begin{eqnarray*}\lefteqn{\frac{\partial}{\partial t}g_{i,k}(\vec{\vartheta},t)=\sum_{j=1}^d q_{ji}\, g_{j,k}(\vec{\vartheta},t) +\sum_{\ell=1}^d q_{\ell k}\, g_{i,\ell}(\vec{\vartheta},t)}\\ &&-\,\mathopen{}\mathclose\bgroup\originalleft(\vartheta_1\alpha_i+\vartheta_2\alpha_k-\frac{1}{2}\vartheta_1^2\sigma_i^2-\frac{1}{2}\vartheta_2^2\sigma_k^2\aftergroup\egroup\originalright)g_{i,k}(\vec{\vartheta},t) -\vartheta_1\gamma_i\,\frac{\partial}{\partial \vartheta_1}g_{i,k}(\vec{\vartheta},t) -\vartheta_2\gamma_k\,\frac{\partial}{\partial \vartheta_2}g_{i,k}(\vec{\vartheta},t), \end{eqnarray*} or in self-evident matrix notation, suppressing the arguments $\vec{\vartheta}$ and $t$, \begin{eqnarray*}\lefteqn{\frac{\partial G}{\partial t}= Q^{\rm T}G+GQ-\vartheta_1 \,{\rm diag}\{{\boldsymbol \alpha}\} G -\vartheta_2 G\,{\rm diag}\{{\boldsymbol \alpha}\}}\\ &&+\,\frac{1}{2}\vartheta_1^2 \,{\rm diag}\{{\boldsymbol \sigma}^2\} G +\frac{1}{2}\vartheta_2^2 G\,{\rm diag}\{{\boldsymbol \sigma}^2\} -\vartheta_1 \,{\rm diag}\{{\boldsymbol \gamma}\} \frac{\partial G}{\partial \vartheta_1} -\vartheta_2 \frac{\partial G}{\partial \vartheta_2}\,{\rm diag}\{{\boldsymbol \gamma}\}. \end{eqnarray*}
This matrix-valued system of {\sc pde}\,s can be converted into its vector-valued counterpart. Define the $d^2$-dimensional vector $\check{\boldsymbol g}(\vec{\vartheta},t):={\rm vec}(G(\vec{\vartheta},t)).$ Recall the definitions of the Kronecker sum (denoted by `$\oplus$') and the Kronecker product (denoted by `$\otimes$'). Using the relations ${\rm vec}(ABC)=(C^{\rm T}\otimes A){\rm vec}(B)$ and $A\oplus B= A\otimes I+I\otimes B$, for matrices $A$, $B$, and $C$ of appropriate dimensions, we obtain the vector-valued {\sc pde} \begin{eqnarray*}\lefteqn{\hspace{5mm}\frac{\partial \check {\vec{g}}}{\partial t}= (Q^{\rm T}\oplus Q^{\rm T})\check{\vec{g}} -\vartheta_1 (I\otimes {\rm diag}\{\vec{\alpha}\})\check{\vec{g}} -\vartheta_2 ( {\rm diag}\{\vec{\alpha}\}\otimes I)\check{\vec{g}}}
\\ &&+\,\frac{\vartheta_1^2}{2} (I\otimes {\rm diag}\{\vec{\sigma}^2\})\check{\vec{g}} +\frac{\vartheta_2^2 }{2}( {\rm diag}\{\vec{\sigma}^2\}\otimes I)\check{\vec{g}} -\vartheta_1 (I\otimes {\rm diag}\{\vec{\gamma}\})\frac{\partial \check {\vec{g}}}{\partial \vartheta_1} -\vartheta_2 ( {\rm diag}\{\vec{\gamma}\}\otimes I)\frac{\partial \check {\vec{g}}}{\partial \vartheta_2}, \end{eqnarray*} again suppressing the arguments $\vec{\vartheta}$ and $t$.
It is clear how this procedure should be extended to $K\in\{3,4,\ldots\}$, but, as mentioned above, we do not include this because of the cumbersome notation needed.
\iffalse $\rhd$ {\it MM: here we should decide to maintain this approach, or to include an operator-based approach. My current feeling would be to include a last section with general results, in which also the operator-based approach can find its way...}\fi
\subsection{Explicit computations for two-dimensional case} We now present more explicit expressions relating to the case that $d=2$. Define $q:=q_1+q_2$. Suppose the system starts off at $(M(0),X(0)) = (m_0,2)$. Throughout this example we use the notation
\[g_i(\vartheta,t,j):= {\mathbb E}\mathopen{}\mathclose\bgroup\originalleft(e^{-\vartheta M(t)} 1\{X(t)=j\}\,|\,X(0)=i\aftergroup\egroup\originalright).\] The theory of this section yields the following system of partial differential equations: \[\frac{\partial}{\partial t} g_{2}(t, \vartheta, 1)+\vartheta\gamma_1\,\frac{\partial}{\partial \vartheta} g_{2}(t, \vartheta, 1)= \mathopen{}\mathclose\bgroup\originalleft(-q_{1}-\vartheta \alpha_{1}+\frac{1}{2}\vartheta^{2} \sigma_{1}^{2}\aftergroup\egroup\originalright) g_{2}(t, \vartheta, 1)+q_2 g_{2}(t, \vartheta, 2) ,\] \[\frac{\partial}{\partial t} g_{2}(t, \vartheta, 2)+\vartheta\gamma_2\,\frac{\partial}{\partial \vartheta} g_{2}(t, \vartheta, 2)= \mathopen{}\mathclose\bgroup\originalleft(-q_{2}-\vartheta \alpha_{2}+\frac{1}{2}\vartheta^{2} \sigma_{2}^{2}\aftergroup\egroup\originalright) g_{2}(t, \vartheta, 2)+q_1 g_{2}(t, \vartheta, 1) ,\] with conditions (realizing that $\pi_i=q_i/q$) \[ \mathopen{}\mathclose\bgroup\originalleft( \begin{array}{cc} g_{2}(0, \vartheta, 1) \\ g_{2}(0, \vartheta, 2)\end{array} \aftergroup\egroup\originalright) =\mathopen{}\mathclose\bgroup\originalleft( \begin{array}{cc} 0 \\ e^{-\vartheta x} \end{array} \aftergroup\egroup\originalright), \:\:\:\: \mathopen{}\mathclose\bgroup\originalleft( \begin{array}{cc} g_{2}(t, 0, 1) \\ g_{2}(t, 0, 2)\end{array} \aftergroup\egroup\originalright) =\mathopen{}\mathclose\bgroup\originalleft( \begin{array}{cc} \pi_1-\pi_1e^{-qt}\\ \pi_2+\pi_1 e^{-qt}\end{array}\aftergroup\egroup\originalright), \] and $\vartheta \in {\mathbb R}$ and $t\in [0, \infty)$.
In the special case that $q_1=0$ (so that state 2 is transient, and state 1 is absorbing), the system of differential equations decouples; the second of the above two partial differential equations can be solved using the method of characteristics. Routine calculations lead to \[ g_{2}(t, \vartheta, 2)=\exp \mathopen{}\mathclose\bgroup\originalleft(-\vartheta m_0 e^{-\gamma_{2} t}-q_{2}t-\frac{\alpha_{2}}{\gamma_{2}}(\vartheta-\vartheta e^{-\gamma_{2}t})+ \frac{\sigma^{2}_{2}}{4\gamma_{2}}(\vartheta^{2}-\vartheta^{2}e^{-2\gamma_{2}t})\aftergroup\egroup\originalright). \] Now the first equation of the two partial differential equations can be solved as well, with the distinguishing feature that now we have a non-homogeneous (rather than a homogeneous) single-dimensional partial differential equation. It can be verified that it is solved by \begin{eqnarray*} g_{2}(t, \vartheta, 1)&=& q_{2}\exp\mathopen{}\mathclose\bgroup\originalleft(-\frac{\alpha_{1}}{\gamma_{1}}\vartheta+ \frac{\sigma_{1}^{2}}{4\gamma_{1}}\vartheta^{2}\aftergroup\egroup\originalright)\times\\ &&\hspace{2cm}\int_{0}^{t}g_{2}(s, \vartheta e^{-\gamma_{1}(t-s)}, 2) \exp\mathopen{}\mathclose\bgroup\originalleft(\frac{\alpha_{1}}{\gamma_{1}}\vartheta e^{-\gamma_{1}(t-s)}-\frac{\sigma_{1}^{2}}{4\gamma_{1}}\vartheta^{2}e^{-2\gamma_{1}(t-s)}\aftergroup\egroup\originalright){\rm d} s. \end{eqnarray*}
\section{Parameter scaling}\label{Sec:TS}
So far we have characterized the distribution of $M(t)$ in terms of an algorithm to determine moments, and a {\sc pde} for the Fourier-Laplace transform. In other words, so far we have not presented any explicit results on the distribution of $M(t)$ itself. In this section we consider asymptotic regimes in which this {\rm is} possible; these regimes can be interpreted as parameter scalings.
More specifically, in this section we consider the following two scaled versions of the {\sc mmou} model. \begin{itemize} \item[$\rhd$] In the first we (linearly) speed up the background process (that is, we replace $Q\mapsto NQ$ or, equivalently, $X(t) \mapsto X(Nt)$). Our main result is that, as $N\to\infty$, the {\sc mmou} essentially experiences the time-averaged parameters, i.e., $\alpha_\infty:={\boldsymbol \pi}^{\rm T}{\boldsymbol\alpha}$, $\gamma_\infty:={\boldsymbol \pi}^{\rm T}{\boldsymbol\gamma}$ and $\sigma_\infty^2:={\boldsymbol \pi}^{\rm T}{\boldsymbol\sigma^2}$. As a consequence, it behaves as an {\sc ou} process with these parameters. \item[$\rhd$] The second regime considered concerns a {\it simultaneous} scaling of the background process and the {\sc ou} processes. This is done as in Section \ref{SPECC}: $Q$ on the one hand, and ${\boldsymbol\alpha}$ and ${\boldsymbol\sigma^2}$ on the other hand are scaled at {\it different} rates: we replace ${\boldsymbol\alpha}\mapsto N^h{\boldsymbol\alpha}$ and ${\boldsymbol\sigma^2}\mapsto N^h{\boldsymbol\sigma^2}$, but $Q\mapsto N Q$ for some $h\geqslant 0$). We obtain essentially two regimes, in line with the observations in Section \ref{SPECC}. \end{itemize} As mentioned above, we are particularly interested in the limiting behavior in the regime that $N$ grows large. It is shown that the process $M(t)$, which we now denote as $M^{[N]}(t)$ to stress the dependence on $N$, converges to the solution of a specific {\sc sde}. Importantly, we establish {\it weak convergence}, i.e., in the sense of convergence at the process level; our result can be seen as the counterpart of the result for Markov-modulated infinite-server queues in \cite{DAVE}.
We consider sequences of {\sc mmou} processes, indexed by ${N}$, subject to the following scaling: \(Q \mapsto {N} Q\); \(\boldsymbol\alpha \mapsto {N}^h \boldsymbol\alpha \); \(\boldsymbol\sigma \mapsto {N}^{h/2} \boldsymbol\sigma\), where $h \geqslant 0$; note that by appropriately choosing $h$ we enter the two regimes described above as we let $N$ grow large (see Corollaries \ref{C1} and \ref{C2}). The definitions of $M(t)$, ${\boldsymbol Z}(t)$ and ${\boldsymbol K}(t)$ (the latter two having been defined in Section \ref{TB}) then take the following form (where superscripts are being used to make the dependence on ${N}$ and $h$ explicit):
\begin{equation} \mathrm{d} M^{[N,h]}(t) = ({N}^h \boldsymbol\alpha - \boldsymbol\gamma M^{[N,h]}(t))^\mathrm{T} {\boldsymbol Z}\hN(t)\, \mathrm{d} t + {N}^{h/2} \boldsymbol\sigma^\mathrm{T} {\boldsymbol Z}\hN(t)\, \mathrm{d} B(t), \end{equation}
and
\begin{equation} \mathrm{d} {\boldsymbol Z}\hN(t) = {N} Q^\mathrm{T} {\boldsymbol Z}\hN(t)\, \mathrm{d} t + \mathrm{d} {\boldsymbol K}\hN(t) . \label{eq:KsN} \end{equation}
We keep the initial condition $M^{[N,h]}(0)$ at a fixed level $M(0)$. Let, with the definitions of ${\alpha_\infty}, \gamma_\infty,$ and $\sigma^2_\infty$ given above, the `average path' $\varrho(t)$ be defined by the {\sc ode} \[ \mathrm{d} \varrho(t) = (\alpha_\infty - \gamma_\infty \varrho(t)) \mathrm{d} t,\,\, \varrho(0)=\mathbf{1}_{\{h=0\}}M(0), \] such that we have \[ \varrho(t) = e^{-\gamma_\infty t}\varrho(0)+ \frac{\alpha_\infty}{\gamma_\infty} (1 - e^{-\gamma_\infty t}). \] It is possible to show that $\varrho(t)$ coincides with $\lim_{N\to\infty}N^{-h}\mathbb{E} M^{[N,h]}(t)$, in particular we have the initial value $\varrho(0)=\lim_{N\to\infty}\mathbb{E} N^{-h}M(0)=\mathbf{1}_{\{h=0\}}M(0)$.
We can now state the main theorem of this section.
\begin{theorem}\label{THS} Under the scaling \(Q \mapsto {N} Q\); \(\boldsymbol\alpha \mapsto {N}^h \boldsymbol\alpha \); \(\boldsymbol\sigma \mapsto {N}^{h/2} \boldsymbol\sigma \),
we have that the scaled and centered process \(\hat M^{[N,h]}(t)\), as defined through \[ \hat M^{[N,h]}(t) := {N}^{-\beta} (M^{[N,h]}(t) - {N}^h\varrho(t)), \] converges weakly to the solution of the following {\sc sde}: \[ \mathrm{d} \hat M(t) = - \gamma_\infty \hat M(t) \mathrm{d} t + \sqrt{ \sigma^2_\infty \mathbf{1}_{\{h\leqslant1 \}}+ {V}'(t) \mathbf{1}_{\{h\geqslant 1 \}}}\mathrm{d} B(t),\,\:\:\:\:\hat M(0)=0. \] where \(\beta:=\max\{h/2,h-1/2\}\), $B$ a Brownian motion, and
\begin{equation} \label{defv} {V}(t) := \int_0^t (\boldsymbol\alpha - \boldsymbol\gamma\varrho(s))^\mathrm{T} (\mathrm{diag}\{{\boldsymbol \pi}\} D+D^\mathrm{T} \mathrm{diag}\{{\boldsymbol \pi}\})(\boldsymbol\alpha - \boldsymbol\gamma \varrho(s)){\rm d}s. \end{equation} \end{theorem}
Before proving this result, we observe that the above theorem provides us with the limiting behavior in the two regimes described at the beginning of this section. In the first corollary we simply take $h=0.$
\begin{corollary}\label{C1} Under the scaling \(Q \mapsto {N} Q\), with \(\boldsymbol\alpha\) and \(\boldsymbol\sigma\) kept at their original values, we have that $M^{[N,0]}(t)$ converges weakly to a process ${\mathscr M}_1(t)$, which is an (ordinary, i.e., non-modulated) {\sc ou} process with parameters \((\alpha_\infty, \gamma_\infty, \sigma_\infty)\), defined through the {\sc sde} \[ \mathrm{d} {\mathscr M}_1(t) = (\alpha_\infty - \gamma_\infty {\mathscr M}_1 (t))\mathrm{d} t + \sigma_\infty \mathrm{d} B(t). \] \end{corollary}
The second corollary describes the situation in which both the background process and the {\sc ou} process are scaled, but at different rates. We explicitly characterize the limiting behaviour in each of the three resulting regimes.
\begin{corollary}\label{C2} Under the scaling \(Q \mapsto {N} Q\); \(\boldsymbol\alpha \mapsto {N}^h \boldsymbol\alpha \); \(\boldsymbol\sigma \mapsto {N}^{h/2} \boldsymbol\sigma \), we have that $\hat M^{[N,h]}(t)$ converges weakly to a process ${\mathscr M}_2(t)$, defined through one of the following {\sc sde}\,s: if \,$0<h<1$, then \[\mathrm{d} {\mathscr M}_2(t) = - \gamma_\infty {\mathscr M}_2(t)\, \mathrm{d} t + \sigma_\infty \mathrm{d} B(t),\] if $h=1$, then \[\mathrm{d} {\mathscr M}_2(t) = - \gamma_\infty {\mathscr M}_2(t)\, \mathrm{d} t + \sqrt{\sigma^2_\infty +{V}'(t)}\mathrm{d} B(t), \] and if $h>1$, then \[\mathrm{d} {\mathscr M}_2(t) = - \gamma_\infty {\mathscr M}_2 (t)\,\mathrm{d} t +\sqrt{{V}'(t)} \, \mathrm{d} B(t).\] \end{corollary}
These corollaries are trivial consequences of Thm.\ \ref{THS}, and therefore we direct our attention to the proof of this main theorem itself. We remark that Corollary \ref{C2} confirms an observation we made in Section~\ref{TB}: for $h<1$ the system essentially behaves as an non-modulated {\sc ou} process, while for $h>1$ the background process plays a role through its deviation matrix $D$.
\\ In the proof of Theorem~\ref{THS} we need an auxiliary result, which we present first.
\begin{lemma}\label{lemmah} Let the $d$-dimensional row vectors ${\boldsymbol \Psi}^{[N]}$ be a sequence of predictable processes such that ${\boldsymbol \Psi}^{[N]}(t)\to{\boldsymbol \Psi}(t)$ in probability uniformly on compact sets, i.e., as $N\to\infty$,
\[\sup_{t\leq T}|{\boldsymbol \Psi}^{[N]}(t)-{\boldsymbol \Psi}(t)|\to 0\] in probability for every $T>0$; here ${\boldsymbol \Psi}$ is deterministic, satisfying $\int_0^t {\boldsymbol \Psi}(s){\boldsymbol \Psi}(s)^\mathrm{T}\,\mathrm{d} s<\infty$ for every $t>0$. Furthermore, let $\vec{X}^{[N]}$ be continuous semimartingales that converge weakly to a $d$-dimensional scaled Brownian motion $\boldsymbol B$ with quadratic variation $\langle{\boldsymbol B}\rangle_t=Ct$ (where $C\in\mathbb{R}^{d\times d}$).
Then, as $N\to\infty$, the stochastic integrals \[\int_0^\cdot {\boldsymbol \Psi}^{[N]}(s)\,\mathrm{d} \vec{X}^{[N]}(s)\] converge weakly to the time-inhomogeneous Brownian motion $B^{\boldsymbol \Psi}:=\int_0^\cdot {\boldsymbol \Psi}(s)\,\mathrm{d} \boldsymbol B(s)$ with quadratic variation \[ \langle B^{\boldsymbol \Psi}\rangle_t=\int_0^t{\boldsymbol \Psi}(s)C{\boldsymbol \Psi}(s)^\mathrm{T}\,\mathrm{d} s. \]
\end{lemma}
The claim of Lemma \ref{lemmah} essentially follows from \cite[Thm. VI.6.22]{JS}. To check the condition of the cited theorem, one needs weak convergence of the pair $({\boldsymbol \Psi}^{[N]}, \vec{X}^{[N]})$, but this is guaranteed by the uniform convergence in probability of the ${\boldsymbol \Psi}^{[N]}(t)$.
\iffalse \begin{proof} Consider the following process: \begin{equation}\mathrm{d}\Phi^{[N,h]}(t) := {N}^{h/2-\beta} \sum_{k=1}^d \sigma_k Z_k\hN(t) \mathrm{d} B(t) + {N}^{-\beta} \sum_{k=1}^d \tilde M_k^{[N,h]}(t) \mathrm{d} L_k\hN(t) . \label{dphi}\end{equation}
Clearly, this is a local martingale, as linear combinations preserve the local martingale property and locally bounded, predictable processes integrated with respect to local martingales are themselves local martingales.
By plugging in the definitions of the $M^{[N,h]}$ and $L_k\hN$, and applying the relation between $M^{[N,h]}(t)$ and $\hat M^{[N,h]}(t)$, we obtain \begin{align*} \mathrm{d}\Phi^{[N,h]}(t) & = \, \mathrm{d} M^{[N,h]}(t) - ({N}^h \alpha_\infty -\gamma_\infty M^{[N,h]}(t)) \mathrm{d} t + {N}^{-1-\beta} \sum_{j=1}^d \sum_{k=1}^d D_{jk} \tilde M_k\hN(t) \mathrm{d} Z_j\hN(t). \\
& = \,\mathrm{d} \hat M^{[N,h]}(t) + \gamma_\infty \hat M^{[N,h]}(t)\mathrm{d} t + {N}^{-1-\beta} \sum_{j=1}^d \sum_{k=1}^d D_{jk}\tilde M_k^{[N,h]}(t) \mathrm{d} Z_j\hN(t), \end{align*} We denote the last term by $\mathrm{d} H^{[N,h]}(t)$, and observe that it converges to $0$ as ${N}\to\infty$ (to this end, recall that \({N}^{-h} \tilde M_k^{[N,h]}(t) \to \alpha_k - \gamma_k \varrho(t)\) as \({N}\to\infty\), and observe that directly from the definition of $\beta$ it follows that $h-1-\beta<0$).
We apply the martingale central limit theorem \cite[Ch.~7, Thm.~1.4]{ETHIERKURTZ} to the sequence of local martingales $\Phi^{[N,h]}(t)$. As we have that \[ {\mathbb E} \sup_{0\leq t\leq T} \mathopen{}\mathclose\bgroup\originalleft( \Phi^{[N,h]}(t) - \Phi^{[N,h]}(t-)\aftergroup\egroup\originalright) \to 0\] for every $T>0$ as ${N}\to\infty$, we must find the predictable quadratic variation $\langle \Phi^{[N,h]} \rangle_t$. From (\ref{dphi}), \begin{align*} \mathrm{d} \langle \Phi^{[N,h]} \rangle_t = {N}^{h-2\beta} \sum_{k=1}^d \sigma_k^2 Z_k\hN(t) \mathrm{d} t
+ {N}^{-2\beta} \sum_{j=1}^d\sum_{k=1}^d \tilde M_j^{[N,h]}(t)\tilde M_k^{[N,h]}(t) \mathrm{d} \langle L_j\hN,L_k\hN\rangle_t. \end{align*} As a result, $\langle \Phi^{[N,h]} \rangle_t$ consists of two terms, corresponding to the two terms in the previous display. The first of these terms is, as $N\to\infty$, proportional to ${N}^{h-2\beta} \sigma_\infty^2$ due to the ergodic theorem. The second term requires a bit of additional work. In Lemma \ref{LB} in Appendix~\ref{app-convergence}, we cover the convergence of \(N\, \langle L_j\hN,L_k\hN\rangle_t\), and we already established the convergence of \(N^{-h}\tilde M^{[N,h]}(t)\). We now invoke the continuous mapping theorem on the mapping \(F\): \[ F[m_1,m_2,\ell](t) := \int_0^t m_1(s) m_2(s) \mathrm{d} \ell(s), \] which is indeed continuous for continuous functions $m_1, m_2, \ell$. It follows that the second term is of the order $N^{2h-2\beta-1}$, with the corresponding proportionality constant being equal to \[\int_0^t \sum_{j=1}^d\sum_{k=1}^d \mathopen{}\mathclose\bgroup\originalleft(\alpha_j - \gamma_j \varrho(s)\aftergroup\egroup\originalright) \mathopen{}\mathclose\bgroup\originalleft( \alpha_k - \gamma_k \varrho(s)\aftergroup\egroup\originalright) \mathopen{}\mathclose\bgroup\originalleft(\pi_jD_{jk}+\pi_kD_{kj}\aftergroup\egroup\originalright){\rm d}s,\] which we recognize as $V(t)$. The sum of both terms therefore behaves essentially polynomially, with degree \[\max\{h-2\beta,2h-2\beta-1\}=\max\{h,2h-1\}-2\beta= 0;\] the first term contributes if $h\leqslant 1$, and the second term if $h\geqslant 1$. It thus follows that \[ \langle \Phi^{[N,h]} \rangle_t \to \sigma^2_\infty 1_{\{h\leqslant1 \}}+ V(t) 1_{\{h\geqslant 1 \}}, \] and as such by the {\sc m-clt} that $\Phi^{[N,h]}$ converges weakly to $\Phi$, defined as \begin{equation*}
\Phi(t) := B\mathopen{}\mathclose\bgroup\originalleft(\sigma^2_\infty 1_{\{h\leqslant1 \}} + V(t) 1_{\{h\geqslant 1\}}\aftergroup\egroup\originalright) = \sqrt{\sigma^2_\infty 1_{\{h\leqslant1 \}}+ V(t) 1_{\{h\geqslant 1\}}} B(t), \end{equation*} where $B(t)$ is a standard Brownian motion.
The last part of the proof consists of converting this limiting process of $\Phi^{[N,h]}$ into one for $\hat M^{[N,h]}$. To this end, consider \begin{align*}
\mathrm{d} \mathopen{}\mathclose\bgroup\originalleft(e^{\gamma_\infty t} \hat M^{[N,h]}(t)\aftergroup\egroup\originalright) & = e^{\gamma_\infty t} \mathrm{d} \hat M^{[N,h]}(t) +
\gamma_\infty e^{\gamma_\infty t} \hat M^{[N,h]}(t) \mathrm{d} t \\
& = e^{\gamma_\infty t} \mathrm{d} \Phi^{[N,h]}(t) + e^{\gamma_\infty} \mathrm{d} H^{[N,h]}(t), \end{align*} where we recall that $\mathrm{d} H^{[N,h]}(t)$ vanishes as $N\to\infty$. From this we see that if $\Phi^{[N,h]}(t)$ converges in distribution, then so does $\hat M^{[N,h]}(t)$; moreover, it is clear that its limit is the unique solution of the {\sc sde} in the claim of the proof. \end{proof} \fi
We now proceed with the proof of Thm.\ \ref{THS}.
\begin{proof}
The proof of Thm.\ \ref{THS} consists of 4 steps.
$\rhd$ {\it Step} 1. We describe the dynamics of the process $\hat M^{[N,h]}(t)$ through \begin{align*} \mathrm{d}\hat M^{[N,h]}(t) & =N^{h-\beta}(\boldsymbol\alpha-\rho(t)\boldsymbol\gamma)^\mathrm{T}(\vec{Z}^{[N]}(t)-{\boldsymbol \pi})\,\mathrm{d} t+N^{h/2-\beta}\vec{\boldsymbol\sigma}^\mathrm{T}{\m Z}^{[N]}_t\mathrm{d} B(t) - \boldsymbol\gamma^\mathrm{T} {\m Z}^{[N]}_t\hat M^{[N,h]}(t)\,\mathrm{d} t \\ & =: N^{h-\beta-\half}\mathrm{d} G^{[N]}(t)+N^{h/2-\beta}\mathrm{d}\hat{B}^{[N]}(t)- \boldsymbol\gamma^\mathrm{T} {\m Z}^{[N]}_t\hat M^{[N,h]}(t)\,\mathrm{d} t. \end{align*} Defining ${\boldsymbol \zeta}^{[N]}(t):=\int_0^t{\m Z}^{[N]}(s)\,\mathrm{d} s$ and $Y^{[N,h]}(t):=e^{\boldsymbol\gamma^\mathrm{T}{\boldsymbol \zeta}^{[N]}(t)}\hat M^{[N,h]}(t)$, one obtains \begin{align}\label{eq:y}
\mathrm{d} Y^{[N,h]}(t) & = N^{h-\beta-\half}e^{\boldsymbol\gamma^\mathrm{T}{\boldsymbol \zeta}^{[N]}_t}\mathrm{d} G^{[N]}(t)+N^{h/2-\beta}e^{\boldsymbol\gamma^\mathrm{T}{\boldsymbol \zeta}^{[N]}_t}\mathrm{d}\hat{B}^{[N]}(t). \end{align} In the next two steps we analyze the two terms in the right hand side of \eqref{eq:y}.
$\rhd$ {\it Step} 2. We first consider the first term on the right hand side of \eqref{eq:y}. To analyze it, we need the functional central limit theorem for the martingale ${\vec{K}}_{\circ}^{[N]}:=\vec{K}^{[N]}/\sqrt{N}.$ From the proof of Prop.~\ref{prop:nnd} we know that \[ \frac{1}{N}\langle {\vec{K}}_\circ^{[N]}\rangle_t=\int_0^t\mathopen{}\mathclose\bgroup\originalleft(\mathrm{diag}\{Q^\mathrm{T} \vec{Z}^{[N]}(s)\}-Q^\mathrm{T}\mathrm{diag}\{\vec{Z}^{[N]}(s)\}-\mathrm{diag}\{\vec{Z}^{[N]}(s)\}Q\aftergroup\egroup\originalright)\,\mathrm{d} s, \] which by the ergodic theorem converges to $-Q^\mathrm{T}\mathrm{diag}\{\vec{{\boldsymbol \pi}}\}-\mathrm{diag}\{\vec{{\boldsymbol \pi}}\}Q$. As the jumps of ${\vec{K}}_\circ^{[N]}$ are of order $O(1/\sqrt{N})$, the martingale central limit theorem (see e.g.\ \cite[Thm.~VIII.3.11]{JS} or \cite[Thm.~7.1.4]{ETHIERKURTZ}) gives the weak convergence of ${\vec{K}}_\circ^{[N]}$ to a $d$-dimensional scaled Brownian motion ${\boldsymbol B}_\circ$ with \[\langle\boldsymbol{B}_\circ\rangle_t=-\mathopen{}\mathclose\bgroup\originalleft(Q^\mathrm{T}\mathrm{diag}\{\vec{{\boldsymbol \pi}}\}+\mathrm{diag}\{\vec{{\boldsymbol \pi}}\}Q\aftergroup\egroup\originalright)\,t.\] Moreover, we then also deduce the weak convergence of the process $\vec{Z}^{[N,Q]}:=\sqrt{N}\int_0^\cdot Q^{\rm T}\vec{Z}^{[N]}(s)\,{\rm d}s.$ to $-\boldsymbol{B}_\circ$, and hence to $\boldsymbol{B}_\circ$ as well.
\begin{itemize} \item[$\circ$] We first apply Lemma \ref{lemmah} with the choice (with $D$ denoting the deviation matrix) \[ {\boldsymbol \Psi}^{[N]}(t) := -(\boldsymbol\alpha-\rho(t)\boldsymbol\gamma)^\mathrm{T} D^\mathrm{T}, \:\:\:\:\: X^{[N]} := \vec{Z}^{[N,Q]}, \] to the process \[G^{[N]}=\sqrt{N}\int_0^\cdot (\boldsymbol\alpha-\rho(s)\boldsymbol\gamma)^\mathrm{T} (\vec{Z}^{[N]}(s)-{\boldsymbol \pi})\,{\rm d}s=-\sqrt{N}\int_0^\cdot (\boldsymbol\alpha-\rho(s)\boldsymbol\gamma)^\mathrm{T} (QD)^\mathrm{T} \vec{Z}^{[N]}(s)\,{\rm d}s,\] where the last equality follows from $QD=\mathbf{1}{\boldsymbol \pi}^\mathrm{T}-I$ (see the proof of Prop.~\ref{prop:nnd}). Note that ${\boldsymbol \Psi}^{[N]}(t)={\boldsymbol \Psi}(t)$ for all $N$, and therefore it is immediate that the weak limit can be identified as a continuous Gaussian martingale $G$, where it turns out that $\langle G\rangle_t=V(t),$ with $V(t)$ defined in (\ref{defv}), which again follows from the proof of Prop.~\ref{prop:nnd}.
\item[$\circ$]
In the next step we consider the processes $\int_0^\cdot{\Psi}^{[N]}(s)\,\mathrm{d} G^{[N]}(s)$, with ${\Psi}^{[N]}(s):=\exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \zeta}^{[N]}(s))$. As these processes are increasing, we have the a.s.\ convergence of \[\sup_{s\leq T}\,\mathopen{}\mathclose\bgroup\originalleft|\,\exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \zeta}^{[N]}(s))-\exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \pi}\,s)\,\aftergroup\egroup\originalright|\to 0\] as $N\to\infty$, by combining the ergodic theorem with \cite[Thm.\ VI.2.15(c)]{JS} (which states that pointwise convergence of increasing functions to a continuous limit implies uniform convergence on compacts). As an immediate consequence of the above and Lemma~\ref{lemmah}, we obtain the weak convergence of $\int_0^\cdot \exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \zeta}^{[N]}(s))\,\mathrm{d} G^{[N]}(s)$ to $\int_0^\cdot \exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \pi}\,s)\,\mathrm{d} G(s)=\int_0^\cdot \exp(\gamma_\infty s)\,\mathrm{d} G(s)$. \end{itemize}
$\rhd$ {\it Step} 3. We now consider the second term on the right hand side of \eqref{eq:y}. For the Brownian term $\hat{B}^{[N]}$ we have by the martingale central limit theorem weak convergence to the Gaussian martingale $\hat{B}$, with quadratic variation $\langle\hat{B}\rangle_t=\sigma^2_\infty t$. The convergence of $\int_0^\cdot \exp(\boldsymbol\gamma^{\rm T} {\boldsymbol \zeta}^{[N]}(s))\,\mathrm{d} \hat{B}^{[N]}(s)$ can be handled as above to obtain weak convergence to the Gaussian martingale $\int_0^\cdot \exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \pi} s)\,\mathrm{d} \hat{B}(s)=\int_0^\cdot \exp(\gamma_\infty s)\,\mathrm{d} \hat{B}(s)$.
$\rhd$ {\it Step} 4. In order to finally obtain the weak limit of $Y^{[N,h]}$ we use\[ h-\beta-\half =\frac{1}{2}\min\{h-1,0\},\:\:\:\:\: \frac{h}{2}-\beta =\frac{1}{2}\min\{1-h,0\}. \]
Clearly, for $h<1$ we have convergence of $Y^{[N,h]}$ to $\int_0^\cdot \exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \pi} s)\,\mathrm{d} \hat{B}(s)$, whereas for $h>1$ we have convergence to $\int_0^\cdot \exp(\boldsymbol\gamma^\mathrm{T} {\boldsymbol \pi}\,s)\,\mathrm{d} G(s)$. For $h=1$ we get weak convergence to the sum of these. To see this, recall that the weak convergence of the $G^{[N]}$ was based on properties of the Markov chain, whereas the convergence of the $B^{[N]}$ resulted from considerations involving the Brownian motion $B$, and these basic processes are independent. Note further that $Y^{[N,h]}(0)=N^{-\beta}M(0)-N^{h-\beta}\mathbf{1}_{\{h=0\}}M(0)\to 0$. Combining these results, we find that $Y^{[N,h]}$ converges to a Gaussian martingale $Y$ given by \[
Y(t)=
\int_0^t e^{\gamma_\infty s}(\mathbf{1}_{\{h\leqslant 1\}}\,\mathrm{d} \hat{B}(s)+\mathbf{1}_{\{h\geqslant 1\}}\,\mathrm{d} G(s)), \] and hence the $\hat{M}^{[N,h]}$ converge weakly to the limit $\hat{M}$ given by $\hat{M}(t)=e^{-\gamma_\infty t}Y(t)$, and this process satisfies the {\sc sde} \[ \mathrm{d} \hat{M}(t)=-\gamma_\infty \hat{M}(t)\,\mathrm{d} t+(\mathbf{1}_{\{h\leqslant 1\}}\,\mathrm{d} \hat{B}(t)+\mathbf{1}_{\{h\geqslant 1\}}\,\mathrm{d} G(t)). \] In this equation the (continuous, Gaussian) martingale has quadratic variation $\mathbf{1}_{\{h\leqslant 1\}}\sigma_\infty^2 t+ \mathbf{1}_{\{h\geqslant 1\}}V(t) $. Hence we can identify its distribution with that of \[ \int_0^\cdot\sqrt{\mathbf{1}_{\{h\leqslant 1\}}\sigma_\infty^2+\mathbf{1}_{\{h\geqslant 1\}}{V}'(s)}\,\mathrm{d} B(s), \] where $B$ is a standard Brownian motion. This finishes the proof. \end{proof}
\iffalse We already came across {\it deviation matrices} earlier in this paper. This section heavily relies on this concept, and also on the related concept of {\it fundamental matrices}; see e.g.\ for more background \cite{CS}. Recall that the deviation matrix $D=(D_{ij})_{i,j=1}^d$ of the finite-state Markov $X(\cdot)$ is defined through \[D_{ij}:=\int_0^\infty (p_{ij}(t)-\pi_j){\rm d}t,\] or, in matrix notation, $D=\int_0^\infty (e^{Qt}-\Pi){\rm d}t$, with $\Pi:= \vec{1}\vec{\pi}^{\rm T}.$ The fundamental matrix $F$ is given by $F:=D+\Pi.$ A number of standard identities play a role below, in particular $QF=FQ=\Pi-I$ and $\Pi F=F\Pi=\Pi.$ \fi
\iffalse \subsection{Time scaling of the background process}\label{61} \footnote{\tt {\footnotesize MM: from this moment on I didn't change anything, apart from a few notational issues. As I understood it, Koen will rephrase the results in terms of weak convergence results, i.e., convergence at the path level to the solution of specific {\sc sde}\,s. Is it correct that you can do that in both scaling regimes, i.e., the ones of both Section 5.1 and 5.2?}} \footnote{\tt {\footnotesize MM: as I want to used superscripts of the type $^{(N)}$ in Section 6, to denote the multiple individual {\sc ou} processes, I chose to replace it in this section by $^{[N]}$.}} In this subsection, we speed up the background process by replacing $X(t)$ by $X(Nt)$, which is equivalent to the scaling $Q\mapsto NQ$. The main result of this subsection is that we show that under this scaling $M^{[N]}(t)$ (we add the superscript to emphasize the dependence on $N$) converges in distribution to an ordinary (that is, non-modulated) {\sc ou} process at time $t$, as $N\to\infty$.
\newcommand{\hspace{-.25mm}}{\hspace{-.25mm}}
We assume that the process starts at level $M ^{[N]} (0) = M_0$ at time $0$, where $M_0$ has a Normal distribution with mean $a$ and variance $b^2$ and is independent of the background process and the Brownian motion. In this case $M ^{[N]} (t)$ has a Normal distribution with random mean \begin{align*} \mu(t;N) &:= M_0 \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{0}^{t} \gamma_{X (Nr)} {\rm d} r \aftergroup\egroup\originalright) + \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X (Nr)} \, {\rm d} r \aftergroup\egroup\originalright) \alpha_{X(Ns)} \, {\rm d} s \intertext{and random variance} v(t;N) &:= \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_{X(Nr)} \, {\rm d} r \aftergroup\egroup\originalright) \sigma^{2}_{X(Ns)} \, {\rm d} s. \end{align*} In particular, it holds that ${\mathbb E} \exp ( {\rm i} \theta M ^{[N]} (t) ) = {\mathbb E} \exp ( {\rm i} \theta \mu(t;N) - \tfrac{1}{2} \theta^2 v(t;N) )$. It follows from Lemma~\ref{lem:intasconv} that $\mu(t;N) \to \mu^{\star}(t)$ and $v(t;N) \to v^{\star}(t)$ a.s.\ for $N \to \infty$, where \[ \mu^{\star}(t) := M_0 e^{-\gamma_\infty t} + \int_{0}^{t} e^{-\gamma_\infty (t-s)} \alpha_\infty \, {\rm d} s,\:\:\: v^{\star}(t) := \int_{0}^{t} e^{ -2 \gamma_\infty (t-s) } \sigma^2_\infty \, {\rm d} s. \] Notice that $\mu^{\star}(t)$ is a random variable and $v^{\star}(t)$ is a constant. Because the norm of $\exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta M ^{[N]} (t) \aftergroup\egroup\originalright)$ is bounded by $1$, the Dominated Convergence Theorem gives \begin{align*} \lim_{N \to \infty} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta M ^{[N]} (t) \aftergroup\egroup\originalright) &= \lim_{N \to \infty} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta \mu(t;N) - \tfrac{1}{2} \theta^2 v(t;N) \aftergroup\egroup\originalright) \\ &= {\mathbb E} \lim_{N \to \infty} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta \mu(t;N) - \tfrac{1}{2} \theta^2 v(t;N) \aftergroup\egroup\originalright)\\ &= {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta \mu^{\star}(t) - \tfrac{1}{2} \theta^2 v^{\star}(t) \aftergroup\egroup\originalright). \end{align*} Using the fact that $M_0 \sim \mathcal{N} (a , b^2 )$ and appealing to L\'evy's continuity theorem (see \cite[Section 18.1]{WILL}), we arrive at the following result. \begin{proposition} \label{PP} Impose the scaling $Q\mapsto NQ$. For $N \to \infty$, the random variable $M^{[N]}(t)$ converges in distribution to a Normal distribution with mean $\varrho(t)$ and variance $v(t)$, where \begin{align*} \varrho(t) := a e^{-\gamma_\infty t} + \frac{\alpha_\infty}{\gamma_\infty}(1-e^{-\gamma_\infty t}), \:\:\:\: v(t) := b^2 e^{-2\gamma_\infty t} + \frac{\sigma_\infty^2}{2\gamma_\infty}(1-e^{-2\gamma_\infty t}). \end{align*} \end{proposition}
Notice that the distribution featuring in this result is the marginal distribution at time $t$ of an {\sc ou} process with parameters $\alpha_\infty$, $\gamma_\infty$, and $\sqrt{\sigma^2_\infty}$, started at level $M_0$. A similar analysis can be done for the {\it steady-state} level $M^{[N]}$; this random variable converges (as $N\to\infty$) to a Normal distribution with mean $\varrho(\infty)$ and variance $v(\infty)$.
\subsection{Time scaling of the background process and OU processes} As mentioned above, we now scale ${\boldsymbol\alpha}\mapsto N{\boldsymbol\alpha}$, ${\boldsymbol\sigma^2}\mapsto N{\boldsymbol\sigma^2}$, and $Q\mapsto N^fQ$, for some $f>0$. The main result of this subsection is a central limit theorem for $M^{[N]}(t)$. The reasoning for its steady-state counterpart $M^{[N]}$ is analogous; therefore, we just state the result and leave out the derivation.
For notational simplicity we assume that the process starts off at level $M^{[N]}(0) = 0$, but it will be clear that the analysis also applies to the case $M^{[N]}(0) = M_0$, with $M_0$ an independent random variable. Under the present scaling, the random variable $M^{[N]}(t)$ has a Normal distribution with random mean \begin{align*} \mu(t;N) &= \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X (N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) N \alpha_{X(N^{f} s)} \, {\rm d} s \intertext{and random variance} v(t;N) &= \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_{X(N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) N \sigma^{2}_{X(N^{f} s)} \, {\rm d} s. \end{align*}
Let $\varrho:=\alpha_\infty/\gamma_\infty$ and $\varrho(t):= \varrho\,(1-e^{-\gamma_\infty t})$. Define $\beta:=\max\{1/2,1-f/2\}$. Then \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{- \beta} \mathopen{}\mathclose\bgroup\originalleft( M ^{[N]} (t) - N \varrho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) = {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{-\beta} \mathopen{}\mathclose\bgroup\originalleft( \mu(t;N) - N \varrho (t) \aftergroup\egroup\originalright) - \tfrac{1}{2} \theta^2 N^{-2\beta} v(t;N) \aftergroup\egroup\originalright). \end{align*} Now observe that \begin{align*} N^{-2\beta} v(t;N) = N^{1-2\beta} \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_{X(N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) \sigma^{2}_{X(N^{f} s)} \, {\rm d} s \end{align*} and that \begin{align*} \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_{X(N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) \sigma^{2}_{X(N^{f} s)} \, {\rm d} s \; \xrightarrow{{\rm a.s.}} \; \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_\infty \, {\rm d} r \aftergroup\egroup\originalright) \sigma^{2}_\infty \, {\rm d} s \end{align*} for $N \to \infty$, according to Lemma~\ref{lem:intasconv}. Since $1-2\beta < 0$ if $f \in (0,1)$ and $1-2\beta = 0$ if $f \geq 1$, it follows that \begin{align} \label{eq:varconv} N^{-2\beta} v(t;N) \; \xrightarrow{{\rm a.s.}} \; \begin{cases} 0 &\text{ if } f \in (0,1)\\ \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( -2 \int_{s}^{t} \gamma_\infty \, {\rm d} r \aftergroup\egroup\originalright) \sigma^{2}_\infty \, {\rm d} s &\text{ if } f \in [1,\infty)\end{cases} \end{align} for $N \to \infty$. Notice that in any case $N^{-2\beta} v(t;N)$ converges a.s.\ to a constant.
Using elementary calculus, we may write $N^{-\beta} \mathopen{}\mathclose\bgroup\originalleft( \mu(t;N) - N \varrho (t) \aftergroup\egroup\originalright) = N^{1-\beta-f/2} G ^{[N]}(t)$, where \begin{align*} G ^{[N]} (t) := N^{f/2} \int_{0}^{t} \mathopen{}\mathclose\bgroup\originalleft( \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X (N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) \alpha_{X(N^{f} s)} - \exp \mathopen{}\mathclose\bgroup\originalleft( - \gamma_\infty (t-s) \aftergroup\egroup\originalright) \alpha_\infty \aftergroup\egroup\originalright) \, {\rm d} s. \end{align*} According to Lemma~\ref{lem:mcclt}, the random variable $G ^{[N]}(t)$ converges in distribution to a Normal distribution with mean $0$ and variance $\tfrac{\Phi_D (t)}{\gamma_\infty}$, where \begin{align*} \Phi_D (t):=2 \gamma_\infty \int_0^t e^{-2\gamma_{\infty} (t-s) } \sum_{i=1}^d\sum_{j=1}^d \pi_i (\alpha_i-\varrho(s)\gamma_i)D_{ij} (\alpha_j-\varrho(s)\gamma_j) \, {\rm d}s. \end{align*} Clearly, $1-\beta-f/2 = 0$ if $f \in (0,1]$ and $1-\beta-f/2 < 0$ if $f > 1$. Then Slutsky's lemma implies that \begin{align} \label{eq:meanconv} N^{-\beta} \mathopen{}\mathclose\bgroup\originalleft( \mu(t;N) - N \varrho (t) \aftergroup\egroup\originalright) \; = \; N^{1-\beta-f/2} G ^{[N]}(t) \; \xrightarrow{\text{d}} \; \begin{cases} \mathcal{N} \mathopen{}\mathclose\bgroup\originalleft( 0 , \tfrac{\Phi_D (t)}{\gamma_\infty} \aftergroup\egroup\originalright) & \text{ if } f \in (0,1]\\ 0 & \text{ if } f \in (1,\infty) \end{cases} \end{align} for $N \to \infty$.
Recall that \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{- \beta} \mathopen{}\mathclose\bgroup\originalleft( M ^{[N]} (t) - N \varrho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) = {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{-\beta} \mathopen{}\mathclose\bgroup\originalleft( \mu(t;N) - N \varrho (t) \aftergroup\egroup\originalright) - \tfrac{1}{2} \theta^2 N^{-2\beta} v(t;N) \aftergroup\egroup\originalright). \end{align*} It follows from Equation~\eqref{eq:varconv} that $- \tfrac{1}{2} \theta^2 N^{-2\beta} v(t;N) \xrightarrow{\text{a.s.}} - \tfrac{1}{2} \theta^2 \frac{\sigma^2_\infty}{2\gamma_\infty}\mathopen{}\mathclose\bgroup\originalleft(1-e^{-2\gamma_\infty t}\aftergroup\egroup\originalright)1_{\{f\geqslant 1\}}$, which is a constant. We may rewrite the result in Equation~\eqref{eq:meanconv} as $N^{-\beta} \mathopen{}\mathclose\bgroup\originalleft( \mu(t;N) - N \varrho (t) \aftergroup\egroup\originalright) \xrightarrow{\text{d}} \mathcal{N} \mathopen{}\mathclose\bgroup\originalleft( 0 , \tfrac{\Phi_D (t)}{\gamma_\infty} 1_{\{f\leqslant 1\}} \aftergroup\egroup\originalright)$. Now using Lemma~\ref{lem:cfconv} together with these observations, it follows that \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{- \beta} \mathopen{}\mathclose\bgroup\originalleft( M ^{[N]} (t) - N \varrho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \xrightarrow{} \exp \mathopen{}\mathclose\bgroup\originalleft( - \tfrac{1}{2} \theta^2 \sigma^2 (t) \aftergroup\egroup\originalright), \end{align*} where \begin{align*} \sigma^2 (t) := \frac{\Phi_D (t)}{\gamma_\infty}1_{\{f\leqslant 1\}}+\frac{\sigma^2_\infty}{2\gamma_\infty}\mathopen{}\mathclose\bgroup\originalleft(1-e^{-2\gamma_\infty t}\aftergroup\egroup\originalright)1_{\{f\geqslant 1\}}. \end{align*} L\'evy's continuity theorem now implies the main result of this subsection, which is formulated in the following statement. \begin{theorem} Impose the scaling ${\boldsymbol\alpha}\mapsto N{\boldsymbol\alpha}$, ${\boldsymbol\sigma^2}\mapsto N{\boldsymbol\sigma^2}$, and $Q\mapsto N^fQ$, for some $f>0$. Then the random variable \[\frac{M^{[N]} (t) -N \varrho (t)}{N^\beta}\] converges in distribution to a Normal distribution with mean $0$ and variance $\sigma^2(t)$ as $N \to \infty$. \end{theorem}
We now present the main result for the stationary case. As mentioned, the techniques used to prove this are very similar to those of the transient case and we leave out the derivation. Defining \begin{align*} \Phi_D &:=\sum_{i=1}^d\sum_{j=1}^d \pi_i (\alpha_i-\varrho\gamma_i)D_{ij} (\alpha_j-\varrho\gamma_j) \intertext{and} \sigma^2 &:= \frac{\Phi_D}{\gamma_\infty}1_{\{f\leqslant 1\}}+\frac{\sigma^2_\infty}{2\gamma_\infty}1_{\{f\geqslant 1\}}, \end{align*} we get the following result. \begin{theorem} Impose the scaling ${\boldsymbol\alpha}\mapsto N{\boldsymbol\alpha}$, ${\boldsymbol\sigma^2}\mapsto N{\boldsymbol\sigma^2}$, and $Q\mapsto N^fQ$, for some $f>0$. Then the random variable \[\frac{M^{[N]}-N\varrho}{N^\beta}\] converges in distribution to a Normal distribution with mean $0$ and variance $\sigma^2$ as $N \to \infty$. \end{theorem} \fi
\newcommand{^{\rm T}}{^{\rm T}}
\newcommand{^{(j)}}{^{(j)}} \newcommand{^{(k)}}{^{(k)}} \newcommand{^{(j,k)}}{^{(j,k)}} \newcommand{{\ha}}{^{(1)}} \newcommand{{\hb}}{^{(2)}}
\section{Multiple MMOU processes driven by the same background process} {In this section, we consider a single background process $X$, taking as before values in $\{1,\ldots,d\}$, modulating {\it multiple} {\sc ou} processes. Suppose there are $J\in{\mathbb N}$ such processes, with parameters $(\vec{\alpha}^{(1)},\vec{\gamma}^{(1)},\vec{\sigma}^{(1)})$ up to $(\vec{\alpha}^{(J)},\vec{\gamma}^{(J)},\vec{\sigma}^{(J)})$. It is further assumed that the {\sc ou} processes are driven by {\it independent} Brownian motions $B_1(\cdot).\ldots, B_J(\cdot)$.} Combining the above, this leads to the $J$ coupled {\sc sde}\,s \[{\rm d}{M_j(t)} = \mathopen{}\mathclose\bgroup\originalleft(\alpha^{(j)}_{X(t)}-\gamma^{(j)}_{X(t)}{M_j(t)}\aftergroup\egroup\originalright){\rm d}t +\sigma^{(j)}_{X(t)} \,{\rm d}B_j(t),\] for $j=1,\ldots,J.$ We call the process a $J$-{\sc mmou} process.
Interestingly, this construction yields $J$ components that have common features, as they react to the same background process, as well as component-specific features, as a consequence of the fact that the driving Brownian motions are independent. This model is particularly useful in settings with multidimensional stochastic processes whose components are affected by the same external factors.
An example of a situation where this idea can be exploited is that of multiple asset prices reacting to the (same) state of the economy, which could be represented by a background process (for instance with two states, that is, alternating between a `good' and a `bad' state). In this way the dependence between the individual components can be naturally modeled. In mathematical finance, one of the key challenges is to develop models that incorporate the correlation between the individual components in a sound way. Some proposals were to simplistic, ignoring too many relevant details, while others correspond with models with overly many parameters, with its repercussions in terms of the calibration that needs to be performed.
Another setting in which such a coupling may offer a natural modeling framework is that of a wireless network. Channel conditions may be modeled as alternating between various levels, and users' transmission rates may react in a similar way to these fluctuations.
Many of the results derived in the previous sections, covering the case $J=1$, can be generalized to the situation of $J$-{\sc mmou} processes described above. To avoid unnecessary repetition, we restrict ourselves to a few of these extensions. In particular, we present (i)~the counterpart of Thm.\ \ref{PROP}, stating that $\vec{M}(t)$ is, conditionally on the path of the background process, multivariate Normally distributed; (ii)~some explicit calculations for the means and (co-)variances for certain special cases; (iii)~the generalization of the {\sc pde} of Thm.\ \ref{PDEth}, (iv) explicit expressions for the steady-state (mixed) moments. Procedures for transient moments, and scaling results (such as a $J$-dimensional {\sc clt}) are not included in this paper, but can be developed as in the single-dimensional case.
\subsection{Conditional Normality}
First we condition on the path $(X(s), s\in [0,t]).$ It is evident that, under this conditioning, the individual components of ${\vec{M}}(t)$ are independent. The following result describes this setting in greater detail.
\iffalse
{\begin{proposition}\label{PROP_MULT}Denote by $X$ the path $(X(s), s\in [0,t]).$ $(\vec{M}(t)\,|\,X)$ has a multivariate Normal distribution with random parameters $(\mbox{\sc m}^{(1)},\ldots,\mbox{\sc m}^{(J)})$ and $(\mbox{\sc s}^{(j,k)})_{j,k=1}^J$ given by
\[{\mbox{\sc m}}^{(j)}:={\mathbb E}(M_j(t)\,|\,X)=m_0 ^{(j)} \exp\mathopen{}\mathclose\bgroup\originalleft({-\int_0^t\gamma^{(j)}_{X(s)}{\rm d}s}\aftergroup\egroup\originalright)+\int_0^t\exp\mathopen{}\mathclose\bgroup\originalleft({-\int_s^t \gamma^{(j)}_{X(r)}{\rm d}r}\aftergroup\egroup\originalright)\alpha^{(j)}_{X(s)}\,{\rm d}s\]
and $\mbox{\sc s}^{(j,k)}:={\mathbb C}{\rm ov}(M_j(t),M_k(t)\,|\,X)=0$, while for $j=k$,
\[\mbox{\sc s}^{(j,j)}:={\mathbb V}{\rm ar}(M_j(t)\,|\,X)=\int_0^t\exp\mathopen{}\mathclose\bgroup\originalleft({-2\int_s^t \gamma^{(j)}_{X(r)}{\rm d}r}\aftergroup\egroup\originalright)(\sigma^{(j)}_{X(s)})^2\,{\rm d}s.\] \end{proposition}} \fi
\begin{proposition}\label{PROP2} Define $\Gamma ^{(j)}(t) := \int_{0}^{t} \gamma^{(j)}_{X (s)} \, {\rm d} s$, for $j=1,\ldots,J.$ Then the $J$-dimensional stochastic process $(\vec{M}(t))_{t \geqslant 0}$ given by \begin{align*} M^{(j)} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = M^{(j)}_0 e^{ - \Gamma^{(j)} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) } + \int_{0}^{t} e^{ - \mathopen{}\mathclose\bgroup\originalleft( \Gamma^{(j)} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma^{(j)} \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \alpha^{(j)}_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} s + \int_{0}^{t} e^{ - \mathopen{}\mathclose\bgroup\originalleft( \Gamma^{(j)} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma^{(j)} \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \sigma^{(j)}_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \end{align*} is the unique $J$-{\sc mmou} process with initial condition $\vec{M}_0$.
Conditional on the process $X$, the random vector $\vec{M} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)$ has a multivariate Normal distribution with, for $j=1,\ldots,J$, random mean \[ \mu^{(j)} \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = M_0^{(j)} \exp\mathopen{}\mathclose\bgroup\originalleft({-\Gamma ^{(j)}(t) }\aftergroup\egroup\originalright)+\int_0^t\exp\mathopen{}\mathclose\bgroup\originalleft({- (\Gamma ^{(j)}(t) -\Gamma ^{(j)}(s)) }\aftergroup\egroup\originalright)\alpha^{(j)}_{X(s)}\,{\rm d}s\] and random covariance $v^{(j,k)}(t)=0$ if $j\not=k$ and \[ v ^{(j,j)}\mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \int_{0}^{t} \exp\mathopen{}\mathclose\bgroup\originalleft({-2 (\Gamma ^{(j)}(t) -\Gamma ^{(j)}(s)) }\aftergroup\egroup\originalright)\mathopen{}\mathclose\bgroup\originalleft(\sigma^{(j)}_{X(s)}\aftergroup\egroup\originalright)^2\,{\rm d}s. \] \end{proposition}
\subsection{Mean and (co-)variance}
The mean and (co-)variance of $\vec{M}(t)$ for $J$-{\sc mmou} can be computed relying on stochastic integration theory, with a procedure similar to the one relied on in Section~\ref{TB}; we do not include the resulting expressions.
{We consider in greater detail the special case that $\gamma_i^{(j)}\equiv \gamma^{(j)}$ for all $i\in\{1,\ldots,d\}$ (as in Section~\ref{TB}), because in this situation expressions simplify greatly. The means and variances can be found as in Prop.~\ref{PROP}; we now point out how to compute the covariance $v_t^{(j,k)}:={\mathbb C}{\rm ov}(M^{(j)}(t), M^{(k)}(t))$ (with $j\not=k$), relying on the {\it law of total covariance}. We write, in self-evident notation,
\[v_t^{(j,k)}={\mathbb E}({\mathbb C}{\rm ov}(M^{(j)}(t), M^{(k)}(t)\,|\,X))+
{\mathbb C}{\rm ov}({\mathbb E}(M^{(j)}(t)\,|\,X), {\mathbb E}(M^{(k)}(t)\,|\,X)).\] The first term obviously cancels (cf.\ Prop.\ \ref{PROP2}), while the second reads \begin{eqnarray*}\lefteqn{\hspace{-1cm}\frac{1}{\gamma^{(j)}+\gamma^{(k)}}\mathopen{}\mathclose\bgroup\originalleft(\sum_{i_1=1}^d\sum_{i_2=1}^d \alpha^{(j)}_{i_1}\alpha_{i_2}^{(k)}\int_0^t\mathopen{}\mathclose\bgroup\originalleft(e^{-\gamma^{(k)} v}-e^{-(\gamma^{(j)}+\gamma^{(k)})t+\gamma^{(j)} v}\aftergroup\egroup\originalright)\pi_{i_1}(p_{i_1i_2}(v)-\pi_{i_2}){\rm d}v\aftergroup\egroup\originalright.}\\ &&\mathopen{}\mathclose\bgroup\originalleft.\sum_{i_1=1}^d\sum_{i_2=1}^d \alpha^{(k)}_{i_1}\alpha_{i_2}^{(j)}\int_0^t\mathopen{}\mathclose\bgroup\originalleft(e^{-\gamma^{(j)} v}-e^{-(\gamma^{(k)}+\gamma^{(j)})t+\gamma^{(k)} v}\aftergroup\egroup\originalright)\pi_{i_1}(p_{i_1i_2}(v)-\pi_{i_2}){\rm d}v\aftergroup\egroup\originalright) .\end{eqnarray*} We consider two limiting regimes. \begin{itemize} \item[$\rhd$] For $t\to\infty$, it is readily checked that there is convergence to \[\frac{1}{\gamma^{(j)}+\gamma^{(k)}}\mathopen{}\mathclose\bgroup\originalleft((\vec{\alpha}^{(j)})^{\rm T}{\rm diag}\{\vec{\pi}\}D(\gamma^{(k)})\vec{\alpha}^{(k)}+ (\vec{\alpha}^{(k)})^{\rm T}{\rm diag}\{\vec{\pi}\}D(\gamma^{(j)})\vec{\alpha}^{(j)}\aftergroup\egroup\originalright).\] \item[$\rhd$] Apply, as before, the scaling ${\boldsymbol\alpha}\mapsto N^h{\boldsymbol\alpha}$, ${\boldsymbol\sigma^2}\mapsto N^h{\boldsymbol\sigma^2}$, and $Q\mapsto NQ$ for some $h>0$. We obtain that the covariance, for $N$ large, behaves as \[\mathopen{}\mathclose\bgroup\originalleft(\frac{1-e^{-(\gamma ^{(j)}+\gamma^{(k)})t}}{\gamma^{(j)}+\gamma^{(k)}}\aftergroup\egroup\originalright)\mathopen{}\mathclose\bgroup\originalleft(2N^{2h-1}(\vec{\alpha}^{(j)})^{\rm T}{\rm diag}\{\vec{\pi}\}D\vec{\alpha}^{(k)}\aftergroup\egroup\originalright).\] \end{itemize}}
{\begin{Ex} {\rm We now provide explicit results for $t\to\infty$ for the case $d=2,J=2$. It can be verified that, with $q_1:=q_{12}$, $q_2:=q_{21}$ and $q:=q_1+q_2$, \[D(\gamma^{(j)})=\frac{1}{q(q+\gamma^{(j)})}\mathopen{}\mathclose\bgroup\originalleft(\begin{array}{rr} q_2&-q_2\\ -q_1&q_1\end{array}\aftergroup\egroup\originalright).\] It is a matter of elementary calculus to show that the steady-state covariance is \[{\mathbb C}{\rm ov}(M_1, M_2) =\frac{1}{\gamma\ha+\gamma\hb}\frac{q_1q_2}{q^2}\frac{2q+\gamma\ha+\gamma\hb}{(q+\gamma\ha)(q+\gamma\hb)} \mathopen{}\mathclose\bgroup\originalleft((\alpha_1\hb-\alpha_2\hb)(\alpha_1\ha-\alpha_2\ha)\aftergroup\egroup\originalright) \] whereas, for $j=1,2$, \[{\mathbb V}{\rm ar}\,M_j=\frac{q_1(\sigma_2^{(j)})^2+q_2(\sigma_1^{(j)})^2}{2\gamma^{(j)} q}+\frac{1}{\gamma^{(j)}}\frac{q_1q_2}{q^2(q+\gamma^{(j)})}\mathopen{}\mathclose\bgroup\originalleft(\alpha_1^{(j)}-\alpha_2^{(j)}\aftergroup\egroup\originalright)^2.\] These expressions enable us to compute the correlation coefficient between $M_1$ and $M_2$. For the special case that $\vec{\sigma}\ha=\vec{\sigma}\hb=\vec{0}$, we obtain, modulo its sign, \[\sqrt{\frac{\gamma\ha\gamma\hb}{(q+\gamma\ha)(q+\gamma\hb)}}\frac{2q+\gamma\ha+\gamma\hb}{\gamma\ha+\gamma\hb},\] which can be verified to be smaller than 1. }\end{Ex}}
\subsection{Transient behavior: partial differential equations}
In order to uniquely characterize the joint distribution of $\vec{M}(t)$, we now set up a system of partial differential equations for the objects \[g_i(\vec{\vartheta},t):= {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft(e^{\sum_{j=1}^J \vartheta_j M^{(j)}(t) } 1\{X(t)=i\}\aftergroup\egroup\originalright),\] with $i\in\{1,\ldots,d\}.$ Relying on the machinery used when establishing the system of {\sc pde}\,s featuring in Thm.\ \ref{PDEth}, we obtain that ${\partial {\boldsymbol g}(\vec{\vartheta},t)}/{\partial t}$ equals \[Q^{\rm T}{\boldsymbol g}(\vec{\vartheta},t)- \sum_{j=1}^J\mathopen{}\mathclose\bgroup\originalleft(\vartheta_j\,{\rm diag}\{{\boldsymbol \alpha}^{(j)}\}-\frac{1}{2}\vartheta_j^2{\rm diag}\{({\boldsymbol \sigma}^{(j)})^2\}\aftergroup\egroup\originalright) {\boldsymbol g}(\vec{\vartheta},t)-\sum_{j=1}^J\vartheta_j\,{\rm diag}\{{\boldsymbol \gamma}^{(j)}\}\,\frac{\partial}{\partial \vartheta_j}{\boldsymbol g}(\vec{\vartheta},t). \] \iffalse The corresponding initial conditions are ${\boldsymbol g}(\vec{0},t)={\boldsymbol p}_t$ and \[{\boldsymbol g}(\vec{\vartheta},0) = e^{-\sum_{j=1}^J\vartheta_j m_0^{(j)}}{\boldsymbol p}_0.\]\fi
\subsection{Recursive scheme for higher order moments}
The above system of {\sc pde}\,s can be used to determine all (transient and stationary) moments related to $J$-{\sc mmou}. We restrict ourselves to the stationary moments here. Define $\vec{h}_{\vec{k}}= (h_{1,\vec{k}},\ldots,h_{d,\vec{k}})^{\rm T},$ where \[h_{i,\vec{k}}:= {\mathbb E}\mathopen{}\mathclose\bgroup\originalleft((-1)^{\sum_{j=1}^J k_j} (M^{(1)})^{k_1}\cdots (M^{(J)})^{k_J}1\{X=i\}\aftergroup\egroup\originalright).\] Observe that $\vec{h}_{\vec{0}} =\vec{\pi}.$ With techniques similar to those applied earlier, $\vec{e}_j\in{\mathbb R}^J$ denoting the $j$-th unit vector, we obtain the recursion \begin{eqnarray*}\vec{h}_{\vec{k}} &=& \mathopen{}\mathclose\bgroup\originalleft(Q^{\rm T}-\sum_{j=1}^J k_j\,{\rm diag}\{{\boldsymbol \gamma}^{(j)}\}\aftergroup\egroup\originalright)^{-1}\\ &&\times\: \mathopen{}\mathclose\bgroup\originalleft(\sum_{j=1}^J k_j\,{\rm diag}\{{\boldsymbol \alpha}^{(j)}\} \vec{h}_{\vec{k}-\vec{e}_j} -\frac{1}{2}\sum_{j=1}^J k_j(k_j-1)\,{\rm diag}\{({\boldsymbol \sigma}^{(j)})^2\} \vec{h}_{\vec{k}-2\vec{e}_j}\aftergroup\egroup\originalright).\end{eqnarray*} This procedure allows us to compute all mixed moments, thus facilitating the calculation of covariances as well. In the situation of $J=2$, for instance, we find that \[{\mathbb E}M^{(1)}M^{(2)} = \vec{1}\mathopen{}\mathclose\bgroup\originalleft(Q^{\rm T}-{\rm diag}\{{\boldsymbol \gamma}\ha\}- {\rm diag}\{{\boldsymbol \gamma}\hb\}\aftergroup\egroup\originalright)^{-1} \mathopen{}\mathclose\bgroup\originalleft( {\rm diag}\{{\boldsymbol \alpha}\ha\}\vec{h}_{0,1}+ {\rm diag}\{{\boldsymbol \alpha}\hb\}\vec{h}_{1,0} \aftergroup\egroup\originalright),\] where $\vec{h}_{0,1}$ and $\vec{h}_{1,0}$ follow from the analysis presented in Section 5.
\begin{remark} {\rm The model proposed in this section describes a $J$-dimensional stochastic process with dependent components. In many situations, the dimension $d$ can be chosen relatively small (see for instance \cite{BAN,DAV}), whereas $J$ tends to be large (e.g., in the context of asset prices). Importantly, the $\frac{1}{2}J(J+1)=O(J^2)$ entries of the covariance matrix of ${\vec{M}}(t)$ (or its stationary counterpart $\vec{M}$) are endogenously determined by the model, and need not be estimated from data. Instead, this approach requires the calibration of just the $d(d-1)$ entries of the $Q$-matrix, as well as the $3dJ$ parameters of the underlying {\sc ou} processes, totaling $O(J)$ parameters. We conclude that, as a consequence, this framework offers substantial potential advantages. }\end{remark}
\section{Discussion and concluding remarks} This paper has presented a set of results on {\sc mmou}, ranging from procedures to compute moments and a {\sc pde} for the Fourier-Laplace transform, to weak convergence results under specific scalings and a multivariate extension in which multiple {\sc mmou}\,s are modulated by the same background process. Although a relatively large number of aspects is covered, there are many issues that still need to be studied. One such area concerns the large-deviations behavior under specific scalings, so as to obtain the counterparts of the results obtained in e.g.\ \cite{BMT2, JMKO, JM} for the Markov-modulated infinite-server queue.
It is further remarked that in this paper we looked at an regime-switching version of the {\sc ou} process, but of course we could have considered various other processes. One option is the Markov-modulated version of the so-called Cox-Ingersoll-Ross ({\sc cir}) process: \[ {\rm d} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \mathopen{}\mathclose\bgroup\originalleft( \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} - \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \, {\rm d} t + \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)}\sqrt{M(t)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright). \] Some results we have established for {\sc mmou} have their immediate {\sc mmcir} counterpart, while for others there are crucial differences. It is relatively straightforward to adapt the procedure used in Section \ref{FLT}, to set up a system of {\sc pde}\,s for the Fourier-Laplace transforms (essentially based on It\^{o}'s rule). Interestingly, the recursions to generate all moments are now one-step (rather than two-step) recursions. A further objective would be to see to what extent the results of our paper generalize to more general classes of diffusions; see e.g.\ \cite{GANG}.
\appendix
\section{Existence and basic properties of MMOU}\label{sec:mmouexist} In this appendix we provide background and formal underpinnings of results presented in Section \ref{MOD}. Throughout we work with a given probability space $\mathopen{}\mathclose\bgroup\originalleft( \Omega , \mathcal{F} , \mathbb{P} \aftergroup\egroup\originalright)$ on which a random variable $M_0$, a standard Brownian motion $B$, and a continuous-time Markov process $X$ with finite state space are defined. It is assumed that $M_0$, $X$ and $B$ are independent. Denote the natural filtrations of $X$ and $B$ by $( \mathcal{F}_{t}^{X} )_{t \geqslant 0}$ and $( \mathcal{F}_{t}^{B} )_{t \geqslant 0}$, respectively. As before, the state space of $X$ is $\mathopen{}\mathclose\bgroup\originalleft\lbrace 1 , \ldots , d \aftergroup\egroup\originalright\rbrace$ for some $d\in{\mathbb N}$, and we let $\alpha_{i} \in \mathbb{R}$, $\gamma_{i}>0$ and $\sigma_{i} \in \mathbb{R}$ for $i \in \mathopen{}\mathclose\bgroup\originalleft\lbrace 1 , \ldots , d \aftergroup\egroup\originalright\rbrace$. We start by the definition of {\sc mmou}, cf.\ Equation (\ref{SIE:intMMOU}).
\begin{definition} A stochastic process $M$ is called an {\sc mmou} process with initial condition $M_0$ if \begin{align} \label{eq:defmmou} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) &= M_0 + \int_{0}^{t} \mathopen{}\mathclose\bgroup\originalleft( \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} - \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} M \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \, {\rm d} s + \int_{0}^{t} \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \end{align} for all $t \geq 0$. \end{definition}
To show existence of an {\sc mmou} process, we first need a filtration $\mathopen{}\mathclose\bgroup\originalleft( \mathcal{H}_t \aftergroup\egroup\originalright)_{t \geqslant 0}$ that satisfies the usual conditions and with respect to which $X$ is adapted and $B$ is a Brownian motion. Define the multivariate process $Y$ by $Y_t = \mathopen{}\mathclose\bgroup\originalleft( M_0 , X_t , B_t \aftergroup\egroup\originalright)$. Its natural filtration is given by $\mathcal{F}_{t}^{Y} = \sigma \mathopen{}\mathclose\bgroup\originalleft( M_0 , \mathcal{F}_{t}^{X} , \mathcal{F}_{t}^{B} \aftergroup\egroup\originalright)$. Using the independence assumptions, it is easily verified that $Y$ is a Markov process with respect to $\mathcal{F}_{t}^{Y}$ and that $B$ is a Brownian motion with respect to this filtration. In addition, $Y$ is a Feller process. This is an immediate result of the independence assumptions and the fact that $M_0$ (viewed as a stochastic process), $X$ and $B$ are Feller processes.
Now define the augmented filtration $\mathopen{}\mathclose\bgroup\originalleft( \mathcal{H}_t \aftergroup\egroup\originalright)_{t \geqslant 0}$ via $\mathcal{H}_t = \sigma \mathopen{}\mathclose\bgroup\originalleft( \mathcal{F}_{t}^{Y} , \mathcal{N} \aftergroup\egroup\originalright)$, where $\mathcal{N}$ consists of all $F \subset \Omega$ such that there exists $G \in \mathcal{F}_{\infty}^{Y}$ with $F \subset G$ and $\mathbb{P} \mathopen{}\mathclose\bgroup\originalleft( G \aftergroup\egroup\originalright) = 0$. Since $Y$ has c\`{a}dl\`{a}g paths, it follows from \cite[Prop. III.2.10]{RY} that $\mathopen{}\mathclose\bgroup\originalleft( \mathcal{H}_t \aftergroup\egroup\originalright)_{t \geqslant 0}$ satisfies the usual conditions. Relative to this filtration, the process $B$ is a Brownian motion \cite[Th.~2.7.9]{KS} and $Y$ is a Feller process \cite[p.~92]{KS}.
We now verify in detail the validity of Thm.\ \ref{PROP}. To construct an {\sc mmou} process, define the stochastic process \begin{align*} \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) &:= \int_{0}^{t} \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} s, \end{align*} which is clearly adapted to $\mathopen{}\mathclose\bgroup\originalleft( \mathcal{H}_t \aftergroup\egroup\originalright)_{t \geqslant 0}$. The continuous stochastic process \begin{equation} \label{eq:gammarepr} M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = M_0 e^{ - \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} + \int_{0}^{t} e^{- \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) }\alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} s + \int_{0}^{t} e^{- \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) }\sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \end{equation} is well defined and adapted to $\mathopen{}\mathclose\bgroup\originalleft( \mathcal{H}_{t} \aftergroup\egroup\originalright)_{t \geqslant 0}$, too. Using similar techniques as in the construction of ordinary {\sc ou} (cf.\ \cite[Ch.~V.5]{RW}), one verifies that $M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)$ satisfies Equation~\eqref{eq:defmmou}, so the stochastic process $M$, as given by (\ref{eq:gammarepr}), is an {\sc mmou} process.
Now we would like to know whether a process that satisfies the stochastic differential equation~\eqref{eq:defmmou} is unique. Of course, uniqueness up to indistinguishability is the strongest form of uniqueness we can get. We will show that this holds for {\sc mmou}. To this end, suppose we have two {\sc mmou} processes $M^{(1)}$ and $M^{(2)}$, i.e., \begin{align*} M^{(i)}(t) = M_0 + \int_{0}^{t} \mathopen{}\mathclose\bgroup\originalleft( \alpha_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} - \gamma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} M^{(i)} \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \, {\rm d} s + \int_{0}^{t} \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright), \qquad i \in \mathopen{}\mathclose\bgroup\originalleft\lbrace 1,2 \aftergroup\egroup\originalright\rbrace. \end{align*} Then $V (t) := M^{(1)} (t) - M^{(2)} (t)$ satisfies \begin{align*} V(t) = - \int_{0}^{t} \gamma_{X(s)} V(s) \, {\rm d} s \end{align*} with initial condition $V(0) = 0$, on a measurable set $\Omega^{\star}$ that has probability $1$. If $V(t) = 0$ for all $t \geq 0$ for every $\omega \in \Omega^{\star}$, then $M^{(1)}$ and $M^{(2)}$ are indistinguishable. This is indeed the case, as a direct consequence of \cite[Th.~I.5.1]{HALE} and \cite[Th.~I.5.3]{HALE}. Consequently, every {\sc mmou} process admits a representation as in Equation~\eqref{eq:gammarepr}.
For fixed $t \geq 0$ we would like to know the distribution of $M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)$. Let, for a given $\Gamma(t)$, $\mu(t)$ and $v(t)$ be given by (\ref{rmu}) and (\ref{rv}), respectively. Observe that we may write \[M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) = \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) + \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright).\]
Using the independence assumptions and standard properties of integrals with respect to Brownian motion, it is easily verified that \begin{eqnarray*} {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ e^ { {\rm i} \theta M \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)} \middle\vert \mathcal{F}_{\infty}^{X} \aftergroup\egroup\originalright] &= &{\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta \mathopen{}\mathclose\bgroup\originalleft( \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) + \int_{0}^{t}e^{- \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \middle\vert \mathcal{F}_{\infty}^{X} \aftergroup\egroup\originalright]\\ &=& e^{ {\rm i} \theta \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) } {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta \mathopen{}\mathclose\bgroup\originalleft( \int_{0}^{t} e^{- \mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)} \, {\rm d} B \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \middle\vert \mathcal{F}_{\infty}^{X} \aftergroup\egroup\originalright]\\ &=& e^{ {\rm i} \theta \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) }\exp \mathopen{}\mathclose\bgroup\originalleft( - \tfrac{1}{2} \theta^2 \int_{0}^{t} e^{- 2\mathopen{}\mathclose\bgroup\originalleft( \Gamma \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) - \Gamma \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) } \sigma_{X \mathopen{}\mathclose\bgroup\originalleft( s \aftergroup\egroup\originalright)}^2 \, {\mathrm d} s \aftergroup\egroup\originalright)\\ &=& e^{ {\rm i} \theta \mu \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright)- \tfrac{1}{2} \theta^2 v \mathopen{}\mathclose\bgroup\originalleft( t \aftergroup\egroup\originalright) } ,\end{eqnarray*}which implies the Normality claim in Thm.\ \ref{PROP}.
\iffalse \section{Some convergence results for finite Markov chains} In this appendix, we establish a technical result needed in Section \ref{Sec:TS}. \label{app-convergence} \begin{lemma} \label{LB} As $N\to\infty$, we have $N\langle L_k\hN, L_\ell\hN \rangle_t\to (\pi_l D_{k\ell} + \pi_\ell D_{\ell k}) t.$ \end{lemma}
\begin{proof} By the product rule, we have \[{N}^{-1} \mathrm{d}\mathopen{}\mathclose\bgroup\originalleft(Z_i\hN(t) Z_j\hN(t) \aftergroup\egroup\originalright) = {N}^{-1} Z_i\hN(t)\mathrm{d} Z_j\hN(t) + {N}^{-1} Z_j\hN(t)\mathrm{d} Z_i\hN(t) + {N}^{-1} \mathrm{d} \mathopen{}\mathclose\bgroup\originalleft[Z\hN_i, Z\hN_j \aftergroup\egroup\originalright]_t. \] Making use of the fact that $Z\hN_i(t)Z\hN_j(t) = Z\hN_i(t) 1_{\{i=j\}}$ and of formula \eqref{eq:KsN}, we obtain after rearranging that \begin{align*} {N}^{-1}Z\hN_i(t)&\mathrm{d} K\hN_j(t) + {N}^{-1}Z\hN_j(t)\mathrm{d} K\hN_i(t) \\ & = -{N}^{-1} \mathrm{d}\mathopen{}\mathclose\bgroup\originalleft[Z\hN_i, Z\hN_j\aftergroup\egroup\originalright]_t - Z\hN_i(t) q_{ij} \mathrm{d} t - Z\hN_j(t) q_{ji} \mathrm{d} t + {N}^{-1}\mathrm{d} Z\hN_i(t) 1_{\{i=j\}}. \end{align*} Note that the two terms on the left-hand side are local martingales, and as the difference between the optional and the predictable quadratic variation is a local martingale, we can apply the martingale central limit theorem to the local martingale \[ -{N}^{-1} \mathrm{d}\mathopen{}\mathclose\bgroup\originalleft\langle Z\hN_i, Z\hN_j\aftergroup\egroup\originalright\rangle_t - Z\hN_i(t) q_{ij} \mathrm{d} t - Z\hN_j(t) q_{ji} \mathrm{d} t + {N}^{-1}\mathrm{d} Z\hN_i(t) 1_{\{i=j\}},\] and thus we establish that, as $N\to\infty$, for $i\not=j$ \[N^{-1} \mathopen{}\mathclose\bgroup\originalleft\langle Z\hN_i, Z\hN_j\aftergroup\egroup\originalright\rangle_t \to -\mathopen{}\mathclose\bgroup\originalleft(\pi_iq_{ij}+\pi_j q_{ji}\aftergroup\egroup\originalright)t;\] it is readily verified that this claim also applies when $i=j.$ Then observe that \[ \mathrm{d}\langle L_k\hN, L_\ell\hN \rangle_t = N^{-2}\sum_{i=1}^d\sum_{j=1}^d D_{ik}D_{j\ell} \,\mathrm{d} \langle Z\hN_i, Z\hN_j\rangle_t .\] From $QD=\Pi-I$ it follows that $-\sum_{j=1}^d q_{ij}D_{j\ell}= 1_{\{i=\ell\}} -\pi_\ell$ and $ -\sum_{i=1}^d q_{ji}D_{ik} = 1_{\{j=k\}} -\pi_k,$ and consequently we have that \[-\sum_{i=1}^d\sum_{j=1}^d D_{ik}D_{j\ell} \mathopen{}\mathclose\bgroup\originalleft(\pi_iq_{ij}+\pi_j q_{ji}\aftergroup\egroup\originalright) = \pi_\ell D_{\ell k}+ \pi_kD_{k\ell},\] which implies the stated. \end{proof} \fi
\iffalse \section{Some convergence results} \footnote{\tt {\footnotesize MM: this appendix have not touched.}} In this section we will prove three convergence results that are repeatedly used in the time scaling analysis in Section~\ref{Sec:TS}. Consider an irreducible continuous-time Markov chain $(X(t))_{t\geqslant 0}$ with finite state space $\{1,\ldots,d\}$. Its generator matrix is denoted by $Q = \mathopen{}\mathclose\bgroup\originalleft( q_{ij} \aftergroup\egroup\originalright)_{i,j=1}^{d}$ and the (unique) invariant distribution corresponding to $Q$ is denoted by the column vector ${\boldsymbol \pi}$. Let $\alpha : \{1,\ldots,d\} \to \mathbb{R}$ and $\gamma : \{1,\ldots,d\} \to \mathbb{R}$ and define $\alpha_\infty := \sum_{i=1}^d \pi_i \alpha_i$ and $\gamma_\infty := \sum_{i=1}^d \pi_i \gamma_i$. \begin{lemma} \label{lem:intasconv} Let $t \in [0,\infty)$. For $N \to \infty$ it holds that \begin{align*} \int_{0}^{t} \exp\mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X\mathopen{}\mathclose\bgroup\originalleft({N r}\aftergroup\egroup\originalright)} \, {\rm d} r \aftergroup\egroup\originalright) \alpha_{X\mathopen{}\mathclose\bgroup\originalleft({N s}\aftergroup\egroup\originalright)} \, {\rm d} s \xrightarrow{{\rm a.s.}} \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \gamma_\infty (t-s) \aftergroup\egroup\originalright) \alpha_\infty \, {\rm d} s. \end{align*} \end{lemma} \begin{proof} Fix some $t \in [0,\infty)$. It follows from \cite[Th.\ VI.3.1]{ASM} that \begin{align*} \int_{s}^{t} \gamma_{X(Nr)} \, {\rm d} r = \int_{0}^{t} \gamma_{X(Nr)} \, {\rm d} r - \int_{0}^{s} \gamma_{X(Nr)} \, {\rm d} r \to \gamma_\infty (t-s) \end{align*} for $N \to \infty$ and any $0 \leq s \leq t$ a.s. Let $\Omega^{\star}$ denote a measurable set with $\mathbb{P} \mathopen{}\mathclose\bgroup\originalleft( \Omega^{\star} \aftergroup\egroup\originalright) = 1$ on which this convergence holds true.
From now on, we work with fixed $\omega \in \Omega^{\star}$. Clearly, for $N \to \infty$ and any $0 \leq s \leq t$ we have $\exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X(N r)} \, {\rm d} r \aftergroup\egroup\originalright) \to \exp \mathopen{}\mathclose\bgroup\originalleft( - \gamma_\infty (t-s) \aftergroup\egroup\originalright)$ . The Dominated Convergence Theorem then implies that \begin{align*} \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X(N r)} \, {\rm d} r \aftergroup\egroup\originalright) \alpha_{X(N s)} \, {\rm d} s - \int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft( - \gamma_\infty (t-s) \aftergroup\egroup\originalright) \alpha_{X(N s)} \, {\rm d} s \to 0 \end{align*} for $N \to \infty$, so to complete the proof it suffices to show that $\int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft(\gamma_\infty s \aftergroup\egroup\originalright) \alpha_{X(N s)} \, {\rm d} s$ converges to $\int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft(\gamma_\infty s \aftergroup\egroup\originalright) \alpha_\infty \, {\rm d} s$.
To keep the proof relatively compact, we only treat the case $\alpha_\infty > 0$ and $\gamma_\infty > 0$. Proofs for the other cases can be handled using the same method. Let $m \in \mathbb{N}$ and $N$ be fixed. Writing $t^{m}_{k} = \tfrac{2^k}{2^m} t$, we have \begin{align*} \sum_{k=1}^{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty s^{+}_{k,m} (N) \aftergroup\egroup\originalright) \int_{t^{m}_{k-1}}^{t^{m}_{k}} \alpha_{X(Ns)} \, {\rm d} s &\geq \int_{0}^{t} \exp(\gamma_\infty s) \alpha_{X(Ns)} \, {\rm d} s\\ &\geq \sum_{k=1}^{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty s^{-}_{k,m} (N) \aftergroup\egroup\originalright) \int_{t^{m}_{k-1}}^{t^{m}_{k}} \alpha_{X(Ns)} \, {\rm d} s, \end{align*} where the $s^{+}_{k,m} (N) \in \mathopen{}\mathclose\bgroup\originalleft[ t^{m}_{k-1} , t^{m}_{k} \aftergroup\egroup\originalright]$ are chosen such that the upper bound is maximized and the $s^{-}_{k,m} (N) \in \mathopen{}\mathclose\bgroup\originalleft[ t^{m}_{k-1} , t^{m}_{k} \aftergroup\egroup\originalright]$ such that the lower bound is minimized. It is easy to see that $s^{\pm}_{k,m} (N) \in \mathopen{}\mathclose\bgroup\originalleft\lbrace t^{m}_{k-1} , t^{m}_{k} \aftergroup\egroup\originalright\rbrace$.
Keeping $m$ fixed and taking $N \to \infty$, we get $ s^{+}_{k,m} (N) \to t^{m}_{k}$ and $ s^{-}_{k,m} (N) \to t^{m}_{k-1}$, where we use that $\alpha_\infty > 0$, $\gamma_\infty > 0$ and $\int_{t^{m}_{k-1}}^{t^{m}_{k}} \alpha_{X(Ns)} \, {\rm d} s \to \alpha_\infty / 2^m$. Invoking the Dominated Convergence Theorem once again, we obtain \begin{align*} \lim_{N \to \infty} \sum_{k=1}^{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty s^{+}_{k,m} (N) \aftergroup\egroup\originalright) \int_{t^{m}_{k-1}}^{t^{m}_{k}} \alpha_{X(Ns)} \, {\rm d} s &= \sum_{k=1}^{2^m} \tfrac{1}{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty t^{m}_{k} \aftergroup\egroup\originalright) \alpha_\infty \intertext{and} \lim_{N \to \infty} \sum_{k=1}^{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty s^{-}_{k,m} (N) \aftergroup\egroup\originalright) \int_{t^{m}_{k-1}}^{t^{m}_{k}} \alpha_{X(Ns)} \, {\rm d} s &= \sum_{k=1}^{2^m} \tfrac{1}{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty t^{m}_{k-1} \aftergroup\egroup\originalright) \alpha_\infty, \end{align*} so that \begin{align*} \sum_{k=1}^{2^m} \tfrac{1}{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty t^{m}_{k} \aftergroup\egroup\originalright) \alpha_\infty &\geq \limsup_{N \to \infty} \int_{0}^{t} \exp(\gamma_\infty s) \alpha_{X(Ns)} \, {\rm d} s\\ &\geq \liminf_{N \to \infty} \int_{0}^{t} \exp(\gamma_\infty s) \alpha_{X(Ns)} \, {\rm d} s \geq \sum_{k=1}^{2^m} \tfrac{1}{2^m} \exp \mathopen{}\mathclose\bgroup\originalleft( \gamma_\infty t^{m}_{k-1} \aftergroup\egroup\originalright) \alpha_\infty. \end{align*} Now taking $m \to \infty$, it follows that both the upper bound and the lower bound converge to the integral $\int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft(\gamma_\infty s \aftergroup\egroup\originalright) \alpha_\infty \, {\rm d} s$. Hence, $\lim_{N \to \infty} \int_{0}^{t} \exp(\gamma_\infty s) \alpha_{X(Ns)} \, {\rm d} s$ exists and equals $\int_{0}^{t} \exp \mathopen{}\mathclose\bgroup\originalleft(\gamma_\infty s \aftergroup\egroup\originalright) \alpha_\infty \, {\rm d} s$. As noted before, this suffices to prove the lemma. \end{proof}
The result of Lemma~\ref{lem:intasconv} also holds with the exponential function replaced by a general continuous function. The proof of this result works in the same way as the proof of Lemma~\ref{lem:intasconv}, but is notationally more complicated. These complications can be avoided in the proof of Lemma~\ref{lem:intasconv}, because the exponential function is strictly convex.
\begin{lemma} \label{lem:cfconv} Consider sequences of real-valued random variables $Y , Y_1 , Y_2 , \ldots$ and $Z_1 , Z_2 , \ldots$ that are defined on some common probability space. Assume that $ Z_N \leq K$ a.s.\ for every $N \in \mathbb{N}$ and some $K \in \mathbb{R}$ and that $Z_N \xrightarrow{{\rm a.s.}} c$ for some $c \in \mathopen{}\mathclose\bgroup\originalleft( -\infty , K \aftergroup\egroup\originalright]$. Then $Y_{N} \xrightarrow{{\rm d}} Y$ if and only if \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_N + Z_N \aftergroup\egroup\originalright) \to {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y + c \aftergroup\egroup\originalright) \end{align*} for every $\theta \in \mathbb{R}$ as $N \to \infty$. \end{lemma} \begin{proof} Suppose that $Y_{N} \xrightarrow{{\rm d}} Y$ and fix $\theta \in {\mathbb R}$. Since $Z_N \xrightarrow{{\rm a.s.}} c$ by assumption, we have $\mathopen{}\mathclose\bgroup\originalleft( Y_N , Z_N \aftergroup\egroup\originalright) \xrightarrow{{\rm d}} \mathopen{}\mathclose\bgroup\originalleft( Y , c \aftergroup\egroup\originalright)$. But then ${\mathbb E} f \mathopen{}\mathclose\bgroup\originalleft( Y_N , Z_N \aftergroup\egroup\originalright) \to {\mathbb E} f \mathopen{}\mathclose\bgroup\originalleft( Y , c \aftergroup\egroup\originalright)$ for every bounded, continuous function $f$. In particular, this holds for the bounded, continuous function $f (y,z) = \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta y + z \aftergroup\egroup\originalright)$ defined on the domain ${\mathbb R} \times \mathopen{}\mathclose\bgroup\originalleft( -\infty , K \aftergroup\egroup\originalright]$.
Conversely, suppose that ${\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_N + Z_N \aftergroup\egroup\originalright) \to {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y + c \aftergroup\egroup\originalright)$ for every $\theta \in \mathbb{R}$ as $N \to \infty$. Fix $\theta \in {\mathbb R}$ and write \begin{align*} \begin{split} {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_{N} \aftergroup\egroup\originalright) - \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y \aftergroup\egroup\originalright) \aftergroup\egroup\originalright] &= {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( c - Z_{N} \aftergroup\egroup\originalright) \exp \mathopen{}\mathclose\bgroup\originalleft( -c \aftergroup\egroup\originalright) \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_{N} + Z_{N} \aftergroup\egroup\originalright) - \exp \mathopen{}\mathclose\bgroup\originalleft( -c \aftergroup\egroup\originalright) \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_{N} + Z_{N} \aftergroup\egroup\originalright) \aftergroup\egroup\originalright]\\ &\qquad + {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( -c \aftergroup\egroup\originalright) \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_{N} + Z_{N} \aftergroup\egroup\originalright) - \exp \mathopen{}\mathclose\bgroup\originalleft( -c \aftergroup\egroup\originalright) \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y + c \aftergroup\egroup\originalright) \aftergroup\egroup\originalright]. \end{split} \end{align*} The first expectation goes to zero by the Dominated Convergence Theorem and the second goes to zero by assumption. Then ${\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y_N \aftergroup\egroup\originalright) \to {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta Y \aftergroup\egroup\originalright)$ for every $\theta \in {\mathbb R}$, so $Y_{N} \xrightarrow{{\rm d}} Y$. \end{proof} In general, the conclusion of Lemma~\ref{lem:cfconv} does not hold if we drop the assumption that $Z_N \leq K$ a.s. Consider the probability space $\mathopen{}\mathclose\bgroup\originalleft( [0,1] , \mathcal{B}[0,1] , \lambda \aftergroup\egroup\originalright)$, where $\lambda$ denotes Lebesgue measure. Take $0 = Y = Y_1 = Y_2 = \ldots$ and $Z_N = N 1_{[0,1/N]}$. Then $Z_N \xrightarrow{{\rm a.s.}} 0$, but $\int_{[0,1]} \exp(Z_N) \, {\rm d} \lambda = \exp(N) / N \to \infty$.
\begin{lemma} \label{lem:mcclt} Let $f > 0$ and $t \geq 0$. For $N \to \infty$, the random variable \begin{align*} N^{f/2} \int_{0}^{t} \mathopen{}\mathclose\bgroup\originalleft( \exp \mathopen{}\mathclose\bgroup\originalleft( - \int_{s}^{t} \gamma_{X (N^{f} r)} \, {\rm d} r \aftergroup\egroup\originalright) \alpha_{X(N^{f} s)} - \exp \mathopen{}\mathclose\bgroup\originalleft( - \gamma_\infty (t-s) \aftergroup\egroup\originalright) \alpha_\infty \aftergroup\egroup\originalright) \, {\rm d} s \end{align*} converges in distribution to a Normal distribution with mean $0$ and variance \begin{align*} \Psi_{D} := 2 \int_0^t e^{-2\gamma_{\infty} (t-s) } \sum_{i=1}^d\sum_{j=1}^d \pi_i (\alpha_i-\varrho(s)\gamma_i)D_{ij} (\alpha_j-\varrho(s)\gamma_j) \, {\rm d}s, \end{align*} where $\varrho(s) = \tfrac{\alpha_{\infty}}{\gamma_{\infty}} \mathopen{}\mathclose\bgroup\originalleft( 1 - e^{-\gamma_{\infty} s} \aftergroup\egroup\originalright)$. \end{lemma} \begin{proof} Clearly, it suffices to show the convergence for $f = 1/2$. We will prove this lemma using a central limit theorem for a Markov-modulated infinite-server queue. To be more precise, consider the setup of Model I in \cite{BMT} where the arrival rates are given by $\alpha_1 , \ldots , \alpha_d$ and the hazard rates by $\gamma_1 , \ldots , \gamma_d$. Now impose the scaling $\alpha_i \mapsto N \alpha_i$ and $q_{ij} \mapsto \sqrt{N} q_{ij}$. (Recall that scaling $q_{ij} \mapsto \sqrt{N} q_{ij}$ is equivalent to replacing $X(s)$ by $X (\sqrt{N}s)$.)
Given $N$, denote the number of jobs in the system at time $t$ by $U ^{[N]} (t)$. According to \cite{BMT}, the random variable $U ^{[N]} (t)$ has a Poisson distribution with random parameter \begin{align*} \psi_{X} (t ; N) = N \int_{0}^{t} \alpha_{X (\sqrt{N} s)} e^{-\int_{s}^{t} \gamma_{X (\sqrt{N} s)} \, {\rm d} r} \, {\rm d} s. \end{align*} To prove the lemma, we have to show that $N^{1/4} \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{N} \psi_{X} (t ; N) - \varrho (t) \aftergroup\egroup\originalright)$ converges to a Normal distribution with mean $0$ and variance $\Psi_{D}$.
In \cite{BMT} it is shown that $N^{-3/4} \mathopen{}\mathclose\bgroup\originalleft( U ^{[N]} (t) - N \rho (t) \aftergroup\egroup\originalright)$ converges in distribution to a Normal distribution with mean $0$ and variance $\Psi_{D}$. Hence, it holds that \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{-3/4} \mathopen{}\mathclose\bgroup\originalleft( U ^{[N]} (t) - N \rho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \to \exp \mathopen{}\mathclose\bgroup\originalleft( - \tfrac{1}{2} \theta^2 \Psi_{D} \aftergroup\egroup\originalright) \end{align*} for all $\theta \in {\mathbb R}$. Since $U ^{[N]} (t)$ has a Poisson distribution with random parameter $\psi_{X} (t ; N)$, we obtain \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{-3/4} \mathopen{}\mathclose\bgroup\originalleft( U ^{[N]} (t) - N \rho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) &= \\ \exp \mathopen{}\mathclose\bgroup\originalleft( - {\rm i} \theta N^{1/4} \varrho (t) \aftergroup\egroup\originalright) {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( \psi_{X} (t ; N) \mathopen{}\mathclose\bgroup\originalleft[ \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{-3/4} \aftergroup\egroup\originalright) - 1 \aftergroup\egroup\originalright] \aftergroup\egroup\originalright) &=\\ \exp \mathopen{}\mathclose\bgroup\originalleft( - {\rm i} \theta N^{1/4} \varrho (t) \aftergroup\egroup\originalright) {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( \psi_{X} (t ; N) \mathopen{}\mathclose\bgroup\originalleft[ \frac{{\rm i} \theta}{N^{3/4}} + O \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{N \sqrt{N}} \aftergroup\egroup\originalright) \aftergroup\egroup\originalright] \aftergroup\egroup\originalright) &=\\ {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{1/4} \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{N} \psi_{X} (t ; N) - \varrho (t) \aftergroup\egroup\originalright) + \psi_{X} (t ; N) \cdot O \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{\sqrt{N}} \aftergroup\egroup\originalright) \aftergroup\egroup\originalright). \end{align*} Observe that $\psi_{X} (t ; N)$ is a.s.\ bounded by a constant for all $N \in \mathbb{N}$, so Lemma~\ref{lem:cfconv} implies that \begin{align*} {\mathbb E} \exp \mathopen{}\mathclose\bgroup\originalleft( {\rm i} \theta N^{1/4} \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{N} \psi_{X} (t ; N) - \varrho (t) \aftergroup\egroup\originalright) \aftergroup\egroup\originalright) \to \exp \mathopen{}\mathclose\bgroup\originalleft( - \tfrac{1}{2} \theta^2 \Psi_{D} \aftergroup\egroup\originalright) \end{align*} for all $\theta \in {\mathbb R}$. L\'evy's continuity theorem (see \cite[Section 18.1]{WILL}) now implies that the random variable $N^{1/4} \mathopen{}\mathclose\bgroup\originalleft( \tfrac{1}{N} \psi_{X} (t ; N) - \varrho (t) \aftergroup\egroup\originalright)$ converges to a Normal distribution with mean $0$ and variance $\Psi_{D}$, as required. \end{proof} \fi
{\small
}
\end{document}
\section{Removed original parts}
\subsection{Recursive schemes for determining moments}
The objective of this section is to set up a recursive scheme to generate all transient moments, that is, the expected value of $M(t)^k$, for any $k\in\{1,2,\ldots\}$, jointly with the indicator function $1\{X(t)=i\}$.
The central notion in this section is \[h_{i,k}(t):=\lim_{\vartheta\downarrow 0}\frac{\partial^{k}}{\partial\vartheta^k}\,g_i(\vartheta,t)= {\mathbb E} \mathopen{}\mathclose\bgroup\originalleft((-1)^k\,M(t)^k\, 1\{X(t)=i\}\aftergroup\egroup\originalright);\] we write $\vec{h}_k(t)= (h_{1,k}(t),\ldots,h_{d,k}(t))^{\rm T}.$ Observe that $\vec{h}_{k}(0) = (-1)^k\,m_0^k\,\vec{p}_0.$
It requires an elementary verification to check that, for given scalars $A,B$ and a given function $F(\cdot)$, for any $k\in\{2,3,\ldots\}$, \begin{eqnarray*}\frac{\partial^{k}}{\partial\vartheta^k}\mathopen{}\mathclose\bgroup\originalleft(\mathopen{}\mathclose\bgroup\originalleft(A\vartheta+ B\vartheta^2\aftergroup\egroup\originalright)F(\vartheta)\aftergroup\egroup\originalright)&=& \mathopen{}\mathclose\bgroup\originalleft(A\vartheta +B\vartheta^2\aftergroup\egroup\originalright)\frac{\partial^{k}}{\partial\vartheta^k}\,F(\vartheta)\\&& +\,k\mathopen{}\mathclose\bgroup\originalleft(A+2B\vartheta\aftergroup\egroup\originalright)\frac{\partial^{k-1}}{\partial\vartheta^{k-1}}\,F(\vartheta)+ B\,k(k-1)\frac{\partial^{k-2}}{\partial\vartheta^{k-2}}\,F(\vartheta), \end{eqnarray*} given the derivatives under consideration are well defined. By a direct application of Thm.\ \ref{PDEth} we thus obtain, for any $k\in\{1,2,\ldots\}$, \[h'_{i,k}(t) = \sum_{j=1}^d q_{ji} h_{j,k}(t) - k\alpha_i h_{i,k-1}(t)+\frac{\sigma_i^2}{2}k(k-1)h_{i,k-2}(t)-k\gamma_i h_{i,k}(t),\] where $h_{i,0}(t) = {\mathbb P}(X(t)=i).$
From the above we can now set up a recursive scheme to compute all transient moments $h_{i,k}(t)$, for $i\in\{1,\ldots,d\}$, $k\in\{0,1\ldots\}$, and $t\geqslant 0$; this procedure resembles the one for the Markov-modulated infinite-server queue, as presented in \cite{OCP}. At any step of the recursion an inhomogeneous system of linear differential equations needs to be solved, as follows. Define, for $k\in\{1,2,\ldots\}$, \[\bar h_{i,k}(t):= - k\alpha_i h_{i,k-1}(t)+\frac{\sigma_i^2}{2}k(k-1)h_{i,k-2}(t)\] (where the last term in the right-hand side obviously vanishes if $k=1$); $\vec{\bar{h}}_{k}(\cdot)$ is defined analogously to $\vec{{h}}_{k}(\cdot)$. Then, recalling $\bar Q_{k\vec{\gamma}}:= {Q}^{\rm T}- k\,{\rm diag}\{\vec{\gamma}\}$, we find (in vector notation) \[\vec{h}_k(t) = e^{\bar Q_{k\vec{\gamma}}t} \vec{h}_k(0) + \int_0^t e^{\bar Q_{k\vec{\gamma}}(t-s)} \vec{\bar{h}}_{k}(s)\, {\rm d}s.\] Observe that in step $k$ of this recursion, the function ${\bar{\vec{h}}}_{k}(s)$ is known.
Considering the {\it stationary} moments $\vec{h}_k:=\vec{h}_k(\infty)$, we obtain an ordinary recursion, in line with the one derived by Xing {\it et al.} \cite{XING}. For any $k\in\{2,3,\ldots\}$ the system of linear equations \[ \bar Q_{k\vec{\gamma}} \vec{h}_k = k\,{\rm diag}\{\vec{\alpha}\} \vec{h}_{k-1}- \frac{1}{2}k(k-1) \,{\rm diag}\{\vec{\sigma}^2\}\vec{h}_{k-2}.\] needs to be solved; for $k=1$ we have the linear system $\bar Q_{\vec{\gamma}} \vec{h}_1 = k\,{\rm diag}\{\vec{\alpha}\} \vec{h}_{0},$ where $\vec{h}_{0} = \vec{\pi}.$
We now point out how to compute the covariance \[c(t,u) :={\mathbb C}{\rm ov}\,(M(t), M(t+u)),\] for $t,u\geqslant 0.$ To this end, we first observe that \[c(t,u) =\frac{1}{2}\mathopen{}\mathclose\bgroup\originalleft({\mathbb V}{\rm ar}\,(M(t)+M(t+u))-v_t-v_{t+u}\aftergroup\egroup\originalright).\] Also, \[{\mathbb V}{\rm ar}\,(M(t)+M(t+u)) ={\mathbb E}\mathopen{}\mathclose\bgroup\originalleft((M(t)+M(t+u))^2\aftergroup\egroup\originalright)-(\mu_t+\mu_{t+u})^2.\] As we already developed schemes to compute $\mu_t$ and $v_t$, for $t\geqslant 0$ in Section \ref{TB}, we are left with determining the second moment of $M(t)+M(t+u)$. To this end, we set up a system of {\sc pde}\,s for \[f_{i,k}({\vartheta},{t}) := {\mathbb E} e^{-\vartheta(M(t)+M(t+u))} 1\{X(t)=i,X(t+u)=k\},\] for $u\geqslant 0$ fixed, and $i,k\in\{1,\ldots,d\}.$ Define $F(\vartheta,t)$ as the $d\times d$ matrix $(f_{i,k}({\vartheta},{t}))_{i,k=1}^d$, and $\check{\vec{f}}(\vartheta,t):={\rm vec}(F(\vartheta,t)).$ It follows from an argumentation similar to the one in Section \ref{TBPDE}, that \begin{eqnarray*}\frac{\partial \check {\vec{f}}}{\partial t}&=& (Q^{\rm T}\oplus Q^{\rm T})\check{\vec{f}} -\vartheta ({\rm diag}\{\vec{\alpha}\}\oplus {\rm diag}\{\vec{\alpha}\})\check{\vec{f}} \\ &&+\,\frac{\vartheta^2}{2} ({\rm diag}\{\vec{\sigma}^2\}\oplus {\rm diag}\{\vec{\sigma}^2\})\check{\vec{f}} -\vartheta ({\rm diag}\{\vec{\gamma}\}\oplus {\rm diag}\{\vec{\gamma}\})\frac{\partial \check {\vec{f}}}{\partial \vartheta}, \end{eqnarray*} suppressing the arguments ${\vartheta}$ and $t$. Realize that \[{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft((M(t)+M(t+u))\,1\{X(t)=i,X(t+u)=j\aftergroup\egroup\originalright) =-\lim_{\vartheta\downarrow 0} \frac{\partial}{\partial \vartheta} f_{i,k}(\vartheta,t),\] and \[{\mathbb E}\mathopen{}\mathclose\bgroup\originalleft((M(t)+M(t+u))^2\,1\{X(t)=i,X(t+u)=j\aftergroup\egroup\originalright) =\lim_{\vartheta\downarrow 0} \frac{\partial^2}{\partial \vartheta^2} f_{i,k}(\vartheta,t),\] which can be found by differentiating the above {\sc pde} once and twice, respectively and take the limit $\vartheta\downarrow 0$; both result in an elementary inhomogeneous system of linear differential equations. These can be solved by imposing the appropriate initial conditions.
\subsection{PDE stuff}
For $K=1$, the object of interest is \[g_i(\vartheta,t) := {\mathbb E} e^{-\vartheta M(t)} 1\{X(t)=i\},\] for $i=1,\ldots,d$; realize that, without loss of generality, we have taken $t_1=0.$ We set up a system of partial differential equations applying the usual `$\Delta t$-argument', as follows. Let $U_i(\cdot)$ denote an {\sc ou} process with positive parameters $\alpha_i,\gamma_i$, and $\sigma_i^2$. By conditioning on the state of the system $\Delta t$ time units earlier, we readily obtain, up to an error of $o(\Delta t)$, \begin{eqnarray}\nonumber g_i(\vartheta,t)&=&\sum_{j\not=i} q_{ji}\Delta t\cdot g_j(\vartheta,t)+ \mathopen{}\mathclose\bgroup\originalleft(1-q_{i}\Delta t\aftergroup\egroup\originalright)\cdot\\
&&\label{di}\hspace{-21mm}\int_{-\infty}^\infty\int_{-\infty}^\infty e^{-\vartheta (x+y)} {\mathbb P}(M(t-\Delta t)\in {\rm d} x, X(t-\Delta t)=i){\mathbb P}(U_i(\Delta t) -U_i(0) \in {\rm d} y\,|\,U_i(0)=x). \end{eqnarray} Conditioning on $\{U_i(0)=x\}$, applying known results for the transient distribution of the {\sc ou} process, $U_i( t) -U_i(0)$ obeys a Normal distribution with mean $m_i$ and variance $s_i^2,$ where \[(m_i,s_i^2):=\mathopen{}\mathclose\bgroup\originalleft(\mathopen{}\mathclose\bgroup\originalleft(\frac{\alpha_i}{\gamma_i}-x\aftergroup\egroup\originalright)(1-e^{-\gamma_i t}),\frac{\sigma_i^2}{2\gamma_i}(1-e^{-2\gamma_i t})\aftergroup\egroup\originalright).\] Recall that a Normally distributed random variable with mean $\mu$ and variance $\sigma^2$ has Laplace transform $e^{-\vartheta\mu+\frac{1}{2}\vartheta^2\sigma^2}.$ Using this relation, we first evaluate the integral over $y$: \begin{eqnarray*}
\lefteqn{\hspace{-1cm}\int_{-\infty}^\infty e^{-\vartheta y}{\mathbb P}(U_i(\Delta t) -U_i(0) \in {\rm d} y\,|\,U_i(0)=x) }\\&=&\exp\mathopen{}\mathclose\bgroup\originalleft(-\vartheta\mathopen{}\mathclose\bgroup\originalleft(\frac{\alpha_i}{\gamma_i}-x\aftergroup\egroup\originalright)(1-e^{-\gamma_i \Delta t})+\frac{1}{2}\vartheta^2\frac{\sigma_i^2}{2\gamma_i}(1-e^{-2\gamma_i \Delta t})\aftergroup\egroup\originalright). \end{eqnarray*} This expression can be rewritten, for $\Delta t\downarrow 0$, as \[\exp\mathopen{}\mathclose\bgroup\originalleft(-\vartheta(\alpha_i - x\gamma_i)\Delta t +\frac{1}{2}\vartheta^2 \sigma_i^2 \Delta t+o(\Delta t)\aftergroup\egroup\originalright)=1-\vartheta(\alpha_i - x\gamma_i)\Delta t +\frac{1}{2}\vartheta^2 \sigma_i^2 \Delta t+o(\Delta t).\] As an immediate consequence, the double integral in (\ref{di}) equals, up to terms of $o(\Delta t)$, \begin{eqnarray*}\lefteqn{\hspace{-1cm}\int_{-\infty}^\infty e^{-\vartheta x}\mathopen{}\mathclose\bgroup\originalleft(1-\vartheta(\alpha_i - x\gamma_i)\Delta t +\frac{1}{2}\vartheta^2 \sigma_i^2 \Delta t\aftergroup\egroup\originalright){\mathbb P}(M(t-\Delta t)\in {\rm d} x, X(t-\Delta t)=i)}\\ &=&g_i(\vartheta,t-\Delta t)\mathopen{}\mathclose\bgroup\originalleft(1-\mathopen{}\mathclose\bgroup\originalleft(\vartheta\alpha_i-\frac{1}{2}\vartheta^2\sigma_i^2\aftergroup\egroup\originalright)\Delta t\aftergroup\egroup\originalright) -\vartheta\gamma_i\Delta t\frac{\partial}{\partial \vartheta}g_i(\vartheta,t).\end{eqnarray*} Rearranging, it is found that, up to an $o(1)$ error, \[\frac{g_i(\vartheta,t)-g_i(\vartheta,t-\Delta t)}{\Delta t}=\sum_{j=1}^d q_{ji}\cdot g_j(\vartheta,t)-\mathopen{}\mathclose\bgroup\originalleft(\vartheta\alpha_i-\frac{1}{2}\vartheta^2\sigma_i^2\aftergroup\egroup\originalright)g_i(\vartheta,t-\Delta t) -\vartheta\gamma_i\,\frac{\partial}{\partial \vartheta}g_i(\vartheta,t).\] By letting $\Delta t\downarrow 0$, we obtain the system of {\sc pde}\,s: \[\frac{\partial}{\partial t}g_i(\vartheta,t)=\sum_{j=1}^d q_{ji}\, g_j(\vartheta,t)-\mathopen{}\mathclose\bgroup\originalleft(\vartheta\alpha_i-\frac{1}{2}\vartheta^2\sigma_i^2\aftergroup\egroup\originalright)g_i(\vartheta,t) -\vartheta\gamma_i\,\frac{\partial}{\partial \vartheta}g_i(\vartheta,t).\] In self-evident matrix notation, we have obtained the following result.
\end{document} | arXiv |
\begin{document}
\title{Arithmetic actions on cyclotomic function fields} \begin{abstract} We derive the group structure for cyclotomic function fields obtained by applying the Carlitz action for extensions of an initial constant field. The tame and wild structures are isolated to describe the Galois action on differentials. We show that the associated invariant rings are not polynomial. \end{abstract}
\section{Introduction}
Let $\mathbb{F}_q$ denote the finite field of $q$ elements, where $q = p^r$ is a power of the prime integer $p$. Let $d$ be a nonnegative integer. Consider the rational function field $\mathbb{F}_{q^d}(T)$. The Carlitz action for $\mathbb{F}_{q^d}$ is defined as $$ C_{q^d}(T)(u) = Tu + u^{q^d}, \quad u\in \overline{\mathbb{F}_q(T)}. $$ This defines an action by $T$, which may be extended $\mathbb{F}_{q^d}$-linearly to an action by elements of $\mathbb{F}_{q^d}[T]$, according to \begin{equation}\label{Carlitzaction} M = \sum a_i T^i\in \mathbb{F}_{q^d}[T], \qquad C_{q^d}(M)(u) = M {*}_du=\sum a_i C_{q^d}^i(T)(u). \end{equation} The Carlitz $M$-torsion points $C_{q^d}[M]$ are then the torsion $\mathbb{F}_{q^d}$-modules within the algebraic closure $\overline{\mathbb{F}_{q^d}(T)}$ via this action. We note that this does depend upon the choice of $d$. Henceforth, for a polynomial $M \in \mathbb{F}_{q^d}[T]$, we let $K_{q^d,M}$ denote the \emph{cyclotomic function field} for $\mathbb{F}_{q^d}$ and $M$, which is obtained by adjoining to $\mathbb{F}_{q^d}(T)$ the Carlitz $M$-torsion points $C_{q^d}[M]$. These function fields are called \emph{cyclotomic} as they are derived from an exponential function in positive characteristic and enjoy many of the same properties of the classical cyclotomic extensions of $\mathbb{Q}$ \cite[Chapter 12]{salvador2007topics}.
We suppose henceforth that $M \in \mathbb{F}_q[T]$ and that $M$ splits over $\mathbb{F}_{q^d}[T]$. As in \cite{Ward}, one may determine explicitly the holomorphic differentials for $K_{q^d,M}$. Here, we relate this situation to the original cyclotomic function field $K_{q,M}$. We first prove the essential result:
\begin{theorem} \label{inclusion} $K_{q,M} \subset K_{q^d,M}$. \end{theorem}
This allows us to understand the differentials of $K_{q,M}$ in terms of those of $K_{q^d,M}$ by examining Galois covers. Henceforth, we denote $$H_{q^d,M}:=\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d} K_{q,M}).$$ One then obtains naturally the following tower of fields: \begin{equation} \label{fig:tower} \xymatrix{
& K_{q^d,M} \ar@{-}[dd] \ar@{-}[dl]_{H_{q^d,M}} \\
\mathbb{F}_{q^d}K_{q,M} \ar@{-}[d] \ar@{-}[dr] & \\
K_{q,M} \ar@{-}[dr] & \mathbb{F}_{q^d}(T) \ar@{-}[d] \\
& \mathbb{F}_q(T) } \end{equation} The group $H_{q^d,M}$ was studied by Chapman \cite{Chapman} when $M \in \mathbb{F}_q[T]$ is square-free, in order to give a normal integral basis of the ring of integers of $K_{q,M}$ over $\mathbb{F}_q[T]$. This cannot be done in the same fashion if $M$ contains a square $P^2$ of an irreducible polynomial $P \in \mathbb{F}_q[T]$, as under the wild ramification at $P$ in $K_{q,M}$ the integer ring is no longer a free $\mathbb{F}_q[T]$ module. Here, we study $H_{q^d,M}$ more generally, as the genus is invariant under constant extensions, so that identification of the space of differentials of $K_{q,M}$ reduces to identifying those differentials of $K_{q^d,M}$ which are fixed by the action of $H_{q^d,M}$.
The Frobenius map on $\mathbb{F}_{q^d}/\mathbb{F}_q$ permutes the roots of $M$, and the group $H_{q^d,M}$ is nontrivial: Even in the case where $M = P$ is irreducible over $\mathbb{F}_q[T]$ and $\deg(M) = d$, $|H_{q^d,M}|=(q^d-1)^{d-1}$. The group $H_{q^d,M}$ may be described in a simple, explicit way in terms of the Carlitz action. The abelian Galois group $\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d}(T))$ is naturally a $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_{q})$-module, and denoting $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_{q})=\langle \sigma\rangle$, the group $H_{q^d,M}$ may be described as \[ H_{q^d,M}= (\sigma-1)\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d}(T)). \] This is proven in Lemma \ref{Kummerfun}. In general, the absolute Galois group $\hat{\mathbb{Z}}=\mathrm{Gal}(\bar{\mathbb{F}}_q/\mathbb{F}_q)$ acts on the cyclotomic function fields, and this action may be precisely described using the group structure of $H_{q^d,M}$. This point of view, where the {\em arithmetic} part of a Galois group is acting on the {\em geometric} part, is a unifying notion. One may see, for example, the seminal article of Y. Ihara \cite{IharaProfinite}.
We devote Section 2 to the description of $H_{q^d,M}$. In Section 3, we examine the tame structures arising within this group and give an explicit Kummer generator of the tame part of $H_{q^d,M}$. Section 4 describes the wild component of $H_{q^d,M}$, including the higher ramification groups and different. Cyclotomic function fields may also be viewed as towers of Kummer and Artin-Schreier extensions, whose form we give in Section 5. Section 6 describes the Galois module structure of the differentials of $K_{q,M}$. We concern ourselves with the group $H_{q^d,M}$ as its invariants yield differentials on the constant extension $\mathbb{F}_{q^d} K_{q,M}$ of $K_{q,M}$, and constant extensions do not alter the genus, so that it suffices to give a description of the differentials of $\mathbb{F}_{q^d} K_{q,M}$ in order to understand the Galois module structures for $K_{q,M}$. The holomorphic differentials are comprised of products of generators of the Carlitz torsion modules. In order to compute the $H_{q^d,M}$-invariant differentials, we will employ modular invariant theory. For fixed $q^d$ and $M$, our constructions provide an algorithm for the computation of invariants and holomorphic differentials for the function field $K_{q,M}$. As we show in Section 6, the invariant ring for the algebra of Carlitz generators is not polynomial. This shows that a closed formula for a basis for holomorphic differentials will be quite complicated in general, despite that it can be done when $M$ splits over $\mathbb{F}_q$ \cite{Ward}.
\section{Preliminary results}
\subsection{Inclusions of cyclotomic function fields} We now give the proof of Theorem \ref{inclusion}.
\begin{proof}[Proof of Theorem \ref{inclusion}] For a global field $K$, let $S(L/K)$ denote the collection of places of $K$ which split completely in $L$. By Bauer's theorem \cite[Theorem 11.5.1]{salvador2007topics}, we have for a global function field $K$ and two Galois extensions $L_1$ and $L_2$ of $K$ that $$L_2 \subset L_1 \Leftrightarrow S(L_1/K) \subset S(L_2/K).$$ Thus, the extension $K_{q,M}$ is contained in $K_{q^d,M}$ if, and only if, the places of $\mathbb{F}_q(T)$ which split in $K_{q^d,M}$ also split in $K_{q,M}$. For a place $\mathfrak{p}$ of $\mathbb{F}_q(T)$, we let $\mathfrak{P}$ denote a place of $K_{q,M}$ above $\mathfrak{p}$, $\mathfrak{p}_{q^d}$ a place of $\mathbb{F}_{q^d}(T)$ above $\mathfrak{p}$, and $\mathfrak{P}_{q^d}$ a place of $K_{q^d,M}$ above $\mathfrak{p}$. If $\mathfrak{p}$ denotes a place of $K = \mathbb{F}_q(T)$ which splits completely in $K_{q^d,M}$, then we have $$[\mathfrak{O}_{\mathfrak{P}_{q^d}}/\mathfrak{P}_{q^d}:\mathfrak{o}_{\mathfrak{p}}/\mathfrak{p}] = 1,$$ where $\mathfrak{O}_{\mathfrak{P}_{q^d}}$ denotes the valuation ring for $\mathfrak{P}_{q^d}$ in $K_{q^d,M}$ and $\mathfrak{P}_{q^d}$ its maximal ideal, $\mathfrak{o}_{\mathfrak{p}}$ the valuation ring for $\mathfrak{p}$ in $K$ and $\mathfrak{p}$ its maximal ideal. In the analogous notation, we thus have $$[\mathfrak{O}_{\mathfrak{P}_{q^d}}/\mathfrak{P}_{q^d}:\mathfrak{o}_{\mathfrak{p}_{q^d}}/\mathfrak{p}_{q^d}][\mathfrak{o}_{\mathfrak{p}_{q^d}}/\mathfrak{p}_{q^d}: \mathfrak{o}_{\mathfrak{p}}/\mathfrak{p}] = 1.$$ In particular, it follows that $$[\mathfrak{O}_{\mathfrak{P}_{q^d}}/\mathfrak{P}_{q^d}:\mathfrak{o}_{\mathfrak{p}_{q^d}}/\mathfrak{p}_{q^d}] = 1,$$ and that the place $\mathfrak{p}_{q^d}$ of $\mathbb{F}_{q^d}(T)$ is completely split in $K_{q^d,M}$. Notice that $\mathfrak{p}$ cannot be infinity, as infinity is not split in cyclotomic extensions (the ramification index is the size of the constant field minus one \cite[Theorem 12.4.6]{salvador2007topics}). It follows that the place $\mathfrak{p}_{q^d}$ is associated with an irreducible polynomial $P_{q^d} \in \mathbb{F}_{q^d}[T]$. By cyclotomic function field theory, for example, Proposition 12.5.2 of Villa-Salvador \cite{salvador2007topics}, the inertia degree of $\mathfrak{p}_{q^d}$ is equal to the order of $P_{q^d}$ modulo $M$. In fact, we may write $$P = \prod_{i=1}^k P_i$$ in $\mathbb{F}_{q^d}[T]$, where $P$ is associated with $\mathfrak{p}$ in $\mathbb{F}_q[T]$ and the polynomials $P_i$ are the (distinct) factors of $P$ in $\mathbb{F}_{q^d}(T)$. We also know that the finite places of $\mathbb{F}_{q^d}$ which divide $M$ ramify in $K_{q^d,M}$, and hence are not completely split. Also, we know that $P_{q^d} = P_i$ for some $i$, but also that $P_{q^d}$ was an arbitrary choice of place, which could be done as the extensions we consider are all Galois. Thus $(P_i,M)=1$ for all $i=1,\ldots,k$, from which it follows that $(P,M) = 1$. By cyclotomic function field theory, we also know that the order of $P$ modulo $M$ in $\mathbb{F}_q[T]$ is equal to the inertia degree of $\mathfrak{p}$ in $K_{q,M}$. For each $i = 1,\ldots,k$, let $o_{h,i}$ denote the order of $P_i$ modulo $M$ in $\mathbb{F}_{q^d}[T]$. Thus $$P_i^{o_{h,i}} \equiv 1 \mod M, \quad i=1,\ldots,k.$$ We may then write $P_i^{o_{h,i}} - 1 = FM$ for some $F \in \mathbb{F}_{q^d}[T]$. As the Galois action of $\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)$ is transitive, it follows that for any $j = 1,\ldots,k$, there exists $\sigma \in \text{Gal}(\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T))$ such that $\sigma(P_i) = P_j$. It follows that $$P_j^{o_{h,i}} - 1 =\sigma(P_i)^{o_{h,i}} - 1 = \sigma(P_i^{o_{h,i}}) - 1 = \sigma(P_i^{o_{h,i}} - 1) = \sigma(FM) = \sigma(F)M,$$ where $\sigma(F) \in \mathbb{F}_{q^d}[T]$ by definition of the Galois action of $\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)$. It follows by symmetry that the order of each $P_i$ modulo $M$ is the same. We therefore set $o_h := o_{h,i}$ for $i=1,\ldots,k$. It follows from this that $$P^{o_h} = \left(\prod_{i=1}^k P_i\right)^{o_h} =\prod_{i=1}^k P_i^{o_h} \equiv \prod_{i=1}^k 1 = 1 \mod M,$$ and hence the order $o_P$ of $P$ modulo $M$ is at most $o_h$. As the polynomials $P_i$, $i=1,\ldots,k$ are completely split in $K_{q^d,M}$, it follows from the cyclotomic theory that $o_h = 1$, and thus $o_P \leq o_h = 1$. Thus, the place $\mathfrak{p}$ associated with $P$ is completely split in $K_{q,M}$. We have thus shown that if a place $\mathfrak{p}$ of $K = \mathbb{F}_q(T)$ splits completely in $K_{q^d,M}$, then it must also split completely in $K_{q,M}$. Hence, by Bauer's theorem, it follows that $K_{q,M} \subset K_{q^d,M}$. \end{proof} Henceforth, as we frequently distinguish between $\mathbb{F}_q[T]$ and $\mathbb{F}_{q^d}[T]$, we denote $A_1 := \mathbb{F}_q[T]$ and $A_d:=\mathbb{F}_{q^d}[T]$. The following properties of Galois extensions may be easily deduced from the previous theorem (see also \cite[Chapter 12]{salvador2007topics}). \begin{itemize} \item $\mathrm{Gal}(\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)) \cong\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ \item $\mathrm{Gal}(K_{q,M}/\mathbb{F}_q(T))\cong (A_1/MA_1)^*$. \item $\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d}(T))\cong (A_d/MA_d)^*$. \item $\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_q(T)) \cong (A_d/MA_d)^*\times \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$. \end{itemize} We now fix a basis $1=v_1,\ldots,v_d$ of $\mathbb{F}_{q^d}$ as a vector space over $\mathbb{F}_q$, and we write \[ A_d\cong A_1 \oplus v_2A_1 \oplus \cdots \oplus v_dA_1. \] As $M\in A_1$ by definition, we then have \[ A_d/M A_d \cong A_1/MA_1 \oplus v_2A_1/MA_1 \oplus \cdots \oplus v_dA_1/MA_1. \] Also, the group $\mathrm{Gal}(K_{q^d,M}/K_{q,M})$ fits in the short exact sequence \[ 1 \rightarrow \mathrm{Gal}(K_{q^d,M}/K_{q,M}) \rightarrow (A_d/MA_d)^* \times \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q) \rightarrow (A_1/MA_1)^* \rightarrow 1. \] For ease of notation, we define $G_{q^d,M}:=\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d}(T))$. It is well-known that \begin{equation}\label{isomorphism}
G_{q^d,M} \cong
\left(A_d/M A_d\right)^*, \end{equation} where the Galois action is induced by the Carlitz action by elements of $(\mathbb{F}_{q^d}[T]/M)^*$. The Galois inclusion $\mathbb{F}_q(T) \subset \mathbb{F}_{q^d}(T) \subset K_{q^d,M}$ gives rise to another short exact sequence: \[ \xymatrix{
1
\rightarrow \mathrm{Gal}(K_{q^d,M}
/\mathbb{F}_{q^d}(T)) \ar@{=}[d] \ar[r] &
\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q}(T)) \ar[r]^-\pi&
\mathrm{Gal}(\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)) \ar@{=}[d] \rightarrow 1
\\
G_{q^d,M} & & \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q) } \] By standard arguments of group theory, the Galois group $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ acts by conjugation on $G_{q^d,M}$ in terms of an inverse section of the map $\pi$. We note that as the group $G_{q^d,M}$ is abelian, this action is well defined, i.e., independent of the choice of the section of $\pi$.
\subsection{The group $G_{q^d,P}$ as a $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$-module} \label{frobAC} We identify each divisor $D\in (A_d/MA_d)^*$ with the element $\rho_D \in G_{q^d,M}$ under the isomorphism \eqref{isomorphism}. The natural action of
$\sigma \in \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ on $\rho_D$ is given by conjugation.
As such, we have
\[
\sigma \rho_D \sigma^{-1}=\rho_{\sigma (D)},
\]
where $\sigma(D)$ simply denotes the image of $D\in A_d$ under the natural action of $\sigma$ in $\mathbb{F}_{q^d}$. We have $$ \rho_D (u):=D *_d u=u^{q^s} + b_{s-1}u^{q^{s-1}}+ \cdots + Du,$$ so that $$\sigma \rho_D \sigma^{-1}(u) =u^{q^s} + \sigma(b_{s-1})u^{q^{s-1}}+ \cdots + \sigma(D)u,
$$ where $*_d$ denotes the Carlitz action over $\mathbb{F}_{q^d}(T)$. In what follows, we emphasise that $G_{q,M}=\mathrm{Gal}(K_{q,M}/\mathbb{F}_{q}(T))$ is isomorphic to $\mathrm{Gal}(\mathbb{F}_{q^d}K_{q,M}/\mathbb{F}_{q^d}(T))$, as one may deduce from the tower of fields given in \eqref{fig:tower}.
\begin{lemma} \label{Kummerfun} The group $H_{q^d,M}=\mathrm{Gal}(K_{q^{d},M}/\mathbb{F}_{q^d}K_{q,M})$ in the short exact sequence \begin{equation} \label{sesH} 1 \rightarrow H_{q^d,M} \rightarrow {G}_{q^d,M} \rightarrow G_{q,M} \rightarrow 1 \end{equation} satisfies for $\sigma\in \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ \begin{enumerate}
\item $\sigma(H_{q^d,M})=H_{q^d,M}$
\item $H_{q^d,M}=(\sigma-1)G_{q^d,M}$. \end{enumerate} \end{lemma} \begin{proof} \begin{enumerate}
\item The natural action on subgroups of a Galois groups is the conjugation action. The field $$\mathbb{F}_{q^d}K_{q,M} =K_{q^d,M}^{H_{q^d,M}}$$ is a subfield of $K_{q^d,M}$ which is invariant, albeit not pointwise, under the action of $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$. Let $\sigma$ be a generator of the cyclic group $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$. As both
$$\sigma(\mathbb{F}_{q^d} K_{q,M})=K_{q^d,M}^{\sigma H_{q^d,M}\sigma^{-1}}\text{ and }\sigma(\mathbb{F}_{q^d} K_{q,M})=\mathbb{F}_{q^d} K_{q,M},$$ we have that $\sigma H_{q^d,M} \sigma^{-1}=H_{q^d,M}$.
\item
We will prove first that $(\sigma-1)D \in H_{q^d,M}$ for each element $D \in G_{q^d,M}$. The group $G_{q^d,M}$ consists of classes of invertible elements $D\in \mathbb{F}_{q^d}[T] $ modulo $M$. Let $\sigma\in \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ be a generator of the cyclic Galois group. As $G_{q,M}$ is the Galois group of a geometric extension, it follows that the group $G_{q,M}=G_{q^d,M}/H_{q^d,M}$ is pointwise $\sigma$-invariant. Thus $\sigma(D)/D \in H_{q^d,M}$.
Since the group $G_{q^d,M}$ is abelian, the map \[ \xymatrix@R-2pc{
G_{q^d,M} \ar[r]^\Phi & G_{q^d,M} \\
\alpha \ar@{|->}[r] & \sigma(\alpha)\alpha^{-1} } \] is a group homomorphism. The kernel of $\Phi$ consists of elements $D\in G_{q^d,M}\cong \left(\mathbb{F}_{q^d}[T]/M \right)^*$ which are left invariant under the action of $\sigma$, hence it is isomorphic to $G_{q,M}$. On the other hand, we have proven that $\mathrm{Im}(\Phi) \subset H_{q^d,M}$.
Thus $|\mathrm{Im}(\Phi)|=|G_{q^d,M}|/|G_{q,M}|$. Since by definition $|G_{q,M}|=|G_{q^d,M}|/|H_{q^d,M}|$, we obtain $|\mathrm{Im}(\Phi)|=|H_{q^d,M}|$, and we arrive at \[ H_{q^d,M}= (\sigma-1) G_{q^d,M}, \] concluding the proof. \end{enumerate} \end{proof} \begin{remark} The group $G_{q^d,M}$ is naturally a $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$-module. The group $G_{q,M}$ is the space of coinvariants \[ G_{q,M}=(G_{q^d,M})_{\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)}= \frac{G_{q^d,M}}{(\sigma-1)G_{q^d,M} }. \] \end{remark}
\subsection{Reduction to irreducible factors of $M$} We now reduce the computation of the structure of the group $H_{q^d,M}$ to the study of the corresponding groups for the irreducible components of $M$. Let $M\in \mathbb{F}_q[T]$ be of degree $k$, with factorization in $\mathbb{F}_q[T]$ \[ M=\prod_{j=1}^r M_j^{\alpha_j}, \]
where the polynomials $M_j$ are irreducible, monic and of degree $s_j|d$. In the finite field $\mathbb{F}_{q^d}$, the polynomials $M_j \in \mathbb{F}_q[T]$ factor into linear factors in $\mathbb{F}_{q^d}[T]$. We write \[ M=\prod_{j=1}^r \prod_{i=1}^{s_j} (T-\rho_{i,j})^{\alpha_j}, \qquad \qquad \rho_{i,j} \in \mathbb{F}_{q^d}. \] The field $K_{q,M}$ is the compositum of the fields $K_{q,M_j^{\alpha_j}}$, each of which is, in turn, a subfield of $K_{q^d,M_j^{\alpha_j}}$. This yields the following diagram: \[ \xymatrix@C=.5pc{
& & K_{q^d,M} \ar@{-}[dd] \ar@{-}[dll] \ar@{-}[dl] \ar@{-}[dr] \ar@{-}[drr]
& & \\ K_{q^d,M_1^{\alpha_1}} \ar@{-}[dd]_{H_{q^d,M_1^{\alpha_1}}} & K_{q^d,M_2^{\alpha_2}} \ar@{-}[dd]_{H_{q^d,M_2^{\alpha_2}}}&
& K_{q^d,M_{r-1}^{\alpha_{r-1}}} \ar@{-}[dd]^{H_{q^d,M_{r-1}^{\alpha_{r-1}}}}
& K_{q^d,M_{r}^{\alpha_r}}
\ar@{-}[dd]^{H_{q^d,M_r^{\alpha_r}}}
\\
& & { \mathbb{F}_{q^d} K_{q,M}\ar@{-}[rd] \ar@{-}[rrd] \ar@{-}[ld] \ar@{-}[lld]} & &
\\ \mathbb{F}_{q^d}K_{q,M_1^{\alpha_1}} & \mathbb{F}_{q^d}K_{q,M_2^{\alpha_2}} & \cdots & \mathbb{F}_{q^d}K_{q,M_{r-1}^{\alpha_{r-1}}} & \mathbb{F}_{q^d}K_{q,M_r^{\alpha_r}} \\
& & { \mathbb{F}_{q^d}(T)} \ar@{-}[ull] \ar@{-}[ul] \ar@{-}[ur] \ar@{-}[urr]
& & } \] We have \[
\mathrm{Gal}(K_{q^d,M}/\mathbb{F}_{q^d}(T))\cong
{\bigtimes}_{j=1}^r \mathrm{Gal}(K_{q^d,M_j^{a_j}}/\mathbb{F}_{q^d}(T)) \] and \[
H_{q^d,M}= {\bigtimes}_{j=1}^r H_{q^d,M_j^{a_j}}. \]
The problem of determining the structure of the group $H_{q^d,M}$ may therefore be reduced to determination of each of the groups $H_{q^d,M_i^{\alpha_i}}$. This means that we may assume $M$ to be a power $P^\alpha$ of an irreducible polynomial $P \in \mathbb{F}_q[T]$. Thus, as a consequence of Lemma \ref{Kummerfun}, we now study the group $G_{q^d,P}$, where $P$ is an irreducible polynomial in $\mathbb{F}_q[T]$ of degree $s | d$. The splitting field of $P$ is equal to $\mathbb{F}_{q^s}$. By definition, we have the following short exact sequence: \begin{equation} \label{ses-Galois} 1 \rightarrow P_{q^d,P^\alpha} \rightarrow G_{q^d,P^\alpha} \rightarrow G_{q^d,P} \rightarrow 1, \end{equation} where \[
P_{q^d,P^\alpha}=\{D \in \mathbb{F}_{q^d}[T] \mod P^\alpha, D\equiv 1 \mod P\}. \] The field $K_{q^d,P^\alpha}$ is the compositum of a generalised Artin-Schreier extension with the Kummer extension $K_{q^d,P}/\mathbb{F}_{q^d}(T)$. The subfield $\mathbb{F}_{q^d} K_{q,P^\alpha}$ has a similar decomposition, into a generalised Artin-Schreier extension with Galois group $\mathbb{Z}/q^{\alpha-1}\mathbb{Z}$ with the Kummer extension $\mathbb{F}_{q^d}K_{q,P}/\mathbb{F}_{q^d}(T)$. We have the following tower of fields: \[ \xymatrix{
& K_{q^d,P^\alpha} \ar@{-}[dr] \ar@{-}[dl] \ar@{-}[d] &
\\ K_{q^d,P} \ar@{-}[d] & \mathbb{F}_{q^d}K_{q,P^\alpha} \ar@{-}[dr] \ar@{-}[ld] & K_{q^d,P^\alpha}^{G_{q^d,P}} \ar@{-}[d] \\ \mathbb{F}_{q^d}K_{q,P} \ar@{-}[dr]& & \mathbb{F}_{q^d}K_{q,P^\alpha}^{G_{q,P}} \ar@{-}[dl] \\ & \mathbb{F}_{q^d}(T) } \] \begin{lemma} \label{Fi} Let $\sigma\in \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$, and for each $i=1,\ldots,\alpha$, let $$ F_i:=K_{q,P^i}^{G_{q,P}}. $$ Then for each $i=1,\ldots,\alpha$, the generator $\sigma$ of the Galois group $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ satisfies \begin{enumerate}
\item
$\sigma(K_{q^d,P^i})=K_{q^d,P^i}$.
\item
$\sigma(F_i)=F_i$. \end{enumerate} \end{lemma}
\begin{proof} By construction, we have $\sigma(\mathbb{F}_{q^d}(T))=\mathbb{F}_{q^d}(T)$ and
$\sigma(K_{q^d,P^i})=K_{q^d,P^i}$, for each $i=1,\ldots,\alpha$. The Galois group $\mathrm{Gal}(K_{q^d,P^\alpha}/\mathbb{F}_{q^d}(T))$ is congruent to the direct product of the cyclic group $\mathbb{F}_{q^d}^*$ with the $p$-group $\mathrm{Gal}(F_\alpha/\mathbb{F}_{q^d}(T))$. By definition, we have that $\mathbb{F}_{q^d}(T) \subset \sigma(F_\alpha) \subset K_{q^d,P^\alpha}$, whence $\sigma(F_\alpha)$ corresponds to a Galois group $H$ which is isomorphic to a cyclic group of order $q^d-1$. As there is a unique such subgroup in $\mathrm{Gal}(K_{q^d,P^\alpha}/\mathbb{F}_{q^d}(T))$, it follows that $\sigma(F_\alpha)=F_\alpha$.
The result for $F_i$ for each $i=1,\ldots, \alpha-1$ follows by induction. \end{proof}
We note that property (2) in Lemma \ref{Fi} implies that $(\sigma-1)G_{q^d,P}$ corresponds to a subgroup of $H_{q^d,P}$, and by order comparisons, we obtain that the unique such submodule of $G_{q^d,P}$ is given by the image of the map $\sigma-1$. For a realisation of a Kummer model of $K_{q,P}$, we refer to Section \ref{KummerSection}.
\section{Tame structure} \label{KummerSection}
In order to understand $H_{q^d,P}$, we will describe the character group of $G_{q^d,P}$ using the torsion of the Carlitz module. For an introduction to Kummer theory of extensions the reader is reffered to \cite{Jacobson2}. Let $P=\prod_{i=1}^s (T-\rho_i)$ be the decomposition of the irreducible polynomial $P\in \mathbb{F}_q[T]$ in $\mathbb{F}_{q^d}[T]$. We know by prime decomposition \cite[Chapter 12]{salvador2007topics} that \begin{equation}\label{Chinese} C_{q^d}[P]=\bigoplus_{i=1}^{ s} C_{q^d}[T-\rho_i]. \end{equation} The torsion modules $C_{q^d}[T-\rho_i]$ are defined as \[ C_{q^d}[T-\rho_i]:=\{z \in \overline{\mathbb{F}_q(T)}: z^{q^d}+(T-\rho_i)z=0 \}. \] Let $\lambda_i$ be a generator of $C_{q^d}[T-\rho_i]$ as an $A_d$-module. Then $\lambda_i$ satisfies the equation \begin{equation}
\label{lambdaKummer}
\lambda_i^{q^d-1}=-(T-\rho_i). \end{equation} \begin{lemma}
\label{Galdact}
Let $\sigma$ be a generator of the cyclic group $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$. Then
\[
\sigma(\lambda_i)=
\begin{cases}
\zeta_{\sigma,i} \lambda_{i+1} & \mbox{ if } 1 \leq i< {s}\\
\zeta_{\sigma,d} \lambda_1 & \mbox{ if } i={s},
\end{cases}
\]
where $\zeta_{\sigma,i}$ is a $(q^{d}-1)$st root of unity, which depends on both $\sigma$ and $i$. \end{lemma} \begin{proof} Consider the action of $\sigma$ on \eqref{lambdaKummer}. If $i< s$, then \[ (\sigma \lambda_i)^{q^d-1}=-\sigma(T-\rho_i)=-(T-\sigma(\rho_i))=-(T-\sigma_{i+1})=\lambda_{i+1}^{q^d-1}. \] The result follows in this case. The proof for $i=s$ is the same, except that $\sigma(\rho_s)=\rho_1$. \end{proof} On the other hand, the action of $G_{q^d,P}$ on $\lambda_i$ is given by multiplication by elements in $\mathbb{F}_{q^d}^*$. Indeed, if $f\in \mathbb{F}_{q^d}[T]$ and $(f,P)=1$, then $f(\rho_i) \neq 0$ for all $i=1,\ldots,s$. By definition of the Carlitz action $*_d$, and the fact that $\lambda_i$ is a $(T-\rho_i)$-torsion point it follows that \begin{equation} \label{*daction} \sigma_f \lambda_i= f *_d \lambda_i=f(\rho_i)\cdot \lambda_i. \end{equation} We note that $f(\rho_i) \in \mathbb{F}_{q^d}$, whence $f(\rho_i)^{q^d-1}=1$. \begin{definition}
Let $\zeta$ be a fixed choice of primitive $(q^{d}-1)$st root of unity. We define the dual elements $\{\sigma_k^*\} \in G_{q^d,P}^*$ such that
\[
\sigma_k^*(\sigma_\ell)=
\begin{cases}
1 & \mbox{ if } k\neq \ell \\
\zeta & \mbox{ if } k=\ell.
\end{cases}
\] \end{definition}
\begin{remark} As $s \mid d$ we have that $(q^s-1) \mid (q^d-1)$. The element $$\zeta_1:=\zeta^{\frac{q^d-1}{q^s-1}}$$ generates a cyclic subgroup of $G_{q^d,P}$ of order $q^s-1$. \end{remark}
\begin{lemma} For each $i_0 = 1,\ldots,s$, consider the polynomials
\[
f_{i_0}(x):=\left(1-
\prod_{\substack{i=1 \\ i\neq i_0}}^{s} (x-\rho_i)\right)=1-\frac{P(x)}{x-\rho_{i_0}} \in \mathbb{F}_{q^d}[x].
\] Then
\[
\sigma_{f_{i_0}}*_d \lambda_j=
\left(1-
\prod_{\substack{i=1 \\ i\neq i_0}}^{{s}} (\rho_{j}-\rho_i)
\right)
\cdot \lambda_j.
\] \end{lemma} \begin{proof} The proof follows immediately from \eqref{*daction}. \end{proof} \begin{lemma} For each $i_0=1,\ldots,s$, consider the elements \[ Z_{i_0}:=\left(1-
\prod_{\substack{i=1 \\ i\neq i_0}}^{s} (\rho_{i_0}-\rho_i)
\right). \] Then \[ Z_{i_0}=Z_1^{q^{i_0-1}}. \] Furthermore, the elements $Z_{i_0}$ are primitive $(q^{s}-1)$st roots of unity. \end{lemma} \begin{proof} The number of generators of a cyclic group of order $q^{s}-1$ is equal to $\phi(q^{s}-1)$, where $\phi$ denotes the Euler totient function. Furthermore, it is well-known that ${s} \mid \phi(q^{s}-1)$. We find,
recall that $\rho_1=\zeta_1$ and $\rho_i=\zeta_1^{q^{i-1}}$ for $1\leq i \leq {s}-1$,
\begin{align*}
Z_{i_0} & = \left(1-\prod_{\substack{i=1 \\ i\neq i_0}}^{{{s}}}
(\zeta_1^{q^{i_0-1}}-\zeta_1^{q^{i-1}})
\right) \\
&= \left(1-\prod_{i=2 }^{{{s}}}
(\zeta_1^{q^{i_0-1}}-\zeta_1^{q^{i+i_0-2}})
\right)\\
& = \left(1-\prod_{i=2 }^{{{s}}}
(\zeta_1-\zeta_1^{q^{i-1}})
\right)^{q^{i_0-1}}
= Z_1^{q^{i_0-1}},
\end{align*}
which concludes the proof. \end{proof} Recall that each generator $\lambda_i$ of $C_{q^d}[T-\rho_i]$ satisfies \eqref{lambdaKummer}. The elements $\lambda_i$ define characters $\sigma_{\lambda_i}^*=\chi_{\lambda_i}$ by Kummer theory, which are given by \[ \sigma_{\lambda_i}^*(\sigma)=\lambda_i^{\sigma}\lambda_i^{-1}, \] for each $\sigma \in G_{q^d,P}$. In particular, we find that \[ \sigma_{\lambda_i}^*(\sigma_{f_j})=\lambda_{i}^{\sigma_{f_j}} \lambda_{i}^{-1}= \begin{cases} Z_1^{q^{j-1}} & \mbox{ if } i= j \\ 1 & \mbox{ if } i \neq j. \end{cases} \] We now write $Z_1=\zeta_1^\alpha$ for some $\alpha \in \mathbb{N}$, $(\alpha,q^{{s}}-1)=1$. The character group of $G_{q^d,P}$ is non-canonically isomorphic to $G_{q^d,P}$. Moreover, letting {$n = q^s - 1$}, the quotient map in \eqref{sesH} gives \[G_{q^d,P} \rightarrow \mathbb{Z}/n \mathbb{Z} \rightarrow 1,\] which by duality yields the injection of the cyclic group $\mathbb{Z}/n\mathbb{Z}$ \[ 1 \rightarrow \mathbb{Z}/n\mathbb{Z} \rightarrow G_{q^d,P}^*. \] For each $i=1,\ldots,{{s}}$, let $\sigma_i$ be chosen generators of the $i$th direct summand in the decomposition given in \eqref{Chinese} of the group $G_{q^d,P}$, and consider a dual basis $\sigma^*_i$ of $G_{q^d,P}^*$ such that \[\sigma_i^* \sigma_j=\delta_{ij} \rho_1{=\delta_{ij}\zeta_1 },\] where $\delta_{ij}$ is Kronecker's $\delta$. An injection $$\iota: \langle g \rangle=\mathbb{Z}/n\mathbb{Z}\rightarrow G_{q^d,P}^*$$ is described by giving the coordinates of the generator $g$, i.e., \begin{equation} \label{define-chara} \iota(g)=\prod_{i=1}^{{s}} \left( \sigma_i^*\right)^{ \frac{q^d-1}{q^s-1}b_i}. \end{equation} Furthermore, the element $\iota(g)$ has order $n$ if, and only if, at least one of the integers $b_i$ is prime to $n$. Also, the character $\iota(g)$ given in \eqref{define-chara} is associated (via the Kummer correspondence) to the element \begin{equation} \label{L}
L=\prod_{i=1}^{{s}}
\lambda_i^{\frac{q^d-1}{q^s-1}b_i}, \mbox{ which satisfies } L^{q^s-1}=
(-1)^s
\prod_{i=1}^{{s}} (T-\rho_i)^{b_i}. \end{equation}
\begin{lemma} \label{KummerGen} For each $i=1,\ldots,{{s}}$, the exponent $b_i$ in \eqref{L} may be explicitly and recursively determined. \end{lemma} \begin{proof} For the Frobenius generator $\sigma$ of the cyclic group $\mathrm{Gal}(\mathbb{F}_{q^{{s}}}/\mathbb{F}_q)$ and $L$ as defined in \eqref{L}, the element $\sigma(L)$ generates the Kummer extension and by the theory of Kummer extensions it has the form \[ \sigma(L)=L^{\mu} a^{q^{{s}}-1}, \] for some $\mu\in \mathbb{N}$ such that $(\mu,q^{{s}}-1)=1$ and some $a\in \mathbb{F}_{q^d}(T)$. This implies that \[ \lambda_1^{b_s}\prod_{i=2}^{{{s}}} \lambda_i^{b_{i-1}} =\prod_{i=1}^{{s}} \lambda_i^{b_i \mu} a^{q^{{s}}-1}, \] which in turn implies for each $i = 2,\ldots,{s}$ that \[ b_{i-1}=\mu b_i \mod q^{{s}}-1 \] and also that \[ b_{{s}}=\mu b_1 \mod q^{{s}}-1. \] We let $\mu'$ be the inverse of $\mu$ modulo $q^d-1$. This yields \begin{align}
\notag b_1 \mu' & \equiv b_2 \mod q^{{s}}-1 \\
\notag b_2 \mu' & \equiv b_3 \mod q^{{s}}-1 \\
\label{lasteq1} \cdots & \cdots \\
\notag b_{{{s}}-1} \mu' &\equiv b_{{s}} \mod q^{{s}}-1 \\
\notag b_{{s}} \mu' & \equiv b_1 \mod q^{{s}}-1. \end{align} Therefore, $b_i = (\mu')^{i-1} b_1$ for each $i=2,\ldots,{{s}}$. As $b_{{s}}=(\mu')^{{{s}}-1}b_1$ \eqref{lasteq1} implies that \[ (\mu')^{{s}} \equiv 1 \mod q^{{s}}-1. \] We can thus select $\mu'=q$ to obtain the appropriate value of
$\mu' \mod (q^{{s}}-1)$. It may also be assumed without loss that $b_1=1$. \end{proof}
\noindent We have thus proven the following result. \begin{proposition} The model of the function field $\mathbb{F}_{q^d} K_{q,P}$ is given by the Kummer extension: \begin{equation} \label{TameKummer} L^{q^{{s}}-1}= (-1)^s \prod_{i=1}^{{s}} \left( T-\zeta_1^{q^{i-1}} \right)^{q^i}. \end{equation} \end{proposition} The Galois module structure for differentials of such extensions is known by the work of Boseck \cite{Boseck}. In Kummer extensions of $\mathbb{F}_{q^d}(T)$ of the form $y^n=\prod_{\nu=1}^d (T-a_i)^{b_i}$, $a_i\in \mathbb{F}_{q^d}$ the places $T-a_i$ are ramified with ramification index \[
e_i=\frac{q^{{s}}-1}{(q^{{s}}-1,b_i)}, \] see \cite{Ko}. Furthermore, by the theory of Carlitz torsion modules, we may also easily see that there is ramification over all places corresponding to the linear factors $T-\rho_i$ of $P$ in $A_d$. It follows that $(b_i,q^{{s}}-1)=1$, for each $i=1,\ldots,{{s}}$. As there is ramification of degree $q-1$ at infinity in $K_{q,P}/\mathbb{F}_q(T)$, we obtain \[ \sum_{\nu=1}^{{s}} b_i=1+q+\cdots +q^{{{s}}-1}. \] We have the following tower of fields and ramified places over $\mathbb{F}_{q^d}(T)$: \[ \xymatrix@C=.8pc{ K_{q^d,M} \ar@{-}[d] & B_{1,1} \cdots B_{1,q^s-1} \ar@{-}[d]^{\frac{q^d-1}{q^s-1}} & \cdots & B_{s,1} \cdots B_{s,q^s-1} \ar@{-}[d]^{\frac{q^d-1}{q^s-1}} & Q_1,\ldots Q_{t} \ar@{-}[d]^{\frac{q^d-1}{q-1}} \\
\mathbb{F}_{q^d} K_{q,M} \ar@{-}[d]_{\mathbb{F}_{q^{{s}}}^*} & B_{1} & \cdots & B_{{s}} &
B_{\infty,1}, \ldots B_{\infty,\frac{q^{{s}}-1}{q-1}} \\ \mathbb{F}_{q^d}(T) & P_1 \ar@{-}[u]^{q^{{s}}-1} & \cdots & P_{{s}} \ar@{-}[u]^{q^{{s}}-1} & P_\infty \ar@{-}[u]^{q-1} } \] { \begin{remark} \label{no-rem} In the special case $s=d$, there is no ramification over $B_1,\ldots,B_s$ in the extension $K_{q^d,P}/\mathbb{F}_{q^d} K_{q,P}$. \end{remark} }
\section{Wild structure}
We now proceed to the case $M=P^\alpha$, where $P \in \mathbb{F}_q[T]$ is again an irreducible polynomial of degree $s\mid d$. By previous arguments, it is easily seen that the abelian Galois group $\mathrm{Gal}(K_{q^d,P^\alpha}/\mathbb{F}_q(T))$ may be written as the direct product \[ \mathrm{Gal}(K_{q^d,P^\alpha}/\mathbb{F}_q(T))\cong G_{q^d,P} \times P_{q^d,P^\alpha}, \] where \[ P_{q^d,P^\alpha}=\{D \in \mathbb{F}_{q^d}[T] \mod P^\alpha, D\equiv 1 \mod P\}. \] There is a very precise way to describe the group $P_{q^d,P^\alpha}$, which is also used in the elementary proof of the Kronecker-Weber theorem for rational function fields \cite{Salas-Torres}. \begin{proposition}[Proposition 5.1 \cite{Salas-Torres}] \label{ab-p-grp} Let $r$ be a positive integer. The group $P_{q^r,P^\alpha}$ is an abelian $p$-group. Let $v_{q^r,n}(\alpha)$ denote the number of cyclic groups of order $p^n$ in the decomposition of $P_{q^r,P^\alpha}$, where $s=\deg P$. Then\begin{equation*} v_{q^r,n}(\alpha)=\frac{q^{rs\big(\alpha-\genfrac\lceil\rceil{0.5pt}1{\alpha} {p^n}\big)}-q^{rs\big(\alpha-\genfrac\lceil\rceil{0.5pt}1{\alpha} {p^{n-1}}\big)}}{p^{n-1}(p-1\big)}= \frac{q^{rs\big(\alpha-\genfrac\lceil\rceil{0.5pt}1{\alpha} {p^{n-1}}\big)}\big(q^{rs\big(\genfrac\lceil\rceil{0.5pt}1{\alpha}{p^{n-1}} -\genfrac\lceil\rceil{0.5pt}1{\alpha}{p^{n}}\big)}-1\big)}{p^{n-1}(p-1)}, \end{equation*} where $\lceil x\rceil$ denotes the ceiling function on $\mathbb{Q}$, i.e., the minimum integer greater than or equal to $x$. \end{proposition} In particular, Proposition \ref{ab-p-grp} holds for both $P_{q,P^\alpha}$ and $P_{q^d,P^\alpha}$ by setting $r = 1$ and $r = d$, respectively. For the Kummer extensions $P_{q,P}$ and $P_{q^d,P}$, we must realise the Galois group \[ H'_{q^d,P^\alpha}:=\mathrm{Gal}\left(K_{q^d,P^\alpha}^{G_{q^d,P}}/\mathbb{F}_{q^d}K_{q,P^\alpha}^{G_{q,P}}\right). \] For this, we obtain the exact sequence \[ 0 \rightarrow H'_{q^d,P^\alpha} \rightarrow \mathrm{Gal}(K_{q^d,P^\alpha}^{G_{q^d,P}}/\mathbb{F}_{q^d}(T)) \rightarrow \mathrm{Gal}(\mathbb{F}_{q^d}K_{q,P^\alpha}^{G_{q,P}} / \mathbb{F}_{q^d}(T)) \rightarrow 0, \] where the structure of the abelian $p$-group $$P_{q,P^\alpha}= \mathrm{Gal}(\mathbb{F}_{q^d} K_{q,P^\alpha}^{G_{q,P}} / \mathbb{F}_{q^d}(T))$$ is given by Proposition \ref{ab-p-grp}. \begin{corollary} $H'_{q^d,P^{\alpha}}=(\sigma-1)P_{q^d,P^\alpha}$. \end{corollary} \begin{proof} This follows in the same manner as Lemma \ref{Kummerfun}, as $\sigma(H'_{q^d,P^\alpha})=H'_{q^d,P^\alpha}$ and $(\sigma-1)D \in H'_{q^d,P^\alpha}$ for every $D\in P_{q^d,P^\alpha}$. \end{proof}
In the extension $K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}$, there is generally wild ramification: According to \cite[Proposition 12.4.5]{salvador2007topics}, the place at infinity is ramified in the extension $\mathbb{F}_{q^d} K_{q,P^\alpha}$ with index $q-1$ and in the extension $K_{q^d,P^\alpha}$ with ramification index $q^d-1$. Moreover, the ramification degree of $P$ in the extension $\mathbb{F}_{q^d}K_{q,P^\alpha} /\mathbb{F}_{q^d}(T)$ is equal to {$q^{s\alpha}-q^{s(\alpha-1)}$}, while the ramification degree of $P$ in extension $K_{q^d,P^\alpha}/\mathbb{F}_{q^d}(T)$ is given by $q^{d\alpha}-q^{d(\alpha-1)}$ \cite[Proposition 12.3.14]{salvador2007topics}, whence the ramification in extension $K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}$ is given by \[ { e=\frac{q^{d\alpha}-q^{d(\alpha-1)}}{q^{s\alpha}-q^{s(\alpha-1)}}=q^{(d-s)(\alpha-1)}\frac{q^{d}-1}{q^s-1}. } \] We thus obtain the following diagram, where $s=(q^{d\alpha}-q^{d(\alpha-1)})/(q-1)$: \[ \xymatrix@C=1.3pc{
K_{q^{d},P^\alpha} \ar@{-}[d]^H & P' \ar@{-}[d]^e
& \infty_{1,1}, \ldots, \infty_{1,q-1} \ar@{-}[d]^{\frac{q^d-1}{q-1}}
& & \infty_{s,1}, \ldots, \infty_{s,q-1} \ar@{-}[d]^{\frac{q^d-1}{q-1}}& \\
\mathbb{F}_{q^d}K_{q,P^\alpha} \ar@{-}[d] & P_1 \ar@{-}[d]
& \infty_1 \ar@{-}[rd]^{q-1} & \ldots &\infty_{s} \ar@{-}[ld]_{q-1} \\
\mathbb{F}_{q^d}(T) & P & & \infty & } \] The irreducible polynomial $P$ factors in $\mathbb{F}_{q^d}$ as \begin{equation} \label{factorisation} P(T)=\prod_{i=1}^{s}(T-\zeta_1^{q^{i-1}}), \end{equation} where $\zeta_1$ is a primitive $(q^s-1)$st root of 1. We denote $P_i = T-\zeta_1^{q^{i-1}}$ ($i=1,\ldots,s$).
\begin{lemma} The quotient $A_d/P^\alpha$ is $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$-equivariantly isomorphic to the direct sum of vector spaces: \[ A_d/P^\alpha= \left(A_1/P \right)^\alpha. \] The group of units $(A_d/P^\alpha)^*$ satisfies \[ (A_d/P^\alpha)^*= (A_d/P)^* \oplus \left( A_d/P\right)^{\alpha-1}. \] \end{lemma} \begin{proof} It is clear that the following sequence is exact: \begin{equation} \label{reduce-power} 0 \rightarrow P^{\alpha-1}/P^\alpha \rightarrow A_1/P^\alpha \rightarrow A_1/P^{\alpha-1} \rightarrow 1. \end{equation} Therefore, we can prove by induction that \[ (A_d/P^\alpha)= A_d/P \oplus P/P^2 \oplus P^2/P^3 \oplus \cdots \oplus P^{\alpha-1}/P^\alpha. \] On the other hand, the map \begin{align*} A_d/P & \rightarrow P^i/P^{i+1} \\
f \mod P & \mapsto f\cdot P^i \mod P^{i+1} \end{align*} is a $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$-equivariant isomorphism, since $P^i$ is a $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$-invariant element. \end{proof} Let $f \in A_d/P^\alpha$. Consider the class $f_0$ of $f$ modulo $P^{\alpha-1}$, i.e., \[ f \mod P^\alpha \equiv f_0 + P^{\alpha-1} f_1 \mod P^\alpha, \qquad f \mod P^{\alpha-1} \equiv f_0 \mod P^{\alpha-1}. \] We consider now the multiplication \begin{align*} f\cdot g &\equiv (f_0 + P^{\alpha-1} f_1 ) (g_0+ P^{\alpha-1}g_1) \\ & \equiv f_0 g_0 + ( \bar{f}_0 g_1+ f_1 \bar{g}_0 )P^{\alpha-1} \mod P^{\alpha}, \end{align*} where $\bar{f}_0,\bar{g}_0$ denote the classes of $f_0,g_0 \mod P$. It is clear by induction that $f$ is invertible if, and only if, $\bar{f}_0\equiv f \mod P$ is invertible. We define the following filtration: \begin{equation} \label{Nt-def} N_t:=\{ D \mod P^\alpha : D \equiv 1 \mod P^t\}. \end{equation} The group $N_1$ is the wild part of $(A_d/P^\alpha)^*$. We have the following short exact sequence \[ 1 \rightarrow N_{t+1} \rightarrow N_{t} \rightarrow P^t/P^{t+1} \rightarrow 1, \] where the group structure on $N_t$ is multiplicative while the structure on $P^t/P^{t+1}$ is additive. The wild part of $H_{q^d,P^\alpha}$ consists of elements of the form $\sigma(D)D^{-1}$ in $N_1$, where $D\in N_1$. The filtration of $N_1$ \[ N_1 \supset N_2 \supset \cdots N_i \supset \cdots \] induces a filtration on $H_{q^d,P^\alpha}$: \[ H^1=H_{q^d,P^\alpha}\cap N_1 \supset H^2=H_{q^d,P^\alpha} \cap N_2 \supset \cdots \supset H^i=H_{q^d,P^\alpha} \cap N_i \supset \cdots \] We observe that \[ \frac{H^i}{H^{i+1}}=\{ \sigma(D)D^{-1} \mod H^{i+1}: D \in H^i\}, \] and the latter group can be identified with the image of the operator $(\sigma-1)(f)$ in the additive group $P^i/P^{i+1}\cong A_d/P$.
\begin{lemma} \label{H-filt} The space $A_d/P \cong \oplus_{i=1}^s \mathbb{F}_{q^d}$. An element $f\in A_d/P$ is mapped to the coordinates $(f(\zeta),f(\zeta^q),\ldots,f(\zeta^{q^{s-1}})) \in \oplus_{i=1}^s \mathbb{F}_{q^d}$. The action of the operator $\sigma-1$ on the coordinates $(x_1,\ldots,x_s) \in \oplus_{i=1}^s \mathbb{F}_{q^d}$ is given by: \[ \xymatrix{ (x_1,\ldots,x_s) \ar[r]^-{\sigma-1} & (x_s^{q}-x_1, x_1^q-x_2, \ldots, x_{s-1}^q-x_s). } \] \end{lemma} The kernel of $\sigma-1$ consists of elements $(x_1,\ldots,x_s)$ such that \[ x_1\in \mathbb{F}_{q^d}: x_i=x_1^{q^{i-1}}, \; i=2,\ldots, s. \] Clearly this set has $q^d$ elements since all elements are determined by the value of $x_1$. Therefore, the image of $\sigma-1$ has exactly $q^{d(s-1)}$ elements.
\begin{remark} Given an $H_{q^d,P^\alpha}$-module $\mathcal{M}$, the space of invariants $\mathcal{M}^H$ is given by \[ \mathcal{M}^{H_{q^d,P^\alpha}}= \left( \left( \mathcal{M}^{H_{q^d,P^\alpha}^\alpha} \right)^{H_{q^d,P^\alpha}^{\alpha-1}/H_{q^d,P^\alpha}^\alpha } \cdots \right)^{H_{q^d,P^\alpha}^1/H_{q^d,P^\alpha}^2}. \] Since $H^\alpha=H^\alpha/H^{\alpha+1}$, we can apply recursively the computation of Lemma \ref{H-filt} in order to compute $H_{q^d,P^\alpha}$-invariants. \end{remark}
We now turn to ramification groups and the computation of the different. For each $i \in \mathbb{Z}$ with $i \geq -1$, the
$i$th ramification group of $\mathfrak{P}|\mathfrak{p}$ is defined as $$
G_{i}(\mathfrak{P}|\mathfrak{p}) = \{\sigma \in G_{q^d,P^\alpha}\;| \; v_\mathfrak{P}(\sigma(x) - x) \geq i+1\text{ for all } x \in \mathfrak{O}_\mathfrak{P}\},$$ where $\mathfrak{O}_\mathfrak{P}$ denotes the valuation ring at $\mathfrak{P}$. We denote $G_i = G_i(\mathfrak{P}|\mathfrak{p})$.
\begin{proposition} \label{filtration} \begin{enumerate} \item The groups $N_k$ defined in \eqref{Nt-def} have order $q^{ds(\alpha-k)}$ for $1\leq k \leq n$ and correspond to the upper ramification filtration at $\mathfrak{P}|\mathfrak{p}$. \item We have \begin{itemize}
\item $G_0= G_{q^d,P^\alpha}$,
\item $G_i= N_k$ for all $q^{d(k-1)} \leq i \leq q^{dk} - 1$ and $1 \leq k \leq \alpha-1$, and
\item $G_i = N_\alpha = \mathrm{Id}$ for all $i \geq q^{d(\alpha-1)}$. \end{itemize}\end{enumerate} \end{proposition} \begin{proof} \begin{enumerate} \item \cite[Prop. 2.2]{Keller}. \item This follows by the relation between upper and lower ramification filtrations \cite[IV. sec. 3]{SeL}. \end{enumerate} \end{proof}
By Proposition \ref{filtration}, the lower ramification filtration is given by \begin{align*} G_0 & > G_1=\cdots=G_{q^{d}-1}=N_1 \\
& > G_{q^{d}}=\cdots=G_{q^{2d}-1}=N_2 \\
& > G_{q^{2ds}}=\cdots = G_{q^{3d}-1}=N_3 \\
& > \qquad \qquad \cdots \\
& > G_{q^{d(\alpha-2)}}
=\cdots=G_{q^{d(\alpha-1)}}=N_{\alpha-1} \\ & > \{1\}. \end{align*} The ramification filtration for the group $H_{q^d,P^\alpha}$ may be found by intersecting $H_{q^d,P^\alpha}$ with $G_i$, so that \[
H_i:=G_i \cap H_{q^d,P^\alpha},\qquad |H_i|= \begin{cases} (q^{d}-1)^{s-1} q^{d(s-1)(\alpha-1)} & \text{ if } i=0 \\ q^{d(s-1)(\alpha-i)} & \text{ if } i \geq 1. \end{cases} \] We now determine the different $\mathfrak{D}_{K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}}$ of $K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}$. \begin{proposition} \label{prop:47}
$$\mathfrak{D}_{K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}} = \prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P}^A \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^B,$$ where $s=\deg P$, $s\mid d$, \begin{align} \label{Aeq}
A &=({\alpha q^{d\alpha}- (\alpha+1)q^{d(\alpha-1)}}) - ( {\alpha q^{s\alpha} - (\alpha+1)q^{s(\alpha-1)}})\frac{q^{d\alpha } - q^{d(\alpha -1)}}{q^{\alpha s}-q^{(\alpha -1)s}} \\\notag & = \frac{q^{d (\alpha -1)} \left(q^d-q^s\right)}{q^s-1}, \end{align}
and \begin{equation} \label{Beq} B = (q^d - 2) - (q-2) \frac{q^d-1}{q-1} = q\left(\frac{q^{d-1} - 1}{q-1}\right). \end{equation} \end{proposition}
\begin{proof} As the extension $K_{q^d,P}/\mathbb{F}_q(T)$ is separable, we may employ \cite[Theorem 5.7.15]{salvador2007topics}: Among separable extensions $K \subset L \subset M$ of global fields, we have the functorial identity \begin{equation} \label{differentfunct}\mathfrak{D}_{M/K} = \mathfrak{D}_{M/L} \text{con}_{L/M}(\mathfrak{D}_{L/K}), \end{equation} where $\mathrm{con}_{L/M}$ denotes the conorm map of the corresponding fields $L,M$, see \cite[5.3]{salvador2007topics}. We consider the two towers $$\mathbb{F}_q(T) \subset K_{q,P^\alpha } \subset \mathbb{F}_{q^d} K_{q,P^\alpha } \subset K_{q^d,P^\alpha } \quad \text{ and }\quad \mathbb{F}_q(T) \subset \mathbb{F}_{q^d}(T) \subset K_{q^d,P^\alpha }.$$ We may now proceed with computations within each of these towers. \begin{enumerate}
\item $\mathbb{F}_q(T) \subset K_{q,P^\alpha }$. The different $\mathfrak{D}_{K_{q,P^\alpha }/\mathbb{F}_q(T)}$ is given by \cite[prop. 12.7.1]{salvador2007topics}
$$\mathfrak{D}_{K_{q,P^\alpha }/\mathbb{F}_q(T)} = \mathfrak{P}^{\alpha q^{s\alpha } - (\alpha +1)q^{s(\alpha -1)}} \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{q-2}, $$ where $\mathfrak{P}$ is the unique place of $K_{q,P^\alpha }$ above the place $\mathfrak{p}$ of $\mathbb{F}_q(T)$ associated with $P$. \item $ \mathbb{F}_{q^d} K_{q,P^\alpha }/ K_{q,P^\alpha }$ is unramified at all places of $K_{q,P^\alpha }$, whence $$\mathfrak{D}_{\mathbb{F}_{q^d} K_{q,P^\alpha } /K_{q,P^\alpha }} = (1).$$ \item $\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)$ is also unramified at all places of $\mathbb{F}_q(T)$, whence $$\mathfrak{D}_{\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)} = (1).$$
\item For the extension $K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)$: As $s | d$ and the polynomial $P$ thus splits completely in $\mathbb{F}_{q^d}[T]$, we denote each linear factor of $P$ in $\mathbb{F}_{q^d}[T]$ by $\wp_i$, so that $P = \prod_{i=1}^s \wp_i$. We obtain \cite[Thm. 12.7.2]{salvador2007topics}
$$\mathfrak{D}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)} = \left[\prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P} \right]^{\alpha q^{d\alpha }- (\alpha +1)q^{d(\alpha -1)}} \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{q^d-2}.$$ \end{enumerate}
By \eqref{differentfunct}, we may therefore write $\mathfrak{D}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d} K_{q,P^\alpha }}$ as \begin{align*} \notag \mathfrak{D}^{-1}&_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d} K_{q,P^\alpha }} = \mathfrak{D}_{K_{q^d,P^\alpha }/\mathbb{F}_q(T)}^{-1} \text{con}_{\mathbb{F}_{q^d}K_{q,P}/K_{q^d,P^\alpha }}(\mathfrak{D}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/\mathbb{F}_q(T)}) \\ \notag &= \left(\mathfrak{D}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)} \text{con}_{\mathbb{F}_{q^d}(T)/K_{q^d,P^\alpha }}(\mathfrak{D}_{\mathbb{F}_{q^d}(T)/\mathbb{F}_q(T)})\right)^{-1} \\
\notag & \qquad \qquad \qquad \times \text{con}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/K_{q^d,P^\alpha }}(\mathfrak{D}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/\mathbb{F}_q(T)}) \\\notag &= \mathfrak{D}^{-1}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)}\text{con}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/K_{q^d,P^\alpha }}(\mathfrak{D}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/\mathbb{F}_q(T)}) \\\notag &= \mathfrak{D}^{-1}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)}\text{con}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/K_{q^d,P^\alpha }}( \mathfrak{D}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/K_{q,P^\alpha }} \\
\notag & \qquad \qquad \qquad \qquad \times \text{con}_{K_{q,P^\alpha }/\mathbb{F}_{q^d} K_{q,P^\alpha }}(\mathfrak{D}_{K_{q,P^\alpha }/\mathbb{F}_q(T)}))
\\ &= \mathfrak{D}^{-1}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)}\text{con}_{\mathbb{F}_{q^d} K_{q,P^\alpha }/K_{q^d,P^\alpha }}( \text{con}_{K_{q,P^\alpha }/\mathbb{F}_{q^d} K_{q,P^\alpha }}(\mathfrak{D}_{K_{q,P^\alpha }/\mathbb{F}_q(T)})) \\\notag &= \mathfrak{D}^{-1}_{K_{q^d,P^\alpha }/\mathbb{F}_{q^d}(T)} \text{con}_{K_{q,P^\alpha }/K_{q^d,P^\alpha }}(\mathfrak{D}_{K_{q,P^\alpha }/\mathbb{F}_q(T)}) \\\notag & = \left[\prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P} \right]^{-({\alpha q^{d\alpha }- (\alpha +1)q^{d(\alpha -1)}})} \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{-(q^d-2)} \\\notag & \qquad \qquad\qquad\qquad\qquad \times \text{con}_{K_{q,P^\alpha }/K_{q^d,P^\alpha }}\left(\mathfrak{P}^{{\alpha q^{s\alpha } - (\alpha +1)q^{s(\alpha -1)}}} \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{q-2}\right) \\\notag &= \left[\prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P} \right]^{-({\alpha q^{d\alpha }- (\alpha +1)q^{d(\alpha -1)}})} \prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{-(q^d-2)} \\\notag & \qquad\qquad\qquad \times \left[\prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P}^{{\alpha q^{s\alpha } - (\alpha +1)q^{s(\alpha -1)}}}\right]^{\frac{q^{d\alpha } - q^{d(\alpha -1)}}{q^{\alpha s}-q^{(\alpha -1)s}}} \left[\prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}^{q-2}\right]^{\frac{q^d-1}{q-1}}.\end{align*} The result follows.
\end{proof}
\section{Tower structures}
\label{WTCM} We now examine cyclotomic function fields as composites of towers of Kummer and Artin-Schreier extensions. Let $P \in \mathbb{F}_q[T]$ be irreducible, whence $P$ possesses only simple roots. We assume once more that $\deg{P}=s \mid d$. We now give the recursive definition for the cyclotomic function field $K_{q^d,(T-\rho)^\alpha}$.
\begin{lemma} Let $(T - \rho) \in A_d$ be a factor of $P$, where $\rho\in \mathbb{F}_{q^s}\cong A_1/P$. Then the field $K_{q^d,(T - \rho)^\alpha}$ may be described recursively by a tower of composita of explicitly determined Kummer and Artin-Schreier extensions over $\mathbb{F}_{q^d}(T)$. \end{lemma} \begin{proof} We first consider the case $\alpha = 2$, i.e., the cyclotomic function field $K_{q^d,(T-\rho)^2}$ generated over $\mathbb{F}_{q^d}(T)$ by the torsion points of $(T-\rho)^2$. By definition of the Carlitz action $*_d$, we have \begin{align*} (T-\rho)*_d u &= u^{q^d}+(T-\rho) u \\ (T-\rho)^2*_du & = u^{q^{2d}}+ \left( (T-\rho)^{q^d}+(T-\rho) \right) u^{q^d} + (T-\rho)^2 u. \end{align*} We denote $X=(T-\rho)*_du$. The equation \[ (T-\rho)*_dX=X^{q^d}+(T-\rho)X=0 \] implies that either $X=0$ or $X^{q^d-1}=-(T-\rho)$. Let $\lambda$ be a solution of the second equation, so that $\lambda^{q^d-1}=-(T-\rho)$. The general torsion point for $(T-\rho)^2$ over $\mathbb{F}_{q^d}$ may then be described by the equation \[ u^{q^d}+ (T-\rho)u =\lambda. \] We set $u=U\lambda$, which yields \[ U^{q^d}\lambda^{q^d}-\lambda^{q^d-1} \lambda U=\lambda, \] whence we obtain \begin{equation} \label{U-def} U^{q^d}-U=-\frac{1}{T-\rho}. \end{equation} We have thus constructed the following tower of fields: \[ \xymatrix{
& K_{q^d,(T-\rho)^2} \ar@{-}[dr] \ar@{-}[dl] & \\
\frac{\mathbb{F}_{q^d}(T)[U]}{\langle U^{q^d}-U=-\frac{1}{T-\rho} \rangle} \ar@{-}[dr] & &
\frac{\mathbb{F}_{q^d}(T)[\lambda]}{\langle\lambda^{q^d-1}=-(T-\rho)\rangle} \ar@{-}[dl] \\
& \mathbb{F}_{q^d}(T) & } \] The field $K_{q^d,(T-\rho)^2}$ is therefore the compositum of a Kummer extension and an Artin-Schreier extension, where a root $u$ of the torsion point equation $(T-\rho)^2*_du$ is given by $u=U\lambda$. One may now easily proceed inductively: Let $U_2:=U$ be the element given in \eqref{U-def}, and let $u_2=U_2\lambda$. A solution of $(T-\rho)^3*_du_3=0$ is then given by \[ u_3^{q^d}+(T-\rho)u_3=u_2. \] We set $U_3=u_3/\lambda$. This yields $U_3^{q^d}\lambda^{q^d}- \lambda^{q^d-1}\lambda U_3=u_2$, which in turn implies that \[ U_3^{q^d}-U_3=-{ \frac{U_2}{T-\rho} }. \] (We note that $u_2/\lambda^{q^d-1}=U_2$.) In this way, we may build a tower of successive Artin-Schreier extensions. We have thus obtained the extended diagram \begin{equation} \label{compositediagram} \xymatrix{
& K_{q^d,(T-\rho)^\alpha} \ar@{-}[dr] \ar@{-}[ddddl] \ar@{.}[dd]&
\\
& &
\frac{\mathbb{F}_{q^d}(T)[U_\alpha]}{\langle U_\alpha^{q^d}-U_\alpha={-\frac{U_{\alpha-1}}{T - \rho}} \rangle} \ar@{.}[dd]\\
& K_{q^d,(T-\rho)^3} \ar@{-}[dr] \ar@{-}[ddl] \ar@{-}[d]
& \\
& K_{q^d,(T-\rho)^2} \ar@{-}[dr] \ar@{-}[dl] \ar@{-}[d]
&
\frac{\mathbb{F}_{q^d}(T)[U_3]}{\langle U_3^{q^d}-U_3={-\frac{U_2}{T-\rho}} \rangle} \ar@{-}[d]
\\
\mathbb{F}_{q^{d}}(T)(\lambda) \ar@{-}[dr]_{\text{Kummer}} & K_{q^d,(T-\rho)} \ar@{=}[l]
&
\frac{\mathbb{F}_{q^d}(T)[U_2]}{\langle U_2^{q^d}-U_2={-\frac{1}{T-\rho}}\rangle} \ar@{-}[dl]\\
& \mathbb{F}_{q^d}(T) & } \end{equation} This completes the proof. \end{proof}
Within the diagram \eqref{compositediagram}, we have described the Kummer model of the extension $\mathbb{F}_{q^d}K_{q,P^\alpha}/\mathbb{F}_{q^d}(T)$. By the arguments of \S 2 on Kummer covers, it thus remains to describe the Artin-Schreier-Witt model of the extension $$K_{q^d,P^\alpha}^{\mathbb{F}_{q^d}^*}/\mathbb{F}_{q^d}(T).$$ We may therefore prove the following corollary. \begin{corollary} Let $P \in \mathbb{F}_q[T]$ be irreducible of degree $s\mid d$. Then the field $K_{q^d,P^\alpha}^{\mathbb{F}_{q^d}^*}$ may be described recursively by a tower of composita of explicitly determined Artin-Schreier extensions over $\mathbb{F}_{q^d}(T)$. \end{corollary} \begin{proof} For each linear factor $T-\rho_i$ of $P$, we consider the generating elements $U_j^{(i)}$, $j = 1,\ldots,\alpha$, of the fields $K_{q^d,(T-\rho_i)^\alpha}$, each of which satisfies the equation \[ \left( U_j^{(i)} \right)^p- U_j^{(i)} = U_{j-1}^{(i)}. \] By the Chinese remainder theorem once more, we obtain an equality with the compositum \[ K_{q^d,P^\alpha}^{\mathbb{F}_{q^d}^*} = \prod_{i=1}^{{s}} K_{q^d,(T-\rho_i)^\alpha}^{\mathbb{F}_{q^d}^*}. \] As before, let $\sigma$ be a generator of the cyclic group $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_{q})$ such that $\sigma (\rho_i)=\rho_{i+1}$, for each $i=1,\ldots,{{s}}-1$, and $\sigma(\rho_{{s}})=\rho_1$. For each $i=1,\ldots,{{s}}-1$, we have $$\sigma(U_2^{(i)})=U_2^{(i+1)}-a_i, \qquad \qquad a_i\in \mathbb{F}_{q^d}.$$ We may normalise without loss the selection of elements $U_2^{(i)}$ so that $$\sigma(U_2^{(i)})=U_2^{(i+1)}.$$ Proceeding inductively, we thus obtain \[ \sigma(U_{j}^{(i)})=U_{j}^{(i+1)} \qquad\qquad j = 2,\ldots,\alpha. \] By the correspondence of Artin-Schreier extensions to additive characters, we know that the field $\mathbb{F}_{q^d}K_{q,P^2}^{\mathbb{F}_{q}^*}$ is given by an Artin-Schreier equation \[ y^{q^d}-y=\sum_{i=1}^{{s}} \frac{b_i}{U_1^{(i)}}, \qquad \qquad U_1^{(i)}=T-\rho_i. \] On the other hand, the field $K_{q,P^{2}}$ is invariant under the action of the generator $\sigma$. It follows that there exists an element $c_i \in \mathbb{F}_{q^d}(T)$ such that \[ \sigma\left(\sum_{i=1}^{{s}} \frac{b_i}{U_1^{(i)}}\right)= \sum_{i=1}^{{s}} \frac{b_i}{U_1^{(i+1)}}+ c_i^p-c_i. \] By uniqueness of partial fraction expansions, this yields that $b_1=b_2=\cdots=b_{{s}}$. In order to consider the higher powers $j = 3,\ldots,\alpha$, one may then proceed inductively, or alternatively, via a standard Witt vector construction \cite{Hazewinkel}. \end{proof}
\section{Galois module structure}
The space of holomorphic differentials $H^0(X,\Omega_X)$ for the curve $X$ corresponding to the cyclotomic function field $K_{q^d,M}$ if $\mathbb{F}_{q^d}$ is selected big enough so that $M$ splits in $\mathbb{F}_{q^d}$ are known, see \cite{Ward}. Our strategy in computing holomorphic differentials $H^0(Y,\Omega_Y)$ for the curve $Y$ corresponding to $K_{q,M}$, where $M$ does not split in $\mathbb{F}_q$ is to consider the Galois cover $X\rightarrow Y$ with Galois group $H=H_{q,M}$ and reduce holomorphic differentials of $X$ to holomorphic differentials of $Y$. We will prove that we have the inclusions \begin{equation} \label{inclusions} H^0(Y,\Omega_Y) \subset L_Y(\Omega(D)) =H^0(X,\Omega_X)^H, \end{equation} where $L_Y(\Omega(D))$ is a space of non-holomorphic differentials allowing poles on a certain explicitly given divisor $D$. Our proposed strategy is to approach the structure of $L_Y(\Omega(D))$ using the inclusions of eq. (\ref{inclusions}. We have to compute the $H$-invariant differentials of $H^0(X,\Omega_X)$ and then select the holomorphic ones among them.
Let us start in a more general setting. Consider a Galois ramified cover $\pi:X\rightarrow Y$ of projective complete nonsingular curves defined over the field $k=\mathbb{F}_{q^d}$ with Galois group $H$, and let $df$ be a differential on $Y$. Let $\pi^*$ denote the pullback and $k(X),k(Y)$ be the functions fields of the curves $X,Y$. We will follow a multiplicative notation for the divisors. A divisor $D=\prod_{i=1}^t P_i^{a_i}$, where $P_i$ are prime divisors and
$a_i\in \mathbb{N}$ will be called integral. The divisor $\mathrm{div}_X(\pi^*(df))$ of $\pi^*(df)$ in $X$ is given by \[ \mathrm{div}_X(\pi^*(df))= \pi^* \mathrm{div}_Y(df)\cdot R_{X/Y}, \] where $R_{X/Y}$ is the ramification divisor, see \cite[IV.2]{Hartshorne:77}. This allows us to compute holomorphic differentials on $X$ via functions $g\in k(X)$ such that $ \mathrm{div}_X(g)\cdot\mathrm{div}_X(\pi^*df)$ is holomorphic \cite[sec. 3]{Boseck}. $H$-invariant differentials on $X$ correspond to meromorphic differentials $\Omega_Y(\mathcal{D})$ of $Y$ with a well-prescribed set of poles and pole orders, where $\mathcal{D}$ is a divisor which can be explicitly prescribed.
We let $\mathfrak{I}_X$ (resp. $\mathfrak{I}_Y$) denote the collection of integral divisors of $X$ (resp. $Y$). Let $df$ be a differential of $Y$, and let \[ R_{X/Y}=\prod_{i=1}^s \prod_{Q_{\nu,i} \mapsto P_i} Q_{\nu,i}^{\delta_{i}} \] be the ramification divisor of $X/Y$, where $\delta_i \in \mathbb{Z}$ is the exponent of the different. \begin{lemma} The space of $H$-invariant differentials in $X$ is isomorphic to the vector space \begin{align} \label{H-inv} L_Y\left( \Omega_Y \left(\prod_{i=1}^s (P_i)_Y^{\left\lfloor \frac{\delta_i}{e_i}\right\rfloor } \right)\right) &= \left\{ g\in k(Y): \mathrm{div}_Y(g) \cdot \mathrm{div}_Y({df}) \prod_{i=1}^s (P_i)_Y^{\left\lfloor \frac{\delta_i}{e_i}\right\rfloor } \in \mathfrak{I}_Y \right\} \\ & = L_Y(\mathcal{D}) \label{invariants1} \end{align} \end{lemma} \begin{proof}
An $H$-invariant differential on $X$ is given by $h df, $ where $h,f \in k(Y)$. We observe that $\omega=h df$ is holomorphic if, and only if, the divisor
\[\mathrm{div}_X(\omega)=\mathrm{div}_X(h)\mathrm{div}_X(\pi^*(df)) \in \mathfrak{I}_X.
\]
By taking the pushforward and using the fact that applying $\pi_* \pi^*$ is equivalent to raising to the $|H|$ power
we compute that \[ \pi_* (\mathrm{div}_X(\omega ))=
\mathrm{div}_Y(h)^{|H|}\cdot \mathrm{div}_Y(df)^{|H|}
\cdot \mathrm{div}_Y(\pi_*(R_{X/Y})),
\] and $\omega$ is holomorphic if and only if $\pi_*(\omega) \in \mathfrak{I}_Y$. An easy computation yields that \[
\mathrm{div}_Y(\pi_*(R_{X/Y}))=\prod_{i=1}^s (P_i)_Y^{\delta_i \frac{|H|}{e_i}}, \] where $\delta_i$ is the differential exponent at $P_i$, and therefore, the set of $H$-invariant differentials can be identified with the space of functions given in eq. (\ref{H-inv}). \end{proof} Assume now that $X$ and $Y$ are the curves corresponding to the function fields
$K_{q^d,P^\alpha}$ and $\mathbb{F}_{q^d} K_{q,P^\alpha}$, respectively. We will take $f=T$ and we will compute the ingredients of lemma \ref{H-inv}.
We will compute the divisor in $Y$ of $dT$. We know that \begin{equation} \label{divisorT} \mathrm{div}_Y(dT)= \prod_{i=1}^{s}
\prod_{\mathfrak{P}|P_i} {\mathfrak{P}_i}^S \prod_{Q \mid \mathfrak{p}_\infty} Q^{q-2} \cdot \text{con}_{\mathbb{F}_q(T)/\mathbb{F}_{q^d}K_{q,P^\alpha}}(\mathfrak{p}_\infty^{-2}), \end{equation} where $S=\alpha q^\alpha-(\alpha+1)q^{\alpha-1}$ \cite[prop. 12.7.2]{salvador2007topics}.
Recall also the value of the different divisor we have computed in proposition \ref{prop:47} $\mathfrak{D} = \mathfrak{D}_{K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}} $
$$\mathfrak{D}_{K_{q^d,P^\alpha}/\mathbb{F}_{q^d} K_{q,P^\alpha}} = \left(\prod_{i=1}^s \prod_{\mathfrak{P}|\wp_i} \mathfrak{P}\right)^{\frac{q^{d (\alpha-1)} \left(q^d-q^s\right)}{q^s-1}} \left(\prod_{\mathfrak{B}|\mathfrak{p}_\infty} \mathfrak{B}\right)^{q\left(\frac{q^{d-1} - 1}{q-1}\right)}.$$ \begin{remark} In the special case that $s=d$, ramification is tame in the extension $K_{q^d,P^\alpha}/\mathbb{F}_{q^d}K_{q,P^\alpha}$, so that $\mathcal{D}=0$ and the invariant elements thus satisfy $L_X(\Omega_X)^H=L_Y(\Omega_X)$. \end{remark}
By the computation of the second author in \cite[p.46]{Ward} A holomorphic differential on $X$ is given by a differential of the form \begin{equation} \label{hol13} \omega= \prod_{i=1}^{{s}} \prod_{k=2}^\alpha \lambda_{i,k}^{\mu_{i,k}} \lambda_{i,1}^{-\mu_{i,1}} dT, \end{equation} where $\lambda_{i,k}$ are generators of the Carlitz torsion modules $C_{q^d}[P_i^k]$ of the factors of $M=\prod_{i=1}^r P_i^{n_i}$, and $\mu_{i,k}$ satisfy certain inequalities, see \cite[eq. (22)]{Ward}.
By the Chinese remainder theorem, the class of an element $D \in \mathbb{F}_{q^d}[T]$ modulo $$P^\alpha = \prod_{i=1}^s P_i^\alpha$$ determined by the classes $D \mod P_i^\alpha$. Moreover, a class $D \mod P_i^\alpha$ can be expressed as a $P_i$-adic series \[ D \mod P_i^\alpha = a_{i,0} +a_{i,1} P_i + a_{i,2} P_i^2 + \cdots a_{i,\alpha-1} P_i^{\alpha-1} \mod P_i^\alpha, \] where $a_{i,j} \in \mathbb{F}_{q^d}$ for all $1\leq i \leq s$ and $0 \leq j \leq \alpha-1$. The action of $D$ on $\lambda_{i,k}$ is determined by its $P_i$-adic decomposition. We also have for each $k=1,\ldots,\alpha$ that \begin{align} \left(\sum_{\ell=0}^{\alpha-1} a_{i,\ell} P_i^\ell\right)*_d \lambda_{i,k} &= \left(\sum_{\ell=0}^{\alpha-1} a_{i,\ell} P_i^\ell P_i^{\alpha-k} \right) *_d \lambda_{i,\alpha} \nonumber \\ &= \left(\sum_{\ell=0}^{\alpha-1} a_{i,\ell} P_i^{\alpha- k + \ell} \right) *_d \lambda_{i,\alpha} \label{actionl} \\ &= \sum_{\ell=0}^{\alpha-1} a_{i,\ell} \left(P_i^{\alpha- k + \ell} *_d \lambda_{i,\alpha}\right) \nonumber \\ &= \sum_{\ell=0}^{\alpha-1} a_{i,\ell} \lambda_{i,k-\ell},\nonumber \end{align} where we define $\lambda_{i,m} := 0$ whenever $m \leq 0$.
The action described in \eqref{actionl} gives rise to a representation
\begin{eqnarray}\notag \rho:(\mathbb{F}_{q^d}(T)/P^\alpha)^* & \longrightarrow & \mathrm{GL}(\alpha,\mathbb{F}_{q^d}) \\ \sum_{\ell=0}^{\alpha-1} a_\ell P^\ell & \mapsto & \begin{pmatrix} \label{actionMatrixav} a_0 & a_1 & \cdots & a_{\alpha-2} & a_{\alpha-1} \\ 0 & a_0 & a_1 & \cdots & a_{\alpha-2} \\ \vdots & 0 & \ddots & \ddots & \vdots\\ \vdots & & \ddots & a_0 & a_1\\ 0 & \cdots & \cdots & 0 & a_0 \end{pmatrix}. \end{eqnarray} Upper triangular matrices of the form \eqref{actionMatrixav} are known as {\em Toeplitz} matrices. In this way, we obtain a representation of $\mathbb{F}_{q^d}^*$ inside the algebraic subgroup of upper triangular matrices $T_\alpha(\mathbb{F}_{q^d})$ given by the ideal of relations \[ I:=\langle T_{i,i+\mu}-T_{j,j+\mu} \text{ for all } 1\leq i \leq \alpha \text{ and } 0\leq j \leq n-1\rangle, \] i.e., the algebraic group given by the affine coordinate ring \[ k[T_{i,j},\det(T_{i,j})^{-1}]/\langle T_{i,j}: i> j, I\rangle \] and the corresponding finite group of Lie type defined by the fixed points of the $d$-th power of the Frobenius. \begin{definition} Let $\Delta T_\alpha$ denote the subgroup of $T_\alpha(\mathbb{F}_{q^d})$ consisting of matrices given as in \eqref{actionMatrixav}. \end{definition}
\begin{remark}\label{select} Let $M \in \mathbb{F}_q[T]$ be arbitrary and nonzero. An element $f$ is invariant under the action of $H_{q^d,M}$ if, and only if, \begin{equation} \label{comp-cond} \boxed{ \sigma_D \circ \sigma(x)=\sigma \circ\sigma_D(x), \text{ for all } D\in \mathbb{F}_{q^d}[T]/M. } \end{equation} We now recall a classical result of descent theory. From a cohomological point of view, there is a natural action of $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q)$ on the $\mathbb{F}_{q^d}$-vector space $$V=H^0(K_{q^d,M},\Omega_{K_{q^d,M}}).$$ Let us consider a basis $\{\omega_1,\ldots,\omega_g\}$ of $V$, where $g$ denotes the genus of $K_{q^d,M}$. Define the map \begin{eqnarray*} \mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_q) &\rightarrow & \mathrm{GL}(V) \\ \sigma &\mapsto & \rho(\sigma): v \mapsto v^{\sigma} \end{eqnarray*} For each basis element $\omega_i$, $1\leq i \leq g$ we write \[ \omega_i^\sigma= \sum_{\nu=1}^g \rho(\sigma)_{\nu,i} \omega_\nu. \] Then, since $(\omega_i^{\sigma_1})^{\sigma_2}=\omega^{\sigma_1\sigma_2}$, we have \[ \omega_i^{\sigma_1 \sigma_2}=\sum_{\nu,\mu=1}^{g} \rho(\sigma_1)^{\sigma_2}_{\nu,i} \rho(\sigma_2)_{\mu,\nu} \omega_\mu \] so that the function $\rho$ satisfies the cocycle condition $\rho(\sigma_1\sigma_2)=\rho(\sigma_1)^{\sigma_2} \rho(\sigma_2).$ The multidimensional Hilbert's 90 theorem asserts that there is an element $\wp \in GL(V)$ such that $\rho(\sigma)=\wp^{-1}\wp^\sigma$. Moreover, the elements $\omega_i'=\omega_i \wp^{-1}$ are $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_{q})$-invariant since \[ (\omega_i \wp^{-1})^\sigma=(\omega_i^\sigma)(\wp^{-1})^\sigma= \omega_i \rho(\sigma)( \wp^{-1})^\sigma=\omega_i \wp^{-1}\wp^\sigma(\wp^{-1})^\sigma=\omega_i \wp^{-1}. \] From now on $\{\omega_i\}_{i=1,\ldots,g}$ denotes an $\mathrm{Gal}(\mathbb{F}_{q^d}/\mathbb{F}_{q})$-invariant basis. An arbitrary element $\omega \in V $ is written as \[ \omega= \sum_{i=1}^g a_i \omega_i \] and the action of $\sigma_D$ with respect to this basis is given by a representation \begin{eqnarray*} G_{q^d,M} & \rightarrow & GL(V) \\
\sigma_D & \mapsto & A(\sigma_D)=:A_D \end{eqnarray*} The condition of \eqref{comp-cond} is now expressed as the matrix condition \[ A_D \begin{pmatrix} a_1^q \\ \vdots \\a_g^q \end{pmatrix} =A_D^q \begin{pmatrix} a_1^q \\ \vdots \\a_g^q \end{pmatrix} \Leftrightarrow A_D^{q^{d-1}} \begin{pmatrix} a_1 \\ \vdots \\a_g \end{pmatrix} =A_D \begin{pmatrix} a_1 \\ \vdots \\a_g \end{pmatrix}. \] Equivalently, the common eigenspace in $V$ of the eigenvalue 1 of all matrices of the form $A_D^{q^{d-1}-1}$ gives the space of $H_{q^d,M}$-invariant differentials. The space $L_Y(\Omega_Y(\mathcal{D}))$, see \eqref{invariants1} consists of meromorphic differentials with allowed poles at $\mathcal{D}$, and it is only necessary to select the holomorphic differentials among these. \end{remark}
We now return to the case $M = P^\alpha$ and examine invariant rings. The group $\Delta T_\alpha$ is clearly abelian. The action of \eqref{actionMatrixav} has an extension to the polynomial ring $\mathbb{F}_{q^d}[\lambda_{i,0},\ldots,\lambda_{i,\alpha-1}]$. Consider the vector space of polynomials of multidegree, which we denote by $\mathrm{mdeg}$, bounded by $(\mu_0,\ldots,\mu_{\alpha-1})$: \[ W_{\bar{\mu}}:=\{ f \in \mathbb{F}_{q^d}[\lambda_0,\ldots,\lambda_{\alpha-1}] : \mathrm{mdeg}(f) \leq (\mu_0,\ldots,\mu_{\alpha-1}) \} \qquad (\bar{\mu} = (\mu_0,\ldots,\mu_{\alpha-1})). \] The space $W_{\bar{\mu}}$ inherits a unique representation of the group $(\mathbb{F}_{q^d}(T)/P^\alpha)^*$. Therefore, we obtain \begin{equation} \label{secondInvariant} H^0(Y,\Omega_Y) \subset L_Y(\Omega_Y(\mathcal{D}))= W_{\bar{\mu}}^{H_{q^d,P^\alpha}}. \end{equation} We thus consider the polynomial ring $\mathbb{F}_{q^d}[\lambda_0,\ldots,\lambda_{\alpha-1}]$ equipped with the natural extension of the linear action of \eqref{actionl} which is represented by the matrix in \eqref{actionMatrixav}. The space of invariants $\mathbb{F}_{q^d}[\lambda_0,\ldots,\lambda_{\alpha-1}]^{H_{q^d,P^\alpha}}$ is a finitely generated ring.
Consider the subgroup $H < \mathrm{GL}(\alpha,\mathbb{F}_{q^d})$ which consists of unitriangular elements of the form \eqref{actionMatrixav}, corresponding to the wild component of the cover $X \rightarrow Y$. Let us view the particular case of $\mathrm{GL}(3,\mathbb{F}_3)$, in order to simplify the presentation. In this case, the subgroup $H$ of Toeplitz matrices take the form \[ \sigma = \begin{pmatrix} 1 & a & b \\ 0 & 1 & a \\ 0 & 0 & 1
\end{pmatrix}, \qquad\qquad a,b \in \mathbb{F}_3.\] Viewing this matrix as acting on the ring $\mathbb{F}_3[x,y,z]$, we find $\sigma(x) = x$, and $$\sigma(y^3 - y x^2) = y^3 + a^3 x^2 - y x^2 - a x^3 = y^3 + a x^2 - y x^2 - a x^3 = y^3 - y x^2.$$ By modular representation theory \cite[Corollary 3.1.6]{CampWeh}, a homogeneous system of parameters $\{f,g,h\}$ for $\mathbb{F}_3[x,y,z]$ satisfies $$\mathbb{F}_3[f,g,h] = \mathbb{F}_3[x,y,z]^H$$ if, and only if, $$\deg(f) \deg(g) \deg(h) = |H|.$$ By definition, $|H| = 9$. Also by definition, we have $$\sigma(y) = y + ax,$$ so any invariant involving $y$ must have degree at least $q$. The same is true for $z$ as $$\sigma(z) = z + ay + bx.$$ As the invariant for $x$ is already of minimal degree (one), it follows that the remaining two invariants must be of degree $3 \mid 9$ if $\mathbb{F}_3[x,y,z]^H$ is polynomial. Let us then examine the action of $\sigma$ on all homogeneous terms of degree $3$ in the variables $x$, $y$, and $z$: \begin{center}{\tiny
$$ \begin{array}{||c |c| c| c |c||}
\hline
\text{Element} & \text{Constant} & x & x^2 & x^3 \\
\hline\hline
x^3 & 0 & 0 & 0& 0 \\
\hline
y^3 & 0 & 0 & 0 & a \\
\hline
z^3 & a y^3 & 0 & 0 & b \\
\hline
x^2 y & 0 & 0 & 0 & a \\
\hline
xy^2 & 0 & 0 & 2ay & a^2 \\
\hline
x^2 z & 0 & 0 & ay & b \\
\hline
x z^2 & 0 & a^2 y^2 + 2 a y z + z^2 & 2 a b y + 2 b z & b^2 \\
\hline
y^2 z & a y^3 + y^2 z & 2 a^2 y^2 + b y^2 + 2 a y z & a^3 y + 2 a b y + a^2 z & a^2 b \\
\hline
y z^2 & a^2 y^3 + 2 a y^2 z + y z^2 & a^3 y^2 + 2 a b y^2 + 2 a^2 y z + 2 b y z + a z^2 & 2 a^2 b y + b^2 y + 2 a b z & a b^2 \\
\hline
xyz & 0 & a y^2 + y z & a^2 y + b y + a z & ab \\
\hline \end{array}$$} \emph{The table of remainder coefficients via the $H$-action.} \end{center} Note that we are only considering the remainder coefficients, as the unitriangular action always returns an expansion containing the original element (the left-hand column). Clearly $f=x$ is the first invariant. The invariant of minimal degree containing $y$ is equal to the aforementioned $y^3 - y x^2$. It remains then to find the third invariant of degree $3$, which must contain the variable $z$. Examination of the coefficients in $x^3$, we find that there are only two other terms with equal coefficients: $x^2 z$ and $z^3$. But if an invariant contains these two terms, then as $x^2 z$ has a coefficient of $ay$ on $x^2$, it follows that it must contain another term with a coefficient equal to a multiply of $ay$ on $x^2$. The occurs in only one element: $x y^2$. But the coefficient of $x^3$ on $x y^2$ is equal to $a^2$, which matches no other terms of degree 3. Thus there is no invariant of degree 3 containing the element $z$. This argument may be easily generalised to our case of $\mathrm{GL}(\alpha,\mathbb{F}_{q^d})$. We thus obtain:
\begin{theorem} Let $H$ be the subgroup of upper unitriangular Toeplitz matrices in $\mathrm{GL}(\alpha,\mathbb{F}_{q^d})$. The ring of invariants $\mathbb{F}_{q^d}[\lambda_0,\ldots,\lambda_{\alpha-1}]^H$ is not polynomial. \end{theorem}
By Lemma \ref{Kummerfun}, we have $H_{q^d,P^\alpha}=(\sigma-1)G_{q^d,P^\alpha}$. When $\alpha = 3$, for example, an element of $H_{q^d,P^\alpha}$ takes the form (up to the tame part, i.e., a diagonal multiple)
\begin{align}\label{sigma-1}\notag \begin{pmatrix} 1 & \sigma(a) & \sigma(b) \\ 0 & 1 & \sigma(a) \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & a & b \\ 0 & 1 & a \\ 0 & 0 & 1 \end{pmatrix}^{-1}&=\begin{pmatrix} 1 & a^q & b^q\\ 0 & 1 & a^q \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & a & b \\ 0 & 1 & a \\ 0 & 0 & 1 \end{pmatrix}^{-1}\\ & = \left( \begin{array}{ccc}
1 & a^q-a & a\big(a^q-a\big)+b^q-b \\
0 & 1 & a^q-a \\
0 & 0 & 1 \\ \end{array} \right). \end{align} This may be easily generalised to arbitrary $\alpha$:
\begin{proposition} The upper diagonal entries of matrices for elements of $H_{q^d,P^\alpha}$ are $\mathbb{F}_{q^d}$-multiples of Frobenius differences $x^q - x$ $(x \in \mathbb{F}_{q^d})$. \end{proposition}
An explicit description of the holomorphic differentials of $K_{q,P^\alpha}$ requires computation of classical binomial coefficients occurring in the $H_{q^d,P^\alpha}$-action on the canonical basis consisting of elements of the form \eqref{hol13}. Although it would be desirable, no basis of cyclotomic holomorphic differentials is currently known which allows a description of this action in terms of the function field binomial coefficients $\bfrac{M}{i}_{q^d}$ appearing in the expansion of the additive Carlitz action \eqref{Carlitzaction}
$$C_{q^d}(M)(u) = \sum a_i \tau_{q^d}^i (u) = \sum_{i=0}^{\deg(M)} \bfrac{M}{i}_{q^d} u^{q^{di}}.$$ This fact is owed to linear dependence between terms: The Carlitz $M$-torsion module $C_{q^d}[M]$ is too small as an $\mathbb{F}_{q^d}$-vector space of dimension equal $\deg(M)$, far from sufficient to match genus growth \cite[Proposition 12.7.1]{salvador2007topics}. We leave this as an open question for a future work.
\end{document} | arXiv |
/[escript]/trunk/doc/inversion/Regularization.tex
Contents of /trunk/doc/inversion/Regularization.tex
Wed Dec 5 05:32:22 2012 UTC (7 years, 1 month ago) by caltinay
File MIME type: application/x-tex
A bit of doco cleanup.
1 \chapter{Regularization}\label{Chp:ref:regularization}
3 The general cost function $J_{total}$ to be minimized has some of the cost
4 function $J_{forward}$ measuring the defect of the result from the
5 forward model with the data, and the cost function $J_{reg}$ introducing the
6 regularization into the problem and makes sure that a unique answer exists.
7 The regularization term is a function of, possibly vector-valued, level set
8 function $m$ which represents the physical properties to be represented and is,
9 from a mathematical point of view, the unknown of the inversion problem.
10 It is the intention that the values of $m$ are between zero and one and that
11 actual physical values are created from a mapping before being fed into a
12 forward model. In general the cost function $J_{reg}$ is defined as
13 \begin{equation}\label{EQU:REG:1}
14 J_{reg}(m) = \frac{1}{2} \int_{\Omega}
15 \sum_{k} \mu^{(0)}_k \cdot s^{(0)}_k \cdot m_k^2 + \mu^{(1)}_{ki} \cdot s^{(1)}_{ki} \cdot L_i^2 \cdot m_{k,i} \cdot m_{k,i}
16 + \sum_{l<k} \mu^{(c)}_{lk} \cdot s^{(c)}_{lk} \cdot L^4 \cdot \sigma(m_l,m_k) dx
17 \end{equation}
18 where $s^{(0)}_k$, $s^{(1)}_{ki}$ and $s^{(c)}_{lk}$ are scaling factors with
19 values between zero and one (limits including).
20 They may vary with their location within the domain $\Omega$.
21 $L_i$ is the width of the domain in $x_i$ direction and $L^2=L_i \cdot L_i$.
22 $\sigma$ is a given symmetric, non-negative cross correlation function.
23 We use
25 \sigma(a,b) = ( a_{,i} \cdot a_{,i}) \cdot ( b_{,i} \cdot b_{,i}) - ( a_{,i} \cdot b_{,i})^2
27 Notice that the cross correlation function is measuring the angle between the
28 surface normals of contours of level set functions.
29 So minimizing the cost function will align the surface normals of the contours.
30 The additional weight factors $\mu^{(0)}_k$, $ \mu^{(1)}_{ki}$ and
31 $\mu^{(c)}_{lk}$ are between zero and one and constant across the domain.
32 They are potentially modified during the inversion in order to improve the
33 balance between the different terms in the cost function.
34 Notice that values for $\mu^{(0)}_k$, $ \mu^{(1)}_{ki}$ and $\mu^{(c)}_{lk}$
35 are relevant for which the values of the corresponding entries in scaling
36 factors $s^{(0)}_k$, $s^{(1)}_{ki}$ and $s^{(c)}_{lk}$ are non-zero.
37 Also notice that the factors $L^4$ and $L_i^2$ take care of any length scale changes.
38 With the notation
40 \begin{array}{rcl}
41 \widehat{s}^{(0)}_k & = & \mu^{(0)}_k \cdot w^{(0)}_k \\
42 \widehat{s}^{(1)}_{ki} & = & \mu^{(1)}_{ki} \cdot w^{(1)}_{ki} \cdot L_i^2 \\
43 \widehat{s}^{(c)}_{lk} & = & \mu^{c}_{lk} \cdot w^{(c)}_{lk} \cdot L^4 \\
44 \end{array}
46 with $k<l$ we can write
47 \begin{equation}\label{EQU:REG:1b}
48 J_{reg}(m) = \frac{1}{2} \int_{\Omega} \left(
49 \sum_{k} \widehat{s}^{(0)}_k \cdot m_k^2 + \widehat{s}^{(1)}_{ki} \cdot m_{k,i} \cdot m_{k,i}
50 + \sum_{l<k} \widehat{s}^{(c)}_{lk} \cdot \sigma(m_l,m_k) \right) dx
52 We need to provide the derivative $\frac{ \partial J_{reg}}{\partial q}$ of
53 the cost function $J_{reg}$ with respect to a given direction $q$ which equals
54 zero at locations where $m$ is assumed to be zero.
55 The derivative is given as
57 \frac{ \partial J_{reg}}{\partial q}(m) =
58 \int_{\Omega} Y_k \cdot q_k + X_{k,i} q_{k,i} dx
60 where
64 For a single-valued level set function this takes the form
67 \mu^{reg} \int_{\Omega} \omega \cdot m \cdot q + \omega_i \cdot L_i^2 \cdot m_{,i} \cdot q_{,i} dx
69 So we can represent the gradient $\nabla J_{reg}$ of the cost function
70 $J_{reg}$ by the pair of values $(Y,X)$ where we set
72 Y=\mu^{reg} \cdot \omega \cdot m \mbox{ and } X_i = \mu^{reg} \cdot \omega_i \cdot L_i^2 \cdot m_{,i}
74 and
75 \begin{equation}\label{EQU:REG:3c}
76 \frac{ \partial J_{reg}}{\partial q}(m) = [ \nabla J_{reg}(m), q ] =
77 \int_{\Omega} Y \cdot q + X_i \cdot q_{,i} dx
79 where $[.,.]$ is called the dual product.
83 ==============================================================
85 where $<.,.>$ is an inner product. If the level set function $m$ has several components $m_j$ the inner product $<.>$ is given
86 in the form
87 $\omega^{(k)}$ and $\omega^{(k)}_i$ are fixed non-negative weighting factors and $\mu^{reg}_k$ are weighting factors
88 which may be modified during the inversion. $L_i$ is the length of the domain in $x_i$ direction. In the special case that
89 the level set function $m$ has a single component the inner product takes the form
91 <p,q> =
92 \mu^{reg} \int_{\Omega} \omega \cdot p \cdot q + \omega_i \cdot L_i^2 \cdot p_{,i} \cdot q_{,i} dx
94 In practice it is assumed that the level set function is known to be zero in certain regions in the domain. Typically these regions
95 corresponds to region above the surface or regions explored by drilling.
97 We need to provide the derivative of the cost function $J_{reg}$ with respect to a given direction $q$ which equals zero at locations
98 where $m$ is assumed to be zero. For a single-valued
99 level set function th is takes the form
100 \begin{equation}\label{EQU:REG:3}
101 \frac{ \partial J_{reg}}{\partial q}(m) =
102 \mu^{reg} \int_{\Omega} \omega \cdot m \cdot q + \omega_i \cdot L_i^2 \cdot m_{,i} \cdot q_{,i} dx
103 \end{equation}
104 So we can represent the gradient $\nabla J_{reg}$ of the cost function $J_{reg}$ by the pair of values $(Y,X)$ where we set
105 \begin{equation}\label{EQU:REG:3b}
106 Y=\mu^{reg} \cdot \omega \cdot m \mbox{ and } X_i = \mu^{reg} \cdot \omega_i \cdot L_i^2 \cdot m_{,i}
109 \begin{equation}\label{EQU:REG:3c}
110 \frac{ \partial J_{reg}}{\partial q}(m) = [ \nabla J_{reg}(m), q ] =
111 \int_{\Omega} Y \cdot q + X_i \cdot q_{,i} dx
113 where $[.,.]$ is called the dual product.
115 For a multi-valued level set function an additional correlation term is introduced into the cost function $J_{total}$:
117 J_{reg}(m) = \frac{1}{2} < m, m > + \frac{1}{2} \sum_{k,l} \mu_{kl}^{sec} \cdot \int_{\Omega} \sigma(m_k,m_l) dx
119 where $sigma$ is a given symmetric, non-negative correlation function, and $\mu_{kl}^{sec}$ are symmetric, weighting factors
120 ($\mu_{kl}^{sec} = \mu_{lk}^{sec}$, $\mu_{kk}^{sec}=0$) which may
121 be altered during the inversion. We use the correlation function
123 \sigma(a,b) = \frac{L^2}{2} \cdot ( ( a_{,i} \cdot a_{,i}) \cdot ( b_{,i} \cdot b_{,i}) - ( a_{,i} \cdot b_{,i})^2 )
125 with $L=L_i \cdot L_i$. Minimizing $J_{reg}(m)$ is minimizing the angle between the surface normals of the contours formed by
126 two level set function. the derivative of the cost function $J_{reg}$ with respect to a given direction $q$ which equals zero at locations
127 where $m$ is assumed to be zero:
129 \begin{array}{ll}
130 \displaystyle{\frac{ \partial J_{reg}}{\partial q}(m)} =
131 \displaystyle{\sum_{k} \mu^{reg}_k \int_{\Omega} \omega^{(k)} \cdot m_k \cdot q_k + \omega^{(k)}_i \cdot L_i^2 \cdot m_{k,i} \cdot q_{k,i} dx } \\
132 + \displaystyle{\sum_{k,l} \mu_{kl}^{sec} \cdot {L^2} \int_{\Omega} ( m_{k,i} \cdot q_{k,i}) \cdot ( m_{l,j} \cdot m_{l,j}) - ( m_{k,j} \cdot m_{l,j}) \cdot ( q_{l,i} \cdot m_{k,i}) } dx
133 \end{array}
135 Similar to the single-case we can represent
136 the gradient $\nabla J_{reg}$ of the cost function $J_{reg}$ by the pair of values $(Y,X)$ where we set
138 Y_k= \mu^{reg}_k \cdot \omega^{(k)} \cdot m_k
142 X_{ki} = \mu^{reg}_k \cdot \omega^{(k)} \cdot L_i^2 \cdot m_{k,i} +
143 \sum_{l} \mu_{kl}^{sec} \cdot {L^2} \cdot ( ( m_{l,j} \cdot m_{l,j}) \cdot m_{k,i} - ( m_{l,j} \cdot m_{k,j}) \cdot m_{l,i} )
148 \int_{\Omega} Y_j \cdot q_j + X_{ki} \cdot q_{k,i} dx
150 where $[.,.]$ is the dual product.
152 We also need to provide an approximation of the inverse of the Hessian operator which provides a
153 level set function $h$ for a given value $r$ represented by the pair of values $(Y,X)$. If one ignores the correlation function
154 the inner product defines the Hessian operator of the cost function. In this approach we set
156 < p, h > = [p, r]
158 for all $p$. This problem can be solved using \escript \class{LinearPDE} class by setting
160 \begin{array}{rcl}
161 A_{ij} & =& (\omega_i \cdot L_i^2) \cdot \delta_{ij} \\
162 D & = & \mu^{reg} \cdot \omega
165 and $X$ and $Y$ as defined by $r$ for the case of a single-valued level set function.
166 For a vector-valued level-set function one sets:
169 A_{kilj} & = & (\mu^{reg}_l \omega^{(l)}_i L_i^2) \cdot \delta_{kl} \cdot \delta_{ij} \\
170 D_{kl} & = & \mu^{reg}_l \cdot \omega^{(l)} \delta_{kl} \omega
173 ====================================================
174 \begin{classdesc}{Regularization}{domain
175 \optional{, s0=\None}
177 \optional{, sc=\None}
178 \optional{, location_of_set_m=Data()}
179 \optional{, numLevelSets=1}
180 \optional{, useDiagonalHessianApproximation=\True}
181 \optional{, tol=1e-8}}
182 opens a linear, steady, second order PDE on the \member{domain}.
183 The parameters \member{numEquations} and \member{numSolutions} give the number
184 of equations and the number of solution components.
185 If \member{numEquations} and \member{numSolutions} are non-positive, then the
186 number of equations and the number of solutions, respectively, stay undefined
187 until a coefficient is defined.
188 \end{classdesc}
192 \section{The general regularization class}
193 \begin{classdesc}{RegularizationBase}{} | CommonCrawl |
Nataša Jonoska
Nataša Jonoska (Macedonian: Наташа Јоноска, pronounced [na'taʃa jɔ'noska]; born 1961,[1] also spelled Natasha Jonoska) is a Macedonian mathematician and professor at the University of South Florida known for her work in DNA computing.[2] Her research is about how biology performs computation, "in particular using formal models such as cellular or other finite types of automata, formal language theory symbolic dynamics, and topological graph theory to describe molecular computation."[3]
Nataša Jonoska
Born1961 (1961)
EducationSs. Cyril and Methodius University of Skopje
Binghamton University
AwardsRosenberg Tulip Award in DNA Computing, 2007
Scientific career
FieldsMathematics, Computer science, DNA computing
InstitutionsUniversity of South Florida
ThesisSynchronizing Representations of Sofic Systems (1993)
Websiteshell.cas.usf.edu/~jonoska/
She received her bachelor's degree in mathematics and computer science from Ss. Cyril and Methodius University of Skopje in Yugoslavia (now North Macedonia) in 1984. She earned her PhD in mathematics from the State University of New York at Binghamton in 1993 with the dissertation "Synchronizing Representations of Sofic Systems".[2] Her dissertation advisor was Tom Head.[4]
In 2007, she won the Rosenberg Tulip Award in DNA Computing for her work in applications of Automata theory and graph theory to DNA nanotechnology.[5] She was elected a AAAS Fellow in 2014[6] for advancements in understanding information processing in molecular self-assembly.[4] She is a board member for many journals including Theoretical Computer Science,[7] the International Journal of Foundations of Computer Science, Computability, and Natural Computing.[2] In 2022 she was awarded a Simons Fellowship.[8]
Notable publications
• J. Chen, N. Jonoska, G. Rozenberg, (eds). Nanotechnology: Science and Computing, Springer- Verlag 2006.
• N. Jonoska, Gh. Paun, G. Rozenberg, (eds.). Aspects of Molecular Computing LNCS 2950, Springer-Verlag 2004.
• N. Jonoska, N.C. Seeman, (eds.). DNA Computing, Revised papers from the 7th International Meeting on DNA-Based Computers, LNCS 2340, Springer-Verlag 2002.
References
1. Birth year from Library of Congress catalog entry, retrieved 2018-12-10.
2. "Nataša Jonoska". USF Department of Mathematics & Statistics. Retrieved 2017-03-02.
3. Jonoska, Nataša. Discrete and Topological Models in Molecular Biology. Springer.
4. "Mathematical Sciences Graduate Newsletter". Binghamton University. 2016-06-30. Archived from the original on 2017-03-07. Retrieved 2017-03-07.
5. "The Rosenberg Tulip Award in DNA Computing". ISNSCE. 2015-12-23. Archived from the original on 2017-03-03. Retrieved 2017-03-02.
6. "Jonoska, Natasha". American Association for the Advancement of Science. 2016-08-01. Archived from the original on 2017-03-07. Retrieved 2017-03-07.
7. "Theoretical Computer Science Editorial Board". Retrieved March 2, 2017.
8. "2022 Simons Fellows in Mathematics and Theoretical Physics Announced". Simons Foundation. 2022-02-18. Retrieved 2022-07-04.
External links
• dblp computer science bibliography
Authority control
International
• ISNI
• VIAF
National
• France
• BnF data
• Germany
• Israel
• United States
• Netherlands
Academics
• DBLP
• MathSciNet
• Mathematics Genealogy Project
• zbMATH
Other
• IdRef
| Wikipedia |
\begin{document}
\thispagestyle{empty}
\begin{center}
\resizebox{\linewidth}{!}{ \textbf{\Large Nonlinear analysis with endlessly continuable functions}}
\end{center}
\begin{center}
{\large Shingo \textsc{Kamimoto} and David \textsc{Sauzin}}
\end{center}
\begin{abstract}
We give estimates for the convolution product of an arbitrary number
of endlessly continuable functions. This allows us to deal with
nonlinear operations for the corresponding resurgent series,
e.g. substitution into a convergent power series.
\end{abstract}
\section{Introduction}\label{sec:0}
This is an announcement of our forthcoming paper \cite{KS}, the main subject of which is the ring structure of the space~$\mathscr R$ of \emph{resurgent} formal series.
Recall that~$\mathscr R$ is the subspace of the ring of formal series $\C[[z]]$ defined as
\beglab{eqdefgR}
\mathscr R \coloneqq \mathcal{B}^{-1}(\C\delta \oplus \hat\mathscr R),
\end{equation}
where
$\mathcal{B} \colon\thinspace \C[[z]] \to \C\delta \oplus \C[[\zeta]]$
is the formal Borel transform, defined by
\beglab{eqdefcB}
\tilde\varphi(z) = \sum_{j=0}^{\infty} \varphi_j z^{j}
\mapsto
\mathcal{B}(\tilde\varphi)(\zeta) = \varphi_0\delta + \hat\varphi(\zeta),
\enspace \text{with}\; \;
\hat\varphi(\zeta) \coloneqq \sum_{j=1}^{\infty} \varphi_j \frac{\zeta^{j-1}}{(j-1)!},
\end{equation}
and $\hat\mathscr R$ is the subspace of~$\C[[\zeta]]$ consisting of all convergent power series which are ``endlessly continuable''
in the following sense:
\begin{dfn} \label{defendlesscont}
A convergent power series $\hat\varphi\in\C\{\zeta\}$ is said to be
\emph{endlessly continuable} if, for every real $L>0$, there exists a
finite subset~$F_L$ of~$\C$ such that~$\hat\varphi$ can be
analytically continued along every Lipschitz path
$\gamma \colon\thinspace [0,1] \to \C$
of length $<L$
such that $\gamma(0)=0$ and $\gamma\big( (0,1] \big) \subset \C\setminus F_L$.
\end{dfn}
Resurgence theory was invented by J.~\'Ecalle in the early 1980s \cite{E} and has many applications in the study of holomorphic dynamical systems, analytic differential equations, WKB analysis, etc.
Here, we are dealing with a simplified version, inspired by \cite{CNP}, which is sufficient for most applications
(our definition of endlessly continuable functions is slightly more restrictive than the one in \cite{CNP}, which is itself less general than the definition of ``functions without a cut'' on which is based \cite{E}
-- see also \cite{DO}).
We are interested in nonlinear operations in the space of formal series, like substitution of one or several series without constant term $\tilde\varphi_1,\ldots, \tilde\varphi_r$ into a power series $F(w_1,\ldots,w_r)$, defined as
\beglab{eqdefsubstF}
F(\tilde\varphi_1,\ldots,\tilde\varphi_r) \coloneqq \sum_{k\in\N^r}
c_k \, \tilde\varphi_1^{k_1} \cdots \tilde\varphi_r^{k_r}
\end{equation}
for $F = \sum_{k\in\N^r} c_k \, w_1^{k_1} \cdots w_r^{k_r}$.
One of the main results of \cite{KS} is
\begin{thm} \label{thmsubstgR}
Let $r\ge1$ be an integer.
Then, for any convergent power series $F(w_1,\ldots,w_r) \in \C\{w_1,\ldots,w_r\}$
and for any resurgent series $\tilde\varphi_1,\ldots,\tilde\varphi_r \in \mathscr R$ without constant term,
\[
F(\tilde\varphi_1,\ldots,\tilde\varphi_r) \in \mathscr R.
\]
\end{thm}
It is the aim of this announcement to outline the idea of the proof, based on the notion of ``discrete filtered sets'' and quantitative estimates for the convolution of endless continuable functions.
Recall that the convolution in $\C[[\zeta]]$, defined as
$\hat\varphi_1 * \hat\varphi_2 \coloneqq
\mathcal{B}\big( \mathcal{B}^{-1}(\hat\varphi_1) \cdot \mathcal{B}^{-1}(\hat\varphi_2) \big)$
({\emph{i.e.}}\ the mere counterpart via~$\mathcal{B}$ of multiplication of formal series without constant term), takes the following form for convergent power series:
\begin{multline*}
\hat\varphi_1,\hat\varphi_2 \in \C\{\zeta\} \quad\Rightarrow\quad
\hat\varphi_1*\hat\varphi_2(\zeta) = \int_0^\zeta \hat\varphi_1(\zeta_1) \hat\varphi_2(\zeta-\zeta_1)\,{\mathrm d}\zeta_1 \\
\enspace\text{for}\;
\abs{\zeta} < \min\{ \operatorname{RCV}(\hat\varphi_1), \operatorname{RCV}(\hat\varphi_2) \},
\end{multline*}
where $\operatorname{RCV}(\,\cdot\,)$ is a notation for the radius of convergence of a power series.
The symbol~$\delta$ which appears in~\eqref{eqdefgR} and~\eqref{eqdefcB} is nothing but the convolution unit (obtained from $(\C[[\zeta]],*)$ by adjunction of unit);
convolution makes $\C\delta\oplus\C[[\zeta]]$ a ring (isomorphic to the ring of formal series $\C[[z]]$), of which $\C\delta\oplus\C\{\zeta\}$ is a subring.
It is proved in \cite{DO} that the convolution product of two endlessly continuable functions is endlessly continuable, hence
$\C\delta\oplus\hat\mathscr R$ is a subring of $\C\delta\oplus\C\{\zeta\}$
and $\mathscr R$ is a subring of $\C[[z]]$.
However, to reach the conclusions of Theorem~\ref{thmsubstgR}, precise estimates on the convolution product of an arbitrary number of endlessly continuable functions are needed,
so as to prove the convergence of the series of holomorphic functions
$\sum c_k \, \hat\varphi_1^{*k_1} * \cdots * \hat\varphi_r^{*k_r}$
and to check its endless continuability.
\begin{rem} \label{remOmcontrestr}
Let $\Omega$ be a nonempty closed discrete subset of~$\C$.
If a convergent power series~$\hat\varphi$ meets the requirement of Definition~\ref{defendlesscont} with
\beglab{eqdefOmLrestr}
F_L = \{\, \omega \in \Omega \mid \abs{\omega} \le L \,\}
\quad\text{for each $L>0$,}
\end{equation}
then it is said to be \emph{$\Omega$-continuable}.
Pulling back this definition by~$\mathcal{B}$, we obtain the definition of an \emph{$\Omega$-resurgent series}, which is a particular case of resurgent series.
It is proved in \cite{SFunkEkva} that the space of $\Omega$-continuable functions is closed under convolution if and only if $\Omega$ is stable under addition.
Under that assumption, the space of $\Omega$-resurgent series is thus a subring of $\C[[z]]$; nonlinear analysis with $\Omega$-resurgent series is dealt with in \cite{NLresur}, where an analogue of Theorem~\ref{thmsubstgR} is proved for them.
\end{rem}
Our study of endlessly continuable functions and our proof of Theorem~\ref{thmsubstgR} are based on the notion of ``$\Omega$-continuable function'', where $\Omega$ is a ``discrete
filtered set'' in the sense of \cite{DO};
this is a generalization of the situation described in Remark~\ref{remOmcontrestr}, so that the meaning
of $\Omega$-continuability will now be more extended ($\Omega$ will stand for a family of finite sets $(\Omega_L)_{L\ge0}$ not necessarily of the form~\eqref{eqdefOmLrestr}).
The plan of the paper is as follows.
Discrete filtered sets and the corresponding $\Omega$-continuable functions are defined in Section~\ref{sec:dfs},
where we give a refined version of the main result, Theorem~\ref{thmsubstOmgR}.
Then, in Section~\ref{sec:pfthm}, we state Theorem~\ref{thm:1.12} which gives precise estimates for the convolution product of an arbitrary number of $\Omega$-continuable functions, and show how this implies Theorem~\ref{thmsubstOmgR}.
Finally, in Section~\ref{sec:isot}, we sketch the main step of the proof of Theorem~\ref{thm:1.12}.
\section{Discrete filtered sets and $\Omega$-resurgent series}\label{sec:dfs}
\subsection{$\Omega$-continuable functions and $\Omega$-resurgent series}
We use the notations
\[
\N = \{0,1,2,\ldots\}, \qquad
\R_{\geq0} = \{\lambda\in\R\ |\ \lambda\geq0\}.
\]
\begin{dfn}[Adapted from \cite{CNP},\cite{DO}]
A \emph{discrete filtered set}, or \emph{d.f.s.}\ for short, is a family $\Omega = (\Omega_L)_{L\in\R_{\geq0}}$ of subsets of~$\C$ such that
\begin{enumerate}[i)]
\item
$\Omega_L$ is a finite set for each $L\in\R_{\geq0}$,
\item
$\Omega_{L_1}\subseteq \Omega_{L_2}$ for $L_1\leq L_2$,
\item
there exists $\delta>0$ such that $\Omega_\delta=\O$.
\end{enumerate}
Given a d.f.s.~$\Omega$, we set
\[
\mathcal{S}_\Omega \coloneqq \big\{ (\lambda,\omega)\in\R_{\geq0}\times\C \mid \omega\in\Omega_\lambda \big\}
\]
and define $\overline\mathcal{S}_\Omega$ as the closure of $\mathcal{S}_\Omega$ in $\R_{\geq0}\times\C$. We then call
\[
\mathcal{M}_\Omega \coloneqq \big(\R_{\geq0}\times\C\big) \setminus \overline\mathcal{S}_\Omega
\quad \text{(open subset of $\R_{\geq0}\times\C$)}
\]
the \emph{allowed open set} associated with~$\Omega$.
\end{dfn}
\begin{dfn} \label{defOmallowedpaths}
We denote by~$\Pi$ the set of all Lipschitz paths
$\gamma \colon\thinspace [0,t_*] \to \C$ such that $\gamma(0)=0$, with some real $t_*\ge0$ depending on~$\gamma$.
We then denote by $\gamma_{|t} \in \Pi$ the restriction of~$\gamma$ to the interval $[0,t]$ for any $t\in[0,t_*]$, and by $L(\gamma)$ the total length of~$\gamma$.
Given a d.f.s.~$\Omega$, we call \emph{$\Omega$-allowed path} any $\gamma\in\Pi$ such that
\[
\big( L(\gamma_{|t}), \gamma(t) \big) \in \mathcal{M}_\Omega
\enspace\text{for all $t$.}
\]
We denote by $\Pi_\Omega$ the set of all $\Omega$-allowed paths.
\end{dfn}
\begin{dfn} \label{defOmcontOmres}
Given a d.f.s.~$\Omega$, we call \emph{$\Omega$-continuable function} a holomorphic germ $\hat\varphi \in \C\{\zeta\}$ which can be analytically continued along any path $\gamma\in\Pi_{\Omega}$.
We denote by~$\hat\mathscr R_\Omega$ the set of all $\Omega$-continuable functions and define
\[
\mathscr R_\Omega \coloneqq \mathcal{B}^{-1} \big( \C\delta \oplus \hat\mathscr R_\Omega \big)
\]
to be the set of \emph{$\Omega$-resurgent} series.
\end{dfn}
\begin{exa} \label{exacloseddiscOm}
Given a closed discrete subset~$\Omega$ of~$\C$, the formula $\tilde\Omega_L \coloneqq \{\, \omega \in \Omega \mid \abs{\omega} \le L \,\}$ for $L\in\R_{\geq0}$ defines a d.f.s.~$\tilde\Omega$.
Then the notion of $\Omega$-continuability defined in Remark~\ref{remOmcontrestr} agrees with the notion of $\tilde\Omega$-continuability of Definition~\ref{defOmcontOmres}.
Thus we can identify the set~$\Omega$ and the d.f.s.~$\tilde\Omega$.
\end{exa}
The relation between the $\Omega$-continuable functions or the $\Omega$-resurgent series of Definition~\ref{defOmcontOmres} and the resurgent series or the endlessly continuable functions of Section~\ref{sec:0} is as follows:
\begin{prp} \label{propidgROmgR}
A formal series $\tilde\varphi\in\C[[z]]$ is resurgent if and only if there exists a d.f.s.~$\Omega$ such that $\tilde\varphi$ is $\Omega$-resurgent.
Correspondingly,
\beglab{eqidentitygROmgR}
\hat\mathscr R = \bigcup_{\Omega\in\{\text{d.f.s.}\}} \hat\mathscr R_\Omega.
\end{equation}
\end{prp}
The proof of Proposition~\ref{propidgROmgR} is outlined in Section~\ref{sec:pfprpRes}.
\begin{rem} \label{reminclusdfs}
Observe that
\[
\Omega \subset \Omega' \quad\Rightarrow\quad
\mathscr R_\Omega \subset \mathscr R_{\Omega'},
\]
where the symbol $\subset$ in the left-hand side stands for the partial order defined by $\Omega_L \subset \Omega'_L$ for each~$L$.
Indeed, $\Omega\subset\Omega'$ implies $\mathcal{S}_\Omega\subset\mathcal{S}_{\Omega'}$, hence
$\mathcal{M}_{\Omega'} \subset \mathcal{M}_\Omega$ and $\Pi_{\Omega'} \subset \Pi_\Omega$.
\end{rem}
\begin{rem}
Obviously, entire functions are always $\Omega$-continuable:
$\mathscr O(\C) \subset \hat\mathscr R_\Omega$ for all d.f.s.~$\Omega$
(e.g.\ because $\mathscr O(\C) = \hat\mathscr R_{\O}$, denoting by~$\O$ the trivial d.f.s.).
The inclusion is not necessarily strict for a non-trivial d.f.s.\
In fact, one can show that
\[
\hat\mathscr R_\Omega = \mathscr O(\C)
\quad \Leftrightarrow \quad
\forall L>0,\; \exists L'>L\; \text{such that} \;
\Omega_{L'} \subset \{\, \omega\in\C \mid \abs{\omega} < L \,\}.
\]
A simple example where this happens is when $\Omega_L=\O$ for $0\le L<2$ and $\Omega_L = \{1\}$ for $L\ge2$.
\end{rem}
\subsection{Sums of discrete filtered sets} \label{sec:sumsdsf}
The proof of the following lemma is easy and left to the reader.
\begin{lmm}
Let~$\Omega$ and~$\Omega'$ be two d.f.s.\
Then the formula
\[
(\Omega *\Omega')_L \coloneqq \{\, \omega_1+\omega_2 \mid
\omega_1\in\Omega_{L_1}, \omega_2\in\Omega'_{L_2}, L_1+L_2=L \, \}
\cup\Omega_{L}\cup\Omega'_{L}
\quad\text{for $L\in\R_{\geq0}$}
\]
defines a d.f.s.\ $\Omega*\Omega'$.
The law~$*$ on the set of all d.f.s.\ is commutative and associative.
The formula $\Omega^{*n} \coloneqq
\underbrace{ \Omega* \cdots*\Omega }_{\text{$n$ times}}$
(for $n\ge1$) defines an inductive system and
\[
\Omega^{*\infty} \coloneqq \varinjlim_n\ \Omega^{*n}
\]
is a d.f.s.
\end{lmm}
We call $\Omega*\Omega'$ the \emph{sum} of the d.f.s.~$\Omega$ and~$\Omega'$.
In \cite{DO} the following is claimed:
\begin{thm}[\cite{DO}]\label{thm:DO}
Assume that $\Omega$ and $\Omega'$ are d.f.s.\ and $\tilde\varphi\in\mathscr R_\Omega$,
$\tilde\psi\in\mathscr R_{\Omega'}$.
Then the product series $\tilde\varphi \cdot\tilde\psi$ is $\Omega*\Omega'$-resurgent.
\end{thm}
In view of Proposition~\ref{propidgROmgR}, a direct consequence of Theorem~\ref{thm:DO} is
\begin{crl}
The space of resurgent formal series~$\mathscr R$ is a subring of the ring
of formal series $\C[[z]]$. \end{crl}
Similarly, in view of Proposition~\ref{propidgROmgR}, Theorem~\ref{thmsubstgR} is a direct consequence of
\begin{thm} \label{thmsubstOmgR}
Let $r\ge1$ be integer and let $\Omega_1$, \ldots, $\Omega_r$ be d.f.s.\
Then for any convergent power series $F(w_1,\ldots,w_r) \in \C\{w_1,\ldots,w_r\}$
and for any $\tilde\varphi_1,\ldots,\tilde\varphi_r \in \C[[z]]$ without constant term, one has
\[
\tilde\varphi_1 \in \mathscr R_{\Omega_1}, \ldots, \tilde\varphi_r \in \mathscr R_{\Omega_r}
\quad \Rightarrow \quad
F(\tilde\varphi_1,\ldots,\tilde\varphi_r) \in \mathscr R_{\Omega^*},
\]
where $\Omega^* \coloneqq (\Omega_1 * \cdots * \Omega_r)^{*\infty}$.
\end{thm}
The proof of Theorem~\ref{thmsubstOmgR} is outlined in Sections~\ref{sec:pfthm} and~\ref{sec:isot}.
Theorem~\ref{thm:DO} may be viewed as a particular case of Theorem~\ref{thmsubstOmgR} (by taking $F(w_1,w_2)=w_1 w_2$).
The proof of the former theorem consists in checking that, for $\hat\varphi\in\hat\mathscr R_\Omega$ and $\hat\psi \in \hat\mathscr R_{\Omega'}$, the convolution product $\hat\varphi*\hat\psi$ can be analytically continued along the paths of $\Pi_{\Omega*\Omega'}$ and thus belongs to $\hat\mathscr R_{\Omega*\Omega'}$.
In the situation of Theorem~\ref{thmsubstOmgR}, with the notation~\eqref{eqdefsubstF}, we have
$\hat\psi_k \coloneqq c_k \, \hat\varphi_1^{*k_1} * \cdots * \hat\varphi_r^{*k_r} \in \hat\mathscr R_{\Omega^*}$
for each nonzero $k\in\N^r$, but some analysis is required to prove the convergence of the series $\sum\hat\psi_k$ of $\Omega^*$-continuable functions in~$\hat\mathscr R_{\Omega^*}$;
what we need is a precise estimate for the convolution product of an arbitrary number of endlessly continuable functions,
and this will be the content of Theorem~\ref{thm:1.12}.
In the particular case of a closed discrete subset~$\Omega$ of~$\C$ assumed to be stable under the addition and viewed as a d.f.s.\ as in Example~\ref{exacloseddiscOm}, we have $\Omega^{*\infty} = \Omega$
and Theorem~\ref{thm:1.12} was proved for that case in \cite{NLresur}.
One of the main purposes of \cite{KS} is to extend the techniques of \cite{NLresur} to the more general setting of endlessly continuable functions.
\subsection{Upper closure of a d.f.s.\ and sketch of proof of
Proposition~\ref{propidgROmgR}} \label{sec:pfprpRes}
The proof of Proposition~\ref{propidgROmgR} makes use of the notion of ``upper closure'' of a d.f.s., which allows to simplify a bit the definition of $\Omega$-allowedness for a path, and thus of $\Omega$-continuability for a holomorphic germ.
\begin{dfn}
We call \emph{upper closure} of a d.f.s.~$\Omega$ the family of sets $\tilde\Omega = (\tilde\Omega)_{L\ge0}$ defined by
\[
\tilde\Omega_L \coloneqq \bigcap_{\varepsilon>0} \Omega_{L+\varepsilon}
\quad\text{for every $L\in\R_{\geq0}$.}
\]
\end{dfn}
Notice that $\Omega \subset \tilde\Omega$.
\begin{lmm} \label{lemclosOm}
Let $\Omega$ be a d.f.s.\
Then its upper closure~$\tilde\Omega$ is a d.f.s., and there exists a real sequence $(L_n)_{n\ge0}$ such that
$0=L_0 < L_1 < L_2 < \cdots$
and
\[
L_n < L < L_{n+1}
\quad \Rightarrow \quad
\tilde\Omega_{L_n} = \tilde\Omega_L = \Omega_L
\]
for every integer $n\ge0$.
\end{lmm}
\begin{lmm} \label{lemOmallowedness}
Let $\Omega$ be a d.f.s.. Then
\beglab{eqovcSOmcStiOm}
\overline\mathcal{S}_\Omega = \mathcal{S}_{\tilde\Omega}.
\end{equation}
Consequently, $\Omega$-allowedness admits the following characterization:
for a path $\gamma\in\Pi$,
\begin{align*}
\gamma \in \Pi_\Omega
\quad&\Leftrightarrow\quad
\text{for all $t$,}\;\,
\gamma(t) \in \C \setminus \tilde\Omega_{L(\gamma_{|t})} \\[1ex]
&\Leftrightarrow\quad
\text{for all $t$,\; $\exists n$ such that}\;\,
L(\gamma_{|t}) < L_{n+1}
\enspace\text{and}\enspace
\gamma(t) \in \C \setminus \tilde\Omega_{L_n}
\end{align*}
(with the notation of Lemma~\ref{lemclosOm}).
\end{lmm}
The proofs of Lemma~\ref{lemclosOm} and Lemma~\ref{lemOmallowedness} are easy; see \cite{KS} for the details.
Notice that, given~$\Omega$ and $\gamma\in\Pi_\Omega$, it may be impossible to find \emph{one} real $L\ge L(\gamma)$ such that $\gamma(t) \in \C\setminus\tilde\Omega_L$ for \emph{all} $t>0$.
Take for instance~$\Omega$ defined by $\Omega_L \coloneqq \O$ for $0\le L < 2$ and $\Omega_L \coloneqq \{1,2\}$ for $L\ge2$ (so $\Omega = \tilde\Omega$ in that case),
and $\gamma\in\Pi_\Omega$ following the line segment $[0,3/2]$, then winding once around~$2$ and ending at~$3/2$:
no ``uniform''~$L$ can be found for that path.
Observe that, in that example, there exists $\hat\varphi\in\hat\mathscr R_\Omega$ with an analytic continuation along~$\gamma$ such that the resulting holomorphic germ at~$3/2$ is singular at~$1$ (but~$1$ is not singular for the principal branch of~$\hat\varphi$).
This is why the proof of Proposition~\ref{propidgROmgR} requires a bit of work.
\begin{proof}[Sketch of the proof of Proposition~\ref{propidgROmgR}]
It is sufficient to prove~\eqref{eqidentitygROmgR}.
Suppose $\hat\varphi \in \hat\mathscr R_\Omega$ for a certain d.f.s.~$\Omega$ and let $L>0$.
Then~$\hat\varphi$ meets the requirement of Definition~\ref{defendlesscont} with $F_L = \tilde\Omega_L$,
hence $\hat\varphi\in\hat\mathscr R$.
Thus $\hat\mathscr R_\Omega \subset \hat\mathscr R$.
Suppose now $\hat\varphi\in\hat\mathscr R$.
In view of Definition~\ref{defendlesscont}, we have $\delta \coloneqq \operatorname{RCV}(\hat\varphi) >0$ and, for each positive integer~$n$, we can choose a finite set~$F_{n}$ such that
\begin{eq-text} \label{eqpropertyFnde}
the germ~$\hat\varphi$ can be analytically continued along any path $\gamma\colon\thinspace[0,1]\to\C$ of~$\Pi$ such that $L(\gamma) < (n+1)\delta$ and $\gamma\big( (0,1] \big) \subset \C\setminus F_{n}$.
\end{eq-text}
Let $F_0\coloneqq \O$. The property~\eqref{eqpropertyFnde} holds for $n=0$ too.
For every real $L\ge0$, we set
\[
\Omega_L \coloneqq \bigcup_{k=0}^n F_{k}
\qquad \text{with $n \coloneqq \floor{L/\delta}$.}
\]
One can check that $\Omega\coloneqq (\Omega_L)_{L\in\R_{\geq0}}$ is a d.f.s.\ which coincides with its upper closure.
In \cite{KS}, it is shown with the help of Lemma~\ref{lemOmallowedness} that $\hat\varphi\in\hat\mathscr R_\Omega$.
\end{proof}
\section{The Riemann surface~$X_\Omega$ -- an estimate
for the convolution product of several $\Omega$-continuable functions} \label{sec:pfthm}
As announced in Section~\ref{sec:sumsdsf}, we will now state a theorem from which Theorem~\ref{thmsubstOmgR} and thus Theorem~\ref{thmsubstgR} follow.
A few preliminaries are necessary.
In all this section we suppose that~$\Omega$ is a fixed d.f.s.\
\begin{dfn}[ Adapted from \cite{DO}]
We call \textit{$\Omega$-endless Rieman surface} any triple $(X,\mathfrak{p},\un{0})$ such that
$X$ is a connected Riemann surface,
$\mathfrak{p} \colon\thinspace X \to \C$ is a local biholomorphism,
$\un{0} \in \mathfrak{p}^{-1}(0)$,
and any path $\gamma \colon\thinspace [0,t_*] \to \C$ of~$\Pi_\Omega$ has a lift
$\un{\ga} \colon\thinspace [0,t_*] \to X$ such that $\un{\ga}(0) = \un{0}$.
\end{dfn}
Notice that, given $\gamma \in \Pi_\Omega$, the lift~$\un{\ga}$ is unique (because the fibres of~$\mathfrak{p}$ are discrete).
It is shown in \cite{KS} how, among all $\Omega$-endless Riemann surfaces, one can construct an object $(X_{\Omega},\mathfrak{p}_\Omega,\un{0}_\Omega)$ which is cofinal in the following sense:
\begin{prp} \label{lemuniversalXOm}
There exists an $\Omega$-endless Riemann surface $(X_{\Omega},\mathfrak{p}_\Omega,\un{0}_\Omega)$ such that, for any $\Omega$-endless Riemann surface $(\tilde X,\tilde\mathfrak{p},\tilde\un{0})$, there is a local biholomorphism $\mathfrak{q} \colon\thinspace X_\Omega \to \tilde X$ such that $\mathfrak{q}(\un{0}_\Omega)=\tilde\un{0}$ and the diagram
\[
\begin{xy} (0,20) *{X_{\Omega}}, (30,20) *{\tilde X}, (15,0) *{\C}, {(6,20) \ar (24,20)}, {(2,16) \ar (13,4)}, {(28,16) \ar (17,4)},
(14,23) *{\mathfrak{q}},
(3,10) *{\mathfrak{p}_\Omega},
(27,10) *{\tilde\mathfrak{p}}
\end{xy}
\]
is commutative.
The $\Omega$-endless Riemann surface $(X_{\Omega},\mathfrak{p}_\Omega,\un{0}_\Omega)$ is unique up to isomorphism
and $X_\Omega$ is simply connected.
\end{prp}
The reader is referred to \cite{KS} for the proof.
Notice that in particular, for any d.f.s.~$\Omega'$ such that $\Omega\subset\Omega'$ as in Remark~\ref{reminclusdfs},
Proposition~\ref{lemuniversalXOm} yields a local biholomorphism $\mathfrak{q} \colon\thinspace X_{\Omega'}\to X_{\Omega}$.
For an arbitrary connected Riemann surface~$X$, we denote by~$\mathscr O_X$ the sheaf of holomorphic functions on~$X$.
If $\mathfrak{p} \colon\thinspace X \to \C$ is a local biholomorphism, then there is a natural morphism
$\mathfrak{p}^* \colon\thinspace \mathfrak{p}^{-1}\mathscr O_{\C} \to \mathscr O_X$.
Recall that $\mathfrak{p}^{-1}\mathscr O_{\C}$ is a sheaf on~$X$, whose stalk at a point $\un\zeta_* \in \mathfrak{p}^{-1}(\zeta_*)$ is
$\big( \mathfrak{p}^{-1}\mathscr O_{\C} \big)_{\un\zeta_*} = \mathscr O_{\C,\mathfrak{p}(\un\zeta_*)} \cong \C\{\zeta-\zeta_*\}$.
\begin{lmm}
Let $\hat\varphi \in \C\{\zeta\} = \mathscr O_{\C,0}$.
Then the following properties are equivalent:
\begin{enumerate}[{\rm i)}]
\item
$\hat\varphi\in\mathscr O_{\C,0}$ is $\Omega$-continuable,
\item
$\mathfrak{p}_\Omega^*\hat\varphi \in \mathscr O_{X_{\Omega},\un{0}_\Omega}$ can be analytically continued along any path on $X_{\Omega}$,
\item
$\mathfrak{p}_\Omega^*\hat\varphi \in \mathscr O_{X_{\Omega},\un{0}_\Omega}$ can be extended to
$\Gamma(X_{\Omega},\mathscr O_{X_{\Omega}})$.
\end{enumerate}
\end{lmm}
So, the morphism~$\mathfrak{p}_\Omega^*$ allows us to identify an $\Omega$-continuable function with a function holomorphic on the whole of the Riemann surface~$X_\Omega$:
\[
\restr{\mathfrak{p}_\Omega^*}{\hat\mathscr R_\Omega} \colon\thinspace
\hat\mathscr R_\Omega \xrightarrow{\smash{\ensuremath{\sim}}} \Gamma(X_{\Omega},\mathscr O_{X_{\Omega}}).
\]
The reader is referred to \cite{KS} for the details.
\begin{nota}
For $\delta>0$ small enough so that $\Omega_\delta=\O$ and for $L>0$, we set
\begin{gather*}
\Pi_\Omega^{\delta,L} \coloneqq \big\{\, \gamma\in\Pi \mid
L(\gamma) \le L \;\;\text{and}\;\;
\abs{ L(\gamma_{|t})-\lambda }^2 + \abs{ \gamma(t)-\omega }^2 \ge \delta^2
\;\, \text{for all $(\lambda,\omega)\in\mathcal{S}_\Omega$ and $t$} \,\big\}, \\[1ex]
K_{\Omega}^{\delta,L} \coloneqq \big\{\, \un\zeta\in X_\Omega \mid
\exists t_*\ge0 \;\,\text{and}\;\, \exists \gamma \colon\thinspace [0,t_*] \to \C
\;\text{path of $\Pi_\Omega^{\delta,L}$ such that
$\un\zeta = \un{\ga}(t_*)$}
\,\big\}.
\end{gather*}
\end{nota}
The condition $\Omega_\delta=\O$ is meant to ensure that
$\Pi_\Omega^{\delta,L}$ is a nonempty subset of $\Pi_\Omega$ and hence
$K_\Omega^{\delta,L}$ is a nonempty compact subset of~$X_\Omega$.
In fact, with the notation of Lemma~\ref{lemclosOm}, $\Omega_\delta=\O$ as soon as $\delta<L_1$ and then, for every $\gamma\in\Pi$,
\[
L(\gamma)+\delta \le L_1
\quad \Rightarrow \quad
\gamma \in \Pi_\Omega^{\delta,L}
\enspace \text{for all $L \ge L(\gamma)$.}
\]
(In particular, if $L+\delta\le L_1$, then $\Pi_\Omega^{\delta,L}$ consists exactly of the paths of~$\Pi$ which have length $\le L$.)
Notice that, if $\Omega_\delta = \O$, then $\Omega^{*n}_\delta=\O$ for all $n\ge1$ and $\Omega^{*\infty}_\delta=\O$.
On the other hand, for a given d.f.s.~$\Omega$, the family $(K_\Omega^{\delta,L})_{\delta,L>0}$ yields an exhaustion of~$X_\Omega$ by compact subsets.
We are now ready to state the main result of this section,
which is the analytical core of our study of the convolution of endelssly continuable functions:
\begin{thm}\label{thm:1.12}
Let $\Omega$ be a d.f.s.\ and let $\delta,L>0$ be reals such that $\Omega_{2\delta}=\O$.
Then there exist $c,\delta'>0$ such that $\delta'\le\delta$ and, for every integer $n\ge1$ and for every
$\hat f_1, \ldots, \hat f_n \in \hat\mathscr R_\Omega$,
the function $1*\hat f_{1}*\cdots *\hat f_{n}$ belongs to $\hat\mathscr R_{\Omega^{*n}}$
and satisfies the following estimates:
\beglab{1.11}
\sup_{K_{\Omega^{*n}}^{\delta,L}} \abs*{
\mathfrak{p}_{\Omega^{*n}}^* \big( 1*\hat f_{1}*\cdots *\hat f_{n}\big )
}
\leq
\frac{c ^n}{n!}
\ \sup_{\substack{ L\pp1,\ldots,L\pp n>0 \\ L\pp 1+\cdots+L\pp n=L}}
\ \sup_{K_{\Omega}^{\delta',L\pp 1}} \abs{ \mathfrak{p}_\Omega^{*} \hat f_1 }
\, \cdots
\sup_{K_{\Omega}^{\delta',L\pp n}} \abs{ \mathfrak{p}_\Omega^{*} \hat f_n }.
\end{equation}
\end{thm}
The main step of the proof of Theorem~\ref{thm:1.12} is sketched in Section~\ref{sec:isot}
(possible values for~$c$ and~$\delta'$ are indicated in~\eqref{eqdefdepcthmestim};
the point is that they depend on~$\Omega$, $\delta$ and~$L$, but not on~$n$ nor on $\hat f_1, \ldots, \hat f_n$).
The full proof of Theorem~\ref{thm:1.12} is in \cite{KS}.
\begin{proof}[Theorem~\ref{thm:1.12} implies
Theorem~\ref{thmsubstOmgR}]
Let $r\ge1$ and let $\Omega_1,\ldots,\Omega_r$ be d.f.s.\
Let
$\Omega \coloneqq \Omega_1 * \cdots * \Omega_r$,
so that $\Omega_i \subset \Omega$ and $\hat\mathscr R_{\Omega_i} \subset \hat\mathscr R_\Omega$ for $i=1,\ldots,r$.
Let $F \in \C\{w_1,\ldots,w_r\}$. Denote its coefficients by $(c_k)_{k\in\N^r}$ as in~\eqref{eqdefsubstF} and pick $C,\Lambda>0$ such that
$\abs{c_k} \le C \Lambda^{\abs{k}}$ for all~$k$,
with the notation $\abs{k} \coloneqq k_1+\cdots+k_r$.
Let $\tilde\varphi_1,\ldots\tilde\varphi_r$ be formal series without constant term such that $\hat\varphi_i \coloneqq \mathcal{B}\tilde\varphi_i \in \mathscr R_{\Omega_i}$ for each~$i$.
We get the uniform convergence of
$\sum c_k\, \mathfrak{p}_{\Omega^{*\infty}}^* (1*\hat\varphi_1^{*k_1}*\cdots*\hat\varphi^{*k_r})$
on every compact subset of~$X_{\Omega^{*\infty}}$ by means of estimates of the form
\[
\sup_{K_{\Omega^{*\infty}}^{\delta,L}} \abs{ c_k\,\mathfrak{p}_{\Omega^{*\infty}}^* (1*\hat\varphi_1^{*k_1}*\cdots*\hat\varphi^{*k_r}) }
\le
\sup_{K_{\Omega^{*n}}^{\delta,L}} \abs{ c_k\,\mathfrak{p}_{\Omega^{*n}}^* (1*\hat\varphi_1^{*k_1}*\cdots*\hat\varphi^{*k_r}) }
\le
C \Lambda^n \cdot \frac{c^n}{n!} \cdot M^n,
\]
where $\delta,L>0$ with $\Omega_{2\delta}=\O$, $n\coloneqq \abs{k} \ge1$,
$M \coloneqq \sup_{1\le i\le r}\, \sup_{K_{\Omega}^{\delta',L}} \abs{ \mathfrak{p}_\Omega^{*} \hat\varphi_i }$,
and the positive reals~$c$ and~$\delta'$ stem from Theorem~\ref{thm:1.12}.
\end{proof}
\section{Sketch of the proof of Theorem~\ref{thm:1.12} -- construction
of adapted deformations of the identity} \label{sec:isot}
\subsection{Preliminaries}
Let $\Omega$ be a d.f.s.\
Recall from Definition~\ref{defOmallowedpaths} and~\ref{defOmcontOmres} that $\Omega$-continuability is defined by means of the allowed open subset $\mathcal{M}_\Omega$ of $\R_{\geq0}\times\C$ associated with~$\Omega$, and of paths $\gamma\in\Pi$ which satisfy
\[
\tilde\gamma(t) \coloneqq \big( L(\gamma_{|t}), \gamma(t) \big) \in \mathcal{M}_\Omega
\quad\text{for all $t$.}
\]
The latter condition is $\gamma\in\Pi_\Omega$.
Conversely, notice that
\begin{eq-text} \label{eqtextcharacOmalltiga}
if $t \in [0,t_*] \mapsto
\tilde\gamma(t) = \big( \lambda(t),\gamma(t) \big) \in \mathcal{M}_\Omega$
is a piecewise $C^1$ path such that $\tilde\gamma(0)=(0,0)$ and
$\lambda'(t) = \abs{\gamma'(t)}$ for a.e.~$t$, then $\gamma\in\Pi_\Omega$.
\end{eq-text}
Recall from Section~\ref{sec:pfthm} that, if $\gamma \colon\thinspace [0,t_*] \to \C$ is a path of~$\Pi_\Omega$, then there is a unique path
$\un{\ga} \colon\thinspace [0,t_*] \to X_\Omega$ such that $\un{\ga}(0)=\un{0}_\Omega$ and $\mathfrak{p}_\Omega\circ\un{\ga} = \gamma$.
We fix $\rho>0$ such that $\Omega_{2\rho}=\O$ and set
\[ U \coloneqq \{\, \zeta\in\C \mid \abs{\zeta} < 2\rho \,\}. \]
For every $\zeta\in U$, the path $\gamma_\zeta \colon\thinspace t\in[0,1] \mapsto t\zeta$ is in~$\Pi_\Omega$ and the formula
\[
\zeta \in U \mapsto \mathscr L(\zeta) \coloneqq \un{\ga}_\zeta(1) \in X_\Omega
\]
defines a holomorphic section~$\mathscr L$ of~$\mathfrak{p}_\Omega$ on~$U$.
Let $\un{U} \coloneqq \mathscr L(U)$: this is an open subset of~$X_\Omega$ containing~$\un{0}_\Omega$ and we have mutually inverse biholomorphisms
\[
\mathscr L \colon\thinspace U \xrightarrow{\smash{\ensuremath{\sim}}} \un{U}, \qquad
\restr{\mathfrak{p}_\Omega}{\un{U}} \colon\thinspace \un{U} \xrightarrow{\smash{\ensuremath{\sim}}} U.
\]
\begin{nota} \label{notesimplexn}
For any $n\ge1$, we denote by~$\Delta_n$ the $n$-dimensional simplex
\[
\Delta_n \coloneqq \{\, (s_1,\ldots,s_n)\in\R^n \mid s_1,\ldots,s_n\ge0
\;\text{and}\;
s_1 +\cdots + s_n \le 1 \,\}
\]
with the standard orientation, and by $[\Delta_n]\in\mathscr E_n(\R^n)$ the corresponding integration current.
For every $\zeta\in U$, we consider the map
\[
{\vec{\mathscr D}}(\zeta) \colon\thinspace
\vec s = (s_1,\ldots,s_n) \mapsto
{\vec{\mathscr D}}(\zeta,\vec s) \coloneqq \big( \mathscr L(s_1\zeta),\ldots,\mathscr L(s_n\zeta) \big) \in \un{U}^n \subset X_\Omega^n,
\]
defined in a neighbourhood of~$\Delta_n$ in~$\R^n$,
and denote by ${\vec{\mathscr D}}(\zeta)_\# [\Delta_n] \in \mathscr E_n(X_\Omega^n)$ the push-forward of~$[\Delta_n]$ by~${\vec{\mathscr D}}(\zeta)$.
\end{nota}
The reader is referred to \cite{NLresur} for the notations and notions related to integration currents.
Let $n\ge1$, $\hat f_1,\ldots, \hat f_n \in \hat\mathscr R_\Omega$ and
$\hat g \coloneqq 1*\hat f_1 * \cdots * \hat f_n$.
Our starting point is
\begin{lmm}[\cite{NLresur}]
Let
\[ \beta \coloneqq (\mathfrak{p}_\Omega^*\hat f_1)\big(\un\zeta_1\big) \cdots (\mathfrak{p}_\Omega^*\hat f_n)\big(\un\zeta_n\big) \,
{\mathrm d}\un\zeta_1 \wedge \cdots \wedge {\mathrm d}\un\zeta_n, \]
where we denote by ${\mathrm d}\un\zeta_1 \wedge \cdots \wedge {\mathrm d}\un\zeta_n$ the pullback of the $n$-form ${\mathrm d}\zeta_1 \wedge \cdots \wedge {\mathrm d}\zeta_n$ in $X_\Omega^n$ by $\mathfrak{p}^{\otimes n} \colon\thinspace X_\Omega^n \to \C^n$.
Then
\[
\zeta \in U \quad\Rightarrow\quad
\hat g(\zeta) =
{\vec{\mathscr D}}(\zeta)_\# [\Delta_n](\beta).
\]
\end{lmm}
\subsection{$\gamma$-adapted deformations of the identity}
Let $L>0$ and $\delta \in (0,\rho)$. Let $\gamma \colon\thinspace [0,1] \to \C$ be a path of $\Pi_{\Omega^{*n}}^{\delta,L} \subset \Pi_{\Omega^{*n}}$.
We want to study the analytic continuation of~$\hat g$ along~$\gamma$, which amounts to studying
$(\mathfrak{p}_{\Omega^{*n}}^*\hat g)\big( \un{\ga}(t) \big)$,
where~$\un{\ga}$ is the lift of~$\gamma$ in $X_{\Omega^{*n}}$ which starts at~$\un{0}_{\Omega^{*n}}$.
Without loss of generality, we may assume that there exists $a\in(0,1)$ such that
\[
0 < \abs{\gamma(a)} < \rho, \qquad
\gamma(t) = \tfrac{t}{a}\gamma(a) \enspace\text{for $t\in[0,a]$,}
\qquad \text{$\restr{\gamma}{[a,1]}$ is $C^1$.}
\]
\begin{dfn}
For $\zeta \in \C$ and $1\le i\le n$, we set
\begin{align*}
\mathcal{N}(\zeta) &\coloneqq \big\{\, \big(\un\zeta_1,\ldots,\un\zeta_n\big) \in X_\Omega^n \mid
\mathfrak{p}_\Omega\big(\un\zeta_1\big) + \cdots + \mathfrak{p}_\Omega\big(\un\zeta_n\big) = \zeta \,\big\},
\\[1ex]
\mathcal{N}_i &\coloneqq \big\{\, \big(\un\zeta_1,\ldots,\un\zeta_n\big) \in X_\Omega^n \mid \un\zeta_i = \un{0}_\Omega \,\big\}.
\end{align*}
We call \emph{$\gamma$-adapted deformation of the identity on~$\un V$}
any family $(\Psi_t)_{t\in[a,1]}$ of maps
\[
\Psi_t \colon\thinspace \un V \to X_\Omega^n,
\]
where~$\un V$ is a neighbourhood of ${\vec{\mathscr D}}\big( \gamma(a) \big)(\Delta_n)$ in~$X_\Omega^n$,
such that
$\Psi_a = \mathop{\hbox{{\rm Id}}}\nolimits$,
the map
$\big(t,\vec{\un\ze}\big) \in [a,1] \times \un V \mapsto
\Psi_t\big(\vec{\un\ze}\big) \in X_\Omega^n$
is locally Lipschitz,
and for any $t\in [a,1]$ and $i=1,\ldots,n$,
\begin{align*}
\vec{\un\ze} \in \mathcal{N}\big(\gamma(a)\big) \quad & \Rightarrow \quad
\Psi_t\big(\vec{\un\ze}\big) \in \mathcal{N}\big(\gamma(t)\big), \\
\vec{\un\ze} \in \mathcal{N}_i \quad & \Rightarrow \quad
\Psi_t\big(\vec{\un\ze}\big) \in \mathcal{N}_i.
\end{align*}
\end{dfn}
The above notion is a slight generalization of the ``$\gamma$-adapted origin-fixing isotopies'' which appear in \cite[Def.~5.1]{NLresur}.
Adapting the proof of \cite[Prop.~5.2]{NLresur}, we get
\begin{prp}[\cite{NLresur}]
If $(\Psi_t)_{t\in[a,1]}$ is a $\gamma$-adapted deformation of the identity, then
\beglab{eqconthatgugat}
(\mathfrak{p}_{\Omega^{*n}}^*\hat g)\big( \un{\ga}(t) \big) =
\big( \Psi_t \circ {\vec{\mathscr D}}\big( \gamma(a) \big) \big)_\# [\Delta_n](\beta)
\qquad\text{for $t\in[a,1]$.}
\end{equation}
\end{prp}
Notice that, with the notations
\beglab{eqdefunzeitzeit}
\big(
\un\zeta_1^t, \ldots, \un\zeta_n^t
\big) \coloneqq
\Psi_t\circ {\vec{\mathscr D}}\big( \gamma(a) \big) \colon\thinspace \Delta_n \to X_\Omega^n,
\qquad \zeta_i^t \coloneqq \mathfrak{p}_\Omega \circ \un\zeta_i^t \quad\text{for $1\le
i\le n$,}
\end{equation}
formula~\eqref{eqconthatgugat} can be rewritten as
\beglab{eqconthatgugatbis}
(\mathfrak{p}_{\Omega^{*n}}^*\hat g)\big( \un{\ga}(t) \big) =
\int_{\Delta_n}
(\mathfrak{p}_\Omega^*\hat f_1)\big(\un\zeta_1^t\big) \cdots (\mathfrak{p}_\Omega^*\hat f_n)\big(\un\zeta_n^t\big)
\operatorname{det}\bigg[ \frac{\partial\zeta_i^t}{\partial s_j}\bigg]_{1\le i,j\le n}
\, {\mathrm d} s_1 \cdots {\mathrm d} s_n
\end{equation}
(for each~$t$, the partial derivatives $\frac{\partial\zeta_i^t}{\partial s_j}$ exist almost everywhere on~$\Delta_n$ by Rademacher's theorem, for the functions $\vec s \mapsto \zeta_i^t(\vec s)$ are Lipschitz).
\subsection{Sketch of the proof of Theorem~\ref{thm:1.12}}
We define a function $\eta\ge0$ by the formula
\[
v = (\lambda,\xi) \in \mathcal{M}_\Omega \mapsto
\eta(v) \coloneqq \operatorname{dist}\big( (\lambda,\xi), \{ (0,0) \} \cup \overline\mathcal{S}_\Omega \big),
\]
where $\operatorname{dist}(\cdot,\cdot)$ is a notation for the Euclidean distance in $\R\times\C \simeq \R^3$.
The following three lemmas allow to prove Theorem~\ref{thm:1.12}.
The reader is referred to \cite{KS} for their proofs.
\begin{lmm}
The function~$D$ defined by the formula
\[
D\big(t,(v_1,\ldots,v_n)\big) \coloneqq
\eta(v_1) + \cdots + \eta(v_n) +
\operatorname{dist}\big( \big( L(\gamma_{|t}),\gamma(t) \big), v_1+\cdots+v_n \big)
\]
is everywhere positive on $[a,1] \times \mathcal{M}_\Omega^n$ and the formula
\beglab{eqdefvecX}
\vec X(t,\vec v) = \left| \begin{aligned}
X_1 &\coloneqq \frac{\eta(v_1)}{D(t,\vec v)} \big( \abs{\gamma'(t)}, \gamma'(t) \big)\\
& \qquad \vdots \\[1ex]
X_n &\coloneqq \frac{\eta(v_1)}{D(t,\vec v)} \big( \abs{\gamma'(t)}, \gamma'(t) \big)
\end{aligned} \right.
\end{equation}
defines a non-autonomous vector field
$\vec X(t,\vec v) \in T_{\vec v} \big( \mathcal{M}_\Omega^n \big) \simeq (\R\times\C)^n$
on $[a,1]\times\mathcal{M}_\Omega^n$,
which admits a flow map $\Phi_t \colon\thinspace \mathcal{M}_\Omega^n \to \mathcal{M}_\Omega^n$ between time~$a$ and time~$t$
for every $t\in [a,1]$.
\end{lmm}
\begin{lmm}
One can define a $\gamma$-adapted deformation of the identity $(\Psi_t)_{t\in[a,1]}$ on~$\un{U}^n$ as follows:
for every $\vec{\un\ze} = \big( \mathscr L(\zeta_1),\ldots \mathscr L(\zeta_n) \big) \in \un{U}^n$ and $i \in \{1,\ldots,n\}$,
we set $v_j \coloneqq (\abs{\zeta_j},\zeta_j)$ for each $j\in\{1,\ldots,n\}$
and define a path $\tilde\gamma_{i,\vec{\un\ze}} \colon\thinspace [0,1] \to \mathcal{M}_\Omega$ by
\[
t \in [0,a] \enspace\Rightarrow\enspace
\tilde\gamma_{i,\vec{\un\ze}}(t) \coloneqq \tfrac{t}{a} v_i,
\qquad
t \in [a,1] \enspace\Rightarrow\enspace
\tilde\gamma_{i,\vec{\un\ze}}(t) \coloneqq \pi_i \circ \Phi_t(v_1,\ldots, v_n),
\]
where $\pi_i \colon\thinspace \mathcal{M}_\Omega^n \to \mathcal{M}_\Omega$ is the projection onto the $i^{\text{th}}$ factor;
then, by virtue of~\eqref{eqtextcharacOmalltiga},
the $\C$-projection of $\tilde\gamma_{i,\vec{\un\ze}}$ is
a path $\gamma_{i,\vec{\un\ze}} \in \Pi_\Omega$, and we set
\[
\Psi_t\big(\vec{\un\ze}\big) \coloneqq \big(
\un{\ga}_{1,\vec{\un\ze}}(t), \ldots, \un{\ga}_{n,\vec{\un\ze}}(t)
\big) \in X_\Omega^n
\quad \text{for $t\in[a,1]$.}
\]
\end{lmm}
\begin{lmm} \label{lemestimdet}
Consider the functions
$\vec s \in \Delta_n \mapsto
v_i^a(\vec s) \coloneqq \big(
s_i\abs{\gamma(a)}, s_i\gamma(a)
\big) \in \mathcal{M}_\Omega$ for $1\le i \le n$ and,
for each $t\in [a,1]$,
\[
(v_1^t, \ldots, v_n^t) \coloneqq \Phi_t \circ (v_1^a, \ldots, v_n^a)
\colon\thinspace \Delta_n \to \mathcal{M}_\Omega^n.
\]
Suppose $|\gamma(a)|>\delta$ and let
\[
\mathcal{M}_\Omega^{\delta,L} \coloneqq \big\{\,
(\lambda,\zeta) \in \R_{\geq0}\times\C \mid
\lambda\leq L \;\;\text{and}\;\;
\operatorname{dist}\big( (\lambda,\zeta), u \big) \ge \delta
\;\, \text{for all $u\in\{ (0,0) \} \cup \overline\mathcal{S}_\Omega$}
\,\big\}.
\]
Then
\begin{equation}
(v_1^t, \ldots, v_n^t)(\Delta_n) \subset
\bigcup_{L\pp 1+\cdots+L\pp n=L(\gamma_{|t})}
\mathcal{M}_\Omega^{\delta(t),L\pp 1}
\times\cdots\times
\mathcal{M}_\Omega^{\delta(t),L\pp n},
\end{equation}
where
$\delta(t) \coloneqq
\frac12 \rho\,\mathrm e^{-2\sqrt{2}\delta^{-1}(L(\gamma_{|t}) - \abs{\gamma(a)})}$.
Moreover, for each~$i$, the $\C$-projection of~$v_i^t$ is a Lipschitz function $\zeta_i^t \colon\thinspace \Delta_n \to \C$ and the almost everywhere defined partial derivatives
$\frac{\partial\zeta_i^t}{\partial s_j}$
satisfy
\[
\abs*{\operatorname{det}\bigg[ \frac{\partial\zeta_i^t}{\partial s_j}\bigg]_{1\le i,j\le n}}
\le \big( c(t) \big)^n,
\]
where
$c(t) \coloneqq
\abs{\gamma(a)} \,\mathrm e^{3\sqrt{2}\delta^{-1}(L(\gamma_{|t}) - \abs{\gamma(a)})}$.
\end{lmm}
We set
\beglab{eqdefdepcthmestim}
\delta' \coloneqq
\frac12 \rho\,\mathrm e^{-2\sqrt{2}\delta^{-1} L},
\qquad
c \coloneqq
\abs{\gamma(a)} \,\mathrm e^{3\sqrt{2}\delta^{-1} L},
\end{equation}
so that $\delta' \le \delta(t)$
and $c \ge c(t)$ for all $t\in[a,1]$.
Theorem~\ref{thm:1.12} follows from the previous estimates and the identity~\eqref{eqconthatgugatbis}
(the functions~$\zeta_i^t$ in~\eqref{eqdefunzeitzeit} and in
Lemma~\ref{lemestimdet} are indeed the same).
\noindent {\em Acknowledgements.}
{This work has been supported by Grant-in-Aid for JSPS Fellows Grant Number 15J06019, French National Research Agency reference ANR-12-BS01-0017 and Laboratoire Hypathie A*Midex.}
\noindent
Shingo \textsc{Kamimoto}\\ Department of Mathematics, Hiroshima University, Hiroshima 739-8526, Japan.
\noindent
David \textsc{Sauzin}\\ Laboratorio Fibonacci, CNRS--CRM Ennio De
Giorgi SNS Pisa, Italy.\\
{\itshape Current address}: IMCCE, CNRS--Observatoire de Paris, France.
\begin{flushright}
\textit{\small August 21, 2015. Revised February 25, 2016.}
\end{flushright}
\end{document} | arXiv |
Hamilton's Principle
Hamilton's principle states that a dynamic system always follows a path such that its action integral is stationary (that is, maximum or minimum).
Why should the action integral be stationary? On what basis did Hamilton state this principle?
lagrangian-formalism variational-principle action
tsudottsudot
$\begingroup$ It should be noted that this is "Hamilton's principle", that is is not exactly the same as "Hamiltonian [classical] mechanics" (ie, where an actual Hamiltonian is involved) and that is as nothing specific about QM. $\endgroup$ – Cedric H. Nov 2 '10 at 20:40
$\begingroup$ In the Euler Lagrange equations. The neccesary condition L to be an extremal point is it satisfies the EL eqs. So Hamilton's principle is not actually a principle. You can think in QED, in QM,... but it is just because a mathematical reason. $\endgroup$ – Dog_69 Mar 22 '18 at 18:29
The notes from week 1 of John Baez's course in Lagrangian mechanics give some insight into the motivations for action principles.
The idea is that least action might be considered an extension of the principle of virtual work. When an object is in equilibrium, it takes zero work to make an arbitrary small displacement on it, i. e. the dot product of any small displacement vector and the force is zero (in this case because the force itself is zero).
When an object is accelerating, if we add in an "inertial force" equal to $\,-ma\,$, then a small, arbitrary, time-dependent displacement from the objects true trajectory would again have zero dot product with $\,F-ma,\,$ the true force and inertial force added. This gives
$$(F-ma)\cdot \delta q(t) = 0$$
From there, a few calculations found in the notes lead to the stationary action integral.
Baez discusses D'Alembert more than Hamilton, but either way it's an interesting look into the origins of the idea.
MarianD
Mark EichenlaubMark Eichenlaub
$\begingroup$ Note that the principle of virtual work is called D'Alembert principle: en.wikipedia.org/wiki/D%27Alembert%27s_principle $\endgroup$ – Cedric H. Nov 4 '10 at 19:23
There is also Feynman's approach, i.e. least action is true classically just because it is true quantum mechanically, and classical physics is best considered as an approximation to the underlying quantum approach. See http://www.worldscibooks.com/physics/5852.html or http://www.eftaylor.com/pub/call_action.html .
Basically, the whole thing is summarized in a nutshell in Richard P. Feynman, The Feynman Lectures on Physics (Addison–Wesley, Reading, MA, 1964), Vol. II, Chap. 19. (I think, please correct me if I'm wrong here). The fundamental idea is that the action integral defines the quantum mechanical amplitude for the position of the particle, and the amplitude is stable to interference effects (-->has nonzero probability of occurrence) only at extrema or saddle points of the action integral. The particle really does explore all alternative paths probabilistically.
You likely want to read Feynman's Lectures on Physics anyway, so you might as well start now. :-)
sigoldberg1sigoldberg1
$\begingroup$ Feynman's Lectures on Physics are good, but best read after to have properly learnt the subject, in order to provide new/further insight, I feel. $\endgroup$ – Noldorin Jan 18 '11 at 22:31
As you can see from the image below, you want the variation of the action integral to be a minimum, therefore $\displaystyle \frac{\delta S}{\delta q}$ must be $0$. Otherwise, you are not taking the true path between $q_{t_{1}}$ and $q_{t_{2}}$ but a slightly longer path. However, even following $\delta S=0$, as you know, you might end up with another extremum.
Following the link from j.c., you can find On a General Method on Dynamics, which probably answers your question regarding Hamilton's reasoning. I haven't read it but almost surely it is worthwhile.
Robert SmithRobert Smith
$\begingroup$ This seems like a tautological answer as it is precisely Hamilton's principle which is used to arrive at the above picture in the first place. $\endgroup$ – Casimir Oct 18 '15 at 7:41
$\begingroup$ Maybe you were taught Hamilton's principle and arrived at that picture as an explanation, but the picture is perfectly general. It describes the variation of a function with fixed end points. $\endgroup$ – Robert Smith Oct 18 '15 at 16:44
I generally tell the story that the action principle is another way of getting at the same differential equations -- so at the level of mechanics, the two are equivalent. However, when it comes to quantum field theory, the description in terms of path integrals over the exponentiated action is essential when considering instanton effects. So eventually one finds that the formulation in terms of actions is more fundamental, and more physically sound.
But still, people don't have a "feel" for action the way they have a feel for energy.
Eric ZaslowEric Zaslow
Let us remember that the equations of motion with initial conditions $q(0), (dq/dt)(0)$ were advanced first and the least action principle was formulated later, as a sequence. Although beautiful and elegant mathematically, the least action principle uses some future, "boundary" condition $q(t_2)$, which is unknown physically. There is no least action principle operating only with the initial conditions.
Moreover, it is implied that the equations have physical solutions. This is so in the Classical Mechanics but is wrong in the Classical Electrodynamics. So, even derived from formally correct "principle", the equations may be wrong on physical and mathematical level. In this respect, formulating the right physical equations is a more fundamental task for physicists than relying on some "principle" of obtaining equations "automatically". It is we physicists who are responsible for correctly formulating equations.
In CED, QED, and QFT one has to "repair on go" the wrong solutions just because the physics was guessed and initially implemented incorrectly.
P.S. I would like to show how in reality the system "chooses" its trajectory: if at $t = 0$ the particle has a momentum $p(t)$, then at the next time $t+dt$ it has the momentum $p(t) + F(t)\cdot dt$. This increment is quite local in time, it is determined by the present force value $F(t)$ so no future "boundary" condition can determine it. The trajectory is not "chosen" from virtual ones; it is "drawn" by the instant values of force, coordinate, and velocity.
$\begingroup$ I like to think that both options are merely mathematical models and so none is more real. Neither the system chooses its trajectory nor the future determines the least action path. The non-locality of QM leads to similar doubts. $\endgroup$ – Eduardo Guerras Valera Nov 1 '12 at 6:34
$\begingroup$ Amazingly, there is now a least action principle operating only with the initial conditions! prl.aps.org/abstract/PRL/v110/i17/e174301 $\endgroup$ – wnoise Apr 23 '13 at 7:52
$\begingroup$ Here is a free arXiv version. Without reading the article in detail, it smells like a classical Keldysh formalism, cf. this and this Phys.SE posts. $\endgroup$ – Qmechanic♦ Jun 15 '13 at 22:07
Instead of specifying the initial position and momentum just like we have done in Newton's formalism, let's reformulate our question as following:
If we choose to specify the initial and final positions: $\textbf{What path does the particle take?}$
Let's assert we can recover the Newton's formalism by the following formalism, so-called Lagrangian formalism or Hamiltonian principle.
To each path illstrated on above figure, we assign a number which we call the action
$$S[\vec{r}(t)] = \int_{t_1}^{t_2}dt \left(\dfrac{1}{2}m\dot{\vec{r}}^2-V(\vec{r})\right)$$
where this integrand is the difference between the kinetic energy and the potential energy.
$\textbf{Hamilton's principle claims}$: The true path taken by the particle is an extremum of S.
$\textbf{Proof:}$
1.Change the path slightly:
$$\vec{r}(t) \rightarrow \vec{r}(t) +\delta \vec{r}(t)$$
2.Keep the end points of the path fixed:
$$ \delta \vec{r}(t_1) = \delta \vec{r}(t_2) = 0 $$
3.Take the variation of the action $S$:
finally, you will get
$$ \delta S = \int_{t_1}^{t_2} \left[-m\ddot{\vec{r}} - \nabla V\right] \cdot \delta \vec{r} $$
The condition that the path we started with is an extremum of the action is
$$\delta S = 0$$
which should hold for all changes $\delta \vec{r}(t)$ that we make to the path.The only way this can happen is if the expression in $[\cdots]$ is zero. This means
$$ m\ddot{\vec{r}} = -\nabla V$$
Now we recognize this as $\textbf{Newton's equations}$. Requiring that the action is extremized is equivalent to requiring that the path obeys Newton's equations.
For more details you could read this pdf lecture.
$\begingroup$ If we see a particle constrained to move on a sphere, we get to paths one is a maximum or a minimum. I feel a particle follows path of least action but the mathematical equation δS=0 does give us an ambiguous answer, but a certain part of this answer contains a path of least action in it. You can see Arfken and Weber. $\endgroup$ – Chetan Waghela Aug 27 '18 at 5:25
Not the answer you're looking for? Browse other questions tagged lagrangian-formalism variational-principle action or ask your own question.
Does Action in Classical Mechanics have a Interpretation?
Proof of Hamilton's principle
What is the principle of least action?
Why are action principles so powerful and widely applicable?
Why is there a Lagrangian?
Intuition behind the use of the Principle of Stationary Action in Classical Field Theory
How can the action can describe a movement? What is the argument behind?
How principle of least action?
Why the Principle of Least Action?
Good reading on the Keldysh formalism
Type of stationary point in Hamilton's principle
Multiple classical paths from Hamilton's principle
How Hamilton's Principle was found?
Confusion regarding the principle of least action in Landau & Lifshitz "The Classical Theory of Fields"
When is the principle of stationary action not the principle of least action?
The Nambu-Goto action how do we know the Hamilton's principle applies?
How does Hamilton's Principle give us the path taken? | CommonCrawl |
\begin{document}
\title{Convergence rate for eigenvalues of the elastic Neumann--Poincar\'e operator on smooth and real analytic boundaries in two dimensions\thanks{\footnotesize This work was supported by NRF grants No. 2016R1A2B4011304 and 2017R1A4A1014735, and by A3 Foresight Program among China (NSF), Japan (JSPS), and Korea (NRF 2014K2A2A6000567)}}
\author{Kazunori Ando\thanks{Department of Electrical and Electronic Engineering and Computer Science, Ehime University, Ehime 790-8577, Japan. Email: {\tt [email protected]}.} \and Hyeonbae Kang\thanks{Department of Mathematics and Institute of Applied Mathematics, Inha University, Incheon 22212, S. Korea. Email: {\tt [email protected]}.} \and Yoshihisa Miyanishi\thanks{Center for Mathematical Modeling and Data Science, Osaka University, Osaka 560-8531, Japan. Email: {\tt [email protected]}.}}
\date{\today} \maketitle
\begin{abstract} The elastic Neumann--Poincar\'e operator is a boundary integral operator associated with the Lam\'e system of linear elasticity. It is known that if the boundary of a planar domain is smooth enough, it has eigenvalues converging to two different points determined by Lam\'e parameters. We show that eigenvalues converge at a polynomial rate on smooth boundaries and the convergence rate is determined by smoothness of the boundary. We also show that they converge at an exponential rate if the boundary of the domain is real analytic. \end{abstract}
\noindent{\footnotesize {\bf Key words}. Lam\'e system, linear elasticity, Neumann--Poincar\'e operator, eigenvalues, convergence rate, smooth boundary, real analytic boundary}
\section{Introduction}
In this paper we study the convergence rate of the elastic Neumann--Poincar\'e (abbreviated by NP) operator defined on the boundary of a two-dimensional bounded domain.
The elastic NP operator, which is also commonly called the double layer potential, arises naturally when solving boundary value problems for the Lam\'e system of linear elasticity using Layer potentials. The Lam\'e system is defined by \begin{equation}\label{lame} \mathcal{L}_{\lambda,\mu} := \mu \Delta + (\lambda+\mu) \nabla \nabla\cdot, \end{equation} where $(\lambda,\mu)$ denotes the pair of Lam\'e parameters. While a precise definition will given in the next section, we mention, as an example, that the solution to the Neumann problem on a bounded domain $\Omega$, namely, $\mathcal{L}_{\lambda,\mu} {\bf u} =0$ in $\Omega$ and $\partial_\nu{\bf u}={\bf g}$ on $\partial\Omega$ ($\partial_\nu$ denotes the conormal derivative), is given by $$ {\bf u}({\bf x}) = {\bf S} (-1/2 {\bf I} + {\bf K}^*)^{-1}[{\bf g}]({\bf x}), \quad {\bf x} \in \Omega, $$ where ${\bf I}$ is the identity operator, ${\bf S}$ is the single layer potential, ${\bf K}$ is the elastic NP operator on $\partial\Omega$, and ${\bf K}^*$ is its adjoint on $L^2$-space (see, for example, \cite{DKV-Duke-88}).
As observed in the above mentioned paper, the elastic NP operator defined on the boundary $\partial\Omega$ of the domain $\Omega$ is not compact on either $L^2(\partial\Omega)^2$ or $H^{1/2}(\partial\Omega)^2$ (the Sobolev space of order $1/2$) even if $\partial\Omega$ is smooth. However, it is recently discovered in \cite{AJKKY} that if the two-dimensional region $\Omega$ has the $C^{1, \alpha}$ boundary for some $\alpha>0$, then the elastic NP operator ${\bf K}$ is polynomially compact, more precisely, \begin{equation}\label{statcompact} {\bf K}^2 - k_0^2 {\bf I} \ \mbox{ is compact on $H^{1/2}(\partial\Omega)^2$}, \end{equation} where the number $k_0$ is defined by \begin{equation}\label{Gkdef} k_0 = \frac{\mu}{2(2\mu+\lambda)}. \end{equation} As a consequence, it is shown that the spectrum of ${\bf K}$ on $H^{1/2}(\partial\Omega)^2$ consists of two sets of eigenvalues converging to $\pm k_0$, respectively. The purpose of this paper is to investigate the convergence rates of eigenvalues.
The electro-static NP operator, which is the counterpart of the elastic NP operator for the Laplace operator, has much simpler spectral structure. If $\partial\Omega$ is $C^{1,\alpha}$ ($\alpha>0$), then the electro-static NP operator is compact and has eigenvalues converging to $0$. Quantitative estimates of the decay rate of NP eigenvalues has been obtained:
Suppose that the NP eigenvalues $\{ \lambda_j \}$ are arranged in such a way that $| \lambda_1 | = | \lambda_2| \ge | \lambda_3 | = | \lambda_4 | \ge \cdots$. It is helpful to mention that if $\lambda$ is an eigenvalue of the electro-static NP operator in two dimensions, so is $-\lambda$ \cite{BM}. It is proved in \cite{MS} that if the boundary of the domain is $C^k$ ($k \ge 2 $), then \begin{equation}\label{eigenest-smooth}
|\lambda_j| = o(j^{d}) \quad \text{ as } j \to \infty, \end{equation} for any $d > - k + 3/2$ (see also \cite{JL}). If $\partial\Omega$ is real analytic, then it is proved in \cite{AKM-JIE} that for any $\epsilon < \epsilon_{\partial\Omega}$ there is a constant $C$ such that \begin{equation}\label{eigenest}
|\lambda_{2n-1}|=|\lambda_{2n}| \le Ce^{-n\epsilon} \end{equation} for all $n$. Here $\epsilon_{\partial\Omega}$ is the modified maximal Grauert radius of $\partial\Omega$ (see subsection \ref{subsec:complex} of this paper for the definition of the modified maximal Grauert radius of $\partial\Omega$). Moreover, it is proved by a few examples that the estimate \eqnref{eigenest} is optimal.
In this paper we extend the results for the electro-static NP operator to the elastic one. Let $\Omega$ be a simply connected bounded domain in $\mathbb{R}^2$ with $C^{1, \alpha}$ boundary for some $\alpha>0$, and let $\lambda_j^{\pm}$ be eigenvalues of the elastic NP operator ${\bf K}$ accumulating to $\pm k_0$, respectively. We show that $\lambda_j^{\pm}$ converges to $\pm k_0$ at a polynomial rate on smooth boundaries (Theorem \ref{thm:smooth}), and at an exponential rate on real analytic boundaries (Theorem \ref{analytic decay}). It is worth mentioning that the polynomial and exponential rates obtained in this paper may not be optimal, in particular, the exponential rate is not. We include a brief discussion on this in Conclusion at the end of this paper.
In order to obtain results of this paper, we utilize a number of important ingredients. Among them are a result of J. Delgado and M. Ruzhansky \cite{DR} which relates the regularity of the integral kernel with the Schatten class where the operator belongs, a result of Gilfeather \cite{G} on the decomposition of polynomially compact operators, Weyl's inequality on singular values and eigenvalues, and the Weyl-Courant min-max principle.
This paper is organized as follows. In section \ref{sec:pre} we review derivation of the result \eqnref{statcompact} and show some regularities of the integral kernel of the elastic NP operator using a complex parametrization. Section \ref{sec:poly} is to deal with the polynomial convergence on smooth boundaries, and Section \ref{sec:exp} is for the exponential convergence on real analytic boundaries. This paper ends with a short conclusion.
\section{Prelimaries}\label{sec:pre}
\subsection{Elasto-static NP operator}
In this subsection we briefly review the result \eqnref{statcompact} as well as some preliminary results for the investigation of this paper.
Let ${\bf \GG} = \left( \Gamma_{ij} \right)_{i, j = 1}^2$ be the Kelvin matrix of fundamental solutions to the Lam\'{e} operator in two dimensions, namely, \begin{equation}\label{Kelvin}
\Gamma_{ij}({\bf x}) = \frac{\alpha_1}{2 \pi} \delta_{ij} \ln{|{\bf x}|} - \frac{\alpha_2}{2 \pi} \displaystyle \frac{x_i x_j}{|{\bf x}| ^2}, \end{equation} where \begin{equation}
\alpha_1 = \frac{1}{2} \left( \frac{1}{\mu} + \frac{1}{2 \mu + \lambda} \right) \quad\mbox{and}\quad \alpha_2 = \frac{1}{2} \left( \frac{1}{\mu} - \frac{1}{2 \mu + \lambda} \right). \end{equation} Then the NP operator for the Lam\'e system is defined by \begin{equation}\label{BK} {\bf K} [{\bf f}] ({\bf x}) := \mbox{p.v.} \int_{\partial \Omega} \partial_{\nu_{\bf y}} {\bf \Gamma} ({\bf x}-{\bf y}) {\bf f}({\bf y}) d \sigma({\bf y}) \quad \mbox{a.e. } {\bf x} \in \partial \Omega. \end{equation} Here, p.v. stands for the Cauchy principal value, and the conormal derivative on $\partial \Omega$ corresponding to the Lam\'e operator $\mathcal{L}_{\lambda,\mu}$ is defined to be \begin{equation}\label{conormal} \partial_\nu {\bf u} := (\mathbb{C} {\bf u}) {\bf n} = \lambda (\nabla \cdot {\bf u}) {\bf n} + \mu \left( \nabla {\bf u} + \nabla {\bf u}^\top \right) {\bf n} \quad \mbox{on } \partial \Omega, \end{equation} where ${\bf n}$ is the outward unit normal to $\partial \Omega$ and the superscript $\top$ denotes transpose of a matrix. The conormal derivative $\partial_{\nu_{\bf y}}{\bf \GG} ({\bf x}-{\bf y})$ of the Kelvin matrix with respect to ${\bf y}$-variables is defined by \begin{equation}\label{kerdef} \partial_{\nu_{\bf y}}{\bf \GG} ({\bf x}-{\bf y}) {\bf b} = \partial_{\nu_{\bf y}} ({\bf \GG} ({\bf x}-{\bf y}) {\bf b}) \end{equation} for any constant vector ${\bf b}$.
It is shown in \cite{AJKKY} that \begin{equation}\label{funddecomp} \partial_{\nu_{\bf y}}{\bf \GG}({\bf x}-{\bf y})= 2k_0 {\bf K}_1({\bf x},{\bf y}) - {\bf K}_2({\bf x},{\bf y}), \end{equation} where $k_0$ is the number given in \eqnref{Gkdef} and \begin{align}
{\bf K}_1({\bf x},{\bf y}) &= \frac{{\bf n}_{\bf y} ({\bf x}-{\bf y})^\top - ({\bf x}-{\bf y}) {\bf n}_{\bf y}^\top}{2\pi |{\bf x}-{\bf y}|^{2}}
= \frac{1}{2\pi |{\bf x}-{\bf y}|^2} \begin{bmatrix} 0 & K({\bf x},{\bf y}) \\ - K({\bf x},{\bf y}) & 0 \end{bmatrix} , \\
{\bf K}_2({\bf x},{\bf y}) &= \frac{\mu}{2\mu+\lambda} \frac{( {\bf x}-{\bf y}) \cdot {\bf n}_{\bf y} }{2\pi |{\bf x}-{\bf y}|^2} {\bf I} + \frac{2(\mu+ \lambda)}{2\mu+\lambda} \frac{( {\bf x}-{\bf y}) \cdot {\bf n}_{\bf y} }{2\pi |{\bf x}-{\bf y}|^{4}} ({\bf x}-{\bf y})({\bf x}-{\bf y})^\top . \label{BKtwo} \end{align} Here and throughout the paper ${\bf I}$ is the $2 \times 2$ identity matrix as the identity operator.
We define ${\bf T}_j$, $j=1, 2$, to be the operator defined by the integral kernel ${\bf K}_j$, namely, \begin{equation} {\bf T}_j [\mbox{\boldmath $\Gvf$}]({\bf x}):= \text{p.v.} \int_{\partial\Omega} {\bf K}_j({\bf x},{\bf y}) \mbox{\boldmath $\Gvf$}({\bf y}) \, d \sigma({\bf y}), \quad {\bf x} \in \partial\Omega. \end{equation} Observe that \begin{equation} K({\bf x},{\bf y}):= - n_2({\bf y}) (x_1-y_1) + n_1({\bf y}) (x_2-y_2). \end{equation} Using this fact, it is proved in \cite{AJKKY} that \begin{equation}\label{BTone} {\bf T}_1 = \frac{1}{2} \begin{bmatrix}0 & -\mathcal{H} \\ \mathcal{H} & 0 \end{bmatrix} + \begin{bmatrix}0 & \mathcal{K} \mathcal{H} \\ -\mathcal{K} \mathcal{H} & 0 \end{bmatrix}, \end{equation} where $\mathcal{H}$ is the Hilbert transformation on $\partial\Omega$ and $\mathcal{K}$ is the electro-static NP operator, namely, \begin{equation}\label{electro}
\mathcal{K}[\psi]({\bf x}):= \frac{1}{2\pi} \int_{\partial \Omega} \frac{( {\bf y}-{\bf x}) \cdot {\bf n}_{\bf y}}{|{\bf x}-{\bf y}|^2} \psi({\bf y}) \, d\sigma({\bf y}), \quad {\bf x} \in \partial\Omega. \end{equation} Let \begin{equation}
{\bf H} =
\begin{bmatrix}
0 & - \mathcal{H} \\
\mathcal{H} & 0
\end{bmatrix}, \end{equation} and \begin{equation}
{\bf B} =
\begin{bmatrix}
\mathcal{K} & 0 \\
0 & \mathcal{K}
\end{bmatrix}. \end{equation} Then we have the following relation from \eqnref{funddecomp} and \eqnref{BTone}: \begin{equation}\label{BKBHBB}
{\bf K} = k_0 {\bf H} - 2k_0 {\bf B} {\bf H} - {\bf T}_2. \end{equation}
Let us denote the integral kernel of $\mathcal{K}$ by $K_0$, namely, \begin{equation}\label{Kzero}
K_0({\bf x},{\bf y}) = \frac{1}{2\pi} \frac{( {\bf y}-{\bf x}) \cdot {\bf n}_{\bf y}}{|{\bf x}-{\bf y}|^2} . \end{equation} If $\partial\Omega$ is $C^{1,\alpha}$, then $$
|K_0({\bf x},{\bf y})| \le C |{\bf x}-{\bf y}|^{-1+\alpha} $$ for some constant $C$. Thus, if $\alpha>0$, then $\mathcal{K}$ is compact, and so is ${\bf B}$. Since the term ${\bf K}_2$ has $K_0$ as factors as one can see from \eqnref{BKtwo}, we infer that ${\bf T}_2$ is compact. Thus, $2k_0 {\bf B} {\bf H} + {\bf T}_2$ is compact. Since $\mathcal{H}^2=-I$ and hence ${\bf H}^2={\bf I}$, \eqnref{statcompact} follows.
The elastic NP operator ${\bf K}$ can be realized as a self-adjoint operator on $H^{1/2}(\partial\Omega)^2$ by introducing a new inner product in the same way as for the symmetrization of the electro-static NP operator in \cite{KPS}. In fact, let ${\bf S}$ be the single layer potential for the Lam\'e system, namely, $$ {\bf S}[\mbox{\boldmath $\Gvf$}]({\bf x})= \int_{\partial\Omega} {\bf \GG}({\bf x}-{\bf y}) \mbox{\boldmath $\Gvf$}({\bf y}) d\sigma({\bf y}). $$ Even though there are some domains $\Omega$ such that ${\bf S}$ may have one-dimensional null space as a mapping from $H^{-1/2}(\partial\Omega)^2$ into $H^{1/2}(\partial\Omega)^2$, if we dilate the domain in such a case, then ${\bf S}: H^{-1/2}(\partial\Omega)^2 \to H^{1/2}(\partial\Omega)^2$ becomes invertible. Since the elastic NP operator is invariant under dilation, we may assume without loss of generality that ${\bf S}$ is invertible from the beginning. Let $\langle \cdot, \cdot \rangle$ denote the $H^{1/2}-H^{-1/2}$ duality pairing, and define \begin{equation}\label{star} \langle \mbox{\boldmath $\Gvf$}, \mbox{\boldmath $\Gy$} \rangle_* := \langle \mbox{\boldmath $\Gvf$}, {\bf S}^{-1}[\mbox{\boldmath $\Gy$}] \rangle \end{equation} for $\mbox{\boldmath $\Gvf$}, \mbox{\boldmath $\Gy$} \in H^{1/2}(\partial\Omega)^2$. It is actually an inner product on $H^{1/2}(\partial\Omega)^2$, and the elastic NP operator ${\bf K}$ is self-adjoint with respect to this inner product, which is a consequence of the Plemelj's symmetrization principle, namely, \begin{equation}\label{plemelj} {\bf S}{\bf K}^*={\bf K}{\bf S} . \end{equation} See \cite{AJKKY} and references therein. Since ${\bf K}$ is self-adjoint, we can infer from \eqnref{statcompact} that there are two nonempty sequences of eigenvalues converging to $k_0$ and $-k_0$.
\subsection{Complex parametrization of the NP operator}\label{subsec:complex}
In this section we derive some regularity estimates of the integral kernel of the operator ${\bf K} - k_0 {\bf H}= - 2k_0 {\bf B} {\bf H} - {\bf T}_2$ appearing in \eqnref{BKBHBB}. For that purpose, it is convenient to use a complex parametrization of $\partial\Omega$.
Let $S^1$ be the unit circle and $Q: S^1 \rightarrow \partial \Omega \subset{\mathbb{C}}$ be a regular parametrization of $\partial\Omega$. Here and afterwards we identify $\mathbb{R}^2$ with the complex plane $\mathbb{C}$. Let \begin{equation} q(t):=Q(e^{it}), \quad t \in \mathbb{R} . \end{equation} Then $q$ is $C^{k,\alpha}$ if $\partial\Omega$ is $C^{k,\alpha}$ smooth, and is real analytic if $\partial\Omega$ is. Moreover, $q$ is a $2\pi$-periodic function, namely, $q(t + 2\pi) = q(t)$.
Suppose that $\partial\Omega$ is real analytic. Then $Q$ admits an extension as an analytic mapping from an annulus
\begin{equation} A_\epsilon:= \{ \tau \in {\mathbb{C}}\; :\; e^{-\epsilon}<|\tau|<e^{\epsilon}\; \} \label{analytic_annulus} \end{equation} for some $\epsilon>0$ onto a tubular neighborhood of $\partial\Omega$ in $\mathbb{C}$. The function $q$ is an analytic function from $\mathbb{R} \times i (-\epsilon, \epsilon)$ onto a tubular neighborhood of $\partial\Omega$.
For a real analytic parametrization $q$ of $\partial\Omega$, we consider the numbers $\epsilon$ such that $q$ satisfies an additional condition: $$ \mbox{(G)} \quad \mbox{if $q(t)=q(s)$ for $t \in [-\pi, \pi) \times i (-\epsilon, \epsilon)$ and $s \in [-\pi, \pi)$, then $t=s$}. $$ It is worth emphasizing that the condition (G) is weaker than univalence. It only requires that $q$ attains values $q(s)$ for $s \in [-\pi, \pi)$ only at $s$: The condition (G) is equivalent to the fact that the only points that the function $q: \mathbb{R} \times i (- \epsilon, \epsilon) \to \mathbb{C}$ maps to $\partial \Omega$ are those on the real line. Since $Q$ is one-to-one on $\partial \Omega$, the extended function is univalent in $A_\epsilon$ if $\epsilon$ is sufficiently small. Therefore, the condition (G) is fulfilled if $\epsilon$ is small. We denote the supremum of such $\epsilon$ by $\epsilon_q$ and call it the modified maximal Grauert radius of $q$. We emphasize that $\epsilon_q$ may differ depending on the parametrization $q$. The supremum of $\epsilon_q$ over all regular real analytic parametrizations $q$ of $\partial\Omega$ is called the {\it modified maximal Grauert radius} of $\partial\Omega$ and it is shown in \cite{AKM-JIE} that the electro-static NP eigenvalues converges to $0$ at the rate of $o(e^{-\epsilon j})$ as $j \to \infty$ for any $\epsilon$ less than the modified maximal Grauert radius of $\partial\Omega$.
There is a special parametrization of $\partial\Omega$ (and such a parametrization will be used in this paper). Let $U$ be the unit disk and $\Phi:U \to \Omega$ be a Riemann mapping, namely, a univalent mapping from $U$ onto $\Omega$ ($\Omega$ is assumed to be simply connected). If $\partial\Omega$ is $C^{k,\alpha}$, then $\Phi$ can be extended as an injective $C^{k,\alpha}$ mapping from $\overline{U}$ onto $\overline{\Omega}$ (see \cite[Theorem 3.6]{Pomm}). If $\partial\Omega$ is real analytic, then $\Phi$ is extended as an analytic function in a neighborhood of $\overline{U}$ (see \cite[Proposition 3.1]{Pomm}). Thus, assuming that $\partial\Omega$ is $C^{k,\alpha}$, we may take $Q=\Phi$ on $S^1=\partial U$ and $q$ accordingly. For convenience, we call such a parametrization by the name `a parametrization by a Riemann mapping $\Phi$'.
Let $q$ be a $2\pi$-periodic parametrization of $\partial\Omega$. Let $T_q(t,s)$ be the integral kernel of the operator $2k_0 {\bf B} {\bf H} + {\bf T}_2$ after parametrization by $q$, namely, \begin{equation}\label{Tq} (2k_0 {\bf B} {\bf H} + {\bf T}_2)[\mbox{\boldmath $\Gvf$}](q(t)) = \int_{-\pi}^\pi T_q(t,s) \mbox{\boldmath $\Gvf$}(q(s))ds. \end{equation} Since $T_q(t, s)$ is $2\pi$-periodic with respect to the $t$ variable, it admits the Fourier series expansion: \begin{equation}\label{fourier}
T_q(t, s)=\sum_{k\in {\mathbb{Z}}} a_k^q(s) e^{ikt}, \quad a_k^q(s) = \frac{1}{2\pi} \int_{-\pi}^{\pi} T_q(t, s) e^{-ikt} dt. \end{equation} We emphasize that $T_q$ is a $2\times 2$ matrix-valued function, and so is $a_k^q(s)$.
We obtain the following proposition.
\begin{prop}\label{extension} Let $\Omega$ be a simply connected bounded domain in $\mathbb{R}^2$. \begin{itemize} \item[{\rm (i)}] If $\partial\Omega$ is $C^{k,\alpha}$ for some $k$ and $0 \le \alpha <1$ satisfying $k+\alpha >2$, then the integral kernels of the operators ${\bf B}$ and ${\bf T}_2$ are $C^{k-2,\alpha}$-smooth in both $t$ and $s$ variables. \item[{\rm (ii)}] If $\partial\Omega$ is real analytic, let $q$ be the parametrization of $\partial\Omega$ by a Riemann mapping of $\Omega$, and $T_q$ be the parametrized kernel given by {\rm \eqnref{Tq}} and $a_k^q$ be its Fourier coefficient defined by {\rm \eqnref{fourier}}. For any $0 < \epsilon < \epsilon_q$ {\rm ($\epsilon_q$ is the modified maximal Grauert radius of $q$)} there is a constant $C$ such that \begin{equation}\label{Fourier_coeff_estimate}
| a_k^q(s) | \le C e^{-\epsilon |k|}
\end{equation} for all integer $k$ and $s \in [-\pi, \pi)$. Here $| a_k^q(s) |$ denotes the maximum of its entries in absolute value. \end{itemize} \end{prop}
\noindent {\sl Proof}. \ Write the operator ${\bf T}_2$ as \begin{equation}\label{T21T22}
{\bf T}_2 = \frac{\mu}{2 \mu + \lambda} {\bf T}_{2, 1} + \frac{2 \left( \mu + \lambda \right)}{2 \mu + \lambda} {\bf T}_{2, 2}, \end{equation} where the definition of each operator is clear from \eqnref{BKtwo}. In particular, ${\bf T}_{2,1} = \mathcal{K} {\bf I}$ where $\mathcal{K}$ is the electro-static NP operator.
It is known that the integral kernel of $\mathcal{K}$ admits an analytic extension to the maximal Grauert tube. In fact, if we let ${\bf x}=q(t)$ and ${\bf y}=q(s)$ for ${\bf x}, {\bf y} \in\partial\Omega$ where $q$ is a regular parametrization of $\partial\Omega$ (either $C^{k,\alpha}$ or real analytic), then the outward unit normal vector ${\bf n}_{\bf y}$ is given by $-i q'(s)/|q'(s)|$ and $d\sigma({\bf y})=|q'(s)|ds$. Using notation \eqnref{Kzero}, the parametrized kernel denoted by $A_q(t,s)$ is given by \begin{equation}\label{Kq}
A_q(t,s)=K_0({\bf x},{\bf y}) |q'(t)| = \frac{1}{4\pi i} \Big[\frac{q'(t)}{q(t)-q(s)}-\frac{\overline{q'(t)}}{\overline{q(t)} - \overline{q(s)} } \Big] .
\end{equation} It is shown in \cite{AKM-JIE, MS} that $A_q(t,s)$ is $C^{k-2,\alpha}$ if $\partial\Omega$ is $C^{k,\alpha}$, and if $\partial\Omega$ is real analytic, then $A_q(t,s)$ extends as an analytic function in $|\Im s|< \epsilon_q$. As a consequence, it is proved that for any $0 < \epsilon < \epsilon_q$ there is a constant $C$ such that \begin{equation}\label{aest}
\left| \frac{1}{2\pi} \int_{-\pi}^{\pi} A_q(t, s) e^{-ikt} dt \right| \le C e^{-\epsilon |k|} \end{equation} for all integer $k$ and $s \in [-\pi, \pi)$. Here we review the proof of \eqnref{aest} in \cite{AKM-JIE} since the same argument is repeatedly used.
If $k>0$, then we take a rectangular contour $R$ with the clockwise orientation in $\mathbb{R} \times i(-\epsilon_q, \epsilon_q)$: $$ R = R_1\cup R_2\cup R_3\cup R_4 := [-\pi, \pi]\cup [\pi, \pi-i\epsilon] \cup [\pi-i\epsilon, -\pi-i\epsilon] \cup [-\pi-i \epsilon, -\pi]. $$ Since $A_q(t, s)$ is analytic in $\mathbb{R} \times i(-\epsilon_q, \epsilon_q)$ and $2\pi$-periodic with respect to the $t$ variable, we have \begin{align*}
0= \int_{R} A_q(t, s) e^{-ikt} dt = \Big\{\int_{R_1}+\int_{R_3} \Big\} A_q(t, s) e^{-ikt} dt , \end{align*} which implies \begin{equation*}
\int_{-\pi}^{\pi} A_q(t, s) e^{-ikt} dt =-\int_{R_3} A_q(t, s) e^{-ikt} dt =-\int_{\pi - i\epsilon}^{-\pi - i\epsilon} A_q(t, s) e^{-ikt} dt. \end{equation*}
Since $|A_q(t, s)|$ is bounded for all $s \in \mathbb{R}$ and $t \in R_3$, \eqnref{aest} for $k>0$ follows. \eqnref{aest} for $k<0$ can be proved similarly, and the $k = 0$ case is obvious.
We now look into the operator ${\bf T}_{2, 2}$. If we use the same parametrization, then the parametrized kernel of ${\bf T}_{2, 2}$, which is denoted by $K_{2,2}(t,s)$, is given by \begin{align*}
K_{2,2}(t,s) &:= \frac{\left( {\bf x} - {\bf y} \right) \cdot {\bf n}_y}{2 \pi \left| {\bf x} - {\bf y} \right|^4} \left( {\bf x} - {\bf y} \right) \left( {\bf x} - {\bf y} \right)^\top |q'(s)| \\
&= 2 q'(s) A_q(t,s) \frac{(q(t)-q(s))\otimes (q(t)-q(s)) }{|q(t)-q(s)|^2}. \end{align*} Here $(q(t)-q(s))\otimes (q(t)-q(s))$ denotes the tensor product, that is, \begin{align*} &(q(t)-q(s))\otimes (q(t)-q(s)) \\ & = \begin{bmatrix}
|\Re(q(t)-q(s))|^2 & \Re(q(t)-q(s))\Im(q(t)-q(s)) \\
\Re(q(t)-q(s))\Im(q(t)-q(s)) & |\Im(q(t)-q(s))|^2
\end{bmatrix}. \end{align*} One can easily see from this formula that the function $$
R(t,s):=\frac{(q(t)-q(s))\otimes (q(t)-q(s)) }{|q(t)-q(s)|^2} $$ is $C^{k-1, \alpha}$ if $\partial\Omega$ is $C^{k, \alpha}$. Moreover, letting $q^{*}(s)=\overline{q(\overline{s})}$, we have \begin{align*}
|q(t)-q(s)|^2&=(\overline{q(t)}-{q^{*}(s)})(q(t)-q(s)), \\ \Re{(q(t)-q(s))}&=\frac{q(t)-q(s)+\overline{q(t)}-q^{*}(s)}{2}, \\ \Im{(q(t)-q(s))}&=\frac{q(t)-q(s)-\overline{q(t)}+q^{*}(s)}{2i} \end{align*}
for real $s, t$. These identities show that $R(t,s)$ as a function of $s$ is analytic in $|\Im s| <\epsilon_q$ for each fixed $t$. Thus $K_{2, 2}(t,s)$ is $C^{k-2, \alpha}$ if $\partial\Omega$ is $C^{k, \alpha}$, and extends analytically to $|\Im s| <\epsilon_q$ if $q$ is real analytic. The estimate \eqnref{Fourier_coeff_estimate} for $K_{2,2}(t,s)$ can be derived in the same way to derive the estimate for $A_q$ above. It is worthy mentioning that the facts proved so far hold for any parametrization $q$, not just for a parametrization by a Riemann mapping.
The operator $2k_0 {\bf B} {\bf H} +{\bf T}_2$ is expressed in terms of $\mathcal{K}$, $\mathcal{K}\mathcal{H}$, and ${\bf T}_{22}$. Thus we need to prove \eqnref{Fourier_coeff_estimate} for the operator $\mathcal{K}\mathcal{H}$. For that purpose, we use a parametrization $q$ by a Riemann mapping, say $\Phi$. Note that the function $f+i\mathcal{H} [f]$ extends analytically in $\Omega$. Let $\mathcal{H}_0$ be the Hilbert transform on $U$, the unit disc. Then, $f\circ \Phi +i \mathcal{H}_0[ f\circ \Phi]$ extends analytically in $U$, and so does $(f +i \mathcal{H}[f]) \circ \Phi$. Thus we have, after adjusting a constant, \begin{equation}\label{Hzero} \mathcal{H}[f] \circ\Phi = \mathcal{H}_0[f\circ \Phi]. \end{equation} The Hilbert transform on the circle can be computed explicitly. In fact, we have \begin{equation}\label{Hilbert} \mathcal{H}_0[e^{ikt}]= -i(\mbox{sgn} \,k) e^{ikt} \quad\mbox{for all } k \neq 0. \end{equation} In particular, we see that $\mathcal{H}_0$ is skew-symmetric, namely, \begin{equation}\label{skew} \int_{-\pi}^\pi f(t) \mathcal{H}_0[g](t) dt = - \int_{-\pi}^\pi \mathcal{H}_0[f](t) g(t) dt \end{equation} for any square integrable functions $f$ and $g$ on $[-\pi,\pi]$. Therefore, we have \begin{align*} \mathcal{K}\mathcal{H}[f](\Phi(\xi)) &=\int_{\partial\Omega} K_0(\Phi(\xi), y) \mathcal{H}[f](y)\, d\sigma(y) \\
&=\int_{\partial U} K_0(\Phi(\xi), \Phi(\omega)) (\mathcal{H} f)(\Phi(\omega)) |\Phi'(\omega)| d\sigma(\omega) \\
&=\int_{\partial U} K_0(\Phi(\xi), \Phi(\omega)) \mathcal{H}_0 [f \circ \Phi](\omega)|\Phi'(\omega)| d\sigma(\omega) \\
&=-\int_{\partial U} \mathcal{H}_0 [K_0(\Phi(\xi), \Phi(\cdot)) |\Phi'(\cdot)|](\omega) (f \circ \Phi)(\omega) d\sigma(\omega). \end{align*} We then infer that the parametrized kernel of $\mathcal{K}\mathcal{H}$, which is denoted by $B_q(t,s)$, is given by $$
B_q(t,s)= -\mathcal{H}_0 [K_0(\Phi(e^{it}), \Phi(\cdot)) |\Phi'(\cdot)|](e^{is}). $$ Thanks to \eqnref{Kq}, we have $$ B_q(t,s)= -\mathcal{H}_0 [A_q(t,\cdot)](e^{is}). $$ To show \eqnref{Fourier_coeff_estimate} for $B_q(t,s)$, we observe that \begin{align*} \frac{1}{2\pi} \int_{-\pi}^{\pi} B_q(t, s) e^{-ikt} dt = \frac{1}{2\pi} \int_{-\pi}^{\pi} A_q(t,s) \mathcal{H}_0[e^{-ikt}] dt. \end{align*} It then follows from \eqnref{Hilbert} that \begin{align*} \frac{1}{2\pi} \int_{-\pi}^{\pi} B_q(t, s) e^{-ikt} dt = \frac{i\mbox{sgn}\, k}{2\pi} \int_{-\pi}^{\pi} A_q(t,s) e^{-ikt} dt. \end{align*} Thus \eqnref{Fourier_coeff_estimate} for $B_q(t,s)$ follows from \eqnref{aest}, and the proof is complete.
\ensuremath{\square}
\section{Polynomial convergence on smooth boundaries}\label{sec:poly}
In this section, we prove the following theorem:
\begin{thm}\label{thm:smooth} If $\partial\Omega$ is $C^{k, \alpha}$ with $k+\alpha > 2$ and $0\leq \alpha <1$, then eigenvalues $\lambda_j^{\pm}$ of the elastic NP operator ${\bf K}$ converging to $\pm k_0$ satisfy \begin{equation} \lambda_j^{\pm} = \pm k_0 + o(j^{d}) \quad \text{as}\; j\rightarrow \infty \end{equation} for any $d>-(k+\alpha)+3/2$. \end{thm}
\subsection{Schatten classes}
Recall that every compact operator $L$ on a separable Hilbert space takes the canonical form $$ L\psi=\sum_{j=1}^{\infty} \alpha_j \langle \psi, v_j \rangle u_j $$ for some orthonormal basis $\{u_j\}$ and $\{v_j\}$, where $\alpha_j$ are singular values of $L$ (i.e., eigenvalues of $(L^*L)^{1/2}$), and $\langle \cdot, \cdot \rangle$ is the inner product. The singular values are non-negative, and we denote the $p$-Schatten (quasi)-norm of $L$ by \begin{equation}\label{Schattennorm} \Vert L \Vert_{S^p}= \left( \sum_{j=1}^{\infty} \alpha_j^p \right)^{1/p}. \end{equation}
If $p \ge 1$, then (\ref{Schattennorm}) defines a norm. For $0<p<1$, (\ref{Schattennorm}) does not define a norm but it is a unitary invariant functional which is a `quasi-norm' in the sense that instead of the triangle inequality we have \begin{equation}\label{Minkowski} \Vert L +M \Vert_{S^p}\leq 2^{1/p-1}(\Vert L \Vert_{S^p}+\Vert M \Vert_{S^p}), \quad 0<p<1. \end{equation} Further, we have the H\"older inequality: \begin{equation}\label{Holder} \Vert LM \Vert_{S^r}\leq \Vert L \Vert_{S^p} \Vert M \Vert_{S^q} \end{equation} for $0<p, q \le \infty$ with $1/p+1/q=1/r$ (see, e.g., \cite{DR,Si}). \begin{lem}\label{lem:1} If operators $A, B, C, D$ on a separable Hilbert space $H$ are in the Schatten class $S_r$, then the operator ${\bf R}$, defined by
\begin{equation*}
{\bf R} =
\begin{bmatrix}
A & B \\
C & D
\end{bmatrix},
\end{equation*} is in the same Schatten class $S_r$ on the Hilbert space $H \times H$. \end{lem}
\noindent {\sl Proof}. \ Since the Schatten (quasi)-norm is unitary invariant, we have \begin{equation*} \Big\Vert \begin{bmatrix}
O & B \\
O & O
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Big\Vert \begin{bmatrix}
O & B \\
O & O
\end{bmatrix} \begin{bmatrix}
O & I \\
I & O
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Big\Vert \begin{bmatrix}
B & O \\
O & O
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Vert B \Vert_{S^r}, \end{equation*} and \begin{equation*} \Big\Vert \begin{bmatrix}
O & O \\
C & O
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Big\Vert \begin{bmatrix}
O & O \\
C & O
\end{bmatrix} \begin{bmatrix}
O & I \\
I & O
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Big\Vert \begin{bmatrix}
O & O \\
O & C
\end{bmatrix} \Big\Vert_{S_r(H \times H)} =\Vert C \Vert_{S^r}. \end{equation*} From the inequality (\ref{Minkowski}), we have \begin{align*} \Vert {\bf R} \Vert_{S_r(H \times H)}\leq C_1( \Vert A \Vert_{S^r}+\Vert B \Vert_{S^r}+ \Vert C \Vert_{S^r}+\Vert D \Vert_{S^r})< +\infty \end{align*} for some constant $C_1$, as desired.
\ensuremath{\square}
Here we invoke the result \cite[Theorem 3.6]{DR} which states that if $E(x, y)\in H_{x, y}^{\mu_1, \mu_2}(\partial\Omega \times \partial\Omega)$ (the Sobolev space of order $\mu_1$ in $x$-variable and $\mu_2$ in $y$-variable), then the integral operator $\mathcal{E}$ on $L^2(\partial\Omega)$ defined by the integral kernel $E(x, y)$ is in the Schatten classes $S_{r}(L^2(\partial\Omega))$ for $r>\frac{2}{1+2(\mu_1+\mu_2)}$. Suppose that $\partial\Omega$ is $C^{k,\alpha}$ with $k + \alpha >2$. According to Proposition \ref{extension} (i), the integral kernels of ${\bf B}$ and ${\bf T}_2$, which are $2 \times 2$ matrix-valued functions, are $C^{k-2, \alpha}$-smooth in both $t$ and $s$ variables. Thus each component of ${\bf B}$ and ${\bf T}_2$ is in the Schatten class $S_r$ for $r>\frac{2}{1+2(k-2+\alpha)}=\frac{2}{2k+2\alpha-3}$ by letting $\mu_1+\mu_2=k-2+\alpha$. We then infer from Lemma \ref{lem:1} that ${\bf B}$ and ${\bf T}_2$ themselves are in the same Schatten class $S_r$. Since ${\bf H}$ is a bounded operator on $L^2(\partial \Omega)^2$ and the Schatten class $S_r$ is an ideal on the space of all the bounded operators, $2k_0{\bf B} {\bf H} + {\bf T}_2$ is in the Schatten class $S_r$ for $r>\frac{2}{2k+2\alpha-3}$.
Let us introduce an invertible linear transform on $L^2(\partial\Omega)^2$ : \begin{equation}\label{BPdef} {\bf P}=\frac{1}{\sqrt{2}}\begin{bmatrix} I & \mathcal{H} \\ \mathcal{H} & {I} \end{bmatrix} . \end{equation} Since $\mathcal{H}^2=-I$, we have \begin{equation} {\bf P}^{-1}=\frac{1}{\sqrt{2}}\begin{bmatrix} I & -\mathcal{H} \\ -\mathcal{H} & {I} \end{bmatrix}. \end{equation} It follows from \eqnref{BKBHBB} that \begin{equation}\label{PinvKP} {\bf P}^{-1} {\bf K} {\bf P} = k_0\begin{bmatrix} I & 0 \\ 0 & -{I} \end{bmatrix} -{\bf Q} , \end{equation} where \begin{equation}\label{BS1} {\bf Q} := {\bf P}^{-1} (2k_0{\bf B} {\bf H} + {\bf T}_2) {\bf P}. \end{equation} Since $2k_0{\bf B} {\bf H} + {\bf T}_2$ belongs to the Schatten class $S_r$ for $r>\frac{2}{2k+2\alpha-3}$, so does ${\bf Q}$.
Let us now recall the result \cite[Theorem 1]{G} on the decomposition of polynomially compact operators, of which the following is a special case: \begin{thm} Let $A$ be a polynomially compact operator on a Hilbert space $H$ with minimal polynomial $p(z)=(z-k_0)(z+k_0)$. Then the Hilbert space $H$ is decomposed into the direct sum $H=H_{k_0}\bigoplus H_{-k_0}$, and the operators $A-k_0 I$ and $A+k_0 I$ are compact on $H_{k_0}$ and $H_{-k_0}$, respectively. \end{thm}
In the above, the decomposition can be explicitly given by \begin{equation}\label{Hdecom} H_{k_0}=E_{k_0}H \quad\mbox{and}\quad H_{-k_0}=E_{-k_0}H, \end{equation} where \begin{align} E_{k_0} &:= \frac{1}{2\pi i} \int_{\partial (k_0)} (A-\lambda I)^{-1} d\lambda, \label{Ekzero}\\ E_{-k_0} &:= \frac{1}{2\pi i} \int_{\partial (-k_0)} (A-\lambda I)^{-1} d\lambda . \label{Ekzero2} \end{align} Here $\partial(k_0)$ and $\partial(-k_0)$ denote disjoint contours around $k_0$ and $-k_0$ satisfying $\sigma(K) \subset \text{int}(\partial(k_0))\cup \text{int}(\partial(-k_0))$. We emphasize that the $E_{\pm k_0}={\bf I}$ on $H_{\pm k_0}$, respectively.
We now apply the decomposition to the operator $A={\bf P}^{-1}{\bf K}{\bf P}$. According to \eqnref{PinvKP}, we have \begin{equation}\label{PKPI} {\bf P}^{-1}{\bf K}{\bf P}-\lambda {\bf I} =\begin{bmatrix} (k_0-\lambda)I & 0 \\ 0 & {(-k_0-\lambda)I} \end{bmatrix} -{\bf Q} . \end{equation} Using the partial Neumann series, we have \begin{align*} &({\bf P}^{-1}{\bf K}{\bf P}-\lambda {\bf I})^{-1} \\ &=\left( \begin{bmatrix} (k_0-\lambda)I & 0 \\ 0 & {(-k_0-\lambda)I} \end{bmatrix} -{\bf Q} \right)^{-1} \\ &= \begin{bmatrix} (k_0-\lambda)I & 0 \\ 0 & {(-k_0-\lambda)I} \end{bmatrix}^{-1} \left( {\bf I} - \begin{bmatrix} (k_0-\lambda)I & 0 \\ 0 & {(-k_0-\lambda)I} \end{bmatrix}^{-1} {\bf Q} \right)^{-1} \\ & = C(\lambda) \left[ {\bf I} + C(\lambda) {\bf Q} + A(\lambda) \right], \end{align*} where \begin{equation}\label{CGl} C(\lambda):= \begin{bmatrix} \displaystyle \frac{1}{k_0-\lambda} I & 0 \\ 0 & \displaystyle \frac{-1}{k_0+\lambda} I \end{bmatrix} \end{equation} and \begin{equation}\label{AGl} A(\lambda)=\left( C(\lambda) {\bf Q}\right)^2 \left({\bf I}- C(\lambda) {\bf Q} \right)^{-1}= \left({\bf I}- C(\lambda) {\bf Q} \right)^{-1}\left( C(\lambda) {\bf Q}\right)^2. \end{equation}
We now prove that $E_{k_0}$ defined by \eqnref{Ekzero} with $A= {\bf P}^{-1}{\bf K}{\bf P}$ is of the form \begin{equation}\label{EkzeroNP} E_{k_0} = \begin{bmatrix} -I & 0 \\ 0 & 0 \end{bmatrix} +{\bf Q}_{k_0}, \end{equation} where ${\bf Q}_{k_0}$ is in the same Schatten class as ${\bf Q}^2$. In fact, one can see immediately that $$ \frac{1}{2\pi i}\int_{\partial (k_0)} C(\lambda) d\lambda = \begin{bmatrix} -I & 0 \\ 0 & 0 \end{bmatrix}. $$ We also have $$ \frac{1}{2\pi i} \int_{\partial (k_0)} C(\lambda)^2 {\bf Q} d\lambda = 0. $$
Let \begin{equation} {\bf Q}_{k_0}:= \frac{1}{2\pi i}\int_{\partial (k_0)} C(\lambda)A(\lambda) \, d\lambda, \end{equation} and we show that ${\bf Q}_{k_0}$ is in the same Schatten class as ${\bf Q}^2$. In fact, if we denote the matrix operator ${\bf Q}$ as ${\bf Q}=(Q_{ij})_{i, j=1, 2}$, then we find \begin{equation}\label{tildeS} {\bf Q} C(\lambda) =C(\lambda){\bf Q}+(\frac{-1}{k_0+\lambda}-\frac{1}{k_0-\lambda}) \begin{bmatrix} O & Q_{12} \\ -Q_{21} & O \end{bmatrix}=:C(\lambda){\bf Q}+B(\lambda){\bf R}. \end{equation} Therefore, \begin{align*} C(\lambda)A(\lambda)&=C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1}\left( C(\lambda) {\bf Q}\right)^2 \\ &=C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)^2 {\bf Q}^2 +C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)B(\lambda) {\bf R}{\bf Q}. \end{align*} Since ${\bf Q}^2$ and ${\bf R}{\bf Q}$ are independent of $\lambda$, we have \begin{align} {\bf Q}_{k_0}=&\left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)^2 d\lambda\right) {\bf Q}^2 \nonumber \\ & + \left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)B(\lambda) d\lambda\right) {\bf R}{\bf Q}. \label{BSkzero} \end{align} Since $\mbox{dist}(\partial(k_0), \lambda_j) > c_0$ for some $c_0>0$ for all eigenvalues $\lambda_j$ of ${\bf P}^{-1}{\bf K}{\bf P}$, $\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1}$ is bounded independently of $\lambda \in \partial(k_0)$, namely, $$
\| \left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} \| \le C $$ for some $C$ independent of $\lambda$. Therefore operator-valued functions $C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)^2$ and $C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)B(\lambda)$ are bounded and continuous in $\lambda \in \partial(k_0)$, and hence \begin{align*} \Big\Vert \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)^2 d\lambda \Big\Vert + \Big\Vert \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)B(\lambda) d\lambda \Big\Vert \le C \end{align*} for some $C$ (see, for example, \cite[\S 5, Theorem 1]{Yosida}).
Suppose that ${\bf Q}$ belongs to the Schatten class $S_p$ for some $p$. Then by the definition of ${\bf R}$ in \eqnref{tildeS}, we see that ${\bf R}\in S_p$, and \eqref{Holder} shows that ${\bf Q}^2, {\bf R}{\bf Q} \in S_{p/2}$. It then follows from \eqref{Minkowski} that \begin{align*} \left\Vert {\bf Q}_{k_0} \right\Vert_{S_{p/2}} \leq C_p \Big( &\Big\Vert \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)^2 d\lambda \Big\Vert \Vert {\bf Q}^2\Vert_{S_{p/2}} \\ + &\Big\Vert \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) {\bf Q} \right)^{-1} C(\lambda)B(\lambda) d\lambda \Big\Vert \Vert {\bf R}{\bf Q} \Vert_{S_{p/2}}\Big) < +\infty. \end{align*} Thus, ${\bf Q}_{k_0} \in S_{p/2}$.
In short, we showed that $E_{k_0}$ is of the form \eqnref{EkzeroNP}, and that if ${\bf Q} \in S_p$, then ${\bf Q}_{k_0} \in S_{p/2}$ (${\bf Q}^2$ also belongs to the same class). Similarly, one can show that \begin{equation} E_{-k_0} := \frac{1}{2\pi i} \int_{\partial(-k_0)} ({\bf P}^{-1}{\bf K}{\bf P}-\lambda {\bf I})^{-1} d\lambda =\begin{bmatrix} 0 & 0 \\ 0 & -I \end{bmatrix} +{\bf Q}_{-k_0}, \end{equation} where ${\bf Q}_{-k_0} \in S_{p/2}$ if ${\bf Q} \in S_p$.
We are now ready to prove Theorem \ref{thm:smooth}.
\noindent{\sl Proof of Theorem \ref{thm:smooth}}. Let us consider the operator ${\bf P}^{-1} {\bf K} {\bf P}-k_0 {\bf I}$ on $H_{k_0}:= E_{k_0}(L^2(\partial\Omega)^2)$ where $E_{k_0}$ is of the form in \eqnref{EkzeroNP}. In view of \eqnref{PKPI}, we have \begin{align} ({\bf P}^{-1} {\bf K} {\bf P} -k_0 {\bf I}) E_{k_0} & = \left( k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} -{\bf Q} \right) \left(\begin{bmatrix} -I & 0 \\ 0 & 0 \end{bmatrix} +{\bf Q}_{k_0}\right) \nonumber \\ &= {\bf Q} \begin{bmatrix} I & 0 \\ 0 & 0 \end{bmatrix} + k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} {\bf Q}_{k_0}\quad \text{mod}\ S_r. \label{BSSk} \end{align} This operator is in Schatten class $S_r$ with $r>\frac{2}{2k+2\alpha-3}$.
Here we invoke a result: If a self-adjoint operator $A$ on a Hilbert space belong to the Schatten class $S_r$, then its singular values $a_j$ satisfy $$ a_j= O(j^{-1/r +\epsilon}) \quad \mbox{as } j \to \infty, $$ for any $\epsilon >0$. See, for example, \cite{MR, Si} for a proof of this fact. Since $E_{k_0}={\bf I}$ on $H_{k_0}$ in \eqnref{BSSk}, the singular values of ${\bf P}^{-1}{\bf K} {\bf P}-k_0 {\bf I}$ on $H_{k_0}$, denoted by $\alpha_j^+$, satisfy \begin{equation} \alpha^{+}_j =o(j^{d}) \quad \mbox{as } j \to \infty, \end{equation} for any $d>-(k+\alpha)+3/2$. Let $\kappa_j$ be eigenvalues of ${\bf P}^{-1}{\bf K} {\bf P}-k_0 {\bf I}$ on $H_{k_0}$ enumerated in decreasing order in absolute values. By Weyl's inequality \cite{Si}, $\kappa_j$ satisfies $$
\sum_{j} |\kappa_j |^r \le \sum_{j} |\alpha_j |^r $$ as long as the righthand side is finite. Thus we have $$ \kappa_j=o(j^{d}) \quad \mbox{as } j \to \infty, $$ for any $d>-(k+\alpha)+3/2$. Since $\lambda_j^+$ are eigenvalues of ${\bf K}$ on $H^{1/2}(\partial\Omega)^2$ while $\kappa_j$ are eigenvalues of ${\bf P}^{-1}{\bf K} {\bf P}-k_0 {\bf I}$ on $L^2(\partial\Omega)^2$, we have $\{\lambda_j^+ -k_0 \} \subset \{\kappa_j \}$, and thus \begin{equation} \lambda^{+}_j -k_0=o(j^{d}) \quad \mbox{as } j \to \infty, \end{equation} for any $d>-(k+\alpha)+3/2$, as desired.
For the space $H_{-k_0}$, similarly we have \begin{equation} \lambda^{-}_j +k_0=o(j^{d}) \quad \mbox{as } j \to \infty, \end{equation} for any $d>-(k+\alpha)+3/2$. This completes the proof.
\ensuremath{\square}
\section{Exponential decay on analytic boundaries}\label{sec:exp}
We now consider the case of analytic boundaries.
Suppose that $\partial\Omega$ is real analytic and let $\Phi:U \to \Omega$ be a Riemann mapping. Let $q$ be the parametrization of $\partial\Omega$ by $\Phi$, namely, $q(s)=\Phi(e^{is})$, and let $\epsilon_q$ be the maximal Grauert radius of $q$. For $\mbox{\boldmath $\Gy$} \in H^{1/2}(\partial\Omega)^2$, let ${\bf f}(s):= \mbox{\boldmath $\Gy$}(q(s))$. By \eqnref{Hzero}, we have $$ {\bf P}[\mbox{\boldmath $\Gy$}](q(s))= \frac{1}{\sqrt{2}}\begin{bmatrix} \psi_1 (q(s))+ \mathcal{H}[\psi_2](q(s)) \\ \mathcal{H}[\psi_1](q(s)) + \psi_2 (q(s)) \end{bmatrix} = \widetilde{{\bf P}}[{\bf f}](s), $$ where \begin{equation}\label{tildeBP} \widetilde{{\bf P}}=\frac{1}{\sqrt{2}}\begin{bmatrix} I & \mathcal{H}_0 \\ \mathcal{H}_0 & {I} \end{bmatrix}. \end{equation}
With $T_q(t,s)$ defined in \eqnref{Tq}, let $$ {\bf V}[{\bf f}](t):= \int_{-\pi}^\pi {T}_q(t,s) {\bf f}(s) ds. $$ Then, it follows from \eqnref{Tq}, \eqnref{fourier} and \eqnref{BS1} that $$ {\bf Q}[\mbox{\boldmath $\Gy$}](q(t)) = \widetilde{{\bf P}}^{-1} {\bf V} \widetilde{{\bf P}} [{\bf f}](t). $$ If we write \begin{equation}\label{tildeT} {\bf Q} [\mbox{\boldmath $\Gy$}](q(t)) =: \int_{-\pi}^\pi \widetilde{T}_q(t,s) {\bf f}(s) ds \end{equation} and \begin{equation}\label{fourier2} \widetilde{T}_q(t, s)=:\sum_{k\in {\mathbb{Z}}} \tilde{a}_k^q(s) e^{ikt}, \end{equation} then \begin{align*} \int_{-\pi}^{\pi} \tilde{a}_k^q(s) (\mbox{\boldmath $\Gy$} \circ q)(s) ds &= \frac{1}{2\pi} \int_{-\pi}^{\pi} e^{-ikt} {\bf Q} [\mbox{\boldmath $\Gy$}](q(t)) dt \\ &= \frac{1}{2\pi} \int_{-\pi}^{\pi} \widetilde{{\bf P}} [e^{-ikt}I] {\bf V} \widetilde{{\bf P}} [{\bf f}](t) dt, \end{align*} where the last equality holds thanks to \eqnref{skew} because $$ \widetilde{{\bf P}}^{-1}=\frac{1}{\sqrt{2}}\begin{bmatrix} I & -\mathcal{H}_0 \\ -\mathcal{H}_0 & {I} \end{bmatrix}. $$ Because of \eqnref{Hilbert}, we have $$ \widetilde{{\bf P}} [e^{-ikt}I] = e^{-ikt} P_k , $$ where \begin{equation} P_k:= \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & i\mbox{sgn} \,k \\ i\mbox{sgn} \,k & 1 \end{bmatrix} . \end{equation} Therefore, \begin{align*} \int_{-\pi}^{\pi} \tilde{a}_k^q(s) {\bf f} (s) ds &= P_k \int_{-\pi}^{\pi} e^{-ikt} {\bf V} \widetilde{{\bf P}} [{\bf f}](t) dt \\ &= P_k \int_{-\pi}^{\pi} a_k^q(s) \widetilde{{\bf P}} [{\bf f}](s) ds \\ &= P_k \int_{-\pi}^{\pi} \frac{1}{\sqrt 2}\begin{bmatrix} a_{11}^{k}-\mathcal{H}_0(a_{12}^k) & a_{12}^{k}-\mathcal{H}_0(a_{11}^k)\\ a_{21}^k-\mathcal{H}_0(a_{22}^k) & a_{22}^k-\mathcal{H}_0(a_{21}^k) \end{bmatrix} {\bf f}(s) ds. \end{align*} Here we denote the matrix elements of $a_k^q(s)$ by $a_{ij}^k$ $(i, j=1, 2)$. Since above relation holds for all ${\bf f}$, we conclude that \begin{equation}\label{tildeform} \tilde{a}_k^q(s)=\frac{1}{\sqrt 2}P_k \begin{bmatrix} a_{11}^{k}-\mathcal{H}_0(a_{12}^k) & a_{12}^{k}-\mathcal{H}_0(a_{11}^k)\\ a_{21}^k-\mathcal{H}_0(a_{22}^k) & a_{22}^k-\mathcal{H}_0(a_{21}^k) \end{bmatrix}. \end{equation}
For $\mbox{\boldmath $\Gy$} \in H^{1/2}(\partial\Omega)^2$, let ${\bf f} = \mbox{\boldmath $\Gy$} \circ q$. Then ${\bf f} \in H^{1/2}(\mathbb{T})^2$, namely, ${\bf f} \in H^{1/2}([-\pi, \pi])^2$ and $2\pi$-periodic. Let \begin{equation}\label{wideBS} \widetilde{{\bf Q}}[{\bf f}](t):= {\bf Q}[\mbox{\boldmath $\Gy$}](q(t)). \end{equation} Then we see from \eqnref{tildeT} and \eqnref{fourier2} that \begin{equation} \widetilde{{\bf Q}}[{\bf f}](t)= \sum_{k\in {\mathbb{Z}}} e^{ikt} \frac{1}{2\pi} \int_{-\pi}^{\pi} \tilde{a}_k^q(s) {\bf f}(s) ds. \end{equation}
For a positive integer $n$ define the finite truncation $\widetilde{{\bf Q}}_n$ of $\widetilde{{\bf Q}}$ by \begin{equation}\label{finitetrunc}
\widetilde{{\bf Q}}_n[{\bf f}](t):= \sum_{|k| < n} e^{ikt} \frac{1}{2\pi} \int_{-\pi}^{\pi} \tilde{a}_k^q(s) {\bf f}(s) ds. \end{equation} Then $\widetilde{{\bf Q}}_n$ is of rank $2(2n-1)$. Moreover, we have \begin{align*}
\|(\widetilde{{\bf Q}} - \widetilde{{\bf Q}}_n)[{\bf f}]\|_{H^{1/2}(\mathbb{T})^2} & \le C \sum_{|k| \ge n} |k| \left| \int_{-\pi}^{\pi} \tilde{a}_k^q(s) {\bf f}(s) ds \right| \\
& \le C \sum_{|k| \ge n} |k| \| \tilde{a}_k^q \|_{H^{-1/2}(\mathbb{T})^4} \|{\bf f} \|_{H^{1/2}(\mathbb{T})^2} . \end{align*} Since the Hilbert transform $\mathcal{H}_0$ is bounded on $L^2(\mathbb{T})$, we have from \eqnref{Fourier_coeff_estimate}, \eqnref{tildeBP} and \eqnref{tildeform} that for any $\epsilon < \epsilon_q$ there exist $C_1$ and $C_2$ such that $$
\| \tilde{a}_k^q \|_{H^{-1/2}(\mathbb{T})^4} \le \| \tilde{a}_k^q \|_{L^2(\mathbb{T})^4} \le C_1 \| {a}_k^q \|_{L^2(\mathbb{T})^4} \le C_2 e^{-\epsilon |k|} $$ for all $k$. Thus, $$
\|(\widetilde{{\bf Q}} - \widetilde{{\bf Q}}_n)[{\bf f}]\|_{H^{1/2}(\mathbb{T})^2} \le C_2 \sum_{|k| \ge n} |k| e^{-\epsilon |k|} \|{\bf f} \|_{H^{1/2}(\mathbb{T})^2} \le C_2 e^{-\epsilon n}. $$ In short, we have \begin{equation}\label{trunc}
\|(\widetilde{{\bf Q}} - \widetilde{{\bf Q}}_n) \| \le C_2 e^{-\epsilon n} \end{equation} for any $\epsilon < \epsilon_q$.
We are now at the position to state and prove the second main theorem of this paper. The proof relies on the Weyl-Courant min-max principle which we state below for readers' sake (see, for example, \cite{MR728688} for a proof).
\begin{lem}\label{lem:W-C_minimax1} Let $\mathcal{T}$ be a compact symmetric operator on a Hilbert space, whose eigenvalues $\{ \kappa_n \}_{n = 1}^\infty$ are arranged as \begin{equation}\label{order}
| \kappa_1 | \ge | \kappa_2 | \ge \cdots \ge | \kappa_n | \ge \cdots. \end{equation} If $\mathcal{T}_n$ is an operator of rank less than or equal to $n$, then $$
\Vert \mathcal{T} - \mathcal{T}_n \Vert \ge | \kappa_{n + 1} |. $$ \end{lem}
The following theorem is the second main result of this paper.
\begin{thm}\label{analytic decay} Suppose that $\partial\Omega$ is real analytic. Let $q$ be a parametrization of $\partial\Omega$ by a Riemann mapping and let $\epsilon_q$ be its modified maximal Grauert radius. Then, eigenvalues $\lambda_j^{\pm}$ of the elastic NP operator ${\bf K}$ converging to $\pm k_0$ satisfy \begin{equation}\label{expdecay} \lambda^{\pm}_j = \pm k_0+ o(e^{-\epsilon j}) \quad \text{as}\; j\rightarrow \infty \end{equation} for any $\epsilon <\epsilon_q/8$ . \end{thm}
\noindent {\sl Proof}. \ Let ${\bf P}$ be the operator define by \eqnref{BPdef}, and define similarly to \eqnref{star} an inner product for $\mbox{\boldmath $\Gvf$}, \mbox{\boldmath $\Gy$} \in H^{1/2}(\partial\Omega)^2$ by $$ \langle \mbox{\boldmath $\Gvf$}, \mbox{\boldmath $\Gy$} \rangle_{**} :=\langle \mbox{\boldmath $\Gvf$}, {\bf P}^{-1} {\bf S}^{-1} {\bf P} \mbox{\boldmath $\Gy$} \rangle, $$ where ${\bf S}$ is the single layer potential. Since ${\bf P}$ is an invertible operator on $H^{1/2}(\partial\Omega)^2$, it is indeed an inner product on $H^{1/2}(\partial\Omega)^2$.
The operator ${\bf P}^{-1} {\bf K} {\bf P}$ is self-adjoint with respect to $\langle \cdot, \cdot \rangle_{**}$ by Plemelji's symmetrization principle \eqnref{plemelj}. Let $H_{k_0}$ and $H_{-k_0}$ be defined according to \eqnref{Hdecom} with $H= H^{1/2}(\partial\Omega)^2$. Then ${\bf P}^{-1} {\bf K} {\bf P}$ maps $H_{k_0}$ into itself. Since $E_{k_0}$ is the identity on $H_{k_0}$, it follows from \eqnref{BSSk} that if $\mbox{\boldmath $\Gvf$} \in H_{k_0}$, then \begin{align*} ({\bf P}^{-1} {\bf K} {\bf P} -k_0 {\bf I})[\mbox{\boldmath $\Gvf$}] = ({\bf P}^{-1} {\bf K} {\bf P} -k_0 {\bf I}) E_{k_0} [\mbox{\boldmath $\Gvf$}] = \left({\bf Q} \begin{bmatrix} I & 0 \\ 0 & 0 \end{bmatrix} + k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} {\bf Q}_{k_0} \right) [\mbox{\boldmath $\Gvf$}]. \end{align*} Thus the operator $$ {\bf Q} \begin{bmatrix} I & 0 \\ 0 & 0 \end{bmatrix} + k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} {\bf Q}_{k_0} $$ is self-adjoint on $H_{k_0}$.
For $\mbox{\boldmath $\Gvf$} \in H_{k_0}$ let ${\bf f}=\mbox{\boldmath $\Gvf$}\circ q$, and denote the collection of such functions by $\widetilde{H}_{k_0}$. Equip $\widetilde{H}_{k_0}$ with the inner product \begin{equation}\label{inner3} \langle {\bf f}, {\bf g} \rangle_{**} := \langle \mbox{\boldmath $\Gvf$}, \mbox{\boldmath $\Gy$} \rangle_{**}, \end{equation} where ${\bf f} = \mbox{\boldmath $\Gvf$}\circ q$ and ${\bf g}= \mbox{\boldmath $\Gy$}\circ q$. Having \eqnref{BSkzero} in mind, we define \begin{align*} \widetilde{{\bf Q}}_{k_0}= &\left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) \widetilde{\bf Q} \right)^{-1} C(\lambda)^2 d\lambda\right) \widetilde{\bf Q}^2 \nonumber \\ & + \left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) \widetilde{\bf Q} \right)^{-1} C(\lambda)B(\lambda) d\lambda\right) \widetilde{\bf R} \widetilde{\bf Q}, \end{align*} where $\widetilde{{\bf Q}}$ is defined by \eqnref{wideBS} and $\widetilde{\bf R}$ is defined similarly, and define \begin{equation} \mathcal{T}:= \widetilde{{\bf Q}} \begin{bmatrix} I & 0 \\ 0 & 0 \end{bmatrix} + k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} \widetilde{{\bf Q}}_{k_0} . \end{equation} Then $\mathcal{T}$ is self-adjoint on $\widetilde{H}_{k_0}$ with respect to the inner product \eqnref{inner3}.
Using the finite truncation $\widetilde{{\bf Q}}_n$ of $\widetilde{{\bf Q}}$, we define \begin{align*} \widetilde{{\bf Q}}_{k_0,n}:= &\left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) \widetilde{\bf Q} \right)^{-1} C(\lambda)^2 d\lambda\right) \widetilde{\bf Q} \widetilde{\bf Q}_n \nonumber \\ & + \left(\frac{1}{2\pi i} \int_{\partial(k_0)}C(\lambda)\left({\bf I}- C(\lambda) \widetilde{\bf Q} \right)^{-1} C(\lambda)B(\lambda) d\lambda\right) \widetilde{\bf R} \widetilde{\bf Q}_n, \end{align*} and \begin{equation} \mathcal{T}_n:= \widetilde{{\bf Q}}_n \begin{bmatrix} I & 0 \\ 0 & 0 \end{bmatrix} + k_0 \begin{bmatrix} 0 & 0 \\ 0 & -2{I} \end{bmatrix} \widetilde{{\bf Q}}_{k_0,n} . \end{equation} Since $\widetilde{{\bf Q}}_n$ is of rank $2(2n-1)$, $\mathcal{T}_n$ is of rank at most $4(2n-1)$. Moreover, we have from \eqnref{trunc} that \begin{equation}\label{trunc2}
\| \mathcal{T}-\mathcal{T}_n \| \le C \|\widetilde{{\bf Q}} - \widetilde{{\bf Q}}_n \| \le C e^{-\epsilon n}. \end{equation}
Let $\{ \kappa_n \}_{n = 1}^\infty$ be eigenvalues of $\mathcal{T}$ on $\widetilde{H}_{k_0}$ arranged according to \eqnref{order}. Then Lemma \ref{lem:W-C_minimax1} and \eqnref{trunc2} show that $$
|\kappa_{4(2n-1)+1}| \le C e^{-\epsilon n}, $$ and this inequality holds for all $\epsilon < \epsilon_q$. In other words, we have \begin{equation}
|\kappa_{k}| \le C e^{-\epsilon k/8}, \end{equation}
This completes the proof of \eqnref{expdecay} for $\lambda_j^+$. Similarly one can prove \eqnref{expdecay} for $\lambda_j^-$.
\ensuremath{\square}
\section*{Conclusion}
It is proved in this paper that eigenvalues of the elastic NP operator on $\partial\Omega$, the boundary of a planar domain $\Omega$, converge to $\pm k_0$ at a polynomial rate if $\partial\Omega$ is smooth, and at an exponential rate if $\partial\Omega$ is real analytic. Moreover, quantitative convergence rates are derived.
It is shown in \cite{AJKKY} that on the ellipse $x^2/a^2+y^2/b^2=1$ ($a \ge b$) \begin{equation}\label{123}
|\lambda^+_j - k_0| \approx C n e^{- n \rho} \quad\mbox{and}\quad |\lambda^-_j + k_0| \approx C n e^{- 2 n \rho}, \end{equation} where $$ \rho= \log \frac{a+b}{a-b}. $$ This $\rho$ is the modified maximal Grauert radius of the parametrization $q(t) = a \cos{t} + ib \sin{t}$ of the ellipse (see Example 2 in \cite{AKM-JIE}). This example shows that the convergence rate \eqnref{expdecay} is not optimal. In particular, \eqnref{123} shows that the convergence rates of eigenvalues at $k_0$ and $-k_0$ are different. But the method of this paper cannot catch such a difference. It is quite interesting and challenging to clarify such a difference in convergence rates for general domains with real analytic boundaries. Optimality of the convergence rate on smooth boundaries also requires further investigation.
In three dimensions elastic NP eigenvalues consist of three subsequences converging to $k_0$, $0$ and $-k_0$ \cite{AKM, KK}. It is a challenging problem to find convergence rates in three dimensions and Weyl asymptotics of the convergence. In connection with this problem we refer readers to recent work of Miyanishi \cite{Miya} and Miyanishi-Rosneblum \cite{MR} where Weyl asymptotics for the eigenvalues for the electro-static NP operator.
\end{document} | arXiv |
Population difference gratings created on vibrational transitions by nonoverlapping subcycle THz pulses
Your article has downloaded
Similar articles being viewed by others
Carousel with three slides shown at a time. Use the Previous and Next buttons to navigate three slides at a time, or the slide dot buttons at the end to jump three slides at a time.
Modifying angular and polarization selection rules of high-order harmonics by controlling electron trajectories in k-space
Yasuyuki Sanari, Tomohito Otobe, … Hideki Hirori
Asymmetries in ionization of atomic superposition states by ultrashort laser pulses
J. Venzke, A. Becker & A. Jaron-Becker
Analysis of a q-deformed hyperbolic short laser pulse in a multi-level atomic system
N. Boutabba, S. Grira & H. Eleuch
Sub-cycle coherent control of ionic dynamics via transient ionization injection
Qian Zhang, Hongqiang Xie, … Zengxiu Zhao
Propagation of optically tunable coherent radiation in a gas of polar molecules
Piotr Gładysz, Piotr Wcisło & Karolina Słowik
Amplification of intense light fields by nearly free electrons
Mary Matthews, Felipe Morales, … Misha Ivanov
Role of Van Hove singularities and effective mass anisotropy in polarization-resolved high harmonic spectroscopy of silicon
Pawan Suthar, František Trojánek, … Martin Kozák
Field-resolved high-order sub-cycle nonlinearities in a terahertz semiconductor laser
J. Riepl, J. Raab, … R. Huber
Strong-field coherent control of isolated attosecond pulse generation
Yudong Yang, Roland E. Mainz, … Franz X. Kärtner
Rostislav Arkhipov1,2,3,
Anton Pakhomov2,
Mikhail Arkhipov1,2,
Ihar Babushkin4,5,6,
Ayhan Demircan4,5,
Uwe Morgner4,5 &
Nikolay Rosanov2,3
Scientific Reports volume 11, Article number: 1961 (2021) Cite this article
Optical physics
Terahertz optics
We study theoretically a possibility of creation and ultrafast control (erasing, spatial frequency multiplication) of population density gratings in a multi-level resonant medium having a resonance transition frequency in the THz range. These gratings are produced by subcycle THz pulses coherently interacting with a nonlinear medium, without any need for pulses to overlap, thereby utilizing an indirect pulse interaction via an induced coherent polarization grating. High values of dipole moments of the transitions in the THz range facilitate low field strength of the needed THz excitation. Our results clearly show this possibility in multi-level resonant media. Our theoretical approach is based on an approximate analytical solution of time-dependent Schrödinger equation (TDSE) using perturbation theory. Remarkably, as we show here, quasi-unipolar subcycle pulses allow more efficient excitation of higher quantum levels, leading to gratings with a stronger modulation depth. Numerical simulations, performed for THz resonances of the \(H_20\) molecule using Bloch equations for density matrix elements, are in agreement with analytical results in the perturbative regime. In the strong-field non-perturbative regime, the spatial shape of the gratings becomes non-harmonic. A possibility of THz radiation control using such gratings is discussed. The predicted phenomena open novel avenues in THz spectroscopy of molecules with unipolar and quasi-unipolar THz light bursts and allow for better control of ultra-short THz pulses.
Generation of few-cycle THz pulses (0.1–10 THz) have attracted considerable interest over the past decades1,2,3,4 due to the growing number of applications in science and technology. For example, THz pulses are used for spectroscopy, since the THz range includes rotational and vibrational resonances of large molecules as well as transitions in various dielectrics and semiconductor structures3,4,5,6,7,8,9,10. They have a huge potential in other applications such as medicine, wireless communication systems, charge particles acceleration etc3,4. Nowadays, THz pulses up to subcycle duration became available1,2,3,4. Such durations can be much shorter than the relaxation times \(T_1\) and \(T_2\) of the resonant medium. That is, so called coherent interaction regime takes place, and effects of resonant light-matter interactions such as Rabi oscillations may arise11. If a resonant medium interacts coherently with a train of few-cycle pulses and the pulses do not overlap in the medium, population density gratings can be created in a two-level medium as it was shown in optical range using long nanosecond12,13,14, femtosecond and attosecond pulses15,16,17 as well as in THz range using multi-cycle THz18 pulses.
Such gratings are based on interaction between the pulses without an actual overlap, taking place indirectly, via oscillations of macroscopic polarization of the medium. The first pulse prepares the medium in a coherent superposition of the ground and excited states. This superposition exists within the time scale of \(T_2\), until destroyed by decoherence. If a second pulse enters the medium within this time, it interacts with this induced atomic polarization, and in this way an inversion grating can be formed. This is in contrast to the traditional approach in which such gratings are generated as a result of interference of two or more long quasimonochromatic overlapping beams19.
The possibility of ultrafast creation and control of optical gratings by attosecond-long single-cycle and subcycle optical pulse trains was studied in15,16,17. However, generation of attosecond pulses with single-cycle and subcycle pulse duration requires a complicated setup. Besides, in the optical range, the field strengths needed to facilitate the effective interaction are extremely high (\(~10^4-10^5\) ESU \(\approx 10^6-10^7\) V/cm), which makes practical implementation even more complicated. In contrast, in the THz range, subcycle pulses can be generated much easier1,2,3,4.
Next, the pump power needed to realize coherent interactions in THz range is several orders of magnitude lower, provided that high THz vibrational transitions possess huge dipole moments \(d_{12}\)20,21. The latter allows using THz pulses experimentally available to date, and field strengths, significantly lower than in the optical range. It worth to note that practically available subcycle THz pulses often contain a burst of single polarity and a big tail of opposite polarity and small amplitude1,2,3,4,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38. Action of such quasi-unipolar pulses is nearly the same as the true unipolar ones38.
Generation of unipolar and quasi-unipolar pulses and their applications in optics is a subject of active discussions22,23,24,25,26,27,28,29,30, see also recent review31 and references therein. These pulses, due to their unipolar character, effectively transfer their energy to charged particles, resulting in novel applications, including highly effective ionization and control of Rydberg atoms32,33,34, effective attosecond pulse generation35, effective excitation and ultra-fast control of electron wave packets dynamics23,36,37,38, charge acceleration39, holographic recording40 and others.
As we mentioned above, in previous works of the authors15,16,17 grating dynamics was studied in the optical range using few-cycle pulses in a two-level medium. However, due to broad spectral content of few-cycle pulses taking into account multilevel character of the system is of high importance. Some remarks on the possibility of grating formation in multi-level systems in the optical range were shortly reported in a prior work16,41. However, a detailed analysis of grating dynamics under such circumstances was up to now still missing. In this paper, we study a possibility of population density grating formation on vibrational THz resonance transitions in three- and multi-level media, assuming high values of transition dipole moments (tens to hundreds Debyes), created by subcycle THz pulses. We consider a possibility to use short quasi-unipolar subcycle pulses for grating formation, because they allow more effective excitation and control of quantum state population23,36,37,38. In previous studies, only bipolar few-cycle pulses were considered in this context15,16.
For the theoretical analysis of the multi-level system in question we use the standard perturbation approach for the time-dependent Schrödinger equation (TDSE) for "small" electric field amplitude. For numerical simulations, we use the Bloch equations for density matrix elements of a three-level medium. For analytical studies, we model the multi-level system as a quantum harmonic oscillator (HO) with equidistant levels assuming resonance frequency in THz range and high values of dipole moments of the resonant transitions. In spite of the fact, that our theoretical analysis is quite general, some particular examples will be mentioned.
To realize coherent light-matter interactions, the Rabi frequency \(\Omega _R=d_{12}E_0/\hbar\) (\(d_{12}\) is the transition dipole moment, \(E_0\) is the electric field amplitude) should be larger than the inverse polarization relaxation time \(T_2\), \(\Omega _R > 1/T_2\) and the pulse duration \(\tau _p <T_2\). First, most of molecules have vibration resonances in THz range6,7,8,9,10 and low energy states can be modelled, to some level of approximation, using quantum HO42. In our analysis below we consider a water molecule \(H_2O\) having resonances in the interval 0.5–1 THz43,44. Other examples are Rydberg atoms with large quantum numbers \(n>>1\)—they also have large dipole moments45, can be arranged to possess long life times46 and resonance transitions in THz range32,33,34,45. Next, it is shown47 that the confinement potential of an electron in nanostructures and quantum dots (QD) for energy below the Fermi level is approximately parabolic, thus, the HO model can be used in this case. QD media can have extremely high values of transition dipole moments (tens-hundreds Debye) as well as \(T_2\) at low temperatures as high as hundreds ns48,49; they also can be used for THz generation50. Furthermore, quantum cascade lasers can generate THz radiation51. Semiconductor nanostructures used in such devices have very high dipole moments (tens of Debye) and can operate as three-level systems52,53. In some media like crystals, containing impurities of rare-earth ions, the values of \(T_2\) at low temperatures can approach extremely high values - from several seconds to several hours54.
There is another advantage of creating grating on vibrations transitions in THz range: In quantum HO in the first order perturbation approach, only the transition from the ground state to the 1st excited state is possible, in contrast to, for instance, 1/r potential. As we see here, this significantly reduces the probability of excitation of higher order levels, even if we go into nonperturbative regime with HO.
Furthermore, creation of the gratings on vibrational transitions in different systems opens novel opportunities in THz ultra-fast spectroscopy. For instance, diffraction of a weak probe pulse on such gratings can be used for spectroscopic measurements of \(T_2\) – a task which is otherwise proved to be quite difficult experimentally12,13,14. As we show below, such gratings can be also used for control of THz radiation, for instance ultrafast pulse reshaping using fast mirrors.
This paper is organized as follows. First, in "Classical picture of grating formation in a system of classical HOs", for a deeper understanding of the idea of grating formation, we consider aclassical picture of the gratings arising in a medium consisting of classical harmonic oscillators (HO). In "Multi-level vibration system: weak THz field strength" we consider a grating formation in a multi-level system using perturbation theory for TDSE, when the THz field strength is low. Here we use a \(\delta\)-pulse approximation, valid when the pulse duration is smaller than the inverse transition period of the medium. After this, pulses of finite duration are considered. In "Numerical simulations" we perform numerical simulations for three-level HO using parameters for \(H_2O\) molecule. A possibility of THz radiation control by the gratings is considered in the "Control of long THz pulses". Finally, concluding remarks are drawn.
Classical picture of grating formation in a system of classical HOs
The simplest setup with four THz pulses counter-propagating in a medium to create a grating. Inset shows a 4-level HO molecular medium with the eigenfrequency \(\omega _0\). This figure was created with Paint application for Windows and converted to eps using online convertor (https://image.online-convert.com/ru/convert-to-eps).
First, we consider the classical picture of a grating formation. Let a dielectric resonant medium consist of linear classical harmonic oscillators, non-interacting with each other and having eigen-frequency \(\omega _0\), distributed along z-axis, see Fig. 1. The displacement of the oscillator at point z is governed by the following equation (neglecting damping of oscillations):
$$\begin{aligned} {\ddot{X}}(z,t) + \omega _0^2 X(z,t)=q/m E(z,t) \end{aligned}$$
Here q is the electron charge and m the oscillator mass. Let the medium be excited by a pair of extremely-short pulses with duration much smaller than the medium proper oscillations period \(T_0=2\pi /\omega _0\). In this approximation, and for simplicity assuming the electric field in the form of two delta pulses \(E(t)=S_0 \left[ \delta (t)+\delta (t-\Delta )\right]\), counter-propagating as shown in Fig. 1, with the delay \(\Delta (z)\) depending on the oscillator position z. We assume low enough density of the oscillators on the string, i.e., changing of the pulse shape during the propagation is negligible. Under the action of such kick-like excitation, the medium starts to harmonically oscillate at the eigen-frequency \(\omega _0\). It can be easily shown that the response of the medium can be represented as55
$$\begin{aligned} X(z,t)&= {} X_0 \sin \omega _0t, t<\Delta , \nonumber \\&= {} X_0 \sin \omega _0t+ X_0 \sin (\omega _0(t-\Delta )) =X_0\cos \left( \omega _0\Delta /2\right) \sin \left( \omega _0t+\omega _0\Delta /2\right) , t>\Delta . \end{aligned}$$
From the last expression it is seen that after arrival of the second pulse, the amplitude of the displacement periodically depends on the pulse-to-pulse delay \(~\cos \left( \omega _0\Delta /2\right)\). This can be interpreted as periodic grating formation in the system of classical oscillators. In the next section, we consider the corresponding quantum picture.
Multi-level vibration system: weak THz field strength
Theoretical approach
In the previous studies we predicted population density gratings formation in a two-level medium15,16,17. However, subcycle pulses have broadband spectra and two-level approximation can be inapplicable. In this section we consider a multi-level vibration system, namely, a quantum harmonic oscillator (HO). The HO model is commonly used as a simplest model for theoretical description of molecular vibrations42.
Interaction of a subcycle pulse with a quantum system with arbitrary configuration of states is governed by the TDSE describing the evolution of the wave function \(\psi\)42:
$$\begin{aligned} i\hbar \frac{\partial \psi }{\partial t} = \Big [ {{\hat{H}}}_0 + V(t) \Big ] \psi . \end{aligned}$$
\({{\hat{H}}}_0\) is the intrinsic Hamiltonian of the unperturbed system, and \(V(t)=-qxE(t)\) is the interaction potential with the excitating pulse in the dipole approximation. The wave functions of the eigenstates are the eigenfunctions of the intrinsic Hamiltonian \({{\hat{H}}}_0\) and given by42:
$$\begin{aligned} \psi _n(x) = \Big (\frac{m\omega _0}{\pi \hbar } \Big )^{1/4} \frac{1}{\sqrt{2^n n!}} e^{-\frac{m \omega _0 x^2}{2 \hbar }} H_n\Big ( x \sqrt{\frac{m \omega _0}{\hbar }}\Big ), \end{aligned}$$
where \(H_n\Big (x\sqrt{\frac{m \omega _0}{\hbar }}\Big )\) - Hermite polynomials of order n. The general solution of the TDSE (3) can be written as a superposition of eigenstates \(\psi _n\) with the amplitudes \(a_n\):
$$\begin{aligned} \psi (x,t)=\sum _n a_n(t) \psi _n(x). \end{aligned}$$
Let us assume that the system was initially in the ground state with \(n=0\) and the pulse amplitude is small. The amplitudes of the eigenstates can be easily calculated in the 1st order of the perturbation theory42:
$$\begin{aligned} a^{I}_{n}=-\frac{i}{\hbar }\int V_{0n}e^{i\omega _{0}t}dt. \end{aligned}$$
The transition probability of a HO from the ground state of the discrete spectrum to the n-th state \(w_{0n}\) is given by \(|a^{I}_{n}|^2\)42:
$$\begin{aligned} w_{0n}=\frac{1}{\hbar ^2} \Big | \int V_{0n}e^{i\omega _{0}t}dt \Big |^2. \end{aligned}$$
\(V_{0n}\) is the matrix element of the perturbation operator, which is expressed through the matrix element of the dipole moment \(d_{n,n+1}\) as:
$$\begin{aligned} V_{n,n+1} = - d_{n,n+1} E(t). \end{aligned}$$
For HO, the matrix \(d_{n,n+1}\) is given by42:
$$\begin{aligned} d_{n,n+1}= q \sqrt{\frac{\hbar n(n+1)}{2m\omega _0}}. \end{aligned}$$
Other matrix elements are zero, because in HO only transitions between neighbouring states are possible. That is, in the 1st order perturbation approach, only transition from the ground state to the 1st excited state has nonzero probability, i.e.,
$$\begin{aligned} w_{01}=\frac{q^2}{2m\omega _0\hbar } \Big | \int E(t)e^{i\omega _{0}t}dt \Big |^2. \end{aligned}$$
This allows us to consider HO as an effective two-level medium, as least in perturbative approximation. This gives rise to high-contrast grating formation only on the first transition \(0-1\) of the vibrational spectrum.
Population density grating formation and their control using \(\delta\)-pulses
Before providing detailed analysis of the grating dynamics let us consider for simplicity interaction of a HO with a \(\delta\)-pulse. A validity of this approximation follows from the fact that experimentally obtained subcycle pulse shape contains a short burst of electric field (half-wave) of one polarity and a long damped tail of small amplitude of the opposite polarity1,2,3,4,22,23,24,25,26,27,28,29,30. In view of the small amplitude of the tail, the main contribution is given by the strong half-wave part38. Assuming, that the pulse duration is smaller than all resonant transition periods in the atom/molecule, we can describe our driving field as a set of delta-function-like pulses:
$$\begin{aligned} E(t)=\sum _n S_{E,n}\delta (t-\Delta _{n}), \end{aligned}$$
having the time delays \(\Delta _n\) and electric pulse area \(S_{E,n}=\int E_n(t)dt\)56, \(E_n\) is the electric field of the n-th pulse.
In the case of a spatially extended medium, one can consider a string of atoms distributed along the z axis. If the concentration of atoms in such a string is relatively small, one may neglect nonlinear pulse shape modification due to propagation effects. A setup for a grating formation in the case with four pulses is shown in Fig. 1 (similar scheme was used earlier for a two-level medium15,16). The first pulse propagates in the medium from left to right, whereas the second one travels from right to left, after the 1st one already left the medium, so that the pulses do not overlap in the medium. Under these conditions, the delay between two pulses is constantly changing with time. The 3rd pulse propagates after the 2nd one in the same direction. The 4th pulse travels in the same direction as the 1st one after 3rd pulse left the medium. To track this situation without directly solving the wave equation, we may consider every point separately. In such consideration, the difference from one point to another in z-direction is mapped to the delay between two pulses \(\Delta \sim z/c\). Thus, we can consider a single-atom response and calculate the populations of the levels in dependence on the delay between two ultra-short pulses in order to show the existence of a grating as well as to estimate its properties.
First, consider the action of two pulses propagating in the opposite directions as shown in Fig. 1:
$$\begin{aligned} E(t)=S_0 \left[ \delta (t) + \delta (t-\Delta )\right] , \end{aligned}$$
where \(\Delta\) is the delay between two pulses. Using Eq. (7) and performing integration it is easy to obtain an expression for the transition probability \(w_{01}\) (the only nonzero one, according to Eq. (8)):
$$\begin{aligned} w_{01}=2\frac{d^2_{01}S^2_{0}}{\hbar ^2} \left( 1+\cos \omega _{01} \Delta \right) . \end{aligned}$$
From Eq. (12), the periodic dependence of the transition probability on the delay between the pulses \(\Delta\) is seen. Since in the case of an extended medium, the delay \(\Delta \sim z/c\) determines the time of arrival of the second pulse to a point of the medium with coordinate z, Eq. (12) shows a possibility of a periodic grating formation in the medium. Equation (12) is valid for any multi-level quantum system, when the concentration of particles is small and the change in the pulse shape during the propagation process can be neglected. However, formula Eq. (12) was obtained in the perturbation theory in the weak-field approximation. The case of an arbitrary strong driving field will be considered below.
We now show a possibility of erasing and spatial frequency multiplication of the gratings. Suppose that the system interacts with three pulses, see Fig. 1:
$$\begin{aligned} E(t)=S_0 \left[ \delta (t)+\delta (t-\Delta )+ \delta (t-\Delta -\Delta _{23})\right] , \end{aligned}$$
where \(\Delta _{23}\) is the delay between the 2nd and the 3rd pulse. Using Eq. (7) for the transition probability it is easy to obtain
$$\begin{aligned} w_{01}=\frac{d^2_{01}S^2_{0}}{\hbar ^2} |1+e^{i\omega _{01}\Delta } + e^{i\omega _{01}\Delta }e^{i\omega _{01}\Delta _{23}}|^2. \end{aligned}$$
From Eq. (14) it is seen that when \(e^{i\omega _{01}\Delta _{23}}=-1\), the 3rd pulse erases the grating since the probability of transition does not depend on the delay and thus on the spatial position.
Next, let the system interact with the 4th pulse (see Fig. 1):
$$\begin{aligned} E(t)=S_0 \left[ \delta (t)+\delta (t-\Delta )+ \delta (t-\delta -\Delta _{23}) + \delta (t-\Delta _{23}-\Delta _{34})\right] , \end{aligned}$$
where \(\Delta _{34}\) - delay between the 3rd and the 4th pulse. For the transition probability we obtain:
$$\begin{aligned} w_{01}=\frac{d^2_{01}S^2_{0}}{\hbar ^2} |1+e^{i\omega _{01}\Delta } + e^{i\omega _{01}\Delta }e^{i\omega _{01}\Delta _{23}} + e^{i\omega _{01}\Delta }e^{i\omega _{01}\Delta _{23}}e^{i\omega _{01}\Delta _{34}}|^2. \end{aligned}$$
We now show the possibility of the multiplication of the spatial frequency of the gratings analogously as it is done in a two-level system15. We choose the following values of the delays between pulses: \(\Delta _{23}=\pi /\omega _{01} +2\pi k /\omega _{01}\), that is \(e^{i\omega _{01}\Delta _{23}}=-1)\) and \(\Delta _{34}=\Delta +2\pi k / \omega _{01}\), where \(k=0,2,4,6\) Hence, from Eq. (16) it is easy to obtain:
$$\begin{aligned} w_{01}=\frac{d^2_{01}S^2_{0}}{\hbar ^2} |1-e^{2i\omega _{01}\Delta }|^2 = 2\frac{d^2_{01}S^2_{0}}{\hbar ^2} \left( 1 - \cos 2\omega _{01}\Delta \right) . \end{aligned}$$
From Eq. (17) it is seen that the spatial frequency of the gratings is multiplied by a factor of two. Thus, we showed that by selecting the delay between the pulses it is possible to control period of the multi-level-based grating.
Population density grating formation using subcycle THz pulses of finite duration
Dependence of the population of the 1st excited state \(w_{01}\) on the pulse duration \(\tau _p\) and the amplitude \(E_0\) calculated for \(H_2O\) molecule. Other parameters: \(\Delta =3\) ps, \(\omega _0/2\pi =0.97\) THz, \(d_{01}=19.2\) Debye. This figure was created with Matlab R2016b (www.mathworks.com).
Using Eq. (7), we show a possibility of existence of population density gratings in HO-type systems for the pulses of finite duration. As we mentioned above, experimentally obtained half-cycle THz pulses contain a strong half-wave of high amplitude and a long weak tail of the opposite polarity1,2,3,4. It was shown in38, that the impact of this tail can be neglected, provided that its amplitude is small, and duration is larger than the width of the main half-wave. Hence, we first neglect for simplicity this tail and consider the impact on the system of two Gaussian pulses given by:
$$\begin{aligned} E(t)=E_0\exp \left( -{t}^2/\tau _p^2\right) + E_0\exp \left( -(t-\Delta )^2/\tau _p^2\right) , \end{aligned}$$
where \(\Delta\) is the time delay between two pulses. In the subsequent analysis we include the tail into consideration. Substituting Eq. (18) into Eq. (7) and taking account that \(\int e^{ibx-ax^2}dx=\sqrt{\frac{\pi }{a}}e^{\frac{-b^2}{4a}}\), we obtain
$$\begin{aligned} w_{01}=\frac{2 \pi q^2 E_0^2\tau _p^2}{m\hbar \omega _0}\exp \frac{-\omega _0^2\tau _p^2}{2}\left( 1+\cos \omega _0\Delta \right) , \end{aligned}$$
where we have explicitly used Eq. (8) for \(d_{01}\) as well as denoted the transition frequency \(0 \rightarrow 1\) as \(\omega _0 = \omega _{01}\). Expression Eq. (19) is proportional to the square of the field strength \(E_0\) and at the first glance it seems that probability \(w_{01}\) can be very high at large field amplitudes. However, Eq. (19) was obtained using perturbation approach and is valid when the electric field amplitude is small, i.e. \(q^2E_0^2\pi \tau _p^2/m \ll \hbar \omega _0\). From Eq. (19) one can also see that the periodic dependence of the transition probability (population of the first excited state) on the delay between pulses \(\Delta\) is similar to the case of \(\delta\)-function-like pulses considered earlier. The modulation depth of the grating is proportional to the square of the electric field amplitude of the pulse. Formula Eq. (19) can be interpreted as a harmonic inversion grating created by a pair of counter-propagating subcycle pulses in a spatially-extended medium. Thus, in the case of the pulses with finite duration the existence of the inversion gratings is also possible.
We apply the theory developed above to a \(H_2O\) molecule. It has isolated resonances in the THz range, in particular, around 0.97-0.99 THz according to experimental results of43. Below we take \(\omega _0/2\pi \approx 0.97\) THz . Using the value for the "characteristic radius" of water \(R=4\) Angstrom44, we estimate transition dipole moment as \(d_{01}=qR=19.2\) Debye (q is the electron charge). The two-dimensional diagram in Fig. 2 illustrates the dependence of the 1st excited state population \(w_{01}\) Eq. (19) for water molecules vs the pulse duration \(\tau _p\) and the pulse amplitude \(E_0\) for \(\Delta =3\) fs. The maximal probability value \(w_{01}\) at the fixed delay \(\Delta\) is determined by the term \(\tau _p^2\exp \frac{-\omega _0^2\tau _p^2}{2}\). For small pulse durations (shorter than the transition period, \(\omega _0\tau _p \ll 1\)) this term increases with increase of \(\tau _p\), reaching its maximum value at certain point. With the particular parameters mentioned above, \(w_{01}\) reaches its maximum at the pulse duration \(\tau _p\) of around 200 fs. When the pulse duration becomes larger than the transition period, \(\omega _0\tau _p \gg 1\), the population \(w_{01}\) tends to zero. It means, that an unipolar pulse with a duration smaller than the inverse transition frequency (\(\omega _0\tau _p \ll 1\)) acts more effectively than a long unipolar one with a larger duration and the same amplitude. This statement is valid in general case of quasi unipolar ones, see below.
It can be also seen, that the modulation depth of the gratings significantly depends on the duration of the incident pulses and their amplitudes. It is also seen from Fig. 2 that for creation of gratings, electric fields of small amplitude of \(\sim\) kV/cm are sufficient, what can be easily reached in practice1,2,3,4.
Since the HO model is used to describe molecular vibrations (more precisely, low excited vibration states), and the oscillation frequencies of the molecules could lie in the THz region, the analytical result Eq. (19) clearly shows the possibility of a grating creating in molecular systems using a pair of THz subcycle pulses with experimentally available strengths, several orders of magnitude lower than in the optical range.
Now, we proceed further to take into account the tails of the Gaussian pulses. We assume, instead of Eq. (18), the following more general expression for the exciting field:
$$\begin{aligned} E(t)=E_0\exp \left( -{t}^2/\tau _p^2\right) \cos (\Omega t + \varphi _1) + E_0\exp \left( -(t-\Delta )^2/\tau _p^2\right) \cos (\Omega (t-\Delta ) + \varphi _2), \end{aligned}$$
with the carrier-wave frequency \(\Omega\) and the carrier-envelope phase (CEP) \(\varphi _i\). For clarity, we assume below CEP for all pulses in the sequence to be fixed \(\varphi _i = \varphi = \text {const}\), i.e., that the pulses are coming from a CEP-stabilized laser pulse source. The electric pulse area for such pulses is given as:
$$\begin{aligned} S_E = \sqrt{\pi } E_0 \tau _p \exp \left( - \Omega ^2 \tau _p^2 / 4\right) \cos \varphi , \end{aligned}$$
so that these pulses can be safely treated as unipolar ones if \(\Omega \tau _p \sim 1\) or even \(\Omega \tau _p \ll 1\) and \(\varphi \ne \pm \pi /2\).
Substituting now Eq. (20) into Eq. (7) and performing integration we find:
$$\begin{aligned} w_{01}=\frac{\pi q^2 E_0^2\tau _p^2}{m\hbar \omega _0} \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ) \left( 1+\cos \omega _0\Delta \right) . \end{aligned}$$
Equation (22) again yields a periodic dependence of the transition probability \(w_{01}\) (population of the first excited state) on the delay \(\Delta\) similarly to Eq. (19) above. Moreover, Eq. (19) contains some interesting peculiarities. When CEP \(\varphi = \pm \pi /2\), i.e. the exciting pulses are strictly bipolar according to Eq. (21) and \(S_E = 0\), the population gratings still arise, even though they have smaller modulation depth. The dependence of the modulation amplitude on the duration and CEP of the pump pulses is determined from Eq. (22) by the following factor:
$$\begin{aligned} \kappa = \omega _0^2 \tau _p^2 \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ), \end{aligned}$$
where we have introduce the factor \(\omega _0^2\) to make the parameter \(\kappa\) dimensionless. Figure 3 illustrates the dependence of this parameter on CEP \(\varphi\) and the pulse duration \(\tau _p\). One can see that \(\kappa\) achieves its maximal value at \(\tau _p \approx 0.4\) ps and \(\cos \varphi = 1\). Also, it is worth noting that in the limit \(\Omega \rightarrow 0\) Eq. (22) coincides with Eq. (12).
It is also seen from Fig. 3 that the grating modulation depth is larger for subcycle pulses (\(\Omega \tau _p \ll 1\)) than for multi-cycle ones, and it is smaller for bipolar pulses (when \(\varphi =\pi /2\) and the pulse area \(S_E=0\)). This fact is in agreement with our previous results, which showed that quasi-unipolar subcycle pulses allow more efficient nonresonant excitation of quantum systems with respect to single-cycle and multi-cycle ones37,38.
Dependence of the parameter \(\kappa\) from Eq. (23) on the carrier-envelope phase (CEP) \(\varphi\) and the pulse duration \(\tau _p\); other parameters: \(\omega _0/2\pi = 0.97\) THz, \(\Omega = 2 \cdot 10^{12}\) \(\hbox {s}^{-1}\). This figure was created with Matlab R2018a (www.mathworks.com).
Let us check now the results of the previous section for the sequence of three and four pump pulses. For three pulses we have the exciting electric field in the form:
$$\begin{aligned} E(t)&= {} E_0\exp \left( -{t}^2/\tau _p^2\right) \cos (\Omega t + \varphi ) + E_0\exp \left( -(t-\Delta )^2/\tau _p^2\right) \cos (\Omega (t-\Delta ) + \varphi )\\& \quad +E_0\exp \left( -(t - \Delta - \Delta _{23})^2/\tau _p^2\right) \cos (\Omega (t-\Delta - \Delta _{23}) + \varphi ), \end{aligned}$$
and Eq. (7) gives:
$$\begin{aligned} w_{01}&= {} \frac{\pi q^2 E_0^2\tau _p^2}{2 m\hbar \omega _0} \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ) \nonumber \\\times & {} \Big ( 3 + 2 \cos \omega _0\Delta + 2 \cos \omega _0 (\Delta + \Delta _{23}) + 2 \cos \omega _0\Delta _{23} \Big ). \end{aligned}$$
If we choose \(\Delta _{23}=\pi /\omega _{0} +2\pi n \omega _{0}\), Eq. (24) reduces to:
$$\begin{aligned} w_{01}=\frac{\pi q^2 E_0^2\tau _p^2}{2 m\hbar \omega _0} \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ), \end{aligned}$$
i.e., the third pulse erases the population grating and we get a constant value of \(w_{01}\) along the medium. Finally, when we add the fourth pulse:
$$\begin{aligned} E(t)&= {} E_0\exp \left( -{t}^2/\tau _p^2\right) \cos (\Omega t + \varphi ) + E_0\exp \left( -(t-\Delta )^2/\tau _p^2\right) \cos (\Omega (t-\Delta ) + \varphi )\\& \quad + E_0\exp \left( -(t - \Delta - \Delta _{23})^2/\tau _p^2\right) \cos (\Omega (t-\Delta - \Delta _{23}) + \varphi ) \\& \quad + E_0\exp \left( -(t - \Delta - \Delta _{23} - \Delta _{34} )^2/\tau _p^2\right) \cos (\Omega (t-\Delta - \Delta _{23} - \Delta _{34}) + \varphi ), \end{aligned}$$
and we obtain with Eq. (7):
$$\begin{aligned} w_{01}= & {} \frac{\pi q^2 E_0^2\tau _p^2}{2 m\hbar \omega _0} \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ) \Big (4 + 2 \cos \omega _0\Delta + 2 \cos \omega _0 (\Delta + \Delta _{23})\nonumber \\&+ 2 \cos \omega _0\Delta _{23} + 2 \cos \omega _0 (\Delta + \Delta _{23} + \Delta _{34}) + 2 \cos \omega _0 (\Delta _{23} + \Delta _{34}) + 2 \cos \omega _0\Delta _{34} \Big ). \end{aligned}$$
As we choose the delays between pulses: \(\Delta _{23}=\pi /\omega _{0} +2 \pi n/ \omega _{0}\) and \(\Delta _{34} = \Delta + 2\pi n/ \omega _{0}\) with integer n, we get the following population grating:
$$\begin{aligned} w_{01}=\frac{\pi q^2 E_0^2\tau _p^2}{m\hbar \omega _0} \exp \frac{- (\omega _0^2 + \Omega ^2) \tau _p^2}{2} \Big ( \cosh \left( \omega _0 \Omega \tau _p^2\right) + \cos 2 \varphi \Big ) \left( 1-\cos 2 \omega _0\Delta \right) , \end{aligned}$$
i.e., the spatial frequency of the grating is multiplied by factor of 2.
Numerical simulations
To check our analytical theory and observe, what happens in the nonperturbative regime, we solve numerically a system of Bloch equations for density-matrix element, which models interaction of a three-level medium with THz pulses:
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{21}= & {} -\rho _{21}/T_{21}-i \omega _{21} \rho _{21} - i \frac{ d_{21} E}{\hbar } ( \rho _{22} - \rho _{11} ) - i \frac{ d_{13} E}{\hbar } \rho _{32} + i \frac{ d_{23} E}{\hbar } \rho _{31}, \end{aligned}$$
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{32}= & {} -\rho _{23}/T_{32} -i \omega _{32} \rho _{32} - i \frac{ d_{32} E}{\hbar } ( \rho _{33} - \rho _{22} ) - i \frac{ d_{21} E}{\hbar } \rho _{31} + i \frac{ d_{13} E}{\hbar } \rho _{21}, \end{aligned}$$
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{31}&= {} -\rho _{31}/T_{31} -i \omega _{31} \rho _{31} - i \frac{ d_{31} E}{\hbar } ( \rho _{33} - \rho _{11} ) - i \frac{ d_{21} E}{\hbar } \rho _{32} + i \frac{ d_{23} E}{\hbar } \rho _{21}, \end{aligned}$$
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{11}&= \rho _{22}/T_{22}+\rho _{33}/T_{33}+{} i \frac{ d_{21} E}{\hbar } ( \rho _{21} - \rho _{21}^* ) - i \frac{ d_{13} E}{\hbar } (\rho _{13} - \rho _{13}^*), \end{aligned}$$
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{22}&= {} -\rho _{22}/T_{22} -i \frac{ d_{21} E}{\hbar } ( \rho _{21} - \rho _{21}^* ) - i \frac{ d_{23} E}{\hbar } (\rho _{23} - \rho _{23}^*), \end{aligned}$$
$$\begin{aligned} \frac{\partial }{\partial t} \rho _{33}&= {} -\rho _{33}/T_{33}+ i \frac{ d_{13} E}{\hbar } ( \rho _{13} - \rho _{13}^* ) + i \frac{ d_{23} E}{\hbar } (\rho _{23} - \rho _{23}^*). \end{aligned}$$
Equations (27)–(29) describe the evolution of off-diagonal elements of the density matrix \(\rho _{21}, \rho _{32}, \rho _{31}\), which are associated with the polarization of the medium. Equations (30)–(32) describe the evolution of diagonal elements of the density matrix \(\rho _{11}\), \(\rho _{22}\), \(\rho _{33}\), which have the meaning of populations of the first, second and third levels, correspondingly. Parameters \(d_{21}, d_{23}, d_{13}\) are the dipole moments of the corresponding transitions, \(\omega _{21}\), \(\omega _{32}\), \(\omega _{31}\) are the transition frequencies. In our case, we consider a three-level HO medium, so \(\omega _{21}=\omega _{32}=\omega _0\) and \(\omega _{31}\)=\(2\omega _0\), \(d_{13}=0\). Equations (27)–(29) also contain relaxation times of the non-diagonal elements of the density matrix \(T_{21}\), \(T_{32}\), \(T_{31}\), and population lifetimes of the 2nd and 3rd levels respectively \(T_{22}\) and \(T_{33}\). We performed series of numerical simulations for both low and high THz field amplitudes.
Low-power THz fields
Equation (19) was obtained using perturbation approach valid for low field strength. In the 1st order perturbation approach, only probability transition \(w_{01}\) is non-vanishing. This is because transition dipole moments in HO \(d_{0,n}=0\) for n larger than 1. Numerical simulations (see below) showed that populations of higher levels are 10-100 times lower than the populations of the 2nd level \(w_{01}\). This fact enables the possibility of creating the high contrast grating on the main transition \(0 \rightarrow 1\) neglecting other transitions using weak THz field values.
To confirm this statement, we performed numerical simulations using system of density matrix equations (27)–(32) with a pair of Gaussian pulses (18). Figure 4 shows the behaviour of the populations \(\rho _{11}\) (a), \(\rho _{22}\) (b), and \(\rho _{33}\) (c) versus the delay \(\Delta\) for the water molecule and \(E_0=15\) kV/cm assuming infinite relaxation times. The influence of finite relaxation times will be studied in the next section. It can be seen from Fig. 4b that the grating obtained numerically has the same shape and roughly the same amplitude as predicted by Eq. (19). Besides, the population of the 3rd level \(\rho _{33}\) is 10 times smaller than \(\rho _{32}\).
Dependence of the populations \(\rho _{11}\) (a), \(\rho _{22}\) (b), and \(\rho _{33}\) (c) on the delay \(\Delta\) between two Gaussian THz pulses for the \(H_2O\) molecule. Blue circles show the result of the numerical simulations, red solid line show the analytical results obtained from Eq. (19). Parameters: \(E_0=15 000\) V/cm, \(\tau _p=150\) fs, \(d_{12}=19.2\) Debye, \(\omega _0/2\pi =0.97\) THz, all the relaxation times \(T_{ik}=\infty\). This figure was created with Matlab R2016b (www.mathworks.com).
High-power THz fields
Dependence of the populations difference \(\rho _{11}-\rho _{22}\) (a), \(\rho _{11}-\rho _{33}\) (b), \(\rho _{22}-\rho _{33}\) (c) on the delay \(\Delta\) between two Gaussian THz pulses and time t for parameters of the \(H_20\) molecule (\(\omega _0/2\pi =0.97\) THz, \(d_{12}=19.2\) Debye). Other parameters: \(E_0= 150\) kV/cm, \(\tau _p=150\) fs, \(T_{22}=T_{33}=250\) ps, \(T_{21}=T_{32}=T_{31}=5\) ps. This figure was created with Matlab R2016b (www.mathworks.com).
To study the grating dynamics in the high-power field we performed a series of the numerical simulations of the Bloch equations described above at different pump field strengths and durations. Figure 5 shows the behaviour of the populations difference \(\rho _{11}-\rho _{22}\) (a), \(\rho _{11}-\rho _{33}\) (b), \(\rho _{22}-\rho _{33}\) (c) versus the delay \(\Delta\) between two Gaussian THz pulses and time t for the \(H_20\) molecule (\(\omega _0/2\pi =0.97\) THz, \(d_{12}=19.2\) Debye) for the following parameters: \(E_0=150\) kV/cm, \(\tau _p=150\) fs. Typical lifetimes of the vibrational levels \(T_1\) and coherence times \(T_2\) of vibration states are in the ps range57,58. We take relaxation population lifetimes \(T_{22}=T_{33}=250\) ps and coherence lifetimes \(T_{21}=T_{32}=T_{31}=5\) ps57,58.
One can see noticeable differences to the case of low field strength described above. The grating shape is not harmonic anymore, and has complex peak structure in contrast to the weak-field case. Also in contrast to the case of the two-level system, where both analytical and numerical solutions predict harmonic shape only15,16. Next, due to finite values of the relaxation times, the grating modulation depth decreases dramatically with time.
To summarize the results of these sections, we see that using THz pulses and vibrational transitions introduces many differences and advantages with respect to the previously studied case of optical field excitation. It allows reducing field strength using experimentally available subcycle THz fields. One can use only the transition \(0 \rightarrow 1\) for grating formation in the weak-field case. The shape of the grating can be controlled by increasing the field strength, in contrast to the case of a two-level medium, where grating shape was always harmonic.
Control of long THz pulses
In this section, we describe an application of the gratings described above, to control propagation of THz pulses. As it follows from the Bloch equations, the modification of polarization in the linear regime corresponding to a density grating of full contrast (\(|\rho _{22}-\rho _{11}|=2\)) is
$$\begin{aligned} |\delta P| = 2T_2d_{12}^2NE/\hbar , \end{aligned}$$
where N is the atomic density. Taking into account that \(\delta P = \varepsilon _0 \chi E\), we have \(|\chi |=2d_{12}^2NT_2/(\hbar \varepsilon _0)\), and therefore the refractive index modification
$$\begin{aligned} \delta n \approx \delta \chi /2 = \frac{d_{12}^2T_2N}{\varepsilon _0\hbar }. \end{aligned}$$
A refractive index grating is a powerful tool to make highly frequency-selective reflection of THz radiation, fully controllable on the single-cycle (picosecond) time scale. As an example, in Fig. 6 we show the dependence of reflection on a wavelength resulting from a grating containing 1000 oscillation periods, each having the length 75 \(\mu\)m in a gas with atmospheric pressure consisting of active molecules, which thus creates a density grating with the contrast \(\delta n \approx 10^{-3}\). The reflection is calculated using the standard multilevel approach59: The ABCD matrix of a single layer of size h for the normal incidence is
$$\begin{aligned} M(h) = \begin{pmatrix} \cos {(k_0nh)} &{} -\frac{i}{p}\sin {(k_0nh)} \\ -ip\sin {(k_0nh)} &{} \cos {(k_0nh)} \end{pmatrix}, \end{aligned}$$
where \(k_0\) is the wavevector in vacuum, n is the refractive index, \(p=\sqrt{\epsilon }\). For our calculation we have taken \(\lambda /4\) layers with interleaving layers of the refractive index \(n_1=1-\delta n/2\) and \(n_1=1+\delta n/2\). Multiplying the matrices for all layer gives the resulting reflection. Although an analytic expression exists for the whole such product59, we find more useful direct numerical multiplication.
Reflection of a long weak narrow-line probe pulse in dependence on its wavelength from a grating containing 1000 periods (\(75\,\mu \hbox {m}\) each) in a medium with 1 bar pressure of the active molecules. The inset shows schematically a CW wave modulated by switching on and off the grating dynamically as a function of time. This figure was created in Phython 2.7, preinstalled with Ubuntu linux 18.04.05 (https://ubuntu.com/).
The refractive index grating can be used in various ways. The key advantage is a possibility of fast switching on the single-cycle level. An example shown in the inset to Fig. 6 is a fast amplitude modulation of a THz CW wave allowing to encode information into it.
To summarize, we studied theoretically the possibility of population density grating formation created by subcycle THz pulses in a molecular medium having resonant transitions in THz range. The pulses interact with the molecules coherently and do not overlap in the medium. The amplitude of the grating can be controlled either by tuning the pump amplitude or by an additional pulse. The grating modulation depth is proportional to the square of the THz field amplitude but is also influenced by the coherence times in the medium.
In the case of a multi-level system, using the first order of the perturbation theory in the weak-field approximation, we studied the grating dynamics created by two, three and four subcycle pulses. The possibility of a grating creation and their ultrafast control (erasing and spatial frequency multiplication) in multi-level system excited by subcycle pulses has been shown. A possible scheme of a setup for a grating formation and their control using four counter-propagating pulses on vibrations transitions in a \(H_2O\) molecule without overlap in the medium was considered.
Our analysis revealed significant advantages of a grating creation in the THz range with respect to the optical range considered earlier. Because of high dipole moments in the THz range, one needs significantly smaller field amplitudes than in the optical range, of the order of kV/cm. This opens a new opportunity for an ultrafast THz spectroscopy with subcycle THz pulses to determine the resonance frequencies and the corresponding dephasing \(T_2\) and relaxation \(T_1\) times via diffraction of a weak probe pulse on the induced gratings12,13,14. The investigated phenomenon can be also used for creation of ultrafast beam deflectors and switches on molecular systems in the THz range.
As we have seen, somewhat counter-intuitively, the HO model in the perturbative regime provides lower excitation probabilities of the higher states than, for instance, the atomic potential 1/r, and thus the quality of the grating in the molecular case is better than in the case of an atom. This was supported also by non-perturbative simulations with the Bloch equations.
Numerical simulations performed for the parameters of \(H_2O\) molecules and analytical results revealed that in the low-field case gratings have a harmonic shape. But in the strong-field case, when the perturbation approach is not valid anymore, the grating shape differs dramatically from the harmonic one. It has complex peak structure, since the level populations in the medium undergo multiple Rabi floppings over the pulse duration.
The obtained results also indicate a possibility of effective grating creation by quasi-unipolar subcycle THz pulses with respect to bipolar few-cycle ones. This efficient grating creation occurs in spite of the broad spectrum of the subcycle pulses covering many resonances at once, and non-resonant interaction with the molecule transitions. This result opens novel opportunities in ultrafast spectroscopy in the THz range with unipolar half-cycle pulses.
Roskos, H. G., Thomson, M. D., Kress, M. & Loeffler, T. Broadband THz emission from gas plasmas induced by femtosecond optical pulses: From fundamentals to applications. Laser Photon. Rev. 1, 349 (2007).
Article ADS CAS Google Scholar
Reiman, K. Table-top sources of ultrashort THz pulses. Rep. Progr. Phys. 70, 1597 (2007).
Article ADS Google Scholar
Lepeshov, S., Gorodetsky, A., Krasnok, A., Rafailov, E. & Belov, P. Enhancement of terahertz photoconductive antenna operation by optical nanoantennas. Laser Phot. Rev. 11(1), 1600199 (2016).
Fülöp, J. A., Tzortzakis, S. & Kampfrath, T. Laser-driven strong-field terahertz sources. Adv. Opt. Mater. 8(3), 1900681 (2020).
Ferguson, B. & Zhang, X. C. Materials for terahertz science and technology. Nat. Mater. 1(1), 26–33 (2002).
Article ADS CAS PubMed Google Scholar
Jepsen, P. U., Cooke, D. G. & Koch, M. Terahertz spectroscopy and imaging-Modern techniques and applications. Laser Photon. Rev. 5(1), 124–166 (2011).
Parrott, E. P. & Zeitler, J. A. Terahertz time-domain and low-frequency Raman spectroscopy of organic materials. Appl. Spec. 69(1), 1–25 (2015).
Zeitler, J. A. et al. Terahertz pulsed spectroscopy and imaging in the pharmaceutical setting—a review. J. Pharm. Pharmacol. 59, 209 (2007).
Williams, J. C. & Twieg, R. J. Broadband terahertz characterization of the refractive index and absorption of some important polymeric and organic electro-optic materials. J. Appl. Phys. 109, 043505 (2011).
Murakami, H., Toyota, Y., Nishi, T. & Nashima, S. Terahertz absorption spectroscopy of protein-containing reverse micellar solution. Chem. Phys. Lett. 519, 105 (2012).
Allen, L. & Eberly, J. H. Optical Resonance and Two-level Atoms (Wiley, New York, 1975).
Abella, I. D., Kurnit, N. A. & Hartmann, S. R. Photon echoes. Phys. Rev. 141, 391 (1966).
Shtyrkov, E. I., Lobkov, V. S. & Yarmukhametov, N. G. Grating induces in ruby by interference of atomic states. JETP Lett. 27, 648 (1978).
ADS Google Scholar
Shtyrkov, E. I. Optical echo holography. Opt. Spectr. 114(1), 96 (2013).
Arkhipov, R. M. et al. Ultrafast creation and control of population density gratings via ultraslow polarization waves. Opt. Lett. 41, 4983 (2016).
Arkhipov, R. M. et al. Population density gratings induced by few-cycle optical pulses in a resonant medium. Sci. Rep. 7, 12467 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Arkhipov, R. M., Arkhipov, M. V., Pakhomov, A. V., Babushkin, I. & Rosanov, N. N. Light-induced spatial gratings created by unipolar attosecond pulses coherently interacting with a resonant medium. Laser Phys. Lett. 14, 095402 (2017).
Arkhipov, R. M., Pakhomov, A. V., Arkhipov, M. V., Babushkin, I. & Rosanov, N. N. Population difference gratings induced in a resonant medium by a pair of short terahertz nonoverlapping pulses. Opt. Spectrosc. 125(4), 586 (2018).
Eichler, H. J., Günter, P. & Pohl, D. W. Laser-Induced Dynamic Gratings (Springer, Berlin, 1981).
Dolgaleva, K., Materikina, D. V., Boyd, R. W. & Kozlov, S. A. Prediction of an extremely large nonlinear refractive index for crystals at terahertz frequencies. Phys. Rev. A 92, 023809 (2015).
Tcypkin, A. N. et al. High Kerr nonlinearity of water in THz spectral range. Opt. Express 27, 10419 (2019).
Kozlov, V. V., Rosanov, N. N., De Angelis, C. & Wabnitz, S. Generation of unipolar pulses from nonunipolar optical pulses in a nonlinear medium. Phys. Rev. A 84, 023818 (2011).
Hassan, M. T. et al. Optical attosecond pulses and tracking the nonlinear response of bound electrons. Nature 530, 66 (2016).
Pakhomov, A. V. et al. All-optical control of unipolar pulse generation in a resonant medium with nonlinear field coupling. Phys. Rev. A 95, 013804 (2017).
Arkhipov, M. V. et al. Generation of unipolar half-cycle pulses via unusual reflection of a single-cycle pulse from an optically thin metallic or dielectric layer. Opt. Lett. 42, 2189 (2017).
Efimenko, E. S., Sychugin, S. A., Tsarev, M. V. & Bakunov, M. I. Quasistatic precursors of ultrashort laser pulses in electro-optic crystals. Phys. Rev. A 98, 013842 (2018).
Tsarev, M. V. & Bakunov, M. I. Tilted-pulse-front excitation of strong quasistatic precursors. Opt. Express 27, 5154 (2019).
Pakhomov, A. V. et al. Unusual terahertz waveforms from a resonant medium controlled by diffractive optical elements. Sc. Rep. 9, 7444 (2019).
Wu, H.-C. & Meyer-ter Vehn, J. Giant half-cycle attosecond pulses. Nat. Photon. 6, 304 (2012).
Xu, J. et al. Terawatt-scale optical half-cycle attosecond pulses. Sci. Rep. 8, 2669 (2018).
Article ADS PubMed PubMed Central CAS Google Scholar
Arkhipov, R. M., Arkhipov, M. V. & Rosanov, N. N. Unipolar light: Existence, generation, propagation, and impact on microobjects. Quant. Electron. 50(9), 801 (2020).
Jones, R. R., You, D. & Bucksbaum, P. H. Ionization of Rydberg atoms by subpicosecond half-cycle electromagnetic pulses. Phys. Rev. Lett. 70(9), 1236 (1993).
Wesdorp, C., Robicheaux, F. & Noordam, L. D. Displacing rydberg electrons: The mono-cycle nature of half-cycle pulses. Phys. Rev. Lett. 87(8), 083001 (2001).
Wetzels, A. et al. Rydberg state ionization by half-cycle-pulse excitation: Strong kicks create slow electrons. Phys. Rev. Lett. 89(27), 273003 (2002).
Pan, Y., Zhao, S.-F. & Zhou, X.-X. Generation of isolated sub-40-as pulses from gas-phase CO molecules using an intense few-cycle chirped laser and a unipolar pulse. Phys. Rev. A 87, 035805 (2013).
Chai, X. et al. Subcycle terahertz nonlinear optics. Phys. Rev. Lett. 121, 143901 (2018).
Arkhipov, R. M. et al. Unipolar subcycle pulse-driven nonresonant excitation of quantum systems. Opt. Lett. 44, 1202 (2019).
Arkhipov, R. M. et al. Selective ultrafast control of multi-level quantum systems by subcycle and unipolar pulses. Opt. Express 28(11), 17020–17034 (2020).
Rosanov, N. N. & Vysotina, N. V. Direct acceleration of a charge in vacuum by linearly polarized radiation pulses. J. Exp. Theor. Phys. 130, 52–55 (2020).
Arkhipov, R. M., Arkhipov, M. V. & Rosanov, N. N. On the possibility of holographic recording in the absence of coherence between a reference beam and a beam scattered by an object. JETP Lett. 111(9), 484–488 (2020).
Arkhipov, R. M., Arkhipov, M. V., Pakhomov, A. V. & Rosanov, N. N. Population gratings produced in a quantum system by a pair of sub-cycle pulses. Quant. Electron. 49(10), 958 (2019).
Landau, L. D. & Lifshitz, E. M. Quantum Mech. (Pergamon, Oxford, 1974).
Van Exter, M., Fattinger, C. & Grischkowsky, D. Terahertz time-domain spectroscopy of water vapor. Opt. Lett. 14(20), 1128–1130 (1989).
Heyden, M. et al. Dissecting the THz spectrum of liquid water from first principles via correlations in time and space. Proc. Natl. Acad. Sci. 107(27), 12068–12073 (2010).
Lee, Y.S. Terahertz Spectroscopy of Atoms and Molecules, In: Principles of Terahertz Science and Technology. Springer, Boston, MA (2009).
Zhang, H. et al. Autler-Townes splitting of a cascade system in ultracold cesium Rydberg atoms. Phys. Rev. A 87(3), 033835 (2013).
Bednarek, S., Szafran, B. & Adamowski, J. Theoretical description of electronic properties of vertical gated quantum dots. Phys. Rev. B 64, 195303 (2001).
Borri, P. et al. Ultralong dephasing time in InGaAs quantum dots. Phys. Rev. Lett. 87(15), 157401 (2001).
Bayer, M. & Forchel, A. Temperature dependence of the exciton homogeneous linewidth in In060 Ga 040 As/GaAs self-assembled quantum dots. Phys. Rev. B 65(4), 041308 (2002).
Leyman, R. R. et al. Quantum dot materials for terahertz generation applications. Laser Photon. Rev. 10(5), 772–779 (2016).
Scalari, G. et al. THz and sub-THz quantum cascade lasers. Laser Photon. Rev. 3, 45–66 (2009).
Choi, H. et al. Time-resolved investigations of electronic transport dynamics in quantum cascade lasers based on diagonal lasing transition. IEEE J. Quantum Electron. 45, 307–321 (2009).
Choi, H. et al. Ultrafast Rabi flopping and coherent pulse propagation in a quantum cascade laser. Nat. Photon. 4(10), 706–710 (2010).
Babbit, W. R. & Mossberg, T. Time-domain frequency-selective optical data storage in a solid-state material. Opt. Commun. 65, 185 (1988).
Akhmanov, S. A. & Nikitin, S. Y. Physical Optics (Clarendon Press, Oxford, 1997).
Rosanov, N. N., Arkhipov, R. M. & Arkhipov, M. V. On laws of conservation in the electrodynamics of continuous media (on the occasion of the 100th anniversary of the SI Vavilov State Optical Institute). Physics-Uspekhi 61(12), 1227 (2018).
Maier, M. Applications of stimulated Raman scattering. Appl. Phys. 11(3), 209–231 (1976).
Akhmanov, S. A. & Koroteev, N. I. Methods of Nonlinear Optics in Light Scattering Spectroscopy (Nauka, Moscow, 1981).
Born, M. & Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (Elsevier, Amsterdam, 2013).
Open Access funding enabled and organized by Projekt DEAL. R.A. thanks Russian Science Foundation, project 19-72-00012 for the financial support (analytical and numerical study of gratings formation). I.B., U.M. and A.D. are thankful to the Deutsche Forscunggemeinschaft (DFG) projects BA 4156/4-2, MO 850-19/2 and MO 850-23/1, as well as to Germany's Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453).
St. Petersburg State University, Saint Petersburg, Russian Federation
Rostislav Arkhipov & Mikhail Arkhipov
ITMO University, Saint Petersburg, Russian Federation
Rostislav Arkhipov, Anton Pakhomov, Mikhail Arkhipov & Nikolay Rosanov
Ioffe Institute, Saint Petersburg, Russian Federation
Rostislav Arkhipov & Nikolay Rosanov
University of Hannover, Hannover, Germany
Ihar Babushkin, Ayhan Demircan & Uwe Morgner
Cluster of Excellence PhoenixD (Photonics, Optics, and Engineering—Innovation Across Disciplines), Hannover, Germany
Max Born Institute, Berlin, Germany
Ihar Babushkin
Rostislav Arkhipov
Anton Pakhomov
Mikhail Arkhipov
Ayhan Demircan
Uwe Morgner
Nikolay Rosanov
R. A. and A. P. provided analytical theory, R. A., A. P., I. B. and M. A. performed numerical simulations, I. B., A. D., U. M. and N. R. analysed the results and participated in the discussions, article formulation and writing. All authors reviewed the manuscript.
Correspondence to Ihar Babushkin.
Arkhipov, R., Pakhomov, A., Arkhipov, M. et al. Population difference gratings created on vibrational transitions by nonoverlapping subcycle THz pulses. Sci Rep 11, 1961 (2021). https://doi.org/10.1038/s41598-021-81275-8
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Intense ultra-short pulses from femtosecond to attosecond
About Scientific Reports
Guide to referees
Scientific Reports (Sci Rep) ISSN 2045-2322 (online) | CommonCrawl |
Define the operation $a\nabla b = 2 + b^a$. What is the value of $(1\nabla 2) \nabla 3$?
We see that
$$1\nabla 2=2+2^1=4$$
Then,
$$4\nabla 3=2+3^4=83$$
So the answer is $\boxed{83}$. | Math Dataset |
\begin{document}
\begin{abstract} Discrete exterior calculus (DEC) is a framework for constructing discrete versions of exterior differential calculus objects, and is widely used in computer graphics, computational topology, and discretizations of the Hodge-Laplace operator and other related partial differential equations. However, a rigorous convergence analysis of DEC has always been lacking; as far as we are aware, the only convergence proof of DEC so far appeared is for the scalar Poisson problem in two dimensions, and it is based on reinterpreting the discretization as a finite element method.
Moreover, even in two dimensions, there have been some puzzling numerical experiments reported in the literature, apparently suggesting that there is convergence without consistency.
In this paper, we develop a general independent framework for analyzing issues such as convergence of DEC without relying on theories of other discretization methods, and demonstrate its usefulness by establishing convergence results for DEC beyond the Poisson problem in two dimensions. Namely, we prove that DEC solutions to the scalar Poisson problem in arbitrary dimensions converge pointwise to the exact solution at least linearly with respect to the mesh size. We illustrate the findings by various numerical experiments, which show that the convergence is in fact of second order when the solution is sufficiently regular. The problems of explaining the second order convergence, and of proving convergence for general $p$-forms remain open. \end{abstract}
\maketitle
\section{Introduction} \label{s:intro}
The main objective of this paper is to establish convergence of discrete exterior calculus approximations on unstructured triangulations for the scalar Poisson problem in general dimensions. There are several approaches to extending the exterior calculus to discrete spaces; What we mean by {\em discrete exterior calculus} (DEC) in this paper is the approach put forward by Anil Hirani and his collaborators, cf. \parencite{Hirani03,Desbrun2005}. Since its conception, DEC has found many applications and has been extended in various directions, including general relativity \parencite{Frau06}, electrodynamics \parencite{Stern2007}, linear elasticity \parencite{Yavari08}, computational modeling \parencite{Desbrun2008}, port-Hamiltonian systems \parencite{SSS2012}, digital geometry processing \parencite{Crane2013}, Darcy flow \parencite{HNC15}, and the Navier-Stokes equations \parencite{MHS16}. However, a rigorous convergence analysis of DEC has always been lacking; As far as we are aware, the only convergence proof of DEC so far appeared is for the scalar Poisson problem in two dimensions, and it is based on reinterpreting the discretization as a finite element method, cf. \parencite{HPW06}. In the current paper, we develop a general independent framework for analyzing issues such as convergence of DEC without relying on theories established for other discretization methods, and demonstrate its usefulness by proving that DEC solutions to the scalar Poisson problem in arbitrary dimensions converge to the exact solution as the mesh size tends to $0$.
Developing an original framework to study the convergence of DEC allows us to explore to what extent the theory is compatible in the sense of \parencite{arnold2006}. At the turn of the millennium, compatibility appeared as a conducive paradigm for stability. In this spirit, we here reproduce at the discrete level a standard variational technique in the analysis of PDEs based on the use of the Poincar\'e inequality.
In what follows, we would like to describe our results in more detail. Let $K_h$ be a family of $n$-dimensional completely well-centered simplicial complexes triangulating a $n$-dimensional polytope $\mathcal{P}$ in $\mathbb{R}^n$, with the parameter $h>0$ representing the diameter of a typical simplex in the complex. Let $\Delta_h=\delta_h\dif_{\,h}+\dif_{\,h}\delta_h$ be their associated discrete Hodge-Laplace operators, where the discrete exterior derivatives $\dif_{\,h}$ and the codifferentials $\delta_h=(-1)^{n(k-1)+1}\star_h\dif_{\,h}\star_h$ are defined as in \parencite{Desbrun2005,Hirani03} up to a sign. Denote by $C^k(K_h)$ the space of $k$-cochains over $K_h$. In this paper, we study the convergence of solutions $\omega_h\in C^k(K_h)$ solving discrete Hodge-Laplace Dirichlet problems of the form \begin{equation}\label{eq: Discrete Poisson Dirichlet} \begin{cases} \Delta_h \omega_h = R_h f& \mbox{in } K_h\\ \omega_h=R_h g& \mbox{on } \partial K_h, \end{cases} \end{equation} where $f$ and $g$ are differential forms, and $R_h$ is the deRham operator, cf. \parencite{Whitney57}. It is shown in \parencite{Xu04,Xu04b} that under {\em very} special symmetry assumptions on $K_h$, the consistency estimate \begin{equation*}
\|\Delta_h R_h \omega - R_h\Delta \omega\|_{\infty}= O(h^2) \end{equation*} holds for sufficiently smooth functions $\omega$. However, as the numerical experiments from \parencite{Xu04,Nong04} revealed, this does \textit{not} hold for general triangulations. In Section~\ref{s:consistency}, we show that a common shape regularity assumption on $K_h$ can only guarantee \begin{equation}\label{eq: consistency estimate}
\|\Delta_h R_h \omega - R_h\Delta \omega\| = O(1)+O(h) \end{equation}
for sufficiently smooth functions $\omega$, in both the maximum $\|\cdot\|_\infty$ and discrete $L^2$-norm $\|\cdot\|_h$.
Although the consistency estimate \eqref{eq: consistency estimate} is not adequate for the Lax-Richtmyer framework, by making use of a special structure of the error term itself, we are able to establish convergence for $0$-forms in general dimensions. Namely, we prove in Section \ref{s:stability} that the approximations $u_h\in C^0(K_h)$ obtained from solving (\ref{eq: Discrete Poisson Dirichlet}) still satisfy \begin{equation}\label{intro convergence}
\|\omega_h-R_h \omega\|_h = O(h) , \qquad\text{and}\qquad
\|\dif\,(\omega_h-R_h \omega)\|_h=O(h) , \end{equation} where $\omega\in C^2(\mathcal{P})$ is the solution of the corresponding continuous Poisson problem with source term $f$ and boundary condition $g$. We remark that a convergence proof in 2 dimensions can be obtained by reinterpreting the discrete problem as arising from affine finite elements, cf. \parencite{HPW06,Wardetzky08}, which shows that the first quantity in \eqref{intro convergence} should indeed be $O(h^2)$ if the exact solution is sufficiently regular. This is consistent with the numerical experiments from \parencite{Nong04}, and moreover, in Section \ref{s:numerics}, we report some numerical experiments in 3 dimensions, which suggest that one has $O(h^2)$ convergence in general dimensions. Therefore, our $O(h)$ convergence result for $0$-forms should be considered only as a first step towards a complete theoretical understanding of the convergence behavior of discrete exterior calculus. Apart from explaining the $O(h^2)$ convergence for $0$-forms, proving convergence for general $p$-forms remains as an important open problem.
This paper is organized as follows. In the next section, we review the basic notions of discrete exterior calculus, not only to fix notations, but also to discuss issues such as the boundary of a dual cell in detail to clarify some inconsistencies existing in the current literature. Then in Section~\ref{s:consistency}, we treat the consistency question, and in Section~\ref{s:stability}, we establish stability of DEC for the scalar Poisson problem. Our main result \eqref{intro convergence} is proved in Section~\ref{s:stability}. We end the paper by reporting on some numerical experiments, in Section \ref{s:numerics}.
\section{Discrete environment}
We review the basic definitions involved in discrete exterior calculus that are needed for the purposes of this work. Readers unaquainted with these discrete structures are encouraged to go over the material covered in the important works cited below. The shape regularity condition that we impose on our triangulations is discussed in Subsection \ref{subs: Discrete Structures}, and a new definition for the boundary of a dual cell is introduced in Subsection \ref{subs: Discrete Operators}.
\subsection{Simplicial complexes and regular triangulations} \label{subs: Discrete Structures}
The basic geometric objects upon which DEC is designed are borrowed from algebraic topology. While the use of cube complexes is discussed in \parencite{BH12}, we here consider simplices to be the main building blocks of the theory. The following definitions are given in \parencite{Desbrun2005} and can also be found in any introductory textbook on simplicial homology.
By a \textit{$k$-simplex} in $\mathbb{R}^n$, we mean the $k$-dimensional convex span
\begin{equation*}
\sigma=\left.\lbrack v_0,...,v_k\rbrack=\left\{\sum_{i=0}^k a_i v_i\right\vert v_i\in\mathbb{R}^n, a_i\geq0,\sum_{i=0}^k a_i =1\right\},
\end{equation*} where $v_0,...,v_k$ are affinely independent. We denote its circumcenter by $c(\sigma)$. Any $\ell$-simplex $\tau$ defined from a nonempty subset of these vertices is said to be a face of $\sigma$, and we denote this partial ordering by $\sigma\succ\tau$. We write $\vert\sigma\vert$ for the $k$-dimensional volume of a $k$-simplex $\sigma$ and adopt the convention that the volume of a vertex is $1$. The plane of $\tau$ is defined as the smallest affine subspace of $\mathbb{R}^n$ containing $\tau$ and is denoted by $P(\tau)$. A simplicial \textit{$n$-complex} $K$ in $\mathbb{R}^n$ is a collection of $n$-simplices in $\mathbb{R}^n$ such that: \begin{itemize}
\item Every face of a simplex in $K$ is in $K$;
\item The intersection of any two simplices of $K$ is either empty or a face of both. \end{itemize} It is well-centered if the the circumcenter of a simplex of any dimension is contained in the interior of that simplex. If the set of simplices of a complex $L$ is a subset of the simplices of another complex $K$, then $L$ is called a \textit{subcomplex} of $K$. We denote by $\Delta_k(L)$ the set of all elementary $k$-simplices of $L$. The \textit{star} of a $k$-simplex $\sigma \in K$ is defined as the set $\text{St}(\sigma)=\{\rho\in K \vert \sigma \prec \rho\}$. $\text{St}(\sigma)$ is not closed under taking faces in general. It is thus useful to define the closed star $\overline{\text{St}}(\sigma)$ to be the smallest subcomplex of $K$ containing $\text{St}(\sigma)$. We denote the free abelian group generated by a basis consisting of the oriented k-simplices by $C_k(K)$. This is the space of finite formal sums of $k$-simplices with coefficients in $\mathbb{Z}$. Elements of $C_k(K)$ are called \textit{$k$-chains}. More generally, we will write $\oplus_kC_k(K)$ for the space of finite formal sums of elements in $\cup_k C_k(K)$ with coefficients in $\mathbb{F}_2$. The \textit{boundary} of a $k$-chain is obtained using the linear operator $\partial:\oplus_k C_k(K)\longrightarrow \oplus_k C_{k-1}(K)$ defined on a simplex $[v_0,...,v_k]\in K$ by \begin{equation*} \partial\lbrack v_0,...,v_k\rbrack = \sum_{i=0}^k (-1)^i \lbrack v_0,...,\hat{v_i},...,v_k\rbrack. \end{equation*}
Any simplicial $n$-complex $K$ in $\mathbb{R}^n$ such that $\cup_{\sigma\in\Delta_n(K)}\sigma=\mathcal{P}$ is called a \textit{triangulation} of $\mathcal{P}$. We consider in this work families of well-centered triangulations $K_h$ in which each complex is indexed by the size $h>0$ of its longest edge. We write $\gamma_{\tau}$ for the radius of the largest $\dim(\tau)$-ball contained in $\tau$. The following condition imposed on $K_h$ is common in the finite element literature, see, e.g., \parencite{Ciarlet02}. We suppose there exists a shape regularity constant $C_{reg}>0$, independent of $h$, such that for all simplex $\sigma$ in $K_h$, \begin{equation*} \mathrm{diam}(\sigma)\leq C_{\text{reg}}\,\gamma_{\sigma}. \end{equation*} A family of triangulations satisfying this condition is said to be \textit{regular}. Important consequences of this regularity assumption will later follow from the next lemma. \begin{lemma}\label{lem: bounded number of simplices} Let $\{K_h\}$ be a regular family of simplicial complexes triangulating an $n$-dimensional polytope $\mathcal{P}$ in $\mathbb{R}^n$. Then there exists a positive constant $C_{\#}$, independent of $h$, such that \begin{equation*} \#\left\{\sigma\in\Delta_n(K_h) : \sigma\in \overline{\mathrm{St}}(\tau)\right\}\leq C_{\#},\,\,\,\,\,\forall\,\tau\in\Delta_k(K_h). \end{equation*} \end{lemma} \begin{proof} If $\tau\prec\sigma$, then $\sigma$ contains all the vertices of $\tau$. It is thus sufficient to consider the case where $\tau$ is a vertex. Let $v$ be a vertex in $K_h$, and suppose $\sigma\in\overline{\text{St}}(v)$. Let $B_\sigma$ be the $n$-dimensional ball of radius $\gamma_\sigma$ contained in $\sigma$. The set $A=\cup_{\eta\in\Delta_{k-1}(\sigma)}\eta\cap B_{\sigma}\cap\text{St}(\sigma)$ contains exactly $n$ points in $\mathbb{R}^n$. The argument \begin{equation*} \theta=\min_{A}\arctan \left(\frac{\gamma_{\sigma}}{\vert x - v\vert}\right) \end{equation*} is thus well-defined, and it satisfies $\theta\geq \arctan\left(1/C_{\text{reg}}\right)$ by the regularity assumption. Consider an $n$-dimensional cone of height $\gamma_{\sigma}$, apex $v$ and aperture $2\theta$ contained in $\sigma$. Its generatrix determine a spherical cap $V_\sigma$ on the hypersphere $S_{\sigma}$ of radius $h$ centered at $v$. The intersection of spherical caps determined by cones contained in distinct simplices is countable. Therefore, there can be at most \begin{equation*} \frac{\mathrm{vol} (S_{\sigma})}{V(\arctan\left(1/C_{\text{reg}}\right))} = 2\pi\left(\int_0^{\arctan(1/C_{\text{reg}})}\sin^n(t)dt\right)^{-1} \end{equation*} of them, and only so many distinct $n$-simplices containing $v$ as a result. \end{proof}
\subsection{Combinatorial orientation and duality}\label{sec: Combinatorial Orientation and Duality} A triangulation stands as a geometric discretization of a polytopic domain, but it ought to be equipped with a meaningful notion of orientation if a compatible discrete calculus is to be defined on its simplices. We outline below the exposition found in \parencite{Hirani03}.
We felt the need to review the definitions of Subsection \ref{subs: Discrete Structures} partly to be able to stress the fact that the expression of a $k$-simplex $\sigma$ comes naturally with an ordering of its vertices. Defining two orderings to be equivalent if they differ by an even permutation yields two equivalence classes called \textit{orientations}. The vertices themselves are dimensionless. As such, they are given no orientation. By interpreting a permutation $\rho$ of the vertices in $\sigma$ as an ordering for the basis vectors $v_{\rho(1)}-v_{\rho(0)},v_{\rho(2)}-v_{\rho(1)},...,v_{\rho(k)}-v_{\rho(k-1)}$, we see that these equivalence classes coincide with the ones obtained when the affine space $P(\sigma)$ is endowed with an orientation in the usual sense. A simplex is thus oriented by its plane and vice versa. The planes of the $(k-1)$-faces of $\sigma$ inherits an orientation as subspaces of $P(\sigma)$. Correspondingly, we establish that the \textit{induced orientation} by $[v_0,...,v_k]$ on the $(k-1)$-face $v_0,...,\hat{v_i},...,v_k$ is the same as the orientation of $[v_0,...,\hat{v_i},...,v_k]$ if $i$ is even, while the opposite orientation is assigned otherwise. Two $k$-simplices $\sigma$ and $\tau$ in $\mathbb{R}^n$ are hence comparable if $P(\sigma)=P(\tau)$, or if they share a ($k-1$)-face. In the first case, the \textit{relative orientation} $\text{sign}(\sigma,\tau)=\pm 1$ of the two simplices is $+1$ when their bases yield the same orientation of the plane and $-1$ otherwise. The induced orientation on the common face is similarly used to establish relative orientation in the second case. The mechanics of orientation are conveniently captured by the structure of exterior algebra. For example, $v_1-v_0\wedge ... \wedge v_k-v_{k-1}$ could be used to represent the orientation of $\lbrack v_0,...,v_k\rbrack$. From now on, we will always assume that $K_h$ is well-centered and that all its $n$-simplices are positively oriented with respect to each other. The orientations of lower dimensional simplices are chosen independently.
We are now ready to introduce the final important objects pertaining to the discrete domain before we move on to the functional aspects of DEC. Denote by $D_h$ the smallest simplicial $n$-complex in $\mathbb{R}^n$ containing every simplex of the form $[c(v),...,c(\tau),...,c(\sigma)]$, where the simplices $v\prec ...\prec\tau\prec ...\prec \sigma$ belong to $K_h$. Let $\ast: \oplus_kC_k(K_h)\longrightarrow \oplus_kC_{n-k}(D_h)$ be the homomorphism acting on $\tau\in K_h$ by \begin{equation*}\label{def: circumcentric duality operator} \ast\tau = \sum_{\tau\prec...\prec\sigma}\pm_{\sigma,...,\tau}[c(\tau),...,c(\sigma)], \end{equation*} where $\pm_{\sigma,...,\tau}=\mathrm{sign}\left(\lbrack v,...,c\left(\tau\right)], \tau\right) \mathrm{sign}\left(\lbrack v,...,c\left(\sigma\right)\rbrack, \sigma\right)$. We define the \textit{oriented circumcentric dual} of $K_h$ by $\ast K_h=\{\ast\tau \,\vert\, \tau\in K_h\}$ (see Figure \ref{fig: example of dual}). Note that the space $C_{n-k}(\ast K_h)$ of finite formal sums of ($n-k$)-dimensional elements of $\ast K_h$ with integer coefficients is a subgroup of $C_{n-k}(D_h)$ onto which the restriction of $\ast$ to $C_k(K_h)$ is an isomorphism. In fact, since a simplex whose vertices are $c(\tau),...,c(\sigma)$ is oriented in the above formula to satisfy $ P(\tau)\times P(c(\tau),...,c(\sigma))\sim \sigma$, we effortlessly extend the definition of $\ast$ to $\oplus_k C_k(\ast K_h)$ as well by defining $\ast\ast\tau=(-1)^{k(n-k)}\tau$ for every simplex $\tau\in\Delta_k(K_h)$, $k=1,...,n$. \begin{figure}
\caption{Boundary and interior faces are perpendicular to their duals. On the left is shown a $1$-dimensional complex in blue and its dual in red. On the right, each shade of grey indicates a $2$-dimensional simplex in $D_h$. The dual of the vertex $\sigma$ is a complex of these simplices, and its boundary is colored in red.}
\label{fig: example of dual}
\end{figure}\
\subsection{Discrete operators}\label{subs: Discrete Operators}
A strength of discrete exterior calculus is foreseen in the following objects. The theory is built on a natural and intuitive notion of discrete differential forms having a straightforward implementation. We call \textit{$k$-cochains} the elements of the space $C^k(K_h) = \text{Hom}(C_k(K_h), \mathbb{R})$, and define $\oplus_kC^k(K_h)$, $C^k(\ast K_h)$ and $\oplus_kC^k(\ast K_h)$ as expected. The \textit{discrete Hodge star} is an isomorphism $\star_h:\oplus_k C^{k}(K_h)\longrightarrow \oplus_kC^{n-k}(\ast K_h)$ satisfying \begin{equation*}\label{def: Hodge star} \langle \star_h\omega_h,\ast\sigma\rangle = \frac{\vert\ast\sigma\vert}{\vert\sigma\vert}\langle \omega_h,\sigma\rangle,\,\,\,\,\,\forall\,\omega\in K_h. \end{equation*} In complete formal analogy, we further impose that \begin{equation*} \langle \star_h\star_h\omega_h,\ast\ast\sigma\rangle = \left(\frac{\vert\ast\sigma\vert}{\vert\sigma\vert}\right)^{-1}\langle \star_h\omega_h,\ast\sigma\rangle,\,\,\,\,\,\forall\,\omega\in K_h. \end{equation*} In other words, $\langle \star_h\star_h\omega_h,\sigma\rangle=(-1)^{k(n-k)}\langle \star_h\star_h\omega_h,\ast\ast\sigma\rangle=(-1)^{k(n-k)}\langle \omega_h,\sigma\rangle$ for all $k$-cochains $\omega_h$, and as a consequence $\star_h\star_h=(-1)^{k(n-k)}$ on $C^k(K_h)$. The spaces $C^k(K_h)$ are finite dimensional Hilbert spaces when equipped with the discrete inner product \begin{equation*} \left(\alpha_h,\beta_h\right)_h=\sum_{\tau\in\Delta_k(K_h)}\langle\alpha_h,\tau\rangle\langle\star_h\beta_h,\ast\tau\rangle,\,\,\,\,\,\alpha_h,\beta_h\in C^k(K_h). \end{equation*} A compatible definition of the discrete $L^2$-norm on the dual triangulation is also chosen by enforcing the Hodge star to be an isometry. The norm in the following definition is obtained from the inner product \begin{equation*} \left(\star\alpha_h,\star\beta_h\right)_h=\sum_{\tau\in\Delta_k(K_h)}\langle\star\alpha_h,\ast\tau\rangle\langle\star_h\star_h\beta_h,\ast\ast\tau\rangle,\,\,\,\,\,\star\alpha_h,\star\beta_h\in C^k(\ast K_h), \end{equation*} which is immediatly seen to satisfy $\left(\alpha_h,\beta_h\right)_h=\left(\star\alpha_h,\star\beta_h\right)_h$. \begin{definition}
The discrete $L^2$-norm on $C^k(\ast K_h)$ is defined by
\begin{equation*}
\|\star\omega_h\|^2_h = \sum_{\tau\in\Delta_k(K_h)}\left(\frac{\vert\ast\tau\vert}{\vert\tau\vert}\right)^{-1}\langle\star_h\omega_h,\ast\tau\rangle^2,\,\,\,\,\, \omega_h\in C^k(\ast K_h).
\end{equation*} \end{definition}
The last step towards a full discretization of the Hodge-Laplace operator is to discretize the exterior derivative. While requiring that \begin{equation*}
\langle \dif\omega_h,\tau\rangle =\langle \omega_h,\partial\tau\rangle,\,\,\,\,\,\forall\,\tau\in K_h, \end{equation*} readily defines a \textit{discrete exterior derivative} $\dif_{\,h}:\oplus_kC^k(K_h)\longrightarrow \oplus_kC^{k+1}(K_h)$ that satisfies Stokes' theorem, we need to make precise what is meant by the boundary of a dual element if we hope to define the exterior derivative on $C^k(\ast K_h)$ similarly. We examine the case of a $k$-simplex $\tau=\pm_{\tau}[v_0,...,v_k]$ in $K_h$. It is sufficient to restrict our attention to an $n$-dimensional simplex $\sigma$ to which $\tau$ is a face. We assume that the orientation of $\sigma$ is consistent with $ \left(v_1-v_0\right)\wedge\left(v_2-v_1\right)\wedge...\wedge\left(v_n-v_{n-1}\right), $ and thereon begin our study. The orientation of $\tau$ is represented by $ \pm_{\tau}\left(v_1-v_0\right)\wedge...\wedge\left(v_k-v_{k-1}\right) $. We have seen that enforcing the orientation of its circumcentric dual $ \ast\tau=\pm_{\ast\tau}[c(\tau),c([v_0,...,v_{k+1}]),...,c(\sigma)] $ to satisfy the definition given in Section \ref{sec: Combinatorial Orientation and Duality} is equivalent to requiring that $ \pm_{\tau}\pm_{\ast \tau}\left(v_1-v_0\right)\wedge...\wedge\left(v_n-v_{n-1}\right) \sim \sigma $. Consequently, $\pm_{\tau}=\pm_{\ast \tau}$ by hypothesis (i.e. the signs agree), and we obtain $ \ast\tau\sim \pm_{\tau}\left(v_{k+1}-v_k\right)\wedge...\wedge\left(v_n-v_{n-1}\right) $. Since similar equivalences hold for any $(k+1)$-face $\eta=\pm_{\eta}[v_0,...,v_{k+1}]$ of $\sigma$, the orientation induced by $\eta$ on the face $v_0,...,v_k$ is defined to be the same as the orientation of \begin{equation*} (-1)^{k+1}\pm_{\eta}\pm_{\tau}\tau \sim(-1)^{k+1}\pm_{\eta}\left(v_1-v_0\right)\wedge...\wedge\left(v_{k}-v_{k-1}\right). \end{equation*} Therefore, choosing $\pm_{\text{old}}=(-1)^{k+1}\pm_{\eta}\pm_{\tau}$ makes the induced orientation of $\pm_{\text{old}}\eta$ on that face consistent with the orientation of $\tau$, and yields on the one hand that the orientation of $c(\eta)$, ..., $c(\sigma)$ as a piece of $\ast\pm_{\text{old}}\eta$ is given by \begin{equation*} (-1)^{k+1}\pm_{\tau}(\pm_{\eta})^2\left(v_{k+2}-v_{k+1}\right)\wedge...\wedge\left(v_n-v_{n-1}\right). \end{equation*}
On the other hand, $P\left(\pm_{\text{new}}\left(\ast\pm_{\text{old}}\eta\right)\right)$ is a subspace of codimension $1$ in $P(\ast\tau)$. As such, it inherits a boundary orientation in the usual sense through the assignement \begin{equation*} P(\ast\tau)\sim\pm_{\text{new}}(-1)^{k+1}\pm_{\tau}\overrightarrow{\nu}\wedge\left(v_{k+2}-v_{k+1}\right)\wedge...\wedge\left(v_n-v_{n-1}\right), \end{equation*} where $\overrightarrow{\nu}$ is any vector pointing away from $P(\ast\eta)$. Since by hypothesis $\overrightarrow{\nu}=(v_{k+1}-v_k)$ is a valid choice of outward vector, we conclude that the above compatible relation holds if and only if $\pm_{\text{new}}=(-1)^{k+1}$. The claim that the following new definition for the boundary of a dual element is suited for integration by parts rests on the later observation.
\begin{figure}
\caption{This figure illustates the exposition of Section \ref{subs: Discrete Operators}. The plane in which the triangle lies is a representation for the $n$-dimensional plane of $\sigma$, while the dotted line represents $P(\tau)$.}
\end{figure}
\begin{definition}\label{def: boundary of dual} The linear operator $\partial: \oplus_kC_{n-k}\left(\ast K_h,\mathbb{Z}\right)\longrightarrow \oplus C_{n-k-1}\left(\ast K_h,\mathbb{Z}\right)$, which we call the \textit{dual boundary operator}, is defined as the linear operator acting on the dual of $\tau=[v_0,...,v_k]\in K_h$ by \begin{equation*} \partial\ast\tau = (-1)^{k+1} \sum_{\eta\succ\tau}\ast\eta, \end{equation*} where $\eta$ is a $(k+1)$-simplex in $K_h$ oriented so that the induced orientation of $\eta$ on the face $v_0,...,v_k$ is consistent with the orientation of $\tau$. \end{definition}
\begin{example} Let $\sigma=\lbrack v_0,v_1,v_2\rbrack$ be an oriented $2$-simplex. The $2$-dimensional dual of $\tau=v_0$ is given by \begin{equation*} \ast \tau = \pm_{v_0,\lbrack v_0,v_1\rbrack,\sigma}\lbrack v_0,c\left(\lbrack v_0,v_1\rbrack\right), c(\sigma) \rbrack +\pm_{v_0,\lbrack v_0,v_2\rbrack,\sigma}\lbrack v_0,c\left(\lbrack v_0,v_2\rbrack\right), c(\sigma) \rbrack, \end{equation*} where by definition \begin{align*} \pm_{v_0,\lbrack v_0,v_1\rbrack,\sigma} &= \mathrm{sign}\left(\lbrack v_0,c\left(\lbrack v_0,v_1\rbrack\right), c(\sigma) \rbrack, \sigma\right) = 1;\\ \pm_{v_0,\lbrack v_0,v_2\rbrack,\sigma} &= \mathrm{sign}\left(\lbrack v_0,c\left(\lbrack v_0,v_2\rbrack\right), c(\sigma) \rbrack, \sigma\right) = -1. \end{align*} The orientation of the boundary edges of $\ast\tau$ with endpoints $c([v_0,v_2])$, $c(\sigma)$ and $c([v_0,v_1])$, $c(\sigma)$ are compatible with integration by parts if they are assigned an orientation equivalent to the one given in the above expression. Yet, from the definition of the boundary of a dual cell as found in the literature, \begin{align*} \partial\ast\tau &= \ast \left((-1)[v_0,v_1]\right)+\ast\left((-1)[v_0,v_2]\right)\\ & = \ast [v_1,v_0] + \ast [v_2,v_0]\\ &= \pm_{[v_1,v_0],\sigma}[c(v_0,v_2),c(\sigma)] +\pm_{[v_2,v_0],\sigma}[c(v_0,v_1),c(\sigma)], \end{align*} where \begin{align*} \pm_{[v_1,v_0],\sigma} &= \mathrm{sign}\left([v_0,c([v_1,v_0])],[v_1,v_0]\right) \cdot\mathrm{sign}\left(\lbrack v_0,c\left(\lbrack v_0,v_1\rbrack\right),c(\sigma)\rbrack,\sigma\right)= (-1)(+1)=-1; \\ \pm_{[v_2,v_0]\sigma} &= \mathrm{sign}\left([v_0,c([v_2,v_0])],[v_2,v_0]\right) \cdot\mathrm{sign}\left(\lbrack v_0,c\left(\lbrack v_0,v_2\rbrack\right),c(\sigma)\rbrack,\sigma\right)= (-1)(-1)=+1. \end{align*} We illustrate this example in Figure \ref{fig: example 2d dual}.
\begin{figure}
\caption{In red is shown the orientation of the boundary of $\ast\tau$ as obtained from definition \ref{def: boundary of dual}. The blue vectors represent the orientation as obtained from the definition found in the current literature, which differs from the compatible orientation by a multiple of $(-1)^{1+0}=-1$.}
\label{fig: example 2d dual}
\end{figure} \end{example}
Using Definition \ref{def: boundary of dual}, we can now resolutely extend the exterior derivative to $$\oplus_kC^{n-k}(\ast K_h)$$ by defining it as the homomorphism satisfying \begin{equation*} \langle \dif\star_h\omega_h,\ast\tau\rangle =\langle \star_h\omega_h,\partial\ast\tau\rangle,\,\,\,\,\,\forall\,\tau\in K_h. \end{equation*}
\section{Consistency} \label{s:consistency}
In this section, we develop a framework to address consistency questions for operators such as the Hodge-Laplace operator. We begin by proving a preliminary lemma which reduces the question of consistency of the Hodge-Laplace operator to the one of consistency of the Hodge star. We then proceed with a demonstration of the latter, and derive bounds on the norms of various discrete operators.
We denote by $C^r\Lambda^k(\mathcal{O})$ the space of differential $k$-forms $\omega$ on an open set $\mathcal{O}\subset\mathbb{R}^n$ such that the function \begin{equation*} x\mapsto \omega_x(X_1(x),...,X_k(x)) \end{equation*}
is $r$ times continuously differentiable for every $k$-tuples $X_1,...,X_k$ of smooth vector fields on $\mathcal{O}$. Given an $n$-polytope $\mathcal{Q}$, say an $n$-dimensional subcomplex of $K_h$, we write $C^r\Lambda^k(\mathcal{Q})$ for the set of differential $k$-forms obtained by restricting to $\mathcal{Q}$ a differential form in $C^r\Lambda^k(\mathcal{O})$, where $\mathcal{O}$ is any open set in $\mathbb{R}^n$ containing $\mathcal{Q}$. The `exact' discrete representatives for solutions of the continuous problems corresponding to (\ref{eq: Discrete Poisson Dirichlet}) are constructed using the {\em deRham map} $R_h$ defined on $C\Lambda^k(\mathcal{P})$ by
\begin{equation*}
\langle R_h\omega, s \rangle = \int_{s}\omega,
\end{equation*}
where $s$ is a $k$-dimensional simplex in $K_h$ or the dual of a $(n-k)$-dimensional one. The next lemma depends on the extremely convenient property that $\dif_{\,h}R_h= R_h\dif\,$. \begin{lemma}\label{lem: reducing consistency} Given $\omega\in C^2\Lambda^k(\mathcal{P})$, we have \begin{multline*} \Delta_h R_h\omega - R_h \Delta \omega = \star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega +\left(\star_h R_h - R_h\star\right)d\star d\omega \\ +\dif_{\,h}\left(\star_hR_h-R_h\star\right)d\star \omega +\dif_{\,h} \star_h \dif_{\,h} \left(\star_h R_h -R_h \star\right)\omega. \end{multline*} \end{lemma} \begin{proof} Consider the explicit expression \begin{multline*} \Delta_h R_h\omega - R_h \Delta \omega = \left(\delta_h \dif_{\,h}+\dif_{\,h} \delta_h\right)R_h\omega -R_h\left(\delta \dif+\dif \delta\right)\omega \\ = \left(\star_h \dif_{\,h} \star_h \dif_{\,h} R_h - R_h \star \dif \star \dif\right)\omega+ \left(\dif_{\,h} \star_h \dif_{\,h}\star_h R_h - R_h \dif\star \dif\star\right)\omega \end{multline*} of the discrete Hodge-Laplace operator. Substituting $$ \star_h \dif_{\,h} R_h \omega = \star_h R_h \dif \omega= \star_h R_h \dif \omega -R_h \star \dif \omega+R_h \star \dif \omega= \left(\star_h R_h-R_h \star \right)\dif\omega +R_h \star \dif\omega $$ in the first summand, we obtain \begin{align*} \star_h \dif_{\,h} \star_h \dif_{\,h} R_h \omega - R_h \star \dif \star \dif \omega &= \star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega + \star_h \dif_{\,h} R_h \star d\omega - R_h \star \dif \star \dif\omega \\ &= \star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega +\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega. \end{align*} The second summand can be rewritten as \begin{align*} \left(\dif_{\,h} \star_h \dif_{\,h}\star_h R_h - R_h \dif\star \dif\star\right)\omega &= \dif_{\,h}\left(\star_h \dif_{\,h}\star_h R_h - R_h \star \dif\star\right)\omega \\ &= \dif_{\,h}\left(\star_h \dif_{\,h}\star_h R_h-\star_h R_h \dif \star +\star_h R_h \dif \star-R_h \star \dif\star\right) \omega \\ &= \dif_{\,h}\left(\star_hR_h-R_h\star\right)\dif\star \omega +\dif_{\,h}\left(\star_h \dif_{\,h} \star_h R_h - \star_h R_h \dif\star\right)\omega. \end{align*} The desired equality then follows from the identity \begin{equation*} \left(\star_h \dif_{\,h} \star_h R_h - \star_h R_h \dif\star\right)\omega = \left(\star_h \dif_{\,h} \star_h R_h - \star_h \dif_{\,h} R_h\star\right)\omega = \star_h \dif_{\,h} \left(\star_h R_h -R_h \star\right)\omega , \end{equation*} which completes the proof. \end{proof}
Given a $n$-simplex $\sigma$ and a $k$-dimensional face $\tau\prec\sigma$, the subspaces $P(\tau)$ and $P(\ast\tau)$ of $\mathbb{R}^n$ are perpendicular and satisfy $P(\tau)\times P(\ast\tau)=P(\sigma)$. Since the the discrete hodge star maps $k$-cochains on $K_h$ to $(n-k)$-cochains on the dual mesh $\ast K_h$, it captures the geometric gist of its classical Hodge operator $\star$, which acts on wedge products of orthonormal covectors as $\star (\dif\lambda_{\rho(1)}\wedge \dif\lambda_{\rho(2)}\wedge...\wedge \dif\lambda_{\rho(k)}) =\mathrm{sign}(\rho)\,\dif\lambda_{\rho(k+1)}\wedge \dif\lambda_{\rho(k+2)}\wedge...\wedge \dif\lambda_{\rho(n)}$.
We hope to exploit this correspondence to estimate the consistency of $\star_h$. By definition, the deRham map directly relates the integral of a differential $k$-form $\omega$ over a $k$-dimensional simplex $\tau$ of $K_h$ with the value of its discrete representative at $\tau$. But one can also integrate any differential $(n-k)$-form, in particular $\star\omega$, over $\ast\tau$. This suggests that simple approximation arguments could be used to compare $\langle R_h\star\omega,\ast\tau\rangle$ with $\langle\star_h\omega_h,\ast\tau\rangle$, since the latter is defined as a scaling of the aforesaid integral $\omega_h=R_h\omega$ by the area factor $\vert\ast \tau\vert/\vert \tau\vert$, which is also naturally related to those very integrals under consideration.
The technique we use is best illustrated in low dimensions. Let $p=(p_1,p_2)$ be a vertex of a triangulation $K_h$ embedded in $\mathbb{R}^2$. For a function $f$ on $\mathbb{R}^2$, we have $\star f=f\dif x\wedge \dif y$. On the one hand, $\langle R_h f, p \rangle$ is simply the evaluation of $f$ at $p$. One the other hand, if $f$ is differentiable, then a Taylor expansion around $p$ yields \begin{align*} \langle R_h\star f,\ast p \rangle &= \iint_{\ast p} f \dif A\\ &= \iint_{\ast p} f(p) + ((x,y)-(p_1,p_2))^TDf(p)+O(h^2)\dif A\\ &= \vert\ast p\vert f(p) + O(h^3). \end{align*} Relying on our convention that $\vert p\vert=1$, we conclude that \begin{equation}\label{eq: consistency prototype estimate} \langle R_h\star f,\ast p \rangle - \langle \star_hR_h f, \ast p \rangle = \langle R_h\star f,\ast p \rangle - \vert\ast p\vert f(p) = O(h^3). \end{equation}
This argument is used in the next theorem as a prototype which we generalize in order to derive estimates for differential forms of higher order in arbitrary dimensions.
\begin{theorem}\label{thm:consistency estimate}
Let $\sigma$ be a $n$-simplex, and suppose $\tau\prec\sigma$ is $k$-dimensional. Then
\begin{equation*}
\langle \star_h R_h \omega , \ast\tau \rangle = \langle R_h\star\omega,\ast\tau\rangle+ O\left(h^{n+1}/(\gamma_{\tau})^k\right),\,\,\,\,\,\omega\in C^1\Lambda^k(\sigma).
\end{equation*} \end{theorem} \begin{proof}
Denote by $\Sigma(k,n)$ the set of strictly increasing maps $\{1,...,k\}\longrightarrow\{1,...,n\}$. Since $P(\tau)\perp P(\ast\tau)$ and $P(\tau)\times P(\ast\tau)=\mathbb{R}^n$, we can choose orthonormal vectors $t_i=x_i-c(\tau)$, $x_i\in \mathbb{R}^n$, such that $\{t_i\}_{i=1,...,k}$ and $\{t_i\}_{i=k+1,..,n}$ are bases for $P(\tau)$ and $P(\ast\tau)$ respectively. Let $\dif\lambda_1,...,\dif\lambda_n$ be a basis for $\text{Alt}^n\mathbb{R}^n$ dual to $\{t_i\}_{i=1,...,n}$. We write $\mathrm{vol}_{\tau}$ for $\dif\lambda_1\wedge...\wedge\dif\lambda_k$ and $\mathrm{vol}_{\ast\tau}$ for $\dif\lambda_{k+1}\wedge...\wedge\dif\lambda_n$.
Following the argument which led to (\ref{eq: consistency prototype estimate}), we approximate the integral $\langle R_h\omega,\tau\rangle$ of a differential $k$-form $\omega=\sum_{\rho\in\Sigma(k,n)}f_{\rho}(\dif\lambda)_\rho$ over $\tau$ using Taylor expansion. This yields
\begin{equation*}
\int_{\tau}\sum_{\rho\in\Sigma(k,n)}f_{\rho}(\dif\lambda)_\rho
=\int_{\tau} f_{1,...,k}\mathrm{vol}_{\tau}
=\vert \tau \vert f_{1,...,k}\left(c(\tau)\right)+O(h^{k+1}).
\end{equation*}
We find similarly that
\begin{equation*}
\langle R_h\star \omega, \ast\tau \rangle
= \int_{\ast \tau}\sum_{\rho\in\sum(k,n)}f_{\rho}\star(\dif\lambda)_{\rho}
=\int_{\ast\tau} f_{1,...,k}\mathrm{vol}_{\ast\tau}
=\vert\ast\tau\vert f_{1,...,k}\left(c(\tau)\right)+O(h^{n-k+1}).
\end{equation*}
Combining these two equations, we get
\begin{align*}
\langle R_h\star \omega, \ast\tau \rangle &=\frac{\vert\ast\tau\vert}{\vert\tau\vert}\langle R_h\omega,\tau\rangle +O\left(h^{n+1}/(\gamma_{\tau})^k\right)+O(h^{n-k+1})\\
&=\langle\star_h R_h\omega,\ast\tau\rangle+O\left(h^{n+1}/(\gamma_{\tau})^k\right) ,
\end{align*} which completes the proof. \end{proof}
\begin{corollary}\label{cor: consistency of hodge star on dual}
Integrating on the dual mesh, we obtain
\begin{equation*}
\langle\star_h R_h (\star\omega),\tau\rangle = \langle R_h\star(\star\omega), \tau\rangle + O(h^{k+1}),\,\,\,\,\, \omega\in C^1\Lambda^k(\mathcal{P}),
\end{equation*}
when $K_h$ is regular. \end{corollary} \begin{proof}
Using Theorem \ref{thm:consistency estimate}, we find that
\begin{align*}
\langle\star_h R_h (\star\omega),\tau\rangle &= (-1)^{k(n-k)}\langle\star_h R_h (\star\omega),\ast\ast\tau\rangle\\
&= (-1)^{k(n-k)}\left(\frac{\vert\ast\tau\vert}{\vert\tau\vert}\right)^{-1}\langle R_h (\star\omega),\ast\tau\rangle\\
&= (-1)^{k(n-k)}\left(\frac{\vert\ast\tau\vert}{\vert\tau\vert}\right)^{-1}\left(\frac{\vert\ast\tau\vert}{\vert\tau\vert}\langle R_h\omega,\tau\rangle +O(h^{n-k+1})\right)\\
&= \langle R_h \star \left(\star\omega\right),\tau\rangle + O(h^{k+1}).
\end{align*} \end{proof}
\begin{comment} \begin{theorem}\label{cor: consistency first estimate} Let $\sigma$ be a $n$-simplex, and suppose $\tau\prec\sigma$ is $k$-dimensional. Then \begin{equation*} \langle \star_h R_h \omega , \ast\tau \rangle = \langle\star\omega,\ast\tau\rangle+ O\left(h^{n+1}/(\gamma_{\tau})^k\right),\,\,\,\,\,\omega\in\Lambda^k(\sigma). \end{equation*} \end{theorem} \begin{proof} Denote by $\Sigma(k,n)$ the set of strictly increasing maps $\{1,...,k\}\longrightarrow\{1,...,n\}$. Let $\sigma=[v_0,...,v_n]$ and assume $\tau$ is an orientation of the face $v_0,...,v_k$. Let $\dif\lambda_1,...,\dif\lambda_k$ be a basis for $\text{Alt}^k(\tau)$ dual to $t_i=v_i-v_0$, $i=1,...,n$, i.e. the vectors $t_1,...t_k$ form a basis for $P(\tau)$ and satisfy $\dif\lambda_1\wedge...\wedge\dif\lambda_k(t_1,...,t_n)=1$. Under these hypotheses, \begin{equation*} \vert \tau \vert = \vert\det\left(v_1-v_0,...,v_k-v_0\right)\vert =\vert\det\left(t_1,...,t_k\right)\vert =\frac{1}{k!}\mathrm{vol}_\sigma(t_1,...,t_n). \end{equation*} In the spirit of the argument which led to (\ref{eq: consistency prototype estimate}), we now approximate the integral of a differential $k$-form $\omega=\sum_{\rho\in\Sigma(k,n)}f_{\rho}(\dif\lambda)_\rho$ over $\tau$ by \begin{equation*} \langle\omega,\tau\rangle=\int_{\tau}\sum_{\rho\in\Sigma(k,n)}f_{\rho}(\dif\lambda)_\rho =\frac{1}{\vert \tau\vert k!}\int_{\tau} f_{1,...,k}\mathrm{vol}_{\tau} =\frac{f_{1,...,k}\left(c(\tau)\right)}{k!}+O(h^{k+1}). \end{equation*} Moreover, since $P(\tau)\perp P(\ast\tau)$, \begin{equation*} \langle\star \omega, \ast\tau \rangle = \int_{\ast \tau}\sum_{\rho\in\sum(k,n)}f_{\rho}\star(\dif\lambda)_{\rho} =\frac{\vert\ast\tau\vert f_{1,...,k}\left(c(\tau)\right)}{\vert \tau\vert k!}+O(h^{n-k+1}). \end{equation*} Combining these two equations, \begin{align*} \langle\star \omega, \ast\tau \rangle &=\frac{\vert\ast\tau\vert}{\vert\tau\vert}\langle\omega,\tau\rangle +O\left(h^{n+1}/(\gamma_{\tau})^k\right)+O(h^{n-k+1})\\ &=\langle\star R_h\omega,\ast\tau\rangle+O\left(h^{n+1}/(\gamma_{\tau})^k\right). \end{align*} \end{proof} \end{comment}
\begin{corollary}\label{cor: consistency of hodge star} The estimate \begin{equation*}
\| \star_h R_h \omega - R_h \star \omega \|_\infty = O(h^{n-k+1}),\,\,\,\,\, \omega\in C^1\Lambda^k(\mathcal{P}) \end{equation*} holds when $K_h$ is regular. \end{corollary}
\begin{corollary}\label{cor: consistency of hodge star L2}
The estimate
\begin{equation*}
\| \star_h R_h \omega - R_h \star \omega \|_h= O(h),\,\,\,\,\, \omega\in C^1\Lambda^k(\mathcal{P})
\end{equation*}
holds when $K_h$ is regular. \end{corollary} \begin{proof} Using Theorem \ref{thm:consistency estimate}, we estimate directly \begin{align*}
\| \star_h R_h \omega - R_h \star \omega \|_h^2 &= \sum_{\tau\in\Delta_k(K_h)}\left(\frac{\ast\tau}{\tau}\right)^{-1}\langle \star_h R_h \omega - R_h \star \omega,\ast\tau\rangle^2\\ &\leq C\sum_{\tau\in\Delta_k(K_h)}\left(\frac{\ast\tau}{\tau}\right)^{-1}\left( h^{n-k+1}\right)^2\\ & \lesssim \sum_{\tau\in\Delta_k(K_h)} h^{n+2}\\ &\lesssim h^2, \end{align*} where the last inequality is obtained from the fact that $\#\{\tau:\tau\in\Delta_k(K_h)\}\sim h^n$, which is a consequence of the regularity assumption. \end{proof}
Finally, the following Corollary is of special importance. It's proof is similar to the one used for Corollary \ref{cor: consistency of hodge star L2}.
\begin{corollary} \label{cor: consistency of hodge star L2 on the dual}
The estimate
\begin{equation*}
\| \left(\star_h R_h - R_h \star\right) \left(\star\omega\right) \|_h= O(h),\,\,\,\,\, \omega\in C^1\Lambda^k(\mathcal{P})
\end{equation*}
holds when $K_h$ is regular. \end{corollary} \begin{proof}
\begin{align*}
\| \left(\star_h R_h \omega - R_h \star\right) \left(\star\omega\right) \|^2_h &= \sum_{\tau\in\Delta_k(K_h)}\langle\left(\star_h R_h \omega - R_h \star\right) \left(\star\omega\right),\tau\rangle \langle \star_h\left(\star_h R_h \omega - R_h \star\right) \left(\star\omega\right),\ast\tau\rangle\\
&=\sum_{\tau\in\Delta_k(K_h)}\frac{\vert\ast\tau\vert}{\vert\tau\vert}\langle\left(\star_h R_h \omega - R_h \star\right) \left(\star\omega\right),\tau\rangle^2\\
&\lesssim \sum_{\tau\in\Delta_k(K_h)} h^{n-2k}\left(h^{k+1}\right)\\
&\lesssim h^2.
\end{align*} \end{proof}
As claimed, we see that estimates on the norm of the operators defined in Section \ref{subs: Discrete Operators} would finally allow one to use the above corollaries to find related bounds on the consistency expression given in Lemma \ref{lem: reducing consistency}. In particular, since
\begin{equation}\label{eq: Hodge-Laplace on functions}
\Delta_h\omega_h=\delta_h\dif_{\,h}\omega_h,\,\,\,\,\, \omega_h\in C^0(K_h),
\end{equation}
it is sufficient for the Hodge-Laplace problem on $0$-forms to evaluate the operator norm of the discrete exterior derivative and of the discrete Hodge star over $C^k(\ast K_h)$, $k=1,...,n$. Namely, from (\ref{eq: Hodge-Laplace on functions}) and the proof of Lemma \ref{lem: reducing consistency}, the consistency error of the Hodge-Laplace restricted to $0$-forms $\omega$ can be written as \begin{equation*} \Delta_h R_h\omega - R_h \Delta \omega = \star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega +\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega. \end{equation*} The following estimates mainly rely on Lemma \ref{lem: bounded number of simplices}, and on the regularity assumption imposed on $K_h$. Indeed, for $\omega_h \in \Delta_k(K_h)$, the inequality \begin{equation}\label{eq: op maximum norm exterior derivative over dual}
\|\dif_{\,h}\star_h\omega_h\|_{\infty}\leq C\|\star_h\omega_h\|_\infty, \end{equation} is a direct consequence of the former, whereas \begin{equation}\label{eq: op maximum norm Hodge star over dual}
\|\star_h\star_h\omega_h\|_{\infty}\sim h^{2k-n}\|\star_h\omega_h\|_{\infty} \end{equation} is immediately obtained from the latter. While \begin{equation}\label{eq: op L2 norm Hodge star over dual}
\|\star_h\|_{\mathcal{L}\left((C^k(\ast K_h),\|\cdot\|_h),(C^{n-k}(K_h),\|\cdot\|_h)\right)}= 1 \end{equation} is merely a statement about the Hodge star being an isometry, the last required estimate is derived from
\begin{align}
\|\dif_{\,h} \star_h\omega_h\|_h^2 & = \sum_{\eta\in\Delta_{k-1}(K_h)}\left(\frac{\vert\ast\eta\vert}{\vert\eta\vert}\right)^{-1}\langle\star_h\omega_h,\partial\ast\eta\rangle^2 \nonumber\\
&=\sum_{\eta\in\Delta_{k-1}(K_h)}\,\,\sum_{\substack{\tau\in\Delta_k(K_h),\\\tau\succ\eta}}\left(\frac{\vert\ast\eta\vert}{\vert\eta\vert}\right)^{-1}\langle\star_h\omega_h,\ast\tau\rangle^2 \nonumber\\
&\leq Ch^{-2}\|\star_h\omega_h\|_h. \label{eq: op L2 norm exterior derivative over dual}
\end{align} Finally, by combining the estimates (\ref{eq: op maximum norm exterior derivative over dual}), (\ref{eq: op maximum norm Hodge star over dual}), (\ref{eq: op L2 norm Hodge star over dual}) and (\ref{eq: op L2 norm exterior derivative over dual}), with corollaries \ref{cor: consistency of hodge star on dual}, \ref{cor: consistency of hodge star}, \ref{cor: consistency of hodge star L2} and \ref{cor: consistency of hodge star L2 on the dual}, we infer \begin{align*}
\|\star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega\|_h &\leq \|\star_h\|_{\mathcal{L}\left((C^k(\ast K_h),\|\cdot\|_h),(C^{n-k}(K_h),\|\cdot\|_h)\right)}\|\dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega\|_h\\
&\lesssim h^{-1} \|\left(\star_h R_h-R_h \star \right)\dif\omega\|_h\\ &\lesssim h^{-1}h = O(1), \end{align*}
\begin{align*}
\|\star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega\|_{\infty} &\lesssim h^{2k-n}\|\dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega\|_{\infty}\\
&\lesssim h^{2k-n} \|\left(\star_h R_h-R_h \star \right)\dif\omega\|_{\infty}\\ & \lesssim h^{2k-n}h^{n-k} = O(h^{k}), \end{align*}
\begin{equation*}
\|\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega\|_h = O(h), \end{equation*} and \begin{align*}
\|\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega\|_\infty = O(h^{k+1}). \end{align*}
We have proved the following.
\begin{corollary}\label{c: consistency bound} If $K_h$ is regular, then \begin{equation*} \begin{split} \Delta_h R_h\omega - R_h \Delta \omega &= \star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega +\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega \\ &= O(1)+O(h) , \end{split} \end{equation*} for $\omega\in C^2\Lambda^0(\mathcal{P})$, in both the maximum and discrete $L^2$-norm. \end{corollary}
Note that in the displayed equation above, we have used the notation $O(1)+O(h)$ to convey information on the individual sizes of the two terms appearing in the right hand side of the first line. In fact, the preceding corollary will not be employed in what follows, since it yields the consistency error of $O(1)$. However, the techniques we have used to estimate the individual terms and operator norms will prove to be fruitful.
\section{Stability and convergence} \label{s:stability}
We carry on with a proof of the first order convergence estimates \begin{equation*}
\|u_h-R_h u\|_h = O(h)\,\,\,\,\,\text{and}\,\,\,\,\, \|\dif\,(u_h-R_h u)\|_h=O(h), \end{equation*} previously stated in (\ref{intro convergence}). The demonstration is based on the discrete variational form of the Poisson problem (\ref{eq: Discrete Poisson Dirichlet}). Its expression can be derived efficiently using the next proposition.
\begin{proposition}\label{prop: adjoint of exterior derivative}
If $\omega_h\in C^{k}(K_h)$ and $\eta_h\in C^{k+1}(K_h)$, then
\begin{equation}
\left(\dif_{\,h}\omega_h,\eta_h \right)_h = \left( \omega_h,\delta_h\eta_h\right)_h.
\end{equation} \end{proposition} \begin{proof}
It is sufficient to consider the case where $\omega_h(\tau)=1$ on a $k$-simplex $\tau$ in $K_h$ and vanishes otherwise. On the one hand,
\begin{equation}\label{adjoint derivative equation}
\left(\dif_{\,h}\omega_h,\eta_h \right)_h = \sum_\sigma\langle\omega_h, \partial\sigma\rangle\langle \star_h\eta_h, \ast\sigma\rangle =\langle\omega_h,\tau\rangle \sum_{\sigma\succ\tau}\langle\star\eta_h,\ast\sigma\rangle,
\end{equation}
where $\sigma$ is a $(k+1$)-simplex oriented so that it is consistent with the induced orientation on $\tau$. On the other hand, since $\delta_h = (-1)^{k}\star_h^{-1}\dif_{\,h}\star_h$ on $k$-cochains, it follows from definition \ref{def: boundary of dual} that
\begin{equation*}
\left(\omega_h,\delta_h\eta_h\right)_h = (-1)^{k+1}\langle\omega_h,\tau\rangle\langle \dif_{\,h}\star_h\eta_h, \ast\tau\rangle = \langle\omega_h,\tau\rangle\sum_{\sigma\succ\tau}\langle \star\eta_h, \ast\sigma\rangle,
\end{equation*}
where $\sigma$ is oriented as in (\ref{adjoint derivative equation}). \end{proof} Before we do so however, we prove a discrete Poincar\'e-like inequality for $0$-cochains that is essential to the argument. The inequality is established by comparing the discrete norm of these cochains with the continuous $L^2$-norm of Whitney forms \begin{equation*} \phi_\tau = k!\sum_{i=0}^k (-1)^i\lambda_i\dif\lambda_1\wedge...\wedge\widehat{\dif\lambda_i}\wedge...\wedge\dif\lambda_k,\,\,\,\,\,\tau\in\Delta_k(K_h), \end{equation*} where $\lambda_i$ is the piecewise linear hat function evaluating to $1$ at the $i$th vertex of $\tau$ and $0$ at every other vertices of $K_h$. Setting \begin{equation*} W_h\omega_h = \sum_{\tau}\omega_h(\tau)\phi_\tau,\,\,\,\,\, \forall \tau\in\Delta_k(K_h), \end{equation*} for all $\omega_h\in C^k(K_h)$ defines linear maps $W_h$, called Whitney maps, which have the key property that $W_h\dif_{\,h}\omega_h=\dif W_h\omega_h$. \begin{theorem}\label{thm: equivalence with Whitney forms}
Let $K_h$ be a family of regular triangulations. There exist two positive constants $c_1$ and $c_2$, independent of $h$, satisfying
\begin{equation*}
c_1 \|\omega_h\|_h \leq \|W_h\omega_h\|_{L^2\Lambda^k(K_h)}\leq c_2\|\omega_h\|_h, \,\,\,\,\, \omega_h\in C^k(K_h).
\end{equation*} \end{theorem} \begin{proof}
We proceed using a scaling argument. Suppose $\sigma=[v_0,...,v_n]\in\Delta_n(K_h)$, and assume $\tau\prec\sigma$ is an orientation of the face $v_0,...,v_k$. Let $\{\lambda_i\}$ be the barycentric coordinate functions associated to the vertices of $\sigma$ (these are the piecewise linear hat functions used in the definition of Whitney forms). The $1$-forms $\dif\lambda_0,...,\widehat{\dif\lambda_{\ell}},...,\dif\lambda_n$ are a basis for $\text{Alt}^n(\mathbb{R}^n)$ dual to $t^{\ell}_i=v_i-v_{\ell}$, $i=1,...,n$, i.e. the vectors $t^{\ell}_1,...t^{\ell}_n$ form a basis for $P(\sigma)$ and satisfy $\dif\lambda_1\wedge...\wedge \widehat{\lambda_{\ell}}\wedge...\wedge\dif\lambda_n(t^{\ell}_1,...,t^{\ell}_n)=1$. In this setting, it follows in general that for any oriented face $\rho=[v_{\rho(0)},...,v_{\rho(m)}]$ of $\sigma$,
\begin{multline*}
\vert \rho \vert = \vert\det\left(v_{\rho(1)}-v_{\rho(0)},...,v_{\rho(m)}-v_{\rho(0)}\right)\vert\\
=\vert\det\left(t^{\rho(0)}_1,...,t^{\rho(0)}_m\right)\vert
=\pm_{\rho}\frac{1}{m!}\mathrm{vol}_\rho(t^{\rho(0)}_1,...,t^{\rho(0)}_n).
\end{multline*} In other words, \begin{equation}\label{eq: change of basis simplex} \dif\lambda_{\rho(1)}\wedge...\wedge \widehat{\dif\lambda_{\rho(0)}} \wedge...\wedge\dif\lambda_{\rho(m)}=\pm_{\rho}\frac{1}{\vert\rho\vert m!}\mathrm{vol}_{\rho}, \end{equation} where $\pm_{\rho}$ depends on the orientation of $\rho$.
Now let $\hat{\sigma}$ denote the standard $n$-simplex in $\mathbb{R}^n$, and consider an affine transformation $F:\hat{\sigma}\longrightarrow\sigma$ of the form $F=B+b$, where $B:\mathbb{R}^n\longrightarrow\mathbb{R}^n$ is a linear map and $b\in\mathbb{R}^n$ a vector. We compute the pullback $\hat{\phi_{\tau}}=F^*\phi_{\tau}$ of a Whitney $k$-form $\phi_{\tau}$ using (\ref{eq: change of basis simplex}). To lighten notation, we write $\hat{\tau}=F^{-1}(\tau)$ and $B_{\hat{\tau}}=B\vert_{P(\hat{\tau})}$. We evaluate directly
\begin{align*}
\left(F^* \phi_\tau\right)_x &= k!\sum_{i=0}^k \frac{\pm_i\lambda_{i}\circ F}{k!\vert\tau\vert}F^*\mathrm{vol}_{\tau} \\
&= k!\sum_{i=0}^k (-1)^i\left(\lambda_{i}\circ F\right) \vert\det B_{\hat{\tau}}\vert\bigwedge_{\substack{\ell=0\\ \ell\neq i}}^k \dif\lambda_{\ell} \\
&= \vert\det B_{\hat{\tau}}\vert\left(\phi_{\tau}\right)_{F(x)}.
\end{align*} A change of variables then yields
\begin{align*}
\int_{\sigma}\|\sum_{\tau}\omega_h(\tau)\phi_{\tau}\|^2 \mathrm{vol}_{\sigma}&= \int_{\sigma}\|\sum_{\tau}\frac{\omega_h(\tau)}{\vert \det B_{\hat{\tau}}\vert}(\hat{\phi}_{\tau})_{F^{-1}}\|^2\mathrm{vol}_{\sigma}\\
&= \vert\det B\vert\int_{\hat{\sigma}}\|\sum_{\tau}\frac{\omega_h(\tau)}{\vert \det B_{\hat{\tau}}\vert}\hat{\phi}_{\tau}\|^2\mathrm{vol}_{\hat{\sigma}}.
\end{align*}
Using the equivalence of norms on finite dimensional Banach spaces and the regularity assumption on $K_h$, we therefore conclude that
\begin{equation*}
\|W_h\omega_h\|^2_{L^2\Lambda^k(\sigma)}\sim \vert\det B\vert\sum_{\tau}\left(\frac{\omega_h(\tau)}{\vert \det B_{\hat{\tau}}\vert}\right)^2
\sim h^{n-2k}\sum_{\tau}\omega_h(\tau)^2
\sim \|\omega_h\|_h^2,
\end{equation*}
where the equivalences do not depend on $h$. \end{proof}
\begin{corollary}\label{cor: poincare}
There exists a constant $C$, independent of $h$, such that the discrete Poincar\'e inequality
\begin{equation*}
\|\omega_h\|_h \leq C\|\dif_{\,h}\omega_h\|_h
\end{equation*}
holds for all $\omega_h\in C^0(K_h)$ such that $\omega_h = 0$ on $\partial K_h$. \end{corollary} \begin{proof}
Using Theorem \ref{thm: equivalence with Whitney forms} and the Poincar\'e inequality, we have
\begin{equation}
\|\omega_h\|_h\lesssim\|W_h\omega_h\|_h\lesssim\|\dif W_h\omega_h\|_{L^2\Lambda^k(K_h)}=\| W_h\dif_{\,h}\omega_h\|_{L^2\Lambda^k(K_h)}\lesssim\|\dif_{\,h}\omega_h\|_h ,
\end{equation}
which establishes the proof. \end{proof}
The argument is twofold. We first restrict our attention in (\ref{eq: Discrete Poisson Dirichlet}) to the homogeneous boundary condition $g=0$, and introduce in a second breath inhomogeneous Dirichlet conditions. Consider the following variational formulations.
Suppose that $\nu_h\in C^0(K_h)$ vanishes everywhere but at a vertex $p$. For all $\omega_h \in C^0(K_h)$, we have \begin{equation*} \left(\delta_h\dif_{\,h}\omega_h,\nu_h\right)_h - \left( R_h f,\nu_h\right)_h = \nu_h(p)\vert\ast p\vert\left( \langle\delta_h\dif_{\,h}\omega_h,p\rangle - \langle R_hf,p\rangle\right). \end{equation*} In other words, $\Delta_h\omega_h = R_h f$ if and only if $\left( \delta_hd_h\omega_h,\nu_h\right)_h = \left( R_h f,\nu_h\right)_h$ for all $\nu_h$. By Proposition \ref{prop: adjoint of exterior derivative}, we may thus equivalently find a discrete function $\omega_h$ vanishing on $\partial K_h$ such that \begin{equation}\label{eq: critical solutions} \left(\dif\omega_h,\dif_{\,h}\nu_h\right) = \left(R_h f,\nu_h\right)_h \end{equation} for all $0$-cochains $\nu_h$ satisfying the homogeneous boundary condition. Note that this problem in turn reduces to the one of minimizing the energy functional \begin{equation*}\label{eq: energy} E_h(\nu_h)= \frac{1}{2}\left(\dif_{\,h}\nu_h,\dif_{\,h}\nu_h\right)_h-\left(R_hf,\nu_h\right)_h \end{equation*} over the same collection of $\nu_h$. Indeed a direct computation shows that $\omega_h$ satisfies (\ref{eq: critical solutions}) if and only if $\frac{\dif}{\dif\epsilon}\big\vert_{\epsilon = 0}E_h\left(\omega_h+\epsilon \nu_h\right) = 0$ for all these $\nu_h$, in which case we further conclude from \begin{equation*} E_h\left(\omega_h+\nu_h\right)= \underbrace{\frac{1}{2}\left(\dif_{\,h}\omega_h,\dif_{\,h}\omega_h\right)_h}_{\geq 0}+\underbrace{\left(\omega_h,\nu_h\right)_h-\left(R_hf,\omega_h\right)_h}_{= 0\text{ by (\ref{eq: critical solutions})}}+\underbrace{\frac{1}{2}\left(\nu_h,\nu_h\right)_h-\left(R_hf,\nu_h\right)_h}_{E_h(\nu_h)} \end{equation*} that $\omega_h$ is a minimizer. Since $\left(\dif_{\,h}u_h,\dif_{\,h}u_h\right)_h=0$ if and only if $u_h$ is constant, $\delta_h\dif_{\,h}$ is invertible over the space of discrete functions vanishing on $\partial K_h$. The existence and uniqueness of a solution to (\ref{eq: critical solutions}) is thus guaranteed for all $h$.
Using Corollary \ref{cor: poincare} in (\ref{eq: critical solutions}) and assuming $R_hf$ is not identically $0$ (the case with trivial solution $\omega_h=0$), we obtain \begin{equation*}
\left(\dif_{\,h}\omega_h,\dif_{\,h}\omega_h\right)_h\leq\|\omega_h\|_h\|R_hf\|_h\leq C\|\dif_{\,h}\omega_h\|_h\|R_hf\|_h, \end{equation*} and another application of that corollary finally yields the stability estimate \begin{equation*}
\|\omega_h\|_h\leq C \|R_hf\|_h. \end{equation*}
Unfortunately, convergence cannot be obtained with an application of the Lax-Richtmyer theorem with this estimate and the consistency bound derived in Corollary \ref{c: consistency bound}. However, Proposition \ref{prop: adjoint of exterior derivative} comes to our rescue. Given a solution $\omega$ to the associated continuous problem, it allows us to use the expression for $\Delta_h$ given in Lemma \ref{lem: reducing consistency} to evaluate the error $e_h=R_h\omega-\omega_h$ with \begin{align*} \left(\dif_{\,h}e_h,\dif_{\,h}e_h\right)_h&=\left(\Delta_he_h,e_h\right)_h\\ &= \left(\star_h \dif_{\,h}\left(\star_h R_h-R_h \star \right)\dif\omega,e_h\right)_h +\left(\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega,e_h\right)_h\\ &=\left(\star_h^{-1}\left(\star_h R_h-R_h \star \right)\dif\omega,\dif_{\,h}e_h\right)_h + \left(\left(\star_h R_h - R_h\star\right)\dif\star \dif\omega,e_h\right)_h\\
&\leq Ch\|\dif_{\,h} e\|_h+Ch\|e_h\|_h, \end{align*} where the last inequality was obtained from an application of Corollary \ref{cor: consistency of hodge star L2}, (\ref{eq: op L2 norm Hodge star over dual}) and the second to last estimate in Corollary \ref{c: consistency bound}. Using the discrete Poincar\'e-like inequality again completes the proof of the homogeneous case of the following theorem. \begin{mdframed} \begin{theorem} The unique discrete solution $\omega_h\in C^0(K_h)$ of problem (\ref{eq: Discrete Poisson Dirichlet}) stated for $0$-forms over a regular triangulation $K_h$ satisfy \begin{equation*}
\|e_h\|_h\leq C\|\dif_{\, h}e_h\|_h= O(h). \end{equation*} \end{theorem} \end{mdframed}
As one would expect, the case of inhomogeneous boundary conditions reduces to the homogeneous one. Given $g_h\neq \vec{0}$, the Poisson problem is to find $\omega_h$ in the affine space $\{g+\eta_h\vert\, \eta_h\in C^0(K_h), \eta_h = 0\, \text{on}\,\,\, \partial K_h\}$ satisfying (\ref{eq: critical solutions}). That is, we are looking for $u_h\in C^0(K_h)\cap\{\eta_h:\eta_h\vert_{\partial K_h}=0\}$ satisfying \begin{equation}\label{eq: critical solutions inhomogeneous} \left(\dif_{\,h}u_h,\dif_{\,h}\nu_h\right)_h= \left(R_hf, \nu_h \right)_h - \left(\dif_{\, h}g_h,\dif_{\, h}\nu_h\right)_h = F(u_h,\nu_h), \end{equation} for all $\nu_h$ vanishing on the boundary, which is equivalent to the previous homogeneous problem, but with the linear functional $F:C^0(K_h)\times C^0(K_h)\longrightarrow \mathbb{R}$ on the right hand side. Repeating the previous arguments, we obtain the stability estimate \begin{equation}
\|u_h\|_h\leq C\left( \|R_hf\|_h+\|\dif_{\, h} g_h\|_h\right). \end{equation} The rest of the proof goes through similarly, so that the solution $\omega_h=g_h+u_h$ to (\ref{eq: Discrete Poisson Dirichlet}) with inhomogeneous boundary condition $g$ is first order convergent.
\section{Numerical experiments} \label{s:numerics}
In this section, we report on some numerical experiments performed over two and three dimensional triangulations. The discrete solutions are computed from the inverse of $\Delta_h$ built as a compound of the operators defined in Section \ref{subs: Discrete Operators}. The volumes needed to implement the Hodge stars as diagonal matrices $\star^h_k$ are computed in a standard way. The matrices $\dif^{\,h}_{\,k-1,\text{Primal}}=(\partial^h_{k})^T$ acting on vector representations of cochains (denoted by $[\cdot]$) in $C^{k-1}(K_h)$ are created using the algorithm suggested in \parencite{BH12}. By construction, the orientation of $\dif^{\,h}_{\,k-1,\text{Primal}}[\tau]\in\Delta_{k}(K_h)$ is therefore consistent with the orientation of the $(k-1)$-simplex $\tau$. Hence, it is suitably oriented for definition \ref{def: boundary of dual} to imply \begin{align*} \left(\dif^{\,h}_{\,\,n-k,\text{Dual}}\star^h_k\lbrack\omega_h\rbrack\right)^T \lbrack\tau\rbrack&= \langle \dif_{\,h}\star_h\omega_h, \ast\tau\rangle\\ &=(-1)^k\sum_{\eta\succ\tau}\langle\star_h\omega_h,\ast\eta\rangle\\ &= (-1)^k\left(\star_h^k[\omega_h]\right)^T\dif^{\,h}_{\,k-1,\text{Primal}}[\tau]\\ &=(-1)^k\left((\dif^{\,h}_{\,k-1,\text{Primal}})^T\star_h^k[\omega_h]\right)^T[\tau] \end{align*} for all $\omega_h\in C^k(K_h)$ and $\tau\in\Delta_{k-1}(K_h)$. This proves the practical definition \begin{equation*} \dif^{\,h}_{\,\,n-k,\text{Dual}}=(-1)^k\left(\dif^{\,h}_{\,k-1,\text{Primal}}\right)^T = (-1)^k \partial^h_k \end{equation*} given in \parencite{Desbrun2008}, which we use in the following.
\subsection{Experiments in two dimensions} Convergence of DEC solutions for $0$-forms is first studied over two types of convex polygons. Non-convex polygons are then used to evaluate the consequences of a lack of regularity caused by re-entrant corners.
\subsubsection{Regular polygons}\label{Regular n-gons} We conduct numerical experiments on refinements of the form $\{K_{c\cdot2^{-i}}\}_{i=0}^N$ of the wheel graph $W_{5}$ whose boundary is a regular pentagon. Triangulation of the pentagonal domain is performed by recursively subdividing each elementary $2$-simplex of the initial complex into its four inscribed subtriangles delimited by the graph of its medial triangle and its boundary. We illustrate the process in Figure \ref{fig: W5 Initial Mesh}.
A discrete solution to the Hodge-Laplace Dirichlet problem with trigonometric exact solution $u(x,y)=x^2\sin(y)$ over this complex is displayed along with its error function in Figure \ref{results convex polygons}. The size of the errors for its collection of refinements with $N=9$ is found in different discrete norms in Table \ref{table: Integral Errors Pentagon Trig}. The results show second order convergence both in the discrete $L^2$ and $H^1$ norms. Other cases where the initial primal triangulation is designed from a wheel graph on $n+1$ vertices are also considered. In particular, repeating the experiment on regular $n$-gons with $6\leq n \leq 8$ yields the same asymptotics.
\begin{figure}
\caption{Initial complex $K_c$}
\label{fig: W5 Initial Mesh}
\end{figure}
\begin{figure}\label{results convex polygons}
\end{figure}
\begin{table} \scalebox{0.70}{
\begin{tabular}{|c||c|c|c|c|c|c|} \hline
$i$ &$e_i^\infty=\|e_{C\cdot 2^{-i}}\|_{\infty}$& $\log\left(e_i^\infty/e^\infty_{i-1}\right)$ & $e^{H^1_d}=\|\dif e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$& $\log\left(e_i^{H^1_d}/e^{H^1_d}_{i-1}\right)$ & $e^{L_d^2}=\|e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$ & $\log\left(e_i^{L^2_d}/e^{L^2_d}_{i-1}\right)$ \\ \hline 0 & 1.561251e-17 & - & 2.975694e-17 & - & 1.487847e-17 & -\\ \hline 1 & 3.202794e-03 & -4.754362e+01 & 1.072846e-02 & -4.835714e+01 & 2.821094e-03 & -4.743002e+01\\ \hline 2 & 7.836073e-04 & 2.031128e+00 & 2.879579e-03 & 1.897512e+00 & 6.332754e-04 & 2.155350e+00\\ \hline 3 & 1.956510e-04 & 2.001848e+00 & 7.353114e-04 & 1.969431e+00 & 1.532456e-04 & 2.046987e+00\\ \hline 4 & 4.891893e-05 & 1.999818e+00 & 1.849975e-04 & 1.990850e+00 & 3.798925e-05 & 2.012183e+00\\ \hline 5 & 1.227086e-05 & 1.995157e+00 & 4.633277e-05 & 1.997401e+00 & 9.477213e-06 & 2.003057e+00\\ \hline 6 & 3.067823e-06 & 1.999949e+00 & 1.158895e-05 & 1.999283e+00 & 2.368052e-06 & 2.000762e+00\\ \hline 7 & 7.669629e-07 & 1.999987e+00 & 2.897627e-06 & 1.999806e+00 & 5.919350e-07 & 2.000190e+00\\ \hline 8 & 1.917491e-07 & 1.999937e+00 & 7.244331e-07 & 1.999948e+00 & 1.479789e-07 & 2.000047e+00\\ \hline
\end{tabular}
}
\caption{Experiment of Subsection \ref{Regular n-gons} with $u(x,y)=x^2\sin(y)$. The terms $C\cdot2^{-i}\in\mathbb{R}$ indicates the values of $h$ in $\|\cdot\|_h$.}\label{table: Integral Errors Pentagon Trig}
\end{table}
\subsubsection{Rectangular domains}\label{Rectangular Domains} Three different types of regular triangulations were used to investigate convergence of DEC solutions over the unit square. These appear as degenerate examples of circumcentric complexes in which the circumcenters lie on the hypotenuses of the primal triangles. Examples of these triangulations are shown in Figure \ref{fig: Triangulations of the Square}.
The computations carried over the unit square produce results similar to the ones previously obtained in Subsection \ref{Regular n-gons}. \begin{figure}
\caption{Three regular triangulations of the square.}
\label{fig: Triangulations of the Square}
\end{figure}
\subsubsection{Unstructured meshes}\label{sub: Asymmetric Convex Polygons} Second order convergence in all norm is also observed for unstructured meshes on convex polygons. The discrete solutions behaved similarly over non-convex polygons when the solution is smooth enough. One example of a primal domain over which the algorithm was tested is shown in Figure \ref{fig:asymmetric mesh}.
\begin{figure}
\caption{Initial complex $K_c$}
\caption{Unstructured triangulations were refined as in Subsection \ref{Regular n-gons}.}
\label{fig:asymmetric mesh}
\end{figure}
\subsubsection{Non-convex polygons}\label{concave Polygons} We study the convergence behavior of DEC when a reentrant corner is present along the boundary of the primal complex. More precisely, we consider re-entrant corners with various angles, leading to the exact solutions $u\in H^{1+\mu}(\mathcal{P})$, $0<\mu<1$, which lack $H^2$ regularity.
Elected candidates for $u\in H^{1+\mu}(\mathcal{P})$ were harmonic functions of the form $r^{\mu}\sin(\mu\theta)$. These functions suit the model of Figure \ref{fig: Pentagon with Corner} (A) for $\mu=\pi/(2\pi -\beta)=\pi/\alpha$ and the result of the experiments can found in Table \ref{table: Integral Errors Pentagon Corner 5/8}. The initial triangulation for this case is also plotted along its first refinement in Figure \ref{fig: Pentagon with Corner}. The refinement algorithm of Subsection \ref{Regular n-gons} was used. Other experiments were performed and led to the empirical observation that $\|u-u_h\|_h\sim h^{2\mu}$ and $\|\dif\,(u-u_h)\|_h\sim h^{\mu}$. This convergence behavior is precisely what would be expected when a finite element method is applied to the same problem, which may be explained by the fact that our discretization is equivalent to a finite element method, cf. \parencite{HPW06,Wardetzky08}
\begin{figure}
\caption{Model of exact solutions}
\caption{Initial complex $K_c$}
\caption{We design an exact solution $u\in H^{1+\mu}(\mathcal{P})$, $0<\mu<1$, such that $\Delta u = 0$ in $\mathcal{P}$ and $u=0$ on the dotted piece of the boundary $\Gamma$ drawn in (A). The red boundary shown in (B) and (C) corresponds to a concave cycle of $W_5$ on which calculations were conducted. This is an instance of the case where $\alpha=8\pi/5$ in (A). The constant $c$ was fixed as in Figure \ref{fig: W5 Initial Mesh}.}
\label{fig: Pentagon with Corner}
\end{figure}
\begin{figure}\label{results nonconvex polygons}
\end{figure}
\begin{table}
\scalebox{0.70}{
\begin{tabular}{|c||c|c|c|c|c|c|} \hline
$i$ &$e_i^\infty=\|e_{C\cdot 2^{-i}}\|_{\infty}$& $\log\left(e_i^\infty/e^\infty_{i-1}\right)$ & $e^{H^1_d}=\|\dif e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$& $\log\left(e_i^{H^1_d}/e^{H^1_d}_{i-1}\right)$ & $e^{L_d^2}=\| e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$ & $\log\left(e_i^{L^2_d}/e^{L^2_d}_{i-1}\right)$ \\ \hline 0 & 0 & - & 0 & - & 0 & - \\ \hline 1 & 3.402738e-02 & - & 8.467970e-02 & - & 2.346479e-02 & - \\ \hline 2 & 3.194032e-02 & 9.131748e-02 & 6.533106e-02 & 3.742472e-01 & 1.353817e-02 & 7.934654e-01 \\ \hline 3 & 2.346298e-02 & 4.449927e-01 & 4.496497e-02 & 5.389676e-01 & 6.570546e-03 & 1.042947e+00 \\ \hline 4 & 1.595752e-02 & 5.561491e-01 & 2.983035e-02 & 5.920204e-01 & 2.970932e-03 & 1.145097e+00 \\ \hline 5 & 1.054876e-02 & 5.971636e-01 & 1.952228e-02 & 6.116590e-01 & 1.299255e-03 & 1.193231e+00 \\ \hline 6 & 6.894829e-03 & 6.134867e-01 & 1.270715e-02 & 6.194814e-01 & 5.584503e-04 & 1.218184e+00 \\ \hline 7 & 4.485666e-03 & 6.201927e-01 & 8.252738e-03 & 6.226958e-01 & 2.377754e-04 & 1.231830e+00 \\ \hline 8 & 2.912660e-03 & 6.229847e-01 & 5.354822e-03 & 6.240341e-01 & 1.007013e-04 & 1.239517e+00 \\ \hline \end{tabular} }
\caption{Experiment of Subsection \ref{concave Polygons} with $r^{\mu}\sin(\mu\theta)$, $\mu=5/8$. The terms $C\cdot2^{-i}\in\mathbb{R}$ indicates the values of $h$ in $\|\cdot\|_h$.}\label{table: Integral Errors Pentagon Corner 5/8} \end{table}
\subsection{Three dimensional case}\label{sub: 3-Dimensional Triangulations}
As explained in \parencite{VanderZee2008}, it is not an easy task in general to generate and refine tetrahedral meshes of $3$-dimensional arbitrary convex domains without altering its circumcentric quality. The next example is a degenerate case: the circumcenters of the tetrahedra used to triangulate the cube lies on lower dimensional simplices, but it does allow for a better control over the step size in $h$ (and thus for a better evaluation of the convergence rate), because the mesh can be refined recursively by gluing smaller copies of itself filling the cuboidal domain. The triangulation is displayed in Figure \ref{cubic mesh}. Again, a second order convergence in all norms similar to the results of Subsection \ref{Regular n-gons} is obtained and presented in Table \ref{table: errors cubic}.
\begin{table}
\scalebox{0.70}{
\begin{tabular}{|c||c|c|c|c|c|c|}
\hline
$i$ &$e_i^\infty=\|e_{C\cdot 2^{-i}}\|_{\infty}$& $\log\left(e_i^\infty/e^\infty_{i-1}\right)$ & $e^{H^1_d}=\|\dif e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$& $\log\left(e_i^{H^1_d}/e^{H^1_d}_{i-1}\right)$ & $e^{L_d^2}=\|e_{C\cdot 2^{-i}}\|_{C\cdot 2^{-i}}$ & $\log\left(e_i^{L^2_d}/e^{L^2_d}_{i-1}\right)$ \\ \hline 0 & 8.586493e-04 & - & 1.487224e-03 & - & 3.035784e-04 & -\\ \hline 1 & 2.666725e-04 & 1.687000e+00 & 6.216886e-04 & 1.258358e+00 & 1.156983e-04 & 1.391702e+00 \\ \hline 2 & 7.122948e-05 & 1.904523e+00 & 1.774812e-04 & 1.808526e+00 & 3.166206e-05 & 1.869540e+00 \\ \hline 3 & 1.835021e-05 & 1.956678e+00 & 4.594339e-05 & 1.949737e+00 & 8.083333e-06 & 1.969733e+00 \\ \hline 4 & 4.621759e-06 & 1.989283e+00 & 1.158904e-05 & 1.987096e+00 & 2.031176e-06 & 1.992635e+00 \\ \hline
\end{tabular}
}
\caption{Experiment of Subsection \ref{sub: 3-Dimensional Triangulations} with $u(x,y)=x^2\sin(y)+\cos(z)$.The terms $C\cdot2^{-i}\in\mathbb{R}$ indicates the values of $h$ in $\|\cdot\|_h$.}\label{table: errors cubic} \end{table}
\begin{figure}
\caption{Initial complex $K_c$}
\caption{The initial 3-dimensional primal triangulation and its first refinement are shown. A sequence of finer triangulations was created by gluing at each step $4$ smaller copies of the previous refinement into the initial cubic domain.}
\label{cubic mesh}
\end{figure}
\section{Conclusion}
This paper fills a gap in the current literature, which has yet to offer any theoretical validation regarding the convergence of discrete exterior calculus approximations for PDE problems in general dimensions. Namely, we prove that discrete exterior calculus approximations to the scalar Poisson problem converge at least linearly with respect to the mesh size for quasi-uniform triangulations in arbitrary dimensions. Nevertheless, it must be emphasized that this {\em first order} convergence result is only partially satisfactory.
In accordance with \parencite{Nong04}, the numerical experiments of Section \ref{s:numerics} display pointwise {\em second order} convergence of the discrete solutions over unstructured triangulations. The same behavior was observed also for the discrete $L^2$ norm. The challenges of explaining the second order convergence, and of proving convergence for general $p$-forms persist.
Due emphasis must be given to the role played by compatibility in obtaining this result. The reliable framework of the continuous setting was reproduced at the discrete level to a sufficient extent so as to successfully provide a theorem of stability comparable to the one found in the classical PDEs literature. This makes another convincing case for the study and development of structure preserving discretization in general.
An accessory consequence of our investigations is the technical modification of the combinatorial definition for the boundary of a dual cell currently found in the early literature. We suggest that it is presently only compatible with the continuous theory up to a sign, and that accounting for the latter yields a new definition which agrees with the algorithms later described in \parencite{Desbrun2008}. A compatible extension of the usual discrete $L^2$-norm to $C^k(\ast K_h)$ was also explicitly introduced.
\section*{Acknowledgments}
This paper is the first author's first research article, and he would like to thank his family for its unwavering support on his journey to become a scientist. The second author would like to thank Gerard Awanou (UI Chicago) for his insights offered during the initial stage of this project, and Alan Demlow (TAMU) for a discussion on interpreting some of the numerical experiments. This work is supported by NSERC Discovery Grant, and NSERC Discovery Accelerator Supplement Program. During the course of this work, the second author was also partially supported by the Mongolian Higher Education Reform Project L2766-MON.
\nocite{*} \printbibliography
\end{document} | arXiv |
Hijaluronski fileri
Botox – botulinum toksin
Aparativni tretmani
Radiotalasni lifting
Mezoterapija bez igala
Mikrodermoabrazija
Lipo laser
Beauty tretmani
Dermaroler
n value of steel
децембар 2, 2020 Uncategorized 0 Comments
Cast Iron: Coated : 0.010: 0.013: 0.014: Uncoated: 0.011: 0.014: 0.016: 4. Easily access valuable industry resources now with full access to the digital edition of The FABRICATOR. Of the similar books on the market today, none explain in detail why one steel is comparable to another. Perhaps the person was familiar with equations such as that used to calculate carbon equivalent (CE) used to predict the relative difficulty of welding. Structural steel grades are designed with specific chemical compositions and mechanical properties formulated for particular applications. natural channels with stones and weeds: 0.035. very poor natural channels Use it. A/V measures the rate of temperature increase of a steel cross section by the ratio of the heated surface area to the volume. 24 in. Tensile / yield strengths and ductilities for some of the plain carbon and low alloy steels are given in the following mechanical properties of steel chart. References Cast irom, ASTM A48, structural steel fro bridges and structures, ASTM A7. 11/27/2020 . The processes used to strengthen the metal also reduce the n-value. S355 steel is a structural steel with a specified minimum yield strength of 355 N/mm². Value of a 1943 Steel Penny . When metal alloys are cold worked, their yield strength increases. The N value (standard Penetration test) value is widely used in Geotechnical Engineering designs especially in India and nearby countries. • Some higher strength steel specifications require a spread of 10,000 or 20,000 PSI between the yield strength and tensile strength. © 2020 FMA Communications, Inc. All rights reserved. Recycle steel today! Anisotropy is, more importantly, also caused by preferred crystallographic orientation or "texture" in the steel. The test-piece has an initial width of 10 mm, thickness of 1.4 mm and gauge length of 50 mm. Use it. (2) For lined corrugated metal pipe, a composite roughness coefficient may be computed using the procedures outlined in the HDS No. The total value, or equity value, is then the sum of the present value of the future cash flows, which in this case is AU$7.2b. Pipe-arches approx-imately have the same roughness characteristics as their equivalent round pipes. After metals have reached their elastic limit and plastically deform they experience strain hardening, which can increase the strength within the final products application. The value of the strain hardening exponent lies between 0 and 1. Last month this column emphasized that our traditional steels have work-hardening exponents (n-values) that remain constant during deformation. Fabricators & Manufacturers Association, Intl. 12/1/2020 11:23:56 PM212.129.35.138. N The higher the n-value, the steeper the stress-strain curve in the uniform elongation region of the tensile test. Wrought Iron: Black : 0.012: 0.014: 0.015: Galvanized: 0.013: 0.016: 0.017: 5. The U value of Steel is 26.2 or an R value of .0382. Compared to the current share price of AU$14.9, the company appears around fair value at the time of writing. The greater the spread between the yield and tensile strengths, the steeper will be the stress-strain curve and the higher the n-value. 2135 Point Blvd., Elgin, IL 60123 (815) 399-8700. 10 in. Events Events Events . Is there a of obtaining the n-value from only that single piece of data? The test-piece has an initial width of 10 mm, thickness of 1.4 mm and gauge length of 50 mm. For structural design it is standard practice to consider the unit weight of structural steel equal to γ = 78.5 kN/m 3 and the density of structural steel approximately ρ = 7850 kg/m 3. It is likely to gradually replace the use of Hp/A. N/mm2 is not SI. Location B indicates the maximum, n-value expected when the minimum yield strength is specified. A value of 0 means that a material is a perfectly plastic solid, while a value of 1 represents a 100% elastic solid. N/A: 11/27/2020: an hour ago . 2. It depends according to the deformation grade applied. It should be noted that, for submerged sands, the SPT-N value needs to be reduced (N red) using the following relationship for SPT-N values exceeding 15. The sheet thickness is retained as specimen thickness, while the parallel length is obtained by milling or punching operations. Strain is the "deformation of a solid due to stress" - change in dimension divided by the original value of the dimension - and can be expressed as. A number of these issues are reviewed this month. DENSITY OF STEEL. Most metals have a n value between 0.10 and 0.50. n-Value The strain hardening exponent n is a measure of the response of metallic materials after cold working. Events Events Our major market-leading conferences and events offer optimum networking opportunities to all participants while adding great value to their business. • Can you explain why specifying the minimum yield strength of higher strength steels limits the maximum n-value? ε = dL / L (1) where. Conversions - Above 480 °C (900 °F), the value of the modulus of elasticity decreases rapidly. Often the n-value is ignored because it seems too complex. While the yield strength may increase slightly, a major reduction in the n-value will take place. Get to know the n-value. For years the n-values were only good to two decimal places. The intersection is the maximum n-value. 15 in. Physical Requirement: All steels have same modulus.. 200 to 210 GPa, or (in your units) those numbers times 1000. Absolutely. For the last decade, a large number of steel producers have improved their process control procedures so the n-value throughout most of the coil varies in the third decimal place. 1) Mild Steel Bars: Mild steel bars can be supplied in two grades . It really does not care what caused the difference. 2.25 2.05 Er value 9.6 Yield Strength, Tensile Strength and Ductility Values for Steels at Room Temperature: Material: Yield Strength: Tensile Strength % Elong. roughness than for annually corrugated steel pipe. Modulus of Elasticity Young's Modulus Strength for Metals - Iron and Steel as the young's modulus or elastic modulus of steel varies by the alloying additions in the steel. Stress is force per unit area and can be expressed as. These conversion charts are provided for guidance only as each scales uses different methods of measuring hardness. This table shows approximate hardness of steel using Brinell, Rockwell B and C and Vickers scales. Using the r-values in the three directions, two other important parameters are calculated. Concrete: Easily access valuable industry resources now with full access to the digital edition of The WELDER. steel, which has higher ductility and is capable of being formed into a wide variety of shapes. • Sometimes a coil is received that fails in a severe stretch area, while other coils form successfully. 10 in. Source: Admet Inc. Ductility is defined as the ability of a material to deform plastically before fracturing. If you have any comments or questions about the glossary, please contact Dan Davis, editor-in-chief of The FABRICATOR. Mexico Metalforming Technology Conference. AHSS are complex, sophisticated materials, with carefully selected chemical compositions and multiphase microstructures resulting from precisely controlled heating and cooling processes. Likewise, the TS/YS ratio will increase with the increased spread. Steel Trade Graphs Steel Trade Graphs. It got great weldability and machinability, let us see more mechanical details of this steel. Reply. I think N/mm^2 is then MPa since (10^–3)^2, inverted is 10^6. Determine the K and n values. • Is n-value a super-property that combines different material properties to assess formability? The arrow B represents the minimum specified yield strength. Material Properties of S355 Steel - An Overview S355 is a non-alloy European standard (EN 10025-2) structural steel, most commonly used after S235 where more strength is needed. TEHRAN, Nov. 29 (MNA) – The export value of steel products of the country exceeded $1.5 billion in the first seven months of the current Iranian calendar year (from March 21 to Oct. 22). The following table lists the buy price (what you can expect to pay to a dealer to purchase the coin) and sell value (what you can expect a dealer to pay you if you sell the coin). P: 216-901-8800 | F: 216-901-9669 36 in. The higher the Hp/A, the faster the steel section heats up and so the greater the thickness of fire protection material required. of the steel exposed to the fire and the mass of the steel section. To obtain a higher n value, one would have to reduce the yield strength below the specification. Hope this helps. When a custom metal fabricator launches a product, Modern material handling in the structural fab shop, The 4 components of reliable systems in stamping, Q&A: How sensors and controls help stampers adapt to the new normal, 5 ways to handle stamping, die cutting waste streams automatically, Second-gen Michigan stamper proves out her mettle through prototyping, Consumables Corner: Diagnosing the obvious and not-so-obvious causes of porosity, Jim's Cover Pass: Face masks are the new necessary shop PPE, Jim's Cover Pass: How to help new welders decode blueprints, Consumables Corner: How to diagnose and prevent weld cracking, Minibike enthusiasts make the most of miscellaneous metals, Helping manufacturers maintain the momentum of innovation, Planning a way out of the pandemic chaos for business owners, Tube manufacturer invests in flexible, automated mill technology, 7 maneras de repensar el flujo de trabajo en la oficina, Perfeccionando una soldadura de proyección en acero de ultra-alta resistencia, La forma y manipulación del rayo lleva la soldadura láser a sus límites, Report: Environmental impacts of metal 3D printing, Satair 3D-prints first flightworthy spare part for Airbus A320ceo, Army looks to 3D-print spare parts to speed aging equipment's return to duty, Software Webinar Series Session 4: Digital Transformation, Predictive Analytics to Solve Scheduling, The FABRICATOR's Technology Summit & Tours, Hastings Air Energy Control, Inc. - Controlled Process Ventilation: Save Money, Save Lives. The mechanical properties of the coil ends may be different because they undergo different processing conditions compared to locations interior to the coil. Cement: Neat Surface: 0.010: 0.011: 0.013: Mortar: 0.011: 0.013: 0.015: 7. The n-value is determined by tensile stress and strain values; while for the r-value calculation the specimen section measurement is also required. In essence, steel is composed of iron and carbon, although it is the amount of carbon, as well as the level of impurities and additional alloying elements that determine the properties of each steel grade. The limiting value is dependent on material, but is generally between 5 and 6. Modulus of Elasticity for Metals. and Larger This exposure to n-value generates a variety of questions about its importance, measurement, source, application and other sometimes fine details. φ in terms of 'N' or Dr φ= 20N +15o r φ=28o +15D Point resistance from SPT 4 N D 0.4 N L qp (tsf) = ≤ ⋅ ⋅ ⋅ N = avg value for 10D above and 4D below pile tip 10D 4D Q 1For a given initial φ unit point resistance for bored piles =1/3 to 1/2 of driven piles, and bulbous piles driven with great impact At ambient temperature between (160 to 200) MPa. They are worth about 10 to 13 cents each in circulated condition, and as much as 50 cents or more if uncirculated.. They simply appear together in a list of steels. Standard ASTM E8 Tensile Specimen. The n-value is measured over a strain range from 10 to 20 percent, 7 to 15 percent or 10 percent to UTS. 24 in. Steel prices saw some correction in the last week of November following a massive rally that pushed prices to an eleven-month high of 4,125 Yuan/MT as construction activity in China is expected to slow when the weather turns colder. steel (or more) that may stand alone in the structure or that is one of many pieces in an assembly or shipping piece. Definitions. Haihong International Trade (HK) CO., Limited. A good knowledge of the basic mechanical properties of these steels is needed for a satisfactory use of them. See Note 5. The Young's modulus of the steel is 19 × 10¹⁰ N/m². Long-term readers of The Science of Forming column and attendees at PMA metalforming seminars are acutely aware of the emphasis given to the workhardening of metals and the workhardening exponent or n-value. This usually indicates that the computer has been allowed to calculate a large number of decimal places that are not meaningful nor scientifically accurate. For low-carbon steels that have a single microstructure of ferrite, a historical data band can be constructed (See graph). Your test locations most likely are from blanks within the coil. electroslag, forged ring/ block,etc. Internal … Steel: Lockbar and welded: 0.010: 0.012: 0.014: Riveted and spiral: 0.013: 0.016: 0.017: 3. A higher ratio means more stretchability. Average n values range from 0.035 (steel) or 0.036 (aluminum) for 5-foot-diameter pipes to 0.033 for pipes of 18 feet or greater diameter. 36 in. a)Mild steel bars grade-I designated as Fe 410-S or Grade 60 b) Mild steel bars grade-II designated as Fe-410-o or Grade 40 . The n-value will print with the rest of the data if the n-value switch is turned on. Is the third decimal place accurate? Comparing steel standards is not an exact science, so the biggest challenge of preparing such a book was deciding on the "rules of comparison." Get your online quote today! Inflation Fear and Green Hope Drive Investors Into Copper. Many translated example sentences containing "value of steel" – German-English dictionary and search engine for German translations. n-value, also known as the strain hardening exponent, is the measure of a metal's response to cold working. Young's modulus of carbon steels (mild, medium and high), alloy steels, stainless steels and tool steels are given in the following table in GPA and ksi. 2-2/3" x 1/2" Annular 8 in. "exact" uses full enumeration of all sample splits with resulting standardized Steel statistics to obtain the exact \(P\)-value. Would this be a low n-value problem? It will become your most powerful trouble-shooter for sheetmetal stretch failures. 2) Medium Tensile Steel Bars designated as Fe- 540-w-ht or Grade 75 . Supply Condition : As Rolled, Normalized Rolling, Furnace Normalizing, … mighthaveverydifferentvalues.Nevertheless,intheabsenceof the stress-strain data for thematerial itself, the assumption, that the data derived from the testsof theshort columns may logically Stainless Steel, Special Steel, Compressor Blading, Turbine Blading, Superalloy Supplier. If the property data are acquired automatically during a tensile test and processed by computer software, most of the new property calculation codes automatically compute n-value. Corrugated Steel Pipe—Manning's "n" Value 60 in. The time dependent deformation due to heavy load over time is known as creep.. Delta r (∆ r) is called the "planar anisotropy parameter" in the formula: ∆ r = (r 0 + r 90 - 2r 45)/2. Corrugated Steel Pipe—Manning's "n" Value 60 in. Structural steel is a standard construction material made from specific grades of steel and formed in a range of industry-standard cross-sectional shapes (or 'Sections'). The n-Value, i.e. In cold-formed steel construction, the use of a range of thin, high strength steels (0.35 mm thickness and 550 MPa yield stress) has increased significantly in recent times. but low carbon steel varies a range of 20.59*104 Mpa and pre hardened steels 19.14*104 Mpa ; Creep. It is the ratio of the stress and the strain of a material. Design values of structural steel material properties Nominal values of structural steel yield strength and ultimate strength For structural design according to Eurocode 3 (EN1993-1-1), the nominal values of the yield strength f y and the ultimate strength f u for structural steel are obtained as a simplification from EN1993-1-1 Table 3.1 , which is reproduced above in tabular format. The n-value is the amount of strengthening for each increment of straining. According to the World Steel Association, there are over 3,500 different grades of steel, encompassing unique physical, chemical, and environmental properties. A typical value of the modulus of elasticity: - at 200 °C (400 °F) is about 193 GPa (28 × 10 6 psi); - at 360 °C (680 °F), 179 GPa (26 × 10 6 psi); - at 445 °C (830 °F), 165 GPa (24 × 10 6 psi); - and at 490 °C (910 °F), 152 GPa (22 × 10 6 psi). The Lankford coefficient (also called Lankford value, R-value, or plastic strain ratio) is a measure of the plastic anisotropy of a rolled sheet metal.This scalar quantity is used extensively as an indicator of the formability of recrystallized low-carbon steel sheets. • The n-values for a coil of steel often are given to three decimal places. TENSILE - YIELD STRENGTH OF STEEL CHART. 2-2/3" x 1/2" Annular 8 in. Strength [] Yield strengtYield strength is the most common property that the designer will need as it is the basis used for most of the rules given in design codes.In European Standards for structural carbon steels (including weathering steel), the primary designation relates to the yield strength, e.g. Other possibilities include a different chemistry, different processing, or even shipment of the wrong coil. For the last decade, a large number of steel producers have improved their process control procedures so the n-value throughout most of the coil varies in the third decimal place. C. MECHANICAL PROPERTIES OF CARBON AND STAINLESS STEEL 360 Table C.1: Nominal values of yield strength f y and ultimate tensile strength f u for hot rolled structural steel Standard and steel grade Nominal thickness of the element t [mm] t 40mm 40mm < t 80mm f y [N/mm 2] f u [N/mm ] f y [N/mm 2] f u [N/mm 2] EN 10025-2 S235 235 360 215 360 S275 275 430 255 410 6363 Oak Tree Blvd. Metric is Pascals, N/m^2. 4140 Steel Uses. If the steel is C15, with the material at 900°C 144 MPa, while at 1200°C 65 MPa. There is a complex equation based on the tensile strength/yield strength ratio. The n-value is the one property of sheetmetal that helps the most in evaluating its relative stretchability. Could the 2020s turn out like the 2010s for metal fabricators? ε = strain (m/m, in/in) dL = elongation or compression (offset) of object (m, in) L = length of object (m, in) Stress - σ. 1 MPa = 10 6 Pa = 1 N/mm 2 = 145.0 psi (lbf/in 2); Fatigue limit, endurance limit, and fatigue strength are used to describe the amplitude (or range) of cyclic stress that can be applied to the material without causing fatigue failure. Pipe, Angles, Expanded Metal, Flat bars, Rounds,Channels and Rebar products. The n-value is determined by tensile stress and strain values; while for the r-value calculation the specimen section measurement is also required. A typical S-N curve corresponding to this type of material is shown Curve A in Figure 1. FINISHLINE All-In-One Deburring & Finishing Solution. The work-hardening exponent of sheet steel which indicates how much the material strengthens when the material is deformed. 18 in. Accoding to The ASHRAE Handbook - Fundamentals 2005 Chapter 39 Table 3. σ = F / A (2) where. A value of 0 means that a … This function uses pairwise Wilcoxon tests, comparing a common control sample with each of several treatment samples, in a multiple comparison fashion. The steel has a 6-inch pitch and a 2-inch rise; aluminum has a 9-inch pitch and a 2.5-inch rise. Study it. Steel traded at USD 711 per metric ton on 6 November, which was up 12.7% from the same day in the prior month. Easily access valuable industry resources now with full access to the digital edition of The Tube & Pipe Journal. Get to know the n-value. Enjoy full access to the digital edition of STAMPING Journal, which serves the metal stamping market with the latest technology advancements, best practices, and industry news. However, a fourth or fifth decimal place n-values are … 12 in. A reduction in impurities such as C and N and addition of stabi- ... n-value 0.19 0.18 0.46 Table 3 r-value and forming properties NSSC 180 SUS304 r-value average 1.4 1.0 L.D.R. Steel Hardness Conversion Table. S355 J2+N Steel Plate Grade Specification : Material: Material En-10025-2 Steel Plate , S355 J2+N Steel Plate Standard: EN 10025-2:2004 Item: Offshore & Structural Steel Plate Width: 1000mm-4500mm Thickness: 5mm-150mm Length: 3000mm-18000mm Surface treatment: Bare, galvanized coated or as customer's requirements. Steel's Multiple Comparison Wilcoxon Tests. Is there some other of estimating n-value? At Value Steel & Pipe we're all about offering high-quality product to our customers at some of the industry's most competitive prices.We specialize in sourcing and selling excess stock materials such as Mild Steel Plate, H.S.S. SAE AISI 4140 Alloy Steel. The value of the strain hardening exponent lies between 0 and 1. Various strengthening mechanisms are employed to achieve a range of strength, ductility, toughness, and fatigue properties. ... S355J2+N/M is the direct EN equivalent of ASTM A572 GR 50. Checking the n-value of the problem coil would be a good first step. a - Minimum specified value of the American Society of Testing Materials. Easily access valuable industry resources now with full access to the digital edition of The Fabricator en Español. TEL:+86-816-3646575 FAX: +86-816-3639422 Study it. 48 in. Why is there a difference? Value of a 1943 Steel Penny . "simulated" uses Nsim simulated standardized Steel statistics based on random splits of the pooled samples into samples of sizes \(n_1, \ldots, n_k\), to estimate the \(P\)-value. An example might be: I have never heard this type of question asked before last month. AHSS are complex, sophisticated materials, with carefully selected chemical compositions and multiphase microstructures resulting from precisely controlled heating and cooling processes. Enjoy full access to the digital edition of The Additive Report to learn how to use additive manufacturing technology to increase operational efficiency and improve the bottom line. Gage marks spaced at 2 inches are applied with a punch. • The n-values for a coil of steel often are given to three decimal places. Tests show somewhat higher n values for this metal and type of construction than for riveted construction. Your steel supplier must run its tests from the coil ends. For this reason, some of the new advanced higher strength steels have complex microstructures that allow higher n-values for the same strength. N = 0.5(N 1 + N 2) Where N 1 is the smallest SPT-N values over the two effective diameters below the toe level N 2 is the average SPT-N value over 10 effective diameters below the pile toe. Oil Retreats on Signs of OPEC+ Discord Ahead of Key Meeting. | Independence | Ohio 44131-2500 1.3 Forming Properties of Steel 9 1.3.1 Stretchability Index: n-values 11 1.3.2 Drawability index: r-values 14 1.4 Ultrasonic Measurements of r-values: Ultra-Form 19 1.4.1 Review 19 1.4.2 Ultra-Form's Description 22 1.4.3 Other Recent Advances 24 1.5 The Present Research 24 CHAPTER 2. Specimens are obtained from the strip or sheet at set angles with respect to the lamination direction which affects the r-value. A steel mill or service center sometimes will correct poor shape with an extra heavy temper pass. Title: Microsoft Word - IB 4001 Mannings n Value Research.doc Author: SCMcKeen Created Date: 12/28/2005 3:43:44 PM Cold working is the plastic deformation of metal below its recrystallization temperature and this is used in many manufacturing processes, such as wire drawing, forging and rolling. This problem is highlighted as point A in the graph. The N value (standard Penetration test) value is widely used in Geotechnical Engineering designs especially in India and nearby countries. Pipe-arches approx-imately have the same roughness characteristics as their equivalent round pipes. • Our tensile test machine does not compute the n-value. n-value noun. LOW CARBON STEELS 28 We have to convert it into dyne/cm². MF, © Copyright 2020 - PMA Services, Inc. It should be noted that in European design standards, the section factor is presented as A/V which has the same numerical value … and Larger Young's modulus of steel at room temperature is typically between 190 GPa (27500 ksi) and 215 GPa (31200 ksi). In the final step we divide the equity value by the number of shares outstanding. The density of steel is in the range of 7.75 and 8.05 g/cm 3 (7750 and 8050 kg/m 3 or 0.280 and 0.291 lb/in 3).The theoretical density of mild steel (low-carbon steel) is about 7.87 g/cm 3 (0.284 lb/in 3).. Density of carbon steels, alloy steels, tool steels and stainless steels are shown below in g/cm 3, kg/m 3 and lb/in 3. EU Quota Tracking EU Quota Tracking. 12 in. roughness than for annually corrugated steel pipe. Fortunately, the n-value is not that complicated, but is a primary metal property measured directly during a tensile test. They are worth about 10 to 13 cents each in circulated condition, and as much as 50 cents or more if uncirculated.. The unit weight of structural steel is specified in the design standard EN 1991-1-1 Table A.4 between 77.0 kN/m 3 and 78.5 kN/m 3. Steel has little or no resistance to heat transfer. However, a fourth or fifth decimal place n-values are sometimes published. Excessive stretching leads to local necking and tearing of the stamping. The following table lists the buy price (what you can expect to pay to a dealer to purchase the coin) and sell value (what you can expect a dealer to pay you if you sell the coin). Steel Pipe, Ungalvanized: 0.015 — Cast Iron Pipe: 0.015 — Clay Sewer Pipe: 0.013 — Polymer Concrete Grated Line Drain: 0.011: 0.010 – 0.013: Notes: (1) Tabulated n-values apply to circular pipes flowing full except for the grated line drain. Guaranteed. For years the n-values were only good to two decimal places. characteristic of steel and titanium in benign environmental conditions. • How much additional tensile testing is required to obtain the n-value? 15 in. We know that the relationship between dyne and Newton is, 1 Newton = 10⁵ dyne. • We run n-value tests on some of our blanks, but the results are different from those provided by our steel supplier. 0 0. measurement of a material's capacity to resist heat flow from one side 18 in. Steel (USA) Price Outlook Prices for hot-rolled coil U.S. steel continued to soar in recent weeks, hitting a one-year high, amid strong manufacturing activity data in China and the U.S in October. The upper curve is the maximum expected n-value as a function of yield strength. Corrugated Metal: Subdrain: 0.017: 0.019: 0.021: Stormdrain: 0.021: 0.024: 0.030: 6. Steel - Coal-tar enamel: 0.010: Steel - smooth: 0.012: Steel - New unlined: 0.011: Steel - Riveted: 0.019: Vitrified clay sewer pipe: 0.013 - 0.015: Wood - planed: 0.012: Wood - unplaned: 0.013: Wood stave pipe, small diameter: 0.011 - 0.012: Wood stave pipe, large diameter: 0.012 - 0.013 Determine the K and n values. A more truthful reason is a lack of understanding. Is this related to the n-value? Highest price of steel per pound in all of Florida. 48 in. PRESS HARDENABLE STEELS (PHS) Press Hardenable Steel (PHS), commonly referred to as Mn22B5 or 15B22, is available as Cold Rolled full hard or annealed and tempered. 12:00 AM . Usually none. And also 1 m² = 10⁴ cm². SAE 4140 (AISI 4140 steel) is a Cr-Mo series (Chrome molybdenum series) low alloy steel, this material has high strength and hardenability, good toughness, small deformation during quenching, high creep strength and long-lasting strength at high temperature. A more truthful reason is a lack of understanding. And stainless steel is about 4% lower. This shows the steel with the 20,000 PSI spread will have more stretchability than the steel with only a 10,000 PSI spread. The work-hardening exponent of sheet steel which indicates how much the material strengthens when the material is deformed. Structural steel is a standard construction material made from specific grades of steel and formed in a range of industry-standard cross-sectional shapes (or 'Sections'). Detailer – a person or entity that is charged with the production of the advanced bill of materials, final bill of materials, and the production of all shop drawings necessary to purchase, fabricate and erect structural steel. It will become your most powerful trouble-shooter for sheetmetal stretch failures. The graph shows why this relationship happens. The n-value decreases with increasing yield strength. They provide a quick checklist to those very familiar with the n-value, and an introduction for those less active in the field. S355JR can be supplied as steel plate/ sheet, round steel bar, steel tube/pipe, steel stripe, steel billet, steel ingot, steel wire rods. If the exact value of n is not needed, two or more material samples can be compared using just the TS/YS ratio if none of the samples have any yield point elongation (YPE). Point A shows a steel sample with an n-value below the expected value. Various strengthening mechanisms are employed to achieve a range of strength, ductility, toughness, and fatigue properties. Structural rivet steel , ASTM A141; high-strength structural rivet steel, ASTM A195 . The die reacts to the properties of the incoming blank. Is the third decimal place accurate? Call now! Specimens are obtained from the strip or sheet at set angles with respect to the lamination direction which affects the r-value. N umerous research programmes show that some types of fully stressed steel sections can achieve a 30 minute fire resistance without ... factor is presented as A/V which has the same numerical value as Hp/A. strain hardening exponent, has been shown to correlate with stretch forming behavior, while the r m is a measure of deep-drawing capability. Often the n-value is ignored because it seems too complex.
Apple Snail Louisiana, Amadeus To Sabre Commands, Radial Fan Blower, Baby Shop High Chair, Texas Flowering Tree Identification, Walking To New Orleans Lyrics And Chords, Stamp Drawing Images, How Long Does It Take To Get Hired At Popeyes,
Our Essential Oils Can Help You Relieve Stress
Review: 100% Organic Argan Oil
Loose Curls Hair Tutorial
sr..org
REKLI SU O NAMA
Visoki profesionalizam i prijateljsko okruženje. Dr Drago i Gorica, pobednička ekipa!
Sanja Mirosavljevic
Mezoterapija lica je fantastičan tretman. Moje lice sada izgleda kao kada se vratim sa dugog i lepog odmora.
Julija Korda
Divni!!!
Dejana Dea Živković
Jako profesionalna ekipa. Svaka čast. Sve pohvale za dr. Dragu i Goricu koji su divni.
Danka Milićević
Najbolji,najprofesionalniji i najljubazniji tim!!! Preporucujem svima!
Ksenija Savić
Uroša Martinovića br. 11 (A Blok)
(+381) 060 0 300 888
[email protected]
Mi na drustvenim mrezama
Matijasevic Estetik 2016 | CommonCrawl |
Journal of Dynamics & Games
July 2018 , Volume 5 , Issue 3
Select all articles
Export/Reference:
Imperfectly competitive markets, trade unions and inflation: Do imperfectly competitive markets transmit more inflation than perfectly competitive ones? A theoretical appraisal
Luis C. Corchón
2018, 5(3): 189-201 doi: 10.3934/jdg.2018012 +[Abstract](1818) +[HTML](324) +[PDF](458.0KB)
In this paper we study the theoretical plausibility of the conjecture that inflation arises because imperfectly competitive markets (ICM in the sequel) translate cost pushes in large price increases. We define two different measures of inflation transmission. We compared these measures in several models of ICM and in perfectly competitive markets (PCM in the sequel). In each case we find a necessary and sufficient condition for an ICM to transmit more inflation -according to the two measures-than that transmitted by a PCM.
Luis C. Corch\u00F3n. Imperfectly competitive markets, trade unions and inflation: Do imperfectly competitive markets transmit more inflation than perfectly competitive ones? A theoretical appraisal. Journal of Dynamics & Games, 2018, 5(3): 189-201. doi: 10.3934\/jdg.2018012.
Equivalences between two matching models: Stability
Paola B. Manasero
2018, 5(3): 203-221 doi: 10.3934/jdg.2018013 +[Abstract](1858) +[HTML](385) +[PDF](442.62KB)
We study the equivalences between two matching models, where the agents in one side of the market, the workers, have responsive preferences on the set of agents of the other side, the firms. We modify the firms' preferences on subsets of workers and define a function between the set of many-to-many matchings and the set of related many-to-one matchings. We prove that this function restricted to the set of stable matchings is bijective and that preserves the stability of the corresponding matchings in both models. Using this function, we prove that for the many-to-many problem with substitutable preferences for the firms and responsive preferences for the workers, the set of stable matchings is non-empty and has a lattice structure.
Paola B. Manasero. Equivalences between two matching models: Stability. Journal of Dynamics & Games, 2018, 5(3): 203-221. doi: 10.3934\/jdg.2018013.
Critical transitions and Early Warning Signals in repeated Cooperation Games
Christian Hofer, Georg Jäger and Manfred Füllsack
Scanning a system's dynamics for critical transitions, i.e. sudden shifts from one system state to another, with the methodology of Early Warning Signals has been shown to yield promising results in many scientific fields. So far however, such investigations focus on aggregated system dynamics modeled with equation-based methods. In this paper the methodology of Early Warning Signals is applied to critical transitions found in the context of Cooperation Games. Since equation-based methods are not well suited to account for interactions in game theoretic settings, an agent-based model of a repeated Cooperation Game is used to generate data. We find that Early Warning Signals can be detected in agent-based simulations of such systems.
Christian Hofer, Georg J\u00E4ger, Manfred F\u00FCllsack. Critical transitions and Early Warning Signals in repeated Cooperation Games. Journal of Dynamics & Games, 2018, 5(3): 223-230. doi: 10.3934\/jdg.2018014.
Strategic delegation effects on Cournot and Stackelberg competition
Nickolas J. Michelacakis
This paper compares the outcomes of two three-stage games of two firms competing for quantity with managerial delegation. In fact, we prove that simultaneous choice of managers by the proprietors of the firms followed by Stackelberg-type competition is equivalent to sequential choice of managers followed by Cournot-type competition. We prove equivalence in a general setting, namely, when the duopolistic model is characterised by a non-linear inverse demand function of the form \begin{document}$p_i = a-(q_i)^n-γ (q_j)^n$\end{document}, \begin{document}$i,j = 1,2$\end{document} and \begin{document}$n∈\mathbb{N}$\end{document}.
Nickolas J. Michelacakis. Strategic delegation effects on Cournot and Stackelberg competition. Journal of Dynamics & Games, 2018, 5(3): 231-242. doi: 10.3934\/jdg.2018015.
A bare-bones mathematical model of radicalization
C. Connell McCluskey and Manuele Santoprete
Radicalization is the process by which people come to adopt increasingly extreme political or religious ideologies. While radical thinking is by no means problematic in itself, it becomes a threat to national security when it leads to violence. We introduce a simple compartmental model (similar to epidemiology models) to describe the radicalization process. We then extend the model to allow for multiple ideologies. Our approach is similar to the one used in the study of multi-strain diseases. Based on our models, we assess several strategies to counter violent extremism.
C. Connell McCluskey, Manuele Santoprete. A bare-bones mathematical model of radicalization. Journal of Dynamics & Games, 2018, 5(3): 243-264. doi: 10.3934\/jdg.2018016.
RSS this journal
Tex file preparation
Abstracted in
Add your name and e-mail address to receive news of forthcoming issues of this journal:
Select the journal
Select Journals | CommonCrawl |
Monad (category theory)
In category theory, a branch of mathematics, a monad (also triple, triad, standard construction and fundamental construction)[1] is a monoid in the category of endofunctors of some fixed category. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes, the denotational semantics of imperative programming languages, and in functional programming languages, allowing languages with non-mutable states to do things such as simulate for-loops; see Monad (functional programming).
Not to be confused with Monad (homological algebra).
Introduction and definition
A monad is a certain type of endofunctor. For example, if $F$ and $G$ are a pair of adjoint functors, with $F$ left adjoint to $G$, then the composition $G\circ F$ is a monad. If $F$ and $G$ are inverse functors, the corresponding monad is the identity functor. In general, adjunctions are not equivalences—they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of $F\circ G$, is discussed under the dual theory of comonads.
Formal definition
Throughout this article $C$ denotes a category. A monad on $C$ consists of an endofunctor $T\colon C\to C$ together with two natural transformations: $\eta \colon 1_{C}\to T$ (where $1_{C}$ denotes the identity functor on $C$) and $\mu \colon T^{2}\to T$ (where $T^{2}$ is the functor $T\circ T$ from $C$ to $C$). These are required to fulfill the following conditions (sometimes called coherence conditions):
• $\mu \circ T\mu =\mu \circ \mu T$ (as natural transformations $T^{3}\to T$); here $T\mu $ and $\mu T$ are formed by "horizontal composition"
• $\mu \circ T\eta =\mu \circ \eta T=1_{T}$ (as natural transformations $T\to T$; here $1_{T}$ denotes the identity transformation from $T$ to $T$).
We can rewrite these conditions using the following commutative diagrams:
See the article on natural transformations for the explanation of the notations $T\mu $ and $\mu T$, or see below the commutative diagrams not using these notions:
The first axiom is akin to the associativity in monoids if we think of $\mu $ as the monoid's binary operation, and the second axiom is akin to the existence of an identity element (which we think of as given by $\eta $). Indeed, a monad on $C$ can alternatively be defined as a monoid in the category $\mathbf {End} _{C}$ whose objects are the endofunctors of $C$ and whose morphisms are the natural transformations between them, with the monoidal structure induced by the composition of endofunctors.
The power set monad
The power set monad is a monad ${\mathcal {P}}$ on the category $\mathbf {Set} $: For a set $A$ let $T(A)$ be the power set of $A$ and for a function $f\colon A\to B$ let $T(f)$ be the function between the power sets induced by taking direct images under $f$. For every set $A$, we have a map $\eta _{A}\colon A\to T(A)$, which assigns to every $a\in A$ the singleton $\{a\}$. The function
$\mu _{A}\colon T(T(A))\to T(A)$
takes a set of sets to its union. These data describe a monad.
Remarks
The axioms of a monad are formally similar to the monoid axioms. In fact, monads are special cases of monoids, namely they are precisely the monoids among endofunctors $\operatorname {End} (C)$, which is equipped with the multiplication given by composition of endofunctors.
Composition of monads is not, in general, a monad. For example, the double power set functor ${\mathcal {P}}\circ {\mathcal {P}}$ does not admit any monad structure.[2]
Comonads
The categorical dual definition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a category $C$ is a monad for the opposite category $C^{\mathrm {op} }$. It is therefore a functor $U$ from $C$ to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.
Monads are to monoids as comonads are to comonoids. Every set is a comonoid in a unique way, so comonoids are less familiar in abstract algebra than monoids; however, comonoids in the category of vector spaces with its usual tensor product are important and widely studied under the name of coalgebras.
Terminological history
The notion of monad was invented by Roger Godement in 1958 under the name "standard construction". Monad has been called "dual standard construction", "triple", "monoid" and "triad".[3] The term "monad" is used at latest 1967, by Jean Bénabou.[4][5]
Examples
Identity
The identity functor on a category $C$ is a monad. Its multiplication and unit are the identity function on the objects of $C$.
Monads arising from adjunctions
Any adjunction
$F:C\rightleftarrows D:G$
gives rise to a monad on C. This very widespread construction works as follows: the endofunctor is the composite
$T=G\circ F.$
This endofunctor is quickly seen to be a monad, where the unit map stems from the unit map $\operatorname {id} _{C}\to G\circ F$ of the adjunction, and the multiplication map is constructed using the counit map of the adjunction:
$T^{2}=G\circ F\circ G\circ F\xrightarrow {G\circ {\text{counit}}\circ F} G\circ F=T.$
In fact, any monad can be found as an explicit adjunction of functors using the Eilenberg–Moore category $C^{T}$ (the category of $T$-algebras).[6]
Double dualization
The double dualization monad, for a fixed field k arises from the adjunction
$(-)^{*}:\mathbf {Vect} _{k}\rightleftarrows \mathbf {Vect} _{k}^{op}:(-)^{*}$
where both functors are given by sending a vector space V to its dual vector space $V^{*}:=\operatorname {Hom} (V,k)$. The associated monad sends a vector space V to its double dual $V^{**}$. This monad is discussed, in much greater generality, by Kock (1970).
Closure operators on partially ordered sets
For categories arising from partially ordered sets $(P,\leq )$ (with a single morphism from $x$ to $y$ if and only if $x\leq y$), then the formalism becomes much simpler: adjoint pairs are Galois connections and monads are closure operators.
Free-forgetful adjunctions
For example, let $G$ be the forgetful functor from the category Grp of groups to the category Set of sets, and let $F$ be the free group functor from the category of sets to the category of groups. Then $F$ is left adjoint of $G$. In this case, the associated monad $T=G\circ F$ takes a set $X$ and returns the underlying set of the free group $\mathrm {Free} (X)$. The unit map of this monad is given by the maps
$X\to T(X)$
including any set $X$ into the set $\mathrm {Free} (X)$ in the natural way, as strings of length 1. Further, the multiplication of this monad is the map
$T(T(X))\to T(X)$
made out of a natural concatenation or 'flattening' of 'strings of strings'. This amounts to two natural transformations. The preceding example about free groups can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg–Moore algebras), so monads can also be seen as generalizing varieties of universal algebras.
Another monad arising from an adjunction is when $T$ is the endofunctor on the category of vector spaces which maps a vector space $V$ to its tensor algebra $T(V)$, and which maps linear maps to their tensor product. We then have a natural transformation corresponding to the embedding of $V$ into its tensor algebra, and a natural transformation corresponding to the map from $T(T(V))$ to $T(V)$ obtained by simply expanding all tensor products.
Codensity monads
Under mild conditions, functors not admitting a left adjoint also give rise to a monad, the so-called codensity monad. For example, the inclusion
$\mathbf {FinSet} \subset \mathbf {Set} $
does not admit a left adjoint. Its codensity monad is the monad on sets sending any set X to the set of ultrafilters on X. This and similar examples are discussed in Leinster (2013).
Monads used in denotational semantics
The following monads over the category of sets are used in denotational semantics of imperative programming languages, and analogous constructions are used in functional programming.
The maybe monad
The endofunctor of the maybe or partiality monad adds a disjoint point:[7]
$(-)_{*}:\mathbf {Set} \to \mathbf {Set} $
$X\mapsto X\cup \{*\}$
The unit is given by the inclusion of a set $X$ into $X_{*}$:
$\eta _{X}:X\to X_{*}$
$x\mapsto x$
The multiplication maps elements of $X$ to themselves, and the two disjoint points in $(X_{*})_{*}$ to the one in $X_{*}$.
In both functional programming and denotational semantics, the maybe monad models partial computations, that is, computations that may fail.
The state monad
Given a set $S$, the endofunctor of the state monad maps each set $X$ to the set of functions $S\to S\times X$. The component of the unit at $X$ maps each element $x\in X$ to the function
$\eta _{X}(x):S\to S\times X$
$s\mapsto (s,x)$
The multiplication maps the function $f:S\to S\times (S\to S\times X),s\mapsto (s',f')$ to the function
$\mu _{X}(f):S\to S\times X$
$s\mapsto f'(s')$
In functional programming and denotational semantics, the state monad models stateful computations.
The environment monad
Given a set $E$, the endofunctor of the reader or environment monad maps each set $X$ to the set of functions $E\to X$. Thus, the endofunctor of this monad is exactly the hom functor $\mathrm {Hom} (E,-)$. The component of the unit at $X$ maps each element $x\in X$ to the constant function $e\mapsto x$.
In functional programming and denotational semantics, the environment monad models computations with access to some read-only data.
The list and set monads
The list or nondeterminism monad maps a set X to the set of finite sequences (i.e., lists) with elements from X. The unit maps an element x in X to the singleton list [x]. The multiplication concatenates a list of lists into a single list.
In functional programming, the list monad is used to model nondeterministic computations. The covariant powerset monad is also known as the set monad, and is also used to model nondeterministic computation.
Algebras for a monad
See also: F-algebra and pseudoalgebra
Given a monad $(T,\eta ,\mu )$ on a category $C$, it is natural to consider $T$-algebras, i.e., objects of $C$ acted upon by $T$ in a way which is compatible with the unit and multiplication of the monad. More formally, a $T$-algebra $(x,h)$ is an object $x$ of $C$ together with an arrow $h\colon Tx\to x$ of $C$ called the structure map of the algebra such that the diagrams
and
commute.
A morphism $f\colon (x,h)\to (x',h')$ of $T$-algebras is an arrow $f\colon x\to x'$ of $C$ such that the diagram
commutes. $T$-algebras form a category called the Eilenberg–Moore category and denoted by $C^{T}$.
Algebras over the free group monad
For example, for the free group monad discussed above, a $T$-algebra is a set $X$ together with a map from the free group generated by $X$ towards $X$ subject to associativity and unitality conditions. Such a structure is equivalent to saying that $X$ is a group itself.
Algebras over the distribution monad
Another example is the distribution monad ${\mathcal {D}}$ on the category of sets. It is defined by sending a set $X$ to the set of functions $f:X\to [0,1]$ with finite support and such that their sum is equal to $1$. In set-builder notation, this is the set
${\mathcal {D}}(X)=\left\{f:X\to [0,1]:{\begin{matrix}\#{\text{supp}}(f)<+\infty \\\sum _{x\in X}f(x)=1\end{matrix}}\right\}$
By inspection of the definitions, it can be shown that algebras over the distribution monad are equivalent to convex sets, i.e., sets equipped with operations $x+_{r}y$ for $r\in [0,1]$ subject to axioms resembling the behavior of convex linear combinations $rx+(1-r)y$ in Euclidean space.[8]
Algebras over the symmetric monad
Another useful example of a monad is the symmetric algebra functor on the category of $R$-modules for a commutative ring $R$.
${\text{Sym}}^{\bullet }(-):{\text{Mod}}(R)\to {\text{Mod}}(R)$
sending an $R$-module $M$ to the direct sum of symmetric tensor powers
${\text{Sym}}^{\bullet }(M)=\bigoplus _{k=0}^{\infty }{\text{Sym}}^{k}(M)$
where ${\text{Sym}}^{0}(M)=R$. For example, ${\text{Sym}}^{\bullet }(R^{\oplus n})\cong R[x_{1},\ldots ,x_{n}]$ where the $R$-algebra on the right is considered as a module. Then, an algebra over this monad are commutative $R$-algebras. There are also algebras over the monads for the alternating tensors ${\text{Alt}}^{\bullet }(-)$ and total tensor functors $T^{\bullet }(-)$ giving anti-symmetric $R$-algebras, and free $R$-algebras, so
${\begin{aligned}{\text{Alt}}^{\bullet }(R^{\oplus n})&=R(x_{1},\ldots ,x_{n})\\{\text{T}}^{\bullet }(R^{\oplus n})&=R\langle x_{1},\ldots ,x_{n}\rangle \end{aligned}}$
where the first ring is the free anti-symmetric algebra over $R$ in $n$-generators and the second ring is the free algebra over $R$ in $n$-generators.
Commutative algebras in E-infinity ring spectra
There is an analogous construction for commutative $\mathbb {S} $-algebras[9]pg 113 which gives commutative $A$-algebras for a commutative $\mathbb {S} $-algebra $A$. If ${\mathcal {M}}_{A}$ is the category of $A$-modules, then the functor $\mathbb {P} :{\mathcal {M}}_{A}\to {\mathcal {M}}_{A}$ :{\mathcal {M}}_{A}\to {\mathcal {M}}_{A}} is the monad given by
$\mathbb {P} (M)=\bigvee _{j\geq 0}M^{j}/\Sigma _{j}$
where
$M^{j}=M\wedge _{A}\cdots \wedge _{A}M$
$j$-times. Then there is an associated category ${\mathcal {C}}_{A}$ of commutative $A$-algebras from the category of algebras over this monad.
Monads and adjunctions
As was mentioned above, any adjunction gives rise to a monad. Conversely, every monad arises from some adjunction, namely the free–forgetful adjunction
$T(-):C\rightleftarrows C^{T}:{\text{forget}}$
whose left adjoint sends an object X to the free T-algebra T(X). However, there are usually several distinct adjunctions giving rise to a monad: let $\mathbf {Adj} (C,T)$ be the category whose objects are the adjunctions $(F,G,e,\varepsilon )$ such that $(GF,e,G\varepsilon F)=(T,\eta ,\mu )$ and whose arrows are the morphisms of adjunctions that are the identity on $C$. Then the above free–forgetful adjunction involving the Eilenberg–Moore category $C^{T}$ is a terminal object in $\mathbf {Adj} (C,T)$. An initial object is the Kleisli category, which is by definition the full subcategory of $C^{T}$ consisting only of free T-algebras, i.e., T-algebras of the form $T(x)$ for some object x of C.
Monadic adjunctions
Given any adjunction $(F:C\to D,G:D\to C,\eta ,\varepsilon )$ with associated monad T, the functor G can be factored as
$D{\stackrel {\tilde {G}}{\to }}C^{T}{\stackrel {\text{forget}}{\to }}C,$
i.e., G(Y) can be naturally endowed with a T-algebra structure for any Y in D. The adjunction is called a monadic adjunction if the first functor ${\tilde {G}}$ yields an equivalence of categories between D and the Eilenberg–Moore category $C^{T}$.[10] By extension, a functor $G\colon D\to C$ is said to be monadic if it has a left adjoint $F$ forming a monadic adjunction. For example, the free–forgetful adjunction between groups and sets is monadic, since algebras over the associated monad are groups, as was mentioned above. In general, knowing that an adjunction is monadic allows one to reconstruct objects in D out of objects in C and the T-action.
Beck's monadicity theorem
Beck's monadicity theorem gives a necessary and sufficient condition for an adjunction to be monadic. A simplified version of this theorem states that G is monadic if it is conservative (or G reflects isomorphisms, i.e., a morphism in D is an isomorphism if and only if its image under G is an isomorphism in C) and C has and G preserves coequalizers.
For example, the forgetful functor from the category of compact Hausdorff spaces to sets is monadic. However the forgetful functor from all topological spaces to sets is not conservative since there are continuous bijective maps (between non-compact or non-Hausdorff spaces) that fail to be homeomorphisms. Thus, this forgetful functor is not monadic.[11] The dual version of Beck's theorem, characterizing comonadic adjunctions, is relevant in different fields such as topos theory and topics in algebraic geometry related to descent. A first example of a comonadic adjunction is the adjunction
$-\otimes _{A}B:\mathbf {Mod} _{A}\rightleftarrows \mathbf {Mod} _{B}:\operatorname {forget} $
for a ring homomorphism $A\to B$ between commutative rings. This adjunction is comonadic, by Beck's theorem, if and only if B is faithfully flat as an A-module. It thus allows to descend B-modules, equipped with a descent datum (i.e., an action of the comonad given by the adjunction) to A-modules. The resulting theory of faithfully flat descent is widely applied in algebraic geometry.
Uses
Monads are used in functional programming to express types of sequential computation (sometimes with side-effects). See monads in functional programming, and the more mathematically oriented Wikibook module b:Haskell/Category theory.
Monads are used in the denotational semantics of impure functional and imperative programming languages.[12][13]
In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic via closure operators, interior algebras, and their relation to models of S4 and intuitionistic logics.
Generalization
It is possible to define monads in a 2-category $C$. Monads described above are monads for $C=\mathbf {Cat} $.
See also
• Distributive law between monads
• Lawvere theory
• Monad (functional programming)
• Polyad
• Strong monad
References
1. Barr, Michael; Wells, Charles (1985), "Toposes, Triples and Theories" (PDF), Grundlehren der mathematischen Wissenschaften, Springer-Verlag, vol. 278, pp. 82 and 120, ISBN 0-387-96115-1.
2. Klin; Salamanca (2018), "Iterated Covariant Powerset is not a Monad", Electronic Notes in Theoretical Computer Science, 341: 261–276, doi:10.1016/j.entcs.2018.11.013
3. Mac Lane 1978, p. 138. sfn error: no target: CITEREFMac_Lane1978 (help)
4. Bénabou, Jean (1967). Bénabou, J.; Davis, R.; Dold, A.; Isbell, J.; MacLane, S.; Oberst, U.; Roos, J. -E. (eds.). "Introduction to bicategories". Reports of the Midwest Category Seminar. Lecture Notes in Mathematics. Berlin, Heidelberg: Springer. 47: 1–77. doi:10.1007/BFb0074299. ISBN 978-3-540-35545-8.
5. "RE: Monads". Gmane. 2009-04-04. Archived from the original on 2015-03-26.
6. Riehl, Emily. "Category Theory in Context" (PDF). p. 162. Archived (PDF) from the original on 5 Apr 2021.
7. Riehl 2017, p. 155.
8. Świrszcz, T. (1974), "Monadic functors and convexity", Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys., 22: 39–42, MR 0390019, Jacobs, Bart (2010), "Convexity, Duality and Effects", Theoretical Computer Science, IFIP Advances in Information and Communication Technology, vol. 323, pp. 1–19, doi:10.1007/978-3-642-15240-5_1, ISBN 978-3-642-15239-9
9. Basterra, M. (1999-12-15). "André–Quillen cohomology of commutative S-algebras". Journal of Pure and Applied Algebra. 144 (2): 111–143. doi:10.1016/S0022-4049(98)00051-6. ISSN 0022-4049.
10. MacLane (1978) uses a stronger definition, where the two categories are isomorphic rather than equivalent.
11. MacLane (1978, §§VI.3, VI.9)
12. Wadler, Philip (1993). Broy, Manfred (ed.). "Monads for functional programming". Program Design Calculi. NATO ASI Series. Berlin, Heidelberg: Springer. 118: 233–264. doi:10.1007/978-3-662-02880-3_8. ISBN 978-3-662-02880-3. "The concept of a monad, which arises from category theory, has been applied by Moggi to structure the denotational semantics of programming languages."
13. Mulry, Philip S. (1998-01-01). "Monads in Semantics". Electronic Notes in Theoretical Computer Science. US-Brazil Joint Workshops on the Formal Foundations of Software Systems. 14: 275–286. doi:10.1016/S1571-0661(05)80241-5. ISSN 1571-0661.
Further reading
• Barr, Michael; Wells, Charles (1999), Category Theory for Computing Science (PDF)
• Godement, Roger (1958), Topologie Algébrique et Théorie des Faisceaux., Actualités Sci. Ind., Publ. Math. Univ. Strasbourg, vol. 1252, Paris: Hermann, pp. viii+283 pp
• Kock, Anders (1970), "On Double Dualization Monads", Mathematica Scandinavica, 27: 151, doi:10.7146/math.scand.a-10995
• Leinster, Tom (2013), "Codensity and the ultrafilter monad", Theory and Applications of Categories, 28: 332–370, arXiv:1209.3606, Bibcode:2012arXiv1209.3606L
• MacLane, Saunders (1978), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5, doi:10.1007/978-1-4757-4721-8, ISBN 978-1-4419-3123-8
• Pedicchio, Maria Cristina; Tholen, Walter, eds. (2004). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory. Encyclopedia of Mathematics and Its Applications. Vol. 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. Zbl 1034.18001.
• Riehl, Emily (2017), Category Theory in Context, ISBN 9780486820804
• Turi, Daniele (1996–2001), Category Theory Lecture Notes (PDF)
External links
• Monads, five short lectures (with one appendix).
• John Baez's This Week's Finds in Mathematical Physics (Week 89) covers monads in 2-categories.
| Wikipedia |
\begin{document}
\preprint{ } \title[G\"{o}ppert-Mayer and the SFA]{Low-frequency failure of the G\"{o}ppert-Mayer gauge transformation and consequences for the Strong-Field Approximation} \author{H. R. Reiss} \affiliation{Max Born Institute, 12489 Berlin, Germany} \affiliation{American University, Washington, DC 20016-8058, USA}
\pacs{32.80.Rm, 33.80.Rv, 42.50.Hz, 33.20.Xx}
\begin{abstract} The G\"{o}ppert-Mayer (GM) gauge transformation, of central importance in atomic, molecular, and optical physics since it connects the length gauge and the velocity gauge, becomes unphysical as the field frequency declines towards zero. This is not consequential for theories of transverse fields, but it is the underlying reason for the failure of gauge invariance in the dipole-approximation version of the Strong-Field Approximation (SFA). This failure of the GM gauge transformation explains why the length gauge is preferred in analytical approximation methods for fields that possess a constant electric field as a zero-frequency limit.
\end{abstract} \date[9 September 2015]{} \maketitle
The Strong-Field Approximation (SFA) is the basic analytical method for the treatment of the interaction of nonperturbatively strong laser fields with atoms and molecules, but it is known to be gauge-dependent. It is important to note from the outset that results obtained herein apply only to theories that make \textit{a priori} use of the dipole approximation. Such theories are identifiable by the fact that a zero-frequency limit exists, and that this limit corresponds to a constant electric field. In other words, this work applies only to longitudinal fields. Thus theories that are derived from propagating-wave formalisms are excluded, since such transverse-field theories have extremely low-frequency radio waves as a low frequency limit.
Gauge dependence of the SFA is probably shown most clearly in Ref. \cite{bmb}, where the length gauge (LG) results are plausible, but the velocity gauge (VG) results are not. This long-known lack of gauge invariance has led to statements of alarm, such as \textquotedblleft\textit{... the SFA is not gauge invariant, which is really bad news for a theory.}.\textquotedblright \ \cite{mishajmo} (emphasis from the original.) Another expression of concern is: \textquotedblleft...how can a noninvariant theory be used for the calculation of observables?\textquotedblright\ \cite{poprtun}.
The approach taken here for examination of the gauge problem is entirely general, with no dependence on the particular properties of any problem or class of problems beyond the statement that the field is treated as a longitudinal field (or the equivalent statement that the field has a zero-frequency limit corresponding to a static electric field). We start with a re-derivation of the known result \cite{hrjmo,hrtun} that the static electric field can be described only within a unique gauge if all physical constraints are to be satisfied. A nominally alternative gauge is discarded on the grounds that it violates the physical condition that a charged particle in a static electric field represents a system for which total energy is conserved. It is then shown that this unphysical gauge arises from a G\"{o}ppert-Mayer (GM) gauge transformation from the length gauge to the velocity gauge as applied to an oscillatory electric field in the zero frequency limit. This establishes the unphysical nature of the GM gauge transformation when zero frequency is a possibility. This is consequential in that photoelectron spectra that extend to zero frequency are a necessary part of any strong-field, nonperturbative problem. The GM gauge transformation from the LG to the VG is thus shown to be unphysical in the zero-frequency limit, leaving the LG as the only physical alternative. The two constraints of strong fields and the accessibility of a zero-frequency limit are all that is necessary to confirm the LG as the only physical gauge for the SFA in the form appropriate to oscillatory electric fields.
Consider a static electric field with the amplitude $E_{0}$. It is known from electrostatics that this field can be specified by the scalar and vector potentials \begin{equation} \phi=-\mathbf{r\cdot E}_{0},\quad\mathbf{A}=0. \label{a} \end{equation} A gauge transformation can be accomplished by a scalar generating function $\Lambda$ subject only to the constraint that the generating function satisfy the homogeneous wave equation \begin{equation} \partial^{\mu}\partial_{\mu}\Lambda=0. \label{b} \end{equation} The 4-vector potential following from a gauge transformation is \begin{equation} \widetilde{A}^{\mu}=A^{\mu}+\partial^{\mu}\Lambda, \label{c} \end{equation} which is equivalent to the transformed scalar and 3-vector potentials \begin{align} \widetilde{\phi} & =\phi+\frac{1}{c}\partial_{t}\Lambda,\label{d}\\ \widetilde{\mathbf{A}} & =\mathbf{A}-\mathbf{\nabla}\Lambda. \label{e} \end{align} It is well-known that the representation of a static electric field by a scalar potential alone, as in Eq.(\ref{a}) can be gauge-transformed so that the field can be described by a vector potential alone by using the generating function \begin{equation} \Lambda=ct\mathbf{r\cdot E}_{0}, \label{f} \end{equation} which leads to the new potentials \begin{equation} \widetilde{\phi}=0,\quad\widetilde{\mathbf{A}}=-ct\mathbf{E}_{0}. \label{g} \end{equation} The potentials in Eq. (\ref{g}) are unphysical in the sense that a charged particle subject to those potentials is described by Lagrangian and Hamiltonian functions that possess explicit time dependence; and explicit time dependence of these system functions is a clear indicator that total energy is not conserved. This contrasts with the time independence of the potentials in Eq.(\ref{a}), signifying energy conservation.
The formal foundations for Noether's Theorem connecting symmetries with physical conservation laws are expressed in terms of the Lagrangian function. (See, for example, Ref. \cite{goldstein}.) The potentials (\ref{a}) lead to a Lagrangian that has no explicit dependence on time, and thereby demonstrates energy conservation, whereas the potentials (\ref{g}) signify a Lagrangian that depends explicitly on the time, and is thus unphysical.
The GM gauge transformation is usually expressed in terms of the vector potential that arises after the transformation. That is, the generator of the GM gauge transformation is usually written as \begin{equation} \Lambda^{GM}=-\mathbf{r\cdot}\widetilde{\mathbf{A}}.\label{g1} \end{equation} This is exactly what follows from Eqs. (\ref{f}) and (\ref{g}), so the above discussion amounts to concluding that the GM gauge transformation is unphysical when $\omega=0$.
Problems described by nonperturbative methods such as tunneling methods \cite{kel,nr,ppt,adk}, have spectra that are always inclusive of zero frequency. This is straightforward to describe within the LG, but the extension to $\omega\rightarrow0$ defies treatment within the VG.
The failure of the GM gauge transformation has no significance for transverse fields, such as laser fields. Such fields are propagating fields that do not have a zero frequency limit in the same sense as longitudinal fields. Propagating fields have extremely low-frequency radio fields as the limit when $\omega\rightarrow0$ \cite{hr101,hrtun}. The limit point of $\omega=0$ cannot be achieved for a variety of (inter-related) reasons: propagation is not defined when $\omega=0$; the magnetic field must always have the same magnitude as the electric field (in Gaussian units), so it can never be set to zero when the electric field is nonzero; $\omega\rightarrow0$ implies wavelength $\lambda\rightarrow\infty$; the ponderomotive energy $U_{p}$ for a transverse field is proportional to $1/\omega^{2}$, so infinite energy must be supplied; there is no gauge freedom at all for propagating fields \cite{hrjmo,hrtun}; and so on.
The overall conclusion is that the LG is the sole physical gauge for oscillatory electric fields when the zero-frequency limit must be considered.
I thank Prof. D. Bauer of Rostock University for useful discussions.
\end{document} | arXiv |
\begin{definition}[Definition:Angle Inscribed in Circle]
:300px
Let $AB$ and $BC$ be two chords of a circle which meet at $B$.
The angle $\angle ABC$ is the '''angle inscribed at $B$ (with respect to $A$ and $C$)'''.
Category:Definitions/Circles
\end{definition} | ProofWiki |
Maier's matrix method
Maier's matrix method is a technique in analytic number theory due to Helmut Maier that is used to demonstrate the existence of intervals of natural numbers within which the prime numbers are distributed with a certain property. In particular it has been used to prove Maier's theorem (Maier 1985) and also the existence of chains of large gaps between consecutive primes (Maier 1981). The method uses estimates for the distribution of prime numbers in arithmetic progressions to prove the existence of a large set of intervals where the number of primes in the set is well understood and hence that at least one of the intervals contains primes in the required distribution.
The method
The method first selects a primorial and then constructs an interval in which the distribution of integers coprime to the primorial is well understood. By looking at copies of the interval translated by multiples of the primorial an array (or matrix) of integers is formed where the rows are the translated intervals and the columns are arithmetic progressions where the difference is the primorial. By Dirichlet's theorem on arithmetic progressions the columns will contain many primes if and only if the integer in the original interval was coprime to the primorial. Good estimates for the number of small primes in these progressions due to (Gallagher 1970) allows the estimation of the primes in the matrix which guarantees the existence of at least one row or interval with at least a certain number of primes.
References
• Maier, Helmut (1985), "Primes in short intervals", The Michigan Mathematical Journal, 32 (2): 221–225, doi:10.1307/mmj/1029003189
• Maier, Helmut (1981), "Chains of large gaps between consecutive primes", Advances in Mathematics, 39 (3): 257–269, doi:10.1016/0001-8708(81)90003-7
• Gallagher, Patrick (1970), "A large sieve density estimate near σ=1", Inventiones Mathematicae, 11 (4): 329–339, doi:10.1007/BF01403187
| Wikipedia |
A novel image encryption framework based on markov map and singular value decomposition
Gaurav Bhatnagar1, Q. M. Jonathan Wu1, Balasubramanian Raman2• Institutions (2)
University of Windsor1, Indian Institute of Technology Roorkee2
22 Jun 2011-pp 286-296
TL;DR: A novel yet simple encryption technique is proposed based on toral automorphism, Markov map and singular value decomposition (SVD) and a reliable decryption scheme is proposed to construct original image from encrypted image.
Abstract: In this paper, a novel yet simple encryption technique is proposed based on toral automorphism, Markov map and singular value decomposition (SVD). The core idea of the proposed scheme is to scramble the pixel positions by the means of toral automorphism and then encrypting the scrambled image using Markov map and SVD. The combination of Markov map and SVD changed the pixels values significantly in order to confuse the relationship among the pixels. Finally, a reliable decryption scheme is proposed to construct original image from encrypted image. Experimental results demonstrate the efficiency and robustness of the proposed scheme.
What's unique about this paper?
Discrete fractional wavelet transform and its application to multiple encryption
01 Feb 2013-Information Sciences
TL;DR: A novel encryption scheme is proposed for securing multiple images during communication and transmission over insecure channel by discretizing continuous fractional wavelet transform and chaotic maps.
Abstract: The fractional wavelet transform is a useful mathematical transformation that generalizes the most prominent tool in signal and image processing namely wavelet transform by rotation of signals in the time-frequency plane. The definition of discrete fractional wavelet transform is not reported yet in the literature. Therefore, a definition of the discrete fractional wavelet transform is consolidated by discretizing continuous fractional wavelet transform in the proposed work. Possible applications of the transform are in transient signal processing, image analysis, image transmission, biometrics, image compression etc. In this paper, image transmission is chosen as the primary application and hence a novel encryption scheme is proposed for securing multiple images during communication and transmission over insecure channel. The proposed multiple image encryption scheme is consolidated by fractional wavelet transform and chaotic maps. First, all the images are encrypted followed by their sharing. The sharing process is done considering numerical techniques by making the sharing process a system of linear equations. Experimental results and security analysis demonstrate the efficiency and robustness of the proposed primary application.
ECG Data Encryption Then Compression Using Singular Value Decomposition
Ting Yu Liu1, Kuan Jen Lin1, Hsi Chun Wu1• Institutions (1)
Fu Jen Catholic University1
01 May 2018-IEEE Journal of Biomedical and Health Informatics
TL;DR: Experimental results prove the first ETC approach for processing ECG data using the singular value decomposition technique to be an effective technique for assuring data security as well as compression performance forECG data.
Abstract: Electrocardiogram (ECG) monitoring systems are widely used in healthcare. ECG data must be compressed for transmission and storage. Furthermore, there is a need to be able to directly process biomedical signals in encrypted domains to ensure the protection of patients' privacy. Existing encryption-then-compression (ETC) approaches for multimedia using the state-of-the-art encryption techniques inevitably sacrifice the compression efficiency or signal quality. This paper presents the first ETC approach for processing ECG data. The proposed approach not only can protect data privacy but also provide the same quality of the reconstructed signals without sacrificing the compression efficiency relative to unencrypted compressions. Specifically, the singular value decomposition technique is used to compress the data such that the proposed system can provide quality-control compressed data, even though the data has been encrypted. Experimental results prove the proposed system to be an effective technique for assuring data security as well as compression performance for ECG data.
Cites methods from "A novel image encryption framework ..."
...In [30], the SVD is exploited to produce an orthogonal key matrix which is used to encrypt images....
A new image encryption based on chaotic systems and singular value decomposition
Ahmed A. Abd El-Latif1, Ahmed A. Abd El-Latif2, Li Li2, Ning Wang2, Qiong Li2, Xiamu Niu2 - Show less +2 more • Institutions (2)
Menoufia University1, Harbin Institute of Technology2
TL;DR: Simulation results justify the feasibility of the proposed scheme in image encryption purpose and show the ability to enforce security in chaotic systems and singular value decomposition.
Abstract: This paper presents an efficient image encryption scheme based on chaotic systems and singular value decomposition. In this scheme, the image pixel's positions are scrambled using chaotic systems with variable control parameters. To further enforce the security, the pixel gray values are modified using a combination between singular value decomposition (SVD) and chaotic polynomial map. Simulation results justify the feasibility of the proposed scheme in image encryption purpose.
...Scrambling is done by various methods based on toral automorphism ([3]), two or high-dimentional chaotic system with fixed control parameters [4] etc....
..., and the diffusion is done through the diffusion cipher like chaos based methods ([2-5]), DNA based methods ([6]), and other assorted methods [7, ....
...[3] Considered items Bhantnagar et al....
...3 Resistance to differential attack To test the influence of a one-pixel change in cipher image, two common measures [1-5] are used, i....
An efficient & secure encryption scheme for biometric data using holmes map & singular value decomposition
Garima Mehta1, Malay Kishore Dutta1, Pyung Soo Kim2• Institutions (2)
Guru Gobind Singh Indraprastha University1, Korea Polytechnic University2
TL;DR: Experimental results shows that the proposed algorithm is lossless in nature, robust against statistical attacks and has high key sensitivity, and low PSNR values indicate thatThe proposed algorithm provides a high level of perceptual security for the biometric data.
Abstract: In the recent past we have been facing security challenges towards the transmission of biometric data over unsecured data channels. A lot of techniques have been developed and implemented for the secure transmission of the data. Taking the security concept in mind we introduce an efficient method based on chaotic theory for secured data transmission. The core idea of the proposed method is to shuffle the adjacent pixel correlation using the combination of Arnold Cat Map, Holmes Map and Singular Value Decomposition (SVD). The pixel values are scrambled using the Arnold Cat Map and further Holmes Map and SVD are used to alter the pixel values to complicate the relationship. Finally, decryption method is proposed to reconstruct the original data from encrypted data. Performance of proposed algorithm has been experimentally analyzed using statistical attack analysis, key sensitivity analysis and Peak Signal to Noise Ratio (PSNR). Experimental results shows that the proposed algorithm is lossless in nature, robust against statistical attacks and has high key sensitivity. Further low PSNR values indicate that the proposed algorithm provides a high level of perceptual security for the biometric data.
Cites background from "A novel image encryption framework ..."
...Although lot of research has been done in field of chaotic theory [6, 7] but still there is need for more robustness and perceptual security to make encryption schemes more efficient and secured....
...Experimental results of the proposed algorithm indicates significant reduction of the correlation coefficient among adjacent pixels and significantly low PSNR values[6] makes it difficult to retrieve the original image from its encrypted one without the knowledge of correct decryption key....
A secure image encryption algorithm based on polar decomposition
Satendra Pal Singh1, Gaurav Bhatnagar1, Dharmendra Kumar Gurjar1• Institutions (1)
Indian Institute of Technology, Jodhpur1
TL;DR: A novel image encryption technique is proposed based on reference sets with some prime numbers and polar decomposition using a recursive random number generation process, and a reliable decryption process has been presented to reconstruct the original image.
Abstract: In this paper, a novel image encryption technique is proposed based on reference sets with some prime numbers and polar decomposition. In this technique, a primary secret key and reference sets are used in the generation of feature vector using a recursive random number generation (RRNG) process. This feature vector is then used for encryption process. Finally, a reliable decryption process has been presented to reconstruct the original image. The Simulated results demonstrate the efficiency and robustness of the proposed technique.
...In [7], the authors have proposed an encryption framework based on singular value decomposition (SVD)....
A universal image quality index
Zhou Wang, Alan C. Bovik1• Institutions (1)
University of Texas at Austin1
07 Aug 2002-IEEE Signal Processing Letters
TL;DR: Although the new index is mathematically defined and no human visual system model is explicitly employed, experiments on various image distortion types indicate that it performs significantly better than the widely used distortion metric mean squared error.
Abstract: We propose a new universal objective image quality index, which is easy to calculate and applicable to various image processing applications. Instead of using traditional error summation methods, the proposed index is designed by modeling any image distortion as a combination of three factors: loss of correlation, luminance distortion, and contrast distortion. Although the new index is mathematically defined and no human visual system model is explicitly employed, our experiments on various image distortion types indicate that it performs significantly better than the widely used distortion metric mean squared error. Demonstrative images and an efficient MATLAB implementation of the algorithm are available online at http://anchovy.ece.utexas.edu//spl sim/zwang/research/quality_index/demo.html.
"A novel image encryption framework ..." refers methods in this paper
...Peak signal to noise ration (PSNR), spectral distortion (SD), normalized singular value similarity (NSvS) [17] and Universal Image Quality Index (UIQ) [ 18 ] are used as the objective metrics to evaluate proposed technique....
Singular value decomposition and least squares solutions
Gene H. Golub1, C. Reinsch2• Institutions (2)
Stanford University1, Munich University of Applied Sciences2
01 Apr 1970-Numerische Mathematik
TL;DR: The decomposition of A is called the singular value decomposition (SVD) and the diagonal elements of ∑ are the non-negative square roots of the eigenvalues of A T A; they are called singular values.
Abstract: Let A be a real m×n matrix with m≧n. It is well known (cf. [4]) that $$A = U\sum {V^T}$$ (1) where $${U^T}U = {V^T}V = V{V^T} = {I_n}{\text{ and }}\sum {\text{ = diag(}}{\sigma _{\text{1}}}{\text{,}} \ldots {\text{,}}{\sigma _n}{\text{)}}{\text{.}}$$ The matrix U consists of n orthonormalized eigenvectors associated with the n largest eigenvalues of AA T , and the matrix V consists of the orthonormalized eigenvectors of A T A. The diagonal elements of ∑ are the non-negative square roots of the eigenvalues of A T A; they are called singular values. We shall assume that $${\sigma _1} \geqq {\sigma _2} \geqq \cdots \geqq {\sigma _n} \geqq 0.$$ Thus if rank(A)=r, σ r+1 = σ r+2=⋯=σ n = 0. The decomposition (1) is called the singular value decomposition (SVD).
"A novel image encryption framework ..." refers background in this paper
...In linear algebra, the singular value decomposition(SVD) [ 14 ] is an important factorization of a rectangular real or complex matrix with many applications in signal/image processing and statistics....
Book•DOI•
Numerische Mathematik 1
Josef Stoer
Chaos-based image encryption algorithm ✩
Zhi-Hong Guan1, Fangjun Huang1, Wenjie Guan2• Institutions (2)
Huazhong University of Science and Technology1, University of Waterloo2
10 Oct 2005-Physics Letters A
TL;DR: In this Letter, a new image encryption scheme is presented, in which shuffling the positions and changing the grey values of image pixels are combined to confuse the relationship between the cipher-image and the plain-image.
Abstract: In this Letter, a new image encryption scheme is presented, in which shuffling the positions and changing the grey values of image pixels are combined to confuse the relationship between the cipher-image and the plain-image. Firstly, the Arnold cat map is used to shuffle the positions of the image pixels in the spatial-domain. Then the discrete output signal of the Chen's chaotic system is preprocessed to be suitable for the grayscale image encryption, and the shuffled image is encrypted by the preprocessed signal pixel by pixel. The experimental results demonstrate that the key space is large enough to resist the brute-force attack and the distribution of grey values of the encrypted image has a random-like behavior.
A new image encryption algorithm based on hyper-chaos
Tiegang Gao1, Zengqiang Chen1• Institutions (1)
Nankai University1
21 Jan 2008-Physics Letters A
TL;DR: The experimental results demonstrate that the suggested encryption algorithm of image has the advantages of large key space and high security, and moreover, the distribution of grey values of the encrypted y image has a random-like behavior.
Abstract: This Letter presents a new image encryption scheme, which employs an image total shuffling matrix to shuffle the positions of image pixels and then uses a hyper-chaotic system to confuse the relationship between the plain-image and the cipher-image. The experimental results demonstrate that the suggested encryption algorithm of image has the advantages of large key space and high security, and moreover, the distribution of grey values of the encrypted y image has a random-like behavior.
Selective image encryption based on pixels of interest and singular value decomposition
01 Jul 2012-Digital Signal Processing
Gaurav Bhatnagar, Q. M. Jonathan Wu
Ahmed A. Abd El-Latif, Ahmed A. Abd El-Latif, Li Li, Ning Wang, Qiong Li, Xiamu Niu - Show less +3 more
Garima Mehta, Malay Kishore Dutta, Pyung Soo Kim
SVD-based image compression, encryption, and identity authentication algorithm on cloud
01 Oct 2019-Iet Image Processing
Changzhi Yu, Hengjian Li, Wang Xiyu
A novel image encryption scheme based on 3D bit matrix and chaotic map with Markov properties
01 Mar 2019-Egyptian Informatics Journal
Meng Ge, Ruisong Ye | CommonCrawl |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.