bigcode/jupyter-parsed · Datasets at Hugging Face

d0e5097964502d053a63dd51603eb8bf26107b3f

117,500

ipynb

Jupyter Notebook

Reset Put Option.ipynb

briangodwinlim/Financial-Math

f8425cb1f873a35b0c9abb02cb87fdc713c1b891

[ "MIT" ]

null

Reset Put Option.ipynb

briangodwinlim/Financial-Math

f8425cb1f873a35b0c9abb02cb87fdc713c1b891

[ "MIT" ]

null

Reset Put Option.ipynb

briangodwinlim/Financial-Math

f8425cb1f873a35b0c9abb02cb87fdc713c1b891

[ "MIT" ]

1

2021-11-12T04:40:45.000Z

24.271845

540

0.348996

[ [ [ "# Reset Put Option\n\nA reset put option is similar to a standard put option except that the exercise price is reset equal to the stock price on the pre-specified reset date if this stock price exceeds the original exercise price. Unlike the standard put option, a Reset put option has a stochastic strike price. On issue date, the reset put option has a strike price equal to the stock price. However, if the stock price exceeds the original strike price on a pre-specified future reset date, then the strike price is reset to the current strike price.\n\nThis notebook proposes three approaches to pricing the exotic option: the binomial tree approach, Monte Carlo simulation approach, and the closed form solution. The presentation accompanying this notebook can be found in my [website](https://www.brianlim.xyz/files/Reset%20Put%20Option.pdf).\n\nTo read more about Reset Put Option, you can refer to the paper by [Gray and Whaley (1999)](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.8221&rep=rep1&type=pdf).", "_____no_output_____" ], [ "## Load Libraries\n\nFirst, we import the necessary libraries", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\nfrom scipy.stats import multivariate_normal as mvn\nfrom scipy.stats import norm\nimport plotly.express as px\nimport plotly.io as pio\npio.templates.default = \"plotly_white\"", "_____no_output_____" ] ], [ [ "## Binomial Tree\n\nFor the binomial tree implementation, instead of doing the naive approach of doing path dependent options, we can optimize our calculations since we are only concerned with the value at $T_1$. The formula used is from [Shparber and Resheff (2004)](https://www.researchgate.net/publication/240390357_Valuation_of_Cliquet_Options).\n\n$$p_0 = e^{-rT_2} \\sum_{j=0}^{n_1}\\sum_{i=j}^{n_2-n_1+j} \\frac{n_1! (n_2 - n_1)!}{j! (n_1 - j)! (i - j)! (n_2 - n_1 - i + j)!} p^i (1-p)^{n_2-i} \\max(S_0 - S_0 u^{i}d^{n_2-i}, S_0 u^{j}d^{n_1-j} - S_0 u^i d^{n_2-i}, 0)$$\n\nTo further optimize the performance of this implementation, we can use the recursive form of the combination function and apply dynamic programming.\n\n$${n \\choose r} = {{n-1} \\choose {r}} + {{n-1} \\choose {r-1}}$$", "_____no_output_____" ] ], [ [ "memo = [[-1 for _ in range(1000)] for _ in range(1000)]\n\ndef choose(n,r):\n if r > n or r < 0:\n return 0\n elif n == 1:\n return 1\n elif memo[n][r] == -1:\n memo[n][r] = choose(n-1, r-1) + choose(n-1, r)\n return memo[n][r]\n \ndef BT_option_price(S0, T2, n1, n2, r, q, sigma):\n dt = T2 / n2\n u = np.exp( sigma * np.sqrt(dt))\n d = np.exp(- sigma * np.sqrt(dt))\n pu = (np.exp( (r - q) * dt) - d) / (u - d)\n pd = (u - np.exp( (r - q) * dt)) / (u - d)\n\n ans = 0\n for j in range(n1+1):\n for i in range(j, n2 - n1 + j + 1):\n ans += (\n choose(n1, j) * choose (n2 - n1, i - j) * pow(pu, i) * pow(pd, n2 - i) *\n max(\n S0 - S0 * pow(u, i) * pow(d, n2 - i),\n S0 * pow(u, j) * pow(d, n1 - j) - S0 * pow(u, i) * pow(d, n2 - i),\n 0\n )\n )\n \n return np.exp(-r * T2) * ans", "_____no_output_____" ], [ "print(\"Binomial Tree: \", BT_option_price(\n S0 = 100, \n T2 = 1, \n n1 = 500, \n n2 = 1000, \n r = 0.1, \n q = 0.05, \n sigma = 0.3)\n)", "Binomial Tree: 11.50392391907085\n" ] ], [ [ "## Monte Carlo Simulation\n\nFor the Monte Carlo Simulation, we will use the discretized GBM to determine trajectories of the stock price. The discretized GBM is given as\n$$S_{t + \\Delta t} = S_t \\left[1 + (r - q) \\Delta t + \\sigma \\sqrt{\\Delta t} Z\\right],$$\nwhere $Z \\sim N(0,1)$. After simulating each trajectory, we get the present value of the mean of the payoffs.", "_____no_output_____" ] ], [ [ "def generate_trajectory(S0, T2, n2, r, q, sigma):\n dt = T2 / n2\n trajectory = [S0]\n for _ in range (n2):\n trajectory.append(\n trajectory[-1] * (1 + ( r - q ) * dt + sigma * np.sqrt(dt) * np.random.randn())\n )\n return trajectory\n\ndef MC_option_price(S0, T2, n1, n2, r, q, sigma):\n res = []\n for _ in range(100000):\n tmp = generate_trajectory(S0, T2, n2, r, q, sigma)\n res.append( max(max(S0, tmp[n1]) - tmp[-1] ,0) )\n return np.exp(- r * T2) * np.mean(res)", "_____no_output_____" ], [ "print(\"Monte Carlo: \", MC_option_price(\n S0 = 100, \n T2 = 1, \n n1 = 50, \n n2 = 100, \n r = 0.1,\n q = 0.05,\n sigma = 0.3)\n)", "Monte Carlo: 11.524762360429376\n" ] ], [ [ "## Closed Form\n\nAccording to [Gray and Whaley (1999)](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.8221&rep=rep1&type=pdf), the closed form of the reset put option price is \n\\begin{align*}\n p_0 &= S_0 e^{-qT_1 -r(T_2-T_1)} N(a_1) N(-c_2) - S_0 e^{-qT_2} N(a_1) N(-c_1) \\\\\n & \\qquad + S_0 e^{-rT_2} N_2\\left(-b_2, -a_2, \\sqrt{\\frac{T_1}{T_2}}\\right) - S_0 e^{-qT_2} N_2\\left(-b_1, -a_1, \\sqrt{\\frac{T_1}{T_2}}\\right),\n\\end{align*}\n\nwhere \n\\begin{align*}\n& a_1 = \\dfrac{(r-q+\\frac{1}{2}\\sigma^2)T_1}{\\sigma\\sqrt{T_1}}, a_2 = a_1 - \\sigma\\sqrt{T_1},\\\\\n& b_1 = \\dfrac{(r-q+\\frac{1}{2}\\sigma^2)T_2}{\\sigma\\sqrt{T_2}}, b_2 = b_1 - \\sigma\\sqrt{T_2}, \\\\\n& c_1 = \\dfrac{(r-q+\\frac{1}{2}\\sigma^2)(T_2-T_1)}{\\sigma\\sqrt{T_2-T_1}}, c_2 = c_1 - \\sigma\\sqrt{T_2-T_1}.\n\\end{align*}", "_____no_output_____" ] ], [ [ "def closed_form_option_price(S0, T1, T2, r, q, sigma):\n a1 = ( (r - q + 0.5 * sigma**2) * T1 ) / (sigma * np.sqrt(T1))\n a2 = ( (r - q - 0.5 * sigma**2) * T1 ) / (sigma * np.sqrt(T1))\n b1 = ( (r - q + 0.5 * sigma**2) * T2 ) / (sigma * np.sqrt(T2))\n b2 = ( (r - q - 0.5 * sigma**2) * T2 ) / (sigma * np.sqrt(T2))\n c1 = ( (r - q + 0.5 * sigma**2) * (T2 - T1) ) / (sigma * np.sqrt(T2 - T1))\n c2 = ( (r - q - 0.5 * sigma**2) * (T2 - T1) ) / (sigma * np.sqrt(T2 - T1))\n \n rho = np.sqrt(T1 / T2)\n Sigma = np.array(\n [[1, rho],\n [rho, 1]]\n )\n\n return (\n S0 * np.exp(-q * T1 - r * (T2 - T1)) * norm.cdf(a1) * norm.cdf(-c2)\n - S0 * np.exp(-q * T2) * norm.cdf(a1) * norm.cdf(-c1)\n + S0 * np.exp(-r * T2) * mvn.cdf(np.array([-b2, -a2]), mean = np.zeros(2), cov = Sigma)\n - S0 * np.exp(-q * T2) * mvn.cdf(np.array([-b1, -a1]), mean = np.zeros(2), cov = Sigma)\n )", "_____no_output_____" ], [ "print(\"Closed Form: \", closed_form_option_price(\n S0 = 100, \n T1 = 0.5, \n T2 = 1, \n r = 0.1, \n q = 0.05,\n sigma = 0.3)\n)", "Closed Form: 11.509604706054052\n" ] ], [ [ "## Sensitivity Analysis\n\nNext, we can perform a sensitivity analysis on the exotic option and compare its valuation against a vanilla European put option.", "_____no_output_____" ] ], [ [ "def vanilla_price(S0, T, r, q, sigma):\n d1 = ( (r - q + 0.5 * sigma**2) * T ) / (sigma * np.sqrt(T))\n d2 = ( (r - q - 0.5 * sigma**2) * T ) / (sigma * np.sqrt(T))\n \n return (\n S0 * np.exp(-r * T) * norm.cdf(-d2)\n - S0 * np.exp(- q * T) * norm.cdf(-d1)\n )", "_____no_output_____" ] ], [ [ "### Reset Date\n\nFirst, we perform sensitivity analysis on the reset date.", "_____no_output_____" ] ], [ [ "df = []\nfor T1 in np.linspace(0.0001,0.9999,50):\n df.append([\n T1,\n closed_form_option_price(S0 = 100, T1 = T1, \n T2 = 1, r = 0.1, q = 0.05, sigma = 0.3),\n vanilla_price(S0 = 100, T = 1, r = 0.1, q = 0.05, sigma = 0.3)\n ])\ndf = pd.DataFrame(df, columns = [\"Reset Date\", \"Reset Put Option\", \"Put Option\"])\ndf = df.melt(id_vars = [\"Reset Date\"])\npx.line(df, x = \"Reset Date\", y = \"value\", color = \"variable\", \n labels = {\"value\" : \"Price\", \"variable\" : \"Type\"})", "_____no_output_____" ] ], [ [ "### Risk-Free Rate\n\nNext, we perform sensitivity analysis on the risk-free rate.", "_____no_output_____" ] ], [ [ "df = []\nfor r in np.linspace(0,0.2,50):\n df.append([\n r,\n closed_form_option_price(S0 = 100, T1 = 0.5, \n T2 = 1, r = r, q = 0.05, sigma = 0.3),\n vanilla_price(S0 = 100, T = 1, r = r, q = 0.05, sigma = 0.3)\n ])\ndf = pd.DataFrame(df, columns = [\"Risk-Free Rate\", \"Reset Put Option\", \"Put Option\"])\ndf = df.melt(id_vars = [\"Risk-Free Rate\"])\npx.line(df, x = \"Risk-Free Rate\", y = \"value\", color = \"variable\", \n labels = {\"value\" : \"Price\", \"variable\" : \"Type\"})", "_____no_output_____" ] ], [ [ "### Dividend Yield\n\nAfterwards, we perform sensitivity analysis on the dividend yield.", "_____no_output_____" ] ], [ [ "df = []\nfor q in np.linspace(0,0.1,50):\n df.append([\n q,\n closed_form_option_price(S0 = 100, T1 = 0.5, \n T2 = 1, r = 0.1, q = q, sigma = 0.3),\n vanilla_price(S0 = 100, T = 1, r = 0.1, q = q, sigma = 0.3)\n ])\ndf = pd.DataFrame(df, columns = [\"Dividend Yield\", \"Reset Put Option\", \"Put Option\"])\ndf = df.melt(id_vars = [\"Dividend Yield\"])\npx.line(df, x = \"Dividend Yield\", y = \"value\", color = \"variable\", \n labels = {\"value\" : \"Price\", \"variable\" : \"Type\"})", "_____no_output_____" ] ], [ [ "### Volatility\n\nFinally, we perform sensitivity analysis on the volatility.", "_____no_output_____" ] ], [ [ "df = []\nfor sigma in np.linspace(0.0001,0.5,50):\n df.append([\n sigma,\n closed_form_option_price(S0 = 100, T1 = 0.5, \n T2 = 1, r = 0.1, q = 0.05, sigma = sigma),\n vanilla_price(S0 = 100, T = 1, r = 0.1, q = 0.05, sigma = sigma)\n ])\ndf = pd.DataFrame(df, columns = [\"Volatility\", \"Reset Put Option\", \"Put Option\"])\ndf = df.melt(id_vars = [\"Volatility\"])\npx.line(df, x = \"Volatility\", y = \"value\", color = \"variable\", \n labels = {\"value\" : \"Price\", \"variable\" : \"Type\"})", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e51817791d9272569fa53347ddb46aefbf872d

4,015

ipynb

Jupyter Notebook

files/transcripts/txtTOjson.ipynb

fastai/ethics.fast.ai

f00d48fe0bbeeead089ba788fab771ce5bbfb446

[ "Apache-2.0" ]

44

2020-03-06T00:27:03.000Z

2022-02-26T21:06:03.000Z

files/transcripts/txtTOjson.ipynb

fastai/ethics.fast.ai

f00d48fe0bbeeead089ba788fab771ce5bbfb446

[ "Apache-2.0" ]

4

2021-05-04T21:37:04.000Z

2021-09-28T01:05:06.000Z

files/transcripts/txtTOjson.ipynb

fastai/ethics.fast.ai

f00d48fe0bbeeead089ba788fab771ce5bbfb446

[ "Apache-2.0" ]

5

2020-08-30T04:57:11.000Z

2021-06-18T06:57:11.000Z

21.356383

90

0.463263

[ [ [ "from datetime import datetime\nimport pathlib\nimport json", "_____no_output_____" ], [ "list((pathlib.Path()/'srv1').iterdir())", "_____no_output_____" ], [ "txtfiles = list((pathlib.Path()/'textfiles').iterdir())", "_____no_output_____" ], [ "txtfiles", "_____no_output_____" ], [ "def make_json(txtfile):\n my_dict = {}\n with txtfile.open() as f:\n cnt = 0\n for line in f:\n if (cnt%3)==0:\n a = line\n a[0].split(',.')\n b = a.split(',')[0]\n dt = datetime.strptime(b.split('.')[0], '%H:%M:%S')\n tm = f'{dt.hour*60 + dt.minute:02d}' + \":\" + f'{dt.second:02d}'\n if (cnt%3)==1:\n txt = line.strip()\n if (cnt%3)==2:\n my_dict[tm] = txt\n cnt += 1\n json.dump(my_dict, txtfile.with_suffix('.json').open('w'), indent=2)", "_____no_output_____" ], [ "for txtfile in txtfiles:\n make_json(txtfile)", "_____no_output_____" ], [ "json.dump()", "_____no_output_____" ], [ "a = '0:00:00.000,0:00:04.440\\n'", "_____no_output_____" ], [ "a[0].split(',.')\nb = a.split(',')[0]\ndt = datetime.strptime(b.split('.')[0], '%H:%M:%S')\nf'{dt.hour + dt.minute:02d}' + \":\" + f'{dt.second:02d}'", "_____no_output_____" ], [ "dt.minute", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e523e2dcf0f5468c11ddc91f6eb4cb8b9df90e

831,937

ipynb

Jupyter Notebook

01 Simulated Annealing/02 200 bar Truss/01 Notebooks/SA-02-02 200 bar Truss Case 3 in groupings.ipynb

mjamezquidilla/Optimization-Practices

9baf65b7da1ab217de473aa4cd07a409b59e0c58

[ "MIT" ]

1

2021-03-14T21:47:38.000Z

01 Simulated Annealing/02 200 bar Truss/01 Notebooks/SA-02-02 200 bar Truss Case 3 in groupings.ipynb

mjamezquidilla/Optimization-Practices

9baf65b7da1ab217de473aa4cd07a409b59e0c58

[ "MIT" ]

null

01 Simulated Annealing/02 200 bar Truss/01 Notebooks/SA-02-02 200 bar Truss Case 3 in groupings.ipynb

mjamezquidilla/Optimization-Practices

9baf65b7da1ab217de473aa4cd07a409b59e0c58

[ "MIT" ]

null

1,480.314947

445,335

0.805366

[ [ [ "from pysead import Truss_2D\nimport numpy as np\nfrom random import random\nimport matplotlib.pyplot as plt ", "_____no_output_____" ], [ "# initialize node dictionary\nnodes = {}\n\n# compute distances\ndistances_1 = np.arange(0,5*240,240)\ndistances_2 = np.arange(0,9*120,120)\n\n# from node 1 to node 5\nfor i, distance in enumerate(distances_1):\n nodes.update({i+1: [distance, 360+144*10]})\n\n# from node 6 to node 14\nfor i, distance in enumerate(distances_2):\n nodes.update({i+6: [distance, 360+144*9]})\n\n# from node 15 to node 19\nfor i, distance in enumerate(distances_1):\n nodes.update({i+15: [distance, 360+144*8]})\n\n# from node 20 to node 28\nfor i, distance in enumerate(distances_2):\n nodes.update({i+20: [distance, 360+144*7]})\n\n# from node 29 to node 33\nfor i, distance in enumerate(distances_1):\n nodes.update({i+29: [distance, 360+144*6]})\n\n# from node 34 to node 42\nfor i, distance in enumerate(distances_2):\n nodes.update({i+34: [distance, 360+144*5]})\n\n# from node 43 to node 47\nfor i, distance in enumerate(distances_1):\n nodes.update({i+43: [distance, 360+144*4]})\n\n# from node 48 to node 56\nfor i, distance in enumerate(distances_2):\n nodes.update({i+48: [distance, 360+144*3]}) \n\n# from node 57 to node 61\nfor i, distance in enumerate(distances_1):\n nodes.update({i+57: [distance, 360+144*2]})\n\n# from node 62 to node 70\nfor i, distance in enumerate(distances_2):\n nodes.update({i+62: [distance, 360+144*1]})\n\n# from node 71 to node 75\nfor i, distance in enumerate(distances_1):\n nodes.update({i+71: [distance, 360]})\n\nnodes.update({76:[240,0], 77:[120*6,0]})", "_____no_output_____" ], [ "elements = {1:[1,2], 2:[2,3], 3:[3,4], 4:[4,5],\n 5:[6,1], 6:[7,1], 7:[7,2], 8:[8,2], 9:[9,2], 10:[9,3], 11:[10,3], 12:[11,3], 13:[11,4], 14:[12,4], 15:[13,4], 16:[13,5], 17:[14,5],\n 18:[6,7], 19:[7,8], 20:[8,9], 21:[9,10], 22:[10,11], 23:[11,12], 24:[12,13], 25:[13,14],\n 26:[15,6], 27:[15,7], 28:[16,7], 29:[16,8], 30:[16,9], 31:[17,9], 32:[17,10], 33:[17,11], 34:[18,11], 35:[18,12], 36:[18,13], 37:[19,13], 38:[19,14],\n 39:[15,16], 40:[16,17], 41:[17,18], 42:[18,19],\n 43:[20,15], 44:[21,15], 45:[21,16], 46:[22,16], 47:[23,16], 48:[23,17], 49:[24,17], 50:[25,17], 51:[25,18], 52:[26,18], 53:[27,18], 54:[27,19], 55:[28,19],\n 56:[20,21], 57:[21,22], 58:[22,23], 59:[23,24], 60:[24,25], 61:[25,26], 62:[26,27], 63:[27,28],\n 64:[29,20], 65:[29,21], 66:[30,21], 67:[30,22], 68:[30,23], 69:[31,23], 70:[31,24], 71:[31,25], 72:[32,25], 73:[32,26], 74:[32,27], 75:[33,27], 76:[33,28],\n 77:[29,30], 78:[30,31], 79:[31,32], 80:[32,33],\n 81:[34,29], 82:[35,29], 83:[35,30], 84:[36,30], 85:[37,30], 86:[37,31], 87:[38,31], 88:[39,31], 89:[39,32], 90:[40,32], 91:[41,32], 92:[41,33], 93:[42,33],\n 94:[34,35], 95:[35,36], 96:[36,37], 97:[37,38], 98:[38,39], 99:[39,40], 100:[40,41], 101:[41,42],\n 102:[43,34], 103:[43,35], 104:[44,35], 105:[44,36], 106:[44,37], 107:[45,37], 108:[45,38], 109:[45,39], 110:[46,39], 111:[46,40], 112:[46,41], 113:[47,41], 114:[47,42],\n 115:[43,44], 116:[44,45], 117:[45,46], 118:[46,47], 119:[48,43], 120:[49,43], 121:[49,44], 122:[50,44], 123:[51,44], 124:[51,45], 125:[52,45], 126:[53,45], 127:[53,46], 128:[54,46], 129:[55,46], 130:[55,47], 131:[56,47],\n 132:[48,49], 133:[49,50], 134:[50,51], 135:[51,52], 136:[52,53], 137:[53,54], 138:[54,55], 139:[55,56], 140:[57,48], 141:[57,49], 142:[58,49], 143:[58,50], 144:[58,51], 145:[59,51], 146:[59,52], 147:[59,53], 148:[60,53], 149:[60,54], 150:[60,55], 151:[61,55], 152:[61,56],\n 153:[57,58], 154:[58,59], 155:[59,60], 156:[60,61],\n 157:[62,57], 158:[63,57], 159:[63,58], 160:[64,58], 161:[65,58], 162:[65,59], 163:[66,59], 164:[67,59], 165:[67,60], 166:[68,60], 167:[69,60], 168:[69,61], 169:[70,61],\n 170:[62,63], 171:[63,64], 172:[64,65], 173:[65,66], 174:[66,67], 175:[67,68], 176:[68,69], 177:[69,70],\n 178:[71,62], 179:[71,63], 180:[72,63], 181:[72,64], 182:[72,65], 183:[73,65], 184:[73,66], 185:[73,67], 186:[74,67], 187:[74,68], 188:[74,69], 189:[75,69], 190:[75,70],\n 191:[71,72], 192:[72,73], 193:[73,74], 194:[74,75],\n 195:[76,71], 196:[76,72], 197:[76,73], 198:[77,73], 199:[77,74], 200:[77,75]}", "_____no_output_____" ], [ "supports = {76:[1,1], 77:[1,1]}\nelasticity = {key: 30_000 for key in elements}", "_____no_output_____" ], [ "forces = {key: [0,-10] for key in [1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 15, 16, 17, 18, 19, 20, 22, 24, 26, 28, 29, 30, 31, 32, 33, 34, 36, 38, 40, 42, 43, 44, 45, 46, 47, 48, 50, 52, 54, 56, 57, 58, 59, 60, 61, 62, 64, 66, 68, 70, 71,72, 73, 74,75]}\nforces.update({key: [1,-10] for key in [1,6,15,20,29,34,43,48,57,62,71]})", "_____no_output_____" ], [ "def Truss_solver(cross_sectional_areas):\n cross_area = {key: cross_sectional_areas[key - 1] for key in elements}\n\n Two_Hundred_Truss_Case_1 = Truss_2D(nodes = nodes,\n elements= elements,\n supports= supports,\n forces = forces,\n elasticity= elasticity,\n cross_area= cross_area)\n\n Two_Hundred_Truss_Case_1.Solve()\n\n return (Two_Hundred_Truss_Case_1.member_lengths_, Two_Hundred_Truss_Case_1.member_stresses_, Two_Hundred_Truss_Case_1.displacements_)\n", "_____no_output_____" ] ], [ [ "## Step 2: Define Objective Function", "_____no_output_____" ] ], [ [ "def Objective_Function(areas):\n \n member_lengths, member_stresses, node_displacements = Truss_solver(areas) \n total_area = np.array(areas)\n total_member_lengths = []\n \n for length in member_lengths:\n total_member_lengths.append(member_lengths[length])\n\n total_member_lengths = np.array(total_member_lengths)\n\n weight = total_area.dot(np.array(total_member_lengths))\n\n weight = weight.sum() * 0.283 # lb/in^3\n\n return (weight, member_stresses, node_displacements)", "_____no_output_____" ] ], [ [ "## Step 3: Define Constraints", "_____no_output_____" ] ], [ [ "def stress_constraint(stress_new):\n if stress_new > 30 or stress_new < -30:\n stress_counter = 1\n else:\n stress_counter = 0\n \n return stress_counter", "_____no_output_____" ], [ "def displacement_constraint(node_displacement_new): \n x = node_displacement_new[0]\n y = node_displacement_new[1]\n if x > 0.5 or x < -0.5:\n displacement_counter = 1\n elif y > 0.5 or y < -0.5:\n displacement_counter = 1\n else:\n displacement_counter = 0\n\n return displacement_counter", "_____no_output_____" ] ], [ [ "Step 4: Define Algorithm", "_____no_output_____" ], [ "Step 4.1: Initialize Parameters", "_____no_output_____" ] ], [ [ "D = [0.100, 0.347, 0.440, 0.539, 0.954, 1.081, 1.174, 1.333, 1.488,\n1.764, 2.142, 2.697, 2.800, 3.131, 3.565, 3.813, 4.805, 5.952, 6.572,\n7.192, 8.525, 9.300, 10.850, 13.330, 14.290, 17.170, 19.180, 23.680,\n28.080, 33.700]", "_____no_output_____" ], [ "def closest(list_of_areas, area_values_list):\n for i, area_value in enumerate(area_values_list):\n idx = (np.abs(list_of_areas - area_value)).argmin() \n area_values_list[i] = list_of_areas[idx]\n return area_values_list", "_____no_output_____" ], [ "cross_area_groupings = {1:[1,4], 2:[2,3], 3:[5,17], 4:[6,16], 5:[7,15], 6:[8,14], 7:[9,13], 8:[10,12], 9:[11], 10:[132,139,170,177,18,25,56,63],\n 11:[19,20,23,24], 12:[21,22], 13:[26,38], 14:[27,37], 15:[28,36], 16:[29,35], 17:[30,34], 18:[31,33], 19:[32], 20:[39,42],\n 21:[40,41], 22:[43,55], 23:[44,54], 24:[45,53], 25:[46,52], 26:[47,51], 27:[48,50], 28:[49], 29:[57,58,61,62], 30:[59,60],\n 31:[64,76], 32:[65,75], 33:[66,74], 34:[67,73], 35:[68,72], 36:[69,71], 37:[70], 38:[77,80], 39:[78,79], 40:[81,93],\n 41:[82,92], 42:[83,91], 43:[84,90], 44:[85,89], 45:[86,88], 46:[87], 47:[95,96,99,100], 48:[97,98], 49:[102,114], 50:[103,113],\n 51:[104,112], 52:[105,111], 53:[106,110], 54:[107, 109], 55:[108], 56:[115,118], 57:[116,117], 58:[119,131], 59:[120,130], 60:[121,129],\n 61:[122,128], 62:[123,127], 63:[124,126], 64:[125], 65:[133,134,137,138], 66:[135,136], 67:[140,152], 68:[141,151], 69:[142,150], 70:[143,149],\n 71:[144,148], 72:[145,147], 73:[146], 74:[153,156], 75:[154,155], 76:[157,169], 77:[158,168], 78:[159,167], 79:[160,166], 80:[161,165],\n 81:[162,164], 82:[163], 83:[171,172,175,176], 84:[173,174], 85:[178,190], 86:[179,189], 87:[180,188], 88:[181,187], 89:[182,186], 90:[183,185],\n 91:[184], 92:[191,194], 93:[192,193], 94:[195,200], 95:[196,199], 96:[197,198], 97:[94,101]}", "_____no_output_____" ], [ "area_old = [35 for i in range(len(elements))]", "_____no_output_____" ], [ "# intermediate variables \nk = 0.05 # move variable's constant\nM = 1000 # number of loops to be performed\nT0 = 10000 # initial temperature\nN = 20 # initial number of neighbors per search space loop\nalpha = 0.85 # cooling parameter", "_____no_output_____" ], [ "temp = [] # storing of values for the temperature per loop M\nmin_weight = [] # storing best value of the objective function per loop M\narea_list = [] # storing x values per loop for plotting purposes", "_____no_output_____" ], [ "def Random_Number_Check(objective_old, objective_new, Init_temp):\n return 1/((np.exp(objective_old - objective_new)) / Init_temp)", "_____no_output_____" ], [ "%%time \nfor m in range(M):\n for n in range(N):\n # generate random area from choices\n # create random area array from area choices\n area_random_array = np.random.choice(D,len(cross_area_groupings))\n\n # create dictionary from random array\n cross_area_dict = {key+1: area_random_array[key] for key in range(len(area_random_array))}\n\n # create dictionary from cross area dictionary that follows the groupings dictionary\n cross_area = {}\n for group in cross_area_groupings:\n value = cross_area_dict[group]\n for element in cross_area_groupings[group]:\n dict_append = {element: value}\n cross_area.update(dict_append)\n # Sort the cross area groupings dictionary in asending order\n cross_area = {k: v for k, v in sorted(cross_area.items(), key=lambda item: item[0])}\n \n # flatten the cross area groupings dictionary to a list\n area_new = []\n for area in cross_area:\n area_new.append(cross_area[area])\n \n area_new = np.array(area_new)\n\n for i,area in enumerate(area_old):\n random_area = random()\n if random_area >= 0.5:\n area_new[i] = k*random_area\n else:\n area_new[i] = -k*random_area \n \n for i, area in enumerate(area_old):\n area_new[i] = area_old[i] + area_new[i]\n closest(D,area_new)\n\n weight_computed, stresses_new, node_displacement_new = Objective_Function(area_new)\n weight_old, _, _ = Objective_Function(area_old)\n\n check = Random_Number_Check(weight_computed, weight_old, T0)\n random_number = random()\n\n # Contraint 1: stresses should be within 25ksi and -25ksi\n stress_counter = []\n for j in stresses_new:\n stress_counter.append(stress_constraint(stresses_new[j]))\n stress_counter = sum(stress_counter)\n\n # Constraint 2: Node Displacement should be limited to -2in and 2in\n displacement_counter = 0\n for k in node_displacement_new:\n displacement_counter = displacement_counter + displacement_constraint(node_displacement_new[k])\n\n if stress_counter >= 1 or displacement_counter >= 1:\n area_old = area_old\n else: \n if weight_computed <= weight_old:\n area_old = area_new\n elif random_number <= check:\n area_old = area_new\n else:\n area_old = area_old\n\n temp.append(T0)\n min_weight.append(weight_old)\n area_list.append(area_old)\n \n T0 = alpha * T0", "Wall time: 18min 55s\n" ], [ "plt.figure(figsize=[12,6])\nplt.grid(True)\nplt.xlabel('Iterations')\nplt.ylabel('Weight')\nplt.title('Iterations VS Weight')\nplt.plot(min_weight)", "_____no_output_____" ], [ "area_list[-1]", "_____no_output_____" ], [ "cross_area = {key: area_list[-1][key-1] for key in elements}\n\nTwo_Hundred_Truss_Case_1 = Truss_2D(nodes = nodes,\n elements= elements,\n supports= supports,\n forces = forces,\n elasticity= elasticity,\n cross_area= cross_area)\n\nTwo_Hundred_Truss_Case_1.Solve()", "_____no_output_____" ], [ "Two_Hundred_Truss_Case_1.Draw_Truss_Displacements(figure_size=[15,25])", "_____no_output_____" ], [ "Two_Hundred_Truss_Case_1.displacements_", "_____no_output_____" ], [ "weight, _, _ = Objective_Function(area_list[-1])\nweight", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e525c0526bc1d8f764002b2a19da75f3e8d757

9,531

ipynb

Jupyter Notebook

notebooks/test_bfcnn.ipynb

NikolasMarkou/blind_image_denoising

9c2e0b70838156ba2f58c362e60898bc9c718759

[ "MIT" ]

9

2021-03-23T09:33:34.000Z

2022-01-29T09:33:34.000Z

notebooks/test_bfcnn.ipynb

NikolasMarkou/blind_image_denoising

9c2e0b70838156ba2f58c362e60898bc9c718759

[ "MIT" ]

null

notebooks/test_bfcnn.ipynb

NikolasMarkou/blind_image_denoising

9c2e0b70838156ba2f58c362e60898bc9c718759

[ "MIT" ]

null

30.257143

303

0.529116

[ [ [ "import os\nimport sys\nimport keras\nimport numpy as np\nimport tensorflow as tf\nfrom keras import datasets\nimport matplotlib\nimport matplotlib.pyplot as plt\n\nsys.path.append(os.getcwd() + \"/../\")\n\nfrom bfcnn import BFCNN, collage, get_conv2d_weights", "_____no_output_____" ], [ "# setup environment\nos.environ[\"TF_CPP_MIN_LOG_LEVEL\"] = \"3\"\ntf.compat.v1.disable_eager_execution()\ntf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)", "_____no_output_____" ], [ "# get dataset \n(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()\nx_train = x_train.astype(np.float32)\nx_train = np.expand_dims(x_train, axis=3)\nx_test = x_test.astype(np.float32)\nx_test = np.expand_dims(x_test, axis=3)", "_____no_output_____" ], [ "EPOCHS = 10\nFILTERS = 32\nNO_LAYERS = 5\nMIN_STD = 1.0\nMAX_STD = 100.0\nLR_DECAY = 0.9\nLR_INITIAL = 0.1\nBATCH_SIZE = 64\nCLIP_NORMAL = 1.0\nINPUT_SHAPE = (28, 28, 1)\nPRINT_EVERY_N_BATCHES = 2000", "_____no_output_____" ], [ "# build model\nmodel = \\\n BFCNN(\n input_dims=INPUT_SHAPE,\n no_layers=NO_LAYERS,\n filters=FILTERS,\n kernel_regularizer=keras.regularizers.l2(0.001))", "_____no_output_____" ], [ "# train dataset\ntrained_model, history = \\\n BFCNN.train(\n model=model, \n input_dims=INPUT_SHAPE,\n dataset=x_train,\n epochs=EPOCHS,\n batch_size=BATCH_SIZE,\n min_noise_std=MIN_STD,\n max_noise_std=MAX_STD,\n lr_initial=LR_INITIAL,\n lr_decay=LR_DECAY,\n print_every_n_batches=PRINT_EVERY_N_BATCHES)\n", "2021-04-02 17:02:03,771 INFO custom_callbacks.py:__init__:88] deleting existing training image in ./training/images\n2021-04-02 17:02:03,773 INFO model.py:train:326] begin training\n" ], [ "matplotlib.use(\"nbAgg\")\n\n# summarize history for loss\nplt.figure(figsize=(15,5))\nplt.plot(history.history[\"loss\"],\n marker=\"o\",\n color=\"red\", \n linewidth=3, \n markersize=6)\nplt.grid(True)\nplt.title(\"model loss\")\nplt.ylabel(\"loss\")\nplt.xlabel(\"epoch\")\nplt.legend([\"train\"], loc=\"upper right\")\nplt.show()", "_____no_output_____" ], [ "from math import log10\n\n# calculate mse for different std\nsample_test = x_test[0:1024,:,:,:]\nsample_test_mse = []\nsample_train = x_train[0:1024,:,:,:]\nsample_train_mse = []\nsample_std = []\n\nfor std_int in range(0, int(MAX_STD), 5):\n std = float(std_int)\n #\n noisy_sample_test = sample_test + np.random.normal(0.0, std, sample_test.shape)\n noisy_sample_test = np.clip(noisy_sample_test, 0.0, 255.0)\n results_test = trained_model.model.predict(noisy_sample_test)\n mse_test = np.mean(np.power(sample_test - results_test, 2.0))\n sample_test_mse.append(mse_test)\n #\n noisy_sample_train = sample_train + np.random.normal(0.0, std, sample_train.shape)\n noisy_sample_train = np.clip(noisy_sample_train, 0.0, 255.0)\n results_train = trained_model.model.predict(noisy_sample_train)\n mse_train = np.mean(np.power(sample_train - results_train, 2.0))\n sample_train_mse.append(mse_train)\n #\n sample_std.append(std)", "_____no_output_____" ], [ "matplotlib.use(\"nbAgg\")\n\n# summarize history for loss\nplt.figure(figsize=(16,8))\nplt.plot(sample_std,\n [20 * log10(255) -10 * log10(m) for m in sample_test_mse],\n color=\"red\",\n linewidth=2)\nplt.plot(sample_std,\n [20 * log10(255) -10 * log10(m) for m in sample_train_mse],\n color=\"green\", \n linewidth=2)\nplt.grid(True)\nplt.title(\"Peak Signal-to-Noise Ratio\")\nplt.ylabel(\"PSNR\")\nplt.xlabel(\"Additive normal noise standard deviation\")\nplt.legend([\"test\", \"train\"], loc=\"lower right\")\nplt.show()", "_____no_output_____" ], [ "# draw test samples, predictions and diff\nmatplotlib.use(\"nbAgg\")\n\nsample = x_test[0:64,:,:,:]\nnoisy_sample = sample + np.random.normal(0.0, MAX_STD, sample.shape)\nnoisy_sample = np.clip(noisy_sample, 0.0, 255.0)\nresults = trained_model.model.predict(noisy_sample)\n \nplt.figure(figsize=(14,14))\nplt.subplot(2, 2, 1)\nplt.imshow(collage(sample), cmap=\"gray_r\") \nplt.subplot(2, 2, 2)\nplt.imshow(collage(noisy_sample), cmap=\"gray_r\") \nplt.subplot(2, 2, 3)\nplt.imshow(collage(results), cmap=\"gray_r\") \nplt.subplot(2, 2, 4)\nplt.imshow(collage(np.abs(sample - results)), cmap=\"gray_r\") \nplt.show() ", "_____no_output_____" ], [ "trained_model.save(\"./model.h5\")", "_____no_output_____" ], [ "m = trained_model.model\n\nweights = get_conv2d_weights(m)\n\nmatplotlib.use(\"nbAgg\")\nplt.figure(figsize=(14,5))\nplt.grid(True)\nplt.hist(x=weights, bins=500, range=(-0.4,+0.4), histtype=\"bar\", log=True)\nplt.show()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e53b955ae720413915a014e0bfb817af7750c1

66,944

ipynb

Jupyter Notebook

docs/reports/report5_metadata.ipynb

ShNadi/OkCupid-project

5eca6571e5c2a65c9cc185fadd24b0724a3cbb1b

[ "MIT" ]

null

docs/reports/report5_metadata.ipynb

ShNadi/OkCupid-project

5eca6571e5c2a65c9cc185fadd24b0724a3cbb1b

[ "MIT" ]

null

docs/reports/report5_metadata.ipynb

ShNadi/OkCupid-project

5eca6571e5c2a65c9cc185fadd24b0724a3cbb1b

[ "MIT" ]

null

83.367372

14,096

0.779861

[ [ [ "### OkCupid DataSet: Classify using combination of text data and metadata\n### Meeting 5, 03- 03- 2020\n", "_____no_output_____" ], [ "### Recap last meeting's decisions:\n<ol>\n <p>Meeting 4, 28- 01- 2020</p>\n <li> Approach 1: </li>\n <ul>\n <li>Merge classs 1, 3 and 5</li>\n <li>Under sample class 6 </li>\n <li> Merge classes 6, 7, 8</li>\n </ul> \n <li> Approach 2:</li>\n <ul>\n <li>Merge classs 1, 3 and 5 as class 1</li> \n <li> Merge classes 6, 7, 8 as class 8</li>\n <li>Under sample class 8 </li>\n </ul> \n <li> collect metadata: </li>\n <ul>\n <li> Number of misspelled </li>\n <li> Number of unique words </li>\n <li> Avg no wordlength </li>\n </ul> \n \n \n\n</ol>", "_____no_output_____" ], [ "## Education level summary\n\n<ol>\n <p></p>\n <img src=\"rep2_image/count_diag.JPG\"> \n\n</ol>\n \n<ol>\n <p></p>\n <img src=\"rep2_image/count_table.JPG\"> \n\n</ol>\n\n## Logistic regression after removing minority classes and undersampling\n<ol>\n <p></p>\n <img src=\"rep2_image/log1.JPG\"> \n\n</ol>\n\n## Merge levels: \n- Merge classs 1, 3 and 5 as class 1\n- Merge classes 6, 7, 8 as class 8\n- weight classes while classifying using Logistic regression\n<ol>\n <p></p>\n <img src=\"rep2_image/count_table2.JPG\"> \n\n</ol>\n\n\n\n<ol>\n <p></p>\n ### Logistic regression with undersampling\n <img src=\"rep2_image/log_undersampling.JPG\"> \n\n</ol>\n\n<ol>\n <p></p>\n ### Logistic regression with weighting\n <img src=\"rep2_image/log_weight.JPG\"> \n\n</ol>\n\n\n", "_____no_output_____" ], [ "### Add metadata to the dataset", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport matplotlib.pyplot as plt\nfrom sklearn.feature_extraction.text import CountVectorizer\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.naive_bayes import MultinomialNB\nfrom sklearn.metrics import accuracy_score\nfrom sklearn.multiclass import OneVsRestClassifier\nfrom sklearn.metrics import confusion_matrix\nfrom sklearn.feature_extraction.text import TfidfVectorizer\nimport seaborn as sns\nfrom sklearn.metrics import classification_report\nfrom sklearn.preprocessing import StandardScaler\nfrom sklearn import preprocessing\nfrom sklearn.preprocessing import FunctionTransformer\nfrom sklearn.pipeline import Pipeline\nfrom sklearn.multiclass import OneVsRestClassifier\nfrom sklearn.linear_model import LogisticRegression\nfrom sklearn.pipeline import FeatureUnion\nfrom collections import Counter\nfrom sklearn.naive_bayes import MultinomialNB\nimport numpy as np\nimport itertools\nimport matplotlib.pyplot as plt\nimport matplotlib.cm as cm\nfrom sklearn.utils import resample\n", "_____no_output_____" ], [ "\ndef plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):\n \"\"\"\n This function prints and plots the confusion matrix.\n Normalization can be applied by setting `normalize=True`.\n \"\"\"\n if normalize:\n cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]\n print(\"Normalized confusion matrix\")\n else: \n print('Confusion matrix, without normalization')\n \n print(cm)\n\n plt.imshow(cm, interpolation='nearest', cmap=cmap)\n plt.title(title)\n plt.colorbar()\n tick_marks = np.arange(len(classes))\n plt.xticks(tick_marks, classes, rotation=45)\n plt.yticks(tick_marks, classes)\n \n fmt = '.2f' if normalize else 'd'\n thresh = cm.max() / 2.\n for i, j in itertools.product(range(cm.shape[0])\n , range(cm.shape[1])):\n plt.text(j, i, format(cm[i, j], fmt),\n horizontalalignment=\"center\",\n color=\"white\" if cm[i, j] > thresh else \"black\")\n plt.tight_layout()\n plt.ylabel('True label')\n plt.xlabel('Predicted label')\n ", "_____no_output_____" ], [ "df = pd.read_csv (r'../../../data/processed/stylo_cupid2.csv')\ndf.columns", "_____no_output_____" ], [ "# import readability\n# from tqdm._tqdm_notebook import tqdm_notebook\n# tqdm_notebook.pandas()\n\n# def text_readability(text):\n# results = readability.getmeasures(text, lang='en')\n# return results['readability grades']['FleschReadingEase']\n \n# df['readability'] = df.progress_apply(lambda x:text_readability(x['text']), axis=1)\n\n", "_____no_output_____" ], [ "df.head()", "_____no_output_____" ], [ "# Read metadata dataset to dataframe\n\n# df = pd.read_csv (r'../../../data/processed/stylo_cupid2.csv')\n\ndf['sex'].mask(df['sex'].isin(['m']) , 0.0, inplace=True)\ndf['sex'].mask(df['sex'].isin(['f']) , 1.0, inplace=True)\n# print(df['sex'].value_counts())\n\ndf['isced'].mask(df['isced'].isin([3.0, 5.0]) , 1.0, inplace=True)\ndf['isced'].mask(df['isced'].isin([6.0, 7.0]) , 8.0, inplace=True)\n\n# # Separate majority and minority classes\n# df_majority = df[df.isced==8.0]\n# df_minority = df[df.isced==1.0]\n \n# # Downsample majority class\n# df_majority_downsampled = resample(df_majority, \n# replace=False, # sample without replacement\n# n_samples=10985, # to match minority class\n# random_state=123) # reproducible results\n \n# # Combine minority class with downsampled majority class\n# df = pd.concat([df_majority_downsampled, df_minority])\n\n\n\nprint(sorted(Counter(df['isced']).items()))\ndf = df.dropna(subset=['clean_text', 'isced'])\n\ncorpus = df[['clean_text', 'count_char','count_word', '#anwps', 'count_punct', 'avg_wordlength', 'count_misspelled', 'word_uniqueness', 'age', 'sex']]\ntarget = df[\"isced\"]\n\n# vectorization\nX_train, X_val, y_train, y_val = train_test_split(corpus, target, train_size=0.75, stratify=target,\n test_size=0.25, random_state = 0)\n\n\nget_text_data = FunctionTransformer(lambda x: x['clean_text'], validate=False)\nget_numeric_data = FunctionTransformer(lambda x: x[['count_char','count_word', '#anwps', 'count_punct', 'avg_wordlength', 'count_misspelled', 'word_uniqueness', 'age', 'sex']], validate=False)\n\n", "[(1.0, 10985), (8.0, 38958)]\n" ], [ "# Solver = lbfgs\n# merge vectorized text data and scaled numeric data\nprocess_and_join_features = Pipeline([\n ('features', FeatureUnion([\n ('numeric_features', Pipeline([\n ('selector', get_numeric_data),\n ('scaler', preprocessing.StandardScaler())\n \n ])),\n ('text_features', Pipeline([\n ('selector', get_text_data),\n ('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))\n ]))\n ])),\n ('clf', LogisticRegression(random_state=0,max_iter=1000, solver='lbfgs', penalty='l2', class_weight='balanced'))\n])\n\n\n\n# merge vectorized text data and scaled numeric data\nprocess_and_join_features.fit(X_train, y_train)\npredictions = process_and_join_features.predict(X_val)\n\n\nprint(\"Final Accuracy for Logistic: %s\"% accuracy_score(y_val, predictions))\ncm = confusion_matrix(y_val,predictions)\nplt.figure()\nplot_confusion_matrix(cm, classes=[0,1], normalize=False,\n title='Confusion Matrix')\nprint(classification_report(y_val, predictions))", "Final Accuracy for Logistic: 0.83559009694736\nConfusion matrix, without normalization\n[[1558 1187]\n [ 865 8871]]\n precision recall f1-score support\n\n 1.0 0.64 0.57 0.60 2745\n 8.0 0.88 0.91 0.90 9736\n\n accuracy 0.84 12481\n macro avg 0.76 0.74 0.75 12481\nweighted avg 0.83 0.84 0.83 12481\n\n" ], [ "from sklearn.model_selection import cross_val_predict\nfrom sklearn.metrics import confusion_matrix\n\n\n# scores = cross_val_score(process_and_join_features, X_train, y_train, cv=5)\n# print(scores)\n# print(scores.mean())\n\nprocess_and_join_features.fit(X_train, y_train)\n\ny_pred = cross_val_predict(process_and_join_features, corpus, target, cv=5)\n", "_____no_output_____" ], [ "conf_mat = confusion_matrix(target, y_pred)\nprint(conf_mat)", "[[ 6266 4714]\n [ 3389 35555]]\n" ], [ "from sklearn.model_selection import cross_val_score, cross_val_predict\n\nscores = cross_val_score(process_and_join_features, corpus, target, cv=5)\nprint(scores)\nprint(scores.mean())", "[0.83755633 0.84076114 0.84036054 0.82934402 0.83974359]\n0.8375531245586328\n" ], [ "from sklearn.model_selection import cross_val_score, cross_val_predict\n\nscores = cross_val_score(process_and_join_features, corpus, target, cv=5)\nprint(scores)\nprint(scores.mean())", "[0.83735603 0.84046069 0.84196294 0.82824236 0.84044471]\n0.8376933489176072\n" ], [ "# Solver = sag\n# merge vectorized text data and scaled numeric data\nprocess_and_join_features = Pipeline([\n ('features', FeatureUnion([\n ('numeric_features', Pipeline([\n ('selector', get_numeric_data),\n ('scaler', preprocessing.StandardScaler())\n \n ])),\n ('text_features', Pipeline([\n ('selector', get_text_data),\n ('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))\n ]))\n ])),\n ('clf', LogisticRegression(random_state=0,max_iter=5000, solver='sag', penalty='l2', class_weight='balanced'))\n])\n\n# \nprocess_and_join_features.fit(X_train, y_train)\npredictions = process_and_join_features.predict(X_val)\n\n\nprint(\"Final Accuracy for Logistic: %s\"% accuracy_score(y_val, predictions))\ncm = confusion_matrix(y_val,predictions)\nplt.figure()\nplot_confusion_matrix(cm, classes=[0,1], normalize=False,\n title='Confusion Matrix')\nprint(classification_report(y_val, predictions))", "Final Accuracy for Logistic: 0.8376732633603077\nConfusion matrix, without normalization\n[[1593 1122]\n [ 904 8862]]\n precision recall f1-score support\n\n 1.0 0.64 0.59 0.61 2715\n 8.0 0.89 0.91 0.90 9766\n\n accuracy 0.84 12481\n macro avg 0.76 0.75 0.75 12481\nweighted avg 0.83 0.84 0.84 12481\n\n" ], [ "# Solver='saga'\n# merge vectorized text data and scaled numeric data\nprocess_and_join_features = Pipeline([\n ('features', FeatureUnion([\n ('numeric_features', Pipeline([\n ('selector', get_numeric_data),\n ('scaler', preprocessing.StandardScaler())\n \n ])),\n ('text_features', Pipeline([\n ('selector', get_text_data),\n ('vec', CountVectorizer(binary=False, ngram_range=(1, 2), lowercase=True))\n ]))\n ])),\n ('clf', LogisticRegression(n_jobs=-1, random_state=0,max_iter=3000, solver='saga', penalty='l2', class_weight='balanced'))\n])\n\n# \nprocess_and_join_features.fit(X_train, y_train)\npredictions = process_and_join_features.predict(X_val)\n\n\nprint(\"Final Accuracy for Logistic: %s\"% accuracy_score(y_val, predictions))\ncm = confusion_matrix(y_val,predictions)\nplt.figure()\nplot_confusion_matrix(cm, classes=[0,1], normalize=False,\n title='Confusion Matrix')\nprint(classification_report(y_val, predictions))", "Final Accuracy for Logistic: 0.8353497315920199\nConfusion matrix, without normalization\n[[1636 1079]\n [ 976 8790]]\n precision recall f1-score support\n\n 1.0 0.63 0.60 0.61 2715\n 8.0 0.89 0.90 0.90 9766\n\n accuracy 0.84 12481\n macro avg 0.76 0.75 0.75 12481\nweighted avg 0.83 0.84 0.83 12481\n\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e53cd60f87cd060cb7968999b623ac615b7f1e

5,222

ipynb

Jupyter Notebook

ipynb/Germany-Nordrhein-Westfalen-LK-Märkischer-Kreis.ipynb

oscovida/oscovida.github.io

c74d6da79feda1b5ccce107ad3acd48cf0e74c1c

[ "CC-BY-4.0" ]

2

2020-06-19T09:16:14.000Z

2021-01-24T17:47:56.000Z

ipynb/Germany-Nordrhein-Westfalen-LK-Märkischer-Kreis.ipynb

oscovida/oscovida.github.io

c74d6da79feda1b5ccce107ad3acd48cf0e74c1c

[ "CC-BY-4.0" ]

8

2020-04-20T16:49:49.000Z

2021-12-25T16:54:19.000Z

ipynb/Germany-Nordrhein-Westfalen-LK-Märkischer-Kreis.ipynb

oscovida/oscovida.github.io

c74d6da79feda1b5ccce107ad3acd48cf0e74c1c

[ "CC-BY-4.0" ]

4

2020-04-20T13:24:45.000Z

2021-01-29T11:12:12.000Z

31.269461

206

0.532555

[ [ [ "# Germany: LK Märkischer Kreis (Nordrhein-Westfalen)\n\n* Homepage of project: https://oscovida.github.io\n* Plots are explained at http://oscovida.github.io/plots.html\n* [Execute this Jupyter Notebook using myBinder](https://mybinder.org/v2/gh/oscovida/binder/master?filepath=ipynb/Germany-Nordrhein-Westfalen-LK-Märkischer-Kreis.ipynb)", "_____no_output_____" ] ], [ [ "import datetime\nimport time\n\nstart = datetime.datetime.now()\nprint(f\"Notebook executed on: {start.strftime('%d/%m/%Y %H:%M:%S%Z')} {time.tzname[time.daylight]}\")", "_____no_output_____" ], [ "%config InlineBackend.figure_formats = ['svg']\nfrom oscovida import *", "_____no_output_____" ], [ "overview(country=\"Germany\", subregion=\"LK Märkischer Kreis\", weeks=5);", "_____no_output_____" ], [ "overview(country=\"Germany\", subregion=\"LK Märkischer Kreis\");", "_____no_output_____" ], [ "compare_plot(country=\"Germany\", subregion=\"LK Märkischer Kreis\", dates=\"2020-03-15:\");\n", "_____no_output_____" ], [ "# load the data\ncases, deaths = germany_get_region(landkreis=\"LK Märkischer Kreis\")\n\n# get population of the region for future normalisation:\ninhabitants = population(country=\"Germany\", subregion=\"LK Märkischer Kreis\")\nprint(f'Population of country=\"Germany\", subregion=\"LK Märkischer Kreis\": {inhabitants} people')\n\n# compose into one table\ntable = compose_dataframe_summary(cases, deaths)\n\n# show tables with up to 1000 rows\npd.set_option(\"max_rows\", 1000)\n\n# display the table\ntable", "_____no_output_____" ] ], [ [ "# Explore the data in your web browser\n\n- If you want to execute this notebook, [click here to use myBinder](https://mybinder.org/v2/gh/oscovida/binder/master?filepath=ipynb/Germany-Nordrhein-Westfalen-LK-Märkischer-Kreis.ipynb)\n- and wait (~1 to 2 minutes)\n- Then press SHIFT+RETURN to advance code cell to code cell\n- See http://jupyter.org for more details on how to use Jupyter Notebook", "_____no_output_____" ], [ "# Acknowledgements:\n\n- Johns Hopkins University provides data for countries\n- Robert Koch Institute provides data for within Germany\n- Atlo Team for gathering and providing data from Hungary (https://atlo.team/koronamonitor/)\n- Open source and scientific computing community for the data tools\n- Github for hosting repository and html files\n- Project Jupyter for the Notebook and binder service\n- The H2020 project Photon and Neutron Open Science Cloud ([PaNOSC](https://www.panosc.eu/))\n\n--------------------", "_____no_output_____" ] ], [ [ "print(f\"Download of data from Johns Hopkins university: cases at {fetch_cases_last_execution()} and \"\n f\"deaths at {fetch_deaths_last_execution()}.\")", "_____no_output_____" ], [ "# to force a fresh download of data, run \"clear_cache()\"", "_____no_output_____" ], [ "print(f\"Notebook execution took: {datetime.datetime.now()-start}\")\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ] ]

d0e54817c264b9c1111505edbfc77d253ef069d6

296,210

ipynb

Jupyter Notebook

solutions/task_4_classification.ipynb

knutzk/handson-ml

3b80038e85e6ea0ac1dc1c4e068f563adca1d760

[ "Apache-2.0" ]

1

2020-05-01T11:20:53.000Z

solutions/task_4_classification.ipynb

knutzk/handson-ml

3b80038e85e6ea0ac1dc1c4e068f563adca1d760

[ "Apache-2.0" ]

null

solutions/task_4_classification.ipynb

knutzk/handson-ml

3b80038e85e6ea0ac1dc1c4e068f563adca1d760

[ "Apache-2.0" ]

null

201.093007

72,632

0.906651

[ [ [ "# Task 4: Classification\n\n_All credit for the code examples of this notebook goes to the book \"Hands-On Machine Learning with Scikit-Learn & TensorFlow\" by A. Geron. Modifications were made and text was added by K. Zoch in preparation for the hands-on sessions._", "_____no_output_____" ], [ "# Setup", "_____no_output_____" ], [ "First, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:", "_____no_output_____" ] ], [ [ "# Common imports\nimport numpy as np\nimport os\n\n# to make this notebook's output stable across runs\nnp.random.seed(42)\n\n# To plot pretty figures\n%matplotlib inline\nimport matplotlib as mpl\nimport matplotlib.pyplot as plt\nmpl.rc('axes', labelsize=14)\nmpl.rc('xtick', labelsize=12)\nmpl.rc('ytick', labelsize=12)\n\n# Function to save a figure. This also decides that all output files \n# should stored in the subdirectorz 'classification'.\nPROJECT_ROOT_DIR = \".\"\nEXERCISE = \"classification\"\n\ndef save_fig(fig_id, tight_layout=True):\n path = os.path.join(PROJECT_ROOT_DIR, \"output\", EXERCISE, fig_id + \".png\")\n print(\"Saving figure\", fig_id)\n if tight_layout:\n plt.tight_layout()\n plt.savefig(path, format='png', dpi=300)", "_____no_output_____" ] ], [ [ "# Preparing the dataset", "_____no_output_____" ], [ "Define a function to sort the dataset into the 'targets' train and test data. This is needed because we want to use the same 60,000 data points for training, and the sam e10,000 data points for testing on every machine (and the dataset provided through Scikit-Learn is already prepared in this way).", "_____no_output_____" ] ], [ [ "def sort_by_target(mnist):\n reorder_train = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[:60000])]))[:, 1]\n reorder_test = np.array(sorted([(target, i) for i, target in enumerate(mnist.target[60000:])]))[:, 1]\n mnist.data[:60000] = mnist.data[reorder_train]\n mnist.target[:60000] = mnist.target[reorder_train]\n mnist.data[60000:] = mnist.data[reorder_test + 60000]\n mnist.target[60000:] = mnist.target[reorder_test + 60000]", "_____no_output_____" ] ], [ [ "Now fetch the dataset using the SciKit-Learn function (this might take a moment ...).", "_____no_output_____" ] ], [ [ "# We need this try/except for different Scikit-Learn versions.\ntry:\n from sklearn.datasets import fetch_openml\n mnist = fetch_openml('mnist_784', version=1, cache=True)\n mnist.target = mnist.target.astype(np.int8) # fetch_openml() returns targets as strings\n sort_by_target(mnist) # fetch_openml() returns an unsorted dataset\nexcept ImportError:\n from sklearn.datasets import fetch_mldata\n mnist = fetch_mldata('MNIST original')\nmnist[\"data\"], mnist[\"target\"]", "_____no_output_____" ] ], [ [ "Let's have a look at what the 'data' key contains: it is a numpy array with one row per instance and one column per feature.", "_____no_output_____" ] ], [ [ "mnist[\"data\"]", "_____no_output_____" ] ], [ [ "And the same for the 'target' key which is an array of labels.", "_____no_output_____" ] ], [ [ "mnist[\"target\"]", "_____no_output_____" ] ], [ [ "Now, let's first define the more useful `x` and `y` aliases for the data and target keys, and let's have a look at the type of data using the `shape` function: we see 70,000 entries in the data array, with 784 features each. The 784 correspond to 28x28 pixels of an image with brightness values between 0 and 255. ", "_____no_output_____" ] ], [ [ "X, y = mnist[\"data\"], mnist[\"target\"]\nX.shape # get some information about its shape", "_____no_output_____" ], [ "28*28 # just a little cross-check we're doing the correct arithmetics here ...", "_____no_output_____" ], [ "X[36000][160:200] # Plot brightness values [160:200] of the random image X[36000].", "_____no_output_____" ] ], [ [ "Now let's have a look at one of the images. We just pick a random image and use the `numpy.reshape()` function to reshape it into an array of 28x28 pixels. Then we can plot it with `matplotlib.pyplot.imshow()`:", "_____no_output_____" ] ], [ [ "some_digit = X[36000]\nsome_digit_image = some_digit.reshape(28, 28)\nplt.imshow(some_digit_image, cmap = mpl.cm.binary,\n interpolation=\"nearest\")\nplt.axis(\"off\")\n\nsave_fig(\"some_digit_plot\")\nplt.show()", "Saving figure some_digit_plot\n" ] ], [ [ "Let's quickly define a function to plot one of the digits, we will need it later down the line. It might also be useful to have a function to plot multiple digits in a batch (we will also use this function later). The following two cells will not produce any output.", "_____no_output_____" ] ], [ [ "def plot_digit(data):\n image = data.reshape(28, 28)\n plt.imshow(image, cmap = mpl.cm.binary,\n interpolation=\"nearest\")\n plt.axis(\"off\")", "_____no_output_____" ], [ "def plot_digits(instances, images_per_row=10, **options):\n size = 28\n images_per_row = min(len(instances), images_per_row)\n images = [instance.reshape(size,size) for instance in instances]\n n_rows = (len(instances) - 1) // images_per_row + 1\n row_images = []\n n_empty = n_rows * images_per_row - len(instances)\n images.append(np.zeros((size, size * n_empty)))\n for row in range(n_rows):\n rimages = images[row * images_per_row : (row + 1) * images_per_row]\n row_images.append(np.concatenate(rimages, axis=1))\n image = np.concatenate(row_images, axis=0)\n plt.imshow(image, cmap = mpl.cm.binary, **options)\n plt.axis(\"off\")", "_____no_output_____" ] ], [ [ "Great, now we can plot multiple digits at once. Let's ignore the details of the `np.r_[]` function and the indexing used within it for now and focus on what it does: it takes ten examples of each digit from the data array, which we can then plot with our `plot_digits()` function.", "_____no_output_____" ] ], [ [ "plt.figure(figsize=(9,9))\nexample_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]\nplot_digits(example_images, images_per_row=10)\nsave_fig(\"more_digits_plot\")\nplt.show()", "Saving figure more_digits_plot\n" ] ], [ [ "Ok, at this point we have a fairly good idea how our data array looks like: we have an array of 70,000 images with 28x28 pixels each. The entries in the array are sorted according to ascending digits, i.e. it starts with images of zeros and ends with images of nines at entry 59,999. Entries `x[60000:]` onwards are meant to be used for testing and again contain images of all digits in ascending order.\n\nBefore starting with binary classification, let's quickly confirm that the labels stored in `y` actually make sense. We previously looked at entry `X[36000]` and it looked like a five. Does `y[36000]` say the same?", "_____no_output_____" ] ], [ [ "y[36000]", "_____no_output_____" ] ], [ [ "Good! As a very last step, let's split train and test and store them separately. Because we also don't want our training to be biased, we should shuffle the entries randomly (i.e. not sort them in ascending order anymore). We can do this with the `np.random.permutation(60000)` function which returns a random permutation of the numbers between zero and 60,000.", "_____no_output_____" ] ], [ [ "X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]", "_____no_output_____" ], [ "import numpy as np\n\nshuffle_index = np.random.permutation(60000)\nX_train, y_train = X_train[shuffle_index], y_train[shuffle_index]", "_____no_output_____" ] ], [ [ "# Binary classifier", "_____no_output_____" ], [ "Before going towards a classifier, which can distinguish _all_ digits, let's start with something simple. Since our random digit `X[36000]` was a five, why not design a classifier that can distinguish fives from other digits? Let's first rewrite our labels from integers to booleans:", "_____no_output_____" ] ], [ [ "y_train_5 = (y_train == 5) # an array of booleans which is 'True' whenever y_train is == 5\ny_test_5 = (y_test == 5)\ny_train_5 # let's look at the array", "_____no_output_____" ] ], [ [ "A good model for the classification is the Stochastic Gradient Descent that was introduced in the lecture. Conveniently, Skiki-Learn already has such a classifier implemented, so let's import it and give it our training data `X_train` with the true labels `y_train_5`.", "_____no_output_____" ] ], [ [ "from sklearn.linear_model import SGDClassifier\n\n# SDG relies on randomness, but by fixing the `random_state` we can get reproducible results.\n# The other values are just to avoid a warning issued by Skikit-Learn ...\nsgd_clf = SGDClassifier(random_state=42, max_iter=5, tol=-np.infty)\nsgd_clf.fit(X_train, y_train_5)", "_____no_output_____" ] ], [ [ "If the training of the classifier was successful, it should be able to predict the label of our example instance `X[36000]` correctly.", "_____no_output_____" ] ], [ [ "sgd_clf.predict([some_digit])", "_____no_output_____" ] ], [ [ "That's good, but it doesn't really give us an idea about the overall performance of the classifier. One good measure for this introduced in the lecture is the cross-validation score. In k-fold cross-validation, the training data is split into k equal subsets. Then the classifier is trained on k-1 sets and evaluated on set k. It's called cross-validation, because this is done for all k possible (and non-redundant) permutations. In case of a 3-fold, this means we train on subsets 1 and 2 and validated on 3, train on 1 and 3 and validate on 2, and train on 2 and 3 and validate on 1. The _score_ represents the prediction accuracy on the validation fold.", "_____no_output_____" ] ], [ [ "from sklearn.model_selection import cross_val_score\ncross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring=\"accuracy\")", "_____no_output_____" ] ], [ [ "While these numbers seem amazingly good, keep in mind, that only 10% of our training data are images of fives, so even a classifier which always predicts 'not five' would reach an accuracy of about 90% ...\n\nIn the following box, maybe you can try to implement the cross validation yourself! The `StratifiedKFold` creates k non-biased subsets of the training data. The input to the `StratifiedKFold.split(X, y)` are the training data `X` (in our case called `X_train`) and the labels (in our case for the five-classifier `y_train_5`). The `sklearn.base.clone` function will help to make a copy of the classifier object.", "_____no_output_____" ] ], [ [ "from sklearn.model_selection import StratifiedKFold\nfrom sklearn.base import clone\n\nskfolds = StratifiedKFold(n_splits=3, random_state=42)\n\nfor train_indices, test_indices in skfolds.split(X_train, y_train_5):\n clone_clf = clone(sgd_clf) # make a clone of the classifier\n # [...] some code is missing here\n X_train_folds = X_train[train_indices]\n y_train_folds = y_train_5[train_indices]\n clone_clf.fit(X_train_folds, y_train_folds)\n \n X_test_fold = X_train[test_indices]\n y_test_fold = y_train_5[test_indices]\n y_pred = clone_clf.predict(X_test_fold)\n \n n_correct = sum(y_pred == y_test_fold)\n print(\"Fraction of correct predictions: %s\" % (n_correct / len(y_pred)))", "Fraction of correct predictions: 0.9502\nFraction of correct predictions: 0.96565\nFraction of correct predictions: 0.96495\n" ] ], [ [ "Let's move on to another performance measure: the confusion matrix. The confusion matrix is a 2x2 matrix and includes the number of true positives, false positives (type-I error), true negatives and false negatives (type-II error). First, let's use another of Scitkit-Learn's functions: `cross_val_predict` takes our classifier, our training data and our true labels, and automatically performs a k-fold cross-validation. It returns an array of the predicted labels.", "_____no_output_____" ] ], [ [ "from sklearn.model_selection import cross_val_predict\n\n# Take our SGD classifer and perform a 3-fold cross-validation.\ny_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)\n\n# Print some of the predicted labels.\nprint(y_train_pred)", "[False False False ... False False False]\n" ] ], [ [ "Using cross-validation always gives us a 'clean', i.e. unbiased estimate of our prediction power, because the performance of the classifier is evaluated on data it hadn't seen during training. Now we have our predicted labels in `y_train_pred` and can compare them to the true labels `y_train_5`. So let's create a confusion matrix.", "_____no_output_____" ] ], [ [ "from sklearn.metrics import confusion_matrix\n\nconfusion_matrix(y_train_5, y_train_pred)", "_____no_output_____" ] ], [ [ "How do we read this? The rows correspond to the _true_ classes, the columns to the _predicted_ classes. So the 53,272 means that about fifty-three thousand numbers that are 'not five' were predicted as such, while 1307 were predicted to be fives. 4344 true fives were predicted to be fives, but 1077 were not. Sometimes it makes sense to normalise the confusion matrix by rows, so that the values in the cells give an idea how large the _fraction_ of correctly and incorrectly predicted instances is. So let's try this:", "_____no_output_____" ] ], [ [ "matrix = confusion_matrix(y_train_5, y_train_pred)\nrow_sums = matrix.sum(axis=1)\nmatrix / row_sums[:, np.newaxis]", "_____no_output_____" ] ], [ [ "There are other metrics to evaluate the performance of classifiers as we saw in the lecture. One example is the _precision_ which is the rate of true positives among all positives. The precision is a measure how many of our predicted positives are _actually_ positives, i.e. it can be calculated as TP / (TP + FP) (TP = true positives, FP = false positives).", "_____no_output_____" ] ], [ [ "from sklearn.metrics import precision_score, recall_score\n\nprint(precision_score(y_train_5, y_train_pred))\n\n# Can you reproduce this value by hand? All info should be in the confusion matrix.\ntp = matrix[1][1]\nfp = matrix[0][1]\nprecision_by_hand = tp / (tp + fp)\nprint(\"By hand: %s\" % precision_by_hand)", "0.7687135020350381\nBy hand: 0.7687135020350381\n" ] ], [ [ "Or in words: 77% of our predicted fives are _actually_ fives, while 23% of the predicted fives are other numbers.\n\nAnother metric, which is often used in conjunction with the _precision_, is the _recall_. The recall is a measure of how many of the true positives as predicted as such, i.e. \"how many true positives do we identify\". It is easy to reach perfect precision if you just make your classifier reject all negatives, but it's impossible to keep a high recall score in that case. Let's look at our classifier's recall:", "_____no_output_____" ] ], [ [ "print(recall_score(y_train_5, y_train_pred))\n\n# Again, it should be straight-forward to make this calculation by hand. Can you try?\ntp = matrix[1][1]\nfn = matrix[1][0]\nrecall_by_hand = tp / (tp + fn)\nprint(\"By hand: %s\" % recall_by_hand)", "0.801328168234643\nBy hand: 0.801328168234643\n" ] ], [ [ "In words: only 80% of the fives are correctly predicted to be fives. Doesn't look as great as the 95% prediction rate, does it? A nice combination for precision and recall is their harmonic mean, usually known (and in the lecture introduced as) the _F_1 score_. The harmonic mean (as opposed to the arithmetic mean) is very sensitive low values, so only a good balance between precision and recall will lead to a high F_1 score. Very conveniently, Scikit-Learn comes with an implementation of the score already, but can you also calculate it by hand?", "_____no_output_____" ] ], [ [ "from sklearn.metrics import f1_score\nprint(f1_score(y_train_5, y_train_pred))\n\n# Once more, it is fairly easy to calculate this by hand. Give it a try!\nf1_score_by_hand = 2 / (1/precision_by_hand + 1/recall_by_hand)\nprint(\"By hand: %s\" % f1_score_by_hand)", "0.7846820809248555\nBy hand: 0.7846820809248556\n" ] ], [ [ "Of course, a balanced precision and recall is not _always_ desirable. Whether you want both to be equally high, depends on the use case. Sometimes, you'd definitely want to classify as many true positives as such, with the tradeoff to have low precision (example: in a test for a virus you want every true positive to know that they might be infected, but you might get a few false positives). In other cases, you might want a high precision with the tradeoff that you don't detect all positives as such (example: it's ok to remove some harmless videos in a video filter, but you don't want harmful content to pass your filter).", "_____no_output_____" ], [ "## Decision function\n\nWhen we use the `predict()` function, our classifier gives a boolean prediction. But how is that prediction done? The classifier calculates a score, called 'decision_function' in Scikit-Learn, and any instance above a certain threshold is classified as 'true', any instance below as 'false'. By retrieving the decision function directly, we can look at different tradeoffs between precision and recall.", "_____no_output_____" ] ], [ [ "y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,\n method=\"decision_function\")\nprint(y_scores) # Print scores to get an idea ...", "[ -434076.49813641 -1825667.15281624 -767086.76186905 ...\n -867191.25267994 -565357.11420164 -366599.16018198]\n" ] ], [ [ "This again gives us a numpy array with 60,000 entries, all of which contain a floating point value with the predicted score. Now, as we've seen before, Scikit-Learn provides many functions out-of-the-box to evaluate classifiers. The following `precision_recall_curve` metric gives us tuples of precision, recall and threshold values based on our training data. It takes the true labels, in our case `y_train_5` and the `y_scores` to calculate these. We can then use thes values to plot curves for precision and recall for different threshold values.", "_____no_output_____" ] ], [ [ "from sklearn.metrics import precision_recall_curve\n\nprecisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)\nprint(precisions)", "[0.09080706 0.09079183 0.09079335 ... 1. 1. 1. ]\n" ], [ "def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):\n plt.plot(thresholds, precisions[:-1], \"b--\", label=\"Precision\", linewidth=2)\n plt.plot(thresholds, recalls[:-1], \"g-\", label=\"Recall\", linewidth=2)\n plt.xlabel(\"Threshold\", fontsize=16)\n plt.legend(loc=\"upper left\", fontsize=16)\n plt.ylim([0, 1])\n\nplt.figure(figsize=(8, 4))\nplot_precision_recall_vs_threshold(precisions, recalls, thresholds)\nplt.xlim([-700000, 700000])\nsave_fig(\"precision_recall_vs_threshold_plot\")\nplt.show()", "Saving figure precision_recall_vs_threshold_plot\n" ] ], [ [ "Looks good! Bonus question: why is the precision curve bumpier than the recall?\n\nLet's assume we want to optimise our classfier for a precision value of 93%. Can you find a good threshold? The below threshold is just a test value and definitely too low. ", "_____no_output_____" ] ], [ [ "threshold = -20000\ny_train_pred_93 = (y_scores > threshold)\nprint(\"precision: %s\" % precision_score(y_train_5, y_train_pred_93))\nprint(\"recall: %s\" % recall_score(y_train_5, y_train_pred_93))", "precision: 0.7297430021280079\nrecall: 0.8223574986164914\n" ] ], [ [ "Sometimes, plotting precision vs. recall can also be helpful.", "_____no_output_____" ] ], [ [ "def plot_precision_vs_recall(precisions, recalls):\n plt.plot(recalls, precisions, \"b-\", linewidth=2)\n plt.xlabel(\"Recall\", fontsize=16)\n plt.ylabel(\"Precision\", fontsize=16)\n plt.axis([0, 1, 0, 1])\n\nplt.figure(figsize=(8, 6))\nplot_precision_vs_recall(precisions, recalls)\nsave_fig(\"precision_vs_recall_plot\")\nplt.show()", "Saving figure precision_vs_recall_plot\n" ] ], [ [ "# ROC curves\n\nBecause it's an extremely common performance measure, we should also have a look at the ROC curve (_receiver operating characteristic_). ROC curves plot true positives vs. false positives, or usually the true positive _rate_ vs. the false positive _rate_. While the first is exactly what we called _recall_ so far, the latter is one minus the _true negative rate_, also called specificity. Let's import the ROC curve from Scikit-Learn, this will give us tuples of FPR, TPR and threshold values again.", "_____no_output_____" ] ], [ [ "from sklearn.metrics import roc_curve\n\nfpr, tpr, thresholds = roc_curve(y_train_5, y_scores)", "_____no_output_____" ] ], [ [ "Now we can plot them:", "_____no_output_____" ] ], [ [ "def plot_roc_curve(fpr, tpr, label=None):\n plt.plot(fpr, tpr, linewidth=2, label=label)\n plt.plot([0, 1], [0, 1], 'k--')\n plt.axis([0, 1, 0, 1])\n plt.xlabel('False Positive Rate', fontsize=16)\n plt.ylabel('True Positive Rate', fontsize=16)\n\nplt.figure(figsize=(8, 6))\nplot_roc_curve(fpr, tpr)\nsave_fig(\"roc_curve_plot\")\nplt.show()", "Saving figure roc_curve_plot\n" ] ], [ [ "It is always desirable to have the curve as close to the top left corner as above. As a measure for this, one usually calculates the _area under curve_. What is the AUC value for a random classifier?", "_____no_output_____" ] ], [ [ "from sklearn.metrics import roc_auc_score\n\nroc_auc_score(y_train_5, y_scores)", "_____no_output_____" ] ], [ [ "# Multiclass classification\n\nSo far we have completely ignored the fact that our training data not only includes fives and 'other digits', but in fact ten different input labels (one for each digit). Multiclass classification will allow us to distinguish each of them individually and predict the _most likely class_ for each instance. Scikit-Learn is clever enough to realise, that our label array `y_train` contains ten different classes, so – without explicitly telling us – it runs ten binary classifiers when we call the `fit()` function on the SGD classifier. Each of these binary classifiers trains one class vs. all others (\"one-versus-all\"). Let's try it out:", "_____no_output_____" ] ], [ [ "sgd_clf.fit(X_train, y_train)", "_____no_output_____" ] ], [ [ "How does it classify our previous example of something that looked like a five?", "_____no_output_____" ] ], [ [ "sgd_clf.predict([some_digit])", "_____no_output_____" ] ], [ [ "Great! But what exactly happens under the hood? It actually calculates ten different scores for the ten different binary classifiers and picks the class with the highest score. We can see this by calling the `decision_function()` as we did earlier:", "_____no_output_____" ] ], [ [ "some_digit_scores = sgd_clf.decision_function([some_digit])\nprint(some_digit_scores) # Print us the array content\nprint(\"Largest entry: %s\" % np.argmax(some_digit_scores)) # Get the index of the largest entry", "[[-311402.62954431 -363517.28355739 -446449.5306454 -183226.61023518\n -414337.15339485 161855.74572176 -452576.39616343 -471957.14962573\n -518542.33997148 -536774.63961222]]\nLargest entry: 5\n" ] ], [ [ "Scikit-Learn even comes with a class to run the one-versus-one approach as well. We can just give it our SGD classifier instance and then call the `fit()` function on it:", "_____no_output_____" ] ], [ [ "from sklearn.multiclass import OneVsOneClassifier\novo_clf = OneVsOneClassifier(sgd_clf)\novo_clf.fit(X_train, y_train)\n\n# What does it predict for our random five?\novo_clf.predict([some_digit])", "_____no_output_____" ] ], [ [ "And how many classifiers does this one-versus-one approach need? Can you come up with the formula?", "_____no_output_____" ] ], [ [ "print(\"Number of estimators: %s\" % len(ovo_clf.estimators_))", "Number of estimators: 45\n" ] ], [ [ "Back to the one-versus-all approach – how good are we? For that, we can calculate the cross-validation score once more to get values for the accuracy. Bear in mind that now we are running a _ten-class_ classification!", "_____no_output_____" ] ], [ [ "cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring=\"accuracy\")", "_____no_output_____" ] ], [ [ "This is not bad at all, although you could probably spend hours optimising the hyperparameters of this model. How good does the onve-versus-one approach perform? Try it out!\n\nLet's look at some other performance measures for the one-versus-all classifier. A good point to start is the confusing matrix.", "_____no_output_____" ] ], [ [ "y_train_pred = cross_val_predict(sgd_clf, X_train, y_train, cv=3)\nconf_mx = confusion_matrix(y_train_pred, y_train)\nconf_mx", "_____no_output_____" ] ], [ [ "Ok, maybe it's better to display this in a plot:", "_____no_output_____" ] ], [ [ "def plot_confusion_matrix(matrix):\n fig = plt.figure(figsize=(8,8))\n ax = fig.add_subplot(111)\n plt.xlabel('Predicted class', fontsize=16)\n plt.ylabel('True class', fontsize=16)\n cax = ax.matshow(matrix)\n fig.colorbar(cax)\n \nplot_confusion_matrix(conf_mx)\nsave_fig(\"confusion_matrix_plot\", tight_layout=False)\nplt.show()", "Saving figure confusion_matrix_plot\n" ] ], [ [ "It's still very hard to see what's going on. So maybe we should (1) normalise the matrix by rows again, (2) \"remove\" all diagonal entries, because those are not interesting for us for the error analysis.", "_____no_output_____" ] ], [ [ "row_sums = conf_mx.sum(axis=1, keepdims=True)\nnorm_conf_mx = conf_mx / row_sums\n\nnp.fill_diagonal(norm_conf_mx, 0)\nplot_confusion_matrix(norm_conf_mx)\nsave_fig(\"confusion_matrix_errors_plot\", tight_layout=False)\nplt.show()", "Saving figure confusion_matrix_errors_plot\n" ] ], [ [ "It seems we're predicting many of the eights wrong. In particular, many of them are predicted to be a five! On the other hand, not many fives are misclassified as eights. Interesting, right? Let's pick out some eights and fives, each of which are either correctly predicted, or predicted as the other class. Maybe looking at the pictures with our \"human learning\" algorithm will see the problem.", "_____no_output_____" ] ], [ [ "cl_a, cl_b = 8, 5 # Define class a and class b for the plot\n\n# Training data from class a, which is predicted as a.\nX_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]\n\n# Training data from class a, which is predicted as b.\nX_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]\n\n# Training data from class b, which is predicted as a.\nX_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]\n\n# Training data from class b, which is predicted as b.\nX_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]\n\nplt.figure(figsize=(8,8))\nplt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)\nplt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)\nplt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)\nplt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)\nsave_fig(\"error_analysis_digits_plot\")\nplt.show()", "Saving figure error_analysis_digits_plot\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e557af0848788b292260029ac3e9b93d1527e1

76,081

ipynb

Jupyter Notebook

wip/nn4.ipynb

ArenasGuerreroJulian/kglab

5c34ff586890b56d25bda6cc2bce3f11ce09065f

[ "MIT" ]

1

2020-10-26T16:45:31.000Z

wip/nn4.ipynb

ArenasGuerreroJulian/kglab

5c34ff586890b56d25bda6cc2bce3f11ce09065f

[ "MIT" ]

null

wip/nn4.ipynb

ArenasGuerreroJulian/kglab

5c34ff586890b56d25bda6cc2bce3f11ce09065f

[ "MIT" ]

null

63.295341

24,214

0.702948

[ [ [ "# \"Build Your First Neural Network with PyTorch\"\n\n * article <https://curiousily.com/posts/build-your-first-neural-network-with-pytorch/>\n * dataset <https://www.kaggle.com/jsphyg/weather-dataset-rattle-package>\n \nrequires `torch 1.4.0`", "_____no_output_____" ] ], [ [ "import os\nfrom os.path import dirname\nimport numpy as np\nimport pandas as pd\nfrom tqdm import tqdm\n\nimport seaborn as sns\nfrom pylab import rcParams\nimport matplotlib.pyplot as plt\nfrom matplotlib import rc\n\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.metrics import confusion_matrix, classification_report\n\nimport torch\nfrom torch import nn, optim\nimport torch.nn.functional as F\n\n%matplotlib inline\n\nsns.set(style='whitegrid', palette='muted', font_scale=1.2)\nHAPPY_COLORS_PALETTE = [\"#01BEFE\", \"#FFDD00\", \"#FF7D00\", \"#FF006D\", \"#93D30C\", \"#8F00FF\"]\nsns.set_palette(sns.color_palette(HAPPY_COLORS_PALETTE))\nrcParams[\"figure.figsize\"] = 12, 8\n\nRANDOM_SEED = 42\nnp.random.seed(RANDOM_SEED)\ntorch.manual_seed(RANDOM_SEED)", "_____no_output_____" ], [ "df = pd.read_csv(dirname(os.getcwd()) + \"/dat/weatherAUS.csv\")\ndf.describe()", "_____no_output_____" ], [ "df.shape", "_____no_output_____" ], [ "# data pre-processing\ncols = [ \"Rainfall\", \"Humidity3pm\", \"Pressure9am\", \"RainToday\", \"RainTomorrow\" ]\ndf = df[cols]\ndf.head()", "_____no_output_____" ], [ "df[\"RainToday\"].replace({\"No\": 0, \"Yes\": 1}, inplace = True)\ndf[\"RainTomorrow\"].replace({\"No\": 0, \"Yes\": 1}, inplace = True)\ndf.head()", "_____no_output_____" ], [ "# drop missing values\ndf = df.dropna(how=\"any\")\ndf.head()", "_____no_output_____" ], [ "sns.countplot(df.RainTomorrow);", "_____no_output_____" ], [ "df.RainTomorrow.value_counts() / df.shape[0]", "_____no_output_____" ], [ "X = df[[\"Rainfall\", \"Humidity3pm\", \"RainToday\", \"Pressure9am\"]]\ny = df[[\"RainTomorrow\"]]\nX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=RANDOM_SEED)", "_____no_output_____" ], [ "X_train = torch.from_numpy(X_train.to_numpy()).float()\nX_test = torch.from_numpy(X_test.to_numpy()).float()\n\ny_train = torch.squeeze(torch.from_numpy(y_train.to_numpy()).float())\ny_test = torch.squeeze(torch.from_numpy(y_test.to_numpy()).float())\n\nprint(X_train.shape, y_train.shape)\nprint(X_test.shape, y_test.shape)", "torch.Size([99751, 4]) torch.Size([99751])\ntorch.Size([24938, 4]) torch.Size([24938])\n" ], [ "class Net (nn.Module):\n def __init__ (self, n_features):\n super(Net, self).__init__()\n self.fc1 = nn.Linear(n_features, 5)\n self.fc2 = nn.Linear(5, 3)\n self.fc3 = nn.Linear(3, 1)\n \n\n def forward (self, x):\n x = F.relu(self.fc1(x))\n x = F.relu(self.fc2(x))\n return torch.sigmoid(self.fc3(x))", "_____no_output_____" ], [ "net = Net(X_train.shape[1])", "_____no_output_____" ], [ "# training\ncriterion = nn.BCELoss()", "_____no_output_____" ], [ "optimizer = optim.Adam(net.parameters(), lr=0.001)", "_____no_output_____" ], [ "# weather forecast\n\ndef calculate_accuracy (y_true, y_pred):\n predicted = y_pred.ge(.5).view(-1)\n return (y_true == predicted).sum().float() / len(y_true)", "_____no_output_____" ], [ "def round_tensor (t, decimal_places=3):\n return round(t.item(), decimal_places)\n\n\nMAX_EPOCH = 5000\n\nfor epoch in range(MAX_EPOCH):\n y_pred = net(X_train)\n y_pred = torch.squeeze(y_pred)\n train_loss = criterion(y_pred, y_train)\n \n if epoch % 100 == 0:\n train_acc = calculate_accuracy(y_train, y_pred)\n \n y_test_pred = net(X_test)\n y_test_pred = torch.squeeze(y_test_pred)\n \n test_loss = criterion(y_test_pred, y_test)\n test_acc = calculate_accuracy(y_test, y_test_pred)\n \n print(\nf'''epoch {epoch}\nTrain set - loss: {round_tensor(train_loss)}, accuracy: {round_tensor(train_acc)}\nTest set - loss: {round_tensor(test_loss)}, accuracy: {round_tensor(test_acc)}\n''')\n \n optimizer.zero_grad()\n train_loss.backward()\n optimizer.step()", "epoch 0\nTrain set - loss: 0.472, accuracy: 0.791\nTest set - loss: 0.473, accuracy: 0.792\n\nepoch 100\nTrain set - loss: 0.474, accuracy: 0.792\nTest set - loss: 0.476, accuracy: 0.793\n\nepoch 200\nTrain set - loss: 0.476, accuracy: 0.793\nTest set - loss: 0.477, accuracy: 0.793\n\nepoch 300\nTrain set - loss: 0.476, accuracy: 0.793\nTest set - loss: 0.477, accuracy: 0.793\n\nepoch 400\nTrain set - loss: 0.474, accuracy: 0.792\nTest set - loss: 0.476, accuracy: 0.793\n\nepoch 500\nTrain set - loss: 0.472, accuracy: 0.792\nTest set - loss: 0.473, accuracy: 0.793\n\nepoch 600\nTrain set - loss: 0.47, accuracy: 0.791\nTest set - loss: 0.471, accuracy: 0.792\n\nepoch 700\nTrain set - loss: 0.468, accuracy: 0.79\nTest set - loss: 0.47, accuracy: 0.791\n\nepoch 800\nTrain set - loss: 0.468, accuracy: 0.789\nTest set - loss: 0.47, accuracy: 0.79\n\nepoch 900\nTrain set - loss: 0.469, accuracy: 0.789\nTest set - loss: 0.47, accuracy: 0.789\n\nepoch 1000\nTrain set - loss: 0.47, accuracy: 0.789\nTest set - loss: 0.471, accuracy: 0.789\n\nepoch 1100\nTrain set - loss: 0.47, accuracy: 0.788\nTest set - loss: 0.471, accuracy: 0.788\n\nepoch 1200\nTrain set - loss: 0.47, accuracy: 0.788\nTest set - loss: 0.471, accuracy: 0.789\n\nepoch 1300\nTrain set - loss: 0.469, accuracy: 0.789\nTest set - loss: 0.47, accuracy: 0.789\n\nepoch 1400\nTrain set - loss: 0.468, accuracy: 0.789\nTest set - loss: 0.469, accuracy: 0.789\n\nepoch 1500\nTrain set - loss: 0.467, accuracy: 0.789\nTest set - loss: 0.468, accuracy: 0.79\n\nepoch 1600\nTrain set - loss: 0.466, accuracy: 0.79\nTest set - loss: 0.467, accuracy: 0.79\n\nepoch 1700\nTrain set - loss: 0.466, accuracy: 0.791\nTest set - loss: 0.467, accuracy: 0.791\n\nepoch 1800\nTrain set - loss: 0.466, accuracy: 0.791\nTest set - loss: 0.467, accuracy: 0.792\n\nepoch 1900\nTrain set - loss: 0.466, accuracy: 0.792\nTest set - loss: 0.467, accuracy: 0.793\n\nepoch 2000\nTrain set - loss: 0.466, accuracy: 0.792\nTest set - loss: 0.467, accuracy: 0.793\n\nepoch 2100\nTrain set - loss: 0.466, accuracy: 0.792\nTest set - loss: 0.467, accuracy: 0.793\n\nepoch 2200\nTrain set - loss: 0.465, accuracy: 0.792\nTest set - loss: 0.466, accuracy: 0.792\n\nepoch 2300\nTrain set - loss: 0.464, accuracy: 0.791\nTest set - loss: 0.466, accuracy: 0.792\n\nepoch 2400\nTrain set - loss: 0.464, accuracy: 0.791\nTest set - loss: 0.465, accuracy: 0.791\n\nepoch 2500\nTrain set - loss: 0.464, accuracy: 0.791\nTest set - loss: 0.465, accuracy: 0.791\n\nepoch 2600\nTrain set - loss: 0.464, accuracy: 0.79\nTest set - loss: 0.465, accuracy: 0.79\n\nepoch 2700\nTrain set - loss: 0.463, accuracy: 0.79\nTest set - loss: 0.465, accuracy: 0.79\n\nepoch 2800\nTrain set - loss: 0.463, accuracy: 0.79\nTest set - loss: 0.465, accuracy: 0.79\n\nepoch 2900\nTrain set - loss: 0.463, accuracy: 0.79\nTest set - loss: 0.464, accuracy: 0.79\n\nepoch 3000\nTrain set - loss: 0.463, accuracy: 0.79\nTest set - loss: 0.464, accuracy: 0.79\n\nepoch 3100\nTrain set - loss: 0.462, accuracy: 0.79\nTest set - loss: 0.464, accuracy: 0.791\n\nepoch 3200\nTrain set - loss: 0.462, accuracy: 0.791\nTest set - loss: 0.463, accuracy: 0.791\n\nepoch 3300\nTrain set - loss: 0.461, accuracy: 0.791\nTest set - loss: 0.463, accuracy: 0.791\n\nepoch 3400\nTrain set - loss: 0.461, accuracy: 0.792\nTest set - loss: 0.463, accuracy: 0.792\n\nepoch 3500\nTrain set - loss: 0.461, accuracy: 0.792\nTest set - loss: 0.462, accuracy: 0.792\n\nepoch 3600\nTrain set - loss: 0.461, accuracy: 0.792\nTest set - loss: 0.462, accuracy: 0.793\n\nepoch 3700\nTrain set - loss: 0.461, accuracy: 0.792\nTest set - loss: 0.462, accuracy: 0.793\n\nepoch 3800\nTrain set - loss: 0.46, accuracy: 0.792\nTest set - loss: 0.462, accuracy: 0.793\n\nepoch 3900\nTrain set - loss: 0.46, accuracy: 0.792\nTest set - loss: 0.461, accuracy: 0.793\n\nepoch 4000\nTrain set - loss: 0.46, accuracy: 0.792\nTest set - loss: 0.461, accuracy: 0.792\n\nepoch 4100\nTrain set - loss: 0.459, accuracy: 0.792\nTest set - loss: 0.461, accuracy: 0.792\n\nepoch 4200\nTrain set - loss: 0.459, accuracy: 0.792\nTest set - loss: 0.46, accuracy: 0.792\n\nepoch 4300\nTrain set - loss: 0.459, accuracy: 0.791\nTest set - loss: 0.46, accuracy: 0.792\n\nepoch 4400\nTrain set - loss: 0.459, accuracy: 0.792\nTest set - loss: 0.46, accuracy: 0.792\n\nepoch 4500\nTrain set - loss: 0.458, accuracy: 0.791\nTest set - loss: 0.46, accuracy: 0.792\n\nepoch 4600\nTrain set - loss: 0.458, accuracy: 0.792\nTest set - loss: 0.459, accuracy: 0.792\n\nepoch 4700\nTrain set - loss: 0.458, accuracy: 0.792\nTest set - loss: 0.459, accuracy: 0.792\n\nepoch 4800\nTrain set - loss: 0.458, accuracy: 0.792\nTest set - loss: 0.459, accuracy: 0.792\n\nepoch 4900\nTrain set - loss: 0.457, accuracy: 0.792\nTest set - loss: 0.459, accuracy: 0.793\n\n" ], [ "# save the model\nMODEL_PATH = \"model.pth\"\ntorch.save(net, MODEL_PATH)", "_____no_output_____" ], [ "# restore model\nnet = torch.load(MODEL_PATH)", "_____no_output_____" ], [ "# evaluation\nclasses = [\"No rain\", \"Raining\"]\n\ny_pred = net(X_test)\ny_pred = y_pred.ge(.5).view(-1).cpu()\ny_test = y_test.cpu()\n\nprint(classification_report(y_test, y_pred, target_names=classes))", " precision recall f1-score support\n\n No rain 0.80 0.99 0.88 19413\n Raining 0.71 0.11 0.19 5525\n\n micro avg 0.79 0.79 0.79 24938\n macro avg 0.75 0.55 0.53 24938\nweighted avg 0.78 0.79 0.73 24938\n\n" ], [ "cm = confusion_matrix(y_test, y_pred)\ndf_cm = pd.DataFrame(cm, index=classes, columns=classes)\n\nhmap = sns.heatmap(df_cm, annot=True, fmt=\"d\")\nhmap.yaxis.set_ticklabels(hmap.yaxis.get_ticklabels(), rotation=0, ha='right')\nhmap.xaxis.set_ticklabels(hmap.xaxis.get_ticklabels(), rotation=30, ha='right')\n\nplt.ylabel('True label')\nplt.xlabel('Predicted label');", "_____no_output_____" ], [ "def will_it_rain (rainfall, humidity, rain_today, pressure):\n t = torch.as_tensor([rainfall, humidity, rain_today, pressure]).float().cpu()\n output = net(t)\n print(\"net(t)\", output.item())\n return output.ge(0.5).item()", "_____no_output_____" ], [ "will_it_rain(rainfall=10, humidity=10, rain_today=True, pressure=2)", "net(t) 0.7304017543792725\n" ], [ "will_it_rain(rainfall=0, humidity=1, rain_today=False, pressure=100)", "net(t) 0.506089448928833\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e5596daa8ebae6f1a7aa6b596300198bb8c6b0

42,550

ipynb

Jupyter Notebook

SoftwareDesign202010_0101.ipynb

zfukuoka/Copying_a_sutra

2d0b1f781fc029ae0108b639e893708a8c45cee2

[ "BSD-2-Clause" ]

null

SoftwareDesign202010_0101.ipynb

zfukuoka/Copying_a_sutra

2d0b1f781fc029ae0108b639e893708a8c45cee2

[ "BSD-2-Clause" ]

null

SoftwareDesign202010_0101.ipynb

zfukuoka/Copying_a_sutra

2d0b1f781fc029ae0108b639e893708a8c45cee2

[ "BSD-2-Clause" ]

null

46.25

21,990

0.678049

[ [ [ "<a href=\"https://colab.research.google.com/github/zfukuoka/Copying_a_sutra/blob/master/SoftwareDesign202010_0101.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "# SoftwareDesign 2020年10月号第1特集 Pythonではじめる統計学\n\n## 第1章統計分析に必須のライブラリ\n", "_____no_output_____" ], [ "### リスト1", "_____no_output_____" ] ], [ [ "import seaborn as sns\n\ntips = sns.load_dataset(\"tips\")\nsns.catplot(\n data=tips, x=\"time\", y=\"tip\", kind=\"violin\"\n)", "_____no_output_____" ] ], [ [ "### リスト2\n\n標本空間が $\\{a_1, \\dotsc, a_n\\}$ であるとき、その算術平均 $(\\displaystyle A)$ は次のとおりに定義される。\n\n$$A = \\frac{1}{n}\\sum_{k=1}^{n} a_k = \\frac{a_1 + a_2 + \\dotsb + a_n}{n}$$\n", "_____no_output_____" ], [ "### NumPy入門", "_____no_output_____" ], [ "#### ndarray型", "_____no_output_____" ] ], [ [ "import numpy as np\n\nint_arr = np.array([1, 2])", "_____no_output_____" ], [ "int_arr.dtype", "_____no_output_____" ], [ "float_arr = np.array([1, 2], dtype=np.float32)", "_____no_output_____" ], [ "float_arr.dtype", "_____no_output_____" ], [ "float_arr.astype(np.int)", "_____no_output_____" ] ], [ [ "#### ndarrayオブジェクト生成", "_____no_output_____" ] ], [ [ "np.arange(3)", "_____no_output_____" ], [ "np.arange(0, 2.5, 0.5)", "_____no_output_____" ], [ "np.zeros(3)", "_____no_output_____" ], [ "np.ones([2, 3])", "_____no_output_____" ], [ "np.random.seed(1)\nnp.random.rand(3,3)", "_____no_output_____" ], [ "arr1 = np.arange(1, 4)\narr1", "_____no_output_____" ], [ "arr2 = np.arange(1, 13).reshape(4, 3)\narr2", "_____no_output_____" ] ], [ [ "#### 要素へのアクセス", "_____no_output_____" ] ], [ [ "arr1[0]", "_____no_output_____" ], [ "arr1[1:3]", "_____no_output_____" ], [ "arr2[0]", "_____no_output_____" ], [ "arr2[1, 2]", "_____no_output_____" ], [ "arr2[0, 1:3]", "_____no_output_____" ], [ "arr1[1] = 10\narr1", "_____no_output_____" ], [ "arr2[1, :2] = 100\narr2", "_____no_output_____" ] ], [ [ "#### ブロードキャスト", "_____no_output_____" ] ], [ [ "li = [1, 2, 3]\n[x + 1 for x in li]", "_____no_output_____" ], [ "arr1 = np.array([1, 2, 3])\narr1 + 1", "_____no_output_____" ], [ "# 前述のコードから続けてそのまま動かすと、テキストと異なる結果になる\n# 恐らく、arr2を途中で変えたことを忘れたか、無視したものと考えられる\n# このため、テキストにはないが改めてarr2の初期化を行う\narr2 = np.arange(1, 13).reshape(4, 3)\narr1 + arr2", "_____no_output_____" ] ], [ [ "#### 関数の適用", "_____no_output_____" ] ], [ [ "np.power(arr1, arr2)", "_____no_output_____" ], [ "abs(np.array([1, -2, 3]))", "_____no_output_____" ], [ "sum(np.array([1, 2, 3]))", "_____no_output_____" ], [ "def my_func(x):\n return x ** 2 + 1\n\nmy_func(arr1)", "_____no_output_____" ] ], [ [ "### pandas入門", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ] ]

d0e559c14ce829ca2b6a007bd0ba14dbf5269dc7

305,583

ipynb

Jupyter Notebook

scraping_tools/trans_markt_scraper_instructions.ipynb

d-v-dlee/super_liga_xg

e3054cadf00755a347d31ce335c567db91e433a7

[ "MIT" ]

3

2019-01-24T07:30:45.000Z

2019-11-28T15:52:44.000Z

scraping_tools/trans_markt_scraper_instructions.ipynb

d-v-dlee/super_liga_xg

e3054cadf00755a347d31ce335c567db91e433a7

[ "MIT" ]

null

scraping_tools/trans_markt_scraper_instructions.ipynb

d-v-dlee/super_liga_xg

e3054cadf00755a347d31ce335c567db91e433a7

[ "MIT" ]

null

42.230929

167

0.470131

[ [ [ "# Scraping transfermarkt by html", "_____no_output_____" ] ], [ [ "from selenium.webdriver import (Chrome, Firefox)\nimport time\n\nimport requests\nfrom bs4 import BeautifulSoup", "_____no_output_____" ], [ "from html_scraper import db", "_____no_output_____" ], [ "players = db['players']", "_____no_output_____" ], [ "player_urls = db['player_urls']", "_____no_output_____" ], [ "browser = Firefox()", "_____no_output_____" ], [ "url = 'https://www.transfermarkt.co.uk/primera-division/startseite/wettbewerb/AR1N'", "_____no_output_____" ], [ "browser.get(url)", "_____no_output_____" ], [ "elems = browser.find_elements_by_class_name(\"vereinprofil_tooltip\")\nurl_links = []\nfor link in elems:\n url = link.get_attribute('href')\n if url not in url_links and 'startseite' in url:\n url_links.append(url)", "_____no_output_____" ], [ "len(url_links)", "_____no_output_____" ], [ "club1 = url_links[0]", "_____no_output_____" ], [ "browser.get(club1)", "_____no_output_____" ] ], [ [ "### Go from club_url to detailed page club_url", "_____no_output_____" ] ], [ [ "detailed_url = []\nfor url in url_links:\n change_url = url.replace('startseite', 'kader')\n url_final = change_url + '/plus/1'\n detailed_url.append(url_final)", "_____no_output_____" ], [ "detailed_url", "_____no_output_____" ] ], [ [ "### old code... skip down to scraping to DBMongo step", "_____no_output_____" ] ], [ [ "from html_scraper import scrape_player_info", "_____no_output_____" ], [ "scrape_player_info(detailed_url, delay=15)", "_____no_output_____" ], [ "db", "_____no_output_____" ], [ "club1 = detailed_url[0]\nbrowser.get(club1)", "_____no_output_____" ], [ "sel = 'td.hauptlink a'\nlink_elements = browser.find_elements_by_css_selector(sel)", "_____no_output_____" ], [ "print(link_elements[0].text)", "Esteban Andrada\n" ], [ "sel = 'td.zentriert'\nlink_elements = browser.find_elements_by_css_selector(sel)", "_____no_output_____" ], [ "print(link_elements[0].text)", "31\n" ], [ "for link in link_elements:\n print(link.text)", "31\nJan 26, 1991 (27)\n\n1,94 m\nright\nAug 6, 2018\n\n30.06.2022\n1\nAug 21, 1995 (23)\n\n1,93 m\nright\nFeb 1, 2017\n\n30.06.2021\n28\nMar 17, 1987 (31)\n\n1,92 m\nright\nOct 6, 2018\n\n31.12.2018\n25\nMar 5, 1997 (21)\n\n1,87 m\nright\n-\n\n30.06.2019\n6\nSep 27, 1993 (25)\n\n1,85 m\nright\nJul 25, 2012\n\n30.06.2021\n24\nNov 3, 1988 (30)\n\n1,86 m\nright\nJul 5, 2018\n\n30.06.2021\n2\nMay 12, 1985 (33)\n\n1,84 m\nright\nJul 1, 2017\n\n30.06.2020\n26\nJan 26, 1999 (19)\n\n1,87 m\nright\nJul 1, 2018\n\n30.06.2021\n18\nFeb 22, 1991 (27)\n\n1,73 m\nleft\nJan 22, 2016\n\n30.06.2019\n3\nJan 15, 1989 (29)\n\n1,80 m\nleft\nJan 4, 2018\n\n30.06.2021\n20\nJul 21, 1994 (24)\n\n1,76 m\nleft\nJul 30, 2018\n\n30.06.2019\n14\nJun 9, 1992 (26)\n\n1,76 m\nright\nJan 22, 2015\n\n31.12.2018\n29\nMay 20, 1991 (27)\n\n1,85 m\nright\nJan 1, 2016\n\n30.06.2020\n4\nAug 18, 1988 (30)\n\n1,70 m\nright\nJan 1, 2018\n\n30.06.2021\n16\nOct 16, 1993 (25)\n\n1,79 m\nright\nAug 25, 2016\n\n30.06.2021\n40\nJan 13, 1998 (20)\n\n1,86 m\nright\n-\n\n-\n15\nDec 28, 1995 (22)\n\n1,72 m\nright\nAug 23, 2017\n\n30.06.2020\n5\nApr 10, 1986 (32)\n\n1,77 m\nright\nJul 24, 2013\n\n30.06.2020\n8\nAug 10, 1985 (33)\n\n1,75 m\nright\nSep 1, 2015\n\n30.06.2020\n39\nFeb 11, 2000 (18)\n\n1,82 m\nright\nJul 1, 2018\n\n-\n30\nNov 16, 1995 (23)\n\n1,76 m\nleft\nJan 26, 2018\n\n31.12.2021\n10\nDec 8, 1992 (25)\n\n1,85 m\nright\nJul 17, 2017\n\n31.12.2018\n7\nJan 21, 1996 (22)\n\n1,74 m\nright\nJul 9, 2014\n\n30.06.2022\n11\nApr 3, 1995 (23)\n\n1,73 m\nright\nJul 18, 2017\n\n31.12.2018\n22\nMay 19, 1996 (22)\n\n1,79 m\nright\nJul 1, 2018\n\n30.06.2023\n32\nFeb 5, 1984 (34)\n\n1,71 m\nright\nJan 6, 2018\n\n31.12.2019\n19\nMar 18, 1987 (31)\n\n1,75 m\nright\nJul 6, 2018\n\n30.06.2021\n9\nMay 17, 1990 (28)\n\n1,77 m\nright\nJul 1, 2016\n\n30.06.2021\n17\nOct 14, 1989 (29)\n\n1,77 m\nright\nAug 7, 2017\n\n30.06.2020\n" ], [ "sel = 'td.rechts.hauptlink'\nlink_elements = browser.find_elements_by_css_selector(sel)", "_____no_output_____" ], [ "test = '£4.05m '\nchars = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'k', 'm', '.']\n''.join(char for char in test if char in chars)", "_____no_output_____" ], [ "player_dict_odd = {}\nfor row in browser.find_elements_by_css_selector(\"tr.odd\"):\n player = row.find_element_by_css_selector('td.hauptlink a').text\n squad_num = row.find_elements_by_css_selector('td.zentriert')[0].text\n birthday = row.find_elements_by_css_selector('td.zentriert')[1].text\n transfer_value = row.find_element_by_css_selector('td.rechts.hauptlink').text\n player_dict_odd[player] = {'squad_num': squad_num, 'birthday': birthday, 'transfer_value': transfer_value}", "_____no_output_____" ], [ "player_dict_odd", "_____no_output_____" ], [ "# player_dict_even = {}\n# for row in browser.find_elements_by_css_selector(\"tr.even\"):\n# player = row.find_element_by_css_selector('td.hauptlink a').text\n# squad_num = row.find_elements_by_css_selector('td.zentriert')[0].text\n# birthday = row.find_elements_by_css_selector('td.zentriert')[1].text\n# # nationality = row.find_element_by_css_selector('td.zentriert.img')\n# transfer_value = row.find_element_by_css_selector('td.rechts.hauptlink').text\n# player_dict_even[player] = {'squad_num': squad_num, 'birthday': birthday, 'transfer_value': transfer_value}", "_____no_output_____" ], [ "# player_dict_even", "_____no_output_____" ], [ "player_dict = {**player_dict_even, **player_dict_odd}", "_____no_output_____" ], [ "len(player_dict)", "_____no_output_____" ], [ "# test = db['test']", "_____no_output_____" ], [ "# test.insert_one(player_dict)", "_____no_output_____" ] ], [ [ "# Scraping to DB Mongo", "_____no_output_____" ] ], [ [ "db_urls = detailed_url.copy()", "_____no_output_____" ], [ "db_urls", "_____no_output_____" ], [ "from html_scraper import get_all_player_data_from_url, team_scrape", "_____no_output_____" ], [ "teams = [get_all_player_data_from_url(url) for url in db_urls]", "_____no_output_____" ], [ "from html_scraper import add_player_to_db\nimport pandas as pd", "_____no_output_____" ], [ "for url in db_urls:\n player_data = get_all_player_data_from_url(url)\n print(url)\n for player in player_data:\n add_player_to_db(player)\n ", "https://www.transfermarkt.co.uk/club-atletico-boca-juniors/kader/verein/189/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/ca-independiente-de-avellaneda/kader/verein/1234/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-river-plate/kader/verein/209/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/racing-club-de-avellaneda/kader/verein/1444/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-san-lorenzo-de-almagro/kader/verein/1775/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-lanus/kader/verein/333/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-velez-sarsfield/kader/verein/1029/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-deportivo-godoy-cruz/kader/verein/12574/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-colon-santa-fe-/kader/verein/1070/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/defensa-y-justicia/kader/verein/2402/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-rosario-central/kader/verein/1418/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/talleres-de-cordoba-ca/kader/verein/3938/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/ca-union-santa-fe/kader/verein/7097/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/estudiantes-de-la-plata/kader/verein/288/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-huracan/kader/verein/2063/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/argentinos-juniors/kader/verein/1030/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-banfield/kader/verein/830/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/belgrano-de-cordoba/kader/verein/2417/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-tigre/kader/verein/11831/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-newells-old-boys/kader/verein/1286/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-tucuman/kader/verein/14554/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-de-gimnasia-y-esgrima-la-plata/kader/verein/1106/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-aldosivi-mdp-/kader/verein/12301/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-san-martin-sj-/kader/verein/10511/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-san-martin-tucuman-/kader/verein/12709/saison_id/2018/plus/1\nhttps://www.transfermarkt.co.uk/club-atletico-patronato/kader/verein/19806/saison_id/2018/plus/1\n" ] ], [ [ "# check db", "_____no_output_____" ] ], [ [ "db.players", "_____no_output_____" ], [ "players = db.players.find()", "_____no_output_____" ], [ "players.count()", "/Users/david/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:1: DeprecationWarning: count is deprecated. Use Collection.count_documents instead.\n \"\"\"Entry point for launching an IPython kernel.\n" ], [ "master_list = []\nfor player in players:\n master_list.append(player)", "_____no_output_____" ], [ "master_list", "_____no_output_____" ], [ "pd.DataFrame(master_list)\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

d0e559dc0065825203e48c78aa21537c02f3563d

668,734

ipynb

Jupyter Notebook

flask_backend/anime_flask/Data/Jupyter/AnimeKNN-Model.ipynb

shafqatshad/AnmieRecommenderSystem

f58d6ab2b3614aa81208ec844ef99963c988c69d

[ "Apache-2.0" ]

null

flask_backend/anime_flask/Data/Jupyter/AnimeKNN-Model.ipynb

shafqatshad/AnmieRecommenderSystem

f58d6ab2b3614aa81208ec844ef99963c988c69d

[ "Apache-2.0" ]

null

flask_backend/anime_flask/Data/Jupyter/AnimeKNN-Model.ipynb

shafqatshad/AnmieRecommenderSystem

f58d6ab2b3614aa81208ec844ef99963c988c69d

[ "Apache-2.0" ]

null

44.606057

26,916

0.324065

[ [ [ "import itertools\nimport numpy as np\nimport matplotlib.pyplot as plt\nfrom matplotlib.ticker import NullFormatter\nimport pandas as pd\nimport numpy as np\nimport matplotlib.ticker as ticker\nfrom sklearn import preprocessing\n%matplotlib inline", "_____no_output_____" ], [ "# Load Data From CSV File\ndf = pd.read_csv('AnimeList.csv')\ncols_id = list(df.columns)\n\n# Clean some anime episodes that havent been updated. From personal experience, animes that are Hentai genre,\n# Ova, Movie, Special anime type mainly have only 1 episode\ndf.loc[(df[\"genre\"]==\"Hentai\") & (df[\"episodes\"]==0),\"episodes\"] = 1\ndf.loc[(df[\"type\"]==\"OVA\") & (df[\"episodes\"]==0),\"episodes\"] = 1\ndf.loc[(df[\"type\"] == \"Movie\") & (df[\"episodes\"]==0), \"episodes\"] = 1\ndf.loc[(df[\"type\"] == \"Special\") & (df[\"episodes\"]==0), \"episodes\"] = 1\n\n# Adjust NaN values\nfor col in cols_id:\n try:\n float(df_filtered[col][0])\n df[col].fillna(df[col].median(),inplace = True)\n except:\n df[col].fillna(0, inplace = True)\ndf.head()", "_____no_output_____" ], [ "# Check number of individual values in each column\ncols_id = list(df.columns)\nfor col in cols_id:\n a = len(df[col].value_counts())\n print(a, col)\n print(\"==============================================================================\")", "14477 title\n==============================================================================\n5607 title_english\n==============================================================================\n13702 title_japanese\n==============================================================================\n8576 title_synonyms\n==============================================================================\n14383 image_url\n==============================================================================\n7 type\n==============================================================================\n16 source\n==============================================================================\n196 episodes\n==============================================================================\n3 status\n==============================================================================\n2 airing\n==============================================================================\n10026 aired_string\n==============================================================================\n9649 aired\n==============================================================================\n301 duration\n==============================================================================\n7 rating\n==============================================================================\n630 score\n==============================================================================\n5908 scored_by\n==============================================================================\n10640 rank\n==============================================================================\n11759 popularity\n==============================================================================\n7810 members\n==============================================================================\n1229 favorites\n==============================================================================\n1039 background\n==============================================================================\n222 premiered\n==============================================================================\n442 broadcast\n==============================================================================\n9420 related\n==============================================================================\n3222 producer\n==============================================================================\n194 licensor\n==============================================================================\n779 studio\n==============================================================================\n4545 genre\n==============================================================================\n4328 opening_theme\n==============================================================================\n5458 ending_theme\n==============================================================================\n" ], [ "df_filtered = df\nnew = pd.DataFrame(df_filtered.groupby(\"type\").size())\nnew.columns = ['count']\nnew = new.sort_values(by = \"count\")\nprint(new)\na = new.index.tolist()\na", " count\ntype \nUnknown 30\nMusic 849\nONA 1144\nSpecial 1948\nMovie 2624\nOVA 3612\nTV 4271\n" ], [ "# Columns with less than 50 distinct values will beconverted to numbers, \n# the values with more population will get higher index value\nfirst_filtered = {}\nfor col in cols_id:\n if len(df_filtered[col].value_counts()) < 50:\n new = pd.DataFrame(df_filtered.groupby(col).size())\n new.columns = ['count']\n new = new.sort_values(by = \"count\")\n a = new.index.tolist()\n converted = {}\n new_id = []\n old_i = {}\n start = 0\n for i in new.values:\n i = int(i)\n if i not in list(old_i.keys()):\n new_id.append(start)\n old_i[i] = start\n converted[a[start]] = start\n start += 1\n else:\n new_id.append(old_i[i])\n print(col)\n print(converted)\n first_filtered[col] = converted\n print(\"=======================\")\n new[\"new_id\"] = new_id\n df_filtered[col] = df_filtered[col].replace(new.index,new.new_id)\nprint(\"All converted attributes: \")\nprint(first_filtered)\ndf_filtered", "type\n{'Unknown': 0, 'Music': 1, 'ONA': 2, 'Special': 3, 'Movie': 4, 'OVA': 5, 'TV': 6}\n=======================\nsource\n{'Radio': 0, 'Digital manga': 1, 'Card game': 2, 'Book': 3, 'Picture book': 4, 'Web manga': 5, '4-koma manga': 6, 'Music': 7, 'Novel': 8, 'Other': 9, 'Light novel': 10, 'Game': 11, 'Visual novel': 12, 'Manga': 13, 'Original': 14, 'Unknown': 15}\n=======================\nstatus\n{'Not yet aired': 0, 'Currently Airing': 1, 'Finished Airing': 2}\n=======================\nairing\n{True: 0, False: 1}\n=======================\nrating\n{'None': 0, 'R+ - Mild Nudity': 1, 'R - 17+ (violence & profanity)': 2, 'Rx - Hentai': 3, 'PG - Children': 4, 'G - All Ages': 5, 'PG-13 - Teens 13 or older': 6}\n=======================\nAll converted attributes: \n{'type': {'Unknown': 0, 'Music': 1, 'ONA': 2, 'Special': 3, 'Movie': 4, 'OVA': 5, 'TV': 6}, 'source': {'Radio': 0, 'Digital manga': 1, 'Card game': 2, 'Book': 3, 'Picture book': 4, 'Web manga': 5, '4-koma manga': 6, 'Music': 7, 'Novel': 8, 'Other': 9, 'Light novel': 10, 'Game': 11, 'Visual novel': 12, 'Manga': 13, 'Original': 14, 'Unknown': 15}, 'status': {'Not yet aired': 0, 'Currently Airing': 1, 'Finished Airing': 2}, 'airing': {True: 0, False: 1}, 'rating': {'None': 0, 'R+ - Mild Nudity': 1, 'R - 17+ (violence & profanity)': 2, 'Rx - Hentai': 3, 'PG - Children': 4, 'G - All Ages': 5, 'PG-13 - Teens 13 or older': 6}}\n" ], [ "# Clean licensor column\nnew_license = []\na = pd.DataFrame(df_filtered.licensor.value_counts())\na.index.name = \"lisence_id\"\nfor count in a.licensor:\n if count < 11:\n new_license.append(1)\n elif 10 < count < 50:\n new_license.append(2)\n elif count == 11105:\n new_license.append(0)\n else:\n new_license.append(3)\na['new_license'] = new_license\ndf_filtered['licensor'] = df_filtered['licensor'].replace(a.index, a.new_license)\ndf_filtered", "_____no_output_____" ], [ "df_filtered.licensor.unique()", "_____no_output_____" ], [ "# Separate genres to columns\nfeatures = pd.concat([df_filtered[\"genre\"].str.get_dummies(sep=\", \")],axis=1)\nfeatures_cols = list(features.columns)\nfor feature_col in features_cols:\n df_filtered[feature_col] = features[feature_col]\ndf_filtered", "_____no_output_____" ], [ "# Convert duration column to number\nimport re\n\nnew_duration = []\nfor time in df_filtered.duration:\n test_string = time\n temp = re.findall(r'\\d+', test_string) \n res = list(map(int, temp))\n if len(res) == 2:\n n = res[1] + 60 * res[0]\n new_duration.append(n)\n elif len(res) == 0:\n new_duration.append(0)\n else:\n new_duration.append(res[0])\ndf_filtered['duration'] = new_duration\ndf_filtered['duration'] = df_filtered.duration.mask(df_filtered.duration == 0, df_filtered['duration'].mean(skipna=True))\ndf_filtered", "_____no_output_____" ], [ "# Convert Premiered Column to Year column and Season Column\nnew_year = []\nseasons = []\nfor time in df_filtered.premiered:\n test_string = str(time)\n temp = re.findall(r'\\d+', test_string) \n res = list(map(int, temp))\n if len(res) == 0:\n new_year.append(0)\n seasons.append(time)\n else:\n new_year.append(res[0])\n seasons.append(str(time).replace(str(res[0]), ''))\n\ndf_filtered['year'] = new_year\ndf_filtered['season'] = seasons\ndf_filtered", "_____no_output_____" ], [ "cols_id = list(df_filtered.columns)\ndf_model = df_filtered[['title']]\ndf_not_use = df_filtered[['title']]\nfor col in cols_id:\n try:\n float(df_filtered[col][0])\n df_model[col] = df_filtered[col]\n except:\n df_not_use[col] = df_filtered[col]\ndf_model.set_index('title')\ndf_not_use.set_index('title')\ndf_model", "/usr/local/share/anaconda3/lib/python3.7/site-packages/ipykernel_launcher.py:9: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n if __name__ == '__main__':\n/usr/local/share/anaconda3/lib/python3.7/site-packages/ipykernel_launcher.py:7: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n import sys\n" ], [ "# I can see that there are some 0 values in episodes column\ndf_noeps = df_model[df_model.episodes == 0]\ndf_noeps.head()", "_____no_output_____" ], [ "# I can see that there are some 0 values in Score column as well\ndf_noscores = df_model[df_model.score == 0]\ndf_noscores.head()", "_____no_output_____" ], [ "# Now i see that in the episodes column and the rating column has some 0 values. Therefore, I tried to find an API\n# called Encyclopedia API to update some missing episodes and ratings values", "_____no_output_____" ], [ "# Check eps and rating for anime Jinki:Extend\n\nimport xml.etree.ElementTree as ET\nimport urllib.request\nfrom xml.etree.ElementTree import fromstring, ElementTree\n\nurl = \"https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime=4658\"\nresponse = urllib.request.urlopen(url).read()\nresponse = response.decode('utf-8')\ntree = ET.fromstring(response)\nfor child in tree:\n element = child.findall('episode')\n print(\"Number of eps: \"+ str(len(element)))\n element = child.find('ratings').attrib\n print(\"Rating: \" + str(element[\"weighted_score\"]))\n ", "Number of eps: 13\nRating: 5.9563\n" ], [ "df_report = pd.read_csv('report.csv')\nanime_id = pd.DataFrame(df_report[['id', 'name']])\nname_ls = list(anime_id.name)\nanime_id.head()", "_____no_output_____" ], [ "# Check for similar missing episodes anime in my data compare to those of their data \n# and update to a new dataframe called update_eps\ndf_report = pd.read_csv('report.csv')\nanime_id = pd.DataFrame(df_report[['id', 'name']])\nname_ls = list(anime_id.name)\nanime_id = anime_id.set_index(['name'])\n\nsimilar_eps = []\neps = []\ncount = 0\nfor n in df_noeps.title:\n url = \"https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime=\"\n if n in name_ls and n != 0:\n similar_eps.append(n)\n try:\n int(anime_id.loc[[n]].id[0])\n new_id = int(anime_id.loc[[n]].id[0])\n url += str(new_id)\n\n response = urllib.request.urlopen(url).read()\n response = response.decode('utf-8')\n tree = ET.fromstring(response)\n for child in tree:\n element = child.findall('episode')\n eps.append(len(element))\n if len(element) != 0:\n count += 1\n except:\n similar_eps.remove(n)\n continue\nupdate_eps = pd.DataFrame(eps, similar_eps, columns = [\"episodes\"])\nprint(str(count) + \" of the missing episodes have been updated\")\nupdate_eps.sort_values(by=[\"episodes\"], ascending = False).head()", "11 of the missing episodes have been updated\n" ], [ "# Check for similar missing scores anime in my data compare to those of their data \n# and update to a new dataframe called update_scores\ndf_report = pd.read_csv('report.csv')\nanime_id = pd.DataFrame(df_report[['id', 'name']])\nname_ls = list(anime_id.name)\nanime_id = anime_id.set_index(['name'])\n\nsimilar_scores = []\nscores = []\ncount = 0\nfor n in df_noscores.title:\n url = \"https://cdn.animenewsnetwork.com/encyclopedia/api.xml?anime=\"\n if n in name_ls and n != 0:\n similar_scores.append(n)\n try:\n int(anime_id.loc[[n]].id[0])\n new_id = int(anime_id.loc[[n]].id[0])\n url += str(new_id)\n\n response = urllib.request.urlopen(url).read()\n response = response.decode('utf-8')\n tree = ET.fromstring(response)\n for child in tree:\n element = child.find('ratings').attrib\n scores.append(float(element[\"weighted_score\"]))\n if float(element[\"weighted_score\"]):\n count += 1\n except:\n similar_scores.remove(n)\n continue\nupdate_scores = pd.DataFrame(scores, similar_scores, columns = ['score'])\nprint(str(count) + \" of the missing scores have been updated\")\nupdate_scores.sort_values(by=['score'], ascending = False).head()", "35 of the missing scores have been updated\n" ], [ "# Now Use the new found values to update the model dataFrame.\nfor name in df_model.title:\n if name in similar_eps:\n df_model.loc[(df_model[\"title\"]==name) & (df_model[\"episodes\"]==0),\"episodes\"] = update_eps.loc[name, \"episodes\"]\n if name in similar_scores:\n df_model.loc[(df_model[\"title\"]==name) & (df_model[\"score\"]==0),\"score\"] = update_scores.loc[name, \"score\"]\n \n# For the remaining 0 episodes anime, I change them to 12 which is an average number of episodes per anime season\ndf_model['episodes']=df_model.episodes.mask(df_model.episodes == 0, 12)", "/usr/local/share/anaconda3/lib/python3.7/site-packages/pandas/core/indexing.py:543: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n self.obj[item] = s\n/usr/local/share/anaconda3/lib/python3.7/site-packages/ipykernel_launcher.py:9: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n if __name__ == '__main__':\n" ], [ "df_not_use.drop(['genre', 'premiered'], axis=1).head()", "_____no_output_____" ], [ "# At this point we have a dataset for model called df_model and the remaining unused dataset called df_not_use", "_____no_output_____" ], [ "# KNN model application", "_____no_output_____" ], [ "# KNN with KNeighborsClassifier to predict anime Score\n# To use scikit-learn library, we have to convert the Pandas data frame to a Numpy array:\n# For this model, I round the score column to integers instead of floats\nscores = []\nfor score in df_model.score:\n scores.append(round(score))\nY = pd.DataFrame(scores)\n\ndf_model1 = df_model\ndf_model2 = df_model\nuse_cols = list(df_model1.columns)\nif 'score' in use_cols:\n use_cols.remove('score')\nif 'title' in use_cols:\n use_cols.remove('title')\nX = df_model1[use_cols].values #.astype(float)\nX[0:5]\ny = Y[0].values\ny[0:5]", "_____no_output_____" ], [ "#Normalize Data\nx = preprocessing.StandardScaler().fit(X).transform(X.astype(float))\nx[0:2]", "_____no_output_____" ], [ "#Train Test Split\nfrom sklearn.model_selection import train_test_split\nX_train, X_test, y_train, y_test = train_test_split( x, y, test_size=0.2, random_state=4)\nprint ('Train set:', X_train.shape, y_train.shape)\nprint ('Test set:', X_test.shape, y_test.shape)", "Train set: (11582, 58) (11582,)\nTest set: (2896, 58) (2896,)\n" ], [ "#K nearest neighbor (K-NN)\nfrom sklearn.neighbors import KNeighborsClassifier\nk = 7\n#Train Model and Predict \nneigh = KNeighborsClassifier(n_neighbors = k, algorithm='auto').fit(X_train,y_train)\nneigh", "_____no_output_____" ], [ "#Predicting\nyhat = neigh.predict(X_test)\nyhat[0:5]", "_____no_output_____" ], [ "#Accuracy evaluation\nfrom sklearn import metrics\nprint(\"Train set Accuracy: \", metrics.accuracy_score(y_train, neigh.predict(X_train)))\nprint(\"Test set Accuracy: \", metrics.accuracy_score(y_test, yhat))", "Train set Accuracy: 0.6616301156967709\nTest set Accuracy: 0.5345303867403315\n" ], [ "#K value\nKs = 10\nmean_acc = np.zeros((Ks-1))\nstd_acc = np.zeros((Ks-1))\nConfustionMx = [];\nfor n in range(1,Ks):\n \n #Train Model and Predict \n neigh = KNeighborsClassifier(n_neighbors = n).fit(X_train,y_train)\n yhat=neigh.predict(X_test)\n mean_acc[n-1] = metrics.accuracy_score(y_test, yhat)\n\n \n std_acc[n-1]=np.std(yhat==y_test)/np.sqrt(yhat.shape[0])\n\nmean_acc", "_____no_output_____" ], [ "#Plot model accuracy for Different number of Neighbors\nplt.plot(range(1,Ks),mean_acc,'g')\nplt.fill_between(range(1,Ks),mean_acc - 1 * std_acc,mean_acc + 1 * std_acc, alpha=0.10)\nplt.legend(('Accuracy ', '+/- 3xstd'))\nplt.ylabel('Accuracy ')\nplt.xlabel('Number of Neighbors (K)')\nplt.tight_layout()\nplt.show()", "_____no_output_____" ], [ "print( \"The best accuracy was with\", mean_acc.max(), \"with k=\", mean_acc.argmax()+1)", "The best accuracy was with 0.5355662983425414 with k= 1\n" ], [ "# Apply Nearest Neighbor model for recommendation", "_____no_output_____" ], [ "from sklearn.neighbors import NearestNeighbors", "_____no_output_____" ], [ "X", "_____no_output_____" ], [ "# Here I use the Nearest Neighbor model to find the nearest 5 similar animes \n# (closest distances between the animes' attributes)\nrec_neigh = NearestNeighbors(n_neighbors=6, algorithm='auto').fit(X)\ndistances, indexs = rec_neigh.kneighbors(X)", "_____no_output_____" ], [ "# Return the Index of the anime if its name is given in full\n# Warning, the name has to be exact, even the upper case letters.\ndef full_id(name):\n try:\n df_model1[df_model1[\"title\"] == name].index.tolist()[0]\n return df_model1[df_model1[\"title\"] == name].index.tolist()[0]\n except:\n return \"This is not a valid full name\"\n\nall_names = list(df_model1.title.values)\n\n# If you only know a part of the anime name, you can get the list of possible full anime names, \n# The input can be lower case\ndef part_id(part):\n for name in all_names:\n if part.lower() in name.lower():\n print(name, all_names.index(name))", "_____no_output_____" ], [ "# Can get similar animes with input of anime name or anime index\n\ndef similar_animes(query=None,id=None):\n if id:\n for id in indexs[id][1:]:\n print(df_model1.iloc[id][\"title\"])\n if query:\n found_id = full_id(query)\n if found_id == \"This is not a valid full name\":\n print(found_id)\n else:\n for id in indexs[found_id][1:]:\n print(df_model1.iloc[id][\"title\"])", "_____no_output_____" ], [ "similar_animes(query=\"Naruto\")", "No Game No Life\nAngel Beats!\nTokyo Ghoul\nCode Geass: Hangyaku no Lelouch\nMirai Nikki (TV)\n" ], [ "# It's well known that Naruto is a very popular anime, therefore, the 5 recommended options are very popular as well and\n# some of them has many episodes and series such as Tokyo Ghoul and Code Geass with lots of fighting scenes.\n# Personally, I would really recommend Angle Beats - a very touching anime", "_____no_output_____" ], [ "# When I put in a strange anime name it will cause error\nsimilar_animes(query=\"Slime\")", "This is not a valid full name\n" ], [ "# Therefore I check the available names for \"slime\"\npart_id(\"slime\")", "Slime Boukenki: Umi da, Yeah! 1090\nTensei shitara Slime Datta Ken 3072\n" ], [ "# After copy paste the name, it works!!\nsimilar_animes(query=\"Slime Boukenki: Umi da, Yeah!\")", "Mugen no Ryvius: Illusion\nMorinaga Nyuugyou x Mary to Majo no Hana\nKingdom of Chaos: Born to Kill\nFushigi na Somera-chan Special\nBamboo Blade: CM Fanfu-Fufe-Fo\n" ], [ "# Now I will set up random user response to predict an anime score", "_____no_output_____" ], [ "# Some of the string attributes are categorized to numbers\nprint(first_filtered)", "{'type': {'Unknown': 0, 'Music': 1, 'ONA': 2, 'Special': 3, 'Movie': 4, 'OVA': 5, 'TV': 6}, 'source': {'Radio': 0, 'Digital manga': 1, 'Card game': 2, 'Book': 3, 'Picture book': 4, 'Web manga': 5, '4-koma manga': 6, 'Music': 7, 'Novel': 8, 'Other': 9, 'Light novel': 10, 'Game': 11, 'Visual novel': 12, 'Manga': 13, 'Original': 14, 'Unknown': 15}, 'status': {'Not yet aired': 0, 'Currently Airing': 1, 'Finished Airing': 2}, 'airing': {True: 0, False: 1}, 'rating': {'None': 0, 'R+ - Mild Nudity': 1, 'R - 17+ (violence & profanity)': 2, 'Rx - Hentai': 3, 'PG - Children': 4, 'G - All Ages': 5, 'PG-13 - Teens 13 or older': 6}}\n" ], [ "print(first_filtered.keys())", "dict_keys(['type', 'source', 'status', 'airing', 'rating'])\n" ], [ "user_qs = []\nfor key in use_cols:\n if key == \"0\":\n break\n user_qs.append(key)\nprint(user_qs)", "['type', 'source', 'episodes', 'status', 'airing', 'duration', 'rating', 'scored_by', 'rank', 'popularity', 'members', 'favorites', 'licensor']\n" ], [ "genres = []\nfor key in use_cols:\n if key not in user_qs:\n genres.append(key)\ngenres.remove('year')\nprint(genres)", "['0', 'Action', 'Adventure', 'Cars', 'Comedy', 'Dementia', 'Demons', 'Drama', 'Ecchi', 'Fantasy', 'Game', 'Harem', 'Hentai', 'Historical', 'Horror', 'Josei', 'Kids', 'Magic', 'Martial Arts', 'Mecha', 'Military', 'Music', 'Mystery', 'Parody', 'Police', 'Psychological', 'Romance', 'Samurai', 'School', 'Sci-Fi', 'Seinen', 'Shoujo', 'Shoujo Ai', 'Shounen', 'Shounen Ai', 'Slice of Life', 'Space', 'Sports', 'Super Power', 'Supernatural', 'Thriller', 'Vampire', 'Yaoi', 'Yuri']\n" ], [ "# Here are the attributes for the user to input\nprint(use_cols)", "['type', 'source', 'episodes', 'status', 'airing', 'duration', 'rating', 'scored_by', 'rank', 'popularity', 'members', 'favorites', 'licensor', '0', 'Action', 'Adventure', 'Cars', 'Comedy', 'Dementia', 'Demons', 'Drama', 'Ecchi', 'Fantasy', 'Game', 'Harem', 'Hentai', 'Historical', 'Horror', 'Josei', 'Kids', 'Magic', 'Martial Arts', 'Mecha', 'Military', 'Music', 'Mystery', 'Parody', 'Police', 'Psychological', 'Romance', 'Samurai', 'School', 'Sci-Fi', 'Seinen', 'Shoujo', 'Shoujo Ai', 'Shounen', 'Shounen Ai', 'Slice of Life', 'Space', 'Sports', 'Super Power', 'Supernatural', 'Thriller', 'Vampire', 'Yaoi', 'Yuri', 'year']\n" ], [ "# Use random to random the user response invarious categories: 'type', 'source', 'status', 'airing', 'rating' and the genres\n# The remaining attributes' default value would be the column's mean value, the anime year is set to 2017\nimport random\nimport numpy\n\nuser_response = {}\ngen_choice = random.randint(1, 5)\ngen_str = \"\"\nfor choice in range(gen_choice):\n gen_str += \", \"\n gen_str += str(random.choice(genres))\ngen_default = []\nfor gen in genres:\n if gen in gen_str:\n gen_default.append(1)\n else:\n gen_default.append(0)\nresponse_default = []\nfor qs in use_cols:\n if qs not in user_qs:\n break\n if qs in first_filtered.keys():\n key_list = list(first_filtered[qs].keys()) \n val_list = list(first_filtered[qs].values()) \n first = random.choice(val_list)\n response_default.append(first)\n user_response[qs] = key_list[val_list.index(first)]\n else:\n response_default.append(df_model1[qs].mean())\n user_response[qs] = df_model1[qs].mean()\nresponse_default.extend(gen_default)\nresponse_default.append(2017)\nuser_response['genre'] = gen_str\nuser_response['year'] = 2017\nprint(\"User input is:\")\nprint(\"\")\nprint(user_response)", "User input is:\n\n{'type': 'TV', 'source': 'Picture book', 'episodes': 12.003246304738223, 'status': 'Finished Airing', 'airing': True, 'duration': 26.237322491727266, 'rating': 'PG - Children', 'scored_by': 11460.02527973477, 'rank': 5739.031634203619, 'popularity': 7220.259566238431, 'members': 22966.402679928167, 'favorites': 311.6496062992126, 'licensor': 0.6075424782428512, 'genre': ', Yaoi, Historical, Space, Parody', 'year': 2017}\n" ], [ "# Return the anime score from the input\ndf2 = pd.DataFrame([response_default], columns=use_cols)\ndf_test = df_model1.append(df2, sort = True)\nX_test = df_test[use_cols].values\nx_test = preprocessing.StandardScaler().fit(X_test).transform(X_test.astype(float))\nscore = neigh.predict([x_test[len(x_test) - 1]])\nprint(\"The predicted anime score is: \" + str(score))", "The predicted anime score is: [7]\n" ], [ "# Here, an anime about Historical and Space for children which originate from Picture book has a decent score (7)\n# This makes sense because this anime seems to be very interesting for children \n# and would attract lots of viewers for education material", "_____no_output_____" ], [ "# Use random to random the user response invarious categories: 'type', 'source', 'status', 'airing', 'rating' and the genres\n# The remaining attributes' default value would be the column's mean value, the anime year is set to 2017\nimport random\nimport numpy\n\nuser_response = {}\ngen_choice = random.randint(1, 5)\ngen_str = \"\"\nfor choice in range(gen_choice):\n gen_str += \", \"\n gen_str += str(random.choice(genres))\ngen_default = []\nfor gen in genres:\n if gen in gen_str:\n gen_default.append(1)\n else:\n gen_default.append(0)\nresponse_default = []\nfor qs in use_cols:\n if qs not in user_qs:\n break\n if qs in first_filtered.keys():\n key_list = list(first_filtered[qs].keys()) \n val_list = list(first_filtered[qs].values()) \n first = random.choice(val_list)\n response_default.append(first)\n user_response[qs] = key_list[val_list.index(first)]\n else:\n response_default.append(df_model1[qs].mean())\n user_response[qs] = df_model1[qs].mean()\nresponse_default.extend(gen_default)\nresponse_default.append(2017)\nuser_response['genre'] = gen_str\nuser_response['year'] = 2017\nprint(\"User input is:\")\nprint(\"\")\nprint(user_response)", "User input is:\n\n{'type': 'TV', 'source': 'Unknown', 'episodes': 12.003246304738223, 'status': 'Not yet aired', 'airing': True, 'duration': 26.237322491727266, 'rating': 'Rx - Hentai', 'scored_by': 11460.02527973477, 'rank': 5739.031634203619, 'popularity': 7220.259566238431, 'members': 22966.402679928167, 'favorites': 311.6496062992126, 'licensor': 0.6075424782428512, 'genre': ', Music', 'year': 2017}\n" ], [ "# Return the anime score from the input\ndf2 = pd.DataFrame([response_default], columns=use_cols)\ndf_test = df_model1.append(df2, sort = True)\nX_test = df_test[use_cols].values\nx_test = preprocessing.StandardScaler().fit(X_test).transform(X_test.astype(float))\nscore = neigh.predict([x_test[len(x_test) - 1]])\nprint(\"The predicted anime score is: \" + str(score))", "The predicted anime score is: [4]\n" ], [ "# Here the anime that has an Unknown source with Music genre and has Rx-Hentai rate (censored info related) has a low score (4)\n# This makes sense because it doesn't sound appealing to watch a porn anime that has music in it", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e56d831316e0fb2d79b3acd7b45603d9f790aa

7,438

ipynb

Jupyter Notebook

Expressions_and_Operations.ipynb

EJ-Capito/CPEN-21A-ECE-2-3

f248d986cb308e9d02fa4e7490bd0c74b4ccb285

[ "Apache-2.0" ]

null

Expressions_and_Operations.ipynb

EJ-Capito/CPEN-21A-ECE-2-3

f248d986cb308e9d02fa4e7490bd0c74b4ccb285

[ "Apache-2.0" ]

null

Expressions_and_Operations.ipynb

EJ-Capito/CPEN-21A-ECE-2-3

f248d986cb308e9d02fa4e7490bd0c74b4ccb285

[ "Apache-2.0" ]

null

21.312321

249

0.379538

[ [ [ "<a href=\"https://colab.research.google.com/github/EJ-Capito/CPEN-21A-ECE-2-3/blob/main/Expressions_and_Operations.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "##Boolean Operators\n", "_____no_output_____" ] ], [ [ "a=1\nb=2\n\nprint(a>b)\nprint(a<b)\nprint(a==b)\nprint(a!=b)", "False\nTrue\nFalse\nTrue\n" ] ], [ [ "##bool() function", "_____no_output_____" ] ], [ [ "print(bool(15))\nprint(bool(True))\nprint(bool(1))\n\nprint(bool(False))\nprint(bool(0))\nprint(bool(None))\nprint(bool([]))", "True\nTrue\nTrue\nFalse\nFalse\nFalse\nFalse\n" ] ], [ [ "##Functions return a Boolean", "_____no_output_____" ] ], [ [ "def myFunction():return False\n\nif myFunction():\n print(\"True\")\nelse:\n print(\"False\")", "False\n" ] ], [ [ "##Arithmetic Operator", "_____no_output_____" ] ], [ [ "print(10>9)\nprint(10<9)\nprint(10==9)\n\nprint(10+5)\nprint(10-5)\nprint(10*5)\nprint(10/5)\nprint(10%5)\nprint(10//3)\nprint(10**2)", "True\nFalse\nFalse\n15\n5\n50\n2.0\n0\n3\n100\n" ] ], [ [ "##Bitwise operators", "_____no_output_____" ] ], [ [ "a=60 #0011 1100\nb=13 #0000 1101\n\nprint(a & b)\nprint(a | b)\nprint(a^b)\n\nprint(a<<2) #0011 1100\nprint(a>>1) #0000 1101", "12\n61\n49\n240\n30\n" ] ], [ [ "##Assignment Operator", "_____no_output_____" ] ], [ [ "a+=3 #Same as a=a+3, a=60+3, a=63\nprint(a)", "63\n" ] ], [ [ "##Logical Operator", "_____no_output_____" ] ], [ [ "a = True\nb = False\n\nprint(a and b)\nprint(a or b)\nprint(not(a or b))\n\nprint(a > b and b > a)\nprint(a==a or b==b)\nprint(not(a==a or b==b))", "False\nTrue\nFalse\nFalse\nTrue\nFalse\n" ] ], [ [ "##Identify Operators", "_____no_output_____" ] ], [ [ "print(a is b)\nprint(a is not b)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e56ff3cdb53099dd199b2acb2e524b438bf6b1

22,165

ipynb

Jupyter Notebook

MNIST_data_set_with_pure_Convolution.ipynb

Jyotiranjan404/Pure-CNN-using-MNIST-dataset

9bb4959b69e2d3fe0c734f15ddb46b9f635f69fb

[ "Apache-2.0" ]

null

MNIST_data_set_with_pure_Convolution.ipynb

Jyotiranjan404/Pure-CNN-using-MNIST-dataset

9bb4959b69e2d3fe0c734f15ddb46b9f635f69fb

[ "Apache-2.0" ]

null

MNIST_data_set_with_pure_Convolution.ipynb

Jyotiranjan404/Pure-CNN-using-MNIST-dataset

9bb4959b69e2d3fe0c734f15ddb46b9f635f69fb

[ "Apache-2.0" ]

null

45.795455

188

0.498308

[ [ [ "import pandas as pd\nimport numpy as np\nimport tensorflow as tf\nfrom tensorflow.keras.models import Sequential\nfrom tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout,Activation,BatchNormalization\nfrom tensorflow.keras.callbacks import ModelCheckpoint \nimport matplotlib.pyplot as plt\n%matplotlib inline\nimport seaborn as sns \nimport keras\nfrom keras.utils import np_utils\nfrom tensorflow.keras.datasets import mnist", "_____no_output_____" ], [ "(X_train, y_train), (X_test, y_test) = mnist.load_data()", "_____no_output_____" ], [ "print(len(X_train))\nprint(len(X_test))", "60000\n10000\n" ], [ "X_train = X_train.astype('float32')/255 #Scaling the data\nX_test = X_test.astype('float32')/255 \n\nprint('X_train shape:', X_train.shape)\nprint(X_train.shape[0], '=train samples')\nprint(X_test.shape[0], '=test samples')", "X_train shape: (60000, 28, 28)\n60000 =train samples\n10000 =test samples\n" ], [ "num_classes = 10 \n# print first ten (integer-valued) training labels\nprint('Integer-valued labels:')\nprint(y_train[:10])\n\n# one-hot encode the labels\n# convert class vectors to binary class matrices\ny_train = np_utils.to_categorical(y_train, num_classes)\ny_test = np_utils.to_categorical(y_test, num_classes)\n\n# print first ten (one-hot) training labels\nprint('One-hot labels:')\nprint(y_train[:10])", "Integer-valued labels:\n[5 0 4 1 9 2 1 3 1 4]\nOne-hot labels:\n[[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]\n [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]\n [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]\n [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]\n [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]\n [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]\n" ], [ "img_rows, img_cols = 28, 28\n\nX_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)\nX_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)\ninput_shape = (img_rows, img_cols, 1)\n\nprint('input_shape: ', input_shape)\nprint('x_train shape:', X_train.shape)", "input_shape: (28, 28, 1)\nx_train shape: (60000, 28, 28, 1)\n" ], [ "model = Sequential()\nmodel.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu', input_shape=(28,28,1))) #26\n\nmodel.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #24 \nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\nmodel.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) # 22\nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\nmodel.add(MaxPooling2D(pool_size=(2, 2))) #11\n\nmodel.add(Conv2D(filters=16,kernel_size=(3,3), activation='relu')) # 9\nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\nmodel.add(Conv2D(filters=10,kernel_size=(1,1), activation='relu')) # 9\nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\nmodel.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #7 \nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\n \nmodel.add(Conv2D(filters=10,kernel_size=(3,3), activation='relu')) #5 \nmodel.add(BatchNormalization())\nmodel.add(Dropout(0.1))\n\n\nmodel.add(Conv2D(filters=10,kernel_size=(5,5))) #1 \n\nmodel.add(Flatten())\nmodel.add(Activation('softmax'))\nmodel.summary()", "Model: \"sequential_2\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\nconv2d_15 (Conv2D) (None, 26, 26, 10) 100 \n_________________________________________________________________\nconv2d_16 (Conv2D) (None, 24, 24, 10) 910 \n_________________________________________________________________\nbatch_normalization_11 (Batc (None, 24, 24, 10) 40 \n_________________________________________________________________\ndropout_11 (Dropout) (None, 24, 24, 10) 0 \n_________________________________________________________________\nconv2d_17 (Conv2D) (None, 22, 22, 10) 910 \n_________________________________________________________________\nbatch_normalization_12 (Batc (None, 22, 22, 10) 40 \n_________________________________________________________________\ndropout_12 (Dropout) (None, 22, 22, 10) 0 \n_________________________________________________________________\nmax_pooling2d_2 (MaxPooling2 (None, 11, 11, 10) 0 \n_________________________________________________________________\nconv2d_18 (Conv2D) (None, 9, 9, 16) 1456 \n_________________________________________________________________\nbatch_normalization_13 (Batc (None, 9, 9, 16) 64 \n_________________________________________________________________\ndropout_13 (Dropout) (None, 9, 9, 16) 0 \n_________________________________________________________________\nconv2d_19 (Conv2D) (None, 9, 9, 10) 170 \n_________________________________________________________________\nbatch_normalization_14 (Batc (None, 9, 9, 10) 40 \n_________________________________________________________________\ndropout_14 (Dropout) (None, 9, 9, 10) 0 \n_________________________________________________________________\nconv2d_20 (Conv2D) (None, 7, 7, 10) 910 \n_________________________________________________________________\nbatch_normalization_15 (Batc (None, 7, 7, 10) 40 \n_________________________________________________________________\ndropout_15 (Dropout) (None, 7, 7, 10) 0 \n_________________________________________________________________\nconv2d_21 (Conv2D) (None, 5, 5, 10) 910 \n_________________________________________________________________\nbatch_normalization_16 (Batc (None, 5, 5, 10) 40 \n_________________________________________________________________\ndropout_16 (Dropout) (None, 5, 5, 10) 0 \n_________________________________________________________________\nconv2d_22 (Conv2D) (None, 1, 1, 10) 2510 \n_________________________________________________________________\nflatten_2 (Flatten) (None, 10) 0 \n_________________________________________________________________\nactivation_2 (Activation) (None, 10) 0 \n=================================================================\nTotal params: 8,140\nTrainable params: 8,008\nNon-trainable params: 132\n_________________________________________________________________\n" ], [ "def scheduler(epoch, lr):\n return round(0.003 * 1/(1 + 0.319 * epoch), 10)\nmodel.compile(loss='categorical_crossentropy', optimizer=tf.keras.optimizers.Adam(lr=0.003), metrics=['accuracy'])\nmodel.fit(X_train, y_train, batch_size=128, epochs=30, verbose=1, validation_data=(X_test, y_test),\n callbacks=[tf.keras.callbacks.LearningRateScheduler(scheduler, verbose=1)])", "/usr/local/lib/python3.7/dist-packages/tensorflow/python/keras/optimizer_v2/optimizer_v2.py:375: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead.\n \"The `lr` argument is deprecated, use `learning_rate` instead.\")\n" ] ], [ [ "Here i run for 30 epochs but in 25 epcohs i got validation accuracy as 99.40%.", "_____no_output_____" ] ], [ [ "", "_____no_output_____" ] ] ]

[ "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e5726309d82938b3d6c01826b590e16046d7f4

11,476

ipynb

Jupyter Notebook

generate_attack_tree_graph.ipynb

gdusan/attack-trees

03876769691f36ab23c892e3ad921518009fd4f8

[ "MIT" ]

null

generate_attack_tree_graph.ipynb

gdusan/attack-trees

03876769691f36ab23c892e3ad921518009fd4f8

[ "MIT" ]

null

generate_attack_tree_graph.ipynb

gdusan/attack-trees

03876769691f36ab23c892e3ad921518009fd4f8

[ "MIT" ]

null

38

118

0.457564

[ [ [ "import collections\nimport json\nimport pprint\nfrom datetime import datetime\nimport pandas as pd\n\n# Notebook to generate attack tree Graphviz file and Emacs Org mode\n# table for attack tree analysis configuration. The input is itemized\n# list of attack tree nodes with mark modifiers.\n\n# Should use Python3.4+\n\n# Name of the attack tree itemized input\ntf = 'at/at-gather-intelligence-about.org'\n# Prefix for the scenario\nprefix = 'N'\n# Not important, internal to grahviz\ncluster_prefix = 'T'\nstep = 2\ntab = 8\ntest = ''\n# Output Graphviz or/and Org table\norg = False\ngraphviz = True\n##### Graphviz params\n## Shape\n#gshape = 'octagon'\n#style=''\ngshape = 'box'\nstyle='rounded'\n\n# Tree implementation, Python magic\ndef tree(): return collections.defaultdict(tree)\n\ndef add_tree(t, keys):\n \"\"\"\n Add elements to the tree\n\n t: tree\n keys: list of elements\n \"\"\"\n for key in keys:\n t = t[key]\n\ndef print_tree(t):\n print(json.dumps(t, indent=2, sort_keys=True))\n \ndef leaf_nodes(tree, k='', current=''):\n \"\"\"\n Finds tree leaf nodes, yields node identifiers build/concatenated\n on the fly\n\n k and current are important only for recursive calls\n yields concatenated node identifiers\n \"\"\"\n current += '.' + k\n path = current.lstrip('.')\n if not tree.keys() and path != '':\n yield path\n for k in tree.keys():\n yield from leaf_nodes(tree[k], k, current)\n\n\n# Open org input file\nwith open(tf) as f:\n test = f.readlines()\n\n#### Itemize list input \nbranches = [] \nlevels = [] \nst = []\n\n# Parse simple/limited org input\n# - st: list of lists, each list has two elements, one the concatenated\n# levels and the other the description of the node\n# - branches: list of branches of the tree, used to build the tree\nfor l in test:\n # Modifiers\n or_join = True\n horizontal = True\n double = False\n triple = False\n red = False\n l = l.strip('\\n')\n l = l.replace('\\t', ' '*tab)\n n = l.split('-')\n if len(n) == 1:\n if st:\n st[-1][1] = st[-1][1] + ' ' + n[0].lstrip()\n continue\n level = int(len(n[0])/step)\n if level == 0:\n pass\n elif level > len(levels):\n levels.append(1)\n elif level == len(levels):\n levels[-1] += 1\n elif level < len(levels):\n levels = levels[:level]\n levels[-1] += 1\n # Parse the label string for the modifiers\n label = n[1].lstrip().rstrip()\n ls = label.split(' ')\n if ls[-1].find('[') >= 0:\n mod = ls[-1]\n # print('found modifier %s' % mod)\n mod = mod.lstrip('[').rstrip(']')\n if len(mod) >= 1 and mod[0] == 'a':\n or_join = False\n if len(mod) >= 2 and mod[1] == 'v':\n horizontal = False\n if mod.find('!') >= 0:\n double = True\n if mod.find('*') >= 0:\n red = True\n # print('modifier join:%s, direction:%s' % (or_join, horizontal))\n label = ' '.join(ls[:-1])\n e = []\n e.append('.'.join(map(str, levels)))\n e.append(label)\n e.append([or_join, horizontal, double, red, triple])\n branches.append('.'.join(map(str, levels)).split('.'))\n st.append(e)\n\n# Fill the tree, uses Python magic \ntr = tree()\nfor b in branches:\n add_tree(tr, b)\n\n# Remove ORs on leaf nodes, subsuboptimal\nfor l in leaf_nodes(tr):\n for e in st:\n if e[0] == l:\n e[2][0] = None\n\n# Build a mapper between the levels and the names\n# Build the list of tree nodes\nat_nodes_mapper = {}\nat_mod_mapper = {}\nat_nodes = [] \nfor e in st:\n den = e[0]\n if not e[0]:\n den = 0\n name = '%s_%s' % (prefix, den)\n label = '<<FONT POINT-SIZE=\"9\">%s<br/>%s</FONT>>' % (prefix, den)\n st = style\n# label = '\\\"%s\\\\n%s\\\"' % (prefix, den)\n (or_join, horizontal, double, red, triple) = e[2]\n template = '\"%s\" [shape=%s, label=%s, label=\"%s\", xlabel=%s];'\n if double:\n template = '\"%s\" [shape=%s, style=%s, peripheries=2, label=\"%s\", xlabel=%s];' \n# template = '\"%s\" [shape=doubleoctagon, label=\"%s\", xlabel=\"%s\"];'\n if red:\n if st:\n st = \"\\\"%s,filled\\\"\" % st\n else:\n st = 'filled' \n template = '\"%s\" [shape=%s, style=%s, fillcolor=red, label=\"%s\", xlabel=%s];'\n at_nodes.append(template % (name, gshape, st, e[1], label))\n at_nodes_mapper[den] = name\n at_mod_mapper[den] = e[2]\n\n#### Graphviz output \n# Graphviz defaults\nor_node = 'node [shape=%s, height=.0001, width=.0001, penwidth=0, label=\"\"]' % gshape\nor_style = '[style=dashed, weight=%s];'\nand_style = '[weight=%s];'\nfull_style = '[dir=full, arrowhead=normal, weight=1000];'\nor_node_def_templ = or_node + ' %s;'\nor_line_templ = '%s ' + or_style\nand_line_templ = '%s ' + and_style\nrank = '{rank=same; %s;}'\n\n# Prints graphviz subgraph\ndef print_graph(path, nodes, or_join=True, horizontal=True):\n if nodes:\n root = False\n if nodes[0] == '':\n root = True\n path = 0\n nodes = nodes[1:]\n weight = 1\n line_templ = or_line_templ\n join_style = or_style\n if not or_join:\n line_templ = and_line_templ\n join_style = and_style \n num_or_nodes = len(nodes)\n nodes_in = ['\"%s_%s\"' % (prefix, n) for n in nodes]\n if path:\n nodes_in = ['\"%s_%s.%s\"' % (prefix, path, n) for n in nodes]\n or_nodes_in = ['\"or%s_%s_%s\"' % (cluster_prefix, path, e) for e in range(0, num_or_nodes)]\n print('subgraph \"cluster_%s%s\" {' % (cluster_prefix, path))\n extra_join_style = join_style % (weight*200)\n join_style = join_style % weight\n if horizontal:\n print('# Horizontal')\n if len(nodes)%2 == 0: # Add to even \n num_or_nodes += 1\n or_nodes_in = ['\"or%s_%s_%s\"' % (cluster_prefix, path, e) for e in range(0, num_or_nodes)]\n print(or_node_def_templ % ', '.join(or_nodes_in))\n print(line_templ % (' -> '.join(or_nodes_in), weight*100))\n print(rank % ', '.join(or_nodes_in))\n print(rank % ', '.join(nodes_in))\n spare = or_nodes_in[int(len(nodes)/2)]\n if len(nodes)%2 == 0: \n or_nodes_in = or_nodes_in[:int(len(or_nodes_in)/2)] + or_nodes_in[int(len(or_nodes_in)/2)+1:]\n assert(len(nodes_in) == len(or_nodes_in))\n for i, n in enumerate(nodes_in):\n print('%s -> %s %s' % (n, or_nodes_in[i], extra_join_style)) \n print('%s -> \"%s\" %s' % (spare, at_nodes_mapper[path], full_style))\n else: \n print('# Vertical')\n print(or_node_def_templ % ', '.join(or_nodes_in))\n print(line_templ % (' -> '.join(or_nodes_in), weight*700))\n assert(len(nodes_in) == len(or_nodes_in))\n for i, n in enumerate(nodes_in):\n print(rank % ', '.join([n, or_nodes_in[i]])) \n for i, n in enumerate(nodes_in):\n print('%s -> %s %s' % (n, or_nodes_in[i], extra_join_style)) \n print('%s -> \"%s\" %s' % (or_nodes_in[-1], at_nodes_mapper[path], full_style))\n print('}')\n print()\n\n# Ascii style tree visualisation\ndef pass_tree(tr, k='', me=''):\n \"\"\"\n Go through the tree and print the concatenated branches\n \"\"\"\n tree = tr\n me += '.' + k\n path = me.lstrip('.')\n print(' '*path.count('.') + '-'*path.count('.') + path)\n for k in tree.keys():\n pass_tree(tree[k], k, me)\n\n# Recursive through graphviz subgraphs\ncluster = 0 \ndef pass_graph(tr, k='', me=''):\n \"\"\"\n Pass through the graph and print it\n \"\"\"\n tree = tr\n me += '.' + k\n path = me.lstrip('.')\n try:\n (or_join, horizontal, double, red, triple) = at_mod_mapper[path]\n print_graph(path, list(tree.keys()), or_join=or_join, horizontal=horizontal)\n except:\n (or_join, horizontal, double, red, triple) = at_mod_mapper[0]\n print_graph(path, list(tree.keys()), or_join=or_join, horizontal=horizontal)\n for k in tree.keys():\n pass_graph(tree[k], k, me)\n\n \nif graphviz:\n # Print Graphviz nodes \n for n in at_nodes:\n print(n) \n\n # Print Graphviz subraphs plot data\n print()\n pass_graph(tr)\n\n\n#### Org mode table \n# Print Org mode style table for nodes analysis\nif org:\n print()\n for e in st:\n den = e[0]\n if not e[0]:\n den = 0\n name = '%s_%s' % (prefix, den)\n print('|%s|%s||||' % (name.replace('_', '+'), e[1]))\n", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code" ] ]

d0e57ba46d43514d96f59b39b36f5cb89ea33ed5

1,479

ipynb

Jupyter Notebook

python/GeometryAG/gaGAmv.ipynb

karng87/nasm_game

a97fdb09459efffc561d2122058c348c93f1dc87

[ "MIT" ]

null

python/GeometryAG/gaGAmv.ipynb

karng87/nasm_game

a97fdb09459efffc561d2122058c348c93f1dc87

[ "MIT" ]

null

python/GeometryAG/gaGAmv.ipynb

karng87/nasm_game

a97fdb09459efffc561d2122058c348c93f1dc87

[ "MIT" ]

null

18.721519

81

0.501014

[ [ [ "import sympy as sm\nimport galgebra.ga as ga\ng3 = ga.Ga('e_x e_y e_z',g=[1,1,1],coords=sm.symbols('x y z',real=True))\ng3.mv()", "_____no_output_____" ], [ "g3.mv()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code" ] ]

d0e5ae310883712b94797739ceab273f2122265f

174,405

ipynb

Jupyter Notebook

Sprawozdania_doswadczenia_Numeryczne/Przyblizanie_stalej_e/prog/program.ipynb

Magikis/University_Projects

bcaf8bd5695cd3809dfd53a922936a64daf51fec

[ "MIT" ]

null

Sprawozdania_doswadczenia_Numeryczne/Przyblizanie_stalej_e/prog/program.ipynb

Magikis/University_Projects

bcaf8bd5695cd3809dfd53a922936a64daf51fec

[ "MIT" ]

null

Sprawozdania_doswadczenia_Numeryczne/Przyblizanie_stalej_e/prog/program.ipynb

Magikis/University_Projects

bcaf8bd5695cd3809dfd53a922936a64daf51fec

[ "MIT" ]

null

280.393891

36,925

0.893896

[ [ [ "empty" ] ] ]

[ "empty" ]

[ [ "empty" ] ]

d0e5b3e5997e06997e90af5a63ed2263867f534e

14,667

ipynb

Jupyter Notebook

Uni_face_model.ipynb

Pierre-code7/face-mask-detection3classes

5fd4e3fa6c9c84064db469fb90f37282482331b1

[ "MIT" ]

null

Uni_face_model.ipynb

Pierre-code7/face-mask-detection3classes

5fd4e3fa6c9c84064db469fb90f37282482331b1

[ "MIT" ]

null

Uni_face_model.ipynb

Pierre-code7/face-mask-detection3classes

5fd4e3fa6c9c84064db469fb90f37282482331b1

[ "MIT" ]

null

36.485075

130

0.510602

[ [ [ "\"Uni Face mask model\"", "_____no_output_____" ], [ "#some important packages\nfrom tensorflow.keras.applications.mobilenet_v2 import preprocess_input\nfrom tensorflow.keras.preprocessing.image import img_to_array\nfrom tensorflow.keras.models import model_from_json\nfrom tensorflow.keras.models import load_model\nfrom imutils.video import VideoStream\nimport numpy as np\nimport argparse\nimport cv2\nimport os", "_____no_output_____" ], [ "# Load your trained model\n\njson_file = open('model_3class.json', 'r')\nloaded_model_json = json_file.read()\njson_file.close()# load json and create model\n\nmodel = model_from_json(loaded_model_json)\n# load weights into new model\nmodel.load_weights(\"model_3class.h5\")\nprint(\"Loaded model from disk\")", "Loaded model from disk\n" ], [ "# load our serialized face detector model from disk\nprint(\"[INFO] loading face detector model...\")\nprototxtPath = 'weights/deploy.prototxt.txt'\nweightsPath = 'weights/res10_300x300_ssd_iter_140000.caffemodel'\nnet = cv2.dnn.readNet(prototxtPath, weightsPath)\n", "[INFO] loading face detector model...\n" ], [ "\"\" \"Application on image // Play with the parameters to choose the right probabilities\"\"\"\n", "_____no_output_____" ], [ "# load the image to test\n#image = cv2.imread('images/pic1.jpeg')\nimage = cv2.imread('inputs/images/img4.jpeg')\norig = image.copy()\n(h, w) = image.shape[:2]\n\n# construct a blob from the image\nblob = cv2.dnn.blobFromImage(image, 1.0, (300, 300),\n\t(104.0, 177.0, 123.0))\n\n# pass the blob through the network and obtain the face detections\nprint(\"[INFO] computing face detections...\")\nnet.setInput(blob)\ndetections = net.forward()\n\n# loop over the detections\nfor i in range(0, detections.shape[2]):\n\t# extract the confidence (i.e., probability) associated with\n\t# the detection\n\tconfidence = detections[0, 0, i, 2]\n\n\t# filter out weak detections by ensuring the confidence is\n\t# greater than the minimum confidence\n\tif confidence > 0.5:\n\t\t# compute the (x, y)-coordinates of the bounding box for\n\t\t# the object\n\t\tbox = detections[0, 0, i, 3:7] * np.array([w, h, w, h])\n\t\t(startX, startY, endX, endY) = box.astype(\"int\")\n\n\t\t# ensure the bounding boxes fall within the dimensions of\n\t\t# the frame\n\t\t(startX, startY) = (max(0, startX), max(0, startY))\n\t\t(endX, endY) = (min(w - 1, endX), min(h - 1, endY))\n\n\t\t# extract the face ROI, convert it from BGR to RGB channel\n\t\t# ordering, resize it to 224x224, and preprocess it\n\t\tface = image[startY:endY, startX:endX]\n\t\tface = cv2.cvtColor(face, cv2.COLOR_BGR2RGB)\n\t\tface = cv2.resize(face, (224, 224))\n\t\tface = img_to_array(face)\n\t\tface = preprocess_input(face)\n\t\tface = np.expand_dims(face, axis=0)\n\n\t\t# pass the face through the model to determine if the face\n\t\t# has a mask or not\n\t\t(notCorrect, mask, withoutMask) = model.predict(face)[0]\n\n\t\t# determine the class label and color we'll use to draw\n\t\t# the bounding box and text\n\t\tif (mask < 0.70 and withoutMask < 0.70) or notCorrect > max(mask, withoutMask):\n\t\t\t label, color = \"Not correct\", (0, 255, 255)\n\t\telif mask > max (withoutMask, notCorrect):\n\t\t\tlabel, color = \"Mask\", (0, 255,0)\n\t\telif withoutMask > max (mask, notCorrect):\n\t\t\tlabel, color = \"No Mask\", (0, 0, 255)\n\t\t# label = \"Mask\" if mask > max (withoutMask, notCorrect) else \"No Mask\"\n\t\t# color = (0, 255, 0) if label == \"Mask\" else (0, 0, 255)\n\n\t\t# include the probability in the label\n\t\tlabel = \"{}: {:.2f}%\".format(label, max(mask, withoutMask) * 100)\n\n\t\t# display the label and bounding box rectangle on the output\n\t\t# frame\n\t\tcv2.putText(image, label, (startX, startY - 10),\n\t\t\tcv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)\n\t\tcv2.rectangle(image, (startX, startY), (endX, endY), color, 2)\n\n#save the output image\ncv2.imwrite('outputs/output_uni.jpg', image)\n# show the output image\ncv2.imshow(\"Output\", image)\ncv2.waitKey(0)\n\ncv2.destroyAllWindows()", "[INFO] computing face detections...\n" ], [ "\"\"\"\" Application on webcam \"\"\"\"", "_____no_output_____" ], [ "def detect_and_predict_mask(frame, faceNet, maskNet):\n\t# grab the dimensions of the frame and then construct a blob\n\t# from it\n\t(h, w) = frame.shape[:2]\n\tblob = cv2.dnn.blobFromImage(frame, 1.0, (300, 300),\n\t\t(104.0, 177.0, 123.0))\n\n\t# pass the blob through the network and obtain the face detections\n\tfaceNet.setInput(blob)\n\tdetections = faceNet.forward()\n\n\t# initialize our list of faces, their corresponding locations,\n\t# and the list of predictions from our face mask network\n\tfaces = []\n\tlocs = []\n\tpreds = []\n\n\t# loop over the detections\n\tfor i in range(0, detections.shape[2]):\n\t\t# extract the confidence (i.e., probability) associated with\n\t\t# the detection\n\t\tconfidence = detections[0, 0, i, 2]\n\n\t\t# filter out weak detections by ensuring the confidence is\n\t\t# greater than the minimum confidence\n\t\tif confidence > 0.5:\n\t\t\t# compute the (x, y)-coordinates of the bounding box for\n\t\t\t# the object\n\t\t\tbox = detections[0, 0, i, 3:7] * np.array([w, h, w, h])\n\t\t\t(startX, startY, endX, endY) = box.astype(\"int\")\n\n\t\t\t# ensure the bounding boxes fall within the dimensions of\n\t\t\t# the frame\n\t\t\t(startX, startY) = (max(0, startX), max(0, startY))\n\t\t\t(endX, endY) = (min(w - 1, endX), min(h - 1, endY))\n\n\t\t\t# extract the face ROI, convert it from BGR to RGB channel\n\t\t\t# ordering, resize it to 224x224, and preprocess it\n\t\t\tface = frame[startY:endY, startX:endX]\n\t\t\tface = cv2.cvtColor(face, cv2.COLOR_BGR2RGB)\n\t\t\tface = cv2.resize(face, (224, 224))\n\t\t\tface = img_to_array(face)\n\t\t\tface = preprocess_input(face)\n\t\t\tface = np.expand_dims(face, axis=0)\n\n\t\t\t# add the face and bounding boxes to their respective\n\t\t\t# lists\n\t\t\tfaces.append(face)\n\t\t\tlocs.append((startX, startY, endX, endY))\n\n\t# only make a predictions if at least one face was detected\n\tif len(faces) > 0:\n\t\t# for faster inference we'll make batch predictions on *all*\n\t\t# faces at the same time rather than one-by-one predictions\n\t\t# in the above `for` loop\n\t\tpreds = maskNet.predict(faces)\n\n\t# return a 2-tuple of the face locations and their corresponding\n\t# locations\n\treturn (locs, preds)\n\n", "_____no_output_____" ], [ "maskNet = model\n\nsize = 4\nwebcam = cv2.VideoCapture(0) #Use camera 0\n\n\n# loop over the frames from the video stream\nwhile True:\n\t# grab the frame from the threaded video stream and resize it\n\t# to have a maximum width of 400 pixels\n\t#frame = vs.read()\n\t#frame = imutils.resize(frame, width=400)\n\n\t(rval, frame) = webcam.read()\n\t#frame = imutils.resize(frame, width=400)\n\tframe = cv2.flip(frame,1,1) #Flip to act as a mirror\n\tframe = cv2.resize(frame, (frame.shape[1] // size, frame.shape[0] // size))# Resize the image to speed up detection\n# detect faces in the frame and determine if they are wearing a\n\t# face mask or not\n\t(locs, preds) = detect_and_predict_mask(frame, net, maskNet)\n\n\t# loop over the detected face locations and their corresponding\n\t# locations\n\tfor (box, pred) in zip(locs, preds):\n\t\t# unpack the bounding box and predictions\n\t\t(startX, startY, endX, endY) = box\n\t\t(notCorrect, mask, withoutMask) = pred\n\n\t\t# determine the class label and color we'll use to draw\n\t\t# the bounding box and text\n\t\tif (mask < 0.70 and withoutMask < 0.70) or notCorrect > max(mask, withoutMask):\n\t\t\t label, color = \"Not correct\", (0, 255, 255)\n\t\telif mask > max (withoutMask, notCorrect):\n\t\t\tlabel, color = \"Mask\", (0, 255,0)\n\t\telif withoutMask > max (mask, notCorrect):\n\t\t\tlabel, color = \"No Mask\", (0, 0, 255)\n\t\t# include the probability in the label\n\t\tlabel = \"{}: {:.2f}%\".format(label, max(notCorrect, mask, withoutMask) * 100)\n\n\t\t# display the label and bounding box rectangle on the output\n\t\t# frame\n\t\tcv2.putText(frame, label, (startX-30, startY - 10),\n\t\t\tcv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)\n\t\tcv2.rectangle(frame, (startX, startY), (endX, endY), color, 2)\n\n\t# show the output frame\n\tcv2.namedWindow(\"LIVE\", cv2.WND_PROP_FULLSCREEN)\n\tcv2.setWindowProperty(\"LIVE\",cv2.WND_PROP_FULLSCREEN,\t\t\tcv2.WINDOW_FULLSCREEN)\n\tcv2.imshow(\"LIVE\", frame)\n\tkey = cv2.waitKey(10)\n\tif key==27:\n\t\tbreak\n# Stop video\nwebcam.release()\n\n# Close all started windows\ncv2.destroyAllWindows()\n", "_____no_output_____" ], [ "# Video", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e5bb58b699714b85d9e57416fff02d1148fc9f

32,920

ipynb

Jupyter Notebook

site/vi/tutorials/keras/classification.ipynb

ilyaspiridonov/docs-l10n

a061a44e40d25028d0a4458094e48ab717d3565c

[ "Apache-2.0" ]

1

2021-09-23T09:56:29.000Z

site/vi/tutorials/keras/classification.ipynb

ilyaspiridonov/docs-l10n

a061a44e40d25028d0a4458094e48ab717d3565c

[ "Apache-2.0" ]

null

site/vi/tutorials/keras/classification.ipynb

ilyaspiridonov/docs-l10n

a061a44e40d25028d0a4458094e48ab717d3565c

[ "Apache-2.0" ]

1

2020-05-31T15:04:18.000Z

32.465483

568

0.50887

[ [ [ "##### Copyright 2018 The TensorFlow Authors.", "_____no_output_____" ] ], [ [ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n# you may not use this file except in compliance with the License.\n# You may obtain a copy of the License at\n#\n# https://www.apache.org/licenses/LICENSE-2.0\n#\n# Unless required by applicable law or agreed to in writing, software\n# distributed under the License is distributed on an \"AS IS\" BASIS,\n# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n# See the License for the specific language governing permissions and\n# limitations under the License.", "_____no_output_____" ], [ "#@title MIT License\n#\n# Copyright (c) 2017 François Chollet\n#\n# Permission is hereby granted, free of charge, to any person obtaining a\n# copy of this software and associated documentation files (the \"Software\"),\n# to deal in the Software without restriction, including without limitation\n# the rights to use, copy, modify, merge, publish, distribute, sublicense,\n# and/or sell copies of the Software, and to permit persons to whom the\n# Software is furnished to do so, subject to the following conditions:\n#\n# The above copyright notice and this permission notice shall be included in\n# all copies or substantial portions of the Software.\n#\n# THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR\n# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,\n# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL\n# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER\n# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING\n# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER\n# DEALINGS IN THE SOFTWARE.", "_____no_output_____" ] ], [ [ "# Phân loại cơ bản: Dự đoán ảnh quần áo giày dép", "_____no_output_____" ], [ "<table class=\"tfo-notebook-buttons\" align=\"left\">\n <td>\n <a target=\"_blank\" href=\"https://www.tensorflow.org/tutorials/keras/classification\"><img src=\"https://www.tensorflow.org/images/tf_logo_32px.png\" />Xem trên TensorFlow.org</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/vi/tutorials/keras/classification.ipynb\"><img src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" />Chạy trên Google Colab</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://github.com/tensorflow/docs-l10n/blob/master/site/vi/tutorials/keras/classification.ipynb\"><img src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" />Xem mã nguồn trên GitHub</a>\n </td>\n <td>\n <a href=\"https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/vi/tutorials/keras/classification.ipynb\"><img src=\"https://www.tensorflow.org/images/download_logo_32px.png\" />Tải notebook</a>\n </td>\n</table>", "_____no_output_____" ], [ "**Lưu ý:** Cộng đồng TensorFlow tại Việt Nam đã và đang dịch những tài liệu này từ nguyên bản tiếng Anh.\nNhững bản dịch này được hoàn thiện dựa trên sự nỗ lực đóng góp từ cộng đồng lập trình viên sử dụng TensorFlow, \nvà điều này có thể không đảm bảo được tính cập nhật của bản dịch đối với [Tài liệu chính thức bằng tiếng Anh](https://www.tensorflow.org/?hl=en) này.\nNếu bạn có bất kỳ đề xuất nào nhằm cải thiện bản dịch này, vui lòng tạo Pull request đến \nkho chứa trên GitHub của [tensorflow/docs-l10n](https://github.com/tensorflow/docs-l10n).\nĐể đăng ký dịch hoặc cải thiện nội dung bản dịch, các bạn hãy liên hệ và đặt vấn đề tại \n[[email protected]](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-vi).", "_____no_output_____" ], [ "Trong hướng dẫn này, chúng ta sẽ huấn luyện một mô hình mạng neuron để phân loại các hình ảnh về quần áo và giày dép.\n\nĐừng ngại nếu bạn không hiểu hết mọi chi tiết, vì chương trình trong hướng dẫn này là một chương trình TensorFlow hoàn chỉnh, và các chi tiết sẽ dần được giải thích ở những phần sau.\n\nHướng dẫn này dùng [tf.keras](https://www.tensorflow.org/guide/keras), một API cấp cao để xây dựng và huấn luyện các mô hình trong TensorFlow.", "_____no_output_____" ] ], [ [ "# TensorFlow and tf.keras\nimport tensorflow as tf\nfrom tensorflow import keras\n\n# Helper libraries\nimport numpy as np\nimport matplotlib.pyplot as plt\n\nprint(tf.__version__)", "_____no_output_____" ] ], [ [ "## Import tập dữ liệu về quần áo và giày dép từ Fashion MNIST", "_____no_output_____" ], [ "Chúng ta sẽ dùng tập dữ liệu về quần áo và giày dép từ [Fashion MNIST](https://github.com/zalandoresearch/fashion-mnist), chứa khoảng 70,000 ảnh đen trắng phân thành 10 loại. Mỗi một ảnh là một loại quần áo hoặc giày dép với độ phân giải thấp (28 by 28 pixel), như hình minh hoạ bên dưới:\n\n<table>\n <tr><td>\n <img src=\"https://tensorflow.org/images/fashion-mnist-sprite.png\"\n alt=\"Fashion MNIST sprite\" width=\"600\">\n </td></tr>\n <tr><td align=\"center\">\n <b>Figure 1.</b> <a href=\"https://github.com/zalandoresearch/fashion-mnist\">Fashion-MNIST samples</a> (by Zalando, MIT License).<br/> \n </td></tr>\n</table>\n\nFashion MNIST là tập dữ liệu được dùng để thay thế cho tập dữ liệu [MNIST](http://yann.lecun.com/exdb/mnist/) kinh điển thường dùng cho các chương trình \"Hello, World\" của machine learning trong lĩnh vực thị giác máy tính. Tập dữ liệu kinh điển vừa đề cập gồm ảnh của các con số (ví dụ 0, 1, 2) được viết tay. Các ảnh này có cùng định dạng tệp và độ phân giải với các ảnh về quần áo và giầy dép chúng ta sắp dùng.\n\nHướng dẫn này sử dụng tập dữ liệu Fashion MNIST, vì đây là một bài toán tương đối phức tạp hơn so với bài toán nhận diện chữ số viết tay. Cả 2 tập dữ liệu (Fashion MNIST và MNIST kinh điển) đều tương đối nhỏ và thường dùng để đảm bảo một giải thuật chạy đúng, phù hợp cho việc kiểm thử và debug.\n\nVới tập dữ liệu này, 60.000 ảnh sẽ được dùng để huấn luyện và 10.000 ảnh sẽ đường dùng để đánh giá khả năng phân loại nhận diện ảnh của mạng neuron. Chúng ta có dùng tập dữ liệu Fashion MNIST trực tiếp từ TensorFlow như sau:", "_____no_output_____" ] ], [ [ "fashion_mnist = keras.datasets.fashion_mnist\n\n(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()", "_____no_output_____" ] ], [ [ "Tập dữ liệu sau khi được tải sẽ trả về 4 mảng NumPy:\n\n* 2 mảng `train_images` và `train_labels` là *tập huấn luyện*. Mô hình sẽ học từ dữ liệu của 2 mảng này.\n* 2 mảng `test_images` vả `test_labels` là *tập kiểm thử*. Sau khi mô hình được huấn luyện xong, chúng ta sẽ chạy thử mô hình với dữ liệu đầu vào từ `test_images` để lấy kết quả, và so sánh kết quả đó với dữ liệu đối ứng từ `test_labels` để đánh giá chất lượng của mạng neuron.\n\nMỗi ảnh là một mảng NumPy 2 chiều, 28x28, với mỗi pixel có giá trị từ 0 đến 255. *Nhãn* là một mảng của các số nguyên từ 0 đến 9, tương ứng với mỗi *lớp* quần áo giày dép:\n\n<table>\n <tr>\n <th>Nhãn</th>\n <th>Lớp</th>\n </tr>\n <tr>\n <td>0</td>\n <td>Áo thun</td>\n </tr>\n <tr>\n <td>1</td>\n <td>Quần dài</td>\n </tr>\n <tr>\n <td>2</td>\n <td>Áo liền quần</td>\n </tr>\n <tr>\n <td>3</td>\n <td>Đầm</td>\n </tr>\n <tr>\n <td>4</td>\n <td>Áo khoác</td>\n </tr>\n <tr>\n <td>5</td>\n <td>Sandal</td>\n </tr>\n <tr>\n <td>6</td>\n <td>Áo sơ mi</td>\n </tr>\n <tr>\n <td>7</td>\n <td>Giày</td>\n </tr>\n <tr>\n <td>8</td>\n <td>Túi xách</td>\n </tr>\n <tr>\n <td>9</td>\n <td>Ủng</td>\n </tr>\n</table>\n\nMỗi ảnh sẽ được gán với một nhãn duy nhất. Vì tên của mỗi lớp không có trong tập dữ liệu, nên chúng ta có thể định nghĩa ở đây để dùng về sau:", "_____no_output_____" ] ], [ [ "class_names = ['Áo thun', 'Quần dài', 'Áo liền quần', 'Đầm', 'Áo khoác',\n 'Sandal', 'Áo sơ mi', 'Giày', 'Túi xách', 'Ủng']", "_____no_output_____" ] ], [ [ "## Khám phá dữ liệu\n\nChúng ta có thể khám phá dữ liệu một chút trước khi huấn luyện mô hình. Câu lệnh sau sẽ cho ta thấy có 60.000 ảnh trong tập huấn luyện, với mỗi ảnh được biểu diễn theo dạng 28x28 pixel:", "_____no_output_____" ] ], [ [ "train_images.shape", "_____no_output_____" ] ], [ [ "Tương tự, tập huấn luyện cũng có 60.000 nhãn đối ứng:", "_____no_output_____" ] ], [ [ "len(train_labels)", "_____no_output_____" ] ], [ [ "Mỗi nhãn là một số nguyên từ 0 đến 9:", "_____no_output_____" ] ], [ [ "train_labels", "_____no_output_____" ] ], [ [ "Có 10.000 ảnh trong tập kiểm thử, mỗi ảnh cũng được biểu diễn ở dãng 28 x 28 pixel:", "_____no_output_____" ] ], [ [ "test_images.shape", "_____no_output_____" ] ], [ [ "Và tập kiểm thử cũng chứa 10,000 nhãn:", "_____no_output_____" ] ], [ [ "len(test_labels)", "_____no_output_____" ] ], [ [ "## Tiền xử lý dữ liệu\n\nDữ liệu cần được tiền xử lý trước khi được dùng để huấn luyện mạng neuron. Phân tích ảnh đầu tiên trong tập dữ liệu, chúng ta sẽ thấy các pixel có giá trị từ 0 đến 255:", "_____no_output_____" ] ], [ [ "plt.figure()\nplt.imshow(train_images[0])\nplt.colorbar()\nplt.grid(False)\nplt.show()", "_____no_output_____" ] ], [ [ "Chúng ta cần tiền xử lý để mỗi một điểm ảnh có giá trị từ 0 đến 1 (có thể hiểu là 0% đến 100%). Để làm điều này, chúng ta chỉ cần lấy giá trị của pixel chia cho 255. Cần lưu ý rằng việc tiền xử lý này phải được áp dụng đồng thời cho cả *tập huấn luyện* và *tập kiểm thử*:", "_____no_output_____" ] ], [ [ "train_images = train_images / 255.0\n\ntest_images = test_images / 255.0", "_____no_output_____" ] ], [ [ "Để chắc chắn việc tiền xử lý diễn ra chính xác, chúng ta có thể in ra 25 ảnh đầu trong *tập huấn luyện* cùng với tên lớp dưới mỗi ảnh.", "_____no_output_____" ] ], [ [ "plt.figure(figsize=(10,10))\nfor i in range(25):\n plt.subplot(5,5,i+1)\n plt.xticks([])\n plt.yticks([])\n plt.grid(False)\n plt.imshow(train_images[i], cmap=plt.cm.binary)\n plt.xlabel(class_names[train_labels[i]])\nplt.show()", "_____no_output_____" ] ], [ [ "## Xây dựng mô hình\n\nĐể xây dựng mạng neuron, chúng tay cần cấu hình các layer của mô hình, và sau đó biên dịch mô hình.", "_____no_output_____" ], [ "### Thiết lập các layers\n\nThành phần cơ bản của một mạng neuron là các *layer*. Các layer trích xuất các điểm đặc biệt từ dữ liệu mà chúng đón nhận. Khi thực hiện tốt, những điểm đặc biệt này mang nhiều ý nghĩa và phục vụ cho toán của chúng ta.\n\nĐa số các mô hình deep learning đều chứa các layer đơn gian được xâu chuỗi lại với nhau. Đa số các layer, ví dụ `tf.keras.layers.Dense`, đều có các trọng số sẽ được học trong quá trình huấn luyện.", "_____no_output_____" ] ], [ [ "model = keras.Sequential([\n keras.layers.Flatten(input_shape=(28, 28)),\n keras.layers.Dense(128, activation='relu'),\n keras.layers.Dense(10, activation='softmax')\n])", "_____no_output_____" ] ], [ [ "Trong mạng neuron trên, lớp đầu tiên, `tf.keras.layers.Flatten`, chuyển đổi định dạng của hình ảnh từ mảng hai chiều (28x28) thành mảng một chiều (28x28 = 784). Tưởng tương công việc của layer này là cắt từng dòng của anh, và ghép nối lại thành một dòng duy nhất nhưng dài gấp 28 lần. Lớp này không có trọng số để học, nó chỉ định dạng lại dữ liệu.\n\nSau layer làm phẳng ảnh (từ 2 chiều thành 1 chiều), phần mạng neuron còn lại gồm một chuỗi hai layer `tf.keras.layers.Dense`. Đây là các layer neuron được kết nối hoàn toàn (mỗi một neuron của layer này kết nối đến tất cả các neuron của lớp trước và sau nó). Layer `Dense` đầu tiên có 128 nút (hoặc neuron). Layer thứ hai (và cuối cùng) là lớp *softmax* có 10 nút, với mỗi nút tương đương với điểm xác suất, và tổng các giá trị của 10 nút này là 1 (tương đương 100%). Mỗi nút chứa một giá trị cho biết xác suất hình ảnh hiện tại thuộc về một trong 10 lớp.\n\n### Biên dịch mô hình\n\nTrước khi mô hình có thể được huấn luyện, chúng ta cần thêm vài chỉnh sửa. Các chỉnh sửa này được thêm vào trong bước *biên dịch* của mô hình:\n\n* *Hàm thiệt hại* — dùng để đo lường mức độ chính xác của mô hình trong quá trình huấn luyện. Chúng ta cần giảm thiểu giá trị của hạm này \"điều khiển\" mô hình đi đúng hướng (thiệt hại càng ít, chính xác càng cao).\n* *Trình tối ưu hoá* — Đây là cách mô hình được cập nhật dựa trên dữ liệu huấn luyện được cung cấp và hàm thiệt hại.\n* *Số liệu* — dùng để theo dõi các bước huấn luyện và kiểm thử. Ví dụ sau dùng *accuracy*, tỉ lệ ảnh được phân loại chính xác.", "_____no_output_____" ] ], [ [ "model.compile(optimizer='adam',\n loss='sparse_categorical_crossentropy',\n metrics=['accuracy'])", "_____no_output_____" ] ], [ [ "## Huấn luyện mô hình\n\nHuấn luyện mô hình mạng neuron cần các bước sau:\n\n1. Cung cấp dữ liệu huấn luyện cho mô hình. Trong ví dụ này, dữ liệu huấn luyện năm trong 2 mảng `train_images` và `train_labels`\n2. Mô hình sẽ học cách liên kết ảnh với nhãn.\n3. Chúng ta sẽ yêu cầu mô hình đưa ra dự đoán từ dữ liệu của tập kiểm thử, trong ví dụ này là mảng `test_images`, sau đó lấy kết quả dự đoán đối chiếu với nhãn trong mảng `test_labels`.\n\nĐể bắt đầu huấn luyện, gọi hàm `model.fit`. Hàm này được đặt tên `fit` vì nó sẽ \"fit\" (\"khớp\") mô hình với dữ liệu huấn luyện:", "_____no_output_____" ] ], [ [ "model.fit(train_images, train_labels, epochs=10)", "_____no_output_____" ] ], [ [ "Trong quá trình huấn luyện, các số liệu như thiệt hại và hay độ chính xác được hiển thị. Với dữ liệu huấn luyện này, mô hình đạt đến độ accuracy vào khoảng 0.88 (88%).", "_____no_output_____" ], [ "## Đánh giá mô hình\n\nTiếp theo, chúng đánh giá các chất lượng của mô hình bằng tập kiểm thử:", "_____no_output_____" ] ], [ [ "test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)\n\nprint('\\nTest accuracy:', test_acc)", "_____no_output_____" ] ], [ [ "Đến thời điểm này, chúng ta thấy rằng độ accuracy của mô hình, khi đánh giá bằng tập kiểm thử, hơi thấp hơn so với số liệu trong quá trình huấn luyện. Khoảng cách giữa hai độ accuracy khi huấn luyện và khi kiểm thử thể hiện sự *overfitting*. Overfitting xảy ra khi một mô hình ML hoạt động kém hơn khi được cung cấp các đầu vào mới, mà mô hình chưa từng thấy trước đây trong quá trình đào tạo.", "_____no_output_____" ], [ "## Đưa ra dự đoán\n\nVới một mô hình đã được đào tạo, chúng ta có thể dùng nó để đưa ra dự đoán với một số ảnh.", "_____no_output_____" ] ], [ [ "predictions = model.predict(test_images)", "_____no_output_____" ] ], [ [ "Ở đây, mô hình sẽ dự đoán nhãn cho từng hình ảnh trong bộ thử nghiệm. Hãy xem dự đoán đầu tiên:", "_____no_output_____" ] ], [ [ "predictions[0]", "_____no_output_____" ] ], [ [ "Trong ví dụ này, dự đoán là một mảng 10 số thực, mỗi số tương ứng với \"độ tự tin\" của mô hình rằng ảnh đó thuộc về nhãn đó. Chúng ta có thể thấy nhãn nào có độ tư tin cao nhất:", "_____no_output_____" ] ], [ [ "np.argmax(predictions[0])", "_____no_output_____" ] ], [ [ "Vậy là mô hình tự tin nhất rằng ảnh này là một loại ủng, hoặc `class_names[9]`. Đối chiếu với nhãn trong tập kiểm thử, ta thấy dự đoán này là đúng:", "_____no_output_____" ] ], [ [ "test_labels[0]", "_____no_output_____" ] ], [ [ "Ta thử vẽ biểu đồ để xem các dự đoán trên cả 10 lớp của mô hình.", "_____no_output_____" ] ], [ [ "def plot_image(i, predictions_array, true_label, img):\n predictions_array, true_label, img = predictions_array, true_label[i], img[i]\n plt.grid(False)\n plt.xticks([])\n plt.yticks([])\n\n plt.imshow(img, cmap=plt.cm.binary)\n\n predicted_label = np.argmax(predictions_array)\n if predicted_label == true_label:\n color = 'blue'\n else:\n color = 'red'\n\n plt.xlabel(\"{} {:2.0f}% ({})\".format(class_names[predicted_label],\n 100*np.max(predictions_array),\n class_names[true_label]),\n color=color)\n\ndef plot_value_array(i, predictions_array, true_label):\n predictions_array, true_label = predictions_array, true_label[i]\n plt.grid(False)\n plt.xticks(range(10))\n plt.yticks([])\n thisplot = plt.bar(range(10), predictions_array, color=\"#777777\")\n plt.ylim([0, 1])\n predicted_label = np.argmax(predictions_array)\n\n thisplot[predicted_label].set_color('red')\n thisplot[true_label].set_color('blue')", "_____no_output_____" ] ], [ [ "Chúng ta có thể nhìn vào ảnh 0th, các dự đoán, và mảng dự đoán.\nNhãn dự đoán đúng màu xanh và nhãn sai màu đỏ. Con số là số phần trăm của các nhãn được dự đoán.", "_____no_output_____" ] ], [ [ "i = 0\nplt.figure(figsize=(6,3))\nplt.subplot(1,2,1)\nplot_image(i, predictions[i], test_labels, test_images)\nplt.subplot(1,2,2)\nplot_value_array(i, predictions[i], test_labels)\nplt.show()", "_____no_output_____" ], [ "i = 12\nplt.figure(figsize=(6,3))\nplt.subplot(1,2,1)\nplot_image(i, predictions[i], test_labels, test_images)\nplt.subplot(1,2,2)\nplot_value_array(i, predictions[i], test_labels)\nplt.show()", "_____no_output_____" ] ], [ [ "Thử vẽ biểu đồ với vài ảnh và dự đoán đi kèm. Chú ý thấy rằng mô hình đôi khi dự đoán sai dù điểm tự tin rất cao.", "_____no_output_____" ] ], [ [ "# Plot the first X test images, their predicted labels, and the true labels.\n# Color correct predictions in blue and incorrect predictions in red.\nnum_rows = 5\nnum_cols = 3\nnum_images = num_rows*num_cols\nplt.figure(figsize=(2*2*num_cols, 2*num_rows))\nfor i in range(num_images):\n plt.subplot(num_rows, 2*num_cols, 2*i+1)\n plot_image(i, predictions[i], test_labels, test_images)\n plt.subplot(num_rows, 2*num_cols, 2*i+2)\n plot_value_array(i, predictions[i], test_labels)\nplt.tight_layout()\nplt.show()", "_____no_output_____" ] ], [ [ "Cuối cùng, dùng mô hình để đưa ra dự đoán về một ảnh duy nhất.", "_____no_output_____" ] ], [ [ "# Grab an image from the test dataset.\nimg = test_images[1]\n\nprint(img.shape)", "_____no_output_____" ] ], [ [ "Các mô hình `tf.keras` được tối ưu hóa để đưa ra dự đoán về một *lô* hoặc bộ sưu tập các ví dụ cùng một lúc. Theo đó, mặc dù bạn đang sử dụng một ảnh duy nhất, bạn cần thêm nó vào list:", "_____no_output_____" ] ], [ [ "# Add the image to a batch where it's the only member.\nimg = (np.expand_dims(img,0))\n\nprint(img.shape)", "_____no_output_____" ] ], [ [ "Dự đoán nhãn cho ảnh này:", "_____no_output_____" ] ], [ [ "predictions_single = model.predict(img)\n\nprint(predictions_single)", "_____no_output_____" ], [ "plot_value_array(1, predictions_single[0], test_labels)\n_ = plt.xticks(range(10), class_names, rotation=45)", "_____no_output_____" ] ], [ [ "`model.predict` trả về một list của lists — mỗi list cho mỗi ảnh trong lô dữ liệu. Lấy dự đoán cho hình ảnh trong lô:", "_____no_output_____" ] ], [ [ "np.argmax(predictions_single[0])", "_____no_output_____" ] ], [ [ "Mô hình dự đoán ảnh này có nhãn là đúng như mong muốn.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e5f58c9d4d26d617e1b12e8ce2b83aec0ee0f2

87,105

ipynb

Jupyter Notebook

Convolution+model+-+Application+-+v1 (1).ipynb

suvam14das/Finger-Sign-detector-using-CNN

0d777587985a03b5408665510cc6c92a798c58b3

[ "MIT" ]

null

Convolution+model+-+Application+-+v1 (1).ipynb

suvam14das/Finger-Sign-detector-using-CNN

0d777587985a03b5408665510cc6c92a798c58b3

[ "MIT" ]

null

Convolution+model+-+Application+-+v1 (1).ipynb

suvam14das/Finger-Sign-detector-using-CNN

0d777587985a03b5408665510cc6c92a798c58b3

[ "MIT" ]

null

98.758503

19,026

0.803513

[ [ [ "# Convolutional Neural Networks: Application\n\nWelcome to Course 4's second assignment! In this notebook, you will:\n\n- Implement helper functions that you will use when implementing a TensorFlow model\n- Implement a fully functioning ConvNet using TensorFlow \n\n**After this assignment you will be able to:**\n\n- Build and train a ConvNet in TensorFlow for a classification problem \n\nWe assume here that you are already familiar with TensorFlow. If you are not, please refer the *TensorFlow Tutorial* of the third week of Course 2 (\"*Improving deep neural networks*\").", "_____no_output_____" ], [ "## 1.0 - TensorFlow model\n\nIn the previous assignment, you built helper functions using numpy to understand the mechanics behind convolutional neural networks. Most practical applications of deep learning today are built using programming frameworks, which have many built-in functions you can simply call. \n\nAs usual, we will start by loading in the packages. ", "_____no_output_____" ] ], [ [ "import math\nimport numpy as np\nimport h5py\nimport matplotlib.pyplot as plt\nimport scipy\nfrom PIL import Image\nfrom scipy import ndimage\nimport tensorflow as tf\nfrom tensorflow.python.framework import ops\nfrom cnn_utils import *\n\n%matplotlib inline\nnp.random.seed(1)", "_____no_output_____" ] ], [ [ "Run the next cell to load the \"SIGNS\" dataset you are going to use.", "_____no_output_____" ] ], [ [ "# Loading the data (signs)\nX_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()", "_____no_output_____" ] ], [ [ "As a reminder, the SIGNS dataset is a collection of 6 signs representing numbers from 0 to 5.\n\n<img src=\"images/SIGNS.png\" style=\"width:800px;height:300px;\">\n\nThe next cell will show you an example of a labelled image in the dataset. Feel free to change the value of `index` below and re-run to see different examples. ", "_____no_output_____" ] ], [ [ "# Example of a picture\nindex = 5\nplt.imshow(X_train_orig[index])\nprint (\"y = \" + str(np.squeeze(Y_train_orig[:,index])))", "y = 4\n" ] ], [ [ "In Course 2, you had built a fully-connected network for this dataset. But since this is an image dataset, it is more natural to apply a ConvNet to it.\n\nTo get started, let's examine the shapes of your data. ", "_____no_output_____" ] ], [ [ "X_train = X_train_orig/255\nX_test = X_test_orig/255\nY_train = convert_to_one_hot(Y_train_orig, 6).T #.T used for transpose\nY_test = convert_to_one_hot(Y_test_orig, 6).T\nprint (\"number of training examples = \" + str(X_train.shape[0]))\nprint (\"number of test examples = \" + str(X_test.shape[0]))\nprint (\"X_train shape: \" + str(X_train.shape))\nprint (\"Y_train shape: \" + str(Y_train.shape))\nprint (\"X_test shape: \" + str(X_test.shape))\nprint (\"Y_test shape: \" + str(Y_test.shape))\nconv_layers = {}", "number of training examples = 1080\nnumber of test examples = 120\nX_train shape: (1080, 64, 64, 3)\nY_train shape: (1080, 6)\nX_test shape: (120, 64, 64, 3)\nY_test shape: (120, 6)\n" ] ], [ [ "### 1.1 - Create placeholders\n\nTensorFlow requires that you create placeholders for the input data that will be fed into the model when running the session.\n\n**Exercise**: Implement the function below to create placeholders for the input image X and the output Y. You should not define the number of training examples for the moment. To do so, you could use \"None\" as the batch size, it will give you the flexibility to choose it later. Hence X should be of dimension **[None, n_H0, n_W0, n_C0]** and Y should be of dimension **[None, n_y]**. [Hint](https://www.tensorflow.org/api_docs/python/tf/placeholder).", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: create_placeholders\n\ndef create_placeholders(n_H0, n_W0, n_C0, n_y):\n \"\"\"\n Creates the placeholders for the tensorflow session.\n \n Arguments:\n n_H0 -- scalar, height of an input image\n n_W0 -- scalar, width of an input image\n n_C0 -- scalar, number of channels of the input\n n_y -- scalar, number of classes\n \n Returns:\n X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype \"float\"\n Y -- placeholder for the input labels, of shape [None, n_y] and dtype \"float\"\n \"\"\"\n\n ### START CODE HERE ### (≈2 lines)\n X = tf.placeholder(tf.float32, shape=(None,n_H0, n_W0, n_C0))\n Y = tf.placeholder(tf.float32, shape=(None, n_y))\n ### END CODE HERE ###\n \n return X, Y", "_____no_output_____" ], [ "X, Y = create_placeholders(64, 64, 3, 6)\nprint (\"X = \" + str(X))\nprint (\"Y = \" + str(Y))", "X = Tensor(\"Placeholder:0\", shape=(?, 64, 64, 3), dtype=float32)\nY = Tensor(\"Placeholder_1:0\", shape=(?, 6), dtype=float32)\n" ] ], [ [ "**Expected Output**\n\n<table> \n<tr>\n<td>\n X = Tensor(\"Placeholder:0\", shape=(?, 64, 64, 3), dtype=float32)\n\n</td>\n</tr>\n<tr>\n<td>\n Y = Tensor(\"Placeholder_1:0\", shape=(?, 6), dtype=float32)\n\n</td>\n</tr>\n</table>", "_____no_output_____" ], [ "### 1.2 - Initialize parameters\n\nYou will initialize weights/filters $W1$ and $W2$ using `tf.contrib.layers.xavier_initializer(seed = 0)`. You don't need to worry about bias variables as you will soon see that TensorFlow functions take care of the bias. Note also that you will only initialize the weights/filters for the conv2d functions. TensorFlow initializes the layers for the fully connected part automatically. We will talk more about that later in this assignment.\n\n**Exercise:** Implement initialize_parameters(). The dimensions for each group of filters are provided below. Reminder - to initialize a parameter $W$ of shape [1,2,3,4] in Tensorflow, use:\n```python\nW = tf.get_variable(\"W\", [1,2,3,4], initializer = ...)\n```\n[More Info](https://www.tensorflow.org/api_docs/python/tf/get_variable).", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: initialize_parameters\n\ndef initialize_parameters():\n \"\"\"\n Initializes weight parameters to build a neural network with tensorflow. The shapes are:\n W1 : [4, 4, 3, 8]\n W2 : [2, 2, 8, 16]\n Returns:\n parameters -- a dictionary of tensors containing W1, W2\n \"\"\"\n \n tf.set_random_seed(1) # so that your \"random\" numbers match ours\n \n ### START CODE HERE ### (approx. 2 lines of code)\n W1 = tf.get_variable(\"W1\", shape= [4, 4, 3, 8], initializer = tf.contrib.layers.xavier_initializer(seed = 0))\n W2 = tf.get_variable(\"W2\", shape= [2, 2, 8, 16], initializer = tf.contrib.layers.xavier_initializer(seed = 0))\n ### END CODE HERE ###\n\n parameters = {\"W1\": W1,\n \"W2\": W2}\n \n return parameters", "_____no_output_____" ], [ "tf.reset_default_graph()\nwith tf.Session() as sess_test:\n parameters = initialize_parameters()\n init = tf.global_variables_initializer()\n sess_test.run(init)\n print(\"W1 = \" + str(parameters[\"W1\"].eval()[1,1,1]))\n print(\"W2 = \" + str(parameters[\"W2\"].eval()[1,1,1]))", "W1 = [ 0.00131723 0.14176141 -0.04434952 0.09197326 0.14984085 -0.03514394\n -0.06847463 0.05245192]\nW2 = [-0.08566415 0.17750949 0.11974221 0.16773748 -0.0830943 -0.08058\n -0.00577033 -0.14643836 0.24162132 -0.05857408 -0.19055021 0.1345228\n -0.22779644 -0.1601823 -0.16117483 -0.10286498]\n" ] ], [ [ "** Expected Output:**\n\n<table> \n\n <tr>\n <td>\n W1 = \n </td>\n <td>\n[ 0.00131723 0.14176141 -0.04434952 0.09197326 0.14984085 -0.03514394 <br>\n -0.06847463 0.05245192]\n </td>\n </tr>\n\n <tr>\n <td>\n W2 = \n </td>\n <td>\n[-0.08566415 0.17750949 0.11974221 0.16773748 -0.0830943 -0.08058 <br>\n -0.00577033 -0.14643836 0.24162132 -0.05857408 -0.19055021 0.1345228 <br>\n -0.22779644 -0.1601823 -0.16117483 -0.10286498]\n </td>\n </tr>\n\n</table>", "_____no_output_____" ], [ "### 1.2 - Forward propagation\n\nIn TensorFlow, there are built-in functions that carry out the convolution steps for you.\n\n- **tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = 'SAME'):** given an input $X$ and a group of filters $W1$, this function convolves $W1$'s filters on X. The third input ([1,f,f,1]) represents the strides for each dimension of the input (m, n_H_prev, n_W_prev, n_C_prev). You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d)\n\n- **tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME'):** given an input A, this function uses a window of size (f, f) and strides of size (s, s) to carry out max pooling over each window. You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/max_pool)\n\n- **tf.nn.relu(Z1):** computes the elementwise ReLU of Z1 (which can be any shape). You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/relu)\n\n- **tf.contrib.layers.flatten(P)**: given an input P, this function flattens each example into a 1D vector it while maintaining the batch-size. It returns a flattened tensor with shape [batch_size, k]. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/flatten)\n\n- **tf.contrib.layers.fully_connected(F, num_outputs):** given a the flattened input F, it returns the output computed using a fully connected layer. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/fully_connected)\n\nIn the last function above (`tf.contrib.layers.fully_connected`), the fully connected layer automatically initializes weights in the graph and keeps on training them as you train the model. Hence, you did not need to initialize those weights when initializing the parameters. \n\n\n**Exercise**: \n\nImplement the `forward_propagation` function below to build the following model: `CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED`. You should use the functions above. \n\nIn detail, we will use the following parameters for all the steps:\n - Conv2D: stride 1, padding is \"SAME\"\n - ReLU\n - Max pool: Use an 8 by 8 filter size and an 8 by 8 stride, padding is \"SAME\"\n - Conv2D: stride 1, padding is \"SAME\"\n - ReLU\n - Max pool: Use a 4 by 4 filter size and a 4 by 4 stride, padding is \"SAME\"\n - Flatten the previous output.\n - FULLYCONNECTED (FC) layer: Apply a fully connected layer without an non-linear activation function. Do not call the softmax here. This will result in 6 neurons in the output layer, which then get passed later to a softmax. In TensorFlow, the softmax and cost function are lumped together into a single function, which you'll call in a different function when computing the cost. ", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: forward_propagation\n\ndef forward_propagation(X, parameters):\n \"\"\"\n Implements the forward propagation for the model:\n CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED\n \n Arguments:\n X -- input dataset placeholder, of shape (input size, number of examples)\n parameters -- python dictionary containing your parameters \"W1\", \"W2\"\n the shapes are given in initialize_parameters\n\n Returns:\n Z3 -- the output of the last LINEAR unit\n \"\"\"\n \n # Retrieve the parameters from the dictionary \"parameters\" \n W1 = parameters['W1']\n W2 = parameters['W2']\n \n ### START CODE HERE ###\n # CONV2D: stride of 1, padding 'SAME'\n Z1 = tf.nn.conv2d(X,W1,strides=[1,1,1,1],padding=\"SAME\")\n \n # RELU\n A1 = tf.nn.relu(Z1)\n \n # MAXPOOL: window 8x8, sride 8, padding 'SAME'\n P1 = tf.nn.max_pool(A1,ksize=[1,8,8,1],strides=[1,8,8,1],padding=\"SAME\")\n \n # CONV2D: filters W2, stride 1, padding 'SAME'\n Z2 = tf.nn.conv2d(P1,W2,strides=[1,1,1,1],padding=\"SAME\")\n \n # RELU\n A2 = tf.nn.relu(Z2)\n \n # MAXPOOL: window 4x4, stride 4, padding 'SAME'\n P2 = tf.nn.max_pool(A2,ksize=[1,4,4,1],strides=[1,4,4,1],padding=\"SAME\")\n \n # FLATTEN\n P2 = tf.contrib.layers.flatten(P2)\n \n # FULLY-CONNECTED without non-linear activation function (not not call softmax).\n # 6 neurons in output layer. Hint: one of the arguments should be \"activation_fn=None\" \n Z3 = tf.contrib.layers.fully_connected(P2, 6,activation_fn= None)\n \n ### END CODE HERE ###=None\n\n return Z3", "_____no_output_____" ], [ "tf.reset_default_graph()\n\nwith tf.Session() as sess:\n np.random.seed(1)\n X, Y = create_placeholders(64, 64, 3, 6)\n parameters = initialize_parameters()\n Z3 = forward_propagation(X, parameters)\n init = tf.global_variables_initializer()\n sess.run(init)\n a = sess.run(Z3, {X: np.random.randn(2,64,64,3), Y: np.random.randn(2,6)})\n print(\"Z3 = \" + str(a))", "Z3 = [[-0.44670227 -1.57208765 -1.53049231 -2.31013036 -1.29104376 0.46852064]\n [-0.17601591 -1.57972014 -1.4737016 -2.61672091 -1.00810647 0.5747785 ]]\n" ] ], [ [ "**Expected Output**:\n\n<table> \n <td> \n Z3 =\n </td>\n <td>\n [[-0.44670227 -1.57208765 -1.53049231 -2.31013036 -1.29104376 0.46852064] <br>\n [-0.17601591 -1.57972014 -1.4737016 -2.61672091 -1.00810647 0.5747785 ]]\n </td>\n</table>", "_____no_output_____" ], [ "### 1.3 - Compute cost\n\nImplement the compute cost function below. You might find these two functions helpful: \n\n- **tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y):** computes the softmax entropy loss. This function both computes the softmax activation function as well as the resulting loss. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits)\n- **tf.reduce_mean:** computes the mean of elements across dimensions of a tensor. Use this to sum the losses over all the examples to get the overall cost. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/reduce_mean)\n\n** Exercise**: Compute the cost below using the function above.", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: compute_cost \n\ndef compute_cost(Z3, Y):\n \"\"\"\n Computes the cost\n \n Arguments:\n Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)\n Y -- \"true\" labels vector placeholder, same shape as Z3\n \n Returns:\n cost - Tensor of the cost function\n \"\"\"\n \n ### START CODE HERE ### (1 line of code)\n cost = tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y)\n ### END CODE HERE ###\n \n return cost", "_____no_output_____" ], [ "tf.reset_default_graph()\n\nwith tf.Session() as sess:\n np.random.seed(1)\n X, Y = create_placeholders(64, 64, 3, 6)\n parameters = initialize_parameters()\n Z3 = forward_propagation(X, parameters)\n cost = compute_cost(Z3, Y)\n init = tf.global_variables_initializer()\n sess.run(init)\n a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})\n a = sess.run(tf.reduce_mean(a))\n print(\"cost = \"+ str(a))", "cost = 2.91034\n" ] ], [ [ "**Expected Output**: \n\n<table>\n <td> \n cost =\n </td> \n \n <td> \n 2.91034\n </td> \n</table>", "_____no_output_____" ], [ "## 1.4 Model \n\nFinally you will merge the helper functions you implemented above to build a model. You will train it on the SIGNS dataset. \n\nYou have implemented `random_mini_batches()` in the Optimization programming assignment of course 2. Remember that this function returns a list of mini-batches. \n\n**Exercise**: Complete the function below. \n\nThe model below should:\n\n- create placeholders\n- initialize parameters\n- forward propagate\n- compute the cost\n- create an optimizer\n\nFinally you will create a session and run a for loop for num_epochs, get the mini-batches, and then for each mini-batch you will optimize the function. [Hint for initializing the variables](https://www.tensorflow.org/api_docs/python/tf/global_variables_initializer)", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: model\n\ndef model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,\n num_epochs = 100, minibatch_size = 64, print_cost = True):\n \"\"\"\n Implements a three-layer ConvNet in Tensorflow:\n CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED\n \n Arguments:\n X_train -- training set, of shape (None, 64, 64, 3)\n Y_train -- test set, of shape (None, n_y = 6)\n X_test -- training set, of shape (None, 64, 64, 3)\n Y_test -- test set, of shape (None, n_y = 6)\n learning_rate -- learning rate of the optimization\n num_epochs -- number of epochs of the optimization loop\n minibatch_size -- size of a minibatch\n print_cost -- True to print the cost every 100 epochs\n \n Returns:\n train_accuracy -- real number, accuracy on the train set (X_train)\n test_accuracy -- real number, testing accuracy on the test set (X_test)\n parameters -- parameters learnt by the model. They can then be used to predict.\n \"\"\"\n \n ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables\n tf.set_random_seed(1) # to keep results consistent (tensorflow seed)\n seed = 3 # to keep results consistent (numpy seed)\n (m, n_H0, n_W0, n_C0) = X_train.shape \n n_y = Y_train.shape[1] \n costs = [] # To keep track of the cost\n \n # Create Placeholders of the correct shape\n ### START CODE HERE ### (1 line)\n X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)\n ### END CODE HERE ###\n\n # Initialize parameters\n ### START CODE HERE ### (1 line)\n parameters = initialize_parameters()\n ### END CODE HERE ###\n \n # Forward propagation: Build the forward propagation in the tensorflow graph\n ### START CODE HERE ### (1 line)\n Z3 = forward_propagation(X, parameters)\n ### END CODE HERE ###\n \n # Cost function: Add cost function to tensorflow graph\n ### START CODE HERE ### (1 line)\n cost = compute_cost(Z3, Y)\n ### END CODE HERE ###\n \n # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.\n ### START CODE HERE ### (1 line)\n optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)\n ### END CODE HERE ###\n \n # Initialize all the variables globally\n init = tf.global_variables_initializer()\n \n # Start the session to compute the tensorflow graph\n with tf.Session() as sess:\n \n # Run the initialization\n sess.run(init)\n \n # Do the training loop\n for epoch in range(num_epochs):\n\n minibatch_cost = 0.\n num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set\n seed = seed + 1\n minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)\n\n for minibatch in minibatches:\n\n # Select a minibatch\n (minibatch_X, minibatch_Y) = minibatch\n # IMPORTANT: The line that runs the graph on a minibatch.\n # Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).\n ### START CODE HERE ### (1 line)\n _ , temp_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})\n ### END CODE HERE ###\n \n minibatch_cost += (sess.run(tf.reduce_mean(temp_cost)) / num_minibatches)\n \n\n # Print the cost every epoch\n if print_cost == True and epoch % 5 == 0:\n print (\"Cost after epoch %i: %f\" % (epoch, minibatch_cost))\n if print_cost == True and epoch % 1 == 0:\n costs.append(minibatch_cost)\n \n \n # plot the cost\n plt.plot(np.squeeze(costs))\n plt.ylabel('cost')\n plt.xlabel('iterations (per tens)')\n plt.title(\"Learning rate =\" + str(learning_rate))\n plt.show()\n\n # Calculate the correct predictions\n predict_op = tf.argmax(Z3, 1)\n correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))\n \n # Calculate accuracy on the test set\n accuracy = tf.reduce_mean(tf.cast(correct_prediction, \"float\"))\n print(accuracy)\n train_accuracy = accuracy.eval({X: X_train, Y: Y_train})\n test_accuracy = accuracy.eval({X: X_test, Y: Y_test})\n print(\"Train Accuracy:\", train_accuracy)\n print(\"Test Accuracy:\", test_accuracy)\n \n # Predict random examples\n index = 10\n Xin = np.array(X_test[[index],:,:,:],dtype=\"float\")\n pred = tf.argmax(Z3,1)\n a = sess.run(pred, {X: Xin})\n print(\"Number = \" + str(a))\n plt.imshow(X_test[index])\n \n return train_accuracy, test_accuracy, parameters", "_____no_output_____" ] ], [ [ "Run the following cell to train your model for 100 epochs. Check if your cost after epoch 0 and 5 matches our output. If not, stop the cell and go back to your code!", "_____no_output_____" ] ], [ [ "_, _, parameters = model(X_train, Y_train, X_test, Y_test)\n\n", "Cost after epoch 0: 1.918090\nCost after epoch 5: 1.545281\nCost after epoch 10: 1.005111\nCost after epoch 15: 0.828035\nCost after epoch 20: 0.684271\nCost after epoch 25: 0.648975\nCost after epoch 30: 0.574304\nCost after epoch 35: 0.557773\nCost after epoch 40: 0.502622\nCost after epoch 45: 0.511315\nCost after epoch 50: 0.432930\nCost after epoch 55: 0.412427\nCost after epoch 60: 0.395395\nCost after epoch 65: 0.421457\nCost after epoch 70: 0.431765\nCost after epoch 75: 0.387242\nCost after epoch 80: 0.377383\nCost after epoch 85: 0.341380\nCost after epoch 90: 0.324428\nCost after epoch 95: 0.335774\n" ] ], [ [ "**Expected output**: although it may not match perfectly, your expected output should be close to ours and your cost value should decrease.\n\n<table> \n<tr>\n <td> \n **Cost after epoch 0 =**\n </td>\n\n <td> \n 1.917929\n </td> \n</tr>\n<tr>\n <td> \n **Cost after epoch 5 =**\n </td>\n\n <td> \n 1.506757\n </td> \n</tr>\n<tr>\n <td> \n **Train Accuracy =**\n </td>\n\n <td> \n 0.940741\n </td> \n</tr> \n\n<tr>\n <td> \n **Test Accuracy =**\n </td>\n\n <td> \n 0.783333\n </td> \n</tr> \n</table>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e5f8d9b6e30462a9ffbab3881702728bf01c15

2,979

ipynb

Jupyter Notebook

Programming/python/theory/recursive_function.ipynb

kwangjunechoi7/TIL

99403791eb77fd9190d7d6f60ade67bb48122b33

[ "MIT" ]

null

Programming/python/theory/recursive_function.ipynb

kwangjunechoi7/TIL

99403791eb77fd9190d7d6f60ade67bb48122b33

[ "MIT" ]

null

Programming/python/theory/recursive_function.ipynb

kwangjunechoi7/TIL

99403791eb77fd9190d7d6f60ade67bb48122b33

[ "MIT" ]

null

30.090909

524

0.524001

[ [ [ "import pandas as pd", "_____no_output_____" ], [ "def words(letters, word=''):\n letters or print(word)\n for letter in letters:\n words(letters - {letter}, word + letter)\n\nwords(set('catdog'))", "_____no_output_____" ], [ "### recursive function \n- 함수 자체를 호출 \n- 종료 조건만 지정\n- 조건에 수렴하지 않을 경우 무한 재귀 발생 \n- 느린 실행\n- 코드의 길이와 변수가 적어 가독성이 높아짐\n- 재사용과 코드의 길이, 유지 보수에 유리 \n- 합병정렬 같은 걸 for 문으로 구성하기는 매우 힘들 것 \n- 작성한 코드가 정확히 동작하는 걸 증명하는 것은 매우 어려움 \n- 재귀함수의 경우 수학적으로 정의한 내용을 그대로 옮기면 재귀 형태의 함수가 되기 때문에 유리\n- 컴파일러가 재귀호출의 문제점을 해결해줄 수 있음", "_____no_output_____" ], [ "data = {'json': [{'type': 'p', 'children': [{'type': 'text', 'data': 'Lorem Ipsum is simply dummy text '}, {'type': 'a', 'attribs': {'href': 'http://example.com'}, 'children': [{'type': 'text', 'data': 'simply dummy text'}]}, {'type': 'text', 'data': ' Lorem Ipsum is simply dummy text 2'}]}, {'type': 'p', 'children': [{'type': 'text', 'data': 'second Lorem Ipsum is simply dummy text'}]}, {'type': 'div', 'children': [{'type': 'text', 'data': 'Third Lorem Ipsum is simply dummy text'}]}, {'type': 'outstream-1'}]}\n\ndef render(d):\n def build_tag(t):\n if t['type'] == 'text':\n return t['data']\n attrs = ''.join(f' {a}=\"{b}\"' for a, b in t.get(\"attribs\", {}).items())\n return f'<{t[\"type\"]}{attrs}>{render(t.get(\"children\", []))}</{t[\"type\"]}>\\n'\n return ''.join(build_tag(i) for i in d)\n\nprint(render(data['json']))", "<p>Lorem Ipsum is simply dummy text <a href=\"http://example.com\">simply dummy text</a>\n Lorem Ipsum is simply dummy text 2</p>\n<p>second Lorem Ipsum is simply dummy text</p>\n<div>Third Lorem Ipsum is simply dummy text</div>\n<outstream-1></outstream-1>\n\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code" ] ]

d0e60734877dff4f68e3a4eccd3a5b94551acfc9

35,065

ipynb

Jupyter Notebook

Chapter05/Activity 15 - Predicting the loss of customers.ipynb

TrainingByPackt/Master-Data-Science-with-Python-

cd5e1bd30a886d8b4ae3e4835bf3c657c29a52a3

[ "MIT" ]

28

2019-06-25T15:03:13.000Z

2022-03-28T20:53:01.000Z

Chapter05/Activity 15 - Predicting the loss of customers.ipynb

TrainingByPackt/Master-Data-Science-with-Python-

cd5e1bd30a886d8b4ae3e4835bf3c657c29a52a3

[ "MIT" ]

null

Chapter05/Activity 15 - Predicting the loss of customers.ipynb

TrainingByPackt/Master-Data-Science-with-Python-

cd5e1bd30a886d8b4ae3e4835bf3c657c29a52a3

[ "MIT" ]

93

2019-06-26T02:34:00.000Z

2022-03-29T16:21:48.000Z

62.504456

9,520

0.702182

[ [ [ "%matplotlib inline", "_____no_output_____" ], [ "import pandas as pd\nimport xgboost as xgb\nimport numpy as np\nfrom sklearn.metrics import accuracy_score\nimport matplotlib.pyplot as plt\nimport graphviz\nfrom sklearn.preprocessing import LabelEncoder", "_____no_output_____" ], [ "data = pd.read_csv(\"data/telco-churn.csv\")", "_____no_output_____" ], [ "data.head()", "_____no_output_____" ], [ "data.shape", "_____no_output_____" ], [ "data.drop('customerID', axis = 1, inplace = True)", "_____no_output_____" ], [ "data.iloc[0]", "_____no_output_____" ], [ "data['gender'] = LabelEncoder().fit_transform(data['gender'])\ndata['Partner'] = LabelEncoder().fit_transform(data['Partner'])\ndata['Dependents'] = LabelEncoder().fit_transform(data['Dependents'])\ndata['PhoneService'] = LabelEncoder().fit_transform(data['PhoneService'])\ndata['MultipleLines'] = LabelEncoder().fit_transform(data['MultipleLines'])\ndata['InternetService'] = LabelEncoder().fit_transform(data['InternetService'])\ndata['OnlineSecurity'] = LabelEncoder().fit_transform(data['OnlineSecurity'])\ndata['OnlineBackup'] = LabelEncoder().fit_transform(data['OnlineBackup'])\ndata['DeviceProtection'] = LabelEncoder().fit_transform(data['DeviceProtection'])\ndata['TechSupport'] = LabelEncoder().fit_transform(data['TechSupport'])\ndata['StreamingTV'] = LabelEncoder().fit_transform(data['StreamingTV'])\ndata['StreamingMovies'] = LabelEncoder().fit_transform(data['StreamingMovies'])\ndata['Contract'] = LabelEncoder().fit_transform(data['Contract'])\ndata['PaperlessBilling'] = LabelEncoder().fit_transform(data['PaperlessBilling'])\ndata['PaymentMethod'] = LabelEncoder().fit_transform(data['PaymentMethod'])\ndata['Churn'] = LabelEncoder().fit_transform(data['Churn'])", "_____no_output_____" ], [ "data.dtypes", "_____no_output_____" ], [ "data.TotalCharges = pd.to_numeric(data.TotalCharges, errors='coerce')", "_____no_output_____" ], [ "X = data.copy()\nX.drop(\"Churn\", inplace = True, axis = 1)\nY = data.Churn", "_____no_output_____" ], [ "X_train, X_test = X[:int(X.shape[0]*0.8)].values, X[int(X.shape[0]*0.8):].values\nY_train, Y_test = Y[:int(Y.shape[0]*0.8)].values, Y[int(Y.shape[0]*0.8):].values", "_____no_output_____" ], [ "train = xgb.DMatrix(X_train, label=Y_train)\ntest = xgb.DMatrix(X_test, label=Y_test)", "_____no_output_____" ], [ "test_error = {}\nfor i in range(20):\n param = {'max_depth':i, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}\n num_round = 50\n model_metrics = xgb.cv(param, train, num_round, nfold = 10)\n test_error[i] = model_metrics.iloc[-1]['test-error-mean']", "_____no_output_____" ], [ "plt.scatter(test_error.keys(),test_error.values())\nplt.xlabel('Max Depth')\nplt.ylabel('Test Error')\nplt.show()", "_____no_output_____" ], [ "param = {'max_depth':4, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}\nnum_round = 300\nmodel_metrics = xgb.cv(param, train, num_round, nfold = 10)", "_____no_output_____" ], [ "plt.scatter(range(300),model_metrics['test-error-mean'], s = 0.7, label = 'Test Error')\nplt.scatter(range(300),model_metrics['train-error-mean'], s = 0.7, label = 'Train Error')\nplt.legend()\nplt.show()", "_____no_output_____" ], [ "param = {'max_depth':4, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}\nnum_round = 100\nmodel = xgb.train(param, train, num_round)\npreds = model.predict(test)\naccuracy = accuracy_score(Y[int(Y.shape[0]*0.8):].values, preds)\nprint(\"Accuracy: %.2f%%\" % (accuracy * 100.0))", "Accuracy: 79.77%\n" ], [ "model.save_model('churn-model.model')", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e61315fd44a906f1a3ab16bde73dd7e73d2044

223,633

ipynb

Jupyter Notebook

Python_Stock/Technical_Indicators/Stochastic_Slow.ipynb

eu90h/Stock_Analysis_For_Quant

5e5e9f9c2a8f4af72e26564bc9d66bd2c90880df

[ "MIT" ]

null

Python_Stock/Technical_Indicators/Stochastic_Slow.ipynb

eu90h/Stock_Analysis_For_Quant

5e5e9f9c2a8f4af72e26564bc9d66bd2c90880df

[ "MIT" ]

null

Python_Stock/Technical_Indicators/Stochastic_Slow.ipynb

eu90h/Stock_Analysis_For_Quant

5e5e9f9c2a8f4af72e26564bc9d66bd2c90880df

[ "MIT" ]

null

202.749773

93,650

0.840936

[ [ [ "# Slow Stochastic", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\nimport matplotlib.pyplot as plt\n\nimport warnings\nwarnings.filterwarnings(\"ignore\")\n\n# yfinance is used to fetch data \nimport yfinance as yf\nyf.pdr_override()", "_____no_output_____" ], [ "# input\nsymbol = 'AAPL'\nstart = '2018-08-01'\nend = '2019-01-01'\n\n# Read data \ndf = yf.download(symbol,start,end)\n\n# View Columns\ndf.head()", "[*********************100%***********************] 1 of 1 downloaded\n" ], [ "n = 14 # number of days\ns = 3 # smoothing\ndf['High_Highest'] = df['Adj Close'].rolling(n).max()\ndf['Low_Lowest'] = df['Adj Close'].rolling(n).min()\ndf['Fast_%K'] = ((df['Adj Close'] - df['Low_Lowest']) / (df['High_Highest'] - df['Low_Lowest'])) * 100\ndf['Slow_%K'] = df['Fast_%K'].rolling(s).mean()\ndf['Slow_%D'] = df['Slow_%K'].rolling(s).mean()", "_____no_output_____" ], [ "df.head(30)", "_____no_output_____" ], [ "fig = plt.figure(figsize=(14,10))\nax1 = plt.subplot(2, 1, 1)\nax1.plot(df['Adj Close'])\nax1.set_title('Stock '+ symbol +' Closing Price')\nax1.set_ylabel('Price')\n\nax2 = plt.subplot(2, 1, 2)\nax2.plot(df['Slow_%K'], label='Slow %K')\nax2.plot(df['Slow_%D'], label='Slow %D')\nax2.text(s='Overbought', x=df.index[30], y=80, fontsize=14)\nax2.text(s='Oversold', x=df.index[30], y=20, fontsize=14)\nax2.axhline(y=80, color='red')\nax2.axhline(y=20, color='red')\nax2.grid()\nax2.set_ylabel('Slow Stochastic')\nax2.legend(loc='best')\nax2.set_xlabel('Date')", "_____no_output_____" ] ], [ [ "## Candlestick with Slow Stochastic", "_____no_output_____" ] ], [ [ "from matplotlib import dates as mdates\nimport datetime as dt\n\ndfc = df.copy()\ndfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']\n#dfc = dfc.dropna()\ndfc = dfc.reset_index()\ndfc['Date'] = mdates.date2num(dfc['Date'].astype(dt.date))\ndfc.head()", "_____no_output_____" ], [ "from mpl_finance import candlestick_ohlc\n\nfig = plt.figure(figsize=(14,10))\nax1 = plt.subplot(2, 1, 1)\ncandlestick_ohlc(ax1,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)\nax1.xaxis_date()\nax1.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))\nax1.grid(True, which='both')\nax1.minorticks_on()\nax1v = ax1.twinx()\ncolors = dfc.VolumePositive.map({True: 'g', False: 'r'})\nax1v.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)\nax1v.axes.yaxis.set_ticklabels([])\nax1v.set_ylim(0, 3*df.Volume.max())\nax1.set_title('Stock '+ symbol +' Closing Price')\nax1.set_ylabel('Price')\n\nax2 = plt.subplot(2, 1, 2)\nax2.plot(df['Slow_%K'], label='Slow %K')\nax2.plot(df['Slow_%D'], label='Slow %D')\nax2.text(s='Overbought', x=df.index[30], y=80, fontsize=14)\nax2.text(s='Oversold', x=df.index[30], y=20, fontsize=14)\nax2.axhline(y=80, color='red')\nax2.axhline(y=20, color='red')\nax2.grid()\nax2.set_ylabel('Slow Stochastic')\nax2.legend(loc='best')\nax2.set_xlabel('Date')", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

d0e615468a024e40ed79c11530d36536e903ccb7

3,449

ipynb

Jupyter Notebook

data/M100-json_builder.ipynb

felixrlopezm/OP_Map

a46f2a18b3d739bebfc700adebc9f8c481af624a

[ "MIT" ]

null

data/M100-json_builder.ipynb

felixrlopezm/OP_Map

a46f2a18b3d739bebfc700adebc9f8c481af624a

[ "MIT" ]

null

data/M100-json_builder.ipynb

felixrlopezm/OP_Map

a46f2a18b3d739bebfc700adebc9f8c481af624a

[ "MIT" ]

1

2022-03-06T18:27:18.000Z

38.322222

170

0.543056

[ [ [ "import json\nimport numpy as np", "_____no_output_____" ], [ "# Element mapping: dictionary with mapping, x_labels and y_labels\n# mapping is square matrix; if no element, use dummy element -666\n\n# Left Hand Side - Upper Skin panels\nlhs_upr_skin_panels = np.array([[200089,200095,200060,200066,200072,200059,200042,200047,200041,200002,-666,-666,-666,-666,-666,-666,-666,-666],\n [200088,200094,200061,200067,200073,200058,200043,200046,200029,200030,200022,200023,200026,200001,-666,-666,-666,-666],\n [200087,200093,200062,200068,200074,200057,200044,200045,200037,200038,200052,200053,200010,200011,200012,200013,200003,200000],\n [200086,200092,200063,200069,200075,200056,200078,200083,200039,200040,200050,200051,200021,200020,200016,200017,200007,200006],\n [200085,200091,200064,200070,200076,200055,200079,200082,200033,200034,200048,200049,200027,200028,200018,200019,200004,200005],\n [200084,200090,200065,200071,200077,200054,200080,200081,200035,200036,200031,200032,200024,200025,200014,200015,200009,200008]])\n\nlhs_upr_skin_panels_dic = {'mapping': lhs_upr_skin_panels.tolist(),\n 'x_labels': ['R1-R2', '', 'R2-R3', '', 'R3-R4', '', 'R4-R5', '', 'R5-R6', '', 'R6-R7', '', 'R7-R8', '', 'R8-R9', '', 'R9-R10', ''],\n 'y_labels': ['FS-S1', 'S1-S2', 'S2-S3', 'S3-S4', 'S4-S5', 'S5-RS']}\n \n# Rib1 web panels\nrib1_web = np.array([[30068,30050,30054,30060,30063,30062],\n [30067,30047,30049,30056,30045,30061],\n [30066,30058,30051,30053,30059,30064],\n [30065,30057,30048,30055,30046,30052]])\n\nrib1_web_dic = {'mapping': rib1_web.tolist(),\n 'x_labels': ['<--FS', '', '', '', '', 'RS-->'],\n 'y_labels': ['upr', '', '', 'lwr']}", "_____no_output_____" ], [ "# Creating an element mapping dictionary of lists\n#elm_mapping = {'lhs_upr_skin_panels': lhs_upr_skin_panels.tolist(), 'rib1_web': rib1_web.tolist()}\n\nelm_mapping = {'lhs_upr_skin_panels': lhs_upr_skin_panels_dic, 'rib1_web': rib1_web_dic}", "_____no_output_____" ], [ "# Saving the dictionary into a json file:\njson.dump(elm_mapping, open( \"MECEA-HTP-mapping-B.json\", 'w' ) )", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code" ] ]

d0e619c2120bd794833f82abcb6ef53f21a68890

52,049

ipynb

Jupyter Notebook

notebooks/continuation/logistic.ipynb

tmiyaji/sgc164

660f61b72a3898f8e287feb464134f5c48f9383e

[ "BSD-3-Clause" ]

3

2021-02-01T15:29:43.000Z

2021-10-01T13:20:21.000Z

notebooks/continuation/logistic.ipynb

tmiyaji/sgc164

660f61b72a3898f8e287feb464134f5c48f9383e

[ "BSD-3-Clause" ]

null

notebooks/continuation/logistic.ipynb

tmiyaji/sgc164

660f61b72a3898f8e287feb464134f5c48f9383e

[ "BSD-3-Clause" ]

1

2020-12-20T07:46:22.000Z

135.898172

43,048

0.880171

[ [ [ "# ロジスティック写像\n\n$$\nf(x, a) = a x (1 - x)\n$$", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pathfollowing as pf\nimport matplotlib.pyplot as plt\nimport seaborn as sns\n%matplotlib inline\nsns.set('poster', 'whitegrid', 'dark', rc={\"lines.linewidth\": 2, 'grid.linestyle': '-'})", "_____no_output_____" ], [ "def func(x, a):\n return np.array([a[0] * x[0] * (1.0 - x[0])])\n\ndef dfdx(x,a):\n return np.array([[a[0]*(1.0 - 2*x[0])]])\n\ndef dfda(x,a):\n return np.array([x[0]*(1.0 - x[0])])", "_____no_output_____" ] ], [ [ "## 不動点の追跡\n\n- $(x, a) = (2/3, 3)$で周期倍分岐が起こる", "_____no_output_____" ] ], [ [ "x=np.array([0.5])\na=np.array([2.0])\nbd,bp,lp,pd=pf.pathfollow(x, a, func, dfdx, dfda,nmax=45, h=0.05, epsr=1.0e-10, epsb=1.0e-10, amin=0.0,amax=4.0,problem='map', quiet=True)", "# parameter arrived at boundary\n" ] ], [ [ "周期倍分岐点", "_____no_output_____" ] ], [ [ "bd[pd[0]]", "_____no_output_____" ] ], [ [ "## 周期点の追跡", "_____no_output_____" ], [ "周期2の周期点の枝に切り替える", "_____no_output_____" ] ], [ [ "v2 = pf.calcSwitchingVectorPD(bd[pd[0]], func, dfdx, dfda, period=2)\nx2=bd[pd[0]]['x']\na2=bd[pd[0]]['a']\nbd2,bp2,lp2, pd2=pf.pathfollow(x2, a2, func, dfdx, dfda, w=v2, nmax=65, h=0.025, epsr=1.0e-10, epsb=1.0e-10, amin=0.0,amax=4.0,problem='map', quiet=True,period=2)", "# parameter arrived at boundary\n" ] ], [ [ "周期点の周期倍分岐", "_____no_output_____" ] ], [ [ "bd2[pd2[0]]", "_____no_output_____" ] ], [ [ "周期4の周期点の枝に切り替える", "_____no_output_____" ] ], [ [ "v4 = pf.calcSwitchingVectorPD(bd2[pd2[0]], func, dfdx, dfda, period=4)\nx4=bd2[pd2[0]]['x']\na4=bd2[pd2[0]]['a']\nbd4,bp4,lp4, pd4=pf.pathfollow(x4, a4, func, dfdx, dfda, w=v4, nmax=65, h=0.0125, epsr=1.0e-10, amin=0.0,amax=4.0,epsb=1.0e-12, problem='map', quiet=True,period=4)", "# parameter arrived at boundary\n" ] ], [ [ "周期8の周期点の枝に切り替える", "_____no_output_____" ] ], [ [ "v8 = pf.calcSwitchingVectorPD(bd4[pd4[0]], func, dfdx, dfda, period=8)\nx8=bd4[pd4[0]]['x']\na8=bd4[pd4[0]]['a']\nbd8,bp8,lp8, pd8=pf.pathfollow(x8, a8, func, dfdx, dfda, w=v8, nmax=130, h=0.00625, epsr=1.0e-10, amin=0.0,amax=4.0,epsb=1.0e-12, problem='map', quiet=True,period=8)", "# parameter arrived at boundary\n" ] ], [ [ "これまでにもとめた周期倍分岐点のパラメータ値$a$", "_____no_output_____" ] ], [ [ "print(bd[pd[0]]['a'], bd2[pd2[0]]['a'], bd4[pd4[0]]['a'], bd8[pd8[0]]['a'])", "[3.] [3.44948974] [3.54409036] [3.56440727]\n" ], [ "print(pd8)", "[7]\n" ], [ "bd_r = np.array([bd[m]['a'][0] for m in range(len(bd))])\nbd_x = np.array([bd[m]['x'][0] for m in range(len(bd))])\nbd_r2 = np.array([bd2[m]['a'][0] for m in range(len(bd2))])\nbd_x2 = np.array([bd2[m]['x'][0] for m in range(len(bd2))])\nbd_r4 = np.array([bd4[m]['a'][0] for m in range(len(bd4))])\nbd_x4 = np.array([bd4[m]['x'][0] for m in range(len(bd4))])\nbd_r8 = np.array([bd8[m]['a'][0] for m in range(len(bd8))])\nbd_x8 = np.array([bd8[m]['x'][0] for m in range(len(bd8))])", "_____no_output_____" ], [ "def f(x,a):\n return a*x*(1-x)\n\nbd_x22 = np.array([f(bd_x2[m], bd_r2[m]) for m in range(len(bd2))])\nbd_x42 = np.array([f(bd_x4[m], bd_r4[m]) for m in range(len(bd4))])\nbd_x43 = np.array([f(bd_x42[m], bd_r4[m]) for m in range(len(bd4))])\nbd_x44 = np.array([f(bd_x43[m], bd_r4[m]) for m in range(len(bd4))])\nbd_x82 = np.array([f(bd_x8[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x83 = np.array([f(bd_x82[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x84 = np.array([f(bd_x83[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x85 = np.array([f(bd_x84[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x86 = np.array([f(bd_x85[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x87 = np.array([f(bd_x86[m], bd_r8[m]) for m in range(len(bd8))])\nbd_x88 = np.array([f(bd_x87[m], bd_r8[m]) for m in range(len(bd8))])", "_____no_output_____" ], [ "fig = plt.figure(figsize=(8, 5))\nax = fig.add_subplot(111)\nax.set_xlim(2,4)\nax.set_ylim(0.2, 1)\nax.set_xlabel(\"$a$\")\nax.set_ylabel(\"$x$\")\nax.plot(bd_r ,bd_x, '-k')\nax.plot(bd_r2, bd_x2, '-k')\nax.plot(bd_r2, bd_x22, '-k')\nax.plot(bd_r4, bd_x4, '-k')\nax.plot(bd_r4, bd_x42, '-k')\nax.plot(bd_r4, bd_x43, '-k')\nax.plot(bd_r4, bd_x44, '-k')\nax.plot(bd_r8, bd_x8, '-k')\nax.plot(bd_r8, bd_x82, '-k')\nax.plot(bd_r8, bd_x83, '-k')\nax.plot(bd_r8, bd_x84, '-k')\nax.plot(bd_r8, bd_x85, '-k')\nax.plot(bd_r8, bd_x86, '-k')\nax.plot(bd_r8, bd_x87, '-k')\nax.plot(bd_r8, bd_x88, '-k')\n# plt.savefig(\"bd_logistic.pdf\", bbox_inches='tight')", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ] ]

d0e6215227d378eb9234291037769afe528af06a

178,620

ipynb

Jupyter Notebook

02-introduction-to-neural-networks-and-tensorflow/introduction-to-neural-networks-and-tensorflow.ipynb

vr140/intro-deep-learning

689ab820e6924bf627c33f857d0b2fb64459d7ea

[ "MIT" ]

1

2018-06-23T18:35:39.000Z

02-introduction-to-neural-networks-and-tensorflow/introduction-to-neural-networks-and-tensorflow.ipynb

vr140/intro-deep-learning

689ab820e6924bf627c33f857d0b2fb64459d7ea

[ "MIT" ]

4

2020-11-13T17:56:25.000Z

2022-02-09T23:57:03.000Z

02-introduction-to-neural-networks-and-tensorflow/introduction-to-neural-networks-and-tensorflow.ipynb

vr140/intro-deep-learning

689ab820e6924bf627c33f857d0b2fb64459d7ea

[ "MIT" ]

null

175.117647

28,658

0.515536

[ [ [ "## Part 2: Introduction to Feed Forward Networks\n\n### 1. What is a neural network?\n\n#### 1.1 Neurons\n\nA neuron is software that is roughly modeled after the neuons in your brain. In software, we model it with an _affine function_ and an _activation function_. \n\nOne type of neuron is the perceptron, which outputs a binary output 0 or 1 given an input [7]:\n\n<img src=\"perceptron.jpg\" width=\"600\" height=\"480\" />\n\nYou can add an activation function to the end isntead of simply thresholding values to clip values from 0 to 1. One common activiation function is the logistic function.\n\n<img src=\"sigmoid_neuron.jpg\" width=\"600\" height=\"480\" />\n\nThe most common activation function used nowadays is the rectified linear unit, which is simply max(0, z) where z = w * x + b, or the neurons output.\n\n#### 1.2 Hidden layers and multi-layer perceptrons\n\nA multi-layer perceptron (MLP) is quite simply layers on these perceptrons that are wired together. The layers between the input layer and the output layer are known as the hidden layers. The below is a four layer network with two hidden layers [7]:\n\n\n<img src=\"hidden_layers.jpg\" width=\"600\" height=\"480\" />", "_____no_output_____" ], [ "### 2. Tensorflow\nTensorflow (https://www.tensorflow.org/install/) is an extremely popular deep learning library built by Google and will be the main library used for of the rest of these notebooks (in the last lesson, we briefly used numpy, a numerical computation library that's useful but does not have deep learning functionality). NOTE: Other popular deep learning libraries include Pytorch and Caffe2. Keras is another popular one, but its API has since been absorbed into Tensorflow. Tensorflow is chosen here because:\n\n* it has the most active community on Github\n* it's well supported by Google in terms of core features\n* it has Tensorflow serving, which allows you to serve your models online (something we'll see in a future notebook)\n* it has Tensorboard for visualization (which we will use in this lesson)\n\nLet's train our first model to get a sense of how powerful Tensorflow can be!", "_____no_output_____" ] ], [ [ "# Some initial setup. Borrowed from:\n# https://github.com/ageron/handson-ml/blob/master/09_up_and_running_with_tensorflow.ipynb\n\n# Common imports\nimport numpy as np\nimport os\nimport tensorflow as tf\n\n# To plot pretty figures\n%matplotlib inline\nimport matplotlib\nimport matplotlib.pyplot as plt\nplt.rcParams['axes.labelsize'] = 14\nplt.rcParams['xtick.labelsize'] = 12\nplt.rcParams['ytick.labelsize'] = 12\n\n# Where to save the figures\nPROJECT_ROOT_DIR = \".\"\nCHAPTER_ID = \"tensorflow\"\n\ndef save_fig(fig_id):\n path = os.path.join(PROJECT_ROOT_DIR, \"images\", CHAPTER_ID, fig_id + \".png\")\n print(\"Saving figure\", fig_id)\n plt.tight_layout()\n plt.savefig(path, format='png', dpi=300)\n\ndef stabilize_output():\n tf.reset_default_graph()\n # needed to avoid the following error: https://github.com/RasaHQ/rasa_core/issues/80\n tf.keras.backend.clear_session()\n tf.set_random_seed(seed=42)\n np.random.seed(seed=42)\n\nprint \"Done\"", "Done\n" ] ], [ [ "Below we will train our first model using the example from the Tensorflow tutorial: https://www.tensorflow.org/tutorials/\n\nThis will show you the basics of training a model!", "_____no_output_____" ] ], [ [ "# The example below is also in https://colab.research.google.com/github/tensorflow/models/blob/master/samples/core/get_started/_index.ipynb\n\n# to ensure relatively stable output across sessions\nstabilize_output()\n\nmnist = tf.keras.datasets.mnist\n# load data (requires Internet connection)\n(x_train, y_train),(x_test, y_test) = mnist.load_data()\nx_train, x_test = x_train / 255.0, x_test / 255.0\n\n# build a model\nmodel = tf.keras.models.Sequential([\n # flattens the input\n tf.keras.layers.Flatten(),\n # 1 \"hidden\" layer with 512 units - more on this in the next notebook\n tf.keras.layers.Dense(512, activation=tf.nn.relu),\n # example of regularization - dropout is a way of dropping hidden units at a certain factor\n # this essentially results in a model averaging across a large set of possible configurations of the hidden layer above\n # and results in model that should generalize better\n tf.keras.layers.Dropout(0.2),\n # 10 because there's possible didigts - 0 to 9\n tf.keras.layers.Dense(10, activation=tf.nn.softmax)\n])\nmodel.compile(optimizer='adam',\n loss='sparse_categorical_crossentropy',\n metrics=['accuracy'])\n# train a model (using 5 epochs -> notice the accuracy improving with each epoch)\nmodel.fit(x_train, y_train, epochs=5)\n\nprint model.metrics_names # see https://keras.io/models/model/ for the full API\n# evaluate model accuracy\nmodel.evaluate(x_test, y_test)", "Epoch 1/5\n60000/60000 [==============================] - 8s 127us/step - loss: 0.2198 - acc: 0.9344\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\nEpoch 2/5\n60000/60000 [==============================] - 8s 127us/step - loss: 0.0970 - acc: 0.9709\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\nEpoch 3/5\n60000/60000 [==============================] - 9s 148us/step - loss: 0.0684 - acc: 0.9781\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\nEpoch 4/5\n60000/60000 [==============================] - 9s 150us/step - loss: 0.0521 - acc: 0.9831\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\nEpoch 5/5\n60000/60000 [==============================] - 9s 149us/step - loss: 0.0428 - acc: 0.9858\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\n['loss', 'acc']\n10000/10000 [==============================] - 0s 47us/step\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\b\n" ] ], [ [ "You should see something similar to [0.06788356024027743, 0.9806]. The first number is the final loss and the second number is the accuracy.\n\nCongratulations, it means you've trained a classifier that classifies digit images in the MNIST Dataset with __98% accuracy__! We'll break down how the model is optimizing to achieve this accuracy below.", "_____no_output_____" ], [ "### 3. More Training of Neural Networks in Tensorflow\n\n#### 3.1: Data Preparation\n\nWe load the CIFAR-10 dataset using the tf.keras API. ", "_____no_output_____" ] ], [ [ "# Borrowed from http://cs231n.github.io/assignments2018/assignment2/\ndef load_cifar10(num_training=49000, num_validation=1000, num_test=10000):\n \"\"\"\n Fetch the CIFAR-10 dataset from the web and perform preprocessing to prepare\n it for the two-layer neural net classifier. These are the same steps as\n we used for the SVM, but condensed to a single function.\n \"\"\"\n # Load the raw CIFAR-10 dataset and use appropriate data types and shapes\n # NOTE: Download will take a few minutes but once downloaded, it should be cached.\n cifar10 = tf.keras.datasets.cifar10.load_data()\n (X_train, y_train), (X_test, y_test) = cifar10\n X_train = np.asarray(X_train, dtype=np.float32)\n y_train = np.asarray(y_train, dtype=np.int32).flatten()\n X_test = np.asarray(X_test, dtype=np.float32)\n y_test = np.asarray(y_test, dtype=np.int32).flatten()\n\n # Subsample the data\n mask = range(num_training, num_training + num_validation)\n X_val = X_train[mask]\n y_val = y_train[mask]\n mask = range(num_training)\n X_train = X_train[mask]\n y_train = y_train[mask]\n mask = range(num_test)\n X_test = X_test[mask]\n y_test = y_test[mask]\n\n # Normalize the data: subtract the mean pixel and divide by std\n mean_pixel = X_train.mean(axis=(0, 1, 2), keepdims=True)\n std_pixel = X_train.std(axis=(0, 1, 2), keepdims=True)\n X_train = (X_train - mean_pixel) / std_pixel\n X_val = (X_val - mean_pixel) / std_pixel\n X_test = (X_test - mean_pixel) / std_pixel\n\n return X_train, y_train, X_val, y_val, X_test, y_test\n\n\n# Invoke the above function to get our data.\n# N - index of the number of datapoints (minibatch size)\n# H - index of the the height of the feature map\n# W - index of the width of the feature map\nNHW = (0, 1, 2)\nX_train, y_train, X_val, y_val, X_test, y_test = load_cifar10()\nprint('Train data shape: ', X_train.shape)\nprint('Train labels shape: ', y_train.shape, y_train.dtype)\nprint('Validation data shape: ', X_val.shape)\nprint('Validation labels shape: ', y_val.shape)\nprint('Test data shape: ', X_test.shape)\nprint('Test labels shape: ', y_test.shape)", "('Train data shape: ', (49000, 32, 32, 3))\n('Train labels shape: ', (49000,), dtype('int32'))\n('Validation data shape: ', (1000, 32, 32, 3))\n('Validation labels shape: ', (1000,))\n('Test data shape: ', (10000, 32, 32, 3))\n('Test labels shape: ', (10000,))\n" ] ], [ [ "#### 3.2 Preparation: Dataset object\n\nBorrowed from CS231N [2], we will define a `Dataset` class for iteration to store data and labels.", "_____no_output_____" ] ], [ [ "class Dataset(object):\n def __init__(self, X, y, batch_size, shuffle=False):\n \"\"\"\n Construct a Dataset object to iterate over data X and labels y\n \n Inputs:\n - X: Numpy array of data, of any shape\n - y: Numpy array of labels, of any shape but with y.shape[0] == X.shape[0]\n - batch_size: Integer giving number of elements per minibatch\n - shuffle: (optional) Boolean, whether to shuffle the data on each epoch\n \"\"\"\n assert X.shape[0] == y.shape[0], 'Got different numbers of data and labels'\n self.X, self.y = X, y\n self.batch_size, self.shuffle = batch_size, shuffle\n\n def __iter__(self):\n N, B = self.X.shape[0], self.batch_size\n idxs = np.arange(N)\n if self.shuffle:\n np.random.shuffle(idxs)\n return iter((self.X[i:i+B], self.y[i:i+B]) for i in range(0, N, B))\n\n\ntrain_dset = Dataset(X_train, y_train, batch_size=64, shuffle=True)\nval_dset = Dataset(X_val, y_val, batch_size=64, shuffle=False)\ntest_dset = Dataset(X_test, y_test, batch_size=64)\nprint \"Done\"", "Done\n" ], [ "# We can iterate through a dataset like this:\nfor t, (x, y) in enumerate(train_dset):\n print(t, x.shape, y.shape)\n if t > 5: break\n \n# You can also optionally set GPU to true if you are working on AWS/Google Cloud (more on that later). For now,\n# we to false\n\n# Set up some global variables\nUSE_GPU = False\n\nif USE_GPU:\n device = '/device:GPU:0'\nelse:\n device = '/cpu:0'\n\n# Constant to control how often we print when training models\nprint_every = 100\n\nprint('Using device: ', device)", "(0, (64, 32, 32, 3), (64,))\n(1, (64, 32, 32, 3), (64,))\n(2, (64, 32, 32, 3), (64,))\n(3, (64, 32, 32, 3), (64,))\n(4, (64, 32, 32, 3), (64,))\n(5, (64, 32, 32, 3), (64,))\n(6, (64, 32, 32, 3), (64,))\n('Using device: ', '/cpu:0')\n" ], [ "# Borrowed fromcs231n.github.io/assignments2018/assignment2/\n# We define a flatten utility function to help us flatten our image data - the 32x32x3 \n# (or 32 x 32 image size with three channels for RGB) flattens into 3072 \ndef flatten(x):\n \"\"\" \n Input:\n - TensorFlow Tensor of shape (N, D1, ..., DM)\n \n Output:\n - TensorFlow Tensor of shape (N, D1 * ... * DM)\n \"\"\"\n N = tf.shape(x)[0]\n return tf.reshape(x, (N, -1))\n\ndef two_layer_fc(x, params):\n \"\"\"\n A fully-connected neural network; the architecture is:\n fully-connected layer -> ReLU -> fully connected layer.\n Note that we only need to define the forward pass here; TensorFlow will take\n care of computing the gradients for us.\n \n The input to the network will be a minibatch of data, of shape\n (N, d1, ..., dM) where d1 * ... * dM = D. The hidden layer will have H units,\n and the output layer will produce scores for C classes.\n\n Inputs:\n - x: A TensorFlow Tensor of shape (N, d1, ..., dM) giving a minibatch of\n input data.\n - params: A list [w1, w2] of TensorFlow Tensors giving weights for the\n network, where w1 has shape (D, H) and w2 has shape (H, C).\n \n Returns:\n - scores: A TensorFlow Tensor of shape (N, C) giving classification scores\n for the input data x.\n \"\"\"\n w1, w2 = params # Unpack the parameters\n x = flatten(x) # Flatten the input; now x has shape (N, D)\n h = tf.nn.relu(tf.matmul(x, w1)) # Hidden layer: h has shape (N, H)\n scores = tf.matmul(h, w2) # Compute scores of shape (N, C)\n return scores\n\ndef two_layer_fc_test():\n # TensorFlow's default computational graph is essentially a hidden global\n # variable. To avoid adding to this default graph when you rerun this cell,\n # we clear the default graph before constructing the graph we care about.\n tf.reset_default_graph()\n hidden_layer_size = 42\n\n # Scoping our computational graph setup code under a tf.device context\n # manager lets us tell TensorFlow where we want these Tensors to be\n # placed.\n with tf.device(device):\n # Set up a placehoder for the input of the network, and constant\n # zero Tensors for the network weights. Here we declare w1 and w2\n # using tf.zeros instead of tf.placeholder as we've seen before - this\n # means that the values of w1 and w2 will be stored in the computational\n # graph itself and will persist across multiple runs of the graph; in\n # particular this means that we don't have to pass values for w1 and w2\n # using a feed_dict when we eventually run the graph.\n x = tf.placeholder(tf.float32)\n w1 = tf.zeros((32 * 32 * 3, hidden_layer_size))\n w2 = tf.zeros((hidden_layer_size, 10))\n \n # Call our two_layer_fc function to set up the computational\n # graph for the forward pass of the network.\n scores = two_layer_fc(x, [w1, w2])\n \n # Use numpy to create some concrete data that we will pass to the\n # computational graph for the x placeholder.\n x_np = np.zeros((64, 32, 32, 3))\n with tf.Session() as sess:\n # The calls to tf.zeros above do not actually instantiate the values\n # for w1 and w2; the following line tells TensorFlow to instantiate\n # the values of all Tensors (like w1 and w2) that live in the graph.\n sess.run(tf.global_variables_initializer())\n \n # Here we actually run the graph, using the feed_dict to pass the\n # value to bind to the placeholder for x; we ask TensorFlow to compute\n # the value of the scores Tensor, which it returns as a numpy array.\n scores_np = sess.run(scores, feed_dict={x: x_np})\n print scores_np\n print(scores_np.shape)\n\ntwo_layer_fc_test()\n# should print a bunch of zeros\n# should print {64, 10}\nprint \"Done\"", "[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]\n(64, 10)\nDone\n" ] ], [ [ "#### 3.3 Training\n\nWe will now train using the gradient descent algorithm explained in the previous notebook. The check_accuracy function below lets us check the accuracy of our neural network.\n\nAs explained in CS231N:\n\n\"The `training_step` function has three basic steps:\n\n1. Compute the loss\n2. Compute the gradient of the loss with respect to all network weights\n3. Make a weight update step using (stochastic) gradient descent.\n\nNote that the step of updating the weights is itself an operation in the computational graph - the calls to `tf.assign_sub` in `training_step` return TensorFlow operations that mutate the weights when they are executed. There is an important bit of subtlety here - when we call `sess.run`, TensorFlow does not execute all operations in the computational graph; it only executes the minimal subset of the graph necessary to compute the outputs that we ask TensorFlow to produce. As a result, naively computing the loss would not cause the weight update operations to execute, since the operations needed to compute the loss do not depend on the output of the weight update. To fix this problem, we insert a **control dependency** into the graph, adding a duplicate `loss` node to the graph that does depend on the outputs of the weight update operations; this is the object that we actually return from the `training_step` function. As a result, asking TensorFlow to evaluate the value of the `loss` returned from `training_step` will also implicitly update the weights of the network using that minibatch of data.\n\nWe need to use a few new TensorFlow functions to do all of this:\n- For computing the cross-entropy loss we'll use `tf.nn.sparse_softmax_cross_entropy_with_logits`: https://www.tensorflow.org/api_docs/python/tf/nn/sparse_softmax_cross_entropy_with_logits\n- For averaging the loss across a minibatch of data we'll use `tf.reduce_mean`:\nhttps://www.tensorflow.org/api_docs/python/tf/reduce_mean\n- For computing gradients of the loss with respect to the weights we'll use `tf.gradients`: https://www.tensorflow.org/api_docs/python/tf/gradients\n- We'll mutate the weight values stored in a TensorFlow Tensor using `tf.assign_sub`: https://www.tensorflow.org/api_docs/python/tf/assign_sub\n- We'll add a control dependency to the graph using `tf.control_dependencies`: https://www.tensorflow.org/api_docs/python/tf/control_dependencies\"", "_____no_output_____" ] ], [ [ "# Borrowed from cs231n.github.io/assignments2018/assignment2/\ndef training_step(scores, y, params, learning_rate):\n \"\"\"\n Set up the part of the computational graph which makes a training step.\n\n Inputs:\n - scores: TensorFlow Tensor of shape (N, C) giving classification scores for\n the model.\n - y: TensorFlow Tensor of shape (N,) giving ground-truth labels for scores;\n y[i] == c means that c is the correct class for scores[i].\n - params: List of TensorFlow Tensors giving the weights of the model\n - learning_rate: Python scalar giving the learning rate to use for gradient\n descent step.\n \n Returns:\n - loss: A TensorFlow Tensor of shape () (scalar) giving the loss for this\n batch of data; evaluating the loss also performs a gradient descent step\n on params (see above).\n \"\"\"\n # First compute the loss; the first line gives losses for each example in\n # the minibatch, and the second averages the losses acros the batch\n losses = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)\n loss = tf.reduce_mean(losses)\n\n # Compute the gradient of the loss with respect to each parameter of the the\n # network. This is a very magical function call: TensorFlow internally\n # traverses the computational graph starting at loss backward to each element\n # of params, and uses backpropagation to figure out how to compute gradients;\n # it then adds new operations to the computational graph which compute the\n # requested gradients, and returns a list of TensorFlow Tensors that will\n # contain the requested gradients when evaluated.\n grad_params = tf.gradients(loss, params)\n \n # Make a gradient descent step on all of the model parameters.\n new_weights = [] \n for w, grad_w in zip(params, grad_params):\n new_w = tf.assign_sub(w, learning_rate * grad_w)\n new_weights.append(new_w)\n\n # Insert a control dependency so that evaluting the loss causes a weight\n # update to happen; see the discussion above.\n with tf.control_dependencies(new_weights):\n return tf.identity(loss)\n\n# Train using stochastic gradient descent without momentum\ndef train(model_fn, init_fn, learning_rate):\n \"\"\"\n Train a model on CIFAR-10.\n \n Inputs:\n - model_fn: A Python function that performs the forward pass of the model\n using TensorFlow; it should have the following signature:\n scores = model_fn(x, params) where x is a TensorFlow Tensor giving a\n minibatch of image data, params is a list of TensorFlow Tensors holding\n the model weights, and scores is a TensorFlow Tensor of shape (N, C)\n giving scores for all elements of x.\n - init_fn: A Python function that initializes the parameters of the model.\n It should have the signature params = init_fn() where params is a list\n of TensorFlow Tensors holding the (randomly initialized) weights of the\n model.\n - learning_rate: Python float giving the learning rate to use for SGD.\n \"\"\"\n # First clear the default graph\n tf.reset_default_graph()\n is_training = tf.placeholder(tf.bool, name='is_training')\n # Set up the computational graph for performing forward and backward passes,\n # and weight updates.\n with tf.device(device):\n # Set up placeholders for the data and labels\n x = tf.placeholder(tf.float32, [None, 32, 32, 3])\n y = tf.placeholder(tf.int32, [None])\n params = init_fn() # Initialize the model parameters\n scores = model_fn(x, params) # Forward pass of the model\n loss = training_step(scores, y, params, learning_rate)\n\n # Now we actually run the graph many times using the training data\n with tf.Session() as sess:\n # Initialize variables that will live in the graph\n sess.run(tf.global_variables_initializer())\n for t, (x_np, y_np) in enumerate(train_dset):\n # Run the graph on a batch of training data; recall that asking\n # TensorFlow to evaluate loss will cause an SGD step to happen.\n feed_dict = {x: x_np, y: y_np}\n loss_np = sess.run(loss, feed_dict=feed_dict)\n \n # Periodically print the loss and check accuracy on the val set\n if t % print_every == 0:\n print('Iteration %d, loss = %.4f' % (t, loss_np))\n check_accuracy(sess, val_dset, x, scores, is_training)\n\n# Helper method for evaluating our model accuracy (note it also runs the computational graph but doesn't update loss)\ndef check_accuracy(sess, dset, x, scores, is_training=None):\n \"\"\"\n Check accuracy on a classification model.\n \n Inputs:\n - sess: A TensorFlow Session that will be used to run the graph\n - dset: A Dataset object on which to check accuracy\n - x: A TensorFlow placeholder Tensor where input images should be fed\n - scores: A TensorFlow Tensor representing the scores output from the\n model; this is the Tensor we will ask TensorFlow to evaluate.\n \n Returns: Nothing, but prints the accuracy of the model\n \"\"\"\n num_correct, num_samples = 0, 0\n for x_batch, y_batch in dset:\n feed_dict = {x: x_batch, is_training: 0}\n scores_np = sess.run(scores, feed_dict=feed_dict)\n y_pred = scores_np.argmax(axis=1)\n num_samples += x_batch.shape[0]\n num_correct += (y_pred == y_batch).sum()\n acc = float(num_correct) / num_samples\n print('Got %d / %d correct (%.2f%%)' % (num_correct, num_samples, 100 * acc))\nprint \"Done\"", "Done\n" ], [ "# Borrowed from cs231n.github.io/assignments2018/assignment2/\n# We initialize the weight matrices for our models using a method known as Kaiming's normalization method [8]\ndef kaiming_normal(shape):\n if len(shape) == 2:\n fan_in, fan_out = shape[0], shape[1]\n elif len(shape) == 4:\n fan_in, fan_out = np.prod(shape[:3]), shape[3]\n return tf.random_normal(shape) * np.sqrt(2.0 / fan_in)\n\n\ndef two_layer_fc_init():\n \"\"\"\n Initialize the weights of a two-layer network (one hidden layer), for use with the\n two_layer_network function defined above.\n \n Inputs: None\n \n Returns: A list of:\n - w1: TensorFlow Variable giving the weights for the first layer\n - w2: TensorFlow Variable giving the weights for the second layer\n \"\"\"\n # Numer of neurons in hidden layer\n hidden_layer_size = 4000\n # Now we initialize the weights of our two layer network using tf.Variable\n # \"A TensorFlow Variable is a Tensor whose value is stored in the graph and persists across runs of the \n # computational graph; however unlike constants defined with `tf.zeros` or `tf.random_normal`, \n # the values of a Variable can be mutated as the graph runs; these mutations will persist across graph runs. \n # Learnable parameters of the network are usually stored in Variables.\"\n w1 = tf.Variable(kaiming_normal((3 * 32 * 32, hidden_layer_size)))\n w2 = tf.Variable(kaiming_normal((hidden_layer_size, 10)))\n return [w1, w2]\nprint \"Done\"", "Done\n" ], [ "# Now we actually train our model with one *epoch* ! We use a learning rate of 0.01\nlearning_rate = 1e-2\ntrain(two_layer_fc, two_layer_fc_init, learning_rate)\n\n# You should see an accuracy of >40% with just one epoch (an epoch in this case consists of 700 iterations\n# of gradient descent but can be tuned)", "Iteration 0, loss = 3.1850\nGot 117 / 1000 correct (11.70%)\nIteration 100, loss = 1.8910\nGot 386 / 1000 correct (38.60%)\nIteration 200, loss = 1.3805\nGot 398 / 1000 correct (39.80%)\nIteration 300, loss = 1.8048\nGot 384 / 1000 correct (38.40%)\nIteration 400, loss = 1.7182\nGot 431 / 1000 correct (43.10%)\nIteration 500, loss = 1.8586\nGot 438 / 1000 correct (43.80%)\nIteration 600, loss = 1.8791\nGot 427 / 1000 correct (42.70%)\nIteration 700, loss = 1.9940\nGot 437 / 1000 correct (43.70%)\n" ] ], [ [ "#### 3.3 Keras\n\nNote in the first cell, we used the tf.keras Sequential API to make a neural network but here we use \"barebones\" Tensorflow. One of the good (and possibly bad) things about Tensorflow is that there are several ways to create a neural network and train it. Here are some possible ways:\n* Barebones tensorflow\n* tf.keras Model API\n* tf.keras Sequential API\n\nHere is a table of comparison borrowed from [2]:\n\n| API | Flexibility | Convenience |\n|---------------|-------------|-------------|\n| Barebone | High | Low |\n| `tf.keras.Model` | High | Medium |\n| `tf.keras.Sequential` | Low | High |\n\n\nNote that with the tf.keras Model API, you have the options of using the **object-oriented API**, where each layer of the neural network is represented as a Python object (like `tf.layers.Dense`) or the **functional API**, where each layer is a Python function (like `tf.layers.dense`). We will only use the Sequential API and skip the Model API in the cells below because we will simply trade off lots of flexiblity for convenience.", "_____no_output_____" ] ], [ [ "# Now we will train the same model using the Sequential API. \n# First we set up our training and model initializiation functions\ndef train_keras(model_init_fn, optimizer_init_fn, num_epochs=1):\n \"\"\"\n Simple training loop for use with models defined using tf.keras. It trains\n a model for one epoch on the CIFAR-10 training set and periodically checks\n accuracy on the CIFAR-10 validation set.\n \n Inputs:\n - model_init_fn: A function that takes no parameters; when called it\n constructs the model we want to train: model = model_init_fn()\n - optimizer_init_fn: A function which takes no parameters; when called it\n constructs the Optimizer object we will use to optimize the model:\n optimizer = optimizer_init_fn()\n - num_epochs: The number of epochs to train for\n \n Returns: Nothing, but prints progress during trainingn\n \"\"\"\n tf.reset_default_graph() \n with tf.device(device):\n # Construct the computational graph we will use to train the model. We\n # use the model_init_fn to construct the model, declare placeholders for\n # the data and labels\n x = tf.placeholder(tf.float32, [None, 32, 32, 3])\n y = tf.placeholder(tf.int32, [None])\n \n # We need a place holder to explicitly specify if the model is in the training\n # phase or not. This is because a number of layers behaves differently in\n # training and in testing, e.g., dropout and batch normalization.\n # We pass this variable to the computation graph through feed_dict as shown below.\n is_training = tf.placeholder(tf.bool, name='is_training')\n \n # Use the model function to build the forward pass.\n scores = model_init_fn(x, is_training)\n\n # Compute the loss like we did in Part II\n loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=scores)\n loss = tf.reduce_mean(loss)\n\n # Use the optimizer_fn to construct an Optimizer, then use the optimizer\n # to set up the training step. Asking TensorFlow to evaluate the\n # train_op returned by optimizer.minimize(loss) will cause us to make a\n # single update step using the current minibatch of data.\n \n # Note that we use tf.control_dependencies to force the model to run\n # the tf.GraphKeys.UPDATE_OPS at each training step. tf.GraphKeys.UPDATE_OPS\n # holds the operators that update the states of the network.\n # For example, the tf.layers.batch_normalization function adds the running mean\n # and variance update operators to tf.GraphKeys.UPDATE_OPS.\n optimizer = optimizer_init_fn()\n update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)\n with tf.control_dependencies(update_ops):\n train_op = optimizer.minimize(loss)\n\n # Now we can run the computational graph many times to train the model.\n # When we call sess.run we ask it to evaluate train_op, which causes the\n # model to update.\n with tf.Session() as sess:\n sess.run(tf.global_variables_initializer())\n t = 0\n for epoch in range(num_epochs):\n print('Starting epoch %d' % epoch)\n for x_np, y_np in train_dset:\n feed_dict = {x: x_np, y: y_np, is_training:1}\n loss_np, _ = sess.run([loss, train_op], feed_dict=feed_dict)\n if t % print_every == 0:\n print('Iteration %d, loss = %.4f' % (t, loss_np))\n check_accuracy(sess, val_dset, x, scores, is_training=is_training)\n print()\n t += 1\n \ndef model_init_fn(inputs, is_training):\n input_shape = (32, 32, 3)\n hidden_layer_size, num_classes = 4000, 10\n initializer = tf.variance_scaling_initializer(scale=2.0)\n layers = [\n tf.layers.Flatten(input_shape=input_shape),\n tf.layers.Dense(hidden_layer_size, activation=tf.nn.relu,\n kernel_initializer=initializer),\n tf.layers.Dense(num_classes, kernel_initializer=initializer),\n ]\n model = tf.keras.Sequential(layers)\n return model(inputs)\n\ndef optimizer_init_fn():\n return tf.train.GradientDescentOptimizer(learning_rate)\nprint \"Done\"", "Done\n" ], [ "# Now the actual training\nlearning_rate = 1e-2\ntrain_keras(model_init_fn, optimizer_init_fn)\n\n# Again, you should see accuracy > 40% after one epoch (700 iterations) of gradient descent", "Starting epoch 0\nIteration 0, loss = 2.8911\nGot 128 / 1000 correct (12.80%)\n()\nIteration 100, loss = 1.8686\nGot 391 / 1000 correct (39.10%)\n()\nIteration 200, loss = 1.3735\nGot 424 / 1000 correct (42.40%)\n()\nIteration 300, loss = 1.7414\nGot 394 / 1000 correct (39.40%)\n()\nIteration 400, loss = 1.6495\nGot 434 / 1000 correct (43.40%)\n()\nIteration 500, loss = 1.7604\nGot 432 / 1000 correct (43.20%)\n()\nIteration 600, loss = 1.8787\nGot 432 / 1000 correct (43.20%)\n()\nIteration 700, loss = 1.8601\nGot 440 / 1000 correct (44.00%)\n()\n" ] ], [ [ "### 4. Backpropagation\n\nYou'll often hear the term \"backpropagation\" or \"backprop,\" which is a way of updating a neural network. Google has a great demo that walks you through the backpropagation algorithm in detail. I encourage you to check it out!\n\nhttps://google-developers.appspot.com/machine-learning/crash-course/backprop-scroll/\n\nSee also this seminar by Geoffrey Hinton, a premier deep learning researcher, on whether the brain can do back-propagation. It's an interesting lecture with relatively : https://www.youtube.com/watch?v=VIRCybGgHts\n\n", "_____no_output_____" ], [ "### 5. References\n\n<pre>\n [1] Fast.ai (http://course.fast.ai/) \n [2] CS231N (http://cs231n.github.io/) \n [3] CS224D (http://cs224d.stanford.edu/syllabus.html) \n [4] Hands on Machine Learning (https://github.com/ageron/handson-ml) \n [5] Deep learning with Python Notebooks (https://github.com/fchollet/deep-learning-with-python-notebooks) \n [6] Deep learning by Goodfellow et. al (http://www.deeplearningbook.org/) \n [7] Neural networks online book (http://neuralnetworksanddeeplearning.com/)\n [8] He et al, *Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification\n*, ICCV 2015, https://arxiv.org/abs/1502.01852\n</pre>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ] ]

d0e62e3e1cd1ee211841a60ff4a22169820eb864

6,508

ipynb

Jupyter Notebook

main.ipynb

krish1237/Flipr-corona

b9f47174532fa77fcca7a7a7051a00aa71ffe282

[ "Apache-2.0" ]

1

2020-07-31T06:05:05.000Z

main.ipynb

krish1237/Flipr-corona

b9f47174532fa77fcca7a7a7051a00aa71ffe282

[ "Apache-2.0" ]

null

main.ipynb

krish1237/Flipr-corona

b9f47174532fa77fcca7a7a7051a00aa71ffe282

[ "Apache-2.0" ]

null

24.01476

104

0.462354

[ [ [ "GETTING DATA", "_____no_output_____" ] ], [ [ "import numpy as np", "_____no_output_____" ], [ "data = np.load(\"./data.npz\")\nX_train = data[\"X_train\"]\nY_train = data[\"Y_train\"]\nX_test = data[\"X_test\"]\nprint(\"Shapes\")\nprint(\"X_train:\",X_train.shape)\nprint(\"Y_train:\",Y_train.shape)\nprint(\"X_test:\",X_test.shape)", "Shapes\nX_train: (10714, 21)\nY_train: (10714,)\nX_test: (14498, 21)\n" ] ], [ [ "COMPILING KERAS MODEL", "_____no_output_____" ] ], [ [ "from tensorflow.keras.layers import Input, Dense\nfrom tensorflow.keras.models import Sequential", "_____no_output_____" ], [ "model = Sequential()\nmodel.add(Dense(32, input_dim=21, kernel_initializer='glorot_uniform',\n bias_initializer='zeros', activation=\"relu\"))\nmodel.add(Dense(64, kernel_initializer='glorot_uniform',\n bias_initializer='zeros', activation=\"relu\"))\nmodel.add(Dense(32, kernel_initializer='glorot_uniform',\n bias_initializer='zeros', activation=\"relu\"))\nmodel.add(Dense(1, kernel_initializer='glorot_uniform',\n bias_initializer='zeros', activation=\"sigmoid\"))", "_____no_output_____" ], [ "model.compile(loss=\"mean_squared_error\", optimizer=\"adam\")", "_____no_output_____" ] ], [ [ "TRAINING MODEL", "_____no_output_____" ] ], [ [ "labels = Y_train.reshape(-1,1)\nepochs = 10\nlabels", "_____no_output_____" ], [ "model.fit(X_train,Y_train.reshape(-1,1), validation_split=0.1, epochs=epochs)", "Train on 9642 samples, validate on 1072 samples\nEpoch 1/10\n9642/9642 [==============================] - 1s 99us/sample - loss: 0.0085 - val_loss: 0.0107\nEpoch 2/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0080 - val_loss: 0.0094\nEpoch 3/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0079 - val_loss: 0.0094\nEpoch 4/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0078 - val_loss: 0.0095\nEpoch 5/10\n9642/9642 [==============================] - 1s 52us/sample - loss: 0.0077 - val_loss: 0.0093\nEpoch 6/10\n9642/9642 [==============================] - 1s 52us/sample - loss: 0.0076 - val_loss: 0.0093\nEpoch 7/10\n9642/9642 [==============================] - 1s 52us/sample - loss: 0.0075 - val_loss: 0.0093\nEpoch 8/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0075 - val_loss: 0.0101\nEpoch 9/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0075 - val_loss: 0.0096\nEpoch 10/10\n9642/9642 [==============================] - 1s 53us/sample - loss: 0.0074 - val_loss: 0.0097\n" ], [ "y_pred = model.predict(X_train)", "_____no_output_____" ], [ "y_pred", "_____no_output_____" ], [ "labels", "_____no_output_____" ], [ "model.save(\"model.h5\")", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

d0e62fa9cb57b2919710370748ffb11702af394a

71,562

ipynb

Jupyter Notebook

notebooks/simple_linear_regression.ipynb

mjbrann4/py-ml

9d310f3ff6eba1356243f6fa2ba44ea29f250d33

[ "MIT" ]

null

notebooks/simple_linear_regression.ipynb

mjbrann4/py-ml

9d310f3ff6eba1356243f6fa2ba44ea29f250d33

[ "MIT" ]

null

notebooks/simple_linear_regression.ipynb

mjbrann4/py-ml

9d310f3ff6eba1356243f6fa2ba44ea29f250d33

[ "MIT" ]

null

259.282609

26,020

0.926665

[ [ [ "# Simple Linear Regression using Basic Python", "_____no_output_____" ] ], [ [ "import numpy as np\nimport random\n\nimport matplotlib.pyplot as plt\nplt.style.use('ggplot')\n%matplotlib inline", "_____no_output_____" ] ], [ [ "## Produce target and feature data", "_____no_output_____" ] ], [ [ "X = np.linspace(1,20,20)\n\n# true function\ny_true = 2*X + 5\n\n# function with noise ('error term')\ny_rand = 2*X + 5 + np.random.randint(-10, 11, len(X))", "_____no_output_____" ], [ "fig, ax = plt.subplots(figsize=(8,5))\nplt.scatter(X, y_rand, color = 'b', s = 20, label = 'Observations') \nplt.plot(X, y_true, color='m', label='True Function')\nplt.xlabel('X')\nplt.ylabel('y')\nplt.legend()\nplt.show()", "_____no_output_____" ] ], [ [ "## OLS", "_____no_output_____" ] ], [ [ "def simple_ols(X, y):\n '''Function to perform simple OLS regression using basic python\n\n Parameters:\n X - single feature np array or list\n y - target np array or list\n '''\n X_bar = np.mean(X)\n y_bar = np.mean(y)\n\n num_list = [(X[i] - X_bar) * (y[i] - y_bar) for i in range(len(X))]\n denom_list = [(X[i] - X_bar)**2 for i in range(len(X))]\n\n # slope\n b1 = sum(num_list) / sum(denom_list)\n\n # intercept\n b0 = y_bar - b1 * X_bar\n \n return b0, b1", "_____no_output_____" ], [ "b0, b1 = simple_ols(X, y_rand)\nprint('slope: ', b1)\nprint('intercept: ', b0)", "slope: 1.7503759398496241\nintercept: 6.421052631578949\n" ], [ "y_est = b1*X + b0", "_____no_output_____" ], [ "# plot residuals\nfig, ax = plt.subplots(figsize=(8,5))\nplt.scatter(X, y_rand, color = 'b', s = 20, label = 'Observations') \nplt.plot(X, y_est, color='g', label='Estimated Function')\nplt.vlines(X,y_est,y_rand, color='b', alpha=0.5)\nplt.xlabel('X')\nplt.ylabel('y')\nplt.title('Good Fit')\nplt.legend()\nplt.show()", "_____no_output_____" ], [ "fig, ax = plt.subplots(figsize=(8,5))\nplt.scatter(X, y_rand, color = 'b', s = 20, label = 'Observations') \nplt.plot(X, y_true, color='m', label='True Function')\nplt.plot(X, y_est, color='g', label='Estimated Function')\nplt.xlabel('X')\nplt.ylabel('y')\nplt.legend()\nplt.show()", "_____no_output_____" ] ], [ [ "## Take 1000 Samples to Verify Estimates are Equal to True Values", "_____no_output_____" ] ], [ [ "samples = [ 2*X + 5 + np.random.randint(-10, 11, len(X)) for i in range(1000) ]", "_____no_output_____" ], [ "betas = [simple_ols(X, s) for s in samples ]", "_____no_output_____" ], [ "# mean of each column in list of betas\nb0_sampled, b1_sampled = np.mean(betas, axis=0)", "_____no_output_____" ], [ "print('slope: ', b0_sampled)\nprint('intercept: ', b1_sampled)", "slope: 5.011063157894742\nintercept: 2.0014939849624045\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

d0e632332cb9ad006b0125f28fc82bf50c91baf4

4,376

ipynb

Jupyter Notebook

starter_code/VacationPy.ipynb

kanikajain1/python-api-challenge

4800572aef4b2027ad9408d38d5e3150f0ee5a80

[ "ADSL" ]

2

2020-07-15T00:18:55.000Z

2020-07-15T00:34:35.000Z

starter_code/VacationPy.ipynb

kanikajain1/python-api-challenge

4800572aef4b2027ad9408d38d5e3150f0ee5a80

[ "ADSL" ]

null

starter_code/VacationPy.ipynb

kanikajain1/python-api-challenge

4800572aef4b2027ad9408d38d5e3150f0ee5a80

[ "ADSL" ]

null

22.10101

156

0.541362

[ [ [ "# VacationPy\n----\n\n#### Note\n* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.", "_____no_output_____" ] ], [ [ "# Dependencies and Setup\nimport matplotlib.pyplot as plt\nimport pandas as pd\nimport numpy as np\nimport requests\nimport gmaps\nimport os\n\n# Import API key\nfrom api_keys import g_key", "_____no_output_____" ] ], [ [ "### Store Part I results into DataFrame\n* Load the csv exported in Part I to a DataFrame", "_____no_output_____" ] ], [ [ "\n", "_____no_output_____" ] ], [ [ "### Humidity Heatmap\n* Configure gmaps.\n* Use the Lat and Lng as locations and Humidity as the weight.\n* Add Heatmap layer to map.", "_____no_output_____" ], [ "### Create new DataFrame fitting weather criteria\n* Narrow down the cities to fit weather conditions.\n* Drop any rows will null values.", "_____no_output_____" ], [ "### Hotel Map\n* Store into variable named `hotel_df`.\n* Add a \"Hotel Name\" column to the DataFrame.\n* Set parameters to search for hotels with 5000 meters.\n* Hit the Google Places API for each city's coordinates.\n* Store the first Hotel result into the DataFrame.\n* Plot markers on top of the heatmap.", "_____no_output_____" ] ], [ [ "# NOTE: Do not change any of the code in this cell\n\n# Using the template add the hotel marks to the heatmap\ninfo_box_template = \"\"\"\n<dl>\n<dt>Name</dt><dd>{Hotel Name}</dd>\n<dt>City</dt><dd>{City}</dd>\n<dt>Country</dt><dd>{Country}</dd>\n</dl>\n\"\"\"\n# Store the DataFrame Row\n# NOTE: be sure to update with your DataFrame name\nhotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]\nlocations = hotel_df[[\"Lat\", \"Lng\"]]", "_____no_output_____" ], [ "# Add marker layer ontop of heat map\n\n\n# Display figure\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ] ]

d0e63c2672ab845b9b58650f23711a4b45421c94

24,084

ipynb

Jupyter Notebook

LR_RF.ipynb

Berend789/Extubation_Failure_Prediction

0848a1fbcee4d3f5bc66c1666edfd629a4e23ec7

[ "MIT" ]

null

LR_RF.ipynb

Berend789/Extubation_Failure_Prediction

0848a1fbcee4d3f5bc66c1666edfd629a4e23ec7

[ "MIT" ]

null

LR_RF.ipynb

Berend789/Extubation_Failure_Prediction

0848a1fbcee4d3f5bc66c1666edfd629a4e23ec7

[ "MIT" ]

null

39.034036

555

0.600648

[ [ [ "import gc\nimport locale\nimport pickle\nimport os\nimport pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport seaborn as sns\n\nfrom matplotlib.colors import ListedColormap\nfrom all_stand_var import conv_dict, lab_cols, used_cols\nfrom all_own_funct import cnfl, value_filtering,y_modelling,x_modelling,evaluate,lin_reg_coef,split_stratified_into_train_val_test\nfrom seaborn import heatmap\nfrom sklearn.metrics import roc_curve, accuracy_score, roc_auc_score\nfrom sklearn.metrics import classification_report, confusion_matrix,average_precision_score,f1_score,roc_curve,roc_auc_score,plot_confusion_matrix\nfrom sklearn.ensemble import RandomForestRegressor,RandomForestClassifier\nfrom matplotlib.backends.backend_pdf import PdfPages\nfrom sklearn.preprocessing import StandardScaler\nfrom sklearn.linear_model import LogisticRegression\nfrom sklearn.ensemble import RandomForestRegressor,RandomForestClassifier\nfrom sklearn.model_selection import RandomizedSearchCV\nfrom scipy.stats import kurtosis\n\nlocale.setlocale(locale.LC_ALL, 'fr_FR')\n\n\n# output folder in which al results are saved\noutput_folder = os.path.join(os.getcwd(), 'Results_LR_RF_v2','1u_Results_no_mis')\nif not os.path.exists(output_folder):\n os.makedirs(output_folder)\n", "C:\\Users\\berend\\Anaconda3\\lib\\site-packages\\numpy\\_distributor_init.py:32: UserWarning: loaded more than 1 DLL from .libs:\nC:\\Users\\berend\\Anaconda3\\lib\\site-packages\\numpy\\.libs\\libopenblas.NOIJJG62EMASZI6NYURL6JBKM4EVBGM7.gfortran-win_amd64.dll\nC:\\Users\\berend\\Anaconda3\\lib\\site-packages\\numpy\\.libs\\libopenblas.PYQHXLVVQ7VESDPUVUADXEVJOBGHJPAY.gfortran-win_amd64.dll\nC:\\Users\\berend\\Anaconda3\\lib\\site-packages\\numpy\\.libs\\libopenblas.WCDJNK7YVMPZQ2ME2ZZHJJRJ3JIKNDB7.gfortran-win_amd64.dll\n stacklevel=1)\n" ], [ "#Create processed dataframe, if not already run LR_build.py\n\"\"\"\nused_cols = ['pat_hosp_id', 'pat_bd', 'pat_datetime', 'AdmissionDate', 'DischargeDate', 'mon_rr', 'mon_hr', 'mon_sat',\n 'mon_etco2', 'vent_m_ppeak','vent_m_peep','vent_m_fio2',\n 'mon_ibp_mean', 'pat_weight_act', 'vent_m_rr', 'vent_m_tv_exp']\ndtype_dict={'vent_cat': 'category','vent_machine':'category','vent_mode':'category'}\ndf_raw=pd.read_csv(r'data\\sorted_bron_date.csv',delimiter=';',converters=conv_dict,usecols=used_cols,dtype=dtype_dict,parse_dates=['pat_bd','pat_datetime','AdmissionDate', 'DischargeDate'],na_values=['NULL','null', 'Null','nUll','nuLl','nulL'],dayfirst=True)\n#df = pp.data_pp_function(df_raw,path=output_folder,timestep='12H')\n#df=df.groupby('Admissionnumber',sort=False).fillna(method='ffill').fillna(method='bfill')\n\"\"\"\n", "_____no_output_____" ], [ "import importlib\nimport LR_build as pp\nimportlib.reload(pp)\n# Load processed dataframe\nf = open(os.path.join('./Results_LR_RF_v2/', 'processed_df.txt'), 'rb')\ndf = pickle.load(f)\nf.close()\n\n\n", "_____no_output_____" ], [ "#informative plots and descriptive information\n\"\"\"\nused_cols = [ 'pat_datetime', 'mon_rr', 'mon_hr', 'mon_sat',\n 'mon_etco2', 'vent_m_fio2', 'vent_m_ppeak','vent_m_peep',\n 'mon_ibp_mean','pat_weight_act','vent_m_rr', 'vent_m_tv_exp','Age']\nfor col in used_cols:\n print(df[col].describe())\n\nprint(df[df.index.get_level_values('pat_hosp_id') == 5407]['Reintub'].value_counts())\nprint(df[df.index.get_level_values('pat_hosp_id') == 5150574]['pat_datetime'].tail(100))\nplt.plot(np.linspace(start=0,stop=720,num=720),df[df.index.get_level_values('pat_hosp_id') == 5407]['vent_m_peep'],'b-')\nplt.plot(np.linspace(start=0,stop=720,num=720),df[df.index.get_level_values('pat_hosp_id')==5150574]['vent_m_tv_exp'],'r-')\nfig=plt.gcf()\nfig.set_size_inches(18.5, 10.5)\nplt.show()\n\"\"\"\n\n", "_____no_output_____" ], [ "# calculate the hour intervals, and also the missingness parameter\ndf=df.reset_index(drop=False)\ndf.info()\ndef index_1hr(group):\n group['tim']=pd.date_range(start='1/1/2018', periods=len(group), freq='1min')\n grouped = pd.Grouper(key='tim', freq='1H')\n group['idx_1hr']=group.groupby(grouped,sort=False).ngroup().add(1)\n group['mis']=(group['pat_datetime'].max()-group['pat_datetime'].min()).total_seconds()/60\n del group['tim']\n return group\n\ndf=df.groupby('Adnum',sort=False,as_index=False).apply(index_1hr)\nprint((df['Adnum'].value_counts()))\nprint(df.info())\ndf['idx_1hr']=df['idx_1hr'].astype(str)\nprint(df['idx_1hr'].unique())\ndf[['mis']]=StandardScaler().fit_transform(df[['mis']])\ndf=df.set_index(['pat_hosp_id','AdmissionDate','DischargeDate'])\n\n\n\n\n\n", "_____no_output_____" ], [ "# Stratified spit of dataframe into train, test and validation\npat=pd.read_excel(r'Results\\admissiondate_v2.xlsx', parse_dates=[\n 'AdmissionDate', 'DischargeDate'])\ngroup=pat.groupby('pat_hosp_id',sort=False).max().reset_index()\ngroup.drop_duplicates('pat_hosp_id',inplace=True)\n\ndf_train,df_val,df_test=split_stratified_into_train_val_test(group, stratify_colname='Reintub',\n frac_train=0.7, frac_val=0.1, frac_test=0.2,\n random_state=1)\n\ntrain_pat=df_train['pat_hosp_id'].unique()\ntest_pat=df_test['pat_hosp_id'].unique()\nval_pat=df_val['pat_hosp_id'].unique()\n\ndf_train = df[df.index.get_level_values('pat_hosp_id').isin(train_pat)]\ndf_val = df[df.index.get_level_values('pat_hosp_id').isin(val_pat)]\ndf_test = df[df.index.get_level_values('pat_hosp_id').isin(test_pat)]\n\n", "_____no_output_____" ], [ "print(df_train.info())\ndef y_modelling(df):\n y = df[['Reintub', 'Adnum', 'idx_1hr']]\n y = y.groupby(['Adnum', 'idx_1hr'], sort=False).agg(['max'])\n y.columns = [\"_\".join(a) for a in y.columns.to_flat_index()]\n y.reset_index(drop=True, inplace=True, level='idx_1hr')\n y = y.reset_index().drop_duplicates().set_index(\n ['Adnum'])\n y = y[~y.index.duplicated(keep='last')]\n y = y.fillna(value=0)\n return y\n# from dataframwe with label per minute, to array with label per admission\nY_TRAIN=y_modelling(df_train)\nY_TEST=y_modelling(df_test)\nY_VAL=y_modelling(df_val)\nY_TRAIN=Y_TRAIN['Reintub_max'].to_numpy()\nY_TEST=Y_TEST['Reintub_max'].to_numpy()\nY_VAL=Y_VAL['Reintub_max'].to_numpy()\nY_TRAIN=np.append(Y_TRAIN,Y_VAL)\n\n", "_____no_output_____" ], [ "def x_modelling(df):\n temp = df[['Age', 'Adnum', 'idx_1hr','pat_weight_act']]\n df = df.drop(['Age','pat_weight_act','Extubation_date','level_0','pat_datetime', 'Reintub'], axis=1)\n df = df.groupby(['Adnum', 'idx_1hr'], sort=False).agg(['mean', 'std',lin_reg_coef])\n df.columns = [\"_\".join(a) for a in df.columns.to_flat_index()]\n df = df.stack().unstack([2, 1])\n df.columns = [\"_\".join(a) for a in df.columns.to_flat_index()]\n df = df.reset_index().drop_duplicates().set_index('Adnum')\n df = df.fillna(method='ffill').fillna(method='bfill')\n\n temp = temp.groupby('Adnum', sort=False).agg(['mean'])\n temp.columns = [\"_\".join(a) for a in temp.columns.to_flat_index()]\n temp = temp.reset_index().drop_duplicates().set_index('Adnum')\n temp = temp[~temp.index.duplicated(keep='last')]\n \"\"\"\n df_temp = df_temp.drop('idx_1hr',axis=1)\n df_temp = df_temp.groupby('Adnum',sort=False).agg([lin_reg_coef])\n df_temp.columns = [\"_\".join(a) for a in df_temp.columns.to_flat_index()]\n df_temp = df_temp.reset_index().drop_duplicates().set_index('Adnum')\n df_temp = df_temp[~df_temp.index.duplicated(keep='last')]\n \"\"\"\n df = df.merge(temp, right_index=True, left_index=True, how='left')\n #df = df.merge(df_temp, right_index=True, left_index=True, how='left')\n del temp\n return df\n\n# Calculate features per admission\nX_TRAIN=x_modelling(df_train)\nX_TEST=x_modelling(df_test)\nX_VAL=x_modelling(df_val)\nprint(X_TRAIN.info())\nprint(X_TEST.info())\nX_TRAIN=X_TRAIN.fillna(value=0)\nX_VAL=X_VAL.fillna(value=0)\nX_TEST=X_TEST.fillna(value=0)\n\n\nX_TRAIN=X_TRAIN.append(X_VAL)", "_____no_output_____" ], [ "# Save Train and test data to file\nf = open(os.path.join(output_folder, 'x_train.txt'), 'wb')\npickle.dump(X_TRAIN, f)\nf.close()\n\nf = open(os.path.join(output_folder, 'x_test.txt'), 'wb')\npickle.dump(X_TEST, f)\nf.close()\n\nf = open(os.path.join(output_folder, 'y_train.txt'), 'wb')\npickle.dump(Y_TRAIN, f)\nf.close()\n\nf = open(os.path.join(output_folder, 'y_test.txt'), 'wb')\npickle.dump(Y_TEST, f)\nf.close()", "_____no_output_____" ], [ "# Randomised search for random forest mode\n# Number of trees in random forest\nn_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]\n# Number of features to consider at every split\nmax_features = ['auto', 'sqrt']\n# Maximum number of levels in tree\nmax_depth = [int(x) for x in np.linspace(10, 50, num = 11)]\nmax_depth.append(None)\n# Minimum number of samples required to split a node\nmin_samples_split = [2, 5, 10]\n# Minimum number of samples required at each leaf node\nmin_samples_leaf = [1, 2, 4]\n# Method of selecting samples for training each tree\nbootstrap = [True, False]\n# Create the random grid\nrandom_grid = {'n_estimators': n_estimators,\n 'max_features': max_features,\n 'max_depth': max_depth,\n 'min_samples_split': min_samples_split,\n 'min_samples_leaf': min_samples_leaf,\n 'bootstrap': bootstrap}\n\n# Use the random grid to search for best hyperparameters\n# First create the base model to tune\nrf = RandomForestClassifier()\n# Random search of parameters, using 3 fold cross validation, \n# search across 100 different combinations, and use all available cores\nrf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 20, cv = 3, verbose=2, random_state=42, n_jobs = -1)\n# Fit the random search model\nrf_random.fit(X_TRAIN, Y_TRAIN)\n\n\n\n", "_____no_output_____" ], [ "# Evaluate the base model vs the optimized model\n\nbase_model = RandomForestClassifier(n_estimators = 10, random_state = 42,max_depth=10)\nbase_model.fit(X_TRAIN, Y_TRAIN)\nbase_accuracy = evaluate(base_model, X_TEST, Y_TEST,'base_accuracy RF',output_folder)\n\nbest_random = rf_random.best_estimator_\nrandom_accuracy = evaluate(best_random, X_TEST,Y_TEST,'Best_random RF',output_folder)\n\nif base_accuracy > random_accuracy:\n best_random = base_model", "_____no_output_____" ], [ "# Create AUROC plot, confusion matrix and other results\n\nfrom all_own_funct import roc_auc_ci\ntry:\n pdf = PdfPages(os.path.join(output_folder,f\"Figures_all_.pdf\"))\nexcept PermissionError:\n os.remove(os.path.join(output_folder,f\"Figures_all.pdf\"))\n os.remove(os.path.join(output_folder,f\"Result_scores_all.txt\"))\nclf = best_random\ny_pred_clas=clf.predict(X_TEST)\n\n# Predict the probabilities, function depends on used classifier\ntry:\n y_pred_prob=clf.predict_proba(X_TEST)\n y_pred_prob=y_pred_prob[:,1]\nexcept:\n try:\n y_pred_prob=clf.decision_function(X_TEST)\n except:\n y_pred_prob=y_pred_clas\n\nreport=classification_report(Y_TEST,y_pred_clas,target_names=['No Reintubation','Reintubation'])\nscore=clf.score(X_TEST,Y_TEST)\naverage_precision = average_precision_score(Y_TEST, y_pred_prob)\nf1_s=f1_score(Y_TEST, y_pred_clas)\n\n# write scoring metrics to file\nwith open(os.path.join(output_folder,f\"Result_scores_all.txt\"),'a') as file:\n file.write(f\"Results for RF on training set\\n\\n\")\n file.write(f\"Classification report \\n {report} \\n\")\n file.write(f\"Hold_out_scores {score} \\n\")\n file.write(f\"Average precision score {average_precision} \\n\")\n file.write(f\"F1 score {f1_s} \\n\\n\\n\")\n\nplot_confusion_matrix(clf,X_TEST,Y_TEST)\nplt.title(f\"Confusion matrix of random forrest\")\nfig=plt.gcf()\npdf.savefig(fig)\nplt.close(fig)\n\nfpr, tpr, _ = roc_curve(Y_TEST, y_pred_prob)\nauc = roc_auc_score(Y_TEST, y_pred_prob)\n\n\n# 95%CI calculation using bootstrapping\nn_bootstraps = 2000\nrng_seed = 42 # control reproducibility\nbootstrapped_scores = []\n\nrng = np.random.RandomState(rng_seed)\nfor i in range(n_bootstraps):\n # bootstrap by sampling with replacement on the prediction indices\n indices = rng.randint(0, len(y_pred_prob), len(y_pred_prob))\n if len(np.unique(Y_TEST[indices])) < 2:\n # We need at least one positive and one negative sample for ROC AUC\n # to be defined: reject the sample\n continue\n\n score = roc_auc_score(Y_TEST[indices], y_pred_prob[indices])\n bootstrapped_scores.append(score)\n #print(\"Bootstrap #{} ROC area: {:0.3f}\".format(i + 1, score))\n\nsorted_scores = np.array(bootstrapped_scores)\nsorted_scores.sort()\n\n# Computing the lower and upper bound of the 90% confidence interval\n# You can change the bounds percentiles to 0.025 and 0.975 to get\n# a 95% confidence interval instead.\nconfidence_lower = sorted_scores[int(0.05 * len(sorted_scores))]\nconfidence_upper = sorted_scores[int(0.95 * len(sorted_scores))]\nwith open(os.path.join(output_folder,f\"Result_scores_all.txt\"),'a') as file:\n file.write(\"\\nConfidence interval for the score: [{:0.3f} - {:0.3}]\\n\".format(\n confidence_lower, confidence_upper))\na=roc_auc_ci(Y_TEST,y_pred_prob)\nprint(a)\n\n\nplt.plot(fpr,tpr,label=f\"auc={auc}\",linewidth=1.5,markersize=1)\n\nplt.legend(loc=4,fontsize='xx-small')\nplt.title(f'ROC of Random Forrest hour data')\nplt.xlabel('False Positive Rate')\nplt.ylabel('True Positive Rate')\naxes = plt.gca()\naxes.set_xlim([0,1])\naxes.set_ylim([0,1])\nfig=plt.gcf()\npdf.savefig(fig)\nplt.close(fig)\n", "_____no_output_____" ], [ "# Hyperparameters for Logistic Regression\n# The solvers\nsolver =['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']\n# Class weight optimizer\nclass_weight=[{0:0.1,1:0.9},'balanced',None]\n# Penalty\npenalty=['l1', 'l2', 'elasticnet', None]\n# Inverse of regularization strength\nC=np.logspace(-3,3,7)\n# Bootsrapping\nbootstrap = [True, False]\n# Create the random grid\nrandom_grid = {'solver':solver,\n 'class_weight':class_weight,\n 'penalty':penalty,\n 'C':C,\n 'penalty':penalty}", "_____no_output_____" ], [ "# First create the base model to tune\nlr = LogisticRegression(max_iter=500)\n# Random search of parameters, using 3 fold cross validation, \n# search across 60 different combinations, and use all available cores\nlr_random = RandomizedSearchCV(estimator = lr , param_distributions = random_grid, n_iter = 20, cv = 3, verbose=2, random_state=42, n_jobs = -1)\n# Fit the random search model\nlr_random.fit(X_TRAIN, Y_TRAIN)", "_____no_output_____" ], [ "# Evaluate the models based on AUROC\nbase_model_lr = LogisticRegression(max_iter=500)\nbase_model_lr.fit(X_TRAIN, Y_TRAIN)\nbase_accuracy_lr = evaluate(base_model, X_TEST, Y_TEST,'base_model LR',output_folder)\n\nbest_random_lr = lr_random.best_estimator_\nrandom_accuracy_lr = evaluate(best_random, X_TEST,Y_TEST,'Best random LR',output_folder)\n\nif base_accuracy_lr > random_accuracy_lr:\n best_random_lr = base_model_lr", "_____no_output_____" ], [ "# Create AUROC plot, confusion matrix and other results for Logistic regression\n\nclf = best_random_lr\n\ny_pred_clas=clf.predict(X_TEST)\n# Predict the probabilities, function depends on used classifier\n\ntry:\n y_pred_prob=clf.predict_proba(X_TEST)\n y_pred_prob=y_pred_prob[:,1]\nexcept:\n try:\n y_pred_prob=clf.decision_function(X_TEST)\n except:\n y_pred_prob=y_pred_clas\n\nreport=classification_report(Y_TEST,y_pred_clas,target_names=['No Reintubation','Reintubation'])\nscore=clf.score(X_TEST,Y_TEST)\naverage_precision = average_precision_score(Y_TEST, y_pred_prob)\nf1_s=f1_score(Y_TEST, y_pred_clas)\n\nwith open(os.path.join(output_folder,f\"Result_scores_all.txt\"),'a') as file:\n file.write(f\"Results for LR on training\\n\\n\")\n file.write(f\"Classification report \\n {report} \\n\")\n file.write(f\"Hold_out_scores {score} \\n\")\n file.write(f\"Average precision score {average_precision} \\n\")\n file.write(f\"F1 score {f1_s} \\n\\n\\n\")\n\nplot_confusion_matrix(clf,X_TEST,Y_TEST)\nplt.title(f\"Confusion matrix of logistic regression\")\nfig=plt.gcf()\npdf.savefig(fig)\nplt.close(fig)\n\nfpr, tpr, _ = roc_curve(Y_TEST, y_pred_prob)\nauc = roc_auc_score(Y_TEST, y_pred_prob)\n\n\nn_bootstraps = 2000\nrng_seed = 42 # control reproducibility\nbootstrapped_scores = []\n\nrng = np.random.RandomState(rng_seed)\nfor i in range(n_bootstraps):\n # bootstrap by sampling with replacement on the prediction indices\n indices = rng.randint(0, len(y_pred_prob), len(y_pred_prob))\n if len(np.unique(Y_TEST[indices])) < 2:\n # We need at least one positive and one negative sample for ROC AUC\n # to be defined: reject the sample\n continue\n\n score = roc_auc_score(Y_TEST[indices], y_pred_prob[indices])\n bootstrapped_scores.append(score)\n #print(\"Bootstrap #{} ROC area: {:0.3f}\".format(i + 1, score))\n\nsorted_scores = np.array(bootstrapped_scores)\nsorted_scores.sort()\n\n# Computing the lower and upper bound of the 90% confidence interval\n# You can change the bounds percentiles to 0.025 and 0.975 to get\n# a 95% confidence interval instead.\nconfidence_lower = sorted_scores[int(0.05 * len(sorted_scores))]\nconfidence_upper = sorted_scores[int(0.95 * len(sorted_scores))]\nwith open(os.path.join(output_folder,f\"Result_scores_all.txt\"),'a') as file:\n file.write(\"\\nConfidence interval for the score: [{:0.3f} - {:0.3}]\\n\".format(\n confidence_lower, confidence_upper))\n\na=roc_auc_ci(Y_TEST,y_pred_prob)\nprint(a)\n\nplt.plot(fpr,tpr,label=f\"auc={auc}\",linewidth=1.5,markersize=1)\n\n\nplt.legend(loc=4,fontsize='xx-small')\nplt.title(f'ROC of Logistic Regression data')\nplt.xlabel('False Positive Rate')\nplt.ylabel('True Positive Rate')\naxes = plt.gca()\naxes.set_xlim([0,1])\naxes.set_ylim([0,1])\nfig=plt.gcf()\npdf.savefig(fig)\nplt.close(fig)\npdf.close()\n", "_____no_output_____" ], [ "# Save the best models\nimport pickle\nf = open(os.path.join(output_folder,'ran_for.sav'), 'wb')\npickle.dump(best_random, f)\nf.close()\n\nf = open(os.path.join(output_folder,'log_reg.sav'), 'wb')\npickle.dump(best_random_lr, f)\nf.close()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e641cf2308646b9137660202f75bb78fd3d52b

196,449

ipynb

Jupyter Notebook

notebooks/hydrostatic_balance.ipynb

Pearl-Ayem/ATSC_Course_Work

c075d166c235ac4e68a4b77750e02b2a5e77abd0

[ "MIT" ]

null

notebooks/hydrostatic_balance.ipynb

Pearl-Ayem/ATSC_Course_Work

c075d166c235ac4e68a4b77750e02b2a5e77abd0

[ "MIT" ]

null

notebooks/hydrostatic_balance.ipynb

Pearl-Ayem/ATSC_Course_Work

c075d166c235ac4e68a4b77750e02b2a5e77abd0

[ "MIT" ]

null

320.995098

91,369

0.916279

[ [ [ "<h1>Table of Contents<span class=\"tocSkip\"></span></h1>\n<div class=\"toc\"><ul class=\"toc-item\"><li><span><a href=\"#Scale-heights-for-typical-atmospheric-soundings\" data-toc-modified-id=\"Scale-heights-for-typical-atmospheric-soundings-1\"><span class=\"toc-item-num\">1  </span>Scale heights for typical atmospheric soundings</a></span><ul class=\"toc-item\"><li><span><a href=\"#Plot-McClatchey's-US-Standard-Atmospheres\" data-toc-modified-id=\"Plot-McClatchey's-US-Standard-Atmospheres-1.1\"><span class=\"toc-item-num\">1.1  </span>Plot McClatchey's US Standard Atmospheres</a></span><ul class=\"toc-item\"><li><span><a href=\"#Reading-the-soundings-files-into-pandas\" data-toc-modified-id=\"Reading-the-soundings-files-into-pandas-1.1.1\"><span class=\"toc-item-num\">1.1.1  </span>Reading the soundings files into pandas</a></span></li></ul></li></ul></li><li><span><a href=\"#Use-pd.DataFrame.head-to-see-first-5-lines\" data-toc-modified-id=\"Use-pd.DataFrame.head-to-see-first-5-lines-2\"><span class=\"toc-item-num\">2  </span>Use pd.DataFrame.head to see first 5 lines</a></span><ul class=\"toc-item\"><li><ul class=\"toc-item\"><li><span><a href=\"#Plot--temp-and-vapor-mixing-ratio-rmix-($\\rho_{H2O}/\\rho_{air}$)\" data-toc-modified-id=\"Plot--temp-and-vapor-mixing-ratio-rmix-($\\rho_{H2O}/\\rho_{air}$)-2.0.1\"><span class=\"toc-item-num\">2.0.1  </span>Plot temp and vapor mixing ratio rmix ($\\rho_{H2O}/\\rho_{air}$)</a></span></li></ul></li><li><span><a href=\"#Calculating-scale-heights-for-temperature-and-air-density\" data-toc-modified-id=\"Calculating-scale-heights-for-temperature-and-air-density-2.1\"><span class=\"toc-item-num\">2.1  </span>Calculating scale heights for temperature and air density</a></span><ul class=\"toc-item\"><li><span><a href=\"#How-do-$\\overline{H_p}$-and-$\\overline{H_\\rho}$-compare-for-the-tropical-sounding?\" data-toc-modified-id=\"How-do-$\\overline{H_p}$-and-$\\overline{H_\\rho}$-compare-for-the-tropical-sounding?-2.1.1\"><span class=\"toc-item-num\">2.1.1  </span>How do $\\overline{H_p}$ and $\\overline{H_\\rho}$ compare for the tropical sounding?</a></span></li><li><span><a href=\"#How-well-do-these-average-values-represent-the-pressure-and-density-profiles?\" data-toc-modified-id=\"How-well-do-these-average-values-represent-the-pressure-and-density-profiles?-2.1.2\"><span class=\"toc-item-num\">2.1.2  </span>How well do these average values represent the pressure and density profiles?</a></span></li><li><span><a href=\"#Assignment-for-Tuesday\" data-toc-modified-id=\"Assignment-for-Tuesday-2.1.3\"><span class=\"toc-item-num\">2.1.3  </span>Assignment for Tuesday</a></span></li></ul></li></ul></li></ul></div>", "_____no_output_____" ], [ "# Scale heights for typical atmospheric soundings", "_____no_output_____" ], [ "## Plot McClatchey's US Standard Atmospheres\n\nThere are five different average profiles for the tropics, subarctic summer, subarctic winter, midlatitude summer, midlatitude winter. These are called the US Standard Atmospheres. This notebook shows how to read and plot the soundings, and calculate the pressure and density scale heights.", "_____no_output_____" ] ], [ [ "from matplotlib import pyplot as plt\nimport matplotlib.ticker as ticks\nimport numpy as np\nimport a301\nfrom pathlib import Path\nimport pandas as pd\nimport pprint", "_____no_output_____" ], [ "soundings_folder= a301.test_dir / Path('soundings')\nsounding_files = list(soundings_folder.glob(\"*csv\"))", "_____no_output_____" ] ], [ [ "### Reading the soundings files into pandas\n\nThere are five soundings.\nThe soundings have six columns and 33 rows (i.e. 33 height levels). The variables are\n z, press, temp, rmix, den, o3den -- where rmix is the mixing ratio of water vapor, den is the dry air density and o3den is the ozone density. The units are \n m, pa, K, kg/kg, kg/m^3, kg/m^3\n \n I will read the 6 column soundings into a [pandas (panel data) DataFrame](http://pandas.pydata.org/pandas-docs/stable/dsintro.html), which is like a matrix except the columns can be accessed by column name in addition to column number. The main advantage for us is that it's easier to keep track of which variables we're plotting\n \n", "_____no_output_____" ] ], [ [ "name_dict=dict()\nsound_dict=dict()\nfor item in sounding_files:\n name_dict[item.stem]=item\npprint.pprint(name_dict)\n\nfor item in sounding_files:\n sound_dict[item.stem]=pd.read_csv(item)", "{'midsummer': PosixPath('/Users/phil/repos/a301_code/test_data/soundings/midsummer.csv'),\n 'midwinter': PosixPath('/Users/phil/repos/a301_code/test_data/soundings/midwinter.csv'),\n 'subsummer': PosixPath('/Users/phil/repos/a301_code/test_data/soundings/subsummer.csv'),\n 'subwinter': PosixPath('/Users/phil/repos/a301_code/test_data/soundings/subwinter.csv'),\n 'tropics': PosixPath('/Users/phil/repos/a301_code/test_data/soundings/tropics.csv')}\n" ] ], [ [ "# Use pd.DataFrame.head to see first 5 lines", "_____no_output_____" ] ], [ [ "for key,value in sound_dict.items():\n print(f\"sounding: {key}\\n{sound_dict[key].head()}\")", "sounding: tropics\n Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101300.0 300.0 0.01900 1.1670 5.600000e-08\n1 1 1000.0 90400.0 294.0 0.01300 1.0640 5.600000e-08\n2 2 2000.0 80500.0 288.0 0.00929 0.9689 5.400000e-08\n3 3 3000.0 71500.0 284.0 0.00470 0.8756 5.100000e-08\n4 4 4000.0 63300.0 277.0 0.00266 0.7951 4.700000e-08\nsounding: subsummer\n Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101000.0 287.0 0.00910 1.2200 4.900000e-08\n1 1 1000.0 89600.0 282.0 0.00600 1.1100 5.400000e-08\n2 2 2000.0 79290.0 276.0 0.00420 0.9971 5.600000e-08\n3 3 3000.0 70000.0 271.0 0.00269 0.8985 5.800001e-08\n4 4 4000.0 61600.0 266.0 0.00165 0.8077 6.000000e-08\nsounding: subwinter\n Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101300.0 257.1 0.001200 1.3720 4.100000e-08\n1 1 1000.0 88780.0 259.1 0.001200 1.1930 4.100000e-08\n2 2 2000.0 77750.0 255.9 0.001030 1.0580 4.100000e-08\n3 3 3000.0 67980.0 252.7 0.000747 0.9366 4.300000e-08\n4 4 4000.0 59320.0 247.7 0.000459 0.8339 4.500000e-08\nsounding: midwinter\n Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101800.000 272.2 0.00350 1.3010 6.000000e-08\n1 1 1000.0 89730.000 268.7 0.00250 1.1620 5.400000e-08\n2 2 2000.0 78970.000 265.2 0.00180 1.0370 4.900000e-08\n3 3 3000.0 69380.000 261.7 0.00116 0.9230 4.900000e-08\n4 4 4000.0 60809.996 255.7 0.00069 0.8282 4.900000e-08\nsounding: midsummer\n Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101300.0 294.0 0.01400 1.1910 6.000000e-08\n1 1 1000.0 90200.0 290.0 0.00930 1.0800 6.000000e-08\n2 2 2000.0 80200.0 285.0 0.00585 0.9757 6.000000e-08\n3 3 3000.0 71000.0 279.0 0.00343 0.8846 6.200001e-08\n4 4 4000.0 62800.0 273.0 0.00189 0.7998 6.400000e-08\n" ] ], [ [ "We use these keys to get a dataframe with 6 columns, and 33 levels. Here's an example for the midsummer sounding", "_____no_output_____" ] ], [ [ "midsummer=sound_dict['midsummer']\nprint(midsummer.head())\nlist(midsummer.columns)", " Unnamed: 0 z press temp rmix den o3den\n0 0 0.0 101300.0 294.0 0.01400 1.1910 6.000000e-08\n1 1 1000.0 90200.0 290.0 0.00930 1.0800 6.000000e-08\n2 2 2000.0 80200.0 285.0 0.00585 0.9757 6.000000e-08\n3 3 3000.0 71000.0 279.0 0.00343 0.8846 6.200001e-08\n4 4 4000.0 62800.0 273.0 0.00189 0.7998 6.400000e-08\n" ] ], [ [ "### Plot temp and vapor mixing ratio rmix ($\\rho_{H2O}/\\rho_{air}$)", "_____no_output_____" ] ], [ [ "%matplotlib inline\nplt.style.use('ggplot')\nmeters2km=1.e-3\nplt.close('all')\nfig,(ax1,ax2)=plt.subplots(1,2,figsize=(11,8))\nfor a_name,df in sound_dict.items():\n ax1.plot(df['temp'],df['z']*meters2km,label=a_name)\n ax1.set(ylim=(0,40),title='Temp soundings',ylabel='Height (km)',\n xlabel='Temperature (K)')\n\n ax2.plot(df['rmix']*1.e3,df['z']*meters2km,label=a_name)\n ax2.set(ylim=(0,8),title='Vapor soundings',ylabel='Height (km)',\n xlabel='vapor mixing ratio (g/kg)')\nax1.legend();", "_____no_output_____" ] ], [ [ "## Calculating scale heights for temperature and air density", "_____no_output_____" ], [ "Here is equation 1 of the [hydrostatic balance notes](http://clouds.eos.ubc.ca/~phil/courses/atsc301/hydrostat.html#equation-hydro)", "_____no_output_____" ], [ "$$\\frac{ 1}{\\overline{H_p}} = \\overline{ \\left ( \\frac{1 }{H} \\right )} = \\frac{\\int_{0 }^{z}\\!\\frac{1}{H} dz^\\prime }{z-0} $$\n\nwhere\n\n$$H=R_d T/g$$", "_____no_output_____" ], [ "and here is the Python code to do that integral:", "_____no_output_____" ] ], [ [ "g=9.8 #don't worry about g(z) for this exercise\nRd=287. #kg/m^3\ndef calcScaleHeight(T,p,z):\n \"\"\"\n Calculate the pressure scale height H_p\n \n Parameters\n ----------\n \n T: vector (float)\n temperature (K)\n \n p: vector (float) of len(T)\n pressure (pa)\n \n z: vector (float) of len(T\n height (m)\n \n Returns\n -------\n \n Hbar: vector (float) of len(T)\n pressure scale height (m)\n \n \"\"\"\n dz=np.diff(z)\n TLayer=(T[1:] + T[0:-1])/2.\n oneOverH=g/(Rd*TLayer)\n Zthick=z[-1] - z[0]\n oneOverHbar=np.sum(oneOverH*dz)/Zthick\n Hbar = 1/oneOverHbar\n return Hbar", "_____no_output_____" ] ], [ [ "Similarly, equation (5) of the [hydrostatic balance notes](http://clouds.eos.ubc.ca/~phil/courses/atsc301/hydrostat.html#equation-hydro)\nis:\n\n$$\\frac{d\\rho }{\\rho} = - \\left ( \\frac{1 }{H} + \n \\frac{1 }{T} \\frac{dT }{dz} \\right ) dz \\equiv - \\frac{dz }{H_\\rho} $$\n \nWhich leads to \n\n$$\\frac{ 1}{\\overline{H_\\rho}} = \\frac{\\int_{0 }^{z}\\!\\left [ \\frac{1}{H} + \\frac{1 }{T} \\frac{dT }{dz} \\right ] dz^\\prime }{z-0} $$\n\nand the following python function:\n", "_____no_output_____" ] ], [ [ "def calcDensHeight(T,p,z):\n \"\"\"\n Calculate the density scale height H_rho\n \n Parameters\n ----------\n \n T: vector (float)\n temperature (K)\n \n p: vector (float) of len(T)\n pressure (pa)\n \n z: vector (float) of len(T\n height (m)\n \n Returns\n -------\n \n Hbar: vector (float) of len(T)\n density scale height (m)\n \"\"\"\n dz=np.diff(z)\n TLayer=(T[1:] + T[0:-1])/2.\n dTdz=np.diff(T)/np.diff(z)\n oneOverH=g/(Rd*TLayer) + (1/TLayer*dTdz)\n Zthick=z[-1] - z[0]\n oneOverHbar=np.sum(oneOverH*dz)/Zthick\n Hbar = 1/oneOverHbar\n return Hbar", "_____no_output_____" ] ], [ [ "### How do $\\overline{H_p}$ and $\\overline{H_\\rho}$ compare for the tropical sounding?", "_____no_output_____" ] ], [ [ "sounding='tropics'\n#\n# grab the dataframe and get the sounding columns\n#\ndf=sound_dict[sounding]\nz=df['z'].values\nTemp=df['temp'].values\npress=df['press'].values", "_____no_output_____" ], [ "#\n# limit calculation to bottom 10 km\n#\nhit=z<10000.\nzL,pressL,TempL=(z[hit],press[hit],Temp[hit])\nrhoL=pressL/(Rd*TempL)\nHbar= calcScaleHeight(TempL,pressL,zL)\nHrho= calcDensHeight(TempL,pressL,zL)\nprint(\"pressure scale height for the {} sounding is {:5.2f} km\".format(sounding,Hbar*1.e-3))\nprint(\"density scale height for the {} is {:5.2f} km\".format(sounding,Hrho*1.e-3))", "pressure scale height for the tropics sounding is 7.96 km\ndensity scale height for the tropics is 9.74 km\n" ] ], [ [ "### How well do these average values represent the pressure and density profiles?", "_____no_output_____" ] ], [ [ "theFig,theAx=plt.subplots(1,1)\ntheAx.semilogy(Temp,press/100.)\n#\n# need to flip the y axis since pressure decreases with height\n#\ntheAx.invert_yaxis()\ntickvals=[1000,800, 600, 400, 200, 100, 50,1]\ntheAx.set_yticks(tickvals)\nmajorFormatter = ticks.FormatStrFormatter('%d')\ntheAx.yaxis.set_major_formatter(majorFormatter)\ntheAx.set_yticklabels(tickvals)\ntheAx.set_ylim([1000.,50.])\ntheAx.set_title('{} temperature profile'.format(sounding))\ntheAx.set_xlabel('Temperature (K)')\ntheAx.set_ylabel('pressure (hPa)');", "_____no_output_____" ] ], [ [ "Now check the hydrostatic approximation by plotting the pressure column against\n\n$$p(z) = p_0 \\exp \\left (-z/\\overline{H_p} \\right )$$\n\nvs. the actual sounding p(T):", "_____no_output_____" ] ], [ [ "fig,theAx=plt.subplots(1,1)\nhydroPress=pressL[0]*np.exp(-zL/Hbar)\ntheAx.plot(pressL/100.,zL/1000.,label='sounding')\ntheAx.plot(hydroPress/100.,zL/1000.,label='hydrostat approx')\ntheAx.set_title('height vs. pressure for tropics')\ntheAx.set_xlabel('pressure (hPa)')\ntheAx.set_ylabel('height (km)')\ntheAx.set_xlim([500,1000])\ntheAx.set_ylim([0,5])\ntickVals=[500, 600, 700, 800, 900, 1000]\ntheAx.set_xticks(tickVals)\ntheAx.set_xticklabels(tickVals)\ntheAx.legend(loc='best');", "_____no_output_____" ] ], [ [ "Again plot the hydrostatic approximation\n\n$$\\rho(z) = \\rho_0 \\exp \\left (-z/\\overline{H_\\rho} \\right )$$\n\nvs. the actual sounding $\\rho(z)$:", "_____no_output_____" ] ], [ [ "fig,theAx=plt.subplots(1,1)\nhydroDens=rhoL[0]*np.exp(-zL/Hrho)\ntheAx.plot(rhoL,zL/1000.,label='sounding')\ntheAx.plot(hydroDens,zL/1000.,label='hydrostat approx')\ntheAx.set_title('height vs. density for the tropics')\ntheAx.set_xlabel('density ($kg\\,m^{-3}$)')\ntheAx.set_ylabel('height (km)')\ntheAx.set_ylim([0,5])\ntheAx.legend(loc='best');", "_____no_output_____" ] ], [ [ "<a name=\"oct7assign\"></a>\n\n### Assignment for Tuesday\n\nAdd cells to this notebook to:\n\n1\\. Print out the density and pressure scale heights for each of the five soundings\n\n2\\. Define a function that takes a sounding dataframe and returns the \"total precipitable water\", which is defined as:\n\n$$W = \\int_0^{z_{top}} \\rho_v dz $$\n\nDo a change of units to convert $kg\\,m^{-2}$ to $cm\\,m^{-2}$ using the density of liquid water (1000 $kg\\,m^{-3}$) -- that is, turn the kg of water in the 1 square meter column into cubic meters and turn that into $cm/m^{-2}$\n\n3\\. Use your function to print out W for all five soundings", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e6530e9b60561ab10b969d0c7bede80da97766

645

ipynb

Jupyter Notebook

.ipynb_checkpoints/ene.015-checkpoint.ipynb

nsuberi/RW_Raster_Getters

86905219f43a05420a055f750b267db62a08fea8

[ "MIT" ]

null

.ipynb_checkpoints/ene.015-checkpoint.ipynb

nsuberi/RW_Raster_Getters

86905219f43a05420a055f750b267db62a08fea8

[ "MIT" ]

null

.ipynb_checkpoints/ene.015-checkpoint.ipynb

nsuberi/RW_Raster_Getters

86905219f43a05420a055f750b267db62a08fea8

[ "MIT" ]

null

19.545455

127

0.575194

[ [ [ "Solar Energy Potential\tene.015\thttp://www.vaisala.com/en/energy/Documents/WEA-ERG-3TIER-Global%20Solar%20Validation.pdf", "_____no_output_____" ] ] ]

[ "markdown" ]

[ [ "markdown" ] ]

d0e65416098041d47ac2ca44dfc63077582e54de

141,024

ipynb

Jupyter Notebook

Codes/Final (SVM SVC template ).ipynb

masudurHimel/ML---APS-Failure-at-Scania-Trucks-Data-Set

28ce0f07da1b72616107316f7e77f2f6d7b64673

[ "MIT" ]

null

Codes/Final (SVM SVC template ).ipynb

masudurHimel/ML---APS-Failure-at-Scania-Trucks-Data-Set

28ce0f07da1b72616107316f7e77f2f6d7b64673

[ "MIT" ]

null

Codes/Final (SVM SVC template ).ipynb

masudurHimel/ML---APS-Failure-at-Scania-Trucks-Data-Set

28ce0f07da1b72616107316f7e77f2f6d7b64673

[ "MIT" ]

1

2019-07-19T15:35:22.000Z

85.313975

42,108

0.769373

[ [ [ "import pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nimport warnings\nwarnings.filterwarnings(\"ignore\")\n%matplotlib inline\nsns.set_style('whitegrid')\nfrom sklearn.linear_model import LogisticRegression\nfrom sklearn.metrics import classification_report\nfrom sklearn.metrics import confusion_matrix\nfrom sklearn.model_selection import cross_val_predict,cross_val_score\nfrom sklearn.metrics import roc_auc_score,roc_curve\nfrom sklearn.model_selection import train_test_split\nfrom sklearn import metrics\nfrom sklearn.metrics import mean_squared_error\nfrom sklearn.svm import SVC", "_____no_output_____" ], [ "training_data = pd.read_csv(\"../Data/aps_failure_training_set.csv\",na_values=\"na\")\ntraining_data.head()", "_____no_output_____" ] ], [ [ "# Preprocessing", "_____no_output_____" ] ], [ [ "plt.figure(figsize=(20,12))\nsns.heatmap(training_data.isnull(),yticklabels=False,cbar=False,cmap = 'viridis')", "_____no_output_____" ] ], [ [ "# Missing value handling", "_____no_output_____" ], [ "We are going to use different approches with missing values:\n\n1. Removing the column having 80% missing values (**Self intuition)\n2. Keeping all the features\n3. Later, we will try to implement some feature engineering \n\n\n**For the rest of the missing values, we are replacing them with their mean() for now (**Ref) ", "_____no_output_____" ], [ "<big><b>Second Approach</b>", "_____no_output_____" ] ], [ [ "sample_training_data = training_data\nsample_training_data.fillna(sample_training_data.mean(),inplace=True)\n\n#after replacing with mean()\n\nplt.figure(figsize=(20,12))\nsns.heatmap(sample_training_data.isnull(),yticklabels=False,cbar=False,cmap='viridis')", "_____no_output_____" ], [ "#as all the other values are numerical except Class column so we can replace them with 1 and 0\n\nsample_training_data = sample_training_data.replace('neg',0)\nsample_training_data = sample_training_data.replace('pos',1)\n\nsample_training_data.head()", "_____no_output_____" ] ], [ [ "# Testing Data preprocessing", "_____no_output_____" ] ], [ [ "testing_data = pd.read_csv(\"../Data/aps_failure_test_set.csv\",na_values=\"na\")\ntesting_data.head()", "_____no_output_____" ], [ "sample_testing_data = testing_data\nsample_testing_data.fillna(sample_testing_data.mean(),inplace=True)\n\n#after replacing with mean()\n\nplt.figure(figsize=(20,12))\nsns.heatmap(sample_testing_data.isnull(),yticklabels=False,cbar=False,cmap='viridis')", "_____no_output_____" ], [ "#as all the other values are numerical except Class column so we can replace them with 1 and 0\n\nsample_testing_data = sample_testing_data.replace('neg',0)\nsample_testing_data = sample_testing_data.replace('pos',1)\n\nsample_testing_data.head()", "_____no_output_____" ] ], [ [ "# Implemented Methods ", "_____no_output_____" ] ], [ [ "def getCost(y_test,prediction):\n '''\n evaluate the total cost without modified threshold\n '''\n tn, fp, fn, tp = confusion_matrix(y_test,prediction).ravel()\n confusionData = [[tn,fp],[fn,tp]]\n print(\"Confusion Matrix\\n\")\n print(pd.DataFrame(confusionData,columns=['FN','FP'],index=['TN','TP']))\n cost = 10*fp+500*fn\n values = {'Score':[cost],'Number of Type 1 faults':[fp],'Number of Type 2 faults':[fn]}\n print(\"\\n\\nCost\\n\")\n print(pd.DataFrame(values))", "_____no_output_____" ], [ "def getCostWithThreshold(X_test,y_test,prediction,threshold,model):\n \"\"\"\n evaluate the total cost with modified threshold\n model = model instance\n \"\"\"\n THRESHOLD = threshold #optimal one chosen from the roc curve\n thresholdPrediction = np.where(model.predict_proba(X_test)[:,1] > THRESHOLD, 1,0)\n tn, fp, fn, tp = confusion_matrix(y_test,thresholdPrediction).ravel()\n cost = 10*fp+500*fn\n values = {'Score':[cost],'Number of Type 1 faults':[fp],'Number of Type 2 faults':[fn]}\n pd.DataFrame(values)", "_____no_output_____" ], [ "def aucForThreshold(X_test,y_test,model):\n \"\"\"\n return roc auc curve for determining the optimal threshold\n model = desired model's instance\n \"\"\"\n from sklearn.metrics import roc_auc_score,roc_curve\n logit_roc_auc = roc_auc_score(y_test, model.predict_proba(X_test)[:,1])\n fpr, tpr, thresholds = roc_curve(y_test,model.predict_proba(X_test)[:,1])\n plt.figure()\n plt.plot(fpr, tpr, label='Logistic Regression (area = %0.2f)' % logit_roc_auc)\n plt.plot([0, 1], [0, 1],'r--')\n plt.xlim([0.0, 1.0])\n plt.ylim([0.0, 1.0])\n plt.xlabel('False Positive Rate')\n plt.ylabel('True Positive Rate')\n plt.title('Receiver operating characteristic')\n plt.legend(loc=\"upper center\")\n plt.savefig('Log_ROC')\n\n\n # create the axis of thresholds (scores)\n ax2 = plt.gca().twinx()\n ax2.plot(fpr, thresholds, markeredgecolor='g',linestyle='dashed', color='g',label = 'Threshold')\n ax2.set_ylabel('Threshold',color='g')\n ax2.set_ylim([thresholds[-1],thresholds[0]])\n ax2.set_xlim([fpr[0],fpr[-1]])\n plt.legend(loc=\"lower right\")\n plt.savefig('roc_and_threshold.png')\n plt.show()", "_____no_output_____" ], [ "def evaluationScored(y_test,prediction):\n acc = metrics.accuracy_score(y_test, prediction)\n r2 = metrics.r2_score(y_test, prediction)\n f1 = metrics.f1_score(y_test, prediction)\n mse = metrics.mean_squared_error(y_test, prediction)\n values = {'Accuracy Score':[acc],'R2':[r2],'F1':[f1],'MSE':[mse]}\n print(\"\\n\\nScores\")\n print (pd.DataFrame(values))\n ", "_____no_output_____" ] ], [ [ "# Model implementation with Cross validation", "_____no_output_____" ] ], [ [ "X = sample_training_data.drop('class',axis=1)\ny = sample_training_data['class']", "_____no_output_____" ], [ "CV_prediction = cross_val_predict(SVC(),X,y,cv = 5)", "_____no_output_____" ], [ "CV_score = cross_val_score(SVC(),X,y,cv = 5)", "_____no_output_____" ], [ "#mean cross validation score \nnp.mean(CV_score)", "_____no_output_____" ], [ "print(classification_report(y,CV_prediction))", "_____no_output_____" ], [ "evaluationScores(y,CV_prediction)", "_____no_output_____" ], [ "CV_prediction = cross_val_predict(SVC(),X,y,cv = 10)", "_____no_output_____" ], [ "print(classification_report(y,CV_prediction))", "_____no_output_____" ], [ "evaluationScores(y,CV_prediction)", "_____no_output_____" ] ], [ [ "# Try with test train split", "_____no_output_____" ] ], [ [ "X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)", "_____no_output_____" ], [ "svc_model = SVC()", "_____no_output_____" ], [ "svc_model.fit(X_train,y_train)", "_____no_output_____" ], [ "trainingPrediction = svc_model.predict(X_test)", "_____no_output_____" ], [ "evaluationScored(y_test,trainingPrediction)", "\n\nScores\n Accuracy Score R2 F1 MSE\n0 0.982833 -0.017467 0.0 0.017167\n" ], [ "getCost(y_test,trainingPrediction)", "Confusion Matrix\n\n FN FP\nTN 17691 0\nTP 309 0\n\n\nCost\n\n Score Number of Type 1 faults Number of Type 2 faults\n0 154500 0 309\n" ] ], [ [ "<b>With threshold</b>", "_____no_output_____" ] ], [ [ "aucForThreshold(X_test,y_test,svc_model)", "_____no_output_____" ], [ "#need to implement\ngetCostWithThreshold(X_test,y_test,trainingPrediction,threshold,svc_model)", "_____no_output_____" ] ], [ [ "<b>With Gridsearch</b>", "_____no_output_____" ] ], [ [ "param_grid = {'C': [0.1,1], 'gamma': [1,0.1], 'kernel': ['rbf']} ", "_____no_output_____" ], [ "from sklearn.model_selection import GridSearchCV", "_____no_output_____" ], [ "grid = GridSearchCV(SVC(),param_grid,refit=True,verbose=3)", "_____no_output_____" ], [ "#fitting again\ngrid.fit(X_train,y_train)", "Fitting 3 folds for each of 4 candidates, totalling 12 fits\n[CV] C=0.1, gamma=1, kernel=rbf ......................................\n" ], [ "grid.best_params_", "_____no_output_____" ], [ "grid.best_estimator_", "_____no_output_____" ], [ "grid_predictions = grid.predict(X_test)", "_____no_output_____" ], [ "evaluationScored(y_test,grid_predictions)", "\n\nScores\n Accuracy Score R2 F1 MSE\n0 0.982833 -0.017467 0.0 0.017167\n" ], [ "getCost(y_test,grid_predictions)", "Confusion Matrix\n\n FN FP\nTN 17691 0\nTP 309 0\n\n\nCost\n\n Score Number of Type 1 faults Number of Type 2 faults\n0 154500 0 309\n" ], [ "aucForThreshold(X_test,y_test,grid)", "_____no_output_____" ], [ "#need to implement\ngetCostWithThreshold(X_test,y_test,trainingPrediction,threshold,grid)", "_____no_output_____" ] ], [ [ "# Testing Data implementation ", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ] ]

d0e65b780f010e92a6f5ea8c30a38953f1a176b4

294,296

ipynb

Jupyter Notebook

notebooks/transfer learning - cats vs dogs.ipynb

quanhua92/TensorFlow-2.x-Cheatsheet

9978d127d265a50f4fb78b19f621f265733b383e

[ "MIT" ]

1

2020-09-16T20:13:36.000Z

notebooks/transfer learning - cats vs dogs.ipynb

quanhua92/TensorFlow-2.x-Cheatsheet

9978d127d265a50f4fb78b19f621f265733b383e

[ "MIT" ]

null

notebooks/transfer learning - cats vs dogs.ipynb

quanhua92/TensorFlow-2.x-Cheatsheet

9978d127d265a50f4fb78b19f621f265733b383e

[ "MIT" ]

1

2020-04-02T09:38:40.000Z

567.044316

194,428

0.944634

[ [ [ "import tensorflow as tf\n\nprint(tf.__version__)", "2.1.0\n" ], [ "import tensorflow_datasets as tfds\n\nprint(tfds.__version__)", "1.3.2\n" ] ], [ [ "# Get dataset", "_____no_output_____" ] ], [ [ "SPLIT_WEIGHTS = (8, 1, 1)\nsplits = tfds.Split.TRAIN.subsplit(weighted=SPLIT_WEIGHTS)\n\n(raw_train, raw_validation, raw_test), metadata = tfds.load('cats_vs_dogs', \n split=list(splits),\n with_info=True,\n as_supervised=True)", "_____no_output_____" ], [ "print(metadata.features)", "FeaturesDict({\n 'image': Image(shape=(None, None, 3), dtype=tf.uint8),\n 'image/filename': Text(shape=(), dtype=tf.string),\n 'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=2),\n})\n" ], [ "import matplotlib.pyplot as plt\n\n%matplotlib inline\n\nget_label_name = metadata.features['label'].int2str\n\nfor image, label in raw_train.take(2):\n plt.figure()\n plt.imshow(image)\n plt.title(get_label_name(label))", "_____no_output_____" ] ], [ [ "# Prepare input pipelines", "_____no_output_____" ] ], [ [ "IMG_SIZE = 160\nBATCH_SIZE = 32\nSHUFFLE_BUFFER_SIZE = 1000", "_____no_output_____" ], [ "def normalize_img(image, label):\n image = tf.cast(image, tf.float32)\n image = (image / 127.5) - 1.0\n image = tf.image.resize(image, (IMG_SIZE, IMG_SIZE))\n return image, label", "_____no_output_____" ], [ "ds_train = raw_train.map(normalize_img)\nds_validation = raw_validation.map(normalize_img)\nds_test = raw_test.map(normalize_img)", "_____no_output_____" ], [ "ds_train = ds_train.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)\nds_validation = ds_validation.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)\nds_test = ds_test.batch(BATCH_SIZE)", "_____no_output_____" ] ], [ [ "# Get pretrained model", "_____no_output_____" ] ], [ [ "base_model = tf.keras.applications.MobileNetV2(input_shape=(IMG_SIZE, IMG_SIZE, 3),\n include_top=False,\n weights='imagenet')", "_____no_output_____" ], [ "base_model.trainable = False", "_____no_output_____" ], [ "model = tf.keras.Sequential([\n base_model,\n tf.keras.layers.GlobalAveragePooling2D(),\n tf.keras.layers.Dense(1)\n])", "_____no_output_____" ], [ "model.summary()", "Model: \"sequential\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\nmobilenetv2_1.00_160 (Model) (None, 5, 5, 1280) 2257984 \n_________________________________________________________________\nglobal_average_pooling2d (Gl (None, 1280) 0 \n_________________________________________________________________\ndense (Dense) (None, 1) 1281 \n=================================================================\nTotal params: 2,259,265\nTrainable params: 1,281\nNon-trainable params: 2,257,984\n_________________________________________________________________\n" ] ], [ [ "# (Optional): Use Tensorflow Hub", "_____no_output_____" ] ], [ [ "import tensorflow_hub as hub\nprint(hub.__version__)", "0.8.0.dev\n" ], [ "feature_extractor_url = \"https://tfhub.dev/google/imagenet/mobilenet_v2_035_160/classification/4\"\nbase_model = hub.KerasLayer(feature_extractor_url, input_shape=(IMG_SIZE, IMG_SIZE, 3), trainable=False)", "_____no_output_____" ], [ "model = tf.keras.Sequential([\n base_model,\n tf.keras.layers.Dense(1)\n])", "_____no_output_____" ], [ "model.summary()", "Model: \"sequential_1\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\nkeras_layer (KerasLayer) (None, 1001) 1692489 \n_________________________________________________________________\ndense_1 (Dense) (None, 1) 1002 \n=================================================================\nTotal params: 1,693,491\nTrainable params: 1,002\nNon-trainable params: 1,692,489\n_________________________________________________________________\n" ] ], [ [ "# Compile model", "_____no_output_____" ] ], [ [ "base_learning_rate = 1e-4\n\nmodel.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),\n loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),\n metrics=['accuracy'])", "_____no_output_____" ] ], [ [ "# Evaluate random model", "_____no_output_____" ] ], [ [ "loss0, accuracy0 = model.evaluate(ds_validation)", " 73/Unknown - 5s 72ms/step - loss: 1.1503 - accuracy: 0.4358" ] ], [ [ "# Train model", "_____no_output_____" ] ], [ [ "initial_epochs = 3\n\nhistory = model.fit(ds_train,\n epochs=initial_epochs,\n validation_data=ds_validation)", "Epoch 1/3\n582/582 [==============================] - 27s 46ms/step - loss: 0.5690 - accuracy: 0.7017 - val_loss: 0.4069 - val_accuracy: 0.8022\nEpoch 2/3\n582/582 [==============================] - 23s 40ms/step - loss: 0.3905 - accuracy: 0.8111 - val_loss: 0.3690 - val_accuracy: 0.8302\nEpoch 3/3\n582/582 [==============================] - 24s 41ms/step - loss: 0.3612 - accuracy: 0.8270 - val_loss: 0.3482 - val_accuracy: 0.8366\n" ] ], [ [ "# Fine-tune", "_____no_output_____" ] ], [ [ "base_model.trainable = True", "_____no_output_____" ], [ "base_learning_rate = 1e-5\n\nmodel.compile(optimizer=tf.keras.optimizers.RMSprop(lr=base_learning_rate),\n loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),\n metrics=['accuracy'])", "_____no_output_____" ], [ "model.summary()", "Model: \"sequential_1\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\nkeras_layer (KerasLayer) (None, 1001) 1692489 \n_________________________________________________________________\ndense_1 (Dense) (None, 1) 1002 \n=================================================================\nTotal params: 1,693,491\nTrainable params: 1,679,411\nNon-trainable params: 14,080\n_________________________________________________________________\n" ], [ "fine_tune_epochs = 3\ntotal_epochs = initial_epochs + fine_tune_epochs\n\nhistory_fine = model.fit(ds_train,\n epochs=total_epochs,\n initial_epoch=history.epoch[-1],\n validation_data=ds_validation)", "Epoch 3/6\n582/582 [==============================] - 56s 95ms/step - loss: 0.3367 - accuracy: 0.8987 - val_loss: 0.2620 - val_accuracy: 0.9366\nEpoch 4/6\n582/582 [==============================] - 48s 82ms/step - loss: 0.2734 - accuracy: 0.9287 - val_loss: 0.2230 - val_accuracy: 0.9483\nEpoch 5/6\n582/582 [==============================] - 47s 81ms/step - loss: 0.2495 - accuracy: 0.9378 - val_loss: 0.2128 - val_accuracy: 0.9547\nEpoch 6/6\n582/582 [==============================] - 47s 81ms/step - loss: 0.2357 - accuracy: 0.9432 - val_loss: 0.2045 - val_accuracy: 0.9599\n" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

d0e6621ba1b990ce8c9551414fd73381bd5feb53

7,195

ipynb

Jupyter Notebook

6-machine-learning/Problem-1.ipynb

HabibMrad/mmtf-workshop-2018

ed94f0d2d47c7f9ea82894e9e7e9ccf860c7f30b

[ "Apache-2.0" ]

1

2019-09-21T09:44:35.000Z

6-machine-learning/Problem-1.ipynb

HabibMrad/mmtf-workshop-2018

ed94f0d2d47c7f9ea82894e9e7e9ccf860c7f30b

[ "Apache-2.0" ]

null

6-machine-learning/Problem-1.ipynb

HabibMrad/mmtf-workshop-2018

ed94f0d2d47c7f9ea82894e9e7e9ccf860c7f30b

[ "Apache-2.0" ]

null

27.461832

166

0.472689

[ [ [ "# Problem 1\nApply your skills to classify protein foldType with Decision Tree Classifier\n\n## Imports", "_____no_output_____" ] ], [ [ "from mmtfPyspark.ml import SparkMultiClassClassifier, datasetBalancer \nfrom pyspark.sql import SparkSession\nfrom pyspark.sql.functions import *\nimport mltoolkit", "_____no_output_____" ] ], [ [ "## Configure Spark Session", "_____no_output_____" ] ], [ [ "spark = SparkSession.builder.appName(\"Problem-1\").getOrCreate()", "_____no_output_____" ] ], [ [ "## TODO-1: Read in data from parquet file", "_____no_output_____" ] ], [ [ "parquetFile = './input_features/'\ndata = # Your Code Here #", "_____no_output_____" ] ], [ [ "## TODO-2: Select alpha, beta, alpha+beta foldtypes", "_____no_output_____" ] ], [ [ "data = # Your Code Here #\nprint(f\"Total number of data: {data.count()}\")", "Total number of data: 2390\n" ] ], [ [ "## TODO-3: Downsample data", "_____no_output_____" ] ], [ [ "label = 'foldType'\n\ndata = # Your Code Here #\nprint(f\"Dataset size (balanced) : {data.count()}\")\n \ndata.groupby(label).count().show()", "Dataset size (balanced) : 1266\n+--------+-----+\n|foldType|count|\n+--------+-----+\n| beta| 626|\n| alpha| 640|\n+--------+-----+\n\n" ] ], [ [ "## TODO-4: Decision Tree Classifier with PySpark", "_____no_output_____" ] ], [ [ "from pyspark.ml.classification import DecisionTreeClassifier\n\ndtc = # Your Code Here: Make Decision Tree Classifier Class #\nmcc = # Your Code Here: Use MulticlassClassifier wrapper on dtc#\nmatrics = # Your Code Here: fit data#\nfor k,v in matrics.items(): print(f\"{k}\\t{v}\")", "\n Class\tTrain\tTest\nalpha\t562\t78\nbeta\t561\t65\n\nSample predictions: DecisionTreeClassifier\n+----------------+-----------+----------+---------+--------+--------------------+------------+-------------+--------------------+----------+--------------+\n|structureChainId| alpha| beta| coil|foldType| features|indexedLabel|rawPrediction| probability|prediction|predictedLabel|\n+----------------+-----------+----------+---------+--------+--------------------+------------+-------------+--------------------+----------+--------------+\n| 2PW8.I|0.048387095|0.30645162|0.6451613| beta|[0.34626930754166...| 1.0| [13.0,322.0]|[0.03880597014925...| 1.0| beta|\n| 4Q1Q.B| 0.0| 0.5| 0.5| beta|[-0.1299340440187...| 1.0| [13.0,322.0]|[0.03880597014925...| 1.0| beta|\n| 5F6L.J| 0.0|0.21052632|0.7894737| beta|[0.28061876961818...| 1.0| [23.0,1.0]|[0.95833333333333...| 0.0| alpha|\n| 5INB.B| 0.0|0.18181819|0.8181818| beta|[0.20785025656223...| 1.0| [33.0,2.0]|[0.94285714285714...| 0.0| alpha|\n| 1OGO.X|0.034965035|0.42482516|0.5402098| beta|[0.00471779905128...| 1.0| [13.0,322.0]|[0.03880597014925...| 1.0| beta|\n+----------------+-----------+----------+---------+--------+--------------------+------------+-------------+--------------------+----------+--------------+\nonly showing top 5 rows\n\nTotal time taken: 4.23888897895813\n\nMethod\tDecisionTreeClassifier\nAUC\t0.8371794871794872\nF\t0.8390496581875636\nAccuracy\t0.8391608391608392\nPrecision\t0.8390211449942462\nRecall\t0.8391608391608392\nFalse Positive Rate\t0.16480186480186482\nTrue Positive Rate\t0.8391608391608392\n\t\nConfusion Matrix\n['alpha', 'beta']\nDenseMatrix([[67., 11.],\n [12., 53.]])\n" ] ], [ [ "## BONUS: Decision Tree Classifier with sklearn", "_____no_output_____" ] ], [ [ "from sklearn.tree import DecisionTreeClassifier\n\ndf = # Your Code Here: convert data to Pandas Dataframe #\ndtc = # Your Code Here: Make Decision Tree Classifier Class #\nmcc = # Your Code Here: Use MulticlassClassifier wrapper on dtc#\nmatrics = # Your Code Here: fit data#\nfor k,v in matrics.items(): print(f\"{k}\\t{v}\")", "\n Class\tTrain\tTest\n\nbeta\t568\t58\n\nalpha\t571\t69\n\nTotal time taken: 0.08887577056884766\n\nMethods\tDecisionTreeClassifier\nAUC\t0.7906046976511744\nF Score\t0.7938931297709925\nAccuracy\t0.7874015748031497\nPrecision\t0.8387096774193549\nRecall\t0.7536231884057971\nFalse Positive Rate\t0.16129032258064516\nTrue Positive Rate\t0.7384615384615385\n\t\nConfusion Matrix\n['beta' 'alpha']\n[[48 10]\n [17 52]]\n" ], [ "spark.stop()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

d0e672120e0f949450c661830f0f6c331d9bafec

107,707

ipynb

Jupyter Notebook

nbs/40_tabular.core.ipynb

yijinlee/fastai2

4c3556c3c3cdafef774f50613a51f09e653e0dc0

[ "Apache-2.0" ]

null

nbs/40_tabular.core.ipynb

yijinlee/fastai2

4c3556c3c3cdafef774f50613a51f09e653e0dc0

[ "Apache-2.0" ]

null

nbs/40_tabular.core.ipynb

yijinlee/fastai2

4c3556c3c3cdafef774f50613a51f09e653e0dc0

[ "Apache-2.0" ]

null

32.688012

173

0.415043

[ [ [ "#default_exp tabular.core", "_____no_output_____" ], [ "#export\nfrom fastai2.torch_basics import *\nfrom fastai2.data.all import *", "_____no_output_____" ], [ "from nbdev.showdoc import *", "_____no_output_____" ], [ "#export\npd.set_option('mode.chained_assignment','raise')", "_____no_output_____" ] ], [ [ "# Tabular core\n\n> Basic function to preprocess tabular data before assembling it in a `DataLoaders`.", "_____no_output_____" ], [ "## Initial preprocessing", "_____no_output_____" ] ], [ [ "#export\ndef make_date(df, date_field):\n \"Make sure `df[date_field]` is of the right date type.\"\n field_dtype = df[date_field].dtype\n if isinstance(field_dtype, pd.core.dtypes.dtypes.DatetimeTZDtype):\n field_dtype = np.datetime64\n if not np.issubdtype(field_dtype, np.datetime64):\n df[date_field] = pd.to_datetime(df[date_field], infer_datetime_format=True)", "_____no_output_____" ], [ "df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24']})\nmake_date(df, 'date')\ntest_eq(df['date'].dtype, np.dtype('datetime64[ns]'))", "_____no_output_____" ], [ "#export\ndef add_datepart(df, field_name, prefix=None, drop=True, time=False):\n \"Helper function that adds columns relevant to a date in the column `field_name` of `df`.\"\n make_date(df, field_name)\n field = df[field_name]\n prefix = ifnone(prefix, re.sub('[Dd]ate$', '', field_name))\n attr = ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear', 'Is_month_end', 'Is_month_start',\n 'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start']\n if time: attr = attr + ['Hour', 'Minute', 'Second']\n for n in attr: df[prefix + n] = getattr(field.dt, n.lower())\n df[prefix + 'Elapsed'] = field.astype(np.int64) // 10 ** 9\n if drop: df.drop(field_name, axis=1, inplace=True)\n return df", "_____no_output_____" ], [ "df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24']})\ndf = add_datepart(df, 'date')\ntest_eq(df.columns, ['Year', 'Month', 'Week', 'Day', 'Dayofweek', 'Dayofyear', 'Is_month_end', 'Is_month_start', \n 'Is_quarter_end', 'Is_quarter_start', 'Is_year_end', 'Is_year_start', 'Elapsed'])\ndf.head()", "_____no_output_____" ], [ "#export\ndef _get_elapsed(df,field_names, date_field, base_field, prefix):\n for f in field_names:\n day1 = np.timedelta64(1, 'D')\n last_date,last_base,res = np.datetime64(),None,[]\n for b,v,d in zip(df[base_field].values, df[f].values, df[date_field].values):\n if last_base is None or b != last_base:\n last_date,last_base = np.datetime64(),b\n if v: last_date = d\n res.append(((d-last_date).astype('timedelta64[D]') / day1))\n df[prefix + f] = res\n return df", "_____no_output_____" ], [ "#export\ndef add_elapsed_times(df, field_names, date_field, base_field):\n \"Add in `df` for each event in `field_names` the elapsed time according to `date_field` grouped by `base_field`\"\n field_names = list(L(field_names))\n #Make sure date_field is a date and base_field a bool\n df[field_names] = df[field_names].astype('bool')\n make_date(df, date_field)\n\n work_df = df[field_names + [date_field, base_field]]\n work_df = work_df.sort_values([base_field, date_field])\n work_df = _get_elapsed(work_df, field_names, date_field, base_field, 'After')\n work_df = work_df.sort_values([base_field, date_field], ascending=[True, False])\n work_df = _get_elapsed(work_df, field_names, date_field, base_field, 'Before')\n\n for a in ['After' + f for f in field_names] + ['Before' + f for f in field_names]:\n work_df[a] = work_df[a].fillna(0).astype(int)\n\n for a,s in zip([True, False], ['_bw', '_fw']):\n work_df = work_df.set_index(date_field)\n tmp = (work_df[[base_field] + field_names].sort_index(ascending=a)\n .groupby(base_field).rolling(7, min_periods=1).sum())\n tmp.drop(base_field,1,inplace=True)\n tmp.reset_index(inplace=True)\n work_df.reset_index(inplace=True)\n work_df = work_df.merge(tmp, 'left', [date_field, base_field], suffixes=['', s])\n work_df.drop(field_names,1,inplace=True)\n return df.merge(work_df, 'left', [date_field, base_field])", "_____no_output_____" ], [ "df = pd.DataFrame({'date': ['2019-12-04', '2019-11-29', '2019-11-15', '2019-10-24'],\n 'event': [False, True, False, True], 'base': [1,1,2,2]})\ndf = add_elapsed_times(df, ['event'], 'date', 'base')\ndf", "_____no_output_____" ], [ "#export\ndef cont_cat_split(df, max_card=20, dep_var=None):\n \"Helper function that returns column names of cont and cat variables from given `df`.\"\n cont_names, cat_names = [], []\n for label in df:\n if label == dep_var: continue\n if df[label].dtype == int and df[label].unique().shape[0] > max_card or df[label].dtype == float:\n cont_names.append(label)\n else: cat_names.append(label)\n return cont_names, cat_names", "_____no_output_____" ] ], [ [ "## Tabular -", "_____no_output_____" ] ], [ [ "#export\nclass _TabIloc:\n \"Get/set rows by iloc and cols by name\"\n def __init__(self,to): self.to = to\n def __getitem__(self, idxs):\n df = self.to.items\n if isinstance(idxs,tuple):\n rows,cols = idxs\n cols = df.columns.isin(cols) if is_listy(cols) else df.columns.get_loc(cols)\n else: rows,cols = idxs,slice(None)\n return self.to.new(df.iloc[rows, cols])", "_____no_output_____" ], [ "#export\nclass Tabular(CollBase, GetAttr, FilteredBase):\n \"A `DataFrame` wrapper that knows which cols are cont/cat/y, and returns rows in `__getitem__`\"\n _default,with_cont='procs',True\n def __init__(self, df, procs=None, cat_names=None, cont_names=None, y_names=None, y_block=None, splits=None,\n do_setup=True, device=None, inplace=False, reduce_memory=True):\n if inplace and splits is not None and pd.options.mode.chained_assignment is not None:\n warn(\"Using inplace with splits will trigger a pandas error. Set `pd.options.mode.chained_assignment=None` to avoid it.\")\n if not inplace: df = df.copy()\n if splits is not None: df = df.iloc[sum(splits, [])]\n self.dataloaders = delegates(self._dl_type.__init__)(self.dataloaders)\n super().__init__(df)\n\n self.y_names,self.device = L(y_names),device\n if y_block is None and self.y_names:\n # Make ys categorical if they're not numeric\n ys = df[self.y_names]\n if len(ys.select_dtypes(include='number').columns)!=len(ys.columns): y_block = CategoryBlock()\n else: y_block = RegressionBlock()\n if y_block is not None and do_setup:\n if callable(y_block): y_block = y_block()\n procs = L(procs) + y_block.type_tfms\n self.cat_names,self.cont_names,self.procs = L(cat_names),L(cont_names),Pipeline(procs)\n self.split = len(df) if splits is None else len(splits[0])\n if reduce_memory: \n if len(self.cat_names) > 0: self.reduce_cats() \n if len(self.cont_names) > 0: self.reduce_conts()\n if do_setup: self.setup()\n\n def new(self, df):\n return type(self)(df, do_setup=False, reduce_memory=False, y_block=TransformBlock(),\n **attrdict(self, 'procs','cat_names','cont_names','y_names', 'device'))\n \n def subset(self, i): return self.new(self.items[slice(0,self.split) if i==0 else slice(self.split,len(self))])\n def copy(self): self.items = self.items.copy(); return self\n def decode(self): return self.procs.decode(self)\n def decode_row(self, row): return self.new(pd.DataFrame(row).T).decode().items.iloc[0]\n def reduce_cats(self): self.train[self.cat_names] = self.train[self.cat_names].astype('category')\n def reduce_conts(self): self[self.cont_names] = self[self.cont_names].astype(np.float32)\n def show(self, max_n=10, **kwargs): display_df(self.new(self.all_cols[:max_n]).decode().items)\n def setup(self): self.procs.setup(self)\n def process(self): self.procs(self)\n def loc(self): return self.items.loc\n def iloc(self): return _TabIloc(self)\n def targ(self): return self.items[self.y_names]\n def x_names (self): return self.cat_names + self.cont_names\n def n_subsets(self): return 2\n def y(self): return self[self.y_names[0]]\n def new_empty(self): return self.new(pd.DataFrame({}, columns=self.items.columns))\n def to_device(self, d=None):\n self.device = d\n return self\n \n def all_col_names (self): \n ys = [n for n in self.y_names if n in self.items.columns]\n return self.x_names + self.y_names if len(ys) == len(self.y_names) else self.x_names\n\nproperties(Tabular,'loc','iloc','targ','all_col_names','n_subsets','x_names','y')", "_____no_output_____" ], [ "#export\nclass TabularPandas(Tabular):\n def transform(self, cols, f, all_col=True): \n if not all_col: cols = [c for c in cols if c in self.items.columns]\n if len(cols) > 0: self[cols] = self[cols].transform(f)", "_____no_output_____" ], [ "#export\ndef _add_prop(cls, nm):\n @property\n def f(o): return o[list(getattr(o,nm+'_names'))]\n @f.setter\n def fset(o, v): o[getattr(o,nm+'_names')] = v\n setattr(cls, nm+'s', f)\n setattr(cls, nm+'s', fset)\n\n_add_prop(Tabular, 'cat')\n_add_prop(Tabular, 'cont')\n_add_prop(Tabular, 'y')\n_add_prop(Tabular, 'x')\n_add_prop(Tabular, 'all_col')", "_____no_output_____" ], [ "df = pd.DataFrame({'a':[0,1,2,0,2], 'b':[0,0,0,0,1]})\nto = TabularPandas(df, cat_names='a')\nt = pickle.loads(pickle.dumps(to))\ntest_eq(t.items,to.items)\ntest_eq(to.all_cols,to[['a']])", "_____no_output_____" ], [ "#export\nclass TabularProc(InplaceTransform):\n \"Base class to write a non-lazy tabular processor for dataframes\"\n def setup(self, items=None, train_setup=False): #TODO: properly deal with train_setup\n super().setup(getattr(items,'train',items), train_setup=False)\n # Procs are called as soon as data is available\n return self(items.items if isinstance(items,Datasets) else items)", "_____no_output_____" ], [ "#export\ndef _apply_cats (voc, add, c):\n if not is_categorical_dtype(c):\n return pd.Categorical(c, categories=voc[c.name][add:]).codes+add\n return c.cat.codes+add #if is_categorical_dtype(c) else c.map(voc[c.name].o2i)\ndef _decode_cats(voc, c): return c.map(dict(enumerate(voc[c.name].items)))", "_____no_output_____" ], [ "#export\nclass Categorify(TabularProc):\n \"Transform the categorical variables to that type.\"\n order = 1\n def setups(self, to):\n self.classes = {n:CategoryMap(to.iloc[:,n].items, add_na=(n in to.cat_names)) for n in to.cat_names}\n\n def encodes(self, to): to.transform(to.cat_names, partial(_apply_cats, self.classes, 1))\n def decodes(self, to): to.transform(to.cat_names, partial(_decode_cats, self.classes))\n def __getitem__(self,k): return self.classes[k]", "_____no_output_____" ], [ "#export\n@Categorize\ndef setups(self, to:Tabular):\n if len(to.y_names) > 0:\n self.vocab = CategoryMap(getattr(to, 'train', to).iloc[:,to.y_names[0]].items)\n self.c = len(self.vocab)\n return self(to)\n\n@Categorize\ndef encodes(self, to:Tabular):\n to.transform(to.y_names, partial(_apply_cats, {n: self.vocab for n in to.y_names}, 0), all_col=False)\n return to\n\n@Categorize\ndef decodes(self, to:Tabular):\n to.transform(to.y_names, partial(_decode_cats, {n: self.vocab for n in to.y_names}), all_col=False)\n return to", "_____no_output_____" ], [ "show_doc(Categorify, title_level=3)", "_____no_output_____" ], [ "df = pd.DataFrame({'a':[0,1,2,0,2]})\nto = TabularPandas(df, Categorify, 'a')\ncat = to.procs.categorify\ntest_eq(cat['a'], ['#na#',0,1,2])\ntest_eq(to['a'], [1,2,3,1,3])\nto.show()", "_____no_output_____" ], [ "df1 = pd.DataFrame({'a':[1,0,3,-1,2]})\nto1 = to.new(df1)\nto1.process()\n#Values that weren't in the training df are sent to 0 (na)\ntest_eq(to1['a'], [2,1,0,0,3])\nto2 = cat.decode(to1)\ntest_eq(to2['a'], [1,0,'#na#','#na#',2])", "_____no_output_____" ], [ "#test with splits\ncat = Categorify()\ndf = pd.DataFrame({'a':[0,1,2,3,2]})\nto = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]])\ntest_eq(cat['a'], ['#na#',0,1,2])\ntest_eq(to['a'], [1,2,3,0,3])", "_____no_output_____" ], [ "df = pd.DataFrame({'a':pd.Categorical(['M','H','L','M'], categories=['H','M','L'], ordered=True)})\nto = TabularPandas(df, Categorify, 'a')\ncat = to.procs.categorify\ntest_eq(cat['a'], ['#na#','H','M','L'])\ntest_eq(to.items.a, [2,1,3,2])\nto2 = cat.decode(to)\ntest_eq(to2['a'], ['M','H','L','M'])", "_____no_output_____" ], [ "#test with targets\ncat = Categorify()\ndf = pd.DataFrame({'a':[0,1,2,3,2], 'b': ['a', 'b', 'a', 'b', 'b']})\nto = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]], y_names='b')\ntest_eq(to.vocab, ['a', 'b'])\ntest_eq(to['b'], [0,1,0,1,1])\nto2 = to.procs.decode(to)\ntest_eq(to2['b'], ['a', 'b', 'a', 'b', 'b'])", "_____no_output_____" ], [ "#test with targets and train\ncat = Categorify()\ndf = pd.DataFrame({'a':[0,1,2,3,2], 'b': ['a', 'b', 'a', 'c', 'b']})\nto = TabularPandas(df, cat, 'a', splits=[[0,1,2],[3,4]], y_names='b')\ntest_eq(to.vocab, ['a', 'b'])", "_____no_output_____" ], [ "#export\nclass NormalizeTab(TabularProc):\n \"Normalize the continuous variables.\"\n order = 2\n def setups(self, dsets): self.means,self.stds = dsets.conts.mean(),dsets.conts.std(ddof=0)+1e-7\n def encodes(self, to): to.conts = (to.conts-self.means) / self.stds\n def decodes(self, to): to.conts = (to.conts*self.stds ) + self.means", "_____no_output_____" ], [ "#export\n@Normalize\ndef setups(self, to:Tabular):\n self.means,self.stds = getattr(to, 'train', to).conts.mean(),getattr(to, 'train', to).conts.std(ddof=0)+1e-7\n return self(to)\n\n@Normalize\ndef encodes(self, to:Tabular):\n to.conts = (to.conts-self.means) / self.stds\n return to\n\n@Normalize\ndef decodes(self, to:Tabular):\n to.conts = (to.conts*self.stds ) + self.means\n return to", "_____no_output_____" ], [ "norm = Normalize()\ndf = pd.DataFrame({'a':[0,1,2,3,4]})\nto = TabularPandas(df, norm, cont_names='a')\nx = np.array([0,1,2,3,4])\nm,s = x.mean(),x.std()\ntest_eq(norm.means['a'], m)\ntest_close(norm.stds['a'], s)\ntest_close(to['a'].values, (x-m)/s)", "_____no_output_____" ], [ "df1 = pd.DataFrame({'a':[5,6,7]})\nto1 = to.new(df1)\nto1.process()\ntest_close(to1['a'].values, (np.array([5,6,7])-m)/s)\nto2 = norm.decode(to1)\ntest_close(to2['a'].values, [5,6,7])", "_____no_output_____" ], [ "norm = Normalize()\ndf = pd.DataFrame({'a':[0,1,2,3,4]})\nto = TabularPandas(df, norm, cont_names='a', splits=[[0,1,2],[3,4]])\nx = np.array([0,1,2])\nm,s = x.mean(),x.std()\ntest_eq(norm.means['a'], m)\ntest_close(norm.stds['a'], s)\ntest_close(to['a'].values, (np.array([0,1,2,3,4])-m)/s)", "_____no_output_____" ], [ "#export\nclass FillStrategy:\n \"Namespace containing the various filling strategies.\"\n def median (c,fill): return c.median()\n def constant(c,fill): return fill\n def mode (c,fill): return c.dropna().value_counts().idxmax()", "_____no_output_____" ], [ "#export\nclass FillMissing(TabularProc):\n \"Fill the missing values in continuous columns.\"\n def __init__(self, fill_strategy=FillStrategy.median, add_col=True, fill_vals=None):\n if fill_vals is None: fill_vals = defaultdict(int)\n store_attr(self, 'fill_strategy,add_col,fill_vals')\n\n def setups(self, dsets):\n missing = pd.isnull(dsets.conts).any()\n self.na_dict = {n:self.fill_strategy(dsets[n], self.fill_vals[n])\n for n in missing[missing].keys()}\n\n def encodes(self, to):\n missing = pd.isnull(to.conts)\n for n in missing.any()[missing.any()].keys():\n assert n in self.na_dict, f\"nan values in `{n}` but not in setup training set\"\n for n in self.na_dict.keys():\n to[n].fillna(self.na_dict[n], inplace=True)\n if self.add_col:\n to.loc[:,n+'_na'] = missing[n]\n if n+'_na' not in to.cat_names: to.cat_names.append(n+'_na')", "_____no_output_____" ], [ "show_doc(FillMissing, title_level=3)", "_____no_output_____" ], [ "fill1,fill2,fill3 = (FillMissing(fill_strategy=s) \n for s in [FillStrategy.median, FillStrategy.constant, FillStrategy.mode])\ndf = pd.DataFrame({'a':[0,1,np.nan,1,2,3,4]})\ndf1 = df.copy(); df2 = df.copy()\ntos = (TabularPandas(df, fill1, cont_names='a'),\n TabularPandas(df1, fill2, cont_names='a'),\n TabularPandas(df2, fill3, cont_names='a'))\ntest_eq(fill1.na_dict, {'a': 1.5})\ntest_eq(fill2.na_dict, {'a': 0})\ntest_eq(fill3.na_dict, {'a': 1.0})\n\nfor t in tos: test_eq(t.cat_names, ['a_na'])\n\nfor to_,v in zip(tos, [1.5, 0., 1.]):\n test_eq(to_['a'].values, np.array([0, 1, v, 1, 2, 3, 4]))\n test_eq(to_['a_na'].values, np.array([0, 0, 1, 0, 0, 0, 0]))", "_____no_output_____" ], [ "fill = FillMissing() \ndf = pd.DataFrame({'a':[0,1,np.nan,1,2,3,4], 'b': [0,1,2,3,4,5,6]})\nto = TabularPandas(df, fill, cont_names=['a', 'b'])\ntest_eq(fill.na_dict, {'a': 1.5})\ntest_eq(to.cat_names, ['a_na'])\ntest_eq(to['a'].values, np.array([0, 1, 1.5, 1, 2, 3, 4]))\ntest_eq(to['a_na'].values, np.array([0, 0, 1, 0, 0, 0, 0]))\ntest_eq(to['b'].values, np.array([0,1,2,3,4,5,6]))", "_____no_output_____" ] ], [ [ "## TabularPandas Pipelines -", "_____no_output_____" ] ], [ [ "procs = [Normalize, Categorify, FillMissing, noop]\ndf = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4]})\nto = TabularPandas(df, procs, cat_names='a', cont_names='b')\n\n#Test setup and apply on df_main\ntest_eq(to.cat_names, ['a', 'b_na'])\ntest_eq(to['a'], [1,2,3,2,2,3,1])\ntest_eq(to['b_na'], [1,1,2,1,1,1,1])\nx = np.array([0,1,1.5,1,2,3,4])\nm,s = x.mean(),x.std()\ntest_close(to['b'].values, (x-m)/s)\ntest_eq(to.classes, {'a': ['#na#',0,1,2], 'b_na': ['#na#',False,True]})", "_____no_output_____" ], [ "#Test apply on y_names\ndf = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})\nto = TabularPandas(df, procs, 'a', 'b', y_names='c')\n\ntest_eq(to.cat_names, ['a', 'b_na'])\ntest_eq(to['a'], [1,2,3,2,2,3,1])\ntest_eq(to['b_na'], [1,1,2,1,1,1,1])\ntest_eq(to['c'], [1,0,1,0,0,1,0])\nx = np.array([0,1,1.5,1,2,3,4])\nm,s = x.mean(),x.std()\ntest_close(to['b'].values, (x-m)/s)\ntest_eq(to.classes, {'a': ['#na#',0,1,2], 'b_na': ['#na#',False,True]})\ntest_eq(to.vocab, ['a','b'])", "_____no_output_____" ], [ "df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,1,np.nan,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})\nto = TabularPandas(df, procs, 'a', 'b', y_names='c')\n\ntest_eq(to.cat_names, ['a', 'b_na'])\ntest_eq(to['a'], [1,2,3,2,2,3,1])\ntest_eq(df.a.dtype,int)\ntest_eq(to['b_na'], [1,1,2,1,1,1,1])\ntest_eq(to['c'], [1,0,1,0,0,1,0])", "_____no_output_____" ], [ "df = pd.DataFrame({'a':[0,1,2,1,1,2,0], 'b':[0,np.nan,1,1,2,3,4], 'c': ['b','a','b','a','a','b','a']})\nto = TabularPandas(df, procs, cat_names='a', cont_names='b', y_names='c', splits=[[0,1,4,6], [2,3,5]])\n\ntest_eq(to.cat_names, ['a', 'b_na'])\ntest_eq(to['a'], [1,2,2,1,0,2,0])\ntest_eq(df.a.dtype,int)\ntest_eq(to['b_na'], [1,2,1,1,1,1,1])\ntest_eq(to['c'], [1,0,0,0,1,0,1])", "_____no_output_____" ], [ "#export\ndef _maybe_expand(o): return o[:,None] if o.ndim==1 else o", "_____no_output_____" ], [ "#export\nclass ReadTabBatch(ItemTransform):\n def __init__(self, to): self.to = to\n\n def encodes(self, to):\n if not to.with_cont: res = (tensor(to.cats).long(),)\n else: res = (tensor(to.cats).long(),tensor(to.conts).float())\n ys = [n for n in to.y_names if n in to.items.columns]\n if len(ys) == len(to.y_names): res = res + (tensor(to.targ),)\n if to.device is not None: res = to_device(res, to.device)\n return res\n\n def decodes(self, o):\n o = [_maybe_expand(o_) for o_ in to_np(o) if o_.size != 0]\n vals = np.concatenate(o, axis=1)\n try: df = pd.DataFrame(vals, columns=self.to.all_col_names)\n except: df = pd.DataFrame(vals, columns=self.to.x_names)\n to = self.to.new(df)\n return to", "_____no_output_____" ], [ "#export\n@typedispatch\ndef show_batch(x: Tabular, y, its, max_n=10, ctxs=None):\n x.show()", "_____no_output_____" ], [ "from torch.utils.data.dataloader import _MultiProcessingDataLoaderIter,_SingleProcessDataLoaderIter,_DatasetKind\n_loaders = (_MultiProcessingDataLoaderIter,_SingleProcessDataLoaderIter)", "_____no_output_____" ], [ "#export\n@delegates()\nclass TabDataLoader(TfmdDL):\n do_item = noops\n def __init__(self, dataset, bs=16, shuffle=False, after_batch=None, num_workers=0, **kwargs):\n if after_batch is None: after_batch = L(TransformBlock().batch_tfms)+ReadTabBatch(dataset)\n super().__init__(dataset, bs=bs, shuffle=shuffle, after_batch=after_batch, num_workers=num_workers, **kwargs)\n\n def create_batch(self, b): return self.dataset.iloc[b]\n\nTabularPandas._dl_type = TabDataLoader", "_____no_output_____" ] ], [ [ "## Integration example", "_____no_output_____" ] ], [ [ "path = untar_data(URLs.ADULT_SAMPLE)\ndf = pd.read_csv(path/'adult.csv')\ndf_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()\ndf_test.drop('salary', axis=1, inplace=True)\ndf_main.head()", "_____no_output_____" ], [ "cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']\ncont_names = ['age', 'fnlwgt', 'education-num']\nprocs = [Categorify, FillMissing, Normalize]\nsplits = RandomSplitter()(range_of(df_main))", "_____no_output_____" ], [ "to = TabularPandas(df_main, procs, cat_names, cont_names, y_names=\"salary\", splits=splits)", "_____no_output_____" ], [ "dls = to.dataloaders()\ndls.valid.show_batch()", "_____no_output_____" ], [ "to.show()", "_____no_output_____" ], [ "row = to.items.iloc[0]\nto.decode_row(row)", "_____no_output_____" ], [ "to_tst = to.new(df_test)\nto_tst.process()\nto_tst.items.head()", "_____no_output_____" ], [ "tst_dl = dls.valid.new(to_tst)\ntst_dl.show_batch()", "_____no_output_____" ] ], [ [ "## Other target types", "_____no_output_____" ], [ "### Multi-label categories", "_____no_output_____" ], [ "#### one-hot encoded label", "_____no_output_____" ] ], [ [ "def _mock_multi_label(df):\n sal,sex,white = [],[],[]\n for row in df.itertuples():\n sal.append(row.salary == '>=50k')\n sex.append(row.sex == ' Male')\n white.append(row.race == ' White')\n df['salary'] = np.array(sal)\n df['male'] = np.array(sex)\n df['white'] = np.array(white)\n return df", "_____no_output_____" ], [ "path = untar_data(URLs.ADULT_SAMPLE)\ndf = pd.read_csv(path/'adult.csv')\ndf_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()\ndf_main = _mock_multi_label(df_main)", "_____no_output_____" ], [ "df_main.head()", "_____no_output_____" ], [ "#export\n@EncodedMultiCategorize\ndef encodes(self, to:Tabular): return to\n\n@EncodedMultiCategorize\ndef decodes(self, to:Tabular):\n to.transform(to.y_names, lambda c: c==1)\n return to", "_____no_output_____" ], [ "cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']\ncont_names = ['age', 'fnlwgt', 'education-num']\nprocs = [Categorify, FillMissing, Normalize]\nsplits = RandomSplitter()(range_of(df_main))\ny_names=[\"salary\", \"male\", \"white\"]", "_____no_output_____" ], [ "%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names=y_names, y_block=MultiCategoryBlock(encoded=True, vocab=y_names), splits=splits)", "CPU times: user 101 ms, sys: 4.01 ms, total: 105 ms\nWall time: 103 ms\n" ], [ "dls = to.dataloaders()\ndls.valid.show_batch()", "_____no_output_____" ] ], [ [ "#### Not one-hot encoded", "_____no_output_____" ] ], [ [ "def _mock_multi_label(df):\n targ = []\n for row in df.itertuples():\n labels = []\n if row.salary == '>=50k': labels.append('>50k')\n if row.sex == ' Male': labels.append('male')\n if row.race == ' White': labels.append('white')\n targ.append(' '.join(labels))\n df['target'] = np.array(targ)\n return df", "_____no_output_____" ], [ "path = untar_data(URLs.ADULT_SAMPLE)\ndf = pd.read_csv(path/'adult.csv')\ndf_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()\ndf_main = _mock_multi_label(df_main)", "_____no_output_____" ], [ "df_main.head()", "_____no_output_____" ], [ "@MultiCategorize\ndef encodes(self, to:Tabular): \n #to.transform(to.y_names, partial(_apply_cats, {n: self.vocab for n in to.y_names}, 0))\n return to\n \n@MultiCategorize\ndef decodes(self, to:Tabular): \n #to.transform(to.y_names, partial(_decode_cats, {n: self.vocab for n in to.y_names}))\n return to", "_____no_output_____" ], [ "cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']\ncont_names = ['age', 'fnlwgt', 'education-num']\nprocs = [Categorify, FillMissing, Normalize]\nsplits = RandomSplitter()(range_of(df_main))", "_____no_output_____" ], [ "%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names=\"target\", y_block=MultiCategoryBlock(), splits=splits)", "CPU times: user 106 ms, sys: 3.41 ms, total: 110 ms\nWall time: 108 ms\n" ], [ "to.procs[2].vocab", "_____no_output_____" ] ], [ [ "### Regression", "_____no_output_____" ] ], [ [ "#export\n@RegressionSetup\ndef setups(self, to:Tabular): \n if self.c is not None: return\n self.c = len(to.y_names)\n return to\n\n@RegressionSetup\ndef encodes(self, to:Tabular): return to\n\n@RegressionSetup\ndef decodes(self, to:Tabular): return to", "_____no_output_____" ], [ "path = untar_data(URLs.ADULT_SAMPLE)\ndf = pd.read_csv(path/'adult.csv')\ndf_main,df_test = df.iloc[:10000].copy(),df.iloc[10000:].copy()\ndf_main = _mock_multi_label(df_main)", "_____no_output_____" ], [ "cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']\ncont_names = ['fnlwgt', 'education-num']\nprocs = [Categorify, FillMissing, Normalize]\nsplits = RandomSplitter()(range_of(df_main))", "_____no_output_____" ], [ "%time to = TabularPandas(df_main, procs, cat_names, cont_names, y_names='age', splits=splits)", "CPU times: user 107 ms, sys: 444 µs, total: 108 ms\nWall time: 106 ms\n" ], [ "to.procs[-1].means", "_____no_output_____" ], [ "dls = to.dataloaders()\ndls.valid.show_batch()", "_____no_output_____" ] ], [ [ "## Not being used now - for multi-modal", "_____no_output_____" ] ], [ [ "class TensorTabular(Tuple):\n def get_ctxs(self, max_n=10, **kwargs):\n n_samples = min(self[0].shape[0], max_n)\n df = pd.DataFrame(index = range(n_samples))\n return [df.iloc[i] for i in range(n_samples)]\n\n def display(self, ctxs): display_df(pd.DataFrame(ctxs))\n\nclass TabularLine(pd.Series):\n \"A line of a dataframe that knows how to show itself\"\n def show(self, ctx=None, **kwargs): return self if ctx is None else ctx.append(self)\n\nclass ReadTabLine(ItemTransform):\n def __init__(self, proc): self.proc = proc\n\n def encodes(self, row):\n cats,conts = (o.map(row.__getitem__) for o in (self.proc.cat_names,self.proc.cont_names))\n return TensorTabular(tensor(cats).long(),tensor(conts).float())\n\n def decodes(self, o):\n to = TabularPandas(o, self.proc.cat_names, self.proc.cont_names, self.proc.y_names)\n to = self.proc.decode(to)\n return TabularLine(pd.Series({c: v for v,c in zip(to.items[0]+to.items[1], self.proc.cat_names+self.proc.cont_names)}))\n\nclass ReadTabTarget(ItemTransform):\n def __init__(self, proc): self.proc = proc\n def encodes(self, row): return row[self.proc.y_names].astype(np.int64)\n def decodes(self, o): return Category(self.proc.classes[self.proc.y_names][o])", "_____no_output_____" ], [ "# tds = TfmdDS(to.items, tfms=[[ReadTabLine(proc)], ReadTabTarget(proc)])\n# enc = tds[1]\n# test_eq(enc[0][0], tensor([2,1]))\n# test_close(enc[0][1], tensor([-0.628828]))\n# test_eq(enc[1], 1)\n\n# dec = tds.decode(enc)\n# assert isinstance(dec[0], TabularLine)\n# test_close(dec[0], pd.Series({'a': 1, 'b_na': False, 'b': 1}))\n# test_eq(dec[1], 'a')\n\n# test_stdout(lambda: print(show_at(tds, 1)), \"\"\"a 1\n# b_na False\n# b 1\n# category a\n# dtype: object\"\"\")", "_____no_output_____" ] ], [ [ "## Export -", "_____no_output_____" ] ], [ [ "#hide\nfrom nbdev.export import notebook2script\nnotebook2script()", "Converted 00_torch_core.ipynb.\nConverted 01_layers.ipynb.\nConverted 02_data.load.ipynb.\nConverted 03_data.core.ipynb.\nConverted 04_data.external.ipynb.\nConverted 05_data.transforms.ipynb.\nConverted 06_data.block.ipynb.\nConverted 07_vision.core.ipynb.\nConverted 08_vision.data.ipynb.\nConverted 09_vision.augment.ipynb.\nConverted 09b_vision.utils.ipynb.\nConverted 09c_vision.widgets.ipynb.\nConverted 10_tutorial.pets.ipynb.\nConverted 11_vision.models.xresnet.ipynb.\nConverted 12_optimizer.ipynb.\nConverted 13_callback.core.ipynb.\nConverted 13a_learner.ipynb.\nConverted 13b_metrics.ipynb.\nConverted 14_callback.schedule.ipynb.\nConverted 14a_callback.data.ipynb.\nConverted 15_callback.hook.ipynb.\nConverted 15a_vision.models.unet.ipynb.\nConverted 16_callback.progress.ipynb.\nConverted 17_callback.tracker.ipynb.\nConverted 18_callback.fp16.ipynb.\nConverted 18a_callback.training.ipynb.\nConverted 19_callback.mixup.ipynb.\nConverted 20_interpret.ipynb.\nConverted 20a_distributed.ipynb.\nConverted 21_vision.learner.ipynb.\nConverted 22_tutorial.imagenette.ipynb.\nConverted 23_tutorial.vision.ipynb.\nConverted 24_tutorial.siamese.ipynb.\nConverted 24_vision.gan.ipynb.\nConverted 30_text.core.ipynb.\nConverted 31_text.data.ipynb.\nConverted 32_text.models.awdlstm.ipynb.\nConverted 33_text.models.core.ipynb.\nConverted 34_callback.rnn.ipynb.\nConverted 35_tutorial.wikitext.ipynb.\nConverted 36_text.models.qrnn.ipynb.\nConverted 37_text.learner.ipynb.\nConverted 38_tutorial.text.ipynb.\nConverted 40_tabular.core.ipynb.\nConverted 41_tabular.data.ipynb.\nConverted 42_tabular.model.ipynb.\nConverted 43_tabular.learner.ipynb.\nConverted 44_tutorial.tabular.ipynb.\nConverted 45_collab.ipynb.\nConverted 46_tutorial.collab.ipynb.\nConverted 50_tutorial.datablock.ipynb.\nConverted 60_medical.imaging.ipynb.\nConverted 61_tutorial.medical_imaging.ipynb.\nConverted 65_medical.text.ipynb.\nConverted 70_callback.wandb.ipynb.\nConverted 71_callback.tensorboard.ipynb.\nConverted 72_callback.neptune.ipynb.\nConverted 73_callback.captum.ipynb.\nConverted 74_callback.cutmix.ipynb.\nConverted 97_test_utils.ipynb.\nConverted 99_pytorch_doc.ipynb.\nConverted index.ipynb.\nConverted tutorial.ipynb.\n" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e67a51cfd6132989c517c55bd45430f6d2f4f3

5,992

ipynb

Jupyter Notebook

A1.Optimization/Optimization_student.ipynb

ML4DS/ML4all

7336489dcb87d2412ad62b5b972d69c98c361752

[ "MIT" ]

27

2016-11-30T17:34:00.000Z

2022-03-23T23:11:48.000Z

A1.Optimization/Optimization_student.ipynb

ML4DS/ML4all

7336489dcb87d2412ad62b5b972d69c98c361752

[ "MIT" ]

5

2019-08-12T18:28:49.000Z

2019-11-26T11:01:39.000Z

A1.Optimization/Optimization_student.ipynb

ML4DS/ML4all

7336489dcb87d2412ad62b5b972d69c98c361752

[ "MIT" ]

14

2016-11-30T17:34:18.000Z

2021-09-15T09:53:32.000Z

23.40625

248

0.529873

[ [ [ "# Optimización ", "_____no_output_____" ], [ " Author: Jesús Cid-Sueiro\n Jerónimo Arenas-García\n \n Versión: 0.1 (2019/09/13)\n 0.2 (2019/10/02): Solutions added", "_____no_output_____" ], [ "## Exercise: compute the minimum of a real-valued function\n\nThe goal of this exercise is to implement and test optimization algorithms for the minimization of a given function. Gradient descent and Newton's method will be explored.\n\nOur goal it so find the minimizer of the real-valued function\n$$\nf(w) = - w exp(-w)\n$$\nbut the whole code will be easily modified to try with other alternative functions.\n\nYou will need to import some libraries (at least, `numpy` and `matplotlib`). Insert below all the imports needed along the whole notebook. Remind that numpy is usually abbreviated as np and `matplotlib.pyplot` is usually abbreviated as `plt`.", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "### Part 1: The function and its derivatives.\n\n**Question 1.1**: Implement the following three methods:\n\n* Method **`f`**: given $w$, it returns the value of function $f(w)$.\n* Method **`df`**: given $w$, it returns the derivative of $f$ at $w$\n* Medhod **`d2f`**: given $w$, it returns the second derivative of $f$ at $w$\n", "_____no_output_____" ] ], [ [ "# Funcion f\n# <SOL>\n# </SOL>\n\n# First derivative\n# <SOL>\n# </SOL>\n\n# Second derivative\n# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "### Part 2: Gradient descent.\n\n**Question 2.1**: Implement a method **`gd`** that, given `w` and a learning rate parameter `rho` applies a single iteration of the gradien descent algorithm\n", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "**Question 2.2**: Apply the gradient descent to optimize the given function. To do so, start with an initial value $w=0$ and iterate $20$ times. Save two lists:\n\n* A list of succesive values of $w_n$\n* A list of succesive values of the function $f(w_n)$.", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "**Question 2.3**: Plot, in a single figure:\n\n* The given function, for values ranging from 0 to 20.\n* The sequence of points $(w_n, f(w_n))$.", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "You can check the effect of modifying the value of the learning rate.", "_____no_output_____" ], [ "### Part 2: Newton's method.\n\n**Question 3.1**: Implement a method **`newton`** that, given `w` and a learning rate parameter `rho` applies a single iteration of the Newton's method\n", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "**Question 3**: Apply the Newton's method to optimize the given function. To do so, start with an initial value $w=0$ and iterate $20$ times. Save two lists:\n\n* A list of succesive values of $w_n$\n* A list of succesive values of the function $f(w_n)$.", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "**Question 4**: Plot, in a single figure:\n\n* The given function, for values ranging from 0 to 20.\n* The sequence of points $(w_n, f(w_n))$.", "_____no_output_____" ] ], [ [ "# <SOL>\n# </SOL>", "_____no_output_____" ] ], [ [ "You can check the effect of modifying the value of the learning rate.", "_____no_output_____" ], [ "### Part 3: Optimize other cost functions", "_____no_output_____" ], [ "Now you are ready to explore these optimization algorithms with other more sophisticated functions. Try with them.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ] ]

d0e6836edb675ce464f9633ca7e2bb268eb4d054

10,880

ipynb

Jupyter Notebook

exps/04_CNN_baseline/test.ipynb

pzinemanas/sed_endtoend

71e177e0d785e026ebcdb242f35af1e49ddd3128

[ "MIT" ]

null

exps/04_CNN_baseline/test.ipynb

pzinemanas/sed_endtoend

71e177e0d785e026ebcdb242f35af1e49ddd3128

[ "MIT" ]

null

exps/04_CNN_baseline/test.ipynb

pzinemanas/sed_endtoend

71e177e0d785e026ebcdb242f35af1e49ddd3128

[ "MIT" ]

null

40.446097

292

0.604136

[ [ [ "# Test S-CNN baseline", "_____no_output_____" ] ], [ [ "%load_ext autoreload\n%autoreload 2\n\nimport numpy as np\nimport os\nimport librosa\nimport glob\nimport sys\n\nsys.path.insert(0,'../..')\nfrom sed_endtoend.cnn.model import build_custom_cnn\nfrom sed_endtoend.data_generator import DataGenerator\n\nos.environ[\"CUDA_VISIBLE_DEVICES\"]=\"1\"\n\nfrom params import *\n\n# files parameters\nNfiles = None\nresume = False\nload_subset = Nfiles", "Using TensorFlow backend.\n" ], [ "params = {'sequence_time': sequence_time, 'sequence_hop_time':sequence_hop_time,\n 'label_list':label_list,'audio_hop':audio_hop, 'audio_win':audio_win,\n 'n_fft':n_fft,'sr':sr,'mel_bands':mel_bands,'normalize':normalize_data, \n 'frames':frames,'get_annotations':get_annotations, 'dataset': dataset}\n\nsequence_frames = int(np.ceil(sequence_time*sr/audio_hop))\n\n# Datasets\nlabels = {}# Labels\n\ntest_files = sorted(glob.glob(os.path.join(audio_folder,'test', '*.wav')))\nval_files = sorted(glob.glob(os.path.join(audio_folder,'validate', '*.wav')))\n\nif load_subset is not None:\n test_files = test_files[:load_subset]\n val_files = val_files[:load_subset]\n\ntest_labels = {}\ntest_mel = {}\nval_labels = {}\nval_mel = {}\n\nfor n,id in enumerate(test_files):\n labels[id] = os.path.join(label_folder, 'test',os.path.basename(id).replace('.wav','.txt'))\nfor id in val_files:\n labels[id] = os.path.join(label_folder, 'validate',os.path.basename(id).replace('.wav','.txt'))\n\nparams['sequence_hop_time'] = sequence_time # To calculate F1_1s \n \n# Generators\nprint('Making test generator')\ntest_generator = DataGenerator(test_files, labels, **params)\n\nprint('Making validation generator')\nvalidation_generator = DataGenerator(val_files, labels, **params)\n\nprint('Getting validation data')\n\n_,_,mel_val,y_val = validation_generator.return_all()\n\nprint('Getting test data')\n\n_,_,mel_test,y_test = test_generator.return_all()", "Making test generator\nMaking validation generator\nGetting validation data\n0.0 %\n10.0 %\n20.0 %\n30.0 %\n40.0 %\n50.0 %\n60.0 %\n70.0 %\n80.0 %\n90.0 %\nGetting test data\n0.0 %\n10.0 %\n20.0 %\n30.0 %\n40.0 %\n50.0 %\n60.0 %\n70.0 %\n80.0 %\n90.0 %\n" ], [ "print('\\nTesting model...')\n\nsequence_samples = int(sequence_time*sr)\n\nmodel = build_custom_cnn(n_freq_cnn=mel_bands, n_frames_cnn=sequence_frames,large_cnn=large_cnn)\n\nweights_best_file = os.path.join(expfolder, 'weights_best.hdf5')\nmodel.load_weights(weights_best_file)\n\nmodel.summary()\n\ny_test_predicted = model.predict(mel_test)\ny_val_predicted = model.predict(mel_val)\n\nnp.save(os.path.join(expfolder, 'y_val_predicted.npy'),y_val_predicted)\nnp.save(os.path.join(expfolder, 'y_val.npy'),y_val)\n\nnp.save(os.path.join(expfolder, 'y_test_predict.npy'),y_test_predicted)\nnp.save(os.path.join(expfolder, 'y_test.npy'),y_test)\n\nprint(\"[Done]\")", "WARNING: Logging before flag parsing goes to stderr.\nW1003 16:16:21.528877 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:74: The name tf.get_default_graph is deprecated. Please use tf.compat.v1.get_default_graph instead.\n\nW1003 16:16:21.538780 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:517: The name tf.placeholder is deprecated. Please use tf.compat.v1.placeholder instead.\n\nW1003 16:16:21.582764 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:133: The name tf.placeholder_with_default is deprecated. Please use tf.compat.v1.placeholder_with_default instead.\n\nW1003 16:16:21.595330 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:4138: The name tf.random_uniform is deprecated. Please use tf.random.uniform instead.\n\nW1003 16:16:21.603944 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:3976: The name tf.nn.max_pool is deprecated. Please use tf.nn.max_pool2d instead.\n\nW1003 16:16:21.612474 140711985211136 deprecation_wrapper.py:119] From /home/pzinemanas/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:174: The name tf.get_default_session is deprecated. Please use tf.compat.v1.get_default_session instead.\n\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code" ] ]

d0e683732647b0b83436e2a0d90b632018bb587e

922,269

ipynb

Jupyter Notebook

content/sections/section3/notebook/cs109a_section_3.ipynb

songdavidb/2019-CS109A

5cd50e7a3f84b0d6b6668fb80732fb91bfec6cea

[ "MIT" ]

null

content/sections/section3/notebook/cs109a_section_3.ipynb

songdavidb/2019-CS109A

5cd50e7a3f84b0d6b6668fb80732fb91bfec6cea

[ "MIT" ]

null

content/sections/section3/notebook/cs109a_section_3.ipynb

songdavidb/2019-CS109A

5cd50e7a3f84b0d6b6668fb80732fb91bfec6cea

[ "MIT" ]

null

369.795108

591,460

0.907253

[ [ [ "# <img style=\"float: left; padding-right: 10px; width: 45px\" src=\"https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png\"> CS109A Introduction to Data Science \n\n## Standard Section 3: Multiple Linear Regression and Polynomial Regression \n\n**Harvard University**<br/>\n**Fall 2019**<br/>\n**Instructors**: Pavlos Protopapas, Kevin Rader, and Chris Tanner<br/>\n**Section Leaders**: Marios Mattheakis, Abhimanyu (Abhi) Vasishth, Robbert (Rob) Struyven<br/>\n\n<hr style='height:2px'>", "_____no_output_____" ] ], [ [ "#RUN THIS CELL \nimport requests\nfrom IPython.core.display import HTML\nstyles = requests.get(\"http://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css\").text\nHTML(styles)", "_____no_output_____" ] ], [ [ "For this section, our goal is to get you familiarized with Multiple Linear Regression. We have learned how to model data with kNN Regression and Simple Linear Regression and our goal now is to dive deep into Linear Regression.\n\nSpecifically, we will: \n \n- Load in the titanic dataset from seaborn\n- Learn a few ways to plot **distributions** of variables using seaborn\n- Learn about different **kinds of variables** including continuous, categorical and ordinal\n- Perform single and multiple linear regression\n- Learn about **interaction** terms\n- Understand how to **interpret coefficients** in linear regression\n- Look at **polynomial** regression\n- Understand the **assumptions** being made in a linear regression model\n- (Extra): look at some cool plots to raise your EDA game", "_____no_output_____" ], [ "![meme](../fig/meme.png)", "_____no_output_____" ] ], [ [ "# Data and Stats packages\nimport numpy as np\nimport pandas as pd\n\n# Visualization packages\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nsns.set()", "_____no_output_____" ] ], [ [ "# Extending Linear Regression\n\n## Working with the Titanic Dataset from Seaborn\n\nFor our dataset, we'll be using the passenger list from the Titanic, which famously sank in 1912. Let's have a look at the data. Some descriptions of the data are at https://www.kaggle.com/c/titanic/data, and here's [how seaborn preprocessed it](https://github.com/mwaskom/seaborn-data/blob/master/process/titanic.py).\n\nThe task is to build a regression model to **predict the fare**, based on different attributes.\n\nLet's keep a subset of the data, which includes the following variables: \n\n- age\n- sex\n- class\n- embark_town\n- alone\n- **fare** (the response variable)", "_____no_output_____" ] ], [ [ "# Load the dataset from seaborn \ntitanic = sns.load_dataset(\"titanic\")\ntitanic.head()", "_____no_output_____" ], [ "# checking for null values\nchosen_vars = ['age', 'sex', 'class', 'embark_town', 'alone', 'fare']\ntitanic = titanic[chosen_vars]\ntitanic.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 891 entries, 0 to 890\nData columns (total 6 columns):\nage 714 non-null float64\nsex 891 non-null object\nclass 891 non-null category\nembark_town 889 non-null object\nalone 891 non-null bool\nfare 891 non-null float64\ndtypes: bool(1), category(1), float64(2), object(2)\nmemory usage: 29.8+ KB\n" ] ], [ [ "**Exercise**: check the datatypes of each column and display the statistics (min, max, mean and any others) for all the numerical columns of the dataset.", "_____no_output_____" ] ], [ [ "## your code here\ntitanic.dtypes\ntitanic.describe()\n", "_____no_output_____" ], [ "# %load 'solutions/sol1.py'\n", "_____no_output_____" ] ], [ [ "**Exercise**: drop all the non-null *rows* in the dataset. Is this always a good idea?", "_____no_output_____" ] ], [ [ "## your code here\ntitanic = titanic.dropna(axis=0)\ntitanic.info()\n\n#inputation is an alternative to addressing null values", "<class 'pandas.core.frame.DataFrame'>\nInt64Index: 712 entries, 0 to 890\nData columns (total 6 columns):\nage 712 non-null float64\nsex 712 non-null object\nclass 712 non-null category\nembark_town 712 non-null object\nalone 712 non-null bool\nfare 712 non-null float64\ndtypes: bool(1), category(1), float64(2), object(2)\nmemory usage: 29.3+ KB\n" ], [ "# %load 'solutions/sol2.py'", "_____no_output_____" ] ], [ [ "Now let us visualize the response variable. A good visualization of the distribution of a variable will enable us to answer three kinds of questions:\n\n- What values are central or typical? (e.g., mean, median, modes)\n- What is the typical spread of values around those central values? (e.g., variance/stdev, skewness)\n- What are unusual or exceptional values (e.g., outliers)", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(24, 6))\nax = ax.ravel()\n\nsns.distplot(titanic['fare'], ax=ax[0])\nax[0].set_title('Seaborn distplot')\nax[0].set_ylabel('Normalized frequencies')\n\nsns.violinplot(x='fare', data=titanic, ax=ax[1])\nax[1].set_title('Seaborn violin plot')\nax[1].set_ylabel('Frequencies')\n\nsns.boxplot(x='fare', data=titanic, ax=ax[2])\nax[2].set_title('Seaborn box plot')\nax[2].set_ylabel('Frequencies')\nfig.suptitle('Distribution of count');", "_____no_output_____" ] ], [ [ "How do we interpret these plots?", "_____no_output_____" ], [ "## Train-Test Split", "_____no_output_____" ] ], [ [ "from sklearn.model_selection import train_test_split\n\ntitanic_train, titanic_test = train_test_split(titanic, train_size=0.7, random_state=99)\ntitanic_train = titanic_train.copy()\ntitanic_test = titanic_test.copy()\nprint(titanic_train.shape, titanic_test.shape)", "(498, 6) (214, 6)\n" ] ], [ [ "## Simple one-variable OLS", "_____no_output_____" ], [ "**Exercise**: You've done this before: make a simple model using the OLS package from the statsmodels library predicting **fare** using **age** using the training data. Name your model `model_1` and display the summary", "_____no_output_____" ] ], [ [ "from statsmodels.api import OLS\nimport statsmodels.api as sm", "_____no_output_____" ], [ "# Your code here\n\n", "_____no_output_____" ], [ "# %load 'solutions/sol3.py'\nage_ca = sm.add_constant(titanic_train['age'])\nmodel_1 = OLS(titanic_train['fare'], age_ca).fit()\nmodel_1.summary()", "C:\\Users\\davidsong\\Anaconda3\\envs\\109a\\lib\\site-packages\\numpy\\core\\fromnumeric.py:2389: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.\n return ptp(axis=axis, out=out, **kwargs)\n" ] ], [ [ "## Dealing with different kinds of variables", "_____no_output_____" ], [ "In general, you should be able to distinguish between three kinds of variables: \n\n1. Continuous variables: such as `fare` or `age`\n2. Categorical variables: such as `sex` or `alone`. There is no inherent ordering between the different values that these variables can take on. These are sometimes called nominal variables. Read more [here](https://stats.idre.ucla.edu/other/mult-pkg/whatstat/what-is-the-difference-between-categorical-ordinal-and-interval-variables/). \n3. Ordinal variables: such as `class` (first > second > third). There is some inherent ordering of the values in the variables, but the values are not continuous either. \n\n*Note*: While there is some inherent ordering in `class`, we will be treating it like a categorical variable.", "_____no_output_____" ] ], [ [ "titanic_orig = titanic_train.copy()", "_____no_output_____" ] ], [ [ "Let us now examine the `sex` column and see the value counts.", "_____no_output_____" ] ], [ [ "titanic_train['sex'].value_counts()", "_____no_output_____" ] ], [ [ "**Exercise**: Create a column `sex_male` that is 1 if the passenger is male, 0 if female. The value counts indicate that these are the two options in this particular dataset. Ensure that the datatype is `int`.", "_____no_output_____" ] ], [ [ "# your code here\ntitanic_train['sex_male'] = (titanic_train.sex == 'male').astype(int)\ntitanic_train['sex_male'].value_counts()\n", "_____no_output_____" ], [ "# %load 'solutions/sol4.py'", "_____no_output_____" ] ], [ [ "Do we need a `sex_female` column, or a `sex_others` column? Why or why not?\n\nNow, let us look at `class` in greater detail.", "_____no_output_____" ] ], [ [ "titanic_train['class_Second'] = (titanic_train['class'] == 'Second').astype(int)\ntitanic_train['class_Third'] = 1 * (titanic_train['class'] == 'Third') # just another way to do it\n\ntitanic_train['class_Second'].value_counts()\ntitanic_train['class_Third'].value_counts()", "_____no_output_____" ], [ "titanic_train.info()", "<class 'pandas.core.frame.DataFrame'>\nInt64Index: 498 entries, 278 to 805\nData columns (total 9 columns):\nage 498 non-null float64\nsex 498 non-null object\nclass 498 non-null category\nembark_town 498 non-null object\nalone 498 non-null bool\nfare 498 non-null float64\nsex_male 498 non-null int32\nclass_Second 498 non-null int32\nclass_Third 498 non-null int32\ndtypes: bool(1), category(1), float64(2), int32(3), object(2)\nmemory usage: 26.4+ KB\n" ], [ "# This function automates the above:\ntitanic_train_copy = pd.get_dummies(titanic_train, columns=['sex', 'class'], drop_first=True)\ntitanic_train_copy.head()", "_____no_output_____" ] ], [ [ "## Linear Regression with More Variables", "_____no_output_____" ], [ "**Exercise**: Fit a linear regression including the new sex and class variables. Name this model `model_2`. Don't forget the constant!", "_____no_output_____" ] ], [ [ "# your code here\n\n", "_____no_output_____" ], [ "# %load 'solutions/sol5.py'\nmodel_2 = sm.OLS(titanic_train['fare'], \n sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third']])).fit()\n\n# add constant just once for B0 value)\n\nmodel_2.summary()", "_____no_output_____" ] ], [ [ "### Interpreting These Results", "_____no_output_____" ], [ "1. Which of the predictors do you think are important? Why?\n2. All else equal, what does being male do to the fare?\n\n### Going back to the example from class\n\n![male_female](../fig/male_female.png)\n\n3. What is the interpretation of $\\beta_0$ and $\\beta_1$?\n\nBeta 0 = male; beta 1 = male - female (difference b/w male and female)", "_____no_output_____" ], [ "## Exploring Interactions", "_____no_output_____" ] ], [ [ "sns.lmplot(x=\"age\", y=\"fare\", hue=\"sex\", data=titanic_train, size=6)", "C:\\Users\\davidsong\\Anaconda3\\envs\\109a\\lib\\site-packages\\seaborn\\regression.py:546: UserWarning: The `size` paramter has been renamed to `height`; please update your code.\n warnings.warn(msg, UserWarning)\n" ] ], [ [ "The slopes seem to be different for male and female. What does that indicate?\n\nLet us now try to add an interaction effect into our model.", "_____no_output_____" ] ], [ [ "# It seemed like gender interacted with age and class. Can we put that in our model?\ntitanic_train['sex_male_X_age'] = titanic_train['age'] * titanic_train['sex_male']\n\nmodel_3 = sm.OLS(\n titanic_train['fare'],\n sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age']])\n).fit()\nmodel_3.summary()", "_____no_output_____" ] ], [ [ "**What happened to the `age` and `male` terms?**", "_____no_output_____" ] ], [ [ "# It seemed like gender interacted with age and class. Can we put that in our model?\ntitanic_train['sex_male_X_class_Second'] = titanic_train['age'] * titanic_train['class_Second']\ntitanic_train['sex_male_X_class_Third'] = titanic_train['age'] * titanic_train['class_Third']\n\nmodel_4 = sm.OLS(\n titanic_train['fare'],\n sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age', \n 'sex_male_X_class_Second', 'sex_male_X_class_Third']])\n).fit()\nmodel_4.summary()", "_____no_output_____" ] ], [ [ "## Polynomial Regression \n\n![poly](../fig/poly.png)", "_____no_output_____" ], [ "Perhaps we now believe that the fare also depends on the square of age. How would we include this term in our model?", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots(figsize=(12,6))\nax.plot(titanic_train['age'], titanic_train['fare'], 'o')\nx = np.linspace(0,80,100)\nax.plot(x, x, '-', label=r'$y=x$')\nax.plot(x, 0.04*x**2, '-', label=r'$y=c x^2$')\nax.set_title('Plotting Age (x) vs Fare (y)')\nax.set_xlabel('Age (x)')\nax.set_ylabel('Fare (y)')\nax.legend();", "_____no_output_____" ] ], [ [ "**Exercise**: Create a model that predicts fare from all the predictors in `model_4` + the square of age. Show the summary of this model. Call it `model_5`. Remember to use the training data, `titanic_train`.", "_____no_output_____" ] ], [ [ "# your code here\n\n", "_____no_output_____" ], [ "# %load 'solutions/sol6.py'\ntitanic_train['age^2'] = titanic_train['age'] **2\nmodel_5 = sm.OLS(\n titanic_train['fare'],\n sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age', \n 'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])\n).fit()\nmodel_5.summary()", "_____no_output_____" ] ], [ [ "## Looking at All Our Models: Model Selection", "_____no_output_____" ], [ "What has happened to the $R^2$ as we added more features? Does this mean that the model is better? (What if we kept adding more predictors and interaction terms? **In general, how should we choose a model?** We will spend a lot more time on model selection and learn about ways to do so as the course progresses.", "_____no_output_____" ] ], [ [ "models = [model_1, model_2, model_3, model_4, model_5]\nfig, ax = plt.subplots(figsize=(12,6))\nax.plot([model.df_model for model in models], [model.rsquared for model in models], 'x-')\nax.set_xlabel(\"Model degrees of freedom\")\nax.set_title('Model degrees of freedom vs training $R^2$')\nax.set_ylabel(\"$R^2$\");", "_____no_output_____" ] ], [ [ "**What about the test data?**\n\nWe added a lot of columns to our training data and must add the same to our test data in order to calculate $R^2$ scores.", "_____no_output_____" ] ], [ [ "# Added features for model 1\n# Nothing new to be added\n\n# Added features for model 2\ntitanic_test = pd.get_dummies(titanic_test, columns=['sex', 'class'], drop_first=True)\n\n# Added features for model 3\ntitanic_test['sex_male_X_age'] = titanic_test['age'] * titanic_test['sex_male']\n\n# Added features for model 4\ntitanic_test['sex_male_X_class_Second'] = titanic_test['age'] * titanic_test['class_Second']\ntitanic_test['sex_male_X_class_Third'] = titanic_test['age'] * titanic_test['class_Third']\n\n# Added features for model 5\ntitanic_test['age^2'] = titanic_test['age'] **2", "_____no_output_____" ] ], [ [ "**Calculating R^2 scores**", "_____no_output_____" ] ], [ [ "from sklearn.metrics import r2_score\n\nr2_scores = []\ny_preds = []\ny_true = titanic_test['fare']\n\n# model 1\ny_preds.append(model_1.predict(sm.add_constant(titanic_test['age'])))\n\n# model 2\ny_preds.append(model_2.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third']])))\n\n# model 3\ny_preds.append(model_3.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third', \n 'sex_male_X_age']])))\n\n# model 4\ny_preds.append(model_4.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third', \n 'sex_male_X_age', 'sex_male_X_class_Second', \n 'sex_male_X_class_Third']])))\n\n# model 5\ny_preds.append(model_5.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', \n 'class_Third', 'sex_male_X_age', \n 'sex_male_X_class_Second', \n 'sex_male_X_class_Third', 'age^2']])))\n\nfor y_pred in y_preds:\n r2_scores.append(r2_score(y_true, y_pred))\n \nmodels = [model_1, model_2, model_3, model_4, model_5]\nfig, ax = plt.subplots(figsize=(12,6))\nax.plot([model.df_model for model in models], r2_scores, 'x-')\nax.set_xlabel(\"Model degrees of freedom\")\nax.set_title('Model degrees of freedom vs test $R^2$')\nax.set_ylabel(\"$R^2$\");", "_____no_output_____" ] ], [ [ "## Regression Assumptions. Should We Even Regress Linearly?", "_____no_output_____" ], [ "![linear regression](../fig/linear_regression.png)", "_____no_output_____" ], [ "**Question**: What are the assumptions of a linear regression model? \n\nWe find that the answer to this question can be found on closer examimation of $\\epsilon$. What is $\\epsilon$? It is assumed that $\\epsilon$ is normally distributed with a mean of 0 and variance $\\sigma^2$. But what does this tell us?\n\n1. Assumption 1: Constant variance of $\\epsilon$ errors. This means that if we plot our **residuals**, which are the differences between the true $Y$ and our predicted $\\hat{Y}$, they should look like they have constant variance and a mean of 0. We will show this in our plots.\n2. Assumption 2: Independence of $\\epsilon$ errors. This again comes from the distribution of $\\epsilon$ that we decide beforehand.\n3. Assumption 3: Linearity. This is an implicit assumption as we claim that Y can be modeled through a linear combination of the predictors. **Important Note:** Even though our predictors, for instance $X_2$, can be created by squaring or cubing another variable, we still use them in a linear equation as shown above, which is why polynomial regression is still a linear model.\n4. Assumption 4: Normality. We assume that the $\\epsilon$ is normally distributed, and we can show this in a histogram of the residuals.\n\n**Exercise**: Calculate the residuals for model 5, our most recent model. Optionally, plot and histogram these residuals and check the assumptions of the model.", "_____no_output_____" ] ], [ [ "# your code here\n\n", "_____no_output_____" ], [ "# %load 'solutions/sol7.py'\npredictors = sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age', \n 'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])\ny_hat = model_5.predict(predictors)\nresiduals = titanic_train['fare'] - y_hat\n\n# plotting\nfig, ax = plt.subplots(ncols=2, figsize=(16,5))\nax = ax.ravel()\nax[0].set_title('Plot of Residuals')\nax[0].scatter(y_hat, residuals, alpha=0.2)\nax[0].set_xlabel(r'$\\hat{y}$')\nax[0].set_ylabel('residuals')\n\nax[1].set_title('Histogram of Residuals')\nax[1].hist(residuals, alpha=0.7)\nax[1].set_xlabel('residuals')\nax[1].set_ylabel('frequency');\n\n# Mean of residuals\nprint('Mean of residuals: {}'.format(np.mean(residuals)))", "Mean of residuals: 4.582536938043967e-13\n" ] ], [ [ "**What can you say about the assumptions of the model?**", "_____no_output_____" ], [ "----------------\n### End of Standard Section\n---------------", "_____no_output_____" ], [ "## Extra: Visual exploration of predictors' correlations\n\nThe dataset for this problem contains 10 simulated predictors and a response variable. ", "_____no_output_____" ] ], [ [ "# read in the data \ndata = pd.read_csv('../data/dataset3.txt')\ndata.head()", "_____no_output_____" ], [ "# this effect can be replicated using the scatter_matrix function in pandas plotting\nsns.pairplot(data);", "_____no_output_____" ] ], [ [ "Predictors x1, x2, x3 seem to be perfectly correlated while predictors x4, x5, x6, x7 seem correlated.", "_____no_output_____" ] ], [ [ "data.corr()", "_____no_output_____" ], [ "sns.heatmap(data.corr())", "_____no_output_____" ] ], [ [ "## Extra: A Handy Matplotlib Guide", "_____no_output_____" ], [ "![](https://i.imgur.com/XTzSuoR.png)\nsource: http://matplotlib.org/faq/usage_faq.html\n\nSee also [this](http://matplotlib.org/faq/usage_faq.html) matplotlib tutorial.", "_____no_output_____" ], [ "![violin plot](../fig/violin.png)\n\nSee also [this](https://mode.com/blog/violin-plot-examples) violin plot tutorial.", "_____no_output_____" ], [ "---", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ] ]

d0e68e043c36251dc429885bf4df1229bf4c870e

30,456

ipynb

Jupyter Notebook

Machine_Learning/algorithms/SOFTMAX.ipynb

Mendes1302/Data_Science

1d364ab2bf1f68f62bb2d9453d2897fef3f03484

[ "MIT" ]

4

2021-07-29T18:11:36.000Z

2021-11-23T23:46:21.000Z

Machine_Learning/algorithms/SOFTMAX.ipynb

Mendes1302/Data_Science

1d364ab2bf1f68f62bb2d9453d2897fef3f03484

[ "MIT" ]

null

Machine_Learning/algorithms/SOFTMAX.ipynb

Mendes1302/Data_Science

1d364ab2bf1f68f62bb2d9453d2897fef3f03484

[ "MIT" ]

null

182.371257

16,489

0.700749

[ [ [ "import torch\nimport torch.nn as nn\nimport numpy as np\nimport matplotlib.pyplot as plt\n\n# PREPARAÇÃO DOS DADOS\n\n# Datapoints (NOTAS)\nx_numpy = np.array([2,4,3,5,7,2,9,4,10,9,4,6,1,5,6,9,8,3, 1, 5, 6, 5,2, 7, 8, 2,5,9, 10,2,1,3,8,5,6,5])\n# 3 classes (0=reprovados, 1=recuperação, 2=aprovados) \ny_numpy = np.array([0,0,0,1,2,0,2,0,2,2,0,1,0,1,1,2,1,0,0,1,1,1,0,2,2,0,1,2,2,0,0,0,2,1,1,1])\n\nx = torch.from_numpy(x_numpy.astype(np.float32))\ny = torch.from_numpy(y_numpy.astype(np.float32))\ny = y.long()\nx = x.view(x.shape[0], 1)\n\nprint(x.shape)\nprint(y.shape)\nprint(y)", "torch.Size([36, 1])\ntorch.Size([36])\ntensor([0, 0, 0, 1, 2, 0, 2, 0, 2, 2, 0, 1, 0, 1, 1, 2, 1, 0, 0, 1, 1, 1, 0, 2,\n 2, 0, 1, 2, 2, 0, 0, 0, 2, 1, 1, 1])\n" ], [ "# CLASS DE REGRESSÃO LOGÍSTICA\n\nclass RegressaoSoftmax(nn.Module):\n def __init__(self, n_input, n_output):\n super(RegressaoSoftmax, self).__init__()\n self.Linear = nn.Linear(n_input, n_output)\n\n def forward(self, x):\n return self.Linear(x)\n\n\n# DEFINICIÇÃO DE MODELO\ninput_size = 1\noutput_size = 3\nmodel = RegressaoSoftmax(input_size, output_size)\n\n# DEFINIÇÃO DA FUNÇAO DE CUSTO E OTIMIZADOR\nlearning_rate = 0.02\ncriterion = nn.CrossEntropyLoss()\noptimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)\n\n# LOOP DE TREINAMENTO\nnum_epochs = 5500\ncontador_custo = []\nfor epoch in range(num_epochs):\n #forward pass and loos\n y_hat = model(x) \n loss = criterion(y_hat, y)\n contador_custo.append(loss)\n #print(y_hat)\n\n #backward pass (calcular gradientes)\n loss.backward()\n\n #update (atualizar os pesos)\n optimizer.step()\n\n \n #limpar o otimizador\n optimizer.zero_grad()\n\n\n\n# PLOTANDO O GRÁFICO DA FUNÇÃO DE CUSTO\nprint(\"GRÁFICO DA FUNÇÃO DE CUSTO\")\nplt.plot(contador_custo, 'b')\nplt.show()", "GRÁFICO DA FUNÇÃO DE CUSTO\n" ], [ "# fazer predição de teste\nteste = np.array([4, 9, 7, 2, 6, 5, 4.9, 4.5])\nt_teste = torch.from_numpy(teste.astype(np.float32))\nt_teste = t_teste.view(t_teste.shape[0], 1)\n\nwith torch.no_grad():\n predicoes = model(t_teste)\n print (np.argmax(predicoes, axis=1).flatten())", "tensor([0, 2, 2, 0, 1, 1, 1, 1])\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code" ] ]

d0e692d8ddcea935896e50c20a9819c3beed9bae

1,805

ipynb

Jupyter Notebook

ML-week/py_ds/Aggregate data with Pandas.ipynb

gopala-kr/a-wild-week-in-ai

5b6735b60e4ddc0c181cbc55763600aa659f5b49

[ "MIT" ]

62

2018-08-01T04:06:25.000Z

2021-11-22T13:22:34.000Z

ML-week/py_ds/Aggregate data with Pandas.ipynb

gopala-kr/a-wild-week-in-ai

5b6735b60e4ddc0c181cbc55763600aa659f5b49

[ "MIT" ]

null

ML-week/py_ds/Aggregate data with Pandas.ipynb

gopala-kr/a-wild-week-in-ai

5b6735b60e4ddc0c181cbc55763600aa659f5b49

[ "MIT" ]

25

2018-09-15T19:12:03.000Z

2021-05-19T17:01:59.000Z

20.280899

133

0.539058

[ [ [ "import pandas as pd", "_____no_output_____" ], [ "df = pd.read_csv('data/MonthlyProductSales.csv')", "_____no_output_____" ], [ "# yearly sales summary\ndf.groupby(df['Month of Order Date'].str[:4]).describe().reset_index().rename(columns={'Month of Order Date': 'Year of Order'})", "_____no_output_____" ], [ "# yearly product sales totals\ndf_export = df.groupby([df['Month of Order Date'].str[:4], 'Product Name']).sum().reset_index()\ndf_export.rename(columns={'Month of Order Date': 'Year of Order'})", "_____no_output_____" ], [ "# overall product sales totals\ndf.groupby('Product Name').sum().reset_index()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code" ] ]

d0e694dc16cd3e164f6b48c526f9894d0ca3e1b3

42,965

ipynb

Jupyter Notebook

ex3_cnn_da.ipynb

swag-kaust/dda_pytorch

818f2baeffa618ee121ff69d689823206eb3bbbf

[ "MIT" ]

2

2021-08-18T13:07:35.000Z

2021-12-21T17:53:55.000Z

ex3_cnn_da.ipynb

swag-kaust/dda_pytorch

818f2baeffa618ee121ff69d689823206eb3bbbf

[ "MIT" ]

null

ex3_cnn_da.ipynb

swag-kaust/dda_pytorch

818f2baeffa618ee121ff69d689823206eb3bbbf

[ "MIT" ]

null

52.015738

15,848

0.68884

[ [ [ "# Example 3. CNN + DDA\nHere, we train the same CNN as in previous notebook but applying the Direct Domain Adaptation method (DDA) to reduce the gap between MNIST and MNIST-M datasets. \n\n-------\nThis code is modified from [https://github.com/fungtion/DANN_py3](https://github.com/fungtion/DANN_py3). ", "_____no_output_____" ] ], [ [ "import os\nimport sys\nimport tqdm\nimport random\nimport numpy as np\nfrom numpy.fft import rfft2, irfft2, fftshift, ifftshift\n\nimport torch.backends.cudnn as cudnn\nimport torch.optim as optim\nimport torch.nn as nn\nimport torch.utils.data\nfrom torchvision import datasets\nfrom torchvision import transforms\n\nfrom components.data_loader import GetLoader\nfrom components.model import CNNModel\nfrom components.test import test\nimport components.shared as sd", "_____no_output_____" ], [ "# os.environ[\"CUDA_VISIBLE_DEVICES\"] = \"2\"", "_____no_output_____" ] ], [ [ "### Init paths", "_____no_output_____" ] ], [ [ "# Paths to datasets\nsource_dataset_name = 'MNIST'\ntarget_dataset_name = 'mnist_m'\nsource_image_root = os.path.join('dataset', source_dataset_name)\ntarget_image_root = os.path.join('dataset', target_dataset_name)\nos.makedirs('./dataset', exist_ok=True)\n\n# Where to save outputs\nmodel_root = './out_ex3_cnn_da'\nos.makedirs(model_root, exist_ok=True)", "_____no_output_____" ] ], [ [ "### Init training", "_____no_output_____" ] ], [ [ "cuda = True\ncudnn.benchmark = True\n\n# Hyperparameters\nlr = 1e-3\nbatch_size = 128\nimage_size = 28\nn_epoch = 100\n\n# manual_seed = random.randint(1, 10000)\nmanual_seed = 222\nrandom.seed(manual_seed)\ntorch.manual_seed(manual_seed)\nprint(f'Random seed: {manual_seed}')", "Random seed: 222\n" ] ], [ [ "### Data", "_____no_output_____" ] ], [ [ "# Transformations / augmentations\nimg_transform_source = transforms.Compose([\n transforms.Resize(image_size),\n transforms.ToTensor(),\n transforms.Normalize(mean=(0.1307,), std=(0.3081,)),\n transforms.Lambda(lambda x: x.repeat(3, 1, 1)),\n])\n\nimg_transform_target = transforms.Compose([\n transforms.Resize(image_size),\n transforms.ToTensor(),\n transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))\n])\n\n# Load MNIST dataset\ndataset_source = datasets.MNIST(\n root='dataset',\n train=True,\n transform=img_transform_source,\n download=True\n)\n\n# Load MNIST-M dataset\ntrain_list = os.path.join(target_image_root, 'mnist_m_train_labels.txt')\ndataset_target = GetLoader(\n data_root=os.path.join(target_image_root, 'mnist_m_train'),\n data_list=train_list,\n transform=img_transform_target\n)", "_____no_output_____" ] ], [ [ "# Direct Domain Adaptation (DDA)", "_____no_output_____" ], [ "## Average auto-correlation\nFor entire dataset", "_____no_output_____" ] ], [ [ "def get_global_acorr_for_loader(loader):\n \"\"\" The average auto-correlation of all images in the dataset \"\"\"\n global_acorr = np.zeros((3, 28, 15), dtype=np.complex128)\n prog_bar = tqdm.tqdm(loader)\n for data, _ in prog_bar:\n data_f = np.fft.rfft2(data, s=data.shape[-2:], axes=(-2, -1))\n # Auto-correlation is multiplication with the conjucate of self\n # in frequency domain\n global_acorr += data_f * np.conjugate(data_f)\n global_acorr /= len(loader)\n print(global_acorr.shape)\n return np.fft.fftshift(global_acorr)\n\ndef route_to(fname):\n \"\"\" Shortcut for routing to the save folder \"\"\"\n return os.path.join(model_root, fname)\n\n# Compute global acorr if not in the folder, load otherwise\nif not 'gacorr_dst_tr.npy' in os.listdir(model_root):\n print('Save global acorr')\n gacorr_dst_tr = get_global_acorr_for_loader(dataset_target)\n gacorr_src_tr = get_global_acorr_for_loader(dataset_source)\n np.save(route_to('gacorr_dst_tr.npy'), gacorr_dst_tr)\n np.save(route_to('gacorr_src_tr.npy'), gacorr_src_tr)\nelse:\n print('Load global acorr')\n gacorr_dst_tr = np.load(route_to('gacorr_dst_tr.npy'))\n gacorr_src_tr = np.load(route_to('gacorr_src_tr.npy'))", "Load global acorr\n" ] ], [ [ "## Average cross-correlation\nPick a random pixel(-s) from each image in the dataset and average", "_____no_output_____" ] ], [ [ "# Window size\ncrop_size = 1\nprint(f'Use the crop size for xcorr = {crop_size}')", "Use the crop size for xcorr = 1\n" ], [ "def crop_ref(x, n=1, edge=5):\n \"\"\"Crop a window from the image\n Args:\n x(np.ndarray): image [c, h, w]\n n(int): window size\n edge(int): margin to avoid from edges of the image\n \"\"\"\n if n % 2 == 0: n+=1;\n k = int((n - 1) / 2)\n nz, nx = x.shape[-2:]\n dim1 = np.random.randint(0+k+edge, nz-k-edge)\n dim2 = np.random.randint(0+k, nx-k)\n out = x[..., dim1-k:dim1+k+1, dim2-k:dim2+k+1]\n return out\n\n# crop_ref(np.ones((2, 100, 100)), n=5).shape", "_____no_output_____" ], [ "def get_global_xcorr_for_loader(loader, crop_size=1):\n # Init the placeholder for average\n rand_pixel = np.zeros((3, crop_size, crop_size))\n \n # Loop over all images in the dataset\n prog_bar = tqdm.tqdm(loader)\n for data, _ in prog_bar:\n rand_pixel += np.mean(crop_ref(data, crop_size).numpy(), axis=0)\n rand_pixel /= len(loader)\n \n # Place the mean pixel into center of an empty image\n c, h ,w = data.shape\n mid_h, mid_w = int(h // 2), int(w // 2)\n embed = np.zeros_like(data)\n embed[..., mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel\n global_xcorr = np.fft.rfft2(embed, s=data.shape[-2:], axes=(-2, -1))\n return np.fft.fftshift(global_xcorr)\n\n\n# Compute global xcorr if not in the folder, load otherwise\nif not 'gxcorr_dst_tr.npy' in os.listdir(model_root):\n# if True:\n print('Save global xcorr')\n gxcorr_dst_tr = get_global_xcorr_for_loader(dataset_target, crop_size)\n gxcorr_src_tr = get_global_xcorr_for_loader(dataset_source, crop_size)\n np.save(route_to('gxcorr_dst_tr.npy'), gxcorr_dst_tr)\n np.save(route_to('gxcorr_src_tr.npy'), gxcorr_src_tr)\nelse:\n print('Load global xcorr')\n gxcorr_dst_tr = np.load(route_to('gxcorr_dst_tr.npy'))\n gxcorr_src_tr = np.load(route_to('gxcorr_src_tr.npy'))", "Load global xcorr\n" ] ], [ [ "## Train Loader", "_____no_output_____" ] ], [ [ "def flip_channels(x):\n \"\"\"Reverse polarity of random channels\"\"\"\n flip_matrix = np.random.choice([-1, 1], 3)[..., np.newaxis, np.newaxis] \n return (x * flip_matrix).astype(np.float32)\n\ndef shuffle_channels(x):\n \"\"\"Change order of channels\"\"\"\n return np.random.permutation(x)\n\ndef normalize_channels(x):\n \"\"\"Map data to [-1,1] range. The scaling after conv(xcorr, acorr) is not \n suitable for image processing so this function fixes it\"\"\"\n cmin = np.min(x, axis=(-2,-1))[..., np.newaxis, np.newaxis]\n x -= cmin\n cmax = np.max(np.abs(x), axis=(-2,-1))[..., np.newaxis, np.newaxis]\n x /= cmax\n x *= 2\n x -= 1\n return x.astype(np.float32)", "_____no_output_____" ], [ "class DDALoaderTrain(torch.utils.data.Dataset):\n def __init__(self, loader1, avg_acorr2, p=0.5, crop_size=1):\n super().__init__()\n self.loader1 = loader1\n self.avg_acorr2 = avg_acorr2\n self.p = p\n self.crop_size = crop_size\n \n def __len__(self):\n return len(self.loader1)\n \n def __getitem__(self, item):\n # Get main data (data, label)\n data, label = self.loader1.__getitem__(item)\n data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))\n \n # Get random pixel from another data from the same dataset\n random_index = np.random.randint(0, len(self.loader1))\n another_data, _ = self.loader1.__getitem__(random_index)\n rand_pixel = crop_ref(another_data, self.crop_size)\n \n # Convert to Fourier domain\n c, h ,w = another_data.shape\n mid_h, mid_w = int(h // 2), int(w // 2)\n embed = np.zeros_like(another_data)\n embed[:, mid_h:mid_h+1, mid_w:mid_w+1] = rand_pixel\n pixel_fft = np.fft.rfft2(embed, s=another_data.shape[-2:], axes=(-2, -1))\n pixel_fft = np.fft.fftshift(pixel_fft)\n \n # Cross-correlate the data sample with the random pixel from the same dataset\n xcorr = data_fft * np.conjugate(pixel_fft)\n\n # Convolve the ruslt with the auto-correlation of another dataset\n conv = xcorr * self.avg_acorr2\n\n # Reverse Fourier domain and map channels to [-1, 1] range\n data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))\n data_da = normalize_channels(data_da)\n \n # Apply data augmentations\n if np.random.rand() < self.p:\n data_da = flip_channels(data_da)\n if np.random.rand() < self.p:\n data_da = shuffle_channels(data_da)\n \n # Return a pair of data / label\n return data_da.astype(np.float32), label", "_____no_output_____" ], [ "dataset_source = DDALoaderTrain(dataset_source, gacorr_dst_tr)\ndataset_target = DDALoaderTrain(dataset_target, gacorr_src_tr)\n\ndummy_data, dummy_label = dataset_source.__getitem__(0)\nprint('Image shape: {}\\t Label: {}'.format(dummy_data.shape, dummy_label))", "Image shape: (3, 28, 28)\t Label: 5\n" ] ], [ [ "# Test Loader", "_____no_output_____" ] ], [ [ "class DDALoaderTest(torch.utils.data.Dataset):\n def __init__(self, loader1, avg_acorr2, avg_xcorr1):\n super().__init__()\n self.loader1 = loader1\n self.avg_acorr2 = avg_acorr2\n self.avg_xcorr1 = avg_xcorr1\n \n def __len__(self):\n return len(self.loader1)\n \n def __getitem__(self, item):\n data, label = self.loader1.__getitem__(item)\n data_fft = fftshift(rfft2(data, s=data.shape[-2:], axes=(-2, -1)))\n \n xcorr = data_fft * np.conjugate(self.avg_xcorr1)\n conv = xcorr * self.avg_acorr2\n\n data_da = fftshift(irfft2(ifftshift(conv), axes=(-2, -1)))\n data_da = normalize_channels(data_da)\n return data_da.astype(np.float32), label", "_____no_output_____" ] ], [ [ "Re-define the test function so it accounts for the average cross-correlation and auto-correlation from source and target datasets", "_____no_output_____" ] ], [ [ "def test(dataset_name, model_root, crop_size=1):\n image_root = os.path.join('dataset', dataset_name) \n if dataset_name == 'mnist_m':\n test_list = os.path.join(image_root, 'mnist_m_test_labels.txt')\n dataset = GetLoader(\n data_root=os.path.join(image_root, 'mnist_m_test'),\n data_list=test_list,\n transform=img_transform_target\n )\n \n if not 'gxcorr_dst_te.npy' in os.listdir(model_root):\n print('Save global acorr and xcorr')\n # acorr\n gacorr_src_te = get_global_acorr_for_loader(dataset)\n np.save(route_to('gacorr_src_te.npy'), gacorr_src_te)\n # xcorr\n gxcorr_dst_te = get_global_xcorr_for_loader(dataset, crop_size)\n np.save(route_to('gxcorr_dst_te.npy'), gxcorr_dst_te)\n else:\n gacorr_src_te = np.load(route_to('gacorr_src_te.npy'))\n gxcorr_dst_te = np.load(route_to('gxcorr_dst_te.npy'))\n \n # Init loader for MNIST-M\n dataset = DDALoaderTest(dataset, gacorr_src_te, gxcorr_dst_te)\n else:\n dataset = datasets.MNIST(\n root='dataset',\n train=False,\n transform=img_transform_source,\n )\n if not 'gxcorr_src_te.npy' in os.listdir(model_root):\n print('Save global acorr and xcorr')\n # acorr\n gacorr_dst_te = get_global_acorr_for_loader(dataset)\n np.save(route_to('gacorr_dst_te.npy'), gacorr_dst_te)\n # xcorr\n gxcorr_src_te = get_global_xcorr_for_loader(dataset, crop_size)\n np.save(route_to('gxcorr_src_te.npy'), gxcorr_src_te)\n else:\n gacorr_dst_te = np.load(route_to('gacorr_dst_te.npy'))\n gxcorr_src_te = np.load(route_to('gxcorr_src_te.npy'))\n \n # Init loader for MNIST\n dataset = DDALoaderTest(dataset, gacorr_dst_te, gxcorr_src_te)\n\n dataloader = torch.utils.data.DataLoader(\n dataset=dataset,\n batch_size=batch_size,\n shuffle=False,\n num_workers=8\n )\n\n \"\"\" test \"\"\"\n my_net = torch.load(os.path.join(model_root, 'mnist_mnistm_model_epoch_current.pth'))\n my_net = my_net.eval()\n\n if cuda:\n my_net = my_net.cuda()\n\n len_dataloader = len(dataloader)\n data_target_iter = iter(dataloader)\n\n i = 0\n n_total = 0\n n_correct = 0\n\n while i < len_dataloader:\n # test model using target data\n data_target = data_target_iter.next()\n t_img, t_label = data_target\n\n _batch_size = len(t_label)\n\n if cuda:\n t_img = t_img.cuda()\n t_label = t_label.cuda()\n\n class_output, _ = my_net(input_data=t_img, alpha=0)\n pred = class_output.data.max(1, keepdim=True)[1]\n n_correct += pred.eq(t_label.data.view_as(pred)).cpu().sum()\n n_total += _batch_size\n i += 1\n\n accu = n_correct.data.numpy() * 1.0 / n_total\n return accu", "_____no_output_____" ] ], [ [ "# Training", "_____no_output_____" ] ], [ [ "dataloader_source = torch.utils.data.DataLoader(\n dataset=dataset_source,\n batch_size=batch_size,\n shuffle=True,\n num_workers=8)\n\ndataloader_target = torch.utils.data.DataLoader(\n dataset=dataset_target,\n batch_size=batch_size,\n shuffle=True,\n num_workers=8)", "_____no_output_____" ], [ "class CNNModel(nn.Module):\n def __init__(self):\n super(CNNModel, self).__init__()\n self.feature = nn.Sequential()\n self.feature.add_module('f_conv1', nn.Conv2d(3, 64, kernel_size=5))\n self.feature.add_module('f_bn1', nn.BatchNorm2d(64))\n self.feature.add_module('f_pool1', nn.MaxPool2d(2))\n self.feature.add_module('f_relu1', nn.ReLU(True))\n self.feature.add_module('f_conv2', nn.Conv2d(64, 50, kernel_size=5))\n self.feature.add_module('f_bn2', nn.BatchNorm2d(50))\n self.feature.add_module('f_drop1', nn.Dropout2d())\n self.feature.add_module('f_pool2', nn.MaxPool2d(2))\n self.feature.add_module('f_relu2', nn.ReLU(True))\n\n self.class_classifier = nn.Sequential()\n self.class_classifier.add_module('c_fc1', nn.Linear(50 * 4 * 4, 100))\n self.class_classifier.add_module('c_bn1', nn.BatchNorm1d(100))\n self.class_classifier.add_module('c_relu1', nn.ReLU(True))\n self.class_classifier.add_module('c_drop1', nn.Dropout())\n self.class_classifier.add_module('c_fc2', nn.Linear(100, 100))\n self.class_classifier.add_module('c_bn2', nn.BatchNorm1d(100))\n self.class_classifier.add_module('c_relu2', nn.ReLU(True))\n self.class_classifier.add_module('c_fc3', nn.Linear(100, 10))\n self.class_classifier.add_module('c_softmax', nn.LogSoftmax(dim=1))\n\n def forward(self, input_data, alpha):\n input_data = input_data.expand(input_data.data.shape[0], 3, 28, 28)\n feature = self.feature(input_data)\n feature = feature.view(-1, 50 * 4 * 4)\n\n class_output = self.class_classifier(feature)\n\n return class_output, 0", "_____no_output_____" ], [ "# load model\nmy_net = CNNModel()\n\n# setup optimizer\noptimizer = optim.Adam(my_net.parameters(), lr=lr)\n\nloss_class = torch.nn.NLLLoss()\n\nif cuda:\n my_net = my_net.cuda()\n loss_class = loss_class.cuda()\n\nfor p in my_net.parameters():\n p.requires_grad = True", "_____no_output_____" ], [ "# Record losses for each epoch (used in compare.ipynb)\nlosses = {'test': {'acc_bw': [], 'acc_color': []}}\nname_losses = 'losses.pkl'", "_____no_output_____" ], [ "if not name_losses in os.listdir(model_root):\n# if True:\n # training\n best_accu_t = 0.0\n for epoch in range(n_epoch):\n\n len_dataloader = min(len(dataloader_source), len(dataloader_target))\n data_source_iter = iter(dataloader_source)\n data_target_iter = iter(dataloader_target)\n\n for i in range(len_dataloader):\n\n p = float(i + epoch * len_dataloader) / n_epoch / len_dataloader\n alpha = 2. / (1. + np.exp(-10 * p)) - 1\n\n # training model using source data\n data_source = data_source_iter.next()\n s_img, s_label = data_source\n\n my_net.zero_grad()\n batch_size = len(s_label)\n\n if cuda:\n s_img = s_img.cuda()\n s_label = s_label.cuda()\n\n class_output, _ = my_net(input_data=s_img, alpha=alpha)\n err_s_label = loss_class(class_output, s_label)\n\n err = err_s_label\n err.backward()\n optimizer.step()\n\n sys.stdout.write('\\r epoch: %d, [iter: %d / all %d], err_s_label: %f' \\\n % (epoch, i + 1, len_dataloader, err_s_label.data.cpu().numpy()))\n sys.stdout.flush()\n torch.save(my_net, '{0}/mnist_mnistm_model_epoch_current.pth'.format(model_root))\n\n print('\\n')\n accu_s = test(source_dataset_name, model_root)\n print('Accuracy of the %s dataset: %f' % ('mnist', accu_s))\n accu_t = test(target_dataset_name, model_root)\n print('Accuracy of the %s dataset: %f\\n' % ('mnist_m', accu_t))\n\n losses['test']['acc_bw'].append(accu_s)\n losses['test']['acc_color'].append(accu_t)\n\n if accu_t > best_accu_t:\n best_accu_s = accu_s\n best_accu_t = accu_t\n torch.save(my_net, '{0}/mnist_mnistm_model_epoch_best.pth'.format(model_root))\n\n print('============ Summary ============= \\n')\n print('Accuracy of the %s dataset: %f' % ('mnist', best_accu_s))\n print('Accuracy of the %s dataset: %f' % ('mnist_m', best_accu_t))\n print('Corresponding model was save in ' + model_root + '/mnist_mnistm_model_epoch_best.pth')\n sd.save_dict(os.path.join(model_root, 'losses.pkl'), losses)\nelse:\n path_losses = os.path.join(model_root, name_losses)\n print(f'Losses from previous run found!')\n losses = sd.load_dict(path_losses)\n sd.plot_curves(losses)", "Losses from previous run found!\nLoad dict from ./out_ex3_cnn_da/losses.pkl\n" ], [ "print('============ Summary ============= \\n')\nprint('Accuracy of the %s dataset: %f' % ('mnist', max(losses['test']['acc_bw'])))\nprint('Accuracy of the %s dataset: %f' % ('mnist_m', max(losses['test']['acc_color'])))\nprint('Corresponding model was saved into ' + model_root + '/mnist_mnistm_model_epoch_best.pth')", "============ Summary ============= \n\nAccuracy of the mnist dataset: 0.990200\nAccuracy of the mnist_m dataset: 0.734141\nCorresponding model was saved into ./out_ex3_cnn_da/mnist_mnistm_model_epoch_best.pth\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

d0e6bb6757b0e01b8ca85352cd9d1b0f6e5fa5e1

510,359

ipynb

Jupyter Notebook

Time Series Forecasting Apple (1).ipynb

DheerajKumar97/Apple-Stock-Price-Forecasting

31987b441d24d1e200fa41d44610c52c2b678ab1

[ "MIT" ]

null

Time Series Forecasting Apple (1).ipynb

DheerajKumar97/Apple-Stock-Price-Forecasting

31987b441d24d1e200fa41d44610c52c2b678ab1

[ "MIT" ]

null

Time Series Forecasting Apple (1).ipynb

DheerajKumar97/Apple-Stock-Price-Forecasting

31987b441d24d1e200fa41d44610c52c2b678ab1

[ "MIT" ]

null

226.826222

82,092

0.879371

[ [ [ "import numpy as np\nimport pandas as pd\nimport matplotlib.pyplot as plt\nimport seaborn as sns", "_____no_output_____" ], [ "df = pd.read_csv(\"E:\\Downlload\\AAPL.csv\")\ndf", "_____no_output_____" ], [ "df1 = df[['Date','Close']]\ndf1", "_____no_output_____" ], [ "df1 = df1.rename(columns={\"Close\":'Close'})\ndf1", "_____no_output_____" ], [ "df1 = df1.set_index(['Date'])\ndf1", "_____no_output_____" ], [ "import math\ndata = df1.diff()\ndata = data[1:]", "_____no_output_____" ], [ "from statsmodels.graphics.tsaplots import plot_acf\nplot_acf(df1)\nplt.title('ACF Before Diff')", "_____no_output_____" ], [ "plot_acf(data)\nplt.title('ACF After Diff')", "_____no_output_____" ], [ "#df.plot(figsize=(15,5),color='red')\nplt.rcParams[\"figure.figsize\"] = 15,8\nplt.title('price history')\nplt.plot(data['Close'],color = 'black',linewidth=4)\nplt.xlabel('Date',fontsize=18)\nplt.ylabel('Open Price $',fontsize=18)\nax = plt.axes()\nax.set_facecolor(\"orange\")\nplt.show()", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:7: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n import sys\n" ], [ "dataset = data.values\ntraining_data_len = math.ceil(len(dataset)*.8)\ntraining_data_len", "_____no_output_____" ], [ "from sklearn.preprocessing import MinMaxScaler\nscaler = MinMaxScaler(feature_range=(0,1))\nscaled_data = scaler.fit_transform(dataset)\nscaled_data", "_____no_output_____" ], [ "train_data = scaled_data[0:training_data_len,:]\nx_train=[]\ny_train=[]\nfor i in range(60,len(train_data)):\n x_train.append(train_data[i-60:i,0])\n y_train.append(train_data[i,0])\n if i<= 61:\n print(x_train)\n print(y_train)\n print()", "[array([0.48762909, 0.3443299 , 0.7089351 , 0.54501739, 0.48419273,\n 0.62714796, 0.52817896, 0.53402082, 0.31443316, 0.26838513,\n 0.51993136, 0.52542975, 0.28934737, 0.54158099, 0.24261169,\n 0.68969118, 0.59312743, 0.51030937, 0.72955363, 0.53264621,\n 0.41374614, 0.38556689, 0.34604822, 0.52886642, 0.35841935,\n 0.52061879, 0.51065308, 0.36872877, 0.63951913, 0.40378019,\n 0.40378047, 0.48900369, 0.57903767, 0.3718217 , 0.39347081,\n 0.39862576, 0.42989711, 0.45463945, 0.43883189, 0.34089354,\n 0.66735409, 0.27353984, 0.33951918, 0.25085905, 0.46460509,\n 0.09896927, 0.70824768, 0.31134023, 0.61924432, 0.42336783,\n 0.4927838 , 0.30068738, 0.50927878, 0.41237126, 0.72577352,\n 0.46391767, 0.50309294, 0.14982823, 0.68866032, 0.39828181])]\n[0.49140918978291176]\n\n[array([0.48762909, 0.3443299 , 0.7089351 , 0.54501739, 0.48419273,\n 0.62714796, 0.52817896, 0.53402082, 0.31443316, 0.26838513,\n 0.51993136, 0.52542975, 0.28934737, 0.54158099, 0.24261169,\n 0.68969118, 0.59312743, 0.51030937, 0.72955363, 0.53264621,\n 0.41374614, 0.38556689, 0.34604822, 0.52886642, 0.35841935,\n 0.52061879, 0.51065308, 0.36872877, 0.63951913, 0.40378019,\n 0.40378047, 0.48900369, 0.57903767, 0.3718217 , 0.39347081,\n 0.39862576, 0.42989711, 0.45463945, 0.43883189, 0.34089354,\n 0.66735409, 0.27353984, 0.33951918, 0.25085905, 0.46460509,\n 0.09896927, 0.70824768, 0.31134023, 0.61924432, 0.42336783,\n 0.4927838 , 0.30068738, 0.50927878, 0.41237126, 0.72577352,\n 0.46391767, 0.50309294, 0.14982823, 0.68866032, 0.39828181]), array([0.3443299 , 0.7089351 , 0.54501739, 0.48419273, 0.62714796,\n 0.52817896, 0.53402082, 0.31443316, 0.26838513, 0.51993136,\n 0.52542975, 0.28934737, 0.54158099, 0.24261169, 0.68969118,\n 0.59312743, 0.51030937, 0.72955363, 0.53264621, 0.41374614,\n 0.38556689, 0.34604822, 0.52886642, 0.35841935, 0.52061879,\n 0.51065308, 0.36872877, 0.63951913, 0.40378019, 0.40378047,\n 0.48900369, 0.57903767, 0.3718217 , 0.39347081, 0.39862576,\n 0.42989711, 0.45463945, 0.43883189, 0.34089354, 0.66735409,\n 0.27353984, 0.33951918, 0.25085905, 0.46460509, 0.09896927,\n 0.70824768, 0.31134023, 0.61924432, 0.42336783, 0.4927838 ,\n 0.30068738, 0.50927878, 0.41237126, 0.72577352, 0.46391767,\n 0.50309294, 0.14982823, 0.68866032, 0.39828181, 0.49140919])]\n[0.49140918978291176, 0.24845378818158445]\n\n" ], [ "x_train,y_train = np.array(x_train),np.array(y_train)", "_____no_output_____" ], [ "x_train=np.reshape(x_train,(x_train.shape[0],x_train.shape[1],1))\nx_train.shape", "_____no_output_____" ], [ "from keras.models import Sequential\nfrom keras.layers import Dense, LSTM\nmodel = Sequential()\nmodel.add(LSTM(50,return_sequences=True, input_shape=(x_train.shape[1],1)))\nmodel.add(LSTM(50,return_sequences=False))\nmodel.add(Dense(25))\nmodel.add(Dense(1))", "Using TensorFlow backend.\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:526: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n _np_qint8 = np.dtype([(\"qint8\", np.int8, 1)])\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:527: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n _np_quint8 = np.dtype([(\"quint8\", np.uint8, 1)])\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:528: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n _np_qint16 = np.dtype([(\"qint16\", np.int16, 1)])\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:529: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n _np_quint16 = np.dtype([(\"quint16\", np.uint16, 1)])\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:530: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n _np_qint32 = np.dtype([(\"qint32\", np.int32, 1)])\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\framework\\dtypes.py:535: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.\n np_resource = np.dtype([(\"resource\", np.ubyte, 1)])\n" ], [ "model.compile(optimizer=\"adam\",loss=\"mean_squared_error\")", "_____no_output_____" ], [ "model.fit(x_train,y_train,batch_size=1,epochs=1)", "WARNING:tensorflow:From C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\tensorflow\\python\\ops\\math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\nInstructions for updating:\nUse tf.cast instead.\nEpoch 1/1\n87/87 [==============================] - 7s 83ms/step - loss: 0.0229\n" ], [ "test_data = scaled_data[training_data_len - 60:,:]\nx_test =[]\ny_test = dataset[training_data_len:,:]\nfor i in range(60,len(test_data)):\n x_test.append(test_data[i-60:i,0])", "_____no_output_____" ], [ "x_test = np.array(x_test)\nprint(x_test.shape)\nx_test = np.reshape(x_test,(x_test.shape[0],x_test.shape[1],1))\nprint(x_test.shape)", "(36, 60)\n(36, 60, 1)\n" ], [ "predictions = model.predict(x_test)\npredictions = scaler.inverse_transform(predictions)", "_____no_output_____" ], [ "rmse = np.sqrt(np.mean(predictions - y_test)**2)\nrmse", "_____no_output_____" ], [ "train = data[:training_data_len]\nvalid = data[training_data_len:]\nvalid['predictions'] = predictions\nplt.figure(figsize=(16,6))\nplt.title('model')\nplt.xlabel('Date' , fontsize=18)\nplt.ylabel('Close price' , fontsize=18)\nplt.plot(train['Close'],color = 'black',linewidth=4)\nplt.plot(valid['Close'],color = 'red',linewidth=4)\nplt.grid()\nax = plt.axes()\nax.set_facecolor(\"orange\")", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:3: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy\n This is separate from the ipykernel package so we can avoid doing imports until\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:11: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n # This is added back by InteractiveShellApp.init_path()\n" ], [ "x = df.values\nx.size", "_____no_output_____" ], [ "train = x[0:150]\ntest = x[150:]", "_____no_output_____" ], [ "train,test", "_____no_output_____" ], [ "predictions=[]", "_____no_output_____" ], [ "from statsmodels.tsa.ar_model import AR\nfrom sklearn.metrics import mean_squared_error\nmodel_ar = AR(train)\nmodel_ar_fit = model_ar.fit()", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\ar_model.py:691: FutureWarning: \nstatsmodels.tsa.AR has been deprecated in favor of statsmodels.tsa.AutoReg and\nstatsmodels.tsa.SARIMAX.\n\nAutoReg adds the ability to specify exogenous variables, include time trends,\nand add seasonal dummies. The AutoReg API differs from AR since the model is\ntreated as immutable, and so the entire specification including the lag\nlength must be specified when creating the model. This change is too\nsubstantial to incorporate into the existing AR api. The function\nar_select_order performs lag length selection for AutoReg models.\n\nAutoReg only estimates parameters using conditional MLE (OLS). Use SARIMAX to\nestimate ARX and related models using full MLE via the Kalman Filter.\n\nTo silence this warning and continue using AR until it is removed, use:\n\nimport warnings\nwarnings.filterwarnings('ignore', 'statsmodels.tsa.ar_model.AR', FutureWarning)\n\n warnings.warn(AR_DEPRECATION_WARN, FutureWarning)\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\base\\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency W-MON will be used.\n % freq, ValueWarning)\n" ], [ "AR_prediction=model_ar_fit.predict(start =120, end =154)\nAR_prediction", "_____no_output_____" ], [ "model_ar_fit.summary()", "_____no_output_____" ], [ "train = data[:training_data_len]\nvalid = data[training_data_len:]\nvalid['AR_predictions'] = AR_prediction\nplt.plot(train,color = 'black',linewidth=4)\nplt.plot(valid,color = 'Red',linewidth=4)\nplt.title(\"Train vs AR_Predictions\")\nplt.grid()\nax = plt.axes()\nax.set_facecolor(\"orange\")", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:3: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy\n This is separate from the ipykernel package so we can avoid doing imports until\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:8: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n \n" ], [ "from statsmodels.tsa.arima_model import ARIMA\nmodel_arima = ARIMA(train,order=(3,1,1))\nmodel_arima_fit = model_arima.fit()\nmodel_arima_fit", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\base\\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency W-MON will be used.\n % freq, ValueWarning)\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\base\\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency W-MON will be used.\n % freq, ValueWarning)\n" ], [ "pred = model_arima_fit.forecast(steps=36)[0]\npred", "_____no_output_____" ], [ "model_arima_fit.summary()", "_____no_output_____" ], [ "len(train),len(valid)", "_____no_output_____" ], [ "len(pred)", "_____no_output_____" ], [ "train = data[:training_data_len]\nvalid = data[training_data_len:]\nvalid['ARIMA_predictions'] = pred\nplt.plot(train,color = 'black',linewidth=4)\nplt.plot(valid,color = 'Red',linewidth=4)\nplt.title(\"Train vs ARIMA_Predictions\")\nplt.grid()\nax = plt.axes()\nax.set_facecolor(\"orange\")", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:3: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy\n This is separate from the ipykernel package so we can avoid doing imports until\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:8: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n \n" ], [ "from statsmodels.tsa.statespace.sarimax import SARIMAX \n \nmodel_sarimax = SARIMAX(train, order = (1, 1, 1), seasonal_order =(2, 1, 1, 12)) \n\nmodel_sarimax_fit = model_sarimax.fit()", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\base\\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency W-MON will be used.\n % freq, ValueWarning)\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\base\\tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency W-MON will be used.\n % freq, ValueWarning)\n" ], [ "sr_pred = model_sarimax_fit.predict(start =151, end =186,typ = 'levels',dynamic =True)\nlen(sr_pred)", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\statsmodels\\tsa\\statespace\\kalman_filter.py:2014: ValueWarning: Dynamic prediction specified to begin during out-of-sample forecasting period, and so has no effect.\n ' effect.', ValueWarning)\n" ], [ "model_sarimax_fit.summary()", "_____no_output_____" ], [ "train = data[:training_data_len]\nvalid = data[training_data_len:]\nvalid['SARIMAX_predictions'] = sr_pred\nplt.plot(train,color = 'black',linewidth=4)\nplt.plot(valid,color = 'Red',linewidth=4)\nplt.title(\"Train vs SARIMAX_predictions\")\nplt.grid()\nax = plt.axes()\nax.set_facecolor(\"orange\")", "C:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:3: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame.\nTry using .loc[row_indexer,col_indexer] = value instead\n\nSee the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy\n This is separate from the ipykernel package so we can avoid doing imports until\nC:\\Users\\DELL\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:8: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n \n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e6cdb7c704e2ac49b0b58d75edf923035ef169

5,017

ipynb

Jupyter Notebook

notebooks/Lidar_comparison_AGU_2019/ERW_snow_on.ipynb

jomey/raster_compare

5199005d01f569e187e944d62af0ea70c383d16a

[ "MIT" ]

1

2021-11-13T12:59:53.000Z

notebooks/Lidar_comparison_AGU_2019/ERW_snow_on.ipynb

jomey/raster_compare

5199005d01f569e187e944d62af0ea70c383d16a

[ "MIT" ]

null

notebooks/Lidar_comparison_AGU_2019/ERW_snow_on.ipynb

jomey/raster_compare

5199005d01f569e187e944d62af0ea70c383d16a

[ "MIT" ]

null

25.596939

101

0.565876

[ [ [ "## Swow On and Free Scenes", "_____no_output_____" ] ], [ [ "from plot_helpers import *\n\nplt.style.use('fivethirtyeight')", "_____no_output_____" ], [ "casi_data = PixelClassifier(CASI_DATA, CLOUD_MASK, VEGETATION_MASK)\nhillshade = RasterFile(HILLSHADE, band_number=1).band_values()\n\nsnow_on_diff_data = RasterFile(SNOW_ON_DIFF, band_number=1)\nband_values_snow_on_diff = snow_on_diff_data.band_values()\nband_values_snow_on_diff_mask = band_values_snow_on_diff.mask.copy()\n\nsnow_free_diff_data = RasterFile(SNOW_FREE_DIFF, band_number=1)\nband_values_snow_free_diff = snow_free_diff_data.band_values()\nband_values_snow_free_diff_mask = band_values_snow_free_diff.mask.copy()", "_____no_output_____" ] ], [ [ "## Snow Pixels comparison", "_____no_output_____" ] ], [ [ "band_values_snow_free_diff.mask = casi_data.snow_surfaces(band_values_snow_free_diff_mask)\nband_values_snow_on_diff.mask = casi_data.snow_surfaces(band_values_snow_on_diff_mask)\n\nax = box_plot_compare(\n [\n band_values_snow_free_diff,\n band_values_snow_on_diff,\n ],\n [\n 'SfM Bare Ground\\n- Lidar Bare Ground', \n 'SfM Snow\\n- Lidar Snow', \n ],\n)\nax.set_ylabel('$\\Delta$ Elevation (m)')\nax.set_ylim([-1, 1]);", "_____no_output_____" ], [ "color_map = LinearSegmentedColormap.from_list(\n 'snow_pixels',\n ['royalblue', 'none'],\n N=2\n)\n\nplt.figure(figsize=(6,6), dpi=150)\nplt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)\nplt.imshow(\n band_values_snow_on_diff.mask,\n cmap=color_map,\n)\nset_axes_style(plt.gca())\nplt.xticks([])\nplt.yticks([]);", "_____no_output_____" ] ], [ [ "## Stable Ground", "_____no_output_____" ] ], [ [ "lidar_data = RasterFile(LIDAR_SNOW_DEPTH, band_number=1)\nband_values_lidar = lidar_data.band_values()\n\nsfm_data = RasterFile(SFM_SNOW_DEPTH, band_number=1)\nband_values_sfm = sfm_data.band_values()", "_____no_output_____" ], [ "band_values_lidar.mask = casi_data.stable_surfaces(band_values_lidar.mask)\nband_values_sfm.mask = casi_data.stable_surfaces(band_values_sfm.mask)\nband_values_snow_on_diff.mask = casi_data.stable_surfaces(band_values_snow_on_diff_mask)\nband_values_snow_free_diff.mask = casi_data.stable_surfaces(band_values_snow_free_diff_mask)\n\ndata_sources = [\n band_values_lidar,\n band_values_sfm,\n band_values_snow_on_diff,\n band_values_snow_free_diff,\n]\n\nlabels=[\n 'Lidar Snow\\n Depth',\n 'SfM Snow\\n Depth',\n 'Snow On\\n Scenes',\n 'Bare Ground\\n Scenes',\n]\n\nax = box_plot_compare(data_sources, labels)\n\nax.set_ylim([-1.2, 1.2]);", "_____no_output_____" ], [ "color_map = LinearSegmentedColormap.from_list(\n 'snow_pixels',\n ['sienna', 'none'],\n N=2\n)\n\n\nplt.figure(figsize=(6,6), dpi=150)\nplt.imshow(hillshade, cmap='gray', clim=(1, 255), alpha=0.5)\nplt.imshow(\n band_values_snow_on_diff.mask,\n cmap=color_map,\n)\nset_axes_style(plt.gca())\nplt.xticks([])\nplt.yticks([]);", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

d0e6d8eb4814e807b3472da02a44ca55529f9e0e

3,472

ipynb

Jupyter Notebook

benchmark and comparison/pigeonhole_optimization_comparison.ipynb

MossGoblin/crystal_sort

eba57f0863f3e7a7dea67b5b3190d1cd671753b3

[ "MIT" ]

1

2021-06-08T11:36:06.000Z

benchmark and comparison/pigeonhole_optimization_comparison.ipynb

MossGoblin/crystal_sort

eba57f0863f3e7a7dea67b5b3190d1cd671753b3

[ "MIT" ]

null

benchmark and comparison/pigeonhole_optimization_comparison.ipynb

MossGoblin/crystal_sort

eba57f0863f3e7a7dea67b5b3190d1cd671753b3

[ "MIT" ]

null

24.624113

165

0.542051

[ [ [ "import numpy as np\nfrom datetime import datetime\nimport crystal_sort\nimport math", "_____no_output_____" ], [ "def get_rand_set(min: int, max: int, size: int):\n set = np.random.randint(min, max, size=size)\n set = set.tolist()\n return set", "_____no_output_____" ], [ "min = 0\nmax = 10000\nsize = 10000", "_____no_output_____" ], [ "input_bucket = get_rand_set(min, max, size)", "_____no_output_____" ], [ "start_sort_nopgh = datetime.utcnow()\noutput_bucket_nopgh = crystal_sort.sort(input_bucket, False)\nend_sort_nopgh = datetime.utcnow()", "_____no_output_____" ], [ "start_sort_pgh = datetime.utcnow()\noutput_bucket_pgh = crystal_sort.sort(input_bucket, True)\nend_sort_pgh = datetime.utcnow()", "_____no_output_____" ], [ "if output_bucket_pgh == sorted(input_bucket) and output_bucket_nopgh == sorted(input_bucket):\n nophg_time = end_sort_nopgh - start_sort_nopgh\n phg_time = end_sort_pgh - start_sort_pgh\n mag = max - min\n size_str = str(size)\n mag_str = str(mag)\n if len(mag_str) > len(size_str):\n padding = len(mag_str)\n else:\n padding = len(size_str)\n size_str = size_str.rjust(padding + len('value mag: '))\n mag_str = mag_str.rjust(padding + len('size: '))\n print(f'size: {size_str}')\n print(f'value mag: {mag_str}')\n print(f'(values: {min}..{max})')\n print('without / with pigeonhole optimization ')\n print(f'time: {nophg_time} / {phg_time} ({phg_time / nophg_time * 100:.2f} %)')\nelse:\n print('FAIL')", "size: 10000\nvalue mag: 10000\n(values: 0..10000)\nwithout / with pigeonhole optimization \ntime: 0:00:02.218382 / 0:00:00.005002 (0.23 %)\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ] ]

d0e6df7b87a6916f828dd2d3b7e29a62a4ad5d44

89,993

ipynb

Jupyter Notebook

.ipynb_checkpoints/Tutorial-checkpoint.ipynb

nuriale207/preprocesspack

cc06a9cb79c5e3b392371fcd8d1ccf7185e71821

[ "MIT" ]

null

.ipynb_checkpoints/Tutorial-checkpoint.ipynb

nuriale207/preprocesspack

cc06a9cb79c5e3b392371fcd8d1ccf7185e71821

[ "MIT" ]

null

.ipynb_checkpoints/Tutorial-checkpoint.ipynb

nuriale207/preprocesspack

cc06a9cb79c5e3b392371fcd8d1ccf7185e71821

[ "MIT" ]

null

89.27877

19,196

0.752825

[ [ [ "This tutorial provides simple examples to learn how to use the functions provided by Preprocesspack package. First we are going to load the modules needed.", "_____no_output_____" ] ], [ [ "from preprocesspack import utils, Attribute, DataSet, graphics", "_____no_output_____" ] ], [ [ "First we are going to create an Attribute object. There are several ways of creating an object. In this example we have created three Attributes.", "_____no_output_____" ] ], [ [ "attr=Attribute.Attribute(name=\"age\",vector=[34,16,78,90,12])\nattrContinuous=Attribute.Attribute(name=\"mark\",vector=[1.2,3.4,6.7,8.9,4.7])\nattrPass=Attribute.Attribute(name=\"pass\",vector=[0,0,1,1,0])\n\nattr.printAttribute()", "age\n34\n16\n78\n90\n12\n" ] ], [ [ "\nTo create a DataSet we can add a previously defined attribute or pass a vector. The name of each column will be the attribute name.", "_____no_output_____" ] ], [ [ "ds=DataSet.DataSet([],name=\"Students\")\nds.addAttribute(attr)\nds.addAttribute(attrContinuous)\nds.addAttribute(attrPass)\nds.printDataSet()", "age \tmark \tpass \t\n34\t\t1.2\t\t0\t\t\n16\t\t3.4\t\t0\t\t\n78\t\t6.7\t\t1\t\t\n90\t\t8.9\t\t1\t\t\n12\t\t4.7\t\t0\t\t\n\n" ] ], [ [ "From now on the tutorial will focus in how to use the preprocesspack in an external DataSet. We will use a DataSet called wine data that includes the information (alcohol quantity, color intensity, magnesium...) of two wine types. In this step we have loaded the data from a csv file using loadDataSet function. This function loads the csv file content into a DataSet. In this example the loaded file is separated by , and the first row works as the column name for the file.", "_____no_output_____" ] ], [ [ "wineData=DataSet.loadDataSet(\"wine_data_reduced.csv\")\nwineData.printDataSet()", "Class \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t14.23\t\t1.71\t\t2.43\t\t15.6\t\t127\t\t2.8\t\t\n0\t\t13.2\t\t1.78\t\t2.14\t\t11.2\t\t100\t\t2.65\t\t\n0\t\t13.16\t\t2.36\t\t2.67\t\t18.6\t\t101\t\t2.8\t\t\n0\t\t14.37\t\t1.95\t\t2.5\t\t16.8\t\t113\t\t3.85\t\t\n0\t\t13.24\t\t2.59\t\t2.87\t\t21.0\t\t118\t\t2.8\t\t\n0\t\t14.2\t\t1.76\t\t2.45\t\t15.2\t\t112\t\t3.27\t\t\n0\t\t14.39\t\t1.87\t\t2.45\t\t14.6\t\t96\t\t2.5\t\t\n0\t\t14.06\t\t2.15\t\t2.61\t\t17.6\t\t121\t\t2.6\t\t\n0\t\t14.83\t\t1.64\t\t2.17\t\t14.0\t\t97\t\t2.8\t\t\n0\t\t13.86\t\t1.35\t\t2.27\t\t16.0\t\t98\t\t2.98\t\t\n0\t\t14.1\t\t2.16\t\t2.3\t\t18.0\t\t105\t\t2.95\t\t\n0\t\t14.12\t\t1.48\t\t2.32\t\t16.8\t\t95\t\t2.2\t\t\n0\t\t13.75\t\t1.73\t\t2.41\t\t16.0\t\t89\t\t2.6\t\t\n0\t\t14.75\t\t1.73\t\t2.39\t\t11.4\t\t91\t\t3.1\t\t\n0\t\t14.38\t\t1.87\t\t2.38\t\t12.0\t\t102\t\t3.3\t\t\n0\t\t13.63\t\t1.81\t\t2.7\t\t17.2\t\t112\t\t2.85\t\t\n0\t\t14.3\t\t1.92\t\t2.72\t\t20.0\t\t120\t\t2.8\t\t\n0\t\t13.83\t\t1.57\t\t2.62\t\t20.0\t\t115\t\t2.95\t\t\n0\t\t14.19\t\t1.59\t\t2.48\t\t16.5\t\t108\t\t3.3\t\t\n0\t\t13.64\t\t3.1\t\t2.56\t\t15.2\t\t116\t\t2.7\t\t\n1\t\t12.37\t\t0.94\t\t1.36\t\t10.6\t\t88\t\t1.98\t\t\n1\t\t12.33\t\t1.1\t\t2.28\t\t16.0\t\t101\t\t2.05\t\t\n1\t\t12.64\t\t1.36\t\t2.02\t\t16.8\t\t100\t\t2.02\t\t\n1\t\t13.67\t\t1.25\t\t1.92\t\t18.0\t\t94\t\t2.1\t\t\n1\t\t12.37\t\t1.13\t\t2.16\t\t19.0\t\t87\t\t3.5\t\t\n1\t\t12.17\t\t1.45\t\t2.53\t\t19.0\t\t104\t\t1.89\t\t\n1\t\t12.37\t\t1.21\t\t2.56\t\t18.1\t\t98\t\t2.42\t\t\n1\t\t13.11\t\t1.01\t\t1.7\t\t15.0\t\t78\t\t2.98\t\t\n1\t\t12.37\t\t1.17\t\t1.92\t\t19.6\t\t78\t\t2.11\t\t\n1\t\t13.34\t\t0.94\t\t2.36\t\t17.0\t\t110\t\t2.53\t\t\n1\t\t12.21\t\t1.19\t\t1.75\t\t16.8\t\t151\t\t1.85\t\t\n1\t\t12.29\t\t1.61\t\t2.21\t\t20.4\t\t103\t\t1.1\t\t\n1\t\t13.86\t\t1.51\t\t2.67\t\t25.0\t\t86\t\t2.95\t\t\n1\t\t13.49\t\t1.66\t\t2.24\t\t24.0\t\t87\t\t1.88\t\t\n1\t\t12.99\t\t1.67\t\t2.6\t\t30.0\t\t139\t\t3.3\t\t\n1\t\t11.96\t\t1.09\t\t2.3\t\t21.0\t\t101\t\t3.38\t\t\n1\t\t11.66\t\t1.88\t\t1.92\t\t16.0\t\t97\t\t1.61\t\t\n1\t\t13.03\t\t0.9\t\t1.71\t\t16.0\t\t86\t\t1.95\t\t\n1\t\t11.84\t\t2.89\t\t2.23\t\t18.0\t\t112\t\t1.72\t\t\n1\t\t12.33\t\t0.99\t\t1.95\t\t14.8\t\t136\t\t1.9\t\t\n1\t\t12.7\t\t3.87\t\t2.4\t\t23.0\t\t101\t\t2.83\t\t\n\n" ] ], [ [ "The first step with this DataSet will be to discretize the Alcohol and Magnesium columns of the data, as it can be easily noticed that both can be divided into three intervals. DataSet and Attribute objects can be discretized using the function discretize. This function computes two types of discretization: on the one hand, by assigning the \"EW\" value to the type parameter equal width discretization is computed. On the other hand, assigning \"EF\" value to the parameter computes equal width discretization. Num.bins parameter indicates how many intervals are going to be made. In the following example we will compute an equal width discretization of the both columns (2 and 6). Moreover, we will compute an Equal Frecuency discretization in the last attribute, using num.bins=5", "_____no_output_____" ] ], [ [ "\nwineData=wineData.discretize(3,\"EW\",[1,5])\nwineData=wineData.discretize(5,\"EF\",[6])\nwineData.printDataSet()", "8\n16\n24\n32\n40\nClass \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t(13.773333333333333, inf)\t\t1.71\t\t2.43\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.78\t\t2.14\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.36\t\t2.67\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.95\t\t2.5\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.59\t\t2.87\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.76\t\t2.45\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.45\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.15\t\t2.61\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.64\t\t2.17\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.35\t\t2.27\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.16\t\t2.3\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.48\t\t2.32\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.73\t\t2.41\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.73\t\t2.39\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.38\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.81\t\t2.7\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.92\t\t2.72\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.57\t\t2.62\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.59\t\t2.48\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t3.1\t\t2.56\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.94\t\t1.36\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.1\t\t2.28\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.36\t\t2.02\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.25\t\t1.92\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.13\t\t2.16\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.45\t\t2.53\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.21\t\t2.56\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.01\t\t1.7\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.17\t\t1.92\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.94\t\t2.36\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.19\t\t1.75\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.61\t\t2.21\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(13.773333333333333, inf)\t\t1.51\t\t2.67\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.66\t\t2.24\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.67\t\t2.6\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.09\t\t2.3\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.88\t\t1.92\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.9\t\t1.71\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t2.89\t\t2.23\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.99\t\t1.95\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t3.87\t\t2.4\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "Single attributes can also be discretized:\n", "_____no_output_____" ] ], [ [ "attr=Attribute.Attribute(name=\"age\",vector=[34,16,78,90,12])\nage_category=attr.discretize(2,\"EW\")\nage_category.printAttribute()\n", "age\n(-inf, 51.0)\n(-inf, 51.0)\n(51.0, inf)\n(51.0, inf)\n(-inf, 51.0)\n" ] ], [ [ "The function normalize is used to normalize the data or an attribute. When applied to a DataSet, columns parameter indicate to which columns the normalization have to be applied. In this case I will apply it to the following columns: 2,3,4,6. ", "_____no_output_____" ] ], [ [ "wineDataNormalized=wineData.normalize([2,3,4,6])\nwineDataNormalized.printDataSet()", "Class \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t(13.773333333333333, inf)\t\t1.71\t\t2.43\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.78\t\t2.14\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.36\t\t2.67\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.95\t\t2.5\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.59\t\t2.87\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.76\t\t2.45\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.45\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.15\t\t2.61\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.64\t\t2.17\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.35\t\t2.27\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.16\t\t2.3\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.48\t\t2.32\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.73\t\t2.41\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.73\t\t2.39\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.38\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.81\t\t2.7\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.92\t\t2.72\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.57\t\t2.62\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.59\t\t2.48\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t3.1\t\t2.56\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.94\t\t1.36\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.1\t\t2.28\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.36\t\t2.02\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.25\t\t1.92\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.13\t\t2.16\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.45\t\t2.53\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.21\t\t2.56\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.01\t\t1.7\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.17\t\t1.92\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.94\t\t2.36\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.19\t\t1.75\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.61\t\t2.21\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(13.773333333333333, inf)\t\t1.51\t\t2.67\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.66\t\t2.24\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.67\t\t2.6\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.09\t\t2.3\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.88\t\t1.92\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.9\t\t1.71\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t2.89\t\t2.23\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.99\t\t1.95\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t3.87\t\t2.4\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "If the columns parameter is empty and the normalize function is applied to the hole DataSet it will return the original attribute if applied to categorical attributes and will normalize the rest.", "_____no_output_____" ] ], [ [ "wineDataNormalized=wineData.normalize()\nwineDataNormalized.printDataSet()", "Class \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t(13.773333333333333, inf)\t\t1.71\t\t2.43\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.78\t\t2.14\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.36\t\t2.67\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.95\t\t2.5\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.59\t\t2.87\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.76\t\t2.45\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.45\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.15\t\t2.61\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.64\t\t2.17\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.35\t\t2.27\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.16\t\t2.3\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.48\t\t2.32\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.73\t\t2.41\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.73\t\t2.39\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.38\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.81\t\t2.7\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.92\t\t2.72\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.57\t\t2.62\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.59\t\t2.48\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t3.1\t\t2.56\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.94\t\t1.36\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.1\t\t2.28\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.36\t\t2.02\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.25\t\t1.92\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.13\t\t2.16\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.45\t\t2.53\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.21\t\t2.56\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.01\t\t1.7\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.17\t\t1.92\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.94\t\t2.36\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.19\t\t1.75\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.61\t\t2.21\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(13.773333333333333, inf)\t\t1.51\t\t2.67\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.66\t\t2.24\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.67\t\t2.6\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.09\t\t2.3\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.88\t\t1.92\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.9\t\t1.71\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t2.89\t\t2.23\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.99\t\t1.95\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t3.87\t\t2.4\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "Single attributes can also be normalized. If the attribute is categorical the result will be the original attribute", "_____no_output_____" ] ], [ [ "attrNorm=attrContinuous.normalize()\nattrNorm.printAttribute()\n\nattrNorm=age_category.normalize()\nattrNorm.printAttribute()\n", "mark\n0.0\n1.8333333333333335\n4.583333333333334\n6.416666666666667\n2.916666666666667\nage\n(-inf, 51.0)\n(-inf, 51.0)\n(51.0, inf)\n(51.0, inf)\n(-inf, 51.0)\n" ] ], [ [ "To standardize the data or an attribute the function standardize can be used. When applied to a DataSet, columns parameter indicate to which columns the normalization have to be applied. In this case I will apply it to the following columns: 2,3,4,6.\n", "_____no_output_____" ] ], [ [ "wineDataStandardized=wineData.standardize([2,3,4,6])\nwineDataStandardized.printDataSet()", "Class \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t(13.773333333333333, inf)\t\t1.71\t\t2.43\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.78\t\t2.14\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.36\t\t2.67\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.95\t\t2.5\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.59\t\t2.87\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.76\t\t2.45\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.45\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.15\t\t2.61\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.64\t\t2.17\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.35\t\t2.27\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.16\t\t2.3\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.48\t\t2.32\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.73\t\t2.41\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.73\t\t2.39\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.38\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.81\t\t2.7\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.92\t\t2.72\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.57\t\t2.62\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.59\t\t2.48\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t3.1\t\t2.56\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.94\t\t1.36\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.1\t\t2.28\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.36\t\t2.02\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.25\t\t1.92\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.13\t\t2.16\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.45\t\t2.53\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.21\t\t2.56\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.01\t\t1.7\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.17\t\t1.92\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.94\t\t2.36\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.19\t\t1.75\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.61\t\t2.21\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(13.773333333333333, inf)\t\t1.51\t\t2.67\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.66\t\t2.24\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.67\t\t2.6\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.09\t\t2.3\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.88\t\t1.92\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.9\t\t1.71\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t2.89\t\t2.23\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.99\t\t1.95\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t3.87\t\t2.4\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "If the columns parameter is empty and the standardize function is applied to the hole DataSet it will return the original attribute if applied to categorical attributes and will standardize the rest.", "_____no_output_____" ] ], [ [ "wineDataStandardized=wineData.standardize()\nwineDataStandardized.printDataSet()", "Class \tAlcohol \tMalid ac\tAsh \tAlcalini\tMagnesiu\t Total p\t\n0\t\t(13.773333333333333, inf)\t\t1.71\t\t2.43\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.78\t\t2.14\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.36\t\t2.67\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.95\t\t2.5\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t2.59\t\t2.87\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.76\t\t2.45\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.45\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.15\t\t2.61\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.64\t\t2.17\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.35\t\t2.27\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t2.16\t\t2.3\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.48\t\t2.32\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.73\t\t2.41\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.73\t\t2.39\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.87\t\t2.38\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t1.81\t\t2.7\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.92\t\t2.72\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.57\t\t2.62\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(13.773333333333333, inf)\t\t1.59\t\t2.48\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n0\t\t(12.716666666666667, 13.773333333333333)\t\t3.1\t\t2.56\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.94\t\t1.36\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.1\t\t2.28\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.36\t\t2.02\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.25\t\t1.92\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.13\t\t2.16\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.45\t\t2.53\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.21\t\t2.56\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.01\t\t1.7\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.17\t\t1.92\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.94\t\t2.36\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.19\t\t1.75\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.61\t\t2.21\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(13.773333333333333, inf)\t\t1.51\t\t2.67\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.66\t\t2.24\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t1.67\t\t2.6\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.09\t\t2.3\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t1.88\t\t1.92\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(12.716666666666667, 13.773333333333333)\t\t0.9\t\t1.71\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t2.89\t\t2.23\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t0.99\t\t1.95\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n1\t\t(-inf, 12.716666666666667)\t\t3.87\t\t2.4\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "Single attributes can also be standardized. If the attribute is categorical the result will be the original attribute", "_____no_output_____" ] ], [ [ "attrStd=attrContinuous.standardize()\nattrStd.printAttribute()\n\nattrStd=age_category.standardize()\nattrStd.printAttribute()\n", "mark\n-1.4248840017881383\n-0.5955864346098569\n0.6483599161575655\n1.4776574833358471\n-0.10554696309541775\nage\n(-inf, 51.0)\n(-inf, 51.0)\n(51.0, inf)\n(51.0, inf)\n(-inf, 51.0)\n" ] ], [ [ "Entropy function computes the entropy of an Attribute or a complete DataSet. In the case of continuous variables it returns None. The entropy of a given DataSet can be plotted using the entropyPlot function. In the following example we have computed the entropy of the Wine Data dataset, as there are only 4 categorical or discrete variables we have only 4 results.", "_____no_output_____" ] ], [ [ "print(str(wineData.entropy()))\ngraphics.entropyPlot(wineData)", "[0.9995708393473224, 1.5788720570183736, None, None, None, 1.3247497144200895, 1.4552137931890252]\n" ] ], [ [ "The entropy of single attributes can also be computed. If the attribute is not categorical the result will be None.", "_____no_output_____" ] ], [ [ "print(attrContinuous.entropy())\nprint (age_category.entropy())", "None\n0.9709505944546686\n" ] ], [ [ "The package also includes a function to compute the variance of a DataDet or an Attribute. The variance function returns a vector with the variance of each column of the DataSet or a value in the case of the Attribute. If the attribute is a factor it will return None.", "_____no_output_____" ] ], [ [ "print(wineData.variance())", "[0.2498512790005949, None, 0.37029541939321836, 0.10231171921475313, 13.642629387269485, None, None]\n" ] ], [ [ "The variance function can also be applied to Attributes.\n", "_____no_output_____" ] ], [ [ "print(attrContinuous.variance())\nprint (age_category.variance())", "7.0376\nNone\n" ] ], [ [ "In order to analyze the relation between the data, the correlation function computes the correlation between the Attribute pairs of a DataSet. It calculates the correlation matrix between continuous variables and the mutual information between categorical ones. In the case where one of the variables is categorical and the other one discrete a discretization is computed in the continuous one. The parameters of the correlation function are the DataSet, num.bins and discretizationType. The default value of the last two is 3 and \"EW\". In the following example the correlation between the standardized wineData DataSet is computed.\n", "_____no_output_____" ] ], [ [ "print(wineDataStandardized.correlation())", "[[ 1. 0.40036882 -0.360096 -0.52998158 0.34937507 0.0582239\n 0.10514007]\n [ 0.40036882 1.09439071 0.10264858 0.12943356 0.0694872 0.02751501\n 0.1561628 ]\n [-0.360096 0.10264858 1. 0.48744897 0.17908969 0.12763826\n 0.10179586]\n [-0.52998158 0.12943356 0.48744897 1. 0.39673597 0.0910056\n 0.11043564]\n [ 0.34937507 0.0694872 0.17908969 0.39673597 1. 0.12342519\n 0.0645761 ]\n [ 0.0582239 0.02751501 0.12763826 0.0910056 0.12342519 0.91824653\n 0.01192319]\n [ 0.10514007 0.1561628 0.10179586 0.11043564 0.0645761 0.01192319\n 1.00867734]]\n" ] ], [ [ "With the correlationPlot function the correlation can be displayed graphically. The plot type used for that is a HeatMap that is darker where the correlation between the Attributes is higher.", "_____no_output_____" ] ], [ [ " graphics.correlationPlot(wineDataStandardized)", "_____no_output_____" ] ], [ [ "Another useful function of this package is the filter function. This function removes from the data the attributes with a correlation above the given threshold. If a function is passed through FUN parameter is given the filter function will apply the function to the data and remove the attributes that have a higher score than the threshold for the given function. Inverse parameter indicates whether the attributes have to be behind the thresshold in order to be removed, its default value is False. In the following example, first the attributes with a correlation higher than 0.4 are removed: Class.\n", "_____no_output_____" ] ], [ [ "filteredWineData=wineDataStandardized.filter(0.4)\nfilteredWineData.printDataSet()", "Alcohol \tMalid ac\tAlcalini\tMagnesiu\t Total p\t\n(13.773333333333333, inf)\t\t1.71\t\t15.6\t\t(126.66666666666666, inf)\t\t(2.8, 3.5)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.78\t\t11.2\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t2.36\t\t18.6\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n(13.773333333333333, inf)\t\t1.95\t\t16.8\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n(12.716666666666667, 13.773333333333333)\t\t2.59\t\t21.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n(13.773333333333333, inf)\t\t1.76\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n(13.773333333333333, inf)\t\t1.87\t\t14.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(13.773333333333333, inf)\t\t2.15\t\t17.6\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(13.773333333333333, inf)\t\t1.64\t\t14.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n(13.773333333333333, inf)\t\t1.35\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(13.773333333333333, inf)\t\t2.16\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n(13.773333333333333, inf)\t\t1.48\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.73\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(13.773333333333333, inf)\t\t1.73\t\t11.4\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(13.773333333333333, inf)\t\t1.87\t\t12.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.81\t\t17.2\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n(13.773333333333333, inf)\t\t1.92\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.8, 3.5)\t\t\n(13.773333333333333, inf)\t\t1.57\t\t20.0\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n(13.773333333333333, inf)\t\t1.59\t\t16.5\t\t(102.33333333333333, 126.66666666666666)\t\t(2.95, inf)\t\t\n(12.716666666666667, 13.773333333333333)\t\t3.1\t\t15.2\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t0.94\t\t10.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.1\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.36\t\t16.8\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.25\t\t18.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.13\t\t19.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(-inf, 12.716666666666667)\t\t1.45\t\t19.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.21\t\t18.1\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.01\t\t15.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(-inf, 12.716666666666667)\t\t1.17\t\t19.6\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t0.94\t\t17.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.19\t\t16.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t1.61\t\t20.4\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(13.773333333333333, inf)\t\t1.51\t\t25.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.66\t\t24.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t1.67\t\t30.0\t\t(126.66666666666666, inf)\t\t(2.95, inf)\t\t\n(-inf, 12.716666666666667)\t\t1.09\t\t21.0\t\t(-inf, 102.33333333333333)\t\t(2.95, inf)\t\t\n(-inf, 12.716666666666667)\t\t1.88\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(12.716666666666667, 13.773333333333333)\t\t0.9\t\t16.0\t\t(-inf, 102.33333333333333)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t2.89\t\t18.0\t\t(102.33333333333333, 126.66666666666666)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t0.99\t\t14.8\t\t(126.66666666666666, inf)\t\t(-inf, 2.8)\t\t\n(-inf, 12.716666666666667)\t\t3.87\t\t23.0\t\t(-inf, 102.33333333333333)\t\t(2.8, 3.5)\t\t\n\n" ] ], [ [ "In the following example the attributes with a variance higher than 2 will be removed. If we compute the variance we see that the attributes that have to be removed are the fifth (Alcalinity of ash) and the 11th one (Color intensity).", "_____no_output_____" ] ], [ [ "import numpy as np\nprint(wineData.variance())\nfilteredWineData=wineData.filter(13,np.mean)\nfilteredWineData.printDataSet()", "[None, 0.37029541939321836, 13.642629387269485, None, None]\n" ] ], [ [ "Using the RocAuc function the area behind the ROC curve can be calculated. The RocAuc function takes as parameters: a DataSet, a variable and a class index and returns the area behind the ROC curve. In order to visualize the curve, the function RocPlot plots the Roc curve of the given variable index. In the example the Iris dataset is loaded and the roc", "_____no_output_____" ] ], [ [ " print(ds.rocAuc(1,2))\ngraphics.rocPlot(ds,1,2)", "-0.6666666666666667\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e6e9d38d3e1716bde84d5ad8fa5e243457f28f

72,128

ipynb

Jupyter Notebook

Jupyter Notebooks/CpG islands Hidden Markov Model.ipynb

thierrygrimm/CpGIslandHMM

ec4258de387e82d19103e426194dedc146aa19fd

[ "MIT" ]

null

Jupyter Notebooks/CpG islands Hidden Markov Model.ipynb

thierrygrimm/CpGIslandHMM

ec4258de387e82d19103e426194dedc146aa19fd

[ "MIT" ]

null

Jupyter Notebooks/CpG islands Hidden Markov Model.ipynb

thierrygrimm/CpGIslandHMM

ec4258de387e82d19103e426194dedc146aa19fd

[ "MIT" ]

1

2022-02-01T15:14:54.000Z

143.395626

31,040

0.873586

[ [ [ "# Modelling CpG islands with Hidden Markov Models", "_____no_output_____" ], [ "<h1>Table of Contents<span class=\"tocSkip\"></span></h1>\n<div class=\"toc\"><ul class=\"toc-item\"><li><span><a href=\"#Introduction\" data-toc-modified-id=\"Introduction-1\"><span class=\"toc-item-num\">1  </span>Introduction</a></span><ul class=\"toc-item\"><li><span><a href=\"#General\" data-toc-modified-id=\"General-1.1\"><span class=\"toc-item-num\">1.1  </span>General</a></span></li><li><span><a href=\"#Viterbi,-Forward/Backward-Algorithm\" data-toc-modified-id=\"Viterbi,-Forward/Backward-Algorithm-1.2\"><span class=\"toc-item-num\">1.2  </span>Viterbi, Forward/Backward Algorithm</a></span></li></ul></li><li><span><a href=\"#Imports\" data-toc-modified-id=\"Imports-2\"><span class=\"toc-item-num\">2  </span>Imports</a></span></li><li><span><a href=\"#Matrices\" data-toc-modified-id=\"Matrices-3\"><span class=\"toc-item-num\">3  </span>Matrices</a></span></li><li><span><a href=\"#Forward-Algorithm\" data-toc-modified-id=\"Forward-Algorithm-4\"><span class=\"toc-item-num\">4  </span>Forward Algorithm</a></span></li><li><span><a href=\"#Backward-Algorithm\" data-toc-modified-id=\"Backward-Algorithm-5\"><span class=\"toc-item-num\">5  </span>Backward Algorithm</a></span></li><li><span><a href=\"#Test-Sequence\" data-toc-modified-id=\"Test-Sequence-6\"><span class=\"toc-item-num\">6  </span>Test Sequence</a></span></li><li><span><a href=\"#Test-Sequence-Modification\" data-toc-modified-id=\"Test-Sequence-Modification-7\"><span class=\"toc-item-num\">7  </span>Test Sequence Modification</a></span></li></ul></div>", "_____no_output_____" ], [ "## Introduction", "_____no_output_____" ], [ "### General", "_____no_output_____" ], [ "We model CpG islands by creating a Hidden Markov Model of the 1st order.\nThe model assumes the presence of two “hidden” states: **CpG island** and **nonCpG island**.", "_____no_output_____" ], [ "We estimate parameters of the model by calculating **transition, emission and initiation** probabilities. For this use sequences from the file “Sequences.txt” with the known location of CpG islands described in the file “Keys.txt”. \n\nEach line of the file “Sequences.txt” corresponds to a single sequence of bases “A”, “T”, “G” and “C”. The file contains 500 sequences in total. \n\nThe file “Keys.txt” specifies states of sequence bases: “+” – the base belongs to a CpG island, “-” – the base does not belong to a CpG island. ", "_____no_output_____" ], [ "Note that in this exercise we do not require that the emission of the base at the\nposition i depends on the base at the position i+1.\n\n\nlook in most probable state for an observation", "_____no_output_____" ], [ "### Viterbi, Forward/Backward Algorithm", "_____no_output_____" ], [ "1. **Transition probability:** go from state k to state l: 𝑎𝑎𝑘𝑘,𝑙𝑙 = 𝑃𝑃(𝜋𝜋𝑖𝑖 = 𝑙𝑙 | 𝜋𝜋𝑖𝑖−1 = 𝑘𝑘) \n\n\n2. **Emission probabilities:** emit a base 𝛽𝛽 at state l: 𝑒𝑒𝑙𝑙(𝛽𝛽) = 𝑃𝑃(𝑥𝑥𝑖𝑖 = 𝛽𝛽 | 𝜋𝜋𝑖𝑖 = 𝑙𝑙) \n\n\n3. **Initiation probability:** genomic sequence starts at certain state (CpG or non-CpG)", "_____no_output_____" ], [ "## Imports", "_____no_output_____" ] ], [ [ "from matplotlib.patches import Rectangle\nimport re\nimport random\nimport pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\n%matplotlib inline", "_____no_output_____" ], [ "transitions = np.zeros((2, 2)) # +- / +-\nemissions = np.zeros((4, 2)) # +- / ACTG\ninitiations = np.zeros((1, 2)) # +- / Probability", "_____no_output_____" ] ], [ [ "## Matrices", "_____no_output_____" ] ], [ [ "sequences = pd.read_csv('Sequences.txt', header=None)[0]\nkeys = pd.read_csv('keys.txt', header=None)[0]\nkeys_ohe = [x.replace('+', \"1\").replace('-', \"0\") for x in keys] # binary\ntotals = [60278, 29119]\n\n# Transition Array\nfor i in range(2):\n for x in range(2):\n query = str(i)+str(x)\n transitions[i][x] = np.sum(\n [len(re.findall('(?=%s)' % query, keys_ohe[n])) for n in range(len(keys))])/totals[i]\n\nprint('Transitions: -+ / -+')\nprint(transitions)\nprint('\\n')\nnon_cpgs = [[m.start() for m in re.finditer('0', n)] for n in keys_ohe]\ncpgs = [[m.start() for m in re.finditer('1', n)] for n in keys_ohe]\n\ncp_nuc = [[sequences[r][i] for i in cpgs[r]] for r in range(len(sequences))]\nnon_cp_nuc = [[sequences[r][i] for i in non_cpgs[r]]\n for r in range(len(sequences))]\nstates = [non_cp_nuc, cp_nuc]\nnucs = ['A', 'T', 'G', 'C']\ntotals2 = [np.sum([len(x) for x in non_cp_nuc]),\n np.sum([len(x) for x in cp_nuc])]\n\n# Emisssion Array\nfor nuc in range(len(nucs)):\n for state in range(len(states)):\n emissions[nuc][state] = np.sum(\n [n.count(nucs[nuc]) for n in states[state]])/totals2[state]\n\nprint('Emissions: ATGC/-+')\nprint(emissions)\nprint('\\n')\n\n# Initiation Array (occurence in sequence)\npos = np.sum([int(n[0]) for n in keys_ohe])\ninitiations = [pos/500, 1-pos/500]\n\nprint('Initiations: -+/Probabilites')\nprint(initiations)", "Transitions: -+ / -+\n[[0.9871429 0.0128571 ]\n [0.02558467 0.97441533]]\n\n\nEmissions: ATGC/-+\n[[0.25910751 0.14164113]\n [0.26115618 0.14501192]\n [0.24023989 0.35263875]\n [0.23949642 0.36070821]]\n\n\nInitiations: -+/Probabilites\n[0.442, 0.558]\n" ] ], [ [ "Using Viterbi algorithm we find the most likely assignment of CpG islands in the\n“Test_sequence”.", "_____no_output_____" ], [ "## Forward Algorithm", "_____no_output_____" ] ], [ [ "def forward(sequence, initmat, a, e):\n states = [0, 1]\n seqlen = len(sequence)\n f = [[0]*seqlen, [0]*seqlen]\n ptr = [[0]*seqlen]\n nucleotide = {\"A\": 0, \"T\": 1, \"G\": 2, \"C\": 3}\n for k in states:\n f[k][0] = initmat[k]*e[k][nucleotide[sequence[0]]]\n for i in range(1, seqlen):\n for k in states:\n # Sum of both last previous probs*transitions for each state\n f[k][i] = f[states[0]][i-1]*a[states[0]][k]\n # Remaining state\n for l in states[1:]:\n f[k][i] += f[l][i-1]*a[l][k]\n f[k][i] = f[k][i]*e[k][nucleotide[sequence[i]]]\n return f", "_____no_output_____" ] ], [ [ "## Backward Algorithm", "_____no_output_____" ] ], [ [ "def backward(sequence, initmat, a, e):\n\n states = [0, 1]\n seqlen = len(sequence)\n b = [[0]*seqlen, [0]*seqlen]\n nucleotide = {\"A\": 0, \"T\": 1, \"C\": 2, \"G\": 3}\n\n for k in states:\n b[k][-1] = 1\n\n for i in np.arange(seqlen-2, -1, -1):\n # -1 for index shift, -1 for second last column\n\n for k in states:\n b[k][i] = b[states[0]][i+1] * a[k][states[0]] * \\\n e[states[0]][nucleotide[sequence[i+1]]]\n\n # Remaining state\n for l in states[1:]:\n b[k][i] += b[l][i+1]*a[k][l]*e[l][nucleotide[sequence[i+1]]]\n b[k][i] = b[k][i]\n\n start = 0\n for k in states:\n start += b[k][0]*e[k][nucleotide[sequence[0]]]*initmat[k]\n\n return b", "_____no_output_____" ] ], [ [ "## Test Sequence", "_____no_output_____" ] ], [ [ "test_sequence=\"AACAATAATTTTGTTCTCCAATATAATCATCGACGCGTCGCGACGCGCGGGGGCGCCGGGTGACCCTATACTTCACTTGAATGCCATCCG\"", "_____no_output_____" ], [ "states = [0,1]\nstart_p = [0.558, 0.442]\ntrans_p = [[0.9871429, 0.0128571], [0.02558467, 0.97441533]]\nemit_p = [[0.25910751, 0.26115618, 0.24023989, 0.23949642],\n [0.14164113, 0.14501192, 0.35263875, 0.36070821]]", "_____no_output_____" ] ], [ [ "For every base of the “Test_sequence” calculate the probability to be in a CpG island. Use Forward and Backward algorithms. Calculate the probability of the “Test_sequence” using Forward and Backward algorithms. Obtained values should be the same. Plot the result: x-axis defines the position of the base, the y-axis defines the probability of the base to be in a CpG island.", "_____no_output_____" ] ], [ [ "f1 = forward(test_sequence, start_p, trans_p, emit_p)\nb1 = backward(test_sequence, start_p, trans_p, emit_p)\nprobs = np.multiply(f1, b1) / np.sum(f1, axis=0)[-1]\n\nisland = [\"-\"]*len(test_sequence)\nstate=np.argmax(probs1,axis=0)\nfor i in range(len(test_sequence)):\n if state[i]==1: \n island[i]=\"+\" \nprint('Most likely states: ' + \"\".join(island))\n\n", "Most likely states: --------------------------------++++++++++++++++++++++++++++++++--------------------------\n" ], [ "plt.figure(figsize=(16, 3))\nplt.plot(probs[1], label='Probability')\nplt.title('Probability Estimates for CpG Island')\nplt.xlabel('Base Position')\nplt.ylabel('Probability')\nplt.legend(loc='best')\nplt.show()", "_____no_output_____" ] ], [ [ "## Test Sequence Modification", "_____no_output_____" ], [ "Change a single letter of the “Test_sequence” from G to T (red):", "_____no_output_____" ] ], [ [ "test_sequence2=\"AACAATAATTTTGTTCTCCAATATAATCATCGACGCGTCGCGACTCGCGGGGGCGCCGGGTGACCCTATACTTCACTTGAATGCCATCCG\"", "_____no_output_____" ], [ "f2 = forward(test_sequence2, start_p, trans_p, emit_p)\nb2 = backward(test_sequence2, start_p, trans_p, emit_p)\nprobs2 = np.multiply(f2, b2) / np.sum(f2, axis=0)[-1]\n\nisland2 = [\"-\"]*len(test_sequence2)\nstate2=np.argmax(probs2,axis=0)\nfor i in range(len(test_sequence2)):\n if state2[i]==1: \n island2[i]=\"+\" \nprint('Most likely states: ' + \"\".join(island2))", "Most likely states: ---------------------------------+++++++++++++++++++++++++++++++--------------------------\n" ], [ "plt.figure(figsize=(16, 3))\nplt.plot(probs[1], label='Original')\nplt.plot(probs2[1], label='Modified')\nplt.title('Modified Probability Estimates of CpG Island')\nplt.xlabel('Base Position')\nplt.ylabel('Probability')\nplt.legend(loc='best')\nplt.show()", "_____no_output_____" ] ], [ [ "Run Viterbi, Forward and Backward algorithms for the modified “Test_sequence”. For every base of the “Test_sequence” calculate the probability to be in a CpG island. Discuss the impact of the modification of one letter of the “Test_sequence” on the performance of Viterbi algorithm and on the probability of bases to belong to a CpG island.", "_____no_output_____" ], [ "**Answer:**\n\nChanging a single nucleotide affects neighbors because we use the forward/backward algorithm.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ] ]

d0e6eb4cd9ebe4e70d6367f672c2aa638bcf5eb1

96,546

ipynb

Jupyter Notebook

notebooks/logistic_training.ipynb

schaber/direct_capstone

f7b015c3f7c70bd0114a842117d0964edf7a0c35

[ "MIT" ]

null

notebooks/logistic_training.ipynb

schaber/direct_capstone

f7b015c3f7c70bd0114a842117d0964edf7a0c35

[ "MIT" ]

5

2020-06-17T18:23:11.000Z

2020-06-17T18:24:31.000Z

notebooks/logistic_training.ipynb

schaber/direct_capstone

f7b015c3f7c70bd0114a842117d0964edf7a0c35

[ "MIT" ]

1

2020-04-30T19:42:06.000Z

244.420253

15,916

0.92734

[ [ [ "import sys\nsys.path.append('../modules')\nimport likelihood_predictor\nfrom likelihood_predictor import PlastPredictor\nimport numpy as np\nimport pandas as pd\nimport seaborn as sns\nimport matplotlib.pyplot as plt\nimport matplotlib.cm as cm\nfrom scipy.stats import zscore\nimport pickle", "_____no_output_____" ], [ "pl_full = pd.read_pickle('../database/plasticizer_data_v10_polarity.pkl')\npl_pol = pd.concat([pl_full[pl_full.columns[1:195]], pl_full['Polarity']], axis=1)\nall_cols = pl_pol.columns.to_numpy()\npl_data = pl_pol[all_cols].to_numpy()\nlin_data = pd.read_pickle('../database/linolein_test.pkl')\nlin_data['Polarity'] = 0.048856\nlin_data = lin_data[all_cols].to_numpy()\norg_full = pd.read_pickle('../database/org_polarity_v2.pkl')", "_____no_output_____" ], [ "psim1 = open(\"pubs_similarity.txt\", 'r')\npsim11 = [line.rstrip('\\n') for line in psim1]\npsim2 = open(\"pubs_othersim.txt\", 'r')\npsim22 = [line.rstrip('\\n') for line in psim2]", "_____no_output_____" ], [ "org_full\norg_full['Dsim'] = psim11\norg_full['Nasim'] = psim22", "_____no_output_____" ], [ "org_full = org_full.sort_values(by ='Dsim')", "_____no_output_____" ], [ "org_full = org_full[:5000]\norg_data = org_full[all_cols].to_numpy()", "_____no_output_____" ], [ "pp = PlastPredictor()\npp_model = pp.fit_model(pl_data, org_data)", "_____no_output_____" ], [ "clf_file = 'savemodel.pkl'\nscaler_file = 'savescaler.pkl'\npp.save_model(clf_file, scaler_file)", "_____no_output_____" ], [ "org_acc = pp.predict(org_data, type='binary', class_id='neg')\npl_acc = pp.predict(pl_data, type='binary', class_id='pos')\nlin_prob = pp.predict(lin_data)\norg_acc, pl_acc, lin_prob", "_____no_output_____" ], [ "pl_probs = pp.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs = pp.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()", "_____no_output_____" ], [ "sns.distplot(pl_probs, hist=False)\nsns.distplot(org_probs, hist=False)\nplt.show()", "_____no_output_____" ], [ "p1=PlastPredictor(reg_param=0.9)\np1.fit_model(pl_data, org_data)\n\norg_acc = p1.predict(org_data, type='binary', class_id='neg')\npl_acc = p1.predict(pl_data, type='binary', class_id='pos')\nlin_prob = p1.predict(lin_data)\n\npl_probs2 = p1.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs2 = p1.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()\n\n\nsns.distplot(pl_probs2, hist=False)\nsns.distplot(org_probs2, hist=False)\nplt.show()", "_____no_output_____" ], [ "p1=PlastPredictor(reg_param=0.6)\np1.fit_model(pl_data, org_data)\n\norg_acc = p1.predict(org_data, type='binary', class_id='neg')\npl_acc = p1.predict(pl_data, type='binary', class_id='pos')\nlin_prob = p1.predict(lin_data)\n\npl_probs2 = p1.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs2 = p1.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()\n\n\nsns.distplot(pl_probs2, hist=False)\nsns.distplot(org_probs2, hist=False)\nplt.show()", "_____no_output_____" ], [ "p1=PlastPredictor(reg_param=0.4)\np1.fit_model(pl_data, org_data)\n\norg_acc = p1.predict(org_data, type='binary', class_id='neg')\npl_acc = p1.predict(pl_data, type='binary', class_id='pos')\nlin_prob = p1.predict(lin_data)\n\npl_probs2 = p1.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs2 = p1.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()\n\n\nsns.distplot(pl_probs2, hist=False)\nsns.distplot(org_probs2, hist=False)\nplt.show()", "_____no_output_____" ], [ "p1=PlastPredictor(reg_param=0.2)\np1.fit_model(pl_data, org_data)\n\norg_acc = p1.predict(org_data, type='binary', class_id='neg')\npl_acc = p1.predict(pl_data, type='binary', class_id='pos')\nlin_prob = p1.predict(lin_data)\n\npl_probs2 = p1.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs2 = p1.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()\n\n\nsns.distplot(pl_probs2, hist=False)\nsns.distplot(org_probs2, hist=False)\nplt.show()", "_____no_output_____" ], [ "p1=PlastPredictor(reg_param=0.1)\np1.fit_model(pl_data, org_data)\n\norg_acc = p1.predict(org_data, type='binary', class_id='neg')\npl_acc = p1.predict(pl_data, type='binary', class_id='pos')\nlin_prob = p1.predict(lin_data)\n\npl_probs2 = p1.predict(pl_data)\npl_smiles = pl_full['SMILES'].to_numpy()\norg_probs2 = p1.predict(org_data)\norg_smiles = org_full['SMILES'].to_numpy()\n\n\nsns.distplot(pl_probs2, hist=False)\nsns.distplot(org_probs2, hist=False)\nplt.show()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e6ebd865e03e94be333972adfc2cc18ba4024f

378,319

ipynb

Jupyter Notebook

Model backlog/Models/Train/87-cassava-leaf-effnetb5-scl-2020-2-aux-512x512.ipynb

dimitreOliveira/Cassava-Leaf-Disease-Classification

22a42e840875190e2d8cd1c838d1aef7b956f39f

[ "MIT" ]

8

2021-02-18T22:35:19.000Z

2021-03-29T07:59:10.000Z

Model backlog/Models/Train/87-cassava-leaf-effnetb5-scl-2020-2-aux-512x512.ipynb

dimitreOliveira/Cassava-Leaf-Disease-Classification

22a42e840875190e2d8cd1c838d1aef7b956f39f

[ "MIT" ]

null

Model backlog/Models/Train/87-cassava-leaf-effnetb5-scl-2020-2-aux-512x512.ipynb

dimitreOliveira/Cassava-Leaf-Disease-Classification

22a42e840875190e2d8cd1c838d1aef7b956f39f

[ "MIT" ]

3

2021-03-27T13:48:23.000Z

2021-07-26T13:05:35.000Z

238.687066

175,200

0.901406

[ [ [ "## Dependencies", "_____no_output_____" ] ], [ [ "!pip install --quiet efficientnet", "\u001b[33mWARNING: You are using pip version 20.1.1; however, version 21.0 is available.\r\nYou should consider upgrading via the '/opt/conda/bin/python3.7 -m pip install --upgrade pip' command.\u001b[0m\r\n" ], [ "import warnings, time\nfrom kaggle_datasets import KaggleDatasets\nfrom sklearn.model_selection import KFold\nfrom sklearn.metrics import classification_report, confusion_matrix, accuracy_score\nfrom tensorflow.keras import optimizers, Sequential, losses, metrics, Model\nfrom tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint\nimport efficientnet.tfkeras as efn\nfrom cassava_scripts import *\nfrom scripts_step_lr_schedulers import *\nimport tensorflow_addons as tfa\n\n\nseed = 0\nseed_everything(seed)\nwarnings.filterwarnings('ignore')", "_____no_output_____" ] ], [ [ "### Hardware configuration", "_____no_output_____" ] ], [ [ "# TPU or GPU detection\n# Detect hardware, return appropriate distribution strategy\nstrategy, tpu = set_up_strategy()\n\nAUTO = tf.data.experimental.AUTOTUNE\nREPLICAS = strategy.num_replicas_in_sync\nprint(f'REPLICAS: {REPLICAS}')\n\n\n# Mixed precision\nfrom tensorflow.keras.mixed_precision import experimental as mixed_precision\npolicy = mixed_precision.Policy('mixed_bfloat16')\nmixed_precision.set_policy(policy)\n\n# XLA\ntf.config.optimizer.set_jit(True)", "Running on TPU grpc://10.0.0.2:8470\nREPLICAS: 8\n" ] ], [ [ "# Model parameters", "_____no_output_____" ] ], [ [ "BATCH_SIZE = 64 * REPLICAS #32 * REPLICAS\nLEARNING_RATE = 3e-5 * REPLICAS # 1e-5 * REPLICAS\nEPOCHS_CL = 5\nEPOCHS = 15\nHEIGHT = 512\nWIDTH = 512\nHEIGHT_DT = 512\nWIDTH_DT = 512\nCHANNELS = 3\nN_CLASSES = 5\nN_FOLDS = 5\nFOLDS_USED = 1\nES_PATIENCE = 5", "_____no_output_____" ] ], [ [ "# Load data", "_____no_output_____" ] ], [ [ "database_base_path = '/kaggle/input/cassava-leaf-disease-classification/'\ntrain = pd.read_csv(f'{database_base_path}train.csv')\nprint(f'Train samples: {len(train)}')\n\nGCS_PATH = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-center-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord)\nGCS_PATH_EXT = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-external-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) (External)\nGCS_PATH_CLASSES = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-classes-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) by classes\nGCS_PATH_EXT_CLASSES = KaggleDatasets().get_gcs_path(f'cassava-leaf-disease-tfrecords-classes-ext-{HEIGHT_DT}x{WIDTH_DT}') # Center croped and resized (50 TFRecord) (External) by classes\n\n\nFILENAMES_COMP = tf.io.gfile.glob(GCS_PATH + '/*.tfrec')\n# FILENAMES_2019 = tf.io.gfile.glob(GCS_PATH_EXT + '/*.tfrec')\n\n# FILENAMES_COMP_CBB = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CBB*.tfrec')\n# FILENAMES_COMP_CBSD = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CBSD*.tfrec')\n# FILENAMES_COMP_CGM = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CGM*.tfrec')\n# FILENAMES_COMP_CMD = tf.io.gfile.glob(GCS_PATH_CLASSES + '/CMD*.tfrec')\n# FILENAMES_COMP_Healthy = tf.io.gfile.glob(GCS_PATH_CLASSES + '/Healthy*.tfrec')\n\n# FILENAMES_2019_CBB = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CBB*.tfrec')\n# FILENAMES_2019_CBSD = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CBSD*.tfrec')\n# FILENAMES_2019_CGM = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CGM*.tfrec')\n# FILENAMES_2019_CMD = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/CMD*.tfrec')\n# FILENAMES_2019_Healthy = tf.io.gfile.glob(GCS_PATH_EXT_CLASSES + '/Healthy*.tfrec')\n\nTRAINING_FILENAMES = FILENAMES_COMP\nNUM_TRAINING_IMAGES = count_data_items(TRAINING_FILENAMES)\n\nprint(f'GCS: train images: {NUM_TRAINING_IMAGES}')\ndisplay(train.head())", "Train samples: 21397\nGCS: train images: 21395\n" ] ], [ [ "# Augmentation", "_____no_output_____" ] ], [ [ "def data_augment(image, label):\n# p_rotation = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_spatial = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_rotate = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_pixel_1 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_pixel_2 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_pixel_3 = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n# p_shear = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_crop = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n p_cutout = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n \n# # Shear\n# if p_shear > .2:\n# if p_shear > .6:\n# image = transform_shear(image, HEIGHT, shear=20.)\n# else:\n# image = transform_shear(image, HEIGHT, shear=-20.)\n \n# # Rotation\n# if p_rotation > .2:\n# if p_rotation > .6:\n# image = transform_rotation(image, HEIGHT, rotation=45.)\n# else:\n# image = transform_rotation(image, HEIGHT, rotation=-45.)\n \n # Flips\n image = tf.image.random_flip_left_right(image)\n image = tf.image.random_flip_up_down(image)\n if p_spatial > .75:\n image = tf.image.transpose(image)\n \n # Rotates\n if p_rotate > .75:\n image = tf.image.rot90(image, k=3) # rotate 270º\n elif p_rotate > .5:\n image = tf.image.rot90(image, k=2) # rotate 180º\n elif p_rotate > .25:\n image = tf.image.rot90(image, k=1) # rotate 90º\n \n # Pixel-level transforms\n if p_pixel_1 >= .4:\n image = tf.image.random_saturation(image, lower=.7, upper=1.3)\n if p_pixel_2 >= .4:\n image = tf.image.random_contrast(image, lower=.8, upper=1.2)\n if p_pixel_3 >= .4:\n image = tf.image.random_brightness(image, max_delta=.1)\n \n # Crops\n if p_crop > .6:\n if p_crop > .9:\n image = tf.image.central_crop(image, central_fraction=.5)\n elif p_crop > .8:\n image = tf.image.central_crop(image, central_fraction=.6)\n elif p_crop > .7:\n image = tf.image.central_crop(image, central_fraction=.7)\n else:\n image = tf.image.central_crop(image, central_fraction=.8)\n elif p_crop > .3:\n crop_size = tf.random.uniform([], int(HEIGHT*.6), HEIGHT, dtype=tf.int32)\n image = tf.image.random_crop(image, size=[crop_size, crop_size, CHANNELS])\n \n image = tf.image.resize(image, size=[HEIGHT, WIDTH])\n\n if p_cutout > .5:\n image = data_augment_cutout(image)\n \n return image, label", "_____no_output_____" ] ], [ [ "## Auxiliary functions", "_____no_output_____" ] ], [ [ "# CutOut\ndef data_augment_cutout(image, min_mask_size=(int(HEIGHT * .1), int(HEIGHT * .1)), \n max_mask_size=(int(HEIGHT * .125), int(HEIGHT * .125))):\n p_cutout = tf.random.uniform([], 0, 1.0, dtype=tf.float32)\n \n if p_cutout > .85: # 10~15 cut outs\n n_cutout = tf.random.uniform([], 10, 15, dtype=tf.int32)\n image = random_cutout(image, HEIGHT, WIDTH, \n min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)\n elif p_cutout > .6: # 5~10 cut outs\n n_cutout = tf.random.uniform([], 5, 10, dtype=tf.int32)\n image = random_cutout(image, HEIGHT, WIDTH, \n min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)\n elif p_cutout > .25: # 2~5 cut outs\n n_cutout = tf.random.uniform([], 2, 5, dtype=tf.int32)\n image = random_cutout(image, HEIGHT, WIDTH, \n min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=n_cutout)\n else: # 1 cut out\n image = random_cutout(image, HEIGHT, WIDTH, \n min_mask_size=min_mask_size, max_mask_size=max_mask_size, k=1)\n\n return image", "_____no_output_____" ], [ "# Datasets utility functions\ndef random_crop(image, label):\n \"\"\"\n Resize and reshape images to the expected size.\n \"\"\"\n image = tf.image.random_crop(image, size=[HEIGHT, WIDTH, CHANNELS])\n return image, label\n\ndef prepare_image(image, label):\n \"\"\"\n Resize and reshape images to the expected size.\n \"\"\"\n image = tf.image.resize(image, [HEIGHT, WIDTH])\n image = tf.reshape(image, [HEIGHT, WIDTH, CHANNELS])\n return image, label\n\ndef center_crop_(image, label, height_rs, width_rs, height=HEIGHT_DT, width=WIDTH_DT, channels=3):\n image = tf.reshape(image, [height, width, channels]) # Original shape\n \n h, w = image.shape[0], image.shape[1]\n if h > w:\n image = tf.image.crop_to_bounding_box(image, (h - w) // 2, 0, w, w)\n else:\n image = tf.image.crop_to_bounding_box(image, 0, (w - h) // 2, h, h)\n \n image = tf.image.resize(image, [height_rs, width_rs]) # Expected shape\n return image, label\n\n\ndef read_tfrecord_(example, labeled=True, n_classes=5):\n \"\"\"\n 1. Parse data based on the 'TFREC_FORMAT' map.\n 2. Decode image.\n 3. If 'labeled' returns (image, label) if not (image, name).\n \"\"\"\n if labeled:\n TFREC_FORMAT = {\n 'image': tf.io.FixedLenFeature([], tf.string), \n 'target': tf.io.FixedLenFeature([], tf.int64), \n }\n else:\n TFREC_FORMAT = {\n 'image': tf.io.FixedLenFeature([], tf.string), \n 'image_name': tf.io.FixedLenFeature([], tf.string), \n }\n example = tf.io.parse_single_example(example, TFREC_FORMAT)\n image = decode_image(example['image'])\n if labeled:\n label_or_name = tf.cast(example['target'], tf.int32)\n # One-Hot Encoding needed to use \"categorical_crossentropy\" loss\n# label_or_name = tf.one_hot(tf.cast(label_or_name, tf.int32), n_classes)\n else:\n label_or_name = example['image_name']\n return image, label_or_name\n\ndef get_dataset(filenames, labeled=True, ordered=False, repeated=False, \n cached=False, augment=False):\n \"\"\"\n Return a Tensorflow dataset ready for training or inference.\n \"\"\"\n \n ignore_order = tf.data.Options()\n if not ordered:\n ignore_order.experimental_deterministic = False\n dataset = tf.data.Dataset.list_files(filenames)\n dataset = dataset.interleave(tf.data.TFRecordDataset, num_parallel_calls=AUTO)\n else:\n dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTO)\n \n dataset = dataset.with_options(ignore_order)\n \n dataset = dataset.map(lambda x: read_tfrecord_(x, labeled=labeled), num_parallel_calls=AUTO)\n \n if augment:\n dataset = dataset.map(data_augment, num_parallel_calls=AUTO)\n \n dataset = dataset.map(scale_image, num_parallel_calls=AUTO)\n dataset = dataset.map(prepare_image, num_parallel_calls=AUTO)\n \n \n if labeled:\n dataset = dataset.map(conf_output, num_parallel_calls=AUTO)\n \n \n if not ordered:\n dataset = dataset.shuffle(2048)\n if repeated:\n dataset = dataset.repeat()\n \n dataset = dataset.batch(BATCH_SIZE)\n \n if cached:\n dataset = dataset.cache()\n dataset = dataset.prefetch(AUTO)\n return dataset\n\ndef conf_output(image, label):\n \"\"\"\n Configure the output of the dataset.\n \"\"\"\n aux_label = [0.]\n aux_2_label = [0.]\n# if tf.math.argmax(label, axis=-1) == 4: # Healthy\n if label == 4: # Healthy\n aux_label = [1.]\n# if tf.math.argmax(label, axis=-1) == 3: # CMD\n if label == 3: # CMD\n aux_2_label = [1.]\n return (image, (label, aux_label, aux_2_label))", "_____no_output_____" ] ], [ [ "# Training data samples (with augmentation)", "_____no_output_____" ] ], [ [ "# train_dataset = get_dataset(FILENAMES_COMP, ordered=True, augment=True)\n# train_iter = iter(train_dataset.unbatch().batch(20))\n\n# display_batch_of_images(next(train_iter))\n# display_batch_of_images(next(train_iter))", "_____no_output_____" ] ], [ [ "# Model", "_____no_output_____" ] ], [ [ "def encoder_fn(input_shape):\n inputs = L.Input(shape=input_shape, name='input_image')\n base_model = efn.EfficientNetB5(input_tensor=inputs, \n include_top=False, \n weights='noisy-student', \n pooling=None)\n \n outputs = L.GlobalAveragePooling2D()(base_model.output)\n model = Model(inputs=inputs, outputs=outputs)\n return model\n\ndef add_projection_head(input_shape, encoder):\n inputs = L.Input(shape=input_shape, name='input_image')\n features = encoder(inputs)\n outputs = L.Dense(128, activation='relu', name='projection_head', dtype='float32')(features)\n \n model = Model(inputs=inputs, outputs=outputs)\n return model\n\ndef classifier_fn(input_shape, N_CLASSES, encoder, trainable=True):\n for layer in encoder.layers:\n layer.trainable = trainable\n \n inputs = L.Input(shape=input_shape, name='input_image')\n \n features = encoder(inputs)\n features = L.Dropout(.5)(features)\n features = L.Dense(1000, activation='relu')(features)\n features = L.Dropout(.5)(features)\n \n output = L.Dense(N_CLASSES, activation='softmax', name='output', dtype='float32')(features)\n output_healthy = L.Dense(1, activation='sigmoid', name='output_healthy', dtype='float32')(features)\n output_cmd = L.Dense(1, activation='sigmoid', name='output_cmd', dtype='float32')(features)\n \n model = Model(inputs=inputs, outputs=[output, output_healthy, output_cmd])\n return model", "_____no_output_____" ], [ "temperature = 0.1\n\nclass SupervisedContrastiveLoss(losses.Loss):\n def __init__(self, temperature=0.1, name=None):\n super(SupervisedContrastiveLoss, self).__init__(name=name)\n self.temperature = temperature\n\n def __call__(self, labels, feature_vectors, sample_weight=None):\n # Normalize feature vectors\n feature_vectors_normalized = tf.math.l2_normalize(feature_vectors, axis=1)\n # Compute logits\n logits = tf.divide(\n tf.matmul(\n feature_vectors_normalized, tf.transpose(feature_vectors_normalized)\n ),\n temperature,\n )\n return tfa.losses.npairs_loss(tf.squeeze(labels), logits)", "_____no_output_____" ] ], [ [ "### Learning rate schedule", "_____no_output_____" ] ], [ [ "lr_start = 1e-8\nlr_min = 1e-6\nlr_max = LEARNING_RATE\nnum_cycles = 1\nwarmup_epochs = 3\nhold_max_epochs = 0\ntotal_epochs = EPOCHS\nstep_size = (NUM_TRAINING_IMAGES//BATCH_SIZE)\nhold_max_steps = hold_max_epochs * step_size\ntotal_steps = total_epochs * step_size\nwarmup_steps = warmup_epochs * step_size\n\n\ndef lrfn(total_steps, warmup_steps=0, lr_start=1e-4, lr_max=1e-3, lr_min=1e-4, num_cycles=1.):\n @tf.function\n def cosine_with_hard_restarts_schedule_with_warmup_(step):\n \"\"\" Create a schedule with a learning rate that decreases following the\n values of the cosine function with several hard restarts, after a warmup\n period during which it increases linearly between 0 and 1.\n \"\"\"\n\n if step < warmup_steps:\n lr = (lr_max - lr_start) / warmup_steps * step + lr_start\n else:\n progress = (step - warmup_steps) / (total_steps - warmup_steps)\n lr = lr_max * (0.5 * (1.0 + tf.math.cos(np.pi * ((num_cycles * progress) % 1.0))))\n if lr_min is not None:\n lr = tf.math.maximum(lr_min, float(lr))\n return lr\n return cosine_with_hard_restarts_schedule_with_warmup_\n\nlrfn_fn = lrfn(total_steps, warmup_steps, lr_start, lr_max, lr_min, num_cycles)\nrng = [i for i in range(total_steps)]\ny = [lrfn_fn(tf.cast(x, tf.float32)) for x in rng]\n\nsns.set(style='whitegrid')\nfig, ax = plt.subplots(figsize=(20, 6))\nplt.plot(rng, y)\n\nprint(f'{total_steps} total steps and {step_size} steps per epoch')\nprint(f'Learning rate schedule: {y[0]:.3g} to {max(y):.3g} to {y[-1]:.3g}')", "615 total steps and 41 steps per epoch\nLearning rate schedule: 1e-08 to 0.00024 to 1e-06\n" ] ], [ [ "# Training", "_____no_output_____" ] ], [ [ "skf = KFold(n_splits=N_FOLDS, shuffle=True, random_state=seed)\noof_pred = []; oof_labels = []; oof_names = []; oof_folds = []; history_list = []; oof_embed = []\n\nfor fold,(idxT, idxV) in enumerate(skf.split(np.arange(15))):\n if fold >= FOLDS_USED:\n break\n if tpu: tf.tpu.experimental.initialize_tpu_system(tpu)\n K.clear_session()\n print(f'\\nFOLD: {fold+1}')\n print(f'TRAIN: {idxT} VALID: {idxV}')\n\n # Create train and validation sets\n TRAIN_FILENAMES = tf.io.gfile.glob([GCS_PATH + '/Id_train%.2i*.tfrec' % x for x in idxT])\n# FILENAMES_COMP_CBB = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CBB%.2i*.tfrec' % x for x in idxT])\n# FILENAMES_COMP_CBSD = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CBSD%.2i*.tfrec' % x for x in idxT])\n# FILENAMES_COMP_CGM = tf.io.gfile.glob([GCS_PATH_CLASSES + '/CGM%.2i*.tfrec' % x for x in idxT])\n# FILENAMES_COMP_Healthy = tf.io.gfile.glob([GCS_PATH_CLASSES + '/Healthy%.2i*.tfrec' % x for x in idxT])\n \n np.random.shuffle(TRAIN_FILENAMES)\n \n VALID_FILENAMES = tf.io.gfile.glob([GCS_PATH + '/Id_train%.2i*.tfrec' % x for x in idxV])\n \n ct_train = count_data_items(TRAIN_FILENAMES)\n ct_valid = count_data_items(VALID_FILENAMES)\n \n step_size = (ct_train // BATCH_SIZE)\n warmup_steps = (warmup_epochs * step_size)\n total_steps = (total_epochs * step_size)\n total_steps_cl = (EPOCHS_CL * step_size)\n warmup_steps_cl = 1\n \n \n ### Pre-train the encoder\n print('Pre-training the encoder using \"Supervised Contrastive\" Loss')\n with strategy.scope():\n encoder = encoder_fn((None, None, CHANNELS))\n encoder_proj = add_projection_head((None, None, CHANNELS), encoder)\n encoder_proj.summary()\n\n lrfn_fn = lrfn(total_steps, warmup_steps, lr_start, lr_max, lr_min, num_cycles)\n# optimizer = optimizers.SGD(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)), \n# momentum=0.95, nesterov=True)\n optimizer = optimizers.Adam(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)))\n encoder_proj.compile(optimizer=optimizer, \n loss=SupervisedContrastiveLoss(temperature))\n \n es = EarlyStopping(patience=ES_PATIENCE, restore_best_weights=True, \n monitor='val_loss', mode='max', verbose=1)\n history_enc = encoder_proj.fit(x=get_dataset(TRAIN_FILENAMES, repeated=True, augment=True), \n validation_data=get_dataset(VALID_FILENAMES, ordered=True), \n steps_per_epoch=step_size, \n# callbacks=[es], \n batch_size=BATCH_SIZE, \n epochs=EPOCHS,\n verbose=2).history\n\n \n ### Train the classifier with the frozen encoder\n print('Training the classifier with the frozen encoder')\n \n with strategy.scope():\n model = classifier_fn((None, None, CHANNELS), N_CLASSES, encoder, trainable=False)\n model.summary()\n\n lrfn_fn = lrfn(total_steps_cl, warmup_steps_cl, lr_start, lr_max, lr_min, num_cycles)\n# optimizer = optimizers.SGD(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)), \n# momentum=0.95, nesterov=True)\n optimizer = optimizers.Adam(learning_rate=lambda: lrfn_fn(tf.cast(optimizer.iterations, tf.float32)))\n model.compile(optimizer=optimizer, \n loss={'output': losses.SparseCategoricalCrossentropy(), \n 'output_healthy': losses.BinaryCrossentropy(), \n 'output_cmd': losses.BinaryCrossentropy()},\n loss_weights={'output': 1., \n 'output_healthy': .1, \n 'output_cmd': .1}, \n metrics={'output': metrics.SparseCategoricalAccuracy(), \n 'output_healthy': metrics.BinaryAccuracy(), \n 'output_cmd': metrics.BinaryAccuracy()})\n \n model_path = f'model_{fold}.h5'\n chkpt = ModelCheckpoint(model_path, mode='max', \n monitor='val_output_sparse_categorical_accuracy', \n save_best_only=True, save_weights_only=True)\n \n history = model.fit(x=get_dataset(TRAIN_FILENAMES, repeated=True, augment=True), \n validation_data=get_dataset(VALID_FILENAMES, ordered=True), \n steps_per_epoch=step_size, \n callbacks=[chkpt], \n epochs=EPOCHS_CL, \n verbose=2).history\n \n \n ### RESULTS\n print(f\"#### FOLD {fold+1} OOF Accuracy = {np.max(history['val_output_sparse_categorical_accuracy']):.3f}\")\n \n history_list.append(history)\n # Load best model weights\n model.load_weights(model_path)\n\n # OOF predictions\n ds_valid = get_dataset(VALID_FILENAMES, ordered=True)\n oof_folds.append(np.full((ct_valid), fold, dtype='int8'))\n oof_labels.append([target[0].numpy() for img, target in iter(ds_valid.unbatch())])\n x_oof = ds_valid.map(lambda image, target: image)\n oof_pred.append(np.argmax(model.predict(x_oof)[0], axis=-1))\n # OOF names\n ds_valid_names = get_dataset(VALID_FILENAMES, labeled=False, ordered=True)\n oof_names.append(np.array([img_name.numpy().decode('utf-8') for img, img_name in iter(ds_valid_names.unbatch())]))\n oof_embed.append(encoder.predict(x_oof)) # OOF embeddings", "\nFOLD: 1\nTRAIN: [ 0 2 3 4 5 7 9 10 11 12 13 14] VALID: [1 6 8]\nPre-training the encoder using \"Supervised Contrastive\" Loss\nDownloading data from https://github.com/qubvel/efficientnet/releases/download/v0.0.1/efficientnet-b5_noisy-student_notop.h5\n115261440/115255328 [==============================] - 3s 0us/step\nModel: \"model_1\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\ninput_image (InputLayer) [(None, None, None, 3)] 0 \n_________________________________________________________________\nmodel (Model) (None, 2048) 28513520 \n_________________________________________________________________\nprojection_head (Dense) (None, 128) 262272 \n=================================================================\nTotal params: 28,775,792\nTrainable params: 28,603,056\nNon-trainable params: 172,736\n_________________________________________________________________\nEpoch 1/15\n33/33 - 113s - loss: 5.2375 - val_loss: 4.3300\nEpoch 2/15\n33/33 - 61s - loss: 4.0034 - val_loss: 3.9327\nEpoch 3/15\n33/33 - 65s - loss: 3.8120 - val_loss: 3.7829\nEpoch 4/15\n33/33 - 65s - loss: 3.6911 - val_loss: 3.6853\nEpoch 5/15\n33/33 - 64s - loss: 3.6240 - val_loss: 3.6188\nEpoch 6/15\n33/33 - 62s - loss: 3.5820 - val_loss: 3.5979\nEpoch 7/15\n33/33 - 66s - loss: 3.5495 - val_loss: 3.5783\nEpoch 8/15\n33/33 - 64s - loss: 3.5320 - val_loss: 3.5620\nEpoch 9/15\n33/33 - 65s - loss: 3.5097 - val_loss: 3.5496\nEpoch 10/15\n33/33 - 64s - loss: 3.4976 - val_loss: 3.5317\nEpoch 11/15\n33/33 - 62s - loss: 3.4827 - val_loss: 3.5264\nEpoch 12/15\n33/33 - 64s - loss: 3.4742 - val_loss: 3.5344\nEpoch 13/15\n33/33 - 66s - loss: 3.4783 - val_loss: 3.5348\nEpoch 14/15\n33/33 - 64s - loss: 3.4565 - val_loss: 3.5341\nEpoch 15/15\n33/33 - 61s - loss: 3.4684 - val_loss: 3.5337\nTraining the classifier with the frozen encoder\nModel: \"model_2\"\n__________________________________________________________________________________________________\nLayer (type) Output Shape Param # Connected to \n==================================================================================================\ninput_image (InputLayer) [(None, None, None, 0 \n__________________________________________________________________________________________________\nmodel (Model) (None, 2048) 28513520 input_image[0][0] \n__________________________________________________________________________________________________\ndropout (Dropout) (None, 2048) 0 model[2][0] \n__________________________________________________________________________________________________\ndense (Dense) (None, 1000) 2049000 dropout[0][0] \n__________________________________________________________________________________________________\ndropout_1 (Dropout) (None, 1000) 0 dense[0][0] \n__________________________________________________________________________________________________\noutput (Dense) (None, 5) 5005 dropout_1[0][0] \n__________________________________________________________________________________________________\noutput_healthy (Dense) (None, 1) 1001 dropout_1[0][0] \n__________________________________________________________________________________________________\noutput_cmd (Dense) (None, 1) 1001 dropout_1[0][0] \n==================================================================================================\nTotal params: 30,569,527\nTrainable params: 2,056,007\nNon-trainable params: 28,513,520\n__________________________________________________________________________________________________\nEpoch 1/5\n33/33 - 113s - output_sparse_categorical_accuracy: 0.8271 - output_healthy_binary_accuracy: 0.8179 - output_healthy_loss: 0.3953 - loss: 0.5718 - output_cmd_loss: 0.3635 - output_loss: 0.4959 - output_cmd_binary_accuracy: 0.8593 - val_output_sparse_categorical_accuracy: 0.8789 - val_output_healthy_binary_accuracy: 0.9152 - val_output_healthy_loss: 0.2270 - val_loss: 0.4328 - val_output_cmd_loss: 0.1588 - val_output_loss: 0.3942 - val_output_cmd_binary_accuracy: 0.9535\nEpoch 2/5\n33/33 - 62s - output_sparse_categorical_accuracy: 0.9022 - output_healthy_binary_accuracy: 0.9168 - output_healthy_loss: 0.1968 - loss: 0.3399 - output_cmd_loss: 0.1357 - output_loss: 0.3067 - output_cmd_binary_accuracy: 0.9631 - val_output_sparse_categorical_accuracy: 0.8794 - val_output_healthy_binary_accuracy: 0.9327 - val_output_healthy_loss: 0.1842 - val_loss: 0.4020 - val_output_cmd_loss: 0.1416 - val_output_loss: 0.3694 - val_output_cmd_binary_accuracy: 0.9542\nEpoch 3/5\n33/33 - 66s - output_sparse_categorical_accuracy: 0.9018 - output_healthy_binary_accuracy: 0.9324 - output_healthy_loss: 0.1709 - loss: 0.3287 - output_cmd_loss: 0.1247 - output_loss: 0.2992 - output_cmd_binary_accuracy: 0.9628 - val_output_sparse_categorical_accuracy: 0.8817 - val_output_healthy_binary_accuracy: 0.9341 - val_output_healthy_loss: 0.1719 - val_loss: 0.3906 - val_output_cmd_loss: 0.1405 - val_output_loss: 0.3594 - val_output_cmd_binary_accuracy: 0.9537\nEpoch 4/5\n33/33 - 62s - output_sparse_categorical_accuracy: 0.9042 - output_healthy_binary_accuracy: 0.9353 - output_healthy_loss: 0.1648 - loss: 0.3289 - output_cmd_loss: 0.1226 - output_loss: 0.3001 - output_cmd_binary_accuracy: 0.9635 - val_output_sparse_categorical_accuracy: 0.8817 - val_output_healthy_binary_accuracy: 0.9348 - val_output_healthy_loss: 0.1689 - val_loss: 0.3887 - val_output_cmd_loss: 0.1403 - val_output_loss: 0.3577 - val_output_cmd_binary_accuracy: 0.9535\nEpoch 5/5\n33/33 - 64s - output_sparse_categorical_accuracy: 0.9014 - output_healthy_binary_accuracy: 0.9345 - output_healthy_loss: 0.1623 - loss: 0.3264 - output_cmd_loss: 0.1219 - output_loss: 0.2980 - output_cmd_binary_accuracy: 0.9629 - val_output_sparse_categorical_accuracy: 0.8817 - val_output_healthy_binary_accuracy: 0.9353 - val_output_healthy_loss: 0.1685 - val_loss: 0.3884 - val_output_cmd_loss: 0.1403 - val_output_loss: 0.3576 - val_output_cmd_binary_accuracy: 0.9533\n#### FOLD 1 OOF Accuracy = 0.882\n" ] ], [ [ "## Model loss graph", "_____no_output_____" ] ], [ [ "for fold, history in enumerate(history_list):\n print(f'\\nFOLD: {fold+1}')\n plot_metrics(history, acc_name='output_sparse_categorical_accuracy')", "\nFOLD: 1\n" ] ], [ [ "# Model evaluation", "_____no_output_____" ] ], [ [ "y_true = np.concatenate(oof_labels)\ny_pred = np.concatenate(oof_pred)\nfolds = np.concatenate(oof_folds)\nnames = np.concatenate(oof_names)\n\nacc = accuracy_score(y_true, y_pred)\nprint(f'Overall OOF Accuracy = {acc:.3f}')\n\ndf_oof = pd.DataFrame({'image_id':names, 'fold':fold, \n 'target':y_true, 'pred':y_pred})\ndf_oof.to_csv('oof.csv', index=False)\ndisplay(df_oof.head())\n\nprint(classification_report(y_true, y_pred, target_names=CLASSES))", "Overall OOF Accuracy = 0.882\n" ] ], [ [ "# Confusion matrix", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots(1, 1, figsize=(20, 12))\ncfn_matrix = confusion_matrix(y_true, y_pred, labels=range(len(CLASSES)))\ncfn_matrix = (cfn_matrix.T / cfn_matrix.sum(axis=1)).T\ndf_cm = pd.DataFrame(cfn_matrix, index=CLASSES, columns=CLASSES)\nax = sns.heatmap(df_cm, cmap='Blues', annot=True, fmt='.2f', linewidths=.5).set_title('Train', fontsize=30)\nplt.show()", "_____no_output_____" ] ], [ [ "# Visualize embeddings outputs", "_____no_output_____" ] ], [ [ "y_true = np.concatenate(oof_labels)\ny_pred = np.concatenate(oof_pred)\ny_embeddings = np.concatenate(oof_embed)\n\nvisualize_embeddings(y_embeddings, y_true)", "_____no_output_____" ] ], [ [ "# Visualize predictions", "_____no_output_____" ] ], [ [ "# train_dataset = get_dataset(TRAINING_FILENAMES, ordered=True)\n# x_samp, y_samp = dataset_to_numpy_util(train_dataset, 18)\n# y_samp = np.argmax(y_samp, axis=-1)\n\n# x_samp_1, y_samp_1 = x_samp[:9,:,:,:], y_samp[:9]\n# samp_preds_1 = model.predict(x_samp_1, batch_size=9)\n# display_9_images_with_predictions(x_samp_1, samp_preds_1, y_samp_1)\n\n# x_samp_2, y_samp_2 = x_samp[9:,:,:,:], y_samp[9:]\n# samp_preds_2 = model.predict(x_samp_2, batch_size=9)\n# display_9_images_with_predictions(x_samp_2, samp_preds_2, y_samp_2)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e6f15735334755bb94d1f30231c4f3abc68047

21,329

ipynb

Jupyter Notebook

strings/strings4-sol.ipynb

DavidLeoni/softpython-

f832762e60556b2b3be13f2befbfb5343716a81a

[ "CC-BY-4.0" ]

2

2021-04-28T08:31:14.000Z

2021-08-13T19:43:55.000Z

strings/strings4-sol.ipynb

DavidLeoni/softpython-

f832762e60556b2b3be13f2befbfb5343716a81a

[ "CC-BY-4.0" ]

14

2020-07-13T16:36:31.000Z

2021-12-08T16:47:54.000Z

strings/strings4-sol.ipynb

DavidLeoni/softpython-it

f832762e60556b2b3be13f2befbfb5343716a81a

[ "CC-BY-4.0" ]

null

30.339972

476

0.532655

[ [ [ "# Ricordati di eseguire questa cella con Shift+Invio\n\nimport sys\nsys.path.append('../')\nimport jupman", "_____no_output_____" ] ], [ [ "# Stringhe 4 - iterazione e funzioni\n\n## [Scarica zip esercizi](../_static/generated/strings.zip)\n\n[Naviga file online](https://github.com/DavidLeoni/softpython-it/tree/master/strings)\n\n", "_____no_output_____" ], [ "### Che fare\n\n- scompatta lo zip in una cartella, dovresti ottenere qualcosa del genere: \n\n```\n\nstrings\n strings1.ipynb \n strings1-sol.ipynb \n strings2.ipynb\n strings2-sol.ipynb\n strings3.ipynb\n strings3-sol.ipynb\n jupman.py \n```\n\n<div class=\"alert alert-warning\">\n\n**ATTENZIONE**: Per essere visualizzato correttamente, il file del notebook DEVE essere nella cartella szippata.\n</div>\n\n- apri il Jupyter Notebook da quella cartella. Due cose dovrebbero aprirsi, prima una console e poi un browser. Il browser dovrebbe mostrare una lista di file: naviga la lista e apri il notebook `strings1.ipynb`\n- Prosegui leggendo il file degli esercizi, ogni tanto al suo interno troverai delle scritte **ESERCIZIO**, che ti chiederanno di scrivere dei comandi Python nelle celle successive. Gli esercizi sono graduati per difficoltà, da una stellina ✪ a quattro ✪✪✪✪\n\n\nScorciatoie da tastiera:\n\n* Per eseguire il codice Python dentro una cella di Jupyter, premi `Control+Invio`\n* Per eseguire il codice Python dentro una cella di Jupyter E selezionare la cella seguente, premi `Shift+Invio`\n* Per eseguire il codice Python dentro una cella di Jupyter E creare una nuova cella subito dopo, premi `Alt+Invio`\n* Se per caso il Notebook sembra inchiodato, prova a selezionare `Kernel -> Restart`\n\n", "_____no_output_____" ], [ "## Esercizi con le funzioni\n\n\n<div class=\"alert alert-warning\">\n\n**ATTENZIONE: Gli esercizi seguenti richiedono di conoscere:**\n\n<ul>\n<li>Tutti gli esercizi sulle stringhe precedenti</li>\n<li>[Controllo di flusso](https://it.softpython.org/#control-flow)</li>\n<li>[Funzioni](https://it.softpython.org/functions/functions-sol.html)</li>\n</ul>\n<br/>\n\n**Se sei alle prime armi con la programmazione, ti conviene saltarli e ripassare in seguito**\n</div>", "_____no_output_____" ], [ "### lung\n\n✪ a. Scrivi una funzione `lung1(stringa)` in cui data una stringa, RITORNI quanto è lunga la stringa. Usa `len` Per esempio, con la stringa `\"ciao\"`, la vostra funzione dovrebbe ritornare `4` mentre con `\"hi\"` dovrebbe ritornare `2`\n\n```python\n>>> x = lung1(\"ciao\")\n>>> x\n4\n```\n\n✪ b. Scrivi una funzione `lung2` che come prima calcola la lunghezza della stringa, ma SENZA usare `len` (usa un ciclo `for`)\n\n```python\n>>> y = lung2(\"mondo\")\n>>> y\n5\n```", "_____no_output_____" ] ], [ [ "# scrivi qui\n\n# versione con len, più veloce perchè python assieme ad una stringa mantiene sempre in memoria \n# il numero della lunghezza immediatamente disponibile\n\ndef lung1(stringa):\n return len(stringa)\n\n# versione con contatore, più lenta\ndef lung2(parola):\n contatore = 0\n for lettera in parola:\n contatore = contatore + 1\n return contatore", "_____no_output_____" ] ], [ [ "### contin\n\n✪ Scrivi la funzione `contin(parola, stringa)`, che RITORNA `True` se `parola` contiene la `stringa` indicata, altrimenti RITORNA `False` \n \n- Usa l'operatore `in`\n\n\n\n```python\n>>> x = contin('carpenteria', 'ent')\n>>> x\nTrue\n>>> y = contin('carpenteria', 'zent')\n>>> y\nFalse\n```", "_____no_output_____" ] ], [ [ "# scrivi qui\n\ndef contin(parola, stringa):\n return stringa in parola", "_____no_output_____" ] ], [ [ "### invertilet\n\n✪ Scrivi la funzione `invertilet(primo, secondo)` che prende in input due stringhe di lunghezza maggiore di 3, e RESTITUISCE una nuova stringa in cui le parole sono concatenate e separate da uno spazio, le ultime lettere delle due parole sono invertite. Questo significa che passando in input 'ciao' e 'world', la funzione dovrebbe restituire 'ciad worlo'\n\nSe le stringhe non sono di lunghezza adeguata, il programma STAMPA _errore!_\n\nSUGGERIMENTO: usa _le slice_\n\n\n```python\n>>> x = invertilet('hi','mondo')\n'errore!'\n>>> x\nNone\n>>> x = invertilet('cirippo', 'bla')\n'errore!'\n>>> x\nNone\n```\n", "_____no_output_____" ] ], [ [ "# scrivi qui\n\ndef invertilet(primo,secondo):\n if len(primo) <= 3 or len(secondo) <=3:\n print(\"errore!\")\n else:\n return primo[:-1] + secondo[-1] + \" \" + secondo[:-1] + primo[-1]\n", "_____no_output_____" ] ], [ [ "### nspazio\n\n✪ Scrivi la funzione `nspazio` che data una stringa in input, RITORNA una nuova stringa in\ncui l’n-esimo carattere è uno spazio. Per esempio, data la stringa 'largamente' e il carattere all'indice 5, il programma deve RITORNARE `'larga ente'`. Nota: se il numero \ndovesse essere troppo grande (i.e., la parola ha 6 caratteri e chiedo di rimuovere \nil numero 9), il programma STAMPA _errore!_\n\n```python\n>>> x = nspazio('largamente', 5)\n>>> x\n'larga ente'\n\n>>> x = nspazio('ciao', 9)\nerrore!\n>>> x\nNone\n\n>>> x = nspazio('ciao', 4)\nerrore!\n>>> x\nNone\n```", "_____no_output_____" ] ], [ [ "# scrivi qui\n\ndef nspazio(parola, indice):\n if indice >= len(parola):\n print(\"errore!\")\n return parola[:indice]+' '+parola[indice+1:]\n\n#nspazio(\"largamente\", 5)", "_____no_output_____" ] ], [ [ "### inifin\n\n✪ Scrivi un programma in Python prende una stringa, e se la stringa ha una lunghezza maggiore di 4, il programma STAMPA le prime e le ultime due lettere. Altrimenti, nel caso in cui la lunghezza della stringa sia minore di 4, STAMPA `voglio almeno 4 caratteri`. Per esempio, passando alla funzione `\"ciaomondo\"`, la funzione dovrebbe stampare `\"cido\"`. Passando `\"ciao\"` dovrebbe stampare `ciao` e passando `\"hi\"` dovrebbe stampare `voglio almeno 4 caratteri`\n\n```python\n>>> inifin('ciaomondo')\ncido\n\n>>> inifin('hi')\nVoglio almeno 4 caratteri\n```", "_____no_output_____" ] ], [ [ "# scrivi qui\n\ndef inifin(stringa):\n if len(stringa) >= 4:\n print(stringa[:2] + stringa[-2:])\n else:\n print(\"Voglio almeno 4 caratteri\")\n ", "_____no_output_____" ] ], [ [ "### scambia\n\nScrivere una funzione che data una stringa, inverte il primo e l’ultimo carattere, e STAMPA il risultato.\n\nQuindi, data la stringa “mondo”, il programma stamperà “oondm”\n\n```python\n>>> scambia('mondo')\noondm\n```", "_____no_output_____" ] ], [ [ "# scrivi qui\n\ndef scambia(stringa):\n print(stringa[-1] + stringa[1:-1] + stringa[0])", "_____no_output_____" ] ], [ [ "## Esercizi con eccezioni e test\n\n\n\n<div class=\"alert alert-warning\">\n\n**ATTENZIONE: Gli esercizi seguenti richiedono di conoscere:**\n\n<ul>\n<li>[Controllo di flusso](https://it.softpython.org/#control-flow)</li>\n<li>[Funzioni](https://it.softpython.org/functions/functions-sol.html)</li>\n<li>**e anche**: [Eccezioni e test con assert](https://it.softpython.org/errors-and-testing/errors-and-testing-sol.html)\n</ul>\n<br/>\n<strong>Se sei alle prime armi con la programmazione, ti conviene saltarli e ripassare in seguito</strong>\n</div>\n\n", "_____no_output_____" ], [ "### halet\n\n✪ RITORNA `True` se parola contiene lettera, `False` altrimenti\n \n- usare ciclo `while`", "_____no_output_____" ] ], [ [ "def halet(parola, lettera):\n #jupman-raise\n indice = 0 # inizializziamo indice\n while indice < len(parola):\n if parola[indice] == lettera:\n return True # abbiamo trovato il carattere, possiamo interrompere la ricerca\n indice += 1 # è come scrivere indice = indice + 1\n # se arriviamo DOPO il while, c'è una sola ragione:\n # non abbiamo trovato nulla, quindi dobbiamo ritornare False\n return False\n #/jupman-raise\n\n\n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n\nassert halet(\"ciao\", 'a')\nassert not halet(\"ciao\", 'A')\nassert halet(\"ciao\", 'c') \nassert not halet(\"\", 'a')\nassert not halet(\"ciao\", 'z')\n# FINE TEST", "_____no_output_____" ] ], [ [ "### conta\n\n✪ RITORNA il numero di occorrenze di lettera in parola\n\nNOTA: NON VOGLIO UNA STAMPA, VOGLIO CHE *RITORNI* IL VALORE!\n \n- Usare ciclo for in ", "_____no_output_____" ] ], [ [ "\ndef conta(parola, lettera):\n #jupman-raise\n occorrenze = 0\n for carattere in parola:\n # print(\"carattere corrente = \", carattere) # le print di debug sono ammesse\n if carattere == lettera:\n # print(\"trovata occorrenza !\") # le print di debug sono ammesse\n occorrenze += 1\n return occorrenze # L'IMPORTANTE E' _RITORANRE_ IL VALORE COME DA TESTO DELL'ESERCIZIO !!!!!\n #/jupman-raise\n \n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n\nassert conta(\"ciao\", \"z\") == 0 \nassert conta(\"ciao\", \"c\") == 1\nassert conta(\"babbo\", \"b\") == 3\nassert conta(\"\", \"b\") == 0\nassert conta(\"ciao\", \"C\") == 0 \n# FINE TEST", "_____no_output_____" ] ], [ [ "### contiene_minuscola\n\n✪ Esercizio ripreso dall' Esercizio 4 del libro Pensare in Python Capitolo Stringhe\nleggere in fondo qua: https://davidleoni.github.io/ThinkPythonItalian/html/thinkpython2009.html\n \n- RITORNA True se la parola contiene almeno una lettera minuscola\n- RITORNA False altrimenti\n\n- Usare ciclo `while`", "_____no_output_____" ] ], [ [ "\ndef contiene_minuscola(s):\n #jupman-raise\n i = 0\n while i < len(s):\n if s[i] == s[i].lower():\n return True\n i += 1\n return False\n #/jupman-raise\n \n\n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n\nassert contiene_minuscola(\"David\") \nassert contiene_minuscola(\"daviD\")\nassert not contiene_minuscola(\"DAVID\")\nassert not contiene_minuscola(\"\")\nassert contiene_minuscola(\"a\")\nassert not contiene_minuscola(\"A\")", "_____no_output_____" ] ], [ [ "### dialetto\n\n✪✪ Esiste un dialetto in cui tutte le “a” devono per forza essere precedute da una “g”. Nel caso una parola dovesse contenere “a” _non_ preceduta da una “g”, possiamo dire con certezza che questa parola non fa parte di quel dialetto. Scrivere una funzione che data una parola, RITORNI `True` se la parola rispetta le regole del dialetto, `False` altrimenti. \n\n```python\n>>> dialetto(\"ammot\")\nFalse\n>>> print(dialetto(\"paganog\")\nFalse\n>>> print(dialetto(\"pgaganog\")\nTrue\n>>> print(dialetto(\"ciao\")\nFalse\n>>> dialetto(\"cigao\")\nTrue\n>>> dialetto(\"zogava\")\nFalse\n>>> dialetto(\"zogavga\")\nTrue\n```", "_____no_output_____" ] ], [ [ "\n\ndef dialetto(parola):\n #jupman-raise\n n = 0\n for i in range(0,len(parola)):\n if parola[i] == \"a\":\n if i == 0 or parola[i - 1] != \"g\":\n return False\n return True\n #/jupman-raise\n\n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n \nassert dialetto(\"a\") == False\nassert dialetto(\"ab\") == False\nassert dialetto(\"ag\") == False\nassert dialetto(\"ag\") == False\nassert dialetto(\"ga\") == True\nassert dialetto(\"gga\") == True\nassert dialetto(\"gag\") == True\nassert dialetto(\"gaa\") == False\nassert dialetto(\"gaga\") == True\nassert dialetto(\"gabga\") == True\nassert dialetto(\"gabgac\") == True\nassert dialetto(\"gabbgac\") == True\nassert dialetto(\"gabbgagag\") == True\n# FINE TEST", "_____no_output_____" ] ], [ [ "### contavoc \n\n✪✪ Data una stringa, scrivere una funzione che conti il numero di vocali. \nSe il numero di vocali è pari RITORNA il numero di vocali, altrimenti solleva l'eccezione `ValueError`\n\t\n```python \n>>> conta_vocali(\"asso\") \n2\n>>> conta_vocali(\"ciao\")\n---------------------------------------------------------------------------\nValueError Traceback (most recent call last)\n<ipython-input-15-058310342431> in <module>()\n 16 contavoc(\"arco\")\n---> 19 contavoc(\"ciao\")\n\nValueError: Vocali dispari !\n```", "_____no_output_____" ] ], [ [ "\ndef contavoc(parola):\n #jupman-raise\n n_vocali = 0\n\n vocali = [\"a\",\"e\",\"i\",\"o\",\"u\"]\n\n for lettera in parola:\n if lettera.lower() in vocali:\n n_vocali = n_vocali + 1\n\n if n_vocali % 2 == 0:\n return n_vocali\n else:\n raise ValueError(\"Vocali dispari !\")\n #/jupman-raise\n \n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n \nassert contavoc(\"arco\") == 2\nassert contavoc(\"scaturire\") == 4\n\ntry:\n contavoc(\"ciao\") # con questa stringa ci attendiamo che sollevi l'eccezione ValueError\n raise Exception(\"Non dovrei arrivare fin qui !\")\nexcept ValueError: # se solleva l'eccezione ValueError,si sta comportando come previsto e non facciamo niente\n pass\n\ntry:\n contavoc(\"aiuola\") # con questa stringa ci attendiamo che sollevi l'eccezione ValueError\n raise Exception(\"Non dovrei arrivare fin qui !\")\nexcept ValueError: # se solleva l'eccezione ValueError,si sta comportando come previsto e non facciamo niente\n pass\n\n", "_____no_output_____" ] ], [ [ "### palindroma\n\n✪✪✪ Una parola è palindroma quando è esattamente la stessa se letta al contrario\n\nScrivi una funzione che RITORNA `True` se una parola è palindroma, `False` altrimenti\n\n* assumi che la stringa vuota sia palindroma\n\nEsempio: \n\n```python\n>>> x = palindroma('radar')\n>>> x\nTrue\n>>> x = palindroma('scatola')\n>>> x\nFalse\n\n```", "_____no_output_____" ] ], [ [ "\ndef palindroma(parola):\n #jupman-raise\n for i in range(len(parola) // 2):\n if parola[i] != parola[len(parola)- i - 1]:\n return False\n \n return True # nota che è FUORI dal for: superati tutti i controlli,\n # possiamo concludere che la parola è palindroma\n #/jupman-raise\n \n# INIZIO TEST - NON TOCCARE ! \n# se hai scritto tutto il codice giusto, ed esegui la cella, python non dovrebbe lanciare AssertionError\n\nassert palindroma('') == True # assumiamo che la stringa vuota sia palindroma\nassert palindroma('a') == True\nassert palindroma('aa') == True\nassert palindroma('ab') == False\nassert palindroma('aba') == True\nassert palindroma('bab') == True\nassert palindroma('bba') == False\nassert palindroma('abb') == False\nassert palindroma('abba') == True\nassert palindroma('baab') == True\nassert palindroma('abbb') == False\nassert palindroma('bbba') == False\nassert palindroma('radar') == True\nassert palindroma('scatola') == False\n\n# FINE TEST\n ", "_____no_output_____" ] ], [ [ "## Prosegui\n\nContinua con le [challenges](https://it.softpython.org/strings/strings5-chal.html)", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e70469ad7b3135e135fec124d4d0e738dd3ab7

586,702

ipynb

Jupyter Notebook

financial_planning.ipynb

kary2003/5_financial_planning

11ddc3ab01f567eab683efff10f1debbec5c2009

[ "ADSL" ]

null

financial_planning.ipynb

kary2003/5_financial_planning

11ddc3ab01f567eab683efff10f1debbec5c2009

[ "ADSL" ]

null

financial_planning.ipynb

kary2003/5_financial_planning

11ddc3ab01f567eab683efff10f1debbec5c2009

[ "ADSL" ]

null

86.30509

129,004

0.714959

[ [ [ "## Unit 5 - Financial Planning", "_____no_output_____" ] ], [ [ " %%capture \n# Initial imports\nimport os\nimport requests\nimport pandas as pd\nfrom dotenv import load_dotenv\nimport alpaca_trade_api as tradeapi\nfrom MCForecastTools import MCSimulation\n", "_____no_output_____" ], [ " # Load .env enviroment variables\nload_dotenv()", "_____no_output_____" ] ], [ [ "## Part 1 - Personal Finance Planner", "_____no_output_____" ] ], [ [ "# Set monthly household income\nmonthly_income = 12000", "_____no_output_____" ] ], [ [ "### Collect Crypto Prices Using the requests Library", "_____no_output_____" ] ], [ [ " # Current amount of crypto assets\nmy_btc = 1.2\nmy_eth = 5.3", "_____no_output_____" ], [ " # Crypto API URLs\nbtc_url = \"https://api.alternative.me/v2/ticker/Bitcoin/?convert=USD\"\neth_url = \"https://api.alternative.me/v2/ticker/Ethereum/?convert=USD\"", "_____no_output_____" ], [ "requests.get(btc_url)\nbtc_url_data = requests.get(btc_url)\nbtc_data = btc_url_data.json()\n\nrequests.get(eth_url)\neth_url_data = requests.get(eth_url)\neth_data = eth_url_data.json()\n\n# Fetch current BTC price\ncurrent = float(btc_data['data']['1']['quotes']['USD']['price'])\n\n# Fetch current ETH price\ncurrent2 = float(eth_data['data']['1027']['quotes']['USD']['price'])\n\n# Compute current value of my crpto\nmy_btc_value = my_btc * current\nmy_eth_value = my_eth * current2\n\nprint(f\"The current value of your {my_btc} BTC is ${my_btc_value:0.2f}\")\nprint(f\"The current value of your {my_eth} ETH is ${my_eth_value:0.2f}\")", "The current value of your 1.2 BTC is $18422.15\nThe current value of your 5.3 ETH is $2369.84\n" ] ], [ [ "### Collect Investments Data Using Alpaca: SPY (stocks) and AGG (bonds)", "_____no_output_____" ] ], [ [ " # Current amount of shares\nmy_agg = 200\nmy_spy = 50", "_____no_output_____" ], [ " # Set Alpaca API key and secret\nalpaca_api_key = os.getenv(\"ALPACA_API_KEY\")\nalpaca_secret_key = os.getenv(\"ALPACA_SECRET_KEY\")\n\n# Create the Alpaca API object\nalpaca = tradeapi.REST(\n alpaca_api_key,\n alpaca_secret_key,\n api_version=\"v2\"\n)", "_____no_output_____" ], [ "# Set timeframe to '1D' for Alpaca API\ntimeframe = \"1D\"\n\nstart_date = pd.Timestamp(\"2020-10-21\", tz=\"America/New_York\").isoformat()\nend_date = pd.Timestamp(\"2020-10-21\", tz=\"America/New_York\").isoformat()\n# today_now = pd.Timestamp.today().isoformat()\n\n# Set the tickers\ntickers = [\"AGG\", \"SPY\"]\n\n# Get current closing prices for SPY and AGG\ndf_ticker = alpaca.get_barset(\n tickers,\n timeframe,\n start=start_date,\n end=end_date\n).df\n\ndf_ticker.head()", "_____no_output_____" ], [ "# Create and empty DataFrame for closing prices\nclosing_prices = pd.DataFrame()\n\n# Pick AGG and SPY close prices\nclosing_prices[\"AGG\"] = df_ticker[\"AGG\"][\"close\"]\nclosing_prices[\"SPY\"] = df_ticker[\"SPY\"][\"close\"]\n\nclosing_prices\n# Drop the time component of the date\nclosing_prices.index = closing_prices.index.date\nclosing_prices.head()\n\nagg_close_price = closing_prices['AGG'][0]\nspy_close_price = closing_prices['SPY'][0]\n\nprint(f\"Current AGG closing price: ${agg_close_price:0.2f}\")\nprint(f\"Current SPY closing price: ${spy_close_price:0.2f}\")", "Current AGG closing price: $117.52\nCurrent SPY closing price: $342.69\n" ], [ " # Compute the current value of shares\nmy_spy_value = spy_close_price * my_spy\nmy_agg_value = agg_close_price * my_agg\n# Print current value of share\nprint(f\"The current value of your {my_spy} SPY shares is ${my_spy_value:0.2f}\")\nprint(f\"The current value of your {my_agg} AGG shares is ${my_agg_value:0.2f}\")", "The current value of your 50 SPY shares is $17134.50\nThe current value of your 200 AGG shares is $23503.00\n" ] ], [ [ "#### Savings Health Analysis", "_____no_output_____" ] ], [ [ "# Create savings DataFrame\nshares = my_spy_value + my_agg_value\ncrypto = my_btc_value + my_eth_value\n\nsavings = [['shares',shares],['crypto', crypto]]\n\ndf_savings = pd.DataFrame(savings, columns =['','amount'])\ndf_savings.set_index(df_savings[''], inplace=True)\n\n# Use the `drop` function to drop specific columns\ndf_savings.drop(columns=[''], inplace=True)\ndf_savings", "_____no_output_____" ], [ " %%capture \ndf_savings = pd.DataFrame({\"Amount\": [shares, crypto]},\n index=['Shares', 'Crypto'])\nplot = df_savings.plot.pie(subplots=True)", "_____no_output_____" ], [ "# Set ideal emergency fund\nemergency_fund = monthly_income * 3\n\n# Calculate total amount of savings\nmy_savings = shares + crypto\n\n# Validate saving health\nif my_savings > emergency_fund:\n print(\"Congratulations! You have enough money in your emergency fund.\")\nelse:\n print(\"Your need more funds\")", "Congratulations! You have enough money in your emergency fund.\n" ] ], [ [ "#### Part 2 - Retirement Planning\nMonte Carlo Simulation", "_____no_output_____" ] ], [ [ "# Set start and end dates of five years back from today.\n# Sample results may vary from the solution based on the time frame chosen\nstart_date1 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()\nend_date1 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()", "_____no_output_____" ], [ " # Get 5 years' worth of historical data for SPY and AGG!\n# Set the tickers\nticker = [\"AGG\", \"SPY\"]\n \ndf_stock_data = alpaca.get_barset(\n ticker,\n timeframe,\n start=start_date1,\n end=end_date1\n).df\n\n# Display sample data\ndf_stock_data.head().append(df_stock_data.tail())", "_____no_output_____" ], [ "# ?MCSimulation", "_____no_output_____" ], [ " # Configuring a Monte Carlo simulation to forecast 30 years cumulative returnss\nMC_30year = MCSimulation(\n portfolio_data = df_stock_data,\n weights = [.40,.60],\n num_simulation = 500,\n num_trading_days = 252*30\n)", "_____no_output_____" ], [ "MC_30year.portfolio_data.head()", "_____no_output_____" ], [ "MC_30year.calc_cumulative_return()", "Running Monte Carlo simulation number 0.\nRunning Monte Carlo simulation number 10.\nRunning Monte Carlo simulation number 20.\nRunning Monte Carlo simulation number 30.\nRunning Monte Carlo simulation number 40.\nRunning Monte Carlo simulation number 50.\nRunning Monte Carlo simulation number 60.\nRunning Monte Carlo simulation number 70.\nRunning Monte Carlo simulation number 80.\nRunning Monte Carlo simulation number 90.\nRunning Monte Carlo simulation number 100.\nRunning Monte Carlo simulation number 110.\nRunning Monte Carlo simulation number 120.\nRunning Monte Carlo simulation number 130.\nRunning Monte Carlo simulation number 140.\nRunning Monte Carlo simulation number 150.\nRunning Monte Carlo simulation number 160.\nRunning Monte Carlo simulation number 170.\nRunning Monte Carlo simulation number 180.\nRunning Monte Carlo simulation number 190.\nRunning Monte Carlo simulation number 200.\nRunning Monte Carlo simulation number 210.\nRunning Monte Carlo simulation number 220.\nRunning Monte Carlo simulation number 230.\nRunning Monte Carlo simulation number 240.\nRunning Monte Carlo simulation number 250.\nRunning Monte Carlo simulation number 260.\nRunning Monte Carlo simulation number 270.\nRunning Monte Carlo simulation number 280.\nRunning Monte Carlo simulation number 290.\nRunning Monte Carlo simulation number 300.\nRunning Monte Carlo simulation number 310.\nRunning Monte Carlo simulation number 320.\nRunning Monte Carlo simulation number 330.\nRunning Monte Carlo simulation number 340.\nRunning Monte Carlo simulation number 350.\nRunning Monte Carlo simulation number 360.\nRunning Monte Carlo simulation number 370.\nRunning Monte Carlo simulation number 380.\nRunning Monte Carlo simulation number 390.\nRunning Monte Carlo simulation number 400.\nRunning Monte Carlo simulation number 410.\nRunning Monte Carlo simulation number 420.\nRunning Monte Carlo simulation number 430.\nRunning Monte Carlo simulation number 440.\nRunning Monte Carlo simulation number 450.\nRunning Monte Carlo simulation number 460.\nRunning Monte Carlo simulation number 470.\nRunning Monte Carlo simulation number 480.\nRunning Monte Carlo simulation number 490.\n" ], [ "# Plot simulation outcomes\nline_plot = MC_30year.plot_simulation()\n\n# Save the plot for future usage\nline_plot.get_figure().savefig(\"MC_30year_sim_plot.png\", bbox_inches=\"tight\")", "_____no_output_____" ], [ "# Plot probability distribution and confidence intervals\ndist_plot = MC_30year.plot_distribution()\n\n# Save the plot for future usage\ndist_plot.get_figure().savefig('MC_30year_dist_plot.png',bbox_inches='tight')", "_____no_output_____" ], [ " # Fetch summary statistics from the Monte Carlo simulation results\ntbl = MC_30year.summarize_cumulative_return()\n\n# Print summary statistics\nprint(tbl)", "count 500.000000\nmean 11.345167\nstd 7.313115\nmin 1.943399\n25% 6.058662\n50% 9.757410\n75% 14.528162\nmax 55.313315\n95% CI Lower 2.754306\n95% CI Upper 31.080523\nName: 7560, dtype: float64\n" ] ], [ [ "#### Given an initial investment of $20,000, what is the expected portfolio return in dollars at the 95% lower and upper confidence intervals?", "_____no_output_____" ] ], [ [ " # Set initial investment\ninitial_investment = 20000\n\n# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $20,000\nci_lower = round(tbl[8]*20000,2)\nci_upper = round(tbl[9]*20000,2)\n\n# Print results\nprint(f\"There is a 95% chance that an initial investment of ${initial_investment} in the portfolio\"\n f\" over the next 30 years will end within in the range of\"\n f\" ${ci_lower} and ${ci_upper}\")", "There is a 95% chance that an initial investment of $20000 in the portfolio over the next 30 years will end within in the range of $55086.12 and $621610.45\n" ] ], [ [ "#### How would a 50% increase in the initial investment amount affect the expected portfolio return in dollars at the 95% lower and upper confidence intervals", "_____no_output_____" ] ], [ [ "# Set initial investment\ninitial_investment1 = 20000 * 1.5\n\n# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $30,000\nci_lower1 = round(tbl[8]*(20000*1.5),2)\nci_upper1 = round(tbl[9]*(20000*1.5),2)\n\n# Print results\nprint(f\"There is a 95% chance that an initial investment of ${initial_investment1} in the portfolio\"\n f\" over the next 30 years will end within in the range of\"\n f\" ${ci_lower1} and ${ci_upper1}\")", "There is a 95% chance that an initial investment of $30000.0 in the portfolio over the next 30 years will end within in the range of $82629.18 and $932415.68\n" ] ], [ [ "#### Optional Challenge - Early Retirement\nFive Years Retirement Option", "_____no_output_____" ] ], [ [ "# Configuring a Monte Carlo simulation to forecast 5 years cumulative returns\nstart_date5 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()\nend_date5 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()\nticker5 = [\"AGG\", \"SPY\"]\n \nfive_stock_data = alpaca.get_barset(\n ticker5,\n timeframe,\n start=start_date5,\n end=end_date5\n).df\n\n# Display sample data\nMC_fiveyear = MCSimulation(\n portfolio_data = five_stock_data,\n weights = [.40,.60],\n num_simulation = 500,\n num_trading_days = 252*5\n)", "_____no_output_____" ], [ "# Running a Monte Carlo simulation to forecast 5 years cumulative returns\nMC_fiveyear.calc_cumulative_return()", "Running Monte Carlo simulation number 0.\nRunning Monte Carlo simulation number 10.\nRunning Monte Carlo simulation number 20.\nRunning Monte Carlo simulation number 30.\nRunning Monte Carlo simulation number 40.\nRunning Monte Carlo simulation number 50.\nRunning Monte Carlo simulation number 60.\nRunning Monte Carlo simulation number 70.\nRunning Monte Carlo simulation number 80.\nRunning Monte Carlo simulation number 90.\nRunning Monte Carlo simulation number 100.\nRunning Monte Carlo simulation number 110.\nRunning Monte Carlo simulation number 120.\nRunning Monte Carlo simulation number 130.\nRunning Monte Carlo simulation number 140.\nRunning Monte Carlo simulation number 150.\nRunning Monte Carlo simulation number 160.\nRunning Monte Carlo simulation number 170.\nRunning Monte Carlo simulation number 180.\nRunning Monte Carlo simulation number 190.\nRunning Monte Carlo simulation number 200.\nRunning Monte Carlo simulation number 210.\nRunning Monte Carlo simulation number 220.\nRunning Monte Carlo simulation number 230.\nRunning Monte Carlo simulation number 240.\nRunning Monte Carlo simulation number 250.\nRunning Monte Carlo simulation number 260.\nRunning Monte Carlo simulation number 270.\nRunning Monte Carlo simulation number 280.\nRunning Monte Carlo simulation number 290.\nRunning Monte Carlo simulation number 300.\nRunning Monte Carlo simulation number 310.\nRunning Monte Carlo simulation number 320.\nRunning Monte Carlo simulation number 330.\nRunning Monte Carlo simulation number 340.\nRunning Monte Carlo simulation number 350.\nRunning Monte Carlo simulation number 360.\nRunning Monte Carlo simulation number 370.\nRunning Monte Carlo simulation number 380.\nRunning Monte Carlo simulation number 390.\nRunning Monte Carlo simulation number 400.\nRunning Monte Carlo simulation number 410.\nRunning Monte Carlo simulation number 420.\nRunning Monte Carlo simulation number 430.\nRunning Monte Carlo simulation number 440.\nRunning Monte Carlo simulation number 450.\nRunning Monte Carlo simulation number 460.\nRunning Monte Carlo simulation number 470.\nRunning Monte Carlo simulation number 480.\nRunning Monte Carlo simulation number 490.\n" ], [ " # Plot simulation outcomes\nline_plot_5 = MC_fiveyear.plot_simulation()\n\n# Save the plot for future usage\nline_plot_5.get_figure().savefig(\"MC_fiveyear_sim_plot.png\", bbox_inches=\"tight\")", "_____no_output_____" ], [ "# Plot probability distribution and confidence intervals\ndist_plot_5 = MC_fiveyear.plot_distribution()\n\n# Save the plot for future usage\ndist_plot_5.get_figure().savefig('MC_fiveyear_dist_plot.png',bbox_inches='tight')", "_____no_output_____" ], [ "# Fetch summary statistics from the Monte Carlo simulation results\ntbl_five = MC_fiveyear.summarize_cumulative_return()\n\n# Print summary statistics\nprint(tbl_five)", "count 500.000000\nmean 1.498154\nstd 0.411890\nmin 0.606598\n25% 1.204727\n50% 1.453940\n75% 1.747834\nmax 3.353604\n95% CI Lower 0.877865\n95% CI Upper 2.382144\nName: 1260, dtype: float64\n" ], [ "# Set initial investment\ninitial_investment_five = 60000\n\n# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $60,000\nci_lower_five = round(tbl_five[8]*60000,2)\nci_upper_five = round(tbl_five[9]*60000,2)\n\n# Print results\nprint(f\"There is a 95% chance that an initial investment of ${initial_investment_five} in the portfolio\"\n f\" over the next 5 years will end within in the range of\"\n f\" ${ci_lower_five} and ${ci_upper_five}\")", "There is a 95% chance that an initial investment of $60000 in the portfolio over the next 5 years will end within in the range of $52671.88 and $142928.62\n" ] ], [ [ " ##### Ten Years Retirement Option", "_____no_output_____" ] ], [ [ " # Configuring a Monte Carlo simulation to forecast 10 years cumulative returns\n\nstart_date_10 = pd.Timestamp('2015-10-21', tz='America/New_York').isoformat()\nend_date_10 = pd.Timestamp('2020-10-21', tz='America/New_York').isoformat()\nticker_10 = [\"AGG\", \"SPY\"]\n \nten_stock_data = alpaca.get_barset(\n ticker_10,\n timeframe,\n start=start_date_10,\n end=end_date_10\n).df\n\n# Display sample data\nMC_tenyear = MCSimulation(\n portfolio_data = ten_stock_data,\n weights = [.40,.60],\n num_simulation = 500,\n num_trading_days = 252*10\n)", "_____no_output_____" ], [ " # Running a Monte Carlo simulation to forecast 10 years cumulative returns\nMC_tenyear.calc_cumulative_return()", "Running Monte Carlo simulation number 0.\nRunning Monte Carlo simulation number 10.\nRunning Monte Carlo simulation number 20.\nRunning Monte Carlo simulation number 30.\nRunning Monte Carlo simulation number 40.\nRunning Monte Carlo simulation number 50.\nRunning Monte Carlo simulation number 60.\nRunning Monte Carlo simulation number 70.\nRunning Monte Carlo simulation number 80.\nRunning Monte Carlo simulation number 90.\nRunning Monte Carlo simulation number 100.\nRunning Monte Carlo simulation number 110.\nRunning Monte Carlo simulation number 120.\nRunning Monte Carlo simulation number 130.\nRunning Monte Carlo simulation number 140.\nRunning Monte Carlo simulation number 150.\nRunning Monte Carlo simulation number 160.\nRunning Monte Carlo simulation number 170.\nRunning Monte Carlo simulation number 180.\nRunning Monte Carlo simulation number 190.\nRunning Monte Carlo simulation number 200.\nRunning Monte Carlo simulation number 210.\nRunning Monte Carlo simulation number 220.\nRunning Monte Carlo simulation number 230.\nRunning Monte Carlo simulation number 240.\nRunning Monte Carlo simulation number 250.\nRunning Monte Carlo simulation number 260.\nRunning Monte Carlo simulation number 270.\nRunning Monte Carlo simulation number 280.\nRunning Monte Carlo simulation number 290.\nRunning Monte Carlo simulation number 300.\nRunning Monte Carlo simulation number 310.\nRunning Monte Carlo simulation number 320.\nRunning Monte Carlo simulation number 330.\nRunning Monte Carlo simulation number 340.\nRunning Monte Carlo simulation number 350.\nRunning Monte Carlo simulation number 360.\nRunning Monte Carlo simulation number 370.\nRunning Monte Carlo simulation number 380.\nRunning Monte Carlo simulation number 390.\nRunning Monte Carlo simulation number 400.\nRunning Monte Carlo simulation number 410.\nRunning Monte Carlo simulation number 420.\nRunning Monte Carlo simulation number 430.\nRunning Monte Carlo simulation number 440.\nRunning Monte Carlo simulation number 450.\nRunning Monte Carlo simulation number 460.\nRunning Monte Carlo simulation number 470.\nRunning Monte Carlo simulation number 480.\nRunning Monte Carlo simulation number 490.\n" ], [ " # Plot simulation outcomes\nline_plot_10= MC_tenyear.plot_simulation()\n\n# Save the plot for future usage\nline_plot_10.get_figure().savefig(\"MC_tenyear_sim_plot.png\", bbox_inches=\"tight\")", "_____no_output_____" ], [ "# Plot probability distribution and confidence intervals\ndist_plot_10 = MC_tenyear.plot_distribution()\n\n# Save the plot for future usage\ndist_plot_10.get_figure().savefig('MC_tenyear_dist_plot.png',bbox_inches='tight')", "_____no_output_____" ], [ "# Fetch summary statistics from the Monte Carlo simulation results\ntbl_ten = MC_tenyear.summarize_cumulative_return()\n\n# Print summary statistics\nprint(tbl_ten)", "count 500.000000\nmean 2.200078\nstd 0.843440\nmin 0.726255\n25% 1.586855\n50% 2.064024\n75% 2.608526\nmax 6.699747\n95% CI Lower 1.037354\n95% CI Upper 4.245572\nName: 2520, dtype: float64\n" ], [ "# Set initial investment\ninitial_investment_ten = 60000\n\n# Use the lower and upper `95%` confidence intervals to calculate the range of the possible outcomes of our $60,000\nci_lower_ten = round(tbl_ten[8]*60000,2)\nci_upper_ten = round(tbl_ten[9]*60000,2)\n\n# Print results\nprint(f\"There is a 95% chance that an initial investment of ${initial_investment_ten} in the portfolio\"\n f\" over the next 10 years will end within in the range of\"\n f\" ${ci_lower_ten} and ${ci_upper_ten}\")", "There is a 95% chance that an initial investment of $60000 in the portfolio over the next 10 years will end within in the range of $62241.22 and $254734.34\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

d0e71455ca4e0e3267c447ed61ce345539b1983d

6,718

ipynb

Jupyter Notebook

PreProcessingTable.ipynb

vapatinagy/topic_modeling_bsc2019

9cc61613c58b78ecf6ca5d2ed59a2a16f4cb7421

[ "MIT" ]

null

PreProcessingTable.ipynb

vapatinagy/topic_modeling_bsc2019

9cc61613c58b78ecf6ca5d2ed59a2a16f4cb7421

[ "MIT" ]

null

PreProcessingTable.ipynb

vapatinagy/topic_modeling_bsc2019

9cc61613c58b78ecf6ca5d2ed59a2a16f4cb7421

[ "MIT" ]

null

31.688679

207

0.526943

[ [ [ "# IMPORT PACKAGES\nimport spacy, string\nnlp = spacy.load('de_core_news_sm')\nfrom spacy.lang.de import German", "_____no_output_____" ], [ "# LOAD DATA S.T. 1 LINE IN XLSX = 1 DOCUMENT\ndef load (path):\n data_raw = open(path + '.csv', encoding = 'utf-8').read().replace('\\\"', '').replace('\\ufeff', '')\n data_1row_1string = data_raw.split('\\n')\n \n data_list_remove_empty_last_line = []\n for row in range(0, len(data_1row_1string)-1):\n data_list_remove_empty_last_line.append(data_1row_1string[row])\n \n data_1row_stringlist = [row.split(';') for row in data_list_remove_empty_last_line]\n \n print('data from ' + path + ' is loaded')\n return data_1row_stringlist", "_____no_output_____" ], [ "# EXTRACT TRANSCRIPTIONS\ndef extract (data_1row_stringlist):\n column1 = [row[0] for row in data_1row_stringlist]\n column1_1row_tokenlist = [nlp(row) for row in column1]\n print('column extraction is done')\n \n return column1_1row_tokenlist", "_____no_output_____" ], [ "# normalization, spacy lemmatization\ndef normalize (column1_1row_tokenlist):\n column1_normalized = []\n for row in column1_1row_tokenlist:\n row_lemmatized = [token.lemma_.lower().replace('ß', 'ss').replace('\\'s', '').replace('’s', '') for token in row if (not token.text.isdigit() and token.is_punct == False and len(token) > 1)]\n column1_normalized.append(row_lemmatized)\n print('spacy normalization is done')\n \n return column1_normalized", "_____no_output_____" ], [ "# optimization with gerTwol\ndef gertwol_optimize (column1_normalized):\n\n gertwol_raw = nlp(open('GERTWOL_LIST.csv', encoding = 'utf-8').read().replace('\\ufeff', ''))\n gertwol_list = [row.text.split(';') for row in gertwol_raw if row.text != '\\n'] \n\n lemma_dict = {}\n for i in range(0, len(gertwol_list)-1): \n row = gertwol_list[i]\n lemma_dict[row[0]] = [row[1]]\n\n column1_gertwoled = []\n j = 0\n with open('GerTwol_check.csv', 'w') as test:\n for row in column1_normalized:\n for i in range (0, len(row)):\n if (row[i] in lemma_dict.keys() and row[i] != lemma_dict[row[i]][0]):\n test.write(row[i] + ': ' + lemma_dict[row[i]][0] + '\\n')\n row[i] = lemma_dict[row[i]][0] #returns value\n j = j + 1\n column1_gertwoled.append(row) \n\n print('gertwol optimization is done, nr of changed items: ' + str(j))\n return column1_gertwoled", "_____no_output_____" ], [ "# REMOVE STOPWORDS\ndef remove_stopwords (column1):\n column1_nostops = []\n stopwords = open('STOPWORDS.csv', encoding = 'utf-8').read().replace('\\ufeff', '').split('\\n')\n\n for row in column1: \n row_nostops = [word for word in row if word not in stopwords]\n column1_nostops.append(row_nostops) \n \n print('stopword removal is done')\n return column1_nostops", "_____no_output_____" ], [ "#insert transcription back to table and print\ndef reinsert_and_save(data_1row_stringlist, column1_normalized, path):\n i = 0\n for row in column1_normalized:\n data_to_string = ''\n for word in row:\n if word.strip() != '':\n data_to_string = data_to_string + word.strip() + ' ' \n data_1row_stringlist[i][0] = data_to_string\n i = i + 1\n \n data_no_empty_record = [row for row in data_1row_stringlist if row[0].strip() != '']\n \n with open(path + 'norm.csv', 'w', encoding = 'utf-8') as doc_out:\n for row in data_no_empty_record:\n for cell in row:\n doc_out.write(cell + ';')\n doc_out.write('\\n')\n print(path + ' output is saved')\n\n return doc_out\n", "_____no_output_____" ], [ "# EXECUTE\npaths = ['./IO_YO/all', './IO_YO/Test']\n\ndoc_in = load(paths[0] + '_in_v2')\ndoc_norm = normalize(extract(doc_in))\ndoc_gert = gertwol_optimize (doc_norm) \n\n#doc_out = reinsert_and_save(doc_in, doc_norm, paths[0] + '_1')\n#doc_out = reinsert_and_save(doc_in, doc_gert, paths[0] + '_2') \n#doc_out = reinsert_and_save(doc_in, remove_stopwords (doc_norm), paths[0] + '_1S') \ndoc_out = reinsert_and_save(doc_in, remove_stopwords (doc_gert), paths[0] + '_2S') ", "data from ./IO_YO/all_in_v2 is loaded\ncolumn extraction is done\nspacy normalization is done\ngertwol optimization is done, nr of changed items: 10259\nstopword removal is done\n./IO_YO/all_2S output is saved\n" ], [ " ", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e71bb66a4997b74880c1fbda8a1d8a347e1053

119,378

ipynb

Jupyter Notebook

archive/python/indexing_in_numpy.ipynb

ajrichards/bayesian-examples

fbd87c6f1613ea516408e9ebc3c9eff1248246e4

[ "BSD-3-Clause" ]

2

2016-01-27T08:51:23.000Z

2017-04-17T02:21:34.000Z

archive/python/indexing_in_numpy.ipynb

ajrichards/notebook

fbd87c6f1613ea516408e9ebc3c9eff1248246e4

[ "BSD-3-Clause" ]

null

archive/python/indexing_in_numpy.ipynb

ajrichards/notebook

fbd87c6f1613ea516408e9ebc3c9eff1248246e4

[ "BSD-3-Clause" ]

null

380.184713

111,040

0.934963

[ [ [ "## Indexing in NumPy\n\n### np.where vs masking\n\n * np.where returns just the indices where the equivalent mask is true\n * this is useful if you need the actual indices (maybe for counts)\n * otherwise the shorthand notation (masking) is perhaps easier\n * np.where returns a tuple\n\n### Why do I care?\n\nYou may need to work directly in NumPy due to the size of your data. NumPy has a number of tricks that can speed up your code. Even if you already knew the **trick** shown here you may like to see some code that can help you compare the speeds of different methods... This is important aspect of performance tuning or more specifically code optimization.\n", "_____no_output_____" ] ], [ [ "import numpy as np\n%matplotlib inline\nx = np.arange(5)\nprint(np.where(x < 3))\nprint(x < 3) ", "(array([0, 1, 2]),)\n[ True True True False False]\n" ] ], [ [ "### Chaining logic statements", "_____no_output_____" ] ], [ [ "x = np.arange(10)\n\ny1 = np.intersect1d(np.where(x > 3),np.where(x<7))\ny2 = np.where((x > 3) & (x < 7))\ny3 = np.where(np.logical_and(x > 3, x < 7))\ny4 = x[(x > 3) & (x < 7)]\nprint(y1,y2,y3,y4)", "[4 5 6] (array([4, 5, 6]),) (array([4, 5, 6]),) [4 5 6]\n" ] ], [ [ "### Random helpful things in NumPy", "_____no_output_____" ] ], [ [ "a = np.array(['a','b','c','c'])\n#a = np.sort(np.unique(a))\nb = np.array(['c','d','e','c','f'])\n\nmask1a = np.in1d(a,b)\nmask1b = [np.where(b==i)[0].tolist() for i in a]\nmask2a = np.in1d(b,a)\nmask2b = [np.where(a==i)[0].tolist() for i in b]\nprint(\"1\")\nprint(mask1a)\nprint(mask1b)\nprint(\"2\")\nprint(mask2a)\nprint(mask2b)", "1\n[False False True True]\n[[], [], [0, 3], [0, 3]]\n2\n[ True False False True False]\n[[2, 3], [], [], [2, 3], []]\n" ] ], [ [ "### How does one array compare to another?\n\nThis example is also the real reason to read this notebook.\n\n```python\na = np.array(['a','b','c'])\nb = np.array(['c','d','e','c','f'])\n```\n * Where do we find elements of a in b?\n * Where do we find elements of b in a?\n * If you can use np.in1d\n \n[np.in1d](http://docs.scipy.org/doc/numpy/reference/generated/numpy.in1d.html) is fast. But alway make sure you understand **when** it can be used before using it.\n\n * if we have a query(a) and a search(b) list it can be helpful if you sort and make unique the query list\n * it also helps to only look for things you can find\n\nYou might be suprised how often this comes up.\n\n * matrix of hospital visits give me only data on subjects from $a$\n * matrix of test scores use only subjects where name is in list $a$ \n", "_____no_output_____" ] ], [ [ "## Get rid of nans\nx = np.array([[1., 2., np.nan, 3., np.nan, np.nan]])\nx[~np.isnan(x)]\n\n## carry around indices\nlabels = np.array(['x' + str(i)for i in range(10)])\nx = np.random.randint(1,14,10)\nsortedInds = np.argsort(x)\nprint(\"sorted labels: %s\"%labels[sortedInds])\n\n## make x have exactly 5 evenly spaced points in the range 11 to 23\nnp.linspace(11,23,5)\n\n## numpy has very efficient set operations\nprint(np.intersect1d(np.array([1,2,3]),np.arange(10)))\n", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\nimport time\n\nsizes = [100,1000,5000,10000]\n\ntimes1,times2,times3 = [],[],[]\n\nfor n1 in sizes:\n n2 = n1 * 100\n a = np.random.randint(0,200,n1)\n b = np.random.randint(0,100,n2)\n b_list = b.tolist()\n \n ## attempt 1\n time_start = time.time()\n a = np.sort(np.unique(a))\n a = a[np.in1d(a,b)]\n times1.append(time.time()-time_start)\n\n ## attempt 2\n time_start = time.time()\n inds2 = [np.where(b==i)[0] for i in a]\n inds2 = [item for sublist in inds2 for item in sublist]\n inds2 = np.sort(np.array(inds2))\n times2.append(time.time()-time_start)\n \n ## attempt 3\n time_start = time.time()\n inds3 = np.array([i for i,x in enumerate(b_list) if x in a])\n inds3.sort()\n times3.append(time.time()-time_start)\n \ntimes1,times2,times3 = [np.array(t) for t in [times1,times2,times3]] \n\nfig = plt.figure(figsize=(6,4),dpi=400)\nax = fig.add_subplot(111)\n\nindex = np.arange(len(sizes))\nbar_width = 0.25\nopacity = 0.4\n\nrects1 = plt.bar(index, times1, bar_width,\n alpha=opacity,\n color='b',\n label='np.in1d')\n\nrects1 = plt.bar(index + bar_width, times2, bar_width,\n alpha=opacity,\n color='k',\n label='np.where')\n\nrects2 = plt.bar(index + (bar_width * 2.0), times3, bar_width,\n alpha=opacity,\n color='c',\n label='list-only')\n\nplt.xlabel('len(query_vector) by method')\nplt.ylabel('Compute time (s)')\nplt.title('Comparing two vectors')\nplt.xticks(index + bar_width + (bar_width/2.0), [str(s) for s in sizes] )\nplt.legend(loc='upper left')\nplt.tight_layout()\nplt.show()\n\n \n ", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

d0e7258cc9888167c9d280d5dc1686a7aa85e8df

233,933

ipynb

Jupyter Notebook

BO_trials/BO_log_scale (2).ipynb

michelleliu1027/Bayesian_PV

5636980ae64712e7bf3c017ea4986fba7b858674

[ "MIT" ]

1

2021-09-08T07:51:19.000Z

BO_trials/BO_log_scale (2).ipynb

michelleliu1027/Bayesian_PV

5636980ae64712e7bf3c017ea4986fba7b858674

[ "MIT" ]

2

2021-09-29T19:11:20.000Z

2021-09-29T23:23:22.000Z

BO_trials/BO_log_scale (2).ipynb

michelleliu1027/Bayesian_PV

5636980ae64712e7bf3c017ea4986fba7b858674

[ "MIT" ]

2

2021-09-19T05:24:32.000Z

2021-12-06T03:39:10.000Z

392.505034

31,034

0.935063

[ [ [ "## Bayesian Optimisation Verification", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\nfrom matplotlib import pyplot as plt\nfrom matplotlib.colors import LogNorm\nfrom scipy.interpolate import interp1d\nfrom scipy import interpolate\nfrom sklearn.gaussian_process import GaussianProcessRegressor\nfrom sklearn.gaussian_process.kernels import RBF, WhiteKernel\nfrom scipy import stats\nfrom scipy.stats import norm\nfrom sklearn.metrics.pairwise import euclidean_distances\nfrom scipy.spatial.distance import cdist\nfrom scipy.optimize import fsolve\nimport math\n\ndef warn(*args, **kwargs):\n pass\nimport warnings\nwarnings.warn = warn", "_____no_output_____" ] ], [ [ "## Trial on TiOx/SiOx\nTempeature vs. S10_HF", "_____no_output_____" ] ], [ [ "#import normal data sheet at 85 C (time:0~5000s) \naddress = 'data/degradation.xlsx'\nx_normal = []\ny_normal = []\ndf = pd.read_excel(address,sheet_name = 'normal data',usecols = [0],names = None,nrows = 5000)\ndf_85 = df.values.tolist()\ndf = pd.read_excel(address,sheet_name = 'normal data',usecols = [3],names = None,nrows = 5000)\ndf_85L = df.values.tolist() \n\n#import smooth data sheet at 85 C (time:0~5000s)\naddress = 'data/degradation.xlsx'\ndf = pd.read_excel(address,sheet_name = 'smooth data',usecols = [0],names = None,nrows = 5000)\ndf_85s = df.values.tolist()\ndf = pd.read_excel(address,sheet_name = 'smooth data',usecols = [3],names = None,nrows = 5000)\ndf_85Ls = df.values.tolist()", "_____no_output_____" ], [ "#import normal data sheet at 120 C (time:0~5000s) \naddress = 'data/degradation.xlsx'\nx_normal = []\ny_normal = []\ndf = pd.read_excel(address,sheet_name = 'normal data',usecols = [0],names = None,nrows = 5000)\ndf_120 = df.values.tolist()\ndf = pd.read_excel(address,sheet_name = 'normal data',usecols = [3],names = None,nrows = 5000)\ndf_120L = df.values.tolist() \n\n#import smooth data sheet at 120 C (time:0~5000s)\naddress = 'data/degradation.xlsx'\ndf = pd.read_excel(address,sheet_name = 'smooth data',usecols = [0],names = None,nrows = 5000)\ndf_120s = df.values.tolist()\ndf = pd.read_excel(address,sheet_name = 'smooth data',usecols = [3],names = None,nrows = 5000)\ndf_120Ls = df.values.tolist()", "_____no_output_____" ], [ "# randomly select 7 points from normal data\nx_normal = np.array(df_120).T\ny_normal = np.array(df_li_L).T \nx_normal = x_normal.reshape((5000))\ny_normal = y_normal.reshape((5000))\n", "_____no_output_____" ], [ "def plot (X,X_,y_mean,y,y_cov,gp,kernel):\n #plot function\n plt.figure()\n plt.plot(X_, y_mean, 'k', lw=3, zorder=9)\n\n plt.fill_between(X_, y_mean - np.sqrt(np.diag(y_cov)),y_mean + np.sqrt(np.diag(y_cov)),alpha=0.5, color='k')\n plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))\n plt.tick_params(axis='y', colors = 'white')\n plt.tick_params(axis='x', colors = 'white')\n plt.ylabel('Lifetime',color = 'white')\n plt.xlabel('Time',color = 'white')\n plt.tight_layout()", "_____no_output_____" ], [ "# Preparing training set\n# For log scaled plot\nx_loop = np.array([1,10,32,100,316,1000,3162])\nX = x_normal[x_loop].reshape(x_loop.size)\ny = y_normal[x_loop]\nX = X.reshape(x_loop.size,1)\nX = np.log10(X)\nMAX_x_value = np.log10(5000)\nX_ = np.linspace(0,MAX_x_value, 5000)\n\n# Kernel setting\nlength_scale_bounds_MAX = 0.5\nlength_scale_bounds_MIN = 1e-4\n\nfor length_scale_bounds_MAX in (0.3,0.5,0.7):\n kernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.00000001)\n gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, y)\n y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)\n plot (X,X_,y_mean,y,y_cov,gp,kernel)", "_____no_output_____" ], [ "# Find the minimum value in the bound\n# 5000 * 5000\n# Find minimum value in the last row as the minimum value for the bound\n\ndef ucb(X , gp, dim, delta):\n \"\"\"\n Calculates the GP-UCB acquisition function values\n Inputs: gp: The Gaussian process, also contains all data\n x:The point at which to evaluate the acquisition function \n Output: acq_value: The value of the aquisition function at point x\n \"\"\"\n mean, var = gp.predict(X[:, np.newaxis], return_cov=True)\n #var.flags['WRITEABLE']=True\n #var[var<1e-10]=0 \n mean = np.atleast_2d(mean).T\n var = np.atleast_2d(var).T \n beta = 2*np.log(np.power(5000,2.1)*np.square(math.pi)/(3*delta))\n return mean - np.sqrt(beta)* np.sqrt(np.diag(var))\n\nacp_value = ucb(X_, gp, 0.1, 5)\nX_min = np.argmin(acp_value[-1])\n\nprint(acp_value[-1,X_min])\nprint(np.argmin(acp_value[-1]))\nprint(min(acp_value[-1]))", "0.1548936251935482\n539\n0.1548936251935482\n" ], [ "# Preparing training set\nx_loop = np.array([1,10,32,100,316,1000,3162])\nX = x_normal[x_loop].reshape(x_loop.size)\ny = y_normal[x_loop]\nX = X.reshape(x_loop.size,1)\nX = np.log10(X)\nMAX_x_value = np.log10(5000)\nX_ = np.linspace(0,MAX_x_value, 5000)\n\n# Kernel setting\nlength_scale_bounds_MAX = 0.4\nlength_scale_bounds_MIN = 1e-4\nkernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.0001)\ngp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, y)\ny_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)\n\nacp_value = ucb(X_, gp, 0.1, 5)\nucb_y_min = acp_value[-1]\nprint (min(ucb_y_min))\nX_min = np.argmin(acp_value[-1])\nprint(acp_value[-1,X_min])\nprint(np.argmin(acp_value[-1]))\nprint(min(acp_value[-1]))\n\nplt.figure()\nplt.plot(X_, y_mean, 'k', lw=3, zorder=9)\nplt.plot(X_, ucb_y_min, 'x', lw=3, zorder=9)\n# plt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')\nplt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))\nplt.tick_params(axis='y', colors = 'white')\nplt.tick_params(axis='x', colors = 'white')\nplt.ylabel('Lifetime',color = 'white')\nplt.xlabel('Time',color = 'white')\nplt.tight_layout()\n", "-1.9993282670112766\n-1.9993282670112766\n653\n-1.9993282670112766\n" ], [ "acp_value = ucb(X_, gp, 0.1, 5)\nX_min = np.argmin(acp_value[-1])\n\nprint(acp_value[-1,X_min])\nprint(np.argmin(acp_value[-1]))\nprint(min(acp_value[-1]))", "-1.0178925921332458\n618\n-1.0178925921332458\n" ], [ "# Iterate i times with mins value point of each ucb bound\n\n# Initiate with 7 data points, apply log transformation to them\nx_loop = np.array([1,10,32,100,316,1000,3162])\nX = x_normal[x_loop].reshape(x_loop.size)\nY = y_normal[x_loop]\nX = X.reshape(x_loop.size,1)\nX = np.log10(X)\nMAX_x_value = np.log10(5000)\nX_ = np.linspace(0,MAX_x_value, 5000)\n# Kernel setting\nlength_scale_bounds_MAX = 0.5\nlength_scale_bounds_MIN = 1e-4\nkernel = 1.0 * RBF(length_scale=20,length_scale_bounds=(length_scale_bounds_MIN, length_scale_bounds_MAX)) + WhiteKernel(noise_level=0.0001)\ngp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, Y)\ny_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)\n\nacp_value = ucb(X_, gp, 0.1, 5)\nucb_y_min = acp_value[-1]\n\nplt.figure()\nplt.plot(X_, y_mean, 'k', lw=3, zorder=9)\nplt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')\nplt.scatter(X[:, 0], Y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))\nplt.tick_params(axis='y', colors = 'white')\nplt.tick_params(axis='x', colors = 'white')\nplt.ylabel('Lifetime',color = 'white')\nplt.xlabel('Time',color = 'white')\nplt.tight_layout()\n\n# Change i to set extra data points\ni=0\n\nwhile i < 5 :\n acp_value = ucb(X_, gp, 0.1, 5)\n ucb_y_min = acp_value[-1]\n index = np.argmin(acp_value[-1])\n\n print(acp_value[-1,X_min])\n print(min(acp_value[-1]))\n\n # Protection to stop equal x value\n while index in x_loop:\n index = index - 50\n x_loop = np.append(x_loop, index)\n x_loop = np.sort(x_loop)\n\n print (x_loop)\n\n X = x_normal[x_loop].reshape(x_loop.size)\n Y = y_normal[x_loop]\n X = X.reshape(x_loop.size,1)\n X = np.log10(X)\n\n gp = GaussianProcessRegressor(kernel=kernel,alpha=0.0).fit(X, Y)\n\n plt.plot(X_, y_mean, 'k', lw=3, zorder=9)\n plt.fill_between(X_, y_mean, ucb_y_min,alpha=0.5, color='k')\n plt.scatter(X[:, 0], Y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))\n plt.tick_params(axis='y', colors = 'white')\n plt.tick_params(axis='x', colors = 'white')\n plt.ylabel('Lifetime',color = 'white')\n plt.xlabel('Time',color = 'white')\n plt.title('cycle %d'%(i), color = 'white')\n plt.tight_layout()\n plt.show()\n\n i+=1\nprint('X:', X, '\\nY:', Y)\ns = interpolate.InterpolatedUnivariateSpline(x_loop,Y)\nx_uni = np.arange(0,5000,1)\ny_uni = s(x_uni)\n# Plot figure\nplt.plot(df_120s,df_120Ls,'-',color = 'gray')\nplt.plot(x_uni,y_uni,'-',color = 'red')\nplt.plot(x_loop, Y,'x',color = 'black')\nplt.tick_params(axis='y', colors = 'white')\nplt.tick_params(axis='x', colors = 'white')\nplt.ylabel('Lifetime',color = 'white')\nplt.xlabel('Time',color = 'white')\nplt.title('cycle %d'%(i+1), color = 'white')\n\n\nplt.show()", "-1.0178925921332458\n-1.0178925921332458\n[ 1 10 32 100 316 618 1000 3162]\n" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e7343384b7e520f3977c157a3ea2e047d76074

114,594

ipynb

Jupyter Notebook

CreditCheck.ipynb

ABPande/MyPythonRepo

51de39aee6c99b6ea2eb47fb199925ee63ca3750

[ "Apache-2.0" ]

null

CreditCheck.ipynb

ABPande/MyPythonRepo

51de39aee6c99b6ea2eb47fb199925ee63ca3750

[ "Apache-2.0" ]

null

CreditCheck.ipynb

ABPande/MyPythonRepo

51de39aee6c99b6ea2eb47fb199925ee63ca3750

[ "Apache-2.0" ]

null

55.763504

8,144

0.598269

[ [ [ "import numpy as np\nimport pandas as pd\nimport matplotlib.pyplot as plt\nimport seaborn as sns\n%matplotlib inline\n\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.tree import DecisionTreeClassifier\nfrom IPython.display import Image\n\nfrom sklearn import tree\nfrom os import system\n\nfrom sklearn.metrics import confusion_matrix, classification_report, accuracy_score", "_____no_output_____" ], [ "credit_df = pd.read_csv(\"credit.csv\")\ncredit_df.head()", "_____no_output_____" ], [ "credit_df.shape", "_____no_output_____" ], [ "credit_df.describe()", "_____no_output_____" ], [ "credit_df.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 1000 entries, 0 to 999\nData columns (total 17 columns):\nchecking_balance 1000 non-null object\nmonths_loan_duration 1000 non-null int64\ncredit_history 1000 non-null object\npurpose 1000 non-null object\namount 1000 non-null int64\nsavings_balance 1000 non-null object\nemployment_duration 1000 non-null object\npercent_of_income 1000 non-null int64\nyears_at_residence 1000 non-null int64\nage 1000 non-null int64\nother_credit 1000 non-null object\nhousing 1000 non-null object\nexisting_loans_count 1000 non-null int64\njob 1000 non-null object\ndependents 1000 non-null int64\nphone 1000 non-null object\ndefault 1000 non-null object\ndtypes: int64(7), object(10)\nmemory usage: 132.9+ KB\n" ], [ "for feature in credit_df.columns:\n if credit_df[feature].dtype == 'object':\n credit_df[feature] = pd.Categorical(credit_df[feature])\ncredit_df.head(5)", "_____no_output_____" ], [ "print(credit_df.checking_balance.value_counts())\nprint(credit_df.credit_history.value_counts())\nprint(credit_df.purpose.value_counts())\nprint(credit_df.savings_balance.value_counts())\nprint(credit_df.employment_duration.value_counts())\nprint(credit_df.other_credit.value_counts())\nprint(credit_df.housing.value_counts())\nprint(credit_df.job.value_counts())\nprint(credit_df.phone.value_counts())", "unknown 394\n< 0 DM 274\n1 - 200 DM 269\n> 200 DM 63\nName: checking_balance, dtype: int64\ngood 530\ncritical 293\npoor 88\nvery good 49\nperfect 40\nName: credit_history, dtype: int64\nfurniture/appliances 473\ncar 337\nbusiness 97\neducation 59\nrenovations 22\ncar0 12\nName: purpose, dtype: int64\n< 100 DM 603\nunknown 183\n100 - 500 DM 103\n500 - 1000 DM 63\n> 1000 DM 48\nName: savings_balance, dtype: int64\n1 - 4 years 339\n> 7 years 253\n4 - 7 years 174\n< 1 year 172\nunemployed 62\nName: employment_duration, dtype: int64\nnone 814\nbank 139\nstore 47\nName: other_credit, dtype: int64\nown 713\nrent 179\nother 108\nName: housing, dtype: int64\nskilled 630\nunskilled 200\nmanagement 148\nunemployed 22\nName: job, dtype: int64\nno 596\nyes 404\nName: phone, dtype: int64\n" ], [ "replace_struc = {\n \"checking_balance\": { \"unknown\": 0, \"< 0 DM\" : -1, \"1 - 200 DM\":1, \"> 200 DM\":2},\n \"credit_history\": { \"good\": 3, \"critical\" : 1, \"poor\":2, \"very good\":4, \"perfect\":5},\n \"savings_balance\": { \"< 100 DM\": 1, \"100 - 500 DM\" : 3, \"500 - 1000 DM\":7.5, \"> 1000 DM\":13, \"unknown\":0},\n \"employment_duration\": { \"< 1 year\": 1, \"1 - 4 years\" : 3, \"4 - 7 years\":5.5, \"> 7 years\":10, \"unemployed\":0},\n \"phone\": { \"no\": 1, \"yes\" : 2},\n \"default\": { \"no\": 0, \"yes\" : 1},\n}\noneHotCols = [\"purpose\", \"housing\", \"other_credit\", \"job\"]", "_____no_output_____" ], [ "credit_df = credit_df.replace(replace_struc)\ncredit_df = pd.get_dummies(credit_df, columns = oneHotCols)\ncredit_df.head(10)", "_____no_output_____" ], [ "credit_df.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 1000 entries, 0 to 999\nData columns (total 29 columns):\nchecking_balance 1000 non-null int64\nmonths_loan_duration 1000 non-null int64\ncredit_history 1000 non-null int64\namount 1000 non-null int64\nsavings_balance 1000 non-null float64\nemployment_duration 1000 non-null float64\npercent_of_income 1000 non-null int64\nyears_at_residence 1000 non-null int64\nage 1000 non-null int64\nexisting_loans_count 1000 non-null int64\ndependents 1000 non-null int64\nphone 1000 non-null int64\ndefault 1000 non-null int64\npurpose_business 1000 non-null uint8\npurpose_car 1000 non-null uint8\npurpose_car0 1000 non-null uint8\npurpose_education 1000 non-null uint8\npurpose_furniture/appliances 1000 non-null uint8\npurpose_renovations 1000 non-null uint8\nhousing_other 1000 non-null uint8\nhousing_own 1000 non-null uint8\nhousing_rent 1000 non-null uint8\nother_credit_bank 1000 non-null uint8\nother_credit_none 1000 non-null uint8\nother_credit_store 1000 non-null uint8\njob_management 1000 non-null uint8\njob_skilled 1000 non-null uint8\njob_unemployed 1000 non-null uint8\njob_unskilled 1000 non-null uint8\ndtypes: float64(2), int64(11), uint8(16)\nmemory usage: 117.3 KB\n" ], [ "x = credit_df.drop(\"default\", axis = 1)\ny = credit_df.pop(\"default\")", "_____no_output_____" ], [ "x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 101)", "_____no_output_____" ], [ "d_tree = DecisionTreeClassifier(criterion = 'gini', random_state = 1)\nd_tree.fit(x_train, y_train)", "_____no_output_____" ], [ "print(d_tree.score(x_train, y_train))\nprint(d_tree.score(x_test, y_test))", "1.0\n0.6566666666666666\n" ], [ "train_char_label = [\"no\", \"yes\"]\nCredit_Tree_File = open(\"credit_tree.dot\", \"w\")\ndot_data = tree.export_graphviz(d_tree, out_file = Credit_Tree_File, feature_names = list(x_train), class_names = list(train_char_label))\nCredit_Tree_File.close()", "_____no_output_____" ], [ "retCode = system(\"dot - Tpng credit_tree.dot -o credit_tree.png\")\nif (retCode > 0):\n print(\"Failed\" + str(retCode))\nelse:\n display(Image(\"credit_tree.png\"))", "Failed1\n" ], [ "d_tree_R = DecisionTreeClassifier(criterion = \"gini\", max_depth = 3, random_state = 1)\nd_tree_R.fit (x_train, y_train)\nprint (d_tree_R.score(x_train,y_train))\nprint (d_tree_R.score(x_test,y_test))", "0.7585714285714286\n0.7233333333333334\n" ], [ "train_char_label = [\"no\", \"yes\"]\nCredit_Tree_File = open(\"credit_tree.dot\", \"w\")\ndot_data = tree.export_graphviz(d_tree_R, out_file = Credit_Tree_File, feature_names = list(x_train), class_names = list(train_char_label))\nCredit_Tree_File.close()", "_____no_output_____" ], [ "retCode = system(\"dot - Tpng credit_tree.dot -o credit_tree.png\")\nif (retCode > 0):\n print(\"Failed\" + str(retCode))\nelse:\n display(Image(\"credit_tree.png\"))", "Failed1\n" ], [ "print (pd.DataFrame(d_tree_R.feature_importances_,columns = [\"Imp\"], index = x_train.columns))", " Imp\nchecking_balance 0.601550\nmonths_loan_duration 0.110975\ncredit_history 0.000000\namount 0.110832\nsavings_balance 0.000000\nemployment_duration 0.000000\npercent_of_income 0.000000\nyears_at_residence 0.000000\nage 0.000000\nexisting_loans_count 0.000000\ndependents 0.000000\nphone 0.000000\npurpose_business 0.000000\npurpose_car 0.000000\npurpose_car0 0.000000\npurpose_education 0.000000\npurpose_furniture/appliances 0.000000\npurpose_renovations 0.000000\nhousing_other 0.000000\nhousing_own 0.000000\nhousing_rent 0.000000\nother_credit_bank 0.051769\nother_credit_none 0.000000\nother_credit_store 0.000000\njob_management 0.124874\njob_skilled 0.000000\njob_unemployed 0.000000\njob_unskilled 0.000000\n" ], [ "print(d_tree_R.score (x_test, y_test))\ny_pred = d_tree_R.predict(x_test)\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, index = [\"No\", \"Yes\"], columns = [\"No\", \"Yes\"])\nplt.figure (figsize = (7,5))\nsns.heatmap(df_cm, annot = True, fmt = \"g\")", "0.7233333333333334\n" ], [ "from sklearn.ensemble import bagging, AdaBoostClassifier\nada_boost = AdaBoostClassifier(base_estimator=d_tree, n_estimators=50, random_state = 1)\nada_boost.fit(x_train, y_train)", "C:\\Users\\abhijit.a.pande\\AppData\\Local\\Continuum\\anaconda3\\lib\\site-packages\\sklearn\\utils\\deprecation.py:144: FutureWarning: The sklearn.ensemble.bagging module is deprecated in version 0.22 and will be removed in version 0.24. The corresponding classes / functions should instead be imported from sklearn.ensemble. Anything that cannot be imported from sklearn.ensemble is now part of the private API.\n warnings.warn(message, FutureWarning)\n" ], [ "from sklearn.ensemble import BaggingClassifier\nbag_ = BaggingClassifier(base_estimator=d_tree, n_estimators=100, random_state = 1)\nbag_.fit(x_train, y_train)", "_____no_output_____" ], [ "y_pred = bag_.predict(x_test)\nprint(bag_.score(x_test, y_test))\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, columns = [\"no\",\"yes\"], index = [\"no\",\"yes\"])\nsns.heatmap(df_cm,annot = True)", "0.76\n" ], [ "y_pred = ada_boost.predict(x_test)\nprint(ada_boost.score(x_test, y_test))\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, columns = [\"no\",\"yes\"], index = [\"no\",\"yes\"])\nsns.heatmap(df_cm,annot = True)", "0.6866666666666666\n" ], [ "ada_boost = AdaBoostClassifier(n_estimators=100, random_state = 1)\nada_boost.fit(x_train, y_train)", "_____no_output_____" ], [ "y_pred = ada_boost.predict(x_test)\nprint(ada_boost.score(x_test, y_test))\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, columns = [\"no\",\"yes\"], index = [\"no\",\"yes\"])\nsns.heatmap(df_cm,annot = True)", "0.7233333333333334\n" ], [ "from sklearn.ensemble import GradientBoostingClassifier\ngrb_ = GradientBoostingClassifier(n_estimators=100, random_state = 1)\ngrb_.fit(x_train, y_train)\ny_pred = grb_.predict(x_test)\nprint(grb_.score(x_test, y_test))\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, columns = [\"no\",\"yes\"], index = [\"no\",\"yes\"])\nsns.heatmap(df_cm,annot = True)", "0.7466666666666667\n" ], [ "from sklearn.ensemble import RandomForestClassifier\nrandom_forest = RandomForestClassifier(n_estimators=100, random_state = 1, max_features = 6)\nrandom_forest.fit(x_train, y_train)\ny_pred = random_forest.predict(x_test)\nprint(random_forest.score(x_test, y_test))\ncm = confusion_matrix(y_test, y_pred, labels = [0,1])\ndf_cm = pd.DataFrame(cm, columns = [\"no\",\"yes\"], index = [\"no\",\"yes\"])\nsns.heatmap(df_cm,annot = True)", "0.76\n" ], [ "ada_boost.predict_proba(x_test)\nbag_.predict_proba(x_test)\ngrb_.predict_proba(x_test)\nrandom_forest.predict_proba(x_test)", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e73ff8652968cec23d4640e2d6c379cf0c8272

14,611

ipynb

Jupyter Notebook

Tutorials/tuto1_Create.ipynb

helene-t/SciDataTool

4374ee2c1a55421af614aac00ba5ac7cf3db1144

[ "Apache-2.0" ]

null

Tutorials/tuto1_Create.ipynb

helene-t/SciDataTool

4374ee2c1a55421af614aac00ba5ac7cf3db1144

[ "Apache-2.0" ]

null

Tutorials/tuto1_Create.ipynb

helene-t/SciDataTool

4374ee2c1a55421af614aac00ba5ac7cf3db1144

[ "Apache-2.0" ]

null

45.095679

429

0.566012

[ [ [ "# How to create Data objects\n\nThe SciDataTool python module has been created to **ease the handling of scientific data**, and considerately simplify plot commands. It unifies the extraction of relevant data (e.g. slices), whether they are stored in the time/space or in the frequency domain. The call to Fourier Transform functions is **transparent**, although it still can be parameterized through the use of a dictionary.\n\nThis tutorial explains the **structure** of the `Data` classes, then shows **how to create axes and fields objects**.\n\nThe following example demonstrates the syntax to **quickly create a 2D data field** (airgap radial flux density) depending on time and angle:", "_____no_output_____" ] ], [ [ "# Add SciDataTool to the Python path\nimport sys\nsys.path.append('..')\n\n# Import useful packages\nfrom os.path import join\nfrom numpy import pi, squeeze\nfrom pandas import ExcelFile, read_excel\n\n# Import SciDataTool modules\nfrom SciDataTool import Data1D, DataTime\n\n# Import scientific data\nfrom Tests import DATA_DIR\nxls_file = ExcelFile(join(DATA_DIR, \"tutorials_data.xlsx\"))\ntime = read_excel(xls_file, sheet_name=\"time\", header=None, nrows=1, squeeze=True).to_numpy()\nangle = read_excel(xls_file, sheet_name=\"angle\", header=None, nrows=1, squeeze=True).to_numpy()\nfield = read_excel(xls_file, sheet_name=\"Br\", header=None, nrows=2016, squeeze=True).to_numpy()\n\n#---------------------------------------------------------------\n# Create Data objects\nTime = Data1D(name=\"time\", unit=\"s\", values=time)\nAngle = Data1D(name=\"angle\", unit=\"rad\", values=angle)\nBr = DataTime(\n name=\"Airgap radial flux density\",\n unit=\"T\",\n symbol=\"B_r\",\n axes=[Time, Angle],\n values=field,\n )\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "Your `Data`objects have been successfully created. Other features of the `SciDataTool` package are also available:\n- reduce storage if an axis is regularly spaced\n- reduce storage if the field presents a symmetry along one of its axes\n- store a field in the frequency domain\n- specifiy normalizations\n\nThese functionalities are described in the following sections.\n\n## 1. Data class structure\nThe `Data` class is composed of:\n- classes describing **axes**: `Data1D`, or `DataLinspace` if the axis is regularly spaced (see [section 2](#How-to-reduce-storage-if-an-axis-is-regularly-spaced))\n- classes describing **fields** stored in the time/space domain (`DataTime`) or in the frequential domain (`DataFreq`)\n\nThe following UML summarizes this structure:\n\n<div>\n<img src=\"_static/UML_Data_Object.png\" width=\"450\"/>\n</div>\n\nThe attributes in red are **mandatory**, those in gray are **optional**. To correctly fill the mandatory attributes, it is advised to follow these principles:\n- `values` is a **numpy array**\n- `axes` is a **list** of `Data1D` or `DataLinspace`\n- `name` is **string** corresponding to a short description of the field, or the \n- `symbol` is a **string** giving the symbol of the field in LaTeX format\n- `unit` is a **string** among the list: `[dimless, m, rad, °, g, s, min, h, Hz, rpm, degC, A, J, W, N, C, T, G, V, F, H, Ohm, At, Wb, Mx]`, with a prefix `[k, h, da, d, c, m, etc.]`. Composed units are also available (e.g. `mm/s^2`). It is best to use such a LaTeX formatting for axis labelling. Other units can be added in [conversions.py](https://github.com/Eomys/SciDataTool/blob/master/Functions/conversions.py).\n- for `Data1D` and `DataLinspace`, `name` + `[unit]` can be used to label axes\n- for `DataTime` and `DataFreq`, `name` can be used as plot title, and `symbol` + `[unit]` as label\n\nWhen a `Data1D` is created, the array `values` is **squeezed** to avoid dimension problems. When a `DataTime` or `DataFreq` is created, `values` is also squeezed, and a `CheckDimError` is raised if **dimensions** of `axes` and `values` do not match.\n\nThe following sections explain how to use the optional attributes to optimize storage.", "_____no_output_____" ], [ "## 2. How to reduce storage if an axis is regularly spaced\nAxes often have a **regular distribution**, so that the use of `DataLinspace` allows to reduce the storage.\n\nA `DataLinspace` object has five properties instead of the `values` array: `initial`, `final`, `step` and `number` allow to define the linspace vector (3 out of these 4 suffice), and `include_endpoint` is a boolean used to indicate whether the final point should be included or not (default `False`).\n\nIn the following example, the angle vector is defined as a linspace:", "_____no_output_____" ] ], [ [ "from SciDataTool import DataLinspace\n\n#---------------------------------------------------------------\n# Create Data objects\nAngle = DataLinspace(\n name=\"angle\",\n unit=\"rad\",\n symmetries={},\n initial=0,\n final=2*pi,\n number=2016,\n )\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "## 3. How to reduce storage if a field presents a symmetry/periodicity\nIf a signal shows a **symmetry** or a **periodicity** along one or several of its axes, it is possible to store only the relevant part of the signal, and save the information necessary to rebuild it within the optional attribute `symmetries`. A repeting signal can either be periodic: $f(t+T)=f(t)$, or antiperiodic: $f(t+T)=-f(t)$. Indeed, we can consider that a symmetric signal is a periodic signal of period $T=N/2$.\n\n`symmetries` is a dictionary containing the **name of the axis** and a **dictionary** of its symmetry (`{\"period\": n}` or `{\"antiperiod\": n}`, with *n* the number of periods in the complete signal. Note that the symmetries dictionary must be shared with the field itself (`DataTime` or `DataFreq`).\n\nIn the following example, the time vector and the field are reduced to one third before being stored.", "_____no_output_____" ] ], [ [ "time_reduced = time[0:time.size//3]\nfield_reduced = field[0:time.size//3,:]\n\n#---------------------------------------------------------------\n# Create Data objects\nTime_reduced = Data1D(name=\"time\", unit=\"s\", symmetries={\"time\": {\"period\": 3}}, values=time_reduced)\nBr_reduced = DataTime(\n name=\"Airgap radial flux density\",\n unit=\"T\",\n symbol=\"B_r\",\n axes=[Time, Angle],\n values=field,\n symmetries={\"time\": {\"period\": 3}},\n )\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "## 4. How to store a field in the frequency domain\nIf one prefers to store data in the frequency domain, for example because most postprocessings will handle spectra, or because a small number of harmonics allow to reduce storage, the `DataFreq` class can be used.\n\nThe definition is similar to the `DataTime` one, with the difference that the axes now have to be **frequencies** or **wavenumbers** and a `DataFreq` object is created.\n\nSince we want to be able to go back to the time/space domain, there must exist a corresponding axis name. For the time being, the existing **correspondances** are:\n + `\"time\"` ↔ `\"freqs\"`\n + `\"angle\"` ↔ `\"wavenumber\"`\n\nThis list is to be expanded, and a possibility to manually add a correspondance will be implemented soon.\n\nIn the following example, a field is stored in a `DataFreq` object.", "_____no_output_____" ] ], [ [ "from SciDataTool import DataFreq\n\n# Import scientific data\nfreqs = read_excel(xls_file, sheet_name=\"freqs\", header=None, nrows=1, squeeze=True).to_numpy()\nwavenumber = read_excel(xls_file, sheet_name=\"wavenumber\", header=None, nrows=1, squeeze=True).to_numpy()\nfield_fft2 = read_excel(xls_file, sheet_name=\"Br_fft2\", header=None, nrows=2016, squeeze=True).to_numpy()\n\n#---------------------------------------------------------------\n# Create Data objects\nFreqs = Data1D(name=\"freqs\", unit=\"Hz\", values=freqs)\nWavenumber = Data1D(name=\"wavenumber\", unit=\"dimless\", values=wavenumber)\nBr_fft = DataFreq(\n name=\"Airgap radial flux density\",\n unit=\"T\",\n symbol=\"B_r\",\n axes=[Freqs, Wavenumber],\n values=field_fft2,\n )\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "## 5. How to specify normalizations (axes or field)\nIf you plan to **normalize** your field or its axes during certain postprocessings (but not all), you might want to store the normalizations values. To do so, you can use the `normalizations` attribute, which is a dictionaray:\n- for a normalization of the **field**, use `\"ref\"` (e.g. `{\"ref\": 0.8}`)\n- for a normalization of an **axis**, use the name of the normalized axis unit (e.g. `{\"elec_order\": 60}`). There is no list of predefined normalized axis units, you simply must make sure to request it when you extract data (see [How to extract slices](https://github.com/Eomys/SciDataTool/tree/master/Tutorials/tuto_Slices.ipynb))\n- to **convert** to a unit which does not exist in the predefined units, and if there exists a proportionality relation, it is also possible to add it in the `normalizations` dictionary (e.g. `{\"nameofmyunit\": 154}`)\n\nThis dictionary can also be updated later.\n\nSee below examples of use of `normalizations`:", "_____no_output_____" ] ], [ [ "#---------------------------------------------------------------\nBr = DataTime(\n name=\"Airgap radial flux density\",\n unit=\"T\",\n symbol=\"B_r\",\n axes=[Time, Angle],\n normalizations={\"ref\": 0.8, \"elec_order\": 60},\n values=field,\n )\nBr.normalizations[\"space_order\"] = 3\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "## 6. How to store a field with multiple components\nIt is more efficient to store all the **components** of a same field (e.g. $x$, $y$, $z$ components of a vector field, phases of a signal, etc.) in the same `Data` object. To do so, the `is_components` key can be used to easily recognize it, and strings can be used as values.", "_____no_output_____" ] ], [ [ "from numpy import roll, array\n\nfieldB = roll(field, 100, axis=0)\nfieldC = roll(field, 200, axis=0)\nnew_field = array([field, fieldB, fieldC])\n\n#---------------------------------------------------------------\nPhases = Data1D(name=\"phases\", unit=\"\", values=[\"Phase A\",\"Phase B\",\"Phase C\"], is_components=True)\nBr = DataTime(\n name=\"Airgap radial flux density\",\n unit=\"T\",\n symbol=\"B_r\",\n axes=[Phases, Time, Angle],\n values=new_field,\n )\n#---------------------------------------------------------------", "_____no_output_____" ] ], [ [ "Now that the `Data` objects have been created, we can:\n- [extract slices](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto2_Slices.ipynb)\n- [compare several fields](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto3_Compare.ipynb)\n- [perform advanced Fourier Transforms](https://nbviewer.jupyter.org/github/Eomys/SciDataTool/blob/master/Tutorials/tuto4_Fourier.ipynb)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e748cf3282cf9fb7f6baafd98c666001913272

8,256

ipynb

Jupyter Notebook

Test 2 Ver 1/Test 2.ipynb

mbardoe/DataScience

98738f9b384634ace18cb3c559714df327300978

[ "MIT" ]

null

Test 2 Ver 1/Test 2.ipynb

mbardoe/DataScience

98738f9b384634ace18cb3c559714df327300978

[ "MIT" ]

null

Test 2 Ver 1/Test 2.ipynb

mbardoe/DataScience

98738f9b384634ace18cb3c559714df327300978

[ "MIT" ]

null

20.691729

307

0.529554

[ [ [ "**On my honor I have neither given nor received any unauthorized aid.**", "_____no_output_____" ], [ "**Your name here**", "_____no_output_____" ], [ "# Test 2\n\nOn this test we are going use a dataset that researchers collected about 649 high school students in Portugal, and attempt to determine how their grades are affected by several of the variables that they collected information about. \n\nP. Cortez and A. Silva. Using Data Mining to Predict Secondary School Student Performance. In A. Brito and J. Teixeira Eds., Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) pp. 5-12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978-9077381-39-7. \n\n\n**As always load up the libraries**", "_____no_output_____" ] ], [ [ "library(dplyr)\nlibrary(ggplot2)", "_____no_output_____" ] ], [ [ "\nWe will load the data using the command:", "_____no_output_____" ] ], [ [ "student<-read.csv(\"student-por.csv\")", "_____no_output_____" ] ], [ [ "## Dataset student\n\nThe student dataset looks at the relationship between variables describing students lives and their performance in Portuguese class. \n\n| Attribute | Explanation|\n|-----------|------------|\n|age|student's age (numeric: from 15 to 22) |\n|studytime|hours studied weekly |\n|Walc| Alcoholic drinks consumed weekly |\n|absences| number of school absences (numeric: from 0 to 32) |\n|G3| final grade (numeric: from 0 to 20, output target)|", "_____no_output_____" ] ], [ [ "str(student)", "'data.frame':\t649 obs. of 5 variables:\n $ age : int 18 17 15 15 16 16 16 17 15 15 ...\n $ studytime: int 2 2 2 3 2 2 2 2 2 2 ...\n $ Walc : int 1 1 3 1 2 2 1 1 1 1 ...\n $ absences : int 4 2 6 0 0 6 0 2 0 0 ...\n $ G3 : int 11 11 12 14 13 13 13 13 17 13 ...\n" ] ], [ [ "### Task 1\n\nCreate a scatterplot that shows the relationship between G3 and Walc.", "_____no_output_____" ], [ "### Task 2 \n\nCreate a linear model that predicts the G3 based on the Walc. **Write a markdown cell that gives the equation that predicts G3 from Walc. Does your calculation indicate that Walc is a useful predictor for G3?**", "_____no_output_____" ], [ "### Task 3\n\n**Create a scatterplot that shows the relationship between the G3 and Walc and add in the line of best fit that you found in Task 2.**", "_____no_output_____" ], [ "### Task 4\n\nCreate a table that shows the correlations between the all the quantitative variables in this dataset. **Write a markdown cell indicating the strength of the correlation between G3 and the other attributes.** ", "_____no_output_____" ], [ "### Task 5\n\nCreate a residual plot for the model that you have found in Task 2. **What does the residual plot say about the model that we have found in Task 2?**", "_____no_output_____" ], [ "### Task 6\n\nCreate a multilinear model for G3 from the attributes in this dataset. Only use those attributes that seem demonstrated to be relevant to G3. **In a markdown cell, write the equation for G3 that is given by your model. And then describe what the is the meaning of the $R^2$ value given by the model.**", "_____no_output_____" ] ], [ [ "\n", "_____no_output_____" ] ], [ [ "\n", "_____no_output_____" ], [ "### Task 7\n\n**Explain what each of the coefficients of your multilinear model from Task 6 mean in context of the dataset.**\n", "_____no_output_____" ], [ "### Task 8\n\n**Make a prediction for the final grade of a student with the attributes described below.**\n\n\n|Attribute|Value|\n|---------|-----|\n|age|19 |\n|studytime|1 |\n|Walc| 4 |\n|absences| 22 |\n", "_____no_output_____" ], [ "### Task 9\n\nBased on information what you know of the model used in the prediction above describe in words (with numerical support) how accurate you believe the prediction to be. ", "_____no_output_____" ], [ "# Extra-Credit\n\nCalculate the z-score of the prediction you made in Task 8.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

d0e74a4ed269b46d120279c4a0a3d542d3fd8e93

47,295

ipynb

Jupyter Notebook

1. Introduction to TensorFlow/AZ/ANN/Image Processing/01_mnist_ann.ipynb

AmirRazaMBA/TensorFlow-Certification

ec0990007cff6daf36beac6d00d95c81cdf80353

[ "MIT" ]

1

2020-11-20T14:46:45.000Z

1. Introduction to TensorFlow/AZ/ANN/Image Processing/01_mnist_ann.ipynb

AmirRazaMBA/TF_786

ec0990007cff6daf36beac6d00d95c81cdf80353

[ "MIT" ]

null

1. Introduction to TensorFlow/AZ/ANN/Image Processing/01_mnist_ann.ipynb

AmirRazaMBA/TF_786

ec0990007cff6daf36beac6d00d95c81cdf80353

[ "MIT" ]

1

2021-11-17T02:40:23.000Z

127.824324

15,932

0.85878

[ [ [ "import numpy as np\nimport matplotlib.pyplot as plt\nimport tensorflow as tf\nfrom sklearn.metrics import classification_report,confusion_matrix\nfrom tensorflow.keras.layers import Input, Dense, Flatten, Dropout\nfrom tensorflow.keras.models import Model", "_____no_output_____" ], [ "mnist = tf.keras.datasets.mnist\n\n(x_train, y_train), (x_test, y_test) = mnist.load_data()\nx_train, x_test = x_train / 255.0, x_test / 255.0\nprint(\"x_train.shape:\", x_train.shape)", "x_train.shape: (60000, 28, 28)\n" ], [ "# Build the model\n\ni = Input(shape=x_train[0].shape)\nx = Flatten()(i)\nx = Dense(128, activation='relu')(x)\nx = Dropout(0.2)(x)\nx = Dense(10, activation='softmax')(x)\n\nmodel = Model(i, x)", "_____no_output_____" ], [ "# Compile the model\nmodel.compile(optimizer='adam',\n loss='sparse_categorical_crossentropy',\n metrics=['accuracy'])\n #metrics=['sparse_categorical_crossentropy','accuracy']) note: sparse data is already in loss data", "_____no_output_____" ], [ "# Train the model\nhistory = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=10)", "Epoch 1/10\n1875/1875 [==============================] - 4s 2ms/step - loss: 0.0426 - accuracy: 0.9854 - val_loss: 0.0731 - val_accuracy: 0.9790\nEpoch 2/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0403 - accuracy: 0.9864 - val_loss: 0.0698 - val_accuracy: 0.9811\nEpoch 3/10\n1875/1875 [==============================] - 4s 2ms/step - loss: 0.0373 - accuracy: 0.9876 - val_loss: 0.0702 - val_accuracy: 0.9808\nEpoch 4/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0349 - accuracy: 0.9883 - val_loss: 0.0783 - val_accuracy: 0.9798\nEpoch 5/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0328 - accuracy: 0.9883 - val_loss: 0.0747 - val_accuracy: 0.9799\nEpoch 6/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0327 - accuracy: 0.9886 - val_loss: 0.0774 - val_accuracy: 0.9811\nEpoch 7/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0314 - accuracy: 0.9894 - val_loss: 0.0818 - val_accuracy: 0.9799\nEpoch 8/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0300 - accuracy: 0.9897 - val_loss: 0.0817 - val_accuracy: 0.9805\nEpoch 9/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0284 - accuracy: 0.9898 - val_loss: 0.0830 - val_accuracy: 0.9805\nEpoch 10/10\n1875/1875 [==============================] - 3s 2ms/step - loss: 0.0269 - accuracy: 0.9906 - val_loss: 0.0879 - val_accuracy: 0.9793\n" ], [ "plt.plot(history.history['loss'], label='loss')\nplt.plot(history.history['val_loss'], label='val_loss')\nplt.legend()", "_____no_output_____" ], [ "# Plot accuracy per iteration\nplt.plot(history.history['accuracy'], label='acc')\nplt.plot(history.history['val_accuracy'], label='val_acc')\nplt.legend()", "_____no_output_____" ], [ "# Evaluate the model\nprint(model.evaluate(x_test, y_test, verbose='False'))", "[0.0879092663526535, 0.9793000221252441]\n" ], [ "# Predictions by the model\np_test = np.argmax(model.predict(x_test), axis=-1) \n# model.predict(x_test) > 0.5).astype(\"int32\")", "_____no_output_____" ], [ "print(classification_report(y_test,p_test))", " precision recall f1-score support\n\n 0 0.99 0.99 0.99 980\n 1 0.99 0.99 0.99 1135\n 2 0.98 0.98 0.98 1032\n 3 0.96 0.99 0.98 1010\n 4 0.98 0.98 0.98 982\n 5 0.98 0.97 0.98 892\n 6 0.98 0.99 0.98 958\n 7 0.97 0.98 0.98 1028\n 8 0.98 0.96 0.97 974\n 9 0.99 0.96 0.98 1009\n\n accuracy 0.98 10000\n macro avg 0.98 0.98 0.98 10000\nweighted avg 0.98 0.98 0.98 10000\n\n" ], [ "print(confusion_matrix(y_test,p_test))", "[[ 969 1 3 0 0 1 4 1 1 0]\n [ 0 1127 3 1 0 0 1 0 3 0]\n [ 3 0 1010 5 2 0 1 5 6 0]\n [ 0 0 2 996 0 3 0 5 3 1]\n [ 0 0 1 0 967 0 7 3 1 3]\n [ 2 1 0 12 1 866 6 2 1 1]\n [ 4 2 0 1 3 3 944 0 1 0]\n [ 1 3 10 2 1 0 0 1007 1 3]\n [ 2 1 2 11 7 6 3 5 936 1]\n [ 2 5 1 5 9 4 1 8 3 971]]\n" ], [ "# Show some misclassified examples\nmisclassified_idx = np.where(p_test != y_test)[0]\ni = np.random.choice(misclassified_idx)\nplt.imshow(x_test[i], cmap='gray')\nplt.title(\"True label: %s Predicted: %s\" % (y_test[i], p_test[i]));", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e750954c314a0968ea9c3e4f3d5c36d6dd0347

527,013

ipynb

Jupyter Notebook

notebooks/legacy/legacy/Explore_raw_MODIS_data.ipynb

tomkimpson/ML4L

ffa8360cb80df25bd6af4fa5cc39b42bd6f405cd

[ "MIT" ]

1

2022-02-23T12:31:56.000Z

notebooks/legacy/legacy/Explore_raw_MODIS_data.ipynb

tomkimpson/ML4L

ffa8360cb80df25bd6af4fa5cc39b42bd6f405cd

[ "MIT" ]

null

notebooks/legacy/legacy/Explore_raw_MODIS_data.ipynb

tomkimpson/ML4L

ffa8360cb80df25bd6af4fa5cc39b42bd6f405cd

[ "MIT" ]

null

453.930233

479,496

0.921027

[ [ [ "# MODIS\n\n\n\nMODIS Terra: https://lpdaac.usgs.gov/products/mod11c1v006/\n\nMODIS Acqua: https://lpdaac.usgs.gov/products/myd11c1v061/\n\nDocs: https://lpdaac.usgs.gov/documents/118/MOD11_User_Guide_V6.pdf", "_____no_output_____" ] ], [ [ "! wget https://e4ftl01.cr.usgs.gov/MOLA/MYD11C1.061/2018.04.19/MYD11C1.A2018109.061.2021330052306.hdf -O /network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf", "--2022-03-18 11:14:00-- https://e4ftl01.cr.usgs.gov/MOLA/MYD11C1.061/2018.04.19/MYD11C1.A2018109.061.2021330052306.hdf\nResolving e4ftl01.cr.usgs.gov (e4ftl01.cr.usgs.gov)... 152.61.133.130, 2001:49c8:4000:127d::133:130\nConnecting to e4ftl01.cr.usgs.gov (e4ftl01.cr.usgs.gov)|152.61.133.130|:443... connected.\nHTTP request sent, awaiting response... 302 Found\nLocation: https://urs.earthdata.nasa.gov/oauth/authorize?scope=uid&app_type=401&client_id=ijpRZvb9qeKCK5ctsn75Tg&response_type=code&redirect_uri=https%3A%2F%2Fe4ftl01.cr.usgs.gov%2Foauth&state=aHR0cHM6Ly9lNGZ0bDAxLmNyLnVzZ3MuZ292L01PTEEvTVlEMTFDMS4wNjEvMjAxOC4wNC4xOS9NWUQxMUMxLkEyMDE4MTA5LjA2MS4yMDIxMzMwMDUyMzA2LmhkZg [following]\n--2022-03-18 11:14:08-- https://urs.earthdata.nasa.gov/oauth/authorize?scope=uid&app_type=401&client_id=ijpRZvb9qeKCK5ctsn75Tg&response_type=code&redirect_uri=https%3A%2F%2Fe4ftl01.cr.usgs.gov%2Foauth&state=aHR0cHM6Ly9lNGZ0bDAxLmNyLnVzZ3MuZ292L01PTEEvTVlEMTFDMS4wNjEvMjAxOC4wNC4xOS9NWUQxMUMxLkEyMDE4MTA5LjA2MS4yMDIxMzMwMDUyMzA2LmhkZg\nResolving urs.earthdata.nasa.gov (urs.earthdata.nasa.gov)... 198.118.243.33, 2001:4d0:241a:4081::89\nConnecting to urs.earthdata.nasa.gov (urs.earthdata.nasa.gov)|198.118.243.33|:443... connected.\nHTTP request sent, awaiting response... 401 Unauthorized\nAuthentication selected: Basic realm=\"Please enter your Earthdata Login credentials. If you do not have a Earthdata Login, create one at https://urs.earthdata.nasa.gov//users/new\"\nReusing existing connection to urs.earthdata.nasa.gov:443.\nHTTP request sent, awaiting response... 302 Found\nLocation: https://e4ftl01.cr.usgs.gov/oauth?code=4254dd31a1b89032c31aca53c64c82b2a3e337eb54cdfcf0f7f900ad8573bd1a&state=aHR0cHM6Ly9lNGZ0bDAxLmNyLnVzZ3MuZ292L01PTEEvTVlEMTFDMS4wNjEvMjAxOC4wNC4xOS9NWUQxMUMxLkEyMDE4MTA5LjA2MS4yMDIxMzMwMDUyMzA2LmhkZg [following]\n--2022-03-18 11:14:09-- https://e4ftl01.cr.usgs.gov/oauth?code=4254dd31a1b89032c31aca53c64c82b2a3e337eb54cdfcf0f7f900ad8573bd1a&state=aHR0cHM6Ly9lNGZ0bDAxLmNyLnVzZ3MuZ292L01PTEEvTVlEMTFDMS4wNjEvMjAxOC4wNC4xOS9NWUQxMUMxLkEyMDE4MTA5LjA2MS4yMDIxMzMwMDUyMzA2LmhkZg\nConnecting to e4ftl01.cr.usgs.gov (e4ftl01.cr.usgs.gov)|152.61.133.130|:443... connected.\nHTTP request sent, awaiting response... 302 Found\nLocation: https://e4ftl01.cr.usgs.gov/MOLA/MYD11C1.061/2018.04.19/MYD11C1.A2018109.061.2021330052306.hdf [following]\n--2022-03-18 11:14:17-- https://e4ftl01.cr.usgs.gov/MOLA/MYD11C1.061/2018.04.19/MYD11C1.A2018109.061.2021330052306.hdf\nConnecting to e4ftl01.cr.usgs.gov (e4ftl01.cr.usgs.gov)|152.61.133.130|:443... connected.\nHTTP request sent, awaiting response... 200 OK\nLength: 48245309 (46M) [application/x-hdf]\nSaving to: ‘/network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf’\n\n/network/group/aopp 100%[===================>] 46.01M 1.67MB/s in 17s \n\n2022-03-18 11:14:42 (2.69 MB/s) - ‘/network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf’ saved [48245309/48245309]\n\n" ], [ "import xarray as xr\nimport rioxarray as rxr\n\nmodis_xarray= rxr.open_rasterio('/network/group/aopp/predict/TIP016_PAXTON_RPSPEEDY/ML4L/MODIS.hdf',masked=True)", "_____no_output_____" ], [ "modis_xarray['Day_view_time']", "_____no_output_____" ], [ "modis_df = modis_xarray.to_dataframe().reset_index()", "_____no_output_____" ], [ "lite = modis_df[['y','x', 'LST_Day_CMG','Day_view_time', 'LST_Night_CMG', 'Night_view_time']]", "_____no_output_____" ], [ "L = lite.dropna().copy()", "_____no_output_____" ], [ "L['T_Day'] = L['LST_Day_CMG']*0.02\nL['T_Night'] = L['LST_Night_CMG']*0.02\nL['Time_Day'] = L['Day_view_time']*0.2\nL['Time_Night'] = L['Night_view_time']*0.2\nL['Time_Day_UTC'] = L['Time_Day'] - L['x']/15", "_____no_output_____" ], [ "window = L.query('-70 < y < 70')", "_____no_output_____" ], [ "w = window.copy()", "_____no_output_____" ], [ "import pandas as pd\n \n#Create time delta to change local to UTC\n#time_delta = pd.to_timedelta(window.x/15,unit='H') \n \n #Convert local satellite time to UTC and round to nearest hour\n # time = (pd.to_datetime([file_date + \" \" + local_times[satellite]]*time_delta.shape[0]) - time_delta).round('H')\n\n\nw['ideal_UTC'] = (pd.to_datetime(\"2022-01-01 13:30\") - pd.to_timedelta(w.x/15))#.dt.time\nw['actual_utc'] = (pd.to_datetime(\"2022-01-01 00:00\") + pd.to_timedelta(w.Time_Day_UTC,unit='hours'))#.dt.time \n#w['dfdf'] = w.ideal_UTC.dt.time\n#w['actual_utc'] = (pd.to_datetime(\"00:00\") + pd.to_timedelta(w.Time_Day_UTC,unit='hours')).dt.time #.dt.components['hours']", "_____no_output_____" ], [ "w['difference'] = pd.to_timedelta(w.ideal_UTC - w.actual_utc,unit='s').dt.total_seconds() / 60", "_____no_output_____" ], [ "w", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\nimport matplotlib.colors as mc\nimport matplotlib.colorbar as cb \n\n#Get all data as vectors\nx = w.x.values\ny = w.y.values\nz1 = w.difference.values\n\ncmap = plt.cm.coolwarm\n#Scatter plot it\n# init the figure\nfig,[ax,cax] = plt.subplots(1,2, gridspec_kw={\"width_ratios\":[50,1]},figsize=(30, 20))\n\nvmin = -1500\nvmax= +1500\nnorm = mc.Normalize(vmin=vmin, vmax=vmax)\n\ncb1 = cb.ColorbarBase(cax, cmap=cmap,norm=norm,orientation='vertical')\n \n \nsc = ax.scatter(x, y,s=1,c=cmap(norm(z1)),linewidths=1, alpha=1)\n\n#ax.set_title(z)\nplt.show()", "_____no_output_____" ], [ "modis_xarray.LST_Day_CMG.data.dropna()", "_____no_output_____" ], [ "t = modis_xarray.Day_view_time.data", "_____no_output_____" ], [ "tt = t.flatten()", "_____no_output_____" ], [ "sum(tt)", "_____no_output_____" ], [ "import numpy as np\ntnn = t[~np.isnan(t)]*0.2", "_____no_output_____" ], [ "len(tnn)", "_____no_output_____" ], [ "min(tnn)", "_____no_output_____" ], [ "max(tnn)", "_____no_output_____" ], [ "np.unique(tnn)", "_____no_output_____" ], [ "[[[-19.0715515614,-1.4393790966],\n [53.2624328136,-1.4393790966],\n [53.2624328136,36.0044133726],\n [-19.0715515614,36.0044133726],\n [-19.0715515614,-1.4393790966]]]", "_____no_output_____" ], [ "-19 56\n\n\n-1.4 36", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e77400118871fbb0d27840a362368bc04ba5e3

70,291

ipynb

Jupyter Notebook

examples/notebooks/solvers/ode-solver.ipynb

deepakdinesh1123/PyBaMM

214a4b1e8fc5da6dc42211572454f31671ac1af2

[ "BSD-3-Clause" ]

1

2022-03-24T01:23:16.000Z

examples/notebooks/solvers/ode-solver.ipynb

deepakdinesh1123/PyBaMM

214a4b1e8fc5da6dc42211572454f31671ac1af2

[ "BSD-3-Clause" ]

1

2022-01-15T03:51:22.000Z

examples/notebooks/solvers/ode-solver.ipynb

deepakdinesh1123/PyBaMM

214a4b1e8fc5da6dc42211572454f31671ac1af2

[ "BSD-3-Clause" ]

null

217.619195

31,096

0.912023

[ [ [ "# ODE solver\n\nIn this notebook, we show some examples of solving an ODE model. For the purposes of this example, we use the Scipy solver, but the syntax remains the same for other solvers", "_____no_output_____" ] ], [ [ "%pip install pybamm -q # install PyBaMM if it is not installed\nimport pybamm\nimport tests\nimport numpy as np\nimport os\nimport matplotlib.pyplot as plt\nfrom pprint import pprint\nos.chdir(pybamm.__path__[0]+'/..')\n\n# Create solver\node_solver = pybamm.ScipySolver()", "Note: you may need to restart the kernel to use updated packages.\n" ] ], [ [ "## Integrating ODEs", "_____no_output_____" ], [ "In PyBaMM, a model is solved by calling a solver with `solve`. This sets up the model to be solved, and then calls the method `_integrate`, which is specific to each solver. We begin by setting up and discretising a model", "_____no_output_____" ] ], [ [ "# Create model\nmodel = pybamm.BaseModel()\nu = pybamm.Variable(\"u\")\nv = pybamm.Variable(\"v\")\nmodel.rhs = {u: -v, v: u}\nmodel.initial_conditions = {u: 2, v: 1}\nmodel.variables = {\"u\": u, \"v\": v}\n\n# Discretise using default discretisation\ndisc = pybamm.Discretisation()\ndisc.process_model(model);", "_____no_output_____" ] ], [ [ "Now the model can be solved by calling `solver.solve` with a specific time vector at which to evaluate the solution", "_____no_output_____" ] ], [ [ "# Solve ########################\nt_eval = np.linspace(0, 5, 30)\nsolution = ode_solver.solve(model, t_eval)\n################################\n\n# Extract u and v\nt_sol = solution.t\nu = solution[\"u\"]\nv = solution[\"v\"]\n\n# Plot\nt_fine = np.linspace(0,t_eval[-1],1000)\n\nfig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))\nax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), \"o\")\nax1.set_xlabel(\"t\")\nax1.legend([\"2*cos(t) - sin(t)\", \"u\"], loc=\"best\")\n\nax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), \"o\")\nax2.set_xlabel(\"t\")\nax2.legend([\"2*sin(t) + cos(t)\", \"v\"], loc=\"best\")\n\nplt.tight_layout()\nplt.show()", "_____no_output_____" ] ], [ [ "Note that, where possible, the solver makes use of the mass matrix and jacobian for the model. However, the discretisation or solver will have created the mass matrix and jacobian algorithmically, using the expression tree, so we do not need to calculate and input these manually.", "_____no_output_____" ], [ "The solution terminates at the final simulation time:", "_____no_output_____" ] ], [ [ "solution.termination", "_____no_output_____" ] ], [ [ "### Events\n\nIt is possible to specify events at which a solution should terminate. This is done by adding events to the `model.events` dictionary. In the following example, we solve the same model as before but add a termination event when `v=-2`.", "_____no_output_____" ] ], [ [ "# Create model\nmodel = pybamm.BaseModel()\nu = pybamm.Variable(\"u\")\nv = pybamm.Variable(\"v\")\nmodel.rhs = {u: -v, v: u}\nmodel.initial_conditions = {u: 2, v: 1}\nmodel.events.append(pybamm.Event('v=-2', v + 2)) # New termination event\nmodel.variables = {\"u\": u, \"v\": v}\n\n# Discretise using default discretisation\ndisc = pybamm.Discretisation()\ndisc.process_model(model)\n\n# Solve ########################\nt_eval = np.linspace(0, 5, 30)\nsolution = ode_solver.solve(model, t_eval)\n################################\n\n# Extract u and v\nt_sol = solution.t\nu = solution[\"u\"]\nv = solution[\"v\"]\n\n# Plot\nt_fine = np.linspace(0,t_eval[-1],1000)\n\nfig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))\nax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), \"o\")\nax1.set_xlabel(\"t\")\nax1.legend([\"2*cos(t) - sin(t)\", \"u\"], loc=\"best\")\n\nax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), \"o\", t_fine, -2 * np.ones_like(t_fine), \"k\")\nax2.set_xlabel(\"t\")\nax2.legend([\"2*sin(t) + cos(t)\", \"v\", \"v = -2\"], loc=\"best\")\n\nplt.tight_layout()\nplt.show()", "_____no_output_____" ] ], [ [ "Now the solution terminates because the event has been reached", "_____no_output_____" ] ], [ [ "solution.termination", "_____no_output_____" ], [ "print(\"event time: \", solution.t_event, \"\\nevent state\", solution.y_event.flatten())", "event time: [3.78510677] \nevent state [-0.99995359 -2. ]\n" ] ], [ [ "## References\n\nThe relevant papers for this notebook are:", "_____no_output_____" ] ], [ [ "pybamm.print_citations()", "[1] Joel A. E. Andersson, Joris Gillis, Greg Horn, James B. Rawlings, and Moritz Diehl. CasADi – A software framework for nonlinear optimization and optimal control. Mathematical Programming Computation, 11(1):1–36, 2019. doi:10.1007/s12532-018-0139-4.\n[2] Charles R. Harris, K. Jarrod Millman, Stéfan J. van der Walt, Ralf Gommers, Pauli Virtanen, David Cournapeau, Eric Wieser, Julian Taylor, Sebastian Berg, Nathaniel J. Smith, and others. Array programming with NumPy. Nature, 585(7825):357–362, 2020. doi:10.1038/s41586-020-2649-2.\n[3] Valentin Sulzer, Scott G. Marquis, Robert Timms, Martin Robinson, and S. Jon Chapman. Python Battery Mathematical Modelling (PyBaMM). ECSarXiv. February, 2020. doi:10.1149/osf.io/67ckj.\n[4] Pauli Virtanen, Ralf Gommers, Travis E. Oliphant, Matt Haberland, Tyler Reddy, David Cournapeau, Evgeni Burovski, Pearu Peterson, Warren Weckesser, Jonathan Bright, and others. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nature Methods, 17(3):261–272, 2020. doi:10.1038/s41592-019-0686-2.\n\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e795cfb24f8bda2ef6c4406f36a6cf3c965470

368,700

ipynb

Jupyter Notebook

notebook/Template.ipynb

danni2019/JAB

83fdc19cc054c83479fca41b21db3c2e6960e8f4

[ "MIT" ]

18

2021-05-14T03:58:52.000Z

2022-03-12T15:50:35.000Z

notebook/Template.ipynb

danni2019/time_series_analysis

83fdc19cc054c83479fca41b21db3c2e6960e8f4

[ "MIT" ]

null

notebook/Template.ipynb

danni2019/time_series_analysis

83fdc19cc054c83479fca41b21db3c2e6960e8f4

[ "MIT" ]

11

2021-05-14T02:52:30.000Z

2022-03-14T15:55:47.000Z

319.774501

158,104

0.921958

[ [ [ "## 初始化", "_____no_output_____" ] ], [ [ "import sys,os \nroot_path = os.path.abspath('../../../../')\nsys.path.append(root_path)\nroot_path", "_____no_output_____" ], [ "import pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nimport src.features.factors.consolidate_factor as cf\nimport src.visualization.plotting as pt", "_____no_output_____" ] ], [ [ "## 整理数据", "_____no_output_____" ] ], [ [ "fp = root_path + \"/xxx.parquet\" # 需要用到的其它类型的数据\nmf = pd.read_parquet(fp)", "_____no_output_____" ], [ "md_fp = root_path + \"/data/example/IF/md.parquet\" # 需要用到的行情数据\nmd = pd.read_parquet(md_fp)", "_____no_output_____" ], [ "df = pd.concat([mf, md], axis=1).dropna(axis=0) # 将数据源进行整合", "_____no_output_____" ], [ "df['return'] = df['close'].diff() # 基准收益", "_____no_output_____" ] ], [ [ "## 生成因子", "_____no_output_____" ], [ "## 设置因子的类型、名称、参数值", "_____no_output_____" ] ], [ [ "factor_type = 'tmom'\nfactor_signature = 'xxx'\nparam_signatures = [560, 720, 960, 1200, 1800]\nraw_factor_name = f\"factor_{factor_type}_{factor_signature}\"\nraw_factor_name", "_____no_output_____" ], [ "def factor_tmom_xxx(df: pd.DataFrame, w) -> pd.Series:\n \"\"\"\n 最好在这里规范描述因子逻辑，以便后期整理\n \"\"\"\n df['factor'] = df['return'].rolling(w).mean() / df['return'].rolling(w).max() # 生成因子\n return df['factor']", "_____no_output_____" ] ], [ [ "## 开启一个循环，用以检验因子在不同参数下的表现", "_____no_output_____" ] ], [ [ "# set signal shift\nsig_shift = 1", "_____no_output_____" ], [ "compare_df, compare_df_2 = pd.DataFrame(), pd.DataFrame()\nfor i in param_signatures:\n factor = factor_tmom_xxx(df, i)\n signal = np.sign(factor)\n ret_cumsum_df = pd.DataFrame((df['return'] * signal.shift(sig_shift)).cumsum(), columns=[i])\n ret_df = pd.DataFrame((df['return'] * signal.shift(sig_shift)), columns=[i])\n compare_df = pd.concat([compare_df, ret_cumsum_df], axis=1)\n compare_df_2 = pd.concat([compare_df_2, ret_df], axis=1)\ncompare_df['benchmark'] = base_return.cumsum()\ncompare_df['close'] = df['close']\ncompare_df_2['benchmark'] = base_return", "_____no_output_____" ], [ "compare_df.plot(figsize=(16,9), secondary_y='close')", "_____no_output_____" ], [ "compare_df.drop(columns=['close'], inplace=True)\nvol_on_return = pd.DataFrame((compare_df - compare_df.mean()).std(), columns=['volitility'])\nfinal_return = pd.DataFrame(compare_df.iloc[-1])\nfinal_return.columns = ['return']\nsample_df = pd.concat([vol_on_return, final_return], axis=1)\nsample_df.plot(kind='bar', secondary_y='volitility', figsize=(16,9))", "_____no_output_____" ], [ "compare_df.describe()", "_____no_output_____" ], [ "compare_df_2.describe()", "_____no_output_____" ] ], [ [ "## 选取你认为表现比较好的因子，将因子函数固化", "_____no_output_____" ] ], [ [ "param_signature = 1200\nfactor_name = f\"factor_{factor_type}_{factor_signature}_{param_signature}\"\nfactor_name", "_____no_output_____" ] ], [ [ "#### 现在，你的因子函数应该有固定的参数，而非传入参数。", "_____no_output_____" ] ], [ [ "def factor_tmom_xxx_1200(df: pd.DataFrame):\n \"\"\"\n 衡量北向资金净买入量在1200期内的投票结果\n \"\"\"\n df['factor'] = df['return'].rolling(w).mean() / df['return'].rolling(w).max() # 生成因子\n return df['factor']", "_____no_output_____" ], [ "factor = factor_tmom_xxx_1200(df)", "_____no_output_____" ] ], [ [ "## 再次对固化的因子进行回测检验", "_____no_output_____" ] ], [ [ "# set signal shift\nsig_shift = 1", "_____no_output_____" ] ], [ [ "## 确认因子转换为信号的逻辑", "_____no_output_____" ] ], [ [ "signal = np.sign(factor)", "_____no_output_____" ] ], [ [ "## 确认回测结果", "_____no_output_____" ] ], [ [ "(df['return'] * signal.shift(sig_shift)).cumsum().describe()", "_____no_output_____" ], [ "(df['return'] * signal.shift(sig_shift)).cumsum().plot(figsize=(16,9))", "_____no_output_____" ], [ "data = pd.DataFrame([factor.shift(sig_shift), base_return]).T\ndata.columns = ['factor', 'return']\nfig = plt.figure(figsize=(16,9))\nsns.scatterplot(data=data, x='factor', y='return')", "_____no_output_____" ], [ "data = pd.DataFrame([signal.shift(sig_shift), base_return]).T\ndata.columns = ['signal', 'return']\nfig = plt.figure(figsize=(16,9))\nsns.scatterplot(data=data, x='signal', y='return')", "_____no_output_____" ] ], [ [ "-----------------", "_____no_output_____" ], [ "# <font color=red>CAUTION! </font>\n#### <font color=red>YOU ARE ABOUT TO CONSOLIDATE A FACTOR FUNCTION AND ITS DATA. </font>\n#### <font color=red>ENTER FOLLOWING STEPS WITH CAUTION!</font>", "_____no_output_____" ], [ "-------------------------", "_____no_output_____" ], [ "## consolidate factor", "_____no_output_____" ] ], [ [ "cf.record_source(factor_tmom_xxx_1200)", "_____no_output_____" ] ], [ [ "## set instrument name:", "_____no_output_____" ] ], [ [ "instrument = 'IF'", "_____no_output_____" ] ], [ [ "## save factor to parquet", "_____no_output_____" ] ], [ [ "factor_df = pd.DataFrame(factor)\nfactor_df.columns=['factor']\nfactor_df", "_____no_output_____" ], [ "factor_fp = root_path + f\"/factor/{instrument}/\"\n# os.mkdir(factor_fp)\ncf.save_factor(factor_df, factor_fp, factor_name)", "_____no_output_____" ] ], [ [ "## save signal to parquet", "_____no_output_____" ] ], [ [ "signal_df = pd.DataFrame(signal)\nsignal_df.columns=['signal']\nsignal_df", "_____no_output_____" ], [ "signal_fp = root_path + f\"/signal/{instrument}\"\n# os.mkdir(signal_fp)\ncf.save_signal(signal_df, signal_fp, factor_name)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

d0e7a334f4aee8b4dbf5362a6997c15d691ed3dc

28,555

ipynb

Jupyter Notebook

notebooks/12.Testing_3_all.ipynb

muhdlaziem/DR

74bd52ad5c000966590e8d91c9c2f2682a3fa0a0

[ "MIT" ]

5

2020-10-05T04:30:47.000Z

2021-12-18T11:17:10.000Z

notebooks/12.Testing_3_all.ipynb

muhdlaziem/DR

74bd52ad5c000966590e8d91c9c2f2682a3fa0a0

[ "MIT" ]

7

2020-09-16T08:42:22.000Z

2022-03-12T00:49:02.000Z

notebooks/12.Testing_3_all.ipynb

muhdlaziem/DR

74bd52ad5c000966590e8d91c9c2f2682a3fa0a0

[ "MIT" ]

2

2020-09-20T05:21:14.000Z

2020-11-05T14:29:58.000Z

33.475967

483

0.463001

[ [ [ "<a href=\"https://colab.research.google.com/github/muhdlaziem/DR/blob/master/Testing_3_all.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ] ], [ [ "from google.colab import drive\ndrive.mount('/gdrive')\n%cd /gdrive/'My Drive'/", "Go to this URL in a browser: https://accounts.google.com/o/oauth2/auth?client_id=947318989803-6bn6qk8qdgf4n4g3pfee6491hc0brc4i.apps.googleusercontent.com&redirect_uri=urn%3aietf%3awg%3aoauth%3a2.0%3aoob&scope=email%20https%3a%2f%2fwww.googleapis.com%2fauth%2fdocs.test%20https%3a%2f%2fwww.googleapis.com%2fauth%2fdrive%20https%3a%2f%2fwww.googleapis.com%2fauth%2fdrive.photos.readonly%20https%3a%2f%2fwww.googleapis.com%2fauth%2fpeopleapi.readonly&response_type=code\n\nEnter your authorization code:\n··········\nMounted at /gdrive\n/gdrive/My Drive\n" ], [ "%tensorflow_version 1.x\n\n# import libraries\nimport json\nimport math\nfrom tqdm import tqdm, tqdm_notebook\nimport gc\nimport warnings\nimport os\n\nimport cv2\nfrom PIL import Image\n\nimport pandas as pd\nimport scipy\nimport matplotlib.pyplot as plt\n\nfrom keras import backend as K\nfrom keras import layers\nfrom keras.applications.densenet import DenseNet121\nfrom keras.callbacks import Callback, ModelCheckpoint\nfrom keras.preprocessing.image import ImageDataGenerator\nfrom keras.models import Sequential\nfrom keras.optimizers import Adam\n\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.metrics import cohen_kappa_score, accuracy_score\nimport numpy as np\n\nwarnings.filterwarnings(\"ignore\")\n\n%matplotlib inline", "TensorFlow 1.x selected.\n" ], [ "# Image size\nim_size = 320", "_____no_output_____" ], [ "import pandas as pd\n# %cd diabetic-retinopathy-resized/\nDR = pd.read_csv('/gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/label_for_out_MYRRC_data2_256x256.csv')\nDR.head()", "_____no_output_____" ], [ "def preprocess_image(image_path, desired_size=224):\n img = cv2.imread(image_path)\n img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)\n #img = crop_image_from_gray(img)\n img = cv2.resize(img, (desired_size,desired_size))\n img = cv2.addWeighted(img,4,cv2.GaussianBlur(img, (0,0), desired_size/40) ,-4 ,128)\n \n return img", "_____no_output_____" ], [ "# testing set\n%cd /gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/image\nN = DR.shape[0]\nx_test = np.empty((N, im_size, im_size, 3), dtype=np.uint8)\n\nfor i, image_id in enumerate(tqdm_notebook(DR['file'])):\n x_test[i, :, :, :] = preprocess_image(\n f'{image_id}',\n desired_size = im_size\n )", "/gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/image\n" ], [ "y_test = pd.get_dummies(DR['class']).values\n\nprint(y_test.shape)\nprint(x_test.shape)", "(60, 3)\n(60, 320, 320, 3)\n" ], [ "y_test_multi = np.empty(y_test.shape, dtype=y_test.dtype)\ny_test_multi[:, 2] = y_test[:, 2]\n\nfor i in range(1, -1, -1):\n y_test_multi[:, i] = np.logical_or(y_test[:, i], y_test_multi[:, i+1])\n\nprint(\"Y_test multi: {}\".format(y_test_multi.shape))", "Y_test multi: (60, 3)\n" ], [ "# from keras.models import load_model\nimport tensorflow as tf\n\nmodel = tf.keras.models.load_model('/gdrive/My Drive/diabetic-retinopathy-resized/resized_train_cropped/denseNet_3_all.h5')\nmodel.summary()", "WARNING:tensorflow:From /tensorflow-1.15.2/python3.6/tensorflow_core/python/ops/resource_variable_ops.py:1630: calling BaseResourceVariable.__init__ (from tensorflow.python.ops.resource_variable_ops) with constraint is deprecated and will be removed in a future version.\nInstructions for updating:\nIf using Keras pass *_constraint arguments to layers.\nWARNING:tensorflow:From /tensorflow-1.15.2/python3.6/tensorflow_core/python/ops/nn_impl.py:183: where (from tensorflow.python.ops.array_ops) is deprecated and will be removed in a future version.\nInstructions for updating:\nUse tf.where in 2.0, which has the same broadcast rule as np.where\nModel: \"sequential_1\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\ndensenet121 (Model) (None, 10, 10, 1024) 7037504 \n_________________________________________________________________\nglobal_average_pooling2d_1 ( (None, 1024) 0 \n_________________________________________________________________\ndropout_1 (Dropout) (None, 1024) 0 \n_________________________________________________________________\ndense_1 (Dense) (None, 3) 3075 \n=================================================================\nTotal params: 7,040,579\nTrainable params: 6,956,931\nNon-trainable params: 83,648\n_________________________________________________________________\n" ], [ "y_val_pred = model.predict(x_test) ", "_____no_output_____" ], [ "def compute_score_inv(threshold):\n y1 = y_val_pred > threshold\n y1 = y1.astype(int).sum(axis=1) - 1\n y2 = y_test_multi.sum(axis=1) - 1\n score = cohen_kappa_score(y1, y2, weights='quadratic')\n \n return 1 - score\n\nsimplex = scipy.optimize.minimize(\n compute_score_inv, 0.5, method='nelder-mead'\n)\n\nbest_threshold = simplex['x'][0]\n\ny1 = y_val_pred > best_threshold\ny1 = y1.astype(int).sum(axis=1) - 1\n# y1 = np.where(y1==2,1,y1)\n# y1 = np.where(y1==3,2,y1)\n# y1 = np.where(y1==4,2,y1)\n\ny2 = y_test_multi.sum(axis=1) - 1\nscore = cohen_kappa_score(y1, y2, weights='quadratic')\nprint('Threshold: {}'.format(best_threshold))\nprint('Validation QWK score with best_threshold: {}'.format(score))\n\ny1 = y_val_pred > .5\ny1 = y1.astype(int).sum(axis=1) - 1\n# y1 = np.where(y1==2,1,y1)\n# y1 = np.where(y1==3,2,y1)\n# y1 = np.where(y1==4,2,y1)\nscore = cohen_kappa_score(y1, y2, weights='quadratic')\nprint('Validation QWK score with .5 threshold: {}'.format(score))", "Threshold: 0.5\nValidation QWK score with best_threshold: 0.8205128205128205\nValidation QWK score with .5 threshold: 0.8205128205128205\n" ], [ "from sklearn.metrics import classification_report, confusion_matrix\ny_best = y_val_pred > best_threshold\ny_best = y_best.astype(int).sum(axis=1) - 1\n# y_best = np.where(y_best==2,1,y_best)\n# y_best = np.where(y_best==3,2,y_best)\n# y_best = np.where(y_best==4,2,y_best)\n\nprint('Confusion Matrix')\nprint(confusion_matrix(y_best, y2))\nprint('Classification Report')\ntarget_names = ['No DR', 'Moderate', 'Severe']\nprint(classification_report(y_best, y2, target_names=target_names))", "Confusion Matrix\n[[17 3 1]\n [ 3 16 3]\n [ 0 1 16]]\nClassification Report\n precision recall f1-score support\n\n No DR 0.85 0.81 0.83 21\n Moderate 0.80 0.73 0.76 22\n Severe 0.80 0.94 0.86 17\n\n accuracy 0.82 60\n macro avg 0.82 0.83 0.82 60\nweighted avg 0.82 0.82 0.81 60\n\n" ], [ "print(y_best)\nprint(y2)", "[0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 2 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1\n 1 1 1 2 2 2 2 2 0 2 2 1 1 2 2 2 2 2 2 1 2 2 2]\n[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\n 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]\n" ], [ "DR['predicted'] = y_best\nDR.to_excel(\"/gdrive/My Drive/diabetic-retinopathy-resized/MadamAmeliaSample/result_3_all.xlsx\")", "_____no_output_____" ], [ "", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e7a7b60dce8d0c6091f2c17aef10c5db7b6692

73,015

ipynb

Jupyter Notebook

processing/TF_Sample.ipynb

Wapiti08/Analysis_Ransome_with_GAN

f908ec77b4df1029b10fd4f8a9e94daf1b4bbf7b

[ "MIT" ]

2

2021-10-09T11:44:46.000Z

2022-03-11T15:22:58.000Z

processing/TF_Sample.ipynb

Wapiti08/Analysis_Ransome_with_GAN

f908ec77b4df1029b10fd4f8a9e94daf1b4bbf7b

[ "MIT" ]

null

processing/TF_Sample.ipynb

Wapiti08/Analysis_Ransome_with_GAN

f908ec77b4df1029b10fd4f8a9e94daf1b4bbf7b

[ "MIT" ]

1

2022-03-11T15:23:02.000Z

41.866399

203

0.467356

[ [ [ "import pickle\nimport sys\n", "_____no_output_____" ], [ "# process the normal registry data\nnormal_file_path = './dataset/normal_registry_total.pkl'\nwith open(normal_file_path, 'rb') as fr:\n normal_data = pickle.load(fr, encoding=\"bytes\")\n\n# process the ransom registry data\nransom_file_path = './dataset/ransom_registry_total.pkl'\nwith open(ransom_file_path, 'rb') as fr:\n ransom_data = pickle.load(fr, encoding=\"bytes\")", "_____no_output_____" ], [ "# Preprocessing for lowercase\nimport numpy as np\n\n# lowercase all the data\nnormal_data = np.char.lower(normal_data)\nransom_data = np.char.lower(ransom_data)", "_____no_output_____" ], [ "# calculate the weights\nfrom collections import Counter\n\ndef string_frequency(strings):\n total_len = len(strings)\n weights_dict = {}\n strings_dict = Counter(strings)\n print(len(strings_dict.keys()))\n for key, value in strings_dict.items():\n weights_dict[key] = round(value/total_len, 6)\n return weights_dict\n", "_____no_output_____" ], [ "normal_weights_dict = string_frequency(normal_data)\nransom_weights_dict = string_frequency(ransom_data)", "4685\n6452\n" ], [ "# sort the dict according to the weights\nnormal_query_weights = sorted(normal_weights_dict.items(), key=lambda x: x[1], reverse=True)\nransom_query_weights = sorted(ransom_weights_dict.items(), key=lambda x: x[1], reverse=True)", "_____no_output_____" ], [ "normal_query_weights[:50]", "_____no_output_____" ], [ "ransom_query_weights[:50]", "_____no_output_____" ], [ "import pandas as pd\n# write to dataframe\nnormal_df = pd.DataFrame(normal_query_weights, columns=['features', 'weights'])\nnormal_rank = range(1,len(normal_weights_dict)+1)\nnormal_df['rank']=normal_rank", "_____no_output_____" ], [ "# write to dataframe\nransom_df = pd.DataFrame(ransom_query_weights, columns=['features', 'weights'])\nransom_rank = range(1,len(ransom_weights_dict)+1)\nransom_df['rank'] = ransom_rank", "_____no_output_____" ], [ "ransom_df", "_____no_output_____" ], [ "ransom_df[ransom_df['weights']>0.0006]", "_____no_output_____" ], [ "df1 = ransom_df[ransom_df['weights']>0.0007]\ndf1", "_____no_output_____" ], [ "pd.concat([df1, normal_df], axis=1, join='inner')\nfeature_ranks = df1.merge(normal_df, on=['features'])\nfeature_ranks_com = feature_ranks[['features','rank_x','rank_y']]\nfeature_ranks_com", "_____no_output_____" ], [ "feature_final = feature_ranks_com[feature_ranks_com['rank_y']>35]\nfeature_final", "_____no_output_____" ], [ "feature_final.reset_index()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e7af858eefdb8126f42e2425fd6d1dfcd81515

181,527

ipynb

Jupyter Notebook

feature_sets.ipynb

DillipKS/MLCC_assignments

f673112fc6f96cd3e09fa0caf84e15ca6b705a37

[ "Apache-2.0" ]

2

2018-08-23T09:59:31.000Z

2018-08-23T09:59:32.000Z

feature_sets.ipynb

DillipKS/MLCC_assignments

f673112fc6f96cd3e09fa0caf84e15ca6b705a37

[ "Apache-2.0" ]

null

feature_sets.ipynb

DillipKS/MLCC_assignments

f673112fc6f96cd3e09fa0caf84e15ca6b705a37

[ "Apache-2.0" ]

null

103.375285

57,096

0.736177

[ [ [ "[View in Colaboratory](https://colab.research.google.com/github/DillipKS/MLCC_assignments/blob/master/feature_sets.ipynb)", "_____no_output_____" ], [ "#### Copyright 2017 Google LLC.", "_____no_output_____" ] ], [ [ "# Licensed under the Apache License, Version 2.0 (the \"License\");\n# you may not use this file except in compliance with the License.\n# You may obtain a copy of the License at\n#\n# https://www.apache.org/licenses/LICENSE-2.0\n#\n# Unless required by applicable law or agreed to in writing, software\n# distributed under the License is distributed on an \"AS IS\" BASIS,\n# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n# See the License for the specific language governing permissions and\n# limitations under the License.", "_____no_output_____" ] ], [ [ "# Feature Sets", "_____no_output_____" ], [ "**Learning Objective:** Create a minimal set of features that performs just as well as a more complex feature set", "_____no_output_____" ], [ "So far, we've thrown all of our features into the model. Models with fewer features use fewer resources and are easier to maintain. Let's see if we can build a model on a minimal set of housing features that will perform equally as well as one that uses all the features in the data set.", "_____no_output_____" ], [ "## Setup\n\nAs before, let's load and prepare the California housing data.", "_____no_output_____" ] ], [ [ "from __future__ import print_function\n\nimport math\n\nfrom IPython import display\nfrom matplotlib import cm\nfrom matplotlib import gridspec\nfrom matplotlib import pyplot as plt\nimport numpy as np\nimport pandas as pd\nfrom sklearn import metrics\nimport tensorflow as tf\nfrom tensorflow.python.data import Dataset\n\ntf.logging.set_verbosity(tf.logging.ERROR)\npd.options.display.max_rows = 10\npd.options.display.float_format = '{:.1f}'.format\n\ncalifornia_housing_dataframe = pd.read_csv(\"https://storage.googleapis.com/mledu-datasets/california_housing_train.csv\", sep=\",\")\n\ncalifornia_housing_dataframe = california_housing_dataframe.reindex(\n np.random.permutation(california_housing_dataframe.index))", "_____no_output_____" ], [ "def preprocess_features(california_housing_dataframe):\n \"\"\"Prepares input features from California housing data set.\n\n Args:\n california_housing_dataframe: A Pandas DataFrame expected to contain data\n from the California housing data set.\n Returns:\n A DataFrame that contains the features to be used for the model, including\n synthetic features.\n \"\"\"\n selected_features = california_housing_dataframe[\n [\"latitude\",\n \"longitude\",\n \"housing_median_age\",\n \"total_rooms\",\n \"total_bedrooms\",\n \"population\",\n \"households\",\n \"median_income\"]]\n processed_features = selected_features.copy()\n # Create a synthetic feature.\n processed_features[\"rooms_per_person\"] = (\n california_housing_dataframe[\"total_rooms\"] /\n california_housing_dataframe[\"population\"])\n return processed_features\n\ndef preprocess_targets(california_housing_dataframe):\n \"\"\"Prepares target features (i.e., labels) from California housing data set.\n\n Args:\n california_housing_dataframe: A Pandas DataFrame expected to contain data\n from the California housing data set.\n Returns:\n A DataFrame that contains the target feature.\n \"\"\"\n output_targets = pd.DataFrame()\n # Scale the target to be in units of thousands of dollars.\n output_targets[\"median_house_value\"] = (\n california_housing_dataframe[\"median_house_value\"] / 1000.0)\n return output_targets", "_____no_output_____" ], [ "# Choose the first 12000 (out of 17000) examples for training.\ntraining_examples = preprocess_features(california_housing_dataframe.head(12000))\ntraining_targets = preprocess_targets(california_housing_dataframe.head(12000))\n\n# Choose the last 5000 (out of 17000) examples for validation.\nvalidation_examples = preprocess_features(california_housing_dataframe.tail(5000))\nvalidation_targets = preprocess_targets(california_housing_dataframe.tail(5000))\n\n# Double-check that we've done the right thing.\nprint(\"Training examples summary:\")\ndisplay.display(training_examples.describe())\nprint(\"Validation examples summary:\")\ndisplay.display(validation_examples.describe())\n\nprint(\"Training targets summary:\")\ndisplay.display(training_targets.describe())\nprint(\"Validation targets summary:\")\ndisplay.display(validation_targets.describe())", "Training examples summary:\n" ] ], [ [ "## Task 1: Develop a Good Feature Set\n\n**What's the best performance you can get with just 2 or 3 features?**\n\nA **correlation matrix** shows pairwise correlations, both for each feature compared to the target and for each feature compared to other features.\n\nHere, correlation is defined as the [Pearson correlation coefficient](https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient). You don't have to understand the mathematical details for this exercise.\n\nCorrelation values have the following meanings:\n\n * `-1.0`: perfect negative correlation\n * `0.0`: no correlation\n * `1.0`: perfect positive correlation", "_____no_output_____" ] ], [ [ "correlation_dataframe = training_examples.copy()\ncorrelation_dataframe[\"target\"] = training_targets[\"median_house_value\"]\n\ncorrelation_dataframe.corr()", "_____no_output_____" ] ], [ [ "Features that have strong positive or negative correlations with the target will add information to our model. We can use the correlation matrix to find such strongly correlated features.\n\nWe'd also like to have features that aren't so strongly correlated with each other, so that they add independent information.\n\nUse this information to try removing features. You can also try developing additional synthetic features, such as ratios of two raw features.\n\nFor convenience, we've included the training code from the previous exercise.", "_____no_output_____" ] ], [ [ "def construct_feature_columns(input_features):\n \"\"\"Construct the TensorFlow Feature Columns.\n\n Args:\n input_features: The names of the numerical input features to use.\n Returns:\n A set of feature columns\n \"\"\" \n return set([tf.feature_column.numeric_column(my_feature)\n for my_feature in input_features])", "_____no_output_____" ], [ "def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):\n \"\"\"Trains a linear regression model.\n \n Args:\n features: pandas DataFrame of features\n targets: pandas DataFrame of targets\n batch_size: Size of batches to be passed to the model\n shuffle: True or False. Whether to shuffle the data.\n num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely\n Returns:\n Tuple of (features, labels) for next data batch\n \"\"\"\n \n # Convert pandas data into a dict of np arrays.\n features = {key:np.array(value) for key,value in dict(features).items()} \n \n # Construct a dataset, and configure batching/repeating.\n ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit\n ds = ds.batch(batch_size).repeat(num_epochs)\n\n # Shuffle the data, if specified.\n if shuffle:\n ds = ds.shuffle(10000)\n \n # Return the next batch of data.\n features, labels = ds.make_one_shot_iterator().get_next()\n return features, labels", "_____no_output_____" ], [ "def train_model(\n learning_rate,\n steps,\n batch_size,\n training_examples,\n training_targets,\n validation_examples,\n validation_targets):\n \"\"\"Trains a linear regression model.\n \n In addition to training, this function also prints training progress information,\n as well as a plot of the training and validation loss over time.\n \n Args:\n learning_rate: A `float`, the learning rate.\n steps: A non-zero `int`, the total number of training steps. A training step\n consists of a forward and backward pass using a single batch.\n batch_size: A non-zero `int`, the batch size.\n training_examples: A `DataFrame` containing one or more columns from\n `california_housing_dataframe` to use as input features for training.\n training_targets: A `DataFrame` containing exactly one column from\n `california_housing_dataframe` to use as target for training.\n validation_examples: A `DataFrame` containing one or more columns from\n `california_housing_dataframe` to use as input features for validation.\n validation_targets: A `DataFrame` containing exactly one column from\n `california_housing_dataframe` to use as target for validation.\n \n Returns:\n A `LinearRegressor` object trained on the training data.\n \"\"\"\n\n periods = 10\n steps_per_period = steps / periods\n\n # Create a linear regressor object.\n my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)\n my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)\n linear_regressor = tf.estimator.LinearRegressor(\n feature_columns=construct_feature_columns(training_examples),\n optimizer=my_optimizer\n )\n \n # Create input functions.\n training_input_fn = lambda: my_input_fn(training_examples, \n training_targets[\"median_house_value\"], \n batch_size=batch_size)\n predict_training_input_fn = lambda: my_input_fn(training_examples, \n training_targets[\"median_house_value\"], \n num_epochs=1, \n shuffle=False)\n predict_validation_input_fn = lambda: my_input_fn(validation_examples, \n validation_targets[\"median_house_value\"], \n num_epochs=1, \n shuffle=False)\n\n # Train the model, but do so inside a loop so that we can periodically assess\n # loss metrics.\n print(\"Training model...\")\n print(\"RMSE (on training data):\")\n training_rmse = []\n validation_rmse = []\n for period in range (0, periods):\n # Train the model, starting from the prior state.\n linear_regressor.train(\n input_fn=training_input_fn,\n steps=steps_per_period,\n )\n # Take a break and compute predictions.\n training_predictions = linear_regressor.predict(input_fn=predict_training_input_fn)\n training_predictions = np.array([item['predictions'][0] for item in training_predictions])\n \n validation_predictions = linear_regressor.predict(input_fn=predict_validation_input_fn)\n validation_predictions = np.array([item['predictions'][0] for item in validation_predictions])\n \n # Compute training and validation loss.\n training_root_mean_squared_error = math.sqrt(\n metrics.mean_squared_error(training_predictions, training_targets))\n validation_root_mean_squared_error = math.sqrt(\n metrics.mean_squared_error(validation_predictions, validation_targets))\n # Occasionally print the current loss.\n print(\" period %02d : %0.2f\" % (period, training_root_mean_squared_error))\n # Add the loss metrics from this period to our list.\n training_rmse.append(training_root_mean_squared_error)\n validation_rmse.append(validation_root_mean_squared_error)\n print(\"Model training finished.\")\n\n \n # Output a graph of loss metrics over periods.\n plt.ylabel(\"RMSE\")\n plt.xlabel(\"Periods\")\n plt.title(\"Root Mean Squared Error vs. Periods\")\n plt.tight_layout()\n plt.plot(training_rmse, label=\"training\")\n plt.plot(validation_rmse, label=\"validation\")\n plt.legend()\n\n return linear_regressor", "_____no_output_____" ] ], [ [ "Spend 5 minutes searching for a good set of features and training parameters. Then check the solution to see what we chose. Don't forget that different features may require different learning parameters.", "_____no_output_____" ] ], [ [ "#\n# Your code here: add your features of choice as a list of quoted strings.\n#\nminimal_features = [\"median_income\", \"rooms_per_person\"]\n\nassert minimal_features, \"You must select at least one feature!\"\n\nminimal_training_examples = training_examples[minimal_features]\nminimal_validation_examples = validation_examples[minimal_features]\n\n#\n# Don't forget to adjust these parameters.\n#\ntrain_model(\n learning_rate=0.03,\n steps=500,\n batch_size=10,\n training_examples=minimal_training_examples,\n training_targets=training_targets,\n validation_examples=minimal_validation_examples,\n validation_targets=validation_targets)", "Training model...\nRMSE (on training data):\n period 00 : 204.30\n period 01 : 172.09\n period 02 : 142.18\n period 03 : 115.27\n period 04 : 94.83\n period 05 : 85.87\n period 06 : 84.60\n period 07 : 84.73\n period 08 : 84.56\n period 09 : 84.51\nModel training finished.\n" ] ], [ [ "### Solution\n\nClick below for a solution.", "_____no_output_____" ] ], [ [ "minimal_features = [\n \"median_income\",\n \"latitude\",\n]\n\nminimal_training_examples = training_examples[minimal_features]\nminimal_validation_examples = validation_examples[minimal_features]\n\n_ = train_model(\n learning_rate=0.01,\n steps=500,\n batch_size=5,\n training_examples=minimal_training_examples,\n training_targets=training_targets,\n validation_examples=minimal_validation_examples,\n validation_targets=validation_targets)", "_____no_output_____" ] ], [ [ "## Task 2: Make Better Use of Latitude\n\nPlotting `latitude` vs. `median_house_value` shows that there really isn't a linear relationship there.\n\nInstead, there are a couple of peaks, which roughly correspond to Los Angeles and San Francisco.", "_____no_output_____" ] ], [ [ "plt.scatter(training_examples[\"latitude\"], training_targets[\"median_house_value\"])", "_____no_output_____" ] ], [ [ "**Try creating some synthetic features that do a better job with latitude.**\n\nFor example, you could have a feature that maps `latitude` to a value of `|latitude - 38|`, and call this `distance_from_san_francisco`.\n\nOr you could break the space into 10 different buckets. `latitude_32_to_33`, `latitude_33_to_34`, etc., each showing a value of `1.0` if `latitude` is within that bucket range and a value of `0.0` otherwise.\n\nUse the correlation matrix to help guide development, and then add them to your model if you find something that looks good.\n\nWhat's the best validation performance you can get?", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE: Train on a new data set that includes synthetic features based on latitude.\n\ntrain_lat_bins = [0,0,0,0,0,0,0,0,0,0] #bins for a unit latitude range\n\nfor lat in training_examples[\"latitude\"]:\n if int(lat)==32: train_lat_bins[0]+=1\n elif int(lat)==33: train_lat_bins[1]+=1\n elif int(lat)==34: train_lat_bins[2]+=1\n elif int(lat)==35: train_lat_bins[3]+=1\n elif int(lat)==36: train_lat_bins[4]+=1\n elif int(lat)==37: train_lat_bins[5]+=1\n elif int(lat)==38: train_lat_bins[6]+=1\n elif int(lat)==39: train_lat_bins[7]+=1\n elif int(lat)==40: train_lat_bins[8]+=1\n elif int(lat)==41: train_lat_bins[9]+=1\n\ntrain_lat_bins", "_____no_output_____" ], [ "val_lat_bins = [0,0,0,0,0,0,0,0,0,0] #bins for a unit latitude range\n\nfor lat in validation_examples[\"latitude\"]:\n if int(lat)==32: val_lat_bins[0]+=1\n elif int(lat)==33: val_lat_bins[1]+=1\n elif int(lat)==34: val_lat_bins[2]+=1\n elif int(lat)==35: val_lat_bins[3]+=1\n elif int(lat)==36: val_lat_bins[4]+=1\n elif int(lat)==37: val_lat_bins[5]+=1\n elif int(lat)==38: val_lat_bins[6]+=1\n elif int(lat)==39: val_lat_bins[7]+=1\n elif int(lat)==40: val_lat_bins[8]+=1\n elif int(lat)==41: val_lat_bins[9]+=1\nval_lat_bins", "_____no_output_____" ], [ "", "_____no_output_____" ] ], [ [ "### Solution\n\nClick below for a solution.", "_____no_output_____" ], [ "Aside from `latitude`, we'll also keep `median_income`, to compare with the previous results.\n\nWe decided to bucketize the latitude. This is fairly straightforward in Pandas using `Series.apply`.", "_____no_output_____" ] ], [ [ "LATITUDE_RANGES = zip(range(32, 44), range(33, 45))\n\ndef select_and_transform_features(source_df):\n selected_examples = pd.DataFrame()\n selected_examples[\"median_income\"] = source_df[\"median_income\"]\n for r in LATITUDE_RANGES:\n selected_examples[\"latitude_%d_to_%d\" % r] = source_df[\"latitude\"].apply(\n lambda l: 1.0 if l >= r[0] and l < r[1] else 0.0)\n return selected_examples\n\nselected_training_examples = select_and_transform_features(training_examples)\nselected_validation_examples = select_and_transform_features(validation_examples)", "_____no_output_____" ], [ "selected_training_examples.head()", "_____no_output_____" ], [ "_ = train_model(\n learning_rate=0.03,\n steps=500,\n batch_size=10,\n training_examples=selected_training_examples,\n training_targets=training_targets,\n validation_examples=selected_validation_examples,\n validation_targets=validation_targets)", "Training model...\nRMSE (on training data):\n period 00 : 207.06\n period 01 : 177.35\n period 02 : 149.11\n period 03 : 123.33\n period 04 : 101.95\n period 05 : 88.18\n period 06 : 84.82\n period 07 : 84.22\n period 08 : 83.85\n period 09 : 83.69\nModel training finished.\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ] ]

d0e7b0ffbd5e3e8bb0fba0883d0f2fe8564f9f49

55,367

ipynb

Jupyter Notebook

HeroesOfPymoli/HeroesOfPymoli_starter.HW.ipynb

cmills39/pandas-challenge

d7313dd3b860d8bb8413d5aa7eb7615328520fb5

[ "ADSL" ]

null

HeroesOfPymoli/HeroesOfPymoli_starter.HW.ipynb

cmills39/pandas-challenge

d7313dd3b860d8bb8413d5aa7eb7615328520fb5

[ "ADSL" ]

null

HeroesOfPymoli/HeroesOfPymoli_starter.HW.ipynb

cmills39/pandas-challenge

d7313dd3b860d8bb8413d5aa7eb7615328520fb5

[ "ADSL" ]

null

26.440783

158

0.354345

[ [ [ "### Note\n* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.", "_____no_output_____" ] ], [ [ "# Dependencies and Setup\nimport pandas as pd\n\n# File to Load (Remember to Change These)\nHeroesOfPymoli = \"Resources/purchase_data.csv\"\n\n# Read Purchasing File and store into Pandas data frame\nHoP_df = pd.read_csv(HeroesOfPymoli)\nHoP_df.head()", "_____no_output_____" ] ], [ [ "## Player Count", "_____no_output_____" ], [ "* Display the total number of players\n", "_____no_output_____" ] ], [ [ "Player_Count = HoP_df[\"SN\"].nunique()\nPlayer_Count", "_____no_output_____" ], [ "data = {'Total Players':[Player_Count]}\nPC_df = pd.DataFrame(data)\nPC_df", "_____no_output_____" ] ], [ [ "## Purchasing Analysis (Total)", "_____no_output_____" ], [ "* Run basic calculations to obtain number of unique items, average price, etc.\n\n\n* Create a summary data frame to hold the results\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display the summary data frame\n", "_____no_output_____" ] ], [ [ "# Number of Unique Items\nU_Items_Count = HoP_df[\"Item ID\"].nunique()\nU_Items_Count", "_____no_output_____" ], [ "#Average Price\nAverage_Price = HoP_df[\"Price\"].mean()\nAverage_Price", "_____no_output_____" ], [ "#Total Number of Purchases\nNumber_P = HoP_df[\"Purchase ID\"].count()\nNumber_P\n", "_____no_output_____" ], [ "#Total Revenue\nT_Revenue= Number_P * Average_Price\nT_Revenue", "_____no_output_____" ], [ "PAdata = {'Number of Unique Items':[U_Items_Count], 'Average Price':[Average_Price], 'Number of Purchases' :[Number_P], 'Total Revenue' :[T_Revenue]}\nPA_df = pd.DataFrame(PAdata)\nPA_df", "_____no_output_____" ] ], [ [ "## Gender Demographics", "_____no_output_____" ], [ "* Percentage and Count of Male Players\n\n\n* Percentage and Count of Female Players\n\n\n* Percentage and Count of Other / Non-Disclosed\n\n\n", "_____no_output_____" ] ], [ [ "#Count of Players\nG_Players_df = HoP_df.loc[1:, [\"SN\",\"Gender\",\"Price\",\"Purchase ID\"]]\nGP=G_Players_df.drop_duplicates()\nGP", "_____no_output_____" ], [ "Gender_Count=GP['Gender'].value_counts()\nGender_Count", "_____no_output_____" ], [ "Percent_of_Players= (Gender_Count / Player_Count)*100\nPercent_of_Players", "_____no_output_____" ], [ "GAdata = {'Total Count':[Gender_Count], 'Percentage of Players':[Percent_of_Players]}\nGA_df = pd.DataFrame(GAdata)\nGA_df", "_____no_output_____" ] ], [ [ "\n## Purchasing Analysis (Gender)", "_____no_output_____" ], [ "* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender\n\n\n\n\n* Create a summary data frame to hold the results\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display the summary data frame", "_____no_output_____" ] ], [ [ "# Purchase analysis\nPurchase_Analysis_df = HoP_df.loc[ 1:,[\"Gender\",\"Price\",]]\nPurchase_Analysis_df", "_____no_output_____" ], [ "PA_Count = Purchase_Analysis_df['Gender'].value_counts()\nPA_Count", "_____no_output_____" ], [ "#AVG purchase price per member\nAvg_Purchase_Price = HoP_df.loc[ 1:,[\"Price\"]]\nAvg_Purchase_Price.mean()", "_____no_output_____" ] ], [ [ "## Age Demographics", "_____no_output_____" ], [ "* Establish bins for ages\n\n\n* Categorize the existing players using the age bins. Hint: use pd.cut()\n\n\n* Calculate the numbers and percentages by age group\n\n\n* Create a summary data frame to hold the results\n\n\n* Optional: round the percentage column to two decimal points\n\n\n* Display Age Demographics Table\n", "_____no_output_____" ] ], [ [ "Age_df = HoP_df.loc[1:, [\"SN\",\"Age\"]]\nAG=Age_df.drop_duplicates()\nAgeD=pd.DataFrame(AG)\nAgeD", "_____no_output_____" ], [ "#Establish Bins\nbins= [0,10,15,20,25,30,35,40,100]\n\ngroup_names = [\"<10\",\"10-14\",\"15-19\",\"20-24\",\"25-29\",\"30-34\",\"35-39\",\"40+\"]\n\nAgeD[\"age ranges\"] = pd.cut(AgeD[\"Age\"], bins, labels=group_names)\n\nAgeD.head()", "_____no_output_____" ], [ "#Total Counts\nTotal_Count = AgeD['age ranges'].value_counts()\nTotal_Count", "_____no_output_____" ], [ "#Percentage of Players\nPercent_of_GPlayers= (Total_Count / Player_Count)*100\nPercent_of_GPlayers", "_____no_output_____" ] ], [ [ "## Purchasing Analysis (Age)", "_____no_output_____" ], [ "* Bin the purchase_data data frame by age\n\n\n* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below\n\n\n* Create a summary data frame to hold the results\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display the summary data frame", "_____no_output_____" ] ], [ [ "PurchaseAnalysis_df = HoP_df.loc[1:, [\"SN\",\"Age\",\"Price\",\"Purchase ID\"]]\nPurchaseAnalysis_df", "_____no_output_____" ], [ "P_Analysis=PurchaseAnalysis_df.drop_duplicates()\nPurchaseAS=pd.DataFrame(PurchaseAnalysis_df)\nPurchaseAS", "_____no_output_____" ], [ "#Establish Bins\nbins= [0,10,15,20,25,30,35,40,100]\n\ngroup_names = [\"<10\",\"10-14\",\"15-19\",\"20-24\",\"25-29\",\"30-34\",\"35-39\",\"40+\"]\n\nPurchaseAS[\"age ranges\"] = pd.cut(PurchaseAS[\"Age\"], bins, labels=group_names)\n\nPurchaseAS", "_____no_output_____" ], [ "PA_age_Count = PurchaseAS['age ranges'].value_counts()\nPA_age_Count", "_____no_output_____" ] ], [ [ "## Top Spenders", "_____no_output_____" ], [ "* Run basic calculations to obtain the results in the table below\n\n\n* Create a summary data frame to hold the results\n\n\n* Sort the total purchase value column in descending order\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display a preview of the summary data frame\n\n", "_____no_output_____" ] ], [ [ "T_Spenders_df = HoP_df.loc[1:, [\"SN\",\"Price\"]]\nT_Spenders_df ", "_____no_output_____" ], [ "#Cant figure this out\nT_Spenders1_df = T_Spenders_df.()\nT_Spenders1_df", "_____no_output_____" ] ], [ [ "## Most Popular Items", "_____no_output_____" ], [ "* Retrieve the Item ID, Item Name, and Item Price columns\n\n\n* Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value\n\n\n* Create a summary data frame to hold the results\n\n\n* Sort the purchase count column in descending order\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display a preview of the summary data frame\n\n", "_____no_output_____" ] ], [ [ "PopItems_df = HoP_df.loc[1:, [\"Item Name\",\"Price\",\"Item ID\"]]\nPopItems_df", "_____no_output_____" ], [ "#???\nPopItems1_df = PopItems_df.groupby(by=\"Item Name\")\nPopItems1_df", "_____no_output_____" ] ], [ [ "## Most Profitable Items", "_____no_output_____" ], [ "* Sort the above table by total purchase value in descending order\n\n\n* Optional: give the displayed data cleaner formatting\n\n\n* Display a preview of the data frame\n\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ] ]

d0e7c5d93cee052c12a5885d83a03c79e9b18127

366,126

ipynb

Jupyter Notebook

Pop_Segmentation.ipynb

ahmed14-cell/population-segmentation

af69d8f91a4d66747997885b2168dd0dcd59caef

[ "MIT" ]

null

Pop_Segmentation.ipynb

ahmed14-cell/population-segmentation

af69d8f91a4d66747997885b2168dd0dcd59caef

[ "MIT" ]

null

Pop_Segmentation.ipynb

ahmed14-cell/population-segmentation

af69d8f91a4d66747997885b2168dd0dcd59caef

[ "MIT" ]

null

65.909271

25,388

0.715341

[ [ [ "# Population Segmentation with SageMaker\n\nIn this notebook, we'll employ two, unsupervised learning algorithms to do **population segmentation**. Population segmentation aims to find natural groupings in population data that reveal some feature-level similarities between different regions in the US.\n\nUsing **principal component analysis** (PCA) you will reduce the dimensionality of the original census data. Then, we'll use **k-means clustering** to assign each US county to a particular cluster based on where a county lies in component space. How each cluster is arranged in component space can tell us which US counties are most similar and what demographic traits define that similarity; this information is most often used to inform targeted, marketing campaigns that want to appeal to a specific group of people. This cluster information is also useful for learning more about a population by revealing patterns between regions that you otherwise may not have noticed.\n\n### US Census Data\n\nWe'll be using data collected by the [US Census](https://en.wikipedia.org/wiki/United_States_Census), which aims to count the US population, recording demographic traits about labor, age, population, and so on, for each county in the US. \n### Machine Learning Workflow\n\nTo implement population segmentation, we'll go through a number of steps:\n* Data loading and exploration\n* Data cleaning and pre-processing \n* Dimensionality reduction with PCA\n* Feature engineering and data transformation\n* Clustering transformed data with k-means\n* Extracting trained model attributes and visualizing k clusters\n\nThese tasks make up a complete, machine learning workflow from data loading and cleaning to model deployment.\n\n---", "_____no_output_____" ], [ "First, import the relevant libraries into this SageMaker notebook. ", "_____no_output_____" ] ], [ [ "# data managing and display libs\nimport pandas as pd\nimport numpy as np\nimport os\nimport io\n\nimport matplotlib.pyplot as plt\nimport matplotlib\n%matplotlib inline ", "_____no_output_____" ], [ "# sagemaker libraries\nimport boto3\nimport sagemaker", "_____no_output_____" ] ], [ [ "## Loading the Data from Amazon S3\n\nThis particular dataset is already in an Amazon S3 bucket; you can load the data by pointing to this bucket and getting a data file by name. \n\n> You can interact with S3 using a `boto3` client.", "_____no_output_____" ] ], [ [ "# boto3 client to get S3 data\ns3_client = boto3.client('s3')\nbucket_name='aws-sagemaker-census-segmentation'", "_____no_output_____" ] ], [ [ "Take a look at the contents of this bucket; get a list of objects that are contained within the bucket and print out the names of the objects. You should see that there is one file, 'Census_Data_for_SageMaker.csv'.", "_____no_output_____" ] ], [ [ "# get a list of objects in the bucket\nobj_list=s3_client.list_objects(Bucket=bucket_name)\n\n# print object(s)in S3 bucket\nfiles=[]\nfor contents in obj_list['Contents']:\n files.append(contents['Key'])\n \nprint(files)", "['Census_Data_for_SageMaker.csv']\n" ], [ "# there is one file --> one key\nfile_name=files[0]\n\nprint(file_name)", "Census_Data_for_SageMaker.csv\n" ] ], [ [ "Retrieve the data file from the bucket with a call to `client.get_object()`.", "_____no_output_____" ] ], [ [ "# get an S3 object by passing in the bucket and file name\ndata_object = s3_client.get_object(Bucket=bucket_name, Key=file_name)\n\n# what info does the object contain?\ndisplay(data_object)", "_____no_output_____" ], [ "# information is in the \"Body\" of the object\ndata_body = data_object[\"Body\"].read()\nprint('Data type: ', type(data_body))", "Data type: <class 'bytes'>\n" ] ], [ [ "This is a `bytes` datatype, which you can read it in using [io.BytesIO(file)](https://docs.python.org/3/library/io.html#binary-i-o).", "_____no_output_____" ] ], [ [ "# read in bytes data\ndata_stream = io.BytesIO(data_body)\n\n# create a dataframe\ncounties_df = pd.read_csv(data_stream, header=0, delimiter=\",\") \ncounties_df.head()", "_____no_output_____" ] ], [ [ "## Exploratory Data Analysis (EDA)\n\nNow that we've loaded in the data, it is time to clean it up, explore it, and pre-process it. Data exploration is one of the most important parts of the machine learning workflow because it allows you to notice any initial patterns in data distribution and features that may inform how you proceed with modeling and clustering the data.\n\n### Explore data & drop any incomplete rows of data\n\nWhen you first explore the data, it is good to know what you are working with. How many data points and features are you starting with, and what kind of information can you get at a first glance? In this notebook, we will use complete data points to train a model. So, our first exercise will be to investigate the shape of this data and implement a simple, data cleaning step: dropping any incomplete rows of data.\n\nYou should be able to answer the **question**: How many data points and features are in the original, provided dataset? (And how many points are left after dropping any incomplete rows?)", "_____no_output_____" ] ], [ [ "# print out stats about data\nprint('Original data stats:\\n', counties_df.shape)\n# drop any incomplete rows of data, and create a new df\nclean_counties_df = counties_df.dropna()\nprint('Cleaned data stats:\\n', clean_counties_df.shape)", "Original data stats:\n (3220, 37)\nCleaned data stats:\n (3218, 37)\n" ] ], [ [ "### Create a new DataFrame, indexed by 'State-County'\n\nEventually, you'll want to feed these features into a machine learning model. Machine learning models need numerical data to learn from and not categorical data like strings (State, County). So, you'll reformat this data such that it is indexed by region and you'll also drop any features that are not useful for clustering.\n\nTo complete this task, perform the following steps, using your *clean* DataFrame, generated above:\n1. Combine the descriptive columns, 'State' and 'County', into one, new categorical column, 'State-County'. \n2. Index the data by this unique State-County name.\n3. After doing this, drop the old State and County columns and the CensusId column, which does not give us any meaningful demographic information.\n\nAfter completing this task, you should have a DataFrame with 'State-County' as the index, and 34 columns of numerical data for each county. You should get a resultant DataFrame that looks like the following (truncated for display purposes):\n```\n TotalPop\t Men\t Women\tHispanic\t...\n \nAlabama-Autauga\t55221\t 26745\t28476\t2.6 ...\nAlabama-Baldwin\t195121\t95314\t99807\t4.5 ...\nAlabama-Barbour\t26932\t 14497\t12435\t4.6 ...\n...\n\n```", "_____no_output_____" ] ], [ [ "# index data by 'State-County'\nclean_counties_df.index = clean_counties_df['State'] + '-' + clean_counties_df['County']", "_____no_output_____" ], [ "# drop the old State and County columns, and the CensusId column\n# clean df should be modified or created anew\nclean_counties_df = clean_counties_df.drop(['State', 'County', 'CensusId'], axis=1)\nclean_counties_df.head()", "_____no_output_____" ] ], [ [ "Now, what features do you have to work with?", "_____no_output_____" ] ], [ [ "# features\nfeatures_list = clean_counties_df.columns.values\nprint('Features: \\n', features_list)", "Features: \n ['TotalPop' 'Men' 'Women' 'Hispanic' 'White' 'Black' 'Native' 'Asian'\n 'Pacific' 'Citizen' 'Income' 'IncomeErr' 'IncomePerCap' 'IncomePerCapErr'\n 'Poverty' 'ChildPoverty' 'Professional' 'Service' 'Office' 'Construction'\n 'Production' 'Drive' 'Carpool' 'Transit' 'Walk' 'OtherTransp'\n 'WorkAtHome' 'MeanCommute' 'Employed' 'PrivateWork' 'PublicWork'\n 'SelfEmployed' 'FamilyWork' 'Unemployment']\n" ] ], [ [ "## Visualizing the Data\n\nIn general, you can see that features come in a variety of ranges, mostly percentages from 0-100, and counts that are integer values in a large range. Let's visualize the data in some of our feature columns and see what the distribution, over all counties, looks like.\n\nThe below cell displays **histograms**, which show the distribution of data points over discrete feature ranges. The x-axis represents the different bins; each bin is defined by a specific range of values that a feature can take, say between the values 0-5 and 5-10, and so on. The y-axis is the frequency of occurrence or the number of county data points that fall into each bin. I find it helpful to use the y-axis values for relative comparisons between different features.\n\nBelow, I'm plotting a histogram comparing methods of commuting to work over all of the counties. I just copied these feature names from the list of column names, printed above. I also know that all of these features are represented as percentages (%) in the original data, so the x-axes of these plots will be comparable.", "_____no_output_____" ] ], [ [ "# transportation (to work)\ntransport_list = ['Drive', 'Carpool', 'Transit', 'Walk', 'OtherTransp']\nn_bins = 30 # can decrease to get a wider bin (or vice versa)\n\nfor column_name in transport_list:\n ax=plt.subplots(figsize=(6,3))\n # get data by column_name and display a histogram\n ax = plt.hist(clean_counties_df[column_name], bins=n_bins)\n title=\"Histogram of \" + column_name\n plt.title(title, fontsize=12)\n plt.show()", "_____no_output_____" ] ], [ [ "### EXERCISE: Create histograms of your own\n\nCommute transportation method is just one category of features. If you take a look at the 34 features, you can see data on profession, race, income, and more. Display a set of histograms that interest you!\n", "_____no_output_____" ] ], [ [ "# create a list of features that you want to compare or examine\nmy_list = ['Hispanic', 'White', 'Black', 'Native', 'Asian']\nn_bins = 50\n\n# histogram creation code is similar to above\nfor column_name in my_list:\n ax=plt.subplots(figsize=(6,3))\n # get data by column_name and display a histogram\n ax = plt.hist(clean_counties_df[column_name], bins=n_bins)\n title=\"Histogram of \" + column_name\n plt.title(title, fontsize=12)\n plt.show()", "_____no_output_____" ], [ "# create a list of features that you want to compare or examine\nmy_list = ['WorkAtHome', 'Employed', 'SelfEmployed', 'Unemployment']\nn_bins = 50\n\n# histogram creation code is similar to above\nfor column_name in my_list:\n ax=plt.subplots(figsize=(6,3))\n # get data by column_name and display a histogram\n ax = plt.hist(clean_counties_df[column_name], bins=n_bins)\n title=\"Histogram of \" + column_name\n plt.title(title, fontsize=12)\n plt.show()", "_____no_output_____" ] ], [ [ "### Normalize the data\n\nYou need to standardize the scale of the numerical columns in order to consistently compare the values of different features. You can use a [MinMaxScaler](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) to transform the numerical values so that they all fall between 0 and 1.", "_____no_output_____" ] ], [ [ "# scale numerical features into a normalized range, 0-1\n# store them in this dataframe\nfrom sklearn.preprocessing import MinMaxScaler\n\nmin_max = MinMaxScaler()\n\ncounties_scaled = pd.DataFrame(min_max.fit_transform(clean_counties_df))\n\ncounties_scaled.columns = clean_counties_df.columns\ncounties_scaled.index = clean_counties_df.index\ncounties_scaled.head()", "_____no_output_____" ], [ "counties_scaled.describe()", "_____no_output_____" ] ], [ [ "---\n# Data Modeling\n\n\nNow, the data is ready to be fed into a machine learning model!\n\nEach data point has 34 features, which means the data is 34-dimensional. Clustering algorithms rely on finding clusters in n-dimensional feature space. For higher dimensions, an algorithm like k-means has a difficult time figuring out which features are most important, and the result is, often, noisier clusters.\n\nSome dimensions are not as important as others. For example, if every county in our dataset has the same rate of unemployment, then that particular feature doesn’t give us any distinguishing information; it will not help t separate counties into different groups because its value doesn’t *vary* between counties.\n\n> Instead, we really want to find the features that help to separate and group data. We want to find features that cause the **most variance** in the dataset!\n\nSo, before I cluster this data, I’ll want to take a dimensionality reduction step. My aim will be to form a smaller set of features that will better help to separate our data. The technique I’ll use is called PCA or **principal component analysis**\n\n## Dimensionality Reduction\n\nPCA attempts to reduce the number of features within a dataset while retaining the “principal components”, which are defined as *weighted*, linear combinations of existing features that are designed to be linearly independent and account for the largest possible variability in the data! You can think of this method as taking many features and combining similar or redundant features together to form a new, smaller feature set.\n\nWe can reduce dimensionality with the built-in SageMaker model for PCA.", "_____no_output_____" ], [ "### Roles and Buckets\n\n> To create a model, you'll first need to specify an IAM role, and to save the model attributes, you'll need to store them in an S3 bucket.\n\nThe `get_execution_role` function retrieves the IAM role you created at the time you created your notebook instance. Roles are essentially used to manage permissions and you can read more about that [in this documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html). For now, know that we have a FullAccess notebook, which allowed us to access and download the census data stored in S3.\n\nYou must specify a bucket name for an S3 bucket in your account where you want SageMaker model parameters to be stored. Note that the bucket must be in the same region as this notebook. You can get a default S3 bucket, which automatically creates a bucket for you and in your region, by storing the current SageMaker session and calling `session.default_bucket()`.", "_____no_output_____" ] ], [ [ "from sagemaker import get_execution_role\n\nsession = sagemaker.Session() # store the current SageMaker session\n\n# get IAM role\nrole = get_execution_role()\nprint(role)", "arn:aws:iam::204421427803:role/service-role/AmazonSageMaker-ExecutionRole-20210421T105651\n" ], [ "# get default bucket\nbucket_name = session.default_bucket()\nprint(bucket_name)\nprint()", "sagemaker-us-east-1-204421427803\n\n" ] ], [ [ "## Define a PCA Model\n\nTo create a PCA model, I'll use the built-in SageMaker resource. A SageMaker estimator requires a number of parameters to be specified; these define the type of training instance to use and the model hyperparameters. A PCA model requires the following constructor arguments:\n\n* role: The IAM role, which was specified, above.\n* train_instance_count: The number of training instances (typically, 1).\n* train_instance_type: The type of SageMaker instance for training.\n* num_components: An integer that defines the number of PCA components to produce.\n* sagemaker_session: The session used to train on SageMaker.\n\nDocumentation on the PCA model can be found [here](http://sagemaker.readthedocs.io/en/latest/pca.html).\n\nBelow, I first specify where to save the model training data, the `output_path`.", "_____no_output_____" ] ], [ [ "# define location to store model artifacts\nprefix = 'counties'\n\noutput_path='s3://{}/{}/'.format(bucket_name, prefix)\n\nprint('Training artifacts will be uploaded to: {}'.format(output_path))", "Training artifacts will be uploaded to: s3://sagemaker-us-east-1-204421427803/counties/\n" ], [ "# define a PCA model\nfrom sagemaker import PCA\n\n# this is current features - 1\n# you'll select only a portion of these to use, later\nN_COMPONENTS=33\n\npca_SM = PCA(role=role,\n train_instance_count=1,\n train_instance_type='ml.c4.xlarge',\n output_path=output_path, # specified, above\n num_components=N_COMPONENTS, \n sagemaker_session=session)\n", "train_instance_count has been renamed in sagemaker>=2.\nSee: https://sagemaker.readthedocs.io/en/stable/v2.html for details.\ntrain_instance_type has been renamed in sagemaker>=2.\nSee: https://sagemaker.readthedocs.io/en/stable/v2.html for details.\n" ] ], [ [ "### Convert data into a RecordSet format\n\nNext, prepare the data for a built-in model by converting the DataFrame to a numpy array of float values.\n\nThe *record_set* function in the SageMaker PCA model converts a numpy array into a **RecordSet** format that is the required format for the training input data. This is a requirement for _all_ of SageMaker's built-in models. The use of this data type is one of the reasons that allows training of models within Amazon SageMaker to perform faster, especially for large datasets.", "_____no_output_____" ] ], [ [ "# convert df to np array\ntrain_data_np = counties_scaled.values.astype('float32')\n\n# convert to RecordSet format\nformatted_train_data = pca_SM.record_set(train_data_np)", "_____no_output_____" ] ], [ [ "## Train the model\n\nCall the fit function on the PCA model, passing in our formatted, training data. This spins up a training instance to perform the training job.\n\nNote that it takes the longest to launch the specified training instance; the fitting itself doesn't take much time.", "_____no_output_____" ] ], [ [ "%%time\n\n# train the PCA mode on the formatted data\npca_SM.fit(formatted_train_data)", "Defaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\nDefaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\n" ] ], [ [ "## Accessing the PCA Model Attributes\n\nAfter the model is trained, we can access the underlying model parameters.\n\n### Unzip the Model Details\n\nNow that the training job is complete, you can find the job under **Jobs** in the **Training** subsection in the Amazon SageMaker console. You can find the job name listed in the training jobs. Use that job name in the following code to specify which model to examine.\n\nModel artifacts are stored in S3 as a TAR file; a compressed file in the output path we specified + 'output/model.tar.gz'. The artifacts stored here can be used to deploy a trained model.", "_____no_output_____" ] ], [ [ "# Get the name of the training job, it's suggested that you copy-paste\n# from the notebook or from a specific job in the AWS console\n\ntraining_job_name='pca-2021-04-21-10-18-40-888'\n\n# where the model is saved, by default\nmodel_key = os.path.join(prefix, training_job_name, 'output/model.tar.gz')\nprint(model_key)\n\n# download and unzip model\nboto3.resource('s3').Bucket(bucket_name).download_file(model_key, 'model.tar.gz')\n\n# unzipping as model_algo-1\nos.system('tar -zxvf model.tar.gz')\nos.system('unzip model_algo-1')", "counties/pca-2021-04-21-10-18-40-888/output/model.tar.gz\n" ] ], [ [ "### MXNet Array\n\nMany of the Amazon SageMaker algorithms use MXNet for computational speed, including PCA, and so the model artifacts are stored as an array. After the model is unzipped and decompressed, we can load the array using MXNet.\n\nYou can take a look at the MXNet [documentation, here](https://aws.amazon.com/mxnet/).", "_____no_output_____" ] ], [ [ "import mxnet as mx\n\n# loading the unzipped artifacts\npca_model_params = mx.ndarray.load('model_algo-1')\n\n# what are the params\nprint(pca_model_params)", "{'s': \n[1.7896362e-02 3.0864021e-02 3.2130770e-02 3.5486195e-02 9.4831578e-02\n 1.2699370e-01 4.0288666e-01 1.4084760e+00 1.5100485e+00 1.5957943e+00\n 1.7783760e+00 2.1662524e+00 2.2966361e+00 2.3856051e+00 2.6954880e+00\n 2.8067985e+00 3.0175958e+00 3.3952675e+00 3.5731301e+00 3.6966958e+00\n 4.1890211e+00 4.3457499e+00 4.5410376e+00 5.0189657e+00 5.5786467e+00\n 5.9809699e+00 6.3925138e+00 7.6952214e+00 7.9913125e+00 1.0180052e+01\n 1.1718245e+01 1.3035975e+01 1.9592180e+01]\n<NDArray 33 @cpu(0)>, 'v': \n[[ 2.46869749e-03 2.56468095e-02 2.50773830e-03 ... -7.63925165e-02\n 1.59879066e-02 5.04589686e-03]\n [-2.80601848e-02 -6.86634064e-01 -1.96283013e-02 ... -7.59587288e-02\n 1.57304872e-02 4.95312130e-03]\n [ 3.25766727e-02 7.17300594e-01 2.40726061e-02 ... -7.68136829e-02\n 1.62378680e-02 5.13597298e-03]\n ...\n [ 1.12151138e-01 -1.17030945e-02 -2.88011521e-01 ... 1.39890045e-01\n -3.09406728e-01 -6.34506866e-02]\n [ 2.99992133e-02 -3.13433539e-03 -7.63589665e-02 ... 4.17341813e-02\n -7.06735924e-02 -1.42857227e-02]\n [ 7.33537527e-05 3.01008171e-04 -8.00925500e-06 ... 6.97060227e-02\n 1.20169498e-01 2.33626723e-01]]\n<NDArray 34x33 @cpu(0)>, 'mean': \n[[0.00988273 0.00986636 0.00989863 0.11017046 0.7560245 0.10094159\n 0.0186819 0.02940491 0.0064698 0.01154038 0.31539047 0.1222766\n 0.3030056 0.08220861 0.256217 0.2964254 0.28914267 0.40191284\n 0.57868284 0.2854676 0.28294644 0.82774544 0.34378946 0.01576072\n 0.04649627 0.04115358 0.12442778 0.47014 0.00980645 0.7608103\n 0.19442631 0.21674445 0.0294168 0.22177474]]\n<NDArray 1x34 @cpu(0)>}\n" ] ], [ [ "## PCA Model Attributes\n\nThree types of model attributes are contained within the PCA model.\n\n* **mean**: The mean that was subtracted from a component in order to center it.\n* **v**: The makeup of the principal components; (same as ‘components_’ in an sklearn PCA model).\n* **s**: The singular values of the components for the PCA transformation. This does not exactly give the % variance from the original feature space, but can give the % variance from the projected feature space.\n \nWe are only interested in v and s. \n\nFrom s, we can get an approximation of the data variance that is covered in the first `n` principal components. The approximate explained variance is given by the formula: the sum of squared s values for all top n components over the sum over squared s values for _all_ components:\n\n\\begin{equation*}\n\\frac{\\sum_{n}^{ } s_n^2}{\\sum s^2}\n\\end{equation*}\n\nFrom v, we can learn more about the combinations of original features that make up each principal component.\n", "_____no_output_____" ] ], [ [ "# get selected params\ns=pd.DataFrame(pca_model_params['s'].asnumpy())\nv=pd.DataFrame(pca_model_params['v'].asnumpy())", "_____no_output_____" ] ], [ [ "## Data Variance\n\nOur current PCA model creates 33 principal components, but when we create new dimensionality-reduced training data, we'll only select a few, top n components to use. To decide how many top components to include, it's helpful to look at how much **data variance** the components capture. For our original, high-dimensional data, 34 features captured 100% of our data variance. If we discard some of these higher dimensions, we will lower the amount of variance we can capture.\n\n### Tradeoff: dimensionality vs. data variance\n\nAs an illustrative example, say we have original data in three dimensions. So, three dimensions capture 100% of our data variance; these dimensions cover the entire spread of our data. The below images are taken from the PhD thesis, [“Approaches to analyse and interpret biological profile data”](https://publishup.uni-potsdam.de/opus4-ubp/frontdoor/index/index/docId/696) by Matthias Scholz, (2006, University of Potsdam, Germany).\n\n<img src='notebook_ims/3d_original_data.png' width=35% />\n\nNow, you may also note that most of this data seems related; it falls close to a 2D plane, and just by looking at the spread of the data, we can visualize that the original, three dimensions have some correlation. So, we can instead choose to create two new dimensions, made up of linear combinations of the original, three dimensions. These dimensions are represented by the two axes/lines, centered in the data. \n\n<img src='notebook_ims/pca_2d_dim_reduction.png' width=70% />\n\nIf we project this in a new, 2D space, we can see that we still capture most of the original data variance using *just* two dimensions. There is a tradeoff between the amount of variance we can capture and the number of component-dimensions we use to represent our data.\n\nWhen we select the top n components to use in a new data model, we'll typically want to include enough components to capture about 80-90% of the original data variance. In this project, we are looking at generalizing over a lot of data and we'll aim for about 80% coverage.", "_____no_output_____" ], [ "**Note**: The _top_ principal components, with the largest s values, are actually at the end of the s DataFrame. Let's print out the s values for the top n, principal components.", "_____no_output_____" ] ], [ [ "# looking at top 5 components\nn_principal_components = 5\n\nstart_idx = N_COMPONENTS - n_principal_components # 33-n\n\n# print a selection of s\nprint(s.iloc[start_idx:, :])", " 0\n28 7.991313\n29 10.180052\n30 11.718245\n31 13.035975\n32 19.592180\n" ] ], [ [ "### Calculate the explained variance\n\nIn creating new training data, you'll want to choose the top n principal components that account for at least 80% data variance. \n\nComplete a function, `explained_variance` that takes in the entire array `s` and a number of top principal components to consider. Then return the approximate, explained variance for those top n components. \n\nFor example, to calculate the explained variance for the top 5 components, calculate s squared for *each* of the top 5 components, add those up and normalize by the sum of *all* squared s values, according to this formula:\n\n\\begin{equation*}\n\\frac{\\sum_{5}^{ } s_n^2}{\\sum s^2}\n\\end{equation*}\n\n> Using this function, you should be able to answer the **question**: What is the smallest number of principal components that captures at least 80% of the total variance in the dataset?", "_____no_output_____" ] ], [ [ "# Calculate the explained variance for the top n principal components\n# you may assume you have access to the global var N_COMPONENTS\ndef explained_variance(s, n_top_components):\n '''Calculates the approx. data variance that n_top_components captures.\n :param s: A dataframe of singular values for top components; \n the top value is in the last row.\n :param n_top_components: An integer, the number of top components to use.\n :return: The expected data variance covered by the n_top_components.'''\n \n # your code here\n start_idx = N_COMPONENTS - n_top_components\n exp_var = np.square(s.iloc[start_idx:, :]).sum() / np.square(s).sum()\n return exp_var[0]\n pass\n", "_____no_output_____" ] ], [ [ "### Test Cell\n\nTest out your own code by seeing how it responds to different inputs; does it return a reasonable value for the single, top component? What about for the top 5 components?", "_____no_output_____" ] ], [ [ "# test cell\nn_top_components = 8 # select a value for the number of top components\n\n# calculate the explained variance\nexp_variance = explained_variance(s, n_top_components)\nprint('Explained variance: ', exp_variance)", "Explained variance: 0.83158576\n" ] ], [ [ "As an example, you should see that the top principal component accounts for about 32% of our data variance! Next, you may be wondering what makes up this (and other components); what linear combination of features make these components so influential in describing the spread of our data?\n\nBelow, let's take a look at our original features and use that as a reference.", "_____no_output_____" ] ], [ [ "# features\nfeatures_list = counties_scaled.columns.values\nprint('Features: \\n', features_list)", "Features: \n ['TotalPop' 'Men' 'Women' 'Hispanic' 'White' 'Black' 'Native' 'Asian'\n 'Pacific' 'Citizen' 'Income' 'IncomeErr' 'IncomePerCap' 'IncomePerCapErr'\n 'Poverty' 'ChildPoverty' 'Professional' 'Service' 'Office' 'Construction'\n 'Production' 'Drive' 'Carpool' 'Transit' 'Walk' 'OtherTransp'\n 'WorkAtHome' 'MeanCommute' 'Employed' 'PrivateWork' 'PublicWork'\n 'SelfEmployed' 'FamilyWork' 'Unemployment']\n" ] ], [ [ "## Component Makeup\n\nWe can now examine the makeup of each PCA component based on **the weightings of the original features that are included in the component**. The following code shows the feature-level makeup of the first component.\n\nNote that the components are again ordered from smallest to largest and so I am getting the correct rows by calling N_COMPONENTS-1 to get the top, 1, component.", "_____no_output_____" ] ], [ [ "import seaborn as sns\n\ndef display_component(v, features_list, component_num, n_weights=10):\n \n # get index of component (last row - component_num)\n row_idx = N_COMPONENTS-component_num\n\n # get the list of weights from a row in v, dataframe\n v_1_row = v.iloc[:, row_idx]\n v_1 = np.squeeze(v_1_row.values)\n\n # match weights to features in counties_scaled dataframe, using list comporehension\n comps = pd.DataFrame(list(zip(v_1, features_list)), \n columns=['weights', 'features'])\n\n # we'll want to sort by the largest n_weights\n # weights can be neg/pos and we'll sort by magnitude\n comps['abs_weights']=comps['weights'].apply(lambda x: np.abs(x))\n sorted_weight_data = comps.sort_values('abs_weights', ascending=False).head(n_weights)\n\n # display using seaborn\n ax=plt.subplots(figsize=(10,6))\n ax=sns.barplot(data=sorted_weight_data, \n x=\"weights\", \n y=\"features\", \n palette=\"Blues_d\")\n ax.set_title(\"PCA Component Makeup, Component #\" + str(component_num))\n plt.show()\n", "_____no_output_____" ], [ "# display makeup of first component\nnum=8\ndisplay_component(v, counties_scaled.columns.values, component_num=num, n_weights=20)", "_____no_output_____" ] ], [ [ "# Deploying the PCA Model\n\nWe can now deploy this model and use it to make \"predictions\". Instead of seeing what happens with some test data, we'll actually want to pass our training data into the deployed endpoint to create principal components for each data point. \n\nRun the cell below to deploy/host this model on an instance_type that we specify.", "_____no_output_____" ] ], [ [ "%%time\n# this takes a little while, around 7mins\npca_predictor = pca_SM.deploy(initial_instance_count=1, \n instance_type='ml.t2.medium')", "Defaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\n" ] ], [ [ "We can pass the original, numpy dataset to the model and transform the data using the model we created. Then we can take the largest n components to reduce the dimensionality of our data.", "_____no_output_____" ] ], [ [ "# pass np train data to the PCA model\ntrain_pca = pca_predictor.predict(train_data_np)", "_____no_output_____" ], [ "# check out the first item in the produced training features\ndata_idx = 0\nprint(train_pca[data_idx])", "label {\n key: \"projection\"\n value {\n float32_tensor {\n values: 0.0002009272575378418\n values: 0.0002455431967973709\n values: -0.0005782842636108398\n values: -0.0007815659046173096\n values: -0.00041911262087523937\n values: -0.0005133943632245064\n values: -0.0011316537857055664\n values: 0.0017268601804971695\n values: -0.005361668765544891\n values: -0.009066537022590637\n values: -0.008141040802001953\n values: -0.004735097289085388\n values: -0.00716288760304451\n values: 0.0003725700080394745\n values: -0.01208949089050293\n values: 0.02134685218334198\n values: 0.0009293854236602783\n values: 0.002417147159576416\n values: -0.0034637749195098877\n values: 0.01794189214706421\n values: -0.01639425754547119\n values: 0.06260128319263458\n values: 0.06637358665466309\n values: 0.002479255199432373\n values: 0.10011336207389832\n values: -0.1136140376329422\n values: 0.02589476853609085\n values: 0.04045158624649048\n values: -0.01082391943782568\n values: 0.1204797774553299\n values: -0.0883558839559555\n values: 0.16052711009979248\n values: -0.06027412414550781\n }\n }\n}\n\n" ] ], [ [ "### Create a transformed DataFrame\n\nFor each of our data points, get the top n component values from the list of component data points, returned by our predictor above, and put those into a new DataFrame.\n\nYou should end up with a DataFrame that looks something like the following:\n```\n c_1\t c_2\t c_3\t c_4\t c_5\t ...\nAlabama-Autauga\t-0.060274\t0.160527\t-0.088356\t 0.120480\t-0.010824\t...\nAlabama-Baldwin\t-0.149684\t0.185969\t-0.145743\t-0.023092\t-0.068677\t...\nAlabama-Barbour\t0.506202\t 0.296662\t 0.146258\t 0.297829\t0.093111\t...\n...\n```", "_____no_output_____" ] ], [ [ "# create dimensionality-reduced data\ndef create_transformed_df(train_pca, counties_scaled, n_top_components):\n ''' Return a dataframe of data points with component features. \n The dataframe should be indexed by State-County and contain component values.\n :param train_pca: A list of pca training data, returned by a PCA model.\n :param counties_scaled: A dataframe of normalized, original features.\n :param n_top_components: An integer, the number of top components to use.\n :return: A dataframe, indexed by State-County, with n_top_component values as columns. \n '''\n # create a dataframe of component features, indexed by State-County\n \n # your code here\n df = pd.DataFrame()\n for data in train_pca:\n comp = data.label['projection'].float32_tensor.values\n df = df.append([list(comp)])\n \n df.index = counties_scaled.index\n \n start_idx = N_COMPONENTS - n_top_components\n df = df.iloc[:, start_idx:]\n \n return df.iloc[:, ::-1]\n pass\n", "_____no_output_____" ] ], [ [ "Now we can create a dataset where each county is described by the top n principle components that we analyzed earlier. Each of these components is a linear combination of the original feature space. We can interpret each of these components by analyzing the makeup of the component, shown previously.\n\n### Define the `top_n` components to use in this transformed data\n\nYour code should return data, indexed by 'State-County' and with as many columns as `top_n` components.\n\nYou can also choose to add descriptive column names for this data; names that correspond to the component number or feature-level makeup.", "_____no_output_____" ] ], [ [ "## Specify top n\ntop_n = 8\n\n# call your function and create a new dataframe\ncounties_transformed = create_transformed_df(train_pca, counties_scaled, n_top_components=top_n)\n\n## TODO: Add descriptive column names\ncols = ['col_1', 'col_2', 'col_3', 'col_4', 'col_5', 'col_6', 'col_7', 'col_8']\ncounties_transformed.columns = cols\n# print result\ncounties_transformed.head()", "_____no_output_____" ] ], [ [ "### Delete the Endpoint!\n\nNow that we've deployed the mode and created our new, transformed training data, we no longer need the PCA endpoint.\n\nAs a clean up step, you should always delete your endpoints after you are done using them (and if you do not plan to deploy them to a website, for example).", "_____no_output_____" ] ], [ [ "# delete predictor endpoint\nsession.delete_endpoint(pca_predictor.endpoint)", "The endpoint attribute has been renamed in sagemaker>=2.\nSee: https://sagemaker.readthedocs.io/en/stable/v2.html for details.\n" ] ], [ [ "---\n# Population Segmentation \n\nNow, you’ll use the unsupervised clustering algorithm, k-means, to segment counties using their PCA attributes, which are in the transformed DataFrame we just created. K-means is a clustering algorithm that identifies clusters of similar data points based on their component makeup. Since we have ~3000 counties and 34 attributes in the original dataset, the large feature space may have made it difficult to cluster the counties effectively. Instead, we have reduced the feature space to 7 PCA components, and we’ll cluster on this transformed dataset.", "_____no_output_____" ], [ "### Define a k-means model\n\nYour task will be to instantiate a k-means model. A `KMeans` estimator requires a number of parameters to be instantiated, which allow us to specify the type of training instance to use, and the model hyperparameters. \n\nYou can read about the required parameters, in the [`KMeans` documentation](https://sagemaker.readthedocs.io/en/stable/kmeans.html); note that not all of the possible parameters are required.\n", "_____no_output_____" ], [ "### Choosing a \"Good\" K\n\nOne method for choosing a \"good\" k, is to choose based on empirical data. A bad k would be one so *high* that only one or two very close data points are near it, and another bad k would be one so *low* that data points are really far away from the centers.\n\nYou want to select a k such that data points in a single cluster are close together but that there are enough clusters to effectively separate the data. You can approximate this separation by measuring how close your data points are to each cluster center; the average centroid distance between cluster points and a centroid. After trying several values for k, the centroid distance typically reaches some \"elbow\"; it stops decreasing at a sharp rate and this indicates a good value of k. The graph below indicates the average centroid distance for value of k between 5 and 12.\n\n<img src='notebook_ims/elbow_graph.png' width=50% />\n\nA distance elbow can be seen around 8 when the distance starts to increase and then decrease at a slower rate. This indicates that there is enough separation to distinguish the data points in each cluster, but also that you included enough clusters so that the data points aren’t *extremely* far away from each cluster.", "_____no_output_____" ] ], [ [ "# define a KMeans estimator\nfrom sagemaker import KMeans\n\nn_clusters = 7\nkmeans_est = KMeans(role=role,\n sagemaker_session=session,\n instance_count=1,\n instance_type='ml.c4.xlarge',\n output_path=output_path,\n k=n_clusters)", "_____no_output_____" ] ], [ [ "### Create formatted, k-means training data\n\nJust as before, you should convert the `counties_transformed` df into a numpy array and then into a RecordSet. This is the required format for passing training data into a `KMeans` model.", "_____no_output_____" ] ], [ [ "# convert the transformed dataframe into record_set data\ntraining_data_np = counties_transformed.values.astype('float32')\ntraining_data = kmeans_est.record_set(training_data_np)", "_____no_output_____" ] ], [ [ "### Train the k-means model\n\nPass in the formatted training data and train the k-means model.", "_____no_output_____" ] ], [ [ "%%time\n# train kmeans\nkmeans_est.fit(training_data)", "Defaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\nDefaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\n" ] ], [ [ "### Deploy the k-means model\n\nDeploy the trained model to create a `kmeans_predictor`.\n", "_____no_output_____" ] ], [ [ "%%time\n# deploy the model to create a predictor\nkmeans_predictor = kmeans_est.deploy(initial_instance_count=1, instance_type='ml.t2.medium')", "Defaulting to the only supported framework/algorithm version: 1. Ignoring framework/algorithm version: 1.\n" ] ], [ [ "### Pass in the training data and assign predicted cluster labels\n\nAfter deploying the model, you can pass in the k-means training data, as a numpy array, and get resultant, predicted cluster labels for each data point.", "_____no_output_____" ] ], [ [ "# get the predicted clusters for all the kmeans training data\n\ncluster_info = kmeans_predictor.predict(training_data_np)", "_____no_output_____" ] ], [ [ "## Exploring the resultant clusters\n\nThe resulting predictions should give you information about the cluster that each data point belongs to.\n\nYou should be able to answer the **question**: which cluster does a given data point belong to?", "_____no_output_____" ] ], [ [ "# print cluster info for first data point\ndata_idx = 0\n\nprint('County is: ', counties_transformed.index[data_idx])\nprint()\nprint(cluster_info[data_idx])", "County is: Alabama-Autauga\n\nlabel {\n key: \"closest_cluster\"\n value {\n float32_tensor {\n values: 4.0\n }\n }\n}\nlabel {\n key: \"distance_to_cluster\"\n value {\n float32_tensor {\n values: 0.3278287351131439\n }\n }\n}\n\n" ] ], [ [ "### Visualize the distribution of data over clusters\n\nGet the cluster labels for each of our data points (counties) and visualize the distribution of points over each cluster.", "_____no_output_____" ] ], [ [ "# get all cluster labels\ncluster_labels = [c.label['closest_cluster'].float32_tensor.values[0] for c in cluster_info]", "_____no_output_____" ], [ "# count up the points in each cluster\ncluster_df = pd.DataFrame(cluster_labels)[0].value_counts()\n\nprint(cluster_df)", "4.0 978\n1.0 775\n2.0 423\n6.0 354\n5.0 322\n0.0 260\n3.0 106\nName: 0, dtype: int64\n" ] ], [ [ "Now, you may be wondering, what do each of these clusters tell us about these data points? To improve explainability, we need to access the underlying model to get the cluster centers. These centers will help describe which features characterize each cluster.", "_____no_output_____" ], [ "### Delete the Endpoint!\n\nNow that you've deployed the k-means model and extracted the cluster labels for each data point, you no longer need the k-means endpoint.", "_____no_output_____" ] ], [ [ "# delete kmeans endpoint\nsession.delete_endpoint(kmeans_predictor.endpoint)", "The endpoint attribute has been renamed in sagemaker>=2.\nSee: https://sagemaker.readthedocs.io/en/stable/v2.html for details.\n" ] ], [ [ "---\n# Model Attributes & Explainability\n\nExplaining the result of the modeling is an important step in making use of our analysis. By combining PCA and k-means, and the information contained in the model attributes within a SageMaker trained model, you can learn about a population and remark on some patterns you've found, based on the data.", "_____no_output_____" ], [ "### Access the k-means model attributes\n\nExtract the k-means model attributes from where they are saved as a TAR file in an S3 bucket.\n\nYou'll need to access the model by the k-means training job name, and then unzip the file into `model_algo-1`. Then you can load that file using MXNet, as before.", "_____no_output_____" ] ], [ [ "# download and unzip the kmeans model file\n# use the name model_algo-1\ntraining_job_name='kmeans-2021-04-21-14-23-50-011'\n\nmodel_key = os.path.join(prefix, training_job_name, 'output/model.tar.gz')\nprint(model_key)\nboto3.resource('s3').Bucket(bucket_name).download_file(model_key, 'model.tar.gz')\n\nos.system('tar -zxvf model.tar.gz')\nos.system('unzip model_algo-1')", "counties/kmeans-2021-04-21-14-23-50-011/output/model.tar.gz\n" ], [ "# get the trained kmeans params using mxnet\nkmeans_model_params = mx.ndarray.load('model_algo-1')\n\nprint(kmeans_model_params)", "[\n[[ 2.58064777e-01 -1.65894613e-01 -1.04465716e-01 -1.35486513e-01\n 1.03924178e-01 -1.08686484e-01 -8.16875845e-02 -2.35025808e-02]\n [-2.51183987e-01 -2.47022919e-02 -2.59090755e-02 -3.94684374e-02\n -1.28233312e-02 -2.87618302e-02 7.08517572e-03 -2.10537948e-02]\n [ 3.26939464e-01 2.11919174e-01 4.73352224e-02 2.46492922e-01\n 7.80158266e-02 -5.03628440e-02 3.61014754e-02 -2.20772400e-02]\n [ 1.15437484e+00 -2.67059535e-01 -1.83272630e-01 -3.75311702e-01\n -7.30814040e-02 6.50314614e-02 9.27247480e-02 -2.98950449e-02]\n [-6.96733519e-02 1.08055830e-01 1.33947924e-01 -7.20595196e-02\n -3.05895992e-02 3.85349803e-02 -2.33015679e-02 1.01805180e-02]\n [-1.10012732e-01 -4.45521057e-01 1.13024041e-01 1.49700969e-01\n 1.31083652e-05 1.37050338e-02 2.59297192e-02 3.89263853e-02]\n [-1.38011888e-01 6.29474223e-02 -3.91312391e-01 5.94821125e-02\n -3.68069038e-02 6.09904826e-02 1.90805877e-03 4.27541025e-02]]\n<NDArray 7x8 @cpu(0)>]\n" ] ], [ [ "There is only 1 set of model parameters contained within the k-means model: the cluster centroid locations in PCA-transformed, component space.\n\n* **centroids**: The location of the centers of each cluster in component space, identified by the k-means algorithm. \n", "_____no_output_____" ] ], [ [ "# get all the centroids\ncluster_centroids=pd.DataFrame(kmeans_model_params[0].asnumpy())\ncluster_centroids.columns=counties_transformed.columns\n\ndisplay(cluster_centroids)", "_____no_output_____" ] ], [ [ "### Visualizing Centroids in Component Space\n\nYou can't visualize 7-dimensional centroids in space, but you can plot a heatmap of the centroids and their location in the transformed feature space. \n\nThis gives you insight into what characteristics define each cluster. Often with unsupervised learning, results are hard to interpret. This is one way to make use of the results of PCA + clustering techniques, together. Since you were able to examine the makeup of each PCA component, you can understand what each centroid represents in terms of the PCA components.", "_____no_output_____" ] ], [ [ "# generate a heatmap in component space, using the seaborn library\nplt.figure(figsize = (12,9))\nax = sns.heatmap(cluster_centroids.T, cmap = 'YlGnBu')\nax.set_xlabel(\"Cluster\")\nplt.yticks(fontsize = 16)\nplt.xticks(fontsize = 16)\nax.set_title(\"Attribute Value by Centroid\")\nplt.show()", "_____no_output_____" ] ], [ [ "If you've forgotten what each component corresponds to at an original-feature-level, that's okay! You can use the previously defined `display_component` function to see the feature-level makeup.", "_____no_output_____" ] ], [ [ "# what do each of these components mean again?\n# let's use the display function, from above\ncomponent_num=7\ndisplay_component(v, counties_scaled.columns.values, component_num=component_num)", "_____no_output_____" ] ], [ [ "### Natural Groupings\n\nYou can also map the cluster labels back to each individual county and examine which counties are naturally grouped together.", "_____no_output_____" ] ], [ [ "# add a 'labels' column to the dataframe\ncounties_transformed['labels']=list(map(int, cluster_labels))\n\n# sort by cluster label 0-6\nsorted_counties = counties_transformed.sort_values('labels', ascending=True)\n# view some pts in cluster 0\nsorted_counties.head(20)", "_____no_output_____" ] ], [ [ "You can also examine one of the clusters in more detail, like cluster 1, for example. A quick glance at the location of the centroid in component space (the heatmap) tells us that it has the highest value for the `comp_6` attribute. You can now see which counties fit that description.", "_____no_output_____" ] ], [ [ "# get all counties with label == 1\ncluster=counties_transformed[counties_transformed['labels']==1]\ncluster.head()", "_____no_output_____" ] ], [ [ "## Final Cleanup!\n\n* Double check that you have deleted all your endpoints.\n* I'd also suggest manually deleting your S3 bucket, models, and endpoint configurations directly from your AWS console.\n\nYou can find thorough cleanup instructions, [in the documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/ex1-cleanup.html).", "_____no_output_____" ], [ "---\n# Conclusion\n\nYou have just walked through a machine learning workflow for unsupervised learning, specifically, for clustering a dataset using k-means after reducing the dimensionality using PCA. By accessing the underlying models created within SageMaker, you were able to improve the explainability of your model and draw insights from the resultant clusters. \n\nUsing these techniques, you have been able to better understand the essential characteristics of different counties in the US and segment them into similar groups, accordingly.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ] ]

d0e7c61f2b5feef5962dbca9b04c8370bbf5dd3a

100,774

ipynb

Jupyter Notebook

notebooks/Semantic_Search.ipynb

KewalMishra/VR

3f5bc7ea5d493394c7c4aafabc86849c8faf2bbf

[ "MIT" ]

1

2021-02-10T07:29:59.000Z

notebooks/Semantic_Search.ipynb

KewalMishra/VR

3f5bc7ea5d493394c7c4aafabc86849c8faf2bbf

[ "MIT" ]

1

2021-01-31T05:22:53.000Z

notebooks/Semantic_Search.ipynb

KewalMishra/VR

3f5bc7ea5d493394c7c4aafabc86849c8faf2bbf

[ "MIT" ]

1

2021-02-01T16:09:55.000Z

47.289535

960

0.56714

[ [ [ "<a href=\"https://colab.research.google.com/github/desaibhargav/VR/blob/main/notebooks/Semantic_Search.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "## **Dependencies**", "_____no_output_____" ] ], [ [ "!pip install -U -q sentence-transformers\n!git clone https://github.com/desaibhargav/VR.git", "\u001b[K |████████████████████████████████| 71kB 9.4MB/s \n\u001b[K |████████████████████████████████| 1.8MB 29.8MB/s \n\u001b[K |████████████████████████████████| 1.2MB 56.2MB/s \n\u001b[K |████████████████████████████████| 2.9MB 55.3MB/s \n\u001b[K |████████████████████████████████| 890kB 50.5MB/s \n\u001b[?25h Building wheel for sentence-transformers (setup.py) ... \u001b[?25l\u001b[?25hdone\n Building wheel for sacremoses (setup.py) ... \u001b[?25l\u001b[?25hdone\nCloning into 'VR'...\nremote: Enumerating objects: 142, done.\u001b[K\nremote: Counting objects: 100% (142/142), done.\u001b[K\nremote: Compressing objects: 100% (109/109), done.\u001b[K\nremote: Total 142 (delta 66), reused 71 (delta 19), pack-reused 0\u001b[K\nReceiving objects: 100% (142/142), 4.63 MiB | 8.66 MiB/s, done.\nResolving deltas: 100% (66/66), done.\n" ] ], [ [ "## **Imports**", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport numpy as np\nimport torch\nimport time\n\nfrom typing import Generator\nfrom sentence_transformers import SentenceTransformer, CrossEncoder, util\nfrom VR.backend.chunker import Chunker", "_____no_output_____" ] ], [ [ "## **Dataset**", "_____no_output_____" ] ], [ [ "# load scrapped data (using youtube_client.py)\ndataset = pd.read_pickle('VR/datasets/youtube_scrapped.pickle')\n\n# split transcripts of videos to smaller blocks or chunks (using chunker.py)\nchunked = Chunker(chunk_by='length', expected_threshold=100, min_tolerable_threshold=75).get_chunks(dataset)\n\n# finally, create dataset\ndataset_untagged = dataset.join(chunked).drop(columns=['subtitles', 'timestamps'])\ndf = dataset_untagged.copy().dropna()\nprint(f\"Average length of block: {df.length_of_block.mean()}, Standard Deviation: {df.length_of_block.std()}\")", "Average length of block: 107.33691183188671, Standard Deviation: 12.755147492715611\n" ] ], [ [ "## **Semantic Search**\n\n---\n\nThe idea is to compute embeddings of the query (entered by user) and use cosine similarity to find the `top_k` most similar blocks. \n\nBlocks are nothing but the entire video transcript (big string) split into fixed length strings (small strings, ~100 words). \n\n---\n\nThe reason for such a design choice was threefold, handled by `chunker.py` (refer the repo):\n\n1. First and foremost, some videoes can be very long (over ~40 minutes) which means the transcript for the same is a **massive** string, and we need to avoid hitting the processing length limits of pre-trained models. \n\n2. Secondly, and more importantly, it is always good to maintain the inputs at a length on which the models being used were trained (to stay as close as poossible to the training set for optimum results).\n\n3. But perhaps, most importantly, the purpose for splitting transcripts to blocks is so that the recommendations can be targeted to a snippet within a video. The vision is to recommend many snippets from various videoes highly relevant to the query, rather than entire videoes themselves in which matching snippets have been found (which may sometimes be long and the content may not always be related to the query).\n\n---", "_____no_output_____" ] ], [ [ "# request to enable GPU \nif not torch.cuda.is_available():\n print(\"Warning: No GPU found. Please add GPU to your notebook\")", "_____no_output_____" ], [ "# load model (to encode the dataset)\nbi_encoder = SentenceTransformer('paraphrase-distilroberta-base-v1')\n\n# number of blocks we want to retrieve with the bi-encoder\ntop_k = 200 \n\n# the bi-encoder will retrieve 50 blocks (top_k). \n# we use a cross-encoder, to re-rank the results list to improve the quality.\ncross_encoder = CrossEncoder('cross-encoder/ms-marco-electra-base')", "100%|██████████| 306M/306M [00:11<00:00, 25.7MB/s]\n" ], [ "# encode dataset\ncorpus_embeddings = bi_encoder.encode(df.block.to_list(), convert_to_tensor=True, show_progress_bar=True)\n\n# send corpus embeddings to GPU\ncorpus_embeddings = torch.tensor(corpus_embeddings).cuda()", "_____no_output_____" ], [ "# this function will search the dataset for passages that answer the query\ndef search(query):\n start_time = time.time()\n\n # encode the query using the bi-encoder and find potentially relevant passages\n question_embedding = bi_encoder.encode(query, convert_to_tensor=True)\n\n # send query embeddings to GPU\n question_embedding = question_embedding.cuda()\n\n # perform sematic search by computing cosine similarity between corpus and query embeddings\n # return top_k highest similarity matches\n hits = util.semantic_search(question_embedding, corpus_embeddings, top_k=top_k)[0]\n\n # now, score all retrieved passages with the cross_encoder\n cross_inp = [[query, df.block.to_list()[hit['corpus_id']]] for hit in hits]\n cross_scores = cross_encoder.predict(cross_inp)\n\n # sort results by the cross-encoder scores\n for idx in range(len(cross_scores)):\n hits[idx]['cross-score'] = cross_scores[idx]\n hits = sorted(hits, key=lambda x: x['cross-score'], reverse=True)\n end_time = time.time()\n\n # print output of top-5 hits (for iteractive environments only)\n print(f\"Input query: {query}\")\n print(f\"Results (after {round(end_time - start_time, 2)} seconds):\")\n for hit in hits[0:10]:\n print(\"\\t{:.3f}\\t{}\".format(hit['cross-score'], df.block.to_list()[hit['corpus_id']].replace(\"\\n\", \" \")))", "_____no_output_____" ] ], [ [ "## **Try some queries!**", "_____no_output_____" ] ], [ [ "query = \"I feel lost in life. I feel like there is no purpose of living. How should I deal with this?\"\nsearch(query)", "Input query: I feel lost in life. I feel like there is no purpose of living. How should I deal with this?\nResults (after 4.19 seconds):\n\t0.959\tIt is the pettiness of one’s mind that it’ll seek a meaning because psychologically you will feel kind of unconnected with life if you don’t have a purpose and a meaning. People are constantly trying to create these false purposes. Now, they were quite fine and happy. Suddenly, they got married. Now the purpose is the other person. Then they have children. Now they become miserable with each other. Now the whole purpose that I go through all this misery is because the children. Like this, it goes on. These are things that you’re causing and holding these as purposes of life and is there a God-given purpose? What if God does not know you exist? No, I am just asking, by chance. (Laughter) I am saying in this huge cosmos, for which God is supposed to be the Creator and the manager of these hundred billion galaxies, in that this tiny little planet\n\t0.949\tAt least I could not figure till I was twenty-five, why the hell I have to go through education, so (Laughs) I didn’t go through much education because what is the purpose? Well somebody has a purpose for you. The purpose of life is that this life should find full expression. The purpose of life is not that this life should serve this or that. Every creature on the planet is always trying to become a full-fledged life. That is the aspiration of the human being also. But now we have made that thing of longing to become full-fledged life to find expression only in economic ways. The only way, you can be something in the world is, you have to be economically… you must be success in the economic field. This type of education will smother human genius. Nothing new or truly wonderful will happen. We are only thinking of how to use everything.\n\t0.946\tif you know this one thing all the time, you will see you got your GPS on. There is really no problem, you will never get lost. It doesn’t matter who says what, what kind of situations you are put into, you are never ever lost because you are life sensitive. This is all this life needs that this has to become life sensitive Right now we have developed a psychological structure which has got nothing to do with life. It’s got something to do with the social scene, got nothing to do with the life. Thank you very much (Applause). I think Are we okay? Because people were looking at their watches so I thought I have exceeded my time. Moderator: That was the last question we were taking. If you have any other questions you can put it up on social media. Sadhguru, we would like to thank you so much… Sadhguru: Don’t, don’t, don’t (Laughs).\n\t0.930\tIf every moment of your life becomes absolutely exuberant If every moment of your life becomes absolutely exuberant and bursting within you, ‘Why?’ would be a ridiculous question, isn't it? So this, we can... we can put some enthusiasm into your life saying, ‘God is testing you’ or ‘God is kissing you… hmm? So they will tell you many things. I am telling you, there is no purpose to your life. If you do not realize the exuberance of your existence, you can invent purposes. If you realize the exuberance of this existence, if you experience the ecstasy of being here then who the hell is bothered about the purpose?\n\t0.928\tSo I wondered if the purpose of life is to just live and to live it fully according to my whim and fancy because this is one thing I know I have with me. So, my question is, is the purpose…was I right in thinking that the purpose in life is just to live it fully? Sadhguru: One hundred percent! Live it fully! But living it fully does not mean party every evening. Living it fully means before you fall dead, you must explore all dimensions of life. Nothing that’s possible for a human being should go un-experienced. If you are talking about living fully in that sense, you are on the dot! But later on you added, “according to my whim and fancy”, that’s a problem. Because your whims are not yours, they are social fads. Either you are doing what everybody is doing, or in reaction, you are doing what nobody is doing.\n\t0.926\tQuestioner: What’s… what’s for me the purpose of life, if you can give an insight on that? Thank you. Sadhguru: Isn't it fantastic that if there is no purpose, you have nothing to fulfill, you can just live? Hmm? No, but you want a purpose and not a simple purpose, you want a God-given purpose. (Laughter) It's very dangerous. People who think they have a God-given purpose are doing the cruelest things on the planet. Yes or no? They are doing the most horrible things and they’ve always been doing the most horrible things because when you have a God-given purpose, life here becomes less important than your purpose. No, life is important. Life is important - when I say life, I am not talking about your family, your work, what you do, what you do not do, you party I am not talking about that as life. This is life, isn't it?\n\t0.915\tHow should we deal with that discontent and loneliness? Sadhguru: On one level, many questions are aimed towards, how can I be free from this and that? Another level, you are asking, how can I bind myself to something or somebody? You must decide, what is the highest value in your life - freedom or bondage? Please, I would like to hear that word. Participant: Freedom! Sadhguru: Oh, freedom, hmm! But if you are free, you feel lost. If you go into the mountains and you are totally free, that is, nobody around, nothing around, you’re just in the empty space of the mountains, you don’t feel free, you think you are lost. So to handle freedom, it needs a certain clarity and strength. Most people cannot handle freedom. They are always trying to bind themselves, but only talking freedom all the time. If you really set them free, they will suffer immensely.\n\t0.913\tintense and beautiful is your experience of life. So don’t make too much fuss about it. You’re acting as if you’re going to lose something. No. There is nothing to lose, nothing to gain because you come and you go. You may think, “Oh my life, my life!” No, it’s… your life on this planet is like a pop-up – on the computer screen you have seen these pop-ups? You are just a pop-up and pop-out. In the meantime, will you rise and shine is the only question, all right? So, if… any way you shine, sometimes you may be seen by people, sometimes you may not be seen by people, the important is you… you are shining within yourself and that’s all that matters. If people have eyes, they will see it; if they have no eyes, they won’t see it, that’s their problem. But, you are living an intense and profound life, that’s\n\t0.882\ttrudging through life everyday eating, sleeping, same rubbish. What is the point? There is no point, unless you’re touched by something, some magic of life if it doesn’t touch you either in the form of love or in the form of a flower or in the form of something within you. If something doesn’t sparkle within you definitely there is a question whether I should live or not, isn’t it? And we are taking humanity in that direction with this overload of information. Information is not knowing, information is just garbage collection. You just gather things which don’t mean anything to you. You look smart in a tea party but you’re not smart with life, okay. If you’re smart with life you must be blissful, isn’t it (Laughs)? If you’re really smart with life you must be joyful and blissful. Isn’t it so? You’re only smart in a tea party\n\t0.842\twhen I say oblivious to life, I want you to look at this right now you cannot even call yourself as a living being, because most of the time what is happening with you is just thought and emotion. Thought and emotion is just psychological drama, it has no existential relevance. Here a thousand people can sit here and live in thousand different worlds right now, that means nobody is in reality. Nobody is living, everybody is thinking about life. Psychological space, what happens, has unfortunately overtaken the existential process of life. You do not experience life, you’re only thinking and reacting to situations around you. Thought and emotion is dominating everything. So, right now today morning sun came up on time you don’t think much about that “Okay so what?” (Laughter) No, you need to understand, if sun does not come up tomorrow morning, within eighteen hours all life on this planet will largely seize as we know it.\n" ], [ "query = \"I just recently became a parent and I am feeling very nervous. What is the best way to bring up a child?\"\nsearch(query)", "Input query: I just recently became a parent and I am feeling very nervous. What is the best way to bring up a child?\nResults (after 2.34 seconds):\n\t0.561\tSadhguru, what should be the role of a good parent in today's world? See, parenthood is a very funny thing You're trying to do something that nobody has ever known how to do it well Yes? Nobody has ever known what is the best way to parent their children Even if you have 12 children, you are still learning You may raise eleven properly the twelfth one can give you works, you know? So.. But you want to do your best what is the best thing you can do? One foremost thing I would say is First thing is to work upon yourself a little bit.\n\t0.052\tit doesn’t matter what their problem is. If you leave that level of openness and friendship with them, if they come to you first, there is every possibility that they won’t get lost on something, isn't it? Especially in a society like this, where the moment the child steps out, you don’t know what influences are going to catch him up. The most important thing is this: the parents should get off their pedestal and start treating them as equals and this has to happen right from childhood, you know; that he never sees you as somebody who is pushing him around\n\t0.031\tSimply it’ll come in the form of life or maybe it’ll come in the form of your children - the price. Yes, it’ll be very unfortunate to see that. I am saying this - a very cruel thing to say to any parent, but I am saying this because it’s a very cruel thing to parent a child. The child doesn’t need that, but please see in so many ways, you’re doing everything possible to see that he remains dependent on you in some way or the other. You are not thinking of liberating him. So, the moment you start working,\n\t0.028\tThey’re observing what you do and how you are, isn’t it? So, if you want to raise children, please raise yourself - don’t worry about the children don’t worry about the children just raise yourself into a wonderful human being, make yourself that, it will reflect. It cannot go wrong, but there’s no guarantee. (Laughter) Like in… everything in life, there’s no guarantee because there may be some other stronger influence on the street side, isn’t it? (Laughs)\n\t0.027\tIf you bring up a child free of prejudice in a loving,very open atmosphere, generally, they do well, but there is no guarantee Because there are other influences in the society You don't know into whose hands they'll fall tomorrow morning You don't know into whose hands they'll fall tomorrow morning Yes? You may be doing your best Tomorrow morning into whose hands your child will fall, there is no insurance or guarantee That's a risk that you're taking always But the only thing is - did you do your best or not? That's all there is to life\n\t0.023\twhat would be the best kind of parents to have ? If you look back, you would know very clearly. If you are a parent, the important thing is, please don’t stand on a big pedestal. The only qualification you have is you just came here a few years early. That’s the only mistake you’ve done. Yes. When you say, “I wish I was young,” what it means is, “I made the mistake of coming too early.” So this is the only qualification adults have, that they came here a few years earlier than the younger people. This doesn’t qualify you to advice about everything in the universe. It doesn’t.\n\t0.023\tNo, you don’t need information about your child. You need involvement. With involvement you’ll bring that life to its best. It need not be as good as somebody else or as bad as somebody else because it’s a unique life. Is there one life like another? Participants: No. Sadhguru: It’s a unique life. So, but from… right from day one we are comparing it to another life and trying to make it like that one. This is a very cruel process for the child. A child never understands what the hell the parents want (Laughter). I never understood. Nobody ever explained to me why the hell I should go to the school.\n\t0.021\tgenerally they grow up. Of course you want to provide opportunities for them. Each one of us can provide opportunities only to the extent it's available to us, isn't it? Yes? You cannot provide an opportunity for which you don't have access You will always do according to your limitations I am sure in that area you will do your best, but the important thing is what kind of human beings or brats you raise? For that, what kind of human being are you is an extremely important part of raising children So if your wife became pregnant, it's time for transformation for you\n\t0.019\tSo always having a son was most important. He will be around; If you die, he will do the necessary things so that your liberation will happen. So in pursuit of liberation unknowingly they bore you. Now it's time you remind them. This is an important duty for a child. As your parents are aging, and if they don’t have the sense to come to their senses, you must bring sense to them. You must remind them like I just now reminded you, you’re one year closer to the grave – your parents are much closer than you, isn't it?\n\t0.018\tWe have to equip the child to live in the modern world and still not mess him up with the nonsense that's happening in the name of modernity. So it is a much bigger challenge today than what it was then. And at that time, once the parents gave the children to the guru, they left him there, in complete his authority. Now the parents are very nosey, you know (Laughter)? They won't leave the children full. They want to… constantly meddle with that, they want to put their own stuff into it. All those issues are there, so it’s much more complex today than it was in the gurukul.\n" ], [ "query = \"I had a divorce. I feel like a failure. How should I handle this heartbreak?\"\nsearch(query)", "Input query: I had a divorce. I feel like a failure. How should I handle this heartbreak?\nResults (after 2.41 seconds):\n\t0.323\tBut for some reason, you have come to that situation where this is this has to happen - you need to understand this, that divorce essentially means you have chosen to kill something, which is a part of you, because what you call as myself is just a certain volume of memory. Now, to how to conduct this gracefully? Most people think the best way to conduct a divorce is immediately jump into another relationship and another relationship of the same kind. No, you will cause much more struggle and turmoil within the system by doing that. It’s extremely important\n\t0.109\tripping it apart is almost like tearing yourself apart. Even though you might have begun to almost come to a place, where you can’t stand the person anymore, still it hurts, simply because you’re trying to rip out a memory, which is you, because you are a bundle of memory. If one does the necessary spiritual sadhana, if one does sufficient inner work to establish these energies, which is yourself You’re only divorcing your spouse, you need not divorce yourself. But you need to understand this, you have already divorced yourself. You’re quite divorced from your own self. Your existence has been nurtured\n\t0.059\tBut at the same time, the very fact that you’re going through your divorce means you want to be finished with that memory in some way. Maybe not erase that memory but someone who was a spouse, someone who was a in many ways a part of your life, slowly, for whatever reason, you have begun to experience them as a baggage that you’re unwilling to carry. So, you want to keep the baggage aside but you find the baggage is not something that you voluntarily carry, it is something that compulsively sticks to you. So when whatever sticks to you compulsively,\n\t0.024\tnothing wrong with it. That's wonderful too. You got divorced, is it wrong? No, that's also wonderful. It is just that you make misery out of everything that's what is wrong. You just address that one issue everything will be settled. That's what we are looking at. How not to make misery out of everything? If this one thing is settled everything is settled, isn't it? Yes? If you know how to walk through this world joyfully through marriage and divorce and celibacy and everything, if you know how to walk through this joyfully, what is the problem? Whatever you do is beautiful, isn't it? (Laughs) That comes\n\t0.004\tSo don’t go that way. This is an opportunity somebody is opening up a spiritual dimension for you really, somebody is making you realize how fragile all these things are; they can cheat you, they can run away, they can divorce you or they can fall dead, isn’t it? If they fall dead you wouldn’t think he cheated me, would you think? No but whichever way you’re denied, isn’t it? The important thing is you’re denied something. How he did it, is not the problem, he denied you something either by death or divorce or cheating or whatever you call it\n\t0.004\tif she reaches a point where she’s ready to overcome it, but she feels guilty to let it go because it has troubled her for a very, very long time, and not just her, the ones around her as well. So, is it right to let it go at that point or like… how does one deal with a situation like this? Sadhguru: See, I think this struggle is coming from a misunderstanding that something either unpleasant or terrible that one may encounter in one’s life – it can just happen to anybody in so many different ways - if it happens, people think they must forget it,\n\t0.003\twhether you like it or you don’t like it. Otherwise you shouldn’t get into those projects, you don’t walk into a project, drop it half way and walk away, isn’t it? Juhi Chawla: Yes. It’s your choice but at least choose consciously. You don’t have to get married because everybody is getting married, you don’t have to talk about marriage and divorce in same breath as if they come together (Laughter). This is a completely an American idea, you’re thinking of marriage and divorce together nobody thought of divorce in this country till recently, isn’t it? Juhi Chawla: Yes. Sadhguru: So, if it happens, Sadhguru: So, if it happens, if something happens something truly went wrong between two people and they have to separate that will any way inevitably happen. You don’t have to plan it at the time of wedding (Laughter). why should you ever talk about marriage and divorce in one breath? It's a crime\n\t0.003\tyou must understand, it’s a minimum twenty year project whether you like it or you don’t like it. Otherwise you shouldn’t get into those projects, you don’t walk into a project, drop it half way and walk away, isn’t it? They have their benefits and they have their problems. It’s your choice but at least choose consciously. You don’t have to get married because everybody is getting married, you don’t have to talk about marriage and divorce in same breath as if they come together (Laughter). This is a completely an American idea, you’re thinking of marriage and divorce together\n\t0.002\tnobody thought of divorce in this country till recently, isn’t it? Why should you ever talk about marriage and divorce in one breath? It’s… it’s a crime. It’s really a crime to think on those lines. But if it so happens something truly went wrong between two people and they have to separate that will any way inevitably happen. You don’t have to plan it at the time of wedding (Laughter). Questioner: Namaskaram Sadhguru. NamaskaramJuhi Mam. you mentioned about survival and you talked about aesthetics of life. I would like I would request you to elaborate on aesthetics of life\n\t0.002\tabout four-and-a-half hours had passed. For the first time in my adult life, tears – me and tears were impossible – tears are flowing to a point my shirt is all wet. I’ve always been peaceful and happy, life is working out the way I want, I’m young and successful and no problems. It is just that every cell in my body was bursting with ecstasy. Tears are just dripping like this. So when I shook my skeptical head and asked what’s happening to me, the only thing that my mind could tell me was, maybe I’m going off my rocker.\n" ], [ "query = \"How to be confident while making big decisions in life?\"\nsearch(query)", "Input query: How to be confident while making big decisions in life?\nResults (after 2.63 seconds):\n\t0.984\tsomebody says “I am doing this.” somebody says “I am doing this.” So one thing that all of you should do before you make big decisions in your life is, withdraw from these pressures of peers, professors, parents, everybody. Just spend three days to one week by yourself. Look at it, what is it that you really want to do? Not under pressure from other people. What does this life want to do? Do that! It doesn't matter what other people think about it (Applause)\n\t0.692\t“I do not know,” the longing to know, the seeking to know and the possibility of knowing becomes a living reality. Whatever you don’t know, you believe. If you believe whatever you do not know, you will become confident without clarity. Confidence without clarity is a disastrous process. Where there is no clarity, it is better there is hesitation. If clarity comes, let’s do everything. If there is no clarity, we should at least hesitate. If you have confidence without clarity, it becomes disastrous. This is what belief systems are giving people. People believe something, suddenly they are confident. It doesn’t matter how much disaster it causes to themselves or to everybody around them\n\t0.154\tYou know how a banker is with you (Laughter). So, this is a confidence building process. But confidence without clarity is a disastrous process. What you need is clarity. Confidence means you can’t see but you’re confident. This is a dangerous way to go. This is what… This is a continuous disaster. See, it doesn’t take thousands of years to figure out simple aspects of life. I’m saying… Now Suhel is going at these things – anger, hatred, all kinds of prejudice against each other – with great vehemence about it. What I’m saying is, these are simple things in a human being.\n\t0.114\tThumbnail: Head or Heart, which one to listen to? Moderator (Abhijeet): Namaskaram, Sadhguruji. The first question that I want to ask is actually related to me. I’m the... I’m in the last year of engineering, so now there is a very big decision that I have to make now and people have told me that if I take decisions from my heart I'll be successful in life. So… but there lies a problem. The problem is that I am… I don't know which... which thought is coming from my heart and which thought is coming from my brain. So how can I figure out like\n\t0.110\tgoing on, how do I be positive? And at that time, clarity seems more important than positivity. So how do we place the two? Sadhguru: So what they're calling it as positive is confidence. “Have confidence. Don't worry.” Confidence without clarity is a disaster (Laughter). Yes. If you cannot see clearly, at least you must be hesitant. If you are confident, you're going to walk into something. By chance you may escape sometimes. But what comes your way you don't know. So it's not about being positive, negative. The important thing is, at this stage in your life you just focus\n\t0.057\ta natural upsurge of energy will happen it activates the lumbar region of the spine in a tremendous way strengthens the muscles along the spine the sharpness of your intellect you will see you can see a difference happening just because you're doing a simple few things ultimately whatever whatever you wish to do in your life how much clarity do you have is all there is isn't it about anything yes or no if you don't have clarity you will try to make it up with confidence confidence is a very poor substitute for clarity it's like there's a busy highway\n\t0.048\tNo, we must tell them we don't know, you don't know, maybe we can push our knowing one step forward in this generation. It'll be fantastic. Hmm? One step forward from where we are. But faith means you just believe. Everything you do not know you believe. What belief does to you is, it gives you confidence without clarity. This’s a disaster. Confidence without clarity is a disastrous process. Because if your vision is not clear, at least you must be hesitant, isn't it? You cannot see and you're confident, we know where you're going. Yes or no? You're very serious lot. Can I tell you a joke at least (Laughter)?\n\t0.038\tSadhguru: As you said, to anchor our lives. Now that is... that is the decision that every human being has to make. Do you want to be anchored or do you want to set sail? That is a decision that everybody has to make. If you’re looking for confidence, if you’re looking for stability, then you have to anchor yourself to something. If you’re looking to go far, then anchoring will not help. Traditions, all traditions – with all due respect to all of them – particularly traditions that are coming from India and also elsewhere - I’m... I’m not in any way an expert on… to make a comment on the traditions\n\t0.031\tThe moment you form an opinion, that means you’re not open to anything else, isn’t it? Whether it’s about a person or yourself or about the life around you, you don’t form any kind of opinion or conclusion. Conclusion means death. Yes? Life means no conclusion - you’re looking. Instead of sharpening your vision, you’re drawing a conclusion because conclusion brings a certain certainty, it brings a certain confidence. The moment you believe something, you are confident. Confidence without clarity is a disaster. It’s better to see clearly rather than just believe something. If you believe something, it gives you confidence and sometimes it works unfortunately.\n\t0.024\tBut to exercise this choice, you have to be in a certain way within yourself. Within yourself, you are in a certain state of equanimity, balance and exuberance, that no matter what life throws at you, you will make it into a wonderful possibility. Life can throw all kinds of horrible things. Don’t underestimate life, it can do things to you, tch yes? It can… It can do all kinds of things to you. Most unexpected time, it will throw something at you that you did not imagine possible. The more active you are, more unexpected things happen to you (Laughs). Yes.\n" ] ], [ [ "## **Semantic Search x Auxiliary Features**\n\nThis section is under active development. \n\n---\n\nThis purpose of this section is to explore two primary frontiers:\n\n1. Just semantic search yields satisfactory results, but comes at the cost of compute power. The bottleneck for compute power is the cross-encoder step. This section explores how to reduce the search area, so that semantic search (by the cross-encoder) is performed over a small number blocks, significantly cutting down on the recommendation time. \n\n2. Other than the content itself, several other features such as video statistics (views, likes, dislikes), video titles, video descriptions, video tags present in the dataset can be leveraged to improve the recommendations. \n\n---\n\n", "_____no_output_____" ] ], [ [ "", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e7eb3b1c400d1ca9b0431d37a054d218896946

103,730

ipynb

Jupyter Notebook

code/chap07-all-exercises.ipynb

JeffreyMinucci/ThinkBayes2

69ec0789fdbb98e0283a22e8955c5a997552289d

[ "MIT" ]

null

code/chap07-all-exercises.ipynb

JeffreyMinucci/ThinkBayes2

69ec0789fdbb98e0283a22e8955c5a997552289d

[ "MIT" ]

null

code/chap07-all-exercises.ipynb

JeffreyMinucci/ThinkBayes2

69ec0789fdbb98e0283a22e8955c5a997552289d

[ "MIT" ]

1

2018-08-04T17:36:10.000Z

120.616279

29,658

0.873441

[ [ [ "# Think Bayes: Chapter 7\n\nThis notebook presents code and exercises from Think Bayes, second edition.\n\nCopyright 2016 Allen B. Downey\n\nMIT License: https://opensource.org/licenses/MIT", "_____no_output_____" ] ], [ [ "from __future__ import print_function, division\n\n% matplotlib inline\nimport warnings\nwarnings.filterwarnings('ignore')\n\nimport math\nimport numpy as np\n\nfrom thinkbayes2 import Pmf, Cdf, Suite, Joint\nimport thinkplot", "_____no_output_____" ] ], [ [ "## Warm-up exercises", "_____no_output_____" ], [ "**Exercise:** Suppose that goal scoring in hockey is well modeled by a \nPoisson process, and that the long-run goal-scoring rate of the\nBoston Bruins against the Vancouver Canucks is 2.9 goals per game.\nIn their next game, what is the probability\nthat the Bruins score exactly 3 goals? Plot the PMF of `k`, the number\nof goals they score in a game.", "_____no_output_____" ] ], [ [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ] ], [ [ "**Exercise:** Assuming again that the goal scoring rate is 2.9, what is the probability of scoring a total of 9 goals in three games? Answer this question two ways:\n\n1. Compute the distribution of goals scored in one game and then add it to itself twice to find the distribution of goals scored in 3 games.\n\n2. Use the Poisson PMF with parameter $\\lambda t$, where $\\lambda$ is the rate in goals per game and $t$ is the duration in games.", "_____no_output_____" ] ], [ [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ] ], [ [ "**Exercise:** Suppose that the long-run goal-scoring rate of the\nCanucks against the Bruins is 2.6 goals per game. Plot the distribution\nof `t`, the time until the Canucks score their first goal.\nIn their next game, what is the probability that the Canucks score\nduring the first period (that is, the first third of the game)?\n\nHint: `thinkbayes2` provides `MakeExponentialPmf` and `EvalExponentialCdf`.", "_____no_output_____" ] ], [ [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ] ], [ [ "**Exercise:** Assuming again that the goal scoring rate is 2.8, what is the probability that the Canucks get shut out (that is, don't score for an entire game)? Answer this question two ways, using the CDF of the exponential distribution and the PMF of the Poisson distribution.", "_____no_output_____" ] ], [ [ "# Solution goes here", "_____no_output_____" ], [ "# Solution goes here", "_____no_output_____" ] ], [ [ "## The Boston Bruins problem\n\nThe `Hockey` suite contains hypotheses about the goal scoring rate for one team against the other. The prior is Gaussian, with mean and variance based on previous games in the league.\n\nThe Likelihood function takes as data the number of goals scored in a game.", "_____no_output_____" ] ], [ [ "from thinkbayes2 import MakeNormalPmf\nfrom thinkbayes2 import EvalPoissonPmf\n\nclass Hockey(Suite):\n \"\"\"Represents hypotheses about the scoring rate for a team.\"\"\"\n\n def __init__(self, label=None):\n \"\"\"Initializes the Hockey object.\n\n label: string\n \"\"\"\n mu = 2.8\n sigma = 0.3\n\n pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)\n Suite.__init__(self, pmf, label=label)\n \n def Likelihood(self, data, hypo):\n \"\"\"Computes the likelihood of the data under the hypothesis.\n\n Evaluates the Poisson PMF for lambda and k.\n\n hypo: goal scoring rate in goals per game\n data: goals scored in one game\n \"\"\"\n lam = hypo\n k = data\n like = EvalPoissonPmf(k, lam)\n return like", "_____no_output_____" ] ], [ [ "Now we can initialize a suite for each team:", "_____no_output_____" ] ], [ [ "suite1 = Hockey('bruins')\nsuite2 = Hockey('canucks')", "_____no_output_____" ] ], [ [ "Here's what the priors look like:", "_____no_output_____" ] ], [ [ "thinkplot.PrePlot(num=2)\nthinkplot.Pdf(suite1)\nthinkplot.Pdf(suite2)\nthinkplot.Config(xlabel='Goals per game',\n ylabel='Probability')", "_____no_output_____" ] ], [ [ "And we can update each suite with the scores from the first 4 games.", "_____no_output_____" ] ], [ [ "suite1.UpdateSet([0, 2, 8, 4])\nsuite2.UpdateSet([1, 3, 1, 0])\n\nthinkplot.PrePlot(num=2)\nthinkplot.Pdf(suite1)\nthinkplot.Pdf(suite2)\nthinkplot.Config(xlabel='Goals per game',\n ylabel='Probability')\n\nsuite1.Mean(), suite2.Mean()", "_____no_output_____" ] ], [ [ "To predict the number of goals scored in the next game we can compute, for each hypothetical value of $\\lambda$, a Poisson distribution of goals scored, then make a weighted mixture of Poissons:", "_____no_output_____" ] ], [ [ "from thinkbayes2 import MakeMixture\nfrom thinkbayes2 import MakePoissonPmf\n\ndef MakeGoalPmf(suite, high=10):\n \"\"\"Makes the distribution of goals scored, given distribution of lam.\n\n suite: distribution of goal-scoring rate\n high: upper bound\n\n returns: Pmf of goals per game\n \"\"\"\n metapmf = Pmf()\n\n for lam, prob in suite.Items():\n pmf = MakePoissonPmf(lam, high)\n metapmf.Set(pmf, prob)\n\n mix = MakeMixture(metapmf, label=suite.label)\n return mix", "_____no_output_____" ] ], [ [ "Here's what the results look like.", "_____no_output_____" ] ], [ [ "goal_dist1 = MakeGoalPmf(suite1)\ngoal_dist2 = MakeGoalPmf(suite2)\n\nthinkplot.PrePlot(num=2)\nthinkplot.Pmf(goal_dist1)\nthinkplot.Pmf(goal_dist2)\nthinkplot.Config(xlabel='Goals',\n ylabel='Probability',\n xlim=[-0.7, 11.5])\n\ngoal_dist1.Mean(), goal_dist2.Mean()", "_____no_output_____" ] ], [ [ "Now we can compute the probability that the Bruins win, lose, or tie in regulation time.", "_____no_output_____" ] ], [ [ "diff = goal_dist1 - goal_dist2\np_win = diff.ProbGreater(0)\np_loss = diff.ProbLess(0)\np_tie = diff.Prob(0)\n\nprint('Prob win, loss, tie:', p_win, p_loss, p_tie)", "Prob win, loss, tie: 0.4579997823117246 0.37029032604107404 0.1717098916472006\n" ] ], [ [ "If the game goes into overtime, we have to compute the distribution of `t`, the time until the first goal, for each team. For each hypothetical value of $\\lambda$, the distribution of `t` is exponential, so the predictive distribution is a mixture of exponentials.", "_____no_output_____" ] ], [ [ "from thinkbayes2 import MakeExponentialPmf\n\ndef MakeGoalTimePmf(suite):\n \"\"\"Makes the distribution of time til first goal.\n\n suite: distribution of goal-scoring rate\n\n returns: Pmf of goals per game\n \"\"\"\n metapmf = Pmf()\n\n for lam, prob in suite.Items():\n pmf = MakeExponentialPmf(lam, high=2.5, n=1001)\n metapmf.Set(pmf, prob)\n\n mix = MakeMixture(metapmf, label=suite.label)\n return mix", "_____no_output_____" ] ], [ [ "Here's what the predictive distributions for `t` look like.", "_____no_output_____" ] ], [ [ "time_dist1 = MakeGoalTimePmf(suite1) \ntime_dist2 = MakeGoalTimePmf(suite2)\n \nthinkplot.PrePlot(num=2)\nthinkplot.Pmf(time_dist1)\nthinkplot.Pmf(time_dist2) \nthinkplot.Config(xlabel='Games until goal',\n ylabel='Probability')\n\ntime_dist1.Mean(), time_dist2.Mean()", "_____no_output_____" ] ], [ [ "In overtime the first team to score wins, so the probability of winning is the probability of generating a smaller value of `t`:", "_____no_output_____" ] ], [ [ "p_win_in_overtime = time_dist1.ProbLess(time_dist2)\np_adjust = time_dist1.ProbEqual(time_dist2)\np_win_in_overtime += p_adjust / 2\nprint('p_win_in_overtime', p_win_in_overtime)", "p_win_in_overtime 0.5241451046185259\n" ] ], [ [ "Finally, we can compute the overall chance that the Bruins win, either in regulation or overtime.", "_____no_output_____" ] ], [ [ "p_win_overall = p_win + p_tie * p_win_in_overtime\nprint('p_win_overall', p_win_overall)", "p_win_overall 0.5480006814331824\n" ] ], [ [ "## Exercises", "_____no_output_____" ], [ "**Exercise:** To make the model of overtime more correct, we could update both suites with 0 goals in one game, before computing the predictive distribution of `t`. Make this change and see what effect it has on the results.", "_____no_output_____" ] ], [ [ "# Solution goes here", "_____no_output_____" ] ], [ [ "**Exercise:** In the final match of the 2014 FIFA World Cup, Germany defeated Argentina 1-0. What is the probability that Germany had the better team? What is the probability that Germany would win a rematch?\n\nFor a prior distribution on the goal-scoring rate for each team, use a gamma distribution with parameter 1.3.", "_____no_output_____" ], [ "**Exercise:** In the 2014 FIFA World Cup, Germany played Brazil in a semifinal match. Germany scored after 11 minutes and again at the 23 minute mark. At that point in the match, how many goals would you expect Germany to score after 90 minutes? What was the probability that they would score 5 more goals (as, in fact, they did)?\n\nNote: for this one you will need a new suite that provides a Likelihood function that takes as data the time between goals, rather than the number of goals in a game. ", "_____no_output_____" ], [ "**Exercise:** Which is a better way to break a tie: overtime or penalty shots?", "_____no_output_____" ], [ "**Exercise:** Suppose that you are an ecologist sampling the insect population in a new environment. You deploy 100 traps in a test area and come back the next day to check on them. You find that 37 traps have been triggered, trapping an insect inside. Once a trap triggers, it cannot trap another insect until it has been reset.\nIf you reset the traps and come back in two days, how many traps do you expect to find triggered? Compute a posterior predictive distribution for the number of traps.", "_____no_output_____" ], [ "#### Exercise 7-1.\nIf buses arrive at a bus stop every 20 minutes, and you arrive at the bus stop at a random\ntime, your wait time until the bus arrives is uniformly distributed from 0 to 20\nminutes.\n\nBut in reality, there is variability in the time between buses. Suppose you are waiting\nfor a bus, and you know the historical distribution of time between buses. Compute\nyour distribution of wait times.\n\nHint: Suppose that the time between buses is either 5 or 10 minutes with equal probability.\nWhat is the probability that you arrive during one of the 10 minute intervals?\n\nI solve a version of this problem in the next chapter.", "_____no_output_____" ], [ "#### Exercise 7-2.\nSuppose that passengers arriving at the bus stop are well-modeled by a Poisson process\nwith parameter λ. If you arrive at the stop and find 3 people waiting, what is your\nposterior distribution for the time since the last bus arrived.\nI solve a version of this problem in the next chapter.", "_____no_output_____" ], [ "#### Exercise 7-4.\nSuppose you are the manager of an apartment building with 100 light bulbs in common\nareas. It is your responsibility to replace light bulbs when they break.\n\nOn January 1, all 100 bulbs are working. When you inspect them on February 1, you\nfind 3 light bulbs out. If you come back on April 1, how many light bulbs do you\nexpect to find broken?\n\nIn the previous exercise, you could reasonably assume that an event is equally likely at\nany time. For light bulbs, the likelihood of failure depends on the age of the bulb.\nSpecifically, old bulbs have an increasing failure rate due to evaporation of the filament.\n\nThis problem is more open-ended than some; you will have to make modeling decisions.\nYou might want to read about the Weibull distribution (http://en.wikipedia.org/\nwiki/Weibull_distribution). Or you might want to look around for information about\nlight bulb survival curves.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

d0e7fbb566b988b96483a182b0b5466a72af2195

165,888

ipynb

Jupyter Notebook

src/graphene_adsorbed_phases.ipynb

DelMaestroGroup/papers-code-BoseHubbardModelHeAdsorptionGraphene

ef8ff4ce20349ead1b432000b5039ba0301001ea

[ "MIT" ]

null

src/graphene_adsorbed_phases.ipynb

DelMaestroGroup/papers-code-BoseHubbardModelHeAdsorptionGraphene

ef8ff4ce20349ead1b432000b5039ba0301001ea

[ "MIT" ]

null

src/graphene_adsorbed_phases.ipynb

DelMaestroGroup/papers-code-BoseHubbardModelHeAdsorptionGraphene

ef8ff4ce20349ead1b432000b5039ba0301001ea

[ "MIT" ]

null

49.386127

6,484

0.503502

[ [ [ "# Adsorbed Phases on Graphene", "_____no_output_____" ] ], [ [ "import numpy as np\nimport matplotlib.pyplot as plt\nfrom graphenetools import gt\nimport re,glob,os,sys\nfrom scipy.signal import argrelextrema\nimport dgutils.colors as colortools\nimport dgutils.pypov as pypov\nfrom collections import defaultdict\nimport importlib\nfrom PIL import Image,ImageOps\n\nfrom vapory import *\nπ = np.pi\n\n%matplotlib inline\n%config InlineBackend.figure_format = 'svg'\ncolors = plt.rcParams['axes.prop_cycle'].by_key()['color']\n\n# plot style\nplot_style = {'notebook':'../include/notebook.mplstyle','aps':'../include/aps.mplstyle'}\nplt.style.reload_library()\nplt.style.use(plot_style['notebook'])\nfigsize = plt.rcParams['figure.figsize']\n\nincluded = [\"colors.inc\",\"textures.inc\",\"functions.inc\"]\nfilename = \"../plots/graphene_cell.pov\"", "_____no_output_____" ] ], [ [ "## Setting the colors", "_____no_output_____" ] ], [ [ "blue = colortools.hex_to_rgb('#0073CD')\ngrey = colortools.hex_to_rgb('#a7a7a7')\nbrown = colortools.hex_to_rgb('#e9b68c')\nbrown = colortools.hex_to_rgb('#926f34')\ngreen = colortools.hex_to_rgb('#15A05E')\nred = colortools.hex_to_rgb('#8c0a07')", "_____no_output_____" ] ], [ [ "## Construct the graphene lattice, $\\sqrt{3}\\times\\sqrt{3}$ adsorbant and bonds", "_____no_output_____" ] ], [ [ "# lattice vectors\naₒ = 1.42\na = (aₒ/2)*np.array([[np.sqrt(3),-np.sqrt(3)],[3,3]])\n\n#√3 x √3\nθ = π/6\nR = np.array([[np.cos(θ),-np.sin(θ)],[np.sin(θ),np.cos(θ)]])\nα = np.matmul(R,np.sqrt(3)*a)\n\n# basis vectors\nb = aₒ*np.array([[np.sqrt(3)/2,0],[1/2,1]])\n\n# Box size\nL = [8,8]", "_____no_output_____" ], [ "import sympy\nsympy.init_printing(use_unicode=True)\nsympy.Matrix(α)", "_____no_output_____" ] ], [ [ "### The Lattice", "_____no_output_____" ] ], [ [ "C_positions = []\nG_centers = []\nhex_centers = []\nfor n1 in range(-12,12):\n for n2 in range(-12,12):\n G_centers.append(n1*α[:,0] + n2*α[:,1])\n C_positions.append(n1*a[:,0] + n2*a[:,1] + b[:,0])\n C_positions.append(n1*a[:,0] + n2*a[:,1] + b[:,1])\n hex_centers.append(n1*a[:,0] + n2*a[:,1])\n\nC_positions = np.array(C_positions)\nG_centers = np.array(G_centers)\nhex_centers = np.array(hex_centers)\n\nC_positions_big = np.array(C_positions[np.intersect1d(np.where(np.abs(C_positions[:,0])<2*L[0])[0],np.where(np.abs(C_positions[:,1])<1.9*L[1])[0])])\nHe_positions_big = np.array(G_centers[np.intersect1d(np.where(np.abs(G_centers[:,0])<2*L[0])[0],np.where(np.abs(G_centers[:,1])<1.8*L[1])[0])])\nhex_centers_big = np.array(hex_centers[np.intersect1d(np.where(np.abs(hex_centers[:,0])<2*L[0])[0],np.where(np.abs(hex_centers[:,1])<1.8*L[1])[0])])\n\nC_positions = np.array(C_positions[np.intersect1d(np.where(np.abs(C_positions[:,0])<L[0])[0],np.where(np.abs(C_positions[:,1])<L[1])[0])])\nHe_positions = np.array(G_centers[np.intersect1d(np.where(np.abs(G_centers[:,0])<L[0])[0],np.where(np.abs(G_centers[:,1])<L[1])[0])])\nhex_centers = np.array(hex_centers[np.intersect1d(np.where(np.abs(hex_centers[:,0])<L[0])[0],np.where(np.abs(hex_centers[:,1])<L[1])[0])])", "_____no_output_____" ], [ "fig,ax = plt.subplots()\nax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')\nax.scatter(He_positions[:,0],He_positions[:,1], s=8, color='b')\n\nax.set_aspect('equal')\nax.set_xlabel('x / Å')\nax.set_ylabel('y / Å')", "_____no_output_____" ] ], [ [ "### Visualizing the Lattice Vectors", "_____no_output_____" ] ], [ [ "fig,ax = plt.subplots()\n#ax.scatter(He_positions[:,0],He_positions[:,1], s=8, color='b')\n\nax.annotate(\"\",\n xy=(a[0,0], a[1,0]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='k'),\n )\nax.annotate(r\"$\\vec{a}_1$\",\n xy=(a[0,0], a[1,0]), xycoords='data',\n xytext=(1, 1), textcoords='offset points',\n )\n\nax.annotate(\"\",\n xy=(a[0,1], a[1,1]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='r'),\n )\nax.annotate(r\"$\\vec{a}_2$\",\n xy=(a[0,1], a[1,1]), xycoords='data',\n xytext=(1, 1), textcoords='offset points', color='r'\n )\n\nax.annotate(\"\",\n xy=(b[0,0], b[1,0]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='b'),\n )\n\nax.annotate(r\"$\\vec{b}_1$\",\n xy=(b[0,0], b[1,0]), xycoords='data',\n xytext=(2, 2), textcoords='offset points', color='b'\n )\n\nax.annotate(\"\",\n xy=(b[0,1], b[1,1]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='g'),\n )\nax.annotate(r\"$\\vec{b}_2$\",\n xy=(b[0,1], b[1,1]), xycoords='data',\n xytext=(2, 2), textcoords='offset points', color='g'\n )\n\nax.annotate(\"\",\n xy=(α[0,0], α[1,0]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='y'),\n )\nax.annotate(r\"$\\vec{\\alpha}_1$\",\n xy=(α[0,0], α[1,0]), xycoords='data',\n xytext=(2, 2), textcoords='offset points', color='y'\n )\n\nax.annotate(\"\",\n xy=(α[0,1], α[1,1]), xycoords='data',\n xytext=(0, 0), textcoords='data',\n arrowprops=dict(arrowstyle=\"->\",\n connectionstyle=\"arc3\",ec='y',zorder=-10),\n )\nax.annotate(r\"$\\vec{\\alpha}_2$\",\n xy=(α[0,1], α[1,1]), xycoords='data',\n xytext=(2, 2), textcoords='offset points', color='y',zorder=-10\n )\n\nax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')\n\n\nax.set_aspect('equal')\nax.set_xlim(-6,6)\nax.set_ylim(-1,6)\nax.set_xlabel('x / Å')\nax.set_ylabel('y / Å')", "_____no_output_____" ] ], [ [ "### The Bonds", "_____no_output_____" ] ], [ [ "bonds = np.empty([0,4])\nfig,ax = plt.subplots()\n\nNG = len(C_positions)\nfor i in range(NG):\n ri = C_positions[i]\n for j in range(i,NG):\n rj = C_positions[j]\n d = np.linalg.norm(ri-rj)\n if d > 0.1 and d < (aₒ+0.1):\n ax.plot([ri[0],rj[0]],[ri[1],rj[1]],'-', zorder=-1, lw=0.5,color=grey)\n bonds = np.vstack((bonds,[ri[0],rj[0],ri[1],rj[1]]))\n \nax.scatter(C_positions[:,0],C_positions[:,1], s=4, color='k')\nax.scatter(He_positions[:,0],He_positions[:,1], s=8, color=blue)\nax.set_aspect('equal')\nax.set_xlabel('x / Å')\nax.set_ylabel('y / Å')", "_____no_output_____" ], [ "x,y = C_positions[:,0],C_positions[:,1]\nx1,x2,y1,y2 = bonds[:,0],bonds[:,1],bonds[:,2],bonds[:,3]", "_____no_output_____" ] ], [ [ "## Create a graphic of the dual triangular lattice", "_____no_output_____" ] ], [ [ "dual_bonds = np.empty([0,4])\n\nNA = len(hex_centers)\nfor i in range(NA):\n ri = hex_centers[i]\n for j in range(i,NA):\n rj = hex_centers[j]\n d = np.linalg.norm(ri-rj)\n if d > 0.1 and d < (np.sqrt(3)*aₒ+0.1):\n dual_bonds = np.vstack((dual_bonds,[ri[0],rj[0],ri[1],rj[1]]))", "_____no_output_____" ] ], [ [ "## Images of Adsorbed Phases\n### Setting the colors and sizes for some objects", "_____no_output_____" ] ], [ [ "col_C = Texture(Finish('ambient','0.2','diffuse','0.8'),Pigment('color',brown,'transmit',0.0))\ncol_bond = Texture(Finish('phong','0.2'),Pigment('color',brown,'transmit',0.0))\ncol_He = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',0.0))\ncol_He_link = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',0.6))\n\ncol_box = Texture(Finish('specular',0.5,'roughness',0.001,\n 'ambient',0,'diffuse',0.6,'conserve_energy'),\n Pigment('color','Gray','transmit',0.0))\n\ncol_int = Texture(Finish('specular',0.5,'roughness',0.001,\n 'ambient',0,'diffuse',0.6,'conserve_energy'),\n Pigment('color','Gray','transmit',0.5))\n\ncol_floor = Texture(Pigment('color','White','transmit',0.0))\n\n\nr_C = 0.30 # radius of C-atoms in graphene\nr_He = 3*r_C #/2.258# radius of He-atoms ", "_____no_output_____" ] ], [ [ "## C1/3 Solid\n### Generate the graphene lattice", "_____no_output_____" ] ], [ [ "sphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]\ncylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]\nsphere.extend([Sphere([cr[0],1.1, cr[1]], r_He, col_He) for cr in He_positions])", "_____no_output_____" ] ], [ [ "### Output image to disk", "_____no_output_____" ] ], [ [ "cam = Camera('location',[0,75,0],'look_at',[0,0,0])\nbg = Background(\"color\", \"White\",'transmit',1.0)\nlights = [LightSource( [0,80,0], 'color','White','parallel')]\n#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])\n\nobj = [bg] + lights + sphere + cylinder \n\nscene = Scene(camera=cam,objects=obj,included=included)\n#scene.render('ipython', width=400, height=200,remove_temp=False)\n\nfilename = '../plots/graphene_solid.png'\npovstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,\n output_alpha=True,remove_temp=False)\n\n# autocrop the image\nimage = Image.open(filename)\ncropped = image.crop(image.getbbox())\ncropped.save(filename)", "_____no_output_____" ] ], [ [ "## Superfluid", "_____no_output_____" ] ], [ [ "import importlib\nimportlib.reload(vapory)", "_____no_output_____" ], [ "# graphene\nsphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]\ncylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]\n\n# Helium\natoms = [Sphere([cr[0],1.1, cr[1]], r_He/3.0, col_He_link) for cr in hex_centers]", "_____no_output_____" ], [ "bonds = []\nsphere_path = []\nnum_atoms = hex_centers.shape[0]\nnum_points = 21\nnum_shift = 2\ns = ''\n\nrmin = 0.4*r_He/3.0\nrmax = 0.8*r_He/3.0\nm = (rmax-rmin)/int(num_points/2)\n\nfor i in range(num_atoms):\n r1 = hex_centers[i,:]\n for j in range(i,num_atoms):\n r2 = hex_centers[j,:]\n Δr = r2-r1\n if Δr[0]**2 + Δr[1]**2 <= 1.05*3*aₒ**2:\n if Δr[1] > 0 or (Δr[1]< 0.001 and Δr[0] > 0):\n path = pypov.generate_linear_path(r1,r2,num_points)\n s = '\\n'\n for n in range(num_shift,num_points-num_shift):\n rad = m*np.abs((n-int(num_points/2)))+rmin\n \n loc = [path[n][0]+np.random.uniform(low=-0.001,high=0.001),1.1,path[n][1]+np.random.uniform(low=-0.001,high=0.001)]\n s += vectorize(loc) + f', {rad}'\n if n < num_points-1-num_shift:\n s += ',\\n'\n else:\n s+= '\\n'\n \n s += str(format_if_necessary(col_He_link))\n bonds.append(Macro(\"sphere_sweep\",f\"linear_spline\\n{num_points-2*num_shift}\",s)) ", "_____no_output_____" ], [ "cam = Camera('location',[0,75,0],'look_at',[0,0,0])\nbg = Background(\"color\", \"White\",'transmit',1.0)\nlights = [LightSource( [0,20,0], 'color','White','parallel')]\n#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])\n\nobj = [bg] + lights + sphere + cylinder + [Merge(*bonds,*atoms)]\n\nscene = Scene(camera=cam,objects=obj,included=included)\n#scene.render('ipython', width=400, height=200,remove_temp=False)\n\nfilename = '../plots/graphene_superfluid.png'\npovstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,\n output_alpha=True,remove_temp=False)\n\n# autocrop the image\nimage = Image.open(filename)\ncropped = image.crop(image.getbbox())\ncropped.save(filename)", "_____no_output_____" ] ], [ [ "## Supersolid", "_____no_output_____" ] ], [ [ "# graphene\nsphere = [Sphere([x[i],0, y[i]], r_C, col_C) for i in range(len(x))]\ncylinder = [Cylinder([x1[i],0.0,y1[i]],[x2[i],0.0,y2[i]], 0.075,col_bond) for i in range(len(x1))]\n\n# Helium\natoms = [Sphere([cr[0],1.1, cr[1]], r_He/4.0, col_He_link) for cr in hex_centers]\n\natoms.extend([Sphere([cr[0],1.1, cr[1]], r_He/2.0, col_He) for cr in He_positions])", "_____no_output_____" ], [ "bonds = []\nsphere_path = []\nnum_atoms = hex_centers.shape[0]\nnum_points = 21\nnum_shift = 2\ns = ''\n\nrmin = 0.4*r_He/4.0\nrmax = 0.8*r_He/4.0\nm = (rmax-rmin)/int(num_points/2)\n\nfor i in range(num_atoms):\n r1 = hex_centers[i,:]\n for j in range(i,num_atoms):\n r2 = hex_centers[j,:]\n Δr = r2-r1\n if Δr[0]**2 + Δr[1]**2 <= 1.05*3*aₒ**2:\n if Δr[1] > 0 or (Δr[1]< 0.001 and Δr[0] > 0):\n path = pypov.generate_linear_path(r1,r2,num_points)\n s = '\\n'\n for n in range(num_shift,num_points-num_shift):\n rad = m*np.abs((n-int(num_points/2)))+rmin\n \n loc = [path[n][0]+np.random.uniform(low=-0.001,high=0.001),1.1,path[n][1]+np.random.uniform(low=-0.001,high=0.001)]\n s += vectorize(loc) + f', {rad}'\n if n < num_points-1-num_shift:\n s += ',\\n'\n else:\n s+= '\\n'\n \n s += str(format_if_necessary(col_He_link))\n bonds.append(Macro(\"sphere_sweep\",f\"linear_spline\\n{num_points-2*num_shift}\",s)) ", "_____no_output_____" ], [ "cam = Camera('location',[0,75,0],'look_at',[0,0,0])\nbg = Background(\"color\", \"White\",'transmit',1.0)\nlights = [LightSource( [0,20,0], 'color','White','parallel')]\n#lights.extend([LightSource( [0,75,0], 'color','White shadowless')])\n\nobj = [bg] + lights + sphere + cylinder + [Merge(*bonds,*atoms)]\n\nscene = Scene(camera=cam,objects=obj,included=included)\n#scene.render('ipython', width=400, height=200,remove_temp=False)\n\nfilename = '../plots/graphene_supersolid.png'\npovstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,\n output_alpha=True,remove_temp=False)\n\n# autocrop the image\nimage = Image.open(filename)\ncropped = image.crop(image.getbbox())\ncropped.save(filename)", "_____no_output_____" ] ], [ [ "## Suspended Wetting\n\nWe first construct the bonds for the larger graphene lattice used in wetting.", "_____no_output_____" ] ], [ [ "bonds_big = np.empty([0,4])\n\nNG_big = len(C_positions_big)\nfor i in range(NG_big):\n ri = C_positions_big[i]\n for j in range(i,NG_big):\n rj = C_positions_big[j]\n d = np.linalg.norm(ri-rj)\n if d > 0.1 and d < (aₒ+0.1):\n bonds_big = np.vstack((bonds_big,[ri[0],rj[0],ri[1],rj[1]]))\n\nx_big,y_big = C_positions_big[:,0],C_positions_big[:,1]\nx1_big,x2_big,y1_big,y2_big = bonds_big[:,0],bonds_big[:,1],bonds_big[:,2],bonds_big[:,3]", "_____no_output_____" ], [ "# graphene\nsphere = [Sphere([x_big[i],0, y_big[i]], r_C, col_C) for i in range(len(x_big))]\ncylinder = [Cylinder([x1_big[i],0.0,y1_big[i]],[x2_big[i],0.0,y2_big[i]], 0.075,col_bond) for i in range(len(x1_big))]", "_____no_output_____" ], [ "atoms = []\nzspace = 1.1\n\nr_He = 1.2*r_C\n\nfor n in range(1,12):\n\n if n == 1: \n shift = 0.05\n else:\n shift = 0.1\n \n for i,cr in enumerate(He_positions_big):\n ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2)\n if ccx < -2*L[0]:\n ccx += 4*L[0]\n \n ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n)\n ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)\n \n if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1]:\n atoms.append(Sphere([ccx,ccz,ccy], r_He, col_He))\n \n # shift to get 2/3 filling\n ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2) + a[0,0]\n if ccx < -2*L[0]:\n ccx += 4*L[0]\n ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n) + a[1,0]\n ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)\n \n if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1]:\n atoms.append(Sphere([ccx,ccz,ccy], r_He, col_He))\n\n# now do the vapor\nvapor = False\n\nif vapor:\n n_min = n\n n_max = n+8\n\n trans = pypov.linear([n_min,0.1],[n_max,0.9])\n lin_shift = pypov.linear([n_min,0.1],[n_max,0.5])\n freq = pypov.linear([n_min,2/3],[n_max,0.1])\n rad = pypov.linear([n_min,r_He],[n_max,0.4*r_He])\n\n for n in range(n_min,n_max):\n shift = lin_shift(n)\n\n col_He_gas = Texture(Finish('phong','0.9','phong_size',400),Pigment('color',green,'transmit',trans(n)))\n for i,cr in enumerate(hex_centers_big):\n ccx = cr[0] + np.random.uniform(low=-shift*n, high=shift*n) - np.sqrt(3)*aₒ*(n%2)\n ccy = cr[1] + np.random.uniform(low=-shift*n, high=shift*n)\n ccz = n*zspace + np.random.uniform(low=-shift*n, high=shift*n)\n\n if np.abs(ccx) < 2*L[0] and np.abs(ccy) < 2*L[1] and np.random.random() < freq(n):\n atoms.append(Sphere([ccx,ccz,ccy], rad(n), col_He_gas))", "_____no_output_____" ], [ "cam = Camera('location',[0,25,-80],'look_at',[0,0,0])\nbg = Background(\"color\", \"White\",'transmit',1.0)\nlights = [LightSource( [0,25,-80], 'color','White shadowless')]\n\n# cam = Camera('location',[0,80,0],'look_at',[0,0,0])\n# bg = Background(\"color\", \"White\",'transmit',1.0)\n# lights = [LightSource( [0,80,0], 'color','White','parallel')]\n\nobj = [bg] + lights + sphere + cylinder + atoms \n\nscene = Scene(camera=cam,objects=obj,included=included)\n\nfilename = '../plots/graphene_suspended.png'\npovstring = scene.render(filename, width=3600, height=3600,quality=11,antialiasing=0.2,\n output_alpha=True,remove_temp=False)\n\n# autocrop the image\nimage = Image.open(filename)\ncropped = image.crop(image.getbbox())\ncropped.save(filename)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

d0e7fc374ca2e3d05f075b58cad89d00bab27cdf

20,679

ipynb

Jupyter Notebook

examples/usgs-earthquakes.ipynb

Swanson-Hysell/mapboxgl-jupyter

814b47e592df6418d39c0a2d70269bb08c3cc554

[ "MIT" ]

1

2018-05-10T17:55:53.000Z

examples/usgs-earthquakes.ipynb

Janmanjay/mapboxgl-jupyter

630f3a7ab565fad9596f535a9fd2db678cfc9e6c

[ "MIT" ]

null

examples/usgs-earthquakes.ipynb

Janmanjay/mapboxgl-jupyter

630f3a7ab565fad9596f535a9fd2db678cfc9e6c

[ "MIT" ]

null

36.278947

331

0.468978

[ [ [ "# USGS Earthquakes with the Mapboxgl-Jupyter Python Library\nhttps://github.com/mapbox/mapboxgl-jupyter", "_____no_output_____" ] ], [ [ "# Python 3.5+ only!\nimport asyncio\nfrom aiohttp import ClientSession\nimport json, geojson, os, time\nimport pandas as pd\nfrom datetime import datetime, timedelta\nfrom mapboxgl.viz import *\nfrom mapboxgl.utils import *\nimport pysal.esda.mapclassify as mapclassify", "_____no_output_____" ], [ "# Get Data from the USGS API\ndata = []\n\nasync def fetch(url, headers, params, session):\n async with session.get(url, headers=headers, params=params) as resp:\n tempdata = await resp.json()\n data.append(tempdata)\n return tempdata\n \nasync def bound_fetch(sem, url, headers, params, session):\n # Getter function with semaphore.\n async with sem:\n await fetch(url, headers, params, session)\n\nasync def get_quakes(param_list, headers):\n # Store tasks to run\n tasks = []\n \n # create instance of Semaphore\n sem = asyncio.Semaphore(1000)\n \n # Generate URL from parameters\n endpoint = '/query'\n url = '{base_url}{endpoint}'.format(base_url=base_url, endpoint=endpoint)\n \n async with ClientSession() as session:\n for i in range(len(param_list)):\n task = asyncio.ensure_future(bound_fetch(sem, url, headers, param_list[i], session))\n tasks.append(task)\n responses = await asyncio.gather(*tasks)\n return responses\n \ndef create_params(starttime, endtime, minmagnitude):\n return {\n 'format': 'geojson', \n 'starttime': starttime,\n 'endtime': endtime,\n 'minmagnitude': minmagnitude\n }", "_____no_output_____" ], [ "# Default parameters \nbase_url = 'https://earthquake.usgs.gov/fdsnws/event/1'\nHEADERS = {\n 'user-agent': ('Mozilla/5.0 (Macintosh; Intel Mac OS X 10_10_5) '\n 'AppleWebKit/537.36 (KHTML, like Gecko) '\n 'Chrome/45.0.2454.101 Safari/537.36'),\n}\n\n# Make a list of data to get in a date range\napi_args = []\nstartdate = '2012-01-01'\ndate = datetime.strptime(startdate, \"%Y-%m-%d\")\nfor i in range(1000):\n low = datetime.strftime(date + timedelta(days=i*10), \"%Y-%m-%d\")\n high = datetime.strftime(date + timedelta(days=(i+1)*10), \"%Y-%m-%d\")\n api_args.append(create_params(low, high, 2))", "_____no_output_____" ], [ "#Run api queries for all queries generated\nloop = asyncio.get_event_loop()\nfuture = asyncio.ensure_future(get_quakes(api_args, HEADERS))\ntemp = loop.run_until_complete(future)", "_____no_output_____" ], [ "#Collect results into a Pandas dataframe\n\nkeep_props = ['felt', 'mag', 'magType', 'place', 'time', 'tsunami', 'longitude', 'latitude']\ndf = pd.DataFrame(columns=keep_props, index=[0])\nfeatures = []\n\nfor fc in data:\n for f in fc['features']:\n feature = {}\n for k in f['properties']:\n if k in keep_props:\n feature[k] = f['properties'][k]\n feature['longitude'] = f['geometry']['coordinates'][0]\n feature['latitude'] = f['geometry']['coordinates'][1]\n feature['timestamp'] = time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(feature['time']/1000))\n features.append(feature)\n \ndf = pd.DataFrame.from_dict(features) ", "_____no_output_____" ], [ "print(df.shape)\ndf.head(1)", "(198308, 9)\n" ] ], [ [ "# Set your Mapbox access token.\nSet a MAPBOX_ACCESS_TOKEN environment variable, or copy your token to use this notebook.\n\nIf you do not have a Mapbox access token, sign up for an account at https://www.mapbox.com/\n\nIf you already have an account, you can grab your token at https://www.mapbox.com/account/", "_____no_output_____" ] ], [ [ "token = os.getenv('MAPBOX_ACCESS_TOKEN')", "_____no_output_____" ], [ "# Generate a geojson file from the dataframe \n\ndf_to_geojson(df, filename='points.geojson', precision=4, lon='longitude', lat='latitude',\n properties=['mag','timestamp'])", "_____no_output_____" ], [ "# Create the visualization\n#Calculate the visualization to create\ncolor_breaks = mapclassify.Natural_Breaks(df['mag'], k=6, initial=0).bins\ncolor_stops = create_color_stops(color_breaks, colors='YlOrRd')\n\nradius_breaks = mapclassify.Natural_Breaks(df['mag'], k=6, initial=0).bins\nradius_stops = create_radius_stops(radius_breaks, 1, 10)\n\n\nviz = GraduatedCircleViz('https://dl.dropbox.com/s/h4xjjlc9ggnr88b/earthquake-points-180223.geojson', #'points.geojson',\n color_property = 'mag',\n color_stops = color_stops,\n radius_property = 'mag',\n radius_stops = radius_stops,\n opacity=0.8,\n below_layer='waterway-label',\n zoom=2,\n center= [-95, 37],\n access_token=token)\nviz.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

d0e7fc65b13c48821af74ffb536c38936571acde

6,098

ipynb

Jupyter Notebook

15 BST-1/15.7 isBST (Another solution).ipynb

suhassuhas/Coding-Ninjas---Data-Structures-and-Algorithms-in-Python

e660d5a83b80df9cb67b2d06f2b5ba182586f3da

[ "Unlicense" ]

4

2021-09-09T06:52:31.000Z

2022-01-09T00:05:11.000Z

15 BST-1/15.7 isBST (Another solution).ipynb

rishitbhojak/Coding-Ninjas---Data-Structures-and-Algorithms-in-Python

3b5625df60f7ac554fae58dc8ea9fd42012cbfae

[ "Unlicense" ]

null

15 BST-1/15.7 isBST (Another solution).ipynb

rishitbhojak/Coding-Ninjas---Data-Structures-and-Algorithms-in-Python

3b5625df60f7ac554fae58dc8ea9fd42012cbfae

[ "Unlicense" ]

5

2021-09-15T13:49:32.000Z

2022-01-20T20:37:46.000Z

26.982301

81

0.467366

[ [ [ "Using min and max in another way\nJust passing minrange and maxrange\n\n r\n / \\\n / \\\n min, r-1 r, max ", "_____no_output_____" ] ], [ [ "import queue\nclass BinaryTreeNode:\n def __init__(self, data):\n self.data = data\n self.left = None\n self.right = None\n\ndef minTree(root):\n if root == None:\n return 1000000\n leftMin = minTree(root.left)\n rightMin = minTree(root.right)\n return min(leftMin, rightMin, root.data)\n\ndef maxTree(root):\n if root == None: \n return -10000000\n leftMax = maxTree(root.left)\n rightMax = maxTree(root.right)\n return max(leftMax, rightMax, root.data)\n\ndef isBST(root):\n if root == None:\n return True\n leftMax = maxTree(root.left)\n rightMin = minTree(root.right)\n if root.data > rightMin or root.data <= leftMax:\n return False\n\n isLeftBST = isBST(root.left)\n isRightBST = isBST(root.right)\n\n return isLeftBST and isRightBST\n\ndef isBST2(root):\n if root == None:\n return 1000000, -1000000, True\n leftMin, leftMax, isLeftBST = isBST2(root.left)\n rightMin, rightMax, isRightBST = isBST2(root.right)\n \n minimum = min(leftMin, rightMin, root.data)\n maximum = max(leftMax, rightMax, root.data)\n \n isTreeBST = True\n \n if root.data <= leftMax or root.data > rightMin:\n isTreeBST = False\n if not(isLeftBST) or not(isRightBST):\n isTreeBST = False\n \n return minimum, maximum, isTreeBST\n \ndef isBST3(root, min_range, max_range):\n if root == None:\n return True\n if root.data < min_range or root.data > max_range:\n return False\n \n isLeftWithinConstraints = isBST3(root.left, min_range, root.data -1)\n isRightWithinConstraints = isBST3(root.right, root.data, max_range)\n \n return isLeftWithinConstraints and isRightWithinConstraints\n \n \n\ndef printTreeDetailed(root):\n if root == None:\n return\n print(root.data, end = \":\")\n\n if root.left is not None:\n print(root.left.data, end = \",\")\n\n if root.right is not None:\n print(root.right.data, end = \" \")\n\n print()\n printTreeDetailed(root.left)\n printTreeDetailed(root.right)\n \ndef takeLevelWiseTreeInput():\n q = queue.Queue()\n print(\"Enter root\")\n rootData = int(input())\n if rootData == -1:\n return None\n root = BinaryTreeNode(rootData)\n q.put(root)\n \n while (not(q.empty())):\n current_node = q.get()\n \n print(\"Enter left child of \", current_node.data)\n leftChildData = int(input())\n if leftChildData != -1:\n leftChild = BinaryTreeNode(leftChildData)\n current_node.left = leftChild\n q.put(leftChild)\n \n print(\"Enter right child of \", current_node.data)\n rightChildData = int(input())\n if rightChildData != -1:\n rightChild = BinaryTreeNode(rightChildData)\n current_node.right = rightChild\n q.put(rightChild)\n \n return root", "_____no_output_____" ], [ "root = takeLevelWiseTreeInput()\nprintTreeDetailed(root)\nisBST3(root, -10000, 10000)", "Enter root\n4\nEnter left child of 4\n2\nEnter right child of 4\n6\nEnter left child of 2\n1\nEnter right child of 2\n3\nEnter left child of 6\n5\nEnter right child of 6\n7\nEnter left child of 1\n-1\nEnter right child of 1\n-1\nEnter left child of 3\n-1\nEnter right child of 3\n-1\nEnter left child of 5\n-1\nEnter right child of 5\n-1\nEnter left child of 7\n-1\nEnter right child of 7\n-1\n4:2,6 \n2:1,3 \n1:\n3:\n6:5,7 \n5:\n7:\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ] ]

d0e8000d1d7079c8f98fd212d327dec685e2b63e

17,709

ipynb

Jupyter Notebook

advanced/MLP.ipynb

saitoicepp/ppcc2021_DeepLearning

ba679567a9648584ada2394c4219f891d9af60bd

[ "Apache-2.0" ]

null

advanced/MLP.ipynb

saitoicepp/ppcc2021_DeepLearning

ba679567a9648584ada2394c4219f891d9af60bd

[ "Apache-2.0" ]

null

advanced/MLP.ipynb

saitoicepp/ppcc2021_DeepLearning

ba679567a9648584ada2394c4219f891d9af60bd

[ "Apache-2.0" ]

null

31.123023

149

0.573324

[ [ [ "# Tensorflowが使うCPUの数を制限します。(VMを使う場合)\n%env OMP_NUM_THREADS=1\n%env TF_NUM_INTEROP_THREADS=1\n%env TF_NUM_INTRAOP_THREADS=1\n\nfrom tensorflow.config import threading\nnum_threads = 1\nthreading.set_inter_op_parallelism_threads(num_threads)\nthreading.set_intra_op_parallelism_threads(num_threads)\n\n#ライブラリのインポート\n%matplotlib inline\nimport numpy as np\nimport matplotlib.pyplot as plt", "_____no_output_____" ] ], [ [ "## MLP モデルのKerasによる実装\n基礎編で使った2次元データを基に、MLPモデルをTensorflow/Kerasで書いてみます。", "_____no_output_____" ] ], [ [ "\n\n# 二次元ガウス分布と一様分布\ndef getDataset2():\n state = np.random.get_state()\n np.random.seed(0) # 今回はデータセットの乱数を固定させます。\n\n nSignal = 100 # 生成するシグナルイベントの数\n nBackground = 1000 # 生成するバックグラウンドイベントの数\n\n # データ点の生成\n xS = np.random.multivariate_normal([1.0, 0], [[1, 0], [0, 1]], size=nSignal) # 平均(x1,x2) = (1.0, 0.0)、分散=1の２次元ガウス分布\n tS = np.ones(nSignal) # Signalは1にラベリング\n xB = np.random.uniform(low=-5, high=5, size=(nBackground, 2)) # (-5, +5)の一様分布\n tB = np.zeros(nBackground) # Backgroundは0にラベリング\n\n # 2つのラベルを持つ学習データを1つにまとめる\n x = np.concatenate([xS, xB])\n t = np.concatenate([tS, tB]).reshape(-1, 1)\n # データをランダムに並び替える\n p = np.random.permutation(len(x))\n x = x[p]\n t = t[p]\n\n np.random.set_state(state)\n\n return x, t\n\n\n# ラベル t={0,1}を持つデータ点のプロット\ndef plotDataPoint(x, t):\n # シグナル/バックグラウンドの抽出\n xS = x[t[:, 0] == 1] # シグナルのラベルだけを抽出\n xB = x[t[:, 0] == 0] # バックグラウンドのラベルだけを抽出\n\n # プロット\n plt.scatter(xS[:, 0], xS[:, 1], label='Signal', c='red', s=10) # シグナルをプロット\n plt.scatter(xB[:, 0], xB[:, 1], label='Background', c='blue', s=10) # バックグラウンドをプロット\n plt.xlabel('x1') # x軸ラベルの設定\n plt.ylabel('x2') # y軸ラベルの設定\n plt.legend() # legendの表示\n plt.show()\n\n\n# prediction関数の等高線プロット (fill)\ndef PlotPredictionContour(prediction, *args):\n # 等高線を描くためのメッシュの生成\n x1, x2 = np.mgrid[-5:5:100j, -5:5:100j] # x1 = (-5, 5), x2 = (-5, 5) の範囲で100点x100点のメッシュを作成\n x1 = x1.flatten() # 二次元配列を一次元配列に変換 ( shape=(100, 100) => shape(10000, ))\n x2 = x2.flatten() # 二次元配列を一次元配列に変換 ( shape=(100, 100) => shape(10000, ))\n x = np.array([x1, x2]).T\n\n # 関数predictionを使って入力xから出力yを計算し、等高線プロットを作成\n y = prediction(x, *args)\n cs = plt.tricontourf(x[:, 0], x[:, 1], y.flatten(), levels=10)\n plt.colorbar(cs)\n", "_____no_output_____" ] ], [ [ "中間層が2層、それぞれの層のノード数がそれぞれ3つ、1つのMLPを構成します。", "_____no_output_____" ] ], [ [ "from tensorflow.keras.models import Sequential\nfrom tensorflow.keras.layers import Dense\nfrom tensorflow.keras.optimizers import SGD\n\n# データ点の取得\nx, t = getDataset2()\n\n# モデルの定義\nmodel = Sequential([\n Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n\n# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法\nmodel.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=1.0))\n\n# トレーニング\nmodel.fit(\n x=x,\n y=t,\n batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。\n epochs=3000, # 学習のステップ数\n verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される\n)\n\n# プロット\n## パーセプトロンの出力を等高線プロット\nPlotPredictionContour(model.predict)\n\n## データ点をプロット\nplotDataPoint(x, t)\n", "_____no_output_____" ] ], [ [ "`Dense` は1層の隠れ層を作成する関数です。\n`Dense`の詳細は[公式のドキュメント](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense)を参照することでわかります。\nドキュメントを見ると、\n```python\ntf.keras.layers.Dense(\n units, activation=None, use_bias=True,\n kernel_initializer='glorot_uniform',\n bias_initializer='zeros', kernel_regularizer=None,\n bias_regularizer=None, activity_regularizer=None, kernel_constraint=None,\n bias_constraint=None, **kwargs\n)\n```\nのような引数を持つことがわかります。また、各引数の意味は、\n* `units`:\tPositive integer, dimensionality of the output space.\n* `activation`:\tActivation function to use. If you don't specify anything, no activation is applied (ie. \"linear\" activation: a(x) = x).\n* `use_bias`:\tBoolean, whether the layer uses a bias vector.\n* `kernel_initializer`:\tInitializer for the kernel weights matrix.\n* `bias_initializer`:\tInitializer for the bias vector.\n* `kernel_regularizer`:\tRegularizer function applied to the kernel weights matrix.\n* `bias_regularizer`:\tRegularizer function applied to the bias vector.\n* `activity_regularizer`:\tRegularizer function applied to the output of the layer (its \"activation\").\n* `kernel_constraint`:\tConstraint function applied to the kernel weights matrix.\n* `bias_constraint`:\tConstraint function applied to the bias vector.\n\nのようになっています。隠れ層のノード数、重みの初期化方法、正規化方法、制約方法などを指定できることがわかります。\n知らない関数を使うときは、必ずドキュメントを読んで、関数の入出力、引数、デフォルトの値などを確認するようにしましょう。\n例えばこのDense関数は\n```python\nDense(units=10)\n```\nのように、`units`(ノード数)だけを指定すれば動作しますが、その場合、暗に活性化関数は適用されず、重みの初期化は`glorot_uniform`で行われます。\n\n`input_dim`は最初の層だけに対して必要となります。\n", "_____no_output_____" ], [ "Keras Model (上の例では`model`)は`summary`関数を使用することで、その構成が確認できます。", "_____no_output_____" ] ], [ [ "model.summary()", "_____no_output_____" ] ], [ [ "このモデルは、１層目の隠れ層の出力が3, 学習可能なパラメータ数が9, 2層目の隠れ層の出力が1, 学習可能なパラメータ数が4 であることがわかります。\"Output Shape\"の\"None\"はサイズが未確定であることを表しています。ここでは、バッチサイズ用の次元になります。", "_____no_output_____" ], [ "モデルの構成図を作ってくれる便利なAPIも存在します。", "_____no_output_____" ] ], [ [ "from tensorflow.keras.utils import plot_model\nplot_model(model, to_file='model.png', show_shapes=True)", "_____no_output_____" ] ], [ [ "層の数を増やしてみましょう。新たな層を重ねることで層の数を増やすことができます。\n```python\nmodel = Sequential([\n Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid') # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid') # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n```", "_____no_output_____" ] ], [ [ "model = Sequential([\n Dense(units=3, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=3, activation='sigmoid'), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n\nmodel.summary()", "_____no_output_____" ] ], [ [ "モデルのパラメータの数が増えていることがわかります。\n\n次に、ノードの数を増やしてみましょう。", "_____no_output_____" ] ], [ [ "model = Sequential([\n Dense(units=128, activation='sigmoid', input_dim=2), # ノード数が3の層を追加。活性化関数はシグモイド関数。\n Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。\n Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。\n Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。\n Dense(units=128, activation='sigmoid'), # ノード数が128の層を追加。活性化関数はシグモイド関数。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n\nmodel.summary()", "_____no_output_____" ] ], [ [ "パラメータの数が大きく増えたことがわかります。\nMLPにおいては、パラメータの数は、ノード数の2乗で増加します。", "_____no_output_____" ], [ "このモデルを使って学習させてみましょう。", "_____no_output_____" ] ], [ [ "# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法\nmodel.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.01))\n\n# トレーニング\nmodel.fit(\n x=x,\n y=t,\n batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。\n epochs=3000, # 学習のステップ数\n verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される\n)\n\n# プロット\n## パーセプトロンの出力を等高線プロット\nPlotPredictionContour(model.predict)\n\n## データ点をプロット\nplotDataPoint(x, t)", "_____no_output_____" ] ], [ [ "これまでは活性化関数としてシグモイド関数(`sigmoid`)を使っていました。昔はsigmoid関数やtanh関数がよく使われていましたが、最近はReLU関数がよく使われます。\n$$\n ReLU = \\begin{cases}\n x & (x \\geq 0) \\\\\n 0 & (x < 0)\n \\end{cases}\n$$\n\nReLUが好まれる理由については、別の資料を参照してください。\n\nReLUを使って学習がどのようになるか確認してみましょう。", "_____no_output_____" ] ], [ [ "from tensorflow.keras.models import Sequential\nfrom tensorflow.keras.layers import Dense\nfrom tensorflow.keras.optimizers import SGD\n\n# データ点の取得\nx, t = getDataset2()\n\n# モデルの定義\nmodel = Sequential([\n Dense(units=128, activation='relu', input_dim=2), # ノード数が3の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n\n# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法\nmodel.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.01))\n\n# トレーニング\nmodel.fit(\n x=x,\n y=t,\n batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。\n epochs=3000, # 学習のステップ数\n verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される\n)\n\n# プロット\n## パーセプトロンの出力を等高線プロット\nPlotPredictionContour(model.predict)\n\n## データ点をプロット\nplotDataPoint(x, t)", "_____no_output_____" ] ], [ [ "深層学習をトレーニングするにあたって、最適化関数(optimizer)も非常に重要な要素です。\n確率的勾配降下法(SGD)の他によく使われるアルゴリズムとして adam があります。\nadamを使ってみると、どのようになるでしょうか。", "_____no_output_____" ] ], [ [ "from tensorflow.keras.models import Sequential\nfrom tensorflow.keras.layers import Dense\nfrom tensorflow.keras.optimizers import SGD\n\n# データ点の取得\nx, t = getDataset2()\n\n# モデルの定義\nmodel = Sequential([\n Dense(units=128, activation='relu', input_dim=2), # ノード数が3の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=128, activation='relu'), # ノード数が128の層を追加。活性化関数はReLU。\n Dense(units=1, activation='sigmoid') # ノード数が1の層を追加。活性化関数はシグモイド関数。\n])\n\n# 誤差関数としてクロスエントロピーを指定。最適化手法は(確率的)勾配降下法\nmodel.compile(loss='binary_crossentropy', optimizer='adam')\n\n# トレーニング\nmodel.fit(\n x=x,\n y=t,\n batch_size=len(x), # バッチサイズ。一回のステップで全てのデータを使うようにする。\n epochs=3000, # 学習のステップ数\n verbose=0, # 1とするとステップ毎に誤差関数の値などが表示される\n)\n\n# プロット\n## パーセプトロンの出力を等高線プロット\nPlotPredictionContour(model.predict)\n\n## データ点をプロット\nplotDataPoint(x, t)", "_____no_output_____" ] ], [ [ "## Keras モデルの定義方法\nKerasモデルを定義する方法はいくつかあります。\n最も簡単なのが`Sequential`を使った方法で、これまでの例では全てこの方法でモデルを定義してきました。\n一方で、少し複雑なモデルを考えると、`Sequential`モデルで対応できなくなってきます。\n一例としてResidual Network(ResNet)で使われるskip connectionを考えてみます。\nskip connectionは\n$$\ny = f_2(f_1(x) + x)\n$$\nのように、入力を２つの経路に分け、片方はMLP、もう片方はそのまま後ろのレイヤーに接続するつなげ方です。\nこのようなモデルは、途中入出力の分岐があるため、`Sequential`モデルでは実装できません。\nかわりに`Function API`を使うとこれを実装することができます。\n\n`Functional API`では以下のようにしてモデルを定義します。", "_____no_output_____" ] ], [ [ "from tensorflow.keras import Input, Model\ninput = Input(shape=(2,))\nx = Dense(units=128, activation='relu')(input)\nx = Dense(units=128, activation='relu')(x)\nx = Dense(units=128, activation='relu')(x)\nx = Dense(units=128, activation='relu')(x)\nx = Dense(units=128, activation='relu')(x)\noutput = Dense(units=1, activation='sigmoid')(x)\nmodel = Model(input, output)", "_____no_output_____" ] ], [ [ "入力(`Input`)をモジュールに順々に適用していき、\n```python\nx = Dense()(x)\n```\n最終的な出力(`output`)とはじめの入力を使って`Model`クラスを定義する、という流れになっています。\n\n`Functional API`でskip connectionを実装すると、以下のようになります。", "_____no_output_____" ] ], [ [ "from tensorflow.keras import Input, Model\nfrom tensorflow.keras.layers import Add\ninput = Input(shape=(2,))\nx = Dense(units=128, activation='relu')(input)\nz = Dense(units=128, activation='relu')(x)\nx = Add()([x, z])\nz = Dense(units=128, activation='relu')(x)\nx = Add()([x, z])\noutput = Dense(units=1, activation='sigmoid')(x)\nmodel = Model(input, output)\n\nfrom tensorflow.keras.utils import plot_model\nplot_model(model, to_file='model.png', show_shapes=True)", "_____no_output_____" ] ], [ [ "Kerasモデルを定義する方法として、`Model`クラスのサブクラスを作る方法もあります。\n`Model`クラスをカスタマイズすることができるので、特殊な学習をさせたいときなど、高度な深層学習モデルを扱うときに使われることもあります。", "_____no_output_____" ] ], [ [ "# Modelクラスを継承して新しいクラスを作成します\nfrom tensorflow.keras import Model\nclass myModel(Model):\n def __init__(self):\n super().__init__()\n self.dense_1 = Dense(units=128, activation='relu')\n self.dense_2 = Dense(units=128, activation='relu')\n self.dense_3 = Dense(units=128, activation='relu')\n self.dense_4 = Dense(units=128, activation='relu')\n self.dense_5 = Dense(units=128, activation='relu')\n self.dense_6 = Dense(units=1, activation='sigmoid')\n\n def call(self, inputs):\n x = self.dense_1(inputs)\n x = self.dense_2(x)\n x = self.dense_3(x)\n x = self.dense_4(x)\n x = self.dense_5(x)\n x = self.dense_6(x)\n return x\n\nmodel = myModel()\n", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e8044538977005f082cf58b649bfbe8600726e

4,346

ipynb

Jupyter Notebook

SDED-Ragic/workspace.ipynb

lanesharman/OpenDoors

c601fc067a4def1aea2d67995ce9f3baa8386501

[ "Apache-2.0" ]

null

SDED-Ragic/workspace.ipynb

lanesharman/OpenDoors

c601fc067a4def1aea2d67995ce9f3baa8386501

[ "Apache-2.0" ]

null

SDED-Ragic/workspace.ipynb

lanesharman/OpenDoors

c601fc067a4def1aea2d67995ce9f3baa8386501

[ "Apache-2.0" ]

null

27.681529

142

0.47515

[ [ [ "import requests\nimport pandas\nimport config", "_____no_output_____" ], [ "table_id = '1'\ngroup_name = 'test2'\n\n\nurl = 'https://www.ragic.com/ccedatabase/%s/%s?api&APIKey=%s' % (group_name, table_id, config.api)\n\nr = requests.get(url)\nr.json()\n", "_____no_output_____" ], [ "class RagicTools():\n def __init__(self, table_id, group_name, api):\n self.table_id = table_id\n self.group_name = group_name\n self.api = api\n self.url = 'https://www.ragic.com/ccedatabase/%s/%s?api&APIKey=%s' % (self.group_name, self.table_id, self.api)\n def get_table(self):\n '''\n gets table passed into constructor \n '''\n r = requests.get(self.url)\n return r.json()\n \n def add_entry(self, entry):\n '''\n entry must look like this: \n files = {\n '1000114': (None, '8'),\n '1000115': (None, 'column 1-2-3'),\n '1000116': (None, 'column 2-2'),\n '1000117': (None, 'column 3-2')\n }\n where the keys are the column ids that can be found in ragic\n adds entry to table\n '''\n \n r = requests.post(url, files = entry)\n return r.json()\n\n def delete_entry(self, row_id):\n '''\n deletes row in current table in \n '''\n row_id = str(row_id)\n url = 'https://www.ragic.com/ccedatabase/%s/%s/%s?api&APIKey=%s' % (self.group_name, self.table_id, row_id, self.api)\n r = requests.delete(url)\n return r.json()\n\n def update_entry(self, row_id, updated_entry):\n '''\n updates given row with new data in group\n entry must look like this:\n updated_entry = {\n '1000114': (None, '9'),\n '1000115': (None, 'updated'),\n '1000116': (None, 'from'),\n '1000117': (None, 'script')\n }\n\n '''\n row_id = str(row_id)\n url = 'https://www.ragic.com/ccedatabase/%s/%s/%s?api&APIKey=%s' % (self.group_name, self.table_id, row_id, self.api) \n r = requests.post(url, updated_entry)\n return r.json()\n \n def get_table_id(self):\n return self.table_id\n def get_group(self):\n return self.group_name\n \n\n", "_____no_output_____" ], [ "# pandas.DataFrame(test_json).transpose()[['_ragicId', 'T1-ID', 'T11','T12','T13']].set_index('_ragicId')", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code" ] ]

d0e8190121fc81279e0a3b43a8d014a4a6749589

84,108

ipynb

Jupyter Notebook

FINAL_CODE/Model_LSTM.ipynb

rafsunshuvo/Thesis

57917688d74253b3bebe545b12eecf51f18ecba2

[ "MIT" ]

null

FINAL_CODE/Model_LSTM.ipynb

rafsunshuvo/Thesis

57917688d74253b3bebe545b12eecf51f18ecba2

[ "MIT" ]

null

FINAL_CODE/Model_LSTM.ipynb

rafsunshuvo/Thesis

57917688d74253b3bebe545b12eecf51f18ecba2

[ "MIT" ]

null

70.383264

15,798

0.640403

[ [ [ "<a href=\"http://colab.research.google.com/github/dipanjanS/nlp_workshop_odsc19/blob/master/Module05%20-%20NLP%20Applications/Project07C%20-%20Text%20Classification%20Deep%20Learning%20Sequential%20Models%20LSTMs.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ] ], [ [ "!nvidia-smi", "Wed Feb 2 16:16:49 2022 \n+-----------------------------------------------------------------------------+\n| NVIDIA-SMI 495.46 Driver Version: 460.32.03 CUDA Version: 11.2 |\n|-------------------------------+----------------------+----------------------+\n| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |\n| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |\n| | | MIG M. |\n|===============================+======================+======================|\n| 0 Tesla T4 Off | 00000000:00:04.0 Off | 0 |\n| N/A 39C P0 27W / 70W | 298MiB / 15109MiB | 0% Default |\n| | | N/A |\n+-------------------------------+----------------------+----------------------+\n \n+-----------------------------------------------------------------------------+\n| Processes: |\n| GPU GI CI PID Type Process name GPU Memory |\n| ID ID Usage |\n|=============================================================================|\n| No running processes found |\n+-----------------------------------------------------------------------------+\n" ], [ "!pip install contractions\n!pip install textsearch\n!pip install tqdm\nimport nltk\nnltk.download('punkt')", "Requirement already satisfied: contractions in /usr/local/lib/python3.7/dist-packages (0.1.66)\nRequirement already satisfied: textsearch>=0.0.21 in /usr/local/lib/python3.7/dist-packages (from contractions) (0.0.21)\nRequirement already satisfied: anyascii in /usr/local/lib/python3.7/dist-packages (from textsearch>=0.0.21->contractions) (0.3.0)\nRequirement already satisfied: pyahocorasick in /usr/local/lib/python3.7/dist-packages (from textsearch>=0.0.21->contractions) (1.4.2)\nRequirement already satisfied: textsearch in /usr/local/lib/python3.7/dist-packages (0.0.21)\nRequirement already satisfied: pyahocorasick in /usr/local/lib/python3.7/dist-packages (from textsearch) (1.4.2)\nRequirement already satisfied: anyascii in /usr/local/lib/python3.7/dist-packages (from textsearch) (0.3.0)\nRequirement already satisfied: tqdm in /usr/local/lib/python3.7/dist-packages (4.62.3)\n[nltk_data] Downloading package punkt to /root/nltk_data...\n[nltk_data] Package punkt is already up-to-date!\n" ], [ "import pandas as pd\nimport numpy as np\n\n# fix random seed for reproducibility\nseed = 42\nnp.random.seed(seed)", "_____no_output_____" ], [ "import zipfile\nfrom google.colab import drive\ndrive.mount(\"/content/drive\")\nz= zipfile.ZipFile(\"/content/drive/MyDrive/Colab Notebooks/YouTube-Spam-Collection-v1.zip\")\nPsy=pd.read_csv(z.open(\"Youtube01-Psy.csv\"))\nKatyPerry =pd.read_csv(z.open(\"Youtube02-KatyPerry.csv\"))\nLMFAQ =pd.read_csv(z.open(\"Youtube03-LMFAO.csv\"))\nEminem =pd.read_csv(z.open(\"Youtube04-Eminem.csv\"))\nShakira =pd.read_csv(z.open(\"Youtube05-Shakira.csv\"))\nframes = [Psy,LMFAQ,Eminem,Shakira,KatyPerry]\ndataset = pd.concat(frames)\ndataset.head(10)", "Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount(\"/content/drive\", force_remount=True).\n" ], [ "\ndataset.info()", "<class 'pandas.core.frame.DataFrame'>\nInt64Index: 1956 entries, 0 to 349\nData columns (total 5 columns):\n # Column Non-Null Count Dtype \n--- ------ -------------- ----- \n 0 COMMENT_ID 1956 non-null object\n 1 AUTHOR 1956 non-null object\n 2 DATE 1711 non-null object\n 3 CONTENT 1956 non-null object\n 4 CLASS 1956 non-null int64 \ndtypes: int64(1), object(4)\nmemory usage: 91.7+ KB\n" ], [ "\ndataset.head()", "_____no_output_____" ], [ "# build train and test datasets\nreviews = dataset['CONTENT'].values\nsentiments = dataset['CLASS'].values\n\ntrain_reviews = reviews[:3500]\ntrain_sentiments = sentiments[:3500]\n\ntest_reviews = reviews[3500:]\ntest_sentiments = sentiments[3500:]", "_____no_output_____" ], [ "import contractions\nfrom bs4 import BeautifulSoup\nimport numpy as np\nimport re\nimport tqdm\nimport unicodedata\n\n\ndef strip_html_tags(text):\n soup = BeautifulSoup(text, \"html.parser\")\n [s.extract() for s in soup(['iframe', 'script'])]\n stripped_text = soup.get_text()\n stripped_text = re.sub(r'[\\r|\\n|\\r\\n]+', '\\n', stripped_text)\n return stripped_text\n\ndef remove_accented_chars(text):\n text = unicodedata.normalize('NFKD', text).encode('ascii', 'ignore').decode('utf-8', 'ignore')\n return text\n\ndef pre_process_corpus(docs):\n norm_docs = []\n for doc in tqdm.tqdm(docs):\n doc = strip_html_tags(doc)\n doc = doc.translate(doc.maketrans(\"\\n\\t\\r\", \" \"))\n doc = doc.lower()\n doc = remove_accented_chars(doc)\n doc = contractions.fix(doc)\n # lower case and remove special characters\\whitespaces\n doc = re.sub(r'[^a-zA-Z0-9\\s]', '', doc, re.I|re.A)\n doc = re.sub(' +', ' ', doc)\n doc = doc.strip() \n norm_docs.append(doc)\n \n return norm_docs", "_____no_output_____" ], [ "%%time\n\nnorm_train_reviews = pre_process_corpus(train_reviews)\nnorm_test_reviews = pre_process_corpus(test_reviews)", " 0%| | 0/1956 [00:00<?, ?it/s]/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://twitter.com/GBphotographyGB\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://ubuntuone.com/40beUutVu2ZKxK4uTgPZ8K\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://hackfbaccountlive.com/?ref=4604617\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://binbox.io/1FIRo#123\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://thepiratebay.se/torrent/6381501/Timothy_Sykes_Collection\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.gcmforex.com/partners/aw.aspx?Task=JoinT2&AffiliateID=9107\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/teeLaLaLa\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.twitch.tv/zxlightsoutxz\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://flipagram.com/f/LUkA1QMrhF\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.gofundme.com/gvr7xg\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://soundcloud.com/jackal-and-james/wrap-up-the-night\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.surveymonkey.com/s/CVHMKLT\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/pages/Mathster-WP/1495323920744243?ref=hl\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://hackfbaccountlive.com/?ref=5242575\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/FUDAIRYQUEEN?pnref=story\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n 72%|███████▏ | 1410/1956 [00:00<00:00, 7007.38it/s]/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.twitch.tv/daconnormc\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/photo.php?fbid=543627485763966&l=0d878a889c\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.bubblews.com/news/6401116-vps-solutions\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://shhort.com/a?r=HuPwEH5ab\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://shhort.com/a?r=G8iX5cTKd\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://shhort.com/a?r=Jt2ufxHxc\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.reverbnation.com/slicknick313/songs\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://viralangels.com/user/d4aaacwk\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://vimeo.com/107297364\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/pages/Komedi-burda-gel/775510675841486\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/profile.php?id=100007085325116\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://vimeo.com/106865403\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://minhateca.com.br/mauro-sp2013/Filmes+Series+Desenhos+Animes+Mp3+etc\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/antrobofficial\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://hackfbaccountlive.com/?ref=4344749\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://soundcloud.com/j-supt-fils-du-son/fucking-hostile\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://www.facebook.com/myfunnyriddles\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"http://www.wattpad.com/story/26032883-she-can-love-you-good\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n/usr/local/lib/python3.7/dist-packages/bs4/__init__.py:336: UserWarning: \"https://binbox.io/DNCkM#qT4Q1JB1\" looks like a URL. Beautiful Soup is not an HTTP client. You should probably use an HTTP client like requests to get the document behind the URL, and feed that document to Beautiful Soup.\n ' that document to Beautiful Soup.' % decoded_markup\n100%|██████████| 1956/1956 [00:00<00:00, 6945.09it/s]\n0it [00:00, ?it/s]" ] ], [ [ "## Preprocessing\n\nTo prepare text data for our deep learning model, we transform each review into a sequence.\nEvery word in the review is mapped to an integer index and thus the sentence turns into a sequence of numbers.\n\nTo perform this transformation, keras provides the ```Tokenizer```", "_____no_output_____" ] ], [ [ "import tensorflow as tf\n\nt = tf.keras.preprocessing.text.Tokenizer(oov_token='<UNK>')\n# fit the tokenizer on the documents\nt.fit_on_texts(norm_train_reviews)\nt.word_index['<PAD>'] = 0", "_____no_output_____" ], [ "max([(k, v) for k, v in t.word_index.items()], key = lambda x:x[1]), min([(k, v) for k, v in t.word_index.items()], key = lambda x:x[1]), t.word_index['<UNK>']", "_____no_output_____" ], [ "train_sequences = t.texts_to_sequences(norm_train_reviews)\ntest_sequences = t.texts_to_sequences(norm_test_reviews)", "_____no_output_____" ], [ "print(\"Vocabulary size={}\".format(len(t.word_index)))\nprint(\"Number of Documents={}\".format(t.document_count))", "Vocabulary size=4118\nNumber of Documents=1956\n" ], [ "import matplotlib.pyplot as plt\n%matplotlib inline\n\ntrain_lens = [len(s) for s in train_sequences]\ntest_lens = [len(s) for s in test_sequences]\n\nfig, ax = plt.subplots(1,2, figsize=(12, 6))\nh1 = ax[0].hist(train_lens)\nh2 = ax[1].hist(test_lens)", "_____no_output_____" ], [ "MAX_SEQUENCE_LENGTH = 1000", "_____no_output_____" ] ], [ [ "", "_____no_output_____" ] ], [ [ "# pad dataset to a maximum review length in words\nX_train = tf.keras.preprocessing.sequence.pad_sequences(train_sequences, maxlen=MAX_SEQUENCE_LENGTH)\nX_test = tf.keras.preprocessing.sequence.pad_sequences(test_sequences, maxlen=MAX_SEQUENCE_LENGTH)\nX_train.shape, X_test.shape", "_____no_output_____" ] ], [ [ "### Encoding Labels\n\n", "_____no_output_____" ] ], [ [ "from sklearn.preprocessing import LabelEncoder\n\nle = LabelEncoder()\nnum_classes=2 # positive -> 1, negative -> 0", "_____no_output_____" ], [ "y_train = le.fit_transform(train_sentiments)\ny_test = le.transform(test_sentiments)", "_____no_output_____" ], [ "VOCAB_SIZE = len(t.word_index)", "_____no_output_____" ] ], [ [ "# LSTM Model", "_____no_output_____" ] ], [ [ "EMBEDDING_DIM = 300 # dimension for dense embeddings for each token\nLSTM_DIM = 128 # total LSTM units\n\nmodel = tf.keras.models.Sequential()\nmodel.add(tf.keras.layers.Embedding(input_dim=VOCAB_SIZE, output_dim=EMBEDDING_DIM, input_length=MAX_SEQUENCE_LENGTH))\nmodel.add(tf.keras.layers.SpatialDropout1D(0.1))\nmodel.add(tf.compat.v1.keras.layers.CuDNNLSTM(LSTM_DIM, return_sequences=False))\nmodel.add(tf.keras.layers.Dense(256, activation='relu'))\nmodel.add(tf.keras.layers.Dense(1, activation=\"sigmoid\"))\n\nmodel.compile(loss=\"binary_crossentropy\", optimizer=\"adam\",\n metrics=[\"accuracy\"])\nmodel.summary()", "Model: \"sequential_1\"\n_________________________________________________________________\n Layer (type) Output Shape Param # \n=================================================================\n embedding_1 (Embedding) (None, 1000, 300) 1235400 \n \n spatial_dropout1d_1 (Spatia (None, 1000, 300) 0 \n lDropout1D) \n \n cu_dnnlstm_1 (CuDNNLSTM) (None, 128) 220160 \n \n dense_2 (Dense) (None, 256) 33024 \n \n dense_3 (Dense) (None, 1) 257 \n \n=================================================================\nTotal params: 1,488,841\nTrainable params: 1,488,841\nNon-trainable params: 0\n_________________________________________________________________\n" ] ], [ [ "## Train Model", "_____no_output_____" ] ], [ [ "Metrics = [tf.keras.metrics.BinaryAccuracy(name = 'accuracy'),\n tf.keras.metrics.Precision(name = 'precision'),\n tf.keras.metrics.Recall(name = 'recall')\n ]", "_____no_output_____" ], [ "# compiling our model\nmodel.compile(optimizer ='adam',\n loss = 'binary_crossentropy',\n metrics = Metrics)", "_____no_output_____" ], [ "batch_size = 100\nhistory=model.fit(X_train, y_train, epochs=5, batch_size=batch_size, \n shuffle=True, validation_split=0.1, verbose=1)", "Epoch 1/5\n18/18 [==============================] - 2s 90ms/step - loss: 0.0122 - accuracy: 0.9983 - precision: 0.9978 - recall: 0.9989 - val_loss: 0.3582 - val_accuracy: 0.8520 - val_precision: 0.8554 - val_recall: 0.8068\nEpoch 2/5\n18/18 [==============================] - 2s 87ms/step - loss: 0.0064 - accuracy: 0.9989 - precision: 0.9989 - recall: 0.9989 - val_loss: 0.4340 - val_accuracy: 0.8469 - val_precision: 0.8452 - val_recall: 0.8068\nEpoch 3/5\n18/18 [==============================] - 2s 94ms/step - loss: 0.0025 - accuracy: 0.9994 - precision: 1.0000 - recall: 0.9989 - val_loss: 0.6222 - val_accuracy: 0.8469 - val_precision: 0.8222 - val_recall: 0.8409\nEpoch 4/5\n18/18 [==============================] - 2s 87ms/step - loss: 8.1755e-04 - accuracy: 1.0000 - precision: 1.0000 - recall: 1.0000 - val_loss: 0.7594 - val_accuracy: 0.8418 - val_precision: 0.8434 - val_recall: 0.7955\nEpoch 5/5\n18/18 [==============================] - 2s 87ms/step - loss: 4.7767e-04 - accuracy: 1.0000 - precision: 1.0000 - recall: 1.0000 - val_loss: 0.7190 - val_accuracy: 0.8418 - val_precision: 0.8434 - val_recall: 0.7955\n" ], [ "from matplotlib import pyplot", "_____no_output_____" ], [ "pyplot.subplot(211)\npyplot.title('Loss')\npyplot.plot(history.history['loss'], label='train')\npyplot.plot(history.history['val_loss'], label='test')\npyplot.legend()\n# plot accuracy during training\npyplot.subplot(212)\npyplot.title('Accuracy')\npyplot.plot(history.history['accuracy'], label='train')\npyplot.plot(history.history['val_accuracy'], label='test')\npyplot.legend()\npyplot.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ] ]

d0e82097a35c8e5acd4aa893dc78082eee37f5e7

7,226

ipynb

Jupyter Notebook

docs/_downloads/695ce7a76ce07582023a85d63a717ce2/saving_and_loading_models_for_inference.ipynb

Baescott/PyTorch-tutorials-kr

613e87c4a652779ab73c5c9381b6b2426ada9885

[ "BSD-3-Clause" ]

1

2021-07-08T12:37:20.000Z

docs/_downloads/695ce7a76ce07582023a85d63a717ce2/saving_and_loading_models_for_inference.ipynb

Baescott/PyTorch-tutorials-kr

613e87c4a652779ab73c5c9381b6b2426ada9885

[ "BSD-3-Clause" ]

null

docs/_downloads/695ce7a76ce07582023a85d63a717ce2/saving_and_loading_models_for_inference.ipynb

Baescott/PyTorch-tutorials-kr

613e87c4a652779ab73c5c9381b6b2426ada9885

[ "BSD-3-Clause" ]

null

51.614286

1,532

0.596872

[ [ [ "%matplotlib inline", "_____no_output_____" ] ], [ [ "\nSaving and loading models for inference in PyTorch\n==================================================\nThere are two approaches for saving and loading models for inference in\nPyTorch. The first is saving and loading the ``state_dict``, and the\nsecond is saving and loading the entire model.\n\nIntroduction\n------------\nSaving the model’s ``state_dict`` with the ``torch.save()`` function\nwill give you the most flexibility for restoring the model later. This\nis the recommended method for saving models, because it is only really\nnecessary to save the trained model’s learned parameters.\nWhen saving and loading an entire model, you save the entire module\nusing Python’s\n`pickle <https://docs.python.org/3/library/pickle.html>`__ module. Using\nthis approach yields the most intuitive syntax and involves the least\namount of code. The disadvantage of this approach is that the serialized\ndata is bound to the specific classes and the exact directory structure\nused when the model is saved. The reason for this is because pickle does\nnot save the model class itself. Rather, it saves a path to the file\ncontaining the class, which is used during load time. Because of this,\nyour code can break in various ways when used in other projects or after\nrefactors.\nIn this recipe, we will explore both ways on how to save and load models\nfor inference.\n\nSetup\n-----\nBefore we begin, we need to install ``torch`` if it isn’t already\navailable.\n\n\n::\n\n pip install torch\n\n\n\n", "_____no_output_____" ], [ "Steps\n-----\n\n1. Import all necessary libraries for loading our data\n2. Define and intialize the neural network\n3. Initialize the optimizer\n4. Save and load the model via ``state_dict``\n5. Save and load the entire model\n\n1. Import necessary libraries for loading our data\n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n\nFor this recipe, we will use ``torch`` and its subsidiaries ``torch.nn``\nand ``torch.optim``.\n\n\n", "_____no_output_____" ] ], [ [ "import torch\nimport torch.nn as nn\nimport torch.optim as optim", "_____no_output_____" ] ], [ [ "2. Define and intialize the neural network\n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n\nFor sake of example, we will create a neural network for training\nimages. To learn more see the Defining a Neural Network recipe.\n\n\n", "_____no_output_____" ] ], [ [ "class Net(nn.Module):\n def __init__(self):\n super(Net, self).__init__()\n self.conv1 = nn.Conv2d(3, 6, 5)\n self.pool = nn.MaxPool2d(2, 2)\n self.conv2 = nn.Conv2d(6, 16, 5)\n self.fc1 = nn.Linear(16 * 5 * 5, 120)\n self.fc2 = nn.Linear(120, 84)\n self.fc3 = nn.Linear(84, 10)\n\n def forward(self, x):\n x = self.pool(F.relu(self.conv1(x)))\n x = self.pool(F.relu(self.conv2(x)))\n x = x.view(-1, 16 * 5 * 5)\n x = F.relu(self.fc1(x))\n x = F.relu(self.fc2(x))\n x = self.fc3(x)\n return x\n\nnet = Net()\nprint(net)", "_____no_output_____" ] ], [ [ "3. Initialize the optimizer\n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n\nWe will use SGD with momentum.\n\n\n", "_____no_output_____" ] ], [ [ "optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)", "_____no_output_____" ] ], [ [ "4. Save and load the model via ``state_dict``\n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n\nLet’s save and load our model using just ``state_dict``.\n\n\n", "_____no_output_____" ] ], [ [ "# Specify a path\nPATH = \"state_dict_model.pt\"\n\n# Save\ntorch.save(net.state_dict(), PATH)\n\n# Load\nmodel = Net()\nmodel.load_state_dict(torch.load(PATH))\nmodel.eval()", "_____no_output_____" ] ], [ [ "A common PyTorch convention is to save models using either a ``.pt`` or\n``.pth`` file extension.\n\nNotice that the ``load_state_dict()`` function takes a dictionary\nobject, NOT a path to a saved object. This means that you must\ndeserialize the saved state_dict before you pass it to the\n``load_state_dict()`` function. For example, you CANNOT load using\n``model.load_state_dict(PATH)``.\n\nRemember too, that you must call ``model.eval()`` to set dropout and\nbatch normalization layers to evaluation mode before running inference.\nFailing to do this will yield inconsistent inference results.\n\n5. Save and load entire model\n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n\nNow let’s try the same thing with the entire model.\n\n\n", "_____no_output_____" ] ], [ [ "# Specify a path\nPATH = \"entire_model.pt\"\n\n# Save\ntorch.save(net, PATH)\n\n# Load\nmodel = torch.load(PATH)\nmodel.eval()", "_____no_output_____" ] ], [ [ "Again here, remember that you must call model.eval() to set dropout and\nbatch normalization layers to evaluation mode before running inference.\n\nCongratulations! You have successfully saved and load models for\ninference in PyTorch.\n\nLearn More\n----------\n\nTake a look at these other recipes to continue your learning:\n\n- `Saving and loading a general checkpoint in PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_and_loading_a_general_checkpoint.html>`__\n- `Saving and loading multiple models in one file using PyTorch <https://pytorch.org/tutorials/recipes/recipes/saving_multiple_models_in_one_file.html>`__\n\n", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e8423b31babd0f20e1b590007f705f68fbfde3

7,201

ipynb

Jupyter Notebook

DeepLearning/pytorch/Autograd.ipynb

MikoyChinese/learn

c482b1e84496279935b5bb2cfc1e6d78e2868c63

[ "Apache-2.0" ]

null

DeepLearning/pytorch/Autograd.ipynb

MikoyChinese/learn

c482b1e84496279935b5bb2cfc1e6d78e2868c63

[ "Apache-2.0" ]

null

DeepLearning/pytorch/Autograd.ipynb

MikoyChinese/learn

c482b1e84496279935b5bb2cfc1e6d78e2868c63

[ "Apache-2.0" ]

null

26.769517

336

0.551312

[ [ [ "## Autograd: automatic differentiation\n\nCentral to all neural networks in PyTorch is the `autograd` package. Let's first briefly visit this, and we will then go to train our first neural network.\n\nThe `autograd` package provides automatic differentiation for all operation on Tensors. It is a define-by-run framework, which means that your backprop is defined by how your code is run, and that every single iteration can be different.\n\nLet us see this in more simple terms with some examples.", "_____no_output_____" ], [ "#### Tensor\n\n`torch.Tensor` is the central class of the package. If you set its attribute `.requires_grad` as True, it starts to track all operations on it. When you finish your computation you can call `.backward()` and have all the gradients computed automatically. The gradient for this tensor will be accumulated into `.grad` attribute.\n\nTo stop a tensor from tracking history, you can call `.detach()` to detach it from the computation history, and to prevent future computation from being tracked.\n\nTo prevent tracking history (and using memory), you can also wrap the code block in `with torch.no_grad():`. This can be particularly helpful when evaluating a model because the model may have trainable parameters with `requires_grad=True`, but for which we don’t need the gradients.\n\nThere’s one more class which is very important for autograd implementation - a `Function`.\n\n`Tensor` and `Function` are interconnected and build up an acyclic graph, that encodes a complete history of computation. Each tensor has a `.grad_fn` attribute that references a `Function` that has created the `Tensor` (except for Tensors created by the user - their `grad_fn` is None).\n\nIf you want to compute the derivatives, you can call `.backward()` on a `Tensor`. If `Tensor` is a scalar (i.e. it holds a one element data), you don’t need to specify any arguments to `backward()`, however if it has more elements, you need to specify a `gradient` argument that is a tensor of matching shape.", "_____no_output_____" ] ], [ [ "import torch\n\n# Create a tensor and set `requires_grad=True` to track computation with it.\nx = torch.ones(2, 2, requires_grad=True)\nprint(x)\n\n# Do a tensor operation:\ny = x + 2\nprint(y)\n\n# y was created as a result of an operation, so it has a grad_fn\nprint(y.grad_fn)\n\nz = y * y * 3\nout = z.mean()\nprint(z, out)", "tensor([[1., 1.],\n [1., 1.]], requires_grad=True)\ntensor([[3., 3.],\n [3., 3.]], grad_fn=<AddBackward0>)\n<AddBackward0 object at 0x7f2f53a06828>\ntensor([[27., 27.],\n [27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)\n" ], [ "a = torch.randn(2, 2)\na = ((a * 3) / (a -1))\n\nprint(a.requires_grad)\na.requires_grad_(True)\nprint(a.requires_grad)\nb = (a * a).sum()\nprint(b.grad_fn)", "False\nTrue\n<SumBackward0 object at 0x7f2f536585f8>\n" ], [ "out.backward()\nprint(x.grad)", "tensor([[4.5000, 4.5000],\n [4.5000, 4.5000]])\n" ], [ "x = torch.randn(3 ,requires_grad=True)\n\ny = x * 2\nwhile y.data.norm() < 1000:\n y *= 2\n \nprint(y)", "tensor([ -736.4083, 477.7849, -1220.2983], grad_fn=<MulBackward0>)\n" ], [ "v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)\ny.backward(v)\nprint(x.grad)", "tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])\n" ], [ "# You can also stop autograd from tracking history on Tensors\n# with .requires_grad=True either by wrapping the code block in with torch.no_grad():\n\nprint(x.requires_grad)\nprint((x ** 2).requires_grad)\n\nwith torch.no_grad():\n print((x ** 2).requires_grad)", "True\nTrue\nFalse\n" ], [ "# Or by using .detach() to get a new Tensor with the same content but that does not require gradients:\n\nprint(x.requires_grad)\ny = x.detach()\nprint(y.requires_grad)\nprint(x.eq(y).all())", "True\nFalse\ntensor(1, dtype=torch.uint8)\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ] ]

d0e856d1ff9a75ce90c1369a00a94d3281e5d9c1

411,340

ipynb

Jupyter Notebook

Chapter05/Exercise5.02/Exercise5.02.ipynb

thoolihan/The-Deep-Learning-with-PyTorch-Workshop

16fc18f96736eaaa25802b9f34ec39198c76c05d

[ "MIT" ]

16

2020-07-23T17:54:06.000Z

2022-03-29T06:21:25.000Z

Chapter05/Exercise5.02/Exercise5.02.ipynb

PacktWorkshops/Applied-Deep-Learning-with-PyTorch

bcfe00b2a2c6ec5b823d40ee801d5332346f0ca8

[ "MIT" ]

4

2021-03-19T13:28:57.000Z

2022-01-13T02:50:08.000Z

Chapter05/Exercise5.02/Exercise5.02.ipynb

PacktWorkshops/Applied-Deep-Learning-with-PyTorch

bcfe00b2a2c6ec5b823d40ee801d5332346f0ca8

[ "MIT" ]

28

2020-02-19T16:57:59.000Z

2022-03-14T07:57:51.000Z

2,350.514286

210,548

0.966016

[ [ [ "## Exercise 5.01", "_____no_output_____" ] ], [ [ "import numpy as np\nimport torch\nfrom torch import nn, optim\nfrom PIL import Image\nimport matplotlib.pyplot as plt\nfrom torchvision import transforms, models", "_____no_output_____" ], [ "imsize = 224\n\nloader = transforms.Compose([\n transforms.Resize(imsize), \n transforms.ToTensor(),\n transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225))])", "_____no_output_____" ], [ "def image_loader(image_name):\n image = Image.open(image_name)\n image = loader(image).unsqueeze(0)\n return image", "_____no_output_____" ], [ "content_img = image_loader(\"images/dog.jpg\")\nstyle_img = image_loader(\"images/matisse.jpg\")", "_____no_output_____" ], [ "unloader = transforms.Compose([\n transforms.Normalize((-0.485/0.229, -0.456/0.224, -0.406/0.225), (1/0.229, 1/0.224, 1/0.225)),\n transforms.ToPILImage()])", "_____no_output_____" ], [ "def tensor2image(tensor):\n image = tensor.clone() \n image = image.squeeze(0) \n image = unloader(image)\n return image", "_____no_output_____" ], [ "plt.figure()\nplt.imshow(tensor2image(content_img))\nplt.title(\"Content Image\")\nplt.show()\n\nplt.figure()\nplt.imshow(tensor2image(style_img))\nplt.title(\"Style Image\")\nplt.show()", "_____no_output_____" ] ], [ [ "## Exercise 5.02", "_____no_output_____" ] ], [ [ "model = models.vgg19(pretrained=True).features\n\nfor param in model.parameters():\n param.requires_grad_(False)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e86347ccc63ff6664936dea89493eb0d49ca98

64,075

ipynb

Jupyter Notebook

tutorials/chemistry/05_Sampling_potential_energy_surfaces.ipynb

azeemba/qiskit-tutorials

b138746092c967883fc363f7102226969bbf0507

[ "Apache-2.0" ]

1

2020-09-01T15:42:59.000Z

tutorials/chemistry/05_Sampling_potential_energy_surfaces.ipynb

azeemba/qiskit-tutorials

b138746092c967883fc363f7102226969bbf0507

[ "Apache-2.0" ]

null

tutorials/chemistry/05_Sampling_potential_energy_surfaces.ipynb

azeemba/qiskit-tutorials

b138746092c967883fc363f7102226969bbf0507

[ "Apache-2.0" ]

2

2019-11-04T01:23:31.000Z

2020-03-08T17:28:31.000Z

119.766355

23,964

0.862489

[ [ [ "# Sampling the potential energy surface ", "_____no_output_____" ], [ "## Introduction \n\nThis interactive notebook demonstrates how to utilize the Potential Energy Surface (PES) samplers algorithm of qiskit chemistry to generate the dissociation profile of a molecule. We use the Born-Oppenhemier Potential Energy Surface (BOPES)and demonstrate how to exploit bootstrapping and extrapolation to reduce the total number of function evaluations in computing the PES using the Variational Quantum Eigensolver (VQE). \n", "_____no_output_____" ] ], [ [ "# import common packages\nimport numpy as np\nimport pandas as pd\nimport matplotlib.pyplot as plt\nfrom functools import partial\n\n# qiskit\nfrom qiskit.aqua import QuantumInstance\nfrom qiskit import BasicAer\nfrom qiskit.aqua.algorithms import NumPyMinimumEigensolver, VQE, IQPE\nfrom qiskit.aqua.components.optimizers import SLSQP\nfrom qiskit.circuit.library import ExcitationPreserving\nfrom qiskit import BasicAer\nfrom qiskit.aqua.algorithms import NumPyMinimumEigensolver, VQE\nfrom qiskit.aqua.components.optimizers import SLSQP\n\n# chemistry components\nfrom qiskit.chemistry.components.initial_states import HartreeFock\nfrom qiskit.chemistry.components.variational_forms import UCCSD\nfrom qiskit.chemistry.drivers import PySCFDriver, UnitsType\nfrom qiskit.chemistry.core import Hamiltonian, TransformationType, QubitMappingType\nfrom qiskit.aqua.algorithms import VQAlgorithm, VQE, MinimumEigensolver\nfrom qiskit.chemistry.transformations import FermionicTransformation\nfrom qiskit.chemistry.drivers import PySCFDriver\nfrom qiskit.chemistry.algorithms.ground_state_solvers import GroundStateEigensolver\nfrom qiskit.chemistry.algorithms.pes_samplers.bopes_sampler import BOPESSampler\nfrom qiskit.chemistry.drivers.molecule import Molecule\nfrom qiskit.chemistry.algorithms.pes_samplers.extrapolator import *\n\nimport warnings\nwarnings.simplefilter('ignore', np.RankWarning)", "_____no_output_____" ] ], [ [ "Here, we use the H2 molecule as a model sysem for testing.", "_____no_output_____" ] ], [ [ "ft = FermionicTransformation()\ndriver = PySCFDriver()\nsolver = VQE(quantum_instance=\n QuantumInstance(backend=BasicAer.get_backend('statevector_simulator')))\nme_gsc = GroundStateEigensolver(ft, solver)", "_____no_output_____" ], [ "stretch1 = partial(Molecule.absolute_stretching, atom_pair=(1, 0))\nmol = Molecule(geometry=[('H', [0., 0., 0.]),\n ('H', [0., 0., 0.3])],\n degrees_of_freedom=[stretch1],\n )\n\n# pass molecule to PSYCF driver\ndriver = PySCFDriver(molecule=mol)", "_____no_output_____" ], [ "print(mol.geometry)", "[('H', [0.0, 0.0, 0.0]), ('H', [0.0, 0.0, 0.3])]\n" ] ], [ [ "### Make a perturbation to the molecule along the absolute_stretching dof", "_____no_output_____" ] ], [ [ "mol.perturbations = [0.2]\nprint(mol.geometry)\n\nmol.perturbations = [0.6]\nprint(mol.geometry)", "[('H', [0.0, 0.0, 0.0]), ('H', [0.0, 0.0, 0.8999999999999999])]\n[('H', [0.0, 0.0, 0.0]), ('H', [0.0, 0.0, 0.5])]\n" ] ], [ [ "# Calculate bond dissociation profile using BOPES Sampler\n\nHere, we pass the molecular information and the VQE to a built-in type called the BOPES Sampler. The BOPES Sampler allows the computation of the potential energy surface for a specified set of degrees of freedom/points of interest.", "_____no_output_____" ], [ "## First we compare no bootstrapping vs bootstrapping \n\nBootstrapping the BOPES sampler involves utilizing the optimal variational parameters for a given degree of freedom, say r (ex. interatomic distance) as the initial point for VQE at a later degree of freedom, say r + $\\epsilon$. By default, if boostrapping is set to True, all previous optimal parameters are used as initial points for the next runs.", "_____no_output_____" ] ], [ [ "stretch1 = partial(Molecule.absolute_stretching, atom_pair=(1, 0))\nmol = Molecule(geometry=[('H', [0., 0., 0.]),\n ('H', [0., 0., 0.3])],\n degrees_of_freedom=[stretch1],\n )\n\n# pass molecule to PSYCF driver\ndriver = PySCFDriver(molecule=mol)\n\n# Specify degree of freedom (points of interest)\npoints = np.linspace(0.1, 2, 20)\nresults_full = {} # full dictionary of results for each condition\nresults = {} # dictionary of (point,energy) results for each condition\nconditions = {False: 'no bootstrapping', True: 'bootstrapping'}\n\n\nfor value, bootstrap in conditions.items():\n # define instance to sampler\n bs = BOPESSampler(\n gss=me_gsc\n ,bootstrap=value\n ,num_bootstrap=None\n ,extrapolator=None)\n # execute\n res = bs.sample(driver,points)\n results_full[f'{bootstrap}'] = res.raw_results\n results[f'points_{bootstrap}'] = res.points\n results[f'energies_{bootstrap}'] = res.energies", "_____no_output_____" ] ], [ [ "# Compare to classical eigensolver\n", "_____no_output_____" ] ], [ [ "# define numpy solver\nsolver_numpy = NumPyMinimumEigensolver()\nme_gsc_numpy = GroundStateEigensolver(ft, solver_numpy)\nbs_classical = BOPESSampler(\n gss=me_gsc_numpy\n ,bootstrap=False\n ,num_bootstrap=None\n ,extrapolator=None)\n# execute\nres_np = bs_classical.sample(driver, points)\nresults_full['np'] = res_np.raw_results\nresults['points_np'] = res_np.points\nresults['energies_np'] = res_np.energies", "_____no_output_____" ] ], [ [ "## Plot results", "_____no_output_____" ] ], [ [ "fig = plt.figure()\nfor value, bootstrap in conditions.items():\n plt.plot(results[f'points_{bootstrap}'], results[f'energies_{bootstrap}'], label = f'{bootstrap}')\nplt.plot(results['points_np'], results['energies_np'], label = 'numpy')\nplt.legend()\nplt.title('Dissociation profile')\nplt.xlabel('Interatomic distance')\nplt.ylabel('Energy')", "_____no_output_____" ] ], [ [ "# Compare number of evaluations", "_____no_output_____" ] ], [ [ "for condition, result_full in results_full.items():\n print(condition)\n print('Total evaluations for ' + condition + ':')\n sum = 0\n for key in result_full:\n if condition is not 'np':\n sum += result_full[key]['raw_result']['cost_function_evals']\n else:\n sum = 0\n print(sum)", "no bootstrapping\nTotal evaluations for no bootstrapping:\n1714\nbootstrapping\nTotal evaluations for bootstrapping:\n1266\nnp\nTotal evaluations for np:\n0\n" ] ], [ [ "# Extrapolation \n\nHere, an extrapolator added that will try to fit each (param,point) set to some specified function and suggest an initial parameter set for the next point (degree of freedom). \n\n- Extrapolator is based on an external extrapolator that sets the 'window', that is, the number of previous points to use for extrapolation, while the internal extrapolator proceeds with the actual extrapolation.\n- In practice, the user sets the window by specifies an integer value to num_bootstrap - which also the number of previous points to use for bootstrapping. Additionally, the external extrapolator defines the space within how to extrapolate - here PCA, clustering and the standard window approach. \n\nIn practice, if no extrapolator is defined and bootstrapping is True, then all previous points will be bootstrapped. If an extrapolator list is defined and no points are specified for bootstrapping, then the extrapolation will be done based on all previous points.", "_____no_output_____" ], [ "1. Window Extrapolator: An extrapolator which wraps another extrapolator, limiting the internal extrapolator's ground truth parameter set to a fixed window size\n2. PCA Extrapolator: A wrapper extrapolator which reduces the points' dimensionality with PCA, performs extrapolation in the transformed pca space, and untransforms the results before returning.\n3. Sieve Extrapolator: A wrapper extrapolator which performs an extrapolation, then clusters the extrapolated parameter values into two large and small clusters, and sets the small clusters' parameters to zero.\n4. Polynomial Extrapolator: An extrapolator based on fitting each parameter to a polynomial function of a user-specified degree.\n5. Differential Extrapolator: An extrapolator based on treating each param set as a point in space, and performing regression to predict the param set for the next point. A user-specified degree also adds derivatives to the values in the point vectors which serve as features in the training data for the linear regression.", "_____no_output_____" ], [ "## Here we test two different extrapolation techniques", "_____no_output_____" ] ], [ [ "# define different extrapolators\ndegree = 1\nextrap_poly = Extrapolator.factory(\"poly\", degree = degree)\nextrap_diff = Extrapolator.factory(\"diff_model\", degree = degree)\nextrapolators = {'poly': extrap_poly, 'diff_model': extrap_diff}\n\nfor key in extrapolators:\n extrap_internal = extrapolators[key]\n extrap = Extrapolator.factory(\"window\", extrapolator = extrap_internal)\n # define extrapolator\n # BOPES sampler\n bs_extr = BOPESSampler(\n gss=me_gsc\n ,bootstrap=True\n ,num_bootstrap=None\n ,extrapolator=extrap)\n # execute\n res = bs_extr.sample(driver, points)\n \n results_full[f'{key}']= res.raw_results\n results[f'points_{key}'] = res.points\n results[f'energies_{key}'] = res.energies\n", "_____no_output_____" ] ], [ [ "## Plot results", "_____no_output_____" ] ], [ [ "fig = plt.figure()\nfor value, bootstrap in conditions.items():\n plt.plot(results[f'points_{bootstrap}'], results[f'energies_{bootstrap}'], label = f'{bootstrap}')\nplt.plot(results['points_np'], results['energies_np'], label = 'numpy')\nfor condition in extrapolators.keys():\n print(condition)\n plt.plot(results[f'points_{condition}'], results[f'energies_{condition}'], label = condition)\nplt.legend()\nplt.title('Dissociation profile')\nplt.xlabel('Interatomic distance')\nplt.ylabel('Energy')", "poly\ndiff_model\n" ] ], [ [ "# Compare number of evaluations", "_____no_output_____" ] ], [ [ "for condition, result_full in results_full.items():\n print(condition)\n print('Total evaluations for ' + condition + ':')\n sum = 0\n for key in results_full[condition].keys():\n if condition is not 'np':\n sum += results_full[condition][key]['raw_result']['cost_function_evals']\n else:\n sum = 0\n print(sum)", "no bootstrapping\nTotal evaluations for no bootstrapping:\n1714\nbootstrapping\nTotal evaluations for bootstrapping:\n1266\nnp\nTotal evaluations for np:\n0\npoly\nTotal evaluations for poly:\n715\ndiff_model\nTotal evaluations for diff_model:\n928\n" ], [ "import qiskit.tools.jupyter\n%qiskit_version_table\n%qiskit_copyright", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

d0e876c2f5cb741ffcd87af5adb4290712539b94

157,047

ipynb

Jupyter Notebook

weight-initialization/weight_initialization_exercise.ipynb

tengwu27/udacity-deep-learning

d9fd347b4ca35b268cd8622b7d40dd147ad0e93d

[ "MIT" ]

null

weight-initialization/weight_initialization_exercise.ipynb

tengwu27/udacity-deep-learning

d9fd347b4ca35b268cd8622b7d40dd147ad0e93d

[ "MIT" ]

1

2022-02-10T02:33:06.000Z

weight-initialization/weight_initialization_exercise.ipynb

tengwu27/udacity-deep-learning

d9fd347b4ca35b268cd8622b7d40dd147ad0e93d

[ "MIT" ]

null

205.290196

47,252

0.892102

[ [ [ "# Weight Initialization\nIn this lesson, you'll learn how to find good initial weights for a neural network. Weight initialization happens once, when a model is created and before it trains. Having good initial weights can place the neural network close to the optimal solution. This allows the neural network to come to the best solution quicker. \n\n<img src=\"notebook_ims/neuron_weights.png\" width=40%/>\n\n\n## Initial Weights and Observing Training Loss\n\nTo see how different weights perform, we'll test on the same dataset and neural network. That way, we know that any changes in model behavior are due to the weights and not any changing data or model structure. \n> We'll instantiate at least two of the same models, with _different_ initial weights and see how the training loss decreases over time, such as in the example below. \n\n<img src=\"notebook_ims/loss_comparison_ex.png\" width=60%/>\n\nSometimes the differences in training loss, over time, will be large and other times, certain weights offer only small improvements.\n\n### Dataset and Model\n\nWe'll train an MLP to classify images from the [Fashion-MNIST database](https://github.com/zalandoresearch/fashion-mnist) to demonstrate the effect of different initial weights. As a reminder, the FashionMNIST dataset contains images of clothing types; `classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']`. The images are normalized so that their pixel values are in a range [0.0 - 1.0). Run the cell below to download and load the dataset.\n\n---\n#### EXERCISE\n\n[Link to normalized distribution, exercise code](#normalex)\n\n---", "_____no_output_____" ], [ "### Import Libraries and Load [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)", "_____no_output_____" ] ], [ [ "import torch\nimport numpy as np\nfrom torchvision import datasets\nimport torchvision.transforms as transforms\nfrom torch.utils.data.sampler import SubsetRandomSampler\n\n# number of subprocesses to use for data loading\nnum_workers = 0\n# how many samples per batch to load\nbatch_size = 100\n# percentage of training set to use as validation\nvalid_size = 0.2\n\n# convert data to torch.FloatTensor\ntransform = transforms.ToTensor()\n\n# choose the training and test datasets\ntrain_data = datasets.FashionMNIST(root='data', train=True,\n download=True, transform=transform)\ntest_data = datasets.FashionMNIST(root='data', train=False,\n download=True, transform=transform)\n\n# obtain training indices that will be used for validation\nnum_train = len(train_data)\nindices = list(range(num_train))\nnp.random.shuffle(indices)\nsplit = int(np.floor(valid_size * num_train))\ntrain_idx, valid_idx = indices[split:], indices[:split]\n\n# define samplers for obtaining training and validation batches\ntrain_sampler = SubsetRandomSampler(train_idx)\nvalid_sampler = SubsetRandomSampler(valid_idx)\n\n# prepare data loaders (combine dataset and sampler)\ntrain_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,\n sampler=train_sampler, num_workers=num_workers)\nvalid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, \n sampler=valid_sampler, num_workers=num_workers)\ntest_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size, \n num_workers=num_workers)\n\n# specify the image classes\nclasses = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', \n 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']", "_____no_output_____" ] ], [ [ "### Visualize Some Training Data", "_____no_output_____" ] ], [ [ "import matplotlib.pyplot as plt\n%matplotlib inline\n \n# obtain one batch of training images\ndataiter = iter(train_loader)\nimages, labels = dataiter.next()\nimages = images.numpy()\n\n# plot the images in the batch, along with the corresponding labels\nfig = plt.figure(figsize=(25, 4))\nfor idx in np.arange(20):\n ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])\n ax.imshow(np.squeeze(images[idx]), cmap='gray')\n ax.set_title(classes[labels[idx]])", "/Users/tengwu/opt/anaconda3/envs/deep-learning/lib/python3.7/site-packages/ipykernel_launcher.py:12: MatplotlibDeprecationWarning: Passing non-integers as three-element position specification is deprecated since 3.3 and will be removed two minor releases later.\n if sys.path[0] == '':\n" ] ], [ [ "## Define the Model Architecture\n\nWe've defined the MLP that we'll use for classifying the dataset.\n\n### Neural Network\n<img style=\"float: left\" src=\"notebook_ims/neural_net.png\" width=50%/>\n\n\n* A 3 layer MLP with hidden dimensions of 256 and 128. \n\n* This MLP accepts a flattened image (784-value long vector) as input and produces 10 class scores as output.\n---\nWe'll test the effect of different initial weights on this 3 layer neural network with ReLU activations and an Adam optimizer. \n\nThe lessons you learn apply to other neural networks, including different activations and optimizers.", "_____no_output_____" ], [ "---\n## Initialize Weights\nLet's start looking at some initial weights.\n### All Zeros or Ones\nIf you follow the principle of [Occam's razor](https://en.wikipedia.org/wiki/Occam's_razor), you might think setting all the weights to 0 or 1 would be the best solution. This is not the case.\n\nWith every weight the same, all the neurons at each layer are producing the same output. This makes it hard to decide which weights to adjust.\n\nLet's compare the loss with all ones and all zero weights by defining two models with those constant weights.\n\nBelow, we are using PyTorch's [nn.init](https://pytorch.org/docs/stable/nn.html#torch-nn-init) to initialize each Linear layer with a constant weight. The init library provides a number of weight initialization functions that give you the ability to initialize the weights of each layer according to layer type.\n\nIn the case below, we look at every layer/module in our model. If it is a Linear layer (as all three layers are for this MLP), then we initialize those layer weights to be a `constant_weight` with bias=0 using the following code:\n>```\nif isinstance(m, nn.Linear):\n nn.init.constant_(m.weight, constant_weight)\n nn.init.constant_(m.bias, 0)\n```\n\nThe `constant_weight` is a value that you can pass in when you instantiate the model.", "_____no_output_____" ] ], [ [ "import torch.nn as nn\nimport torch.nn.functional as F\n\n# define the NN architecture\nclass Net(nn.Module):\n def __init__(self, hidden_1=256, hidden_2=128, constant_weight=None):\n super(Net, self).__init__()\n # linear layer (784 -> hidden_1)\n self.fc1 = nn.Linear(28 * 28, hidden_1)\n # linear layer (hidden_1 -> hidden_2)\n self.fc2 = nn.Linear(hidden_1, hidden_2)\n # linear layer (hidden_2 -> 10)\n self.fc3 = nn.Linear(hidden_2, 10)\n # dropout layer (p=0.2)\n self.dropout = nn.Dropout(0.2)\n \n # initialize the weights to a specified, constant value\n if(constant_weight is not None):\n for m in self.modules():\n if isinstance(m, nn.Linear):\n nn.init.constant_(m.weight, constant_weight)\n nn.init.constant_(m.bias, 0)\n \n \n def forward(self, x):\n # flatten image input\n x = x.view(-1, 28 * 28)\n # add hidden layer, with relu activation function\n x = F.relu(self.fc1(x))\n # add dropout layer\n x = self.dropout(x)\n # add hidden layer, with relu activation function\n x = F.relu(self.fc2(x))\n # add dropout layer\n x = self.dropout(x)\n # add output layer\n x = self.fc3(x)\n return x\n", "_____no_output_____" ] ], [ [ "### Compare Model Behavior\n\nBelow, we are using `helpers.compare_init_weights` to compare the training and validation loss for the two models we defined above, `model_0` and `model_1`. This function takes in a list of models (each with different initial weights), the name of the plot to produce, and the training and validation dataset loaders. For each given model, it will plot the training loss for the first 100 batches and print out the validation accuracy after 2 training epochs. *Note: if you've used a small batch_size, you may want to increase the number of epochs here to better compare how models behave after seeing a few hundred images.* \n\nWe plot the loss over the first 100 batches to better judge which model weights performed better at the start of training. **I recommend that you take a look at the code in `helpers.py` to look at the details behind how the models are trained, validated, and compared.**\n\nRun the cell below to see the difference between weights of all zeros against all ones.", "_____no_output_____" ] ], [ [ "# initialize two NN's with 0 and 1 constant weights\nmodel_0 = Net(constant_weight=0)\nmodel_1 = Net(constant_weight=1)", "_____no_output_____" ], [ "import helpers\nimport importlib\nimportlib.reload(helpers)\n\n# put them in list form to compare\nmodel_list = [(model_0, 'All Zeros'),\n (model_1, 'All Ones')]\n\n\n# plot the loss over the first 100 batches\nhelpers.compare_init_weights(model_list, \n 'All Zeros vs All Ones', \n train_loader,\n valid_loader)", "_____no_output_____" ] ], [ [ "As you can see the accuracy is close to guessing for both zeros and ones, around 10%.\n\nThe neural network is having a hard time determining which weights need to be changed, since the neurons have the same output for each layer. To avoid neurons with the same output, let's use unique weights. We can also randomly select these weights to avoid being stuck in a local minimum for each run.\n\nA good solution for getting these random weights is to sample from a uniform distribution.", "_____no_output_____" ], [ "### Uniform Distribution\nA [uniform distribution](https://en.wikipedia.org/wiki/Uniform_distribution) has the equal probability of picking any number from a set of numbers. We'll be picking from a continuous distribution, so the chance of picking the same number is low. We'll use NumPy's `np.random.uniform` function to pick random numbers from a uniform distribution.\n\n>#### [`np.random_uniform(low=0.0, high=1.0, size=None)`](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.uniform.html)\n>Outputs random values from a uniform distribution.\n\n>The generated values follow a uniform distribution in the range [low, high). The lower bound minval is included in the range, while the upper bound maxval is excluded.\n\n>- **low:** The lower bound on the range of random values to generate. Defaults to 0.\n- **high:** The upper bound on the range of random values to generate. Defaults to 1.\n- **size:** An int or tuple of ints that specify the shape of the output array.\n\nWe can visualize the uniform distribution by using a histogram. Let's map the values from `np.random_uniform(-3, 3, [1000])` to a histogram using the `helper.hist_dist` function. This will be `1000` random float values from `-3` to `3`, excluding the value `3`.", "_____no_output_____" ] ], [ [ "import importlib\nimportlib.reload(helpers)\nhelpers.hist_dist('Random Uniform (low=-3, high=3)', np.random.uniform(-3, 3, [1000]))", "_____no_output_____" ] ], [ [ "The histogram used 500 buckets for the 1000 values. Since the chance for any single bucket is the same, there should be around 2 values for each bucket. That's exactly what we see with the histogram. Some buckets have more and some have less, but they trend around 2.\n\nNow that you understand the uniform function, let's use PyTorch's `nn.init` to apply it to a model's initial weights.\n\n### Uniform Initialization, Baseline\n\n\nLet's see how well the neural network trains using a uniform weight initialization, where `low=0.0` and `high=1.0`. Below, I'll show you another way (besides in the Net class code) to initialize the weights of a network. To define weights outside of the model definition, you can:\n>1. Define a function that assigns weights by the type of network layer, *then* \n2. Apply those weights to an initialized model using `model.apply(fn)`, which applies a function to each model layer.\n\nThis time, we'll use `weight.data.uniform_` to initialize the weights of our model, directly.", "_____no_output_____" ] ], [ [ "# takes in a module and applies the specified weight initialization\ndef weights_init_uniform(m):\n classname = m.__class__.__name__\n # for every Linear layer in a model..\n if classname.find('Linear') != -1:\n # apply a uniform distribution to the weights and a bias=0\n m.weight.data.uniform_(0.0, 1.0)\n m.bias.data.fill_(0)", "_____no_output_____" ], [ "# create a new model with these weights\nmodel_uniform = Net()\nmodel_uniform.apply(weights_init_uniform)", "_____no_output_____" ], [ "# evaluate behavior \nhelpers.compare_init_weights([(model_uniform, 'Uniform Weights')], \n 'Uniform Baseline', \n train_loader,\n valid_loader)", "_____no_output_____" ] ], [ [ "---\nThe loss graph is showing the neural network is learning, which it didn't with all zeros or all ones. We're headed in the right direction!\n\n## General rule for setting weights\nThe general rule for setting the weights in a neural network is to set them to be close to zero without being too small. \n>Good practice is to start your weights in the range of $[-y, y]$ where $y=1/\\sqrt{n}$ \n($n$ is the number of inputs to a given neuron).\n\nLet's see if this holds true; let's create a baseline to compare with and center our uniform range over zero by shifting it over by 0.5. This will give us the range [-0.5, 0.5).", "_____no_output_____" ] ], [ [ "# takes in a module and applies the specified weight initialization\ndef weights_init_uniform_center(m):\n classname = m.__class__.__name__\n # for every Linear layer in a model..\n if classname.find('Linear') != -1:\n # apply a centered, uniform distribution to the weights\n m.weight.data.uniform_(-0.5, 0.5)\n m.bias.data.fill_(0)\n\n# create a new model with these weights\nmodel_centered = Net()\nmodel_centered.apply(weights_init_uniform_center)", "_____no_output_____" ] ], [ [ "Then let's create a distribution and model that uses the **general rule** for weight initialization; using the range $[-y, y]$, where $y=1/\\sqrt{n}$ .\n\nAnd finally, we'll compare the two models.", "_____no_output_____" ] ], [ [ "# takes in a module and applies the specified weight initialization\ndef weights_init_uniform_rule(m):\n classname = m.__class__.__name__\n # for every Linear layer in a model..\n if classname.find('Linear') != -1:\n # get the number of the inputs\n n = m.in_features\n y = 1.0/np.sqrt(n)\n m.weight.data.uniform_(-y, y)\n m.bias.data.fill_(0)\n\n# create a new model with these weights\nmodel_rule = Net()\nmodel_rule.apply(weights_init_uniform_rule)", "_____no_output_____" ], [ "# compare these two models\nmodel_list = [(model_centered, 'Centered Weights [-0.5, 0.5)'), \n (model_rule, 'General Rule [-y, y)')]\n\n# evaluate behavior \nhelpers.compare_init_weights(model_list, \n '[-0.5, 0.5) vs [-y, y)', \n train_loader,\n valid_loader)", "_____no_output_____" ] ], [ [ "This behavior is really promising! Not only is the loss decreasing, but it seems to do so very quickly for our uniform weights that follow the general rule; after only two epochs we get a fairly high validation accuracy and this should give you some intuition for why starting out with the right initial weights can really help your training process!\n\n---\n\nSince the uniform distribution has the same chance to pick *any value* in a range, what if we used a distribution that had a higher chance of picking numbers closer to 0? Let's look at the normal distribution.\n\n### Normal Distribution\nUnlike the uniform distribution, the [normal distribution](https://en.wikipedia.org/wiki/Normal_distribution) has a higher likelihood of picking number close to it's mean. To visualize it, let's plot values from NumPy's `np.random.normal` function to a histogram.\n\n>[np.random.normal(loc=0.0, scale=1.0, size=None)](https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.normal.html)\n\n>Outputs random values from a normal distribution.\n\n>- **loc:** The mean of the normal distribution.\n- **scale:** The standard deviation of the normal distribution.\n- **shape:** The shape of the output array.", "_____no_output_____" ] ], [ [ "helpers.hist_dist('Random Normal (mean=0.0, stddev=1.0)', np.random.normal(0, 2, size=[1000]))", "_____no_output_____" ] ], [ [ "Let's compare the normal distribution against the previous, rule-based, uniform distribution.\n\n<a id='normalex'></a>\n#### TODO: Define a weight initialization function that gets weights from a normal distribution \n> The normal distribution should have a mean of 0 and a standard deviation of $y=1/\\sqrt{n}$", "_____no_output_____" ] ], [ [ "## complete this function\ndef weights_init_normal(m):\n '''Takes in a module and initializes all linear layers with weight\n values taken from a normal distribution.'''\n \n classname = m.__class__.__name__\n # for every Linear layer in a model\n # m.weight.data shoud be taken from a normal distribution\n # m.bias.data should be 0\n if classname.find('Linear') != -1:\n # get the number of the inputs\n n = m.in_features\n y = 1.0/np.sqrt(n)\n m.weight.data.normal_(0, y)\n m.bias.data.fill_(0)\n ", "_____no_output_____" ], [ "## -- no need to change code below this line -- ##\n\n# create a new model with the rule-based, uniform weights\nmodel_uniform_rule = Net()\nmodel_uniform_rule.apply(weights_init_uniform_rule)\n\n# create a new model with the rule-based, NORMAL weights\nmodel_normal_rule = Net()\nmodel_normal_rule.apply(weights_init_normal)", "_____no_output_____" ], [ "# compare the two models\nmodel_list = [(model_uniform_rule, 'Uniform Rule [-y, y)'), \n (model_normal_rule, 'Normal Distribution')]\n\n# evaluate behavior \nhelpers.compare_init_weights(model_list, \n 'Uniform vs Normal', \n train_loader,\n valid_loader)", "_____no_output_____" ] ], [ [ "The normal distribution gives us pretty similar behavior compared to the uniform distribution, in this case. This is likely because our network is so small; a larger neural network will pick more weight values from each of these distributions, magnifying the effect of both initialization styles. In general, a normal distribution will result in better performance for a model.\n", "_____no_output_____" ], [ "---\n\n### Automatic Initialization\n\nLet's quickly take a look at what happens *without any explicit weight initialization*.", "_____no_output_____" ] ], [ [ "## Instantiate a model with _no_ explicit weight initialization \nmodel_no_rule = Net()\n\n# create a new model with the rule-based, uniform weights\nmodel_uniform_rule = Net()\nmodel_uniform_rule.apply(weights_init_uniform_rule)\n\n# create a new model with the rule-based, NORMAL weights\nmodel_normal_rule = Net()\nmodel_normal_rule.apply(weights_init_normal)\n\n# compare the two models\nmodel_list = [(model_uniform_rule, 'Uniform Rule [-y, y)'), \n (model_normal_rule, 'Normal Distribution'),\n (model_no_rule, 'no')]\n\n# evaluate behavior \nhelpers.compare_init_weights(model_list, \n 'Uniform vs Normal', \n train_loader,\n valid_loader)", "_____no_output_____" ], [ "## evaluate the behavior using helpers.compare_init_weights\n\n", "_____no_output_____" ] ], [ [ "As you complete this exercise, keep in mind these questions:\n* What initializaion strategy has the lowest training loss after two epochs? What about highest validation accuracy?\n* After testing all these initial weight options, which would you decide to use in a final classification model?", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ] ]

d0e88d02d8ea6c7ca0dc44005b763a48055c5f76

832,426

ipynb

Jupyter Notebook

notebooks/Assumptions.ipynb

victordalla/regression-diagnosis

d0dd04de0dac801726113a93f2a6c833307333ca

[ "MIT" ]

null

notebooks/Assumptions.ipynb

victordalla/regression-diagnosis

d0dd04de0dac801726113a93f2a6c833307333ca

[ "MIT" ]

null

notebooks/Assumptions.ipynb

victordalla/regression-diagnosis

d0dd04de0dac801726113a93f2a6c833307333ca

[ "MIT" ]

null

1,668.188377

180,860

0.957

[ [ [ "%load_ext autoreload\n%autoreload 2", "_____no_output_____" ], [ "from os import path\nimport sys, inspect\ncurrent_dir = path.dirname(path.abspath(inspect.getfile(inspect.currentframe())))\nparent_dir = path.dirname(current_dir)\nsys.path.insert(0, parent_dir) \n\nimport numpy as np\nimport pandas as pd\nimport statsmodels.formula.api as smf\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nsns.set()\n\n\nfrom nu_aesthetics.single_colors import brand, design\nfrom matplotlib.cm import register_cmap\n\n\nfrom support.shared_consts import *\nfrom support.utils import *", "_____no_output_____" ] ], [ [ "# Model\n\n$Y = \\beta_0 + \\beta_1 x_1 + \\dots + \\beta_k x_k + \\epsilon$\n\n$\\epsilon_i$ i.i.d. $N(0, 1)$\n\n$E = Y - \\hat{Y}$", "_____no_output_____" ], [ "## Canonical X", "_____no_output_____" ], [ "$Y = 6 + 1.3 x + \\epsilon$\n\n$\\epsilon_i$ i.i.d. $N(0, 1)$", "_____no_output_____" ] ], [ [ "x = x_fix.copy()\ne = e_fix.copy()\ny = y_fix.copy()\ndata = pd.DataFrame({\"x\": x, \"e\": e, \"y\": y})\n\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nprint(regressor.summary())\nax = plot_lmreg(data=data)\nplt.savefig(f\"../imgs/simul_model_canonical.png\", bbox_inches=\"tight\")\nplt.show()\n\ndata[\"pred\"] = predict(regressor, data)\nplot_resid(regressor, data)\nplt.savefig(f\"../imgs/simul_resid_canonical.png\", bbox_inches=\"tight\")\nplt.show()", " OLS Regression Results \n==============================================================================\nDep. Variable: y R-squared: 0.556\nModel: OLS Adj. R-squared: 0.555\nMethod: Least Squares F-statistic: 373.7\nDate: Tue, 25 May 2021 Prob (F-statistic): 1.57e-54\nTime: 13:10:35 Log-Likelihood: -1599.5\nNo. Observations: 300 AIC: 3203.\nDf Residuals: 298 BIC: 3210.\nDf Model: 1 \nCovariance Type: nonrobust \n==============================================================================\n coef std err t P>|t| [0.025 0.975]\n------------------------------------------------------------------------------\nIntercept 7.6801 3.360 2.285 0.023 1.067 14.293\nx 1.2881 0.067 19.332 0.000 1.157 1.419\n==============================================================================\nOmnibus: 1.939 Durbin-Watson: 2.048\nProb(Omnibus): 0.379 Jarque-Bera (JB): 1.745\nSkew: 0.080 Prob(JB): 0.418\nKurtosis: 2.663 Cond. No. 58.5\n==============================================================================\n\nNotes:\n[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.\n" ] ], [ [ "## Model validity\n\nNormality: the OLS is `robust`, having its `validity` even when their assumptions are false - hypothesis tests and confidence intervals are approximately correct for **non-normal large samples**.<br/>\nThe OLS might not be `efficient`, specially for **heavy-tailed** distributed errors. \nWhen the errors have a **skewed distribution**, the mean is no more a good measure of centrality and this compromises the `interpretation` of the OLS coefficients even though they might be valid. The remedy to this is usually a transformation on $Y$ to make it more symmetrical.", "_____no_output_____" ], [ "**Non linearity on covariate**\n\n$Y = 6 + 1.3 x ^2 + \\epsilon$", "_____no_output_____" ] ], [ [ "x = x_fix.copy() / 10\ne = e_fix.copy()\ny = true_params[\"b0\"] + true_params[\"b1\"] * x**2 + e\ndata = pd.DataFrame({\"x\": x, \"e\": e, \"y\": y})\n\nprint(\"Model: y ~ x\")\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nax = plot_lmreg(data=data, x=\"x\", y=\"y\", lowess=True)\nplt.savefig(f\"../imgs/simul_model_nonlin_cov_false.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\nplot_resid(regressor, data)\nplt.savefig(f\"../imgs/simul_resid_nonlin_cov_false.png\", bbox_inches=\"tight\")\nplt.show()\n\n\nprint(\"Model: y ~ x**2\")\ndata[\"x2\"] = data[\"x\"]**2\nregressor = smf.ols(formula=\"y ~ x2\", data=data).fit()\nax = plot_lmreg(data=data, x=\"x2\", y=\"y\", lowess=True)\nplt.savefig(f\"../imgs/simul_model_nonlin_cov_true.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data, x=\"x2\")\nplot_resid(regressor, data, x=\"x2\")\nplt.savefig(f\"../imgs/simul_resid_nonlin_cov_true.png\", bbox_inches=\"tight\")\nplt.show()", "Model: y ~ x\n" ] ], [ [ "**Non linearity on response**\n\n$Y^2 = 6 + 1.3 x + \\epsilon$", "_____no_output_____" ] ], [ [ "setting = \"canonical\"\n\nx = x_fix.copy()\ne = e_fix.copy()\ny = 100+true_params[\"b0\"] + true_params[\"b1\"] * x + e\ny = y**2\ndata = pd.DataFrame({\"x\": x, \"e\": e, \"y\": y})\n\nprint(\"Model: y ~ x\")\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nax = plot_lmreg(data=data, x=\"x\", y=\"y\", lowess=True)\nplt.savefig(f\"../imgs/simul_model_nonlin_y_false.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\ndata[\"qresid\"] = calculate_qresid(regressor, data)\nplot_resid(regressor, data)\nplt.savefig(f\"../imgs/simul_resid_nonlin_y_false.png\", bbox_inches=\"tight\")\nplt.show()\n\n\nprint(\"Model: sqrt(y) ~ x\")\ndata[\"sqrt_y\"] = np.sqrt(data[\"y\"])\nregressor = smf.ols(formula=\"sqrt_y ~ x\", data=data).fit()\nax = plot_lmreg(data=data, x=\"x\", y=\"sqrt_y\", lowess=True)\nplt.savefig(f\"../imgs/simul_model_nonlin_y_true.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\ndata[\"qresid\"] = calculate_qresid(regressor, data, y=\"sqrt_y\")\nplot_resid(regressor, data, y=\"sqrt_y\")\nplt.savefig(f\"../imgs/simul_resid_nonlin_y_true.png\", bbox_inches=\"tight\")\nplt.show()", "Model: y ~ x\n" ] ], [ [ "**Non independent**\n\nPositive-correlated data in a same with independent data between days.", "_____no_output_____" ] ], [ [ "x = x_fix.copy()\ndata = pd.DataFrame({\"x\": x, \"e\": None, \"y\": None})\ndata[\"date\"] = pd.Series(range(n//5)).sample(n, replace=True, random_state=0).values\nfor idx, [group, df_group] in enumerate(data.groupby(\"date\")):\n m = len(df_group)\n cov = np.full((m, m), 0.9 * true_params[\"scale\"]**2)\n np.fill_diagonal(cov, true_params[\"scale\"]**2)\n np.random.seed(idx)\n data.loc[data[\"date\"] == group, \"e\"] = np.random.multivariate_normal(np.zeros(m), cov, 1)[0]\n# e = np.random.normal(0, true_params[\"scale\"], 1)\n# np.random.seed(seed)\n# data.loc[data[\"date\"] == group, \"e\"] = e + np.random.normal(0, true_params[\"scale\"]/2, m)\ndata[\"y\"] = true_params[\"b0\"] + true_params[\"b1\"] * data[\"x\"] + data[\"e\"]\ndata = data.astype(\"float\")\n\nprint(\"Model: y ~ x\")\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nprint(regressor.summary())\nax = plot_lmreg(data=data, x=\"x\", y=\"y\")\nplt.savefig(f\"../imgs/simul_model_dep.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\nplot_resid(regressor, data.set_index(\"date\"))\nplt.savefig(f\"../imgs/simul_resid_dep.png\", bbox_inches=\"tight\")\nplt.show()\n\n\nprint(\"Model: y ~ x; aggregated residuals\")\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nprint(regressor.summary())\nax = plot_lmreg(data=data, x=\"x\", y=\"y\")\nplt.savefig(f\"../imgs/simul_model_dep_agg.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\ndata = data.groupby(\"date\").mean()\nplot_resid(regressor, data.set_index(\"x\"))\nplt.savefig(f\"../imgs/simul_resid_dep_agg.png\", bbox_inches=\"tight\")\nplt.show()\n\n\nprint(\"Model: y ~ date\")\ndata = data.groupby(\"date\").mean().reset_index()\nregressor = smf.ols(formula=\"y ~ date\", data=data).fit()\nprint(regressor.summary())\nax = plot_lmreg(data=data, x=\"date\", y=\"y\", lowess=True)\nplt.savefig(f\"../imgs/simul_model_dep_date.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data, x=\"date\")\nplot_resid(regressor, data.set_index(\"date\"), x=\"date\")\nplt.savefig(f\"../imgs/simul_resid_dep_date.png\", bbox_inches=\"tight\")\nplt.show()", "_____no_output_____" ] ], [ [ "**Non-constant variance**", "_____no_output_____" ] ], [ [ "setting = \"canonical\"\n\nx = x_fix.copy()\ne = e_fix.copy()\nmu = 100 + true_params[\"b1\"] * x\ne = (mu)**0.5 * e\ny = true_params[\"b0\"] + true_params[\"b1\"] * x + e\ndata = pd.DataFrame({\"x\": x, \"e\": e, \"y\": y})\n\nprint(\"Model: y ~ x\")\nregressor = smf.ols(formula=\"y ~ x\", data=data).fit()\nax = plot_lmreg(data=data, x=\"x\", y=\"y\")\nsns.regplot(x=\"x\",y=\"y\", data=data, ax=ax,\n lowess=True, scatter=False,\n color=brand.NU_DARK_PURPLE_MATPLOT, line_kws={\"linestyle\": \"--\"})\nplt.savefig(f\"../imgs/simul_model_nonconst_var.png\", bbox_inches=\"tight\")\nplt.show()\ndata[\"pred\"] = predict(regressor, data)\ndata[\"qresid\"] = calculate_qresid(regressor, data)\nplot_resid(regressor, data)\nplt.savefig(f\"../imgs/simul_model_nonconst_var.png\", bbox_inches=\"tight\")\nplt.show()", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e89d0884656fcc4611ddb9621fc96475ac2ab4

351,422

ipynb

Jupyter Notebook

Lab8.ipynb

leolinxup6/tf-

2792226afcaf43446e2af229116b14d4c7f70847

[ "MIT" ]

45

2019-09-07T01:24:50.000Z

2022-03-01T03:26:44.000Z

Lab8.ipynb

leolinxup6/tf-

2792226afcaf43446e2af229116b14d4c7f70847

[ "MIT" ]

null

Lab8.ipynb

leolinxup6/tf-

2792226afcaf43446e2af229116b14d4c7f70847

[ "MIT" ]

42

2019-08-22T23:04:15.000Z

2022-03-30T23:00:04.000Z

294.569992

126,280

0.875557

[ [ [ "# 實驗：實作InceptionV3網路架構", "_____no_output_____" ], [ "<table class=\"tfo-notebook-buttons\" align=\"left\">\n <td>\n <a target=\"_blank\" href=\"https://colab.research.google.com/github/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb\"><img src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" />Run in Google Colab</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://github.com/taipeitechmmslab/MMSLAB-TF2/blob/master/Lab8.ipynb\"><img src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" />View source on GitHub</a>\n </td>\n</table>", "_____no_output_____" ], [ "### Import必要套件", "_____no_output_____" ] ], [ [ "import numpy as np\nimport matplotlib.pyplot as plt\nimport tensorflow as tf", "_____no_output_____" ] ], [ [ "---\n## Keras Applications\n### 創建InceptionV3網路架構\n- 輸入大小(預設)：(299, 299, 3)\n- 權重(預設)：`imagenet`\n- 輸出類別(預設)：1000個類別", "_____no_output_____" ] ], [ [ "model = tf.keras.applications.InceptionV3(include_top=True, weights='imagenet')", "Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/inception_v3/inception_v3_weights_tf_dim_ordering_tf_kernels.h5\n96116736/96112376 [==============================] - 22s 0us/step\n" ] ], [ [ "透過`model.summary`可以察看網路模型的每一層資訊：", "_____no_output_____" ] ], [ [ "model.summary()", "Model: \"inception_v3\"\n__________________________________________________________________________________________________\nLayer (type) Output Shape Param # Connected to \n==================================================================================================\ninput_1 (InputLayer) [(None, 299, 299, 3) 0 \n__________________________________________________________________________________________________\nconv2d (Conv2D) (None, 149, 149, 32) 864 input_1[0][0] \n__________________________________________________________________________________________________\nbatch_normalization (BatchNorma (None, 149, 149, 32) 96 conv2d[0][0] \n__________________________________________________________________________________________________\nactivation (Activation) (None, 149, 149, 32) 0 batch_normalization[0][0] \n__________________________________________________________________________________________________\nconv2d_1 (Conv2D) (None, 147, 147, 32) 9216 activation[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_1 (BatchNor (None, 147, 147, 32) 96 conv2d_1[0][0] \n__________________________________________________________________________________________________\nactivation_1 (Activation) (None, 147, 147, 32) 0 batch_normalization_1[0][0] \n__________________________________________________________________________________________________\nconv2d_2 (Conv2D) (None, 147, 147, 64) 18432 activation_1[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_2 (BatchNor (None, 147, 147, 64) 192 conv2d_2[0][0] \n__________________________________________________________________________________________________\nactivation_2 (Activation) (None, 147, 147, 64) 0 batch_normalization_2[0][0] \n__________________________________________________________________________________________________\nmax_pooling2d (MaxPooling2D) (None, 73, 73, 64) 0 activation_2[0][0] \n__________________________________________________________________________________________________\nconv2d_3 (Conv2D) (None, 73, 73, 80) 5120 max_pooling2d[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_3 (BatchNor (None, 73, 73, 80) 240 conv2d_3[0][0] \n__________________________________________________________________________________________________\nactivation_3 (Activation) (None, 73, 73, 80) 0 batch_normalization_3[0][0] \n__________________________________________________________________________________________________\nconv2d_4 (Conv2D) (None, 71, 71, 192) 138240 activation_3[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_4 (BatchNor (None, 71, 71, 192) 576 conv2d_4[0][0] \n__________________________________________________________________________________________________\nactivation_4 (Activation) (None, 71, 71, 192) 0 batch_normalization_4[0][0] \n__________________________________________________________________________________________________\nmax_pooling2d_1 (MaxPooling2D) (None, 35, 35, 192) 0 activation_4[0][0] \n__________________________________________________________________________________________________\nconv2d_8 (Conv2D) (None, 35, 35, 64) 12288 max_pooling2d_1[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_8 (BatchNor (None, 35, 35, 64) 192 conv2d_8[0][0] \n__________________________________________________________________________________________________\nactivation_8 (Activation) (None, 35, 35, 64) 0 batch_normalization_8[0][0] \n__________________________________________________________________________________________________\nconv2d_6 (Conv2D) (None, 35, 35, 48) 9216 max_pooling2d_1[0][0] \n__________________________________________________________________________________________________\nconv2d_9 (Conv2D) (None, 35, 35, 96) 55296 activation_8[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_6 (BatchNor (None, 35, 35, 48) 144 conv2d_6[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_9 (BatchNor (None, 35, 35, 96) 288 conv2d_9[0][0] \n__________________________________________________________________________________________________\nactivation_6 (Activation) (None, 35, 35, 48) 0 batch_normalization_6[0][0] \n__________________________________________________________________________________________________\nactivation_9 (Activation) (None, 35, 35, 96) 0 batch_normalization_9[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d (AveragePooli (None, 35, 35, 192) 0 max_pooling2d_1[0][0] \n__________________________________________________________________________________________________\nconv2d_5 (Conv2D) (None, 35, 35, 64) 12288 max_pooling2d_1[0][0] \n__________________________________________________________________________________________________\nconv2d_7 (Conv2D) (None, 35, 35, 64) 76800 activation_6[0][0] \n__________________________________________________________________________________________________\nconv2d_10 (Conv2D) (None, 35, 35, 96) 82944 activation_9[0][0] \n__________________________________________________________________________________________________\nconv2d_11 (Conv2D) (None, 35, 35, 32) 6144 average_pooling2d[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_5 (BatchNor (None, 35, 35, 64) 192 conv2d_5[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_7 (BatchNor (None, 35, 35, 64) 192 conv2d_7[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_10 (BatchNo (None, 35, 35, 96) 288 conv2d_10[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_11 (BatchNo (None, 35, 35, 32) 96 conv2d_11[0][0] \n__________________________________________________________________________________________________\nactivation_5 (Activation) (None, 35, 35, 64) 0 batch_normalization_5[0][0] \n__________________________________________________________________________________________________\nactivation_7 (Activation) (None, 35, 35, 64) 0 batch_normalization_7[0][0] \n__________________________________________________________________________________________________\nactivation_10 (Activation) (None, 35, 35, 96) 0 batch_normalization_10[0][0] \n__________________________________________________________________________________________________\nactivation_11 (Activation) (None, 35, 35, 32) 0 batch_normalization_11[0][0] \n__________________________________________________________________________________________________\nmixed0 (Concatenate) (None, 35, 35, 256) 0 activation_5[0][0] \n activation_7[0][0] \n activation_10[0][0] \n activation_11[0][0] \n__________________________________________________________________________________________________\nconv2d_15 (Conv2D) (None, 35, 35, 64) 16384 mixed0[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_15 (BatchNo (None, 35, 35, 64) 192 conv2d_15[0][0] \n__________________________________________________________________________________________________\nactivation_15 (Activation) (None, 35, 35, 64) 0 batch_normalization_15[0][0] \n__________________________________________________________________________________________________\nconv2d_13 (Conv2D) (None, 35, 35, 48) 12288 mixed0[0][0] \n__________________________________________________________________________________________________\nconv2d_16 (Conv2D) (None, 35, 35, 96) 55296 activation_15[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_13 (BatchNo (None, 35, 35, 48) 144 conv2d_13[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_16 (BatchNo (None, 35, 35, 96) 288 conv2d_16[0][0] \n__________________________________________________________________________________________________\nactivation_13 (Activation) (None, 35, 35, 48) 0 batch_normalization_13[0][0] \n__________________________________________________________________________________________________\nactivation_16 (Activation) (None, 35, 35, 96) 0 batch_normalization_16[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_1 (AveragePoo (None, 35, 35, 256) 0 mixed0[0][0] \n__________________________________________________________________________________________________\nconv2d_12 (Conv2D) (None, 35, 35, 64) 16384 mixed0[0][0] \n__________________________________________________________________________________________________\nconv2d_14 (Conv2D) (None, 35, 35, 64) 76800 activation_13[0][0] \n__________________________________________________________________________________________________\nconv2d_17 (Conv2D) (None, 35, 35, 96) 82944 activation_16[0][0] \n__________________________________________________________________________________________________\nconv2d_18 (Conv2D) (None, 35, 35, 64) 16384 average_pooling2d_1[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_12 (BatchNo (None, 35, 35, 64) 192 conv2d_12[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_14 (BatchNo (None, 35, 35, 64) 192 conv2d_14[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_17 (BatchNo (None, 35, 35, 96) 288 conv2d_17[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_18 (BatchNo (None, 35, 35, 64) 192 conv2d_18[0][0] \n__________________________________________________________________________________________________\nactivation_12 (Activation) (None, 35, 35, 64) 0 batch_normalization_12[0][0] \n__________________________________________________________________________________________________\nactivation_14 (Activation) (None, 35, 35, 64) 0 batch_normalization_14[0][0] \n__________________________________________________________________________________________________\nactivation_17 (Activation) (None, 35, 35, 96) 0 batch_normalization_17[0][0] \n__________________________________________________________________________________________________\nactivation_18 (Activation) (None, 35, 35, 64) 0 batch_normalization_18[0][0] \n__________________________________________________________________________________________________\nmixed1 (Concatenate) (None, 35, 35, 288) 0 activation_12[0][0] \n activation_14[0][0] \n activation_17[0][0] \n activation_18[0][0] \n__________________________________________________________________________________________________\nconv2d_22 (Conv2D) (None, 35, 35, 64) 18432 mixed1[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_22 (BatchNo (None, 35, 35, 64) 192 conv2d_22[0][0] \n__________________________________________________________________________________________________\nactivation_22 (Activation) (None, 35, 35, 64) 0 batch_normalization_22[0][0] \n__________________________________________________________________________________________________\nconv2d_20 (Conv2D) (None, 35, 35, 48) 13824 mixed1[0][0] \n__________________________________________________________________________________________________\nconv2d_23 (Conv2D) (None, 35, 35, 96) 55296 activation_22[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_20 (BatchNo (None, 35, 35, 48) 144 conv2d_20[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_23 (BatchNo (None, 35, 35, 96) 288 conv2d_23[0][0] \n__________________________________________________________________________________________________\nactivation_20 (Activation) (None, 35, 35, 48) 0 batch_normalization_20[0][0] \n__________________________________________________________________________________________________\nactivation_23 (Activation) (None, 35, 35, 96) 0 batch_normalization_23[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_2 (AveragePoo (None, 35, 35, 288) 0 mixed1[0][0] \n__________________________________________________________________________________________________\nconv2d_19 (Conv2D) (None, 35, 35, 64) 18432 mixed1[0][0] \n__________________________________________________________________________________________________\nconv2d_21 (Conv2D) (None, 35, 35, 64) 76800 activation_20[0][0] \n__________________________________________________________________________________________________\nconv2d_24 (Conv2D) (None, 35, 35, 96) 82944 activation_23[0][0] \n__________________________________________________________________________________________________\nconv2d_25 (Conv2D) (None, 35, 35, 64) 18432 average_pooling2d_2[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_19 (BatchNo (None, 35, 35, 64) 192 conv2d_19[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_21 (BatchNo (None, 35, 35, 64) 192 conv2d_21[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_24 (BatchNo (None, 35, 35, 96) 288 conv2d_24[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_25 (BatchNo (None, 35, 35, 64) 192 conv2d_25[0][0] \n__________________________________________________________________________________________________\nactivation_19 (Activation) (None, 35, 35, 64) 0 batch_normalization_19[0][0] \n__________________________________________________________________________________________________\nactivation_21 (Activation) (None, 35, 35, 64) 0 batch_normalization_21[0][0] \n__________________________________________________________________________________________________\nactivation_24 (Activation) (None, 35, 35, 96) 0 batch_normalization_24[0][0] \n__________________________________________________________________________________________________\nactivation_25 (Activation) (None, 35, 35, 64) 0 batch_normalization_25[0][0] \n__________________________________________________________________________________________________\nmixed2 (Concatenate) (None, 35, 35, 288) 0 activation_19[0][0] \n activation_21[0][0] \n activation_24[0][0] \n activation_25[0][0] \n__________________________________________________________________________________________________\nconv2d_27 (Conv2D) (None, 35, 35, 64) 18432 mixed2[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_27 (BatchNo (None, 35, 35, 64) 192 conv2d_27[0][0] \n__________________________________________________________________________________________________\nactivation_27 (Activation) (None, 35, 35, 64) 0 batch_normalization_27[0][0] \n__________________________________________________________________________________________________\nconv2d_28 (Conv2D) (None, 35, 35, 96) 55296 activation_27[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_28 (BatchNo (None, 35, 35, 96) 288 conv2d_28[0][0] \n__________________________________________________________________________________________________\nactivation_28 (Activation) (None, 35, 35, 96) 0 batch_normalization_28[0][0] \n__________________________________________________________________________________________________\nconv2d_26 (Conv2D) (None, 17, 17, 384) 995328 mixed2[0][0] \n__________________________________________________________________________________________________\nconv2d_29 (Conv2D) (None, 17, 17, 96) 82944 activation_28[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_26 (BatchNo (None, 17, 17, 384) 1152 conv2d_26[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_29 (BatchNo (None, 17, 17, 96) 288 conv2d_29[0][0] \n__________________________________________________________________________________________________\nactivation_26 (Activation) (None, 17, 17, 384) 0 batch_normalization_26[0][0] \n__________________________________________________________________________________________________\nactivation_29 (Activation) (None, 17, 17, 96) 0 batch_normalization_29[0][0] \n__________________________________________________________________________________________________\nmax_pooling2d_2 (MaxPooling2D) (None, 17, 17, 288) 0 mixed2[0][0] \n__________________________________________________________________________________________________\nmixed3 (Concatenate) (None, 17, 17, 768) 0 activation_26[0][0] \n activation_29[0][0] \n max_pooling2d_2[0][0] \n__________________________________________________________________________________________________\nconv2d_34 (Conv2D) (None, 17, 17, 128) 98304 mixed3[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_34 (BatchNo (None, 17, 17, 128) 384 conv2d_34[0][0] \n__________________________________________________________________________________________________\nactivation_34 (Activation) (None, 17, 17, 128) 0 batch_normalization_34[0][0] \n__________________________________________________________________________________________________\nconv2d_35 (Conv2D) (None, 17, 17, 128) 114688 activation_34[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_35 (BatchNo (None, 17, 17, 128) 384 conv2d_35[0][0] \n__________________________________________________________________________________________________\nactivation_35 (Activation) (None, 17, 17, 128) 0 batch_normalization_35[0][0] \n__________________________________________________________________________________________________\nconv2d_31 (Conv2D) (None, 17, 17, 128) 98304 mixed3[0][0] \n__________________________________________________________________________________________________\nconv2d_36 (Conv2D) (None, 17, 17, 128) 114688 activation_35[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_31 (BatchNo (None, 17, 17, 128) 384 conv2d_31[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_36 (BatchNo (None, 17, 17, 128) 384 conv2d_36[0][0] \n__________________________________________________________________________________________________\nactivation_31 (Activation) (None, 17, 17, 128) 0 batch_normalization_31[0][0] \n__________________________________________________________________________________________________\nactivation_36 (Activation) (None, 17, 17, 128) 0 batch_normalization_36[0][0] \n__________________________________________________________________________________________________\nconv2d_32 (Conv2D) (None, 17, 17, 128) 114688 activation_31[0][0] \n__________________________________________________________________________________________________\nconv2d_37 (Conv2D) (None, 17, 17, 128) 114688 activation_36[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_32 (BatchNo (None, 17, 17, 128) 384 conv2d_32[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_37 (BatchNo (None, 17, 17, 128) 384 conv2d_37[0][0] \n__________________________________________________________________________________________________\nactivation_32 (Activation) (None, 17, 17, 128) 0 batch_normalization_32[0][0] \n__________________________________________________________________________________________________\nactivation_37 (Activation) (None, 17, 17, 128) 0 batch_normalization_37[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_3 (AveragePoo (None, 17, 17, 768) 0 mixed3[0][0] \n__________________________________________________________________________________________________\nconv2d_30 (Conv2D) (None, 17, 17, 192) 147456 mixed3[0][0] \n__________________________________________________________________________________________________\nconv2d_33 (Conv2D) (None, 17, 17, 192) 172032 activation_32[0][0] \n__________________________________________________________________________________________________\nconv2d_38 (Conv2D) (None, 17, 17, 192) 172032 activation_37[0][0] \n__________________________________________________________________________________________________\nconv2d_39 (Conv2D) (None, 17, 17, 192) 147456 average_pooling2d_3[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_30 (BatchNo (None, 17, 17, 192) 576 conv2d_30[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_33 (BatchNo (None, 17, 17, 192) 576 conv2d_33[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_38 (BatchNo (None, 17, 17, 192) 576 conv2d_38[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_39 (BatchNo (None, 17, 17, 192) 576 conv2d_39[0][0] \n__________________________________________________________________________________________________\nactivation_30 (Activation) (None, 17, 17, 192) 0 batch_normalization_30[0][0] \n__________________________________________________________________________________________________\nactivation_33 (Activation) (None, 17, 17, 192) 0 batch_normalization_33[0][0] \n__________________________________________________________________________________________________\nactivation_38 (Activation) (None, 17, 17, 192) 0 batch_normalization_38[0][0] \n__________________________________________________________________________________________________\nactivation_39 (Activation) (None, 17, 17, 192) 0 batch_normalization_39[0][0] \n__________________________________________________________________________________________________\nmixed4 (Concatenate) (None, 17, 17, 768) 0 activation_30[0][0] \n activation_33[0][0] \n activation_38[0][0] \n activation_39[0][0] \n__________________________________________________________________________________________________\nconv2d_44 (Conv2D) (None, 17, 17, 160) 122880 mixed4[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_44 (BatchNo (None, 17, 17, 160) 480 conv2d_44[0][0] \n__________________________________________________________________________________________________\nactivation_44 (Activation) (None, 17, 17, 160) 0 batch_normalization_44[0][0] \n__________________________________________________________________________________________________\nconv2d_45 (Conv2D) (None, 17, 17, 160) 179200 activation_44[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_45 (BatchNo (None, 17, 17, 160) 480 conv2d_45[0][0] \n__________________________________________________________________________________________________\nactivation_45 (Activation) (None, 17, 17, 160) 0 batch_normalization_45[0][0] \n__________________________________________________________________________________________________\nconv2d_41 (Conv2D) (None, 17, 17, 160) 122880 mixed4[0][0] \n__________________________________________________________________________________________________\nconv2d_46 (Conv2D) (None, 17, 17, 160) 179200 activation_45[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_41 (BatchNo (None, 17, 17, 160) 480 conv2d_41[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_46 (BatchNo (None, 17, 17, 160) 480 conv2d_46[0][0] \n__________________________________________________________________________________________________\nactivation_41 (Activation) (None, 17, 17, 160) 0 batch_normalization_41[0][0] \n__________________________________________________________________________________________________\nactivation_46 (Activation) (None, 17, 17, 160) 0 batch_normalization_46[0][0] \n__________________________________________________________________________________________________\nconv2d_42 (Conv2D) (None, 17, 17, 160) 179200 activation_41[0][0] \n__________________________________________________________________________________________________\nconv2d_47 (Conv2D) (None, 17, 17, 160) 179200 activation_46[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_42 (BatchNo (None, 17, 17, 160) 480 conv2d_42[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_47 (BatchNo (None, 17, 17, 160) 480 conv2d_47[0][0] \n__________________________________________________________________________________________________\nactivation_42 (Activation) (None, 17, 17, 160) 0 batch_normalization_42[0][0] \n__________________________________________________________________________________________________\nactivation_47 (Activation) (None, 17, 17, 160) 0 batch_normalization_47[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_4 (AveragePoo (None, 17, 17, 768) 0 mixed4[0][0] \n__________________________________________________________________________________________________\nconv2d_40 (Conv2D) (None, 17, 17, 192) 147456 mixed4[0][0] \n__________________________________________________________________________________________________\nconv2d_43 (Conv2D) (None, 17, 17, 192) 215040 activation_42[0][0] \n__________________________________________________________________________________________________\nconv2d_48 (Conv2D) (None, 17, 17, 192) 215040 activation_47[0][0] \n__________________________________________________________________________________________________\nconv2d_49 (Conv2D) (None, 17, 17, 192) 147456 average_pooling2d_4[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_40 (BatchNo (None, 17, 17, 192) 576 conv2d_40[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_43 (BatchNo (None, 17, 17, 192) 576 conv2d_43[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_48 (BatchNo (None, 17, 17, 192) 576 conv2d_48[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_49 (BatchNo (None, 17, 17, 192) 576 conv2d_49[0][0] \n__________________________________________________________________________________________________\nactivation_40 (Activation) (None, 17, 17, 192) 0 batch_normalization_40[0][0] \n__________________________________________________________________________________________________\nactivation_43 (Activation) (None, 17, 17, 192) 0 batch_normalization_43[0][0] \n__________________________________________________________________________________________________\nactivation_48 (Activation) (None, 17, 17, 192) 0 batch_normalization_48[0][0] \n__________________________________________________________________________________________________\nactivation_49 (Activation) (None, 17, 17, 192) 0 batch_normalization_49[0][0] \n__________________________________________________________________________________________________\nmixed5 (Concatenate) (None, 17, 17, 768) 0 activation_40[0][0] \n activation_43[0][0] \n activation_48[0][0] \n activation_49[0][0] \n__________________________________________________________________________________________________\nconv2d_54 (Conv2D) (None, 17, 17, 160) 122880 mixed5[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_54 (BatchNo (None, 17, 17, 160) 480 conv2d_54[0][0] \n__________________________________________________________________________________________________\nactivation_54 (Activation) (None, 17, 17, 160) 0 batch_normalization_54[0][0] \n__________________________________________________________________________________________________\nconv2d_55 (Conv2D) (None, 17, 17, 160) 179200 activation_54[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_55 (BatchNo (None, 17, 17, 160) 480 conv2d_55[0][0] \n__________________________________________________________________________________________________\nactivation_55 (Activation) (None, 17, 17, 160) 0 batch_normalization_55[0][0] \n__________________________________________________________________________________________________\nconv2d_51 (Conv2D) (None, 17, 17, 160) 122880 mixed5[0][0] \n__________________________________________________________________________________________________\nconv2d_56 (Conv2D) (None, 17, 17, 160) 179200 activation_55[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_51 (BatchNo (None, 17, 17, 160) 480 conv2d_51[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_56 (BatchNo (None, 17, 17, 160) 480 conv2d_56[0][0] \n__________________________________________________________________________________________________\nactivation_51 (Activation) (None, 17, 17, 160) 0 batch_normalization_51[0][0] \n__________________________________________________________________________________________________\nactivation_56 (Activation) (None, 17, 17, 160) 0 batch_normalization_56[0][0] \n__________________________________________________________________________________________________\nconv2d_52 (Conv2D) (None, 17, 17, 160) 179200 activation_51[0][0] \n__________________________________________________________________________________________________\nconv2d_57 (Conv2D) (None, 17, 17, 160) 179200 activation_56[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_52 (BatchNo (None, 17, 17, 160) 480 conv2d_52[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_57 (BatchNo (None, 17, 17, 160) 480 conv2d_57[0][0] \n__________________________________________________________________________________________________\nactivation_52 (Activation) (None, 17, 17, 160) 0 batch_normalization_52[0][0] \n__________________________________________________________________________________________________\nactivation_57 (Activation) (None, 17, 17, 160) 0 batch_normalization_57[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_5 (AveragePoo (None, 17, 17, 768) 0 mixed5[0][0] \n__________________________________________________________________________________________________\nconv2d_50 (Conv2D) (None, 17, 17, 192) 147456 mixed5[0][0] \n__________________________________________________________________________________________________\nconv2d_53 (Conv2D) (None, 17, 17, 192) 215040 activation_52[0][0] \n__________________________________________________________________________________________________\nconv2d_58 (Conv2D) (None, 17, 17, 192) 215040 activation_57[0][0] \n__________________________________________________________________________________________________\nconv2d_59 (Conv2D) (None, 17, 17, 192) 147456 average_pooling2d_5[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_50 (BatchNo (None, 17, 17, 192) 576 conv2d_50[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_53 (BatchNo (None, 17, 17, 192) 576 conv2d_53[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_58 (BatchNo (None, 17, 17, 192) 576 conv2d_58[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_59 (BatchNo (None, 17, 17, 192) 576 conv2d_59[0][0] \n__________________________________________________________________________________________________\nactivation_50 (Activation) (None, 17, 17, 192) 0 batch_normalization_50[0][0] \n__________________________________________________________________________________________________\nactivation_53 (Activation) (None, 17, 17, 192) 0 batch_normalization_53[0][0] \n__________________________________________________________________________________________________\nactivation_58 (Activation) (None, 17, 17, 192) 0 batch_normalization_58[0][0] \n__________________________________________________________________________________________________\nactivation_59 (Activation) (None, 17, 17, 192) 0 batch_normalization_59[0][0] \n__________________________________________________________________________________________________\nmixed6 (Concatenate) (None, 17, 17, 768) 0 activation_50[0][0] \n activation_53[0][0] \n activation_58[0][0] \n activation_59[0][0] \n__________________________________________________________________________________________________\nconv2d_64 (Conv2D) (None, 17, 17, 192) 147456 mixed6[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_64 (BatchNo (None, 17, 17, 192) 576 conv2d_64[0][0] \n__________________________________________________________________________________________________\nactivation_64 (Activation) (None, 17, 17, 192) 0 batch_normalization_64[0][0] \n__________________________________________________________________________________________________\nconv2d_65 (Conv2D) (None, 17, 17, 192) 258048 activation_64[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_65 (BatchNo (None, 17, 17, 192) 576 conv2d_65[0][0] \n__________________________________________________________________________________________________\nactivation_65 (Activation) (None, 17, 17, 192) 0 batch_normalization_65[0][0] \n__________________________________________________________________________________________________\nconv2d_61 (Conv2D) (None, 17, 17, 192) 147456 mixed6[0][0] \n__________________________________________________________________________________________________\nconv2d_66 (Conv2D) (None, 17, 17, 192) 258048 activation_65[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_61 (BatchNo (None, 17, 17, 192) 576 conv2d_61[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_66 (BatchNo (None, 17, 17, 192) 576 conv2d_66[0][0] \n__________________________________________________________________________________________________\nactivation_61 (Activation) (None, 17, 17, 192) 0 batch_normalization_61[0][0] \n__________________________________________________________________________________________________\nactivation_66 (Activation) (None, 17, 17, 192) 0 batch_normalization_66[0][0] \n__________________________________________________________________________________________________\nconv2d_62 (Conv2D) (None, 17, 17, 192) 258048 activation_61[0][0] \n__________________________________________________________________________________________________\nconv2d_67 (Conv2D) (None, 17, 17, 192) 258048 activation_66[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_62 (BatchNo (None, 17, 17, 192) 576 conv2d_62[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_67 (BatchNo (None, 17, 17, 192) 576 conv2d_67[0][0] \n__________________________________________________________________________________________________\nactivation_62 (Activation) (None, 17, 17, 192) 0 batch_normalization_62[0][0] \n__________________________________________________________________________________________________\nactivation_67 (Activation) (None, 17, 17, 192) 0 batch_normalization_67[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_6 (AveragePoo (None, 17, 17, 768) 0 mixed6[0][0] \n__________________________________________________________________________________________________\nconv2d_60 (Conv2D) (None, 17, 17, 192) 147456 mixed6[0][0] \n__________________________________________________________________________________________________\nconv2d_63 (Conv2D) (None, 17, 17, 192) 258048 activation_62[0][0] \n__________________________________________________________________________________________________\nconv2d_68 (Conv2D) (None, 17, 17, 192) 258048 activation_67[0][0] \n__________________________________________________________________________________________________\nconv2d_69 (Conv2D) (None, 17, 17, 192) 147456 average_pooling2d_6[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_60 (BatchNo (None, 17, 17, 192) 576 conv2d_60[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_63 (BatchNo (None, 17, 17, 192) 576 conv2d_63[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_68 (BatchNo (None, 17, 17, 192) 576 conv2d_68[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_69 (BatchNo (None, 17, 17, 192) 576 conv2d_69[0][0] \n__________________________________________________________________________________________________\nactivation_60 (Activation) (None, 17, 17, 192) 0 batch_normalization_60[0][0] \n__________________________________________________________________________________________________\nactivation_63 (Activation) (None, 17, 17, 192) 0 batch_normalization_63[0][0] \n__________________________________________________________________________________________________\nactivation_68 (Activation) (None, 17, 17, 192) 0 batch_normalization_68[0][0] \n__________________________________________________________________________________________________\nactivation_69 (Activation) (None, 17, 17, 192) 0 batch_normalization_69[0][0] \n__________________________________________________________________________________________________\nmixed7 (Concatenate) (None, 17, 17, 768) 0 activation_60[0][0] \n activation_63[0][0] \n activation_68[0][0] \n activation_69[0][0] \n__________________________________________________________________________________________________\nconv2d_72 (Conv2D) (None, 17, 17, 192) 147456 mixed7[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_72 (BatchNo (None, 17, 17, 192) 576 conv2d_72[0][0] \n__________________________________________________________________________________________________\nactivation_72 (Activation) (None, 17, 17, 192) 0 batch_normalization_72[0][0] \n__________________________________________________________________________________________________\nconv2d_73 (Conv2D) (None, 17, 17, 192) 258048 activation_72[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_73 (BatchNo (None, 17, 17, 192) 576 conv2d_73[0][0] \n__________________________________________________________________________________________________\nactivation_73 (Activation) (None, 17, 17, 192) 0 batch_normalization_73[0][0] \n__________________________________________________________________________________________________\nconv2d_70 (Conv2D) (None, 17, 17, 192) 147456 mixed7[0][0] \n__________________________________________________________________________________________________\nconv2d_74 (Conv2D) (None, 17, 17, 192) 258048 activation_73[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_70 (BatchNo (None, 17, 17, 192) 576 conv2d_70[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_74 (BatchNo (None, 17, 17, 192) 576 conv2d_74[0][0] \n__________________________________________________________________________________________________\nactivation_70 (Activation) (None, 17, 17, 192) 0 batch_normalization_70[0][0] \n__________________________________________________________________________________________________\nactivation_74 (Activation) (None, 17, 17, 192) 0 batch_normalization_74[0][0] \n__________________________________________________________________________________________________\nconv2d_71 (Conv2D) (None, 8, 8, 320) 552960 activation_70[0][0] \n__________________________________________________________________________________________________\nconv2d_75 (Conv2D) (None, 8, 8, 192) 331776 activation_74[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_71 (BatchNo (None, 8, 8, 320) 960 conv2d_71[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_75 (BatchNo (None, 8, 8, 192) 576 conv2d_75[0][0] \n__________________________________________________________________________________________________\nactivation_71 (Activation) (None, 8, 8, 320) 0 batch_normalization_71[0][0] \n__________________________________________________________________________________________________\nactivation_75 (Activation) (None, 8, 8, 192) 0 batch_normalization_75[0][0] \n__________________________________________________________________________________________________\nmax_pooling2d_3 (MaxPooling2D) (None, 8, 8, 768) 0 mixed7[0][0] \n__________________________________________________________________________________________________\nmixed8 (Concatenate) (None, 8, 8, 1280) 0 activation_71[0][0] \n activation_75[0][0] \n max_pooling2d_3[0][0] \n__________________________________________________________________________________________________\nconv2d_80 (Conv2D) (None, 8, 8, 448) 573440 mixed8[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_80 (BatchNo (None, 8, 8, 448) 1344 conv2d_80[0][0] \n__________________________________________________________________________________________________\nactivation_80 (Activation) (None, 8, 8, 448) 0 batch_normalization_80[0][0] \n__________________________________________________________________________________________________\nconv2d_77 (Conv2D) (None, 8, 8, 384) 491520 mixed8[0][0] \n__________________________________________________________________________________________________\nconv2d_81 (Conv2D) (None, 8, 8, 384) 1548288 activation_80[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_77 (BatchNo (None, 8, 8, 384) 1152 conv2d_77[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_81 (BatchNo (None, 8, 8, 384) 1152 conv2d_81[0][0] \n__________________________________________________________________________________________________\nactivation_77 (Activation) (None, 8, 8, 384) 0 batch_normalization_77[0][0] \n__________________________________________________________________________________________________\nactivation_81 (Activation) (None, 8, 8, 384) 0 batch_normalization_81[0][0] \n__________________________________________________________________________________________________\nconv2d_78 (Conv2D) (None, 8, 8, 384) 442368 activation_77[0][0] \n__________________________________________________________________________________________________\nconv2d_79 (Conv2D) (None, 8, 8, 384) 442368 activation_77[0][0] \n__________________________________________________________________________________________________\nconv2d_82 (Conv2D) (None, 8, 8, 384) 442368 activation_81[0][0] \n__________________________________________________________________________________________________\nconv2d_83 (Conv2D) (None, 8, 8, 384) 442368 activation_81[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_7 (AveragePoo (None, 8, 8, 1280) 0 mixed8[0][0] \n__________________________________________________________________________________________________\nconv2d_76 (Conv2D) (None, 8, 8, 320) 409600 mixed8[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_78 (BatchNo (None, 8, 8, 384) 1152 conv2d_78[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_79 (BatchNo (None, 8, 8, 384) 1152 conv2d_79[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_82 (BatchNo (None, 8, 8, 384) 1152 conv2d_82[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_83 (BatchNo (None, 8, 8, 384) 1152 conv2d_83[0][0] \n__________________________________________________________________________________________________\nconv2d_84 (Conv2D) (None, 8, 8, 192) 245760 average_pooling2d_7[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_76 (BatchNo (None, 8, 8, 320) 960 conv2d_76[0][0] \n__________________________________________________________________________________________________\nactivation_78 (Activation) (None, 8, 8, 384) 0 batch_normalization_78[0][0] \n__________________________________________________________________________________________________\nactivation_79 (Activation) (None, 8, 8, 384) 0 batch_normalization_79[0][0] \n__________________________________________________________________________________________________\nactivation_82 (Activation) (None, 8, 8, 384) 0 batch_normalization_82[0][0] \n__________________________________________________________________________________________________\nactivation_83 (Activation) (None, 8, 8, 384) 0 batch_normalization_83[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_84 (BatchNo (None, 8, 8, 192) 576 conv2d_84[0][0] \n__________________________________________________________________________________________________\nactivation_76 (Activation) (None, 8, 8, 320) 0 batch_normalization_76[0][0] \n__________________________________________________________________________________________________\nmixed9_0 (Concatenate) (None, 8, 8, 768) 0 activation_78[0][0] \n activation_79[0][0] \n__________________________________________________________________________________________________\nconcatenate (Concatenate) (None, 8, 8, 768) 0 activation_82[0][0] \n activation_83[0][0] \n__________________________________________________________________________________________________\nactivation_84 (Activation) (None, 8, 8, 192) 0 batch_normalization_84[0][0] \n__________________________________________________________________________________________________\nmixed9 (Concatenate) (None, 8, 8, 2048) 0 activation_76[0][0] \n mixed9_0[0][0] \n concatenate[0][0] \n activation_84[0][0] \n__________________________________________________________________________________________________\nconv2d_89 (Conv2D) (None, 8, 8, 448) 917504 mixed9[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_89 (BatchNo (None, 8, 8, 448) 1344 conv2d_89[0][0] \n__________________________________________________________________________________________________\nactivation_89 (Activation) (None, 8, 8, 448) 0 batch_normalization_89[0][0] \n__________________________________________________________________________________________________\nconv2d_86 (Conv2D) (None, 8, 8, 384) 786432 mixed9[0][0] \n__________________________________________________________________________________________________\nconv2d_90 (Conv2D) (None, 8, 8, 384) 1548288 activation_89[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_86 (BatchNo (None, 8, 8, 384) 1152 conv2d_86[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_90 (BatchNo (None, 8, 8, 384) 1152 conv2d_90[0][0] \n__________________________________________________________________________________________________\nactivation_86 (Activation) (None, 8, 8, 384) 0 batch_normalization_86[0][0] \n__________________________________________________________________________________________________\nactivation_90 (Activation) (None, 8, 8, 384) 0 batch_normalization_90[0][0] \n__________________________________________________________________________________________________\nconv2d_87 (Conv2D) (None, 8, 8, 384) 442368 activation_86[0][0] \n__________________________________________________________________________________________________\nconv2d_88 (Conv2D) (None, 8, 8, 384) 442368 activation_86[0][0] \n__________________________________________________________________________________________________\nconv2d_91 (Conv2D) (None, 8, 8, 384) 442368 activation_90[0][0] \n__________________________________________________________________________________________________\nconv2d_92 (Conv2D) (None, 8, 8, 384) 442368 activation_90[0][0] \n__________________________________________________________________________________________________\naverage_pooling2d_8 (AveragePoo (None, 8, 8, 2048) 0 mixed9[0][0] \n__________________________________________________________________________________________________\nconv2d_85 (Conv2D) (None, 8, 8, 320) 655360 mixed9[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_87 (BatchNo (None, 8, 8, 384) 1152 conv2d_87[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_88 (BatchNo (None, 8, 8, 384) 1152 conv2d_88[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_91 (BatchNo (None, 8, 8, 384) 1152 conv2d_91[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_92 (BatchNo (None, 8, 8, 384) 1152 conv2d_92[0][0] \n__________________________________________________________________________________________________\nconv2d_93 (Conv2D) (None, 8, 8, 192) 393216 average_pooling2d_8[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_85 (BatchNo (None, 8, 8, 320) 960 conv2d_85[0][0] \n__________________________________________________________________________________________________\nactivation_87 (Activation) (None, 8, 8, 384) 0 batch_normalization_87[0][0] \n__________________________________________________________________________________________________\nactivation_88 (Activation) (None, 8, 8, 384) 0 batch_normalization_88[0][0] \n__________________________________________________________________________________________________\nactivation_91 (Activation) (None, 8, 8, 384) 0 batch_normalization_91[0][0] \n__________________________________________________________________________________________________\nactivation_92 (Activation) (None, 8, 8, 384) 0 batch_normalization_92[0][0] \n__________________________________________________________________________________________________\nbatch_normalization_93 (BatchNo (None, 8, 8, 192) 576 conv2d_93[0][0] \n__________________________________________________________________________________________________\nactivation_85 (Activation) (None, 8, 8, 320) 0 batch_normalization_85[0][0] \n__________________________________________________________________________________________________\nmixed9_1 (Concatenate) (None, 8, 8, 768) 0 activation_87[0][0] \n activation_88[0][0] \n__________________________________________________________________________________________________\nconcatenate_1 (Concatenate) (None, 8, 8, 768) 0 activation_91[0][0] \n activation_92[0][0] \n__________________________________________________________________________________________________\nactivation_93 (Activation) (None, 8, 8, 192) 0 batch_normalization_93[0][0] \n__________________________________________________________________________________________________\nmixed10 (Concatenate) (None, 8, 8, 2048) 0 activation_85[0][0] \n mixed9_1[0][0] \n concatenate_1[0][0] \n activation_93[0][0] \n__________________________________________________________________________________________________\navg_pool (GlobalAveragePooling2 (None, 2048) 0 mixed10[0][0] \n__________________________________________________________________________________________________\npredictions (Dense) (None, 1000) 2049000 avg_pool[0][0] \n==================================================================================================\nTotal params: 23,851,784\nTrainable params: 23,817,352\nNon-trainable params: 34,432\n__________________________________________________________________________________________________\n" ] ], [ [ "將網路模型儲存到TensorBoard上：", "_____no_output_____" ] ], [ [ "model_tb = tf.keras.callbacks.TensorBoard(log_dir='lab8-logs-inceptionv3-keras')\nmodel_tb.set_model(model)", "_____no_output_____" ] ], [ [ "### 資料前處理和輸出解碼", "_____no_output_____" ], [ "使用別人提供的模型預測，需要注意兩件事情，1)訓練時的資料前處理，2)輸出結果對應到的類別。\n\nKeras很貼心的提供每個模型相對應的資料預處理和輸出解碼的函式。\n- preprocess_input：網路架構的影像前處理(注意：每一個模型在訓練時做的資料正規化並不會相同，例如：VGG、ResNet-50輸入影像為0~255的數值，而inception_v3、xception輸入影像為-1~1的數值)。\n- decode_predictions：對應網路架構的輸出解碼。", "_____no_output_____" ], [ "Import資料預處理和輸出解碼的函式：", "_____no_output_____" ] ], [ [ "from tensorflow.keras.applications.inception_v3 import preprocess_input\nfrom tensorflow.keras.applications.inception_v3 import decode_predictions", "_____no_output_____" ] ], [ [ "### 預測輸出結果", "_____no_output_____" ], [ "創建影像讀取的函式：讀取影像，並將影像大小縮放大299x299x3的尺寸。", "_____no_output_____" ] ], [ [ "def read_img(img_path, resize=(299,299)):\n img_string = tf.io.read_file(img_path) # 讀取檔案\n img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼\n img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小\n # 將影像格式增加到4維(batch, height, width, channels)，模型預測要求格式\n img_decode = tf.expand_dims(img_decode, axis=0)\n return img_decode", "_____no_output_____" ] ], [ [ "從資料夾中讀取一張影像（elephant.jpg）作為測試：", "_____no_output_____" ] ], [ [ "img_path = 'image/elephant.jpg'\nimg = read_img(img_path) # 透過剛創建的函式讀取影像\nplt.imshow(tf.cast(img, tf.uint8)[0]) # 透過matplotlib顯示圖片需將影像轉為Integers", "_____no_output_____" ] ], [ [ "預測結果：", "_____no_output_____" ] ], [ [ "img = preprocess_input(img) # 影像前處理\npreds = model.predict(img) # 預測圖片\nprint(\"Predicted:\", decode_predictions(preds, top=3)[0]) # 輸出預測最高的三個類別", "Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/imagenet_class_index.json\n40960/35363 [==================================] - 0s 0us/step\nPredicted: [('n02504458', 'African_elephant', 0.8037864), ('n01871265', 'tusker', 0.121638976), ('n02504013', 'Indian_elephant', 0.0042992695)]\n" ] ], [ [ "---\n## TensorFlow Hub\n\nInstall:\n```\npip install tensorflow-hub\n```\n\nSearch:\nhttps://tfhub.dev/", "_____no_output_____" ] ], [ [ "import tensorflow as tf\nimport tensorflow_hub as hub", "_____no_output_____" ] ], [ [ "### 創建Inception V3模型\n\nModel:\nhttps://tfhub.dev/google/tf2-preview/inception_v3/classification/2\n\nnum_classes = 1001 classes of the classification from the original training\n \nImage:height x width = 299 x 299 pixels, 3 RGB color values in the range 0~1\n\nlabels file: https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt", "_____no_output_____" ] ], [ [ "# Inception V3預訓練模型的URL\nmodule_url = \"https://tfhub.dev/google/tf2-preview/inception_v3/classification/4\"\n\n# 創建一個Sequential Model，網路模型裡面包含了Inception V3網路層\nmodel = tf.keras.Sequential([\n # hub.KerasLayer將載入的Inception V3模型封裝成網路層(Keras Layer)\n hub.KerasLayer(module_url, \n input_shape=(299, 299, 3), # 模型輸入大小\n output_shape=(1001, ), # 模型輸出大小\n name='Inception_v3') # 網路層名稱\n])", "_____no_output_____" ], [ "model.summary()", "Model: \"sequential\"\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\nInception_v3 (KerasLayer) (None, 1001) 23853833 \n=================================================================\nTotal params: 23,853,833\nTrainable params: 0\nNon-trainable params: 23,853,833\n_________________________________________________________________\n" ] ], [ [ "### 資料前處理和輸出解碼", "_____no_output_____" ], [ "創建資料前處理函式：", "_____no_output_____" ] ], [ [ "def read_img(img_path, resize=(299,299)):\n img_string = tf.io.read_file(img_path) # 讀取檔案\n img_decode = tf.image.decode_image(img_string) # 將檔案以影像格式來解碼\n img_decode = tf.image.resize(img_decode, resize) # 將影像resize到網路輸入大小\n img_decode = img_decode / 255.0 # 對影像做正規畫，將數值縮放到0~1之間\n # 將影像格式增加到4維(batch, height, width, channels)，模型預測要求格式\n img_decode = tf.expand_dims(img_decode, axis=0) # \n return img_decode", "_____no_output_____" ] ], [ [ "創建輸出解碼器：", "_____no_output_____" ] ], [ [ "# 下載ImageNet 的標籤檔\nlabels_path = tf.keras.utils.get_file('ImageNetLabels.txt', 'https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt')\n# 讀取標籤檔中的數據\nwith open(labels_path) as file:\n lines = file.read().splitlines()\nprint(lines) # 顯示讀取的標籤\n\nimagenet_labels = np.array(lines) # 將標籤轉成numpy array做為網路輸出的解碼器", "Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt\n16384/10484 [==============================================] - 0s 0us/step\n['background', 'tench', 'goldfish', 'great white shark', 'tiger shark', 'hammerhead', 'electric ray', 'stingray', 'cock', 'hen', 'ostrich', 'brambling', 'goldfinch', 'house finch', 'junco', 'indigo bunting', 'robin', 'bulbul', 'jay', 'magpie', 'chickadee', 'water ouzel', 'kite', 'bald eagle', 'vulture', 'great grey owl', 'European fire salamander', 'common newt', 'eft', 'spotted salamander', 'axolotl', 'bullfrog', 'tree frog', 'tailed frog', 'loggerhead', 'leatherback turtle', 'mud turtle', 'terrapin', 'box turtle', 'banded gecko', 'common iguana', 'American chameleon', 'whiptail', 'agama', 'frilled lizard', 'alligator lizard', 'Gila monster', 'green lizard', 'African chameleon', 'Komodo dragon', 'African crocodile', 'American alligator', 'triceratops', 'thunder snake', 'ringneck snake', 'hognose snake', 'green snake', 'king snake', 'garter snake', 'water snake', 'vine snake', 'night snake', 'boa constrictor', 'rock python', 'Indian cobra', 'green mamba', 'sea snake', 'horned viper', 'diamondback', 'sidewinder', 'trilobite', 'harvestman', 'scorpion', 'black and gold garden spider', 'barn spider', 'garden spider', 'black widow', 'tarantula', 'wolf spider', 'tick', 'centipede', 'black grouse', 'ptarmigan', 'ruffed grouse', 'prairie chicken', 'peacock', 'quail', 'partridge', 'African grey', 'macaw', 'sulphur-crested cockatoo', 'lorikeet', 'coucal', 'bee eater', 'hornbill', 'hummingbird', 'jacamar', 'toucan', 'drake', 'red-breasted merganser', 'goose', 'black swan', 'tusker', 'echidna', 'platypus', 'wallaby', 'koala', 'wombat', 'jellyfish', 'sea anemone', 'brain coral', 'flatworm', 'nematode', 'conch', 'snail', 'slug', 'sea slug', 'chiton', 'chambered nautilus', 'Dungeness crab', 'rock crab', 'fiddler crab', 'king crab', 'American lobster', 'spiny lobster', 'crayfish', 'hermit crab', 'isopod', 'white stork', 'black stork', 'spoonbill', 'flamingo', 'little blue heron', 'American egret', 'bittern', 'crane', 'limpkin', 'European gallinule', 'American coot', 'bustard', 'ruddy turnstone', 'red-backed sandpiper', 'redshank', 'dowitcher', 'oystercatcher', 'pelican', 'king penguin', 'albatross', 'grey whale', 'killer whale', 'dugong', 'sea lion', 'Chihuahua', 'Japanese spaniel', 'Maltese dog', 'Pekinese', 'Shih-Tzu', 'Blenheim spaniel', 'papillon', 'toy terrier', 'Rhodesian ridgeback', 'Afghan hound', 'basset', 'beagle', 'bloodhound', 'bluetick', 'black-and-tan coonhound', 'Walker hound', 'English foxhound', 'redbone', 'borzoi', 'Irish wolfhound', 'Italian greyhound', 'whippet', 'Ibizan hound', 'Norwegian elkhound', 'otterhound', 'Saluki', 'Scottish deerhound', 'Weimaraner', 'Staffordshire bullterrier', 'American Staffordshire terrier', 'Bedlington terrier', 'Border terrier', 'Kerry blue terrier', 'Irish terrier', 'Norfolk terrier', 'Norwich terrier', 'Yorkshire terrier', 'wire-haired fox terrier', 'Lakeland terrier', 'Sealyham terrier', 'Airedale', 'cairn', 'Australian terrier', 'Dandie Dinmont', 'Boston bull', 'miniature schnauzer', 'giant schnauzer', 'standard schnauzer', 'Scotch terrier', 'Tibetan terrier', 'silky terrier', 'soft-coated wheaten terrier', 'West Highland white terrier', 'Lhasa', 'flat-coated retriever', 'curly-coated retriever', 'golden retriever', 'Labrador retriever', 'Chesapeake Bay retriever', 'German short-haired pointer', 'vizsla', 'English setter', 'Irish setter', 'Gordon setter', 'Brittany spaniel', 'clumber', 'English springer', 'Welsh springer spaniel', 'cocker spaniel', 'Sussex spaniel', 'Irish water spaniel', 'kuvasz', 'schipperke', 'groenendael', 'malinois', 'briard', 'kelpie', 'komondor', 'Old English sheepdog', 'Shetland sheepdog', 'collie', 'Border collie', 'Bouvier des Flandres', 'Rottweiler', 'German shepherd', 'Doberman', 'miniature pinscher', 'Greater Swiss Mountain dog', 'Bernese mountain dog', 'Appenzeller', 'EntleBucher', 'boxer', 'bull mastiff', 'Tibetan mastiff', 'French bulldog', 'Great Dane', 'Saint Bernard', 'Eskimo dog', 'malamute', 'Siberian husky', 'dalmatian', 'affenpinscher', 'basenji', 'pug', 'Leonberg', 'Newfoundland', 'Great Pyrenees', 'Samoyed', 'Pomeranian', 'chow', 'keeshond', 'Brabancon griffon', 'Pembroke', 'Cardigan', 'toy poodle', 'miniature poodle', 'standard poodle', 'Mexican hairless', 'timber wolf', 'white wolf', 'red wolf', 'coyote', 'dingo', 'dhole', 'African hunting dog', 'hyena', 'red fox', 'kit fox', 'Arctic fox', 'grey fox', 'tabby', 'tiger cat', 'Persian cat', 'Siamese cat', 'Egyptian cat', 'cougar', 'lynx', 'leopard', 'snow leopard', 'jaguar', 'lion', 'tiger', 'cheetah', 'brown bear', 'American black bear', 'ice bear', 'sloth bear', 'mongoose', 'meerkat', 'tiger beetle', 'ladybug', 'ground beetle', 'long-horned beetle', 'leaf beetle', 'dung beetle', 'rhinoceros beetle', 'weevil', 'fly', 'bee', 'ant', 'grasshopper', 'cricket', 'walking stick', 'cockroach', 'mantis', 'cicada', 'leafhopper', 'lacewing', 'dragonfly', 'damselfly', 'admiral', 'ringlet', 'monarch', 'cabbage butterfly', 'sulphur butterfly', 'lycaenid', 'starfish', 'sea urchin', 'sea cucumber', 'wood rabbit', 'hare', 'Angora', 'hamster', 'porcupine', 'fox squirrel', 'marmot', 'beaver', 'guinea pig', 'sorrel', 'zebra', 'hog', 'wild boar', 'warthog', 'hippopotamus', 'ox', 'water buffalo', 'bison', 'ram', 'bighorn', 'ibex', 'hartebeest', 'impala', 'gazelle', 'Arabian camel', 'llama', 'weasel', 'mink', 'polecat', 'black-footed ferret', 'otter', 'skunk', 'badger', 'armadillo', 'three-toed sloth', 'orangutan', 'gorilla', 'chimpanzee', 'gibbon', 'siamang', 'guenon', 'patas', 'baboon', 'macaque', 'langur', 'colobus', 'proboscis monkey', 'marmoset', 'capuchin', 'howler monkey', 'titi', 'spider monkey', 'squirrel monkey', 'Madagascar cat', 'indri', 'Indian elephant', 'African elephant', 'lesser panda', 'giant panda', 'barracouta', 'eel', 'coho', 'rock beauty', 'anemone fish', 'sturgeon', 'gar', 'lionfish', 'puffer', 'abacus', 'abaya', 'academic gown', 'accordion', 'acoustic guitar', 'aircraft carrier', 'airliner', 'airship', 'altar', 'ambulance', 'amphibian', 'analog clock', 'apiary', 'apron', 'ashcan', 'assault rifle', 'backpack', 'bakery', 'balance beam', 'balloon', 'ballpoint', 'Band Aid', 'banjo', 'bannister', 'barbell', 'barber chair', 'barbershop', 'barn', 'barometer', 'barrel', 'barrow', 'baseball', 'basketball', 'bassinet', 'bassoon', 'bathing cap', 'bath towel', 'bathtub', 'beach wagon', 'beacon', 'beaker', 'bearskin', 'beer bottle', 'beer glass', 'bell cote', 'bib', 'bicycle-built-for-two', 'bikini', 'binder', 'binoculars', 'birdhouse', 'boathouse', 'bobsled', 'bolo tie', 'bonnet', 'bookcase', 'bookshop', 'bottlecap', 'bow', 'bow tie', 'brass', 'brassiere', 'breakwater', 'breastplate', 'broom', 'bucket', 'buckle', 'bulletproof vest', 'bullet train', 'butcher shop', 'cab', 'caldron', 'candle', 'cannon', 'canoe', 'can opener', 'cardigan', 'car mirror', 'carousel', \"carpenter's kit\", 'carton', 'car wheel', 'cash machine', 'cassette', 'cassette player', 'castle', 'catamaran', 'CD player', 'cello', 'cellular telephone', 'chain', 'chainlink fence', 'chain mail', 'chain saw', 'chest', 'chiffonier', 'chime', 'china cabinet', 'Christmas stocking', 'church', 'cinema', 'cleaver', 'cliff dwelling', 'cloak', 'clog', 'cocktail shaker', 'coffee mug', 'coffeepot', 'coil', 'combination lock', 'computer keyboard', 'confectionery', 'container ship', 'convertible', 'corkscrew', 'cornet', 'cowboy boot', 'cowboy hat', 'cradle', 'crane', 'crash helmet', 'crate', 'crib', 'Crock Pot', 'croquet ball', 'crutch', 'cuirass', 'dam', 'desk', 'desktop computer', 'dial telephone', 'diaper', 'digital clock', 'digital watch', 'dining table', 'dishrag', 'dishwasher', 'disk brake', 'dock', 'dogsled', 'dome', 'doormat', 'drilling platform', 'drum', 'drumstick', 'dumbbell', 'Dutch oven', 'electric fan', 'electric guitar', 'electric locomotive', 'entertainment center', 'envelope', 'espresso maker', 'face powder', 'feather boa', 'file', 'fireboat', 'fire engine', 'fire screen', 'flagpole', 'flute', 'folding chair', 'football helmet', 'forklift', 'fountain', 'fountain pen', 'four-poster', 'freight car', 'French horn', 'frying pan', 'fur coat', 'garbage truck', 'gasmask', 'gas pump', 'goblet', 'go-kart', 'golf ball', 'golfcart', 'gondola', 'gong', 'gown', 'grand piano', 'greenhouse', 'grille', 'grocery store', 'guillotine', 'hair slide', 'hair spray', 'half track', 'hammer', 'hamper', 'hand blower', 'hand-held computer', 'handkerchief', 'hard disc', 'harmonica', 'harp', 'harvester', 'hatchet', 'holster', 'home theater', 'honeycomb', 'hook', 'hoopskirt', 'horizontal bar', 'horse cart', 'hourglass', 'iPod', 'iron', \"jack-o'-lantern\", 'jean', 'jeep', 'jersey', 'jigsaw puzzle', 'jinrikisha', 'joystick', 'kimono', 'knee pad', 'knot', 'lab coat', 'ladle', 'lampshade', 'laptop', 'lawn mower', 'lens cap', 'letter opener', 'library', 'lifeboat', 'lighter', 'limousine', 'liner', 'lipstick', 'Loafer', 'lotion', 'loudspeaker', 'loupe', 'lumbermill', 'magnetic compass', 'mailbag', 'mailbox', 'maillot', 'maillot', 'manhole cover', 'maraca', 'marimba', 'mask', 'matchstick', 'maypole', 'maze', 'measuring cup', 'medicine chest', 'megalith', 'microphone', 'microwave', 'military uniform', 'milk can', 'minibus', 'miniskirt', 'minivan', 'missile', 'mitten', 'mixing bowl', 'mobile home', 'Model T', 'modem', 'monastery', 'monitor', 'moped', 'mortar', 'mortarboard', 'mosque', 'mosquito net', 'motor scooter', 'mountain bike', 'mountain tent', 'mouse', 'mousetrap', 'moving van', 'muzzle', 'nail', 'neck brace', 'necklace', 'nipple', 'notebook', 'obelisk', 'oboe', 'ocarina', 'odometer', 'oil filter', 'organ', 'oscilloscope', 'overskirt', 'oxcart', 'oxygen mask', 'packet', 'paddle', 'paddlewheel', 'padlock', 'paintbrush', 'pajama', 'palace', 'panpipe', 'paper towel', 'parachute', 'parallel bars', 'park bench', 'parking meter', 'passenger car', 'patio', 'pay-phone', 'pedestal', 'pencil box', 'pencil sharpener', 'perfume', 'Petri dish', 'photocopier', 'pick', 'pickelhaube', 'picket fence', 'pickup', 'pier', 'piggy bank', 'pill bottle', 'pillow', 'ping-pong ball', 'pinwheel', 'pirate', 'pitcher', 'plane', 'planetarium', 'plastic bag', 'plate rack', 'plow', 'plunger', 'Polaroid camera', 'pole', 'police van', 'poncho', 'pool table', 'pop bottle', 'pot', \"potter's wheel\", 'power drill', 'prayer rug', 'printer', 'prison', 'projectile', 'projector', 'puck', 'punching bag', 'purse', 'quill', 'quilt', 'racer', 'racket', 'radiator', 'radio', 'radio telescope', 'rain barrel', 'recreational vehicle', 'reel', 'reflex camera', 'refrigerator', 'remote control', 'restaurant', 'revolver', 'rifle', 'rocking chair', 'rotisserie', 'rubber eraser', 'rugby ball', 'rule', 'running shoe', 'safe', 'safety pin', 'saltshaker', 'sandal', 'sarong', 'sax', 'scabbard', 'scale', 'school bus', 'schooner', 'scoreboard', 'screen', 'screw', 'screwdriver', 'seat belt', 'sewing machine', 'shield', 'shoe shop', 'shoji', 'shopping basket', 'shopping cart', 'shovel', 'shower cap', 'shower curtain', 'ski', 'ski mask', 'sleeping bag', 'slide rule', 'sliding door', 'slot', 'snorkel', 'snowmobile', 'snowplow', 'soap dispenser', 'soccer ball', 'sock', 'solar dish', 'sombrero', 'soup bowl', 'space bar', 'space heater', 'space shuttle', 'spatula', 'speedboat', 'spider web', 'spindle', 'sports car', 'spotlight', 'stage', 'steam locomotive', 'steel arch bridge', 'steel drum', 'stethoscope', 'stole', 'stone wall', 'stopwatch', 'stove', 'strainer', 'streetcar', 'stretcher', 'studio couch', 'stupa', 'submarine', 'suit', 'sundial', 'sunglass', 'sunglasses', 'sunscreen', 'suspension bridge', 'swab', 'sweatshirt', 'swimming trunks', 'swing', 'switch', 'syringe', 'table lamp', 'tank', 'tape player', 'teapot', 'teddy', 'television', 'tennis ball', 'thatch', 'theater curtain', 'thimble', 'thresher', 'throne', 'tile roof', 'toaster', 'tobacco shop', 'toilet seat', 'torch', 'totem pole', 'tow truck', 'toyshop', 'tractor', 'trailer truck', 'tray', 'trench coat', 'tricycle', 'trimaran', 'tripod', 'triumphal arch', 'trolleybus', 'trombone', 'tub', 'turnstile', 'typewriter keyboard', 'umbrella', 'unicycle', 'upright', 'vacuum', 'vase', 'vault', 'velvet', 'vending machine', 'vestment', 'viaduct', 'violin', 'volleyball', 'waffle iron', 'wall clock', 'wallet', 'wardrobe', 'warplane', 'washbasin', 'washer', 'water bottle', 'water jug', 'water tower', 'whiskey jug', 'whistle', 'wig', 'window screen', 'window shade', 'Windsor tie', 'wine bottle', 'wing', 'wok', 'wooden spoon', 'wool', 'worm fence', 'wreck', 'yawl', 'yurt', 'web site', 'comic book', 'crossword puzzle', 'street sign', 'traffic light', 'book jacket', 'menu', 'plate', 'guacamole', 'consomme', 'hot pot', 'trifle', 'ice cream', 'ice lolly', 'French loaf', 'bagel', 'pretzel', 'cheeseburger', 'hotdog', 'mashed potato', 'head cabbage', 'broccoli', 'cauliflower', 'zucchini', 'spaghetti squash', 'acorn squash', 'butternut squash', 'cucumber', 'artichoke', 'bell pepper', 'cardoon', 'mushroom', 'Granny Smith', 'strawberry', 'orange', 'lemon', 'fig', 'pineapple', 'banana', 'jackfruit', 'custard apple', 'pomegranate', 'hay', 'carbonara', 'chocolate sauce', 'dough', 'meat loaf', 'pizza', 'potpie', 'burrito', 'red wine', 'espresso', 'cup', 'eggnog', 'alp', 'bubble', 'cliff', 'coral reef', 'geyser', 'lakeside', 'promontory', 'sandbar', 'seashore', 'valley', 'volcano', 'ballplayer', 'groom', 'scuba diver', 'rapeseed', 'daisy', \"yellow lady's slipper\", 'corn', 'acorn', 'hip', 'buckeye', 'coral fungus', 'agaric', 'gyromitra', 'stinkhorn', 'earthstar', 'hen-of-the-woods', 'bolete', 'ear', 'toilet tissue']\n" ] ], [ [ "### 預測輸出結果", "_____no_output_____" ], [ "從資料夾中讀取一張影像（elephant.jpg）作為測試：", "_____no_output_____" ] ], [ [ "img_path = 'image/elephant.jpg'\nimg = read_img(img_path) # 透過剛創建的函式讀取影像\nplt.imshow(img[0])", "_____no_output_____" ] ], [ [ "預測結果：", "_____no_output_____" ] ], [ [ "preds = model.predict(img) # 預測圖片\nindex = np.argmax(preds) # 取得預測結果最大的Index\nprint(\"Predicted:\", imagenet_labels[index]) # 透過解碼器將輸出轉成標籤", "Predicted: African elephant\n" ] ], [ [ "顯示最好的三個預測：", "_____no_output_____" ] ], [ [ "# 取得預測結果最大的三個indexs\ntop3_indexs = np.argsort(preds)[0, ::-1][:3] \nprint(\"Predicted:\", imagenet_labels[top3_indexs]) # 透過解碼器將輸出轉成標籤", "Predicted: ['African elephant' 'tusker' 'Indian elephant']\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e8a35d7856b48ee9a84aeb407dbec4d42865c4

849,084

ipynb

Jupyter Notebook

TEMA-2/Clase12_DistribucionesProbabilidad.ipynb

anehik/SPF-2020-II-G1

349569575d8a905f67ef5103c935b7208666857f

[ "MIT" ]

null

TEMA-2/Clase12_DistribucionesProbabilidad.ipynb

anehik/SPF-2020-II-G1

349569575d8a905f67ef5103c935b7208666857f

[ "MIT" ]

null

TEMA-2/Clase12_DistribucionesProbabilidad.ipynb

anehik/SPF-2020-II-G1

349569575d8a905f67ef5103c935b7208666857f

[ "MIT" ]

1

2022-03-29T18:09:54.000Z

1,074.789873

166,936

0.953356

[ [ [ "# Distribuciones de probabilidad", "_____no_output_____" ] ], [ [ "# Importamos librerías a trabajar en todas las simulaciones\nimport matplotlib.pyplot as plt\nimport numpy as np\nfrom itertools import cycle # Librería para hacer ciclos\nimport scipy.stats as st # Librería estadística\nfrom math import factorial as fac # Importo la operación factorial\n\n%matplotlib inline", "_____no_output_____" ] ], [ [ "## 1. Distrución de probabilidad uniforme\n$X\\sim U(a,b)$ Parámetros $a,b \\rightarrow $ intervalo\n$$\\textbf{Función de densidad de probabilidad}\\\\f(x)=\\begin{cases}\\frac{1}{b-a} & a\\leq x \\leq b\\\\0& \\text{otro caso}\\end{cases}$$ \n$$ \\textbf{Función de distribución de probabilidad}\\\\F(x)=\\begin{cases}0& x<a\\\\\\frac{x-a}{b-a} & a\\leq x \\leq b\\\\1& x\\geq b\\end{cases}$$\n![imagen.png](attachment:imagen.png)", "_____no_output_____" ], [ "### Uso en python", "_____no_output_____" ] ], [ [ "a,b=1,2 # Interval\nU = np.random.uniform(a,b)\nU\n\nst.uniform.rvs(loc=a, scale=b, size=2)", "_____no_output_____" ] ], [ [ "## 2. Distribución normal\n$X\\sim N(\\mu,\\sigma^2)$ Parámetros: Media=$\\mu$ y varianza=$\\sigma^2$\n$$ \\textbf{Función de densidad de probabilidad}\\\\ f(x)= \\frac{1}{\\sigma\\sqrt{2\\pi}}e^{\\frac{-(x-\\mu)^2}{2\\sigma^2}}$$\n$$ \\textbf{Función de distribución de probabilidad}\\\\ F(x)= \\frac{1}{\\sigma\\sqrt(2\\pi)}\\int_{-\\infty}^{x}e^{\\frac{-(v-\\mu)^2}{2\\sigma^2}}dv$$\n![imagen.png](attachment:imagen.png)\n", "_____no_output_____" ], [ "### Propiedades\n![imagen.png](attachment:imagen.png)", "_____no_output_____" ], [ "### Estandarización de variables aleatorias normales\n\nComo consecuencia de que la función normal es simétrica en $\\mu$ es posible relacionar todas las variables aleatorias normales con la distribución normal estándar.\n\nSi $X\\sim N(\\mu ,\\sigma ^{2})$, entonces\n$$Z = \\frac{X - \\mu}{\\sigma}$$\n\nes una variable aleatoria normal estándar: $Z\\sim N(0,1)$.\n\n### El Teorema del Límite Central\nEl Teorema del límite central establece que bajo ciertas condiciones (como pueden ser independientes e idénticamente distribuidas con varianza finita), la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal. **(Hablar de la importancia del uso)**\n\n### Incidencia\nCuando en un fenómeno se sospecha la presencia de un gran número de pequeñas causas actuando de forma aditiva e independiente es razonable pensar que las observaciones serán \"normales\". **(Debido al TLC)** \n\nHay causas que pueden actuar de forma multiplicativa (más que aditiva). En este caso, la suposición de normalidad no está justificada y es el logaritmo de la variable en cuestión el que estaría normalmente distribuido. **(log-normal)**.\n\n### Ejemplo de aplicación\nEn variables financieras, el modelo de Black-Scholes, el cúal es empleado para estimar el valor actual de una opción europea para la compra (Call), o venta (Put), de acciones en una fecha futura, supone normalidad en algunas variables económicas. ver:https://es.wikipedia.org/wiki/Modelo_de_Black-Scholes para información adicional.\n\n> Referencia: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_normal", "_____no_output_____" ], [ "### Uso en python", "_____no_output_____" ] ], [ [ "mu, sigma = 0, 0.1 # mean and standard deviation\nN = np.random.normal(mu, sigma,5)\nN\nst.norm.rvs(loc=a, scale=sigma, size=5)", "_____no_output_____" ] ], [ [ "## 3. Distribución exponencial\n$X\\sim Exp(\\beta)$ Parámetros: Media $\\beta>0$ o tasa = $\\lambda = 1/\\beta$\n\n$$\\textbf{Función de densidad de probabilidad}\\\\f(x) = \\frac{1}{\\beta} e^{-\\frac{x}{\\beta}}$$\n$$\\textbf{Función de distribución de probabilidad}\\\\F(x) = 1-e^{-\\frac{x}{\\beta}}$$\n![imagen.png](attachment:imagen.png)\n\n### Ejemplos\nEjemplos para la distribución exponencial **es la distribución de la longitud de los intervalos de una variable continua que transcurren entre dos sucesos**, que se distribuyen según la distribución de Poisson.\n\n - El tiempo transcurrido en un centro de llamadas hasta recibir la primera llamada del día se podría modelar como una exponencial.\n - El intervalo de tiempo entre terremotos (de una determinada magnitud) sigue una distribución exponencial.\n - Supongamos una máquina que produce hilo de alambre, la cantidad de metros de alambre hasta encontrar una falla en el alambre se podría modelar como una exponencial.\n - En fiabilidad de sistemas, un dispositivo con tasa de fallo constante sigue una distribución exponencial.\n \n### Relaciones\nLa suma de k variables aleatorias independientes de distribución exponencial con parámetro $\\lambda$ es una variable aleatoria de distribución de Erlang.\n\n> Referencia: https://en.wikipedia.org/wiki/Exponential_distribution", "_____no_output_____" ], [ "### Uso en python", "_____no_output_____" ] ], [ [ "beta = 4\nE = np.random.exponential(beta,1)\nE\nst.expon", "_____no_output_____" ] ], [ [ "## 4. Distribución erlang\nParámetros: Tamaño $k \\in \\mathbb{N}$, escala=$\\frac{1}{\\beta}$\n$$\\textbf{Función de densidad de probabilidad}\\\\f(x)=x^{k-1}\\frac{e^{-x/\\beta}}{\\beta^k\\Gamma(k)}\\equiv x^{k-1}\\frac{e^{-x/\\beta}}{\\beta^k(k-1)!}$$\n\n$$\\textbf{Función de distribución de probabilidad}\\\\F(x)=1-\\sum_{n=0}^{k-1}\\frac{1}{n!}e^{-\\frac{1}{\\beta}x}\\big(\\frac{x}{\\beta}\\big)^n$$\n![imagen.png](attachment:imagen.png)\n\n### Simplificaciones\nLa distribución Erlang con tamaño $k=1$ se simplifica a una distribución exponencial. Esta es una distribución de la suma de $k$ variables exponenciales donde cada una tiene media $\\beta$ \n\n### Ocurrencia\n**Tiempos de espera**\n\nLos eventos que ocurren de forma independiente con una tasa promedio se modelan con un proceso de Poisson. Los tiempos de espera entre k ocurrencias del evento son distribuidos Erlang. (La cuestión relacionada con el número de eventos en una cantidad de tiempo dada descrita por una distribución de Poisson).\n\nLas fórmulas de Erlang se han utilizado en economía de negocios para describir los tiempos entre compras de un activo.\n\n> Referencia: https://en.wikipedia.org/wiki/Erlang_distribution", "_____no_output_____" ], [ "### Uso en python", "_____no_output_____" ] ], [ [ "N = 10000 # Número de muestras\nk,scale = 3,1/4 # Parámetros de la distribución \n\nE1 = st.erlang.rvs(k,scale=scale,size=N)\nE2 = np.random.gamma(k,scale,N) # Erlang como caso particular de la distribución gamma\n\nplt.figure(1,figsize=[12,4])\nplt.subplot(121)\nplt.hist(E1,50,density=True,label='Usando Lib. scipy')\nplt.legend()\nplt.subplot(122)\nplt.hist(E2,50,density=True,label='Usando Lib. numpy')\nplt.legend()\nplt.show()", "_____no_output_____" ] ], [ [ "## 5. Distribución binomial\n$X\\sim B(n,p)$ Parámetros: $n$ y $p$\n$$\\textbf{Función de densidad de probabilidad}\\\\p_i=P(X=i)={n \\choose i}p^i(1-p)^{n-i}= \\frac{n!}{i!(n-i)!}p^i(1-p)^{n-i},\\quad i=0,1,\\cdots,n$$\n>Recordar:$$p_{i+1}=\\frac{n-i}{i+1}\\frac{p}{1-p} p_i $$\n\n$$\\textbf{Función de distribución de probabilidad}\\\\F(x)=\\sum_{i=0}^{k-1}\\frac{n!}{i!(n-i)!}p^i(1-p)^{n-i}$$", "_____no_output_____" ], [ "## Método vectorizado", "_____no_output_____" ] ], [ [ "# Función que calcula la probabilidad acumulada optimizada\ndef proba_binomial(n:'Cantidad de ensayos',p:'Probabilidad de los eventos',\n N:'Cantidad de puntos a graficar'):\n Pr = np.zeros(N)\n Pr[0] = (1-p)**n\n def pr(i):\n nonlocal Pr\n c = p/(1-p)\n Pr[i+1]=(c*(n-i)/(i+1))*Pr[i]\n \n # Lleno el vector Pr usando compresión de listas\n [pr(i) for i in range(N-1)]\n return Pr", "_____no_output_____" ], [ "# Comprobación de función creada\n# Distintos parámetros para graficar la función binomial\nn = [50,100,150]\n# Parámetro p de la dristribución\np = 0.5\n# Resultado usando método convencional\nP = list(map(lambda x,n: proba_binomial(n,p,100),range(len(n)),n))\nP = np.asmatrix(P)\nprint(P.shape)\n\ndef grafica_distribucion_prob(P:'Matriz de probabilidades binomiales'):\n # Gráfica de densidad de probabilidad\n fig,(ax1,ax2) = plt.subplots(1,2)\n fig.set_figwidth(10)\n ax1.plot(P.T,'o',markersize=3)\n ax1.legend(['n=50','n=100','n=150'])\n ax1.set_title('Densidad de probabilidad')\n # ax1.show()\n\n # Probabilidad acumulada\n F = np.cumsum(P,axis=1)\n # plt.figure(2)\n ax2.plot(F.T,'o',markersize=3)\n ax2.legend(['n=%d'%n[0],'n=%d'%n[1],'n=%d'%n[2]])\n ax2.set_title('Distribución acumulada')\n\n plt.show()\nst.binom \n# Gráfica del método convencional y vectorizado\ngrafica_distribucion_prob(P)", "(3, 100)\n" ] ], [ [ "### Características\nLa distribución binomial es una distribución de probabilidad discreta que cuenta el número de éxitos en una secuencia de **n ensayos de Bernoulli independientes entre sí**, con una probabilidad `fija` p de ocurrencia del éxito entre los ensayos. A lo que se denomina «éxito», tiene una probabilidad de ocurrencia p y al otro, «fracaso», tiene una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se designa por $X$ a la variable que mide el número de éxitos que se han producido en los n experimentos. \n\nCuando se dan estas circunstancias, se dice que la variable $X$ sigue una distribución de probabilidad binomial, y se denota $X\\sim B(n,p)$.\n\n### Ejemplo\nSupongamos que se lanza un dado (con 6 caras) 51 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una $X \\sim B(51, 1/6)$ y la probabilidad sería $P(X=20)$:\n\n$$P(X=20)={51 \\choose 20}(1/6)^{20}(1-1/6)^{51-20} $$", "_____no_output_____" ] ], [ [ "n = 51; p=1/6; X=20\nprint('P(X=20)=',st.binom(n,p).pmf(X))", "P(X=20)= 7.444834157690862e-05\n" ] ], [ [ "### Relaciones con otras variables aleatorias\n\nSi n tiende a infinito y p es tal que el producto entre ambos parámetros tiende a $\\lambda$, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro $\\lambda$.\n\nPor último, se cumple que cuando $p =0.5$ y n es muy grande (usualmente se exige que $n\\geq 30$) la distribución binomial puede aproximarse mediante la distribución normal, con parámetros $\\mu=np,\\sigma^2=np(1-p)$.\n\n> Referencia: https://en.wikipedia.org/wiki/Binomial_distribution", "_____no_output_____" ] ], [ [ "p = .5; n = 50\nmu = n*p; sigma = np.sqrt(n*p*(1-p))\n\n# Usando nuetra función creada\nBi = proba_binomial(n,p,n)\nplt.figure(1,figsize=[10,5])\nplt.subplot(121)\nplt.plot(Bi,'o')\nplt.title('Distribución binomial n=%i,p=%0.2f'%(n,p))\n\n# Usando la función de la librería scipy para graficar la normal\nx = np.arange(0,n)\nBi_norm = st.norm.pdf(x,loc=mu,scale=sigma)\nplt.subplot(122)\nplt.plot(Bi_norm,'o')\nplt.title('Distribución~normal(np,np(1-p))')\nplt.show()", "_____no_output_____" ] ], [ [ "## 6. Distribución Poisson\nParámetros: media=$\\lambda>0 \\in \\mathbb{R}$, N°Ocurrencias = k\n\n - k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).\n - λ es un parámetro positivo que representa el <font color ='red'>**número de veces que se espera que ocurra el fenómeno durante un intervalo dado**</font>. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40\n\n$$\\textbf{Función de densidad de probabilidad}\\\\p(k)=\\frac{\\lambda^k e^{-\\lambda}}{k!},\\quad k\\in \\mathbb{N}$$\n\n### Aplicación\nEl número de sucesos en un intervalo de tiempo dado es una variable aleatoria de distribución de Poisson donde $\\lambda$ es la media de números de sucesos en este intervalo.\n\n### Relación con distribución Erlang o Gamma\nEl tiempo hasta que ocurre el suceso número k en un proceso de Poisson de intensidad $\\lambda$ es una variable aleatoria con distribución gamma o (lo mismo) con distribución de Erlang con $ \\beta =1/\\lambda $\n\n### Aproximación normal\nComo consecuencia del teorema central del límite, para valores grandes de $\\lambda$ , una variable aleatoria de Poisson X puede aproximarse por otra normal, con parámetros $\\mu=\\sigma^2=\\lambda$. Por otro lado, si el cociente \n$$Y=\\frac{X-\\lambda}{\\sqrt{\\lambda}}$$\nconverge a una distribución normal de media 0 y varianza 1.\n\n### Ejemplo\nSi el 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, para obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson. En este caso concreto, k es 5 y, λ, el valor esperado de libros defectuosos es el 2% de 400, es decir, 8. Por lo tanto, la probabilidad buscada es\n$$P(5;8)={\\frac {8^{5}e^{-8}}{5!}}=0,092$$\n\n> Referencia: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson", "_____no_output_____" ] ], [ [ "k=5; Lamda = 8\nprint('P(5;8)=',st.poisson(Lamda).pmf(k))", "P(5;8)= 0.09160366159257921\n" ] ], [ [ "## Usando el paquete estadístico `stats`", "_____no_output_____" ] ], [ [ "# Parámetros\nLamda = [8,20]\nk=np.arange(0,40); \n\n# Distribución de probabilidad\nP = np.array([st.poisson(Lamda[i]).pmf(k) for i in range(len(Lamda))])\n\n# Distribución de probabilidad acumulada\nP_acum = np.array([st.poisson(Lamda[i]).cdf(k) for i in range(len(Lamda))])\n\nfig,[ax1,ax2] = plt.subplots(1,2,sharey=False,figsize=[12,4])\nax1.plot(P.T,'o',markersize=3)\nax1.legend(['$\\lambda$=%d'%i for i in Lamda])\nax1.title.set_text('Distribución de probabilidad')\n\nax2.plot(P_acum.T,'o',markersize=3)\n[ax2.hlines(P_acum[i,:],range(len(k)),range(1,len(k)+1)) for i in range(len(Lamda))]\nplt.legend(['$\\lambda$=%d'%i for i in Lamda])\nax2.title.set_text('Distribución de probabilidad')\n\nplt.show()\n# P_acum.shape", "_____no_output_____" ] ], [ [ "## Usando las expresiones matemáticas", "_____no_output_____" ] ], [ [ "import scipy.special as sps \n\np = lambda k,l:(l**k*np.exp(-l))/sps.gamma(k+1)\nk = np.arange(0,50)\nl = [1,10,20,30]\nP = np.asmatrix(list(map(lambda x:p(k,x*np.ones(len(k))),l))).T\nprint(P.shape)\nplt.figure(1,figsize=[12,4])\nplt.subplot(121)\nplt.plot(P,'o',markersize=3)\nplt.legend(['$\\lambda$=%d'%i for i in l])\nplt.title('Distribución de probabilidad')\n\n# Probabilidad acumulada \nP_ac = np.cumsum(P,axis=0)\n\nplt.subplot(122)\nplt.plot(P_ac,'o',markersize=3)\n[plt.hlines(P_ac[:,i],range(len(P_ac)),range(1,len(P_ac)+1)) for i in range(len(l))]\nplt.legend(['$\\lambda$=%d'%i for i in l])\nplt.title('Distribución de probabilidad acumulada')\nplt.show()", "(50, 4)\n" ] ], [ [ "![imagen.png](attachment:imagen.png)", "_____no_output_____" ], [ "## 7. Distribuciónn triangular\nParámetros: \n - a : $a\\in (-\\infty ,\\infty)$\n - b : $b > a$ \n - c : $a\\leq c\\leq b$\n - Soporte: $a\\leq x\\leq b$ \n\n$$\\textbf{Función de densidad de probabilidad}\\\\f(x|a,b,c)={\\begin{cases}{\\frac {2(x-a)}{(b-a)(c-a)}}&{\\text{para }}a\\leq x<c,\\\\[4pt]{\\frac {2}{b-a}}&{\\text{para }}x=c,\\\\[4pt]{\\frac {2(b-x)}{(b-a)(b-c)}}&{\\text{para }}c<x\\leq b,\\\\[4pt]0&{\\text{para otros casos}}\\end{cases}}$$\n\n\n$$\\textbf{Función de distribución de probabilidad}\\\\F(x|a,b,c)={\\begin{cases}{0}&{\\text{para }}x\\leq a,\\\\[4pt]{\\frac {(x-a)^2}{(b-a)(c-a)}}&{\\text{para }}a< x\\leq c,\\\\[4pt]{1-\\frac{(b-x)^2}{(b-a)(b-c)}}&{\\text{para }}c<x< b,\\\\[4pt]1&{\\text{para }}b\\leq x\\end{cases}}$$\n\n![imagen.png](attachment:imagen.png)\n\n### Uso de la distribución triangular\nLa distribución triangular es habitualmente empleada como una descripción subjetiva de una población para la que sólo se cuenta con una cantidad limitada de datos muestrales y, especialmente en casos en que la relación entre variables es conocida pero los **datos son escasos** (posiblemente porque es alto el costo de recolectarlos). Está basada en un conocimiento del mínimo y el máximo como el del valor modal. Por estos motivos, la Distribución Triangular ha sido denominada como la de \"falta de precisión\" o de información.\n\n> Referencia: https://en.wikipedia.org/wiki/Triangular_distribution", "_____no_output_____" ], [ "# <font color ='red'> Tarea (Opcional)\nGenerar valores aleatorios para la siguiente distribución de probabilidad\n $$f(x)=\\begin{cases}\\frac{2}{(c-a)(b-a)}(x-a), & a\\leq x \\leq b\\\\ \\frac{-2}{(c-a)(c-b)}(x-c),& b\\leq x \\leq c \\end{cases}$$ con a=1; b=2; c=5\n1. Usando el método de la transformada inversa.\n2. Usando el método de aceptación y rechazo.\n3. En la librería `import scipy.stats as st` hay una función que genera variables aleatorias triangulares `st.triang.pdf(x, c, loc, scale)` donde \"c,loc,scale\" son los parámetros de esta distribución (similares a los que nuestra función se llaman a,b,c, PERO NO IGUALES). Explorar el help de python para encontrar la equivalencia entre los parámetros \"c,loc,scale\" y los parámetros de nuestra función con parámetros \"a,b,c\". La solución esperada es como se muestra a continuación:\n![imagen.png](attachment:imagen.png)\n\n4. Generar 1000 variables aleatorias usando la función creada en el punto 2 y usando la función `st.triang.rvs` y graficar el histograma en dos gráficas diferentes de cada uno de los conjuntos de variables aleatorios creado. Se espera algo como esto:\n", "_____no_output_____" ], [ "![imagen.png](attachment:imagen.png)", "_____no_output_____" ], [ "### La pongo como opcional por que puede aparecer en un quiz o un examen.\n\n# <font color ='red'>Tarea distribuciones de probabilidad:</font>\n\nLa tarea debe de realizarse en grupos, los cuales están nombrados en la siguiente tabla. La tarea consiste en modificar una de las páginas que corresponde a el grupo conformado, por ejemplo si eres el grupo 1, debes de modificar la página que corresponde a tu grupo, no ninguna de las otras páginas. En dicha página les voy a pedir que respondan a cada una de las siguientes pregutas, para el próximo viernes 9 de octubre, donde consultan acerca de cada una de las distribuciones de probabilidad asignadas. Lo que necesito que consulten es:\n\n1. Explicación del uso de cada distribución de probabilidad.\n\n2. Utilizar recursos audiovisuales, como videos, tablas, gifts, imágenes, enlace externos, etc, los cuales desde esta plataforma de canvas es posible introducir, en donde expliquen de la forma mas amigable y simple posible, las aplicaciones y usos de las distribuciones de probabilidad asignadas.\n\n3. Consultar en libros, internet, aplicaciones de como usar dichas distribuciones, por qué usarlas y posibles aplicaciones en finanzas.\n\n4. También pueden poner la descripción matemática de dichas distribuciones. Noten que pueden ingresar código latex para poder ingresar ecuaciones y demás.\n\n5. Poner pantallazos del código y resultados de como usar dicha función de distribución de probabilidad en python. Algo como esto\n> Distribución poisson\n> - Distribución de probabilidad y distribución acumulada (usando el paquete estadístico stats)\n> ![imagen.png](attachment:imagen.png)", "_____no_output_____" ], [ "> - Gráficas para distintos parámetros en este caso $\\lambda = [8,30]$\n> ![imagen.png](attachment:imagen.png)\n\n6. ¿Cómo pudieran responder la pregunta P(X<b)=** ? Para el caso de la distribución poisson exploren el comando `st.poisson(Lamda).ppf(b)`\n\nLa calificación estará basada, en la creatividad y el manejo que tengan de cada una de sus distribuciones de probabilidad a la hora de la exposición.\n", "_____no_output_____" ], [ "<script>\n $(document).ready(function(){\n $('div.prompt').hide();\n $('div.back-to-top').hide();\n $('nav#menubar').hide();\n $('.breadcrumb').hide();\n $('.hidden-print').hide();\n });\n</script>\n\n<footer id=\"attribution\" style=\"float:right; color:#808080; background:#fff;\">\nCreated with Jupyter by Oscar David Jaramillo Zuluaga\n</footer>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

d0e8b53a6e4541617c527200a440c88159cd2ebc

7,059

ipynb

Jupyter Notebook

pycocoEvalDemo.ipynb

alitariq-syed/mmdetection

76a592a855515e9ff147f5c0caeea02bcfc5437b

[ "Apache-2.0" ]

null

pycocoEvalDemo.ipynb

alitariq-syed/mmdetection

76a592a855515e9ff147f5c0caeea02bcfc5437b

[ "Apache-2.0" ]

null

pycocoEvalDemo.ipynb

alitariq-syed/mmdetection

76a592a855515e9ff147f5c0caeea02bcfc5437b

[ "Apache-2.0" ]

null

40.803468

1,614

0.59371

[ [ [ "%matplotlib inline\nimport matplotlib.pyplot as plt\nfrom pycocotools.coco import COCO\nfrom pycocotools.cocoeval import COCOeval\nimport numpy as np\nimport skimage.io as io\nimport pylab\npylab.rcParams['figure.figsize'] = (10.0, 8.0)", "_____no_output_____" ], [ "annType = ['segm','bbox','keypoints']\nannType = annType[1] #specify type here\nprefix = 'person_keypoints' if annType=='keypoints' else 'instances'\nprint ('Running demo for *%s* results.'%(annType))", "Running demo for *bbox* results.\n" ], [ "#initialize COCO ground truth api\n\nannFile = 'data/TBX11K/annotations/json/TBX11K_val_only_tb.json'\ncocoGt=COCO(annFile)", "loading annotations into memory...\nDone (t=0.00s)\ncreating index...\nindex created!\n" ], [ "cocoGt.dataset", "_____no_output_____" ], [ "#initialize COCO detections api\nresFile='100_results.json'\ncocoDt=cocoGt.loadRes(resFile)", "Loading and preparing results...\n" ], [ "imgIds=sorted(cocoGt.getImgIds())\nimgIds=imgIds[0:100]\nimgId = imgIds[np.random.randint(100)]", "_____no_output_____" ], [ "# running evaluation\ncocoEval = COCOeval(cocoGt,cocoDt,annType)\ncocoEval.params.imgIds = imgIds\ncocoEval.evaluate()\ncocoEval.accumulate()\ncocoEval.summarize()", "Running per image evaluation... \nDONE (t=0.46s).\nAccumulating evaluation results... \nDONE (t=0.38s).\n Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.505\n Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.697\n Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.573\n Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.586\n Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.519\n Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.501\n Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.387\n Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.594\n Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.595\n Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.640\n Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.566\n Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.564\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ] ]

d0e8b73ee2588cce2f7f989b350dfdcf8d010ddc

5,823

ipynb

Jupyter Notebook

polymer_brushes/FreeformVFP-example.ipynb

arm61/refnx-models

cfddcf811babe3ad2e5a21666b310af6f41238e7

[ "BSD-3-Clause" ]

1

2020-03-27T01:45:32.000Z

polymer_brushes/FreeformVFP-example.ipynb

arm61/refnx-models

cfddcf811babe3ad2e5a21666b310af6f41238e7

[ "BSD-3-Clause" ]

2

2019-12-13T04:14:50.000Z

2020-08-06T05:22:12.000Z

polymer_brushes/FreeformVFP-example.ipynb

arm61/refnx-models

cfddcf811babe3ad2e5a21666b310af6f41238e7

[ "BSD-3-Clause" ]

5

2018-11-02T04:10:45.000Z

2021-07-12T14:10:05.000Z

25.651982

127

0.541989

[ [ [ "%matplotlib notebook\n\nimport pickle\nimport numpy as np\nimport matplotlib.pyplot as plt\n\nfrom refnx.reflect import SLD, Slab, ReflectModel, MixedReflectModel\nfrom refnx.dataset import ReflectDataset as RD\nfrom refnx.analysis import Objective, CurveFitter, PDF, Parameter, process_chain, load_chain\n\nfrom FreeformVFP import FreeformVFP", "_____no_output_____" ], [ "# Version numbers allow you to repeat the analysis on your computer and obtain identical results.\nimport refnx, scipy\nrefnx.version.version, np.version.version, scipy.version.version", "_____no_output_____" ] ], [ [ "# Load data\nThree datasets are included, pNIPAM at 25 °C, 32.5 °C and 40 °C. \n\npNIPAM is thermoresponsive; the 25 °C is a swollen, diffuse layer, whilst the 40 °C data is a collapsed slab.", "_____no_output_____" ] ], [ [ "data = RD(\"pNIPAM brush in d2o at 25C.dat\")\n# data = RD(\"pNIPAM brush in d2o at 32C.dat\")\n# data = RD(\"pNIPAM brush in d2o at 40C.dat\")", "_____no_output_____" ] ], [ [ "# Define materials and slab components\n\nFor simplicity some parameters that may normally have been allowed to vary have been set to predetermined optimum values.", "_____no_output_____" ] ], [ [ "si = SLD(2.07, 'si')\nsio2 = SLD(2.9, 'sio2')\nd2o = SLD(6.23 , 'd2o')\npolymer = SLD(0.81, 'polymer')\n\nsi_l = si(0, 0)\nsio2_l = sio2(20, 4.8)\nd2o_l = d2o(0, 0)", "_____no_output_____" ] ], [ [ "# Create the freeform component", "_____no_output_____" ] ], [ [ "NUM_KNOTS = 4\n\n#Polymer layer 1\npolymer_0 = polymer(2, 0.5)\n\n# Polymer-Solvent interface (spline)\npolymer_vfp = FreeformVFP(adsorbed_amount=120,\n vff=[0.6] * NUM_KNOTS,\n dzf=[1/(NUM_KNOTS + 1)] * (NUM_KNOTS + 1),\n polymer_sld=polymer, \n name='freeform vfp',\n left_slabs=[polymer_0])", "_____no_output_____" ] ], [ [ "# Set parameter bounds", "_____no_output_____" ] ], [ [ "sio2.real.setp(vary=True, bounds=(2.8, 3.47))\n\npolymer_0.thick.setp(vary=True, bounds=(2, 20))\npolymer_0.vfsolv.setp(vary=True, bounds=(0.1, 0.7))\n\npolymer_vfp.adsorbed_amount.setp(vary=True, bounds=(100, 130))\n\n\n# We can enforce monotonicity through the bounds we place on the fractional volume fraction changes.\nenforce_mono = True\n\nif enforce_mono:\n bounds = (0.1, 1)\nelse:\n bounds = (0.1, 1.5)\n\n# Here we set the bounds on the knot locations\nfor idx in range(NUM_KNOTS):\n polymer_vfp.vff[idx].setp(vary=True, bounds=bounds)\n polymer_vfp.dzf[idx].setp(vary=True, bounds=(0.05, 1))\n\npolymer_vfp.dzf[-1].setp(vary=True, bounds=(0.05, 1))\n\npolymer_vfp.dzf[0].setp(vary=True, bounds=(0.005, 1))", "_____no_output_____" ] ], [ [ "# Create the structure, model, objective", "_____no_output_____" ] ], [ [ "structure = si_l | sio2_l | polymer_0 | polymer_vfp | d2o_l\n\n# contracting the slab representation reduces computation time.\nstructure.contract = 1.5\n\nmodel = ReflectModel(structure)\nmodel.bkg.setp(vary=True, bounds=(1e-6, 1e-5))\nobjective = Objective(model, data)", "_____no_output_____" ], [ "fitter= CurveFitter(objective)\nfitter.fit('differential_evolution');", "_____no_output_____" ], [ "fig, [ax_vfp, ax_sld, ax_refl] = plt.subplots(1, 3, figsize=(10,3), dpi=90)\nz = np.linspace(-50, 1750, 2000)\n\nax_vfp.plot(*polymer_vfp.profile())\nax_sld.plot(*structure.sld_profile(z))\nax_refl.plot(data.x, objective.generative())\nax_refl.errorbar(data.x, data.y, yerr=data.y_err)\n\nax_refl.set_yscale('log')\n\nfig.tight_layout()", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

d0e8ca508506dac424a2ccf0998e4f6a4f21756c

36,606

ipynb

Jupyter Notebook

notebooks/MR/d_undersampled_reconstructions.ipynb

mastergari/SIRF-Exercises

0d89f8765d0f1a06e66bc1f54267999d35f9cdae

[ "Apache-2.0" ]

7

2020-11-19T17:04:18.000Z

2022-02-04T19:00:05.000Z

notebooks/MR/d_undersampled_reconstructions.ipynb

mastergari/SIRF-Exercises

0d89f8765d0f1a06e66bc1f54267999d35f9cdae

[ "Apache-2.0" ]

88

2020-06-04T08:52:53.000Z

2021-07-15T16:54:33.000Z

notebooks/MR/d_undersampled_reconstructions.ipynb

SynerBI/SIRF-Exercises

b78988c1539b9ae888ab4efbcdd32c2b972626de

[ "Apache-2.0" ]

8

2020-06-19T12:56:24.000Z

2022-03-31T11:54:43.000Z

30.91723

429

0.577692

[ [ [ "# Iterative reconstruction of undersampled MR data\n\nThis demonstration shows how to hande undersampled data\nand how to write a simple iterative reconstruction algorithm with\nthe acquisition model.\n\nThis demo is a 'script', i.e. intended to be run step by step in a\nPython notebook such as Jupyter. It is organised in 'cells'. Jupyter displays these\ncells nicely and allows you to run each cell on its own.", "_____no_output_____" ], [ "First version: 27th of March 2019 \nUpdated: 26nd of June 2021 \nAuthor: Johannes Mayer, Christoph Kolbitsch\n\nCCP SyneRBI Synergistic Image Reconstruction Framework (SIRF). \nCopyright 2015 - 2017 Rutherford Appleton Laboratory STFC. \nCopyright 2015 - 2017 University College London. \nCopyright 2015 - 2017, 2019, 2021 Physikalisch-Technische Bundesanstalt.\n\nThis is software developed for the Collaborative Computational\nProject in Positron Emission Tomography and Magnetic Resonance imaging\n(http://www.ccppetmr.ac.uk/).\n\nLicensed under the Apache License, Version 2.0 (the \"License\");\nyou may not use this file except in compliance with the License.\nYou may obtain a copy of the License at\n http://www.apache.org/licenses/LICENSE-2.0\nUnless required by applicable law or agreed to in writing, software\ndistributed under the License is distributed on an \"AS IS\" BASIS,\nWITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\nSee the License for the specific language governing permissions and\nlimitations under the License.", "_____no_output_____" ] ], [ [ "#%% make sure figures appears inline and animations works\n%matplotlib notebook\n\n# Setup the working directory for the notebook\nimport notebook_setup\nfrom sirf_exercises import cd_to_working_dir\ncd_to_working_dir('MR', 'd_undersampled_reconstructions')", "_____no_output_____" ], [ "__version__ = '0.1.0'\n\n# import engine module\nimport sirf.Gadgetron as pMR\nfrom sirf.Utilities import examples_data_path\nfrom sirf_exercises import exercises_data_path\n\n# import further modules\nimport os, numpy\n\nimport matplotlib.pyplot as plt\nimport matplotlib.animation as animation\n\nfrom tqdm.auto import trange", "_____no_output_____" ] ], [ [ "### Undersampled Reconstruction\n#### Goals of this notebook:\n\n- Write a fully sampled reconstruction on your own.\n- Obtain knowledge of how to deal with undersampled data.\n- User SIRF and Gadgetron to perform a GRAPPA reconstruction.\n- Implement an iterative parallel imaging SENSE reconstruction algorithm from scratch.\n", "_____no_output_____" ] ], [ [ "# This is just an auxiliary function\ndef norm_array( arr ):\n min_a = abs(arr).min()\n max_a = abs(arr).max()\n\n return (arr - min_a)/(max_a - min_a)\n ", "_____no_output_____" ] ], [ [ "### Time to get warmed up again:\nSince we deal with undersampled data in this last section, we need to compare it to a reference.\nSo we need to reconstruct the fully sampled dataset we encountered before.\n\nThis is an ideal opportunity to test what we learned and employ the `pMR.FullSampledReconstructor` class from before.", "_____no_output_____" ], [ "### Programming Task: Fully sampled reconstruction\n\n__Please write code that does the following:__\n- create a variable called `full_acq_data` of type `pMR.AcquisitionData` from the file `ptb_resolutionphantom_fully_ismrmrd.h5`\n- create a variable called `prep_full_data` and assign it the preprocessed data by calling the function `pMR.preprocess_acquisition_data` on our variable `full_acq_data`\n- create a variable called `recon` of type `pMR.FullySampledReconstructor()`\n- call the `set_input` method of `recon` on `prep_full_data` to assign our fully sampled dataset to our reconstructor\n- call the `process()` method of `recon` without arguments. \n- create a variable called `fs_image` and assign it the output of the `get_output` method of `recon`\n\n__Hint:__ if you call a function without arguments, don't forget the empty parenthesis.\n\n#### Don't look at the solution before you tried! \n", "_____no_output_____" ] ], [ [ "# YOUR CODE GOES HERE\n\n\n\n\n\n\n", "_____no_output_____" ], [ "# VALIDATION CELL\nfs_image_array = fs_image.as_array()\nfs_image_array = norm_array(fs_image_array)\n\nfig = plt.figure()\nplt.set_cmap('gray')\nax = fig.add_subplot(1,1,1)\nax.imshow( abs(fs_image_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('Fully sampled reconstruction')\nax.axis('off')", "_____no_output_____" ], [ "# Solution Cell. Don't look if you didn't try!\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\ndata_path = exercises_data_path('MR', 'PTB_ACRPhantom_GRAPPA')\nfilename_full_file = os.path.join(data_path, 'ptb_resolutionphantom_fully_ismrmrd.h5')\n\nfull_acq_data = pMR.AcquisitionData(filename_full_file)\nprep_full_data = pMR.preprocess_acquisition_data(full_acq_data)\n\nrecon = pMR.FullySampledReconstructor()\nrecon.set_input(prep_full_data)\nrecon.process()\nfs_image = recon.get_output()", "_____no_output_____" ], [ "# VALIDATION CELL\nfs_image_array = fs_image.as_array()\nfs_image_array = norm_array(fs_image_array)\n\nfig = plt.figure()\nplt.set_cmap('gray')\nax = fig.add_subplot(1,1,1)\nax.imshow( abs(fs_image_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('Fully sampled reconstruction')\nax.axis('off')", "_____no_output_____" ], [ "# LOADING AND PREPROCESSING DATA FOR THIS SET\nfilename_grappa_file = os.path.join(data_path, 'ptb_resolutionphantom_GRAPPA4_ismrmrd.h5')\nacq_data = pMR.AcquisitionData(filename_grappa_file)\npreprocessed_data = pMR.preprocess_acquisition_data(acq_data)\npreprocessed_data.sort()\n", "_____no_output_____" ], [ "print('Is the data we loaded undersampled? %s' % preprocessed_data.is_undersampled())", "_____no_output_____" ], [ "#%% RETRIEVE K-SPACE DATA\nk_array = preprocessed_data.as_array()\nprint('Size of k-space %dx%dx%d' % k_array.shape)", "_____no_output_____" ], [ "#%% SELECT VIEW DATA FROM DIFFERENT COILS\nprint('Size of k-space %dx%dx%d' % k_array.shape)\n\nnum_channels = k_array.shape[1]\nprint(num_channels)\nk_array = norm_array(k_array)\n\n\nfig = plt.figure()\nplt.set_cmap('gray')\nfor c in range(num_channels):\n ax = fig.add_subplot(2,num_channels//2,c+1)\n ax.imshow(abs(k_array[:,c,:]), vmin=0, vmax=0.05)\n ax.set_title('Coil '+str(c+1))\n ax.axis('off')\n", "_____no_output_____" ] ], [ [ "This looks pretty similar to what we had before, so we should be good.", "_____no_output_____" ] ], [ [ "# we define a quick fft with sos coil combination to do a standard reconstruction.\ndef our_fft( k_array ):\n image_array = numpy.zeros(k_array.shape, numpy.complex128)\n for c in range(num_channels):\n image_array[:,c,:] = numpy.fft.fftshift( numpy.fft.ifft2( numpy.fft.ifftshift(k_array[:,c,:])))\n# image_array = image_array/image_array.max() \n image_array = numpy.sqrt(numpy.sum(numpy.square(numpy.abs(image_array)),1))\n\n return image_array", "_____no_output_____" ], [ "# now we make a FFT of the data we looked at and compare it to our fully sampled image\nimage_array_sos = our_fft(k_array)\nimage_array_sos = norm_array(image_array_sos)\n\n\nfig = plt.figure()\nax = fig.add_subplot(1,2,1)\nax.imshow(abs(image_array_sos), vmin=0, vmax=1)\nax.set_title('Undersampled')\nax.axis('off')\n\nax = fig.add_subplot(1,2,2)\nax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('Fully sampled')\nax.axis('off')\n", "_____no_output_____" ] ], [ [ "### Question: \nPlease answer the following question for yourself:\n - Why is the undersampled reconstruction squeezed, but covers the whole FOV?\n", "_____no_output_____" ] ], [ [ "# NOW LET'S LOOK WHICH PARTS ARE SAMPLED AND WHICH ARE LEFT OUT\n# kspace_encode_step_1 gives the phase encoding steps which were performed\nwhich_pe = preprocessed_data.get_ISMRMRD_info('kspace_encode_step_1')\n\nprint('The following Phase Encoding (PE) points were sampled: \\n')\nprint(which_pe)", "_____no_output_____" ] ], [ [ "#### Observation: approximately 3 out of 4 phase encoding steps are missing.", "_____no_output_____" ] ], [ [ "# Fill an array with 1 only if a datapoint was acquired\nsampling_mask = numpy.zeros([256,256])\n\nfor pe in which_pe:\n sampling_mask[pe,:] = 1\n\n# PLOT THE SAMPLING MASK \nfig = plt.figure()\nplt.set_cmap('gray')\nax = fig.add_subplot(1,1,1)\nax.imshow( sampling_mask, vmin=0, vmax=1)\nax.set_title('Sampling pattern of a GRAPPA acquisition')\nplt.xlabel('Frequency encoding')\nplt.ylabel('Phase encoding')\n#ax.axis('off')", "_____no_output_____" ] ], [ [ "We notice that $112 = \\frac{256}{4} + 48$.\nThis means the around the center of k-space is densely sampled containing 48 readout lines.\nThe outside of k-space is undersampled by a factor of 4.", "_____no_output_____" ], [ "### Workaround: 'zero-fill' the k-space data\nSince the artifacts seem to be related to the shape of the data, let's just unsqueeze the shape into the correct one. \nSomehow we need to supply more datapoints to our FFT. But can we just add datapoints? This will corrupt the data!\n\nActually, a Fourier transform is just a sum weighted by a phase:\n\n$$\nf(x) = \\sum_k e^{j k x} \\cdot F(k)\n$$\n\nSo it does not mind if we add a data point $F(k) = 0$ at a position we didn't sample!\n\nThis means we make a larger array, __add our data in the correct spots__, and the gaps we fill with zeros. The correct spots are given by our sampling mask!", "_____no_output_____" ] ], [ [ "k_shape = [sampling_mask.shape[0], num_channels, sampling_mask.shape[1]]\nzf_k_array = numpy.zeros(k_shape, numpy.complex128)\n\nfor i in range(k_array.shape[0]):\n zf_k_array[which_pe[i],:,:] = k_array[i,:,:]\n\n\nfig = plt.figure()\nplt.set_cmap('gray')\nfor c in range(num_channels):\n ax = fig.add_subplot(2,num_channels//2,c+1)\n ax.imshow(abs(zf_k_array[:,c,:]), vmin=0, vmax=0.05)\n ax.set_title('Coil '+str(c+1))\n ax.axis('off')\n\n\n ", "_____no_output_____" ], [ "# Reconstruct the zero-filled data and take a look\nzf_recon = our_fft( zf_k_array)\nzf_recon = norm_array(zf_recon)\n\n\nfig = plt.figure()\nax = fig.add_subplot(1,2,1)\nax.imshow(abs(zf_recon), vmin=0, vmax=1)\nax.set_title('Zero-filled Undersampled ')\nax.axis('off')\n\n\nax = fig.add_subplot(1,2,2)\nax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('Fully Sampled ')\nax.axis('off')\n", "_____no_output_____" ] ], [ [ "### Observation: \nBummer. Now the shape is correct, however the artifacts are still present. \n\n - What artifacts appear in the zero-filled reconstruction?\n - Why are they artifacts all fine-lined?\n - How come they only appear in one direction?\n\nTo get rid of these we will need some parallel imaging techniques.", "_____no_output_____" ], [ "### Coil Sensitivity Map computation\nParallel imaging, this has something to do with exploiting the spatially varying coil sensitivities. \n", "_____no_output_____" ] ], [ [ "# WHICH COILMAPS DO WE GET FROM THIS DATASET?\ncsm = pMR.CoilSensitivityData()\ncsm.smoothness = 50\ncsm.calculate(preprocessed_data)\ncsm_array = numpy.squeeze(csm.as_array())\n\ncsm_array = csm_array.transpose([1,0,2])\n\nfig = plt.figure()\nplt.set_cmap('jet')\nfor c in range(csm_array.shape[1]):\n ax = fig.add_subplot(2,num_channels//2,c+1)\n ax.imshow(abs(csm_array[:,c,:]))\n ax.set_title('Coil '+str(c+1))\n ax.axis('off')\nplt.set_cmap('gray')", "_____no_output_____" ] ], [ [ "### Question: \nIn practice we would want to use a weighted sum (WS) coil combination technique so any artifacts in the coilmap would directly translate into the combined image. But we didn't see any of the high frequency artifacts!\n\nPlease answer the following question:\n\n\n- Why are there are artifacts in the reconstruction but not in the coilmaps? \n", "_____no_output_____" ], [ "We learned before, that parallel imaging is easily able to get rid of undersampling factor R=4.\nBut to have enough information to estimate coilmaps the center must be fully sampled. \n\nErgo a perfect acceleration by R=4 is not possible, one needs to spends some time to sample the center densely, to obtain coil sensitivities. Still, $\\frac{112}{256} = 0.44$, we acquired 56% faster.\n\n### GRAPPA Reconstruction\nGRAPPA is a parallel imaging technique which promises to get rid of undersampling artifacts. \nSo let's use one of our SIRF classes and see what it can do!", "_____no_output_____" ] ], [ [ "# WE DO A GRAPPA RECONSTRUCTION USING SIRF\n\nrecon = pMR.CartesianGRAPPAReconstructor()\nrecon.set_input(preprocessed_data)\nrecon.compute_gfactors(False)\nprint('---\\n reconstructing...')\n\nrecon.process()\n# for undersampled acquisition data GRAPPA computes Gfactor images\n# in addition to reconstructed ones\ngrappa_images = recon.get_output()\ngrappa_images_array = grappa_images.as_array()\ngrappa_images_array = norm_array(grappa_images_array)", "_____no_output_____" ], [ "# PLOT THE RESULTS\nfig = plt.figure(figsize=(9, 4))\n\nax = fig.add_subplot(1,3,1)\nax.imshow(abs(zf_recon), vmin=0, vmax=1)\nax.set_title('Zero-filled Undersampled ')\nax.axis('off')\n\nax = fig.add_subplot(1,3,2)\nax.imshow(abs(grappa_images_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('GRAPPA')\nax.axis('off')\n\nax = fig.add_subplot(1,3,3)\nax.imshow(abs(fs_image_array[0,:,:]), vmin=0, vmax=1)\nax.set_title('Fully Sampled')\nax.axis('off')\nplt.tight_layout()", "_____no_output_____" ] ], [ [ "__Well, that was very little code to perform a difficult task!__ That is because we sent our data off to The Gadgetron and they did all the work.\n### Question:\nIn what respect did a GRAPPA reconstruction:\n\n * improve the resulting image?\n * deterioate the resulting image?\n", "_____no_output_____" ], [ "# GREAT! Now we want to develop our own algorithm and be better than the GRAPPA reconstruction!\n## Urgh, let's rather not because we are annoyed by how much code we have to write all the time! Zero filling, coil combining, inverse FFTs. Frankly: terrible!\n\nWe want to capture our entire imaging and reconstruction process in one single object and don't care about data structure. Also we don't want to have to sum over coil channels all the time and take care of zero filling, this is just too much work! ", "_____no_output_____" ], [ "When we want to develop some reconstruction algorithm, we want to be able to go from an image $x$ __forward__ to k-space data $y$:\n$$ E: x \\rightarrow y,$$\nimplicitly performing multiplication of the image with the coil sensitivities $C_c$ for each channel $c$ and performing an FFT:\n\n$$\nE x = y_c = \\mathcal{F}( C_c \\cdot x).\n$$\n\nIn iterative image reconstruction we often to apply the so-called __backward__ or __adjoint__ to transform the k-space data into image space. This bundles doing the zero-filling, inverse FFT, and coil combination into one operation:\n$$ E^H: y \\rightarrow x,$$\nimplicitly performing everything: \n$$\nE^H y = x = \\sum_c C_c^*\\mathcal{F}^{-1}(y) \n$$\n\n$E^H$ in this case is the hermitian conjugate of the complex valued operator $E$. It is the combination of transposing and complex conjugation of a matrix: $ E^H = (E^T)^* $. Note, that this is not generally the inverse: $ E^H \\neq E^{-1}$ ", "_____no_output_____" ], [ "### Enter: AcquisitionModel\n\nIn SIRF there exists something called `AcquisitionModel`, in the literature also referenced as and Encoding operator $E$, *E* for encoding.", "_____no_output_____" ] ], [ [ "# NOW WE GENERATE THE ACQUISITION MODEL\nE = pMR.AcquisitionModel(preprocessed_data, grappa_images)", "_____no_output_____" ], [ "# We need help again to see what this thing here can do\nhelp(E)", "_____no_output_____" ], [ "# to supply coil info to the acquisition model we use the dedicated method\nE.set_coil_sensitivity_maps(csm)\n\n# Now we can hop back from k-space into image space in just one line:\naq_model_image = E.backward( preprocessed_data )", "_____no_output_____" ] ], [ [ "Well this is not much code any more. Suddenly implementing our own iterative algorithm seems feasible!\n### QUESTION\nBEFORE YOU RUN THE NEXT CELL AND LOOK AT THE PLOT:\nIn the next plot the image stored in `aq_model_image_array` will be shown, i.e. $x = E^H y$. \nBased on the discussion what the AcquisitionModel E does, what do you expect the reconstruction to look like?\n- Is it squeezed or is it the correct size?\n- Does it contain artifacts? If so, which ones?", "_____no_output_____" ] ], [ [ "aq_model_image_array = norm_array(aq_model_image.as_array())\n\nfig = plt.figure()\nplt.set_cmap('gray')\nax = fig.add_subplot(1,1,1)\nax.imshow(abs(aq_model_image_array[0,:,:]))\nax.set_title('Result Backward Method of E ')\nax.axis('off')", "_____no_output_____" ] ], [ [ "__Well, bummer again, the artifacts are still there!__ Of course, the acquisition model is just a compact version of our above code. We need something smarter to kill them off. But it got a bit more homogeneous, due to the weighted coil combination. ", "_____no_output_____" ], [ "# Image Reconstruction as an Inverse Problem\n## Iterative Parallel Imaging Reconstruction\n\nIn order to employ parallel imagaing, we should look at image reconstruction as an inverse problem.\nBy \"image reconstruction\" we actually mean to achieve the following equality:\n$$ E x = y,$$ or equivalently\n$$ E^H E \\, x = E^H y,$$ \nwhere $E$ is the encoding operator $x$ is the true image object and $y$ is the MR raw data we acquired. \nThe task of image reconstruction boils down to optimizing the following function:\n$$ \\mathcal{C}(x) = \\frac{1}{2} \\bigl{|} \\bigl{|} E \\, x - y \\bigr{|} \\bigr{|}_2^2 \\\\\n\\tilde{x} = \\min_x \\mathcal{C}(x)\n$$\nTo iteratively find the minimum of this cost function, $\\tilde{x}$, we need to go through steps of the kind:\n1. have a first guess for our image (usually an empty image)\n2. generate k-space data from this guess and compute the discrepancy to our acquired data (i.e. evaluate the cost fuction).\n3. update our image guess based on the computed discrepancy s.t. the cost will be lowered. \n\n__By iterating steps 2 and 3 many times we will end up at $\\tilde{x}$.__\n\nIs that going to be better than a GRAPPA reconstruction? ", "_____no_output_____" ], [ "## Implementing Conjugate Gradient Descent SENSE\n\nConjugate Gradient (CG) optimization is such an iterative procedure which will quickly result in finding $\\tilde{x}$.\nWe can study the corresponding [Wikipedia Article](https://en.wikipedia.org/wiki/Conjugate_gradient_method#Description_of_the_problem_addressed_by_conjugate_gradients).\n\nThis looks like our thang! \n\nFor that we need to write a bit of code:\n- We already have this encoding operator `E` defined where we can go from image to k-space and back.\n- Now we need to implement our first guess\n- and somehow we loop through steps 2 and 3 updating our image s.t. the costs are lowered.\n\nThey want to compute x in $Ax = b$, we want to compute x in $E^H E x = E^H y$. \nThis means we need to translate what it says on Wikipedia:\n- $x$ = reconstructed image\n- $A$ = $E^HE$\n- $b$ = $E^H y$\n", "_____no_output_____" ], [ "### Programming task\nPlease write code executing the following task:\n- define a fuction named `A_operator`\n- it should have one single argument `image`\n- it should return $E^H( E (image))$ \n\n__Hint 1:__ We defined `E` already. Use it methods `forward` and `backward`. `forward` goes from image space to k-space and `backward` the other way round. \n__Hint 2:__ Short reminder on the syntax. The function should look like: \n```\ndef function_name( arugment_name):\n variable = code_that_does_something_with ( argument_name )\n return variable\n```", "_____no_output_____" ] ], [ [ "# Write your code here (this is as much space as you need!)\n# make sure the name of your function is A_operator\n\n\n\n", "_____no_output_____" ], [ "# Don't look at the solution before you tried! \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# With this guy we will write our optimization\ndef A_operator( image ):\n return E.backward( E.forward(image) )", "_____no_output_____" ] ], [ [ "#### Back to Wikipedia!\nNow we have all the tools we need. Now let's write the code to optimize our cost function iteratively. \nWe don't care too much about maths, but we want the [algorithm](https://en.wikipedia.org/wiki/Conjugate_gradient_method#The_resulting_algorithm).\n", "_____no_output_____" ] ], [ [ "# our images should be the same shape as the GRAPPA output\nrecon_img = grappa_images \n\n# since we have no knowledge at all of what the image is we start from zero\nzero_array = recon_img.as_array()\nzero_array.fill(0)\nrecon_img.fill(zero_array)\n\n# now name the variables the same as in the Wikipedia article:\nx = recon_img\ny = preprocessed_data\n", "_____no_output_____" ] ], [ [ "### Programming task: Initialize Iterative Reconstruction\nPlease write code executing the following task:\n- Initialize a variable `r` with `r` = $b - Ax$ (`r` stands for residual). \n__Hint 0:__ Remember: $b=E^H y$. Don't forget we just defined the A operator!\n- Print the type of `r` using Pythons built-in `type` and `print` function. What type of r do you expect? Is it an image, or is it acquisition data?\n- After you wrote these two lines run your cell pressing `Ctrl+Enter`, to get the output of the print statement. This will tell you the class of `r`.\n- Afterwards, initialize a variable named `rr` with `rr` = $r^\\dagger r$. (`rr` stands for r times r). `rr` is the value of the cost function by the way. \n__Hint 1:__ No need to access any numpy arrays! Objects of type `sirf.Gadgetron.ImageData` have the method called ` norm()` giving you the square root of the quantity we are looking for. \n__Hint 2:__ Python-Power: $c=a^b$ $\\equiv$ `c = a**b`. \n- Initialize a variable `rr0` with the value of `rr` to store the starting norm of the residuals.\n- Initialize a variable `p` with the value of `r`.", "_____no_output_____" ] ], [ [ "## WRITE YOUR CODE IN THIS CELL\n## Please make sure to name the variables correctly\n\n", "_____no_output_____" ], [ "##### Don't look at the solution before you tried! #############################\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n############################################################################\n# this is our first residual\nr = E.backward( y ) - A_operator(x)\n\n# print the type\nprint('The type of r is: ' + str( type(r) ) ) \n\n# this is our cost function at the start\nrr = r.norm() ** 2\nrr0 = rr\n\n# initialize p\np = r\n", "_____no_output_____" ], [ "# now we write down the algorithm\n\n# how many iterative steps do we want\n# how low should the cost be\nnum_iter = 15\nsufficiently_small = 1e-7", "_____no_output_____" ], [ "#prep a container to store the updated image after each iteration, this is just for plotting reasons!\ndata_shape = numpy.array( x.as_array().shape )\ndata_shape[0] = num_iter\narray_with_iterations = numpy.zeros(data_shape, numpy.complex128)", "_____no_output_____" ], [ "# HERE WE RUN THE LOOP.\n\nprint('Cost for k = 0: ' + str( rr/ rr0) )\nwith trange(num_iter) as iters:\n for k in iters:\n\n Ap = A_operator( p )\n\n alpha = rr / Ap.dot(p)\n\n x = x + alpha * p\n\n r = r - alpha * Ap\n\n beta = r.norm()**2 / rr\n rr = r.norm()**2\n\n p = r + beta * p\n\n relative_residual = numpy.sqrt(rr/rr0)\n\n array_with_iterations[k,:,:] = x.as_array()\n iters.write('Cost for k = ' +str(k+1) + ': ' + str(relative_residual) )\n iters.set_postfix(cost=relative_residual)\n\n if( relative_residual < sufficiently_small ):\n iters.write('We achieved our desired accuracy. Stopping iterative reconstruction')\n break\n\n\nif k is num_iter-1: \n print('Reached maximum number of iterations. Stopping reconstruction.')", "_____no_output_____" ], [ "# See how the reconstructed image evolves\nfig = plt.figure()\nims = []\nfor i in range(k):\n im = plt.imshow(abs( array_with_iterations[i,:,:]), animated=True)\n ims.append([im])\n\nani = animation.ArtistAnimation(fig, ims, interval=500, blit=True, repeat_delay=0)\nplt.show() \n ", "_____no_output_____" ], [ "## now check out the final result as a still image\nrecon_arr = norm_array( x.as_array())\n\nplt.set_cmap('gray')\nfig = plt.figure()\nax = fig.add_subplot(1,1,1)\nax.imshow(abs(recon_arr[0,:,:]))\nax.set_title('SENSE RECONSTRUCTION')\nax.axis('off')", "_____no_output_____" ], [ "# Let's Plot\nrecon_arr = x.as_array()\n\nfig = plt.figure(figsize=(9, 9))\n\nax = fig.add_subplot(2,2,1)\nax.imshow(abs(aq_model_image_array[0,:,:]))\nax.set_title('UNDERSAMPLED RECONSTRUCTION')\nax.axis('off')\n\nax = fig.add_subplot(2,2,2)\nax.imshow(abs(grappa_images_array[0,:,:]))\nax.set_title('GRAPPA RECONSTRUCTION')\nax.axis('off')\n\nax = fig.add_subplot(2,2,3)\nax.imshow(abs(recon_arr[0,:,:]))\nax.set_title('SENSE RECONSTRUCTION')\nax.axis('off')\n\nax = fig.add_subplot(2,2,4)\nax.imshow(abs(fs_image_array[0,:,:]))\nax.set_title('FULLY SAMPLED RECONSTRUCTION')\nax.axis('off')\n\nplt.tight_layout()", "_____no_output_____" ] ], [ [ "### Question: Evaluation SENSE Reconstruction\n[So what is better, GRAPPA or SENSE?](https://www.youtube.com/watch?v=XVCtkzIXYzQ) \n\nPlease answer the following questions:\n- Where is the noise coming from? \n- Why has not every high-frequency artifact vanished?", "_____no_output_____" ], [ "And if you had typed the above code into your computer in 2001 and written a [paper](https://scholar.google.de/scholar?hl=de&as_sdt=0%2C5&q=Advances+in+sensitivity+encoding+with+arbitrary+k%E2%80%90space+trajectories&btnG=) on it, then 18 years later you had a good 1000 citations (plus 6k from the [previous one](https://scholar.google.de/scholar?hl=de&as_sdt=0%2C5&q=SENSE%3A+sensitivity+encoding+for+fast+MRI&btnG=)).\n\n", "_____no_output_____" ], [ "### Undersampled Reconstruction\n#### Recap:\n\nIn this notebook you\n- wrote your own fully sampled recon using SIRF.\n- saw the undersampling structure of GRAPPA files\n- discovered high-frequency undersampling artifacts.\n- implemented our own version of SENSE and beat (?) GRAPPA.\n", "_____no_output_____" ], [ "### Fin\n\nThis was the last exercise. We hoped you learned some new things about MRI and had a pleasant experience with SIRF and Python. \nSee you later!\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ] ]

d0e8e7d494dc811f0ad3a4b863ec917f7f54ea9e

466,482

ipynb

Jupyter Notebook

hw1/knn.ipynb

hexiang-hu/cs231n-practice

42c9ea3ff1fafd8dce7838c9afbb06a071292bfd

[ "MIT" ]

6

2018-09-07T10:17:42.000Z

2020-10-28T01:47:06.000Z

hw1/knn.ipynb

hexiang-hu/cs231n-practice

42c9ea3ff1fafd8dce7838c9afbb06a071292bfd

[ "MIT" ]

null

hw1/knn.ipynb

hexiang-hu/cs231n-practice

42c9ea3ff1fafd8dce7838c9afbb06a071292bfd

[ "MIT" ]

4

2018-08-04T06:56:41.000Z

2020-03-30T01:33:01.000Z

83.003915

311

0.824825

[ [ [ "# k-Nearest Neighbor (kNN) exercise\n\n*Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*\n\nThe kNN classifier consists of two stages:\n\n- During training, the classifier takes the training data and simply remembers it\n- During testing, kNN classifies every test image by comparing to all training images and transfering the labels of the k most similar training examples\n- The value of k is cross-validated\n\nIn this exercise you will implement these steps and understand the basic Image Classification pipeline, cross-validation, and gain proficiency in writing efficient, vectorized code.", "_____no_output_____" ] ], [ [ "# Run some setup code for this notebook.\n\nimport random\nimport numpy as np\nfrom cs231n.data_utils import load_CIFAR10\nimport matplotlib.pyplot as plt\n\n# This is a bit of magic to make matplotlib figures appear inline in the notebook\n# rather than in a new window.\n%matplotlib inline\nplt.rcParams['figure.figsize'] = (10.0, 8.0) \n# set default size of plots\nplt.rcParams['image.interpolation'] = 'nearest'\nplt.rcParams['image.cmap'] = 'gray'\n\n# Some more magic so that the notebook will reload external python modules;\n# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython\n%load_ext autoreload\n%autoreload 2", "_____no_output_____" ], [ "# Load the raw CIFAR-10 data.\ncifar10_dir = 'cs231n/datasets/cifar-10-batches-py'\nX_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)\n\n# As a sanity check, we print out the size of the training and test data.\nprint 'Training data shape: ', X_train.shape\nprint 'Training labels shape: ', y_train.shape\nprint 'Test data shape: ', X_test.shape\nprint 'Test labels shape: ', y_test.shape", "Training data shape: (50000, 32, 32, 3)\nTraining labels shape: (50000,)\nTest data shape: (10000, 32, 32, 3)\nTest labels shape: (10000,)\n" ], [ "# Visualize some examples from the dataset.\n# We show a few examples of training images from each class.\nclasses = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']\nnum_classes = len(classes)\nsamples_per_class = 7\nfor y, cls in enumerate(classes):\n idxs = np.flatnonzero(y_train == y)\n # select $samples_per_class different samples from a class\n idxs = np.random.choice(idxs, samples_per_class, replace=False)\n for i, idx in enumerate(idxs):\n plt_idx = i * num_classes + y + 1\n plt.subplot(samples_per_class, num_classes, plt_idx)\n plt.imshow(X_train[idx].astype('uint8'))\n plt.axis('off')\n if i == 0:\n plt.title(cls)\nplt.show()", "_____no_output_____" ], [ "# Subsample the data for more efficient code execution in this exercise\nnum_training = 5000\nmask = range(num_training)\nX_train = X_train[mask]\ny_train = y_train[mask]\n\nnum_test = 500\nmask = range(num_test)\nX_test = X_test[mask]\ny_test = y_test[mask]", "_____no_output_____" ], [ "# Reshape the image data into rows\nX_train = np.reshape(X_train, (X_train.shape[0], -1))\nX_test = np.reshape(X_test, (X_test.shape[0], -1))\nprint X_train.shape, X_test.shape", "(5000, 3072) (500, 3072)\n" ], [ "from cs231n.classifiers import KNearestNeighbor\n\n# Create a kNN classifier instance. \n# Remember that training a kNN classifier is a noop: \n# the Classifier simply remembers the data and does no further processing \nclassifier = KNearestNeighbor()\nclassifier.train(X_train, y_train)", "_____no_output_____" ] ], [ [ "We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps: \n\n1. First we must compute the distances between all test examples and all train examples. \n2. Given these distances, for each test example we find the k nearest examples and have them vote for the label\n\nLets begin with computing the distance matrix between all training and test examples. For example, if there are **Ntr** training examples and **Nte** test examples, this stage should result in a **Nte x Ntr** matrix where each element (i,j) is the distance between the i-th test and j-th train example.\n\nFirst, open `cs231n/classifiers/k_nearest_neighbor.py` and implement the function `compute_distances_two_loops` that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.", "_____no_output_____" ] ], [ [ "\n# Open cs231n/classifiers/k_nearest_neighbor.py and implement\n# compute_distances_two_loops.\n\n# Test your implementation:\ndists = classifier.compute_distances_two_loops(X_test)\n\nprint dists.shape", "(500, 5000)\n" ], [ "# We can visualize the distance matrix: each row is a single test example and\n# its distances to training examples\nplt.imshow(dists, interpolation='none')", "_____no_output_____" ] ], [ [ "**Inline Question #1:** Notice the structured patterns in the distance matrix. \n\n- What is the cause behind the distinctly visible rows? \n- What causes the columns?", "_____no_output_____" ], [ "**Your Answer**: \n* Each test image will have variant L2 distance to the training images\n* Each training image have distinct L2 distance to the test images \n\n", "_____no_output_____" ] ], [ [ "# Now implement the function predict_labels and run the code below:\n# We use k = 1 (which is Nearest Neighbor).\ny_test_pred = classifier.predict_labels(dists, k=1)\n\n# Compute and print the fraction of correctly predicted examples\nnum_correct = np.sum(y_test_pred == y_test)\naccuracy = float(num_correct) / num_test\nprint 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)", "Got 137 / 500 correct => accuracy: 0.274000\n" ], [ "# Now lets speed up distance matrix computation by using partial vectorization\n# with one loop. Implement the function compute_distances_one_loop and run the\n# code below:\ndists_one = classifier.compute_distances_one_loop(X_test)\n\n# To ensure that our vectorized implementation is correct, we make sure that it\n# agrees with the naive implementation. There are many ways to decide whether\n# two matrices are similar; one of the simplest is the Frobenius norm. In case\n# you haven't seen it before, the Frobenius norm of two matrices is the square\n# root of the squared sum of differences of all elements; in other words, reshape\n# the matrices into vectors and compute the Euclidean distance between them.\ndifference = np.linalg.norm(dists - dists_one, ord='fro')\nprint 'Difference was: %f' % (difference, )\nif difference < 0.001:\n print 'Good! The distance matrices are the same'\nelse:\n print 'Uh-oh! The distance matrices are different'", "Difference was: 0.000000\nGood! The distance matrices are the same\n" ], [ "# Now implement the fully vectorized version inside compute_distances_no_loops\n# and run the code\n\ndists_two = classifier.compute_distances_no_loops(X_test)\n\n# check that the distance matrix agrees with the one we computed before:\ndifference = np.linalg.norm(dists - dists_two, ord='fro')\nprint 'Difference was: %f' % (difference, )\nif difference < 0.001:\n print 'Good! The distance matrices are the same'\nelse:\n print 'Uh-oh! The distance matrices are different'", "Difference was: 0.000000\nGood! The distance matrices are the same\n" ], [ "# Let's compare how fast the implementations are\ndef time_function(f, *args):\n \"\"\"\n Call a function f with args and return the time (in seconds) that it took to execute.\n \"\"\"\n import time\n tic = time.time()\n f(*args)\n toc = time.time()\n return toc - tic\n\ntwo_loop_time = time_function(classifier.compute_distances_two_loops, X_test)\nprint 'Two loop version took %f seconds' % two_loop_time\n\none_loop_time = time_function(classifier.compute_distances_one_loop, X_test)\nprint 'One loop version took %f seconds' % one_loop_time\n\nno_loop_time = time_function(classifier.compute_distances_no_loops, X_test)\nprint 'No loop version took %f seconds' % no_loop_time\n\n# you should see significantly faster performance with the fully vectorized implementation", "Two loop version took 52.685231 seconds\nOne loop version took 44.575945 seconds\nNo loop version took 0.529489 seconds\n" ] ], [ [ "### Cross-validation\n\nWe have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.", "_____no_output_____" ] ], [ [ "num_folds = 5\nk_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]\n\nX_train_folds = []\ny_train_folds = []\n################################################################################\n# TODO: #\n# Split up the training data into folds. After splitting, X_train_folds and #\n# y_train_folds should each be lists of length num_folds, where #\n# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #\n# Hint: Look up the numpy array_split function. #\n################################################################################\nidxes = range(num_training)\nidx_folds = np.array_split(idxes, num_folds)\nfor idx in idx_folds:\n# mask = np.ones(num_training, dtype=bool)\n# mask[idx] = False\n# X_train_folds.append( (X_train[mask], X_train[~mask]) )\n# y_train_folds.append( (y_train[mask], y_train[~mask]) )\n X_train_folds.append( X_train[idx] )\n y_train_folds.append( y_train[idx] )\n \n# A dictionary holding the accuracies for different values of k that we find\n# when running cross-validation. After running cross-validation,\n# k_to_accuracies[k] should be a list of length num_folds giving the different\n# accuracy values that we found when using that value of k.\nk_to_accuracies = {}\n\n\n################################################################################\n# TODO: #\n# Perform k-fold cross validation to find the best value of k. For each #\n# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #\n# where in each case you use all but one of the folds as training data and the #\n# last fold as a validation set. Store the accuracies for all fold and all #\n# values of k in the k_to_accuracies dictionary. #\n################################################################################\nimport sys\nclassifier = KNearestNeighbor()\nVerbose = False\nfor k in k_choices:\n if Verbose: print \"processing k=%f\" % k\n else: sys.stdout.write('.')\n k_to_accuracies[k] = list()\n for num in xrange(num_folds):\n if Verbose: print \"processing fold#%i/%i\" % (num, num_folds)\n \n X_cv_train = np.vstack( [ X_train_folds[x] for x in xrange(num_folds) if x != num ])\n y_cv_train = np.hstack( [ y_train_folds[x].T for x in xrange(num_folds) if x != num ])\n \n X_cv_test = X_train_folds[num]\n y_cv_test = y_train_folds[num]\n\n # train k-nearest neighbor classifier\n classifier.train(X_cv_train, y_cv_train)\n \n # calculate trained matrix\n dists = classifier.compute_distances_no_loops(X_cv_test)\n \n y_cv_test_pred = classifier.predict_labels(dists, k=k)\n # Compute and print the fraction of correctly predicted examples\n num_correct = np.sum(y_cv_test_pred == y_cv_test)\n k_to_accuracies[k].append( float(num_correct) / y_cv_test.shape[0] )\n\n################################################################################\n# END OF YOUR CODE #\n################################################################################\n\n# Print out the computed accuracies\nfor k in sorted(k_to_accuracies):\n for accuracy in k_to_accuracies[k]:\n print 'k = %d, accuracy = %f' % (k, accuracy)", ".." ], [ "# plot the raw observations\nfor k in k_choices:\n accuracies = k_to_accuracies[k]\n plt.scatter([k] * len(accuracies), accuracies)\n\n# plot the trend line with error bars that correspond to standard deviation\naccuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])\naccuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])\nplt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)\nplt.title('Cross-validation on k')\nplt.xlabel('k')\nplt.ylabel('Cross-validation accuracy')\nplt.show()", "_____no_output_____" ], [ "# Based on the cross-validation results above, choose the best value for k, \n# retrain the classifier using all the training data, and test it on the test\n# data.\nbest_k = 6\n\nclassifier = KNearestNeighbor()\nclassifier.train(X_train, y_train)\ny_test_pred = classifier.predict(X_test, k=best_k)\n\n# Compute and display the accuracy\nnum_correct = np.sum(y_test_pred == y_test)\naccuracy = float(num_correct) / num_test\nprint 'Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy)", "Got 141 / 500 correct => accuracy: 0.282000\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

d0e90d424caa4f011cf6bb81fb124eddf2596f37

529,062

ipynb

Jupyter Notebook

10_AUDIO/03_FORCED_ALIGNMENT_WAV2VEC2/01_Forced_Alignment_Wav2Vec2.ipynb

CrispenGari/pytorch-python

e5e8f8d48aa17ed4eb2236e53cbea78d6beeacf6

[ "MIT" ]

1

2021-11-08T07:37:16.000Z

10_AUDIO/03_FORCED_ALIGNMENT_WAV2VEC2/01_Forced_Alignment_Wav2Vec2.ipynb

CrispenGari/pytorch-python

e5e8f8d48aa17ed4eb2236e53cbea78d6beeacf6

[ "MIT" ]

null

10_AUDIO/03_FORCED_ALIGNMENT_WAV2VEC2/01_Forced_Alignment_Wav2Vec2.ipynb

CrispenGari/pytorch-python

e5e8f8d48aa17ed4eb2236e53cbea78d6beeacf6

[ "MIT" ]

1

2021-11-22T17:52:50.000Z

449.500425

90,169

0.928093

[ [ [ "### Forced Alignment with Wav2Vec2\n\nIn this notebook we are going to follow [this pytorch tutorial](https://pytorch.org/tutorials/intermediate/forced_alignment_with_torchaudio_tutorial.html) to align script to speech with torchaudio using the CTC segmentation algorithm described in [ CTC-Segmentation of Large Corpora for German End-to-end Speech Recognition](https://arxiv.org/abs/2007.09127)\n\n\nThe process of alignment looks like the following.\n\n1. Estimate the frame-wise label probability from audio waveform\nGenerate the trellis matrix which represents the probability of labels aligned at time step.\n2. Find the most likely path from the trellis matrix.\n3. In this example, we use torchaudio’s Wav2Vec2 model for acoustic feature extraction.\n\n\n### Installation of `tourchaudio`", "_____no_output_____" ] ], [ [ "!pip install torchaudio", "\u001b[K |██████████████████████████████▎ | 834.1 MB 1.3 MB/s eta 0:00:37tcmalloc: large alloc 1147494400 bytes == 0x5625b25b6000 @ 0x7f581be12615 0x5625790604cc 0x56257914047a 0x5625790632ed 0x562579154e1d 0x5625790d6e99 0x5625790d19ee 0x562579064bda 0x5625790d6d00 0x5625790d19ee 0x562579064bda 0x5625790d3737 0x562579155c66 0x5625790d2daf 0x562579155c66 0x5625790d2daf 0x562579155c66 0x5625790d2daf 0x562579065039 0x5625790a8409 0x562579063c52 0x5625790d6c25 0x5625790d19ee 0x562579064bda 0x5625790d3737 0x5625790d19ee 0x562579064bda 0x5625790d2915 0x562579064afa 0x5625790d2c0d 0x5625790d19ee\n\u001b[K |████████████████████████████████| 881.9 MB 19 kB/s \n\u001b[?25hRequirement already satisfied: typing-extensions in /usr/local/lib/python3.7/dist-packages (from torch==1.10.0->torchaudio) (3.7.4.3)\nInstalling collected packages: torch, torchaudio\n Attempting uninstall: torch\n Found existing installation: torch 1.9.0+cu111\n Uninstalling torch-1.9.0+cu111:\n Successfully uninstalled torch-1.9.0+cu111\n\u001b[31mERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.\ntorchvision 0.10.0+cu111 requires torch==1.9.0, but you have torch 1.10.0 which is incompatible.\ntorchtext 0.10.0 requires torch==1.9.0, but you have torch 1.10.0 which is incompatible.\u001b[0m\nSuccessfully installed torch-1.10.0 torchaudio-0.10.0\n" ] ], [ [ "### Imports", "_____no_output_____" ] ], [ [ "import os, requests, torch, torchaudio, IPython\nfrom dataclasses import dataclass\nimport matplotlib.pyplot as plt", "_____no_output_____" ], [ "SPEECH_URL = 'https://download.pytorch.org/torchaudio/test-assets/Lab41-SRI-VOiCES-src-sp0307-ch127535-sg0042.flac'\nSPEECH_FILE = 'speech.flac'\n\nif not os.path.exists(SPEECH_FILE):\n with open(SPEECH_FILE, 'wb') as file:\n with requests.get(SPEECH_URL) as resp:\n resp.raise_for_status()\n file.write(resp.content)\n ", "_____no_output_____" ] ], [ [ "### Generate frame-wise label probability\n\nThe first step is to generate the label class porbability of each aduio frame. We can use a ``Wav2Vec2`` model that is trained for ASR.\n\n``torchaudio`` provides easy access to pretrained models with associated labels.\n\n**Note:** In the subsequent sections, we will compute the probability in log-domain to avoid numerical instability. For this purpose, we normalize the emission with ``log_softmax``.\n\n", "_____no_output_____" ] ], [ [ "bundle = torchaudio.pipelines.WAV2VEC2_ASR_BASE_960H\nmodel = bundle.get_model()\nlabels = bundle.get_labels()\nwith torch.inference_mode():\n waveform, _ = torchaudio.load(SPEECH_FILE)\n emissions, _ = model(waveform)\n emissions = torch.log_softmax(emissions, dim=-1)\n\nemission = emissions[0].cpu().detach()", "_____no_output_____" ] ], [ [ "### Visualization", "_____no_output_____" ] ], [ [ "print(labels)\nplt.imshow(emission.T)\nplt.colorbar()\nplt.title(\"Frame-wise class probability\")\nplt.xlabel(\"Time\")\nplt.ylabel(\"Labels\")\nplt.show()", "('<s>', '<pad>', '</s>', '<unk>', '|', 'E', 'T', 'A', 'O', 'N', 'I', 'H', 'S', 'R', 'D', 'L', 'U', 'M', 'W', 'C', 'F', 'G', 'Y', 'P', 'B', 'V', 'K', \"'\", 'X', 'J', 'Q', 'Z')\n" ] ], [ [ "### Generate alignment probability (trellis)\n\nFrom the emission matrix, next we generate the trellis which represents\nthe probability of transcript labels occur at each time frame.\n\nTrellis is 2D matrix with time axis and label axis. The label axis\nrepresents the transcript that we are aligning. In the following, we use\n$t$ to denote the index in time axis and $j$ to denote the\nindex in label axis. $c_j$ represents the label at label index\n$j$.\n\nTo generate, the probability of time step $t+1$, we look at the\ntrellis from time step $t$ and emission at time step $t+1$.\nThere are two path to reach to time step $t+1$ with label\n$c_{j+1}$. The first one is the case where the label was\n$c_{j+1}$ at $t$ and there was no label change from\n$t$ to $t+1$. The other case is where the label was\n$c_j$ at $t$ and it transitioned to the next label\n$c_{j+1}$ at $t+1$.\n\nThe follwoing diagram illustrates this transition.\n\n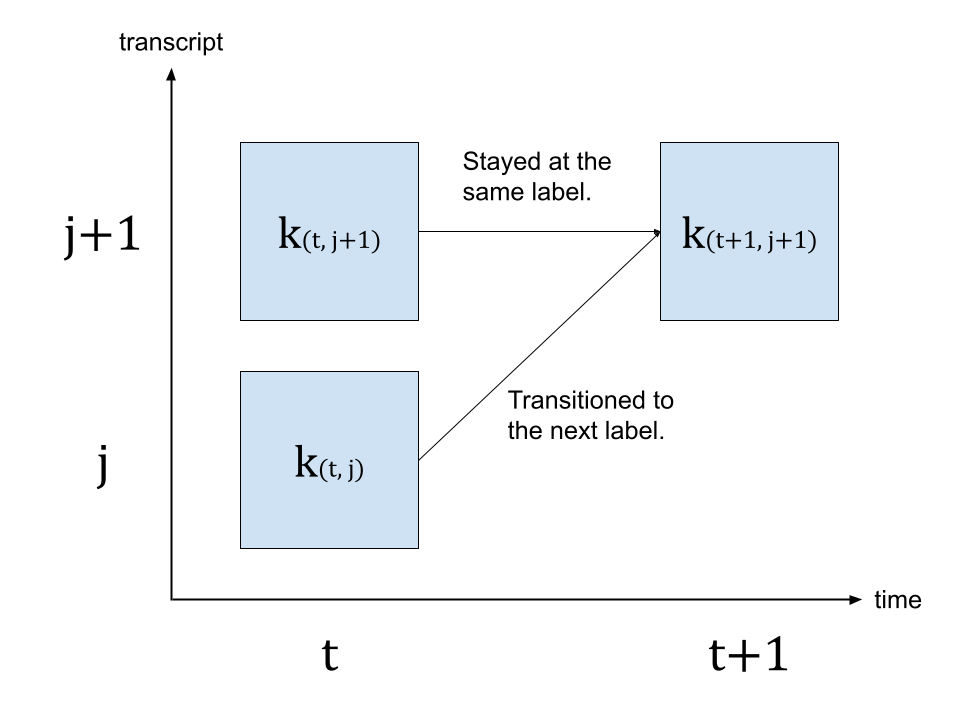![](https://download.pytorch.org/torchaudio/tutorial-assets/ctc-forward.png)\n\n\nSince we are looking for the most likely transitions, we take the more\nlikely path for the value of $k_{(t+1, j+1)}$, that is\n\n$ k_{(t+1, j+1)} = max( k_{(t, j)} p(t+1, c_{j+1}), k_{(t, j+1)} p(t+1,\nrepeat) ) $\n\nwhere $k$ represents is trellis matrix, and $p(t, c_j)$\nrepresents the probability of label $c_j$ at time step $t$.\n$repeat$ represents the blank token from CTC formulation. (For the\ndetail of CTC algorithm, please refer to the `Sequence Modeling with CTC\n[distill.pub] <https://distill.pub/2017/ctc/>`__)", "_____no_output_____" ] ], [ [ "transcript = 'I|HAD|THAT|CURIOSITY|BESIDE|ME|AT|THIS|MOMENT'\ndictionary = {c: i for i, c in enumerate(labels)}", "_____no_output_____" ], [ "tokens = [dictionary[c] for c in transcript]\nprint(list(zip(transcript, tokens)))", "[('I', 10), ('|', 4), ('H', 11), ('A', 7), ('D', 14), ('|', 4), ('T', 6), ('H', 11), ('A', 7), ('T', 6), ('|', 4), ('C', 19), ('U', 16), ('R', 13), ('I', 10), ('O', 8), ('S', 12), ('I', 10), ('T', 6), ('Y', 22), ('|', 4), ('B', 24), ('E', 5), ('S', 12), ('I', 10), ('D', 14), ('E', 5), ('|', 4), ('M', 17), ('E', 5), ('|', 4), ('A', 7), ('T', 6), ('|', 4), ('T', 6), ('H', 11), ('I', 10), ('S', 12), ('|', 4), ('M', 17), ('O', 8), ('M', 17), ('E', 5), ('N', 9), ('T', 6)]\n" ], [ "def get_trellis(emission, tokens, blank_id=0):\n num_frame = emission.size(0)\n num_tokens = len(tokens)\n\n # Trellis has extra diemsions for both time axis and tokens.\n # The extra dim for tokens represents <SoS> (start-of-sentence)\n # The extra dim for time axis is for simplification of the code.\n trellis = torch.full((num_frame+1, num_tokens+1), -float('inf'))\n trellis[:, 0] = 0\n for t in range(num_frame):\n trellis[t+1, 1:] = torch.maximum(\n # Score for staying at the same token\n trellis[t, 1:] + emission[t, blank_id],\n # Score for changing to the next token\n trellis[t, :-1] + emission[t, tokens],\n )\n return trellis\n\ntrellis = get_trellis(emission, tokens)", "_____no_output_____" ], [ "trellis", "_____no_output_____" ] ], [ [ "### Visualization.", "_____no_output_____" ] ], [ [ "plt.imshow(trellis[1:, 1:].T, origin='lower')\nplt.annotate(\"- Inf\", (trellis.size(1) / 5, trellis.size(1) / 1.5))\nplt.colorbar()\nplt.show()", "_____no_output_____" ] ], [ [ ">In the above visualization, we can see that there is a trace of high probability crossing the matrix diagonally.", "_____no_output_____" ], [ "### Find the most likely path (backtracking)\n\nOnce the trellis is generated, we will traverse it following the\nelements with high probability.\n\nWe will start from the last label index with the time step of highest\nprobability, then, we traverse back in time, picking stay\n($c_j \\rightarrow c_j$) or transition\n($c_j \\rightarrow c_{j+1}$), based on the post-transition\nprobability $k_{t, j} p(t+1, c_{j+1})$ or\n$k_{t, j+1} p(t+1, repeat)$.\n\nTransition is done once the label reaches the beginning.\n\nThe trellis matrix is used for path-finding, but for the final\nprobability of each segment, we take the frame-wise probability from\nemission matrix.\n", "_____no_output_____" ] ], [ [ "@dataclass\nclass Point:\n token_index: int\n time_index: int\n score: float", "_____no_output_____" ], [ "def backtrack(trellis, emission, tokens, blank_id=0):\n # Note:\n # j and t are indices for trellis, which has extra dimensions\n # for time and tokens at the beginning.\n # When refering to time frame index `T` in trellis,\n # the corresponding index in emission is `T-1`.\n # Similarly, when refering to token index `J` in trellis,\n # the corresponding index in transcript is `J-1`.\n j = trellis.size(1) - 1\n t_start = torch.argmax(trellis[:, j]).item()\n\n path = []\n for t in range(t_start, 0, -1):\n # 1. Figure out if the current position was stay or change\n # Note (again):\n # `emission[J-1]` is the emission at time frame `J` of trellis dimension.\n # Score for token staying the same from time frame J-1 to T.\n stayed = trellis[t-1, j] + emission[t-1, blank_id]\n # Score for token changing from C-1 at T-1 to J at T.\n changed = trellis[t-1, j-1] + emission[t-1, tokens[j-1]]\n\n # 2. Store the path with frame-wise probability.\n prob = emission[t-1, tokens[j-1] if changed > stayed else 0].exp().item()\n # Return token index and time index in non-trellis coordinate.\n path.append(Point(j-1, t-1, prob))\n\n # 3. Update the token\n if changed > stayed:\n j -= 1\n if j == 0:\n break\n else:\n raise ValueError('Failed to align')\n return path[::-1]\n\npath = backtrack(trellis, emission, tokens)\nprint(path)", "[Point(token_index=0, time_index=30, score=0.9999842643737793), Point(token_index=0, time_index=31, score=0.9847016334533691), Point(token_index=0, time_index=32, score=0.9999707937240601), Point(token_index=0, time_index=33, score=0.15400736033916473), Point(token_index=1, time_index=34, score=0.9999173879623413), Point(token_index=1, time_index=35, score=0.6080494523048401), Point(token_index=2, time_index=36, score=0.9997720122337341), Point(token_index=2, time_index=37, score=0.9997127652168274), Point(token_index=3, time_index=38, score=0.9999357461929321), Point(token_index=3, time_index=39, score=0.9861611127853394), Point(token_index=4, time_index=40, score=0.9238568544387817), Point(token_index=4, time_index=41, score=0.9257279634475708), Point(token_index=4, time_index=42, score=0.01566161774098873), Point(token_index=5, time_index=43, score=0.9998378753662109), Point(token_index=6, time_index=44, score=0.9988442659378052), Point(token_index=6, time_index=45, score=0.10147518664598465), Point(token_index=7, time_index=46, score=0.9999426603317261), Point(token_index=7, time_index=47, score=0.9999946355819702), Point(token_index=8, time_index=48, score=0.9979604482650757), Point(token_index=8, time_index=49, score=0.03603147715330124), Point(token_index=8, time_index=50, score=0.061637770384550095), Point(token_index=9, time_index=51, score=4.3353440560167655e-05), Point(token_index=10, time_index=52, score=0.999980092048645), Point(token_index=10, time_index=53, score=0.9967095851898193), Point(token_index=10, time_index=54, score=0.9999257326126099), Point(token_index=11, time_index=55, score=0.9999982118606567), Point(token_index=11, time_index=56, score=0.9990686774253845), Point(token_index=11, time_index=57, score=0.9999996423721313), Point(token_index=11, time_index=58, score=0.9999996423721313), Point(token_index=11, time_index=59, score=0.845763087272644), Point(token_index=12, time_index=60, score=0.9999995231628418), Point(token_index=12, time_index=61, score=0.9996013045310974), Point(token_index=13, time_index=62, score=0.999998927116394), Point(token_index=13, time_index=63, score=0.003524808445945382), Point(token_index=13, time_index=64, score=1.0), Point(token_index=13, time_index=65, score=1.0), Point(token_index=14, time_index=66, score=0.9999916553497314), Point(token_index=14, time_index=67, score=0.9971591234207153), Point(token_index=14, time_index=68, score=0.9999990463256836), Point(token_index=14, time_index=69, score=0.9999991655349731), Point(token_index=14, time_index=70, score=0.9999998807907104), Point(token_index=14, time_index=71, score=0.9999998807907104), Point(token_index=14, time_index=72, score=0.9999881982803345), Point(token_index=14, time_index=73, score=0.0114297391846776), Point(token_index=15, time_index=74, score=0.9999978542327881), Point(token_index=15, time_index=75, score=0.9996137022972107), Point(token_index=15, time_index=76, score=0.999998927116394), Point(token_index=15, time_index=77, score=0.9727506041526794), Point(token_index=16, time_index=78, score=0.999998927116394), Point(token_index=16, time_index=79, score=0.9949339032173157), Point(token_index=16, time_index=80, score=0.999998927116394), Point(token_index=16, time_index=81, score=0.9999121427536011), Point(token_index=17, time_index=82, score=0.9999775886535645), Point(token_index=17, time_index=83, score=0.657644510269165), Point(token_index=17, time_index=84, score=0.9984305500984192), Point(token_index=18, time_index=85, score=0.9999874830245972), Point(token_index=18, time_index=86, score=0.9993744492530823), Point(token_index=18, time_index=87, score=0.9999988079071045), Point(token_index=18, time_index=88, score=0.10424047708511353), Point(token_index=19, time_index=89, score=0.9999969005584717), Point(token_index=19, time_index=90, score=0.39786556363105774), Point(token_index=20, time_index=91, score=0.9999933242797852), Point(token_index=20, time_index=92, score=1.698678829598066e-06), Point(token_index=20, time_index=93, score=0.9861364364624023), Point(token_index=21, time_index=94, score=0.9999960660934448), Point(token_index=21, time_index=95, score=0.999272882938385), Point(token_index=21, time_index=96, score=0.9993410706520081), Point(token_index=22, time_index=97, score=0.9999983310699463), Point(token_index=22, time_index=98, score=0.9999971389770508), Point(token_index=22, time_index=99, score=0.9999997615814209), Point(token_index=22, time_index=100, score=0.9999995231628418), Point(token_index=23, time_index=101, score=0.9999732971191406), Point(token_index=23, time_index=102, score=0.9983218312263489), Point(token_index=23, time_index=103, score=0.9999992847442627), Point(token_index=23, time_index=104, score=0.9999997615814209), Point(token_index=23, time_index=105, score=1.0), Point(token_index=23, time_index=106, score=1.0), Point(token_index=23, time_index=107, score=0.9998630285263062), Point(token_index=24, time_index=108, score=0.9999982118606567), Point(token_index=24, time_index=109, score=0.9988585710525513), Point(token_index=25, time_index=110, score=0.9999798536300659), Point(token_index=25, time_index=111, score=0.8573576807975769), Point(token_index=26, time_index=112, score=0.9999847412109375), Point(token_index=26, time_index=113, score=0.9870267510414124), Point(token_index=26, time_index=114, score=1.9051107301493175e-05), Point(token_index=27, time_index=115, score=0.9999794960021973), Point(token_index=27, time_index=116, score=0.9998255372047424), Point(token_index=28, time_index=117, score=0.9999991655349731), Point(token_index=28, time_index=118, score=0.9999734163284302), Point(token_index=28, time_index=119, score=0.0009003716404549778), Point(token_index=29, time_index=120, score=0.9993481040000916), Point(token_index=29, time_index=121, score=0.9975457787513733), Point(token_index=29, time_index=122, score=0.00030507598421536386), Point(token_index=30, time_index=123, score=0.9999344348907471), Point(token_index=30, time_index=124, score=6.078748810978141e-06), Point(token_index=31, time_index=125, score=0.9833143949508667), Point(token_index=32, time_index=126, score=0.9974581599235535), Point(token_index=32, time_index=127, score=0.000824039860162884), Point(token_index=33, time_index=128, score=0.9965156316757202), Point(token_index=33, time_index=129, score=0.01746312528848648), Point(token_index=34, time_index=130, score=0.9989173412322998), Point(token_index=35, time_index=131, score=0.9999698400497437), Point(token_index=35, time_index=132, score=0.9999842643737793), Point(token_index=36, time_index=133, score=0.9997640252113342), Point(token_index=36, time_index=134, score=0.5100255012512207), Point(token_index=37, time_index=135, score=0.9998302459716797), Point(token_index=37, time_index=136, score=0.08518796414136887), Point(token_index=37, time_index=137, score=0.004072554875165224), Point(token_index=38, time_index=138, score=0.9999814033508301), Point(token_index=38, time_index=139, score=0.012051521800458431), Point(token_index=38, time_index=140, score=0.9999979734420776), Point(token_index=38, time_index=141, score=0.0005779753555543721), Point(token_index=39, time_index=142, score=0.9999068975448608), Point(token_index=39, time_index=143, score=0.9999960660934448), Point(token_index=39, time_index=144, score=0.9999980926513672), Point(token_index=40, time_index=145, score=0.9999915361404419), Point(token_index=40, time_index=146, score=0.9971166849136353), Point(token_index=40, time_index=147, score=0.9981797933578491), Point(token_index=41, time_index=148, score=0.9999310970306396), Point(token_index=41, time_index=149, score=0.9879536628723145), Point(token_index=41, time_index=150, score=0.9997628331184387), Point(token_index=42, time_index=151, score=0.9999535083770752), Point(token_index=43, time_index=152, score=0.9999716281890869), Point(token_index=44, time_index=153, score=0.6811626553535461)]\n" ] ], [ [ "### Visualization", "_____no_output_____" ] ], [ [ "def plot_trellis_with_path(trellis, path):\n # To plot trellis with path, we take advantage of 'nan' value\n trellis_with_path = trellis.clone()\n for i, p in enumerate(path):\n trellis_with_path[p.time_index, p.token_index] = float('nan')\n plt.imshow(trellis_with_path[1:, 1:].T, origin='lower')\n\nplot_trellis_with_path(trellis, path)\nplt.title(\"The path found by backtracking\")\nplt.show()", "_____no_output_____" ] ], [ [ "Looking good. Now this path contains repetations for the same labels, so let’s merge them to make it close to the original transcript.\n\nWhen merging the multiple path points, we simply take the average probability for the merged segments.\n\n\n", "_____no_output_____" ] ], [ [ "# Merge the labels\n@dataclass\nclass Segment:\n label: str\n start: int\n end: int\n score: float\n\n def __repr__(self):\n return f\"{self.label}\\t({self.score:4.2f}): [{self.start:5d}, {self.end:5d})\"\n\n @property\n def length(self):\n return self.end - self.start\n\ndef merge_repeats(path):\n i1, i2 = 0, 0\n segments = []\n while i1 < len(path):\n while i2 < len(path) and path[i1].token_index == path[i2].token_index:\n i2 += 1\n score = sum(path[k].score for k in range(i1, i2)) / (i2 - i1)\n segments.append(Segment(transcript[path[i1].token_index], path[i1].time_index, path[i2-1].time_index + 1, score))\n i1 = i2\n return segments\n\nsegments = merge_repeats(path)\nfor seg in segments:\n print(seg)", "I\t(0.78): [ 30, 34)\n|\t(0.80): [ 34, 36)\nH\t(1.00): [ 36, 38)\nA\t(0.99): [ 38, 40)\nD\t(0.62): [ 40, 43)\n|\t(1.00): [ 43, 44)\nT\t(0.55): [ 44, 46)\nH\t(1.00): [ 46, 48)\nA\t(0.37): [ 48, 51)\nT\t(0.00): [ 51, 52)\n|\t(1.00): [ 52, 55)\nC\t(0.97): [ 55, 60)\nU\t(1.00): [ 60, 62)\nR\t(0.75): [ 62, 66)\nI\t(0.88): [ 66, 74)\nO\t(0.99): [ 74, 78)\nS\t(1.00): [ 78, 82)\nI\t(0.89): [ 82, 85)\nT\t(0.78): [ 85, 89)\nY\t(0.70): [ 89, 91)\n|\t(0.66): [ 91, 94)\nB\t(1.00): [ 94, 97)\nE\t(1.00): [ 97, 101)\nS\t(1.00): [ 101, 108)\nI\t(1.00): [ 108, 110)\nD\t(0.93): [ 110, 112)\nE\t(0.66): [ 112, 115)\n|\t(1.00): [ 115, 117)\nM\t(0.67): [ 117, 120)\nE\t(0.67): [ 120, 123)\n|\t(0.50): [ 123, 125)\nA\t(0.98): [ 125, 126)\nT\t(0.50): [ 126, 128)\n|\t(0.51): [ 128, 130)\nT\t(1.00): [ 130, 131)\nH\t(1.00): [ 131, 133)\nI\t(0.75): [ 133, 135)\nS\t(0.36): [ 135, 138)\n|\t(0.50): [ 138, 142)\nM\t(1.00): [ 142, 145)\nO\t(1.00): [ 145, 148)\nM\t(1.00): [ 148, 151)\nE\t(1.00): [ 151, 152)\nN\t(1.00): [ 152, 153)\nT\t(0.68): [ 153, 154)\n" ] ], [ [ "### Visualization", "_____no_output_____" ] ], [ [ "def plot_trellis_with_segments(trellis, segments, transcript):\n # To plot trellis with path, we take advantage of 'nan' value\n trellis_with_path = trellis.clone()\n for i, seg in enumerate(segments):\n if seg.label != '|':\n trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')\n\n plt.figure()\n plt.title(\"Path, label and probability for each label\")\n ax1 = plt.axes()\n ax1.imshow(trellis_with_path.T, origin='lower')\n ax1.set_xticks([])\n\n for i, seg in enumerate(segments):\n if seg.label != '|':\n ax1.annotate(seg.label, (seg.start + .7, i + 0.3))\n ax1.annotate(f'{seg.score:.2f}', (seg.start - .3, i + 4.3))\n\n plt.figure()\n plt.title(\"Probability for each label at each time index\")\n ax2 = plt.axes()\n xs, hs = [], []\n for p in path:\n label = transcript[p.token_index]\n if label != '|':\n xs.append(p.time_index + 1)\n hs.append(p.score)\n\n for seg in segments:\n if seg.label != '|':\n ax2.axvspan(seg.start+.4, seg.end+.4, color='gray', alpha=0.2)\n ax2.annotate(seg.label, (seg.start + .8, -0.07))\n\n ax2.bar(xs, hs, width=0.5)\n ax2.axhline(0, color='black')\n ax2.set_position(ax1.get_position())\n ax2.set_xlim(ax1.get_xlim())\n ax2.set_ylim(-0.1, 1.1)\n\nplot_trellis_with_segments(trellis, segments, transcript)\nplt.show()", "/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:10: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n # Remove the CWD from sys.path while we load stuff.\n/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:21: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n" ] ], [ [ "Looks good. Now let’s merge the words. The Wav2Vec2 model uses ``'|'`` as the word boundary, so we merge the segments before each occurance of ``'|'``.", "_____no_output_____" ] ], [ [ "# Merge words\ndef merge_words(segments, separator='|'):\n words = []\n i1, i2 = 0, 0\n while i1 < len(segments):\n if i2 >= len(segments) or segments[i2].label == separator:\n if i1 != i2:\n segs = segments[i1:i2]\n word = ''.join([seg.label for seg in segs])\n score = sum(seg.score * seg.length for seg in segs) / sum(seg.length for seg in segs)\n words.append(Segment(word, segments[i1].start, segments[i2-1].end, score))\n i1 = i2 + 1\n i2 = i1\n else:\n i2 += 1\n return words\n\nword_segments = merge_words(segments)\nfor word in word_segments:\n print(word)", "I\t(0.78): [ 30, 34)\nHAD\t(0.84): [ 36, 43)\nTHAT\t(0.52): [ 44, 52)\nCURIOSITY\t(0.89): [ 55, 91)\nBESIDE\t(0.94): [ 94, 115)\nME\t(0.67): [ 117, 123)\nAT\t(0.66): [ 125, 128)\nTHIS\t(0.70): [ 130, 138)\nMOMENT\t(0.97): [ 142, 154)\n" ] ], [ [ "### Visualization", "_____no_output_____" ] ], [ [ "trellis_with_path = trellis.clone()\nfor i, seg in enumerate(segments):\n if seg.label != '|':\n trellis_with_path[seg.start+1:seg.end+1, i+1] = float('nan')\n\nplt.imshow(trellis_with_path[1:, 1:].T, origin='lower')\nax1 = plt.gca()\nax1.set_yticks([])\nax1.set_xticks([])\n\n\nfor word in word_segments:\n plt.axvline(word.start - 0.5)\n plt.axvline(word.end - 0.5)\n\nfor i, seg in enumerate(segments):\n if seg.label != '|':\n plt.annotate(seg.label, (seg.start, i + 0.3))\n plt.annotate(f'{seg.score:.2f}', (seg.start , i + 4), fontsize=8)\n\nplt.show()\n\n# The original waveform\nratio = waveform.size(1) / (trellis.size(0) - 1)\nplt.plot(waveform[0])\nfor word in word_segments:\n x0 = ratio * word.start\n x1 = ratio * word.end\n plt.axvspan(x0, x1, alpha=0.1, color='red')\n plt.annotate(f'{word.score:.2f}', (x0, 0.8))\n\nfor seg in segments:\n if seg.label != '|':\n plt.annotate(seg.label, (seg.start * ratio, 0.9))\n\nax2 = plt.gca()\nxticks = ax2.get_xticks()\nplt.xticks(xticks, xticks / bundle.sample_rate)\nplt.xlabel('time [second]')\nax2.set_position(ax1.get_position())\nax2.set_yticks([])\nax2.set_ylim(-1.0, 1.0)\nax2.set_xlim(0, waveform.size(-1))\nplt.show()\n\n# Generate the audio for each segment\nprint(transcript)\nIPython.display.display(IPython.display.Audio(SPEECH_FILE))\nfor i, word in enumerate(word_segments):\n x0 = int(ratio * word.start)\n x1 = int(ratio * word.end)\n filename = f\"{i}_{word.label}.wav\"\n torchaudio.save(filename, waveform[:, x0:x1], bundle.sample_rate)\n print(f\"{word.label}: {x0 / bundle.sample_rate:.3f} - {x1 / bundle.sample_rate:.3f}\")\n IPython.display.display(IPython.display.Audio(filename))", "_____no_output_____" ], [ "", "_____no_output_____" ], [ "", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

d0e911a4a9256964e31c557fe4fce4991cce2e84

248,238

ipynb

Jupyter Notebook

Day16/Day16.ipynb

freddykao/Opencv_for_kaggle

f99c6985eda98551852b63e6d505b1aa6e6b01f9

[ "MIT" ]

null

Day16/Day16.ipynb

freddykao/Opencv_for_kaggle

f99c6985eda98551852b63e6d505b1aa6e6b01f9

[ "MIT" ]

null

Day16/Day16.ipynb

freddykao/Opencv_for_kaggle

f99c6985eda98551852b63e6d505b1aa6e6b01f9

[ "MIT" ]

null

395.283439

210,492

0.915915

[ [ [ "\"\"\"Keras-ImageDataGenerator\n『本次練習內容』\n學習使用Keras-ImageDataGenerator 與 Imgaug 做圖像增強\n『本次練習目的』\n熟悉Image Augmentation的實作方法\n瞭解如何導入Imgae Augmentation到原本NN架構中\"\"\"", "_____no_output_____" ], [ "from keras.models import Sequential\nfrom keras.layers import Convolution2D\nfrom keras.layers import MaxPooling2D\nfrom keras.layers import Flatten\nfrom keras.layers import Dense\nfrom keras.layers import Dropout\nfrom keras.layers import BatchNormalization\nfrom keras.datasets import cifar10\nimport numpy as np\nimport tensorflow as tf\nfrom sklearn.preprocessing import OneHotEncoder\n\n(x_train, y_train), (x_test, y_test) = cifar10.load_data()\n\nprint(x_train.shape) #(50000, 32, 32, 3)\n\n## Normalize Data\ndef normalize(X_train,X_test):\n mean = np.mean(X_train,axis=(0,1,2,3))\n std = np.std(X_train, axis=(0, 1, 2, 3))\n X_train = (X_train-mean)/(std+1e-7)\n X_test = (X_test-mean)/(std+1e-7) \n return X_train, X_test,mean,std\n \n \n## Normalize Training and Testset \nx_train, x_test,mean_train,std_train = normalize(x_train, x_test) \n\n## OneHot Label 由(None, 1)-(None, 10)\n## ex. label=2,變成[0,0,1,0,0,0,0,0,0,0]\none_hot=OneHotEncoder()\ny_train=one_hot.fit_transform(y_train).toarray()\ny_test=one_hot.transform(y_test).toarray()", "(50000, 32, 32, 3)\n" ], [ "classifier=Sequential()\ninput_shape=(32,32,3)\n\n#卷積組合\nclassifier.add(Convolution2D(filters =32 ,kernel_size=(3,3),input_shape=input_shape,padding =\"same\"))#32,3,3,input_shape=(32,32,3),activation='relu''\nclassifier.add(BatchNormalization(momentum=0.8))\n\n'''自己決定MaxPooling2D放在哪裡'''\n#classifier.add(MaxPooling2D(pool_size=(2,2)))\n\n#卷積組合\nclassifier.add(Convolution2D(filters =32 ,kernel_size=(3,3),input_shape=input_shape,padding =\"same\"))#32,3,3,input_shape=(32,32,3),activation='relu''\nclassifier.add(BatchNormalization(momentum=0.8))\n\n#flatten\nclassifier.add(Flatten())\n\n#FC\nclassifier.add(Dense(80)) #output_dim=100,activation=relu\n\n#輸出\nclassifier.add(Dense(output_dim=10,activation='relu'))\n\n#超過兩個就要選categorical_crossentrophy\nclassifier.compile(optimizer = 'adam', loss = 'categorical_crossentropy', metrics = ['accuracy'])\nclassifier.fit(x_train,y_train,batch_size=100,epochs=100)", "C:\\Users\\fredd\\Anaconda3\\lib\\site-packages\\ipykernel_launcher.py:22: UserWarning: Update your `Dense` call to the Keras 2 API: `Dense(activation=\"relu\", units=10)`\n" ], [ "from keras.preprocessing.image import ImageDataGenerator\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport cv2\n%matplotlib inline\n\n##定義使用的Augmentation\nimg_gen = ImageDataGenerator(\nhorizontal_flip=True)\n\nwidth=224\nheight=224\nbatch_size=4\n\nimg = cv2.imread('Tano.JPG') \nimg = cv2.resize(img, (224,224))##改變圖片尺寸\nimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR，轉成RGB\nimg_origin=img.copy()\nimg= np.array(img, dtype=np.float32)\nimg_combine=np.array([img,img,img,img],dtype=np.uint8) ##輸入generator要是四維，(224,224,3)變成(4,224,224,3)\nbatch_gen = img_gen.flow(img_combine, batch_size=4)\nassert next(batch_gen).shape==(batch_size, width, height, 3)\n\nplt.figure(figsize=(20,10))\ni = 1\nfor batch in batch_gen:\n plt.subplot(1, 5, 1)\n plt.imshow(img_origin) ##原圖\n plt.subplot(1, 5, i+1)\n plt.imshow(batch[0, :, :, :].astype(np.uint8))\n plt.imshow(batch[1, :, :, :].astype(np.uint8))\n plt.imshow(batch[2, :, :, :].astype(np.uint8))\n plt.imshow(batch[3, :, :, :].astype(np.uint8))\n plt.axis('off')\n i += 1\n if i > 4:\n break # or the generator would loop infinitely", "C:\\Users\\fredd\\Anaconda3\\lib\\site-packages\\ipykernel_launcher.py:27: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.\n" ], [ "\ntrain_datagen = ImageDataGenerator(rescale = 2,shear_range = 0.2,zoom_range = 0.2,horizontal_flip = True)\n#Test Generator，只需要Rescale，不需要其他增強\ntest_datagen = ImageDataGenerator(rescale = 1./255)\n\n#將路徑給Generator，自動產生Label\ntraining_set = train_datagen.flow_from_directory('training_set',\n target_size = (64, 64),\n batch_size = 32,\n class_mode = 'categorical')\n\ntest_set = test_datagen.flow_from_directory('test_set',\n target_size = (64, 64),\n batch_size = 32,\n class_mode = 'categorical')\n \n#訓練\nclassifier.fit_generator(training_set,steps_per_epoch = 250,nb_epoch = 25,\n validation_data = valid_set,validation_steps = 63)", "Found 46 images belonging to 2 classes.\nFound 30 images belonging to 2 classes.\n" ], [ "#預測新照片\nfrom keras.preprocessing import image as image_utils\ntest_image = image_utils.load_img('dataset/new_images/new_picture.jpg', target_size=(224, 224))\ntest_image = image_utils.img_to_array(test_image)\ntest_image = np.expand_dims(test_image, axis=0) \n\nresult = classifier.predict_on_batch(test_image)", "_____no_output_____" ], [ "from imgaug import augmenters as iaa\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport cv2\n\nimg = cv2.imread('Tano.JPG') \nimg = cv2.resize(img, (224,224))##改變圖片尺寸\nimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR，轉成RGB\nimg_origin=img.copy()\nimg= np.array(img, dtype=np.float32)\n\nimages = np.random.randint(0, 255, (5, 224, 224, 3), dtype=np.uint8)##創造一個array size==(5, 224, 224, 3)\n\nflipper = iaa.Fliplr(1.0) #水平翻轉機率==1.0\nimages[0] = flipper.augment_image(img) \n\nvflipper = iaa.Flipud('''填入''') #垂直翻轉機率40%\nimages[1] = vflipper.augment_image(img) \n\nblurer = iaa.GaussianBlur(3.0)\nimages[2] = blurer.augment_image(img) # 高斯模糊圖像( sigma of 3.0)\n\ntranslater = iaa.Affine(translate_px={\"x\": -16}) #向左橫移16個像素\nimages[3] = translater.augment_image(img) \n\nscaler = iaa.Affine(scale={\"y\":'''填入'''}) # 縮放照片，區間(0.8-1.2倍)\nimages[4] = scaler.augment_image(img)\n\ni=1\nplt.figure(figsize=(20,20))\nfor image in images:\n plt.subplot(1, 6, 1)\n plt.imshow(img_origin.astype(np.uint8))\n plt.subplot(1, 6, i+1)\n plt.imshow(image.astype(np.uint8))\n plt.axis('off')\n i+=1", "_____no_output_____" ], [ "\"\"\"第二Part\n打包多種Augmentation\n請學員自行練習新增以及改變Augmentation內容\n可參考Github: https://github.com/aleju/imgaug\"\"\"", "_____no_output_____" ], [ "import numpy as np\nimport imgaug as ia\nimport imgaug.augmenters as iaa\nimport matplotlib.pyplot as plt\n%matplotlib inline\n\n##輸入照片\nimg = cv2.imread('Tano.JPG') \nimg = cv2.resize(img, (224,224))##改變圖片尺寸\nimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR，轉成RGB\nimg_origin=img.copy()\nimg= np.array(img, dtype=np.float32)\n\nimg_combine=np.array([img,img,img,img],dtype=np.float32) \n\nsometimes = lambda aug: iaa.Sometimes(0.5, aug) # Sometimes(0.5, ...) 代表每次都有50%的機率運用不同的Augmentation\n\n##包裝想運用之圖像強化方式\nseq = iaa.Sequential([\n iaa.Crop(px=(0, 16)),\n iaa.Fliplr(0.4), \n sometimes(iaa.CropAndPad(\n percent=(-0.05, 0.1),\n pad_mode=ia.ALL,\n pad_cval=(0, 255)\n )),\n sometimes(iaa.Affine(\n scale={\"x\": (0.8, 1.2), \"y\": (0.8, 1.2)}, \n translate_percent={\"x\": (-0.2, 0.2), \"y\": (-0.2, 0.2)}, \n rotate=(-10, 10),\n shear=(-8, 8), \n order=[0, 1], \n cval=(0, 255),\n mode=ia.ALL \n )),\n sometimes(iaa.Superpixels(p_replace=(0, 1.0), n_segments=(20, 200))), # convert images into their superpixel representation\n sometimes(iaa.OneOf([\n iaa.GaussianBlur((0, 3.0)), # blur images \n iaa.AverageBlur(k=(1,3)), # blur image using local means with kernel sizes between 1 and 3\n iaa.MedianBlur(k=(3, 5)), # blur image using local medians with kernel sizes between 3 and 5\n ])),\n sometimes(iaa.Sharpen(alpha=(0, 0.2), lightness=(0.1, 0.4))), # sharpen images\n sometimes(iaa.Emboss(alpha=(0, 0.3), strength=(0, 0.5))), # emboss images\n ],random_order=True)\n\n\n\nimages_aug = seq.augment_images(img_combine) ## Image Augmentation\n\n##畫出來\ni=1\nplt.figure(figsize=(20,20))\nfor image in images_aug:\n plt.subplot(1, 5, 1)\n plt.imshow(img_origin.astype(np.uint8))\n plt.subplot(1, 5, i+1)\n plt.imshow(image.astype(np.uint8))\n plt.axis('off')\n i+=1", "_____no_output_____" ], [ "#包裝自定義Augmentation 與 Imgaug Augmentation", "_____no_output_____" ], [ "from PIL import Image\nimport os\nimport pickle\nimport numpy as np\nimport cv2\nimport glob\nimport pandas as pd\nimport time\nimport random\nimport imgaug as ia\nimport imgaug.augmenters as iaa\n\n'''隨機改變亮度''' \nclass RandomBrightness(object):\n '''Function to randomly make image brighter or darker\n Parameters\n ----------\n delta: float\n the bound of random.uniform distribution\n '''\n def __init__(self, delta=16):\n assert 0 <= delta <= 255\n self.delta = delta\n\n def __call__(self, image):\n delta = random.uniform(-self.delta, self.delta)\n if random.randint(0, 1):\n image = image + delta\n image = np.clip(image, 0.0, 255.0)\n return image\n \n'''隨機改變對比'''\nclass RandomContrast(object):\n '''Function to strengthen or weaken the contrast in each image\n Parameters\n ----------\n lower: float\n lower bound of random.uniform distribution\n upper: float\n upper bound of random.uniform distribution\n '''\n def __init__(self, lower=0.5, upper=1.5):\n assert upper >= lower, \"contrast upper must be >= lower.\"\n assert lower >= 0, \"contrast lower must be non-negative.\"\n self.lower = lower\n self.upper = upper\n\n def __call__(self, image):\n alpha = random.uniform(self.lower, self.upper)\n if random.randint(0, 1):\n image = image * alpha\n image = np.clip(image, 0.0, 255.0)\n return image\n \n'''包裝所有Augmentation'''\nclass Compose(object):\n def __init__(self, transforms):\n self.transforms = transforms\n\n def __call__(self, image):\n for t in self.transforms:\n image= t(image)\n return image\n\n'''包裝Imgaug'''\nclass ImgAugSequence(object):\n def __init__(self, sequence):\n self.sequence = sequence\n\n def __call__(self, image):\n image = self.sequence.augment_image(image)\n \n return image\n \nclass TrainAugmentations(object):\n def __init__(self):\n #Define imgaug.augmenters Sequential transforms\n sometimes = lambda aug: iaa.Sometimes(0.4, aug) # applies the given augmenter in 50% of all cases\n\n img_seq = iaa.Sequential([\n sometimes(iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.03*255), per_channel=0.5)),\n sometimes(iaa.ContrastNormalization((0.5, 2.0), per_channel=1),),\n sometimes(iaa.Sharpen(alpha=(0, 0.2), lightness=(0.1, 0.4))), # sharpen images\n sometimes(iaa.Emboss(alpha=(0, 0.3), strength=(0, 0.5))), # emboss images\n ],random_order=True)\n \n self.aug_pipeline = Compose([\n RandomBrightness(16), #make image brighter or darker\n RandomContrast(0.9, 1.1), #strengthen or weaken the contrast in each image\n ImgAugSequence(img_seq),\n ])\n \n\n def __call__(self, image):\n image= self.aug_pipeline(image)\n return image\n \nAugmenation=TrainAugmentations()", "_____no_output_____" ], [ "import numpy as np\nimport imgaug as ia\nimport imgaug.augmenters as iaa\nimport matplotlib.pyplot as plt\n%matplotlib inline\n\n##輸入照片\nimg = cv2.imread('Tano.JPG') \nimg = cv2.resize(img, (224,224))##改變圖片尺寸\nimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) #Cv2讀進來是BGR，轉成RGB\n\noutput=Augmenation(img) \n\n##畫出來\nplt.figure(figsize=(10,10))\nfor image in images_aug:\n plt.imshow(output.astype(np.uint8))\n plt.axis('off')", "_____no_output_____" ], [ "#鎖住隨機性-主要用在Semantic segmentation中", "_____no_output_____" ], [ "class MaskAugSequence(object):\n def __init__(self, sequence):\n self.sequence = sequence\n\n def __call__(self, image, mask):\n sequence = self.sequence.to_deterministic() ##用來關閉隨機性\n image = sequence.augment_image(image)\n mask = sequence.augment_image(mask)\n image, mask= image.astype(np.float32), mask.astype(np.float32)\n return image, mask", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e91645b9718de99b4f6137f57126c29356d08e

53,903

ipynb

Jupyter Notebook

GRS.ipynb

hoangkimkhai276/recsys

0c48ed382e45d7b11ce98aa15411b74819310f46

[ "BSD-4-Clause-UC" ]

1

2021-11-18T16:05:33.000Z

GRS.ipynb

hoangkimkhai276/No-name-1---DKE--Recsys-2021

0c48ed382e45d7b11ce98aa15411b74819310f46

[ "BSD-4-Clause-UC" ]

null

GRS.ipynb

hoangkimkhai276/No-name-1---DKE--Recsys-2021

0c48ed382e45d7b11ce98aa15411b74819310f46

[ "BSD-4-Clause-UC" ]

null

32.807669

245

0.405543

[ [ [ "import pandas as pd\nimport random", "_____no_output_____" ] ], [ [ "### Read the data", "_____no_output_____" ] ], [ [ "movies_df = pd.read_csv('mymovies.csv')\nratings_df = pd.read_csv('myratings.csv')", "_____no_output_____" ] ], [ [ "### Select the data\nThe recommender system should avoid bias, for example, the recommender system should not recommend movie with just 1 rating which is also a 5-star rating. But should recommend movies with more ratings.\nTherefore, we only take into account movies with at least 200 ratings and users who have at least rated 50 movies.", "_____no_output_____" ] ], [ [ "user_threshold = 50\nmovie_threshold = 200\nfiltered_users = ratings_df['user'].value_counts()>=user_threshold\nfiltered_users = filtered_users[filtered_users].index.tolist()\n\nfiltered_movies = ratings_df['item'].value_counts()>=movie_threshold\nfiltered_movies = filtered_movies[filtered_movies].index.tolist()\n\nfiltered_df = ratings_df[(ratings_df['user'].isin(filtered_users)) & (ratings_df['item'].isin(filtered_movies))]", "_____no_output_____" ], [ "display(filtered_df)", "_____no_output_____" ] ], [ [ "### Select a group of n random users\nHere we let n = 5, we select 5 random users from the filtered dataset", "_____no_output_____" ] ], [ [ "#Select a random group of user\nuser_ids = filtered_df['user'].unique()\ngroup_users_ids = random.sample(list(user_ids), 5)", "_____no_output_____" ], [ "group_users_ids", "_____no_output_____" ] ], [ [ "### Select rated and unrated movies for the given group\nWe now can get the rated movies all users in the groups, and from that, we can also get the unrated movies for the whole group of 5 ", "_____no_output_____" ] ], [ [ "selected_group_rating = ratings_df.loc[ratings_df['user'].isin(group_users_ids)]\ngroup_rated_movies_ids = selected_group_rating['item'].unique()\ngroup_unrated_movies_ids = set(movies_df['item']) - set(group_rated_movies_ids)\ngroup_rated_movies_df = movies_df.loc[movies_df['item'].isin(group_rated_movies_ids)]\ngroup_unrated_movies_df = movies_df.loc[movies_df['item'].isin(group_unrated_movies_ids)]", "_____no_output_____" ], [ "group_rated_movies_df", "_____no_output_____" ], [ "group_unrated_movies_df", "_____no_output_____" ] ], [ [ "### Calculate expected ratings for unrated movies\nFor each users, we need to calculate the expected ratings for the user's unrated movies. To calculate unrated ratings, we first need to train\nan algorithm, here, the SVD algorithm from Surprise is used\n", "_____no_output_____" ] ], [ [ "from surprise import Reader, Dataset, SVD\nfrom surprise.model_selection.validation import cross_validate", "_____no_output_____" ] ], [ [ "We perform 5-fold cross validation on the whole ratings dataset to see how well SVD will perform", "_____no_output_____" ] ], [ [ "reader = Reader()\ndata = Dataset.load_from_df(ratings_df[['user', 'item', 'rating']], reader)\nsvd = SVD()\ncross_validate(svd, data, measures=['RMSE', 'MAE'], cv=5, verbose=True)", "Evaluating RMSE, MAE of algorithm SVD on 5 split(s).\n\n Fold 1 Fold 2 Fold 3 Fold 4 Fold 5 Mean Std \nRMSE (testset) 0.8776 0.8791 0.8701 0.8678 0.8708 0.8731 0.0044 \nMAE (testset) 0.6764 0.6764 0.6677 0.6680 0.6679 0.6713 0.0042 \nFit time 9.63 9.58 9.44 9.52 9.58 9.55 0.06 \nTest time 0.17 0.16 0.22 0.23 0.16 0.19 0.03 \n" ] ], [ [ "Next, We train the SVD model on the dataset", "_____no_output_____" ] ], [ [ "trainset = data.build_full_trainset()\nsvd = svd.fit(trainset)", "_____no_output_____" ], [ "def predict(user):\n unrated_movies = list(group_unrated_movies_df['item'].unique())\n pred = pd.DataFrame()\n i = 0\n for item in unrated_movies:\n pred = pred.append({'user':user,'item': item, 'predicted_rating':svd.predict(user, item)[3]}, ignore_index=True)\n return pred\n \n", "_____no_output_____" ], [ "users_rating = []\nfor user in group_users_ids:\n prediction = predict(user)\n prediction = prediction.sort_values('predicted_rating')\n prediction = prediction.merge(movies_df, on= 'item')\n users_rating.append(prediction[['user','item','title','predicted_rating']])", "_____no_output_____" ] ], [ [ "The algorithm will iterate through 5 users, for each user, it will calculate the predicted rating for each unrated movie. Then the algorithm combines the predicted ratings of 5 users into one big dataset, to perform aggregation calculation", "_____no_output_____" ] ], [ [ "final = pd.concat([df for df in users_rating], ignore_index = True)", "_____no_output_____" ], [ "final", "_____no_output_____" ] ], [ [ "### Additive Strategy", "_____no_output_____" ] ], [ [ "additive = final.copy()\nadditive= additive.groupby(['item','title']).sum()\nadditive = additive.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\nadditive", "_____no_output_____" ] ], [ [ "### Most Pleasure Strategy", "_____no_output_____" ] ], [ [ "most_pleasure = final.copy()", "_____no_output_____" ], [ "most_pleasure = final.copy()\nmost_pleasure= most_pleasure.groupby(['item','title']).max()\nmost_pleasure = most_pleasure.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\nmost_pleasure", "_____no_output_____" ] ], [ [ "### Least Misery Strategy", "_____no_output_____" ] ], [ [ "least_misery = final.copy()\nleast_misery = final.copy()\nleast_misery= least_misery.groupby(['item','title']).min()\nleast_misery = least_misery.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\nleast_misery", "_____no_output_____" ], [ "def fairness():\n titles = []\n for uid in group_users_ids:\n data = final.loc[final['user'] == uid]\n data = data.sort_values(by = 'predicted_rating', ascending = False).reset_index().iloc[0]['title']\n titles.append([uid,data])\n return titles", "_____no_output_____" ], [ "tt = fairness()\nprint(tt)", "[[387, '12 angry men'], [384, 'eternal sunshine of the spotless mind'], [460, 'amadeus'], [76, \"guess who's coming to dinner\"], [151, 'kiss kiss bang bang']]\n" ], [ "def gen_rec_and_explain():\n most_pleasure = final.copy()\n most_pleasure= most_pleasure.groupby(['item','title']).max()\n most_pleasure = most_pleasure.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\n most_pleasure_movie = most_pleasure.iloc[0:5]['title']\n least_misery = final.copy()\n least_misery= least_misery.groupby(['item','title']).min()\n least_misery = least_misery.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\n least_misery_movie = least_misery.iloc[0:5]['title']\n additive = final.copy()\n additive= additive.groupby(['item','title']).sum()\n additive = additive.sort_values(by=\"predicted_rating\", ascending=False).reset_index()\n additive_movie = additive.iloc[0:5]['title']\n fairnesss = fairness()\n print(\"#FAIR\")\n for uid, title in fairnesss:\n print(\"The movie {} is the most favorite movie of user {}\".format(title, uid))\n print(\"#ADD: \")\n print(\"The movies: {} was recommended to you because they have highest additive rating within your group\".format(list(additive_movie)))\n print(\"#LEAST: \")\n print(\"The movies: {} was recommended to you because they are everyones' preferences \".format(list(least_misery_movie)))\n print(\"#MOST: \")\n print(\"The movies: {} was recommended to you because they are the most loved\".format(list(most_pleasure_movie)))\n", "_____no_output_____" ], [ "gen_rec_and_explain()", "#FAIR\nThe movie 12 angry men is the most favorite movie of user 387\nThe movie eternal sunshine of the spotless mind is the most favorite movie of user 384\nThe movie amadeus is the most favorite movie of user 460\nThe movie guess who's coming to dinner is the most favorite movie of user 76\nThe movie kiss kiss bang bang is the most favorite movie of user 151\n#ADD: \nThe movies: ['eternal sunshine of the spotless mind', 'kiss kiss bang bang', \"guess who's coming to dinner\", 'ran', \"schindler's list\"] was recommended to you because they have highest additive rating within your group\n#LEAST: \nThe movies: ['eternal sunshine of the spotless mind', \"guess who's coming to dinner\", 'dead poets society', 'ran', \"all the president's men\"] was recommended to you because they are everyones' preferences \n#MOST: \nThe movies: ['kiss kiss bang bang', 'amadeus', 'whiplash', \"schindler's list\", 'saving private ryan'] was recommended to you because they are the most loved\n" ], [ "import itertools\nfrom lenskit.algorithms import Recommender\nfrom lenskit.algorithms.user_knn import UserUser\n\nuser_user = UserUser(15, min_nbrs=3) # Minimum (3) and maximum (15) number of neighbors to consider\nrecsys = Recommender.adapt(user_user)\nrecsys.fit(ratings_df)\ngroup_unseen_df = pd.DataFrame(list(itertools.product(group_users_ids, group_unrated_movies_ids)), columns=['user', 'item'])\ngroup_unseen_df['predicted_rating'] = recsys.predict(group_unseen_df)\ngroup_unseen_df = group_unseen_df.loc[group_unseen_df['predicted_rating'].notnull()]\ndisplay(group_unseen_df)", "_____no_output_____" ], [ "group_unseen_df", "_____no_output_____" ], [ "group_unseen_df.groupby('item').sum()", "_____no_output_____" ], [ "additive_df = group_unseen_df.groupby('item').sum()\nadditive_df = additive_df.join(movies_df['title'], on='item')\nadditive_df = additive_df.sort_values(by=\"predicted_rating\", ascending=False).reset_index()[['item', 'title', 'predicted_rating']]\ndisplay(additive_df.head(10))", "_____no_output_____" ], [ "additive_df = group_unseen_df.groupby('item').sum()", "_____no_output_____" ], [ "additive_df", "_____no_output_____" ], [ "movies_df.loc[movies_df['item'] == 177593]", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e91f3341576120c3ab2f0f84549c60fe0605d5

11,823

ipynb

Jupyter Notebook

Data Structures/Recursion/Call stack.ipynb

gmendozah/Data-Structures-and-Algorithms

07474db45acfe42855cc0f4cc968c0564b2cb91a

[ "MIT" ]

5

2021-10-08T11:21:08.000Z

2022-01-24T22:40:03.000Z

Data Structures/Recursion/Call stack.ipynb

gmendozah/Data-Structures-and-Algorithms

07474db45acfe42855cc0f4cc968c0564b2cb91a

[ "MIT" ]

null

Data Structures/Recursion/Call stack.ipynb

gmendozah/Data-Structures-and-Algorithms

07474db45acfe42855cc0f4cc968c0564b2cb91a

[ "MIT" ]

3

2021-12-13T06:50:58.000Z

2022-02-05T03:38:49.000Z

35.398204

356

0.606445

[ [ [ "# Call stacks and recursion\nIn this notebook, we'll take a look at *call stacks*, which will provide an opportunity to apply some of the concepts we've learned about both stacks and recursion.", "_____no_output_____" ], [ "### What is a *call stack*?\n\nWhen we use functions in our code, the computer makes use of a data structure called a **call stack**. As the name suggests, a *call stack* is a type of stack—meaning that it is a *Last-In, First-Out* (LIFO) data structure.\n\nSo it's a type of stack—but a stack of *what*, exactly? \n\nEssentially, a *call stack* is a stack of *frames* that are used for the *functions* that we are calling. When we call a function, say `print_integers(5)`, a *frame* is created in memory. All the variables local to the function are created in this memory frame. And as soon as this frame is created, it's pushed onto the call stack.\n\nThe frame that lies at the top of the call stack is executed first. And as soon as the function finishes executing, this frame is discarded from the *call stack*. \n", "_____no_output_____" ], [ "### An example\n\nLet's consider the following function, which simply takes two integers and returns their sum", "_____no_output_____" ] ], [ [ "def add(num_one, num_two):\n output = num_one + num_two\n return output", "_____no_output_____" ], [ "result = add(5, 7)\nprint(result)", "12\n" ] ], [ [ "Before understanding what happens when a function is executed, it is important to remind ourselves that whenever an expression such as `product = 5 * 7` is evaluated, the right hand side of the `=` sign is evaluted first. When the right-hand side is completely evaluated, the result is stored in the variable name mentioned in the left-hand side. \n\nWhen Python executes line 1 in the previous cell (`result = add(5, 7)`), the following things happen in memory:\n\n\n* A frame is created for the `add` function. This frame is then pushed onto the *call stack*. We do not have to worry about this because Python takes care of this for us. \n\n\n* Next, the parameters `num_one` and `num_two` get the values `5` and `7`, respectively\n\nIf we run this code in Python tutor website [http://pythontutor.com/](http://pythontutor.com/) , we can get a nice visualization of what's happening \"behind the scenes\" in memory:\n\n<img src='./stack-frame-resources/01.png'>\n\n\n* Python then moves on to the first line of the function. The first line of the function is\n \n output = num_one + num_two\n \n Here an expression is being evaluated and the result is stored in a new variable. The expression here is sum of two numbers the result of which is stored in the variable `output`. We know that whenever an expression is evaluated, the right-hand side of the `= sign` is evaluated first. So, the numbers `5 and 7` will be added first.\n \n \n* Once the right-hand side is completely evaluated, then the assignment operation happens i.e. now the result of `5 + 7` will be stored in the variable `output`.\n<img src='./stack-frame-resources/02.png'> \n\n\n* In the next line, we are returning this value. \n\n return output\n \n Python acknowledged this return statement. \n <img src='./stack-frame-resources/03.png'>\n \n \n* Now the last line of the function has been executed. Therefore, this function can now be discarded from the stack frame. Also, the right-hand side of the expression `result = add(5, 7)` has finished evaluation. Now, the result of this evaluation will be stored in the variable `result`.\n\n <img src='./stack-frame-resources/04.png'>\n", "_____no_output_____" ], [ "\nNow the next question is how does this behave like a stack?\nThe answer is pretty simple. We know that a stack is a Last-In First-Out (LIFO) structure, meaning the latest element inserted in the stack is the first to be removed. \n\nYou can play more with such \"behind-the-scenes\" of code execution on the Python tutor website: http://pythontutor.com/\n\n### Another example\n\nHere's another example. Let's say we have a function `add()` which adds two integers and then prints a custom message for us using the `custom_print()` function.", "_____no_output_____" ] ], [ [ "def add(num_one, num_two):\n output = num_one + num_two\n custom_print(output, num_one, num_two)\n return output\n\ndef custom_print(output, num_one, num_two):\n print(\"The sum of {} and {} is: {}\".format(num_one, num_two, output))\n \nresult = add(5, 7) ", "The sum of 5 and 7 is: 12\n" ] ], [ [ "What happens \"behind-the-scenes\" when `add()` is called, as in `result = add(5, 7)`?\n\nFeel free to play with this on the Python tutor website. Here are a few points which might help aid the understanding.\n\n* We know that when add function is called using `result = add(5, 7)`, a frame is created in the memory for the `add()` function. This frame is then pushed onto the call stack.\n\n\n* Next, the two numbers are added and their result is stored in the variable `output`. \n\n\n* On the next line we have a new function call - `custom_print(output, num_one, num_two)`. It's obvious that a new frame should be created for this function call as well. You must have realized that this new frame is now pushed into the call stack. \n\n* We also know that the function which is at the top of the call stack is the one which Python executes. So, our `custom_print(output, num_one, num_two)` will now be executed. \n\n\n* Python executes this function and as soon as it is finished with execution, the frame for `custom_print(output, num_one, num_two)` is discarded. If you recall, this is the LIFO behavior that we have discussed while studying stacks. \n\n\n* Now, again the frame for `add()` function is at the top. Python resumes operation just after the line where it had left and returns the `output`. ", "_____no_output_____" ], [ "### Call Stack and Recursion", "_____no_output_____" ], [ "#### Problem Statement\n\nConsider the following problem:\n\nGiven a positive integer `n`, write a function, `print_integers`, that uses recursion to print all numbers from `n` to `1`. \n\nFor example, if `n` is `4`, the function shuld print `4 3 2 1`. \n\nIf we use iteration, the solution to the problem is simple. We can simply start at `4` and use a loop to print all numbers till `1`. However, instead of using an interative approach, our goal is to solve this problem using recursion.", "_____no_output_____" ] ], [ [ "def print_integers(n):\n # TODO: Complete the function so that it uses recursion to print all integers from n to 1\n if n <= 0:\n return\n print(n)\n print_integers(n - 1)", "_____no_output_____" ] ], [ [ "<span class=\"graffiti-highlight graffiti-id_0usbivt-id_8peifb7\"><i></i><button>Show Solution</button></span>", "_____no_output_____" ] ], [ [ "print_integers(5)", "5\n4\n3\n2\n1\n" ] ], [ [ "Now let's consider what happens in the call stack when `print_integers(5)` is called. ", "_____no_output_____" ], [ "* As expected, a frame will be created for the `print_integers()` function and pushed onto the call stack. \n\n\n* Next, the parameter `n` gets the value `5`. \n\n\n* Following this, the function starts executing. The base condition is checked. For `n = 5`, the base case is `False`, so we move forward and print the value of `n`.\n\n\n* In the next line, `print_integers()` is called again. This time it is called with the argument `n - 1`. The value of `n` in the current frame is `5`. So this new function call takes place with value `4`. Again, a new frame is created. **Note that for every new call a new frame will be created.** This frame is pushed onto the top of the stack. \n\n\n* Python now starts executing this frame. Again the base case is checked. It's `False` for `n = 4`. Following this, the `n` is printed and then `print_integers()` is called with argument `n - 1 = 3`. \n\n\n* The process keeps on like this until we hit the base case. When `n <= 0`, we return from the frame without calling the function `print_integers()` again. Because we have returned from the function call, the frame is discarded from the call stack and the next frame resumes execution right after the line where we left off. ", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ] ]

d0e92c60b4285e740d2959e79dcc562d2abe93a6

467,210

ipynb

Jupyter Notebook

Results_Summary.ipynb

RajArPatra/MIDAS-tassk-2

5023a60e523049ddf29665171df335e75d1e046c

[ "MIT" ]

null

Results_Summary.ipynb

RajArPatra/MIDAS-tassk-2

5023a60e523049ddf29665171df335e75d1e046c

[ "MIT" ]

null

Results_Summary.ipynb

RajArPatra/MIDAS-tassk-2

5023a60e523049ddf29665171df335e75d1e046c

[ "MIT" ]

null

162.225694

121,042

0.838462

[ [ [ "<a href=\"https://colab.research.google.com/github/RajArPatra/MIDAS-task-2/blob/main/Results_Summary.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "Libraries", "_____no_output_____" ] ], [ [ "from sklearn.preprocessing import StandardScaler,MinMaxScaler\nimport pandas as pd\nimport torchvision\nimport os\nimport numpy as np\nfrom skimage import io,transform as ts\nimport torch\nfrom torchvision import transforms\nfrom torch.utils.data import Dataset\nimport torch\nimport torch.nn as nn\nimport torch.nn.functional as F\nfrom PIL import Image\nimport imgaug as ia\nimport imgaug.augmenters as iaa\nfrom sklearn.decomposition import PCA\nfrom sklearn.manifold import TSNE\nimport matplotlib.pyplot as plt\n\nfrom torch.autograd import Variable\nimport distutils\nfrom distutils import dir_util\nfrom torch.utils.data.sampler import SubsetRandomSampler\nfrom torch.utils.tensorboard import SummaryWriter\n", "_____no_output_____" ] ], [ [ "Mount Drive", "_____no_output_____" ] ], [ [ "from google.colab import drive\ndrive.mount('/content/drive')", "Mounted at /content/drive\n" ] ], [ [ "# PART 1", "_____no_output_____" ], [ "Training and evaluation for part1 for whole of 62 classes", "_____no_output_____" ] ], [ [ "run_train(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part1',0,70,10,False)", " Epoch: 0 Iter: 0 Average train loss: 4.2706\n Epoch: 0 Iter: 100 Average train loss: 4.5716\n\n\n====> After epoch 0 \n====>Epoch Time: 0m 34s\n====>Average train loss: 4.5318 \n\n\n Epoch: 1 Iter: 0 Average train loss: 4.4155\n Epoch: 1 Iter: 100 Average train loss: 4.3727\n\n\n====> After epoch 1 \n====>Epoch Time: 0m 34s\n====>Average train loss: 4.3441 \n\n\n Epoch: 2 Iter: 0 Average train loss: 4.5803\n Epoch: 2 Iter: 100 Average train loss: 4.2247\n\n\n====> After epoch 2 \n====>Epoch Time: 0m 33s\n====>Average train loss: 4.1836 \n\n\n Epoch: 3 Iter: 0 Average train loss: 4.2621\n Epoch: 3 Iter: 100 Average train loss: 4.0549\n\n\n====> After epoch 3 \n====>Epoch Time: 0m 34s\n====>Average train loss: 4.0082 \n\n\n Epoch: 4 Iter: 0 Average train loss: 3.9282\n Epoch: 4 Iter: 100 Average train loss: 3.8463\n\n\n====> After epoch 4 \n====>Epoch Time: 0m 34s\n====>Average train loss: 3.8120 \n\n\n Epoch: 5 Iter: 0 Average train loss: 4.0263\n Epoch: 5 Iter: 100 Average train loss: 3.6955\n\n\n====> After epoch 5 \n====>Epoch Time: 0m 34s\n====>Average train loss: 3.6667 \n\n\n Epoch: 6 Iter: 0 Average train loss: 3.3101\n Epoch: 6 Iter: 100 Average train loss: 3.4915\n\n\n====> After epoch 6 \n====>Epoch Time: 0m 34s\n====>Average train loss: 3.4873 \n\n\n Epoch: 7 Iter: 0 Average train loss: 3.4153\n Epoch: 7 Iter: 100 Average train loss: 3.3418\n\n\n====> After epoch 7 \n====>Epoch Time: 0m 34s\n====>Average train loss: 3.3017 \n\n\n Epoch: 8 Iter: 0 Average train loss: 3.1431\n Epoch: 8 Iter: 100 Average train loss: 3.1543\n\n\n====> After epoch 8 \n====>Epoch Time: 0m 33s\n====>Average train loss: 3.1385 \n\n\n Epoch: 9 Iter: 0 Average train loss: 2.8556\n Epoch: 9 Iter: 100 Average train loss: 3.0656\n\n\n====> After epoch 9 \n====>Epoch Time: 0m 34s\n====>Average train loss: 3.0318 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_9.th\n Epoch: 10 Iter: 0 Average train loss: 2.9760\n Epoch: 10 Iter: 100 Average train loss: 2.9238\n\n\n====> After epoch 10 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.9077 \n\n\n Epoch: 11 Iter: 0 Average train loss: 2.9216\n Epoch: 11 Iter: 100 Average train loss: 2.7740\n\n\n====> After epoch 11 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.7946 \n\n\n Epoch: 12 Iter: 0 Average train loss: 3.1660\n Epoch: 12 Iter: 100 Average train loss: 2.7025\n\n\n====> After epoch 12 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.6610 \n\n\n Epoch: 13 Iter: 0 Average train loss: 2.8336\n Epoch: 13 Iter: 100 Average train loss: 2.5210\n\n\n====> After epoch 13 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.5632 \n\n\n Epoch: 14 Iter: 0 Average train loss: 2.4175\n Epoch: 14 Iter: 100 Average train loss: 2.4956\n\n\n====> After epoch 14 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.4791 \n\n\n Epoch: 15 Iter: 0 Average train loss: 2.7437\n Epoch: 15 Iter: 100 Average train loss: 2.4557\n\n\n====> After epoch 15 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.4172 \n\n\n Epoch: 16 Iter: 0 Average train loss: 1.6853\n Epoch: 16 Iter: 100 Average train loss: 2.3637\n\n\n====> After epoch 16 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.3836 \n\n\n Epoch: 17 Iter: 0 Average train loss: 2.2992\n Epoch: 17 Iter: 100 Average train loss: 2.2967\n\n\n====> After epoch 17 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.2923 \n\n\n Epoch: 18 Iter: 0 Average train loss: 2.2061\n Epoch: 18 Iter: 100 Average train loss: 2.1914\n\n\n====> After epoch 18 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.1899 \n\n\n Epoch: 19 Iter: 0 Average train loss: 1.7530\n Epoch: 19 Iter: 100 Average train loss: 2.2050\n\n\n====> After epoch 19 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.1985 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_19.th\n Epoch: 20 Iter: 0 Average train loss: 2.2722\n Epoch: 20 Iter: 100 Average train loss: 2.0822\n\n\n====> After epoch 20 \n====>Epoch Time: 0m 33s\n====>Average train loss: 2.1015 \n\n\n Epoch: 21 Iter: 0 Average train loss: 1.7934\n Epoch: 21 Iter: 100 Average train loss: 2.1013\n\n\n====> After epoch 21 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.0897 \n\n\n Epoch: 22 Iter: 0 Average train loss: 2.0732\n Epoch: 22 Iter: 100 Average train loss: 2.0328\n\n\n====> After epoch 22 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.0356 \n\n\n Epoch: 23 Iter: 0 Average train loss: 1.9140\n Epoch: 23 Iter: 100 Average train loss: 2.0175\n\n\n====> After epoch 23 \n====>Epoch Time: 0m 34s\n====>Average train loss: 2.0062 \n\n\n Epoch: 24 Iter: 0 Average train loss: 1.9305\n Epoch: 24 Iter: 100 Average train loss: 1.9236\n\n\n====> After epoch 24 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.9464 \n\n\n Epoch: 25 Iter: 0 Average train loss: 1.8548\n Epoch: 25 Iter: 100 Average train loss: 1.9129\n\n\n====> After epoch 25 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.9142 \n\n\n Epoch: 26 Iter: 0 Average train loss: 1.7801\n Epoch: 26 Iter: 100 Average train loss: 1.8804\n\n\n====> After epoch 26 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.8771 \n\n\n Epoch: 27 Iter: 0 Average train loss: 2.1546\n Epoch: 27 Iter: 100 Average train loss: 1.8582\n\n\n====> After epoch 27 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.8557 \n\n\n Epoch: 28 Iter: 0 Average train loss: 1.4878\n Epoch: 28 Iter: 100 Average train loss: 1.8010\n\n\n====> After epoch 28 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.8113 \n\n\n Epoch: 29 Iter: 0 Average train loss: 1.4982\n Epoch: 29 Iter: 100 Average train loss: 1.7325\n\n\n====> After epoch 29 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.7467 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_29.th\n Epoch: 30 Iter: 0 Average train loss: 1.8057\n Epoch: 30 Iter: 100 Average train loss: 1.7495\n\n\n====> After epoch 30 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.7658 \n\n\n Epoch: 31 Iter: 0 Average train loss: 1.3992\n Epoch: 31 Iter: 100 Average train loss: 1.7161\n\n\n====> After epoch 31 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.7387 \n\n\n Epoch: 32 Iter: 0 Average train loss: 2.0202\n Epoch: 32 Iter: 100 Average train loss: 1.7176\n\n\n====> After epoch 32 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.7354 \n\n\n Epoch: 33 Iter: 0 Average train loss: 1.5017\n Epoch: 33 Iter: 100 Average train loss: 1.7133\n\n\n====> After epoch 33 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.6953 \n\n\n Epoch: 34 Iter: 0 Average train loss: 1.7382\n Epoch: 34 Iter: 100 Average train loss: 1.6455\n\n\n====> After epoch 34 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.6525 \n\n\n Epoch: 35 Iter: 0 Average train loss: 2.0696\n Epoch: 35 Iter: 100 Average train loss: 1.7021\n\n\n====> After epoch 35 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.6816 \n\n\n Epoch: 36 Iter: 0 Average train loss: 2.5728\n Epoch: 36 Iter: 100 Average train loss: 1.6140\n\n\n====> After epoch 36 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.6055 \n\n\n Epoch: 37 Iter: 0 Average train loss: 1.6955\n Epoch: 37 Iter: 100 Average train loss: 1.6405\n\n\n====> After epoch 37 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.6122 \n\n\n Epoch: 38 Iter: 0 Average train loss: 1.4047\n Epoch: 38 Iter: 100 Average train loss: 1.5643\n\n\n====> After epoch 38 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.5579 \n\n\n Epoch: 39 Iter: 0 Average train loss: 1.2658\n Epoch: 39 Iter: 100 Average train loss: 1.5637\n\n\n====> After epoch 39 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.5543 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_39.th\n Epoch: 40 Iter: 0 Average train loss: 1.7455\n Epoch: 40 Iter: 100 Average train loss: 1.5628\n\n\n====> After epoch 40 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.5495 \n\n\n Epoch: 41 Iter: 0 Average train loss: 1.5163\n Epoch: 41 Iter: 100 Average train loss: 1.5286\n\n\n====> After epoch 41 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.5177 \n\n\n Epoch: 42 Iter: 0 Average train loss: 1.6754\n Epoch: 42 Iter: 100 Average train loss: 1.4990\n\n\n====> After epoch 42 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.5092 \n\n\n Epoch: 43 Iter: 0 Average train loss: 1.1545\n Epoch: 43 Iter: 100 Average train loss: 1.5048\n\n\n====> After epoch 43 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.4845 \n\n\n Epoch: 44 Iter: 0 Average train loss: 1.4095\n Epoch: 44 Iter: 100 Average train loss: 1.4640\n\n\n====> After epoch 44 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.4776 \n\n\n Epoch: 45 Iter: 0 Average train loss: 1.8122\n Epoch: 45 Iter: 100 Average train loss: 1.4810\n\n\n====> After epoch 45 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.4799 \n\n\n Epoch: 46 Iter: 0 Average train loss: 1.4935\n Epoch: 46 Iter: 100 Average train loss: 1.4196\n\n\n====> After epoch 46 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.4045 \n\n\n Epoch: 47 Iter: 0 Average train loss: 1.6696\n Epoch: 47 Iter: 100 Average train loss: 1.3611\n\n\n====> After epoch 47 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3989 \n\n\n Epoch: 48 Iter: 0 Average train loss: 1.4419\n Epoch: 48 Iter: 100 Average train loss: 1.4051\n\n\n====> After epoch 48 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.4227 \n\n\n Epoch: 49 Iter: 0 Average train loss: 1.4235\n Epoch: 49 Iter: 100 Average train loss: 1.3219\n\n\n====> After epoch 49 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3724 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_49.th\n Epoch: 50 Iter: 0 Average train loss: 1.1337\n Epoch: 50 Iter: 100 Average train loss: 1.3999\n\n\n====> After epoch 50 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.3855 \n\n\n Epoch: 51 Iter: 0 Average train loss: 1.6260\n Epoch: 51 Iter: 100 Average train loss: 1.3536\n\n\n====> After epoch 51 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3746 \n\n\nEpoch 52: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 52 Iter: 0 Average train loss: 1.2478\n Epoch: 52 Iter: 100 Average train loss: 1.3507\n\n\n====> After epoch 52 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3472 \n\n\n Epoch: 53 Iter: 0 Average train loss: 1.2118\n Epoch: 53 Iter: 100 Average train loss: 1.3167\n\n\n====> After epoch 53 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3204 \n\n\n Epoch: 54 Iter: 0 Average train loss: 1.7790\n Epoch: 54 Iter: 100 Average train loss: 1.3115\n\n\n====> After epoch 54 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.2874 \n\n\n Epoch: 55 Iter: 0 Average train loss: 1.0593\n Epoch: 55 Iter: 100 Average train loss: 1.2808\n\n\n====> After epoch 55 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.2700 \n\n\n Epoch: 56 Iter: 0 Average train loss: 0.8728\n Epoch: 56 Iter: 100 Average train loss: 1.3185\n\n\n====> After epoch 56 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.3100 \n\n\n Epoch: 57 Iter: 0 Average train loss: 1.0899\n Epoch: 57 Iter: 100 Average train loss: 1.2720\n\n\n====> After epoch 57 \n====>Epoch Time: 0m 34s\n====>Average train loss: 1.2843 \n\n\nEpoch 58: reducing learning rate of group 0 to 2.5000e-05.\n Epoch: 58 Iter: 0 Average train loss: 1.6466\n Epoch: 58 Iter: 100 Average train loss: 1.2823\n\n\n====> After epoch 58 \n====>Epoch Time: 0m 33s\n====>Average train loss: 1.2680 \n\n\n Epoch: 59 Iter: 0 Average train loss: 1.4900\n Epoch: 59 Iter: 100 Average train loss: 1.3042\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part1/epoch_59.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 55 \n====>conv Time: 1907.9600670337677\n====>Average train loss: 1.2845 +-0.0171\n" ], [ "\nprint('Train_accuracy:'.format(acc_meter.value())", "Train_accuracy: 0.8620967741935484\n" ], [ "train_labels,train_preds = get_all_preds(model, train_loader)\ncm = confusion_matrix(train_labels, train_preds.argmax(dim=1))\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[35 0 0 ... 0 0 0]\n [ 0 21 0 ... 0 0 0]\n [ 0 0 31 ... 0 0 0]\n ...\n [ 0 0 0 ... 29 4 0]\n [ 0 0 0 ... 0 36 0]\n [ 0 0 0 ... 0 0 39]]\n" ] ], [ [ "Training and evaluation for part1 for (0-9) classes", "_____no_output_____" ] ], [ [ "run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_(0-9)_part1',0,100,10,False)", " Epoch: 0 Iter: 0 Average train loss: 3.0626\n\n\n====> After epoch 0 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.6124 \n\n\n Epoch: 1 Iter: 0 Average train loss: 2.2847\n\n\n====> After epoch 1 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.5068 \n\n\n Epoch: 2 Iter: 0 Average train loss: 2.2013\n\n\n====> After epoch 2 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.5091 \n\n\n Epoch: 3 Iter: 0 Average train loss: 2.5242\n\n\n====> After epoch 3 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.4903 \n\n\n Epoch: 4 Iter: 0 Average train loss: 2.3181\n\n\n====> After epoch 4 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.3724 \n\n\n Epoch: 5 Iter: 0 Average train loss: 1.9034\n\n\n====> After epoch 5 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.3534 \n\n\n Epoch: 6 Iter: 0 Average train loss: 2.6350\n\n\n====> After epoch 6 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.3031 \n\n\n Epoch: 7 Iter: 0 Average train loss: 2.5244\n\n\n====> After epoch 7 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.2935 \n\n\n Epoch: 8 Iter: 0 Average train loss: 2.5626\n\n\n====> After epoch 8 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.3366 \n\n\n Epoch: 9 Iter: 0 Average train loss: 2.4721\n\n\n====> After epoch 9 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.2416 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_(0-9)_part2/epoch_9.th\n Epoch: 10 Iter: 0 Average train loss: 1.9041\n\n\n====> After epoch 10 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.1231 \n\n\n Epoch: 11 Iter: 0 Average train loss: 2.3573\n\n\n====> After epoch 11 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.1247 \n\n\n Epoch: 12 Iter: 0 Average train loss: 1.9363\n\n\n====> After epoch 12 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.0631 \n\n\n Epoch: 13 Iter: 0 Average train loss: 1.8311\n\n\n====> After epoch 13 \n====>Epoch Time: 0m 5s\n====>Average train loss: 2.0873 \n\n\n Epoch: 14 Iter: 0 Average train loss: 2.1637\n\n\n====> After epoch 14 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.9010 \n\n\n Epoch: 15 Iter: 0 Average train loss: 2.1711\n\n\n====> After epoch 15 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.8220 \n\n\n Epoch: 16 Iter: 0 Average train loss: 1.8091\n\n\n====> After epoch 16 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.7712 \n\n\n Epoch: 17 Iter: 0 Average train loss: 2.0727\n\n\n====> After epoch 17 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.7782 \n\n\n Epoch: 18 Iter: 0 Average train loss: 1.4791\n\n\n====> After epoch 18 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.7424 \n\n\n Epoch: 19 Iter: 0 Average train loss: 2.0179\n\n\n====> After epoch 19 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.6800 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_(0-9)_part2/epoch_19.th\n Epoch: 20 Iter: 0 Average train loss: 1.6131\n\n\n====> After epoch 20 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.6074 \n\n\n Epoch: 21 Iter: 0 Average train loss: 1.6685\n\n\n====> After epoch 21 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.5771 \n\n\n Epoch: 22 Iter: 0 Average train loss: 1.5168\n\n\n====> After epoch 22 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.5498 \n\n\n Epoch: 23 Iter: 0 Average train loss: 1.5960\n\n\n====> After epoch 23 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.4721 \n\n\n Epoch: 24 Iter: 0 Average train loss: 1.2318\n\n\n====> After epoch 24 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.4698 \n\n\n Epoch: 25 Iter: 0 Average train loss: 1.6567\n\n\n====> After epoch 25 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.4396 \n\n\n Epoch: 26 Iter: 0 Average train loss: 1.5029\n\n\n====> After epoch 26 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.3314 \n\n\n Epoch: 27 Iter: 0 Average train loss: 1.1729\n\n\n====> After epoch 27 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.3471 \n\n\n Epoch: 28 Iter: 0 Average train loss: 1.6663\n\n\n====> After epoch 28 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.2466 \n\n\n Epoch: 29 Iter: 0 Average train loss: 0.9937\n\n\n====> After epoch 29 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.2562 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_(0-9)_part2/epoch_29.th\n Epoch: 30 Iter: 0 Average train loss: 1.2143\n\n\n====> After epoch 30 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.2682 \n\n\nEpoch 31: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 31 Iter: 0 Average train loss: 1.3690\n\n\n====> After epoch 31 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.1838 \n\n\n Epoch: 32 Iter: 0 Average train loss: 1.1040\n\n\n====> After epoch 32 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.1227 \n\n\n Epoch: 33 Iter: 0 Average train loss: 1.1226\n\n\n====> After epoch 33 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.2015 \n\n\n Epoch: 34 Iter: 0 Average train loss: 1.0789\n\n\n====> After epoch 34 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0844 \n\n\n Epoch: 35 Iter: 0 Average train loss: 1.0896\n\n\n====> After epoch 35 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.1123 \n\n\n Epoch: 36 Iter: 0 Average train loss: 1.1859\n\n\n====> After epoch 36 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0968 \n\n\nEpoch 37: reducing learning rate of group 0 to 2.5000e-05.\n Epoch: 37 Iter: 0 Average train loss: 1.3166\n\n\n====> After epoch 37 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0754 \n\n\n Epoch: 38 Iter: 0 Average train loss: 1.6061\n\n\n====> After epoch 38 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.1325 \n\n\n Epoch: 39 Iter: 0 Average train loss: 0.7750\n\n\n====> After epoch 39 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0848 \n\n\nEpoch 40: reducing learning rate of group 0 to 1.2500e-05.\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_(0-9)_part2/epoch_39.th\n Epoch: 40 Iter: 0 Average train loss: 0.4486\n\n\n====> After epoch 40 \n====>Epoch Time: 0m 5s\n====>Average train loss: 0.9671 \n\n\n Epoch: 41 Iter: 0 Average train loss: 1.2151\n\n\n====> After epoch 41 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0862 \n\n\n Epoch: 42 Iter: 0 Average train loss: 0.7912\n\n\n====> After epoch 42 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0010 \n\n\nEpoch 43: reducing learning rate of group 0 to 6.2500e-06.\n Epoch: 43 Iter: 0 Average train loss: 0.7319\n\n\n====> After epoch 43 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0129 \n\n\n Epoch: 44 Iter: 0 Average train loss: 1.5016\n\n\n====> After epoch 44 \n====>Epoch Time: 0m 5s\n====>Average train loss: 1.0318 \n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_(0-9)_part2/epoch_44.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 40 \n====>conv Time: 223.8778576850891\n====>Average train loss: 1.0198 +-0.0440\n" ], [ "acc_meter=AverageValueMeter()\nmodel.eval()\nfor batch_idx, (data,label) in enumerate(train_loader):\n data = data.to(device)\n label=label.to(device)\n data = data.expand(-1, 3, -1, -1)\n output= model(data)\n \n \n r=accuracy_fn(output.data,label.data,(1,3,5))\n acc_meter.add(r[0].item())\nprint('Train_accuracy:{}'.format(acc_meter.value()))", "Train_accuracy:0.84\n" ], [ "cm=conf(model,train_loader,10)\ncm=cm.cpu().numpy().astype('uint64')\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[26 2 1 2 2 0 7 0 0 0]\n [ 0 36 1 1 1 0 0 1 0 0]\n [ 0 0 37 0 1 0 1 1 0 0]\n [ 0 2 0 30 1 0 3 0 1 3]\n [ 0 0 0 0 35 0 2 0 0 3]\n [ 0 0 0 2 1 34 2 0 0 1]\n [ 0 0 0 0 1 0 38 0 1 0]\n [ 0 0 0 0 3 0 0 33 0 4]\n [ 0 0 0 0 1 0 2 0 37 0]\n [ 0 2 0 0 2 0 0 0 1 35]]\n" ] ], [ [ "# Part 2 ", "_____no_output_____" ], [ "Training and Evaluation Metrics for part2 without pretrained weights", "_____no_output_____" ] ], [ [ "run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part2_nopre3',0,100,10,False,1)", " Epoch: 0 Iter: 0 Average train loss: 2.4773\n Epoch: 0 Iter: 1000 Average train loss: 1.2459\n Epoch: 0 Iter: 2000 Average train loss: 0.9317\n Epoch: 0 Iter: 3000 Average train loss: 0.7897\n Epoch: 0 Iter: 0 Average val loss: 0.4479 Acc1: 0.81 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 0 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.7204 \n====> Average val loss: 0.2254 Acc1: 0.94 Acc3: 0.99 Acc5: 1.00\n\n\n Epoch: 1 Iter: 0 Average train loss: 0.7511\n Epoch: 1 Iter: 1000 Average train loss: 0.3844\n Epoch: 1 Iter: 2000 Average train loss: 0.3714\n Epoch: 1 Iter: 3000 Average train loss: 0.3578\n Epoch: 1 Iter: 0 Average val loss: 0.0402 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 1 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.3513 \n====> Average val loss: 0.0796 Acc1: 0.98 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 2 Iter: 0 Average train loss: 0.4488\n Epoch: 2 Iter: 1000 Average train loss: 0.2881\n Epoch: 2 Iter: 2000 Average train loss: 0.2852\n Epoch: 2 Iter: 3000 Average train loss: 0.2781\n Epoch: 2 Iter: 0 Average val loss: 0.0855 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 2 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.2746 \n====> Average val loss: 0.0591 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 3 Iter: 0 Average train loss: 0.4817\n Epoch: 3 Iter: 1000 Average train loss: 0.2462\n Epoch: 3 Iter: 2000 Average train loss: 0.2409\n Epoch: 3 Iter: 3000 Average train loss: 0.2368\n Epoch: 3 Iter: 0 Average val loss: 0.0360 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 3 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.2329 \n====> Average val loss: 0.0443 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 4 Iter: 0 Average train loss: 0.4532\n Epoch: 4 Iter: 1000 Average train loss: 0.2100\n Epoch: 4 Iter: 2000 Average train loss: 0.2059\n Epoch: 4 Iter: 3000 Average train loss: 0.2045\n Epoch: 4 Iter: 0 Average val loss: 0.0162 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 4 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.2009 \n====> Average val loss: 0.0364 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 5 Iter: 0 Average train loss: 0.1002\n Epoch: 5 Iter: 1000 Average train loss: 0.1850\n Epoch: 5 Iter: 2000 Average train loss: 0.1836\n Epoch: 5 Iter: 3000 Average train loss: 0.1827\n Epoch: 5 Iter: 0 Average val loss: 0.0099 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 5 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1820 \n====> Average val loss: 0.0297 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 6 Iter: 0 Average train loss: 0.1503\n Epoch: 6 Iter: 1000 Average train loss: 0.1698\n Epoch: 6 Iter: 2000 Average train loss: 0.1674\n Epoch: 6 Iter: 3000 Average train loss: 0.1658\n Epoch: 6 Iter: 0 Average val loss: 0.0029 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 6 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1664 \n====> Average val loss: 0.0255 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 7 Iter: 0 Average train loss: 0.0615\n Epoch: 7 Iter: 1000 Average train loss: 0.1560\n Epoch: 7 Iter: 2000 Average train loss: 0.1555\n Epoch: 7 Iter: 3000 Average train loss: 0.1548\n Epoch: 7 Iter: 0 Average val loss: 0.0403 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 7 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1531 \n====> Average val loss: 0.0279 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 8 Iter: 0 Average train loss: 0.0623\n Epoch: 8 Iter: 1000 Average train loss: 0.1512\n Epoch: 8 Iter: 2000 Average train loss: 0.1502\n Epoch: 8 Iter: 3000 Average train loss: 0.1478\n Epoch: 8 Iter: 0 Average val loss: 0.0126 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 8 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1473 \n====> Average val loss: 0.0218 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 9 Iter: 0 Average train loss: 0.1863\n Epoch: 9 Iter: 1000 Average train loss: 0.1427\n Epoch: 9 Iter: 2000 Average train loss: 0.1399\n Epoch: 9 Iter: 3000 Average train loss: 0.1374\n Epoch: 9 Iter: 0 Average val loss: 0.0040 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 9 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1374 \n====> Average val loss: 0.0213 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_nopre3/epoch_9.th\n Epoch: 10 Iter: 0 Average train loss: 0.3356\n Epoch: 10 Iter: 1000 Average train loss: 0.1286\n Epoch: 10 Iter: 2000 Average train loss: 0.1283\n Epoch: 10 Iter: 3000 Average train loss: 0.1284\n Epoch: 10 Iter: 0 Average val loss: 0.0018 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 10 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1272 \n====> Average val loss: 0.0199 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 11 Iter: 0 Average train loss: 0.2217\n Epoch: 11 Iter: 1000 Average train loss: 0.1192\n Epoch: 11 Iter: 2000 Average train loss: 0.1223\n Epoch: 11 Iter: 3000 Average train loss: 0.1231\n Epoch: 11 Iter: 0 Average val loss: 0.0152 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 11 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1223 \n====> Average val loss: 0.0210 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 12 Iter: 0 Average train loss: 0.1053\n Epoch: 12 Iter: 1000 Average train loss: 0.1255\n Epoch: 12 Iter: 2000 Average train loss: 0.1223\n Epoch: 12 Iter: 3000 Average train loss: 0.1216\n Epoch: 12 Iter: 0 Average val loss: 0.4409 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 12 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1207 \n====> Average val loss: 0.0181 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 13 Iter: 0 Average train loss: 0.2598\n Epoch: 13 Iter: 1000 Average train loss: 0.1176\n Epoch: 13 Iter: 2000 Average train loss: 0.1138\n Epoch: 13 Iter: 3000 Average train loss: 0.1148\n Epoch: 13 Iter: 0 Average val loss: 0.0055 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 13 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1152 \n====> Average val loss: 0.0160 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 14 Iter: 0 Average train loss: 0.0127\n Epoch: 14 Iter: 1000 Average train loss: 0.1081\n Epoch: 14 Iter: 2000 Average train loss: 0.1091\n Epoch: 14 Iter: 3000 Average train loss: 0.1079\n Epoch: 14 Iter: 0 Average val loss: 0.0026 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 14 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1072 \n====> Average val loss: 0.0176 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 15 Iter: 0 Average train loss: 0.0212\n Epoch: 15 Iter: 1000 Average train loss: 0.1066\n Epoch: 15 Iter: 2000 Average train loss: 0.1044\n Epoch: 15 Iter: 3000 Average train loss: 0.1069\n Epoch: 15 Iter: 0 Average val loss: 0.0149 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 15 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1063 \n====> Average val loss: 0.0187 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 16: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 16 Iter: 0 Average train loss: 0.0265\n Epoch: 16 Iter: 1000 Average train loss: 0.0942\n Epoch: 16 Iter: 2000 Average train loss: 0.0941\n Epoch: 16 Iter: 3000 Average train loss: 0.0919\n Epoch: 16 Iter: 0 Average val loss: 0.0023 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 16 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0928 \n====> Average val loss: 0.0163 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 17 Iter: 0 Average train loss: 0.1757\n Epoch: 17 Iter: 1000 Average train loss: 0.0901\n Epoch: 17 Iter: 2000 Average train loss: 0.0905\n Epoch: 17 Iter: 3000 Average train loss: 0.0913\n Epoch: 17 Iter: 0 Average val loss: 0.0007 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 17 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0920 \n====> Average val loss: 0.0161 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_nopre3/epoch_17.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 13 \n====>conv Time: 630.5595891475677\n====>Average train loss: 0.0170 +-0.0012\n" ], [ "acc_meter=AverageValueMeter()\nmodel.eval()\nfor batch_idx, (data,label) in enumerate(test_loader):\n data = data.to(device)\n label=label.to(device)\n data = data.expand(-1, 3, -1, -1)\n output= model(data)\n \n \n r=accuracy_fn(output.data,label.data,(1,3,5))\n acc_meter.add(r[0].item())\nprint('Test_accuracy:{}'.format(acc_meter.value()))", "Test_accuracy:0.9957000000000005\n" ], [ "cm=conf(model,train_loader,10)\ncm=cm.cpu().numpy().astype('uint64')\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[5920 0 0 1 0 0 2 0 0 0]\n [ 0 6731 0 0 0 1 3 6 1 0]\n [ 0 10 5938 1 0 0 2 6 1 0]\n [ 1 0 0 6117 0 7 1 2 2 1]\n [ 0 2 0 0 5830 0 1 3 0 6]\n [ 0 0 0 2 0 5413 4 0 1 1]\n [ 2 0 0 0 2 1 5913 0 0 0]\n [ 0 5 1 0 1 0 0 6256 0 2]\n [ 1 1 0 0 1 4 2 1 5837 4]\n [ 0 0 0 1 16 3 0 2 0 5927]]\n" ] ], [ [ "Training and Evaluation Metrics for part2 with pretrained weights from part 1", "_____no_output_____" ] ], [ [ "run_pre(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part2_pre3',0,100,10,False,1)", " Epoch: 0 Iter: 0 Average train loss: 2.4606\n Epoch: 0 Iter: 1000 Average train loss: 0.9732\n Epoch: 0 Iter: 2000 Average train loss: 0.7794\n Epoch: 0 Iter: 3000 Average train loss: 0.6809\n Epoch: 0 Iter: 0 Average val loss: 0.1013 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 0 \n====>Epoch Time: 0m 46s\n====>Average train loss: 0.6301 \n====> Average val loss: 0.1604 Acc1: 0.97 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 1 Iter: 0 Average train loss: 0.4502\n Epoch: 1 Iter: 1000 Average train loss: 0.3853\n Epoch: 1 Iter: 2000 Average train loss: 0.3702\n Epoch: 1 Iter: 3000 Average train loss: 0.3568\n Epoch: 1 Iter: 0 Average val loss: 0.0950 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 1 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.3451 \n====> Average val loss: 0.0900 Acc1: 0.98 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 2 Iter: 0 Average train loss: 0.2567\n Epoch: 2 Iter: 1000 Average train loss: 0.2933\n Epoch: 2 Iter: 2000 Average train loss: 0.2823\n Epoch: 2 Iter: 3000 Average train loss: 0.2750\n Epoch: 2 Iter: 0 Average val loss: 0.0173 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 2 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.2701 \n====> Average val loss: 0.0504 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 3 Iter: 0 Average train loss: 0.2361\n Epoch: 3 Iter: 1000 Average train loss: 0.2374\n Epoch: 3 Iter: 2000 Average train loss: 0.2354\n Epoch: 3 Iter: 3000 Average train loss: 0.2305\n Epoch: 3 Iter: 0 Average val loss: 0.0081 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 3 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.2266 \n====> Average val loss: 0.0462 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 4 Iter: 0 Average train loss: 0.0673\n Epoch: 4 Iter: 1000 Average train loss: 0.2045\n Epoch: 4 Iter: 2000 Average train loss: 0.2053\n Epoch: 4 Iter: 3000 Average train loss: 0.2022\n Epoch: 4 Iter: 0 Average val loss: 0.0206 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 4 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1980 \n====> Average val loss: 0.0383 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 5 Iter: 0 Average train loss: 0.0656\n Epoch: 5 Iter: 1000 Average train loss: 0.1873\n Epoch: 5 Iter: 2000 Average train loss: 0.1849\n Epoch: 5 Iter: 3000 Average train loss: 0.1821\n Epoch: 5 Iter: 0 Average val loss: 0.0187 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 5 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1808 \n====> Average val loss: 0.0301 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 6 Iter: 0 Average train loss: 0.0723\n Epoch: 6 Iter: 1000 Average train loss: 0.1657\n Epoch: 6 Iter: 2000 Average train loss: 0.1680\n Epoch: 6 Iter: 3000 Average train loss: 0.1673\n Epoch: 6 Iter: 0 Average val loss: 0.1116 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 6 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1649 \n====> Average val loss: 0.0261 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 7 Iter: 0 Average train loss: 0.2546\n Epoch: 7 Iter: 1000 Average train loss: 0.1584\n Epoch: 7 Iter: 2000 Average train loss: 0.1552\n Epoch: 7 Iter: 3000 Average train loss: 0.1563\n Epoch: 7 Iter: 0 Average val loss: 0.0056 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 7 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1537 \n====> Average val loss: 0.0266 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 8 Iter: 0 Average train loss: 0.0921\n Epoch: 8 Iter: 1000 Average train loss: 0.1493\n Epoch: 8 Iter: 2000 Average train loss: 0.1471\n Epoch: 8 Iter: 3000 Average train loss: 0.1451\n Epoch: 8 Iter: 0 Average val loss: 0.0233 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 8 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1442 \n====> Average val loss: 0.0219 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 9 Iter: 0 Average train loss: 0.0253\n Epoch: 9 Iter: 1000 Average train loss: 0.1449\n Epoch: 9 Iter: 2000 Average train loss: 0.1400\n Epoch: 9 Iter: 3000 Average train loss: 0.1379\n Epoch: 9 Iter: 0 Average val loss: 0.0301 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 9 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1387 \n====> Average val loss: 0.0225 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_pre3/epoch_9.th\n Epoch: 10 Iter: 0 Average train loss: 0.0350\n Epoch: 10 Iter: 1000 Average train loss: 0.1255\n Epoch: 10 Iter: 2000 Average train loss: 0.1294\n Epoch: 10 Iter: 3000 Average train loss: 0.1305\n Epoch: 10 Iter: 0 Average val loss: 0.1121 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 10 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1307 \n====> Average val loss: 0.0217 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 11 Iter: 0 Average train loss: 0.0424\n Epoch: 11 Iter: 1000 Average train loss: 0.1252\n Epoch: 11 Iter: 2000 Average train loss: 0.1225\n Epoch: 11 Iter: 3000 Average train loss: 0.1220\n Epoch: 11 Iter: 0 Average val loss: 0.0142 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 11 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1220 \n====> Average val loss: 0.0231 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 12 Iter: 0 Average train loss: 0.1533\n Epoch: 12 Iter: 1000 Average train loss: 0.1193\n Epoch: 12 Iter: 2000 Average train loss: 0.1169\n Epoch: 12 Iter: 3000 Average train loss: 0.1193\n Epoch: 12 Iter: 0 Average val loss: 0.0258 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 12 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.1200 \n====> Average val loss: 0.0183 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 13 Iter: 0 Average train loss: 0.0177\n Epoch: 13 Iter: 1000 Average train loss: 0.1149\n Epoch: 13 Iter: 2000 Average train loss: 0.1154\n Epoch: 13 Iter: 3000 Average train loss: 0.1161\n Epoch: 13 Iter: 0 Average val loss: 0.0015 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 13 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1146 \n====> Average val loss: 0.0179 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 14 Iter: 0 Average train loss: 0.0989\n Epoch: 14 Iter: 1000 Average train loss: 0.1071\n Epoch: 14 Iter: 2000 Average train loss: 0.1094\n Epoch: 14 Iter: 3000 Average train loss: 0.1101\n Epoch: 14 Iter: 0 Average val loss: 0.1808 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 14 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1103 \n====> Average val loss: 0.0171 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 15 Iter: 0 Average train loss: 0.2554\n Epoch: 15 Iter: 1000 Average train loss: 0.1054\n Epoch: 15 Iter: 2000 Average train loss: 0.1057\n Epoch: 15 Iter: 3000 Average train loss: 0.1069\n Epoch: 15 Iter: 0 Average val loss: 0.0012 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 15 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.1061 \n====> Average val loss: 0.0183 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 16 Iter: 0 Average train loss: 0.0810\n Epoch: 16 Iter: 1000 Average train loss: 0.1021\n Epoch: 16 Iter: 2000 Average train loss: 0.1007\n Epoch: 16 Iter: 3000 Average train loss: 0.1008\n Epoch: 16 Iter: 0 Average val loss: 0.0056 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 16 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0999 \n====> Average val loss: 0.0202 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 17: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 17 Iter: 0 Average train loss: 0.0544\n Epoch: 17 Iter: 1000 Average train loss: 0.0980\n Epoch: 17 Iter: 2000 Average train loss: 0.0970\n Epoch: 17 Iter: 3000 Average train loss: 0.0955\n Epoch: 17 Iter: 0 Average val loss: 0.0006 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 17 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0939 \n====> Average val loss: 0.0166 Acc1: 0.99 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 18 Iter: 0 Average train loss: 0.2423\n Epoch: 18 Iter: 1000 Average train loss: 0.0886\n Epoch: 18 Iter: 2000 Average train loss: 0.0887\n Epoch: 18 Iter: 3000 Average train loss: 0.0895\n Epoch: 18 Iter: 0 Average val loss: 0.0022 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 18 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0905 \n====> Average val loss: 0.0154 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 19 Iter: 0 Average train loss: 0.0831\n Epoch: 19 Iter: 1000 Average train loss: 0.0874\n Epoch: 19 Iter: 2000 Average train loss: 0.0894\n Epoch: 19 Iter: 3000 Average train loss: 0.0873\n Epoch: 19 Iter: 0 Average val loss: 0.0146 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 19 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0875 \n====> Average val loss: 0.0153 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_pre3/epoch_19.th\n Epoch: 20 Iter: 0 Average train loss: 0.0292\n Epoch: 20 Iter: 1000 Average train loss: 0.0874\n Epoch: 20 Iter: 2000 Average train loss: 0.0867\n Epoch: 20 Iter: 3000 Average train loss: 0.0893\n Epoch: 20 Iter: 0 Average val loss: 0.0005 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 20 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0878 \n====> Average val loss: 0.0157 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 21 Iter: 0 Average train loss: 0.0758\n Epoch: 21 Iter: 1000 Average train loss: 0.0851\n Epoch: 21 Iter: 2000 Average train loss: 0.0840\n Epoch: 21 Iter: 3000 Average train loss: 0.0838\n Epoch: 21 Iter: 0 Average val loss: 0.0008 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 21 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0844 \n====> Average val loss: 0.0146 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 22 Iter: 0 Average train loss: 0.0874\n Epoch: 22 Iter: 1000 Average train loss: 0.0806\n Epoch: 22 Iter: 2000 Average train loss: 0.0833\n Epoch: 22 Iter: 3000 Average train loss: 0.0833\n Epoch: 22 Iter: 0 Average val loss: 0.0014 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 22 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0835 \n====> Average val loss: 0.0143 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 23 Iter: 0 Average train loss: 0.0735\n Epoch: 23 Iter: 1000 Average train loss: 0.0814\n Epoch: 23 Iter: 2000 Average train loss: 0.0817\n Epoch: 23 Iter: 3000 Average train loss: 0.0819\n Epoch: 23 Iter: 0 Average val loss: 0.0008 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 23 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0824 \n====> Average val loss: 0.0154 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 24 Iter: 0 Average train loss: 0.0994\n Epoch: 24 Iter: 1000 Average train loss: 0.0786\n Epoch: 24 Iter: 2000 Average train loss: 0.0775\n Epoch: 24 Iter: 3000 Average train loss: 0.0790\n Epoch: 24 Iter: 0 Average val loss: 0.0010 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 24 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0782 \n====> Average val loss: 0.0171 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 25: reducing learning rate of group 0 to 2.5000e-05.\n Epoch: 25 Iter: 0 Average train loss: 0.0994\n Epoch: 25 Iter: 1000 Average train loss: 0.0757\n Epoch: 25 Iter: 2000 Average train loss: 0.0775\n Epoch: 25 Iter: 3000 Average train loss: 0.0775\n Epoch: 25 Iter: 0 Average val loss: 0.1189 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 25 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0775 \n====> Average val loss: 0.0142 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 26 Iter: 0 Average train loss: 0.0725\n Epoch: 26 Iter: 1000 Average train loss: 0.0728\n Epoch: 26 Iter: 2000 Average train loss: 0.0736\n Epoch: 26 Iter: 3000 Average train loss: 0.0740\n Epoch: 26 Iter: 0 Average val loss: 0.0004 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 26 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0748 \n====> Average val loss: 0.0159 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 27 Iter: 0 Average train loss: 0.2483\n Epoch: 27 Iter: 1000 Average train loss: 0.0747\n Epoch: 27 Iter: 2000 Average train loss: 0.0760\n Epoch: 27 Iter: 3000 Average train loss: 0.0747\n Epoch: 27 Iter: 0 Average val loss: 0.0010 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 27 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0753 \n====> Average val loss: 0.0136 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 28 Iter: 0 Average train loss: 0.0073\n Epoch: 28 Iter: 1000 Average train loss: 0.0731\n Epoch: 28 Iter: 2000 Average train loss: 0.0733\n Epoch: 28 Iter: 3000 Average train loss: 0.0745\n Epoch: 28 Iter: 0 Average val loss: 0.0010 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 28 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0745 \n====> Average val loss: 0.0139 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 29 Iter: 0 Average train loss: 0.0152\n Epoch: 29 Iter: 1000 Average train loss: 0.0705\n Epoch: 29 Iter: 2000 Average train loss: 0.0713\n Epoch: 29 Iter: 3000 Average train loss: 0.0717\n Epoch: 29 Iter: 0 Average val loss: 0.0058 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 29 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0732 \n====> Average val loss: 0.0139 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 30: reducing learning rate of group 0 to 1.2500e-05.\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_pre3/epoch_29.th\n Epoch: 30 Iter: 0 Average train loss: 0.0572\n Epoch: 30 Iter: 1000 Average train loss: 0.0768\n Epoch: 30 Iter: 2000 Average train loss: 0.0749\n Epoch: 30 Iter: 3000 Average train loss: 0.0735\n Epoch: 30 Iter: 0 Average val loss: 0.0013 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 30 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0736 \n====> Average val loss: 0.0133 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 31 Iter: 0 Average train loss: 0.1351\n Epoch: 31 Iter: 1000 Average train loss: 0.0726\n Epoch: 31 Iter: 2000 Average train loss: 0.0744\n Epoch: 31 Iter: 3000 Average train loss: 0.0714\n Epoch: 31 Iter: 0 Average val loss: 0.0018 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 31 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0715 \n====> Average val loss: 0.0135 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 32 Iter: 0 Average train loss: 0.0335\n Epoch: 32 Iter: 1000 Average train loss: 0.0723\n Epoch: 32 Iter: 2000 Average train loss: 0.0694\n Epoch: 32 Iter: 3000 Average train loss: 0.0683\n Epoch: 32 Iter: 0 Average val loss: 0.0005 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 32 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0690 \n====> Average val loss: 0.0142 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 33: reducing learning rate of group 0 to 6.2500e-06.\n Epoch: 33 Iter: 0 Average train loss: 0.0263\n Epoch: 33 Iter: 1000 Average train loss: 0.0709\n Epoch: 33 Iter: 2000 Average train loss: 0.0713\n Epoch: 33 Iter: 3000 Average train loss: 0.0706\n Epoch: 33 Iter: 0 Average val loss: 0.0006 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 33 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0697 \n====> Average val loss: 0.0132 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 34 Iter: 0 Average train loss: 0.0118\n Epoch: 34 Iter: 1000 Average train loss: 0.0667\n Epoch: 34 Iter: 2000 Average train loss: 0.0642\n Epoch: 34 Iter: 3000 Average train loss: 0.0674\n Epoch: 34 Iter: 0 Average val loss: 0.0007 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 34 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0672 \n====> Average val loss: 0.0134 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 35 Iter: 0 Average train loss: 0.0198\n Epoch: 35 Iter: 1000 Average train loss: 0.0685\n Epoch: 35 Iter: 2000 Average train loss: 0.0696\n Epoch: 35 Iter: 3000 Average train loss: 0.0679\n Epoch: 35 Iter: 0 Average val loss: 0.0008 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 35 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0682 \n====> Average val loss: 0.0132 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nEpoch 36: reducing learning rate of group 0 to 3.1250e-06.\n Epoch: 36 Iter: 0 Average train loss: 0.0196\n Epoch: 36 Iter: 1000 Average train loss: 0.0720\n Epoch: 36 Iter: 2000 Average train loss: 0.0714\n Epoch: 36 Iter: 3000 Average train loss: 0.0708\n Epoch: 36 Iter: 0 Average val loss: 0.0009 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 36 \n====>Epoch Time: 0m 44s\n====>Average train loss: 0.0691 \n====> Average val loss: 0.0137 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\n Epoch: 37 Iter: 0 Average train loss: 0.0402\n Epoch: 37 Iter: 1000 Average train loss: 0.0632\n Epoch: 37 Iter: 2000 Average train loss: 0.0661\n Epoch: 37 Iter: 3000 Average train loss: 0.0669\n Epoch: 37 Iter: 0 Average val loss: 0.0775 Acc1: 0.94 Acc3: 1.00 Acc5: 1.00\n\n\n====> After epoch 37 \n====>Epoch Time: 0m 45s\n====>Average train loss: 0.0672 \n====> Average val loss: 0.0142 Acc1: 1.00 Acc3: 1.00 Acc5: 1.00\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part2_pre3/epoch_37.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 33 \n====>conv Time: 1534.2143957614899\n====>Average train loss: 0.0135 +-0.0004\n" ], [ "acc_meter=AverageValueMeter()\nmodel.eval()\nfor batch_idx, (data,label) in enumerate(test_loader):\n data = data.to(device)\n label=label.to(device)\n data = data.expand(-1, 3, -1, -1)\n output= model(data)\n \n \n r=accuracy_fn(output.data,label.data,(1,3,5))\n acc_meter.add(r[0].item())\nprint('Test_accuracy:{}'.format(acc_meter.value()))", "Test_accuracy:0.9954999999999997\n" ], [ "def conf(model,test_loader,n_class):\n nb_classes = n_class\n model.to(device)\n model.eval()\n confusion_matrix = torch.zeros(nb_classes, nb_classes)\n with torch.no_grad():\n for i, (inputs, classes) in enumerate(test_loader):\n inputs = inputs.to(device)\n inputs=inputs.expand(-1, 3, -1, -1)\n classes = classes.to(device)\n outputs = model(inputs)\n _, preds = torch.max(outputs, 1)\n for t, p in zip(classes.view(-1), preds.view(-1)):\n confusion_matrix[t.long(), p.long()] += 1\n return confusion_matrix", "_____no_output_____" ], [ "cm=conf(model,train_loader,10)\ncm=cm.cpu().numpy().astype('uint64')\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[5923 0 0 0 0 0 0 0 0 0]\n [ 0 6738 0 0 0 0 0 4 0 0]\n [ 0 1 5955 0 0 0 0 2 0 0]\n [ 0 0 0 6127 0 3 0 0 0 1]\n [ 0 2 0 0 5833 0 0 2 0 5]\n [ 0 0 0 2 0 5418 1 0 0 0]\n [ 1 0 0 0 0 0 5917 0 0 0]\n [ 0 5 0 0 0 0 0 6260 0 0]\n [ 0 0 0 0 0 0 0 0 5849 2]\n [ 0 0 0 0 3 1 0 1 0 5944]]\n" ] ], [ [ "# Part 3", "_____no_output_____" ], [ "Training and Evaluation Metrics for part3 without pretrained weights", "_____no_output_____" ] ], [ [ "run(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part3_nopre',0,100,10,False,1)", " Epoch: 0 Iter: 0 Average train loss: 3.1254\n Epoch: 0 Iter: 1000 Average train loss: 2.4200\n Epoch: 0 Iter: 2000 Average train loss: 2.4051\n Epoch: 0 Iter: 3000 Average train loss: 2.3953\n Epoch: 0 Iter: 0 Average val loss: 2.3099 Acc1: 0.00 Acc3: 0.00 Acc5: 0.19\n\n\n====> After epoch 0 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3896 \n====> Average val loss: 2.3095 Acc1: 0.12 Acc3: 0.24 Acc5: 0.44\n\n\n Epoch: 1 Iter: 0 Average train loss: 2.3351\n Epoch: 1 Iter: 1000 Average train loss: 2.3667\n Epoch: 1 Iter: 2000 Average train loss: 2.3626\n Epoch: 1 Iter: 3000 Average train loss: 2.3607\n Epoch: 1 Iter: 0 Average val loss: 2.3241 Acc1: 0.00 Acc3: 0.12 Acc5: 0.25\n\n\n====> After epoch 1 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3574 \n====> Average val loss: 2.3221 Acc1: 0.02 Acc3: 0.16 Acc5: 0.35\n\n\n Epoch: 2 Iter: 0 Average train loss: 2.3581\n Epoch: 2 Iter: 1000 Average train loss: 2.3496\n Epoch: 2 Iter: 2000 Average train loss: 2.3464\n Epoch: 2 Iter: 3000 Average train loss: 2.3435\n Epoch: 2 Iter: 0 Average val loss: 2.3091 Acc1: 0.00 Acc3: 0.19 Acc5: 0.25\n\n\n====> After epoch 2 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3430 \n====> Average val loss: 2.3121 Acc1: 0.01 Acc3: 0.19 Acc5: 0.40\n\n\nEpoch 3: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 3 Iter: 0 Average train loss: 2.3922\n Epoch: 3 Iter: 1000 Average train loss: 2.3336\n Epoch: 3 Iter: 2000 Average train loss: 2.3348\n Epoch: 3 Iter: 3000 Average train loss: 2.3332\n Epoch: 3 Iter: 0 Average val loss: 2.3063 Acc1: 0.06 Acc3: 0.38 Acc5: 0.56\n\n\n====> After epoch 3 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3325 \n====> Average val loss: 2.3107 Acc1: 0.01 Acc3: 0.18 Acc5: 0.36\n\n\n Epoch: 4 Iter: 0 Average train loss: 2.2592\n Epoch: 4 Iter: 1000 Average train loss: 2.3264\n Epoch: 4 Iter: 2000 Average train loss: 2.3280\n Epoch: 4 Iter: 3000 Average train loss: 2.3277\n Epoch: 4 Iter: 0 Average val loss: 2.3092 Acc1: 0.06 Acc3: 0.12 Acc5: 0.44\n\n\n====> After epoch 4 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3267 \n====> Average val loss: 2.3090 Acc1: 0.01 Acc3: 0.19 Acc5: 0.43\n\n\n Epoch: 5 Iter: 0 Average train loss: 2.2277\n Epoch: 5 Iter: 1000 Average train loss: 2.3185\n Epoch: 5 Iter: 2000 Average train loss: 2.3210\n Epoch: 5 Iter: 3000 Average train loss: 2.3210\n Epoch: 5 Iter: 0 Average val loss: 2.3070 Acc1: 0.00 Acc3: 0.31 Acc5: 0.44\n\n\n====> After epoch 5 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3208 \n====> Average val loss: 2.3094 Acc1: 0.01 Acc3: 0.14 Acc5: 0.37\n\n\n Epoch: 6 Iter: 0 Average train loss: 2.3179\n Epoch: 6 Iter: 1000 Average train loss: 2.3218\n Epoch: 6 Iter: 2000 Average train loss: 2.3203\n Epoch: 6 Iter: 3000 Average train loss: 2.3199\n Epoch: 6 Iter: 0 Average val loss: 2.3040 Acc1: 0.00 Acc3: 0.19 Acc5: 0.31\n\n\n====> After epoch 6 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3187 \n====> Average val loss: 2.3116 Acc1: 0.01 Acc3: 0.14 Acc5: 0.35\n\n\nEpoch 7: reducing learning rate of group 0 to 2.5000e-05.\n Epoch: 7 Iter: 0 Average train loss: 2.2484\n Epoch: 7 Iter: 1000 Average train loss: 2.3159\n Epoch: 7 Iter: 2000 Average train loss: 2.3153\n Epoch: 7 Iter: 3000 Average train loss: 2.3148\n Epoch: 7 Iter: 0 Average val loss: 2.3056 Acc1: 0.00 Acc3: 0.19 Acc5: 0.56\n\n\n====> After epoch 7 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3149 \n====> Average val loss: 2.3106 Acc1: 0.02 Acc3: 0.15 Acc5: 0.36\n\n\n Epoch: 8 Iter: 0 Average train loss: 2.5084\n Epoch: 8 Iter: 1000 Average train loss: 2.3113\n Epoch: 8 Iter: 2000 Average train loss: 2.3129\n Epoch: 8 Iter: 3000 Average train loss: 2.3132\n Epoch: 8 Iter: 0 Average val loss: 2.3107 Acc1: 0.00 Acc3: 0.06 Acc5: 0.31\n\n\n====> After epoch 8 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3128 \n====> Average val loss: 2.3105 Acc1: 0.01 Acc3: 0.13 Acc5: 0.39\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part3_nopre/epoch_8.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 4 \n====>conv Time: 315.5340414047241\n====>Average train loss: 2.3102 +-0.0010\n" ], [ "acc_meter=AverageValueMeter()\nmodel.eval()\nfor batch_idx, (data,label) in enumerate(test_loader):\n data = data.to(device)\n label=label.to(device)\n data = data.expand(-1, 3, -1, -1)\n output= model(data)\n \n \n r=accuracy_fn(output.data,label.data,(1,3,5))\n acc_meter.add(r[0].item())\nprint('Test_accuracy:{}'.format(acc_meter.value()))", "Test_accuracy:0.0116\n" ], [ "cm=conf(model,train_loader,10)\ncm=cm.cpu().numpy().astype('uint64')\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[3362 12 19 76 130 78 446 136 1539 182]\n [3431 38 35 188 127 74 433 187 1040 254]\n [3193 24 43 209 98 53 467 170 1541 211]\n [3058 29 36 220 127 87 377 205 1645 253]\n [3178 17 36 190 123 86 480 152 1399 253]\n [3117 35 27 207 128 78 420 202 1685 240]\n [3018 30 35 177 132 91 518 166 1654 216]\n [3218 33 40 196 108 54 467 198 1345 295]\n [3081 16 26 194 120 110 403 143 1780 256]\n [3041 24 32 209 82 78 385 212 1652 279]]\n" ] ], [ [ "Training and Evaluation Metrics for part3 with pretrained weights from part1", "_____no_output_____" ] ], [ [ "run_pre(model,criterion,optimizer,scheduler,'/content/drive/MyDrive/Model_files','task2/BMCNN_part3_pre2',0,100,10,False,1)", " Epoch: 0 Iter: 0 Average train loss: 2.7048\n Epoch: 0 Iter: 1000 Average train loss: 2.4365\n Epoch: 0 Iter: 2000 Average train loss: 2.4062\n Epoch: 0 Iter: 3000 Average train loss: 2.3940\n Epoch: 0 Iter: 0 Average val loss: 2.3724 Acc1: 0.00 Acc3: 0.12 Acc5: 0.38\n\n\n====> After epoch 0 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3884 \n====> Average val loss: 2.3522 Acc1: 0.01 Acc3: 0.13 Acc5: 0.28\n\n\n Epoch: 1 Iter: 0 Average train loss: 2.3908\n Epoch: 1 Iter: 1000 Average train loss: 2.3586\n Epoch: 1 Iter: 2000 Average train loss: 2.3600\n Epoch: 1 Iter: 3000 Average train loss: 2.3576\n Epoch: 1 Iter: 0 Average val loss: 2.3236 Acc1: 0.00 Acc3: 0.00 Acc5: 0.25\n\n\n====> After epoch 1 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3561 \n====> Average val loss: 2.3253 Acc1: 0.01 Acc3: 0.12 Acc5: 0.31\n\n\n Epoch: 2 Iter: 0 Average train loss: 2.2772\n Epoch: 2 Iter: 1000 Average train loss: 2.3468\n Epoch: 2 Iter: 2000 Average train loss: 2.3460\n Epoch: 2 Iter: 3000 Average train loss: 2.3427\n Epoch: 2 Iter: 0 Average val loss: 2.3230 Acc1: 0.00 Acc3: 0.12 Acc5: 0.50\n\n\n====> After epoch 2 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3422 \n====> Average val loss: 2.3229 Acc1: 0.02 Acc3: 0.13 Acc5: 0.30\n\n\n Epoch: 3 Iter: 0 Average train loss: 2.1830\n Epoch: 3 Iter: 1000 Average train loss: 2.3323\n Epoch: 3 Iter: 2000 Average train loss: 2.3314\n Epoch: 3 Iter: 3000 Average train loss: 2.3303\n Epoch: 3 Iter: 0 Average val loss: 2.3085 Acc1: 0.00 Acc3: 0.19 Acc5: 0.31\n\n\n====> After epoch 3 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3301 \n====> Average val loss: 2.3081 Acc1: 0.02 Acc3: 0.19 Acc5: 0.48\n\n\n Epoch: 4 Iter: 0 Average train loss: 2.3128\n Epoch: 4 Iter: 1000 Average train loss: 2.3263\n Epoch: 4 Iter: 2000 Average train loss: 2.3238\n Epoch: 4 Iter: 3000 Average train loss: 2.3216\n Epoch: 4 Iter: 0 Average val loss: 2.3149 Acc1: 0.00 Acc3: 0.12 Acc5: 0.38\n\n\n====> After epoch 4 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3217 \n====> Average val loss: 2.3104 Acc1: 0.00 Acc3: 0.18 Acc5: 0.41\n\n\n Epoch: 5 Iter: 0 Average train loss: 2.2517\n Epoch: 5 Iter: 1000 Average train loss: 2.3180\n Epoch: 5 Iter: 2000 Average train loss: 2.3156\n Epoch: 5 Iter: 3000 Average train loss: 2.3149\n Epoch: 5 Iter: 0 Average val loss: 2.3135 Acc1: 0.00 Acc3: 0.12 Acc5: 0.25\n\n\n====> After epoch 5 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3143 \n====> Average val loss: 2.3137 Acc1: 0.02 Acc3: 0.14 Acc5: 0.33\n\n\nEpoch 6: reducing learning rate of group 0 to 5.0000e-05.\n Epoch: 6 Iter: 0 Average train loss: 2.2459\n Epoch: 6 Iter: 1000 Average train loss: 2.3076\n Epoch: 6 Iter: 2000 Average train loss: 2.3087\n Epoch: 6 Iter: 3000 Average train loss: 2.3076\n Epoch: 6 Iter: 0 Average val loss: 2.3081 Acc1: 0.06 Acc3: 0.12 Acc5: 0.19\n\n\n====> After epoch 6 \n====>Epoch Time: 1m 2s\n====>Average train loss: 2.3064 \n====> Average val loss: 2.3147 Acc1: 0.02 Acc3: 0.14 Acc5: 0.38\n\n\n Epoch: 7 Iter: 0 Average train loss: 2.3043\n Epoch: 7 Iter: 1000 Average train loss: 2.3081\n Epoch: 7 Iter: 2000 Average train loss: 2.3071\n Epoch: 7 Iter: 3000 Average train loss: 2.3070\n Epoch: 7 Iter: 0 Average val loss: 2.3125 Acc1: 0.00 Acc3: 0.12 Acc5: 0.25\n\n\n====> After epoch 7 \n====>Epoch Time: 1m 3s\n====>Average train loss: 2.3066 \n====> Average val loss: 2.3104 Acc1: 0.00 Acc3: 0.15 Acc5: 0.42\n\n\nSAVE MODEL to /content/drive/MyDrive/Model_files/task2/BMCNN_part3_pre2/epoch_7.th\n" ], [ "print('====> After epoch {} '.format(con.epoch))\nprint('====>conv Time: {}'.format(con.time))\n#print('====>conv Time: {}'.format(con.time))\nprint('====>Average train loss: {:.4f} +-{:.4f}'.format(\n con.meter.value()[0],con.meter.value()[1]))", "====> After epoch 3 \n====>conv Time: 253.81242299079895\n====>Average train loss: 2.3114 +-0.0027\n" ], [ "acc_meter=AverageValueMeter()\nmodel.eval()\nfor batch_idx, (data,label) in enumerate(test_loader):\n data = data.to(device)\n label=label.to(device)\n data = data.expand(-1, 3, -1, -1)\n output= model(data)\n \n \n r=accuracy_fn(output.data,label.data,(1,3,5))\n acc_meter.add(r[0].item())\nprint('Test_accuracy:{}'.format(acc_meter.value()))", "Test_accuracy:0.004200000000000006\n" ], [ "cm=conf(model,train_loader,10)\ncm=cm.cpu().numpy().astype('uint64')\nplt.figure(figsize=(10,10))\nplot_confusion_matrix(cm, lst1)", "Confusion matrix, without normalization\n[[2875 94 1825 16 320 22 195 13 171 449]\n [2918 88 1458 21 377 38 59 41 199 608]\n [2649 78 2031 20 382 32 175 50 142 450]\n [2694 63 1870 26 431 34 183 48 188 500]\n [2715 84 1684 13 452 29 197 39 149 552]\n [2692 88 1995 19 428 33 199 47 136 502]\n [2680 80 1984 21 335 32 188 35 162 520]\n [2536 79 1897 18 426 22 166 48 137 625]\n [2684 94 1961 20 369 30 153 44 223 551]\n [2786 92 1650 21 423 34 177 49 174 588]]\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

d0e9493d3487c9965dab8f0be313b152d88dd4e6

270,464

ipynb

Jupyter Notebook

_notebooks/2020-03-18-case-count-estimation-us-states.ipynb

maximelefrancois86/covid19-dashboard

162e2b0c0de27ac5cc7a233e0e1c8b25cfd15062

[ "Apache-2.0" ]

null

_notebooks/2020-03-18-case-count-estimation-us-states.ipynb

maximelefrancois86/covid19-dashboard

162e2b0c0de27ac5cc7a233e0e1c8b25cfd15062

[ "Apache-2.0" ]

null

_notebooks/2020-03-18-case-count-estimation-us-states.ipynb

maximelefrancois86/covid19-dashboard

162e2b0c0de27ac5cc7a233e0e1c8b25cfd15062

[ "Apache-2.0" ]

null

124.867959

70,476

0.741951

[ [ [ "# How many cases of COVID-19 does each U.S. state really have?\n> Reported U.S. case counts are based on the number of administered tests. Since not everyone is tested, this number is biased. We use Bayesian techniques to estimate the true number of cases.\n\n- author: Joseph Richards\n- image: images/covid-state-case-estimation.png\n- hide: false\n- comments: true\n- categories: [MCMC, US, states, cases]\n- permalink: /covid-19-us-case-estimation/\n- toc: false", "_____no_output_____" ] ], [ [ "#hide\n\n# Setup and imports\n%matplotlib inline\n\nimport warnings\nwarnings.simplefilter('ignore')\n\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport pandas as pd\nimport pymc3 as pm\nimport requests\n\nfrom IPython.display import display, Markdown", "_____no_output_____" ], [ "#hide\n\n# Data utilities:\n\ndef get_statewise_testing_data():\n '''\n Pull all statewise data required for model fitting and\n prediction\n\n Returns:\n * df_out: DataFrame for model fitting where inclusion\n requires testing data from 7 days ago\n * df_pred: DataFrame for count prediction where inclusion\n only requires testing data from today\n '''\n\n # Pull testing counts by state:\n out = requests.get('https://covidtracking.com/api/states')\n df_out = pd.DataFrame(out.json())\n df_out.set_index('state', drop=True, inplace=True)\n\n # Pull time-series of testing counts:\n ts = requests.get('https://covidtracking.com/api/states/daily')\n df_ts = pd.DataFrame(ts.json())\n\n # Get data from last week\n date_last_week = df_ts['date'].unique()[7]\n df_ts_last_week = _get_test_counts(df_ts, df_out.index, date_last_week)\n df_out['num_tests_7_days_ago'] = \\\n (df_ts_last_week['positive'] + df_ts_last_week['negative'])\n df_out['num_pos_7_days_ago'] = df_ts_last_week['positive']\n\n # Get data from today:\n df_out['num_tests_today'] = (df_out['positive'] + df_out['negative'])\n\n # State population:\n df_pop = pd.read_excel(('https://github.com/jwrichar/COVID19-mortality/blob/'\n 'master/data/us_population_by_state_2019.xlsx?raw=true'),\n skiprows=2, skipfooter=5)\n r = requests.get(('https://raw.githubusercontent.com/jwrichar/COVID19-mortality/'\n 'master/data/us-state-name-abbr.json'))\n state_name_abbr_lookup = r.json()\n \n df_pop.index = df_pop['Geographic Area'].apply(\n lambda x: str(x).replace('.', '')).map(state_name_abbr_lookup)\n df_pop = df_pop.loc[df_pop.index.dropna()]\n\n df_out['total_population'] = df_pop['Total Resident\\nPopulation']\n\n # Tests per million people, based on today's test coverage\n df_out['tests_per_million'] = 1e6 * \\\n (df_out['num_tests_today']) / df_out['total_population']\n df_out['tests_per_million_7_days_ago'] = 1e6 * \\\n (df_out['num_tests_7_days_ago']) / df_out['total_population']\n\n # People per test:\n df_out['people_per_test'] = 1e6 / df_out['tests_per_million']\n df_out['people_per_test_7_days_ago'] = \\\n 1e6 / df_out['tests_per_million_7_days_ago']\n\n # Drop states with messed up / missing data:\n # Drop states with missing total pop:\n to_drop_idx = df_out.index[df_out['total_population'].isnull()]\n print('Dropping %i/%i states due to lack of population data: %s' %\n (len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))\n df_out.drop(to_drop_idx, axis=0, inplace=True)\n\n df_pred = df_out.copy(deep=True) # Prediction DataFrame\n\n # Criteria for model fitting:\n # Drop states with missing test count 7 days ago:\n to_drop_idx = df_out.index[df_out['num_tests_7_days_ago'].isnull()]\n print('Dropping %i/%i states due to lack of tests: %s' %\n (len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))\n df_out.drop(to_drop_idx, axis=0, inplace=True)\n # Drop states with no cases 7 days ago:\n to_drop_idx = df_out.index[df_out['num_pos_7_days_ago'] == 0]\n print('Dropping %i/%i states due to lack of positive tests: %s' %\n (len(to_drop_idx), len(df_out), ', '.join(to_drop_idx)))\n df_out.drop(to_drop_idx, axis=0, inplace=True)\n\n # Criteria for model prediction:\n # Drop states with missing test count today:\n to_drop_idx = df_pred.index[df_pred['num_tests_today'].isnull()]\n print('Dropping %i/%i states in prediction data due to lack of tests: %s' %\n (len(to_drop_idx), len(df_pred), ', '.join(to_drop_idx)))\n df_pred.drop(to_drop_idx, axis=0, inplace=True)\n # Cast counts to int\n df_pred['negative'] = df_pred['negative'].astype(int)\n df_pred['positive'] = df_pred['positive'].astype(int)\n\n return df_out, df_pred\n\ndef _get_test_counts(df_ts, state_list, date):\n\n ts_list = []\n for state in state_list:\n state_ts = df_ts.loc[df_ts['state'] == state]\n # Back-fill any gaps to avoid crap data gaps\n state_ts.fillna(method='bfill', inplace=True)\n\n record = state_ts.loc[df_ts['date'] == date]\n ts_list.append(record)\n\n df_ts = pd.concat(ts_list, ignore_index=True)\n return df_ts.set_index('state', drop=True)\n", "_____no_output_____" ], [ "#hide\n\n# Model utilities\n\ndef case_count_model_us_states(df):\n\n # Normalize inputs in a way that is sensible:\n\n # People per test: normalize to South Korea\n # assuming S.K. testing is \"saturated\"\n ppt_sk = np.log10(51500000. / 250000)\n df['people_per_test_normalized'] = (\n np.log10(df['people_per_test_7_days_ago']) - ppt_sk)\n\n n = len(df)\n\n # For each country, let:\n # c_obs = number of observed cases\n c_obs = df['num_pos_7_days_ago'].values\n # c_star = number of true cases\n\n # d_obs = number of observed deaths\n d_obs = df[['death', 'num_pos_7_days_ago']].min(axis=1).values\n # people per test\n people_per_test = df['people_per_test_normalized'].values\n\n covid_case_count_model = pm.Model()\n\n with covid_case_count_model:\n\n # Priors:\n mu_0 = pm.Beta('mu_0', alpha=1, beta=100, testval=0.01)\n # sig_0 = pm.Uniform('sig_0', lower=0.0, upper=mu_0 * (1 - mu_0))\n alpha = pm.Bound(pm.Normal, lower=0.0)(\n 'alpha', mu=8, sigma=3, shape=1)\n beta = pm.Bound(pm.Normal, upper=0.0)(\n 'beta', mu=-1, sigma=1, shape=1)\n # beta = pm.Normal('beta', mu=0, sigma=1, shape=3)\n sigma = pm.HalfNormal('sigma', sigma=0.5, testval=0.1)\n # sigma_1 = pm.HalfNormal('sigma_1', sigma=2, testval=0.1)\n\n # Model probability of case under-reporting as logistic regression:\n mu_model_logit = alpha + beta * people_per_test\n tau_logit = pm.Normal('tau_logit',\n mu=mu_model_logit,\n sigma=sigma,\n shape=n)\n tau = np.exp(tau_logit) / (np.exp(tau_logit) + 1)\n\n c_star = c_obs / tau\n\n # Binomial likelihood:\n d = pm.Binomial('d',\n n=c_star,\n p=mu_0,\n observed=d_obs)\n\n return covid_case_count_model", "_____no_output_____" ], [ "#hide\n\ndf, df_pred = get_statewise_testing_data()\n\n# Initialize the model:\nmod = case_count_model_us_states(df)\n\n# Run MCMC sampler\nwith mod:\n trace = pm.sample(500, tune=500, chains=1)", "Dropping 4/56 states due to lack of population data: AS, GU, MP, VI\nDropping 0/52 states due to lack of tests: \nDropping 0/52 states due to lack of positive tests: \nDropping 0/52 states in prediction data due to lack of tests: \n" ], [ "#hide_input\n\nn = len(trace['beta'])\n\n# South Korea:\nppt_sk = np.log10(51500000. / 250000)\n\n\n# Compute predicted case counts per state right now\nlogit_now = pd.DataFrame([\n pd.Series(np.random.normal((trace['alpha'][i] + trace['beta'][i] * (np.log10(df_pred['people_per_test']) - ppt_sk)),\n trace['sigma'][i]), index=df_pred.index)\n for i in range(len(trace['beta']))])\nprob_missing_now = np.exp(logit_now) / (np.exp(logit_now) + 1) \n\npredicted_counts_now = np.round(df_pred['positive'] / prob_missing_now.mean(axis=0)).astype(int)\n\npredicted_counts_now_lower = np.round(df_pred['positive'] / prob_missing_now.quantile(0.975, axis=0)).astype(int)\npredicted_counts_now_upper = np.round(df_pred['positive'] / prob_missing_now.quantile(0.025, axis=0)).astype(int)\n\ncase_increase_percent = list(map(lambda x, y: (((x - y) / float(y))),\n predicted_counts_now, df_pred['positive']))\n\ndf_summary = pd.DataFrame(\n data = {\n 'Cases Reported': df_pred['positive'],\n 'Cases Estimated': predicted_counts_now,\n 'Percent Increase': case_increase_percent,\n 'Tests per Million People': df_pred['tests_per_million'].round(1),\n 'Cases Estimated (range)': list(map(lambda x, y: '(%i, %i)' % (round(x), round(y)),\n predicted_counts_now_lower, predicted_counts_now_upper)),\n 'Cases per Million': ((df_pred['positive'] / df_pred['total_population']) * 1e6),\n 'Positive Test Rate': (df_pred['positive'] / (df_pred['positive'] + df_pred['negative']))\n },\n index=df_pred.index)\n\nfrom datetime import datetime\ndisplay(Markdown(\"## Summary for the United States on %s:\" % str(datetime.today())[:10]))\ndisplay(Markdown(f\"**Reported Case Count:** {df_summary['Cases Reported'].sum():,}\"))\ndisplay(Markdown(f\"**Predicted Case Count:** {df_summary['Cases Estimated'].sum():,}\"))\ncase_increase_percent = 100. * (df_summary['Cases Estimated'].sum() - df_summary['Cases Reported'].sum()) / df_summary['Cases Estimated'].sum()\ndisplay(Markdown(\"**Percentage Underreporting in Case Count:** %.1f%%\" % case_increase_percent))", "_____no_output_____" ], [ "#hide\ndf_summary.loc[:, 'Ratio'] = df_summary['Cases Estimated'] / df_summary['Cases Reported']\ndf_summary.columns = ['Reported Cases', 'Est Cases', '% Increase',\n 'Tests per Million', 'Est Range',\n 'Cases per Million', 'Positive Test Rate',\n 'Ratio']\n\ndf_display = df_summary[['Reported Cases', 'Est Cases', 'Est Range', 'Ratio',\n 'Tests per Million', 'Cases per Million',\n 'Positive Test Rate']].copy()", "_____no_output_____" ] ], [ [ "## COVID-19 Case Estimates, by State\n\n### Definition Of Fields:\n\n- **Reported Cases**: The number of cases reported by each state, which is a function of how many tests are positive.\n- **Est Cases**: The predicted number of cases, accounting for the fact that not everyone is tested.\n- **Est Range**: The 95% confidence interval of the predicted number of cases.\n- **Ratio**: `Estimated Cases` divided by `Reported Cases`.\n- **Tests per Million**: The number of tests administered per one million people. The less tests administered per capita, the larger the difference between reported and estimated number of cases, generally.\n- **Cases per Million**: The number of **reported** cases per on million people.\n- **Positive Test Rate**: The **reported** percentage of positive tests.", "_____no_output_____" ] ], [ [ "#hide_input\ndf_display.sort_values(\n by='Est Cases', ascending=False).style.background_gradient(\n cmap='Oranges').format(\n {'Ratio': \"{:.1f}\"}).format(\n {'Tests per Million': \"{:.1f}\"}).format(\n {'Cases per Million': \"{:.1f}\"}).format(\n {'Positive Test Rate': \"{:.0%}\"})", "_____no_output_____" ], [ "#hide_input\n\ndf_plot = df_summary.copy(deep=True)\n\n# Compute predicted cases per million\ndf_plot['predicted_counts_now_pm'] = 1e6 * (\n df_pred['positive'] / prob_missing_now.mean(axis=0)) / df_pred['total_population']\n\ndf_plot['predicted_counts_now_lower_pm'] = 1e6 * (\n df_pred['positive'] / prob_missing_now.quantile(0.975, axis=0))/ df_pred['total_population']\ndf_plot['predicted_counts_now_upper_pm'] = 1e6 * (\n df_pred['positive'] / prob_missing_now.quantile(0.025, axis=0))/ df_pred['total_population']\n\ndf_plot.sort_values('predicted_counts_now_pm', ascending=False, inplace=True)\n\nxerr = [\n df_plot['predicted_counts_now_pm'] - df_plot['predicted_counts_now_lower_pm'], \n df_plot['predicted_counts_now_upper_pm'] - df_plot['predicted_counts_now_pm']]\n\nfig, axs = plt.subplots(1, 1, figsize=(15, 15))\nax = plt.errorbar(df_plot['predicted_counts_now_pm'], range(len(df_plot)-1, -1, -1),\n xerr=xerr, fmt='o', elinewidth=1, label='Estimate')\nax = plt.yticks(range(len(df_plot)), df_plot.index[::-1])\nax = plt.errorbar(df_plot['Cases per Million'], range(len(df_plot)-1, -1, -1),\n xerr=None, fmt='.', color='k', label='Reported')\nax = plt.xlabel('COVID-19 Case Counts Per Million People', size=20)\nax = plt.legend(fontsize='xx-large', loc=4)\nax = plt.grid(linestyle='--', color='grey', axis='x')", "_____no_output_____" ] ], [ [ "## Appendix: Model Diagnostics \n\n### Derived relationship between Test Capacity and Case Under-reporting\n\nPlotted is the estimated relationship between test capacity (in terms of people per test -- larger = less testing) and the likelihood a COVID-19 case is reported (lower = more under-reporting of cases).\n\nThe lines represent the posterior samples from our MCMC run (note the x-axis is plotted on a log scale). The rug plot shows the current test capacity for each state (black '|') and the capacity one week ago (cyan '+'). For comparison, South Korea's testing capacity is currently at the very left of the graph (200 people per test).", "_____no_output_____" ] ], [ [ "#hide_input\n\n# Plot pop/test vs. Prob of case detection for all posterior samples:\nx = np.linspace(0.0, 4.0, 101)\nlogit_pcase = pd.DataFrame([\n trace['alpha'][i] + trace['beta'][i] * x\n for i in range(n)])\npcase = np.exp(logit_pcase) / (np.exp(logit_pcase) + 1)\n\nfig, ax = plt.subplots(1, 1, figsize=(14, 9))\nfor i in range(n):\n ax = plt.plot(10**(ppt_sk + x), pcase.iloc[i], color='grey', lw=.1, alpha=.5)\n plt.xscale('log')\n plt.xlabel('State-wise population per test', size=14)\n plt.ylabel('Probability a true case is detected', size=14)\n\n# rug plots:\nax=plt.plot(df_pred['people_per_test'], np.zeros(len(df_pred)),\n marker='|', color='k', ls='', ms=20,\n label='U.S. State-wise Test Capacity Now')\nax=plt.plot(df['people_per_test_7_days_ago'], np.zeros(len(df)),\n marker='+', color='c', ls='', ms=10,\n label='U.S. State-wise Test Capacity 7 Days Ago')\nax = plt.legend(fontsize='x-large')", "_____no_output_____" ] ], [ [ "## About this Analysis\n\nThis analysis was done by [Joseph Richards](https://twitter.com/joeyrichar).\n\nThis project[^1] uses the testing rates per state from [https://covidtracking.com/](https://covidtracking.com/), which reports case counts and mortality by state. This is used to **estimate the number of unreported (untested) COVID-19 cases in each U.S. state.**\n\nThe analysis makes a few assumptions:\n\n1. The probability that a case is reported by a state is a function of the number of tests run per person in that state. Hence the degree of under-reported cases is a function of tests run per capita.\n2. The underlying mortality rate is the same across every state.\n3. Patients take time to succumb to COVID-19, so the mortality counts *today* reflect the case counts *7 days ago*. E.g., mortality rate = (cumulative deaths today) / (cumulative cases 7 days ago).\n\nThe model attempts to find the most likely relationship between state-wise test volume (per capita) and under-reporting, such that the true underlying mortality rates between the individual states are as similar as possible. The model simultaneously finds the most likely posterior distribution of mortality rates, the most likely *true* case count per state, and the test volume vs. case underreporting relationship.\n\n[^1]: Full details about the model are available at: https://github.com/jwrichar/COVID19-mortality", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

d0e95338821dffe57f221337b146e09f75836723

709,984

ipynb

Jupyter Notebook

Notebook.ipynb

toogy/pendigits-hmm

03382e1457941714439d40b67e53eaf117fe4d08

[ "MIT" ]

null

Notebook.ipynb

toogy/pendigits-hmm

03382e1457941714439d40b67e53eaf117fe4d08

[ "MIT" ]

null

Notebook.ipynb

toogy/pendigits-hmm

03382e1457941714439d40b67e53eaf117fe4d08

[ "MIT" ]

null

1,329.558052

229,130

0.947782

[ [ [ "%matplotlib inline\n%pylab inline", "Populating the interactive namespace from numpy and matplotlib\n" ], [ "from parsing import parser, digit\nfrom plotting import plotter, voronoi\nfrom analysis import training, sampling, testing, classify\nfrom config import settings\n\nimport warnings\nwarnings.filterwarnings('ignore')", "_____no_output_____" ], [ "n_observation_classes = 256\nn_hidden_states = 30\nn_iter = 10000\ntol = 0.1", "_____no_output_____" ], [ "parse = parser.Parser();\ntrain_digits = parse.parse_file('data/pendigits-train');\ntest_digits = parse.parse_file('data/pendigits-test')", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (5, 5);\nplotter.plot_digit(train_digits[6], True)", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (15, 6);\nplotter.plot_digits_heatmap(train_digits, True);", "_____no_output_____" ], [ "centroids = training.get_digit_kmeans_centroids(train_digits, n_observation_classes - 3)", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (10, 10);\nvoronoi.plot_centroids(centroids);", "_____no_output_____" ], [ "training.set_digit_observations(train_digits, centroids, n_observation_classes)", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (5, 5);\nplotter.plot_digit_observations(train_digits[11], centroids, n_observation_classes, True)", "_____no_output_____" ], [ "hidden_markov_models = training.train_hmm(train_digits, n_observation_classes, n_hidden_states, n_iter, tol)", "_____no_output_____" ], [ "samplings = sampling.get_samplings(hidden_markov_models, n_observation_classes, centroids, 100)", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (5, 5);\nplotter.plot_digit(samplings[2][8], True)", "_____no_output_____" ], [ "pylab.rcParams['figure.figsize'] = (15, 6);\nplotter.plot_digit_samples_heatmap(samplings)", "_____no_output_____" ], [ "test_labels_probabilities = classify.get_labels_probabilities(test_digits, hidden_markov_models, centroids, n_observation_classes, n_hidden_states,\n n_iter, tol, True, True, \"test_labels_probabilities.dat\")", "_____no_output_____" ], [ "test_classifier = classify.WeightedClassifier(test_digits, test_labels_probabilities)\nprediction_matrix = test_classifier.get_prediction_matrix()\nfor row in prediction_matrix:\n print(row)", "[328, 0, 0, 0, 1, 0, 1, 0, 33, 0]\n[1, 282, 49, 1, 0, 1, 0, 5, 14, 11]\n[0, 22, 326, 0, 3, 0, 0, 9, 3, 1]\n[0, 5, 0, 312, 0, 4, 0, 2, 2, 11]\n[0, 5, 12, 0, 160, 0, 2, 0, 160, 24]\n[0, 0, 2, 0, 0, 73, 5, 0, 193, 62]\n[3, 3, 0, 0, 0, 0, 310, 0, 18, 2]\n[0, 55, 20, 23, 0, 0, 0, 24, 51, 191]\n[0, 1, 0, 0, 0, 9, 0, 0, 307, 19]\n[0, 10, 0, 0, 1, 6, 0, 1, 6, 312]\n" ], [ "test_classifier.print_classification_performance()", "total classification accuracy : 69.60251644266515\nlabel 1 : 90.35812672176309\nlabel 2 : 77.47252747252747\nlabel 3 : 89.56043956043956\nlabel 4 : 92.85714285714286\nlabel 5 : 44.07713498622589\nlabel 6 : 21.791044776119403\nlabel 7 : 92.26190476190476\nlabel 8 : 6.593406593406593\nlabel 9 : 91.36904761904762\nlabel 0 : 92.85714285714286\n" ], [ "gaussian_hidden_markov_models = training.train_gaussian_hmm(train_digits, n_hidden_states, n_iter, tol)", "_____no_output_____" ], [ "for i in range(0, 10):\n print(classify.get_gaussian_hmm_probability(test_digits[0], gaussian_hidden_markov_models[i]))", "-85.3174667263\n-304.582351302\n-212.766422804\n-82.5324956152\n-28.4598359226\n-293.374894692\n-172.812791103\n9.64127185866\n-16.3436783895\n-142.691638808\n" ], [ "gaussian_test_labels_probabilities = classify.get_gaussian_labels_probabilities(test_digits, gaussian_hidden_markov_models, n_observation_classes, n_hidden_states,\n n_iter, tol, True, True, \"gaussian_test_labels_probabilities.dat\")", "_____no_output_____" ], [ "gaussian_test_classifier = classify.GaussianClassifier(test_digits, gaussian_test_labels_probabilities)\nprediction_matrix = gaussian_test_classifier.get_prediction_matrix()\nfor row in prediction_matrix:\n print(row)", "[332, 0, 0, 0, 4, 0, 0, 0, 27, 0]\n[1, 306, 45, 0, 0, 0, 1, 5, 2, 4]\n[0, 12, 350, 0, 1, 0, 0, 1, 0, 0]\n[0, 3, 0, 324, 0, 0, 0, 3, 0, 6]\n[0, 2, 0, 0, 328, 2, 0, 0, 15, 16]\n[0, 2, 0, 0, 0, 315, 0, 0, 14, 4]\n[6, 0, 0, 0, 0, 0, 329, 0, 1, 0]\n[0, 38, 0, 0, 1, 0, 0, 323, 0, 2]\n[0, 0, 0, 0, 0, 2, 0, 0, 327, 7]\n[0, 8, 0, 0, 1, 0, 0, 2, 2, 323]\n" ], [ "gaussian_test_classifier.print_classification_performance()", "total classification accuracy : 93.13697454961395\nlabel 1 : 91.46005509641873\nlabel 2 : 84.06593406593407\nlabel 3 : 96.15384615384616\nlabel 4 : 96.42857142857143\nlabel 5 : 90.35812672176309\nlabel 6 : 94.02985074626865\nlabel 7 : 97.91666666666667\nlabel 8 : 88.73626373626374\nlabel 9 : 97.32142857142857\nlabel 0 : 96.13095238095238\n" ] ], [ [ "# Dynamic Time Warping\n\n\\begin{equation}\ny = \\mathop{\\arg\\,\\max}\\limits{l \\in L} \\frac{1}{n_l} \\sum_{i = 0}^{n_l} \\text{fastdtw\\_distance}(x_i^l, x_{\\text{test}})\n\\end{equation}", "_____no_output_____" ] ], [ [ "import dtw\n\nprint(dtw.score())", "0.898484415213\n" ] ] ]

[ "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

d0e954d155bff46fb1f8b8ffc100e5837f365ec5

148,103

ipynb

Jupyter Notebook

lab2.ipynb

nushtosh/python-data-analysis

bbfe0aa42b48872a3dbf3f43e8018a390db4f7f9

[ "Apache-2.0" ]

null

lab2.ipynb

nushtosh/python-data-analysis

bbfe0aa42b48872a3dbf3f43e8018a390db4f7f9

[ "Apache-2.0" ]

null

lab2.ipynb

nushtosh/python-data-analysis

bbfe0aa42b48872a3dbf3f43e8018a390db4f7f9

[ "Apache-2.0" ]

null

125.830926

21,360

0.839882

[ [ [ "import os\n\nos.chdir(\"C:\\\\Users\\\\olya\\\\Downloads\")\n\nimport pandas as pd\nimport numpy as np\nimport matplotlib\nimport matplotlib.pyplot as plt\n%matplotlib inline", "_____no_output_____" ], [ "AH = pd.read_csv('PRODUCT_LIST.CSV', sep=\";\",encoding='Windows-1251', header = 0, index_col=False)\ndf = pd.read_csv('SALE_LIST.csv', sep=\";\",encoding='Windows-1251', header = 0, index_col=False)", "_____no_output_____" ], [ "df.head()", "_____no_output_____" ], [ "AH.head()", "_____no_output_____" ], [ "AH.rename(columns = {'Product_code':'product_code'}, inplace = True)", "_____no_output_____" ], [ "mergeList = AH.merge(df, on=['product_code'])", "_____no_output_____" ], [ "topm = mergeList[mergeList['rest_code'] == 'Мечта'].sort_values('product_count', ascending = False)\ntopo = mergeList[mergeList['rest_code'] == 'Озерный'].sort_values('product_count', ascending = False)", "_____no_output_____" ], [ "topm", "_____no_output_____" ], [ "top5m = list(topm.groupby('Product_name')['product_count'].sum().sort_values(ascending = False).head(5).index.values)\nprint(top5m)", "['Кофе Латте 300мл', 'Кофе КАПУЧИНО 150мл', 'Кофе АМЕРИКАНО 90мл', 'Кофе ЭСПРЕССО 30 мл', 'Раф кофе 300мл']\n" ], [ "topm[topm['Product_name'].isin(top5m)].groupby('Product_name')['product_count'].sum().plot.bar()", "_____no_output_____" ], [ "topm['product_count'].sum()", "_____no_output_____" ], [ "topm[topm['Product_name'].isin(top5m)].boxplot(column='product_count',by='Product_name')\nplt.xticks(rotation=90)", "_____no_output_____" ], [ "topo", "_____no_output_____" ], [ "top5o = list(topo.groupby('Product_name')['product_count'].sum().sort_values(ascending = False).head(5).index.values)\nprint(top5o)", "['Кофе КАПУЧИНО 150мл', 'Кофе Латте 300мл', 'Кофе ЭСПРЕССО 30 мл', 'Кофе АМЕРИКАНО 90мл', 'Раф кофе 300мл']\n" ], [ "topo[topo['Product_name'].isin(top5o)].groupby('Product_name')['product_count'].sum().plot.bar()", "_____no_output_____" ], [ "topm[topm['Product_name'].isin(top5m)].boxplot(column='product_count',by='Product_name')\nplt.xticks(rotation=90)", "_____no_output_____" ], [ "gtopm=topm[topm['Product_name'].isin(top5m)].groupby('Product_name')['product_count'].sum().plot.bar(alpha=0.5,color='red')\ngtopo=topo[topo['Product_name'].isin(top5o)].groupby('Product_name')['product_count'].sum().plot.bar(alpha=0.6)\nplt.legend(['Мечта','Озерный'])", "_____no_output_____" ], [ "topm['product_count'].sum()\n", "_____no_output_____" ], [ "topo['product_count'].sum()", "_____no_output_____" ], [ "df1=pd.DataFrame(data={'product_count':[topm['product_count'].sum(),topo['product_count'].sum()]},index=['Мечта','Озерный'])\ndf1.plot.bar()", "_____no_output_____" ], [ "df", "_____no_output_____" ], [ "df.boxplot(column='product_count', by='rest_code')", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e96d54560fb204d75678afeb8e7bdb4c320575

3,820

ipynb

Jupyter Notebook

notebooks/Cavity Length Determiner.ipynb

garrekstemo/pistachio

ca357f73b11c25fea984b6bfd068a13852797553

[ "MIT" ]

1

2021-04-19T23:51:26.000Z

notebooks/Cavity Length Determiner.ipynb

garrekds/pistachio

ca357f73b11c25fea984b6bfd068a13852797553

[ "MIT" ]

null

notebooks/Cavity Length Determiner.ipynb

garrekds/pistachio

ca357f73b11c25fea984b6bfd068a13852797553

[ "MIT" ]

null

28.507463

239

0.593194

[ [ [ "# Cavity Length Determiner\n\nUse this notebook to find peak positions in a spectrum and use the free spectral range, along with the known or calculated material refractive index, to determine the cavity length in vacuum. The *must* be done at 0-degree incidence.", "_____no_output_____" ] ], [ [ "import ipywidgets as widgets\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nimport pandas as pd\nfrom scipy import signal\nfrom ruamel_yaml import YAML\nimport data_io\nimport material_properties as mp\nimport pmath\n\nyaml = YAML()\nsns.set_theme(context='notebook', style='whitegrid', palette='dark')\n%matplotlib widget", "_____no_output_____" ], [ "data_directory = 'path/to/angle/resolved/data/directory/'\nangle_data, absorbance_data = data_io.get_angle_data_from_dir(data_directory)\n\nprint('Loading data from:')\nprint(data_directory, '\\n')\nprint('Angles in range: [', angle_data[0][0], ',', angle_data[-1][0], ']')", "_____no_output_____" ], [ "angle, wavenumber, intensity = angle_data[0]\n\nlb = 500\nub = 8000\nmask = (wavenumber >= lb) & (wavenumber <= ub)\nwavenumber = wavenumber[mask]\nintensity = intensity[mask]\npeaks_in_interval = signal.find_peaks(intensity, height=1.0, distance=500)[0]\nnumber_of_peaks = len(peaks_in_interval)\npeak_pos_x = [wavenumber[p] for p in peaks_in_interval]\npeak_pos_y = [intensity[p] for p in peaks_in_interval]\npeaks_data = pd.DataFrame({'Peaks': peak_pos_x})", "_____no_output_____" ], [ "# Plot the selected spectrum or a subrange\nfig, ax = plt.subplots()\n\nax.plot(wavenumber, intensity)\nax.scatter(peak_pos_x, peak_pos_y, color='orange')\n\nax.set_title(\"Spectrum subrange at {} degrees\\n{} peaks\".format(angle, number_of_peaks))\nax.set_xlabel(r'Wavenumber (cm$^{-1}$)')\nax.set_ylabel('Transmittance (%)')\nplt.show()", "_____no_output_____" ], [ "# Check the peak spacing statistics.\npeaks_data.diff().describe()", "_____no_output_____" ], [ "concentration = sample['Concentration']\nsolvent_refractive_index = 1.0 \nsolute_refractive_index = 1.0\nn_eff = pmath.refractive_line(concentration, solvent_refractive_index, solute_refractive_index, 0.0, neat_solute_concentration)\nL_cav = float(10**4 / (2 * n_eff * peaks_data.diff().mean()))\n\nprint('Concentration:', concentration, 'mol/L')\nprint('Refractive index:', n_eff)\nprint('Cavity length:', L_cav, 'micrometers')", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

d0e975aa7398e8f352559ee667a8a7c4812c2a00

2,373

ipynb

Jupyter Notebook

assignments/assignment02/ProjectEuler6.ipynb

edwardd1/phys202-2015-work

b91da6959223a82c4c0b8030c92a789234a4b6b9

[ "MIT" ]

null

assignments/assignment02/ProjectEuler6.ipynb

edwardd1/phys202-2015-work

b91da6959223a82c4c0b8030c92a789234a4b6b9

[ "MIT" ]

null

assignments/assignment02/ProjectEuler6.ipynb

edwardd1/phys202-2015-work

b91da6959223a82c4c0b8030c92a789234a4b6b9

[ "MIT" ]

null

21.378378

138

0.501475

[ [ [ "# Project Euler: Problem 6", "_____no_output_____" ], [ "https://projecteuler.net/problem=6\n\nThe sum of the squares of the first ten natural numbers is,\n\n$$1^2 + 2^2 + ... + 10^2 = 385$$\n\nThe square of the sum of the first ten natural numbers is,\n\n$$(1 + 2 + ... + 10)^2 = 552 = 3025$$\n\nHence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is 3025 − 385 = 2640.", "_____no_output_____" ] ], [ [ "#Pretty simple process. I summed all the y's up and squared the sum and then I subtracted each x^2 (1-100) from that result.\nx = 0\ny = 0\nn = 0\nwhile (y < 100):\n y = y + 1\n n = n + y\n#print (y)\n#print (n)\nn = (n ** 2)\nwhile (x < 100):\n x = x + 1\n n = n - (x ** 2)\n#print (x)\nprint (n)\n#raise NotImplementedError()", "25164150\n" ], [ "# This cell will be used for grading, leave it at the end of the notebook.", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code" ] ]

d0e97e2144bbd590ab4cc6f4a2f11b069ec8e2eb

646,491

ipynb

Jupyter Notebook

docs/source/notebooks/GLM-logistic.ipynb

JvParidon/pymc3

f60dc1db74df3c54d707761e9dc054a7fdf0435c

[ "Apache-2.0" ]

2

2020-05-29T07:10:45.000Z

2021-04-07T06:43:52.000Z

docs/source/notebooks/GLM-logistic.ipynb

JvParidon/pymc3

f60dc1db74df3c54d707761e9dc054a7fdf0435c

[ "Apache-2.0" ]

null

docs/source/notebooks/GLM-logistic.ipynb

JvParidon/pymc3

f60dc1db74df3c54d707761e9dc054a7fdf0435c

[ "Apache-2.0" ]

1

2019-01-02T09:02:18.000Z

272.321398

288,324

0.886028

[ [ [ "# GLM: Logistic Regression\n\n* This is a reproduction with a few slight alterations of [Bayesian Log Reg](http://jbencook.github.io/portfolio/bayesian_logistic_regression.html) by J. Benjamin Cook\n\n* Author: Peadar Coyle and J. Benjamin Cook\n* How likely am I to make more than $50,000 US Dollars?\n* Exploration of model selection techniques too - I use WAIC to select the best model. \n* The convenience functions are all taken from Jon Sedars work.\n* This example also has some explorations of the features so serves as a good example of Exploratory Data Analysis and how that can guide the model creation/ model selection process. ", "_____no_output_____" ] ], [ [ "%matplotlib inline\nimport pandas as pd\nimport numpy as np\nimport pymc3 as pm\nimport matplotlib.pyplot as plt\nimport seaborn\nimport warnings\nwarnings.filterwarnings('ignore')\nfrom collections import OrderedDict\nfrom time import time\n\nimport numpy as np\nimport pandas as pd\nimport matplotlib.pyplot as plt\n\nfrom scipy.optimize import fmin_powell\nfrom scipy import integrate\n\nimport theano as thno\nimport theano.tensor as T", "_____no_output_____" ], [ "def run_models(df, upper_order=5):\n ''' \n Convenience function:\n Fit a range of pymc3 models of increasing polynomial complexity. \n Suggest limit to max order 5 since calculation time is exponential.\n '''\n \n models, traces = OrderedDict(), OrderedDict()\n\n for k in range(1,upper_order+1):\n\n nm = 'k{}'.format(k)\n fml = create_poly_modelspec(k)\n\n with pm.Model() as models[nm]:\n\n print('\\nRunning: {}'.format(nm))\n pm.glm.GLM.from_formula(fml, df, family=pm.glm.families.Normal())\n\n traces[nm] = pm.sample(2000, chains=1, init=None, tune=1000) \n \n return models, traces\n\ndef plot_traces(traces, retain=1000):\n ''' \n Convenience function:\n Plot traces with overlaid means and values\n '''\n \n ax = pm.traceplot(traces[-retain:], figsize=(12,len(traces.varnames)*1.5),\n lines={k: v['mean'] for k, v in pm.summary(traces[-retain:]).iterrows()})\n\n for i, mn in enumerate(pm.summary(traces[-retain:])['mean']):\n ax[i,0].annotate('{:.2f}'.format(mn), xy=(mn,0), xycoords='data'\n ,xytext=(5,10), textcoords='offset points', rotation=90\n ,va='bottom', fontsize='large', color='#AA0022')\n \ndef create_poly_modelspec(k=1):\n ''' \n Convenience function:\n Create a polynomial modelspec string for patsy\n '''\n return ('income ~ educ + hours + age ' + ' '.join(['+ np.power(age,{})'.format(j) \n for j in range(2,k+1)])).strip()", "_____no_output_____" ] ], [ [ "The [Adult Data Set](http://archive.ics.uci.edu/ml/datasets/Adult) is commonly used to benchmark machine learning algorithms. The goal is to use demographic features, or variables, to predict whether an individual makes more than \\\\$50,000 per year. The data set is almost 20 years old, and therefore, not perfect for determining the probability that I will make more than \\$50K, but it is a nice, simple dataset that can be used to showcase a few benefits of using Bayesian logistic regression over its frequentist counterpart.\n\n\nThe motivation for myself to reproduce this piece of work was to learn how to use Odd Ratio in Bayesian Regression.", "_____no_output_____" ] ], [ [ "data = pd.read_csv(\"https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data\", header=None, names=['age', 'workclass', 'fnlwgt', \n 'education-categorical', 'educ', \n 'marital-status', 'occupation',\n 'relationship', 'race', 'sex', \n 'captial-gain', 'capital-loss', \n 'hours', 'native-country', \n 'income'])", "_____no_output_____" ], [ "data.head(10)", "_____no_output_____" ] ], [ [ "## Scrubbing and cleaning\nWe need to remove any null entries in Income. \nAnd we also want to restrict this study to the United States.", "_____no_output_____" ] ], [ [ "data = data[~pd.isnull(data['income'])]", "_____no_output_____" ], [ "data[data['native-country']==\" United-States\"]", "_____no_output_____" ], [ "income = 1 * (data['income'] == \" >50K\")\nage2 = np.square(data['age'])", "_____no_output_____" ], [ "data = data[['age', 'educ', 'hours']]\ndata['age2'] = age2\ndata['income'] = income", "_____no_output_____" ], [ "income.value_counts()", "_____no_output_____" ] ], [ [ "## Exploring the data \nLet us get a feel for the parameters. \n* We see that age is a tailed distribution. Certainly not Gaussian!\n* We don't see much of a correlation between many of the features, with the exception of Age and Age2. \n* Hours worked has some interesting behaviour. How would one describe this distribution? \n", "_____no_output_____" ] ], [ [ "g = seaborn.pairplot(data)", "_____no_output_____" ], [ "# Compute the correlation matrix\ncorr = data.corr()\n\n# Generate a mask for the upper triangle\nmask = np.zeros_like(corr, dtype=np.bool)\nmask[np.triu_indices_from(mask)] = True\n\n# Set up the matplotlib figure\nf, ax = plt.subplots(figsize=(11, 9))\n\n# Generate a custom diverging colormap\ncmap = seaborn.diverging_palette(220, 10, as_cmap=True)\n\n# Draw the heatmap with the mask and correct aspect ratio\nseaborn.heatmap(corr, mask=mask, cmap=cmap, vmax=.3,\n linewidths=.5, cbar_kws={\"shrink\": .5}, ax=ax)", "_____no_output_____" ] ], [ [ "We see here not many strong correlations. The highest is 0.30 according to this plot. We see a weak-correlation between hours and income \n(which is logical), we see a slighty stronger correlation between education and income (which is the kind of question we are answering).", "_____no_output_____" ], [ "## The model\nWe will use a simple model, which assumes that the probability of making more than $50K \nis a function of age, years of education and hours worked per week. We will use PyMC3 \ndo inference. \n\nIn Bayesian statistics, we treat everything as a random variable and we want to know the posterior probability distribution of the parameters\n(in this case the regression coefficients)\nThe posterior is equal to the likelihood $$p(\\theta | D) = \\frac{p(D|\\theta)p(\\theta)}{p(D)}$$\n\nBecause the denominator is a notoriously difficult integral, $p(D) = \\int p(D | \\theta) p(\\theta) d \\theta $ we would prefer to skip computing it. Fortunately, if we draw examples from the parameter space, with probability proportional to the height of the posterior at any given point, we end up with an empirical distribution that converges to the posterior as the number of samples approaches infinity. \n\nWhat this means in practice is that we only need to worry about the numerator. \n\nGetting back to logistic regression, we need to specify a prior and a likelihood in order to draw samples from the posterior. We could use sociological knowledge about the effects of age and education on income, but instead, let's use the default prior specification for GLM coefficients that PyMC3 gives us, which is $p(θ)=N(0,10^{12}I)$. This is a very vague prior that will let the data speak for themselves.\n\nThe likelihood is the product of n Bernoulli trials, $\\prod^{n}_{i=1} p_{i}^{y} (1 - p_{i})^{1-y_{i}}$,\nwhere $p_i = \\frac{1}{1 + e^{-z_i}}$, \n\n$z_{i} = \\beta_{0} + \\beta_{1}(age)_{i} + \\beta_2(age)^{2}_{i} + \\beta_{3}(educ)_{i} + \\beta_{4}(hours)_{i}$ and $y_{i} = 1$ if income is greater than 50K and $y_{i} = 0$ otherwise. \n\nWith the math out of the way we can get back to the data. Here I use PyMC3 to draw samples from the posterior. The sampling algorithm used is NUTS, which is a form of Hamiltonian Monte Carlo, in which parameteres are tuned automatically. Notice, that we get to borrow the syntax of specifying GLM's from R, very convenient! I use a convenience function from above to plot the trace infromation from the first 1000 parameters. ", "_____no_output_____" ] ], [ [ "with pm.Model() as logistic_model:\n pm.glm.GLM.from_formula('income ~ age + age2 + educ + hours', data, family=pm.glm.families.Binomial())\n trace_logistic_model = pm.sample(2000, chains=1, init=None, tune=1000)", "Sequential sampling (1 chains in 1 job)\nNUTS: [hours, educ, age2, age, Intercept]\n100%|██████████| 3000/3000 [10:03<00:00, 4.97it/s]\nOnly one chain was sampled, this makes it impossible to run some convergence checks\n" ], [ "plot_traces(trace_logistic_model, retain=1000)", "_____no_output_____" ] ], [ [ "## Some results \nOne of the major benefits that makes Bayesian data analysis worth the extra computational effort in many circumstances is that we can be explicit about our uncertainty. Maximum likelihood returns a number, but how certain can we be that we found the right number? Instead, Bayesian inference returns a distribution over parameter values.\n\nI'll use seaborn to look at the distribution of some of these factors. ", "_____no_output_____" ] ], [ [ "plt.figure(figsize=(9,7))\ntrace = trace_logistic_model[1000:]\nseaborn.jointplot(trace['age'], trace['educ'], kind=\"hex\", color=\"#4CB391\")\nplt.xlabel(\"beta_age\")\nplt.ylabel(\"beta_educ\")\nplt.show()", "_____no_output_____" ] ], [ [ "So how do age and education affect the probability of making more than $$50K?$ To answer this question, we can show how the probability of making more than $50K changes with age for a few different education levels. Here, we assume that the number of hours worked per week is fixed at 50. PyMC3 gives us a convenient way to plot the posterior predictive distribution. We need to give the function a linear model and a set of points to evaluate. We will pass in three different linear models: one with educ == 12 (finished high school), one with educ == 16 (finished undergrad) and one with educ == 19 (three years of grad school).", "_____no_output_____" ] ], [ [ "# Linear model with hours == 50 and educ == 12\nlm = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] + \n samples['age']*x + \n samples['age2']*np.square(x) + \n samples['educ']*12 + \n samples['hours']*50)))\n\n# Linear model with hours == 50 and educ == 16\nlm2 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] + \n samples['age']*x + \n samples['age2']*np.square(x) + \n samples['educ']*16 + \n samples['hours']*50)))\n\n# Linear model with hours == 50 and educ == 19\nlm3 = lambda x, samples: 1 / (1 + np.exp(-(samples['Intercept'] + \n samples['age']*x + \n samples['age2']*np.square(x) + \n samples['educ']*19 + \n samples['hours']*50)))", "_____no_output_____" ] ], [ [ "\nEach curve shows how the probability of earning more than $ 50K$ changes with age. The red curve represents 19 years of education, the green curve represents 16 years of education and the blue curve represents 12 years of education. For all three education levels, the probability of making more than $50K increases with age until approximately age 60, when the probability begins to drop off. Notice that each curve is a little blurry. This is because we are actually plotting 100 different curves for each level of education. Each curve is a draw from our posterior distribution. Because the curves are somewhat translucent, we can interpret dark, narrow portions of a curve as places where we have low uncertainty and light, spread out portions of the curve as places where we have somewhat higher uncertainty about our coefficient values.", "_____no_output_____" ] ], [ [ "# Plot the posterior predictive distributions of P(income > $50K) vs. age\npm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm, samples=100, color=\"blue\", alpha=.15)\npm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm2, samples=100, color=\"green\", alpha=.15)\npm.plot_posterior_predictive_glm(trace, eval=np.linspace(25, 75, 1000), lm=lm3, samples=100, color=\"red\", alpha=.15)\n\nimport matplotlib.lines as mlines\nblue_line = mlines.Line2D(['lm'], [], color='b', label='High School Education')\ngreen_line = mlines.Line2D(['lm2'], [], color='g', label='Bachelors')\nred_line = mlines.Line2D(['lm3'], [], color='r', label='Grad School')\nplt.legend(handles=[blue_line, green_line, red_line], loc='lower right')\nplt.ylabel(\"P(Income > $50K)\")\nplt.xlabel(\"Age\")\nplt.show()", "_____no_output_____" ], [ "b = trace['educ']\nplt.hist(np.exp(b), bins=20, normed=True)\nplt.xlabel(\"Odds Ratio\")\nplt.show()", "_____no_output_____" ] ], [ [ "\nFinally, we can find a credible interval (remember kids - credible intervals are Bayesian and confidence intervals are frequentist) for this quantity. This may be the best part about Bayesian statistics: we get to interpret credibility intervals the way we've always wanted to interpret them. We are 95% confident that the odds ratio lies within our interval!", "_____no_output_____" ] ], [ [ "lb, ub = np.percentile(b, 2.5), np.percentile(b, 97.5)\n\nprint(\"P(%.3f < O.R. < %.3f) = 0.95\" % (np.exp(lb),np.exp(ub)))", "P(1.378 < O.R. < 1.414) = 0.95\n" ] ], [ [ "## Model selection \n\nOne question that was immediately asked was what effect does age have on the model, and why should it be $age^2$ versus age? We'll run the model with a few changes to see what effect higher order terms have on this model in terms of WAIC. ", "_____no_output_____" ] ], [ [ "models_lin, traces_lin = run_models(data, 4)", "\nRunning: k1\n" ], [ "dfwaic = pd.DataFrame(index=['k1','k2','k3','k4'], columns=['lin'])\ndfwaic.index.name = 'model'\n\nfor nm in dfwaic.index:\n dfwaic.loc[nm, 'lin'] = pm.waic(traces_lin[nm],models_lin[nm])[0]\n\n\ndfwaic = pd.melt(dfwaic.reset_index(), id_vars=['model'], var_name='poly', value_name='waic')\n\ng = seaborn.factorplot(x='model', y='waic', col='poly', hue='poly', data=dfwaic, kind='bar', size=6)", "_____no_output_____" ] ], [ [ "WAIC confirms our decision to use age^2. ", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ] ]

d0e9970191b496d0707938aeb56f7566b1719e81

504,659

ipynb

Jupyter Notebook

MC/MC Prediction.ipynb

ksang/reinforcement-learning

eae329add8cf9c5834ab26a7fec77ddbe336a135

[ "MIT" ]

null

MC/MC Prediction.ipynb

ksang/reinforcement-learning

eae329add8cf9c5834ab26a7fec77ddbe336a135

[ "MIT" ]

null

MC/MC Prediction.ipynb

ksang/reinforcement-learning

eae329add8cf9c5834ab26a7fec77ddbe336a135

[ "MIT" ]

null

2,601.335052

134,836

0.961542

[ [ [ "%matplotlib inline\n\nimport gym\nimport matplotlib\nimport numpy as np\nimport sys\n\nfrom collections import defaultdict\n\nif \"../\" not in sys.path:\n sys.path.append(\"../\") \nfrom lib.envs.blackjack import BlackjackEnv\nfrom lib import plotting\n\nmatplotlib.style.use('ggplot')", "_____no_output_____" ], [ "env = BlackjackEnv()", "_____no_output_____" ], [ "def mc_prediction(policy, env, num_episodes, discount_factor=1.0):\n \"\"\"\n Monte Carlo prediction algorithm. Calculates the value function\n for a given policy using sampling.\n \n Args:\n policy: A function that maps an observation to action probabilities.\n env: OpenAI gym environment.\n num_episodes: Number of episodes to sample.\n discount_factor: Gamma discount factor.\n \n Returns:\n A dictionary that maps from state -> value.\n The state is a tuple and the value is a float.\n \"\"\"\n\n # Keeps track of sum and count of returns for each state\n # to calculate an average. We could use an array to save all\n # returns (like in the book) but that's memory inefficient.\n returns_sum = defaultdict(float)\n returns_count = defaultdict(float)\n \n # The final value function\n V = defaultdict(float)\n \n for i_episode in range(num_episodes):\n observation = env.reset()\n episode = []\n for t in range(100):\n action = policy(observation)\n next_state, reward, done, _ = env.step(action)\n episode.append((observation, reward))\n if done:\n break\n observation = next_state\n states = set([x[0] for x in episode])\n for state in states:\n first_occurence_idx = next(i for i,x in enumerate(episode)\n if x[0] == state)\n G = sum([x[1]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])\n returns_sum[state] += G\n returns_count[state] += 1\n V[state] = returns_sum[state]/returns_count[state]\n return V ", "_____no_output_____" ], [ "def sample_policy(observation):\n \"\"\"\n A policy that sticks if the player score is > 20 and hits otherwise.\n \"\"\"\n score, dealer_score, usable_ace = observation\n return 0 if score >= 20 else 1", "_____no_output_____" ], [ "V_10k = mc_prediction(sample_policy, env, num_episodes=10000)\nplotting.plot_value_function(V_10k, title=\"10,000 Steps\")\n\nV_500k = mc_prediction(sample_policy, env, num_episodes=500000)\nplotting.plot_value_function(V_500k, title=\"500,000 Steps\")", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code" ] ]

d0e999b222d6de3d8d93fcb8bca43f4bbec6d51f

690,202

ipynb

Jupyter Notebook

src/notebook.ipynb

LorenzoTinfena/spotify-music-analysis

2846f83c1f257ffd7c83d207f6e1ddb1a3e1d9a1

[ "MIT" ]

null

src/notebook.ipynb

LorenzoTinfena/spotify-music-analysis

2846f83c1f257ffd7c83d207f6e1ddb1a3e1d9a1

[ "MIT" ]

null

src/notebook.ipynb

LorenzoTinfena/spotify-music-analysis

2846f83c1f257ffd7c83d207f6e1ddb1a3e1d9a1

[ "MIT" ]

null

1,865.410811

239,029

0.784725

[ [ [ "# Indian food analysis\n\nFirstly please read docs.md\n\n## Table of contents\n* Data preparation\n * Load original dataset into dataframes\n * Data cleansing\n * Save dataset\n * Load cleansed dataset\n* Analysis\n * Top 30 popular songs of all time\n * Analyze by a single song\n * Analyze track duration with frequency distribution chart\n * Analyze average track details by year\n\n## Data preparation\n### Load original dataset into dataframes\n\nfonte: https://www.kaggle.com/yamaerenay/spotify-dataset-19212020-160k-tracks", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\n\n# read dataset from csv\ndf_data_by_song : pd.DataFrame = pd.read_csv('dataset/original/data.csv', index_col='name')\ndf_data_by_artist : pd.DataFrame = pd.read_csv('dataset/original/data_by_artist.csv', index_col='artists')\ndf_data_by_genres : pd.DataFrame = pd.read_csv('dataset/original/data_by_genres.csv', index_col='genres')\ndf_data_by_year : pd.DataFrame = pd.read_csv('dataset/original/data_by_year.csv', index_col='year')\ndf_data_w_genres : pd.DataFrame = pd.read_csv('dataset/original/data_w_genres.csv', index_col='artists')", "_____no_output_____" ], [ "# show dataset\nprint(f'data_by_song:\\tPK: {df_data_by_song.index.name}\\t{str(list(df_data_by_song.columns))}')\nprint(f'data_by_artist:\\tPK: {df_data_by_artist.index.name}\\t{str(list(df_data_by_artist.columns))}')\nprint(f'data_by_genres:\\tPK: {df_data_by_genres.index.name}\\t{str(list(df_data_by_genres.columns))}')\nprint(f'data_by_year:\\tPK: {df_data_by_year.index.name}\\t{str(list(df_data_by_year.columns))}')\nprint(f'data_w_genres:\\tPK: {df_data_w_genres.index.name}\\t{str(list(df_data_w_genres.columns))}')", "data_by_song:\tPK: name\t['valence', 'year', 'acousticness', 'artists', 'danceability', 'duration_ms', 'energy', 'explicit', 'id', 'instrumentalness', 'key', 'liveness', 'loudness', 'mode', 'popularity', 'release_date', 'speechiness', 'tempo']\ndata_by_artist:\tPK: artists\t['mode', 'count', 'acousticness', 'danceability', 'duration_ms', 'energy', 'instrumentalness', 'liveness', 'loudness', 'speechiness', 'tempo', 'valence', 'popularity', 'key']\ndata_by_genres:\tPK: genres\t['mode', 'acousticness', 'danceability', 'duration_ms', 'energy', 'instrumentalness', 'liveness', 'loudness', 'speechiness', 'tempo', 'valence', 'popularity', 'key']\ndata_by_year:\tPK: year\t['mode', 'acousticness', 'danceability', 'duration_ms', 'energy', 'instrumentalness', 'liveness', 'loudness', 'speechiness', 'tempo', 'valence', 'popularity', 'key']\ndata_w_genres:\tPK: artists\t['genres', 'acousticness', 'danceability', 'duration_ms', 'energy', 'instrumentalness', 'liveness', 'loudness', 'speechiness', 'tempo', 'valence', 'popularity', 'key', 'mode', 'count']\n" ] ], [ [ "### Data cleansing\n", "_____no_output_____" ] ], [ [ "# some fixes\ndf_data_by_song = df_data_by_song.drop(columns=['id'])\ndf_data_by_artist.index.name = 'artist'\ndf_data_by_genres.index.name = 'genre'\ndf_data_w_genres.index.name = 'artist'", "_____no_output_____" ], [ "# reorder columns\ndf_data_by_song = df_data_by_song[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness', 'artists', 'year', 'explicit', 'release_date']]\ndf_data_by_artist = df_data_by_artist[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'count']]\ndf_data_by_genres = df_data_by_genres[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness']]\ndf_data_by_year = df_data_by_year[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness']]\ndf_data_w_genres = df_data_w_genres[['popularity', 'danceability', 'valence', 'duration_ms', 'energy', 'acousticness', 'instrumentalness', 'liveness', 'key', 'loudness', 'tempo', 'mode', 'speechiness', 'count', 'genres']]", "_____no_output_____" ] ], [ [ "### Savedataset", "_____no_output_____" ] ], [ [ "df_data_by_song.to_csv('dataset/cleansed/data_by_song.csv')\ndf_data_by_artist.to_csv('dataset/cleansed/data_by_artist.csv')\ndf_data_by_genres.to_csv('dataset/cleansed/data_by_genres.csv')\ndf_data_by_year.to_csv('dataset/cleansed/data_by_year.csv')\ndf_data_w_genres.to_csv('dataset/cleansed/data_w_genres.csv')", "_____no_output_____" ] ], [ [ "### Load cleansed dataset", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nimport numpy as np\n\ndf_data_by_song : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_song.csv', index_col='name')\ndf_data_by_artist : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_artist.csv', index_col='artist')\ndf_data_by_genres : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_genres.csv', index_col='genre')\ndf_data_by_year : pd.DataFrame = pd.read_csv('dataset/cleansed/data_by_year.csv', index_col='year')\ndf_data_w_genres : pd.DataFrame = pd.read_csv('dataset/cleansed/data_w_genres.csv', index_col='artist')", "_____no_output_____" ] ], [ [ "## Analysis\n### Top 30 popular songs of all time\nyou can choose by and ascending or dicending", "_____no_output_____" ] ], [ [ "by = 'loudness' # choices: popularity duration_ms key loudness tempo year\nascending = False\n\nimport matplotlib.pyplot as plt\n\ndf_data_by_song_tops = df_data_by_song.sort_values(by=by, ascending=ascending).head(30)\n\nfig, ax = plt.subplots(figsize=(10, 10))\nax.barh(list(df_data_by_song_tops.index.values), df_data_by_song_tops[by])\nax.invert_yaxis()\nplt.title('Most ingredient used')\nplt.show()", "_____no_output_____" ] ], [ [ "### Analyze by a single song\nyou can choose song_name", "_____no_output_____" ] ], [ [ "song_name = 'Stasera... Che Sera! - 1991 - Remaster;'\n\nimport matplotlib.pyplot as plt\nfrom lib.complexRadar import ComplexRadar\n\nif song_name not in df_data_by_song.index:\n raise IndexError('Song doesn\\'t exist')\n\nsong = df_data_by_song.loc[song_name]\n\nif isinstance(song, pd.DataFrame): #if multiple song with same name, song is a Dataframe, so I have to save only the first row as pd.Series\n song = song.iloc[0]\n\n# duration milliseconds to seconds\nsong = song.rename({'duration_ms' : 'duration_s'})\nsong['duration_s'] = song['duration_s'] / 1000\n\n# print release date\nprint('Release date: ' + song['release_date'])\nprint()\n\n# print artists details\nimport ast\nprint('Artists: ')\nprint()\nfor artist in ast.literal_eval(song['artists']):\n print('name: ' + artist)\n if artist in df_data_by_artist.index:\n print(df_data_by_artist.loc[artist].to_string())\n print()\n\n# print track details\nprint('track details:')\nsong: pd.Series = song.drop(index=['artists', 'release_date'])\n\nvariables = list(song.index)\ndata = list(song.values)\nranges = [(0, 100), (0, 1), (0, 1), (0, 6000), # popularity danceability valence duration_s\n (0, 1), (0, 1), (0, 1), (0, 1), # energy acousticness instrumentalness liveness\n (0, 11), (-60, 4), (-1, 250), (0, 1), # key loudness tempo mode\n (0, 1), (1921, 2020), (0, 1)] # speechiness year explicit\n\n# plotting\nfig = plt.figure(figsize=(6, 6))\nradar = ComplexRadar(fig, variables, ranges)\nradar.plot(data)\nradar.fill(data, alpha=0.2)\nplt.show()\n", "Release date: 1976\n\nArtists: \n\nname: Matia Bazar\npopularity 43.000000\ndanceability 0.644500\nvalence 0.642000\nduration_ms 229809.000000\nenergy 0.576000\nacousticness 0.186500\ninstrumentalness 0.002713\nliveness 0.161600\nkey 6.000000\nloudness -13.872500\ntempo 119.247000\nmode 0.000000\ncount 4.000000\n\ntrack details:\n" ] ], [ [ "### Analyze track duration with frequency distribution chart", "_____no_output_____" ] ], [ [ "X = df_data_by_song.rename(columns={'duration_ms' : 'duration_s'})\nX=X['duration_s'].loc[X['duration_s'] < 800000] / 10**3\n\n# plotting\nplt.figure(figsize=(20, 5))\nsns.distplot(X)\nplt.show()", "_____no_output_____" ] ], [ [ "### Analyze average track details by year\nyou can choose by which detail", "_____no_output_____" ] ], [ [ "by = 'duration_ms' #choices: popularity, duration_ms, key, loudness, tempo\n\ndf_data_by_song : pd.DataFrame = df_data_by_song \ndata = df_data_by_song[[by, 'year']].groupby(by='year').mean()\nX = data.index\nY = data[by].values\n\n# plotting\nfig, ax = plt.subplots()\nax.plot(X, Y)\nax.grid()\nax.set_xlabel('year')\nax.set_ylabel(by)\nfig.set_size_inches(20, 5)\nfig.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

d0e9a4abb182109ac1f381e30f031b8dca88243c

663,948

ipynb

Jupyter Notebook

deeplearning/chainercv/augmentation_bbox.ipynb

terasakisatoshi/pythonCodes

baee095ecee96f6b5ec6431267cdc6c40512a542

[ "MIT" ]

null

deeplearning/chainercv/augmentation_bbox.ipynb

terasakisatoshi/pythonCodes

baee095ecee96f6b5ec6431267cdc6c40512a542

[ "MIT" ]

null

deeplearning/chainercv/augmentation_bbox.ipynb

terasakisatoshi/pythonCodes

baee095ecee96f6b5ec6431267cdc6c40512a542

[ "MIT" ]

null

2,329.642105

139,952

0.963422

[ [ [ "import chainercv\nfrom chainercv import utils\nfrom chainercv.visualizations import vis_bbox, vis_point, vis_image\nimport numpy as np\nfrom scipy import ndimage\n\n%matplotlib inline", "/Users/terasakisatoshi/.pyenv/versions/miniconda3-3.19.0/lib/python3.5/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.\n from ._conv import register_converters as _register_converters\n" ], [ "import cv2\n\n\ndef imread(path, mod='chainercv'):\n if mod == 'chainercv':\n return chainercv.utils.read_image(path)\n else:\n img = cv2.imread(path)\n img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)\n # HWC -> CHW\n return img.transpose(2, 0, 1)", "_____no_output_____" ], [ "img = imread(\"lena.png\")\nvis_image(img)", "_____no_output_____" ], [ "r_eye = [115, 115]\nl_eye = [115, 140]\npoints = np.array([r_eye, l_eye])\nvis_point(img, points)", "_____no_output_____" ], [ "bbox = [[100, 100, 160, 150]]\nvis_bbox(img, bbox)", "_____no_output_____" ], [ "def rotate_point(point_yx, degree, center_yx):\n offset_x, offset_y = center_yx\n shift = point_yx - center_yx\n shift_y, shift_x = shift[:, 0], shift[:, 1]\n cos_rad = np.cos(np.deg2rad(degree))\n sin_rad = np.sin(np.deg2rad(degree))\n qx = offset_x + cos_rad * shift_x + sin_rad * shift_y\n qy = offset_y - sin_rad * shift_x + cos_rad * shift_y\n return np.array([qy, qx]).transpose()\n\n\ndef rot_image(img, degree):\n # CHW => HWC\n img = img.transpose(1, 2, 0)\n rot = ndimage.rotate(img, degree, reshape=False)\n # HWC => CHW\n rot = rot.transpose(2, 0, 1)\n return rot\n\n\ndef rotate(img, keypoints, bbox, degree):\n new_keypoints = []\n center_yx = np.array(img.shape[1:])/2\n for points in keypoints:\n rot_points = rotate_point(np.array(points),\n degree,\n center_yx)\n new_keypoints.append(rot_points)\n\n new_bbox = []\n for x, y, w, h in bbox:\n points = np.array([[y+h/2, x+w/2]])\n ry, rx = rotate_point(points,\n degree,\n center_yx)[0]\n new_bbox.append([rx-w/2, ry-h/2, w, h])\n\n rot = rot_image(img, degree)\n return rot, new_keypoints, new_bbox", "_____no_output_____" ], [ "r_eye = [115, 115]\nl_eye = [115, 140]\npoints = np.array([r_eye, l_eye])\nkeypoints = [\n points\n]\n\nb = [100, 100, 160, 150] # ymin,xmin,ymax,ymax\nb = [100, 100, 50, 60] # y,x,w,h\nbbox = [\n np.asarray(b)\n]\nrot, rot_keypoints, rot_bbox = rotate(img, keypoints, bbox, 50)\nvis_point(rot, rot_keypoints[0])", "_____no_output_____" ], [ "rot_bbox = [[y, x, y+h, x+w] for x, y, w, h in rot_bbox]\nvis_bbox(rot, rot_bbox)", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code" ] ]

d0e9a9d3774fe394c466b275cbb09ecb6ed0b4a7

478,585

ipynb

Jupyter Notebook

acc-models-ps-master/scenarios/lhc_proton/0_injection/MADX_example_ps_inj_lhc.ipynb

HaroonRafique/PS_Lattice_SC_Optimisation

9a798bca455f524239fc0772ff50bf67e2142371

[ "MIT" ]

null

acc-models-ps-master/scenarios/lhc_proton/0_injection/MADX_example_ps_inj_lhc.ipynb

HaroonRafique/PS_Lattice_SC_Optimisation

9a798bca455f524239fc0772ff50bf67e2142371

[ "MIT" ]

null

acc-models-ps-master/scenarios/lhc_proton/0_injection/MADX_example_ps_inj_lhc.ipynb

HaroonRafique/PS_Lattice_SC_Optimisation

9a798bca455f524239fc0772ff50bf67e2142371

[ "MIT" ]

null

92.947174

329,116

0.776819

[ [ [ "from cpymad.madx import Madx\nimport numpy as np\nimport matplotlib.pyplot as plt \nimport matplotlib\n\n%config InlineBackend.figure_format = 'retina'\nplt.rcParams[\"mathtext.fontset\"] = \"cm\"\n\nmatplotlib.rcParams.update({'font.size': 15})\nmatplotlib.rc('font',**{'family':'serif'})", "_____no_output_____" ] ], [ [ "# Setting up the MAD-X environment", "_____no_output_____" ] ], [ [ "madx = Madx()\nmadx.command.beam('PARTICLE=PROTON, PC = 2.14;')\nmadx.input('BRHO := BEAM->PC * 3.3356;')\n# call sequence of main units\nmadx.call('/eos/home-a/ahuschau/www/test-acc-models/repository/PS/2019/PS_MU.seq')\n# call sequence of straight section elements\nmadx.call('/eos/home-a/ahuschau/www/test-acc-models/repository/PS/2019/PS_SS.seq')\n# call general strength file\nmadx.call('/eos/home-a/ahuschau/www/test-acc-models/repository/PS/2019/PS.str')\nmadx.call('ps_inj_lhc.str')", "\n ++++++++++++++++++++++++++++++++++++++++++++\n + MAD-X 5.04.02 (64 bit, Linux) +\n + Support: [email protected], http://cern.ch/mad +\n + Release date: 2018.10.03 +\n + Execution date: 2019.08.19 09:29:57 +\n ++++++++++++++++++++++++++++++++++++++++++++\n/**********************************************************************************\n\n* PLACEHOLDERS: \n\n* NOTE: reference to CDS note to be written to summarize changes\n\n* TODO: at each occurrence an action still has to be done\n\n************************************************************************************/\n\n\n\n/**********************************************************************************\n\n*\n\n* Elements description and sequence file for each PS main unit (MU).\n\n*\n\n* Summary of changes with respect to previous versions available at NOTE\n\n*\n\n* 11/06/2019 - Alexander Huschauer\n\n************************************************************************************/\n\n\n\n\n\n/************************************************************************************\n\n*\n\n* DEFINITION OF FOCUSING AND DEFOCUSING HALF-UNITS OF THE MU \n\n*\n\n*************************************************************************************/\n\n\n\n/************************************************************************************\n\n* \t\t\t\t\t\t\t F HALF-UNITS \t\t\t\t\t \n\n*************************************************************************************/\n\n\n\nLF = +2.1260;\t\t\t\t! iron length of F half-unit\n\nDLF := +0.0715925; ! theoretical bending length correction; value has been rounded on drawing PS_LM___0013 (MU01 assembly) to 0.0716 m\n\nL_F = LF + DLF;\t\t\t\t! total magnetic length\n\n\n\n! yoke inside\n\nANGLE_F := 0.03135884818; \t! angle calculated according to EQ.? in NOTE\n\nK1_F := +0.05872278;\t\t! TODO: quadrupole gradient to be rematched for the bare machine\n\nK2_F := 0.0;\t\t\t\t! to be potentially used instead of allocating the PFW sextupole to multipoles\n\n\n\n/************************************************************************************\n\n* \t\t\t\t\t\t\t D HALF-UNITS \t\t\t\t\t \n\n*************************************************************************************/\n\n\n\nLD = +2.1340; \t! iron length of D half-unit\n\nDLD := +0.0715925; ! theoretical bending length correction; value has been rounded on drawing PS_LM___0013 (MU01 assembly) to 0.0716 m\n\nL_D = LD + DLD;\t\t\t\t! total magnetic length\n\n\n\n! yoke inside\n\nANGLE_D := 0.03147300489; \t! angle calculated according to EQ.? in (CDS NOTE)\n\nK1_D := -0.05872278;\t\t! TODO: quadrupole gradient to be rematched for the bare machine\n\nK2_D := 0.0;\t\t\t\t! to be potentially used instead of allocating the PFW sextupole to multipoles\n\n\n\n/************************************************************************************\n\n*\n\n* MULTIPOLES INSIDE THE MAIN UNITS REPRESENTING THE POLE FACE WINDINGS \n\n*\t\t (TODO: explanation for new multipole description to be added in NOTE)\n\n*\n\n*************************************************************************************/\n\n\n\n! TODO: discuss whether inside or outside yoke description should still be retained\n\n! ideally, information from the magnetic model to be incorporated here\n\n! TODO: explain disappearance of the junction, being replaced by only a MULTIPOLE\n\n\n\nMP_F: MULTIPOLE, knl := {0, 0, MPK2, MPK3_F, MPK4_F, MPK5_F};\n\nMP_J: MULTIPOLE, knl := {0, 0, MPK2_J, 0, MPK4_J, MPK5_J};\n\nMP_D: MULTIPOLE, knl := {0, 0, MPK2, MPK3_D, MPK4_D, MPK5_D};\n\n\n\n/************************************************************************************\n\n*\n\n* DEFINITION OF HORIZONTAL ORBIT CORRECTORS REPRESENTING THE BACKLEG WINDINGS \n\n*\n\n*************************************************************************************/\n\n\n\n! In reality each DHZ corresponds to a cable around the yoke of two adjacent MUs. \n\n! For example, PR.DHZXX provides a correction along MU(XX-1) and MUXX.\n\n! In this model, the effect of each PR.DHZXX is represented by kicks at the location \n\n! of the juntion of MU(XX-1) and MUXX.\n\n\n\nPR.DHZ01: HKICKER, KICK := KDHZ01;\n\nPR.DHZ03: HKICKER, KICK := KDHZ03;\n\nPR.DHZ05: HKICKER, KICK := KDHZ05;\n\nPR.DHZ07: HKICKER, KICK := KDHZ07;\n\nPR.DHZ09: HKICKER, KICK := KDHZ09;\n\nPR.DHZ11: HKICKER, KICK := KDHZ11;\n\nPR.DHZ13: HKICKER, KICK := KDHZ13;\n\nPR.DHZ15: HKICKER, KICK := KDHZ15;\n\nPR.DHZ17: HKICKER, KICK := KDHZ17;\n\nPR.DHZ19: HKICKER, KICK := KDHZ19;\n\nPR.DHZ21: HKICKER, KICK := KDHZ21;\n\nPR.DHZ23: HKICKER, KICK := KDHZ23;\n\nPR.DHZ25: HKICKER, KICK := KDHZ25;\n\nPR.DHZ27: HKICKER, KICK := KDHZ27;\n\nPR.DHZ29: HKICKER, KICK := KDHZ29;\n\nPR.DHZ31: HKICKER, KICK := KDHZ31;\n\nPR.DHZ33: HKICKER, KICK := KDHZ33;\n\nPR.DHZ35: HKICKER, KICK := KDHZ35;\n\nPR.DHZ37: HKICKER, KICK := KDHZ37;\n\nPR.DHZ39: HKICKER, KICK := KDHZ39;\n\nPR.DHZ41: HKICKER, KICK := KDHZ41;\n\nPR.DHZ43: HKICKER, KICK := KDHZ43;\n\nPR.DHZ45: HKICKER, KICK := KDHZ45;\n\nPR.DHZ47: HKICKER, KICK := KDHZ47;\n\nPR.DHZ49: HKICKER, KICK := KDHZ49;\n\nPR.DHZ51: HKICKER, KICK := KDHZ51;\n\nPR.DHZ53: HKICKER, KICK := KDHZ53;\n\nPR.DHZ55: HKICKER, KICK := KDHZ55;\n\nPR.DHZ57: HKICKER, KICK := KDHZ57;\n\nPR.DHZ59: HKICKER, KICK := KDHZ59;\n\nPR.DHZ61: HKICKER, KICK := KDHZ61;\n\nPR.DHZ63: HKICKER, KICK := KDHZ63;\n\nPR.DHZ65: HKICKER, KICK := KDHZ65;\n\nPR.DHZ67: HKICKER, KICK := KDHZ67;\n\nPR.DHZ69: HKICKER, KICK := KDHZ69;\n\nPR.DHZ71: HKICKER, KICK := KDHZ71;\n\nPR.DHZ73: HKICKER, KICK := KDHZ73;\n\nPR.DHZ75: HKICKER, KICK := KDHZ75;\n\nPR.DHZ77: HKICKER, KICK := KDHZ77;\n\nPR.DHZ79: HKICKER, KICK := KDHZ79;\n\nPR.DHZ81: HKICKER, KICK := KDHZ81;\n\nPR.DHZ83: HKICKER, KICK := KDHZ83;\n\nPR.DHZ85: HKICKER, KICK := KDHZ85;\n\nPR.DHZ87: HKICKER, KICK := KDHZ87;\n\nPR.DHZ89: HKICKER, KICK := KDHZ89;\n\nPR.DHZ91: HKICKER, KICK := KDHZ91;\n\nPR.DHZ93: HKICKER, KICK := KDHZ93;\n\nPR.DHZ95: HKICKER, KICK := KDHZ95;\n\nPR.DHZ97: HKICKER, KICK := KDHZ97;\n\nPR.DHZ99: HKICKER, KICK := KDHZ99;\n\n\n\n/************************************************************************************\n\n*\n\n* \t\t\t\t\t\tDEFINITION OF EACH MU \n\n*\n\n*************************************************************************************/\n\n\n\n!R ! D-F unit, yoke outside\n\n!S ! F-D unit, yoke outside\n\n!T ! F-D unit, yoke inside\n\n!U ! D-F unit, yoke inside\n\n\n\nMU_L = L_F + L_D;\t\t! Total magnetic length of one MU\n\nPR.BH.F: SBEND, L = L_F, ANGLE := ANGLE_F, K1 := K1_F, K2 := K2_F;\n\nPR.BH.D: SBEND, L = L_D, ANGLE := ANGLE_D, K1 := K1_D, K2 := K2_D;\n\n\n\nPR.BHT01: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ01, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU02: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ03, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT03: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ03, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR04: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ05, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT05: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ05, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR06: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ07, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS07: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ07, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR08: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ09, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT09: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ09, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR10: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ11, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS11: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ11, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR12: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ13, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS13: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ13, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU14: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ15, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT15: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ15, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU16: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ17, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT17: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ17, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU18: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ19, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS19: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ19, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR20: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ21, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT21: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ21, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR22: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ23, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT23: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ23, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU24: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ25, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT25: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ25, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR26: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ27, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS27: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ27, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU28: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ29, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT29: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ29, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR30: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ31, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT31: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ31, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR32: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ33, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS33: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ33, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR34: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ35, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT35: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ35, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR36: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ37, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT37: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ37, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR38: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ39, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT39: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ39, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU40: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ41, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT41: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ41, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR42: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ43, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT43: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ43, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR44: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ45, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT45: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ45, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR46: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ47, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS47: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ47, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR48: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ49, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT49: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ49, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR50: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ51, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT51: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ51, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR52: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ53, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS53: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ53, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR54: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ55, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT55: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ55, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU56: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ57, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT57: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ57, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU58: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ59, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT59: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ59, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU60: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ61, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT61: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ61, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU62: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ63, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT63: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ63, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU64: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ65, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT65: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ65, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR66: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ67, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS67: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ67, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU68: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ69, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT69: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ69, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR70: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ71, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT71: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ71, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR72: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ73, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS73: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ73, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU74: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ75, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT75: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ75, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR76: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ77, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT77: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ77, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR78: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ79, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS79: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ79, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR80: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ81, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT81: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ81, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR82: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ83, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS83: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ83, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR84: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ85, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT85: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ85, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR86: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ87, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS87: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ87, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHU88: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ89, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT89: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ89, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR90: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ91, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT91: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ91, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR92: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ93, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS93: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ93, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR94: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ95, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT95: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ95, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR96: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ97, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHT97: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ97, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR98: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ99, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHS99: SEQUENCE, L = MU_L;\n\n MP_F, AT = 0.0;\n\n PR.BH.F, AT = L_F/2;\n\n MP_J, AT = L_F;\n\n PR.DHZ99, AT = L_F;\n\n PR.BH.D, AT = L_F + L_D/2;\n\n MP_D, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\nPR.BHR00: SEQUENCE, L = MU_L;\n\n MP_D, AT = 0.0;\n\n PR.BH.D, AT = L_D/2;\n\n MP_J, AT = L_D;\n\n PR.DHZ01, AT = L_D;\n\n PR.BH.F, AT = L_D + L_F/2;\n\n MP_F, AT = MU_L;\n\nENDSEQUENCE;\n\n\n\n\n\n\n\n\n\n\n\n\n\n! TODO: remove all descriptions starting with ++, as those cause errors in MAD-X\n\n!++HEAD++\n\n /**********************************************************************************\n\n *\n\n * PS version STUDY in MAD X SEQUENCE format\n\n * Generated the 07-JUN-2019 18:23:18 from LHCLAYOUT@EDMSDB Database\n\n *\n\n * Generated from LHCLAYOUT@EDMSDB since 10/04/2017 P.Le Roux\n\n ************************************************************************************/\n\n! TODO: remove description\n\n!++END_HEAD+++\n\n\n\n! TODO: remove description\n\n!++ELEMENTS++\n\n\n\n/************************************************************************************/\n\n/* TYPES DEFINITION */\n\n/************************************************************************************/\n\n\n\n//---------------------- DRIFT ---------------------------------------------\n\nBFA : DRIFT , L := 1; ! Bending magnet. Fast bumper\n\nKFA__001 : DRIFT , L := 1; ! Fast Kicker\n\nKFA__002 : DRIFT , L := .8; ! Fast Kicker\n\nKFA__003 : DRIFT , L := 2.4; ! Fast Kicker\n\nKFB : DRIFT , L := 1; ! kicker (Damper)\n\nMCVAAWAP : DRIFT , L := .2; ! Corrector magnet, dipole vertical, type 202\n\nSEH__001 : DRIFT , L := 1; ! Electrostatic septum (ejection).\n\nSMH__001 : DRIFT , L := 2.4; ! Septum Magnet Horizontal\n\nSMH__003 : DRIFT , L := .8; ! Septum Magnet Horizontal\n\nSMH__004 : DRIFT , L := 1.2; ! Septum Magnet Horizontal\n\nTDI__001 : DRIFT , L := 1; ! Internal beam dump (PS)\n\n//---------------------- HKICKER ---------------------------------------------\n\nBLG : HKICKER , L := .2; ! Dipole magnet, bumper horizontal, type 213\n\nKFA__004 : HKICKER , L := .888; ! Fast Kicker\n\nKFA__005 : HKICKER , L := 0; ! Fast Kicker\n\nMCHBAWWP : HKICKER , L := .2; ! Corrector magnet, dipole horizontal, type 205\n\nMCHBBWWP : HKICKER , L := .2; ! Corrector magnet, dipole horizontal, type 206\n\nMDBBBCWP : HKICKER , L := .2; ! Dipole magnet, bumper horizontal, type 209\n\nMDBCAWWP : HKICKER , L := .2; ! Dipole magnet, bumper vertical, type 210\n\nSMH__007 : HKICKER , L := 0; ! Septum Magnet Horizontal\n\n//---------------------- INSTRUMENT ---------------------------------------------\n\nMSG : INSTRUMENT , L := 0; ! SEM grid\n\n//---------------------- MARKER ---------------------------------------------\n\nTDIRB001 : MARKER , L := 0; ! Internal Beam Dump, Retarding, type B\n\nTPS : MARKER , L := 0; ! Septum Shielding (Absorber)\n\nVVS : MARKER , L := 0; ! Vacuum Sector Valve (PS Complex)\n\n//---------------------- MONITOR ---------------------------------------------\n\nBCT : MONITOR , L := 0; ! Beam current transformer\n\nBCTF : MONITOR , L := 0; ! Fast Beam Current Transformers\n\nBCW_A : MONITOR , L := 0; ! Beam Wall Current monitor type A\n\nBGIHA : MONITOR , L := 0; ! Beam Gas Ionisation Horizontal, type A\n\nBPMTS : MONITOR , L := 1; ! 2 planes Stripline BPM with 4 long electrodes for PS Tune\n\nBPUNO : MONITOR , L := 0; ! Beam Position, Normal Pick-up\n\nBPUWA : MONITOR , L := 0; ! Beam Position Pickup, Wideband, type A\n\nBSGW : MONITOR , L := 0; ! SEM Grid with Wire\n\nBTVMA001 : MONITOR , L := 0; ! Beam observation TV, with Magnetic coupling, type A, variant 001\n\nBTVMF005 : MONITOR , L := 0; ! Beam TV Motorised Flip, variant 005\n\nBTVPL001 : MONITOR , L := 0; ! Beam observation TV Pneumatic Linear, variant 001\n\nBWSRB : MONITOR , L := 0; ! Beam Wire Scanner, Rotational, type B\n\nMTV : MONITOR , L := 0; ! TV screen (scintillation monitor)\n\nUDP : MONITOR , L := 1; ! Pick-ups (p.u. electrode). damper\n\nUFB : MONITOR , L := 0; ! Feedback pick-up.\n\nULF : MONITOR , L := 0; ! Low Frequency pick-up\n\nULG : MONITOR , L := 0; ! Closed orbit. Large pick-up\n\nUPH__001 : MONITOR , L := 0; ! Pick-up (p.u. electrode). Beam control, phase.\n\nURL : MONITOR , L := 0; ! Pick-up (p.u. electrode). Beam control, radial.\n\nURP : MONITOR , L := 0; ! Pick-up (p.u. electrode). Resistive position.\n\nURS : MONITOR , L := 0; ! Pick-up (p.u. electrode). Wide band, resistive.(wall current moniteur).\n\nUSP : MONITOR , L := 0; ! Pick-ups (p.u. electrode). Special (low intensity)\n\n//---------------------- MULTIPOLE ---------------------------------------------\n\nMM_AAIAP : MULTIPOLE , L := 0; ! Multipole magnet, type 403\n\nMU_HRCWP : MULTIPOLE , L := 4.403185; ! Main unit, multipole, PS type R\n\nMU_HSCWP : MULTIPOLE , L := 4.403185; ! Main unit, multipole, PS type S\n\nMU_HTCWP : MULTIPOLE , L := 4.403185; ! Main unit, multipole, PS type T\n\nMU_HUCWP : MULTIPOLE , L := 4.403185; ! Main unit, multipole, PS type U\n\n\n\n! TODO: implement actual length for each magnetic element\n\n! length of type 802 according to MTE design report\n\n! verify length of type MTE, closer to 0.5 m (initially 0.48 m) according to specififcations\n\n//---------------------- OCTUPOLE ---------------------------------------------\n\nMONAAFWP : OCTUPOLE , L := 0.22; ! Octupole magnet, type 802\n\nMONDAFWP : OCTUPOLE , L := .5; ! Octupole magnet, type MTE\n\n//---------------------- PLACEHOLDER ---------------------------------------------\n\nMDBCCWWC : PLACEHOLDER , L := .36; ! Dipole magnet, bumper horizontal, type IPM\n\n//---------------------- QUADRUPOLE ---------------------------------------------\n\nMQNAAIAP : QUADRUPOLE , L := 0; ! Quadrupole magnet, type 401\n\nMQNABIAP : QUADRUPOLE , L := 0; ! Quadrupole magnet, type 402\n\nMQNBAFAP : QUADRUPOLE , L := .2; ! Quadrupole magnet, type 406\n\nMQNBCAWP : QUADRUPOLE , L := .2; ! Quadrupole magnet, type 407\n\nMQNBDAAP : QUADRUPOLE , L := .2; ! Quadrupole magnet, type 408\n\nMQNCAAWP : QUADRUPOLE , L := .3; ! Quadrupole magnet, type 409\n\nMQNCHAWP : QUADRUPOLE , L := .2; ! Quadrupole magnet, type 414\n\nMQSAAIAP : QUADRUPOLE , L := 0; ! Quadrupole magnet, skew, type 404\n\n//---------------------- RFCAVITY ---------------------------------------------\n\nAARFB : RFCAVITY , L := 1; ! RF CAVITY 40/80 MHZ\n\n\n\n! TODO: verify length of 10 MHz cavities, see EDMS 1265845\n\nACC10 : RFCAVITY , L := 2.39; ! 10 MHz radio frequency cavity\n\n\n\n! TODO: correct length of 20 MHz cavities to 1.0 m (in LDB also the responsible is incorrect, should be somebody from BE-RF)\n\nACC20 : RFCAVITY , L := 1.0; ! 20 MHz radio frequency cavity\n\n\n\n! TODO: correct length of 200 MHz to 0.40 m\n\nACC200 : RFCAVITY , L := .40; ! RF Cavity 200 MHz\n\n\n\n! TODO: correct length of 40 MHz cavities to 1.0 m\n\nACC40 : RFCAVITY , L := .99; ! 40 MHz radio frequency cavity\n\nACWFA : RFCAVITY , L := .88; ! Accelerating Cavities - Wide-band - Finemet - Type A (for PSring)\n\n//---------------------- SEXTUPOLE ---------------------------------------------\n\n!TODO: verify magnetic length of type 608 - changed according to MTE design report\n\nMXNBAFWP : SEXTUPOLE , L := .195; ! Sextupole Magnet, type 608\n\nMXNCAAWP : SEXTUPOLE , L := 0; ! Sextupole Magnet, type 610\n\nMX_AAIAP : SEXTUPOLE , L := 0; ! Sextupole Magnet, type 601\n\nMX_ABIAP : SEXTUPOLE , L := 0; ! Sextupole magnet, type 602\n\n\n\n! TODO: remove return statement here\n\n!return;\n\n\n\n! TODO: remove description\n\n!++END_ELEMENTS++\n\n\n\n! TODO: remove description\n\n!++SEQUENCE++\n\n\n\n/************************************************************************************/\n\n/* PS STRAIGHTSECTION */\n\n/************************************************************************************/\n\n\n\nPS01: SEQUENCE, L=3;\n\n PR.XSE01.A : MXNBAFWP , AT = .42 , SLOT_ID = 2369746;\n\n PR.XSE01.B : MXNBAFWP , AT = .675 , SLOT_ID = 2369747;\n\nENDSEQUENCE;\n\n\n\nPS02: SEQUENCE, L=1.6;\n\n PA.UFB02 : BPUNO , AT = .0934, SLOT_ID = 2253327;\n\n PA.CWB02 : ACWFA , AT = .775 , SLOT_ID = 10338559;\n\n PR.MM02 : MM_AAIAP , AT = 1.47 , SLOT_ID = 8178825;\n\nENDSEQUENCE;\n\n\n\nPS03: SEQUENCE, L=1.6;\n\n PR.BPM03 : BPUNO , AT = .0934, SLOT_ID = 2253342; ! Position is based on optics definition\n\n PR.BCW03.A : BCW_A , AT = .5137, SLOT_ID = 36269910; ! Position is an estimate\n\n PR.BCW03.B : BCW_A , AT = 1.036, SLOT_ID = 36269911; ! Position is an estimate\n\n PR.MM03 : MM_AAIAP , AT = 1.47 , SLOT_ID = 5365801; ! Position is based on optics definition\n\nENDSEQUENCE;\n\n\n\nPS04: SEQUENCE, L=1.6;\n\n PE.KFA04 : KFA__004 , AT = .694 , SLOT_ID = 2369736;\n\n PR.MM04 : MM_AAIAP , AT = 1.47 , SLOT_ID = 5365802;\n\nENDSEQUENCE;\n\n\n\nPS05: SEQUENCE, L=1.6;\n\n PR.BPM05 : BPUNO , AT = .0934, SLOT_ID = 2253375;\n\n PE.QKE16.05 : MQNCHAWP , AT = .436 , SLOT_ID = 2253376;\n\n PR.DHZOC05 : MDBCAWWP , AT = .929 , SLOT_ID = 8178824;\n\n PR.QFN05 : MQNAAIAP , AT = 1.47 , SLOT_ID = 2253379;\n\nENDSEQUENCE;\n\n\n\nPS06: SEQUENCE, L=3;\n\n! TODO: correct position of PR.QDW06 (should be at the end of PS06 - I have manually inserted it below for the time being)\n\n! PR.QDW06 : MQNABIAP , AT = -14.1, SLOT_ID = 2253399;\n\n\n\n! TODO: correct positions of 200 MHz cavities, as they are overlapping (where to find proper position information?)\n\n! PA.C200.06.A : ACC200 , AT = .5455, SLOT_ID = 2253393;\n\n! PA.C200.06.B : ACC200 , AT = .9195, SLOT_ID = 2253394;\n\n! PA.C200.06.C : ACC200 , AT = 1.293, SLOT_ID = 2253395;\n\n! PA.C200.06.D : ACC200 , AT = 1.667, SLOT_ID = 2253396;\n\n! PA.C200.06.E : ACC200 , AT = 2.041, SLOT_ID = 2253397;\n\n! PA.C200.06.F : ACC200 , AT = 2.415, SLOT_ID = 2253398; \n\n\n\n PA.C200.06.A : ACC200 , AT = .4, SLOT_ID = 2253393;\n\n PA.C200.06.B : ACC200 , AT = .8, SLOT_ID = 2253394;\n\n PA.C200.06.C : ACC200 , AT = 1.2, SLOT_ID = 2253395;\n\n PA.C200.06.D : ACC200 , AT = 1.6, SLOT_ID = 2253396;\n\n PA.C200.06.E : ACC200 , AT = 2., SLOT_ID = 2253397;\n\n PA.C200.06.F : ACC200 , AT = 2.4, SLOT_ID = 2253398;\n\n\n\n ! TODO: verify position \n\n PR.QDW06 : MQNABIAP , AT = 2.859, SLOT_ID = 2253399;\n\nENDSEQUENCE;\n\n\n\nPS07: SEQUENCE, L=1.6;\n\n PR.BPM07 : ULG , AT = .0934, SLOT_ID = 2253413;\n\n PR.XSE07 : MXNCAAWP , AT = .6252, SLOT_ID = 2253414;\n\n PR.QTRTB07 : MQNCAAWP , AT = 1.115, SLOT_ID = 2253416;\n\n PR.QSK07 : MQSAAIAP , AT = 1.471, SLOT_ID = 2253417;\n\nENDSEQUENCE;\n\n\n\nPS08: SEQUENCE, L=1.6;\n\n PR.C80.08 : AARFB , AT = .775 , SLOT_ID = 2253431;\n\n PR.MM08 : MM_AAIAP , AT = 1.475, SLOT_ID = 5365803;\n\nENDSEQUENCE;\n\n\n\nPS09: SEQUENCE, L=1.6;\n\n PE.BFA09.P : BFA , AT = .775 , SLOT_ID = 2253447;\n\n! TODO: remove BFA staircase as it is overlapping with the pedestal and won't be there any more after LS2\n\n! PE.BFA09.S : BFA , AT = .775 , SLOT_ID = 10413798;\n\n PR.QFN09 : MQNAAIAP , AT = 1.459, SLOT_ID = 2253449;\n\nENDSEQUENCE;\n\n\n\nPS10: SEQUENCE, L=1.6;\n\n PR.BPM10 : BPUNO , AT = .0934, SLOT_ID = 2253463;\n\n PR.XSK10 : MX_AAIAP , AT = .78 , SLOT_ID = 10414023; ! Position is approximate\n\n PR.VVS10 : VVS , AT = 1.25 , SLOT_ID = 13720377; ! Position is estimated\n\n PR.QDN10 : MQNAAIAP , AT = 1.475, SLOT_ID = 2253464;\n\nENDSEQUENCE;\n\n\n\nPS11: SEQUENCE, L=3;\n\n PA.C10.11 : ACC10 , AT = 1.509, SLOT_ID = 2253478;\n\nENDSEQUENCE;\n\n\n\nPS12: SEQUENCE, L=1.6;\n\n PR.UEP12 : ULG , AT = .0934, SLOT_ID = 2253493;\n\n PR.RAL12 : TDIRB001 , AT = .3077, SLOT_ID = 8178823;\n\n PE.BSW12 : MCHBAWWP , AT = .6990, SLOT_ID = 2253494;\n\n PR.DVT12 : MCVAAWAP , AT = .9550, SLOT_ID = 2253495;\n\nENDSEQUENCE;\n\n\n\nPS13: SEQUENCE, L=1.6;\n\n PR.BPM13 : BPUNO , AT = .0934, SLOT_ID = 2253509;\n\n PE.KFA13 : KFA__004 , AT = .694 , SLOT_ID = 2369737;\n\nENDSEQUENCE;\n\n\n\nPS14: SEQUENCE, L=1.6;\n\n PR.XSK14 : MX_ABIAP , AT = .6231, SLOT_ID = 10414025;\n\n PE.BSW14 : MCHBAWWP , AT = 1.091, SLOT_ID = 2253524;\n\nENDSEQUENCE;\n\n\n\nPS15: SEQUENCE, L=1.6;\n\n PR.BPM15 : ULG , AT = .0895, SLOT_ID = 2253538;\n\n PE.TPS15 : TPS , AT = .7766, SLOT_ID = 6894625;\n\nENDSEQUENCE;\n\n\n\nPS16: SEQUENCE, L=3;\n\n! TODO: BTV16 is overlapping with SMH16, changed position to 0.2 m (instead of .3585 m) \n\n PE.BTV16 : MTV , AT = .2, SLOT_ID = 2253555;\n\n ! TODO: verify position of SMH16 as drawing PS_LM___0042 indicates central position of 1.505 m\n\n PE.SMH16 : SMH__001 , AT = 1.472, SLOT_ID = 2253556;\n\nENDSEQUENCE;\n\n\n\nPS17: SEQUENCE, L=1.6;\n\n PR.BPM17 : ULG , AT = .445 , SLOT_ID = 2253570;\n\n PR.QFW17 : MQNABIAP , AT = 1.470, SLOT_ID = 2253572;\n\nENDSEQUENCE;\n\n\n\nPS18: SEQUENCE, L=1.6;\n\n PA.UPH18 : UPH__001 , AT = .0934, SLOT_ID = 2253586;\n\n PR.DHZOC18 : MCHBAWWP , AT = .4173, SLOT_ID = 2253587;\n\n PR.QDW18 : MQNABIAP , AT = 1.469, SLOT_ID = 2253588;\n\nENDSEQUENCE;\n\n\n\nPS19: SEQUENCE, L=1.6;\n\n PE.BSW23.19 : MCHBAWWP , AT = .6327, SLOT_ID = 2253605;\n\n PR.QTRDA19 : MQNBAFAP , AT = 1.033, SLOT_ID = 2253606;\n\n PR.QSK19 : MQSAAIAP , AT = 1.480, SLOT_ID = 2253607;\n\nENDSEQUENCE;\n\n\n\nPS20: SEQUENCE, L=1.6;\n\n PR.BPM20 : BPUNO , AT = .0934, SLOT_ID = 2253621;\n\n PE.BSW20 : MCHBAWWP , AT = .4653, SLOT_ID = 2253622;\n\n PR.VVS20 : VVS , AT = 1.25 , SLOT_ID = 13720428; ! Position is an estimate\n\n PR.MM20 : MM_AAIAP , AT = 1.470, SLOT_ID = 5365804;\n\nENDSEQUENCE;\n\n\n\nPS21: SEQUENCE, L=3;\n\n PE.KFA21 : KFA__004 , AT = 2.094, SLOT_ID = 2369738;\n\n PR.QFN21 : MQNAAIAP , AT = 2.859, SLOT_ID = 2253643;\n\nENDSEQUENCE;\n\n\n\nPS22: SEQUENCE, L=1.6;\n\n PA.URL22 : URL , AT = .0934, SLOT_ID = 2253657;\n\n PI.BSW26.22 : MCHBBWWP , AT = .4662, SLOT_ID = 2253658;\n\n PE.BSW22 : MCHBAWWP , AT = .7562, SLOT_ID = 2253659;\n\n PR.DVT22 : MCVAAWAP , AT = 1.093, SLOT_ID = 2253660;\n\n PR.QDW22 : MQNABIAP , AT = 1.491, SLOT_ID = 2253661;\n\nENDSEQUENCE;\n\n\n\nPS23: SEQUENCE, L=1.6;\n\n PR.BPM23 : BPUNO , AT = .0934, SLOT_ID = 2253675;\n\n PE.SEH23 : SEH__001 , AT = .7748, SLOT_ID = 2253676;\n\n PR.QSK23 : MQSAAIAP , AT = 1.470, SLOT_ID = 2253678;\n\nENDSEQUENCE;\n\n\n\nPS24: SEQUENCE, L=1.6;\n\n PR.DVT24 : MCVAAWAP , AT = .8146, SLOT_ID = 2253692;\n\n PR.QSK24 : MQSAAIAP , AT = 1.471, SLOT_ID = 2253693;\n\nENDSEQUENCE;\n\n\n\nPS25: SEQUENCE, L=1.6;\n\n! TODO: verify position of PR.BPM25 - I assume it is at the same position as the other PUs (see also EDMS 223648) \n\n! PR.BPM25 : ULG , AT = -.093, SLOT_ID = 2253707;\n\n PR.BPM25 : ULG , AT = .0934, SLOT_ID = 2253707;\n\n PE.QKE16.25 : MQNCHAWP , AT = .5206, SLOT_ID = 2253708;\n\nENDSEQUENCE;\n\n\n\nPS26: SEQUENCE, L=3;\n\n PI.SMH26 : SMH__007 , AT = 1.788, SLOT_ID = 2253724;\n\n PI.BTV26 : BTVPL001 , AT = 1.788, SLOT_ID = 2253725;\n\n PI.BSF26 : MSG , AT = 1.788, SLOT_ID = 2253726;\n\nENDSEQUENCE;\n\n\n\nPS27: SEQUENCE, L=1.6;\n\n PR.BPM27 : ULG , AT = .0934, SLOT_ID = 2253740;\n\n PR.QTRDA27 : MQNBAFAP , AT = .4748, SLOT_ID = 2253741;\n\n PE.BSW23.27 : MCHBAWWP , AT = 1.105, SLOT_ID = 2253744;\n\n PR.QFW27 : MQNABIAP , AT = 1.469, SLOT_ID = 2253745;\n\nENDSEQUENCE;\n\n\n\nPS28: SEQUENCE, L=1.6;\n\n PI.KFA28 : KFA__005 , AT = .775 , SLOT_ID = 2253760;\n\n PR.QDW28 : MQNABIAP , AT = 1.471, SLOT_ID = 2253761;\n\nENDSEQUENCE;\n\n\n\nPS29: SEQUENCE, L=1.6;\n\n PR.QSE29 : MQNCAAWP , AT = .626 , SLOT_ID = 2253775;\n\n PR.QTRDB29 : MQNBAFAP , AT = 1.081, SLOT_ID = 2253777;\n\n PR.QSK29 : MQSAAIAP , AT = 1.47 , SLOT_ID = 2253778;\n\nENDSEQUENCE;\n\n\n\nPS30: SEQUENCE, L=1.6;\n\n PR.BPM30 : ULG , AT = .0934, SLOT_ID = 2253792;\n\n PR.DVT30 : MCVAAWAP , AT = .5465, SLOT_ID = 2253793;\n\n PI.BSW26.30 : MCHBBWWP , AT = .9505, SLOT_ID = 2253794;\n\n PR.VVS30 : VVS , AT = 1.21 , SLOT_ID = 13720429; ! Position is an estimate\n\n PR.QSK30 : MQSAAIAP , AT = 1.488, SLOT_ID = 2253795;\n\nENDSEQUENCE;\n\n\n\nPS31: SEQUENCE, L=3;\n\n PR.QFW31 : MQNABIAP , AT = 2.870, SLOT_ID = 2253811;\n\nENDSEQUENCE;\n\n\n\nPS32: SEQUENCE, L=1.6;\n\n PR.UFB32 : UFB , AT = .2999, SLOT_ID = 2253825; ! Not connected\n\n PR.QDW32 : MQNABIAP , AT = 1.471, SLOT_ID = 2253826;\n\nENDSEQUENCE;\n\n\n\nPS33: SEQUENCE, L=1.6;\n\n PR.BPM33 : ULG , AT = .0934, SLOT_ID = 2253840;\n\n PI.QLB33 : MQNCHAWP , AT = .52 , SLOT_ID = 47643341;\n\n PA.UFB33 : UFB , AT = 1.18 , SLOT_ID = 2253842; ! Not connected\n\n PR.QSK33 : MQSAAIAP , AT = 1.469, SLOT_ID = 2253843;\n\nENDSEQUENCE;\n\n\n\nPS34: SEQUENCE, L=1.6;\n\n PR.BCT34 : BCT , AT = .775 , SLOT_ID = 2253858;\n\n PR.MM34 : MM_AAIAP , AT = 1.470, SLOT_ID = 5365805;\n\nENDSEQUENCE;\n\n\n\nPS35: SEQUENCE, L=1.6;\n\n PR.BPM35 : BPUNO , AT = .0934, SLOT_ID = 2253874;\n\n PR.QFN35 : MQNAAIAP , AT = 1.459, SLOT_ID = 2253877;\n\nENDSEQUENCE;\n\n\n\nPS36: SEQUENCE, L=3;\n\n PA.URL36 : URL , AT = .0934, SLOT_ID = 2253891;\n\n PA.C10.36 : ACC10 , AT = 1.475, SLOT_ID = 2253892;\n\n PR.QDN36 : MQNAAIAP , AT = 2.863, SLOT_ID = 2253893;\n\nENDSEQUENCE;\n\n\n\nPS37: SEQUENCE, L=1.6;\n\n PR.BPM37 : BPUNO , AT = .0934, SLOT_ID = 2253907;\n\n PR.QTRDB37 : MQNBDAAP , AT = .4407, SLOT_ID = 2253908;\n\n PA.UPH37 : BPUNO , AT = 1.180, SLOT_ID = 2253910;\n\n PR.MM37 : MM_AAIAP , AT = 1.459, SLOT_ID = 5365806;\n\nENDSEQUENCE;\n\n\n\nPS38: SEQUENCE, L=1.6;\n\n PA.UPH38 : UPH__001 , AT = .0934, SLOT_ID = 2253926;\n\n PR.BCT38 : BCTF , AT = .775 , SLOT_ID = 2253927;\n\n PR.MM38 : MM_AAIAP , AT = 1.470, SLOT_ID = 5365807;\n\nENDSEQUENCE;\n\n\n\nPS39: SEQUENCE, L=1.6;\n\n PR.XNO39.A : MXNBAFWP , AT = .398 , SLOT_ID = 2369739;\n\n PR.ONO39 : MONDAFWP , AT = .7745, SLOT_ID = 2369740;\n\n PR.XNO39.B : MXNBAFWP , AT = 1.151, SLOT_ID = 2369741;\n\n PR.QFN39 : MQNAAIAP , AT = 1.459, SLOT_ID = 2253944;\n\nENDSEQUENCE;\n\n\n\nPS40: SEQUENCE, L=1.6;\n\n PR.BPM40 : BPUNO , AT = .0934, SLOT_ID = 2253958;\n\n PI.BSW40 : MDBBBCWP , AT = .472 , SLOT_ID = 2253959;\n\n PR.ODN40 : MONAAFWP , AT = .802 , SLOT_ID = 2253960;\n\n PR.VVS40 : VVS , AT = 1.251, SLOT_ID = 13720430; ! Position is an estimate\n\n PR.QDN40 : MQNAAIAP , AT = 1.481, SLOT_ID = 2253961;\n\nENDSEQUENCE;\n\n\n\nPS41: SEQUENCE, L=3;\n\n PR.QTRTA41 : MQNBCAWP , AT = 1.475, SLOT_ID = 2253976;\n\n PR.QSK41 : MQSAAIAP , AT = 2.895, SLOT_ID = 2253977;\n\nENDSEQUENCE;\n\n\n\nPS42: SEQUENCE, L=1.6;\n\n PI.BTV42.A : BTVMA001 , AT = 0 , SLOT_ID = 42854779;\n\n !TODO: position to be verified\n\n PI.BSW42 : MDBBBCWP , AT = .472 ;\n\n PI.BSF42 : MSG , AT = 1.47 , SLOT_ID = 2253993; ! Slot type is to be checked\n\nENDSEQUENCE;\n\n\n\nPS43: SEQUENCE, L=1.6;\n\n PR.BPM43 : ULG , AT = .0934, SLOT_ID = 2254008;\n\n PI.BSW43 : MDBBBCWP , AT = .5362, SLOT_ID = 2254009;\n\n PR.QSK43 : MQSAAIAP , AT = 1.495, SLOT_ID = 2254011;\n\nENDSEQUENCE;\n\n\n\nPS44: SEQUENCE, L=1.6;\n\n PI.BSW44 : MDBBBCWP , AT = 1.073, SLOT_ID = 2254026;\n\n PR.MM44 : MM_AAIAP , AT = 1.473, SLOT_ID = 5365808;\n\nENDSEQUENCE;\n\n\n\nPS45: SEQUENCE, L=1.6;\n\n PR.BPM45 : BPUNO , AT = .0934, SLOT_ID = 2254042;\n\n PI.KFA45 : KFA__002 , AT = .775 , SLOT_ID = 2254043;\n\n PR.QFN45 : MQNAAIAP , AT = 1.459, SLOT_ID = 2254045;\n\nENDSEQUENCE;\n\n\n\nPS46: SEQUENCE, L=3;\n\n PA.C10.46 : ACC10 , AT = 1.475, SLOT_ID = 2254059;\n\n PR.QDN46 : MQNAAIAP , AT = 2.873, SLOT_ID = 2254060;\n\nENDSEQUENCE;\n\n\n\nPS47: SEQUENCE, L=1.6;\n\n PR.BPM47 : BPUNO , AT = .0934, SLOT_ID = 2254074;\n\n PR.TDI47 : TDI__001 , AT = .775 , SLOT_ID = 2254075;\n\n PR.QSK47 : MQSAAIAP , AT = 1.495, SLOT_ID = 2254077;\n\nENDSEQUENCE;\n\n\n\nPS48: SEQUENCE, L=1.6;\n\n PI.BSG48 : BSGW , AT = .0934, SLOT_ID = 2254091;\n\n PR.TDI48 : TDI__001 , AT = .775 , SLOT_ID = 2254092;\n\n PR.QSK48 : MQSAAIAP , AT = 1.496, SLOT_ID = 2254093;\n\nENDSEQUENCE;\n\n\n\nPS49: SEQUENCE, L=1.6;\n\n PI.QLB49 : MQNCHAWP , AT = .52 , SLOT_ID = 47643342;\n\n PR.QTRTA49 : MQNCAAWP , AT = 1.093, SLOT_ID = 2254108;\n\n PR.QFN49 : MQNAAIAP , AT = 1.481, SLOT_ID = 2254109;\n\nENDSEQUENCE;\n\n\n\nPS50: SEQUENCE, L=1.6;\n\n PR.BPM50 : BPUNO , AT = .0934, SLOT_ID = 2254123;\n\n PR.ODN50 : MONAAFWP , AT = .9725, SLOT_ID = 2254124;\n\n PR.VVS50 : VVS , AT = 1.302, SLOT_ID = 13720431; ! Position is an estimate\n\n PR.QDN50 : MQNAAIAP , AT = 1.470, SLOT_ID = 2254125;\n\nENDSEQUENCE;\n\n\n\nPS51: SEQUENCE, L=3;\n\n PA.URL51 : URL , AT = .0934, SLOT_ID = 2254139;\n\n PA.C10.51 : ACC10 , AT = 1.475, SLOT_ID = 2254140;\n\nENDSEQUENCE;\n\n\n\nPS52: SEQUENCE, L=1.6;\n\n PI.BSG52 : BSGW , AT = .0934, SLOT_ID = 2254155;\n\n PR.ODN52.A : MONAAFWP , AT = .5155, SLOT_ID = 10430397; ! Position is estimated\n\n PR.XSK52 : MX_AAIAP , AT = .75 , SLOT_ID = 10414027; ! Position estimated after installation of new octupole in the same straight section\n\n PR.ODN52.B : MONAAFWP , AT = .9955, SLOT_ID = 2254156; ! Position is estimated\n\n PR.QSK52 : MQSAAIAP , AT = 1.496, SLOT_ID = 2253994; ! Moved from Section 42 according to ECR: PS-VC-EC-0001\n\nENDSEQUENCE;\n\n\n\nPS53: SEQUENCE, L=1.6;\n\n PR.BPM53 : BPUNO , AT = .0934, SLOT_ID = 2254170;\n\n PE.BSW57.53 : MCHBBWWP , AT = .8333, SLOT_ID = 2254171;\n\n PR.MM53 : MM_AAIAP , AT = 1.469, SLOT_ID = 5365809;\n\nENDSEQUENCE;\n\n\n\nPS54: SEQUENCE, L=1.6;\n\n PI.BSG54 : BSGW , AT = .0934, SLOT_ID = 2254188;\n\n PR.BPM54 : BPUNO , AT = .3615, SLOT_ID = 10414030; ! Position is estimated!\n\n PR.BWSH54 : BWSRB , AT = .8035, SLOT_ID = 2254189;\n\n PR.MM54 : MM_AAIAP , AT = 1.470, SLOT_ID = 5365810;\n\nENDSEQUENCE;\n\n\n\nPS55: SEQUENCE, L=1.6;\n\n PR.BPM55 : BPUNO , AT = .0934, SLOT_ID = 2254205;\n\n PR.XNO55.A : MXNBAFWP , AT = .3981, SLOT_ID = 2254206; ! Estimated position\n\n PR.ONO55 : MONDAFWP , AT = .7746, SLOT_ID = 2369742;\n\n PR.XNO55.B : MXNBAFWP , AT = 1.151, SLOT_ID = 2254207; ! Estimated position\n\n PR.QFN55 : MQNAAIAP , AT = 1.459, SLOT_ID = 2254209;\n\nENDSEQUENCE;\n\n\n\nPS56: SEQUENCE, L=3;\n\n! TODO: position of cavity to be corrected (I assumed the same position as it is for other C10 cavities - tbc)\n\n! PA.C10.56 : ACC10 , AT = .775 , SLOT_ID = 2254223;\n\n PA.C10.56 : ACC10 , AT = 1.475 , SLOT_ID = 2254223;\n\n PR.QDW56 : MQNABIAP , AT = 2.859, SLOT_ID = 2254224;\n\nENDSEQUENCE;\n\n\n\nPS57: SEQUENCE, L=1.6;\n\n PR.BPM57 : ULG , AT = .0934, SLOT_ID = 2254238;\n\n PE.BTV57 : BTVMF005 , AT = .3584, SLOT_ID = 2254242;\n\n PE.SMH57 : SMH__003 , AT = .775 , SLOT_ID = 2254240;\n\n PR.QSK57 : MQSAAIAP , AT = 1.496, SLOT_ID = 2254241;\n\nENDSEQUENCE;\n\n\n\nPS58: SEQUENCE, L=1.6;\n\n PR.XSK58 : MX_ABIAP , AT = .755 , SLOT_ID = 10414032; ! Position is an estimate!\n\n PR.QSK58 : MQSAAIAP , AT = 1.481, SLOT_ID = 2254256;\n\nENDSEQUENCE;\n\n\n\nPS59: SEQUENCE, L=1.6;\n\n PR.BSW57.59 : MCHBAWWP , AT = .4454, SLOT_ID = 2254271;\n\n PR.QFW59 : MQNABIAP , AT = 1.470, SLOT_ID = 2254273;\n\nENDSEQUENCE;\n\n\n\nPS60: SEQUENCE, L=1.6;\n\n PR.BPM60 : ULG , AT = .0934, SLOT_ID = 2254287;\n\n PR.DHZOC60 : MCHBBWWP , AT = .434 , SLOT_ID = 2254288;\n\n PR.XNO60 : MXNBAFWP , AT = .85 , SLOT_ID = 10428678; ! Position is an estimate\n\n PR.VVS60 : VVS , AT = 1.209, SLOT_ID = 13720432; ! Position is an estimate\n\n PR.QDW60 : MQNABIAP , AT = 1.475, SLOT_ID = 2254289;\n\nENDSEQUENCE;\n\n\n\nPS61: SEQUENCE, L=3;\n\n! TODO: verify positions of all elements as they are overlapping (I arbitrarily moved them to avoid overlapping)\n\n! PR.QTRDB61 : MQNBAFAP , AT = .4323, SLOT_ID = 2254304;\n\n! PE.SMH61 : SMH__004 , AT = .995 , SLOT_ID = 2254307;\n\n! PR.BSW57.61 : BLG , AT = 1.855, SLOT_ID = 2254305; \n\n\n\n PR.QTRDB61 : MQNBAFAP , AT = .4323, SLOT_ID = 2254304;\n\n PE.SMH61 : SMH__004 , AT = 1.195 , SLOT_ID = 2254307;\n\n PR.BSW57.61 : BLG , AT = 1.955, SLOT_ID = 2254305;\n\nENDSEQUENCE;\n\n\n\n! TODO: include this SS at extraction from LDB even if empty\n\nPS62: SEQUENCE, L=1.6;\n\nENDSEQUENCE;\n\n\n\nPS63: SEQUENCE, L=1.6;\n\n PR.BPM63 : ULG , AT = .3685, SLOT_ID = 2254334;\n\nENDSEQUENCE;\n\n\n\nPS64: SEQUENCE, L=1.6;\n\n PR.BPM64 : BPUNO , AT = .357 , SLOT_ID = 42548391; ! Position is to be checked\n\n PR.BWSV64 : BWSRB , AT = .803 , SLOT_ID = 2254349; ! Position is to be confirmed\n\n PR.MM64 : MM_AAIAP , AT = 1.470, SLOT_ID = 5365829;\n\nENDSEQUENCE;\n\n\n\nPS65: SEQUENCE, L=1.6;\n\n PR.BPM65 : BPUNO , AT = .0934, SLOT_ID = 2254365;\n\n PR.BWSH65 : BWSRB , AT = .803 , SLOT_ID = 2369743;\n\nENDSEQUENCE;\n\n\n\nPS66: SEQUENCE, L=3;\n\n PA.C10.66 : ACC10 , AT = 1.475, SLOT_ID = 2254380;\n\nENDSEQUENCE;\n\n\n\nPS67: SEQUENCE, L=1.6;\n\n PR.BPM67 : BPUNO , AT = .0934, SLOT_ID = 2254394;\n\n PR.BSW57.67 : MCHBBWWP , AT = .4422, SLOT_ID = 2254395;\n\n PR.QFN67 : MQNAAIAP , AT = 1.469, SLOT_ID = 2254398;\n\nENDSEQUENCE;\n\n\n\nPS68: SEQUENCE, L=1.6;\n\n PA.UPH68 : UPH__001 , AT = .0934, SLOT_ID = 2254412;\n\n PR.BPM68 : BPUNO , AT = .357 , SLOT_ID = 10414035;\n\n PR.BWSH68 : BWSRB , AT = .803 , SLOT_ID = 10414037;\n\n PR.QDN68 : MQNAAIAP , AT = 1.462, SLOT_ID = 2254413;\n\nENDSEQUENCE;\n\n\n\nPS69: SEQUENCE, L=1.6;\n\n PR.BQS69 : ULF , AT = .0934, SLOT_ID = 2254427;\n\n PR.QTRDB69 : MQNBDAAP , AT = 1.160, SLOT_ID = 2254429;\n\n PR.MM69 : MM_AAIAP , AT = 1.459, SLOT_ID = 5365811;\n\nENDSEQUENCE;\n\n\n\nPS70: SEQUENCE, L=1.6;\n\n PR.BPM70 : BPUNO , AT = .0934, SLOT_ID = 2254445;\n\n PR.ODN70.A : MONAAFWP , AT = .6305, SLOT_ID = 10430399; ! Position is an estimate\n\n PR.ODN70.B : MONAAFWP , AT = .978 , SLOT_ID = 2254446;\n\n PR.VVS70 : VVS , AT = 1.344, SLOT_ID = 13720433; ! Position is an estimate\n\n PR.MM70 : MM_AAIAP , AT = 1.469, SLOT_ID = 5365812;\n\nENDSEQUENCE;\n\n\n\nPS71: SEQUENCE, L=3;\n\n PE.KFA71 : KFA__003 , AT = 1.472, SLOT_ID = 2254462;\n\n PR.QFN71 : MQNAAIAP , AT = 2.859, SLOT_ID = 2254464;\n\nENDSEQUENCE;\n\n\n\nPS72: SEQUENCE, L=1.6;\n\n PR.BQS72 : ULF , AT = .0934, SLOT_ID = 2254478;\n\n PR.BQL72 : BPMTS , AT = .775 , SLOT_ID = 6078900;\n\n PR.QDN72 : MQNAAIAP , AT = 1.472, SLOT_ID = 2254479;\n\nENDSEQUENCE;\n\n\n\nPS73: SEQUENCE, L=1.6;\n\n PR.BPM73 : BPUNO , AT = .0934, SLOT_ID = 2254493;\n\n PR.QTRTA73 : MQNBCAWP , AT = .4542, SLOT_ID = 2254494;\n\n PR.QSK73 : MQSAAIAP , AT = 1.469, SLOT_ID = 2254497;\n\nENDSEQUENCE;\n\n\n\nPS74: SEQUENCE, L=1.6;\n\n PR.MM74 : MM_AAIAP , AT = 1.467, SLOT_ID = 5365813;\n\nENDSEQUENCE;\n\n\n\nPS75: SEQUENCE, L=1.6;\n\n PR.BPM75 : BPUNO , AT = .0934, SLOT_ID = 2254526;\n\nENDSEQUENCE;\n\n\n\nPS76: SEQUENCE, L=3;\n\n PA.URL76 : URL , AT = .0934, SLOT_ID = 10410423;\n\n PA.C10.76 : ACC10 , AT = 1.475, SLOT_ID = 2254542;\n\n PR.MM76 : MM_AAIAP , AT = 2.872, SLOT_ID = 5365830;\n\nENDSEQUENCE;\n\n\n\nPS77: SEQUENCE, L=1.6;\n\n PR.BPM77 : BPUNO , AT = .0934, SLOT_ID = 2254558;\n\n PA.C40.77 : ACC40 , AT = .775 , SLOT_ID = 2254560;\n\n PR.QFN77 : MQNAAIAP , AT = 1.481, SLOT_ID = 2254561;\n\nENDSEQUENCE;\n\n\n\nPS78: SEQUENCE, L=1.6;\n\n PA.C40.78 : ACC40 , AT = .775 , SLOT_ID = 2254575;\n\n PR.QDN78 : MQNAAIAP , AT = 1.472, SLOT_ID = 2254576;\n\nENDSEQUENCE;\n\n\n\nPS79: SEQUENCE, L=1.6;\n\n PE.KFA79 : KFA__001 , AT = .696 , SLOT_ID = 2254591;\n\n PR.VVS79 : VVS , AT = 1.25 , SLOT_ID = 13720434; ! Position is an estimate\n\n PR.MM79 : MM_AAIAP , AT = 1.472, SLOT_ID = 5365814;\n\nENDSEQUENCE;\n\n\n\nPS80: SEQUENCE, L=1.6;\n\n PR.BPM80 : BPUNO , AT = .0934, SLOT_ID = 2254607;\n\n PA.C20.80 : ACC20 , AT = .775 , SLOT_ID = 2254608;\n\n PR.MM80 : MM_AAIAP , AT = 1.472, SLOT_ID = 5365815;\n\nENDSEQUENCE;\n\n\n\nPS81: SEQUENCE, L=3;\n\n PA.C10.81 : ACC10 , AT = 1.475, SLOT_ID = 2254624;\n\n PR.QFN81 : MQNAAIAP , AT = 2.881, SLOT_ID = 2254626;\n\nENDSEQUENCE;\n\n\n\nPS82: SEQUENCE, L=1.6;\n\n! TODO: the BGI magnet and detector are overlapping here. I think it would be best to remove the magnet and only include the instrument PS.BGI82 in the sequence.\n\n! PR.MDB82 : MDBCCWWC , AT = .775 , SLOT_ID = 41442239; ! Position is not mechancially accurate, and based upon being at the centre of the optics defined straight section\n\n PR.BGI82 : BGIHA , AT = .775 , SLOT_ID = 41479404; ! Position is not mechanically accurate. Placed at the centre of the optics defined straight section.\n\n PR.QDN82 : MQNAAIAP , AT = 1.480, SLOT_ID = 2254641;\n\nENDSEQUENCE;\n\n\n\nPS83: SEQUENCE, L=1.6;\n\n PR.BPM83 : ULG , AT = .0934, SLOT_ID = 2254655;\n\n PR.USP83 : USP , AT = .775 , SLOT_ID = 2254656;\n\n PR.MM83 : MM_AAIAP , AT = 1.472, SLOT_ID = 5365816;\n\nENDSEQUENCE;\n\n\n\nPS84: SEQUENCE, L=1.6;\n\n PR.MM84 : MM_AAIAP , AT = 1.480, SLOT_ID = 5365817;\n\nENDSEQUENCE;\n\n\n\nPS85: SEQUENCE, L=1.6;\n\n PR.BPM85 : ULG , AT = .0934, SLOT_ID = 2254689;\n\n PR.BWSV85 : BWSRB , AT = .803 , SLOT_ID = 2254690;\n\n PR.QFN85 : MQNAAIAP , AT = 1.481, SLOT_ID = 2254692;\n\nENDSEQUENCE;\n\n\n\nPS86: SEQUENCE, L=3;\n\n PA.C10.86 : ACC10 , AT = 1.475, SLOT_ID = 2254706;\n\n PR.QDN86 : MQNAAIAP , AT = 2.880, SLOT_ID = 2254707;\n\nENDSEQUENCE;\n\n\n\nPS87: SEQUENCE, L=1.6;\n\n PR.BPM87 : BPUNO , AT = .0934, SLOT_ID = 2254721;\n\n PR.QTRDA87 : MQNBDAAP , AT = .4167, SLOT_ID = 2254722;\n\n PR.QSE87 : MQNCAAWP , AT = .843 , SLOT_ID = 2254724;\n\n PR.MM87 : MM_AAIAP , AT = 1.472, SLOT_ID = 5365818;\n\nENDSEQUENCE;\n\n\n\nPS88: SEQUENCE, L=1.6;\n\n PA.UPH88 : UPH__001 , AT = .0934, SLOT_ID = 2254740;\n\n PR.C80.88 : AARFB , AT = .775 , SLOT_ID = 2254741;\n\n PR.MM88 : MM_AAIAP , AT = 1.481, SLOT_ID = 5365819;\n\nENDSEQUENCE;\n\n\n\nPS89: SEQUENCE, L=1.6;\n\n PR.C80.89 : AARFB , AT = .775 , SLOT_ID = 2254758;\n\n PR.QFN89 : MQNAAIAP , AT = 1.481, SLOT_ID = 2254759;\n\nENDSEQUENCE;\n\n\n\nPS90: SEQUENCE, L=1.6;\n\n PR.BPM90 : BPUNO , AT = .0934, SLOT_ID = 2254773;\n\n PR.BPMW90 : BPUWA , AT = .4216, SLOT_ID = 42401369; ! Absolute position is not mechanically accurate. It is positioned using the design drawings of the section, and using the optics file position for the centre of PR.ODN90 as the cumulative distance reference\n\n PR.ODN90 : MONAAFWP , AT = .9892, SLOT_ID = 2254774;\n\n PR.VVS90 : VVS , AT = 1.251, SLOT_ID = 13720435; ! Position is an estimate\n\n PR.QDN90 : MQNAAIAP , AT = 1.472, SLOT_ID = 2254775;\n\nENDSEQUENCE;\n\n\n\nPS91: SEQUENCE, L=3;\n\n PA.C10.91 : ACC10 , AT = 1.475, SLOT_ID = 2254789;\n\n PR.MM91 : MM_AAIAP , AT = 2.881, SLOT_ID = 5365820;\n\nENDSEQUENCE;\n\n\n\nPS92: SEQUENCE, L=1.6;\n\n PR.C20.92 : ACC20 , AT = .775 , SLOT_ID = 2254806;\n\n PR.QSK92 : MQSAAIAP , AT = 1.503, SLOT_ID = 2254807;\n\nENDSEQUENCE;\n\n\n\nPS93: SEQUENCE, L=1.6;\n\n PR.BPM93 : ULG , AT = .0934, SLOT_ID = 2254821;\n\n PR.USP93 : UDP , AT = .775 , SLOT_ID = 2254822;\n\n PR.QSK93 : MQSAAIAP , AT = 1.495, SLOT_ID = 2254824;\n\nENDSEQUENCE;\n\n\n\nPS94: SEQUENCE, L=1.6;\n\n PR.XNO94 : MXNBAFWP , AT = .7706, SLOT_ID = 10428460; ! Position is an estimate\n\n PR.UWB94 : BPUWA , AT = 1.125, SLOT_ID = 2254839;\n\n PR.MM94 : MM_AAIAP , AT = 1.480, SLOT_ID = 5365821;\n\nENDSEQUENCE;\n\n\n\nPS95: SEQUENCE, L=1.6;\n\n PR.BPM95 : BPUNO , AT = .0934, SLOT_ID = 2254855;\n\n PR.UWB95 : URS , AT = .4624, SLOT_ID = 2254856;\n\n PR.QTRDA95 : MQNBDAAP , AT = 1.122, SLOT_ID = 2254858;\n\n PR.QFN95 : MQNAAIAP , AT = 1.481, SLOT_ID = 2254859;\n\nENDSEQUENCE;\n\n\n\nPS96: SEQUENCE, L=3;\n\n PA.URL96 : URL , AT = .0934, SLOT_ID = 2254873;\n\n PA.C10.96 : ACC10 , AT = 1.475, SLOT_ID = 2254874;\n\n PR.QDN96 : MQNAAIAP , AT = 2.880, SLOT_ID = 2254875;\n\nENDSEQUENCE;\n\n\n\nPS97: SEQUENCE, L=1.6;\n\n PR.BPM97 : BPUNO , AT = .0934, SLOT_ID = 2254889;\n\n PR.KFB97 : KFB , AT = .775 , SLOT_ID = 2254890;\n\n PR.MM97 : MM_AAIAP , AT = 1.481, SLOT_ID = 5365822;\n\nENDSEQUENCE;\n\n\n\nPS98: SEQUENCE, L=1.6;\n\n PR.UFB98 : BPUNO , AT = .0934, SLOT_ID = 2254907;\n\n PR.MM98 : MM_AAIAP , AT = 1.473, SLOT_ID = 5365823;\n\nENDSEQUENCE;\n\n\n\nPS99: SEQUENCE, L=1.6;\n\n PR.QTRTB99.A : MQNBCAWP , AT = .6532, SLOT_ID = 2254926;\n\n PR.QTRTB99.B : MQNBCAWP , AT = 1.078, SLOT_ID = 5706126;\n\n PR.QFN99 : MQNAAIAP , AT = 1.472, SLOT_ID = 2254927;\n\nENDSEQUENCE;\n\n\n\nPS00: SEQUENCE, L=1.6;\n\n PR.BPM00 : BPUNO , AT = .0934, SLOT_ID = 2254941;\n\n PR.WCM00 : URP , AT = .5092, SLOT_ID = 2254942;\n\n PR.ODN00 : MONAAFWP , AT = .9508, SLOT_ID = 2254943;\n\n PR.VVS00 : VVS , AT = 1.251, SLOT_ID = 13720436; ! Position is an estimate\n\n PR.QDN00 : MQNAAIAP , AT = 1.472, SLOT_ID = 2254944;\n\nENDSEQUENCE;\n\n\n\n\n\n/************************************************************************************/\n\n/* PS Sectors */\n\n/************************************************************************************/\n\n\n\n! TODO: modify incorrect MU lengths in LDB to avoid that the magnet is positioned at 3.0000000005\n\n! TODO: remove SLOT_IDs for sequence descriptions (PSXX and PR.BHXXX) as SLOT_ID only exists for elements but not for sequences in MAD-X\n\n! TODO: modify length of each sector to be 62.83185 instead of 62.831853\n\n! TODO: correct positions of SS and BH*\n\n\n\nSEC01 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS01 , AT = 0. ;!, SLOT_ID = 2194390;\n\n PR.BHT01 , AT = 3. ;!, SLOT_ID = 2253018;\n\n PS02 , AT = 7.403185 ;!, SLOT_ID = 2194392;\n\n PR.BHU02 , AT = 9.003185 ;!, SLOT_ID = 2253020;\n\n PS03 , AT = 13.40637 ;!, SLOT_ID = 2194394;\n\n PR.BHT03 , AT = 15.00637 ;!, SLOT_ID = 2253022;\n\n PS04 , AT = 19.409555 ;!, SLOT_ID = 2194396;\n\n PR.BHR04 , AT = 21.009555 ;!, SLOT_ID = 2253024;\n\n PS05 , AT = 25.41274 ;!, SLOT_ID = 2194398;\n\n PR.BHT05 , AT = 27.01274 ;!, SLOT_ID = 2253026;\n\n PS06 , AT = 31.415925 ;!, SLOT_ID = 2194400;\n\n PR.BHR06 , AT = 34.415925 ;!, SLOT_ID = 2253028;\n\n PS07 , AT = 38.81911 ;!, SLOT_ID = 2194402;\n\n PR.BHS07 , AT = 40.41911 ;!, SLOT_ID = 2253030;\n\n PS08 , AT = 44.822295 ;!, SLOT_ID = 2194404;\n\n PR.BHR08 , AT = 46.422295 ;!, SLOT_ID = 2253032;\n\n PS09 , AT = 50.82548 ;!, SLOT_ID = 2194406;\n\n PR.BHT09 , AT = 52.42548 ;!, SLOT_ID = 2253034;\n\n PS10 , AT = 56.828665 ;!, SLOT_ID = 2194408;\n\n PR.BHR10 , AT = 58.428665 ;!, SLOT_ID = 2253036;\n\nENDSEQUENCE;\n\n\n\nSEC02 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS11 , AT = 0. ;!, SLOT_ID = 2194410;\n\n PR.BHS11 , AT = 3. ;!, SLOT_ID = 2253038;\n\n PS12 , AT = 7.403185 ;!, SLOT_ID = 2194412;\n\n PR.BHR12 , AT = 9.003185 ;!, SLOT_ID = 2253040;\n\n PS13 , AT = 13.40637 ;!, SLOT_ID = 2194414;\n\n PR.BHS13 , AT = 15.00637 ;!, SLOT_ID = 2253042;\n\n PS14 , AT = 19.409555 ;!, SLOT_ID = 2194416;\n\n PR.BHU14 , AT = 21.009555 ;!, SLOT_ID = 2253044;\n\n PS15 , AT = 25.41274 ;!, SLOT_ID = 2194418;\n\n PR.BHT15 , AT = 27.01274 ;!, SLOT_ID = 2253046;\n\n PS16 , AT = 31.415925 ;!, SLOT_ID = 2194420;\n\n PR.BHU16 , AT = 34.415925 ;!, SLOT_ID = 2253048;\n\n PS17 , AT = 38.81911 ;!, SLOT_ID = 2194422;\n\n PR.BHT17 , AT = 40.41911 ;!, SLOT_ID = 2253050;\n\n PS18 , AT = 44.822295 ;!, SLOT_ID = 2194424;\n\n PR.BHU18 , AT = 46.422295 ;!, SLOT_ID = 2253052;\n\n PS19 , AT = 50.82548 ;!, SLOT_ID = 2194426;\n\n PR.BHS19 , AT = 52.42548 ;!, SLOT_ID = 2253054;\n\n PS20 , AT = 56.828665 ;!, SLOT_ID = 2194428;\n\n PR.BHR20 , AT = 58.428665 ;!, SLOT_ID = 2253056;\n\nENDSEQUENCE;\n\n\n\nSEC03 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS21 , AT = 0. ;!, SLOT_ID = 2194430;\n\n PR.BHT21 , AT = 3. ;!, SLOT_ID = 2253058;\n\n PS22 , AT = 7.403185 ;!, SLOT_ID = 2194432;\n\n PR.BHR22 , AT = 9.003185 ;!, SLOT_ID = 2253060;\n\n PS23 , AT = 13.40637 ;!, SLOT_ID = 2194434;\n\n PR.BHT23 , AT = 15.00637 ;!, SLOT_ID = 2253062;\n\n PS24 , AT = 19.409555 ;!, SLOT_ID = 2194436;\n\n PR.BHU24 , AT = 21.009555 ;!, SLOT_ID = 2253064;\n\n PS25 , AT = 25.41274 ;!, SLOT_ID = 2194438;\n\n PR.BHT25 , AT = 27.01274 ;!, SLOT_ID = 2253066;\n\n PS26 , AT = 31.415925 ;!, SLOT_ID = 2194440;\n\n PR.BHR26 , AT = 34.415925 ;!, SLOT_ID = 2253068;\n\n PS27 , AT = 38.81911 ;!, SLOT_ID = 2194442;\n\n PR.BHS27 , AT = 40.41911 ;!, SLOT_ID = 2253070;\n\n PS28 , AT = 44.822295 ;!, SLOT_ID = 2194444;\n\n PR.BHU28 , AT = 46.422295 ;!, SLOT_ID = 2253072;\n\n PS29 , AT = 50.82548 ;!, SLOT_ID = 2194446;\n\n PR.BHT29 , AT = 52.42548 ;!, SLOT_ID = 2253074;\n\n PS30 , AT = 56.828665 ;!, SLOT_ID = 2194448;\n\n PR.BHR30 , AT = 58.428665 ;!, SLOT_ID = 2253076;\n\nENDSEQUENCE;\n\n\n\nSEC04 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS31 , AT = 0. ;!, SLOT_ID = 2194450;\n\n PR.BHT31 , AT = 3. ;!, SLOT_ID = 2253078;\n\n PS32 , AT = 7.403185 ;!, SLOT_ID = 2194452;\n\n PR.BHR32 , AT = 9.003185 ;!, SLOT_ID = 2253080;\n\n PS33 , AT = 13.40637 ;!, SLOT_ID = 2194454;\n\n PR.BHS33 , AT = 15.00637 ;!, SLOT_ID = 2253082;\n\n PS34 , AT = 19.409555 ;!, SLOT_ID = 2194456;\n\n PR.BHR34 , AT = 21.009555 ;!, SLOT_ID = 2253084;\n\n PS35 , AT = 25.41274 ;!, SLOT_ID = 2194458;\n\n PR.BHT35 , AT = 27.01274 ;!, SLOT_ID = 2253086;\n\n PS36 , AT = 31.415925 ;!, SLOT_ID = 2194460;\n\n PR.BHR36 , AT = 34.415925 ;!, SLOT_ID = 2253088;\n\n PS37 , AT = 38.81911 ;!, SLOT_ID = 2194462;\n\n PR.BHT37 , AT = 40.41911 ;!, SLOT_ID = 2253090;\n\n PS38 , AT = 44.822295 ;!, SLOT_ID = 2194464;\n\n PR.BHR38 , AT = 46.422295 ;!, SLOT_ID = 2253092;\n\n PS39 , AT = 50.82548 ;!, SLOT_ID = 2194466;\n\n PR.BHT39 , AT = 52.42548 ;!, SLOT_ID = 2253094;\n\n PS40 , AT = 56.828665 ;!, SLOT_ID = 2194468;\n\n PR.BHU40 , AT = 58.428665 ;!, SLOT_ID = 2253096;\n\nENDSEQUENCE;\n\n\n\nSEC05 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS41 , AT = 0. ;!, SLOT_ID = 2194470;\n\n PR.BHT41 , AT = 3. ;!, SLOT_ID = 2253098;\n\n PS42 , AT = 7.403185 ;!, SLOT_ID = 2194472;\n\n PR.BHR42 , AT = 9.003185 ;!, SLOT_ID = 2253100;\n\n PS43 , AT = 13.40637 ;!, SLOT_ID = 2194474;\n\n PR.BHT43 , AT = 15.00637 ;!, SLOT_ID = 2253102;\n\n PS44 , AT = 19.409555 ;!, SLOT_ID = 2194476;\n\n PR.BHR44 , AT = 21.009555 ;!, SLOT_ID = 2253104;\n\n PS45 , AT = 25.41274 ;!, SLOT_ID = 2194478;\n\n PR.BHT45 , AT = 27.01274 ;!, SLOT_ID = 2253106;\n\n PS46 , AT = 31.415925 ;!, SLOT_ID = 2194480;\n\n PR.BHR46 , AT = 34.415925 ;!, SLOT_ID = 2253108;\n\n PS47 , AT = 38.81911 ;!, SLOT_ID = 2194482;\n\n PR.BHS47 , AT = 40.41911 ;!, SLOT_ID = 2253110;\n\n PS48 , AT = 44.822295 ;!, SLOT_ID = 2194484;\n\n PR.BHR48 , AT = 46.422295 ;!, SLOT_ID = 2253112;\n\n PS49 , AT = 50.82548 ;!, SLOT_ID = 2194486;\n\n PR.BHT49 , AT = 52.42548 ;!, SLOT_ID = 2253114;\n\n PS50 , AT = 56.828665 ;!, SLOT_ID = 2194488;\n\n PR.BHR50 , AT = 58.428665 ;!, SLOT_ID = 2253116;\n\nENDSEQUENCE;\n\n\n\nSEC06 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS51 , AT = 0. ;!, SLOT_ID = 2194490;\n\n PR.BHT51 , AT = 3. ;!, SLOT_ID = 2253118;\n\n PS52 , AT = 7.403185 ;!, SLOT_ID = 2194492;\n\n PR.BHR52 , AT = 9.003185 ;!, SLOT_ID = 2253120;\n\n PS53 , AT = 13.40637 ;!, SLOT_ID = 2194494;\n\n PR.BHS53 , AT = 15.00637 ;!, SLOT_ID = 2253122;\n\n PS54 , AT = 19.409555 ;!, SLOT_ID = 2194496;\n\n PR.BHR54 , AT = 21.009555 ;!, SLOT_ID = 2253124;\n\n PS55 , AT = 25.41274 ;!, SLOT_ID = 2194498;\n\n PR.BHT55 , AT = 27.01274 ;!, SLOT_ID = 2253126;\n\n PS56 , AT = 31.415925 ;!, SLOT_ID = 2194500;\n\n PR.BHU56 , AT = 34.415925 ;!, SLOT_ID = 2253128;\n\n PS57 , AT = 38.81911 ;!, SLOT_ID = 2194502;\n\n PR.BHT57 , AT = 40.41911 ;!, SLOT_ID = 2253130;\n\n PS58 , AT = 44.822295 ;!, SLOT_ID = 2194504;\n\n PR.BHU58 , AT = 46.422295 ;!, SLOT_ID = 2253132;\n\n PS59 , AT = 50.82548 ;!, SLOT_ID = 2194506;\n\n PR.BHT59 , AT = 52.42548 ;!, SLOT_ID = 2253134;\n\n PS60 , AT = 56.828665 ;!, SLOT_ID = 2194508;\n\n PR.BHU60 , AT = 58.428665 ;!, SLOT_ID = 2253136;\n\nENDSEQUENCE;\n\n\n\nSEC07 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS61 , AT = 0. ;!, SLOT_ID = 2194510;\n\n PR.BHT61 , AT = 3. ;!, SLOT_ID = 2253138;\n\n PS62\t , AT = 7.403185 ;!;\n\n PR.BHU62 , AT = 9.003185 ;!, SLOT_ID = 2253140;\n\n PS63 , AT = 13.40637 ;!, SLOT_ID = 2194514;\n\n PR.BHT63 , AT = 15.00637 ;!, SLOT_ID = 2253142;\n\n PS64 , AT = 19.409555 ;!, SLOT_ID = 2194516;\n\n PR.BHU64 , AT = 21.009555 ;!, SLOT_ID = 2253144;\n\n PS65 , AT = 25.41274 ;!, SLOT_ID = 2194518;\n\n PR.BHT65 , AT = 27.01274 ;!, SLOT_ID = 2253146;\n\n PS66 , AT = 31.415925 ;!, SLOT_ID = 2194520;\n\n PR.BHR66 , AT = 34.415925 ;!, SLOT_ID = 2253148;\n\n PS67 , AT = 38.81911 ;!, SLOT_ID = 2194522;\n\n PR.BHS67 , AT = 40.41911 ;!, SLOT_ID = 2253150;\n\n PS68 , AT = 44.822295 ;!, SLOT_ID = 2194524;\n\n PR.BHU68 , AT = 46.422295 ;!, SLOT_ID = 2253152;\n\n PS69 , AT = 50.82548 ;!, SLOT_ID = 2194526;\n\n PR.BHT69 , AT = 52.42548 ;!, SLOT_ID = 2253154;\n\n PS70 , AT = 56.828665 ;!, SLOT_ID = 2194528;\n\n PR.BHR70 , AT = 58.428665 ;!, SLOT_ID = 2253156;\n\nENDSEQUENCE;\n\n\n\nSEC08 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS71 , AT = 0. ;!, SLOT_ID = 2194530;\n\n PR.BHT71 , AT = 3. ;!, SLOT_ID = 2253158;\n\n PS72 , AT = 7.403185 ;!, SLOT_ID = 2194532;\n\n PR.BHR72 , AT = 9.003185 ;!, SLOT_ID = 2253160;\n\n PS73 , AT = 13.40637 ;!, SLOT_ID = 2194534;\n\n PR.BHS73 , AT = 15.00637 ;!, SLOT_ID = 2253162;\n\n PS74 , AT = 19.409555 ;!, SLOT_ID = 2194536;\n\n PR.BHU74 , AT = 21.009555 ;!, SLOT_ID = 2253164;\n\n PS75 , AT = 25.41274 ;!, SLOT_ID = 2194538;\n\n PR.BHT75 , AT = 27.01274 ;!, SLOT_ID = 2253166;\n\n PS76 , AT = 31.415925 ;!, SLOT_ID = 2194540;\n\n PR.BHR76 , AT = 34.415925 ;!, SLOT_ID = 2253168;\n\n PS77 , AT = 38.81911 ;!, SLOT_ID = 2194542;\n\n PR.BHT77 , AT = 40.41911 ;!, SLOT_ID = 2253170;\n\n PS78 , AT = 44.822295 ;!, SLOT_ID = 2194544;\n\n PR.BHR78 , AT = 46.422295 ;!, SLOT_ID = 2253172;\n\n PS79 , AT = 50.82548 ;!, SLOT_ID = 2194546;\n\n PR.BHS79 , AT = 52.42548 ;!, SLOT_ID = 2253174;\n\n PS80 , AT = 56.828665 ;!, SLOT_ID = 2194548;\n\n PR.BHR80 , AT = 58.428665 ;!, SLOT_ID = 2253176;\n\nENDSEQUENCE;\n\n\n\nSEC09 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS81 , AT = 0. ;!, SLOT_ID = 2194550;\n\n PR.BHT81 , AT = 3. ;!, SLOT_ID = 2253178;\n\n PS82 , AT = 7.403185 ;!, SLOT_ID = 2194552;\n\n PR.BHR82 , AT = 9.003185 ;!, SLOT_ID = 2253180;\n\n PS83 , AT = 13.40637 ;!, SLOT_ID = 2194554;\n\n PR.BHS83 , AT = 15.00637 ;!, SLOT_ID = 2253182;\n\n PS84 , AT = 19.409555 ;!, SLOT_ID = 2194556;\n\n PR.BHR84 , AT = 21.009555 ;!, SLOT_ID = 2253184;\n\n PS85 , AT = 25.41274 ;!, SLOT_ID = 2194558;\n\n PR.BHT85 , AT = 27.01274 ;!, SLOT_ID = 2253186;\n\n PS86 , AT = 31.415925 ;!, SLOT_ID = 2194560;\n\n PR.BHR86 , AT = 34.415925 ;!, SLOT_ID = 2253188;\n\n PS87 , AT = 38.81911 ;!, SLOT_ID = 2194562;\n\n PR.BHS87 , AT = 40.41911 ;!, SLOT_ID = 2253190;\n\n PS88 , AT = 44.822295 ;!, SLOT_ID = 2194564;\n\n PR.BHU88 , AT = 46.422295 ;!, SLOT_ID = 2253192;\n\n PS89 , AT = 50.82548 ;!, SLOT_ID = 2194566;\n\n PR.BHT89 , AT = 52.42548 ;!, SLOT_ID = 2253194;\n\n PS90 , AT = 56.828665 ;!, SLOT_ID = 2194568;\n\n PR.BHR90 , AT = 58.428665 ;!, SLOT_ID = 2253196;\n\nENDSEQUENCE;\n\n\n\nSEC00 : SEQUENCE, REFER=ENTRY, L = 62.83185;\n\n PS91 , AT = 0. ;!, SLOT_ID = 2194570;\n\n PR.BHT91 , AT = 3. ;!, SLOT_ID = 2253198;\n\n PS92 , AT = 7.403185 ;!, SLOT_ID = 2194572;\n\n PR.BHR92 , AT = 9.003185 ;!, SLOT_ID = 2253200;\n\n PS93 , AT = 13.40637 ;!, SLOT_ID = 2194574;\n\n PR.BHS93 , AT = 15.00637 ;!, SLOT_ID = 2253202;\n\n PS94 , AT = 19.409555 ;!, SLOT_ID = 2194576;\n\n PR.BHR94 , AT = 21.009555 ;!, SLOT_ID = 2253204;\n\n PS95 , AT = 25.41274 ;!, SLOT_ID = 2194578;\n\n PR.BHT95 , AT = 27.01274 ;!, SLOT_ID = 2253206;\n\n PS96 , AT = 31.415925 ;!, SLOT_ID = 2194580;\n\n PR.BHR96 , AT = 34.415925 ;!, SLOT_ID = 2253208;\n\n PS97 , AT = 38.81911 ;!, SLOT_ID = 2194582;\n\n PR.BHT97 , AT = 40.41911 ;!, SLOT_ID = 2253210;\n\n PS98 , AT = 44.822295 ;!, SLOT_ID = 2194584;\n\n PR.BHR98 , AT = 46.422295 ;!, SLOT_ID = 2253212;\n\n PS99 , AT = 50.82548 ;!, SLOT_ID = 2194586;\n\n PR.BHS99 , AT = 52.42548 ;!, SLOT_ID = 2253214;\n\n PS00 , AT = 56.828665 ;!, SLOT_ID = 2194588;\n\n PR.BHR00 , AT = 58.428665 ;!, SLOT_ID = 2253216;\n\nENDSEQUENCE;\n\n\n\n\n\n/************************************************************************************/\n\n/* PS Sequence */\n\n/************************************************************************************/\n\n\n\n! TODO: account for the initial offset of -0.3 m in LDB (also to be agreed with SU)\n\n! TODO: remove SLOT_IDs for sequence descriptions (PSXX and PR.BHXXX) as SLOT_ID only exists for elements but not for sequences in MAD-X\n\n! TODO: correct positions of sectors\n\n\n\nPS : SEQUENCE, REFER=ENTRY, L = 628.3185;\n\n SEC01, AT = 0.0 ;!, SLOT_ID = 2186614;\n\n SEC02, AT = 62.83185 ;!, SLOT_ID = 2186615;\n\n SEC03, AT = 125.6637 ;!, SLOT_ID = 2186616;\n\n SEC04, AT = 188.49555 ;!, SLOT_ID = 2186617;\n\n SEC05, AT = 251.3274 ;!, SLOT_ID = 2186618;\n\n SEC06, AT = 314.15925 ;!, SLOT_ID = 2186619;\n\n SEC07, AT = 376.9911 ;!, SLOT_ID = 2186620;\n\n SEC08, AT = 439.82295 ;!, SLOT_ID = 2186621;\n\n SEC09, AT = 502.6548 ;!, SLOT_ID = 2186622;\n\n SEC00, AT = 565.48665 ;!, SLOT_ID = 2186623;\n\nENDSEQUENCE;\n\n\n\nreturn;\n\n" ] ], [ [ "# Performing a PTC Twiss", "_____no_output_____" ] ], [ [ "madx.command.use(sequence = 'PS')\nmadx.command.ptc_create_universe()\nmadx.command.ptc_create_layout('time=false, model=2, exact=true, method=6, nst=5')\nmadx.command.ptc_twiss('closed_orbit, icase=56, no=4, slice_magnets')\nmadx.command.ptc_end", "Determined SECTOR NMUL MAX : 2\n MAD-X Beam Parameters\n Energy : 0.233665E+01\n Kinetic Energy : 0.139838E+01\n Particle Rest Mass : 0.938272E+00\n Momentum : 0.214000E+01\n Setting MADx with \n energy 2.3366545526771887 \n method 6\n Num. of steps 5\n charge 1.0000000000000000 \n Length of machine: 628.31850000000065 \n The machine is a RING\n ------------------------------------ PTC Survey ------------------------------------\n Before start: 0.0000000000000000 0.0000000000000000 0.0000000000000000 \n Before end: 0.0000000000000000 0.0000000000000000 0.0000000000000000 \n After start: 0.0000000000000000 0.0000000000000000 0.0000000000000000 \n After end: -2.6953046045052886E-010 0.0000000000000000 -1.7950787967180304E-008\n ************ State Summary ****************\n MADTHICK=>KIND = 37 MATRIX-KICK-MATRIX \n Rectangular Bend: input arc length (rho alpha) \n Default integration method 6\n Default integration steps 5\n This is a proton \n EXACT_MODEL = TRUE \n TOTALPATH = 0\n RADIATION = FALSE\n STOCHASTIC = FALSE\n ENVELOPE = FALSE\n NOCAVITY = TRUE \n TIME = FALSE\n FRINGE = FALSE\n PARA_IN = FALSE\n ONLY_2D = FALSE\n ONLY_4D = FALSE\n DELTA = FALSE\n SPIN = FALSE\n MODULATION = FALSE\n RAMPING = FALSE\n ACCELERATE = FALSE\n\n++++++ table: ptc_twiss_summary\n\n length alpha_c alpha_c_p alpha_c_p2 \n 628.3185 0.02673251283 0.07111328055 -0.3652636934 \n\n alpha_c_p3 eta_c gamma_tr q1 \n -0.1576956755 -0.1345059185 6.116177884 0.2454672837 \n\n q2 dq1 dq2 qs \n 0.2836600762 -5.346466499 -7.163152557 0 \n\n beta_x_min beta_x_max beta_y_min beta_y_max \n 11.71269282 22.59565706 11.64196647 22.44394696 \n\n beta11min beta11max beta12min beta12max \n 11.71269282 22.59565706 0 0 \n\n beta13min beta13max beta21min beta21max \n 0 0 0 0 \n\n beta22min beta22max beta23min beta23max \n 11.64196647 22.44394696 0 0 \n\n beta31min beta31max beta32min beta32max \n 0 0 0 0 \n\n beta33min beta33max disp1min disp1max \n 0 0 0 3.047668437 \n\n disp2min disp2max disp3min disp3max \n -0.3361144192 0.3361144192 0 0 \n\n disp4min disp4max deltap orbit_x \n 0 0 0 0 \n\n orbit_px orbit_y orbit_py orbit_pt \n 0 0 0 0 \n\n orbit_t xcorms ycorms pxcorms \n 0 0 0 0 \n\n pycorms tcorms ptcorms xcomax \n 0 0.1378029567 0 0 \n\n ycomax pxcomax pycomax tcomax \n 0 0 0 2.209343819e-14 \n\n ptcomax xcomin ycomin pxcomin \n 0 0 0 0 \n\n pycomin tcomin ptcomin \n 0 -1.912 0 \n" ] ], [ [ "# Print non-zero entries of the PTC Twiss summary table", "_____no_output_____" ] ], [ [ "twiss = madx.table['ptc_twiss_summary']\nfor k in twiss.keys():\n if twiss[k][0] > 0:\n print(k + ' = ' + str(twiss[k][0]))", "length = 628.3185000000026\nalpha_c = 0.02673251283033799\nalpha_c_p = 0.07111328054643197\ngamma_tr = 6.1161778841446335\nq1 = 0.24546728367615464\nq2 = 0.28366007619895556\nbeta_x_min = 11.712692822201694\nbeta_x_max = 22.595657062401727\nbeta_y_min = 11.641966474678512\nbeta_y_max = 22.443946960176095\nbeta11min = 11.712692822201694\nbeta11max = 22.595657062401727\nbeta22min = 11.641966474678512\nbeta22max = 22.443946960176095\ndisp1max = 3.0476684372260223\ndisp2max = 0.336114419191337\ntcorms = 0.1378029566709518\ntcomax = 2.2093438190040615e-14\n" ] ], [ [ "# Plot the optics functions", "_____no_output_____" ] ], [ [ "twiss = madx.table['ptc_twiss']\n\nf, ax = plt.subplots(1,figsize = (12,7))\n\nax.plot(twiss.S, twiss.BETA11, color = 'darkblue', label = r'$\\beta_x$', linewidth = 1)\nax.plot(twiss.S, twiss.BETA22, color = 'firebrick', label = r'$\\beta_y$', linewidth = 1)\nax.plot(twiss.S, twiss.DISP1*0-100, 'k', label = r'$D_x$')\n\nax2 = ax.twinx()\nax2.plot(twiss.S, twiss.DISP1, 'k', label = r'$D_x$', linewidth = 1)\n\ny = [6, 24]\ndx = [2, 6]\n\nax.set_xlim(0, 2*np.pi*100)\nax.set_ylim(y)\n\nax2.set_ylim(dx)\n\nax.set_xlabel('s [m]')\nax.set_ylabel(r'$\\beta_{x,y}$ [m]')\nax2.set_ylabel(r'$D_x$ [m]')\n\nax.legend(frameon = False, ncol = 3, loc = 'upper center', bbox_to_anchor=(0.5, 1.12))", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]