question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
successful-pairs-of-spells-and-potions | Python 3 || 7 lines, binary search || T/S: 94% / 81% | python-3-7-lines-binary-search-ts-94-81-cnyzn | \nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n\n n, ans = len(potions), []\n | Spaulding_ | NORMAL | 2023-04-02T15:41:35.890514+00:00 | 2024-06-13T03:48:09.270724+00:00 | 1,161 | false | ```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n\n n, ans = len(potions), []\n potions.sort()\n \n for s in spells:\n num = success//s + bool(success%s)\n idx = bisect_left(potions, num)\n ans.append(n-idx)\n\n return ans\n```\n[https://leetcode.com/problems/successful-pairs-of-spells-and-potions/submissions/1286592686/](https://leetcode.com/problems/successful-pairs-of-spells-and-potions/submissions/1286592686/)\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(*N*), in which *N* ~ `len(potions)`. | 9 | 0 | ['Python3'] | 0 |
successful-pairs-of-spells-and-potions | Simple C++ Binary Search :) | simple-c-binary-search-by-scaar-7x0u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- the approach that is used here is binary search.\n- So first we sort th | Scaar | NORMAL | 2023-04-02T12:15:44.029058+00:00 | 2023-04-02T12:15:44.029093+00:00 | 105 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- the approach that is used here is `binary search`.\n- So first we `sort` the potions.\n- then we traverse through `every element in spell` and multiply it to the potions.\n- and because our potions is `sorted` we can apply binary search now.\n- so by doing that we can get the minimum element in `potions` which has multiplication `>=` to our success.\n- when we get that element then every element from its right or is bigger than that element is gonna pass.\n- so we push the `total size of potions - index of minimum success element`.\n- after doing it for all the elements in `spells`, we return the answer\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: `O(nlog(n+m))` #correct me if i\'m wrong cause not sure perfectly :)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n`Upvote ! It just takes 1 click :)`\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> ans;\n int n= spells.size();\n int m = potions.size();\n sort(potions.begin(), potions.end());\n for (int i=0;i<n;i++){\n int spell = spells[i];\n int start = 0;\n int end = m-1;\n while(start<=end){\n int mid = start + (end-start)/2;\n long long product = (long) spell * potions[mid];\n if(product>=success){\n end = mid-1;\n } \n else{\n start = mid+1;\n }\n }\n ans.push_back(m-start);\n \n }\n return ans;\n \n }\n};\n```\n | 9 | 0 | ['Binary Search', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Binary Search | binary-search-by-virendra115-0iaz | \npublic int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n for(int i=0;i<spells.length;i++){\n | virendra115 | NORMAL | 2022-06-11T16:02:30.930952+00:00 | 2022-06-11T16:02:30.930987+00:00 | 1,224 | false | ```\npublic int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n for(int i=0;i<spells.length;i++){\n int l=0,h=potions.length;\n while(l<h){\n int mid = (l+h)/2;\n if(1L*spells[i]*potions[mid]>=success){\n h=mid;\n }else{\n l=mid+1;\n }\n }\n spells[i]=potions.length-l;\n }\n return spells;\n }\n``` | 9 | 0 | ['Java'] | 3 |
successful-pairs-of-spells-and-potions | ✅ EASY || 💯 BEATS-PROOF || 🌟 C++ || 🧑💻 BEGINNER FRIENDLY || 🙂 DETAILED EXPLANATION | easy-beats-proof-c-beginner-friendly-det-izo2 | \n\n# \uD83C\uDF1F PROOF\n---\n\n\n---\n\n\n\n# \uD83C\uDF1F Intuition\n---\n Describe your first thoughts on how to solve this problem. \n#### The problem requ | mukund_rakholiya | NORMAL | 2024-11-20T10:59:50.078361+00:00 | 2024-11-20T11:00:48.549513+00:00 | 692 | false | ```\n```\n# \uD83C\uDF1F PROOF\n---\n\n\n---\n```\n```\n\n# \uD83C\uDF1F Intuition\n---\n<!-- Describe your first thoughts on how to solve this problem. -->\n#### The problem requires counting the number of potions that can form a "successful" pair with each spell. Instead of brute force, which would be inefficient due to the constraints, we optimize using:\n\n1. **Sorting and binary search, or**\n2. **A frequency array approach to preprocess the count of successful potions.**\n\n#### Here, the code utilizes a frequency array to calculate the number of potions greater than or equal to a required value efficiently.\n```\n```\n# \uD83C\uDF1F Approach\n---\n<!-- Describe your approach to solving the problem. -->\n1. **Preprocessing Potions**:\n\n - Use an array `postfix[]` where `postfix[i]` represents the count of potions with strength greater than or equal to `i`.\n - Traverse the potions array to update counts in `postfix[]`.\nProcess `postfix[]` in reverse to calculate cumulative frequencies.\n\n2. **Processing Spells**:\n\n - For each spell, calculate the minimum potion strength (`val`) required for a successful pair:\n - `val = ceil(success / spell)`.\n - Efficiently handle the division to avoid floating-point issues using `(success + spell - 1) / spell`.\n - Retrieve the count of potions greater than or equal to `val` from `postfix[]`.\n\n3. **Update Spells In-place**:\n\n - Modify the `spells` array to store the result directly, avoiding additional space for the output.\n\n\n```\n```\n# \uD83C\uDF1F Complexity\n---\n- ### Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- **O(n + m + maxPotionStrength):**\n- **O(m) for updating `postfix`[].**\n- **O(maxPotionStrength) for cumulative counts.**\n- **O(n) for iterating over `spells`.**\n---\n- ### Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(maxPotionStrength) for the `postfix[]` array.**\n```\n```\n# \uD83C\uDF1F Code\n---\n```cpp []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions,\n long long success) {\n int max_val = 0;\n\n for (auto& potion : potions)\n max_val = max(max_val, potion);\n\n int postfix[max_val + 1];\n\n memset(postfix, 0, sizeof(postfix));\n\n for (auto& potion : potions)\n postfix[potion]++;\n\n for (int i = max_val - 1; i >= 0; --i)\n postfix[i] += postfix[i + 1];\n\n for (int i = 0; i < spells.size(); ++i) {\n long long val = success / (long long)spells[i];\n\n if (success % (long long)spells[i] != 0)\n val++;\n\n spells[i] = val <= max_val ? postfix[val] : 0;\n }\n\n return spells;\n }\n};\n```\n\n```\n```\n---\n\n\n\n---\n```\n```\n | 8 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'C++'] | 9 |
successful-pairs-of-spells-and-potions | ✅C++ || EASY Binary Search | c-easy-binary-search-by-chiikuu-8wex | Code\n\nclass Solution {\n #define ll long long\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long c) {\n sort(p.begi | CHIIKUU | NORMAL | 2023-04-02T09:02:42.597241+00:00 | 2023-04-02T09:02:42.597299+00:00 | 1,420 | false | # Code\n```\nclass Solution {\n #define ll long long\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long c) {\n sort(p.begin(),p.end());\n vector<int>an;\n for(int i=0;i<s.size();i++){\n int d=0;\n ll g=c/s[i];\n if(c%s[i])g++;\n int f=lower_bound(p.begin(),p.end(),g)-p.begin();\n d += p.size()-f;\n an.push_back(d);\n }\n return an;\n }\n};\n```\n\n | 8 | 1 | ['Binary Search', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | 2300. Successful Pairs of Spells and Potions EASY 96.70% Fast | 2300-successful-pairs-of-spells-and-poti-x0ka | \n\n# Intuition\nThe task is to determine, for each spell, how many potions can be paired with it such that the product of the spell\'s power and the potion\'s | k-arsyn28 | NORMAL | 2024-06-18T18:36:49.404795+00:00 | 2024-06-18T18:36:49.404813+00:00 | 472 | false | \n\n# Intuition\nThe task is to determine, for each spell, how many potions can be paired with it such that the product of the spell\'s power and the potion\'s power meets or exceeds a given success threshold. By sorting the potions, we can efficiently use binary search to find the smallest potion that, when multiplied with the current spell, meets the threshold.\n# Approach\n**Sort the Potions:** Start by sorting the list of potion powers. This allows us to use binary search to quickly find the minimum potion power that can pair successfully with a given spell.\n\n**Binary Search for Each Spell:** For each spell in the list of spells, perform a binary search on the sorted potions to find the smallest index where the product of the spell\'s power and the potion\'s power is at least the success threshold.\n\n**Calculate Successful Pairs:** The number of successful pairs for a given spell is then the number of potions from the found index to the end of the potions list. This is computed as the total number of potions minus the found index.\n\n**Store Results:** Store the result for each spell in a result list, which is returned at the end.\n# Complexity\n- Time complexity: **O(n\u2217log(m))**\n- Space complexity: **O(n)**\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long suc) {\n\n sort(p.begin(),p.end());\n vector<int>ans;\n int m = p.size();\n int n = s.size();\n int idx = 0;\n for(int i=0;i<n;i++)\n {\n int l=0;\n int r=m-1;\n int idx=m;\n while(l<=r){\n int mid = l+(r-l)/2;\n if(static_cast<long long>(s[i])*p[mid] >= suc)\n {\n r=mid-1;\n idx = mid;\n }\n else{\n l = mid+1;\n }\n }\n ans.push_back(max(m-idx,0));\n }\n return ans;\n }\n};\n``` | 7 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | C++ | EASY EXPLANATION | BEGINNER FRIENDLY | WITHOUT BS🙂 | c-easy-explanation-beginner-friendly-wit-lelj | Intuition\nWE WILL SORT SPELLS IN DESCENDING ORDER AND POTIONS IN ASCENDING ORDER . SO THAT EVERY TIME I CHECK FOR A GIVEN SPELL ,I DON\'T HAVE TO TRAVERSE FROM | codman_1 | NORMAL | 2023-04-02T06:11:06.210609+00:00 | 2023-04-02T06:24:54.567347+00:00 | 784 | false | # Intuition\nWE WILL SORT SPELLS IN DESCENDING ORDER AND POTIONS IN ASCENDING ORDER . SO THAT EVERY TIME I CHECK FOR A GIVEN SPELL ,I DON\'T HAVE TO TRAVERSE FROM BEGINNING . It will start from some index k .\n\nAND ALSO.\nIF ANY GREATER SPELL IS NOT ABLE TO MAKE SUCCESS FROM POTIONS ,THEN \nNO SPELL AFTER THAT WILL GIVE ANY SUCCESS . THEREFORE \n\n```\nif(flag==0)break;\n```\n\n# Approach\nSEE CODE WITH COMMENTS . YOU WILL SURELY GET IT .\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& ss, vector<int>& p, long long suc) {\n vector<int>s=ss;// TO MAKE USE OF ITS SORTED(DESCENDING) FORM .\n unordered_map<int,int>mpp;// TO STORE SPELL WITH THEIR SUCCESS.\n vector<int>ans; // FINAL RESULT WILL BE STORED .\n\n sort(p.begin(),p.end());\n\n sort(s.begin(),s.end(),greater<int>()); // SORTING IN DESCENDING .\n\n int n=s.size();int n2=p.size();\n // K IS USED FOR NEW INDEX FROM WHERE NEXT SPELL SHOULD CHECK IN POTION FOR THEIR SUCCESS .\n int k=0;\n\n for(int i=0;i<n;i++){\n\n bool flag=0;// for check if any spell is making success or not.\n\n for(int j=k;j<n2;j++){\n // 1LL for avoiding overflow of int .\n if(1LL*s[i]*p[j]>=suc){\n k=j; // storing new index for next spell to traverse.\n flag=1;\n mpp[s[i]]=n2-j;// storing success of current spell.\n break;\n }\n }\n // if spell is not making success ,break;\n if(flag==0){ break; } \n }\n\n for(int i=0;i<n;i++){\n // if spell was making any success .It had stored in mpp.\n if(mpp.count(ss[i]))ans.push_back(mpp[ss[i]]);\n\n else ans.push_back(0);\n }\n\n return ans;\n }\n};\n```\nCODE BY :) AMAN MAURYA \nTHANK YOU \n\nUPVOTE IF YOU FOUND IT EASY OR DIFFERENT .\n\n | 7 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | [Java] Easy solution using Binary search || O(n*logn) | java-easy-solution-using-binary-search-o-9z8s | O(n*log(n)) / O(1)\n\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n \n for(int i | 2000shivam659 | NORMAL | 2022-06-13T12:22:03.490762+00:00 | 2022-06-13T14:12:12.205291+00:00 | 762 | false | **O(n*log(n)) / O(1)**\n```\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n \n for(int i = 0; i < spells.length; i++) {\n int l = 0, r = potions.length;\n \n while(l < r) {\n int m = l + (r - l) / 2;\n \n if((long)spells[i]*potions[m] >= success)\n r = m;\n else\n l = m + 1;\n }\n \n spells[i] = potions.length - l;\n }\n \n return spells;\n }\n```\n*Comment down, If you have any doubt.*\n**Upvote^, If you liked it.** | 7 | 0 | ['Binary Tree', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | Solution By Dare2Solve | Detailed Explanation | Clean Code | solution-by-dare2solve-detailed-explanat-fcnw | Explanation []\nauthorslog.com/blog/ZzthSLHX8W\n\n# Code\n\ncpp []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& | Dare2Solve | NORMAL | 2024-08-22T18:20:48.135733+00:00 | 2024-08-22T18:20:48.135801+00:00 | 772 | false | ```Explanation []\nauthorslog.com/blog/ZzthSLHX8W\n```\n# Code\n\n```cpp []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<long long> arr; // Use long long to handle large numbers\n for (int potion : potions) {\n arr.push_back(ceil(success / (double)potion)); // Ensure double division for accurate results\n }\n sort(arr.begin(), arr.end());\n\n vector<int> res;\n for (int spell : spells) {\n int l = 0, r = arr.size() - 1, M = 0;\n while (l <= r) {\n int m = l + (r - l) / 2;\n if (arr[m] <= spell) {\n l = m + 1;\n M = l;\n } else {\n r = m - 1;\n }\n }\n res.push_back(M);\n }\n\n return res;\n }\n};\n\n```\n\n```python []\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n arr = [math.ceil(success / potion) for potion in potions]\n arr.sort()\n\n res = []\n for spell in spells:\n l, r, M = 0, len(arr) - 1, 0\n while l <= r:\n m = (l + r) // 2\n if arr[m] <= spell:\n l = m + 1\n M = l\n else:\n r = m - 1\n res.append(M)\n\n return res\n\n```\n\n```java []\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n List<Long> arr = new ArrayList<>();\n for (int potion : potions) {\n arr.add((long) Math.ceil((double) success / potion)); // Use long for large numbers\n }\n Collections.sort(arr);\n\n int[] res = new int[spells.length];\n for (int i = 0; i < spells.length; i++) {\n int spell = spells[i];\n int l = 0, r = arr.size() - 1, M = 0;\n while (l <= r) {\n int m = l + (r - l) / 2;\n if (arr.get(m) <= spell) {\n l = m + 1;\n M = l;\n } else {\n r = m - 1;\n }\n }\n res[i] = M;\n }\n\n return res;\n }\n}\n\n```\n\n```javascript []\nvar successfulPairs = function(spells, potions, success) {\n let arr = [];\n for(let potion of potions) {\n arr.push(Math.ceil(success / potion));\n }\n arr.sort((a,b) => a-b);\n const n = arr.length;\n console.log(arr);\n\n const res = [];\n for(let spell of spells) {\n let l=0, r=n-1, M=0;\n while(l<=r) {\n let m = Math.floor((l+r)/2);\n if(arr[m] <= spell) {\n l = m+1;\n M = l;\n } else {\n r = m-1;\n }\n }\n res.push(M);\n } \n return res;\n};\n``` | 6 | 0 | ['Array', 'Two Pointers', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
successful-pairs-of-spells-and-potions | Powerful Binary search Approach | powerful-binary-search-approach-by-ganji-ic5w | \n# Time Complexity----->O(NLogN)\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n | GANJINAVEEN | NORMAL | 2023-04-03T17:44:22.001098+00:00 | 2023-04-03T17:44:22.001139+00:00 | 325 | false | \n# Time Complexity----->O(NLogN)\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n list1=[]\n potions.sort()\n // some test cases are not sorted\n for s in spells:\n // binary search on left most value i.e greater than success\n left,right,index=0,len(potions)-1,len(potions)# index is len(potions) in worst case where no values matches with potions values\n while left<=right:\n mid=(left+right)//2\n if s*potions[mid]>=success:\n right=mid-1\n index=mid\n else:\n left=mid+1\n // add all possible values by total length -index\n list1.append(len(potions)-index)\n return list1\n \n```\n# please upvote me it would encourage me alot\n\n | 6 | 0 | ['Python3'] | 0 |
successful-pairs-of-spells-and-potions | C# Prefix Sum O(m + n) time O(1) space | c-prefix-sum-om-n-time-o1-space-by-harro-hsju | Intuition\nTo get to success we need to check if we can compensate potion power with our spell power. So we need to calculate neededSpellCost for each potion. A | HarrowinG | NORMAL | 2023-04-02T09:39:52.006241+00:00 | 2023-04-02T09:39:52.006278+00:00 | 1,055 | false | # Intuition\nTo get to ```success``` we need to check if we can compensate potion power with our spell power. So we need to calculate ```neededSpellCost``` for each potion. As it is an integer division we need to add 1 when it can\'t be divided to satisfy the requirement. After that we can see which spell can be used with which potion to make needed power.\n\n# Approach\n```neededSpellCost``` can be quite big, such that we won\'t have any possible spell at all, such cases just ignored.\n\nDuring the calculation of ```neededSpellCost``` we starting to build up our ```prefixSum```. After the loop on potions we will have ```prefixSum``` sloted with the number of each spell required.\n\nBut any ```k``` spell power can also be used to cover any less powerful spell. So we are going through ```prefixSum``` and accumulate it.\n\nLast run just goes through potions and sees how many each potion can cover.\n\n# Complexity\n- Time complexity: ```O(m + n + 100000)``` => ```O(m + n)```\n\n- Space complexity: ```O(100000)``` => ```O(1)```\n\n# Code C#\n```\npublic class Solution {\n public int[] SuccessfulPairs(int[] spells, int[] potions, long success)\n {\n var limit = 100001;\n var prefixSum = new int[limit];\n for (var i = 0; i < potions.Length; i++)\n {\n var neededSpellCost = success % potions[i] == 0\n ? success / potions[i]\n : success / potions[i] + 1;\n\n if (neededSpellCost < limit)\n prefixSum[neededSpellCost]++;\n }\n\n for (var i = 1; i < prefixSum.Length; i++)\n prefixSum[i] += prefixSum[i - 1];\n\n var result = new int[spells.Length];\n for (var i = 0; i < spells.Length; i++)\n result[i] = prefixSum[spells[i]];\n\n return result;\n }\n}\n``` | 6 | 0 | ['Prefix Sum', 'C#'] | 1 |
successful-pairs-of-spells-and-potions | Python Solution Explained | python-solution-explained-by-vi_ek-ivls | \'\'\'\n\n def successfulPairs(self, spells: List[int], potions: List[int], s: int) -> List[int]:\n q=[]\n potions.sort() | vi_ek | NORMAL | 2022-06-11T17:49:26.043189+00:00 | 2022-06-11T17:49:26.043231+00:00 | 911 | false | \'\'\'\n\n def successfulPairs(self, spells: List[int], potions: List[int], s: int) -> List[int]:\n q=[]\n potions.sort() #Sort the potion array\n a=len(potions)\n for i in spells:\n count=0\n l=0 #We have to find a value which is less than (success/i) in sorted array \n r=len(potions) # binary seach will give index of that point and onwards that index all are \n x=s/i #greater values \n while l<r:\n mid=l+(r-l)//2\n if potions[mid]>=x:\n r=mid\n else:\n l=mid+1\n \n count=(a-l) #Last - index that came with binary search\n q.append(count)\n return q\n\'\'\' | 6 | 0 | ['Binary Search', 'Tree', 'C', 'Python'] | 1 |
successful-pairs-of-spells-and-potions | Python 3 | Math, Binary Search | Explanation | python-3-math-binary-search-explanation-t8wy5 | Explanation\n- The order of potions doesn\'t matter, we just need to find out how many potion can form a successful pair with the current spell\n\t- Thus, we ca | idontknoooo | NORMAL | 2022-06-11T17:41:22.360730+00:00 | 2022-06-11T17:45:32.190588+00:00 | 709 | false | ### Explanation\n- The order of `potions` doesn\'t matter, we just need to find out how many potion can form a *successful* pair with the current *spell*\n\t- Thus, we can sort `potions` to make a faster binary search\n- We can\'t use spell to multiply each potion, it takes a long time `O(mn)`; \n\t- Instead, we can use `success` to divided by the current *spell*, which is a `O(1)` operation\n- If `success % spell == 0`, then we want to include `success // spell`\n\t- Thus, we will use a `bisect_left`\n- Otherwise, we don\'t want to include `success // spell`\n\t- Thus, we will use a `bisect_right`\n- `n - idx` is the number of *successful* potions with the current *spell*\n- Time: `O(nlgm), n = len(spells), m = len(potions)`\n### Implementation\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n ans, n = [], len(potions)\n for spell in spells:\n val = success // spell\n if success % spell == 0:\n idx = bisect.bisect_left(potions, val)\n else: \n idx = bisect.bisect_right(potions, val)\n ans.append(n - idx)\n return ans\n``` | 6 | 0 | ['Math', 'Binary Search', 'Python', 'Python3'] | 1 |
successful-pairs-of-spells-and-potions | Python Two Pointers Solution w/ sorting (WITHOUT binary search) | python-two-pointers-solution-w-sorting-w-6tum | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea is to initially sort both the spells and potions array, and then initialize a | nelsonh15 | NORMAL | 2023-04-02T23:01:36.559855+00:00 | 2023-04-02T23:15:16.867976+00:00 | 447 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to initially sort both the ```spells``` and ```potions``` array, and then initialize a variable called ```p``` at the last element of ```potions```. ```p``` will only move from right to left, while another pointer, ```s```, will iterate through ```spells``` from left to right. We will check if ``` spells[s]*potions[p] >= success ```. If so, keep on moving the ```p``` pointer to the left until that condition fails. Record the result once that condition fails for each iteration of ```spells```.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Since the order of our ```spells``` array is important in order to return the number of potions that will form a successful pair with each element in ```spell```, we will recreate the ```spells``` list as a nested list that stores each of its elements and its index.\n```Ex. spells = [5,1,3] -> spells = [[5,0],[1,1],[3,2]]```\n2. Sort both ```spells``` and ```potions```.\n3. Initialize ```result``` and ```p``` to ```[0]*len(spells)``` and ```len(potions)-1```, respectively. The ```result``` array will be returned in the end.\n4. Run a for-loop on ```spells``` and for each iteration, we run a while-loop that checks if ```spells[s][0]*potions[p] >= success```. If so, we decrement the ```p``` pointer until that condition fails. There\'s no point in checking further since we already found the potion with the least strength that will form a successful pair for the ```spell[s]``` spell.\n5. Once the while-loop breaks, we can compute the number of potions that will form a successful pair by doing ```len(potions)-p-1``` and replace the element\'s value in ```result``` on the ```spells[s][1]``` index.\n\n# Complexity\n- Time complexity: **O(nlog(n)+mlog(m)+n)** because we sorted both input lists and iterate through ```spells```\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n spells = [[spells[i],i] for i in range(len(spells))]\n spells.sort()\n potions.sort()\n\n result = [0]*len(spells)\n p = len(potions)-1\n for s in range(len(spells)):\n while p >= 0 and spells[s][0]*potions[p] >= success:\n p -= 1\n result[spells[s][1]] = len(potions)-p-1\n\n return result\n``` | 5 | 0 | ['Array', 'Two Pointers', 'Sorting', 'Counting', 'Python3'] | 1 |
successful-pairs-of-spells-and-potions | 🚨 [JavaScript][php] - Beats 100% - Binary Search - faster than other solutions | javascriptphp-beats-100-binary-search-fa-qavq | \n# Approach\nHere is my approach to solving the problem using a binary search:\n\n First, we sort the potions array in ascending order. This ensures that the s | hobobobo256 | NORMAL | 2023-04-02T17:37:51.117222+00:00 | 2023-04-02T17:37:51.117256+00:00 | 721 | false | \n# Approach\nHere is my approach to solving the problem using a binary search:\n\n* First, we sort the potions array in ascending order. This ensures that the smallest potions are at the front of the\n array.\n\n* Then, we iterate over the spells array. For each spell, we perform _a binary search_ on the potions array to find the\n first potion that is greater than or equal to the _success_ value.\n\n* The number of potions that are greater than or equal to the spell\'s power is the number of successful pairs that can\n be formed with that spell.\n* We add this number to the pairs result array.\n* We continue this process until we have iterated over all of the spells.\n* Finally, we return the pairs array.\n\n# Complexity\n\nThe **time complexity** of the algorithm is O(n log m), where n is the number of potions, and m is the number of spells.\nThis is because the algorithm sorts the potions array in O(n log n) time and performs a binary search on the potions\narray for each spell, which takes O(n*log m) time. => O( (n+m) * log m) => O(n log m)\n\nThe **space complexity** of the algorithm is O(1), since the algorithm only requires a constant amount of space to store\nthe\npotions array, the spells array, the success value, and the pairs array.\n\n```javascript []\n/**\n * Binary search approach O((n+m)*log(m))\n *\n * @param {number[]} spells\n * @param {number[]} potions\n * @param {number} success\n * @return {number[]}\n */\nvar successfulPairs = function (spells, potions, success) {\n const pairs = [];\n potions.sort((a, b) => a - b);\n const spellsLength = spells.length;\n const potionsLength = potions.length;\n\n for (let i = 0; i < spellsLength; i++) {\n let count = 0;\n // binary search\n let left = 0;\n let right = potionsLength - 1;\n while (left <= right) {\n // const mid = Math.floor((left + right) / 2);\n const mid = (left + right) >> 1;\n if (spells[i] * potions[mid] >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n count = potionsLength - left;\n pairs.push(count);\n }\n return pairs;\n };\n```\n\n```php []\nclass Solution\n{\n /**\n * @param Integer[] $spells\n * @param Integer[] $potions\n * @param Integer $success\n * @return Integer[]\n */\n function successfulPairs(array $spells, array $potions, int $success): array {\n $pairsResult = [];\n $potionsCount = count($potions);\n $spellsCount = count($spells);\n sort($potions);\n // binary search\n for ($i = 0; $i < $spellsCount; $i++) {\n $left = 0;\n $right = $potionsCount - 1;\n while ($left <= $right) {\n $mid = ($left + $right) >> 1;\n if ($spells[$i] * $potions[$mid] >= $success) {\n $right = $mid - 1;\n } else {\n $left = $mid + 1;\n }\n }\n $pairsResult[$i] = $potionsCount - $left;\n }\n return $pairsResult;\n }\n}\n```\n\n```javascript []\n/**\n * Binary search approach with with small optimization\n *\n * @param {number[]} spells\n * @param {number[]} potions\n * @param {number} success\n * @return {number[]}\n */\nvar successfulPairs = function (spells, potions, success) {\n const pairs = [];\n potions.sort((a, b) => a - b);\n const spellsLength = spells.length;\n const potionsLength = potions.length;\n\n let maxSpellValueWithZeroSuccess = 0; // Optimize - max value of a spell that will never be successful\n\n for (let i = 0; i < spellsLength; i++) {\n let count = 0;\n if (spells[i] > maxSpellValueWithZeroSuccess) {\n // binary search\n let left = 0;\n let right = potionsLength - 1;\n while (left <= right) {\n const mid = (left + right) >> 1;\n if (spells[i] * potions[mid] >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n count = potionsLength - left;\n if (count == 0) maxSpellValueWithZeroSuccess = spells[i];\n }\n pairs.push(count);\n }\n return pairs;\n };\n```\n\n##### Thanks for reading! If you have any questions or suggestions, please leave a comment below. I would love to hear your thoughts! \uD83D\uDE0A\n### **Please upvote if you found this post helpful! \uD83D\uDE4F** | 5 | 0 | ['Binary Search', 'PHP', 'JavaScript'] | 3 |
successful-pairs-of-spells-and-potions | [Kotlin] Binary search | kotlin-binary-search-by-dzmtr-veuj | \nimport kotlin.math.ceil\n\nclass Solution {\n fun successfulPairs(spells: IntArray, potions: IntArray, success: Long): IntArray {\n val res = IntArray(s | dzmtr | NORMAL | 2023-04-02T12:20:56.732014+00:00 | 2023-04-02T12:20:56.732060+00:00 | 48 | false | ```\nimport kotlin.math.ceil\n\nclass Solution {\n fun successfulPairs(spells: IntArray, potions: IntArray, success: Long): IntArray {\n val res = IntArray(spells.size)\n potions.sort()\n\n fun findIndex(target: Long): Int {\n var lo = 0\n var hi = potions.lastIndex\n\n while (lo < hi) {\n val mid = lo + (hi - lo) / 2\n if (potions[mid] >= target) hi = mid else lo = mid + 1\n }\n return hi\n }\n\n for (i in spells.indices) {\n val target = ceil(success / spells[i].toDouble()).toLong()\n if (potions.last() < target) continue\n res[i] = potions.lastIndex - findIndex(target = target) + 1\n }\n\n return res\n}\n}\n```\n\n___\nTime: O(n*logn) - cost for sort\nSpace: O(n) - cost of result array\n___\n\n\n\n | 5 | 0 | ['Binary Search', 'Kotlin'] | 0 |
successful-pairs-of-spells-and-potions | Binary Search | Intuition explained with example | binary-search-intuition-explained-with-e-i378 | Intuition\n Describe your first thoughts on how to solve this problem. \nIf we sort the potions array and find the minimum index where the product is greater th | nidhiii_ | NORMAL | 2023-04-02T06:14:47.348241+00:00 | 2023-04-02T06:24:49.698869+00:00 | 887 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we sort the potions array and find the minimum index where the product is greater than or equal to success, then we can be sure that the rest of the potions array will give product greater than or equal to success only.\n\nTo solve this kind of problem, we can use Binary Search. We can search in the range 0 to potions.size() and update the range according to whether the mid-value is enough or not.\n\n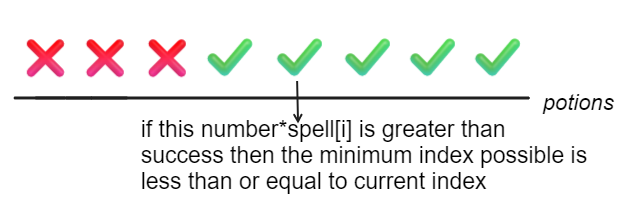\n\nThe condition would be:\n``` \nspell[i]*potions[j]>=success\n=> potions[j]>=success/spell[i] (as success can be a large number)\n```\nNow we need to find the index where this condition is satisfied for the first time.\n# Example\nLet\'s say we have the following inputs:\n```\nspells = [2, 3, 4]\npotions = [1, 2, 3, 4, 5]\nsuccess = 5\n```\n\nAfter sorting potions, we have:\n```\npotions = [1, 2, 3, 4, 5]\n```\n\nFor num = spell[0] = 2, we call binary search. \n```\nsuccess/num = 2.5 \nThe index of the first element in potions that is >= 2.5 is 2.\nTherefore, we append size-idx = 5-2 = 3 to the ans vector.\n```\nFor num = 3:\n```\nsuccess/num = 1.67\nThe index of the first element in potions that is >= 1.67 is 1.\nTherefore, we append n-idx = 5-1 = 4 to the ans vector.\n```\n\nFor num = 4:\n```\nThe index of the first element in potions that is g>= 1.25 is 0.\nTherefore, we append n-idx = 5-0 = 5 to the ans vector.\n```\nThe final ans vector:\n```\n[3, 4, 5]\nindicating that there are 3 successful pairs for num = 2, \n4 successful pairs for num = 3, \nand 5 successful pairs for num = 4.\n```\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(mlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int binarySearch(int num, vector<int>& potions, long long success){\n int left=0, right=potions.size()-1;\n double curr=(double)success/num; \n while(left<right){\n int mid=left+(right-left)/2;\n if(potions[mid]>=curr){ \n right=mid; // set right to mid to search for lower indices\n }\n else left=mid+1; // else set left to mid+1 to search for higher indices\n }\n if(potions[right]>=curr) return right; // if any element has product greater than or equal to success\n else return -1; // else potion with success probability not fount\n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int>ans;\n int n=potions.size();\n sort(potions.begin(),potions.end()); \n for(int num:spells){\n int idx=binarySearch(num,potions,success); // find index where condition is satisfied for the first time\n if(idx==-1) ans.push_back(0); // if potion with success probability not found, add 0\n else ans.push_back(n-idx); // else, n-idx would be the number of pairs that satisfy the condition\n }\n return ans; \n }\n};\n\n``` | 5 | 0 | ['Binary Search', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Clear C# Binary Search beats 95.4% | clear-c-binary-search-beats-954-by-need_-96oo | Intuition\n Describe your first thoughts on how to solve this problem. \nAfter sort potions, this problem becomes to: for each spells[i], find the first index i | need_what | NORMAL | 2023-04-02T03:31:56.960069+00:00 | 2023-04-02T03:31:56.960101+00:00 | 582 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter sort potions, this problem becomes to: for each spells[i], find the first index in potions that spells[i] * potions[index] >= success. Then the pair that spells[i] can form is potions.Length - index\n\nFind the first index match a condition is a typical binary search question.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mlogm + nlogm)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\npublic class Solution {\n public int[] SuccessfulPairs(int[] spells, int[] potions, long success) {\n Array.Sort(potions);\n int[] retval = new int[spells.Length];\n for(int i = 0; i < spells.Length; i++)\n {\n int l = 0, r = potions.Length - 1;\n int leftMostIdx = -1;\n while(l <= r)\n {\n int m = (l + r) / 2;\n if (((long)spells[i]) * potions[m] >= success)\n {\n leftMostIdx = m;\n r = m - 1;\n }\n else l = m + 1;\n }\n retval[i] = leftMostIdx == -1 ? 0 : potions.Length - leftMostIdx;\n }\n\n return retval; \n }\n}\n``` | 5 | 0 | ['C#'] | 0 |
successful-pairs-of-spells-and-potions | JAVA || Easy Solution Using Binary Search || Beginner friendly || Using Map | java-easy-solution-using-binary-search-b-zp1a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shivrastogi | NORMAL | 2023-04-02T01:05:09.528664+00:00 | 2023-04-02T01:05:09.528687+00:00 | 2,466 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n \n Map<Integer, int[]> duplicates;\n\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int[] pairs = new int[spells.length];\n Arrays.sort(potions);\n int ind = 0;\n duplicates = new HashMap<>();\n for (int i = 0; i < potions.length; i++) {\n if (duplicates.containsKey(potions[i])) {\n int[] idx = duplicates.get(potions[i]);\n duplicates.put(potions[i], new int[]{idx[0], i});\n } else duplicates.put(potions[i], new int[]{i});\n }\n\n for (int s : spells) {\n int idx = bs(potions, (long) Math.ceil((double) success / s));\n if (idx >= 0) {\n pairs[ind++] = potions.length - idx;\n } else {\n pairs[ind++] = 0;\n }\n }\n return pairs;\n }\n\n private int bs(int[] potions, long value) {\n int l = 0, h = potions.length - 1;\n while (l < h) {\n int mid = l + (h - l) / 2;\n if (value < potions[mid]) {\n h = mid;\n } else if (value > potions[mid]) {\n l = mid + 1;\n } else if (value == potions[mid]) {\n return duplicates.get(potions[mid])[0];\n }\n }\n\n return potions[l] < value ? -1 : l;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | ✅C++ | ✅Use Binary Search | ✅Efficient solution | c-use-binary-search-efficient-solution-b-ewuv | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) \n {\n int sn = spells.size | Yash2arma | NORMAL | 2022-06-12T05:52:14.509715+00:00 | 2023-04-02T05:45:19.193588+00:00 | 654 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) \n {\n int sn = spells.size();\n int pn = potions.size();\n vector<int> ans; //stores answer\n \n sort(potions.begin(), potions.end()); //sort potions for binary search\n \n for(auto it : spells)\n {\n int left=0, right=pn-1, mid; //define left, right and mid pointers\n \n while(left<=right) //iterate until right is lesser than left\n {\n mid = (left+right)>>1; \n \n if((long long)it*potions[mid] >= success) right=mid-1;\n \n else left=mid+1;\n }\n ans.push_back(pn-left);\n }\n return ans;\n \n }\n};\n```\n\n# Please upvote if you like this approach :) | 5 | 0 | ['Binary Search', 'C', 'Sorting', 'Binary Tree', 'C++'] | 1 |
successful-pairs-of-spells-and-potions | 🧪🧙♂️ Successful Pairs of Spells and Potions – Binary Search Brew! ⚡️ | successful-pairs-of-spells-and-potions-b-j0se | 💡 IntuitionYou’re given two arrays:spells[i] = power of the i-th spellpotions[j] = strength of the j-th potion
You need to count how many potions can be paired | NAVNEETkharb | NORMAL | 2025-04-05T16:42:03.839958+00:00 | 2025-04-05T16:42:03.839958+00:00 | 144 | false | # 💡 Intuition
You’re given two arrays:
spells[i] = power of the i-th spell
potions[j] = strength of the j-th potion
You need to count how many potions can be paired with each spell such that:
spell[i] * potion[j] ≥ success
---
# 🚀 Approach – Sort & Binary Search Combo! 🧠
To efficiently count how many potions will succeed with a given spell, we:
1️⃣ Sort the potions array
2️⃣ For each spell, use binary search to find the first potion that satisfies spell * potion ≥ success
3️⃣ All potions from that point to the end of the array are valid ✅
---
# 🧭 Steps
Sort the potions array (once).
For each spell:
Binary search to find the lowest index where `spell * potion ≥ success`
The count is `potions.length - index`
Store the result for each spell.
---
# ⏱ Time & Space Complexity
Time Complexity:
- Sorting potions: O(m log m)
- For each spell: O(log m) binary search
- Total: O(n log m) ✅
Space Complexity: O(1) extra space (excluding output array)
---
# Code
```java []
class Solution {
public int[] successfulPairs(int[] spells, int[] potions, long success) {
int n = spells.length, m = potions.length;
Arrays.sort(potions);
int[] pairs = new int[n];
for(int i = 0; i<n; i++){
int low = 0, high = m-1;
while(low<=high){
int mid = low+(high-low)/2;
long num = (long)spells[i]*potions[mid];
if(num>=success) high = mid-1;
else low = mid+1;
}
pairs[i] = m - (high+1);
}
return pairs;
}
}
```
```C++ []
class Solution {
public:
vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {
sort(potions.begin(), potions.end());
int m = potions.size();
vector<int> res;
for (int spell : spells) {
int low = 0, high = m - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
long long product = (long long) spell * potions[mid];
if (product >= success) {
high = mid - 1;
} else {
low = mid + 1;
}
}
res.push_back(m - (high + 1));
}
return res;
}
};
```
```python []
from bisect import bisect_left
class Solution:
def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:
potions.sort()
m = len(potions)
res = []
for spell in spells:
target = (success + spell - 1) // spell # Ceiling division to avoid float
idx = bisect_left(potions, target)
res.append(m - idx)
return res
```
---
# 🎯 Summary
Combining sorting and binary search is a game-changer when you need to count elements that satisfy a condition efficiently. A perfect blend of logic and optimization 🔥
# If this made it easier for you, don’t forget to UPVOTE ⬆️ and share with your network. Let's learn together! 🙌💬
| 4 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'Python', 'C++', 'Java'] | 1 |
successful-pairs-of-spells-and-potions | Go simple solution | go-simple-solution-by-khangtn1-31lg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | khangtn1 | NORMAL | 2023-09-30T14:20:05.006091+00:00 | 2023-09-30T14:21:23.286064+00:00 | 209 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O((m+n)*logm)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npackage main\n\nimport "sort"\n\nfunc successfulPairs(spells []int, potions []int, success int64) []int {\n\tsort.Ints(potions)\n\tres := []int{}\n\tfor i := 0; i < len(spells); i++ {\n\t\tl, r := 0, len(potions)-1\n\t\tfor l <= r {\n\t\t\tm := l + (r-l)/2\n\t\t\tif int64(spells[i]*potions[m]) < success {\n\t\t\t\tl = m + 1\n\t\t\t} else {\n\t\t\t\tr = m - 1\n\t\t\t}\n\t\t}\n\t\tres = append(res, len(potions)-l)\n\t}\n\treturn res\n}\n\n``` | 4 | 0 | ['Go'] | 0 |
successful-pairs-of-spells-and-potions | Java. Binary Search. Spells and Potions | java-binary-search-spells-and-potions-by-moyo | \n\nclass Solution {\n public int search(int[] nums, long target, long sel) {\n int start = 0;\n int finish = nums.length - 1;\n int med | red_planet | NORMAL | 2023-04-02T20:43:50.512477+00:00 | 2023-04-02T20:43:50.512523+00:00 | 1,025 | false | \n```\nclass Solution {\n public int search(int[] nums, long target, long sel) {\n int start = 0;\n int finish = nums.length - 1;\n int med;\n if (target < nums[start] * sel) return start;\n if (target > nums[finish] * sel) return nums.length;\n\n while (start < finish && nums[start] < nums[finish])\n {\n if (target == nums[start] * sel) return start;\n med = (start + finish) / 2;\n if (target > nums[med] * sel)\n start = med + 1;\n else\n finish = med;\n\n }\n if (nums[start] * sel == target) return start;\n if (nums[start] * sel < target)\n return start + 1;\n else\n return start;\n }\n\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n HashMap<Integer, Integer> dict = new HashMap<>();\n Arrays.sort(potions);\n int [] answ = new int[spells.length];\n for (int i = 0; i < spells.length; i++) {\n if (!dict.containsKey(spells[i]))\n dict.put(spells[i], potions.length - search(potions, success, spells[i]));\n answ[i] = dict.get(spells[i]);\n }\n return answ;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | Binary Search for Success. | binary-search-for-success-by-shahscript-2jdf | Intuition\n Describe your first thoughts on how to solve this problem. \nUsing Binary Search for suucess.\n\n# Approach\n Describe your approach to solving the | shahscript | NORMAL | 2023-04-02T19:25:02.112066+00:00 | 2023-04-02T19:25:02.112099+00:00 | 253 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing Binary Search for suucess.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort the array.\n- Binary Search to locate the dividing element.\n- Dividing element is where the product is just started to get greater.\n For Ex.\n spell = 5,\n potions = [1,2,3,4,5]\n success = 16\n then, dividing element = 4 (index = 3);\n- subtracting the index with the length.\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*log(M) + MlogM)\n*MlogM for Sorting.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n\n\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] arr, int[] arr1, long suc) {\n int[] res = new int[arr.length];\n Arrays.sort(arr1);\n int l, r, mid;\n long t;\n for (int i = 0; i < arr.length; i++) {\n l = 0;\n r = arr1.length - 1;\n while (l <= r) {\n mid = (l + r) / 2;\n t = arr[i];\n if (arr1[mid] * t >= suc) {\n r = mid - 1;\n if(r==-1){\n res[i] = arr1.length;\n }\n } else if (arr1[mid] * t < suc) {\n if (mid + 1 < arr1.length && arr1[mid + 1] * t >= suc) {\n res[i] = arr1.length - (mid + 1);\n break;\n }\n l = mid + 1;\n }\n }\n }\n\n return res;\n }\n}\n\n``` | 4 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | C++ ✅✅ Easy LOWER BOUND 2023 short sol MUST WATCH. | c-easy-lower-bound-2023-short-sol-must-w-lezs | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long t) {\n sort(p.begin(),p.end());\n vector<in | dynamo_518 | NORMAL | 2023-04-02T17:02:15.695679+00:00 | 2023-04-02T17:02:15.695714+00:00 | 1,000 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long t) {\n sort(p.begin(),p.end());\n vector<int> ans; \n int x; long long y;\n for(auto &it:s) {\n y = t / it;\n x = p.end() - lower_bound(p.begin(),p.end(),y * it >= t ? y : y + 1);\n ans.push_back(x);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['C', 'Sorting', 'Binary Tree'] | 1 |
successful-pairs-of-spells-and-potions | Easy and fast C++ Solution with full explanation | easy-and-fast-c-solution-with-full-expla-pmgb | Intuition\nsorting the potions array to reduce the number of operations to search(binary search) for the element whose product with ith spell is greater than or | technoreck | NORMAL | 2023-04-02T06:59:22.570842+00:00 | 2023-04-02T07:03:58.288677+00:00 | 888 | false | # Intuition\nsorting the potions array to reduce the number of operations to search(binary search) for the element whose product with ith spell is greater than or equal to the success.\n\n# Approach\n1. sort `potions` array.\n2. use `binary search` to search for the element whose product with that spell is equal or just greater than `success`.\n3. count all the elements after that element *(including that element)* in `potions` array as all the elements after this element are greater than it and hence will result in greater product than `success`.\n4. store that count in an `ans` vector.\n5. return `ans`.\n\n# Complexity\n- Time complexity:\n`O(n*logm)`\n\n- Space complexity:\n`O(n)`\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size();\n int m = potions.size();\n sort(potions.begin(), potions.end());\n vector<int> ans;\n for(auto &i: spells){\n int j = 0;\n int k = m-1;\n while(j<=k){\n int mid = (j+k)/2;\n int long x = potions[mid];\n if(i*x<success){\n j = mid + 1;\n }\n else{\n k = mid - 1;\n }\n }\n ans.push_back(m-k-1);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Array', 'Binary Search', 'Sorting', 'C++'] | 1 |
successful-pairs-of-spells-and-potions | python3 Solution | python3-solution-by-motaharozzaman1996-u59f | \n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n N=len(pot | Motaharozzaman1996 | NORMAL | 2023-04-02T04:11:56.216778+00:00 | 2023-04-02T04:11:56.216809+00:00 | 1,698 | false | \n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n N=len(potions)\n ans=[]\n for s in spells:\n target=(success-1)//s\n index=bisect.bisect_right(potions,target)\n ans.append(N-index)\n \n return ans \n``` | 4 | 0 | ['Python', 'Python3'] | 2 |
successful-pairs-of-spells-and-potions | 🗓️ Daily LeetCoding Challenge April, Day 2 | daily-leetcoding-challenge-april-day-2-b-pxj4 | This problem is the Daily LeetCoding Challenge for April, Day 2. Feel free to share anything related to this problem here! You can ask questions, discuss what y | leetcode | OFFICIAL | 2023-04-02T00:00:23.491056+00:00 | 2023-04-02T00:00:23.491124+00:00 | 6,742 | false | This problem is the Daily LeetCoding Challenge for April, Day 2.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/successful-pairs-of-spells-and-potions/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 0 approach in the official solution</summary>
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 4 | 0 | [] | 18 |
successful-pairs-of-spells-and-potions | ✅C++ || Binary Search || Explanation with Comments | c-binary-search-explanation-with-comment-vx4a | Please Upvote If It Helps\n\n\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) \n {\ | mayanksamadhiya12345 | NORMAL | 2022-06-11T19:56:14.635500+00:00 | 2022-06-11T19:56:14.635530+00:00 | 461 | false | **Please Upvote If It Helps**\n\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) \n {\n // declare a vector of size spell that will store our ans\n int n = spells.size();\n int m = potions.size();\n vector<int> ans(n,0);\n \n // sort the potions fir applying the binary search\n sort(potions.begin(),potions.end());\n \n int i = 0; // it will help in storing the ans\n \n // start iterating over the spells\n for(auto& x : spells)\n {\n int l = 0;\n int r = m-1;\n int mid;\n \n // binary search\n while(l <= r)\n {\n mid = (l+r)>>1;\n \n // if it gives our need then reduce the window to the left side for cheking more \n if((long long)x*potions[mid] >= success)\n r = mid-1;\n \n // if not then check to the right side\n else\n l = mid+1;\n }\n ans[i] = m-l; // storing the answer (total size - not needed size)\n i++;\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['C'] | 0 |
successful-pairs-of-spells-and-potions | [C++] | Binary search | short and simple logic | c-binary-search-short-and-simple-logic-b-ap4n | For each spell,\nneed = success * 1.0 / spell\nBinary search the index of first potion >= need in the sorted potions.\nThe number of potions that are successful | synapse50 | NORMAL | 2022-06-11T17:39:01.493478+00:00 | 2022-06-11T17:45:15.548535+00:00 | 605 | false | For each spell,\n**need = success * 1.0 / spell**\nBinary search the index of **first potion >= need** in the sorted potions.\nThe number of potions that are successful are **potions.length - index**\n```\nvector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(),potions.end());\n long long need;\n vector<int> ans;\n for(int spell:spells){\n need=ceil(success*1.0/spell);\n ans.push_back(potions.end()-lower_bound(potions.begin(),potions.end(),need));\n }\n return ans;\n }\n```\n*-----please upvote-----* | 4 | 0 | ['C', 'Binary Tree'] | 0 |
successful-pairs-of-spells-and-potions | Python||Binary Search||Explanation | pythonbinary-searchexplanation-by-nandha-xbcx | I Was Also One Of The Person Who Got TLE At The First Attempt\n\nThe Straight Forward Approach was to multiply each and every value of potion with the every val | nandhan11 | NORMAL | 2022-06-11T16:38:05.105249+00:00 | 2022-06-11T16:40:27.362015+00:00 | 470 | false | I Was Also One Of The Person Who Got TLE At The First Attempt\n\nThe Straight Forward Approach was to multiply each and every value of potion with the every value of spell and count the values which are greater than success and append to the answer array. This was one of the common solution which every one thinks of..\n\nThe Solution For Me Which Got Accepted Was After Using Binary Search With Sorting Array.\n\nLet Us See How It Worked For Me..\n\nSuppose spell = [5,1,3] potions = [1,2,3,4,5] success = 7\n\nConsider First Element Of Spell - 5 the least number that makes 5 after multiplying results to greater than or equal to 7 that is obviously 2 - So the resultant value will be 4 \n\nConsider Second Element Of Spell -1 The Smallest Number That Makes Greater Than or equal to 7 is 7 but it is not in the array so the resultant value will be 0\n\nConsider Last Element Of Spell - 3 The Smallest Number That Makes 3 Greater Than Or Equal To 7 is 3 - So the Resultant Value will be 3\n\nSimilarly For Every Value in Spell If We Are Able To Find The Smaller Value Which After Multiplying Makes Greater Than Success Value And Then We Had To Find The Left Most Index Which Will Be Suitable For Placing The Obtained Value In The Potions Will Result Us Answer.\n\nThis is my following Code For The Problem..\n\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n result = self.function(spells,potions,success)\n return result\n \n def function(self,arr1,arr2,success):\n n2 = len(arr2)\n arr2.sort() #Sorting Enables Us To Do Binary Search\n ans = []\n for i in arr1:\n val = math.ceil(success/i) #Finding the Value Of Portion With Least Strength So That It Can Be Greater Than Success\n idx = bisect.bisect_left(arr2,val) #Finding The Left Most Index So That The Value Can Be Inserted\n res = n2-idx+1 #Calculating the remaining numbers after finding the suitable index\n ans.append(res-1)\n return ans\n```\n\nPlease Upvote If You Like The Explanation..\uD83D\uDE0A\n\n\nHappy LeetCoding!!!! | 4 | 1 | ['Sorting', 'Binary Tree', 'Python'] | 1 |
successful-pairs-of-spells-and-potions | c++ solution using binary search | c-solution-using-binary-search-by-dilips-44lx | \nclass Solution {\npublic:\n int find(vector<int>&nums,long long val,long long max_val)\n {\n int l=0;\n int r=nums.size()-1;\n int | dilipsuthar17 | NORMAL | 2022-06-11T16:31:40.841845+00:00 | 2022-06-11T16:31:40.841876+00:00 | 232 | false | ```\nclass Solution {\npublic:\n int find(vector<int>&nums,long long val,long long max_val)\n {\n int l=0;\n int r=nums.size()-1;\n int ans=0;\n int n=nums.size();\n while(l<=r)\n {\n int mid=(l+r)/2;\n if((1ll)*nums[mid]*val>=max_val)\n {\n ans=n-mid;\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n return ans;\n }\n vector<int> successfulPairs(vector<int>& s, vector<int>& nums, long long success) \n {\n int n=s.size();\n vector<int>ans;\n sort(nums.begin(),nums.end());\n for(int i=0;i<n;i++)\n {\n int val=find(nums,s[i],success);\n ans.push_back(val);\n }\n return ans;\n }\n};\n``` | 4 | 2 | ['C', 'Binary Tree', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Beats 93.22% in C++ | Binary Search Algorithm | beats-9322-in-c-binary-search-algorithm-gmimr | Code\ncpp []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n \n int | SPA111 | NORMAL | 2024-08-22T14:36:25.614584+00:00 | 2024-08-22T14:36:25.614618+00:00 | 684 | false | # Code\n```cpp []\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n \n int n = spells.size();\n int m = potions.size();\n vector<int> pairs;\n\n sort(potions.begin(), potions.end());\n\n for(int i = 0; i < n; i++)\n pairs.push_back(m - (lower_bound(potions.begin(), potions.end(), (double)success / spells[i]) - potions.begin()));\n\n return pairs;\n }\n};\n``` | 3 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | [ Python ] | Simple & Clean Solution using Binary Search | python-simple-clean-solution-using-binar-9ixa | Code\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n ans = []\n potions.sor | yash_visavadia | NORMAL | 2023-04-29T18:42:22.079116+00:00 | 2023-04-29T18:42:22.079140+00:00 | 419 | false | # Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n ans = []\n potions.sort()\n\n n = len(potions)\n for s in spells:\n ind = bisect_left(potions, success / s)\n ans.append(n - ind)\n return ans\n```\n\n## Binary Search\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n ans = []\n potions.sort()\n\n n = len(potions)\n for s in spells:\n l, r = 0, n - 1\n while l <= r:\n mid = (l + r) >> 1\n if potions[mid] * s >= success:\n r = mid - 1\n else:\n l = mid + 1\n ans.append(n - l)\n return ans\n``` | 3 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'Python3'] | 0 |
successful-pairs-of-spells-and-potions | C++ Solution | c-solution-by-pranto1209-z5cw | Approach\n Describe your approach to solving the problem. \n Binary Search\n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n | pranto1209 | NORMAL | 2023-04-02T20:29:46.078566+00:00 | 2023-08-03T12:43:30.162138+00:00 | 428 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n Binary Search\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N * log M)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = potions.size();\n sort(potions.begin(), potions.end());\n vector<int> ans;\n for(auto x: spells) {\n int l = 0, r = n - 1;\n while(l <= r) {\n int mid = (l + r) / 2;\n if(1ll * potions[mid] * x < success) l = mid + 1;\n else r = mid - 1;\n }\n ans.push_back(n - l);\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | Java | Binary Search | Clean code | Beats > 87% | java-binary-search-clean-code-beats-87-b-7bp2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | judgementdey | NORMAL | 2023-04-02T19:47:26.597339+00:00 | 2023-04-02T19:52:43.140819+00:00 | 43 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O((m+n) * log(m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log(m))$$ used by the sort algorithm in Java\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n var n = spells.length;\n var m = potions.length;\n var pairs = new int[n];\n \n Arrays.sort(potions);\n\n for (var i=0; i<n; i++) {\n var minPotion = (int) Math.ceil((double) success / spells[i]);\n\n if (minPotion > potions[m-1]) continue;\n\n var l = 0;\n var r = m-1;\n\n while (l < r) {\n var mid = l + (r-l) / 2;\n\n if (potions[mid] < minPotion) l = mid+1;\n else r = mid;\n }\n pairs[i] = m-l;\n }\n return pairs;\n }\n}\n```\nIf you like my solution, please upvote it! | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | Master the Art of Spell and Potion Pairing: A TypeScript Binary Search Approach (100% / 87.50%) | master-the-art-of-spell-and-potion-pairi-wpvo | Intuition\nGiven two arrays representing the strengths of spells and potions, our task is to find the number of successful pairs for each spell. A pair is consi | polyym | NORMAL | 2023-04-02T14:50:51.483934+00:00 | 2023-04-02T14:50:51.483964+00:00 | 172 | false | # Intuition\nGiven two arrays representing the strengths of spells and potions, our task is to find the number of successful pairs for each spell. A pair is considered successful if the product of the strengths of the spell and the potion is at least equal to a given `success` value. To solve this problem efficiently, we can take advantage of a binary search algorithm on the sorted potions array for each spell.\n\n# Approach\n1. **Sort the potions array:** First, we sort the potions array in ascending order. This enables us to perform binary search on the array later in the process. Sorting takes $$O(m * log(m))$$ time, where m is the length of the potions array.\n2. **Define a binary search function:** We create a binary search function that takes an array and a target value as inputs. The function iterates over the array and finds the index where the target value should be inserted while maintaining the sorted order of the array. This function has a time complexity of $$O(log(m))$$ as it is applied to the sorted potions array.\n3. **Iterate over spells:** For each spell in the spells array, we calculate the minimum potion strength required to form a successful pair. To do this, we divide the `success` value by the strength of the current spell and round up to the nearest integer. This gives us the minimum potion strength that, when multiplied by the current spell strength, will produce a product greater than or equal to the `success` value. We then use the binary search function to find the index where this minimum potion strength should be inserted in the sorted potions array.\n4. **Calculate the number of successful pairs:** The number of successful pairs for a given spell is the difference between the length of the potions array and the index found using binary search. This is because all the potions at the index and to the right of it in the sorted array have a strength greater than or equal to the minimum potion strength required for a successful pair with the current spell.\n5. **Return an array with the results:** Finally, we return an array with the number of successful pairs for each spell by mapping over the spells array and performing the above steps for each element. The returned array has the same length as the input spells array.\n\n# Complexity\nTime complexity: $$O(n\u2217log(m))$$, where n is the length of the spells array and m is the length of the potions array. This complexity is due to sorting the potions array in $$O(m * log(m))$$ time and performing binary search on the potions array for each spell in $$O(n * log(m))$$ time.\nSpace complexity: $$O(1)$$, as we only use a constant amount of additional memory for temporary variables.\n\n# Code\n```\n/**\n * Performs binary search on a sorted array to find the index where the target value should be inserted.\n * \n * @param arr - A sorted array of numbers.\n * @param target - The target number to be searched for.\n * @returns The index where the target value should be inserted to maintain the sorted order.\n */\nfunction binarySearch(arr: number[], target: number): number {\n let left = 0;\n let right = arr.length - 1;\n\n // Iterate until the left and right pointers converge.\n while (left <= right) {\n const mid = left + Math.floor((right - left) / 2);\n\n if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n\n // Return the index where the target value should be inserted.\n return left;\n}\n\n/**\n * Calculates the number of successful pairs of spells and potions.\n * A spell and potion pair is considered successful if the product of their strengths is at least `success`.\n *\n * @param spells - An array of integers representing the strengths of the spells.\n * @param potions - An array of integers representing the strengths of the potions.\n * @param success - An integer representing the minimum product of spell and potion strengths required for success.\n * @returns An array of integers representing the number of potions that will form a successful pair with each spell.\n */\nfunction successfulPairs(spells: number[], potions: number[], success: number): number[] {\n // Sort the potions list in ascending order to allow for efficient binary search.\n potions.sort((a, b) => a - b);\n\n // Iterate over each spell in the spells list and use binary search to find the index of the first potion\n // that forms a successful pair, then calculate the number of successful pairs for each spell.\n // The map function creates a new array with the results of calling the provided function on every element in the original spells array.\n return spells.map(\n // Calculate the minimum potion strength required to form a successful pair\n // with the current spell, and use binary search to find the index where the target value should be inserted.\n (spell) => potions.length - binarySearch(potions, Math.ceil(success / spell))\n );\n}\n```\n\n | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'TypeScript'] | 0 |
successful-pairs-of-spells-and-potions | Day92||Binary Search very Easy Solution | day92binary-search-very-easy-solution-by-whuz | Intuition and Approach\nWe have implemented Binary Search to Solve the problem\n\nSo, Condition to use binary tree is that array must be sorted\n\nSo, we used t | Rarma | NORMAL | 2023-04-02T14:13:02.383186+00:00 | 2023-04-02T14:13:02.383230+00:00 | 719 | false | # Intuition and Approach\nWe have implemented Binary Search to Solve the problem\n\nSo, Condition to use binary tree is that array must be sorted\n\nSo, we used the inbuilt sort function.\n\nNow to solve the problem many of you have already tried to do it in O(n^2) order (Code given below) but it is giving the TLE.\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& po, long long success) {\n vector<int> v;\n int count=0;\n\n for(int i=0;i<s.size();i++){\n for(int j=0;j<po.size();j++){\n if(s[i]*po[j] >= success){\n count++;\n }\n }\n v.push_back(count);\n count=0;\n }\n return v;\n }\n};\n```\n(In above approach we are simply calulating the product of two array and comparing it to Success)\nSo, to overcome the TLE we have to think a way to minimize our search space and hence Binary Search came into play\n\nThere is an **Observation** for sorted array which is that if a current potion muliplied with current spell and if it greater than Success then all elements ahead of that position will be a satisfiable answer.\n```\ne.g. spells=[5,3,1] , potion=[1,2,3,4,5] , Success=7\nAns: 5*1=5, 5*2=10, 5*3=15, 5*4=20, 5*5=25\n |\n |--from here, all ahead value will be greater than Success\nSimilarly, 3*1=3, 3*2=6, 3*3=9...\n |\n |--from here, all value satisfy the Success\n*Hence, we have to calculate or find the leftmost value which satisfies \nthe relation.\n```\nSo, We are using binary search to find that value by using the condition you can check it in the code.\n\n**Upvote If you like.**\n# Complexity\n- Time complexity:O(n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& po, long long success) {\n vector<int> v;\n //sorting the potion array\n sort(po.begin(),po.end());\n\n for(int i=0;i<s.size();i++){\n int count=0;\n int l=0,r=po.size()-1;\n int mid=l + (r-l)/2;\n //Using Binary Search on potion array\n while(l<=r){\n if(s[i]*1ll*po[mid] >= success){//1LL is securely integer overflow\n count=po.size()-mid;\n r=mid-1;\n }\n else{\n l=mid+1;\n }\n mid= l + (r-l)/2;\n }\n v.push_back(count);\n }\n \n return v;\n }\n};\n``` | 3 | 0 | ['Math', 'Binary Search', 'Sorting', 'C++'] | 2 |
successful-pairs-of-spells-and-potions | BINARY SEARCH || C++ || PLEASE UPVOTE | binary-search-c-please-upvote-by-satyam2-e4w0 | Intuition\nCan be done in binary search.\n\n# Approach\nStarting with the sorting of potions , After that getting the element till which (spells[i]*potions[mid | satyam2805singh | NORMAL | 2023-04-02T12:18:42.855109+00:00 | 2023-04-02T12:18:42.855146+00:00 | 85 | false | # Intuition\nCan be done in binary search.\n\n# Approach\nStarting with the sorting of potions , After that getting the element till which (spells[i]*potions[mid]) is greater than success and store those elements in pairs[i].\nThe submission shall be taken care of for long long type casting.\n\n# Complexity\n- Time complexity:\nO(nlogm)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n=spells.size(),m=potions.size();\n \n \n sort(potions.begin(),potions.end());\n vector<int> pairs(n);\n for(int i=0;i<n;i++){\n int c=0,l=0,r=m-1;\n while(l<=r){\n \n int mid=l+(r-l)/2;\n if((long long)spells[i]*(long long)potions[mid]>=success){\n r=mid-1;\n \n }\n else{\n l=mid+1;\n }\n }\n pairs[i]=m-1-r;\n }\n\n \n return pairs;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | Simple 14 lines of code in O(n logn)✔ | simple-14-lines-of-code-in-on-logn-by-ha-3l46 | NOTE:\nPlease go through the Intution and Approach before jumping to the code. You will definitely get it!\nSuggested to write things on notebook while reading. | harsh6176 | NORMAL | 2023-04-02T10:35:22.967781+00:00 | 2023-04-02T10:35:22.967827+00:00 | 152 | false | # NOTE:\n**Please go through the Intution and Approach before jumping to the code. You will definitely get it!**\nSuggested to write things on notebook while reading.\n\n# Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn the question, we can see a basic pattern that we have to search a value for every element in spell. If we do this searching linearly for all n elements of spell (m times).\n\nIt will give us complexity of `O(n*m)`. This complexity can be reduced to `O(n * logm)` by using binary search. But before that we have to sort the array potions.\n```C++ []\nsort(potions.begin(), potions.end()); // sorting array of potions\n```\n\nNow, it is given in the question that we have to find the number of elements in potions that multiply with spell[i] to give value >= success.\n\nIn simple words: \n$$spells[i] * potions[j] >= success$$\n\nTaking spells[i] on R.H.S. we get:\n$$potions[j] >= success / spells[i]$$\n\nSo minimum possible value of potion for spells[i] is `success / spells[i]`. Now, it is clear that we have to find **$$lower bound$$** in our already sorted array of potions. And we know, all the elements after this lower bound in the potions array will be greater (as the array is sorted in increasing order), so we will get the answer by doing m - lower bound.\n```\nans[i] = m - lower_bound_ind;\n```\nPlease check the code below.\n\n\n\n# Complexity\n- Time complexity: O(n logm)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote if it was helpfull.!\uD83D\uDE03\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size(), m = potions.size();\n sort(potions.begin(), potions.end());\n vector<int> ans(n);\n for (int i{}; i<n; ++i){\n long long potion = ceil((double)success/spells[i]);\n int lower_bound_ind = lower_bound(potions.begin(), potions.end(), potion) - potions.begin();\n ans[i] = m-lower_bound_ind;\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Array', 'Math', 'Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Easy Java || Binary Search || Beats 85% | easy-java-binary-search-beats-85-by-hars-ui7b | Intuition\nSolution using basic Binary Search\n\n# Approach\n1. sort the potion array\n2. now iterate for the spell array\n3. binary search the index where the | harshverma2702 | NORMAL | 2023-04-02T10:29:32.833329+00:00 | 2023-04-02T10:29:32.833361+00:00 | 79 | false | # Intuition\nSolution using basic Binary Search\n\n# Approach\n1. sort the potion array\n2. now iterate for the spell array\n3. binary search the index where the multiple of spell*potion>=success\n4. now from that index onwards rest potions will be surely >=success because they are arranged in increasing order\n# Complexity\n- Time complexity:\nO(NlogM)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] s, int[] p, long sus) {\n Arrays.sort(p);\n int n = s.length;\n int m = p.length;\n int[] ans = new int[n];\n for(int i=0;i<n;i++){\n ans[i] =m-search(p,sus,m,s[i]);\n }\n return ans;\n }\n\n int search(int[] p ,long t ,int size, int given){\n int s =0;\n int e = size-1;\n while(s<=e){\n int mid = (s+e)/2;\n long mul = (long)given*p[mid];\n if(mul>=t){\n e = mid-1;\n }else{\n s = mid+1;\n }\n\n }\n return s;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | Simple Commented C++ | Binary Search | simple-commented-c-binary-search-by-sour-tjs4 | ```\nclass Solution {\npublic:\n vector successfulPairs(vector& spells, vector& potions, long long success) {\n // Sort the potions array as we will u | SourabCodes | NORMAL | 2023-04-02T09:23:58.144955+00:00 | 2023-04-02T09:23:58.145014+00:00 | 167 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n // Sort the potions array as we will use binary search here...\n sort(potions.begin(),potions.end());\n \n // Declaring the answer array...\n vector<int> ans(spells.size(),0);\n \n for(int i = 0; i < spells.size(); i++){\n long long n = spells[i];\n \n // the required element can be calculated as follows...\n long long int req = (success/n) + (success%n != 0);\n \n // if the required element is found then all the elements greater than "req" will satisfy the condition...\n int indx = lower_bound(potions.begin(),potions.end(),req) - potions.begin();\n \n // taking all elements greater than and equal to "req"...\n ans[i] = potions.size() - indx;\n \n }\n \n return ans;\n \n }\n}; | 3 | 0 | ['C', 'Binary Tree'] | 0 |
successful-pairs-of-spells-and-potions | Easy Python solution using || Bisect | easy-python-solution-using-bisect-by-lal-4rkk | Code\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n lst=[]\n potions.sort( | Lalithkiran | NORMAL | 2023-04-02T09:13:30.723397+00:00 | 2023-04-02T09:13:30.723430+00:00 | 345 | false | # Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n lst=[]\n potions.sort()\n ln=len(potions)\n for i in spells:\n t = bisect_left(potions, success/i)\n lst.append(ln-t)\n return lst\n``` | 3 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Python3'] | 0 |
successful-pairs-of-spells-and-potions | ✅✅ Binary Search Approach || Java Solution | binary-search-approach-java-solution-by-k8kcc | \n# Java Code\n\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int pairs[] = new int[spells.length];\ | pratham31 | NORMAL | 2023-04-02T08:04:46.570383+00:00 | 2023-04-02T08:05:13.711389+00:00 | 362 | false | \n# Java Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int pairs[] = new int[spells.length];\n\n Arrays.sort(potions);\n\n for(int i = 0; i < spells.length; i++)\n {\n int start = 0, end = potions.length-1;\n while(start <= end)\n {\n int mid = start + (end - start)/2;\n if(potions[mid] * (long)spells[i] >= success)\n {\n end = mid - 1;\n }\n else\n {\n start = mid + 1;\n }\n }\n pairs[i] = potions.length - start;\n }\n\n return pairs;\n }\n}\n```\n\n# PLEASE UPVOTE \uD83D\uDC4D | 3 | 0 | ['Two Pointers', 'Binary Search', 'Sorting', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | Easy Explanation , Binary search Approach 🔥⬆️ | easy-explanation-binary-search-approach-2f3yc | Approach\n1. Brute Force approach to solve this problem is to use a nested loop, where the outer loop iterates over the "spells" vector and the inner loop itera | ishaanchoudhary | NORMAL | 2023-04-02T07:44:14.415996+00:00 | 2023-04-02T07:44:14.416025+00:00 | 40 | false | # Approach\n1. Brute Force approach to solve this problem is to use a **nested loop**, where the outer loop iterates over the "spells" vector and the inner loop iterates over the "potions" vector. For each pair (s, p), the product s * p is checked against the target. If the product is greater than or equal to the target, then the pair is considered successful and the count is incremented.\nHowever, this approach has a time complexity of **O(n^2)**, which is inefficient for large values of n.\n2. A more efficient approach is to first sort the "potions" vector in non-decreasing order. This allows us to perform ***binary search*** on the sorted "potions" vector to ***find the index of the last element*** that satisfies the condition ***s * p >= target*** for a given s->element.\n Then, for each element s in the "spells" vector, we can use binary search to find the number of elements in the "potions" vector that satisfy the condition s * p >= target. This can be done by finding the index of the last element in the "potions" vector that satisfies the condition using binary search, and subtracting this index from the total number of elements in the "potions" vector.\n\n# Complexity\n- Time complexity: O(n log n)\n- Space Complexity: O(n)\n# Code\n```\nclass Solution {\npublic:\n int getPairCount(vector<int>& potions, int& spell, long long& target)\n {\n int n = potions.size(), bestIdx = n;\n int low = 0, high = n - 1;\n \n while(low <= high)\n {\n int mid = low + (high - low) / 2;\n long long product = (long long)spell * potions[mid];\n \n if (product >= target)\n {\n bestIdx = mid;\n high = mid - 1;\n }\n else low = mid + 1;\n }\n \n return (n - bestIdx);\n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success)\n {\n int n = spells.size();\n vector<int>v(n);\n sort(potions.begin(), potions.end());\n for (int i = 0; i < n; i++) \n ans[i] = getPairCount(potions, spells[i], success);\n \n return v;\n }\n};\n``` | 3 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 1 |
successful-pairs-of-spells-and-potions | [Python3] One line solution. | python3-one-line-solution-by-geka32-uylb | Code\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n return potions.sort() or [len | geka32 | NORMAL | 2023-04-02T07:35:14.991212+00:00 | 2023-04-02T07:35:14.991252+00:00 | 920 | false | # Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n return potions.sort() or [len(potions) - bisect_left(potions, -(-success // spell)) for spell in spells]\n\n``` | 3 | 0 | ['Python3'] | 2 |
successful-pairs-of-spells-and-potions | Java Solution for beginners. With simple explanation and some additional tips | java-solution-for-beginners-with-simple-ygjqw | Intuition\nBinary Search\n\n# Approach\nStep 1 : Sort potions \nStep 2 : get number of pair of successful potions and spells by using binary search. Try finding | shashwat1712 | NORMAL | 2023-04-02T07:25:13.809007+00:00 | 2023-04-02T09:37:45.307825+00:00 | 480 | false | # Intuition\nBinary Search\n\n# Approach\nStep 1 : Sort potions \nStep 2 : get number of pair of successful potions and spells by using binary search. Try finding smallest element in potions which can give you successful pair by subtracting index of samllest element by length of potions.\nStep 3 : store all the value in ans[] and return ans.\n\n\n# Tips\n1. In below code you can store ans[] values into spells[] which can help you reduce space complexity from O(n) to O(1). \n\n2. Instead of using function couSuc you can do binary search in for loop instead to save some more time. \n\n# Advantages\n1. This approach gives you consistent result and it is favorable for very large array. \n\n2. This code can be done in space complexity of O(1) instead of O(n). which makes it space efficient. \n\n# Disadvantages\n1. It is slower for small array. two Poiner method is favorable for smaler array\n\n# Complexity\n- Time complexity:\n O(n log n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n Arrays.sort(potions);\n int ans[] = new int[spells.length];\n for(int i=0;i<spells.length;i++){\n ans[i]=couSuc(spells[i],potions,success);\n }\n return ans;\n }\n private int couSuc(int a, int[] arr, long b){\n int start=0,end=arr.length;\n while(start<end){\n int mid=start+(end-start)/2;\n if((long)arr[mid]*a>=b){\n end=mid;\n }\n else{\n start=mid+1;\n }\n }\n return arr.length-start;\n }\n}\n``` | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | Sorting + Binary Search + Explaination||✅Easy Java solution||Beginner Friendly🔥 | sorting-binary-search-explainationeasy-j-s9aa | Intuition\n Describe your first thoughts on how to solve this problem. \nSort the potions array and then use binary search on potions array to get the that elem | deepVashisth | NORMAL | 2023-04-02T07:03:41.476411+00:00 | 2023-04-02T07:04:09.508803+00:00 | 94 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSort the potions array and then use binary search on potions array to get the that element whose elements of right part of the array will be greater than or equal to success given because if that particular element excceds success then all element from right will be also excceds.\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n = spells.length;\n int m = potions.length;\n int ans[] = new int[n];\n Arrays.sort(potions);\n for(int i = 0 ; i < n; i ++){\n int spell = spells[i];\n int low = 0;\n int high = m - 1;\n while(low <= high){\n int mid = (high - low)/2 + low;\n long product = (long)spell * (long)potions[mid];\n if(product >= success){\n high = mid - 1;\n }else{\n low = mid + 1;\n }\n }\n ans[i] = m - low;\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Binary Search', 'Sorting', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | C++ solution || with explanation || Let's code it💻 | c-solution-with-explanation-lets-code-it-a0zn | Upvote if you found this solution helpful\uD83D\uDD25\n\n# Approach\nThe first approach which comes to mind after reading the question is to traverse the Potion | piyusharmap | NORMAL | 2023-04-02T05:28:59.346860+00:00 | 2023-04-02T05:28:59.346905+00:00 | 325 | false | # Upvote if you found this solution helpful\uD83D\uDD25\n\n# Approach\nThe first approach which comes to mind after reading the question is to traverse the Potions array for each spell and count the number of pairs which satisfies the given condition, but this method leads to TLE because the time complexity for this will be O(n x m) where both n and m are of order 10^5.\nSo, the optimized approach is to reduce the number of calculations we are doing for each spell.\nIf we think for second we can deduce that by sorting the list of potions and using binary search to traverse the list we can reduce our calculations in a significant way.\n\nNOTE: Keep in mind to convert the product of spell and potion to LONG LONG before further moving with calculations\n\n# Code\n```\nclass Solution {\npublic:\n\n int countPairs(int spell, vector<int> &potions, long long success){\n int n = potions.size();\n int index = n;\n int start = 0;\n int end = n-1;\n\n while(start <= end){\n int mid = start + (end-start)/2;\n\n //if the product of potion and spell satisfies the condition, move the end pointer to mid-1 because we need to find the first element for which the product of spell and potion is greater than success\n if((long long)potions[mid]*spell >= success){\n index = mid;\n end = mid-1;\n }\n\n //if the product is less than the success value move to start pointer to mid+1\n if((long long)potions[mid]*spell < success)\n start = mid+1;\n }\n\n return n-index;\n }\n\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> ans(spells.size());\n\n //sorting the potions list\n sort(potions.begin(), potions.end());\n\n //for each spell find the number of potions which can satisfy the condition\n for(int i=0; i<spells.size(); i++)\n ans[i] = countPairs(spells[i], potions, success);\n\n return ans;\n }\n};\n``` | 3 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | JavaScript, Java, C and Python solution with time complexity of O(n log m) | javascript-java-c-and-python-solution-wi-xq7p | \n\n# Approach\nSort the potions array in descending order.\nCreate an empty hash map map to store the results.\nFor each element in the spells array:\na. If th | Aryan_rajput_ | NORMAL | 2023-04-02T05:22:26.709860+00:00 | 2023-04-02T05:22:26.709922+00:00 | 373 | false | \n\n# Approach\nSort the potions array in descending order.\nCreate an empty hash map map to store the results.\nFor each element in the spells array:\na. If the element is not in the map, calculate the value of success / spells[i] and find the position of the first element in the sorted potions array that is greater than or equal to this value using a binary search. Store this position in len and add it to the res array. Also store len in the map against spells[i].\nb. If the element is already in the map, retrieve the value of len from the map and add it to the res array.\nReturn the res array.\n\n# Complexity\n- Time complexity: O(n log m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m + n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# JavaCsript\n```\n/**\n * @param {number[]} spells\n * @param {number[]} potions\n * @param {number} success\n * @return {number[]}\n */\n var successfulPairs = function(spells, potions, success) {\n let res = [];\n potions.sort((a, b) => b-a);\n let map = new Map();\n \n for(let i=0; i<spells.length; i++){\n if(!map.has(spells[i])){\n let s = success / spells[i];\n let len = search(potions, s);\n res.push(len);\n map.set(spells[i], len);\n }else{\n let len = map.get(spells[i]);\n res.push(len);\n }\n }\n \n return res;\n};\n\nfunction search(potions, target){\n let res = 0;\n let left = 0;\n let right = potions.length-1;\n while(left <= right){\n let mid = Math.floor((left + right) / 2);\n if(potions[mid] < target){\n right = mid - 1;\n }else{\n left = mid + 1;\n res = mid + 1;\n }\n }\n\n return res;\n}\n```\n# Java\n```\npublic class SuccessfulPairs {\n public static int[] successfulPairs(int[] spells, int[] potions, int success) {\n ArrayList<Integer> res = new ArrayList<>();\n int[] sortedPotions = potions.clone();\n Arrays.sort(sortedPotions);\n Map<Integer, Integer> map = new HashMap<>();\n\n for(int i=0; i<spells.length; i++){\n if(!map.containsKey(spells[i])){\n int s = success / spells[i];\n int len = search(sortedPotions, s);\n res.add(len);\n map.put(spells[i], len);\n }else{\n int len = map.get(spells[i]);\n res.add(len);\n }\n }\n\n int[] result = new int[res.size()];\n for(int i=0; i<res.size(); i++){\n result[i] = res.get(i);\n }\n return result;\n }\n\n public static int search(int[] potions, int target){\n int res = 0;\n int left = 0;\n int right = potions.length-1;\n while(left <= right){\n int mid = (left + right) / 2;\n if(potions[mid] < target){\n right = mid - 1;\n }else{\n left = mid + 1;\n res = mid + 1;\n }\n }\n\n return res;\n }\n}\n```\n# C\n```\n\n\nint search(int* potions, int potionsSize, int target){\n int res = 0;\n int left = 0;\n int right = potionsSize-1;\n while(left <= right){\n int mid = (left + right) / 2;\n if(potions[mid] < target){\n right = mid - 1;\n }else{\n left = mid + 1;\n res = mid + 1;\n }\n }\n\n return res;\n}\n\nint* successfulPairs(int* spells, int spellsSize, int* potions, int potionsSize, int success, int* returnSize) {\n int* res = malloc(spellsSize * sizeof(int));\n int* sortedPotions = malloc(potionsSize * sizeof(int));\n memcpy(sortedPotions, potions, potionsSize * sizeof(int));\n qsort(sortedPotions, potionsSize, sizeof(int), (const void *)compare);\n int* map = calloc(spellsSize, sizeof(int));\n\n for(int i=0; i<spellsSize; i++){\n if(map[spells[i]] == 0){\n int s = success / spells[i];\n int len = search(sortedPotions, potionsSize, s);\n res[i] = len;\n map[spells[i]] = len;\n }else{\n int len = map[spells[i]];\n res[i] = len;\n }\n }\n \n free(map);\n free(sortedPotions);\n *returnSize = spellsSize;\n return res;\n}\n\nint compare(const void * a, const void * b) {\n return (*(int*)b - *(int*)a);\n}\n```\n# Python\n```\nfrom typing import List\nimport bisect\n\ndef successfulPairs(spells: List[int], potions: List[int], success: int) -> List[int]:\n res = []\n sortedPotions = sorted(potions, reverse=True)\n map = {}\n\n for i in range(len(spells)):\n if spells[i] not in map:\n s = success / spells[i]\n len = bisect.bisect_left(sortedPotions, s)\n res.append(len)\n map[spells[i]] = len\n else:\n len = map[spells[i]]\n res.append(len)\n\n return res\n``` | 3 | 0 | ['C', 'Python', 'Java', 'JavaScript'] | 1 |
successful-pairs-of-spells-and-potions | Python short and clean 2-liner. Functional programming. | python-short-and-clean-2-liner-functiona-e1z2 | Approach\n1. Sort potions into, say s_potions.\n\n2. For each spells, say x, binary-search for insertion index i in s_potions.\n\n3. Return len(potions) - i.\n\ | darshan-as | NORMAL | 2023-04-02T05:03:09.114918+00:00 | 2023-04-02T05:03:09.114955+00:00 | 291 | false | # Approach\n1. Sort `potions` into, say `s_potions`.\n\n2. For each `spells`, say `x`, binary-search for insertion index `i` in `s_potions`.\n\n3. Return `len(potions) - i`.\n\n# Complexity\n- Time complexity: $$O((m + n) * log(n))$$\n\n- Space complexity: $$O(m + n)$$\n\nwhere,\n`m is number of spells`,\n`n is number of potions`.\n\n# Code\nWIth currying (partial functions):\n```python\nclass Solution:\n def successfulPairs(self, spells: list[int], potions: list[int], success: int) -> list[int]:\n f = partial(bisect.bisect_left, sorted(potions))\n return (len(potions) - f(success / x) for x in spells)\n\n\n```\nWithout using currying (partial functions):\n```python\nclass Solution:\n def successfulPairs(self, spells: list[int], potions: list[int], success: int) -> list[int]:\n s_potions = sorted(potions)\n return (len(potions) - bisect.bisect_left(s_potions, success / x) for x in spells)\n\n\n``` | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'Python', 'Python3'] | 0 |
successful-pairs-of-spells-and-potions | Sort + Binary Search | C++ | sort-binary-search-c-by-tusharbhart-og4f | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = potions.size();\n | TusharBhart | NORMAL | 2023-04-02T04:02:38.547545+00:00 | 2023-04-02T04:02:38.547577+00:00 | 1,579 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = potions.size();\n vector<int> ans;\n sort(potions.begin(), potions.end());\n\n for(int i : spells) {\n int pos = lower_bound(potions.begin(), potions.end(), ceil((double)success / i)) - potions.begin();\n ans.push_back(n - pos);\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Easy Solution Implemented with more one language. | easy-solution-implemented-with-more-one-rvj2u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Mustafa-Moghazy | NORMAL | 2023-04-02T01:27:04.796646+00:00 | 2023-04-02T01:27:04.796679+00:00 | 895 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++ Code\n```\nclass Solution {\npublic:\n int BS(int t, vector<int>& p, long long success){\n long long l = 0, r = p.size()-1, mid = -1;\n while(l<=r){\n mid = (l+r)/2;\n if( (long long)t*p[mid] < success )\n l = mid+1;\n else\n r = mid-1;\n }\n return l;\n }\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size(), p = potions.size(), temp;\n vector<int> ans(n, 0);\n sort(potions.begin(), potions.end());\n for(int i=0; i<n; ++i){\n temp = BS( spells[i] , potions, success );\n ans[i] = (temp == p) ? 0 : p-temp;\n }\n return ans;\n }\n};\n```\n# Java Code \n```\nclass Solution {\n public int BS(int t, int[] p, long success){\n int l = 0, r = p.length-1, mid;\n while(l<=r){\n mid = (l+r)/2;\n if( (long)t*p[mid] < success )\n l = mid+1;\n else\n r = mid-1;\n }\n return l;\n }\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n = spells.length, p = potions.length, temp;\n int[] ans = new int[n];\n Arrays.sort(potions);\n for(int i=0; i<n; ++i){\n temp = BS(spells[i], potions, success);\n ans[i] = (temp == p)? 0 : p - temp;\n }\n return ans;\n }\n}\n```\n# JavaScript Code\n```\n/**\n * @param {number[]} spells\n * @param {number[]} potions\n * @param {number} success\n * @return {number[]}\n */\nconst BS = ( t, p, success)=>{\n let l = 0, r = p.length-1, mid;\n while(l<=r){\n mid = parseInt( (l+r)/2 );\n if( t*p[mid] < success ){\n l = mid+1;\n }else{\n r = mid-1;\n }\n }\n return l;\n}\n\nvar successfulPairs = function(spells, potions, success) {\n let n = spells.length, p = potions.length, temp;\n let ans = new Array(n);\n potions.sort((a, b)=> a - b);\n for(let i=0; i<n; ++i){\n temp = BS( spells[i], potions, success);\n console.log(temp);\n ans[i] = (temp == p)? 0 : p-temp;\n }\n return ans;\n};\n``` | 3 | 0 | ['C++', 'Java', 'JavaScript'] | 0 |
successful-pairs-of-spells-and-potions | Swift | Binary Search | swift-binary-search-by-upvotethispls-bwmg | Binary Search (accepted answer)\n\nclass Solution {\n func successfulPairs(_ spells: [Int], _ potions: [Int], _ success: Int) -> [Int] {\n let potions | UpvoteThisPls | NORMAL | 2023-04-02T01:16:25.357001+00:00 | 2023-04-02T20:12:34.087734+00:00 | 138 | false | **Binary Search (accepted answer)**\n```\nclass Solution {\n func successfulPairs(_ spells: [Int], _ potions: [Int], _ success: Int) -> [Int] {\n let potions = potions.sorted()\n \n return spells.map { spell in\n var (left, right) = (0, potions.count)\n while left < right {\n let mid = (left+right)/2\n (left, right) = spell * potions[mid] >= success ? (left, mid) : (mid+1, right)\n }\n return potions.count - left\n }\n }\n}\n``` | 3 | 0 | ['Swift'] | 1 |
successful-pairs-of-spells-and-potions | JS, binary search with comments | js-binary-search-with-comments-by-bagiry-b3oo | Intuition\nTo achieve we don\'t have to calcualate every spell * potion. If we sort potions then have to find the firs potion which satisfies our conditions. Al | bagiryan | NORMAL | 2023-04-02T00:34:12.980217+00:00 | 2023-04-02T00:38:16.177045+00:00 | 547 | false | # Intuition\nTo achieve we don\'t have to calcualate every spell * potion. If we sort potions then have to find the firs potion which satisfies our conditions. All next potions will satisfy as well.\n\n# Approach\n - Sort potions ascending order\n - for each spell find that minimum number which would be bigger than success after multiplying on it\n - find the index of the first potion which is equal or more than that number\n\n# Complexity\n- Time complexity: O(n*log(n) + n*log(m))\n\n- Space complexity: O(1)\n\n# Code\n```\n/**\n * @param {number[]} spells\n * @param {number[]} potions\n * @param {number} success\n * @return {number[]}\n */\nvar successfulPairs = function(spells, potions, success) {\n // Sort potions asc order for binary search\n potions.sort((a, b) => a - b);\n const ans = [];\n for (const spell of spells) {\n // this number will help us to find the index of the first potion which is equal or more than that number\n const rel = success / spell;\n let left = 0, right = potions.length - 1;\n // standard binary search\n while (left <= right) {\n const mid = Math.floor((left + right) / 2);\n if (potions[mid] < rel) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n // the answer for this number would be the difference between the potions leng and the index\n ans.push(potions.length - left);\n }\n return ans;\n};\n``` | 3 | 0 | ['JavaScript'] | 0 |
successful-pairs-of-spells-and-potions | C++ || Sort and Lower Bound | c-sort-and-lower-bound-by-sosuke23-bibl | Code\n\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long success) {\n int n = s.size(), m = p.size(); | Sosuke23 | NORMAL | 2023-04-02T00:07:08.088381+00:00 | 2023-04-02T00:07:08.088425+00:00 | 747 | false | # Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long success) {\n int n = s.size(), m = p.size();\n sort(p.begin(), p.end());\n vector<int> res(n);\n for (int i = 0; i < n; i += 1) {\n long long x = (success + s[i] - 1) / s[i];\n if (x > p.back()) continue;\n auto it = lower_bound(p.begin(), p.end(), (int)x);\n res[i] = m - (it - p.begin());\n }\n return res;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | ✅Easiest & Best Solution in C++ || BinarySearch✅ | easiest-best-solution-in-c-binarysearch-ma23p | Complexity\n- Time complexity:\nO(nlogm)\n\n- Space complexity:\nO(1)\n\n# Code\nPlease Upvote if u liked my Solution\uD83D\uDE42\n\nclass Solution {\npublic:\n | aDish_21 | NORMAL | 2022-10-27T20:11:41.787762+00:00 | 2022-10-27T20:11:41.787807+00:00 | 467 | false | # Complexity\n- Time complexity:\nO(nlogm)\n\n- Space complexity:\nO(1)\n\n# Code\n**Please Upvote if u liked my Solution**\uD83D\uDE42\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n=spells.size(),m=potions.size();\n vector<int> pairs;\n sort(potions.begin(),potions.end());\n for(int i=0;i<n;i++){\n if(spells[i]>=success){\n pairs.push_back(m);\n continue;\n }\n int ll=0,ul=m-1,mid;\n while(ll<=ul){\n mid =ll+(ul-ll)/2;\n long long product=(long long)potions[mid]*spells[i];\n if(product>=success)\n ul=mid-1;\n else\n ll=mid+1;\n }\n pairs.push_back(m-ll);\n }\n return pairs;\n }\n};\n```\n**Happy LeetCoding\uD83D\uDCAF\nPlease Upvote** | 3 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | JS | Binary search | Runtime: 83.33% | js-binary-search-runtime-8333-by-diff64-dkyn | \nvar successfulPairs = function(spells, potions, success) {\n\tlet res = [];\n\tpotions.sort((a, b) => a - b);\n\tfor (let i = 0; i < spells.length; i++) {\n\t | Diff64 | NORMAL | 2022-08-18T13:53:55.642475+00:00 | 2022-08-18T13:53:55.642529+00:00 | 563 | false | ```\nvar successfulPairs = function(spells, potions, success) {\n\tlet res = [];\n\tpotions.sort((a, b) => a - b);\n\tfor (let i = 0; i < spells.length; i++) {\n\t\tlet h = potions.length-1, l = 0, mid;\n\t\twhile (l <= h) {\n\t\t\tmid = ~~(l + (h-l)/2);\n\t\t\tif (spells[i] * potions[mid] >= success) h = mid-1;\n\t\t\telse l = mid+1;\n\t\t}\n\t\tres[i] = potions.length-1 - h;\n\t}\n\treturn res;\n};\n``` | 3 | 0 | ['Binary Tree', 'JavaScript'] | 0 |
successful-pairs-of-spells-and-potions | O(N+M) Approach || C++ || Without binary Search and sort || Easy || Faster | onm-approach-c-without-binary-search-and-x24e | \nclass Solution {\npublic:\n \n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int maxi = 0;\n | bit_changes | NORMAL | 2022-06-11T19:27:50.157042+00:00 | 2022-06-11T19:28:16.655642+00:00 | 399 | false | ```\nclass Solution {\npublic:\n \n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int maxi = 0;\n unordered_map<int,int> dp;\n for(int i = 0 ; i<potions.size() ; i++){\n dp[potions[i]]++;\n maxi = max(potions[i],maxi);\n }\n \n vector<int> refer(maxi+1);\n \n refer[refer.size()-1] = dp[refer.size()-1];\n \n for(int i = refer.size()-2 ; i >= 0 ; i--){\n refer[i] = refer[i+1] + dp[i];\n }\n \n vector<int> result(spells.size());\n \n for(int i = 0 ; i < spells.size() ; i++){\n double t1 = success;\n double t2 = spells[i];\n long long temp = ceil(t1/t2);\n if(temp > maxi){\n result[i] = 0;\n continue;\n }\n result[i]= refer[temp];\n }\n return result;\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | [Rust] Native binary search solution | rust-native-binary-search-solution-by-ni-6145 | rust\nuse std::cmp::Ordering;\n\nimpl Solution {\n pub fn successful_pairs(spells: Vec<i32>, mut potions: Vec<i32>, success: i64) -> Vec<i32> {\n let | night-crawler | NORMAL | 2022-06-11T17:01:53.706944+00:00 | 2022-06-12T15:48:24.610004+00:00 | 189 | false | ```rust\nuse std::cmp::Ordering;\n\nimpl Solution {\n pub fn successful_pairs(spells: Vec<i32>, mut potions: Vec<i32>, success: i64) -> Vec<i32> {\n let num_potions = potions.len() as i32;\n potions.sort_unstable();\n\n let mut result = vec![0; spells.len()];\n\n for (i, spell) in spells.into_iter().enumerate() {\n let left = potions\n .binary_search_by(|&potion| match (potion as i64 * spell as i64).cmp(&success) {\n Ordering::Less => Ordering::Less,\n // treat equal element as greater so that the BS will always terminate with\n // Error() containing the index of element that is greater or equal to one we\n // searched for\n Ordering::Equal => Ordering::Greater,\n Ordering::Greater => Ordering::Greater,\n })\n .unwrap_err() as i32;\n\n result[i] = (num_potions - left) as i32;\n }\n\n result\n }\n}\n```\n\nBinary search example:\n\n```rust\n#[test]\nfn test6() {\n\t// 4 is missing\n\tlet sample = vec![1, 2, 3, 5, 6, 7, 7];\n\tlet left = sample\n\t\t.binary_search_by(|&potion| match potion.cmp(&4) {\n\t\t\tOrdering::Less => Ordering::Less,\n\t\t\tOrdering::Equal => Ordering::Greater,\n\t\t\tOrdering::Greater => Ordering::Greater,\n\t\t})\n\t\t.unwrap_err();\n\tassert_eq!(sample[left], 5);\n\n\tlet left = sample\n\t\t.binary_search_by(|&potion| match potion.cmp(&3) {\n\t\t\tOrdering::Less => Ordering::Less,\n\t\t\tOrdering::Equal => Ordering::Greater,\n\t\t\tOrdering::Greater => Ordering::Greater,\n\t\t})\n\t\t.unwrap_err();\n\tassert_eq!(sample[left], 3);\n}\n```\n\nEquivalent for:\n\n```rust\nimpl Solution {\n pub fn successful_pairs(spells: Vec<i32>, mut potions: Vec<i32>, success: i64) -> Vec<i32> {\n let num_potions = potions.len();\n potions.sort_unstable();\n\n let mut result = vec![0; spells.len()];\n\n for (i, spell) in spells.into_iter().enumerate() {\n let mut left = 0;\n let mut right = num_potions;\n\n while left < right {\n let mid = left + (right - left) / 2;\n if spell as i64 * potions[mid] as i64 >= success {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n result[i] = (num_potions - left) as i32;\n }\n\n result\n }\n}\n``` | 3 | 0 | ['Binary Tree', 'Rust'] | 3 |
successful-pairs-of-spells-and-potions | JAVA || Clean Code || Binary Search | java-clean-code-binary-search-by-rachelg-u0xp | \nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n \n Arrays.sort(potions);\n int[] res=ne | rachelgupta7codenirvana | NORMAL | 2022-06-11T16:57:14.396328+00:00 | 2022-06-11T16:57:14.396357+00:00 | 441 | false | ```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n \n Arrays.sort(potions);\n int[] res=new int[spells.length];\n \n for(int i=0;i<spells.length;i++)\n {\n int count=binarySearch(spells[i],potions,success);\n res[i]=count;\n }\n \n return res;\n }\n \n public static int binarySearch(int spell, int[] potions, long success)\n {\n int i=0;\n int j=potions.length-1;\n int n=potions.length;\n \n int res=0;\n \n while(i<=j)\n {\n int mid=(i+j)/2;\n \n if((spell*1.0)*potions[mid]>=success)\n {\n res=n-mid;\n j=mid-1;\n }\n \n else\n {\n i=mid+1;\n }\n }\n \n return res;\n }\n}\n``` | 3 | 0 | ['Binary Search', 'Java'] | 2 |
successful-pairs-of-spells-and-potions | Successful Pairs of spells and Potions | successful-pairs-of-spells-and-potions-b-by1k | Easy approach Binary search --\nPlease Upvote\n\n\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long ss) {\n | BibhabenduMukherjee | NORMAL | 2022-06-11T16:50:15.879491+00:00 | 2022-06-11T16:50:55.281152+00:00 | 101 | false | **Easy approach Binary search --**\n**Please Upvote**\n\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long ss) {\n sort(p.begin() , p.end());\n vector<long long> res(s.size());\n for(int i = 0 ; i< s.size() ; ++i){\n res[i] = (ss/s[i]);\n }\n \n vector<int> ans;\n for(int i = 0 ; i < s.size() ; ++i){\n \n if(ss <= 1LL*res[i]*s[i] ){\n int ind = lower_bound(p.begin() , p.end() , res[i]) - p.begin() ; \n ans.push_back(p.size() - ind);\n }else{\n int ind = upper_bound(p.begin() , p.end() , res[i]) - p.begin() ;\n \n ans.push_back(p.size() - ind);\n } \n \n }\n \n return ans;\n \n }\n};\n\n``` | 3 | 1 | ['Binary Tree'] | 0 |
successful-pairs-of-spells-and-potions | C++ || EASY TO UNDERSTAND || Ultimate Binary Search Solution | c-easy-to-understand-ultimate-binary-sea-s9nm | \n#define ll long long int\n#define ld long double\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& p, long long su | aarindey | NORMAL | 2022-06-11T16:05:58.865720+00:00 | 2022-06-11T16:05:58.865757+00:00 | 154 | false | ```\n#define ll long long int\n#define ld long double\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& p, long long success) {\n sort(p.begin(),p.end());\n ll n=p.size();\n\n vector<int> ans;\n for(int x:spells)\n {\n ll up=ceil((success)/(1.0*x));\n ll idx=lower_bound(p.begin(),p.end(),up)-p.begin();\n if(idx==n)\n {\n ans.push_back(0);\n }\n else\n ans.push_back(n-idx);\n }\n return ans;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 3 | 1 | [] | 1 |
successful-pairs-of-spells-and-potions | Binary Search | Python | Easy to understand | binary-search-python-easy-to-understand-8vo8o | Idea:\nThe pretty straightforward solution, sort potions and for each spell find an index of minimal potions that will make success and we know that everything | dilshodbek | NORMAL | 2022-06-11T16:05:52.116014+00:00 | 2022-06-11T16:05:52.116076+00:00 | 211 | false | Idea:\nThe pretty straightforward solution, sort potions and for each spell find an index of minimal potions that will make success and we know that everything greater will make a success too. \n\n\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n ans = []\n for i in spells:\n cur = success/i\n ans.append(len(potions)-bisect.bisect_left(potions, cur))\n return ans\n``` | 3 | 0 | [] | 1 |
successful-pairs-of-spells-and-potions | Priority queue || C++ || Max-heap || Easy-Understanding || Simple | priority-queue-c-max-heap-easy-understan-4pip | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> ans;\n | itzyash_01 | NORMAL | 2022-06-11T16:03:59.932279+00:00 | 2022-06-11T16:03:59.932311+00:00 | 218 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n vector<int> ans;\n priority_queue<int> pq;\n unordered_map<int,int> mp;\n for(int i=0;i<potions.size();i++)\n pq.push(potions[i]);\n vector<int> spells1=spells;\n sort(spells.begin(),spells.end());\n int cnt=0;\n for(int i=0;i<=spells.size()-1;i++)\n {\n while(!pq.empty())\n {\n int x=pq.top();\n if((long long) x* (long long) spells[i]>=success) {cnt++; pq.pop();}\n else\n break;\n }\n mp[spells[i]]=cnt;\n }\n for(int i=0;i<spells.size();i++)\n {\n ans.push_back(mp[spells1[i]]);\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | Sort potions and apply Binary Search || C++ || Sorting 🟩 | sort-potions-and-apply-binary-search-c-s-v3vr | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long k) {\n sort(potions.begin(),potions.end | VIPul1 | NORMAL | 2022-06-11T16:03:14.158059+00:00 | 2022-06-11T16:13:49.284373+00:00 | 254 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long k) {\n sort(potions.begin(),potions.end());\n int n = spells.size(), m = potions.size();\n int i = 0, j = 0;\n vector<int> res;\n for(int i=0;i<n;i++){\n int l = 0, h = m;\n long long c1 = spells[i];\n while(l<h){\n int mid = (l+h)/2;\n long long c2 = potions[mid];\n long long cur = c1*c2;\n if(cur<k) l = mid+1;\n else if(cur>=k) h = mid;\n }\n res.push_back(m-h);\n }\n return res;\n }\n};\n``` | 3 | 0 | ['C', 'Sorting'] | 1 |
successful-pairs-of-spells-and-potions | Ceil + binary search | ceil-binary-search-by-slow_code-oyxz | \ttypedef long long ll;\n\tclass Solution {\n\tpublic:\n\t\tvector successfulPairs(vector& spells, vector& portions, long long success) {\n\t\t\tsort(begin(port | Slow_code | NORMAL | 2022-06-11T16:00:41.184095+00:00 | 2022-06-11T16:02:58.622632+00:00 | 276 | false | \ttypedef long long ll;\n\tclass Solution {\n\tpublic:\n\t\tvector<int> successfulPairs(vector<int>& spells, vector<int>& portions, long long success) {\n\t\t\tsort(begin(portions),end(portions));\n\t\t\tvector<int>res;\n\t\t\tint m = portions.size();\n\t\t\tfor(auto num:spells){\n\t\t\t\tif(success/num>=100001){\n\t\t\t\t\tres.push_back(0);\n\t\t\t\t\tcontinue;\n\t\t\t\t}\n\t\t\t\tint n = success/num + (success%num!=0);\n\t\t\t\tint i = lower_bound(begin(portions),end(portions),n)-begin(p);\n\t\t\t\tres.push_back(m-i);\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\t}; | 3 | 0 | [] | 0 |
successful-pairs-of-spells-and-potions | Python Binary Search EASY TO UNDERSTAND SOLUTION | python-binary-search-easy-to-understand-uj207 | \n# Code\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n n = len(spells)\n | chrishardin | NORMAL | 2024-08-18T22:57:00.521826+00:00 | 2024-08-18T22:57:00.521864+00:00 | 98 | false | \n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n n = len(spells)\n m = len(potions)\n pairs = [0] * n\n\n # Info from question\n # spells[i] = strength of i\n # potion[j] = strength of j\n # product of strength is at least success\n # pairs[i] is number of potions that will form a successful pair with ith spell\n\n # Algo\n # Use binary search to get the mid potion\n # while low <= high\n # - if mid >= success, increment by (m-mid) since mid->m would all be greaterthan\n # if it is, increment pairs[i]\n\n # Sort potions before the order does not matter\n potions.sort()\n\n # Iterate over spells\n for i in range(n):\n # Get low and high variables for binary search\n low = 0\n high = m\n # While low is less than high, keep looping\n while low < high:\n # get mid\n mid = (low + high) // 2\n # Check if product is higher than success\n if spells[i] * potions[mid] >= success:\n pairs[i] += (high-mid)\n high = mid\n else:\n # We are at the bottom of the list\n if low == mid:\n break\n # Everything before mid would not pass success, so we move up\n low = mid\n return pairs\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'Python3'] | 0 |
successful-pairs-of-spells-and-potions | Counting Successful Spell-Potion Pairs Using Binary Search (100% Runtime Efficiency) | counting-successful-spell-potion-pairs-u-5ibk | Intuition\nThe function calculates the number of successful pairs between each spell and a potion. A pair is considered successful if the product of the spell a | authxth | NORMAL | 2024-08-18T13:42:39.947434+00:00 | 2024-08-18T13:42:39.947484+00:00 | 332 | false | # Intuition\nThe function calculates the number of successful pairs between each spell and a potion. A pair is considered successful if the product of the spell and potion values is greater than or equal to a given success threshold. To efficiently find these pairs, binary search is employed after sorting the potions array.\n\n\n# Approach\n1. **Sort Potions**: Begin by sorting the `potions` array. This allows for efficient searching using binary search.\n2. **Binary Search for Each Spell**:\n - For each spell, determine the smallest index in the `potions` array such that the product of the spell and the potion at that index meets or exceeds the success threshold.\n - Use binary search to find this index efficiently. The idea is to minimize the number of comparisons by halving the search space in each iteration.\n - The number of successful pairs for each spell is then the total number of potions minus the found index.\n3. **Store Results**: Append the result for each spell to the `ans` array.\n\n\n# Complexity\n- **Time complexity**: $O(nlogm)$, where n is the number of spells and m is the number of potions. Sorting the potions array takes $O(mlogm)$, and each binary search operation for a spell is $O(logm)$, leading to the overall complexity.\n\n- **Space complexity**: $O(1)$ for the binary search and $O(n)$ for storing the results in the `ans` array.\n\n# Code\n```\nfunction successfulPairs(spells: number[], potions: number[], success: number): number[] {\n potions.sort((a, b) => a - b);\n const m = potions.length;\n const ans: number[] = [];\n for (const v of spells) {\n let left = 0;\n let right = m;\n while (left < right) {\n const mid = (left + right) >> 1;\n if (v * potions[mid] >= success) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n ans.push(m - left);\n }\n return ans;\n}\n``` | 2 | 0 | ['TypeScript'] | 0 |
successful-pairs-of-spells-and-potions | ✅💯🔥Simple Code📌🚀| 🔥✔️Easy to understand🎯 | 🎓🧠Beginner friendly🔥| O(N logM) Time Comp.💀💯 | simple-code-easy-to-understand-beginner-lxd6g | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | atishayj4in | NORMAL | 2024-07-20T18:01:31.454748+00:00 | 2024-08-01T18:58:45.370545+00:00 | 251 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n = spells.length;\n int m = potions.length;\n int[] pairs = new int[n];\n Arrays.sort(potions);\n for (int i = 0; i < n; i++) {\n int spell = spells[i];\n int left = 0;\n int right = m - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n long product = (long) spell * potions[mid];\n if (product >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n pairs[i] = m - left;\n }\n return pairs;\n }\n}\n\n```\n\n | 2 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'C', 'Sorting', 'Python', 'C++', 'Java'] | 0 |
successful-pairs-of-spells-and-potions | Easy Binary Search Approach | easy-binary-search-approach-by-codered23-uf3w | \n\n# Complexity\n- Time complexity:\nO(n logm)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] | codeRed23 | NORMAL | 2024-06-29T13:47:28.084124+00:00 | 2024-06-29T13:47:28.084156+00:00 | 147 | false | \n\n# Complexity\n- Time complexity:\nO(n logm)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n=spells.length;\n int m=potions.length;\n int[] arr= new int[n];\n Arrays.sort(potions);\n for(int i=0;i<n;i++){\n long spell=spells[i];\n long lo=0;\n long hi=m-1;\n long lb=-1;\n while(hi>=lo){\n long mid=lo+(hi-lo)/2;\n long pair=spell*potions[(int)mid];\n if(pair>=success){\n lb=mid;\n hi=mid-1;\n }else lo=mid+1;\n }if(lb!=-1) arr[i]+=m-lb;\n }\n return arr;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | Beats 89% || C++ solution using binary search and sorting | beats-89-c-solution-using-binary-search-u5i8y | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yashu761 | NORMAL | 2024-06-25T10:12:55.360334+00:00 | 2024-06-25T10:12:55.360368+00:00 | 492 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO((m+n)logm) sorting potions vector -> mlogm and applying binary search on potions for every spell nlogm\n\n- Space complexity:\nO(n) ans vector for return the results\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions,\n long long success) {\n\n // sort the potions and apply binary search in it for every spells\n vector<int> ans;\n sort(potions.begin(), potions.end());\n\n int n = potions.size();\n int lower = 0, higher = n - 1,index;\n long long temp ;\n for (int i = 0; i < spells.size(); i++) {\n temp= spells[i];\n \n // usign binary search find the first index where success is found\n if (temp * potions[n - 1] < success) {\n ans.push_back(0);\n continue;\n }\n\n lower = 0, higher = n - 1;\n\n while (lower <higher) {\n index = lower+(-lower + higher) / 2;\n\n if ((long long)(temp * potions[index]) < success) \n lower = index + 1;\n else\n higher = index ;\n }\n \n ans.push_back(n-lower);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | 🔥Simple and easy approach using lower_bound | simple-and-easy-approach-using-lower_bou-ao4i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sparsh_7637 | NORMAL | 2024-06-18T20:29:05.320390+00:00 | 2024-06-18T20:29:05.320425+00:00 | 55 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(nlog(n))$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long num) {\n sort(p.begin(), p.end());\n int n = s.size();\n int m = p.size();\n vector<int> ans;\n\n for (int i = 0; i < n; i++) {\n long long a = s[i];\n long long requiredPotion = (num + a - 1) / a; \n auto it = lower_bound(p.begin(), p.end(), requiredPotion);\n ans.push_back(p.end() - it);\n }\n\n return ans;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | ✅ Easy C++ Solution | easy-c-solution-by-moheat-ex61 | Code\n\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size( | moheat | NORMAL | 2024-05-31T08:22:24.828211+00:00 | 2024-05-31T08:22:24.828245+00:00 | 125 | false | # Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n = spells.size();\n int m = potions.size();\n\n vector<int> v;\n\n sort(potions.begin(),potions.end());\n\n for(int i=0;i<n;i++)\n {\n long long spell = spells[i];\n\n int start = 0;\n int end = m;\n while(start < end)\n {\n int mid = start + (end - start)/2;\n if(spell * potions[mid] >= success)\n {\n end = mid;\n }\n else\n {\n start = mid + 1;\n }\n }\n v.push_back(m - start);\n }\n return v;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | ✅Easy C++ Solution(Only 5 lines) || For Beginners 📌🔥🔥📌 | easy-c-solutiononly-5-lines-for-beginner-bxo6 | \n\n\n# Please upvote of you found the solution helpful.\uD83D\uDE4F\uD83C\uDFFB\n\n# Code\n\nclass Solution {\npublic:\n vector<int> successfulPairs(vector< | Gaurav_Tomar | NORMAL | 2024-04-27T05:38:36.496493+00:00 | 2024-04-27T05:38:36.496529+00:00 | 280 | false | \n\n\n# ***Please upvote of you found the solution helpful.\uD83D\uDE4F\uD83C\uDFFB***\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& s, vector<int>& p, long long suc) {\n sort(p.begin(),p.end()); int n=s.size();\n vector<int>ans(n);\n for(int i=0;i<n;i++)\n ans[i]=p.end()-upper_bound(p.begin(),p.end(),(long long)ceil((suc*1.0)/s[i])-1);\n return ans;\n }\n};\n``` | 2 | 0 | ['Binary Search', 'C++'] | 0 |
successful-pairs-of-spells-and-potions | C++ | O((N+M)*LogM TC Solution | Binary Search on solution space | c-onmlogm-tc-solution-binary-search-on-s-tyza | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), poti | theCuriousCoder | NORMAL | 2024-04-27T05:09:10.077904+00:00 | 2024-04-27T05:09:10.077923+00:00 | 4 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(), potions.end());\n int n = spells.size(), m = potions.size();\n vector<int> output;\n for(int i = 0; i<n; i++) {\n if (spells[i]*1ll*potions[m-1] < success) {\n output.push_back(0);\n continue;\n } \n \n if (spells[i]*1ll*potions[0] >= success) {\n output.push_back(m);\n continue;\n }\n // find min index such that spells[i]*potions[idx] >= success\n int lo = -1; // min impossible value;\n int hi = m-1; // max possible value\n \n while(hi - lo > 1) {\n int mid = lo + (hi-lo)/2;\n if (spells[i]*1ll*potions[mid] >= success) {\n hi = mid;\n } else {\n lo = mid;\n }\n }\n output.push_back(m-(lo+1));\n }\n return output;\n }\n};\n``` | 2 | 0 | [] | 0 |
successful-pairs-of-spells-and-potions | [Python] Binary Search | python-binary-search-by-lshigami-adu7 | \n\n# Code\n\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n def BinarySearch(nums,x | lshigami | NORMAL | 2024-03-18T07:56:31.045473+00:00 | 2024-03-18T07:56:31.045505+00:00 | 645 | false | \n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n def BinarySearch(nums,x):\n l=0\n r=len(nums)-1\n while l<=r:\n m=(l+r)//2\n if nums[m]>=x:\n r=m-1\n elif nums[m]<x:\n l=m+1\n return r+1\n ans=[]\n res=0\n potions.sort()\n n=len(potions )\n for i in range (0,len(spells)):\n res=0\n index=BinarySearch(potions,success/spells[i])\n print(index)\n if index<=n:\n res=n-index\n ans.append(res)\n return ans\n\n``` | 2 | 0 | ['Python3'] | 0 |
successful-pairs-of-spells-and-potions | Simple pythonic solution | simple-pythonic-solution-by-burkh4rt-ks5t | Code\npython\nclass Solution:\n def successfulPairs(\n self, spells: List[int], potions: List[int], success: int\n ) -> List[int]:\n n, _ = | burkh4rt | NORMAL | 2024-01-20T04:15:29.372627+00:00 | 2024-01-20T04:15:29.372658+00:00 | 400 | false | # Code\n```python\nclass Solution:\n def successfulPairs(\n self, spells: List[int], potions: List[int], success: int\n ) -> List[int]:\n n, _ = len(potions), potions.sort()\n return [n - bisect_left(potions, success / s) for s in spells]\n``` | 2 | 0 | ['Python3'] | 0 |
successful-pairs-of-spells-and-potions | hashmap + stack approach Beats 99.87% + Explaination 🔥✅ | hashmap-stack-approach-beats-9987-explai-vat1 | \n# Approach\n So we need to sort the potion array , why ? Because when we loop through the potion array we want to store the number of integers are infront of | LovinsonDieujuste | NORMAL | 2024-01-13T22:52:38.810855+00:00 | 2024-01-13T22:52:38.810876+00:00 | 469 | false | \n# Approach\n So we need to sort the ```potion``` array , why ? Because when we loop through the ``` potion``` array we want to store the number of integers are infront of `potion[i]` \n\nFor Example: ```potions = [5,2,4,3,1]``` \nWhen we sort it we get this ```[1,2,3,4,5]```\nNow we know that 5 numbers are greater or equal to number ``1`` \nAnd we know that 4 numbers are greater or equal to number ```2```\nAlso we know that 3 numbers are greater or equal to number ```3```\nAnd so on...\nWhy is this important ? Let me explain\n\nLets say ```spells = [5,1,3], potions = [1,1,3,4,5], success = 7```\nand our ```spell[i] = 5``` \nset our bar = ```success / spell[i]``` so ```bar = 7 / 5 | 1.4``` then we know that our ```potion[i]``` have to be greater or equal to ```bar``` in order to succeed, since we are working with integers and not float then we can use ```ceil``` to round it up so ```bar = 2```\n\nNow our ```1st``` for loop should cause our hashmap to look like this ```hashmap = {1: 5, 3: 3, 4: 2, 5: 1}``` keep in mind ```trace```, it will be use to store the order of the sorted number. We\'ll use ```trace``` later in the ```2nd``` for loop.\n\nNow to make our ```lookup``` variable in the ```2nd``` for loop , this variable will be use to store how many integers are in front of bar if ```bar = i```.\n\nNow our lookup look like this ```lookup = [5,5,3,3,2,1] ```\nBoom youre done \u2705 now we can loop through ```spell```\n\n ```spell[0] = 5``` Now we have to set our bar to, ```bar = ceil(7 / 5 | 1.4) = 2``` Now we go to ```lookup[2] = 3``` which means if the ```bar = 2``` then 3 integers are greater or equal to 2, If the bar is greater then the length of ```lookup``` that means ```0``` integers are greater or equal to the bar so we add ```0``` in our ```stack``` if the bar is a negative number then we know that ```all``` of our integers is greater than the bar so we can add ```lookup[0] | len(potions) ```\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n pointer = 0\n trace = []\n hashmap ={}\n stack = []\n length = len(potions)\n lookup = []\n \n\n for idx, num in enumerate(potions):\n if num in hashmap:\n continue\n hashmap[num] = length - idx\n trace.append(num)\n \n for i in range(potions[-1] + 1):\n Pnum = trace[pointer]\n if i not in hashmap:\n \n lookup.append(hashmap[Pnum])\n continue\n \n lookup.append(hashmap[Pnum])\n pointer +=1\n \n for spell in spells:\n bar = ceil(success / spell)\n if bar > len(lookup) - 1:\n stack.append(0)\n elif bar < 0:\n stack.append(lookup[0])\n else:\n stack.append(lookup[bar])\n\n return stack\n\n\n``` | 2 | 0 | ['Hash Table', 'Stack', 'Python3'] | 1 |
successful-pairs-of-spells-and-potions | [Binary Search] Easy Solution in Python | binary-search-easy-solution-in-python-by-jrrr | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hongyingyue | NORMAL | 2024-01-05T07:24:30.449811+00:00 | 2024-01-05T07:24:30.449846+00:00 | 199 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n res = [0] * len(spells)\n potions.sort()\n\n for i in range(len(spells)):\n # find the smallest value to reach in spells\n needed = success//spells[i] + bool(success % spells[i])\n\n l, r = 0, len(potions) # r should start with len(potions) to give a full range from 0 to len(potions) to l\n while l < r:\n mid = l + (r - l) // 2\n if potions[mid] < needed:\n l = mid + 1\n else:\n r = mid\n res[i] = len(potions) - l\n\n return res\n``` | 2 | 0 | ['Python3'] | 0 |
successful-pairs-of-spells-and-potions | 🔥🔥Easy Solutions in Java || Beats 75.85% | easy-solutions-in-java-beats-7585-by-ans-c39t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AnsH29 | NORMAL | 2023-10-20T02:26:53.621588+00:00 | 2023-10-20T02:26:53.621608+00:00 | 649 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] successfulPairs(int[] spells, int[] potions, long success) {\n int n = spells.length;\n int m = potions.length;\n int[] pairs = new int[n];\n Arrays.sort(potions);\n for (int i = 0; i < n; i++) {\n int spell = spells[i];\n int left = 0;\n int right = m - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n long product = (long) spell * potions[mid];\n if (product >= success) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n pairs[i] = m - left;\n }\n return pairs;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
successful-pairs-of-spells-and-potions | Successful Pairs of Spells and Potions C++ solution | successful-pairs-of-spells-and-potions-c-q70a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rissabh361 | NORMAL | 2023-09-07T05:16:05.637716+00:00 | 2023-09-07T05:16:05.637743+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n=potions.size();\n sort(potions.begin(), potions.end());\n vector<int> ans;\n for(long it: spells)\n {\n int start=0;\n int end=n-1;\n int count=0;\n \n while(start<=end)\n {\n int mid=(start+end)/2;\n if(it*potions[mid]>=success)\n {\n count+=end-mid+1;\n end=mid-1;\n }\n else\n start=mid+1;\n }\n ans.push_back(count);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
successful-pairs-of-spells-and-potions | C++ | | Binary Search | c-binary-search-by-rhythm_jain-9dyy | \nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n=potions.size();\n | rhythm_jain_ | NORMAL | 2023-07-17T10:14:32.226251+00:00 | 2023-07-17T10:14:32.226272+00:00 | 15 | false | ```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n int n=potions.size();\n sort(potions.begin(), potions.end());\n vector<int> ans;\n for(long it: spells)\n {\n int start=0;\n int end=n-1;\n int count=0;\n \n while(start<=end)\n {\n int mid=(start+end)/2;\n if(it*potions[mid]>=success)\n {\n count+=end-mid+1;\n end=mid-1;\n }\n else\n start=mid+1;\n }\n ans.push_back(count);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Binary Search', 'Sorting', 'Binary Tree', 'C++'] | 1 |
successful-pairs-of-spells-and-potions | (sorting-->mlogm) and (traverse+binary serach--> nlogm) solution | sorting-mlogm-and-traversebinary-serach-mvo27 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Leximoberg | NORMAL | 2023-07-09T02:47:46.684202+00:00 | 2023-07-09T02:47:46.684222+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {\n sort(potions.begin(),potions.end());\n int n=spells.size();\n vector<int>pairs(n,0);\n int m=potions.size();\n for(int i=0;i<n;i++){\n int l=0,r=m-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(1LL*potions[mid]*spells[i]>=success){\n r=mid-1;\n\n }\n else{\n l=mid+1;\n }\n }\n pairs[i]=m-l;\n\n }\n return pairs;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.