problem
stringlengths 18
4.46k
| answer
stringlengths 1
942
| pass_at_n
float64 0.08
0.92
|
|---|---|---|
In a right trapezoid \(ABCD\), the sum of the lengths of the bases \(AD\) and \(BC\) is equal to its height \(AB\). In what ratio does the angle bisector of \(\angle ABC\) divide the lateral side \(CD\)?
|
1:1
| 0.875 |
In the Cartesian coordinate system $xOy$, the ellipse $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ $(a > b > 0)$ has left and right foci at $F_{1}$ and $F_{2}$, respectively. The chords $ST$ and $UV$ of the ellipse are parallel to the $x$-axis and $y$-axis, respectively, and intersect at point $P$. The lengths of segments $PU$, $PS$, $PV$, and $PT$ are $1$, $2$, $3$, and $6$, respectively. The area of the triangle $\triangle P F_{1} F_{2}$ is...
|
\sqrt{15}
| 0.375 |
Let \( H \) be the orthocenter of \( \triangle ABC \), and \( 3 \overrightarrow{HA} + 4 \overrightarrow{HB} + 5 \overrightarrow{HC} = \mathbf{0} \). Determine \( \cos \angle AHB \).
|
-\frac{\sqrt{6}}{6}
| 0.375 |
A circle touches the longer leg of a right triangle, passes through the vertex of the opposite acute angle, and has its center on the hypotenuse of the triangle. What is the radius of the circle if the lengths of the legs are 5 and 12?
|
\frac{65}{18}
| 0.75 |
In what numeral system is the number 11111 a perfect square?
|
B = 3
| 0.375 |
A function \( f(x) \) defined on \(\mathbb{R}\) satisfies the following conditions for any real number \( x \):
$$
\begin{array}{l}
f(x+3) \leqslant f(x) + 3, \\
f(x+2) \geqslant f(x) + 2,
\end{array}
$$
and \( f(1) = 2 \). Let \( a_{n} = f(n) \) for \( n \in \mathbb{Z}_{+} \). Find:
$$
f(2015) =
$$
|
2016
| 0.375 |
By multiplying four numbers, Nina obtained a result whose units digit is 0. What numbers did she multiply and what was the result, if the factors are consecutive prime numbers?
|
210
| 0.75 |
If the centroid of the inscribed triangle \( ABC \) of the curve \( y^{2}=4 \sqrt{2} x \) is its focus \( F \), then
\[ |FA|^{2} + |FB|^{2} + |FC|^{2} = \]
|
27
| 0.875 |
Given that $P$ is any point on the ellipse $\frac{x^{2}}{16}+\frac{y^{2}}{15}=1$, and $EF$ is any diameter of the circle $\odot N:(x-1)^{2}+y^{2}=4$, find the range of values for $\overrightarrow{P E} \cdot \overrightarrow{P F}$.
|
[5, 21]
| 0.75 |
Let \( f:[0,1] \rightarrow \mathbb{R} \) be continuous and satisfy:
\[
\begin{aligned}
b f(2 x) & = f(x), & & 0 \leq x \leq 1/2 ; \\
f(x) & = b + (1-b) f(2 x - 1), & & 1/2 \leq x \leq 1,
\end{aligned}
\]
where \( b=\frac{1+c}{2+c}, \, c>0 \). Show that \( 0 < f(x) - x < c \) for every \( x \), \( 0 < x < 1 \).
|
0 < f(x) - x <c
| 0.875 |
Given triangles \(ABC\) and \(A'B'C'\) with areas of 1 and 2025, respectively. It is known that rays \(AB\) and \(A'B'\) are parallel and go in opposite directions. The same is true for pairs \(BC\) and \(B'C'\), \(CA\) and \(C'A'\). Let \(A''\), \(B''\), and \(C''\) be the midpoints of segments \(AA'\), \(BB'\), and \(CC'\). Find the area of triangle \(A''B''C''\).
|
484
| 0.875 |
Given that quadrilateral \(ABCD\) is an isosceles trapezoid with \(AB \parallel CD\), \(AB = 6\), and \(CD = 16\). Triangle \(ACE\) is a right-angled triangle with \(\angle AEC = 90^\circ\), and \(CE = BC = AD\). Find the length of \(AE\).
|
4\sqrt{6}
| 0.5 |
Two spheres with radius \( r \) are externally tangent to each other. Three spheres with radius \( R \) are externally tangent to each other, with each one tangent to the other two. Each of these spheres is also externally tangent to the first two spheres.
Find the relationship between \( R \) and \( r \).
|
R = 6r
| 0.5 |
Consider the cut lines formed in the initial 100 x 100 square. It is easy to see that cutting the folded square once corresponds to multiple parallel lines cut in the initial square, where the distance between these lines is no less than 2 (since at least one fold line must pass between any two cut lines). Thus, there are no more than 50 such lines, and they divide the square into at most 51 rectangles. With two such cuts, a maximum of $51^{2}=2601$ parts can be formed, as each rectangle from the first division can be split into no more than 51 parts in the second cut. An example with 2601 parts can be achieved by folding the square so that the fold lines form a 2 x 2 grid and then cutting the resulting folded 2 x 2 square along its two central lines.
|
2601
| 0.875 |
Person A, Person B, and Person C start from point $A$ to point $B$. Person A starts at 8:00, Person B starts at 8:20, and Person C starts at 8:30. They all travel at the same speed. After Person C has been traveling for 10 minutes, Person A is exactly halfway between Person B and point $B$, and at that moment, Person C is 2015 meters away from point $B$. Find the distance between points $A$ and $B$.
|
2418
| 0.75 |
Find the remainder when the integer
$$
1 \times 3 \times 5 \times 7 \times \cdots \times 2003 \times 2005
$$
is divided by 1000.
|
375
| 0.875 |
There are apples in a closed bag. Three friends tried to lift the bag and guess how many fruits were inside. The first guessed that there were 20 apples, the second thought there were 22, and the third guessed 25. When they opened the bag, it turned out that one of them was off by 1, another by 3, and the third by 6. How many apples were in the bag? Find all possible answers.
|
19
| 0.75 |
$AB$ is the diameter of a circle, $BC$ is the tangent. The secant $AC$ is divided by the circle at point $D$ into two equal parts. Find the angle $DAB$.
|
45^\circ
| 0.875 |
The numbers 0 and 1 are placed in the cells of the table as shown in the figure.
| 0 | 1 | 0 | 0 |
| - | - | - | - |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
Permissible actions:
- Add one to all numbers in a row;
- Add one to all numbers in a column;
- Add one to all numbers along a line parallel to any diagonal (in particular, you can add one to the number in any corner cell).
Is it possible, as a result of several such actions, to obtain a table in which all numbers are equal?
|
\text{No}
| 0.625 |
Given that the real part of the expansion of \((1 + \mathrm{i} x)^{4n + 2}\) (where \(x \in \mathbb{R}\)) is a polynomial in \(x\), find the sum of the coefficients of this polynomial.
|
0
| 0.75 |
Kermit the frog enjoys hopping around the infinite square grid in his backyard. It takes him 1 Joule of energy to hop one step north, south, east, or west. He wakes up one morning on the grid with 100 Joules of energy, and hops till he falls asleep with 0 energy. How many different places could he have gone to sleep?
|
10201
| 0.25 |
Given the sets \(A=\left\{(x, y) \mid (x-3)^{2}+(y-4)^{2} \leqslant\left(\frac{5}{2}\right)^{2}\right\}\) and \(B=\left\{(x, y) \mid (x-4)^{2}+(y-5)^{2}>\left(\frac{5}{2}\right)^{2}\right\}\), find the number of lattice points in the set \(A \cap B\).
|
7
| 0.5 |
Let \( A = \{a^2, a+1, -3\} \) and \( B = \{a-3, 2a-1, a^2+1\} \), and suppose \( A \cap B = \{-3\} \). Find the value of the real number \( a \).
|
-1
| 0.875 |
Let \( f(x) = ax + b \) (where \( a \) and \( b \) are real numbers), \( f_1(x) = f(x) \), \( f_{n+1}(x) = f(f_n(x)) \) for \( n=1, 2, 3, \cdots \). Given that \( 2a + b = -2 \) and \( f_k(x) = -243x + 244 \), find \( k \).
|
5
| 0.875 |
Given the real numbers \(\alpha\) and \(\beta\) that satisfy the following system of equations:
\[
\begin{cases}
\alpha^{3} - 3\alpha^{2} + 5\alpha - 17 = 0 \\
\beta^{3} - 3\beta^{2} + 5\beta + 11 = 0
\end{cases}
\]
find the value of \(\alpha + \beta\).
|
2
| 0.875 |
Given three circles, each with a radius of 3, and centers at \((14, 92)\), \((17, 76)\), and \((19, 84)\), find the absolute value of the slope of a line passing through the point \((17, 76)\) such that the sum of the areas of the parts of the circles on one side of the line is equal to the sum of the areas of the parts of the circles on the other side of the line.
|
24
| 0.75 |
In the figure, $ABCD$ is a square, $ADE$ is an equilateral triangle and $E$ is a point outside of the square $ABCD$. If $\angle AEB=\alpha^{\circ}$, determine the value of $\alpha$.
|
15
| 0.125 |
In triangle $ABC$ with an acute angle at vertex $A$, an angle bisector $AE$ and an altitude $BH$ are drawn. It is known that $\angle AEB = 45^{\circ}$. Find the angle $EHC$.
|
45^\circ
| 0.875 |
Given real numbers \( x \) and \( y \) satisfying the equation \(\frac{x^{2}}{3}+y^{2}=1\), find the range of values of
$$
P=|2x+y-4|+|4-x-2y|.
$$
|
[2, 14]
| 0.75 |
Given a positive integer $d$ which is square-free, and a fundamental solution $(x_{0}, y_{0})$ to the equation $x^{2} - d y^{2} = 1$. Find the positive integer solutions $(x, y)$ to this equation such that all prime factors of $x$ divide $x_{0}$.
|
(x_0, y_0)
| 0.5 |
Let \( M_n \) be the set of \( n \)-digit pure decimals in decimal notation \( 0.\overline{a_1a_2\cdots a_n} \), where \( a_i \) can only take the values 0 or 1 for \( i=1,2,\cdots,n-1 \), and \( a_n = 1 \). Let \( T_n \) be the number of elements in \( M_n \), and \( S_n \) be the sum of all elements in \( M_n \). Find \( \lim_{n \rightarrow \infty} \frac{S_n}{T_n} \).
|
\frac{1}{18}
| 0.75 |
An isosceles triangle \( \triangle ABC \) is given with \( AB = BC \). Point \( E \) is marked on the ray \( BA \) beyond point \( A \), and point \( D \) is marked on the side \( BC \). It is known that:
\[
\angle ADC = \angle AEC = 60^\circ, \quad AD = CE = 13
\]
Find the length of segment \( AE \), given that \( DC = 9 \).
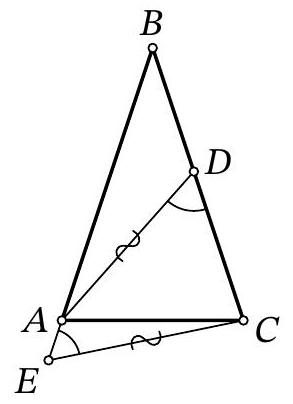
|
4
| 0.25 |
A line \( l \) passes through the focus \( F \) of the parabola \( y^2 = 4x \) and intersects the parabola at points \( A \) and \( B \). Point \( M \) is given as \( (4,0) \). Extending \( AM \) and \( BM \) intersects the parabola again at points \( C \) and \( D \), respectively. Find the value of \(\frac{S_{\triangle CDM}}{S_{\triangle ABM}}\).
|
16
| 0.625 |
11 gardeners are planting trees. 2 of them are planting trees on Street A, and the remaining 9 are planting trees on Street B. In the evening, they return to their dormitory.
Gardener A says: "Although there are fewer of us, we spent the same amount of time as you did."
Gardener B says: "Although there are more of us, the length of our street is 5 times the length of your street."
If the intervals at which they plant the trees are the same and each gardener plants the same number of trees, planting only on one side of the road and including both ends of the street, how many trees did these 11 gardeners plant in total?
|
44
| 0.875 |
A tourist travels from point \(A\) to point \(B\) in 1 hour and 56 minutes. The route from \(A\) to \(B\) first goes uphill, then on flat terrain, and finally downhill. What is the length of the flat terrain if the tourist's speed downhill is 6 km/h, uphill is 4 km/h, and on flat terrain is 5 km/h, and the total distance between \(A\) and \(B\) is \(x\) km? The distances uphill and on flat terrain are both whole numbers of kilometers.
|
3
| 0.875 |
1) \(\lim _{x \rightarrow 2}\left(\frac{1}{x-2}-\frac{4}{x^{2}-4}\right)\)
2) \(\lim _{x \rightarrow +\infty}\left(x-\sqrt{x^{2}+5x}\right)\)
3) \(\lim \left(\sqrt{\operatorname{tg}^{2} \alpha+\sec \alpha-\operatorname{tg} \alpha}\right)\)
4) \(\lim _{x \rightarrow 0}(2 \operatorname{cosec} 2x - \operatorname{ctg} x)\)
|
0
| 0.25 |
Let \( LOVER \) be a convex pentagon such that \( LOVE \) is a rectangle. Given that \( OV = 20 \) and \( LO = VE = RE = RL = 23 \), compute the radius of the circle passing through \( R, O \), and \( V \).
|
23
| 0.25 |
Find the point \( M' \) that is symmetric to the point \( M \) with respect to the line.
$$
\begin{aligned}
& M(0, 2, 1) \\
& \frac{x-1.5}{2} = \frac{y}{-1} = \frac{z-2}{1}
\end{aligned}
$$
|
(-1, 0, 1)
| 0.75 |
How many solutions does the equation
$$
\left\lfloor\frac{x}{20}\right\rfloor=\left\lfloor\frac{x}{17}\right\rfloor
$$
have over the set of positive integers?
Here, $\lfloor a\rfloor$ denotes the greatest integer less than or equal to \(a\).
|
56
| 0.625 |
In each cell of a \(5 \times 5\) table, a natural number is written with invisible ink. It is known that the sum of all the numbers equals 200, and the sum of three numbers located inside any \(1 \times 3\) rectangle equals 23. What is the value of the central number in the table?
|
16
| 0.375 |
There are 21 towns. Each airline runs direct flights between every pair of towns in a group of five. What is the minimum number of airlines needed to ensure that at least one airline runs direct flights between every pair of towns?
|
21
| 0.625 |
The lateral face of a regular quadrilateral pyramid forms a $45^{\circ}$ angle with the base plane. Find the angle between the adjacent lateral faces.
|
120^\circ
| 0.125 |
In triangle \( ABC \), \( AB = 86 \) and \( AC = 97 \). A circle with center at point \( A \) and radius \( AB \) intersects side \( BC \) at points \( B \) and \( X \). Given that both \( BX \) and \( CX \) have integer lengths, what is the length of \( BC \)?
|
61
| 0.875 |
Let \( x = \sin^4\left(\frac{\pi}{8}\right) + \cos^4\left(\frac{\pi}{8}\right) + \sin^4\left(\frac{7\pi}{8}\right) + \cos^4\left(\frac{7\pi}{8}\right) \). Find the value of \( 36x \).
|
54
| 0.75 |
Call a \(2n\)-digit base-10 number special if we can split its digits into two sets of size \(n\) such that the sum of the numbers in the two sets is the same. Let \(p_{n}\) be the probability that a randomly-chosen \(2n\)-digit number is special. (We allow leading zeros in \(2n\)-digit numbers). The sequence \(p_{n}\) converges to a constant \(c\). Find \(c\).
|
\frac{1}{2}
| 0.875 |
Let $ABC$ be an isosceles triangle with $A$ as the vertex, $D$ the midpoint of $[BC]$, and $\Gamma$ a circle centered at $D$ tangent to $[AB]$ and $[AC]$. Let $M \in [AB]$ and $N \in [AC]$ be such that $[MN]$ is tangent to $\Gamma$.
Show that $BD^2 = BM \times CN$.
|
BD^2 = BM \times CN
| 0.875 |
The four positive integers \(a, b, c, d\) satisfy \(a < b < c < d\). When the sums of the six pairs of these integers are calculated, the six answers are all different and the four smallest sums are 6, 8, 12, and 21. What is the value of \(d\)?
|
20
| 0.75 |
Let \( f \) be the function that maps a positive integer to the sum of its digits when written in base 10. For example, \( f(537)=15 \). Calculate \( f\left(f\left(f\left(4444^{4444}\right)\right)\right) \).
|
7
| 0.625 |
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} \sqrt{n+2}(\sqrt{n+3}-\sqrt{n-4})$$
|
\frac{7}{2}
| 0.5 |
In an isosceles triangle with a lateral side of 100 and a base of 60, a circle is inscribed. Find the distance between the points of tangency located on the lateral sides.
|
42
| 0.75 |
A board for playing "Battleship" has a size of $10 \times 10$. What is the maximum number of ships with a size of $1 \times 4$ that can be placed on it?
|
24
| 0.25 |
If the fraction \(\frac{p}{q}\) (where \( p, q \in \mathbf{Z}_{+} \)) is converted into a decimal as
\[
\frac{p}{q} = 0.198 \cdots,
\]
then, when \( q \) takes its minimum value, what is \( p+q \)?
|
121
| 0.5 |
Find the value of $\cos ^{4} \frac{\pi}{16}+\cos ^{4} \frac{3 \pi}{16}+\cos ^{4} \frac{5 \pi}{16}+\cdots+\cos ^{4} \frac{15 \pi}{16}$.
|
3
| 0.5 |
Suppose there are 997 points given in a plane. If every two points are joined by a line segment with its midpoint colored in red, show that there are at least 1991 red points in the plane. Can you find a special case with exactly 1991 red points?
|
1991
| 0.5 |
For any positive integer \( n \), let \( D_n \) denote the set of all positive divisors of \( n \). Define \( f_i(n) (i=1,2) \) as the number of elements in the set
\[ F_i(n) = \{ a \in D_n \mid a \equiv i \pmod{4} \} \]
Find the smallest positive integer \( m \) such that
\[ 2f_1(m) - f_2(m) = 2017. \]
|
2 \times 5^{2016}
| 0.25 |
Compute
$$
\int_{1}^{\sqrt{3}} x^{2 x^{2}+1}+\ln \left(x^{2 x^{2 x^{2}+1}}\right) d x. \text{ }$$
|
13
| 0.25 |
Given that \( z \) is a complex number, \( |z| = 1 \), and \( u = z^{4} - z^{3} - 3z^{2}i - z + 1 \). Find the maximum value of \( |u| \) and the complex number \( z \) when the maximum value is achieved.
|
5
| 0.875 |
A palindrome is a number, word, or text that reads the same backward as forward. How much time in a 24-hour day display palindromes on a clock, showing time from 00:00:00 to 23:59:59?
|
96
| 0.25 |
Find all real polynomials \(P\) such that \(P(0) = 0\) and \(P(X^2 + 1) = P(X)^2 + 1\).
|
P(X) = X
| 0.5 |
Given \(a, b, c \in \mathbf{R}^{+}\) (positive real numbers) such that \(a b c + a + c = b\), determine the maximum value of \(p = \frac{2}{a^{2}+1} - \frac{2}{b^{2}+1} + \frac{3}{c^{2}+1}\).
|
\frac{10}{3}
| 0.125 |
A swimmer swims against the current of a river and encounters an empty boat drifting with the current. Continuing to swim against the current for another $t$ minutes after the encounter, the swimmer then turns back and catches up with the boat $s$ meters from the point where they met. Find the speed of the river current.
|
\frac{s}{2 t}
| 0.875 |
Snow White entered a room with a round table surrounded by 30 chairs. Some of the chairs were occupied by dwarfs. It turned out that Snow White couldn't sit in a way such that no one was sitting next to her. What is the minimum number of dwarfs that could have been at the table? Explain how the dwarfs must have been seated.
|
10
| 0.875 |
An \(n \times m\) maze is an \(n \times m\) grid in which each cell is one of two things: a wall, or a blank. A maze is solvable if there exists a sequence of adjacent blank cells from the top left cell to the bottom right cell going through no walls. (In particular, the top left and bottom right cells must both be blank.) Determine the number of solvable \(2 \times 2\) mazes.
|
3
| 0.625 |
Given 100 distinct prime numbers \( p_{1}, p_{2}, \cdots, p_{100} \), let \( N=p_{1}^{2}+p_{2}^{2}+\cdots+p_{100}^{2} \). What is the remainder when \( N \) is divided by 3?
|
1
| 0.375 |
Let \(ABC\) be a triangle with \(AB = 13\), \(BC = 14\), and \(CA = 15\). Let \(I_A\), \(I_B\), and \(I_C\) be the \(A\), \(B\), and \(C\) excenters of this triangle, respectively, and let \(O\) be the circumcenter of the triangle. Let \(\gamma_A\), \(\gamma_B\), and \(\gamma_C\) be the corresponding excircles and \(\omega\) be the circumcircle. \(X\) is one of the intersections between \(\gamma_A\) and \(\omega\). Likewise, \(Y\) is an intersection of \(\gamma_B\) and \(\omega\), and \(Z\) is an intersection of \(\gamma_C\) and \(\omega\). Compute
\[
\cos \angle OXI_A + \cos \angle OYI_B + \cos \angle OZI_C.
\]
|
-\frac{49}{65}
| 0.125 |
Solve in integers: \(6x^2 + 5xy + y^2 = 6x + 2y + 7\). Specify the answer for which the value \(|x| + |y|\) is the largest. Write the answer in the form \((x; y)\).
|
(-8 ; 25)
| 0.5 |
Let \( P(x) \) be a polynomial of degree 2008 with leading coefficient 1 such that
\[ P(0) = 2007, \; P(1) = 2006, \; P(2) = 2005, \ldots, P(2007) = 0. \]
Determine the value of \( P(2008) \). You may use factorials in your answer.
|
2008! - 1
| 0.875 |
Find the smallest positive number $\alpha$ such that there exists a positive number $\beta$ for which the inequality $\sqrt{1+x} + \sqrt{1-x} \leq 2 - \frac{x^{\alpha}}{\beta}$ holds for $0 \leq x \leq 1$.
|
2
| 0.75 |
It is known that \(a^{2} b + a^{2} c + b^{2} a + b^{2} c + c^{2} a + c^{2} b + 3 a b c = 30\) and \(a^{2} + b^{2} + c^{2} = 13\).
Find \(a + b + c\).
|
5
| 0.875 |
Let the ellipse be given by \(\frac{x^{2}}{5}+\frac{y^{2}}{4}=1\). The locus of the intersection points of two mutually perpendicular tangents to the ellipse is \(C\). Tangents \(PA\) and \(PB\) to the curve \(C\) intersect at point \(P\), touching the curve at points \(A\) and \(B\) respectively. Find the minimum value of \(\overrightarrow{PA} \cdot \overrightarrow{PB}\).
|
18 \sqrt{2} - 27
| 0.625 |
Given three numbers \(a, b, c\) such that \(a \times b = 24\), \(a \times c = 36\), and \(b \times c = 54\), find the value of \(a + b + c\).
|
19
| 0.75 |
Does there exist \( n > 1 \) such that the set of positive integers may be partitioned into \( n \) non-empty subsets so that if we take an arbitrary element from every set but one, then their sum belongs to the remaining set?
|
\text{No}
| 0.5 |
Determine the number of roots of the equation:
$$
\left(21 x - 11 + \frac{\sin x}{100}\right) \cdot \sin(6 \arcsin x) \cdot \sqrt{(\pi - 6x)(\pi + x)} = 0
$$
|
7
| 0.125 |
What is the largest $n$ for which the numbers $1,2, \ldots, 14$ can be colored in red and blue so that for any number $k=1,2, \ldots, n$, there are a pair of blue numbers and a pair of red numbers, each pair having a difference equal to $k$?
|
11
| 0.375 |
A circle is inscribed in a triangle, and the points of tangency with the sides of the triangle are connected to each other. A new circle is inscribed in the resulting triangle, and the points of tangency with its sides are the vertices of a third triangle, which has the same angles as the original triangle. Find these angles.
|
60^\circ
| 0.125 |
A sequence of two distinct numbers is extended in two ways: one to form a geometric progression and the other to form an arithmetic progression. The third term of the geometric progression coincides with the tenth term of the arithmetic progression. With which term of the arithmetic progression does the fourth term of the geometric progression coincide?
|
74
| 0.875 |
\( n \) is a positive integer that is not greater than 100 and not less than 10, and \( n \) is a multiple of the sum of its digits. How many such \( n \) are there?
|
24
| 0.375 |
We consider 2015 lines in a plane, no two of which are parallel and no three of which meet at a single point. Let $E$ be the set of their intersection points.
We want to assign a color to each point in $E$ such that any two points on the same line, whose connecting segment contains no other points from $E$, are colored differently.
What is the minimum number of colors needed to achieve such a coloring?
|
3
| 0.125 |
On side \(AD\) of rectangle \(ABCD\), there is a point \(E\). On segment \(EC\), there is such a point \(M\) that \(AB=BM\) and \(AE=EM\). Find the length of side \(BC\), given that \(ED=16\) and \(CD=12\).
|
20
| 0.875 |
In each cell of a $5 \times 5$ table, a natural number is written with invisible ink. It is known that the sum of all the numbers is 200, and the sum of the three numbers within any $1 \times 3$ rectangle is 23. What is the value of the central number in the table?
|
16
| 0.25 |
For the infinite sequence of numbers \( x_{1}, x_{2}, x_{3}, \ldots \), the relationship \( x_{n} = x_{n-1} \cdot x_{n-3} \) holds for all natural numbers \( n \geq 4 \). It is known that \( x_{1} = 1 \), \( x_{2} = 1 \), and \( x_{3} = -1 \). Find \( x_{2022} \).
|
1
| 0.375 |
A player throws a fair die (with each number from 1 to 6 having an equal probability of 1/6 and each throw being independent) repeatedly until their total score is greater than or equal to \( n \). Let \( p(n) \) be the probability that their final score is exactly \( n \). Find \( \lim_{n \to \infty} p(n) \).
|
\frac{2}{7}
| 0.375 |
Find all functions \( f: \mathbb{R}_{+}^{*} \longrightarrow \mathbb{R}_{+}^{*} \) such that for every \( x \in \mathbb{R}_{+}^{*} \), there exists exactly one \( y \in \mathbb{R}_{+}^{*} \) such that:
\[
x f(y) + y f(x) \leq 2
\]
|
f(x) = \frac{1}{x}
| 0.75 |
A plane parallel to the base of a quadrilateral pyramid with a volume of 81 cuts off a smaller pyramid with a volume of 3. Find the volume of the pyramid whose four vertices coincide with the vertices of the section and whose fifth vertex lies in the plane of the base of the larger pyramid.
|
6
| 0.5 |
The diagonals of a trapezoid are mutually perpendicular, and one of them is equal to 17. Find the area of the trapezoid if its height is 15.
|
\frac{4335}{16}
| 0.25 |
Let the three sides of a triangle be integers \( l \), \( m \), and \( n \) with \( l > m > n \). It is known that \( \left\{\frac{3^l}{10^4}\right\} = \left\{\frac{3^m}{10^4}\right\} = \left\{\frac{3^n}{10^4}\right\} \), where \( \{x\} \) denotes the fractional part of \( x \). Determine the minimum value of the perimeter of the triangle.
|
3003
| 0.625 |
In a school chess tournament, boys and girls competed, with the number of boys being 5 times the number of girls. According to the tournament rules, each player played against every other player twice. How many players participated in total, given that the boys scored exactly twice as many points as the girls? (A win in a chess game counts as 1 point, a draw counts as 0.5 points, and a loss counts as 0 points.)
|
6 \text{ players}
| 0.75 |
The square \(ABCD\) is to be decomposed into \(n\) nonoverlapping triangles, all of whose angles are acute. Find the smallest integer \(n\) for which there exists a solution to this problem and construct at least one decomposition for this \(n\). Additionally, answer whether it is possible to require that (at least) one of these triangles has a perimeter less than an arbitrarily given positive number.
|
8
| 0.75 |
To determine the smallest value of \( n \) for which the following system of equations has a solution:
$$
\left\{\begin{array}{l}
\sin x_{1}+\sin x_{2}+\cdots+\sin x_{n}=0, \\
\sin x_{1}+2 \sin x_{2}+\cdots+n \sin x_{n}=100
\end{array}\right.
$$
|
20
| 0.5 |
Let $\Gamma$ be a circle with chord $[BC]$. Let $A$ be the midpoint of the arc $\overparen{BC}$. From point $A$, draw two arbitrary chords $[AD]$ and $[AE]$ which intersect the segment $[BC]$ at $F$ and $G$ respectively. Show that the quadrilateral $DFGE$ is cyclic.
|
DFGE
| 0.375 |
In a regular truncated quadrilateral pyramid with the height of the lateral face \( a \), a sphere can be inscribed. Find the area of its lateral surface.
|
4a^2
| 0.75 |
Find a three-digit number whose square is a six-digit number, such that each subsequent digit from left to right is greater than the previous one.
|
367
| 0.25 |
Given that the function \( f(x) \) is monotonically increasing on \([2,+\infty)\), and for any real number \( x \), \( f(2+x)=f(2-x) \) always holds. If \( f\left(1-2 x^{2}\right)<f\left(1+2 x-x^{2}\right) \), determine the range of values for \( x \).
|
(-2, 0)
| 0.625 |
A triangular prism \( ABC A_1 B_1 C_1 \) with the base \( ABC \) and lateral edges \( AA_1, BB_1, CC_1 \) is intersected by a plane passing through points \( E, F, C \), where point \( E \) is the midpoint of edge \( AA_1 \), and point \( F \) lies on edge \( BB_1 \) such that \( BF:FB_1 = 1:2 \). Find the volume of the part of the prism \( ABC A_1 B_1 C_1 \) that is enclosed between the intersecting plane and the base of this prism, given that the volume of the prism is \( V \).
|
\frac{5}{18} V
| 0.25 |
Take a standard set of dominoes and remove all duplicates and blanks. Then consider the remaining 15 dominoes as fractions. The dominoes are arranged in such a way that the sum of all fractions in each row equals 10. However, unlike proper fractions, you are allowed to use as many improper fractions (such as \(\frac{4}{3}, \frac{5}{2}, \frac{6}{1}\)) as you wish, as long as the sum in each row equals 10.
|
10
| 0.125 |
Given complex numbers \( z \) and \( \omega \) satisfying the following two conditions:
1. \( z + \omega + 3 = 0 \);
2. \( |z|, 2, |\omega| \) form an arithmetic sequence.
Is there a maximum value for \( \cos(\arg z - \arg \omega) \)? If so, find it.
|
\frac{1}{8}
| 0.75 |
Given the equation:
\[ A = \operatorname{ctg}\left(\frac{11 \pi}{4}+\frac{1}{2} \arccos \frac{2 b}{a}\right)+\operatorname{ctg}\left(\frac{11 \pi}{4}-\frac{1}{2} \arccos \frac{2 b}{a}\right) \]
Find the value of \( A \).
|
-\frac{a}{b}
| 0.875 |
One of the diagonals of an inscribed quadrilateral is a diameter of its circumscribed circle.
Verify that the intersections $E$ and $F$ of the lines perpendicular to $A$ and $C$, respectively, to the line $BD$, satisfy:
$$
DE = BF
$$
|
DE = BF
| 0.75 |
Given a finite set \( A \), there exists a function \( f: \mathbf{N}^{*} \rightarrow A \) with the following property: if \( i, j \in \mathbf{N}^{*} \) and \( |i-j| \) is a prime number, then \( f(i) \neq f(j) \). What is the minimum number of elements that the set \( A \) must have?
|
4
| 0.875 |
What is the largest number of natural numbers less than 50 that can be chosen so that any two of them are relatively prime?
|
16
| 0.5 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.