path
stringlengths 7
265
| concatenated_notebook
stringlengths 46
17M
|
|---|---|
Density Dataframe for Systolic BP, Diastolic BP, Steel HR, Weight.ipynb
|
###Markdown
Part 1: Systolic Analysis 1a) Data-preprocessing To remove insignificant data, I first make a dataframe of patients who have multiple systolic measurements in a single day. I then check the elapsed time between all such measurements, and for those that were recorded less than 10 minutes apart, I simply use the first value and discard the second value. I then use this dataframe along with the original dataframe to obtain a new dataframe with only significant measurements.
###Code
# Checking for multiple values, creating csv of multiple values
c = datawithtime[datawithtime.type_measurement == 'Systolic blood pressure']
c = c.sort_values('date_measurement')
c.reset_index(inplace=True)
del c['index']
import csv
df = pd.DataFrame(index=[], columns=[]) # dataframe to store measurements with repeated dates
for i in range(0, len(e)):
d = c[c.email == e[i]]
d.reset_index(inplace=True)
del d['index']
d
d.date_measurement
d['date_without_time'] = d['date_measurement'].str[0:10] # new column for date w/o time
d
bool_series = d.duplicated('date_without_time', keep = False) # bool series for duplicated dates
if any(bool_series) == True:
duplicates = d[bool_series] # temporary dataframe of duplicates per patient
duplicates.reset_index(inplace=True)
del duplicates['index']
df = pd.concat([df, duplicates])
#display(duplicates)
#duplicates.to_csv('Systolic duplicates.csv', mode='a', header=True, index=False)
df = df.reset_index(drop=True) # all systolic measurements that have repeated dates (shows date without time as well)
# Getting rid of insignificant measurements
df['elapsed_hours'] = np.nan # create new column in df
for i in range(1,len(df)):
if df.email[i] == df.email[i-1] and df.date_without_time[i] == df.date_without_time[i-1]: # if row email and date match previous row
diff1 = datetime.strptime(df.date_measurement[i], '%Y-%m-%d %H:%M:%S') - datetime.strptime(df.date_measurement[i-1], '%Y-%m-%d %H:%M:%S') # finding time difference
if diff1.days == 0 and diff1.seconds < 600: # if difference is less than 10 minutes apart
df.loc[i, 'elapsed_hours'] = 0
if diff1.days == 0 and diff1.seconds >= 600:
hours = diff1.seconds/3600
df.loc[i, 'elapsed_hours'] = hours
# df now shows elapsed hours where 0 means insignificant (duplicate) value
# Getting rid of rows with 0 so that df now has only meaningful values
droplist = []
for i in range(0, len(df)):
if df.elapsed_hours[i] == 0:
droplist.append(i)
droplist
df.drop(droplist, inplace=True)
df = df.reset_index(drop=True) # removed meaningless (< 10 mins) values from df
#df.to_csv('systolic_density_without_duplicates.csv')
# Updating dataframe to only show meaningful systolic measurements
droplist = [] # Creating new droplist to update dataframe
# For each patient in df, look at date_without_time and remove rows for those dates from datawithtimeSys
# First make new dataframe called datawithtimeSys to continue analysis
datawithtimeSys = datawithtime[datawithtime.type_measurement == 'Systolic blood pressure']
datawithtimeSys = datawithtimeSys.reset_index(drop=True) # resetting indices for for-loop
for i in range(0, len(e)):
tempdf = df[df.email == e[i]] # get dates from here
tempdfdates = list(set(tempdf.date_without_time)) # unique duplicate date list for a single patient
for j in range(0, len(tempdfdates)):
for k in range(0, len(datawithtimeSys)):
if datawithtimeSys.email[k] == e[i] and datawithtimeSys.date_measurement[k][0:10] == tempdfdates[j]:
droplist.append(k)
# Dropping rows with duplicate data dates
datawithtimeSys.drop(droplist, inplace=True) # all duplicates dropped
datawithtimeSys = datawithtimeSys.sort_values('email') # sorting by email
# Merging duplicates with non-duplicates into new dataframe: densitylist
densitylist = pd.concat([datawithtimeSys, df], ignore_index=True, sort=False)
densitylist = densitylist.sort_values('email')
densitylist = densitylist.reset_index(drop=True) # updated dataframe for Systolic density analysis
###Output
_____no_output_____
###Markdown
1b) Systolic analysisI use these results to conduct analysis of systolic blood pressure measurements (from day 0 to day 30) for each patient and update results into the densitydf dataframe. The rows of densitydf correspond to each patient, while the columns are the analyses conducted. Further explanation of each column can be found in the file titled 'Columns'.
###Code
# First get every patient's start date to 30 days
# Then create empty list, append measurement values if date falls in 30 day interval
# Length of list = density
day1binarylistsys = [] # 1 if systolic < 130, else 0
day1binarylistdia = [] # 1 if diastolic < 80, else 0
day30binarylistsys = [] # 1 if systolic < 130, else 0
day30binarylistdia = [] # 1 if diastolic < 80, else 0
edate.date_used[0] # edate has starting dates as timestamps
for i in range(0, len(e)): # for all patients
dlist = [] # all measurements from 0 to 30 days
datelist = [] # 30 dates from start to end
stdlist = [] # each element = # of data points for that date; total 30 elements
startdate = 0
enddate = 0
# Setting everyone's start date, end date (after 30 days)
for j in range(0,len(edate)):
if edate.email[j] == e[i]:
startdate = edate.date_used[j]
enddate = edate.date_used[j] + timedelta(days=30)
# Creating list of 30 dates for std (elements are dates from start date to end date)
def daterange(date1, date2):
for n in range(int ((date2 - date1).days)+1):
yield date1 + timedelta(n)
for dt in daterange(startdate, enddate):
datelist.append(dt)
# Updating dlist and calculating binary outcome
day1data = [0]
day30data = [0]
for z in range(0, len(densitylist)):
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') <= enddate:
dlist.append(densitylist.value_measurement[z])
# Updating day1data
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') == startdate:
day1data.append(densitylist.value_measurement[z])
# Updating day30data
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') == enddate:
day30data.append(densitylist.value_measurement[z])
# Calculating binary outcome
outcome1 = 0 # for first datapoint
outcome2 = 0 # for last datapoint
if len(dlist) != 0:
day1mean = sum(day1data)/(len(day1data)-1)
day30mean = sum(day30data)/(len(day30data)-1)
if day1mean < 130 and day1mean != 0:
outcome1 = 1
elif day1mean >= 130:
outcome1 = 0
else: # AKA if value = 0 (no data)
outcome1 = np.nan
if day30mean < 130 and day30mean != 0:
outcome2 = 1
elif day30mean >= 130:
outcome2 = 0
else: # AKA if value = 0 (no data)
outcome2 = np.nan
else:
outcome1 = np.nan
outcome2 = np.nan
day1binarylistsys.append(outcome1)
day30binarylistsys.append(outcome2)
# Updating stdlist
for m in range(0, len(datelist)):
count = 0
for n in range(0, len(densitylist)):
if densitylist.email[n] == e[i] and datetime.strptime(densitylist.date_measurement[n][0:10], '%Y-%m-%d') == datelist[m]:
count = count + 1
stdlist.append(count)
density = len(dlist)
# Calculating risk score
sum1 = []
sum2 = []
score = 0
for k in range(0,len(dlist)):
if dlist[k] > 140:
sum1.append(dlist[k] - 140)
if dlist[k] < 100:
sum2.append(100 - dlist[k])
score = (sum(sum1) + sum(sum2))/density
average = sum(stdlist)/31
if density > 1: # if patient has more than 1 datapoint
std = statistics.stdev(dlist)
else:
std = np.nan
# Inputting values into dataframe
for w in range(0,len(densitydf)):
if densitydf.email[w] == e[i]:
densitydf.at[w, 'average_BP_data_per_day'] = average
densitydf.at[w,'std_BP_data_per_day'] = statistics.stdev(stdlist) # std for data volume per day over 30 days
densitydf.at[w,'BP_density'] = density
densitydf.at[w,'systolic_mean'] = mean(dlist)
densitydf.at[w,'systolic_std'] = std # std for systolic values
densitydf.at[w,'systolic_risk_score'] = score
#print(dlist)
#print(('{0} density: {1}'.format(e[i], density)))
#print(('{0} score: {1}'.format(e[i], score)))
#print(('{0} average: {1}'.format(e[i], average)))
#print(datelist)
#print(stdlist)
densitydf.head()
###Output
_____no_output_____
###Markdown
Part 2: Diastolic Analysis 2a) Data-preprocessing I use the same approach as I did in Part 1. To remove insignificant data, I first make a dataframe of patients who have multiple diastolic measurements in a single day. I then check the elapsed time between all such measurements, and for those that were recorded less than 10 minutes apart, I simply use the first value and discard the second value. I then use this dataframe along with the original dataframe to obtain a new dataframe with only significant measurements.
###Code
# Checking for multiple values, creating csv of multiple values
c = datawithtime[datawithtime.type_measurement == 'Diastolic blood pressure']
c = c.sort_values('date_measurement')
c.reset_index(inplace=True)
del c['index']
import csv
df = pd.DataFrame(index=[], columns=[])
for i in range(0, len(e)):
d = c[c.email == e[i]]
d.reset_index(inplace=True)
del d['index']
d
d.date_measurement
d['date_without_time'] = d['date_measurement'].str[0:10] # new column for date w/o time
d
bool_series = d.duplicated('date_without_time', keep = False) # bool series for duplicated dates
if any(bool_series) == True:
duplicates = d[bool_series] # temporary dataframe of duplicates per patient
duplicates.reset_index(inplace=True)
del duplicates['index']
df = pd.concat([df, duplicates])
#display(duplicates)
#duplicates.to_csv('Diastolic duplicates.csv', mode='a', header=True, index=False)
df = df.reset_index(drop=True)
# Getting rid of insignificant measurements
df['elapsed_hours'] = np.nan
for i in range(1,len(df)):
if df.email[i] == df.email[i-1] and df.date_without_time[i] == df.date_without_time[i-1]: #duplicates
diff1 = datetime.strptime(df.date_measurement[i], '%Y-%m-%d %H:%M:%S') - datetime.strptime(df.date_measurement[i-1], '%Y-%m-%d %H:%M:%S')
if diff1.days == 0 and diff1.seconds < 600: #less than 10 minutes
df.loc[i, 'elapsed_hours'] = 0
if diff1.days == 0 and diff1.seconds >= 600:
hours = diff1.seconds/3600
df.loc[i, 'elapsed_hours'] = hours
# Getting rid of rows with 0 so that df now has only meaningful values
droplist = []
for i in range(0, len(df)):
if df.elapsed_hours[i] == 0:
droplist.append(i)
droplist
df.drop(droplist, inplace=True)
df = df.reset_index(drop=True)
#df.to_csv('Diastolic_density.csv')
# Updating dataframe to only show meaningful diastolic measurements
droplist = []
# For each patient in df, look at date_without_time and remove rows for those dates from datawithtimeDia
datawithtimeDia = datawithtime[datawithtime.type_measurement == 'Diastolic blood pressure']
datawithtimeDia = datawithtimeDia.reset_index(drop=True)
for i in range(0, len(e)):
tempdf = df[df.email == e[i]] # get dates from here
tempdfdates = list(set(tempdf.date_without_time)) # unique duplicate date list for a single patient
for j in range(0, len(tempdfdates)):
for k in range(0, len(datawithtimeDia)):
if datawithtimeDia.email[k] == e[i] and datawithtimeDia.date_measurement[k][0:10] == tempdfdates[j]:
droplist.append(k)
# Dropping rows with duplicate data dates
datawithtimeDia.drop(droplist, inplace=True) # dropping insignificant values
datawithtimeDia = datawithtimeDia.sort_values('email')
# Merging duplicates with non-duplicates into new dataframe: densitylist
densitylist = pd.concat([datawithtimeDia, df], ignore_index=True, sort=False)
densitylist = densitylist.sort_values('email')
densitylist = densitylist.reset_index(drop=True)
###Output
_____no_output_____
###Markdown
2b) Diastolic analysisI use the same approach as I did in Part 1. I use these results to conduct analysis of diastolic blood pressure measurements (from day 0 to day 30) for each patient and update results into the densitydf dataframe. The rows of densitydf correspond to each patient, while the columns are the analyses conducted. Further explanation of each column can be found in the file titled 'Columns'. In addition, I calculate new risk scores for Diastolic measurements, using different measurement ranges provided by my principal investigator. This is denoted 'risk score v2'. I also fill out the blood pressure binary outcomes for each patient, and update densitydf accordingly.
###Code
# Note: no datelist, since avg data per day for blood pressure was already computed in Systolic analysis
for i in range(0, len(e)):
dlist = []
startdate = 0
enddate = 0
for j in range(0,len(edate)):
if edate.email[j] == e[i]:
startdate = edate.date_used[j]
enddate = edate.date_used[j] + timedelta(days=30)
# Updating dlist and calculating binary outcome
day1data = [0]
day30data = [0]
for z in range(0, len(densitylist)):
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') <= enddate:
dlist.append(densitylist.value_measurement[z])
# Updating day1data
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') == startdate:
day1data.append(densitylist.value_measurement[z])
# Updating day30data
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') == enddate:
day30data.append(densitylist.value_measurement[z])
# Calculating binary outcome
outcome1 = 0 # for first datapoint
outcome2 = 0 # for last datapoint
if len(dlist) != 0:
day1mean = sum(day1data)/(len(day1data)-1)
day30mean = sum(day30data)/(len(day30data)-1)
if day1mean < 80 and day1mean != 0:
outcome1 = 1
elif day1mean >= 80:
outcome1 = 0
else: # AKA if value = 0 (no data)
outcome1 = np.nan
if day30mean < 80 and day30mean != 0:
outcome2 = 1
elif day30mean >= 80:
outcome2 = 0
else: # AKA if value = 0 (no data)
outcome2 = np.nan
else:
outcome1 = np.nan
outcome2 = np.nan
#print(day1data, day30data)
day1binarylistdia.append(outcome1)
day30binarylistdia.append(outcome2)
density = len(dlist)
# Calculating risk score
sum1 = []
sum2 = []
score = 0
for k in range(0,len(dlist)):
if dlist[k] > 80:
sum1.append(dlist[k] - 80)
if dlist[k] < 60:
sum2.append(60 - dlist[k])
score = (sum(sum1) + sum(sum2))/density
# Calculating risk score v2
sum3 = []
sum4 = []
score2 = 0
for k in range(0,len(dlist)):
if dlist[k] > 85:
sum3.append(dlist[k] - 85)
if dlist[k] < 60:
sum4.append(60 - dlist[k])
score2 = (sum(sum3) + sum(sum4))/density
average = sum(stdlist)/31
if density > 1:
std = statistics.stdev(dlist)
else:
std = np.nan
# Inputting values into dataframe
for w in range(0,len(densitydf)):
if densitydf.email[w] == e[i]:
densitydf.at[w,'diastolic_mean'] = mean(dlist)
densitydf.at[w,'diastolic_std'] = std
densitydf.at[w,'diastolic_risk_score'] = score
densitydf.at[w,'diastolic_risk_score_v2'] = score2
#print(dlist)
#print(('{0} density: {1}'.format(e[i], density)))
#print(('{0} score: {1}'.format(e[i], score)))
#print(('{0} average: {1}'.format(e[i], average)))
# Inputting binary outcome for BP
for w in range(0,len(densitydf)):
# Binary outcome start
if day1binarylistsys[w] == 1 and day1binarylistdia[w] == 1:
densitydf.at[w,'Binary_outcome_BP_start'] = 1
elif day1binarylistsys[w] == np.nan:
densitydf.at[w,'Binary_outcome_BP_start'] = np.nan
elif day1binarylistdia[w] == np.nan:
densitydf.at[w,'Binary_outcome_BP_start'] = np.nan
else:
densitydf.at[w,'Binary_outcome_BP_start'] = 0
# Binary outcome end
if day30binarylistsys[w] == 1 and day30binarylistdia[w] == 1:
densitydf.at[w,'Binary_outcome_BP_end'] = 1
elif day30binarylistsys[w] == np.nan:
densitydf.at[w,'Binary_outcome_BP_end'] = np.nan
elif day30binarylistdia[w] == np.nan:
densitydf.at[w,'Binary_outcome_BP_end'] = np.nan
else:
densitydf.at[w,'Binary_outcome_BP_end'] = 0
densitydf.head()
###Output
_____no_output_____
###Markdown
Part 3: HR (Steel) Analysis For HR (Steel) measurements, I knew from my visualizations (number of data for days) that there were no dates with more than one measurement per patient, which meant that there was no need to compare time stamps for each patient to remove insignificant values. Therefore, I just had to remove all measurements with a value of 0, and was able to directly proceed with my analyses and input the results into densitydf. In addition, I calculate new risk scores for HR (Steel) measurements, using different measurement ranges provided by my principal investigator. This is denoted 'risk score v2'. I also fill out the HR (Steel) binary outcomes for each patient, and update densitydf accordingly.
###Code
hrlist = data[data.type_measurement == 'Heart rate - from Steel HR - Average over the day']
hrlist = hrlist.reset_index(drop=True)
droplist = []
for i in range(0, len(hrlist)):
if hrlist.value_measurement[i] == 0:
droplist.append(i)
hrlist.drop(droplist, inplace=True)
hrlist = hrlist.reset_index(drop=True) # got rid of 0 values in hrlist
for i in range(0, len(e)):
dlist = []
datelist = [] # 30 dates from start to end
stdlist = [] # each element = # of data points per day; total 30 elements
startdate = 0
enddate = 0
for j in range(0,len(edate)):
if edate.email[j] == e[i]:
startdate = edate.date_used[j]
enddate = edate.date_used[j] + timedelta(days=30)
# Creating list of 30 dates for std
def daterange(date1, date2):
for n in range(int ((date2 - date1).days)+1):
yield date1 + timedelta(n)
for dt in daterange(startdate, enddate):
datelist.append(dt)
# Updating dlist and calculating binary outcome
day1data = [0]
day30data = [0]
for z in range(0, len(hrlist)):
if hrlist.email[z] == e[i] and datetime.strptime(hrlist.date_measurement[z][0:10], '%Y-%m-%d') <= enddate:
dlist.append(hrlist.value_measurement[z])
# Updating day1data
if hrlist.email[z] == e[i] and datetime.strptime(hrlist.date_measurement[z][0:10], '%Y-%m-%d') == startdate:
day1data.append(hrlist.value_measurement[z])
# Updating day30data
if hrlist.email[z] == e[i] and datetime.strptime(hrlist.date_measurement[z][0:10], '%Y-%m-%d') == enddate:
day30data.append(hrlist.value_measurement[z])
#print(day1data, day30data)
# Calculating binary outcome
outcome1 = 0 # for first datapoint
outcome2 = 0 # for last datapoint
if len(dlist) != 0:
day1mean = sum(day1data)/(len(day1data)-1)
day30mean = sum(day30data)/(len(day30data)-1)
if day1mean < 70 and day1mean != 0:
outcome1 = 1
if day1mean >= 70:
outcome1 = 0
if day1mean == 0: # AKA if there's no data
outcome1 = np.nan
if day30mean < 70 and day30mean != 0:
outcome2 = 1
if day30mean >= 70:
outcome2 = 0
if day30mean == 0: # AKA if there's no data
outcome2 = np.nan
else:
outcome1 = np.nan
outcome2 = np.nan
# Updating stdlist
for m in range(0, len(datelist)):
count = 0
for n in range(0, len(hrlist)):
if hrlist.email[n] == e[i] and datetime.strptime(hrlist.date_measurement[n][0:10], '%Y-%m-%d') == datelist[m]:
count = count + 1
stdlist.append(count)
density = len(dlist)
# Calculating risk score
sum1 = []
sum2 = []
score = 0
for k in range(0,len(dlist)):
if dlist[k] > 90:
sum1.append(dlist[k] - 90)
if dlist[k] < 60:
sum2.append(60 - dlist[k])
score = (sum(sum1) + sum(sum2))/density
# Calculating risk score v2
sum3 = []
sum4 = []
score2 = 0
for k in range(0,len(dlist)):
if dlist[k] > 100:
sum3.append(dlist[k] - 100)
if dlist[k] < 60:
sum4.append(60 - dlist[k])
score2 = (sum(sum3) + sum(sum4))/density
average = sum(stdlist)/31
if density > 1:
std = statistics.stdev(dlist)
else:
std = np.nan
# Inputting values into dataframe
for w in range(0,len(densitydf)):
if densitydf.email[w] == e[i]:
densitydf.at[w, 'average_HR_data_per_day'] = average
densitydf.at[w,'std_HR_data_per_day'] = statistics.stdev(stdlist)
densitydf.at[w,'Steel_HR_density'] = density
densitydf.at[w,'Steel_HR_mean'] = mean(dlist)
densitydf.at[w,'Steel_HR_std'] = std
densitydf.at[w,'Steel_HR_risk_score'] = score
densitydf.at[w,'Steel_HR_risk_score_v2'] = score2
densitydf.at[w,'Binary_outcome_HR_start'] = outcome1
densitydf.at[w,'Binary_outcome_HR_end'] = outcome2
#print(dlist)
#print(('{0} density: {1}'.format(e[i], density)))
#print(('{0} score: {1}'.format(e[i], score)))
#print(('{0} average: {1}'.format(e[i], average)))
densitydf.head()
###Output
_____no_output_____
###Markdown
Part 4: Weight Analysis 4a) Data-preprocessing I use the same approach as I did in Part 1 and 2. To remove insignificant data, I first make a dataframe of patients who have multiple weight measurements in a single day. I then check the elapsed time between all such measurements, and for those that were recorded less than 10 minutes apart, I simply use the first value and discard the second value. I then use this dataframe along with the original dataframe to obtain a new dataframe with only significant measurements.
###Code
# Checking for multiple values, creating csv of multiple values
c = datawithtime[datawithtime.type_measurement == 'Weight']
c = c.sort_values('date_measurement')
c.reset_index(inplace=True)
del c['index']
import csv
df = pd.DataFrame(index=[], columns=[])
for i in range(0, len(e)):
d = c[c.email == e[i]]
d.reset_index(inplace=True)
del d['index']
d
d.date_measurement
d['date_without_time'] = d['date_measurement'].str[0:10] # new column for date w/o time
d
bool_series = d.duplicated('date_without_time', keep = False) # bool series for duplicated dates
if any(bool_series) == True:
duplicates = d[bool_series] # temporary dataframe of duplicates per patient
duplicates.reset_index(inplace=True)
del duplicates['index']
df = pd.concat([df, duplicates])
#display(duplicates)
duplicates.to_csv('Weight duplicates.csv', mode='a', header=True, index=False)
df = df.reset_index(drop=True)
# Getting rid of insignificant measurements
df['elapsed_hours'] = np.nan
for i in range(1,len(df)):
if df.email[i] == df.email[i-1] and df.date_without_time[i] == df.date_without_time[i-1]: #duplicates
diff1 = datetime.strptime(df.date_measurement[i], '%Y-%m-%d %H:%M:%S') - datetime.strptime(df.date_measurement[i-1], '%Y-%m-%d %H:%M:%S')
if diff1.days == 0 and diff1.seconds < 600: #less than 10 minutes
df.loc[i, 'elapsed_hours'] = 0
if diff1.days == 0 and diff1.seconds >= 600:
hours = diff1.seconds/3600
df.loc[i, 'elapsed_hours'] = hours
# Getting rid of rows with 0 so that df now has only meaningful values
droplist = []
for i in range(0, len(df)):
if df.elapsed_hours[i] == 0:
droplist.append(i)
droplist
df.drop(droplist, inplace=True)
df = df.reset_index(drop=True)
#df.to_csv('Weight_density.csv')
# Updating dataframe to only show meaningful weight measurements
droplist = []
# For each patient in df, look at date_without_time and remove rows for those dates from datawithtimeW
datawithtimeW = datawithtime[datawithtime.type_measurement == 'Weight']
datawithtimeW = datawithtimeW.reset_index(drop=True)
for i in range(0, len(e)):
tempdf = df[df.email == e[i]] # get dates from here
tempdfdates = list(set(tempdf.date_without_time)) # unique duplicate date list for a single patient
for j in range(0, len(tempdfdates)):
for k in range(0, len(datawithtimeW)):
if datawithtimeW.email[k] == e[i] and datawithtimeW.date_measurement[k][0:10] == tempdfdates[j]:
droplist.append(k)
# Dropping rows with duplicate data dates
datawithtimeW.drop(droplist, inplace=True) # dropping insignificant values
datawithtimeW = datawithtimeW.sort_values('email')
# Merging duplicates with non-duplicates into new dataframe: densitylist
densitylist = pd.concat([datawithtimeW, df], ignore_index=True, sort=False)
densitylist = densitylist.sort_values('email')
densitylist = densitylist.reset_index(drop=True)
###Output
_____no_output_____
###Markdown
4b) Weight analysisI use the same approach as I did in Part 1 and 2. I use these results to conduct analysis of weight measurements (from day 0 to day 30) for each patient and update results into the densitydf dataframe. The rows of densitydf correspond to each patient, while the columns are the analyses conducted. Further explanation of each column can be found in the file titled 'Columns'.
###Code
for i in range(0, len(e)): # for all patients
dlist = [] # all measurements from 0 to 30 days
datelist = [] # 30 dates from start to end
stdlist = [] # each element = # of data points for that date; total 30 elements
startdate = 0
enddate = 0
# Setting everyone's start date, end date (after 30 days)
for j in range(0,len(edate)):
if edate.email[j] == e[i]:
startdate = edate.date_used[j]
enddate = edate.date_used[j] + timedelta(days=30)
# Creating list of 30 dates for std (elements are dates from start date to end date)
def daterange(date1, date2):
for n in range(int ((date2 - date1).days)+1):
yield date1 + timedelta(n)
for dt in daterange(startdate, enddate):
datelist.append(dt)
# Updating dlist
for z in range(0, len(densitylist)):
if densitylist.email[z] == e[i] and datetime.strptime(densitylist.date_measurement[z][0:10], '%Y-%m-%d') <= enddate:
dlist.append(densitylist.value_measurement[z])
# Updating stdlist
for m in range(0, len(datelist)):
count = 0
for n in range(0, len(densitylist)):
if densitylist.email[n] == e[i] and datetime.strptime(densitylist.date_measurement[n][0:10], '%Y-%m-%d') == datelist[m]:
count = count + 1
stdlist.append(count)
density = len(dlist)
# Calculating risk score
#sum1 = []
#sum2 = []
#score = 0
#for k in range(0,len(dlist)):
# if dlist[k] > 140:
# sum1.append(dlist[k] - 140)
# if dlist[k] < 100:
# sum2.append(100 - dlist[k])
# score = (sum(sum1) + sum(sum2))/density
average = sum(stdlist)/31
if density > 1: # if patient has more than 1 datapoint
std = statistics.stdev(dlist)
else:
std = np.nan
# Inputting values into dataframe
for w in range(0,len(densitydf)):
if densitydf.email[w] == e[i]:
densitydf.at[w, 'average_Weight_data_per_day'] = average
densitydf.at[w,'std_Weight_data_per_day'] = statistics.stdev(stdlist) # std for data volume per day over 30 days
densitydf.at[w,'Weight_density'] = density
densitydf.at[w,'Weight_mean'] = mean(dlist)
densitydf.at[w,'Weight_std'] = std # std for Weight values
densitydf.at[w,'Weight_risk_score'] = np.nan
#densitydf.head()
densitydf.to_csv('density_dataframe.csv')
###Output
_____no_output_____
|
Reproducibility of published results/Evaluating the burden of COVID-19 in Bahia, Brazil: A modeling analysis of 14.8 million individuals/script/.ipynb_checkpoints/SEIRHUD-checkpoint.ipynb
|
###Markdown
Run SEIRHUD
###Code
from model import SEIRHUD
import csv
import numpy as np
import pandas as pd
import time
import warnings
from tqdm import tqdm
warnings.filterwarnings('ignore')
data = pd.read_csv("../data/data.csv")
data.head()
def bootWeig(series, times):
series = np.diff(series)
series = np.insert(series, 0, 1)
results = []
for i in range(0,times):
results.append(np.random.multinomial(n = sum(series), pvals = series/sum(series)))
return np.array(results)
#using bootstrap to
infeclists = bootWeig(data["infec"], 500)
deathslists = bootWeig(data["dthcm"], 500)
#Define empty lists to recive results
ypred = []
dpred = []
upred = []
hpred = []
spred = []
epred = []
beta1 = []
beta2 = []
gammaH = []
gammaU = []
delta = []
h = []
ia0 = []
e0 = []
#define fixed parameters:
kappa = 1/4
p = 0.2
gammaA = 1/3.5
gammaS = 1/4
muH = 0.15
muU = 0.4
xi = 0.53
omega_U = 0.29
omega_H = 0.14
N = 14873064
bound = ([0,0,0,1/14,1/14,0,0.05,0,0,0],[1.5,1,30,1/5,1/5,1,0.35,10/N,10/N,10/N])
for cases, deaths in tqdm(zip(infeclists, deathslists)):
model = SEIRHUD(tamanhoPop = N, numeroProcessadores = 8)
model.fit(x = range(1,len(data["infec"]) + 1),
y = np.cumsum(cases),
d = np.cumsum(deaths),
pesoMorte = 0.5,
bound = bound,
kappa = kappa,
p = p,
gammaA = gammaA,
gammaS = gammaS,
muH = muH,
muU = muU,
xi = xi,
omegaU = omega_U,
omegaH = omega_H,
stand_error = True,
)
results = model.predict(range(1,len(data["infec"]) + 200))
coef = model.getCoef()
#Append predictions
ypred.append(results["pred"])
dpred.append(results["death"])
hpred.append(results["hosp"])
upred.append(results["UTI"])
spred.append(results["susceptible"])
epred.append(results["exposed"])
#append parameters
beta1.append(coef["beta1"])
beta2.append(coef["beta2"])
gammaH.append(coef["gammaH"])
gammaU.append(coef["gammaU"])
delta.append(coef["delta"])
h.append(coef["h"])
ia0.append(coef["ia0"])
e0.append(coef["e0"])
def getConfidenceInterval(series, length):
series = np.array(series)
#Compute mean value
meanValue = [np.mean(series[:,i]) for i in range(0,length)]
#Compute deltaStar
deltaStar = meanValue - series
#Compute lower and uper bound
deltaL = [np.quantile(deltaStar[:,i], q = 0.025) for i in range(0,length)]
deltaU = [np.quantile(deltaStar[:,i], q = 0.975) for i in range(0,length)]
#Compute CI
lowerBound = np.array(meanValue) + np.array(deltaL)
UpperBound = np.array(meanValue) + np.array(deltaU)
return [meanValue, lowerBound, UpperBound]
#Get confidence interval for prediction
for i, pred in tqdm(zip([ypred, dpred, upred, hpred, epred, spred],
["Infec", "deaths", "UTI", "Hosp", "exposed", "susceptible"])):
Meanvalue, lowerBound, UpperBound = getConfidenceInterval(i, len(data["infec"]) + 199)
df = pd.DataFrame.from_dict({pred + "_mean": Meanvalue,
pred + "_lb": lowerBound,
pred + "_ub": UpperBound})
df.to_csv("../results/" + pred + ".csv", index = False)
#Exprort parametes
parameters = pd.DataFrame.from_dict({"beta1": beta1,
"beta2": beta2,
"gammaH": gammaH,
"gammaU": gammaU,
"delta": delta,
"h": h,
"ia0":ia0,
"e0": e0})
parameters.to_csv("../results/Parameters.csv", index = False)
###Output
_____no_output_____
|
Lernphase/SW03/Skript.ipynb
|
###Markdown
Aufgabe 3.4 kann erst später gelöst werden
###Code
norm.cdf(x=27, loc=32, scale=6)
1-norm.cdf(x=0.9, loc=0, scale=0.45)
norm.cdf(x=0.9, loc=1.8, scale=0.45)
a,b = norm.cdf(x=[0.2485,0.2515], loc=0.2508, scale=0.0015)
b-a
norm.cdf(x=0.2515, loc=0.2508, scale=0.0005) - norm.cdf(x=0.2485, loc=0.2508, scale=0.0005)
norm.cdf(x=0.2515, loc=0.2500, scale=0.0005) - norm.cdf(x=0.2485, loc=0.2500, scale=0.0005)
norm.ppf(q=0.9)
norm.cdf(x=2)
norm.cdf(x=-2)
norm.cdf(x=2)+norm.cdf(x=-2)
from scipy.integrate import quad
f = lambda x: 1/10 - x/200
ans, _ = quad(f, 0, 5)
print(ans)
print(5/10 - 25/400)
###Output
_____no_output_____
|
notebooks/00.0-download-datasets/2.0-bengalese-finch-koumura-et-al.ipynb
|
###Markdown
Download the song dataset from Katahira et al- Data location: https://datadryad.org/resource/doi:10.5061/dryad.6pt8g
###Code
%load_ext autoreload
%autoreload 2
from avgn.downloading.download import download_tqdm
from avgn.utils.paths import DATA_DIR
from avgn.utils.general import unzip_file
data_urls = [
('https://ndownloader.figshare.com/articles/3470165/versions/1', 'all_files.zip'),
]
output_loc = DATA_DIR/"raw/koumura/"
for url, filename in data_urls:
download_tqdm(url, output_location=output_loc/filename)
for
###Output
_____no_output_____
|
Homework/Homework 3/pandas-exercise.ipynb
|
###Markdown
Homework 3 - Pandas
###Code
# Load required modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from grader import grader_1
%matplotlib inline
###Output
_____no_output_____
###Markdown
Pandas Introduction Reading File 1.1) Read the CSV file called 'data3.csv' into a dataframe called df. Data description* Data source: http://www.fao.org/nr/water/aquastat/data/query/index.html* Data, units:* GDP, current USD (CPI adjusted)* NRI, mm/yr* Population density, inhab/km^2* Total area of the country, 1000 ha = 10km^2* Total Population, unit 1000 inhabitants
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.2) Display the first 10 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.3) Display the column names.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.4) Use iloc to display the first 3 rows and first 4 columns.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Data Preprocessing 2.1) Find all the rows that have 'NaN' in the 'Symbol' column. Display first 5 rows. Hint : You might have to use a mask
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.2) Now, we will try to get rid of the NaN valued rows and columns. First, drop the column 'Other' which only has 'NaN' values. Then drop all other rows that have any column with a value 'NaN'. Store the result in place. Then display the last 5 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.3) For our analysis we do not want all the columns in our dataframe. Lets drop all the redundant columns/ features. **Drop columns**: **Area Id, Variable Id, Symbol**. Save the new dataframe as df1. Display the first 5 rows of the new dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.4) Display all the unique values in your new dataframe for each of the columns: Area, Variable Name, Year.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.5) Display some basic statistical details like percentile, mean, std etc. of our dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Plot 3.1) Plot a bar graph showing the count for each unique value in the column 'Area'. Give it a title.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Extract specific statistics from the preprocessed data: 4.1) Create a dataframe 'dftemp' to store rows where Area is 'Iceland'. Display the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
4.2) Store the years (with the same format as 2.5) when the National Rainfall Index (NRI) was greater than 900 and less than 950 in Iceland in a dataframe named "df_years". Use the dataframe you created in the previous question 'dftemp' to calcuate it.
###Code
# your code here
df_years = #code
###Output
_____no_output_____
###Markdown
Submit homework Run the following code block if you're ready to submit the homework
###Code
grader_1(df_years) #do not edit
###Output
_____no_output_____
###Markdown
Homework 3 - Pandas
###Code
# Load required modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
###Output
_____no_output_____
###Markdown
Pandas Introduction Reading File 1.1) Read the CSV file called 'data3.csv' into a dataframe called df. Data description* Data source: http://www.fao.org/nr/water/aquastat/data/query/index.html* Data, units:* GDP, current USD (CPI adjusted)* NRI, mm/yr* Population density, inhab/km^2* Total area of the country, 1000 ha = 10km^2* Total Population, unit 1000 inhabitants
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.2) Display the first 10 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.3) Display the column names.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.4) Use iloc to display the first 3 rows and first 4 columns.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Data Preprocessing 2.1) Find all the rows that have 'NaN' in the 'Symbol' column. Display first 5 rows. Hint : You might have to use a mask
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.2) Now, we will try to get rid of the NaN valued rows and columns. First, drop the column 'Other' which only has 'NaN' values. Then drop all other rows that have any column with a value 'NaN'. Store the result in place. Then display the last 5 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.3) For our analysis we do not want all the columns in our dataframe. Lets drop all the redundant columns/ features. **Drop columns**: **Area Id, Variable Id, Symbol**. Save the new dataframe as df1. Display the first 5 rows of the new dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.4) Display all the unique values in your new dataframe for each of the columns: Area, Variable Name, Year.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.5) Display some basic statistical details like percentile, mean, std etc. of our dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Plot 3.1) Plot a bar graph showing the count for each unique value in the column 'Area'. Give it a title.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Extract specific statistics from the preprocessed data: 4.1) Create a dataframe 'dftemp' to store rows where Area is 'Iceland'. Display the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
4.2) Print the years (with the same format as 2.5) when the National Rainfall Index (NRI) was greater than 900 and less than 950 in Iceland. Use the dataframe you created in the previous question 'dftemp'.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Homework 3 - Pandas
###Code
# Load required modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from grader import grader_1
%matplotlib inline
###Output
_____no_output_____
###Markdown
Pandas Introduction Reading File 1.1) Read the CSV file called 'data3.csv' into a dataframe called df. Data description* Data source: http://www.fao.org/nr/water/aquastat/data/query/index.html* Data, units:* GDP, current USD (CPI adjusted)* NRI, mm/yr* Population density, inhab/km^2* Total area of the country, 1000 ha = 10km^2* Total Population, unit 1000 inhabitants
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.2) Display the first 10 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.3) Display the column names.
###Code
# your code here
###Output
_____no_output_____
###Markdown
1.4) Use iloc to display the first 3 rows and first 4 columns.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Data Preprocessing 2.1) Find all the rows that have 'NaN' in the 'Symbol' column. Display first 5 rows. Hint : You might have to use a mask
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.2) Now, we will try to get rid of the NaN valued rows and columns. First, drop the column 'Other' which only has 'NaN' values. Then drop all other rows that have any column with a value 'NaN'. Store the result in place. Then display the last 5 rows of the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.3) For our analysis we do not want all the columns in our dataframe. Lets drop all the redundant columns/ features. **Drop columns**: **Area Id, Variable Id, Symbol**. Save the new dataframe as df1. Display the first 5 rows of the new dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.4) Display all the unique values in your new dataframe for each of the columns: Area, Variable Name, Year.
###Code
# your code here
###Output
_____no_output_____
###Markdown
2.5) Display some basic statistical details like percentile, mean, std etc. of our dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Plot 3.1) Plot a bar graph showing the count for each unique value in the column 'Area'. Give it a title.
###Code
# your code here
###Output
_____no_output_____
###Markdown
Extract specific statistics from the preprocessed data: 4.1) Create a dataframe 'dftemp' to store rows where Area is 'Iceland'. Display the dataframe.
###Code
# your code here
###Output
_____no_output_____
###Markdown
4.2) Store the years (with the same format as 2.5) when the National Rainfall Index (NRI) was greater than 900 and less than 950 in Iceland in a dataframe named "df_years". Use the dataframe you created in the previous question 'dftemp' to calcuate it.
###Code
# your code here
df_years = #code
###Output
_____no_output_____
###Markdown
Submit homework Run the following code block if you're ready to submit the homework
###Code
grader_1(df_years) #do not edit
###Output
_____no_output_____
|
notebooks/layers/pooling/GlobalAveragePooling1D.ipynb
|
###Markdown
GlobalAveragePooling1D **[pooling.GlobalAveragePooling1D.0] input 6x6**
###Code
data_in_shape = (6, 6)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(260)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (6, 6)
in: [-0.806777, -0.564841, -0.481331, 0.559626, 0.274958, -0.659222, -0.178541, 0.689453, -0.028873, 0.053859, -0.446394, -0.53406, 0.776897, -0.700858, -0.802179, -0.616515, 0.718677, 0.303042, -0.080606, -0.850593, -0.795971, 0.860487, -0.90685, 0.89858, 0.617251, 0.334305, -0.351137, -0.642574, 0.108974, -0.993964, 0.051085, -0.372012, 0.843766, 0.088025, -0.598662, 0.789035]
out shape: (6,)
out: [0.063218, -0.244091, -0.269288, 0.050485, -0.141549, -0.032765]
###Markdown
**[pooling.GlobalAveragePooling1D.1] input 3x7**
###Code
data_in_shape = (3, 7)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(261)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (3, 7)
in: [0.601872, -0.028379, 0.654213, 0.217731, -0.864161, 0.422013, 0.888312, -0.714141, -0.184753, 0.224845, -0.221123, -0.847943, -0.511334, -0.871723, -0.597589, -0.889034, -0.544887, -0.004798, 0.406639, -0.35285, 0.648562]
out shape: (7,)
out: [-0.23662, -0.367389, 0.111391, -0.00273, -0.435155, -0.14739, 0.221717]
###Markdown
**[pooling.GlobalAveragePooling1D.2] input 8x4**
###Code
data_in_shape = (8, 4)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(262)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (8, 4)
in: [-0.215694, 0.441215, 0.116911, 0.53299, 0.883562, -0.535525, -0.869764, -0.596287, 0.576428, -0.689083, -0.132924, -0.129935, -0.17672, -0.29097, 0.590914, 0.992098, 0.908965, -0.170202, 0.640203, 0.178644, 0.866749, -0.545566, -0.827072, 0.420342, -0.076191, 0.207686, -0.908472, -0.795307, -0.948319, 0.683682, -0.563278, -0.82135]
out shape: (4,)
out: [0.227348, -0.112345, -0.244185, -0.027351]
###Markdown
export for Keras.js tests
###Code
print(json.dumps(DATA))
###Output
{"pooling.GlobalAveragePooling1D.0": {"input": {"data": [-0.806777, -0.564841, -0.481331, 0.559626, 0.274958, -0.659222, -0.178541, 0.689453, -0.028873, 0.053859, -0.446394, -0.53406, 0.776897, -0.700858, -0.802179, -0.616515, 0.718677, 0.303042, -0.080606, -0.850593, -0.795971, 0.860487, -0.90685, 0.89858, 0.617251, 0.334305, -0.351137, -0.642574, 0.108974, -0.993964, 0.051085, -0.372012, 0.843766, 0.088025, -0.598662, 0.789035], "shape": [6, 6]}, "expected": {"data": [0.063218, -0.244091, -0.269288, 0.050485, -0.141549, -0.032765], "shape": [6]}}, "pooling.GlobalAveragePooling1D.1": {"input": {"data": [0.601872, -0.028379, 0.654213, 0.217731, -0.864161, 0.422013, 0.888312, -0.714141, -0.184753, 0.224845, -0.221123, -0.847943, -0.511334, -0.871723, -0.597589, -0.889034, -0.544887, -0.004798, 0.406639, -0.35285, 0.648562], "shape": [3, 7]}, "expected": {"data": [-0.23662, -0.367389, 0.111391, -0.00273, -0.435155, -0.14739, 0.221717], "shape": [7]}}, "pooling.GlobalAveragePooling1D.2": {"input": {"data": [-0.215694, 0.441215, 0.116911, 0.53299, 0.883562, -0.535525, -0.869764, -0.596287, 0.576428, -0.689083, -0.132924, -0.129935, -0.17672, -0.29097, 0.590914, 0.992098, 0.908965, -0.170202, 0.640203, 0.178644, 0.866749, -0.545566, -0.827072, 0.420342, -0.076191, 0.207686, -0.908472, -0.795307, -0.948319, 0.683682, -0.563278, -0.82135], "shape": [8, 4]}, "expected": {"data": [0.227348, -0.112345, -0.244185, -0.027351], "shape": [4]}}}
###Markdown
GlobalAveragePooling1D **[pooling.GlobalAveragePooling1D.0] input 6x6**
###Code
data_in_shape = (6, 6)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(input=layer_0, output=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(260)
data_in = 2 * np.random.random(data_in_shape) - 1
print('')
print('in shape:', data_in_shape)
print('in:', format_decimal(data_in.ravel().tolist()))
result = model.predict(np.array([data_in]))
print('out shape:', result[0].shape)
print('out:', format_decimal(result[0].ravel().tolist()))
###Output
in shape: (6, 6)
in: [-0.806777, -0.564841, -0.481331, 0.559626, 0.274958, -0.659222, -0.178541, 0.689453, -0.028873, 0.053859, -0.446394, -0.53406, 0.776897, -0.700858, -0.802179, -0.616515, 0.718677, 0.303042, -0.080606, -0.850593, -0.795971, 0.860487, -0.90685, 0.89858, 0.617251, 0.334305, -0.351137, -0.642574, 0.108974, -0.993964, 0.051085, -0.372012, 0.843766, 0.088025, -0.598662, 0.789035]
out shape: (6,)
out: [0.063218, -0.244091, -0.269288, 0.050485, -0.141549, -0.032765]
###Markdown
**[pooling.GlobalAveragePooling1D.1] input 3x7**
###Code
data_in_shape = (3, 7)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(input=layer_0, output=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(261)
data_in = 2 * np.random.random(data_in_shape) - 1
print('')
print('in shape:', data_in_shape)
print('in:', format_decimal(data_in.ravel().tolist()))
result = model.predict(np.array([data_in]))
print('out shape:', result[0].shape)
print('out:', format_decimal(result[0].ravel().tolist()))
###Output
in shape: (3, 7)
in: [0.601872, -0.028379, 0.654213, 0.217731, -0.864161, 0.422013, 0.888312, -0.714141, -0.184753, 0.224845, -0.221123, -0.847943, -0.511334, -0.871723, -0.597589, -0.889034, -0.544887, -0.004798, 0.406639, -0.35285, 0.648562]
out shape: (7,)
out: [-0.23662, -0.367389, 0.111391, -0.00273, -0.435155, -0.14739, 0.221717]
###Markdown
**[pooling.GlobalAveragePooling1D.2] input 8x4**
###Code
data_in_shape = (8, 4)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(input=layer_0, output=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(262)
data_in = 2 * np.random.random(data_in_shape) - 1
print('')
print('in shape:', data_in_shape)
print('in:', format_decimal(data_in.ravel().tolist()))
result = model.predict(np.array([data_in]))
print('out shape:', result[0].shape)
print('out:', format_decimal(result[0].ravel().tolist()))
###Output
in shape: (8, 4)
in: [-0.215694, 0.441215, 0.116911, 0.53299, 0.883562, -0.535525, -0.869764, -0.596287, 0.576428, -0.689083, -0.132924, -0.129935, -0.17672, -0.29097, 0.590914, 0.992098, 0.908965, -0.170202, 0.640203, 0.178644, 0.866749, -0.545566, -0.827072, 0.420342, -0.076191, 0.207686, -0.908472, -0.795307, -0.948319, 0.683682, -0.563278, -0.82135]
out shape: (4,)
out: [0.227348, -0.112345, -0.244185, -0.027351]
###Markdown
GlobalAveragePooling1D **[pooling.GlobalAveragePooling1D.0] input 6x6**
###Code
data_in_shape = (6, 6)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(260)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (6, 6)
in: [-0.806777, -0.564841, -0.481331, 0.559626, 0.274958, -0.659222, -0.178541, 0.689453, -0.028873, 0.053859, -0.446394, -0.53406, 0.776897, -0.700858, -0.802179, -0.616515, 0.718677, 0.303042, -0.080606, -0.850593, -0.795971, 0.860487, -0.90685, 0.89858, 0.617251, 0.334305, -0.351137, -0.642574, 0.108974, -0.993964, 0.051085, -0.372012, 0.843766, 0.088025, -0.598662, 0.789035]
out shape: (6,)
out: [0.063218, -0.244091, -0.269288, 0.050485, -0.141549, -0.032765]
###Markdown
**[pooling.GlobalAveragePooling1D.1] input 3x7**
###Code
data_in_shape = (3, 7)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(261)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (3, 7)
in: [0.601872, -0.028379, 0.654213, 0.217731, -0.864161, 0.422013, 0.888312, -0.714141, -0.184753, 0.224845, -0.221123, -0.847943, -0.511334, -0.871723, -0.597589, -0.889034, -0.544887, -0.004798, 0.406639, -0.35285, 0.648562]
out shape: (7,)
out: [-0.23662, -0.367389, 0.111391, -0.00273, -0.435155, -0.14739, 0.221717]
###Markdown
**[pooling.GlobalAveragePooling1D.2] input 8x4**
###Code
data_in_shape = (8, 4)
L = GlobalAveragePooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(262)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalAveragePooling1D.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
###Output
in shape: (8, 4)
in: [-0.215694, 0.441215, 0.116911, 0.53299, 0.883562, -0.535525, -0.869764, -0.596287, 0.576428, -0.689083, -0.132924, -0.129935, -0.17672, -0.29097, 0.590914, 0.992098, 0.908965, -0.170202, 0.640203, 0.178644, 0.866749, -0.545566, -0.827072, 0.420342, -0.076191, 0.207686, -0.908472, -0.795307, -0.948319, 0.683682, -0.563278, -0.82135]
out shape: (4,)
out: [0.227348, -0.112345, -0.244185, -0.027351]
###Markdown
export for Keras.js tests
###Code
import os
filename = '../../../test/data/layers/pooling/GlobalAveragePooling1D.json'
if not os.path.exists(os.path.dirname(filename)):
os.makedirs(os.path.dirname(filename))
with open(filename, 'w') as f:
json.dump(DATA, f)
print(json.dumps(DATA))
###Output
{"pooling.GlobalAveragePooling1D.0": {"input": {"data": [-0.806777, -0.564841, -0.481331, 0.559626, 0.274958, -0.659222, -0.178541, 0.689453, -0.028873, 0.053859, -0.446394, -0.53406, 0.776897, -0.700858, -0.802179, -0.616515, 0.718677, 0.303042, -0.080606, -0.850593, -0.795971, 0.860487, -0.90685, 0.89858, 0.617251, 0.334305, -0.351137, -0.642574, 0.108974, -0.993964, 0.051085, -0.372012, 0.843766, 0.088025, -0.598662, 0.789035], "shape": [6, 6]}, "expected": {"data": [0.063218, -0.244091, -0.269288, 0.050485, -0.141549, -0.032765], "shape": [6]}}, "pooling.GlobalAveragePooling1D.1": {"input": {"data": [0.601872, -0.028379, 0.654213, 0.217731, -0.864161, 0.422013, 0.888312, -0.714141, -0.184753, 0.224845, -0.221123, -0.847943, -0.511334, -0.871723, -0.597589, -0.889034, -0.544887, -0.004798, 0.406639, -0.35285, 0.648562], "shape": [3, 7]}, "expected": {"data": [-0.23662, -0.367389, 0.111391, -0.00273, -0.435155, -0.14739, 0.221717], "shape": [7]}}, "pooling.GlobalAveragePooling1D.2": {"input": {"data": [-0.215694, 0.441215, 0.116911, 0.53299, 0.883562, -0.535525, -0.869764, -0.596287, 0.576428, -0.689083, -0.132924, -0.129935, -0.17672, -0.29097, 0.590914, 0.992098, 0.908965, -0.170202, 0.640203, 0.178644, 0.866749, -0.545566, -0.827072, 0.420342, -0.076191, 0.207686, -0.908472, -0.795307, -0.948319, 0.683682, -0.563278, -0.82135], "shape": [8, 4]}, "expected": {"data": [0.227348, -0.112345, -0.244185, -0.027351], "shape": [4]}}}
|
Metdat-science/Pertemuan 6 - 23 Februari 2022/Data Understanding-Visualisasi.ipynb
|
###Markdown
Belajar memahami data dengan melihat visualisasi-nya Pie Chart
###Code
import matplotlib.pyplot as plt
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
plt.pie(data, labels = rasa,)
plt.show
rasa = ('coklat', 'strawberry', 'vanila', 'keju', 'white coffee')
data = (12, 15, 3, 10, 5)
plt.pie(data, labels = rasa,)
plt.show
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
plt.pie(data, labels = rasa, autopct = '%1.1f%%')
plt.show
rasa = ('coklat', 'strawberry', 'vanila', 'keju', 'white coffee')
data = (12, 15, 3, 10, 5)
plt.pie(data, labels = rasa, autopct = '%1.2f%%' ) #jika 2 angka dibelakang koma
plt.show
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
warna = ('#D2691E', '#FF0000', '#00FFFF')
plt.pie(data, labels = rasa, autopct = '%1.1f%%', colors=warna)
plt.show
#Explode
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
warna = ('#D2691E', '#FF0000', '#00FFFF')
highlight = (0,0,0.1)
plt.pie(data, labels = rasa, autopct = '%1.1f%%', colors=warna, explode = highlight)
plt.show
#Shadow
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
warna = ('#D2691E', '#FF0000', '#00FFFF')
highlight = (0,0,0.1)
plt.pie(data, labels = rasa, autopct = '%1.1f%%', colors=warna, explode = highlight, shadow = True)
plt.show
rasa = ('coklat', 'strawberry', 'vanila')
data = (12, 15, 3)
warna = ('#D2691E', '#FF0000', '#00FFFF')
highlight = (0,0,0.1)
plt.title ('Survei es krim favorit')
plt.pie(data, labels = rasa, autopct = '%1.1f%%', colors=warna, explode = highlight, shadow = True)
plt.show
#Buat supaya visualisasi menampilkan data es krim yang paling diminati
rasa = ('coklat', 'strawberry', 'vanila', 'keju', 'matcha')
data = (15, 12, 3, 10, 5)
warna = ('#D2691E', '#FF0000', '#00FFFF', '#FFFF00', '#ADFF2F')
highlight = (0.1,0,0,0,0)
plt.title ('Es Krim Paling Diminati')
plt.pie(data, labels = rasa, autopct = '%1.2f%%', colors = warna, explode = highlight, shadow = True ) #jika 2 angka dibelakang koma
plt.show
###Output
_____no_output_____
###Markdown
Bar Chart
###Code
import matplotlib.pyplot as plt
import numpy as np
negara = ('Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada')
populasi = (45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 975000, 273500000, 1250000, 2655000 )
x_koordinat = np.arange(len(negara))
plt.bar(x_koordinat, populasi)
plt.show()
#melihat nama koordinat X dan Y
negara = ('Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada')
populasi = (45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 9750000, 273500000, 1250000, 2655000 )
x_koordinat = np.arange(len(negara))
plt.title ('Populasi 10 Negara menurut Abjad')
plt.bar(x_koordinat, populasi, tick_label=negara)
plt.xticks(rotation=90)
plt.ylabel('Populasi (juta)')
plt.show()
#Sorting kanan ke kiri (besar ke kecil)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
negara = ('Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada')
populasi = (45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 9750000, 273500000, 1250000, 2655000 )
df = pd.DataFrame({'Country' : negara, 'Population':populasi})
df.sort_values(by='Population', inplace = True)
x_koordinat = np.arange(len(negara))
plt.title ('Populasi 10 Negara menurut Abjad')
plt.bar(x_koordinat, df['Population'], tick_label=df['Country'])
plt.xticks(rotation=90)
plt.ylabel('Populasi (juta)')
plt.show()
#Sorting kiri ke kanan (besar ke kecil)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
negara = ('Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada')
populasi = (45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 9750000, 273500000, 1250000, 2655000 )
df = pd.DataFrame({'Country' : negara, 'Population':populasi})
df.sort_values(by='Population', inplace = True, ascending = False)
x_koordinat = np.arange(len(negara))
plt.title ('Populasi 10 Negara menurut Abjad')
plt.bar(x_koordinat, df['Population'], tick_label=df['Country'])
plt.xticks(rotation=90)
plt.ylabel('Populasi (juta)')
plt.show()
#Highlight
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
negara = ('Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada')
populasi = (45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 9750000, 273500000, 1250000, 2655000 )
df = pd.DataFrame({'Country' : negara, 'Population':populasi})
df.sort_values(by='Population', inplace = True)
x_koordinat = np.arange(len(df))
warna = ['#0000FF' for _ in range(len(df))]
warna [-3] = '#FF0000'
#plt.figure(figsize=(20,10)) -> memperbesar gambar
plt.title ('Populasi 10 Negara menurut Abjad')
plt.bar(x_koordinat, df['Population'], tick_label=df['Country'], color=warna)
plt.xticks(rotation=90)
plt.ylabel('Populasi (juta)')
plt.show()
###Output
_____no_output_____
###Markdown
Line Graph
###Code
import matplotlib.pyplot as plt
suhu_c = [15,16,20,30,35,37,40,36,34,32,30,28,25]
jam = [0,2,4,6,8,10,12,14,16,18,20,22,24]
plt.plot(jam, suhu_c, marker='o')
plt.title ('Suhu dalam 1 Hari, 23 Februari 2022')
plt.ylabel('Celcius')
plt.xlabel('Jam')
plt.show
#marker (penanda)
import matplotlib.pyplot as plt
suhu_c = [15,16,20,30,35,37,40,36,34,32,30,28,25]
jam = [0,2,4,6,8,10,12,14,16,18,20,22,24]
plt.plot(jam, suhu_c, marker='o')
plt.title ('Suhu dalam 1 Hari, 23 Februari 2022')
plt.ylabel('Celcius')
plt.xlabel('Jam')
plt.show
import matplotlib.pyplot as plt
suhu_c = [15,16,20,30,35,37,40,36,34,32,30,28,25]
prediksi = [2,2,1,20,15,27,30,26,14,22,21,15,37]
jam = [0,2,4,6,8,10,12,14,16,18,20,22,24]
plt.plot(jam, suhu_c, marker='o')
plt.plot(jam, prediksi, linestyle='--')
plt.title ('Suhu dalam 1 Hari, 23 Februari 2022')
plt.ylabel('Celcius')
plt.xlabel('Jam')
plt.show
###Output
_____no_output_____
###Markdown
Scatter Plot
###Code
import matplotlib.pyplot as plt
#import numpy as np
#import pandas as pd
negara = ['Argentina', 'Belanda', 'Ceko', 'Denmark', 'Finlandia', 'Germany', 'Hongkong', 'Indonesia','Jepang', 'Kanada']
populasi = [45380000, 212600000, 19120000, 5831000, 5531000, 83240000, 9750000, 273500000, 1250000, 2655000 ]
gdp = [383, 1445, 252, 355, 271, 3806, 155, 1058, 5065, 39]
#plt.title ('Suhu dalam 1 Hari, 23 Februari 2022')
#plt.ylabel('Celcius')
#plt.xlabel('Jam')
plt.scatter(populasi,gdp)
plt.show()
###Output
_____no_output_____
###Markdown
Heatmap
###Code
pip install seaborn
import seaborn as sbr
kota = ['Pati', 'Salatiga', 'Semarang', 'Kudus', 'Demak', 'Solo', 'Yogyakarta', 'Purwodadi', 'Tegal', 'Jepara']
bulan = ['Jan', 'Feb', 'Mar', 'Apr', 'Mei', 'Jun', 'Jul','Ags','Sep','Okt','Nov','Des']
temperatur = [[34, 30, 32, 33, 35, 36, 35, 38, 37, 34, 32, 33], #Pati
[30, 20, 42, 23, 27, 26, 25, 33, 32, 29, 35, 37], #Salatiga
[39, 36, 27, 30, 25, 31, 30, 41, 27, 24, 22, 23],#Semarang
[31, 32, 38, 38, 43, 26, 43, 36, 33, 30, 32, 38], #Kudus
[32, 34, 29, 36, 39, 39, 40, 33, 27, 34, 40, 33], #Demak
[33, 30, 26, 34, 37, 36, 38, 38, 36, 32, 37, 32], #Solo
[34, 37, 32, 33, 38, 33, 39, 31, 40, 37, 39, 36], #Yogyaarta
[35, 35, 38, 40, 32, 30, 35, 36, 30, 39, 38, 34], # Purwodadi
[38, 27, 33, 29, 33, 32, 34, 30, 35, 31, 36, 37], # Tegal
[39, 29, 34, 31, 34, 38, 33, 42, 37, 36, 32, 38],] # Jepara
sbr.heatmap(temperatur, yticklabels=kota, xticklabels=bulan)
import seaborn as sbr
kota = ['Pati', 'Salatiga', 'Semarang', 'Kudus', 'Demak', 'Solo', 'Yogyakarta', 'Purwodadi', 'Tegal', 'Jepara']
bulan = ['Jan', 'Feb', 'Mar', 'Apr', 'Mei', 'Jun', 'Jul','Ags','Sep','Okt','Nov','Des']
temperatur = [[34, 30, 32, 33, 35, 36, 35, 38, 37, 34, 32, 33], #Pati
[30, 20, 42, 23, 27, 26, 25, 33, 32, 29, 35, 37], #Salatiga
[39, 36, 27, 30, 25, 31, 30, 41, 27, 24, 22, 23],#Semarang
[31, 32, 38, 38, 43, 26, 43, 36, 33, 30, 32, 38], #Kudus
[32, 34, 29, 36, 39, 39, 40, 33, 27, 34, 40, 33], #Demak
[33, 30, 26, 34, 37, 36, 38, 38, 36, 32, 37, 32], #Solo
[34, 37, 32, 33, 38, 33, 39, 31, 40, 37, 39, 36], #Yogyaarta
[35, 35, 38, 40, 32, 30, 35, 36, 30, 39, 38, 34], # Purwodadi
[38, 27, 33, 29, 33, 32, 34, 30, 35, 31, 36, 37], # Tegal
[39, 29, 34, 31, 34, 38, 33, 42, 37, 36, 32, 38],] # Jepara
sbr.heatmap(temperatur, yticklabels=kota, xticklabels=bulan, cmap = 'coolwarm')
###Output
_____no_output_____
|
docs/_shelved_sphinx_content/specialized_topics/general/dummy_measurement_without_server/measurement_notebook.ipynb
|
###Markdown
Dummy Measurement Without Server README This is an example to illustrate how measurement notebooks could look like.Of course this is easy to convert to a script, if you prefer working with spyder, for example.Some things are not in a state yet that we're fully happy with, they're annotated correspondingly.**TODO:** the initialization could be in a separate script or notebook. That would be useful if multiple notebooks run measurements, for example. Initialization Imports
###Code
# %matplotlib inline
from pprint import pprint
import time
import numpy as np
from matplotlib import pyplot as plt
import h5py
from qcodes import Instrument, Station, find_or_create_instrument
from plottr.data import datadict_storage as dds, datadict as dd
###Output
_____no_output_____
###Markdown
Configuration
###Code
DATADIR = './data/'
###Output
_____no_output_____
###Markdown
Create instruments **TODO:** here we would prefer getting the instruments from the server.
###Code
# Create a new station, close all previous instruments
Instrument.close_all()
station = Station()
from instrumentserver.testing.dummy_instruments.rf import ResonatorResponse
vna = find_or_create_instrument(ResonatorResponse, 'vna')
station.add_component(vna)
vna.resonator_frequency(5e9)
vna.resonator_linewidth(10e6)
from instrumentserver.testing.dummy_instruments.rf import FluxControl
flux = find_or_create_instrument(FluxControl, 'flux', 'vna')
station.add_component(flux)
###Output
Connected to: None vna (serial:None, firmware:None) in 0.01s
###Markdown
Example: Flux tuning a resonator Testing
###Code
# just acquire a trace and plot. The resonance frequency should change when changing the flux.
vna.start_frequency(4e9)
vna.stop_frequency(5.2e9)
vna.npoints(1201)
vna.bandwidth(1e4)
vna.power(-50)
flux.flux(0)
f_vals = vna.frequency()
s11_vals = vna.data()
fig, ax = plt.subplots(1, 1)
ax.plot(f_vals, np.angle(s11_vals))
###Output
_____no_output_____
###Markdown
Measurement BasicsThis is a very simple example for how to use DDH5Writer to save data to hdf5.The basic structure is:1. specify the structure of the data. This is required for two reasons: A, knowing the data structure before actually running measurement code allows to pre-define objects in the data files, which is important for accessing the data from multiple programs (single-writer multi-reader support). B, for all features in live-plotting and analysis to work we need to know the relations between different data objects (like dependent and independent data). 2. use the Writer as context manager to add data (in practice, in some kind of measurement loop). Live plottingYou can use `plottr` to live plot the data (or plot it later). An easy way to do this is by running the `monitr` app from the command line. This assumes that plottr is installed through pip, which should create the required launcher script. Run (and replace ```` with your data directory root):`` $ plottr-monitr ``You should see the monitr window open. On the left you will see all data files in your data directory. If you select a data file, the right hand side will display the contents of that file. you can plot data by right-clicking on a top-level group container and selecting 'Plot ````'.If you activate the ``Auto-plot new`` button in the toolbar, any new data files appearing from this point on will be plotted automatically. The default refresh rate for the monitr app is 2 seconds (can be set a startup as a command line option). Notes**TODO:** This is using the bare file writer. Some things, like setting up the data structure will be made easier, but the new measurement structures are will work in progress.**TODO:** This isn't saving meta data yet, or copying additional files. An easy way to circumvent that for the time being is by inheriting from the DDH5 writer.
###Code
# this is defining the data structure.
data = dd.DataDict(
flux = dict(unit='Phi0'),
frequency = dict(unit='Hz'),
s11 = dict(axes=['flux', 'frequency']), # no unit, complex.
)
data.validate() # this is just for catching mistakes.
with dds.DDH5Writer(basedir=DATADIR, datadict=data, name='FluxSweep') as writer:
for flux_val in np.linspace(-1,1,101):
flux.flux(flux_val)
time.sleep(0.2)
# the writer accepts one line for each data field.
# that means we should reshape the data that each entry has the form [<data>].
# for practical purposes that means that each frequency and s11 data array
# is like one datapoint.
writer.add_data(
flux = [flux_val],
frequency = vna.frequency().reshape(1,-1),
s11 = vna.data().reshape(1,-1),
)
###Output
Data location: ./data/2021-09-01\2021-09-01T144913_aeda4d09-FluxSweep\data.ddh5
###Markdown
Inspecting the dataThis is just to illustrate how to open and look at the data. You often would not actually do that in the measurement notebook.Note that the data is currently also in the memory. **TODO**: an operation mode for not keeping the data in the memory is not implemented yet.To illustrate, we look at the data in the memory, and compare with the file.
###Code
# when we look at the data now, we see it's not on a grid, even though we want the data to be.
pprint(data.structure())
pprint(data.shapes())
# this is detecting the grid in the data
data_as_grid = dd.datadict_to_meshgrid(data)
pprint(data_as_grid.structure())
pprint(data_as_grid.shapes())
flux_data = data_as_grid.data_vals('flux')
frq_data = data_as_grid.data_vals('frequency')
s11_data = data_as_grid.data_vals('s11')
fig, ax = plt.subplots(1, 1)
ax.imshow(
np.angle(s11_data.T),
aspect='auto', origin='lower',
extent=[flux_data.min(), flux_data.max(), frq_data.min(), frq_data.max()]
)
ax.set_xlabel('Flux (phi_0)')
ax.set_ylabel('Frequency (Hz)')
# Loading from file is essentiall the same thing:
data_from_file = dds.datadict_from_hdf5(writer.filepath)
data_as_grid = dd.datadict_to_meshgrid(data_from_file)
flux_data = data_as_grid.data_vals('flux')
frq_data = data_as_grid.data_vals('frequency')
s11_data = data_as_grid.data_vals('s11')
fig, ax = plt.subplots(1, 1)
ax.imshow(
np.angle(s11_data.T),
aspect='auto', origin='lower',
extent=[flux_data.min(), flux_data.max(), frq_data.min(), frq_data.max()]
)
ax.set_xlabel('Flux (phi_0)')
ax.set_ylabel('Frequency (Hz)')
###Output
_____no_output_____
|
example_project.ipynb
|
###Markdown
--- Project for the course in Microeconometrics | Summer 2019, M.Sc. Economics, Bonn University | [Annica Gehlen](https://github.com/amageh) Replication of Jason M. Lindo, Nicholas J. Sanders & Philip Oreopoulos (2010) --- This notebook contains my replication of the results from the following paper:> Lindo, J. M., Sanders, N. J., & Oreopoulos, P. (2010). Ability, gender, and performance standards: Evidence from academic probation. American Economic Journal: Applied Economics, 2(2), 95-117. Downloading and viewing this notebook:* The best way to view this notebook is by downloading it and the repository it is located in from [GitHub](https://github.com/HumanCapitalAnalysis/template-course-project). Other viewing options like _MyBinder_ or _NBViewer_ may have issues with displaying images or coloring of certain parts (missing images can be viewed in the folder [files](https://github.com/HumanCapitalAnalysis/template-course-project/tree/master/files) on GitHub).* The original paper, as well as the data and code provided by the authors can be accessed [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). Information about replication and individual contributions:* For the replication, I try to remain true to the original structure of the paper so readers can easily follow along and compare. All tables and figures are named and labeled as they appear in Lindo et al. (2010).* The tables in my replication appear transposed compared to the original tables to suit my workflow in Python.* For transparency, all sections in the replication that constitute independent contributions by me and are not part of results presented (or include deviations from the methods used) in the paper are marked as _extensions_. Table of Contents1. Introduction2. Theoretical Background3. Identification4. Empirical Strategy5. Replication of Lindo et al. (2010)5.1. Data & Descriptive StatisticsTable 1- Summary statistics5.2. Results5.2.1. Tests of the Validity of the RD Approachi. Extension: Visual Validity CheckExtension | Table - Descriptive Statistics of Treated and Untreated Group Close to the CutoffExtension | Figure - Distribution of Covariates throughout the Probation Cutoffii. Advanced Validity CheckFigure 1 | Distribution of Student Grades Relative to their CutoffTable 2 - Estimated Discontinuities in Observable Characteristics5.2.2. First Year GPAs and Academic ProbationFigure 2 - Porbation Status at the End of First YearTable 3 - Estimated Discontinuity in Probation Status5.2.3. The Immediate Response to Academic ProbationTable 4 - Estimated Effect on the Decision to Leave after the First EvaluationFigure 3 - Stratified Results for Voluntarily Leaving School at the End of the First year5.2.4. The Impact onSubsequent Performancei. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next TermFigure 4 - GPA in the Next Enrolled TermTable 5 - Estimated Discontinuites in Subsequent GPA | Part A - Next Term GPATable 5 - Estimated Discontinuites in Subsequent GPA | Part B - Probability of Placing Above the Cutoff in Next Termii. Formal Bound Analysis on Subsequent GPA (partial extension)Subsequent Performance with 95% Confidence IntervalFormal Bound Analysis from Lindo et al. (2010) (p.110)Replication of Formal Bound Analysis5.2.5. The Impacts on GraduationFigure 5 - Graduation RatesTable 6 - Estimated Effects on GraduationGraduated after 6 years6. Extension: Robustness Checks6.1. A Closer Look at Students' Subsequent Performance.6.1.1. Subsequent Performance and Total Credits in Year 2No summer classesSummer classes6.1.2. Subsequent Cumulative Grade Point Average (CGPA)Effect of Academic Probation on Subsequent CGPAEffect of Academic Probation on the Probability of Achieving a CGPA Above the Cutoff in the Next Term6.2. Bandwidth SensitivityBandwidth sensitivity of the effect of probation on the probability of leaving schoolBandwidth sensitivity of the effect of probation on subsequent GPA7. Conclusion8. References
###Code
%matplotlib inline
import numpy as np
import pandas as pd
import pandas.io.formats.style
import seaborn as sns
import statsmodels as sm
import statsmodels.formula.api as smf
import statsmodels.api as sm_api
import matplotlib as plt
from IPython.display import HTML
from auxiliary.example_project_auxiliary_predictions import *
from auxiliary.example_project_auxiliary_plots import *
from auxiliary.example_project_auxiliary_tables import *
###Output
_____no_output_____
###Markdown
--- 1. Introduction --- Lindo et al. (2010) examine the effects of academic probation on student outcomes using data from Canada. Academic probation is a university policy that aims to improve the performance of the lowest- scoring students. If a student's Grade Point Average (GPA) drops below a certain threshold, the student is placed on academic probation. The probation status serves as a warning and does not entail immediate consequences, however, if students fail to improve their grades during the following term, they face the threat of being suspended from the university. In a more general sense, academic probation may offer insights into how agents respond to negative incentives and the threat of punishment in a real-world context with high stakes. To estimate the causal impact of being placed on probation, Lindo et al. (2010) apply a **regression discontinuity design (RDD)** to data retrieved from three campuses at a large Canadian university. The RDD is motivated by the idea that the students who score just above the threshold for being put on academic probation provide a good counterfactual to the 'treatment group' that scores just below the threshold. In line with the performance standard model that serves as the theoretical framework for the paper, Lindo et al. (2010) find that being placed on probation induces students to drop out but increases the grades of the students who remain in school. The authors also find large heterogeneities in the way different groups of students react to academic probation.**Main variables** | **Treatment** | **Main outcomes** | **Main Covariates** ||-------------------|-------------------------|------------------------|| Academic probation| Drop-out rates | Gender || . | Subsequent performance | HS grades | | . | Graduation rates | Native language | In this notebook, I replicate the results presented in the paper by Lindo et al. (2010). Furthermore, I discuss in detail the identification strategy used by the authors and evaluate the results using multiple robustness checks. My analysis offers general support for the findings of Lindo et al. (2010) and points out some factors which may enable a deeper understanding of the causal relationship explored in the paper. This notebook is structured as follows. In the next section, I present the performance standard model that lays down the theoretical framework for the paper (Section 2). In Section 3, I analyze the identification strategy that Lindo et al. (2010) use to unravel the causal effects of academic probation on student outcomes and Section 4 briefly discusses the empirical strategy the authors use for estimation. Section 5 and Section 6 constitute the core of this notebook. Section 5 shows my replication of the results in the paper and discussion thereof. In Section 6 I conduct various robustness checks and discuss some limitations of the paper. Section 7 offers some concluding remarks. --- 2. Theoretical Background---The underlying framework used for the analysis is a model developed by Bénabou and Tirole (2000) which models agent's responses to a performance standard. While Bénabou and Tirole (2000) model a game between a principal and an agent, Lindo et al. (2010) focus only on the agent to relate the model to the example of academic probation. In the performance standard model, the agents face a choice between three options: 1. **Option 1**: Incurs cost $c_1$ and grants benefit $V_1$ if successful. 2. **Option 2**: Incurs cost $c_2$ and grants benefit $V_2$ if successful. 3. **Neither** option: Incurs 0 cost and 0 benefit. Option 1 has a lower cost and a lower benefit than option 2 such that:\begin{equation} 0 < c_1 < c_2 , 0 < V_1 < V_2.\end{equation}Ability, denoted by $\theta$, translates to the probability of successfully completing either option. Assuming agents have perfect information about their ability, they solve the maximizing problem\begin{equation}max\{0, \theta V_1-c_1, \theta V_2-c_2\}.\end{equation} Let $\underline{\theta}$ be the ability level where the agent is indifferent between neither and option two and let $\bar{\theta}$ be the ability level at which the agent is indifferent between option 1 and option 2. Assuming that\begin{equation}\underline{\theta} \equiv \frac{c_1}{V_1} < \bar{\theta} \equiv \frac{c_2-c_1}{V_2-V1} < 1\end{equation}ensures that both options are optimal for at least some $\theta$.It can be shown that * the lowest ability types ($\theta < \underline{\theta}$) choose neither option,* the highest ability types ($\bar{\theta} < \theta$) choose the difficult option,* the individuals in between the high and low type $\underline{\theta}< \theta < \bar{\theta} $) choose the easier option.If the principal now removes option 1 or makes choosing this option much more costly, then the agent will choose option 2 if and only if\begin{equation}\theta \ge \frac{c_2}{V_2} \equiv \theta^*\end{equation}and choose neither option otherwise. The agents who would have chosen option 1 now split according to ability. Agents with high ability (specifically those with $\theta \in [\theta^*,\bar{\theta}]$) work harder, thereby choosing option 2, while low ability types (those with $\theta \in [\underline{\theta}, \theta^*]$) do not pursue option 2 (and thus choose neither option).In the context of academic probation students face a similar decision and possible courses of action. Students whose GPA is just above the probation cutoff face the full set of options for the next year:1. **Option 1**: Return to school and exhibit low effort and leading to a low GPA2. **Option 2**: Return to school and exhibit high effort with the intent of achieving a high GPA3. **Neither** option: Drop out of universityStudents who score below the probation cutoff face a restricted set of options as the university administration essentially eliminates option 1 by suspending students if they do not improve their grades. Lindo et al. (2010) formulate three testable implications of this theoretical framework: * _Forbidding option 1 will **increase the overall probability of students dropping out**._ * _Forbidding option 1 will **increase the performance of those who return**._ * _Forbidding option 1 will cause **relatively low-ability students to drop out** and **relatively high-ability students to return and work harder**._ --- 3. Identification--- Lindo et al. (2010) in their paper aim to evaluate how academic probation affects students, specifically their probability of dropping out of university and whether it motivates those who remain to improve their grades. Students are placed on probation if their Grade Point Average (GPA) drops below a certain threshold and face the threat of suspension if they fail to improve their GPA in the next term. Students are thus clearly separated into a treated group (who is put on probation) and an untreated group based on their GPA. The causal graph below illustrates the relationship between the assignment variable $X$, treatment $D$ and outcome $Y$. While $X$ (the GPA) directly assigns students to treatment, it may also be linked to student outcomes. Additionally, there may be observables $W$ and unobservables $U$ also affecting $X$,$D$, and $Y$. There are thus multiple backdoor paths that need to be closed in order to isolate the effect of academic probation. Simply controlling for the variables in question, in this case, does not suffice since there are unobservables that we cannot condition on. A randomized experiment, on the other hand, could eliminate selection bias in treatment by randomly assigning probation to students. The research question evaluated in the paper constitutes a classic policy evaluation problem in economics where we try to understand the causal implications of a policy without being able to observe the counterfactual world where the policy is not administered. However, as with many questions in economics, implementing a randomize experiment directly is not a feasible option, especially since we are examing the effect of a penalty whose consequences may affect students for the rest of their lives.Since it is not possible to randomize assignment to treatment, another method is needed to isolate the effects of academic probation on student outcomes. Lindo et al. (2010) apply a regression discontinuity design (RDD) to the problem at hand, a method pioneered by Thistlethwaite and Campbell (1960) in their analysis of the effects of scholarships on student outcomes. In fact, the identification problem in Lindo et al. (2010) is quite similar to that of Thistlethwaite and Campbell (1960) as both papers evaluate the causal effects of an academic policy on student outcomes. However, while the scholarship administered to high performing students in Thistlethwaite and Campbell (1960) constitutes a positive reinforcement for these students, Lindo et al. (2010) examine the effects of a negative reinforcement or penalty on low performing students. This means that, in contrast to Thistlethwaite and Campbell (1960) and many other applications of RD, our treatment group lies _below_ the cutoff and not above it. This does not change the causal inference of this model but it might be confusing to readers familiar with RD designs and should thus be kept in mind. The regression discontinuity design relies on the assumption of local randomization, i.e. the idea that students who score just above the cutoff do not systematically differ from those who score below the cutoff and thus pose an appropriate control group for the students who are placed on probation. This identification strategy relies on the assumption that students are unable to precisely manipulate their grades to score just above or below the probation threshold. Within the neighborhood around the discontinuity threshold, the RDD thus in a sense mimics a randomized experiment. To explain how the use of regression discontinuity allows Lindo et al. (2010) to identify treatment effects, I draw on material provided in Lee and Lemieux (2010) and their discussion on the RDD in the potential outcomes framework. As mentioned above, for each student $i$ we can image a potential outcome where they are placed on probation $Y_i(1)$ and where they are not $Y_i(0)$ but we can never simultaneously observe both outcomes for each student. Since it is impossible to observe treatment effects at the individual level, researchers thus estimate average effects using treatment and control groups. For the RDD this potential outcomes framework translates by imagining there are two underlying relationships between the average student outcome and the assignment variable $X$ (the students' GPA), which are represented by $E[Y_i(1)|X]$ and $E[Y_i(0)|X]$. Since all students who score below the cutoff $c$ are placed on probation, we only observe $E[Y_i(1)|X]$ for those below the cutoff and $E[Y_i(0)|X]$ for those above the cutoff. We can estimate the average treatment effects by taking the difference of the conditional expectations at the cutoff if these underlying functions are continuous throughout the cutoff:\begin{equation}lim_{\epsilon \downarrow 0}E[Y_i|X_i=c+\epsilon] - lim_{\epsilon \uparrow 0} E[Y_i|X_i=c+\epsilon] = E[Y_i(1)-Y_i(0)|X=c].\end{equation}As explained above, this _continuity assumption_ is fulfilled by the RDD because we can assume that students have _imprecise control_ over the assignment variable, their GPA. We can clearly identify the average treatment effects because there is a natural sharp cutoff at the threshold. The treatment administered to students is being confronted with the information that they are placed on probation and the subsequent threat of suspension. Being put on probation does not involve any actions by the students, in fact being assigned to the treatment group already constitutes the treatment in itself. Non-compliers thus do not pose a concern for this research design. As the theoretical framework discussed in the prior section illustrates, students on probation face the decision of dropping out or trying to improve their performance in the next term. While the estimation on effects on dropping out using the regression discontinuity design is relatively straight forward, the estimation of effects for subsequent performance adds additional challenges.The extended causal graph above illustrates how the subsequent performance of students is also affected by whether a student drops out or not. This factor adds additional complexity to the estimation problem because we cannot observe the subsequent GPA for students who drop out after being placed on probation. This factor puts into question the comparability of the treatment and control group in subsequent periods. I address these concerns and possible solutions in later sections of this notebook.Aside from the two main outcomes, Lindo et al. (2010) also examine the effects of academic probation on graduation rates of students. However, since information about student's academic progress over the whole course of their studies is limited in the available data, only very simple analysis is possible. --- 4. Empirical Strategy---The authors examine the impact of being put on probation after the first year in university. The probation status after the first year is a deterministic function of student's GPA, formally\begin{equation}PROB^{year1}_{IC} = 1(GPANORM^{year1}_{IC} < 0),\end{equation}where $PROB^{year1}_{IC}$ represents the probation status of student $i$ at campus $c$ and $GPANORM^{year1}_{IC}$ is the distance between student $i$'s first-year GPA and the probationary cutoff at their respective campus. The distance of first-year GPA from the threshold thus constitutes the *running variable* in this RD design. Normalizing the running variable in this way makes sense because the three campuses have different GPA thresholds for putting students on probation (the threshold at campus 1 and 2 is 1.5, at campus 3 the threshold is 1.6), using the distance from the cutoff as the running variable instead allows Lindo et al. (2010) to pool the data from all three campuses.Applying the regression discontinuity design, the treatment effect for students near the threshold is obtained by comparing the outcomes of students just below the threshold to those just above the threshold.The following equation can be used to estimate the effects of academic probation on subsequent student outcomes:\begin{equation}Y_{ic} = m(GPANORM_{ic}^{year1}) + \delta1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}* $Y_{ic}$ denotes the outcome for student $i$ at campus $c$, * $m(GPANORM_{ic}^{year1})$ is a continuous function of students' standardized first year GPAs,* $1(GPANORM_{ic}^{year1}<0)$ is an indicator function equal to 1 if the student's GPA is below the probation cutoff,* $u_{ic} $ is the error term,* $\delta$ is the coefficient for the estimated impact of being placed on academic probation after the first year.For the regression analysis, Lindo et al. (2010) extend the above equation by an interaction term and a constant:\begin{equation}Y_{ic} = \alpha + \delta1(GPANORM_{ic}^{year1}<0) + \beta(GPANORM_{ic}^{year1}) + \gamma(GPANORM_{ic}^{year1})x 1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}This regression equation does not include covariates because Lindo et al. (2010) implement a split sample analysis for the covariates in the analysis. --- 5. Replication of Lindo et al. (2010)--- 5.1. Data & Descriptive StatisticsLindo et al. (2010) filter the data to meet the following requirements:* Students high school grade measure is not missing,* Students entered university before the year 2004 ( to ensure they can be observed over a 2-year period),* Students are between 17 and 21 years of age at time of entry.* Distance from cutoff is maximally 0.6 (or 1.2).The first three requirements are already fulfilled in the provided data. It should be noted that the high school measure is a student's average GPA in courses that are universally taken by high school students in the province. Thus all students that remain in the sample (84 % of the original data) attended high school in the province. This has the advantage that the high school measurement for all students is very comparable. An additional implication that should be taken note of for later interpretations is that this also implies that all students assessed in the study attended high school in the province. The group of 'nonnative' English speakers thus, for example, does not include students that moved to Canada after completing high school.
###Code
data_1 = pd.read_stata('data/data-performance-standards-1.dta')
data_2 = pd.read_stata('data/data-performance-standards-2.dta')
data = pd.concat([data_1, data_2], axis=1)
data = prepare_data(data)
###Output
_____no_output_____
###Markdown
---**NOTE**: The original data provided by the authors can be found [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). For this replication the data is split into two .dta-files due to size constraints.--- As shown in the graph below, the distance from the cutoff for university GPA in the provided dataset still spans from values of -1.6 to 2.8 as can be seen below. Lindo et al. (2010) use a bandwidth of *(-0.6, 0.6)* for regression results and a bandwidth of *(-1.2, 1.2)* for graphical analysis.
###Code
plot_hist_GPA(data)
# Reduce sample to students within 1.2 points from cutoff.
sample12 = data[abs(data['dist_from_cut']) < 1.2]
sample12.reset_index(inplace=True)
print("A sample of students within 1.2 points from the cuttoff consits of", len(sample12), "observations.")
# Reduce sample to students within 0.6 points from cutoff.
sample06 = data[abs(data['dist_from_cut']) < 0.6]
sample06.reset_index(inplace=True)
print("The final sample includes", len(sample06), "observations.")
###Output
The final sample includes 12530 observations.
###Markdown
Table 1 shows the descriptive statistics of the main student characteristics and outcomes in the restricted sample with a bandwidth of 0.6 from the cutoff. The majority of students are female (62%) and native English speakers (72%). Students in the reduced sample on average placed in the 33rd percentile in high school. It should also be noted that quite a large number of students (35%) are placed on probation after the fist year. An additional 11% are placed on probation after the first year. Table 1- Summary statistics
###Code
create_table1(sample06)
###Output
_____no_output_____
###Markdown
5.2. Results 5.2.1. Tests of the Validity of the RD Approach The core motivation in the application of RD approaches is the idea, that the variation in treatment near the cutoff is random if subjects are unable to control the selection into treatment (Lee & Lemieux, 2010). This condition, if fulfilled, means the RDD can closely emulate a randomized experiment and allows researchers to identify the causal effects of treatment. For evaluating the effects of academic probation on subsequent student outcomes, the RDD is thus a valid approach only if students are not able to precisely manipulate whether they score above or below the cutoff. Lindo et al. (2010) offer multiple arguments to address concerns about nonrandom sorting: 1. The study focuses on first-year students, assuming this group of students is likely to be less familiar with the probation policy on campus. To verify their conjecture, the authors also conducted a survey in an introductory economics course which revealed that around 50 % of students were unsure of the probation cutoff at their campus. They also claim that this analysis showed no relationship between knowledge of probation cutoffs and students' grades. 2. The authors also point out that most first-year courses span the entire year and most of the evaluation takes place at the end of the term which would make it difficult for students to purposely aim for performances slightly above the cutoff for academic probation.3. Finally, and most importantly, the implication of local randomization is testable. If nonrandom sorting were to be a problem, there should be a discontinuity in the distribution of grades at the cutoff with a disproportionate number of students scoring just above the cutoff. Additionally, all the covariates should be continuous throughout the cutoff to ensure that the group above the probation cutoff constitutes a realistic counterfactual for the treated group.In the following section, I first conduct a brief visual and descriptive check of validity before presenting my replication of the validity checks conducted in Lindo et al. (2010). i. Extension: Visual Validity Check To check for discontinuities in the covariates and the distribution of students around the cutoff Lindo et al. (2010) use local linear regression analysis. Before implementing the rather extensive validity check conducted by Lindo et al. (2010) I show in this section that a rather simple descriptive and graphical analysis of the distribution of covariates already supports the assumption they are continuous throughout the threshold. Extension | Table - Descriptive Statistics of Treated and Untreated Group Close to the CutoffThe table below shows the means of the different covariates at the limits of the cutoff from both sides (here within a bandwidth of 0.1 grade points). We can see that the means of the groups below and above the probation cutoff are very similar, even equal for some of the variables.
###Code
cov_descriptives = describe_covariates_at_cutoff(sample06,bandwidth=0.1)
cov_descriptives
###Output
_____no_output_____
###Markdown
Extension | Figure - Distribution of Covariates throughout the Probation CutoffThe figure below shows the means of the nine covariates in bins of size 0.5 (grade points). Similar to the descriptive table shown above, this visualization shows that there seem to be no apparent discontinuities in the distribution of students for any of the observable characteristics (graphs with bins of size 0.1 or 0.025 suggest the same).
###Code
plot_covariates(data=data, descriptive_table=cov_descriptives,bins = 'dist_from_cut_med05')
###Output
_____no_output_____
###Markdown
ii. Advanced Validity Check(as conducted by Lindo et al. (2010)) Figure 1 | Distribution of Student Grades Relative to their Cutoff To test the assumption of local randomization, Lindo et al. (2010) run a local linear regression on the distribution of students throughout the cutoff. As mentioned above, these should be continuous as a jump in the distribution of students around the cutoff would indicate that students can in some way manipulate their GPA to place above the cutoff. For the analysis, the data (containing all observations within 1.2 GPA points from the cutoff) is sorted into bins of size 0.1. The bins contain their lower limit but not their upper limit. To replicate the result from Lindo et al. (2010), I calculate the frequency of each bin and then run a local linear regression with a bandwidth of 0.6 on the size of the bins. Figure 1 shows the bins and the predicted frequency for each bin. The results show that the distribution of grades seems to be continuous around the cutoff, suggesting that we can assume local randomization. This method of testing the validity is especially useful because it could capture the effects of unobservables, whose influence we cannot otherwise test like we test for discontinuities in observable characteristics in the parts above and below. If all observable characteristics would show to be continuous throughout the cutoff but we could still observe a jump in the distribution of students above the cutoff, this would suggest that some unobservable characteristic distinguishes students above and below the probation threshold. Fortunately, the results shown below indicate that this is not the case supporting the RDD as a valid identification strategy.
###Code
bin_frequency_fig1 = calculate_bin_frequency(sample12, "dist_from_cut_med10")
predictions_fig1 = create_bin_frequency_predictions(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), 0.6)
plot_figure1(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), predictions_fig1)
###Output
_____no_output_____
###Markdown
Table 2 - Estimated Discontinuities in Observable Characteristics Table 2 shows the results of local linear regression (using a bandwidth of 0.6) for a range of observable characteristics that are related to student outcomes. Significant discontinuities would indicate that students with certain characteristics might be able to manipulate their grades to score above the probation cutoff. Similar to the descriptive validity checks on covariates in the section, these results additionally support the validity of the RDD. Table 2 shows that the coefficient for scoring below the cutoff is insignificant at the 10% level for all covariates.
###Code
table2_variables = ('hsgrade_pct', 'totcredits_year1', 'age_at_entry', 'male', 'english',
'bpl_north_america','loc_campus1', 'loc_campus2')
regressors = ['const', 'gpalscutoff', 'gpaXgpalscutoff', 'gpaXgpagrcutoff']
table2 = estimate_RDD_multiple_outcomes(sample06, table2_variables, regressors)
table2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
---**NOTE**: My results for 'Male' and 'Age at entry' are switched compared to the table presented in Lindo et al. (2010). Since the results are identical otherwise, I assume this difference stems from an error in the table formatting of the published paper. **NOTE**: The p-values in all regression tables are color-coded to enhance readability:* P-values at the 10% level are magenta,* P-values at the 5 % level are red,* P-values at the 1 % level are orange.The color-coding may not be visible in all viewing options for Jupyter Notebooks (e.g. MyBinder).--- 5.2.2. First Year GPAs and Academic Probation Figure 2 and Table 3 show the estimated discontinuity in probation status. Figure 2 and the first part of Table 3 show the estimated discontinuity for the probation status after the _first year_. The second part of Table 3 presents the results for the estimated effects of scoring below the cutoff on the probability of _ever_ being placed on academic probation.Figure 2 and part 1 of Table 3 verify that the discontinuity at the cutoff is **sharp**, i.e. all students whose GPA falls below the cutoff are placed on probation. For students below the cutoff, the probability of being placed on probation is 1, for students above the cutoff it is 0.It should be noted that the estimated discontinuity at the cutoff is only approximately equal to 1 for all of the different subgroups, as the results in Part 1 of Table 3 show. The authors attribute this fact to administrative errors in the data reportage. Figure 2 - Porbation Status at the End of First Year
###Code
predictions_fig2 = create_predictions(sample12, 'probation_year1', regressors, 0.6)
plot_figure2(sample12, predictions_fig2)
###Output
_____no_output_____
###Markdown
Table 3 - Estimated Discontinuity in Probation StatusTo estimate the discontinuity in probation status, the authors again use a bandwidth of 0.6 from the cutoff. In addition to the whole sample, they also estimate the discontinuities for certain subgroups within the selected bandwidth:* **high school grades below** and **above the median** (here, median refers to the median of the entire dataset (median: *50*) and not the median of the subset of students with a GPA within 0.6 grade points of the probation cutoff (the median for this set would be *28*))* **male** and **female** students* **english** native speakers and students with a different native language (**nonenglish**)
###Code
sample_treat06 = sample06[sample06['dist_from_cut'] < 0]
sample_untreat06 = sample06[sample06['dist_from_cut'] >= 0]
sample06 = pd.concat([sample_untreat06, sample_treat06])
groups_dict_keys = ['All', 'HS Grades < median', 'HS Grades > median', 'Male', 'Female',
'Native English', 'Nonnative English']
groups_dict_columns = ['const', 'lowHS', 'highHS','male', 'female', 'english', 'noenglish']
groups_dict_06 = create_groups_dict(sample06, groups_dict_keys, groups_dict_columns)
###Output
_____no_output_____
###Markdown
**Table 3 | Part 1 - Estimated Discontinuity in Probation Status for Year 1**
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'probation_year1', regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Table 3 | Part 2 - Estimated Discontinuity in Probabtion Status Ever** Part 2 of Table 3 presents the estimated effect of scoring below the cutoff in the first year for _ever_ being placed on probation. The results show that even of those who score slightly above the probation cutoff in year 1, 33 % are placed on probation at some other point in time during their studies. For the different subgroups of students this value varies from 29% (for students with high school grades above the median) up to 36.7% (for the group of males). These results already indicate that we can expect heterogeneities in the way different students react to being placed on academic probation.The fact that it is not unlikely for low performing students just slightly above the cutoff to fall below it later on also underlines these student's fitness as a control group for the purpose of the analysis. Lindo et al. (2010) argue that the controls can be thought of as receiving a much weaker form of treatment than the group that is placed on probation, as scoring just above the cutoff in year 1 does not save students from falling below the cutoff and being placed on probation in subsequent terms.
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'probation_ever',regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
5.2.3. The Immediate Response to Academic Probation Students who have been placed on academic probation enter their next term at university with the threat of suspension in case they fail to improve their grades. Recalling the theoretical framework presented in prior sections, students face the following set of options after each term:1. **Option 1**: Return to school, exhibit low effort and achieving a low GPA,2. **Option 2**: Return to school, exhibit high effort with the intent of achieving a high GPA,3. **Neither** option: Drop out of university.Students on probation face a different set of choices than the students that were not placed on probation as the threat of suspension essentially eliminates option 1. Of course, students could enter the next term, exhibit low effort, and receive low grades, but this would result in suspension. Since both option 1 and option 3 result in the student not continuing school (at least for a certain period of time), students who cannot meet the performance standard (thus leading to suspension) are much better off dropping out and saving themselves the cost of attending university for another term. Table 4 - Estimated Effect on the Decision to Leave after the First Evaluation
###Code
table4 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'left_school', regressors)
table4.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
The results presented in Table 4 and and Figure 3 show the effects of being placed on probation on the probability to drop out of school after the first evaluation. The first row of Table 4 shows the average effect of academic probation on this outcome. The results indicate that, on average, being placed on probation increases the probability of leaving university by 1.8 percentage points. A student on academic probation is thus 44% more likely to drop out than their control group counterpart.The results presented in the rest of Table 4 and and Figure 3 show that the average effect of being placed on probation is also characterized by large heterogeneities between the different subgroups of students. For males and native English speakers, the results, which are significant at the 5% level, show an increase of 3.7 and 2.8 percentage points respectively in the probability of leaving university after being placed on probation after the first evaluation. The results show no significant effects for these group's counterparts, the subgroups of females and nonnative English speakers. Aside from gender and native language, the results also indicate that high school performance seems to play a role in how students react on being placed on probation. For the group of students who scored above the median in high school academic probation roughly doubles the probability of leaving school compared to the control group while there is no such effect for students who scored below the median in high school. Lindo et al. (2010) contribute this finding to a discouragement effect for those students who are placed on probation, which seems to be larger for students who did well in high school. Figure 3 - Stratified Results for Voluntarily Leaving School at the End of the First year
###Code
groups_dict_12 = create_groups_dict(sample12, groups_dict_keys, groups_dict_columns)
predictions_groups_dict = create_fig3_predictions(groups_dict_12, regressors, 0.6)
plot_figure3(groups_dict_12, predictions_groups_dict, groups_dict_keys)
###Output
_____no_output_____
###Markdown
5.2.4. The Impact onSubsequent Performance i. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next Term The next outcome Lindo et al. (2010) analyze is the performance of students who stayed at university for the next term. The theoretical framework presented in Section 2 predicts that those students on probation who stay at university will try to improve their GPA. Indeed, if they do not manage to improve, they will be suspended and could have saved themselves the effort by dropping out.The results presented in Figure 4 and Table 5 show the estimated discontinuity in subsequent GPA. Lindo et al. (2010) find significant results (at the 5% level) for all subgroups, which is an even bigger effect than that of probation on drop out rates, where only some subgroups were affected. Figure 4 - GPA in the Next Enrolled Term
###Code
predictions_fig4 = create_predictions(sample12, 'nextGPA', regressors, 0.6)
plot_figure4(sample12, predictions_fig4)
###Output
_____no_output_____
###Markdown
As part A of Table 5 shows, the average treatment effect on the GPA in the next term is positive for all groups of students. The average student on probation has a GPA increase of 0.23 grade points which is 74% of the control group. The increase is greatest for students who have high school grades below the median. These students increase their GPA by 0.25 grade points on average, 90% more than their control group. This is an interesting finding because the counterpart, students who scored above the median in high school, are especially likely to drop out. Thus high school grades seem to have a large effect on whether students perceive academic probation as discouragement or as an incentive to improve their performance. It should be noted here, that the '*next term*' may not be the next year for all students because some students take summer classes. If students fail to improve their grades during summer classes, they are already suspended after summer and will not enter the second year. Only using grades from the second year would thus omit students who were suspended before even entering the second year. The existence of summer classes may complicate the comparability of students after being put on probation. However, in a footnote Lindo et al. (2010) mention that they find no statistically significant impact of academic probation on the probability that a student enrolls in summer classes and the estimates for subsequent GPA are nearly identical when controlling for whether a student's next term was attending a summer class. ---**NOTE**: Lindo et al. (2010) in this call this the '*improvement*' of students' GPA, however, this phrasing in my opinion could be misleading, as the dependent variable in this analysis is the distance from cutoff in the next term. The results thus capture the increase in subsequent GPA in general and not relative to the GPA in the prior term.--- Table 5 - Estimated Discontinuites in Subsequent GPA | Part A - Next Term GPA
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextGPA', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Table 5 - Estimated Discontinuites in Subsequent GPA | Part B - Probability of Placing Above the Cutoff in Next Term Panel B of Table 5 shows the probability of scoring above the cutoff in the next term. This statistic is very important because it decides whether students on academic probation are suspended after the subsequent term. It is therefore important for students who scored below the cutoff in the first year to not only improve their GPA, but improve it enough to score above the cutoff in the next term. Again academic probation increases the probability of students scoring above the cutoff in the next term for all subgroups.
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextGPA_above_cutoff', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
ii. Formal Bound Analysis on Subsequent GPA (partial extension) As already mentioned in the section on the identification strategy, analyzing outcomes that occur after the immediate reaction to probation (the decision whether to drop out or not) becomes more challenging if we find that students are significantly more or less likely to drop out if they have been placed on academic probation. As discussed in the preceding section, this is the case because some groups of students indeed are more likely to drop out if they have been placed on probation.For the analysis of subsequent GPA, this means that the results become less reliable because there is a group of students (those who dropped out) whose subsequent performance cannot be observed. This can cause the results to be biased. For example, if academic probation causes students with relatively low ability to drop out (which the performance model would predict) then we would find a positive impact on subsequent GPA being solely driven by the fact that the low performers in the treatment group dropped out. If, on the other hand, high ability students were more likely to drop out, the estimates for the impact on subsequent performance would be downward biased.In short, the control group might not be comparable anymore. To test whether the results on subsequent GPA are robust to these concerns, Lindo et al. (2010) use formal bound analysis for the results on subsequent GPA which I present below.In addition to this formal bound analysis, I plot confidence intervals for the results on subsequent GPA. Confidence intervals are a useful way to support the graphical analysis of RDDs and ensure the discontinuity at the threshold does not disappear when new population samples are drawn. The graph below shows the estimates from before including a bootstrap 95% percent confidence interval. The confidence interval around the cutoff shows to be quite small, and the fall in subsequent GPA between the treatment and control group persists even at the borders of the confidence interval. Subsequent Performance with 95% Confidence Interval
###Code
bootstrap_pred = bootstrap_predictions(n=100, data=sample12, outcome='nextGPA', regressors=regressors, bandwidth=0.6)
CI = get_confidence_interval(data=bootstrap_pred, lbound=2.5, ubound=97.5, index_var='dist_from_cut')
predictions_fig4_CI = pd.concat([predictions_fig4, CI[['upper_bound', 'lower_bound']]], axis=1)
plot_figure4_with_CI(data=sample12, pred=predictions_fig4_CI)
###Output
_____no_output_____
###Markdown
---**NOTE**: The confidence intervals presented here are the product of only 100 resampling iterations of the bootstrap because increasing the number of times the data is resampled significantly increases the runtime of this notebook. However, I have tested the bootstrap for up to 1000 iterations and the results do not diverge very much from the version shown here. --- This type of confidence interval, however, does not correct for potential biases in the treatment or control group discussed above because the bootstrap only resamples the original data and therefore can at best achieve the estimate resulting from the original sample. To test the sensitivity to possible nonrandom attrition through specific students dropping out of university, Lindo et al. (2010) perform a formal bound analysis using a trimming procedure proposed by Lee (2009)*. The reasoning for this approach is based on the concerns described above. To find a lower bound of the estimate, Lindo et al. (2010) assume that academic probation causes students who would have performed worse in the next term to drop out. The control group is thus made comparable by dropping the lowest-performing students (in the next term) from the sample, assuming these students would have dropped out had they been placed on probation. To calculate the upper bound estimate, the same share of students is dropped from the upper part of the grade distribution instead. The share of students who need to be dropped is given by the estimated impact of probation on leaving school. For example, in the entire sample students on probation are 1.8 percentage points more likely to drop out, which is 44% of the control mean. Thus, to make the groups comparable again we presumably need to drop 44% more students from the control group than actually dropped out. For groups of students where the estimated impact of probation on leaving school is negative, students from the control group need to be dropped instead (i.e. here the lower bound is given by dropping the top students in the treatment group and the upper bound is given by dropping the bottom students). While all results I have presented in this replication so far are exactly identical to the results from Lindo et al. (2010), I, unfortunately, cannot replicate the results from the formal bound analysis precisely. The description in the paper is brief and the provided STATA code from the authors does not include the formal bound analysis. While referring to methods presented in Lee (2009) has been helpful to understand the trimming procedure, I am unable to replicate the exact numbers presented in Lindo et al. (2010).The table pictured below shows the results of the formal bound analysis presented in Lindo et al. (2010). The authors conclude that the positive effects of academic probation on students' subsequent GPA are too great to be explained by the attrition caused by dropouts. ---**NOTE**: In their paper Lindo et al. (2010) quote _'Lee (2008)'_ which could also refer to a different paper by Lee and Card from 2008 listed in the references. However, since this paper in contrast to the 2009 paper by Lee does not mention formal bound analysis and since Lee (2009) is not mentioned anywhere else in the paper, I am certain this is a citation error.--- Formal Bound Analysis from Lindo et al. (2010) (p.110)  The table below shows my results using the proposed trimming procedure (table is again transposed compared to the original). The overall results are quite similar to the ones presented in Lindo et al. (2010), all estimates presented in Table 5 still lie between the lower and upper bound. It should be noted that in my replication the lower bound estimate for students with high school grades above the median was not significant at the 10% level while the results for all other groups were. Replication of Formal Bound Analysis
###Code
table4['add_leavers'] = round(table4['GPA below cutoff (1)']/table4['Intercept (0)'],2)
add_leavers = table4['add_leavers']
lb_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, True, False)
lower_bound = estimate_RDD_multiple_datasets(lb_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
ub_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, False, True)
upper_bound = estimate_RDD_multiple_datasets(ub_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
bounds = pd.concat([lower_bound.iloc[:,[0,2]],upper_bound.iloc[:,[0,2]]], axis=1)
bounds.columns = pd.MultiIndex.from_product([['Lower Bound Estimate','Upper Bound Estimate',],
['GPA below cutoff (1)', 'Std.err (1)']])
bounds
###Output
_____no_output_____
###Markdown
5.2.5. The Impacts on GraduationAs a third outcome, Lindo et al. (2010) examine the effects of academic probation on students' graduation rates. As already discussed in the previous section, the outcomes that are realized later in time are more complex to examine because of all the different choices a student has made until she or he reaches that outcome. Graduation rates are the product of a dynamic decision-making process that spans throughout the students' time at university. While the study focuses mainly on the effects of being put on probation after the first year, the decision problem described in the theoretical framework can be faced by students at different points during their academic career as students can be placed on probation each term or for multiple terms in a row. There are different ways in which academic probation could affect graduation rates. On the one hand, it could reduce the probability of graduating because probation increases the probability of dropping out and some students who fail to increase their grades are suspended. On the other hand, these students might have graduated either way and thus do not have an effect. Additionally, probation could increase graduation rates because those students who remain improve their performance. Figure 5 - Graduation Rates Figure 5 and Table 6 show the estimated impacts of academic probation after the first year on whether a student has graduated in four, five or six years. The effects are negative for all three options, suggesting that the negative effects discussed above overweigh potential positive effects on graduation rates.
###Code
plot_figure5(sample12,
create_predictions(sample12,'gradin4', regressors, 0.6),
create_predictions(sample12,'gradin5', regressors, 0.6),
create_predictions(sample12,'gradin6', regressors, 0.6))
###Output
_____no_output_____
###Markdown
Table 6 - Estimated Effects on Graduation The effects on graduation rates are insignificant for most subgroups, the group of students with high school grades above the median stands out as being especially negatively affected by being placed on probation in the first year. This group of students sees their probability of graduation within six years reduced by 14.5 percent. Lindo et al. (2010) attribute these results to the fact that this group of students is especially likely to drop out after being put on probation and also on average does not do much better than their counterpart if they continue to attend university.Overall the results on graduation rates are rather limited. This likely stems from the more complex nature in which probation in the first year can affect this outcome later down the line. Unfortunately, most of the data in the provided dataset focus on the first two years of students' time at university (e.g. we only now the GPA of the first two years). Much more information would be needed to uncover the mechanisms in which probation may affect students' probability of graduating within specific timeframes.---**NOTE**: Below I only show the sections of Table 6 that are discussed above as the entire table is quite extensive. The other results presented in Table 6 of the paper can be viewed by uncommenting the code at the end of this section.--- Graduated after 6 years
###Code
table6 = create_table6(groups_dict_06, groups_dict_keys, regressors)
table6.loc[['All','HS Grades > median' ],
'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Code for complete Table 6:**
###Code
# table6.loc[:, 'Graduated after 4 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 5 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
--- 6. Extension: Robustness Checks ---As discussed in my replication of Lindo et al. (2010) above, the authors use a variety of validity and robustness checks to analyze the reliability of their results. Aside from some smaller independent contributions that I already discuss in the replication part for better context, I in this section further analyze subsequent performance and check the bandwidth sensitivity of the results in drop out rates and subsequent GPA. 6.1. A Closer Look at Students' Subsequent Performance. 6.1.1. Subsequent Performance and Total Credits in Year 2 The results from Lindo et al. (2010) presented above show that students are more likely to drop out after being placed on academic probation but those who remain in school tend to improve their GPA above the cutoff in the next term. These results are generally in line with the theoretical framework presented in the paper which predicts that students either drop out or improve their GPA if the cost of not improving in the next term increases. The performance standard model explains these results through students self-selecting between increasing effort and dropping out based on their abilities (which are defined as the probability of meeting the performance standard). Students who are less likely to improve their GPA should thus be more likely to drop out. Unfortunately, it is not possible to test this prediction, as Lindo et al. (2010) emphasize in the paper because the probability of meeting the performance standard is not observed for students who leave school. However, examining the students who remain in school may give some further insights. While Lindo et al. (2010) observe that students have been placed on probation on average improve their performance, it is not clear under which circumstances this is happening. A look at the amount of credits students are taking in their second year may give some insights. The results presented below show that being placed on probation after the first year has a negative effect on the amount of credits students take in the second year for all of the examined subgroups except the group of nonnative English speakers. This is a stark contrast to the first year where both the treatment and control group take almost the same amount of credits (as shown in the section on the validity of the RD Approach).
###Code
predictions_credits_year2 = create_predictions(sample12, 'total_credits_year2', regressors, 0.6)
plot_figure_credits_year2(sample12, predictions_credits_year2)
###Output
_____no_output_____
###Markdown
The results indicate that being placed on probation decreases the total credits taken by the average student in year two by 0.33, around 8% of the control mean. As the table below shows, the results are most prominent for males, native English speakers, and students with high school grades above the median. Interestingly, these are the same groups of students that are most likely to drop out, suggesting that the discouragement effect persists throughout these groups and even those who re-enroll for the next term proceed with caution by taking fewer credits.
###Code
table_total_credits_year2 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,
'total_credits_year2',regressors)
table_total_credits_year2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
When interpreting these results it should be kept in mind that some students' next evaluation takes place during summer classes. Students who have taken summer classes enter their second year already having either passed the next evaluation or not. Those who fell below the cutoff will have been suspended and thus are missing from the data for the second year and those who have passed the threshold in the summer classes are likely not on probation anymore. Estimating the effects of probation on credits taken in the second year separately for both groups shows that those who did not take classes in the summer are more affected than those who did. For the students who took summer classes, the results are only significant for males, students with high school grades above the median and native English speakers. No summer classes
###Code
sample06_nosummer = sample06[sample06.summerreg_year1 == 0]
groups_dict_06_nosummer = create_groups_dict(data=sample06_nosummer, keys=groups_dict_keys,columns=groups_dict_columns)
table_totcred_y2_nosummer = estimate_RDD_multiple_datasets(groups_dict_06_nosummer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_nosummer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Summer classes
###Code
sample06_summer = sample06[sample06.summerreg_year1 == 1]
groups_dict_06_summer = create_groups_dict(sample06_summer,groups_dict_keys,groups_dict_columns)
table_totcred_y2_summer = estimate_RDD_multiple_datasets(groups_dict_06_summer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_summer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
These findings are useful for interpreting the subsequent performance of students because more credits likely signify a larger workload for the student. Instead of increasing their effort, students may just decrease their workload by completing fewer credits in the next term. Unfortunately, we cannot test this in detail because the data doesn't show how many credits students completed in which term. Reducing the sample for the analysis of the subsequent GPA to students who did not attend summer classes and completed 4 credits in the second year (the most frequent amount of credits takeen by this group of students) shows that the effect of scoring below the cutoff in year 1 becomes insignificant for the students who have above-median high school grades and nonnative English speakers. The improvement decreases a bit for some groups like females or students with high school grades below the median but increases for others like males and native english speakers. Overall the results are still highly significant though considering the small window of observations to which the data is reduced in this case. This suggests that while students on probation do seem to take fewer credits in the next year, the improvements to subsequent performance is too great to just be attributed to students decreasing their workload.
###Code
sample06_many_credits = sample06_nosummer[(sample06_nosummer.total_credits_year2 == 4)]
groups_dict_06_manycredits = create_groups_dict(sample06_many_credits,groups_dict_keys,groups_dict_columns)
table_manycredits = estimate_RDD_multiple_datasets(groups_dict_06_manycredits,groups_dict_keys,
'nextGPA',regressors)
table_manycredits.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.1.2. Subsequent Cumulative Grade Point Average (CGPA) An additional factor that might be important for the analysis of subsequent performance is the Cumulative Grade Point Average (CGPA). Lindo et al. (2010) focus their analysis of subsequent performance solely on the grades achieved in the next term. However, in the section on the institutional background in the paper the authors write:>*At all campuses, students on probation can avoid suspension and return to good academic standing by bringing their cumulative GPA up to the cutoff.* (Lindo et al., 2010, p.98).To avoid suspension in the long term, students on probation thus are required to not only score above the cutoff in the next term but to score high enough to bring their CGPA above the probation threshold. Students who score above the threshold in the next term but still have a CGPA below the cutoff remain on probation. Students who fail to bring their GPA above the cutoff (and thus also their CGPA since their first-year GPA and first-year CGPA are the same) are suspended. As the figure and table below show, the positive effects of probation on subsequent performance carry over to students' CGPA as well. Being placed on probation on average increases students' CGPA by 0.07 grade points or 63% of the control mean although the difference is rather difficult to spot visually.
###Code
predictions_nextCGPA = create_predictions(sample12, 'nextCGPA', regressors, 0.6)
plot_nextCGPA(sample12, predictions_nextCGPA)
###Output
_____no_output_____
###Markdown
Effect of Academic Probation on Subsequent CGPA
###Code
table_nextCGPA = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextCGPA', regressors)
table_nextCGPA.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
However, in contrast to the probability of improving the next term GPA above the cutoff, academic probation has no significant effect on the probability of improving the CGPA above the cutoff in the next term except for the group of nonnative English speakers where the probability is actually negative. Indeed, out of all students on probation (within 0.6 grade points of the cutoff), only around 37% improve their next term CGPA above the cutoff. Around 23% improve their GPA above the cutoff but not their CGPA and remain on probation. The other students dropped out or are suspended after the next term. This suggests that the effects of probation span much longer than just the subsequent term for many students, not only indirectly because they have had the experience of being placed on probation but also directly because many of them remain on probation for multiple subsequent terms. These factors underline the points made in previous sections about the complexity of the way academic probation can affect a student's academic career. After being placed on probation a student can take a multitude of different paths, many more than the theoretical framework introduced in Section 2 leads on. A more dynamic approach to estimating the effects of academic probation could likely offer more insights into how students react to this university policy. Effect of Academic Probation on the Probability of Achieving a CGPA Above the Cutoff in the Next Term
###Code
table_nextCGPA_above_cutoff = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextCGPA_above_cutoff',
regressors)
table_nextCGPA_above_cutoff.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.2. Bandwidth Sensitivity As a final robustness check, I evaluate the model at different bandwidths to ensure that results are not limited to one specific sample of students within a particular bandwidth. Lindo et al. (2010) use a distance from the threshold of 0.6 for the main regression analysis and 1.2 for graphical analysis (although the estimated curve at each point relies on a local linear regression with a bandwidth of 0.6 as well). The chosen bandwidth around the cutoff thus captures around 25% of the total range of grades (the GPA values observed in the first year span from 0 to 4.3). Lindo et al. (2010) do not discuss the reasoning behind their choice of bandwidth in detail and do not apply optimal bandwidth selection methods like some other applications of regression discontinuity (Imbens & Lemieux, 2008; Lee & Lemieux, 2010). However, from a heuristic standpoint, this bandwidth choice seems reasonable. Since the cutoff lies at a GPA of 1.5 (1.6 at Campus 3), this bandwidth includes students whose GPA falls roughly between 0.9 and 2.1 grade points, so a range of around one average grade point including the edges. A much larger bandwidth would not make sense because it would include students that are failing every class and students who are achieving passable grades and are thus not very comparable to students who pass or fall below the threshold by a small margin.I evaluate bandwidths of length 0.2 (0.1 distance from cutoff on each side) up to 2.4 (1.2 distance from cutoff on both sides). As Lindo et al. (2010), I choose a maximum bandwidth of 1.2 the reasons explained in the paragraph above. Bandwidth sensitivity of the effect of probation on the probability of leaving school The table below shows the estimated effect of probation on the probability to leave school after the first year using local linear regression (same specification as before) for all bandwidths between 0.1 and 1.2. The bandwidths are on the vertical axis, and the different subgroups are on the horizontal axis of the table. An *x* in the table indicates that the estimate was insignificant at the 10% level and is thus not shown for readability. The table shows that the results for the effects on leaving school are relatively sensitive to bandwidth selection. Estimates of students within only 0.2 grade points of the probation threshold are not significant for any of the groups considered. Results for students with high school grades below the median are only significant for bandwidths between 0.3 and 0.5 while estimates for students with high school grades above the median are only significant between values of 0.5 and 0.7. The results for the other subgroups, on the other hand, seem to be quite robust to bandwidth selection. The findings reported in this table suggest that some results presented in the previous sections should be interpreted carefully. Especially the estimates of students based on high school grades might be driven by some underlying factors that are not observed in this study. These could explain the sensitivity of the results to bandwidth selection.
###Code
bandwidths = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2]
summary_left_school = bandwidth_sensitivity_summary(data, 'left_school',groups_dict_keys, groups_dict_columns, regressors)
summary_left_school.loc[(bandwidths,'probation'),:]
#summary_left_school #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
###Markdown
Bandwidth sensitivity of the effect of probation on subsequent GPA The results for the effects of academic probation on subsequent performance, on the other hand, seem to be quite robust to bandwidth selection. The estimated effects are the highest for most subgroups around the threshold of 0.6 chosen by Lindo et al. (2010) but the effects do not change sign for any subgroup and still remain quite similar.Again, the group of students with high school grades above the median does not show significant results for bandwidths between 0.1 and 0.4 and thus seems to be the most sensitive to bandwidth selection.
###Code
summary_nextGPA = bandwidth_sensitivity_summary(data, 'nextGPA', groups_dict_keys, groups_dict_columns, regressors)
summary_nextGPA.loc[(bandwidths,'probation'),:]
# summary_nextGPA #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
###Markdown
--- Project for the course in Microeconometrics | Summer 2019, M.Sc. Economics, Bonn University | [Annica Gehlen](https://github.com/amageh) Replication of Jason M. Lindo, Nicholas J. Sanders & Philip Oreopoulos (2010) --- This notebook contains my replication of the results from the following paper:> Lindo, J. M., Sanders, N. J., & Oreopoulos, P. (2010). Ability, gender, and performance standards: Evidence from academic probation. American Economic Journal: Applied Economics, 2(2), 95-117. Downloading and viewing this notebook:* The best way to view this notebook is by downloading it and the repository it is located in from [GitHub](https://github.com/HumanCapitalAnalysis/template-course-project). Other viewing options like _MyBinder_ or _NBViewer_ may have issues with displaying images or coloring of certain parts (missing images can be viewed in the folder [files](https://github.com/HumanCapitalAnalysis/template-course-project/tree/master/files) on GitHub).* The original paper, as well as the data and code provided by the authors can be accessed [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). Information about replication and individual contributions:* For the replication, I try to remain true to the original structure of the paper so readers can easily follow along and compare. All tables and figures are named and labeled as they appear in Lindo et al. (2010).* The tables in my replication appear transposed compared to the original tables to suit my workflow in Python.* For transparency, all sections in the replication that constitute independent contributions by me and are not part of results presented (or include deviations from the methods used) in the paper are marked as _extensions_. Table of Contents1. Introduction2. Theoretical Background3. Identification4. Empirical Strategy5. Replication of Lindo et al. (2010)5.1. Data & Descriptive Statistics5.2. Results5.2.1. Tests of the Validity of the RD Approachi. Extension: Visual Validity Checkii. Advanced Validity Check5.2.2. First Year GPAs and Academic Probation5.2.3. The Immediate Response to Academic Probation5.2.4. The Impact onSubsequent Performancei. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next Termii. Formal Bound Analysis on Subsequent GPA (partial extension)5.2.5. The Impacts on Graduation6. Extension: Robustness Checks6.1. A Closer Look at Students' Subsequent Performance.6.1.1. Subsequent Performance and Total Credits in Year 26.1.2. Subsequent Cumulative Grade Point Average (CGPA)6.2. Bandwidth Sensitivity7. Conclusion8. References
###Code
%matplotlib inline
import numpy as np
import pandas as pd
import pandas.io.formats.style
import seaborn as sns
import statsmodels as sm
import statsmodels.formula.api as smf
import statsmodels.api as sm_api
import matplotlib as plt
from IPython.display import HTML
from auxiliary.example_project_auxiliary_predictions import *
from auxiliary.example_project_auxiliary_plots import *
from auxiliary.example_project_auxiliary_tables import *
###Output
_____no_output_____
###Markdown
--- 1. Introduction --- Lindo et al. (2010) examine the effects of academic probation on student outcomes using data from Canada. Academic probation is a university policy that aims to improve the performance of the lowest- scoring students. If a student's Grade Point Average (GPA) drops below a certain threshold, the student is placed on academic probation. The probation status serves as a warning and does not entail immediate consequences, however, if students fail to improve their grades during the following term, they face the threat of being suspended from the university. In a more general sense, academic probation may offer insights into how agents respond to negative incentives and the threat of punishment in a real-world context with high stakes. To estimate the causal impact of being placed on probation, Lindo et al. (2010) apply a **regression discontinuity design (RDD)** to data retrieved from three campuses at a large Canadian university. The RDD is motivated by the idea that the students who score just above the threshold for being put on academic probation provide a good counterfactual to the 'treatment group' that scores just below the threshold. In line with the performance standard model that serves as the theoretical framework for the paper, Lindo et al. (2010) find that being placed on probation induces students to drop out but increases the grades of the students who remain in school. The authors also find large heterogeneities in the way different groups of students react to academic probation.**Main variables** | **Treatment** | **Main outcomes** | **Main Covariates** ||-------------------|-------------------------|------------------------|| Academic probation| Drop-out rates | Gender || . | Subsequent performance | HS grades | | . | Graduation rates | Native language | In this notebook, I replicate the results presented in the paper by Lindo et al. (2010). Furthermore, I discuss in detail the identification strategy used by the authors and evaluate the results using multiple robustness checks. My analysis offers general support for the findings of Lindo et al. (2010) and points out some factors which may enable a deeper understanding of the causal relationship explored in the paper. This notebook is structured as follows. In the next section, I present the performance standard model that lays down the theoretical framework for the paper (Section 2). In Section 3, I analyze the identification strategy that Lindo et al. (2010) use to unravel the causal effects of academic probation on student outcomes and Section 4 briefly discusses the empirical strategy the authors use for estimation. Section 5 and Section 6 constitute the core of this notebook. Section 5 shows my replication of the results in the paper and discussion thereof. In Section 6 I conduct various robustness checks and discuss some limitations of the paper. Section 7 offers some concluding remarks. --- 2. Theoretical Background---The underlying framework used for the analysis is a model developed by Bénabou and Tirole (2000) which models agent's responses to a performance standard. While Bénabou and Tirole (2000) model a game between a principal and an agent, Lindo et al. (2010) focus only on the agent to relate the model to the example of academic probation. In the performance standard model, the agents face a choice between three options: 1. **Option 1**: Incurs cost $c_1$ and grants benefit $V_1$ if successful. 2. **Option 2**: Incurs cost $c_2$ and grants benefit $V_2$ if successful. 3. **Neither** option: Incurs 0 cost and 0 benefit. Option 1 has a lower cost and a lower benefit than option 2 such that:\begin{equation} 0 < c_1 < c_2 , 0 < V_1 < V_2.\end{equation}Ability, denoted by $\theta$, translates to the probability of successfully completing either option. Assuming agents have perfect information about their ability, they solve the maximizing problem\begin{equation}max\{0, \theta V_1-c_1, \theta V_2-c_2\}.\end{equation} Let $\underline{\theta}$ be the ability level where the agent is indifferent between neither and option two and let $\bar{\theta}$ be the ability level at which the agent is indifferent between option 1 and option 2. Assuming that\begin{equation}\underline{\theta} \equiv \frac{c_1}{V_1} < \bar{\theta} \equiv \frac{c_2-c_1}{V_2-V1} < 1\end{equation}ensures that both options are optimal for at least some $\theta$.It can be shown that * the lowest ability types ($\theta < \underline{\theta}$) choose neither option,* the highest ability types ($\bar{\theta} < \theta$) choose the difficult option,* the individuals in between the high and low type $\underline{\theta}< \theta < \bar{\theta} $) choose the easier option.If the principal now removes option 1 or makes choosing this option much more costly, then the agent will choose option 2 if and only if\begin{equation}\theta \ge \frac{c_2}{V_2} \equiv \theta^*\end{equation}and choose neither option otherwise. The agents who would have chosen option 1 now split according to ability. Agents with high ability (specifically those with $\theta \in [\theta^*,\bar{\theta}]$) work harder, thereby choosing option 2, while low ability types (those with $\theta \in [\underline{\theta}, \theta^*]$) do not pursue option 2 (and thus choose neither option).In the context of academic probation students face a similar decision and possible courses of action. Students whose GPA is just above the probation cutoff face the full set of options for the next year:1. **Option 1**: Return to school and exhibit low effort and leading to a low GPA2. **Option 2**: Return to school and exhibit high effort with the intent of achieving a high GPA3. **Neither** option: Drop out of universityStudents who score below the probation cutoff face a restricted set of options as the university administration essentially eliminates option 1 by suspending students if they do not improve their grades. Lindo et al. (2010) formulate three testable implications of this theoretical framework: * _Forbidding option 1 will **increase the overall probability of students dropping out**._ * _Forbidding option 1 will **increase the performance of those who return**._ * _Forbidding option 1 will cause **relatively low-ability students to drop out** and **relatively high-ability students to return and work harder**._ --- 3. Identification--- Lindo et al. (2010) in their paper aim to evaluate how academic probation affects students, specifically their probability of dropping out of university and whether it motivates those who remain to improve their grades. Students are placed on probation if their Grade Point Average (GPA) drops below a certain threshold and face the threat of suspension if they fail to improve their GPA in the next term. Students are thus clearly separated into a treated group (who is put on probation) and an untreated group based on their GPA. The causal graph below illustrates the relationship between the assignment variable $X$, treatment $D$ and outcome $Y$. While $X$ (the GPA) directly assigns students to treatment, it may also be linked to student outcomes. Additionally, there may be observables $W$ and unobservables $U$ also affecting $X$,$D$, and $Y$. There are thus multiple backdoor paths that need to be closed in order to isolate the effect of academic probation. Simply controlling for the variables in question, in this case, does not suffice since there are unobservables that we cannot condition on. A randomized experiment, on the other hand, could eliminate selection bias in treatment by randomly assigning probation to students. The research question evaluated in the paper constitutes a classic policy evaluation problem in economics where we try to understand the causal implications of a policy without being able to observe the counterfactual world where the policy is not administered. However, as with many questions in economics, implementing a randomize experiment directly is not a feasible option, especially since we are examing the effect of a penalty whose consequences may affect students for the rest of their lives.Since it is not possible to randomize assignment to treatment, another method is needed to isolate the effects of academic probation on student outcomes. Lindo et al. (2010) apply a regression discontinuity design (RDD) to the problem at hand, a method pioneered by Thistlethwaite and Campbell (1960) in their analysis of the effects of scholarships on student outcomes. In fact, the identification problem in Lindo et al. (2010) is quite similar to that of Thistlethwaite and Campbell (1960) as both papers evaluate the causal effects of an academic policy on student outcomes. However, while the scholarship administered to high performing students in Thistlethwaite and Campbell (1960) constitutes a positive reinforcement for these students, Lindo et al. (2010) examine the effects of a negative reinforcement or penalty on low performing students. This means that, in contrast to Thistlethwaite and Campbell (1960) and many other applications of RD, our treatment group lies _below_ the cutoff and not above it. This does not change the causal inference of this model but it might be confusing to readers familiar with RD designs and should thus be kept in mind. The regression discontinuity design relies on the assumption of local randomization, i.e. the idea that students who score just above the cutoff do not systematically differ from those who score below the cutoff and thus pose an appropriate control group for the students who are placed on probation. This identification strategy relies on the assumption that students are unable to precisely manipulate their grades to score just above or below the probation threshold. Within the neighborhood around the discontinuity threshold, the RDD thus in a sense mimics a randomized experiment. To explain how the use of regression discontinuity allows Lindo et al. (2010) to identify treatment effects, I draw on material provided in Lee and Lemieux (2010) and their discussion on the RDD in the potential outcomes framework. As mentioned above, for each student $i$ we can image a potential outcome where they are placed on probation $Y_i(1)$ and where they are not $Y_i(0)$ but we can never simultaneously observe both outcomes for each student. Since it is impossible to observe treatment effects at the individual level, researchers thus estimate average effects using treatment and control groups. For the RDD this potential outcomes framework translates by imagining there are two underlying relationships between the average student outcome and the assignment variable $X$ (the students' GPA), which are represented by $E[Y_i(1)|X]$ and $E[Y_i(0)|X]$. Since all students who score below the cutoff $c$ are placed on probation, we only observe $E[Y_i(1)|X]$ for those below the cutoff and $E[Y_i(0)|X]$ for those above the cutoff. We can estimate the average treatment effects by taking the difference of the conditional expectations at the cutoff if these underlying functions are continuous throughout the cutoff:\begin{equation}lim_{\epsilon \downarrow 0}E[Y_i|X_i=c+\epsilon] - lim_{\epsilon \uparrow 0} E[Y_i|X_i=c+\epsilon] = E[Y_i(1)-Y_i(0)|X=c].\end{equation}As explained above, this _continuity assumption_ is fulfilled by the RDD because we can assume that students have _imprecise control_ over the assignment variable, their GPA. We can clearly identify the average treatment effects because there is a natural sharp cutoff at the threshold. The treatment administered to students is being confronted with the information that they are placed on probation and the subsequent threat of suspension. Being put on probation does not involve any actions by the students, in fact being assigned to the treatment group already constitutes the treatment in itself. Non-compliers thus do not pose a concern for this research design. As the theoretical framework discussed in the prior section illustrates, students on probation face the decision of dropping out or trying to improve their performance in the next term. While the estimation on effects on dropping out using the regression discontinuity design is relatively straight forward, the estimation of effects for subsequent performance adds additional challenges.The extended causal graph above illustrates how the subsequent performance of students is also affected by whether a student drops out or not. This factor adds additional complexity to the estimation problem because we cannot observe the subsequent GPA for students who drop out after being placed on probation. This factor puts into question the comparability of the treatment and control group in subsequent periods. I address these concerns and possible solutions in later sections of this notebook.Aside from the two main outcomes, Lindo et al. (2010) also examine the effects of academic probation on graduation rates of students. However, since information about student's academic progress over the whole course of their studies is limited in the available data, only very simple analysis is possible. --- 4. Empirical Strategy---The authors examine the impact of being put on probation after the first year in university. The probation status after the first year is a deterministic function of student's GPA, formally\begin{equation}PROB^{year1}_{IC} = 1(GPANORM^{year1}_{IC} < 0),\end{equation}where $PROB^{year1}_{IC}$ represents the probation status of student $i$ at campus $c$ and $GPANORM^{year1}_{IC}$ is the distance between student $i$'s first-year GPA and the probationary cutoff at their respective campus. The distance of first-year GPA from the threshold thus constitutes the *running variable* in this RD design. Normalizing the running variable in this way makes sense because the three campuses have different GPA thresholds for putting students on probation (the threshold at campus 1 and 2 is 1.5, at campus 3 the threshold is 1.6), using the distance from the cutoff as the running variable instead allows Lindo et al. (2010) to pool the data from all three campuses.Applying the regression discontinuity design, the treatment effect for students near the threshold is obtained by comparing the outcomes of students just below the threshold to those just above the threshold.The following equation can be used to estimate the effects of academic probation on subsequent student outcomes:\begin{equation}Y_{ic} = m(GPANORM_{ic}^{year1}) + \delta1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}* $Y_{ic}$ denotes the outcome for student $i$ at campus $c$, * $m(GPANORM_{ic}^{year1})$ is a continuous function of students' standardized first year GPAs,* $1(GPANORM_{ic}^{year1}<0)$ is an indicator function equal to 1 if the student's GPA is below the probation cutoff,* $u_{ic} $ is the error term,* $\delta$ is the coefficient for the estimated impact of being placed on academic probation after the first year.For the regression analysis, Lindo et al. (2010) extend the above equation by an interaction term and a constant:\begin{equation}Y_{ic} = \alpha + \delta1(GPANORM_{ic}^{year1}<0) + \beta(GPANORM_{ic}^{year1}) + \gamma(GPANORM_{ic}^{year1})x 1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}This regression equation does not include covariates because Lindo et al. (2010) implement a split sample analysis for the covariates in the analysis. --- 5. Replication of Lindo et al. (2010)--- 5.1. Data & Descriptive StatisticsLindo et al. (2010) filter the data to meet the following requirements:* Students high school grade measure is not missing,* Students entered university before the year 2004 ( to ensure they can be observed over a 2-year period),* Students are between 17 and 21 years of age at time of entry.* Distance from cutoff is maximally 0.6 (or 1.2).The first three requirements are already fulfilled in the provided data. It should be noted that the high school measure is a student's average GPA in courses that are universally taken by high school students in the province. Thus all students that remain in the sample (84 % of the original data) attended high school in the province. This has the advantage that the high school measurement for all students is very comparable. An additional implication that should be taken note of for later interpretations is that this also implies that all students assessed in the study attended high school in the province. The group of 'nonnative' English speakers thus, for example, does not include students that moved to Canada after completing high school.
###Code
data_1 = pd.read_stata('data/data-performance-standards-1.dta')
data_2 = pd.read_stata('data/data-performance-standards-2.dta')
data = pd.concat([data_1, data_2], axis=1)
data = prepare_data(data)
###Output
_____no_output_____
###Markdown
---**NOTE**: The original data provided by the authors can be found [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). For this replication the data is split into two .dta-files due to size constraints.--- As shown in the graph below, the distance from the cutoff for university GPA in the provided dataset still spans from values of -1.6 to 2.8 as can be seen below. Lindo et al. (2010) use a bandwidth of *(-0.6, 0.6)* for regression results and a bandwidth of *(-1.2, 1.2)* for graphical analysis.
###Code
plot_hist_GPA(data)
# Reduce sample to students within 1.2 points from cutoff.
sample12 = data[abs(data['dist_from_cut']) < 1.2]
sample12.reset_index(inplace=True)
print("A sample of students within 1.2 points from the cuttoff consits of", len(sample12), "observations.")
# Reduce sample to students within 0.6 points from cutoff.
sample06 = data[abs(data['dist_from_cut']) < 0.6]
sample06.reset_index(inplace=True)
print("The final sample includes", len(sample06), "observations.")
###Output
The final sample includes 12530 observations.
###Markdown
Table 1 shows the descriptive statistics of the main student characteristics and outcomes in the restricted sample with a bandwidth of 0.6 from the cutoff. The majority of students are female (62%) and native English speakers (72%). Students in the reduced sample on average placed in the 33rd percentile in high school. It should also be noted that quite a large number of students (35%) are placed on probation after the fist year. An additional 11% are placed on probation after the first year. Table 1- Summary statistics
###Code
create_table1(sample06)
###Output
_____no_output_____
###Markdown
5.2. Results 5.2.1. Tests of the Validity of the RD Approach The core motivation in the application of RD approaches is the idea, that the variation in treatment near the cutoff is random if subjects are unable to control the selection into treatment (Lee & Lemieux, 2010). This condition, if fulfilled, means the RDD can closely emulate a randomized experiment and allows researchers to identify the causal effects of treatment. For evaluating the effects of academic probation on subsequent student outcomes, the RDD is thus a valid approach only if students are not able to precisely manipulate whether they score above or below the cutoff. Lindo et al. (2010) offer multiple arguments to address concerns about nonrandom sorting: 1. The study focuses on first-year students, assuming this group of students is likely to be less familiar with the probation policy on campus. To verify their conjecture, the authors also conducted a survey in an introductory economics course which revealed that around 50 % of students were unsure of the probation cutoff at their campus. They also claim that this analysis showed no relationship between knowledge of probation cutoffs and students' grades. 2. The authors also point out that most first-year courses span the entire year and most of the evaluation takes place at the end of the term which would make it difficult for students to purposely aim for performances slightly above the cutoff for academic probation.3. Finally, and most importantly, the implication of local randomization is testable. If nonrandom sorting were to be a problem, there should be a discontinuity in the distribution of grades at the cutoff with a disproportionate number of students scoring just above the cutoff. Additionally, all the covariates should be continuous throughout the cutoff to ensure that the group above the probation cutoff constitutes a realistic counterfactual for the treated group.In the following section, I first conduct a brief visual and descriptive check of validity before presenting my replication of the validity checks conducted in Lindo et al. (2010). i. Extension: Visual Validity Check To check for discontinuities in the covariates and the distribution of students around the cutoff Lindo et al. (2010) use local linear regression analysis. Before implementing the rather extensive validity check conducted by Lindo et al. (2010) I show in this section that a rather simple descriptive and graphical analysis of the distribution of covariates already supports the assumption they are continuous throughout the threshold. Extension | Table - Descriptive Statistics of Treated and Untreated Group Close to the CutoffThe table below shows the means of the different covariates at the limits of the cutoff from both sides (here within a bandwidth of 0.1 grade points). We can see that the means of the groups below and above the probation cutoff are very similar, even equal for some of the variables.
###Code
cov_descriptives = describe_covariates_at_cutoff(sample06,bandwidth=0.1)
cov_descriptives
###Output
_____no_output_____
###Markdown
Extension | Figure - Distribution of Covariates throughout the Probation CutoffThe figure below shows the means of the nine covariates in bins of size 0.5 (grade points). Similar to the descriptive table shown above, this visualization shows that there seem to be no apparent discontinuities in the distribution of students for any of the observable characteristics (graphs with bins of size 0.1 or 0.025 suggest the same).
###Code
plot_covariates(data=data, descriptive_table=cov_descriptives,bins = 'dist_from_cut_med05')
###Output
_____no_output_____
###Markdown
ii. Advanced Validity Check(as conducted by Lindo et al. (2010)) Figure 1 | Distribution of Student Grades Relative to their Cutoff To test the assumption of local randomization, Lindo et al. (2010) run a local linear regression on the distribution of students throughout the cutoff. As mentioned above, these should be continuous as a jump in the distribution of students around the cutoff would indicate that students can in some way manipulate their GPA to place above the cutoff. For the analysis, the data (containing all observations within 1.2 GPA points from the cutoff) is sorted into bins of size 0.1. The bins contain their lower limit but not their upper limit. To replicate the result from Lindo et al. (2010), I calculate the frequency of each bin and then run a local linear regression with a bandwidth of 0.6 on the size of the bins. Figure 1 shows the bins and the predicted frequency for each bin. The results show that the distribution of grades seems to be continuous around the cutoff, suggesting that we can assume local randomization. This method of testing the validity is especially useful because it could capture the effects of unobservables, whose influence we cannot otherwise test like we test for discontinuities in observable characteristics in the parts above and below. If all observable characteristics would show to be continuous throughout the cutoff but we could still observe a jump in the distribution of students above the cutoff, this would suggest that some unobservable characteristic distinguishes students above and below the probation threshold. Fortunately, the results shown below indicate that this is not the case supporting the RDD as a valid identification strategy.
###Code
bin_frequency_fig1 = calculate_bin_frequency(sample12, "dist_from_cut_med10")
predictions_fig1 = create_bin_frequency_predictions(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), 0.6)
plot_figure1(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), predictions_fig1)
###Output
_____no_output_____
###Markdown
Table 2 - Estimated Discontinuities in Observable Characteristics Table 2 shows the results of local linear regression (using a bandwidth of 0.6) for a range of observable characteristics that are related to student outcomes. Significant discontinuities would indicate that students with certain characteristics might be able to manipulate their grades to score above the probation cutoff. Similar to the descriptive validity checks on covariates in the section, these results additionally support the validity of the RDD. Table 2 shows that the coefficient for scoring below the cutoff is insignificant at the 10% level for all covariates.
###Code
table2_variables = ('hsgrade_pct', 'totcredits_year1', 'age_at_entry', 'male', 'english',
'bpl_north_america','loc_campus1', 'loc_campus2')
regressors = ['const', 'gpalscutoff', 'gpaXgpalscutoff', 'gpaXgpagrcutoff']
table2 = estimate_RDD_multiple_outcomes(sample06, table2_variables, regressors)
table2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
---**NOTE**: My results for 'Male' and 'Age at entry' are switched compared to the table presented in Lindo et al. (2010). Since the results are identical otherwise, I assume this difference stems from an error in the table formatting of the published paper. **NOTE**: The p-values in all regression tables are color-coded to enhance readability:* P-values at the 10% level are magenta,* P-values at the 5 % level are red,* P-values at the 1 % level are orange.The color-coding may not be visible in all viewing options for Jupyter Notebooks (e.g. MyBinder).--- 5.2.2. First Year GPAs and Academic Probation Figure 2 and Table 3 show the estimated discontinuity in probation status. Figure 2 and the first part of Table 3 show the estimated discontinuity for the probation status after the _first year_. The second part of Table 3 presents the results for the estimated effects of scoring below the cutoff on the probability of _ever_ being placed on academic probation.Figure 2 and part 1 of Table 3 verify that the discontinuity at the cutoff is **sharp**, i.e. all students whose GPA falls below the cutoff are placed on probation. For students below the cutoff, the probability of being placed on probation is 1, for students above the cutoff it is 0.It should be noted that the estimated discontinuity at the cutoff is only approximately equal to 1 for all of the different subgroups, as the results in Part 1 of Table 3 show. The authors attribute this fact to administrative errors in the data reportage. Figure 2 - Porbation Status at the End of First Year
###Code
predictions_fig2 = create_predictions(sample12, 'probation_year1', regressors, 0.6)
plot_figure2(sample12, predictions_fig2)
###Output
_____no_output_____
###Markdown
Table 3 - Estimated Discontinuity in Probation StatusTo estimate the discontinuity in probation status, the authors again use a bandwidth of 0.6 from the cutoff. In addition to the whole sample, they also estimate the discontinuities for certain subgroups within the selected bandwidth:* **high school grades below** and **above the median** (here, median refers to the median of the entire dataset (median: *50*) and not the median of the subset of students with a GPA within 0.6 grade points of the probation cutoff (the median for this set would be *28*))* **male** and **female** students* **english** native speakers and students with a different native language (**nonenglish**)
###Code
sample_treat06 = sample06[sample06['dist_from_cut'] < 0]
sample_untreat06 = sample06[sample06['dist_from_cut'] >= 0]
sample06 = pd.concat([sample_untreat06, sample_treat06])
groups_dict_keys = ['All', 'HS Grades < median', 'HS Grades > median', 'Male', 'Female',
'Native English', 'Nonnative English']
groups_dict_columns = ['const', 'lowHS', 'highHS','male', 'female', 'english', 'noenglish']
groups_dict_06 = create_groups_dict(sample06, groups_dict_keys, groups_dict_columns)
###Output
_____no_output_____
###Markdown
**Table 3 | Part 1 - Estimated Discontinuity in Probation Status for Year 1**
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'probation_year1', regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Table 3 | Part 2 - Estimated Discontinuity in Probabtion Status Ever** Part 2 of Table 3 presents the estimated effect of scoring below the cutoff in the first year for _ever_ being placed on probation. The results show that even of those who score slightly above the probation cutoff in year 1, 33 % are placed on probation at some other point in time during their studies. For the different subgroups of students this value varies from 29% (for students with high school grades above the median) up to 36.7% (for the group of males). These results already indicate that we can expect heterogeneities in the way different students react to being placed on academic probation.The fact that it is not unlikely for low performing students just slightly above the cutoff to fall below it later on also underlines these student's fitness as a control group for the purpose of the analysis. Lindo et al. (2010) argue that the controls can be thought of as receiving a much weaker form of treatment than the group that is placed on probation, as scoring just above the cutoff in year 1 does not save students from falling below the cutoff and being placed on probation in subsequent terms.
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'probation_ever',regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
5.2.3. The Immediate Response to Academic Probation Students who have been placed on academic probation enter their next term at university with the threat of suspension in case they fail to improve their grades. Recalling the theoretical framework presented in prior sections, students face the following set of options after each term:1. **Option 1**: Return to school, exhibit low effort and achieving a low GPA,2. **Option 2**: Return to school, exhibit high effort with the intent of achieving a high GPA,3. **Neither** option: Drop out of university.Students on probation face a different set of choices than the students that were not placed on probation as the threat of suspension essentially eliminates option 1. Of course, students could enter the next term, exhibit low effort, and receive low grades, but this would result in suspension. Since both option 1 and option 3 result in the student not continuing school (at least for a certain period of time), students who cannot meet the performance standard (thus leading to suspension) are much better off dropping out and saving themselves the cost of attending university for another term. Table 4 - Estimated Effect on the Decision to Leave after the First Evaluation
###Code
table4 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'left_school', regressors)
table4.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
The results presented in Table 4 and and Figure 3 show the effects of being placed on probation on the probability to drop out of school after the first evaluation. The first row of Table 4 shows the average effect of academic probation on this outcome. The results indicate that, on average, being placed on probation increases the probability of leaving university by 1.8 percentage points. A student on academic probation is thus 44% more likely to drop out than their control group counterpart.The results presented in the rest of Table 4 and and Figure 3 show that the average effect of being placed on probation is also characterized by large heterogeneities between the different subgroups of students. For males and native English speakers, the results, which are significant at the 5% level, show an increase of 3.7 and 2.8 percentage points respectively in the probability of leaving university after being placed on probation after the first evaluation. The results show no significant effects for these group's counterparts, the subgroups of females and nonnative English speakers. Aside from gender and native language, the results also indicate that high school performance seems to play a role in how students react on being placed on probation. For the group of students who scored above the median in high school academic probation roughly doubles the probability of leaving school compared to the control group while there is no such effect for students who scored below the median in high school. Lindo et al. (2010) contribute this finding to a discouragement effect for those students who are placed on probation, which seems to be larger for students who did well in high school. Figure 3 - Stratified Results for Voluntarily Leaving School at the End of the First year
###Code
groups_dict_12 = create_groups_dict(sample12, groups_dict_keys, groups_dict_columns)
predictions_groups_dict = create_fig3_predictions(groups_dict_12, regressors, 0.6)
plot_figure3(groups_dict_12, predictions_groups_dict, groups_dict_keys)
###Output
_____no_output_____
###Markdown
5.2.4. The Impact onSubsequent Performance i. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next Term The next outcome Lindo et al. (2010) analyze is the performance of students who stayed at university for the next term. The theoretical framework presented in Section 2 predicts that those students on probation who stay at university will try to improve their GPA. Indeed, if they do not manage to improve, they will be suspended and could have saved themselves the effort by dropping out.The results presented in Figure 4 and Table 5 show the estimated discontinuity in subsequent GPA. Lindo et al. (2010) find significant results (at the 5% level) for all subgroups, which is an even bigger effect than that of probation on drop out rates, where only some subgroups were affected. Figure 4 - GPA in the Next Enrolled Term
###Code
predictions_fig4 = create_predictions(sample12, 'nextGPA', regressors, 0.6)
plot_figure4(sample12, predictions_fig4)
###Output
_____no_output_____
###Markdown
As part A of Table 5 shows, the average treatment effect on the GPA in the next term is positive for all groups of students. The average student on probation has a GPA increase of 0.23 grade points which is 74% of the control group. The increase is greatest for students who have high school grades below the median. These students increase their GPA by 0.25 grade points on average, 90% more than their control group. This is an interesting finding because the counterpart, students who scored above the median in high school, are especially likely to drop out. Thus high school grades seem to have a large effect on whether students perceive academic probation as discouragement or as an incentive to improve their performance. It should be noted here, that the '*next term*' may not be the next year for all students because some students take summer classes. If students fail to improve their grades during summer classes, they are already suspended after summer and will not enter the second year. Only using grades from the second year would thus omit students who were suspended before even entering the second year. The existence of summer classes may complicate the comparability of students after being put on probation. However, in a footnote Lindo et al. (2010) mention that they find no statistically significant impact of academic probation on the probability that a student enrolls in summer classes and the estimates for subsequent GPA are nearly identical when controlling for whether a student's next term was attending a summer class. ---**NOTE**: Lindo et al. (2010) in this call this the '*improvement*' of students' GPA, however, this phrasing in my opinion could be misleading, as the dependent variable in this analysis is the distance from cutoff in the next term. The results thus capture the increase in subsequent GPA in general and not relative to the GPA in the prior term.--- Table 5 - Estimated Discontinuites in Subsequent GPA | Part A - Next Term GPA
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextGPA', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Table 5 - Estimated Discontinuites in Subsequent GPA | Part B - Probability of Placing Above the Cutoff in Next Term Panel B of Table 5 shows the probability of scoring above the cutoff in the next term. This statistic is very important because it decides whether students on academic probation are suspended after the subsequent term. It is therefore important for students who scored below the cutoff in the first year to not only improve their GPA, but improve it enough to score above the cutoff in the next term. Again academic probation increases the probability of students scoring above the cutoff in the next term for all subgroups.
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextGPA_above_cutoff', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
ii. Formal Bound Analysis on Subsequent GPA (partial extension) As already mentioned in the section on the identification strategy, analyzing outcomes that occur after the immediate reaction to probation (the decision whether to drop out or not) becomes more challenging if we find that students are significantly more or less likely to drop out if they have been placed on academic probation. As discussed in the preceding section, this is the case because some groups of students indeed are more likely to drop out if they have been placed on probation.For the analysis of subsequent GPA, this means that the results become less reliable because there is a group of students (those who dropped out) whose subsequent performance cannot be observed. This can cause the results to be biased. For example, if academic probation causes students with relatively low ability to drop out (which the performance model would predict) then we would find a positive impact on subsequent GPA being solely driven by the fact that the low performers in the treatment group dropped out. If, on the other hand, high ability students were more likely to drop out, the estimates for the impact on subsequent performance would be downward biased.In short, the control group might not be comparable anymore. To test whether the results on subsequent GPA are robust to these concerns, Lindo et al. (2010) use formal bound analysis for the results on subsequent GPA which I present below.In addition to this formal bound analysis, I plot confidence intervals for the results on subsequent GPA. Confidence intervals are a useful way to support the graphical analysis of RDDs and ensure the discontinuity at the threshold does not disappear when new population samples are drawn. The graph below shows the estimates from before including a bootstrap 95% percent confidence interval. The confidence interval around the cutoff shows to be quite small, and the fall in subsequent GPA between the treatment and control group persists even at the borders of the confidence interval. Subsequent Performance with 95% Confidence Interval
###Code
bootstrap_pred = bootstrap_predictions(n=100, data=sample12, outcome='nextGPA', regressors=regressors, bandwidth=0.6)
CI = get_confidence_interval(data=bootstrap_pred, lbound=2.5, ubound=97.5, index_var='dist_from_cut')
predictions_fig4_CI = pd.concat([predictions_fig4, CI[['upper_bound', 'lower_bound']]], axis=1)
plot_figure4_with_CI(data=sample12, pred=predictions_fig4_CI)
###Output
_____no_output_____
###Markdown
---**NOTE**: The confidence intervals presented here are the product of only 100 resampling iterations of the bootstrap because increasing the number of times the data is resampled significantly increases the runtime of this notebook. However, I have tested the bootstrap for up to 1000 iterations and the results do not diverge very much from the version shown here. --- This type of confidence interval, however, does not correct for potential biases in the treatment or control group discussed above because the bootstrap only resamples the original data and therefore can at best achieve the estimate resulting from the original sample. To test the sensitivity to possible nonrandom attrition through specific students dropping out of university, Lindo et al. (2010) perform a formal bound analysis using a trimming procedure proposed by Lee (2009)*. The reasoning for this approach is based on the concerns described above. To find a lower bound of the estimate, Lindo et al. (2010) assume that academic probation causes students who would have performed worse in the next term to drop out. The control group is thus made comparable by dropping the lowest-performing students (in the next term) from the sample, assuming these students would have dropped out had they been placed on probation. To calculate the upper bound estimate, the same share of students is dropped from the upper part of the grade distribution instead. The share of students who need to be dropped is given by the estimated impact of probation on leaving school. For example, in the entire sample students on probation are 1.8 percentage points more likely to drop out, which is 44% of the control mean. Thus, to make the groups comparable again we presumably need to drop 44% more students from the control group than actually dropped out. For groups of students where the estimated impact of probation on leaving school is negative, students from the control group need to be dropped instead (i.e. here the lower bound is given by dropping the top students in the treatment group and the upper bound is given by dropping the bottom students). While all results I have presented in this replication so far are exactly identical to the results from Lindo et al. (2010), I, unfortunately, cannot replicate the results from the formal bound analysis precisely. The description in the paper is brief and the provided STATA code from the authors does not include the formal bound analysis. While referring to methods presented in Lee (2009) has been helpful to understand the trimming procedure, I am unable to replicate the exact numbers presented in Lindo et al. (2010).The table pictured below shows the results of the formal bound analysis presented in Lindo et al. (2010). The authors conclude that the positive effects of academic probation on students' subsequent GPA are too great to be explained by the attrition caused by dropouts. ---**NOTE**: In their paper Lindo et al. (2010) quote _'Lee (2008)'_ which could also refer to a different paper by Lee and Card from 2008 listed in the references. However, since this paper in contrast to the 2009 paper by Lee does not mention formal bound analysis and since Lee (2009) is not mentioned anywhere else in the paper, I am certain this is a citation error.--- Formal Bound Analysis from Lindo et al. (2010) (p.110)  The table below shows my results using the proposed trimming procedure (table is again transposed compared to the original). The overall results are quite similar to the ones presented in Lindo et al. (2010), all estimates presented in Table 5 still lie between the lower and upper bound. It should be noted that in my replication the lower bound estimate for students with high school grades above the median was not significant at the 10% level while the results for all other groups were. Replication of Formal Bound Analysis
###Code
table4['add_leavers'] = round(table4['GPA below cutoff (1)']/table4['Intercept (0)'],2)
add_leavers = table4['add_leavers']
lb_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, True, False)
lower_bound = estimate_RDD_multiple_datasets(lb_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
ub_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, False, True)
upper_bound = estimate_RDD_multiple_datasets(ub_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
bounds = pd.concat([lower_bound.iloc[:,[0,2]],upper_bound.iloc[:,[0,2]]], axis=1)
bounds.columns = pd.MultiIndex.from_product([['Lower Bound Estimate','Upper Bound Estimate',],
['GPA below cutoff (1)', 'Std.err (1)']])
bounds
###Output
_____no_output_____
###Markdown
5.2.5. The Impacts on GraduationAs a third outcome, Lindo et al. (2010) examine the effects of academic probation on students' graduation rates. As already discussed in the previous section, the outcomes that are realized later in time are more complex to examine because of all the different choices a student has made until she or he reaches that outcome. Graduation rates are the product of a dynamic decision-making process that spans throughout the students' time at university. While the study focuses mainly on the effects of being put on probation after the first year, the decision problem described in the theoretical framework can be faced by students at different points during their academic career as students can be placed on probation each term or for multiple terms in a row. There are different ways in which academic probation could affect graduation rates. On the one hand, it could reduce the probability of graduating because probation increases the probability of dropping out and some students who fail to increase their grades are suspended. On the other hand, these students might have graduated either way and thus do not have an effect. Additionally, probation could increase graduation rates because those students who remain improve their performance. Figure 5 - Graduation Rates Figure 5 and Table 6 show the estimated impacts of academic probation after the first year on whether a student has graduated in four, five or six years. The effects are negative for all three options, suggesting that the negative effects discussed above overweigh potential positive effects on graduation rates.
###Code
plot_figure5(sample12,
create_predictions(sample12,'gradin4', regressors, 0.6),
create_predictions(sample12,'gradin5', regressors, 0.6),
create_predictions(sample12,'gradin6', regressors, 0.6))
###Output
_____no_output_____
###Markdown
Table 6 - Estimated Effects on Graduation The effects on graduation rates are insignificant for most subgroups, the group of students with high school grades above the median stands out as being especially negatively affected by being placed on probation in the first year. This group of students sees their probability of graduation within six years reduced by 14.5 percent. Lindo et al. (2010) attribute these results to the fact that this group of students is especially likely to drop out after being put on probation and also on average does not do much better than their counterpart if they continue to attend university.Overall the results on graduation rates are rather limited. This likely stems from the more complex nature in which probation in the first year can affect this outcome later down the line. Unfortunately, most of the data in the provided dataset focus on the first two years of students' time at university (e.g. we only now the GPA of the first two years). Much more information would be needed to uncover the mechanisms in which probation may affect students' probability of graduating within specific timeframes.---**NOTE**: Below I only show the sections of Table 6 that are discussed above as the entire table is quite extensive. The other results presented in Table 6 of the paper can be viewed by uncommenting the code at the end of this section.--- Graduated after 6 years
###Code
table6 = create_table6(groups_dict_06, groups_dict_keys, regressors)
table6.loc[['All','HS Grades > median' ],
'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Code for complete Table 6:**
###Code
# table6.loc[:, 'Graduated after 4 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 5 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
--- 6. Extension: Robustness Checks ---As discussed in my replication of Lindo et al. (2010) above, the authors use a variety of validity and robustness checks to analyze the reliability of their results. Aside from some smaller independent contributions that I already discuss in the replication part for better context, I in this section further analyze subsequent performance and check the bandwidth sensitivity of the results in drop out rates and subsequent GPA. 6.1. A Closer Look at Students' Subsequent Performance. 6.1.1. Subsequent Performance and Total Credits in Year 2 The results from Lindo et al. (2010) presented above show that students are more likely to drop out after being placed on academic probation but those who remain in school tend to improve their GPA above the cutoff in the next term. These results are generally in line with the theoretical framework presented in the paper which predicts that students either drop out or improve their GPA if the cost of not improving in the next term increases. The performance standard model explains these results through students self-selecting between increasing effort and dropping out based on their abilities (which are defined as the probability of meeting the performance standard). Students who are less likely to improve their GPA should thus be more likely to drop out. Unfortunately, it is not possible to test this prediction, as Lindo et al. (2010) emphasize in the paper because the probability of meeting the performance standard is not observed for students who leave school. However, examining the students who remain in school may give some further insights. While Lindo et al. (2010) observe that students have been placed on probation on average improve their performance, it is not clear under which circumstances this is happening. A look at the amount of credits students are taking in their second year may give some insights. The results presented below show that being placed on probation after the first year has a negative effect on the amount of credits students take in the second year for all of the examined subgroups except the group of nonnative English speakers. This is a stark contrast to the first year where both the treatment and control group take almost the same amount of credits (as shown in the section on the validity of the RD Approach).
###Code
predictions_credits_year2 = create_predictions(sample12, 'total_credits_year2', regressors, 0.6)
plot_figure_credits_year2(sample12, predictions_credits_year2)
###Output
_____no_output_____
###Markdown
The results indicate that being placed on probation decreases the total credits taken by the average student in year two by 0.33, around 8% of the control mean. As the table below shows, the results are most prominent for males, native English speakers, and students with high school grades above the median. Interestingly, these are the same groups of students that are most likely to drop out, suggesting that the discouragement effect persists throughout these groups and even those who re-enroll for the next term proceed with caution by taking fewer credits.
###Code
table_total_credits_year2 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,
'total_credits_year2',regressors)
table_total_credits_year2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
When interpreting these results it should be kept in mind that some students' next evaluation takes place during summer classes. Students who have taken summer classes enter their second year already having either passed the next evaluation or not. Those who fell below the cutoff will have been suspended and thus are missing from the data for the second year and those who have passed the threshold in the summer classes are likely not on probation anymore. Estimating the effects of probation on credits taken in the second year separately for both groups shows that those who did not take classes in the summer are more affected than those who did. For the students who took summer classes, the results are only significant for males, students with high school grades above the median and native English speakers. No summer classes
###Code
sample06_nosummer = sample06[sample06.summerreg_year1 == 0]
groups_dict_06_nosummer = create_groups_dict(data=sample06_nosummer, keys=groups_dict_keys,columns=groups_dict_columns)
table_totcred_y2_nosummer = estimate_RDD_multiple_datasets(groups_dict_06_nosummer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_nosummer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Summer classes
###Code
sample06_summer = sample06[sample06.summerreg_year1 == 1]
groups_dict_06_summer = create_groups_dict(sample06_summer,groups_dict_keys,groups_dict_columns)
table_totcred_y2_summer = estimate_RDD_multiple_datasets(groups_dict_06_summer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_summer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
These findings are useful for interpreting the subsequent performance of students because more credits likely signify a larger workload for the student. Instead of increasing their effort, students may just decrease their workload by completing fewer credits in the next term. Unfortunately, we cannot test this in detail because the data doesn't show how many credits students completed in which term. Reducing the sample for the analysis of the subsequent GPA to students who did not attend summer classes and completed 4 credits in the second year (the most frequent amount of credits takeen by this group of students) shows that the effect of scoring below the cutoff in year 1 becomes insignificant for the students who have above-median high school grades and nonnative English speakers. The improvement decreases a bit for some groups like females or students with high school grades below the median but increases for others like males and native english speakers. Overall the results are still highly significant though considering the small window of observations to which the data is reduced in this case. This suggests that while students on probation do seem to take fewer credits in the next year, the improvements to subsequent performance is too great to just be attributed to students decreasing their workload.
###Code
sample06_many_credits = sample06_nosummer[(sample06_nosummer.total_credits_year2 == 4)]
groups_dict_06_manycredits = create_groups_dict(sample06_many_credits,groups_dict_keys,groups_dict_columns)
table_manycredits = estimate_RDD_multiple_datasets(groups_dict_06_manycredits,groups_dict_keys,
'nextGPA',regressors)
table_manycredits.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.1.2. Subsequent Cumulative Grade Point Average (CGPA) An additional factor that might be important for the analysis of subsequent performance is the Cumulative Grade Point Average (CGPA). Lindo et al. (2010) focus their analysis of subsequent performance solely on the grades achieved in the next term. However, in the section on the institutional background in the paper the authors write:>*At all campuses, students on probation can avoid suspension and return to good academic standing by bringing their cumulative GPA up to the cutoff.* (Lindo et al., 2010, p.98).To avoid suspension in the long term, students on probation thus are required to not only score above the cutoff in the next term but to score high enough to bring their CGPA above the probation threshold. Students who score above the threshold in the next term but still have a CGPA below the cutoff remain on probation. Students who fail to bring their GPA above the cutoff (and thus also their CGPA since their first-year GPA and first-year CGPA are the same) are suspended. As the figure and table below show, the positive effects of probation on subsequent performance carry over to students' CGPA as well. Being placed on probation on average increases students' CGPA by 0.07 grade points or 63% of the control mean although the difference is rather difficult to spot visually.
###Code
predictions_nextCGPA = create_predictions(sample12, 'nextCGPA', regressors, 0.6)
plot_nextCGPA(sample12, predictions_nextCGPA)
###Output
_____no_output_____
###Markdown
Effect of Academic Probation on Subsequent CGPA
###Code
table_nextCGPA = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextCGPA', regressors)
table_nextCGPA.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
However, in contrast to the probability of improving the next term GPA above the cutoff, academic probation has no significant effect on the probability of improving the CGPA above the cutoff in the next term except for the group of nonnative English speakers where the probability is actually negative. Indeed, out of all students on probation (within 0.6 grade points of the cutoff), only around 37% improve their next term CGPA above the cutoff. Around 23% improve their GPA above the cutoff but not their CGPA and remain on probation. The other students dropped out or are suspended after the next term. This suggests that the effects of probation span much longer than just the subsequent term for many students, not only indirectly because they have had the experience of being placed on probation but also directly because many of them remain on probation for multiple subsequent terms. These factors underline the points made in previous sections about the complexity of the way academic probation can affect a student's academic career. After being placed on probation a student can take a multitude of different paths, many more than the theoretical framework introduced in Section 2 leads on. A more dynamic approach to estimating the effects of academic probation could likely offer more insights into how students react to this university policy. Effect of Academic Probation on the Probability of Achieving a CGPA Above the Cutoff in the Next Term
###Code
table_nextCGPA_above_cutoff = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextCGPA_above_cutoff',
regressors)
table_nextCGPA_above_cutoff.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.2. Bandwidth Sensitivity As a final robustness check, I evaluate the model at different bandwidths to ensure that results are not limited to one specific sample of students within a particular bandwidth. Lindo et al. (2010) use a distance from the threshold of 0.6 for the main regression analysis and 1.2 for graphical analysis (although the estimated curve at each point relies on a local linear regression with a bandwidth of 0.6 as well). The chosen bandwidth around the cutoff thus captures around 25% of the total range of grades (the GPA values observed in the first year span from 0 to 4.3). Lindo et al. (2010) do not discuss the reasoning behind their choice of bandwidth in detail and do not apply optimal bandwidth selection methods like some other applications of regression discontinuity (Imbens & Lemieux, 2008; Lee & Lemieux, 2010). However, from a heuristic standpoint, this bandwidth choice seems reasonable. Since the cutoff lies at a GPA of 1.5 (1.6 at Campus 3), this bandwidth includes students whose GPA falls roughly between 0.9 and 2.1 grade points, so a range of around one average grade point including the edges. A much larger bandwidth would not make sense because it would include students that are failing every class and students who are achieving passable grades and are thus not very comparable to students who pass or fall below the threshold by a small margin.I evaluate bandwidths of length 0.2 (0.1 distance from cutoff on each side) up to 2.4 (1.2 distance from cutoff on both sides). As Lindo et al. (2010), I choose a maximum bandwidth of 1.2 the reasons explained in the paragraph above. Bandwidth sensitivity of the effect of probation on the probability of leaving school The table below shows the estimated effect of probation on the probability to leave school after the first year using local linear regression (same specification as before) for all bandwidths between 0.1 and 1.2. The bandwidths are on the vertical axis, and the different subgroups are on the horizontal axis of the table. An *x* in the table indicates that the estimate was insignificant at the 10% level and is thus not shown for readability. The table shows that the results for the effects on leaving school are relatively sensitive to bandwidth selection. Estimates of students within only 0.2 grade points of the probation threshold are not significant for any of the groups considered. Results for students with high school grades below the median are only significant for bandwidths between 0.3 and 0.5 while estimates for students with high school grades above the median are only significant between values of 0.5 and 0.7. The results for the other subgroups, on the other hand, seem to be quite robust to bandwidth selection. The findings reported in this table suggest that some results presented in the previous sections should be interpreted carefully. Especially the estimates of students based on high school grades might be driven by some underlying factors that are not observed in this study. These could explain the sensitivity of the results to bandwidth selection.
###Code
bandwidths = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2]
summary_left_school = bandwidth_sensitivity_summary(data, 'left_school',groups_dict_keys, groups_dict_columns, regressors)
summary_left_school.loc[(bandwidths,'probation'),:]
#summary_left_school #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
###Markdown
Bandwidth sensitivity of the effect of probation on subsequent GPA The results for the effects of academic probation on subsequent performance, on the other hand, seem to be quite robust to bandwidth selection. The estimated effects are the highest for most subgroups around the threshold of 0.6 chosen by Lindo et al. (2010) but the effects do not change sign for any subgroup and still remain quite similar.Again, the group of students with high school grades above the median does not show significant results for bandwidths between 0.1 and 0.4 and thus seems to be the most sensitive to bandwidth selection.
###Code
summary_nextGPA = bandwidth_sensitivity_summary(data, 'nextGPA', groups_dict_keys, groups_dict_columns, regressors)
summary_nextGPA.loc[(bandwidths,'probation'),:]
# summary_nextGPA #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
###Markdown
--- Project for the course in Microeconometrics | Summer 2019, M.Sc. Economics, Bonn University | [Annica Gehlen](https://github.com/amageh) Replication of Masami Imai and Seitaro Takarabe --- This notebook contains my replication of the results from the following paper:> Lindo, J. M., Sanders, N. J., & Oreopoulos, P. (2010). Ability, gender, and performance standards: Evidence from academic probation. American Economic Journal: Applied Economics, 2(2), 95-117. Downloading and viewing this notebook:* The best way to view this notebook is by downloading it and the repository it is located in from [GitHub](https://github.com/HumanCapitalAnalysis/template-course-project). Other viewing options like _MyBinder_ or _NBViewer_ may have issues with displaying images or coloring of certain parts (missing images can be viewed in the folder [files](https://github.com/HumanCapitalAnalysis/template-course-project/tree/master/files) on GitHub).* The original paper, as well as the data and code provided by the authors can be accessed [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). Information about replication and individual contributions:* For the replication, I try to remain true to the original structure of the paper so readers can easily follow along and compare. All tables and figures are named and labeled as they appear in Lindo et al. (2010).* The tables in my replication appear transposed compared to the original tables to suit my workflow in Python.* For transparency, all sections in the replication that constitute independent contributions by me and are not part of results presented (or include deviations from the methods used) in the paper are marked as _extensions_. Table of Contents1. Introduction2. Theoretical Background3. Identification4. Empirical Strategy5. Replication of Lindo et al. (2010)5.1. Data & Descriptive Statistics5.2. Results5.2.1. Tests of the Validity of the RD Approachi. Extension: Visual Validity Checkii. Advanced Validity Check5.2.2. First Year GPAs and Academic Probation5.2.3. The Immediate Response to Academic Probation5.2.4. The Impact onSubsequent Performancei. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next Termii. Formal Bound Analysis on Subsequent GPA (partial extension)5.2.5. The Impacts on Graduation6. Extension: Robustness Checks6.1. A Closer Look at Students' Subsequent Performance.6.1.1. Subsequent Performance and Total Credits in Year 26.1.2. Subsequent Cumulative Grade Point Average (CGPA)6.2. Bandwidth Sensitivity7. Conclusion8. References
###Code
%matplotlib inline
import numpy as np
import pandas as pd
import pandas.io.formats.style
import seaborn as sns
import statsmodels as sm
import statsmodels.formula.api as smf
import statsmodels.api as sm_api
import matplotlib as plt
from IPython.display import HTML
from auxiliary.example_project_auxiliary_predictions import *
from auxiliary.example_project_auxiliary_plots import *
from auxiliary.example_project_auxiliary_tables import *
###Output
_____no_output_____
###Markdown
--- 1. Introduction --- Lindo et al. (2010) examine the effects of academic probation on student outcomes using data from Canada. Academic probation is a university policy that aims to improve the performance of the lowest- scoring students. If a student's Grade Point Average (GPA) drops below a certain threshold, the student is placed on academic probation. The probation status serves as a warning and does not entail immediate consequences, however, if students fail to improve their grades during the following term, they face the threat of being suspended from the university. In a more general sense, academic probation may offer insights into how agents respond to negative incentives and the threat of punishment in a real-world context with high stakes. To estimate the causal impact of being placed on probation, Lindo et al. (2010) apply a **regression discontinuity design (RDD)** to data retrieved from three campuses at a large Canadian university. The RDD is motivated by the idea that the students who score just above the threshold for being put on academic probation provide a good counterfactual to the 'treatment group' that scores just below the threshold. In line with the performance standard model that serves as the theoretical framework for the paper, Lindo et al. (2010) find that being placed on probation induces students to drop out but increases the grades of the students who remain in school. The authors also find large heterogeneities in the way different groups of students react to academic probation.**Main variables** | **Treatment** | **Main outcomes** | **Main Covariates** ||-------------------|-------------------------|------------------------|| Academic probation| Drop-out rates | Gender || . | Subsequent performance | HS grades | | . | Graduation rates | Native language | In this notebook, I replicate the results presented in the paper by Lindo et al. (2010). Furthermore, I discuss in detail the identification strategy used by the authors and evaluate the results using multiple robustness checks. My analysis offers general support for the findings of Lindo et al. (2010) and points out some factors which may enable a deeper understanding of the causal relationship explored in the paper. This notebook is structured as follows. In the next section, I present the performance standard model that lays down the theoretical framework for the paper (Section 2). In Section 3, I analyze the identification strategy that Lindo et al. (2010) use to unravel the causal effects of academic probation on student outcomes and Section 4 briefly discusses the empirical strategy the authors use for estimation. Section 5 and Section 6 constitute the core of this notebook. Section 5 shows my replication of the results in the paper and discussion thereof. In Section 6 I conduct various robustness checks and discuss some limitations of the paper. Section 7 offers some concluding remarks. --- 2. Theoretical Background---The underlying framework used for the analysis is a model developed by Bénabou and Tirole (2000) which models agent's responses to a performance standard. While Bénabou and Tirole (2000) model a game between a principal and an agent, Lindo et al. (2010) focus only on the agent to relate the model to the example of academic probation. In the performance standard model, the agents face a choice between three options: 1. **Option 1**: Incurs cost $c_1$ and grants benefit $V_1$ if successful. 2. **Option 2**: Incurs cost $c_2$ and grants benefit $V_2$ if successful. 3. **Neither** option: Incurs 0 cost and 0 benefit. Option 1 has a lower cost and a lower benefit than option 2 such that:\begin{equation} 0 < c_1 < c_2 , 0 < V_1 < V_2.\end{equation}Ability, denoted by $\theta$, translates to the probability of successfully completing either option. Assuming agents have perfect information about their ability, they solve the maximizing problem\begin{equation}max\{0, \theta V_1-c_1, \theta V_2-c_2\}.\end{equation} Let $\underline{\theta}$ be the ability level where the agent is indifferent between neither and option two and let $\bar{\theta}$ be the ability level at which the agent is indifferent between option 1 and option 2. Assuming that\begin{equation}\underline{\theta} \equiv \frac{c_1}{V_1} < \bar{\theta} \equiv \frac{c_2-c_1}{V_2-V1} < 1\end{equation}ensures that both options are optimal for at least some $\theta$.It can be shown that * the lowest ability types ($\theta < \underline{\theta}$) choose neither option,* the highest ability types ($\bar{\theta} < \theta$) choose the difficult option,* the individuals in between the high and low type $\underline{\theta}< \theta < \bar{\theta} $) choose the easier option.If the principal now removes option 1 or makes choosing this option much more costly, then the agent will choose option 2 if and only if\begin{equation}\theta \ge \frac{c_2}{V_2} \equiv \theta^*\end{equation}and choose neither option otherwise. The agents who would have chosen option 1 now split according to ability. Agents with high ability (specifically those with $\theta \in [\theta^*,\bar{\theta}]$) work harder, thereby choosing option 2, while low ability types (those with $\theta \in [\underline{\theta}, \theta^*]$) do not pursue option 2 (and thus choose neither option).In the context of academic probation students face a similar decision and possible courses of action. Students whose GPA is just above the probation cutoff face the full set of options for the next year:1. **Option 1**: Return to school and exhibit low effort and leading to a low GPA2. **Option 2**: Return to school and exhibit high effort with the intent of achieving a high GPA3. **Neither** option: Drop out of universityStudents who score below the probation cutoff face a restricted set of options as the university administration essentially eliminates option 1 by suspending students if they do not improve their grades. Lindo et al. (2010) formulate three testable implications of this theoretical framework: * _Forbidding option 1 will **increase the overall probability of students dropping out**._ * _Forbidding option 1 will **increase the performance of those who return**._ * _Forbidding option 1 will cause **relatively low-ability students to drop out** and **relatively high-ability students to return and work harder**._ --- 3. Identification--- Lindo et al. (2010) in their paper aim to evaluate how academic probation affects students, specifically their probability of dropping out of university and whether it motivates those who remain to improve their grades. Students are placed on probation if their Grade Point Average (GPA) drops below a certain threshold and face the threat of suspension if they fail to improve their GPA in the next term. Students are thus clearly separated into a treated group (who is put on probation) and an untreated group based on their GPA. The causal graph below illustrates the relationship between the assignment variable $X$, treatment $D$ and outcome $Y$. While $X$ (the GPA) directly assigns students to treatment, it may also be linked to student outcomes. Additionally, there may be observables $W$ and unobservables $U$ also affecting $X$,$D$, and $Y$. There are thus multiple backdoor paths that need to be closed in order to isolate the effect of academic probation. Simply controlling for the variables in question, in this case, does not suffice since there are unobservables that we cannot condition on. A randomized experiment, on the other hand, could eliminate selection bias in treatment by randomly assigning probation to students. The research question evaluated in the paper constitutes a classic policy evaluation problem in economics where we try to understand the causal implications of a policy without being able to observe the counterfactual world where the policy is not administered. However, as with many questions in economics, implementing a randomize experiment directly is not a feasible option, especially since we are examing the effect of a penalty whose consequences may affect students for the rest of their lives.Since it is not possible to randomize assignment to treatment, another method is needed to isolate the effects of academic probation on student outcomes. Lindo et al. (2010) apply a regression discontinuity design (RDD) to the problem at hand, a method pioneered by Thistlethwaite and Campbell (1960) in their analysis of the effects of scholarships on student outcomes. In fact, the identification problem in Lindo et al. (2010) is quite similar to that of Thistlethwaite and Campbell (1960) as both papers evaluate the causal effects of an academic policy on student outcomes. However, while the scholarship administered to high performing students in Thistlethwaite and Campbell (1960) constitutes a positive reinforcement for these students, Lindo et al. (2010) examine the effects of a negative reinforcement or penalty on low performing students. This means that, in contrast to Thistlethwaite and Campbell (1960) and many other applications of RD, our treatment group lies _below_ the cutoff and not above it. This does not change the causal inference of this model but it might be confusing to readers familiar with RD designs and should thus be kept in mind. The regression discontinuity design relies on the assumption of local randomization, i.e. the idea that students who score just above the cutoff do not systematically differ from those who score below the cutoff and thus pose an appropriate control group for the students who are placed on probation. This identification strategy relies on the assumption that students are unable to precisely manipulate their grades to score just above or below the probation threshold. Within the neighborhood around the discontinuity threshold, the RDD thus in a sense mimics a randomized experiment. To explain how the use of regression discontinuity allows Lindo et al. (2010) to identify treatment effects, I draw on material provided in Lee and Lemieux (2010) and their discussion on the RDD in the potential outcomes framework. As mentioned above, for each student $i$ we can image a potential outcome where they are placed on probation $Y_i(1)$ and where they are not $Y_i(0)$ but we can never simultaneously observe both outcomes for each student. Since it is impossible to observe treatment effects at the individual level, researchers thus estimate average effects using treatment and control groups. For the RDD this potential outcomes framework translates by imagining there are two underlying relationships between the average student outcome and the assignment variable $X$ (the students' GPA), which are represented by $E[Y_i(1)|X]$ and $E[Y_i(0)|X]$. Since all students who score below the cutoff $c$ are placed on probation, we only observe $E[Y_i(1)|X]$ for those below the cutoff and $E[Y_i(0)|X]$ for those above the cutoff. We can estimate the average treatment effects by taking the difference of the conditional expectations at the cutoff if these underlying functions are continuous throughout the cutoff:\begin{equation}lim_{\epsilon \downarrow 0}E[Y_i|X_i=c+\epsilon] - lim_{\epsilon \uparrow 0} E[Y_i|X_i=c+\epsilon] = E[Y_i(1)-Y_i(0)|X=c].\end{equation}As explained above, this _continuity assumption_ is fulfilled by the RDD because we can assume that students have _imprecise control_ over the assignment variable, their GPA. We can clearly identify the average treatment effects because there is a natural sharp cutoff at the threshold. The treatment administered to students is being confronted with the information that they are placed on probation and the subsequent threat of suspension. Being put on probation does not involve any actions by the students, in fact being assigned to the treatment group already constitutes the treatment in itself. Non-compliers thus do not pose a concern for this research design. As the theoretical framework discussed in the prior section illustrates, students on probation face the decision of dropping out or trying to improve their performance in the next term. While the estimation on effects on dropping out using the regression discontinuity design is relatively straight forward, the estimation of effects for subsequent performance adds additional challenges.The extended causal graph above illustrates how the subsequent performance of students is also affected by whether a student drops out or not. This factor adds additional complexity to the estimation problem because we cannot observe the subsequent GPA for students who drop out after being placed on probation. This factor puts into question the comparability of the treatment and control group in subsequent periods. I address these concerns and possible solutions in later sections of this notebook.Aside from the two main outcomes, Lindo et al. (2010) also examine the effects of academic probation on graduation rates of students. However, since information about student's academic progress over the whole course of their studies is limited in the available data, only very simple analysis is possible. --- 4. Empirical Strategy---The authors examine the impact of being put on probation after the first year in university. The probation status after the first year is a deterministic function of student's GPA, formally\begin{equation}PROB^{year1}_{IC} = 1(GPANORM^{year1}_{IC} < 0),\end{equation}where $PROB^{year1}_{IC}$ represents the probation status of student $i$ at campus $c$ and $GPANORM^{year1}_{IC}$ is the distance between student $i$'s first-year GPA and the probationary cutoff at their respective campus. The distance of first-year GPA from the threshold thus constitutes the *running variable* in this RD design. Normalizing the running variable in this way makes sense because the three campuses have different GPA thresholds for putting students on probation (the threshold at campus 1 and 2 is 1.5, at campus 3 the threshold is 1.6), using the distance from the cutoff as the running variable instead allows Lindo et al. (2010) to pool the data from all three campuses.Applying the regression discontinuity design, the treatment effect for students near the threshold is obtained by comparing the outcomes of students just below the threshold to those just above the threshold.The following equation can be used to estimate the effects of academic probation on subsequent student outcomes:\begin{equation}Y_{ic} = m(GPANORM_{ic}^{year1}) + \delta1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}* $Y_{ic}$ denotes the outcome for student $i$ at campus $c$, * $m(GPANORM_{ic}^{year1})$ is a continuous function of students' standardized first year GPAs,* $1(GPANORM_{ic}^{year1}<0)$ is an indicator function equal to 1 if the student's GPA is below the probation cutoff,* $u_{ic} $ is the error term,* $\delta$ is the coefficient for the estimated impact of being placed on academic probation after the first year.For the regression analysis, Lindo et al. (2010) extend the above equation by an interaction term and a constant:\begin{equation}Y_{ic} = \alpha + \delta1(GPANORM_{ic}^{year1}<0) + \beta(GPANORM_{ic}^{year1}) + \gamma(GPANORM_{ic}^{year1})x 1(GPANORM_{ic}^{year1}<0) + u_{ic} \end{equation}This regression equation does not include covariates because Lindo et al. (2010) implement a split sample analysis for the covariates in the analysis. --- 5. Replication of Lindo et al. (2010)--- 5.1. Data & Descriptive StatisticsLindo et al. (2010) filter the data to meet the following requirements:* Students high school grade measure is not missing,* Students entered university before the year 2004 ( to ensure they can be observed over a 2-year period),* Students are between 17 and 21 years of age at time of entry.* Distance from cutoff is maximally 0.6 (or 1.2).The first three requirements are already fulfilled in the provided data. It should be noted that the high school measure is a student's average GPA in courses that are universally taken by high school students in the province. Thus all students that remain in the sample (84 % of the original data) attended high school in the province. This has the advantage that the high school measurement for all students is very comparable. An additional implication that should be taken note of for later interpretations is that this also implies that all students assessed in the study attended high school in the province. The group of 'nonnative' English speakers thus, for example, does not include students that moved to Canada after completing high school.
###Code
data_1 = pd.read_stata('data/data-performance-standards-1.dta')
data_2 = pd.read_stata('data/data-performance-standards-2.dta')
data = pd.concat([data_1, data_2], axis=1)
data = prepare_data(data)
###Output
_____no_output_____
###Markdown
---**NOTE**: The original data provided by the authors can be found [here](https://www.aeaweb.org/articles?id=10.1257/app.2.2.95). For this replication the data is split into two .dta-files due to size constraints.--- As shown in the graph below, the distance from the cutoff for university GPA in the provided dataset still spans from values of -1.6 to 2.8 as can be seen below. Lindo et al. (2010) use a bandwidth of *(-0.6, 0.6)* for regression results and a bandwidth of *(-1.2, 1.2)* for graphical analysis.
###Code
plot_hist_GPA(data)
# Reduce sample to students within 1.2 points from cutoff.
sample12 = data[abs(data['dist_from_cut']) < 1.2]
sample12.reset_index(inplace=True)
print("A sample of students within 1.2 points from the cuttoff consits of", len(sample12), "observations.")
# Reduce sample to students within 0.6 points from cutoff.
sample06 = data[abs(data['dist_from_cut']) < 0.6]
sample06.reset_index(inplace=True)
print("The final sample includes", len(sample06), "observations.")
###Output
The final sample includes 12530 observations.
###Markdown
Table 1 shows the descriptive statistics of the main student characteristics and outcomes in the restricted sample with a bandwidth of 0.6 from the cutoff. The majority of students are female (62%) and native English speakers (72%). Students in the reduced sample on average placed in the 33rd percentile in high school. It should also be noted that quite a large number of students (35%) are placed on probation after the fist year. An additional 11% are placed on probation after the first year. Table 1- Summary statistics
###Code
create_table1(sample06)
###Output
_____no_output_____
###Markdown
5.2. Results 5.2.1. Tests of the Validity of the RD Approach The core motivation in the application of RD approaches is the idea, that the variation in treatment near the cutoff is random if subjects are unable to control the selection into treatment (Lee & Lemieux, 2010). This condition, if fulfilled, means the RDD can closely emulate a randomized experiment and allows researchers to identify the causal effects of treatment. For evaluating the effects of academic probation on subsequent student outcomes, the RDD is thus a valid approach only if students are not able to precisely manipulate whether they score above or below the cutoff. Lindo et al. (2010) offer multiple arguments to address concerns about nonrandom sorting: 1. The study focuses on first-year students, assuming this group of students is likely to be less familiar with the probation policy on campus. To verify their conjecture, the authors also conducted a survey in an introductory economics course which revealed that around 50 % of students were unsure of the probation cutoff at their campus. They also claim that this analysis showed no relationship between knowledge of probation cutoffs and students' grades. 2. The authors also point out that most first-year courses span the entire year and most of the evaluation takes place at the end of the term which would make it difficult for students to purposely aim for performances slightly above the cutoff for academic probation.3. Finally, and most importantly, the implication of local randomization is testable. If nonrandom sorting were to be a problem, there should be a discontinuity in the distribution of grades at the cutoff with a disproportionate number of students scoring just above the cutoff. Additionally, all the covariates should be continuous throughout the cutoff to ensure that the group above the probation cutoff constitutes a realistic counterfactual for the treated group.In the following section, I first conduct a brief visual and descriptive check of validity before presenting my replication of the validity checks conducted in Lindo et al. (2010). i. Extension: Visual Validity Check To check for discontinuities in the covariates and the distribution of students around the cutoff Lindo et al. (2010) use local linear regression analysis. Before implementing the rather extensive validity check conducted by Lindo et al. (2010) I show in this section that a rather simple descriptive and graphical analysis of the distribution of covariates already supports the assumption they are continuous throughout the threshold. Extension | Table - Descriptive Statistics of Treated and Untreated Group Close to the CutoffThe table below shows the means of the different covariates at the limits of the cutoff from both sides (here within a bandwidth of 0.1 grade points). We can see that the means of the groups below and above the probation cutoff are very similar, even equal for some of the variables.
###Code
cov_descriptives = describe_covariates_at_cutoff(sample06,bandwidth=0.1)
cov_descriptives
###Output
_____no_output_____
###Markdown
Extension | Figure - Distribution of Covariates throughout the Probation CutoffThe figure below shows the means of the nine covariates in bins of size 0.5 (grade points). Similar to the descriptive table shown above, this visualization shows that there seem to be no apparent discontinuities in the distribution of students for any of the observable characteristics (graphs with bins of size 0.1 or 0.025 suggest the same).
###Code
plot_covariates(data=data, descriptive_table=cov_descriptives,bins = 'dist_from_cut_med05')
###Output
_____no_output_____
###Markdown
ii. Advanced Validity Check(as conducted by Lindo et al. (2010)) Figure 1 | Distribution of Student Grades Relative to their Cutoff To test the assumption of local randomization, Lindo et al. (2010) run a local linear regression on the distribution of students throughout the cutoff. As mentioned above, these should be continuous as a jump in the distribution of students around the cutoff would indicate that students can in some way manipulate their GPA to place above the cutoff. For the analysis, the data (containing all observations within 1.2 GPA points from the cutoff) is sorted into bins of size 0.1. The bins contain their lower limit but not their upper limit. To replicate the result from Lindo et al. (2010), I calculate the frequency of each bin and then run a local linear regression with a bandwidth of 0.6 on the size of the bins. Figure 1 shows the bins and the predicted frequency for each bin. The results show that the distribution of grades seems to be continuous around the cutoff, suggesting that we can assume local randomization. This method of testing the validity is especially useful because it could capture the effects of unobservables, whose influence we cannot otherwise test like we test for discontinuities in observable characteristics in the parts above and below. If all observable characteristics would show to be continuous throughout the cutoff but we could still observe a jump in the distribution of students above the cutoff, this would suggest that some unobservable characteristic distinguishes students above and below the probation threshold. Fortunately, the results shown below indicate that this is not the case supporting the RDD as a valid identification strategy.
###Code
bin_frequency_fig1 = calculate_bin_frequency(sample12, "dist_from_cut_med10")
predictions_fig1 = create_bin_frequency_predictions(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), 0.6)
plot_figure1(bin_frequency_fig1, bin_frequency_fig1.bins.unique().round(4), predictions_fig1)
###Output
_____no_output_____
###Markdown
Table 2 - Estimated Discontinuities in Observable Characteristics Table 2 shows the results of local linear regression (using a bandwidth of 0.6) for a range of observable characteristics that are related to student outcomes. Significant discontinuities would indicate that students with certain characteristics might be able to manipulate their grades to score above the probation cutoff. Similar to the descriptive validity checks on covariates in the section, these results additionally support the validity of the RDD. Table 2 shows that the coefficient for scoring below the cutoff is insignificant at the 10% level for all covariates.
###Code
table2_variables = ('hsgrade_pct', 'totcredits_year1', 'age_at_entry', 'male', 'english',
'bpl_north_america','loc_campus1', 'loc_campus2')
regressors = ['const', 'gpalscutoff', 'gpaXgpalscutoff', 'gpaXgpagrcutoff']
table2 = estimate_RDD_multiple_outcomes(sample06, table2_variables, regressors)
table2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
---**NOTE**: My results for 'Male' and 'Age at entry' are switched compared to the table presented in Lindo et al. (2010). Since the results are identical otherwise, I assume this difference stems from an error in the table formatting of the published paper. **NOTE**: The p-values in all regression tables are color-coded to enhance readability:* P-values at the 10% level are magenta,* P-values at the 5 % level are red,* P-values at the 1 % level are orange.The color-coding may not be visible in all viewing options for Jupyter Notebooks (e.g. MyBinder).--- 5.2.2. First Year GPAs and Academic Probation Figure 2 and Table 3 show the estimated discontinuity in probation status. Figure 2 and the first part of Table 3 show the estimated discontinuity for the probation status after the _first year_. The second part of Table 3 presents the results for the estimated effects of scoring below the cutoff on the probability of _ever_ being placed on academic probation.Figure 2 and part 1 of Table 3 verify that the discontinuity at the cutoff is **sharp**, i.e. all students whose GPA falls below the cutoff are placed on probation. For students below the cutoff, the probability of being placed on probation is 1, for students above the cutoff it is 0.It should be noted that the estimated discontinuity at the cutoff is only approximately equal to 1 for all of the different subgroups, as the results in Part 1 of Table 3 show. The authors attribute this fact to administrative errors in the data reportage. Figure 2 - Porbation Status at the End of First Year
###Code
predictions_fig2 = create_predictions(sample12, 'probation_year1', regressors, 0.6)
plot_figure2(sample12, predictions_fig2)
###Output
_____no_output_____
###Markdown
Table 3 - Estimated Discontinuity in Probation StatusTo estimate the discontinuity in probation status, the authors again use a bandwidth of 0.6 from the cutoff. In addition to the whole sample, they also estimate the discontinuities for certain subgroups within the selected bandwidth:* **high school grades below** and **above the median** (here, median refers to the median of the entire dataset (median: *50*) and not the median of the subset of students with a GPA within 0.6 grade points of the probation cutoff (the median for this set would be *28*))* **male** and **female** students* **english** native speakers and students with a different native language (**nonenglish**)
###Code
sample_treat06 = sample06[sample06['dist_from_cut'] < 0]
sample_untreat06 = sample06[sample06['dist_from_cut'] >= 0]
sample06 = pd.concat([sample_untreat06, sample_treat06])
groups_dict_keys = ['All', 'HS Grades < median', 'HS Grades > median', 'Male', 'Female',
'Native English', 'Nonnative English']
groups_dict_columns = ['const', 'lowHS', 'highHS','male', 'female', 'english', 'noenglish']
groups_dict_06 = create_groups_dict(sample06, groups_dict_keys, groups_dict_columns)
###Output
_____no_output_____
###Markdown
**Table 3 | Part 1 - Estimated Discontinuity in Probation Status for Year 1**
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'probation_year1', regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Table 3 | Part 2 - Estimated Discontinuity in Probabtion Status Ever** Part 2 of Table 3 presents the estimated effect of scoring below the cutoff in the first year for _ever_ being placed on probation. The results show that even of those who score slightly above the probation cutoff in year 1, 33 % are placed on probation at some other point in time during their studies. For the different subgroups of students this value varies from 29% (for students with high school grades above the median) up to 36.7% (for the group of males). These results already indicate that we can expect heterogeneities in the way different students react to being placed on academic probation.The fact that it is not unlikely for low performing students just slightly above the cutoff to fall below it later on also underlines these student's fitness as a control group for the purpose of the analysis. Lindo et al. (2010) argue that the controls can be thought of as receiving a much weaker form of treatment than the group that is placed on probation, as scoring just above the cutoff in year 1 does not save students from falling below the cutoff and being placed on probation in subsequent terms.
###Code
table3_1 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'probation_ever',regressors)
table3_1.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
5.2.3. The Immediate Response to Academic Probation Students who have been placed on academic probation enter their next term at university with the threat of suspension in case they fail to improve their grades. Recalling the theoretical framework presented in prior sections, students face the following set of options after each term:1. **Option 1**: Return to school, exhibit low effort and achieving a low GPA,2. **Option 2**: Return to school, exhibit high effort with the intent of achieving a high GPA,3. **Neither** option: Drop out of university.Students on probation face a different set of choices than the students that were not placed on probation as the threat of suspension essentially eliminates option 1. Of course, students could enter the next term, exhibit low effort, and receive low grades, but this would result in suspension. Since both option 1 and option 3 result in the student not continuing school (at least for a certain period of time), students who cannot meet the performance standard (thus leading to suspension) are much better off dropping out and saving themselves the cost of attending university for another term. Table 4 - Estimated Effect on the Decision to Leave after the First Evaluation
###Code
table4 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'left_school', regressors)
table4.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
The results presented in Table 4 and and Figure 3 show the effects of being placed on probation on the probability to drop out of school after the first evaluation. The first row of Table 4 shows the average effect of academic probation on this outcome. The results indicate that, on average, being placed on probation increases the probability of leaving university by 1.8 percentage points. A student on academic probation is thus 44% more likely to drop out than their control group counterpart.The results presented in the rest of Table 4 and and Figure 3 show that the average effect of being placed on probation is also characterized by large heterogeneities between the different subgroups of students. For males and native English speakers, the results, which are significant at the 5% level, show an increase of 3.7 and 2.8 percentage points respectively in the probability of leaving university after being placed on probation after the first evaluation. The results show no significant effects for these group's counterparts, the subgroups of females and nonnative English speakers. Aside from gender and native language, the results also indicate that high school performance seems to play a role in how students react on being placed on probation. For the group of students who scored above the median in high school academic probation roughly doubles the probability of leaving school compared to the control group while there is no such effect for students who scored below the median in high school. Lindo et al. (2010) contribute this finding to a discouragement effect for those students who are placed on probation, which seems to be larger for students who did well in high school. Figure 3 - Stratified Results for Voluntarily Leaving School at the End of the First year
###Code
groups_dict_12 = create_groups_dict(sample12, groups_dict_keys, groups_dict_columns)
predictions_groups_dict = create_fig3_predictions(groups_dict_12, regressors, 0.6)
plot_figure3(groups_dict_12, predictions_groups_dict, groups_dict_keys)
###Output
_____no_output_____
###Markdown
5.2.4. The Impact onSubsequent Performance i. Main Results for Impact on GPA & Probability of Placing Above Cutoff in the Next Term The next outcome Lindo et al. (2010) analyze is the performance of students who stayed at university for the next term. The theoretical framework presented in Section 2 predicts that those students on probation who stay at university will try to improve their GPA. Indeed, if they do not manage to improve, they will be suspended and could have saved themselves the effort by dropping out.The results presented in Figure 4 and Table 5 show the estimated discontinuity in subsequent GPA. Lindo et al. (2010) find significant results (at the 5% level) for all subgroups, which is an even bigger effect than that of probation on drop out rates, where only some subgroups were affected. Figure 4 - GPA in the Next Enrolled Term
###Code
predictions_fig4 = create_predictions(sample12, 'nextGPA', regressors, 0.6)
plot_figure4(sample12, predictions_fig4)
###Output
_____no_output_____
###Markdown
As part A of Table 5 shows, the average treatment effect on the GPA in the next term is positive for all groups of students. The average student on probation has a GPA increase of 0.23 grade points which is 74% of the control group. The increase is greatest for students who have high school grades below the median. These students increase their GPA by 0.25 grade points on average, 90% more than their control group. This is an interesting finding because the counterpart, students who scored above the median in high school, are especially likely to drop out. Thus high school grades seem to have a large effect on whether students perceive academic probation as discouragement or as an incentive to improve their performance. It should be noted here, that the '*next term*' may not be the next year for all students because some students take summer classes. If students fail to improve their grades during summer classes, they are already suspended after summer and will not enter the second year. Only using grades from the second year would thus omit students who were suspended before even entering the second year. The existence of summer classes may complicate the comparability of students after being put on probation. However, in a footnote Lindo et al. (2010) mention that they find no statistically significant impact of academic probation on the probability that a student enrolls in summer classes and the estimates for subsequent GPA are nearly identical when controlling for whether a student's next term was attending a summer class. ---**NOTE**: Lindo et al. (2010) in this call this the '*improvement*' of students' GPA, however, this phrasing in my opinion could be misleading, as the dependent variable in this analysis is the distance from cutoff in the next term. The results thus capture the increase in subsequent GPA in general and not relative to the GPA in the prior term.--- Table 5 - Estimated Discontinuites in Subsequent GPA | Part A - Next Term GPA
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextGPA', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Table 5 - Estimated Discontinuites in Subsequent GPA | Part B - Probability of Placing Above the Cutoff in Next Term Panel B of Table 5 shows the probability of scoring above the cutoff in the next term. This statistic is very important because it decides whether students on academic probation are suspended after the subsequent term. It is therefore important for students who scored below the cutoff in the first year to not only improve their GPA, but improve it enough to score above the cutoff in the next term. Again academic probation increases the probability of students scoring above the cutoff in the next term for all subgroups.
###Code
table5 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextGPA_above_cutoff', regressors)
table5.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
ii. Formal Bound Analysis on Subsequent GPA (partial extension) As already mentioned in the section on the identification strategy, analyzing outcomes that occur after the immediate reaction to probation (the decision whether to drop out or not) becomes more challenging if we find that students are significantly more or less likely to drop out if they have been placed on academic probation. As discussed in the preceding section, this is the case because some groups of students indeed are more likely to drop out if they have been placed on probation.For the analysis of subsequent GPA, this means that the results become less reliable because there is a group of students (those who dropped out) whose subsequent performance cannot be observed. This can cause the results to be biased. For example, if academic probation causes students with relatively low ability to drop out (which the performance model would predict) then we would find a positive impact on subsequent GPA being solely driven by the fact that the low performers in the treatment group dropped out. If, on the other hand, high ability students were more likely to drop out, the estimates for the impact on subsequent performance would be downward biased.In short, the control group might not be comparable anymore. To test whether the results on subsequent GPA are robust to these concerns, Lindo et al. (2010) use formal bound analysis for the results on subsequent GPA which I present below.In addition to this formal bound analysis, I plot confidence intervals for the results on subsequent GPA. Confidence intervals are a useful way to support the graphical analysis of RDDs and ensure the discontinuity at the threshold does not disappear when new population samples are drawn. The graph below shows the estimates from before including a bootstrap 95% percent confidence interval. The confidence interval around the cutoff shows to be quite small, and the fall in subsequent GPA between the treatment and control group persists even at the borders of the confidence interval. Subsequent Performance with 95% Confidence Interval
###Code
bootstrap_pred = bootstrap_predictions(n=100, data=sample12, outcome='nextGPA', regressors=regressors, bandwidth=0.6)
CI = get_confidence_interval(data=bootstrap_pred, lbound=2.5, ubound=97.5, index_var='dist_from_cut')
predictions_fig4_CI = pd.concat([predictions_fig4, CI[['upper_bound', 'lower_bound']]], axis=1)
plot_figure4_with_CI(data=sample12, pred=predictions_fig4_CI)
###Output
_____no_output_____
###Markdown
---**NOTE**: The confidence intervals presented here are the product of only 100 resampling iterations of the bootstrap because increasing the number of times the data is resampled significantly increases the runtime of this notebook. However, I have tested the bootstrap for up to 1000 iterations and the results do not diverge very much from the version shown here. --- This type of confidence interval, however, does not correct for potential biases in the treatment or control group discussed above because the bootstrap only resamples the original data and therefore can at best achieve the estimate resulting from the original sample. To test the sensitivity to possible nonrandom attrition through specific students dropping out of university, Lindo et al. (2010) perform a formal bound analysis using a trimming procedure proposed by Lee (2009)*. The reasoning for this approach is based on the concerns described above. To find a lower bound of the estimate, Lindo et al. (2010) assume that academic probation causes students who would have performed worse in the next term to drop out. The control group is thus made comparable by dropping the lowest-performing students (in the next term) from the sample, assuming these students would have dropped out had they been placed on probation. To calculate the upper bound estimate, the same share of students is dropped from the upper part of the grade distribution instead. The share of students who need to be dropped is given by the estimated impact of probation on leaving school. For example, in the entire sample students on probation are 1.8 percentage points more likely to drop out, which is 44% of the control mean. Thus, to make the groups comparable again we presumably need to drop 44% more students from the control group than actually dropped out. For groups of students where the estimated impact of probation on leaving school is negative, students from the control group need to be dropped instead (i.e. here the lower bound is given by dropping the top students in the treatment group and the upper bound is given by dropping the bottom students). While all results I have presented in this replication so far are exactly identical to the results from Lindo et al. (2010), I, unfortunately, cannot replicate the results from the formal bound analysis precisely. The description in the paper is brief and the provided STATA code from the authors does not include the formal bound analysis. While referring to methods presented in Lee (2009) has been helpful to understand the trimming procedure, I am unable to replicate the exact numbers presented in Lindo et al. (2010).The table pictured below shows the results of the formal bound analysis presented in Lindo et al. (2010). The authors conclude that the positive effects of academic probation on students' subsequent GPA are too great to be explained by the attrition caused by dropouts. ---**NOTE**: In their paper Lindo et al. (2010) quote _'Lee (2008)'_ which could also refer to a different paper by Lee and Card from 2008 listed in the references. However, since this paper in contrast to the 2009 paper by Lee does not mention formal bound analysis and since Lee (2009) is not mentioned anywhere else in the paper, I am certain this is a citation error.--- Formal Bound Analysis from Lindo et al. (2010) (p.110)  The table below shows my results using the proposed trimming procedure (table is again transposed compared to the original). The overall results are quite similar to the ones presented in Lindo et al. (2010), all estimates presented in Table 5 still lie between the lower and upper bound. It should be noted that in my replication the lower bound estimate for students with high school grades above the median was not significant at the 10% level while the results for all other groups were. Replication of Formal Bound Analysis
###Code
table4['add_leavers'] = round(table4['GPA below cutoff (1)']/table4['Intercept (0)'],2)
add_leavers = table4['add_leavers']
lb_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, True, False)
lower_bound = estimate_RDD_multiple_datasets(lb_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
ub_trimmed_dict_06 = trim_data(groups_dict_06, add_leavers, False, True)
upper_bound = estimate_RDD_multiple_datasets(ub_trimmed_dict_06, groups_dict_keys, 'nextGPA', regressors)
bounds = pd.concat([lower_bound.iloc[:,[0,2]],upper_bound.iloc[:,[0,2]]], axis=1)
bounds.columns = pd.MultiIndex.from_product([['Lower Bound Estimate','Upper Bound Estimate',],
['GPA below cutoff (1)', 'Std.err (1)']])
bounds
###Output
_____no_output_____
###Markdown
5.2.5. The Impacts on GraduationAs a third outcome, Lindo et al. (2010) examine the effects of academic probation on students' graduation rates. As already discussed in the previous section, the outcomes that are realized later in time are more complex to examine because of all the different choices a student has made until she or he reaches that outcome. Graduation rates are the product of a dynamic decision-making process that spans throughout the students' time at university. While the study focuses mainly on the effects of being put on probation after the first year, the decision problem described in the theoretical framework can be faced by students at different points during their academic career as students can be placed on probation each term or for multiple terms in a row. There are different ways in which academic probation could affect graduation rates. On the one hand, it could reduce the probability of graduating because probation increases the probability of dropping out and some students who fail to increase their grades are suspended. On the other hand, these students might have graduated either way and thus do not have an effect. Additionally, probation could increase graduation rates because those students who remain improve their performance. Figure 5 - Graduation Rates Figure 5 and Table 6 show the estimated impacts of academic probation after the first year on whether a student has graduated in four, five or six years. The effects are negative for all three options, suggesting that the negative effects discussed above overweigh potential positive effects on graduation rates.
###Code
plot_figure5(sample12,
create_predictions(sample12,'gradin4', regressors, 0.6),
create_predictions(sample12,'gradin5', regressors, 0.6),
create_predictions(sample12,'gradin6', regressors, 0.6))
###Output
_____no_output_____
###Markdown
Table 6 - Estimated Effects on Graduation The effects on graduation rates are insignificant for most subgroups, the group of students with high school grades above the median stands out as being especially negatively affected by being placed on probation in the first year. This group of students sees their probability of graduation within six years reduced by 14.5 percent. Lindo et al. (2010) attribute these results to the fact that this group of students is especially likely to drop out after being put on probation and also on average does not do much better than their counterpart if they continue to attend university.Overall the results on graduation rates are rather limited. This likely stems from the more complex nature in which probation in the first year can affect this outcome later down the line. Unfortunately, most of the data in the provided dataset focus on the first two years of students' time at university (e.g. we only now the GPA of the first two years). Much more information would be needed to uncover the mechanisms in which probation may affect students' probability of graduating within specific timeframes.---**NOTE**: Below I only show the sections of Table 6 that are discussed above as the entire table is quite extensive. The other results presented in Table 6 of the paper can be viewed by uncommenting the code at the end of this section.--- Graduated after 6 years
###Code
table6 = create_table6(groups_dict_06, groups_dict_keys, regressors)
table6.loc[['All','HS Grades > median' ],
'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
**Code for complete Table 6:**
###Code
# table6.loc[:, 'Graduated after 4 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 5 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
# table6.loc[:, 'Graduated after 6 years'].style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
--- 6. Extension: Robustness Checks ---As discussed in my replication of Lindo et al. (2010) above, the authors use a variety of validity and robustness checks to analyze the reliability of their results. Aside from some smaller independent contributions that I already discuss in the replication part for better context, I in this section further analyze subsequent performance and check the bandwidth sensitivity of the results in drop out rates and subsequent GPA. 6.1. A Closer Look at Students' Subsequent Performance. 6.1.1. Subsequent Performance and Total Credits in Year 2 The results from Lindo et al. (2010) presented above show that students are more likely to drop out after being placed on academic probation but those who remain in school tend to improve their GPA above the cutoff in the next term. These results are generally in line with the theoretical framework presented in the paper which predicts that students either drop out or improve their GPA if the cost of not improving in the next term increases. The performance standard model explains these results through students self-selecting between increasing effort and dropping out based on their abilities (which are defined as the probability of meeting the performance standard). Students who are less likely to improve their GPA should thus be more likely to drop out. Unfortunately, it is not possible to test this prediction, as Lindo et al. (2010) emphasize in the paper because the probability of meeting the performance standard is not observed for students who leave school. However, examining the students who remain in school may give some further insights. While Lindo et al. (2010) observe that students have been placed on probation on average improve their performance, it is not clear under which circumstances this is happening. A look at the amount of credits students are taking in their second year may give some insights. The results presented below show that being placed on probation after the first year has a negative effect on the amount of credits students take in the second year for all of the examined subgroups except the group of nonnative English speakers. This is a stark contrast to the first year where both the treatment and control group take almost the same amount of credits (as shown in the section on the validity of the RD Approach).
###Code
predictions_credits_year2 = create_predictions(sample12, 'total_credits_year2', regressors, 0.6)
plot_figure_credits_year2(sample12, predictions_credits_year2)
###Output
_____no_output_____
###Markdown
The results indicate that being placed on probation decreases the total credits taken by the average student in year two by 0.33, around 8% of the control mean. As the table below shows, the results are most prominent for males, native English speakers, and students with high school grades above the median. Interestingly, these are the same groups of students that are most likely to drop out, suggesting that the discouragement effect persists throughout these groups and even those who re-enroll for the next term proceed with caution by taking fewer credits.
###Code
table_total_credits_year2 = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,
'total_credits_year2',regressors)
table_total_credits_year2.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
When interpreting these results it should be kept in mind that some students' next evaluation takes place during summer classes. Students who have taken summer classes enter their second year already having either passed the next evaluation or not. Those who fell below the cutoff will have been suspended and thus are missing from the data for the second year and those who have passed the threshold in the summer classes are likely not on probation anymore. Estimating the effects of probation on credits taken in the second year separately for both groups shows that those who did not take classes in the summer are more affected than those who did. For the students who took summer classes, the results are only significant for males, students with high school grades above the median and native English speakers. No summer classes
###Code
sample06_nosummer = sample06[sample06.summerreg_year1 == 0]
groups_dict_06_nosummer = create_groups_dict(data=sample06_nosummer, keys=groups_dict_keys,columns=groups_dict_columns)
table_totcred_y2_nosummer = estimate_RDD_multiple_datasets(groups_dict_06_nosummer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_nosummer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
Summer classes
###Code
sample06_summer = sample06[sample06.summerreg_year1 == 1]
groups_dict_06_summer = create_groups_dict(sample06_summer,groups_dict_keys,groups_dict_columns)
table_totcred_y2_summer = estimate_RDD_multiple_datasets(groups_dict_06_summer,groups_dict_keys,
'total_credits_year2',regressors)
table_totcred_y2_summer.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
These findings are useful for interpreting the subsequent performance of students because more credits likely signify a larger workload for the student. Instead of increasing their effort, students may just decrease their workload by completing fewer credits in the next term. Unfortunately, we cannot test this in detail because the data doesn't show how many credits students completed in which term. Reducing the sample for the analysis of the subsequent GPA to students who did not attend summer classes and completed 4 credits in the second year (the most frequent amount of credits takeen by this group of students) shows that the effect of scoring below the cutoff in year 1 becomes insignificant for the students who have above-median high school grades and nonnative English speakers. The improvement decreases a bit for some groups like females or students with high school grades below the median but increases for others like males and native english speakers. Overall the results are still highly significant though considering the small window of observations to which the data is reduced in this case. This suggests that while students on probation do seem to take fewer credits in the next year, the improvements to subsequent performance is too great to just be attributed to students decreasing their workload.
###Code
sample06_many_credits = sample06_nosummer[(sample06_nosummer.total_credits_year2 == 4)]
groups_dict_06_manycredits = create_groups_dict(sample06_many_credits,groups_dict_keys,groups_dict_columns)
table_manycredits = estimate_RDD_multiple_datasets(groups_dict_06_manycredits,groups_dict_keys,
'nextGPA',regressors)
table_manycredits.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.1.2. Subsequent Cumulative Grade Point Average (CGPA) An additional factor that might be important for the analysis of subsequent performance is the Cumulative Grade Point Average (CGPA). Lindo et al. (2010) focus their analysis of subsequent performance solely on the grades achieved in the next term. However, in the section on the institutional background in the paper the authors write:>*At all campuses, students on probation can avoid suspension and return to good academic standing by bringing their cumulative GPA up to the cutoff.* (Lindo et al., 2010, p.98).To avoid suspension in the long term, students on probation thus are required to not only score above the cutoff in the next term but to score high enough to bring their CGPA above the probation threshold. Students who score above the threshold in the next term but still have a CGPA below the cutoff remain on probation. Students who fail to bring their GPA above the cutoff (and thus also their CGPA since their first-year GPA and first-year CGPA are the same) are suspended. As the figure and table below show, the positive effects of probation on subsequent performance carry over to students' CGPA as well. Being placed on probation on average increases students' CGPA by 0.07 grade points or 63% of the control mean although the difference is rather difficult to spot visually.
###Code
predictions_nextCGPA = create_predictions(sample12, 'nextCGPA', regressors, 0.6)
plot_nextCGPA(sample12, predictions_nextCGPA)
###Output
_____no_output_____
###Markdown
Effect of Academic Probation on Subsequent CGPA
###Code
table_nextCGPA = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys, 'nextCGPA', regressors)
table_nextCGPA.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
However, in contrast to the probability of improving the next term GPA above the cutoff, academic probation has no significant effect on the probability of improving the CGPA above the cutoff in the next term except for the group of nonnative English speakers where the probability is actually negative. Indeed, out of all students on probation (within 0.6 grade points of the cutoff), only around 37% improve their next term CGPA above the cutoff. Around 23% improve their GPA above the cutoff but not their CGPA and remain on probation. The other students dropped out or are suspended after the next term. This suggests that the effects of probation span much longer than just the subsequent term for many students, not only indirectly because they have had the experience of being placed on probation but also directly because many of them remain on probation for multiple subsequent terms. These factors underline the points made in previous sections about the complexity of the way academic probation can affect a student's academic career. After being placed on probation a student can take a multitude of different paths, many more than the theoretical framework introduced in Section 2 leads on. A more dynamic approach to estimating the effects of academic probation could likely offer more insights into how students react to this university policy. Effect of Academic Probation on the Probability of Achieving a CGPA Above the Cutoff in the Next Term
###Code
table_nextCGPA_above_cutoff = estimate_RDD_multiple_datasets(groups_dict_06, groups_dict_keys,'nextCGPA_above_cutoff',
regressors)
table_nextCGPA_above_cutoff.style.applymap(color_pvalues, subset=['P-Value (1)', 'P-Value (0)'])
###Output
_____no_output_____
###Markdown
6.2. Bandwidth Sensitivity As a final robustness check, I evaluate the model at different bandwidths to ensure that results are not limited to one specific sample of students within a particular bandwidth. Lindo et al. (2010) use a distance from the threshold of 0.6 for the main regression analysis and 1.2 for graphical analysis (although the estimated curve at each point relies on a local linear regression with a bandwidth of 0.6 as well). The chosen bandwidth around the cutoff thus captures around 25% of the total range of grades (the GPA values observed in the first year span from 0 to 4.3). Lindo et al. (2010) do not discuss the reasoning behind their choice of bandwidth in detail and do not apply optimal bandwidth selection methods like some other applications of regression discontinuity (Imbens & Lemieux, 2008; Lee & Lemieux, 2010). However, from a heuristic standpoint, this bandwidth choice seems reasonable. Since the cutoff lies at a GPA of 1.5 (1.6 at Campus 3), this bandwidth includes students whose GPA falls roughly between 0.9 and 2.1 grade points, so a range of around one average grade point including the edges. A much larger bandwidth would not make sense because it would include students that are failing every class and students who are achieving passable grades and are thus not very comparable to students who pass or fall below the threshold by a small margin.I evaluate bandwidths of length 0.2 (0.1 distance from cutoff on each side) up to 2.4 (1.2 distance from cutoff on both sides). As Lindo et al. (2010), I choose a maximum bandwidth of 1.2 the reasons explained in the paragraph above. Bandwidth sensitivity of the effect of probation on the probability of leaving school The table below shows the estimated effect of probation on the probability to leave school after the first year using local linear regression (same specification as before) for all bandwidths between 0.1 and 1.2. The bandwidths are on the vertical axis, and the different subgroups are on the horizontal axis of the table. An *x* in the table indicates that the estimate was insignificant at the 10% level and is thus not shown for readability. The table shows that the results for the effects on leaving school are relatively sensitive to bandwidth selection. Estimates of students within only 0.2 grade points of the probation threshold are not significant for any of the groups considered. Results for students with high school grades below the median are only significant for bandwidths between 0.3 and 0.5 while estimates for students with high school grades above the median are only significant between values of 0.5 and 0.7. The results for the other subgroups, on the other hand, seem to be quite robust to bandwidth selection. The findings reported in this table suggest that some results presented in the previous sections should be interpreted carefully. Especially the estimates of students based on high school grades might be driven by some underlying factors that are not observed in this study. These could explain the sensitivity of the results to bandwidth selection.
###Code
bandwidths = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2]
summary_left_school = bandwidth_sensitivity_summary(data, 'left_school',groups_dict_keys, groups_dict_columns, regressors)
summary_left_school.loc[(bandwidths,'probation'),:]
#summary_left_school #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
###Markdown
Bandwidth sensitivity of the effect of probation on subsequent GPA The results for the effects of academic probation on subsequent performance, on the other hand, seem to be quite robust to bandwidth selection. The estimated effects are the highest for most subgroups around the threshold of 0.6 chosen by Lindo et al. (2010) but the effects do not change sign for any subgroup and still remain quite similar.Again, the group of students with high school grades above the median does not show significant results for bandwidths between 0.1 and 0.4 and thus seems to be the most sensitive to bandwidth selection.
###Code
summary_nextGPA = bandwidth_sensitivity_summary(data, 'nextGPA', groups_dict_keys, groups_dict_columns, regressors)
summary_nextGPA.loc[(bandwidths,'probation'),:]
# summary_nextGPA #<- uncommenting this code will reveal the table including pvalues
###Output
_____no_output_____
|
src/SVM.ipynb
|
###Markdown
DATA directory
###Code
DIR = Path(r'C:\Users\Abhij\OneDrive\Documents\GitHub\DNA-structure-prediction')
assert DIR.exists()
DATA = DIR/"data"
###Output
_____no_output_____
###Markdown
Helper Functions to read pickled data
###Code
def make_dirs(*, name: str) -> ():
try:
_file = DIR / "data"
os.mkdir(_file / name)
except FileExistsError:
print("Dir exists")
def pkl_it(dataframe, filebase):
with open(DIR / "data" / "pkl" / str(filebase + ".pkl"), "wb") as fh:
dill.dump(dataframe, fh)
return
def unpkl_it(filebase):
with open(DIR / "data" / "pkl" / str(filebase + ".pkl"), "rb") as fh:
return dill.load(fh)
make_dirs(name="results")
make_dirs(name="pkl")
###Output
Dir exists
Dir exists
###Markdown
A flexible helper Class for running different ML algorithms It automatically chooses the best threshold for classification by locating the arg_max (index) of the best F-score
###Code
import logging
from collections import defaultdict
logging.basicConfig(filename=DATA/'results.log', level=logging.INFO)
class Call_Plot():
def __init__(self, sklearn_model=True, model_name="SVM", repeated_k_fold=False):
plt.close()
self.model_name = model_name
self.fig, self.ax = plt.subplots()
self.ax.plot([0,1], [0,1], linestyle='--', label='Random choice')
self.ax.set_xlabel('False Positive Rate', fontsize=12)
self.ax.set_ylabel('True Positive Rate', fontsize=12)
self.fig2, self.ax2 = plt.subplots()
self.ax2.set_xlabel('Recall', fontsize=12)
self.ax2.set_ylabel('Precision', fontsize=12)
self.tprs = []
self.aucs = []
self.mean_fpr = np.linspace(0, 1, 100)
self.no_skill = []
self.sklearn_model = sklearn_model
self.results = defaultdict(list)
self.repeated_k_fold = repeated_k_fold
def Plot(self, data: dict, model, idx):
if self.sklearn_model:
y_pred_val = model.predict_proba(data["X_val"])[:,1]
else:
y_pred_val = model.predict(data["X_val"])
#Precision-Recall
precision, recall, thresholds = precision_recall_curve(data["y_val"], y_pred_val)
no_skill = len(data["y_val"][data["y_val"]==1]) / len(data["y_val"])
self.no_skill.append(no_skill)
avg_pr = average_precision_score(data["y_val"], y_pred_val)
auc_pr = sklearn.metrics.auc(recall, precision)
if self.repeated_k_fold:
self.ax2.plot(recall, precision, marker='.', label=f'Run {(idx)//5+1} Test Fold{(idx)%5+1}: AUC PR={auc_pr:.2f}')
else:
self.ax2.plot(recall, precision, marker='.', label=f'Test Fold{(idx)+1}: AUC PR={auc_pr:.2f}')
# convert to f score
fscore = (2 * precision * recall) / (precision + recall)
# locate the index of the largest f score
ix_pr = np.argmax(fscore)
self.ax2.scatter(recall[ix_pr], precision[ix_pr], marker='o', color='black')
Accuracy = sklearn.metrics.accuracy_score(data["y_val"], np.where(y_pred_val > thresholds[ix_pr], 1, 0))
target_names = ['B-DNA', 'A-DNA']
print(classification_report(data["y_val"], np.where(y_pred_val > thresholds[ix_pr], 1, 0), target_names=target_names))
F1 = sklearn.metrics.f1_score(data["y_val"], np.where(y_pred_val > thresholds[ix_pr], 1, 0))
MCC = sklearn.metrics.matthews_corrcoef(data["y_val"], np.where(y_pred_val > thresholds[ix_pr], 1, 0))
cohen_kappa_score = sklearn.metrics.cohen_kappa_score(data["y_val"], np.where(y_pred_val > thresholds[ix_pr], 1, 0))
logging.info(f'Fold {idx + 1}: Average PR: {avg_pr:.2f} ')
logging.info(f'Fold {idx + 1}: AUC PR: {auc_pr:.2f} ')
logging.info(f'Fold {idx + 1}: Best Threshold_f-score={thresholds[ix_pr]:.2f}, F-Score={fscore[ix_pr]}')
logging.info(f'Fold {idx + 1}: Accuracy: {Accuracy:.2f}')
logging.info(f'Fold {idx + 1}: F1: {F1:.2f}')
logging.info(f'Fold {idx + 1}: MCC: {MCC:.2f}')
#ROC-AUC
fpr, tpr, thresholds_auc = roc_curve(data["y_val"], y_pred_val)
# calculate the g-mean for each threshold
gmeans = np.sqrt(tpr * (1-fpr))
# locate the index of the largest g-mean
ix = np.argmax(gmeans)
if self.repeated_k_fold:
self.ax.plot(fpr, tpr, marker='.',
label=f'Run {(idx)//5+1} Test Fold{(idx)%5+1}: AUC={sklearn.metrics.auc(fpr, tpr):.2f}')
else:
self.ax.plot(fpr, tpr, marker='.',
label=f'Test Fold{(idx)+1}: AUC={sklearn.metrics.auc(fpr, tpr):.2f}')
self.ax.scatter(fpr[ix], tpr[ix], marker='o', color='black')
# axis labels
self.ax.legend(loc="lower left")
# Mean plot
interp_tpr = np.interp(self.mean_fpr, fpr, tpr)
interp_tpr[0] = 0.0
self.tprs.append(interp_tpr)
self.aucs.append(gmeans[ix])
logging.info(f'Fold {idx + 1}: ROC-AUC: {sklearn.metrics.auc(fpr, tpr):.2f}')
logging.info(f'Fold {idx + 1}: Best Threshold_ROC={thresholds_auc[ix]:.2f}, G-Mean_ROC={gmeans[ix]:.2f}')
print("Average PR: ", avg_pr )
print("AUC PR: ", auc_pr)
print('Best Threshold_f-score=%f, F-Score=%.3f' % (thresholds[ix_pr], fscore[ix_pr]))
print("AUC: ", sklearn.metrics.auc(fpr, tpr))
print('Best Threshold_ROC=%f, G-Mean_ROC=%.3f' % (thresholds_auc[ix], gmeans[ix]))
print("Accuracy: ", Accuracy )
print("F1: ", F1 )
print("MCC: ", MCC )
self.results["Average PR"].append(avg_pr)
self.results["AUC PR"].append(auc_pr)
self.results["ROC AUC"].append(sklearn.metrics.auc(fpr, tpr))
self.results["Accuracy"].append(Accuracy)
self.results["F1"].append(F1)
self.results["MCC"].append(MCC)
self.results["cohen_kappa_score"].append(cohen_kappa_score)
def post_Plot(self):
from sklearn.metrics import auc
mean_tpr = np.mean(self.tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(self.mean_fpr, mean_tpr)
std_auc = np.std(self.aucs)
self.ax.plot(self.mean_fpr, mean_tpr, color='b',
label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc),
lw=2, alpha=.8)
std_tpr = np.std(self.tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
self.ax.fill_between(self.mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2,
label=r'$\pm$ 1 std. dev.')
self.ax.legend(loc=(0.45, .05),fontsize='medium')
self.fig.savefig(DIR/"data"/"results"/f"{self.model_name}_AUC_ROC.png", dpi=600)
no_skill = np.mean(np.array(self.no_skill))
self.ax2.plot([0,1], [no_skill,no_skill], linestyle='--', label="Random")
self.ax2.legend(loc=(0.050, .08),fontsize='medium')
self.fig2.savefig(DIR/"data"/"results"/f"{self.model_name}_AUC_PR.png", dpi=600)
###Output
_____no_output_____
###Markdown
Read curated dataset
###Code
curated_data = unpkl_it("curated_dataset")
curated_data
#Check if any sequence has duplicate features
curated_data.drop_duplicates(subset=['AA/TT', 'GG/CC', 'AC/GT',
'CA/TG', 'AT/AT', 'TA/TA', 'AG/CT', 'GA/TC', 'CG/CG', 'GC/GC'], keep='last')
###Output
_____no_output_____
###Markdown
Nested Cross-validation
###Code
from imblearn.combine import SMOTEENN, SMOTETomek
from sklearn.model_selection import RepeatedStratifiedKFold
###Output
_____no_output_____
###Markdown
The function gen_data is a flexible generator that implements outer fold of Nested CV Here, we are using 5-fold stratified Nested cross validation (n_splits = 5)
###Code
def gen_data(data: pd.DataFrame, RESAMPLING: bool=False):
X, y = data.drop(labels="target", axis=1), data["target"]
sss = RepeatedStratifiedKFold(n_splits=5, n_repeats=1, random_state=42)
for train_index, val_index in sss.split(X, y):
smote_tomek = SMOTETomek(random_state=42)
X_resampled, y_resampled = smote_tomek.fit_resample(X.iloc[train_index,:], y.iloc[train_index])
yield {"X_train": X_resampled if RESAMPLING else X.iloc[train_index,:],
"y_train": y_resampled if RESAMPLING else y.iloc[train_index],
"X_val": X.iloc[val_index,:], "y_val": y.iloc[val_index]}
###Output
_____no_output_____
###Markdown
This generator implements inner fold of Nested CV, where we tune hyperparameters.
###Code
def gen_data_for_tuningHP(data: dict, RESAMPLING: bool=True):
X, y = data["X_train"], data["y_train"]
sss = StratifiedShuffleSplit(n_splits=3, test_size=0.3, random_state=42)
for train_index, val_index in sss.split(X, y):
smote_tomek = SMOTETomek(random_state=42)
X_resampled, y_resampled = smote_tomek.fit_resample(X.iloc[train_index,:], y.iloc[train_index])
yield {"X_train": X_resampled if RESAMPLING else X.iloc[train_index,:],
"y_train": y_resampled if RESAMPLING else y.iloc[train_index],
"X_val": X.iloc[val_index,:], "y_val": y.iloc[val_index]}
###Output
_____no_output_____
###Markdown
Helper function: train_test_folds_reader This generator function reads the data from the "train_test_folds" folder and gives the same Train-Test splitsused by us. At each iteration it yields a single split of the dataAlternatively, you can run the `gen_data(curated_data.drop(labels=["item", "sequence"], axis=1), RESAMPLING=False)`, which gives the same split provided that you use the same seed.
###Code
def train_test_folds_reader(*, folder) -> dict:
TRAIN_TEST = Path(folder)
for i in range(5):
yield {"X_train": pd.read_excel(folder/f"train_fold_{i+1}.xls", index_col=0).drop(labels=["target", "sequence", "item"], axis=1),
"y_train": pd.read_excel(folder/f"train_fold_{i+1}.xls", index_col=0)["target"],
"X_val": pd.read_excel(folder/f"test_fold_{i+1}.xls", index_col=0).drop(labels=["target", "sequence", "item"], axis=1),
"y_val": pd.read_excel(folder/f"test_fold_{i+1}.xls", index_col=0)["target"],}
###Output
_____no_output_____
###Markdown
Read the best SVM hyperparameters
###Code
best_svm_params = pd.read_csv(DATA/"tuned_hyperparameters"/"best_svm_params.csv", index_col=0)
best_svm_params
###Output
_____no_output_____
###Markdown
Set up SVM training
###Code
from sklearn.svm import SVC, NuSVC
from sklearn.model_selection import cross_val_score, cross_val_predict
import optuna
from optuna.pruners import HyperbandPruner
import copy
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
def trainer(data, param_updater):
train_x, train_y = data["X_train"], data["y_train"]
param = {
"probability": True,
"class_weight": "balanced",
"random_state": 42,
"verbose": False,
}
param.update(param_updater)
model = SVC(**param)
model = make_pipeline(StandardScaler(), model)
model.fit(train_x, train_y)
return model
###Output
_____no_output_____
###Markdown
Train, Run and evaluate performance of SVM using tuned hyperparametersHere, we use the `train_test_folds_reader(folder=DATA/"train_test_folds")` to yield the same split of data as used us. We then use the tuned hyperparameters (best_svm_params) and convert it into a dictionary. We then train each model and evaluate the performance of each model on each test fold. Note that, alternatively we can also use the `gen_data(curated_data.drop(labels=["item", "sequence"], axis=1), RESAMPLING=False)` will give the same split of data if you use the same seed (42).
###Code
plt.close()
# *************OUTER*************
plot_Model_SVM_test = Call_Plot(repeated_k_fold=False)
for outer_idx, elem in enumerate(train_test_folds_reader(folder=DATA/"train_test_folds")):
# ***********Feed in the best hyperparams for each model************
model = trainer(elem, best_svm_params.T.to_dict()
[f"Model_{outer_idx + 1}"])
plot_Model_SVM_test.Plot(elem, model, outer_idx)
plot_Model_SVM_test.post_Plot()
pd.DataFrame(plot_Model_SVM_test.results)
pd.DataFrame(plot_Model_SVM_test.results).mean()
###Output
_____no_output_____
###Markdown
Running from scratch - Run and evaluate performance of SVM under 5-fold stratified Nested CV
###Code
import optuna
import copy
def objective(data, trial):
train_x, valid_x, train_y, valid_y = data["X_train"], data["X_val"], data["y_train"], data["y_val"]
param = {
"C": trial.suggest_discrete_uniform("C",0.1,1.0,0.1),
"kernel": trial.suggest_categorical("kernel",["rbf",]),
"gamma": trial.suggest_loguniform("gamma", 1e-3, 1e+3),
"probability": True,
"class_weight": "balanced",
"random_state": 42,
"verbose": False,
}
model = SVC(**param)
model = make_pipeline(StandardScaler(), model)
model.fit(train_x, train_y)
return sklearn.metrics.roc_auc_score(valid_y, model.predict(valid_x))
import collections
Trial = collections.namedtuple("Trial",["value", "parameters"])
plt.close()
optuna.logging.set_verbosity(optuna.logging.WARNING)
results = []
outer_models = {}
best_models_svm = {}
hack_svm = {}
# *************OUTER*************
plot_Model_svm = Call_Plot(sklearn_model=True, model_name="SVM", repeated_k_fold=True)
for outer_idx, elem in enumerate(gen_data(curated_data.drop(labels=["item", "sequence"], axis=1), RESAMPLING = False)):
hack_svm[outer_idx] = elem
study_dict = {}
# ***********INNER************
for idx, data_in in enumerate(gen_data_for_tuningHP(elem, RESAMPLING=True)):
study = optuna.create_study(pruner=HyperbandPruner(max_resource="auto"),
direction="maximize")
study.optimize((toolz.curry(objective)(data_in)), n_trials=100)
#print("Number of finished trials: {}".format(len(study.trials)))
trial = study.best_trial
study_dict[idx] = Trial(trial.value, trial.params)
arg_max = max(study_dict, key=lambda d: study_dict[d].value) #max for AUC
best_models_svm[outer_idx] = trainer(elem, study_dict[arg_max].parameters)
plot_Model_svm.Plot(elem, best_models_svm[outer_idx], outer_idx)
plot_Model_svm.post_Plot()
pd.DataFrame(plot_Model_SVM_test.results)
pd.DataFrame(plot_Model_SVM_test.results).mean()
###Output
_____no_output_____
###Markdown
Search with all kernels takes to long. **rbf** perform generally better than other kernels (if using large C value, ie. C = 10).
###Code
params = {
'C': Real(0.1, 100, prior='log-uniform')
}
opt = BayesSearchCV(
estimator=clf,
search_spaces=params,
n_iter=20,
cv=skf,
scoring='f1',
verbose=3,
random_state=42)
opt.fit(bow, y_train.values)
###Output
_____no_output_____
|
_pages/AI/TensorFlow/src/NCIA-CNN/Day_01_04_mnist.ipynb
|
###Markdown
Stocastic Gradient Decent(SGD)* 아래 소스는 weight를 다 돌고 나서 한번에 한다. 안좋은 방법.
###Code
def mnist_sgd():
mnist = input_data.read_data_sets('mnist')
# 784가 feature, 28*28 중에 1개의 pixel이 1의 feature가 된다.
# w = tf.Variable(tf.random_uniform([784, 10]))
# 모델 정확도 높이기 위해 아님 -> 빨리 수렴한다.
# get_variable은 변수가 만들어져 있으면 가져오고 , 없으면 만든다. glorot은 xavier
w = tf.get_variable('w', shape=[784,10], initializer=tf.initializers.glorot_normal())
# w = tf.Variable(tf.contrib.layers.xavier_initializer([784,10]))
# bias는 class의 갯수만큼 정한다.
# b = tf.Variable(tf.random_uniform([10]))
# 정확도 올리기위해
b = tf.Variable(tf.zeros([10]))
ph_x = tf.placeholder(tf.float32)
# (55000, 10) = (55000, 784) @ (784, 10)
z = tf.matmul(ph_x, w) + b
hx = tf.nn.softmax(z)
# tensorflow 2.0d에서 정리 될것, logit=예측 label을 결과괌
# logit에 z를 하는것은 hx를 전달하지 않아도 됨, 자체적으로 함
# 우리의 결과는 ont-hot 백터가 아님으로 sparse_softmax_cross_entropy_with_logits
loss_i = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=z, labels=np.int32(mnist.train.labels))
loss = tf.reduce_mean(loss_i)
# 모델 정확도 높이기 위해 아님 -> 빨리 수렴한다.
# optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train = optimizer.minimize(loss=loss)
# sess로 변수의 값을 알수 있다.
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for i in range(100):
sess.run(train, feed_dict={ph_x: mnist.train.images})
print(i, sess.run(loss, {ph_x: mnist.train.images}))
preds = sess.run(hx, {ph_x: mnist.test.images})
preds_arg = np.argmax(preds, axis=1) # 1: 수평, 0: 수직
# spase일때는 argmax를 가져올필요 없다.
# test_arg = np.argmax(mnist.test.labels, axis=1)
# 파이썬의 list는 broadcasting기능이 없어서, numpy array로 변경
# grades = np.array(['Setosa', 'Versicolor', 'Virginica'])
# print(grades[preds_arg])
# print(preds)
# 1차 혼돈 : 데이터가 섞여 있지 않음으로 인한오류 → shuffle 필요 np.random.shuffle(iris)
# 2차 혼돈 : 돌릴때 마다 위치가 달라져서 ...np.random.seed(1)
print('acc: ', np.mean(preds_arg == mnist.test.labels))
print(preds_arg)
# print(test_arg)
sess.close()
mnist_sgd()
###Output
WARNING:tensorflow:From <ipython-input-3-78923763d920>:2: read_data_sets (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use alternatives such as official/mnist/dataset.py from tensorflow/models.
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:260: maybe_download (from tensorflow.contrib.learn.python.learn.datasets.base) is deprecated and will be removed in a future version.
Instructions for updating:
Please write your own downloading logic.
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\base.py:252: _internal_retry.<locals>.wrap.<locals>.wrapped_fn (from tensorflow.contrib.learn.python.learn.datasets.base) is deprecated and will be removed in a future version.
Instructions for updating:
Please use urllib or similar directly.
Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:262: extract_images (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use tf.data to implement this functionality.
Extracting mnist\train-images-idx3-ubyte.gz
Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:267: extract_labels (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use tf.data to implement this functionality.
Extracting mnist\train-labels-idx1-ubyte.gz
Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.
Extracting mnist\t10k-images-idx3-ubyte.gz
Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.
Extracting mnist\t10k-labels-idx1-ubyte.gz
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\contrib\learn\python\learn\datasets\mnist.py:290: DataSet.__init__ (from tensorflow.contrib.learn.python.learn.datasets.mnist) is deprecated and will be removed in a future version.
Instructions for updating:
Please use alternatives such as official/mnist/dataset.py from tensorflow/models.
WARNING:tensorflow:From C:\Users\shpim\Anaconda3\lib\site-packages\tensorflow\python\framework\op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
0 1.962099
1 1.6237156
2 1.3404368
3 1.1272396
4 0.9743591
5 0.85995346
6 0.7724554
7 0.7066946
8 0.65712285
9 0.6181779
10 0.58579516
11 0.557658
12 0.5330468
13 0.51204383
14 0.4945204
15 0.47987068
16 0.46735656
17 0.4564141
18 0.4466758
19 0.43787408
20 0.42980608
21 0.42236397
22 0.41552272
23 0.40926448
24 0.40352464
25 0.39821044
26 0.3932488
27 0.3886023
28 0.3842514
29 0.38017935
30 0.3763757
31 0.37283567
32 0.3695406
33 0.36644328
34 0.3634831
35 0.3606198
36 0.35785085
37 0.35519588
38 0.35267055
39 0.35027388
40 0.34799495
41 0.3458216
42 0.3437405
43 0.34173772
44 0.33980444
45 0.33794197
46 0.33615747
47 0.334453
48 0.33282074
49 0.33124822
50 0.3297266
51 0.3282517
52 0.32682198
53 0.32543725
54 0.32409838
55 0.32280555
56 0.3215549
57 0.32033998
58 0.31915554
59 0.31800097
60 0.3168782
61 0.31578863
62 0.31473145
63 0.31370446
64 0.31270537
65 0.3117316
66 0.31078118
67 0.30985326
68 0.30894822
69 0.3080661
70 0.3072058
71 0.30636555
72 0.3055441
73 0.3047405
74 0.30395412
75 0.30318466
76 0.30243182
77 0.30169496
78 0.3009731
79 0.30026466
80 0.29956883
81 0.29888558
82 0.29821473
83 0.2975562
84 0.29690948
85 0.29627424
86 0.29564983
87 0.2950359
88 0.29443216
89 0.29383856
90 0.29325476
91 0.29268032
92 0.29211488
93 0.29155806
94 0.29100958
95 0.2904695
96 0.28993732
97 0.28941312
98 0.28889665
99 0.28838766
acc: 0.9219
[7 2 1 ... 4 5 6]
###Markdown
문제 1* 테스트셋의 정확도를 알려주세요.* hint : 데이터를 쪼개쓰는 mini_batch
###Code
def mnist_softmax_mini_batch():
mnist = input_data.read_data_sets('mnist')
# 784가 feature, 28*28 중에 1개의 pixel이 1의 feature가 된다.
# w = tf.Variable(tf.random_uniform([784, 10]))
# 모델 정확도 높이기 위해 아님 -> 빨리 수렴한다.
# get_variable은 변수가 만들어져 있으면 가져오고 , 없으면 만든다. glorot은 xavier
w = tf.get_variable('w2', shape=[784,10], initializer=tf.initializers.glorot_normal())
# w = tf.Variable(tf.contrib.layers.xavier_initializer([784,10]))
# bias는 class의 갯수만큼 정한다.
# b = tf.Variable(tf.random_uniform([10]))
# 정확도 올리기위해
b = tf.Variable(tf.zeros([10]))
ph_x = tf.placeholder(tf.float32)
ph_y = tf.placeholder(tf.int32)
# (55000, 10) = (55000, 784) @ (784, 10)
z = tf.matmul(ph_x, w) + b
hx = tf.nn.softmax(z)
# tensorflow 2.0d에서 정리 될것, logit=예측 label을 결과괌
# logit에 z를 하는것은 hx를 전달하지 않아도 됨, 자체적으로 함
# 우리의 결과는 ont-hot 백터가 아님으로 sparse_softmax_cross_entropy_with_logits
loss_i = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=z, labels=ph_y)
loss = tf.reduce_mean(loss_i)
# 모델 정확도 높이기 위해 아님 -> 빨리 수렴한다.
# optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train = optimizer.minimize(loss=loss)
# sess로 변수의 값을 알수 있다.
sess = tf.Session()
sess.run(tf.global_variables_initializer())
epochs = 10
batch_size = 100 # 출구를 몇개씩 조사할건지
n_iters = mnist.train.num_examples // batch_size # 550
# epcochs를 1번 돌고 념
for i in range(epochs):
c = 0
for j in range(n_iters):
xx, yy = mnist.train.next_batch(batch_size)
sess.run(train, feed_dict={ph_x: xx, ph_y: yy})
c += sess.run(loss, {ph_x: xx, ph_y:yy})
print(i, c/ n_iters)
preds = sess.run(hx, {ph_x: mnist.test.images})
preds_arg = np.argmax(preds, axis=1) # 1: 수평, 0: 수직
# spase일때는 argmax를 가져올필요 없다.
# test_arg = np.argmax(mnist.test.labels, axis=1)
# 파이썬의 list는 broadcasting기능이 없어서, numpy array로 변경
# grades = np.array(['Setosa', 'Versicolor', 'Virginica'])
# print(grades[preds_arg])
# print(preds)
# 1차 혼돈 : 데이터가 섞여 있지 않음으로 인한오류 → shuffle 필요 np.random.shuffle(iris)
# 2차 혼돈 : 돌릴때 마다 위치가 달라져서 ...np.random.seed(1)
print('acc: ', np.mean(preds_arg == mnist.test.labels))
print(preds_arg)
# print(test_arg)
sess.close()
mnist_softmax_mini_batch()
###Output
Extracting mnist\train-images-idx3-ubyte.gz
Extracting mnist\train-labels-idx1-ubyte.gz
Extracting mnist\t10k-images-idx3-ubyte.gz
Extracting mnist\t10k-labels-idx1-ubyte.gz
0 0.34581849932670594
1 0.28294095662507146
2 0.27262380918318574
3 0.2672042059221051
4 0.26281767536293377
5 0.26140581697225573
6 0.2604996431144801
7 0.25685677154497666
8 0.25420204677365044
9 0.25061307678845796
acc: 0.9208
[7 2 1 ... 4 5 6]
###Markdown
멀티 layer
###Code
def mnist_multi_layers():
mnist = input_data.read_data_sets('mnist')
w1 = tf.get_variable('w11', shape=[784, 512], initializer=tf.initializers.glorot_normal())
w2 = tf.get_variable('w22', shape=[512, 256], initializer=tf.initializers.glorot_normal())
w3 = tf.get_variable('w32', shape=[256, 10], initializer=tf.initializers.glorot_normal())
b1 = tf.Variable(tf.zeros([512]))
b2 = tf.Variable(tf.zeros([256]))
b3 = tf.Variable(tf.zeros([ 10]))
ph_x = tf.placeholder(tf.float32)
ph_y = tf.placeholder(tf.int32)
# (55000, 10) = (55000, 784) @ (784, 10)
z1 = tf.matmul(ph_x, w1) + b1
r1 = tf.nn.relu(z1)
z2 = tf.matmul(r1, w2) + b2
r2 = tf.nn.relu(z2)
z3 = tf.matmul(r2, w3) + b3
hx = tf.nn.softmax(z3)
# tensorflow 2.0d에서 정리 될것, logit=예측 label을 결과괌
# logit에 z를 하는것은 hx를 전달하지 않아도 됨, 자체적으로 함
# 우리의 결과는 ont-hot 백터가 아님으로 sparse_softmax_cross_entropy_with_logits
loss_i = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=z3, labels=ph_y)
loss = tf.reduce_mean(loss_i)
# 모델 정확도 높이기 위해 아님 -> 빨리 수렴한다.
# optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train = optimizer.minimize(loss=loss)
# sess로 변수의 값을 알수 있다.
sess = tf.Session()
sess.run(tf.global_variables_initializer())
epochs = 10
batch_size = 100 # 출구를 몇개씩 조사할건지
n_iters = mnist.train.num_examples // batch_size # 550
# epcochs를 1번 돌고 념
for i in range(epochs):
c = 0
for j in range(n_iters):
xx, yy = mnist.train.next_batch(batch_size)
sess.run(train, feed_dict={ph_x: xx, ph_y: yy})
c += sess.run(loss, {ph_x: xx, ph_y:yy})
print(i, c/ n_iters)
preds = sess.run(hx, {ph_x: mnist.test.images})
preds_arg = np.argmax(preds, axis=1) # 1: 수평, 0: 수직
# spase일때는 argmax를 가져올필요 없다.
# test_arg = np.argmax(mnist.test.labels, axis=1)
# 파이썬의 list는 broadcasting기능이 없어서, numpy array로 변경
# grades = np.array(['Setosa', 'Versicolor', 'Virginica'])
# print(grades[preds_arg])
# print(preds)
# 1차 혼돈 : 데이터가 섞여 있지 않음으로 인한오류 → shuffle 필요 np.random.shuffle(iris)
# 2차 혼돈 : 돌릴때 마다 위치가 달라져서 ...np.random.seed(1)
print('acc: ', np.mean(preds_arg == mnist.test.labels))
print(preds_arg)
# print(test_arg)
sess.close()
mnist_multi_layers()
###Output
Extracting mnist\train-images-idx3-ubyte.gz
Extracting mnist\train-labels-idx1-ubyte.gz
Extracting mnist\t10k-images-idx3-ubyte.gz
Extracting mnist\t10k-labels-idx1-ubyte.gz
0 0.17192414816807616
1 0.08467089972712777
2 0.0689768023060804
3 0.056971493860368025
4 0.0562265362912281
5 0.04805349267225459
6 0.0424938825201984
7 0.043625768014674327
8 0.03891693604199893
9 0.032483553080528506
acc: 0.9728
[7 2 1 ... 4 5 6]
|
charts/bubble/data/USEEIO_indicators.ipynb
|
###Markdown
for brief matrix explanations read-> https://github.com/USEPA/USEEIO_API/blob/master/doc/data_format.md Note:If rounding off 8 decimals, ozone depletion, pesticides and a few others would need to switched to scientific notation in the data file. This would allow the files to be reducedUS from 151kb to under 72.7kbGA from 120kb, to under 59.2kb
###Code
#BASE URL AND KEY
#Use the requests library
import csv
import zipfile, io
import os
import pathlib
import requests as r
import pandas as pd
pd.options.display.max_rows = 999
#base_url ='https://api.edap-cluster.com/useeio/api'
base_url ='https://smmtool.app.cloud.gov/api'
api_headers = {}
# api-key for USEEIO
#with open(".USEEIO_API_KEY", 'r') as KEY_FILE:
# api_headers['x-api-key']=KEY_FILE.read()
#api_headers['x-api-key']="PUT_API_KEY_HERE"
# AVAILABLE MODELS
# Show the available models in the native JSON output
models = r.get(base_url+'/models',headers=api_headers)
models_json = models.json()
# MODEL NAME
#Use the first available model
model_name = models_json[0]['id']
#MODEL SECTORS
#Get the sectors
url = base_url+'/'+model_name+'/sectors'
model_sectors = r.get(url,headers=api_headers)
model_sectors_json = model_sectors.json()
#print(model_sectors_json)
model_sector_ids = []
for i in model_sectors_json:
model_sector_ids.append(i['id'])
first_sector_id = model_sector_ids[0]
first_sector_name = model_sectors_json[0]['name']
print('The '+ model_name +' model has ' + str(len(model_sectors_json)) + ' sectors.')
# INDICATORS
url = base_url+'/'+model_name+'/indicators'
model_indictrs_response = r.get(url,headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
HC_indictr_id = model_indictrs_json[8]['id']
model_indictrs_names = []
model_indictrs_ids = []
for i in model_indictrs_json:
model_indictrs_names.append(i['name'])
model_indictrs_ids.append(i['id'])
print('The '+ model_name +' model has ' + str(len(model_indictrs_json)) + ' indicators. The names are:')
print(model_indictrs_names)
model_indictrs_ids
#INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
model_indictrs_json
#In order to get the impacts of total US production, we need to first get the US_production demand vector to use in the calculation
#First get the name by showing all model demand vectors
#DEMAND VECTORS
#See the demand vectors available for the model in their JSON format
demands_response = r.get(base_url+'/'+model_name+'/demands',headers=api_headers)
demands = demands_response.json()
demands
#url = base_url+'/'+model_name+'/demands/2007_us_production'
url = base_url+'/'+model_name+'/demands/2012_US_Production_Complete'
us_production_response = r.get(url,headers=api_headers)
us_production = us_production_response.json()
# A model calculation also requires defining a perspective which is either direct or final
# Direct perspective associated impacts in the sectors in which they occur
# Final perspective rolls up impacts into those products consumed by final consumers
data_to_post = {"perspective": "direct"}
data_to_post["demand"] = us_production
url = base_url+'/'+model_name+'/calculate'
result_response = r.post(url,headers=api_headers,json=data_to_post)
result = result_response.json()
##Old code = uses D matrix
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
# D0 = D0_response.json()
# sorted(D0)
#D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
#D0 = D0_response.json()
# sorted(D0[0])
#
# Collect ALL Indicators from ALL Industr Sectors and Limit to Georgia
#
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
#D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
#D0 = D0_response.json()
#print(D0)
#indicator_data = {}
# Add the industry sector IDs
# indicator_data.update({'industry':model_sector_ids})
#indicator_data.update({'industry_code':[_.split('/')[0] for _ in model_sector_ids]})
#indicator_data.update({'industry_detail':[_.split('/')[1] for _ in model_sector_ids]})
#indicator_data.update({'industry_region':[_.split('/')[2] for _ in model_sector_ids]})
sectors_df = pd.DataFrame(model_sectors_json)
result_df = pd.DataFrame(data=result['data'],columns=result['sectors'],index=result['indicators']).transpose()
#for key, values_list in zip(model_indictrs_ids, result):
# indicator_data.update({key:values_list})
#all_indic_all_indust = pd.DataFrame(data=indicator_data)
# all_indic_all_indust.loc[0:20,['industry_code', 'industry_detail', 'ACID']].sort_values(by='ACID', ascending=False)
formatted_result = pd.merge(sectors_df,result_df,left_on='id',right_index=True)
formatted_result = formatted_result.drop(columns=["id","index","description"])
formatted_result = formatted_result.rename(columns={"code":"industry_code","name":"industry_detail","location":"industry_region"})
formatted_result.head(50)
#all_indic_all_indust.min()
#all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['ENRG'] !=0]
#all_indic_all_indust=all_indic_all_indust.replace(0,0.0000000000000000000000001)
#all_indic_all_indust.min()
#all_indic_all_indust.max()
#all_indic_all_indust.to_csv('indicators_sectors.csv')
formatted_result.to_csv('indicators_sectors.csv')
###Output
_____no_output_____
###Markdown
GAUSEEIO
###Code
# AVAILABLE MODELS
# Show the available models in the native JSON output
models = r.get(base_url+'/models',headers=api_headers)
models_json = models.json()
# MODEL NAME
#Use the first available model
model_name = models_json[1]['id']
#MODEL SECTORS
#Get the sectors
url = base_url+'/'+model_name+'/sectors'
model_sectors = r.get(base_url+'/'+model_name+'/sectors',headers=api_headers)
model_sectors_json = model_sectors.json()
#print(model_sectors_json)
model_sector_ids = []
for i in model_sectors_json:
model_sector_ids.append(i['id'])
first_sector_id = model_sector_ids[0]
first_sector_name = model_sectors_json[0]['name']
print('The '+ model_name +' model has ' + str(len(model_sectors_json)) + ' sectors.')
# INDICATORS
model_indictrs_response = r.get(base_url+'/'+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
HC_indictr_id = model_indictrs_json[8]['id']
model_indictrs_names = []
model_indictrs_ids = []
for i in model_indictrs_json:
model_indictrs_names.append(i['name'])
model_indictrs_ids.append(i['id'])
print('The '+ model_name +' model has ' + str(len(model_indictrs_json)) + ' indicators. The names are:')
print(model_indictrs_names)
model_indictrs_ids
#INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
model_indictrs_json
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
# D0 = D0_response.json()
# sorted(D0)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
# sorted(D0[0])
#
# Collect ALL Indicators from ALL Industr Sectors and Limit to Georgia
#
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
#print(D0)
indicator_data = {}
# Add the industry sector IDs
# indicator_data.update({'industry':model_sector_ids})
indicator_data.update({'industry_code':[_.split('/')[0] for _ in model_sector_ids]})
indicator_data.update({'industry_detail':[_.split('/')[1] for _ in model_sector_ids]})
indicator_data.update({'industry_region':[_.split('/')[2] for _ in model_sector_ids]})
for key, values_list in zip(model_indictrs_ids, D0):
indicator_data.update({key:values_list})
all_indic_all_indust = pd.DataFrame(data=indicator_data)
# all_indic_all_indust.loc[0:20,['industry_code', 'industry_detail', 'ACID']].sort_values(by='ACID', ascending=False)
all_indic_all_indust.head(50)
all_indic_all_indust.min()
all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['ENRG'] !=0]
all_indic_all_indust=all_indic_all_indust.replace(0,0.0000000000000000000000001)
all_indic_all_indust.min()
all_indic_all_indust.max()
all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['industry_region'] =='us-ga']
all_indic_all_indust
all_indic_all_indust.to_csv('indicators_sectors_GA.csv')
###Output
_____no_output_____
###Markdown
for breif matrix explanations read-> https://github.com/USEPA/USEEIO_API/blob/master/doc/data_format.md Note:If rounding off 8 decimals, ozone depletion, pesticides and a few others would need to switched to scientific notation in the data file. This would allow the files to be reducedUS from 151kb to under 72.7kbGA from 120kb, to under 59.2kb
###Code
#BASE URL AND KEY
#Use the requests library
import csv
import zipfile, io
import os
import pathlib
import requests as r
import pandas as pd
pd.options.display.max_rows = 999
base_url ='https://smmtool.app.cloud.gov/api/'
api_headers = {}
# api-key for USEEIO
with open(".USEEIO_API_KEY", 'r') as KEY_FILE:
api_headers['x-api-key']=KEY_FILE.read()
#api_headers['x-api-key']="PUT_API_KEY_HERE"
# AVAILABLE MODELS
# Show the available models in the native JSON output
models = r.get(base_url+'/models',headers=api_headers)
models_json = models.json()
# MODEL NAME
#Use the first available model
model_name = models_json[0]['id']
#MODEL SECTORS
#Get the sectors
model_sectors = r.get(base_url+model_name+'/sectors',headers=api_headers)
model_sectors_json = model_sectors.json()
#print(model_sectors_json)
model_sector_ids = []
for i in model_sectors_json:
model_sector_ids.append(i['id'])
first_sector_id = model_sector_ids[0]
first_sector_name = model_sectors_json[0]['name']
print('The '+ model_name +' model has ' + str(len(model_sectors_json)) + ' sectors.')
# INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
HC_indictr_id = model_indictrs_json[8]['id']
model_indictrs_names = []
model_indictrs_ids = []
for i in model_indictrs_json:
model_indictrs_names.append(i['name'])
model_indictrs_ids.append(i['id'])
print('The '+ model_name +' model has ' + str(len(model_indictrs_json)) + ' indicators. The names are:')
print(model_indictrs_names)
model_indictrs_ids
#INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
model_indictrs_json
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
# D0 = D0_response.json()
# sorted(D0)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
# sorted(D0[0])
#
# Collect ALL Indicators from ALL Industr Sectors and Limit to Georgia
#
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
#print(D0)
indicator_data = {}
# Add the industry sector IDs
# indicator_data.update({'industry':model_sector_ids})
indicator_data.update({'industry_code':[_.split('/')[0] for _ in model_sector_ids]})
indicator_data.update({'industry_detail':[_.split('/')[1] for _ in model_sector_ids]})
indicator_data.update({'industry_region':[_.split('/')[2] for _ in model_sector_ids]})
for key, values_list in zip(model_indictrs_ids, D0):
indicator_data.update({key:values_list})
all_indic_all_indust = pd.DataFrame(data=indicator_data)
# all_indic_all_indust.loc[0:20,['industry_code', 'industry_detail', 'ACID']].sort_values(by='ACID', ascending=False)
all_indic_all_indust.head(50)
all_indic_all_indust.min()
all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['ENRG'] !=0]
all_indic_all_indust=all_indic_all_indust.replace(0,0.0000000000000000000000001)
all_indic_all_indust.min()
all_indic_all_indust.max()
all_indic_all_indust.to_csv('indicators_sectors.csv')
###Output
_____no_output_____
###Markdown
GAUSEEIO
###Code
# AVAILABLE MODELS
# Show the available models in the native JSON output
models = r.get(base_url+'/models',headers=api_headers)
models_json = models.json()
# MODEL NAME
#Use the first available model
model_name = models_json[1]['id']
#MODEL SECTORS
#Get the sectors
model_sectors = r.get(base_url+model_name+'/sectors',headers=api_headers)
model_sectors_json = model_sectors.json()
#print(model_sectors_json)
model_sector_ids = []
for i in model_sectors_json:
model_sector_ids.append(i['id'])
first_sector_id = model_sector_ids[0]
first_sector_name = model_sectors_json[0]['name']
print('The '+ model_name +' model has ' + str(len(model_sectors_json)) + ' sectors.')
# INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
HC_indictr_id = model_indictrs_json[8]['id']
model_indictrs_names = []
model_indictrs_ids = []
for i in model_indictrs_json:
model_indictrs_names.append(i['name'])
model_indictrs_ids.append(i['id'])
print('The '+ model_name +' model has ' + str(len(model_indictrs_json)) + ' indicators. The names are:')
print(model_indictrs_names)
model_indictrs_ids
#INDICATORS
model_indictrs_response = r.get(base_url+model_name+'/indicators',headers=api_headers)
model_indictrs_json = model_indictrs_response.json()
model_indictrs_json
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
# D0 = D0_response.json()
# sorted(D0)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
# sorted(D0[0])
#
# Collect ALL Indicators from ALL Industr Sectors and Limit to Georgia
#
# D0_response = r.get(base_url+model_name+'/matrix/D?row=0',headers=api_headers)
D0_response = r.get(base_url+model_name+'/matrix/D',headers=api_headers)
D0 = D0_response.json()
#print(D0)
indicator_data = {}
# Add the industry sector IDs
# indicator_data.update({'industry':model_sector_ids})
indicator_data.update({'industry_code':[_.split('/')[0] for _ in model_sector_ids]})
indicator_data.update({'industry_detail':[_.split('/')[1] for _ in model_sector_ids]})
indicator_data.update({'industry_region':[_.split('/')[2] for _ in model_sector_ids]})
for key, values_list in zip(model_indictrs_ids, D0):
indicator_data.update({key:values_list})
all_indic_all_indust = pd.DataFrame(data=indicator_data)
# all_indic_all_indust.loc[0:20,['industry_code', 'industry_detail', 'ACID']].sort_values(by='ACID', ascending=False)
all_indic_all_indust.head(50)
all_indic_all_indust.min()
all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['ENRG'] !=0]
all_indic_all_indust=all_indic_all_indust.replace(0,0.0000000000000000000000001)
all_indic_all_indust.min()
all_indic_all_indust.max()
all_indic_all_indust=all_indic_all_indust[all_indic_all_indust['industry_region'] =='us-ga']
all_indic_all_indust
all_indic_all_indust.to_csv('indicators_sectors_GA.csv')
###Output
_____no_output_____
|
03_Grouping/Regiment/Exercises_SolvedbySelf.ipynb
|
###Markdown
Regiment Introduction:Special thanks to: http://chrisalbon.com/ for sharing the dataset and materials. Step 1. Import the necessary libraries
###Code
import pandas as pd
import numpy as np
###Output
_____no_output_____
###Markdown
Step 2. Create the DataFrame with the following values:
###Code
raw_data = {'regiment': ['Nighthawks', 'Nighthawks', 'Nighthawks', 'Nighthawks', 'Dragoons', 'Dragoons', 'Dragoons', 'Dragoons', 'Scouts', 'Scouts', 'Scouts', 'Scouts'],
'company': ['1st', '1st', '2nd', '2nd', '1st', '1st', '2nd', '2nd','1st', '1st', '2nd', '2nd'],
'name': ['Miller', 'Jacobson', 'Ali', 'Milner', 'Cooze', 'Jacon', 'Ryaner', 'Sone', 'Sloan', 'Piger', 'Riani', 'Ali'],
'preTestScore': [4, 24, 31, 2, 3, 4, 24, 31, 2, 3, 2, 3],
'postTestScore': [25, 94, 57, 62, 70, 25, 94, 57, 62, 70, 62, 70]}
###Output
_____no_output_____
###Markdown
Step 3. Assign it to a variable called regiment. Don't forget to name each column
###Code
regiment = pd.DataFrame(raw_data, columns = list(raw_data.keys()))
regiment.head()
###Output
_____no_output_____
###Markdown
Step 4. What is the mean preTestScore from the regiment Nighthawks?
###Code
regiment[regiment['regiment']=='Nighthawks']['preTestScore'].mean()
###Output
_____no_output_____
###Markdown
Step 5. Present general statistics by company
###Code
regiment.groupby('company').describe()
###Output
_____no_output_____
###Markdown
Step 6. What is the mean of each company's preTestScore?
###Code
regiment.groupby('company')['preTestScore'].mean()
###Output
_____no_output_____
###Markdown
Step 7. Present the mean preTestScores grouped by regiment and company
###Code
regiment.groupby(['regiment','company'])['preTestScore'].mean()
###Output
_____no_output_____
###Markdown
Step 8. Present the mean preTestScores grouped by regiment and company without heirarchical indexing
###Code
regiment.groupby(['regiment','company'])['preTestScore'].mean().unstack()
###Output
_____no_output_____
###Markdown
Step 9. Group the entire dataframe by regiment and company
###Code
regiment.groupby(['regiment','company']).head()
###Output
_____no_output_____
###Markdown
Step 10. What is the number of observations in each regiment and company
###Code
regiment.groupby(['regiment','company']).count().unstack()
regiment.groupby(['regiment','company']).size()
###Output
_____no_output_____
###Markdown
Step 11. Iterate over a group and print the name and the whole data from the regiment
###Code
for i in regiment.groupby('regiment'):
print(i)
###Output
_____no_output_____
|
Siamese-networks-medium-triplet.ipynb
|
###Markdown
One Shot Learning with Siamese NetworksThis is the jupyter notebook that accompanies ImportsAll the imports are defined here
###Code
%matplotlib inline
import torchvision
import torchvision.datasets as dset
import torchvision.transforms as transforms
from torch.utils.data import DataLoader,Dataset
import matplotlib.pyplot as plt
import torchvision.utils
import numpy as np
import random
from PIL import Image
import torch
from torch.autograd import Variable
import PIL.ImageOps
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
###Output
_____no_output_____
###Markdown
Helper functionsSet of helper functions
###Code
def imshow(img,text=None,should_save=False):
npimg = img.numpy()
plt.axis("off")
if text:
plt.text(75, 8, text, style='italic',fontweight='bold',
bbox={'facecolor':'white', 'alpha':0.8, 'pad':10})
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
def show_plot(iteration,loss):
plt.plot(iteration,loss)
plt.show()
###Output
_____no_output_____
###Markdown
Configuration ClassA simple class to manage configuration
###Code
class Config():
training_dir = "./data/faces/training/"
testing_dir = "./data/faces/testing/"
train_batch_size = 64
train_number_epochs = 100
###Output
_____no_output_____
###Markdown
Custom Dataset ClassThis dataset generates a pair of images. 0 for geniune pair and 1 for imposter pair
###Code
class SiameseNetworkDataset(Dataset):
def __init__(self,imageFolderDataset,transform=None,should_invert=True):
self.imageFolderDataset = imageFolderDataset
self.transform = transform
self.should_invert = should_invert
def __getitem__(self,index):
img0_tuple = random.choice(self.imageFolderDataset.imgs)
while True:
#keep looping till the same class image is found
img1_tuple = random.choice(self.imageFolderDataset.imgs)
if img0_tuple[1]==img1_tuple[1]:
break
while True:
#keep looping till a different class image is found
img2_tuple = random.choice(self.imageFolderDataset.imgs)
if img0_tuple[1] !=img2_tuple[1]:
break
img0 = Image.open(img0_tuple[0])
img1 = Image.open(img1_tuple[0])
img2 = Image.open(img2_tuple[0])
img0 = img0.convert("L")
img1 = img1.convert("L")
img2 = img2.convert("L")
if self.should_invert:
img0 = PIL.ImageOps.invert(img0)
img1 = PIL.ImageOps.invert(img1)
img2 = PIL.ImageOps.invert(img2)
if self.transform is not None:
img0 = self.transform(img0)
img1 = self.transform(img1)
img2 = self.transform(img2)
return img0, img1, img2
def __len__(self):
return len(self.imageFolderDataset.imgs)
###Output
_____no_output_____
###Markdown
Using Image Folder Dataset
###Code
folder_dataset = dset.ImageFolder(root=Config.training_dir)
siamese_dataset = SiameseNetworkDataset(imageFolderDataset=folder_dataset,
transform=transforms.Compose([transforms.Resize((100,100)),
transforms.ToTensor()
])
,should_invert=False)
print(len(siamese_dataset))
len_valid = 37*0
len_train = len(siamese_dataset) - len_valid
siamese_dataset, test_dataset = torch.utils.data.random_split(siamese_dataset, [len_train, len_valid])
###Output
370
###Markdown
Visualising some of the dataThe top row and the bottom row of any column is one pair. The 0s and 1s correspond to the column of the image.1 indiciates dissimilar, and 0 indicates similar.
###Code
vis_dataloader = DataLoader(siamese_dataset,
shuffle=True,
num_workers=8,
batch_size=8)
dataiter = iter(vis_dataloader)
example_batch = next(dataiter)
concatenated = torch.cat((example_batch[0],example_batch[1]),0)
concatenated = torch.cat((concatenated,example_batch[2]),0)
imshow(torchvision.utils.make_grid(concatenated))
###Output
_____no_output_____
###Markdown
Neural Net DefinitionWe will use a standard convolutional neural network
###Code
class SiameseNetwork(nn.Module):
def __init__(self):
super(SiameseNetwork, self).__init__()
self.cnn1 = nn.Sequential(
nn.ReflectionPad2d(1),
nn.Conv2d(1, 4, kernel_size=3),
nn.ReLU(inplace=True),
nn.BatchNorm2d(4),
nn.ReflectionPad2d(1),
nn.Conv2d(4, 8, kernel_size=3),
nn.ReLU(inplace=True),
nn.BatchNorm2d(8),
nn.ReflectionPad2d(1),
nn.Conv2d(8, 8, kernel_size=3),
nn.ReLU(inplace=True),
nn.BatchNorm2d(8),
)
self.fc1 = nn.Sequential(
nn.Linear(8*100*100, 500),
nn.ReLU(inplace=True),
nn.Linear(500, 500),
nn.ReLU(inplace=True),
nn.Linear(500, 5))
def forward_once(self, x):
output = self.cnn1(x)
output = output.view(output.size()[0], -1)
output = self.fc1(output)
return output
def forward(self, input1, input2, input3):
output1 = self.forward_once(input1)
output2 = self.forward_once(input2)
output3 = self.forward_once(input3)
return output1, output2, output3
###Output
_____no_output_____
###Markdown
Training Time!
###Code
train_dataloader = DataLoader(siamese_dataset,
shuffle=True,
num_workers=8,
batch_size=Config.train_batch_size)
net = SiameseNetwork().cuda()
criterion = torch.nn.TripletMarginLoss(margin=2.0,p=2)
optimizer = optim.Adam(net.parameters(),lr = 0.0005 )
counter = []
loss_history = []
iteration_number= 0
for epoch in range(0,Config.train_number_epochs):
for i, data in enumerate(train_dataloader,0):
img0, img1, img2 = data
img0, img1, img2 = img0.cuda(), img1.cuda(), img2.cuda()
optimizer.zero_grad()
output1,output2,output3 = net(img0,img1,img2)
loss_triplet = criterion(output1,output2,output3)
loss_triplet.backward()
optimizer.step()
if i %10 == 0 :
print("Epoch number {}\n Current loss {}\n".format(epoch,loss_triplet.item()))
iteration_number +=10
counter.append(iteration_number)
loss_history.append(loss_triplet.item())
show_plot(counter,loss_history)
###Output
Epoch number 0
Current loss 1.9760570526123047
Epoch number 1
Current loss 0.20188213884830475
Epoch number 2
Current loss 0.8885836005210876
Epoch number 3
Current loss 0.2169375717639923
Epoch number 4
Current loss 0.024289488792419434
Epoch number 5
Current loss 0.2693146765232086
Epoch number 6
Current loss 0.0
Epoch number 7
Current loss 0.0
Epoch number 8
Current loss 0.28175562620162964
Epoch number 9
Current loss 0.3968459665775299
Epoch number 10
Current loss 0.0
Epoch number 11
Current loss 0.0
Epoch number 12
Current loss 0.5303159952163696
Epoch number 13
Current loss 0.22767633199691772
Epoch number 14
Current loss 0.28010064363479614
Epoch number 15
Current loss 0.4042849838733673
Epoch number 16
Current loss 0.0
Epoch number 17
Current loss 0.0
Epoch number 18
Current loss 0.0
Epoch number 19
Current loss 0.1590598225593567
Epoch number 20
Current loss 0.09468108415603638
Epoch number 21
Current loss 0.0
Epoch number 22
Current loss 0.0
Epoch number 23
Current loss 0.0
Epoch number 24
Current loss 0.3086915612220764
Epoch number 25
Current loss 0.0
Epoch number 26
Current loss 0.0
Epoch number 27
Current loss 0.4594113826751709
Epoch number 28
Current loss 0.09872758388519287
Epoch number 29
Current loss 0.0
Epoch number 30
Current loss 0.0
Epoch number 31
Current loss 0.0
Epoch number 32
Current loss 0.0
Epoch number 33
Current loss 0.10054752230644226
Epoch number 34
Current loss 0.20497757196426392
Epoch number 35
Current loss 0.0
Epoch number 36
Current loss 0.25365936756134033
Epoch number 37
Current loss 0.0
Epoch number 38
Current loss 0.0
Epoch number 39
Current loss 0.0
Epoch number 40
Current loss 0.0
Epoch number 41
Current loss 0.7255319356918335
Epoch number 42
Current loss 0.0
Epoch number 43
Current loss 0.0
Epoch number 44
Current loss 0.0
Epoch number 45
Current loss 0.40389859676361084
Epoch number 46
Current loss 0.0
Epoch number 47
Current loss 0.0
Epoch number 48
Current loss 0.0
Epoch number 49
Current loss 0.0
Epoch number 50
Current loss 0.0
Epoch number 51
Current loss 0.30493801832199097
Epoch number 52
Current loss 0.0
Epoch number 53
Current loss 0.0
Epoch number 54
Current loss 0.049722909927368164
Epoch number 55
Current loss 0.20186275243759155
Epoch number 56
Current loss 0.0
Epoch number 57
Current loss 0.0
Epoch number 58
Current loss 0.0
Epoch number 59
Current loss 0.0
Epoch number 60
Current loss 0.0
Epoch number 61
Current loss 0.3806462287902832
Epoch number 62
Current loss 0.0
Epoch number 63
Current loss 0.13078629970550537
Epoch number 64
Current loss 0.0
Epoch number 65
Current loss 0.20559167861938477
Epoch number 66
Current loss 0.0
Epoch number 67
Current loss 0.0
Epoch number 68
Current loss 0.26312780380249023
Epoch number 69
Current loss 0.29392653703689575
Epoch number 70
Current loss 0.0
Epoch number 71
Current loss 0.0
Epoch number 72
Current loss 0.0
Epoch number 73
Current loss 0.0
Epoch number 74
Current loss 0.4233527183532715
Epoch number 75
Current loss 0.19520169496536255
Epoch number 76
Current loss 0.0
Epoch number 77
Current loss 0.5378351211547852
Epoch number 78
Current loss 0.0
Epoch number 79
Current loss 0.12065374851226807
Epoch number 80
Current loss 0.3406674861907959
Epoch number 81
Current loss 0.0
Epoch number 82
Current loss 0.0
Epoch number 83
Current loss 0.0
Epoch number 84
Current loss 0.13378310203552246
Epoch number 85
Current loss 0.0
Epoch number 86
Current loss 0.0
Epoch number 87
Current loss 0.0
Epoch number 88
Current loss 0.0
Epoch number 89
Current loss 0.0
Epoch number 90
Current loss 0.0
Epoch number 91
Current loss 0.20789432525634766
Epoch number 92
Current loss 0.3616853952407837
Epoch number 93
Current loss 0.0
Epoch number 94
Current loss 0.6088879108428955
Epoch number 95
Current loss 0.2575113773345947
Epoch number 96
Current loss 0.0
Epoch number 97
Current loss 0.0
Epoch number 98
Current loss 0.0
Epoch number 99
Current loss 0.4747195243835449
###Markdown
Some simple testingThe last 3 subjects were held out from the training, and will be used to test. The Distance between each image pair denotes the degree of similarity the model found between the two images. Less means it found more similar, while higher values indicate it found them to be dissimilar.
###Code
folder_dataset_test = dset.ImageFolder(root=Config.testing_dir)
siamese_dataset = SiameseNetworkDataset(imageFolderDataset=folder_dataset_test,
transform=transforms.Compose([transforms.Resize((100,100)),
transforms.ToTensor()
])
,should_invert=False)
test_dataloader = DataLoader(siamese_dataset,num_workers=6,batch_size=1,shuffle=True)
dataiter = iter(test_dataloader)
for i in range(5):
x0,x1,x2 = next(dataiter)
concatenated_ap = torch.cat((x0,x1),0)
concatenated_an = torch.cat((x0,x2),0)
output1,output2,output3 = net(Variable(x0).cuda(),Variable(x1).cuda(),Variable(x2).cuda())
euclidean_distance_ap = F.pairwise_distance(output1, output2)
euclidean_distance_an = F.pairwise_distance(output1, output3)
imshow(torchvision.utils.make_grid(concatenated_ap),'Dissimilarity: {:.2f}'.format(euclidean_distance_ap.item()))
imshow(torchvision.utils.make_grid(concatenated_an),'Dissimilarity: {:.2f}'.format(euclidean_distance_an.item()))
dataiter = iter(test_dataloader)
correct = 0
total = 0
threshold = 130
ap_dist_list = []
an_dist_list = []
with torch.no_grad():
for x0,x1,x2 in dataiter:
output1,output2,output3 = net(Variable(x0).cuda(),Variable(x1).cuda(),Variable(x2).cuda())
euclidean_distance_ap = F.pairwise_distance(output1, output2)
euclidean_distance_an = F.pairwise_distance(output1, output3)
ap_dist_list.append(euclidean_distance_ap.item())
an_dist_list.append(euclidean_distance_an.item())
if euclidean_distance_ap.item() <= threshold:
correct += 1
if euclidean_distance_an.item() > threshold:
correct += 1
total += 2
# correct += sum([i<=threshold for i in ap_dist_list])
# correct += sum([i>threshold for i in an_dist_list])
print('Max euclidean distance for anchor and positive: ', max(ap_dist_list))
print('Min euclidean distance for anchor and negative: ', min(an_dist_list))
print('Average euclidean distance for anchor and positive: %.2f, %.2f' % (np.mean(ap_dist_list), np.std(ap_dist_list)))
print('Average euclidean distance for anchor and negative: %.2f, %.2f' % (np.mean(an_dist_list), np.std(an_dist_list)))
print('Accuracy of the network on the test images: %d %%' % (
100 * correct / total))
folder_dataset_test = dset.ImageFolder(root=Config.testing_dir)
siamese_dataset = SiameseNetworkDataset(imageFolderDataset=folder_dataset_test,
transform=transforms.Compose([transforms.Resize((100,100)),
transforms.ToTensor()
])
,should_invert=False)
test_dataloader = DataLoader(siamese_dataset,num_workers=6,batch_size=1,shuffle=True)
@torch.no_grad()
def get_margin(net):
max_ap_dist = -np.inf
min_an_dist = np.inf
dataiter = iter(test_dataloader)
for x0,x1,x2 in dataiter:
output1,output2,output3 = net(Variable(x0).cuda(),Variable(x1).cuda(),Variable(x2).cuda())
euclidean_distance_ap = F.pairwise_distance(output1, output2)
euclidean_distance_an = F.pairwise_distance(output1, output3)
if euclidean_distance_ap.item() >= max_ap_dist:
max_ap_dist = euclidean_distance_ap.item()
if euclidean_distance_an.item() < min_an_dist:
min_an_dist = euclidean_distance_an.item()
return max_ap_dist, min_an_dist
def get_normalized_margin(net):
ap_dist_list = []
an_dist_list = []
for i in range(50):
max_ap_dist, min_an_dist = get_margin(net)
ap_dist_list.append(max_ap_dist)
an_dist_list.append(min_an_dist)
print('Anchor and postivie average maximum distance is ', np.mean(ap_dist_list))
print('Anchor and negative average maximum distance is ', np.mean(an_dist_list))
print('Normalized margin %.2f %%' % (100*(1 - np.mean(ap_dist_list)/np.mean(an_dist_list))))
get_normalized_margin(net)
###Output
Anchor and postivie average maximum distance is 85.31850852966309
Anchor and negative average maximum distance is 99.9259080505371
Normalized margin 14.62 %
|
create_blob.ipynb
|
###Markdown
Create a binary blob for an OAK-device from an object detection API model
This notebook is used to convert a TF model (more specifically one created using the object detection API) to a `.blob`-file used by OAK-devices.
There are two main steps to do this:
1. Convert the TF model into the OpenVINO intermediate representation (IR)
2. Compile the OpenVINO IR into a Myriad binary (`.blob`-file)
This notebook is based on these tutorials:
- https://docs.openvinotoolkit.org/latest/openvino_docs_MO_DG_prepare_model_convert_model_tf_specific_Convert_Object_Detection_API_Models.html
- https://docs.luxonis.com/en/latest/pages/tutorials/local_convert_openvino/compile-the-model Options
You may need to change these according to your paths and the model used.
For the `TRANSFORMATION_CONFIG` have a look at the [OpenVINO documentation](https://docs.openvinotoolkit.org/latest/openvino_docs_MO_DG_prepare_model_convert_model_tf_specific_Convert_Object_Detection_API_Models.html).
###Code
# Options
import os
MODEL_DIR = "./exported_models/ssd_mobilenet_v2_fpnlite_320x320/"
SAVED_MODEL = os.path.join(MODEL_DIR, "saved_model")
PIPELINE_CONFIG = os.path.join(MODEL_DIR, "pipeline.config")
OPENVINO_DIR = "/opt/intel/openvino_2021"
TRANSFORMATION_CONFIG = os.path.join(OPENVINO_DIR, "deployment_tools/model_optimizer/extensions/front/tf/ssd_support_api_v2.4.json")
###Output
_____no_output_____
###Markdown
Step 0: Install Prequisites (OpenVINO)
This assumes you are using Ubuntu (or any other distribution using the APT package manager, e.g. Debian).
For other ways to install OpenVINO refere to their [website](https://software.intel.com/content/www/us/en/develop/tools/openvino-toolkit/download.html) Add Intel OpenVINO GPG-key
###Code
!curl https://apt.repos.intel.com/openvino/2021/GPG-PUB-KEY-INTEL-OPENVINO-2021 -o openvino.gpg
!sudo apt-key add openvino.gpg
###Output
_____no_output_____
###Markdown
Add the repository
###Code
!echo "deb https://apt.repos.intel.com/openvino/2021/ all main"| sudo tee /etc/apt/sources.list.d/intel-openvino-2021.list
!sudo apt update
###Output
_____no_output_____
###Markdown
Install the package
###Code
!sudo apt -y install intel-openvino-dev-ubuntu20-2021.4.582
###Output
_____no_output_____
###Markdown
Install other OpenVINO dependencies/prerequisites
###Code
%cd /opt/intel/openvino_2021/deployment_tools/model_optimizer/install_prerequisites
!./install_prerequisites.sh
%cd
###Output
_____no_output_____
###Markdown
Step 1: Convert the model to OpenVINO IR Setup OpenVINO environment
###Code
!source {OPENVINO_DIR}/bin/setupvars.sh
###Output
_____no_output_____
###Markdown
Convert the model to OpenVINO IR
Use the `mo_tf.py` tool to convert a TF-model to OpenVINO IR.
This will generate three files: `saved_model.xml`, `saved_model.bin` and `saved_model.mapping`.
Options are:
- `saved_model_dir` should point to the `saved_model`-directory of the exported (frozen) model.
- `tensorflow_object_detection_api_pipeline_config` should point to the `pipeline.conf` file used to create the model.
- `transformation_config` points to a special config that helps the optimizer to convert the model. There are already some configs provided by OpenVINO. For more info check out [this](https://docs.openvinotoolkit.org/latest/openvino_docs_MO_DG_prepare_model_convert_model_tf_specific_Convert_Object_Detection_API_Models.html)
- `reverse_input_channels` is used to invert the order of the input channels, i.e. `RGB BGR`.
This is required if the model was trained with one order and you want to use inference with the other
###Code
!python3 {OPENVINO_DIR}/deployment_tools/model_optimizer/mo_tf.py --saved_model_dir {SAVED_MODEL} \
--tensorflow_object_detection_api_pipeline_config {PIPELINE_CONFIG} \
--transformations_config {TRANSFORMATION_CONFIG} \
--reverse_input_channels
###Output
_____no_output_____
###Markdown
Compile the IR to Myriad code for execution on the OAK-device
The OAK device cannot execute the OpenVINO IR directly so we have to compile it to a Myriad binary.
This takes as input the OpenVINO IR and generates a `saved_model.blob`-file.
###Code
!{OPENVINO_DIR}/deployment_tools/tools/compile_tool/compile_tool -m saved_model.xml -ip U8 -d MYRIAD -VPU_NUMBER_OF_SHAVES 6 -VPU_NUMBER_OF_CMX_SLICES 6
###Output
_____no_output_____
|
session-1/Session_1_first.ipynb
|
###Markdown
###Code
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
# creates our empty model then we start adding our neurons to it
model = Sequential();
# Dense is the type of layer we are adding.
# For now, don't worry about what layers are, we will explain soon!
# The most important thing is the units and input_dim parameters.
# This means we have only one neuron that accepts only one input.
model.add(Dense(units=1,input_dim=1))
# Build our model and setting which optimizer we will use and which loss function
model.compile(optimizer="sgd", loss = "mean_squared_error")
import numpy as np
# simple function Y = 2X - 3
xs = np.array([-1, 0, 1,2,3,4],dtype=float)
ys = np.array([-5,-3,-1,1,3,5],dtype=float)
model.fit(xs, ys,epochs=500)
print(model.predict([10.0]))
weights = model.layers[0].get_weights()[0]
bias = model.layers[0].get_weights()[1]
print("W1 = {0}".format(weights))
print("b = {0}".format(bias))
###Output
W1 = [[1.9999682]]
b = [-2.9999015]
|
PaperPlots/3_PartonShower_1step_ideal_topology.ipynb
|
###Markdown
Test of PS_Fullmodel_1step by LBNL (Slimming level 1) Setteing of circuits
###Code
import warnings
warnings.simplefilter('ignore')
from sample_algorithm.onestepSim_LBNL import runQuantum
circuit_LBNL1 = runQuantum(gLR=1,dophisplit=1)
from transpiler.optimization import slim
example1 = slim.circuit_optimization( circuit=circuit_LBNL1, slim_level=1, work_register = 'w', cut='high')
circuit_LBNL1_op = example1.slim()
circuit_LBNL1 = runQuantum(gLR=1,dophisplit=1)
from qiskit import(
QuantumCircuit,
execute,
Aer)
from qiskit.visualization import plot_histogram
from qiskit import *
def statevector(circ):
circ.remove_final_measurements()
simulator = Aer.get_backend('statevector_simulator')
job = execute(circ, simulator)
result = job.result()
statevector = result.get_statevector(circ)
return qiskit.quantum_info.Statevector(statevector).probabilities_dict()
###Output
_____no_output_____
###Markdown
New Optimizer vs Qiskit Before slimming
###Code
print(circuit_LBNL1.depth(), ',', circuit_LBNL1.__len__())
print('Gate counts:', circuit_LBNL1.count_ops())
circuit_LBNL1_basis = circuit_LBNL1.decompose()
print(circuit_LBNL1_basis.depth(), ',', circuit_LBNL1_basis.__len__())
print('Gate counts:', circuit_LBNL1_basis.count_ops())
###Output
309 , 493
Gate counts: OrderedDict([('cx', 187), ('t', 112), ('tdg', 84), ('h', 56), ('u3', 33), ('u1', 14), ('measure', 6), ('barrier', 1)])
###Markdown
After slimming
###Code
print(circuit_LBNL1_op.depth(), ',', circuit_LBNL1_op.__len__())
print('Gate counts:', circuit_LBNL1_op.count_ops())
circuit_LBNL1_op_basis = circuit_LBNL1_op.decompose()
print(circuit_LBNL1_op_basis.depth(), ',', circuit_LBNL1_op_basis.__len__())
print('Gate counts:', circuit_LBNL1_op_basis.count_ops())
circuit=circuit_LBNL1_op
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, simulator, shots=81920)
result = job.result()
counts = result.get_counts(circuit)
print(counts)
plot_histogram(counts,number_to_keep=None)
statevector(circuit_LBNL1_op)
print(81920*(0.14101480996166701))
print(81920*(0.13079599534594055))
print(81920*0.627151054356188)
print(81920*0.10103814033620448)
###Output
11551.933232059762
10714.80793873945
51376.21437285892
8277.044456341871
###Markdown
New Optimizer vs tket
###Code
from pytket.qiskit import qiskit_to_tk, tk_to_qiskit
from pytket.passes import (RemoveRedundancies, CommuteThroughMultis, CliffordSimp, RebaseIBM, O2Pass,
FullPeepholeOptimise, EulerAngleReduction, USquashIBM, SynthesiseIBM, PauliSimp,
GuidedPauliSimp, OptimisePhaseGadgets, SquashHQS, FlattenRegisters, KAKDecomposition,
RepeatPass, SequencePass)
from pytket import OpType
###Output
_____no_output_____
###Markdown
Before slimming
###Code
def passes2(circ_tk):
pass_list=[EulerAngleReduction(OpType.Rz, OpType.Rx),
RemoveRedundancies(),
GuidedPauliSimp(),
SquashHQS(),
FlattenRegisters(),
OptimisePhaseGadgets(),
KAKDecomposition(),
USquashIBM(),
CliffordSimp(),
FullPeepholeOptimise()]
RebaseIBM().apply(circ_tk)
CommuteThroughMultis().apply(circ_tk)
circ_tk_qiskit_copy = tk_to_qiskit(circ_tk)
circ_tk_copy = qiskit_to_tk(circ_tk_qiskit_copy)
best_pass = RebaseIBM()
mini = tk_to_qiskit(circ_tk).__len__()
for a_pass in pass_list:
#print(tk_to_qiskit(circ_tk_copy).__len__())
a_pass.apply(circ_tk_copy)
if circ_tk_copy.n_gates < mini :
mini = circ_tk_copy.n_gates
best_pass = a_pass
circ_tk_qiskit_copy = tk_to_qiskit(circ_tk)
circ_tk_copy = qiskit_to_tk(circ_tk_qiskit_copy)
best_pass.apply(circ_tk)
return circ_tk
circ = circuit_LBNL1
mystate_reduct_tk = qiskit_to_tk(circ)
RebaseIBM().apply(mystate_reduct_tk)
while tk_to_qiskit(mystate_reduct_tk).__len__() != tk_to_qiskit(passes2(mystate_reduct_tk)).__len__() :
mystate_reduct_tk = passes2(mystate_reduct_tk)
mystate_reduct_qiskit=tk_to_qiskit(mystate_reduct_tk)
print(mystate_reduct_qiskit.depth(), ',', mystate_reduct_qiskit.__len__())
print('Gate counts:', mystate_reduct_qiskit.count_ops())
circuit=mystate_reduct_qiskit
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, simulator, shots=81920)
result = job.result()
counts = result.get_counts(circuit)
print(counts)
plot_histogram(counts,number_to_keep=None)
for key,value in statevector(mystate_reduct_qiskit).items():
if value > 0.0000001:
print(key,value)
print(81920*(0.14101480996166776))
print(81920*(0.1307959953459411))
print(81920*0.6271510543561895)
print(81920*0.1010381403362049)
###Output
11551.933232059822
10714.807938739496
51376.21437285904
8277.044456341904
###Markdown
After slimming
###Code
circ = circuit_LBNL1_op
mystate_reduct_tk = qiskit_to_tk(circ)
RebaseIBM().apply(mystate_reduct_tk)
while tk_to_qiskit(mystate_reduct_tk).__len__() != tk_to_qiskit(passes2(mystate_reduct_tk)).__len__() :
mystate_reduct_tk = passes2(mystate_reduct_tk)
mystate_reduct_qiskit_op=tk_to_qiskit(mystate_reduct_tk)
print(mystate_reduct_qiskit_op.depth(), ',', mystate_reduct_qiskit_op.__len__())
print('Gate counts:', mystate_reduct_qiskit_op.count_ops())
circuit=mystate_reduct_qiskit_op
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, simulator, shots=81920)
result = job.result()
counts = result.get_counts(circuit)
print(counts)
plot_histogram(counts,number_to_keep=None)
for key,value in statevector(mystate_reduct_qiskit_op).items():
if value > 0.0000001:
print(key,value)
print(81920*(0.1410148099616668))
print(81920*(0.13079599534594022))
print(81920*0.6271510543561889)
print(81920*0.10103814033620487)
###Output
11551.933232059744
10714.807938739423
51376.214372858994
8277.044456341902
###Markdown
Conclusion・qiskit+my_optimizer > qiskit・tket+my_optimizer > tket
###Code
circ_list = [circuit_LBNL1_basis, circuit_LBNL1_op_basis, mystate_reduct_qiskit, mystate_reduct_qiskit_op]
depth_list = [circuit_LBNL1_basis.depth(), circuit_LBNL1_op_basis.depth(), mystate_reduct_qiskit.depth(),
mystate_reduct_qiskit_op.depth()]
import matplotlib.pyplot as plt
import numpy as np
n = 4
index = np.arange(n)
fig, ax = plt.subplots()
bar_width = 0.1
alpha = 0.8
name_list=['Original','My_optimizer','tket','tket+My_optimizer']
for i,circ in enumerate(circ_list):
native_gate_num =[depth_list[i],0,0,0]
for key,value in circ.count_ops().items():
if key == 'cx':
native_gate_num[2] += value
native_gate_num[1] += value
elif key != 'barrier' and key != 'measure':
native_gate_num[3] += value
native_gate_num[1] += value
plt.bar(index + i*bar_width, native_gate_num, bar_width, alpha=alpha ,label=name_list[i])
print(native_gate_num)
plt.ylim([0,500])
plt.title('Ideal Topology') # グラフのタイトル plt.xlabel('x')
plt.ylabel('Counts')
plt.xticks(index + 2.5*bar_width, ('Depth','Number of all gates','CX', 'U1,U2,U3'))
plt.grid(axis = 'y')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=10)
plt.show()
###Output
[309, 486, 187, 299]
[83, 114, 61, 53]
[279, 360, 185, 175]
[68, 88, 50, 38]
|
Diabetes Predictor [RF-KNN-Grid]/Female Pima Indian Diabetes.ipynb
|
###Markdown
NN Models Base model (basic Sequential) 1/4
###Code
from sklearn.model_selection import train_test_split
X = df.drop("Outcome", axis=1).values
y = df["Outcome"].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
#1/3 of set due to low amount of records
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
df.shape
model = Sequential()
model.add(Dense(9, activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(5, activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(3, activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(1, activation="sigmoid"))
model.compile(optimizer="adam", loss="binary_crossentropy")
from tensorflow.keras.callbacks import EarlyStopping
early_stop = EarlyStopping(monitor="val_loss", patience=8)
model.fit(X_train_scaled, y_train, validation_data=(X_test_scaled, y_test),
epochs=400, callbacks=[early_stop])
model.summary()
metrics = pd.DataFrame(model.history.history)
metrics.plot()
predictions = model.predict_classes(X_test_scaled)
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
###Output
[[152 5]
[ 68 29]]
precision recall f1-score support
0 0.69 0.97 0.81 157
1 0.85 0.30 0.44 97
accuracy 0.71 254
macro avg 0.77 0.63 0.62 254
weighted avg 0.75 0.71 0.67 254
###Markdown
KNN model 2/4
###Code
from sklearn.neighbors import KNeighborsClassifier
error_rate = []
for k in range(1, 40):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train_scaled, y_train)
pred_k = knn.predict(X_test_scaled)
error_rate.append(np.mean(pred_k != y_test))
np.array(error_rate)
np.argmin(error_rate)
knn = KNeighborsClassifier(n_neighbors=18)
knn.fit(X_train_scaled, y_train)
knn_preds = knn.predict(X_test_scaled)
print(confusion_matrix(y_test, knn_preds))
print(classification_report(y_test, knn_preds))
#performed slightly worse overall than the base model
###Output
[[144 13]
[ 54 43]]
precision recall f1-score support
0 0.73 0.92 0.81 157
1 0.77 0.44 0.56 97
accuracy 0.74 254
macro avg 0.75 0.68 0.69 254
weighted avg 0.74 0.74 0.72 254
###Markdown
Logistic Regression with GridSearch model 3/4
###Code
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
param_grid = {"penalty":['l1', 'l2', 'elasticnet', 'none'],
"tol":[0.0001, 0.0005, 0.001, 0.0002],
"C":[1.0, 0.5, 2, 0.2],
"solver":['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']}
grid = GridSearchCV(LogisticRegression(), param_grid=param_grid, verbose=1)
grid.fit(X_train_scaled, y_train)
grid.best_estimator_
grid.best_params_
lmgrid_preds = grid.best_estimator_.predict(X_test_scaled)
print(confusion_matrix(y_test, lmgrid_preds))
print(classification_report(y_test, lmgrid_preds))
#a slight improvement on the base model
###Output
[[142 15]
[ 45 52]]
precision recall f1-score support
0 0.76 0.90 0.83 157
1 0.78 0.54 0.63 97
accuracy 0.76 254
macro avg 0.77 0.72 0.73 254
weighted avg 0.77 0.76 0.75 254
###Markdown
RandomForest with GridSearch model 4/4
###Code
from sklearn.ensemble import RandomForestClassifier
rf_param_grid = {"n_estimators":[10,40,100,200],
"max_depth":[None,10,20,60,80],
"min_samples_split":[2,6,8,10,12],
"min_samples_leaf":[1,2,4],
"max_features":['auto','sqrt']}
rf_grid = GridSearchCV(RandomForestClassifier(), param_grid=rf_param_grid, verbose=1)
rf_grid.fit(X_train_scaled, y_train)
rf_grid.best_estimator_
rf_preds = rf_grid.best_estimator_.predict(X_test_scaled)
print(confusion_matrix(y_test, rf_preds))
print(classification_report(y_test, rf_preds))
#slightly better performance than the base model,
#but marginally worse than the logistic model
###Output
[[138 19]
[ 41 56]]
precision recall f1-score support
0 0.77 0.88 0.82 157
1 0.75 0.58 0.65 97
accuracy 0.76 254
macro avg 0.76 0.73 0.74 254
weighted avg 0.76 0.76 0.76 254
|
jupyter-example/jupyter-example-sol.ipynb
|
###Markdown
Jupyter example [Download exercises zip](../_static/generated/jupyter-example.zip)[Browse files online](https://github.com/DavidLeoni/jupman/tree/master/jupyter-example)Example of notebook for exercises in Jupyter files. **For python files based example and more, see** [Python example](../python-example/python-example.ipynb) What to do- unzip exercises in a folder, you should get something like this: ```jupyter-example jupyter-example.ipynb jupyter-example-sol.ipynb jupman.py my_lib.py```**WARNING**: to correctly visualize the notebook, it MUST be in an unzipped folder !- open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook `jupyter-example/jupyter-example.ipynb`- Go on reading that notebook, and follow instuctions inside.Shortcut keys:- to execute Python code inside a Jupyter cell, press `Control + Enter`- to execute Python code inside a Jupyter cell AND select next cell, press `Shift + Enter`- to execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press `Alt + Enter`- If the notebooks look stuck, try to select `Kernel -> Restart`
###Code
# REMEMBER TO IMPORT jupman !
# This cell needs to be executed only once, you can usually find it at the beginning of the worksheets
import sys
sys.path.append('../')
import jupman
x = [1,2,3]
y = x
jupman.pytut()
y = [1,2,3]
w = y[0]
jupman.pytut()
###Output
_____no_output_____
###Markdown
Exercise 1Implement `inc` function:
###Code
#jupman-strip
def helper(x):
return x + 1
#/jupman-strip
def inc(x):
#jupman-raise
return helper(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 2Implement `upper` function
###Code
#jupman-strip
def helper2(x):
return x.upper()
#/jupman-strip
def upper(x):
#jupman-raise
return helper2(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 3Note everything *after* the 'write here' comment will be discarded. Note you can put how many spaces you want in the comment
###Code
w = 5
# write here
x = 5 + 6
y = 6.4
z = x / y
###Output
_____no_output_____
###Markdown
Exercise 4Shows how to completely remove the content of a solution cell (including the solution comment) **EXERCISE**: write a function that prints 'hello'
###Code
# SOLUTION
def f():
print('hello')
###Output
_____no_output_____
###Markdown
Jupyter example [Download exercises zip](../_static/generated/jupyter-example.zip)[Browse files online](https://github.com/DavidLeoni/jupman/tree/master/jupyter-example)Example of notebook for exercises in Jupyter files. **For python files based example and more, see** [Python example](../python-example/python-example.ipynb) What to do- unzip exercises in a folder, you should get something like this: ```jupyter-example jupyter-example.ipynb jupyter-example-sol.ipynb jupman.py my_lib.py```**WARNING**: to correctly visualize the notebook, it MUST be in an unzipped folder !- open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook `jupyter-example/jupyter-example.ipynb`- Go on reading that notebook, and follow instuctions inside.Shortcut keys:- to execute Python code inside a Jupyter cell, press `Control + Enter`- to execute Python code inside a Jupyter cell AND select next cell, press `Shift + Enter`- to execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press `Alt + Enter`- If the notebooks look stuck, try to select `Kernel -> Restart`
###Code
# REMEMBER TO IMPORT jupman !
# This cell needs to be executed only once, you can usually find it at the beginning of the worksheets
import sys
sys.path.append('../')
import jupman
x = [1,2,3]
y = x
jupman.pytut()
y = [1,2,3]
w = y[0]
jupman.pytut()
###Output
_____no_output_____
###Markdown
Exercise 1Implement `inc` function:
###Code
#jupman-strip
def helper(x):
return x + 1
#/jupman-strip
def inc(x):
#jupman-raise
return helper(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 2Implement `upper` function
###Code
#jupman-strip
def helper2(x):
return x.upper()
#/jupman-strip
def upper(x):
#jupman-raise
return helper2(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 3Note everything *after* the 'write here' comment will be discarded. Note you can put how many spaces you want in the comment
###Code
w = 5
# write here
x = 5 + 6
y = 6.4
z = x / y
###Output
_____no_output_____
###Markdown
Exercise 4Shows how to completely remove the content of a solution cell (including the solution comment) **EXERCISE**: write a function that prints 'hello'
###Code
# SOLUTION
def f():
print('hello')
###Output
_____no_output_____
###Markdown
Jupyter example [Download exercises zip](../_static/generated/jupyter-example.zip)[Browse files online](https://github.com/DavidLeoni/jupman/tree/master/jupyter-example)Example of notebook for exercises in Jupyter files. **For python files based example and more, see** [Python example](../python-example/python-example.ipynb) What to do- unzip exercises in a folder, you should get something like this: ```jupyter-example jupyter-example.ipynb jupyter-example-sol.ipynb jupman.py my_lib.py```**WARNING**: to correctly visualize the notebook, it MUST be in an unzipped folder !- open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook `jupyter-example/jupyter-example.ipynb`- Go on reading that notebook, and follow instuctions inside.Shortcut keys:- to execute Python code inside a Jupyter cell, press `Control + Enter`- to execute Python code inside a Jupyter cell AND select next cell, press `Shift + Enter`- to execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press `Alt + Enter`- If the notebooks look stuck, try to select `Kernel -> Restart`
###Code
# REMEMBER TO IMPORT jupman !
# This cell needs to be executed only once, you can usually find it at the beginning of the worksheets
import sys
sys.path.append('../')
import jupman
x = [1,2,3]
y = x
jupman.pytut()
y = [1,2,3]
w = y[0]
jupman.pytut()
###Output
_____no_output_____
###Markdown
Exercise 1Implement `inc` function:
###Code
#jupman-strip
def helper(x):
return x + 1
#/jupman-strip
def inc(x):
#jupman-raise
return helper(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 2Implement `upper` function
###Code
#jupman-strip
def helper2(x):
return x.upper()
#/jupman-strip
def upper(x):
#jupman-raise
return helper2(x)
#/jupman-raise
###Output
_____no_output_____
###Markdown
Exercise 3Note everything *after* the 'write here' comment will be discarded. Note you can put how many spaces you want in the comment
###Code
w = 5
# write here
x = 5 + 6
y = 6.4
z = x / y
###Output
_____no_output_____
###Markdown
Exercise 4Shows how to completely remove the content of a solution cell (including the solution comment) **EXERCISE**: write a function that prints 'hello'
###Code
# SOLUTION
def f():
print('hello')
###Output
_____no_output_____
|
jupyter/Pandas analysis.ipynb
|
###Markdown
Use PANDAS to perform analysis.
###Code
import pandas as pd
p1 = pd.read_csv("../big_test/0_4:9500000-10500000.EAS", sep = " ", header=None)
print(p1.shape)
p2 = pd.read_csv('../big_test/0_4:9500000-10500000.EUR', sep=" ", header=None)
p2[[0,2]]
#print(p2.shape)
p3 = pd.merge(p1,p2,how="outer", on=0)
#p3
###Output
(4314, 3)
|
preprocessing/csr_experience_ETL.ipynb
|
###Markdown
Data preparation for the machine learning modelThis file reads in the biographies from S&P Capital IQ and the manually researched DEF 14A statement biographies and chooses 150 random samples from the S&P Capital IQ dataset and 50 random samples from the DEF 14A dataset as the training sample for the fine-tuning of the Longformer model.These 200 training samples will be manually reviewed and social and/or environmental experience will be flagged so that this dataset can then be used to train the Longformer model which will classify the remaining biographies.
###Code
from google.colab import drive
drive.mount('/content/drive')
import numpy as np
import pandas as pd
from glob import glob
import re
import math
from numpy.random import RandomState
# diplay columns without truncation
pd.set_option('display.max_columns', 500)
# diplay rows without truncation
# pd.set_option('display.max_rows', 1000)
###Output
_____no_output_____
###Markdown
Reading in data
###Code
# reading in the excel files with the directors' biographies
file_path = r''
all_files = glob(file_path + '/content/drive/My Drive/director-csr/directors/*.xls')
list_df = []
for file in all_files:
df_file = pd.read_excel(file, skiprows=7) # skipping the first 7 rows above the header
list_df.append(df_file)
df_directors = pd.concat(list_df, axis=0, ignore_index=True)
# reading in the constituents file of the S&P 500 Index
comp_excel = pd.ExcelFile('/content/drive/My Drive/director-csr/Reuters/SP500.xlsx')
sheet_names = ['2015', '2014', '2013', '2012', '2011']
df_dict = {}
for sheet in sheet_names:
df_temp = pd.read_excel(comp_excel, sheet)
df_dict[sheet] = df_temp
df_dict.keys()
df_dict['2015'].head()
###Output
_____no_output_____
###Markdown
Merging biographies and companies
###Code
# renaming the dataframe columns for the 2015 constitutents list of df_dict
df_sp500 = df_dict['2015'].rename(columns={'TICKER SYMBOL': 'ticker', 'NAME.1': 'comp_name'})
# dropping irrelevant and duplicate columns
df_sp500.drop(columns=['Type', 'NAME', 'ISIN CODE'], inplace=True)
# convert all comp_name to lower case
df_sp500['comp_name'] = df_sp500['comp_name'].apply(lambda x: x.lower())
df_sp500.head()
# first 5 rows of the dataframe
df_directors.head()
# renaming some df columns
df_directors = df_directors.rename(columns={'Person Name': 'name',
'Company Name [Any Professional Record] [Current Matching Results]': 'comp_name',
'Exchange:Ticker': 'ticker',
'Biographies': 'bio'
})
# dropping unnecessary columns for now
df_dir_upper = df_directors[['name', 'ticker', 'bio']]
# list of all the columns in the directors dataframe
list(df_directors.columns)
# check how many entries don't have a company ticker
df_dir_upper[df_dir_upper['ticker'] == '-'].count()
# clean up the ticker column and remove the stock exchange information
df_dir_upper.loc[:, 'ticker'] = df_dir_upper['ticker'].apply(lambda x: x.split(':')[1] if ':' in x else x).copy()
# how many unique companies are included in this dataset
comp_numb = len(df_dir_upper['ticker'].unique().tolist())
print('Number of unique companies in dataframe:', comp_numb)
# how many directors are in this dataframe
df_dir_upper.shape
# checking for duplicate entries
print('Number of unique directors in dataframe:', len(df_dir_upper['bio'].unique()))
# creating new dataframe that only includes the directors of S&P500 companies
df_dir_sp500 = df_sp500.merge(df_dir_upper, on='ticker')
df_dir_sp500
###Output
_____no_output_____
###Markdown
Writing the merged S&P500 and director biographies dataframe to an Excel file
###Code
# writing to Excel file
df_dir_sp500.to_excel('/content/drive/My Drive/director-csr/sp500_biographies_2015.xlsx')
###Output
_____no_output_____
###Markdown
Randomly selecting 100 examples for manual review and train, val, test datasets
###Code
# generate 100 numbers randomly
number_42 = RandomState(42)
train_100 = number_42.randint(0,1413,100)
train_100 = list(train_100)
print(train_100)
# check for duplicates
len(set(train_100))
# remove duplicates
train_100 = list(set(train_100))
###Output
_____no_output_____
###Markdown
Unfortunately, the above list of random integers contains 3 duplicates which were not filtered out before the manual review started. Therefore, a list of three random integers will be generated to add these to the list of 97 to get a full 100 samples.
###Code
# generate additional 3 random integers
number_21 = RandomState(21)
train_3 = number_21.randint(0,1413,3)
train_3 = list(train_3)
train_3
# check the two lists for duplicates now
train_100.extend(train_3)
len(set(train_100))
# add an additional of 50 examples because 100 examples were too little
number_13 = RandomState(13)
train_50 = number_13.randint(0,1413,55)
train_50 = list(train_50)
# check for duplicates in train_50
len(set(train_50))
# check for duplicates between the previous 100 examples and the 50 new examples
duplicates = set(train_100) & set(train_50)
print('Duplicates in train_50:', duplicates)
# remove the duplicates from train_50
train_50 = set(train_50) - set(duplicates)
print('Unique values in train_50 after deletion:', len(set(train_50)))
print('Duplicates in both train_100 and train_50 after deletion:', set(train_50) & set(train_100))
###Output
Duplicates in train_50: {1184, 1267, 166}
Unique values in train_50 after deletion: 50
Duplicates in both train_100 and train_50 after deletion: set()
###Markdown
Because the above list of numbers contains 53 items, the three duplicates can be disregarded and we will still have 150 examples in total
###Code
# combine the 100 with the 50 new examples
train_100.extend(train_50)
# get the randomly chosen
train_df = df_dir_sp500.iloc[train_100,:]
train_df.head()
# final check for duplicates
len(train_df.index)
###Output
_____no_output_____
###Markdown
Write biography review sample from S&P Capital IQ to Excel file An important thing to note: I will export this dataframe to an excel file and manually review these biographies to get training and testing data sets.I will tag everything as 1 in the target values if the words match something that could be CSR-related. Even if it is green washing or could be green washing. The machine won't know that just from the words. Once I have tagged, trained, tested, and run the model and I get results back, then I will check whether the flagged people are actually green/social.In 1282 "adult literacy and workforce development" was found and coded as 1 for social. This should be included in the keyword list in the thesis.
###Code
# write the dataframe to an Excel file
train_df_bio = train_df[['bio']]
train_df_bio.to_excel('/content/drive/My Drive/director-csr/review_data/train_150.xlsx')
###Output
_____no_output_____
###Markdown
Create manual review sample from director data that was manually researched from DEF 14AsWhen I first created the above manual review sample of biographies from the S&P Capital IQ biography dataset, I was under the impression that all of the relevant directors in my overall analysis sample were included in it. However, it turned out after I gathered the board membership data and cleaned the data (in the `biography_matching.ipynb` notebook) that only about ~ 1200 directors were included. Therefore, I had to manually research the remaining ~ 4100 directors and their biographies from DEF 14As. The structure, layout and content of the biographies from the S&P Capital IQ dataset and the DEF 14As are very similar. Because certain formulations differ, such as mentioning of committee memberships, I will create another manual review sample from the DEF 14A biographies including 50 samples so that my machine learning model will have seen both types of biographies in the training phase.
###Code
# read in the overall director sample including their biographies
dir_sample_df = pd.read_excel('/content/drive/My Drive/director-csr/complete_sample.xlsx')
dir_sample_df.drop(columns=['Unnamed: 0'], inplace=True)
dir_sample_df.head()
# shape of the director dataframe
dir_sample_df.shape
# clean the sp500 bio data so that it will compare to the cleaned bios in the dir_sample_df
train_df['bio'] = train_df['bio'].apply(lambda x: x.replace('\n', ' '))
train_df['bio'] = train_df['bio'].apply(lambda x: x.replace('\t', ' '))
train_df['bio'] = train_df['bio'].apply(lambda x: re.sub('\s+', ' ', x).strip())
# how many unique directors are included in this sample
num_unique_dirs = len(list(dir_sample_df['unique_dir_id'].unique()))
print('Unique directors included in dataset:', num_unique_dirs)
unique_dirs_df = dir_sample_df[~dir_sample_df.duplicated(subset=['unique_dir_id'], keep='first')]
# shape of the dataframe including bios used in SP Capital IQ review sample
print(unique_dirs_df.shape)
unique_dirs_df = unique_dirs_df[~unique_dirs_df['biographies'].isin(train_df['bio'].values)]
# shape of the dataframe after removing the bios used in SP Capital IQ review sample
print(unique_dirs_df.shape)
# directors not in the S&P Capital IQ dataset
num_dirs_new = unique_dirs_df.shape[0]
# all unique indices
unique_index = unique_dirs_df.index
unique_index
# randomly select 150 samples
number_21 = RandomState(21)
train_50 = number_21.randint(0,num_dirs_new,50)
train_50 = list(train_50)
print(train_50)
# get the review sample
train_50_review = unique_dirs_df.iloc[train_50, :]
train_50_review.head()
# write the dataframe to an Excel file
train_50_review = train_50_review[['biographies']]
train_50_review.to_excel('/content/drive/My Drive/director-csr/review_data/train_second_50.xlsx')
###Output
_____no_output_____
|
reference/approximate/quantum_chemistry.ipynb
|
###Markdown
Trusted Notebook" width="250 px" align="left"> _*VQE algorithm: Application to quantum chemistry*_ The latest version of this notebook is available on https://github.com/QISKit/qiskit-tutorial.*** ContributorsAntonio Mezzacapo, Jay Gambetta IntroductionOne of the most compelling possibilities of quantum computation is the the simulation of other quantum systems. Quantum simulation of quantum systems encompasses a wide range of tasks, including most significantly: 1. Simulation of the time evolution of quantum systems.2. Computation of ground state properties. These applications are especially useful when considering systems of interacting fermions, such as molecules and strongly correlated materials. The computation of ground state properties of fermionic systems is the starting point for mapping out the phase diagram of condensed matter Hamiltonians. It also gives access to the key question of electronic structure problems in quantum chemistry, namely reaction rates. The focus of this notebook is on molecular systems, which are considered to be the ideal bench test for early-stage quantum computers, due to their relevance in chemical applications despite relatively modest sizes. Formally, the ground state problem asks the following:For some physical Hamiltonian *H*, find the smallest eigenvalue $E_G$, such that $H|\psi_G\rangle=E_G|\psi_G\rangle$, where $|\Psi_G\rangle$ is the eigenvector corresponding to $E_G$. It is known that in general this problem is intractable, even on a quantum computer. This means that we cannot expect an efficient quantum algorithm that prepares the ground state of general local Hamiltonians. Despite this limitation, for specific Hamiltonians of interest it might be possible, given physical constraints on the interactions, to solve the above problem efficiently. Currently, at least four different methods exist to approach this problem:1. Quantum phase estimation: Assuming that we can approximately prepare the state $|\psi_G\rangle$, this routine uses controlled implementations of the Hamiltonian to find its smallest eigenvalue. 2. Adiabatic theorem of quantum mechanics: The quantum system is adiabatically dragged from being the ground state of a trivial Hamiltonian to the one of the target problem, via slow modulation of the Hamiltonian terms. 3. Dissipative (non-unitary) quantum operation: The ground state of the target system is a fixed point. The non-trivial assumption here is the implementation of the dissipation map on quantum hardware. 4. Variational quantum eigensolvers: Here we assume that the ground state can be represented by a parameterization containing a relatively small number of parameters.In this notebook we focus on the last method, as this is most likely the simplest to be realized on near-term devices. The general idea is to define a parameterization $|\psi(\boldsymbol\theta)\rangle$ of quantum states, and minimize the energy $$E(\boldsymbol\theta) = \langle \psi(\boldsymbol\theta)| H |\psi(\boldsymbol\theta)\rangle,$$ The key ansatz is that the number of parameters $|\boldsymbol\theta^*|$ that minimizes the energy function scales polynomially with the size (e.g., number of qubits) of the target problem. Then, any local fermionic Hamiltonian can be mapped into a sum over Pauli operators $P_i$, $$H\rightarrow H_P = \sum_i^M w_i P_i,$$ and the energy corresponding to the state $|\psi(\boldsymbol\theta\rangle$, $E(\boldsymbol\theta)$, can be estimated by sampling the individual Pauli terms $P_i$ (or sets of them that can be measured at the same time) on a quantum computer$$E(\boldsymbol\theta) = \sum_i^M w_i \langle \psi(\boldsymbol\theta)| P_i |\psi(\boldsymbol\theta)\rangle.$$ Last, some optimization technique has to be devised in order to find the optimal value of parameters $\boldsymbol\theta^*$, such that $|\psi(\boldsymbol\theta^*)\rangle\equiv|\psi_G\rangle$. Fermionic HamiltoniansThe Hamiltonians describing systems of interacting fermions can be expressed in second quantization language, considering fermionic creation (annihilation) operators $a^\dagger_\alpha(a_\alpha)$, relative to the $\alpha$-th fermionic mode. In the case of molecules, the $\alpha$ labels stand for the different atomic or molecular orbitals. Within the second-quantization framework, a generic molecular Hamiltonian with $M$ orbitals can be written as $$H =H_1+H_2=\sum_{\alpha, \beta=0}^{M-1} t_{\alpha \beta} \, a^\dagger_{\alpha} a_{\beta} +\frac{1}{2} \sum_{\alpha, \beta, \gamma, \delta = 0}^{M-1} u_{\alpha \beta \gamma \delta}\, a^\dagger_{\alpha} a^\dagger_{\gamma} a_{\delta} a_{\beta},$$with the one-body terms representing the kinetic energy of the electrons and the potential energy that they experience in the presence of the nuclei, $$ t_{\alpha\beta}=\int d\boldsymbol x_1\Psi_\alpha(\boldsymbol{x}_1) \left(-\frac{\boldsymbol\nabla_1^2}{2}+\sum_{i} \frac{Z_i}{|\boldsymbol{r}_{1i}|}\right)\Psi_\beta (\boldsymbol{x}_1),$$and their interactions via Coulomb forces $$ u_{\alpha\beta\gamma\delta}=\int\int d \boldsymbol{x}_1 d \boldsymbol{x}_2 \Psi_\alpha^*(\boldsymbol{x}_1)\Psi_\beta(\boldsymbol{x}_1)\frac{1}{|\boldsymbol{r}_{12}|}\Psi_\gamma^*(\boldsymbol{x}_2)\Psi_\delta(\boldsymbol{x}_2),$$where we have defined the nuclei charges $Z_i$, the nuclei-electron and electron-electron separations $\boldsymbol{r}_{1i}$ and $\boldsymbol{r}_{12}$, the $\alpha$-th orbital wavefunction $\Psi_\alpha(\boldsymbol{x}_1)$, and we have assumed that the spin is conserved in the spin-orbital indices $\alpha,\beta$ and $\alpha,\beta,\gamma,\delta$. Molecules considered in this notebook and mapping to qubitsWe consider in this notebook the optimization of two potential energy surfaces, for the hydrogen and lithium hydride molecules, obtained using the STO-3G basis. The molecular Hamiltonians are computed as a function of their interatomic distance, then mapped to two- (H$_2$) and four- (LiH$_2$) qubit problems, via elimination of core and high-energy orbitals and removal of $Z_2$ symmetries. Approximate universal quantum computing for quantum chemisty problemsIn order to find the optimal parameters $\boldsymbol\theta^*$, we set up a closed optimization loop with a quantum computer, based on some stochastic optimization routine. Our choice for the variational ansatz is a deformation of the one used for the optimization of classical combinatorial problems, with the inclusion of $Z$ rotation together with the $Y$ ones. The optimization algorithm for fermionic Hamiltonians is similar to the one for combinatorial problems, and can be summarized as follows: 1. Map the fermionic Hamiltonian $H$ to a qubit Hamiltonian $H_P$.2. Choose the maximum depth of the quantum circuit (this could be done adaptively).3. Choose a set of controls $\boldsymbol\theta$ and make a trial function $|\psi(\boldsymbol\theta)\rangle$. The difference with the combinatorial problems is the insertion of additional parametrized $Z$ single-qubit rotations.4. Evaluate the energy $E(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H_P|~\psi(\boldsymbol\theta)\rangle$ by sampling each Pauli term individually, or sets of Pauli terms that can be measured in the same tensor product basis.5. Use a classical optimizer to choose a new set of controls.6. Continue until the energy has converged, hopefully close to the real solution $\boldsymbol\theta^*$ and return the last value of $E(\boldsymbol\theta)$. Note that, as opposed to the classical case, in the case of a quantum chemistry Hamiltonian one has to sample over non-computational states that are superpositions, and therefore take advantage of using a quantum computer in the sampling part of the algorithm. Motivated by the quantum nature of the answer, we also define a variational trial ansatz in this way: $$|\psi(\boldsymbol\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle$$where $U_\mathrm{entangler}$ is a collection of cPhase gates (fully entangling gates), $U_\mathrm{single}(\boldsymbol\theta) = \prod_{i=1}^n Y(\theta_{i})Z(\theta_{n+i})$ are single-qubit $Y$ and $Z$ rotation, $n$ is the number of qubits and $m$ is the depth of the quantum circuit. References and additional details:[1] A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow, and J. M. Gambetta, *Hardware-efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets*, Nature 549, 242 (2017), and references therein.
###Code
# Checking the version of PYTHON; we only support > 3.5
import sys
if sys.version_info < (3,5):
raise Exception('Please use Python version 3.5 or greater.')
# useful additional packages
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from scipy import linalg as la
from functools import partial
# importing the QISKit
from qiskit import QuantumProgram
import Qconfig
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# import optimization tools
from qiskit.tools.apps.optimization import trial_circuit_ryrz, SPSA_optimization, SPSA_calibration
from qiskit.tools.apps.optimization import Hamiltonian_from_file, make_Hamiltonian
from qiskit.tools.apps.optimization import eval_hamiltonian, group_paulis
# Ignore warnings due to chopping of small imaginary part of the energy
import warnings
warnings.filterwarnings('ignore')
###Output
_____no_output_____
###Markdown
Optimization of H2 at bond lengthIn this first part of the notebook we show the optimization of the H$_2$ Hamiltonian in the STO-3G basis at the bond length of 0.735 Angstrom. After mapping it to a four-qubit system with a binary-tree transformation, two spin-parity symmetries are modded out, leading to a two-qubit Hamiltonian. The energy of the mapped Hamiltonian obtained is then minimized using the variational ansatz described in the introduction, and a stochastic perturbation simultaneous approximation (SPSA) gradient descent method.
###Code
n=2
m=6
device='local_qasm_simulator'
initial_theta=np.random.randn(2*n*m)
entangler_map={0: [1]} # the map of two-qubit gates with control at key and target at values
shots=1
max_trials=100
ham_name='H2/H2Equilibrium.txt'
# Exact Energy
pauli_list=Hamiltonian_from_file(ham_name)
H=make_Hamiltonian(pauli_list)
exact=np.amin(la.eig(H)[0]).real
print('The exact ground state energy is:')
print(exact)
pauli_list_grouped=group_paulis(pauli_list)
# Optimization
Q_program = QuantumProgram()
Q_program.set_api(Qconfig.APItoken,Qconfig.config["url"])
def cost_function(Q_program,H,n,m,entangler_map,shots,device,theta):
return eval_hamiltonian(Q_program,H,trial_circuit_ryrz(n,m,theta,entangler_map,None,False),shots,device).real
initial_c=0.01
target_update=2*np.pi*0.1
save_step = 20
if shots ==1:
SPSA_params=SPSA_calibration(partial(cost_function,Q_program,H,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
output=SPSA_optimization(partial(cost_function,Q_program,H,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1);
else:
SPSA_params=SPSA_calibration(partial(cost_function,Q_program,pauli_list_grouped,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
output=SPSA_optimization(partial(cost_function,Q_program,pauli_list_grouped,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1);
plt.plot(np.arange(0, max_trials,save_step),output[2],label='E(theta_plus)')
plt.plot(np.arange(0, max_trials,save_step),output[3],label='E(theta_minus)')
plt.plot(np.arange(0, max_trials,save_step),np.ones(max_trials//save_step)*output[0],label='Final Energy')
plt.plot(np.arange(0, max_trials,save_step),np.ones(max_trials//save_step)*exact,label='Exact Energy')
plt.legend()
plt.xlabel('Trial state')
plt.ylabel('Energy')
###Output
_____no_output_____
###Markdown
Optimizing the potential energy surface The optimization considered previously is now performed for two molecules, H$_2$ and LiH, for different interatomic distances, and the correspoding nuclei Coulomb repulsion is added in order to obtain a potential energy surface.
###Code
# MOLECULE PARAMETERS
molecule='H2' # name of the molecule: options are H2 or LiH
if molecule=='H2':
n=2 # qubits
Z1=1
Z2=1
min_distance=.2
max_distance=4
number_of_points=39
elif molecule=='LiH':
n=4 # qubits
Z1=1
Z2=3
min_distance=.5
max_distance=5
number_of_points=46
# OPTIMIZATION PARAMETERS
run_optimization=True # Choose True or False. False just plots the exact potential energy surface
def cost_function(Q_program,H,n,m,entangler_map,shots,device,theta):
return eval_hamiltonian(Q_program,H,trial_circuit_ryrz(n,m,theta,entangler_map,None,False),shots,device).real
m=3 # depth (number of layers of sq gates - # entanglers is this number -1)
device='local_qasm_simulator'
initial_theta=np.random.randn(2*n*m) # initial angles
entangler_map={0: [1]} # the map of two-qubit gates with control at key and target at values
shots=1
max_trials=200
initial_c = 0.01
target_update = 2*np.pi*0.1
save_step = 250 #Setting larger than max_trials to suppress the output at every function call
#################### COMPUTING THE POTENTIAL ENERGY SURFACE ###################
mol_distance=np.zeros(number_of_points)
coulomb_repulsion=np.zeros(number_of_points)
electr_energy=np.zeros(number_of_points)
electr_energy_optimized=np.zeros(number_of_points)
Q_program = QuantumProgram()
Q_program.set_api(Qconfig.APItoken,Qconfig.config["url"])
for i in range(number_of_points):
# %%%%%%%%%%%%% Coulomb Repulsion For Diatomic Molecules %%%%%%%%%%%%%%%%%%%%%%
mol_distance[i]=np.around((min_distance+(max_distance-min_distance)*i/(number_of_points-1)),2)
distance=mol_distance[i]/0.529177
coulomb_repulsion[i]=Z1*Z2/distance
# exact diagonalization
ham_text=molecule+'/PESMap'+str(i)+'atdistance'+str(mol_distance[i])+'.txt'
pauli_list=Hamiltonian_from_file(ham_text)
H=make_Hamiltonian(pauli_list)
pauli_list_grouped = group_paulis(pauli_list)
eigen=la.eig(H)
electr_energy[i]=np.amin(eigen[0])
# optimization
if run_optimization:
print('\nOPTIMIZING HAMILTONIAN # '+str(i)+' AT INTERATOMIC DISTANCE ' + str(mol_distance[i]) + ' ANGSTROM\n')
if shots !=1:
H=group_paulis(pauli_list)
SPSA_params = SPSA_calibration(partial(cost_function,Q_program,H,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
electr_energy_optimized[i] = SPSA_optimization(partial(cost_function,Q_program,H,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1)[0];
plt.plot(mol_distance,electr_energy+coulomb_repulsion,label='Exact')
if run_optimization:
plt.plot(mol_distance,electr_energy_optimized+coulomb_repulsion,label='Optimized')
plt.xlabel('Atomic distance (Angstrom)')
plt.ylabel('Energy')
plt.legend()
%run "../version.ipynb"
###Output
_____no_output_____
###Markdown
Trusted Notebook" width="250 px" align="left"> _*VQE algorithm: Application to quantum chemistry*_ The latest version of this notebook is available on https://github.com/QISKit/qiskit-tutorial.*** ContributorsAntonio Mezzacapo, Jay Gambetta IntroductionOne of the most compelling possibilities of quantum computation is the the simulation of other quantum systems. Quantum simulation of quantum systems encompasses a wide range of tasks, including most significantly: 1. Simulation of the time evolution of quantum systems.2. Computation of ground state properties. These applications are especially useful when considering systems of interacting fermions, such as molecules and strongly correlated materials. The computation of ground state properties of fermionic systems is the starting point for mapping out the phase diagram of condensed matter Hamiltonians. It also gives access to the key question of electronic structure problems in quantum chemistry - namely, reaction rates. The focus of this notebook is on molecular systems, which are considered to be the ideal bench test for early-stage quantum computers, due to their relevance in chemical applications despite relatively modest sizes. Formally, the ground state problem asks the following:For some physical Hamiltonian *H*, find the smallest eigenvalue $E_G$, such that $H|\psi_G\rangle=E_G|\psi_G\rangle$, where $|\Psi_G\rangle$ is the eigenvector corresponding to $E_G$. It is known that in general this problem is intractable, even on a quantum computer. This means that we cannot expect an efficient quantum algorithm that prepares the ground state of general local Hamiltonians. Despite this limitation, for specific Hamiltonians of interest it might be possible, given physical constraints on the interactions, to solve the above problem efficiently. Currently, at least four different methods exist to approach this problem:1. Quantum phase estimation: Assuming that we can approximately prepare the state $|\psi_G\rangle$, this routine uses controlled implementations of the Hamiltonian to find its smallest eigenvalue. 2. Adiabatic theorem of quantum mechanics: The quantum system is adiabatically dragged from being the ground state of a trivial Hamiltonian to the one of the target problem, via slow modulation of the Hamiltonian terms. 3. Dissipative (non-unitary) quantum operation: The ground state of the target system is a fixed point. The non-trivial assumption here is the implementation of the dissipation map on quantum hardware. 4. Variational quantum eigensolvers: Here we assume that the ground state can be represented by a parameterization containing a relatively small number of parameters.In this notebook we focus on the last method, as this is most likely the simplest to be realized on near-term devices. The general idea is to define a parameterization $|\psi(\boldsymbol\theta)\rangle$ of quantum states, and minimize the energy $$E(\boldsymbol\theta) = \langle \psi(\boldsymbol\theta)| H |\psi(\boldsymbol\theta)\rangle,$$ The key ansatz is that the number of parameters $|\boldsymbol\theta^*|$ that minimizes the energy function scales polynomially with the size (e.g., number of qubits) of the target problem. Then, any local fermionic Hamiltonian can be mapped into a sum over Pauli operators $P_i$, $$H\rightarrow H_P = \sum_i^M w_i P_i,$$ and the energy corresponding to the state $|\psi(\boldsymbol\theta\rangle$, $E(\boldsymbol\theta)$, can be estimated by sampling the individual Pauli terms $P_i$ (or sets of them that can be measured at the same time) on a quantum computer: $$E(\boldsymbol\theta) = \sum_i^M w_i \langle \psi(\boldsymbol\theta)| P_i |\psi(\boldsymbol\theta)\rangle.$$ Last, some optimization technique must be devised in order to find the optimal value of parameters $\boldsymbol\theta^*$, such that $|\psi(\boldsymbol\theta^*)\rangle\equiv|\psi_G\rangle$. Fermionic HamiltoniansThe Hamiltonians describing systems of interacting fermions can be expressed in second quantization language, considering fermionic creation (annihilation) operators $a^\dagger_\alpha(a_\alpha)$, relative to the $\alpha$-th fermionic mode. In the case of molecules, the $\alpha$ labels stand for the different atomic or molecular orbitals. Within the second-quantization framework, a generic molecular Hamiltonian with $M$ orbitals can be written as $$H =H_1+H_2=\sum_{\alpha, \beta=0}^{M-1} t_{\alpha \beta} \, a^\dagger_{\alpha} a_{\beta} +\frac{1}{2} \sum_{\alpha, \beta, \gamma, \delta = 0}^{M-1} u_{\alpha \beta \gamma \delta}\, a^\dagger_{\alpha} a^\dagger_{\gamma} a_{\delta} a_{\beta},$$with the one-body terms representing the kinetic energy of the electrons and the potential energy that they experience in the presence of the nuclei, $$ t_{\alpha\beta}=\int d\boldsymbol x_1\Psi_\alpha(\boldsymbol{x}_1) \left(-\frac{\boldsymbol\nabla_1^2}{2}+\sum_{i} \frac{Z_i}{|\boldsymbol{r}_{1i}|}\right)\Psi_\beta (\boldsymbol{x}_1),$$and their interactions via Coulomb forces $$ u_{\alpha\beta\gamma\delta}=\int\int d \boldsymbol{x}_1 d \boldsymbol{x}_2 \Psi_\alpha^*(\boldsymbol{x}_1)\Psi_\beta(\boldsymbol{x}_1)\frac{1}{|\boldsymbol{r}_{12}|}\Psi_\gamma^*(\boldsymbol{x}_2)\Psi_\delta(\boldsymbol{x}_2),$$where we have defined the nuclei charges $Z_i$, the nuclei-electron and electron-electron separations $\boldsymbol{r}_{1i}$ and $\boldsymbol{r}_{12}$, the $\alpha$-th orbital wavefunction $\Psi_\alpha(\boldsymbol{x}_1)$, and we have assumed that the spin is conserved in the spin-orbital indices $\alpha,\beta$ and $\alpha,\beta,\gamma,\delta$. Molecules considered in this notebook and mapping to qubitsWe consider in this notebook the optimization of two potential energy surfaces, for the hydrogen and lithium hydride molecules, obtained using the STO-3G basis. The molecular Hamiltonians are computed as a function of their interatomic distance, then mapped to two-(H$_2$) and four-(LiH$_2$) qubit problems, via elimination of core and high-energy orbitals and removal of $Z_2$ symmetries. Approximate universal quantum computing for quantum chemisty problemsIn order to find the optimal parameters $\boldsymbol\theta^*$, we set up a closed optimization loop with a quantum computer, based on some stochastic optimization routine. Our choice for the variational ansatz is a deformation of the one used for the optimization of classical combinatorial problems, with the inclusion of $Z$ rotation together with the $Y$ ones. The optimization algorithm for fermionic Hamiltonians is similar to the one for combinatorial problems, and can be summarized as follows: 1. Map the fermionic Hamiltonian $H$ to a qubit Hamiltonian $H_P$.2. Choose the maximum depth of the quantum circuit (this could be done adaptively).3. Choose a set of controls $\boldsymbol\theta$ and make a trial function $|\psi(\boldsymbol\theta)\rangle$. The difference with the combinatorial problems is the insertion of additional parametrized $Z$ single-qubit rotations.4. Evaluate the energy $E(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)~|H_P|~\psi(\boldsymbol\theta)\rangle$ by sampling each Pauli term individually, or sets of Pauli terms that can be measured in the same tensor product basis.5. Use a classical optimizer to choose a new set of controls.6. Continue until the energy has converged, hopefully close to the real solution $\boldsymbol\theta^*$, and return the last value of $E(\boldsymbol\theta)$. Note that, as opposed to the classical case, in the case of a quantum chemistry Hamiltonian one has to sample over non-computational states that are superpositions, and therefore take advantage of using a quantum computer in the sampling part of the algorithm. Motivated by the quantum nature of the answer, we also define a variational trial ansatz in this way: $$|\psi(\boldsymbol\theta)\rangle = [U_\mathrm{single}(\boldsymbol\theta) U_\mathrm{entangler}]^m |+\rangle$$where $U_\mathrm{entangler}$ is a collection of cPhase gates (fully entangling gates), $U_\mathrm{single}(\boldsymbol\theta) = \prod_{i=1}^n Y(\theta_{i})Z(\theta_{n+i})$ are single-qubit $Y$ and $Z$ rotation, $n$ is the number of qubits and $m$ is the depth of the quantum circuit. References and additional details:[1] A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow, and J. M. Gambetta, *Hardware-efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets*, Nature 549, 242 (2017), and references therein.
###Code
# useful additional packages
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from scipy import linalg as la
from functools import partial
# importing the QISKit
from qiskit import QuantumProgram
import Qconfig
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# import optimization tools
from qiskit.tools.apps.optimization import trial_circuit_ryrz, SPSA_optimization, SPSA_calibration
from qiskit.tools.apps.optimization import Hamiltonian_from_file, make_Hamiltonian
from qiskit.tools.apps.optimization import eval_hamiltonian, group_paulis
# Ignore warnings due to chopping of small imaginary part of the energy
import warnings
warnings.filterwarnings('ignore')
###Output
_____no_output_____
###Markdown
Optimization of H$_2$ at bond lengthIn this first part of the notebook we show the optimization of the H$_2$ Hamiltonian in the STO-3G basis at the bond length of 0.735 Angstrom. After mapping it to a four-qubit system with a binary-tree transformation, two spin-parity symmetries are modded out, leading to a two-qubit Hamiltonian. The energy of the mapped Hamiltonian obtained is then minimized using the variational ansatz described in the introduction, and a stochastic perturbation simultaneous approximation (SPSA) gradient descent method.
###Code
n=2
m=6
device='local_qasm_simulator'
initial_theta=np.random.randn(2*n*m)
entangler_map = Q_program.get_backend_configuration(device)['coupling_map'] # the map of two-qubit gates with control at key and target at values
if entangler_map == 'all-to-all':
entangler_map = {i: [j for j in range(n) if j != i] for i in range(n)}
shots=1
max_trials=100
ham_name='H2/H2Equilibrium.txt
#ham_name="LIH/LiHEquilibrium.txt" #For optimization of LiH at bond length
# Exact Energy
pauli_list=Hamiltonian_from_file(ham_name)
H=make_Hamiltonian(pauli_list)
exact=np.amin(la.eig(H)[0]).real
print('The exact ground state energy is:')
print(exact)
pauli_list_grouped=group_paulis(pauli_list)
# Optimization
Q_program = QuantumProgram()
Q_program.set_api(Qconfig.APItoken,Qconfig.config["url"])
def cost_function(Q_program,H,n,m,entangler_map,shots,device,theta):
return eval_hamiltonian(Q_program,H,trial_circuit_ryrz(n,m,theta,entangler_map,None,False),shots,device).real
initial_c=0.01
target_update=2*np.pi*0.1
save_step = 20
if shots ==1:
SPSA_params=SPSA_calibration(partial(cost_function,Q_program,H,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
output=SPSA_optimization(partial(cost_function,Q_program,H,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1);
else:
SPSA_params=SPSA_calibration(partial(cost_function,Q_program,pauli_list_grouped,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
output=SPSA_optimization(partial(cost_function,Q_program,pauli_list_grouped,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1);
plt.plot(np.arange(0, max_trials,save_step),output[2],label='E(theta_plus)')
plt.plot(np.arange(0, max_trials,save_step),output[3],label='E(theta_minus)')
plt.plot(np.arange(0, max_trials,save_step),np.ones(max_trials//save_step)*output[0],label='Final Energy')
plt.plot(np.arange(0, max_trials,save_step),np.ones(max_trials//save_step)*exact,label='Exact Energy')
plt.legend()
plt.xlabel('Trial state')
plt.ylabel('Energy')
###Output
_____no_output_____
###Markdown
Optimizing the potential energy surface The optimization considered previously is now performed for two molecules, H$_2$ and LiH, for different interatomic distances, and the correspoding nuclei Coulomb repulsion is added in order to obtain a potential energy surface.
###Code
# MOLECULE PARAMETERS
molecule='H2' # name of the molecule: options are H2 or LiH
if molecule=='H2':
n=2 # qubits
Z1=1
Z2=1
min_distance=.2
max_distance=4
number_of_points=39
elif molecule=='LiH':
n=4 # qubits
Z1=1
Z2=3
min_distance=.5
max_distance=5
number_of_points=46
# OPTIMIZATION PARAMETERS
run_optimization=True # Choose True or False. False just plots the exact potential energy surface
def cost_function(Q_program,H,n,m,entangler_map,shots,device,theta):
return eval_hamiltonian(Q_program,H,trial_circuit_ryrz(n,m,theta,entangler_map,None,False),shots,device).real
m=3 # depth (number of layers of sq gates - # entanglers is this number -1)
device='local_qasm_simulator'
initial_theta=np.random.randn(2*n*m) # initial angles
entangler_map = Q_program.get_backend_configuration(device)['coupling_map'] # the map of two-qubit gates with control at key and target at values
if entangler_map == 'all-to-all':
entangler_map = {i: [j for j in range(n) if j != i] for i in range(n)}
shots=1
max_trials=200
initial_c = 0.01
target_update = 2*np.pi*0.1
save_step = 250 #Setting larger than max_trials to suppress the output at every function call
#################### COMPUTING THE POTENTIAL ENERGY SURFACE ###################
mol_distance=np.zeros(number_of_points)
coulomb_repulsion=np.zeros(number_of_points)
electr_energy=np.zeros(number_of_points)
electr_energy_optimized=np.zeros(number_of_points)
Q_program = QuantumProgram()
Q_program.set_api(Qconfig.APItoken,Qconfig.config["url"])
for i in range(number_of_points):
# %%%%%%%%%%%%% Coulomb Repulsion For Diatomic Molecules %%%%%%%%%%%%%%%%%%%%%%
mol_distance[i]=np.around((min_distance+(max_distance-min_distance)*i/(number_of_points-1)),2)
distance=mol_distance[i]/0.529177
coulomb_repulsion[i]=Z1*Z2/distance
# exact diagonalization
ham_text=molecule+'/PESMap'+str(i)+'atdistance'+str(mol_distance[i])+'.txt'
pauli_list=Hamiltonian_from_file(ham_text)
H=make_Hamiltonian(pauli_list)
pauli_list_grouped = group_paulis(pauli_list)
eigen=la.eig(H)
electr_energy[i]=np.amin(eigen[0])
# optimization
if run_optimization:
print('\nOPTIMIZING HAMILTONIAN # '+str(i)+' AT INTERATOMIC DISTANCE ' + str(mol_distance[i]) + ' ANGSTROM\n')
if shots !=1:
H=group_paulis(pauli_list)
SPSA_params = SPSA_calibration(partial(cost_function,Q_program,H,n,m,entangler_map,
shots,device),initial_theta,initial_c,target_update,25)
electr_energy_optimized[i] = SPSA_optimization(partial(cost_function,Q_program,H,n,m,entangler_map,shots,device),
initial_theta,SPSA_params,max_trials,save_step,1)[0];
plt.plot(mol_distance,electr_energy+coulomb_repulsion,label='Exact')
if run_optimization:
plt.plot(mol_distance,electr_energy_optimized+coulomb_repulsion,label='Optimized')
plt.xlabel('Atomic distance (Angstrom)')
plt.ylabel('Energy')
plt.legend()
%run "../version.ipynb"
###Output
_____no_output_____
|
Tutorial 2 - The target function.ipynb
|
###Markdown
Tutorial 2 - The Target FunctionIn this tutorial, we show how to define a target phase-matching function (PMF) and compute the corresponding target amplitude function.
###Code
import numpy as np
import matplotlib.pyplot as plt
from custom_poling.core.target import Target
from custom_poling.core.crystal import Crystal
# Crystal properties
domain_width = 0.01
number_domains = 1000
L = number_domains * domain_width
k0 = np.pi / domain_width
# Numerical integration parameters
dk = 0.1
k_array = np.arange(k0-10,k0+10,dk)
dz = 0.1
# Create a crystal object
crystal = Crystal(domain_width,number_domains)
domain_middles = crystal.domain_middles
#Define and plot the target function
std = L/10.
target_pmf = lambda k:1j*std*np.sqrt(2)/(np.pi*np.sqrt(np.pi))*np.exp(-(k-k0)**2/(2*std**2))*np.exp(1j * L/2 * k)
target = Target(target_pmf,k_array)
target.plot_pmf()
# Compute and plot the target amplitude
target.compute_amplitude(k0,domain_middles,dz)
target.plot_amplitude()
###Output
_____no_output_____
|
Installation Test.ipynb
|
###Markdown
Check Your InstallationEverything below should work in the online version of this notebook. To verify your installation, try opening a copy of this notebook on your computer. First download a copy by right-clicking on the name of this notebook in the file browser (side bar on the left - click on the folder icon if you've closed it). Select "Download." Now run jupyter on your computer and browse to the file. Verify that all of the cells run correctly. In particular, make sure animations and widgets work.
###Code
# see if required packages are installed
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import ipywidgets as widgets
from IPython import display
# try an integration
def f(x): return x**2
I, err = integrate.quad(f, 0, 1)
print(I)
# make a plot
theta = np.linspace(0, 2*np.pi, 200)
plt.plot(theta, np.sin(theta))
plt.show()
###Output
_____no_output_____
###Markdown
Check WidgetsEven if installed correctly, widgets don't work in some web browsers (specifically Internet Explorer). Try a recent version of Chrome, Firefox, etc.
###Code
def plotter(phi):
plt.plot(theta, np.sin(theta + phi))
plt.show()
slider = widgets.FloatSlider(min=0, max=2*np.pi)
gui = widgets.interactive(plotter, phi=slider)
display.display(gui)
###Output
_____no_output_____
###Markdown
Check AnimationsMacOS can have issues. The root of the problem is that conda's version of [ffmpeg](https://ffmpeg.org/download.html) doesn't always work. In the past, students have had success installing in via [Homebrew](https://brew.sh/) (install Homebrew then run `brew install ffmpeg` in a terminal).
###Code
fig = plt.figure()
line, = plt.plot([])
plt.xlim(0, 2*np.pi)
plt.ylim(-1.1, 1.1)
def update(frame):
line.set_data(theta, np.sin(theta + frame/100*2*np.pi))
anim = FuncAnimation(fig, update, frames=100, interval=20)
video = anim.to_html5_video()
html= display.HTML(video)
display.display(html)
plt.close()
###Output
_____no_output_____
###Markdown
Checking Behavior of Graded Cells
###Code
# did you download grading_helper.py?
import grading_helper
%%graded
# this cell should turn blue when run
%%tests
# this cell should turn yellow when run
%%graded
x = 1
%%tests
# this cell should turn green when run
grading_helper.equal(x, 1)
%%tests
# this cell should turn red and show an error when run
grading_helper.equal(x, 2)
###Output
_____no_output_____
###Markdown
Debugging In Jupyter1. Inspect State with Print Statements2. Interrupt Execution3. Recover from Errors
###Code
x = 3
x = 4
print(x)
x = 6
while (x < 100):
x = x + 1
print(x)
###Output
_____no_output_____
|
_build/jupyter_execute/Module4/m4_05.ipynb
|
###Markdown
Building and Training Convolutional Neural Networks (CNNs) with Pytorch This lecture includes:1. Build CNNs2. Train MNIST with CNNs3. Train CIFAR10 with CNNs4. Improve the test accuracy * Normalize the data * Weight decay * learning rate schedule 1. Build CNNs Convolutional Layer
###Code
import torch
import torch.nn as nn
#stride default value: 1
#padding default vaule: 0
conv1 = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, stride=1, padding=0)
class model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 1, 3)
self.conv2 = nn.Conv2d(1, 2, 3)
self.conv3 = nn.Conv2d(3, 2, 3)
my_model=model()
print(my_model.conv1.weight.size()) # (out_channels, in_channels, kernel_size, kernel_size)
print(my_model.conv2.weight.size()) # (out_channels, in_channels, kernel_size, kernel_size)
print(my_model.conv3.weight.size()) # (out_channels, in_channels, kernel_size, kernel_size)
x = torch.randn(1, 1, 4, 4) # batch_size=1, channel =1, image size = 4 * 4
print(x)
print(my_model(x))
###Output
_____no_output_____
###Markdown
Pooling
###Code
import torch.nn.functional as F
out = F.max_pool2d(input, kernel_size)
out = F.avg_pool2d(input, kernel_size)
x = torch.tensor([[[1,3,2,1],[1,3,2,1],[2,1,1,1],[3,5,1,1]]],dtype=float)
print(x)
max_x = F.max_pool2d(x,2)
print(max_x)
avg_x = F.avg_pool2d(x,2)
print(avg_x)
###Output
tensor([[[1., 3., 2., 1.],
[1., 3., 2., 1.],
[2., 1., 1., 1.],
[3., 5., 1., 1.]]], dtype=torch.float64)
tensor([[[3., 2.],
[5., 1.]]], dtype=torch.float64)
tensor([[[2.0000, 1.5000],
[2.7500, 1.0000]]], dtype=torch.float64)
###Markdown
2. Train MNIST with CNNs
###Code
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torch.nn.functional as F
use_cuda = torch.cuda.is_available()
print('Use GPU?', use_cuda)
# Define a LeNet-5
# Note that we need to reshape MNIST imgaes 28*28 to 32*32
class model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16*5*5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
out = F.relu(self.conv1(x))
out = F.avg_pool2d(out, 2)
out = F.relu(self.conv2(out))
out = F.avg_pool2d(out, 2)
# out.size() = [batch_size, channels, size, size], -1 here means channels*size*size
# out.view(out.size(0), -1) is similar to out.reshape(out.size(0), -1), but more efficient
# Think about why we need to reshape the out?
out = out.view(out.size(0), -1)
out = F.relu(self.fc1(out))
out = F.relu(self.fc2(out))
out = self.fc3(out)
return out
minibatch_size = 128
num_epochs = 2
lr = 0.1
# Step 1: Define a model
my_model =model()
if use_cuda:
my_model = my_model.cuda()
# Step 2: Define a loss function and training algorithm
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(my_model.parameters(), lr=lr)
# Step 3: load dataset
MNIST_transform = torchvision.transforms.Compose([torchvision.transforms.Resize((32, 32)),
torchvision.transforms.ToTensor()])
trainset = torchvision.datasets.MNIST(root='./data', train= True, download=True, transform=MNIST_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=minibatch_size)
testset = torchvision.datasets.MNIST(root='./data', train= False, download=True, transform=MNIST_transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=len(testset))
#Step 4: Train the NNs
# One epoch is when an entire dataset is passed through the neural network only once.
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(trainloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
# Forward pass to get the loss
outputs = my_model(images)
loss = criterion(outputs, labels)
# Backward and compute the gradient
optimizer.zero_grad()
loss.backward() #backpropragation
optimizer.step() #update the weights/parameters
# Training accuracy
correct = 0
total = 0
for i, (images, labels) in enumerate(trainloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
outputs = my_model(images)
p_max, predicted = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicted == labels).sum()
training_accuracy = float(correct)/total
# Test accuracy
correct = 0
total = 0
for i, (images, labels) in enumerate(testloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
outputs = my_model(images)
p_max, predicted = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicted == labels).sum()
test_accuracy = float(correct)/total
print('Epoch: {}, the training accuracy: {}, the test accuracy: {}' .format(epoch+1,training_accuracy,test_accuracy))
###Output
Use GPU? False
Epoch: 1, the training accuracy: 0.8597166666666667, the test accuracy: 0.8699
Epoch: 2, the training accuracy: 0.9314, the test accuracy: 0.9323
###Markdown
3. Train CIFAR10 with CNNs
###Code
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torch.nn.functional as F
use_cuda = torch.cuda.is_available()
print('Use GPU?', use_cuda)
class model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 6, 5) # change the input channels from 1 to 3
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16*5*5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
out = F.relu(self.conv1(x))
out = F.avg_pool2d(out, 2)
out = F.relu(self.conv2(out))
out = F.avg_pool2d(out, 2)
# out.size() = [batch_size, channels, size, size], -1 here means channels*size*size
# out.view(out.size(0), -1) is similar to out.reshape(out.size(0), -1), but more efficient
# Think about why we need to reshape the out?
out = out.view(out.size(0), -1)
out = F.relu(self.fc1(out))
out = F.relu(self.fc2(out))
out = self.fc3(out)
return out
minibatch_size = 128
num_epochs = 2
lr = 0.1
# Step 1: Define a model
my_model =model()
if use_cuda:
my_model = my_model.cuda()
# Step 2: Define a loss function and training algorithm
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(my_model.parameters(), lr=lr)
# Step 3: load dataset
CIFAR10_transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=CIFAR10_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=minibatch_size, shuffle=True)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=CIFAR10_transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False)
# classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
#Step 4: Train the NNs
# One epoch is when an entire dataset is passed through the neural network only once.
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(trainloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
# Forward pass to get the loss
outputs = my_model(images)
loss = criterion(outputs, labels)
# Backward and compute the gradient
optimizer.zero_grad()
loss.backward() #backpropragation
optimizer.step() #update the weights/parameters
# Training accuracy
correct = 0
total = 0
for i, (images, labels) in enumerate(trainloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
outputs = my_model(images)
p_max, predicted = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicted == labels).sum()
training_accuracy = float(correct)/total
# Test accuracy
correct = 0
total = 0
for i, (images, labels) in enumerate(testloader):
if use_cuda:
images = images.cuda()
labels = labels.cuda()
outputs = my_model(images)
p_max, predicted = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicted == labels).sum()
test_accuracy = float(correct)/total
print('Epoch: {}, the training accuracy: {}, the test accuracy: {}' .format(epoch+1,training_accuracy,test_accuracy))
###Output
Use GPU? False
Files already downloaded and verified
Files already downloaded and verified
Epoch: 1, the training accuracy: 0.1918, the test accuracy: 0.1957
Epoch: 2, the training accuracy: 0.3463, the test accuracy: 0.3463
###Markdown
4. Improve the test accuracy Normalize the data with the mean and standard deviation of the dataset$$ \tilde{x}[i,j,:,:] = \frac{x[i,j,:,:]-mean[j]}{std[j]},~~~~i=1,2,...,60000,~~~~j=1,2,3$$.
###Code
CIFAR10_transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize(mean=(0.4914, 0.4822, 0.4465), std=(0.2023, 0.1994, 0.2010))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=CIFAR10_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=minibatch_size, shuffle=True)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=CIFAR10_transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=1, shuffle=False)
###Output
Files already downloaded and verified
Files already downloaded and verified
###Markdown
Weight decay Define the loss function with $\ell_2$ regularization:$$L(\theta) :=\frac{1}{N} \sum_{j=1}^N\ell(y_j, h(x_j; \theta)) + + \lambda (\|\theta\|_2^2).$$The parameter $\lambda$ is called "weight_decay" in Pytorch.
###Code
optimizer = optim.SGD(my_model.parameters(), lr=lr, weight_decay = 0.0001)
# weight_decay is usually small. Two suggested values: 0.0001, 0.00001
###Output
_____no_output_____
###Markdown
Learning rate schedule
###Code
def adjust_learning_rate(optimizer, epoch, init_lr):
#lr = 1.0 / (epoch + 1)
lr = init_lr * 0.1 ** (epoch // 10) # epoch // 10, calculate the quotient
for param_group in optimizer.param_groups:
param_group['lr'] = lr
return lr
init_lr = 1
optimizer = optim.SGD(my_model.parameters(), lr=init_lr, weight_decay = 0.0001)
num_epochs = 30
init_lr = 1
for epoch in range(num_epochs):
current_lr = adjust_learning_rate(optimizer, epoch, init_lr)
print('Epoch: {}, Learning rate: {}'.format(epoch+1,current_lr))
###Output
Epoch: 1, Learning rate: 1.0
Epoch: 2, Learning rate: 1.0
Epoch: 3, Learning rate: 1.0
Epoch: 4, Learning rate: 1.0
Epoch: 5, Learning rate: 1.0
Epoch: 6, Learning rate: 1.0
Epoch: 7, Learning rate: 1.0
Epoch: 8, Learning rate: 1.0
Epoch: 9, Learning rate: 1.0
Epoch: 10, Learning rate: 1.0
Epoch: 11, Learning rate: 0.1
Epoch: 12, Learning rate: 0.1
Epoch: 13, Learning rate: 0.1
Epoch: 14, Learning rate: 0.1
Epoch: 15, Learning rate: 0.1
Epoch: 16, Learning rate: 0.1
Epoch: 17, Learning rate: 0.1
Epoch: 18, Learning rate: 0.1
Epoch: 19, Learning rate: 0.1
Epoch: 20, Learning rate: 0.1
Epoch: 21, Learning rate: 0.010000000000000002
Epoch: 22, Learning rate: 0.010000000000000002
Epoch: 23, Learning rate: 0.010000000000000002
Epoch: 24, Learning rate: 0.010000000000000002
Epoch: 25, Learning rate: 0.010000000000000002
Epoch: 26, Learning rate: 0.010000000000000002
Epoch: 27, Learning rate: 0.010000000000000002
Epoch: 28, Learning rate: 0.010000000000000002
Epoch: 29, Learning rate: 0.010000000000000002
Epoch: 30, Learning rate: 0.010000000000000002
###Markdown
Reading material1. LeNet-5: https://engmrk.com/lenet-5-a-classic-cnn-architecture/2. torch.nn.Conv2d: https://pytorch.org/docs/stable/nn.html?highlight=conv2dtorch.nn.Conv2d3. Understand Convolutions:https://medium.com/apache-mxnet/convolutions-explained-with-ms-excel-465d6649831cf17ehttps://medium.com/apache-mxnet/multi-channel-convolutions-explained-with-ms-excel-9bbf8eb77108https://gfycat.com/plasticmenacingdegu (Optional material) How to compute the mean and standard deviation of CIFAR10 dataset?
###Code
import numpy as np
CIFAR10_transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=CIFAR10_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=len(trainset), shuffle=True)
mean = 0.
std = 0.
for i, (images, labels) in enumerate(trainloader):
batch_samples = images.size(0) # batch size (the last batch can have smaller size!)
images = images.view(batch_samples, images.size(1), -1)
mean = images.mean(2).sum(0)
std = images.std(2).sum(0)
mean /= len(trainloader.dataset)
std /= len(trainloader.dataset)
print('mean:', mean.numpy())
print('std1:', std.numpy())
###Output
Files already downloaded and verified
mean: [0.49140054 0.48215687 0.44652957]
std1: [0.20230146 0.19941428 0.20096211]
|
In class code week 6.ipynb
|
###Markdown
To get the reading library's to load a csv file. (got one from Geostats)
###Code
import pandas
import numpy
import csv
###Output
_____no_output_____
###Markdown
This is something we had to look up in Google to figure out how to do.
###Code
df = pandas.read_csv('meanAnnualPrecipitation.csv')
###Output
_____no_output_____
###Markdown
pandas assumes that you want to read a certain way. If you type "print(df)" it is a raw output of df. But if you just use "df" then you get a pretty little table with headers.
###Code
df
###Output
_____no_output_____
###Markdown
"okay python" you have a column named 'd13C', give me those values. We give a variable, file [column header] "dot" values.
###Code
Q_df = df['d13C'].values
print(type(Q_df))
Q_df.shape
###Output
<class 'numpy.ndarray'>
###Markdown
now we can compute some stats from that.
###Code
Q_df.mean()
Q_df.max()
Q_df.min()
Q_df.std()
###Output
_____no_output_____
###Markdown
Note that this is a reason why pandas is popular. This can take "messy" data and make it pretty and readable. This could be useful for data like what we download from "DryCreek" Working in class soloTry getting this data to plot, and see if you need it
###Code
import matplotlib.pyplot
image = matplotlib.pyplot.imshow(Q_df)
matplotlib.pyplot.show()
###Output
_____no_output_____
###Markdown
Okay, first attempt didn't work.
###Code
#plot.set_ylabel('d13C')
matplotlib.pyplot.plot(Q_df,'g-')
matplotlib.pyplot.show()
###Output
_____no_output_____
###Markdown
This is data from TreeLine up at DryCreek. To get pandas to 'ignore' the first few rows, put a flag in as "skiprows =" and then the number of rows.
###Code
TL = pandas.read_csv('Treeline_HrlySummary_2016.csv', skiprows=19)
TL
Q_TL = TL['NetRadiation-Watts/m2'].values
print(type(Q_TL))
Q_TL.shape
matplotlib.pyplot.plot(Q_TL,'g-')
matplotlib.pyplot.show()
USACE = pandas.read_csv('NDHUB.ArmyCorps_0.csv')
USACE
Q_USACE = USACE['ACRES'].values
print(type(Q_USACE))
Q_TL.shape
matplotlib.pyplot.plot(Q_USACE,'g-')
matplotlib.pyplot.show()
###Output
<class 'numpy.ndarray'>
|
homeworks/D063/Day_063_HW.ipynb
|
###Markdown
作業* 在精簡深度學習的方式上 : 卷積類神經 (CNN) 採用像素遠近,而遞歸類神經 (RNN) 採用著則是時間遠近* 那麼,既然有著類似的設計精神,兩者是否有可能互換應用呢?
###Code
可以互換應用,簡單來說就是把輸入的時間維度跟空間維度互換,不過還是得考慮是否合適。
###Output
_____no_output_____
|
example/word-mover/load-word-mover-distance.ipynb
|
###Markdown
What is word mover distance? between two documents in a meaningful way, even when they have no words in common. It uses vector embeddings of words. It been shown to outperform many of the state-of-the-art methods in k-nearest neighbors classification.You can read more about word mover distance from [Word Distance between Word Embeddings](https://towardsdatascience.com/word-distance-between-word-embeddings-cc3e9cf1d632).**Closest to 0 is better**.
###Code
left_sentence = 'saya suka makan ayam'
right_sentence = 'saya suka makan ikan'
left_token = left_sentence.split()
right_token = right_sentence.split()
w2v_wiki = malaya.word2vec.load_wiki()
w2v_wiki = malaya.word2vec.word2vec(w2v_wiki['nce_weights'],w2v_wiki['dictionary'])
fasttext_wiki, ngrams = malaya.fast_text.load_wiki()
fasttext_wiki = malaya.fast_text.fast_text(fasttext_wiki['embed_weights'],
fasttext_wiki['dictionary'], ngrams)
###Output
_____no_output_____
###Markdown
Using word2vec
###Code
malaya.word_mover.distance(left_token, right_token, w2v_wiki)
malaya.word_mover.distance(left_token, left_token, w2v_wiki)
###Output
_____no_output_____
###Markdown
Using fast-text
###Code
malaya.word_mover.distance(left_token, right_token, fasttext_wiki)
malaya.word_mover.distance(left_token, left_token, fasttext_wiki)
###Output
_____no_output_____
###Markdown
Why word mover distance? Maybe you heard about skipthought or siamese network to train sentences similarity, but both required a good corpus plus really slow to train. Malaya provided both models to train your own text similarity, can check here, [Malaya text-similarity](https://malaya.readthedocs.io/en/latest/Similarity.html)`word2vec` or `fast-text` are really good to know semantic definitions between 2 words, like below,
###Code
w2v_wiki.n_closest(word = 'anwar', num_closest=8, metric='cosine')
###Output
_____no_output_____
###Markdown
So we got some suggestion from the interface included distance between 0-1, closest to 1 is better.Now let say I want to compare similarity between 2 sentences, and using vectors representation from our word2vec and fast-text.I got, `rakyat sebenarnya sukakan mahathir`, and `rakyat sebenarnya sukakan najib`
###Code
mahathir = 'rakyat sebenarnya sukakan mahathir'
najib = 'rakyat sebenarnya sukakan najib'
malaya.word_mover.distance(mahathir.split(), najib.split(), w2v_wiki)
###Output
_____no_output_____
###Markdown
0.9, quite good. What happen if we make our sentence quite polarity ambigious for najib? (Again, this is just example)
###Code
mahathir = 'rakyat sebenarnya sukakan mahathir'
najib = 'rakyat sebenarnya gilakan najib'
malaya.word_mover.distance(mahathir.split(), najib.split(), w2v_wiki)
###Output
_____no_output_____
###Markdown
We just changed `sukakan` with `gilakan`, but our word2vec representation based on `rakyat sebenarnya ` not able to correlate same polarity, real definition of `gilakan` is positive polarity, but word2vec learnt `gilakan` is negative or negate. Soft modeWhat happened if a word is not inside vectorizer dictionary? `malaya.word_mover.distance` will throw an exception.
###Code
left = 'tyi'
right = 'qwe'
malaya.word_mover.distance(left.split(), right.split(), w2v_wiki)
###Output
_____no_output_____
###Markdown
So if use `soft = True`, if the word is not inside vectorizer, it will find the nearest word.
###Code
left = 'tyi'
right = 'qwe'
malaya.word_mover.distance(left.split(), right.split(), w2v_wiki, soft = True)
###Output
_____no_output_____
###Markdown
Load expanderWe want to expand shortforms based on `malaya.normalize.spell` by using word mover distance. If our vector knows that `mkn` semantically similar to `makan` based on `saya suka mkn ayam` sentence, word mover distance will become closer.It is really depends on our vector, and word2vec may not able to understand shortform, so we will use fast-text to fix `OUT-OF-VOCAB` problem.
###Code
malays = malaya.load_malay_dictionary()
wiki, ngrams = malaya.fast_text.load_wiki()
fast_text_embed = malaya.fast_text.fast_text(wiki['embed_weights'],wiki['dictionary'],ngrams)
expander = malaya.word_mover.expander(malays, fast_text_embed)
string = 'y u xsuka makan HUSEIN kt situ tmpt'
another = 'i mmg xska mknn HUSEIN kampng tempt'
expander.expand(string)
expander.expand(another)
###Output
_____no_output_____
|
code/research-similarity.ipynb
|
###Markdown
Данные
###Code
df = pd.read_csv('data/features/education_field_of_study_classes.csv', index_col=0)
df['Class'].value_counts()
plt.figure(figsize=(10,6))
plt.title('Top 1 and top 2 semilarity metric')
df['top1'].hist(bins=20, color='r', alpha=0.3, label='top 1')
df['top2'].hist(bins=20, color='b', alpha=0.3, label='top 2')
plt.xlim(0, 1)
plt.legend()
plt.show()
df = pd.read_csv('data/important/company_list.csv', index_col=0)
df[['city', 'number_of_rounds', 'exit_type']].sample(5).reset_index()
df = pd.read_csv('data/features/education_field_of_study_classes.csv', index_col=0)
df[['education_field_of_study']].value_counts().head(30)
###Output
_____no_output_____
|
notebooks/04_layers.ipynb
|
###Markdown
Layers> Custom activations, layers, and layer blocks are contained in this module.
###Code
#hide
from nbdev.showdoc import *
%load_ext autoreload
%autoreload 2
%matplotlib inline
# export
from abc import abstractmethod, ABC
import copy
from einops.layers.torch import Rearrange
from functools import partial
import numpy as np
from operator import add, truediv, sub
import torch
import torch.nn as nn
import torch.nn.functional as F
from htools import add_docstring
from incendio.core import BaseModel
from incendio.data import probabilistic_hash_tensor
from incendio.utils import concat, weighted_avg, identity
# Used for testing only.
from collections import defaultdict, Counter
from itertools import chain
import matplotlib.pyplot as plt
import pandas as pd
from torch.utils.data import Dataset, DataLoader
from htools import assert_raises, InvalidArgumentError, smap
from incendio.data import probabilistic_hash_item
import pandas_htools
###Output
/Users/hmamin/anaconda3/lib/python3.7/site-packages/ipykernel/ipkernel.py:287: DeprecationWarning: `should_run_async` will not call `transform_cell` automatically in the future. Please pass the result to `transformed_cell` argument and any exception that happen during thetransform in `preprocessing_exc_tuple` in IPython 7.17 and above.
and should_run_async(code)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'ends' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'ends' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'filter_by_count' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'grouped_mode' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'impute' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'target_encode' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'top_categories' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'vcounts' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'pprint' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'pprint' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'lambda_sort' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'lambda_sort' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:31: UserWarning: registration of accessor <class 'pandas_flavor.register.register_dataframe_method.<locals>.inner.<locals>.AccessorMethod'> under name 'coalesce' for type <class 'pandas.core.frame.DataFrame'> is overriding a preexisting attribute with the same name.
register_dataframe_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'stringify' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
/Users/hmamin/anaconda3/lib/python3.7/site-packages/pandas_flavor/register.py:53: UserWarning: registration of accessor <class 'pandas_flavor.register.register_series_method.<locals>.inner.<locals>.AccessorMethod'> under name 'is_list_col' for type <class 'pandas.core.series.Series'> is overriding a preexisting attribute with the same name.
register_series_accessor(method.__name__)(AccessorMethod)
###Markdown
Activations
###Code
# export
class GRelu(nn.Module):
"""Generic ReLU."""
def __init__(self, leak=0.0, max=float('inf'), sub=0.0):
super().__init__()
self.leak = leak
self.max = max
self.sub = sub
def forward(self, x):
"""Check which operations are necessary to save computation."""
x = F.leaky_relu(x, self.leak) if self.leak else F.relu(x)
if self.sub:
x -= self.sub
if self.max:
x = torch.clamp(x, max=self.max)
return x
def __repr__(self):
return f'GReLU(leak={self.leak}, max={self.max}, sub={self.sub})'
# export
JRelu = GRelu(leak=.1, sub=.4, max=6.0)
# export
class Mish(nn.Module):
"""OOP form of mish activation.
Mish: A Self Regularized Non-Monotonic Neural Activation Function
https://arxiv.org/pdf/1908.08681v1.pdf
"""
def __init__(self):
super().__init__()
def forward(self, x):
return x * torch.tanh(F.softplus(x))
# export
def mish(x):
"""Functional form of mish activation.
Mish: A Self Regularized Non-Monotonic Neural Activation Function
https://arxiv.org/pdf/1908.08681v1.pdf
Parameters
----------
x: torch.Tensor[float]
Input tensor.
Returns
-------
torch.Tensor[float]: Tensor of same shape as input x.
"""
return x * torch.tanh(F.softplus(x))
def plot_activations(z, a, mode='scatter', **kwargs):
"""Plot an input tensor and its corresponding activations. Both tensors
will be flattened for plotting.
Parameters
----------
z: tf.Tensor
Tensor containing values to plot on the x axis (we can often think of
this as the output of a linear layer, where z=f(x) and a=mish(z)).
a: tf.Tensor
Tensor containing values to plot on y axis.
mode: str
'scatter' for scatter plot or 'plot' for line plot.
kwargs: Values to be passed to the matplotlib plotting function, such as
's' when in 'scatter' mode or 'lw' in 'plot' mode.
Returns
-------
None
"""
plt_func = getattr(plt, mode)
kwargs = kwargs or {}
if mode == 'scatter' and not kwargs:
kwargs = {'s': .75}
plt_func(z.numpy().flatten(), a.numpy().flatten(), **kwargs)
plt.axvline(0, lw=.5, alpha=.5)
plt.axhline(0, lw=.5, alpha=.5)
plt.show()
x = torch.arange(-5, 5, .05)
a = mish(x)
plot_activations(x, a, 'plot')
###Output
_____no_output_____
###Markdown
Layer Blocks
###Code
# export
class ConvBlock(nn.Module):
"""Create a convolutional block optionally followed by a batch norm layer.
"""
def __init__(self, c_in, c_out, kernel_size=3, norm=True, activation=JRelu,
**kwargs):
"""
Parameters
-----------
c_in: int
# of input channels.
c_out: int
# of output channels.
kernel_size: int
Size of kernel in conv2d layer. An integer argument will be used
as both the height and width.
norm: bool
If True, include a batch norm layer after the conv layer. If False,
no norm layer will be used. Note that batch norm has learnable
affine parameters which remove the need for a bias in the preceding
conv layer. When batch norm is not used, however, the conv layer
will include a bias term.
activation: nn.Module
Activation function to use at the end of the convolutional block.
(In some cases such as our ResBlock implementation, we pass in None
so that an extra addition can be performed before the final
activation.) Do not use the functional form here as it will be
added to a sequential object. This is an object, not a class.
kwargs: any
Additional keyword args are passed to Conv2d. Useful kwargs include
stride, and padding (see pytorch docs for nn.Conv2d).
"""
super().__init__()
self.norm = norm
layers = [nn.Conv2d(c_in, c_out, kernel_size, bias=not norm, **kwargs)]
if norm:
layers.append(nn.BatchNorm2d(c_out))
if activation is not None:
layers.append(activation)
self.block = nn.Sequential(*layers)
def forward(self, x):
return self.block(x)
conv = ConvBlock(3, 5, norm=False)
conv
x = torch.rand(2, 3, 4, 4)
conv(x).shape
# export
class ResBlock(nn.Module):
def __init__(self, c_in, kernel_size=3, norm=True, activation=JRelu,
stride=1, padding=1, skip_size=2, **kwargs):
"""Residual block using 2D convolutional layers. Note that kernel_size,
stride, and pad must be selected such that the height and width of
the input remain the same.
Parameters
-----------
c_in: int
# of input channels.
kernel_size: int
Size of filter used in convolution. Default 3 (which becomes 3x3).
norm: bool
Specifies whether to include a batch norm layer after each conv
layer.
activation: callable
Activation function to use.
stride: int
# of pixels the filter moves between each convolution. Default 1.
padding: int
Pixel padding around the input. Default 1.
skip_size: int
Number of conv blocks inside the skip connection (default 2).
ResNet paper notes that skipping a single layer did not show
noticeable improvements.
kwargs: any
Additional kwargs to pass to ConvBlock which will in turn pass them
to Conv2d. If you accidentally pass in a 'c_out', it will be
removed since we need all dimensions to remain unchanged.
"""
super().__init__()
# Ensure we don't accidentally pass in a different c_out.
kwargs.pop('c_out', None)
self.skip_size = skip_size
self.layers = nn.ModuleList([
ConvBlock(c_in, c_in, kernel_size=kernel_size, norm=norm,
activation=None, stride=stride, padding=padding,
**kwargs)
for i in range(skip_size)
])
self.activation = activation
def forward(self, x):
x_out = x
for i, layer in enumerate(self.layers):
x_out = layer(x_out)
# Final activation must be applied after addition.
if i != self.skip_size - 1:
x_out = self.activation(x_out)
return self.activation(x + x_out)
ResBlock(4)
ResBlock(4, norm=False)
# export
@add_docstring(nn.Conv2d)
class ReflectionPaddedConv2d(nn.Module):
"""Conv2d only allows padding_mode of `zeros` or `circular`. This
layer is a quick way for us to use reflection padding.
"""
def __init__(self, in_channels, out_channels, padding=1,
kernel_size=3, **kwargs):
"""Do not specify a padding mode.
"""
super().__init__()
if 'padding_mode' in kwargs:
raise InvalidArgumentError('Remove `padding_mode` from arguments.')
self.reflect = nn.ReflectionPad2d(padding)
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size,
padding=0)
def forward(self, x):
x = self.reflect(x)
return self.conv(x)
def show_img(img):
plt.imshow(img.permute(1, 2, 0) / 255)
plt.show()
rconv = ReflectionPaddedConv2d(3, 3, kernel_size=1, padding=2)
rconv
x = torch.randint(255, (1, 3, 3, 3)).float()
show_img(x[0])
x2 = rconv.reflect(x)
show_img(x2[0])
# Tests
assert nn.Conv2d.__doc__ in ReflectionPaddedConv2d.__doc__
with assert_raises(InvalidArgumentError):
ReflectionPaddedConv2d(3, 3, padding_mode='zeros')
# export
class SmoothSoftmaxBase(nn.Module):
"""Parent class of SmoothSoftmax and SmoothLogSoftmax (softmax or log
softmax with temperature baked in). There shouldn't be a need to
instantiate this class directly.
"""
def __init__(self, log=False, temperature='auto', dim=-1):
"""
Parameters
----------
log: bool
If True, use log softmax (if this is the last activation in a
network, it can be followed by nn.NLLLoss). If False, use softmax
(this is more useful if you're doing something attention-related:
no standard torch loss functions expect softmax outputs). This
argument is usually passed implicitly by the higher level interface
provided by the child classes.
temperature: float or str
If a float, this is the temperature to divide activations by before
applying the softmax. Values larger than 1 soften the distribution
while values between 0 and 1 sharpen it. If str ('auto'), this will
compute the square root of the last dimension of x's shape the
first time the forward method is called and use that for subsequent
calls.
dim: int
The dimension to compute the softmax over.
"""
super().__init__()
self.temperature = None if temperature == 'auto' else temperature
self.act = nn.LogSoftmax(dim=dim) if log else nn.Softmax(dim=dim)
def forward(self, x):
"""
Parameters
----------
x: torch.float
Returns
-------
torch.float: Same shape as x.
"""
# Slightly odd way to do this but we're trying to avoid an extra if
# statement because temperature only needs to be set once and we could
# plausibly call this method millions of times during training.
try:
return self.act(x.div(self.temperature))
except TypeError:
self.temperature = np.sqrt(x.shape[-1])
return self.forward(x)
except Exception as e:
raise e
# export
class SmoothSoftmax(SmoothSoftmaxBase):
def __init__(self, temperature='auto', dim=-1):
super().__init__(log=False, temperature=temperature, dim=dim)
# export
class SmoothLogSoftmax(SmoothSoftmaxBase):
def __init__(self, temperature='auto', dim=-1):
super().__init__(log=True, temperature=temperature, dim=dim)
# export
class SpatialSoftmax(nn.Module):
"""Apply softmax over the height and width dimensions of a batch of image
tensors (or image-like tensors). Concretely, inputs will usually have
shape (batch size, channels, height, width), while outputs will have the
same shape but values for each feature map will now sum to 1. Essentially,
we now have a heatmap of what region in each image to focus on.
"""
def __init__(self, temperature='auto', log=False):
super().__init__()
cls = SmoothLogSoftmax if log else SmoothSoftmax
self.act = cls(temperature)
def forward(self, x):
# Should work on any tensor with shape (bs, ..., h, w).
flattened = self.act(x.view(*x.shape[:-2], -1))
return flattened.view(*x.shape)
# export
class Dropin(nn.Module):
"""Additive dropout. This injects small amounts of noise into a model
in the form of randomly generated floats from a zero-centered
gaussian distribution (variance can be adjusted). This does nothing
in eval mode. Unlike Dropout, this does not scale weights during
training since it does not bias them in any direction.
"""
def __init__(self, scale=.5):
"""
Parameters
----------
scale: float
Used to scale the magnitude of the random noise. Keep in mind
that the scalar term is square rooted, so the relationship
will not be linear. Relatively large values (e.g. 1.0) will have
a stronger regularizing effect, while small values (e.g. 0.1)
will have a slight regularizing effect. There is no max value
enforced, so it's up to the user to select a reasonable value.
"""
super().__init__()
self.scale = scale
def forward(self, x):
if not self.training:
return x
# Storing noise allows us to run diagnostics.
self.noise = torch.randn_like(x) * np.sqrt(self.scale / x.shape[-1])
return x + self.noise
class Net(nn.Module):
def __init__(self):
super().__init__()
self.drop = Dropin()
def forward(self, x):
return self.drop(x)
net = Net()
x = torch.randn(8, 128, 128, 3)
assert np.corrcoef(net(x).flatten(), x.flatten())[0][1] > .9
net.eval()
assert torch.eq(net(x), x).all()
assert not net.drop.training
def simulate_activation_stats(scale=1.0, trials=10_000):
act_stats = defaultdict(list)
noise_stats = defaultdict(list)
drop = Dropin(scale)
for _ in range(trials):
x = torch.randn(3, 4, dtype=torch.float)
z = drop(x)
noise = drop.noise
noise_stats['mean'].append(noise.mean())
noise_stats['std'].append(noise.std())
noise_stats['act_corr'].append(
np.corrcoef(z.flatten(), noise.flatten())[0][1]
)
act_stats['mean'].append(z.mean())
act_stats['std'].append(z.std())
act_stats['x_corr'].append(
np.corrcoef(z.flatten(), x.flatten())[0][1]
)
return pd.DataFrame(dict(
act={k: np.mean(v).round(4) for k, v in act_stats.items()},
noise={k: np.mean(v).round(4) for k, v in noise_stats.items()}
))
for scale in [10, 1, .75, .5, .25, .1]:
print('\n', scale)
simulate_activation_stats(scale, 1_000).pprint()
# export
class LinearSkipBlock(nn.Module):
"""This lets us easily create residual block equivalents with linear
layers.
"""
def __init__(self, x_dim, layer_dims, op, activation=mish):
"""
Parameters
----------
x_dim: int
Size of input tensor.
layer_dims: Iterable[int]
Size of each layer. The length of this list will be the skip size
(2 is probably a reasonable starting point).
op: function
This will be called on the input x and the processed x in the
forward method. This is a concatenation for dense blocks and an
addition for residual blocks, but any operation is possible.
activation: callable
Activation function or callable class. This will be applied after
each layer. The final activation is applied after the `op`
function.
"""
super().__init__()
self.skip_size = len(layer_dims)
self.activation = activation
self.layers = nn.ModuleList([nn.Linear(d_in, d_out) for d_in, d_out
in zip([x_dim]+list(layer_dims),
layer_dims)])
self.op = op
def forward(self, x):
out = x
for i, layer in enumerate(self.layers, 1):
out = layer(out)
if i < self.skip_size: out = self.activation(out)
return self.activation(self.op(x, out))
# export
class LinearResBlock(LinearSkipBlock):
"""Equivalent of ResNet block with linear layers."""
def __init__(self, x_dim, hidden_dims, activation=mish):
if hidden_dims[-1] != x_dim:
raise InvalidArgumentError(
'Last hidden dimension must match input dimension.'
)
super().__init__(x_dim, hidden_dims, add, activation)
# export
class LinearDenseBlock(LinearSkipBlock):
"""Equivalent of DenseNet block with linear layers."""
def __init__(self, x_dim, hidden_dims, activation=mish):
super().__init__(x_dim, hidden_dims, concat, activation)
# export
class WeightedLinearResBlock(LinearSkipBlock):
"""Like a LinearResBlock but takes a weighted average of the input and
output rather than adding them. Addition gives them equal weight and we
may want to weight the output more heavily.
"""
def __init__(self, x_dim, hidden_dims, weights=(.25, .75),
activation=mish):
super().__init__(x_dim, hidden_dims,
partial(weighted_avg, weights=list(weights)),
activation)
# export
class SkipConnection(nn.Module):
"""More generalized version of skip connection. Eventually maybe rewrite
various res/dense/weighted conv blocks with this.
Examples
--------
>> x = torch.randn(3, 4)
>> dense = nn.Linear(4, 2)
>> dense(x).shape
torch.Size([3, 2])
>> skip = SkipConnection(dense, op='cat')
>> skip(x).shape
torch.Size([3, 6])
>> skip = SkipConnection(dense, op='add')
>> skip(x).shape
RuntimeError: The size of tensor a (4) must match the size of tensor b (2)
at non-singleton dimension 1
"""
def __init__(self, block, op='add', input_weight=None):
"""
Parameters
----------
block: nn.Module
A torch layer/model that takes in some input x (and optionally
other args/kwargs) and performs some computations on it. When
using op='add', this should output a tensor with the same shape
as its first input.
op: str
One of ('add', 'cat', 'weighted_avg'). This determines how the
input will be attached to the output. If you choose 'cat',
concatenation will occur over the last axis and input will precede
output.
input_weight: float or None
If op='weighted_avg', you must provide a float in (0, 1) that
determines how heavily to weight the input x. For example, 0.2
means the output of `block` will be much more heavily weighted
than the input tensor, while 0.5 is equivalent to computing the
mean (and in most cases is essentially equivalent to computing
the sum).
"""
super().__init__()
self.block = block
if op == 'add':
self.op = torch.add
elif op == 'cat':
self.op = self._cat
elif op == 'weighted_avg':
if input_weight is None or input_weight <= 0 or input_weight >= 1:
raise ValueError('input_weight must be a float in (0, 1) '
'when op="weighted".')
self.weights = input_weight, 1-input_weight
self.op = self._weighted_avg
else:
raise ValueError('op must be in ("add", "cat", "weighted_avg").')
def forward(self, x, *args, **kwargs):
"""
Parameters
----------
x: torch.Tensor
This first item is considered to be the input which will be
combined with the output of self.block.
args, kwargs: any
Additional args will be forwarded to self.block.
Returns
-------
torch.Tensor: Should have same shape as x unless you're making use of
broadcasting, which should rarely be needed here.
"""
return self.op(x, self.block(x, *args, **kwargs))
@staticmethod
def _cat(x1, x2):
"""Wrapper since torch.cat has a different interface than torch.add
(list of args vs. *args).
"""
return torch.cat([x1, x2], dim=-1)
def _weighted_avg(x1, x2):
"""In our use case, the first tensor will be the original input tensor
and the second will be the output of self.block.
"""
return self.weights[0]*x1 + self.weights[1]*x2
###Output
_____no_output_____
###Markdown
Embeddings and Encodings
###Code
# export
def trunc_normal_(x, mean=0.0, std=1.0):
"""Ported from fastai to remove dependency:
Truncated normal initialization.
From https://discuss.pytorch.org/t/implementing-truncated-normal-initializer/4778/12
"""
return x.normal_().fmod_(2).mul_(std).add_(mean)
# export
class InitializedEmbedding(nn.Embedding):
"""Same as nn.Embedding but with truncated normal initialization. This
also differs from fastai's Embedding class in that it allows padding.
"""
def reset_parameters(self):
with torch.no_grad():
trunc_normal_(self.weight, std=.01)
if self.padding_idx is not None:
torch.zero_(self.weight[self.padding_idx])
InitializedEmbedding(4, 3, 0).weight
InitializedEmbedding(4, 3, 3).weight
InitializedEmbedding(4, 3).weight
# export
class BloomEmbedding(nn.Module):
"""Bloom Embedding layer for memory-efficient word representations.
Each word is encoded by a combination of rows of the embedding
matrix. The number of rows can therefore be far lower than the number
of words in our vocabulary while still providing unique representations.
The reduction in rows allows us to use memory in other ways: a larger
embedding dimension, more or larger layers after the embedding,
larger batch sizes, etc.
Note that if hashing is done in the Dataset, we could use a simple
nn.EmbeddingBag to achieve the same thing. Many users have reported
poor performance with this layer though (especially on CPU, but in some
cases on GPU) so I stick with the standard Embedding. We also bake in
the truncated normal intialization provided by fastai, with a slight tweak
to allow a row for padding.
"""
def __init__(self, n_emb=251, emb_dim=100, n_hashes=4, padding_idx=0,
pre_hashed=False):
"""
Parameters
----------
n_emb: int
Number of rows to create in the embedding matrix. A prime
number is recommended. Lower numbers will be more
memory-efficient but increase the chances of collisions.
emb_dim: int
Size of each embedding. If emb_dim=100, each word will
be represented by a 100-dimensional vector.
n_hashes: int
This determines the number of hashes that will be taken
for each word index, and as a result, the number of rows
that will be summed to create each unique representation.
The higher the number, the lower the chances of a collision.
padding_idx: int or None
If an integer is provided, this will set aside the corresponding
row in the embedding matrix as a vector of zeros. If None, no
padding vector will be allocated.
pre_hashed: bool
Pass in True if the input tensor will already be hashed by the
time it enters this layer (you may prefer pre-compute the hashes
in the Dataset to save computation time during training). In this
scenario, the layer is a simple embedding bag with mode "sum".
Pass in False if the inputs will be word indices that have not yet
been hashed. In this case, hashing will be done inside the
`forward` call.
Suggested values for a vocab size of ~30,000:
| n_emb | n_hashes | unique combos |
|-------|----------|---------------|
| 127 | 5 | 29,998 |
| 251 | 4 | 29,996 |
| 997 | 3 | 29,997 |
| 5,003 | 2 | 29,969 |
"""
super().__init__()
self.n_emb = n_emb
self.emb = InitializedEmbedding(n_emb, emb_dim, padding_idx)
self.n_hashes = n_hashes
self.pad_idx = padding_idx
self.pre_hashed = pre_hashed
self.process_fn = identity if pre_hashed else \
partial(probabilistic_hash_tensor, n_buckets=n_emb,
n_hashes=n_hashes, pad_idx=padding_idx)
# Makes interface consistent with nn.Embedding. Don't change name.
self.embedding_dim = self.emb.embedding_dim
def forward(self, x):
"""
Parameters
----------
x: torch.LongTensor
Input tensor of word indices (bs x seq_len) if pre_hashed is
False. Hashed indices (bs x seq_len x n_hashes) if pre_hashed is
False.
Returns
-------
torch.FloatTensor: Words encoded with combination of embeddings.
(bs x seq_len x emb_dim)
"""
# If not pre-hashed: (bs, seq_len) -> hash -> (bs, seq_len, n_hashes)
hashed = self.process_fn(x)
# (bs, seq_len, n_hashes, emb_dim) -> sum -> (bs, seq_len, emb_dim)
return self.emb(hashed).sum(-2)
class Data(Dataset):
def __init__(self, sentences, labels, seq_len):
x = [s.split(' ') for s in sentences]
self.w2i = self.make_w2i(x)
self.seq_len = seq_len
self.x = self.encode(x)
self.y = torch.tensor(labels)
def __getitem__(self, i):
return self.x[i], self.y[i]
def __len__(self):
return len(self.y)
def make_w2i(self, tok_rows):
return {k: i for i, (k, v) in
enumerate(Counter(chain(*tok_rows)).most_common(), 1)}
def encode(self, tok_rows):
enc = np.zeros((len(tok_rows), self.seq_len), dtype=int)
for i, row in enumerate(tok_rows):
trunc = [self.w2i.get(w, 0) for w in row[:self.seq_len]]
enc[i, :len(trunc)] = trunc
return torch.tensor(enc)
sents = [
'I walked to the store so I hope it is not closed.',
'The theater is closed today and the sky is grey.',
'His dog is brown while hers is grey.'
]
labels = [0, 1, 1]
ds = Data(sents, labels, 10)
ds[1]
dl = DataLoader(ds, batch_size=3)
x, y = next(iter(dl))
x, y
x, y = next(iter(dl))
x, y
be = BloomEmbedding(11, 4)
be.emb.weight
x
# (bs x seq_len) -> (bs -> seq_len -> emb_size)
y = be(x)
y.shape
y[0]
###Output
_____no_output_____
###Markdown
Below, we show by step how to get from x to y. This is meant to demonstrate the basic mechanism, not to show how PyTorch actually implements this under the hood. Let's look at a single row of x, corresponding to 1 sentence where each word is mapped to its index in the vocabulary.
###Code
x[0]
###Output
_____no_output_____
###Markdown
Next, we hash each item.
###Code
hashed = [probabilistic_hash_item(i.item(), 11, int, 4) for i in x[0]]
hashed
###Output
_____no_output_____
###Markdown
Then use each row of hashed integers to index into the embedding weight matrix.
###Code
output = []
for row in hashed:
row_out = be.emb.weight[row]
output.append(row_out)
output = torch.stack(output)
print(output.shape)
output[:2]
###Output
torch.Size([10, 4, 4])
###Markdown
Finally, we sum up the embedding rows. Above, each word is represented by four rows of the embedding matrix. After summing, we get a single vector for each word.
###Code
output = output.sum(-2)
output
###Output
_____no_output_____
###Markdown
Notice that the values now match the output of our embedding layer.
###Code
assert torch.isclose(output, y[0]).all()
###Output
_____no_output_____
###Markdown
Axial encodings are intended to work as positional embeddings for transformer-like architectures. It's possible they could work for word embeddings as well, similar to our use of Bloom embeddings. However, the standard version of axial encodings results in similar vectors for adjacent indices - this makes some sense for positional indices, but for word indices it might require some additional preprocessing. For example, we could compress word embeddings down to 1 dimension and sort them, or simply sort by number of occurrences in our corpus which could be considered to be doing the same thing. Large chunks of the outputs vectors will be shared among different inputs, whereas Bloom embeddings seem like they would have a greater capacity to avoid this issue.
###Code
# export
class AxialEncoding(nn.Module):
"""Axial encodings. These are intended to encode position in a sequence
(e.g. index in a sentence). It's possible we could adapt these for use as
word embeddings but this would likely require some experimentation (for
example, words would likely need to be sorted in a thoughtful manner
(e.g. pre-trained embeddings compressed to 1D?) since adjacent inputs will
share half of their encodings).
"""
def __init__(self, vocab_dim, emb_dim, pad_idx=None):
"""
Parameters
----------
vocab_dim: int
Number of words in vocab (or max sequence length if being used for
positional encodings).
emb_dim: int
Size of embedding vectors (often numbers like 50, 100, 300).
pad_idx: int or None
If necessary, pass in an integer to represent padding. Otherwise
no rows are reserved for padding.
"""
super().__init__()
if emb_dim % 2 != 0:
raise ValueError('emb_dim must be an even number.')
self.v = self._decompose_mult(vocab_dim)
self.e = self._decompose_add(emb_dim)
self.emb = nn.ModuleList(InitializedEmbedding(self.v, self.e, pad_idx)
for _ in range(2))
# Makes interface consistent with nn.Embedding. Don't change name.
self.embedding_dim = self.e * 2
def _decompose_mult(self, dim):
return int(np.ceil(np.sqrt(dim)))
def _decompose_add(self, dim):
return int(np.ceil(dim / 2))
def forward(self, idx):
return torch.cat([self.emb[0](idx%self.v), self.emb[1](idx//self.v)],
dim=-1)
# export
class MultiAxialEncoding(nn.Module):
"""Adapted axial encodings to allow for more than 2 embedding matrices.
These are intended to encode position in a sequence (e.g. index in a
sentence) but might work as word embeddings. This version may be better
suited for that use case because using more blocks results in fewer shared
numbers in the output vectors of adjacent inputs.
Some experimentation is still required for this use case (for
example, words would likely need to be sorted in a thoughtful manner
(e.g. pre-trained embeddings compressed to 1D?) since adjacent inputs will
share half of their encodings).
I made this separate from AxialEncoding (at least for now) since I made a
few tweaks to the original design to make this possible and I wanted to
preserve the option to use the simpler, well-tested method
(AxialEncoding). Here, we use a probabilistic hashing scheme to map each
input to multiple embedding rows, while the original design uses
x%v and x//v.
"""
def __init__(self, vocab_dim, emb_dim, n_blocks=2, pre_hashed=False,
pad_idx=None):
super().__init__()
# Must set n_blocks before computing v or e.
self.n_blocks = n_blocks
self.v = self._decompose_mult(vocab_dim)
self.e = self._decompose_add(emb_dim)
self.pre_hashed = pre_hashed
# Must set emb blocks before defining process_fn.
self.emb = nn.ModuleList(InitializedEmbedding(self.v, self.e, pad_idx)
for _ in range(n_blocks))
self.process_fn = identity if pre_hashed else \
partial(probabilistic_hash_tensor, n_buckets=self.v,
n_hashes=len(self.emb), pad_idx=pad_idx)
# Makes interface consistent with nn.Embedding. Don't change name.
self.embedding_dim = self.e * self.n_blocks
def _decompose_mult(self, dim):
return int(np.ceil(dim ** (1 / self.n_blocks)))
def _decompose_add(self, dim):
return int(np.ceil(dim // self.n_blocks))
def forward(self, idx):
# Hashed shape: (bs, seq_len, n_hashes)
xhash = self.process_fn(idx)
# Each embedding takes in a tensor of shape (bs, seq_len).
res_blocks = [e(hashed.squeeze()) for e, hashed in
zip(self.emb, torch.chunk(xhash, xhash.shape[0], -1))]
return torch.cat(res_blocks, dim=-1)
def reduction_ratio(ax, vocab_size, emb_dim):
"""For testing purposes. Lets us compare the number of weights in a
traditional embedding matrix vs. the number of weights in our axial
encoding.
"""
normal_n = vocab_size * emb_dim
ax_n = sum(e.weight.numel() for e in ax.emb)
print('Normal embedding weights:', normal_n)
print('Axial encoding weights:', ax_n)
print('Difference:', normal_n - ax_n)
print('Ratio:', normal_n / ax_n)
vocab_size = 30_000
emb_dim = 100
bs = 12
ax = AxialEncoding(vocab_size, emb_dim)
x = torch.randint(0, vocab_size, (bs, 2))
print(x.shape)
ax
res = ax(x)
print(res.shape)
reduction_ratio(ax, vocab_size, emb_dim)
vocab_size = 30_000
emb_dim = 100
bs = 12
ax = MultiAxialEncoding(vocab_size, emb_dim, 4)
x = torch.randint(0, vocab_size, (bs, 2))
print(x.shape)
ax
res1 = ax(x)
res1.shape
vocab_size = 30_000
emb_dim = 100
bs = 12
ax_pre = MultiAxialEncoding(vocab_size, emb_dim, 4, pre_hashed=True)
ax_pre
###Output
_____no_output_____
###Markdown
By setting the weights of our pre-hashed embedding to the weights of our hashing embedding, we can check that the outputs are ultimately the same.
###Code
for e, e_pre in zip(ax.emb, ax_pre.emb):
e_pre.weight.data = e.weight.data
xhash = probabilistic_hash_tensor(x, 14, 4)
res2 = ax_pre(xhash)
res2.shape
(res1 == res2).all()
reduction_ratio(ax_pre, vocab_size, emb_dim)
###Output
Normal embedding weights: 3000000
Axial encoding weights: 1400
Difference: 2998600
Ratio: 2142.8571428571427
###Markdown
I imagine that as we increase `n_blocks`, there's likely a point where we simply won't have enough weights to encode the amount of information that's present in the data. It would take some experimentation to find where that line is, however.
###Code
ax_large = MultiAxialEncoding(vocab_size, emb_dim, 8, pre_hashed=True)
ax_large
reduction_ratio(ax_large, vocab_size, emb_dim)
###Output
Normal embedding weights: 3000000
Axial encoding weights: 384
Difference: 2999616
Ratio: 7812.5
###Markdown
AttentionSome GPT2-esque layers. These were mostly intuition-building exercises - more thoroughly tested implementations likely exist in Huggingface.
###Code
# export
class Projector(nn.Module):
"""Project input into multiple spaces. Used in DotProductAttention to
generate queries/keys/values.
"""
def __init__(self, n_in, n_out_single=None, spaces=3):
"""
Parameters
----------
n_in: int
Size of input feature dimension, where input is (bs, n_in) or
(bs, seq_len, n_in). If the latter, this ONLY transforms the last
dimension. If you want to take multiple dimensions of information
into account simultaneously, you can flatten the input prior to
passing it in.
n_out_single: int or None
This determines the size of the feature dimension in each new
space. By default, this will be the same as n_in.
spaces: int
Number of spaces to project the input into. Default is 3 because
we commonly use this to generate queries, keys, and values for
attention computations.
"""
super().__init__()
self.spaces = spaces
self.n_in = n_in
self.n_out_single = n_out_single or n_in
self.spaces = spaces
self.n_out = self.n_out_single * self.spaces
self.fc = nn.Linear(self.n_in, self.n_out)
def forward(self, x):
"""
Parameters
----------
x: torch.Tensor
Shape (bs, n_in) or (bs, seq_len, n_in).
Returns
-------
tuple[torch.Tensor]: Tuple of `spaces` tensors where each tensor has
shape (bs, n_out_single) or (bs, seq_len, n_out_single), depending on
the input shape.
"""
return self.fc(x).chunk(self.spaces, dim=-1)
# export
class DotProductAttention(nn.Module):
"""GPT2-style attention block. This was mostly an intuition-building
exercise - in practice, Huggingface provides layers that should probably
be used instead.
"""
def __init__(self, n_in, n_out=None, nf=None, n_heads=12,
temperature='auto', p1=0.1, p2=0.1, return_attn=False):
"""
Parameters
----------
n_in: int
Last dimension of input, usually embedding dimension.
n_out: int or None
Size of output vectors. By default, this will be the same as the
input.
nf: int or None
Size ("nf = number of features") of queries/keys/values.
By default, this will be the same as n_in. Must be divisible by
n_heads.
n_heads: int
Number of attention heads to use. nf must be divisible
by this as each projected vector will be divided evenly among
each head.
temperature: str or float
If str, must be "auto", meaning softmax inputs will be scaled by
sqrt(n_proj_single). You can also specify a float, where values
<1 sharpen the distribution (usually not what we want here) and
values greater than one soften it (allowing attention head to
route more information from multiple neurons rather than almost
all from one).
p1: float
Value in (0.0, 1.0) setting the dropout probability on the
attention weights.
p2: float
Value in (0.0, 1.0) setting dropout probability following the
output layer.
return_attn: bool
If True, the `forward` method will return a tuple of
(output, attention_weights) tensors. If False (the default), just
return the output tensor.
"""
super().__init__()
nf = nf or n_in
n_out = n_out or n_in
assert nf % n_heads == 0, \
'n_proj_single must be divisible by n_heads'
self.proj_in = Projector(n_in, nf, spaces=3)
# Reshape so hidden dimension is split equally between each head.
self.head_splitter = Rearrange('bs seq (heads f) -> bs heads seq f',
heads=n_heads)
self.soft = SmoothSoftmax(temperature)
self.drop_attn = nn.Dropout(p1)
# Concatenate output of each head.
self.head_merger = Rearrange('bs heads seq f -> bs seq (heads f)')
self.fc_out = nn.Linear(nf, n_out)
self.drop_out = nn.Dropout(p2)
# Non-layer attributes.
self.n_heads = n_heads
self.temperature = temperature
self.p1 = p1
self.p2 = p2
self.return_attn = return_attn
def forward(self, x):
"""
Parameters
----------
x: torch.Tensor
Shape (bs, seq_len, n_in). n_in will usually be the sum of
embedding dimensions (word and positional). For other problems
(e.g. web browsing sequence classificaiton), this might include
other features about the page at time step T.
"""
q, k, v = map(self.head_splitter, self.proj_in(x))
scores = q @ k.transpose(-2, -1)
weights = self.drop_attn(self.soft(scores))
x = weights @ v
x = self.head_merger(x)
x = self.drop_out(self.fc_out(x))
return (x, weights) if self.return_attn else x
###Output
_____no_output_____
###Markdown
Model Bases
###Code
# export
class SiameseBase(BaseModel, ABC):
"""Parent class to implement a Siamese network or triplet network (or any
network that passes n inputs of the same shape through a shared encoder).
It concatenates the items into a single batch so the encoder's forward
method (implemented as self._forward) only needs to be called once.
"""
def forward(self, *xb):
bs = xb[0].shape[0]
xb = self._forward(torch.cat(xb, dim=0))
return xb.view(bs, -1, *xb.shape[1:])
@abstractmethod
def _forward(self, xb):
"""Forward pass for a single batch of x. Note that the batch dimension
here will be batch_size * n, where n is the number of images in a
single example (e.g. n=2 for a traditional Siamese Network, but you
can go arbitrarily high).
"""
raise NotImplementedError
bs, c, h, w = 4, 3, 8, 8
n = 3
xb = [torch.randn(bs, c, h, w) for _ in range(n)]
smap(*xb)
class TripletNet(SiameseBase):
def __init__(self, c_in=3):
super().__init__()
self.conv = nn.Conv2d(c_in, 16, kernel_size=3, stride=2)
self.pool = nn.AdaptiveAvgPool2d((1, 1))
def _forward(self, xb):
print(xb.shape)
xb = self.conv(xb)
print(xb.shape)
xb = self.pool(xb)
print(xb.shape)
xb = xb.squeeze(-1).squeeze(-1)
print(xb.shape)
return xb
###Output
_____no_output_____
###Markdown
In this example, each image is encoded as a 16D vector. We have 3 images per row and 4 rows per batch so we end up with a tensor of shape (4, 3, 16). Notice we only perform 1 forward pass: while we could simply define a separate encoder and pass each image through it separately (e.g. `[self.encoder(x) for x in xb]`), this becomes rather slow if n is large or if our encoder is enormous.
###Code
tnet = TripletNet()
yh = tnet(*xb)
yh.shape
###Output
torch.Size([12, 3, 8, 8])
torch.Size([12, 16, 3, 3])
torch.Size([12, 16, 1, 1])
torch.Size([12, 16])
###Markdown
Our name TripletNet was slightly misleading here: the network can actually handle any choice of n. For instance, here we use it as a Siamese Net.
###Code
yh = tnet(*xb[:2])
yh.shape
###Output
torch.Size([8, 3, 8, 8])
torch.Size([8, 16, 3, 3])
torch.Size([8, 16, 1, 1])
torch.Size([8, 16])
###Markdown
It is often useful to extract intermediate activations from a model. We provide a convenient way to make a new model do this (or convert an existing Sequential model to do this).
###Code
# export
class SequentialWithActivations(nn.Sequential):
def __init__(self, *args, return_idx=()):
"""Create a sequential model that also returns activations from one or
more intermediate layers.
Parameters
----------
args: nn.Modules
Just like a Sequential model: pass in 1 or more layers in the
order you want them to process inputs.
return_idx: Iterable[int]
Indices of which layer outputs to return. Do not include the final
layer since that is always returned automatically. Activations
will be returned in increasing order by index - if you create a 4
layer network and pass in return_idx=[2, 0], your output will
still be [layer_0_acts, layer_2_acts, final_layer_acts].
We recommend passing in indices in the expected return order to
avoid confusion.
"""
super().__init__(*args)
assert all(i < len(args) - 1 for i in return_idx), 'All ids in ' \
'return_idx must correspond to layers before the final layer, ' \
'which is always returned.'
self.return_idx = set(return_idx)
def forward(self, x):
"""
Returns
-------
Tuple[torch.Tensor]: N tensors where the first N-1 correspond to
self.return_idx (sorted in ascending order) and the last item is the
output of the final layer.
"""
res = []
for i, module in enumerate(self):
x = module(x)
if i in self.return_idx: res.append(x)
return (*res, x)
@classmethod
def from_sequential(cls, model, return_idx=()):
"""Convert a standard Sequential model to a MultiOutputSequential.
Parameters
----------
model: nn.Sequential
return_idx: Iterable[int]
Indices of which layer outputs to return. Do not include the final
layer since that is always returned automatically.
"""
model = copy.deepcopy(model)
return cls(*list(model), return_idx=return_idx)
###Output
_____no_output_____
|
Jupyter_Notebooks/Gathering_Data_Final.ipynb
|
###Markdown
For data from current time, we use the praw to get submissions. But since the number of submissions are limited, and the Reddit API removed its timestamp feature, to get previous year data we make use of the Reddit Data made available by Jason Michael Baumgartner using Google BigQuery.So, two approaches are used to collect data. Part I:Import the libraries needed for Reddit Data Collection :1. praw - (“Python Reddit API Wrapper”, a python package that allows for simple access to reddit's API.)2. pandas - open source data analysis and manipulation tool3. matplotlib and seaborn to visualise data
###Code
import praw
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
###Output
_____no_output_____
###Markdown
Create a Reddit instance to access the data
###Code
reddit=praw.Reddit(client_id='',
client_secret='',
username='',
password='',
user_agent=''
)
###Output
_____no_output_____
###Markdown
Get the subreddit - r/india and create a list to hold the all the flair needed. ( The allowed flairs are mentioned - https://www.reddit.com/r/india/wiki/rules )
###Code
subreddit=reddit.subreddit('india')
flair_list=['AskIndia','Non-Political','Scheduled','Photography','Science/Technology','Politics','Business/Finance','Policy/Economy','Sports','Food']
###Output
_____no_output_____
###Markdown
Check the attributes available with the submissions available in a subreddit to see which ones can be used as features.
###Code
submissions=subreddit.search(flair_list[0],limit=1)
for submission in submissions:
print(dir(submission))
###Output
['STR_FIELD', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattr__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_chunk', '_comments_by_id', '_fetch', '_fetch_data', '_fetch_info', '_fetched', '_kind', '_reddit', '_reset_attributes', '_safely_add_arguments', '_url_parts', '_vote', 'all_awardings', 'allow_live_comments', 'approved_at_utc', 'approved_by', 'archived', 'author', 'author_flair_background_color', 'author_flair_css_class', 'author_flair_richtext', 'author_flair_template_id', 'author_flair_text', 'author_flair_text_color', 'author_flair_type', 'author_fullname', 'author_patreon_flair', 'author_premium', 'awarders', 'banned_at_utc', 'banned_by', 'can_gild', 'can_mod_post', 'category', 'clear_vote', 'clicked', 'comment_limit', 'comment_sort', 'comments', 'content_categories', 'contest_mode', 'created', 'created_utc', 'crosspost', 'delete', 'disable_inbox_replies', 'discussion_type', 'distinguished', 'domain', 'downs', 'downvote', 'duplicates', 'edit', 'edited', 'enable_inbox_replies', 'flair', 'fullname', 'gild', 'gilded', 'gildings', 'hidden', 'hide', 'hide_score', 'id', 'id_from_url', 'is_crosspostable', 'is_meta', 'is_original_content', 'is_reddit_media_domain', 'is_robot_indexable', 'is_self', 'is_video', 'likes', 'link_flair_background_color', 'link_flair_css_class', 'link_flair_richtext', 'link_flair_template_id', 'link_flair_text', 'link_flair_text_color', 'link_flair_type', 'locked', 'mark_visited', 'media', 'media_embed', 'media_only', 'mod', 'mod_note', 'mod_reason_by', 'mod_reason_title', 'mod_reports', 'name', 'no_follow', 'num_comments', 'num_crossposts', 'num_reports', 'over_18', 'parent_whitelist_status', 'parse', 'permalink', 'pinned', 'post_hint', 'preview', 'pwls', 'quarantine', 'removal_reason', 'removed_by', 'removed_by_category', 'reply', 'report', 'report_reasons', 'save', 'saved', 'score', 'secure_media', 'secure_media_embed', 'selftext', 'selftext_html', 'send_replies', 'shortlink', 'spoiler', 'stickied', 'subreddit', 'subreddit_id', 'subreddit_name_prefixed', 'subreddit_subscribers', 'subreddit_type', 'suggested_sort', 'thumbnail', 'thumbnail_height', 'thumbnail_width', 'title', 'total_awards_received', 'treatment_tags', 'unhide', 'unsave', 'ups', 'upvote', 'url', 'user_reports', 'view_count', 'visited', 'whitelist_status', 'wls']
###Markdown
Create a pandas adataframe to hold the attributes to save and use for further investigation
###Code
df=pd.DataFrame(columns=['flair','title','author','text','url','comments','score','domain'])
###Output
_____no_output_____
###Markdown
Create a for loop to get the information for the various Flair and store them into the database (max. 200 for each flair)
###Code
for flair in flair_list:
list_of_submission=subreddit.search(flair,limit=200)
for submission in list_of_submission:
if not submission.stickied:
comments=""
submission.comments.replace_more(limit=0)
comment_list=submission.comments.list()
for comment in comment_list:
comments=comments+'\n'+comment.body
df=df.append({'flair':flair,'title':submission.title,'author':submission.author,'text':submission.selftext,'url':submission.url,'comments':comments,'score':submission.score,'domain':submission.domain},ignore_index=True)
###Output
_____no_output_____
###Markdown
Save the database obtained into a csv file for further use during the project.
###Code
#df.to_csv(r'reddit_flair.csv',index=False)
df.to_csv(r'reddit_flair3.csv',index=False)
###Output
_____no_output_____
###Markdown
(Ran twice between a span of few days to get more recent data and saved the data from different days in different files, therefore one is commented out.) Part II:Use Google BigQuery to get data from the dataset.
###Code
import numpy as np
import pandas as pd
from google.cloud import bigquery
import praw
import os
import datetime
os.environ["GOOGLE_APPLICATION_CREDENTIALS"]=r""
reddit=praw.Reddit(client_id='',
client_secret='',
username='',
password='',
user_agent=''
)
client=bigquery.Client()
QUERY_POSTS=(
'SELECT * '
'FROM `fh-bigquery.reddit_posts.201*`'
'WHERE subreddit = "india" and link_flair_text in ("AskIndia","Non-Political","Scheduled","Photography","Science/Technology","Politics","Business/Finance","Policy/Economy","Sports","Food") '
'LIMIT 100000'
)
query_job = client.query(QUERY_POSTS)
query = query_job.result().to_dataframe()
keep = []
data = query
data.to_csv(r'reddit_flair2.csv',index=False)
###Output
_____no_output_____
###Markdown
To take specific features from the dataset only. And then to get a max. of 2000 entries.
###Code
df2=pd.read_csv('reddit_flair2.csv')
df3=df2[['link_flair_text','title','author','selftext','url','id','score','domain']]
keep = []
data = df3
flairs = ['AskIndia','Non-Political','Scheduled','Photography','Science/Technology','Politics','Business/Finance','Policy/Economy','Sports','Food']
for flair in flairs:
l = len(df3[df3['link_flair_text'] == flair])
if l > 2000:
l = 2000
idx = list(df3[df3['link_flair_text'] == flair]['id'])
lst = np.random.choice(idx, l, replace=False)
for item in lst:
keep.append(item)
df4 = df3[df3['id'].isin(keep)]
###Output
_____no_output_____
###Markdown
The above snippet only got us the posts. We now need the comments too. For this we will use praw.
###Code
def getcomments(id_num):
submission=reddit.submission(id=id_num)
submission.comments.replace_more(limit=0)
sub_comments=''
for i,comment in enumerate(submission.comments):
sub_comments+=comment.body
if i==10:
break
return sub_comments
df4['comments']=df4['id'].apply(getcomments)
df4[['id','comments']].head()
print('done')
df4.to_csv('out.csv')
###Output
_____no_output_____
###Markdown
The data is now collected and stored. The recent data is stored in reddit_flair and reddit_flair3 and the data from previous year is saved in out.csv .Now, we combine all the different data and save it in final_db_2.csv
###Code
df1_1=pd.read_csv('reddit_flair3.csv')
df1_2=pd.read_csv('reddit_flair.csv')
df1=pd.concat([df1_1,df1_2],ignore_index=True)
df2=pd.read_csv('out.csv')
df2.drop('Unnamed: 0',axis=1,inplace=True)
df2.drop('id',axis=1,inplace=True)
df2.rename(columns={"selftext": "text","link_flair_text":"flair"},inplace=True)
df_final=pd.concat([df1,df2],ignore_index=True)
df_final.to_csv('final_db_2.csv',index=False)
###Output
_____no_output_____
###Markdown
After the EDA in the next notebook,we see that the dataset is very imbalanced. So oversampling is done here and it is stored in corrected_dataset.csv
###Code
df=pd.read_csv('final_db_2.csv')
df_final=pd.concat([
df,
df[df['flair']=='Scheduled'].sample(n=550),
df[df['flair']=='Food'].sample(n=600),
df[df['flair']=='Photography']
])
df_final=pd.concat([
df_final,
df_final[df_final['flair']=='Photography'].sample(n=500),
])
df_final.to_csv('corrected_dataset.csv')
###Output
_____no_output_____
|
see_food_data_prep.ipynb
|
###Markdown
Create Buckets for the Categories
###Code
grains = ['Wheat and products','Rice (Milled Equivalent)','Barley and products','Maize and products',
'Millet and products','Cereals, Other', 'Sorghum and products', 'Oats', 'Rye and products',
'Cereals - Excluding Beer', 'Infant food']
meat = ['Meat, Aquatic Mammals','Pigmeat', 'Animal fats', 'Offals','Meat', 'Fats, Animals, Raw', 'Offals, Edible']
seafood = ['Aquatic Products, Other','Aquatic Animals, Others','Molluscs, Other', 'Cephalopods','Crustaceans',
'Marine Fish, Other','Pelagic Fish','Demersal Fish','Fish, Seafood','Freshwater Fish',
'Meat, Other','Bovine Meat', 'Poultry Meat', 'Mutton & Goat Meat']
dairy = ['Milk - Excluding Butter', 'Eggs', 'Cream', 'Butter, Ghee']
alcohol = ['Beverages, Fermented','Alcoholic Beverages', 'Beverages, Alcoholic', 'Beer','Wine' ]
fruit = ['Plantains','Grapefruit and products','Lemons, Limes and products','Fruits - Excluding Wine',
'Fruits, Other','Grapes and products (excl wine)', 'Dates', 'Pineapples and products',
'Apples and products', 'Bananas', 'Citrus, Other','Oranges, Mandarines', 'Coconuts - Incl Copra']
veggies = ['Aquatic Plants','Pimento','Onions','Soyabeans','Peas','Beans','Vegetables', 'Pulses', 'Vegetables, Other',
'Tomatoes and products', 'Olives (including preserved)', 'Pulses, Other and products']
root = ['Yams', 'Roots, Other','Sweet potatoes','Cassava and products','Starchy Roots',
'Potatoes and products']
seed_nut = ['Cottonseed', 'Sunflower seed','Palm kernels','Rape and Mustardseed',
'Groundnuts (Shelled Eq)','Treenuts','Sesame seed', 'Nuts and products']
oils = ['Ricebran Oil','Palmkernel Oil', 'Coconut Oil','Fish, Liver Oil','Fish, Body Oil','Maize Germ Oil',
'Oilcrops, Other', 'Vegetable Oils','Oilcrops', 'Oilcrops Oil, Other', 'Olive Oil',
'Sesameseed Oil', 'Cottonseed Oil', 'Rape and Mustard Oil', 'Palm Oil', 'Sunflowerseed Oil',
'Groundnut Oil','Soyabean Oil']
spices_sweetners = ['Sugar non-centrifugal','Spices','Cloves', 'Sugar & Sweeteners','Sugar Crops', 'Spices, Other',
'Pepper', 'Honey', 'Sweeteners, Other','Sugar (Raw Equivalent)', 'Sugar beet', 'Sugar cane']
coffee = ['Coffee and products']
tea = ['Tea (including mate)']
cocoa = ['Cocoa Beans and products']
###Output
_____no_output_____
###Markdown
Apply this to the CSV
###Code
food_groups = [grains, meat, seafood, dairy, alcohol, fruit, veggies, root, seed_nut, oils,
spices_sweetners, coffee, tea, cocoa]
fg_names = ['grains', 'meat', 'seafood', 'dairy', 'alcohol', 'fruit', 'veggies', 'root', 'seed_nut', 'oils',
'spices_sweetners', 'coffee', 'tea', 'cocoa']
for n, fg in enumerate(food_groups):
for f in fg:
food['Item'].replace(f,fg_names[n], inplace=True)
food = pd.DataFrame(food.groupby(['Area', 'Area Abbreviation', 'latitude', 'longitude','Item'], as_index=False).sum())
food = pd.DataFrame(food.groupby(['Area', 'Area Abbreviation', 'latitude', 'longitude','Item'], as_index=False).sum())
food["id"] = food.index
food_long = pd.wide_to_long(food, ["Y"], i="id", j="year")
year = food_long.index.get_level_values('year')
food_long["year"] = year
food_long.reset_index(drop=True, inplace=True)
food_long.drop(["Item Code", "latitude", "longitude", "Element Code", "Area Code"], axis=1, inplace=True)
food_long = food_long[["Area", "Area Abbreviation", "year", "Item", "Y"]]
food_long.head()
###Output
_____no_output_____
###Markdown
All Categories Added
###Code
foodall = pd.DataFrame(food.groupby(['Area', 'Area Abbreviation', 'latitude', 'longitude'], as_index=False).sum())
foodall["Item"] = np.array("all")
foodall.head()
foodall["id"] = foodall.index
foodall_long = pd.wide_to_long(foodall, ["Y"], i="id", j="year")
year = foodall_long.index.get_level_values('year')
foodall_long["year"] = year
foodall_long.reset_index(drop=True, inplace=True)
foodall_long.drop(["Item Code", "latitude", "longitude", "Element Code", "Area Code"], axis=1, inplace=True)
foodall_long = foodall_long[["Area", "Area Abbreviation", "year", "Item", "Y"]]
foodall_long = foodall_long.fillna(0)
foodall_long.head()
###Output
_____no_output_____
###Markdown
Append Dataframes
###Code
food_final = food_long.append(foodall_long, ignore_index=True, verify_integrity=True)
food_final = food_final.sort_values(["Area", "year"], axis=0)
###Output
_____no_output_____
###Markdown
Fix Mislabeled Codes
###Code
food_final.loc[food_final.Area == 'Bahamas', "Area Abbreviation"] = 'BHS'
food_final.loc[food_final.Area == 'The former Yugoslav Republic of Macedonia', "Area Abbreviation"] = 'MKD'
food_final.loc[food_final.Area == 'China, Taiwan Province of', "Area Abbreviation"] = 'TWN'
food_final.loc[food_final.Area == 'China, Macao SAR', "Area Abbreviation"] = 'MAC'
food_final.loc[food_final.Area == 'China, Hong Kong SAR', "Area Abbreviation"] = 'HKG'
###Output
_____no_output_____
###Markdown
Export to csv
###Code
food_final.to_csv("food_final.csv")
###Output
_____no_output_____
|
courseware/heat-transport.ipynb
|
###Markdown
Heat transportThis notebook is part of [The Climate Laboratory](https://brian-rose.github.io/ClimateLaboratoryBook) by [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany. ____________ 1. Spatial patterns of insolation and surface temperature____________Let's take a look at seasonal and spatial pattern of insolation and compare this to the zonal average surface temperatures.
###Code
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import climlab
from climlab import constants as const
# Calculate daily average insolation as function of latitude and time of year
lat = np.linspace( -90., 90., 500 )
days = np.linspace(0, const.days_per_year, 365 )
Q = climlab.solar.insolation.daily_insolation( lat, days )
## daily surface temperature from NCEP reanalysis
ncep_url = "http://www.esrl.noaa.gov/psd/thredds/dodsC/Datasets/ncep.reanalysis.derived/"
ncep_temp = xr.open_dataset( ncep_url + "surface_gauss/skt.sfc.day.1981-2010.ltm.nc", decode_times=False)
#url = 'http://apdrc.soest.hawaii.edu:80/dods/public_data/Reanalysis_Data/NCEP/NCEP/clima/'
#skt_path = 'surface_gauss/skt'
#ncep_temp = xr.open_dataset(url+skt_path)
ncep_temp_zon = ncep_temp.skt.mean(dim='lon')
fig = plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(121)
CS = ax1.contour( days, lat, Q , levels = np.arange(0., 600., 50.) )
ax1.clabel(CS, CS.levels, inline=True, fmt='%r', fontsize=10)
ax1.set_title('Daily average insolation', fontsize=18 )
ax1.contourf ( days, lat, Q, levels=[-100., 0.], colors='k' )
ax2 = fig.add_subplot(122)
CS = ax2.contour( (ncep_temp.time - ncep_temp.time[0])/const.hours_per_day, ncep_temp.lat,
ncep_temp_zon.T, levels=np.arange(210., 310., 10. ) )
ax2.clabel(CS, CS.levels, inline=True, fmt='%r', fontsize=10)
ax2.set_title('Observed zonal average surface temperature', fontsize=18 )
for ax in [ax1,ax2]:
ax.set_xlabel('Days since January 1', fontsize=16 )
ax.set_ylabel('Latitude', fontsize=16 )
ax.set_yticks([-90,-60,-30,0,30,60,90])
ax.grid()
###Output
_____no_output_____
###Markdown
This figure reveals something fairly obvious, but still worth thinking about:**Warm temperatures are correlated with high insolation**. It's warm where the sun shines.More specifically, we can see a few interesting details here:- The seasonal cycle is weakest in the tropics and strongest in the high latitudes.- The warmest temperatures occur slighly NORTH of the equator- The highest insolation occurs at the poles at summer solstice. The local surface temperature does not correlate perfectly with local insolation for two reasons:- the climate system has heat capacity, which buffers some of the seasonal variations- the climate system moves energy around in space! ____________ 2. Calculating Radiative-Convective Equilibrium as a function of latitude____________As a first step to understanding the effects of **heat transport by fluid motions** in the atmosphere and ocean, we can calculate **what the surface temperature would be without any motion**.Let's calculate a **radiative-convective equilibrium** state for every latitude band. Putting realistic insolation into an RCMThis code demonstrates how to create a model with both latitude and vertical dimensions.
###Code
# A two-dimensional domain
state = climlab.column_state(num_lev=30, num_lat=40, water_depth=10.)
# Specified relative humidity distribution
h2o = climlab.radiation.ManabeWaterVapor(name='Fixed Relative Humidity', state=state)
# Hard convective adjustment
conv = climlab.convection.ConvectiveAdjustment(name='Convective Adjustment', state=state, adj_lapse_rate=6.5)
# Daily insolation as a function of latitude and time of year
sun = climlab.radiation.DailyInsolation(name='Insolation', domains=state['Ts'].domain)
# Couple the radiation to insolation and water vapor processes
rad = climlab.radiation.RRTMG(name='Radiation',
state=state,
specific_humidity=h2o.q,
albedo=0.125,
insolation=sun.insolation,
coszen=sun.coszen)
model = climlab.couple([rad,sun,h2o,conv], name='RCM')
print( model)
model.compute_diagnostics()
fig, ax = plt.subplots()
ax.plot(model.lat, model.insolation)
ax.set_xlabel('Latitude')
ax.set_ylabel('Insolation (W/m2)');
###Output
_____no_output_____
###Markdown
This new insolation process uses the same code we've already been working with to compute realistic distributions of insolation. Here we are using```climlab.radiation.DailyInsolation```but there is also```climlab.radiation.AnnualMeanInsolation```for models in which you prefer to suppress the seasonal cycle and prescribe a time-invariant insolation. The following code will just integrate the model forward in four steps in order to get snapshots of insolation at the solstices and equinoxes.
###Code
# model is initialized on Jan. 1
# integrate forward just under 1/4 year... should get about to the NH spring equinox
model.integrate_days(31+28+22)
Q_spring = model.insolation.copy()
# Then forward to NH summer solstice
model.integrate_days(31+30+31)
Q_summer = model.insolation.copy()
# and on to autumnal equinox
model.integrate_days(30+31+33)
Q_fall = model.insolation.copy()
# and finally to NH winter solstice
model.integrate_days(30+31+30)
Q_winter = model.insolation.copy()
fig, ax = plt.subplots()
ax.plot(model.lat, Q_spring, label='Spring')
ax.plot(model.lat, Q_summer, label='Summer')
ax.plot(model.lat, Q_fall, label='Fall')
ax.plot(model.lat, Q_winter, label='Winter')
ax.legend()
ax.set_xlabel('Latitude')
ax.set_ylabel('Insolation (W/m2)');
###Output
_____no_output_____
###Markdown
This just serves to demonstrate that the `DailyInsolation` process is doing something sensible. Note that we could also pass different orbital parameters to this subprocess. They default to present-day values, which is what we are using here. Find the steady seasonal cycle of temperature in radiative-convective equilibrium
###Code
model.integrate_years(4.)
model.integrate_years(1.)
###Output
Integrating for 365 steps, 365.2422 days, or 1.0 years.
Total elapsed time is 5.97411799622278 years.
###Markdown
All climlab `Process` objects have an attribute called `timeave`. This is a dictionary of time-averaged diagnostics, which are automatically calculated during the most recent call to `integrate_years()` or `integrate_days()`.
###Code
model.timeave.keys()
###Output
_____no_output_____
###Markdown
Here we use the `timeave['insolation']` to plot the annual mean insolation. (We know it is the *annual* average because the last call to `model.integrate_years` was for exactly 1 year)
###Code
fig, ax = plt.subplots()
ax.plot(model.lat, model.timeave['insolation'])
ax.set_xlabel('Latitude')
ax.set_ylabel('Insolation (W/m2)')
###Output
_____no_output_____
###Markdown
Compare annual average temperature in RCE to the zonal-, annual mean observations.
###Code
# Plot annual mean surface temperature in the model,
# compare to observed annual mean surface temperatures
fig, ax = plt.subplots()
ax.plot(model.lat, model.timeave['Ts'], label='RCE')
ax.plot(ncep_temp_zon.lat, ncep_temp_zon.mean(dim='time'), label='obs')
ax.set_xticks(range(-90,100,30))
ax.grid(); ax.legend();
###Output
_____no_output_____
###Markdown
Our modeled RCE state is **far too warm in the tropics**, and **too cold in the mid- to high latitudes.** Vertical structure of temperature: comparing RCE to observations
###Code
# Observed air temperature from NCEP reanalysis
## The NOAA ESRL server is shutdown! January 2019
ncep_air = xr.open_dataset( ncep_url + "pressure/air.mon.1981-2010.ltm.nc", decode_times=False)
#air = xr.open_dataset(url+'pressure/air')
#ncep_air = air.rename({'lev':'level'})
level_ncep_air = ncep_air.level
lat_ncep_air = ncep_air.lat
Tzon = ncep_air.air.mean(dim=('time','lon'))
# Compare temperature profiles in RCE and observations
contours = np.arange(180., 350., 15.)
fig = plt.figure(figsize=(14,6))
ax1 = fig.add_subplot(1,2,1)
cax1 = ax1.contourf(lat_ncep_air, level_ncep_air, Tzon+const.tempCtoK, levels=contours)
fig.colorbar(cax1)
ax1.set_title('Observered temperature (K)')
ax2 = fig.add_subplot(1,2,2)
field = model.timeave['Tatm'].transpose()
cax2 = ax2.contourf(model.lat, model.lev, field, levels=contours)
fig.colorbar(cax2)
ax2.set_title('RCE temperature (K)')
for ax in [ax1, ax2]:
ax.invert_yaxis()
ax.set_xlim(-90,90)
ax.set_xticks([-90, -60, -30, 0, 30, 60, 90])
###Output
_____no_output_____
###Markdown
Again, this plot reveals temperatures that are too warm in the tropics, too cold at the poles throughout the troposphere.Note however that the **vertical temperature gradients** are largely dictated by the convective adjustment in our model. We have parameterized this gradient, and so we can change it by changing our parameter for the adjustment.We have (as yet) no parameterization for the **horizontal** redistribution of energy in the climate system. TOA energy budget in RCE equilibriumBecause there is no horizontal energy transport in this model, the TOA radiation budget should be closed (net flux is zero) at all latitudes.Let's check this by plotting time-averaged shortwave and longwave radiation:
###Code
fig, ax = plt.subplots()
ax.plot(model.lat, model.timeave['ASR'], label='ASR')
ax.plot(model.lat, model.timeave['OLR'], label='OLR')
ax.set_xlabel('Latitude')
ax.set_ylabel('W/m2')
ax.legend(); ax.grid()
###Output
_____no_output_____
###Markdown
Indeed, the budget is (very nearly) closed everywhere. Each latitude is in energy balance, independent of every other column. ____________ 3. Observed and modeled TOA radiation budget____________ We are going to look at the (time average) TOA budget as a function of latitude to see how it differs from the RCE state we just plotted.Ideally we would look at actual satellite observations of SW and LW fluxes. Instead, here we will use the NCEP Reanalysis for convenience. But bear in mind that the radiative fluxes in the reanalysis are a model-generated product, they are not really observations. TOA budget from NCEP Reanalysis
###Code
# Get TOA radiative flux data from NCEP reanalysis
# downwelling SW
dswrf = xr.open_dataset(ncep_url + '/other_gauss/dswrf.ntat.mon.1981-2010.ltm.nc', decode_times=False)
#dswrf = xr.open_dataset(url + 'other_gauss/dswrf')
# upwelling SW
uswrf = xr.open_dataset(ncep_url + '/other_gauss/uswrf.ntat.mon.1981-2010.ltm.nc', decode_times=False)
#uswrf = xr.open_dataset(url + 'other_gauss/uswrf')
# upwelling LW
ulwrf = xr.open_dataset(ncep_url + '/other_gauss/ulwrf.ntat.mon.1981-2010.ltm.nc', decode_times=False)
#ulwrf = xr.open_dataset(url + 'other_gauss/ulwrf')
ASR = dswrf.dswrf - uswrf.uswrf
OLR = ulwrf.ulwrf
ASRzon = ASR.mean(dim=('time','lon'))
OLRzon = OLR.mean(dim=('time','lon'))
ticks = [-90, -60, -30, 0, 30, 60, 90]
fig, ax = plt.subplots()
ax.plot(ASRzon.lat, ASRzon, label='ASR')
ax.plot(OLRzon.lat, OLRzon, label='OLR')
ax.set_ylabel('W/m2')
ax.set_xlabel('Latitude')
ax.set_xlim(-90,90); ax.set_ylim(50,310)
ax.set_xticks(ticks);
ax.set_title('Observed annual mean radiation at TOA')
ax.legend(); ax.grid();
###Output
_____no_output_____
###Markdown
We find that ASR does NOT balance OLR in most locations. Across the tropics the absorbed solar radiation exceeds the longwave emission to space. The tropics have a **net gain of energy by radiation**.The opposite is true in mid- to high latitudes: **the Earth is losing energy by net radiation to space** at these latitudes. TOA budget from the control CESM simulationLoad data from the fully coupled CESM control simulation that we've used before.
###Code
casenames = {'cpl_control': 'cpl_1850_f19',
'cpl_CO2ramp': 'cpl_CO2ramp_f19',
'som_control': 'som_1850_f19',
'som_2xCO2': 'som_1850_2xCO2',
}
# The path to the THREDDS server, should work from anywhere
basepath = 'http://thredds.atmos.albany.edu:8080/thredds/dodsC/CESMA/'
# For better performance if you can access the roselab_rit filesystem (e.g. from JupyterHub)
#basepath = '/roselab_rit/cesm_archive/'
casepaths = {}
for name in casenames:
casepaths[name] = basepath + casenames[name] + '/concatenated/'
# make a dictionary of all the CAM atmosphere output
atm = {}
for name in casenames:
path = casepaths[name] + casenames[name] + '.cam.h0.nc'
print('Attempting to open the dataset ', path)
atm[name] = xr.open_dataset(path)
lat_cesm = atm['cpl_control'].lat
ASR_cesm = atm['cpl_control'].FSNT
OLR_cesm = atm['cpl_control'].FLNT
# extract the last 10 years from the slab ocean control simulation
# and the last 20 years from the coupled control
nyears_slab = 10
nyears_cpl = 20
clim_slice_slab = slice(-(nyears_slab*12),None)
clim_slice_cpl = slice(-(nyears_cpl*12),None)
# For now we're just working with the coupled control simulation
# Take the time and zonal average
ASR_cesm_zon = ASR_cesm.isel(time=clim_slice_slab).mean(dim=('lon','time'))
OLR_cesm_zon = OLR_cesm.isel(time=clim_slice_slab).mean(dim=('lon','time'))
###Output
_____no_output_____
###Markdown
Now we can make the same plot of ASR and OLR that we made for the observations above.
###Code
fig, ax = plt.subplots()
ax.plot(lat_cesm, ASR_cesm_zon, label='ASR')
ax.plot(lat_cesm, OLR_cesm_zon, label='OLR')
ax.set_ylabel('W/m2')
ax.set_xlabel('Latitude')
ax.set_xlim(-90,90); ax.set_ylim(50,310)
ax.set_xticks(ticks);
ax.set_title('CESM control simulation: Annual mean radiation at TOA')
ax.legend(); ax.grid();
###Output
_____no_output_____
###Markdown
Essentially the same story as the reanalysis data: there is a **surplus of energy across the tropics** and a net **energy deficit in mid- to high latitudes**.There are two locations where ASR = OLR, near about 35º in both hemispheres. ____________ 4. The energy budget for a zonal band____________ The basic ideaThrough most of the previous notes we have been thinking about **global averages**.We've been working with an energy budget that looks something like this: When we start thinking about regional climates, we need to modify our budget to account for the **additional heating or cooling** due to **transport** in and out of the column: Conceptually, the additional energy source is the difference between what's coming in and what's going out:$$ h = \mathcal{H}_{in} - \mathcal{H}_{out} $$where $h$ is a **dynamic heating rate** in W m$^{-2}$. A more careful budgetLet’s now consider a thin band of the climate system, of width $\delta \phi$ , and write down a careful energy budget for it.  Let $\mathcal{H}(\phi)$ be the total rate of northward energy transport across the latitude line $\phi$, measured in Watts (usually PW).So the transport into the band is $\mathcal{H}(\phi)$, and the transport out is just $\mathcal{H}(\phi + \delta \phi)$The dynamic heating rate looks like$$ h = \frac{\text{transport in} - \text{transport out}}{\text{area of band}} $$ The surface area of the latitude band is$$ A = \text{Circumference} ~\times ~ \text{north-south width} $$$$ A = 2 \pi a \cos \phi ~ \times ~ a \delta \phi $$$$ A = 2 \pi a^2 \cos\phi ~ \delta\phi $$ So we can write the heating rate as$$\begin{align*}h &= \frac{\mathcal{H}(\phi) - \mathcal{H}(\phi+\delta\phi)}{2 \pi a^2 \cos\phi ~ \delta\phi} \\ &= -\frac{1}{2 \pi a^2 \cos\phi} \left( \frac{\mathcal{H}(\phi+\delta\phi) - \mathcal{H}(\phi)}{\delta\phi} \right)\end{align*}$$ Writing it this way, we can see that if the width of the band $\delta \phi$ becomes very small, then the quantity in parentheses is simply the **derivative** $d\mathcal{H}/d\phi$. The **dynamical heating rate** in W m$^{-2}$ is thus$$ h = - \frac{1}{2 \pi a^2 \cos\phi } \frac{\partial \mathcal{H}}{\partial \phi} $$which is the **convergence of energy transport** into this latitude band: the difference between what's coming in and what's going out. ____________ 5. Calculating heat transport from the steady-state energy budget____________If we can **assume that the budget is balanced**, i.e. assume that the system is at equilibrium and there is negligible heat storage, then we can use the energy budget to infer $\mathcal{H}$ from a measured (or modeled) TOA radiation imbalance:The balanced budget is$$ ASR + h = OLR $$(i.e. the **sources** balance the **sinks**)which we can substitute in for $h$ and rearrange to write as$$ \frac{\partial \mathcal{H}}{\partial \phi} = 2 \pi ~a^2 \cos\phi ~ \left( \text{ASR} - \text{OLR} \right) = 2 \pi ~a^2 \cos\phi ~ R_{TOA} $$where for convenience we write $R_{TOA} = ASR - OLR$, the net downward flux at the top of atmosphere. Now integrate from the South Pole ($\phi = -\pi/2$):$$ \int_{-\pi/2}^{\phi} \frac{\partial \mathcal{H}}{\partial \phi^\prime} d\phi^\prime = 2 \pi ~a^2 \int_{-\pi/2}^{\phi} \cos\phi^\prime ~ R_{TOA} d\phi^\prime $$$$ \mathcal{H}(\phi) - \mathcal{H}(-\pi/2) = 2 \pi ~a^2 \int_{-\pi/2}^{\phi} \cos\phi^\prime ~ R_{TOA} d\phi^\prime $$ Our boundary condition is that the transport must go to zero at the pole. We therefore have a formula for calculating the heat transport at any latitude, by integrating the imbalance from the South Pole:$$ \mathcal{H}(\phi) = 2 \pi ~a^2 \int_{-\pi/2}^{\phi} \cos\phi^\prime ~ R_{TOA} d\phi^\prime $$ What about the boundary condition at the other pole? We must have $\mathcal{H}(\pi/2) = 0$ as well, because a non-zero transport at the pole is not physically meaningful.Notice that if we apply the above formula and integrate all the way to the other pole, we then have$$ \mathcal{H}(\pi/2) = 2 \pi ~a^2 \int_{-\pi/2}^{\pi/2} \cos\phi^\prime ~ R_{TOA} d\phi^\prime $$ This is an integral of the radiation imbalance weighted by cosine of latitude. In other words, this is **proportional to the area-weighted global average energy imbalance**.We started by assuming that this imbalance is zero.If the **global budget is balanced**, then the physical boundary condition of no-flux at the poles is satisfied. ____________ 6. Poleward heat transport in the CESM____________ Here we will code up a function that performs the above integration.
###Code
def inferred_heat_transport(energy_in, lat=None, latax=None):
'''Compute heat transport as integral of local energy imbalance.
Required input:
energy_in: energy imbalance in W/m2, positive in to domain
As either numpy array or xarray.DataArray
If using plain numpy, need to supply these arguments:
lat: latitude in degrees
latax: axis number corresponding to latitude in the data
(axis over which to integrate)
returns the heat transport in PW.
Will attempt to return data in xarray.DataArray if possible.
'''
from scipy import integrate
from climlab import constants as const
if lat is None:
try: lat = energy_in.lat
except:
raise InputError('Need to supply latitude array if input data is not self-describing.')
lat_rad = np.deg2rad(lat)
coslat = np.cos(lat_rad)
field = coslat*energy_in
if latax is None:
try: latax = field.get_axis_num('lat')
except:
raise ValueError('Need to supply axis number for integral over latitude.')
# result as plain numpy array
integral = integrate.cumtrapz(field, x=lat_rad, initial=0., axis=latax)
result = (1E-15 * 2 * np.math.pi * const.a**2 * integral)
if isinstance(field, xr.DataArray):
result_xarray = field.copy()
result_xarray.values = result
return result_xarray
else:
return result
###Output
_____no_output_____
###Markdown
Let's now use this to calculate the total northward heat transport from our control simulation with the CESM:
###Code
fig, ax = plt.subplots()
ax.plot(lat_cesm, inferred_heat_transport(ASR_cesm_zon - OLR_cesm_zon))
ax.set_ylabel('PW')
ax.set_xticks(ticks)
ax.grid()
ax.set_title('Total northward heat transport inferred from CESM control simulation')
###Output
_____no_output_____
|
Python/statistics_with_Python/07_Regression/Smart_Alex/Task2_Supermodel.ipynb
|
###Markdown
Reading Data
###Code
data = pd.read_csv('/home/atrides/Desktop/R/statistics_with_Python/07_Regression/Data_Files/Supermodel.dat', sep='\t')
data.head()
fig = plt.figure(figsize=(30,12))
ax1=plt.subplot(131)
coef =np.polyfit(data['age'], data['salary'],1)
poly1d_fn = np.poly1d(coef)
_=plt.plot(data['age'],data['salary'],'co' , data['age'], poly1d_fn(data['age']), '--k')
_=ax1.set_title('salary vs age', fontdict={'fontsize': 18, 'fontweight': 'medium'})
ax2=plt.subplot(132)
coef =np.polyfit(data['years'], data['salary'],1)
poly1d_fn = np.poly1d(coef)
_=plt.plot(data['years'],data['salary'],'co' , data['years'], poly1d_fn(data['years']), '--k')
_=ax2.set_title('salary vs experience', fontdict={'fontsize': 18, 'fontweight': 'medium'})
ax3 = plt.subplot(133)
coef =np.polyfit(data['beauty'], data['salary'],1)
poly1d_fn = np.poly1d(coef)
_=plt.plot(data['beauty'],data['salary'],'co' , data['beauty'], poly1d_fn(data['beauty']), '--k')
_=ax3.set_title('salary vs beauty', fontdict={'fontsize': 18, 'fontweight': 'medium'})
###Output
_____no_output_____
###Markdown
Fitting Model
###Code
m01 = sm.ols('salary~age', data=data)
res_1 = m01.fit()
res_1.summary()
m02 = sm.ols('salary~age+years', data=data)
res_2 = m02.fit()
res_2.summary()
m03 = sm.ols('salary~age+years+beauty', data=data)
res_3 = m03.fit()
res_3.summary()
###Output
_____no_output_____
###Markdown
Comparing Models
###Code
from statsmodels.stats.anova import anova_lm
anova_res = anova_lm(res_1, res_2, res_3)
print(anova_res)
###Output
df_resid ssr df_diff ss_diff F Pr(>F)
0 229.0 49742.554716 0.0 NaN NaN NaN
1 228.0 48555.607734 1.0 1186.946982 5.589655 0.018906
2 227.0 48202.790126 1.0 352.817608 1.661514 0.198711
###Markdown
It seems that including beauty as a predictor in our model doesn't improves the model much as we can see from aic, bic , r_squared and adjusted r_squared. Checking For Outlier Influence
###Code
from statsmodels.stats.outliers_influence import OLSInfluence
summary_frame = OLSInfluence(res_2).summary_frame()
summary_frame.head()
summary_frame = summary_frame[['cooks_d','standard_resid', 'student_resid', 'hat_diag' ]]
summary_frame.head()
resid = pd.DataFrame(data['salary'] - res_2.fittedvalues)
resid.columns = ['residual']
dfbeta = pd.DataFrame(pd.DataFrame(OLSInfluence(res_2).dfbeta)[0])
dfbeta.columns = ['dfbeta']
cov_ratio = pd.DataFrame(OLSInfluence(res_2).cov_ratio)
cov_ratio.columns = ['cov_ratio']
df_ = [data, resid, summary_frame, dfbeta]
from functools import reduce
final_summary = reduce(lambda left,right: pd.merge(left,right, left_index=True, right_index=True), df_)
final_summary.head()
large_resid = final_summary[(final_summary['standard_resid']>=2) | (final_summary['standard_resid']<=-2)]
large_resid = pd.merge(large_resid, cov_ratio, how = 'left', right_index=True, left_index=True)
large_resid
k = 2 #number of predictors
n = len(data)#number of objervations
average_leverage = (k+1)/n
average_leverage
cvr_limit_high = 1+3*average_leverage
cvr_limit_low = 1-3*average_leverage
(cvr_limit_low, cvr_limit_high)
###Output
_____no_output_____
###Markdown
doctored data , i.e removing large_resid points from data to see how the output changes
###Code
df_new = data.merge(large_resid, how='left', indicator=True)
df_new = df_new[df_new['_merge'] == 'left_only']
df_new.head()
df_new.reset_index(inplace=True,drop=True)
res_2.summary()
m04 = sm.ols('salary~age+years', data=df_new)
res_4 = m04.fit()
res_4.summary()
fig = plt.figure(figsize=(20,10))
a1=plt.subplot(122)
coef =np.polyfit(df_new['age'], df_new['salary'],1)
poly1d_fn = np.poly1d(coef)
_=plt.plot(df_new['age'],df_new['salary'],'co' , df_new['age'], poly1d_fn(df_new['age']), '--k')
_=a1.set_ylim([-10,100])
_=a1.set_title('salary vs age in doctored data', fontdict={'fontsize': 18, 'fontweight': 'medium'})
a2=plt.subplot(121)
coef =np.polyfit(data['age'], data['salary'],1)
poly1d_fn = np.poly1d(coef)
_=plt.plot(data['age'],data['salary'],'co' , data['age'], poly1d_fn(data['age']), '--k')
_=a2.set_ylim([-10,100])
_=a2.set_title('salary vs age in original data', fontdict={'fontsize': 18, 'fontweight': 'medium'})
###Output
_____no_output_____
###Markdown
In this case it seems that the line outliers affect our model to some extent!¶ Testing Assumptions
###Code
from statsmodels.stats.stattools import durbin_watson
durbin_watson(res_2.resid)
from statsmodels.tools.tools import add_constant
from statsmodels.stats.outliers_influence import variance_inflation_factor
df_ = add_constant(data)
df_.drop(['salary'],axis=1, inplace=True)
df_.head()
vif = pd.Series([variance_inflation_factor(df_.values, i)
for i in range(1, df_.shape[1])],
index=df_.columns[1:])
vif
avg_vif = np.mean(vif)
avg_vif
fig,ax = plt.subplots(figsize=(6, 4))
ax = plt.hist(final_summary['student_resid'],density=True,bins=30, edgecolor='black', linewidth=1.4)
plt.xlabel('student_resid', fontsize=14)
plt.show()
# performing shapiro-wilk test for checking the normality of errors
st.shapiro(final_summary['standard_resid'])
###Output
_____no_output_____
###Markdown
error deviates from normality
###Code
prediction = pd.DataFrame(res_2.fittedvalues)
prediction.columns = ['predicted']
prediction.head()
prediction['standarized_prediction'] = (prediction['predicted']-prediction['predicted'].mean())/prediction['predicted'].std()
prediction.head()
_ = sns.scatterplot(x= final_summary['standard_resid'], y = prediction['standarized_prediction'] )
_ = plt.axhline(y=0)
_=pg.qqplot(final_summary['standard_resid'])
###Output
_____no_output_____
|
docs/source/jupyter_notebooks.ipynb
|
###Markdown
Jupyter Notebooks Acknowledgements The material in this tutorial is specific to PYNQ. Wherever possible, however, it re-uses generic documentation describing Jupyter notebooks. In particular, we have re-used content from the following example notebooks:1. What is the Jupyter Notebook?1. Notebook Basics1. Running Code1. Markdown CellsThe original notebooks and further example notebooks are available at [Jupyter documentation](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/examples_index.html). Introduction If you are reading this documentation from the webpage, you should note that the webpage is a static html version of the notebook from which it was generated. If the PYNQ platform is available, you can open this notebook from the getting_started folder in the PYNQ Jupyter landing page. The Jupyter Notebook is an **interactive computing environment** that enables users to author notebook documents that include:* Live code* Interactive widgets* Plots* Narrative text* Equations* Images* VideoThese documents provide a **complete and self-contained record of a computation** that can be converted to various formats and shared with others electronically, using version control systems (like git/[GitHub](http://github.com)) or [nbviewer.jupyter.org](http://nbviewer.jupyter.org). Components The Jupyter Notebook combines three components:* **The notebook web application**: An interactive web application for writing and running code interactively and authoring notebook documents.* **Kernels**: Separate processes started by the notebook web application that runs users' code in a given language and returns output back to the notebook web application. The kernel also handles things like computations for interactive widgets, tab completion and introspection. * **Notebook documents**: Self-contained documents that contain a representation of all content in the notebook web application, including inputs and outputs of the computations, narrative text, equations, images, and rich media representations of objects. Each notebook document has its own kernel. Notebook web application The notebook web application enables users to:* **Edit code in the browser**, with automatic syntax highlighting, indentation, and tab completion/introspection.* **Run code from the browser**, with the results of computations attached to the code which generated them.* See the results of computations with **rich media representations**, such as HTML, LaTeX, PNG, SVG, PDF, etc.* Create and use **interactive JavaScript widgets**, which bind interactive user interface controls and visualizations to reactive kernel side computations.* Author **narrative text** using the [Markdown](https://daringfireball.net/projects/markdown/) markup language.* Build **hierarchical documents** that are organized into sections with different levels of headings.* Include mathematical equations using **LaTeX syntax in Markdown**, which are rendered in-browser by [MathJax](http://www.mathjax.org/). Kernels The Notebook supports a range of different programming languages. For each notebook that a user opens, the web application starts a kernel that runs the code for that notebook. Each kernel is capable of running code in a single programming language. There are kernels available in the following languages:* Python https://github.com/ipython/ipython* Julia https://github.com/JuliaLang/IJulia.jl* R https://github.com/takluyver/IRkernel* Ruby https://github.com/minrk/iruby* Haskell https://github.com/gibiansky/IHaskell* Scala https://github.com/Bridgewater/scala-notebook* node.js https://gist.github.com/Carreau/4279371* Go https://github.com/takluyver/igoPYNQ is written in Python, which is the default kernel for Jupyter Notebook, and the only kernel installed for Jupyter Notebook in the PYNQ distribution. Kernels communicate with the notebook web application and web browser using a JSON over ZeroMQ/WebSockets message protocol that is described [here](http://ipython.org/ipython-doc/dev/development/messaging.html). Most users don't need to know about these details, but its important to understand that kernels run on Zynq, while the web browser serves up an interface to that kernel. Notebook Documents Notebook documents contain the **inputs and outputs** of an interactive session as well as **narrative text** that accompanies the code but is not meant for execution. **Rich output** generated by running code, including HTML, images, video, and plots, is embedded in the notebook, which makes it a complete and self-contained record of a computation. When you run the notebook web application on your computer, notebook documents are just **files** on your local filesystem with a **.ipynb** extension. This allows you to use familiar workflows for organizing your notebooks into folders and sharing them with others. Notebooks consist of a **linear sequence of cells**. There are four basic cell types:* **Code cells:** Input and output of live code that is run in the kernel* **Markdown cells:** Narrative text with embedded LaTeX equations* **Heading cells:** Deprecated. Headings are supported in Markdown cells* **Raw cells:** Unformatted text that is included, without modification, when notebooks are converted to different formats using nbconvertInternally, notebook documents are [JSON](http://en.wikipedia.org/wiki/JSON) data with binary values [base64](http://en.wikipedia.org/wiki/Base64) encoded. This allows them to be **read and manipulated programmatically** by any programming language. Because JSON is a text format, notebook documents are version control friendly.**Notebooks can be exported** to different static formats including HTML, reStructeredText, LaTeX, PDF, and slide shows ([reveal.js](http://lab.hakim.se/reveal-js/)) using Jupyter's `nbconvert` utility. Some of documentation for Pynq, including this page, was written in a Notebook and converted to html for hosting on the project's documentation website. Furthermore, any notebook document available from a **public URL or on GitHub can be shared** via [nbviewer](http://nbviewer.ipython.org). This service loads the notebook document from the URL and renders it as a static web page. The resulting web page may thus be shared with others **without their needing to install the Jupyter Notebook**.GitHub also renders notebooks, so any Notebook added to GitHub can be viewed as intended. Notebook Basics The Notebook dashboard The Notebook server runs on the ARM® processor of the board. You can open the notebook dashboard by navigating to [pynq:9090](http://pynq:9090) when your board is connected to the network. The dashboard serves as a home page for notebooks. Its main purpose is to display the notebooks and files in the current directory. For example, here is a screenshot of the dashboard page for an example directory:  The top of the notebook list displays clickable breadcrumbs of the current directory. By clicking on these breadcrumbs or on sub-directories in the notebook list, you can navigate your filesystem.To create a new notebook, click on the "New" button at the top of the list and select a kernel from the dropdown (as seen below).  Notebooks and files can be uploaded to the current directory by dragging a notebook file onto the notebook list or by the "click here" text above the list.The notebook list shows green "Running" text and a green notebook icon next to running notebooks (as seen below). Notebooks remain running until you explicitly shut them down; closing the notebook's page is not sufficient.  To shutdown, delete, duplicate, or rename a notebook check the checkbox next to it and an array of controls will appear at the top of the notebook list (as seen below). You can also use the same operations on directories and files when applicable.  To see all of your running notebooks along with their directories, click on the "Running" tab:  This view provides a convenient way to track notebooks that you start as you navigate the file system in a long running notebook server. Overview of the Notebook UI If you create a new notebook or open an existing one, you will be taken to the notebook user interface (UI). This UI allows you to run code and author notebook documents interactively. The notebook UI has the following main areas:* Menu* Toolbar* Notebook area and cellsThe notebook has an interactive tour of these elements that can be started in the "Help:User Interface Tour" menu item. Modal editor The Jupyter Notebook has a modal user interface which means that the keyboard does different things depending on which mode the Notebook is in. There are two modes: edit mode and command mode. Edit mode Edit mode is indicated by a green cell border and a prompt showing in the editor area:  When a cell is in edit mode, you can type into the cell, like a normal text editor. Enter edit mode by pressing `Enter` or using the mouse to click on a cell's editor area. Command mode Command mode is indicated by a grey cell border with a blue left margin:  When you are in command mode, you are able to edit the notebook as a whole, but not type into individual cells. Most importantly, in command mode, the keyboard is mapped to a set of shortcuts that let you perform notebook and cell actions efficiently. For example, if you are in command mode and you press `c`, you will copy the current cell - no modifier is needed.Don't try to type into a cell in command mode; unexpected things will happen! Enter command mode by pressing `Esc` or using the mouse to click *outside* a cell's editor area. Mouse navigation All navigation and actions in the Notebook are available using the mouse through the menubar and toolbar, both of which are above the main Notebook area:  Cells can be selected by clicking on them with the mouse. The currently selected cell gets a grey or green border depending on whether the notebook is in edit or command mode. If you click inside a cell's editor area, you will enter edit mode. If you click on the prompt or output area of a cell you will enter command mode.If you are running this notebook in a live session on the board, try selecting different cells and going between edit and command mode. Try typing into a cell. If you want to run the code in a cell, you would select it and click the `play` button in the toolbar, the "Cell:Run" menu item, or type Ctrl + Enter. Similarly, to copy a cell you would select it and click the `copy` button in the toolbar or the "Edit:Copy" menu item. Ctrl + C, V are also supported.Markdown and heading cells have one other state that can be modified with the mouse. These cells can either be rendered or unrendered. When they are rendered, you will see a nice formatted representation of the cell's contents. When they are unrendered, you will see the raw text source of the cell. To render the selected cell with the mouse, and execute it. (Click the `play` button in the toolbar or the "Cell:Run" menu item, or type Ctrl + Enter. To unrender the selected cell, double click on the cell. Keyboard Navigation There are two different sets of keyboard shortcuts: one set that is active in edit mode and another in command mode.The most important keyboard shortcuts are `Enter`, which enters edit mode, and `Esc`, which enters command mode.In edit mode, most of the keyboard is dedicated to typing into the cell's editor. Thus, in edit mode there are relatively few shortcuts. In command mode, the entire keyboard is available for shortcuts, so there are many more. The `Help`->`Keyboard Shortcuts` dialog lists the available shortcuts. Some of the most useful shortcuts are:1. Basic navigation: `enter`, `shift-enter`, `up/k`, `down/j`2. Saving the notebook: `s`2. Change Cell types: `y`, `m`, `1-6`, `t`3. Cell creation: `a`, `b`4. Cell editing: `x`, `c`, `v`, `d`, `z`5. Kernel operations: `i`, `0` (press twice) Running Code First and foremost, the Jupyter Notebook is an interactive environment for writing and running code. The notebook is capable of running code in a wide range of languages. However, each notebook is associated with a single kernel. Pynq, and this notebook is associated with the IPython kernel, which runs Python code. Code cells allow you to enter and run code Run a code cell using `Shift-Enter` or pressing the `play` button in the toolbar above. The button displays *run cell, select below* when you hover over it.
###Code
a = 10
print(a)
###Output
_____no_output_____
###Markdown
There are two other keyboard shortcuts for running code:* `Alt-Enter` runs the current cell and inserts a new one below.* `Ctrl-Enter` run the current cell and enters command mode. Managing the Kernel Code is run in a separate process called the Kernel. The Kernel can be interrupted or restarted. Try running the following cell and then hit the `stop` button in the toolbar above. The button displays *interrupt kernel* when you hover over it.
###Code
import time
time.sleep(10)
###Output
_____no_output_____
###Markdown
Cell menu The "Cell" menu has a number of menu items for running code in different ways. These includes:* Run and Select Below* Run and Insert Below* Run All* Run All Above* Run All Below Restarting the kernels The kernel maintains the state of a notebook's computations. You can reset this state by restarting the kernel. This is done from the menu bar, or by clicking on the corresponding button in the toolbar. sys.stdout The stdout and stderr streams are displayed as text in the output area.
###Code
print("Hello from Pynq!")
###Output
_____no_output_____
###Markdown
Output is asynchronous All output is displayed asynchronously as it is generated in the Kernel. If you execute the next cell, you will see the output one piece at a time, not all at the end.
###Code
import time, sys
for i in range(8):
print(i)
time.sleep(0.5)
###Output
_____no_output_____
###Markdown
Large outputs To better handle large outputs, the output area can be collapsed. Run the following cell and then single- or double- click on the active area to the left of the output:
###Code
for i in range(50):
print(i)
###Output
_____no_output_____
###Markdown
Jupyter Notebooks Acknowledgements The material in this tutorial is specific to PYNQ. Wherever possible, however, it re-uses generic documentation describing Jupyter notebooks. In particular, we have re-used content from the following example notebooks:1. What is the Jupyter Notebook?1. Notebook Basics1. Running Code1. Markdown CellsThe original notebooks and further example notebooks are available at [Jupyter documentation](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/examples_index.html). Introduction If you are reading this documentation from the webpage, you should note that the webpage is a static html version of the notebook from which it was generated. If the PYNQ platform is available, you can open this notebook from the getting_started folder in the PYNQ Jupyter landing page. The Jupyter Notebook is an **interactive computing environment** that enables users to author notebook documents that include:* Live code* Interactive widgets* Plots* Narrative text* Equations* Images* VideoThese documents provide a **complete and self-contained record of a computation** that can be converted to various formats and shared with others electronically, using version control systems (like git/[GitHub](http://github.com)) or [nbviewer.jupyter.org](http://nbviewer.jupyter.org). Components The Jupyter Notebook combines three components:* **The notebook web application**: An interactive web application for writing and running code interactively and authoring notebook documents.* **Kernels**: Separate processes started by the notebook web application that runs users' code in a given language and returns output back to the notebook web application. The kernel also handles things like computations for interactive widgets, tab completion and introspection. * **Notebook documents**: Self-contained documents that contain a representation of all content in the notebook web application, including inputs and outputs of the computations, narrative text, equations, images, and rich media representations of objects. Each notebook document has its own kernel. Notebook web application The notebook web application enables users to:* **Edit code in the browser**, with automatic syntax highlighting, indentation, and tab completion/introspection.* **Run code from the browser**, with the results of computations attached to the code which generated them.* See the results of computations with **rich media representations**, such as HTML, LaTeX, PNG, SVG, PDF, etc.* Create and use **interactive JavaScript widgets**, which bind interactive user interface controls and visualizations to reactive kernel side computations.* Author **narrative text** using the [Markdown](https://daringfireball.net/projects/markdown/) markup language.* Build **hierarchical documents** that are organized into sections with different levels of headings.* Include mathematical equations using **LaTeX syntax in Markdown**, which are rendered in-browser by [MathJax](http://www.mathjax.org/). Kernels The Notebook supports a range of different programming languages. For each notebook that a user opens, the web application starts a kernel that runs the code for that notebook. Each kernel is capable of running code in a single programming language. There are kernels available in the following languages:* Python https://github.com/ipython/ipython* Julia https://github.com/JuliaLang/IJulia.jl* R https://github.com/takluyver/IRkernel* Ruby https://github.com/minrk/iruby* Haskell https://github.com/gibiansky/IHaskell* Scala https://github.com/Bridgewater/scala-notebook* node.js https://gist.github.com/Carreau/4279371* Go https://github.com/takluyver/igoPYNQ is written in Python, which is the default kernel for Jupyter Notebook, and the only kernel installed for Jupyter Notebook in the PYNQ distribution. Kernels communicate with the notebook web application and web browser using a JSON over ZeroMQ/WebSockets message protocol that is described [here](http://ipython.org/ipython-doc/dev/development/messaging.html). Most users don't need to know about these details, but its important to understand that kernels run on Zynq, while the web browser serves up an interface to that kernel. Notebook Documents Notebook documents contain the **inputs and outputs** of an interactive session as well as **narrative text** that accompanies the code but is not meant for execution. **Rich output** generated by running code, including HTML, images, video, and plots, is embedded in the notebook, which makes it a complete and self-contained record of a computation. When you run the notebook web application on your computer, notebook documents are just **files** on your local filesystem with a **.ipynb** extension. This allows you to use familiar workflows for organizing your notebooks into folders and sharing them with others. Notebooks consist of a **linear sequence of cells**. There are four basic cell types:* **Code cells:** Input and output of live code that is run in the kernel* **Markdown cells:** Narrative text with embedded LaTeX equations* **Heading cells:** Deprecated. Headings are supported in Markdown cells* **Raw cells:** Unformatted text that is included, without modification, when notebooks are converted to different formats using nbconvertInternally, notebook documents are [JSON](http://en.wikipedia.org/wiki/JSON) data with binary values [base64](http://en.wikipedia.org/wiki/Base64) encoded. This allows them to be **read and manipulated programmatically** by any programming language. Because JSON is a text format, notebook documents are version control friendly.**Notebooks can be exported** to different static formats including HTML, reStructeredText, LaTeX, PDF, and slide shows ([reveal.js](http://lab.hakim.se/reveal-js/)) using Jupyter's `nbconvert` utility. Some of documentation for Pynq, including this page, was written in a Notebook and converted to html for hosting on the project's documentation website. Furthermore, any notebook document available from a **public URL or on GitHub can be shared** via [nbviewer](http://nbviewer.ipython.org). This service loads the notebook document from the URL and renders it as a static web page. The resulting web page may thus be shared with others **without their needing to install the Jupyter Notebook**.GitHub also renders notebooks, so any Notebook added to GitHub can be viewed as intended. Notebook Basics The Notebook dashboard The Notebook server runs on the ARM® processor of the PYNQ-Z1. You can open the notebook dashboard by navigating to [pynq:9090](http://pynq:9090) when your board is connected to the network. The dashboard serves as a home page for notebooks. Its main purpose is to display the notebooks and files in the current directory. For example, here is a screenshot of the dashboard page for an example directory:  The top of the notebook list displays clickable breadcrumbs of the current directory. By clicking on these breadcrumbs or on sub-directories in the notebook list, you can navigate your filesystem.To create a new notebook, click on the "New" button at the top of the list and select a kernel from the dropdown (as seen below).  Notebooks and files can be uploaded to the current directory by dragging a notebook file onto the notebook list or by the "click here" text above the list.The notebook list shows green "Running" text and a green notebook icon next to running notebooks (as seen below). Notebooks remain running until you explicitly shut them down; closing the notebook's page is not sufficient.  To shutdown, delete, duplicate, or rename a notebook check the checkbox next to it and an array of controls will appear at the top of the notebook list (as seen below). You can also use the same operations on directories and files when applicable.  To see all of your running notebooks along with their directories, click on the "Running" tab:  This view provides a convenient way to track notebooks that you start as you navigate the file system in a long running notebook server. Overview of the Notebook UI If you create a new notebook or open an existing one, you will be taken to the notebook user interface (UI). This UI allows you to run code and author notebook documents interactively. The notebook UI has the following main areas:* Menu* Toolbar* Notebook area and cellsThe notebook has an interactive tour of these elements that can be started in the "Help:User Interface Tour" menu item. Modal editor The Jupyter Notebook has a modal user interface which means that the keyboard does different things depending on which mode the Notebook is in. There are two modes: edit mode and command mode. Edit mode Edit mode is indicated by a green cell border and a prompt showing in the editor area:  When a cell is in edit mode, you can type into the cell, like a normal text editor. Enter edit mode by pressing `Enter` or using the mouse to click on a cell's editor area. Command mode Command mode is indicated by a grey cell border with a blue left margin:  When you are in command mode, you are able to edit the notebook as a whole, but not type into individual cells. Most importantly, in command mode, the keyboard is mapped to a set of shortcuts that let you perform notebook and cell actions efficiently. For example, if you are in command mode and you press `c`, you will copy the current cell - no modifier is needed.Don't try to type into a cell in command mode; unexpected things will happen! Enter command mode by pressing `Esc` or using the mouse to click *outside* a cell's editor area. Mouse navigation All navigation and actions in the Notebook are available using the mouse through the menubar and toolbar, both of which are above the main Notebook area:  Cells can be selected by clicking on them with the mouse. The currently selected cell gets a grey or green border depending on whether the notebook is in edit or command mode. If you click inside a cell's editor area, you will enter edit mode. If you click on the prompt or output area of a cell you will enter command mode.If you are running this notebook in a live session on the PYNQ-Z1, try selecting different cells and going between edit and command mode. Try typing into a cell. If you want to run the code in a cell, you would select it and click the `play` button in the toolbar, the "Cell:Run" menu item, or type Ctrl + Enter. Similarly, to copy a cell you would select it and click the `copy` button in the toolbar or the "Edit:Copy" menu item. Ctrl + C, V are also supported.Markdown and heading cells have one other state that can be modified with the mouse. These cells can either be rendered or unrendered. When they are rendered, you will see a nice formatted representation of the cell's contents. When they are unrendered, you will see the raw text source of the cell. To render the selected cell with the mouse, and execute it. (Click the `play` button in the toolbar or the "Cell:Run" menu item, or type Ctrl + Enter. To unrender the selected cell, double click on the cell. Keyboard Navigation There are two different sets of keyboard shortcuts: one set that is active in edit mode and another in command mode.The most important keyboard shortcuts are `Enter`, which enters edit mode, and `Esc`, which enters command mode.In edit mode, most of the keyboard is dedicated to typing into the cell's editor. Thus, in edit mode there are relatively few shortcuts. In command mode, the entire keyboard is available for shortcuts, so there are many more. The `Help`->`Keyboard Shortcuts` dialog lists the available shortcuts. Some of the most useful shortcuts are:1. Basic navigation: `enter`, `shift-enter`, `up/k`, `down/j`2. Saving the notebook: `s`2. Change Cell types: `y`, `m`, `1-6`, `t`3. Cell creation: `a`, `b`4. Cell editing: `x`, `c`, `v`, `d`, `z`5. Kernel operations: `i`, `0` (press twice) Running Code First and foremost, the Jupyter Notebook is an interactive environment for writing and running code. The notebook is capable of running code in a wide range of languages. However, each notebook is associated with a single kernel. Pynq, and this notebook is associated with the IPython kernel, which runs Python code. Code cells allow you to enter and run code Run a code cell using `Shift-Enter` or pressing the `play` button in the toolbar above. The button displays *run cell, select below* when you hover over it.
###Code
a = 10
print(a)
###Output
_____no_output_____
###Markdown
There are two other keyboard shortcuts for running code:* `Alt-Enter` runs the current cell and inserts a new one below.* `Ctrl-Enter` run the current cell and enters command mode. Managing the Kernel Code is run in a separate process called the Kernel. The Kernel can be interrupted or restarted. Try running the following cell and then hit the `stop` button in the toolbar above. The button displays *interrupt kernel* when you hover over it.
###Code
import time
time.sleep(10)
###Output
_____no_output_____
###Markdown
Cell menu The "Cell" menu has a number of menu items for running code in different ways. These includes:* Run and Select Below* Run and Insert Below* Run All* Run All Above* Run All Below Restarting the kernels The kernel maintains the state of a notebook's computations. You can reset this state by restarting the kernel. This is done from the menu bar, or by clicking on the corresponding button in the toolbar. sys.stdout The stdout and stderr streams are displayed as text in the output area.
###Code
print("Hello from Pynq!")
###Output
_____no_output_____
###Markdown
Output is asynchronous All output is displayed asynchronously as it is generated in the Kernel. If you execute the next cell, you will see the output one piece at a time, not all at the end.
###Code
import time, sys
for i in range(8):
print(i)
time.sleep(0.5)
###Output
_____no_output_____
###Markdown
Large outputs To better handle large outputs, the output area can be collapsed. Run the following cell and then single- or double- click on the active area to the left of the output:
###Code
for i in range(50):
print(i)
###Output
_____no_output_____
###Markdown
Jupyter Notebooks Acknowledgements The material in this tutorial is specific to PYNQ. Wherever possible, however, it re-uses generic documentation describing Jupyter notebooks. In particular, we have re-used content from the following example notebooks:1. What is the Jupyter Notebook?1. Notebook Basics1. Running Code1. Markdown CellsThe original notebooks and further example notebooks are available at [Jupyter documentation](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/examples_index.html). Introduction If you are reading this documentation from the webpage, you should note that the webpage is a static html version of the notebook from which it was generated. If the PYNQ platform is available, you can open this notebook from the getting_started folder in the PYNQ Jupyter landing page. The Jupyter Notebook is an **interactive computing environment** that enables users to author notebook documents that include:* Live code* Interactive widgets* Plots* Narrative text* Equations* Images* VideoThese documents provide a **complete and self-contained record of a computation** that can be converted to various formats and shared with others electronically, using version control systems (like git/[GitHub](http://github.com)) or [nbviewer.jupyter.org](http://nbviewer.jupyter.org). Components The Jupyter Notebook combines three components:* **The notebook web application**: An interactive web application for writing and running code interactively and authoring notebook documents.* **Kernels**: Separate processes started by the notebook web application that runs users' code in a given language and returns output back to the notebook web application. The kernel also handles things like computations for interactive widgets, tab completion and introspection. * **Notebook documents**: Self-contained documents that contain a representation of all content in the notebook web application, including inputs and outputs of the computations, narrative text, equations, images, and rich media representations of objects. Each notebook document has its own kernel. Notebook web application The notebook web application enables users to:* **Edit code in the browser**, with automatic syntax highlighting, indentation, and tab completion/introspection.* **Run code from the browser**, with the results of computations attached to the code which generated them.* See the results of computations with **rich media representations**, such as HTML, LaTeX, PNG, SVG, PDF, etc.* Create and use **interactive JavaScript widgets**, which bind interactive user interface controls and visualizations to reactive kernel side computations.* Author **narrative text** using the [Markdown](https://daringfireball.net/projects/markdown/) markup language.* Build **hierarchical documents** that are organized into sections with different levels of headings.* Include mathematical equations using **LaTeX syntax in Markdown**, which are rendered in-browser by [MathJax](http://www.mathjax.org/). Kernels The Notebook supports a range of different programming languages. For each notebook that a user opens, the web application starts a kernel that runs the code for that notebook. Each kernel is capable of running code in a single programming language. There are kernels available in the following languages:* Python https://github.com/ipython/ipython* Julia https://github.com/JuliaLang/IJulia.jl* R https://github.com/takluyver/IRkernel* Ruby https://github.com/minrk/iruby* Haskell https://github.com/gibiansky/IHaskell* Scala https://github.com/Bridgewater/scala-notebook* node.js https://gist.github.com/Carreau/4279371* Go https://github.com/takluyver/igoPYNQ is written in Python, which is the default kernel for Jupyter Notebook, and the only kernel installed for Jupyter Notebook in the PYNQ distribution. Kernels communicate with the notebook web application and web browser using a JSON over ZeroMQ/WebSockets message protocol that is described [here](http://ipython.org/ipython-doc/dev/development/messaging.html). Most users don't need to know about these details, but its important to understand that kernels run on Zynq, while the web browser serves up an interface to that kernel. Notebook Documents Notebook documents contain the **inputs and outputs** of an interactive session as well as **narrative text** that accompanies the code but is not meant for execution. **Rich output** generated by running code, including HTML, images, video, and plots, is embedded in the notebook, which makes it a complete and self-contained record of a computation. When you run the notebook web application on your computer, notebook documents are just **files** on your local filesystem with a **.ipynb** extension. This allows you to use familiar workflows for organizing your notebooks into folders and sharing them with others. Notebooks consist of a **linear sequence of cells**. There are four basic cell types:* **Code cells:** Input and output of live code that is run in the kernel* **Markdown cells:** Narrative text with embedded LaTeX equations* **Heading cells:** Deprecated. Headings are supported in Markdown cells* **Raw cells:** Unformatted text that is included, without modification, when notebooks are converted to different formats using nbconvertInternally, notebook documents are [JSON](http://en.wikipedia.org/wiki/JSON) data with binary values [base64](http://en.wikipedia.org/wiki/Base64) encoded. This allows them to be **read and manipulated programmatically** by any programming language. Because JSON is a text format, notebook documents are version control friendly.**Notebooks can be exported** to different static formats including HTML, reStructeredText, LaTeX, PDF, and slide shows ([reveal.js](http://lab.hakim.se/reveal-js/)) using Jupyter's `nbconvert` utility. Some of documentation for Pynq, including this page, was written in a Notebook and converted to html for hosting on the project's documentation website. Furthermore, any notebook document available from a **public URL or on GitHub can be shared** via [nbviewer](http://nbviewer.ipython.org). This service loads the notebook document from the URL and renders it as a static web page. The resulting web page may thus be shared with others **without their needing to install the Jupyter Notebook**.GitHub also renders notebooks, so any Notebook added to GitHub can be viewed as intended. Notebook Basics The Notebook dashboard The Notebook server runs on the ARM® processor of the board. You can open the notebook dashboard by navigating to [pynq:9090](http://pynq:9090) when your board is connected to the network. The dashboard serves as a home page for notebooks. Its main purpose is to display the notebooks and files in the current directory. For example, here is a screenshot of the dashboard page for an example directory:  The top of the notebook list displays clickable breadcrumbs of the current directory. By clicking on these breadcrumbs or on sub-directories in the notebook list, you can navigate your filesystem.To create a new notebook, click on the "New" button at the top of the list and select a kernel from the dropdown (as seen below).  Notebooks and files can be uploaded to the current directory by dragging a notebook file onto the notebook list or by the "click here" text above the list.The notebook list shows green "Running" text and a green notebook icon next to running notebooks (as seen below). Notebooks remain running until you explicitly shut them down; closing the notebook's page is not sufficient.  To shutdown, delete, duplicate, or rename a notebook check the checkbox next to it and an array of controls will appear at the top of the notebook list (as seen below). You can also use the same operations on directories and files when applicable.  To see all of your running notebooks along with their directories, click on the "Running" tab:  This view provides a convenient way to track notebooks that you start as you navigate the file system in a long running notebook server. Overview of the Notebook UI If you create a new notebook or open an existing one, you will be taken to the notebook user interface (UI). This UI allows you to run code and author notebook documents interactively. The notebook UI has the following main areas:* Menu* Toolbar* Notebook area and cellsThe notebook has an interactive tour of these elements that can be started in the "Help:User Interface Tour" menu item. Modal editor The Jupyter Notebook has a modal user interface which means that the keyboard does different things depending on which mode the Notebook is in. There are two modes: edit mode and command mode. Edit mode Edit mode is indicated by a green cell border and a prompt showing in the editor area:  When a cell is in edit mode, you can type into the cell, like a normal text editor. Enter edit mode by pressing `Enter` or using the mouse to click on a cell's editor area. Command mode Command mode is indicated by a grey cell border with a blue left margin:  When you are in command mode, you are able to edit the notebook as a whole, but not type into individual cells. Most importantly, in command mode, the keyboard is mapped to a set of shortcuts that let you perform notebook and cell actions efficiently. For example, if you are in command mode and you press `c`, you will copy the current cell - no modifier is needed.Don't try to type into a cell in command mode; unexpected things will happen! Enter command mode by pressing `Esc` or using the mouse to click *outside* a cell's editor area. Mouse navigation All navigation and actions in the Notebook are available using the mouse through the menubar and toolbar, both of which are above the main Notebook area:  Cells can be selected by clicking on them with the mouse. The currently selected cell gets a grey or green border depending on whether the notebook is in edit or command mode. If you click inside a cell's editor area, you will enter edit mode. If you click on the prompt or output area of a cell you will enter command mode.If you are running this notebook in a live session on the board, try selecting different cells and going between edit and command mode. Try typing into a cell. If you want to run the code in a cell, you would select it and click the `play` button in the toolbar, the "Cell:Run" menu item, or type Ctrl + Enter. Similarly, to copy a cell you would select it and click the `copy` button in the toolbar or the "Edit:Copy" menu item. Ctrl + C, V are also supported.Markdown and heading cells have one other state that can be modified with the mouse. These cells can either be rendered or unrendered. When they are rendered, you will see a nice formatted representation of the cell's contents. When they are unrendered, you will see the raw text source of the cell. To render the selected cell with the mouse, and execute it. (Click the `play` button in the toolbar or the "Cell:Run" menu item, or type Ctrl + Enter. To unrender the selected cell, double click on the cell. Keyboard Navigation There are two different sets of keyboard shortcuts: one set that is active in edit mode and another in command mode.The most important keyboard shortcuts are `Enter`, which enters edit mode, and `Esc`, which enters command mode.In edit mode, most of the keyboard is dedicated to typing into the cell's editor. Thus, in edit mode there are relatively few shortcuts. In command mode, the entire keyboard is available for shortcuts, so there are many more. The `Help`->`Keyboard Shortcuts` dialog lists the available shortcuts. Some of the most useful shortcuts are:1. Basic navigation: `enter`, `shift-enter`, `up/k`, `down/j`2. Saving the notebook: `s`2. Change Cell types: `y`, `m`, `1-6`, `t`3. Cell creation: `a`, `b`4. Cell editing: `x`, `c`, `v`, `d`, `z`5. Kernel operations: `i`, `0` (press twice) Running Code First and foremost, the Jupyter Notebook is an interactive environment for writing and running code. The notebook is capable of running code in a wide range of languages. However, each notebook is associated with a single kernel. Pynq, and this notebook is associated with the IPython kernel, which runs Python code. Code cells allow you to enter and run code Run a code cell using `Shift-Enter` or pressing the `play` button in the toolbar above. The button displays *run cell, select below* when you hover over it.
###Code
a = 10
print(a)
###Output
_____no_output_____
###Markdown
There are two other keyboard shortcuts for running code:* `Alt-Enter` runs the current cell and inserts a new one below.* `Ctrl-Enter` run the current cell and enters command mode. Managing the Kernel Code is run in a separate process called the Kernel. The Kernel can be interrupted or restarted. Try running the following cell and then hit the `stop` button in the toolbar above. The button displays *interrupt kernel* when you hover over it.
###Code
import time
time.sleep(10)
###Output
_____no_output_____
###Markdown
Cell menu The "Cell" menu has a number of menu items for running code in different ways. These includes:* Run and Select Below* Run and Insert Below* Run All* Run All Above* Run All Below Restarting the kernels The kernel maintains the state of a notebook's computations. You can reset this state by restarting the kernel. This is done from the menu bar, or by clicking on the corresponding button in the toolbar. sys.stdout The stdout and stderr streams are displayed as text in the output area.
###Code
print("Hello from Pynq!")
###Output
_____no_output_____
###Markdown
Output is asynchronous All output is displayed asynchronously as it is generated in the Kernel. If you execute the next cell, you will see the output one piece at a time, not all at the end.
###Code
import time, sys
for i in range(8):
print(i)
time.sleep(0.5)
###Output
_____no_output_____
###Markdown
Large outputs To better handle large outputs, the output area can be collapsed. Run the following cell and then single- or double- click on the active area to the left of the output:
###Code
for i in range(50):
print(i)
###Output
_____no_output_____
###Markdown
Jupyter Notebooks Acknowledgements The material in this tutorial is specific to PYNQ. Wherever possible, however, it re-uses generic documentation describing Jupyter notebooks. In particular, we have re-used content from the following example notebooks:1. What is the Jupyter Notebook?1. Notebook Basics1. Running Code1. Markdown CellsThe original notebooks and further example notebooks are available at [Jupyter documentation](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/examples_index.html). Introduction If you are reading this documentation from the webpage, you should note that the webpage is a static html version of the notebook from which it was generated. If the PYNQ platform is available, you can open this notebook from the getting_started folder in the PYNQ Jupyter landing page. The Jupyter Notebook is an **interactive computing environment** that enables users to author notebook documents that include:* Live code* Interactive widgets* Plots* Narrative text* Equations* Images* VideoThese documents provide a **complete and self-contained record of a computation** that can be converted to various formats and shared with others electronically, using version control systems (like git/[GitHub](http://github.com)) or [nbviewer.jupyter.org](http://nbviewer.jupyter.org). Components The Jupyter Notebook combines three components:* **The notebook web application**: An interactive web application for writing and running code interactively and authoring notebook documents.* **Kernels**: Separate processes started by the notebook web application that runs users' code in a given language and returns output back to the notebook web application. The kernel also handles things like computations for interactive widgets, tab completion and introspection. * **Notebook documents**: Self-contained documents that contain a representation of all content in the notebook web application, including inputs and outputs of the computations, narrative text, equations, images, and rich media representations of objects. Each notebook document has its own kernel. Notebook web application The notebook web application enables users to:* **Edit code in the browser**, with automatic syntax highlighting, indentation, and tab completion/introspection.* **Run code from the browser**, with the results of computations attached to the code which generated them.* See the results of computations with **rich media representations**, such as HTML, LaTeX, PNG, SVG, PDF, etc.* Create and use **interactive JavaScript widgets**, which bind interactive user interface controls and visualizations to reactive kernel side computations.* Author **narrative text** using the [Markdown](https://daringfireball.net/projects/markdown/) markup language.* Build **hierarchical documents** that are organized into sections with different levels of headings.* Include mathematical equations using **LaTeX syntax in Markdown**, which are rendered in-browser by [MathJax](http://www.mathjax.org/). Kernels The Notebook supports a range of different programming languages. For each notebook that a user opens, the web application starts a kernel that runs the code for that notebook. Each kernel is capable of running code in a single programming language. There are kernels available in the following languages:* Python https://github.com/ipython/ipython* Julia https://github.com/JuliaLang/IJulia.jl* R https://github.com/takluyver/IRkernel* Ruby https://github.com/minrk/iruby* Haskell https://github.com/gibiansky/IHaskell* Scala https://github.com/Bridgewater/scala-notebook* node.js https://gist.github.com/Carreau/4279371* Go https://github.com/takluyver/igoPYNQ is written in Python, which is the default kernel for Jupyter Notebook, and the only kernel installed for Jupyter Notebook in the PYNQ distribution. Kernels communicate with the notebook web application and web browser using a JSON over ZeroMQ/WebSockets message protocol that is described [here](http://ipython.org/ipython-doc/dev/development/messaging.html). Most users don't need to know about these details, but its important to understand that kernels run on Zynq, while the web browser serves up an interface to that kernel. Notebook Documents Notebook documents contain the **inputs and outputs** of an interactive session as well as **narrative text** that accompanies the code but is not meant for execution. **Rich output** generated by running code, including HTML, images, video, and plots, is embedded in the notebook, which makes it a complete and self-contained record of a computation. When you run the notebook web application on your computer, notebook documents are just **files** on your local filesystem with a **.ipynb** extension. This allows you to use familiar workflows for organizing your notebooks into folders and sharing them with others. Notebooks consist of a **linear sequence of cells**. There are four basic cell types:* **Code cells:** Input and output of live code that is run in the kernel* **Markdown cells:** Narrative text with embedded LaTeX equations* **Heading cells:** Deprecated. Headings are supported in Markdown cells* **Raw cells:** Unformatted text that is included, without modification, when notebooks are converted to different formats using nbconvertInternally, notebook documents are [JSON](http://en.wikipedia.org/wiki/JSON) data with binary values [base64](http://en.wikipedia.org/wiki/Base64) encoded. This allows them to be **read and manipulated programmatically** by any programming language. Because JSON is a text format, notebook documents are version control friendly.**Notebooks can be exported** to different static formats including HTML, reStructeredText, LaTeX, PDF, and slide shows ([reveal.js](http://lab.hakim.se/reveal-js/)) using Jupyter's `nbconvert` utility. Some of documentation for Pynq, including this page, was written in a Notebook and converted to html for hosting on the project's documentation website. Furthermore, any notebook document available from a **public URL or on GitHub can be shared** via [nbviewer](http://nbviewer.ipython.org). This service loads the notebook document from the URL and renders it as a static web page. The resulting web page may thus be shared with others **without their needing to install the Jupyter Notebook**.GitHub also renders notebooks, so any Notebook added to GitHub can be viewed as intended. Notebook Basics The Notebook dashboard The Notebook server runs on the ARM® processor of the board. You can open the notebook dashboard by navigating to [pynq:9090](http://pynq:9090) when your board is connected to the network. The dashboard serves as a home page for notebooks. Its main purpose is to display the notebooks and files in the current directory. For example, here is a screenshot of the dashboard page for an example directory:  The top of the notebook list displays clickable breadcrumbs of the current directory. By clicking on these breadcrumbs or on sub-directories in the notebook list, you can navigate your filesystem.To create a new notebook, click on the "New" button at the top of the list and select a kernel from the dropdown (as seen below).  Notebooks and files can be uploaded to the current directory by dragging a notebook file onto the notebook list or by the "click here" text above the list.The notebook list shows green "Running" text and a green notebook icon next to running notebooks (as seen below). Notebooks remain running until you explicitly shut them down; closing the notebook's page is not sufficient.  To shutdown, delete, duplicate, or rename a notebook check the checkbox next to it and an array of controls will appear at the top of the notebook list (as seen below). You can also use the same operations on directories and files when applicable.  To see all of your running notebooks along with their directories, click on the "Running" tab:  This view provides a convenient way to track notebooks that you start as you navigate the file system in a long running notebook server. Overview of the Notebook UI If you create a new notebook or open an existing one, you will be taken to the notebook user interface (UI). This UI allows you to run code and author notebook documents interactively. The notebook UI has the following main areas:* Menu* Toolbar* Notebook area and cellsThe notebook has an interactive tour of these elements that can be started in the "Help:User Interface Tour" menu item. Modal editor The Jupyter Notebook has a modal user interface which means that the keyboard does different things depending on which mode the Notebook is in. There are two modes: edit mode and command mode. Edit mode Edit mode is indicated by a green cell border and a prompt showing in the editor area:  When a cell is in edit mode, you can type into the cell, like a normal text editor. Enter edit mode by pressing `Enter` or using the mouse to click on a cell's editor area. Command mode Command mode is indicated by a grey cell border with a blue left margin:  When you are in command mode, you are able to edit the notebook as a whole, but not type into individual cells. Most importantly, in command mode, the keyboard is mapped to a set of shortcuts that let you perform notebook and cell actions efficiently. For example, if you are in command mode and you press `c`, you will copy the current cell - no modifier is needed.Don't try to type into a cell in command mode; unexpected things will happen! Enter command mode by pressing `Esc` or using the mouse to click *outside* a cell's editor area. Mouse navigation All navigation and actions in the Notebook are available using the mouse through the menubar and toolbar, both of which are above the main Notebook area:  Cells can be selected by clicking on them with the mouse. The currently selected cell gets a grey or green border depending on whether the notebook is in edit or command mode. If you click inside a cell's editor area, you will enter edit mode. If you click on the prompt or output area of a cell you will enter command mode.If you are running this notebook in a live session on the board, try selecting different cells and going between edit and command mode. Try typing into a cell. If you want to run the code in a cell, you would select it and click the `play` button in the toolbar, the "Cell:Run" menu item, or type Ctrl + Enter. Similarly, to copy a cell you would select it and click the `copy` button in the toolbar or the "Edit:Copy" menu item. Ctrl + C, V are also supported.Markdown and heading cells have one other state that can be modified with the mouse. These cells can either be rendered or unrendered. When they are rendered, you will see a nice formatted representation of the cell's contents. When they are unrendered, you will see the raw text source of the cell. To render the selected cell with the mouse, and execute it. (Click the `play` button in the toolbar or the "Cell:Run" menu item, or type Ctrl + Enter. To unrender the selected cell, double click on the cell. Keyboard Navigation There are two different sets of keyboard shortcuts: one set that is active in edit mode and another in command mode.The most important keyboard shortcuts are `Enter`, which enters edit mode, and `Esc`, which enters command mode.In edit mode, most of the keyboard is dedicated to typing into the cell's editor. Thus, in edit mode there are relatively few shortcuts. In command mode, the entire keyboard is available for shortcuts, so there are many more. The `Help`->`Keyboard Shortcuts` dialog lists the available shortcuts. Some of the most useful shortcuts are:1. Basic navigation: `enter`, `shift-enter`, `up/k`, `down/j`2. Saving the notebook: `s`2. Change Cell types: `y`, `m`, `1-6`, `t`3. Cell creation: `a`, `b`4. Cell editing: `x`, `c`, `v`, `d`, `z`5. Kernel operations: `i`, `0` (press twice) Running Code First and foremost, the Jupyter Notebook is an interactive environment for writing and running code. The notebook is capable of running code in a wide range of languages. However, each notebook is associated with a single kernel. Pynq, and this notebook is associated with the IPython kernel, which runs Python code. Code cells allow you to enter and run code Run a code cell using `Shift-Enter` or pressing the `play` button in the toolbar above. The button displays *run cell, select below* when you hover over it.
###Code
a = 10
print(a)
###Output
_____no_output_____
###Markdown
There are two other keyboard shortcuts for running code:* `Alt-Enter` runs the current cell and inserts a new one below.* `Ctrl-Enter` run the current cell and enters command mode. Managing the Kernel Code is run in a separate process called the Kernel. The Kernel can be interrupted or restarted. Try running the following cell and then hit the `stop` button in the toolbar above. The button displays *interrupt kernel* when you hover over it.
###Code
import time
time.sleep(10)
###Output
_____no_output_____
###Markdown
Cell menu The "Cell" menu has a number of menu items for running code in different ways. These includes:* Run and Select Below* Run and Insert Below* Run All* Run All Above* Run All Below Restarting the kernels The kernel maintains the state of a notebook's computations. You can reset this state by restarting the kernel. This is done from the menu bar, or by clicking on the corresponding button in the toolbar. sys.stdout The stdout and stderr streams are displayed as text in the output area.
###Code
print("Hello from Pynq!")
###Output
_____no_output_____
###Markdown
Output is asynchronous All output is displayed asynchronously as it is generated in the Kernel. If you execute the next cell, you will see the output one piece at a time, not all at the end.
###Code
import time, sys
for i in range(8):
print(i)
time.sleep(0.5)
###Output
_____no_output_____
###Markdown
Large outputs To better handle large outputs, the output area can be collapsed. Run the following cell and then single- or double- click on the active area to the left of the output:
###Code
for i in range(50):
print(i)
###Output
_____no_output_____
|
notebooks/.ipynb_checkpoints/train_embeddings-checkpoint.ipynb
|
###Markdown
Info* Main Dataset: [S&P 500 stock data](https://www.kaggle.com/camnugent/sandp500)* Download detailes for each company: [S&P 500 Companies with Financial Information](https://datahub.io/core/s-and-p-500-companies-financialsresource-s-and-p-500-companies-financials_zip)Stock prices are flutuated in every day. So, in each day, put those stocks in order of price change to one sentence. Then, with certain window size, each stock will show up with highly related stock frequently, because they tend to move their prices together. Source: [stock2vec repo](https://github.com/kh-kim/stock2vec) Imports
###Code
import pandas as pd
import numpy as np
import operator
import sys
from gensim.models import Word2Vec
from sklearn.decomposition import PCA
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm, tree
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from matplotlib import pyplot
import matplotlib.patches as mpatches
import seaborn as sns
###Output
_____no_output_____
###Markdown
Helper Functions
###Code
def sort_dict(mydict, reversed=False):
return sorted(mydict.items(), key=operator.itemgetter(1), reverse=reversed)
###Output
_____no_output_____
###Markdown
Read Data
###Code
# Companies description
desc_df = pd.read_csv('../notebooks/content/constituents.csv')
print('\nCompanies Details')
print(desc_df.head())
# stocks details
stocks_df = pd.read_csv('../notebooks/content/stocks_data/all_stocks_5yr.csv')#, parse_dates=['date'])
print('\nCompanies Stocks')
print(stocks_df.head())
###Output
Companies Details
Symbol Name Sector
0 MMM 3M Company Industrials
1 AOS A.O. Smith Corp Industrials
2 ABT Abbott Laboratories Health Care
3 ABBV AbbVie Inc. Health Care
4 ACN Accenture plc Information Technology
Companies Stocks
date open high low close volume Name
0 2013-02-08 15.07 15.12 14.63 14.75 8407500 AAL
1 2013-02-11 14.89 15.01 14.26 14.46 8882000 AAL
2 2013-02-12 14.45 14.51 14.10 14.27 8126000 AAL
3 2013-02-13 14.30 14.94 14.25 14.66 10259500 AAL
4 2013-02-14 14.94 14.96 13.16 13.99 31879900 AAL
###Markdown
Preprocess
###Code
# dicitonary for companies name and sector
companies_names = {symbol:name for symbol, name in desc_df[['Symbol', 'Name']].values}
companies_sector = {symbol:sector for symbol, sector in desc_df[['Symbol', 'Sector']].values}
# get all companies symbols
symbols = stocks_df['Name'].values
dates = set(stocks_df['date'].values)
dates = sorted(dates)
# store each individual date and all it's stocks
dates_dictionary = {date:{} for date in dates}
###Output
_____no_output_____
###Markdown
Data for Word EmbeddingsFor each date in out dataset we rearrange each company in ascending order based on the **change in price**.Formula for **change in price** [source](https://pocketsense.com/calculate-market-price-change-common-stock-4829.html):* (closing_price - opening_price) / opening_priceWe can change the formula to use highest price and lowest price. This si something we will test out.
###Code
# calculate price change for each stock and sort them in each day
for date, symbol, op, cl, in stocks_df[['date', 'Name', 'open', 'close']].values:
# CHANGE IN PRICE: (closing_price - opening_price) / opening_price
dates_dictionary[date][symbol] = (cl - op)/op
# sort each day reverse order
dates_dictionary = {date:sort_dict(dates_dictionary[date]) for date in dates}
stocks_w2v_data = [[value[0] for value in dates_dictionary[date]] for date in dates]
# print sample
print(stocks_w2v_data[0])
###Output
['MCO', 'MNST', 'SPGI', 'JNPR', 'AAL', 'BBY', 'INTU', 'SRCL', 'SCHW', 'MCHP', 'FLR', 'CL', 'ILMN', 'PVH', 'FB', 'M', 'IRM', 'VAR', 'DAL', 'BA', 'IT', 'BAC', 'EXC', 'ETR', 'XRX', 'O', 'LEN', 'LB', 'KLAC', 'PWR', 'RJF', 'HUM', 'C', 'VFC', 'EL', 'GLW', 'DHI', 'NEM', 'AEE', 'RMD', 'PG', 'RHT', 'RHI', 'MAS', 'EFX', 'DPS', 'IVZ', 'KSU', 'AES', 'NFLX', 'AXP', 'SIG', 'MU', 'TDG', 'RF', 'HIG', 'FDX', 'VZ', 'IDXX', 'PNC', 'T', 'LUK', 'ABBV', 'TRV', 'DVA', 'KMI', 'CTSH', 'CRM', 'FCX', 'ADM', 'PFE', 'CTAS', 'AMG', 'EQT', 'CCL', 'DGX', 'AKAM', 'NEE', 'GT', 'PEP', 'GPS', 'HCA', 'KO', 'NFX', 'COF', 'PDCO', 'BF.B', 'LEG', 'MET', 'SWK', 'NLSN', 'HRS', 'MDLZ', 'ARE', 'PEG', 'HP', 'CMS', 'ICE', 'DRI', 'MYL', 'SO', 'KMB', 'AJG', 'GRMN', 'DFS', 'BBT', 'CLX', 'PAYX', 'AFL', 'ETN', 'MKC', 'CSCO', 'NRG', 'ANSS', 'UAA', 'NI', 'KORS', 'K', 'TIF', 'UTX', 'GE', 'F', 'NVDA', 'DLR', 'BRK.B', 'NWL', 'EMR', 'A', 'ES', 'AIZ', 'PPL', 'NKE', 'JEC', 'AEP', 'DTE', 'SEE', 'ED', 'ABT', 'WY', 'HSIC', 'WU', 'PCG', 'RTN', 'QCOM', 'AIG', 'FFIV', 'COP', 'KSS', 'GM', 'DISCK', 'AVGO', 'NTRS', 'GD', 'XOM', 'HSY', 'ADS', 'SJM', 'MMC', 'OKE', 'LLY', 'PLD', 'CMCSA', 'CVS', 'MSI', 'TSS', 'DUK', 'WEC', 'ULTA', 'ETFC', 'FMC', 'PCAR', 'MAC', 'TMK', 'BLL', 'GWW', 'ALL', 'MO', 'CBOE', 'AAPL', 'EIX', 'AMZN', 'TSN', 'LRCX', 'STT', 'LNT', 'SBAC', 'AGN', 'NSC', 'VIAB', 'ARNC', 'FE', 'OXY', 'EXPE', 'NDAQ', 'USB', 'CINF', 'IPG', 'WM', 'SWKS', 'V', 'PHM', 'ADSK', 'D', 'SNPS', 'TAP', 'BEN', 'L', 'MOS', 'EBAY', 'SYY', 'RE', 'CNP', 'MRK', 'XYL', 'ROK', 'WHR', 'MMM', 'PBCT', 'HOG', 'XEL', 'DOV', 'MLM', 'BDX', 'CF', 'LUV', 'CHK', 'MON', 'EXPD', 'VRTX', 'CME', 'GIS', 'ADP', 'HCN', 'HON', 'AVY', 'BK', 'FITB', 'TROW', 'CI', 'APC', 'SHW', 'AMD', 'WBA', 'CAG', 'MAA', 'WMT', 'TJX', 'COST', 'ORCL', 'LNC', 'ACN', 'JNJ', 'AMP', 'SCG', 'TRIP', 'SNI', 'ROST', 'WMB', 'NTAP', 'ANTM', 'LH', 'VRSK', 'ZION', 'FL', 'CTL', 'RL', 'FISV', 'INTC', 'CHTR', 'WYN', 'AWK', 'XRAY', 'TPR', 'TGT', 'KR', 'GGP', 'GPC', 'MCD', 'CMA', 'DIS', 'COL', 'MTB', 'PH', 'ESS', 'BIIB', 'LLL', 'GS', 'IFF', 'WFC', 'EXR', 'UDR', 'MDT', 'KMX', 'HCP', 'MCK', 'CA', 'UNP', 'AME', 'BAX', 'ROP', 'ALXN', 'AOS', 'CHRW', 'CVX', 'APA', 'JPM', 'CAH', 'BLK', 'PPG', 'PNW', 'LMT', 'VRSN', 'CCI', 'LOW', 'GOOGL', 'REGN', 'EQR', 'HD', 'XEC', 'COG', 'HBAN', 'HRL', 'SRE', 'AAP', 'NOC', 'STZ', 'MSFT', 'IP', 'PRU', 'KEY', 'RRC', 'XL', 'PKI', 'FRT', 'UPS', 'CAT', 'BSX', 'TWX', 'JCI', 'ABC', 'DE', 'REG', 'MTD', 'GPN', 'RSG', 'NUE', 'BXP', 'SLG', 'CMI', 'PFG', 'ESRX', 'IBM', 'LYB', 'PM', 'ORLY', 'TMO', 'PNR', 'PX', 'APD', 'DISCA', 'AON', 'PKG', 'SYK', 'SBUX', 'JBHT', 'HAL', 'VTR', 'PSX', 'HBI', 'EW', 'CBS', 'PGR', 'TSCO', 'UNH', 'ALGN', 'HES', 'VMC', 'RCL', 'MS', 'AVB', 'PCLN', 'FBHS', 'SPG', 'SLB', 'DRE', 'TEL', 'NOV', 'URI', 'MAR', 'DHR', 'FIS', 'EMN', 'ZBH', 'DG', 'NCLH', 'FTI', 'CSX', 'MA', 'ISRG', 'DISH', 'VNO', 'WAT', 'NBL', 'VLO', 'COO', 'PSA', 'MRO', 'PRGO', 'CMG', 'AYI', 'FAST', 'ECL', 'CB', 'HII', 'CELG', 'STI', 'APH', 'ITW', 'CBG', 'TXT', 'AMGN', 'MHK', 'HRB', 'XLNX', 'UNM', 'ALK', 'ALB', 'CDNS', 'GILD', 'HST', 'BMY', 'CTXS', 'AZO', 'JWN', 'AMAT', 'FLS', 'CERN', 'CPB', 'HOLX', 'KIM', 'OMC', 'SYMC', 'WDC', 'AET', 'DVN', 'UHS', 'UAL', 'ATVI', 'CNC', 'AMT', 'CHD', 'INCY', 'STX', 'MAT', 'EA', 'FLIR', 'BWA', 'TXN', 'LKQ', 'ADBE', 'ADI', 'EQIX', 'ZTS', 'MPC', 'EOG', 'WYNN', 'IR', 'YUM', 'HAS', 'CXO', 'SNA', 'ANDV', 'PXD', 'MGM', 'DLTR', 'AIV']
###Markdown
Train Word Embeddings
###Code
stocks_ordered = [[value[0] for value in dates_dictionary[date]] for date in dates]
def plot_cm(y_true, y_pred, class_names):
cm = confusion_matrix(y_true, y_pred)
fig, ax = pyplot.subplots(figsize=(20, 15))
ax = sns.heatmap(
cm,
annot=True,
fmt="d",
cmap=sns.diverging_palette(230, 30, n=9),
ax=ax,
annot_kws={"fontsize":20}
)
ax.xaxis.set_ticks_position('top')
ax.xaxis.set_label_position('top')
pyplot.ylabel('Actual', fontsize = 20)
pyplot.xlabel('Predicted', fontsize = 20)
ax.set_title('Confusion Matrix', fontsize = 40, y = -.02)
ax.set_xticklabels(class_names, fontsize=20, rotation=90)
ax.set_yticklabels(class_names, rotation=0, fontsize = 20)
b, t = pyplot.ylim() # discover the values for bottom and top
b += 0.5 # Add 0.5 to the bottom
t -= 0.5 # Subtract 0.5 from the top
pyplot.ylim(b, t) # update the ylim(bottom, top) values
pyplot.show() # ta-da! '''
# train model
featureNumber = 15
labels = ['Industrials' ,'Health Care' ,'Information Technology' ,'Utilities','Financials','Materials',
'Consumer Discretionary','Real Estate', 'Consumer Staples','Energy',
'Telecommunication Services']
for j in range(4,6):
model = Word2Vec(stocks_w2v_data, min_count=1, size=j)
print(model)
words = list(model.wv.vocab)
X = model[model.wv.vocab]
Y = list()
for word in words:
Y.append(companies_sector[word])
train, test, train_labels, test_labels = train_test_split(X, Y, test_size=0.33, random_state=42)
classifiers = []
# Initialize our classifiers
#model1 = GaussianNB()
#classifiers.append(model1)
model2 = svm.SVC(gamma = 1, C = 1)
classifiers.append(model2)
#model3 = tree.DecisionTreeClassifier()
#classifiers.append(model3)
#model4 = RandomForestClassifier()
#classifiers.append(model4)
# Train our classifier
for clf in classifiers:
clf.fit(train, train_labels)
y_pred= clf.predict(test)
acc = accuracy_score(test_labels, y_pred)
print("Accuracy is ", acc)
plot_cm(test_labels,y_pred,labels)
#classifier = gnb.fit(train, train_labels)
#preds = gnb.predict(test)
#print(accuracy_score(test_labels, preds))
np.set_printoptions(threshold=sys.maxsize)
# fit a 2d PCA model to the vectors
words = list(model.wv.vocab)
X = model[model.wv.vocab]
pca = PCA(n_components=2)
result = pca.fit_transform(X)
'''
with open("../notebooks/output/features.txt", 'w') as featureFile:
for i in range(0,505):
featureFile.write(words[i])
featureFile.write(", ")
featureFile.write(companies_sector[words[i]])
featureFile.write(", Feature Numbers: ")
for j in range(0,15):
featureFile.write(str(model[model.wv.vocab][i,j]))
featureFile.write(" ")
featureFile.write("\n")
'''
sectors = ['Industrials' ,'Health Care' ,'Information Technology' ,'Utilities','Financials','Materials',
'Consumer Discretionary','Real Estate', 'Consumer Staples','Energy',
'Telecommunication Services']
'''
with open("../notebooks/output/averageFeatures.txt", 'w') as averageFile:
for k in range(0, len(sectors)):
companiesInSector = 0
averages = []
for i in range (0, featureNumber):
averages.append(0.0)
for i in range(0,505):
if companies_sector[words[i]] == sectors[k]:
companiesInSector += 1
for j in range(0,featureNumber):
averages[j] += model[model.wv.vocab][i,j]
for i in range (0,featureNumber):
averages[i] /= companiesInSector;
averageFile.write(sectors[k])
averageFile.write(" Average Feature Numbers: ")
averageFile.write("\n")
for i in range(0, featureNumber):
averageFile.write(str(averages[i]) + " ")
averageFile.write("\n\n")
'''
newResultX = []
newResultY = []
newWords = list()
newWordToken = ""
with open('../notebooks/content/stocks.txt') as stockFile:
contents = stockFile.read()
for i in range(0,505):
newWordToken = "%" + words[i] + "%"
if newWordToken in contents:
newWords.append(words[i])
newResultX.append(result[i,0])
newResultY.append(result[i,1])
#Increase Size of Figure
pyplot.figure(num=None, figsize=(20, 14), dpi=80, facecolor='w', edgecolor='k')
#Colors
sector_color_dict = {'Industrials':'red','Health Care':'orange','Information Technology':'yellow','Utilities':'green',
'Financials':'blue','Materials':'purple','Consumer Discretionary':'cyan','Real Estate':'magenta',
'Consumer Staples':'pink','Energy':'brown','Telecommunication Services':'gray'}
cvec = [sector_color_dict[companies_sector[word]] for word in newWords]
# create a scatter plot of the projection
pyplot.scatter(newResultX[:], newResultY[:], c = cvec)
#Names the Labels
for i, word in enumerate(newWords):
pyplot.annotate(companies_names[word], xy=(newResultX[i], newResultY[i]), fontsize = 12)
#Legend
red_patch=mpatches.Patch(color='red', label='Industrials')
orange_patch=mpatches.Patch(color='orange', label='Health Care')
yellow_patch=mpatches.Patch(color='yellow', label='Information Technology')
green_patch=mpatches.Patch(color='green', label='Utilities')
blue_patch=mpatches.Patch(color='blue', label='Financials')
purple_patch=mpatches.Patch(color='purple', label='Materials')
cyan_patch=mpatches.Patch(color='cyan', label='Consumer Discretionary')
magenta_patch=mpatches.Patch(color='magenta', label='Real Estate')
pink_patch=mpatches.Patch(color='pink', label='Consumer Staples')
brown_patch=mpatches.Patch(color='brown', label='Energy')
gray_patch=mpatches.Patch(color='gray', label='Telecommunication Services')
pyplot.legend(handles=[red_patch,orange_patch,yellow_patch,green_patch,blue_patch,purple_patch,cyan_patch,magenta_patch,
pink_patch,brown_patch,gray_patch],loc='best')
pyplot.show()
'''
pca.fit(X)
eigen_vecs = pca.components_
eigen_vals = pca.explained_variance_
print(eigen_vals)
# Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eigen_pairs.sort(key=lambda k: k[0], reverse=True)
w = np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))
print('Matrix W:\n', w)
'''
target_symb = 'ALXN'
print('Symbol:%s\tName:%s\tSector: %s'%(target_symb, companies_names[target_symb], companies_sector[target_symb]))
top_similar = model.similar_by_word(target_symb, topn=20)
print('Most Similar')
for similar in top_similar:
symb = similar[0]
name = companies_names[symb]
sect = companies_sector[symb]
print('Symbol: %s\tName: %s\t\t\tSector: %s'%(symb, name, sect))
# access vector for one word
print(model['AAL'])
###Output
_____no_output_____
|
notebooks/features/responsible_ai/Interpretability - PDP and ICE explainer.ipynb
|
###Markdown
Partial Dependence (PDP) and Individual Conditional Expectation (ICE) plots Partial Dependence Plot (PDP) and Individual Condition Expectation (ICE) are interpretation methods which describe the average behavior of a classification or regression model. They are particularly useful when the model developer wants to understand generally how the model depends on individual feature values, overall model behavior and do debugging.To practice responsible AI, it is crucial to understand which features drive your model's predictions. This knowledge can facilitate the creation of Transparency Notes, facilitate auditing and compliance, help satisfy regulatory requirements, and improve both transparency and accountability .The goal of this notebook is to show how these methods work for a pretrained model. In this example, we train a classification model with the Adult Census Income dataset. Then we treat the model as an opaque-box model and calculate the PDP and ICE plots for some selected categorical and numeric features. This dataset can be used to predict whether annual income exceeds $50,000/year or not based on demographic data from the 1994 U.S. Census. The dataset we're reading contains 32,561 rows and 14 columns/features.[More info on the dataset here](https://archive.ics.uci.edu/ml/datasets/Adult)We will train a classification model to predict >= 50K or < 50K based on our features.---Python dependencies:matplotlib==3.2.2
###Code
from pyspark.ml import Pipeline
from pyspark.ml.classification import GBTClassifier
from pyspark.ml.feature import VectorAssembler, StringIndexer, OneHotEncoder
import pyspark.sql.functions as F
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from synapse.ml.explainers import ICETransformer
import matplotlib.pyplot as plt
###Output
_____no_output_____
###Markdown
Read and prepare the dataset
###Code
df = spark.read.parquet("wasbs://[email protected]/AdultCensusIncome.parquet")
display(df)
###Output
_____no_output_____
###Markdown
Fit the model and view the predictions
###Code
categorical_features = ["race", "workclass", "marital-status", "education", "occupation", "relationship", "native-country", "sex"]
numeric_features = ["age", "education-num", "capital-gain", "capital-loss", "hours-per-week"]
string_indexer_outputs = [feature + "_idx" for feature in categorical_features]
one_hot_encoder_outputs = [feature + "_enc" for feature in categorical_features]
pipeline = Pipeline(stages=[
StringIndexer().setInputCol("income").setOutputCol("label").setStringOrderType("alphabetAsc"),
StringIndexer().setInputCols(categorical_features).setOutputCols(string_indexer_outputs),
OneHotEncoder().setInputCols(string_indexer_outputs).setOutputCols(one_hot_encoder_outputs),
VectorAssembler(inputCols=one_hot_encoder_outputs+numeric_features, outputCol="features"),
GBTClassifier(weightCol="fnlwgt", maxDepth=7, maxIter=100)])
model = pipeline.fit(df)
###Output
_____no_output_____
###Markdown
Check that model makes sense and has reasonable output. For this, we will check the model performance by calculating the ROC-AUC score.
###Code
data = model.transform(df)
display(data.select('income', 'probability', 'prediction'))
eval_auc = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction")
eval_auc.evaluate(data)
###Output
_____no_output_____
###Markdown
Partial Dependence PlotsPartial dependence plots (PDP) show the dependence between the target response and a set of input features of interest, marginalizing over the values of all other input features. It can show whether the relationship between the target response and the input feature is linear, smooth, monotonic, or more complex. This is relevant when you want to have an overall understanding of model behavior. E.g. Identifying specific age group have a favorable predictions vs other age groups.If you want to learn more please check out the [scikit-learn page on partial dependence plots](https://scikit-learn.org/stable/modules/partial_dependence.htmlpartial-dependence-plots). Setup the transformer for PDP To plot PDP we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `average` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names.Categorical and numeric features can be passed as a list of names. But we can specify parameters for the features by passing a list of dicts where each dict represents one feature. For the numeric features a dictionary can look like this:{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0, "rangeMax": 10000.0, "outputColName": "capital-gain_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numSplits` - the number of splits for the value range for the numeric feature, `rangeMin` - specifies the min value of the range for the numeric feature, `rangeMax` - specifies the max value of the range for the numeric feature, `outputColName` - the name for output column with explanations for the feature.For the categorical features a dictionary can look like this:{"name": "marital-status", "numTopValues": 10, "outputColName": "marital-status_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numTopValues` - the max number of top-occurring values to be included in the categorical feature, `outputColName` - the name for output column with explanations for the feature.
###Code
pdp = ICETransformer(model=model, targetCol="probability", kind="average", targetClasses=[1],
categoricalFeatures=categorical_features, numericFeatures=numeric_features)
###Output
_____no_output_____
###Markdown
PDP transformer returns a dataframe of 1 row * {number features to explain} columns. Each column contains a map between the feature's values and the model's average dependence for the that feature value.
###Code
output_pdp = pdp.transform(df)
display(output_pdp)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
def get_pandas_df_from_column(df, col_name):
keys_df = df.select(F.explode(F.map_keys(F.col(col_name)))).distinct()
keys = list(map(lambda row: row[0], keys_df.collect()))
key_cols = list(map(lambda f: F.col(col_name).getItem(f).alias(str(f)), keys))
final_cols = key_cols
pandas_df = df.select(final_cols).toPandas()
return pandas_df
def plot_dependence_for_categorical(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist= sorted(dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
fig = plt.figure(figsize = figsize)
plt.bar(sortdict.keys(), sortdict.values())
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.show()
def plot_dependence_for_numeric(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist= sorted(dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
fig = plt.figure(figsize = figsize)
plt.plot(list(sortdict.keys()), list(sortdict.values()))
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: "age"We can observe non-linear dependency. The model predicts that income rapidly grows from 24-46 y.o. age, after 46 y.o. model predictions slightly drops and from 68 y.o. remains stable.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, 'age_dependence')
plot_dependence_for_numeric(df_education_num, 'age')
###Output
_____no_output_____
###Markdown
Your results will look like: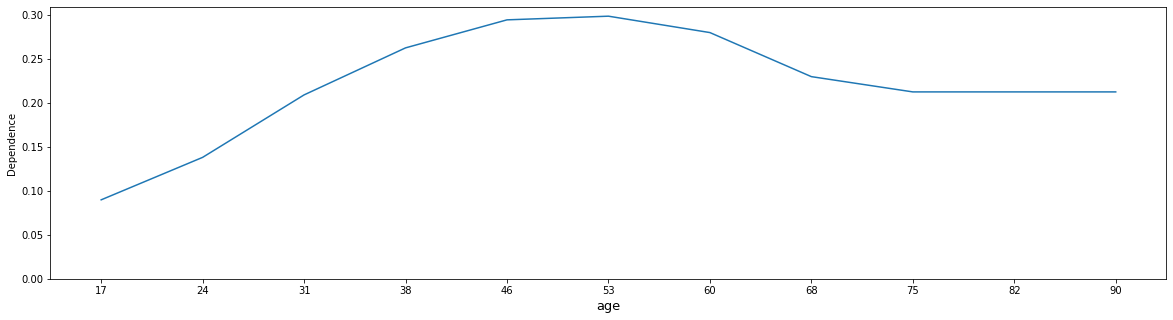 Example 2: "marital-status"The model seems to treat "married-cv-spouse" as one category and tend to give a higher average prediction, and all others as a second category with the lower average prediction.
###Code
df_occupation = get_pandas_df_from_column(output_pdp, 'marital-status_dependence')
plot_dependence_for_categorical(df_occupation, 'marital-status', False, figsize=(30, 5))
###Output
_____no_output_____
###Markdown
Your results will look like: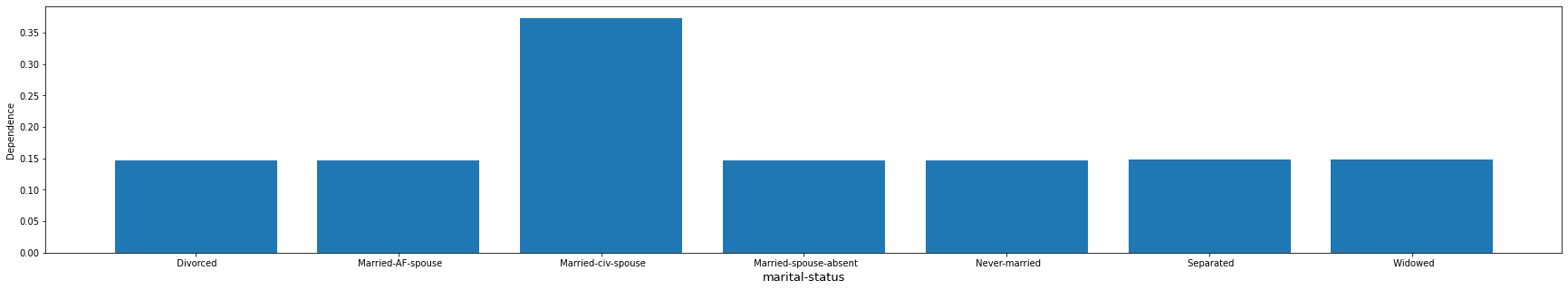 Example 3: "capital-gain"In the first graph, we run PDP with default parameters. We can see that this representation is not super useful because it is not granular enough. By default the range of numeric features are calculated dynamically from the data.In the second graph, we set rangeMin = 0 and rangeMax = 10000 to visualize more granular interpretations for the feature of interest. Now we can see more clearly how the model made decisions in a smaller region.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, 'capital-gain_dependence')
plot_dependence_for_numeric(df_education_num, 'capital-gain_dependence')
###Output
_____no_output_____
###Markdown
Your results will look like:
###Code
pdp_cap_gain = ICETransformer(model=model, targetCol="probability", kind="average", targetClasses=[1],
numericFeatures=[{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0,
"rangeMax": 10000.0}], numSamples=50)
output_pdp_cap_gain = pdp_cap_gain.transform(df)
df_education_num_gain = get_pandas_df_from_column(output_pdp_cap_gain, 'capital-gain_dependence')
plot_dependence_for_numeric(df_education_num_gain, 'capital-gain_dependence')
###Output
_____no_output_____
###Markdown
Your results will look like: ConclusionsPDP can be used to show how features influences model predictions on average and help modeler catch unexpected behavior from the model. Individual Conditional ExpectationICE plots display one line per instance that shows how the instance’s prediction changes when a feature values changes. Each line represents the predictions for one instance if we vary the feature of interest. This is relevant when you want to observe model prediction for instances individually in more details. If you want to learn more please check out the [scikit-learn page on ICE plots](https://scikit-learn.org/stable/modules/partial_dependence.htmlindividual-conditional-expectation-ice-plot). Setup the transformer for ICE To plot ICE we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `individual` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names. For better visualization we set the number of samples to 50.
###Code
ice = ICETransformer(model=model, targetCol="probability", targetClasses=[1],
categoricalFeatures=categorical_features, numericFeatures=numeric_features, numSamples=50)
output = ice.transform(df)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
from math import pi
from collections import defaultdict
def plot_ice_numeric(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
for i in range(num_instances):
plt.plot(col_names, dict_values[i], "k")
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
def plot_ice_categorical(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
angles = [n / float(df.shape[1]) * 2 * pi for n in range(df.shape[1])]
angles += angles [:1]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
ax = plt.subplot(111, polar=True)
plt.xticks(angles[:-1], col_names)
for i in range(num_instances):
values = dict_values[i]
values += values[:1]
ax.plot(angles, values, "k")
ax.fill(angles, values, 'teal', alpha=0.1)
plt.xlabel(col, size=13)
plt.show()
def overlay_ice_with_pdp(df_ice, df_pdp, col, col_int=True, figsize=(20, 5)):
dict_values = defaultdict(list)
col_names_ice = list(df_ice.columns)
num_instances = df_ice.shape[0]
instances_y = {}
i = 0
for col_name in col_names_ice:
for i in range(num_instances):
dict_values[i].append(df_ice[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
for i in range(num_instances):
plt.plot(col_names_ice, dict_values[i], "k")
dict_values_pdp = {}
col_names = list(df_pdp.columns)
for col_name in col_names:
dict_values_pdp[col_name] = df_pdp[col_name][0].toArray()[0]
marklist= sorted(dict_values_pdp.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
plt.plot(col_names_ice, list(sortdict.values()), "r", linewidth=5)
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: Numeric feature: "age"We can overlay the PDP on top of ICE plots. In the graph, the red line shows the PDP plot for the "age" feature, and the black lines show ICE plots for 50 randomly selected observations. The visualization shows that all curves in the ICE plot follow a similar course. This means that the PDP (red line) is already a good summary of the relationships between the displayed feature "age" and the model's average predictions of "income".
###Code
age_df_ice = get_pandas_df_from_column(output, 'age_dependence')
age_df_pdp = get_pandas_df_from_column(output_pdp, 'age_dependence')
overlay_ice_with_pdp(age_df_ice, age_df_pdp, col='age_dependence', figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Your results will look like: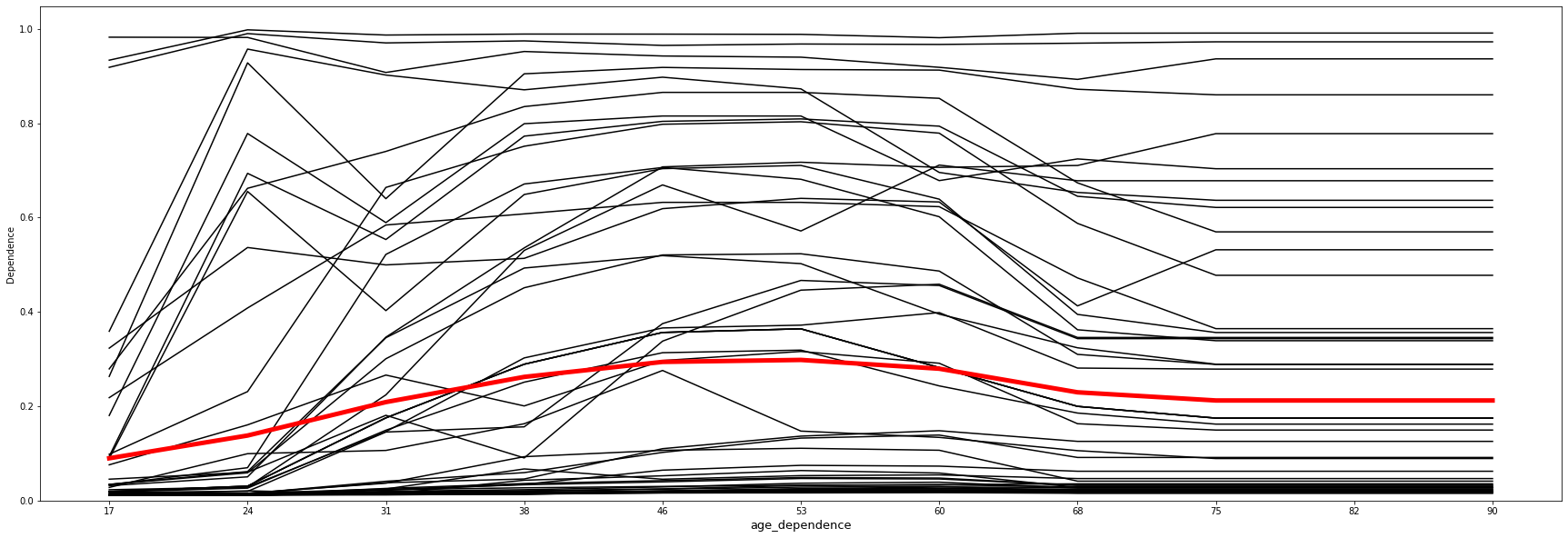 Example 2: Categorical feature: "occupation" For visualization of categorical features, we are using a star plot.- The X-axis here is a circle which is splitted into equal parts, each representing a feature value.- The Y-coordinate shows the dependence values. Each line represents a sample observation.Here we can see that "Farming-fishing" drives the least predictions - because values accumulated near the lowest probabilities, but, for example, "Exec-managerial" seems to have one of the highest impacts for model predictions.
###Code
occupation_dep = get_pandas_df_from_column(output, 'occupation_dependence')
plot_ice_categorical(occupation_dep, 'occupation_dependence', figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Your results will look like: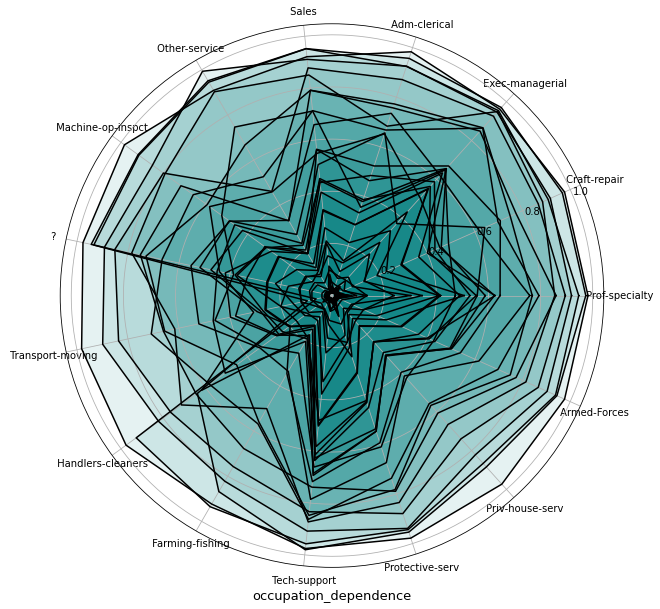 ConclusionsICE plots show model behavior on individual observations. Each line represents the prediction from the model if we vary the feature of interest. PDP-based Feature ImportanceUsing PDP we can calculate a simple partial dependence-based feature importance measure. We note that a flat PDP indicates that varying the feature does not affect the prediction. The more the PDP varies, the more "important" the feature is. If you want to learn more please check out [Christoph M's Interpretable ML Book](https://christophm.github.io/interpretable-ml-book/pdp.htmlpdp-based-feature-importance). Setup the transformer for PDP-based Feature Importance To plot PDP-based feature importance, we first need to set up the instance of `ICETransformer` by setting the `kind` parameter to `feature`. We can then call the `transform` function. `transform` returns a two-column table where the first columns are feature importance values and the second are corresponding features names. The rows are sorted in descending order by feature importance values.
###Code
pdp_based_imp = ICETransformer(model=model, targetCol="probability", kind="feature", targetClasses=[1],
categoricalFeatures=categorical_features, numericFeatures=numeric_features)
output_pdp_based_imp = pdp_based_imp.transform(df)
display(output_pdp_based_imp)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
def plot_pdp_based_imp(df, figsize=(35, 5)):
values_list = list(df.select('pdpBasedDependence').toPandas()['pdpBasedDependence'])
names = list(df.select('featureNames').toPandas()['featureNames'])
dependence_values = []
for vec in values_list:
dependence_values.append(vec.toArray()[0])
fig = plt.figure(figsize = figsize)
plt.bar(names, dependence_values)
plt.xlabel("Feature names", size=13)
plt.ylabel("PDP-based-feature-imporance")
plt.show()
###Output
_____no_output_____
###Markdown
This shows that the features `capital-gain` and `education-num` were the most important for the model, and `sex` and `education` were the least important.
###Code
plot_pdp_based_imp(output_pdp_based_imp)
###Output
_____no_output_____
###Markdown
Partial Dependence (PDP) and Individual Conditional Expectation (ICE) plots Partial Dependence Plot (PDP) and Individual Condition Expectation (ICE) are interpretation methods which describe the average behavior of a classification or regression model. They are particularly useful when the model developer wants to understand generally how the model depends on individual feature values, overall model behavior and do debugging.In terms of [Responsible AI](https://www.microsoft.com/en-us/ai/responsible-ai), understanding which features drive your predictions facilitate the creation of [Transparency Notes](https://docs.microsoft.com/en-us/legal/cognitive-services/language-service/transparency-note), driving not only transparency but accountability while facilitating auditing to meet compliance with regulatory requirements.The goal of this notebook is to show how these methods work for a pretrained model. In this example, we train a classification model with the Adult Census Income dataset. Then we treat the model as an opaque-box model and calculate the PDP and ICE plots for some selected categorical and numeric features. This dataset can be used to predict whether annual income exceeds $50,000/year or not based on demographic data from the 1994 U.S. Census. The dataset we're reading contains 32,561 rows and 14 columns/features.[More info on the dataset here](https://archive.ics.uci.edu/ml/datasets/Adult)We will train a classification model to predict >= 50K or < 50K based on our features.---Python dependencies:matplotlib==3.2.2
###Code
from pyspark.ml import Pipeline
from pyspark.ml.classification import GBTClassifier
from pyspark.ml.feature import VectorAssembler, StringIndexer, OneHotEncoder
import pyspark.sql.functions as F
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from synapse.ml.explainers import ICETransformer
import matplotlib.pyplot as plt
###Output
_____no_output_____
###Markdown
Read and prepare the dataset
###Code
df = spark.read.parquet("wasbs://[email protected]/AdultCensusIncome.parquet")
display(df)
###Output
_____no_output_____
###Markdown
Fit the model and view the predictions
###Code
categorical_features = ["race", "workclass", "marital-status", "education", "occupation", "relationship", "native-country", "sex"]
numeric_features = ["age", "education-num", "capital-gain", "capital-loss", "hours-per-week"]
string_indexer_outputs = [feature + "_idx" for feature in categorical_features]
one_hot_encoder_outputs = [feature + "_enc" for feature in categorical_features]
pipeline = Pipeline(stages=[
StringIndexer().setInputCol("income").setOutputCol("label").setStringOrderType("alphabetAsc"),
StringIndexer().setInputCols(categorical_features).setOutputCols(string_indexer_outputs),
OneHotEncoder().setInputCols(string_indexer_outputs).setOutputCols(one_hot_encoder_outputs),
VectorAssembler(inputCols=one_hot_encoder_outputs+numeric_features, outputCol="features"),
GBTClassifier(weightCol="fnlwgt", maxDepth=7, maxIter=100)])
model = pipeline.fit(df)
###Output
_____no_output_____
###Markdown
Check that model makes sense and has reasonable output. For this, we will check the model performance by calculating the ROC-AUC score.
###Code
data = model.transform(df)
display(data.select('income', 'probability', 'prediction'))
eval_auc = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction")
eval_auc.evaluate(data)
###Output
_____no_output_____
###Markdown
Partial Dependence PlotsPartial dependence plots (PDP) show the dependence between the target response and a set of input features of interest, marginalizing over the values of all other input features. It can show whether the relationship between the target response and the input feature is linear, smooth, monotonic, or more complex. This is relevant when you want to have an overall understanding of model behavior. E.g. Identifying specific age group have a favorable predictions vs other age groups.If you want to learn more please visit [this link](https://scikit-learn.org/stable/modules/partial_dependence.htmlpartial-dependence-plots). Setup the transformer for PDP To plot PDP we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `average` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names.Categorical and numeric features can be passed as a list of names. But we can specify parameters for the features by passing a list of dicts where each dict represents one feature. For the numeric features a dictionary can look like this:{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0, "rangeMax": 10000.0, "outputColName": "capital-gain_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numSplits` - the number of splits for the value range for the numeric feature (default value is 10), `rangeMin` - specifies the min value of the range for the numeric feature, `rangeMax` - specifies the max value of the range for the numeric feature (if not specified, `rangeMin` and `rangeMax` will be computed from the background dataset), `outputColName` - the name for output column with explanations for the feature (default value is input name of the feature + "_dependence").For the categorical features a dictionary can look like this:{"name": "marital-status", "numTopValues": 10, "outputColName": "marital-status_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numTopValues` - the max number of top-occurring values to be included in the categorical feature (default value is 100), `outputColName` - the name for output column with explanations for the feature (default value is input name of the feature + _dependence).
###Code
pdp = ICETransformer(model=model, targetCol="probability", kind="average", targetClasses=[1],
categoricalFeatures=categorical_features, numericFeatures=numeric_features)
###Output
_____no_output_____
###Markdown
PDP transformer returns a dataframe of 1 row * {number features to explain} columns. Each column contains a map between the feature's values and the model's average dependence for the that feature value.
###Code
output_pdp = pdp.transform(df)
display(output_pdp)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
def get_pandas_df_from_column(df, col_name):
keys_df = df.select(F.explode(F.map_keys(F.col(col_name)))).distinct()
keys = list(map(lambda row: row[0], keys_df.collect()))
key_cols = list(map(lambda f: F.col(col_name).getItem(f).alias(str(f)), keys))
final_cols = key_cols
pandas_df = df.select(final_cols).toPandas()
return pandas_df
def plot_dependence_for_categorical(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist= sorted(dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
fig = plt.figure(figsize = figsize)
plt.bar(sortdict.keys(), sortdict.values())
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.show()
def plot_dependence_for_numeric(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist= sorted(dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
fig = plt.figure(figsize = figsize)
plt.plot(list(sortdict.keys()), list(sortdict.values()))
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: "age"We can observe non-linear dependency. The model predicts that income rapidly grows from 24-46 y.o. age, after 46 y.o. model predictions slightly drops and from 68 y.o. remains stable.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, 'age_dependence')
plot_dependence_for_numeric(df_education_num, 'age')
###Output
_____no_output_____
###Markdown
Your results will look like: Example 2: "marital-status"The model seems to treat "married-cv-spouse" as one category and tend to give a higher average prediction, and all others as a second category with the lower average prediction.
###Code
df_occupation = get_pandas_df_from_column(output_pdp, 'marital-status_dependence')
plot_dependence_for_categorical(df_occupation, 'marital-status', False, figsize=(30, 5))
###Output
_____no_output_____
###Markdown
Your results will look like: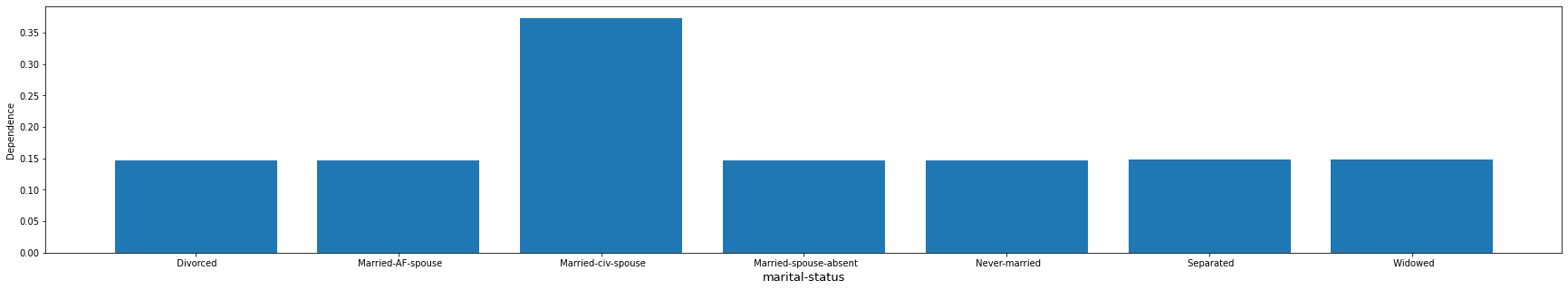 Example 3: "capital-gain"In the first graph, we run PDP with default parameters. We can see that this representation is not super useful because it is not granular enough. By default the range of numeric features are calculated dynamically from the data.In the second graph, we set rangeMin = 0 and rangeMax = 10000 to visualize more granular interpretations for the feature of interest. Now we can see more clearly how the model made decisions in a smaller region.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, 'capital-gain_dependence')
plot_dependence_for_numeric(df_education_num, 'capital-gain_dependence')
###Output
_____no_output_____
###Markdown
Your results will look like:
###Code
pdp_cap_gain = ICETransformer(model=model, targetCol="probability", kind="average", targetClasses=[1],
numericFeatures=[{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0,
"rangeMax": 10000.0}], numSamples=50)
output_pdp_cap_gain = pdp_cap_gain.transform(df)
df_education_num_gain = get_pandas_df_from_column(output_pdp_cap_gain, 'capital-gain_dependence')
plot_dependence_for_numeric(df_education_num_gain, 'capital-gain_dependence')
###Output
_____no_output_____
###Markdown
Your results will look like: ConclusionsPDP can be used to show how features influences model predictions on average and help modeler catch unexpected behavior from the model. Individual Conditional ExpectationICE plots display one line per instance that shows how the instance’s prediction changes when a feature values changes. Each line represents the predictions for one instance if we vary the feature of interest. This is relevant when you want to observe model prediction for instances individually in more details. If you want to learn more please visit [this link](https://scikit-learn.org/stable/modules/partial_dependence.htmlindividual-conditional-expectation-ice-plot). Setup the transformer for ICE To plot ICE we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `individual` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names. For better visualization we set the number of samples to 50.
###Code
ice = ICETransformer(model=model, targetCol="probability", targetClasses=[1],
categoricalFeatures=categorical_features, numericFeatures=numeric_features, numSamples=50)
output = ice.transform(df)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
from math import pi
from collections import defaultdict
def plot_ice_numeric(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
for i in range(num_instances):
plt.plot(col_names, dict_values[i], "k")
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
def plot_ice_categorical(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
angles = [n / float(df.shape[1]) * 2 * pi for n in range(df.shape[1])]
angles += angles [:1]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
ax = plt.subplot(111, polar=True)
plt.xticks(angles[:-1], col_names)
for i in range(num_instances):
values = dict_values[i]
values += values[:1]
ax.plot(angles, values, "k")
ax.fill(angles, values, 'teal', alpha=0.1)
plt.xlabel(col, size=13)
plt.show()
def overlay_ice_with_pdp(df_ice, df_pdp, col, col_int=True, figsize=(20, 5)):
dict_values = defaultdict(list)
col_names_ice = list(df_ice.columns)
num_instances = df_ice.shape[0]
instances_y = {}
i = 0
for col_name in col_names_ice:
for i in range(num_instances):
dict_values[i].append(df_ice[col_name][i].toArray()[0])
fig = plt.figure(figsize = figsize)
for i in range(num_instances):
plt.plot(col_names_ice, dict_values[i], "k")
dict_values_pdp = {}
col_names = list(df_pdp.columns)
for col_name in col_names:
dict_values_pdp[col_name] = df_pdp[col_name][0].toArray()[0]
marklist= sorted(dict_values_pdp.items(), key=lambda x: int(x[0]) if col_int else x[0])
sortdict=dict(marklist)
plt.plot(col_names_ice, list(sortdict.values()), "r", linewidth=5)
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: Numeric feature: "age"We can overlay the PDP on top of ICE plots. In the graph, the red line shows the PDP plot for the "age" feature, and the black lines show ICE plots for 50 randomly selected observations. The visualization will show that all curves follow a similar course. That means that the PDP (red line) is already a good summary of the relationships between the displayed feature "age" and the model's average predictions of "income"
###Code
age_df_ice = get_pandas_df_from_column(output, 'age_dependence')
age_df_pdp = get_pandas_df_from_column(output_pdp, 'age_dependence')
overlay_ice_with_pdp(age_df_ice, age_df_pdp, col='age_dependence', figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Your results will look like: Example 2: Categorical feature: "occupation" For visualization of categorical features, we are using a star plot.- The X-axis here is a circle which is splitted into equal parts, each representing a feature value.- The Y-coordinate shows the dependence values. Each line represents a sample observation.Here we can see that "Farming-fishing" drives the least predictions - because values accumulated near the lowest probabilities, but, for example, "Exec-managerial" seems to have one of the highest impacts for model predictions.
###Code
occupation_dep = get_pandas_df_from_column(output, 'occupation_dependence')
plot_ice_categorical(occupation_dep, 'occupation_dependence', figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Partial Dependence (PDP) and Individual Conditional Expectation (ICE) plots Partial Dependence Plot (PDP) and Individual Condition Expectation (ICE) are interpretation methods which describe the average behavior of a classification or regression model. They are particularly useful when the model developer wants to understand generally how the model depends on individual feature values, overall model behavior and do debugging.To practice responsible AI, it is crucial to understand which features drive your model's predictions. This knowledge can facilitate the creation of Transparency Notes, facilitate auditing and compliance, help satisfy regulatory requirements, and improve both transparency and accountability .The goal of this notebook is to show how these methods work for a pretrained model. In this example, we train a classification model with the Adult Census Income dataset. Then we treat the model as an opaque-box model and calculate the PDP and ICE plots for some selected categorical and numeric features. This dataset can be used to predict whether annual income exceeds $50,000/year or not based on demographic data from the 1994 U.S. Census. The dataset we're reading contains 32,561 rows and 14 columns/features.[More info on the dataset here](https://archive.ics.uci.edu/ml/datasets/Adult)We will train a classification model to predict >= 50K or < 50K based on our features.---Python dependencies:matplotlib==3.2.2
###Code
from pyspark.ml import Pipeline
from pyspark.ml.classification import GBTClassifier
from pyspark.ml.feature import VectorAssembler, StringIndexer, OneHotEncoder
import pyspark.sql.functions as F
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from synapse.ml.explainers import ICETransformer
import matplotlib.pyplot as plt
import os
if os.environ.get("AZURE_SERVICE", None) == "Microsoft.ProjectArcadia":
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
from notebookutils.visualization import display
###Output
_____no_output_____
###Markdown
Read and prepare the dataset
###Code
df = spark.read.parquet(
"wasbs://[email protected]/AdultCensusIncome.parquet"
)
display(df)
###Output
_____no_output_____
###Markdown
Fit the model and view the predictions
###Code
categorical_features = [
"race",
"workclass",
"marital-status",
"education",
"occupation",
"relationship",
"native-country",
"sex",
]
numeric_features = [
"age",
"education-num",
"capital-gain",
"capital-loss",
"hours-per-week",
]
string_indexer_outputs = [feature + "_idx" for feature in categorical_features]
one_hot_encoder_outputs = [feature + "_enc" for feature in categorical_features]
pipeline = Pipeline(
stages=[
StringIndexer()
.setInputCol("income")
.setOutputCol("label")
.setStringOrderType("alphabetAsc"),
StringIndexer()
.setInputCols(categorical_features)
.setOutputCols(string_indexer_outputs),
OneHotEncoder()
.setInputCols(string_indexer_outputs)
.setOutputCols(one_hot_encoder_outputs),
VectorAssembler(
inputCols=one_hot_encoder_outputs + numeric_features, outputCol="features"
),
GBTClassifier(weightCol="fnlwgt", maxDepth=7, maxIter=100),
]
)
model = pipeline.fit(df)
###Output
_____no_output_____
###Markdown
Check that model makes sense and has reasonable output. For this, we will check the model performance by calculating the ROC-AUC score.
###Code
data = model.transform(df)
display(data.select("income", "probability", "prediction"))
eval_auc = BinaryClassificationEvaluator(
labelCol="label", rawPredictionCol="prediction"
)
eval_auc.evaluate(data)
###Output
_____no_output_____
###Markdown
Partial Dependence PlotsPartial dependence plots (PDP) show the dependence between the target response and a set of input features of interest, marginalizing over the values of all other input features. It can show whether the relationship between the target response and the input feature is linear, smooth, monotonic, or more complex. This is relevant when you want to have an overall understanding of model behavior. E.g. Identifying specific age group have a favorable predictions vs other age groups.If you want to learn more please check out the [scikit-learn page on partial dependence plots](https://scikit-learn.org/stable/modules/partial_dependence.htmlpartial-dependence-plots). Setup the transformer for PDP To plot PDP we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `average` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names.Categorical and numeric features can be passed as a list of names. But we can specify parameters for the features by passing a list of dicts where each dict represents one feature. For the numeric features a dictionary can look like this:{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0, "rangeMax": 10000.0, "outputColName": "capital-gain_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numSplits` - the number of splits for the value range for the numeric feature, `rangeMin` - specifies the min value of the range for the numeric feature, `rangeMax` - specifies the max value of the range for the numeric feature, `outputColName` - the name for output column with explanations for the feature.For the categorical features a dictionary can look like this:{"name": "marital-status", "numTopValues": 10, "outputColName": "marital-status_dependance"}Where the required key-value pair is `name` - the name of the numeric feature. Next key-values pairs are optional: `numTopValues` - the max number of top-occurring values to be included in the categorical feature, `outputColName` - the name for output column with explanations for the feature.
###Code
pdp = ICETransformer(
model=model,
targetCol="probability",
kind="average",
targetClasses=[1],
categoricalFeatures=categorical_features,
numericFeatures=numeric_features,
)
###Output
_____no_output_____
###Markdown
PDP transformer returns a dataframe of 1 row * {number features to explain} columns. Each column contains a map between the feature's values and the model's average dependence for the that feature value.
###Code
output_pdp = pdp.transform(df)
display(output_pdp)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
def get_pandas_df_from_column(df, col_name):
keys_df = df.select(F.explode(F.map_keys(F.col(col_name)))).distinct()
keys = list(map(lambda row: row[0], keys_df.collect()))
key_cols = list(map(lambda f: F.col(col_name).getItem(f).alias(str(f)), keys))
final_cols = key_cols
pandas_df = df.select(final_cols).toPandas()
return pandas_df
def plot_dependence_for_categorical(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist = sorted(
dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0]
)
sortdict = dict(marklist)
fig = plt.figure(figsize=figsize)
plt.bar(sortdict.keys(), sortdict.values())
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.show()
def plot_dependence_for_numeric(df, col, col_int=True, figsize=(20, 5)):
dict_values = {}
col_names = list(df.columns)
for col_name in col_names:
dict_values[col_name] = df[col_name][0].toArray()[0]
marklist = sorted(
dict_values.items(), key=lambda x: int(x[0]) if col_int else x[0]
)
sortdict = dict(marklist)
fig = plt.figure(figsize=figsize)
plt.plot(list(sortdict.keys()), list(sortdict.values()))
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: "age"We can observe non-linear dependency. The model predicts that income rapidly grows from 24-46 y.o. age, after 46 y.o. model predictions slightly drops and from 68 y.o. remains stable.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, "age_dependence")
plot_dependence_for_numeric(df_education_num, "age")
###Output
_____no_output_____
###Markdown
Your results will look like: Example 2: "marital-status"The model seems to treat "married-cv-spouse" as one category and tend to give a higher average prediction, and all others as a second category with the lower average prediction.
###Code
df_occupation = get_pandas_df_from_column(output_pdp, "marital-status_dependence")
plot_dependence_for_categorical(df_occupation, "marital-status", False, figsize=(30, 5))
###Output
_____no_output_____
###Markdown
Your results will look like: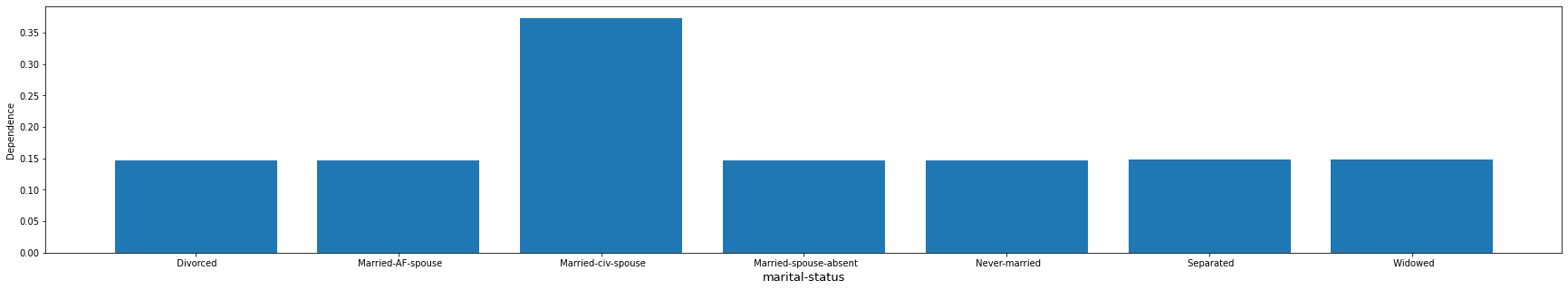 Example 3: "capital-gain"In the first graph, we run PDP with default parameters. We can see that this representation is not super useful because it is not granular enough. By default the range of numeric features are calculated dynamically from the data.In the second graph, we set rangeMin = 0 and rangeMax = 10000 to visualize more granular interpretations for the feature of interest. Now we can see more clearly how the model made decisions in a smaller region.
###Code
df_education_num = get_pandas_df_from_column(output_pdp, "capital-gain_dependence")
plot_dependence_for_numeric(df_education_num, "capital-gain_dependence")
###Output
_____no_output_____
###Markdown
Your results will look like:
###Code
pdp_cap_gain = ICETransformer(
model=model,
targetCol="probability",
kind="average",
targetClasses=[1],
numericFeatures=[
{"name": "capital-gain", "numSplits": 20, "rangeMin": 0.0, "rangeMax": 10000.0}
],
numSamples=50,
)
output_pdp_cap_gain = pdp_cap_gain.transform(df)
df_education_num_gain = get_pandas_df_from_column(
output_pdp_cap_gain, "capital-gain_dependence"
)
plot_dependence_for_numeric(df_education_num_gain, "capital-gain_dependence")
###Output
_____no_output_____
###Markdown
Your results will look like: ConclusionsPDP can be used to show how features influences model predictions on average and help modeler catch unexpected behavior from the model. Individual Conditional ExpectationICE plots display one line per instance that shows how the instance’s prediction changes when a feature values changes. Each line represents the predictions for one instance if we vary the feature of interest. This is relevant when you want to observe model prediction for instances individually in more details. If you want to learn more please check out the [scikit-learn page on ICE plots](https://scikit-learn.org/stable/modules/partial_dependence.htmlindividual-conditional-expectation-ice-plot). Setup the transformer for ICE To plot ICE we need to set up the instance of `ICETransformer` first and set the `kind` parameter to `individual` and then call the `transform` function. For the setup we need to pass the pretrained model, specify the target column ("probability" in our case), and pass categorical and numeric feature names. For better visualization we set the number of samples to 50.
###Code
ice = ICETransformer(
model=model,
targetCol="probability",
targetClasses=[1],
categoricalFeatures=categorical_features,
numericFeatures=numeric_features,
numSamples=50,
)
output = ice.transform(df)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
from math import pi
from collections import defaultdict
def plot_ice_numeric(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize=figsize)
for i in range(num_instances):
plt.plot(col_names, dict_values[i], "k")
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
def plot_ice_categorical(df, col, col_int=True, figsize=(20, 10)):
dict_values = defaultdict(list)
col_names = list(df.columns)
num_instances = df.shape[0]
angles = [n / float(df.shape[1]) * 2 * pi for n in range(df.shape[1])]
angles += angles[:1]
instances_y = {}
i = 0
for col_name in col_names:
for i in range(num_instances):
dict_values[i].append(df[col_name][i].toArray()[0])
fig = plt.figure(figsize=figsize)
ax = plt.subplot(111, polar=True)
plt.xticks(angles[:-1], col_names)
for i in range(num_instances):
values = dict_values[i]
values += values[:1]
ax.plot(angles, values, "k")
ax.fill(angles, values, "teal", alpha=0.1)
plt.xlabel(col, size=13)
plt.show()
def overlay_ice_with_pdp(df_ice, df_pdp, col, col_int=True, figsize=(20, 5)):
dict_values = defaultdict(list)
col_names_ice = list(df_ice.columns)
num_instances = df_ice.shape[0]
instances_y = {}
i = 0
for col_name in col_names_ice:
for i in range(num_instances):
dict_values[i].append(df_ice[col_name][i].toArray()[0])
fig = plt.figure(figsize=figsize)
for i in range(num_instances):
plt.plot(col_names_ice, dict_values[i], "k")
dict_values_pdp = {}
col_names = list(df_pdp.columns)
for col_name in col_names:
dict_values_pdp[col_name] = df_pdp[col_name][0].toArray()[0]
marklist = sorted(
dict_values_pdp.items(), key=lambda x: int(x[0]) if col_int else x[0]
)
sortdict = dict(marklist)
plt.plot(col_names_ice, list(sortdict.values()), "r", linewidth=5)
plt.xlabel(col, size=13)
plt.ylabel("Dependence")
plt.ylim(0.0)
plt.show()
###Output
_____no_output_____
###Markdown
Example 1: Numeric feature: "age"We can overlay the PDP on top of ICE plots. In the graph, the red line shows the PDP plot for the "age" feature, and the black lines show ICE plots for 50 randomly selected observations. The visualization shows that all curves in the ICE plot follow a similar course. This means that the PDP (red line) is already a good summary of the relationships between the displayed feature "age" and the model's average predictions of "income".
###Code
age_df_ice = get_pandas_df_from_column(output, "age_dependence")
age_df_pdp = get_pandas_df_from_column(output_pdp, "age_dependence")
overlay_ice_with_pdp(age_df_ice, age_df_pdp, col="age_dependence", figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Your results will look like: Example 2: Categorical feature: "occupation" For visualization of categorical features, we are using a star plot.- The X-axis here is a circle which is splitted into equal parts, each representing a feature value.- The Y-coordinate shows the dependence values. Each line represents a sample observation.Here we can see that "Farming-fishing" drives the least predictions - because values accumulated near the lowest probabilities, but, for example, "Exec-managerial" seems to have one of the highest impacts for model predictions.
###Code
occupation_dep = get_pandas_df_from_column(output, "occupation_dependence")
plot_ice_categorical(occupation_dep, "occupation_dependence", figsize=(30, 10))
###Output
_____no_output_____
###Markdown
Your results will look like: ConclusionsICE plots show model behavior on individual observations. Each line represents the prediction from the model if we vary the feature of interest. PDP-based Feature ImportanceUsing PDP we can calculate a simple partial dependence-based feature importance measure. We note that a flat PDP indicates that varying the feature does not affect the prediction. The more the PDP varies, the more "important" the feature is. If you want to learn more please check out [Christoph M's Interpretable ML Book](https://christophm.github.io/interpretable-ml-book/pdp.htmlpdp-based-feature-importance). Setup the transformer for PDP-based Feature Importance To plot PDP-based feature importance, we first need to set up the instance of `ICETransformer` by setting the `kind` parameter to `feature`. We can then call the `transform` function. `transform` returns a two-column table where the first columns are feature importance values and the second are corresponding features names. The rows are sorted in descending order by feature importance values.
###Code
pdp_based_imp = ICETransformer(
model=model,
targetCol="probability",
kind="feature",
targetClasses=[1],
categoricalFeatures=categorical_features,
numericFeatures=numeric_features,
)
output_pdp_based_imp = pdp_based_imp.transform(df)
display(output_pdp_based_imp)
###Output
_____no_output_____
###Markdown
Visualization
###Code
# Helper functions for visualization
def plot_pdp_based_imp(df, figsize=(35, 5)):
values_list = list(df.select("pdpBasedDependence").toPandas()["pdpBasedDependence"])
names = list(df.select("featureNames").toPandas()["featureNames"])
dependence_values = []
for vec in values_list:
dependence_values.append(vec.toArray()[0])
fig = plt.figure(figsize=figsize)
plt.bar(names, dependence_values)
plt.xlabel("Feature names", size=13)
plt.ylabel("PDP-based-feature-imporance")
plt.show()
###Output
_____no_output_____
###Markdown
This shows that the features `capital-gain` and `education-num` were the most important for the model, and `sex` and `education` were the least important.
###Code
plot_pdp_based_imp(output_pdp_based_imp)
###Output
_____no_output_____
|
upwork-devs/Pappaterra-Lucia/K8-vmware Project Tracking.ipynb
|
###Markdown
K8-vmware Project Tracking
###Code
%%capture
import sys
!{sys.executable} -m pip install google-auth-oauthlib
!{sys.executable} -m pip install google-api-python-client
!{sys.executable} -m pip install xhtml2pdf
!{sys.executable} -m pip install pdfrw
from modules.presentations import *
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:70% !important; }</style>"))
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')
###Output
_____no_output_____
###Markdown
In this notebook we pull data from this google sheethttps://docs.google.com/spreadsheets/d/13L9OodSo4Gp1vKPKpqEsi8vuoaxefuqhR6adXEvux5o/editgid=0See more related info here:https://docs.google.com/spreadsheets/d/1SetbtWlZC9fEddTbOzlnM36OQYBdtg0bbG4quq9ODKY/editgid=1064322020
###Code
sheet_name='Sheet1'
df = pull_data_from_gsh(sheet_name)
df
create_presentation(df,
file_name='K8-vmware Project Tracking '+sheet_name,
table_title='K8-vmware Project Tracking',
columns_widths=[50, 65, 90, 60, 100, 120, 80, 120])
###Output
_____no_output_____
|
PracticalLabExam_1.ipynb
|
###Markdown
**B**
###Code
import numpy as np
A = np.array ([[1, 2, 3],[4, 5, 6]])
B = np.array ([[1, 2],[3, 4],[5, 6]])
C = np.array ([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
D = np.array ([[1, 2],[3, 4]])
dot = np.dot(A,B)
sum = np.add(D,D)
S = 2*C
print ("A:")
print (dot)
print ("\nB:")
print (sum)
print ("\nC:")
print (S)
print ('Sum of D and D: ')
print (sum)
print ("\nScalar of C")
print (S)
import numpy as np
X = np.array ([[5], [3], [-1]])
print ("Problem 2: ")
print ("\nType:")
print (type(X))
print ("\nDimension:")
print (X.ndim)
print ("\nShape:")
print (X.shape)
###Output
Problem 2:
Type:
<class 'numpy.ndarray'>
Dimension:
2
Shape:
(3, 1)
|
Bioinformatics Stronghold/LEVEL 2/PRTM.ipynb
|
###Markdown
Calculating Protein Mass ProblemIn a weighted alphabet, every symbol is assigned a positive real number called a weight. A string formed from a weighted alphabet is called a weighted string, and its weight is equal to the sum of the weights of its symbols.The standard weight assigned to each member of the 20-symbol amino acid alphabet is the monoisotopic mass of the corresponding amino acid.Given: A protein string P of length at most 1000 aa.Return: The total weight of P. Consult the monoisotopic mass table.
###Code
protein_weight = """
A 71.03711
C 103.00919
D 115.02694
E 129.04259
F 147.06841
G 57.02146
H 137.05891
I 113.08406
K 128.09496
L 113.08406
M 131.04049
N 114.04293
P 97.05276
Q 128.05858
R 156.10111
S 87.03203
T 101.04768
V 99.06841
W 186.07931
Y 163.06333 """.split()
protein_weight_dict = dict(zip(protein_weight[::2],list(map(float,protein_weight[1::2]))))
I = input()
S = 0
for i in I :
S += protein_weight_dict[i]
print("%.3f"%S)
###Output
SKADYEK
821.392
|
StudyNotesOfML/1. Linear regression/Univarible regression-Predict profits for a food truck.ipynb
|
###Markdown
*通过人口数预测利润* 读入数据
###Code
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=('population', 'profit'))
data.head()
###Output
_____no_output_____
###Markdown
查看数据统计信息
###Code
data.describe()
###Output
_____no_output_____
###Markdown
绘制散点图
###Code
data.plot(kind='scatter', x='population', y='profit', figsize=(12, 8))
###Output
_____no_output_____
###Markdown
分离输入输出
###Code
rows = data.shape[0]
cols = data.shape[1]
X = np.mat(np.ones((rows, cols)))
X[:, 1:] = data.iloc[:, :cols - 1].values
X[:10, :]
Y = np.mat(data.iloc[:, 1].values).T
Y[:10, :]
theta = np.mat([0., 0.]).T
theta
###Output
_____no_output_____
###Markdown
损失函数$$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}$$其中:\\[{{h}_{\theta }}\left( x \right)={{\theta }^{T}}X={{\theta }_{0}}{{x}_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}}+...+{{\theta }_{n}}{{x}_{n}}\\]
###Code
def cost_func(X, Y, theta, m):
return np.sum(np.power(X * theta - Y, 2)) / (2 * m)
###Output
_____no_output_____
###Markdown
batch gradient decent(批量梯度下降)$${{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta \right)$$
###Code
def batch_gradient_decent(X, Y, theta, m, alpha=0.01, num_of_iters=1000):
#获取参数数量
num_of_parameters = theta.shape[0]
#保存损失函数值
cost_list = [int(1e9 + 7)]
#用于保存theta的临时向量
theta_tmp = theta.copy()
for i in range(num_of_iters):
bias = X * theta - Y
for j in range(num_of_parameters):
theta_tmp[j, 0] = theta[j, 0] - (alpha / m) * np.sum(np.multiply(bias, X[:, j]))
theta = theta_tmp
cost_val = np.sum(np.power(bias, 2)) / (2 * m)
cost_list.append(cost_val)
cost_list.append(cost_func(X, Y, theta, rows))
return theta, cost_list[1:]
theta, cost_values = batch_gradient_decent(X, Y, theta, rows)
theta
###Output
_____no_output_____
###Markdown
迭代的轮数
###Code
len(cost_values)
###Output
_____no_output_____
###Markdown
最终的损失函数值
###Code
cost_values[-1]
###Output
_____no_output_____
###Markdown
绘制拟合后的曲线
###Code
x = np.mat(np.linspace(np.min(X), np.max(X), 100)).T
x[:10]
y = theta[0, 0] + np.multiply(x, theta[1, 0])
y[:10]
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, y, 'r', label='prediction')
ax.scatter(data.population, data.profit, label='traning data')
ax.legend(loc=2)
ax.set_xlabel('population')
ax.set_ylabel('profit')
ax.set_title('predicted profit vs. population')
###Output
_____no_output_____
###Markdown
绘制损失函数值图像
###Code
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(len(cost_values)), cost_values, 'r')
ax.set_xlabel('iterations')
ax.set_ylabel('cost')
ax.set_title('error vs. training epoch')
###Output
_____no_output_____
###Markdown
使用scikit-learn的线性回归模型
###Code
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, Y)
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
###Output
_____no_output_____
|
travail_pratique/Projet-demo.ipynb
|
###Markdown
Introduction aux réseaux de neurones : Préambule au projetMatériel de cours rédigé par Pascal Germain, 2018************
###Code
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
import torch
from torch import nn
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
###Output
_____no_output_____
###Markdown
Nous vous fournissons quelques fonctions sous la forme d'un module `projetutils`. Vous êtes encouragés à [lire le code source](projetutils.py) et de vous en inspirer pour réaliser votre projet. Chaque fonction est accompagnée d'une courte description en commentaires vous renseignant sur son dessein.
###Code
import projetutils as pr
###Output
_____no_output_____
###Markdown
Préparation des donnéesLa fonction `charger_cifar` permet de charger les données.
###Code
pr.charger_cifar?
###Output
_____no_output_____
###Markdown
Nous vous suggérons de travailler seulement avec les trois premières classes.
###Code
repertoire_cifar = 'cifar/'
classes_cifar = [0, 1, 2]
data_x, data_y = pr.charger_cifar(repertoire_cifar, classes_cifar)
###Output
0 : 1005 images
1 : 974 images
2 : 1032 images
Total : 3011 images
###Markdown
Séparons aléatoirement les données en un ensemble d'apprentissage et un ensemble de test de tailles équivalentes (à l'aide des outils de *scikit-learn*).Nous vous conseillons d'utiliser le même partitionnement des données pour votre projet.
###Code
train_x, test_x, train_y, test_y = train_test_split(data_x, data_y, test_size=0.5, random_state=42)
print('train_x:', train_x.shape)
print('test_x:', test_x.shape)
print('train_y:', train_y.shape)
print('test_y:', test_y.shape)
###Output
train_x: (1505, 3072)
test_x: (1506, 3072)
train_y: (1505,)
test_y: (1506,)
###Markdown
Affichons un échantillon de 40 images sélectionnées aléatoirement dans l'ensemble d'apprentissage. Pour ce faire, nous vous fournissons une fonction `afficher_grille_cifar`.
###Code
indices_aleatoires = np.random.randint(len(train_y), size=40)
pr.afficher_grille_cifar(train_x[indices_aleatoires])
###Output
_____no_output_____
###Markdown
Apprentissage à l'aide d'un réseau de neurones *pleinement connecté* Similairement au TD2, nous utiliserons une classe `ReseauClassifGenerique` pour apprendre notre réseau de neurones, que nous avons bonifié pour permettre d'effectuer la procédure du «early stopping». Pour ce faire, vous devez spécifier les paramètres `fraction_validation` et `patience`. Consultez les commentaires de la classe `ReseauClassifGenerique` pour plus de détails.
###Code
pr.ReseauClassifGenerique?
###Output
_____no_output_____
###Markdown
Un objet `ReseauClassifGenerique` doit être instancié à l'aide d'un paramètre `architecture`. Le module `projetutils` contient un exemple d'architecture pleinement connectée à une couche cachée.
###Code
pr.UneArchiPleinementConnectee?
###Output
_____no_output_____
###Markdown
En combinant les deux classes mentionnées ci-haut, nous pouvons exécuter l'algorithme de descente en gradient. Lors de l'apprentissage, nous affichons la valeur de la fonction objectif pour chaque époque. Si on recourt au «early stopping» (c'est le cas dans l'exemple qui suit), on affiche aussi la précision calculée sur l'ensemble de validation.
###Code
# Créons une architecture prenant une image en entrée (sous la forme d'un vecteur de 3*32*32 éléments),
# possédant 3 sorties (correspondant aux classes «oiseau», «auto», «avion») et 50 neurones sur la couche cachée.
archi_pc = pr.UneArchiPleinementConnectee(nb_entrees=3*32*32, nb_sorties=3, nb_neurones_cachees=50)
# Initialisons le réseau de neurones.
reseau_pc = pr.ReseauClassifGenerique(archi_pc, eta=0.01, alpha=0.1, nb_epoques=500, taille_batch=32,
fraction_validation=.1, patience=20)
# Exécutons l'optimisation
reseau_pc.fit(train_x, train_y)
###Output
[1] 1.05666 | validation: 0.506667 ---> meilleur modèle à ce jour (max_t=21)
[2] 0.97917 | validation: 0.520000 ---> meilleur modèle à ce jour (max_t=22)
[3] 0.91755 | validation: 0.553333 ---> meilleur modèle à ce jour (max_t=23)
[4] 0.87007 | validation: 0.533333
[5] 0.83491 | validation: 0.513333
[6] 0.80878 | validation: 0.540000
[7] 0.78903 | validation: 0.533333
[8] 0.77333 | validation: 0.546667
[9] 0.76027 | validation: 0.560000 ---> meilleur modèle à ce jour (max_t=29)
[10] 0.74885 | validation: 0.560000
[11] 0.73908 | validation: 0.560000
[12] 0.72989 | validation: 0.560000
[13] 0.72092 | validation: 0.560000
[14] 0.71260 | validation: 0.566667 ---> meilleur modèle à ce jour (max_t=34)
[15] 0.70412 | validation: 0.566667
[16] 0.69602 | validation: 0.560000
[17] 0.68831 | validation: 0.573333 ---> meilleur modèle à ce jour (max_t=37)
[18] 0.68088 | validation: 0.573333
[19] 0.67358 | validation: 0.566667
[20] 0.66671 | validation: 0.566667
[21] 0.65984 | validation: 0.566667
[22] 0.65288 | validation: 0.560000
[23] 0.64526 | validation: 0.560000
[24] 0.63852 | validation: 0.560000
[25] 0.63197 | validation: 0.560000
[26] 0.62550 | validation: 0.560000
[27] 0.61927 | validation: 0.566667
[28] 0.61278 | validation: 0.566667
[29] 0.60654 | validation: 0.566667
[30] 0.60044 | validation: 0.566667
[31] 0.59447 | validation: 0.573333
[32] 0.58863 | validation: 0.566667
[33] 0.58263 | validation: 0.586667 ---> meilleur modèle à ce jour (max_t=53)
[34] 0.57615 | validation: 0.580000
[35] 0.57022 | validation: 0.573333
[36] 0.56424 | validation: 0.566667
[37] 0.55833 | validation: 0.573333
[38] 0.55315 | validation: 0.573333
[39] 0.54747 | validation: 0.580000
[40] 0.54198 | validation: 0.586667
[41] 0.53686 | validation: 0.586667
[42] 0.53134 | validation: 0.586667
[43] 0.52649 | validation: 0.600000 ---> meilleur modèle à ce jour (max_t=63)
[44] 0.52168 | validation: 0.606667 ---> meilleur modèle à ce jour (max_t=64)
[45] 0.51663 | validation: 0.606667
[46] 0.51174 | validation: 0.613333 ---> meilleur modèle à ce jour (max_t=66)
[47] 0.50858 | validation: 0.620000 ---> meilleur modèle à ce jour (max_t=67)
[48] 0.50459 | validation: 0.633333 ---> meilleur modèle à ce jour (max_t=68)
[49] 0.49894 | validation: 0.640000 ---> meilleur modèle à ce jour (max_t=69)
[50] 0.49465 | validation: 0.633333
[51] 0.48995 | validation: 0.653333 ---> meilleur modèle à ce jour (max_t=71)
[52] 0.48561 | validation: 0.660000 ---> meilleur modèle à ce jour (max_t=72)
[53] 0.48205 | validation: 0.660000
[54] 0.47573 | validation: 0.666667 ---> meilleur modèle à ce jour (max_t=74)
[55] 0.47144 | validation: 0.666667
[56] 0.46688 | validation: 0.666667
[57] 0.46194 | validation: 0.673333 ---> meilleur modèle à ce jour (max_t=77)
[58] 0.45781 | validation: 0.666667
[59] 0.45500 | validation: 0.673333
[60] 0.45104 | validation: 0.666667
[61] 0.44462 | validation: 0.680000 ---> meilleur modèle à ce jour (max_t=81)
[62] 0.44148 | validation: 0.673333
[63] 0.43510 | validation: 0.686667 ---> meilleur modèle à ce jour (max_t=83)
[64] 0.43155 | validation: 0.680000
[65] 0.42809 | validation: 0.686667
[66] 0.42491 | validation: 0.686667
[67] 0.41990 | validation: 0.686667
[68] 0.41323 | validation: 0.693333 ---> meilleur modèle à ce jour (max_t=88)
[69] 0.41309 | validation: 0.693333
[70] 0.40677 | validation: 0.700000 ---> meilleur modèle à ce jour (max_t=90)
[71] 0.40465 | validation: 0.693333
[72] 0.39780 | validation: 0.693333
[73] 0.39635 | validation: 0.700000
[74] 0.39024 | validation: 0.693333
[75] 0.38392 | validation: 0.700000
[76] 0.38248 | validation: 0.686667
[77] 0.37466 | validation: 0.693333
[78] 0.37052 | validation: 0.700000
[79] 0.36596 | validation: 0.700000
[80] 0.36288 | validation: 0.693333
[81] 0.35850 | validation: 0.700000
[82] 0.35362 | validation: 0.693333
[83] 0.35239 | validation: 0.686667
[84] 0.34564 | validation: 0.673333
[85] 0.34163 | validation: 0.680000
[86] 0.33841 | validation: 0.673333
[87] 0.33429 | validation: 0.660000
[88] 0.32997 | validation: 0.660000
[89] 0.32593 | validation: 0.666667
[90] 0.31948 | validation: 0.660000
=== Optimisation terminée ===
Early stopping à l'époque #70, avec précision en validation de 0.7
###Markdown
Vérifions l'acuité du réseau de neurones pleinement connecté sur l'ensemble test.
###Code
train_pred = reseau_pc.predict(train_x)
test_pred = reseau_pc.predict(test_x)
print('Précision train:', accuracy_score(train_y, train_pred) )
print('Précision test :', accuracy_score(test_y, test_pred))
###Output
Précision train: 0.8332225913621263
Précision test : 0.7297476759628154
###Markdown
La précision sur l'ensemble test devrait se situer entre 70% et 74%, selon les aléas de la descente en gradient stochastique. Vous pouvez répéter l'expérience en exécutant les deux dernières cellules de code. Diagnostique visuel de la descente en gradient La classe `ReseauClassifGenerique` conserve un l'historique des valeurs de la fonction objectif et des valeurs de précision en validation calculées au fil des époques. Nous pouvons ainsi afficher un graphique du comportement de la descente en gradient et éventuellement repérer des problèmes (par exemple, un paramètre `eta` trop élevé induira une oscillation dans la valeur objectif).
###Code
plt.figure(figsize=(16,5))
plt.plot(reseau_pc.liste_objectif, '--', label='Valeur objectif')
plt.plot(reseau_pc.liste_validation, label='Précision en validation')
plt.legend();
###Output
_____no_output_____
###Markdown
Calculer le nombre de paramètres du modèleDans l'énoncé du projet, nous vous demandons de tenir compte du nombre de paramètres que votre réseau de neurones doit optimiser. Nous vous fournissons aussi une fonction `compter_parametres` qui parcourt les structures de données de pyTorch pour obtenir ce nombre de paramètres, et ainsi valider votre calcul.
###Code
pr.compter_parametres(archi_pc.parametres())
###Output
_____no_output_____
###Markdown
**Notez bien:** Votre rapport ne doit pas seulement indiquer le total du nombre de paramètres à optimiser, mais détailler la répartition des paramètres pour chaque couche, en tenant compte de l'architecture de votre réseau.Ainsi, l'architecture pleinement connectée représentée par l'objet `archi_pc` contient $153\, 803$ paramètres, ce qui correspond au total des:* Couche cachée: $[3\,072 \mbox{ entrées}] \times [50 \mbox{ neurones}] + [50 \mbox{ valeurs de biais}] = 153\,650 \mbox{ paramètres}.$* Couche de sortie: $[50 \mbox{ entrées}] \times [3 \mbox{ neurones}] + [3 \mbox{ valeurs de biais}] = 153 \mbox{ paramètres}.$
###Code
(3*32*32)*50+50 + 50*3+3
###Output
_____no_output_____
|
docs/source/user_guide/objectives.ipynb
|
###Markdown
Objectives OverviewOne of the key choices to make when training an ML model is what metric to choose by which to measure the efficacy of the model at learning the signal. Such metrics are useful for comparing how well the trained models generalize to new similar data.This choice of metric is a key component of AutoML because it defines the cost function the AutoML search will seek to optimize. In rayml, these metrics are called **objectives**. AutoML will seek to minimize (or maximize) the objective score as it explores more pipelines and parameters and will use the feedback from scoring pipelines to tune the available hyperparameters and continue the search. Therefore, it is critical to have an objective function that represents how the model will be applied in the intended domain of use.rayml supports a variety of objectives from traditional supervised ML including [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error) for regression problems and [cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) or [area under the ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) for classification problems. rayml also allows the user to define a custom objective using their domain expertise, so that AutoML can search for models which provide the most value for the user's problem. Core ObjectivesUse the `get_core_objectives` method to get a list of which objectives are included with rayml for each problem type:
###Code
from rayml.objectives import get_core_objectives
from rayml.problem_types import ProblemTypes
for objective in get_core_objectives(ProblemTypes.BINARY):
print(objective.name)
###Output
_____no_output_____
###Markdown
rayml defines a base objective class for each problem type: `RegressionObjective`, `BinaryClassificationObjective` and `MulticlassClassificationObjective`. All rayml objectives are a subclass of one of these. Binary Classification Objectives and Thresholds All binary classification objectives have a `threshold` property. Some binary classification objectives like log loss and AUC are unaffected by the choice of binary classification threshold, because they score based on predicted probabilities or examine a range of threshold values. These metrics are defined with `score_needs_proba` set to False. For all other binary classification objectives, we can compute the optimal binary classification threshold from the predicted probabilities and the target.
###Code
from rayml.pipelines import BinaryClassificationPipeline
from rayml.demos import load_fraud
from rayml.objectives import F1
X, y = load_fraud(n_rows=100)
X.ww.init(logical_types={"provider": "Categorical", "region": "Categorical",
"currency": "Categorical", "expiration_date": "Categorical"})
objective = F1()
pipeline = BinaryClassificationPipeline(component_graph=['Simple Imputer', 'DateTime Featurizer', 'One Hot Encoder', 'Random Forest Classifier'])
pipeline.fit(X, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
y_pred_proba = pipeline.predict_proba(X)[True]
pipeline.threshold = objective.optimize_threshold(y_pred_proba, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
###Output
_____no_output_____
###Markdown
Custom ObjectivesOften times, the objective function is very specific to the use-case or business problem. To get the right objective to optimize requires thinking through the decisions or actions that will be taken using the model and assigning a cost/benefit to doing that correctly or incorrectly based on known outcomes in the training data.Once you have determined the objective for your business, you can provide that to rayml to optimize by defining a custom objective function. Defining a Custom Objective FunctionTo create a custom objective class, we must define several elements:* `name`: The printable name of this objective.* `objective_function`: This function takes the predictions, true labels, and an optional reference to the inputs, and returns a score of how well the model performed.* `greater_is_better`: `True` if a higher `objective_function` value represents a better solution, and otherwise `False`.* `score_needs_proba`: Only for classification objectives. `True` if the objective is intended to function with predicted probabilities as opposed to predicted values (example: cross entropy for classifiers).* `decision_function`: Only for binary classification objectives. This function takes predicted probabilities that were output from the model and a binary classification threshold, and returns predicted values.* `perfect_score`: The score achieved by a perfect model on this objective.* `expected_range`: The expected range of values we want this objective to output, which doesn't necessarily have to be equal to the possible range of values. For example, our expected R2 range is from `[-1, 1]`, although the actual range is `(-inf, 1]`. Example: Fraud DetectionTo give a concrete example, let's look at how the [fraud detection](../demos/fraud.ipynb) objective function is built.
###Code
from rayml.objectives.binary_classification_objective import BinaryClassificationObjective
import pandas as pd
class FraudCost(BinaryClassificationObjective):
"""Score the percentage of money lost of the total transaction amount process due to fraud"""
name = "Fraud Cost"
greater_is_better = False
score_needs_proba = False
perfect_score = 0.0
def __init__(self, retry_percentage=.5, interchange_fee=.02,
fraud_payout_percentage=1.0, amount_col='amount'):
"""Create instance of FraudCost
Args:
retry_percentage (float): What percentage of customers that will retry a transaction if it
is declined. Between 0 and 1. Defaults to .5
interchange_fee (float): How much of each successful transaction you can collect.
Between 0 and 1. Defaults to .02
fraud_payout_percentage (float): Percentage of fraud you will not be able to collect.
Between 0 and 1. Defaults to 1.0
amount_col (str): Name of column in data that contains the amount. Defaults to "amount"
"""
self.retry_percentage = retry_percentage
self.interchange_fee = interchange_fee
self.fraud_payout_percentage = fraud_payout_percentage
self.amount_col = amount_col
def decision_function(self, ypred_proba, threshold=0.0, X=None):
"""Determine if a transaction is fraud given predicted probabilities, threshold, and dataframe with transaction amount
Args:
ypred_proba (pd.Series): Predicted probablities
X (pd.DataFrame): Dataframe containing transaction amount
threshold (float): Dollar threshold to determine if transaction is fraud
Returns:
pd.Series: Series of predicted fraud labels using X and threshold
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(ypred_proba, pd.Series):
ypred_proba = pd.Series(ypred_proba)
transformed_probs = (ypred_proba.values * X[self.amount_col])
return transformed_probs > threshold
def objective_function(self, y_true, y_predicted, X):
"""Calculate amount lost to fraud per transaction given predictions, true values, and dataframe with transaction amount
Args:
y_predicted (pd.Series): predicted fraud labels
y_true (pd.Series): true fraud labels
X (pd.DataFrame): dataframe with transaction amounts
Returns:
float: amount lost to fraud per transaction
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(y_predicted, pd.Series):
y_predicted = pd.Series(y_predicted)
if not isinstance(y_true, pd.Series):
y_true = pd.Series(y_true)
# extract transaction using the amount columns in users data
try:
transaction_amount = X[self.amount_col]
except KeyError:
raise ValueError("`{}` is not a valid column in X.".format(self.amount_col))
# amount paid if transaction is fraud
fraud_cost = transaction_amount * self.fraud_payout_percentage
# money made from interchange fees on transaction
interchange_cost = transaction_amount * (1 - self.retry_percentage) * self.interchange_fee
# calculate cost of missing fraudulent transactions
false_negatives = (y_true & ~y_predicted) * fraud_cost
# calculate money lost from fees
false_positives = (~y_true & y_predicted) * interchange_cost
loss = false_negatives.sum() + false_positives.sum()
loss_per_total_processed = loss / transaction_amount.sum()
return loss_per_total_processed
###Output
_____no_output_____
###Markdown
Objectives OverviewOne of the key choices to make when training an ML model is what metric to choose by which to measure the efficacy of the model at learning the signal. Such metrics are useful for comparing how well the trained models generalize to new similar data.This choice of metric is a key component of AutoML because it defines the cost function the AutoML search will seek to optimize. In EvalML, these metrics are called **objectives**. AutoML will seek to minimize (or maximize) the objective score as it explores more pipelines and parameters and will use the feedback from scoring pipelines to tune the available hyperparameters and continue the search. Therefore, it is critical to have an objective function that represents how the model will be applied in the intended domain of use.EvalML supports a variety of objectives from traditional supervised ML including [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error) for regression problems and [cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) or [area under the ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) for classification problems. EvalML also allows the user to define a custom objective using their domain expertise, so that AutoML can search for models which provide the most value for the user's problem. Core ObjectivesUse the `get_core_objectives` method to get a list of which objectives are included with EvalML for each problem type:
###Code
from evalml.objectives import get_core_objectives
from evalml.problem_types import ProblemTypes
for objective in get_core_objectives(ProblemTypes.BINARY):
print(objective.name)
###Output
_____no_output_____
###Markdown
EvalML defines a base objective class for each problem type: `RegressionObjective`, `BinaryClassificationObjective` and `MulticlassClassificationObjective`. All EvalML objectives are a subclass of one of these. Binary Classification Objectives and Thresholds All binary classification objectives have a `threshold` property. Some binary classification objectives like log loss and AUC are unaffected by the choice of binary classification threshold, because they score based on predicted probabilities or examine a range of threshold values. These metrics are defined with `score_needs_proba` set to False. For all other binary classification objectives, we can compute the optimal binary classification threshold from the predicted probabilities and the target.
###Code
from evalml.pipelines import BinaryClassificationPipeline
from evalml.demos import load_fraud
from evalml.objectives import F1
class RFBinaryClassificationPipeline(BinaryClassificationPipeline):
component_graph = ['Simple Imputer', 'DateTime Featurization Component', 'One Hot Encoder', 'Random Forest Classifier']
X, y = load_fraud(n_rows=100)
objective = F1()
pipeline = RFBinaryClassificationPipeline({})
pipeline.fit(X, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
y_pred_proba = pipeline.predict_proba(X)[True]
pipeline.threshold = objective.optimize_threshold(y_pred_proba, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
###Output
_____no_output_____
###Markdown
Custom ObjectivesOften times, the objective function is very specific to the use-case or business problem. To get the right objective to optimize requires thinking through the decisions or actions that will be taken using the model and assigning a cost/benefit to doing that correctly or incorrectly based on known outcomes in the training data.Once you have determined the objective for your business, you can provide that to EvalML to optimize by defining a custom objective function. Defining a Custom Objective FunctionTo create a custom objective class, we must define several elements:* `name`: The printable name of this objective.* `objective_function`: This function takes the predictions, true labels, and an optional reference to the inputs, and returns a score of how well the model performed.* `greater_is_better`: `True` if a higher `objective_function` value represents a better solution, and otherwise `False`.* `score_needs_proba`: Only for classification objectives. `True` if the objective is intended to function with predicted probabilities as opposed to predicted values (example: cross entropy for classifiers).* `decision_function`: Only for binary classification objectives. This function takes predicted probabilities that were output from the model and a binary classification threshold, and returns predicted values.* `perfect_score`: The score achieved by a perfect model on this objective. Example: Fraud DetectionTo give a concrete example, let's look at how the [fraud detection](../demos/fraud.ipynb) objective function is built.
###Code
from evalml.objectives.binary_classification_objective import BinaryClassificationObjective
import pandas as pd
class FraudCost(BinaryClassificationObjective):
"""Score the percentage of money lost of the total transaction amount process due to fraud"""
name = "Fraud Cost"
greater_is_better = False
score_needs_proba = False
perfect_score = 0.0
def __init__(self, retry_percentage=.5, interchange_fee=.02,
fraud_payout_percentage=1.0, amount_col='amount'):
"""Create instance of FraudCost
Arguments:
retry_percentage (float): What percentage of customers that will retry a transaction if it
is declined. Between 0 and 1. Defaults to .5
interchange_fee (float): How much of each successful transaction you can collect.
Between 0 and 1. Defaults to .02
fraud_payout_percentage (float): Percentage of fraud you will not be able to collect.
Between 0 and 1. Defaults to 1.0
amount_col (str): Name of column in data that contains the amount. Defaults to "amount"
"""
self.retry_percentage = retry_percentage
self.interchange_fee = interchange_fee
self.fraud_payout_percentage = fraud_payout_percentage
self.amount_col = amount_col
def decision_function(self, ypred_proba, threshold=0.0, X=None):
"""Determine if a transaction is fraud given predicted probabilities, threshold, and dataframe with transaction amount
Arguments:
ypred_proba (pd.Series): Predicted probablities
X (pd.DataFrame): Dataframe containing transaction amount
threshold (float): Dollar threshold to determine if transaction is fraud
Returns:
pd.Series: Series of predicted fraud labels using X and threshold
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(ypred_proba, pd.Series):
ypred_proba = pd.Series(ypred_proba)
transformed_probs = (ypred_proba.values * X[self.amount_col])
return transformed_probs > threshold
def objective_function(self, y_true, y_predicted, X):
"""Calculate amount lost to fraud per transaction given predictions, true values, and dataframe with transaction amount
Arguments:
y_predicted (pd.Series): predicted fraud labels
y_true (pd.Series): true fraud labels
X (pd.DataFrame): dataframe with transaction amounts
Returns:
float: amount lost to fraud per transaction
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(y_predicted, pd.Series):
y_predicted = pd.Series(y_predicted)
if not isinstance(y_true, pd.Series):
y_true = pd.Series(y_true)
# extract transaction using the amount columns in users data
try:
transaction_amount = X[self.amount_col]
except KeyError:
raise ValueError("`{}` is not a valid column in X.".format(self.amount_col))
# amount paid if transaction is fraud
fraud_cost = transaction_amount * self.fraud_payout_percentage
# money made from interchange fees on transaction
interchange_cost = transaction_amount * (1 - self.retry_percentage) * self.interchange_fee
# calculate cost of missing fraudulent transactions
false_negatives = (y_true & ~y_predicted) * fraud_cost
# calculate money lost from fees
false_positives = (~y_true & y_predicted) * interchange_cost
loss = false_negatives.sum() + false_positives.sum()
loss_per_total_processed = loss / transaction_amount.sum()
return loss_per_total_processed
###Output
_____no_output_____
###Markdown
Objectives OverviewOne of the key choices to make when training an ML model is what metric to choose by which to measure the efficacy of the model at learning the signal. Such metrics are useful for comparing how well the trained models generalize to new similar data.This choice of metric is a key component of AutoML because it defines the cost function the AutoML search will seek to optimize. In EvalML, these metrics are called **objectives**. AutoML will seek to minimize (or maximize) the objective score as it explores more pipelines and parameters and will use the feedback from scoring pipelines to tune the available hyperparameters and continue the search. Therefore, it is critical to have an objective function that represents how the model will be applied in the intended domain of use.EvalML supports a variety of objectives from traditional supervised ML including [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error) for regression problems and [cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) or [area under the ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) for classification problems. EvalML also allows the user to define a custom objective using their domain expertise, so that AutoML can search for models which provide the most value for the user's problem. Core ObjectivesUse the `get_core_objectives` method to get a list of which objectives are included with EvalML for each problem type:
###Code
from evalml.objectives import get_core_objectives
from evalml.problem_types import ProblemTypes
for objective in get_core_objectives(ProblemTypes.BINARY):
print(objective.name)
###Output
_____no_output_____
###Markdown
EvalML defines a base objective class for each problem type: `RegressionObjective`, `BinaryClassificationObjective` and `MulticlassClassificationObjective`. All EvalML objectives are a subclass of one of these. Binary Classification Objectives and Thresholds All binary classification objectives have a `threshold` property. Some binary classification objectives like log loss and AUC are unaffected by the choice of binary classification threshold, because they score based on predicted probabilities or examine a range of threshold values. These metrics are defined with `score_needs_proba` set to False. For all other binary classification objectives, we can compute the optimal binary classification threshold from the predicted probabilities and the target.
###Code
from evalml.pipelines import BinaryClassificationPipeline
from evalml.demos import load_fraud
from evalml.objectives import F1
X, y = load_fraud(n_rows=100)
X.ww.init(logical_types={"provider": "Categorical", "region": "Categorical",
"currency": "Categorical", "expiration_date": "Categorical"})
objective = F1()
pipeline = BinaryClassificationPipeline(component_graph=['Simple Imputer', 'DateTime Featurization Component', 'One Hot Encoder', 'Random Forest Classifier'])
pipeline.fit(X, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
y_pred_proba = pipeline.predict_proba(X)[True]
pipeline.threshold = objective.optimize_threshold(y_pred_proba, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
###Output
_____no_output_____
###Markdown
Custom ObjectivesOften times, the objective function is very specific to the use-case or business problem. To get the right objective to optimize requires thinking through the decisions or actions that will be taken using the model and assigning a cost/benefit to doing that correctly or incorrectly based on known outcomes in the training data.Once you have determined the objective for your business, you can provide that to EvalML to optimize by defining a custom objective function. Defining a Custom Objective FunctionTo create a custom objective class, we must define several elements:* `name`: The printable name of this objective.* `objective_function`: This function takes the predictions, true labels, and an optional reference to the inputs, and returns a score of how well the model performed.* `greater_is_better`: `True` if a higher `objective_function` value represents a better solution, and otherwise `False`.* `score_needs_proba`: Only for classification objectives. `True` if the objective is intended to function with predicted probabilities as opposed to predicted values (example: cross entropy for classifiers).* `decision_function`: Only for binary classification objectives. This function takes predicted probabilities that were output from the model and a binary classification threshold, and returns predicted values.* `perfect_score`: The score achieved by a perfect model on this objective.* `expected_range`: The expected range of values we want this objective to output, which doesn't necessarily have to be equal to the possible range of values. For example, our expected R2 range is from `[-1, 1]`, although the actual range is `(-inf, 1]`. Example: Fraud DetectionTo give a concrete example, let's look at how the [fraud detection](../demos/fraud.ipynb) objective function is built.
###Code
from evalml.objectives.binary_classification_objective import BinaryClassificationObjective
import pandas as pd
class FraudCost(BinaryClassificationObjective):
"""Score the percentage of money lost of the total transaction amount process due to fraud"""
name = "Fraud Cost"
greater_is_better = False
score_needs_proba = False
perfect_score = 0.0
def __init__(self, retry_percentage=.5, interchange_fee=.02,
fraud_payout_percentage=1.0, amount_col='amount'):
"""Create instance of FraudCost
Args:
retry_percentage (float): What percentage of customers that will retry a transaction if it
is declined. Between 0 and 1. Defaults to .5
interchange_fee (float): How much of each successful transaction you can collect.
Between 0 and 1. Defaults to .02
fraud_payout_percentage (float): Percentage of fraud you will not be able to collect.
Between 0 and 1. Defaults to 1.0
amount_col (str): Name of column in data that contains the amount. Defaults to "amount"
"""
self.retry_percentage = retry_percentage
self.interchange_fee = interchange_fee
self.fraud_payout_percentage = fraud_payout_percentage
self.amount_col = amount_col
def decision_function(self, ypred_proba, threshold=0.0, X=None):
"""Determine if a transaction is fraud given predicted probabilities, threshold, and dataframe with transaction amount
Args:
ypred_proba (pd.Series): Predicted probablities
X (pd.DataFrame): Dataframe containing transaction amount
threshold (float): Dollar threshold to determine if transaction is fraud
Returns:
pd.Series: Series of predicted fraud labels using X and threshold
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(ypred_proba, pd.Series):
ypred_proba = pd.Series(ypred_proba)
transformed_probs = (ypred_proba.values * X[self.amount_col])
return transformed_probs > threshold
def objective_function(self, y_true, y_predicted, X):
"""Calculate amount lost to fraud per transaction given predictions, true values, and dataframe with transaction amount
Args:
y_predicted (pd.Series): predicted fraud labels
y_true (pd.Series): true fraud labels
X (pd.DataFrame): dataframe with transaction amounts
Returns:
float: amount lost to fraud per transaction
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(y_predicted, pd.Series):
y_predicted = pd.Series(y_predicted)
if not isinstance(y_true, pd.Series):
y_true = pd.Series(y_true)
# extract transaction using the amount columns in users data
try:
transaction_amount = X[self.amount_col]
except KeyError:
raise ValueError("`{}` is not a valid column in X.".format(self.amount_col))
# amount paid if transaction is fraud
fraud_cost = transaction_amount * self.fraud_payout_percentage
# money made from interchange fees on transaction
interchange_cost = transaction_amount * (1 - self.retry_percentage) * self.interchange_fee
# calculate cost of missing fraudulent transactions
false_negatives = (y_true & ~y_predicted) * fraud_cost
# calculate money lost from fees
false_positives = (~y_true & y_predicted) * interchange_cost
loss = false_negatives.sum() + false_positives.sum()
loss_per_total_processed = loss / transaction_amount.sum()
return loss_per_total_processed
###Output
_____no_output_____
###Markdown
Objectives OverviewOne of the key choices to make when training an ML model is what metric to choose by which to measure the efficacy of the model at learning the signal. Such metrics are useful for comparing how well the trained models generalize to new similar data.This choice of metric is a key component of AutoML because it defines the cost function the AutoML search will seek to optimize. In EvalML, these metrics are called **objectives**. AutoML will seek to minimize (or maximize) the objective score as it explores more pipelines and parameters and will use the feedback from scoring pipelines to tune the available hyperparameters and continue the search. Therefore, it is critical to have an objective function that represents how the model will be applied in the intended domain of use.EvalML supports a variety of objectives from traditional supervised ML including [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error) for regression problems and [cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) or [area under the ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) for classification problems. EvalML also allows the user to define a custom objective using their domain expertise, so that AutoML can search for models which provide the most value for the user's problem. Core ObjectivesUse the `get_core_objectives` method to get a list of which objectives are included with EvalML for each problem type:
###Code
from evalml.objectives import get_core_objectives
from evalml.problem_types import ProblemTypes
for objective in get_core_objectives(ProblemTypes.BINARY):
print(objective.name)
###Output
_____no_output_____
###Markdown
EvalML defines a base objective class for each problem type: `RegressionObjective`, `BinaryClassificationObjective` and `MulticlassClassificationObjective`. All EvalML objectives are a subclass of one of these. Binary Classification Objectives and Thresholds All binary classification objectives have a `threshold` property. Some binary classification objectives like log loss and AUC are unaffected by the choice of binary classification threshold, because they score based on predicted probabilities or examine a range of threshold values. These metrics are defined with `score_needs_proba` set to False. For all other binary classification objectives, we can compute the optimal binary classification threshold from the predicted probabilities and the target.
###Code
from evalml.pipelines import BinaryClassificationPipeline
from evalml.demos import load_fraud
from evalml.objectives import F1
X, y = load_fraud(n_rows=100)
X.ww.init(logical_types={"provider": "Categorical", "region": "Categorical",
"currency": "Categorical", "expiration_date": "Categorical"})
objective = F1()
pipeline = BinaryClassificationPipeline(component_graph=['Simple Imputer', 'DateTime Featurizer', 'One Hot Encoder', 'Random Forest Classifier'])
pipeline.fit(X, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
y_pred_proba = pipeline.predict_proba(X)[True]
pipeline.threshold = objective.optimize_threshold(y_pred_proba, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
###Output
_____no_output_____
###Markdown
Custom ObjectivesOften times, the objective function is very specific to the use-case or business problem. To get the right objective to optimize requires thinking through the decisions or actions that will be taken using the model and assigning a cost/benefit to doing that correctly or incorrectly based on known outcomes in the training data.Once you have determined the objective for your business, you can provide that to EvalML to optimize by defining a custom objective function. Defining a Custom Objective FunctionTo create a custom objective class, we must define several elements:* `name`: The printable name of this objective.* `objective_function`: This function takes the predictions, true labels, and an optional reference to the inputs, and returns a score of how well the model performed.* `greater_is_better`: `True` if a higher `objective_function` value represents a better solution, and otherwise `False`.* `score_needs_proba`: Only for classification objectives. `True` if the objective is intended to function with predicted probabilities as opposed to predicted values (example: cross entropy for classifiers).* `decision_function`: Only for binary classification objectives. This function takes predicted probabilities that were output from the model and a binary classification threshold, and returns predicted values.* `perfect_score`: The score achieved by a perfect model on this objective.* `expected_range`: The expected range of values we want this objective to output, which doesn't necessarily have to be equal to the possible range of values. For example, our expected R2 range is from `[-1, 1]`, although the actual range is `(-inf, 1]`. Example: Fraud DetectionTo give a concrete example, let's look at how the [fraud detection](../demos/fraud.ipynb) objective function is built.
###Code
from evalml.objectives.binary_classification_objective import BinaryClassificationObjective
import pandas as pd
class FraudCost(BinaryClassificationObjective):
"""Score the percentage of money lost of the total transaction amount process due to fraud"""
name = "Fraud Cost"
greater_is_better = False
score_needs_proba = False
perfect_score = 0.0
def __init__(self, retry_percentage=.5, interchange_fee=.02,
fraud_payout_percentage=1.0, amount_col='amount'):
"""Create instance of FraudCost
Args:
retry_percentage (float): What percentage of customers that will retry a transaction if it
is declined. Between 0 and 1. Defaults to .5
interchange_fee (float): How much of each successful transaction you can collect.
Between 0 and 1. Defaults to .02
fraud_payout_percentage (float): Percentage of fraud you will not be able to collect.
Between 0 and 1. Defaults to 1.0
amount_col (str): Name of column in data that contains the amount. Defaults to "amount"
"""
self.retry_percentage = retry_percentage
self.interchange_fee = interchange_fee
self.fraud_payout_percentage = fraud_payout_percentage
self.amount_col = amount_col
def decision_function(self, ypred_proba, threshold=0.0, X=None):
"""Determine if a transaction is fraud given predicted probabilities, threshold, and dataframe with transaction amount
Args:
ypred_proba (pd.Series): Predicted probablities
X (pd.DataFrame): Dataframe containing transaction amount
threshold (float): Dollar threshold to determine if transaction is fraud
Returns:
pd.Series: Series of predicted fraud labels using X and threshold
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(ypred_proba, pd.Series):
ypred_proba = pd.Series(ypred_proba)
transformed_probs = (ypred_proba.values * X[self.amount_col])
return transformed_probs > threshold
def objective_function(self, y_true, y_predicted, X):
"""Calculate amount lost to fraud per transaction given predictions, true values, and dataframe with transaction amount
Args:
y_predicted (pd.Series): predicted fraud labels
y_true (pd.Series): true fraud labels
X (pd.DataFrame): dataframe with transaction amounts
Returns:
float: amount lost to fraud per transaction
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(y_predicted, pd.Series):
y_predicted = pd.Series(y_predicted)
if not isinstance(y_true, pd.Series):
y_true = pd.Series(y_true)
# extract transaction using the amount columns in users data
try:
transaction_amount = X[self.amount_col]
except KeyError:
raise ValueError("`{}` is not a valid column in X.".format(self.amount_col))
# amount paid if transaction is fraud
fraud_cost = transaction_amount * self.fraud_payout_percentage
# money made from interchange fees on transaction
interchange_cost = transaction_amount * (1 - self.retry_percentage) * self.interchange_fee
# calculate cost of missing fraudulent transactions
false_negatives = (y_true & ~y_predicted) * fraud_cost
# calculate money lost from fees
false_positives = (~y_true & y_predicted) * interchange_cost
loss = false_negatives.sum() + false_positives.sum()
loss_per_total_processed = loss / transaction_amount.sum()
return loss_per_total_processed
###Output
_____no_output_____
###Markdown
Objectives OverviewOne of the key choices to make when training an ML model is what metric to choose by which to measure the efficacy of the model at learning the signal. Such metrics are useful for comparing how well the trained models generalize to new similar data.This choice of metric is a key component of AutoML because it defines the cost function the AutoML search will seek to optimize. In EvalML, these metrics are called **objectives**. AutoML will seek to minimize (or maximize) the objective score as it explores more pipelines and parameters and will use the feedback from scoring pipelines to tune the available hyperparameters and continue the search. Therefore, it is critical to have an objective function that represents how the model will be applied in the intended domain of use.EvalML supports a variety of objectives from traditional supervised ML including [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error) for regression problems and [cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) or [area under the ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) for classification problems. EvalML also allows the user to define a custom objective using their domain expertise, so that AutoML can search for models which provide the most value for the user's problem. Core ObjectivesUse the `get_core_objectives` method to get a list of which objectives are included with EvalML for each problem type:
###Code
from evalml.objectives import get_core_objectives
from evalml.problem_types import ProblemTypes
for objective in get_core_objectives(ProblemTypes.BINARY):
print(objective.name)
###Output
_____no_output_____
###Markdown
EvalML defines a base objective class for each problem type: `RegressionObjective`, `BinaryClassificationObjective` and `MulticlassClassificationObjective`. All EvalML objectives are a subclass of one of these. Binary Classification Objectives and Thresholds All binary classification objectives have a `threshold` property. Some binary classification objectives like log loss and AUC are unaffected by the choice of binary classification threshold, because they score based on predicted probabilities or examine a range of threshold values. These metrics are defined with `score_needs_proba` set to False. For all other binary classification objectives, we can compute the optimal binary classification threshold from the predicted probabilities and the target.
###Code
from evalml.pipelines import BinaryClassificationPipeline
from evalml.demos import load_fraud
from evalml.objectives import F1
X, y = load_fraud(n_rows=100)
X.ww.init(logical_types={"provider": "Categorical", "region": "Categorical"})
objective = F1()
pipeline = BinaryClassificationPipeline(component_graph=['Simple Imputer', 'DateTime Featurization Component', 'One Hot Encoder', 'Random Forest Classifier'])
pipeline.fit(X, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
y_pred_proba = pipeline.predict_proba(X)[True]
pipeline.threshold = objective.optimize_threshold(y_pred_proba, y)
print(pipeline.threshold)
print(pipeline.score(X, y, objectives=[objective]))
###Output
_____no_output_____
###Markdown
Custom ObjectivesOften times, the objective function is very specific to the use-case or business problem. To get the right objective to optimize requires thinking through the decisions or actions that will be taken using the model and assigning a cost/benefit to doing that correctly or incorrectly based on known outcomes in the training data.Once you have determined the objective for your business, you can provide that to EvalML to optimize by defining a custom objective function. Defining a Custom Objective FunctionTo create a custom objective class, we must define several elements:* `name`: The printable name of this objective.* `objective_function`: This function takes the predictions, true labels, and an optional reference to the inputs, and returns a score of how well the model performed.* `greater_is_better`: `True` if a higher `objective_function` value represents a better solution, and otherwise `False`.* `score_needs_proba`: Only for classification objectives. `True` if the objective is intended to function with predicted probabilities as opposed to predicted values (example: cross entropy for classifiers).* `decision_function`: Only for binary classification objectives. This function takes predicted probabilities that were output from the model and a binary classification threshold, and returns predicted values.* `perfect_score`: The score achieved by a perfect model on this objective. Example: Fraud DetectionTo give a concrete example, let's look at how the [fraud detection](../demos/fraud.ipynb) objective function is built.
###Code
from evalml.objectives.binary_classification_objective import BinaryClassificationObjective
import pandas as pd
class FraudCost(BinaryClassificationObjective):
"""Score the percentage of money lost of the total transaction amount process due to fraud"""
name = "Fraud Cost"
greater_is_better = False
score_needs_proba = False
perfect_score = 0.0
def __init__(self, retry_percentage=.5, interchange_fee=.02,
fraud_payout_percentage=1.0, amount_col='amount'):
"""Create instance of FraudCost
Arguments:
retry_percentage (float): What percentage of customers that will retry a transaction if it
is declined. Between 0 and 1. Defaults to .5
interchange_fee (float): How much of each successful transaction you can collect.
Between 0 and 1. Defaults to .02
fraud_payout_percentage (float): Percentage of fraud you will not be able to collect.
Between 0 and 1. Defaults to 1.0
amount_col (str): Name of column in data that contains the amount. Defaults to "amount"
"""
self.retry_percentage = retry_percentage
self.interchange_fee = interchange_fee
self.fraud_payout_percentage = fraud_payout_percentage
self.amount_col = amount_col
def decision_function(self, ypred_proba, threshold=0.0, X=None):
"""Determine if a transaction is fraud given predicted probabilities, threshold, and dataframe with transaction amount
Arguments:
ypred_proba (pd.Series): Predicted probablities
X (pd.DataFrame): Dataframe containing transaction amount
threshold (float): Dollar threshold to determine if transaction is fraud
Returns:
pd.Series: Series of predicted fraud labels using X and threshold
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(ypred_proba, pd.Series):
ypred_proba = pd.Series(ypred_proba)
transformed_probs = (ypred_proba.values * X[self.amount_col])
return transformed_probs > threshold
def objective_function(self, y_true, y_predicted, X):
"""Calculate amount lost to fraud per transaction given predictions, true values, and dataframe with transaction amount
Arguments:
y_predicted (pd.Series): predicted fraud labels
y_true (pd.Series): true fraud labels
X (pd.DataFrame): dataframe with transaction amounts
Returns:
float: amount lost to fraud per transaction
"""
if not isinstance(X, pd.DataFrame):
X = pd.DataFrame(X)
if not isinstance(y_predicted, pd.Series):
y_predicted = pd.Series(y_predicted)
if not isinstance(y_true, pd.Series):
y_true = pd.Series(y_true)
# extract transaction using the amount columns in users data
try:
transaction_amount = X[self.amount_col]
except KeyError:
raise ValueError("`{}` is not a valid column in X.".format(self.amount_col))
# amount paid if transaction is fraud
fraud_cost = transaction_amount * self.fraud_payout_percentage
# money made from interchange fees on transaction
interchange_cost = transaction_amount * (1 - self.retry_percentage) * self.interchange_fee
# calculate cost of missing fraudulent transactions
false_negatives = (y_true & ~y_predicted) * fraud_cost
# calculate money lost from fees
false_positives = (~y_true & y_predicted) * interchange_cost
loss = false_negatives.sum() + false_positives.sum()
loss_per_total_processed = loss / transaction_amount.sum()
return loss_per_total_processed
###Output
_____no_output_____
|
examples/kuramoto/watts_strogatz_drivers_K02_zoom.ipynb
|
###Markdown
Experiments for Watts--Strogatz Graph Imports
###Code
%load_ext autoreload
%autoreload 2
import os
import sys
from collections import OrderedDict
import logging
import math
from matplotlib import pyplot as plt
import networkx as nx
import numpy as np
import torch
from torchdiffeq import odeint, odeint_adjoint
sys.path.append('../../')
sys.path.append('../kuramoto_utilities')
# Baseline imports
from gd_controller import AdjointGD
from dynamics_driver import ForwardKuramotoDynamics, BackwardKuramotoDynamics
# Nodec imports
from neural_net import EluTimeControl, TrainingAlgorithm
# Various Utilities
from utilities import evaluate, calculate_critical_coupling_constant, comparison_plot, state_plot
from nnc.helpers.torch_utils.oscillators import order_parameter_cos
logging.getLogger().setLevel(logging.CRITICAL) # set to info to look at loss values etc.
###Output
_____no_output_____
###Markdown
Load graph parametersBasic setup for calculations, graph, number of nodes, etc.
###Code
dtype = torch.float32
device = 'cpu'
graph_type = 'watts_strogatz'
adjacency_matrix = torch.load('../../data/'+graph_type+'_adjacency.pt')
parameters = torch.load('../../data/parameters.pt')
# driver vector is a column vector with 1 value for driver nodes
# and 0 for non drivers.
result_folder = '../../results/' + graph_type + os.path.sep
os.makedirs(result_folder, exist_ok=True)
###Output
_____no_output_____
###Markdown
Load dynamics parametersLoad natural frequencies and initial states which are common for all graphs and also calculate the coupling constant which is different per graph. We use a coupling constant value that is $10%$ of the critical coupling constant value.
###Code
total_time = parameters['total_time']
total_time = 5
natural_frequencies = parameters['natural_frequencies']
critical_coupling_constant = calculate_critical_coupling_constant(adjacency_matrix, natural_frequencies)
coupling_constant = 0.2*critical_coupling_constant
theta_0 = parameters['theta_0']
###Output
_____no_output_____
###Markdown
NODECWe now train NODEC with a shallow neural network. We initialize the parameters in a deterministic manner, and use stochastic gradient descent to train it. The learning rate, number of epochs and neural architecture may change per graph. We use different fractions of driver nodes.
###Code
fractions = np.linspace(0.9,1,10)
order_parameter_mean = []
order_parameter_std = []
samples = 1000
for p in fractions:
sample_arr = []
for i in range(samples):
print(p,i)
driver_nodes = int(p*adjacency_matrix.shape[0])
driver_vector = torch.zeros([adjacency_matrix.shape[0],1])
idx = torch.randperm(len(driver_vector))[:driver_nodes]
driver_vector[idx] = 1
forward_dynamics = ForwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
backward_dynamics = BackwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
neural_net = EluTimeControl([2])
for parameter in neural_net.parameters():
parameter.data = torch.ones_like(parameter.data)/1000 # deterministic init!
train_algo = TrainingAlgorithm(neural_net, forward_dynamics)
best_model = train_algo.train(theta_0, total_time, epochs=3, lr=0.1)
control_trajectory, state_trajectory =\
evaluate(forward_dynamics, theta_0, best_model, total_time, 100)
nn_control = torch.cat(control_trajectory).squeeze().cpu().detach().numpy()
nn_states = torch.cat(state_trajectory).cpu().detach().numpy()
nn_e = (nn_control**2).cumsum(-1)
nn_r = order_parameter_cos(torch.tensor(nn_states)).cpu().numpy()
sample_arr.append(nn_r[-1])
order_parameter_mean.append(np.mean(sample_arr))
order_parameter_std.append(np.std(sample_arr,ddof=1))
order_parameter_mean = np.array(order_parameter_mean)
order_parameter_std = np.array(order_parameter_std)
plt.figure()
plt.errorbar(fractions,order_parameter_mean,yerr=order_parameter_std/np.sqrt(samples),fmt="o")
plt.xlabel(r"fraction of controlled nodes")
plt.ylabel(r"$r(T)$")
plt.tight_layout()
plt.show()
np.savetxt("WS_drivers_K02_zoom.csv",np.c_[order_parameter_mean,order_parameter_std],header="order parameter mean\t order parameter std")
###Output
_____no_output_____
###Markdown
Experiments for Watts--Strogatz Graph Imports
###Code
%load_ext autoreload
%autoreload 2
import os
import sys
from collections import OrderedDict
import logging
import math
from matplotlib import pyplot as plt
import networkx as nx
import numpy as np
import torch
from torchdiffeq import odeint, odeint_adjoint
sys.path.append('../../')
# Baseline imports
from gd_controller import AdjointGD
from dynamics_driver import ForwardKuramotoDynamics, BackwardKuramotoDynamics
# Nodec imports
from neural_net import EluTimeControl, TrainingAlgorithm
# Various Utilities
from utilities import evaluate, calculate_critical_coupling_constant, comparison_plot, state_plot
from nnc.helpers.torch_utils.oscillators import order_parameter_cos
logging.getLogger().setLevel(logging.CRITICAL) # set to info to look at loss values etc.
###Output
The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload
###Markdown
Load graph parametersBasic setup for calculations, graph, number of nodes, etc.
###Code
dtype = torch.float32
device = 'cpu'
graph_type = 'watts_strogatz'
adjacency_matrix = torch.load('../../data/'+graph_type+'_adjacency.pt')
parameters = torch.load('../../data/parameters.pt')
# driver vector is a column vector with 1 value for driver nodes
# and 0 for non drivers.
result_folder = '../../results/' + graph_type + os.path.sep
os.makedirs(result_folder, exist_ok=True)
###Output
_____no_output_____
###Markdown
Load dynamics parametersLoad natural frequencies and initial states which are common for all graphs and also calculate the coupling constant which is different per graph. We use a coupling constant value that is $10%$ of the critical coupling constant value.
###Code
total_time = parameters['total_time']
total_time = 5
natural_frequencies = parameters['natural_frequencies']
critical_coupling_constant = calculate_critical_coupling_constant(adjacency_matrix, natural_frequencies)
coupling_constant = 0.2*critical_coupling_constant
theta_0 = parameters['theta_0']
###Output
_____no_output_____
###Markdown
NODECWe now train NODEC with a shallow neural network. We initialize the parameters in a deterministic manner, and use stochastic gradient descent to train it. The learning rate, number of epochs and neural architecture may change per graph. We use different fractions of driver nodes.
###Code
fractions = np.linspace(0.9,1,10)
order_parameter_mean = []
order_parameter_std = []
samples = 1000
for p in fractions:
sample_arr = []
for i in range(samples):
print(p,i)
driver_nodes = int(p*adjacency_matrix.shape[0])
driver_vector = torch.zeros([adjacency_matrix.shape[0],1])
idx = torch.randperm(len(driver_vector))[:driver_nodes]
driver_vector[idx] = 1
forward_dynamics = ForwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
backward_dynamics = BackwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
neural_net = EluTimeControl([2])
for parameter in neural_net.parameters():
parameter.data = torch.ones_like(parameter.data)/1000 # deterministic init!
train_algo = TrainingAlgorithm(neural_net, forward_dynamics)
best_model = train_algo.train(theta_0, total_time, epochs=3, lr=0.1)
control_trajectory, state_trajectory =\
evaluate(forward_dynamics, theta_0, best_model, total_time, 100)
nn_control = torch.cat(control_trajectory).squeeze().cpu().detach().numpy()
nn_states = torch.cat(state_trajectory).cpu().detach().numpy()
nn_e = (nn_control**2).cumsum(-1)
nn_r = order_parameter_cos(torch.tensor(nn_states)).cpu().numpy()
sample_arr.append(nn_r[-1])
order_parameter_mean.append(np.mean(sample_arr))
order_parameter_std.append(np.std(sample_arr,ddof=1))
order_parameter_mean = np.array(order_parameter_mean)
order_parameter_std = np.array(order_parameter_std)
plt.figure()
plt.errorbar(fractions,order_parameter_mean,yerr=order_parameter_std/np.sqrt(samples),fmt="o")
plt.xlabel(r"fraction of controlled nodes")
plt.ylabel(r"$r(T)$")
plt.tight_layout()
plt.show()
np.savetxt("WS_drivers_K02_zoom.csv",np.c_[order_parameter_mean,order_parameter_std],header="order parameter mean\t order parameter std")
###Output
_____no_output_____
|
Michigan_AppliedDataScienceWithPython/AppliedMachineLearning/Classifier+Visualization.ipynb
|
###Markdown
---_You are currently looking at **version 1.0** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-machine-learning/resources/bANLa) course resource._--- Classifier Visualization PlaygroundThe purpose of this notebook is to let you visualize various classsifiers' decision boundaries.The data used in this notebook is based on the [UCI Mushroom Data Set](http://archive.ics.uci.edu/ml/datasets/Mushroom?ref=datanews.io) stored in `mushrooms.csv`. In order to better vizualize the decision boundaries, we'll perform Principal Component Analysis (PCA) on the data to reduce the dimensionality to 2 dimensions. Dimensionality reduction will be covered in a later module of this course.Play around with different models and parameters to see how they affect the classifier's decision boundary and accuracy!
###Code
%matplotlib notebook
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
df = pd.read_csv('readonly/mushrooms.csv')
df2 = pd.get_dummies(df)
df3 = df2.sample(frac=0.08)
X = df3.iloc[:,2:]
y = df3.iloc[:,1]
pca = PCA(n_components=2).fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(pca, y, random_state=0)
plt.figure(dpi=120)
plt.scatter(pca[y.values==0,0], pca[y.values==0,1], alpha=0.5, label='Edible', s=2)
plt.scatter(pca[y.values==1,0], pca[y.values==1,1], alpha=0.5, label='Poisonous', s=2)
plt.legend()
plt.title('Mushroom Data Set\nFirst Two Principal Components')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.gca().set_aspect('equal')
def plot_mushroom_boundary(X, y, fitted_model):
plt.figure(figsize=(9.8,5), dpi=100)
for i, plot_type in enumerate(['Decision Boundary', 'Decision Probabilities']):
plt.subplot(1,2,i+1)
mesh_step_size = 0.01 # step size in the mesh
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, mesh_step_size), np.arange(y_min, y_max, mesh_step_size))
if i == 0:
Z = fitted_model.predict(np.c_[xx.ravel(), yy.ravel()])
else:
try:
Z = fitted_model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:,1]
except:
plt.text(0.4, 0.5, 'Probabilities Unavailable', horizontalalignment='center',
verticalalignment='center', transform = plt.gca().transAxes, fontsize=12)
plt.axis('off')
break
Z = Z.reshape(xx.shape)
plt.scatter(X[y.values==0,0], X[y.values==0,1], alpha=0.4, label='Edible', s=5)
plt.scatter(X[y.values==1,0], X[y.values==1,1], alpha=0.4, label='Posionous', s=5)
plt.imshow(Z, interpolation='nearest', cmap='RdYlBu_r', alpha=0.15,
extent=(x_min, x_max, y_min, y_max), origin='lower')
plt.title(plot_type + '\n' +
str(fitted_model).split('(')[0]+ ' Test Accuracy: ' + str(np.round(fitted_model.score(X, y), 5)))
plt.gca().set_aspect('equal');
plt.tight_layout()
plt.subplots_adjust(top=0.9, bottom=0.08, wspace=0.02)
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=20)
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(max_depth=3)
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.svm import SVC
model = SVC(kernel='linear')
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.svm import SVC
model = SVC(kernel='rbf', C=1)
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.svm import SVC
model = SVC(kernel='rbf', C=10)
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
from sklearn.neural_network import MLPClassifier
model = MLPClassifier()
model.fit(X_train,y_train)
plot_mushroom_boundary(X_test, y_test, model)
###Output
_____no_output_____
|
tutorials/notebook/cx_site_chart_examples/tagcloud_1.ipynb
|
###Markdown
Example: CanvasXpress tagcloud Chart No. 1This example page demonstrates how to, using the Python package, create a chart that matches the CanvasXpress online example located at:https://www.canvasxpress.org/examples/tagcloud-1.htmlThis example is generated using the reproducible JSON obtained from the above page and the `canvasxpress.util.generator.generate_canvasxpress_code_from_json_file()` function.Everything required for the chart to render is included in the code below. Simply run the code block.
###Code
from canvasxpress.canvas import CanvasXpress
from canvasxpress.js.collection import CXEvents
from canvasxpress.render.jupyter import CXNoteBook
cx = CanvasXpress(
render_to="tagcloud1",
data={
"z": {
"Description": [
"Miles per gallon, a measure of gas mileage",
"Weight of vehicle",
"Drive ratio of the automobile",
"Horsepower",
"Displacement of the car (in cubic inches)",
"Number of cylinders"
]
},
"x": {
"Country": [
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"Japan",
"Japan",
"U.S.",
"Germany",
"Sweden",
"Sweden",
"France",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"Japan",
"Japan",
"U.S.",
"Germany",
"Japan",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"U.S.",
"Japan",
"Italy",
"Germany",
"Japan",
"Germany",
"Germany"
]
},
"y": {
"smps": [
"Buick Estate Wagon",
"Ford Country Squire Wagon",
"Chevy Malibu Wagon",
"Chrysler LeBaron Wagon",
"Chevette",
"Toyota Corona",
"Datsun 510",
"Dodge Omni",
"Audi 5000",
"Volvo 240 GL",
"Saab 99 GLE",
"Peugeot 694 SL",
"Buick Century Special",
"Mercury Zephyr",
"Dodge Aspen",
"AMC Concord D/L",
"Chevy Caprice Classic",
"Ford LTD",
"Mercury Grand Marquis",
"Dodge St Regis",
"Ford Mustang 4",
"Ford Mustang Ghia",
"Mazda GLC",
"Dodge Colt",
"AMC Spirit",
"VW Scirocco",
"Honda Accord LX",
"Buick Skylark",
"Chevy Citation",
"Olds Omega",
"Pontiac Phoenix",
"Plymouth Horizon",
"Datsun 210",
"Fiat Strada",
"VW Dasher",
"Datsun 810",
"BMW 320i",
"VW Rabbit"
],
"vars": [
"MPG",
"Weight",
"Drive_Ratio",
"Horsepower",
"Displacement",
"Cylinders"
],
"data": [
[
16.9,
15.5,
19.2,
18.5,
30,
27.5,
27.2,
30.9,
20.3,
17,
21.6,
16.2,
20.6,
20.8,
18.6,
18.1,
17,
17.6,
16.5,
18.2,
26.5,
21.9,
34.1,
35.1,
27.4,
31.5,
29.5,
28.4,
28.8,
26.8,
33.5,
34.2,
31.8,
37.3,
30.5,
22,
21.5,
31.9
],
[
4.36,
4.054,
3.605,
3.94,
2.155,
2.56,
2.3,
2.23,
2.83,
3.14,
2.795,
3.41,
3.38,
3.07,
3.62,
3.41,
3.84,
3.725,
3.955,
3.83,
2.585,
2.91,
1.975,
1.915,
2.67,
1.99,
2.135,
2.67,
2.595,
2.7,
2.556,
2.2,
2.02,
2.13,
2.19,
2.815,
2.6,
1.925
],
[
2.73,
2.26,
2.56,
2.45,
3.7,
3.05,
3.54,
3.37,
3.9,
3.5,
3.77,
3.58,
2.73,
3.08,
2.71,
2.73,
2.41,
2.26,
2.26,
2.45,
3.08,
3.08,
3.73,
2.97,
3.08,
3.78,
3.05,
2.53,
2.69,
2.84,
2.69,
3.37,
3.7,
3.1,
3.7,
3.7,
3.64,
3.78
],
[
155,
142,
125,
150,
68,
95,
97,
75,
103,
125,
115,
133,
105,
85,
110,
120,
130,
129,
138,
135,
88,
109,
65,
80,
80,
71,
68,
90,
115,
115,
90,
70,
65,
69,
78,
97,
110,
71
],
[
350,
351,
267,
360,
98,
134,
119,
105,
131,
163,
121,
163,
231,
200,
225,
258,
305,
302,
351,
318,
140,
171,
86,
98,
121,
89,
98,
151,
173,
173,
151,
105,
85,
91,
97,
146,
121,
89
],
[
8,
8,
8,
8,
4,
4,
4,
4,
5,
6,
4,
6,
6,
6,
6,
6,
8,
8,
8,
8,
4,
6,
4,
4,
4,
4,
4,
4,
6,
6,
4,
4,
4,
4,
4,
6,
4,
4
]
]
},
"m": {
"Name": "Cars",
"Description": "Measurements on 38 1978-79 model automobiles. The gas mileage in miles per gallon as measured by Consumers Union on a test track. Other values as reported by automobile manufacturer.",
"Reference": "Henderson, H. V. and Velleman, P. F. (1981), Building Regression Models Interactively. Biometrics, 37, 391-411. Data originally collected from Consumer Reports."
}
},
config={
"colorBy": "Country",
"graphType": "TagCloud",
"showTransition": False
},
width=613,
height=613,
events=CXEvents(),
after_render=[],
other_init_params={
"version": 35,
"events": False,
"info": False,
"afterRenderInit": False,
"noValidate": True
}
)
display = CXNoteBook(cx)
display.render(output_file="tagcloud_1.html")
###Output
_____no_output_____
|
002_Numpy.ipynb
|
###Markdown
Numpy
###Code
# Numpy Library
import numpy as np
###Output
_____no_output_____
###Markdown
Import Finance Data (Historical Prices)
###Code
import warnings
warnings.filterwarnings("ignore")
# fix_yahoo_finance is used to fetch data
import fix_yahoo_finance as yf
yf.pdr_override()
# input
symbol = 'AMD'
start = '2014-01-01'
end = '2018-08-27'
# Read data
dataset = yf.download(symbol,start,end)
# View Columns
dataset.head()
# Convert dataset to numpy
# Convert Open dataframe to array
Open_array = np.array(dataset['Open'])
Open_array
print("First element:", Open_array [0])
print("Second element:", Open_array [1])
print("Second last element:", Open_array[-1])
print(Open_array[2:5]) # 3rd to 5th
print(Open_array[:-5]) # beginning to 4th
print(Open_array[5:]) # 6th to end
print(Open_array[:]) # beginning to end
volume = np.array(dataset['Volume'])
# changing first element
volume[0] = 0
print(volume)
# changing 3rd to 5th element
volume[2:5] = np.array([4, 6, 8])
print(volume)
# Add Elements
add_numbers = np.array([1, 2, 3])
np.concatenate((volume, add_numbers))
np.append(volume, add_numbers, axis=0)
# Remove elements
print(volume)
np.delete(volume, 1) # delete the 2nd element
volume = volume.tolist() # Convert tolist() to use remove
volume
volume.remove(0)
print(volume)
print(volume.pop(2)) # Output: 12
print(volume)
###Output
6
[22887200, 4, 8, 30667600, 20840800, 22856100, 42434800, 66613100, 46975600, 45842700, 58702900, 86329500, 29844700, 48095800, 31332300, 27962600, 21765000, 17111700, 13602100, 22280200, 22681000, 14858900, 16072900, 23119700, 21241100, 34198100, 18321300, 13368600, 12387900, 11956700, 14175500, 13276100, 13606800, 10717900, 9173500, 13211700, 18218000, 14643200, 19555800, 10516100, 10740200, 10713000, 55435800, 42135800, 34951400, 14700500, 19803000, 18161500, 20004100, 15273700, 28516900, 23600600, 23871200, 20669500, 14517000, 14799700, 24532000, 13189200, 15386000, 18778800, 14839500, 16802300, 23427000, 24874600, 17339100, 11270300, 21364300, 34428800, 22735100, 21754300, 18173300, 32048100, 102651500, 52806800, 29136300, 27532800, 37810200, 31737100, 14582900, 18419200, 37807300, 14479700, 9015400, 17929300, 22374700, 14550200, 15982900, 14785500, 11224000, 10349600, 18000900, 17166600, 18171000, 15647500, 13369500, 11903100, 9831100, 6922800, 12293800, 8876700, 10030600, 10859500, 10858800, 13286000, 13723800, 8466000, 7597200, 28322100, 20596200, 26709500, 17734600, 26192800, 19445000, 14702400, 10880500, 54721600, 49634100, 20402400, 13844700, 21640500, 16034600, 25850200, 29412600, 20486500, 22521700, 21165500, 41685800, 18462200, 39245000, 22425600, 73046000, 156113700, 61848100, 51309800, 137577700, 34219100, 34004800, 31748200, 27967600, 31793700, 31443400, 36157400, 42981200, 112162900, 33710000, 21493200, 40330600, 16271200, 32712300, 27166900, 29560500, 27369900, 30396800, 26148100, 33349200, 45381300, 23222100, 11986600, 11939800, 8364700, 8998200, 9183900, 7304400, 10331400, 7347200, 12603300, 9600600, 12791400, 6630200, 8396200, 8964800, 13276800, 8086800, 14123900, 18257000, 40156400, 24894600, 16141400, 23030000, 14201400, 16282500, 11792600, 17556500, 12976300, 26857600, 55952200, 33645900, 27904500, 16797000, 17864800, 17720600, 28000000, 69528900, 41062500, 38269400, 39964200, 36924600, 38795400, 75956600, 28711000, 24033800, 23034800, 23731000, 11945800, 13307500, 22878300, 15600900, 13026100, 14704800, 11733600, 12524300, 9635100, 8932900, 7293800, 12593100, 8113500, 15875400, 10915400, 12373000, 12593800, 14967800, 10323300, 15043900, 11311600, 12293900, 11073600, 10553500, 5665000, 16025100, 12438800, 18256500, 14513400, 9479300, 25402100, 22914800, 17690100, 10151600, 21211600, 19636400, 17051600, 12521300, 12423900, 14701500, 15044900, 8274400, 4624000, 4029600, 8527000, 7783700, 11177900, 0, 8878200, 13912500, 12377600, 11136600, 8907600, 9979600, 17907400, 9989900, 17744000, 30192400, 56389300, 46530800, 36169600, 11100700, 36571300, 51805800, 24786200, 17789200, 12908200, 25688700, 22585300, 34829300, 73355600, 38110700, 24133800, 13995100, 11741100, 12975000, 9627600, 8678100, 7273900, 6573600, 10666700, 6323500, 10899400, 6151300, 8680900, 7150200, 15638100, 8644000, 12112800, 11472300, 16785200, 12405900, 10263800, 11772800, 13847200, 8098100, 6132900, 7739900, 11372000, 8819400, 10764800, 7403800, 8724500, 26985300, 28286300, 16810200, 8557500, 7025000, 11196400, 7047600, 8178500, 5738100, 4349000, 7127600, 6184800, 8391500, 13338800, 15281400, 28617300, 53185300, 29126000, 31279400, 27634900, 15130400, 15001200, 13486900, 11448700, 11870200, 11465300, 11662800, 9670100, 12371600, 18492100, 15015600, 9758800, 10046900, 10017500, 7575900, 8865100, 8054800, 4671500, 9588400, 6947700, 7127700, 12845400, 10007800, 17511000, 12354600, 7726200, 6803700, 7101100, 8062300, 11575800, 7349700, 6207600, 12282700, 8161200, 7671000, 4557600, 8627800, 9795000, 27497900, 25400200, 25551700, 19410100, 17919600, 17516700, 18360200, 97054200, 22971500, 19381300, 19375000, 31185900, 20349400, 46418700, 15302900, 23378200, 17520800, 9080900, 15812300, 13517800, 20653300, 28127100, 12142400, 15034500, 16043400, 10641900, 16478400, 11916500, 14614600, 25582200, 15837400, 7733700, 26218200, 14328400, 13236000, 9475000, 7680800, 29926200, 7453700, 8521200, 7839700, 6182100, 9062400, 9751900, 7441200, 13745700, 12529500, 17217400, 12097700, 10715300, 11839300, 10924600, 6503500, 8470700, 6306100, 7154200, 6725300, 6009500, 12547100, 4290400, 31010300, 16458500, 6519400, 4928300, 5831600, 11713900, 5377800, 9975200, 9649200, 11247700, 5644600, 5693100, 7005300, 5708000, 5531700, 7146100, 7595600, 8558400, 7859200, 9198700, 8629100, 7686600, 6698400, 10184300, 27327100, 21544900, 10670800, 5542900, 14944100, 8208400, 9564200, 6313500, 5755600, 6950600, 4474400, 4897100, 5858700, 8705800, 8214600, 4302200, 8997100, 6231200, 6162200, 3532100, 3576800, 5920200, 4149700, 5825100, 9384700, 4704300, 10727100, 4863200, 15859700, 6914800, 2606600, 9924400, 5646400, 7501700, 7059900, 4572600, 8479600, 9055500, 8710000, 13066300, 11890000, 7625700, 7423900, 19543600, 11374100, 17988100, 6876600, 24538700, 30365300, 11900900, 15926600, 15300900, 10046600, 11086100, 32516800, 12972300, 23759400, 22203500, 31822400, 19623600, 17986100, 12749700, 15666600, 21199300, 18978900, 29243600, 26387900, 16245500, 13080900, 11092900, 10833200, 7118400, 11998100, 8816100, 11224100, 9978600, 8278600, 7914400, 11589000, 14626600, 9466100, 7858300, 9957300, 11853400, 13770200, 10823400, 7784100, 9895500, 6710600, 6906200, 5579800, 7911500, 11400300, 9011200, 10845700, 22065300, 15449000, 8754300, 10026900, 13082400, 9603500, 21382400, 33848000, 21573600, 13015700, 29000800, 26330500, 13464900, 10315800, 10167100, 10040200, 7683700, 13566000, 14945900, 9071500, 8257700, 5591100, 9640200, 12473400, 13479200, 8489000, 9045100, 16110100, 8048000, 8935400, 7487500, 8923100, 11719900, 7926100, 13957200, 143265300, 80607900, 36336900, 24186800, 20230000, 17717800, 16972800, 13784800, 8688500, 21529600, 11839300, 16299400, 9411300, 7540300, 9255800, 16470100, 14703800, 20066100, 19506900, 17696900, 13799600, 35434300, 34283900, 24703600, 22611900, 34429600, 25379200, 29696400, 35304700, 17561800, 21329600, 20676200, 16074300, 16219100, 15106500, 13540900, 16757400, 11575300, 34182700, 64894100, 43541300, 35864600, 47943300, 29159200, 36735200, 31025300, 29221400, 33118300, 26124800, 18255900, 16332500, 19392900, 15756700, 28140700, 21027900, 20832500, 14032500, 20050100, 14219300, 38619400, 23439600, 20102400, 40242000, 101838300, 118328600, 81230600, 38514300, 27515600, 22580500, 26729000, 40816400, 23807800, 22393200, 20164000, 21462200, 16772400, 29070700, 13099000, 25466400, 28339400, 26768800, 13791300, 30783300, 75129300, 41519200, 27531100, 22943900, 16451300, 31387900, 16891800, 16088100, 18808800, 22284600, 18538400, 24994600, 57721900, 90693700, 170828000, 78014400, 50819500, 64251100, 52669500, 47829400, 37812400, 28990900, 33450000, 35848200, 61022400, 29875800, 30035900, 27878300, 30746100, 47453100, 30456700, 25770000, 31235600, 27059700, 33059000, 13764700, 32510800, 33592700, 30401700, 66934400, 24261500, 25094200, 29420200, 64607500, 64243500, 52998400, 78862000, 47619300, 37804200, 77261300, 42345900, 39906900, 33852200, 33673600, 32215700, 36999200, 37601100, 38479500, 71749500, 39492200, 29566600, 28909400, 77955700, 124235500, 62336200, 65595900, 71312800, 34583200, 14214100, 25907800, 54831400, 36511900, 56682400, 42398900, 31410100, 92242900, 54897300, 104613000, 60600800, 63342900, 46967800, 46968600, 48871300, 76990000, 46085800, 59314200, 44814100, 36450800, 32216900, 44336500, 71254500, 50147700, 44095400, 55182000, 40781200, 38855200, 34453500, 37128000, 29201600, 39377000, 75244100, 38377500, 70275900, 51797600, 46151300, 27982100, 27905700, 43991200, 61778100, 35866600, 32719200, 37725000, 53704900, 165939300, 116324500, 60036700, 140474100, 158683800, 75942900, 73339900, 54579300, 57413100, 40404300, 33722300, 52502500, 40888000, 66357100, 71505000, 80317600, 46288600, 95422900, 141783000, 73450400, 104330900, 163395900, 117192600, 76666300, 71294700, 45244200, 65142200, 73078100, 52554500, 55179600, 44494800, 224892300, 91565600, 72552700, 61239500, 44549900, 50099500, 42686800, 37420200, 37863500, 44132800, 84566200, 48423700, 58413000, 58816700, 139500100, 70441000, 47178000, 59916600, 37385400, 53442600, 38188200, 37172000, 36491100, 41976100, 25689600, 36120300, 35881000, 36644500, 31327600, 50144600, 68036300, 268336500, 140899400, 77031400, 51759000, 35101100, 51017300, 65995900, 72946500, 56072600, 52565000, 164186900, 160109500, 86900100, 50319700, 78696400, 49799600, 42903900, 33584300, 31907600, 35339000, 42929000, 48002000, 43056200, 66207300, 114998600, 151005900, 88827300, 167454400, 125781800, 87302300, 51909400, 61666000, 59779500, 61803600, 118001500, 188796100, 149594200, 200777300, 101012500, 89319700, 85266900, 87634400, 59267400, 39929100, 99450200, 88927800, 88392100, 78320200, 71102300, 78508400, 111656900, 82084600, 71690800, 78366500, 51957800, 47707500, 51045700, 71014900, 98047400, 236083000, 130303700, 66763800, 69108700, 49149900, 67502200, 52557400, 64254000, 57486800, 47338000, 58861500, 83113400, 63558800, 64236500, 57990300, 64639400, 47371000, 37521700, 58888500, 39033200, 44345400, 37269700, 29732000, 35969600, 33618100, 43933000, 51822100, 53158600, 51445500, 34182400, 35816900, 60886200, 43346100, 54413100, 37210700, 37220200, 50337400, 83517400, 65455200, 102682400, 166821900, 50547000, 84172200, 68302000, 59947200, 35812300, 33926900, 34461100, 85174000, 42303200, 34758600, 28258700, 54032500, 43304000, 38746600, 69874100, 37515800, 34136800, 28995600, 39020300, 33795700, 32538900, 49838000, 84891600, 166762100, 87625400, 115650400, 137785100, 78600000, 66875500, 47942500, 44264300, 96349800, 67900200, 59065000, 76821200, 50209900, 54068300, 37245000, 33524700, 31800400, 56775600, 35960200, 31881700, 23816500, 11035800, 41798300, 65325700, 63333800, 43205000, 42128800, 97328300, 67304100, 38952200, 32665600, 34897000, 29956400, 36211000, 41494800, 29006800, 45462300, 63797700, 43852900, 31420300, 21884300, 50744500, 20437900, 22921800, 18609400, 26678900, 44146300, 154066700, 109503000, 63808900, 63346000, 62560900, 52561200, 38354900, 47149300, 42686600, 38833900, 62086200, 46800700, 34758600, 46417200, 41956400, 42966600, 44239000, 66645400, 91236400, 140977800, 67543300, 79432600, 116568900, 87123200, 55758400, 56471800, 85458200, 63160900, 33661400, 51756800, 59593800, 47332300, 47096500, 40195800, 37886300, 33317600, 42265200, 55975300, 43387500, 63207400, 58123500, 43734800, 46751200, 127603200, 76011200, 89674400, 83748700, 174302600, 80540800, 66373900, 37591000, 53308600, 65116900, 44691700, 59944200, 54844500, 75878500, 68551300, 64832100, 48681400, 64824600, 54891600, 67356900, 65758800, 51087100, 38382600, 42849200, 29169300, 47784400, 38935700, 28875100, 45360300, 42449600, 57841600, 39011900, 42971300, 44992200, 90578000, 145284100, 74347800, 50608800, 43441600, 29267300, 33310600, 47884900, 54001700, 35218400, 49605700, 49744500, 43863700, 50263800, 44183200, 73364000, 38692500, 54063400, 49714200, 43267000, 44388300, 47785700, 43850100, 39578500, 58186400, 46797700, 71677900, 74546000, 56122700, 97089000, 99860300, 81930500, 80737600, 67002600, 90227300, 113048600, 77612200, 104317400, 92542900, 76280600, 95638400, 59257100, 94418400, 54213500, 56014300, 48716800, 41527800, 43398800, 32094000, 40703300, 65101700, 58525500, 37093000, 42544100, 44188100, 40614100, 65275300, 42313500, 40881500, 41267800, 42879800, 44940800, 58201500, 82604900, 192661100, 161903800, 160823400, 118403400, 75495200, 52867100, 53232100, 83579700, 72822600, 52081400, 46536400, 65821100, 81262200, 89195500, 86355700, 69733700, 60616600, 62983200, 55629000, 62002700, 113444100, 164328200, 325058400]
###Markdown
Numpy
###Code
# Numpy Library
import numpy as np
###Output
_____no_output_____
###Markdown
Import Finance Data (Historical Prices)
###Code
import warnings
warnings.filterwarnings("ignore")
# yfinance is used to fetch data
import yfinance as yf
yf.pdr_override()
# input
symbol = 'AMD'
start = '2014-01-01'
end = '2018-08-27'
# Read data
dataset = yf.download(symbol,start,end)
# View Columns
dataset.head()
# Convert dataset to numpy
# Convert Open dataframe to array
Open_array = np.array(dataset['Open'])
Open_array
print("First element:", Open_array [0])
print("Second element:", Open_array [1])
print("Second last element:", Open_array[-1])
print(Open_array[2:5]) # 3rd to 5th
print(Open_array[:-5]) # beginning to 4th
print(Open_array[5:]) # 6th to end
print(Open_array[:]) # beginning to end
volume = np.array(dataset['Volume'])
# changing first element
volume[0] = 0
print(volume)
# changing 3rd to 5th element
volume[2:5] = np.array([4, 6, 8])
print(volume)
# Add Elements
add_numbers = np.array([1, 2, 3])
np.concatenate((volume, add_numbers))
np.append(volume, add_numbers, axis=0)
# Remove elements
print(volume)
np.delete(volume, 1) # delete the 2nd element
volume = volume.tolist() # Convert tolist() to use remove
volume
volume.remove(0)
print(volume)
print(volume.pop(2)) # Output: 12
print(volume)
###Output
6
[22887200, 4, 8, 30667600, 20840800, 22856100, 42434800, 66613100, 46975600, 45842700, 58702900, 86329500, 29844700, 48095800, 31332300, 27962600, 21765000, 17111700, 13602100, 22280200, 22681000, 14858900, 16072900, 23119700, 21241100, 34198100, 18321300, 13368600, 12387900, 11956700, 14175500, 13276100, 13606800, 10717900, 9173500, 13211700, 18218000, 14643200, 19555800, 10516100, 10740200, 10713000, 55435800, 42135800, 34951400, 14700500, 19803000, 18161500, 20004100, 15273700, 28516900, 23600600, 23871200, 20669500, 14517000, 14799700, 24532000, 13189200, 15386000, 18778800, 14839500, 16802300, 23427000, 24874600, 17339100, 11270300, 21364300, 34428800, 22735100, 21754300, 18173300, 32048100, 102651500, 52806800, 29136300, 27532800, 37810200, 31737100, 14582900, 18419200, 37807300, 14479700, 9015400, 17929300, 22374700, 14550200, 15982900, 14785500, 11224000, 10349600, 18000900, 17166600, 18171000, 15647500, 13369500, 11903100, 9831100, 6922800, 12293800, 8876700, 10030600, 10859500, 10858800, 13286000, 13723800, 8466000, 7597200, 28322100, 20596200, 26709500, 17734600, 26192800, 19445000, 14702400, 10880500, 54721600, 49634100, 20402400, 13844700, 21640500, 16034600, 25850200, 29412600, 20486500, 22521700, 21165500, 41685800, 18462200, 39245000, 22425600, 73046000, 156113700, 61848100, 51309800, 137577700, 34219100, 34004800, 31748200, 27967600, 31793700, 31443400, 36157400, 42981200, 112162900, 33710000, 21493200, 40330600, 16271200, 32712300, 27166900, 29560500, 27369900, 30396800, 26148100, 33349200, 45381300, 23222100, 11986600, 11939800, 8364700, 8998200, 9183900, 7304400, 10331400, 7347200, 12603300, 9600600, 12791400, 6630200, 8396200, 8964800, 13276800, 8086800, 14123900, 18257000, 40156400, 24894600, 16141400, 23030000, 14201400, 16282500, 11792600, 17556500, 12976300, 26857600, 55952200, 33645900, 27904500, 16797000, 17864800, 17720600, 28000000, 69528900, 41062500, 38269400, 39964200, 36924600, 38795400, 75956600, 28711000, 24033800, 23034800, 23731000, 11945800, 13307500, 22878300, 15600900, 13026100, 14704800, 11733600, 12524300, 9635100, 8932900, 7293800, 12593100, 8113500, 15875400, 10915400, 12373000, 12593800, 14967800, 10323300, 15043900, 11311600, 12293900, 11073600, 10553500, 5665000, 16025100, 12438800, 18256500, 14513400, 9479300, 25402100, 22914800, 17690100, 10151600, 21211600, 19636400, 17051600, 12521300, 12423900, 14701500, 15044900, 8274400, 4624000, 4029600, 8527000, 7783700, 11177900, 0, 8878200, 13912500, 12377600, 11136600, 8907600, 9979600, 17907400, 9989900, 17744000, 30192400, 56713300, 46530800, 36169600, 11107200, 36571300, 51805800, 24786200, 17790200, 12908200, 25688700, 22592300, 34829300, 73355600, 38300000, 24133800, 13995100, 11741100, 12975000, 9627600, 8678100, 7286100, 6573600, 10666700, 6323500, 10916300, 6151300, 8680900, 7150200, 15638100, 8644000, 12122100, 11472300, 16785200, 12405900, 10312400, 11772800, 13847200, 8098100, 6132900, 7742200, 11385200, 8819400, 10764800, 7450200, 8724500, 26985300, 28286300, 16844100, 8557500, 7025000, 11240500, 7047600, 8178500, 5738100, 4349000, 7127600, 6184800, 8391500, 13364100, 15281400, 28617300, 53185300, 29164300, 31279400, 27634900, 15130400, 15001200, 13486900, 11448700, 11870200, 11465300, 11662800, 9670100, 12371600, 18492100, 15015600, 9758800, 10046900, 10017500, 7575900, 8865100, 8054800, 4732800, 9588400, 6947700, 7127700, 12845400, 10007800, 17511000, 12354600, 7750500, 6803700, 7106000, 8062300, 11575800, 7349700, 6212900, 12282700, 8161200, 7671000, 4557600, 8627800, 9795000, 27497900, 25400200, 25551700, 19410100, 17919600, 17516700, 18360200, 97054200, 22971500, 19381300, 19375000, 31185900, 20349400, 46418700, 15302900, 23378200, 17520800, 9080900, 15812300, 13517800, 20653300, 28127100, 12142400, 15034500, 16043400, 10641900, 16478400, 11916500, 14614600, 25582200, 15837400, 7733700, 26218200, 14328400, 13236000, 9475000, 7680800, 29926200, 7479200, 8521200, 7839700, 6183400, 9062400, 9751900, 7441200, 13745700, 12529500, 17217400, 12097700, 10715300, 11839300, 10924600, 6516000, 8470700, 6306100, 7154200, 6725300, 6009500, 12612300, 4290400, 31010300, 16458500, 6524400, 4928300, 5831600, 11814000, 5377800, 9975200, 9649200, 11247700, 5644600, 5693100, 7005300, 5739500, 5531700, 7146100, 7595600, 8558400, 7859200, 9198700, 8629100, 7686600, 6698400, 10184300, 27327100, 21544900, 10670800, 5584200, 14944100, 8208400, 9564200, 6313500, 5755600, 6950600, 4500400, 4897100, 5858700, 8705800, 8205300, 4302200, 8997100, 6231200, 6162200, 3532100, 3576800, 5920200, 4149700, 5825100, 9384700, 4704300, 10727100, 4863200, 15859700, 6914800, 2606600, 9924400, 5646400, 7501700, 7059900, 4572600, 8479600, 9055500, 8710000, 13069400, 11890000, 7625700, 7423900, 19543600, 11374100, 17988100, 6876600, 24893200, 30365300, 11890900, 16050500, 15300900, 10046600, 11086100, 32516800, 12972300, 23759400, 22203500, 31822400, 19629300, 17986100, 12749700, 15666600, 21199300, 18978900, 29243600, 26387900, 16245500, 13080900, 11097400, 10833200, 7118400, 11998100, 8816100, 11224100, 9978600, 8284800, 7914400, 11589000, 14991500, 9466100, 7858300, 9957300, 11853400, 13770200, 10823400, 7784100, 9895500, 6710600, 6906200, 5614400, 7911500, 11400300, 9011200, 10845700, 22092400, 15449000, 8754300, 10026900, 13082400, 9603500, 21382400, 33848000, 21573600, 13015700, 29000800, 26330500, 13464900, 10315800, 10167100, 10040200, 7683700, 13616200, 14945900, 9071500, 8257700, 5591100, 9640200, 12534600, 13479200, 8489000, 9045100, 16131900, 8048000, 8985300, 7487500, 8938800, 11719900, 7926100, 13957200, 143265300, 80607900, 36336900, 24186800, 20230000, 17717800, 16972800, 13784800, 8688500, 21529600, 11839300, 16299400, 9415100, 7540300, 9255800, 16470100, 14703800, 20066100, 19487500, 17696900, 13799600, 35467000, 34283900, 24703600, 22625700, 34429600, 25379200, 29696400, 35335000, 17561800, 21329600, 20676200, 16074300, 16219100, 15106500, 13500700, 16757400, 11575300, 34182700, 64894100, 43541300, 35864600, 47943300, 29159200, 36735200, 31025300, 29221400, 33118300, 26124800, 18255900, 16332500, 19392900, 15813800, 28140700, 21027900, 20832500, 14032500, 20050100, 14219300, 38619400, 23439600, 20102400, 40242000, 101838300, 118328600, 81230600, 38567300, 27515600, 22580500, 26729000, 40816400, 23807800, 22411000, 20164000, 21462200, 16772400, 29070700, 13240300, 25466400, 28339400, 26768800, 13791300, 30783300, 75129300, 41519200, 27531100, 22943900, 16451300, 31387900, 16916300, 16088100, 18808800, 22284600, 18538400, 24994600, 57721900, 90814700, 170828000, 78014400, 50819500, 64251100, 52669500, 47829400, 37837200, 28990900, 33450000, 35848200, 61022400, 29875800, 30035900, 27878300, 30746100, 47453100, 30456700, 25770000, 31235600, 27059700, 33059000, 13800500, 32510800, 33592700, 30401700, 66934400, 24261500, 25314800, 29420200, 64607500, 64243500, 52998400, 78862000, 47619300, 37804200, 77261300, 42345900, 39906900, 33852200, 33673600, 32215700, 36999200, 37728500, 38479500, 71749500, 39492200, 29596400, 28909400, 78083200, 124235500, 62336200, 65595900, 71312800, 34646000, 14214100, 25907800, 54831400, 36511900, 56682400, 42398900, 31410100, 92242900, 54897300, 104613000, 60600800, 63342900, 46967800, 46968600, 48871300, 77777700, 46085800, 59314200, 44814100, 36450800, 32288200, 44336500, 71254500, 50234300, 44095400, 55182000, 40781200, 38855200, 34453500, 37304800, 29201600, 39377000, 75244100, 38377500, 70491800, 51797600, 46151300, 27982100, 27905700, 43991200, 61778100, 35866600, 32719200, 37725000, 53704900, 165939300, 116324500, 60036700, 140474100, 158683800, 75942900, 73339900, 54579300, 57413100, 40479100, 33722300, 52502500, 40888000, 66357100, 71505000, 80317600, 46288600, 95422900, 141783000, 73450400, 104330900, 163395900, 117192600, 76666300, 71294700, 45244200, 65142200, 73078100, 52554500, 55179600, 44494800, 224892300, 91565600, 72552700, 61239500, 44549900, 50099500, 42686800, 37420200, 37863500, 44132800, 84566200, 48423700, 58413000, 58816700, 139500100, 70441000, 47178000, 59916600, 37385400, 53442600, 38188200, 37172000, 36491100, 41976100, 25689600, 36120300, 35881000, 36644500, 31327600, 50376000, 68036300, 268336500, 140899400, 77031400, 51759000, 35101100, 51017300, 65995900, 72946500, 56072600, 52565000, 164186900, 160109500, 86900100, 50319700, 78696400, 49799600, 42903900, 33584300, 31907600, 35339000, 42929000, 48002000, 43056200, 66207300, 114998600, 151005900, 89515100, 167454400, 125781800, 87302300, 51909400, 61666000, 59779500, 61803600, 118001500, 188796100, 149594200, 200777300, 101012500, 89319700, 85266900, 87634400, 59267400, 39929100, 99450200, 88927800, 88392100, 78320200, 71102300, 78508400, 111656900, 82084600, 71690800, 78366500, 51957800, 47707500, 51045700, 71014900, 98047400, 236083000, 130303700, 66763800, 69108700, 49149900, 67502200, 52557400, 64254000, 57486800, 47338000, 58861500, 83113400, 63558800, 64426100, 57990300, 64639400, 47371000, 37521700, 58888500, 39033200, 44345400, 37269700, 29732000, 35969600, 33618100, 43933000, 51822100, 53158600, 51445500, 34182400, 35816900, 60886200, 43346100, 54413100, 37210700, 37220200, 50337400, 83517400, 65455200, 102682400, 166821900, 50547000, 84172200, 68302000, 59947200, 35812300, 33926900, 34461100, 85174000, 42303200, 34758600, 28258700, 54032500, 43304000, 38746600, 69874100, 37515800, 34136800, 28995600, 39020300, 33795700, 32538900, 49838000, 84891600, 166762100, 87625400, 115650400, 137785100, 78600000, 66875500, 47942500, 44264300, 96349800, 67900200, 59065000, 76821200, 50209900, 54068300, 37245000, 33524700, 31800400, 56775600, 35960200, 31881700, 23816500, 11035800, 41798300, 65325700, 63333800, 43205000, 42128800, 97328300, 67304100, 38952200, 32665600, 34897000, 29956400, 36211000, 41494800, 29006800, 45462300, 63797700, 43852900, 31420300, 21884300, 50744500, 20437900, 22921800, 18609400, 26678900, 44146300, 154066700, 109503000, 63808900, 63346000, 62560900, 52561200, 38354900, 47149300, 42686600, 39020800, 62086200, 46800700, 34758600, 46417200, 41956400, 42966600, 44239000, 66645400, 91236400, 140977800, 67543300, 79432600, 116568900, 87123200, 55758400, 56471800, 85458200, 63160900, 33661400, 51756800, 59593800, 47332300, 47096500, 40195800, 37886300, 33317600, 42265200, 55975300, 43387500, 63207400, 58123500, 43734800, 46751200, 127603200, 76011200, 89674400, 83748700, 174302600, 80540800, 66373900, 37591000, 53308600, 65116900, 44691700, 59944200, 54844500, 75878500, 68551300, 64832100, 48681400, 64824600, 54891600, 67356900, 65758800, 51087100, 38382600, 42849200, 29169300, 47784400, 38935700, 28875100, 45360300, 42449600, 57841600, 39011900, 42971300, 44992200, 90578000, 145284100, 74347800, 50608800, 43441600, 29267300, 33310600, 47884900, 54001700, 35218400, 49605700, 49744500, 43863700, 50263800, 44183200, 73364000, 38692500, 54063400, 49714200, 43267000, 44517800, 47785700, 43850100, 39578500, 58186400, 46797700, 71677900, 74546000, 56122700, 97089000, 99860300, 81930500, 80737600, 67002600, 90227300, 113048600, 77612200, 104317400, 92542900, 76280600, 95638400, 59257100, 94418400, 54213500, 56014300, 48716800, 41527800, 43398800, 32094000, 40703300, 65101700, 58525500, 37093000, 42544100, 44188100, 40614100, 65275300, 42313500, 40881500, 41267800, 42879800, 44940800, 58201500, 82604900, 192661100, 161903800, 160823400, 118403400, 75495200, 52867100, 53232100, 83579700, 72822600, 52081400, 46653400, 65821100, 81411300, 89195500, 86355700, 69733700, 60616600, 62983200, 55629000, 62002700, 113444100, 164328200]
|
08_unit_test_helpers.ipynb
|
###Markdown
Unit Test Helpers> Useful helpers for unit tests
###Code
#export
import pickle
from types import SimpleNamespace
#export
def pickle_object(obj, file_path):
with open(file_path, 'wb') as f:
pickle.dump(obj, f)
def unpickle_object(pickle_path):
with open(pickle_path, 'rb') as f:
return pickle.load(f)
#export
workflow_test_pickles = SimpleNamespace(
workflow_run_response_pickle = r'test_pickles/workflows/run_workflow_response.pkl',
workflow_get_vfs_inputs_response_pickle_path = r'test_pickles/workflows/get_vfs_inputs_response.pkl',
workflow_job_response_pickle_path = r'test_pickles/workflows/workflow_job_response.pkl',
output_asset_response_pickle_path = r'test_pickles/workflows/output_asset_response.pkl',
workflow_download_files_response_pickle_path = r'test_pickles/workflows/download_files_response.pkl',
download_path = 'wf_out_test.csv'
)
#export
jobs_test_pickles = SimpleNamespace(
get_job_by_id = r'test_pickles/jobs/get_job_by_id_response.pkl',
get_log_by_id = r'test_pickles/jobs/get_log_by_id_response.pkl'
)
#export
files_test_pickles = SimpleNamespace(
download_file = r'test_pickles/files/download_file_response.pkl',
upload_file = r'test_pickles/files/upload_file_response.pkl',
upload_duplicate_file = r'test_pickles/files/duplicate_file_upload_response.pkl',
upload_merge_file = r'test_pickles/files/upload_file_merge_response.pkl',
get_file_versions = r'test_pickles/files/get_file_versions_response.pkl',
delete_file = r'test_pickles/files/delete_file_response.pkl',
move_file = r'test_pickles/files/move_file_response.pkl',
copy_file = r'test_pickles/files/copy_file_response.pkl',
restore_deleted = r'test_pickles/files/restore_deleted_file_response.pkl',
restore_deleted_by_path = r'test_pickles/files/restore_deleted_by_path_response.pkl'
)
###Output
_____no_output_____
|
notebooks uni/PC48 - Extra Exercises.ipynb
|
###Markdown
48 - Extra Exercises --- This chapter contains a list of extra exercises. These are meant for exam practice (even though many of them are harder than you would see on an exam), or simply for those who want to continue exercising. In general, I will not tell you which techniques you should use to solve them. Usually there are multiple approaches -- it is up to you to select the most suitable one. Answers are supplied in the next notebook.The exercises may appear in any order -- I intend to keep adding exercises to the end, so later exercises may actually be easier than earlier exercises. Exercise 48.1 For any positive integer `N`, the sum `1 + 2 + 3 + ... + N` is equal to `N*(N+1)/2`. Show this by asking the user for a number `N`, then calculating both the value of the sum, and the outcome of the formula.
###Code
# N(N+1)/2.
###Output
_____no_output_____
###Markdown
Exercise 48.2 Write a program that asks for a number between 100 and 999, with the first digit of the number being different from the last. Let's call this number `ABC`, where `A`, `B`, and `C` are the three digits. Create the number `CBA`, and subtract the lower number from the higher one. Call this number `DEF`, with `D`, `E`, and `F` being the digits. Then create `FED`. Add `DEF` to `FED`, and print the result. For instance, if you start with 321, you create 123, then subtract 123 from 321 to get 198. You reverse 198 to get 891, then add 198 to 891 to get 1089. Test your program with different numbers. What do you notice about the results?
###Code
# Number magic.
###Output
_____no_output_____
###Markdown
Exercise 48.3 Write a program that asks for an integer to use as column size (you can use a minimum of 10). Then take a text, and print that text using a no more words on each line than fit the column size, e.g., if the column size is 40, no more than 40 characters are used on each line (this includes punctuation and whitespaces). Words are not "broken off". After a newline character, you should always go to the next line. For an extra challenge, try to insert spaces in a balanced way so that the column is justified (i.e., all lines are equally long, except for those that end in a new line). Make sure that you can handle column sizes that are less than the maximum word length.In the code block below a text for testing is given.Hints: First split the text into paragraphs, then handle each paragraph separately. For lines that contain only one word, note that you cannot adjust the spacing between words. For lines with only one word that is longer than the column width, you can let the word "stick out". Make sure that you first solve the problem without justification, and then add justification later, as that makes the program quite a bit harder.
###Code
# Creating columns.
text = "And spending four days on the tarmac at Luton airport on a five-day package tour with nothing to eat but \
dried BEA-type sandwiches and you can't even get a drink of Watney's Red Barrel because you're still in England and \
the bloody bar closes every time you're thirsty and there's nowhere to sleep and the kids are crying and vomiting and \
breaking the plastic ashtrays and they keep telling you it'll only be another hour although your plane is still in \
Iceland and has to take some Swedes to Yugoslavia before it can load you up at 3 a.m. in the bloody morning and you \
sit on the tarmac till six because of \"unforeseen difficulties\", i.e. the permanent strike of Air Traffic Control \
in Paris - and nobody can go to the lavatory until you take off at 8, and when you get to Malaga airport everybody's \
swallowing \"enterovioform\" and queuing for the toilets and queuing for the armed customs officers, and queuing for \
the bloody bus that isn't there to take you to the hotel that hasn't yet been finished. And when you finally get to \
the half-built Algerian ruin called the Hotel del Sol by paying half your holiday money to a licensed bandit in a taxi \
you find there's no water in the pool, there's no water in the taps, there's no water in the bog and there's only a \
bleeding lizard in the bidet.\n\
And half the rooms are double booked and you can't sleep anyway because of the permanent twenty-four-hour drilling of \
the foundations of the hotel next door - and you're plagued by appalling apprentice chemists from Ealing pretending to \
be hippies, and middle-class stockbrokers' wives busily buying identical holiday villas in suburban development plots \
just like Esher, in case the Labour government gets in again, and fat American matrons with sloppy-buttocks and \
Hawaiian-patterned ski pants looking for any mulatto male who can keep it up long enough when they finally let it all \
flop out.\n\
And the Spanish Tourist Board promises you that the raging cholera epidemic is merely a case of mild Spanish tummy, \
like the previous outbreak of Spanish tummy in 1660 which killed half London and decimated Europe - and meanwhile the \
bloody Guardia are busy arresting sixteen-year-olds for kissing in the streets and shooting anyone under nineteen who \
doesn't like Franco.\n\
And then on the last day in the airport lounge everyone's comparing sunburns, drinking Nasty Spumante, buying cartons \
of duty free \"cigarillos\" and using up their last pesetas on horrid dolls in Spanish National costume and awful \
straw donkeys and bullfight posters with your name on \"Ordoney, El Cordobes and Brian Pules of Norwich\" and 3-D \
pictures of the Pope and Kennedy and Franco, and everybody's talking about coming again next year and you swear you \
never will although there you are tumbling bleary-eyed out of a tourist-tight antique Iberian airplane..."
###Output
_____no_output_____
###Markdown
Exercise 48.4 Write a program that asks for an integer between zero and 1000 (including zero, excluding 1000), that prints a textual representation of that integer. For instance, if the user enters 513, the output is "five hundred thirteen". Of course, you are not supposed to make one list of 1000 textual representations... otherwise the exercise becomes that you have to do this for all numbers between zero and one billion.
###Code
# Numbers to words.
###Output
_____no_output_____
###Markdown
Exercise 48.5 Write a program that asks for a number, then prints that number in a nicely formatted way according Dutch rules (which are also common in many other European countries), i.e., with periods as thousands-separators, and a comma instead of a decimal point. E.g., the number `-1234567.89` is displayed as `-1.234.567,89`.
###Code
# Mainland formatting.
###Output
_____no_output_____
###Markdown
Exercise 48.6 Write a program that asks the user for a string of characters. Then ask the user for a second string. Remove all the characters that are in the first string from the second string, then print it.
###Code
# General character removal.
###Output
_____no_output_____
###Markdown
Exercise 48.7 Ask the user for a string (which should not contain any spaces) and a sentence. From the sentence, print only those words that contain each of the characters of the string at least once. E.g., if the string is `"sii"` and the sentence is `"There is no business like show business"` then the program should print the words `is`, `business` and `business`. There is no need to remove punctuation or other characters; you can simply split the sentence on its spaces, and consider the list that gets produced a list of the words.
###Code
# Words with particular letters (1).
###Output
_____no_output_____
###Markdown
Exercise 48.8 Ask the user for a string (which should not contain any spaces) and a sentence. From the sentence, print only those words that contain at most two of the characters of the string. E.g., if the string is `"usso"` and the sentence is `"There is no business like show business"` then the program should print the words `There` (which contains none of the characters in the string), `is` (which contains the `s`, which is twice in the string), `no` (which contains an `o`, which is once in the string), and `like` (which contains none of the characters in the string). The word `show` is not printed, as it contains an `s` and an `o`, and since the `s` occurs twice in the string and the `o` once, in total it contains three of the characters in the string. The same holds for `business`, with the `u` and the `s`. There is no need to remove punctuation or other characters; you can simply split the sentence on its spaces, and consider the list that gets produced a list of the words.
###Code
# Words with particular letters (2).
###Output
_____no_output_____
###Markdown
Exercise 48.9 Write a Python program that asks for a sentence, then prints that sentence in three ways, namely: (1) reversed, (2) with each of the words in the sentence reversed, and (3) with the words reversed. There is no need to remove punctuation. For instance, if the sentence is `"Hello, world!"`, you print `"!dlrow ,olleH"`, `",olleH !dlrow"`, and `"world! Hello,"`. There is also no need to preserve multiple spaces between words; you may reduce these to a single space.
###Code
# Contorting a sentence.
###Output
_____no_output_____
###Markdown
Exercise 48.10 Write a program that produces all possible slices from a list, and stores them in a list. For instance, if the list is `[1,2,3]`, then the program produces `[ [], [1], [2], [3], [1,2], [2,3], [1,2,3] ]`. Ordering of the list does not matter.
###Code
# Slices.
###Output
_____no_output_____
###Markdown
Exercise 48.11 Write a program that produces all possible sub-dictionaries from a dictionary, and stores them in a list. For instance, if the dictionary is `{"a":1,"b":2,"c":3}`, the program produces `[ {}, {"a":1}, {"b":2}, {"c":3}, {"a":1,"b":2}, {"a":1,"c":3}, {"b":2,"c":3}, {"a":1,"b":2,"c":3} ]` (the ordering of the list does not matter). Hint: This exercise is quite hard. It looks a lot like the previous exercise, but while the previous one is certainly doable, this one might be beyond your grasp. So I won't blame you if you skip it. To solve it, you have to create all different combinations of keys. There is a function `combinations()` in the `itertools` module that can help you with it. This module is discussed in the chapter on Iterators and Generators, which falls under Object Orientation, but you do not need to know anything about object orientation to understand it. If you do not use `combinations()`, a recursive solution works best. If somebody can think of a simpler way of doing it, I would very much like to hear about it.
###Code
# Sub-dictionaries.
###Output
_____no_output_____
###Markdown
Exercise 48.12 Read the contents of a text file. If there are words in the file that are anagrams of each other, then print those. In case you do not know, an anagram of a word is another word that contains exactly the same letters. E.g., "except" and "expect" are anagrams. Duplicates of words don't count, i.e., you should only report different words. Words only contain letters, and anything that is not a letter should be considered a word boundary. Treat the words case-insensitively.Hint: First think about how you can decide if two words are anagrams of each other. Then think about how you process the file in a smart way. For instance, checking for each word in the file each other word in the file is a very slow process as the time needed to process the file is quadratically related to the length of the file. You better choose a suitable data structure for storing the words.Note: The small text files that I supplied do not contain any anagrams, but the larger ones in the `pcdata` directory contain plenty (sometimes even triple ones, like `won, own, now` or `vile, live, evil`). However, it might be wise to do your initial tests with a file that you create yourself.
###Code
# Anagrams.
###Output
_____no_output_____
###Markdown
Exercise 48.13 Imagine an infinite grid. A person starts in location (0,0) of this grid. When the person walks north, he ends up one Y-coordinate higher, i.e., from (0,0) he moves to (0,1). When the person walks east, he ends up one X-coordinate higher, i.e., from (0,0) he moves to (1,0). When the person walks south, he ends up one Y-coordinate lower, i.e., from (0,0) he moves to (0,-1). When the person walks west, he ends up one X-coordinate lower, i.e., from (0,0) he moves to (-1,0). A "drunkard's walk" entails that a person walks a certain number of moves at random, i.e., after each move he randomly chooses from north, east, south and west the next direction he will move in.Using a simulation in which you let at least 10,000 persons make a random walk of 100 moves, starting from (0,0), estimate the chance that the person ends up at (0,0) again after 100 moves, and estimate the average distance that the person ends up at measured from (0,0) after 100 moves.Hint: The distance from `(0,0)` to `(x,y)` can be calculated as `sqrt( x*x + y*y )`.
###Code
# Drunkard's walk.
###Output
_____no_output_____
###Markdown
Exercise 48.14 Write a program that determines how you can place eight queens on a chess board in such a way that none of them attacks any of the other ones.Hint: Knowing that you need exactly one queen per row and exactly one queen per column, you can express the board as simply a list of eight integers, which are the columns for the queen on the row indicated by the list index. Since all columns must be different, this list contains the integers 0 to 7 once each. This way, you can express all possible configurations of the board as all the possible permutations of the list. You then only need to check these permutations for two queens occupying the same diagonal. As soon as you find one permutation for which the queens are never on the same diagonal, you found a solution. To get all possible permutations of a list, you can use the `permutations()` function from the `itertools` module. This program can be surprisingly short.
###Code
# 8 queens.
###Output
_____no_output_____
###Markdown
Exercise 48.15 Write two functions, one that converts a temperature from Celsius to Fahrenheit, and one that does the reverse. In your main program, ask the user for a temperature as a number followed by a C or an F, then call the appropriate function to convert to the other scale, and display the answer with one decimal. The formula to derive Celsius from Fahrenheit is `C = (5/9) * (F - 32)`.
###Code
# Tempreature conversion.
###Output
_____no_output_____
###Markdown
Exercise 48.16 Pascal's triangle is a construct that starts with a single 1 on the first row, and every row underneath has one more cell, and is shifted half a cell to the left. Each cell contains the number that is the sum of the two cells above it (and if there is only one cell above it, a copy of that cell). This is best visualized; here are the first six rows:`1: 1``2: 1 1``3: 1 2 1``4: 1 3 3 1``5: 1 4 6 4 1``6: 1 5 10 10 5 1`Write a program that prints the first `ROWS` rows of Pascal's triangle (`ROWS` being an integer constant defined at the top of your program). You may simply left-align the output, and use one space between each pair of numbers.
###Code
# Pascal's triangle.
###Output
_____no_output_____
###Markdown
Exercise 48.17 Prime factorization consists of dividing an integer into the prime factors, that multiplied produce the original integer. For instance, the prime factors of 228 are 2, 2, 3, and 19, i.e., `228 = 2 * 2 * 3 * 19`. Write a program that prints all the prime factors of a number that is supplied by the user.
###Code
# Prime factorization.
###Output
_____no_output_____
###Markdown
Exercise 48.18 In the game of Darts, one single dart can obtain different scores: the numbers 1 to 20 (singles), doubles (twice each number in the range 1 to 20), triples (three times each number in the range 1 to 20), and also 25 and 50. The maximum score with three darts is 180 (three times 60). Not all scores below 180 are attainable with three darts. For example, the second-highest possible three-dart score is 177 (namely `2 * 3 * 20 + 3 * 19`). Write a program that prints all scores between 1 and 180 which are not attainable with three or fewer darts (the reason to include "fewer" is that some darts might actually not hit the dart board, so they score zero points).
###Code
# Darts.
###Output
_____no_output_____
###Markdown
Exercise 48.19 The Goldbach conjecture says that every even number greater than 2 can be written as the sum of two primes. This conjecture has not been proven, but it has been checked for values up to one billion billion. Write a program that asks for an even number greater than 2, and then prints two prime numbers of which the sum makes this number. Yourprogram should be able to handle numbers up to 10,000, but may go higher.
###Code
# Goldbach.
###Output
_____no_output_____
###Markdown
Exercise 48.20 Write a program that plays a game. It asks random questions of the form "What is the third letter following F?" or "What is the second letter before X?" The user has to respond with the correct answer; illegal inputs are not counted as wrong answers, but the program simply asks the question again until the user responds with a letter. The program should support all distances from 1 to 10, both before and following the letter. The program asks ten questions, giving feedback after each. At the end, the program gives the user’s performance. Make sure that your program does not ask for letters that do not exist (e.g., the first letter following Z).
###Code
# Letter game.
###Output
_____no_output_____
###Markdown
Exercise 48.21 Write a program that asks for a sentence, and then translates the sentence to Morse. A dictionary containing the Morse alphabet is given below. Sentences should be processed as lower case. If a character in the sentence is not found in the Morse table, then it is considered to be a space. Groups of spaces should be considered a single space. In the translation, spaces are marked with a slash (`/`), while Morse characters are always followed by a space (e.g., `"sos"` is translated as `"... --- ..."` and not as `"...---..."`). If the translation results in an empty string, then make sure to report that explicitly.
###Code
# Morse.
DAH = "-"
DIT = "."
morse = { "a": DIT+DAH, "b": DAH+DIT+DIT+DIT, "c": DAH+DIT+DAH+DIT, "d": DAH+DIT+DIT, "e": DIT, "f": DIT+DIT+DAH+DIT,
"g": DAH+DAH+DIT, "h": DIT+DIT+DIT+DIT, "i": DIT+DIT, "j": DIT+DAH+DAH+DAH, "k": DAH+DIT+DAH, "l": DIT+DAH+DIT+DIT,
"m": DAH+DAH, "n": DAH+DIT, "o": DAH+DAH+DAH, "p": DIT+DAH+DAH+DIT, "q": DAH+DAH+DIT+DAH, "r": DIT+DAH+DIT,
"s": DIT+DIT+DIT, "t": DAH, "u": DIT+DIT+DAH, "v": DIT+DIT+DIT+DAH, "w": DIT+DAH+DAH, "x": DAH+DIT+DIT+DAH,
"y": DAH+DIT+DAH+DAH, "z": DAH+DAH+DIT+DIT, "1": DIT+DAH+DAH+DAH+DAH, "2": DIT+DIT+DAH+DAH+DAH,
"3": DIT+DIT+DIT+DAH+DAH, "4": DIT+DIT+DIT+DIT+DAH, "5": DIT+DIT+DIT+DIT+DIT, "6": DAH+DIT+DIT+DIT+DIT,
"7": DAH+DAH+DIT+DIT+DIT, "8": DAH+DAH+DAH+DIT+DIT, "9": DAH+DAH+DAH+DAH+DIT, "0": DAH+DAH+DAH+DAH+DAH,
".": DIT+DAH+DIT+DAH+DIT+DAH, ",": DAH+DAH+DIT+DIT+DAH+DAH, ":": DAH+DAH+DAH+DIT+DIT+DIT,
"?": DIT+DIT+DAH+DAH+DIT+DIT, "/": DAH+DIT+DIT+DAH+DIT }
###Output
_____no_output_____
###Markdown
Exercise 48.22 Write a program that converts a string, that contains Morse code, to its translation. The Morse characters (which consist of a sequence of dots and dashes) are separated from each other by spaces. Different words in the string are separated from each other by a slash. I.e., the output of the previous exercise can be used as input for this exercise. Note that you probably need a dictionary that uses Morse code as keys; you can build such a dictionary by hand, but a better solution is to use the dictionary from the previous exercise and write some code to invert it (i.e., switch the keys and values). If the string contains something else than dots, dashes, spaces, and slashes, you may just announce that it is not a Morse string and skip the translation. If you find a code that you cannot translate, you can output a hashmark (``) for it.
###Code
# Reverse Morse.
###Output
_____no_output_____
###Markdown
Exercise 48.23 Write a program that asks for a directory name. It then opens all the files in the directory, and scans their contents. It assumes that the files are all text files. For each file that the program scans, it prints the filename, and the number of words in the file. It then prints the ten words from the file that occur the most in the file, with their frequency, in the order highest-frequency to lowest-frequency. In case you have multiple words with the same frequency, of which you can only print some before you get over 10 words, you can choose yourself which ones you print of those.
###Code
# Frequencies.
###Output
_____no_output_____
###Markdown
Exercise 48.24 Write a program that asks for an integer, then prints all divisors of that integer. For instance, if the number is 24, the divisors are 1, 2, 3, 4, 6, 8, 12, and 24.
###Code
# Divisors.
###Output
_____no_output_____
###Markdown
Exercise 48.25 You have five dice, and wish to roll all sixes. You roll all five dice. You then pick out all the sixes, and reroll all the remaining dice. Again, you pick out the sixes, and reroll the dice now remaining. Etcetera. You continue doing this until all dice are showing a six. Write a program that estimates how many rolls on average you need to get all the dice showing a six. Do this by simulating this experiment 100,000 times or more, and calculate the average number of rolls needed.
###Code
# Five sixes.
###Output
_____no_output_____
###Markdown
Exercise 48.26 Fermat’s theorem on the sums of two squares says that an odd prime number (i.e., any prime number except 2) can be expressed as the sum of two squares of integers if and only if the prime number is congruent to 1 (modulo 4); i.e., for an odd prime number `p` you can find integers `x` and `y` so that `p == x*x + y*y` if and only if `p%4 == 1`. Write a program that asks for a positive integer `N`, and then searches for two integers for which the sum of their squares is `N`. If you can find them, print them. If not, print a statement that says so. If `N` is a prime number, your program should print that too, and indicate whether or not your conclusion conflicts with Fermat’s theorem (it should not, of course, but check it anyway – this is a good way to get bugs out of your program).
###Code
# Fermat's theorem.
###Output
_____no_output_____
###Markdown
Exercise 48.27 Write a program that uses a directory (you can define it as a constant at the top of your program). It reads all the words from all the files in that directory, and builds a list of all the five-letter words in those files, whereby each word occurs only once in the list. To make sure that a word like `"doesn"` is not added to the list (which would happen if you consider all non-letters to be word boundaries, and the word `"doesn't"` occurs in a file), do not remove any punctuation from the text before you split it into words. Instead, after splitting the text, remove only punctuation from the start and end of each word. Then check the word to see if it is of length 5, but disallow it if it still contains characters that are not letters. This will avoid the occurrence of `"doesn"`, and neither will a word like `"can't"` get on the list. It will still include a word like `"house."`, after it removes the period from the end.
###Code
# List of five-letter words.
###Output
_____no_output_____
###Markdown
Exercise 48.28 In the television game Lingo, the players have to guess a 5-letter word. They start with one letter given, and then guess words of the correct length. After a guess, any letter that is correct and in the correct place, is marked (in the television show by drawing a square around the letter). Furthermore, any of the remaining letters that is in the sought word, which is not in the correct place, is also marked (in the television show by drawing a circle around the letter). The players have only a limited amount of attempts available to guess the word (usually 5).Write a program that plays Lingo with the user. The program should have a small dictionary of words which it chooses from (you can use the list you got from the previous exercise). The program selects a word to guess, for instance `WATER`. It also randomly selects one of the letters that the user gets "for free", for instance the `A` in the second spot. The user then tries to guess the word. Every time, before the user makes a guess, the program displays the word as far as it is known. This means that it displays the word as a sequence of dashes, one dash for each letter, except that every letter of which the user knows that it is correct and in the correct spot, is displayed as the actual letter. This includes the letter that is given away for free. For instance, if the word is `WATER`, the `A` was given away for free, and the user already guessed an `R` in the last spot, then the word is displayed as `-A--R`.To guess, the user types in a word. The program responds by displaying the guessed word as follows: Every letter that the word contains that is correct and in the correct place, is displayed as an uppercase letter. Every letter of the remaining ones that is correct but not in the correct place, is displayed as a lowercase letter. Finally, all remaining letters are displayed as dashes. For instance, if the word is `WATER` and the user guesses `BARGE`, the program displays `-Ar-e`. The guessing continues until the user guesses the word correctly, or uses up all attempts (after which the program will give the correct answer).Four rules should be noted: (1) if the user makes a mistake, for instance typing a word that is too long or too short, or which contains more than only letters, the program gives an error message and the user can enter a new guess -– this does not count as one of the attempts; (2) the user can enter the word in uppercase or lowercase letters, or even a mix; (3) if the guess contains multiple copies of the same letter, and the word contains that letter but fewer of them, only as many copies of the letter as the word contains are marked -– for instance, if the word is `WATER` and the user guesses `APART`, then only one of the two `A`’s is displayed in the program’s response: `a--rt`; and (4) a correct letter in the correct place has precedence over a correct letter which is not in the correct place –- for instance, if the word is `WATER` and the user guesses `RADAR`, then the program responds with `-A--R`.One rule that is in the "official" Lingo but not in this computer version, is that the player can only guess words that are actually found in the dictionary. To enforce that, you need to load a dictionary with allowed words. That is not impossible, of course, if you have such a dictionary available.
###Code
# Lingo.
###Output
_____no_output_____
###Markdown
Exercise 48.29 The file `wordsEn.txt` is a dictionary that contains over 100,000 words in the English language. Adapt the Lingo program of the previous exercise so that it (1) asks the user the length of the words that they wish to use (minimum 4, maximum 8), (2) sets the number of attempts to the selected word length, (3) chooses a word of the correct length from the dictionary as the answer, and (4) disallows the user from making a guess using a word that is not in the dictionary, or a word that he used before.
###Code
# Complete Lingo.
###Output
_____no_output_____
###Markdown
Exercise 48.30 Use the file `wordsEn.txt` which was provided for the previous exercise. Let the user enter an integer between 1 and 15. Then generate a "word pyramid" of the requested height. A "word pyramid" is a list of words, starting with a word of length 1, followed by a word of length 2, followed by a word of length 3, etc. up to a word with a length that is the height of the pyramid. Each next word has the same letters as the previous word (though not necessarily in the same order) with one extra letter added. For example, here is a word pyramid of height 10:`a``ad``tad``date``tread``traced``catered``racketed``restacked``afterdecks`Of course, you should generate the word pyramid from the supplied dictionary, and preferably you would always generate a pyramid at random, so that you get to see different answers.Note: This exercise is really hard, and you probably need recursion. The limit of 15, by the way, is set because there are no words in the dictionary of 16 letters or more for which a word pyramid is possible.
###Code
# Word pyramid.
###Output
_____no_output_____
###Markdown
Exercise 48.31 Write a program that creates a "magic square" of size 3 by 3. A magic square of this size is three cells wide and three cells high, and each cell contains a number. In this case, the square contains the numbers 1 to 9 each once. The rows, columns, and two biggest diagonals all add up to the same value. Hint: Since the numbers add up to 45, the sum of the nunmbers in each of the rows, columns, and two diagonals must be 15. This means that if you have determined the numbers in the four cells in one of the corners, the whole square is determined. So if you do this with loops, a quadruple-nested loop suffices. Alternatively, you can do it with the `permutations()` function from the `itertools` module, though you have to be smart about it or it will take far too much time.
###Code
# Magic square.
###Output
_____no_output_____
###Markdown
Exercise 48.32 The Towers of Hanoi is a puzzle, which uses three poles, labeled A, B, and C. On pole A there is a stack of discs of varying size; the discs are numbered according to their size. The smallest disc is 1, the next one is 2, the next one is 3, etcetera, up to size `N`. Typical values for `N` are 4 and 5, though in the classic puzzle `N` is supposed to be 64. The discs are stacked on pole A according to their size, the smallest one on top, and the biggest one on the bottom. You now have to move all the discs from pole A to pole C, whereby you have to follow these four rules: (1) you can only move one disc at a time; (2) you can only move discs between the poles; (3) you can only move a disc from a pole if it is on top, and can only move it to the top of another pole; and (4) you can never place a disc on top of a disc that is smaller. Write a program that solves this puzzle for any value of `N` (for testing purposes, `N` should not be chosen higher than 10 or so). Make the program print the solution as a recipe, with lines such as "Move disc 1 from pole A to pole C". At the end, print the number of moves you needed to make, preferably calculated during the process of generating the recipe. A recursive solution is easiest to implement, though an iterative solution is possible too.To think about a recursive solution, consider the following: Solving the Towers of Hanoi with a biggest disc of size 10 is easy if you know how to solve it for size 9. Namely, you use your size-9 procedure to move the top 9 discs to the middle pole, then move the disc of size 10 to the target pole, and finally use the size-9 procedure to move the 9 discs from the middle pole to the target pole. But how do you solve the problem with the biggest disc being size 9? Well, that is simple if you know how to solve it for size 8... You can imagine where this is going. You are reducing the complexity of the problem step by step, until you are at "solving the problem for size 2 is simple if you can solve it for size 1." Solving it for size 1 is trivial: you just move the disc to where it must go. Basically, this comes down to a recursive definition of the solution method: To solve it for size N where you move from pole X to pole Y with Z as temporary pole, you first solve it for size N-1 where you move from pole X to pole Z with pole Y as temporary pole, then move the disc of size N from pole X to pole Y, and finally solve the problem for size N-1 where you move from pole Z to pole Y with pole X as temporary pole.
###Code
# Towers of Hanoi.
###Output
_____no_output_____
###Markdown
Exercise 48.33 A perfect number is a number greater than 1, which is equal to the sum of its divisors (including 1, excluding the number itself). E.g., 6 is a perfect number as its divisors are 1, 2, and 3, and 1+2+3=6. 28 is also a perfect number. Write a program which determines all perfect numbers up to 10,000. There are four of them.
###Code
# Small perfect numbers.
###Output
_____no_output_____
###Markdown
Exercise 48.34 Write a program which determines all perfect numbers up to 1020 (i.e., a 1 followed by 20 zeroes). There are eight of them.Your previous solution will probably far too slow for this. However, you might be able to solve this with the following knowledge:- There are only even perfect numbers in this range (in fact, it is suspected that only even numbers can be perfect)- A Mersenne prime is a prime number of the form `2`p`-1`, whereby `p` is also a prime number- If `q` is a Mersenne prime, then `q(q+1)/2` is a perfect number; moreover, there are no other even perfect numbersFor testing purposes, first check for perfect numbers up to 109. You should find a fifth, beyond the four you found in the previous exercise. The sixth perfect number has 10 digits, the seventh has 12 digits, and the eighth has 19 digits, so you can find them in the range listed. The ninth perfect number has 37 digits, though checking up to 1038 is probably far too slow for Python code.
###Code
# Large perfect numbers.
###Output
_____no_output_____
###Markdown
Exercise 48.35 You have a certain amount of money, expressed as an integer that represents cents (e.g., 1 euro would be expressed as 100). You have a list of coin values. This list is sorted from high to low, with a guaranteed 1 at the end of the list. How many ways are there to pay the amount with these change values? For example, if the amount is 6, and the coins are `[50,20,10,5,2,1]`, then the answer is 5, namely `5+1`, `2+2+2`, `2+2+1+1`, `2+1+1+1+1`, and `1+1+1+1+1+1`. Write a program that calculates such an answer, for any amount, and any list of coins. You do not need to print all the possible combinations, the answer itself suffices. Your program should be able to handle amounts from 1 to 99 at least, with regular coins used in the euro-region (there are 4366 ways to pay out 99 cents this way).
###Code
# Making change.
amount = 6
coins = [50,20,10,5,2,1]
###Output
_____no_output_____
###Markdown
Exercise 48.36 The inconsistent spelling of words is an annoyance; why can't we simplify spelling so that it is easier to learn? Consider the following rules:- If a word ends in a consonant followed by a "y", you can replace the "y" with "ee"; e.g., "shabby" becomes "shabbee"- If a word ends in a consonant followed by "ed", you can replace the "ed" with "t"; e.g., "learned" becomes "learnt"- If a word ends in "gue", you remove the "ue"; e.g., "catalogue" becomes "catalog"- If a word ends in "ough", you replace the "ough" with a single "o": e.g., "although" becomes "altho"- If a word contains a vowel (including "y"), followed by an "s", followed by a vowel (including "y"), you can replace the "s" with a "z"; e.g., "theorise" becomes "theorize"- If a word contains "ae", the "ae" is replaced with a single "e"; e.g., "aesthetic" becomes "esthetic"- If a word ends in "re", the "re" is replaced with "er"; e.g., "sabre" becomes "saber"- If a word ends in "ye", the "ye" is replaced with a single "i"; e.g., "goodbye" becomes "goodbi"- If a word contains "ate", you replace the "ate" with the number "8"; e.g., "later" becomes "l8r"- If a word contains "you", you replace those letters with a single "u"; e.g., "you" becomes "u"- If a word contains "ks", "cs", "kz", or "cz", you replace those letters with an "x"; e.g., "facsimili" becomes "faximili"- If a word ends in "ache", you replace those letters with "ake"; e.g., "headache" becomes "headake"- If a word contains "ea", you replace that with "ee"; e.g., "beat" becomes "beet"- If a word ends in a "d", you replace that "d" with a "t"; e.g., "wood" becomes "woot"Write a program that changes the spelling of a text according to these rules. Make sure that if a word starts with a capital, a replacement retains that capital; e.g., if a sentence starts with "You", you should make it start with "U" (and not "u"). It is a good idea to do this exercise with regular expressions.
###Code
# Modern spelling.
###Output
_____no_output_____
|
Python/Bayesian_test_run.ipynb
|
###Markdown
Trialsgiven rating of 0 - 5, at prequake, quake, postquake of a single site
###Code
n = 100
probs_pre = np.array([0.8, 0.2, 0, 0, 0, 0])
probs_quake = np.array([0.0, 0, 0, 0, 0.2, 0.8])
probs_post = np.array([0, 0, 0.3, 0.2, 0.4, 0.1])
counts_pre = np.random.multinomial(n, probs_pre)
counts_quake = np.random.multinomial(n, probs_quake)
counts_post = np.random.multinomial(n/2, probs_post)
#Convert generated counts to raw scores
def count_to_score(counts):
scores = np.array([])
score = 0
for i in counts:
scores = np.append(scores, i * [score])
score += 1
return scores
scores_pre = count_to_score(counts_pre)
scores_quake = count_to_score(counts_quake)
scores_post = count_to_score(counts_post)
###Output
_____no_output_____
###Markdown
Samplingideas from https://docs.pymc.io/notebooks/updating_priors.html
###Code
# with pm.Model() as dirchlet_multinomial:
# probs = pm.Dirichlet('probs', a=np.ones(6)) # flat prior
# counts = pm.Multinomial('scores', n=n, p=probs, observed=counts_quake)
# trace = pm.sample(1000)
# pm.plot_posterior(trace);
def init_model(D):
with pm.Model() as model_init:
prior = pm.HalfNormal('mu', sd=1)
likelihood = pm.Normal('likelihood', mu=prior, sd=1, observed=D)
trace = pm.sample(1500, chains=1)
return trace
trace = init_model(scores_pre)
pm.traceplot(trace, priors=[pm.HalfNormal.dist(sd=1)]);
pm.plot_posterior(trace);
def from_posterior(param, samples, return_dist=False):
smin, smax = np.min(samples), np.max(samples)
width = smax - smin
x = np.linspace(smin, smax, 100)
y = stats.gaussian_kde(samples)(x)
# what was never sampled should have a small probability but not 0,
# so we'll extend the domain and use linear approximation of density on it
x = np.concatenate([[0], x, [5]])
y = np.concatenate([[0], y, [0]])
if return_dist:
return pm.Interpolated.dist(x, y)
return pm.Interpolated(param, x, y)
def update_prior(D, trace):
with pm.Model() as model:
# Priors are posteriors from previous iteration
prior = from_posterior('mu', trace['mu'])
# Likelihood (sampling distribution) of observations
likelihood = pm.Normal('likelihood', mu=prior, sd=1, observed=D)
# draw 10000 posterior samples
trace = pm.sample(1500, chains=2)
return trace
trace = init_model(scores_pre)
traces = [trace]
for D in [scores_quake, scores_post]:
traces.append(update_prior(D, traces[-1]))
print('Posterior distributions of ' + str(len(traces)) + ' time points.')
cmap = mpl.cm.winter
for param in ['mu']:
plt.figure(figsize=(8, 3))
for update_i, trace in enumerate(traces):
samples = trace[param]
smin, smax = np.min(samples), np.max(samples)
x = np.linspace(smin, smax, 100)
y = stats.gaussian_kde(samples)(x)
plt.plot(x, y, color=cmap(1 - update_i / len(traces)))
#plt.axvline({'alpha': alpha_true, 'beta0': beta0_true, 'beta1': beta1_true}[param], c='k')
plt.ylabel('Frequency')
plt.title(param)
plt.show()
pm.plot_posterior(traces[0]);
pm.plot_posterior(traces[1]);
pm.traceplot(traces[1], priors=[from_posterior('mu', traces[0]['mu'], return_dist=True)]);
pm.traceplot(traces[2], priors=[from_posterior('mu', traces[1]['mu'], return_dist=True)]);
plt.plot(from_posterior('mu', traces[1]['mu'], return_dist=True))
pm.plot_posterior(traces[2]);
###Output
_____no_output_____
###Markdown
Conjugate Model Normal-inverse-Gamma (NIG) prior from https://www.cs.ubc.ca/~murphyk/Papers/bayesGauss.pdf, https://stackoverflow.com/questions/53211277/updating-model-on-pymc3-with-new-observed-data, https://en.wikipedia.org/wiki/Conjugate_prior
###Code
# prior
mu_0 = scores_pre.mean()
nu_0 = scores_pre.shape[0]
alpha_0 = nu_0/2
beta_0 = nu_0 * scores_pre.var() / 2
# # prior
# mu_0 = 57.0
# nu_0 = 80
# alpha_0 = 40
# beta_0 = alpha*5.42**2
# points to compute likelihood at
mu_grid, sd_grid = np.meshgrid(np.linspace(0, 5, 101),
np.linspace(0, 3, 101))
# mu_grid, sd_grid = np.meshgrid(np.linspace(47, 67, 101),
# np.linspace(4, 8, 101))
# normal ~ N(X | mu_0, sigma/sqrt(nu))
logN = stats.norm.logpdf(x=mu_grid, loc=mu_0, scale=sd_grid/np.sqrt(nu_0))
# inv-gamma ~ IG(sigma^2 | alpha, beta)
logIG = stats.invgamma.logpdf(x=sd_grid**2, a=alpha_0, scale=beta_0)
# full log-likelihood
logNIG = logN + logIG
# actually, we'll plot the -log(-log(likelihood)) to get nicer contour
plt.figure(figsize=(8,8))
plt.contourf(mu_grid, sd_grid, -np.log(-logNIG))
plt.xlabel("$\mu$")
plt.ylabel("$\sigma$")
plt.show()
###Output
_____no_output_____
###Markdown
updating parameters
###Code
# precompute some helpful values
n = scores_quake.shape[0]
mu_y = scores_quake.mean()
# updated NIG parameters
mu_n = (nu_0*mu_0 + n*mu_y)/(nu_0 + n)
nu_n = nu_0 + n
alpha_n = alpha_0 + n/2
beta_n = beta_0 + 0.5*(n*nu_0/nu_n)*(mu_y - mu_0)**2 + 0.5*np.square(scores_quake - mu_y).sum()
# np.random.seed(53211277)
# Y1 = np.random.normal(loc=62, scale=7.0, size=20)
# # precompute some helpful values
# n = Y1.shape[0]
# mu_y = Y1.mean()
# # updated NIG parameters
# mu_n = (nu_0*mu_0 + n*mu_y)/(nu_0 + n)
# nu_n = nu_0 + n
# alpha_n = alpha_0 + n/2
# beta_n = beta_0 + 0.5*(n*nu_0/nu_n)*(mu_y - mu_0)**2 + 0.5*np.square(Y1 - mu_y).sum()
# normal ~ N(X | mu_0, sigma/sqrt(nu))
logN = stats.norm.logpdf(x=mu_grid, loc=mu_n, scale=sd_grid/np.sqrt(nu_n))
# inv-gamma ~ IG(sigma^2 | alpha, beta)
logIG = stats.invgamma.logpdf(x=sd_grid**2, a=alpha_n, scale=beta_n)
# full log-likelihood
logNIG = logN + logIG
# actually, we'll plot the -log(-log(likelihood)) to get nicer contour
plt.figure(figsize=(8,8))
plt.contourf(mu_grid, sd_grid, -np.log(-logNIG))
plt.xlabel("$\mu$")
plt.ylabel("$\sigma$")
plt.show()
###Output
_____no_output_____
###Markdown
Wrap as a function
###Code
def define_conj_prior(D, plot=False):
mu_0 = D.mean()
nu_0 = D.shape[0]
alpha_0 = nu_0/2
beta_0 = nu_0 * D.var() / 2
mu_grid, sd_grid = np.meshgrid(np.linspace(0, 5, 101),
np.linspace(0, 3, 101))
logN = stats.norm.logpdf(x=mu_grid, loc=mu_0, scale=sd_grid/np.sqrt(nu_0))
logIG = stats.invgamma.logpdf(x=sd_grid**2, a=alpha_0, scale=beta_0)
logNIG = logN + logIG
if plot:
plt.figure(figsize=(8,8))
plt.contourf(mu_grid, sd_grid, -np.log(-logNIG))
plt.xlabel("$\mu$")
plt.ylabel("$\sigma$")
plt.show()
return (mu_0, nu_0, alpha_0, beta_0)
def update_conj_prior(D, D_prior, plot=False):
mu_0, nu_0, alpha_0, beta_0 = define_conj_prior(D_prior)
n = D.shape[0]
mu_n = D.mean()
mu_n = (nu_0*mu_0 + n*mu_n)/(nu_0 + n)
nu_n = nu_0 + n
alpha_n = alpha_0 + n/2
beta_n = beta_0 + 0.5*(n*nu_0/nu_n)*(mu_n - mu_0)**2 + 0.5*np.square(D - mu_n).sum()
mu_grid, sd_grid = np.meshgrid(np.linspace(0, 5, 101),
np.linspace(0, 3, 101))
logN = stats.norm.logpdf(x=mu_grid, loc=mu_n, scale=sd_grid/np.sqrt(nu_n))
logIG = stats.invgamma.logpdf(x=sd_grid**2, a=alpha_n, scale=beta_n)
logNIG = logN + logIG
if plot:
plt.figure(figsize=(8,8))
plt.contourf(mu_grid, sd_grid, -np.log(-logNIG))
plt.xlabel("$\mu$")
plt.ylabel("$\sigma$")
plt.show()
return (mu_n, nu_n, alpha_n, beta_n)
define_conj_prior(scores_pre, plot=True)
update_conj_prior(scores_quake, scores_pre, plot=True)
update_conj_prior(scores_post, scores_quake, plot=True)
update_conj_prior(np.append(scores_post, scores_post), scores_quake, plot=True)
###Output
_____no_output_____
###Markdown
Multiple sitesSites have different numbers (10, 100, 1000) scores. They are from the same time points (pre, quake, post).(see more https://discourse.pymc.io/t/updating-multivariate-priors/2804/10)
###Code
def gen_samples(n, p):
return count_to_score(np.random.multinomial(n, p))
n = [10, 100, 1000, 10000]
n_sites = len(n)
probs_pre = np.array([0.8, 0.2, 0, 0, 0, 0])
probs_quake = np.array([0.0, 0, 0, 0, 0.2, 0.8])
probs_post = np.array([0, 0, 0.3, 0.2, 0.4, 0.1])
scores_pre_ = [gen_samples(n[i], probs_pre) for i in range(n_sites)]
scores_quake_ = [gen_samples(n[i], probs_quake) for i in range(n_sites)]
scores_post_ = [gen_samples(n[i]/10, probs_post) for i in range(n_sites)]
traces = {}
for site in range(n_sites):
traces[site] = [init_model(scores_pre_[site])]
for Ds in [scores_quake_, scores_post_]:
for site in range(n_sites):
traces[site].append(update_prior(Ds[site], traces[site][-1]))
traces
for site in range(n_sites):
cmap = mpl.cm.winter
trace_ = traces[site]
plt.figure(figsize=(8, 3))
for update_i, trace in enumerate(trace_):
samples = trace['mu']
smin, smax = np.min(samples), np.max(samples)
x = np.linspace(smin, smax, 100)
y = stats.gaussian_kde(samples)(x)
plt.plot(x, y, color=cmap(1 - update_i / len(traces)))
#plt.axvline({'alpha': alpha_true, 'beta0': beta0_true, 'beta1': beta1_true}[param], c='k')
plt.ylabel('Frequency')
plt.title('mu @ n='+str(n[site]))
plt.show()
define_conj_prior(scores_pre_[1], plot=True)
update_conj_prior(scores_quake_[1], scores_pre_[1], plot=True)
update_conj_prior(scores_post_[1], scores_quake_[1], plot=True)
###Output
_____no_output_____
|
notebooks/download_parse_upload_bd.ipynb
|
###Markdown
DeputadosPossíveis valores para o campo Situacao- 'REL' = Renunciou para assumir outro cargo eletivo- 'OUT' = Outros'FAL' = Falecido- 'REN' = Renunciou'LIC' = Licenciado- 'EXE' = No exercíciodo mandato- 'CAS' = Cassado- ' ' = Não categorizad
###Code
'Escolas Estaduais'.upper()
%%time
deputados = alesp_parser.parse_deputados()
tb = bd.Table('deputados','br_sp_alesp')
tb.create(
path='../data/servidores/deputados_alesp.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='pass'
)
tb.publish('replace')
###Output
_____no_output_____
###Markdown
Servidores
###Code
%%time
servidores, liderancas = alesp_parser.parse_servidores()
tb = bd.Table('assessores_parlamentares','br_sp_alesp')
tb.create(
path='../data/servidores/assessores_parlamentares.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='pass'
)
tb.publish('replace')
tb = bd.Table('assessores_lideranca','br_sp_alesp')
tb.create(
path='../data/servidores/assessores_lideranca.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='pass'
)
tb.publish('replace')
servidores.head()
###Output
_____no_output_____
###Markdown
Despesas ALLhttps://www.al.sp.gov.br/dados-abertos/recurso/21
###Code
%%time
despesas_all, despesas_final = alesp_parser.parse_despesas(False)
tb = bd.Table('despesas_gabinete_atual','br_sp_alesp')
tb.create(
path='../data/gastos/despesas_gabinetes_mandato.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='pass'
)
tb.publish('replace')
tb = bd.Table('despesas_gabinete','br_sp_alesp')
tb.create(
path='../data/gastos/despesas_gabinete/',
partitioned=True,
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='pass'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 19/19 [00:53<00:00, 2.83s/it]
###Markdown
Tramitacao https://www.al.sp.gov.br/dados-abertos/grupo/1 AUTORESLista de deputados autores e apoiadores das proposituras.https://www.al.sp.gov.br/dados-abertos/recurso/81
###Code
%%time
alesp_tamitacao_parser.parse_autores(False)
tb = bd.Table('tramitacao_documento_autor','br_sp_alesp')
tb.create(
path='../data/tramitacoes/documento_autor.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:46<00:00, 46.06s/it]
###Markdown
Comissoeshttps://www.al.sp.gov.br/dados-abertos/recurso/43
###Code
%%time
alesp_tamitacao_parser.parse_comissoes(False)
tb = bd.Table('tramitacao_comissoes','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:01<00:00, 1.13s/it]
###Markdown
Deliberações nas ComissõesLista das deliberações sobre as matérias que tramitam nas Comissões Permanentes da Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/52
###Code
%%time
alesp_tamitacao_parser.parse_deliberacoes_comissoes(False)
tb = bd.Table('tramitacao_comissoes_permanentes_deliberacoes','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes_permanentes_deliberacoes.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:05<00:00, 5.71s/it]
###Markdown
Membros de Comissões PermanentesLista de membros das Comissões da Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/45
###Code
%%time
alesp_tamitacao_parser.parse_comissoes_membros(False)
tb = bd.Table('tramitacao_comissoes_membros','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes_membros.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:01<00:00, 1.53s/it]
###Markdown
Natureza do DocumentoLista das naturezas (tipos) dos documentos que fazem parte do Processo Legislativohttps://www.al.sp.gov.br/dados-abertos/recurso/44
###Code
%%time
alesp_tamitacao_parser.parse_naturezasSpl(download=False)
tb = bd.Table('tramitacao_natureza','br_sp_alesp')
tb.create(
path='../data/tramitacoes/naturezasSpl.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:01<00:00, 1.11s/it]
###Markdown
Documentos Palavras ChaveLista de palavras-chave associadas aos documentos e proposituras que tramitam no processo legislativo. Essa indexação é realizada pela Divisão de Biblioteca e Documentação.https://www.al.sp.gov.br/dados-abertos/recurso/42
###Code
%%time
alesp_tamitacao_parser.parse_documento_palavras(False)
tb = bd.Table('tramitacao_documento_palavras_chave','br_sp_alesp')
tb.create(
path='../data/tramitacoes/documento_palavras.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:32<00:00, 32.92s/it]
###Markdown
Index Palavras ChaveLista de palavras-chave que podem ser associadas aos documentos que tramitam no Processo Legislativo no sistema SPL. A lista é definida e a indexação realizada pela equipe do DDI (Departamento de Documentação e Informação) e da DBD (Divisão de Biblioteca e Documentação) Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/41
###Code
%%time
alesp_tamitacao_parser.parse_documento_index_palavras(False)
tb = bd.Table('tramitacao_index_palavras_chave','br_sp_alesp')
tb.create(
path='../data/tramitacoes/index_palavras_chave.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:06<00:00, 6.01s/it]
###Markdown
PareceresRecurso com a lista dos pareceres elaborados nas Comissões das matérias que tramitam ou tramitaram na Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/103http://www.al.sp.gov.br/repositorioDados/processo_legislativo/propositura_parecer.zip
###Code
%%time
alesp_tamitacao_parser.parse_propositura_parecer(False)
tb = bd.Table('tramitacao_propositura_parecer','br_sp_alesp')
tb.create(
path='../data/tramitacoes/propositura_parecer.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:38<00:00, 38.20s/it]
###Markdown
Presença nas ComissõesPresença dos Deputados Estaduais nas reuniões das Comissões Permanentes da Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/53
###Code
%%time
df = alesp_tamitacao_parser.parse_comissoes_permanentes_presencas(False)
tb = bd.Table('tramitacao_comissoes_permanentes_presencas','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes_permanentes_presencas.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:03<00:00, 3.01s/it]
###Markdown
PropositurasLista de proposituras apresentadas pelo Deputados Estaduais e que tramitam ou tramitaram no Processo Legislativo.https://www.al.sp.gov.br/dados-abertos/recurso/56
###Code
%%time
df = alesp_tamitacao_parser.parse_proposituras(False)
tb = bd.Table('tramitacao_proposituras','br_sp_alesp')
tb.create(
path='../data/tramitacoes/proposituras.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [01:02<00:00, 62.02s/it]
###Markdown
Regimes de Tramitação das PropositurasDados dos regimes de tramitação das proposituras.https://www.al.sp.gov.br/dados-abertos/recurso/56
###Code
%%time
alesp_tamitacao_parser.parse_documento_regime(False)
tb = bd.Table('tramitacao_documento_regime','br_sp_alesp')
tb.create(
path='../data/tramitacoes/documento_regime.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:45<00:00, 45.36s/it]
###Markdown
Reuniões de ComissãoLista das reuniões realizadas nas Comissões Permanentes da Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/56
###Code
%%time
alesp_tamitacao_parser.parse_comissoes_permanentes_reunioes(False)
tb = bd.Table('tramitacao_comissoes_permanentes_reunioes','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes_permanentes_reunioes.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:01<00:00, 1.91s/it]
###Markdown
Votações nas ComissõesLista das votações nas deliberações das matérias que tramitam nas Comissões Permanentes da Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/55
###Code
%%time
alesp_tamitacao_parser.parse_comissoes_permanentes_votacoes(False)
tb = bd.Table('tramitacao_comissoes_permanentes_votacoes','br_sp_alesp')
tb.create(
path='../data/tramitacoes/comissoes_permanentes_votacoes.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:20<00:00, 20.03s/it]
###Markdown
--->>> Tramitações atuaishttps://www.al.sp.gov.br/dados-abertos/recurso/221
###Code
%%time
alesp_tamitacao_parser.parse_documento_andamento_atual(False)
tb = bd.Table('tramitacao_documento_andamento_atual','br_sp_alesp')
tb.create(
path='../data/tramitacoes/documento_andamento_atual.csv',
if_table_exists='replace',
if_storage_data_exists='replace',
if_table_config_exists='replace'
)
tb.publish('replace')
###Output
Uploading files: 100%|██████████| 1/1 [00:22<00:00, 22.65s/it]
###Markdown
TramitaçõesRecurso com os andamentos das matérias que tramitam ou tramitaram na Alesp.https://www.al.sp.gov.br/dados-abertos/recurso/101
###Code
# %%time
# alesp_tamitacao_parser.parse_documento_andamento(False)
# tb = bd.Table('tramitacao_documento_andamento','br_sp_alesp')
# tb.create(
# path='../data/tramitacoes/documento_andamento.csv',
# if_table_exists='replace',
# if_storage_data_exists='replace',
# if_table_config_exists='raise'
# )
# tb.publish('replace')
###Output
_____no_output_____
|
doc/jbook_example/jbook_example.ipynb
|
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, (Government of Canada, 2017)1 and (Government of Canada, 2017)2. MethodsThe R programming language (R Core Team, 2019) and the following R packages were usedto perform the analysis: knitr (Xie, 2014), tidyverse (Wickham, 2017), andbookdown (Xie, 2016)_Note: this report is adapted from (Timbers, 2020)._ Results ```{figure} ../../results/horse_pops_plot.png---name: ---```Fig. 1 Horse populations for all provinces in Canada from 1906 - 1972We can see from Fig. 1that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, {cite:p}`horses1` and {cite:p}`horses2`. MethodsThe R programming language {cite:p}`R` and the following R packages were usedto perform the analysis: knitr {cite:p}`knitr`, {cite:p}`tidyverse`, and{cite:p}`bookdown`_Note: this report is adapted from {cite:p}`ttimbers_horses`._ Results ```{figure} ../../results/horse_pops_plot.png---name: horse_pop_plt---Horse populations for all provinces in Canada from 1906 - 1972```We can see from Fig. {numref}`horse_pop_plt`that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, {cite}`horses1, horses2` MethodsThe R programming language {cite}`R` and the following R packages were usedto perform the analysis: knitr {cite}`knitr`, tidyverse {cite}`tidyverse`, andbookdown {cite}`bookdown`_Note: this report is adapted from (Timbers, 2020)._ Results ```{figure} ../../results/horse_pops_plot.png---height: 500pxname: horse_pop---Horse populations for all provinces in Canada from 1906 - 1972```We can see from {ref}`Figure 1 `that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov, display=False)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex, display=False)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, {cite}`horses1`, {cite}`horses2`. MethodsThe R programming language {cite}`R` and the following R packages were used to perform the analysis: knitr {cite}`knitr`, tidyverse, {cite}`tidyverse`, and bookdown {cite}`bookdown`. Note: this report is adapted from {cite}`ttimbers_horses`. Results ```{figure} ../../results/horse_pops_plot.png---figwidth: 500pxname: horse-pop-plot---Horse populations for all provinces in Canada from 1906 - 1972```We can see from {ref}`Fig `that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, (Government of Canada, 2017)1 and (Government of Canada, 2017)2. MethodsThe R programming language (R Core Team, 2019) and the following R packages were usedto perform the analysis: knitr (Xie, 2014), tidyverse (Wickham, 2017), andbookdown (Xie, 2016)_Note: this report is adapted from (Timbers, 2020)._ Results ```{figure} ../../results/horse_pops_plot.png---name: figure_one---Horse populations for all provinces in Canada from 1906 - 1972```We can see from Fig. {numref}`Figure {number} `that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, (Government of Canada, 2017)1 and (Government of Canada, 2017)2. MethodsThe R programming language (R Core Team, 2019) and the following R packages were usedto perform the analysis: knitr (Xie, 2014), tidyverse (Wickham, 2017), andbookdown (Xie, 2016)_Note: this report is adapted from (Timbers, 2020)._ Results ```{figure} ../../results/horse_pops_plot.png---name: ---```Fig. 1 Horse populations for all provinces in Canada from 1906 - 1972We can see from Fig. 1that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
Harry's assignment
###Code
import pandas as pd
from myst_nb import glue
###Output
_____no_output_____
###Markdown
```{tableofcontents} ``` AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, {cite}`horses2` 1 and {cite}`horses1` MethodsThe R programming language (R Core Team, 2019) and the following R packages were usedto perform the analysis: knitr {cite}`knitr`, tidyverse {cite}`tidyverse` , andbookdown {cite}`bookdown`_Note: this report is adapted from {cite}`ttimbers_horses`. Results Horse populations for all provinces in Canada from 1906 - 1972 ```{figure} ../../results/horse_pops_plot.png---name: horse-popsheight: 150px---Horse populations for all provinces in Canada from 1906 - 1972```We can see from {numref}`horse-pops`that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).Specifically, (Government of Canada, 2017)1 and (Government of Canada, 2017)2. MethodsThe R programming language (R Core Team, 2019) and the following R packages were usedto perform the analysis: knitr (Xie, 2014), tidyverse (Wickham, 2017), andbookdown (Xie, 2016)_Note: this report is adapted from (Timbers, 2020)._ Results ```{figure} ../../results/horse_pops_plot.png---name: ---```Fig. 1 Horse populations for all provinces in Canada from 1906 - 1972We can see from Fig. 1that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
###Markdown
AimThis project explores the historical population of horses in Canadabetween 1906 and 1972 for each province. DataHorse population data were sourced from the [Government of Canada's Open Data website](http://open.canada.ca/en/open-data).{cite}`horses1, horses2` MethodsThe R programming language {cite:p}`R` and the following R packages were usedto perform the analysis: knitr {cite:p}`knitr`, tidyverse {cite:p}`tidyverse`, andbookdown {cite:p}`bookdown`_Note: this report is adapted from {cite:p}`ttimbers_horses`._ Results ```{figure} ../../results/horse_pops_plot.png---name: horses-plot---Horse populations for all provinces in Canada from 1906 - 1972```We can see from {numref}`Fig. {number} ` that Ontario, Saskatchewan and Alberta have had the highest horse populations in Canada.All provinces have had a decline in horse populations since 1940.This is likely due to the rebound of the Canadian automotiveindustry after the Great Depression and the Second World War.An interesting follow-up visualisation would be car sales per year for eachProvince over the time period visualised above to further support this hypothesis.
###Code
horses_sd = pd.read_csv("../../results/horses_sd.csv")
largest_sd_prov = str(horses_sd['Province'][0])
glue("largest-sd-prov", largest_sd_prov)
horses_sd_noindex = horses_sd.style.hide_index()
glue("horses-tbl", horses_sd_noindex)
###Output
_____no_output_____
|
appa.ipynb
|
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy Numpy高级应用
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
plt.show()
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
print(np.ones((10, 5)))
np.ones((3, 4, 5), dtype=np.float64).strides
#跨度元祖stride 前进到当前维度下一个元素需要‘跨过’的字节
#分别是[4*5*8(8个字节), 5*8 ,8]
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy numpy数据类型体系
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.uint16.mro()
print(np.issubdtype(ints.dtype, np.number))
print(np.issubdtype(ints.dtype, object))
np.issubdtype(ints.dtype, np.generic)
###Output
True
False
###Markdown
Advanced Array Manipulation 高级数组操作 Reshaping Arrays 数组重塑
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
print(arr.reshape((4, 2)).reshape((2, 4)))
arr = np.arange(12)
print(arr.reshape((4,3), order="C")) #默认C order
arr.reshape((4,3), order="F") #可选Fortran
arr = np.arange(15)
arr.reshape((1,-4, 3)) # 可以给一个维度任意负值,数据自己会判断维度大小
other_arr = np.ones((3, 5))
print(other_arr.shape)
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
print(arr)
f = arr.flatten('F') # 扁平 副本
f[0] = 100
print(arr,f)
r = arr.ravel()#散开 返回源数组的视图
r[0] = 100
print(arr,r)
###Output
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]]
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]] [100 3 6 9 12 1 4 7 10 13 2 5 8 11 14]
[[100 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[ 12 13 14]] [100 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
###Markdown
C Versus Fortran Order C和Fortran顺序
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays 数组的合并和拆分
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
print(np.concatenate([arr1, arr2], axis=0))
np.concatenate([arr1, arr2], axis=1)
print(np.vstack((arr1, arr2)))
np.hstack((arr1, arr2))
np.hstack(arr1)
arr = np.random.randn(7, 7)
print(arr)
al = np.split(arr, [2,4,6])
# first, second, third = np.split(arr, [1, 3]) #0, [1:3], [3:5]
# first,second,third
al
# np.split?
###Output
[[-0.4003 0.4499 0.3996 -0.1516 -2.5579 0.1608 0.0765]
[-0.2972 -1.2943 -0.8852 -0.1875 -0.4936 -0.1154 -0.3507]
[ 0.0447 -0.8978 0.8909 -1.1512 -2.6123 1.1413 -0.8671]
[ 0.3836 -0.437 0.3475 -1.2302 0.5711 0.0601 -0.2255]
[ 1.3497 1.3503 -0.3867 0.866 1.7472 -1.4102 -0.3782]
[-0.3458 0.3801 0.189 1.3233 -2.2646 -0.915 -0.479 ]
[ 1.0472 0.9239 -0.1142 0.4058 0.2885 -0.4348 0.3588]]
###Markdown
Stacking helpers: r_ and c_ 堆叠辅助类:r和c
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
print(np.r_[arr1, arr2]) np.vstack((arr1, arr2))
np.c_[np.r_[arr1, arr2], arr] #np.hstack((ts, arr.reshape(6,1)))
np.c_[np.array([1,2,3])] #可以将(3,) 转化成(1,3)
# np.hstack([1:6, -10:-5])
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat 元素的重复操作:tile和repeat
###Code
arr = np.arange(3)
# arr.repeat(3)
arr, arr*3, arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
print(arr)
arr.repeat(2), arr.repeat(2, axis=0) #axis不设置就扁平化了 因为默认是None不是0
arr.repeat([2, 3], axis=0), arr.repeat([2, 3], axis=1)
arr, np.tile(arr, 2) , np.tile(arr, (1,2)) #奇怪吧
arr, np.tile(arr, (2, 1)), np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put 花式索引的等价函数:take和put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr, arr[inds]
arr.take(inds)
#array([700, 100, 200, 600])
arr.put(inds, 42)
print(arr)#array([ 0, 42, 42, 300, 400, 500, 42, 42, 800, 900])
arr.put(inds, [40, 41, 42, 43])
arr #array([ 0, 41, 42, 300, 400, 500, 43, 40, 800, 900])
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr, arr.take(inds, axis=1), arr.take(inds) #这里axis是None
###Output
_____no_output_____
###Markdown
Broadcasting 广播广播(broadcasting)指的是不同形状的数组之间的算术运算的执行方式。它是一 种非常强大的功能,但也容易令人误解,即使是经验丰富的老手也是如此。将标量 值跟数组合并时就会发生最简单的广播
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
print(arr, arr.mean(0), arr.mean(0).shape)
demeaned = arr - arr.mean(0)#增加.reshape(1,3)也可以
demeaned, demeaned.mean(0)
print(arr)
row_means = arr.mean(1)
print(row_means,
row_means.shape,
row_means.reshape((4, 1)),
np.c_[row_means],
np.c_[row_means].shape == row_means.reshape((4, 1)).shape,
np.c_[row_means] == row_means.reshape((4, 1)) #这两个情况相等
)
demeaned = arr - row_means.reshape((4, 1))
demeaned, demeaned.mean(1)
(arr - np.c_[arr.mean(1)]).mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes 沿其它轴向广播
###Code
arr = np.zeros((4, 4))
arr
arr_3d = arr[:, np.newaxis, :]
arr_3d, arr[:,:,np.newaxis], arr[np.newaxis,:,:]
arr_3d.shape, arr[:,:,np.newaxis].shape, arr[np.newaxis,:,:].shape
arr_1d = np.random.normal(size=3)
arr_1d, arr_1d.shape
arr_1d[:, np.newaxis], arr_1d[:, np.newaxis].shape, np.c_[arr_1d], np.r_[arr_1d]
arr_1d[np.newaxis, :], arr_1d[np.newaxis, :].shape
arr = np.random.randn(3, 4, 5)
print(arr)
depth_means = arr.mean(2)
depth_means, depth_means.shape
#(-0.4522 + 0.7582 -0.5156 -0.5912 + 0.8967)/5
demeaned = arr - depth_means[:, :, np.newaxis]
print(arr)
print(depth_means[:, :, np.newaxis], depth_means[:, :, np.newaxis].shape) #3,4,1
demeaned, demeaned.shape, demeaned.mean(2)
def demean_axis(arr, axis=0):
means = arr.mean(axis)
# This generalizes things like [:, :, np.newaxis] to N dimensions
indexer = [slice(None)] * arr.ndim
indexer[axis] = np.newaxis
return arr - means[indexer]
demean_axis(arr)
###Output
<ipython-input-206-ec87c289fe15>:7: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
return arr - means[indexer]
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting 通过广播设置数组的值
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2]
arr[:2] = [[-1.37], [0.509]]
np.array([[-1.37], [0.509]]).shape
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc高级应用 ufunc Instance Methods ufunc实例方法
###Code
arr = np.arange(10)
np.add.reduce(arr), arr.sum()
arr[::2].sort
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
print(arr)
print(arr[::],arr[::].shape)
print(arr[::2],arr[::2].shape) # 2类似range里的step
arr[::2].sort(1) # sort a few rows 排序1,3,5行
print(arr[::2])
arr
print(arr[:,:-1]) #每行到倒数第一列
print(arr[:, 1:])
arr[:, :-1] < arr[:, 1:]
print(arr[:, :-1] < arr[:, 1:])
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
print(np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)) #整行逻辑与 axis=1
print(np.all(arr[:, :-1] < arr[:, 1:], axis=1))
#logical_and.reduce跟all方法是等价的
arr = np.arange(15).reshape((3, 5))
print(arr)
print(np.add.reduce(arr, axis=1))
print(np.sum(arr, axis=1))
print(np.cumsum(arr, axis=1))
print(np.add.accumulate(arr, axis=1))
arr = np.arange(3).repeat([1, 2, 2])
arr, np.arange(5), np.multiply.outer(arr, np.arange(5)), np.multiply(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
print(x)
print(y)
print(result)
result.shape
#add.reduce/add.reduceat/sum
arr = np.arange(10)
print(np.add.reduce(arr[0:5]), np.add.reduce(arr[5:8]), np.sum(arr[8:]))
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
print(arr)
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
[[ 0 0 0 0 0]
[ 0 1 2 3 4]
[ 0 2 4 6 8]
[ 0 3 6 9 12]]
###Markdown
Writing New ufuncs in Python 编写新的ufunc 自定义
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8)), add_them(np.arange(8), np.arange(8)).dtype
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
add_them(np.arange(8), np.arange(8)), add_them(np.arange(8), np.arange(8)).dtype
arr = np.random.randn(10000)
# %timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
2.97 µs ± 50.5 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
###Markdown
Structured and Record Arrays 结构化和记录式数组
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0], sarr[0]['x'], sarr[0]['y']
sarr['x'], sarr
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields 嵌套dtype和多维字段
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr, arr.shape
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x'], data['y'], data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? 为什么要用结构化数组跟pandas的DataFrame相比,NumPy的结构化数组是一种相对较低级的工具。它 可以将单个内存块解释为带有任意复杂嵌套列的表格型结构。由于数组中的每个元 素在内存中都被表示为固定的字节数,所以结构化数组能够提供非常快速高效的磁 盘数据读写(包括内存映像)、网络传输等功能。 结构化数组的另一个常见用法是,将数据文件写成定长记录字节流,这是C和 C++代码中常见的数据序列化手段(业界许多历史系统中都能找得到)。只要知道 文件的格式(记录的大小、元素的顺序、字节数以及数据类型等),就可以用 np.fromfile将数据读入内存。这种用法超出了本书的范围,知道这点就可以了。 More About Sorting 更多有关排序的话题
###Code
arr = np.random.randn(6)
arr, arr.sort(), arr
#arr.sort()不返回数组,但是会修改数组
arr = np.random.randn(3, 5)
arr
arr[:, 1].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr, np.sort(arr), arr
#np.sort不会修改数组本身,但是会返回一个排序的副本
arr = np.random.randn(3, 5)
arr,arr.sort(axis=1), arr #行排序
arr[:, ::-1] #倒序的语法糖
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort 间接排序:argsort和lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()#1,2,4,3,0
indexer, values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr, arr[:, arr[0].argsort()], arr[0].argsort()
#字典序,就记住用last_name为主排序就完事了
irst_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms 其他供选择的排序算法
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer, values.take(indexer)
###Output
_____no_output_____
###Markdown
 Partially Sorting Arrays 部分排序数组排序的目的之一可能是确定数组中最大或最小的元素。NumPy有两个优化方法, numpy.partition和np.argpartition,可以在第k个最小元素划分的数组
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr, np.partition(arr, 3) #3最小3个 ,-3最大三个
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array 在有序数组中查找元素
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right') #默认左侧
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data, data.shape
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba 用Numba编写快速NumPy函数
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
x = np.random.randn(10000000)
y = np.random.randn(10000000)
%timeit mean_distance(x, y)
# (x - y).mean()
# print(1)
%timeit (x - y).mean()
###Output
51.4 ms ± 2.03 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop```
###Code
import numba as nb
numba_mean_distance = nb.jit(mean_distance)
%timeit numba_mean_distance(x, y)
# @nb.jit
# def mean_distance(x, y):
# nx = len(x)
# result = 0.0
# count = 0
# for i in range(nx):
# result += x[i] - y[i]
# count += 1
# return result / count
###Output
11.3 ms ± 138 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
###Markdown
```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop```
###Code
import numba as nb
numba_mean_distance = nb.jit(mean_distance)
@nb.jit
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
%timeit numba_mean_distance(x, y)
###Output
11.2 ms ± 28.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
###Markdown
```pythonfrom numba import float64, njit =jit(nopython=True)@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()```
###Code
from numba import float64, njit, jit #=jit(nopython=True)
@njit(float64(float64[:], float64[:]))
def mean_distance(x, y):
return (x - y).mean()
%timeit mean_distance(x, y)
###Output
51.4 ms ± 586 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
###Markdown
Creating Custom numpy.ufunc Objects with Numba 用Numba创建自定义numpy.ufunc对象 ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap, mmap.shape
section = mmap[:5]
section
section[:] = np.random.randn(5, 10000)
section[:]
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
# !rm mymmap
###Output
NameError: name 'mmap' is not defined
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
print(arr_c.flags)
print(arr_f.flags)
arr_f.flags.f_contiguous, arr_c.flags.c_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags, '-------', arr_f.flags
arr_c[:50].flags.contiguous, arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy This is a equation $\hat{Y} = \hat{\beta}_{0} + \sum \limits_{j=1}^{p} X_{j}\hat{\beta}_{j}$
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
import datetime
datetime?
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays o表示纵向计算,1表示横向计算
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat 仿真项目数据生成模块中,元素的复制功能得到很好的应用, 首先根据元素特征分布记忆需要生成的数据数量,计算每个特征元素需要生成的数量,生成重复列表 然后根据需要选取数据生成一个随机列表,从生成的重复列表中快速获取随机元素
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
# arr.repeat(2, axis=0)
# arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
# arr
np.tile(arr, 2)
arr
# np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put 快速使用指定索引进行数据获取,在导航模块主线路生成模块中,根据索引快速进行数据获取
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
# 按照指定索引,使用指定数据进行替换
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
# arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
# 使用累加计算
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
arr
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
1.46 ms ± 16.7 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
3.2 µs ± 49.9 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
# argsort获取排序后元素的索引,这个功能很强大,还没想好在哪用
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
# print(last_name[sorter])
# print(first_name[sorter])
zip(last_name[sorter], first_name[sorter])
###Output
<zip object at 0x10e72d7c8>
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array 这个搜索不错,可以直接用于二分查找
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro?
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
# arr.ravel()
# arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
print(arr1,'\n'*3,arr2)
# np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
APPENDIX A.Advanced NumPy 고급 넘파이
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
A.1 ndarray Object Internals_ndarray 객체 구조
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
A.1.1 NumPy dtype Hierarchy 넘파이 D타입 구조
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
A.2 Advanced Array Manipulation 고급 배열 조작 기법 A.2.1 Reshaping Arrays 배열 재형성하기
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
A.2.2 C Versus Fortran Order_ C순서와 포트란 순서
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
A.2.3 Concatenating and Splitting Arrays 배열 이어붙이고 나누기
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_ 배열 쌓기 도우미:r_과 c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
A.2.4 Repeating Elements: tile and repeat 원소 반복하기:반복과 타일
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
A.2.5 Fancy Indexing Equivalents: take and put 팬시 색인:take와 put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
A.3 Broadcasting 브로드캐스팅
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
A.3.1 Broadcasting Over Other Axes 다른 축에 대해 브로드캐스팅하기
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` A.3.2 Setting Array Values by Broadcasting 브로드캐스팅을 이용해서 배열에 값 대입하기
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
A.4 Advanced ufunc Usage 고급 ufunc 사용법 A.4.1 ufunc Instance Methods_ ufunc 인스턴스 메서드
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
A.4.2 Writing New ufuncs in Python 파이썬으로 사용자 정의 ufunc 작성하기
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
A.5 Structured and Record Arrays 구조화된 배열과 레코드 배열
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
A5.1 Nested dtypes and Multidimensional Fields 중첩된 d타입과 다차원 필드
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
A.5.2 Why Use Structured Arrays? 구조화된 배열을 써야 하는 이유 A.6 More About Sorting 정렬에 관하여
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
A.6.1 Indirect Sorts: argsort and lexsort 간접 정렬: argsort와 lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
A.6.2 Alternative Sort Algorithms 대안 정렬 알고리즘
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
A.6.3 Partially Sorting Arrays 배열 일부만 정렬하기
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
A.6.4 numpy.searchsorted: Finding Elements in a Sorted Array 정렬된 배열에서 원소 찾기
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
A.7 Writing Fast NumPy Functions with Numba 넘바를 이용하여 빠른 넘파이 함수 작성하기
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` A.7.1 Creating Custom numpy.ufunc Objects with Numba 넘바를 이용한 사용자 정의 numpy.ufunc 만들기 ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` A.8 Advanced Array Input and Output 고급 배열 입출력 A.8.1 Memory-Mapped Files 메모리 맵 파일
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
A.8.2 HDF5 and Other Array Storage Options 기타 배열 저장 옵션 A.9 Performance Tips 성능 팁 A.9.1 The Importance of Contiguous Memory 인접 메모리의 중요성
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
###Markdown
Advanced NumPy
###Code
import numpy as np
import pandas as pd
np.random.seed(12345)
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
PREVIOUS_MAX_ROWS = pd.options.display.max_rows
pd.options.display.max_rows = 20
np.set_printoptions(precision=4, suppress=True)
###Output
_____no_output_____
###Markdown
ndarray Object Internals
###Code
np.ones((10, 5)).shape
np.ones((3, 4, 5), dtype=np.float64).strides
###Output
_____no_output_____
###Markdown
NumPy dtype Hierarchy
###Code
ints = np.ones(10, dtype=np.uint16)
floats = np.ones(10, dtype=np.float32)
np.issubdtype(ints.dtype, np.integer)
np.issubdtype(floats.dtype, np.floating)
np.float64.mro()
np.issubdtype(ints.dtype, np.number)
###Output
_____no_output_____
###Markdown
Advanced Array Manipulation Reshaping Arrays
###Code
arr = np.arange(8)
arr
arr.reshape((4, 2))
arr.reshape((4, 2)).reshape((2, 4))
arr = np.arange(15)
arr.reshape((5, -1))
other_arr = np.ones((3, 5))
other_arr.shape
arr.reshape(other_arr.shape)
arr = np.arange(15).reshape((5, 3))
arr
arr.ravel()
arr.flatten()
###Output
_____no_output_____
###Markdown
C Versus Fortran Order
###Code
arr = np.arange(12).reshape((3, 4))
arr
arr.ravel()
arr.ravel('F')
###Output
_____no_output_____
###Markdown
Concatenating and Splitting Arrays
###Code
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
np.concatenate([arr1, arr2], axis=0)
np.concatenate([arr1, arr2], axis=1)
np.vstack((arr1, arr2))
np.hstack((arr1, arr2))
arr = np.random.randn(5, 2)
arr
first, second, third = np.split(arr, [1, 3])
first
second
third
###Output
_____no_output_____
###Markdown
Stacking helpers: r_ and c_
###Code
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)
np.r_[arr1, arr2]
np.c_[np.r_[arr1, arr2], arr]
np.c_[1:6, -10:-5]
###Output
_____no_output_____
###Markdown
Repeating Elements: tile and repeat
###Code
arr = np.arange(3)
arr
arr.repeat(3)
arr.repeat([2, 3, 4])
arr = np.random.randn(2, 2)
arr
arr.repeat(2, axis=0)
arr.repeat([2, 3], axis=0)
arr.repeat([2, 3], axis=1)
arr
np.tile(arr, 2)
arr
np.tile(arr, (2, 1))
np.tile(arr, (3, 2))
###Output
_____no_output_____
###Markdown
Fancy Indexing Equivalents: take and put
###Code
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
arr[inds]
arr.take(inds)
arr.put(inds, 42)
arr
arr.put(inds, [40, 41, 42, 43])
arr
inds = [2, 0, 2, 1]
arr = np.random.randn(2, 4)
arr
arr.take(inds, axis=1)
###Output
_____no_output_____
###Markdown
Broadcasting
###Code
arr = np.arange(5)
arr
arr * 4
arr = np.random.randn(4, 3)
arr.mean(0)
demeaned = arr - arr.mean(0)
demeaned
demeaned.mean(0)
arr
row_means = arr.mean(1)
row_means.shape
row_means.reshape((4, 1))
demeaned = arr - row_means.reshape((4, 1))
demeaned.mean(1)
###Output
_____no_output_____
###Markdown
Broadcasting Over Other Axes
###Code
arr - arr.mean(1)
arr - arr.mean(1).reshape((4, 1))
arr = np.zeros((4, 4))
arr_3d = arr[:, np.newaxis, :]
arr_3d.shape
arr_1d = np.random.normal(size=3)
arr_1d[:, np.newaxis]
arr_1d[np.newaxis, :]
arr = np.random.randn(3, 4, 5)
depth_means = arr.mean(2)
depth_means
depth_means.shape
demeaned = arr - depth_means[:, :, np.newaxis]
demeaned.mean(2)
###Output
_____no_output_____
###Markdown
```pythondef demean_axis(arr, axis=0): means = arr.mean(axis) This generalizes things like [:, :, np.newaxis] to N dimensions indexer = [slice(None)] * arr.ndim indexer[axis] = np.newaxis return arr - means[indexer]``` Setting Array Values by Broadcasting
###Code
arr = np.zeros((4, 3))
arr[:] = 5
arr
col = np.array([1.28, -0.42, 0.44, 1.6])
arr[:] = col[:, np.newaxis]
arr
arr[:2] = [[-1.37], [0.509]]
arr
###Output
_____no_output_____
###Markdown
Advanced ufunc Usage ufunc Instance Methods
###Code
arr = np.arange(10)
np.add.reduce(arr)
arr.sum()
np.random.seed(12346) # for reproducibility
arr = np.random.randn(5, 5)
arr[::2].sort(1) # sort a few rows
arr[:, :-1] < arr[:, 1:]
np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
arr = np.arange(15).reshape((3, 5))
np.add.accumulate(arr, axis=1)
arr = np.arange(3).repeat([1, 2, 2])
arr
np.multiply.outer(arr, np.arange(5))
x, y = np.random.randn(3, 4), np.random.randn(5)
result = np.subtract.outer(x, y)
result.shape
arr = np.arange(10)
np.add.reduceat(arr, [0, 5, 8])
arr = np.multiply.outer(np.arange(4), np.arange(5))
arr
np.add.reduceat(arr, [0, 2, 4], axis=1)
###Output
_____no_output_____
###Markdown
Writing New ufuncs in Python
###Code
def add_elements(x, y):
return x + y
add_them = np.frompyfunc(add_elements, 2, 1)
add_them(np.arange(8), np.arange(8))
add_them = np.vectorize(add_elements, otypes=[np.float64])
add_them(np.arange(8), np.arange(8))
arr = np.random.randn(10000)
%timeit add_them(arr, arr)
%timeit np.add(arr, arr)
###Output
_____no_output_____
###Markdown
Structured and Record Arrays
###Code
dtype = [('x', np.float64), ('y', np.int32)]
sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
sarr
sarr[0]
sarr[0]['y']
sarr['x']
###Output
_____no_output_____
###Markdown
Nested dtypes and Multidimensional Fields
###Code
dtype = [('x', np.int64, 3), ('y', np.int32)]
arr = np.zeros(4, dtype=dtype)
arr
arr[0]['x']
arr['x']
dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
data['x']
data['y']
data['x']['a']
###Output
_____no_output_____
###Markdown
Why Use Structured Arrays? More About Sorting
###Code
arr = np.random.randn(6)
arr.sort()
arr
arr = np.random.randn(3, 5)
arr
arr[:, 0].sort() # Sort first column values in-place
arr
arr = np.random.randn(5)
arr
np.sort(arr)
arr
arr = np.random.randn(3, 5)
arr
arr.sort(axis=1)
arr
arr[:, ::-1]
###Output
_____no_output_____
###Markdown
Indirect Sorts: argsort and lexsort
###Code
values = np.array([5, 0, 1, 3, 2])
indexer = values.argsort()
indexer
values[indexer]
arr = np.random.randn(3, 5)
arr[0] = values
arr
arr[:, arr[0].argsort()]
first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
sorter = np.lexsort((first_name, last_name))
sorter
zip(last_name[sorter], first_name[sorter])
###Output
_____no_output_____
###Markdown
Alternative Sort Algorithms
###Code
values = np.array(['2:first', '2:second', '1:first', '1:second',
'1:third'])
key = np.array([2, 2, 1, 1, 1])
indexer = key.argsort(kind='mergesort')
indexer
values.take(indexer)
###Output
_____no_output_____
###Markdown
Partially Sorting Arrays
###Code
np.random.seed(12345)
arr = np.random.randn(20)
arr
np.partition(arr, 3)
indices = np.argpartition(arr, 3)
indices
arr.take(indices)
###Output
_____no_output_____
###Markdown
numpy.searchsorted: Finding Elements in a Sorted Array
###Code
arr = np.array([0, 1, 7, 12, 15])
arr.searchsorted(9)
arr.searchsorted([0, 8, 11, 16])
arr = np.array([0, 0, 0, 1, 1, 1, 1])
arr.searchsorted([0, 1])
arr.searchsorted([0, 1], side='right')
data = np.floor(np.random.uniform(0, 10000, size=50))
bins = np.array([0, 100, 1000, 5000, 10000])
data
labels = bins.searchsorted(data)
labels
pd.Series(data).groupby(labels).mean()
###Output
_____no_output_____
###Markdown
Writing Fast NumPy Functions with Numba
###Code
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
###Output
_____no_output_____
###Markdown
```pythonIn [209]: x = np.random.randn(10000000)In [210]: y = np.random.randn(10000000)In [211]: %timeit mean_distance(x, y)1 loop, best of 3: 2 s per loopIn [212]: %timeit (x - y).mean()100 loops, best of 3: 14.7 ms per loop``` ```pythonIn [213]: import numba as nbIn [214]: numba_mean_distance = nb.jit(mean_distance)``` ```[email protected] mean_distance(x, y): nx = len(x) result = 0.0 count = 0 for i in range(nx): result += x[i] - y[i] count += 1 return result / count``` ```pythonIn [215]: %timeit numba_mean_distance(x, y)100 loops, best of 3: 10.3 ms per loop``` ```pythonfrom numba import float64, njit@njit(float64(float64[:], float64[:]))def mean_distance(x, y): return (x - y).mean()``` Creating Custom numpy.ufunc Objects with Numba ```pythonfrom numba import vectorize@vectorizedef nb_add(x, y): return x + y``` ```pythonIn [13]: x = np.arange(10)In [14]: nb_add(x, x)Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])In [15]: nb_add.accumulate(x, 0)Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])``` Advanced Array Input and Output Memory-Mapped Files
###Code
mmap = np.memmap('mymmap', dtype='float64', mode='w+',
shape=(10000, 10000))
mmap
section = mmap[:5]
section[:] = np.random.randn(5, 10000)
mmap.flush()
mmap
del mmap
mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
mmap
%xdel mmap
!rm mymmap
###Output
_____no_output_____
###Markdown
HDF5 and Other Array Storage Options Performance Tips The Importance of Contiguous Memory
###Code
arr_c = np.ones((1000, 1000), order='C')
arr_f = np.ones((1000, 1000), order='F')
arr_c.flags
arr_f.flags
arr_f.flags.f_contiguous
%timeit arr_c.sum(1)
%timeit arr_f.sum(1)
arr_f.copy('C').flags
arr_c[:50].flags.contiguous
arr_c[:, :50].flags
%xdel arr_c
%xdel arr_f
pd.options.display.max_rows = PREVIOUS_MAX_ROWS
###Output
_____no_output_____
|
code/10.word2vec.ipynb
|
###Markdown
****** Introduction to Word EmbeddingsAnalyzing Meaning through Word Embeddings****** **Using vectors to represent things**- one of the most fascinating ideas in machine learning. - Word2vec is a method to efficiently create word embeddings. - Mikolov et al. (2013). [Efficient Estimation of Word Representations in Vector Space](https://arxiv.org/pdf/1301.3781.pdf) - Mikolov et al. (2013). [Distributed representations of words and phrases and their compositionality](https://arxiv.org/pdf/1310.4546.pdf) ****** The Geometry of CultureAnalyzing Meaning through Word Embeddings******Austin C. Kozlowski; Matt Taddy; James A. Evanshttps://arxiv.org/abs/1803.09288Word embeddings represent **semantic relations** between words as **geometric relationships** between vectors in a high-dimensional space, operationalizing a relational model of meaning consistent with contemporary theories of identity and culture. - Dimensions induced by word differences (e.g. man - woman, rich - poor, black - white, liberal - conservative) in these vector spaces closely correspond to dimensions of cultural meaning, - Macro-cultural investigation with a longitudinal analysis of the coevolution of gender and class associations in the United States over the 20th century The success of these high-dimensional models motivates a move towards "high-dimensional theorizing" of meanings, identities and cultural processes. HistWords HistWords is a collection of tools and datasets for analyzing language change using word vector embeddings. - The goal of this project is to facilitate quantitative research in diachronic linguistics, history, and the digital humanities.- We used the historical word vectors in HistWords to study the semantic evolution of more than 30,000 words across 4 languages. - This study led us to propose two statistical laws that govern the evolution of word meaning https://nlp.stanford.edu/projects/histwords/https://github.com/williamleif/histwords **Diachronic Word Embeddings Reveal Statistical Laws of Semantic Change** Word embeddings quantify 100 years of gender and ethnic stereotypeshttp://www.pnas.org/content/early/2018/03/30/1720347115 The Illustrated Word2vecJay Alammar. https://jalammar.github.io/illustrated-word2vec/ Personality Embeddings> What are you like?**Big Five personality traits**: openness to experience, conscientiousness, extraversion, agreeableness, and neuroticism- the five-factor model (FFM) - **the OCEAN model** - 开放性(openness):具有想象、审美、情感丰富、求异、创造、智能等特质。- 责任心(conscientiousness):显示胜任、公正、条理、尽职、成就、自律、谨慎、克制等特点。- 外倾性(extraversion):表现出热情、社交、果断、活跃、冒险、乐观等特质。- 宜人性(agreeableness):具有信任、利他、直率、依从、谦虚、移情等特质。- 神经质或情绪稳定性(neuroticism):具有平衡焦虑、敌对、压抑、自我意识、冲动、脆弱等情绪的特质,即具有保持情绪稳定的能力。
###Code
# Personality Embeddings: What are you like?
jay = [-0.4, 0.8, 0.5, -0.2, 0.3]
john = [-0.3, 0.2, 0.3, -0.4, 0.9]
mike = [-0.5, -0.4, -0.2, 0.7, -0.1]
###Output
_____no_output_____
###Markdown
Cosine SimilarityThe cosine of two non-zero vectors can be derived by using the Euclidean dot product formula:$$\mathbf{A}\cdot\mathbf{B}=\left\|\mathbf{A}\right\|\left\|\mathbf{B}\right\|\cos\theta$$ $$\text{similarity} = \cos(\theta) = {\mathbf{A} \cdot \mathbf{B} \over \|\mathbf{A}\| \|\mathbf{B}\|} = \frac{ \sum\limits_{i=1}^{n}{A_i B_i} }{ \sqrt{\sum\limits_{i=1}^{n}{A_i^2}} \sqrt{\sum\limits_{i=1}^{n}{B_i^2}} },$$where $A_i$ and $B_i$ are components of vector $A$ and $B$ respectively.
###Code
from numpy import dot
from numpy.linalg import norm
def cos_sim(a, b):
return dot(a, b)/(norm(a)*norm(b))
cos_sim([1, 0, -1], [-1,-1, 0])
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity([[1, 0, -1]], [[-1,-1, 0]])
###Output
_____no_output_____
###Markdown
$$CosineDistance = 1- CosineSimilarity$$
###Code
from scipy import spatial
# spatial.distance.cosine computes
# the Cosine distance between 1-D arrays.
1 - spatial.distance.cosine([1, 0, -1], [-1,-1, 0])
cos_sim(jay, john)
cos_sim(jay, mike)
###Output
_____no_output_____
###Markdown
Cosine similarity works for any number of dimensions. - We can represent people (and things) as vectors of numbers (which is great for machines!).- We can easily calculate how similar vectors are to each other. Word Embeddings Google News Word2VecYou can download Google’s pre-trained model here.- It’s 1.5GB! - It includes word vectors for a vocabulary of 3 million words and phrases - It is trained on roughly 100 billion words from a Google News dataset. - The vector length is 300 features.http://mccormickml.com/2016/04/12/googles-pretrained-word2vec-model-in-python/ Using the **Gensim** library in python, we can - find the most similar words to the resulting vector. - add and subtract word vectors,
###Code
import gensim
# Load Google's pre-trained Word2Vec model.
filepath = '/Users/datalab/bigdata/GoogleNews-vectors-negative300.bin'
model = gensim.models.KeyedVectors.load_word2vec_format(filepath, binary=True)
model['woman'][:10]
model.most_similar('woman')
model.similarity('woman', 'man')
cos_sim(model['woman'], model['man'])
model.most_similar(positive=['woman', 'king'], negative=['man'], topn=5)
###Output
_____no_output_____
###Markdown
$$King- Queen = Man - Woman$$ Now that we’ve looked at trained word embeddings, - let’s learn more about the training process. - But before we get to word2vec, we need to look at a conceptual parent of word embeddings: **the neural language model**. The neural language model“You shall know a word by the company it keeps” J.R. Firth> Bengio 2003 A Neural Probabilistic Language Model. Journal of Machine Learning Research. 3:1137–1155After being trained, early neural language models (Bengio 2003) would calculate a prediction in three steps: The output of the neural language model is a probability score for all the words the model knows. - We're referring to the probability as a percentage here, - but 40% would actually be represented as 0.4 in the output vector. Language Model Training- We get a lot of text data (say, all Wikipedia articles, for example). then- We have a window (say, of three words) that we slide against all of that text.- The sliding window generates training samples for our model As this window slides against the text, we (virtually) generate a dataset that we use to train a model. Instead of only looking two words before the target word, we can also look at two words after it. If we do this, the dataset we’re virtually building and training the model against would look like this:This is called a **Continuous Bag of Words** (CBOW) https://arxiv.org/pdf/1301.3781.pdf Skip-gramInstead of guessing a word based on its context (the words before and after it), this other architecture tries to guess neighboring words using the current word. https://arxiv.org/pdf/1301.3781.pdf The pink boxes are in different shades because this sliding window actually creates four separate samples in our training dataset.- We then slide our window to the next position:- Which generates our next four examples: Negative Sampling And switch it to a model that takes the input and output word, and outputs a score indicating **if they’re neighbors or not** - 0 for “not neighbors”, 1 for “neighbors”. we need to introduce negative samples to our dataset- samples of words that are not neighbors. - Our model needs to return 0 for those samples.- This leads to a great tradeoff of computational and statistical efficiency. Skipgram with Negative Sampling (SGNS) Word2vec Training Process Pytorch word2vec https://github.com/jojonki/word2vec-pytorch/blob/master/word2vec.ipynbhttps://github.com/bamtercelboo/pytorch_word2vec/blob/master/model.py
###Code
# see http://pytorch.org/tutorials/beginner/nlp/word_embeddings_tutorial.html
import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
text = """We are about to study the idea of a computational process.
Computational processes are abstract beings that inhabit computers.
As they evolve, processes manipulate other abstract things called data.
The evolution of a process is directed by a pattern of rules
called a program. People create programs to direct processes. In effect,
we conjure the spirits of the computer with our spells."""
text = text.replace(',', '').replace('.', '').lower().split()
# By deriving a set from `raw_text`, we deduplicate the array
vocab = set(text)
vocab_size = len(vocab)
print('vocab_size:', vocab_size)
w2i = {w: i for i, w in enumerate(vocab)}
i2w = {i: w for i, w in enumerate(vocab)}
# context window size is two
def create_cbow_dataset(text):
data = []
for i in range(2, len(text) - 2):
context = [text[i - 2], text[i - 1],
text[i + 1], text[i + 2]]
target = text[i]
data.append((context, target))
return data
cbow_train = create_cbow_dataset(text)
print('cbow sample', cbow_train[0])
def create_skipgram_dataset(text):
import random
data = []
for i in range(2, len(text) - 2):
data.append((text[i], text[i-2], 1))
data.append((text[i], text[i-1], 1))
data.append((text[i], text[i+1], 1))
data.append((text[i], text[i+2], 1))
# negative sampling
for _ in range(4):
if random.random() < 0.5 or i >= len(text) - 3:
rand_id = random.randint(0, i-1)
else:
rand_id = random.randint(i+3, len(text)-1)
data.append((text[i], text[rand_id], 0))
return data
skipgram_train = create_skipgram_dataset(text)
print('skipgram sample', skipgram_train[0])
class CBOW(nn.Module):
def __init__(self, vocab_size, embd_size, context_size, hidden_size):
super(CBOW, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embd_size)
self.linear1 = nn.Linear(2*context_size*embd_size, hidden_size)
self.linear2 = nn.Linear(hidden_size, vocab_size)
def forward(self, inputs):
embedded = self.embeddings(inputs).view((1, -1))
hid = F.relu(self.linear1(embedded))
out = self.linear2(hid)
log_probs = F.log_softmax(out, dim = 1)
return log_probs
def extract(self, inputs):
embeds = self.embeddings(inputs)
return embeds
class SkipGram(nn.Module):
def __init__(self, vocab_size, embd_size):
super(SkipGram, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embd_size)
def forward(self, focus, context):
embed_focus = self.embeddings(focus).view((1, -1)) # input
embed_ctx = self.embeddings(context).view((1, -1)) # output
score = torch.mm(embed_focus, torch.t(embed_ctx)) # input*output
log_probs = F.logsigmoid(score) # sigmoid
return log_probs
def extract(self, focus):
embed_focus = self.embeddings(focus)
return embed_focus
###Output
_____no_output_____
###Markdown
`torch.mm` Performs a matrix multiplication of the matrices `torch.t` Expects :attr:`input` to be a matrix (2-D tensor) and transposes dimensions 0and 1. Can be seen as a short-hand function for ``transpose(input, 0, 1)``.
###Code
embd_size = 100
learning_rate = 0.001
n_epoch = 30
CONTEXT_SIZE = 2 # 2 words to the left, 2 to the right
def train_cbow():
hidden_size = 64
losses = []
loss_fn = nn.NLLLoss()
model = CBOW(vocab_size, embd_size, CONTEXT_SIZE, hidden_size)
print(model)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
for epoch in range(n_epoch):
total_loss = .0
for context, target in cbow_train:
ctx_idxs = [w2i[w] for w in context]
ctx_var = Variable(torch.LongTensor(ctx_idxs))
model.zero_grad()
log_probs = model(ctx_var)
loss = loss_fn(log_probs, Variable(torch.LongTensor([w2i[target]])))
loss.backward()
optimizer.step()
total_loss += loss.data.item()
losses.append(total_loss)
return model, losses
def train_skipgram():
losses = []
loss_fn = nn.MSELoss()
model = SkipGram(vocab_size, embd_size)
print(model)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
for epoch in range(n_epoch):
total_loss = .0
for in_w, out_w, target in skipgram_train:
in_w_var = Variable(torch.LongTensor([w2i[in_w]]))
out_w_var = Variable(torch.LongTensor([w2i[out_w]]))
model.zero_grad()
log_probs = model(in_w_var, out_w_var)
loss = loss_fn(log_probs[0], Variable(torch.Tensor([target])))
loss.backward()
optimizer.step()
total_loss += loss.data.item()
losses.append(total_loss)
return model, losses
cbow_model, cbow_losses = train_cbow()
sg_model, sg_losses = train_skipgram()
plt.figure(figsize= (10, 4))
plt.subplot(121)
plt.plot(range(n_epoch), cbow_losses, 'r-o', label = 'CBOW Losses')
plt.legend()
plt.subplot(122)
plt.plot(range(n_epoch), sg_losses, 'g-s', label = 'SkipGram Losses')
plt.legend()
plt.tight_layout()
cbow_vec = cbow_model.extract(Variable(torch.LongTensor([v for v in w2i.values()])))
cbow_vec = cbow_vec.data.numpy()
len(cbow_vec[0])
sg_vec = sg_model.extract(Variable(torch.LongTensor([v for v in w2i.values()])))
sg_vec = sg_vec.data.numpy()
len(sg_vec[0])
# 利用PCA算法进行降维
from sklearn.decomposition import PCA
X_reduced = PCA(n_components=2).fit_transform(sg_vec)
# 绘制所有单词向量的二维空间投影
import matplotlib.pyplot as plt
import matplotlib
fig = plt.figure(figsize = (20, 10))
ax = fig.gca()
ax.set_facecolor('black')
ax.plot(X_reduced[:, 0], X_reduced[:, 1], '.', markersize = 1, alpha = 0.4, color = 'white')
# 绘制几个特殊单词的向量
words = list(w2i.keys())
# 设置中文字体,否则无法在图形上显示中文
for w in words:
if w in w2i:
ind = w2i[w]
xy = X_reduced[ind]
plt.plot(xy[0], xy[1], '.', alpha =1, color = 'red')
plt.text(xy[0], xy[1], w, alpha = 1, color = 'white', fontsize = 20)
###Output
_____no_output_____
###Markdown
NGram词向量模型本文件是集智AI学园http://campus.swarma.org 出品的“火炬上的深度学习”第VI课的配套源代码原理:利用一个人工神经网络来根据前N个单词来预测下一个单词,从而得到每个单词的词向量以刘慈欣著名的科幻小说《三体》为例,来展示利用NGram模型训练词向量的方法- 预处理分为两个步骤:1、读取文件、2、分词、3、将语料划分为N+1元组,准备好训练用数据- 在这里,我们并没有去除标点符号,一是为了编程简洁,而是考虑到分词会自动将标点符号当作一个单词处理,因此不需要额外考虑。
###Code
with open("../data/3body.txt", 'r') as f:
text = str(f.read())
import jieba, re
temp = jieba.lcut(text)
words = []
for i in temp:
#过滤掉所有的标点符号
i = re.sub("[\s+\.\!\/_,$%^*(+\"\'””《》]+|[+——!,。?、~@#¥%……&*():]+", "", i)
if len(i) > 0:
words.append(i)
print(len(words))
text[:100]
print(*words[:50])
trigrams = [([words[i], words[i + 1]], words[i + 2]) for i in range(len(words) - 2)]
# 打印出前三个元素看看
print(trigrams[:3])
# 得到词汇表
vocab = set(words)
print(len(vocab))
word_to_idx = {i:[k, 0] for k, i in enumerate(vocab)}
idx_to_word = {k:i for k, i in enumerate(vocab)}
for w in words:
word_to_idx[w][1] +=1
###Output
2000
###Markdown
构造NGram神经网络模型 (三层的网络)1. 输入层:embedding层,这一层的作用是:先将输入单词的编号映射为一个one hot编码的向量,形如:001000,维度为单词表大小。然后,embedding会通过一个线性的神经网络层映射到这个词的向量表示,输出为embedding_dim2. 线性层,从embedding_dim维度到128维度,然后经过非线性ReLU函数3. 线性层:从128维度到单词表大小维度,然后log softmax函数,给出预测每个单词的概率
###Code
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
import torch
class NGram(nn.Module):
def __init__(self, vocab_size, embedding_dim, context_size):
super(NGram, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim) #嵌入层
self.linear1 = nn.Linear(context_size * embedding_dim, 128) #线性层
self.linear2 = nn.Linear(128, vocab_size) #线性层
def forward(self, inputs):
#嵌入运算,嵌入运算在内部分为两步:将输入的单词编码映射为one hot向量表示,然后经过一个线性层得到单词的词向量
embeds = self.embeddings(inputs).view(1, -1)
# 线性层加ReLU
out = F.relu(self.linear1(embeds))
# 线性层加Softmax
out = self.linear2(out)
log_probs = F.log_softmax(out, dim = 1)
return log_probs
def extract(self, inputs):
embeds = self.embeddings(inputs)
return embeds
losses = [] #纪录每一步的损失函数
criterion = nn.NLLLoss() #运用负对数似然函数作为目标函数(常用于多分类问题的目标函数)
model = NGram(len(vocab), 10, 2) #定义NGram模型,向量嵌入维数为10维,N(窗口大小)为2
optimizer = optim.SGD(model.parameters(), lr=0.001) #使用随机梯度下降算法作为优化器
#循环100个周期
for epoch in range(100):
total_loss = torch.Tensor([0])
for context, target in trigrams:
# 准备好输入模型的数据,将词汇映射为编码
context_idxs = [word_to_idx[w][0] for w in context]
# 包装成PyTorch的Variable
context_var = Variable(torch.LongTensor(context_idxs))
# 清空梯度:注意PyTorch会在调用backward的时候自动积累梯度信息,故而每隔周期要清空梯度信息一次。
optimizer.zero_grad()
# 用神经网络做计算,计算得到输出的每个单词的可能概率对数值
log_probs = model(context_var)
# 计算损失函数,同样需要把目标数据转化为编码,并包装为Variable
loss = criterion(log_probs, Variable(torch.LongTensor([word_to_idx[target][0]])))
# 梯度反传
loss.backward()
# 对网络进行优化
optimizer.step()
# 累加损失函数值
total_loss += loss.data
losses.append(total_loss)
print('第{}轮,损失函数为:{:.2f}'.format(epoch, total_loss.numpy()[0]))
###Output
第0轮,损失函数为:56704.61
第1轮,损失函数为:53935.28
第2轮,损失函数为:52241.16
第3轮,损失函数为:51008.51
第4轮,损失函数为:50113.76
第5轮,损失函数为:49434.07
第6轮,损失函数为:48879.33
第7轮,损失函数为:48404.71
第8轮,损失函数为:47983.95
第9轮,损失函数为:47600.01
第10轮,损失函数为:47240.32
第11轮,损失函数为:46897.53
第12轮,损失函数为:46566.24
第13轮,损失函数为:46241.59
第14轮,损失函数为:45920.18
第15轮,损失函数为:45599.50
第16轮,损失函数为:45277.74
第17轮,损失函数为:44953.10
第18轮,损失函数为:44624.41
第19轮,损失函数为:44290.34
第20轮,损失函数为:43950.63
第21轮,损失函数为:43604.48
第22轮,损失函数为:43251.90
第23轮,损失函数为:42891.99
第24轮,损失函数为:42524.64
第25轮,损失函数为:42149.46
第26轮,损失函数为:41766.14
第27轮,损失函数为:41374.89
第28轮,损失函数为:40975.62
第29轮,损失函数为:40568.36
第30轮,损失函数为:40153.31
第31轮,损失函数为:39730.61
第32轮,损失函数为:39300.70
第33轮,损失函数为:38863.39
第34轮,损失函数为:38419.11
第35轮,损失函数为:37968.16
第36轮,损失函数为:37510.99
第37轮,损失函数为:37048.06
第38轮,损失函数为:36579.82
第39轮,损失函数为:36106.78
第40轮,损失函数为:35629.46
第41轮,损失函数为:35148.57
第42轮,损失函数为:34665.39
第43轮,损失函数为:34180.25
第44轮,损失函数为:33693.93
第45轮,损失函数为:33207.48
第46轮,损失函数为:32721.72
第47轮,损失函数为:32237.36
第48轮,损失函数为:31755.00
第49轮,损失函数为:31275.05
第50轮,损失函数为:30798.38
第51轮,损失函数为:30325.62
第52轮,损失函数为:29857.59
第53轮,损失函数为:29394.65
第54轮,损失函数为:28937.08
第55轮,损失函数为:28485.72
第56轮,损失函数为:28041.07
第57轮,损失函数为:27603.33
第58轮,损失函数为:27173.14
第59轮,损失函数为:26750.82
第60轮,损失函数为:26336.92
第61轮,损失函数为:25931.60
第62轮,损失函数为:25534.87
第63轮,损失函数为:25147.07
第64轮,损失函数为:24768.02
第65轮,损失函数为:24397.92
第66轮,损失函数为:24036.68
第67轮,损失函数为:23684.69
第68轮,损失函数为:23341.30
第69轮,损失函数为:23006.46
第70轮,损失函数为:22680.18
第71轮,损失函数为:22361.95
第72轮,损失函数为:22051.86
第73轮,损失函数为:21749.46
第74轮,损失函数为:21454.48
第75轮,损失函数为:21167.06
第76轮,损失函数为:20886.72
第77轮,损失函数为:20613.04
第78轮,损失函数为:20346.13
第79轮,损失函数为:20085.52
第80轮,损失函数为:19831.27
第81轮,损失函数为:19583.16
第82轮,损失函数为:19341.03
第83轮,损失函数为:19104.43
第84轮,损失函数为:18873.11
第85轮,损失函数为:18646.91
第86轮,损失函数为:18425.87
第87轮,损失函数为:18209.80
第88轮,损失函数为:17998.34
第89轮,损失函数为:17791.97
第90轮,损失函数为:17589.94
第91轮,损失函数为:17392.24
第92轮,损失函数为:17199.04
第93轮,损失函数为:17009.97
第94轮,损失函数为:16824.82
第95轮,损失函数为:16643.87
第96轮,损失函数为:16466.76
第97轮,损失函数为:16293.54
第98轮,损失函数为:16123.99
第99轮,损失函数为:15957.75
###Markdown
12m 24s!!!
###Code
# 从训练好的模型中提取每个单词的向量
vec = model.extract(Variable(torch.LongTensor([v[0] for v in word_to_idx.values()])))
vec = vec.data.numpy()
# 利用PCA算法进行降维
from sklearn.decomposition import PCA
X_reduced = PCA(n_components=2).fit_transform(vec)
# 绘制所有单词向量的二维空间投影
import matplotlib.pyplot as plt
import matplotlib
fig = plt.figure(figsize = (20, 10))
ax = fig.gca()
ax.set_facecolor('black')
ax.plot(X_reduced[:, 0], X_reduced[:, 1], '.', markersize = 1, alpha = 0.4, color = 'white')
# 绘制几个特殊单词的向量
words = ['智子', '地球', '三体', '质子', '科学', '世界', '文明', '太空', '加速器', '平面', '宇宙', '信息']
# 设置中文字体,否则无法在图形上显示中文
zhfont1 = matplotlib.font_manager.FontProperties(fname='/Library/Fonts/华文仿宋.ttf', size = 35)
for w in words:
if w in word_to_idx:
ind = word_to_idx[w][0]
xy = X_reduced[ind]
plt.plot(xy[0], xy[1], '.', alpha =1, color = 'red')
plt.text(xy[0], xy[1], w, fontproperties = zhfont1, alpha = 1, color = 'white')
# 定义计算cosine相似度的函数
import numpy as np
def cos_similarity(vec1, vec2):
norm1 = np.linalg.norm(vec1)
norm2 = np.linalg.norm(vec2)
norm = norm1 * norm2
dot = np.dot(vec1, vec2)
result = dot / norm if norm > 0 else 0
return result
# 在所有的词向量中寻找到与目标词(word)相近的向量,并按相似度进行排列
def find_most_similar(word, vectors, word_idx):
vector = vectors[word_to_idx[word][0]]
simi = [[cos_similarity(vector, vectors[num]), key] for num, key in enumerate(word_idx.keys())]
sort = sorted(simi)[::-1]
words = [i[1] for i in sort]
return words
# 与智子靠近的词汇
find_most_similar('智子', vec, word_to_idx)[:10]
###Output
_____no_output_____
###Markdown
Gensim Word2vec
###Code
import gensim as gensim
from gensim.models import Word2Vec
from gensim.models.keyedvectors import KeyedVectors
from gensim.models.word2vec import LineSentence
f = open("../data/三体.txt", 'r')
lines = []
for line in f:
temp = jieba.lcut(line)
words = []
for i in temp:
#过滤掉所有的标点符号
i = re.sub("[\s+\.\!\/_,$%^*(+\"\'””《》]+|[+——!,。?、~@#¥%……&*():;‘]+", "", i)
if len(i) > 0:
words.append(i)
if len(words) > 0:
lines.append(words)
# 调用gensim Word2Vec的算法进行训练。
# 参数分别为:size: 嵌入后的词向量维度;window: 上下文的宽度,min_count为考虑计算的单词的最低词频阈值
model = Word2Vec(lines, size = 20, window = 2 , min_count = 0)
model.wv.most_similar('三体', topn = 10)
# 将词向量投影到二维空间
rawWordVec = []
word2ind = {}
for i, w in enumerate(model.wv.vocab):
rawWordVec.append(model[w])
word2ind[w] = i
rawWordVec = np.array(rawWordVec)
X_reduced = PCA(n_components=2).fit_transform(rawWordVec)
# 绘制星空图
# 绘制所有单词向量的二维空间投影
fig = plt.figure(figsize = (15, 10))
ax = fig.gca()
ax.set_facecolor('black')
ax.plot(X_reduced[:, 0], X_reduced[:, 1], '.', markersize = 1, alpha = 0.3, color = 'white')
# 绘制几个特殊单词的向量
words = ['智子', '地球', '三体', '质子', '科学', '世界', '文明', '太空', '加速器', '平面', '宇宙', '进展','的']
# 设置中文字体,否则无法在图形上显示中文
zhfont1 = matplotlib.font_manager.FontProperties(fname='/Library/Fonts/华文仿宋.ttf', size=26)
for w in words:
if w in word2ind:
ind = word2ind[w]
xy = X_reduced[ind]
plt.plot(xy[0], xy[1], '.', alpha =1, color = 'red')
plt.text(xy[0], xy[1], w, fontproperties = zhfont1, alpha = 1, color = 'yellow')
###Output
_____no_output_____
|
1_Lineare_Regression.ipynb
|
###Markdown
Code-Beispiel: Lineare Regression In diesem Notebook wollen wir mit Hilfe von linearer Regression Vorhersagen auf dem Advertising-Datensatz machen. Ziel ist es anhand von unterschiedlichen Features Vorhersagen über Erkaufserlöse ("Sales") zu machen. Laden des Advertising-Datensatzes Zuerst laden wird die Daten aus der csv-Datei `advertising.csv` in einen Pandas Dataframe. Um den Inhalt zu prüfen, schauen wir uns die ersten paar Zeilen mit Hilfe der `head` Funktion an.
###Code
import pandas as pd
data_raw = pd.read_csv("advertising.csv")
data_raw.head()
###Output
_____no_output_____
###Markdown
Die `head` Funktion zeigt nur die ersten 5 Datenpunkte im Dataframe an. Um zu wissen wie viele Datenpunkte sich im Dataframe befinden, schauen wir auf das `shape` Attribut.
###Code
rows, cols = data_raw.shape
print("Dataframe hat " + str(rows) + " Datenpunkte.")
print("Dataframe hat " + str(cols) + " Spalten.")
###Output
Dataframe hat 200 Datenpunkte.
Dataframe hat 5 Spalten.
###Markdown
Die erste Spalte enthält lediglich einen fortlaufenden Index und wird für die Vorhersage nicht benötigt, sie kann daher entfernt werden.
###Code
data = data_raw.drop(columns=['index'])
data.head()
###Output
_____no_output_____
###Markdown
Als nächstes visualieren wir die Datenpunkte mit Hilfe der `matplotlib`-Library.Dazu erstellten wir einen Plot, welcher auf der x-Achse die `TV`-Daten und auf der y-Achse die `sales`-Daten darstellt.
###Code
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.xlabel("TV Werbebudget (€)")
plt.ylabel("Sales (€)")
plt.show()
###Output
_____no_output_____
###Markdown
Training der linearen Regression Bevor wir mit dem Training beginnen, unterteilten wir die verfügbaren Daten in Trainings- und Testdaten, wobei die Trainingsdaten 80% der ursprünglichen Daten beinhalten sollen und die Testdaten 20%.
###Code
train_data = data.sample(frac=0.8, random_state=0)
test_data = data.drop(train_data.index) # Remove all data in the index column
print('Trainingsdaten')
print(train_data.shape)
print('Testdaten')
print(test_data.shape)
###Output
Trainingsdaten
(160, 4)
Testdaten
(40, 4)
###Markdown
Anschließend trainieren wir auf den Trainingsdaten eine lineare Regression mit dem einen Feature `TV` und dem Label `sales`.
###Code
from sklearn.linear_model import LinearRegression
X_train = train_data['TV'].values.reshape(-1,1) # notwendig wenn nur ein Feature vorhanden ist
y_train = train_data['sales']
reg = LinearRegression()
reg.fit(X_train, y_train) # Praxis aus der Vorlesung
###Output
_____no_output_____
###Markdown
Die lineare Regression ist nun trainiert und das Modell in the `reg` variable verfügbar. Wir können uns nun die Funktionsgeraden ausgeben lassen.
###Code
print(f"Regressionsgerade: y = {reg.intercept_} + {reg.coef_[0]}*TV")
###Output
Regressionsgerade: y = 6.745792674540392 + 0.049503977433492635*TV
###Markdown
Mit dem gerade trainierten Modell können wir nun Vorhersagen auf Datenpunkten machen.
###Code
dataPoint = X_train[0] # erster Datenpunkt aus den Trainingsdaten
prediction = reg.predict(dataPoint.reshape(1, -1)) # Vorhersage auf Datenpunkt
print(f"Bei einem TV-Werbebudget von {dataPoint}€, werden {prediction}€ Umsatz erzielt")
###Output
Bei einem TV-Werbebudget von [69.2]€, werden [10.17146791]€ Umsatz erzielt
###Markdown
Mit dem Modell machen wir nun Vorhersagen auf den Trainingsdaten, um zu visualiesieren wie die trainierte Regressionsgerade aussieht.
###Code
prediction_train = reg.predict(X_train) # Vorhersage auf allen Trainingsdaten zugleich
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.plot(X_train, prediction_train, 'r')
plt.xlabel("TV Werbebudget ($)")
plt.ylabel("Umsatz (Euro)")
plt.show()
###Output
_____no_output_____
###Markdown
Testen des Regressionsmodells Um die Qualität des trainierte Regressionsmodells zu überprüfen, machen wir damit Vorhersagen auf den Testdaten und messen den MSE.
###Code
from sklearn.metrics import mean_squared_error
X_test = test_data['TV'].values.reshape(-1,1)
y_test = test_data['sales']
prediction_test = reg.predict(X_test)
mse_test = mean_squared_error(y_test, prediction_test)
print(f"Mean squared error (MSE) auf Testdaten: {mse_test}")
###Output
Mean squared error (MSE) auf Testdaten: 14.41037265386388
###Markdown
Multidimensionale lineare Regression Im zweiten Schritt erweitern wir die lineare Regression um die beiden Features `radio` und `newspaper`.
###Code
X_train = train_data.drop(columns = ['sales']) # alle Spalten außer Sales
y_train = train_data['sales']
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
print(f"Regression: Y = {reg_all.intercept_} + {reg_all.coef_[0]}*TV + {reg_all.coef_[1]}*radio + {reg_all.coef_[2]}*newspaper")
###Output
Regression: Y = 2.9008471054251572 + 0.04699763711005834*TV + 0.18228777689330944*radio + -0.0012975074726833274*newspaper
###Markdown
Abschließend nutzen wir das neuen Modell um wiederum Vorhersagen auf den Testdaten zu machen.
###Code
X_test = test_data.drop(columns = ['sales'])
y_test = test_data['sales']
predictions = reg_all.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print("Mean squared error (MSE) auf Testdaten: %.2f" % mse)
###Output
Mean squared error (MSE) auf Testdaten: 3.16
###Markdown
Lineare Regression In diesem Notebook werden mittels linearer Regression Vorhersagen auf dem "Advertising"-Datensatz machen. Ziel ist es auf Basis von Werbeausgaben (im Bereich "TV", "Radio" und "Newspaper") Vorhersagen über Verkaufserlöse ("Sales") zu machen. Laden des Advertising-Datensatzes Zuerst laden wird die Daten aus der csv-Datei `advertising.csv` in einen Pandas-DataFrame und schauen uns die Daten kurz an.
###Code
import pandas as pd
data_raw = pd.read_csv("data/advertising.csv")
data_raw.head()
###Output
_____no_output_____
###Markdown
Die `head`-Funktion zeigt nur die ersten 5 Datenpunkte im DataFrame an. Um zu wissen wie viele Datenpunkte sich im DataFrame befinden, schauen wir auf das `shape`-Attribut.
###Code
rows, cols = data_raw.shape
print("Anzahl Zeilen:", rows)
print("Anzahl Spalten:", cols)
###Output
Anzahl Zeilen: 200
Anzahl Spalten: 5
###Markdown
Die erste Spalte enthält lediglich einen fortlaufenden Index und wird für die Vorhersage nicht benötigt, daher wird sie entfernt.
###Code
data = data_raw.drop(columns=['index'])
data.head()
###Output
_____no_output_____
###Markdown
Als nächstes visualieren wir die Datenpunkte mit Hilfe der `matplotlib`-Library.Dazu erstellten wir einen Plot, welcher auf der x-Achse die `TV`-Daten und auf der y-Achse die `sales`-Daten darstellt.
###Code
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.xlabel("TV Werbebudget (€)")
plt.ylabel("Sales (€)")
plt.show()
###Output
_____no_output_____
###Markdown
Training der linearen Regression Als erstes Modell trainieren wir eine lineare Regression mit nur einem Feature. Als Feature wählen wir die Spalte `TV`.Bevor wir mit dem Training beginnen, unterteilten wir die verfügbaren Daten in Trainings- und Testdaten, wobei die Trainingsdaten 80% der ursprünglichen Daten beinhalten sollen und die Testdaten 20%.
###Code
train_data = data.sample(frac=0.8, random_state=0)
test_data = data.drop(train_data.index) # Daten welche nicht in train_data sind
print('Shape der Trainingsdaten:', train_data.shape)
print('Shape der Testdaten:', test_data.shape)
###Output
Shape der Trainingsdaten: (160, 4)
Shape der Testdaten: (40, 4)
###Markdown
Anschließend trainieren wir auf den Trainingsdaten eine lineare Regression mit dem Feature `TV` und dem Label `sales`.Dafür erstellen wir:1. Einen DataFrame mit dem Feature `TV`. Diesen nennen wir `X_train`2. Eine Series mit dem Label. Diese nennen wir `y_train`Um `X_train` als DataFrame und nicht als Series zu erhalten, müssen wir `TV` als Teil einer Liste übergeben. Der folgende Code zeigt den Unterschied:
###Code
X_series = train_data['TV'] # nur TV selektiert
print("Datentyp von X_series:", type(X_series))
X_df = train_data[['TV']] # Liste mit TV als einzigem Element
print("Datentyp von X_df:", type(X_df))
X_train = X_df # Die Features müssen als DataFrame vorliegen und nicht als Series
y_train = train_data['sales']
print("Datentyp von y_train:", type(y_train))
###Output
Datentyp von X_series: <class 'pandas.core.series.Series'>
Datentyp von X_df: <class 'pandas.core.frame.DataFrame'>
Datentyp von y_train: <class 'pandas.core.series.Series'>
###Markdown
Jetzt folgt das eigentliche Training des Modells:
###Code
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X_train, y_train)
###Output
_____no_output_____
###Markdown
Die lineare Regression ist nun trainiert und die Modellgewichte in the `reg`-Variable verfügbar. Wir können uns nun die Regressionsgerade ausgeben lassen.
###Code
print(f"Regressionsgerade: y = {reg.intercept_} + {reg.coef_[0]}*TV")
###Output
Regressionsgerade: y = 6.745792674540395 + 0.04950397743349262*TV
###Markdown
Mit dem trainierten Modell können wir nun Vorhersagen auf einzelnen Datenpunkten machen.
###Code
dataPoint = X_train.iloc[0] # erster Datenpunkt aus den Trainingsdaten
prediction = reg.predict([dataPoint]) # predict-Methode erwartet Liste von Datenpunkten
print(f"Bei einem TV-Werbebudget von {dataPoint[0]}€, werden {prediction[0]}€ Umsatz erzielt.")
###Output
Bei einem TV-Werbebudget von 69.2€, werden 10.171467912938084€ Umsatz erzielt.
###Markdown
Um zu Visualisieren wie die trainierte Regressionsgerade aussieht, machen wir mit dem Modell Vorhersagen auf den Trainingsdatenpunkten.
###Code
prediction_train = reg.predict(X_train) # Vorhersage auf allen Trainingsdaten gleichzeitig
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales']) # Trainingsdatenpunkte
plt.plot(X_train, prediction_train, 'r') # Regressionsgerade
plt.xlabel("TV Werbebudget ($)")
plt.ylabel("Umsatz (Euro)")
plt.show()
###Output
_____no_output_____
###Markdown
Testen des Regressionsmodells Um die Qualität des trainierte Regressionsmodells zu überprüfen, machen wir damit Vorhersagen auf den Testdaten und bestimmen den MSE.
###Code
from sklearn.metrics import mean_squared_error
X_test = test_data[['TV']] # X_test muss ein DateFrame sein
y_test = test_data['sales'] # y_test muss eine Series sein
prediction_test = reg.predict(X_test)
mse_test = mean_squared_error(y_test, prediction_test)
print("Mean squared error (MSE) auf Testdaten:", mse_test)
###Output
Mean squared error (MSE) auf Testdaten: 14.410372653863877
###Markdown
Multidimensionale lineare Regression Wir erweitern nun die lineare Regression indem wir die beiden Features `radio` und `newspaper` zusätzlich benutzen.
###Code
X_train = train_data[["TV", "radio", "newspaper"]]
y_train = train_data['sales']
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
print(f"Regression: Y = {reg_all.intercept_} + {reg_all.coef_[0]}*TV + {reg_all.coef_[1]}*radio + {reg_all.coef_[2]}*newspaper")
###Output
Regression: Y = 2.9008471054251572 + 0.04699763711005833*TV + 0.18228777689330938*radio + -0.0012975074726832771*newspaper
###Markdown
Abschließend nutzen wir das neuen Modell um wiederum Vorhersagen auf den Testdaten zu machen.
###Code
X_test = test_data[["TV", "radio", "newspaper"]]
y_test = test_data['sales']
predictions = reg_all.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print("Mean squared error (MSE) auf Testdaten: %.2f" % mse)
###Output
Mean squared error (MSE) auf Testdaten: 3.16
###Markdown
Code-Beispiel: Lineare Regression In diesem Notebook wollen wir mit Hilfe von linearer Regression Vorhersagen auf dem Advertising-Datensatz machen. Ziel ist es anhand von unterschiedlichen Features Vorhersagen über Erkaufserlöse ("Sales") zu machen. Laden des Advertising-Datensatzes Zuerst laden wird die Daten aus der csv-Datei `advertising.csv` in einen Pandas Dataframe. Um den Inhalt zu prüfen, schauen wir uns die ersten paar Zeilen mit Hilfe der `head` Funktion an.
###Code
import pandas as pd
data_raw = pd.read_csv("advertising.csv")
data_raw.head()
###Output
_____no_output_____
###Markdown
Die `head` Funktion zeigt nur die ersten 5 Datenpunkte im Dataframe an. Um zu wissen wie viele Datenpunkte sich im Dataframe befinden, schauen wir auf die `shape` Variable.
###Code
rows, cols = data_raw.shape
print("Dataframe hat " + str(rows) + " Datenpunkte.")
print("Dataframe hat " + str(cols) + " Attribute.")
###Output
Dataframe hat 200 Datenpunkte.
Dataframe hat 5 Attribute.
###Markdown
Die erste Spalte enthält lediglich einen fortlaufenden Index und wir für die Vorhersage nicht benötigt, sie kann daher entfernt werden.
###Code
data = data_raw.drop(columns=['index'])
data.head()
###Output
_____no_output_____
###Markdown
Als nächstes visualieren wir die Datenpunkte mit Hilfe der `matplotlib`-Library.Dazu erstellten wir einen Plot, welcher auf der x-Achse die `TV`-Daten und auf der y-Achse die `sales`-Daten darstellt.
###Code
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.xlabel("TV Werbebudget (€)")
plt.ylabel("Sales (€)")
plt.show()
###Output
_____no_output_____
###Markdown
Training der linearen Regression Bevor wir mit dem Training beginnen, unterteilten wir die verfügbaren Daten in Trainings- und Testdaten, wobei die Trainingsdaten 80% der ursprünglichen Daten beinhalten sollen und die Testdaten 20%.
###Code
train_data = data.sample(frac=0.8, random_state=0)
test_data = data.drop(train_data.index)
print('Trainingsdaten')
print(train_data.shape)
print('Testdaten')
print(test_data.shape)
###Output
Trainingsdaten
(160, 4)
Testdaten
(40, 4)
###Markdown
Anschließend trainieren wir auf den Trainingsdaten eine lineare Regression mit dem einen Feature `TV` und dem Label `sales`.
###Code
from sklearn.linear_model import LinearRegression
X_train = train_data['TV'].values.reshape(-1,1) # notwendig wenn nur ein Feature vorhanden ist
y_train = train_data['sales']
reg = LinearRegression()
reg.fit(X_train, y_train)
###Output
_____no_output_____
###Markdown
Die lineare Regression ist nun trainiert und das Modell in the `reg` variable verfügbar. Wir können uns nun die Funktionsgeraden ausgeben lassen.
###Code
print(f"Regressionsgerade: y = {reg.intercept_} + {reg.coef_[0]}*TV")
###Output
Regressionsgerade: y = 6.745792674540395 + 0.04950397743349262*TV
###Markdown
Mit dem gerade trainierten Modell können wir nun Vorhersagen auf Datenpunkten machen.
###Code
dataPoint = X_train[0] # erster Datenpunkt aus den Trainingsdaten
prediction = reg.predict(dataPoint.reshape(1, -1)) # Vorhersage auf Datenpunkt
print(f"Bei einem TV-Werbebudget von {dataPoint}€, werden {prediction}€ Umsatz erzielt")
###Output
Bei einem TV-Werbebudget von [69.2]€, werden [10.17146791]€ Umsatz erzielt
###Markdown
Mit dem Modell machen wir nun Vorhersagen auf den Trainingsdaten, um zu visualiesieren wie die trainierte Regressionsgerade aussieht.
###Code
prediction_train = reg.predict(X_train) # Vorhersage auf allen Trainingsdaten zugleich
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.plot(X_train, prediction_train, 'r')
plt.xlabel("TV Werbebudget ($)")
plt.ylabel("Umsatz (Euro)")
plt.show()
###Output
_____no_output_____
###Markdown
Testen des Regressionsmodells Um die Qualität des trainierte Regressionsmodells zu überprüfen, machen wir damit Vorhersagen auf den Testdaten und messen den MSE.
###Code
from sklearn.metrics import mean_squared_error
X_test = test_data['TV'].values.reshape(-1,1)
y_test = test_data['sales']
prediction_test = reg.predict(X_test)
mse_test = mean_squared_error(y_test, prediction_test)
print(f"Mean squared error (MSE) auf Testdaten: {mse_test}")
###Output
Mean squared error (MSE) auf Testdaten: 14.410372653863877
###Markdown
Multidimensionale lineare Regression Im zweiten Schritt erweitern wir die lineare Regression um die beiden Features `radio` und `newspaper`.
###Code
X_train = train_data.drop(columns = ['sales']) # alle Spalten außer Sales
y_train = train_data['sales']
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
print(f"Regression: Y = {reg_all.intercept_} + {reg_all.coef_[0]}*TV + {reg_all.coef_[1]}*radio + {reg_all.coef_[2]}*newspaper")
###Output
Regression: Y = 2.9008471054251572 + 0.04699763711005833*TV + 0.18228777689330938*radio + -0.0012975074726832771*newspaper
###Markdown
Abschließend nutzen wir das neuen Modell um wiederum Vorhersagen auf den Testdaten zu machen.
###Code
X_test = test_data.drop(columns = ['sales'])
y_test = test_data['sales']
predictions = reg_all.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print("Mean squared error (MSE) auf Testdaten: %.2f" % mse)
###Output
Mean squared error (MSE) auf Testdaten: 3.16
###Markdown
Code-Beispiel: Lineare Regression In diesem Notebook wollen wir mit Hilfe von linearer Regression Vorhersagen auf dem Advertising-Datensatz machen. Ziel ist es anhand von unterschiedlichen Features Vorhersagen über Erkaufserlöse ("Sales") zu machen. Laden des Advertising-Datensatzes Zuerst laden wird die Daten aus der csv-Datei `advertising.csv` in einen Pandas Dataframe. Um den Inhalt zu prüfen, schauen wir uns die ersten paar Zeilen mit Hilfe der `head` Funktion an.
###Code
import pandas as pd
data_raw = pd.read_csv("advertising.csv")
data_raw.head()
###Output
_____no_output_____
###Markdown
Die `head` Funktion zeigt nur die ersten 5 Datenpunkte im Dataframe an. Um zu wissen wie viele Datenpunkte sich im Dataframe befinden, schauen wir auf die `shape` Variable.
###Code
rows, cols = data_raw.shape
print("Dataframe hat " + str(rows) + " Datenpunkte.")
print("Dataframe hat " + str(cols) + " Attribute.")
###Output
Dataframe hat 200 Datenpunkte.
Dataframe hat 5 Attribute.
###Markdown
Die erste Spalte enthält lediglich einen fortlaufenden Index und wir für die Vorhersage nicht benötigt, sie kann daher entfernt werden.
###Code
data = data_raw.drop(columns=['index'])
data.head()
###Output
_____no_output_____
###Markdown
Als nächstes visualieren wir die Datenpunkte mit Hilfe der `matplotlib`-Library.Dazu erstellten wir einen Plot, welcher auf der x-Achse die `TV`-Daten und auf der y-Achse die `sales`-Daten darstellt.
###Code
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.xlabel("TV Werbebudget (€)")
plt.ylabel("Sales (€)")
plt.show()
###Output
_____no_output_____
###Markdown
Training der linearen Regression Bevor wir mit dem Training beginnen, unterteilten wir die verfügbaren Daten in Trainings- und Testdaten, wobei die Trainingsdaten 80% der ursprünglichen Daten beinhalten sollen und die Testdaten 20%.
###Code
train_data = data.sample(frac=0.8, random_state=0)
test_data = data.drop(train_data.index)
print('Trainingsdaten')
print(train_data.shape)
print('Testdaten')
print(test_data.shape)
###Output
Trainingsdaten
(160, 4)
Testdaten
(40, 4)
###Markdown
Anschließend trainieren wir auf den Trainingsdaten eine lineare Regression mit dem einen Feature `TV` und dem Label `sales`.
###Code
from sklearn.linear_model import LinearRegression
X_train = train_data['TV'].values.reshape(-1,1) # notwendig wenn nur ein Feature vorhanden ist
y_train = train_data['sales']
reg = LinearRegression()
reg.fit(X_train, y_train)
X_train2 = train_data['radio'].values.reshape(-1,1) # notwendig wenn nur ein Feature vorhanden ist
y_train2 = train_data['sales']
reg2 = LinearRegression()
reg2.fit(X_train2, y_train2)
X_train3 = train_data['newspaper'].values.reshape(-1,1) # notwendig wenn nur ein Feature vorhanden ist
y_train3 = train_data['sales']
reg3 = LinearRegression()
reg3.fit(X_train3, y_train3)
###Output
_____no_output_____
###Markdown
Die lineare Regression ist nun trainiert und das Modell in the `reg` variable verfügbar. Wir können uns nun die Funktionsgeraden ausgeben lassen.
###Code
print(f"Regressionsgerade: y = {reg.intercept_} + {reg.coef_[0]}*TV")
###Output
Regressionsgerade: y = 6.745792674540392 + 0.049503977433492635*TV
###Markdown
Mit dem gerade trainierten Modell können wir nun Vorhersagen auf Datenpunkten machen.
###Code
dataPoint = X_train[0] # erster Datenpunkt aus den Trainingsdaten
prediction = reg.predict(dataPoint.reshape(1, -1)) # Vorhersage auf Datenpunkt
print(f"Bei einem TV-Werbebudget von {dataPoint}€, werden {prediction}€ Umsatz erzielt")
###Output
Bei einem TV-Werbebudget von [69.2]€, werden [10.17146791]€ Umsatz erzielt
###Markdown
Mit dem Modell machen wir nun Vorhersagen auf den Trainingsdaten, um zu visualiesieren wie die trainierte Regressionsgerade aussieht.
###Code
prediction_train = reg.predict(X_train) # Vorhersage auf allen Trainingsdaten zugleich
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.plot(X_train, prediction_train, 'r')
plt.xlabel("TV Werbebudget ($)")
plt.ylabel("Umsatz (Euro)")
plt.show()
###Output
_____no_output_____
###Markdown
Testen des Regressionsmodells Um die Qualität des trainierte Regressionsmodells zu überprüfen, machen wir damit Vorhersagen auf den Testdaten und messen den MSE.
###Code
from sklearn.metrics import mean_squared_error
X_test = test_data['TV'].values.reshape(-1,1)
y_test = test_data['sales']
prediction_test = reg.predict(X_test)
mse_test = mean_squared_error(y_test, prediction_test)
print(f"Mean squared error (MSE) auf Testdaten: {mse_test}")
X_test2 = test_data['radio'].values.reshape(-1,1)
y_test2 = test_data['sales']
prediction_test2 = reg2.predict(X_test2)
mse_test2 = mean_squared_error(y_test2, prediction_test2)
print(f"Mean squared error (MSE) auf Testdaten: {mse_test2}")
X_test3 = test_data['newspaper'].values.reshape(-1,1)
y_test3 = test_data['sales']
prediction_test3 = reg3.predict(X_test3)
mse_test3 = mean_squared_error(y_test3, prediction_test3)
print(f"Mean squared error (MSE) auf Testdaten: {mse_test3}")
###Output
Mean squared error (MSE) auf Testdaten: 14.41037265386388
Mean squared error (MSE) auf Testdaten: 14.678657098022956
Mean squared error (MSE) auf Testdaten: 25.543312576681807
###Markdown
Multidimensionale lineare Regression Im zweiten Schritt erweitern wir die lineare Regression um die beiden Features `radio` und `newspaper`.
###Code
X_train = train_data.drop(columns = ['sales']) # alle Spalten außer Sales
y_train = train_data['sales']
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
print(f"Regression: Y = {reg_all.intercept_} + {reg_all.coef_[0]}*TV + {reg_all.coef_[1]}*radio + {reg_all.coef_[2]}*newspaper")
###Output
Regression: Y = 2.9008471054251572 + 0.04699763711005834*TV + 0.18228777689330944*radio + -0.0012975074726833274*newspaper
###Markdown
Abschließend nutzen wir das neuen Modell um wiederum Vorhersagen auf den Testdaten zu machen.
###Code
X_test = test_data.drop(columns = ['sales'])
y_test = test_data['sales']
predictions = reg_all.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print("Mean squared error (MSE) auf Testdaten: %.2f" % mse)
###Output
Mean squared error (MSE) auf Testdaten: 3.16
###Markdown
Lineare Regression In diesem Notebook werden mittels linearer Regression Vorhersagen auf dem "Advertising"-Datensatz machen. Ziel ist es auf Basis von Werbeausgaben (im Bereich "TV", "Radio" und "Newspaper") Vorhersagen über Verkaufserlöse ("Sales") zu machen. Laden des Advertising-Datensatzes Zuerst laden wird die Daten aus der csv-Datei `advertising.csv` in einen Pandas-DataFrame und schauen uns die Daten kurz an.
###Code
import pandas as pd
data_raw = pd.read_csv("data/advertising.csv")
data_raw.head()
###Output
_____no_output_____
###Markdown
Die `head`-Funktion zeigt nur die ersten 5 Datenpunkte im DataFrame an. Um zu wissen wie viele Datenpunkte sich im DataFrame befinden, schauen wir auf das `shape`-Attribut.
###Code
rows, cols = data_raw.shape
print("Anzahl Zeilen:", rows)
print("Anzahl Spalten:", cols)
###Output
Anzahl Zeilen: 200
Anzahl Spalten: 5
###Markdown
Die erste Spalte enthält lediglich einen fortlaufenden Index und wird für die Vorhersage nicht benötigt, daher wird sie entfernt.
###Code
data = data_raw.drop(columns=['index'])
data.head()
###Output
_____no_output_____
###Markdown
Als nächstes visualieren wir die Datenpunkte mit Hilfe der `matplotlib`-Library.Dazu erstellten wir einen Plot, welcher auf der x-Achse die `TV`-Daten und auf der y-Achse die `sales`-Daten darstellt.
###Code
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales'])
plt.xlabel("TV Werbebudget (€)")
plt.ylabel("Sales (€)")
plt.show()
###Output
_____no_output_____
###Markdown
Training der linearen Regression Als erstes Modell trainieren wir eine lineare Regression mit nur einem Feature. Als Feature wählen wir die Spalte `TV`.Bevor wir mit dem Training beginnen, unterteilten wir die verfügbaren Daten in Trainings- und Testdaten, wobei die Trainingsdaten 80% der ursprünglichen Daten beinhalten sollen und die Testdaten 20%.
###Code
train_data = data.sample(frac=0.8, random_state=0)
test_data = data.drop(train_data.index) # Daten welche nicht in train_data sind
print('Shape der Trainingsdaten:', train_data.shape)
print('Shape der Testdaten:', test_data.shape)
###Output
Shape der Trainingsdaten: (160, 4)
Shape der Testdaten: (40, 4)
###Markdown
Anschließend trainieren wir auf den Trainingsdaten eine lineare Regression mit dem Feature `TV` und dem Label `sales`.Dafür erstellen wir:1. Einen DataFrame mit dem Feature `TV`. Diesen nennen wir `X_train`2. Eine Series mit dem Label. Diese nennen wir `y_train`Um `X_train` als DataFrame und nicht als Series zu erhalten, müssen wir `TV` als Teil einer Liste übergeben. Der folgende Code zeigt den Unterschied:
###Code
X_series = train_data['TV'] # nur TV selektiert
print("Datentyp von X_series:", type(X_series))
X_df = train_data[['TV']] # Liste mit TV als einzigem Element
print("Datentyp von X_df:", type(X_df))
X_train = X_df # Die Features müssen als DataFrame vorliegen und nicht als Series
y_train = train_data['sales']
print("Datentyp von y_train:", type(y_train))
###Output
Datentyp von X_series: <class 'pandas.core.series.Series'>
Datentyp von X_df: <class 'pandas.core.frame.DataFrame'>
Datentyp von y_train: <class 'pandas.core.series.Series'>
###Markdown
Jetzt folgt das eigentliche Training des Modells:
###Code
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X_train, y_train)
###Output
_____no_output_____
###Markdown
Die lineare Regression ist nun trainiert und die Modellgewichte in the `reg`-Variable verfügbar. Wir können uns nun die Regressionsgerade ausgeben lassen.
###Code
print(f"Regressionsgerade: y = {reg.intercept_} + {reg.coef_[0]}*TV")
###Output
Regressionsgerade: y = 6.745792674540394 + 0.04950397743349263*TV
###Markdown
Mit dem trainierten Modell können wir nun Vorhersagen auf einzelnen Datenpunkten machen.
###Code
dataPoint = X_train.iloc[0] # erster Datenpunkt aus den Trainingsdaten
prediction = reg.predict([dataPoint]) # predict-Methode erwartet Liste von Datenpunkten
print(f"Bei einem TV-Werbebudget von {dataPoint[0]}€, werden {prediction[0]}€ Umsatz erzielt.")
###Output
Bei einem TV-Werbebudget von 69.2€, werden 10.171467912938084€ Umsatz erzielt.
###Markdown
Um zu Visualisieren wie die trainierte Regressionsgerade aussieht, machen wir mit dem Modell Vorhersagen auf den Trainingsdatenpunkten.
###Code
prediction_train = reg.predict(X_train) # Vorhersage auf allen Trainingsdaten gleichzeitig
plt.figure(figsize=(16, 8))
plt.scatter(data['TV'], data['sales']) # Trainingsdatenpunkte
plt.plot(X_train, prediction_train, 'r') # Regressionsgerade
plt.xlabel("TV Werbebudget ($)")
plt.ylabel("Umsatz (Euro)")
plt.show()
###Output
_____no_output_____
###Markdown
Testen des Regressionsmodells Um die Qualität des trainierte Regressionsmodells zu überprüfen, machen wir damit Vorhersagen auf den Testdaten und bestimmen den MSE.
###Code
from sklearn.metrics import mean_squared_error
X_test = test_data[['TV']] # X_test muss ein DateFrame sein
y_test = test_data['sales'] # y_test muss eine Series sein
prediction_test = reg.predict(X_test)
mse_test = mean_squared_error(y_test, prediction_test)
print("Mean squared error (MSE) auf Testdaten:", mse_test)
###Output
Mean squared error (MSE) auf Testdaten: 14.41037265386388
###Markdown
Multidimensionale lineare Regression Wir erweitern nun die lineare Regression indem wir die beiden Features `radio` und `newspaper` zusätzlich benutzen.
###Code
X_train = train_data[["TV", "radio", "newspaper"]]
y_train = train_data['sales']
reg_all = LinearRegression()
reg_all.fit(X_train, y_train)
print(f"Regression: Y = {reg_all.intercept_} + {reg_all.coef_[0]}*TV + {reg_all.coef_[1]}*radio + {reg_all.coef_[2]}*newspaper")
###Output
Regression: Y = 2.9008471054251608 + 0.04699763711005833*TV + 0.1822877768933094*radio + -0.0012975074726833402*newspaper
###Markdown
Abschließend nutzen wir das neuen Modell um wiederum Vorhersagen auf den Testdaten zu machen.
###Code
X_test = test_data[["TV", "radio", "newspaper"]]
y_test = test_data['sales']
predictions = reg_all.predict(X_test)
mse = mean_squared_error(y_test, predictions)
print("Mean squared error (MSE) auf Testdaten: %.2f" % mse)
###Output
Mean squared error (MSE) auf Testdaten: 3.16
|
notebooks/BVP_stability.ipynb
|
###Markdown
BVP stability[AMath 585, Winter Quarter 2020](http://staff.washington.edu/rjl/classes/am585w2020/) at the University of Washington. Developed by R.J. LeVeque and distributed under the [BSD license](https://github.com/rjleveque/amath585w2020/blob/master/LICENSE). You are free to modify and use as you please, with attribution.These notebooks are all [available on Github](https://github.com/rjleveque/amath585w2020/).-----Compute the inverse of tridiagonal matrices (augmented by boundary conditions) coming from the BVP $u''(x) = f(x)$.
###Code
%matplotlib inline
from pylab import *
from scipy.sparse import diags
# import a module with a new local name for brevity:
import scipy.sparse.linalg as sp_linalg
###Output
_____no_output_____
###Markdown
Suppress warnings coming from adding new nonzeros in a crc matrix:
###Code
import logging
logging.captureWarnings(True)
###Output
_____no_output_____
###Markdown
Set up the matrixWe will investigate the matrix given in equation (2.43) of the textbook for Dirichlet boundary conditions. This uses the formulation where the standard tridiagonal matrix is augmented by two additional rows for $U_0$ and $U_{m+1}$ that correspond to the equations $U_0 = \alpha$ and $U_1 = \beta$.We will also consider the matrix given at the top of page 32, which is similar but implements a Neumann boundary condition with a second-order accurate one-sided approximation to $u''(x_0)$.**NOTE:** The equation at the bottom of page 31 should have $-\sigma$ on the right hand side, and the matrix at the top of page 32 is incorrect. The first row should correspond to the corrected equation from p. 31. The correct version is: \begin{align*}\frac{1}{h^2} \left[\begin{array}{ccccccccccccccc}-3h/2 & 2h & -h/2\\1&-2&1\\&1&-2&1\\&&&\ddots\\&&&&1&-2&1\\&&&&&0&h^2\end{array}\right]~\left[ \begin{array}{ccccccccccccccc}U_0 \\ U_1 \\ U_2 \\ \vdots \\ U_m \\ U_{m+1}\end{array} \right]= \left[ \begin{array}{ccccccccccccccc}\sigma \\ f(x_1) \\ f(x_2) \\ \vdots \\ f(x_m) \\ \beta\end{array} \right]\end{align*}Note that the first equation in this system approximates $u'(x_0) = \sigma$ with a second-order one-sided difference, and the last equation is simply the Dirichlet BC $u(x_{m+1}) = \beta$. The function below creates such a matrix, and also prints out some information about it, including the norm of the inverse. The `bc` parameter controls whether the left boundary is Dirchlet or Neumann. In the Dirichlet case the first row is simpler, with only one nonzero.
###Code
ax = 0.
bx = 1.
def test_A(m, bc='dirichlet'):
h = (bx-ax) / (m+1)
em = ones(m+2)
em1 = ones(m+1)
A = diags([em1, -2*em, em1], [-1, 0, 1], format='csc')
# fix the first row:
if bc=='dirichlet':
A[0,0] = h**2
A[0,1] = 0.
elif bc=='neumann':
A[0,0] = -3*h/2.
A[0,1] = 2*h
A[0,2] = -h/2. # adding a new nonzero
else:
raise ValueError('Unrecognized bc: %s' % bc)
# fix the last row:
A[m+1,m] = 0.
A[m+1,m+1] = h**2
A = A / h**2
print('m = ', m)
print('A has type %s, of shape %s' % (type(A), A.shape))
Ainv = sp_linalg.inv(A)
normAinv = sp_linalg.norm(Ainv,inf)
print('Infinity norm of Ainv = %g' % normAinv)
return A
###Output
_____no_output_____
###Markdown
Dirichlet boundary conditionsHere's what the matrix looks like for a small value of $m$:
###Code
A = test_A(5, 'dirichlet')
print(A.toarray())
###Output
_____no_output_____
###Markdown
Note that the max-norm of $A^{-1}$ is 1.125. For stability we hope this is uniformly bounded as we increase $m$ (and decrease $h$). In fact we see it is constant:
###Code
A = test_A(99, 'dirichlet')
A = test_A(199, 'dirichlet')
###Output
_____no_output_____
###Markdown
Plot the columns of $A^{-1}$Rather than printing out $A^{-1}$, it is more illuminating to plot the values in each column vs. the row index.From the discussion of Section 2.11 you should know what values to expect for the interior columns of $A^{-1}$ (see Figure 2.1 in the book). The first and last column are plotted separately below since they are scaled differently. Think about what these columns represent in terms of the way we have included the boundary conditions into the matrix formulation.
###Code
m = 5
x = linspace(ax,bx,m+2)
A = test_A(m, bc='dirichlet')
Ainv = sp_linalg.inv(A).toarray()
figure(figsize=(12,5))
subplot(1,2,1)
for j in range(1,m+1):
plot(Ainv[:,j], 'o-', label='column %i' % j)
legend()
xlabel('row index')
ylabel('Ainv value')
subplot(1,2,2)
plot(Ainv[:,0], 'o-', label='column 0')
plot(Ainv[:,m+1], 'o-', label='column %i' % (m+1))
legend()
xlabel('row index')
###Output
_____no_output_____
###Markdown
Neumann boundary conditionsRepeat these tests with Neumman conditions:
###Code
A = test_A(5, 'neumann')
print(A.toarray())
###Output
_____no_output_____
###Markdown
Note that again the max-norm of $A^{-1}$ stays constant as we increase $m$:
###Code
A = test_A(99, bc='neumann')
A = test_A(199, bc='neumann')
###Output
_____no_output_____
###Markdown
Plot the columns of $A^{-1}$Think about why these columns have the form they do.
###Code
m = 5
x = linspace(ax,bx,m+2)
A = test_A(m, bc='neumann')
Ainv = sp_linalg.inv(A).toarray()
figure(figsize=(12,5))
subplot(1,2,1)
for j in range(1,m+1):
plot(Ainv[:,j], 'o-', label='column %i' % j)
legend()
xlabel('row index')
ylabel('Ainv value')
subplot(1,2,2)
plot(Ainv[:,0], 'o-', label='column 0')
plot(Ainv[:,m+1], 'o-', label='column %i' % (m+1))
legend()
xlabel('row index')
###Output
_____no_output_____
|
TrueCompERGenerator.ipynb
|
###Markdown
Generate Rockfall Matrix for True Erosion Rates Syntax`TrueParsPars = TrueCompERGenerator(RunTruePars,RunPars,CalcPars)` Input `RunTruePars` : dictionary containing parameters for constant erosion under the "true" erosion rate. Variables`scenarios` : number of scenarios for the erosion rate/shape value; `total_time` : total time in the model run `MeasPars` : dictionary of size 9 with the information relevant to the run. Output`RunTruePars` : dictionary containing the RunParameters for the true erosion rate runs Variables`RockfallMatrix` : rockfall matrix with the true uniform erosion rate each year (cm) `TrueErosionRates` : output of the true erosion rates (L/T) (cm yr-1); Notes**Date of Creation:** 5. Juli 2021 **Author:** Donovan Dennis **Update:**
###Code
def TrueCompERGenerator(RunTruePars,RunPars,CalcPars):
# bring in the relevant parameters
TrueERs = RunPars['TrueErosionRates']
scenarios = RunTruePars['scenarios']
total_time = RunTruePars['total_time']
# open up a matrix for the annual erosion magnitudes
TrueCompRockfallMatrix = np.empty((scenarios, total_time))
ErosionRates = [0]*scenarios
# loop through the set the eroded amount every year to the respective measured erosion rate
for i in range(scenarios):
TrueCompRockfallMatrix[i,:] = TrueERs[i]
ErosionRates[i] = np.sum(TrueCompRockfallMatrix[i,:]) / total_time
# assign to the parameters dictionary
RunTruePars['RockfallMatrix'] = TrueCompRockfallMatrix
RunTruePars['TrueErosionRates'] = TrueERs
return RunTruePars
###Output
_____no_output_____
|
K_means_Algorithm.ipynb
|
###Markdown
###Code
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import warnings
warnings.filterwarnings('ignore')
iris = load_iris().data
iris = pd.DataFrame(iris)
iris.columns = load_iris().feature_names
iris.head()
import matplotlib.pyplot as plt
import seaborn as sns
def plot_data(X, cluster_label):
return sns.lmplot(
data = X,
x = X.columns[0],
y = X.columns[1],
hue = cluster_label,
fit_reg = False,
legend = False
)
plot_data(iris, None)
plt.show()
k = 10
def centroids_func(X, k):
initial_centroids = X.sample(n = k)
initial_centroids.index = np.arange(1, k + 1)
return initial_centroids
centroids = centroids_func(iris, k)
centroids
def plot_centroids(figure, U):
figure.ax.scatter(
x = U['sepal length (cm)'],
y = U['sepal width (cm)'],
color = 'red',
marker = 'x'
)
# dispalying the position of each centroid in scatterplot
dot_plot = plot_data(iris, None)
plot_centroids(dot_plot, centroids)
# Euclidean distance between it and every centroid.
def assign_cluster(X, U):
m = len(X)
C = pd.DataFrame(np.empty(m), columns = ['label'])
for (i, example) in X.iterrows():
distance = (example - U).apply(np.linalg.norm, axis = 1)
C.loc[i] = (distance ** 2).idxmin()
return C
# lets assign training examples from above to cluster and look at them
labels = assign_cluster(iris, centroids)
dot_plot = plot_data(pd.concat((iris, labels), axis = 1), 'label')
plot_centroids(dot_plot, centroids)
# lets look at the position of new centroid
def updated_centroid(X, C):
joined = pd.concat((X, C), axis = 1)
return joined.groupby('label').mean()
centroids = updated_centroid(iris, labels)
dot_plot = plot_data(pd.concat((iris, labels), axis = 1), 'label')
plot_centroids(dot_plot, centroids)
from scipy.spatial.distance import cdist
from sklearn.cluster import KMeans
ks = range(1, 10)
inertia = []
for i in ks:
model = KMeans(n_clusters= i).fit(iris)
model.fit(iris)
inertia.append(sum(np.min(cdist(iris, model.cluster_centers_, 'euclidean'), axis = 1))/iris.shape[0])
plt.plot(ks, inertia, '-o')
plt.xlabel('number of clusters , k')
plt.ylabel('inertia')
plt.xticks(ks)
plt.show()
from sklearn.metrics import silhouette_score
silhouette_score(iris, labels, metric='euclidean')
# let's pick 3 cluster
dot_plot = plot_data(pd.concat((iris, assign_cluster(iris, centroids_func(iris, 3))), axis = 1), 'label')
plot_centroids(dot_plot, centroids_func(iris, 3))
def plot_data1(X, cluster_label):
return sns.lmplot(
data = X,
x = X.columns[1],
y = X.columns[2],
hue = cluster_label,
fit_reg = False,
legend = False
)
dot_plot = plot_data1(pd.concat((iris, assign_cluster(iris, centroids_func(iris, 3))), axis = 1), 'label')
plot_centroids(dot_plot, centroids_func(iris, 3))
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
xs = iris['sepal length (cm)']
ax.set_xlabel('Sepal Length')
ys = iris['petal length (cm)']
ax.set_ylabel('Petal Length')
zs = iris['petal width (cm)']
ax.set_zlabel('Petal Width')
ax.scatter(xs, ys, zs, s = 50, c = load_iris().target)
plt.show()
# with sklearn kmeans
model = KMeans(n_clusters= 3)
model.fit(iris)
model.predict(iris)
ks = range(1, 10)
inertia = []
for i in ks:
models = KMeans(n_clusters= i)
models.fit(iris)
inertia.append(models.inertia_)
plt.plot(ks, inertia, '-o')
plt.xlabel('number of clusters k')
plt.ylabel('inertia')
plt.xticks(ks)
plt.show()
plt.scatter(iris['sepal length (cm)'], iris['petal length (cm)'], c = model.predict(iris), alpha = 0.5)
centroids = model.cluster_centers_
centroids_x = centroids[:,0]
centroids_y = centroids[:,1]
plt.scatter(centroids_x, centroids_y, marker= '.', s = 50)
zs = iris['petal width (cm)']
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
xs = iris['sepal length (cm)']
ax.set_xlabel('Sepal Length')
ys = iris['petal length (cm)']
ax.set_ylabel('Petal Length')
zs = iris['petal width (cm)']
ax.set_zlabel('Petal Width')
ax.scatter(xs, ys, zs, s = 50, c = model.predict(iris))
plt.show()
###Output
_____no_output_____
|
chapter_2/cross_tables.ipynb
|
###Markdown
total relative frequencies:
###Code
pd.crosstab(tips["tip"], tips["smoker"]).head()
pd.crosstab(tips["tip"], tips["smoker"], normalize = "all", margins= True).head()
pd.crosstab(tips["sex"], tips["day"])
pd.crosstab(tips["sex"], tips["day"], normalize = "all")
pd.crosstab(tips["sex"], tips["day"], normalize = "all", margins=True)
###Output
_____no_output_____
###Markdown
row-wise relative frequencies:
###Code
pd.crosstab(tips["sex"], tips["day"], normalize = 1, margins= True)
###Output
_____no_output_____
###Markdown
column-wise relative frequencies:
###Code
pd.crosstab(tips["sex"], tips["day"], normalize= 0, margins= True)
###Output
_____no_output_____
|
docs/source/example_notebooks/do_sampler_demo.ipynb
|
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect(proceed_when_unidentifiable=True)
###Output
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.causal_identifier:Frontdoor variables for treatment and outcome:[]
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'}
)
###Output
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
_____no_output_____
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect(proceed_when_unidentifiable=True)
###Output
_____no_output_____
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'}
)
###Output
_____no_output_____
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
**FAQ:**- weighting do sampler `dowhy.do_samplers.weighting_sampler.WeightingSampler` 是什么?应该是一个使用倾向得分估计(Logistic Regression) 的判别模型。 Do-sampler 简介--- by Adam Kelleher, Heyang Gong 编译The "do-sampler" is a new feature in DoWhy. 尽管大多数以潜在结果为导向的估算器都专注于估计 the specific contrast $E[Y_0 - Y_1]$, Pearlian inference 专注于更基本的因果量,如反事实结果的分布$P(Y^x = y)$, 它可以用来得出其他感兴趣的统计信息。 通常,很难非参数地表示概率分布。即使可以,您也不想 gloss over finite-sample problems with you data you used to generate it. 考虑到这些问题,我们决定通过使用称为“ do-sampler”的对象从它们中进行采样来表示干预性分布。利用这些样本,我们可以希望 compute finite-sample statistics of our interventional data. 如果我们 bootstrap 许多这样的样本,我们甚至可以期待得到这些统计量的 good sampling distributions. The user should not 这仍然是一个活跃的研究领域,so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, 我们推荐 generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian 干预Following the notion of an intervention in a Pearlian causal model, 我们的 do-samplers 顺序执行如下步骤:1. Disrupt causes2. Make Effective3. Propagate and sample 在第一阶段,我们设想 cutting the in-edges to all of the variables we're intervening on. 在第二阶段,我们将这些变量的值设置为 their interventional quantities。在第三阶段,我们通过模型向前传播该值 to compute interventional outcomes with a sampling procedure.在实践中,我们可以通过多种方式来实现这些步骤。 They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the **weighting do sampler**, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.您可以通过其他方法来实现这三个步骤, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler!我们实现的 do sampler 有三个特点: Statefulness, Integration 和 Specifying interventions. StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default. This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. 我们之前提到的三阶段流程已 is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. (只拟合一次模型) Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler 默认是无需申明的。 The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout DoWhy. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! Demo首先,让我们生成一些数据和一个因果模型。Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
结果比真实的因果效应高 60%. 那么,让我们为这些数据建立因果模型。
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes,
proceed_when_unidentifiable=True)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect()
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['U', 'Z']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'})
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['U', 'Z']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect()
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'})
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect(proceed_when_unidentifiable=True)
###Output
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.causal_identifier:Frontdoor variables for treatment and outcome:[]
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'}
)
###Output
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect()
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'})
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
Do-sampler Introductionby Adam KelleherThe "do-sampler" is a new feature in do-why. While most potential-outcomes oriented estimators focus on estimating the specific contrast $E[Y_0 - Y_1]$, Pearlian inference focuses on more fundamental quantities like the joint distribution of a set of outcomes Y, $P(Y)$, which can be used to derive other statistics of interest.Generally, it's hard to represent a probability distribution non-parametrically. Even if you could, you wouldn't want to gloss over finite-sample problems with you data you used to generate it. With these issues in mind, we decided to represent interventional distributions by sampling from them with an object called to "do-sampler". With these samples, we can hope to compute finite-sample statistics of our interventional data. If we bootstrap many such samples, we can even hope for good sampling distributions for these statistics. The user should note that this is still an area of active research, so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, it's recommended to generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian InterventionsFollowing the notion of an intervention in a Pearlian causal model, our do-samplers implement a sequence of steps:1. Disrupt causes2. Make Effective3. Propagate and sampleIn the first stage, we imagine cutting the in-edges to all of the variables we're intervening on. In the second stage, we set the value of those variables to their interventional quantities. In the third stage, we propagate that value forward through our model to compute interventional outcomes with a sampling procedure.In practice, there are many ways we can implement these steps. They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the weighting do sampler, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.There are other ways you could implement these three steps, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler! StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default.This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. The 3-stage process we mentioned before is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler is stateful by default. The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout do-why. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! DemoFirst, let's generate some data and a causal model. Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
So the naive effect is around 60% high. Now, let's build a causal model for this data.
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect()
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:There are unobserved common causes. Causal effect cannot be identified.
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'})
###Output
/home/amit/python-virtual-envs/env/lib/python3.5/site-packages/sklearn/ensemble/weight_boosting.py:29: DeprecationWarning: numpy.core.umath_tests is an internal NumPy module and should not be imported. It will be removed in a future NumPy release.
from numpy.core.umath_tests import inner1d
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['Z', 'U']
WARNING:dowhy.causal_identifier:There are unobserved common causes. Causal effect cannot be identified.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
**FAQ:**- weighting do sampler `dowhy.do_samplers.weighting_sampler.WeightingSampler` 是什么?应该是一个使用倾向得分估计(Logistic Regression) 的判别模型。 Do-sampler 简介--- by Adam Kelleher, Heyang Gong 编译The "do-sampler" is a new feature in DoWhy. 尽管大多数以潜在结果为导向的估算器都专注于估计 the specific contrast $E[Y_0 - Y_1]$, Pearlian inference 专注于更基本的因果量,如反事实结果的分布$P(Y^x = y)$, 它可以用来得出其他感兴趣的统计信息。 通常,很难非参数地表示概率分布。即使可以,您也不想 gloss over finite-sample problems with you data you used to generate it. 考虑到这些问题,我们决定通过使用称为“ do-sampler”的对象从它们中进行采样来表示干预性分布。利用这些样本,我们可以希望 compute finite-sample statistics of our interventional data. 如果我们 bootstrap 许多这样的样本,我们甚至可以期待得到这些统计量的 good sampling distributions. The user should not 这仍然是一个活跃的研究领域,so you should be careful about being too confident in bootstrapped error bars from do-samplers.Note that do samplers sample from the outcome distribution, and so will vary significantly from sample to sample. To use them to compute outcomes, 我们推荐 generate several such samples to get an idea of the posterior variance of your statistic of interest. Pearlian 干预Following the notion of an intervention in a Pearlian causal model, 我们的 do-samplers 顺序执行如下步骤:1. Disrupt causes2. Make Effective3. Propagate and sample 在第一阶段,我们设想 cutting the in-edges to all of the variables we're intervening on. 在第二阶段,我们将这些变量的值设置为 their interventional quantities。在第三阶段,我们通过模型向前传播该值 to compute interventional outcomes with a sampling procedure.在实践中,我们可以通过多种方式来实现这些步骤。 They're most explicit when we build the model as a linear bayesian network in PyMC3, which is what underlies the MCMC do sampler. In that case, we fit one bayesian network to the data, then construct a new network representing the interventional network. The structural equations are set with the parameters fit in the initial network, and we sample from that new network to get our do sample.In the **weighting do sampler**, we abstractly think of "disrupting the causes" by accounting for selection into the causal state through propensity score estimation. These scores contain the information used to block back-door paths, and so have the same statistics effect as cutting edges into the causal state. We make the treatment effective by selecting the subset of our data set with the correct value of the causal state. Finally, we generated a weighted random sample using inverse propensity weighting to get our do sample.您可以通过其他方法来实现这三个步骤, but the formula is the same. We've abstracted them out as abstract class methods which you should override if you'd like to create your own do sampler!我们实现的 do sampler 有三个特点: Statefulness, Integration 和 Specifying interventions. StatefulnessThe do sampler when accessed through the high-level pandas API is stateless by default. This makes it intuitive to work with, and you can generate different samples with repeated calls to the `pandas.DataFrame.causal.do`. It can be made stateful, which is sometimes useful. 我们之前提到的三阶段流程已 is implemented by passing an internal `pandas.DataFrame` through each of the three stages, but regarding it as temporary. The internal dataframe is reset by default before returning the result.It can be much more efficient to maintain state in the do sampler between generating samples. This is especially true when step 1 requires fitting an expensive model, as is the case with the MCMC do sampler, the kernel density sampler, and the weighting sampler. (只拟合一次模型) Instead of re-fitting the model for each sample, you'd like to fit it once, and then generate many samples from the do sampler. You can do this by setting the kwarg `stateful=True` when you call the `pandas.DataFrame.causal.do` method. To reset the state of the dataframe (deleting the model as well as the internal dataframe), you can call the `pandas.DataFrame.causal.reset` method.Through the lower-level API, the sampler 默认是无需申明的。 The assumption is that a "power user" who is using the low-level API will want more control over the sampling process. In this case, state is carried by internal dataframe `self._df`, which is a copy of the dataframe passed on instantiation. The original dataframe is kept in `self._data`, and is used when the user resets state. IntegrationThe do-sampler is built on top of the identification abstraction used throughout DoWhy. It uses a `dowhy.CausalModel` to perform identification, and builds any models it needs automatically using this identification. Specifying InterventionsThere is a kwarg on the `dowhy.do_sampler.DoSampler` object called `keep_original_treatment`. While an intervention might be to set all units treatment values to some specific value, it's often natural to keep them set as they were, and instead remove confounding bias during effect estimation. If you'd prefer not to specify an intervention, you can set the kwarg like `keep_original_treatment=True`, and the second stage of the 3-stage process will be skipped. In that case, any intervention specified on sampling will be ignored.If the `keep_original_treatment` flag is set to false (it is by default), then you must specify an intervention when you sample from the do sampler. For details, see the demo below! Demo首先,让我们生成一些数据和一个因果模型。Here, Z confounds our causal state, D, with the outcome, Y.
###Code
import os, sys
sys.path.append(os.path.abspath("../../../"))
import numpy as np
import pandas as pd
import dowhy.api
N = 5000
z = np.random.uniform(size=N)
d = np.random.binomial(1., p=1./(1. + np.exp(-5. * z)))
y = 2. * z + d + 0.1 * np.random.normal(size=N)
df = pd.DataFrame({'Z': z, 'D': d, 'Y': y})
(df[df.D == 1].mean() - df[df.D == 0].mean())['Y']
###Output
_____no_output_____
###Markdown
结果比真实的因果效应高 60%. 那么,让我们为这些数据建立因果模型。
###Code
from dowhy import CausalModel
causes = ['D']
outcomes = ['Y']
common_causes = ['Z']
model = CausalModel(df,
causes,
outcomes,
common_causes=common_causes,
proceed_when_unidentifiable=True)
###Output
WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['D'] on outcome ['Y']
###Markdown
Now that we have a model, we can try to identify the causal effect.
###Code
identification = model.identify_effect()
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['U', 'Z']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
###Markdown
Identification works! We didn't actually need to do this yet, since it will happen internally with the do sampler, but it can't hurt to check that identification works before proceeding. Now, let's build the sampler.
###Code
from dowhy.do_samplers.weighting_sampler import WeightingSampler
sampler = WeightingSampler(df,
causal_model=model,
keep_original_treatment=True,
variable_types={'D': 'b', 'Z': 'c', 'Y': 'c'})
###Output
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['U', 'Z']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.
###Markdown
Now, we can just sample from the interventional distribution! Since we set the `keep_original_treatment` flag to `False`, any treatment we pass here will be ignored. Here, we'll just pass `None` to acknowledge that we know we don't want to pass anything.If you'd prefer to specify an intervention, you can just put the interventional value here instead as a list or numpy array.
###Code
interventional_df = sampler.do_sample(None)
(interventional_df[interventional_df.D == 1].mean() - interventional_df[interventional_df.D == 0].mean())['Y']
###Output
_____no_output_____
|
examples/pvtol-lqr-nested.ipynb
|
###Markdown
Vertical takeoff and landing aircraftThis notebook demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. Additional information on this system is available athttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraft System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below:The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).Letting $z=(x,y,\theta, \dot x, \dot y, \dot\theta$), the equations can be written in state space form as:$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -\frac{c}{m} z_4 \\ -g- \frac{c}{m} z_5 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 0 \\ \frac{1}{m} \cos \theta F_1 + \frac{1}{m} \sin \theta F_2 \\ \frac{1}{m} \sin \theta F_1 + \frac{1}{m} \cos \theta F_2 \\ \frac{r}{J} F_1 \end{bmatrix}$$ LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (Linear Systems, Example 6.4) and Chapter 7 (State Feedback, Example 7.9) of [Astrom and Murray](https://fbsbook.org). The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
###Output
_____no_output_____
###Markdown
Choosing equilibrium inputs to be $u_e = (0, mg)$, the dynamics of the system $\frac{dz}{dt}$, and their linearization $A$ about equilibrium point $z_e = (0, 0, 0, 0, 0, 0)$ are given by$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -g \sin z_3 -\frac{c}{m} z_4 \\ g(\cos z_3 - 1)- \frac{c}{m} z_5 \\ 0 \end{bmatrix}\qquadA = \begin{bmatrix} 0 & 0 & 0 &1&0&0\\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&-g&-c/m&0&0 \\ 0&0&0&0&-c/m&0 \\ 0&0&0&0&0&0 \end{bmatrix}$$
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0] # equilibrium point of interest
ue = [0, m*g] # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
# Note that we write A and B here in full generality in case we want
# to test different xe and ue.
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function as$$ J = \int_0^\infty (\xi^T Q_\xi \xi + v^T Q_v v) dt,$$where $\xi = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1])
Qu1a = diag([1, 1])
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K)
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K \xi$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_e = - K(z - z_d) + u_d.$$where $u_e = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$The way we setup the dynamics above, $A$ is already hardcoding $u_d$, so we don't need to include it as an external input. So we just need to cascade the $-K(z-z_d)$ controller with the PVTOL aircraft's dynamics to control it. For didactic purposes, we will cheat in two small ways:- First, we will only interface our controller with the linearized dynamics. Using the nonlinear dynamics would require the `NonlinearIOSystem` functionalities, which we leave to another notebook to introduce.2. Second, as written, our controller requires full state feedback ($K$ multiplies full state vectors $z$), which we do not have access to because our system, as written above, only returns $x$ and $y$ (because of $C$ matrix). Hence, we would need a state observer, such as a Kalman Filter, to track the state variables. Instead, we assume that we have access to the full state.The following code implements the closed loop system:
###Code
# Our input to the system will only be (x_d, y_d), so we need to
# multiply it by this matrix to turn it into z_d.
Xd = matrix([[1,0,0,0,0,0],
[0,1,0,0,0,0]]).T
# Closed loop dynamics
H = ss(A-B*K,B*K*Xd,C,D)
# Step response for the first input
x,t = step(H,input=0,output=0,T=linspace(0,10,100))
# Step response for the second input
y,t = step(H,input=1,output=1,T=linspace(0,10,100))
plot(t,x,'-',t,y,'--')
plot([0, 10], [1, 1], 'k-')
ylabel('Position')
xlabel('Time (s)')
title('Step Response for Inputs')
legend(('Yx', 'Yy'), loc='lower right')
show()
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1])
K1a, X, E = lqr(A, B, Qx1, Qu1a)
H1ax = H = ss(A-B*K1a,B*K1a*Xd,C,D)
Qu1b = (40**2)*diag([1, 1])
K1b, X, E = lqr(A, B, Qx1, Qu1b)
H1bx = H = ss(A-B*K1b,B*K1b*Xd,C,D)
Qu1c = (200**2)*diag([1, 1])
K1c, X, E = lqr(A, B, Qx1, Qu1c)
H1cx = ss(A-B*K1c,B*K1c*Xd,C,D)
[Y1, T1] = step(H1ax, T=linspace(0,10,100), input=0,output=0)
[Y2, T2] = step(H1bx, T=linspace(0,10,100), input=0,output=0)
[Y3, T3] = step(H1cx, T=linspace(0,10,100), input=0,output=0)
plot(T1, Y1.T, 'b-', T2, Y2.T, 'r-', T3, Y3.T, 'g-')
plot([0 ,10], [1, 1], 'k-')
title('Step Response for Inputs')
ylabel('Position')
xlabel('Time (s)')
legend(('Y1','Y2','Y3'),loc='lower right')
axis([0, 10, -0.1, 1.4])
show()
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 (Frequency Domain Design) of [Astrom and Murray](https://fbsbook.org). To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramwhere The controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]) # inner loop (roll)
Po = tf([1], [m, c, 0]) # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200
a = 2
b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1))
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02
b = 5
K = 2
Co = -K*tf([1, 0.3], [1, 10]) # another lead compensator
Lo = -m*g*Po*Co
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po
S = feedback(1, L)
T = feedback(L, 1)
t, y = step(T, T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
show()
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L)
show()
nyquist(L, (0.0001, 1000))
show()
gangof4(Hi*Po, Co)
###Output
_____no_output_____
###Markdown
Vertical takeoff and landing aircraftThis notebook demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. Additional information on this system is available athttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraft System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below:The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).It is convenient to redefine the inputs so that the origin is an equilibrium point of the system with zero input. Letting $u_1 =F_1$ and $u_2 = F_2 - mg$, the equations can be written in state space form as: LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (State Feedback) of [Astrom and Murray](https://fbsbook.org). The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
print("m = %f" % m)
print("J = %f" % J)
print("r = %f" % r)
print("g = %f" % g)
print("c = %f" % c)
###Output
m = 4.000000
J = 0.047500
r = 0.250000
g = 9.800000
c = 0.050000
###Markdown
The linearization of the dynamics near the equilibrium point $x_e = (0, 0, 0, 0, 0, 0)$, $u_e = (0, mg)$ are given by
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0] # equilibrium point of interest
ue = [0, m*g] # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function aswhere $z = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1])
Qu1a = diag([1, 1])
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K)
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K z$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_d = - K(z - z_d) + u_d.$$where $u_d = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$Since the `python-control` package only supports SISO systems, in order to compute the closed loop dynamics, we must extract the dynamics for the lateral and altitude dynamics as individual systems. In addition, we simulate the closed loop dynamics using the step command with $K x_d$ as the input vector (assumes that the "input" is unit size, with $xd$ corresponding to the desired steady state. The following code performs these operations:
###Code
xd = matrix([[1], [0], [0], [0], [0], [0]])
yd = matrix([[0], [1], [0], [0], [0], [0]])
# Indices for the parts of the state that we want
lat = (0,2,3,5)
alt = (1,4)
# Decoupled dynamics
Ax = (A[lat, :])[:, lat] #! not sure why I have to do it this way
Bx, Cx, Dx = B[lat, 0], C[0, lat], D[0, 0]
Ay = (A[alt, :])[:, alt] #! not sure why I have to do it this way
By, Cy, Dy = B[alt, 1], C[1, alt], D[1, 1]
# Step response for the first input
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx)
(Tx, Yx) = step(H1ax, T=linspace(0,10,100))
# Step response for the second input
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy)
(Ty, Yy) = step(H1ay, T=linspace(0,10,100))
plot(Yx.T, Tx, '-', Yy.T, Ty, '--')
plot([0, 10], [1, 1], 'k-')
ylabel('Position')
xlabel('Time (s)')
title('Step Response for Inputs')
legend(('Yx', 'Yy'), loc='lower right')
show()
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1])
K1a, X, E = lqr(A, B, Qx1, Qu1a)
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx)
Qu1b = (40**2)*diag([1, 1])
K1b, X, E = lqr(A, B, Qx1, Qu1b)
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx)
Qu1c = (200**2)*diag([1, 1])
K1c, X, E = lqr(A, B, Qx1, Qu1c)
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx)
[T1, Y1] = step(H1ax, T=linspace(0,10,100))
[T2, Y2] = step(H1bx, T=linspace(0,10,100))
[T3, Y3] = step(H1cx, T=linspace(0,10,100))
plot(Y1.T, T1, 'b-')
plot(Y2.T, T2, 'r-')
plot(Y3.T, T3, 'g-')
plot([0 ,10], [1, 1], 'k-')
title('Step Response for Inputs')
ylabel('Position')
xlabel('Time (s)')
legend(('Y1','Y2','Y3'),loc='lower right')
axis([0, 10, -0.1, 1.4])
show()
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 (Frequency Domain Design) of [Astrom and Murray](https://fbsbook.org). To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramwhere The controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
print("m = %f" % m)
print("J = %f" % J)
print("r = %f" % r)
print("g = %f" % g)
print("c = %f" % c)
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]) # inner loop (roll)
Po = tf([1], [m, c, 0]) # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200
a = 2
b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1))
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02
b = 5
K = 2
Co = -K*tf([1, 0.3], [1, 10]) # another lead compensator
Lo = -m*g*Po*Co
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po
S = feedback(1, L)
T = feedback(L, 1)
t, y = step(T, T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
show()
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L)
show()
nyquist(L, (0.0001, 1000))
show()
gangof4(Hi*Po, Co)
###Output
_____no_output_____
###Markdown
`python-control` Example: Vertical takeoff and landing aircrafthttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraftThis page demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below: The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).It is convenient to redefine the inputs so that the origin is an equilibrium point of the system with zero input. Letting $u_1 =F_1$ and $u_2 = F_2 - mg$, the equations can be written in state space form as: LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (State Feedback) of [http:www.cds.caltech.edu/~murray/amwiki Astrom and Murray]. The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
print("m = %f" % m)
print("J = %f" % J)
print("r = %f" % r)
print("g = %f" % g)
print("c = %f" % c)
###Output
m = 4.000000
J = 0.047500
r = 0.250000
g = 9.800000
c = 0.050000
###Markdown
The linearization of the dynamics near the equilibrium point $x_e = (0, 0, 0, 0, 0, 0)$, $u_e = (0, mg)$ are given by
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0] # equilibrium point of interest
ue = [0, m*g] # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function aswhere $z = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1])
Qu1a = diag([1, 1])
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K)
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K z$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_d = - K(z - z_d) + u_d.$$where $u_d = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$Since the `python-control` package only supports SISO systems, in order to compute the closed loop dynamics, we must extract the dynamics for the lateral and altitude dynamics as individual systems. In addition, we simulate the closed loop dynamics using the step command with $K x_d$ as the input vector (assumes that the "input" is unit size, with $xd$ corresponding to the desired steady state. The following code performs these operations:
###Code
xd = matrix([[1], [0], [0], [0], [0], [0]])
yd = matrix([[0], [1], [0], [0], [0], [0]])
# Indices for the parts of the state that we want
lat = (0,2,3,5)
alt = (1,4)
# Decoupled dynamics
Ax = (A[lat, :])[:, lat] #! not sure why I have to do it this way
Bx, Cx, Dx = B[lat, 0], C[0, lat], D[0, 0]
Ay = (A[alt, :])[:, alt] #! not sure why I have to do it this way
By, Cy, Dy = B[alt, 1], C[1, alt], D[1, 1]
# Step response for the first input
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx)
(Tx, Yx) = step(H1ax, T=linspace(0,10,100))
# Step response for the second input
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy)
(Ty, Yy) = step(H1ay, T=linspace(0,10,100))
plot(Yx.T, Tx, '-', Yy.T, Ty, '--')
plot([0, 10], [1, 1], 'k-')
ylabel('Position')
xlabel('Time (s)')
title('Step Response for Inputs')
legend(('Yx', 'Yy'), loc='lower right')
show()
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1])
K1a, X, E = lqr(A, B, Qx1, Qu1a)
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx)
Qu1b = (40**2)*diag([1, 1])
K1b, X, E = lqr(A, B, Qx1, Qu1b)
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx)
Qu1c = (200**2)*diag([1, 1])
K1c, X, E = lqr(A, B, Qx1, Qu1c)
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx)
[T1, Y1] = step(H1ax, T=linspace(0,10,100))
[T2, Y2] = step(H1bx, T=linspace(0,10,100))
[T3, Y3] = step(H1cx, T=linspace(0,10,100))
plot(Y1.T, T1, 'b-')
plot(Y2.T, T2, 'r-')
plot(Y3.T, T3, 'g-')
plot([0 ,10], [1, 1], 'k-')
title('Step Response for Inputs')
ylabel('Position')
xlabel('Time (s)')
legend(('Y1','Y2','Y3'),loc='lower right')
axis([0, 10, -0.1, 1.4])
show()
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 [Frequency Domain Design](http:www.cds.caltech.edu/~murray/amwiki) of Astrom and Murray. To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramwhere The controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
print("m = %f" % m)
print("J = %f" % J)
print("r = %f" % r)
print("g = %f" % g)
print("c = %f" % c)
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]) # inner loop (roll)
Po = tf([1], [m, c, 0]) # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200
a = 2
b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1))
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02
b = 5
K = 2
Co = -K*tf([1, 0.3], [1, 10]) # another lead compensator
Lo = -m*g*Po*Co
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po
S = feedback(1, L)
T = feedback(L, 1)
t, y = step(T, T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
show()
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L)
show()
nyquist(L, (0.0001, 1000))
show()
gangof4(Hi*Po, Co)
###Output
_____no_output_____
###Markdown
`python-control` Example: Vertical takeoff and landing aircrafthttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraftThis page demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below: The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).It is convenient to redefine the inputs so that the origin is an equilibrium point of the system with zero input. Letting $u_1 =F_1$ and $u_2 = F_2 - mg$, the equations can be written in state space form as:LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (State Feedback) of [http:www.cds.caltech.edu/~murray/amwiki Astrom and Murray]. The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4; # mass of aircraft
J = 0.0475; # inertia around pitch axis
r = 0.25; # distance to center of force
g = 9.8; # gravitational constant
c = 0.05; # damping factor (estimated)
print "m = %f" % m
print "J = %f" % J
print "r = %f" % r
print "g = %f" % g
print "c = %f" % c
###Output
m = 4.000000
J = 0.047500
r = 0.250000
g = 9.800000
c = 0.050000
###Markdown
The linearization of the dynamics near the equilibrium point $x_e = (0, 0, 0, 0, 0, 0)$, $u_e = (0, mg)$ are given by
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0]; # equilibrium point of interest
ue = [0, m*g]; # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function aswhere $z = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1]);
Qu1a = diag([1, 1]);
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K);
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K z$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_d = - K(z - z_d) + u_d.$$where $u_d = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$Since the `python-control` package only supports SISO systems, in order to compute the closed loop dynamics, we must extract the dynamics for the lateral and altitude dynamics as individual systems. In addition, we simulate the closed loop dynamics using the step command with $K x_d$ as the input vector (assumes that the "input" is unit size, with $xd$ corresponding to the desired steady state. The following code performs these operations:
###Code
xd = matrix([[1], [0], [0], [0], [0], [0]]);
yd = matrix([[0], [1], [0], [0], [0], [0]]);
# Indices for the parts of the state that we want
lat = (0,2,3,5);
alt = (1,4);
# Decoupled dynamics
Ax = (A[lat, :])[:, lat]; #! not sure why I have to do it this way
Bx = B[lat, 0]; Cx = C[0, lat]; Dx = D[0, 0];
Ay = (A[alt, :])[:, alt]; #! not sure why I have to do it this way
By = B[alt, 1]; Cy = C[1, alt]; Dy = D[1, 1];
# Step response for the first input
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
(Tx, Yx) = step(H1ax, T=linspace(0,10,100));
# Step response for the second input
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy);
(Ty, Yy) = step(H1ay, T=linspace(0,10,100));
plot(Yx.T, Tx, '-', Yy.T, Ty, '--'); hold(True);
plot([0, 10], [1, 1], 'k-'); hold(True);
ylabel('Position');
xlabel('Time (s)');
title('Step Response for Inputs');
legend(('Yx', 'Yy'), loc='lower right');
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1]); (K1a, X, E) = lqr(A, B, Qx1, Qu1a);
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
Qu1b = (40**2)*diag([1, 1]); (K1b, X, E) = lqr(A, B, Qx1, Qu1b);
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx);
Qu1c = (200**2)*diag([1, 1]); (K1c, X, E) = lqr(A, B, Qx1, Qu1c);
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx);
[T1, Y1] = step(H1ax, T=linspace(0,10,100));
[T2, Y2] = step(H1bx, T=linspace(0,10,100));
[T3, Y3] = step(H1cx, T=linspace(0,10,100));
plot(Y1.T, T1, 'b-'); hold(True);
plot(Y2.T, T2, 'r-'); hold(True);
plot(Y3.T, T3, 'g-'); hold(True);
plot([0 ,10], [1, 1], 'k-'); hold(True);
title('Step Response for Inputs');
ylabel('Position');
xlabel('Time (s)');
legend(('Y1','Y2','Y3'),loc='lower right');
axis([0, 10, -0.1, 1.4]);
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 [Frequency Domain Design](http:www.cds.caltech.edu/~murray/amwiki) of Astrom and Murray. To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramwhere The controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4; # mass of aircraft
J = 0.0475; # inertia around pitch axis
r = 0.25; # distance to center of force
g = 9.8; # gravitational constant
c = 0.05; # damping factor (estimated)
print "m = %f" % m
print "J = %f" % J
print "r = %f" % r
print "g = %f" % g
print "c = %f" % c
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]); # inner loop (roll)
Po = tf([1], [m, c, 0]); # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200; a = 2; b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1));
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02; b = 5; K = 2;
Co = -K*tf([1, 0.3], [1, 10]); # another lead compensator
Lo = -m*g*Po*Co;
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po;
S = feedback(1, L);
T = feedback(L, 1);
t, y = step(T,T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L);
nyquist(L, (0.0001, 1000));
gangof4(Hi*Po, Co);
###Output
_____no_output_____
###Markdown
Vertical takeoff and landing aircraftThis notebook demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. Additional information on this system is available athttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraft System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below:The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).Letting $z=(x,y,\theta, \dot x, \dot y, \dot\theta$), the equations can be written in state space form as:$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -\frac{c}{m} z_4 \\ -g- \frac{c}{m} z_5 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 0 \\ \frac{1}{m} \cos \theta F_1 + \frac{1}{m} \sin \theta F_2 \\ \frac{1}{m} \sin \theta F_1 + \frac{1}{m} \cos \theta F_2 \\ \frac{r}{J} F_1 \end{bmatrix}$$ LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (Linear Systems, Example 6.4) and Chapter 7 (State Feedback, Example 7.9) of [Astrom and Murray](https://fbsbook.org). The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
###Output
_____no_output_____
###Markdown
Choosing equilibrium inputs to be $u_e = (0, mg)$, the dynamics of the system $\frac{dz}{dt}$, and their linearization $A$ about equilibrium point $z_e = (0, 0, 0, 0, 0, 0)$ are given by$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -g \sin z_3 -\frac{c}{m} z_4 \\ g(\cos z_3 - 1)- \frac{c}{m} z_5 \\ 0 \end{bmatrix}\qquadA = \begin{bmatrix} 0 & 0 & 0 &1&0&0\\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&-g&-c/m&0&0 \\ 0&0&0&0&-c/m&0 \\ 0&0&0&0&0&0 \end{bmatrix}$$
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0] # equilibrium point of interest
ue = [0, m*g] # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
# Note that we write A and B here in full generality in case we want
# to test different xe and ue.
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function as$$ J = \int_0^\infty (\xi^T Q_\xi \xi + v^T Q_v v) dt,$$where $\xi = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1])
Qu1a = diag([1, 1])
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K)
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K \xi$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_e = - K(z - z_d) + u_d.$$where $u_e = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$The way we setup the dynamics above, $A$ is already hardcoding $u_d$, so we don't need to include it as an external input. So we just need to cascade the $-K(z-z_d)$ controller with the PVTOL aircraft's dynamics to control it. For didactic purposes, we will cheat in two small ways:- First, we will only interface our controller with the linearized dynamics. Using the nonlinear dynamics would require the `NonlinearIOSystem` functionalities, which we leave to another notebook to introduce.2. Second, as written, our controller requires full state feedback ($K$ multiplies full state vectors $z$), which we do not have access to because our system, as written above, only returns $x$ and $y$ (because of $C$ matrix). Hence, we would need a state observer, such as a Kalman Filter, to track the state variables. Instead, we assume that we have access to the full state.The following code implements the closed loop system:
###Code
# Our input to the system will only be (x_d, y_d), so we need to
# multiply it by this matrix to turn it into z_d.
Xd = matrix([[1,0,0,0,0,0],
[0,1,0,0,0,0]]).T
# Closed loop dynamics
H = ss(A-B*K,B*K*Xd,C,D)
# Step response for the first input
x,t = step(H,input=0,output=0,T=linspace(0,10,100))
# Step response for the second input
y,t = step(H,input=1,output=1,T=linspace(0,10,100))
plot(t,x,'-',t,y,'--')
plot([0, 10], [1, 1], 'k-')
ylabel('Position')
xlabel('Time (s)')
title('Step Response for Inputs')
legend(('Yx', 'Yy'), loc='lower right')
show()
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1])
K1a, X, E = lqr(A, B, Qx1, Qu1a)
H1ax = H = ss(A-B*K1a,B*K1a*Xd,C,D)
Qu1b = (40**2)*diag([1, 1])
K1b, X, E = lqr(A, B, Qx1, Qu1b)
H1bx = H = ss(A-B*K1b,B*K1b*Xd,C,D)
Qu1c = (200**2)*diag([1, 1])
K1c, X, E = lqr(A, B, Qx1, Qu1c)
H1cx = ss(A-B*K1c,B*K1c*Xd,C,D)
[Y1, T1] = step(H1ax, T=linspace(0,10,100), input=0,output=0)
[Y2, T2] = step(H1bx, T=linspace(0,10,100), input=0,output=0)
[Y3, T3] = step(H1cx, T=linspace(0,10,100), input=0,output=0)
plot(T1, Y1.T, 'b-', T2, Y2.T, 'r-', T3, Y3.T, 'g-')
plot([0 ,10], [1, 1], 'k-')
title('Step Response for Inputs')
ylabel('Position')
xlabel('Time (s)')
legend(('Y1','Y2','Y3'),loc='lower right')
axis([0, 10, -0.1, 1.4])
show()
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 (Frequency Domain Design) of [Astrom and Murray](https://fbsbook.org). To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramwhere The controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]) # inner loop (roll)
Po = tf([1], [m, c, 0]) # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200
a = 2
b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1))
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02
b = 5
K = 2
Co = -K*tf([1, 0.3], [1, 10]) # another lead compensator
Lo = -m*g*Po*Co
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po
S = feedback(1, L)
T = feedback(L, 1)
t, y = step(T, T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
show()
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L)
show()
nyquist(L, (0.0001, 1000))
show()
gangof4(Hi*Po, Co)
###Output
_____no_output_____
###Markdown
Vertical takeoff and landing aircraftThis notebook demonstrates the use of the python-control package for analysis and design of a controller for a vectored thrust aircraft model that is used as a running example through the text *Feedback Systems* by Astrom and Murray. This example makes use of MATLAB compatible commands. Additional information on this system is available athttp://www.cds.caltech.edu/~murray/wiki/index.php/Python-control/Example:_Vertical_takeoff_and_landing_aircraft System DescriptionThis example uses a simplified model for a (planar) vertical takeoff and landing aircraft (PVTOL), as shown below:The position and orientation of the center of mass of the aircraft is denoted by $(x,y,\theta)$, $m$ is the mass of the vehicle, $J$ the moment of inertia, $g$ the gravitational constant and $c$ the damping coefficient. The forces generated by the main downward thruster and the maneuvering thrusters are modeled as a pair of forces $F_1$ and $F_2$ acting at a distance $r$ below the aircraft (determined by the geometry of the thrusters).Letting $z=(x,y,\theta, \dot x, \dot y, \dot\theta$), the equations can be written in state space form as:$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -\frac{c}{m} z_4 \\ -g- \frac{c}{m} z_5 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 0 \\ \frac{1}{m} \cos \theta F_1 + \frac{1}{m} \sin \theta F_2 \\ \frac{1}{m} \sin \theta F_1 + \frac{1}{m} \cos \theta F_2 \\ \frac{r}{J} F_1 \end{bmatrix}$$ LQR state feedback controllerThis section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 (Linear Systems, Example 6.4) and Chapter 7 (State Feedback, Example 7.9) of [Astrom and Murray](https://fbsbook.org). The python code listed here are contained the the file pvtol-lqr.py.To execute this example, we first import the libraries for SciPy, MATLAB plotting and the python-control package:
###Code
from numpy import * # Grab all of the NumPy functions
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
%matplotlib inline
###Output
_____no_output_____
###Markdown
The parameters for the system are given by
###Code
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
###Output
_____no_output_____
###Markdown
Choosing equilibrium inputs to be $u_e = (0, mg)$, the dynamics of the system $\frac{dz}{dt}$, and their linearization $A$ about equilibrium point $z_e = (0, 0, 0, 0, 0, 0)$ are given by$$\frac{dz}{dt} = \begin{bmatrix} z_4 \\ z_5 \\ z_6 \\ -g \sin z_3 -\frac{c}{m} z_4 \\ g(\cos z_3 - 1)- \frac{c}{m} z_5 \\ 0 \end{bmatrix}\qquadA = \begin{bmatrix} 0 & 0 & 0 &1&0&0\\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&-g&-c/m&0&0 \\ 0&0&0&0&-c/m&0 \\ 0&0&0&0&0&0 \end{bmatrix}$$
###Code
# State space dynamics
xe = [0, 0, 0, 0, 0, 0] # equilibrium point of interest
ue = [0, m*g] # (note these are lists, not matrices)
# Dynamics matrix (use matrix type so that * works for multiplication)
# Note that we write A and B here in full generality in case we want
# to test different xe and ue.
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Input matrix
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Output matrix
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
###Output
_____no_output_____
###Markdown
To compute a linear quadratic regulator for the system, we write the cost function as$$ J = \int_0^\infty (\xi^T Q_\xi \xi + v^T Q_v v) dt,$$where $\xi = z - z_e$ and $v = u - u_e$ represent the local coordinates around the desired equilibrium point $(z_e, u_e)$. We begin with diagonal matrices for the state and input costs:
###Code
Qx1 = diag([1, 1, 1, 1, 1, 1])
Qu1a = diag([1, 1])
(K, X, E) = lqr(A, B, Qx1, Qu1a); K1a = matrix(K)
###Output
_____no_output_____
###Markdown
This gives a control law of the form $v = -K \xi$, which can then be used to derive the control law in terms of the original variables: $$u = v + u_e = - K(z - z_d) + u_d.$$where $u_e = (0, mg)$ and $z_d = (x_d, y_d, 0, 0, 0, 0)$The way we setup the dynamics above, $A$ is already hardcoding $u_d$, so we don't need to include it as an external input. So we just need to cascade the $-K(z-z_d)$ controller with the PVTOL aircraft's dynamics to control it. For didactic purposes, we will cheat in two small ways:- First, we will only interface our controller with the linearized dynamics. Using the nonlinear dynamics would require the `NonlinearIOSystem` functionalities, which we leave to another notebook to introduce.2. Second, as written, our controller requires full state feedback ($K$ multiplies full state vectors $z$), which we do not have access to because our system, as written above, only returns $x$ and $y$ (because of $C$ matrix). Hence, we would need a state observer, such as a Kalman Filter, to track the state variables. Instead, we assume that we have access to the full state.The following code implements the closed loop system:
###Code
# Our input to the system will only be (x_d, y_d), so we need to
# multiply it by this matrix to turn it into z_d.
Xd = matrix([[1,0,0,0,0,0],
[0,1,0,0,0,0]]).T
# Closed loop dynamics
H = ss(A-B*K,B*K*Xd,C,D)
# Step response for the first input
x,t = step(H,input=0,output=0,T=linspace(0,10,100))
# Step response for the second input
y,t = step(H,input=1,output=1,T=linspace(0,10,100))
plot(t,x,'-',t,y,'--')
plot([0, 10], [1, 1], 'k-')
ylabel('Position')
xlabel('Time (s)')
title('Step Response for Inputs')
legend(('Yx', 'Yy'), loc='lower right')
show()
###Output
_____no_output_____
###Markdown
The plot above shows the $x$ and $y$ positions of the aircraft when it is commanded to move 1 m in each direction. The following shows the $x$ motion for control weights $\rho = 1, 10^2, 10^4$. A higher weight of the input term in the cost function causes a more sluggish response. It is created using the code:
###Code
# Look at different input weightings
Qu1a = diag([1, 1])
K1a, X, E = lqr(A, B, Qx1, Qu1a)
H1ax = H = ss(A-B*K1a,B*K1a*Xd,C,D)
Qu1b = (40**2)*diag([1, 1])
K1b, X, E = lqr(A, B, Qx1, Qu1b)
H1bx = H = ss(A-B*K1b,B*K1b*Xd,C,D)
Qu1c = (200**2)*diag([1, 1])
K1c, X, E = lqr(A, B, Qx1, Qu1c)
H1cx = ss(A-B*K1c,B*K1c*Xd,C,D)
[Y1, T1] = step(H1ax, T=linspace(0,10,100), input=0,output=0)
[Y2, T2] = step(H1bx, T=linspace(0,10,100), input=0,output=0)
[Y3, T3] = step(H1cx, T=linspace(0,10,100), input=0,output=0)
plot(T1, Y1.T, 'b-', T2, Y2.T, 'r-', T3, Y3.T, 'g-')
plot([0 ,10], [1, 1], 'k-')
title('Step Response for Inputs')
ylabel('Position')
xlabel('Time (s)')
legend(('Y1','Y2','Y3'),loc='lower right')
axis([0, 10, -0.1, 1.4])
show()
###Output
_____no_output_____
###Markdown
Lateral control using inner/outer loop designThis section demonstrates the design of loop shaping controller for the vectored thrust aircraft example. This example is pulled from Chapter 11 (Frequency Domain Design) of [Astrom and Murray](https://fbsbook.org). To design a controller for the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. We begin by representing the dynamics using the block diagramThe controller is constructed by splitting the process dynamics and controller into two components: an inner loop consisting of the roll dynamics $P_i$ and control $C_i$ and an outer loop consisting of the lateral position dynamics $P_o$ and controller $C_o$.The closed inner loop dynamics $H_i$ control the roll angle of the aircraft using the vectored thrust while the outer loop controller $C_o$ commands the roll angle to regulate the lateral position.The following code imports the libraries that are required and defines the dynamics:
###Code
from matplotlib.pyplot import * # Grab MATLAB plotting functions
from control.matlab import * # MATLAB-like functions
# System parameters
m = 4 # mass of aircraft
J = 0.0475 # inertia around pitch axis
r = 0.25 # distance to center of force
g = 9.8 # gravitational constant
c = 0.05 # damping factor (estimated)
# Transfer functions for dynamics
Pi = tf([r], [J, 0, 0]) # inner loop (roll)
Po = tf([1], [m, c, 0]) # outer loop (position)
###Output
_____no_output_____
###Markdown
For the inner loop, use a lead compensator
###Code
k = 200
a = 2
b = 50
Ci = k*tf([1, a], [1, b]) # lead compensator
Li = Pi*Ci
###Output
_____no_output_____
###Markdown
The closed loop dynamics of the inner loop, $H_i$, are given by
###Code
Hi = parallel(feedback(Ci, Pi), -m*g*feedback(Ci*Pi, 1))
###Output
_____no_output_____
###Markdown
Finally, we design the lateral compensator using another lead compenstor
###Code
# Now design the lateral control system
a = 0.02
b = 5
K = 2
Co = -K*tf([1, 0.3], [1, 10]) # another lead compensator
Lo = -m*g*Po*Co
###Output
_____no_output_____
###Markdown
The performance of the system can be characterized using the sensitivity function and the complementary sensitivity function:
###Code
L = Co*Hi*Po
S = feedback(1, L)
T = feedback(L, 1)
t, y = step(T, T=linspace(0,10,100))
plot(y, t)
title("Step Response")
grid()
xlabel("time (s)")
ylabel("y(t)")
show()
###Output
_____no_output_____
###Markdown
The frequency response and Nyquist plot for the loop transfer function are computed using the commands
###Code
bode(L)
show()
nyquist(L, (0.0001, 1000))
show()
gangof4(Hi*Po, Co)
###Output
_____no_output_____
|
Notebooks/Chapter19-RNNs/Chapter19-RNNs-1-tanh.ipynb
|
###Markdown
Copyright (c) 2017-21 Andrew GlassnerPermission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. Deep Learning: A Visual Approach by Andrew Glassner, https://glassner.com Order: https://nostarch.com/deep-learning-visual-approach GitHub: https://github.com/blueberrymusic------ What's in this notebookThis notebook is provided as a “behind-the-scenes” look at code used to make some of the figures in this chapter. It is cleaned up a bit from the original code that I hacked together, and is only lightly commented. I wrote the code to be easy to interpret and understand, even for those who are new to Python. I tried never to be clever or even more efficient at the cost of being harder to understand. The code is in Python3, using the versions of libraries as of April 2021. This notebook may contain additional code to create models and images not in the book. That material is included here to demonstrate additional techniques.Note that I've included the output cells in this saved notebook, but Jupyter doesn't save the variables or data that were used to generate them. To recreate any cell's output, evaluate all the cells from the start up to that cell. A convenient way to experiment is to first choose "Restart & Run All" from the Kernel menu, so that everything's been defined and is up to date. Then you can experiment using the variables, data, functions, and other stuff defined in this notebook. Chapter 19: RNNs - Notebook 1: tanh
###Code
import numpy as np
import matplotlib.pyplot as plt
# Make a File_Helper for saving and loading files.
save_files = False
import os, sys, inspect
current_dir = os.path.dirname(os.path.abspath(inspect.getfile(inspect.currentframe())))
sys.path.insert(0, os.path.dirname(current_dir)) # path to parent dir
from DLBasics_Utilities import File_Helper
file_helper = File_Helper(save_files)
def repeat_tanh(x, n):
v = x
for i in range(0, n):
v = np.tanh(v)
return v
# Draw a plot showing the effect of repeating tanh
xs = np.linspace(-8, 8, 500)
plt.plot(xs, repeat_tanh(xs, 1), lw=2, c='red', linestyle='-', label="1 tanh")
plt.plot(xs, repeat_tanh(xs, 2), lw=2, c='blue', linestyle='--', label="2 tanh")
plt.plot(xs, repeat_tanh(xs, 5), lw=2, c='green', linestyle='-.', label="5 tanh")
plt.plot(xs, repeat_tanh(xs, 25), lw=2, c='purple', linestyle=':', label="25 tanh")
plt.legend(loc='best')
plt.xlabel("input")
plt.ylabel("output")
plt.title("Repeated tanh")
file_helper.save_figure('repeated-tanh')
plt.show()
###Output
_____no_output_____
|
HackerRank/Python/Math/Math.ipynb
|
###Markdown
[Polar Coordinates](https://www.hackerrank.com/challenges/polar-coordinates/problem)
###Code
import cmath
c=complex(3,4)
c
c.real
c.imag
abs(c)# (3**2+4**2)**0.5
cmath.phase(c) #angle
import cmath
cx=complex(input())
print(abs(cx))
print(cmath.phase(cx))
###Output
2+4j
###Markdown
[Find Angle MBC](https://www.hackerrank.com/challenges/find-angle/problem)
###Code
import cmath
y,x=float(input()),float(input())
print(round(cmath.phase(complex(x/2,y/2))*180/cmath.pi),'°',sep='')
import numpy as np
np.rint(cmath.phase(complex(x,m))*100)
(x**2+y**2)**0.5/2x
###Output
_____no_output_____
###Markdown
[Triangle Quest 1](https://www.hackerrank.com/challenges/python-quest-1/problem)
###Code
'''
for i in range(1,int(input())): #More than 2 lines will result in 0 score. Do not leave a blank line also
print(f'{i}'*i)
'''
for i in range(int(input())-1): #More than 2 lines will result in 0 score. Do not leave a blank line also
print([1,22,333,4444,55555,666666,7777777,88888888,999999999][i])
###Output
5
###Markdown
[Triangle Quest 2](https://www.hackerrank.com/challenges/triangle-quest-2/problem)
###Code
for i in range(1,int(input())+1): #More than 2 lines will result in 0 score. Do not leave a blank line also
print([0,1, 121, 12321, 1234321, 123454321, 12345654321, 1234567654321, 123456787654321, 12345678987654321][i])
###Output
9
###Markdown
[Mod Divmod](https://www.hackerrank.com/challenges/python-mod-divmod/problem)One of the built-in functions of Python is divmod, which takes two arguments a and c and returns a tuple containing the quotient of a/c first and then the remainder .For example:>>> print divmod(177,10)(17, 7)Here, the integer division is 177/10 => 17 and the modulo operator is 177%10 => 7.
###Code
divmod(177,10)
x,y=int(input()),int(input())
print(x//y,x%y,divmod(x,y),sep='\n')
###Output
177
10
###Markdown
[Power - Mod Power](https://www.hackerrank.com/challenges/python-power-mod-power/problem)So far, we have only heard of Python's powers. Now, we will witness them!Powers or exponents in Python can be calculated using the built-in power function. Call the power function a**b as shown below:>>> pow(a,b) or>>> a**bIt's also possible to calculate a**b%m .>>> pow(a,b,m)
###Code
pow(3,4)
pow(3,4,5)
x,y,z=int(input()),int(input()),int(input())
print(pow(x,y),pow(x,y,z),sep='\n')
###Output
3
4
5
###Markdown
[Integers Come In All Sizes]()
###Code
w,x,y,z=int(input()),int(input()),int(input()),int(input())
print(w**x+y**z)
###Output
9
29
7
27
|
002_Python_String_Methods/008_Python_String_find().ipynb
|
###Markdown
All the IPython Notebooks in this lecture series by Dr. Milan Parmar are available @ **[GitHub](https://github.com/milaan9/02_Python_Datatypes/tree/main/002_Python_String_Methods)** Python String `find()`The **`find()`** method returns the index of first occurrence of the substring (if found). If not found, it returns **-1**.**Syntax**:```pythonstr.find(sub[, start[, end]] )``` `find()` ParametersThe **`find()`** method takes maximum of three parameters:* **sub** - It is the substring to be searched in the **`str`** string.* **start** and **end** (optional) - The range **`str[start:end]`** within which substring is searched. Return Value from `find()`The **`find()`** method returns an integer value:* If the substring exists inside the string, it returns the index of the first occurence of the substring.* If substring doesn't exist inside the string, it returns **-1**. Working of `find()` method
###Code
# Example 1: find() With No start and end Argument
quote = 'Let it be, let it be, let it be'
# first occurance of 'let it'(case sensitive)
result = quote.find('let it')
print("Substring 'let it':", result)
# find returns -1 if substring not found
result = quote.find('small')
print("Substring 'small ':", result)
# How to use find()
if (quote.find('be,') != -1):
print("Contains substring 'be,'")
else:
print("Doesn't contain substring")
# Example 2: find() With start and end Arguments
quote = 'Do small things with great love'
# Substring is searched in 'hings with great love'
print(quote.find('small things', 10))
# Substring is searched in ' small things with great love'
print(quote.find('small things', 2))
# Substring is searched in 'hings with great lov'
print(quote.find('o small ', 10, -1))
# Substring is searched in 'll things with'
print(quote.find('things ', 6, 20))
# Example 3:
s="I Love Python Tutorial"
print(s.find('I'))
print(s.find('I',2))
print(s.find('Love'))
print(s.find('t',2,10))
###Output
0
-1
2
9
|
lessons/pymt/ans/00a_overview.ipynb
|
###Markdown
IntroductionWelcome to the *PyMT* Tutorial.pymt is the Python Modeling Toolkit. It is an Open Source Python package, developed by the [Community Surface Dynamics Modeling System](https://csdms.colorado.edu) (CSDMS), that provides the tools needed for coupling models that expose the [Basic Model Interface](https://bmi.readthedocs.io) (BMI).pymt in three points:* A collection of Earth-surface models* Tools for coupling models of disparate time and space scales* Extensible plug-in framework for adding new models Links* Reference * [Documentation](https://pymt.readthedocs.io) * [Source code](https://github.com/csdms/pymt)* Ask for help * [Issues on GitHub](https://github.com/csdms/pymt/issues) * Attend a live tutorial Tutorial StructureEach section is a separate Jupyter notebook. Within each notebook there is a mixture of text, code, and exercises.If you've not used Jupyter notebooks before, the main things you will want to know,* There are two modes: *command* and *edit** From *command* mode, press `Enter` to change to *edit* mode (and edit the current cell)* From *edit* mode, press `Esc` to change to *command* mode* Press `Shift` + `Enter` to execute the code in the current cellOr, if you would prefer, you can do all of this through the toolbar. Exercise: Print the string, "Hello, World!"
###Code
print("Hello, World!")
# Your code here
###Output
_____no_output_____
###Markdown
IntroductionWelcome to the *PyMT* Tutorial.pymt is the Python Modeling Toolkit. It is an Open Source Python package, developed by the [Community Surface Dynamics Modeling System](https://csdms.colorado.edu) (CSDMS), that provides the tools needed for coupling models that expose the [Basic Model Interface](https://bmi.readthedocs.io) (BMI).pymt in three points:* A collection of Earth-surface models* Tools for coupling models of disparate time and space scales* Extensible plug-in framework for adding new models Links* Reference * [Documentation](https://pymt.readthedocs.io) * [Source code](https://github.com/csdms/pymt)* Ask for help * [Issues on GitHub](https://github.com/csdms/pymt/issues) * Attend a live tutorial Tutorial StructureEach section is a separate Jupyter notebook. Within each notebook there is a mixture of text, code, and exercises.If you've not used Jupyter notebooks before, the main things you will want to know,* There are two modes: *command* and *edit** From *command* mode, press `Enter` to change to *edit* mode (and edit the current cell)* From *edit* mode, press `Esc` to change to *command* mode* Press `Shift` + `Enter` to execute the code in the current cellOr, if you would prefer, you can do all of this through the toolbar. Exercise: Print the string, "Hello, World!"
###Code
print("Hello, World!")
# Your code here
###Output
_____no_output_____
|
Generalized_ODIN.ipynb
|
###Markdown
Setup
###Code
# Grab the initial model weights
!wget -q https://github.com/sayakpaul/Generalized-ODIN-TF/releases/download/v1.0.0/models.tar.gz
!tar xf models.tar.gz
!git clone https://github.com/sayakpaul/Generalized-ODIN-TF
import sys
sys.path.append("Generalized-ODIN-TF")
from scripts import resnet20_odin, resnet20
from tensorflow.keras import layers
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
tf.random.set_seed(42)
np.random.seed(42)
###Output
_____no_output_____
###Markdown
Load CIFAR10
###Code
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
print(f"Total training examples: {len(x_train)}")
print(f"Total test examples: {len(x_test)}")
###Output
Total training examples: 50000
Total test examples: 10000
###Markdown
Define constants
###Code
BATCH_SIZE = 128
EPOCHS = 200
START_LR = 0.1
AUTO = tf.data.AUTOTUNE
###Output
_____no_output_____
###Markdown
Prepare data loaders
###Code
# Augmentation pipeline
simple_aug = tf.keras.Sequential(
[
layers.experimental.preprocessing.RandomFlip("horizontal"),
layers.experimental.preprocessing.RandomRotation(factor=0.02),
layers.experimental.preprocessing.RandomZoom(
height_factor=0.2, width_factor=0.2
),
]
)
# Now, map the augmentation pipeline to our training dataset
train_ds = (
tf.data.Dataset.from_tensor_slices((x_train, y_train))
.shuffle(BATCH_SIZE * 100)
.batch(BATCH_SIZE)
.map(lambda x, y: (simple_aug(x), y), num_parallel_calls=AUTO)
.prefetch(AUTO)
)
# Test dataset
test_ds = (
tf.data.Dataset.from_tensor_slices((x_test, y_test))
.batch(BATCH_SIZE)
.prefetch(AUTO)
)
###Output
_____no_output_____
###Markdown
Utility function for the model
###Code
def get_rn_model(arch, num_classes=10):
n = 2
depth = n * 9 + 2
n_blocks = ((depth - 2) // 9) - 1
# The input tensor
inputs = layers.Input(shape=(32, 32, 3))
x = layers.experimental.preprocessing.Rescaling(scale=1.0 / 127.5, offset=-1)(
inputs
)
# The Stem Convolution Group
x = arch.stem(x)
# The learner
x = arch.learner(x, n_blocks)
# The Classifier for 10 classes
outputs = arch.classifier(x, num_classes)
# Instantiate the Model
model = tf.keras.Model(inputs, outputs)
return model
# First serialize an initial ResNet20 model for reproducibility
# initial_model = get_rn_model(resnet20)
# initial_model.save("initial_model")
initial_model = tf.keras.models.load_model("initial_model")
# Now set the initial model weights of our ODIN model
odin_rn_model = get_rn_model(resnet20_odin)
for rn20_layer, rn20_odin_layer in zip(initial_model.layers[:-2],
odin_rn_model.layers[:-6]):
rn20_odin_layer.set_weights(rn20_layer.get_weights())
###Output
_____no_output_____
###Markdown
Define LR schedule, optimizer, and loss function
###Code
def lr_schedule(epoch):
if epoch < int(EPOCHS * 0.25) - 1:
return START_LR
elif epoch < int(EPOCHS*0.5) -1:
return float(START_LR * 0.1)
elif epoch < int(EPOCHS*0.75) -1:
return float(START_LR * 0.01)
else:
return float(START_LR * 0.001)
lr_callback = tf.keras.callbacks.LearningRateScheduler(lambda epoch: lr_schedule(epoch), verbose=True)
# Optimizer and loss function.
optimizer = tf.keras.optimizers.SGD(learning_rate=START_LR, momentum=0.9)
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
###Output
_____no_output_____
###Markdown
Model training with ResNet20
###Code
odin_rn_model.compile(loss=loss_fn, optimizer=optimizer, metrics=["accuracy"])
history = odin_rn_model.fit(train_ds,
validation_data=test_ds,
epochs=EPOCHS,
callbacks=[lr_callback])
plt.plot(history.history["loss"], label="train loss")
plt.plot(history.history["val_loss"], label="test loss")
plt.grid()
plt.legend()
plt.show()
odin_rn_model.save("odin_rn_model")
_, train_acc = odin_rn_model.evaluate(train_ds, verbose=0)
_, test_acc = odin_rn_model.evaluate(test_ds, verbose=0)
print("Train accuracy: {:.2f}%".format(train_acc * 100))
print("Test accuracy: {:.2f}%".format(test_acc * 100))
###Output
Train accuracy: 99.58%
Test accuracy: 90.70%
###Markdown
Setup
###Code
# Grab the initial model weights
!wget -q https://github.com/sayakpaul/Generalized-ODIN-TF/releases/download/v1.0.0/models.tar.gz
!tar xf models.tar.gz
!git clone https://github.com/sayakpaul/Generalized-ODIN-TF
import sys
sys.path.append("Generalized-ODIN-TF")
from scripts import resnet20_odin, resnet20
from tensorflow.keras import layers
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
tf.random.set_seed(42)
np.random.seed(42)
###Output
_____no_output_____
###Markdown
Load CIFAR10
###Code
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
print(f"Total training examples: {len(x_train)}")
print(f"Total test examples: {len(x_test)}")
###Output
Total training examples: 50000
Total test examples: 10000
###Markdown
Define constants
###Code
BATCH_SIZE = 128
EPOCHS = 200
START_LR = 0.1
AUTO = tf.data.AUTOTUNE
###Output
_____no_output_____
###Markdown
Prepare data loaders
###Code
# Augmentation pipeline
simple_aug = tf.keras.Sequential(
[
layers.experimental.preprocessing.RandomFlip("horizontal"),
layers.experimental.preprocessing.RandomRotation(factor=0.02),
layers.experimental.preprocessing.RandomZoom(
height_factor=0.2, width_factor=0.2
),
]
)
# Now, map the augmentation pipeline to our training dataset
train_ds = (
tf.data.Dataset.from_tensor_slices((x_train, y_train))
.shuffle(BATCH_SIZE * 100)
.batch(BATCH_SIZE)
.map(lambda x, y: (simple_aug(x), y), num_parallel_calls=AUTO)
.prefetch(AUTO)
)
# Test dataset
test_ds = (
tf.data.Dataset.from_tensor_slices((x_test, y_test))
.batch(BATCH_SIZE)
.prefetch(AUTO)
)
###Output
_____no_output_____
###Markdown
Utility function for the model
###Code
def get_rn_model(arch, num_classes=10):
n = 2
depth = n * 9 + 2
n_blocks = ((depth - 2) // 9) - 1
# The input tensor
inputs = layers.Input(shape=(32, 32, 3))
x = layers.experimental.preprocessing.Rescaling(scale=1.0 / 127.5, offset=-1)(
inputs
)
# The Stem Convolution Group
x = arch.stem(x)
# The learner
x = arch.learner(x, n_blocks)
# The Classifier for 10 classes
outputs = arch.classifier(x, num_classes)
# Instantiate the Model
model = tf.keras.Model(inputs, outputs)
return model
# First serialize an initial ResNet20 model for reproducibility
# initial_model = get_rn_model(resnet20)
# initial_model.save("initial_model")
initial_model = tf.keras.models.load_model("initial_model")
# Now set the initial model weights of our ODIN model
odin_rn_model = get_rn_model(resnet20_odin)
for rn20_layer, rn20_odin_layer in zip(initial_model.layers[:-2],
odin_rn_model.layers[:-6]):
rn20_odin_layer.set_weights(rn20_layer.get_weights())
###Output
_____no_output_____
###Markdown
Define LR schedule, optimizer, and loss function
###Code
def lr_schedule(epoch):
if epoch < int(EPOCHS * 0.25) - 1:
return START_LR
elif epoch < int(EPOCHS*0.5) -1:
return float(START_LR * 0.1)
elif epoch < int(EPOCHS*0.75) -1:
return float(START_LR * 0.01)
else:
return float(START_LR * 0.001)
lr_callback = tf.keras.callbacks.LearningRateScheduler(lambda epoch: lr_schedule(epoch), verbose=True)
# Optimizer and loss function.
optimizer = tf.keras.optimizers.SGD(learning_rate=START_LR, momentum=0.9)
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
###Output
_____no_output_____
###Markdown
Model training with ResNet20
###Code
odin_rn_model.compile(loss=loss_fn, optimizer=optimizer, metrics=["accuracy"])
history = odin_rn_model.fit(train_ds,
validation_data=test_ds,
epochs=EPOCHS,
callbacks=[lr_callback])
plt.plot(history.history["loss"], label="train loss")
plt.plot(history.history["val_loss"], label="test loss")
plt.grid()
plt.legend()
plt.show()
odin_rn_model.save("odin_rn_model")
_, train_acc = odin_rn_model.evaluate(train_ds, verbose=0)
_, test_acc = odin_rn_model.evaluate(test_ds, verbose=0)
print("Train accuracy: {:.2f}%".format(train_acc * 100))
print("Test accuracy: {:.2f}%".format(test_acc * 100))
###Output
Train accuracy: 99.58%
Test accuracy: 90.70%
|
samples/DataScience/pos-tagging-neural-nets-keras/pos_tagging_neural_nets_keras.ipynb
|
###Markdown
Part-of-Speech tagging tutorial with the Keras Deep Learning libraryIn this tutorial, you will see how you can use a simple Keras model to train and evaluate an artificial neural network for multi-class classification problems.
###Code
# Ensure reproducibility
import numpy as np
CUSTOM_SEED = 42
np.random.seed(CUSTOM_SEED)
import nltk
nltk.download('treebank')
import random
from nltk.corpus import treebank
sentences = treebank.tagged_sents(tagset='universal')
print('a random sentence: \n-> {}'.format(random.choice(sentences)))
tags = set([tag for sentence in treebank.tagged_sents() for _, tag in sentence])
print('nb_tags: {}\ntags: {}'.format(len(tags), tags))
###Output
nb_tags: 46
tags: {'CC', 'UH', '-LRB-', '$', 'SYM', 'NNS', 'RB', '#', 'NNPS', 'IN', 'RBS', 'VBD', 'MD', 'WP', 'CD', 'VBP', ':', 'WDT', '.', 'DT', 'RBR', 'PRP$', 'JJR', ',', 'VBZ', 'JJS', 'EX', 'VBN', '-NONE-', "''", 'VBG', 'POS', 'NN', 'WRB', '-RRB-', 'FW', 'VB', 'LS', 'PDT', '``', 'NNP', 'JJ', 'TO', 'WP$', 'RP', 'PRP'}
###Markdown
We use approximately 60% of the tagged sentences for training, 20% as the validation set and 20% to evaluate our model.
###Code
train_test_cutoff = int(.80 * len(sentences))
training_sentences = sentences[:train_test_cutoff]
testing_sentences = sentences[train_test_cutoff:]
train_val_cutoff = int(.25 * len(training_sentences))
validation_sentences = training_sentences[:train_val_cutoff]
training_sentences = training_sentences[train_val_cutoff:]
def add_basic_features(sentence_terms, index):
""" Compute some very basic word features.
:param sentence_terms: [w1, w2, ...]
:type sentence_terms: list
:param index: the index of the word
:type index: int
:return: dict containing features
:rtype: dict
"""
term = sentence_terms[index]
return {
'nb_terms': len(sentence_terms),
'term': term,
'is_first': index == 0,
'is_last': index == len(sentence_terms) - 1,
'is_capitalized': term[0].upper() == term[0],
'is_all_caps': term.upper() == term,
'is_all_lower': term.lower() == term,
'prefix-1': term[0],
'prefix-2': term[:2],
'prefix-3': term[:3],
'suffix-1': term[-1],
'suffix-2': term[-2:],
'suffix-3': term[-3:],
'prev_word': '' if index == 0 else sentence_terms[index - 1],
'next_word': '' if index == len(sentence_terms) - 1 else sentence_terms[index + 1]
}
def untag(tagged_sentence):
"""
Remove the tag for each tagged term.
:param tagged_sentence: a POS tagged sentence
:type tagged_sentence: list
:return: a list of tags
:rtype: list of strings
"""
return [w for w, _ in tagged_sentence]
def transform_to_dataset(tagged_sentences):
"""
Split tagged sentences to X and y datasets and append some basic features.
:param tagged_sentences: a list of POS tagged sentences
:param tagged_sentences: list of list of tuples (term_i, tag_i)
:return:
"""
X, y = [], []
for pos_tags in tagged_sentences:
for index, (term, class_) in enumerate(pos_tags):
# Add basic NLP features for each sentence term
X.append(add_basic_features(untag(pos_tags), index))
y.append(class_)
return X, y
###Output
_____no_output_____
###Markdown
For training, validation and testing sentences, we split the attributes into X (input variables) and y (output variables).
###Code
X_train, y_train = transform_to_dataset(training_sentences)
X_test, y_test = transform_to_dataset(testing_sentences)
X_val, y_val = transform_to_dataset(validation_sentences)
###Output
_____no_output_____
###Markdown
Fit our DictVectorizer with our set of features
###Code
from sklearn.feature_extraction import DictVectorizer
dict_vectorizer = DictVectorizer(sparse=False)
dict_vectorizer.fit(X_train + X_test + X_val)
###Output
_____no_output_____
###Markdown
Convert dict features to vectors
###Code
X_train = dict_vectorizer.transform(X_train)
X_test = dict_vectorizer.transform(X_test)
X_val = dict_vectorizer.transform(X_val)
###Output
_____no_output_____
###Markdown
Fit LabelEncoder with our list of classes
###Code
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
label_encoder.fit(y_train + y_test + y_val)
###Output
_____no_output_____
###Markdown
Encode class values as integers
###Code
y_train = label_encoder.transform(y_train)
y_test = label_encoder.transform(y_test)
y_val = label_encoder.transform(y_val)
###Output
_____no_output_____
###Markdown
Convert integers to dummy variables (one hot encoded)
###Code
from keras.utils import np_utils
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
y_val = np_utils.to_categorical(y_val)
###Output
Using TensorFlow backend.
###Markdown
Define a simple Keras sequential model
###Code
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
def build_model(input_dim, hidden_neurons, output_dim):
"""
Construct, compile and return a Keras model which will be used to fit/predict
"""
model = Sequential([
Dense(hidden_neurons, input_dim=input_dim),
Activation('relu'),
Dropout(0.2),
Dense(hidden_neurons),
Activation('relu'),
Dropout(0.2),
Dense(output_dim, activation='softmax')
])
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
return model
###Output
_____no_output_____
###Markdown
Set model parameters and create a new sklearn classifier instance
###Code
from keras.wrappers.scikit_learn import KerasClassifier
model_params = {
'build_fn': build_model,
'input_dim': X_train.shape[1],
'hidden_neurons': 512,
'output_dim': y_train.shape[1],
'epochs': 5,
'batch_size': 256,
'verbose': 1,
'validation_data': (X_val, y_val),
'shuffle': True
}
clf = KerasClassifier(**model_params)
###Output
_____no_output_____
###Markdown
Finally, fit our classifier
###Code
hist = clf.fit(X_train, y_train)
import matplotlib.pyplot as plt
def plot_model_performance(train_loss, train_acc, train_val_loss, train_val_acc):
""" Plot model loss and accuracy through epochs. """
green = '#72C29B'
orange = '#FFA577'
with plt.xkcd():
fig, (ax1, ax2) = plt.subplots(2, figsize=(10, 8))
ax1.plot(range(1, len(train_loss) + 1), train_loss, green, linewidth=5,
label='training')
ax1.plot(range(1, len(train_val_loss) + 1), train_val_loss, orange,
linewidth=5, label='validation')
ax1.set_xlabel('# epoch')
ax1.set_ylabel('loss')
ax1.tick_params('y')
ax1.legend(loc='upper right', shadow=False)
ax1.set_title('Model loss through #epochs', fontweight='bold')
ax2.plot(range(1, len(train_acc) + 1), train_acc, green, linewidth=5,
label='training')
ax2.plot(range(1, len(train_val_acc) + 1), train_val_acc, orange,
linewidth=5, label='validation')
ax2.set_xlabel('# epoch')
ax2.set_ylabel('accuracy')
ax2.tick_params('y')
ax2.legend(loc='lower right', shadow=False)
ax2.set_title('Model accuracy through #epochs', fontweight='bold')
plt.tight_layout()
plt.show()
###Output
_____no_output_____
###Markdown
Plot model performance
###Code
plot_model_performance(
train_loss=hist.history.get('loss', []),
train_acc=hist.history.get('acc', []),
train_val_loss=hist.history.get('val_loss', []),
train_val_acc=hist.history.get('val_acc', [])
)
###Output
/usr/local/lib/python3.5/dist-packages/matplotlib/font_manager.py:1320: UserWarning: findfont: Font family ['xkcd', 'Humor Sans', 'Comic Sans MS'] not found. Falling back to DejaVu Sans
(prop.get_family(), self.defaultFamily[fontext]))
###Markdown
Evaluate model accuracy
###Code
score = clf.score(X_test, y_test, verbose=0)
print('model accuracy: {}'.format(score))
###Output
model accuracy: 0.9657667548280853
###Markdown
Visualize model architecture Finally, save model
###Code
from keras.utils import plot_model
plot_model(clf.model, to_file='tmp/model_structure.png', show_shapes=True)
clf.model.save('/tmp/keras_mlp.h5')
###Output
_____no_output_____
|
Week_3_Assessing_Performance/assign_1_polynomial-regression.ipynb
|
###Markdown
Regression Week 3: Assessing Fit (polynomial regression) In this notebook, we will compare different regression models in order to assess which model fits best. We will be using polynomial regression as a means to examine this topic. In particular, you will:* Write a function to take a Series and a degree and return a DataFrame where each column is the Series to a polynomial value up to the total degree e.g. degree = 3 then column 1 is the Series column 2 is the Series squared and column 3 is the Series cubed* Use matplotlib to visualize polynomial regressions* Use matplotlib to visualize the same polynomial degree on different subsets of the data* Use a validation set to select a polynomial degree* Assess the final fit using test data Importing Libraries
###Code
import os
import zipfile
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('darkgrid')
%matplotlib inline
###Output
_____no_output_____
###Markdown
Unzipping files with house sales data Dataset is from house sales in King County, the region where the city of Seattle, WA is located.
###Code
# Put files in current direction into a list
files_list = [f for f in os.listdir('.') if os.path.isfile(f)]
# Filenames of unzipped files
unzip_files = ['kc_house_data.csv','wk3_kc_house_set_1_data.csv', 'wk3_kc_house_set_2_data.csv',
'wk3_kc_house_set_3_data.csv', 'wk3_kc_house_set_4_data.csv', 'wk3_kc_house_test_data.csv',
'wk3_kc_house_train_data.csv', 'wk3_kc_house_valid_data.csv']
# If upzipped file not in files_list, unzip the file
for filename in unzip_files:
if filename not in files_list:
zip_file = filename + '.zip'
unzipping = zipfile.ZipFile(zip_file)
unzipping.extractall()
unzipping.close
###Output
_____no_output_____
###Markdown
Basics of apply function for Pandas DataFrames Next we're going to write a polynomial function that takes an Series and a maximal degree and returns an DataFrame with columns containing the Series to all the powers up to the maximal degree.The easiest way to apply a power to a Series is to use the .apply() and lambda x: functions. For example to take the example array and compute the third power we can do as follows: (note running this cell the first time may take longer than expected since it loads graphlab)
###Code
tmp = pd.Series([1.0, 2.0, 3.0])
tmp_cubed = tmp.apply(lambda x: x**3)
print tmp
print tmp_cubed
###Output
0 1
1 2
2 3
dtype: float64
0 1
1 8
2 27
dtype: float64
###Markdown
We can create an empty DataFrame using pd.DataFrame() and then add any columns to it with ex_dframe['column_name'] = value. For example we create an empty DataFrame and make the column 'power_1' to be the first power of tmp (i.e. tmp itself).
###Code
ex_dframe = pd.DataFrame()
ex_dframe['power_1'] = tmp
print ex_dframe
print type(ex_dframe)
###Output
power_1
0 1
1 2
2 3
<class 'pandas.core.frame.DataFrame'>
###Markdown
Polynomial_dataframe function Using the hints above complete the following function to create an DataFrame consisting of the powers of a Series up to a specific degree:
###Code
def polynomial_dataframe(feature, degree): # feature is pandas.Series type
# assume that degree >= 1
# initialize the dataframe:
poly_dataframe = pd.DataFrame()
# and set poly_dataframe['power_1'] equal to the passed feature
poly_dataframe['power_1'] = feature
# first check if degree > 1
if degree > 1:
# then loop over the remaining degrees:
for power in range(2, degree+1):
# first we'll give the column a name:
name = 'power_' + str(power)
# assign poly_dataframe[name] to be feature^power; use apply(*)
poly_dataframe[name] = poly_dataframe['power_1'].apply(lambda x: x**power)
return poly_dataframe
###Output
_____no_output_____
###Markdown
To test your function consider the smaller tmp variable and what you would expect the outcome of the following call:
###Code
tmp = pd.Series([1.0, 2.0, 3.0])
print polynomial_dataframe(tmp, 3)
###Output
power_1 power_2 power_3
0 1 1 1
1 2 4 8
2 3 9 27
###Markdown
Visualizing polynomial regression Let's use matplotlib to visualize what a polynomial regression looks like on some real data. First, let's load house sales data
###Code
# Dictionary with the correct dtypes for the DataFrame columns
dtype_dict = {'bathrooms':float, 'waterfront':int, 'sqft_above':int, 'sqft_living15':float,
'grade':int, 'yr_renovated':int, 'price':float, 'bedrooms':float,
'zipcode':str, 'long':float, 'sqft_lot15':float, 'sqft_living':float,
'floors':str, 'condition':int, 'lat':float, 'date':str, 'sqft_basement':int,
'yr_built':int, 'id':str, 'sqft_lot':int, 'view':int}
sales = pd.read_csv('kc_house_data.csv', dtype = dtype_dict)
###Output
_____no_output_____
###Markdown
As in Week 3, we will use the sqft_living variable. For plotting purposes (connecting the dots), you'll need to sort by the values of sqft_living. For houses with identical square footage, we break the tie by their prices.
###Code
sales = sales.sort_values(['sqft_living', 'price'])
sales[['sqft_living', 'price']].head()
###Output
_____no_output_____
###Markdown
Let's start with a degree 1 polynomial using 'sqft_living' (i.e. a line) to predict 'price' and plot what it looks like.
###Code
poly1_data = polynomial_dataframe(sales['sqft_living'], 1)
poly1_data['price'] = sales['price'] # add price to the data since it's the target
poly1_data.head()
###Output
_____no_output_____
###Markdown
Creating feature matrix and output vector to perform linear reggression with Sklearn
###Code
# Note: Must pass list of features to feature matrix X_feat_model_1 for sklearn to work
X_feat_model_1 = poly1_data[ ['power_1'] ]
y_output_model_1 = poly1_data['price']
model_1 = LinearRegression()
model_1.fit(X_feat_model_1, y_output_model_1)
###Output
_____no_output_____
###Markdown
Let's look at the intercept and weight before we plot.
###Code
print model_1.intercept_
print model_1.coef_
###Output
-43580.7430945
[ 280.6235679]
###Markdown
Now, plotting the data and the line learned by linear regression
###Code
plt.figure(figsize=(8,6))
plt.plot(poly1_data['power_1'],poly1_data['price'],'.', label= 'House Price Data')
plt.hold(True)
plt.plot(poly1_data['power_1'], model_1.predict(X_feat_model_1), '-' , label= 'Linear Regression Model')
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('Simple Linear Regression', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
We can see, not surprisingly, that the predicted values all fall on a line, specifically the one with slope 280 and intercept -43579. What if we wanted to plot a second degree polynomial?
###Code
poly2_data = polynomial_dataframe(sales['sqft_living'], 2)
my_features = list(poly2_data) # Get col_names of DataFrame and put in list
poly2_data['price'] = sales['price'] # add price to the data since it's the target
# Creating feature matrix and output vector to perform regression w/ sklearn.
X_feat_model_2 = poly2_data[my_features]
y_output_model_2 = poly2_data['price']
# Creating a LinearRegression Object. Then, performing linear regression on feature matrix and output vector
model_2 = LinearRegression()
model_2.fit(X_feat_model_2, y_output_model_2)
###Output
_____no_output_____
###Markdown
Let's look at the intercept and weights before we plot.
###Code
print model_2.intercept_
print model_2.coef_
plt.figure(figsize=(8,6))
plt.plot(poly2_data['power_1'],poly2_data['price'],'.', label= 'House Price Data')
plt.hold(True)
plt.plot(poly2_data['power_1'], model_2.predict(X_feat_model_2), '-' , label= 'Regression Model')
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('2nd Degree Polynomial Regression', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
The resulting model looks like half a parabola. Try on your own to see what the cubic looks like:
###Code
poly3_data = polynomial_dataframe(sales['sqft_living'], 3)
my_features = list(poly3_data) # Get col_names of DataFrame and put in list
poly3_data['price'] = sales['price'] # add price to the data since it's the target
# Creating feature matrix and output vector to perform regression w/ sklearn.
X_feat_model_3 = poly3_data[my_features]
y_output_model_3 = poly3_data['price']
# Creating a LinearRegression Object. Then, performing linear regression on feature matrix and output vector
model_3 = LinearRegression()
model_3.fit(X_feat_model_3, y_output_model_3)
###Output
_____no_output_____
###Markdown
Looking at intercept and weights before plotting
###Code
print model_3.intercept_
print model_3.coef_
plt.figure(figsize=(8,6))
plt.plot(poly3_data['power_1'],poly3_data['price'],'.', label= 'House Price Data')
plt.hold(True)
plt.plot(poly3_data['power_1'], model_3.predict(X_feat_model_3), '-' , label= 'Regression Model')
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('3rd Degree Polynomial Regression', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
Now try a 15th degree polynomial:
###Code
poly15_data = polynomial_dataframe(sales['sqft_living'], 15)
my_features = list(poly15_data) # Get col_names of DataFrame and put in list
poly15_data['price'] = sales['price'] # add price to the data since it's the target
# Creating feature matrix and output vector to perform regression w/ sklearn.
X_feat_model_15 = poly15_data[my_features]
y_output_model_15 = poly15_data['price']
# Creating a LinearRegression Object. Then, performing linear regression on feature matrix and output vector
model_15 = LinearRegression()
model_15.fit(X_feat_model_15, y_output_model_15)
###Output
_____no_output_____
###Markdown
Looking at intercept and weights before plotting
###Code
print model_15.intercept_
print model_15.coef_
plt.figure(figsize=(8,6))
plt.plot(poly15_data['power_1'],poly15_data['price'],'.', label= 'House Price Data')
plt.hold(True)
plt.plot(poly15_data['power_1'], model_15.predict(X_feat_model_15), '-' , label= 'Regression Model')
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('15th Degree Polynomial Regression', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
What do you think of the 15th degree polynomial? Do you think this is appropriate? If we were to change the data do you think you'd get pretty much the same curve? Let's take a look. Changing the data and re-learning We're going to split the sales data into four subsets of roughly equal size. Then you will estimate a 15th degree polynomial model on all four subsets of the data. Print the coefficients (you should use .print_rows(num_rows = 16) to view all of them) and plot the resulting fit (as we did above). The quiz will ask you some questions about these results. Loading the 4 datasets
###Code
(set_1, set_2) = (pd.read_csv('wk3_kc_house_set_1_data.csv', dtype = dtype_dict), pd.read_csv('wk3_kc_house_set_2_data.csv', dtype = dtype_dict))
(set_3, set_4) = (pd.read_csv('wk3_kc_house_set_3_data.csv', dtype = dtype_dict), pd.read_csv('wk3_kc_house_set_4_data.csv', dtype = dtype_dict))
###Output
_____no_output_____
###Markdown
Making 4 dataframes with 15 features and a price column
###Code
(poly15_set_1, poly15_set_2) = ( polynomial_dataframe(set_1['sqft_living'], 15) , polynomial_dataframe(set_2['sqft_living'], 15) )
(poly15_set_3, poly15_set_4) = ( polynomial_dataframe(set_3['sqft_living'], 15) , polynomial_dataframe(set_4['sqft_living'], 15) )
( poly15_set_1['price'], poly15_set_2['price'] ) = ( set_1['price'] , set_2['price'] )
( poly15_set_3['price'], poly15_set_4['price'] ) = ( set_3['price'] , set_4['price'] )
my_features = list(poly15_set_1) # Put DataFrame col_names in a list. All dataframes have same col_names
( X_feat_set_1, X_feat_set_2 ) = ( poly15_set_1[my_features], poly15_set_2[my_features] )
( X_feat_set_3, X_feat_set_4 ) = ( poly15_set_3[my_features], poly15_set_4[my_features] )
( y_output_set_1, y_output_set_2 ) = ( poly15_set_1['price'], poly15_set_2['price'] )
( y_output_set_3, y_output_set_4 ) = ( poly15_set_3['price'], poly15_set_4['price'] )
# Creating a LinearRegression Object. Then, performing linear regression on feature matrix and output vector
model_deg_15_set_1 = LinearRegression()
model_deg_15_set_2 = LinearRegression()
model_deg_15_set_3 = LinearRegression()
model_deg_15_set_4 = LinearRegression()
model_deg_15_set_1.fit(X_feat_set_1, y_output_set_1)
model_deg_15_set_2.fit(X_feat_set_2, y_output_set_2)
model_deg_15_set_3.fit(X_feat_set_3, y_output_set_3)
model_deg_15_set_4.fit(X_feat_set_4, y_output_set_4)
plt.figure(figsize=(8,6))
plt.plot(poly15_data['power_1'],poly15_data['price'],'.', label= 'House Price Data')
plt.hold(True)
plt.plot(poly15_set_1['power_1'], model_deg_15_set_1.predict(X_feat_set_1), '-' , label= 'Model 1')
plt.plot(poly15_set_2['power_1'], model_deg_15_set_2.predict(X_feat_set_2), '-' , label= 'Model 2')
plt.plot(poly15_set_3['power_1'], model_deg_15_set_3.predict(X_feat_set_3), '-' , label= 'Model 3')
plt.plot(poly15_set_4['power_1'], model_deg_15_set_4.predict(X_feat_set_4), '-' , label= 'Model 4')
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('4 Different 15th Deg. Polynomial Regr. Models', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
**Quiz Question: Is the sign (positive or negative) for power_15 the same in all four models?**
###Code
power_15_coeff = [ model_deg_15_set_1.coef_[-1], model_deg_15_set_2.coef_[-1], model_deg_15_set_3.coef_[-1], model_deg_15_set_4.coef_[-1] ]
print power_15_coeff
print
if all(i > 0 for i in power_15_coeff):
print 'Sign the SAME (Positive) for all 4 models'
elif all(i < 0 for i in power_15_coeff):
print 'Sign the SAME (Negative) for all 4 models'
else:
print 'Sign NOT the same for all 4 models'
###Output
[1.3117216099014014e-87, 8.8062799992843061e-75, 1.1139318003215489e-85, 5.0630590615135435e-74]
Sign the SAME (Positive) for all 4 models
###Markdown
**Quiz Question: (True/False) the plotted fitted lines look the same in all four plots** Fits for 4 different models look very different Selecting a Polynomial Degree Whenever we have a "magic" parameter like the degree of the polynomial there is one well-known way to select these parameters: validation set. (We will explore another approach in week 4).We now load sales dataset split 3-way into training set, test set, and validation set:
###Code
train_data = pd.read_csv('wk3_kc_house_train_data.csv', dtype = dtype_dict)
valid_data = pd.read_csv('wk3_kc_house_valid_data.csv', dtype = dtype_dict)
test_data = pd.read_csv('wk3_kc_house_test_data.csv', dtype = dtype_dict)
# Sorting the Training Data for Plotting
train_data = train_data.sort_values(['sqft_living', 'price'])
train_data[['sqft_living', 'price']].head()
###Output
_____no_output_____
###Markdown
Next you should write a loop that does the following:* For degree in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15] (to get this in python type range(1, 15+1)) * Build an DAtaFrame of polynomial data of train_data['sqft_living'] at the current degree * Add train_data['price'] to the polynomial DataFrame * Learn a polynomial regression model to sqft vs price with that degree on TRAIN data * Compute the RSS on VALIDATION data (here you will want to use .predict()) for that degree and you will need to make a polynomial DataFrame using validation data. * Report which degree had the lowest RSS on validation data
###Code
# poly_deg_dict is a dict which holds poly_features dataframes. key_list is a list of keys for the dicts.
# The keys in key_list are of the form 'poly_deg_i', where i refers to the ith polynomial
poly_deg_dict = {}
key_list = []
# X_feat_dict is a dict with all the feature matrices and y_output_dict is a dict with all the output vectors
X_feat_dict = {}
y_output_dict = {}
# model_poly_deg is a dict which holds all the regression models for the ith polynomial fit
model_poly_deg = {}
# Looping over polynomial features from 1-15
for i in range(1, 15+1, 1):
# Defining key-name and appending key_name to the key_list
key_poly_deg = 'poly_deg_' + str(i)
key_list.append(key_poly_deg)
# Entering each dataframe returned from polynomial_dataframe function into a dict
# Then, saving col_names into a list to do regression w/ these features. Then, adding price column to dataframe
poly_deg_dict[key_poly_deg] = polynomial_dataframe(train_data['sqft_living'], i)
feat_poly_fit = list(poly_deg_dict[key_poly_deg])
poly_deg_dict[key_poly_deg]['price'] = train_data['price']
# Adding feature matrix and output_vector into dicts
X_feat_dict[key_poly_deg] = poly_deg_dict[key_poly_deg][feat_poly_fit]
y_output_dict[key_poly_deg] = poly_deg_dict[key_poly_deg]['price']
# Adding regression models to dicts
model_poly_deg[key_poly_deg] = LinearRegression()
model_poly_deg[key_poly_deg].fit( X_feat_dict[key_poly_deg], y_output_dict[key_poly_deg] )
plt.figure(figsize=(8,6))
plt.plot(train_data['sqft_living'], train_data['price'],'.', label= 'House Price Data')
plt.hold(True)
for i in range(0,5):
leg_label = 'Deg. ' + str(i+1)
plt.plot( poly_deg_dict[key_list[i]]['power_1'], model_poly_deg[key_list[i]].predict(X_feat_dict[key_list[i]]), '-', label = leg_label )
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('Degree 1-5 Polynomial Regression Models', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
plt.figure(figsize=(8,6))
plt.plot(train_data['sqft_living'], train_data['price'],'.', label= 'House Price Data')
plt.hold(True)
for i in range(5,10):
leg_label = 'Deg. ' + str(i+1)
plt.plot( poly_deg_dict[key_list[i]]['power_1'], model_poly_deg[key_list[i]].predict(X_feat_dict[key_list[i]]), '-', label = leg_label )
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('Degree 6-10 Polynomial Regression Models', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
plt.figure(figsize=(8,6))
plt.plot(train_data['sqft_living'], train_data['price'],'.', label= 'House Price Data')
plt.hold(True)
for i in range(10,15):
leg_label = 'Deg. ' + str(i+1)
plt.plot( poly_deg_dict[key_list[i]]['power_1'], model_poly_deg[key_list[i]].predict(X_feat_dict[key_list[i]]), '-', label = leg_label )
plt.hold(False)
plt.legend(loc='upper left', fontsize=16)
plt.xlabel('Living Area (ft^2)', fontsize=16)
plt.ylabel('House Price ($)', fontsize=16)
plt.title('Degree 11-15 Polynomial Regression Models', fontsize=18)
plt.axis([0.0, 14000.0, 0.0, 8000000.0])
plt.show()
###Output
_____no_output_____
###Markdown
**Quiz Question: Which degree (1, 2, …, 15) had the lowest RSS on Validation data?** Now that you have chosen the degree of your polynomial using validation data, compute the RSS of this model on TEST data. Report the RSS on your quiz. First, sorting validation data in case of plotting
###Code
valid_data = valid_data.sort_values(['sqft_living', 'price'])
###Output
_____no_output_____
###Markdown
Now, building a function to compute the RSS
###Code
def get_residual_sum_of_squares(model, data, outcome):
# - data holds the data points with the features (columns) we are interested in performing a linear regression fit
# - model holds the linear regression model obtained from fitting to the data
# - outcome is the y, the observed house price for each data point
# By using the model and applying predict on the data, we return a numpy array which holds
# the predicted outcome (house price) from the linear regression model
model_predictions = model.predict(data)
# Computing the residuals between the predicted house price and the actual house price for each data point
residuals = outcome - model_predictions
# To get RSS, square the residuals and add them up
RSS = sum(residuals*residuals)
return RSS
###Output
_____no_output_____
###Markdown
Now, creating a list of tuples with the values (RSS_deg_i , i). Finding min of list will give min RSS_val and and degree of polynomial
###Code
# First, clearing empty list which will hold tuples
RSS_tup_list = []
# Looping over polynomial features from 1-15
for i in range(1, 15+1, 1):
# Creating dataframe w/ additional features on the validation data. Then, putting these features into a list
valid_data_poly = polynomial_dataframe(valid_data['sqft_living'], i)
feat_val_poly = list(valid_data_poly)
# Using get_residual_sum_of_squares to compute RSS. Using the key_list[i-1] since index starts at 0.
# Each entry of key_list[i-1] contains the key we want for the dict of regression models
RSS_val = get_residual_sum_of_squares(model_poly_deg[key_list[i-1]], valid_data_poly[feat_val_poly], valid_data['price'])
# Appending tuppler with RSS_val and i into RSS_tup_list
RSS_tup_list.append( (RSS_val, i) )
RSS_min = min(RSS_tup_list)
print 'Polynomial Degree with lowest RSS from validation set: ', RSS_min[1]
###Output
Polynomial Degree with lowest RSS from validation set: 6
###Markdown
**Quiz Question: what is the RSS on TEST data for the model with the degree selected from Validation data?** First, sorting test data in case of plotting
###Code
test_data = test_data.sort_values(['sqft_living', 'price'])
###Output
_____no_output_____
###Markdown
Now, finding RSS of polynomial degree 6 on TEST data
###Code
# Creating dataframe w/ additional features on the test data. Then, putting these features into a list
test_data_poly_6 = polynomial_dataframe(test_data['sqft_living'], 6)
feat_val_poly_6 = list(test_data_poly_6)
RSS_test_poly6 = get_residual_sum_of_squares(model_poly_deg[key_list[6-1]], test_data_poly_6[feat_val_poly_6], test_data['price'])
print 'RSS on Test data for Degree 6 Polynomial: ', RSS_test_poly6
###Output
RSS on Test data for Degree 6 Polynomial: 1.35225117491e+14
|
Training_TFKeras_CPU_Distributed/MultiWorker_Notebooks/4.3a-Worker0_Training-InclusiveClassifier-TF_Keras_TFRecord.ipynb
|
###Markdown
Traininig the Inclusive classifier with tf.Keras using data in TFRecord format**tf.keras Inclusive classifier** This notebooks trains a neural network for the particle classifier using the Inclusive Classifier, using as input the list of recunstructed particles with the low level features + the high level features. Data is prepared from Parquet using Apache Spark, and written into TFRecord format. Data in TFRecord format is read from TensorFlow using tf.data and tf.io in tf.keras.To run this notebook we used the following configuration:* *Software stack*: TensorFlow 2.0.0-rc0* *Platform*: CentOS 7, Python 3.6
###Code
import tensorflow as tf
import numpy as np
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import Sequential, Input, Model
from tensorflow.keras.layers import Masking, Dense, Activation, GRU, Dropout, concatenate
tf.version.VERSION
# only needed for TensorFlow 1.x
# tf.enable_eager_execution()
###Output
_____no_output_____
###Markdown
Configure distributed training using tf.distributeThis notebook shows an example of distributed training with tf.keras using 3 concurrent executions on a single machine.The test machine has 24 physical cores it has been notes that a serial execution of the training would leave spare capacity. With distributed training we can "use all the CPU on the box". - TensorFlow MultiWorkerMirroredStrategy is used to distribute the training.- Configuration of the workers is done using the OS enviroment variable **TF_CONFIG**.- **nodes_endpoints** configures the list of machines and ports that will be used. In this example, we use 3 workers on the same machines, you can use this to distribute over multiple machines too- **worker_number** will be unique for each worker, numbering starts from 0- Worker number 0 will be the master. - You need to run the 3 notebooks for the 3 configured workers at the same time (training will only start when all 3 workers are active)
###Code
# Each worker will have a unique worker_number, numbering starts from 0
worker_number=0
nodes_endpoints = ["localhost:12345", "localhost:12346", "localhost:12347", "localhost:12348"]
number_workers = len(nodes_endpoints)
import os
import json
os.environ['TF_CONFIG'] = json.dumps({
'cluster': {
'worker': nodes_endpoints
},
'task': {'type': 'worker', 'index': worker_number}
})
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
###Output
_____no_output_____
###Markdown
Create the Keras model for the inclusive classifier hooking with tf.distribute
###Code
# This implements the distributed stratedy for model
with strategy.scope():
## GRU branch
gru_input = Input(shape=(801,19), name='gru_input')
a = gru_input
a = Masking(mask_value=0.)(a)
a = GRU(units=50,activation='tanh')(a)
gruBranch = Dropout(0.2)(a)
hlf_input = Input(shape=(14), name='hlf_input')
b = hlf_input
hlfBranch = Dropout(0.2)(b)
c = concatenate([gruBranch, hlfBranch])
c = Dense(25, activation='relu')(c)
output = Dense(3, activation='softmax')(c)
model = Model(inputs=[gru_input, hlf_input], outputs=output)
## Compile model
optimizer = 'Adam'
loss = 'categorical_crossentropy'
model.compile(loss=loss, optimizer=optimizer, metrics=["accuracy"] )
model.summary()
###Output
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
gru_input (InputLayer) [(None, 801, 19)] 0
__________________________________________________________________________________________________
masking (Masking) (None, 801, 19) 0 gru_input[0][0]
__________________________________________________________________________________________________
gru (GRU) (None, 50) 10650 masking[0][0]
__________________________________________________________________________________________________
hlf_input (InputLayer) [(None, 14)] 0
__________________________________________________________________________________________________
dropout (Dropout) (None, 50) 0 gru[0][0]
__________________________________________________________________________________________________
dropout_1 (Dropout) (None, 14) 0 hlf_input[0][0]
__________________________________________________________________________________________________
concatenate (Concatenate) (None, 64) 0 dropout[0][0]
dropout_1[0][0]
__________________________________________________________________________________________________
dense (Dense) (None, 25) 1625 concatenate[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 3) 78 dense[0][0]
==================================================================================================
Total params: 12,353
Trainable params: 12,353
Non-trainable params: 0
__________________________________________________________________________________________________
###Markdown
Load test and training data in TFRecord format, using tf.data and tf.io
###Code
PATH = "/local3/lucatests/Data/"
# test dataset
files_test_dataset = tf.data.Dataset.list_files(PATH + "testUndersampled.tfrecord/part-r*", shuffle=False)
# training dataset
files_train_dataset = tf.data.Dataset.list_files(PATH + "trainUndersampled.tfrecord/part-r*", seed=4242)
# tunable
num_parallel_reads=16
test_dataset = files_test_dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE).interleave(
tf.data.TFRecordDataset,
cycle_length=num_parallel_reads,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
train_dataset = files_train_dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE).interleave(
tf.data.TFRecordDataset, cycle_length=num_parallel_reads,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
# Function to decode TF records into the required features and labels
def decode(serialized_example):
deser_features = tf.io.parse_single_example(
serialized_example,
# Defaults are not specified since both keys are required.
features={
'HLF_input': tf.io.FixedLenFeature((14), tf.float32),
'GRU_input': tf.io.FixedLenFeature((801,19), tf.float32),
'encoded_label': tf.io.FixedLenFeature((3), tf.float32),
})
return((deser_features['GRU_input'], deser_features['HLF_input']), deser_features['encoded_label'])
# use for debugging
# for record in test_dataset.take(1):
# print(record)
parsed_test_dataset=test_dataset.map(decode, num_parallel_calls=tf.data.experimental.AUTOTUNE)
parsed_train_dataset=train_dataset.map(decode, num_parallel_calls=tf.data.experimental.AUTOTUNE)
# use for debugging
# Show and example of the parsed data
# for record in parsed_test_dataset.take(1):
# print(record)
# tunable
batch_size = 64 * number_workers
train=parsed_train_dataset.batch(batch_size)
train=train.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
train=train.repeat()
train
num_train_samples=3426083 # there are 3426083 samples in the training dataset
steps_per_epoch=num_train_samples//batch_size
steps_per_epoch
# tunable
test_batch_size = 1024
test=parsed_test_dataset.batch(test_batch_size)
test=test.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
test=test.repeat()
num_test_samples=856090 # there are 856090 samples in the test dataset
validation_steps=num_test_samples//test_batch_size
validation_steps
###Output
_____no_output_____
###Markdown
Train the tf.keras model
###Code
# train the Keras model
# tunable
num_epochs = 6
# callbacks = [ tf.keras.callbacks.TensorBoard(log_dir='./logs') ]
callbacks = []
%time history = model.fit(train, steps_per_epoch=steps_per_epoch, \
validation_data=test, validation_steps=validation_steps, \
epochs=num_epochs, callbacks=callbacks, verbose=1)
PATH="./"
model.save(PATH + "mymodel" + str(worker_number) + ".h5", save_format='h5')
# TF 2.0
# tf.keras.models.save_model(model, PATH + "mymodel" + str(worker_number) + ".tf", save_format='tf')
###Output
_____no_output_____
###Markdown
Training history performance metrics
###Code
%matplotlib notebook
import matplotlib.pyplot as plt
plt.style.use('seaborn-darkgrid')
# Graph with loss vs. epoch
plt.figure()
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='validation')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(loc='upper right')
plt.title("HLF classifier loss")
plt.show()
# Graph with accuracy vs. epoch
%matplotlib notebook
plt.figure()
plt.plot(history.history['accuracy'], label='train')
plt.plot(history.history['val_accuracy'], label='validation')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(loc='lower right')
plt.title("HLF classifier accuracy")
plt.show()
###Output
_____no_output_____
###Markdown
Traininig the Inclusive classifier with tf.Keras using data in TFRecord format**tf.keras Inclusive classifier** This notebooks trains a neural network for the particle classifier using the Inclusive Classifier, using as input the list of recunstructed particles with the low level features + the high level features. Data is prepared from Parquet using Apache Spark, and written into TFRecord format. Data in TFRecord format is read from TensorFlow using tf.data and tf.io in tf.keras.To run this notebook we used the following configuration:* *Software stack*: TensorFlow 2.0.1* *Platform*: CentOS 7, Python 3.6
###Code
import tensorflow as tf
import numpy as np
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import Sequential, Input, Model
from tensorflow.keras.layers import Masking, Dense, Activation, GRU, Dropout, concatenate
tf.version.VERSION
# only needed for TensorFlow 1.x
# tf.enable_eager_execution()
###Output
_____no_output_____
###Markdown
Configure distributed training using tf.distributeThis notebook shows an example of distributed training with tf.keras using 4 concurrent executions on a single machine.The test machine has 24 physical cores it has been notes that a serial execution of the training would leave spare capacity. With distributed training we can "use all the CPU on the box". - TensorFlow MultiWorkerMirroredStrategy is used to distribute the training.- Configuration of the workers is done using the OS enviroment variable **TF_CONFIG**.- **nodes_endpoints** configures the list of machines and ports that will be used. In this example, we use 3 workers on the same machines, you can use this to distribute over multiple machines too- **worker_number** will be unique for each worker, numbering starts from 0- Worker number 0 will be the master. - You need to run the 4 notebooks for the 4 configured workers at the same time (training will only start when all 4 workers are active)
###Code
# Each worker will have a unique worker_number, numbering starts from 0
worker_number=0
nodes_endpoints = ["localhost:12345", "localhost:12346", "localhost:12347", "localhost:12348"]
number_workers = len(nodes_endpoints)
import os
import json
os.environ['TF_CONFIG'] = json.dumps({
'cluster': {
'worker': nodes_endpoints
},
'task': {'type': 'worker', 'index': worker_number}
})
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
###Output
_____no_output_____
###Markdown
Create the Keras model for the inclusive classifier hooking with tf.distribute
###Code
# This implements the distributed stratedy for model
with strategy.scope():
## GRU branch
gru_input = Input(shape=(801,19), name='gru_input')
a = gru_input
a = Masking(mask_value=0.)(a)
a = GRU(units=50,activation='tanh')(a)
gruBranch = Dropout(0.2)(a)
hlf_input = Input(shape=(14), name='hlf_input')
b = hlf_input
hlfBranch = Dropout(0.2)(b)
c = concatenate([gruBranch, hlfBranch])
c = Dense(25, activation='relu')(c)
output = Dense(3, activation='softmax')(c)
model = Model(inputs=[gru_input, hlf_input], outputs=output)
## Compile model
optimizer = 'Adam'
loss = 'categorical_crossentropy'
model.compile(loss=loss, optimizer=optimizer, metrics=["accuracy"] )
model.summary()
###Output
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
gru_input (InputLayer) [(None, 801, 19)] 0
__________________________________________________________________________________________________
masking (Masking) (None, 801, 19) 0 gru_input[0][0]
__________________________________________________________________________________________________
gru (GRU) (None, 50) 10650 masking[0][0]
__________________________________________________________________________________________________
hlf_input (InputLayer) [(None, 14)] 0
__________________________________________________________________________________________________
dropout (Dropout) (None, 50) 0 gru[0][0]
__________________________________________________________________________________________________
dropout_1 (Dropout) (None, 14) 0 hlf_input[0][0]
__________________________________________________________________________________________________
concatenate (Concatenate) (None, 64) 0 dropout[0][0]
dropout_1[0][0]
__________________________________________________________________________________________________
dense (Dense) (None, 25) 1625 concatenate[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 3) 78 dense[0][0]
==================================================================================================
Total params: 12,353
Trainable params: 12,353
Non-trainable params: 0
__________________________________________________________________________________________________
###Markdown
Load test and training data in TFRecord format, using tf.data and tf.io
###Code
PATH = "/local3/lucatests/Data/"
# test dataset
files_test_dataset = tf.data.Dataset.list_files(PATH + "testUndersampled.tfrecord/part-r*", shuffle=False)
# training dataset
files_train_dataset = tf.data.Dataset.list_files(PATH + "trainUndersampled.tfrecord/part-r*", seed=4242)
# tunable
num_parallel_reads=16
test_dataset = files_test_dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE).interleave(
tf.data.TFRecordDataset,
cycle_length=num_parallel_reads,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
train_dataset = files_train_dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE).interleave(
tf.data.TFRecordDataset, cycle_length=num_parallel_reads,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
# Function to decode TF records into the required features and labels
def decode(serialized_example):
deser_features = tf.io.parse_single_example(
serialized_example,
# Defaults are not specified since both keys are required.
features={
'HLF_input': tf.io.FixedLenFeature((14), tf.float32),
'GRU_input': tf.io.FixedLenFeature((801,19), tf.float32),
'encoded_label': tf.io.FixedLenFeature((3), tf.float32),
})
return((deser_features['GRU_input'], deser_features['HLF_input']), deser_features['encoded_label'])
# use for debugging
# for record in test_dataset.take(1):
# print(record)
parsed_test_dataset=test_dataset.map(decode, num_parallel_calls=tf.data.experimental.AUTOTUNE)
parsed_train_dataset=train_dataset.map(decode, num_parallel_calls=tf.data.experimental.AUTOTUNE).cache()
# use for debugging
# Show and example of the parsed data
# for record in parsed_test_dataset.take(1):
# print(record)
# tunable
batch_size = 128 * number_workers
train=parsed_train_dataset.batch(batch_size)
train=train.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
train=train.repeat()
train
num_train_samples=3426083 # there are 3426083 samples in the training dataset
steps_per_epoch=num_train_samples//batch_size
steps_per_epoch
# tunable
test_batch_size = 1024
test=parsed_test_dataset.batch(test_batch_size)
test=test.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
test=test.repeat()
num_test_samples=856090 # there are 856090 samples in the test dataset
validation_steps=num_test_samples//test_batch_size
validation_steps
###Output
_____no_output_____
###Markdown
Train the tf.keras model
###Code
# train the Keras model
# tunable
num_epochs = 6
# callbacks = [ tf.keras.callbacks.TensorBoard(log_dir='./logs') ]
callbacks = []
%time history = model.fit(train, steps_per_epoch=steps_per_epoch, \
epochs=num_epochs, callbacks=callbacks, verbose=1)
# validation_data=test, validation_steps=validation_steps, \
PATH="/local1/lucatests/SparkDLTrigger/Training_TFKeras_Distributed/model/"
model.save(PATH + "mymodel" + str(worker_number) + ".h5", save_format='h5')
###Output
_____no_output_____
###Markdown
Training history performance metrics
###Code
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [16, 10]
plt.style.use('seaborn-darkgrid')
# Graph with loss vs. epoch
plt.figure()
plt.plot(history.history['loss'], label='train')
#plt.plot(history.history['val_loss'], label='validation')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(loc='upper right')
plt.title("HLF classifier loss")
plt.show()
# Graph with accuracy vs. epoch
%matplotlib inline
plt.rcParams['figure.figsize'] = [16, 10]
plt.figure()
plt.plot(history.history['accuracy'], label='train')
#plt.plot(history.history['val_accuracy'], label='validation')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(loc='lower right')
plt.title("HLF classifier accuracy")
plt.show()
###Output
_____no_output_____
|
7-TimeSeries/3-SVR/solution/notebook.ipynb
|
###Markdown
Time series prediction using Support Vector Regressor In this notebook, we demonstrate how to:- prepare 2D time series data for training an SVM regressor model- implement SVR using RBF kernel- evaluate the model using plots and MAPE Importing modules
###Code
import sys
sys.path.append('../../')
import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math
from sklearn.svm import SVR
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape
###Output
_____no_output_____
###Markdown
Preparing data Load data
###Code
energy = load_data('../../data')[['load']]
energy.head(5)
###Output
_____no_output_____
###Markdown
Plot the data
###Code
energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
###Output
_____no_output_____
###Markdown
Create training and testing data
###Code
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
.join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
.plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
###Output
_____no_output_____
###Markdown
Preparing data for training Now, you need to prepare the data for training by performing filtering and scaling of your data.
###Code
train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]
print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)
###Output
Training data shape: (1416, 1)
Test data shape: (48, 1)
###Markdown
Scale the data to be in the range (0, 1).
###Code
scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
train.head(5)
test['load'] = scaler.transform(test)
test.head(5)
###Output
_____no_output_____
###Markdown
Creating data with time-steps For our SVR, we transform the input data to be of the form `[batch, timesteps]`. So, we reshape the existing `train_data` and `test_data` such that there is a new dimension which refers to the timesteps. For our example, we take `timesteps = 5`. So, the inputs to the model are the data for the first 4 timesteps, and the output will be the data for the 5th timestep.
###Code
# Converting to numpy arrays
train_data = train.values
test_data = test.values
# Selecting the timesteps
timesteps=5
# Converting data to 2D tensor
train_data_timesteps=np.array([[j for j in train_data[i:i+timesteps]] for i in range(0,len(train_data)-timesteps+1)])[:,:,0]
train_data_timesteps.shape
# Converting test data to 2D tensor
test_data_timesteps=np.array([[j for j in test_data[i:i+timesteps]] for i in range(0,len(test_data)-timesteps+1)])[:,:,0]
test_data_timesteps.shape
x_train, y_train = train_data_timesteps[:,:timesteps-1],train_data_timesteps[:,[timesteps-1]]
x_test, y_test = test_data_timesteps[:,:timesteps-1],test_data_timesteps[:,[timesteps-1]]
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
###Output
(1412, 4) (1412, 1)
(44, 4) (44, 1)
###Markdown
Creating SVR model
###Code
# Create model using RBF kernel
model = SVR(kernel='rbf',gamma=0.5, C=10, epsilon = 0.05)
# Fit model on training data
model.fit(x_train, y_train[:,0])
###Output
_____no_output_____
###Markdown
Make model prediction
###Code
# Making predictions
y_train_pred = model.predict(x_train).reshape(-1,1)
y_test_pred = model.predict(x_test).reshape(-1,1)
print(y_train_pred.shape, y_test_pred.shape)
###Output
(1412, 1) (44, 1)
###Markdown
Analyzing model performance
###Code
# Scaling the predictions
y_train_pred = scaler.inverse_transform(y_train_pred)
y_test_pred = scaler.inverse_transform(y_test_pred)
print(len(y_train_pred), len(y_test_pred))
# Scaling the original values
y_train = scaler.inverse_transform(y_train)
y_test = scaler.inverse_transform(y_test)
print(len(y_train), len(y_test))
# Extract the timesteps for x-axis
train_timestamps = energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)].index[timesteps-1:]
test_timestamps = energy[test_start_dt:].index[timesteps-1:]
print(len(train_timestamps), len(test_timestamps))
plt.figure(figsize=(25,6))
plt.plot(train_timestamps, y_train, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(train_timestamps, y_train_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.title("Training data prediction")
plt.show()
print('MAPE for training data: ', mape(y_train_pred, y_train)*100, '%')
plt.figure(figsize=(10,3))
plt.plot(test_timestamps, y_test, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(test_timestamps, y_test_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()
print('MAPE for testing data: ', mape(y_test_pred, y_test)*100, '%')
###Output
MAPE for testing data: 1.2623790187854018 %
###Markdown
Full dataset prediction
###Code
# Extracting load values as numpy array
data = energy.copy().values
# Scaling
data = scaler.transform(data)
# Transforming to 2D tensor as per model input requirement
data_timesteps=np.array([[j for j in data[i:i+timesteps]] for i in range(0,len(data)-timesteps+1)])[:,:,0]
print("Tensor shape: ", data_timesteps.shape)
# Selecting inputs and outputs from data
X, Y = data_timesteps[:,:timesteps-1],data_timesteps[:,[timesteps-1]]
print("X shape: ", X.shape,"\nY shape: ", Y.shape)
# Make model predictions
Y_pred = model.predict(X).reshape(-1,1)
# Inverse scale and reshape
Y_pred = scaler.inverse_transform(Y_pred)
Y = scaler.inverse_transform(Y)
plt.figure(figsize=(30,8))
plt.plot(Y, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(Y_pred, color = 'blue', linewidth=1)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()
print('MAPE: ', mape(Y_pred, Y)*100, '%')
###Output
MAPE: 2.0572089029888656 %
|
K-Mode+Bank+Marketing.ipynb
|
###Markdown
K-Mode Clustering on Bank Marketing Dataset The data is related with direct marketing campaigns of a Portuguese banking institution. The marketing campaigns were based on phone calls. Often, more than one contact to the same client was required, in order to access if the product (bank term deposit) would be ('yes') or not ('no') subscribed. **Attribute Information(Categorical):**- age (numeric)- job : type of job (categorical: 'admin.','blue-collar','entrepreneur','housemaid','management','retired','self-employed','services','student','technician','unemployed','unknown')- marital : marital status (categorical: 'divorced','married','single','unknown'; note: 'divorced' means divorced or widowed)- education (categorical: 'basic.4y','basic.6y','basic.9y','high.school','illiterate','professional.course','university.degree','unknown')- default: has credit in default? (categorical: 'no','yes','unknown')- housing: has housing loan? (categorical: 'no','yes','unknown')- loan: has personal loan? (categorical: 'no','yes','unknown')- contact: contact communication type (categorical: 'cellular','telephone') - month: last contact month of year (categorical: 'jan', 'feb', 'mar', ..., 'nov', 'dec')- day_of_week: last contact day of the week (categorical: 'mon','tue','wed','thu','fri')- poutcome: outcome of the previous marketing campaign (categorical: 'failure','nonexistent','success')- UCI Repository:
###Code
# Importing Libraries
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from kmodes.kmodes import KModes
import warnings
warnings.filterwarnings("ignore")
help(KModes)
bank = pd.read_csv('bankmarketing.csv')
bank.head()
bank.columns
bank_cust = bank[['age','job', 'marital', 'education', 'default', 'housing', 'loan','contact','month','day_of_week','poutcome']]
bank_cust.head()
bank_cust['age_bin'] = pd.cut(bank_cust['age'], [0, 20, 30, 40, 50, 60, 70, 80, 90, 100],
labels=['0-20', '20-30', '30-40', '40-50','50-60','60-70','70-80', '80-90','90-100'])
bank_cust.head()
bank_cust = bank_cust.drop('age',axis = 1)
bank_cust.head()
bank_cust.info()
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
bank_cust = bank_cust.apply(le.fit_transform)
bank_cust.head()
# Checking the count per category
job_df = pd.DataFrame(bank_cust['job'].value_counts())
sns.barplot(x=job_df.index, y=job_df['job'])
# Checking the count per category
age_df = pd.DataFrame(bank_cust['age_bin'].value_counts())
sns.barplot(x=age_df.index, y=age_df['age_bin'])
###Output
_____no_output_____
###Markdown
Using K-Mode with "Cao" initialization
###Code
km_cao = KModes(n_clusters=2, init = "Cao", n_init = 1, verbose=1)
fitClusters_cao = km_cao.fit_predict(bank_cust)
# Predicted Clusters
fitClusters_cao
clusterCentroidsDf = pd.DataFrame(km_cao.cluster_centroids_)
clusterCentroidsDf.columns = bank_cust.columns
# Mode of the clusters
clusterCentroidsDf
###Output
_____no_output_____
###Markdown
Using K-Mode with "Huang" initialization
###Code
km_huang = KModes(n_clusters=2, init = "Huang", n_init = 1, verbose=1)
fitClusters_huang = km_huang.fit_predict(bank_cust)
# Predicted clusters
fitClusters_huang
###Output
_____no_output_____
###Markdown
Choosing K by comparing Cost against each K
###Code
cost = []
for num_clusters in list(range(1,5)):
kmode = KModes(n_clusters=num_clusters, init = "Cao", n_init = 1, verbose=1)
kmode.fit_predict(bank_cust)
cost.append(kmode.cost_)
y = np.array([i for i in range(1,5,1)])
plt.plot(y,cost)
## Choosing K=2
km_cao = KModes(n_clusters=2, init = "Cao", n_init = 1, verbose=1)
fitClusters_cao = km_cao.fit_predict(bank_cust)
fitClusters_cao
###Output
_____no_output_____
###Markdown
Combining the predicted clusters with the original DF.
###Code
bank_cust = bank_cust.reset_index()
clustersDf = pd.DataFrame(fitClusters_cao)
clustersDf.columns = ['cluster_predicted']
combinedDf = pd.concat([bank_cust, clustersDf], axis = 1).reset_index()
combinedDf = combinedDf.drop(['index', 'level_0'], axis = 1)
combinedDf.head()
# Data for Cluster1
cluster1 = combinedDf[combinedDf.cluster_predicted==1]
# Data for Cluster0
cluster0 = combinedDf[combinedDf.cluster_predicted==0]
cluster1.info()
cluster0.info()
# Checking the count per category for JOB
job1_df = pd.DataFrame(cluster1['job'].value_counts())
job0_df = pd.DataFrame(cluster0['job'].value_counts())
fig, ax =plt.subplots(1,2,figsize=(20,5))
sns.barplot(x=job1_df.index, y=job1_df['job'], ax=ax[0])
sns.barplot(x=job0_df.index, y=job0_df['job'], ax=ax[1])
fig.show()
age1_df = pd.DataFrame(cluster1['age_bin'].value_counts())
age0_df = pd.DataFrame(cluster0['age_bin'].value_counts())
fig, ax =plt.subplots(1,2,figsize=(20,5))
sns.barplot(x=age1_df.index, y=age1_df['age_bin'], ax=ax[0])
sns.barplot(x=age0_df.index, y=age0_df['age_bin'], ax=ax[1])
fig.show()
print(cluster1['marital'].value_counts())
print(cluster0['marital'].value_counts())
print(cluster1['education'].value_counts())
print(cluster0['education'].value_counts())
###Output
3 4186
2 2572
0 1981
5 1459
1 1033
6 977
7 680
4 7
Name: education, dtype: int64
6 11191
3 5329
5 3784
2 3473
0 2195
1 1259
7 1051
4 11
Name: education, dtype: int64
###Markdown
KPrototype Clustering on Bank marketing dataset
###Code
bank_proto = bank[['job', 'marital', 'education', 'default', 'housing', 'loan','contact','month','day_of_week','poutcome','age','duration','euribor3m']]
bank_proto.isnull().values.any()
bank.duration.mean()
columns_to_normalize = ['age','duration','euribor3m']
columns_to_label = ['job', 'marital', 'education', 'default', 'housing', 'loan','contact','month','day_of_week','poutcome']
bank_proto[columns_to_normalize] = bank_proto[columns_to_normalize].apply(lambda x: (x - x.mean()) / np.std(x))
le = preprocessing.LabelEncoder()
bank_proto[columns_to_label] = bank_proto[columns_to_label].apply(le.fit_transform)
bank_proto.head()
bank_proto_matrix = bank_proto.as_matrix()
from kmodes.kprototypes import KPrototypes
# Running K-Prototype clustering
kproto = KPrototypes(n_clusters=5, init='Cao')
clusters = kproto.fit_predict(bank_proto_matrix, categorical=[0,1,2,3,4,5,6,7,8,9])
bank_proto['clusterID'] = clusters
kproto.cost_
#Choosing optimal K
cost = []
for num_clusters in list(range(1,8)):
kproto = KPrototypes(n_clusters=num_clusters, init='Cao')
kproto.fit_predict(bank_proto_matrix, categorical=[0,1,2,3,4,5,6,7,8,9])
cost.append(kproto.cost_)
plt.plot(cost)
###Output
_____no_output_____
|
ModelSelection/ComparingGaussianMeans.ipynb
|
###Markdown
Chapter 8 - Comparing Gaussian means 8.1 One-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \mu = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu,1/\sigma^2)$$
###Code
# Read data Dr. Smith
Winter = np.array([-0.05,0.41,0.17,-0.13,0.00,-0.05,0.00,0.17,0.29,0.04,0.21,0.08,0.37,
0.17,0.08,-0.04,-0.04,0.04,-0.13,-0.12,0.04,0.21,0.17,0.17,0.17,
0.33,0.04,0.04,0.04,0.00,0.21,0.13,0.25,-0.05,0.29,0.42,-0.05,0.12,
0.04,0.25,0.12])
Summer = np.array([0.00,0.38,-0.12,0.12,0.25,0.12,0.13,0.37,0.00,0.50,0.00,0.00,-0.13,
-0.37,-0.25,-0.12,0.50,0.25,0.13,0.25,0.25,0.38,0.25,0.12,0.00,0.00,
0.00,0.00,0.25,0.13,-0.25,-0.38,-0.13,-0.25,0.00,0.00,-0.12,0.25,
0.00,0.50,0.00])
x = Winter - Summer # allowed because it is a within-subjects design
x = x / np.std(x)
with pm.Model() as model1:
delta = pm.Cauchy('delta', alpha=0, beta=1)
sigma = pm.HalfCauchy('sigma', beta=1)
miu = delta*sigma
xi = pm.Normal('xi', mu=miu, sd=sigma, observed=x)
trace1=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace1[burnin:], varnames=['delta']);
plt.show()
def display_delta(trace, x):
# BFs based on density estimation (using kernel smoothing instead of spline)
from scipy.stats.kde import gaussian_kde
from scipy.stats import cauchy
pm.summary(trace, varnames=['delta'])
tmp = pm.df_summary(trace, varnames=['delta'])
# 95% confidence interval:
x0 = tmp.values[0, 3]
x1 = tmp.values[0, 4]
t_delt = trace['delta'][:]
my_pdf = gaussian_kde(t_delt)
plt.plot(x, my_pdf(x), '--', lw=2.5, alpha=0.6, label='Posterior') # distribution function
plt.plot(x, cauchy.pdf(x), 'r-', lw=2.5, alpha=0.6, label='Prior')
posterior = my_pdf(0) # this gives the pdf at point delta = 0
prior = cauchy.pdf(0) # height of order-restricted prior at delta = 0
BF01 = posterior/prior
print ('the Bayes Factor is %.5f' %(BF01))
plt.plot([0, 0], [posterior, prior], 'k-',
[0, 0], [posterior, prior], 'ko', lw=1.5, alpha=1)
plt.xlabel('Delta')
plt.ylabel('Density')
plt.legend(loc='upper left')
plt.show()
x = np.linspace(-3, 3, 100)
display_delta(trace1, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
0.117 0.156 0.002 [-0.187, 0.413]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.186 0.011 0.120 0.226 0.416
the Bayes Factor is 5.92097
###Markdown
8.2 Order-restricted one-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)_{\mathcal I(-∞,0)}$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \mu = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu,1/\sigma^2)$$
###Code
# Read data Dr. Smith
Winter = np.array([-0.05,0.41,0.17,-0.13,0.00,-0.05,0.00,0.17,0.29,0.04,0.21,0.08,0.37,
0.17,0.08,-0.04,-0.04,0.04,-0.13,-0.12,0.04,0.21,0.17,0.17,0.17,
0.33,0.04,0.04,0.04,0.00,0.21,0.13,0.25,-0.05,0.29,0.42,-0.05,0.12,
0.04,0.25,0.12])
Summer = np.array([0.00,0.38,-0.12,0.12,0.25,0.12,0.13,0.37,0.00,0.50,0.00,0.00,-0.13,
-0.37,-0.25,-0.12,0.50,0.25,0.13,0.25,0.25,0.38,0.25,0.12,0.00,0.00,
0.00,0.00,0.25,0.13,-0.25,-0.38,-0.13,-0.25,0.00,0.00,-0.12,0.25,
0.00,0.50,0.00])
x = Winter - Summer # allowed because it is a within-subjects design
x = x / np.std(x)
with pm.Model() as model2:
delta1 = pm.HalfCauchy('delta1', beta=1)
delta = pm.Deterministic('delta', -delta1)
sigma = pm.HalfCauchy('sigma', beta=1)
miu = delta*sigma
xi = pm.Normal('xi', mu=miu, sd=sigma, observed=x)
trace2=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace2[burnin:], varnames=['delta']);
plt.show()
x = np.linspace(-3, 0, 100)
display_delta(trace2, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
-0.089 0.074 0.001 [-0.236, -0.000]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.275 -0.127 -0.071 -0.030 -0.003
the Bayes Factor is 13.16856
###Markdown
8.3 Two-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)$$$$ \mu \sim \text{Cauchy} (0, 1)$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \alpha = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu+\frac{\alpha}{2},1/\sigma^2)$$$$ y_{i} \sim \text{Gaussian}(\mu-\frac{\alpha}{2},1/\sigma^2)$$
###Code
# Read data
x =np.array([70,80,79,83,77,75,84,78,75,75,78,82,74,81,72,70,75,72,76,77])
y =np.array([56,80,63,62,67,71,68,76,79,67,76,74,67,70,62,65,72,72,69,71])
n1 = len(x)
n2 = len(y)
# Rescale
y = y - np.mean(x)
y = y / np.std(x)
x = (x - np.mean(x)) / np.std(x)
with pm.Model() as model3:
delta = pm.Cauchy('delta', alpha=0, beta=1)
mu = pm.Cauchy('mu', alpha=0, beta=1)
sigma = pm.HalfCauchy('sigma', beta=1)
alpha = delta*sigma
xi = pm.Normal('xi', mu=mu+alpha/2, sd=sigma, observed=x)
yi = pm.Normal('yi', mu=mu-alpha/2, sd=sigma, observed=y)
trace3=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace3[burnin:], varnames=['delta']);
plt.show()
x = np.linspace(-3, 3, 100)
display_delta(trace3, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
1.303 0.357 0.005 [0.623, 2.011]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
0.611 1.059 1.302 1.549 2.006
the Bayes Factor is 0.00467
###Markdown
Chapter 8 - Comparing Gaussian means 8.1 One-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \mu = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu,1/\sigma^2)$$
###Code
# Read data Dr. Smith
Winter = np.array([-0.05,0.41,0.17,-0.13,0.00,-0.05,0.00,0.17,0.29,0.04,0.21,0.08,0.37,
0.17,0.08,-0.04,-0.04,0.04,-0.13,-0.12,0.04,0.21,0.17,0.17,0.17,
0.33,0.04,0.04,0.04,0.00,0.21,0.13,0.25,-0.05,0.29,0.42,-0.05,0.12,
0.04,0.25,0.12])
Summer = np.array([0.00,0.38,-0.12,0.12,0.25,0.12,0.13,0.37,0.00,0.50,0.00,0.00,-0.13,
-0.37,-0.25,-0.12,0.50,0.25,0.13,0.25,0.25,0.38,0.25,0.12,0.00,0.00,
0.00,0.00,0.25,0.13,-0.25,-0.38,-0.13,-0.25,0.00,0.00,-0.12,0.25,
0.00,0.50,0.00])
x = Winter - Summer # allowed because it is a within-subjects design
x = x / np.std(x)
with pm.Model() as model1:
delta = pm.Cauchy('delta', alpha=0, beta=1)
sigma = pm.HalfCauchy('sigma', beta=1)
miu = delta*sigma
xi = pm.Normal('xi', mu=miu, sd=sigma, observed=x)
trace1=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace1[burnin:], varnames=['delta']);
plt.show()
def display_delta(trace, x):
# BFs based on density estimation (using kernel smoothing instead of spline)
from scipy.stats.kde import gaussian_kde
from scipy.stats import cauchy
pm.summary(trace, varnames=['delta'])
tmp = pm.df_summary(trace, varnames=['delta'])
# 95% confidence interval:
x0 = tmp.values[0, 3]
x1 = tmp.values[0, 4]
t_delt = trace['delta'][:]
my_pdf = gaussian_kde(t_delt)
plt.plot(x, my_pdf(x), '--', lw=2.5, alpha=0.6, label='Posterior') # distribution function
plt.plot(x, cauchy.pdf(x), 'r-', lw=2.5, alpha=0.6, label='Prior')
posterior = my_pdf(0) # this gives the pdf at point delta = 0
prior = cauchy.pdf(0) # height of order-restricted prior at delta = 0
BF01 = posterior/prior
print ('the Bayes Factor is %.5f' %(BF01))
plt.plot([0, 0], [posterior, prior], 'k-',
[0, 0], [posterior, prior], 'ko', lw=1.5, alpha=1)
plt.xlabel('Delta')
plt.ylabel('Density')
plt.legend(loc='upper left')
plt.show()
x = np.linspace(-3, 3, 100)
display_delta(trace1, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
0.118 0.156 0.002 [-0.201, 0.412]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.190 0.016 0.116 0.223 0.428
the Bayes Factor is 5.83564
###Markdown
8.2 Order-restricted one-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)_{\mathcal I(-∞,0)}$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \mu = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu,1/\sigma^2)$$
###Code
# Read data Dr. Smith
Winter = np.array([-0.05,0.41,0.17,-0.13,0.00,-0.05,0.00,0.17,0.29,0.04,0.21,0.08,0.37,
0.17,0.08,-0.04,-0.04,0.04,-0.13,-0.12,0.04,0.21,0.17,0.17,0.17,
0.33,0.04,0.04,0.04,0.00,0.21,0.13,0.25,-0.05,0.29,0.42,-0.05,0.12,
0.04,0.25,0.12])
Summer = np.array([0.00,0.38,-0.12,0.12,0.25,0.12,0.13,0.37,0.00,0.50,0.00,0.00,-0.13,
-0.37,-0.25,-0.12,0.50,0.25,0.13,0.25,0.25,0.38,0.25,0.12,0.00,0.00,
0.00,0.00,0.25,0.13,-0.25,-0.38,-0.13,-0.25,0.00,0.00,-0.12,0.25,
0.00,0.50,0.00])
x = Winter - Summer # allowed because it is a within-subjects design
x = x / np.std(x)
with pm.Model() as model2:
delta1 = pm.HalfCauchy('delta1', beta=1)
delta = pm.Deterministic('delta', -delta1)
sigma = pm.HalfCauchy('sigma', beta=1)
miu = delta*sigma
xi = pm.Normal('xi', mu=miu, sd=sigma, observed=x)
trace2=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace2[burnin:], varnames=['delta']);
plt.show()
x = np.linspace(-3, 0, 100)
display_delta(trace2, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
-0.089 0.073 0.001 [-0.237, -0.000]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.276 -0.129 -0.070 -0.031 -0.003
the Bayes Factor is 12.58035
###Markdown
8.3 Two-sample comparison$$ \delta \sim \text{Cauchy} (0, 1)$$$$ \mu \sim \text{Cauchy} (0, 1)$$$$ \sigma \sim \text{Cauchy} (0, 1)_{\mathcal I(0,∞)}$$$$ \alpha = \delta\sigma $$$$ x_{i} \sim \text{Gaussian}(\mu+\frac{\alpha}{2},1/\sigma^2)$$$$ y_{i} \sim \text{Gaussian}(\mu-\frac{\alpha}{2},1/\sigma^2)$$
###Code
# Read data
x =np.array([70,80,79,83,77,75,84,78,75,75,78,82,74,81,72,70,75,72,76,77])
y =np.array([56,80,63,62,67,71,68,76,79,67,76,74,67,70,62,65,72,72,69,71])
n1 = len(x)
n2 = len(y)
# Rescale
y = y - np.mean(x)
y = y / np.std(x)
x = (x - np.mean(x)) / np.std(x)
with pm.Model() as model3:
delta = pm.Cauchy('delta', alpha=0, beta=1)
mu = pm.Cauchy('mu', alpha=0, beta=1)
sigma = pm.HalfCauchy('sigma', beta=1)
alpha = delta*sigma
xi = pm.Normal('xi', mu=mu+alpha/2, sd=sigma, observed=x)
yi = pm.Normal('yi', mu=mu-alpha/2, sd=sigma, observed=y)
trace3=pm.sample(3e3, njobs=2)
burnin=0
pm.traceplot(trace3[burnin:], varnames=['delta']);
plt.show()
x = np.linspace(-3, 3, 100)
display_delta(trace3, x)
###Output
delta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
1.317 0.353 0.005 [0.642, 1.995]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
0.647 1.075 1.313 1.553 2.006
the Bayes Factor is 0.00400
|
pynq_peripherals/modules/grove_light/notebooks/grove_light.ipynb
|
###Markdown
Grove Light sensor module--- Aim* This notebook illustrates how to use available APIs for the Grove Light sensor module on PYNQ-Z2 PMOD and Arduino interfaces. References* [Grove Light sensor](https://www.seeedstudio.com/Grove-Light-Sensor-v1-2-LS06-S-phototransistor.html) * [Grove I2C ADC](https://www.seeedstudio.com/Grove-I2C-ADC.html) * [PYNQ Grove Adapter](https://store.digilentinc.com/pynq-grove-system-add-on-board/)* [Grove Base Shield V2.0](https://www.seeedstudio.com/Base-Shield-V2.html) Last revised* 01 April 2021 + Initial version--- Load _base_ Overlay Note that we load the base bitstream only once to use Grove module with PYNQ Grove Adapter and SEEED Grove Base Shield V2.0Please make sure you run the following cell before running either of the interfaces
###Code
from pynq.overlays.base import BaseOverlay
from pynq_peripherals import ArduinoSEEEDGroveAdapter, PmodGroveAdapter
base = BaseOverlay('base.bit')
###Output
_____no_output_____
###Markdown
Using Grove Light with Grove Base Shield V2.0 (Arduino) Library compilation Make Physical Connections Insert the SEEED Grove Base Shield into the Arduino connector on the board. Connect the Grove Light sensor to A1 connector of the Grove Base Shield. Adapter configuration
###Code
adapter = ArduinoSEEEDGroveAdapter(base.ARDUINO, A1='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.A1
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
_____no_output_____
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
###Markdown
--- Using Grove Light sensor with Grove ADC (Arduino) Make Physical Connections Insert the Grove Base Shield into the Arduino connector on the board. Connect the grove_adc module to one of the connectors labeled I2C. Connect the Grove Light sensor to the grove_adc module. Adapter configuration
###Code
adapter = ArduinoSEEEDGroveAdapter(base.ARDUINO, I2C='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.I2C
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
_____no_output_____
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
###Markdown
--- Using Grove Light sensor with PYNQ Grove Adapter (PMOD) Make Physical Connections Connect the PYNQ Grove Adapter to PMODB connector. Connect the grove_adc module to the G3 connector of the Adapter. Connect the Grove Light sensor to the grove_adc module. Adapter configuration
###Code
adapter = PmodGroveAdapter(base.PMODB, G3='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.G3
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
_____no_output_____
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
###Markdown
Grove Light sensor module--- Aim* This notebook illustrates how to use available APIs for the Grove Light sensor module on PYNQ-Z2 PMOD and Arduino interfaces. References* [Grove Light sensor](https://www.seeedstudio.com/Grove-Light-Sensor-v1-2-LS06-S-phototransistor.html) * [Grove I2C ADC](https://www.seeedstudio.com/Grove-I2C-ADC.html) * [PYNQ Grove Adapter](https://store.digilentinc.com/pynq-grove-system-add-on-board/)* [Grove Base Shield V2.0](https://www.seeedstudio.com/Base-Shield-V2.html) Last revised* 01 April 2021 + Initial version--- Load _base_ Overlay Note that we load the base bitstream only once to use Grove module with PYNQ Grove Adapter and SEEED Grove Base Shield V2.0Please make sure you run the following cell before running either of the interfaces
###Code
from pynq.overlays.base import BaseOverlay
from pynq_peripherals import ArduinoSEEEDGroveAdapter, PmodGroveAdapter
base = BaseOverlay('base.bit')
###Output
_____no_output_____
###Markdown
Using Grove Light with Grove Base Shield V2.0 (Arduino) Library compilation Make Physical Connections Insert the SEEED Grove Base Shield into the Arduino connector on the board. Connect the Grove Light sensor to A1 connector of the Grove Base Shield. Adapter configuration
###Code
adapter = ArduinoSEEEDGroveAdapter(base.ARDUINO, A1='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.A1
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
percentage: 58.53%
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
###Markdown
--- Using Grove Light sensor with Grove ADC (Arduino) Make Physical Connections Insert the Grove Base Shield into the Arduino connector on the board. Connect the grove_adc module to one of the connectors labeled I2C. Connect the Grove Light sensor to the grove_adc module. Adapter configuration
###Code
adapter = ArduinoSEEEDGroveAdapter(base.ARDUINO, I2C='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.I2C
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
percentage: 18.75%
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
###Markdown
--- Using Grove Light sensor with PYNQ Grove Adapter (PMOD) Make Physical Connections Connect the PYNQ Grove Adapter to PMODB connector. Connect the grove_adc module to the G3 connector of the Adapter. Connect the Grove Light sensor to the grove_adc module. Adapter configuration
###Code
adapter = PmodGroveAdapter(base.PMODB, G3='grove_light')
###Output
_____no_output_____
###Markdown
Define device object
###Code
light_sensor = adapter.G3
###Output
_____no_output_____
###Markdown
Reading from the Grove Light sensor
###Code
print('percentage: %.2f%%' % light_sensor.get_intensity())
###Output
percentage: 63.82%
###Markdown
Taking multiple samples at a desired interval and plottingSet numberOfSamples and delayInSeconds to desired values. Vary light intensity manually. Print samples and then plot
###Code
%matplotlib inline
import matplotlib.pyplot as plt
from time import sleep
import numpy as np
import math
numberOfSamples = 20
delayInSeconds = 1
light = np.zeros(numberOfSamples)
for i in range(numberOfSamples):
light[i]=light_sensor.get_intensity()
sleep(delayInSeconds)
plt.plot(range(numberOfSamples), light, 'ro')
plt.title('Light Intensity in Percentage')
plt.axis([0, int(numberOfSamples), 0, 100])
plt.show()
###Output
_____no_output_____
|
docs/samples/logger/knative-eventing/logger_demo.ipynb
|
###Markdown
KfServing KNative Logger demo We create a message dumper KNaive service to print out CloudEvents it receives:
###Code
!pygmentize message-dumper.yaml
!kubectl apply -f message-dumper.yaml
###Output
_____no_output_____
###Markdown
Label the default namespace to activate KNative eventing broker
###Code
!kubectl label namespace default knative-eventing-injection=enabled
###Output
_____no_output_____
###Markdown
Create a knative trigger to pass events to the message logger
###Code
!pygmentize trigger.yaml
!kubectl apply -f trigger.yaml
###Output
_____no_output_____
###Markdown
Create a SkLearn model with associated logger to push events to the message logger URL
###Code
!pygmentize sklearn-logging.yaml
!kubectl apply -f sklearn-logging.yaml
CLUSTER_IPS=!(kubectl -n istio-system get service istio-ingressgateway -o jsonpath='{.status.loadBalancer.ingress[0].ip}')
CLUSTER_IP=CLUSTER_IPS[0]
print(CLUSTER_IP)
SERVICE_HOSTNAMES=!(kubectl get inferenceservice sklearn-iris -o jsonpath='{.status.url}' | cut -d "/" -f 3)
SERVICE_HOSTNAME=SERVICE_HOSTNAMES[0]
print(SERVICE_HOSTNAME)
import requests
def predict(X, name, svc_hostname, cluster_ip):
formData = {
'instances': X
}
headers = {}
headers["Host"] = svc_hostname
res = requests.post('http://'+cluster_ip+'/v1/models/'+name+':predict', json=formData, headers=headers)
if res.status_code == 200:
return res.json()
else:
print("Failed with ",res.status_code)
return []
predict([[6.8, 2.8, 4.8, 1.4]],"sklearn-iris",SERVICE_HOSTNAME,CLUSTER_IP)
!kubectl logs $(kubectl get pod -l serving.knative.dev/configuration=message-dumper -o jsonpath='{.items[0].metadata.name}') user-container
!kubectl delete -f sklearn-logging.yaml
!kubectl delete -f trigger.yaml
!kubectl delete -f message-dumper.yaml
###Output
_____no_output_____
###Markdown
KFServing Knative Logger Demo We create a message dumper Knative service to print out CloudEvents it receives:
###Code
!pygmentize message-dumper.yaml
!kubectl apply -f message-dumper.yaml
###Output
_____no_output_____
###Markdown
Create a channel broker.
###Code
!pygmentize broker.yaml
!kubectl create -f broker.yaml
###Output
_____no_output_____
###Markdown
Create a Knative trigger to pass events to the message logger.
###Code
!pygmentize trigger.yaml
!kubectl apply -f trigger.yaml
###Output
_____no_output_____
###Markdown
Create an sklearn model with associated logger to push events to the message logger URL.
###Code
!pygmentize sklearn-logging.yaml
!kubectl apply -f sklearn-logging.yaml
CLUSTER_IPS=!(kubectl -n istio-system get service istio-ingressgateway -o jsonpath='{.status.loadBalancer.ingress[0].ip}')
CLUSTER_IP=CLUSTER_IPS[0]
print(CLUSTER_IP)
SERVICE_HOSTNAMES=!(kubectl get inferenceservice sklearn-iris -o jsonpath='{.status.url}' | cut -d "/" -f 3)
SERVICE_HOSTNAME=SERVICE_HOSTNAMES[0]
print(SERVICE_HOSTNAME)
import requests
def predict(X, name, svc_hostname, cluster_ip):
formData = {
'instances': X
}
headers = {}
headers["Host"] = svc_hostname
res = requests.post('http://'+cluster_ip+'/v1/models/'+name+':predict', json=formData, headers=headers)
if res.status_code == 200:
return res.json()
else:
print("Failed with ",res.status_code)
return []
predict([[6.8, 2.8, 4.8, 1.4]],"sklearn-iris",SERVICE_HOSTNAME,CLUSTER_IP)
!kubectl logs $(kubectl get pod -l serving.knative.dev/configuration=message-dumper -o jsonpath='{.items[0].metadata.name}') user-container
!kubectl delete -f sklearn-logging.yaml
!kubectl delete -f trigger.yaml
!kubectl delete -f message-dumper.yaml
###Output
_____no_output_____
|
rnnms.ipynb
|
###Markdown
rnnms[][github][][notebook]Author: [tarepan][github]:https://github.com/tarepan/UniversalVocoding[notebook]:https://colab.research.google.com/github/tarepan/UniversalVocoding/blob/main/rnnms.ipynb[tarepan]:https://github.com/tarepan Colab CheckCheck- Google Colaboratory runnning time- GPU type- Python version- CUDA version
###Code
!cat /proc/uptime | awk '{print $1 /60 /60 /24 "days (" $1 "sec)"}'
!head -n 1 /proc/driver/nvidia/gpus/**/information
!python --version
!pip show torch | sed '2!d'
!/usr/local/cuda/bin/nvcc --version | sed '4!d'
###Output
_____no_output_____
###Markdown
Setup Install the package from `tarepan/UniversalVocoding` public repository
###Code
# GoogleDrive
from google.colab import drive
drive.mount('/content/gdrive')
# Dedicated dependencies install
# !pip install "torch==1.10.0" -q # Based on your PyTorch environment
# !pip install "torchaudio==0.10.0" -q # Based on your PyTorch environment
# repository install
!pip uninstall rnnms -y -q
!pip install git+https://github.com/tarepan/UniversalVocoding -q
###Output
_____no_output_____
###Markdown
Training
###Code
# Launch TensorBoard
%load_ext tensorboard
%tensorboard --logdir gdrive/MyDrive/ML_results/rnnms
# Train
!python -m rnnms.main_train \
train.ckpt_log.dir_root=gdrive/MyDrive/ML_results/rnnms \
train.ckpt_log.name_exp=2021 \
train.ckpt_log.name_version=version_1 \
data.adress_data_root=gdrive/MyDrive/ML_data \
# train.model.vocoder.prenet.num_layers=2 \
# # Usage stat
# ## GPU
# !nvidia-smi -l 3
# ## CPU
# !vmstat 5
# !top
###Output
_____no_output_____
|
3.Natural Language Processing in TensorFlow/Week-3/Course_3_Week_3_Lesson_1b.ipynb
|
###Markdown
Multiple Layer LSTM
###Code
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow_datasets as tfds
import tensorflow as tf
print(tf.__version__)
import tensorflow_datasets as tfds
import tensorflow as tf
print(tf.__version__)
# Get the data
dataset, info = tfds.load('imdb_reviews/subwords8k', with_info=True, as_supervised=True)
train_dataset, test_dataset = dataset['train'], dataset['test']
tokenizer = info.features['text'].encoder
BUFFER_SIZE = 10000
BATCH_SIZE = 64
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.padded_batch(BATCH_SIZE, train_dataset.output_shapes)
test_dataset = test_dataset.padded_batch(BATCH_SIZE, test_dataset.output_shapes)
model = tf.keras.Sequential([
tf.keras.layers.Embedding(tokenizer.vocab_size, 64),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.summary()
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
NUM_EPOCHS = 10
history = model.fit(train_dataset, epochs=NUM_EPOCHS, validation_data=test_dataset)
import matplotlib.pyplot as plt
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, 'accuracy')
plot_graphs(history, 'loss')
###Output
_____no_output_____
|
numpy_array_erisim_slicing_altkume_fancyindex_islemleri.ipynb
|
###Markdown
Slicing ile alt kümelere erişme
###Code
a = np.arange(20,30)
a
a[0:3] #slicing bu işte çok da bişeyi yok
a[:3] #üsttekinin aynısı
a[::2] #0dan başladı 1er atkayarak
a[2::2] #2den başlayıp 2şer atlayarak
a = np.random.randint(10, size = (5,5))
a
a[:,0] #vigülden öncesi satırları sonrası sütunları ifade ediyor
#yukarıdan aşağı tüm satırlar ve 0.sütun
a[1:,0] #1.satırdan itibaren aşağıya doğru tüm satırlar ve 0.sütun
a[:,4] #yine aynı şekilde son sütunun tüm satırları
a[0,:] #0.satırın tüm sütunları
a[:2, :3] #2.indexteki satıra kadar ve 3.indexteki sütuna kadar seçildi
a[0:2, 0:3] # bir üsttekinin aynısı zaten karışıklık olmaması için
#böyle kullanmak daha iyi
a
a[0:2, 0:] #ilk 2 satır ve onların tüm sütunları
a[0:, 0:2] #tüm satırların ilk 2 sütunu
a[1:3, 0:2]
#aşağıda göreceğiz ki a[1:3, 0:2]gibi alt kümeler seçip başka bir degere atarsak
#örn alt_kume=a[1:3, 0:2] ; biz bu alt kumede degisiklik yapınca a[]'nın
#orjinalinde de degisiklik oluyor evet biraz garip ama öyle
#örn
a
alt_kume_a = a[0:2, 0:2]
alt_kume_a
alt_kume_a[0,0] = 99
alt_kume_a[1,1] = 99
alt_kume_a
a
#goruldugu gibi orjinal a'da da 99lar geldi
#böyle olmasını istemiyorsak, bu alt kümenin bağımsız
#oldugunu pythona copy()ile söyleriz.
alt_b = a[2:5, 2:5].copy()
alt_b
alt_b[0,0] =99
alt_b[1,1] =99
alt_b[2,2] =99
alt_b
#evet altkumede degisiklik yaptık
a
#ve goruldugu gibi ana kümede degisiklik yok copy()ile
#olusturdugumuz icin
###Output
_____no_output_____
###Markdown
Fancy index
###Code
v = np.arange(0, 30, 3)
v
bu_indexleri_getir = np.array([1,3,5])
v[bu_indexleri_getir]
m = np.arange(9).reshape((3,3))
m
satirda_istenen_indexler = np.array([0,1]) #0.satırve 1.sutun kesisimi
sutunda_istenen_indexler = np.array([1,2]) #1.satır ve 2. sutun kesisimi
m[satirda_istenen_indexler, sutunda_istenen_indexler]
#asagida hem basit index secme hem fancy index kullanacaz
m[0, [1,2]] #sıfırıncı satırın 1.sutun ve 2.sutunla kesisimi
m[0:, [1,2]] #bütün satırlar(bütun yataylar ve 1ve2. sutunun kesisimleri)
c = np.arange(10,20)
c
index = np.array([0,1,2])
index
c[index]
c[index] = 99 #fancy index ile birden fazla indexi secip
#ayni anda degistirdik
c
c[index] = 99 ,100 ,101 #hepsini aynı degere atamak zorunda degiliz
c
###Output
_____no_output_____
|
I Resolving Python with Data Science/Past/01_Data Tables & Basic Concepts of Programming/01practice_data-tables-&-basic-concepts-of-programming.ipynb
|
###Markdown
01 | Data Tables & Basic Concepts of Programming - Subscribe to my [Blog ↗](https://blog.pythonassembly.com/)- Let's keep in touch on [LinkedIn ↗](www.linkedin.com/in/jsulopz) 😄 Discipline to Search Solutions in Google > Apply the following steps when **looking for solutions in Google**:>> 1. **Necesity**: How to load an Excel in Python?> 2. **Search in Google**: by keywords> - `load excel python`> - ~~how to load excel in python~~> 3. **Solution**: What's the `function()` that loads an Excel in Python?> - A Function to Programming is what the Atom to Phisics.> - Every time you want to do something in programming> - **You will need a `function()`** to make it> - Theferore, you must **detect parenthesis `()`**> - Out of all the words that you see in a website> - Because they indicate the presence of a `function()`. Load the Data
###Code
import pandas as pd
df = pd.read_excel('df_mortality_regions.xlsx')
df.head()
###Output
_____no_output_____
###Markdown
Islands Number of Islands
###Code
mask = df.Island == 1
df[mask].shape
df.Island.sum()
df['Island'].sum()
###Output
_____no_output_____
###Markdown
Which region had more Islands?
###Code
df.groupby('Regional indicator')['Island'].sum()
df.groupby('Regional indicator')['Island'].sum().max()
df.groupby('Regional indicator')['Island'].sum().idxmax()
res = df.groupby('Regional indicator')['Island'].sum().sort_values(ascending = False)
res
res.dtypes
res.name
res.values
res.index
res
df.groupby('Regional indicator')['Island'].sum().sort_values(ascending = False)[0]
df.groupby('Regional indicator')['Island'].sum().sort_values(ascending = False)[:1]
df.groupby('Regional indicator')['Island'].sum().sort_values(ascending = False)[:2]
df.groupby('Regional indicator')['Island'].sum().sort_values(ascending = False).head(1)
df.groupby('Regional indicator')['Island'].sum().sort_values().tail(1)
reg = df.groupby('Regional indicator')['Island'].sum().idxmax()
###Output
_____no_output_____
###Markdown
Show all Columns for these Islands
###Code
mask_reg = df['Regional indicator'] == reg
df[mask & mask_reg]
###Output
_____no_output_____
###Markdown
Mean Age of across All Islands?
###Code
df[mask]['Median age'].mean()
????
###Output
Object `??` not found.
###Markdown
Female Heads of State Number of Countries with Female Heads of State
###Code
df['Female head of government'].sum()
###Output
_____no_output_____
###Markdown
Which region had more Female Heads of State?
###Code
df.groupby('Regional indicator')['Female head of government'].sum().sort_values(ascending = False)
reg = df.groupby('Regional indicator')['Female head of government'].sum().idxmax()
###Output
_____no_output_____
###Markdown
Show all Columns for these Countries
###Code
mask_fem = df['Female head of government'] == 1
mask_reg = df['Regional indicator'] == reg
df[mask_fem & mask_reg]
###Output
_____no_output_____
###Markdown
Mean Age of across All Countries?
###Code
df['Median age'].mean()
###Output
_____no_output_____
###Markdown
Show All Columns for the Country with more deaths due to Covid per 100,000 people
###Code
mask = df['COVID-19 deaths per 100,000 population in 2020']>100000
fila = df['COVID-19 deaths per 100,000 population in 2020'].idxmax()
df.loc[fila, :]
pd()
a = 89
a()
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import
fit()
algo.fit()
###Output
_____no_output_____
###Markdown
`algo = ?`
###Code
import sklearn
sklearn.
model = LinearRegression()
model.__dict__
import seaborn as sns
df = sns.load_dataset('mpg')
model.fit(X=df[['weight']], y=df['mpg'])
model.__dict__
mean()
pd.m
df.me
###Output
_____no_output_____
|
Course5/Week1/Building_a_Recurrent_Neural_Network_Step_by_Step_v3a.ipynb
|
###Markdown
Building your Recurrent Neural Network - Step by StepWelcome to Course 5's first assignment! In this assignment, you will implement key components of a Recurrent Neural Network in numpy.Recurrent Neural Networks (RNN) are very effective for Natural Language Processing and other sequence tasks because they have "memory". They can read inputs $x^{\langle t \rangle}$ (such as words) one at a time, and remember some information/context through the hidden layer activations that get passed from one time-step to the next. This allows a unidirectional RNN to take information from the past to process later inputs. A bidirectional RNN can take context from both the past and the future. **Notation**:- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer. - Superscript $(i)$ denotes an object associated with the $i^{th}$ example. - Superscript $\langle t \rangle$ denotes an object at the $t^{th}$ time-step. - **Sub**script $i$ denotes the $i^{th}$ entry of a vector.Example: - $a^{(2)[3]}_5$ denotes the activation of the 2nd training example (2), 3rd layer [3], 4th time step , and 5th entry in the vector. Pre-requisites* We assume that you are already familiar with `numpy`. * To refresh your knowledge of numpy, you can review course 1 of this specialization "Neural Networks and Deep Learning". * Specifically, review the week 2 assignment ["Python Basics with numpy (optional)"](https://www.coursera.org/learn/neural-networks-deep-learning/item/Zh0CU). Be careful when modifying the starter code* When working on graded functions, please remember to only modify the code that is between the```Python START CODE HERE```and```Python END CODE HERE```* In particular, Be careful to not modify the first line of graded routines. These start with:```Python GRADED FUNCTION: routine_name```* The automatic grader (autograder) needs these to locate the function.* Even a change in spacing will cause issues with the autograder. * It will return 'failed' if these are modified or missing." Updates If you were working on the notebook before this update...* The current notebook is version "3a".* You can find your original work saved in the notebook with the previous version name ("v3") * To view the file directory, go to the menu "File->Open", and this will open a new tab that shows the file directory. List of updates* "Forward propagation for the basic RNN", added sections to clarify variable names and shapes: - "Dimensions of $x^{\langle t \rangle}$" - "Hidden State $a$", - "Dimensions of hidden state $a^{\langle t \rangle}$" - "Dimensions of prediction $y^{\langle t \rangle}$"* `rnn_cell_forward`: * Added additional hints. * Updated figure 2.* `rnn_forward` - Set `xt` in a separate line of code to clarify what code is expected; added additional hints. - Clarifies instructions to specify dimensions (2D or 3D), and clarifies variable names. - Additional Hints - Clarifies when the basic RNN works well. - Updated figure 3.* "About the gates" replaced with "overview of gates and states": - Updated to include conceptual description of each gate's purpose, and an explanation of each equation. - Added sections about the cell state, hidden state, and prediction. - Lists variable names that are used in the code, and notes when they differ from the variables used in the equations. - Lists shapes of the variables. - Updated figure 4.* `lstm_forward` - Added instructions, noting the shapes of the variables. - Added hints about `c` and `c_next` to help students avoid copy-by-reference mistakes. - Set `xt` in a separate line to make this step explicit.* Renamed global variables so that they do not conflict with local variables within the function.* Spelling, grammar and wording corrections.* For unit tests, updated print statements and "expected output" for easier comparisons.* Many thanks to mentor Geoff Ladwig for suggested improvements and fixes in the assignments for course 5! Let's first import all the packages that you will need during this assignment.
###Code
import numpy as np
from rnn_utils import *
###Output
_____no_output_____
###Markdown
1 - Forward propagation for the basic Recurrent Neural NetworkLater this week, you will generate music using an RNN. The basic RNN that you will implement has the structure below. In this example, $T_x = T_y$. **Figure 1**: Basic RNN model Dimensions of input $x$ Input with $n_x$ number of units* For a single input example, $x^{(i)}$ is a one-dimensional input vector.* Using language as an example, a language with a 5000 word vocabulary could be one-hot encoded into a vector that has 5000 units. So $x^{(i)}$ would have the shape (5000,). * We'll use the notation $n_x$ to denote the number of units in a single training example. Batches of size $m$* Let's say we have mini-batches, each with 20 training examples. * To benefit from vectorization, we'll stack 20 columns of $x^{(i)}$ examples into a 2D array (a matrix).* For example, this tensor has the shape (5000,20). * We'll use $m$ to denote the number of training examples. * So the shape of a mini-batch is $(n_x,m)$ Time steps of size $T_{x}$* A recurrent neural network has multiple time steps, which we'll index with $t$.* In the lessons, we saw a single training example $x^{(i)}$ (a vector) pass through multiple time steps $T_x$. For example, if there are 10 time steps, $T_{x} = 10$ 3D Tensor of shape $(n_{x},m,T_{x})$* The 3-dimensional tensor $x$ of shape $(n_x,m,T_x)$ represents the input $x$ that is fed into the RNN. Taking a 2D slice for each time step: $x^{\langle t \rangle}$* At each time step, we'll use a mini-batches of training examples (not just a single example).* So, for each time step $t$, we'll use a 2D slice of shape $(n_x,m)$.* We're referring to this 2D slice as $x^{\langle t \rangle}$. The variable name in the code is `xt`. Definition of hidden state $a$* The activation $a^{\langle t \rangle}$ that is passed to the RNN from one time step to another is called a "hidden state." Dimensions of hidden state $a$* Similar to the input tensor $x$, the hidden state for a single training example is a vector of length $n_{a}$.* If we include a mini-batch of $m$ training examples, the shape of a mini-batch is $(n_{a},m)$.* When we include the time step dimension, the shape of the hidden state is $(n_{a}, m, T_x)$* We will loop through the time steps with index $t$, and work with a 2D slice of the 3D tensor. * We'll refer to this 2D slice as $a^{\langle t \rangle}$. * In the code, the variable names we use are either `a_prev` or `a_next`, depending on the function that's being implemented.* The shape of this 2D slice is $(n_{a}, m)$ Dimensions of prediction $\hat{y}$* Similar to the inputs and hidden states, $\hat{y}$ is a 3D tensor of shape $(n_{y}, m, T_{y})$. * $n_{y}$: number of units in the vector representing the prediction. * $m$: number of examples in a mini-batch. * $T_{y}$: number of time steps in the prediction.* For a single time step $t$, a 2D slice $\hat{y}^{\langle t \rangle}$ has shape $(n_{y}, m)$.* In the code, the variable names are: - `y_pred`: $\hat{y}$ - `yt_pred`: $\hat{y}^{\langle t \rangle}$ Here's how you can implement an RNN: **Steps**:1. Implement the calculations needed for one time-step of the RNN.2. Implement a loop over $T_x$ time-steps in order to process all the inputs, one at a time. 1.1 - RNN cellA recurrent neural network can be seen as the repeated use of a single cell. You are first going to implement the computations for a single time-step. The following figure describes the operations for a single time-step of an RNN cell. **Figure 2**: Basic RNN cell. Takes as input $x^{\langle t \rangle}$ (current input) and $a^{\langle t - 1\rangle}$ (previous hidden state containing information from the past), and outputs $a^{\langle t \rangle}$ which is given to the next RNN cell and also used to predict $\hat{y}^{\langle t \rangle}$ rnn cell versus rnn_cell_forward* Note that an RNN cell outputs the hidden state $a^{\langle t \rangle}$. * The rnn cell is shown in the figure as the inner box which has solid lines. * The function that we will implement, `rnn_cell_forward`, also calculates the prediction $\hat{y}^{\langle t \rangle}$ * The rnn_cell_forward is shown in the figure as the outer box that has dashed lines. **Exercise**: Implement the RNN-cell described in Figure (2).**Instructions**:1. Compute the hidden state with tanh activation: $a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a)$.2. Using your new hidden state $a^{\langle t \rangle}$, compute the prediction $\hat{y}^{\langle t \rangle} = softmax(W_{ya} a^{\langle t \rangle} + b_y)$. We provided the function `softmax`.3. Store $(a^{\langle t \rangle}, a^{\langle t-1 \rangle}, x^{\langle t \rangle}, parameters)$ in a `cache`.4. Return $a^{\langle t \rangle}$ , $\hat{y}^{\langle t \rangle}$ and `cache` Additional Hints* [numpy.tanh](https://www.google.com/search?q=numpy+tanh&rlz=1C5CHFA_enUS854US855&oq=numpy+tanh&aqs=chrome..69i57j0l5.1340j0j7&sourceid=chrome&ie=UTF-8)* We've created a `softmax` function that you can use. It is located in the file 'rnn_utils.py' and has been imported.* For matrix multiplication, use [numpy.dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html)
###Code
# GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
"""
Implements a single forward step of the RNN-cell as described in Figure (2)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ### (≈2 lines)
# compute next activation state using the formula given above
a_next = np.tanh(Waa.dot(a_prev) + Wax.dot(xt) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(Wya.dot(a_next) + by)
### END CODE HERE ###
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = \n", a_next_tmp.shape)
print("yt_pred[1] =\n", yt_pred_tmp[1])
print("yt_pred.shape = \n", yt_pred_tmp.shape)
###Output
a_next[4] =
[ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978
-0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape =
(5, 10)
yt_pred[1] =
[ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
0.36920224 0.9966312 0.9982559 0.17746526]
yt_pred.shape =
(2, 10)
###Markdown
**Expected Output**: ```Pythona_next[4] = [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978 -0.18887155 0.99815551 0.6531151 0.82872037]a_next.shape = (5, 10)yt_pred[1] = [ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212 0.36920224 0.9966312 0.9982559 0.17746526]yt_pred.shape = (2, 10)``` 1.2 - RNN forward pass - A recurrent neural network (RNN) is a repetition of the RNN cell that you've just built. - If your input sequence of data is 10 time steps long, then you will re-use the RNN cell 10 times. - Each cell takes two inputs at each time step: - $a^{\langle t-1 \rangle}$: The hidden state from the previous cell. - $x^{\langle t \rangle}$: The current time-step's input data.- It has two outputs at each time step: - A hidden state ($a^{\langle t \rangle}$) - A prediction ($y^{\langle t \rangle}$)- The weights and biases $(W_{aa}, b_{a}, W_{ax}, b_{x})$ are re-used each time step. - They are maintained between calls to rnn_cell_forward in the 'parameters' dictionary. **Figure 3**: Basic RNN. The input sequence $x = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle})$ is carried over $T_x$ time steps. The network outputs $y = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle})$. **Exercise**: Code the forward propagation of the RNN described in Figure (3).**Instructions**:* Create a 3D array of zeros, $a$ of shape $(n_{a}, m, T_{x})$ that will store all the hidden states computed by the RNN.* Create a 3D array of zeros, $\hat{y}$, of shape $(n_{y}, m, T_{x})$ that will store the predictions. - Note that in this case, $T_{y} = T_{x}$ (the prediction and input have the same number of time steps).* Initialize the 2D hidden state `a_next` by setting it equal to the initial hidden state, $a_{0}$.* At each time step $t$: - Get $x^{\langle t \rangle}$, which is a 2D slice of $x$ for a single time step $t$. - $x^{\langle t \rangle}$ has shape $(n_{x}, m)$ - $x$ has shape $(n_{x}, m, T_{x})$ - Update the 2D hidden state $a^{\langle t \rangle}$ (variable name `a_next`), the prediction $\hat{y}^{\langle t \rangle}$ and the cache by running `rnn_cell_forward`. - $a^{\langle t \rangle}$ has shape $(n_{a}, m)$ - Store the 2D hidden state in the 3D tensor $a$, at the $t^{th}$ position. - $a$ has shape $(n_{a}, m, T_{x})$ - Store the 2D $\hat{y}^{\langle t \rangle}$ prediction (variable name `yt_pred`) in the 3D tensor $\hat{y}_{pred}$ at the $t^{th}$ position. - $\hat{y}^{\langle t \rangle}$ has shape $(n_{y}, m)$ - $\hat{y}$ has shape $(n_{y}, m, T_x)$ - Append the cache to the list of caches.* Return the 3D tensor $a$ and $\hat{y}$, as well as the list of caches. Additional Hints- [np.zeros](https://docs.scipy.org/doc/numpy/reference/generated/numpy.zeros.html)- If you have a 3 dimensional numpy array and are indexing by its third dimension, you can use array slicing like this: `var_name[:,:,i]`.
###Code
# GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
### START CODE HERE ###
# initialize "a" and "y_pred" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps of the input 'x' (1 line)
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈2 lines)
xt = x[: ,:,t]
a_next, yt_pred, cache = rnn_cell_forward(xt, a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,4)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][1] = \n", a_tmp[4][1])
print("a.shape = \n", a_tmp.shape)
print("y_pred[1][3] =\n", y_pred_tmp[1][3])
print("y_pred.shape = \n", y_pred_tmp.shape)
print("caches[1][1][3] =\n", caches_tmp[1][1][3])
print("len(caches) = \n", len(caches_tmp))
###Output
a[4][1] =
[-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape =
(5, 10, 4)
y_pred[1][3] =
[ 0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape =
(2, 10, 4)
caches[1][1][3] =
[-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(caches) =
2
###Markdown
**Expected Output**:```Pythona[4][1] = [-0.99999375 0.77911235 -0.99861469 -0.99833267]a.shape = (5, 10, 4)y_pred[1][3] = [ 0.79560373 0.86224861 0.11118257 0.81515947]y_pred.shape = (2, 10, 4)caches[1][1][3] = [-1.1425182 -0.34934272 -0.20889423 0.58662319]len(caches) = 2``` Congratulations! You've successfully built the forward propagation of a recurrent neural network from scratch. Situations when this RNN will perform better:- This will work well enough for some applications, but it suffers from the vanishing gradient problems. - The RNN works best when each output $\hat{y}^{\langle t \rangle}$ can be estimated using "local" context. - "Local" context refers to information that is close to the prediction's time step $t$.- More formally, local context refers to inputs $x^{\langle t' \rangle}$ and predictions $\hat{y}^{\langle t \rangle}$ where $t'$ is close to $t$.In the next part, you will build a more complex LSTM model, which is better at addressing vanishing gradients. The LSTM will be better able to remember a piece of information and keep it saved for many timesteps. 2 - Long Short-Term Memory (LSTM) networkThe following figure shows the operations of an LSTM-cell. **Figure 4**: LSTM-cell. This tracks and updates a "cell state" or memory variable $c^{\langle t \rangle}$ at every time-step, which can be different from $a^{\langle t \rangle}$. Similar to the RNN example above, you will start by implementing the LSTM cell for a single time-step. Then you can iteratively call it from inside a "for-loop" to have it process an input with $T_x$ time-steps. Overview of gates and states - Forget gate $\mathbf{\Gamma}_{f}$* Let's assume we are reading words in a piece of text, and plan to use an LSTM to keep track of grammatical structures, such as whether the subject is singular ("puppy") or plural ("puppies"). * If the subject changes its state (from a singular word to a plural word), the memory of the previous state becomes outdated, so we "forget" that outdated state.* The "forget gate" is a tensor containing values that are between 0 and 1. * If a unit in the forget gate has a value close to 0, the LSTM will "forget" the stored state in the corresponding unit of the previous cell state. * If a unit in the forget gate has a value close to 1, the LSTM will mostly remember the corresponding value in the stored state. Equation$$\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f)\tag{1} $$ Explanation of the equation:* $\mathbf{W_{f}}$ contains weights that govern the forget gate's behavior. * The previous time step's hidden state $[a^{\langle t-1 \rangle}$ and current time step's input $x^{\langle t \rangle}]$ are concatenated together and multiplied by $\mathbf{W_{f}}$. * A sigmoid function is used to make each of the gate tensor's values $\mathbf{\Gamma}_f^{\langle t \rangle}$ range from 0 to 1.* The forget gate $\mathbf{\Gamma}_f^{\langle t \rangle}$ has the same dimensions as the previous cell state $c^{\langle t-1 \rangle}$. * This means that the two can be multiplied together, element-wise.* Multiplying the tensors $\mathbf{\Gamma}_f^{\langle t \rangle} * \mathbf{c}^{\langle t-1 \rangle}$ is like applying a mask over the previous cell state.* If a single value in $\mathbf{\Gamma}_f^{\langle t \rangle}$ is 0 or close to 0, then the product is close to 0. * This keeps the information stored in the corresponding unit in $\mathbf{c}^{\langle t-1 \rangle}$ from being remembered for the next time step.* Similarly, if one value is close to 1, the product is close to the original value in the previous cell state. * The LSTM will keep the information from the corresponding unit of $\mathbf{c}^{\langle t-1 \rangle}$, to be used in the next time step. Variable names in the codeThe variable names in the code are similar to the equations, with slight differences. * `Wf`: forget gate weight $\mathbf{W}_{f}$* `Wb`: forget gate bias $\mathbf{W}_{b}$* `ft`: forget gate $\Gamma_f^{\langle t \rangle}$ Candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$* The candidate value is a tensor containing information from the current time step that **may** be stored in the current cell state $\mathbf{c}^{\langle t \rangle}$.* Which parts of the candidate value get passed on depends on the update gate.* The candidate value is a tensor containing values that range from -1 to 1.* The tilde "~" is used to differentiate the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ from the cell state $\mathbf{c}^{\langle t \rangle}$. Equation$$\mathbf{\tilde{c}}^{\langle t \rangle} = \tanh\left( \mathbf{W}_{c} [\mathbf{a}^{\langle t - 1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{c} \right) \tag{3}$$ Explanation of the equation* The 'tanh' function produces values between -1 and +1. Variable names in the code* `cct`: candidate value $\mathbf{\tilde{c}}^{\langle t \rangle}$ - Update gate $\mathbf{\Gamma}_{i}$* We use the update gate to decide what aspects of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to add to the cell state $c^{\langle t \rangle}$.* The update gate decides what parts of a "candidate" tensor $\tilde{\mathbf{c}}^{\langle t \rangle}$ are passed onto the cell state $\mathbf{c}^{\langle t \rangle}$.* The update gate is a tensor containing values between 0 and 1. * When a unit in the update gate is close to 1, it allows the value of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to be passed onto the hidden state $\mathbf{c}^{\langle t \rangle}$ * When a unit in the update gate is close to 0, it prevents the corresponding value in the candidate from being passed onto the hidden state.* Notice that we use the subscript "i" and not "u", to follow the convention used in the literature. Equation$$\mathbf{\Gamma}_i^{\langle t \rangle} = \sigma(\mathbf{W}_i[a^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_i)\tag{2} $$ Explanation of the equation* Similar to the forget gate, here $\mathbf{\Gamma}_i^{\langle t \rangle}$, the sigmoid produces values between 0 and 1.* The update gate is multiplied element-wise with the candidate, and this product ($\mathbf{\Gamma}_{i}^{\langle t \rangle} * \tilde{c}^{\langle t \rangle}$) is used in determining the cell state $\mathbf{c}^{\langle t \rangle}$. Variable names in code (Please note that they're different than the equations)In the code, we'll use the variable names found in the academic literature. These variables don't use "u" to denote "update".* `Wi` is the update gate weight $\mathbf{W}_i$ (not "Wu") * `bi` is the update gate bias $\mathbf{b}_i$ (not "bu")* `it` is the forget gate $\mathbf{\Gamma}_i^{\langle t \rangle}$ (not "ut") - Cell state $\mathbf{c}^{\langle t \rangle}$* The cell state is the "memory" that gets passed onto future time steps.* The new cell state $\mathbf{c}^{\langle t \rangle}$ is a combination of the previous cell state and the candidate value. Equation$$ \mathbf{c}^{\langle t \rangle} = \mathbf{\Gamma}_f^{\langle t \rangle}* \mathbf{c}^{\langle t-1 \rangle} + \mathbf{\Gamma}_{i}^{\langle t \rangle} *\mathbf{\tilde{c}}^{\langle t \rangle} \tag{4} $$ Explanation of equation* The previous cell state $\mathbf{c}^{\langle t-1 \rangle}$ is adjusted (weighted) by the forget gate $\mathbf{\Gamma}_{f}^{\langle t \rangle}$* and the candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$, adjusted (weighted) by the update gate $\mathbf{\Gamma}_{i}^{\langle t \rangle}$ Variable names and shapes in the code* `c`: cell state, including all time steps, $\mathbf{c}$ shape $(n_{a}, m, T)$* `c_next`: new (next) cell state, $\mathbf{c}^{\langle t \rangle}$ shape $(n_{a}, m)$* `c_prev`: previous cell state, $\mathbf{c}^{\langle t-1 \rangle}$, shape $(n_{a}, m)$ - Output gate $\mathbf{\Gamma}_{o}$* The output gate decides what gets sent as the prediction (output) of the time step.* The output gate is like the other gates. It contains values that range from 0 to 1. Equation$$ \mathbf{\Gamma}_o^{\langle t \rangle}= \sigma(\mathbf{W}_o[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{o})\tag{5}$$ Explanation of the equation* The output gate is determined by the previous hidden state $\mathbf{a}^{\langle t-1 \rangle}$ and the current input $\mathbf{x}^{\langle t \rangle}$* The sigmoid makes the gate range from 0 to 1. Variable names in the code* `Wo`: output gate weight, $\mathbf{W_o}$* `bo`: output gate bias, $\mathbf{b_o}$* `ot`: output gate, $\mathbf{\Gamma}_{o}^{\langle t \rangle}$ - Hidden state $\mathbf{a}^{\langle t \rangle}$* The hidden state gets passed to the LSTM cell's next time step.* It is used to determine the three gates ($\mathbf{\Gamma}_{f}, \mathbf{\Gamma}_{u}, \mathbf{\Gamma}_{o}$) of the next time step.* The hidden state is also used for the prediction $y^{\langle t \rangle}$. Equation$$ \mathbf{a}^{\langle t \rangle} = \mathbf{\Gamma}_o^{\langle t \rangle} * \tanh(\mathbf{c}^{\langle t \rangle})\tag{6} $$ Explanation of equation* The hidden state $\mathbf{a}^{\langle t \rangle}$ is determined by the cell state $\mathbf{c}^{\langle t \rangle}$ in combination with the output gate $\mathbf{\Gamma}_{o}$.* The cell state state is passed through the "tanh" function to rescale values between -1 and +1.* The output gate acts like a "mask" that either preserves the values of $\tanh(\mathbf{c}^{\langle t \rangle})$ or keeps those values from being included in the hidden state $\mathbf{a}^{\langle t \rangle}$ Variable names and shapes in the code* `a`: hidden state, including time steps. $\mathbf{a}$ has shape $(n_{a}, m, T_{x})$* 'a_prev`: hidden state from previous time step. $\mathbf{a}^{\langle t-1 \rangle}$ has shape $(n_{a}, m)$* `a_next`: hidden state for next time step. $\mathbf{a}^{\langle t \rangle}$ has shape $(n_{a}, m)$ - Prediction $\mathbf{y}^{\langle t \rangle}_{pred}$* The prediction in this use case is a classification, so we'll use a softmax.The equation is:$$\mathbf{y}^{\langle t \rangle}_{pred} = \textrm{softmax}(\mathbf{W}_{y} \mathbf{a}^{\langle t \rangle} + \mathbf{b}_{y})$$ Variable names and shapes in the code* `y_pred`: prediction, including all time steps. $\mathbf{y}_{pred}$ has shape $(n_{y}, m, T_{x})$. Note that $(T_{y} = T_{x})$ for this example.* `yt_pred`: prediction for the current time step $t$. $\mathbf{y}^{\langle t \rangle}_{pred}$ has shape $(n_{y}, m)$ 2.1 - LSTM cell**Exercise**: Implement the LSTM cell described in the Figure (4).**Instructions**:1. Concatenate the hidden state $a^{\langle t-1 \rangle}$ and input $x^{\langle t \rangle}$ into a single matrix: $$concat = \begin{bmatrix} a^{\langle t-1 \rangle} \\ x^{\langle t \rangle} \end{bmatrix}$$ 2. Compute all the formulas 1 through 6 for the gates, hidden state, and cell state.3. Compute the prediction $y^{\langle t \rangle}$. Additional Hints* You can use [numpy.concatenate](https://docs.scipy.org/doc/numpy/reference/generated/numpy.concatenate.html). Check which value to use for the `axis` parameter.* The functions `sigmoid()` and `softmax` are imported from `rnn_utils.py`.* [numpy.tanh](https://docs.scipy.org/doc/numpy/reference/generated/numpy.tanh.html)* Use [np.dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html) for matrix multiplication.* Notice that the variable names `Wi`, `bi` refer to the weights and biases of the **update** gate. There are no variables named "Wu" or "bu" in this function.
###Code
# GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
Implement a single forward step of the LSTM-cell as described in Figure (4)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
c_next -- next memory state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
c stands for the cell state (memory)
"""
# Retrieve parameters from "parameters"
Wf = parameters["Wf"] # forget gate weight
bf = parameters["bf"]
Wi = parameters["Wi"] # update gate weight (notice the variable name)
bi = parameters["bi"] # (notice the variable name)
Wc = parameters["Wc"] # candidate value weight
bc = parameters["bc"]
Wo = parameters["Wo"] # output gate weight
bo = parameters["bo"]
Wy = parameters["Wy"] # prediction weight
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
### START CODE HERE ###
# Concatenate a_prev and xt (≈1 line)
concat = np.concatenate((a_prev, xt), axis = 0)
# Compute values for ft (forget gate), it (update gate),
# cct (candidate value), c_next (cell state),
# ot (output gate), a_next (hidden state) (≈6 lines)
ft = sigmoid(np.dot(Wf,concat) + bf) # forget gate
it = sigmoid(np.dot(Wi ,concat) + bi) # update gate
cct = np.tanh(np.dot(Wc ,concat) + bc) # candidate value
c_next = ft * c_prev + it * cct # cell state
ot = sigmoid(np.dot(Wo, concat) + bo) # output gate
a_next = ot * np.tanh(c_next) # hidden state
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.dot(Wy ,a_next) + by)
### END CODE HERE ###
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = ", c_next_tmp.shape)
print("c_next[2] = \n", c_next_tmp[2])
print("c_next.shape = ", c_next_tmp.shape)
print("yt[1] =", yt_tmp[1])
print("yt.shape = ", yt_tmp.shape)
print("cache[1][3] =\n", cache_tmp[1][3])
print("len(cache) = ", len(cache_tmp))
###Output
a_next[4] =
[-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] =
[ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
cache[1][3] =
[-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874
0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache) = 10
###Markdown
**Expected Output**:```Pythona_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482 0.76566531 0.34631421 -0.00215674 0.43827275]a_next.shape = (5, 10)c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942 0.76449811 -0.0981561 -0.74348425 -0.26810932]c_next.shape = (5, 10)yt[1] = [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381 0.00943007 0.12666353 0.39380172 0.07828381]yt.shape = (2, 10)cache[1][3] = [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874 0.07651101 -1.03752894 1.41219977 -0.37647422]len(cache) = 10``` 2.2 - Forward pass for LSTMNow that you have implemented one step of an LSTM, you can now iterate this over this using a for-loop to process a sequence of $T_x$ inputs. **Figure 5**: LSTM over multiple time-steps. **Exercise:** Implement `lstm_forward()` to run an LSTM over $T_x$ time-steps. **Instructions*** Get the dimensions $n_x, n_a, n_y, m, T_x$ from the shape of the variables: `x` and `parameters`.* Initialize the 3D tensors $a$, $c$ and $y$. - $a$: hidden state, shape $(n_{a}, m, T_{x})$ - $c$: cell state, shape $(n_{a}, m, T_{x})$ - $y$: prediction, shape $(n_{y}, m, T_{x})$ (Note that $T_{y} = T_{x}$ in this example). - **Note** Setting one variable equal to the other is a "copy by reference". In other words, don't do `c = a', otherwise both these variables point to the same underlying variable.* Initialize the 2D tensor $a^{\langle t \rangle}$ - $a^{\langle t \rangle}$ stores the hidden state for time step $t$. The variable name is `a_next`. - $a^{\langle 0 \rangle}$, the initial hidden state at time step 0, is passed in when calling the function. The variable name is `a0`. - $a^{\langle t \rangle}$ and $a^{\langle 0 \rangle}$ represent a single time step, so they both have the shape $(n_{a}, m)$ - Initialize $a^{\langle t \rangle}$ by setting it to the initial hidden state ($a^{\langle 0 \rangle}$) that is passed into the function.* Initialize $c^{\langle t \rangle}$ with zeros. - The variable name is `c_next`. - $c^{\langle t \rangle}$ represents a single time step, so its shape is $(n_{a}, m)$ - **Note**: create `c_next` as its own variable with its own location in memory. Do not initialize it as a slice of the 3D tensor $c$. In other words, **don't** do `c_next = c[:,:,0]`.* For each time step, do the following: - From the 3D tensor $x$, get a 2D slice $x^{\langle t \rangle}$ at time step $t$. - Call the `lstm_cell_forward` function that you defined previously, to get the hidden state, cell state, prediction, and cache. - Store the hidden state, cell state and prediction (the 2D tensors) inside the 3D tensors. - Also append the cache to the list of caches.
###Code
# GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (4).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
c -- The value of the cell state, numpy array of shape (n_a, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
"""
# Initialize "caches", which will track the list of all the caches
caches = []
### START CODE HERE ###
Wy = parameters['Wy'] # saving parameters['Wy'] in a local variable in case students use Wy instead of parameters['Wy']
# Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines)
n_x, m, T_x = x.shape[0], x.shape[1], x.shape[2]
n_y, n_a = parameters["Wy"].shape[0], parameters["Wy"].shape[1]
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros((n_a, m))
# loop over all time-steps
for t in range(T_x):
# Get the 2D slice 'xt' from the 3D input 'x' at time step 't'
xt = x[:,:,t]
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Append the cache into caches (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi']= np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][3][6] = ", a_tmp[4][3][6])
print("a.shape = ", a_tmp.shape)
print("y[1][4][3] =", y_tmp[1][4][3])
print("y.shape = ", y_tmp.shape)
print("caches[1][1][1] =\n", caches_tmp[1][1][1])
print("c[1][2][1]", c_tmp[1][2][1])
print("len(caches) = ", len(caches_tmp))
###Output
a[4][3][6] = 0.172117767533
a.shape = (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape = (2, 10, 7)
caches[1][1][1] =
[ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.855544916718
len(caches) = 2
###Markdown
**Expected Output**:```Pythona[4][3][6] = 0.172117767533a.shape = (5, 10, 7)y[1][4][3] = 0.95087346185y.shape = (2, 10, 7)caches[1][1][1] = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139 0.41005165]c[1][2][1] -0.855544916718len(caches) = 2``` Congratulations! You have now implemented the forward passes for the basic RNN and the LSTM. When using a deep learning framework, implementing the forward pass is sufficient to build systems that achieve great performance. The rest of this notebook is optional, and will not be graded. 3 - Backpropagation in recurrent neural networks (OPTIONAL / UNGRADED)In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers do not need to bother with the details of the backward pass. If however you are an expert in calculus and want to see the details of backprop in RNNs, you can work through this optional portion of the notebook. When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in recurrent neural networks you can calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are quite complicated and we did not derive them in lecture. However, we will briefly present them below. 3.1 - Basic RNN backward passWe will start by computing the backward pass for the basic RNN-cell. **Figure 6**: RNN-cell's backward pass. Just like in a fully-connected neural network, the derivative of the cost function $J$ backpropagates through the RNN by following the chain-rule from calculus. The chain-rule is also used to calculate $(\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b})$ to update the parameters $(W_{ax}, W_{aa}, b_a)$. Deriving the one step backward functions: To compute the `rnn_cell_backward` you need to compute the following equations. It is a good exercise to derive them by hand. The derivative of $\tanh$ is $1-\tanh(x)^2$. You can find the complete proof [here](https://www.wyzant.com/resources/lessons/math/calculus/derivative_proofs/tanx). Note that: $ \text{sech}(x)^2 = 1 - \tanh(x)^2$Similarly for $\frac{ \partial a^{\langle t \rangle} } {\partial W_{ax}}, \frac{ \partial a^{\langle t \rangle} } {\partial W_{aa}}, \frac{ \partial a^{\langle t \rangle} } {\partial b}$, the derivative of $\tanh(u)$ is $(1-\tanh(u)^2)du$. The final two equations also follow the same rule and are derived using the $\tanh$ derivative. Note that the arrangement is done in a way to get the same dimensions to match.
###Code
def rnn_cell_backward(da_next, cache):
"""
Implements the backward pass for the RNN-cell (single time-step).
Arguments:
da_next -- Gradient of loss with respect to next hidden state
cache -- python dictionary containing useful values (output of rnn_cell_forward())
Returns:
gradients -- python dictionary containing:
dx -- Gradients of input data, of shape (n_x, m)
da_prev -- Gradients of previous hidden state, of shape (n_a, m)
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dba -- Gradients of bias vector, of shape (n_a, 1)
"""
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ###
# compute the gradient of tanh with respect to a_next (≈1 line)
dtanh = None
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = None
dWax = None
# compute the gradient with respect to Waa (≈2 lines)
da_prev = None
dWaa = None
# compute the gradient with respect to b (≈1 line)
dba = None
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['b'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
gradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])
print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)
###Output
_____no_output_____
###Markdown
**Expected Output**: **gradients["dxt"][1][2]** = -0.460564103059 **gradients["dxt"].shape** = (3, 10) **gradients["da_prev"][2][3]** = 0.0842968653807 **gradients["da_prev"].shape** = (5, 10) **gradients["dWax"][3][1]** = 0.393081873922 **gradients["dWax"].shape** = (5, 3) **gradients["dWaa"][1][2]** = -0.28483955787 **gradients["dWaa"].shape** = (5, 5) **gradients["dba"][4]** = [ 0.80517166] **gradients["dba"].shape** = (5, 1) Backward pass through the RNNComputing the gradients of the cost with respect to $a^{\langle t \rangle}$ at every time-step $t$ is useful because it is what helps the gradient backpropagate to the previous RNN-cell. To do so, you need to iterate through all the time steps starting at the end, and at each step, you increment the overall $db_a$, $dW_{aa}$, $dW_{ax}$ and you store $dx$.**Instructions**:Implement the `rnn_backward` function. Initialize the return variables with zeros first and then loop through all the time steps while calling the `rnn_cell_backward` at each time timestep, update the other variables accordingly.
###Code
def rnn_backward(da, caches):
"""
Implement the backward pass for a RNN over an entire sequence of input data.
Arguments:
da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
caches -- tuple containing information from the forward pass (rnn_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)
dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy array of shape (n_a, n_a)
dba -- Gradient w.r.t the bias, of shape (n_a, 1)
"""
### START CODE HERE ###
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = None
(a1, a0, x1, parameters) = None
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = None
n_x, m = None
# initialize the gradients with the right sizes (≈6 lines)
dx = None
dWax = None
dWaa = None
dba = None
da0 = None
da_prevt = None
# Loop through all the time steps
for t in reversed(range(None)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = None
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = None
dWax += None
dWaa += None
dba += None
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = None
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x_tmp = np.random.randn(3,10,4)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)
da_tmp = np.random.randn(5, 10, 4)
gradients_tmp = rnn_backward(da_tmp, caches_tmp)
print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])
print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)
###Output
_____no_output_____
###Markdown
**Expected Output**: **gradients["dx"][1][2]** = [-2.07101689 -0.59255627 0.02466855 0.01483317] **gradients["dx"].shape** = (3, 10, 4) **gradients["da0"][2][3]** = -0.314942375127 **gradients["da0"].shape** = (5, 10) **gradients["dWax"][3][1]** = 11.2641044965 **gradients["dWax"].shape** = (5, 3) **gradients["dWaa"][1][2]** = 2.30333312658 **gradients["dWaa"].shape** = (5, 5) **gradients["dba"][4]** = [-0.74747722] **gradients["dba"].shape** = (5, 1) 3.2 - LSTM backward pass 3.2.1 One Step backwardThe LSTM backward pass is slightly more complicated than the forward one. We have provided you with all the equations for the LSTM backward pass below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.) 3.2.2 gate derivatives$$d \Gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*(1-\Gamma_o^{\langle t \rangle})\tag{7}$$$$d\tilde c^{\langle t \rangle} = dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * i_t * da_{next} * \tilde c^{\langle t \rangle} * (1-\tanh(\tilde c)^2) \tag{8}$$$$d\Gamma_u^{\langle t \rangle} = dc_{next}*\tilde c^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * \tilde c^{\langle t \rangle} * da_{next}*\Gamma_u^{\langle t \rangle}*(1-\Gamma_u^{\langle t \rangle})\tag{9}$$$$d\Gamma_f^{\langle t \rangle} = dc_{next}*\tilde c_{prev} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * c_{prev} * da_{next}*\Gamma_f^{\langle t \rangle}*(1-\Gamma_f^{\langle t \rangle})\tag{10}$$ 3.2.3 parameter derivatives $$ dW_f = d\Gamma_f^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{11} $$$$ dW_u = d\Gamma_u^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{12} $$$$ dW_c = d\tilde c^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{13} $$$$ dW_o = d\Gamma_o^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{14}$$To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis= 1) axis on $d\Gamma_f^{\langle t \rangle}, d\Gamma_u^{\langle t \rangle}, d\tilde c^{\langle t \rangle}, d\Gamma_o^{\langle t \rangle}$ respectively. Note that you should have the `keep_dims = True` option.Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.$$ da_{prev} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c^{\langle t \rangle} + W_o^T * d\Gamma_o^{\langle t \rangle} \tag{15}$$Here, the weights for equations 13 are the first n_a, (i.e. $W_f = W_f[:n_a,:]$ etc...)$$ dc_{prev} = dc_{next}\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh(c_{next})^2)*\Gamma_f^{\langle t \rangle}*da_{next} \tag{16}$$$$ dx^{\langle t \rangle} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c_t + W_o^T * d\Gamma_o^{\langle t \rangle}\tag{17} $$where the weights for equation 15 are from n_a to the end, (i.e. $W_f = W_f[n_a:,:]$ etc...)**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-17$ below. Good luck! :)
###Code
def lstm_cell_backward(da_next, dc_next, cache):
"""
Implement the backward pass for the LSTM-cell (single time-step).
Arguments:
da_next -- Gradients of next hidden state, of shape (n_a, m)
dc_next -- Gradients of next cell state, of shape (n_a, m)
cache -- cache storing information from the forward pass
Returns:
gradients -- python dictionary containing:
dxt -- Gradient of input data at time-step t, of shape (n_x, m)
da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)
"""
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
### START CODE HERE ###
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = None
n_a, m = None
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = None
dcct = None
dit = None
dft = None
# Code equations (7) to (10) (≈4 lines)
dit = None
dft = None
dot = None
dcct = None
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
dWf = None
dWi = None
dWc = None
dWo = None
dbf = None
dbi = None
dbc = None
dbo = None
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = None
dc_prev = None
dxt = None
### END CODE HERE ###
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
dc_next_tmp = np.random.randn(5,10)
gradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients_tmp["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients_tmp["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
###Output
_____no_output_____
###Markdown
**Expected Output**: **gradients["dxt"][1][2]** = 3.23055911511 **gradients["dxt"].shape** = (3, 10) **gradients["da_prev"][2][3]** = -0.0639621419711 **gradients["da_prev"].shape** = (5, 10) **gradients["dc_prev"][2][3]** = 0.797522038797 **gradients["dc_prev"].shape** = (5, 10) **gradients["dWf"][3][1]** = -0.147954838164 **gradients["dWf"].shape** = (5, 8) **gradients["dWi"][1][2]** = 1.05749805523 **gradients["dWi"].shape** = (5, 8) **gradients["dWc"][3][1]** = 2.30456216369 **gradients["dWc"].shape** = (5, 8) **gradients["dWo"][1][2]** = 0.331311595289 **gradients["dWo"].shape** = (5, 8) **gradients["dbf"][4]** = [ 0.18864637] **gradients["dbf"].shape** = (5, 1) **gradients["dbi"][4]** = [-0.40142491] **gradients["dbi"].shape** = (5, 1) **gradients["dbc"][4]** = [ 0.25587763] **gradients["dbc"].shape** = (5, 1) **gradients["dbo"][4]** = [ 0.13893342] **gradients["dbo"].shape** = (5, 1) 3.3 Backward pass through the LSTM RNNThis part is very similar to the `rnn_backward` function you implemented above. You will first create variables of the same dimension as your return variables. You will then iterate over all the time steps starting from the end and call the one step function you implemented for LSTM at each iteration. You will then update the parameters by summing them individually. Finally return a dictionary with the new gradients. **Instructions**: Implement the `lstm_backward` function. Create a for loop starting from $T_x$ and going backward. For each step call `lstm_cell_backward` and update the your old gradients by adding the new gradients to them. Note that `dxt` is not updated but is stored.
###Code
def lstm_backward(da, caches):
"""
Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).
Arguments:
da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x)
caches -- cache storing information from the forward pass (lstm_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient of inputs, of shape (n_x, m, T_x)
da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
"""
# Retrieve values from the first cache (t=1) of caches.
(caches, x) = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
### START CODE HERE ###
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = None
n_x, m = None
# initialize the gradients with the right sizes (≈12 lines)
dx = None
da0 = None
da_prevt = None
dc_prevt = None
dWf = None
dWi = None
dWc = None
dWo = None
dbf = None
dbi = None
dbc = None
dbo = None
# loop back over the whole sequence
for t in reversed(range(None)):
# Compute all gradients using lstm_cell_backward
gradients = None
# Store or add the gradient to the parameters' previous step's gradient
dx[:,:,t] = None
dWf = None
dWi = None
dWc = None
dWo = None
dbf = None
dbi = None
dbc = None
dbo = None
# Set the first activation's gradient to the backpropagated gradient da_prev.
da0 = None
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
da_tmp = np.random.randn(5, 10, 4)
gradients_tmp = lstm_backward(da_tmp, caches_tmp)
print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
###Output
_____no_output_____
|
notebooks/tutorials/landscape_evolution/river_input_lem/adding_discharge_point_source_to_a_lem.ipynb
|
###Markdown
Adding a discharge point source to a LEM*(Greg Tucker, CSDMS / CU Boulder, fall 2020)*This notebook shows how to add one or more discharge point sources to a Landlab-built landscape evolution model (LEM), using the flow routing components. The basic idea is to modify the `water__unit_flux_in` field to include a large flux (which could be represented as either drainage area or discharge) at one or more locations along the edge of a grid.
###Code
from landlab import RasterModelGrid, imshow_grid
from landlab.components import FlowAccumulator
import numpy as np
###Output
_____no_output_____
###Markdown
Docstring example from `FlowAccumulator`The following is a tiny example from the `FlowAccumulator` documentation:
###Code
mg = RasterModelGrid((5, 4), xy_spacing=(10.0, 10))
topographic__elevation = np.array(
[
0.0,
0.0,
0.0,
0.0,
0.0,
21.0,
10.0,
0.0,
0.0,
31.0,
20.0,
0.0,
0.0,
32.0,
30.0,
0.0,
0.0,
0.0,
0.0,
0.0,
]
)
_ = mg.add_field("topographic__elevation", topographic__elevation, at="node")
mg.set_closed_boundaries_at_grid_edges(True, True, True, False)
fa = FlowAccumulator(mg, "topographic__elevation", flow_director="FlowDirectorSteepest")
runoff_rate = np.arange(mg.number_of_nodes, dtype=float)
rnff = mg.add_field("water__unit_flux_in", runoff_rate, at="node", clobber=True)
fa.run_one_step()
print(mg.at_node["surface_water__discharge"].reshape(5, 4))
# array([ 0., 500., 5200., 0.,
# 0., 500., 5200., 0.,
# 0., 900., 4600., 0.,
# 0., 1300., 2700., 0.,
# 0., 0., 0., 0.])
###Output
_____no_output_____
###Markdown
We can extend this tiny example to show that you can subsequently modify the `rnff` array and it will take effect when you re-run the `FlowAccumulator`:
###Code
rnff[:] = 1.0
fa.run_one_step()
print(mg.at_node["surface_water__discharge"].reshape(5, 4))
###Output
_____no_output_____
###Markdown
Larger exampleIn this example, we create a slightly larger grid, with a surface that slopes down toward the south / bottom boundary. We will introduce a runoff point source at a node in the middle of the top-most non-boundary row.Start by defining some parameters:
###Code
# Parameters
nrows = 41
ncols = 41
dx = 100.0 # grid spacing in m
slope_gradient = 0.01 # gradient of topographic surface
noise_amplitude = 0.2 # amplitude of random noise
input_runoff = 10000.0 # equivalent to a drainage area of 10,000 dx^2 or 10^8 m2
###Output
_____no_output_____
###Markdown
Create grid and topography, and set boundaries:
###Code
# Create a grid, and a field for water input
grid = RasterModelGrid((nrows, ncols), xy_spacing=dx)
# Have just one edge (south / bottom) be open
grid.set_closed_boundaries_at_grid_edges(True, True, True, False)
# Create an elevation field as a ramp with random noise
topo = grid.add_zeros("topographic__elevation", at="node")
topo[:] = slope_gradient * grid.y_of_node
np.random.seed(0)
topo[grid.core_nodes] += noise_amplitude * np.random.randn(grid.number_of_core_nodes)
###Output
_____no_output_____
###Markdown
The `FlowAccumulator` component takes care of identifying drainage directions (here using the D8 method) and calculating the cumulative drainage area and surface water discharge.Note that in this case we are assuming a default runoff value of unity, meaning that the calculated `surface_water__discharge` is actually just drainage area. To introduce the drainage area of a river entering at the top, we will use a large value for runoff. Because we are considering drainage area as the primary variable, with unit "runoff", our input runoff is a dimensionless variable: the number of contributing grid cell equivalents. We will set this to unity at all the nodes in the model except the point-source location.
###Code
# Create a FlowAccumulator component
fa = FlowAccumulator(grid, flow_director="FlowDirectorD8")
# Create a runoff input field, and set one of its nodes to have a large input
runoff = grid.add_ones("water__unit_flux_in", at="node", clobber=True)
top_middle_node = grid.number_of_nodes - int(1.5 * ncols)
runoff[top_middle_node] = input_runoff
fa.run_one_step()
imshow_grid(grid, "surface_water__discharge")
###Output
_____no_output_____
###Markdown
Changing the amount and/or location of inputWe can change the input drainage area / discharge amount or location simply by modifying the `water__unit_flux_in` field. Here we will shift it to the left and double its magnitude.
###Code
runoff[top_middle_node] = 1.0 # go back to being a "regular" node
runoff[top_middle_node - 15] = 2 * input_runoff # shift 15 cells left and double amount
fa.run_one_step()
imshow_grid(grid, "surface_water__discharge")
###Output
_____no_output_____
###Markdown
Note that the `drainage_area` field does not recognize any runoff input. It continues to track *only* the local drainage area:
###Code
imshow_grid(grid, "drainage_area")
###Output
_____no_output_____
###Markdown
This means that you should use the `surface_water__discharge` field rather than the `drainage_area` field, regardless of whether the former is meant to represent discharge (volume per time) or effective drainage area (area). Combining with a Landscape Evolution ModelHere we'll set up a simple LEM that uses the river input.
###Code
from landlab.components import StreamPowerEroder, LinearDiffuser
# Parameters
K = 4.0e-5
D = 0.01
uplift_rate = 0.0001
nrows = 51
ncols = 51
dx = 10.0 # grid spacing in m
slope_gradient = 0.01 # gradient of topographic surface
noise_amplitude = 0.04 # amplitude of random noise
input_runoff = 10000.0 # equivalent to a drainage area of 10,000 dx^2 or 10^6 m2
run_duration = 25.0 / uplift_rate
dt = dx / (K * (dx * dx * input_runoff) ** 0.5)
num_steps = int(run_duration / dt)
print(str(num_steps) + " steps.")
# Create a grid, and a field for water input
grid = RasterModelGrid((nrows, ncols), xy_spacing=dx)
# Have just one edge (south / bottom) be open
grid.set_closed_boundaries_at_grid_edges(True, True, True, False)
# Create an elevation field as a ramp with random noise
topo = grid.add_zeros("topographic__elevation", at="node")
topo[:] = slope_gradient * grid.y_of_node
np.random.seed(0)
topo[grid.core_nodes] += noise_amplitude * np.random.randn(grid.number_of_core_nodes)
# Create components
fa = FlowAccumulator(grid, flow_director="FlowDirectorD8")
sp = StreamPowerEroder(grid, K_sp=K, discharge_field="surface_water__discharge")
ld = LinearDiffuser(grid, linear_diffusivity=D)
runoff = grid.add_ones("water__unit_flux_in", at="node", clobber=True)
top_middle_node = grid.number_of_nodes - int(1.5 * ncols)
runoff[top_middle_node] = input_runoff
for _ in range(num_steps):
topo[grid.core_nodes] += uplift_rate * dt
fa.run_one_step()
ld.run_one_step(dt)
sp.run_one_step(dt)
imshow_grid(grid, topo)
###Output
_____no_output_____
|
naive_forecasting.ipynb
|
###Markdown
Naive forecasting Setup
###Code
import numpy as np
import matplotlib.pyplot as plt
def plot_series(time, series, format="-", start=0, end=None, label=None):
plt.plot(time[start:end], series[start:end], format, label=label)
plt.xlabel("Time")
plt.ylabel("Value")
if label:
plt.legend(fontsize=14)
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def white_noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
###Output
_____no_output_____
###Markdown
Trend and Seasonality
###Code
time = np.arange(4 * 365 + 1)
slope = 0.05
baseline = 10
amplitude = 40
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
noise_level = 5
noise = white_noise(time, noise_level, seed=42)
series += noise
plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()
###Output
_____no_output_____
###Markdown
All right, this looks realistic enough for now. Let's try to forecast it. We will split it into two periods: the training period and the validation period (in many cases, you would also want to have a test period). The split will be at time step 1000.
###Code
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
###Output
_____no_output_____
###Markdown
Naive Forecast
###Code
naive_forecast = series[split_time - 1:-1]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, label="Series")
plot_series(time_valid, naive_forecast, label="Forecast")
###Output
_____no_output_____
###Markdown
Let's zoom in on the start of the validation period:
###Code
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, start=0, end=150, label="Series")
plot_series(time_valid, naive_forecast, start=1, end=151, label="Forecast")
###Output
_____no_output_____
###Markdown
You can see that the naive forecast lags 1 step behind the time series. Now let's compute the mean absolute error between the forecasts and the predictions in the validation period:
###Code
errors = naive_forecast - x_valid
abs_errors = np.abs(errors)
mae = abs_errors.mean()
mae
###Output
_____no_output_____
###Markdown
Naive forecasting
###Code
import numpy as np
import matplotlib.pyplot as plt
def plot_series(time, series, format="-", start=0, end=None, label=None):
plt.plot(time[start:end], series[start:end], format, label=label)
plt.xlabel("Time")
plt.ylabel("Value")
if label:
plt.legend(fontsize=14)
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def white_noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
###Output
_____no_output_____
###Markdown
Trend and Seasonality
###Code
time = np.arange(4 * 365 + 1)
slope = 0.05
baseline = 10
amplitude = 40
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
noise_level = 5
noise = white_noise(time, noise_level, seed=42)
series += noise
plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()
###Output
_____no_output_____
###Markdown
All right, this looks realistic enough for now. Let's try to forecast it. We will split it into two periods: the training period and the validation period (in many cases, you would also want to have a test period). The split will be at time step 1000.
###Code
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
###Output
_____no_output_____
###Markdown
Naive Forecast
###Code
naive_forecast = series[split_time - 1:-1]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, label="Series")
plot_series(time_valid, naive_forecast, label="Forecast")
###Output
_____no_output_____
###Markdown
Let's zoom in on the start of the validation period:
###Code
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, start=0, end=150, label="Series")
plot_series(time_valid, naive_forecast, start=1, end=151, label="Forecast")
###Output
_____no_output_____
###Markdown
You can see that the naive forecast lags 1 step behind the time series. Now let's compute the mean absolute error between the forecasts and the predictions in the validation period:
###Code
errors = naive_forecast - x_valid
abs_errors = np.abs(errors)
mae = abs_errors.mean()
mae
###Output
_____no_output_____
|
1_python/python_review_3.ipynb
|
###Markdown
Python入门(下)1. [简介](简介)2. [函数](函数) [1. 函数的定义](函数的定义) [2. 函数的调用](函数的调用) [3. 函数文档](函数文档) [4. 函数参数](函数参数) [5. 函数的返回值](函数的返回值) [6. 变量作用域](变量作用域) 3. [Lambda-表达式](Lambda-表达式) [1. 匿名函数的定义](匿名函数的定义) [2. 匿名函数的应用](匿名函数的应用) 4. [类与对象](类与对象) [1. 属性和方法组成对象](属性和方法组成对象) [2. self是什么?](self-是什么?) [3. Python的魔法方法](Python-的魔法方法) [4. 公有和私有](公有和私有) [5. 继承](继承) [6. 组合](组合) [7. 类、类对象和实例对象](类、类对象和实例对象) [8. 什么是绑定?](什么是绑定?) [9. 一些相关的内置函数(BIF)](一些相关的内置函数(BIF)) 5. [魔法方法](魔法方法) [1. 基本的魔法方法](基本的魔法方法) [2. 算术运算符](算术运算符) [3. 反算术运算符](反算术运算符) [4. 增量赋值运算](增量赋值运算符) [5. 一元运算符](一元运算符) [6. 属性访问](属性访问) [7. 描述符](描述符) [8. 定制序列](定制序列) [9. 迭代器](迭代器) 简介Python 是一种通用编程语言,其在科学计算和机器学习领域具有广泛的应用。如果我们打算利用 Python 来执行机器学习,那么对 Python 有一些基本的了解就是至关重要的。本 Python 入门系列体验就是为这样的初学者精心准备的。本实验包括以下内容:- 函数 - 函数的定义 - 函数的调用 - 函数文档 - 函数参数 - 函数的返回值 - 变量作用域- Lambda 表达式 - 匿名函数的定义 - 匿名函数的应用- 类与对象 - 对象 = 属性 + 方法 - self 是什么? - Python 的魔法方法 - 公有和私有 - 继承 - 组合 - 类、类对象和实例对象 - 什么是绑定? - 一些相关的内置函数(BIF)- 魔法方法 - 基本的魔法方法 - 算术运算符 - 反算术运算符 - 增量赋值运算符 - 一元运算符 - 属性访问 - 描述符 - 定制序列 - 迭代器 函数 函数的定义还记得 Python 里面“万物皆对象”么?Python 把函数也当成对象,可以从另一个函数中返回出来而去构建高阶函数,比如:参数是函数、返回值是函数。我们首先来介绍函数的定义。- 函数以`def`关键词开头,后接函数名和圆括号()。- 函数执行的代码以冒号起始,并且缩进。- return [表达式] 结束函数,选择性地返回一个值给调用方。不带表达式的return相当于返回`None`。> def functionname (parameters):> "函数_文档字符串"> function_suite> return [expression] 函数的调用【例子】
###Code
def printme(str):
print(str)
printme("我要调用用户自定义函数!") # 我要调用用户自定义函数!
printme("再次调用同一函数") # 再次调用同一函数
temp = printme('hello') # hello
print(temp) # None
###Output
我要调用用户自定义函数!
再次调用同一函数
hello
None
###Markdown
函数文档
###Code
def MyFirstFunction(name):
"函数定义过程中name是形参"
# 因为Ta只是一个形式,表示占据一个参数位置
print('传递进来的{0}叫做实参,因为Ta是具体的参数值!'.format(name))
MyFirstFunction('老马的程序人生')
# 传递进来的老马的程序人生叫做实参,因为Ta是具体的参数值!
print(MyFirstFunction.__doc__)
# 函数定义过程中name是形参
help(MyFirstFunction)
# Help on function MyFirstFunction in module __main__:
# MyFirstFunction(name)
# 函数定义过程中name是形参
###Output
传递进来的老马的程序人生叫做实参,因为Ta是具体的参数值!
函数定义过程中name是形参
Help on function MyFirstFunction in module __main__:
MyFirstFunction(name)
函数定义过程中name是形参
###Markdown
函数参数Python 的函数具有非常灵活多样的参数形态,既可以实现简单的调用,又可以传入非常复杂的参数。从简到繁的参数形态如下:- 位置参数 (positional argument)- 默认参数 (default argument)- 可变参数 (variable argument)- 关键字参数 (keyword argument)- 命名关键字参数 (name keyword argument)- 参数组合**1. 位置参数**> def functionname(arg1):> "函数_文档字符串"> function_suite> return [expression]- `arg1` - 位置参数 ,这些参数在调用函数 (call function) 时位置要固定。**2. 默认参数**> def functionname(arg1, arg2=v):> "函数_文档字符串"> function_suite> return [expression]- `arg2 = v` - 默认参数 = 默认值,调用函数时,默认参数的值如果没有传入,则被认为是默认值。- 默认参数一定要放在位置参数 后面,不然程序会报错。【例子】
###Code
def printinfo(name, age=8):
print('Name:{0},Age:{1}'.format(name, age))
printinfo('小马') # Name:小马,Age:8
printinfo('小马', 10) # Name:小马,Age:10
###Output
Name:小马,Age:8
Name:小马,Age:10
###Markdown
- Python 允许函数调用时参数的顺序与声明时不一致,因为 Python 解释器能够用参数名匹配参数值。【例子】
###Code
def printinfo(name, age):
print('Name:{0},Age:{1}'.format(name, age))
printinfo(age=8, name='小马') # Name:小马,Age:8
###Output
Name:小马,Age:8
###Markdown
**3. 可变参数**顾名思义,可变参数就是传入的参数个数是可变的,可以是 0, 1, 2 到任意个,是不定长的参数。> def functionname(arg1, arg2=v, *args):> "函数_文档字符串"> function_suite> return [expression]- `*args` - 可变参数,可以是从零个到任意个,自动组装成元组。- 加了星号(*)的变量名会存放所有未命名的变量参数。【例子】
###Code
def printinfo(arg1, *args):
print(arg1)
for var in args:
print(var)
printinfo(10) # 10
printinfo(70, 60, 50)
# 70
# 60
# 50
###Output
10
70
60
50
###Markdown
**4. 关键字参数**> def functionname(arg1, arg2=v, *args, **kw):> "函数_文档字符串"> function_suite> return [expression]- `**kw` - 关键字参数,可以是从零个到任意个,自动组装成字典。【例子】
###Code
def printinfo(arg1, *args, **kwargs):
print(arg1)
print(args)
print(kwargs)
printinfo(70, 60, 50)
# 70
# (60, 50)
# {}
printinfo(70, 60, 50, a=1, b=2)
# 70
# (60, 50)
# {'a': 1, 'b': 2}
###Output
70
(60, 50)
{}
70
(60, 50)
{'a': 1, 'b': 2}
###Markdown
「可变参数」和「关键字参数」的同异总结如下:- 可变参数允许传入零个到任意个参数,它们在函数调用时自动组装为一个元组 (tuple)。- 关键字参数允许传入零个到任意个参数,它们在函数内部自动组装为一个字典 (dict)。**5. 命名关键字参数**> def functionname(arg1, arg2=v, *args, *, nkw, **kw):> "函数_文档字符串"> function_suite> return [expression]- `*, nkw` - 命名关键字参数,用户想要输入的关键字参数,定义方式是在nkw 前面加个分隔符 `*`。- 如果要限制关键字参数的名字,就可以用「命名关键字参数」- 使用命名关键字参数时,要特别注意不能缺少参数名。【例子】
###Code
def printinfo(arg1, *, nkw, **kwargs):
print(arg1)
print(nkw)
print(kwargs)
printinfo(70, nkw=10, a=1, b=2)
# 70
# 10
# {'a': 1, 'b': 2}
printinfo(70, 10, a=1, b=2)
# TypeError: printinfo() takes 1 positional argument but 2 were given
###Output
70
10
{'a': 1, 'b': 2}
###Markdown
- 没有写参数名`nwk`,因此 10 被当成「位置参数」,而原函数只有 1 个位置函数,现在调用了 2 个,因此程序会报错。**6. 参数组合**在 Python 中定义函数,可以用位置参数、默认参数、可变参数、命名关键字参数和关键字参数,这 5 种参数中的 4 个都可以一起使用,但是注意,参数定义的顺序必须是:- 位置参数、默认参数、可变参数和关键字参数。- 位置参数、默认参数、命名关键字参数和关键字参数。要注意定义可变参数和关键字参数的语法:- `*args` 是可变参数,`args` 接收的是一个 `tuple`- `**kw` 是关键字参数,`kw` 接收的是一个 `dict`命名关键字参数是为了限制调用者可以传入的参数名,同时可以提供默认值。定义命名关键字参数不要忘了写分隔符 `*`,否则定义的是位置参数。警告:虽然可以组合多达 5 种参数,但不要同时使用太多的组合,否则函数很难懂。 函数的返回值【例子】
###Code
def add(a, b):
return a + b
print(add(1, 2)) # 3
print(add([1, 2, 3], [4, 5, 6])) # [1, 2, 3, 4, 5, 6]
###Output
3
[1, 2, 3, 4, 5, 6]
###Markdown
【例子】
###Code
def back():
return [1, '小马的程序人生', 3.14]
print(back()) # [1, '小马的程序人生', 3.14]
###Output
[1, '小马的程序人生', 3.14]
###Markdown
【例子】
###Code
def back():
return 1, '小马的程序人生', 3.14
print(back()) # (1, '小马的程序人生', 3.14)
###Output
(1, '小马的程序人生', 3.14)
###Markdown
【例子】
###Code
def printme(str):
print(str)
temp = printme('hello') # hello
print(temp) # None
print(type(temp)) # <class 'NoneType'>
###Output
hello
None
<class 'NoneType'>
###Markdown
变量作用域- Python 中,程序的变量并不是在哪个位置都可以访问的,访问权限决定于这个变量是在哪里赋值的。- 定义在函数内部的变量拥有局部作用域,该变量称为局部变量。- 定义在函数外部的变量拥有全局作用域,该变量称为全局变量。- 局部变量只能在其被声明的函数内部访问,而全局变量可以在整个程序范围内访问。【例子】
###Code
def discounts(price, rate):
final_price = price * rate
return final_price
old_price = float(input('请输入原价:')) # 98
rate = float(input('请输入折扣率:')) # 0.9
new_price = discounts(old_price, rate)
print('打折后价格是:%.2f' % new_price) # 88.20
###Output
请输入原价:98
请输入折扣率:0.9
打折后价格是:88.20
###Markdown
- 当内部作用域想修改外部作用域的变量时,就要用到`global`和`nonlocal`关键字了。【例子】
###Code
num = 1
def fun1():
global num # 需要使用 global 关键字声明
print(num) # 1
num = 123
print(num) # 123
fun1()
print(num) # 123
###Output
1
123
123
###Markdown
**内嵌函数**【例子】
###Code
def outer():
print('outer函数在这被调用')
def inner():
print('inner函数在这被调用')
inner() # 该函数只能在outer函数内部被调用
outer()
# outer函数在这被调用
# inner函数在这被调用
###Output
outer函数在这被调用
inner函数在这被调用
###Markdown
**闭包**- 是函数式编程的一个重要的语法结构,是一种特殊的内嵌函数。- 如果在一个内部函数里对外层非全局作用域的变量进行引用,那么内部函数就被认为是闭包。- 通过闭包可以访问外层非全局作用域的变量,这个作用域称为 闭包作用域。【例子】
###Code
def funX(x):
def funY(y):
return x * y
return funY
i = funX(8)
print(type(i)) # <class 'function'>
print(i(5)) # 40
###Output
<class 'function'>
40
###Markdown
【例子】闭包的返回值通常是函数。
###Code
def make_counter(init):
counter = [init]
def inc(): counter[0] += 1
def dec(): counter[0] -= 1
def get(): return counter[0]
def reset(): counter[0] = init
return inc, dec, get, reset
inc, dec, get, reset = make_counter(0)
inc()
inc()
inc()
print(get()) # 3
dec()
print(get()) # 2
reset()
print(get()) # 0
###Output
3
2
0
###Markdown
【例子】 如果要修改闭包作用域中的变量则需要 `nonlocal` 关键字
###Code
def outer():
num = 10
def inner():
nonlocal num # nonlocal关键字声明
num = 100
print(num)
inner()
print(num)
outer()
# 100
# 100
###Output
100
100
###Markdown
**递归**- 如果一个函数在内部调用自身本身,这个函数就是递归函数。【例子】`n! = 1 x 2 x 3 x ... x n`
###Code
# 利用循环
n = 5
for k in range(1, 5):
n = n * k
print(n) # 120
# 利用递归
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
print(factorial(5)) # 120
###Output
120
120
###Markdown
【例子】斐波那契数列 `f(n)=f(n-1)+f(n-2), f(0)=0 f(1)=1`
###Code
# 利用循环
i = 0
j = 1
lst = list([i, j])
for k in range(2, 11):
k = i + j
lst.append(k)
i = j
j = k
print(lst)
# [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
# 利用递归
def recur_fibo(n):
if n <= 1:
return n
return recur_fibo(n - 1) + recur_fibo(n - 2)
lst = list()
for k in range(11):
lst.append(recur_fibo(k))
print(lst)
# [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
###Output
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
###Markdown
【例子】设置递归的层数,Python默认递归层数为 100
###Code
import sys
sys.setrecursionlimit(1000)
###Output
_____no_output_____
###Markdown
Lambda 表达式 匿名函数的定义在 Python 里有两类函数:- 第一类:用 `def` 关键词定义的正规函数- 第二类:用 `lambda` 关键词定义的匿名函数Python 使用 `lambda` 关键词来创建匿名函数,而非`def`关键词,它没有函数名,其语法结构如下:> lambda argument_list: expression- `lambda` - 定义匿名函数的关键词。- `argument_list` - 函数参数,它们可以是位置参数、默认参数、关键字参数,和正规函数里的参数类型一样。- `:`- 冒号,在函数参数和表达式中间要加个冒号。- `expression` - 只是一个表达式,输入函数参数,输出一些值。注意:- `expression` 中没有 return 语句,因为 lambda 不需要它来返回,表达式本身结果就是返回值。- 匿名函数拥有自己的命名空间,且不能访问自己参数列表之外或全局命名空间里的参数。【例子】
###Code
def sqr(x):
return x ** 2
print(sqr)
# <function sqr at 0x000000BABD3A4400>
y = [sqr(x) for x in range(10)]
print(y)
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
lbd_sqr = lambda x: x ** 2
print(lbd_sqr)
# <function <lambda> at 0x000000BABB6AC1E0>
y = [lbd_sqr(x) for x in range(10)]
print(y)
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
sumary = lambda arg1, arg2: arg1 + arg2
print(sumary(10, 20)) # 30
func = lambda *args: sum(args)
print(func(1, 2, 3, 4, 5)) # 15
###Output
<function sqr at 0x00000220081D9E18>
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
<function <lambda> at 0x00000220081FF400>
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
30
15
###Markdown
匿名函数的应用函数式编程 是指代码中每一块都是不可变的,都由纯函数的形式组成。这里的纯函数,是指函数本身相互独立、互不影响,对于相同的输入,总会有相同的输出,没有任何副作用。【例子】非函数式编程
###Code
def f(x):
for i in range(0, len(x)):
x[i] += 10
return x
x = [1, 2, 3]
f(x)
print(x)
# [11, 12, 13]
###Output
[11, 12, 13]
###Markdown
【例子】函数式编程
###Code
def f(x):
y = []
for item in x:
y.append(item + 10)
return y
x = [1, 2, 3]
f(x)
print(x)
# [1, 2, 3]
###Output
[1, 2, 3]
###Markdown
匿名函数 常常应用于函数式编程的高阶函数 (high-order function)中,主要有两种形式:- 参数是函数 (filter, map)- 返回值是函数 (closure)如,在 `filter`和`map`函数中的应用:- `filter(function, iterable)` 过滤序列,过滤掉不符合条件的元素,返回一个迭代器对象,如果要转换为列表,可以使用 `list()` 来转换。【例子】
###Code
odd = lambda x: x % 2 == 1
templist = filter(odd, [1, 2, 3, 4, 5, 6, 7, 8, 9])
print(list(templist)) # [1, 3, 5, 7, 9]
###Output
[1, 3, 5, 7, 9]
###Markdown
- `map(function, *iterables)` 根据提供的函数对指定序列做映射。【例子】
###Code
m1 = map(lambda x: x ** 2, [1, 2, 3, 4, 5])
print(list(m1))
# [1, 4, 9, 16, 25]
m2 = map(lambda x, y: x + y, [1, 3, 5, 7, 9], [2, 4, 6, 8, 10])
print(list(m2))
# [3, 7, 11, 15, 19]
###Output
[1, 4, 9, 16, 25]
[3, 7, 11, 15, 19]
###Markdown
除了 Python 这些内置函数,我们也可以自己定义高阶函数。【例子】
###Code
def apply_to_list(fun, some_list):
return fun(some_list)
lst = [1, 2, 3, 4, 5]
print(apply_to_list(sum, lst))
# 15
print(apply_to_list(len, lst))
# 5
print(apply_to_list(lambda x: sum(x) / len(x), lst))
# 3.0
###Output
15
5
3.0
###Markdown
类与对象 对象 = 属性 + 方法对象是类的实例。换句话说,类主要定义对象的结构,然后我们以类为模板创建对象。类不但包含方法定义,而且还包含所有实例共享的数据。- 封装:信息隐蔽技术我们可以使用关键字 `class` 定义 Python 类,关键字后面紧跟类的名称、分号和类的实现。【例子】
###Code
class Turtle: # Python中的类名约定以大写字母开头
"""关于类的一个简单例子"""
# 属性
color = 'green'
weight = 10
legs = 4
shell = True
mouth = '大嘴'
# 方法
def climb(self):
print('我正在很努力的向前爬...')
def run(self):
print('我正在飞快的向前跑...')
def bite(self):
print('咬死你咬死你!!')
def eat(self):
print('有得吃,真满足...')
def sleep(self):
print('困了,睡了,晚安,zzz')
tt = Turtle()
print(tt)
# <__main__.Turtle object at 0x0000007C32D67F98>
print(type(tt))
# <class '__main__.Turtle'>
print(tt.__class__)
# <class '__main__.Turtle'>
print(tt.__class__.__name__)
# Turtle
tt.climb()
# 我正在很努力的向前爬...
tt.run()
# 我正在飞快的向前跑...
tt.bite()
# 咬死你咬死你!!
# Python类也是对象。它们是type的实例
print(type(Turtle))
# <class 'type'>
###Output
<__main__.Turtle object at 0x000002200820E898>
<class '__main__.Turtle'>
<class '__main__.Turtle'>
Turtle
我正在很努力的向前爬...
我正在飞快的向前跑...
咬死你咬死你!!
<class 'type'>
###Markdown
- 继承:子类自动共享父类之间数据和方法的机制【例子】
###Code
class MyList(list):
pass
lst = MyList([1, 5, 2, 7, 8])
lst.append(9)
lst.sort()
print(lst)
# [1, 2, 5, 7, 8, 9]
###Output
[1, 2, 5, 7, 8, 9]
###Markdown
- 多态:不同对象对同一方法响应不同的行动【例子】
###Code
class Animal:
def run(self):
raise AttributeError('子类必须实现这个方法')
class People(Animal):
def run(self):
print('人正在走')
class Pig(Animal):
def run(self):
print('pig is walking')
class Dog(Animal):
def run(self):
print('dog is running')
def func(animal):
animal.run()
func(Pig())
# pig is walking
###Output
pig is walking
###Markdown
--- self 是什么?Python 的 `self` 相当于 C++ 的 `this` 指针。【例子】
###Code
class Test:
def prt(self):
print(self)
print(self.__class__)
t = Test()
t.prt()
# <__main__.Test object at 0x000000BC5A351208>
# <class '__main__.Test'>
###Output
<__main__.Test object at 0x000002200820EA20>
<class '__main__.Test'>
###Markdown
类的方法与普通的函数只有一个特别的区别 —— 它们必须有一个额外的第一个参数名称(对应于该实例,即该对象本身),按照惯例它的名称是 `self`。在调用方法时,我们无需明确提供与参数 `self` 相对应的参数。【例子】
###Code
class Ball:
def setName(self, name):
self.name = name
def kick(self):
print("我叫%s,该死的,谁踢我..." % self.name)
a = Ball()
a.setName("球A")
b = Ball()
b.setName("球B")
c = Ball()
c.setName("球C")
a.kick()
# 我叫球A,该死的,谁踢我...
b.kick()
# 我叫球B,该死的,谁踢我...
###Output
我叫球A,该死的,谁踢我...
我叫球B,该死的,谁踢我...
###Markdown
--- Python 的魔法方法据说,Python 的对象天生拥有一些神奇的方法,它们是面向对象的 Python 的一切...它们是可以给你的类增加魔力的特殊方法...如果你的对象实现了这些方法中的某一个,那么这个方法就会在特殊的情况下被 Python 所调用,而这一切都是自动发生的...类有一个名为`__init__(self[, param1, param2...])`的魔法方法,该方法在类实例化时会自动调用。【例子】
###Code
class Ball:
def __init__(self, name):
self.name = name
def kick(self):
print("我叫%s,该死的,谁踢我..." % self.name)
a = Ball("球A")
b = Ball("球B")
c = Ball("球C")
a.kick()
# 我叫球A,该死的,谁踢我...
b.kick()
# 我叫球B,该死的,谁踢我...
###Output
我叫球A,该死的,谁踢我...
我叫球B,该死的,谁踢我...
###Markdown
--- 公有和私有在 Python 中定义私有变量只需要在变量名或函数名前加上“__”两个下划线,那么这个函数或变量就会为私有的了。【例子】类的私有属性实例
###Code
class JustCounter:
__secretCount = 0 # 私有变量
publicCount = 0 # 公开变量
def count(self):
self.__secretCount += 1
self.publicCount += 1
print(self.__secretCount)
counter = JustCounter()
counter.count() # 1
counter.count() # 2
print(counter.publicCount) # 2
# Python的私有为伪私有
print(counter._JustCounter__secretCount) # 2
print(counter.__secretCount)
# AttributeError: 'JustCounter' object has no attribute '__secretCount'
###Output
1
2
2
2
###Markdown
【例子】类的私有方法实例
###Code
class Site:
def __init__(self, name, url):
self.name = name # public
self.__url = url # private
def who(self):
print('name : ', self.name)
print('url : ', self.__url)
def __foo(self): # 私有方法
print('这是私有方法')
def foo(self): # 公共方法
print('这是公共方法')
self.__foo()
x = Site('老马的程序人生', 'https://blog.csdn.net/LSGO_MYP')
x.who()
# name : 老马的程序人生
# url : https://blog.csdn.net/LSGO_MYP
x.foo()
# 这是公共方法
# 这是私有方法
x.__foo()
# AttributeError: 'Site' object has no attribute '__foo'
###Output
name : 老马的程序人生
url : https://blog.csdn.net/LSGO_MYP
这是公共方法
这是私有方法
###Markdown
--- 继承Python 同样支持类的继承,派生类的定义如下所示:> class DerivedClassName(BaseClassName):> statement-1> .> .> .> statement-N`BaseClassName`(基类名)必须与派生类定义在一个作用域内。除了类,还可以用表达式,基类定义在另一个模块中时这一点非常有用:> class DerivedClassName(modname.BaseClassName):> statement-1> .> .> .> statement-N【例子】如果子类中定义与父类同名的方法或属性,则会自动覆盖父类对应的方法或属性。
###Code
# 类定义
class people:
# 定义基本属性
name = ''
age = 0
# 定义私有属性,私有属性在类外部无法直接进行访问
__weight = 0
# 定义构造方法
def __init__(self, n, a, w):
self.name = n
self.age = a
self.__weight = w
def speak(self):
print("%s 说: 我 %d 岁。" % (self.name, self.age))
# 单继承示例
class student(people):
grade = ''
def __init__(self, n, a, w, g):
# 调用父类的构函
people.__init__(self, n, a, w)
self.grade = g
# 覆写父类的方法
def speak(self):
print("%s 说: 我 %d 岁了,我在读 %d 年级" % (self.name, self.age, self.grade))
s = student('小马的程序人生', 10, 60, 3)
s.speak()
# 小马的程序人生 说: 我 10 岁了,我在读 3 年级
###Output
小马的程序人生 说: 我 10 岁了,我在读 3 年级
###Markdown
注意:如果上面的程序去掉:`people.__init__(self, n, a, w)`,则输出:` 说: 我 0 岁了,我在读 3 年级`,因为子类的构造方法把父类的构造方法覆盖了。【例子】
###Code
import random
class Fish:
def __init__(self):
self.x = random.randint(0, 10)
self.y = random.randint(0, 10)
def move(self):
self.x -= 1
print("我的位置", self.x, self.y)
class GoldFish(Fish): # 金鱼
pass
class Carp(Fish): # 鲤鱼
pass
class Salmon(Fish): # 三文鱼
pass
class Shark(Fish): # 鲨鱼
def __init__(self):
self.hungry = True
def eat(self):
if self.hungry:
print("吃货的梦想就是天天有得吃!")
self.hungry = False
else:
print("太撑了,吃不下了!")
self.hungry = True
g = GoldFish()
g.move() # 我的位置 9 4
s = Shark()
s.eat() # 吃货的梦想就是天天有得吃!
s.move()
# AttributeError: 'Shark' object has no attribute 'x'
###Output
我的位置 3 8
吃货的梦想就是天天有得吃!
###Markdown
解决该问题可用以下两种方式:- 调用未绑定的父类方法`Fish.__init__(self)`
###Code
class Shark(Fish): # 鲨鱼
def __init__(self):
Fish.__init__(self)
self.hungry = True
def eat(self):
if self.hungry:
print("吃货的梦想就是天天有得吃!")
self.hungry = False
else:
print("太撑了,吃不下了!")
self.hungry = True
###Output
_____no_output_____
###Markdown
- 使用super函数`super().__init__()`
###Code
class Shark(Fish): # 鲨鱼
def __init__(self):
super().__init__()
self.hungry = True
def eat(self):
if self.hungry:
print("吃货的梦想就是天天有得吃!")
self.hungry = False
else:
print("太撑了,吃不下了!")
self.hungry = True
###Output
_____no_output_____
###Markdown
Python 虽然支持多继承的形式,但我们一般不使用多继承,因为容易引起混乱。> class DerivedClassName(Base1, Base2, Base3):> statement-1> .> .> .> statement-N需要注意圆括号中父类的顺序,若是父类中有相同的方法名,而在子类使用时未指定,Python 从左至右搜索,即方法在子类中未找到时,从左到右查找父类中是否包含方法。【例子】
###Code
# 类定义
class People:
# 定义基本属性
name = ''
age = 0
# 定义私有属性,私有属性在类外部无法直接进行访问
__weight = 0
# 定义构造方法
def __init__(self, n, a, w):
self.name = n
self.age = a
self.__weight = w
def speak(self):
print("%s 说: 我 %d 岁。" % (self.name, self.age))
# 单继承示例
class Student(People):
grade = ''
def __init__(self, n, a, w, g):
# 调用父类的构函
People.__init__(self, n, a, w)
self.grade = g
# 覆写父类的方法
def speak(self):
print("%s 说: 我 %d 岁了,我在读 %d 年级" % (self.name, self.age, self.grade))
# 另一个类,多重继承之前的准备
class Speaker:
topic = ''
name = ''
def __init__(self, n, t):
self.name = n
self.topic = t
def speak(self):
print("我叫 %s,我是一个演说家,我演讲的主题是 %s" % (self.name, self.topic))
# 多重继承
class Sample01(Speaker, Student):
a = ''
def __init__(self, n, a, w, g, t):
Student.__init__(self, n, a, w, g)
Speaker.__init__(self, n, t)
# 方法名同,默认调用的是在括号中排前地父类的方法
test = Sample01("Tim", 25, 80, 4, "Python")
test.speak()
# 我叫 Tim,我是一个演说家,我演讲的主题是 Python
class Sample02(Student, Speaker):
a = ''
def __init__(self, n, a, w, g, t):
Student.__init__(self, n, a, w, g)
Speaker.__init__(self, n, t)
# 方法名同,默认调用的是在括号中排前地父类的方法
test = Sample02("Tim", 25, 80, 4, "Python")
test.speak()
# Tim 说: 我 25 岁了,我在读 4 年级
###Output
我叫 Tim,我是一个演说家,我演讲的主题是 Python
Tim 说: 我 25 岁了,我在读 4 年级
###Markdown
组合【例子】
###Code
class Turtle:
def __init__(self, x):
self.num = x
class Fish:
def __init__(self, x):
self.num = x
class Pool:
def __init__(self, x, y):
self.turtle = Turtle(x)
self.fish = Fish(y)
def print_num(self):
print("水池里面有乌龟%s只,小鱼%s条" % (self.turtle.num, self.fish.num))
p = Pool(2, 3)
p.print_num()
# 水池里面有乌龟2只,小鱼3条
###Output
水池里面有乌龟2只,小鱼3条
###Markdown
类、类对象和实例对象类对象:创建一个类,其实也是一个对象也在内存开辟了一块空间,称为类对象,类对象只有一个。> class A(object):> pass实例对象:就是通过实例化类创建的对象,称为实例对象,实例对象可以有多个。【例子】
###Code
class A(object):
pass
# 实例化对象 a、b、c都属于实例对象。
a = A()
b = A()
c = A()
###Output
_____no_output_____
###Markdown
类属性:类里面方法外面定义的变量称为类属性。类属性所属于类对象并且多个实例对象之间共享同一个类属性,说白了就是类属性所有的通过该类实例化的对象都能共享。【例子】
###Code
class A():
a = 0 #类属性
def __init__(self, xx):
A.a = xx #使用类属性可以通过 (类名.类属性)调用。
###Output
_____no_output_____
###Markdown
实例属性:实例属性和具体的某个实例对象有关系,并且一个实例对象和另外一个实例对象是不共享属性的,说白了实例属性只能在自己的对象里面使用,其他的对象不能直接使用,因为`self`是谁调用,它的值就属于该对象。【例子】
###Code
# 创建类对象
class Test(object):
class_attr = 100 # 类属性
def __init__(self):
self.sl_attr = 100 # 实例属性
def func(self):
print('类对象.类属性的值:', Test.class_attr) # 调用类属性
print('self.类属性的值', self.class_attr) # 相当于把类属性 变成实例属性
print('self.实例属性的值', self.sl_attr) # 调用实例属性
a = Test()
a.func()
# 类对象.类属性的值: 100
# self.类属性的值 100
# self.实例属性的值 100
b = Test()
b.func()
# 类对象.类属性的值: 100
# self.类属性的值 100
# self.实例属性的值 100
a.class_attr = 200
a.sl_attr = 200
a.func()
# 类对象.类属性的值: 100
# self.类属性的值 200
# self.实例属性的值 200
b.func()
# 类对象.类属性的值: 100
# self.类属性的值 100
# self.实例属性的值 100
Test.class_attr = 300
a.func()
# 类对象.类属性的值: 300
# self.类属性的值 200
# self.实例属性的值 200
b.func()
# 类对象.类属性的值: 300
# self.类属性的值 300
# self.实例属性的值 100
###Output
类对象.类属性的值: 100
self.类属性的值 100
self.实例属性的值 100
类对象.类属性的值: 100
self.类属性的值 100
self.实例属性的值 100
类对象.类属性的值: 100
self.类属性的值 200
self.实例属性的值 200
类对象.类属性的值: 100
self.类属性的值 100
self.实例属性的值 100
类对象.类属性的值: 300
self.类属性的值 200
self.实例属性的值 200
类对象.类属性的值: 300
self.类属性的值 300
self.实例属性的值 100
###Markdown
注意:属性与方法名相同,属性会覆盖方法。【例子】
###Code
class A:
def x(self):
print('x_man')
aa = A()
aa.x() # x_man
aa.x = 1
print(aa.x) # 1
aa.x()
# TypeError: 'int' object is not callable
###Output
x_man
1
###Markdown
什么是绑定?Python 严格要求方法需要有实例才能被调用,这种限制其实就是 Python 所谓的绑定概念。Python 对象的数据属性通常存储在名为`.__ dict__`的字典中,我们可以直接访问`__dict__`,或利用 Python 的内置函数`vars()`获取`.__ dict__`。【例子】
###Code
class CC:
def setXY(self, x, y):
self.x = x
self.y = y
def printXY(self):
print(self.x, self.y)
dd = CC()
print(dd.__dict__)
# {}
print(vars(dd))
# {}
print(CC.__dict__)
# {'__module__': '__main__', 'setXY': <function CC.setXY at 0x000000C3473DA048>, 'printXY': <function CC.printXY at 0x000000C3473C4F28>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
dd.setXY(4, 5)
print(dd.__dict__)
# {'x': 4, 'y': 5}
print(vars(CC))
# {'__module__': '__main__', 'setXY': <function CC.setXY at 0x000000632CA9B048>, 'printXY': <function CC.printXY at 0x000000632CA83048>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
print(CC.__dict__)
# {'__module__': '__main__', 'setXY': <function CC.setXY at 0x000000632CA9B048>, 'printXY': <function CC.printXY at 0x000000632CA83048>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
###Output
{}
{}
{'__module__': '__main__', 'setXY': <function CC.setXY at 0x000002200822BD08>, 'printXY': <function CC.printXY at 0x000002200822BF28>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
{'x': 4, 'y': 5}
{'__module__': '__main__', 'setXY': <function CC.setXY at 0x000002200822BD08>, 'printXY': <function CC.printXY at 0x000002200822BF28>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
{'__module__': '__main__', 'setXY': <function CC.setXY at 0x000002200822BD08>, 'printXY': <function CC.printXY at 0x000002200822BF28>, '__dict__': <attribute '__dict__' of 'CC' objects>, '__weakref__': <attribute '__weakref__' of 'CC' objects>, '__doc__': None}
###Markdown
一些相关的内置函数(BIF)- `issubclass(class, classinfo)` 方法用于判断参数 class 是否是类型参数 classinfo 的子类。- 一个类被认为是其自身的子类。- `classinfo`可以是类对象的元组,只要class是其中任何一个候选类的子类,则返回`True`。【例子】
###Code
class A:
pass
class B(A):
pass
print(issubclass(B, A)) # True
print(issubclass(B, B)) # True
print(issubclass(A, B)) # False
print(issubclass(B, object)) # True
###Output
True
True
False
True
###Markdown
- `isinstance(object, classinfo)` 方法用于判断一个对象是否是一个已知的类型,类似`type()`。- `type()`不会认为子类是一种父类类型,不考虑继承关系。- `isinstance()`会认为子类是一种父类类型,考虑继承关系。- 如果第一个参数不是对象,则永远返回`False`。- 如果第二个参数不是类或者由类对象组成的元组,会抛出一个`TypeError`异常。【例子】
###Code
a = 2
print(isinstance(a, int)) # True
print(isinstance(a, str)) # False
print(isinstance(a, (str, int, list))) # True
class A:
pass
class B(A):
pass
print(isinstance(A(), A)) # True
print(type(A()) == A) # True
print(isinstance(B(), A)) # True
print(type(B()) == A) # False
###Output
True
False
True
True
True
True
False
###Markdown
- `hasattr(object, name)`用于判断对象是否包含对应的属性。【例子】
###Code
class Coordinate:
x = 10
y = -5
z = 0
point1 = Coordinate()
print(hasattr(point1, 'x')) # True
print(hasattr(point1, 'y')) # True
print(hasattr(point1, 'z')) # True
print(hasattr(point1, 'no')) # False
###Output
True
True
True
False
###Markdown
- `getattr(object, name[, default])`用于返回一个对象属性值。【例子】
###Code
class A(object):
bar = 1
a = A()
print(getattr(a, 'bar')) # 1
print(getattr(a, 'bar2', 3)) # 3
print(getattr(a, 'bar2'))
# AttributeError: 'A' object has no attribute 'bar2'
###Output
1
3
###Markdown
【例子】这个例子很酷!
###Code
class A(object):
def set(self, a, b):
x = a
a = b
b = x
print(a, b)
a = A()
c = getattr(a, 'set')
c(a='1', b='2') # 2 1
###Output
2 1
###Markdown
- `setattr(object, name, value)`对应函数 `getattr()`,用于设置属性值,该属性不一定是存在的。【例子】
###Code
class A(object):
bar = 1
a = A()
print(getattr(a, 'bar')) # 1
setattr(a, 'bar', 5)
print(a.bar) # 5
setattr(a, "age", 28)
print(a.age) # 28
###Output
1
5
28
###Markdown
- `delattr(object, name)`用于删除属性。【例子】
###Code
class Coordinate:
x = 10
y = -5
z = 0
point1 = Coordinate()
print('x = ', point1.x) # x = 10
print('y = ', point1.y) # y = -5
print('z = ', point1.z) # z = 0
delattr(Coordinate, 'z')
print('--删除 z 属性后--') # --删除 z 属性后--
print('x = ', point1.x) # x = 10
print('y = ', point1.y) # y = -5
# 触发错误
print('z = ', point1.z)
# AttributeError: 'Coordinate' object has no attribute 'z'
###Output
x = 10
y = -5
z = 0
--删除 z 属性后--
x = 10
y = -5
###Markdown
- `class property([fget[, fset[, fdel[, doc]]]])`用于在新式类中返回属性值。 - `fget` -- 获取属性值的函数 - `fset` -- 设置属性值的函数 - `fdel` -- 删除属性值函数 - `doc` -- 属性描述信息【例子】
###Code
class C(object):
def __init__(self):
self.__x = None
def getx(self):
return self.__x
def setx(self, value):
self.__x = value
def delx(self):
del self.__x
x = property(getx, setx, delx, "I'm the 'x' property.")
cc = C()
cc.x = 2
print(cc.x) # 2
del cc.x
print(cc.x)
# AttributeError: 'C' object has no attribute '_C__x'
###Output
2
###Markdown
魔法方法魔法方法总是被双下划线包围,例如`__init__`。魔法方法是面向对象的 Python 的一切,如果你不知道魔法方法,说明你还没能意识到面向对象的 Python 的强大。魔法方法的“魔力”体现在它们总能够在适当的时候被自动调用。魔法方法的第一个参数应为`cls`(类方法) 或者`self`(实例方法)。- `cls`:代表一个类的名称- `self`:代表一个实例对象的名称 基本的魔法方法- `__init__(self[, ...])` 构造器,当一个实例被创建的时候调用的初始化方法【例子】
###Code
class Rectangle:
def __init__(self, x, y):
self.x = x
self.y = y
def getPeri(self):
return (self.x + self.y) * 2
def getArea(self):
return self.x * self.y
rect = Rectangle(4, 5)
print(rect.getPeri()) # 18
print(rect.getArea()) # 20
###Output
18
20
###Markdown
- `__new__(cls[, ...])` 在一个对象实例化的时候所调用的第一个方法,在调用`__init__`初始化前,先调用`__new__`。 - `__new__`至少要有一个参数`cls`,代表要实例化的类,此参数在实例化时由 Python 解释器自动提供,后面的参数直接传递给`__init__`。 - `__new__`对当前类进行了实例化,并将实例返回,传给`__init__`的`self`。但是,执行了`__new__`,并不一定会进入`__init__`,只有`__new__`返回了,当前类`cls`的实例,当前类的`__init__`才会进入。【例子】
###Code
class A(object):
def __init__(self, value):
print("into A __init__")
self.value = value
def __new__(cls, *args, **kwargs):
print("into A __new__")
print(cls)
return object.__new__(cls)
class B(A):
def __init__(self, value):
print("into B __init__")
self.value = value
def __new__(cls, *args, **kwargs):
print("into B __new__")
print(cls)
return super().__new__(cls, *args, **kwargs)
b = B(10)
# 结果:
# into B __new__
# <class '__main__.B'>
# into A __new__
# <class '__main__.B'>
# into B __init__
class A(object):
def __init__(self, value):
print("into A __init__")
self.value = value
def __new__(cls, *args, **kwargs):
print("into A __new__")
print(cls)
return object.__new__(cls)
class B(A):
def __init__(self, value):
print("into B __init__")
self.value = value
def __new__(cls, *args, **kwargs):
print("into B __new__")
print(cls)
return super().__new__(A, *args, **kwargs) # 改动了cls变为A
b = B(10)
# 结果:
# into B __new__
# <class '__main__.B'>
# into A __new__
# <class '__main__.A'>
###Output
into B __new__
<class '__main__.B'>
into A __new__
<class '__main__.B'>
into B __init__
into B __new__
<class '__main__.B'>
into A __new__
<class '__main__.A'>
###Markdown
- 若`__new__`没有正确返回当前类`cls`的实例,那`__init__`是不会被调用的,即使是父类的实例也不行,将没有`__init__`被调用。【例子】利用`__new__`实现单例模式。
###Code
class Earth:
pass
a = Earth()
print(id(a)) # 260728291456
b = Earth()
print(id(b)) # 260728291624
class Earth:
__instance = None # 定义一个类属性做判断
def __new__(cls):
if cls.__instance is None:
cls.__instance = object.__new__(cls)
return cls.__instance
else:
return cls.__instance
a = Earth()
print(id(a)) # 512320401648
b = Earth()
print(id(b)) # 512320401648
###Output
2336598724336
2336598528464
2336598467752
2336598467752
###Markdown
- `__new__`方法主要是当你继承一些不可变的 class 时(比如`int, str, tuple`), 提供给你一个自定义这些类的实例化过程的途径。【例子】
###Code
class CapStr(str):
def __new__(cls, string):
string = string.upper()
return str.__new__(cls, string)
a = CapStr("i love lsgogroup")
print(a) # I LOVE LSGOGROUP
###Output
I LOVE LSGOGROUP
###Markdown
- `__del__(self)` 析构器,当一个对象将要被系统回收之时调用的方法。> Python 采用自动引用计数(ARC)方式来回收对象所占用的空间,当程序中有一个变量引用该 Python 对象时,Python 会自动保证该对象引用计数为 1;当程序中有两个变量引用该 Python 对象时,Python 会自动保证该对象引用计数为 2,依此类推,如果一个对象的引用计数变成了 0,则说明程序中不再有变量引用该对象,表明程序不再需要该对象,因此 Python 就会回收该对象。>> 大部分时候,Python 的 ARC 都能准确、高效地回收系统中的每个对象。但如果系统中出现循环引用的情况,比如对象 a 持有一个实例变量引用对象 b,而对象 b 又持有一个实例变量引用对象 a,此时两个对象的引用计数都是 1,而实际上程序已经不再有变量引用它们,系统应该回收它们,此时 Python 的垃圾回收器就可能没那么快,要等专门的循环垃圾回收器(Cyclic Garbage Collector)来检测并回收这种引用循环。【例子】
###Code
class C(object):
def __init__(self):
print('into C __init__')
def __del__(self):
print('into C __del__')
c1 = C()
# into C __init__
c2 = c1
c3 = c2
del c3
del c2
del c1
# into C __del__
###Output
into C __init__
into C __del__
###Markdown
- `__str__(self)`: - 当你打印一个对象的时候,触发`__str__` - 当你使用`%s`格式化的时候,触发`__str__` - `str`强转数据类型的时候,触发`__str__`- `__repr__(self)`: - `repr`是`str`的备胎 - 有`__str__`的时候执行`__str__`,没有实现`__str__`的时候,执行`__repr__` - `repr(obj)`内置函数对应的结果是`__repr__`的返回值 - 当你使用`%r`格式化的时候 触发`__repr__`【例子】
###Code
class Cat:
"""定义一个猫类"""
def __init__(self, new_name, new_age):
"""在创建完对象之后 会自动调用, 它完成对象的初始化的功能"""
self.name = new_name
self.age = new_age
def __str__(self):
"""返回一个对象的描述信息"""
return "名字是:%s , 年龄是:%d" % (self.name, self.age)
def __repr__(self):
"""返回一个对象的描述信息"""
return "Cat:(%s,%d)" % (self.name, self.age)
def eat(self):
print("%s在吃鱼...." % self.name)
def drink(self):
print("%s在喝可乐..." % self.name)
def introduce(self):
print("名字是:%s, 年龄是:%d" % (self.name, self.age))
# 创建了一个对象
tom = Cat("汤姆", 30)
print(tom) # 名字是:汤姆 , 年龄是:30
print(str(tom)) # 名字是:汤姆 , 年龄是:30
print(repr(tom)) # Cat:(汤姆,30)
tom.eat() # 汤姆在吃鱼....
tom.introduce() # 名字是:汤姆, 年龄是:30
###Output
名字是:汤姆 , 年龄是:30
名字是:汤姆 , 年龄是:30
Cat:(汤姆,30)
汤姆在吃鱼....
名字是:汤姆, 年龄是:30
###Markdown
`__str__(self)` 的返回结果可读性强。也就是说,`__str__` 的意义是得到便于人们阅读的信息,就像下面的 '2019-10-11' 一样。`__repr__(self)` 的返回结果应更准确。怎么说,`__repr__` 存在的目的在于调试,便于开发者使用。【例子】
###Code
import datetime
today = datetime.date.today()
print(str(today)) # 2019-10-11
print(repr(today)) # datetime.date(2019, 10, 11)
print('%s' %today) # 2019-10-11
print('%r' %today) # datetime.date(2019, 10, 11)
###Output
2020-08-01
datetime.date(2020, 8, 1)
2020-08-01
datetime.date(2020, 8, 1)
###Markdown
算术运算符类型工厂函数,指的是“不通过类而是通过函数来创建对象”。【例子】
###Code
class C:
pass
print(type(len)) # <class 'builtin_function_or_method'>
print(type(dir)) # <class 'builtin_function_or_method'>
print(type(int)) # <class 'type'>
print(type(list)) # <class 'type'>
print(type(tuple)) # <class 'type'>
print(type(C)) # <class 'type'>
print(int('123')) # 123
# 这个例子中list工厂函数把一个元祖对象加工成了一个列表对象。
print(list((1, 2, 3))) # [1, 2, 3]
###Output
<class 'builtin_function_or_method'>
<class 'builtin_function_or_method'>
<class 'type'>
<class 'type'>
<class 'type'>
<class 'type'>
123
[1, 2, 3]
###Markdown
- `__add__(self, other)`定义加法的行为:`+`- `__sub__(self, other)`定义减法的行为:`-`【例子】
###Code
class MyClass:
def __init__(self, height, weight):
self.height = height
self.weight = weight
# 两个对象的长相加,宽不变.返回一个新的类
def __add__(self, others):
return MyClass(self.height + others.height, self.weight + others.weight)
# 两个对象的宽相减,长不变.返回一个新的类
def __sub__(self, others):
return MyClass(self.height - others.height, self.weight - others.weight)
# 说一下自己的参数
def intro(self):
print("高为", self.height, " 重为", self.weight)
def main():
a = MyClass(height=10, weight=5)
a.intro()
b = MyClass(height=20, weight=10)
b.intro()
c = b - a
c.intro()
d = a + b
d.intro()
if __name__ == '__main__':
main()
# 高为 10 重为 5
# 高为 20 重为 10
# 高为 10 重为 5
# 高为 30 重为 15
###Output
高为 10 重为 5
高为 20 重为 10
高为 10 重为 5
高为 30 重为 15
###Markdown
- `__mul__(self, other)`定义乘法的行为:`*`- `__truediv__(self, other)`定义真除法的行为:`/`- `__floordiv__(self, other)`定义整数除法的行为:`//`- `__mod__(self, other)` 定义取模算法的行为:`%`- `__divmod__(self, other)`定义当被 `divmod()` 调用时的行为- `divmod(a, b)`把除数和余数运算结果结合起来,返回一个包含商和余数的元组`(a // b, a % b)`。【例子】
###Code
print(divmod(7, 2)) # (3, 1)
print(divmod(8, 2)) # (4, 0)
###Output
(3, 1)
(4, 0)
###Markdown
- `__pow__(self, other[, module])`定义当被 `power()` 调用或 `**` 运算时的行为- `__lshift__(self, other)`定义按位左移位的行为:`<<`- `__rshift__(self, other)`定义按位右移位的行为:`>>`- `__and__(self, other)`定义按位与操作的行为:`&`- `__xor__(self, other)`定义按位异或操作的行为:`^`- `__or__(self, other)`定义按位或操作的行为:`|` 反算术运算符反运算魔方方法,与算术运算符保持一一对应,不同之处就是反运算的魔法方法多了一个“r”。当文件左操作不支持相应的操作时被调用。- `__radd__(self, other)`定义加法的行为:`+`- `__rsub__(self, other)`定义减法的行为:`-`- `__rmul__(self, other)`定义乘法的行为:`*`- `__rtruediv__(self, other)`定义真除法的行为:`/`- `__rfloordiv__(self, other)`定义整数除法的行为:`//`- `__rmod__(self, other)` 定义取模算法的行为:`%`- `__rdivmod__(self, other)`定义当被 divmod() 调用时的行为- `__rpow__(self, other[, module])`定义当被 power() 调用或 `**` 运算时的行为- `__rlshift__(self, other)`定义按位左移位的行为:`<<`- `__rrshift__(self, other)`定义按位右移位的行为:`>>`- `__rand__(self, other)`定义按位与操作的行为:`&`- `__rxor__(self, other)`定义按位异或操作的行为:`^`- `__ror__(self, other)`定义按位或操作的行为:`|``a + b`这里加数是`a`,被加数是`b`,因此是`a`主动,反运算就是如果`a`对象的`__add__()`方法没有实现或者不支持相应的操作,那么 Python 就会调用`b`的`__radd__()`方法。【例子】
###Code
class Nint(int):
def __radd__(self, other):
return int.__sub__(other, self) # 注意 self 在后面
a = Nint(5)
b = Nint(3)
print(a + b) # 8
print(1 + b) # -2
###Output
8
-2
###Markdown
增量赋值运算符- `__iadd__(self, other)`定义赋值加法的行为:`+=`- `__isub__(self, other)`定义赋值减法的行为:`-=`- `__imul__(self, other)`定义赋值乘法的行为:`*=`- `__itruediv__(self, other)`定义赋值真除法的行为:`/=`- `__ifloordiv__(self, other)`定义赋值整数除法的行为:`//=`- `__imod__(self, other)`定义赋值取模算法的行为:`%=`- `__ipow__(self, other[, modulo])`定义赋值幂运算的行为:`**=`- `__ilshift__(self, other)`定义赋值按位左移位的行为:`<<=`- `__irshift__(self, other)`定义赋值按位右移位的行为:`>>=`- `__iand__(self, other)`定义赋值按位与操作的行为:`&=`- `__ixor__(self, other)`定义赋值按位异或操作的行为:`^=`- `__ior__(self, other)`定义赋值按位或操作的行为:`|=` 一元运算符- `__neg__(self)`定义正号的行为:`+x`- `__pos__(self)`定义负号的行为:`-x`- `__abs__(self)`定义当被`abs()`调用时的行为- `__invert__(self)`定义按位求反的行为:`~x` 属性访问- `__getattr__(self, name)`: 定义当用户试图获取一个不存在的属性时的行为。- `__getattribute__(self, name)`:定义当该类的属性被访问时的行为(先调用该方法,查看是否存在该属性,若不存在,接着去调用`__getattr__`)。- `__setattr__(self, name, value)`:定义当一个属性被设置时的行为。- `__delattr__(self, name)`:定义当一个属性被删除时的行为。【例子】
###Code
class C:
def __getattribute__(self, item):
print('__getattribute__')
return super().__getattribute__(item)
def __getattr__(self, item):
print('__getattr__')
def __setattr__(self, key, value):
print('__setattr__')
super().__setattr__(key, value)
def __delattr__(self, item):
print('__delattr__')
super().__delattr__(item)
c = C()
c.x
# __getattribute__
# __getattr__
c.x = 1
# __setattr__
del c.x
# __delattr__
###Output
__getattribute__
__getattr__
__setattr__
__delattr__
###Markdown
描述符描述符就是将某种特殊类型的类的实例指派给另一个类的属性。- `__get__(self, instance, owner)`用于访问属性,它返回属性的值。- `__set__(self, instance, value)`将在属性分配操作中调用,不返回任何内容。- `__del__(self, instance)`控制删除操作,不返回任何内容。【例子】
###Code
class MyDecriptor:
def __get__(self, instance, owner):
print('__get__', self, instance, owner)
def __set__(self, instance, value):
print('__set__', self, instance, value)
def __delete__(self, instance):
print('__delete__', self, instance)
class Test:
x = MyDecriptor()
t = Test()
t.x
# __get__ <__main__.MyDecriptor object at 0x000000CEAAEB6B00> <__main__.Test object at 0x000000CEABDC0898> <class '__main__.Test'>
t.x = 'x-man'
# __set__ <__main__.MyDecriptor object at 0x00000023687C6B00> <__main__.Test object at 0x00000023696B0940> x-man
del t.x
# __delete__ <__main__.MyDecriptor object at 0x000000EC9B160A90> <__main__.Test object at 0x000000EC9B160B38>
###Output
__get__ <__main__.MyDecriptor object at 0x0000022008242668> <__main__.Test object at 0x00000220082427B8> <class '__main__.Test'>
__set__ <__main__.MyDecriptor object at 0x0000022008242668> <__main__.Test object at 0x00000220082427B8> x-man
__delete__ <__main__.MyDecriptor object at 0x0000022008242668> <__main__.Test object at 0x00000220082427B8>
###Markdown
定制序列协议(Protocols)与其它编程语言中的接口很相似,它规定你哪些方法必须要定义。然而,在 Python 中的协议就显得不那么正式。事实上,在 Python 中,协议更像是一种指南。**容器类型的协议**- 如果说你希望定制的容器是不可变的话,你只需要定义`__len__()`和`__getitem__()`方法。- 如果你希望定制的容器是可变的话,除了`__len__()`和`__getitem__()`方法,你还需要定义`__setitem__()`和`__delitem__()`两个方法。【例子】编写一个不可改变的自定义列表,要求记录列表中每个元素被访问的次数。
###Code
class CountList:
def __init__(self, *args):
self.values = [x for x in args]
self.count = {}.fromkeys(range(len(self.values)), 0)
def __len__(self):
return len(self.values)
def __getitem__(self, item):
self.count[item] += 1
return self.values[item]
c1 = CountList(1, 3, 5, 7, 9)
c2 = CountList(2, 4, 6, 8, 10)
print(c1[1]) # 3
print(c2[2]) # 6
print(c1[1] + c2[1]) # 7
print(c1.count)
# {0: 0, 1: 2, 2: 0, 3: 0, 4: 0}
print(c2.count)
# {0: 0, 1: 1, 2: 1, 3: 0, 4: 0}
###Output
3
6
7
{0: 0, 1: 2, 2: 0, 3: 0, 4: 0}
{0: 0, 1: 1, 2: 1, 3: 0, 4: 0}
###Markdown
- `__len__(self)`定义当被`len()`调用时的行为(返回容器中元素的个数)。- `__getitem__(self, key)`定义获取容器中元素的行为,相当于`self[key]`。- `__setitem__(self, key, value)`定义设置容器中指定元素的行为,相当于`self[key] = value`。- `__delitem__(self, key)`定义删除容器中指定元素的行为,相当于`del self[key]`。【例子】编写一个可改变的自定义列表,要求记录列表中每个元素被访问的次数。
###Code
class CountList:
def __init__(self, *args):
self.values = [x for x in args]
self.count = {}.fromkeys(range(len(self.values)), 0)
def __len__(self):
return len(self.values)
def __getitem__(self, item):
self.count[item] += 1
return self.values[item]
def __setitem__(self, key, value):
self.values[key] = value
def __delitem__(self, key):
del self.values[key]
for i in range(0, len(self.values)):
if i >= key:
self.count[i] = self.count[i + 1]
self.count.pop(len(self.values))
c1 = CountList(1, 3, 5, 7, 9)
c2 = CountList(2, 4, 6, 8, 10)
print(c1[1]) # 3
print(c2[2]) # 6
c2[2] = 12
print(c1[1] + c2[2]) # 15
print(c1.count)
# {0: 0, 1: 2, 2: 0, 3: 0, 4: 0}
print(c2.count)
# {0: 0, 1: 0, 2: 2, 3: 0, 4: 0}
del c1[1]
print(c1.count)
# {0: 0, 1: 0, 2: 0, 3: 0}
###Output
3
6
15
{0: 0, 1: 2, 2: 0, 3: 0, 4: 0}
{0: 0, 1: 0, 2: 2, 3: 0, 4: 0}
{0: 0, 1: 0, 2: 0, 3: 0}
###Markdown
迭代器- 迭代是 Python 最强大的功能之一,是访问集合元素的一种方式。- 迭代器是一个可以记住遍历的位置的对象。- 迭代器对象从集合的第一个元素开始访问,直到所有的元素被访问完结束。- 迭代器只能往前不会后退。- 字符串,列表或元组对象都可用于创建迭代器:【例子】
###Code
string = 'lsgogroup'
for c in string:
print(c)
'''
l
s
g
o
g
r
o
u
p
'''
for c in iter(string):
print(c)
###Output
l
s
g
o
g
r
o
u
p
l
s
g
o
g
r
o
u
p
###Markdown
【例子】
###Code
links = {'B': '百度', 'A': '阿里', 'T': '腾讯'}
for each in links:
print('%s -> %s' % (each, links[each]))
'''
B -> 百度
A -> 阿里
T -> 腾讯
'''
for each in iter(links):
print('%s -> %s' % (each, links[each]))
###Output
B -> 百度
A -> 阿里
T -> 腾讯
B -> 百度
A -> 阿里
T -> 腾讯
###Markdown
- 迭代器有两个基本的方法:`iter()` 和 `next()`。- `iter(object)` 函数用来生成迭代器。- `next(iterator[, default])` 返回迭代器的下一个项目。- `iterator` -- 可迭代对象- `default` -- 可选,用于设置在没有下一个元素时返回该默认值,如果不设置,又没有下一个元素则会触发 `StopIteration` 异常。【例子】
###Code
links = {'B': '百度', 'A': '阿里', 'T': '腾讯'}
it = iter(links)
while True:
try:
each = next(it)
except StopIteration:
break
print(each)
# B
# A
# T
it = iter(links)
print(next(it)) # B
print(next(it)) # A
print(next(it)) # T
print(next(it)) # StopIteration
###Output
B
A
T
B
A
T
###Markdown
把一个类作为一个迭代器使用需要在类中实现两个魔法方法 `__iter__()` 与 `__next__()` 。- `__iter__(self)`定义当迭代容器中的元素的行为,返回一个特殊的迭代器对象, 这个迭代器对象实现了 `__next__()` 方法并通过 `StopIteration` 异常标识迭代的完成。- `__next__()` 返回下一个迭代器对象。- `StopIteration` 异常用于标识迭代的完成,防止出现无限循环的情况,在 `__next__()` 方法中我们可以设置在完成指定循环次数后触发 `StopIteration` 异常来结束迭代。【例子】
###Code
class Fibs:
def __init__(self, n=10):
self.a = 0
self.b = 1
self.n = n
def __iter__(self):
return self
def __next__(self):
self.a, self.b = self.b, self.a + self.b
if self.a > self.n:
raise StopIteration
return self.a
fibs = Fibs(100)
for each in fibs:
print(each, end=' ')
# 1 1 2 3 5 8 13 21 34 55 89
###Output
1 1 2 3 5 8 13 21 34 55 89
###Markdown
4.10 生成器- 在 Python 中,使用了 `yield` 的函数被称为生成器(generator)。- 跟普通函数不同的是,生成器是一个返回迭代器的函数,只能用于迭代操作,更简单点理解生成器就是一个迭代器。- 在调用生成器运行的过程中,每次遇到 `yield` 时函数会暂停并保存当前所有的运行信息,返回 `yield` 的值, 并在下一次执行 `next()` 方法时从当前位置继续运行。- 调用一个生成器函数,返回的是一个迭代器对象。【例子】
###Code
def myGen():
print('生成器执行!')
yield 1
yield 2
myG = myGen()
for each in myG:
print(each)
'''
生成器执行!
1
2
'''
myG = myGen()
print(next(myG))
# 生成器执行!
# 1
print(next(myG)) # 2
print(next(myG)) # StopIteration
###Output
生成器执行!
1
2
生成器执行!
1
2
###Markdown
【例子】用生成器实现斐波那契数列。
###Code
def libs(n):
a = 0
b = 1
while True:
a, b = b, a + b
if a > n:
return
yield a
for each in libs(100):
print(each, end=' ')
# 1 1 2 3 5 8 13 21 34 55 89
###Output
1 1 2 3 5 8 13 21 34 55 89
|
01_Dive_into_DeepLearning/01_Getting_Started/01_Manipulating_Data_with_ndarray.ipynb
|
###Markdown
Dive into Deep Learning - Getting Started Installation
###Code
!pip install mxnet
###Output
Collecting mxnet
Downloading https://files.pythonhosted.org/packages/35/1d/b27b1f37ba21dde4bb4c84a1b57f4a4e29c576f2a0e6982dd091718f89c0/mxnet-1.3.1-py2.py3-none-win_amd64.whl (21.5MB)
Requirement already satisfied: requests<2.19.0,>=2.18.4 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from mxnet)
Collecting numpy<1.15.0,>=1.8.2 (from mxnet)
Downloading https://files.pythonhosted.org/packages/dc/99/f824a73251589d9fcef2384f9dd21bd1601597fda92ced5882940586ec37/numpy-1.14.6-cp36-none-win_amd64.whl (13.4MB)
Requirement already satisfied: graphviz<0.9.0,>=0.8.1 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from mxnet)
Requirement already satisfied: idna<2.7,>=2.5 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from requests<2.19.0,>=2.18.4->mxnet)
Requirement already satisfied: chardet<3.1.0,>=3.0.2 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from requests<2.19.0,>=2.18.4->mxnet)
Requirement already satisfied: urllib3<1.23,>=1.21.1 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from requests<2.19.0,>=2.18.4->mxnet)
Requirement already satisfied: certifi>=2017.4.17 in c:\users\karti\appdata\local\programs\python\python36\lib\site-packages (from requests<2.19.0,>=2.18.4->mxnet)
Installing collected packages: numpy, mxnet
Found existing installation: numpy 1.15.4
Uninstalling numpy-1.15.4:
Successfully uninstalled numpy-1.15.4
Successfully installed mxnet-1.3.1 numpy-1.14.6
###Markdown
Manipulating Data with ndarray NDArrays are MXNet’s primary tool for storing and transforming data. NDArrays are similar to NumPy’s multi-dimensional array. There are a few advantages:1. NDArrays support asynchronous computation on CPU, GPU, and distributed cloud architectures.2. NDArrays provide support for automatic differentiation Getting Started with ndarrays
###Code
import mxnet as mx
from mxnet import nd
# dir(nd)
# #Vector Operation - Creating a row vector of 10 integers
x = nd.arange(12)
x
# dir(x)
x.shape
x.shape_array()
x.size
y = x.reshape(3,4)
y
x.reshape((3,4))
# #To automatically allow mxnet to figure out the other dimensions need to reshape the data, we could use -1
x.reshape(3,4), x.reshape(3,-1), x.reshape(-1, 4)
# #Working with Tensors i.e. multi-dimensional arrays
nd.zeros((2,3,4))
nd.ones((2,3,4))
arr = [[1,2,3,4], [2,3,4,1], [3,4,1,2], [4,1,2,3]]
nd.array(arr)
# #Generating data from distributions using ndarray
nd.random.normal(0, 1, shape=(3,4))
###Output
_____no_output_____
###Markdown
Operations
###Code
# #Element-wise operations
x = nd.array([1, 2, 4, 8])
y = nd.array([2, 4, 6, 8])
print('x: ', x)
print('y: ', y)
print('x + y', x + y)
print('x - y', x - y)
print('x * y', x * y)
print('x / y', x / y)
# #Matrix Multiplication
x = nd.arange(1,13).reshape((3,4))
y = x.T
print("x: ", x)
print("y: ", y)
print("Dot Product: ", nd.dot(x, y))
# #Comparison Operator
x = nd.arange(1,10).reshape((3,3))
y = x.T
x == y
x, x.sum()
x.norm()
###Output
_____no_output_____
###Markdown
Broadcasting When the shapes of two ndarrays differ, mxnet performs the operations by using the concept of broadcasting on the ndarray with a smaller dimension. Indexing and Slicing is similar to that of Python
###Code
x = nd.arange(1,13).reshape(3,4)
x
x[1:2]
x[1:3]
x[:, 1:3]
x[1,3] = 100
x
x[:, :2] = -10
x
###Output
_____no_output_____
###Markdown
Saving Memory
###Code
x = nd.array([1,1,1])
y = nd.array([1,2,3])
before = id(y)
y = y + x
id(y) == before, id(y), before
###Output
_____no_output_____
###Markdown
In this case, each time we run an operation, like the one above, we would have to allocate memory to the newly created y variable. As the size of the data grows, this becomes undesirable. A better solution would be to update the variables in-place.
###Code
x = nd.array([1,1,1])
y = nd.array([1,2,3])
before = id(y)
y[:] = y + x
id(y) == before, id(y), before
###Output
_____no_output_____
###Markdown
Although, this is comparitively more efficient, the operation y+x would still have to be stored in a buffer.
###Code
x = nd.array([1,1,1])
y = nd.array([1,2,3])
before = id(y)
nd.elemwise_add(x,y, out=y)
id(y) == before, id(y), before
###Output
_____no_output_____
|
Python Advance Programming Assignment/Assignment_05.ipynb
|
###Markdown
Question 1:
###Code
Create a function that takes a number n (integer greater than zero) as an argument,
and returns 2 if n is odd and 8 if n is even.
You can only use the following arithmetic operators:
addition of numbers +, subtraction of numbers -, multiplication of number *, division of number /, and
exponentiation **.
You are not allowed to use any other methods in this challenge (i.e. no if
statements, comparison operators, etc).
Examples
f(1) 2
f(2) 8
f(3) 2
###Output
_____no_output_____
###Markdown
Answer :
###Code
def f(num):
lst = [8,2]
return lst[num-2*int(num/2)]
print(f(1))
print(f(2))
print(f(3))
print(f(99))
print(f(950))
print(f(110))
###Output
2
8
2
2
8
8
###Markdown
Question 2:
###Code
Create a function that returns the majority vote in a list.
A majority vote is an element that occurs > N/2 times in a list (where N is the length of the list).
Examples
majority_vote(["A", "A", "B"]) "A"
majority_vote(["A", "A", "A", "B", "C", "A"]) "A"
majority_vote(["A", "B", "B", "A", "C", "C"]) None
###Output
_____no_output_____
###Markdown
Answer :
###Code
def majority_vote(lst):
count_dic = {}
for i in lst:
if i in count_dic.keys():
count_dic[i] += 1
else:
count_dic[i] = 1
values = list(count_dic.values())
keys = list(count_dic.keys())
max_ = max(values)
if values.count(max_) == 1:
return keys[values.index(max_)]
return None
print(majority_vote(["A", "A", "B"]))
print(majority_vote(["A", "A", "A", "B", "C", "A"]))
print(majority_vote(["A", "B", "B", "A", "C", "C"]))
###Output
A
A
None
###Markdown
Question 3:
###Code
Create a function that takes a string txt and censors any word from a given list lst.
The text removed must be replaced by the given character char.
Examples
censor_string("Today is a Wednesday!", ["Today", "a"], "-") "----- is - Wednesday!"
censor_string("The cow jumped over the moon.", ["cow", "over"], "*") "The *** jumped **** the moon."
censor_string("Why did the chicken cross the road?", ["Did", "chicken",
"road"], "*") "Why *** the ******* cross the ****?"
###Output
_____no_output_____
###Markdown
Answer :
###Code
def censor_string(str_, lst,char):
spl_str_ = re.findall(r"\s|\w+|[^\w\s]", str_)
lower_str = [i.lower() for i in spl_str_]
lower_lst = [i.lower() for i in lst]
cen_str = ""
for i in range(len(lower_str)):
if lower_str[i] in lower_lst:
cen_str += char*len(lower_str[i])
else:
cen_str += spl_str_[i]
return cen_str
print(censor_string("Today is a Wednesday!", ["Today", "a"], "-"))
print(censor_string("The cow jumped over the moon.", ["cow", "over"], "*"))
print(censor_string("Why did the chicken cross the road?", ["Did", "chicken","road"], "*"))
###Output
----- is - Wednesday!
The *** jumped **** the moon.
Why *** the ******* cross the ****?
###Markdown
Question 4:
###Code
In mathematics a Polydivisible Number (or magic number) is a number in
a given number base with digits abcde... that has the following properties:
- Its first digit a is not 0.
- The number formed by its first two digits ab is a multiple of 2.
- The number formed by its first three digits abc is a multiple of 3.
- The number formed by its first four digits abcd is a multiple of 4.
Create a function which takes an integer n and returns True if the given
number is a Polydivisible Number and False otherwise.
Examples
is_polydivisible(1232) True
# 1 / 1 = 1
# 12 / 2 = 6
# 123 / 3 = 41
# 1232 / 4 = 308
is_polydivisible(123220 ) False
# 1 / 1 = 1
# 12 / 2 = 6
# 123 / 3 = 41
# 1232 / 4 = 308
# 12322 / 5 = 2464.4 # Not a Whole Number
# 123220 /6 = 220536.333... # Not a Whole Number
###Output
_____no_output_____
###Markdown
Answer :
###Code
def is_polydivisible(num):
str_ = str(num)
if int(str_[0]) == 0:
return False
lst = [(int(str_[0:i])**i)%i == 0 for i in range(1,len(str_)+1)]
return all(lst)
print(is_polydivisible(1232))
print(is_polydivisible(123220))
###Output
True
False
###Markdown
Question 5:
###Code
Create a function that takes a list of numbers and returns the sum of all
prime numbers in the list.
Examples
sum_primes([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) 17
sum_primes([2, 3, 4, 11, 20, 50, 71]) 87
sum_primes([]) None
###Output
_____no_output_____
###Markdown
Answer :
###Code
import math
def is_prime(n):
if n <= 1:
return False
max_div = math.floor(math.sqrt(n))
for i in range(2, 1 + max_div):
if n % i == 0:
return False
return True
def sum_primes(lst):
if lst == []:
return None
return sum([i for i in lst if is_prime(i)])
print(sum_primes([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]))
print(sum_primes([2, 3, 4, 11, 20, 50, 71]))
print(sum_primes([]))
###Output
17
87
None
|
Copy_of_Assignment6.ipynb
|
###Markdown
Linear Algebra for ECE Laboratory 6 : Matrix Operations Now that you have a fundamental knowledge about representing and operating with vectors as well as the fundamentals of matrices, we'll try to the same operations with matrices and even more. ObjectivesAt the end of this activity you will be able to:1. Be familiar with the fundamental matrix operations.2. Apply the operations to solve intermediate equations.3. Apply matrix algebra in engineering solutions. Discussion
###Code
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
###Output
_____no_output_____
###Markdown
Transposition One of the fundamental operations in matrix algebra is Transposition. The transpose of a matrix is done by flipping the values of its elements over its diagonals. With this, the rows and columns from the original matrix will be switched. So for a matrix $A$ its transpose is denoted as $A^T$. So for example: $$A = \begin{bmatrix} 1 & 2 & 5\\5 & -1 &0 \\ 0 & -3 & 3\end{bmatrix} $$ $$ A^T = \begin{bmatrix} 1 & 5 & 0\\2 & -1 &-3 \\ 5 & 0 & 3\end{bmatrix}$$ This can now be achieved programmatically by using `np.transpose()` or using the `T` method.
###Code
A = np.array ([
[3, 6, 9],
[-4, 8, -12],
[5, 10, 15]
])
A
AT1 = np.transpose(A)
AT1
AT2 = A.T
AT2
np.array_equiv(AT1, AT2)
B = np.array([
[3,6,9,12],
[1,0,2,1],
])
B.shape
np.transpose(B).shape
B.T.shape
###Output
_____no_output_____
###Markdown
Try to create your own matrix (you can try non-squares) to test transposition.
###Code
## Try out your code here.
Z=np.array([
[3,6,9],
[1,0,1]
])
Z.shape
np.transpose(Z).shape
Z.T.shape
ZT = Z.T
ZT
###Output
_____no_output_____
###Markdown
Dot Product / Inner Product If you recall the dot product from laboratory activity before, we will try to implement the same operation with matrices. In matrix dot product we are going to get the sum of products of the vectors by row-column pairs. So if we have two matrices $X$ and $Y$:$$X = \begin{bmatrix}x_{(0,0)}&x_{(0,1)}\\ x_{(1,0)}&x_{(1,1)}\end{bmatrix}, Y = \begin{bmatrix}y_{(0,0)}&y_{(0,1)}\\ y_{(1,0)}&y_{(1,1)}\end{bmatrix}$$The dot product will then be computed as:$$X \cdot Y= \begin{bmatrix} x_{(0,0)}*y_{(0,0)} + x_{(0,1)}*y_{(1,0)} & x_{(0,0)}*y_{(0,1)} + x_{(0,1)}*y_{(1,1)} \\ x_{(1,0)}*y_{(0,0)} + x_{(1,1)}*y_{(1,0)} & x_{(1,0)}*y_{(0,1)} + x_{(1,1)}*y_{(1,1)}\end{bmatrix}$$So if we assign values to $X$ and $Y$:$$X = \begin{bmatrix}1&2\\ 0&1\end{bmatrix}, Y = \begin{bmatrix}-1&0\\ 2&2\end{bmatrix}$$ $$X \cdot Y= \begin{bmatrix} 1*-1 + 2*2 & 1*0 + 2*2 \\ 0*-1 + 1*2 & 0*0 + 1*2 \end{bmatrix} = \begin{bmatrix} 3 & 4 \\2 & 2 \end{bmatrix}$$This could be achieved programmatically using `np.dot()`, `np.matmul()` or the `@` operator.
###Code
X = np.array([
[4,8],
[0,7]
])
Y = np.array([
[-1,0],
[2,2]
])
np.array_equiv(X, Y)
np.dot(X,Y)
X.dot(Y)
X @ Y
np.matmul(X,Y)
D = np.array([
[4,3,2],
[2,1,2],
[2,3,5]
])
E = np.array([
[-2,0,5],
[7,8,9],
[5,6,4]
])
D @ E
D.dot(E)
np.matmul(D, E)
np.dot(D, E)
###Output
_____no_output_____
###Markdown
In matrix dot products there are additional rules compared with vector dot products. Since vector dot products were just in one dimension there are less restrictions. Since now we are dealing with Rank 2 vectors we need to consider some rules: Rule 1: The inner dimensions of the two matrices in question must be the same. So given a matrix $A$ with a shape of $(a,b)$ where $a$ and $b$ are any integers. If we want to do a dot product between $A$ and another matrix $B$, then matrix $B$ should have a shape of $(b,c)$ where $b$ and $c$ are any integers. So for given the following matrices:$$A = \begin{bmatrix}2&4\\5&-2\\0&1\end{bmatrix}, B = \begin{bmatrix}1&1\\3&3\\-1&-2\end{bmatrix}, C = \begin{bmatrix}0&1&1\\1&1&2\end{bmatrix}$$So in this case $A$ has a shape of $(3,2)$, $B$ has a shape of $(3,2)$ and $C$ has a shape of $(2,3)$. So the only matrix pairs that is eligible to perform dot product is matrices $A \cdot C$, or $B \cdot C$.
###Code
A = np.array([
[2, 4, 8],
[5, -2, 5],
[0, 1, 6],
[3,4,5,]
])
B = np.array([
[1,1,0],
[3,3,-9],
[-1,-2,6],
[2,4,6,]
])
C = np.array([
[0,1,1,6],
[1,1,2,5],
[3,-3,2,4]
])
print(A.shape)
print(B.shape)
print(C.shape)
A @ C
B @ C
A @ B
###Output
_____no_output_____
###Markdown
If you would notice the shape of the dot product changed and its shape is not the same as any of the matrices we used. The shape of a dot product is actually derived from the shapes of the matrices used. So recall matrix $A$ with a shape of $(a,b)$ and matrix $B$ with a shape of $(b,c)$, $A \cdot B$ should have a shape $(a,c)$.
###Code
A @ B.T
X = np.array([
[1,2,3,0]
])
Y = np.array([
[1,0,4,-1]
])
print(X.shape)
print(Y.shape)
Y.T @ X
X @ Y.T
###Output
_____no_output_____
###Markdown
And youcan see that when you try to multiply A and B, it returns `ValueError` pertaining to matrix shape mismatch. Rule 2: Dot Product has special propertiesDot products are prevalent in matrix algebra, this implies that it has several unique properties and it should be considered when formulation solutions: 1. $A \cdot B \neq B \cdot A$ 2. $A \cdot (B \cdot C) = (A \cdot B) \cdot C$ 3. $A\cdot(B+C) = A\cdot B + A\cdot C$ 4. $(B+C)\cdot A = B\cdot A + C\cdot A$ 5. $A\cdot I = A$ 6. $A\cdot \emptyset = \emptyset$ I'll be doing just one of the properties and I'll leave the rest to test your skills!
###Code
A = np.array([
[3,2,1],
[4,5,1],
[1,1,1]
])
B = np.array([
[4,1,6],
[4,1,9],
[1,4,8]
])
C = np.array([
[1,1,0],
[0,1,1],
[1,0,1]
])
np.eye(3)
A.dot(np.eye(3))
np.array_equal(A@B, B@A)
E = A @ (B @ C)
E
F = (A @ B) @ C
F
np.array_equal(E, X)
np.array_equiv(E, F)
np.eye(A)
A @ E
z_mat = np.zeros(A.shape)
z_mat
a_dot_z = A.dot(np.zeros(A.shape))
a_dot_z
np.array_equal(a_dot_z,z_mat)
null_mat = np.empty(A.shape, dtype=float)
null = np.array(null_mat,dtype=float)
print(null)
np.allclose(a_dot_z,null)
###Output
[[0. 0.]
[0. 0.]]
###Markdown
Determinant A determinant is a scalar value derived from a square matrix. The determinant is a fundamental and important value used in matrix algebra. Although it will not be evident in this laboratory on how it can be used practically, but it will be reatly used in future lessons.The determinant of some matrix $A$ is denoted as $det(A)$ or $|A|$. So let's say $A$ is represented as:$$A = \begin{bmatrix}a_{(0,0)}&a_{(0,1)}\\a_{(1,0)}&a_{(1,1)}\end{bmatrix}$$We can compute for the determinant as:$$|A| = a_{(0,0)}*a_{(1,1)} - a_{(1,0)}*a_{(0,1)}$$So if we have $A$ as:$$A = \begin{bmatrix}1&4\\0&3\end{bmatrix}, |A| = 3$$But you might wonder how about square matrices beyond the shape $(2,2)$? We can approach this problem by using several methods such as co-factor expansion and the minors method. This can be taught in the lecture of the laboratory but we can achieve the strenuous computation of high-dimensional matrices programmatically using Python. We can achieve this by using `np.linalg.det()`.
###Code
A = np.array([
[3,5],
[7,8]
])
np.linalg.det(A)
B = np.array([
[4,5,7],
[3,9,6],
[2, -2, 7]
])
np.linalg.det(B)
## Now other mathematics classes would require you to solve this by hand,
## and that is great for practicing your memorization and coordination skills
## but in this class we aim for simplicity and speed so we'll use programming
## but it's completely fine if you want to try to solve this one by hand.
B = np.array([
[2,4,6,8],
[1,3,5,7],
[4,-6,8,3],
[6,4,3,9]
])
np.linalg.det(B)
###Output
_____no_output_____
###Markdown
Inverse The inverse of a matrix is another fundamental operation in matrix algebra. Determining the inverse of a matrix let us determine if its solvability and its characteristic as a system of linear equation — we'll expand on this in the nect module. Another use of the inverse matrix is solving the problem of divisibility between matrices. Although element-wise division exists but dividing the entire concept of matrices does not exists. Inverse matrices provides a related operation that could have the same concept of "dividing" matrices.Now to determine the inverse of a matrix we need to perform several steps. So let's say we have a matrix $M$:$$M = \begin{bmatrix}1&7\\-3&5\end{bmatrix}$$First, we need to get the determinant of $M$.$$|M| = (1)(5)-(-3)(7) = 26$$Next, we need to reform the matrix into the inverse form:$$M^{-1} = \frac{1}{|M|} \begin{bmatrix} m_{(1,1)} & -m_{(0,1)} \\ -m_{(1,0)} & m_{(0,0)}\end{bmatrix}$$So that will be:$$M^{-1} = \frac{1}{26} \begin{bmatrix} 5 & -7 \\ 3 & 1\end{bmatrix} = \begin{bmatrix} \frac{5}{26} & \frac{-7}{26} \\ \frac{3}{26} & \frac{1}{26}\end{bmatrix}$$For higher-dimension matrices you might need to use co-factors, minors, adjugates, and other reduction techinques. To solve this programmatially we can use `np.linalg.inv()`.
###Code
M = np.array([
[1,7],
[-3, 5]
])
np.array(M @ np.linalg.inv(M), dtype=int)
P = np.array([
[6, 9, 0],
[4, 2, -1],
[3, 6, 7]
])
Q = np.linalg.inv(P)
Q
P @ Q
## And now let's test your skills in solving a matrix with high dimensions:
N = np.array([
[18,5,23,1,0,33,5],
[0,45,0,11,2,4,2],
[5,9,20,0,0,0,3],
[1,6,4,4,8,43,1],
[8,6,8,7,1,6,1],
[-5,15,2,0,0,6,-30],
[-2,-5,1,2,1,20,12],
])
N_inv = np.linalg.inv(N)
np.array(N @ N_inv,dtype=int)
###Output
_____no_output_____
###Markdown
To validate the wether if the matric that you have solved is really the inverse, we follow this dot product property for a matrix $M$:$$M\cdot M^{-1} = I$$
###Code
squad = np.array([
[1.0, 1.0, 0.5],
[0.7, 0.7, 0.9],
[0.3, 0.3, 1.0]
])
weights = np.array([
[0.2, 0.2, 0.6]
])
p_grade = squad @ weights.T
p_grade
###Output
_____no_output_____
###Markdown
Activity Task 1 Prove and implement the remaining 6 matrix multiplication properties. You may create your own matrices in which their shapes should not be lower than $(3,3)$.In your methodology, create individual flowcharts for each property and discuss the property you would then present your proofs or validity of your implementation in the results section by comparing your result to present functions from NumPy.
###Code
np.array([])
###Output
_____no_output_____
|
_build/jupyter_execute/qaoa-n-queens.ipynb
|
###Markdown
Using QAOA to find solutionsWe start by importing the version of Numpy provided by Pennylane.
###Code
from pennylane import numpy as np
###Output
_____no_output_____
###Markdown
The following line sets the parameter $N$ of the $N$ queens problem. This parameter only needs to be set here, everything downstream is written in terms of this $N$.
###Code
N = 4
###Output
_____no_output_____
###Markdown
The exact cover problem and its generalizationGiven a (countable) set $X$ and a collection $S$ of subsets of $X$, a subcollection $S^\star$ of $S$ is called an exact cover of $X$ if any two sets in $S^\star$ are disjoint, and the union of all sets in $S^\star$ is $X$. We need to find such an exact cover if it exists. We can represent this in matrix form as follows. Let the matrix $M$ have as many rows as there are sets in $S$, and as many columns as there are elements in $X$. For each row of the matrix (corresponding to each set $s$ in $S$), let the $i$th element be $1$ if the corresponding element is in $s$ and zero otherwise. Then, the objective is to find a set of rows such that their sum is the all-ones vector. The set $X$ can be thought of as a set of constraints, and the choice of rows as selections. The objective is then to select a set of rows so that each constraint is satisfied by exactly one selection.The generalized exact cover problem divides $X$ up into two sets. In one set, the constraints must be satisfied by exactly one selection (these are called the primary constraints), while the secondary constraints may be satisfied by at most one (that is, either zero or one) selection. In matrix language, we need to find a set of rows that sum to $1$ in the columns corresponding to the primary constraints and either $0$ or $1$ in the columns corresponding to the secondary constraints. We can frame the $N$ queens problem in this framework as follows. Let the matrix $M$ have $N^2$ columns and $6N - 6$ columns. The first $N$ columns corresponds to the $N$ files (columns) of the chessboard. The next $N$ corresponds to the $N$ ranks (rows). The next $2N - 3$ columns correspond to the diagonals, with the first and last diagonal omitted because they only consist of one square each. Similarly, the last $2N - 3$ columns correspond to the reverse diagonals. Each row $M$ corresponds to a particular position of a queen on the board; it has ones in the columns corresponding to the rank, file, diagonal and reverse diagonal that the square is in, and zeros everywhere else. The objective is to find a selection of rows (or, equivalently, positions of queens) such that they sum to $1$ for each column corresponding to ranks and files (because each rank and file must contain a queen), and either $0$ for $1$ for each column corresponding to a diagonal or a reverse diagonal (because it is not necessary for each diagonal/reverse diagonal to contain a queen).This matrix is generated by the following code. For each row in the matrix (which goes from $1$ to $N^2$ corresponding to the $N^2$ choices of squares), it places a $1$ in the index for the rank, file, diagonal and reverse diagonal of the square, and zeros everywhere else.
###Code
M = np.zeros((N*N, 6*N - 6), requires_grad=False)
for m in range(np.shape(M)[0]):
for n in range(np.shape(M)[1]):
file = m // N
rank = m % N
diagonal = rank - file + (N-1) - 1
rdiagonal = rank + file - 1
if ((n == file
or n == N + rank
or n == 2*N + diagonal
or n == 4*N - 3 + rdiagonal
)
and diagonal >= 0
and diagonal < 2*N - 3
and rdiagonal >= 0
and rdiagonal < 2*N - 3
):
M[m][n] = 1
if n == file or n == N + rank:
M[m][n] = 1
if diagonal >= 0 and diagonal < 2*N - 3:
if n == 2*N + diagonal:
M[m][n] = 1
if rdiagonal >= 0 and rdiagonal < 2*N - 3:
if n == 4*N - 3 + rdiagonal:
M[m][n] = 1
M
###Output
_____no_output_____
###Markdown
As shown in [1], a generalized exact cover problem can be reduced to an exact cover problem by adding a row for each secondary constraint with a $1$ in the corresponding column and zeros everywhere else. The solution to the generalized problem is obtained by taking the solution of the exact problem and picking the original rows that are selected. The following code takes the matrix above defining the generalized problem and creates the matrix for the corresponding exact problem.
###Code
concat = np.concatenate((np.zeros([4*N - 6, 2*N]), np.eye(4*N - 6)), axis=1)
M = np.concatenate((M, concat), axis=0)
M
###Output
_____no_output_____
###Markdown
Setting up the QAOATo apply the QAOA, we need to turn the above problem into one of finding the ground state of an appropriate Hamiltonian. In [2], it is shown how to find the relevant Hamiltonian starting from the matrix defining an exact cover problem. The Hamiltonian is given by $$H = \sum_{i < j} J_{ij} \sigma_i^z \sigma_j^z + \sum_{i} h_i \sigma_i^z,$$where $$J_{rr'} = \frac{1}{2} \sum_{j} M_{rj}M_{r'j}$$and$$h_r = \frac{1}{2} \sum_{i} M_{ri} \left(\sum_{r'} M_{r'i} - 2\right).$$ The following lines compute the matrix $J$ from the matrix $M$ and checks that $J$ is symmetric ($J$ must be Hermitian, and is real since $M$ only has real entries.).
###Code
rows = np.shape(M)[0]
cols = np.shape(M)[1]
J = np.zeros((rows, rows), requires_grad=False)
for i in range(rows):
for j in range(rows):
J[i][j] = (0.5)*np.sum([M[i][f] * M[j][f] for f in range(cols)])
np.allclose(J, np.transpose(J))
###Output
_____no_output_____
###Markdown
The following lines construct the vector $h$ from the matrix $M$.
###Code
h = np.zeros(rows, requires_grad=False)
for r in range(rows):
h[r] = (0.5)*np.sum([M[r][f]*(np.sum([M[s][f] for s in range(rows)]) - 2) for f in range(cols)])
h
###Output
_____no_output_____
###Markdown
We now have everything in place for using QAOA. We need to create the cost and mixer Hamiltonians. We first begin by defining the cost Hamiltonian using the $J$ and $h$ we defined above.
###Code
import pennylane as qml
cost_coeffs = []
cost_observables = []
for j in range(np.shape(J)[0]):
for i in range(j-1):
cost_coeffs.append(J[i][j])
cost_observables.append(qml.PauliZ(i) @ qml.PauliZ(j))
for j in range(np.shape(h)[0]):
cost_coeffs.append(h[j])
cost_observables.append(qml.PauliZ(j))
cost_hamiltonian = qml.Hamiltonian(cost_coeffs, cost_observables, simplify=True)
cost_hamiltonian
###Output
_____no_output_____
###Markdown
The mixer coefficients consist of Pauli $X$ gates acting on the qubits.
###Code
mixer_coeffs = []
mixer_observables = []
for r in range(rows):
mixer_coeffs.append(1)
mixer_observables.append(qml.PauliX(r))
mixer_hamiltonian = qml.Hamiltonian(mixer_coeffs, mixer_observables)
mixer_hamiltonian
###Output
_____no_output_____
###Markdown
OptimizationWe shall use the `qaoa` module from Pennylane and define a layer of the QAOA circuit.
###Code
from pennylane import qaoa
def qaoa_layer(params):
qaoa.cost_layer(params[0], cost_hamiltonian)
qaoa.mixer_layer(params[1], mixer_hamiltonian)
###Output
_____no_output_____
###Markdown
Here we set the depth of the QAOA circuit. As with `N` above, everything downstream is written in terms of this parameter and so to control the number of depths, the only change to be made is here.
###Code
DEPTH = 1
###Output
_____no_output_____
###Markdown
For the circuit, we start with a uniform superposition over the starting qubits and then apply the cost and mixer circuits in succession, as usual for the QAOA.
###Code
wires = range(rows)
depth = DEPTH
def circuit(params):
for w in wires:
qml.Hadamard(wires=w)
qml.layer(qaoa_layer, depth, params)
###Output
_____no_output_____
###Markdown
The cost function is simply the expectation value of the cost Hamiltonian defined above.
###Code
dev = qml.device("default.qubit", wires=wires)
@qml.qnode(dev)
def cost_function(params):
circuit(params)
return qml.expval(cost_hamiltonian)
###Output
_____no_output_____
###Markdown
The parameters are initialized to $0.5$ each (we have not investigated other starting parameter values). We then run the optimizer for $30$ steps using Pennylane.
###Code
optimizer = qml.GradientDescentOptimizer()
steps = 30
params = np.array([[0.5, 0.5] for i in range(depth)], requires_grad=True)
for i in range(steps):
params = optimizer.step(cost_function, params)
print(i, cost_function(params))
print("Optimal Parameters")
print(params)
###Output
_____no_output_____
###Markdown
Next, we use the optimal parameters and sample the qubits corresponding to the rows of the original generalized problem. This data is stored in the `positions` list.
###Code
run_dev = qml.device("default.qubit", wires=wires, shots=1)
@qml.qnode(run_dev)
def optimized_circuit(params):
circuit(params)
return qml.sample(wires=[i for i in range(N*N)])
positions = optimized_circuit(params)
###Output
_____no_output_____
###Markdown
Finally, we create the $N \times N$ chessboard with the queens in the computed positions.
###Code
for i in range(N):
for j in range(N):
if positions[N*i + j] == 1:
print('🟥', end='')
else:
if (i+j) % 2 == 0:
print('⬛', end='')
else:
print('⬜', end='')
print('')
###Output
_____no_output_____
|
workshops/Python-Beginner-Workshop-04.ipynb
|
###Markdown
Welcome to the Beginner Python Workshop **Topic: conditionals (if statements)**This notebook will give you a basic introduction to the Python world. Some of the topics mentioned below is also covered in the [tutorials and tutorial videos](https://github.com/GuckLab/Python-Workshops/tree/main/tutorials)Eoghan O'Connell, Guck Division, MPL, 2021
###Code
# notebook metadata you can ignore!
info = {"workshop": "04",
"topic": ["if statements"],
"version" : "0.0.1"}
###Output
_____no_output_____
###Markdown
How to use this notebook- Click on a cell (each box is called a cell). Hit "shift+enter", this will run the cell!- You can run the cells in any order!- The output of runnable code is printed below the cell.- Check out this [Jupyter Notebook Tutorial video](https://www.youtube.com/watch?v=HW29067qVWk).See the help tab above for more information! What is in this Workshop?In this notebook we cover:- How to use "conditionals" like `if`, `else` and `elif` statements in Python- For more info, check out the related tutorial by Corey Schafer [here](https://www.youtube.com/watch?v=DZwmZ8Usvnk). What is a conditional in PythonA conditional is something that will evaluate to True or False (Boolean). We can check if something is True or False by using an `if` statement.This is the `if` statement syntax:```pythonif conditional: do something (if the above conditional was True)```- The "conditional" above must evaluate to True or False (or something that is Truthy or Falsy).- The indented block of code after the `if` statement will only be executed if the conditional is True.*Syntax notes*:- The second line ( do something ...) must be indented by a tab (4 spaces). - As soon as your code is not indented, it is no longer part of the `if` statement.- There must be a colon ( `:` ) at the end of the `if conditional:` statement.- The double equals sign `==` is used to check for equality. Comparisons that can be used: | Description | Syntax |:--- | :--- | Equal | == || Not equal | != || Greater than | > || Less than | < || Greater or equal | >= || Less or equal | <= || Object identity | is || Data type | isinstance(object, datatype) || other comparisons| and, or, not |
###Code
# import necessary modules
import numpy as np
###Output
_____no_output_____
###Markdown
Some basic examples
###Code
# here is an if statement example
name = True
if name:
print("name is True!")
# we can use slightly different syntax to do (almost) the same thing
if name is True:
print("name is True!")
if name == True:
print("name is True!")
# what if I want to check if it is False?
name = False
# just use the "not" keyword
if not name:
print("name is False!")
if name is False:
print("name is False!")
if name is not True:
print("name is False!")
if name != True:
print("name is False!")
###Output
_____no_output_____
###Markdown
Checking different conditionals
###Code
# we are not just limited to checking Boolean values!
# we can check lots of different conditionals
filename = "M001_010921.rtdc"
# check if the string name is equal to something
if filename == "M001_010921.rtdc":
print("Yes, the names match.")
# check if a string contains some characters
if "010921" in filename:
print(f"Date is correct, processing {filename} ...")
# check if filename variable is a string
if isinstance(filename, str):
print("The 'filename' variable is a string.")
# there are other ways to do this
if type(filename) == str:
print("The 'filename' variable is a string.")
# check if a list is a certain length
values = [2, 5, 7, 2]
if len(values) == 4:
print("There are four items in the list.")
# check if an array is a certain dimensionality
arr = np.array(values)
if arr.ndim == 1:
print("The arr has only one dimension.")
###Output
_____no_output_____
###Markdown
Using the `and`, `or` keywords
###Code
name = "Frodo"
cool_name = True
if name == "Frodo" and cool_name:
print(f"{name} is a cool name.")
values = [2, 5, 7, 2]
if len(values) == 3 or len(values) == 4:
print("These are the length we want!")
###Output
_____no_output_____
###Markdown
Using the `else` statementSyntax:```pythonif conditional: do something (if the above conditional was True)else: do something else (if the above conditional was False) ```*Syntax notes*:- The keyword `else` is used followed by a colon ( `:` )- The indented block after the `else` statement will be executed if the previous conditionals were False.
###Code
# here is an else statement in action
# we will use the same variables as above
values = [2, 5, 7, 2]
if len(values) == 4:
print("There are four items in the list.")
else:
print("This list is strange and should have four items!")
arr = np.array(values)
print(arr)
if arr.ndim == 1:
print("The arr has only one dimension.")
else:
print("I wanted an array with one dimension!")
###Output
_____no_output_____
###Markdown
Using the `elif` statementThe `elif` statement stands for "else if"Syntax:```pythonif conditional: do something (if the above conditional was True)elif different conditional: do something (if the above elif conditional was True and all previous conditions were False)else: do something else (if the above conditionals are all False) ```*Syntax notes*:- The keyword `elif` is used followed by a conditional and a colon ( `:` )- The indented block after the `elif` statement will be executed if the conditional is True.
###Code
# here is an elif statement in action
# we will use the same variables as above
values = [2, 5, 7, 2]
if len(values) == 5:
print("There are five items in the list.")
elif len(values) == 4:
print("Aha, a list with a length of four!")
# we can use if, elif, and else together with many elif
values = [2, 5, 7, 2]
if len(values) == 2:
print("There are two items in the list.")
elif len(values) == 1:
print("Aha, a list with a length of one!")
elif len(values) == 0:
print("This list is empty!")
else:
print("None of the above conditionals were True.")
###Output
_____no_output_____
###Markdown
Difference between `==` and `is`
###Code
a = [1, 2, 3]
b = [1, 2, 3]
print(a == b)
# print(a is b)
# print(id(a))
# print(id(b))
###Output
_____no_output_____
|
20201120/20201116/empirical/individual/.ipynb_checkpoints/DataProcessing-checkpoint.ipynb
|
###Markdown
Data Processing
###Code
import pandas as pd
import numpy as np
import statsmodels.api as sm
# All variables we concern about
columnNames = ["releaseNum", "1968ID", "personNumber", "familyNumber", ""]
# The timeline we care about
years = [1999, 2001, 2003, 2005, 2007]
# The function used to complile all years data into one dataFrame,
# the input "features" is a list of features.
def compile_data_with_features(features, years):
df = pd.DataFrame()
# Loading the data through years
for year in years:
df_sub = pd.read_excel(str(year) + ".xlsx")
df_sub.columns = columnNames
df_sub['year'] = year
df = pd.concat([df, df_sub[['familyID','year'] + features]])
df = df.reset_index(drop = True)
return df
# The function is used to drop the values we do not like in the dataFrame,
# the input "features" and "values" are both list
def drop_values(features, values, df):
for feature in features:
for value in values:
df = df[df[feature] != value]
df = df.reset_index(drop = True)
return df
###Output
_____no_output_____
###Markdown
Summary Statistics
###Code
def summaryStatistics(df, feature, n):
df['quantileRange'] = pd.qcut(df[feature], n, duplicates='drop')
print(df.groupby("quantileRange").participation.mean())
dff = df[df['participation'] == 1]
print(dff.groupby("quantileRange").investmentAmount.mean())
df.groupby("quantileRange").participation.mean().plot(kind='barh').set_xlabel('participation ratio')
return 1
###Output
_____no_output_____
###Markdown
Feature Engineering
###Code
# prepare the combined dataset and set up dummy variables for qualitative data
df = compile_data_with_features(['headCount', 'ageHead', 'maritalStatus', 'employmentStatus',
'liquidWealth', 'race', 'industry' ,'geoCode','incomeHead', "incomeWife",
'foodCost', 'houseCost', 'transCost', 'educationCost', 'childCost', 'healthCost',
'education','farmBusiness', 'checkingSavingAccount', 'debt', 'realEstate','participation',
'investmentAmount', 'vehicle', 'otherAsset', 'annuityIRA',
'wealthWithoutHomeEquity', "wealthWithHomeEquity"], years)
df = drop_values(["ageHead"],[999], df)
df = drop_values(["maritalStatus"],[8,9], df)
df = drop_values(["employmentStatus"],[0, 22, 98, 99], df)
df = drop_values(["liquidWealth"],[999999998,999999999], df)
df = drop_values(["race"],[0,8,9], df)
df = drop_values(["industry"],[999,0], df)
df = drop_values(["education"],[99,0], df)
df["totalExpense"] = df[['foodCost', 'houseCost', 'transCost',
'educationCost', 'childCost', 'healthCost']].sum(axis = 1)
df["laborIncome"] = df["incomeHead"] + df["incomeWife"]
df["costPerPerson"] = df["totalExpense"]/df["headCount"]
df
maritalStatus = ["Married", "neverMarried"]
employmentStatus = ["Working", "Retired", "other"]
race = ["White", "Black","AmericanIndian","Asian","Latino","otherBW","otherRace"]
# Education
# < 8th grade: middle school
# >= 8 and < 12: high scho0l
# >=12 and < 15: college
# >= 15 post graduate
education = ["middleSchool", "highSchool", "college", "postGraduate"]
# Industry
# < 400 manufacturing
# >= 400 and < 500 publicUtility
# >= 500 and < 700 retail
# >= 700 and < 720 finance
# >= 720 and < 900 service
# >= 900 otherIndustry
industry = ["manufacturing", "publicUtility", "retail", "finance", "service", "otherIndustry"]
data = []
for i in range(len(df)):
dataCollect = []
# marital status
if df.iloc[i]["maritalStatus"] == 2:
dataCollect.append(maritalStatus[1])
else:
dataCollect.append(maritalStatus[0])
# employment
if df.iloc[i]["employmentStatus"] == 1:
dataCollect.append(employmentStatus[0])
elif df.iloc[i]["employmentStatus"] == 4:
dataCollect.append(employmentStatus[1])
else:
dataCollect.append(employmentStatus[2])
# race
dataCollect.append(race[int(df.iloc[i]["race"] - 1)])
# Education variable
if df.iloc[i]["education"] < 8:
dataCollect.append(education[0])
elif df.iloc[i]["education"] >= 8 and df.iloc[i]["education"] < 12:
dataCollect.append(education[1])
elif df.iloc[i]["education"] >= 12 and df.iloc[i]["education"] < 15:
dataCollect.append(education[2])
else:
dataCollect.append(education[3])
# industry variable
if df.iloc[i]["industry"] < 400:
dataCollect.append(industry[0])
elif df.iloc[i]["industry"] >= 400 and df.iloc[i]["industry"] < 500:
dataCollect.append(industry[1])
elif df.iloc[i]["industry"] >= 500 and df.iloc[i]["industry"] < 700:
dataCollect.append(industry[2])
elif df.iloc[i]["industry"] >= 700 and df.iloc[i]["industry"] < 720:
dataCollect.append(industry[3])
elif df.iloc[i]["industry"] >= 720 and df.iloc[i]["industry"] < 900:
dataCollect.append(industry[4])
else:
dataCollect.append(industry[5])
data.append(dataCollect)
# Categorical dataFrame
df_cat = pd.DataFrame(data, columns = ["maritalStatus", "employmentStatus", "race", "education", "industry"])
columnNames
rdf = pd.concat([df[["year","participation","annuityIRA", "investmentAmount","ageHead", "liquidWealth",
"laborIncome", "costPerPerson","totalExpense","wealthWithoutHomeEquity", "wealthWithHomeEquity"]],
df_cat[["maritalStatus", "employmentStatus", "education","race", "industry"]]], axis=1)
rdf.columns
# Adjust for inflation.
years = [1999, 2001, 2003, 2005, 2007]
values_at2020 = np.array([1.54, 1.45, 1.39, 1.32, 1.18])
values_at2005 = values_at2020/1.32
values_at2005
quantVariables = ['annuityIRA', 'investmentAmount', 'liquidWealth', 'laborIncome', 'costPerPerson',
'totalExpense', 'wealthWithoutHomeEquity', 'wealthWithHomeEquity']
for i in range(len(rdf)):
for variable in quantVariables:
rdf.at[i, variable] = round(rdf.at[i, variable] * values_at2005[years.index(rdf.at[i,"year"])], 2)
rdf.to_csv('data_inflation_adjusted.csv')
rdf
###Output
_____no_output_____
|
toy-examples/Prediction-ST-OnlineMF-Gdata.ipynb
|
###Markdown
Online Forecasting Matrix Factorization**From**: San Gultekin, John Paisley, 2019. Online forecasting matrix factorization. IEEE Transactions on Signal Processing, 67(5): 1223-1236. Part 1: Model DescriptionSuppose that a multivariate time series can be represented by an $M\times T$ matrix $X$. If $d$ denotes the rank of this matrix, then it is possible to find a $d\times M$ matrix $U$ and a $d\times T$ matrix $V$ such that $X=U^TV$. Since the matrix $V$ is $d\times T$, it corresponds to a compression of the original $M\times T$ matrix $X$. Therefore, the matrix $V$ is itself a multivariate time series, while the matrix $U$ provides the combination coefficients to reconstruct $X$ from $V$.$$U_t=U_{t-1}+\eta_{U,t},\\\boldsymbol{v}_{t}=\theta_1\boldsymbol{v}_{t-1}+\cdots+\theta_P\boldsymbol{v}_{t-P}+\eta_{\boldsymbol{v},t}=\sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}, \\\boldsymbol{x}_{t}=U_{t}^{T}\boldsymbol{v}_{t}+\eta_{\boldsymbol{x},t},$$where $\eta_{U,t}$, $\eta_{\boldsymbol{v},t}$, and $\eta_{\boldsymbol{x},t}$ are white noises. Part 2: Matrix Factorization A. Fixed penalty (FP) constriantIn such online case, at each time a single column of $X$ is observed. Using the above model, at time $t$ we would like to minimize the following loss function$$f\left(U_{t},\boldsymbol{v}_{t}\right)=\left\|\boldsymbol{x}_{t}-U_{t}^{T}\boldsymbol{v}_{t}\right\|_{2}^{2}+\rho_{u}\left\|U_{t}-U_{t-1}\right\|_{F}^{2}+\rho_{v}\left\|\boldsymbol{v}_{t}-\sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}\right\|_{2}^{2}.$$This is called a fixed penalty (FP) matrix factorization in the article.Setting $\rho_{u}\gg\rho_{v}$ means FP will find a solution for which $U_{t}$ is close to $U_{t-1}$, i.e., $U_{t}$ is slowly time-varying. This agrees with the interpretation that, in the batch case $U$ is fixed set of coefficients and $V$ contains the compressed time series.Another caution here is that, setting $\rho_{v}$ high would over-constrain the problem as both $U_{t}$ and $\boldsymbol{v}_{t}$ would be forced to stay close to $U_{t-1}$ and $\sum_{p=1}^{P}\theta_{p}\boldsymbol{v}_{t-p}$ while trying to minimize the approximation error to $\boldsymbol{x}_{t}$. The update equations for FP are$$U_{t}\gets \left(\rho_{u}I+\boldsymbol{v}_{t}\boldsymbol{v}_{t}^{T}\right)^{-1}\left(\rho_{u}U_{t-1}+\boldsymbol{v}_{t}\boldsymbol{x}_{t}^{T}\right), \\\boldsymbol{v}_{t}^{(i)}\gets \left(\rho_{v}I+U_{t}U_{t}^{T}\right)^{-1}\left(\rho_{v}\sum_{p=1}^{P}\theta_{p}\boldsymbol{v}_{t-p}+U_{t}\boldsymbol{x}_{t}\right).$$The FP matrix factorization is summarized in Algorithm 1.>**Drawback**: The fixed penalty approach to matrix factorization suffers from several potential issues. While $\rho_{v}$ can be set to a small number, setting $\rho_{u}$ well has a major impact on performance. It is usually not clear a *priori* while values would yield good results, and often times this may require a large number of cross validations. Another drawback is that $\rho_{u}$ is fixed for the entire data stream. This may not be desirable as changing the regularization level at different time points may improve performance. B. Fixed tolerance (FT) constraintFor the above reasons, it can be useful to allow for time varying, self-tunable regularization. Consider the following optimization problem$$\min_{U_{t},\boldsymbol{v}_{t}}~~\left\|U_{t}-U_{t-1}\right\|_{F}^{2}+\left\|\boldsymbol{v}_{t}-\sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}\right\|_{2}^{2} \\\text{s.t.}~~\left\|\boldsymbol{x}_{t}-U_{t}^{T}\boldsymbol{v}_{t}\right\|_{2}^{2}\leq\epsilon$$where the new parameter $\epsilon$ forces the approximation error to remain below $\epsilon$. The objective function of FT can be optimized by coordinate descent.- Update for $U_{t}$: For a fixed $\boldsymbol{v}_{t}$, the Lagrangian and optimal update for $U_{t}$ are$$\mathcal{L}\left(U_{t},\lambda\right)=\left\|U_{t}-U_{t-1}\right\|_{F}^{2}+\lambda\left\|\boldsymbol{x}_{t}-U_{t}^{T}\boldsymbol{v}_{t}\right\|_{2}^{2}-\lambda\epsilon, \\\implies U_{t}\gets \left(\lambda^{-1}I+\boldsymbol{v}_{t}\boldsymbol{v}_{t}^{T}\right)^{-1}\left(\lambda^{-1}U_{t-1}+\boldsymbol{v}_{t}\boldsymbol{v}_{t}^{T}\right).$$- Update for $\boldsymbol{x}_{t}$: For a fixed $U_{t}$, the Lagrangian and optimal update for $\boldsymbol{v}_{t}$ are$$\mathcal{L}\left(\boldsymbol{v}_{t},\lambda\right)=\left\|\boldsymbol{v}_{t}-\sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}\right\|_{2}^{2}+\lambda\left\|\boldsymbol{x}_{t}-U_{t}^{T}\boldsymbol{x}_{t}\right\|_{2}^{2}-\lambda\epsilon, \\\implies \boldsymbol{v}_{t}\gets \left(\lambda^{-1}I+U_{t}U_{t}^{T}\right)^{-1}\left(\lambda^{-1}\sum_{p=1}^{P}\theta_{p}\boldsymbol{v}_{t-p}+U_{t}\boldsymbol{x}_{t}\right).$$- Optimizing the Lagrange Multiplier $\lambda$: Defining$$c_1=\left\|\boldsymbol{x}_{t}-U_{t-1}\boldsymbol{v}_{t}\right\|_{2}^{2},~c_2=\left\|\boldsymbol{v}_{t}\right\|_{2}^{2},$$and setting the Lagrange multiplier to$$\lambda^{*}=\frac{\sqrt{c_1}}{c_2\sqrt{\epsilon}}-\frac{1}{c_2}$$the optimal update for $U_{t}$ is$$U_{t}\gets \left(I+\lambda^{*}\boldsymbol{v}_{t}\boldsymbol{v}_{t}^{T}\right)^{-1}\left(U_{t-1}+\lambda^{*}\boldsymbol{v}_{t}\boldsymbol{v}_{t}^{T}\right).$$ C. Zero tolerance (ZT) constraintThis case estimates the latent factors $U_{t}$ and $\boldsymbol{v}_{t}$ that are as close to the prior as possible, while allowing no approximation error on $\boldsymbol{x}_{t}$. The optimization problem now becomes$$\min_{U_{t},\boldsymbol{v}_{t}}~~\left\|U_{t}-U_{t-1}\right\|_{F}^{2}+\left\|\boldsymbol{v}_{t}-\sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}\right\|_{2}^{2} \\\text{s.t.}~~U_{t}^{T}\boldsymbol{v}_{t}=\boldsymbol{x}_{t}.$$Optimizing $U_{t}$ given $\boldsymbol{v}_{t}$ can be done with Lagrange multipliers. Following a rescaling, the Lagrangian is given by$$\mathcal{L}\left(\boldsymbol{U}_{t}, \boldsymbol{\lambda}\right)=\frac{1}{2}\left\|\boldsymbol{U}_{t}-\boldsymbol{U}_{t-1}\right\|_{F}^{2}+\boldsymbol{\lambda}^{T}\left(\boldsymbol{x}_{t}-\boldsymbol{U}_{t} \boldsymbol{v}_{t}\right).$$The stationary conditions are$$\begin{aligned} \nabla_{\boldsymbol{U}_{t}} \mathcal{L}\left(\boldsymbol{U}_{t}, \boldsymbol{\lambda}\right) &=0=\boldsymbol{U}_{t}-\boldsymbol{U}_{t-1}+\boldsymbol{v}_{t} \boldsymbol{\lambda}^{T}, \\ \nabla_{\boldsymbol{\lambda}} \mathcal{L}\left(\boldsymbol{U}_{t}, \boldsymbol{\lambda}\right) &=0=\boldsymbol{U}_{t-1}^{T} \boldsymbol{v}_{t}-\boldsymbol{x}_{t}. \end{aligned}$$The solution is then$$\boldsymbol{\lambda}=\frac{\boldsymbol{U}_{t-1}^{T} \boldsymbol{v}_{t}-\boldsymbol{x}_{t}}{\boldsymbol{v}_{t}^{T} \boldsymbol{v}_{t}}, \boldsymbol{U}_{t}=\boldsymbol{U}_{t-1}-\boldsymbol{v}_{t} \boldsymbol{\lambda}^{T}.$$Update $\boldsymbol{v}_{t}$ by$$\boldsymbol{v}_{t} \leftarrow\left(\rho_{v} \boldsymbol{I}+\boldsymbol{U}_{t} \boldsymbol{U}_{t}^{T}\right)^{-1}\left(\rho_{v} \sum_{p=1}^{P}\theta_p\boldsymbol{v}_{t-p}+\boldsymbol{U}_{t} \boldsymbol{x}_{t}\right).$$ Part 3: Optimizing AR CoefficientsLet $\boldsymbol{v}_{t}=\boldsymbol{P}_{t} \boldsymbol{\theta}$ where $\boldsymbol{P}_{t}=\left[\boldsymbol{v}_{t-1} \cdots \boldsymbol{v}_{t-P}\right]$ is a $d\times P$ patch matrix of the provious $P$ columns, then we have$$\widehat{\boldsymbol{\theta}}=\left[\sum_{t=1}^{T} \boldsymbol{P}_{t}^{\top} \boldsymbol{P}_{t}+\boldsymbol{\Sigma}_{\boldsymbol{\theta}}^{-1}\right]^{-1}\left[\sum_{t=1}^{T} \boldsymbol{P}_{t}^{\top} \boldsymbol{v}_{t}\right],$$where we consider the case $\boldsymbol{\Sigma}_{\boldsymbol{\theta}}=r_{0} \boldsymbol{I}$ for a tunable parameter $r_0$.
###Code
import numpy as np
def FP(xt, rho_u, rho_v, Ut_minus, vt_minus, maxiter):
"""Fixed Penalty Matrix Factorization (FP)."""
Ut = Ut_minus
binary_vec = np.zeros(xt.shape)
pos = np.where(xt > 0)
binary_vec[pos] = 1
for i in range(maxiter):
vt = np.matmul(np.linalg.inv(rho_v * np.eye(vt_minus.shape[0])
+ np.matmul(Ut, Ut.T)),
rho_v * vt_minus + np.matmul(Ut, xt))
Ut = np.matmul(np.linalg.inv(rho_u * np.eye(vt_minus.shape[0])
+ np.outer(vt, vt)),
rho_u * Ut_minus + np.outer(vt, xt))
return Ut, vt
def FT(xt, epsilon, rho_v, Ut_minus, vt_minus, maxiter):
"""Fixed Tolerance Matrix Factorization (FT)."""
Ut = Ut_minus
for i in range(maxiter):
vt = np.matmul(np.linalg.inv(rho_v * np.eye(vt_minus.shape[0])
+ np.matmul(Ut, Ut.T)),
rho_v * vt_minus + np.matmul(Ut, xt))
c1 = np.linalg.norm(xt - np.matmul(Ut_minus.T, vt)) ** 2
c2 = np.linalg.norm(vt) ** 2
lambda_star = np.sqrt(c1)/(c2 * np.sqrt(epsilon)) - 1/c2
Ut = np.matmul(np.linalg.inv(np.eye(vt_minus.shape[0])
+ lambda_star * np.outer(vt, vt)),
Ut_minus + lambda_star * np.outer(vt, xt))
return Ut, vt
def ZT(xt, rho_v, Ut_minus, vt_minus, maxiter):
"""Zero Tolerance Matrix Factorization (ZT)."""
Ut = Ut_minus
for i in range(maxiter):
vt = np.matmul(np.linalg.inv(rho_v * np.eye(vt_minus.shape[0])
+ np.matmul(Ut, Ut.T)),
rho_v * vt_minus + np.matmul(Ut, xt))
lambda_vec = (np.matmul(Ut_minus.T, vt) - xt)/(np.linalg.norm(vt) ** 2)
Ut = Ut_minus - np.outer(vt, lambda_vec)
return Ut, vt
def OnlineMF(X, pred_time_steps, d, P, r0, rho_u, epsilon, rho_v, maxiter):
"""Online Forecasting Matrix Factorization."""
binary_mat = np.zeros(X.shape)
pos = np.where(X > 0)
binary_mat[pos] = 1
U0 = np.random.rand(d, X.shape[0])
V0 = np.random.rand(d, X.shape[1])
v0 = np.random.rand(d)
X_new = X[:, 0 : X.shape[1] - pred_time_steps - 1]
for i in range(maxiter):
for m in range(X_new.shape[0]):
U0[:, m] = np.matmul(np.linalg.inv(rho_v * np.eye(d)
+ np.matmul(V0[:, 0 : X_new.shape[1]],
V0[:, 0 : X_new.shape[1]].T)),
np.matmul(V0[:, 0 : X_new.shape[1]], X_new[m, :]))
for n in range(X_new.shape[1]):
V0[:, n] = np.matmul(np.linalg.inv(rho_v * np.eye(d)
+ np.matmul(U0, U0.T)), np.matmul(U0, X_new[:, n]))
pos1 = np.where(X_new > 0)
mat0 = np.zeros((P, P))
vec0 = np.zeros(P)
for t in range(X_new.shape[1] - P):
Pt = V0[:, t : t + P]
mat0 += np.matmul(Pt.T, Pt)
vec0 += np.matmul(Pt.T, V0[:, t + P])
theta_vec = np.matmul(np.linalg.inv(mat0 + np.eye(P)), vec0)
r_l0 = r0 * np.eye(P)
r_r0 = 0
Xt = np.zeros((X.shape[0], pred_time_steps))
Ut = U0
r_lt_minus = r_l0
r_rt_minus = r_r0
for t in range(pred_time_steps):
Ut_minus = Ut
Pt = V0[:, X.shape[1] - pred_time_steps + t - 1 - P : X.shape[1] - pred_time_steps + t - 1]
vt_minus = np.matmul(Pt, theta_vec)
xt = X[:, X.shape[1] - pred_time_steps + t - 1]
Ut, vt = FP(xt, rho_u, rho_v, Ut_minus, vt_minus, maxiter)
V0[:, X.shape[1] - pred_time_steps + t - 1] = vt
r_lt = r_lt_minus + np.matmul(Pt.T, Pt)
r_rt = r_rt_minus + np.matmul(Pt.T, vt)
theta_vec = np.matmul(np.linalg.inv(r_lt), r_rt)
r_lt_minus = r_lt
r_rt_minus = r_rt
Pt0 = V0[:, X.shape[1] - pred_time_steps + t - P : X.shape[1] - pred_time_steps + t]
vt = np.matmul(Pt0, theta_vec)
Xt[:, t] = np.matmul(Ut.T, vt)
if (t + 1) % 20 == 0:
print('Time step: {}'.format(t + 1))
return Xt
###Output
_____no_output_____
###Markdown
Data Organization Part 1: Matrix StructureWe consider a dataset of $m$ discrete time series $\boldsymbol{y}_{i}\in\mathbb{R}^{f},i\in\left\{1,2,...,m\right\}$. The time series may have missing elements. We express spatio-temporal dataset as a matrix $Y\in\mathbb{R}^{m\times f}$ with $m$ rows (e.g., locations) and $f$ columns (e.g., discrete time intervals),$$Y=\left[ \begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1f} \\ y_{21} & y_{22} & \cdots & y_{2f} \\ \vdots & \vdots & \ddots & \vdots \\ y_{m1} & y_{m2} & \cdots & y_{mf} \\ \end{array} \right]\in\mathbb{R}^{m\times f}.$$ Part 2: Tensor StructureWe consider a dataset of $m$ discrete time series $\boldsymbol{y}_{i}\in\mathbb{R}^{nf},i\in\left\{1,2,...,m\right\}$. The time series may have missing elements. We partition each time series into intervals of predifined length $f$. We express each partitioned time series as a matrix $Y_{i}$ with $n$ rows (e.g., days) and $f$ columns (e.g., discrete time intervals per day),$$Y_{i}=\left[ \begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1f} \\ y_{21} & y_{22} & \cdots & y_{2f} \\ \vdots & \vdots & \ddots & \vdots \\ y_{n1} & y_{n2} & \cdots & y_{nf} \\ \end{array} \right]\in\mathbb{R}^{n\times f},i=1,2,...,m,$$therefore, the resulting structure is a tensor $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$.
###Code
import scipy.io
from tensorly import unfold
tensor = scipy.io.loadmat('Guangzhou-data-set/tensor.mat')
tensor = tensor['tensor']
random_matrix = scipy.io.loadmat('Guangzhou-data-set/random_matrix.mat')
random_matrix = random_matrix['random_matrix']
random_tensor = scipy.io.loadmat('Guangzhou-data-set/random_tensor.mat')
random_tensor = random_tensor['random_tensor']
dense_mat = unfold(tensor, 0)
import time
start = time.time()
pred_time_steps = 720
d = 10
P = 144
r0 = 1
rho_u = 1
epsilon = 0.01
rho_v = 1e-4
maxiter = 200
Xt = OnlineMF(dense_mat, pred_time_steps, d, P, r0, rho_u, epsilon, rho_v, maxiter)
small_dense_mat = dense_mat[:, dense_mat.shape[1] - pred_time_steps : dense_mat.shape[1]]
pos = np.where(small_dense_mat > 0)
final_mape = np.sum(np.abs(small_dense_mat[pos] -
Xt[pos])/small_dense_mat[pos])/small_dense_mat[pos].shape[0]
final_rmse = np.sqrt(np.sum((small_dense_mat[pos] -
Xt[pos]) ** 2)/small_dense_mat[pos].shape[0])
print('Final MAPE: {:.6}'.format(final_mape))
print('Final RMSE: {:.6}'.format(final_rmse))
print()
end = time.time()
print('Running time: %d seconds'%(end - start))
import matplotlib.pyplot as plt
plt.figure(figsize = (12, 2.5))
road = 3
plt.plot(Xt[road, :], 'r', small_dense_mat[road, :], 'b')
plt.show()
###Output
_____no_output_____
|
3547_05_Code.ipynb
|
###Markdown
Sebastian Raschka, 2015 Python Machine Learning Essentials Compressing Data via Dimensionality Reduction Note that the optional watermark extension is a small IPython notebook plugin that I developed to make the code reproducible. You can just skip the following line(s).
###Code
%load_ext watermark
%watermark -a 'Sebastian Raschka' -u -d -v -p numpy,scipy,matplotlib,scikit-learn
# to install watermark just uncomment the following line:
#%install_ext https://raw.githubusercontent.com/rasbt/watermark/master/watermark.py
###Output
_____no_output_____
###Markdown
Sections - [Unsupervised dimensionality reduction via principal component analysis](Unsupervised-dimensionality-reduction-via-principal-component-analysis) - [Total and explained variance](Total-and-explained-variance) - [Feature transformation](Feature-transformation) - [Principal component analysis in scikit-learn](Principal-component-analysis-in-scikit-learn)- [Supervised data compression via linear discriminant analysis](Supervised-data-compression-via-linear-discriminant-analysis) - [Computing the scatter matrices](Computing-the-scatter-matrices) - [Selecting linear discriminants for the new feature subspace](Selecting-linear-discriminants-for-the-new-feature-subspace) - [Projecting samples onto the new feature space](Projecting-samples-onto-the-new-feature-space) - [LDA via scikit-learn](LDA-via-scikit-learn)- [Using kernel principal component analysis for nonlinear mappings](Using-kernel-principal-component-analysis-for-nonlinear-mappings) - [Implementing a kernel principal component analysis in Python](Implementing-a-kernel-principal-component-analysis-in-Python) - [Example 1: Separating half-moon shapes](Example-1:-Separating-half-moon-shapes) - [Example 2: Separating concentric circles](Example-2:-Separating-concentric-circles) - [Projecting new data points](Projecting-new-data-points) - [Kernel principal component analysis in scikit-learn](Kernel-principal-component-analysis-in-scikit-learn) Unsupervised dimensionality reduction via principal component analysis [[back to top](Sections)] Loading the *Wine* dataset from Chapter 4.
###Code
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']
df_wine.head()
###Output
_____no_output_____
###Markdown
Splitting the data into 70% training and 30% test subsets.
###Code
from sklearn.cross_validation import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=0)
###Output
_____no_output_____
###Markdown
Standardizing the data.
###Code
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)
###Output
_____no_output_____
###Markdown
Eigendecomposition of the covariance matrix.
###Code
import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\nEigenvalues \n%s' % eigen_vals)
###Output
Eigenvalues
[ 4.8923083 2.46635032 1.42809973 1.01233462 0.84906459 0.60181514
0.52251546 0.08414846 0.33051429 0.29595018 0.16831254 0.21432212
0.2399553 ]
###Markdown
Total and explained variance [[back to top](Sections)]
###Code
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
%matplotlib inline
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/pca1.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
Feature transformation [[back to top](Sections)]
###Code
# Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eigen_pairs.sort(reverse=True)
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print('Matrix W:\n', w)
X_train_pca = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train==l, 0],
X_train_pca[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/pca2.png', dpi=300)
plt.show()
X_train_std[0].dot(w)
###Output
_____no_output_____
###Markdown
Principal component analysis in scikit-learn [[back to top](Sections)]
###Code
from sklearn.decomposition import PCA
pca = PCA()
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_
plt.bar(range(1, 14), pca.explained_variance_ratio_, alpha=0.5, align='center')
plt.step(range(1, 14), np.cumsum(pca.explained_variance_ratio_), where='mid')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.show()
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
plt.scatter(X_train_pca[:,0], X_train_pca[:,1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
###Output
_____no_output_____
###Markdown
Training logistic regression classifier using the first 2 principal components.
###Code
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr = lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/pca3.png', dpi=300)
plt.show()
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/pca4.png', dpi=300)
plt.show()
pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_
###Output
_____no_output_____
###Markdown
Supervised data compression via linear discriminant analysis [[back to top](Sections)] Computing the scatter matrices [[back to top](Sections)] Calculate the mean vectors for each class:
###Code
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1,4):
mean_vecs.append(np.mean(X_train_std[y_train==label], axis=0))
print('MV %s: %s\n' %(label, mean_vecs[label-1]))
###Output
MV 1: [ 0.9259 -0.3091 0.2592 -0.7989 0.3039 0.9608 1.0515 -0.6306 0.5354
0.2209 0.4855 0.798 1.2017]
MV 2: [-0.8727 -0.3854 -0.4437 0.2481 -0.2409 -0.1059 0.0187 -0.0164 0.1095
-0.8796 0.4392 0.2776 -0.7016]
MV 3: [ 0.1637 0.8929 0.3249 0.5658 -0.01 -0.9499 -1.228 0.7436 -0.7652
0.979 -1.1698 -1.3007 -0.3912]
###Markdown
Compute the within-class scatter matrix:
###Code
d = 13 # number of features
S_W = np.zeros((d, d))
for label,mv in zip(range(1, 4), mean_vecs):
class_scatter = np.zeros((d, d)) # scatter matrix for each class
for row in X[y == label]:
row, mv = row.reshape(d, 1), mv.reshape(d, 1) # make column vectors
class_scatter += (row-mv).dot((row-mv).T)
S_W += class_scatter # sum class scatter matrices
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
###Output
Within-class scatter matrix: 13x13
###Markdown
Better: covariance matrix since classes are not equally distributed:
###Code
print('Class label distribution: %s'
% np.bincount(y_train)[1:])
d = 13 # number of features
S_W = np.zeros((d, d))
for label,mv in zip(range(1, 4), mean_vecs):
class_scatter = np.cov(X_train_std[y_train==label].T)
S_W += class_scatter
print('Scaled within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
###Output
Scaled within-class scatter matrix: 13x13
###Markdown
Compute the between-class scatter matrix:
###Code
mean_overall = np.mean(X_train_std, axis=0)
d = 13 # number of features
S_B = np.zeros((d, d))
for i,mean_vec in enumerate(mean_vecs):
n = X[y==i+1, :].shape[0]
mean_vec = mean_vec.reshape(d, 1) # make column vector
mean_overall = mean_overall.reshape(d, 1) # make column vector
S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('Between-class scatter matrix: %sx%s' % (S_B.shape[0], S_B.shape[1]))
###Output
Between-class scatter matrix: 13x13
###Markdown
Selecting linear discriminants for the new feature subspace [[back to top](Sections)] Solve the generalized eigenvalue problem for the matrix $S_W^{-1}S_B$:
###Code
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
###Output
_____no_output_____
###Markdown
Sort eigenvectors in decreasing order of the eigenvalues:
###Code
# Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in decreasing order:\n')
for eigen_val in eigen_pairs:
print(eigen_val[0])
tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)
plt.bar(range(1, 14), discr, alpha=0.5, align='center',
label='individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid',
label='cumulative "discriminability"')
plt.ylabel('"discriminability" ratio')
plt.xlabel('Linear Discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/lda1.png', dpi=300)
plt.show()
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
eigen_pairs[1][1][:, np.newaxis].real))
print('Matrix W:\n', w)
###Output
Matrix W:
[[-0.0707 -0.3778]
[ 0.0359 -0.2223]
[-0.0263 -0.3813]
[ 0.1875 0.2955]
[-0.0033 0.0143]
[ 0.2328 0.0151]
[-0.7719 0.2149]
[-0.0803 0.0726]
[ 0.0896 0.1767]
[ 0.1815 -0.2909]
[-0.0631 0.2376]
[-0.3794 0.0867]
[-0.3355 -0.586 ]]
###Markdown
Projecting samples onto the new feature space [[back to top](Sections)]
###Code
X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train==l, 0],
X_train_lda[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='upper right')
plt.tight_layout()
# plt.savefig('./figures/lda2.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
LDA via scikit-learn [[back to top](Sections)]
###Code
from sklearn.lda import LDA
lda = LDA(n_components=2)
X_train_lda = lda.fit_transform(X_train_std, y_train)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr = lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/lda3.png', dpi=300)
plt.show()
X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/lda4.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
Using kernel principal component analysis for nonlinear mappings [[back to top](Sections)] Implementing a kernel principal component analysis in Python [[back to top](Sections)]
###Code
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF kernel PCA implementation.
Parameters
------------
X: {NumPy ndarray}, shape = [n_samples, n_features]
gamma: float
Tuning parameter of the RBF kernel
n_components: int
Number of principal components to return
Returns
------------
X_pc: {NumPy ndarray}, shape = [n_samples, k_features]
Projected dataset
"""
# Calculate pairwise squared Euclidean distances
# in the MxN dimensional dataset.
sq_dists = pdist(X, 'sqeuclidean')
# Convert pairwise distances into a square matrix.
mat_sq_dists = squareform(sq_dists)
# Compute the symmetric kernel matrix.
K = exp(-gamma * mat_sq_dists)
# Center the kernel matrix.
N = K.shape[0]
one_n = np.ones((N,N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# Obtaining eigenpairs from the centered kernel matrix
# numpy.eigh returns them in sorted order
eigvals, eigvecs = eigh(K)
# Collect the top k eigenvectors (projected samples)
X_pc = np.column_stack((eigvecs[:, -i]
for i in range(1, n_components + 1)))
return X_pc
###Output
_____no_output_____
###Markdown
Example 1: Separating half-moon shapes [[back to top](Sections)]
###Code
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.tight_layout()
# plt.savefig('./figures/half_moon_1.png', dpi=300)
plt.show()
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((50,1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((50,1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
# plt.savefig('./figures/half_moon_2.png', dpi=300)
plt.show()
from matplotlib.ticker import FormatStrFormatter
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50,1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50,1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
ax[0].xaxis.set_major_formatter(FormatStrFormatter('%0.1f'))
ax[1].xaxis.set_major_formatter(FormatStrFormatter('%0.1f'))
plt.tight_layout()
# plt.savefig('./figures/half_moon_3.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
Example 2: Separating concentric circles [[back to top](Sections)]
###Code
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
plt.tight_layout()
# plt.savefig('./figures/circles_1.png', dpi=300)
plt.show()
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y==0, 0], np.zeros((500,1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((500,1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
# plt.savefig('./figures/circles_2.png', dpi=300)
plt.show()
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((500,1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((500,1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
# plt.savefig('./figures/circles_3.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
Projecting new data points [[back to top](Sections)]
###Code
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF kernel PCA implementation.
Parameters
------------
X: {NumPy ndarray}, shape = [n_samples, n_features]
gamma: float
Tuning parameter of the RBF kernel
n_components: int
Number of principal components to return
Returns
------------
X_pc: {NumPy ndarray}, shape = [n_samples, k_features]
Projected dataset
lambdas: list
Eigenvalues
"""
# Calculate pairwise squared Euclidean distances
# in the MxN dimensional dataset.
sq_dists = pdist(X, 'sqeuclidean')
# Convert pairwise distances into a square matrix.
mat_sq_dists = squareform(sq_dists)
# Compute the symmetric kernel matrix.
K = exp(-gamma * mat_sq_dists)
# Center the kernel matrix.
N = K.shape[0]
one_n = np.ones((N,N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# Obtaining eigenpairs from the centered kernel matrix
# numpy.eigh returns them in sorted order
eigvals, eigvecs = eigh(K)
# Collect the top k eigenvectors (projected samples)
alphas = np.column_stack((eigvecs[:,-i] for i in range(1,n_components+1)))
# Collect the corresponding eigenvalues
lambdas = [eigvals[-i] for i in range(1,n_components+1)]
return alphas, lambdas
X, y = make_moons(n_samples=100, random_state=123)
alphas, lambdas = rbf_kernel_pca(X, gamma=15, n_components=1)
x_new = X[25]
x_new
x_proj = alphas[25] # original projection
x_proj
def project_x(x_new, X, gamma, alphas, lambdas):
pair_dist = np.array([np.sum((x_new-row)**2) for row in X])
k = np.exp(-gamma * pair_dist)
return k.dot(alphas / lambdas)
# projection of the "new" datapoint
x_reproj = project_x(x_new, X, gamma=15, alphas=alphas, lambdas=lambdas)
x_reproj
plt.scatter(alphas[y==0, 0], np.zeros((50)),
color='red', marker='^',alpha=0.5)
plt.scatter(alphas[y==1, 0], np.zeros((50)),
color='blue', marker='o', alpha=0.5)
plt.scatter(x_proj, 0, color='black', label='original projection of point X[25]', marker='^', s=100)
plt.scatter(x_reproj, 0, color='green', label='remapped point X[25]', marker='x', s=500)
plt.legend(scatterpoints=1)
plt.tight_layout()
# plt.savefig('./figures/reproject.png', dpi=300)
plt.show()
###Output
_____no_output_____
###Markdown
Kernel principal component analysis in scikit-learn [[back to top](Sections)]
###Code
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
# plt.savefig('./figures/scikit_kpca.png', dpi=300)
plt.show()
###Output
_____no_output_____
|
neural-networks-in-pytorch/convolutional-neural-networks/2_pool_visualization.ipynb
|
###Markdown
Pooling Layer---In this notebook, we add and visualize the output of a maxpooling layer in a CNN. Import the image
###Code
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'images/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# normalize, rescale entries to lie in [0,1]
gray_img = gray_img.astype("float32")/255
# plot image
plt.imshow(gray_img, cmap='gray')
plt.show()
###Output
_____no_output_____
###Markdown
Define and visualize the filters
###Code
import numpy as np
## TODO: Feel free to modify the numbers here, to try out another filter!
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
print('Filter shape: ', filter_vals.shape)
# Defining four different filters,
# all of which are linear combinations of the `filter_vals` defined above
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# For an example, print out the values of filter 1
print('Filter 1: \n', filter_1)
###Output
Filter 1:
[[-1 -1 1 1]
[-1 -1 1 1]
[-1 -1 1 1]
[-1 -1 1 1]]
###Markdown
Define convolutional and pooling layersInitialize a convolutional layer so that it contains all your created filters. Then add a maxpooling layer, [documented here](https://pytorch.org/docs/stable/nn.htmlmaxpool2d), with a kernel size of (4x4) so you can really see that the image resolution has been reduced after this step!
###Code
import torch
import torch.nn as nn
import torch.nn.functional as F
# define a neural network with a convolutional layer with four filters
# AND a pooling layer of size (4, 4)
class Net(nn.Module):
def __init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# assumes there are 4 grayscale filters
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(4, 4)
def forward(self, x):
# calculates the output of a convolutional layer
# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layers
return conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
###Output
Net(
(conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False)
(pool): MaxPool2d(kernel_size=4, stride=4, padding=0, dilation=1, ceil_mode=False)
)
###Markdown
Visualize the output of each filterFirst, we'll define a helper function, `viz_layer` that takes in a specific layer and number of filters (optional argument), and displays the output of that layer once an image has been passed through.
###Code
# helper function for visualizing the output of a given layer
# default number of filters is 4
def viz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1, xticks=[], yticks=[])
# grab layer outputs
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
###Output
_____no_output_____
###Markdown
Let's look at the output of a convolutional layer after a ReLu activation function is applied.
###Code
# plot original image
plt.imshow(gray_img, cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# convert the image into an input Tensor
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
# get all the layers
conv_layer, activated_layer, pooled_layer = model(gray_img_tensor)
# visualize the output of the activated conv layer
viz_layer(activated_layer)
###Output
_____no_output_____
###Markdown
Visualize the output of the pooling layerThen, take a look at the output of a pooling layer. The pooling layer takes as input the feature maps pictured above and reduces the dimensionality of those maps, by some pooling factor, by constructing a new, smaller image of only the maximum (brightest) values in a given kernel area.
###Code
# visualize the output of the pooling layer
viz_layer(pooled_layer)
###Output
_____no_output_____
|
JesseOtradovecLS_DS_111_A_First_Look_at_Data.ipynb
|
###Markdown
Lambda School Data Science - A First Look at Data Lecture - let's explore Python DS libraries and examples!The Python Data Science ecosystem is huge. You've seen some of the big pieces - pandas, scikit-learn, matplotlib. What parts do you want to see more of?
###Code
# TODO - we'll be doing this live, taking requests
# and reproducing what it is to look up and learn things
###Output
_____no_output_____
###Markdown
Assignment - now it's your turnPick at least one Python DS library, and using documentation/examples reproduce in this notebook something cool. It's OK if you don't fully understand it or get it 100% working, but do put in effort and look things up.
###Code
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
#I'm making a particular system of three parabolic equations.
###Output
_____no_output_____
###Markdown
$$\left(\begin{array}{ccc}x_1^2 & x_1 & 1 \\x_2^2 & x_2 & 1 \\x_3^2 & x_3 & 1 \\\end{array}\right)\left(\begin{array}{c}a \\b \\c \\\end{array}\right)=\left(\begin{array}{c}y_1 \\y_2 \\y_3 \\\end{array}\right)$$
###Code
xp = np.array([-2, 1, 4])
yp = np.array([2, -1, 4])
A = np.zeros((3,3))
rhs = np.zeros(3)
for i in range (3):
A[i] = xp [i] **2, xp[i], 1
rhs[i] = yp[i]
print("Array A:")
print(A)
print("rhs:", rhs)
sol=np.linalg.solve(A,rhs)
print("solution is:", sol)
print("specified values of y:", yp)
print("A @ sol:", A @ sol) #this is new syntax
plt.plot(xp,yp,'ro')
x = np.linspace(-3, 5, 100)
y = sol[0] * x ** 2 + sol[1] *x + sol[2]
plt.plot(x,y,'b')
###Output
_____no_output_____
###Markdown
Assignment questionsAfter you've worked on some code, answer the following questions in this text block:1. Describe in a paragraph of text what you did and why, as if you were writing an email to somebody interested but nontechnical.I threw a linearly interdependant system of three parabolic equations into python to solve it and plotted the solution to check my work, along with checking it against the work of the person who made the notebook I'm working with. 2. What was the most challenging part of what you did? Finding the notebook I wanted to work with that was interesting enough to play with but not a research paper on physics... I basically want to do physics research and develop a pipeline for searching for signals in gravitational wave data while at Lambda. 3. What was the most interesting thing you learned? The A @ y syntax works!4. What area would you like to explore with more time? Seriously I spent most of my assignment time debugging zoom and then getting excited about physics papers. I just didn't have time to reproduce any physics results today. Also I need to remember how to tell numpy how to multiply matrices instead of looping like they did in the example. For the exercise. Stretch goals and resourcesFollowing are *optional* things for you to take a look at. Focus on the above assignment first, and make sure to commit and push your changes to GitHub (and since this is the first assignment of the sprint, open a PR as well).- [pandas documentation](https://pandas.pydata.org/pandas-docs/stable/)- [scikit-learn documentation](http://scikit-learn.org/stable/documentation.html)- [matplotlib documentation](https://matplotlib.org/contents.html)- [Awesome Data Science](https://github.com/bulutyazilim/awesome-datascience) - a list of many types of DS resourcesStretch goals:- Find and read blogs, walkthroughs, and other examples of people working through cool things with data science - and share with your classmates!- Write a blog post (Medium is a popular place to publish) introducing yourself as somebody learning data science, and talking about what you've learned already and what you're excited to learn more about.
###Code
###Output
_____no_output_____
###Markdown
Exercises given me by the resourse I'm working with:Consider the following four measurements of the quantity y at time t: (t_0,y_0)=(0,3), (t_1,y_1)=(0.25,1), (t_2,y_2)=(0.5,−3), (t_3,y_3)=(0.75,1). The measurements are part of a wave that may be written asy=a*cos(pi*t)+b*cos(2*pi*t)+c*cos(3*pi*t)+d*cos(4*pi*t)where a, b, c, and d are parameters. Build a system of four linear equations and solve for the four parameters. Creates a plot of the wave for t going from 0 to 1 and show the four measurements with dots.I actually just don't know how to do this exercise because the t isn't just multiplied through, it's in a cosine... So I'm just going to make up an a matrix and multiply it through then follow along with the solution given.
###Code
tp = np.matrix('0; 0.25; 0.5; 0.75')
yp = np.matrix('3;1;-3;1')
A = np.matrix('1,2,3,4;5,6,7,8;2,3,5,6;7,5,4,3')
rhs = yp
sol = np.linalg.solve(A, yp)
print("a,b,c,d:")
print(sol)
###Output
_____no_output_____
###Markdown
ok, right, now just instead of making up the coeffecients for A I just need to multiply through with the cos(n pi t) and we have t. so...
###Code
A = np.zeros((4, 4))
rhs = np.zeros(4)
for i in range(4):
A[i] = np.cos(1 * np.pi * tp[i]), np.cos(2 * np.pi * tp[i]), \
np.cos(3 * np.pi * tp[i]), np.cos(4 * np.pi * tp[i])
sol = np.linalg.solve(A, yp)
print('a,b,c,d: ',sol)
t = np.linspace(0, 1, 100)
#print(t)
y = sol[0] * np.cos(1 * np.pi * t) + sol[1] * np.cos(2 * np.pi * t) + \
sol[2] * np.cos(3 * np.pi * t) + sol[3] * np.cos(4 * np.pi * t)
print ()
plt.plot(t, np.transpose(y), 'b', label='wave')
plt.plot(tp, yp, 'ro', label='data')
plt.show()
###Output
_____no_output_____
|
.ipynb_checkpoints/05-checkpoint.ipynb
|
###Markdown
All the IPython Notebooks in this lecture series are available at https://github.com/rajathkumarmp/Python-Lectures Control Flow Statements If if some_condition: algorithm
###Code
x = 12
if x >10:
print "Hello"
###Output
Hello
###Markdown
If-else if some_condition: algorithm else: algorithm
###Code
x = 12
if x > 10:
print "hello"
else:
print "world"
###Output
hello
###Markdown
if-elif if some_condition: algorithmelif some_condition: algorithmelse: algorithm
###Code
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
else:
print "x=y"
###Output
x<y
###Markdown
if statement inside a if statement or if-elif or if-else are called as nested if statements.
###Code
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
if x==10:
print "x=10"
else:
print "invalid"
else:
print "x=y"
###Output
x<y
x=10
###Markdown
Loops For for variable in something: algorithm
###Code
for i in range(5):
print i
###Output
0
1
2
3
4
###Markdown
In the above example, i iterates over the 0,1,2,3,4. Every time it takes each value and executes the algorithm inside the loop. It is also possible to iterate over a nested list illustrated below.
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
print list1
###Output
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
###Markdown
A use case of a nested for loop in this case would be,
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
for x in list1:
print x
###Output
1
2
3
4
5
6
7
8
9
###Markdown
While while some_condition: algorithm
###Code
i = 1
while i < 3:
print(i ** 2)
i = i+1
print('Bye')
###Output
1
4
Bye
###Markdown
Break As the name says. It is used to break out of a loop when a condition becomes true when executing the loop.
###Code
for i in range(100):
print i
if i>=7:
break
###Output
0
1
2
3
4
5
6
7
###Markdown
Continue This continues the rest of the loop. Sometimes when a condition is satisfied there are chances of the loop getting terminated. This can be avoided using continue statement.
###Code
for i in range(10):
if i>4:
print "The end."
continue
elif i<7:
print i
###Output
0
1
2
3
4
The end.
The end.
The end.
The end.
The end.
###Markdown
List Comprehensions Python makes it simple to generate a required list with a single line of code using list comprehensions. For example If i need to generate multiples of say 27 I write the code using for loop as,
###Code
res = []
for i in range(1,11):
x = 27*i
res.append(x)
print res
###Output
[27, 54, 81, 108, 135, 162, 189, 216, 243, 270]
###Markdown
Since you are generating another list altogether and that is what is required, List comprehensions is a more efficient way to solve this problem.
###Code
[27*x for x in range(1,11)]
###Output
_____no_output_____
###Markdown
That's it!. Only remember to enclose it in square brackets Understanding the code, The first bit of the code is always the algorithm and then leave a space and then write the necessary loop. But you might be wondering can nested loops be extended to list comprehensions? Yes you can.
###Code
[27*x for x in range(1,20) if x<=10]
###Output
_____no_output_____
###Markdown
Let me add one more loop to make you understand better,
###Code
[27*z for i in range(50) if i==27 for z in range(1,11)]
###Output
_____no_output_____
###Markdown
Control Flow Statements If if some_condition: algorithm
###Code
x = 12
if x >10:
print "Hello"
###Output
Hello
###Markdown
If-else if some_condition: algorithm else: algorithm
###Code
x = 12
if x > 10:
print "hello"
else:
print "world"
###Output
hello
###Markdown
if-elif if some_condition: algorithmelif some_condition: algorithmelse: algorithm
###Code
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
else:
print "x=y"
###Output
x<y
###Markdown
if statement inside a if statement or if-elif or if-else are called as nested if statements.
###Code
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
if x==10:
print "x=10"
else:
print "invalid"
else:
print "x=y"
###Output
x<y
x=10
###Markdown
Loops For for variable in something: algorithm
###Code
for i in range(5):
print i
###Output
0
1
2
3
4
###Markdown
In the above example, i iterates over the 0,1,2,3,4. Every time it takes each value and executes the algorithm inside the loop. It is also possible to iterate over a nested list illustrated below.
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
print list1
###Output
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
###Markdown
A use case of a nested for loop in this case would be,
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
for x in list1:
print x
###Output
1
2
3
4
5
6
7
8
9
###Markdown
While while some_condition: algorithm
###Code
i = 1
while i < 3:
print(i ** 2)
i = i+1
print('Bye')
###Output
1
4
Bye
###Markdown
Break As the name says. It is used to break out of a loop when a condition becomes true when executing the loop.
###Code
for i in range(100):
print i
if i>=7:
break
###Output
0
1
2
3
4
5
6
7
###Markdown
Continue This continues the rest of the loop. Sometimes when a condition is satisfied there are chances of the loop getting terminated. This can be avoided using continue statement.
###Code
for i in range(10):
if i>4:
print "The end."
continue
elif i<7:
print i
###Output
0
1
2
3
4
The end.
The end.
The end.
The end.
The end.
###Markdown
List Comprehensions Python makes it simple to generate a required list with a single line of code using list comprehensions. For example If i need to generate multiples of say 27 I write the code using for loop as,
###Code
res = []
for i in range(1,11):
x = 27*i
res.append(x)
print res
###Output
[27, 54, 81, 108, 135, 162, 189, 216, 243, 270]
###Markdown
Since you are generating another list altogether and that is what is required, List comprehensions is a more efficient way to solve this problem.
###Code
[27*x for x in range(1,11)]
###Output
_____no_output_____
###Markdown
That's it!. Only remember to enclose it in square brackets Understanding the code, The first bit of the code is always the algorithm and then leave a space and then write the necessary loop. But you might be wondering can nested loops be extended to list comprehensions? Yes you can.
###Code
[27*x for x in range(1,20) if x<=10]
###Output
_____no_output_____
###Markdown
Let me add one more loop to make you understand better,
###Code
[27*z for i in range(50) if i==27 for z in range(1,11)]
###Output
_____no_output_____
###Markdown
Control Flow Statements If-statements The basic form of the if-statement is:```if some_condition: algorithm```
###Code
x = 12
if x >10:
print("Hello")
###Output
Hello
###Markdown
If-else You can also have an `else` block which is executed if the `if` statement is not true:```pythonif some_condition: do somethingelse: do something else```
###Code
x = 12
if x > 10:
print("hello")
else:
print("world")
###Output
hello
###Markdown
if-elif You can have multiple condition using `elif`. They are tested in order, and the first which evaluates to true is executed. If none evaluate to true, then the optional `else` block is executed (if it exists):```pythonif some_condition: algorithmelif some_condition: algorithmelse: algorithm```
###Code
x = 10
y = 12
if x > y:
print("greater")
elif x < y:
print("less")
else:
print("equal")
###Output
less
###Markdown
if statement inside a `if` statement or `if-elif` or `if-else` are called as nested if statements.
###Code
x = 10
y = 12
if x > y:
print("greater")
elif x < y:
print("less")
if x==10:
print("x=10")
else:
print("invalid")
else:
print("x=y")
###Output
less
x=10
###Markdown
Loops For The main looping construct in Python is the for-loop. It uses the form:```pythonfor item in sequence: algorithm```
###Code
for i in range(5):
print(i)
###Output
0
1
2
3
4
###Markdown
In the above example, i iterates over the 0,1,2,3,4. Every time it takes each value and executes the algorithm inside the loop. It is also possible to iterate over a nested list illustrated below.
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
print(list1)
###Output
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
###Markdown
A use case of a nested for loop in this case would be,
###Code
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
for x in list1:
print(x)
###Output
1
2
3
4
5
6
7
8
9
###Markdown
While While-loops will execute a body as long as some condition is true:```pythonwhile some_condition: algorithm```
###Code
i = 1
while i < 3:
print(i ** 2)
i = i+1
print('Bye')
###Output
1
4
Bye
###Markdown
Break As the name says. It is used to break out of a loop when a condition becomes true when executing the loop.
###Code
for i in range(100):
print(i)
if i>=7:
break
###Output
0
1
2
3
4
5
6
7
###Markdown
Continue This continues the rest of the loop. Sometimes when a condition is satisfied there are chances of the loop getting terminated. This can be avoided using continue statement.
###Code
for i in range(10):
if i>4:
print("The end.")
continue
elif i<7:
print(i)
###Output
0
1
2
3
4
The end.
The end.
The end.
The end.
The end.
###Markdown
List Comprehensions Python makes it simple to generate a required list with a single line of code using list comprehensions. For example If i need to generate multiples of say 27 I write the code using for loop as,
###Code
res = []
for i in range(1,11):
x = 27*i
res.append(x)
res
###Output
_____no_output_____
###Markdown
Since you are generating another list altogether and that is what is required, List comprehensions is a more efficient way to solve this problem.
###Code
[27*x for x in range(1,11)]
###Output
_____no_output_____
###Markdown
That's it! Only remember to enclose it in square brackets Understanding the code, The first bit of the code is always the algorithm and then leave a space and then write the necessary loop. But you might be wondering can nested loops be extended to list comprehensions? Yes you can.
###Code
[27*x for x in range(1,20) if x<=10]
###Output
_____no_output_____
###Markdown
Let me add one more loop to make you understand better,
###Code
[27*z for i in range(50) if i==27 for z in range(1,11)]
###Output
_____no_output_____
|
post-training_static_quantization.ipynb
|
###Markdown
Uploading files
###Code
# captcha dataset:
dataset = tarfile.open('dataset.tar')
dataset.extractall()
dataset.close()
###Output
_____no_output_____
###Markdown
Images from dataset
###Code
data_path = '../datasets/dataset'
plt.figure(figsize=(20, 10))
for i in range(9):
file = random.choice(os.listdir(data_path))
image_path = os.path.join(data_path, file)
img = mimg.imread(image_path)
ax = plt.subplot(3, 3, i + 1)
plt.title(str(file[:-4]), fontsize=20)
plt.imshow(img)
###Output
_____no_output_____
###Markdown
Train and test datasets
###Code
transform = transforms.Compose([
transforms.Resize([224, 224]),
transforms.ToTensor()])
sys.path.append('../scripts')
from dataset_creator import train_test_split
train_dataset = train_test_split(data_path, transform=transform)
test_dataset = train_test_split(data_path, is_train=False, transform=transform)
train_dataloader = DataLoader(train_dataset, batch_size=107, num_workers=0)
test_dataloader = DataLoader(test_dataset, batch_size=1, num_workers=0)
# train_dataset is set to 0.9 part of the initial dataset
len(train_dataset), len(test_dataset)
# Сomponents of captcha texts
numbers = list(str(i) for i in range(10))
letters = list(string.ascii_lowercase)
all_char = numbers + letters
all_char_len = len(all_char)
captcha_len = 5
###Output
_____no_output_____
###Markdown
Model
###Code
model = models.resnet18(pretrained=True)
model.conv1 = torch.nn.Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
model.fc = torch.nn.Linear(in_features=512, out_features=all_char_len * captcha_len, bias=True)
model
###Output
_____no_output_____
###Markdown
Model training
###Code
device = 'cuda'
model.to(device);
loss_function = torch.nn.MultiLabelSoftMarginLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
loss_arr = [] # for visualization of the training loss
def train_model(model, loss_function, optimizer, num_epochs=30):
dataloader = train_dataloader
for epoch in range(num_epochs):
print('Epoch {}/{}:'.format(epoch, num_epochs - 1), flush=True)
for iteration, i in enumerate(dataloader):
img, label_oh, label = i
img = Variable(img).to(device)
labels = Variable(label_oh.float()).to(device)
pred = model(img)
loss = loss_function(pred, labels)
optimizer.zero_grad()
loss_arr.append(float(loss))
loss.backward()
optimizer.step()
return model, loss_arr
train_model(model, loss_function, optimizer)
plt.figure(figsize=(16,8))
plt.plot(range(len(loss_arr)), loss_arr, lw=3, label='loss')
plt.grid(True)
plt.legend( prop={'size': 24})
plt.title('Training loss', fontsize=24)
plt.xlabel('iteration', fontsize=20)
plt.ylabel('loss', fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.show()
torch.save(model.state_dict(), '../models/test_models/resnet18_captcha.pth')
###Output
_____no_output_____
###Markdown
Quantization
###Code
from resnet_quant import resnet18
"""
Resnet_quant is a custom module, where inputs/otnputs are quantized/dequantized using QuantStub/DeQuantStub.
It can be used for quantization/running qauntized models: 'resnet18', 'resnet34', 'resnet50', 'resnet101' and 'resnet152'.
"""
model = resnet18(pretrained=True)
model.conv1 = torch.nn.Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
model.fc = torch.nn.Linear(in_features=512, out_features=all_char_len * captcha_len, bias=True)
checkpoint = torch.load('../models/test_models/resnet18_captcha.pth')
model.load_state_dict(checkpoint)
"""
Here post-training static quantization method is used.
"""
modules_to_fuse = [['conv1', 'bn1'],
['layer1.0.conv1', 'layer1.0.bn1'],
['layer1.0.conv2', 'layer1.0.bn2'],
['layer1.1.conv1', 'layer1.1.bn1'],
['layer1.1.conv2', 'layer1.1.bn2'],
['layer2.0.conv1', 'layer2.0.bn1'],
['layer2.0.conv2', 'layer2.0.bn2'],
['layer2.0.downsample.0', 'layer2.0.downsample.1'],
['layer2.1.conv1', 'layer2.1.bn1'],
['layer2.1.conv2', 'layer2.1.bn2'],
['layer3.0.conv1', 'layer3.0.bn1'],
['layer3.0.conv2', 'layer3.0.bn2'],
['layer3.0.downsample.0', 'layer3.0.downsample.1'],
['layer3.1.conv1', 'layer3.1.bn1'],
['layer3.1.conv2', 'layer3.1.bn2'],
['layer4.0.conv1', 'layer4.0.bn1'],
['layer4.0.conv2', 'layer4.0.bn2'],
['layer4.0.downsample.0', 'layer4.0.downsample.1'],
['layer4.1.conv1', 'layer4.1.bn1'],
['layer4.1.conv2', 'layer4.1.bn2']]
model_quantized = model
model_quantized.eval();
torch.backends.quantized.engine = 'qnnpack'
model_quantized = torch.quantization.fuse_modules(model_quantized, modules_to_fuse)
model_quantized.qconfig = torch.quantization.get_default_qconfig('qnnpack')
torch.quantization.prepare(model_quantized, inplace=True)
model_quantized.eval();
with torch.no_grad():
for m, i in enumerate(train_dataloader):
print(m)
img, label_oh, label = i
img = Variable(img)
model_quantized(img)
torch.quantization.convert(model_quantized, inplace=True)
torch.save(model_quantized.state_dict(), '../models/test_models/resnet18_captcha_quantized.pth')
###Output
_____no_output_____
###Markdown
Test
###Code
def print_size_of_model(model):
torch.save(model.state_dict(), "temp.p")
size=os.path.getsize("temp.p")
print('Size (KB):', size/1e3)
os.remove('temp.p')
def test(model, device, test_loader):
model.to(device)
model.eval();
print_size_of_model(model)
predicted_labels = []
true_labels = []
correct = 0
with torch.no_grad():
for i, (img, label_oh, label) in enumerate(test_dataloader):
img = Variable(img).to(device)
st = time.time()
pred = model(img)
et = time.time()
s_0 = all_char[np.argmax(pred.squeeze().cpu().tolist()[0:all_char_len])]
s_1 = all_char[np.argmax(pred.squeeze().cpu().tolist()[all_char_len:all_char_len * 2])]
s_2 = all_char[np.argmax(pred.squeeze().cpu().tolist()[all_char_len * 2:all_char_len * 3])]
s_3 = all_char[np.argmax(pred.squeeze().cpu().tolist()[all_char_len * 3:all_char_len * 4])]
s_4 = all_char[np.argmax(pred.squeeze().cpu().tolist()[all_char_len * 4:all_char_len * 5])]
captcha = '%s%s%s%s%s' % (s_0, s_1, s_2, s_3, s_4)
true_labels.append(label[0])
predicted_labels.append(captcha)
if label[0] == captcha:
correct += 1
print("========================================= PERFORMANCE =============================================")
print('Accuracy: {}/{} ({:.2f}%)\n'.format(correct, len(test_dataloader), 100. * correct / len(test_dataloader)))
print('Elapsed time = {:0.4f} milliseconds'.format((et - st) * 1000))
print("====================================================================================================")
return predicted_labels, true_labels
"""
LOADING MODELS FROM CHECKPOINTS
"""
# RESNET-18
model = models.resnet18(pretrained=True)
model.conv1 = torch.nn.Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
model.fc = torch.nn.Linear(in_features=512, out_features=all_char_len * captcha_len, bias=True)
checkpoint = torch.load('../models/test_models/resnet18_captcha.pth')
model.load_state_dict(checkpoint)
# QUANTIZED RESNET-18
from resnet_quant import resnet18
modules_to_fuse = [['conv1', 'bn1'],
['layer1.0.conv1', 'layer1.0.bn1'],
['layer1.0.conv2', 'layer1.0.bn2'],
['layer1.1.conv1', 'layer1.1.bn1'],
['layer1.1.conv2', 'layer1.1.bn2'],
['layer2.0.conv1', 'layer2.0.bn1'],
['layer2.0.conv2', 'layer2.0.bn2'],
['layer2.0.downsample.0', 'layer2.0.downsample.1'],
['layer2.1.conv1', 'layer2.1.bn1'],
['layer2.1.conv2', 'layer2.1.bn2'],
['layer3.0.conv1', 'layer3.0.bn1'],
['layer3.0.conv2', 'layer3.0.bn2'],
['layer3.0.downsample.0', 'layer3.0.downsample.1'],
['layer3.1.conv1', 'layer3.1.bn1'],
['layer3.1.conv2', 'layer3.1.bn2'],
['layer4.0.conv1', 'layer4.0.bn1'],
['layer4.0.conv2', 'layer4.0.bn2'],
['layer4.0.downsample.0', 'layer4.0.downsample.1'],
['layer4.1.conv1', 'layer4.1.bn1'],
['layer4.1.conv2', 'layer4.1.bn2']]
torch.backends.quantized.engine = 'qnnpack'
model_quantized = resnet18(pretrained=True)
model_quantized.conv1 = torch.nn.Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
model_quantized.fc = torch.nn.Linear(in_features=512, out_features=all_char_len * captcha_len, bias=True)
model_quantized.qconfig = torch.quantization.get_default_qconfig('qnnpack')
model_quantized.eval();
model_quantized = torch.quantization.fuse_modules(model_quantized, modules_to_fuse)
torch.quantization.prepare(model_quantized, inplace=True)
torch.quantization.convert(model_quantized, inplace=True)
checkpoint = torch.load('../models/test_models/resnet18_captcha_quantized.pth')
model_quantized.load_state_dict(checkpoint)
device = 'cuda'
test(model, device, test_dataloader)
device = 'cpu'
test(model_quantized, device, test_dataloader)
###Output
Size (KB): 11314.005
========================================= PERFORMANCE =============================================
Accuracy: 83/107 (77.57%)
Elapsed time = 182.6580 milliseconds
====================================================================================================
|
start-cse.ipynb
|
###Markdown
CSE - Runtime Starting the CSEExecuting the following command will start a CSE inside the notebook. Changing the Log LevelFor these notebooks the CSE is configured to run in headless mode, which means it will not produce any runtime messages. This is done for better readability of this page.To get more verbose output to see how commands are processed inside the CSE you can replace the last line in the following cell with %run ./acme.py --log-level debug Stopping the CSEOnly one instance of the CSE can run at a time. To stop it you need to *restart* this notebook's kernel from the menu above. **Please be patient. The CSE might take a few seconds to shutdown**. CSE WebUIThe CSE has a WebUI that allows you to see the CSE's resource tree and resources' details.It is available at [http://localhost:8080/webui](http://localhost:8080/webui) .
###Code
# Increase the width of the notebook to accomodate the log output
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
# change to the CSE's directory and start the CSE
%cd -q tools/ACME
%run ./acme.py --headless
###Output
_____no_output_____
###Markdown
CSE - StarterExecuting the following command will start a CSE inside the notebook. Changing the Log LevelTo get more verbose output to see how commands are processed inside the CSE you can replace the last line in the following cell with %run ./acme.py --log-level debug Stopping the CSEOnly one instance of the CSE can run at a time. To stop it just *restart* the notebook's kernel. **Please be patient. The CSE might take a few seconds to shutdown**. CSE WebUIThe CSE has a WebUI that allows you to see the CSE's resource tree and resources' details.It is available at [http://localhost:8080/webui](http://localhost:8080/webui) .
###Code
# Increase the width of the notebook to accomodate the log output
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
# change to the CSE's directory and start the CSE
%cd tools/ACME
%run ./acme.py
###Output
_____no_output_____
|
3-Natural-Lanugage-Processing-in-TensorFlow/week1-sentiment-in-text/Course_3_Week_1_Lesson_2.ipynb
|
###Markdown
Copyright 2019 The TensorFlow Authors.
###Code
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
sentences = [
'I love my dog',
'I love my cat',
'You love my dog!',
'Do you think my dog is amazing?'
]
tokenizer = Tokenizer(num_words = 100, oov_token="<OOV>")
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
sequences = tokenizer.texts_to_sequences(sentences)
padded = pad_sequences(sequences, maxlen=5)
print("\nWord Index = " , word_index)
print("\nSequences = " , sequences)
print("\nPadded Sequences:")
print(padded)
# Try with words that the tokenizer wasn't fit to
test_data = [
'i really love my dog',
'my dog loves my manatee'
]
test_seq = tokenizer.texts_to_sequences(test_data)
print("\nTest Sequence = ", test_seq)
padded = pad_sequences(test_seq, maxlen=10)
print("\nPadded Test Sequence: ")
print(padded)
###Output
_____no_output_____
|
data/5 - XGBoost features originales (0.7468) - CatBoost simple (0.7367).ipynb
|
###Markdown
Lectura de archivos
###Code
%matplotlib inline
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
# Authenticate and create the PyDrive client
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
id = '1FAjcexe-71nGuYIzvnQ46IdXVcqM9cx4'
downloaded = drive.CreateFile({'id': id})
downloaded.GetContentFile('test_values_complete_features.csv')
test_values1 = pd.read_csv('test_values_complete_features.csv', encoding='latin-1', index_col='building_id')
test_values1[test_values1.select_dtypes('O').columns] = test_values1[test_values1.select_dtypes('O').columns].astype('category')
id = '1qs2mEnkqiAqebJE2SvqkrfoV66Edguwr'
downloaded = drive.CreateFile({'id': id})
downloaded.GetContentFile('train_values_complete_features.csv')
train_values1 = pd.read_csv('train_values_complete_features.csv', encoding='latin-1', index_col='building_id')
train_values1[train_values1.select_dtypes('O').columns] = train_values1[train_values1.select_dtypes('O').columns].astype('category')
id='1RUtolRcQlR3RGULttM4ZoQaK_Ouow4gc'
downloaded = drive.CreateFile({'id': id})
downloaded.GetContentFile('train_labels.csv')
train_labels = pd.read_csv('train_labels.csv', encoding='latin-1', dtype={'building_id': 'int64', 'damage_grade': 'int64'}, index_col='building_id')
id='1br3fMwXX_J0XmiXvOm_wfKWvHSj45T3y'
downloaded = drive.CreateFile({'id': id})
downloaded.GetContentFile('train_values.csv')
train_values2 = pd.read_csv('train_values.csv', encoding='latin-1', index_col='building_id')
train_values2[train_values2.select_dtypes('O').columns] = train_values2[train_values2.select_dtypes('O').columns].astype('category')
id = '1kt2VFhgpfRS72wtBOBy1KDat9LanfMZU'
downloaded = drive.CreateFile({'id': id})
downloaded.GetContentFile('test_values.csv')
test_values2 = pd.read_csv('test_values.csv', encoding='latin-1', index_col='building_id')
test_values2[test_values2.select_dtypes('O').columns] = test_values2[test_values2.select_dtypes('O').columns].astype('category')
train_values_complete = train_values1.copy()
test_values_complete = test_values1.copy()
train_values_incomplete = train_values2.copy()
test_values_incomplete = test_values2.copy()
###Output
_____no_output_____
###Markdown
XGBoost (muy buena prueba)
###Code
train_values = train_values_incomplete.copy()
test_values = test_values_incomplete.copy()
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score, confusion_matrix
from sklearn.ensemble import RandomForestClassifier
train_values['legal_ownership_status'].dtype
def get_obj(train, p = False):
obj_types = []
for column in train.columns:
if column in train.select_dtypes('category').columns:
if p: print(column)
obj_types.append(column)
return obj_types
obj_types = get_obj(train_values, True)
def transform_to_int(train, obj_types):
#Assign dictionaries with current values and replacements for each column
d_lsc = {'n':0, 'o':1, 't':2}
d_ft = {'h':0, 'i':1, 'r':2, 'u':3, 'w':4}
d_rt = {'n':0, 'q':1, 'x':2}
d_gft = {'f':0, 'm':1, 'v':2, 'x':3, 'z':4}
d_oft = {'j':0, 'q':1, 's':2, 'x':3}
d_pos = {'j':0, 'o':1, 's':2, 't':3}
d_pc = {'a':0, 'c':1, 'd':2, 'f':3, 'm':4, 'n':5, 'o':6, 'q':7, 's':8, 'u':9}
d_los = {'a':0, 'r':1, 'v':2, 'w':3}
#Each positional index in replacements corresponds to the column in obj_types
replacements = [d_lsc, d_ft, d_rt, d_gft, d_oft, d_pos, d_pc, d_los]
#Replace using lambda Series.map(lambda)
for i,col in enumerate(obj_types):
train[col] = train[col].map(lambda a: replacements[i][a]).astype('int64')
transform_to_int(train_values, obj_types)
x_train, x_test, y_train, y_test = train_test_split(train_values, train_labels)
rcf = RandomForestClassifier()
model = rcf.fit(x_train, y_train)
y_pred = model.predict(x_test)
f1_score(y_test, y_pred,average='micro')
importance = pd.DataFrame({"Feature":list(train_values), "Importance": rcf.feature_importances_}) # build a dataframe with features and their importance
importance = importance.sort_values(by="Importance", ascending=False) #sort by importance
importance
###Output
_____no_output_____
###Markdown
Elimino outliers de los parámetros más importantes
###Code
import textwrap
import matplotlib.cm as colors
top=10
importance_10 = importance.head(top)
a4_dims = (16, 12)
fig, ax = plt.subplots(figsize=a4_dims)
plot=sns.barplot(x=importance_10["Feature"], y=importance_10["Importance"], ax=ax, palette = colors.rainbow(np.linspace(0, 1, top)))
plot.set_xticklabels(plot.get_xticklabels(), rotation=90)
plt.title("15 Most Important Features")
xlocs = plt.xticks()
ax.set_axisbelow(True)
for i in range(top):
texto_fin=""
texto=importance_10['Feature'].tolist()[i]
texto_fin =texto_fin+palabra+"\n"
plt.text(xlocs[0][i],0.005, texto ,ha = "center",rotation=90)
plt.xticks([])
plt.show()
plt.barh(boston.feature_names, rf.feature_importances_)
boxplot_cols=["geo_level_3_id","geo_level_2_id","geo_level_1_id","age", "area_percentage", "height_percentage"]
q=1
plt.figure(figsize=(20,20))
for j in boxplot_cols:
plt.subplot(3,3,q)
ax=sns.boxplot(train_values[j].dropna())
plt.xlabel(j)
q+=1
plt.show()
###Output
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variable as a keyword arg: x. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
###Markdown
Se aprecia que para los de `geo_level_id` no hay outliers, pero para los otros 3 si.
###Code
import scipy
def remove_outliers(df, col_cutoff = 0.01, z_score = 3.5): #define a function to get rid of all outliers of the most important columns
important_cols = importance[importance.Importance>col_cutoff]['Feature'].tolist() #get all columns with importance > 0.01.
df_new = df.copy() #init the new df
for col in important_cols: df_new = df_new[np.abs(scipy.stats.zscore(df_new[col]))<z_score] #removing all rows where a z-score is >3
return df_new
df = pd.concat([train_values, train_labels], axis = 1)
df_new = remove_outliers(df)
y = df_new.pop('damage_grade')
x = df_new
y.value_counts()
###Output
_____no_output_____
###Markdown
Se removieron un montón de valores `damage_grade` = 1 porque eran outliers, lo que no es muy bueno. Acá una justificación del valor elegido para el z_score: Given the size of our dataset, ~ 260,000 samples, considering all variables with z scores > 3, as outliers, corresponding to 0.27% percentile, might be removing some useful data.A z score of 3.5, corresponding with the 0.0465% could also be good enough to remove outliers, while preserving more samples. This way, the original distrbituion between damage grades may be better preserved too.
###Code
def get_original():
df = train_values_incomplete.copy()
#df.drop('building_id', axis =1, inplace=True)
obj_types = get_obj(df)
transform_to_int(df, obj_types)
df['damage_grade'] = train_labels.damage_grade
return df
df = get_original()
#función para volver a dividir df en train_values y train_labels
def get_xy(df):
y = df.pop('damage_grade')
x= df
return x, y
x,y = get_xy(df)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.1, random_state = 42)
def test_model(model, removing = False, col_cutoff = 0.01, z_score = 3.5):
df_train = pd.concat([x_train, y_train], axis = 1) #combine them together, so outliers are simultaneously removed from both
if removing: df_train = remove_outliers(df_train, col_cutoff, z_score)
x, y = get_xy(df_train)
model.fit(x, y)
y_pred = model.predict(x_test)
print(f1_score(y_test, y_pred, average='micro'))
test_model(xgb.XGBRFClassifier()) #xgboost con random forest incluido
test_model(xgb.XGBClassifier()) #xgboost normal
test_model(xgb.XGBClassifier(), True)
xgbc = xgb.XGBClassifier(min_child_weight= 5, learning_rate= 0.1, gamma= 0.05, subsample= 0.8,colsample_bytree= 0.3, colsample_bynode= 0.8,
colsample_bylevel= 0.8, max_depth = 20, n_estimators = 150)
test_model(xgbc)
def submit_model(model, file_name):
test = test_values_incomplete.copy()
transform_to_int(test, get_obj(test))
submission_predictions = model.predict(test)
submission = pd.DataFrame()
submission["building_id"] = test_values_incomplete.reset_index()['building_id']
submission["damage_grade"] = submission_predictions
submission.to_csv(file_name, index=False)
from sklearn.metrics import f1_score
from sklearn.model_selection import train_test_split
from scipy.sparse import coo_matrix, hstack
from sklearn.metrics import f1_score, accuracy_score, confusion_matrix, classification_report
pred = xgbc.predict(x_test)
score = f1_score(y_test, pred, average='micro')
score = accuracy_score(y_test, pred)
cm = confusion_matrix(y_test, pred)
report = classification_report(y_test, pred)
print("f1_micro: ", score, "\n\n")
print(cm, "\n\n")
print(report, "\n\n")
submit_model(xgbc, 'submission_xgb.csv')
###Output
_____no_output_____
###Markdown
CatBoost (muy buena prueba)
###Code
train_values = train_values_incomplete.copy()
test_values = test_values_incomplete.copy()
pip install catboost
from sklearn.metrics import f1_score
from sklearn.model_selection import train_test_split
from scipy.sparse import coo_matrix, hstack
from catboost import CatBoostClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import OneHotEncoder
idx = train_values.shape[0]
data_df = pd.concat([train_values, test_values], sort=False)
drop_colums = ['count_floors_pre_eq']
data_df = data_df.drop(drop_colums,axis = 1)
data_df.shape
cat_features = ['geo_level_1_id', 'geo_level_2_id', 'geo_level_3_id', 'land_surface_condition', 'foundation_type', 'roof_type',
'ground_floor_type', 'other_floor_type', 'position', 'plan_configuration', 'legal_ownership_status']
data_cat = pd.DataFrame(index = data_df.index,
data = data_df,
columns = cat_features)
data_cat.head()
data_cat.shape
data_num = data_df.drop(columns = cat_features)
num_features = data_num.columns
data_num.shape
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder()
enc.fit(data_cat)
data_cat_encoded = enc.transform(data_cat)
data_cat_encoded.shape
scaler = MinMaxScaler()
data_num_scaled = scaler.fit_transform(data_num)
from scipy.sparse import coo_matrix, hstack
data_num_scaled = coo_matrix(data_num_scaled)
data = hstack((data_cat_encoded,data_num_scaled))
data = data.astype(dtype='float16')
X_train = data.tocsr()[:idx]
X_test = data.tocsr()[idx:]
y_train = train_labels['damage_grade'].values
X_train_split, X_valid_split, y_train_split, y_valid_split = train_test_split(X_train, y_train, test_size=0.2, random_state=42)
trainXGB = CatBoostClassifier(learning_rate=0.1,depth=9,iterations=1000,l2_leaf_reg = 1.8)
trainXGB.fit(X_train, y_train)
y_pred = trainXGB.predict(X_valid_split)
print(f1_score(y_valid_split, y_pred, average='micro'))
y_pred = trainXGB.predict(X_test)
predicted_df = pd.DataFrame(y_pred.astype(np.int8), index = test_values.index, columns=['damage_grade'])
predicted_df.to_csv('catboost_submission1.csv')
###Output
_____no_output_____
###Markdown
CatBoost iterando varias pruebas
###Code
train_values = train_values_incomplete.copy()
test_values = test_values_incomplete.copy()
pip install catboost
from sklearn.metrics import f1_score
from sklearn.model_selection import train_test_split
from scipy.sparse import coo_matrix, hstack
from catboost import CatBoostClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import OneHotEncoder
idx = train_values.shape[0]
data_df = pd.concat([train_values, test_values], sort=False)
drop_colums = ['count_floors_pre_eq']
data_df = data_df.drop(drop_colums,axis = 1)
data_df.shape
cat_features = ['geo_level_1_id', 'geo_level_2_id', 'geo_level_3_id', 'land_surface_condition', 'foundation_type', 'roof_type',
'ground_floor_type', 'other_floor_type', 'position', 'plan_configuration', 'legal_ownership_status']
data_cat = pd.DataFrame(index = data_df.index,
data = data_df,
columns = cat_features)
data_cat.head()
data_cat.shape
data_num = data_df.drop(columns = cat_features)
num_features = data_num.columns
data_num.shape
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder()
enc.fit(data_cat)
data_cat_encoded = enc.transform(data_cat)
data_cat_encoded.shape
scaler = MinMaxScaler()
data_num_scaled = scaler.fit_transform(data_num)
from scipy.sparse import coo_matrix, hstack
data_num_scaled = coo_matrix(data_num_scaled)
data = hstack((data_cat_encoded,data_num_scaled))
data = data.astype(dtype='float16')
X_train = data.tocsr()[:idx]
X_test = data.tocsr()[idx:]
y_train = train_labels['damage_grade'].values
X_train_split, X_valid_split, y_train_split, y_valid_split = train_test_split(X_train, y_train, test_size=0.2, random_state=42)
predictions = []
predictions_test = []
for i in range(5):
trainXGB = CatBoostClassifier(learning_rate=0.1,depth=9,iterations=1000,l2_leaf_reg=1.8, random_seed=i)
trainXGB.fit(X_train, y_train)
predictions.append(trainXGB.predict_proba(X_valid_split))
predictions_test.append(trainXGB.predict_proba(X_test))
def avg(preds, iter):
sum1 = 0
sum2 = 0
sum3 = 0
for p in preds:
sum1 += p[iter][0]
sum2 += p[iter][1]
sum3 += p[iter][2]
return [sum1/5, sum2/5, sum3/5]
result = []
for i in range(len(predictions_test[0])):
avg_l = avg(predictions_test, i)
result.append(avg_l)
idxs_winners = []
for r in result:
m = np.max(r)
idx = [i for i,j in enumerate(r) if j == m]
idxs_winners.append(idx[0]+1)
idxs_winners
len(idxs_winners)
predicted_df = pd.DataFrame(predictions_test[3].astype(np.int8), index = test_values.index, columns=['damage_grade'])
#predicted_df.to_csv('catboost_submission2.csv') -> esta es sin predict_proba
predicted_df2 = pd.DataFrame(idxs_winners, index = test_values.index, columns=['damage_grade'])
predicted_df2.to_csv('catboost_submission_avg.csv')
predicted_df2['damage_grade'].value_counts()
###Output
_____no_output_____
|
Solution/Day_06_Solution_v2.ipynb
|
###Markdown
[作業目標]1. [簡答題] 請問下列這三種方法有什麼不同?```print(a.sum()) print(np.sum(a))print(sum(a)) ```2. 請對一個 5x5 的隨機矩陣作正規化的操作。3. 請建立一個長度等於 10 的正整數向量,並且將其中的最大值改成 -1。 作業 1. [簡答題] 請問下列這三種方法有什麼不同?```print(a.sum()) print(np.sum(a))print(sum(a)) ```
###Code
sum() 是 python 內建的函式,所有型態皆可以用。np.sum(a) 跟 a.sum() 是陣列專有的函式,差別在於定義在 np 或是 array 底下。
###Output
_____no_output_____
###Markdown
2. 請對一個 5x5 的隨機矩陣作正規化的操作。
###Code
# 記得先 Import 正確的套件
import numpy as np
# 參考解答
A = np.random.random((5, 5))
A = (A - A.min()) / (A.max() - A.min())
A
###Output
_____no_output_____
###Markdown
3. 請建立一個長度等於 10 的正整數向量,並且將其中的最大值改成 -1。
###Code
Z = np.random.random(10)
Z[Z.argmax()] = -1
print (Z)
###Output
[ 0.29347583 0.59303277 -1. 0.38043546 0.63265939 0.32472618
0.11340241 0.68136955 0.89905432 0.74769935]
|
22.SQL.ipynb
|
###Markdown
**밑바닥부터 시작하는 데이터과학**Data Science from Scratch- https://github.com/joelgrus/data-science-from-scratch/blob/master/first-edition/code-python3/databases.py **23장 데이터베이스와 SQL**Not Quite A Base 를 파이썬으로 간단하게 구현해 보겠습니다
###Code
import math, random, re
from collections import defaultdict
class Table:
def __init__(self, columns):
self.columns = columns
self.rows = []
def __repr__(self): # Table 을 표현하기 위해 다음 행을 출력
return str(self.columns)+"\n"+"\n".join(map(str, self.rows))
def insert(self, row_values):
if len(row_values) != len(self.columns):
raise TypeError("wrong number of elements")
row_dict = dict(zip(self.columns, row_values))
self.rows.append(row_dict)
def update(self, updates, predicate):
for row in self.rows:
if predicate(row):
for column, new_value in updates.items():
row[column] = new_value
# predicate 해당하는 모든 행을 제거
def delete(self, predicate=lambda row: True):
self.rows = [row for row in self.rows if not(predicate(row))]
def select(self, keep_columns=None, additional_columns=None):
if keep_columns is None: # 특정 열이 명시되지 않으면 모든열 출력
keep_columns = self.columns
if additional_columns is None:
additional_columns = {}
# 결과를 저장하기 위한 새로운 Table
result_table = Table(keep_columns + list(additional_columns.keys()))
for row in self.rows:
new_row = [row[column] for column in keep_columns]
for column_name, calculation in additional_columns.items():
new_row.append(calculation(row))
result_table.insert(new_row)
return result_table
# predicate 에 해당하는 행만 반환 합니다
def where(self, predicate=lambda row: True):
where_table = Table(self.columns)
where_table.rows = list(filter(predicate, self.rows))
return where_table
# 첫 num_row 만큼 행을 반환 합니다
def limit(self, num_rows=None):
limit_table = Table(self.columns)
limit_table.rows = (self.rows[:num_rows]
if num_rows is not None
else self.rows)
return limit_table
def group_by(self, group_by_columns, aggregates, having=None):
grouped_rows = defaultdict(list)
# populate groups
for row in self.rows:
key = tuple(row[column] for column in group_by_columns)
grouped_rows[key].append(row)
result_table = Table(group_by_columns + list(aggregates.keys()))
for key, rows in grouped_rows.items():
if having is None or having(rows):
new_row = list(key)
for aggregate_name, aggregate_fn in aggregates.items():
new_row.append(aggregate_fn(rows))
result_table.insert(new_row)
return result_table
def order_by(self, order):
new_table = self.select() # make a copy
new_table.rows.sort(key=order)
return new_table
def join(self, other_table, left_join=False):
join_on_columns = [c for c in self.columns # columns in
if c in other_table.columns] # both tables
additional_columns = [c for c in other_table.columns # columns only
if c not in join_on_columns] # in right table
# all columns from left table + additional_columns from right table
join_table = Table(self.columns + additional_columns)
for row in self.rows:
def is_join(other_row):
return all(other_row[c] == row[c] for c in join_on_columns)
other_rows = other_table.where(is_join).rows
# each other row that matches this one produces a result row
for other_row in other_rows:
join_table.insert([row[c] for c in self.columns] +
[other_row[c] for c in additional_columns])
# if no rows match and it's a left join, output with Nones
if left_join and not other_rows:
join_table.insert([row[c] for c in self.columns] +
[None for c in additional_columns])
return join_table
###Output
_____no_output_____
###Markdown
**1 CREATE TABLE, INSERT**여러 테이블간의 관계를 행렬로 변환할 수 있습니다
###Code
users = Table(["user_id", "name", "num_friends"])
users.insert([0, "Hero", 0])
users.insert([1, "Dunn", 2])
users.insert([2, "Sue", 3])
users.insert([3, "Chi", 3])
users.insert([4, "Thor", 3])
users.insert([5, "Clive", 2])
users.insert([6, "Hicks", 3])
users.insert([7, "Devin", 2])
users.insert([8, "Kate", 2])
users.insert([9, "Klein", 3])
users.insert([10, "Jen", 1])
print("users table : {}".format(users))
###Output
users table : ['user_id', 'name', 'num_friends']
{'user_id': 0, 'name': 'Hero', 'num_friends': 0}
{'user_id': 1, 'name': 'Dunn', 'num_friends': 2}
{'user_id': 2, 'name': 'Sue', 'num_friends': 3}
{'user_id': 3, 'name': 'Chi', 'num_friends': 3}
{'user_id': 4, 'name': 'Thor', 'num_friends': 3}
{'user_id': 5, 'name': 'Clive', 'num_friends': 2}
{'user_id': 6, 'name': 'Hicks', 'num_friends': 3}
{'user_id': 7, 'name': 'Devin', 'num_friends': 2}
{'user_id': 8, 'name': 'Kate', 'num_friends': 2}
{'user_id': 9, 'name': 'Klein', 'num_friends': 3}
{'user_id': 10, 'name': 'Jen', 'num_friends': 1}
###Markdown
**2 UPDATE, SELECT**SQL 데이터를 입력한 뒤 수정, 업데이트를 해야 합니다
###Code
# SELECT
print("users.select()")
print(users.select())
print("users.limit(2)")
print(users.limit(2))
print("users.select(keep_columns=[\"user_id\"])")
print(users.select(keep_columns=["user_id"]))
print('where(lambda row: row["name"] == "Dunn")')
print(users.where(lambda row: row["name"] == "Dunn")
.select(keep_columns=["user_id"]))
def name_len(row):
return len(row["name"])
print('with name_length:')
print(users.select(keep_columns=[],
additional_columns = { "name_length" : name_len }))
print()
###Output
with name_length:
['name_length']
{'name_length': 4}
{'name_length': 4}
{'name_length': 3}
{'name_length': 3}
{'name_length': 4}
{'name_length': 5}
{'name_length': 5}
{'name_length': 5}
{'name_length': 4}
{'name_length': 5}
{'name_length': 3}
###Markdown
**3 GROUP BY**지정된 열에서 **동일한 값을 갖는 행을** 묶어서 **MIN, MAX, COUNT, SUM** 등의 계산을 가능하게 합니다.
###Code
# GROUP BY
def min_user_id(rows):
return min(row["user_id"] for row in rows)
stats_by_length = users \
.select(additional_columns={"name_len" : name_len}) \
.group_by(group_by_columns=["name_len"],
aggregates={ "min_user_id" : min_user_id,
"num_users" : len })
print("stats by length")
print(stats_by_length)
print()
def first_letter_of_name(row):
return row["name"][0] if row["name"] else ""
def average_num_friends(rows):
return sum(row["num_friends"] for row in rows) / len(rows)
def enough_friends(rows):
return average_num_friends(rows) > 1
avg_friends_by_letter = users \
.select(additional_columns={'first_letter' : first_letter_of_name}) \
.group_by(group_by_columns=['first_letter'],
aggregates={ "avg_num_friends" : average_num_friends },
having=enough_friends)
print("avg friends by letter")
print(avg_friends_by_letter)
def sum_user_ids(rows):
return sum(row["user_id"] for row in rows)
user_id_sum = users \
.where(lambda row: row["user_id"] > 1) \
.group_by(group_by_columns=[],
aggregates = {"user_id_sum" : sum_user_ids })
print("user id sum")
print(user_id_sum)
###Output
user id sum
['user_id_sum']
{'user_id_sum': 54}
###Markdown
**4 ORDER BY****사용자의 이름을 알파벳 순서대로 정렬한** 뒤, **앞뒤 2개의 이름만** 얻고싶은 경우에 정렬을 실시합니다
###Code
# ORDER BY
friendliest_letters = avg_friends_by_letter \
.order_by(lambda row: -row["avg_num_friends"]) \
.limit(4)
print("friendliest letters")
print(friendliest_letters)
###Output
friendliest letters
['first_letter', 'avg_num_friends']
{'first_letter': 'S', 'avg_num_friends': 3.0}
{'first_letter': 'T', 'avg_num_friends': 3.0}
{'first_letter': 'C', 'avg_num_friends': 2.5}
{'first_letter': 'K', 'avg_num_friends': 2.5}
###Markdown
**5 JOIN**관계형 데이터베이스 중복이 최소화 되도록 **정규화(normalization)** 작업을 진행합니다
###Code
# JOINs
user_interests = Table(["user_id", "interest"])
user_interests.insert([0, "SQL"])
user_interests.insert([0, "NoSQL"])
user_interests.insert([2, "SQL"])
user_interests.insert([2, "MySQL"])
sql_users = users \
.join(user_interests) \
.where(lambda row:row["interest"] == "SQL") \
.select(keep_columns=["name"])
print("sql users")
print(sql_users)
# counts how many rows have non-None interests
def count_interests(rows):
return len([row for row in rows if row["interest"] is not None])
user_interest_counts = users \
.join(user_interests, left_join=True) \
.group_by(group_by_columns=["user_id"],
aggregates={"num_interests" : count_interests })
print("user interest counts >>>\n{}".format(user_interest_counts))
###Output
user interest counts >>>
['user_id', 'num_interests']
{'user_id': 0, 'num_interests': 2}
{'user_id': 1, 'num_interests': 0}
{'user_id': 2, 'num_interests': 2}
{'user_id': 3, 'num_interests': 0}
{'user_id': 4, 'num_interests': 0}
{'user_id': 5, 'num_interests': 0}
{'user_id': 6, 'num_interests': 0}
{'user_id': 7, 'num_interests': 0}
{'user_id': 8, 'num_interests': 0}
{'user_id': 9, 'num_interests': 0}
{'user_id': 10, 'num_interests': 0}
###Markdown
**6 SUBQURIES**select 의 JOIN 을 할 수 있습니다
###Code
# SUBQUERIES
likes_sql_user_ids = user_interests \
.where(lambda row: row["interest"] == "SQL") \
.select(keep_columns=['user_id'])
likes_sql_user_ids.group_by(group_by_columns=[],
aggregates={"min_user_id":min_user_id })
print("likes sql user ids")
print(likes_sql_user_ids)
###Output
likes sql user ids
['user_id']
{'user_id': 0}
{'user_id': 2}
|
Machine Learning/4. Saving Model Using Pickle and sklearn joblib.ipynb
|
###Markdown
Pickle & Joblib Saving a previous model done by me
###Code
import pandas as pd
import numpy as np
from sklearn import linear_model
df = pd.read_csv('homeprices.csv')
df
model = linear_model.LinearRegression() # Creating linear regression object
model.fit(df[['area']],df[['price']]) # Fitting regression object with dataset values
model.coef_ # m
model.intercept_ # b
model.predict([[5000]])
###Output
_____no_output_____
###Markdown
Save Model To a File Using Python Pickle
###Code
import pickle
with open('model_pickle','wb') as file: # writing in binary mode
pickle.dump(model,file)
###Output
_____no_output_____
###Markdown
Loading saved model
###Code
with open('model_pickle','rb') as file:
prediction_model = pickle.load(file)
prediction_model.coef_
prediction_model.intercept_
prediction_model.predict([[5000]])
###Output
_____no_output_____
###Markdown
Save Model To a File Using sklearn joblib
###Code
from sklearn.externals import joblib
joblib.dump(model, 'model_joblib') # joblib is more efficient when number of numpy array are huge
###Output
c:\users\shaon\appdata\local\programs\python\python37\lib\site-packages\sklearn\externals\joblib\__init__.py:15: FutureWarning: sklearn.externals.joblib is deprecated in 0.21 and will be removed in 0.23. Please import this functionality directly from joblib, which can be installed with: pip install joblib. If this warning is raised when loading pickled models, you may need to re-serialize those models with scikit-learn 0.21+.
warnings.warn(msg, category=FutureWarning)
###Markdown
Loading saved joblib model
###Code
prediction_model2= joblib.load('model_joblib')
prediction_model2.coef_
prediction_model2.intercept_
prediction_model2.predict([[5000]])
###Output
_____no_output_____
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.