Id
stringlengths 1
6
| PostTypeId
stringclasses 7
values | AcceptedAnswerId
stringlengths 1
6
⌀ | ParentId
stringlengths 1
6
⌀ | Score
stringlengths 1
4
| ViewCount
stringlengths 1
7
⌀ | Body
stringlengths 0
38.7k
| Title
stringlengths 15
150
⌀ | ContentLicense
stringclasses 3
values | FavoriteCount
stringclasses 3
values | CreationDate
stringlengths 23
23
| LastActivityDate
stringlengths 23
23
| LastEditDate
stringlengths 23
23
⌀ | LastEditorUserId
stringlengths 1
6
⌀ | OwnerUserId
stringlengths 1
6
⌀ | Tags
list |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
615166
|
1
| null | null |
1
|
16
|
What are not-too-complex methods to perform logistic modeling if some of the predictors are right-censored?
|
Logistic modeling with censored predictors
|
CC BY-SA 4.0
| null |
2023-05-07T18:11:55.993
|
2023-05-07T18:11:55.993
| null | null |
28141
|
[
"censoring"
] |
615167
|
2
| null |
615126
|
3
| null |
Generally, you ask about $E[Q(X,Y)]$ where
$$Q(x,y) = q_{xx}x^2 + q_{yy}y^2 + 2q_{xy}xy = \pmatrix{x&y}\pmatrix{q_{xx}&q_{xy}\\q_{xy}&q_{yy}}\pmatrix{x\\y} = \pmatrix{x&y}\mathbb Q \pmatrix{x\\y}$$
is a homogeneous quadratic form that is represented by the symmetric matrix $\mathbb Q.$ The question concerns the case $q_{xx}=q_{yy}=-1,$ $q_{xy}=1/2.$
Such forms can be diagonalized with orthogonal transformations. That is, there exists an orthogonal matrix $\mathbb O$ ($\mathbb O^\prime \mathbb O = \mathbb I_2$) for which
$$\mathbb O^\prime\, \mathbb Q\, \mathbb O = \pmatrix{\lambda_1&0\\0&\lambda_2}.$$
Therefore, in terms of the linearly transformed variables
$$\pmatrix{U\\V} = \mathbb O^\prime\pmatrix{X\\Y},$$
for which
$$\pmatrix{X\\Y} = \mathbb O \pmatrix{U\\V}\quad\text{and}\quad \pmatrix{X&Y} = \pmatrix{U&V}\mathbb O^\prime$$
(by virtue of the orthogonality of $\mathbb O$), we have
$$\pmatrix{X&Y}\mathbb Q \pmatrix{X\\Y} = \pmatrix{U&V}\mathbb O^\prime\,\mathbb Q\,\mathbb O \pmatrix{U\\V} = \lambda_1 U^2 + \lambda_2 V^2.$$
Linearity of expectation implies
$$E\left[Q(X,Y)\right] = E\left[\pmatrix{X&Y}\mathbb Q \pmatrix{X\\Y}\right] = \lambda_1 E[U^2] + \lambda_2 E[V^2].$$
This generally gives the simplest possible interpretation of $Q:$ it's a weighted sum (or difference) of squares of variables that themselves are simply linear combinations of the original variables. For the form in the question, you can check that $\lambda_1=-1/2$ and $\lambda_2=-3/2$ with
$$U = (X+Y)/\sqrt{2}\quad\text{and}\quad V = (X-Y)/\sqrt{2}.$$
Because all the eigenvalues $\lambda_i$ are negative, this is a negative-definite form: its value is always negative except when $Q$ is evaluated at $(0,0),$ where necessarily the value will be zero.
### Comments
No assumptions are needed for these calculations apart from the existence of the moments in question (which is equivalent to $X$ and $Y$ each having finite variance).
I have italicized all relevant technical terms that will be useful for further research into the mathematics of quadratic forms.
| null |
CC BY-SA 4.0
| null |
2023-05-07T18:28:01.467
|
2023-05-07T18:28:01.467
| null | null |
919
| null |
615168
|
1
| null | null |
0
|
22
|
I have a log-level model and I have trouble with the interpretation when I have an interaction term of two continuous variables.
I came across this when I tried to get the grips of the difference when the covariates are standardized or just centered.
So usually in a log level model I would interpret a one unit increase in x as follows:
A 1 unit increase in x1 leads to a `(exp(b1)-1)*100` per cent increase in y.
My issue now is how to apply the exponential when I have an interaction term.
Say I have a model that is defined as follows:
`log(y) = b1*x1 + b2*x2 + b3(x1*x2)`
How do I know get to the correct interpretation of a one unit increase in x?
is it
a) `(exp(b1)-1)*100 + (exp(b3)-1)*100` or b) `(exp(b1+b3)-1)*100`
Sorry if this is stupid. I just came across this when I worked on a model where I initially had centered continuous variables and later changed them to standardized variables because the interpretation of a 1 standard deviation increase seemed more convenient. However when I did that, I realized that the interpretation doesnt add up.
So I wanted to check if everything is right and compare the two models where the first used centered and the second model used standardised variables.
My assumption was that `sd*(exp(b1)-1)*100` in the centered model was equivalent to `(exp(b1)-1)*100` in the standardised model
which turned out to be true and I was happy. This was basically a double check for me to understand the difference between the two approaches. However, now when I add the interaction term, it did not work out, and I realised that this is probably because I dont fully understand how the approximation with exp() exactly works.
Any help would be very much appreciated.
Below is some example code I generated. I hope this was more or less understandable.
```
set.seed(42)
# Create variables
v1 <- rnorm(n = 1000, mean = 50, sd = 15)
v2 <- rnorm(n = 1000, mean = 50, sd = 15) + 0.3*v1
y <- 0.2*x1+0.4*v2+10
# Center variables
x1 <- scale(v1, scale = F)
x2 <- scale(v2, scale = F)
model1 <- lm(log(y)~x1*x2)
coefs1 <- coef(model1)
#-------------
# Standardise variables
z1 <- scale(v1, scale = T)
z2 <- scale(v2, scale = T)
model2 <- lm(log(y)~z1*z2)
coefs2 <- coef(model2)
#------------
# Those two should be approximately equal
(exp(sd(x1)*coefs1[2])-1)*100
(exp(coefs2[2])-1)*100
# is TRUE
# Interpretation with interaction term does not work out
(exp(sd(x1)*coefs1[2])-1)*100 + (exp(sd(x1)*coefs1[4])-1)*100
(exp(coefs2[2])-1)*100 + (exp(coefs2[4])-1)*100
```
|
Interpretation issues: Interaction term in log-level model
|
CC BY-SA 4.0
| null |
2023-05-07T18:31:01.610
|
2023-05-08T14:49:33.140
| null | null |
314215
|
[
"interaction",
"interpretation"
] |
615169
|
1
| null | null |
1
|
11
|
Is Design Effect (DEFF) possible to be zero?
Note: Design Effect (DEFF) is defined as the ratio of the variance of an estimator
under a certain survey design (non SRS) to the variance of the estimator under
SRS (simple random sampling).
|
Design Effect ZERO
|
CC BY-SA 4.0
| null |
2023-05-07T18:36:44.270
|
2023-05-07T18:36:44.270
| null | null |
387435
|
[
"sampling"
] |
615171
|
1
| null | null |
0
|
13
|
When $(X_n)_{n\in\mathbb N_0}$ is the Markov chain generated by the Metropolis-Hastings algorithm with target density $p$, it is guaranteed that $$\frac1n\sum_{i=0}^{n-1}f(X_i)\xrightarrow{n\to\infty}\int pf.\tag1$$ However, maybe I'm missing something, but consider the simple case of $p=1_{\left[\frac12,1\right)}$ and proposals from $q=1_{\left[0,\frac12\right)}$. Assume, moreover, that $X_0$ is taken from $\left[0,\frac12\right)$. Then the acceptance function is constantly $1$ and hence every proposal will be accepted. That means that $(X_n)_{n\in\mathbb N_0}$ is identically distributed according to $q$. That should mean that $(1)$ cannot hold ... What am I missing?
|
Why does the Metropolis-Hastings algorithm work for proposal density $p=1_{[1/2,1)}$ and proposal density $q=1_{[0,1/2)}$?
|
CC BY-SA 4.0
| null |
2023-05-07T20:05:05.213
|
2023-05-07T20:05:05.213
| null | null |
222528
|
[
"markov-chain-montecarlo",
"metropolis-hastings"
] |
615172
|
1
| null | null |
0
|
16
|
I'm studying the endowment effect through the exchange paradigm. Participants received an object A or B. Then the experimenter asks the participants if they accept to trade their object with the alternative object.
I would like to compare the proportion of participants who refuse to trade A with B, with the proportion of participants who accept to trade B with A. In other words, in a contingency table, I want to compare the proportion of failure of Group 1 with the proportion of success of Group 2. Note that I have a small sample (n < 30).
I don't know tests that allow a direct cross-tabulation comparison like this. I have tried many alternatives (e.g. Fisher's exact test) but they do not allow me to answer this question exactly...
Would you have any ideas or suggestions?
[](https://i.stack.imgur.com/vVMbN.png)
|
Comparing success of group 2 and failure of group 1 (cross-tabulation comparison in contingency table)
|
CC BY-SA 4.0
| null |
2023-05-07T20:05:58.317
|
2023-05-07T20:05:58.317
| null | null |
381165
|
[
"r",
"chi-squared-test",
"proportion",
"fishers-exact-test",
"z-test"
] |
615173
|
1
| null | null |
1
|
35
|
Suppose that Walmart has 1,000 stores. It has a 20% coupon for cereal, and it hypothesizes that the coupon will increase the sales of cereal by 3%.
Walmart put the coupon in 100 stores on 2022-05-01; the other 900 stores continue to have no coupon. Unfortunately, it does NOT have any sales data from before 2022-05-01. The only data that it has is in the post-intervention period (from 2022-05-01 till today).
Assume that I have data on all the confounding variables that you care about.
I was going to use difference-in-difference to estimate the average treatment effect, but I have no pre-intervention data.
What I can do instead to estimate the average treatment effect?
|
Difference-in-difference estimation of average treatment effect with no pre-intervention period
|
CC BY-SA 4.0
| null |
2023-05-07T20:50:35.603
|
2023-05-10T08:00:26.350
|
2023-05-10T08:00:26.350
|
246835
|
269172
|
[
"time-series",
"experiment-design",
"causality",
"difference-in-difference",
"treatment-effect"
] |
615174
|
2
| null |
615137
|
2
| null |
Weights from matching and weighting are closest to `pweights`. They serve the same purpose, which is to shift the distribution of covariates to some target distribution. Sampling weights shift the distribution of variables to resemble that of the sampled population. Propensity score weights for the ATE shift the distribution in each treatment group to resemble that in the full sample. Matching weights for the ATT shift the distribution of the control group to resemble that of the treatment group.
That said, it's best not to try to fit propensity score weights into this categorization. As you said, the point estimates are the same, and all that differs is the standard errors. But you should not be using the standard errors that happen to be produced automatically by Stata. You should use the specific standard error estimator that corresponds to the method you use. Robust (sandwich) standard errors are conservative for propensity score weighting for the ATE, which can be requested using `vce(HC3)`. There are asymptotic standard errors for propensity score weighting when the weights are estimated using logistic regression, which can be requested using `teffects ipw`. For matching without replacement, cluster-robust standard errors are appropriate and can be requested using `vce(subclass)` if `subclass` contains matched pair membership. For matching with replacement, `teffects nnmatch` and `teffects psmatch` have a special standard error estimator that was designed for that method.
| null |
CC BY-SA 4.0
| null |
2023-05-07T21:05:22.733
|
2023-05-07T21:05:22.733
| null | null |
116195
| null |
615175
|
2
| null |
615005
|
2
| null |
This is a book on Generative Models:
>
Tomczak, Jakub M. "Deep Generative Modeling". 2022.
To help readers to choose which models to study I summarize the main classes of Generative Models and provide a brief description of each, which are the resources I studied for an introductory course to Generative Models
# AutoRegressive Models
The image is modeled as a sequence of pixel values. The image distribution $p(x)$ is factorized into a product of conditional distributions and the generation is an autoregressive prediction of the next pixel values based on the previous ones.
## Relevant papers
>
Van Den Oord, Aäron, Nal Kalchbrenner, and Koray Kavukcuoglu. "Pixel recurrent neural networks." International conference on machine learning. PMLR, 2016.
Chen, Xi, et al. "Pixelsnail: An improved autoregressive generative model." International Conference on Machine Learning. PMLR, 2018.
Menick, Jacob, and Nal Kalchbrenner. "Generating high fidelity images with subscale pixel networks and multidimensional upscaling." ICLR (2019)
## Pros
- Simple
- Exact likelihood, allow sampling from the distribution
## Cons
- Does not have a learned representation
- Inference is slow, because of the sequential nature
# Normalizing Flows
Parameterizes $p(x)$ as an invertible deterministic transformation from a base density, such as a standard Gaussian
## Relevant papers
>
Dinh, Laurent, David Krueger, and Yoshua Bengio. ”NICE: Non-linear independent components estimation." ICLR 2015 workshop
Dinh, Laurent, Jascha Sohl-Dickstein, and Samy Bengio. "Density estimation using Real NVP." ICLR 2017
Kingma, Durk P., and Prafulla Dhariwal. "Glow: Generative flow with invertible 1x1 convolutions." Advances in neural information
processing systems 31 (2018)
Papamakarios, George, et al. "Normalizing Flows for Probabilistic Modeling and Inference." J. Mach. Learn. Res. 22.57 (2021): 1-64.
Kobyzev, Ivan, Simon JD Prince, and Marcus A. Brubaker. "Normalizing flows: An introduction and review of current methods." IEEE
Transactions on pattern analysis and machine intelligence 43.11
(2020): 3964-3979.
## Pros
- A very flexible and elegant formulation with exact likelihood
- Allows fast sempling
- Provides a latent representation
## Cons
- Limited freedom in the choice of the architecture, for theoretical (invertibility) and computational constraints
- Latent space needs to have the same dimensionality as the output for invertibility
# Latent Variable Models
Use an encoder network to map inputs onto a low-dimensional latent space and a decoder network to generate images from a latent code
## Relevant papers
>
Kingma, Diederik P., and Max Welling. "Auto-encoding variational bayes." arXiv preprint arXiv:1312.6114 (2013).
Doersch, Carl. "Tutorial on variational autoencoders." arXiv preprint arXiv:1606.05908 (2016).
Kingma, Diederik P., and Max Welling. "An introduction to variational autoencoders." Foundations and Trends® in Machine Learning 12.4
(2019): 307-392.
Higgins et al, $\beta$-vae: Learning Basic Visual Concepts with a Constrained Variational Framework, ICLR 2017
Van Den Oord et al "Neural discrete representation learning." Neurips (2017).
## Pros
- No architecture constraint
- Efficient to learn, flexible
- Allows sampling
## Cons
- Does not have exact likelihood
- Blurry samples if wrongly tuned and without perceptual components in loss
# Generative Adversarial Networks
Train two networks, a generator which produces synthetic data and a discriminator which distinguishes between synthetic and real data
## Relevant papers
>
Goodfellow, Ian et al. Generative Adversarial Networks, NIPS’14
Goodfellow, Ian. Tutorial: Generative Adversarial Networks, NIPS’16
M .Mirza and S. Osindero, "Conditional generative adversarial nets." arXiv preprint arXiv:1411.1784 (2014)
Salimans, Tim, et al. "Improved techniques for training GANs." Advances in neural information processing systems 29 (2016).
Zhu, Jun-Yan, et al. "Unpaired image-to-image translation using cycle-consistent adversarial networks." Proceedings of the IEEE international conference on computer vision. 2017.
Isola, Phillip, et al. "Image-to-image translation with conditional adversarial networks." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017
Jolicoeur-Martineau, Alexia. "The relativistic discriminator: a key element missing from standard GAN." arXiv preprint arXiv:1807.00734 ICLR (2018).
W. Fedus, et al., Many Paths To Equilibrium: Gans Do Not Need To Decrease A Divergence At Every Step, ICLR’18
Schmidhuber, Jürgen. "Generative adversarial networks are special cases of artificial curiosity (1990) and also closely related to predictability minimization (1991)." Neural Networks 127 (2020): 58-66
## Pros
- Sharp, higher resolution outputs compared to the previous classes
- Full freedom in architecture
- Fast sampling
- Latent representation
## Cons
- No likelihood
- Training instability
# Diffusion Models
Learn a denoising process which transforms random noise into an image
## Relevant Papers
>
Sohl-Dickstein, Jascha, et al. "Deep unsupervised learning using nonequilibrium thermodynamics." International Conference on Machine Learning. PMLR, 2015.
Ho, Jonathan, Ajay Jain, and Pieter Abbeel. "Denoising diffusion probabilistic models." Advances in Neural Information Processing Systems 33 (2020): 6840-6851.
Nichol, Alexander Quinn, and Prafulla Dhariwal. "Improved denoising diffusion probabilistic models." International Conference on Machine
Learning. PMLR, 2021.
Ho, Jonathan, et al. "Cascaded Diffusion Models for High Fidelity Image Generation." J. Mach. Learn. Res. 23 (2022): 47-1.
Song, Yang, et al. "Consistency models." arXiv preprint arXiv:2303.01469 (2023).
## Pros
- Stable training
- Great tractability/flexibility trade-off
- High quality samples
## Cons
- Lower likelihood value (even with higher quality results)
- Slow to sample from (Consistency models is an emergent class which aims to alleviate that)
# Text-to-Image generation
Finally, the section where all the hype is, with the previous model classes applied to text-to-image generation
>
Zhang, Han, et al. "Stackgan: Text to photo-realistic image synthesis with stacked generative adversarial networks." Proceedings of the IEEE international conference on computer vision. 2017.
Esser, Patrick, Robin Rombach, and Bjorn Ommer. "Taming transformers for high-resolution image synthesis." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021.
Ramesh, Aditya, et al. "Hierarchical text-conditional image generation with clip latents." arXiv preprint arXiv:2204.06125 (2022).
Saharia, Chitwan, et al. "Photorealistic text-to-image diffusion models with deep language understanding." Advances in Neural Information Processing Systems 35 (2022): 36479-36494.
Rombach, Robin, et al. "High-resolution image synthesis with latent diffusion models." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
| null |
CC BY-SA 4.0
| null |
2023-05-07T21:08:28.793
|
2023-05-07T21:08:28.793
| null | null |
377435
| null |
615176
|
1
| null | null |
0
|
9
|
I am new to generalization techniques in machine learning and I have been experimenting with them recently. I have observed that when I apply them to my model, the performance of the model improves, but the results also become more variable when I try to rebuild the model. For example:
- Regular model has an r squared of: 0.15-0.16
- Models with different generalization techniques have an r squared of: 0.14-0.18
The generalization techniques that I have used are: dropout and weight regularization. My question is whether this increase in variance is related to the randomness associated with these generalization techniques, and if it is normal or if it can be avoided somehow.
|
Does generalization methods in ANN increase variance in results?
|
CC BY-SA 4.0
| null |
2023-05-07T21:21:08.893
|
2023-05-07T21:21:08.893
| null | null |
295963
|
[
"neural-networks",
"regularization",
"dropout",
"generalization"
] |
615177
|
1
| null | null |
1
|
25
|
[](https://i.stack.imgur.com/vFx20.png)
This table shows the results of a Kruskal-Wallis test, but I am not sure what the column values represent. I thought the Kruskal-Wallis test statistic is always positive and that the test merely shows whether there is a difference between groups. In the text, the author makes statements such as:
>
Compared to all other burglary types, census blocks with low single event burglary, low repeat burglary, and low near-repeat burglary (n = 66) displayed significantly lower levels of concentrated disadvantage.
Are these results and conclusions possible with a Kruskal-Wallis test, or are there other analyses incorporated here?
Edit: I searched the full text for mentions of other analyses, but the author only references Kruskal-Wallis being used to create these results.
|
Is this a Kruskal-Wallis Test?
|
CC BY-SA 4.0
| null |
2023-05-07T22:02:09.063
|
2023-05-08T02:36:41.110
|
2023-05-08T02:36:41.110
|
387438
|
387438
|
[
"kruskal-wallis-test"
] |
615178
|
1
| null | null |
0
|
6
|
I am trying to measure the effect of a campaign on the knowledge of a certain disease on population X
method 1: measure the same individual’s knowledge two times once before and once after passing through the campaign
method 2: measure two different groups from the same population, one group has passed though the campaign and the other group have not
what is the difference and why is one better than the other?
|
What is the difference between these two methods of data collection?
|
CC BY-SA 4.0
| null |
2023-05-07T23:00:26.427
|
2023-05-07T23:00:26.427
| null | null |
387443
|
[
"dataset",
"cross-section",
"case-control-study",
"collecting-data"
] |
615179
|
1
| null | null |
0
|
25
|
1. Could you provide an example of how to hypothesize the variance and covariance expectations for a multi-level model with random slopes and random intercepts?
I do not yet have access to my data, so I am unsure how to write the model formula to determine the E[Var] and E[Cov].
I am learning about mixed-effect modeling and need help with developing a hypothesis for the variance. My data will include country, demographic information, region, and a likert scale opinion question to model a metric of poverty.
I plan to use a random slope and random intercept model due to the potential cross-level interactions. A professor has requested that I write up my variance hypotheses for the model. He asked for the variance and covariance expectations at the second level (country).
I don't have access to the data yet and am unsure how to write the variance and covariance expectations. While we've set a list of potential variables, I do not yet know which will be included in the model formula. Since I don't have the model formula or access to the data, I feel unsure of how to write out the variance and covariance expectations.
Thank you!
|
Variance and Covariance Expectations in 2-Level Model with Random slope & intercept
|
CC BY-SA 4.0
| null |
2023-05-07T23:09:38.503
|
2023-05-07T23:09:38.503
| null | null |
387441
|
[
"hypothesis-testing",
"variance",
"multilevel-analysis",
"covariance",
"nested-models"
] |
615181
|
2
| null |
615107
|
1
| null |
Yes - a survey GLM is interpreted in the exact same way as a normal GLM. It's basically just the standard errors / AIC correctly accounting for the clustering etc.
| null |
CC BY-SA 4.0
| null |
2023-05-08T00:29:39.693
|
2023-05-08T00:29:39.693
| null | null |
369002
| null |
615182
|
2
| null |
613560
|
0
| null |
Yt hasn't changed, but its explanation distribution has now changed via the transformed Xt values that are now going into the future. This added explanatory power will be picked up by the regression method and it means other variables other than Xt will have their own influence on Yt reduced, all else equal.
| null |
CC BY-SA 4.0
| null |
2023-05-08T00:44:23.417
|
2023-05-08T00:45:37.407
|
2023-05-08T00:45:37.407
|
387448
|
387448
| null |
615183
|
1
| null | null |
1
|
19
|
Suppose I have 25 dice. I roll them all each day unless the number '6' appears, in which case I discard the die. For example, suppose on day 1, two of the dice roll a 6. I remove them. On the second day, I therefore roll 23 dice. 5 of them land on a 6, so I remove those. On the third day, I roll 18 dice, remove those that land a 6, and so on.
Suppose I have a random variable, $X$, which has three parameters, $k$, $p$, and $n$. $k$ is the total number of dice that have been discarded on or before the $X$th day. $p$ is the probability that an individual die becomes discarded on an arbitrary day (equal to $\frac{1}{6}$ in this example). Finally, $n$ is the number of dice that are rolled each day (25 in this example).
What is the probability distribution of $X$, in terms of its parameters $k$, $p$ and $n$?
Does there exist a standard distribution for $X$? If there was only 1 die, it would be geometrically distributed. If there was one die but you didn't discard the die (simply count the number of 6's), it would be negatively binomially distributed. I'm sure someone has already derived a distribution for this phenomena, but can't locate it. So if anyone knows how to determine the distribution of $X$, that would be great!
|
How to 'generalize' the negative binomial distribution when multiple 'experiments' are being performed simultaneously?
|
CC BY-SA 4.0
| null |
2023-05-08T01:01:57.497
|
2023-05-08T01:01:57.497
| null | null |
224992
|
[
"probability",
"distributions",
"mathematical-statistics"
] |
615184
|
1
| null | null |
0
|
34
|
I'm analysing slightly unbalanced panel data in r (n = 136, T = 9-213, N = 24894) and planning on using fixed or random effects (Hausman test indicates random effects, but high likelihood of omitted variable bias in the model due to lack of available data so unsure whether that means that random should be ruled out in this case?).
This is an example of the model:
```
rm2 <- plm(Assault_rate ~ Private + Sex + Youth, index = c("Institution", "Month_yr"), model = "random", data = panel1)
```
The dependent variable is rate of assaults, and the primary explanatory variable is a binary dummy for privately run institution (12% fall into this category). Other independent variables include male/female institution, youth/juvenile institution. The likely confounding unobserved variables would be staffing levels, funding/expenditure, activities/programs (no data possible for these).
When I try to run tests for cross-sectional dependence it returns NA and the below warning message:
```
Breusch-Pagan LM test for cross-sectional dependence in panels
data: AA_rate ~ Private + Sex + YOI
chisq = NA, df = 9045, p-value = NA
alternative hypothesis: cross-sectional dependence
Warning messages:
1: In cor(wideres, use = "pairwise.complete.obs") :
the standard deviation is zero
2: In pcdres(tres = tres, n = n, w = w, form = paste(deparse(x$formula)), :
Some pairs of individuals (2.9 percent) do not have any or just one time period in common and have been omitted from calculation
```
Does this mean that there is something wrong with my data or model? Is there something fundamentally wrong with this approach that I'm missing?
I am new to this so apologies if I've formatted this incorrectly or missed any important information. Thanks in advance for any advice
I have tried re-specifying the model with different combinations of independent variables, different types of model (pooled, fixed) but get the same warning and NA result.
|
Cross-sectional dependence tests returning NA unbalanced panel
|
CC BY-SA 4.0
| null |
2023-05-08T01:24:55.250
|
2023-05-27T11:23:38.553
|
2023-05-27T11:23:38.553
|
94889
|
387450
|
[
"r",
"regression",
"econometrics",
"panel-data",
"plm"
] |
615186
|
1
| null | null |
1
|
51
|
I am having trouble learning the relevant concepts of t-test.
Even if you search the web or books, the explanation is slightly different, it causes confusion.
(Please understand that I am not a statistics or math major)
[On the requirements of t-test]
(assume we are interested in the mean value of something)
>
Someone say that the population should normally distributed.
>
Someone say that the distribution of sampling mean(for multiple trial of sampling) should be normally distributed. On the other hand, someone say that the each value of samples shoud be normally distributed.
Over many explanations on web, above explanations are mixed, and in some cases the normality test was performed on each sample value prior to performing the t-test, and in other cases, the normality test was performed on the sampling mean (average of samples).
[My Questions]
(1) I think the normal distribution of sampling mean is required to evaluate the possibility of certain t-value appears. (Here, I think that the mean value could explain t-statistic) Which statement among the above is correct?
(2) If the statement:"the normal distribution of sampling mean is required" is true, isn't it always normal distributed as CLT says? Since the distribution of the sampling mean is an imaginary distribution(In practice, we only do one set of sampling), regardless of what n(sample size) and population distribution is, we can imagine infinite trials of sampling, which leads to normal distribution of sampling means.
Then we are conducting our t-test, which evaluates the possibility of our sample t-statistic within that imaginary distribution of t-values. Is this wrong statement?
(3) I am dealing with one-sample t-test. Is there any requirements differences between one-sample and other t-tests?
Please advise an appropriate concept, and every answer would be appreciated.
|
The basic requirements and CLT for one sample t-test
|
CC BY-SA 4.0
| null |
2023-05-08T02:24:38.683
|
2023-05-10T00:20:36.070
|
2023-05-08T02:29:25.600
|
387453
|
387453
|
[
"mathematical-statistics",
"t-test",
"central-limit-theorem"
] |
615187
|
2
| null |
615130
|
2
| null |
#### Preparations
>
Lemma 1. If $X = (X_1, X_2, \ldots, X_d) \sim N_d(0, I_{(d)})$, then
\begin{align}
& E\left[\frac{X_j}{\|X\|}\right] = 0, 1 \leq j \leq d, \\
& E\left[\frac{X_iX_j}{\|X\|^2}\right] =
\begin{cases}
0, & 1 \leq i \neq j \leq d, \\
d^{-1}, & 1 \leq i = j \leq d.
\end{cases}
\end{align}
>
Lemma 2. Suppose an order $n$ matrix $A$ is idempotent and symmetric with $\operatorname{rank}(A) = r$, then there exists an order $n$ orthogonal matrix $P$ such that
\begin{align}
A = P\operatorname{diag}(I_{(r)}, 0)P'.
\end{align}
#### Proof
Without loss of generality, assume $\sigma^2 \equiv 1$. I am also assuming you are only interested in the case $i \neq j$ (the case $i = j$ is similar).
Denote $I_{(n)} - H$ by $\bar{H}$, then $\bar{H}$ is symmetric, idempotent, and $\operatorname{rank}(\bar{H}) = n - p =: r$. By Lemma 2, there exists an order $n$ orthogonal matrix $P$ such that $\bar{H} = P\operatorname{diag}(I_{(r)}, 0)P'$. Denote $P'\varepsilon$ by $X := (\xi, \eta)$, where $\xi \in \mathbb{R}^r$ and $\eta \in \mathbb{R}^{n - r}$. Since $P$ is orthogonal and $\varepsilon\sim N_n(0, I_{(n)})$, it follows that $X \sim N_n(0, I_{(n)})$ and $\xi \sim N_r(0, I_{(r)})$.
Denote the matrix formed by the first $r$ columns of $P$ by $Q$ and the matrix formed by the last $n - r$ columns of $P$ by $R$, then
\begin{align}
& e = \bar{H}\varepsilon = P\operatorname{diag}(I_{(r)}, 0)P'\varepsilon
= \begin{bmatrix} Q & R \end{bmatrix}\begin{bmatrix} \xi \\ 0 \end{bmatrix} = Q\xi. \tag{1} \\
& e'e = \|e\|^2 = \xi'Q'Q\xi = \|\xi\|^2. \tag{2}
\end{align}
Denote the $i$-th row and $j$-th row of $Q$ by $\begin{bmatrix}q_{i1} & \cdots & q_{ir} \end{bmatrix}$ and $\begin{bmatrix}q_{j1} & \cdots & q_{jr} \end{bmatrix}$ respectively, it then follows by $(1)$ and $(2)$ that
\begin{align}
E\left[\frac{e_ie_j}{\|e\|^2}\right]
= E\left[\frac{\sum_{k = 1}^r q_{ik}\xi_k \cdot \sum_{l = 1}^r q_{jl}\xi_l}{\|\xi\|^2}\right], \tag{3}
\end{align}
which by Lemma 1 and $\xi \sim N_r(0, I_{(r)})$ becomes to
\begin{align}
\sum_{k = 1}^r q_{ik}q_{jk}E\left[\frac{\xi_k^2}{\|\xi\|^2} \right] =
r^{-1}\sum_{k = 1}^r q_{ik}q_{jk}. \tag{4}
\end{align}
Finally, $\bar{H} = I_{(n)} - H = QQ'$ implies that
\begin{align}
\sum_{k = 1}^r q_{ik}q_{jk} = \bar{H}(i, j) = -h_{ij}. \tag{5}
\end{align}
Combining $(3), (4), (5)$ yields:
\begin{align}
E\left[\frac{e_ie_j}{\|e\|^2}\right] = -r^{-1}h_{ij},
\end{align}
which immediately gives
\begin{align}
\operatorname{Cov}(r_i, r_j) = \frac{-h_{ij}}{\sqrt{1 - h_{ii}}\sqrt{1 - h_{jj}}}.
\end{align}
---
#### Proof of Lemmas
Lemma 2 is a standard linear algebra result. So I will only discuss how to prove Lemma 1, which is a quite interesting result. Lemma 1 is a corollary of the following well-known theorem of spherical distributions (cf. Theorem 1.5.6 in Aspects of Multivariate Statistical Theory by R. Muirhead):
>
Theorem. If $X$ has an $m$-variate spherical distribution with $P(X = 0) = 0$ and $r = \|X\| = (X'X)^{1/2}, T(X) = \|X\|^{-1}X$, then $T(X)$ is
uniformly distributed on $S_m$ and $T(X)$ and $r$ are independent.
The proof to this theorem is not hard (but might be tedious) by laying out the spherical coordinates of $X$.
To apply this theorem to the proof of Lemma 1, write
\begin{align}
& X_j = \frac{X_j}{\|X\|} \times r, \tag{6} \\
& X_iX_j = \frac{X_iX_j}{\|X\|^2} \times r^2. \tag{7}
\end{align}
Then taking expectations on both sides of $(6), (7)$ and applying the independence of multipliers (by Theorem) finishes the proof.
| null |
CC BY-SA 4.0
| null |
2023-05-08T02:38:39.343
|
2023-05-08T04:00:45.410
|
2023-05-08T04:00:45.410
|
20519
|
20519
| null |
615188
|
2
| null |
615186
|
0
| null |
Think of it this way. If you had an infinite sample, i.e. $n=\infty$, the sample mean would equal the population mean.
But for any finite iid sample of almost any distribution(*), as the sample gets larger and larger, the distribution of the sample mean gets closer and closer to $N(\bar{x},\frac{\sigma}{\sqrt{n}})$, where $\sigma$ is the population SD of the distribution you're drawing from and $\bar{x}$ is the sample mean. This is an asymptotic approximation, meaning the approximation becomes better as $n$ increases. Notice as $n$ approaches infinity, the variance converges to 0
If you have a finite sample from a normal distribution, the mean is t-distributed. This is not an asymptotic approximation. This is an exact result.
If you have a finite sample from a non-normal distribution, you can either use the asymptotic approximation as described above; or use the t-distribution, which has fatter tails than the normal distribution, so can be used to be more conservative. But this can't be theoretically justified, more as a rule-of-thumb some people use.
(*) This includes all distributions with a finite population mean and a finite SD.
| null |
CC BY-SA 4.0
| null |
2023-05-08T02:46:23.530
|
2023-05-08T02:46:23.530
| null | null |
224992
| null |
615189
|
1
| null | null |
0
|
19
|
### Background
When fitting generalised additive models (GAMs) in the past I have used methods for the `mgcv` package outlined in
>
Pedersen EJ, Miller DL, Simpson GL, Ross N (2019) Hierarchical generalized additive models in ecology: an introduction with mgcv. PeerJ 7: e6876.
I am currently transitioning to Bayesian alternatives and preferentially use the `rethinking` package, but have stumbled into some problems when introducing splines to Stan and adding categorical predictor variables.
### MRE
Below I follow
>
McElreath R (2019) Statistical rethinking2: A Bayesian course with examples in R and Stan. Second Edition. Chapman and Hall/CRC
and
>
Kurz S (2023) Statistical rethinking with brms, ggplot2, and the tidyverse: Second edition. https://bookdown.org/content/4857
```
# generate some sinusoidal data
d <- data.frame(x = rep(seq(0, 5 * pi, length.out = 100), 2),
group = rep(c("a", "b"), each = 100))
d$y[1:100] <- 2 * sin(2 * d$x[1:100]) + rnorm(100, 0, 1)
d$y[101:200] <- 5 * sin(3 * d$x[101:200]) + rnorm(100, 0, 0.5)
# generate b splines
knots <- 15
knot_list <- quantile(d$x , probs = seq(0, 1, length.out = knots))
require(splines)
B <- bs(d$x,
knots = knot_list[-c(1, knots)],
degree = 3, intercept = TRUE)
# fit quap model according to McElreath (2019)
require(rethinking)
r.mod <- quap(
alist(
y ~ dnorm(mu, sigma),
mu <- a + B %*% w,
a ~ dnorm(0, 1),
w ~ dnorm(0, 1),
sigma ~ dexp(1)
), data = list(y = d$y, B = B),
start = list(w = rep(0, ncol(B)))
)
precis(r.mod) # model produces parameter estimates
# attempt to fit identical ulam (Stan) model
r.mod.stan <- ulam( # note ulam instead of quap
alist(
y ~ dnorm(mu, sigma),
mu <- a + B %*% w,
a ~ dnorm(0, 1),
w ~ dnorm(0, 1),
sigma ~ dexp(1)
), data = list(y = d$y, B = B),
start = list(w = rep(0, ncol(B))),
chains = 8, cores = 8, iter = 1e4
)
# model fails due to apparently semantic error:
# Ill-typed arguments supplied to assignment operator =: lhs has type real and rhs has type row_vector
# fit brms model according to Kurz (2023)
require(brms)
d$B <- B
b.mod.stan <- brm(data = d,
family = gaussian,
y ~ 1 + B,
prior = c(prior(normal(0, 1), class = Intercept),
prior(normal(0, 1), class = b),
prior(exponential(1), class = sigma)),
iter = 1e4, warmup = 5e3, chains = 4, cores = 4,
seed = 4)
summary(b.mod.stan) # model produces same estimates as quap model
```
### Questions
- Why does the rethinking Stan GAM not run while the brms GAM does?
- How can I incorporate the grouping factor group?
I would appreciate a worked example in `rethinking`.
|
How to fit Bayesian generalised additive models with R and Stan
|
CC BY-SA 4.0
| null |
2023-05-08T02:51:50.573
|
2023-05-10T14:22:43.470
| null | null |
303852
|
[
"bayesian",
"multiple-regression",
"generalized-additive-model",
"brms"
] |
615190
|
1
| null | null |
2
|
46
|
This question is a generalization of another question that I asked [here](https://stats.stackexchange.com/questions/615173/difference-in-difference-estimation-of-average-treatment-effect-with-no-pre-inte).
Suppose that Walmart has 1,000 stores. It has a 20% coupon for cereal, and it hypothesizes that the coupon will increase the sales of cereal by 3%.
Walmart put the coupon in 100 stores on 2022-05-01; the other 900 stores continue to have no coupon. Unfortunately, it does NOT have any sales data from before 2022-05-01. The only data that it has is in the post-intervention period (from 2022-05-01 till today).
Assume that I have data on all the confounding variables that you care about - but ONLY in the post-intervention period.
Given this limitation, is there any method that can estimate the impact of the intervention?
|
Causal inference for intervention with no data in pre-intervention period
|
CC BY-SA 4.0
| null |
2023-05-08T03:56:29.447
|
2023-05-11T14:08:20.917
|
2023-05-11T14:08:20.917
|
269172
|
269172
|
[
"time-series",
"causality",
"treatment-effect"
] |
615191
|
1
| null | null |
1
|
10
|
I have a dataset with counts of birds in two locations over time, and am interested in describing the difference in trends in bird counts between these locations. The counts are conducted by multiple observers, which are included as a random effect. The data is best modelled using generalised poisson or negative binomial distribution (differs per species), and zero-inflation added where indicated by tests using the DHARMa package. Basic model:
```
glmmTMB(total ~ year * location + (1 | observer), family=genpois, data=tmp)
```
When plotted next to the original data, the model fits poorly – with models (strongly) overestimating trend for some species and underestimating for others, compared with the observed data. When fitting the model without the random effect, the model fits well - however, we are interested in the trend over time. The discrepancy appears to be caused by the variance that is attributed to the observer random effect, which perhaps absorbs too much of the time trend information?
We know that there are differences in the quality of the counts between observers and would like to account for this (e.g. not all observers hear the calls of species with higher pitch calls). We do not expect a difference in the trend per observer over time and while there were a few observers that counted birds over two or more periods, most observers only counted one period. Therefore I think we cannot justify using partial pooling by including a random slope per observer. However, including this in the model does seem to reduce (but not eliminate) the bias and improve the fit for some species.
How can I attribute more of the variance currently ascribed to the observer random effect to the fixed effect of interest (trend over time)? Or in what other ways may I be able to reduce the bias in the model fit?
|
Attributing variance to fixed and random effects / partial pooling in glmmTMB
|
CC BY-SA 4.0
| null |
2023-05-08T04:30:33.893
|
2023-05-08T04:30:33.893
| null | null |
387460
|
[
"variance",
"pooling",
"glmmtmb"
] |
615192
|
1
| null | null |
1
|
6
|
I'm trying to understand the RESET Test for Regression Models. We assume that the dependend variable y is a function of the indenpendend variable x. We can write $y=f(x)\approx \beta_0+\beta_1x+\beta_2x^2+\beta_3x^3+\ldots$ because of the Taylor Expansion.
Now my question: Why don't we regress y on $x, x^2, x^3$ and look at the significance of $\beta_2, \beta_3$? Because the Reset Test instead regress y on $x, \hat{y}^2,\hat{y}^3$ ...
I hope someone could explain or give me a hint.
|
Regression Specification Error Test (RESET)
|
CC BY-SA 4.0
| null |
2023-05-08T04:34:59.793
|
2023-05-08T04:34:59.793
| null | null |
387459
|
[
"regression"
] |
615195
|
1
|
615280
| null |
1
|
111
|
I have made the following model in DAGitty:
[](https://i.stack.imgur.com/B8ism.png)
Where X2 is controlled for.
DAGitty says:
>
The total effect cannot be estimated due to adjustment for an intermediate or a descendant of an intermediate.
My understanding is that I can estimate the total effect if I control also for X1, other than X2, as that would block the backdoor path opened by controlling for X2.
Question: Is it possible to find the treatment effect after controlling for X2, e.g. by closing the backdoor path by further controlling for X1?
|
Can controlling for a variable block the backdoor path opened by controlling for a collider?
|
CC BY-SA 4.0
| null |
2023-05-08T05:29:01.313
|
2023-05-09T02:20:26.387
|
2023-05-08T12:37:54.820
|
154990
|
154990
|
[
"causality",
"dag",
"causal-diagram"
] |
615196
|
1
| null | null |
0
|
54
|
Please help me to figure out the final result in a glmmTMB. I used this code
```
model1<-glmmTMB(ctmax ~ lat+ (1|site), dispformula=~lat,data=data)
summary(model1)
```
got this output
```
Family: gaussian ( identity )
Formula: ctmax ~ lat + (1 | site)
Dispersion: ~lat
Data: data
AIC BIC logLik deviance df.resid
1126.1 1146.5 -558.1 1116.1 428
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
site (Intercept) 1.631 1.277
Residual NA NA
Number of obs: 433, groups: site, 21
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 44.69706 1.37032 32.62 <2e-16 ***
lat 0.08627 0.05073 1.70 0.089 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Dispersion model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.17803 0.34125 0.522 0.6019
lat 0.02427 0.01286 1.887 0.0591 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
```
```
|
Which one (conditional or dispersion model) is the final result in glmmTMB?
|
CC BY-SA 4.0
| null |
2023-05-08T06:07:55.793
|
2023-05-08T12:45:41.990
|
2023-05-08T12:21:02.847
|
341520
|
387464
|
[
"heteroscedasticity",
"glmmtmb"
] |
615197
|
2
| null |
615186
|
3
| null |
>
I am having trouble learning the relevant concepts of t-test. Even if you search the web or books, the explanation is slightly different, it causes confusion. (Please understand that I am not a statistics or math major)
Many of the sites and books you're likely to be looking at will contain errors, or at best infelicities of explanation which will lead you to be confused; in many cases it's quite clear that the authors of lots of web pages and even a great many textbooks are themselves no less confused than you are (for all that they appear to have convinced themselves otherwise. You have the distinct advantage over such sources of not having convinced yourself that you understood what you did not.)
I think the first thing to do is to lay out two quite distinct concepts, which too often get conflated:
- What is specifically assumed in order to (algebraically) obtain a t-distribution for the null distribution of the test statistic when $H_0$ is true, and hence for obtaining the exact significance level you seek, and thereby, 'exact' p-values. These assumptions to derive that null distribution of the test statistic are usually called - for obvious reasons - "the assumptions" of the test. If you break those assumptions, you will not get an exact t-distribution for the distribution of that test statistic when $H_0$ is true.
- The weaker conditions under which the t-statistic will have a null distribution which is reasonably approximated by a t-distribution.
There's a difficulty here that should be signalled, in that what's 'reasonable' is very much a case-by-case thing. What you might accept as reasonable for one task and what I might accept as reasonable for that task will differ, and they will probably differ again when we change to some other circumstance.
This distinction is very important for understanding many of the differing claims you'll encounter, and for figuring out whether they make sense as is, whether they make sense in some circumstances (such as adding some conditions) or whether they're pretty much just wrong.
>
Someone say that the population should normally distributed.
This is situation 1 above -- the assumptions under which the t-distribution is derived for the null distribution of the t-test statistic is that the set of random variables representing the sample we plan to draw are independent, identically distributed, normal.
>
Someone say that the distribution of sampling mean(for multiple trial of sampling) should be normally distributed.
- You don't need to run the sampling 'many times'; this is a misconception that many books create. The sample mean of a single sample is a random variable. We can talk about the distribution of that one random variable, and that is indeed the sampling distribution of the mean.
- Strictly, with i.i.d. observations and finite sample size, you can only get a normal distribution for the mean if you started with a normal distribution for each of the values being averaged. The best we can hope for is that the sample mean is approximately normally distributed. We are here talking about whether we're dealing with a sampling distribution that's close enough to use a t-approximation now -- i.e. under situation 2; clearly we aren't in situation 1.
- Even if you have that, note that the t-statistic has both a numerator and a denominator; you can't ignore what happens to the denominator, and you must consider that the statistic is a ratio of the two. The finite-sample distribution of the test statistic depends on the behavior of the ratio of the numerator to the denominator, not just on the numerator.
- To deal with the numerator, people try to invoke the CLT and declare victory, but as we see, it's not quite that simple. We have multiple things to consider there.
- One thing to beware: many books are quite misleading about what the CLT actually says. Indeed many are flat out wrong. Fortunately, some of those books do convey a somewhat different fact -- that in many cases, the distribution of sample means may sometimes be fairly well approximated by a normal distribution (while never actually attaining it). As suggested above, that does not of itself make the t-statistic have a t-distribution.
- Nevertheless, it's often the case that when the numerator is close to normal, the whole statistic is also pretty close to a t-distribution. This is more of an empirical observation than a proven fact, although last I saw, it did seem like we're perhaps getting quite close to having some theorems that will give some conditions under which we can say more about when the sampling distribution of the t-statistic will be within a certain distance (in a specific but useful sense) of the of the t-distribution.
- Skewness and heavy-tailedness are problematic; in particular it's easy (particularly in the case of a one-sided one sample test) for the significance level to be inflated above the chosen significance level with substantial skewness. I've seen a number of real data sets where the distribution was so skewed that samples in the hundreds or even thousands might be required to get good approximate significance levels (though we might easily have different opinions about what's 'good enough' for some situation), and that problem can be greatly increased if you're adjusting for multiple testing (because as you go further into the tail, skewness remains a problem for longer). Heavy tailedness will mostly tend to push down significance levels. This may not seem to be a big problem, but if you think about power it's compounding the power-loss you're already suffering for using a suboptimal statistic by also conducting the test at a lower significance level than you wanted. Sometimes quite considerably lower.
>
On the other hand, someone say that the each value of samples shoud be normally distributed.
This is again, situation 1. In fact I can't see any difference here from the previous thing you said which was situation 1.
>
in some cases the normality test was performed on each sample value prior to performing the t-test, and in other cases, the normality test was performed on the sampling mean (average of samples).
I would not suggest performing a normality test at all. It's answering the wrong question, it leads people to change their hypotheses based on what they discover in the data, and it sometimes leads to some distinctly counter-productive actions.
(That's not to say that I think the assumptions should be ignored, just that this isn't necessarily a great way to go about considering them.)
>
(1) I think the normal distribution of sampling mean is required to evaluate the possibility of certain t-value appears. (Here, I think that the mean value could explain t-statistic)
Please see the explanation above.
>
(2) If the statement:"the normal distribution of sampling mean is required" is true, isn't it always normal distributed as CLT says?
The CLT says nothing like that.
The relevant version of the CLT says (more or less) that in the limit as $n$ goes to infinity, the distribution of the standardized sample mean $(Ȳ−μ)/(σ/√n)$ goes to a standard normal distribution. It does not say that sample means actually have normal distributions at any finite sample size (and in practice this is not so unless you already had normal distributions to begin with).
We're instead dealing with how close to normal a sample mean might be and (again) we should keep in mind that this is not sufficient on its own to establish how good the t-distribution is as an approximation to the null distribution of the test statistic, because a t-statistic is not simply a mean; its denominator is a random quantity, and when you don't start with normal variates, one that is dependent on the numerator.
>
Since the distribution of the sampling mean is an imaginary distribution(In practice, we only do one set of sampling),
Again, you're confused about what's going on. This confusion is caused by books trying very hard to avoid talking about random variables, but then proceeding to assert facts that are really about random variables. Good luck trying to make heads or tails of the result of that!
I'm going to try to at least get you partway (though it's not formally correct, I'll at least try to convey some kind of understanding the distinctions here).
Let's think about the distribution that comes from rolling a fair die. This is a discrete uniform distribution, with probability $\frac16$ on each of the values $1, 2, ..., 6$.
A single die roll has this distribution! Of course, once you observe the outcome of the roll - once we come to consider the observed outcome - we're not discussing a random quantity any more but a realization of it, and it just has a single number as its value; probability doesn't enter into that realized value, probability describes the behavior of the random quantity, rather than the nonrandom observation.
The mean of a single sample is similar; it has a distribution, and we can derive that distribution -- the sampling distribution of the mean. Of course, once you observe the sample, the observed sample mean is the realization of that random value. That observed mean is not itself random, it's a fixed value.
>
Then we are conducting our t-test, which evaluates the possibility of our sample t-statistic within that imaginary distribution of t-values. Is this wrong statement?
The t-statistic is also a random quantity. If the sample values are i.i.d. normal and $H_0$ is true, then the t-statistic has a t-distribution (again, we can talk about the sampling distribution of a t-statistic under some set of conditions). Of course, once you observe the sample, you have a realization of the value of that random quantity, it's just a number.
There's no need to observe many samples for any of this discussion, since we're really talking about the distribution for one sample statistic. One reason you might do that, though, is simply to get an approximate look at what the sampling distribution looks like in a case where you can't readily derive its exact form, by relying on the approach of a sample distribution (e.g. the sample cdf) to the population distribution (population cdf). That is, we might illustrate the approximate shape of the sampling distribution of a single t-statistic, by sampling many of them (and relying on something like the Glivenko-Cantelli theorem, which tells us that the sample cdf of some random quantity converges to the population cdf from which we were obtaining samples of it).
Which is to say, even though any one observed outcome is just a number, nevertheless, the empirical cdf of a large collection of (i.i.d.) samples from the same distribution will approach the population cdf. So such sampling does help us see (in a somewhat rough way) what the distribution of the population looks like that we're sampling, even though we're talking about what the distribution of a single random value would be.
By way of illustration, I don't know what the distribution of a t-statistic will be when sampling from a lognormal distribution. It won't be algebraically tractable and I don't even think its readily doable numerically (though the convolution for the distribution of the numerator would be fairly straightforward). But we can simulate it to get a good idea of what the distribution is like. Here's an example with shape parameter $\sigma=1$, and samples of size $60$. Here I draw a Q-Q plot:
[](https://i.stack.imgur.com/QJoRV.png)
Which shows us that the one-sample t-statistic is pretty left skew; a histogram shows the same thing:
[](https://i.stack.imgur.com/sQrkn.png)
This left skewness might surprise many people, because the numerator of the t-statistic is distinctly right skew. You really can't forget about that denominator in small samples -- it matters!
Now even though we simulated many samples (100,000 samples each of size 60), we should not be confused by this into thinking that we're doing this to find the distribution for many samples; we're doing it to get an approximate picture of the sampling distribution of the t-statistic calculated on a single sample of size 60. That histogram is a reasonably accurate picture of what the density will look like.
[Note that the parent distribution in this case is distinctly less skew than a number of real-life distributions I have dealt with. The ordinary moment-skewness is less than 6.2. That's not small, but considerably bigger skewness than that certainly occurs in practice - and in situations where you might still be interested in inference about means.]
>
(3) I am dealing with one-sample t-test. Is there any requirements differences between one-sample and other t-tests?
Well, yes, in several senses. In situation 1, you have to have more things be simultaneously true for the t-statistic to exactly have a t-distribution when $H_0$ is true (both samples drawn from normal 'populations', independence both within and between samples, equal variances). In situation 2, you're somewhat less sensitive to skewness under $H_0$ when the two populations have the same shape (you can still lower the type I error rate, just as in the one-sample case with a heavier tail), but it's harder to push it up very much above the type I error rate (particularly around $\alpha=0.05$)
If there's anything you'd like clarification on, please indicate where it's required.
Please note that there are a number of relevant posts already on site which will shed more light on your questions and related questions that might arise from the discussion here.
| null |
CC BY-SA 4.0
| null |
2023-05-08T06:09:02.460
|
2023-05-10T00:20:36.070
|
2023-05-10T00:20:36.070
|
805
|
805
| null |
615202
|
1
| null | null |
0
|
6
|
I've come across two different formulas in my studies to calculate the output shape of a convolution.
Below, $I$ is the input image size, $K$ the filter size and $S$ the stride.
$$
\lfloor \frac{I - K + 2P}{S} \rfloor + 1
$$
and
$$
\lfloor \frac{I - K + 2P}{S} + 1 \rfloor
$$
I've computed quite a few examples and I come up with the same results. Are these equivalent?
Edit: Hmm, reasoning I am thinking that they must be equivalent, because the fractional component is only produced by the first term, so that always gets thrown away. The floor of 1 is always 1, so it shouldn't make a difference.
Many thanks in advance!
|
Are the two formulas for computing the output shape of a convolution equivalent? Computing the floor before or after adding $1$?
|
CC BY-SA 4.0
| null |
2023-05-08T08:20:57.580
|
2023-05-08T08:34:19.497
|
2023-05-08T08:34:19.497
|
279126
|
279126
|
[
"conv-neural-network",
"convolution"
] |
615203
|
1
| null | null |
0
|
24
|
Consider $n$ categorical distributions ${\bf X}_i\sim \mathrm{B}(p_{i1}, ..., p_{ik})$ where the outcome of variable $i$ is $\bf e_j$ with probability $p_{ij}$ and ${\bf 0}$ with probability $1-\sum_j p_{ij}$. Let ${\bf S}_n=\sum_i {\bf X}_i$.
Let ${\bf Y}_i\in \Re^k \sim \mathrm{P}(p_{i1}, ..., p_{ik})$ be a poisson multinomial where each coordinate is an independent poisson distribution with rate $p_{ij}$. Let ${\bf T}_n = \sum_i {\bf Y}_i$.
It can be shown by coupling that
$$\sup_A \left| \Pr[{\bf S_n}\in A]-\Pr[{\bf T_n}\in A] \right| \leq \sum_{i=1}^n \left( \sum_{j=1}^k p_{ij}\right)^2$$
Where $A$ is any event in their co-domain.
Problem: Unfortunately, $\left(\sum_{j=1}^k p_{ij}\right)^2$ can be large even if $ \left( \sum_{i=1}^n p_{ij} \right)^2$ is small.
Question: I would like to know if there are similar bounds where the bound is of the form (say) $\sum_{j=1}^k \left( \sum_{i=1}^n p_{ij} \right)^2$ (notice the index interchange). It does not have to be a Poisson bound, but I would like a simpler distribution to work with than ${\bf S}_n$. Also, it doesn't have to be across all events $A$, it could be just a bound for one outcome (as I am not dealing with many outcomes anyways).
|
Approximating sum of categorical random variables with a multinomial poisson distribution
|
CC BY-SA 4.0
| null |
2023-05-08T08:43:14.373
|
2023-05-08T08:43:14.373
| null | null |
181388
|
[
"binomial-distribution",
"poisson-distribution",
"approximation",
"bounds"
] |
615204
|
1
| null | null |
3
|
94
|
I have read on many occasions deep learning practitioners recommending to treat regression problems (with continuous variables) as classification problems, by quantizing the output into bins and using cross-entropy loss instead of L2 loss.
For example these [notes](https://cs231n.github.io/neural-networks-2/#losses) from Stanfords's CS231n class on CNNs:
>
It is important to note that the L2 loss is much harder to optimize than a more stable loss such as Softmax. Intuitively, it requires a very fragile and specific property from the network to output exactly one correct value for each input (and its augmentations). Notice that this is not the case with Softmax, where the precise value of each score is less important: It only matters that their magnitudes are appropriate. Additionally, the L2 loss is less robust because outliers can introduce huge gradients. When faced with a regression problem, first consider if it is absolutely inadequate to quantize the output into bins. [...] Classification has the additional benefit that it can give you a distribution over the regression outputs, not just a single output with no indication of its confidence. If you’re certain that classification is not appropriate, use the L2 but be careful: For example, the L2 is more fragile and applying dropout in the network (especially in the layer right before the L2 loss) is not a great idea.
>
When faced with a regression task, first consider if it is absolutely necessary. Instead, have a strong preference to discretizing your outputs to bins and perform classification over them whenever possible.
Or [Pixel-RNN](https://arxiv.org/abs/1601.06759) which quantizes pixel values into bins:
>
Furthermore, in contrast to previous approaches that model the pixels as continuous values [...], we model the pixels as discrete values using a multinomial distribution implemented with a simple softmax layer. We observe that this approach gives both representational and training advantages for our models.
Treating regression as classification to me seems counter-intuitive, since the model cannot differentiate between a point that has been misclassified to a neighboring bin, vs. a distant bin.
Apart from the few points cited above (allowing for small errors, and being more robust to outliers), is there any theoretical evidence – or at least some intuition – as to why treating regression as classification performs better? Is it purely an optimization issue, because the optimization landscape in classification is easier to navigate than in regression? Or are there any other reasons?
I am mostly asking in the context of deep learning, but am also curious about more general answers.
|
Regression as classification: advantages?
|
CC BY-SA 4.0
| null |
2023-05-08T09:46:46.660
|
2023-05-23T00:53:04.933
|
2023-05-10T15:58:03.243
|
247274
|
82916
|
[
"regression",
"machine-learning",
"neural-networks",
"classification",
"binning"
] |
615205
|
1
|
615209
| null |
14
|
2491
|
This time, I calculated a non-negative dataset which SD is larger than mean
I have seen many people use 'mean ± SD' to show mean and standard deviation.
But I wonder whether we can use that form for non-negative dataset.
The original data can't be lower than 0 but if I use ± it looks can be negative number(like 1 ± 3).
Is their no problem or should I use other way?
|
Can I use 'mean ± SD' for non-negative data when SD is higher than mean?
|
CC BY-SA 4.0
| null |
2023-05-08T09:48:26.427
|
2023-05-16T16:17:29.163
|
2023-05-09T16:23:11.280
|
121522
|
387476
|
[
"mean",
"standard-deviation"
] |
615206
|
1
| null | null |
1
|
10
|
I’m working on a report on length of berth stays for cargo vessels visiting different ports. I would like to be able to benchmark whether vessels in a given fleet (i.e. a customer’s entire fleet of vessels) have shorter/longer berth stays than other vessels calling the same ports.
The length of a berth stay depends on both ship and shore personnel. Hence, when benchmarking in-port efficiency across ports, I need to correct for differences across these ports. My approach has therefore been to derive the average length of the fleet’s berth stay at each port and compare this average to that of all other port calls to the same port (i.e. for all vessels not in my customer’s fleet of vessels). Having done this for each port, I have found the difference in the average port stay between my customer’s fleet and all other vessels. I have then proceeded to weigh each of these differences by the number of fleet port calls to each port in order to arrive at a weighted average difference in berth stay between my customer’s fleet and all other port calls across all the ports in my data sample (I've attached a picture of my equation).
[](https://i.stack.imgur.com/ILLsz.png)
However, I would also like to be able to state whether the weighted average difference in port stay is significantly different between my customer’s fleet and all other vessels. I have been thinking of two different ways to do this:
- Perform a one-sample t-test where I test the null hypothesis that the average fleet berth stay = the average berth stay of all other calls against an alternative hypothesis that these averages are not equal. I would then have a number of observations equal to the number of ports (p). However, this approach would not take into account that the number of observations for each port may be very different, e.g. 100 fleet port calls to Port A and 2 fleet port calls to Port B
- Run an OLS regression where the dependent variable is the length of a port stay and the independent variables would be port (dummy variable to correct for differences in shore personnel efficiency and port infrastructure) and a dummy variable indicating whether the observation is a fleet port call or another vessel. If the latter independent variable is significant, I guess I could then conclude that there is a significant difference in berth stay (i.e. in-port efficiency) between vessels in my customer’s fleet and all other vessels.
Any input would be highly appreciated! Perhaps my entire approach, both the average difference in berth stay and the above two options, is flawed (for instance, the number of observations for other port calls is not accounted for in the weighted average difference in berth stay). My goal is still to say 1) whether there is a significant difference in berth stay between a given fleet of vessels and all other vessels calling the same ports and 2) what the average difference in berth stay is. I’ve attached an example data set for good measure.
[](https://i.stack.imgur.com/SMB8e.png)
I hope someone can help me out. Many thanks for your help
|
Benchmarking vessel in-port efficiency - t-test, OLS regression?
|
CC BY-SA 4.0
| null |
2023-05-08T09:48:32.543
|
2023-05-08T09:48:32.543
| null | null |
387474
|
[
"regression",
"hypothesis-testing",
"statistical-significance",
"inference"
] |
615207
|
1
| null | null |
0
|
15
|
I face with a problem of doing a time series forecasting on multivariate data in the form where different entities have their own 100-day (daily) series of 10 variables, and I'm expected to predict 10-day steps of the response variable in the future.
Now, I'd like to handle "outliers" in the data, and I wonder how to interpret "outliers" in this context. In the case of non-time-series data I'm more confident (of applying Isolation Forest or any other multivariate outlier detection algorithm), but in case of this set of series that is not applicable, because in this case we must consider the respective time series in whole (that is, either the whole series is outlier or inlier, not just one or two steps in the series).
I tried to aggregate each variable of the respective series (like mean/median) and find outliers in these aggregated data, but this is somewhat misleading, as a series could have extremes while it has non-extreme mean/median). Also, I considered qualifying whole series as outlier if there is only one outlier time step among the time flow, but this also seems simplistic, and anyway, too high proportion of the original series would be "outlier" in this way.
What is a proper approach in this problem? Or maybe I should just forget finding outliers at all and try to model on the original data irrespective of the extreme values?
|
How to find (and interpret) outliers in set of time series data?
|
CC BY-SA 4.0
| null |
2023-05-08T09:57:58.350
|
2023-05-08T09:57:58.350
| null | null |
72735
|
[
"time-series",
"outliers",
"data-preprocessing"
] |
615208
|
2
| null |
371236
|
1
| null |
Something like this is possible, although the solution I suggest would not have worked in 2018 at the time this was originally asked.
[SHAP](https://shap.readthedocs.io/en/latest/index.html) package has support for scikit-learn Isolation forests since [2019](https://github.com/slundberg/shap/pull/784), (that same thread for a discussion of precisely what it is SHAP is explaining in the case of an Isolation Forest).
I will give you a concrete example (you will see why that is funny in a minute...). I picked a random dataset for this, [properties of samples of concrete](https://archive.ics.uci.edu/ml/datasets/concrete+compressive+strength). I thought it might be interesting to see what an anomalous sample of concrete looks like, and why it might be considered unusual.
We read in the dataset, fit an Isolation forest, and then explain with the `shap.TreeExplainer` (I will include my complete code at the end).
## SHAP summary plot
[](https://i.stack.imgur.com/ReJZm.png)
Here is the summary plot. Remember, with the isolation forest in scikit-learn, -1 corresponds to anomalies and +1 to the inliers. We should think of low SHAP values as pushing us towards outlier and high SHAP values as pushing us towards inlier.
If we look at slag, we can see that high feature values of slag correspond to a low SHAP value. So we might start to think that samples containing large amounts of slag are unusual. The coarseagg feature is quite interesting - we have high and low feature values for coarseagg corresponding to low SHAP values, and then medium feature values (purple colour) corresponding to higher SHAP values.
We can see this non linear relationship below with a scatter plot `shap.plots.scatter(shap_values[:,"coarseagg"])`.
[](https://i.stack.imgur.com/XtAM5.png)
## Explain individual examples
We can explain individual concrete samples. Here is a force plot of one of the least anomalous samples.
[](https://i.stack.imgur.com/rOKnu.png)
And here is one of the most anomalous samples (outlier).
[](https://i.stack.imgur.com/CC83Q.png)
## Python Code
Notes:
- The SHAP documentation can be hard to follow, with some examples no longer working.
- If you are running this in a Jupyter notebook you may need to explicitly run shap.initjs() at the top of each cell which contains a JS plot otherwise the plot won't render.
```
%pip install shap
import pandas as pd
import shap
from sklearn.ensemble import IsolationForest
# It was easier for me to read in the dataset as a csv which I found on somebody's github
df = pd.read_csv("https://raw.githubusercontent.com/stedy/Machine-Learning-with-R-datasets/master/concrete.csv")
X = df.copy()
clf = IsolationForest(random_state=0).fit(X)
exp = shap.TreeExplainer(clf, X)
shap_values = exp(X)
#Summary plot
shap.initjs()
shap.summary_plot(shap_values, X)
#Scatter plot
shap.plots.scatter(shap_values[:,"coarseagg"])
#Force plot of one of the inliers
shap.initjs()
N=624
shap.force_plot(exp.expected_value, shap_values.values[N],features =X.iloc[N,:] ,feature_names =X.columns)
#Force plot of one of the outliers
shap.initjs()
N=42
shap.force_plot(exp.expected_value, shap_values.values[N],features =X.iloc[N,:] ,feature_names =X.columns)
```
| null |
CC BY-SA 4.0
| null |
2023-05-08T09:58:28.340
|
2023-05-08T09:58:28.340
| null | null |
358991
| null |
615209
|
2
| null |
615205
|
31
| null |
[edited based on helpful feedback in the comments]
It bothers me immensely when people do this. The argument against it is simple: the standard deviation is typically shown to convey information about data distribution (and standard error for a parameter). It achieves this goal well in some situations but not others. If the standard deviation/error implies that negative values are reasonable when you know they are not, it is not helping you communicate accurately. Bimodal distributions are another situation in which mean ± SD/SE is likely to mislead.
So what else can you do? If you're interested in the data distribution, just show the full distributions using density plots, violin plots, histograms, or their alternatives. If you're interested in the uncertainty of a parameter, you could show confidence intervals or the posterior distribution. Unlike standard deviation or standard error, these options can be asymmetric and will communicate the data distribution or uncertainty more accurately.
If you must use a numerical summary for a data distribution without referring to a graph, you could use quartiles instead of mean ± SD.
| null |
CC BY-SA 4.0
| null |
2023-05-08T10:09:26.560
|
2023-05-10T11:40:08.117
|
2023-05-10T11:40:08.117
|
121522
|
121522
| null |
615210
|
2
| null |
615068
|
4
| null |
@John Madden gave a good answer pointing to the root cause of the problem, but adding to it, you should not invert that matrix directly in the first place. Matrix inversion is generally [inefficient](https://gregorygundersen.com/blog/2020/12/09/matrix-inversion/) and [not recommended](https://www.johndcook.com/blog/2010/01/19/dont-invert-that-matrix/) for all kinds of applications. This also applies to Gaussian processes. An efficient algorithm is given by [Rasmussen (2006)](http://gaussianprocess.org/gpml/) as Algorithm 2.1 on p 19:
$$\begin{align}
L &= \operatorname{cholesky}(K + \sigma^2 I) \\
\alpha &= L^\top \backslash (L \backslash y) \\
\mu &= K_{*}^\top \alpha \\
v &= L \backslash K_{*} \\
\Sigma^2 &= K_{**} - v^\top v \\
\end{align}$$
where $K = k(X, X)$, $K_{*} = k(X, X_*)$ and $K_{**} = k(X_*, X_*)$.
| null |
CC BY-SA 4.0
| null |
2023-05-08T10:35:25.840
|
2023-05-08T10:35:25.840
| null | null |
35989
| null |
615211
|
2
| null |
615196
|
2
| null |
Both are final. The conditional model fits the mean, the dispersion models the variance via a log-link(see `help("glmmTMB")`). The variance being related to `lat` shows that a normal linear model would be heteroskedastic.
Your resulting description of `ctmax` is that
$$
ctmax \sim \mathcal N (\mu = 0.08627 \cdot \textrm{lat} + 44.69706 + b_{site}, \sigma^2 = \exp(0.02427 \cdot \textrm{lat} + 0.17803))
$$
with random effect $b_{site}\sim \mathcal N(0, 1.631)$.
Here is an example in R:
```
n <- 5000
x <- rnorm(n)
y <- rnorm(n, mean = 1.5 * x + 4, sd = exp(0.1*x + 0.2))
model1 <- glmmTMB(y ~ x, dispformula = ~ x)
summary(model1)
Family: gaussian ( identity )
Formula: y ~ x
Dispersion: ~x
AIC BIC logLik deviance df.resid
16222.1 16248.1 -8107.0 16214.1 4996
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.99747 0.01750 228.48 <2e-16 ***
x 1.50929 0.01709 88.31 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Dispersion model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.40487 0.02000 20.24 <2e-16 ***
x 0.20827 0.01998 10.42 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
```
| null |
CC BY-SA 4.0
| null |
2023-05-08T10:52:10.463
|
2023-05-08T12:45:41.990
|
2023-05-08T12:45:41.990
|
2126
|
341520
| null |
615212
|
2
| null |
614183
|
2
| null |
As a starting point, I would suggest one option might be to look at implementing a random walk prior on the log-odds of response.
This might not be the best approach but it seems to align with your goals and if nothing else it may be educational and lead you to more fruitful options.
Specifically, if you are assuming discrete time $t$, evenly spaced (e.g. $t = 1, 2, 3, \dots$), then with no loss of generality, you can assume a binomial distribution at each time point:
$$
\begin{aligned}
Y_t &= \mathsf{Bin}(n_t, p_t) \\
\mathsf{logit}(p_0) = \eta_0 &\sim \mathsf{Normal}(\mu_0, \sigma_0) \\
\mathsf{logit}(p_t) = \eta_t &= \eta_{t-1} + \epsilon_t , \quad t \in {1, 2 \dots} \\
\epsilon_t &\sim \mathsf{Normal}(0, \sigma_\epsilon) \\
\sigma_\epsilon &\sim \mathsf{Exponential}(1)
\end{aligned}
$$
where $Y_t$ denotes the number of events at time $t$ out of $n_t$ trials (for which your application would have $Y_t \in \{0, 1\}$ and $n_t = 1$, i.e. Bernoulli). The $\mu_0$ and $\sigma_0$ would be pre-specfied (fixed) based on prior knowledge and the other terms estimated.
To be clear, the first line is the likelihood and then the third line is the first order random walk with $\eta_t$ and $\sigma_\epsilon$ being the parameters of interest.
To implement this, you could use stan [https://mc-stan.org/] or similar. A very basic (and quite naive) implementation is shown below:
```
data {
int N;
int y[N];
int n[N];
int prior_only;
real pri_mu;
real pri_s;
real pri_nu;
}
transformed data {
}
parameters{
real b0;
real b;
vector[N-1] delta;
real<lower=0> nu;
}
transformed parameters{
vector[N] e;
// resp is random walk
e[1] = b0;
for(i in 2:N){e[i] = e[i-1] + delta[i-1] * nu;}
}
model{
target += normal_lpdf(b0 | pri_mu, pri_s);
target += exponential_lpdf(nu | pri_nu);
target += normal_lpdf(delta | 0, 1);
if(!prior_only){target += binomial_logit_lpmf(y | n, e);}
}
generated quantities{
vector[N] p;
p = inv_logit(e);
}
```
which you can run in R with:
```
library("cmdstanr")
library("data.table")
library("ggplot2")
mod1 <- cmdstan_model(<filename here>)
set.seed(1)
K <- 100
epsilon <- rnorm(K-1, 0, 0.1)
eta <- numeric(K)
eta[1] <- qlogis(0.3)
for(i in 2:K){
eta[i] = eta[i-1] + epsilon[i-1]
}
plot(1:K, (eta))
y <- rbinom(K, 50, plogis(eta))
ld <- list(N = K, y = y, n = rep(50, K),
pri_mu = 0, pri_s = 10, pri_nu = 1, prior_only = F)
f1 <- mod1$sample(
data = ld,
chains = 3,iter_sampling = 2000,
adapt_delta = 0.95,
refresh = 0 # print update every 500 iters
)
p <- f1$draws(variables = "p", format = "matrix")
p_mu <- apply(p, 2, mean)
p_025 <- apply(p, 2, function(z)quantile(z, 0.025))
p_975 <- apply(p, 2, function(z)quantile(z, 0.975))
dfig <- data.table(p_mu, p_025, p_975,
p_obs = y/50,
p_tru = plogis(eta),
t = 1:K)
ggplot(dfig, aes(x = t, y = p_mu)) +
geom_ribbon(aes(ymin = p_025, ymax = p_975), alpha = 0.2) +
geom_line() +
geom_point(aes(y = p_obs), col = 2) +
geom_line(aes(y = p_tru), linewidth = 0.4, lty = 2)
```
The above will begin to suffer with large numbers of observations and so may not be suitable for large datasets.
In these cases, you might want to opt for an alternative, such as a penalised-spline or GP approximation (a GP will suffer with large numbers of observations due to the operations that have to be done on the covariance).
The figure shows the inferred probability of response (black line) with the observed data shown as a red points and the underlying true probability of response shown as black dashed line.
[](https://i.stack.imgur.com/FWS1n.png)
The prior serves as a smoother and if this was insufficiently smooth then you could perhaps consider a second order random walk.
Other considerations may relate to whether a drift component is warranted, which it might be by the sounds of your description.
I will leave those for you to look into, should you wish.
| null |
CC BY-SA 4.0
| null |
2023-05-08T11:03:01.890
|
2023-05-08T11:03:01.890
| null | null |
24865
| null |
615213
|
1
| null | null |
2
|
43
|
Can someone please summarise the difference between these 3 boosting algorithms: `AdaBoost vs GBM vs XGB`?
|
AdaBoost vs GBM vs XGB
|
CC BY-SA 4.0
| null |
2023-05-08T11:09:27.003
|
2023-05-08T14:35:24.797
|
2023-05-08T14:35:24.797
|
379489
|
379489
|
[
"machine-learning",
"classification",
"boosting",
"adaboost"
] |
615214
|
1
| null | null |
0
|
25
|
A real-valued feedforward/fully connected neural network with activation function $\sigma : x\in \mathbb R \mapsto \max \{0,x\}\equiv \text{ReLU}(x)$ can formally be seen as a function $f_\theta :\mathcal X\subseteq \mathbb R^{d}\to\mathbb R$ defined by the expression
$$f_{\theta} (x) = A^{(L)}\circ \sigma \circ A^{(L-1)}\circ\ldots\circ \sigma \circ A^{(1)}(x)$$
Where for all $1\le k\le L $, we define $A^{(k)}(x) := W_k x + b_k$ for $W_k,b_k$ respectively weight matrices and bias vectors of appropriate dimensions, and the activation $\sigma$ is applied elementwise. We can aggregate the weights and biases $\big((W_k,b_k)\big)_{l=1}^L $ in a big column vector which we denote $\theta \cong\big((W_k,b_k)\big)_{l=1}^L \in \mathbb R^{p}$ where $p$ is the total number of parameters, and therefore denote by $f_\theta$ the neural network realized by this set of parameters. One can refer to [this paper](https://arxiv.org/pdf/1709.05289.pdf) for a more precise description of this formal representation of deep neural networks as functions.
What I want to ask is the following : for given $x\in\mathcal X$, is there a closed form expression for $\nabla_\theta f_\theta (x) $ ?
I'm aware that I didn't give the explicit representation $\theta$ so the question is a bit ill-posed, but the point is that I am looking for a closed form expression for the derivative of $f_\theta $ with respect to each parameter in $\theta$, i.e. each entry of $W_k$ and $b_k$ for $1\le k\le L$.
I know that in practice, people just use backpropagation so that there is no need to ever compute the whole gradient of $f_\theta (x) $, however I happen to need it for some theoretical investigations. It is possible to go through the algebra carefully and work it out, but it is extremely tedious and I haven't been succesful in deriving a general formula so far.
Is this closed-form expression available somewhere in the literature by any chance ? Since Neural Networks have been around for a while, I would guess (hope) that the answer is yes, but haven't been able to find anything. While I'm at it, I would also be interested in a closed-form expression for the Hessian $\nabla^2_\theta f_\theta(x) $.
Thanks in advance.
|
Closed form expression for the gradient of a fully connected neural network with respect to its parameters
|
CC BY-SA 4.0
| null |
2023-05-08T11:32:35.310
|
2023-05-08T11:32:35.310
| null | null |
305654
|
[
"neural-networks",
"references",
"backpropagation",
"gradient"
] |
615215
|
2
| null |
615195
|
2
| null |
Ok after reading your comments and thinking about for a little bit I both think, that this hypothetical scenario is kind of interesting and that I have a solution for most cases:
When you fit a linear model $Y \sim \beta_T T + \beta_{X2} X2 + \beta_0$, and most generalizations of one, you should also produce a covariance matrix of the estimates $\hat\beta$. We can use this to calculate a coefficient from changes in $\hat\beta_{X2}$ to $\hat\beta_{T}$:
$$
b = \frac{Cov(\hat\beta_{X2}, \hat\beta_T)}{Var(\hat\beta_{X2})} = \frac{\sigma_{\hat\beta_T} \cdot Cor(\hat\beta_{X2}, \hat\beta_T))}{\sigma_{\hat\beta_{X2}}}
$$
Now a change in $\hat\beta_{X2}$, which we will call $\Delta$, will result in $b \cdot\Delta$ change in $\hat\beta_T$. Since we know that the true $\beta_{X2} = 0$ we can use $\Delta = - \hat\beta_{X2}$ and obtain the true estimate $\hat\beta_T -b\cdot\hat\beta_{X2}$.
Let me demonstare with R
```
n <- 10000
treat <- runif(n)
Indi <- rnorm(n, mean = treat) # true treatmet is 1
X1 <- rnorm(n, mean = treat, sd = 0.5)
X2 <- rnorm(n, mean = 1.5*X1 + 0.5*Indi, sd = 2)
# what we we can get:
coef(lm(Indi ~ treat))
#the model
m1 <- lm(Indi ~ treat + X2)
coef(m1)
#covariance of the estimates
vcov(m1)
# correlation coefficient
bX2T <-vcov(m1)["treat", "X2"]/vcov(m1)["X2", "X2"]
# Indi ~ treat reconstructed
bX2T * (-1* coef(m1)["X2"]) + coef(m1)["treat"]
```
This is actually equivalent to fitting $X2 ~ T$ and using that to estimate and add the indirect "effect" that $T$ has via $X2$
| null |
CC BY-SA 4.0
| null |
2023-05-08T11:47:46.817
|
2023-05-08T19:10:17.233
|
2023-05-08T19:10:17.233
|
341520
|
341520
| null |
615216
|
2
| null |
615168
|
1
| null |
The interaction coefficient is the association of the product of the two predictors with outcome, beyond what you would predict based on their individual coefficients. You can't interpret the interaction coefficient without considering both interacting predictors. With interactions, the values of coefficients for one predictor are affected by how its interacting predictors are coded: centering/scaling of continuous predictors, or changing the reference level of a categorical predictor.
Your problem would occur even in a simple linear model without the log/exponentiation issue. Say that $x_1$ and $x_2$ are both centered, and you simply had
$$y=\beta_1 x_1 x_2, $$
with $\beta_1$ the interaction coefficient. Now scale $x_2$ so that $z_2 = x_2/s_2$ and leave $x_1$ alone. Plug in to the above:
$$y=\beta_1 x_1 s_2 z_2= (\beta_1 s_2)x_1 z_2 .$$
The value of the interaction coefficient necessarily changes when you scale $x_2$, from $\beta_1$ to $\beta_1 s_2$. Your approach didn't take that into account.
With an interaction, if you want to estimate the association of a predictor with outcome you must specify values for all predictors with which it interacts. You didn't do that. If you had specified a value for `x2` in the centered-only model and the corresponding value for `z2` in the second (centered and scaled) model, then your estimated associations of `x1` with outcome should agree.
| null |
CC BY-SA 4.0
| null |
2023-05-08T12:07:57.583
|
2023-05-08T14:49:33.140
|
2023-05-08T14:49:33.140
|
28500
|
28500
| null |
615217
|
2
| null |
541078
|
0
| null |
An answer to a question like this can involve several aspects:
- How to fit a half normal distribution (see: https://en.m.wikipedia.org/wiki/Half-normal_distribution#Parameter_estimation )
- How to obtain derived quantities from a half normal distribution (see: https://en.m.wikipedia.org/wiki/Half-normal_distribution#Properties)
- And not the least, whether trying to analyse this problem with a half normal distribution makes sense. There are several discrepancies like the data being described as a discrete distribution (half-normal is continuous) and also the shape of the distribution is a lot different.
In addition the motivation "to find the tails in the distribution and remove them" is unclear and points towards an XY-problem.
(anyways I felt like posting an answer to create a direction for any people that might land on this question in a search; if anybody feels that the first two points do not provide a good answer then ask for more)
| null |
CC BY-SA 4.0
| null |
2023-05-08T12:15:32.747
|
2023-05-08T12:15:32.747
| null | null |
164061
| null |
615218
|
1
| null | null |
0
|
18
|
I ran this code and found the result. Could you please help me to figure out my model follows DHARMa residual?
```
model1<-glmmTMB(ctmax ~ lat+ (1|site), dispformula=~lat,data=data)
summary(model1)
```
Got this result:
[](https://i.stack.imgur.com/vhH3k.png)
|
Whether my model follows the QQ plot and DHARMa residual in glmmTMB?
|
CC BY-SA 4.0
| null |
2023-05-08T12:44:58.747
|
2023-05-08T13:48:07.343
|
2023-05-08T13:48:07.343
|
2126
|
387464
|
[
"diagnostic",
"glmmtmb"
] |
615220
|
1
| null | null |
0
|
25
|
My dataset is composed of various country-level observations over the years. I am interested in the cross-sectionnal dimension of my database rather than the time series aspect. For this reason, I decided to turn this panel dataset into a cross sectional one. To do this, for each variable, I take the mean value of each country over the years. For example, instead of observing Germany's GDP t times, I observe Germany's GDP one time, its value being the mean GDP of Germany over t years.
The problem is, some of my variables are dummies, taking either 0 or 1 as a value (for example, the variable "Democracy" is a dummy). If I use the mean value of "Democracy" for each country as an independant variable in my regression, will the fact that it is not a dummy anymore cause a problem ? If I want to observe the impact of being a democratic country or not on my dependant variable, can I leave this variable as is, or should I find a way to turn this variable back to a dummy ?
|
Can I use the mean value of a dummy variable the same way I would use a dummy variable?
|
CC BY-SA 4.0
| null |
2023-05-08T13:30:36.957
|
2023-05-08T13:30:36.957
| null | null |
382870
|
[
"cross-section"
] |
615221
|
2
| null |
614735
|
3
| null |
I think you're on the right track.
Firstly, the "simple" approach is often called "The Marginal Odds Ratio" or "The Unadjusted Odds Ratio". Marginal here means marginalizing over the other variables as you mentioned. Conversely, the odds ratios obtained from logistic regression might be referred to as "Adjusted Odds Ratios". I will use those terms here.
>
In my opinion, the advantage is that the Odds Ratio calculated using Logistic Regression is "adjusted" to take into account the influence of other variables - whereas the Odds Ratio calculated using the simple way does not take into account the influence of other variables.
This is the main advantage of adjusted estimates, yes. Its very easy to create an example where the marginal estimate might give you the wrong sign, for example.
| null |
CC BY-SA 4.0
| null |
2023-05-08T13:44:26.467
|
2023-05-08T13:44:26.467
| null | null |
111259
| null |
615222
|
1
| null | null |
1
|
23
|
I have a sample of data with n=200 and I would like to predict my descriptive statistics such as mean, Std Dev and 95% CI when I have specific sample size for example n=10 based on the current study.
I assumed my population follows the Normal distribution and I applied t test to calculate CI.
What I have done, I applied random sampling with replacement with n=10 from the original sample and repeated the process 100 times and calculated the mean of each 100 samples then calculate the mean(100 means), sd(100 means) then 95%CI(100 means) to get a good prediction of descriptive statistics for any random sample with size n=10. I was wondering if this approach is correct or not?
Or the other solution could be to get the mean(100 means) and Pooled.Sd(100 sd) then calculate 95%CI.
Could you please give me advise?
Thanks in advance for your help.
|
Estimate overall descriptive statistics (such as mean, Std, CI ) for 100 resampling with same sample size and same population
|
CC BY-SA 4.0
| null |
2023-05-08T13:56:39.810
|
2023-05-08T15:55:12.540
|
2023-05-08T15:55:12.540
|
184917
|
184917
|
[
"descriptive-statistics",
"resampling"
] |
615223
|
1
| null | null |
0
|
32
|
Let $X$ follow normal distribution with mean $\mu_X=10$ and variance $V_X=20$. Let $Y$ follow truncated normal distribution with mean $\mu_Y=-10,V_Y=8$, where $Y\leq 0$ by truncation.
Let $Z=X+Y$. Denote $z_1,\dots, z_N$ be $N$ realizations of $Z$. Now I want to recover $\mu_X,V_X,\mu_Y,V_Y$. Suppose I put appropriate priors on $\mu_X,V_X,\mu_Y,V_Y$.
$Q:$ How do I conduct MCMC posterior sampling for $\mu_X,\mu_Y,V_X,V_Y$? Looking at the likelihood of $Z$, I do not find an easy way to implement Gibbs sampling. Is it possible to conduct MCMC by data augmentation?
|
How to perform MCMC posterior sampling of $X+Y$ random variable?
|
CC BY-SA 4.0
| null |
2023-05-08T14:14:01.347
|
2023-05-08T15:09:43.637
|
2023-05-08T15:09:43.637
|
79469
|
79469
|
[
"self-study",
"bayesian",
"markov-chain-montecarlo",
"data-imputation",
"data-augmentation"
] |
615224
|
1
|
615237
| null |
2
|
83
|
I am testing simulation of the lognormal distribution against the `lung` dataset, as an example of right-censored data, from the `survival` package. Goodness-of-fit tests indicate Weibull provides best fit, but please bear with my example as I try getting my arms around the lognormal distribution too.
When I run the code posted at the bottom, I get the values shown in the image below just before the posted code. Which are the correct parameters for the lognormal distribution, if indeed they are shown below? If not, how would I extract or transform those values? The parameters I am looking for are "σ" for shape parameter (SDEV of the log of the distribution), and "μ" for scale parameter (median of the distribution), consistent with the objective explained in the next paragraph.
My objective is to (A) fit a Kaplain-Meier curve against the fitted `lung` data using those lognormal parameters, (B) run simulations by drawing random samples from a distribution of those lognormal parameters probably using the `mvrnorm()` function of the `MASS` package, and (C) layering (B) against (A) in the same plot in order to show the sensitivity of the survival curve to those parameters as done for another distribution in example: [How to generate multiple forecast simulation paths for survival analysis?](https://stats.stackexchange.com/questions/614198/how-to-generate-multiple-forecast-simulation-paths-for-survival-analysis)
[](https://i.stack.imgur.com/C3TN3.png)
Code:
```
library(survival)
# Fit lognormal distribution to right-censored survival data
fit <- survreg(Surv(time, status) ~ 1, data = lung, dist = "lognormal")
mu <- fit$coef
sigma <- fit$scale
summary(fit)
mu
sigma
```
|
How to extract the correct parameters for the lognormal distribution when using the survreg() function in survival analysis?
|
CC BY-SA 4.0
| null |
2023-05-08T14:21:40.760
|
2023-05-08T15:43:49.800
| null | null |
378347
|
[
"r",
"survival",
"lognormal-distribution",
"parameterization"
] |
615225
|
1
|
615227
| null |
1
|
37
|
I wonder if using a propensity score in the following situation is wrong. Imagine I have the next causal model
$$X = N_x$$
$$Y = f(X, N_y)$$
$$ Z = g(X, Y, N_z)$$
Where $N_z, N_y, N_x$ are independent random variables. One example of such a model is $X$ is race, $Y$ is education $Z$ is income. If I wanted to estimate the causal effect of race on income, for example via ATE, would it be wrong to use propensity score matching?
|
Invalid use of Propensity Score Matching?
|
CC BY-SA 4.0
| null |
2023-05-08T14:21:41.737
|
2023-05-08T14:42:06.830
| null | null |
361051
|
[
"causality",
"propensity-scores",
"treatment-effect",
"causalimpact"
] |
615226
|
1
| null | null |
1
|
18
|
I originally asked this question on stackoverflow [here](https://stackoverflow.com/questions/76200571/visually-show-how-the-effect-of-one-regressor-diminishes-the-effect-and-signific), but was advised to move it to Cross Validated for a more appropriate place to have this discussion.
A commenter pointed out that my situation looks like it could be an example of the [Simpson's Paradox](https://en.wikipedia.org/wiki/Simpson%27s_paradox). While this seems fitting based on the description that "a trend appears in several groups of data but disappears or reverses when the groups are combined", it does not fully explain the phenomenon. To me it seems like the graphs on the Simpson's Paradox page are illustrating an interaction effect, not the impact of controlling for another variable without interaction effects.
I would really appreciate an answer that can also shed some light on what might be going on mathematically as my statistical understanding about what it means to control for a variable and what can cause confounding effects is quite limited. I apologize if because of my lack of knowledge, my question is not as precise as it could be.
My current explanation/idea is that because the effect size of X1 on Y is quite small, adding an even only mildly correlated additional variable will decrease its effect size and significance greatly, to the point where it is no longer significant.
Below is my question.
---
After fitting my regression models, I found that the effect size and significance of one predictor is greatly diminished once I introduce another, dichotomous variable with a strong effect on the response variable. My interpretation is that the new variable's strong effect "overshadows" the one of the other variable. Based on correlation and VIFs, there don't seem to be any multicollinearity issues.
Assuming my interpretation is correct, how could I visually show how the inclusion of the second variable decreases the effect size and significance of the other variable? I thought about doing a scatter plot, but I think it only shows the strong effect of the new variable, not how the new variable influences the old one. What kind of visualization would be useful here? The goal is not to diagnose anything or to necessarily generate additional insight, but rather to make the regression results more intuitive for the reader of my analysis.
I hope that my question is succinct enough to be answered. I realize that it rests on the assumption that my interpretation of my regression is correct. If you have any other feedback aside from what kind of plot would be the best to do what I want, do share it. Thank you!
These are the regression results.
```
> stargazer(m1,m2,type="text")
==============================================
Dependent variable:
----------------------------
Y
(1) (2)
----------------------------------------------
X1 -0.012** -0.006
(0.005) (0.005)
X2 0.750***
(0.132)
Constant 1.438*** 1.074***
(0.094) (0.122)
----------------------------------------------
Observations 56 56
Log Likelihood -133.332 -116.022
Akaike Inf. Crit. 270.664 238.044
==============================================
Note: *p<0.1; **p<0.05; ***p<0.01
```
This is the plot I made which I am not satisfied with yet.
[](https://i.stack.imgur.com/rnATU.png)
Below is the data and code that I am working with.
```
#devtools::install_github("cmartin/ggConvexHull")
library(ggConvexHull)
library(ggplot2)
library(stargazer)
library(car)
# define data
df <- structure(list(Y = c(4L, 0L, 0L, 6L, 6L, 2L, 1L, 9L, 8L, 3L,
6L, 5L, 3L, 5L, 8L, 5L, 2L, 5L, 7L, 7L, 5L, 3L, 7L, 5L, 7L, 8L,
8L, 4L, 4L, 5L, 3L, 4L, 10L, 9L, 2L, 1L, 1L, 3L, 4L, 6L, 3L,
3L, 10L, 7L, 5L, 1L, 2L, 10L, 5L, 3L, 7L, 9L, 6L, 6L, 6L, 2L),
X1 = c(-35, -16, -23, -37, -6, -11, -18, -25, -26, -4, -16,
-26, -13, -29, -33, -1, -6, -2, -28, -5, -1, -4, -2, -11,
-38, -13, -16, -3, -1, -2, -10, -6, -12, -8, -9, -1, -4,
-2, -1, -30, -7, -3, -18, -32, -32, -6, -6, -9, -8, -3, -3,
-7, -9, -5, -4, -9),
X2 = c(0, 0, 0, 0, 1, 0, 0, 1, 1, 0,
0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1,
1, 0, 0, 1, 1, 1, 1, 0)),
row.names = c(NA, -56L),
class = c("tbl_df", "tbl", "data.frame")
)
# create glms
m1 <- glm(Y ~ X1, data=df, family="poisson")
m2 <- glm(Y ~ X1 + X2, data=df, family="poisson")
# there is some correlation
cor(df$X1, df$X2)
# but vifs look okay
vif(m2)
# results show that X1 becomes insignificant when X2 is added
stargazer(m1,m2,type="text")
# plot shows the effect of X2 clearly
# but can it also show the decline in the effect and significance of X1?
p <- ggplot(data=df) +
geom_jitter(aes(x=X1, y=Y, color=factor(X2), shape=factor(X2)),
size=4, alpha=.6, width=0.2, height=0.2) +
geom_convexhull(aes(x=X1, y=Y, fill=factor(X2)),
alpha=.2)
p
```
|
Visually show how the effect of one regressor diminishes the effect and significance of another
|
CC BY-SA 4.0
| null |
2023-05-08T14:35:50.073
|
2023-05-08T14:35:50.073
| null | null |
387002
|
[
"r",
"regression"
] |
615227
|
2
| null |
615225
|
1
| null |
If you're willing to assume this particular causal model, then you don't need to use propensity score matching, or any other backdoor path related method, because the effect of $X$ on $Z$ is not confounded.
See the following from [http://www.dagitty.net/](http://www.dagitty.net/):
[](https://i.stack.imgur.com/G2x4L.png)
Before you go and compute the effect of $X$ on $Z$ in this model though, you should probably consider a model with a different structure. Are you sure you're willing to assume this particular model? For example, are you sure there are no structural factors that affect both the demographics of an area and the income of the people in it?
If you were to imagine such a confounder, you would need to control for it in order to understand the effect of $X$ on $Z$:
[](https://i.stack.imgur.com/QXnza.png)
If you think such a model is true, then propensity score matching on $C$ would make sense.
| null |
CC BY-SA 4.0
| null |
2023-05-08T14:37:03.873
|
2023-05-08T14:42:06.830
|
2023-05-08T14:42:06.830
|
29694
|
29694
| null |
615228
|
1
| null | null |
0
|
15
|
I'm using scikit learn's 'KFoldStratified' for a classification task where I have 64 samples, evenly split across 8 labels. I notice the folds are as follows:
Test 0, 8, 16...
Train 1...7, 9... 15
Where the first element of each label is used in the test set and the remainder in the test set. The same situation is set up for the 2nd element, 3rd element, etc.
I'm curious if there is a way (or if it would be desirable to) create a broader set of splits. For instance in addition to the one above, having a test set with the first element of label 1 and the second element of label 2. I realize these splits add a lot of time to the procedure, but I'm wondering if there is a obvious reason not to do this, and if there isn't, how to approach it (as the KFoldStratified doc doesn't make any apparent mention of this kind of change).
|
K-folds vs 'all possible k-folds'
|
CC BY-SA 4.0
| null |
2023-05-08T14:58:52.300
|
2023-05-08T14:58:52.300
| null | null |
245715
|
[
"cross-validation",
"scikit-learn"
] |
615230
|
2
| null |
237538
|
0
| null |
There is a more model-based view that would be a nice complement to the top answer about SVM. The core insight is to assume a mixture model between positive and negative examples, then learn the mixture fraction separately from the densities. If features for positive examples follow a density $f$ and negative follow a density $g$, you can learn $f$ from the positive examples. Then for the unlabeled examples you know they are a mixture of a known density $f$ with an unknown density $g$, and there are established methods you can use in that situation. For example in FDR control, the density of the test stats is a mixture of a known density (for the null hypotheses) and an unknown density (for the alternative hypotheses). Here are a couple of useful references.
[https://link.springer.com/article/10.1007/s10994-020-05877-5](https://link.springer.com/article/10.1007/s10994-020-05877-5)
[https://cseweb.ucsd.edu/~elkan/posonly.pdf](https://cseweb.ucsd.edu/%7Eelkan/posonly.pdf)
EDIT: a very important assumption of this approach is that the labeled and unlabeled positive examples follow the same distribution. This may not be true in e.g. gene interaction network inference, where important genes may be better-studied and also produce larger effects. Some methods do allow for a biased selection mechanism but the type of bias must be understood in detail.
| null |
CC BY-SA 4.0
| null |
2023-05-08T15:15:00.543
|
2023-05-08T15:20:04.303
|
2023-05-08T15:20:04.303
|
86176
|
86176
| null |
615231
|
1
| null | null |
2
|
34
|
I want to train image segmentation model using U-Net with pretrained ResNet34 as encoder. My dataset is really small, i separate it with
- Train data : 57 images
- Validation data : 16 images
- Test data : 8 images
So, with that data, i want to use image augmentation on train data, but should the validation data be augmented too?
|
Augmenting Image Data on Small Dataset
|
CC BY-SA 4.0
| null |
2023-05-08T15:22:07.510
|
2023-05-08T17:27:09.533
| null | null |
387494
|
[
"neural-networks",
"conv-neural-network",
"data-augmentation"
] |
615232
|
1
| null | null |
1
|
18
|
Context
Assume a game using a fair 6 sided dice ends when one rolls a 6. A random variable N is the total number of throws. N is distributed such that:
$p_N(n) = \frac{5}{6}^{n-1}\frac{1}{6}$
Assume you win 1 point for an even number, and -1 point for an odd number.
$X_i$ is a random variable denoting point's gained from the $i^{th}$ throw s.t. $X_i = 1$ or $X_i = -1$
Random variable $W$ is the total number of points obtained at the end of the game.
$W = \sum_{i=1}^NX_i$
Question:
Why is the moment generating function described as
$M_w(t) = E(e^{tW}) = E(E(e^{tW}|N)) = E(M_{W|N}(t)$)
Specifically I'm interested in the intuition behind the double expectation. Thanks!
|
Double Expectation in Moment Generating Function
|
CC BY-SA 4.0
| null |
2023-05-08T15:27:37.563
|
2023-05-08T15:40:48.597
|
2023-05-08T15:40:48.597
|
377362
|
377362
|
[
"expected-value",
"conditional-expectation",
"moment-generating-function"
] |
615233
|
1
| null | null |
1
|
31
|
I am working on a high-imbalanced (80-20 ratio), high-dimensional dataset (200 sample size, 300 features) where all variables are highly correlated. Can I remove the perfectly correlated (using Pearson's correlation coefficient) variables (6 variables) before cross-validation? Does this cause any information leakage?
|
Can I remove correlated features before cross validation?
|
CC BY-SA 4.0
| null |
2023-05-08T15:29:45.463
|
2023-05-08T17:41:44.033
| null | null |
336916
|
[
"machine-learning",
"correlation",
"cross-validation"
] |
615234
|
1
| null | null |
1
|
17
|
Apologies if this is too simple of a question. I work with population data from the census, which provides a margin of error for all their variables. Reviewers have asked that I account for the MOE in census data but I'm not quite sure how to do that in a regression model. For example, in large census tracts, there can be quite large MOEs (e.g., estimate will be 500 households and the MOE could be 350) while in more dense areas the MOEs tend to be quite small (e.g., estimate 2000 households and the MOE of 100).
To account for MOEs do you transform the data or would you control for it on the right-hand-side of the equation? An example would be helpful too. Is the approach different in a machine learning model? Thank you!!
Edit: Application example
One example application is predicting the rate of renter eviction rate (eviction divided by the number of renters in a tract) based on neighborhood characteristics such as tract median rent, different racial group percentages, and income to name a few explanatory variables.
I would use a negative binomial model in this case given the variance and mean are not equal where the denominator is the offset, eviction counts are the true number of cases in a given tract, and the denominator for the response variable -- renters -- has an MOE. The other explanatory variables of rent, race percentages (a rate of the number of a relative race group divided by the number of renters), and income also have MOE's.
|
How to account for data's margins of error in a regression?
|
CC BY-SA 4.0
| null |
2023-05-08T15:33:14.613
|
2023-05-08T16:48:42.787
|
2023-05-08T16:48:42.787
|
77655
|
77655
|
[
"regression",
"machine-learning",
"controlling-for-a-variable"
] |
615235
|
2
| null |
615233
|
0
| null |
Removing perfectly correlated variables (pairwise Pearson coefficient) is fine. It's like removing a constant feature.
| null |
CC BY-SA 4.0
| null |
2023-05-08T15:37:40.147
|
2023-05-08T17:41:44.033
|
2023-05-08T17:41:44.033
|
204068
|
204068
| null |
615236
|
2
| null |
615231
|
1
| null |
We usually don't touch the validation and test data because modifying them may result in unrealistic performance measurements.
In some cases, people might choose to augment (or in general modify) the validation set, but note that this might even hurt your test performance because the validation and test distributions may diverge and whatever hyper-parameter you optimize for the validation set might not be good for the test set anymore.
Of course, this isn't destined to happen, but the risk associated with modifying your evaluation sets is a non-negligible one.
| null |
CC BY-SA 4.0
| null |
2023-05-08T15:39:38.810
|
2023-05-08T17:27:09.533
|
2023-05-08T17:27:09.533
|
204068
|
204068
| null |
615237
|
2
| null |
615224
|
5
| null |
The `survreg()` function in general fits the following location-scale distribution:
$$g(T)\sim X' \beta + \sigma W, $$
where $g(T)$ is a specified transformation of time (usually but not necessarily a log transformation), $X' \beta $ is the linear predictor based on predictor values $X$ and corresponding regression coefficients $\beta$ (location), $W$ is an underlying standard distribution, and $\sigma$ is the scale parameter specifying the width of the distribution. (Your use of terms "shape" and "scale" isn't consistent with that parameterization.)
For any of the built-in survival distributions you can identify both $g()$ and $W$ with commands like
```
survreg.distributions$lognormal$trans
# function (y)
# log(y)
# <bytecode: 0x7f8f4c5ca898>
# <environment: namespace:survival>
survreg.distributions$lognormal$dist
# [1] "gaussian"
```
to see the model within which coefficients $\beta$ and $\sigma$ will be fit.
Unlike the Weibull survival model, the `survreg()` parameterization of location and scale matches that of the standard R lognormal distribution `plnorm()`, with parameters `meanlog` and `sdlog` matching your `mu` and `sigma`. Add the following code to what you show to compare the observed and modeled results:
```
plot(survfit(Surv(time, status) ~ 1, data = lung))
curve(plnorm(x,meanlog=mu,sdlog=sigma,lower.tail=FALSE),
from=0,to=900,add=TRUE,col="red")
```
| null |
CC BY-SA 4.0
| null |
2023-05-08T15:43:49.800
|
2023-05-08T15:43:49.800
| null | null |
28500
| null |
615238
|
1
| null | null |
0
|
23
|
I have 8 measures: A_1, A_2, A_3, A_4, B_1, B_2, B_3, B_4. I know from the correlation matrix that they are all related. I would like to find the latent variable structure.
Using lavaan in R, I found that the first four variables (A_1, A_2, A_3, A_4) can be explained by one factor/latent variable:
```
mA <- 'fA =~ A_1 + A_2 + A_3 + A_4'
mAfit.o <- cfa(mA, data=dt)
summary(mAfit.o, fit.measures=TRUE)
```
Indeed I obtain as output that:
- Chi-Square for Test User Model is ~.6
- Comparative Fit Index (CFI), Tucker-Lewis Index (TLI) both >.095
- RMSEA < 0.05
Similarly, the second four variables (B_1, B_2, B_3, B_4) can be explained by one factor/latent variable, i.e. the model:
```
mB <- 'fB =~ B_1 + B_2 + B_3 + B_4'
```
has low Chi-Squared, high CFI/TLI and low RMSEA. However, the following models, all have bad performance (high Chi Squared, low CLI/TLI, high RMSEA):
```
mAB1 <- 'fA =~ A_1 + A_2 + A_3 + A_4
fB =~ B_1 + B_2 + B_3 + B_4'
mAB2 <- 'fA =~ A_1 + A_2 + A_3 + A_4
fB =~ B_1 + B_2 + B_3 + B_4
fAB =~ fA+fB'
mAB3 <- 'fAB =~ A_1 + A_2 + A_3 + A_4 + B_1 + B_2 + B_3 + B_4'
```
How should I interpret this?
|
What does it mean if one factor describes four measures, another factor describes other four measures, but both don't describe the eight measures?
|
CC BY-SA 4.0
| null |
2023-05-08T15:44:08.507
|
2023-05-08T15:44:08.507
| null | null |
181921
|
[
"r",
"latent-variable",
"confirmatory-factor",
"lavaan"
] |
615239
|
1
| null | null |
1
|
31
|
Currently I watched the videos (links below) that argues using the normalization (max-min scale) is the bad idea when it comes to the stock prediction. In the videos, the editor aruges that people should use stadardization instead of normalization, becasue in the prediction, you never know the "highest" price and "lowest" price in the future. Therefore,it makes normalization be no sense becuase it will transform the data from 0 to 1 which constrain the model to in this range.
But I found out that in most of papers (includes my own), we use normalization and it just works fine to predict the future. But I am a bit confused now, with his logic, won't all the price or no bound trend prediction has to use standardization? So which should technique should we use? Normalization or standardization?
Video links:
[https://youtu.be/Vfx1L2jh2Ng](https://youtu.be/Vfx1L2jh2Ng)
|
Normalization or standardization in stock prediction
|
CC BY-SA 4.0
| null |
2023-05-08T15:58:50.520
|
2023-05-08T15:58:50.520
| null | null |
382355
|
[
"machine-learning",
"predictive-models",
"normalization",
"standardization"
] |
615240
|
2
| null |
614703
|
1
| null |
If you read the CatBoost paper, you can see that they answer this intuitively. Paraphrasing:
>
The assumption of a time ordering allows you to encode each row with data from the "past", which prevents information from the "future" from leaking into the encoding.
That's the intuitive explanation.
Mathematically:
Iteratively splitting your data into "past" and "future" and conditioning your encoding on the past introduces a significant amount of variance in the encoding of your categories. The variance is like random noise added over the target encoding and partially breaks the relationship between the target and your categorical column.
Partially breaking the relationship prevents target leakage and improves your model's ability to generalise.
This method can also be better than random noise because it doesn't require introducing a prior assumption about the distribution of your category's values.
This combination is powerful and is responsible for Ordered Encoding's success.
| null |
CC BY-SA 4.0
| null |
2023-05-08T16:04:25.157
|
2023-05-08T16:04:25.157
| null | null |
363857
| null |
615241
|
1
| null | null |
0
|
6
|
I'm experimenting with univariate time series using the following approaches that suit time-series analytics in order to transform the data in a way that the inputs to the model are the targets of previous K observations:
1. [lookback period](https://machinelearningmastery.com/lstm-for-time-series-prediction-in-pytorch/), [example1](https://towardsdatascience.com/one-step-predictions-with-lstm-forecasting-hotel-revenues-c9ef0d3ef2df), [example2](https://www.kaggle.com/code/hassanamin/time-series-analysis-using-lstm-keras/notebook)
```
#ِDataset matrix is formed
def create_dataset(df , lookback=1):
data = np.array(df.iloc[:, :-1])
label = np.array(df.iloc[:, -1])
#create X_train and Y_train and MinMaxScaler on Y_train
X = list()
Y = list()
for i in range(lookback , len(data)):
X.append(data[i-lookback:i])
Y.append(label[i])
X = np.array(X)
Y = np.array(Y)
Y=np.expand_dims(Y,-1)
return X,Y
# Lookback period
lookback = 5
X_train, Y_train = create_dataset(train, lookback)
X_val, Y_val = create_dataset(validation, lookback)
X_test, Y_test = create_dataset(test, lookback)
# print(X_train.shape , Y_train.shape) #(155, 5, 1) (155, 1)
# print(X_val.shape, Y_val.shape) #(35, 5, 1) (35, 1)
# print(X_test.shape, Y_test.shape) #(69, 5, 1) (69, 1)
```
2. [transform a time series dataset into a supervised learning dataset](https://machinelearningmastery.com/random-forest-for-time-series-forecasting/) posted by Jason Brownlee:
```
# Finalize model and predict monthly births with random forest
from numpy import asarray
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from sklearn.ensemble import RandomForestRegressor
# transform a time series dataset into a supervised learning dataset
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols = list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
# put it all together
agg = concat(cols, axis=1)
# Drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg.values
# load the dataset
series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
values = series.values
# transform the time series data into supervised learning
train = series_to_supervised(values, n_in=6)
# split into input and output columns
trainX, trainy = train[:, :-1], train[:, -1]
```
Qs: The followings are my question to understand if the abovementioned methods have, e.g. `lookback` or `walk_forward_validation` (WFV) & `series_to_supervised` (STS) have some alignment with used methods on [skforecast](/questions/tagged/skforecast) package.
Q1: What is the difference between these two approaches? (lookback period Vs transform a time series dataset into a supervised learning dataset)
I also tried in meantime `walk_forward_validation()` approach inspired from this [post](https://stackoverflow.com/questions/69442740/multivariate-xgboost-time-series):
>
Walk forward validation is a method for estimating the skill of the model on out-of-sample data. We contrive out of sample, and each time step one out of sample observation becomes in-sample. We can use the same model in ops, as long as the walk-forward is performed each time a new observation is received.
My observation shows no difference between using:
- just series_to_supervised (STS)
- walk_forward_validation (WFV) & series_to_supervised (STS) comparing outputs, especially MAE results, but a bit in quality of forecasting up & downs(could be due to weights during training):

Q2: Does `walk_forward_validation` (WFV) & `series_to_supervised` (STS) are equivalent to the following:
- Recursive multi-step forecasting
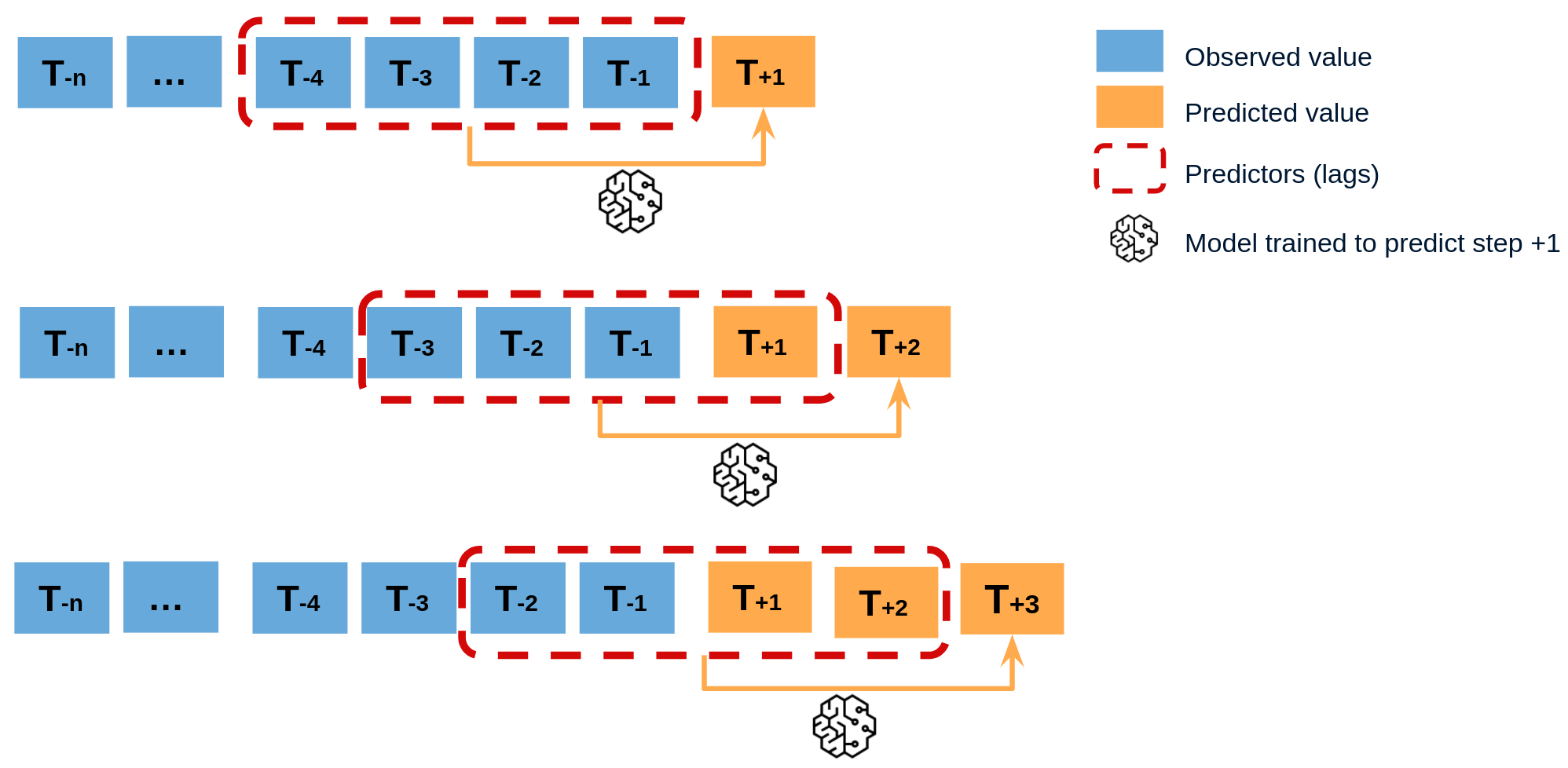
- Direct multi-step forecasting
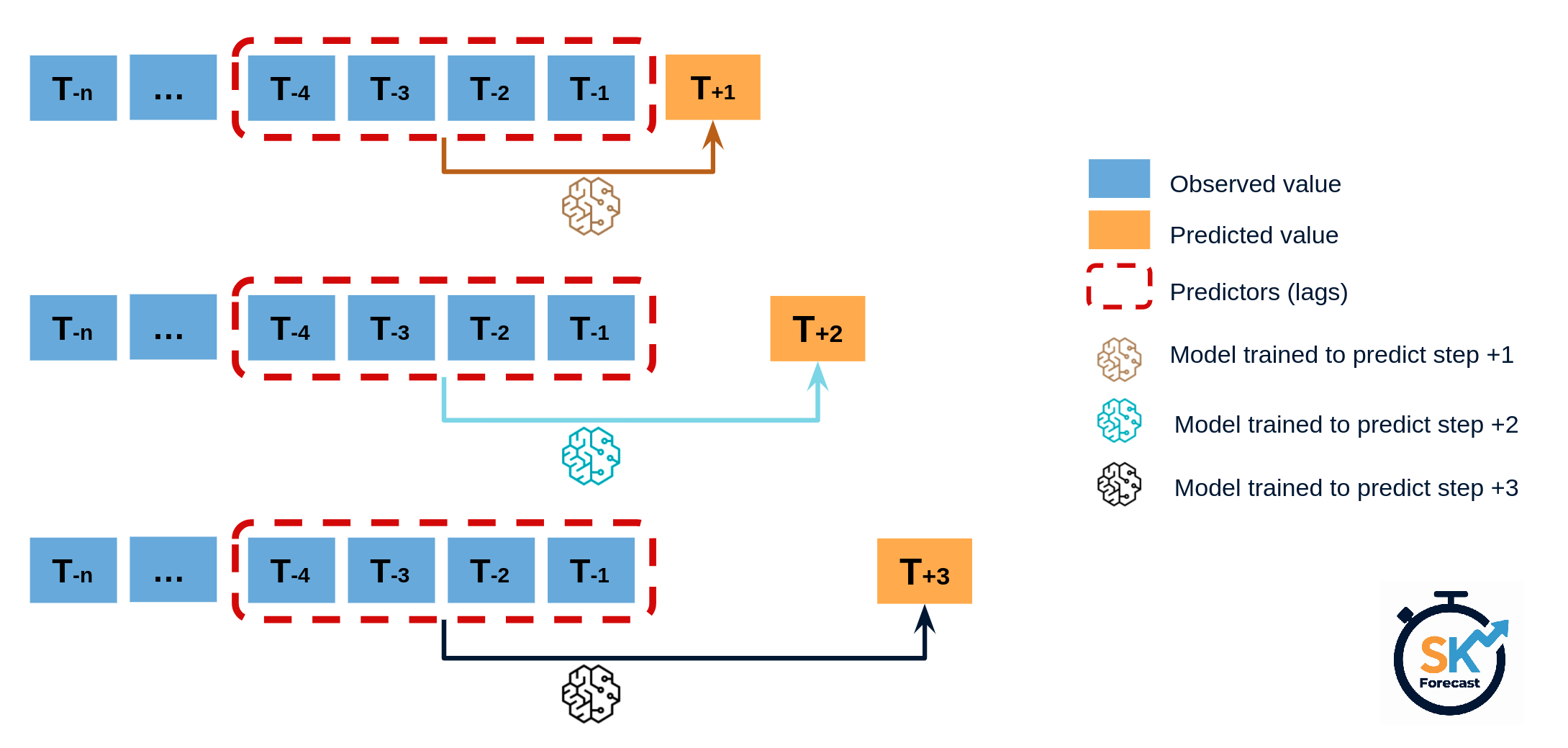
Q3: Is there any alignment/equivalent using `walk_forward_validation` (WFV) & `series_to_supervised` (STS) with one of the following Backtesting ?
- Backtesting with refit and increasing training size (fixed origin)
- Backtesting with refit and fixed training size (rolling origin)
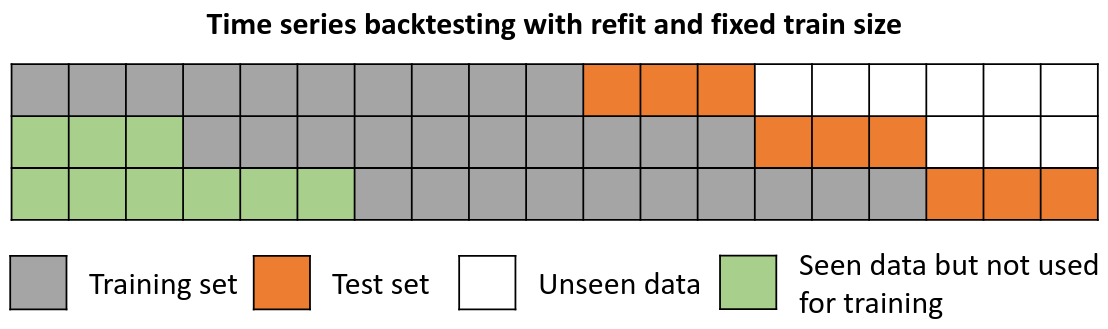
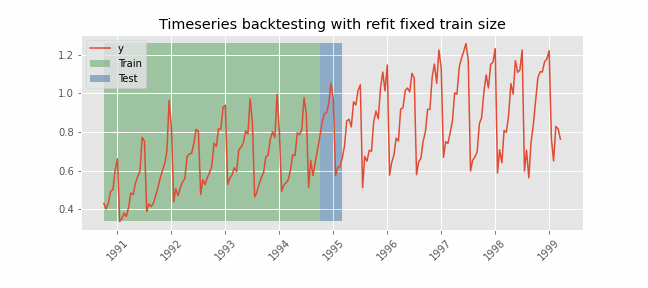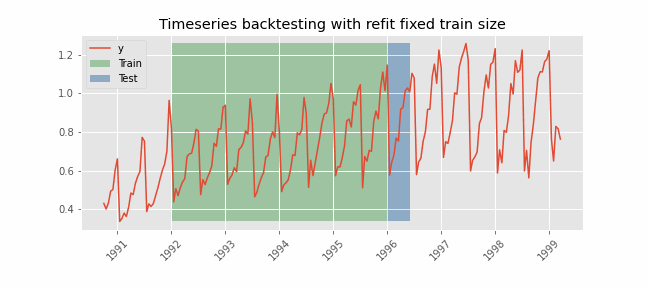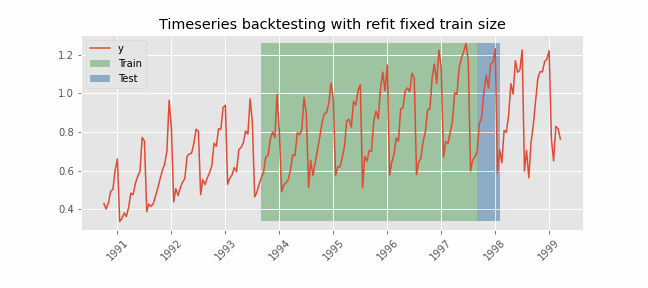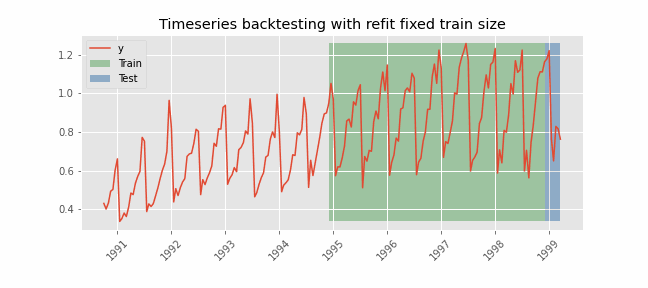
- Backtesting without refit
All pics sources in Q2 & Q3: credit from [Joaquín Amat Rodrigo, Javier Escobar Ortiz](https://www.cienciadedatos.net/documentos/py27-time-series-forecasting-python-scikitlearn.html#Direct-multi-step-forecasting)
|
What is the relationship between walk_forward_validation (WFV)/series_to_supervised (STS) with Direct/Recursive multi-step forecasting & Backtesting
|
CC BY-SA 4.0
| null |
2023-05-08T16:05:00.743
|
2023-05-08T16:05:00.743
| null | null |
240550
|
[
"time-series",
"python",
"forecasting",
"univariate"
] |
615242
|
1
| null | null |
0
|
14
|
I have a question concerning different results between linear regression and the direct effect of mediation analysis.
Indeed, linear regression between predictor X and outcome Y showed a non-significant relationship. However, when I add a mediator within a mediation analysis, the direct effect between X and Y is significant (Indirect and total effects are non-significant). How can I interpret that?
I compute this analysis on JASP.
Thanks
|
Understand inconsistent results between direct effect of mediation analysis and linear regression
|
CC BY-SA 4.0
| null |
2023-05-08T16:07:30.877
|
2023-05-08T16:07:30.877
| null | null |
381165
|
[
"regression",
"linear-model",
"mediation",
"jasp"
] |
615243
|
1
| null | null |
0
|
39
|
[EDIT: had fundamental misunderstanding, rephrasing question - thanks to @whuber for catching that]
I have some pretty simple regressions (linear & logistic) predicting a rate (continuous response var, linear regression) & direction (binary response var, logistic regression) from certain features of the distribution of some measured value. The distribution features are the predictor/explanatory variables.
The measured values are from a sample taken every day, but with different (and quite widely varying) sample sizes on different days, from dozens to thousands (total sample size of ~300k, average ~400/day). The theory is that a combination of features of the distribution each day (e.g. mean, s.d., skew, possibly quantiles) will relate to the relevant rate / direction on that day, so e.g.
`rate ~ mean_x + skew_x`.
Note that the rate / direction are not calculated from the same sample as the explanatory variables - they are observed separately on each day.
Given the range in sample sizes for each day, it seems there should be some way to weight the datapoints based on the sample size for the explanatory variables that day.
I thought weighted regression based on sample sizes (similar to [this previous question](https://stats.stackexchange.com/questions/504572/including-a-weighting-variable-in-a-linear-regression) and [this post](https://www.r-bloggers.com/2015/09/linear-models-with-weighted-observations/)) was appropriate but it seems that's based on sample size of response variables, not explanatory variables, which is the reverse of what I have.
My revised question is thus:
Is it appropriate to include some weighting of datapoints to reflect the differing sample sizes from which the explanatory variables for each datapoint are calculated? and if so, how?
|
Weighting linear / logistic regression data points by explanatory variable sample size
|
CC BY-SA 4.0
| null |
2023-05-08T16:15:05.903
|
2023-05-09T14:05:25.283
|
2023-05-09T14:05:25.283
|
361155
|
361155
|
[
"r",
"regression",
"weighted-regression",
"sample-weighting"
] |
615245
|
1
|
615249
| null |
0
|
68
|
Let $\bf A$ be an $n \times n$ matrix with rank $r$ where $r<n$. How can I get a full-rank approximation for $\bf A$? In other words, I want to find the rank-$n$ $\bf X$ that minimizes the Frobenius norm $\|\bf A-\bf X\|_{\text{F}}$.
|
Full-rank approximation to a square matrix
|
CC BY-SA 4.0
| null |
2023-05-08T16:18:11.057
|
2023-05-08T18:21:09.690
|
2023-05-08T16:36:03.500
|
22311
|
43480
|
[
"optimization",
"matrix",
"ranks",
"constrained-optimization"
] |
615246
|
1
| null | null |
0
|
11
|
I want to run a diff-in-diff regression for a pre-post rollout experiment. Assume for a moment that I have subjects impacted by the experiments.
To validate the trends, I AGGREGATE subjects to a daily basis, and I found a 'PERFECT' (assume this) parallel trends between my control and treatment on a daily basis.
Once I go down to run my diff-in-diff regression, Do I need to run it on:
- A subject basis , i.e. each row is one subject
- A daily basis, i.e. I aggregate the data to a daily basis (the time period where I validate the trend).
- A subject/daily basis, i.e. each row is one day for each particular subject.
|
diff-in-diff regression - parallel assumptions
|
CC BY-SA 4.0
| null |
2023-05-08T16:24:54.030
|
2023-05-08T16:24:54.030
| null | null |
298435
|
[
"hypothesis-testing",
"econometrics",
"causality",
"difference-in-difference"
] |
615247
|
1
| null | null |
0
|
12
|
I have N bootstrapped distributions whose mean and CI i have found. I would like to take a weighted sum of these N distributions(weights sum to 1). The resulting mean would be easy to compute. What would the CI be instead?
Note: The resulting bootstrap histograms look very gaussian and symmetric. But i am not confident to confirm that this will always be the case. So, my questions will be 2 pronged as to what to do in each scenario
Past work:
This [post](https://stats.stackexchange.com/questions/27650/summing-bootstrap-derived-confidence-intervals) talked about something similar. I wasnt sure if this would apply to my case. If it did, would I be right to generate B bootstraps for each of the N distributions and compute the weighted sum for each b-th bootstrap and get B weighted sums. Then do a bootstrap analysis on the B weighted sums to get the final CI?
CONTEXT (not critical but adding it for potential clarity):
I have multiple customers(N) and would like to see the impact of their demand to costs. I focus on n customers and see their effect under 4 demand cases (Zero, Low, Med, High). Taking the simple case of 2 customers, we will have 16 possible demand combinations. Because of the remaining customers (N-2), the total cost of the 2 customers will vary. So i am sampling demands of the N-2 customers and evaluating the total cost under the 16 differenet demand scenarios of the 2 customers. So, I want to see what weights to assign to each of the 16 cases subject to some constraints, so as to find the cheapest average cost.
|
Bootstrapped CI of sum of distributions
|
CC BY-SA 4.0
| null |
2023-05-08T16:29:47.557
|
2023-05-08T16:29:47.557
| null | null |
387497
|
[
"confidence-interval",
"bootstrap"
] |
615248
|
1
|
615254
| null |
1
|
26
|
Let's consider a multi-class classification problem with 4 classes: 0, 1, 2, and 3
F1-Score 'macro'-averaged is calculated like that:
```
F1_macro = 0.25*F1_class0 + 0.25*F1_class1 + 0.25*F1_class2 + 0.25*F1_class3
```
On the other hand, supposing that the relative supports for the classes are:
- class 0: 0.4
- class 1: 0.1
- class 2: 0.4
- class 3: 0.1
F1-Score 'weighted'-averaged is equivalent to:
```
F1_weighted = 0.4*F1_class0 + 0.1*F1_class1 + 0.4*F1_class2 + 0.1*F1_class3
```
Now my question is: does it make sense to consider a customized version of the scores where the weights' values follow an empirical rule? Let's say for example that I am interested in obtaining a model that predicts well minority classes, and in particular class 3. Could the following metric be a valid approach?
```
F1_custom = 0.1*F1_class0 + 0.35*F1_class1 + 0.1*F1_class2 + 0.45*F1_class3
```
I understand that considering the weights as inversely proportional to the relative support could result in overproportional weights in case of severe imbalance, but considering them like that should not be a problem in this sense.
I am aware that there are better metrics, that are also threshold-independent (e.g. AUPRC or AP) that can be extended for a multi-class problem and for which I could also apply this method, but for the moment I am interested in validating this 'custom averaging' method, so I would like to understand if it is feasible for a simple metric like F1-Score and then extend it to other metrics (like AP).
Am I missing something? Why I can not find anything about this topic on internet?
|
Customized F1-Score for multi-class classification
|
CC BY-SA 4.0
| null |
2023-05-08T16:35:24.443
|
2023-05-08T18:47:58.003
|
2023-05-08T18:47:58.003
|
377079
|
377079
|
[
"machine-learning",
"python",
"multi-class",
"confusion-matrix",
"weighted-mean"
] |
615249
|
2
| null |
615245
|
2
| null |
As the simplest example, if we choose $B = t I_n$, then $X = A + B$ and we can make $\| A - (A + B) \|_F = \| B \|_F$ arbitrarily small according to the choice of $t$ such that $|t| > 0$. (But we can't minimize $t$ because the minimum value of $\| B \|_F$ occurs at $t=0$, for which $B$ is not full-rank.)
A wealth of interesting solutions exist for $B$ that are not scalar multiples of the identity matrix.
| null |
CC BY-SA 4.0
| null |
2023-05-08T16:41:56.453
|
2023-05-08T18:21:09.690
|
2023-05-08T18:21:09.690
|
22311
|
22311
| null |
615250
|
1
| null | null |
1
|
62
|
I’m working with big, imbalanced data set for a binary classification challenge. Big in the sense that it’s hard to digest all at once, and imbalanced in the sense that for every positive example there are about 1000 negative examples.
My approach:
- reduce size by down-sample the negative examples in a manner that would result with nearly even good to bad examples ratio (completely balanced data)
- do the classic ML pipeline (EDA, feature extraction and modeling)
- "translate" results/performance metrics back to reflect the original non-sampled / imbalanced data.
I perceived this approach as a reasonably good one, as it results with a manageable data set and points out the signal of positive to negative examples difference.
My question: is that a sensible/methodical approach? Are there pitfalls here? When is this a good/bad idea?
|
Down sampling the big class in imbalanced data
|
CC BY-SA 4.0
| null |
2023-05-08T16:47:33.760
|
2023-05-11T16:51:57.760
| null | null |
387502
|
[
"machine-learning",
"classification",
"unbalanced-classes"
] |
615251
|
2
| null |
615163
|
0
| null |
Let us say the highest order of integration is $d$; usually, $d=1$ though sometimes $d=2$.
- If $d=1$ and there is a single series that is I(1) while the other ones are I(0), you take first differences of that variable and model that together with the other variables using a VAR.
- If $d=1$ and there are two or more I(1) variables, you test for cointegration between them. If they are not cointegrated, you take first differences of them and model them together with I(0) variables using a VAR. If, on the other hand, the I(1) variables are cointegrated, you model them using VECM; you also include the I(0) variables on the side as in this answer. (Watch out that the left hand side of your equations is of the same order of integration as the right hand side.)
- If $d=2$ and there is a single series that is I(2) while the other ones are I(1) and I(0), you take first differences of the I(2) variable and then proceed as in 1., now treating the differenced I(2) variable as a primitive.
- If $d=2$ and there are two or more I(2) variables, you test for cointegration between them. If they are not cointegrated, you take first differences of them and model them together with the other variables as in 1. If, on the other hand, the I(2) variables are cointegrated, you obtain the error correction term(s) and the first-differences of all the I(2) variables and proceed as in (2). This is a bit terse, but trying to cover all cases in detail is quite tedious. (Again, watch out that the left hand side of your equations is of the same order of integration as the right hand side.)
| null |
CC BY-SA 4.0
| null |
2023-05-08T16:54:17.453
|
2023-05-08T16:54:17.453
| null | null |
53690
| null |
615252
|
2
| null |
615250
|
1
| null |
A mantra on here is that class imbalance is not a problem for proper statistical methods, and I agree with this mantra (and have posted variations of it many times). However, class imbalance can result in small amounts of data for the minority class, which is the subject of King and Zeng (2001), discussed [here](https://stats.stackexchange.com/a/559317/247274). Their feeling is that, when it is hard to acquire data, it is possible to be smart about undersampling the majority class and then account for that undersampling later. This way, you keep down the cost of data acquisition without sacrificing the count of minority-class members.
You are not at the data-collection stage, but you do face a similar problem in that you need to use discretion about what data to feed into the model because of hardware limitations. Philosophically, I do not see marked differences between these settings, and the ideas from King and Zeng (2001), which are aligned with the idea behind your plan, apply.
If you really are hardware-constrained and cannot work with the entire set of data, your plan seems as reasonable as any. One change might be to downsample only as much as you need to, rather than targeting balanced classes, since the constraint is the data size and not the balance per se. King and Zeng (2001) might be worth a read, too.
(The ideal scenario would be to use better hardware or buy some time on hardware that can handle it (e.g., AWS), but these need not be realistic for all applications, making it necessary to get clever.)
REFERENCE
[King, Gary, and Langche Zeng. "Logistic regression in rare events data." Political Analysis 9.2 (2001): 137-163.](https://www.jstor.org/stable/pdf/25791637.pdf)
| null |
CC BY-SA 4.0
| null |
2023-05-08T17:01:10.987
|
2023-05-11T10:29:41.883
|
2023-05-11T10:29:41.883
|
247274
|
247274
| null |
615253
|
1
| null | null |
1
|
28
|
I am working on a computer vision problem (chessboard recognition), and my goal is to find the lines that correspond to the chessboard lines. I want to do this via [Hough transform](https://en.wikipedia.org/wiki/Hough_transform), since said lines usually appear as a bunch of clustered points along a sinusoidal curve (although I approximate the curve with a straight line since the vanishing point is usually very far away).
I am able to almost always correctly identifying the two set of lines corresponding to the chessboard, and isolate the straight lines like so:
[](https://i.stack.imgur.com/ajg8A.png)
Now I am facing the problem of correctly identifying the center of the clusters that correspond to the actual chessboard lines: there should be 9 clusters approximately equally spaced along the red line, but some other noise make this clustering task non trivial: for instance, near the edges the cluster appear larger because it detects the outer border of the chessboard that is not actually part of the pattern.
I tried K-Medoids, and sometime it works but sometimes it doesn't, and doesn't take advantage of the fact that I know these clusters should be equally separated.
I tried a gaussian mixture model, specifically the scikit-learn one, but I modified the class to include a term in the log likelihood that is proportional to the entropy of the distances of the gaussians means (to encourage equally distributed distances).
I even tried to come up with a model of 9 gaussians parametrized like
$$P(X|\mu_0,l) \sim \sum_{i=1}^9 \mathcal{N}(\mu_0 + il,\sigma)$$
and tried to maximize the likelihood for $\mu_0$ and $l$ but still the outliers influence the result.
I thought about using some sort of frequency domain approach but I wouldn't really know where to start.
So any suggestion appreciated. Have a great day!
|
What would be the best way to find N clusters equally separated, ignoring outliers?
|
CC BY-SA 4.0
| null |
2023-05-08T17:22:16.223
|
2023-05-08T17:23:11.650
|
2023-05-08T17:23:11.650
|
387507
|
387507
|
[
"clustering",
"computer-vision"
] |
615254
|
2
| null |
615248
|
1
| null |
In principle, there is no problem with defining your custom scores. This can be a custom f1-score that you care about, a customized score obtained from confusion matrix, or some other arbitrary formula. The important thing is, it should make sense regarding your problem.
>
Let's say for example that I am interested in obtaining a model that predicts well minority classes, and in particular class 3. Could the following metric be a valid approach?
F1_custom = 0.1*F1_class0 + 0.45*F1_class1 + 0.1*F1_class2 + 0.35*F1_class3
Regarding this, I'd expect you give more weight to the F1 score of class 3.
>
Am I missing something? Why I can not find anything about this topic on internet?
Maybe you can find more people doing customizations by looking for custom losses defined on confusion matrices. People usually assign a cost of misclassification for each class pair, i.e. $C_{ij}$, and multiply the costs with the entries in the confusion matrix.
| null |
CC BY-SA 4.0
| null |
2023-05-08T18:08:47.750
|
2023-05-08T18:08:47.750
| null | null |
204068
| null |
615255
|
2
| null |
615250
|
0
| null |
People seem to be uncomfortable with deleting any data already collected, even temporarily. In epidemiology, collection of negative cases is often limited to five for each positive case. The theory behind this is that adding a sixth case has very little impact on the standard error of differences between or ratios of statistics from the two kinds of cases.
Subsampling the more common category of cases should be done more often. Choose a ratio that seems sensible and practical from the viewpoint of data analysis and go with it. Five is enough.
If you are not comfortable with five you could also try a larger and smaller number and see if your choice matters much.
If you are concerned about losing information by subsampling then verify any developed models or results either on a larger sample or all the observations.
Supplement any analyses with some descriptive statistics comparing the cases you use with either the total sample or the cases you exclude, checking for surprises or systematic differences. Random sampling should prevent systematic differences.
There is a large literature on this in epidemiology and biostatistics. This is described and discussed in basic methods textbooks in epidemiology.
| null |
CC BY-SA 4.0
| null |
2023-05-08T18:09:13.373
|
2023-05-08T18:09:13.373
| null | null |
154840
| null |
615256
|
1
| null | null |
0
|
15
|
If there is discrete-time batch markovian arrival process with parameter matrices ${\bf D}_k$, $k\geq 0$ then the mean arrival rate per time slot is given by $\lambda={\bf \pi}\sum_{n=0}^\infty n{\bf D}_n{\bf e}$, where ${\bf \pi}$ is stationary vector for D-BMAP and ${\bf e}$ is column vector of all elements one. Now I can't understand how the probability of an arrival in a single slot be same $\lambda$. I think this probability should be ${\bf \pi}\sum_{n=0}^\infty {\bf D}_n{\bf e}$. Please help me to understand. Thank you in advance.
|
For D-BMAP arrival rate per time slot is same as the probability of an arrival in a single slot
|
CC BY-SA 4.0
| null |
2023-05-08T18:31:20.923
|
2023-05-08T19:39:53.713
|
2023-05-08T19:39:53.713
|
211737
|
211737
|
[
"probability",
"mathematical-statistics",
"stochastic-processes",
"markov-process"
] |
615257
|
1
| null | null |
0
|
16
|
I'm really lost in this topic, and I want to ask for help here.
I have a continous variable of interest (X), but also factors that I think they can affect my results (for me the most interesting factor is Sampling site). So, I have made this formula for adonis2:
X ~ Sampling Site + Year + Sex + Age + Sample Type
(Sampling site has 2 levels, Year has 4 categories, Sex has 2, Age has 2, Sample type has 2)
-Are these factors fixed in this way?
-Is this formula right? I know that changing order makes results to be different. Maybe because not all factors have exactly the same n by category? My total n is also <30
Any help/advice/suggestions would be greatly appreciated!!
Thank you in advance!
|
PERMANOVA and random/fixed effects
|
CC BY-SA 4.0
| null |
2023-05-08T18:37:18.793
|
2023-05-08T18:48:58.310
|
2023-05-08T18:48:58.310
|
387509
|
387509
|
[
"mixed-model",
"model",
"fixed-effects-model",
"permutation-test"
] |
615258
|
1
| null | null |
0
|
20
|
I have a complex physically-based biological model which solves partial differential equations to predict the number of individuals in a certain community as a function of temperature, salinity, and chlorophyll concentration. Therefore I have 20 years of daily data for the number of individuals N (i.e., the model output) and measured temperature, salinity, and chlorophyll concentration (i.e., the model inputs). We would like to rank the predictors based on how much they affect the model output. Note that we cannot add and remove predictors from the physically-based model. It will be both unphysical and too computationally expensive.
See below a quick drawing of the model output (N, first plot), and one of the predictors (temperature, T, second plot) for reference. They vary seasonally and there is a clear lag between the two time series.
[](https://i.stack.imgur.com/504CZ.png)
|
Time series analysis: how to rank the ability of predictors to predict physically-based model outputs
|
CC BY-SA 4.0
| null |
2023-05-08T18:41:53.587
|
2023-05-08T23:08:58.477
|
2023-05-08T23:08:58.477
|
271024
|
271024
|
[
"time-series"
] |
615259
|
2
| null |
615258
|
0
| null |
There are a few commonly used ways to "rank" predictors based on "how much".
You can standardize your predicters (z score). The absolute magnitude of each predictor's coefficient will be a standardized effect on the response.
You can, if your model permits it, calculate partial R2 (omega square, eta square) for each coefficient. This will estimate the amount of variation that each predictor accounts for in the nodel.
These two methods roughly tend to agree with each other, but not always. Standardized coefficients can be had for any model. Partial R2 can be trickier to get for some models.
| null |
CC BY-SA 4.0
| null |
2023-05-08T18:48:27.707
|
2023-05-08T18:48:27.707
| null | null |
28141
| null |
615260
|
1
| null | null |
1
|
28
|
Is there a term or name (or better yet, strategies) for the following problem?
Take a 'standard' $k$-armed multi-armed bandit problem (stochastic real rewards, IID pulls for a given arm), but instead of maximizing the mean sum of rewards across $H$ pulls, maximize the mean maximum reward across $H$ pulls.
(I know that classically this is formulated as minimizing regret instead.)
Intuitively, strategies for solving this would have substantially more variance-seeking than strategies for a standard multi-armed bandit problem - if you're in an exploit phase with sufficient pulls left and arm A is known to have a somewhat higher mean, but somewhat lower variance, than arm B, a strategy for a normal multi-armed bandit problem would likely pick A, whereas a strategy for this would likely pick B.
|
Multi-armed bandit with max instead of mean
|
CC BY-SA 4.0
| null |
2023-05-08T19:24:24.533
|
2023-05-20T21:13:46.690
| null | null |
100205
|
[
"multiarmed-bandit"
] |
615263
|
1
| null | null |
1
|
46
|
My data has 5 dependent variables (measured amount of oxygen, halides, nitrogen, sulfur, and organic) and one independent variable with 2 "treatments (flow rate, 1 Lpm or 2 Lpm). The catch is: I have multiple pairs of data for 2 treatments, which are not for the same sample (each pair is its own sample, taken at a different date - see attached picture below).
I would like to evaluate if the flow rate treatment had a significant influence on the results of 5 dependent variables. Would be a classic MANOVA test if not for the fact that I want to know that across all pairs of data. Performing multiple MANOVAs for each pair is not useful because there is not enough measurements for each independent variable (i.e. 2-3 for each dependent variable for each treatment and date).
Any help would be greatly appreciated.
[](https://i.stack.imgur.com/NT5JH.png)
|
Multivariate (5 dependent 1 independent variable) and paired data, multiple samples used. Which statistical test?
|
CC BY-SA 4.0
| null |
2023-05-08T20:13:01.997
|
2023-05-08T22:10:08.963
| null | null |
387514
|
[
"multivariate-analysis",
"paired-data"
] |
615264
|
1
| null | null |
0
|
42
|
I am calculating the odds ratio of a binomial logistic regression model using exp, is there a function to calculate the 95% confidence intervals?
```
model_1 <-svyglm(formula = ACV_COVIDCAR_NEW_1~DMV_H_OPMDCD_combined_factor, design =
data2, family = "binomial" (link="logit"))
summary(model_1)
exp(coef(model_1))
```
|
Logistic regression (binomial) in svyglm, using R, calculating odds ratio and confidence interval
|
CC BY-SA 4.0
| null |
2023-05-08T20:43:00.733
|
2023-05-09T01:11:55.133
| null | null |
387372
|
[
"r"
] |
615265
|
1
| null | null |
0
|
17
|
I like to do feature selection and I am using multiple feature selection algorithms provided by sklearn. What I have done is, use a bunch of feature selection algos and get the score for each feature. This returns a dataframe where the index is the features and columns consists of the scores returned by the different feature selection algorithms. How do I combine these different set of scores and create a single ranking for all the features? After that, what is the best way to select the top K features based on the final aggregated ranking? I am not looking for taking the mean or converting them to ranks and agg based on them. Is there a much better statistical approach? I have read about rank correlation methods like Kendall Tau, Spearman, Concordance correlation coefficient , Borda Count (i implemented this), etc, but I am not exactly sure how to implement them?
|
Feature Selection: Select top best features based on feature scores produced by different algorithms
|
CC BY-SA 4.0
| null |
2023-05-08T21:03:06.850
|
2023-05-08T21:03:06.850
| null | null |
387517
|
[
"correlation",
"python",
"scikit-learn",
"ranking"
] |
615266
|
1
| null | null |
1
|
56
|
I am conducting a meta-analysis and am trying to produce a forest plot displaying the mean weighted effect size with and without the outliers. I looked on so many websites and tried a lot of syntaxes, however, didn't really find anything about what I am looking for.
Assume there are 5 studies in the meta-analysis. Outlier analyses showed that Study 3 is an outlier leading to an overestimation of the mean weighted ES. Accordingly, I calculate a mean ES with (k = 5) and without the outlier (k = 3). I would like to display the studies sorted according to their ES and report both Mean ESs in the forest plot. I would appreciate any help and/or advice.
Study3 Study4 Study5
Mean ES (k = 5) Mean ES (k = 3)
My code:
```
Ishtiaq <- data.frame(
nexp = c(20, 30, 25, 18, 22),
Pain_int_mean = c(-0.5, -0.8, -0.6, -1.2, -0.7),
Pain_int_sd = c(0.2, 0.3, 0.25, 0.18, 0.22),
ncon = c(18, 28, 23, 15, 20),
Pain_con_mean = c(0.3, 0.2, 0.5, 0.4, 0.6),
Pain_con_sd = c(0.15, 0.25, 0.2, 0.18, 0.22),
study_label = c("Study 1", "Study 2", "Study 3", "Study 4", "Study 5")
)
# calculate meta-analysis
Pain_meta <- metacont(nexp, Pain_int_mean, Pain_int_sd, ncon, Pain_con_mean, Pain_con_sd, studlab = study_label, data = Ishtiaq, sm = 'SMD', method.smd = "Hedges", method.tau = "REML")
# create forest plot
F1 = forest.meta(Pain_meta, sortvar = TE, studlab = TRUE, prediction = TRUE,
test.overall.random = T, random = T, fixed = F ,label.right = "Favours control", col.label.right = "black",
label.left = "Favours experimental", col.label.left = "black", col.square = "darkcyan",
col.diamond = "darkblue", col.diamond.lines = "cyan4", col.predict = "red", print.tau2 = F,
mlab = "RE Model for All Studies (k = 5)")
#Remove studies with TE >5
Pain_meta_out_removed <- abs(Pain_meta$TE) > 5
## Then, create the meta-analysis with outliers removed
Pain_meta_no_out = metacont(nexp, Pain_int_mean, Pain_int_sd, ncon, Pain_con_mean, Pain_con_sd, studlab = study_label, data = Ishtiaq[!Pain_meta_out_removed, ], sm = 'SMD', method.smd = "Hedges", method.tau = "REML", random = TRUE, fixed = FALSE)
#add the effect size to original plot
addpoly(Pain_meta_no_out, atransf=exp, mlab="RE Model with Outliers (k = 3)", cex=.75, vi = 'Pain_meta_no_out$TE', sei = 'Pain_meta_no_out$seTE')
```
Error in addpoly.default(Pain_meta_no_out, atransf = exp, mlab = "RE Model with Outliers (k = 3)", :
Length of 'vi' (or 'sei') does not match length of 'x'
|
Forest plot for meta-analysis of continous outcome displaying the mean ES with and without outliers
|
CC BY-SA 4.0
| null |
2023-05-08T21:06:22.817
|
2023-05-09T11:19:39.150
|
2023-05-09T10:46:37.793
|
387512
|
387512
|
[
"meta-analysis",
"metafor",
"forest-plot"
] |
615267
|
1
| null | null |
0
|
17
|
In the following paper ([https://pubmed.ncbi.nlm.nih.gov/33984349/](https://pubmed.ncbi.nlm.nih.gov/33984349/)) the authors perform radiomics feature selection for survival prediction by:
- Bootstrap resampling the dataset x 1000
- Fitting cross-validated LASSO models to each the resampled data sets
- Retaining the 10 most common features with non-zero coefficients across all 1000 models
- Fitting reverse stepwise regression using the ten selected features to the resampled datasets ( the same data sets as generated in step 1)
- Choosing the final features based on the most common cox-regression model.
I would like to replicate this approach (albiet for logistic regression rather than cox-regression).
I am able to use the following R code to obtain the top K features from the Lasso models using the 'boot' library:
```
lasso_Select <- function(x, indices){
x <- x[indices,]
y <- x$Outcome
x = subset(x, select = -Outcome)
x2 <- as.matrix(x)
fit <- glmnet(x2, y , family="binomial",alpha=1, standardize=TRUE)
cv <- cv.glmnet(x2, y, family="binomial",alpha=1, standardize=TRUE)
fit <- glmnet(x2, y, family="binomial",alpha=1, lambda=cv$lambda.min, standardize=TRUE)
return(coef(fit)[,1])
}
myBootstrap <- boot(scaled_train, lasso_Select, R = 1000, parallel = "multicore", ncpus=5)
```
However, I don't believe I can access the individual resampled datasets to then run the multiple logistic regression models and choose the most common. If anyone is able to provide some advice on how best to approach this, it would be much appreciated.
|
Feature Selection Using Bootstrap Resampling, LASSO and Stepwise Regression
|
CC BY-SA 4.0
| null |
2023-05-08T21:06:44.343
|
2023-05-08T21:06:44.343
| null | null |
387518
|
[
"machine-learning",
"cross-validation",
"feature-selection",
"resampling"
] |
615268
|
2
| null |
372013
|
0
| null |
I believe you're missing a $1/b^2$ in the [Hoeffding inequality](https://en.wikipedia.org/wiki/Hoeffding%27s_inequality), which should state:
$$P(\bar{X}-E[\bar{X}] \geq t) \leq e^{-2nt^2/b^2}$$
where $t\geq0$, and $\bar{X}$ denotes the empirical mean of these variables.
Intuitively, Bernstein's inequality uses more information about the distribution of $X$ in its bound, specifically, the variance of $X$, in addition to the bound on the values of $X$. Meanwhile Hoeffding's inequality only relies on the bounds on the values of $X$. Thus we would expect Bernstein's inequality to provide a better bound when the variance of $X$ is small. However, you can compare the upper bounds and see that in some regimes of large variance, Hoeffding's inequality is actually tighter. The gain is not much though, since the variance can be at most $b^2$.
To actually solve the problem, you may want to write Bernstein's inequality in terms of sample means as well:
$$ P(|\bar(X) - E[\bar(X)]| \geq t) \leq 2 \exp(-\frac{nt^2}{2\sigma^2 + (2/3)bt}).$$
(See e.g., Theorem 2 in [these notes](https://zcc1307.github.io/courses/csc588sp21/notes/0126.pdf).)
Then, compare the exponential terms and the desired form $2n^{-\tau}$ and figure out what $t$ should be in terms of $n$ and $\tau$ in order for the desired inequalities to hold.
| null |
CC BY-SA 4.0
| null |
2023-05-08T21:36:53.437
|
2023-05-31T18:59:49.547
|
2023-05-31T18:59:49.547
|
335589
|
335589
| null |
615270
|
2
| null |
615263
|
1
| null |
I'm not confident i know enough to help here, but i'm thinking MANOVA is for 3 or more groups - you just have two groups of scores - i'm thinking a series of Mann-Whitneys - what am i missing here?
| null |
CC BY-SA 4.0
| null |
2023-05-08T22:10:08.963
|
2023-05-08T22:10:08.963
| null | null |
179151
| null |
615271
|
1
|
615867
| null |
0
|
39
|
I have some data that looks like:
|$x_i$ |$y_i$ |
|-----|-----|
|10 |20 |
|11 |21 |
|12 |25 |
|1000 |2001 |
The current method for forecasting an unseen $y'$ based on a known $x'$ is to estimate it as:
$$\hat y' = \frac{1}{n} \sum_{i=1}^n \frac{y_i}{x_i} x'$$
That is, we take the arithmetic mean of the ratio of $y$ to $x$ and apply it to $x'$.
This "model" is specified somewhat informally as a procedure and I'd like to restate it in more formal terms, so that I can determine whether other models that I am considering are generalizations of this model or different models.
So, is there a model of the form $y = \alpha x + \varepsilon$ or maybe $y = \alpha x \varepsilon$ or something, where the maximum likelihood estimator is the arithmetic mean of $y_i/x_i$?
|
The mean of ratios as a regression or MLE
|
CC BY-SA 4.0
| null |
2023-05-08T22:34:51.137
|
2023-05-15T00:38:57.910
| null | null |
346961
|
[
"regression",
"maximum-likelihood",
"ratio"
] |
615272
|
1
| null | null |
1
|
16
|
I am trying to build an ARDL model with the six following variables: `lnNO2`,`lnP`,`lnGDP`,`lnEI`,`lnU` and `lnU2` (one response and five dependent variables). The variables I am using are shown below:
[](https://i.stack.imgur.com/bNf9S.png)
One of the preconditions of an ARDL is that all the variables are either I(0) or I(1). But when I conduct the Zivot-Andrews unit root test on the variables, I obtain strange results: some variables are stationary at levels but not stationary at differences, and some variables are not stationary at levels but are indeed stationary at differences. The variable below is an example:
```
> summary(ur.za(df$lnU, model = "trend")) # No Unit Root
################################
# Zivot-Andrews Unit Root Test #
################################
Call:
lm(formula = testmat)
Residuals:
Min 1Q Median 3Q Max
-0.0041138 -0.0007737 0.0001303 0.0009452 0.0052163
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6331285 0.1229855 5.148 7.84e-06 ***
y.l1 0.8258369 0.0349727 23.614 < 2e-16 ***
trend 0.0028385 0.0006549 4.334 9.95e-05 ***
dt -0.0014855 0.0003439 -4.319 0.000104 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.002034 on 39 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.9998, Adjusted R-squared: 0.9998
F-statistic: 7.967e+04 on 3 and 39 DF, p-value: < 2.2e-16
Teststatistic: -4.98
Critical values: 0.01= -4.93 0.05= -4.42 0.1= -4.11
Potential break point at position: 18
> summary(ur.za(diff(df$lnU), model = "trend")) # Unit Root
################################
# Zivot-Andrews Unit Root Test #
################################
Call:
lm(formula = testmat)
Residuals:
Min 1Q Median 3Q Max
-0.0052449 -0.0002637 -0.0000411 0.0004080 0.0031726
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.691e-03 1.978e-03 2.372 0.0229 *
y.l1 7.811e-01 8.719e-02 8.958 6.63e-11 ***
trend -1.196e-04 4.892e-05 -2.444 0.0193 *
dt 1.944e-04 7.966e-05 2.440 0.0194 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.001116 on 38 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.9445, Adjusted R-squared: 0.9402
F-statistic: 215.8 on 3 and 38 DF, p-value: < 2.2e-16
Teststatistic: -2.511
Critical values: 0.01= -4.93 0.05= -4.42 0.1= -4.11
Potential break point at position: 28
```
As you can clearly see, the variable `lnU` has no unit root (Test Statistic lower that Critical Values), while the variable `diff(lnU)` does have a unit root (Test statistic higher than Critical Value). This situation only occurs for the variables `lnU` and `lnU2`, the other variables are all both level-stationary and difference-stationary.
Question: Will the ARDL model built with those variables be valid, since all the variables are either I(0) or I(1)? Thank you very much in advance.
|
The difference of a variable has a unit root, but the variable itself doesn't
|
CC BY-SA 4.0
| null |
2023-05-08T22:59:49.930
|
2023-05-08T22:59:49.930
| null | null |
180053
|
[
"time-series",
"unit-root",
"ardl"
] |
615273
|
2
| null |
615205
|
-2
| null |
It varies with context, I present one option - "directional standard deviation": compute SD separately above and below mean:

If the goal is a measure of spread of data, this can work.
Arithmetic mean isn't always best - could try median, another averaging metric, or for sparse data, ["sparse mean"](https://github.com/OverLordGoldDragon/StackExchangeAnswers/blob/main/SignalProcessing/Q87355%20-%20audio%2C%20algorithms%20-%20Detecting%20abrupt%20changes/utils87355.py#L109) that I developed and applied on an [audio task](https://dsp.stackexchange.com/a/87512/50076).
```
std = lambda x, x_mean: np.sqrt(1 / len(x) * np.sum((x - x_mean)**2))
x_mean = x.mean()
std_up = std(x[x >= x_mean], x_mean)
std_dn = std(x[x < x_mean], x_mean)
```
This was typed in a hurry and isn't polished; no consideration was given to handling `x == x.mean()` for equivalence with usual SD via constant rescaling, or to whether `<` should be `<=`, but it can be done, refer to [@IgorF.'s answer](https://stats.stackexchange.com/a/615560/239063).
### Clarification
This is simply feature engineering. It has nothing to do with statistical analysis or describing a distribution. SD (standard deviation) is a nonlinear alternative to mean absolute deviation with a quadratic emphasis.
I saw a paper compute SD from 3 samples. I first-authored it and remarked it as ludicrous. Then I figure, it just functions as a spread measure, where another metric wouldn't be much better.
Whether there's better ways to handle asymmetry is a separate topic. Sometimes SD is best for similar reasons it's normally best. I can imagine it being a thresholding feature in skewed non-negative data.
### Connection to question
I read the question, going off of the title and most of the body, as: "I want to use SD but want to stay non-negative". Hence, a premise is, SD is desired - making any objections to SD itself irrelevant. Of course, the question can also read as "alternatives to SD" (as it does in last sentence), but I did say, "I present one option".
More generally, any objections to my metric also hold for SD itself. There's one exception, but often it's an advantage rather than disadvantage: each number in my metric has less confidence per being derived from less data. This can be advantage since, it's more points per sub-distribution. Imagine,

SDD = "standard deviation, directional". For the right-most example, points to right of mean are only a detriment to describing points to left, and the mismatch in distributions can be much worse than shown here (though it does assume "mean" is the right anchor, hence importance of choosing it right).
### Formalizing
@IgorF's answer shows exactly what I intended, minus handling of `x == x.mean()` which I've not considered at the time, and I favor `1/N` over `1/(N-1)`; I build this section off of that. What I dislike about that mean handling is
```
[-2, -1, -1, 0, 1, 1, 2] --> (1.31, 1.31), 1.31
[-2, -1, -1, 1e-15, 1, 1, 2] --> (1.41, 1.31), 1.31
```
showing `--> SDD, SD`. i.e. the sequences barely differ, yet their results differ significantly - that's an instability. SD itself has other such weaknesses, and it's fair to call this one a weakness of SDD; generally, caution is due with mean-based metrics.
If the relative spread of the two sub-distributions is desired, I propose an alternative:
- Replace $\geq$ and $\leq$ with $\gtrapprox$ and $\lessapprox$, as in "points within mean that won't change the pre-normalized SD much", "pre-normalized" meaning without square root and constant rescaling.
- Do this for each side separately.
- Don't double-count - instead, points which qualify both for > mean and ~ mean are counted toward ~ mean alone, and halve the rescaling contribution of the ~ mean points (as in @IgorF.'s). This assures SDD = SD for symmetric distributions.
- "won't change much" becomes a heuristic, and there's many ways to do it - I simply go with abs(x - mean)**2 < current_sd / 50
```
[-2, -1, -1, 0, 1, 1, 2] --> (1.31, 1.31), 1.31
[-2, -1, -1, 1e-15, 1, 1, 2] --> (1.31, 1.31), 1.31
[-2, -1, -1, 3e-1, 1, 1, 2] --> (1.35, 1.29), 1.31
[-2, -1, -1, 5e-1, 1, 1, 2] --> (1.48, 1.19), 1.32
```
It can be made ideal in sense that we can include points based on not changing `sd_up` or `sd_dn` by some percentage, guaranteeing stability, but I've not explored how to do so compute-efficiently.
I've not checked that this satisfies various SD properties exactly, so take with a grain of salt.
### Code
```
import numpy as np
def std_d(x, mean_fn=np.mean, div=50):
# initial estimate
mu = mean_fn(x)
idxs0 = np.where(x < mu)[0]
idxs1 = np.where(x > mu)[0]
sA = np.sum((x[idxs0] - mu)**2)
sB = np.sum((x[idxs1] - mu)**2)
# account for points near mean
idxs0n = np.where(abs(x - mu)**2 < sA/div)[0]
idxs1n = np.where(abs(x - mu)**2 < sB/div)[0]
nmatch0 = sum(1 for b in idxs0n for a in idxs0 if a == b)
nmatch1 = sum(1 for b in idxs1n for a in idxs1 if a == b)
NA = len(idxs0) - nmatch0
NB = len(idxs1) - nmatch1
N0A = len(idxs0n)
N0B = len(idxs1n)
sA += np.sum((x[idxs0n] - mu)**2)
sB += np.sum((x[idxs1n] - mu)**2)
# finalize
kA = 1 / (NA + N0A/2)
kB = 1 / (NB + N0B/2)
sdA = np.sqrt(kA * sA)
sdB = np.sqrt(kB * sB)
return sdA, sdB
x_all = [
[-2, -1, -1, 0, 1, 1, 2],
[-2, -1, -1, 1e-15, 1, 1, 2],
[-2, -1, -1, 3e-1, 1, 1, 2],
[-2, -1, -1, 5e-1, 1, 1, 2],
]
x_all = [np.array(x) for x in x_all]
for x in x_all:
print(std_d(x), x.std())
```
| null |
CC BY-SA 4.0
| null |
2023-05-08T23:29:17.207
|
2023-05-16T16:17:29.163
|
2023-05-16T16:17:29.163
|
239063
|
239063
| null |
615274
|
2
| null |
610372
|
0
| null |
There are a couple of issues with this analysis that I changed since posting this question. If we divide the response variable by the denominator instead of using the offset, we have other distributions available to us (Tweedie, gamma) that allow for other analyses made more difficult with a negative binomial distribution.
The biggest issue, though, is that there is temporal autocorrelation and (potential) nonlinear covariate effects. In the analysis we're currently finalizing (GAMM), we are accounting for temporal autocorrelation and so it would not make sense to include a random effect for the year. But [also 4 years in a random factor would have been too few.](https://stats.stackexchange.com/questions/37647/what-is-the-minimum-recommended-number-of-groups-for-a-random-effects-factor) So it will be included only as a fixed effect. I'm consulting with Dr. Zuur ([highstat.com](https://hightstat.com)) on this analysis, so want to credit him for that.
All this is to say, the super weird residuals flagged problems in our model. We did not ignore those residuals and identified critical factors to include in our model.
| null |
CC BY-SA 4.0
| null |
2023-05-08T23:30:03.410
|
2023-05-12T22:32:20.477
|
2023-05-12T22:32:20.477
|
205125
|
205125
| null |
615275
|
2
| null |
615264
|
1
| null |
Yes - `survey::confint.svyglm`.
| null |
CC BY-SA 4.0
| null |
2023-05-09T01:11:55.133
|
2023-05-09T01:11:55.133
| null | null |
369002
| null |
615276
|
1
|
615288
| null |
1
|
30
|
Is it normal to have different results pattern if data sort is different but the covariances are the same when calculating with propensity score matching in R?
There is data with sample size of about 100.
If I calculate for P-value of the operation time from the data sorted by the operated day, there is no significant difference.
However, it shows significant difference if the imported data is sorted by the operation time descending even though the propensity score is calculated with the same covariances.
Why? and what should be the correct way?
It seems you can manipulate the result by sorting the target item descending even though calculating with the exact same data and the exact same procedure.
|
Is it normal to have different results pattern if data sort is different but the covariances are the same when doing propensity score matching in R?
|
CC BY-SA 4.0
| null |
2023-05-09T01:12:01.067
|
2023-05-09T05:03:10.050
|
2023-05-09T01:35:27.207
|
386592
|
386592
|
[
"r",
"regression",
"logistic",
"propensity-scores"
] |
615277
|
1
| null | null |
0
|
19
|
I'm very new to all this so please bare with me. All advises and corrections are welcome.
Context
I have the following dataset:
```
id,level,condition
#123,1,0
#576,1,0
#663,2,1
#945,1,1
#712,3,0
#981,1,1
#851,3,1
#361,1,1
etc...
```
the id for each user is unique. I have one row per user. The level is the level of engagement for each user. Level 3 represent most engaged user. The condition is an interaction the user did during it’s user journey.
The hypothesis I’d like to validate is that more engaged users are more willing to meet condition (i.e condition = 1).
I have two approaches I can use to validate my hypothesis. I'd like to understand the pros and cons between these two approaches.
Approach #1
From what I understand I can use the Pearson correlation coefficient to demonstrate the correlation between user engagement level and condition. I’m working with BigQuery so I would basically run the following query on my dataset:
```
SELECT
CORR(level, condition)
FROM
my_data_set
```
Let's assume that the dataset is normally distributed for this question.
Approach #2
my second approach would be to sum the condition and divide it by the number of users inside each group. The query would looks like this:
```
SELECT
level,
SUM(condition)/COUNT(*) as ratio
FROM
`my_dataset`
GROUP BY
1
```
from the limited knowledge I have in statistical field the level with the better ratio would be an higher correlation between condition and level of user engagement.
Question
Does the second approche make sense? What are the differences between these two approaches.
|
what is the difference between a multiple group ratio analysis and computing correlation?
|
CC BY-SA 4.0
| null |
2023-05-09T01:14:50.863
|
2023-06-01T05:08:54.177
|
2023-06-01T05:08:54.177
|
121522
|
368573
|
[
"classification",
"correlation"
] |
615278
|
1
| null | null |
1
|
27
|
Consider a normally distributed random variable $X\sim N(\mu,\sigma^2)$.
Since $\Pr[X\leq x]=\Pr[(X-\mu)/\sigma\leq (x-\mu)/\sigma]$, the following equality holds:
$$\Phi(x|\mu, \sigma^2)=\Phi((x-\mu)/\sigma\;|\;0,1)$$
where $\Phi(\cdot|\mu,\sigma^2)$ is a CDF of a normal distribution with mean $\mu$ and variance $\sigma^2$.
That is, we can express a normal CDF using the standard normal CDF.
Here, I thought that an equality $\Pr[X= x]=\Pr[(X-\mu)/\sigma= (x-\mu)/\sigma]$ may also hold and thus $\phi(x|\mu,\sigma^2)=\phi((x-\mu)/\sigma|0,1)$.
However, I checked that this is not true. (In R, `dnorm(3, 2, 3)` $\neq$ `dnorm((3-2)/3)`).
So, why does the equality not hold in the PDF case? and is it possible to express a normal PDF using the standard normal PDF?
|
Expressing a normal PDF using the standard normal PDF
|
CC BY-SA 4.0
| null |
2023-05-09T01:56:08.630
|
2023-05-09T18:34:33.583
| null | null |
375224
|
[
"normal-distribution"
] |
615279
|
1
| null | null |
2
|
34
|
Suppose the distribution F is absolutely continuous. Is there a way to compare (i) the monotonocity of the hazard ratio (i.e., strictly decreasing/increasing); (ii) the skewness of the distribution (i.e., positive or negative); and the concavity or convexity of the survival function.
I have the intuition that a decreasing hazard ratio implies a concave survival function, which, in turn, implies a positive skewness, but do not have a formal proof.
|
Hazard ratio and skewness
|
CC BY-SA 4.0
| null |
2023-05-09T01:56:25.227
|
2023-05-09T04:12:00.237
| null | null |
387525
|
[
"distributions",
"survival",
"skewness",
"hazard"
] |
615280
|
2
| null |
615195
|
3
| null |
The short answer is no - controlling for x1 in this case may mitigate bias, but does not eliminate it: the problem arises because x2 is directly caused by the outcome. You can see this in a simple simulation (Stata code)
```
clear
set obs 1000000
gen t = rnormal()
gen x1 = rnormal() + .5*t
gen y = rnormal() + .5*t
gen x2 = rnormal() +.5*x1 + .5*y
* .5 is the true effect of t on y
reg y t
* condition on x2 ~ estimate t -> y =~ .33
reg y t x2
* condition additionally on x1 ~ estimate t -> y =~ .4
reg y t x2 x1
```
Incidentally, Pearl discusses a similar case, where x2, instead of being caused by y, shares a common cause with y. In that case, controlling for x1 does enable you to obtain the correct treatment effect. See discussion of model 15 (and similar cases in models 14-17) in:
Cinelli, Forney, and Pearl (2022) A crash course in good and bad controls, Sociological Methods and Research
Having said that, it may still be possible to obtain unbiased treatment effect estimates through the use of inverse probability weighting or similar. In the current case, let's imagine that x2 is a binary dropout indicator (0 = remained in study). In this case we can weight our regression with weights = 1/p(x2 = 1 | x1, y), which you can obtain from a logistic regression of x2 on y and x1 or similar. Note that this depends on having fully observed data for y and x1 regardless of the value of x2 - if you don't observe anything when x2 == 1 then the solutions are considerably more complex or may be infeasible. See the following simulation for a demonstration:
```
* Alternative with binary x2
clear
set obs 1000000
gen t = rnormal()
gen x1 = rnormal() + .5*t
gen y = rnormal() + .5*t
gen x2 = rbinomial(1,invlogit(x1 + y))
* .5 is the true effect of t on y
reg y t
* compute inverse probability weights for x2
logit x2 y x1
predict px2, pr
gen ipwx2 = 1/px2
* Unweighted regression is biased as before
reg y t x2
* weighted regressions with x2 as a covariate, adjusting for x1 doesn't matter either way
reg y t x2 [pweight = ipwx2]
reg y t x2 x1 [pweight = ipwx2]
* unweighted/weighted regressions with only x2 == 0 (i.e. if x2 is dropout)
* unweighted regression is biased
reg y t if x2 == 0
* weighted regression ~ unbiased
reg y t if x2 == 0 [pweight = ipwx2]
```
| null |
CC BY-SA 4.0
| null |
2023-05-09T02:20:26.387
|
2023-05-09T02:20:26.387
| null | null |
106580
| null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.